Notes
Article history
The research reported in this issue of the journal was funded by the HS&DR programme or one of its proceeding programmes as project number 09/2001/32. The contractual start date was in September 2010. The final report began editorial review in March 2014 and was accepted for publication in August 2014. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HS&DR editors and production house have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the final report document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
The Dr Foster Unit at Imperial College London is principally funded by Dr Foster Intelligence, an independent health-care information company. The Dr Foster Unit is affiliated with the National Institute for Health Research (NIHR) Imperial Patient Safety Translational Research Centre. Dr Alex Bottle and Professor Paul Aylin are part funded by a grant to the unit from Dr Foster Intelligence outside the submitted work.
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2014. This work was produced by Bottle et al. under the terms of a commissioning contract issued by the Secretary of State for Health. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
Chapter 1 Background and research objectives
Measuring and comparing health-care performance are essential components of driving quality improvement. When comparing patient outcomes such as mortality, it is usually necessary to appropriately adjust for patient factors such as age and disease (collectively known as casemix) using statistical models. The NHS collects a wealth of administrative data that are currently underutilised to support improvements in health-care provision. The aim of this project was to use a core NHS data set, Hospital Episode Statistics (HES), to develop risk-prediction and casemix adjustment models to predict and compare outcomes between health-care units. The outcomes we have chosen are mortality, unplanned readmission, unplanned returns to theatre for selected specialties and non-attendance in outpatients departments (OPDs). As well as patient age and sex, a key casemix factor for risk-adjustment models is comorbidity, which has been measured in various ways, such as the Charlson index,1 that warrant comparison. Modelling for binary outcomes is typically done using logistic regression (LR), but there are a number of machine learning approaches that have been tried and are worth investigating here. Finally, just as statistical methodology has developed, HES itself is expanding and now covers OPD appointments since the financial year 2003/4 and accident and emergency (A&E) attendances since 2007/8. Information from these sources may provide useful information if the data quality is sufficiently high.
In view of all this, the project had these main objectives:
-
to derive robust casemix adjustment models for these outcomes adjusting for available covariates using HES
-
to update the weights and codes for the widely used Charlson index of comorbidity, recalibrate it for the NHS and assess its use for mortality and also non-mortality outcomes
-
to assess if more sophisticated statistical methods based on machine learning such as artificial neural networks (ANNs) outperform traditional LR for risk prediction
-
to assess the usefulness of outpatient data for these models.
The first of these may be considered an overarching aim, with the other three as elements of that aim.
The structure of this report is as follows. Chapter 2, Methods, begins by describing the HES database as held and processed by the Dr Foster Unit at Imperial. It briefly describes the assessment of data quality of the two newer elements used in this project: OPD and A&E records (the Diagnostic Imaging Dataset was released too late for us to obtain it). There are subsections on the outcome measures, particularly the (unplanned) return to theatre (RTT) ones, a review of the literature on comorbidity measures, including a summary of our published systematic review of studies comparing two or more such measures, and the statistical methods for risk adjustment, together with their implementation issues, in particular (re)calibration. That chapter ends by discussing count models as an alternative to considering binary outcomes, particularly readmissions. Chapter 3, Results, begins by giving the results for the updating of the Charlson index using HES data and illustrates the performance of Charlson compared with that of the popular Elixhauser index. It illustrates different methods for incorporating information from prior admissions for two conditions: heart failure (HF) and acute coronary syndrome (ACS). This is followed by a section comparing risk-adjustment methods, which comprises a comparison between LR and machine learning approaches for mortality and readmission. The results of the RTT analyses are then presented. Following a literature review of factors relating to OPD non-attendance, we present the results of the prediction models. Finally, we go beyond the common 28- or 30-day readmission indicator to cover other time periods and future bed-days. We focus on HF patients; the basic results were similar for chronic obstructive pulmonary disease (COPD). Chapter 4 gives the discussion and dissemination activity to date and suggests further research, and Chapter 5 offers some conclusions.
Chapter 2 Methods
Hospital Episode Statistics database
Our unit holds inpatient and day case HES and Secondary Uses Service (SUS) data from 1996/7 to the present with monthly SUS feeds. We apply published HES cleaning rules to the SUS feed. Details of this and our other processing, such as episode and spell linkage, can be found on documents on our website (www1.imperial.ac.uk/publichealth/departments/pcph/research/drfosters/reports/ under ‘HSMR methodology’). HES data cleaning rules may be found on the NHS Information Centre website under HES. Throughout this report, we refer to all these records as ‘HES data’. Briefly, each record in the inpatient part of the database is a finished consultant episode, representing the continuous period of time during which the patient is under the care of a consultant or allied health professional. We link episodes into ‘spells’ (admissions to one provider) and link spells into ‘superspells’, the latter combining any interhospital transfers. We will refer to superspells as ‘admissions’ and in general use them as the unit of analysis throughout.
We hold outpatient HES and SUS data since they became part of HES in 2003/4 and hold A&E records since they became part of HES in 2007/8. The most recent A&E records we had for the project were for 2011/12. The Information Centre’s contractors provide a file to enable us to attach the date and cause of death to HES records, with the latest date of death being August 2011.
We derive a number of fields, in particular the main diagnosis group, the main procedure group and the Carstairs deprivation quintile. We use the Agency for Healthcare Research and Quality (AHRQ) Clinical Classification System (CCS) to turn the International Classification of Diseases, Tenth Edition (ICD-10) codes of the primary diagnosis field into one of 259 diagnosis groups designed for health services research (see www.ahrq.org for details). For procedures, no such system exists for the UK’s Office for Population, Censuses and Surveys (OPCS) procedure codes. Over several years, in conjunction with clinicians, we have created a number of procedure groups. 2 The Carstairs quintile3 is assigned at the super output area geographical level using information from the 2001 census; the necessary 2011 census information was not available in time for this project. Although Carstairs is therefore based on older information than the Index of Multiple Deprivation, its resolution is greater.
We now briefly consider the quality of HES data.
Assessment of inpatient and day case data quality
Submission of HES records is mandatory and coverage is very high, though the frequency and timeliness of submission to SUS varies. Apart from ethnicity, which is fast improving, there are few clearly duplicate records or missing or invalid values in HES for patient identifiers and demographics, dates of admission, discharge or procedure, method of admission and other key fields:2,4 < 1% of records were dropped because of missing values. Most debate around HES data quality concerns the primary and secondary diagnostic and procedure fields. A sample of records is externally audited for its coding and the results published online by trust by the Audit Commission. 5 These reports show that the variation by trusts is notable but narrowing each year. The estimates of coding accuracy in these reports are not sufficiently robust or detailed to allow us to estimate the ‘correct’ level of comorbidity at a given hospital, however. A recent systematic review on this subject by our group6 found coding accuracy to be high (97%), particularly since the introduction of Payment by Results. The Health and Social Care Information Centre have now written two reports on English hospital and social care data (see www.hscic.gov.uk/catalogue/PUB08687 for the first one).
Assessment of outpatient data quality
Unlike with A&E, there is no independent source with which to compare the number of records. We assessed data quality in terms of the proportion of duplicates and the proportion of records with missing values for the primary diagnosis, primary procedure, and date and outcome of attendance (whether the patient attended or not). Most records lacked both a primary procedure (though we cannot ascertain what proportion of OPD appointments actually involved a procedure) and a primary diagnosis field. The use of codes for invalid or unknown was low for the other key fields. The proportion of duplicate records was < 1%, but these should still be removed.
Assessment of accident and emergency data quality
We compared for each hospital the number of electronic records in our data set with counts from the Accident and Emergency Quarterly Monitoring Data Set (QMAE). Overall in the first 2 years of A&E HES, 2007/8 and 2008/9, it was missing more than 6 million of the 19 million attendances reported by QMAE, a shortfall of around a third. As many as 40% of hospitals with A&E departments failed to submit any data. Then 2009/10 saw a jump of around 3 million electronic records to include 16 million out of the 20 million QMAE total, a jump that was maintained but not improved upon in 2010/11. We felt that the shortfall was still too large and therefore decided not to use A&E records in the project. Records for 2011/12 arrived too late for inclusion but may be worth using in future analyses.
Definition of outcome measures and predictors
The two most commonly used mortality measures are in-hospital mortality (any time during the index stay) and 30-day total mortality (in or out of hospital within 30 days of the index admission or procedure date). For readmission, the most commonly used internationally is the 30-day all-cause version; in the UK, 28 days is typically used. Unless otherwise stated, ‘readmission’ as an outcome means within 28 days; for the HF analyses we used 7-, 30-, 90-, 182- and 365-day follow-up periods rather than 28 days.
For HF, the number of admissions and inpatient bed-days during the 365 days following discharge were also counted; these and also the first readmission were split by primary diagnosis into those for HF and those for any other cause (non-HF). OPD non-attendance was simply defined using the ATENTYPE (attendance type) field. The first appointment following inpatient discharge for selected acute conditions was readily identified using dates; of particular interest here was whether or not non-attendance rate varied by the time interval between discharge and the appointment, as if so this would represent an opportunity for the hospitals to reduce missed appointments. The patient’s first new appointment for the specialties of general medicine and general surgery were identified using the field FIRSTATT and also by tracking back 3 years in the database to ensure that this was each patient’s first for that specialty (or at least their first for 3 years).
The construction of the RTT measures followed the same outline for each specialty as for cystectomy in urology. 7 All procedure fields with dates between 1 and 29 days inclusive of the index procedure date, even if performed after transfer or discharge from the index stay, were extracted from the database and inspected by a senior surgeon and clinical coder to determine which were likely to be reinterventions. These can potentially encompass surgical operations, both surgical and non-surgical procedures, including radiological interventions. For orthopaedics, we defined RTT between 1 and 89 days after the index procedure in order to capture infections, which may take a few weeks to develop. The index procedures of hip and knee replacements were each divided into subgroups with advice from a senior surgeon. Hip operations were divided into total with cement, total without cement, hybrid and hip resurfacing. Knee operations were divided into total, unicondylar (or unicompartmental) and patellofemoral replacement, taking into account the national changes in coding practice in 2009/10 regarding Z845 (tibiofemoral joint) and W581 (resurfacing). The small number of otherwise unclassified procedures were excluded. Using laterality Z codes, we matched the RTT to the joint where possible – around 95% of joint procedures had laterality codes.
Potential covariates for the risk-adjustment models were taken from our national monitoring system that uses HES:2 age, sex, deprivation quintile, year, month of admission for respiratory conditions, admission method (elective or emergency if the patient group included both), emergency admissions in the year before the index stay, comorbidities and potentially an interaction between age and comorbidity. For the HF readmission models, we also tried incorporating previous admissions using more sophisticated methods, and we used the number of prior OPD appointments attended and the number missed. HF models also included some procedures. Further details are given in the relevant later sections.
Table 1 summarises which outcomes will be presented for which patient groups.
| Patient group | Outcomes modelled |
|---|---|
| All emergency inpatients combined | Mortality |
| Acute myocardial infarction | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| COPD | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| Stroke | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| HF | Mortality (in-hospital and 30-day total); readmission (7-, 28-, 30-, 90- and 365-day, both all-cause and diagnosis-specific); number of emergency bed-days and readmissions within a year of index discharge (also converted into membership of high-resource ‘buckets’) |
| Pneumonia | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| Fracture of the neck of femur | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| Hip replacement (primary procedure) | Mortality (in-hospital and 30-day total); readmission (7- and 28-day); return to theatre within 90 days |
| Knee replacement (primary procedure) | Mortality (in-hospital and 30-day total); readmission (7- and 28-day); return to theatre within 90 days |
| First-time isolated coronary artery bypass graft (primary procedure) | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| Abdominal aortic aneurysm repair (primary procedure) | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| Colorectal excision (primary procedure) | Mortality (in-hospital and 30-day total); readmission (7- and 28-day) |
| Patients having their first general medical or general surgical OPD appointment | Non-attendance |
| Patients admitted for any of acute myocardial infarction, coronary heart disease, stroke, HF, acute bronchitis, COPD and pneumonia | Non-attendance in first OPD appointment after discharge |
Review of comorbidity indices
The two most commonly used indices are the Charlson1 and Elixhauser,8 originally described using International Classification of Diseases, Ninth Edition (ICD-9) with US data. In each index, points are given for the presence of a set of codes representing diseases associated with higher or sometimes lower risk than if the disease is not present. The points are then summed to give a score for the admission. 9 The Charlson index is now over 20 years old and both indices need calibrating on the data set of interest; to our knowledge, very little has been published from the UK on this. The weights (or scores) for these two indices may be inappropriate for the UK because of differing populations and/or coding practices. We have to date been using an Australian version of Charlson10 in our risk-adjustment models (there are a variety of others for ICD-9), but discussions with clinical coders raised questions over the suitability of some codes when used in the UK. According to their advice, we modified the codes for acute myocardial infarction (AMI) and dementia in particular. 11
A decade or so later, Elixhauser et al. 8 constructed a more extensive index covering 30 conditions. This index was designed for administrative databases such as HES that lack present on admission information, which means that they cannot distinguish between comorbidities and complications that arise during the stay. This is why Elixhauser does not include AMI or stroke, which are both part of Charlson. Some comorbidities were associated with lower risk of mortality and were given negative scores, confirmed in a Canadian analysis. 12 One reason for this was given by Elixhauser: low-risk patients may be given more codes for less acute problems than acutely ill people, for whom coders will focus on problems relevant to the acute situation. The presence of codes for non-life-threatening disease may therefore be a marker for relatively healthy patients.
Including Charlson and Elixhauser, there have been different approaches of selecting sets of comorbidities. The most common typically involved considering the prevalence of each condition and medical expert opinion. 13–17 Gagne et al. 18 and Thombs et al. 19 simply combined all the conditions listed in Elixhauser and the Deyo adaptation of the Charlson index except those conditions thought to be related to the main diagnosis. The simplest approach is to count the number of conditions, thereby giving them equal weight.
To find the best-performing one(s), we conducted a systematic review of multiple comparison studies on comorbidity measures/indices in use with administrative data. The review used a new meta-analytical approach, hypergeometric tests, to identify the best-performing indices. We now briefly outline the search strategy, results and conclusions. Full details may be found elsewhere. 20
The literature search was conducted first using three electronic databases, MEDLINE, EMBASE and PubMed, up to 18 March 2011. Search terms included Charlson, Elixhauser, comorbidity, casemix, case-mix, mortality and morbidity. In addition, the bibliography of the chosen articles and the relevant reviews were searched. 21–25 Two authors independently reviewed the titles and abstracts and the methodology section of the articles and selected the relevant potential articles. All disagreements were resolved by consensus.
Articles were included if administrative data were used and comparisons between predictive performances of at least two indices (perhaps also including common covariates) were made. Articles were excluded if clinical databases without ICD codes were used or if indices were used for the purpose of adjustment only, without any comparison of indices.
The c-statistics and the confidence intervals, or Akaike information criterion (AIC) or other appropriate statistics, were looked at if they were available, to compare the predictive performances of the measures/indices. If c-statistics alone without confidence intervals (or p-values) were provided, an arbitrary ≥ 0.02 cut-off point was chosen to define the difference between two measures/indices as significant.
All mortality outcomes were divided into two major groups: (1) ‘short term’ – all inpatient mortality and any mortality within 30 days of admission; and (2) ‘long term’ – outpatient mortality or that 30 or more days from admission.
After removing duplicates from different databases, we retrieved 1312 studies to review, subsequently reduced to 54 articles eligible for data abstraction. Of these, 90% were carried out in North America.
In summary, for short-term mortality (up to 30 days), the use of empirical weights (of whichever index) or the small group of various other comorbidity measures performed best. For long-term mortality (30+ days), these ‘other measures’, the Romano version of Charlson and the Elixhauser measure performed significantly better. As others have suggested, there may be useful gains if the two indices are combined. In practice, this would mean taking the Elixhauser set and adding dementia if we excluded AMI and stroke (Charlson components), which could occur after admission as complications but whose timing cannot be determined using HES. Following a review of the Sundararajan et al. comorbidity ICD definitions10 by external clinical coders, we amended the Charlson algorithm so that it uses extra codes for AMI and dementia in particular.
Statistical methods
Modelling framework
The terms risk prediction and risk adjustment are closely related despite their differing aims, but a model for predicting mortality, for example, might not include the same set of variables as a risk-adjustment model used to compare hospitals’ mortality rates. Risk prediction values parsimony and interpretability, whereas risk adjustment can focus more on confounder control. Risk-prediction models could encompass factors such as staffing and bed numbers or other factors that are (at least partly) under the hospital’s control, whereas this would be wrong for risk-adjustment models for comparing providers. For the most part we restrict ourselves to adjustment except for part of the HF analysis that covers the prediction of future inpatient activity and for OPD non-attendance prediction.
Prediction of binary outcomes such as mortality or readmission is usually done using LR with records from single institutions. It is therefore prone to problems such as poor reproducibility due to small sample sizes and variations in patient characteristics between study centres. 26 Combining a larger number of institutions would increase the sample size, but the modeller then in principle needs to account for the ‘clustering’ of patients within institutions. The common way of accounting for this is to use multilevel models, particularly with random intercepts for surgeons and hospitals and fixed effects for covariates. For this, we used SAS’s procedure for binary outcomes, PROC GLIMMIX, version 9.2 (SAS Institute Inc., Cary, NC, USA). From this we derived relative risks (RRs) for each hospital using predicted probabilities from only the fixed effects part of the model. 27,28 We used the noblup ilink options within PROC GLIMMIX to achieve this. These RRs are akin to standardised mortality ratios (SMRs), which represent the ratio of the hospital’s rate to the national average rate. The Center for Medicare and Medicaid Services (CMS) in the USA uses empirical Bayes ‘shrunken’ estimates of the SMRs for its publicly reported outcome measures. 29 Confidence intervals for the CMS measures are constructed using a complicated bootstrap procedure. A discussion of the different SMRs calculable from multilevel modelling is given by Mohammed et al. ,30 though the article is unnecessarily critical of mortality measures in general. Several studies have compared the results from fixed and random effects models with regard to provider profiling, in which a key aim is the identification of statistical outliers, especially units with higher than expected mortality. In general, these conclude as Austin et al. 31 did: ‘when the distribution of hospital-specific log-odds of death was normal, random-effects models had greater specificity and positive predictive value than fixed-effects models. However, fixed-effects models had greater sensitivity than random-effects models’ (p. 526).
Bayesian methods in provider profiling are of growing interest, and four such approaches are reviewed by Austin. 32 He concluded that there was often little agreement in the hospital rankings between the methods considered. We will not consider Bayesian methods further.
Multilevel models allow for the estimation of the amount of variation between units at each level, for example between surgeons or hospitals. The residual intraclass correlation coefficient (ICC), a measure of clustering used in hierarchical modelling, expresses the proportion of variability explained by the presence of clusters as, for instance, a hospital level. 33 It is computed as:
where τH is the hospital-level variance and π = 3.14159.
By building up the levels in a hierarchical model, one can assess, for example, how much of the variation in outcomes at hospital level is due to the variation between surgeons or to differences in the distribution of patient factors. In this project, this is particularly useful with surgical outcomes such as RTT, and we will illustrate it for orthopaedics.
Model fitting
The modelling in this project served different purposes, and we therefore took different approaches accordingly. For the comparison of LR and machine learning methods, we needed to mitigate overfitting; in our experience before and during this project, this is not a problem with regression and HES data, and therefore we did not routinely split the data subsets into a training and a testing set. For the comparison of methods, however, we did. For this part of the analysis, we took 2 years of data, randomly split the records into two portions and then recombined them to form a test data set and a training data set so that each of the resulting sets contained a random mix of each year. This was to avoid any effect of the data year itself, for instance on account of national outcome trends or coding changes. We included a binary variable to indicate the year. As the aim was to see to what extent more complex methods can go beyond standard regression, no interactions or non-linear terms were included.
For LR, all candidate covariates were retained: we did not use any stepwise methods given their well-known drawbacks. For the most part we did not test for interactions.
The machine learning methods tend to be slower than LR and, given their complexities, often need an expert as an operator and to choose which implementation to use. While many packages offer ‘out-of-the-box’ ways of running the code, doing so is usually suboptimal, and an expert is needed to make decisions on implementation issues. The sections that follow are therefore the most technical in this report.
Machine learning methods
Logistic regression is familiar to many, easy to use, with easy-to-interpret output consistent across platforms, be it SAS, R or any other. This is in stark contrast to machine learning methods, which may fall into different broad categories. As an alternative to regression, researchers have applied various machine learning methods, especially ANNs and support vector machines (SVMs), and the initial results have been promising. 34–37 There are also various tree-based methods that offer an appealing output that, unlike ANNs and SVMs, shows the relations between predictors. Of these, we consider random forests, as we doubted that our data would benefit from the extra complexity inherent in boosted trees. The essential question here that we tackle is: do these sophisticated methods offer substantial benefits over the humble LR?
These methods have a number of implementation issues and decisions to be taken, as there is much less consensus than for LR. For each method, we now describe these issues and how we addressed them. A short subsection outlines how we assessed the performance of each model. Finally in this chapter, we consider the problem of poor calibration and how, for this comparison of methods set of analyses, we tackled it.
Support vector machines
Support vector machines are designed to find a hypersurface (hyperplane in the linear case) that separates positive outcomes from negative ones (e.g. death vs. survival). SVMs are therefore classifiers. The SVM output is a number detailing how far on one side of the hypersurface or the other a test vector (set of patient characteristics) lies. This number induces an ordering on the data; however, the ordering needs to be recalibrated if one wants a probability estimate. If no hypersurface can be found that separates the data according to outcome, there will be misclassification. The c-parameter controls the leniency of such misclassifications.
For a given set of parameters a SVM is trained on a training set. The trained model is then applied to a test set, and we calculate the c-statistic. A grid-based search is then performed to determine the optimal set of parameters. The optimal parameters depend on the outcome and set of covariates.
A crucial ingredient for SVMs is the so-called kernel, the most prominent ones being linear and Gaussian. We also studied a Mahalanobis distance-based kernel in more detail (see next paragraph), and there are many others which we briefly looked at. There is no uniquely correct choice of kernel. The kernel will contain parameters of its own in addition to C. As mentioned above, another problem is that SVMs generally output not probability estimates but just a rank. This needs to be calibrated in an extra step, which comes with its own issues. Furthermore, care needs to be taken with ‘unbalanced’ data sets. An imbalance in outcome frequencies is common in medical data sets, that is there are usually many more survivors than non-survivors. LR handles this well, but other methods such as SVMs have a tendency to overemphasise the majority class (which is usually survival). This can be solved by either undersampling the majority class (i.e. randomly dropping patients belong to the majority class until the class distribution is balanced) or oversampling the minority class (i.e. counting patients in the minority class several times until numbers are balanced). The SVM code we used implements a similar but somewhat more sophisticated method. It allows the classes to be weighted differently. Since no data are dropped in this process, this method is similar to oversampling but without adding any data, thus not needlessly increasing the data sets. The last point is important, as SVMs are computationally intensive, and speed is a consideration.
Support vector machines work by measuring the similarity, or ‘distance’, of patient characteristics, which are stored as vectors. The problem is: what is a meaningful ‘distance’ in an abstract space of such vectors? How does one compare the presence of, say, diabetes, with the patient’s gender, or either with a 1-year difference in age? There is therefore no natural distance measure. Standard linear or Gaussian kernels are therefore not necessarily the best, and neither are many others, as all the elements of a vector are treated on the same footing. A data-driven distance measure, the Mahalanobis distance,38 does exist, but to implement it directly would be computationally impossible. However, transforming the data by a principal components analysis results in the Euclidian distance measure in the Gaussian kernel becoming the Mahalanobis distance. We also used the transformed data with the linear kernel.
We chose the free package svm-light39 to implement the SVMs. Its advantage is that it is written in C and thus allows for easy implementation of alternative kernels. In general, for a given kernel, a numerical grid search is employed varying the control parameter C and any other kernel parameters if present. Particularly for more complex kernels and limited computer resources, this is prohibitively inefficient. We therefore performed such a grid search for the popular linear kernels (parameter C only) and the Gaussian kernel (parameter C and the width of the Gaussian). We implemented several other kernels, such as Jaccard–Needham, Cosine, Maryland bridge, Correlation, Coulomb, Polynomial and Rogers–Tanimoto. Full testing was not feasible, so we compared the different kernels using only a small subset of the possible parameters (default and similar). We found no indication of any other kernel outperforming the Gaussian kernel and decided not to pursue these other kernels in more detail.
Svm-light was run in ‘regression mode’. In standard mode, that is ‘classification mode’, SVMs yield an optimal hypersurface separating the two classes, such as deaths and survivors. In regression mode the algorithm will try to fit a function so that it comes as close as possible to the outcome values and therefore may contain information in addition to just being on one side or the other of a hypersurface. In practice we did not see much of a difference in SVM performance between ‘regression mode’ and ‘classification mode’.
With the exception of age, all the covariates were binary, so the data are located on the corners of a hypercube. Unsurprisingly, building the model was very slow. Given that one learning run needs to be performed for each combination of SVM parameters, we had to limit each SVM learning run to 24 hours. The resulting model then also contains a large fraction (> 90%) of all data vectors as support vectors – SVM are meant to be able to find a model with few support vectors (support vectors are points that lie on the margins of the separating hyperplanes).
Artificial neural networks
Artificial neural networks come in a multitude of different types. There are far too many adjustable aspects of ANNs to systematically optimise all of them. Hertz et al. discuss important standard implementations of ANNs such as feed-forward and recurrent ANNs, but also unsupervised ANNs such as Kohonen maps. 40 After waning for a few years because of the popularity of SVMs, interest has revived recently under the heading of Deep Learning. 41 We concentrate on what is probably the standard: feed-forward ANNs, which are conceptually quite similar to LR. Whereas in LR a weighted sum feeds into a logit function, in feed-forward ANNs several such structures are fed into a further LR-like computational structure layer by layer. Such ANNs are usually trained using the back-propagation algorithm. This is a local optimisation algorithm. The exact computational methodology for solving the resulting optimisation problem is also not as clear-cut as in LR. One may minimise several different measures such as the Brier score (mean square error), a log-likelihood-based measure as in LR, or some combination of the two, but even then there is no unique solution as is the case in LR. This means that different optimisation methods are used in conjunction with several overall measures, generally resulting in different solutions (local minima) with no unique and obvious choice of the optimal combination. However, the result will usually be a meaningful estimate of a probability. The scoring function which was optimised could interpolate between the mean square error and a LR-like log-likelihood-based measure. This affects the position of the optima and the speed with which they are reached. We chose an equal mix of both. No systematic changes with respect to the result were observed, but some speeding up was observed. For this reason we also added a momentum term and damping into the stepwise updates of the optimisation.
We terminated this procedure at one so-called hidden layer, which is the standard choice. One must decide how many nodes to use. When choosing the number of nodes in the hidden layer, we kept to a common rule of thumb: the number of nodes should be of the order of the square root of the number of variables in the model. Any number of hidden nodes beyond one will give results better than LR. We found that, as long as the number of hidden nodes was greater than two, no systematic changes regarding the c-statistic were observed, so we settled on five as per the rule of thumb. In ANNs as in LR, there is no unique functional form of the non-linear transform, although logit is a common choice.
We added a LR-like direct link from the input layer to the output layer. While this did not improve overall performance it has a few advantages. By setting the links to the hidden layer to zero we are left with a LR-like architecture. The optimisation can then be initialised with a LR solution, which saves time. In addition, back-propagation is then guaranteed to reach an optimum that is at least as good as LR.
Random forests
Random forests is a decision tree-based method. 42 A decision tree is a set of if–then clauses (nodes) with a tree-like structure, with each leaf being a decision on the expected outcome: ‘if (age > 65 years) then if (no diabetes) equals survival’, etc. The trees in random forests use a randomly chosen subset of all explanatory variables at each node. A random forest then consists of many such trees, each one grown on a bootstrapped sample of the training data set (bootstrapping a data set means generating new data sets by drawing from the original one with replacement). The outcome or outcome probability is then derived from a committee decision made by all the trees in the forest. This method may also be combined with other methods. Calibration issues may also be prominent, and there are potentially many parameters to tweak.
Individual trees are grown in the following manner:
-
Sample N cases at random with replacement to create a subset of the data.
-
At each tree node:
-
From the total number of explanatory variables, M, select at random a subset of m explanatory variables.
-
The explanatory variable that provides the best split, according to the classification and regression trees methodology43 or some other objective function, is used to do a binary split on that node.
-
At the next node, choose another m variable at random from all explanatory variables and do the same.
-
For each case, the numbers of trees that ‘vote’ for a particular class (e.g. death) are used as an estimate of the probability of being in that class. In addition to the randomforest package version 4.6–7 (University of California, Berkeley, CA, USA) default of 500 trees and m = sqrt(M), the advice given by Genuer et al. 44 was followed on selecting the number of trees and m.
The random forests were implemented as described by Breiman45 using R version 3.0.2 (The R Foundation for Statistical Computing, Vienna, Austria) and the randomforest package version 4.6–7.
Assessment of model performance
With any risk model comes the need to assess its performance. For binary outcomes, two standard measures for LR are the area under the receiver operating characteristic (ROC) curve, or c-statistic, and the Hosmer–Lemeshow (HL) test output. The former measures discrimination, the ability of the model to predict a higher probability of death for those who died than for those who survived. It is generally considered that values of c above 0.70 represent good discrimination and values above 0.80 represent excellent discrimination. The maximum value obtainable is often quoted as 1 but in fact varies with the distribution of risk in the population (see Cook46 for a full discussion on this statistic). The HL test describes the model’s calibration and divides the data set into risk deciles. The observed and predicted number of events are compared in each decile – which often shows poor calibration at the extremes – and summarised in a chi-squared statistic. It has been criticised for having high type I and II error rates. 47 While a simple plot of observed versus predicted rates may be more useful, we will nonetheless report HL test results because of the large number of models fitted and the need to be concise.
For the HL chi-squared values, we give right-sided p-values. We used 10 bins for the HL test, as is standard. Any constraints of the fitting procedure (e.g. that the total sum of estimated probabilities equals total sum observed events) which reduce the effective number of degrees of freedom apply to the HL test with respect to the training data set. When running LR for a range of patient groups, we used eight degrees of freedom as is standard and as used by SAS. However, in the comparison of methods section, as we present results for the test set, no such constraints exist, and the HL test will be distributed according to the full 10 degrees of freedom.
Recalibration
Being built around a sigmoid output node, ANNs produce output that can be interpreted as a probability estimate, as does LR. The greater variational freedom inherent in the algorithm then means that the result is potentially better calibrated. Therefore we did not recalibrate the ANN output.
Methods that are known to have calibration issues, such as random forests,48 or are not even designed to produce meaningful probability estimates, such as SVMs, have to be recalibrated. We also found a number of the LR models to show overprediction of low risk in particular. As LR may be viewed as an ANN with no hidden nodes, back-propagation is applicable and can be adapted easily to optimise the internal shape parameters of the output node. Adjusting the shape parameters changes the calibration. Standard LR is based on optimising a log-likelihood-based measure and results in perfect overall calibration (i.e. total observed counts equal total predicted counts). Optimising the mean square error does not result in perfect overall calibration. However, the difference in probability estimates using each optimisation scheme encodes the deviance from an optimal model for which the difference would be zero. (This follows from the fact that both measures are so-called ‘strictly proper scoring rules’.) We found that feeding the probability estimates back into a further LR iteration in conjunction with the other covariates improved both discrimination and calibration. This will be labelled ‘LR+’ in the results. Only feeding back in the standard LR probability estimates also improved the final result but to a much lesser degree.
The standard method for recalibration is isotonic regression pool-adjacent-violator algorithm (IR-PAV),49 which we have used throughout. However, this results in a series of steps in the predicted probability curve, which is biologically implausible. Later in the project, we developed a smoothing technique using splines – full details are found elsewhere. 50 To illustrate, the original LR probability estimates for 30-day total mortality following AMI are mapped onto recalibrated estimates for the two methods, compared in Figure 1. The blue ‘diagonal’ line represents no recalibration. The effect of the recalibration is to lower very low probabilities and high probabilities and to push up those in the middle. In other words, LR first over-, then under- and then overestimates probabilities as one moves from low to high values. Depending on the exact use, correct calibration in addition to discrimination may be of importance. Note that the bulk of the patients in this example are to be found between 0.05 and 0.4 so the large discrepancy for very large values affects only few patients.
FIGURE 1.
Comparison of standard (PAV) and alternative (SEP) recalibration methods. Graph (a) shows probabilities up to 0.5; and graph (b) shows the whole data set. SEPs, splined empirical probabilities.
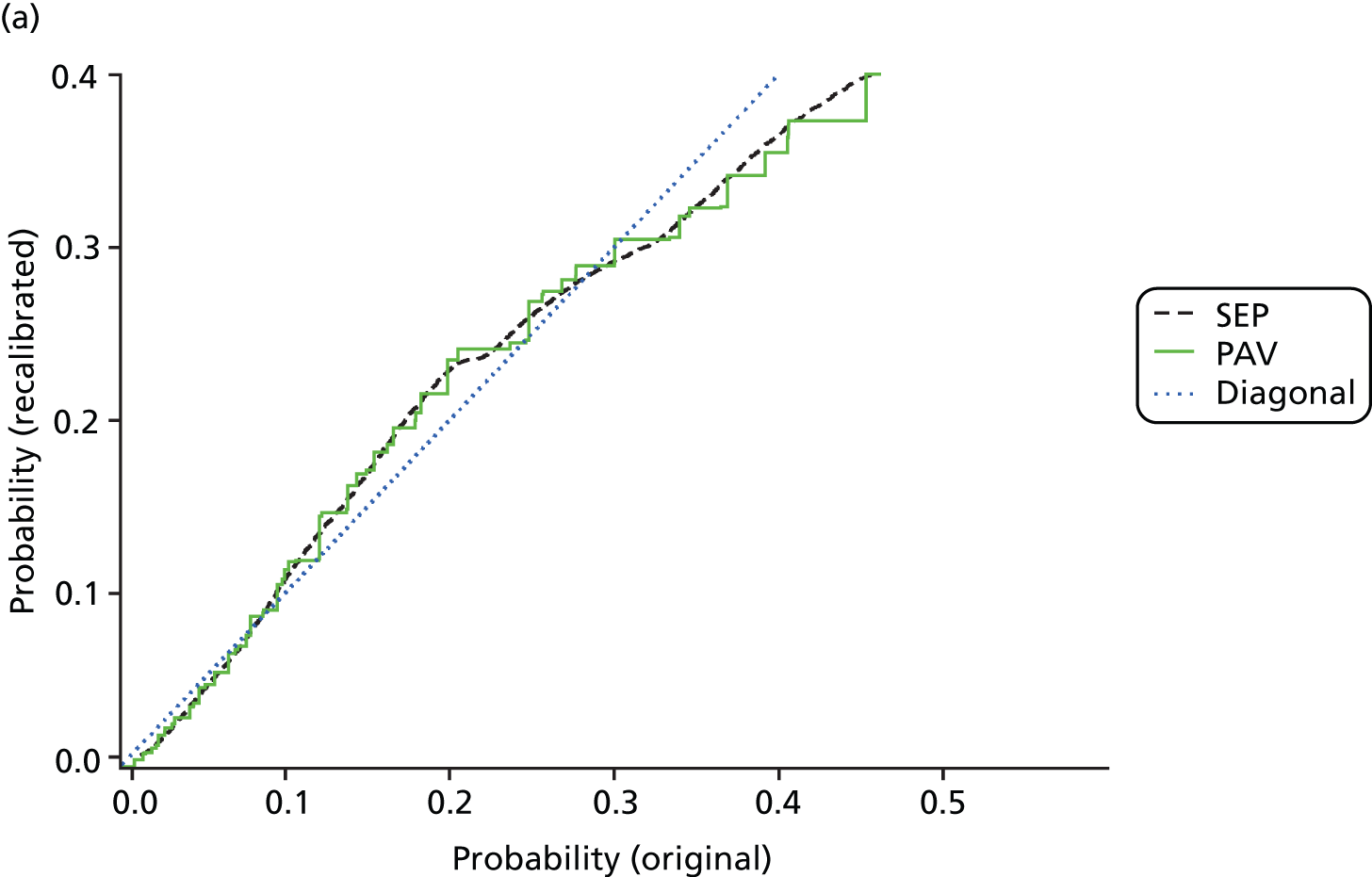
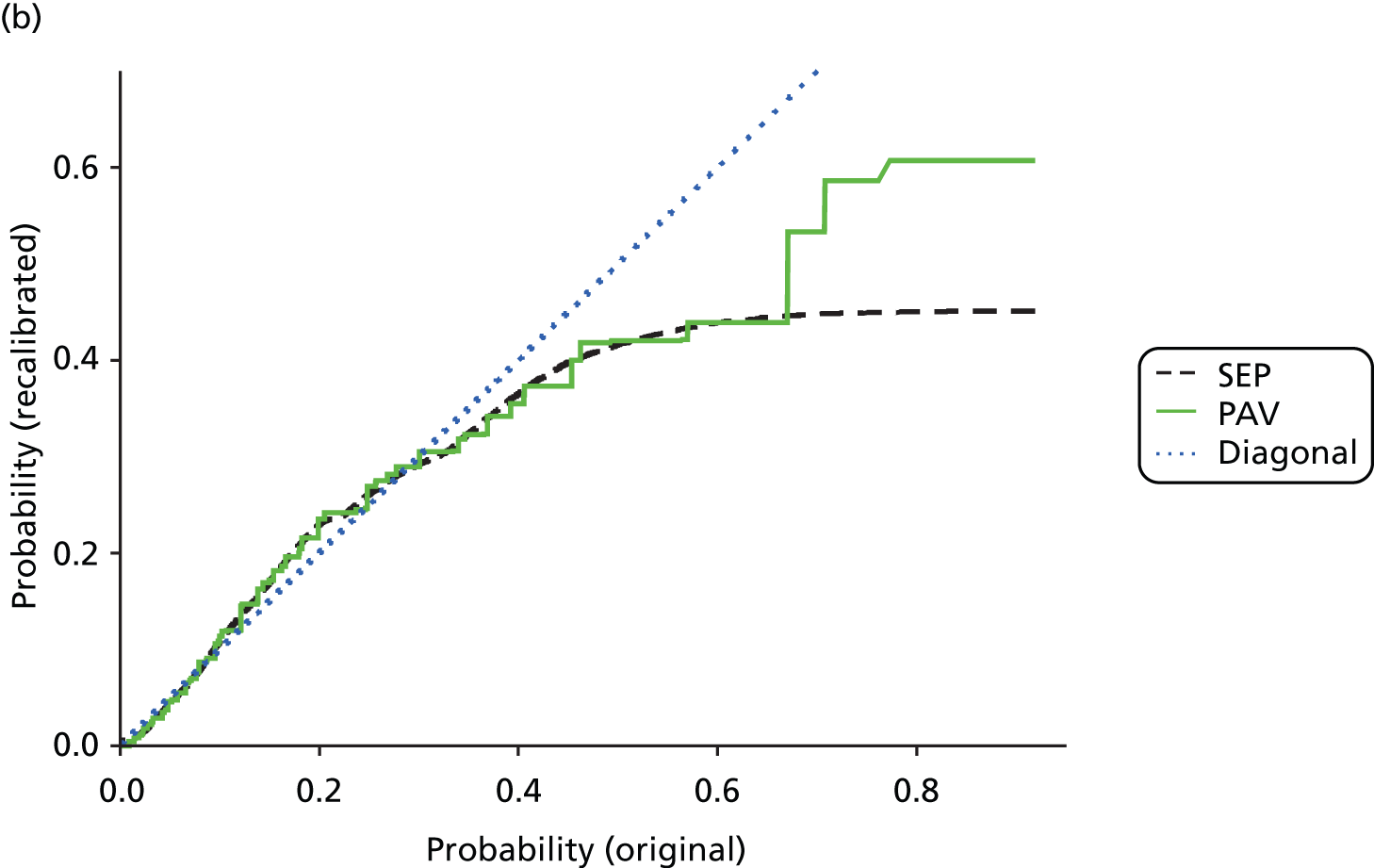
Methods for including information from previous admissions into the prediction models
Many patients, particularly the elderly and those with chronic conditions, have a number of health service contacts. As mentioned before, data quality considerations currently limit the use of A&E attendances (we decided not to use these) and OPD appointments to counting OPD appointments attended and missed; see the last section of Chapter 3. With previous admissions, one may use the procedure and diagnosis information (the latter can be used to augment comorbidity codes as mentioned earlier) and also the timing of them relative to the index contact. A simple but crude approach is to count the number of emergency admissions for any reason within the previous year. 2 To use the primary diagnosis of these previous admissions, one needs to use some grouping algorithm such as the AHRQ’s CCS groups and then combine the infrequent ones. The relative timing, which is recorded in number of days between admission dates, may also be incorporated, as in principle may the duration of each stay.
Intuitively, one may think that a recent readmission better predicts the outcome of the index admission than one that lies further back in time. If we ignore the durations and consider just the fact of admission, then a 3-year lookback period generates roughly 1000 binary variables – one for each day. Determining the effect of each of these variables cannot be done by simply adding them to a LR model. Some aggregation is needed. This also smooths out small time differences (e.g. whether a previous admission is 673 days in the past or 674 is unlikely to be of major significance). We used a two-step process as follows.
First step:
-
We generated the 60 lowest-order orthogonal polynomials of our 1000-dimensional vector space of admission dates. The base polynomial (a horizontal line) then is equivalent to just summing the number of admissions; the next polynomial (a diagonal) translates into a sum weighted by the time difference to the present admission, etc.
-
The value of the sums weighted by these polynomials results in 60 new variables. These were used in a LR model.
-
Using the LR coefficients yields a weighting of polynomials, which results in a single weighted sum that in a LR model would give the same result.
-
As expected, this weighted sum puts about five times greater emphasis on very recent previous admissions than those further in the distant past. The decline in weights occurs over about the first half-year or so.
Second step:
-
The weighted sum above may be used to generate new weighted polynomials. These will give greater prominence in magnitude and resolution to where the weighting is largest, that is to recent admissions. The base polynomial stays the same.
-
One or more such polynomials may now be used as weighted sums to generate variables that can be added to a LR model.
-
We also included a flag for no previous admission within the last 3 years.
To test this, we considered two years of index HF admissions as used in the readmission analyses. Our outcome was unplanned readmission within 28 days. All of these models contained the set of casemix variables used in the comparison of methods above plus the flag for no previous admission. The orthogonal polynomials were generated in SAS using PROC IML, and the weighted sums were implemented in SAS using PROC FCMP.
The effect of the semi-competing risk of death on readmission-type measures
As death precludes subsequent readmission, using LR – which ignores any effect of death either during or following the index discharge – may be potentially misleading. We therefore also applied cause-specific proportional hazards modelling and subdistribution proportional hazards modelling. These two survival analysis methods make different assumptions regarding post-discharge deaths;51,52 other methods exist, but these are the two most widely used. The PSHREG macro in SAS was run for subdistribution hazards. 53 If the odds ratios (ORs) and two sets of hazard ratios all agree, then we can be fairly confident that the effect of post-discharge deaths is minor. For the proportional hazards models we inspected the standard errors and deviance and Schoenfeld residuals; as our focus here was on the validity of using LR as the standard method rather than on the precise specification of a survival analysis model, we did not perform the usual formal tests of proportionality.
As is standard, our analyses of readmissions were restricted to patients discharged alive from their index admission. We did not attempt to take account of deaths during the index admission, and we acknowledge that this is a potential limitation.
Methods for predicting future bed-days in heart failure patients
As well as modelling the first unplanned readmission, as is common practice, we also wanted to consider broader measures of future hospital use. Internationally, the literature on HF readmissions is dominated by studies predicting a single readmission, usually 30-day readmissions,54,55 though some used longer follow-up periods of 90 days56 and 12 months. 57 Braunstein et al. 58 modelled the number of all-cause and HF ambulatory care-sensitive conditions (ACSCs) and all-cause ACSC hospitalisations during 12 months. The ACSC literature tends to focus on trying to predict the high-risk patients. 59,60 Few studies have modelled the number of further admissions. Johnson et al. 61 considered the number of HF-related hospitalisations during 3 years of follow-up using a negative binomial model. Although Chun et al. 62 modelled cardiac and non-cardiac hospitalisations from discharge until death, they took a survival analysis approach that included repeated-events time-to-event analysis. We found no study that considered total future bed-days in HF patients.
Resource-use measures are often characterised by distributions displaying overdispersion and an excess number of zero counts, so a range of count data models including Poisson, negative binomial with quadratic variance function (NB2), zero-inflated Poisson, zero-inflated negative binomial (ZINB), Poisson hurdle and negative binomial hurdle (NBH) models were fitted. The NB2 model allows for overdispersion by relaxing the Poisson model assumption of equal mean and variance. The zero-inflated and hurdle models provide alternative ways of capturing the excess zero counts. The former treats zeroes as arising from one of two sources – always zero and possibly zero – and the latter treats zeroes as arising from only one source. For a review of such models, see Hu et al. 63
Mortality rates in the year after discharge from the index HF admission are high. Accordingly, the number of days the patient survived following discharge from their index HF admission, capped at 365 days, was used as on offset term in the regression models to control for differing opportunity to accrue readmissions and bed-days. 61
‘Buckets’ approach
An alternative approach to modelling the number of bed-days directly is to categorise the count. We assigned patients with a positive number of bed-days to one of five resource-use buckets. The thresholds for each bucket were allocated such that the total resource use (number of patients × number of bed-days) in each bucket was approximately equal. The factors influencing membership of the highest (and two highest) resource-use buckets were examined using LR.
Other modelling details
The models described above assume that observations are independent, so the conditional ICC was calculated to assess the need for models taking account of the clustering of patients in hospitals. We used the same set of covariates as for the first readmission. This time, we also examined the additional value of including specific ICD-10 Z-codes as proxies for care in the community, patient support networks and likely adherence to post-discharge advice. One candidate was the code for living alone, whose recording in HES has been mandatory since 2009.
Nested models were compared using likelihood ratio tests, log-likelihood, AIC and Bayesian information criterion. For pairs of generalised linear models we additionally compared the deviance. Non-nested models were compared using the tests of Vuong64 and Clarke. 65
The mean predicted probability for each count value and observed probabilities were compared graphically. Pearson’s chi-square test and the chi-square goodness of fit test proposed by Cameron and Trivedi (p. 195)66 were not used, as they are not informative with large sample sizes such as ours.
The discrimination and calibration of the logistic models were assessed using the c-statistic and HL statistics respectively.
Chapter 3 Results
We now present results to illustrate the foregoing methods and questions rather than give a large number of tables covering AMI, stroke, HF, COPD, ACS, coronary artery bypass graft (CABG), hip and knee replacements, colorectal surgery and the other patient groups that we analysed. For instance, RTT metrics were defined for colorectal and orthopaedic surgery, and to illustrate this we present results for elective hip and knee replacements. When comparing machine learning and regression, we present results for AMI and colorectal excision.
Adjusting for comorbidity: results from updating the Charlson index
Amending the ICD codes following the expert clinical coder review and literature search led to increases in prevalence for dementia and AMI in particular. Comparison with the original 1987 published weights showed notable declines in relative importance for human immunodeficiency virus (HIV) and increases for dementia, a condition that was not even included in the original 1998 formulation of the Elixhauser index. For illustration, we present the weights derived from 2008/9 inpatients (Table 2).
| Comorbidity variable | Original Charlson weights | Original Charlson codes, new HES-based weights, all inpatients 2008/9 | Amended Charlson codes, new HES-based weights, all inpatients 2008/9 |
|---|---|---|---|
| Cancer | 2 | 5 | 4 |
| Connective tissue disorder | 1 | 3 | 2 |
| Cerebrovascular accident | 1 | 7 | 5 |
| Dementia | 1 | 8 | 7 |
| Diabetes with long-term complications | 2 | 0 | –1 |
| Diabetes without long-term complications | 1 | 2 | 1 |
| Congestive HF | 1 | 8 | 6 |
| HIV | 6 | 0 | 0 |
| Mild or moderate liver disease | 1 | 4 | 4 |
| Pulmonary disease | 1 | 3 | 2 |
| Metastatic cancer | 3 | 8 | 7 |
| AMI | 1 | 5 | 2 |
| Paraplegia | 2 | 1 | 1 |
| Peptic ulcer | 1 | 5 | 4 |
| Peripheral vascular disease | 1 | 4 | 3 |
| Renal disease | 2 | 7 | 5 |
| Severe liver disease | 3 | 11 | 9 |
As we found in our systematic review, Elixhauser generally outperformed Charlson for both mortality and readmissions. To illustrate, Table 3 gives the c-statistic and adjusted R2 values for both indices for AMI and COPD for mortality. More details are given elsewhere. 67
| Measure | Original Charlson codes and weights | Original Charlson codes, empirical weights | Amended Charlson codes, empirical weights | Modified Elixhauser, empirical weights |
|---|---|---|---|---|
| c-statistic | ||||
| All inpatients | 0.719 | 0.726 | 0.757 | 0.799 |
| AMI admissions | 0.624 | 0.641 | 0.654 | 0.668 |
| COPD admissions | 0.577 | 0.601 | 0.611 | 0.646 |
| Adjusted R2 statistic | ||||
| All inpatients | 0.100 | 0.106 | 0.123 | 0.142 |
| AMI admissions | 0.046 | 0.051 | 0.058 | 0.058 |
| COPD admissions | 0.020 | 0.030 | 0.032 | 0.044 |
Incorporating information from prior admissions is often done using a 1-year lookback period but sometimes using a longer one. Table 4 compares the ORs for a set of comorbidities relevant to ACSs when using a 1- and a 5-year lookback and when using none, i.e. when using only the secondary diagnosis codes from the index admission. Some effects were modified when using prior admissions. Overall, a 5-year period offered little benefit over a 1-year period, and a 1-year period offered little over no lookback. Further details are found elsewhere. 67
| Factor | One-year lookback | Five-year lookback | ||
|---|---|---|---|---|
| OR (95% CI) | p-value | OR (95% CI) | p-value | |
| Cancer | 1.50 (1.40 to 1.59) | < 0.001 | 1.25 (1.19 to 1.31) | < 0.001 |
| Atherosclerosis | 0.96 (0.87 to 1.06) | 0.420 | 0.93 (0.86 to 0.99) | 0.034 |
| Valvular disease | 1.81 (1.49 to 2.19) | < 0.001 | 1.76 (1.53 to 2.01) | < 0.001 |
| HF | 1.40 (1.30 to 1.50) | < 0.001 | 1.40 (1.32 to 1.47) | < 0.001 |
| Lower respiratory | 1.34 (1.22 to 1.46) | < 0.001 | 1.30 (1.22 to 1.39) | < 0.001 |
| Diabetes | 1.84 (1.58 to 2.15) | < 0.001 | 1.62 (1.47 to 1.78) | < 0.001 |
| Renal failure | 1.74 (1.52 to 2.00) | < 0.001 | 1.80 (1.63 to 1.99) | < 0.001 |
| Stroke | 1.16 (1.04 to 1.29) | 0.009 | 1.21 (1.13 to 1.29) | < 0.001 |
| Hypertension | 1.33 (1.10 to 1.61) | 0.003 | 1.18 (1.04 to 1.35) | 0.014 |
| Atrial fibrillation | 0.97 (0.87 to 1.08) | 0.554 | 0.90 (0.84 to 0.97) | 0.005 |
| Peripheral vascular disease | 1.43 (1.22 to 1.69) | < 0.001 | 1.42 (1.29 to 1.55) | < 0.001 |
| All other diagnoses | 1.06 (1.03 to 1.09) | < 0.001 | 0.99 (0.96 to 1.02) | 0.369 |
Such lookback approaches ignore the potential impact of the timing in relation to the index admission. More sophisticated approaches using polynomials as described earlier were applied to our HF cohort, and we now give the results.
Including information regarding the timing of previous health service contacts in the prediction models
Since using a straightforward sum for the previous admissions had no great effect in terms of the c-statistic on casemix adjustment, it is unsurprising that the weighted sum we derived did not add much either. This, however, does not mean that previous admissions or the non-constant weights used here are unimportant. Here are the results for 30-day readmission following live discharge from an index HF admission:
-
Without additional variables (i.e. just age, sex, comorbidities, etc.) the c-statistic was 0.579, and the HL test gave a chi-squared of 17.2 (p = 0.025).
-
With a constant sum only for the previous admissions the c-statistic rose to 0.586, and the HL test gave a chi-squared of 17.1 (p = 0.030).
-
With the time-weighted base polynomial for the previous admissions the c-statistic was 0.591, and the HL test gave a slightly improved chi-squared of 11.5 (p = 0.177).
-
The two lowest time-weighted polynomials for the previous admissions yielded a c-statistic of 0.592, and the HL test gave a lower chi-squared of 7.4 (p = 0.499).
-
The three lowest time-weighted polynomials for the previous admissions also yielded a c-statistic of 0.592, and the HL test gave a similar chi-squared of 5.8 (p = 0.675).
-
The four lowest time-weighted polynomials for the previous admissions also yielded a c-statistic of 0.592, and the HL test gave a chi-squared of 5.8 (p = 0.668).
Adding one or two time-weighted polynomials improved the c-statistic by about as much again as did an unweighted sum of previous admissions. This procedure also noticeably improved the calibration. Adding a third polynomial improved the calibration even more, but beyond that we saw no further improvement. We conclude that using these (two or three) time-weighted polynomials was appreciably better than the simple count approach.
Mortality and readmission from logistic regression
Following on from the previous section, we used the Elixhauser set plus dementia to adjust for comorbidity in this section. Model performance in terms of discrimination varied considerably by patient group and outcome (Table 5), with readmissions of any follow-up length being harder to predict than death. Discrimination was generally higher for 28- than for 7-day readmission but similar for the two death outcomes. Because of the large sample sizes, the confidence intervals for the c-statistics were very narrow and are not shown in this report.
| Patient group | 7-day readmission | 28-day readmission | Death | Total 30-day death | ||||
|---|---|---|---|---|---|---|---|---|
| c | HL (p-value) | c | HL (p-value) | c | HL (p-value) | c | HL (p-value) | |
| AMI | 0.623 | 21 (0.006) | 0.644 | 72 | 0.775 | 376 | 0.770 | 361 |
| Stroke | 0.599 | 14 (0.071) | 0.618 | 69 | 0.737 | 707 | 0.732 | 590 |
| HF | 0.600 | 11 (0.165) | 0.618 | 11 (0.166) | 0.684 | 80 | 0.680 | 78 |
| Pneumonia | 0.618 | 60 | 0.657 | 285 | 0.800 | 445 | 0.795 | 459 |
| COPD | 0.650 | 36 | 0.682 | 170 | 0.718 | 73 | 0.714 | 66 |
| FNOF | 0.617 | 38 | 0.624 | 106 | 0.773 | 209 | 0.773 | 183 |
| THR | 0.607 | 5.0 (0.756) | 0.613 | 10 (0.278) | 0.864 | 13 (0.123) | 0.845 | 8.9 (0.348) |
| TKR | 0.615 | 16 (0.039) | 0.61 | 13 (0.111) | 0.811 | 10 (0.273) | 0.804 | 7.5 (0.481) |
| CABG | 0.608 | 8.5 (0.382) | 0.604 | 3.0 (0.933) | 0.835 | 10 (0.237) | 0.830 | 15 (0.061) |
| AAA repair | 0.610 | 2.8 (0.945) | 0.615 | 9.0 (0.339) | 0.770 | 6.3 (0.611) | 0.771 | 4.1 (0.851) |
| Colorectal excision | 0.580 | 9.1 (0.333) | 0.593 | 12 (0.142) | 0.834 | 21 (0.006) | 0.830 | 19 (0.016) |
Calibration was much better for the procedures than for the diagnosis groups. It is common to find that LR models are not always well calibrated, with overprediction of low risk and underprediction of high risk common problems. Where calibration was found to be unacceptable as judged by the HL p-value (though see earlier commentary on this measure), we found overprediction of low risk to be a common explanation. A typical example is given below for 30-day total mortality following AMI. Figure 2 plots the ratio of the observed to predicted deaths.
FIGURE 2.
Ratio of observed to predicted deaths for each risk decile for 30-day mortality following AMI.
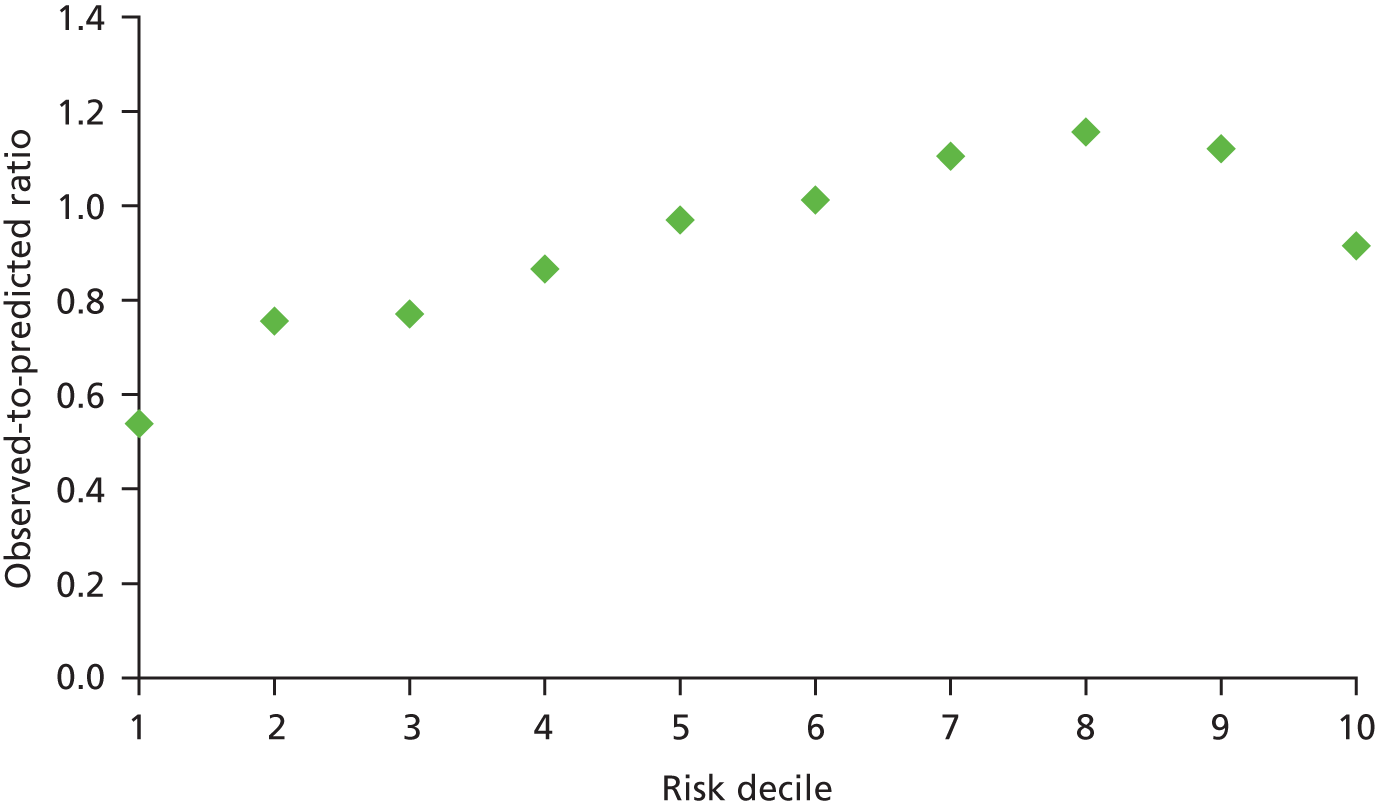
Comparison of methods: logistic regression and machine learning
For the LR models in this section of the analysis, we therefore took output from both the usual LR models and those with the extra recalibration step as described in the earlier recalibration subsection. We compared these with several machine learning approaches. Table 6 gives the resulting discrimination for AMI and elective colorectal surgery for mortality and readmission (results were similar for pneumonia and are not shown). In general, ANNs sometimes gave slightly better c-statistics, but LR performed comparatively well. Overfitting was a problem for the random forests in particular: for example, for AMI mortality, the training set c-statistic reached 0.92, which fell to 0.74 for the test set. For SVMs, only the best results are shown; performance varied by the SVMs’ parameters. In general, we found that overfitting was severe on the raw data for any kernel. However, transforming the data to principal components analysis space, as described earlier, massively reduced overfitting and also stabilised the algorithm. The total predicted outcomes differed from the total observed outcomes because the results are for the test set, whereas any calibration is learnt/trained on the training data set. Even the best method would suffer from at least some such statistical fluctuations.
| Outcome and method | AMI | Colorectal excision | ||||
|---|---|---|---|---|---|---|
| c | HL statistic | p-value | c | HL statistic | p-value | |
| Mortality | ||||||
| LR | 0.773 | 124.5 | < 0.001 | 0.823 | 26.4 | 0.003 |
| LR+ | 0.777 | 17.3 | 0.067 | 0.826 | 51.7 | < 0.001 |
| ANN | 0.777 | 36.4 | < 0.001 | 0.824 | 86.3 | < 0.001 |
| ANN-LR | 0.777 | 36.5 | < 0.001 | 0.826 | 31.9 | < 0.001 |
| SVM linear kernel | 0.771 | 13.4 | 0.201 | 0.806 | 26.8 | 0.003 |
| SVM Gaussian kernel | 0.771 | 8.9 | 0.544 | 0.823 | 49.1 | < 0.001 |
| Random forest | 0.743 | See text | < 0.001 | 0.768 | See text | < 0.001 |
| Readmission | ||||||
| LR | 0.640 | 33.0 | < 0.001 | 0.576 | 8.6 | 0.567 |
| LR+ | 0.638 | 20.2 | 0.027 | 0.570 | 9.6 | 0.479 |
| ANN | 0.638 | 36.5 | < 0.001 | 0.571 | 104.0 | < 0.001 |
| ANN-LR | 0.638 | 42.7 | < 0.001 | 0.570 | 31.9 | < 0.001 |
| SVM linear kernel | 0.637 | 32.0 | < 0.001 | 0.575 | 5.8 | 0.830 |
| SVM Gaussian kernel | 0.636 | 25.1 | 0.005 | 0.578 | 19.7 | 0.032 |
| Random forest | 0.550 | See text | < 0.001 | 0.532 | See text | < 0.001 |
It is noteworthy that random forests suffered more from overfitting than the other methods. This also had repercussions for recalibration: the raw probability estimates were generally too low. In particular we observed that random forests picked up a sizeable number of positive outcomes and grouped them together. Pool adjacent violators recalibration then maps these onto high-probability estimates. Unfortunately, these high probabilities were accurate only on the training data set (overfitting), and hence the corresponding HL test resulted in extremely large chi-squared values, which we have not given in the table.
When these models are used in risk adjustment, the resulting RRs at unit level are also of interest. These were derived by summing the observed and summing the predicted for each hospital and dividing the former sum by the latter sum. Table 7 compares the RRs derived from LR (both standard and recalibrated) with those derived from the other methods for AMI in terms of their funnel plot outlier status. Hospital trusts with at least 50 AMIs in two years were included. The patterns for colorectal surgery were similar and are not shown.
| Outcome and method | Low 95% outliers | High 95% outliers | Low 99.8% outliers | High 99.8% outliers |
|---|---|---|---|---|
| Mortality | ||||
| ANN | 2 | 5 | 1 | 0 |
| ANN-LR | 9 | 3 | 1 | 0 |
| LR | 6 | 3 | 1 | 0 |
| LR+ | 10 | 3 | 1 | 0 |
| SVM linear kernel | 8 | 3 | 1 | 0 |
| SVM Gaussian | 7 | 3 | 1 | 0 |
| Random forest | 19 | 4 | 2 | 0 |
| Readmission | ||||
| ANN | 2 | 0 | 1 | 0 |
| ANN-LR | 3 | 0 | 1 | 0 |
| LR | 4 | 1 | 1 | 0 |
| LR+ | 2 | 0 | 1 | 0 |
| SVM linear kernel | 3 | 1 | 1 | 0 |
| SVM Gaussian | 3 | 1 | 1 | 0 |
| Random forest | 7 | 2 | 1 | 0 |
There were more low than high outliers. In general, there was a lot of similarity between the sets of SMRs themselves and between the numbers of outliers across six of the seven methods. The exception was the random forests, for which recalibration consistently gave the highest total expected count for the four sets (AMI and colorectal, mortality and readmission) and resulted in by far the highest number of hospitals flagged as significantly low on the funnel plots. This was due to overfitting and the assigning of a very high predicted risk to too many patients.
Return-to-theatre metrics for orthopaedics
Following on from our earlier work in urology for cystectomy,7 we give results for total or partial hip replacement (HR) and knee replacement (KR); colorectal excision results may be found elsewhere. 68
There were 260,206 index HR procedures and 286,590 index KR procedures during the 6 years 2007/8 to 2012/13 combined. Because of invalid or unknown consultant team codes, 2153 HRs and 2874 KRs were excluded. A further 112 HRs and 29 KRs were removed at hospitals performing fewer than 30 procedures over the 6 years. This left 260,370 HRs among 2029 surgeons and 315,454 KRs among 2061 surgeons for analysis. Of these, there were 5353 RTTs within 90 days for a rate of 2.1% for HR and 5508 RTTs within 90 days for a rate of 1.8% for KR.
The most common reinterventions were closed reduction of dislocated total prosthetic replacement for HR (34% of the total) and attention to total prosthetic replacement of knee joint not elsewhere classified for KR (28% of the total), the latter mostly representing manipulations under anaesthesia for stiffness. Age, sex and many comorbidities were significant predictors for both index procedures. Age had different relations for hips (ages over 75 years had higher odds) from those for knees (ages under 60 years had higher odds, particularly those under 45 years). Some comorbidities, such as arrhythmias, dementia, obesity, fluid disorders and Parkinson’s disease, were associated with higher odds of RTT for both index procedures, but others, such as liver disease, depression and alcohol abuse, raised the odds only for HR. There was no relation with area deprivation. Hip resurfacing had around half the odds of other hip subgroups; partial knee replacements had around half the odds of other knee subgroups.
Figure 3 shows the variation for RTT following HR by surgeon (the plot for KRs is very similar and is not shown). Because of the known unreliability of consultant codes in HES for unplanned activity, we analysed and give the figures for elective procedures only.
FIGURE 3.
Funnel plot for RTT following HR by surgeon.
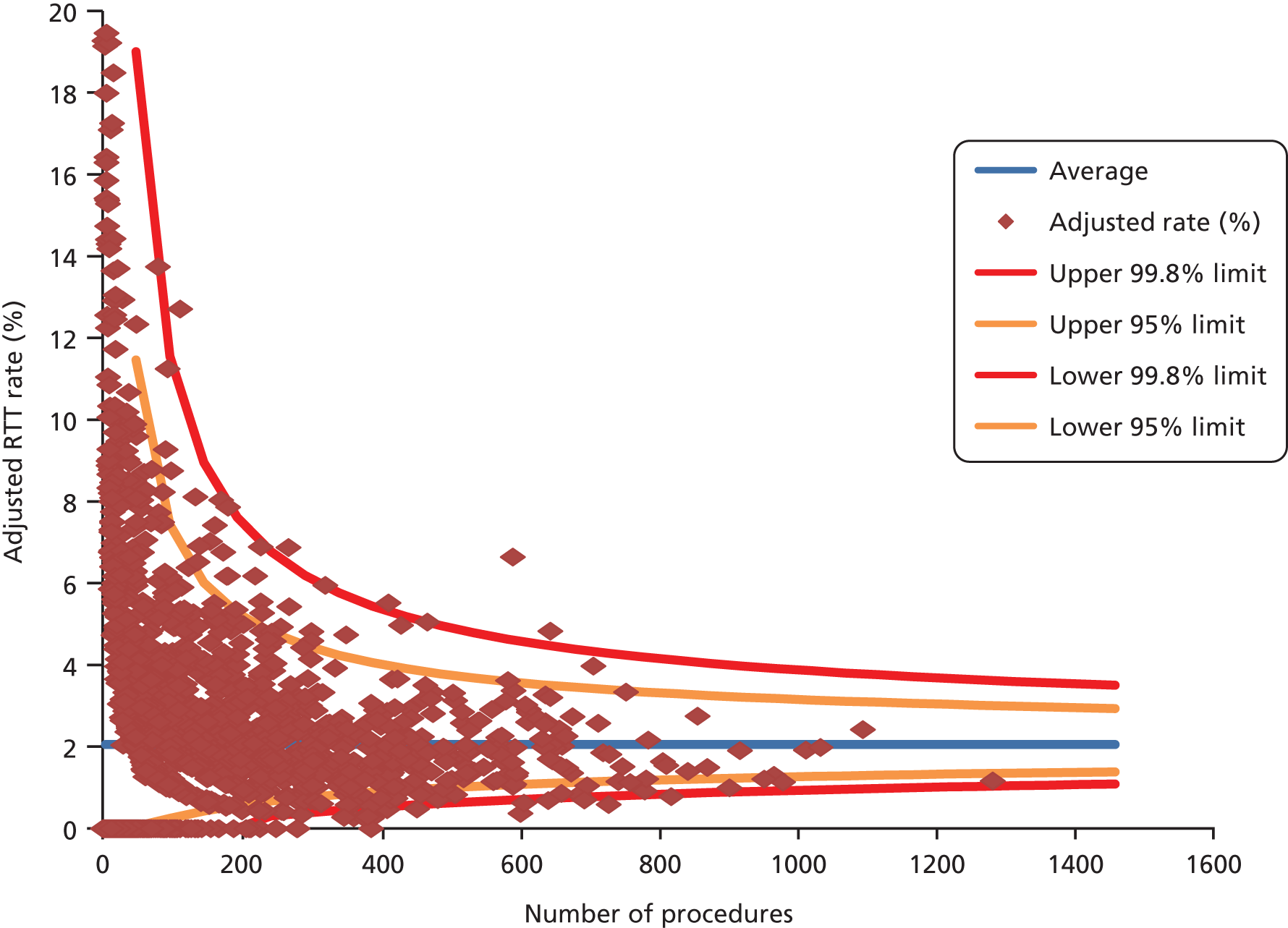
The discrimination of the two models was low (c = 0.61 for HR and 0.60 for KR) but the calibration was acceptable using the HL test (chi-squared 9.2, p = 0.324 for HR, and chi-squared 13.3, p = 0.102 for KR).
Variation by surgeon for HR was similar to that for KR (standard deviation 0.22, Table 8). Patient factors explained little of this for either procedure. Accounting for the hospital explained around a quarter of the variation between surgeons for HR and nearly half (44%) for KR. This suggests that three-quarters of a surgeon’s RTT rate for HR and half their rate for KR are explained by factors other than patient factors or the hospital at which they operate.
| Index procedure and model | AIC | Standard deviation of surgeon effects | % change from surgeon only |
|---|---|---|---|
| HR | |||
| Surgeon only | 51,841 | 0.219 (0.021) | 0 |
| Surgeon + patient factors | 51,153 | 0.210 (0.020) | –4.1 |
| Surgeon + hospital | 51,806 | 0.162 (0.019) | –26.0 |
| Surgeon + hospital + patient factors | 51,124 | 0.160 (0.019) | –26.0 |
| KR | |||
| Surgeon only | 55,094 | 0.220 (0.019) | 0 |
| Surgeon + patient factors | 54,458 | 0.212 (0.019) | –3.6 |
| Surgeon + hospital | 55,000 | 0.123 (0.016) | –44.1 |
| Surgeon + hospital + patient factors | 54,361 | 0.116 (0.016) | –47.3 |
Outpatients department non-attendance
Many reasons for patients missing their OPD appointment have been identified. We now give a brief summary of the literature that is not meant to be exhaustive. Reasons for missing include simple forgetting or confusion over the appointment’s time or location,69 illness severity (either mild, including recovery from symptoms, or severe),70,71 administrative and/or communication errors,69,72–74 being busy or unable to take time off work or arrange child care. 75,76 Previous unsatisfactory experience of health care, such as long waiting times and unhelpful staff with poor communication skills, also has an impact,77,78 as do not being involved in the referral decision-making process69,71 and not understanding the reasons for the appointment. 79 Previous non-attendance is a strong predictor for future behaviour related to attendance,78 with the probability of missing a second appointment being much higher than the probability of not turning up to the first. 75 There is an association between the number of appointments and rates of non-attendance, with high users of outpatient services being more likely to default on an appointment. 78 These patients are likely to have long-term chronic diseases, which may have not changed since their last appointment. 73 Because of this factor, there is often a difference in attendance rates between those attending their first appointment and those attending subsequent follow-up appointments. King et al. 80 found that patients with diabetes and glaucoma felt that, as their condition was stable, missing an appointment was unlikely to harm them.
Several studies have looked at the relation between non-attendance and factors such as demographic information and personal circumstances, for example family size or socioeconomic deprivation. With age, it is likely that non-attendance rates have a bimodal distribution, with young adults and teenagers as well as the elderly being those most likely to miss their appointments. 71 It has been reported that alcoholics, intravenous drug users and those who are pregnant have higher non-attendance rates,75 as well as past and current smokers. 81,82 Patients who are single parents or have children living at home are more likely to be non-attenders. 81 Those with young, large families are also more likely to miss appointments,76,83 as well as those with a poor family support system. 69 Area-level deprivation scores are often strong predictors of non-attendance. 70,84 Gatrad85 found higher rates of non-attendance in Asian populations for both new and follow-up appointments, though these attendance rates improved when culturally specific interventions were introduced.
As well as analysing first-time appointments, we also considered patients recently discharged from inpatient treatment. Just as the time interval between referral and appointment has been found to be a strong predictor of non-attendance,86 so is the time interval between discharge from inpatient admission and the first subsequent outpatient appointment. 70 If there is a lengthy delay then patients are less likely to attend the appointment for a number of reasons, including the appointment being unnecessary as their condition has improved, or simply the patient forgetting the appointment. 78 Two studies found that those waiting more than 2 months from referral to appointment were least likely to attend. 73,87 On the other hand, too short an interval, such as less than 3 days or a week, between referral and appointment had a higher rate of non-attendance, as this short notice does not give patients enough time to reschedule their commitments. 73,79 Hamilton et al. 70 found that, for every 1-week increase in interval, patients were 5–9% more likely to miss their appointment.
While many of the foregoing factors such as personal circumstances are not available in HES, several key ones are, such as age, area-level deprivation, prior non-attendance and time interval between inpatient discharge and the first subsequent appointment. We also used HES to track later hospital activity in our patient cohorts.
Table 9 gives the results for the first appointment in general medical and general surgical OPD; Table 10 gives the same but for the first appointment following inpatient discharge. In both tables, to reduce size, only a few age groups and none of the many diagnosis group and subgroup combinations have been shown.
| Patient factor | OR (95% CI) for general medicine appointments | p-value | OR (95% CI) for general surgery appointments | p-value |
|---|---|---|---|---|
| Age group (years): < 1 (compared with 65–69) | 3.52 (2.67 to 4.63) | < 0.0001 | 2.64 (2.26 to 3.09) | < 0.0001 |
| 1–4 | 3.34 (2.73 to 4.09) | < 0.0001 | 1.82 (1.62 to 2.03) | < 0.0001 |
| 5–9 | 2.26 (1.76 to 2.92) | < 0.0001 | 1.61 (1.42 to 1.83) | < 0.0001 |
| 10–14 | 1.99 (1.60 to 2.48) | < 0.0001 | 1.96 (1.74 to 2.20) | < 0.0001 |
| 15–19 | 2.55 (2.36 to 2.77) | < 0.0001 | 2.86 (2.68 to 3.06) | < 0.0001 |
| 20–24 | 3.06 (2.85 to 3.28) | < 0.0001 | 3.47 (3.29 to 3.66) | < 0.0001 |
| 25–29 | 2.88 (2.69 to 3.08) | < 0.0001 | 3.24 (3.08 to 3.41) | < 0.0001 |
| (rows omitted) | ||||
| 90+ | 1.27 (1.14 to 1.42) | < 0.0001 | 1.58 (1.42 to 1.77) | < 0.0001 |
| Male sex | 1.21 (1.17 to 1.24) | < 0.0001 | 1.29 (1.27 to 1.32) | < 0.0001 |
| Deprivation quintile 2 (compared with least deprived) | 1.06 (1.01 to 1.11) | 0.0238 | 1.07 (1.03 to 1.11) | 0.0002 |
| 3 | 1.25 (1.20 to 1.31) | < 0.0001 | 1.24 (1.19 to 1.28) | < 0.0001 |
| 4 | 1.51 (1.45 to 1.58) | < 0.0001 | 1.60 (1.55 to 1.65) | < 0.0001 |
| 5 (most deprived) | 1.94 (1.86 to 2.03) | < 0.0001 | 2.06 (2.00 to 2.13) | < 0.0001 |
| Waiting (per week) | 1.02 (1.02 to 1.02) | < 0.0001 | 1.03 (1.02 to 1.03) | < 0.0001 |
| Earlier appointments | 0.96 (0.96 to 0.96) | < 0.0001 | 0.97 (0.96 to 0.97) | < 0.0001 |
| Earlier DNAs | 1.32 (1.31 to 1.34) | < 0.0001 | 1.34 (1.33 to 1.35) | < 0.0001 |
| Earlier elective admissions | 0.99 (0.98 to 1.00) | 0.0049 | 0.98 (0.97 to 0.99) | < 0.0001 |
| Earlier emergency admissions | 1.10 (1.09 to 1.11) | < 0.0001 | 1.14 (1.13 to 1.15) | < 0.0001 |
| Earlier total bed-days | 1.01 (1.00 to 1.01) | < 0.0001 | 1.01 (1.00 to 1.01) | < 0.0001 |
| Patient factor | Factor value | OR (95% CI) | p-value |
|---|---|---|---|
| Age (compared with ages 60–64 years) | < 1 | 1.63 (1.41 to 1.89) | < 0.0001 |
| 1–4 | 1.38 (1.19 to 1.59) | < 0.0001 | |
| 5–9 | 1.21 (1.02 to 1.45) | < 0.0001 | |
| 10–14 | 1.49 (1.22 to 1.83) | 0.033 | |
| 15–19 | 1.69 (1.44 to 1.97) | 0.0001 | |
| (rows omitted) | |||
| 85–89 | 1.26 (1.20 to 1.33) | < 0.0001 | |
| 90+ | 1.44 (1.35 to 1.53) | < 0.0001 | |
| Sex | Male | 0.99 (0.97 to 1.01) | 0.375 |
| Charlson comorbidity score | 1.01 (1.01 to 1.02) | < 0.0001 | |
| Number of previous OPD appointments attended | 0.98 (0.98 to 0.98) | < 0.0001 | |
| Number of previous OPD appointments missed | 1.25 (1.24 to 1.26) | < 0.0001 | |
| Number of previous elective admissions | 0.99 (0.98 to 0.99) | < 0.0001 | |
| Number of previous emergency admissions | 1.03 (1.02 to 1.03) | < 0.0001 | |
| LOS of index admission (per night) | 1.01 (1.01 to 1.01) | < 0.0001 | |
| Quintile (compared with least deprived) | 2 | 1.04 (1.00 to 1.08) | 0.073 |
| 3 | 1.21 (1.16 to 1.26) | < 0.0001 | |
| 4 | 1.48 (1.43 to 1.54) | < 0.0001 | |
| 5 (most deprived) | 1.80 (1.74 to 1.87) | < 0.0001 | |
| Completed weeks between discharge and appointment (compared with 12+) | 0 | 1.12 (1.04 to 1.20) | 0.002 |
| 1 | 1.00 (0.93 to 1.08) | 0.982 | |
| 2 | 0.96 (0.89 to 1.03) | 0.248 | |
| 3 | 0.93 (0.86 to 1.00) | 0.046 | |
| 4 | 0.93 (0.86 to 1.00) | 0.048 | |
| 5 | 0.97 (0.90 to 1.05) | 0.421 | |
| 6 | 0.91 (0.84 to 0.98) | 0.016 | |
| 7 | 0.94 (0.87 to 1.02) | 0.124 | |
| 8 | 0.94 (0.86 to 1.02) | 0.136 | |
| 9 | 0.96 (0.88 to 1.05) | 0.360 | |
| 10 | 0.95 (0.87 to 1.04) | 0.289 | |
| 11 | 1.00 (0.91 to 1.01) | 0.947 | |
Odds ratios for each patient factor were very similar whether the index appointment was for general medicine or general surgery. Non-attendance was most likely in the under-30s. Many of the factors found to be important in Table 8 were also important here, with the exception of gender. In addition, index length of stay (LOS), comorbidity (Charlson index) and time interval between discharge and subsequent appointment were also included in the models and were all significant. Following discharge from an inpatient admission, factors were similar whatever acute condition the patient had been admitted for, and therefore all seven conditions have been combined in Table 10.
Key predictors were young and very old age, male gender, deprivation, previous non-attendance and previous emergency admissions. The time interval between discharge and the first appointment thereafter was also a predictor for three of the seven CCS groups: ischaemic heart disease, stroke and HF. Intervals of less than a week had the highest odds of non-attendance. The ‘optimal’ interval for scheduling appointments appeared to be 3–10 weeks for ischaemic heart disease, but no such window was apparent for the other diagnoses considered separately. Combining all seven patient groups suggested that a 6-week interval was optimal, with intervals of 3 and 4 weeks also having significantly lower odds of non-attendance than 12 or more weeks.
The performance of these models was only moderate. Discrimination was 0.67, and there was significant overprediction of low risk.
Patients who did not attend their first post-discharge appointment had more emergency admissions, total inpatient bed-days and further non-attendances in the subsequent year than those who did; however, they had fewer elective admissions and total OPD appointments (Table 11). The means in the two groups varied by index diagnosis group, but the relative differences were consistent. We therefore show the combined figures for all diagnosis groups considered. Although the mean contacts and death rates were lower following a first general medical or general surgical appointment after GP referral, the patterns were the same and are not shown.
| Subsequent outcome | Mean in attenders | Mean in non-attenders | Mean difference (95% CI) | p-value |
|---|---|---|---|---|
| Emergency admissions | 0.81 | 1.04 | –0.24 (–0.26 to –0.22) | < 0.001 |
| Elective admissions | 0.69 | 0.42 | 0.27 (0.25 to 0.29) | < 0.001 |
| Day cases | 0.47 | 0.29 | 0.18 (0.17 to 0.20) | < 0.001 |
| Total inpatient bed-days | 7.8 | 10.1 | –2.31 (–2.54 to –2.07) | < 0.001 |
| Missed appointments | 0.54 | 1.07 | –0.53 (–0.54 to –0.51) | < 0.001 |
| Total appointments, including missed | 6.86 | 5.49 | 1.38 (1.30 to 1.45) | < 0.001 |
| Death rate | 13.7% | 22.4% | –8.8% (–8.4% to –9.2%) | < 0.001 |
Table 11 shows the crude differences between attenders and non-attenders, but the earlier tables showed that the two groups differ in several characteristics that may at least partly confound such unadjusted comparisons. As an example, we ran a LR with death in the year after the index appointment as the outcome, adjusting for the factors in the tables plus the fact of non-attendance as an extra predictor. These models suggested that non-attendance was associated with about a 50% higher odds of death, only slightly reduced from the unadjusted figure.
Other readmission measures and future bed-days: the example of heart failure
During 2008/9 and 2009/10 there were 74,419 live discharges with their first admission with a primary diagnosis of HF. Within 7 days of discharge, 4.7% had an emergency readmission; within a year, around half had been readmitted. A third of these readmissions within 7 days were for HF, dropping to 21% for those within a year. This was matched for patients with an index admission of COPD. Many of the findings for COPD were similar to those for HF. We therefore focus on the HF cohort in this section.
Discrimination was low for all periods of follow-up between 7 and 365 days for either all causes combined or cause-specific measures (c = 0.58 to 0.60). All models were well calibrated (p > 0.10 using HL).
Predictors were similar across all follow-up periods for all-cause readmissions (Table 12) but sometimes differed by cause of readmission (Table 13). Hazard ratios from the two types of survival analysis considered were generally very similar and were also similar to the ORs from hierarchical LR; we therefore present only the latter. Results for 90 and 182 days matched those for 30 and 365 days and are not shown.
| Factor | Value | OR (95% CI) | ||
|---|---|---|---|---|
| Within 7 days | Within 30 days | Within 365 days | ||
| Age group (years) | 18–44 | 1.28 (0.97 to 1.69) | 1.12 (0.93 to 1.34) | 0.86 (0.74 to 0.99) |
| 45–49 | 0.96 (0.68 to 1.35) | 1.11 (0.91 to 1.35) | 1.05 (0.90 to 1.22) | |
| 50–54 | 1.08 (0.83 to 1.40) | 0.95 (0.80 to 1.11) | 0.87 (0.77 to 0.99) | |
| 55–59 | 1.00 (0.80 to 1.24) | 0.93 (0.81 to 1.06) | 0.86 (0.77 to 0.95) | |
| 60–64 | 0.99 (0.82 to 1.19) | 0.96 (0.86 to 1.07) | 0.94 (0.86 to 1.02) | |
| 65–69 | 1 | 1 | 1 | |
| 70–74 | 1.13 (0.97 to 1.31) | 1.04 (0.95 to 1.14) | 1.13 (1.05 to 1.21) | |
| 75–79 | 1.27 (1.11 to 1.46) | 1.15 (1.06 to 1.25) | 1.28 (1.20 to 1.37) | |
| 80–84 | 1.27 (1.11 to 1.45) | 1.11 (1.02 to 1.21) | 1.49 (1.40 to 1.59) | |
| 85–89 | 1.36 (1.18 to 1.56) | 1.21 (1.11 to 1.31) | 1.73 (1.62 to 1.84) | |
| 90+ | 1.49 (1.28 to 1.73) | 1.22 (1.12 to 1.34) | 1.88 (1.75 to 2.03) | |
| Sex | Males | 1.08 (1.02 to 1.15) | 1.00 (0.96 to 1.04) | 0.92 (0.89 to 0.95) |
| Emergency admission | Yes | 1.63 (1.35 to 1.97) | 1.66 (1.48 to 1.87) | 1.70 (1.56 to 1.84) |
| Deprivation quintile (1 is least deprived) | 1 | 1 | 1 | 1 |
| 2 | 1.02 (0.92 to 1.14) | 1.02 (0.95 to 1.08) | 1.03 (0.98 to 1.08) | |
| 3 | 1.06 (0.96 to 1.18) | 1.05 (0.99 to 1.13) | 1.13 (1.08 to 1.19) | |
| 4 | 1.07 (0.97 to 1.19) | 1.06 (0.99 to 1.13) | 1.17 (1.12 to 1.23) | |
| 5 | 1.10 (0.99 to 1.22) | 1.12 (1.05 to 1.19) | 1.27 (1.20 to 1.33) | |
| CABG in year before or during index HF admission | 0.79 (0.57 to 1.08) | 0.76 (0.63 to 0.92) | 0.70 (0.61 to 0.81) | |
| PTCA in year before or during index HF admission | 1.25 (1.02 to 1.52) | 1.20 (1.06 to 1.36) | 1.08 (0.97 to 1.21) | |
| Pacemaker (not CRT) inserted in year before or during index HF admission | 0.92 (0.75 to 1.12) | 0.99 (0.87 to 1.11) | 1.03 (0.93 to 1.13) | |
| CRT inserted in year before or during index HF admission | 0.89 (0.60 to 1.30) | 0.70 (0.54 to 0.90) | 0.84 (0.71 to 0.99) | |
| OPD appointments missed in year before index HF admission | Per appointment | 1.06 (1.02 to 1.10) | 1.09 (1.07 to 1.11) | 1.12 (1.10 to 1.14) |
| OPD appointments attended in year before index HF admission | Per appointment | 1.01 (1.00 to 1.03) | 1.02 (1.01 to 1.03) | 1.04 (1.03 to 1.04) |
| LOS in nights of index HF admission (nights) | 0 | 1 | 1 | 1 |
| 1 | 0.83 (0.72 to 0.95) | 0.96 (0.87 to 1.06) | 0.98 (0.91 to 1.06) | |
| 2 | 0.70 (0.59 to 0.82) | 0.87 (0.78 to 0.97) | 0.94 (0.86 to 1.02) | |
| 3+ | 0.66 (0.59 to 0.74) | 0.91 (0.84 to 0.98) | 0.97 (0.91 to 1.03) | |
| Stroke | 1.33 (1.08 to 1.64) | 1.23 (1.07 to 1.41) | 1.20 (1.06 to 1.35) | |
| Pneumonia | 1.17 (1.06 to 1.29) | 1.19 (1.12 to 1.27) | 1.18 (1.12 to 1.24) | |
| Ischaemic heart disease | 1.13 (1.06 to 1.20) | 1.20 (1.15 to 1.24) | 1.27 (1.23 to 1.31) | |
| Dementia | 1.29 (1.12 to 1.47) | 1.19 (1.09 to 1.31) | 1.11 (1.03 to 1.19) | |
| Arrhythmias | 0.97 (0.91 to 1.03) | 1.04 (1.00 to 1.08) | 1.05 (1.01 to 1.08) | |
| Heart valve disorders | 1.08 (1.00 to 1.16) | 1.07 (1.02 to 1.12) | 1.04 (1.00 to 1.08) | |
| PVD | 1.08 (0.97 to 1.20) | 1.14 (1.07 to 1.22) | 1.16 (1.09 to 1.22) | |
| Hypertension | 0.99 (0.93 to 1.06) | 0.99 (0.95 to 1.03) | 1.03 (1.00 to 1.06) | |
| Chronic lung diseases | 1.27 (1.19 to 1.36) | 1.25 (1.20 to 1.31) | 1.35 (1.30 to 1.40) | |
| Diabetes | 1.07 (1.00 to 1.14) | 1.09 (1.04 to 1.14) | 1.18 (1.14 to 1.22) | |
| Renal disease | 1.22 (1.13 to 1.31) | 1.29 (1.23 to 1.35) | 1.23 (1.19 to 1.28) | |
| Obesity | 0.88 (0.75 to 1.04) | 0.88 (0.80 to 0.97) | 0.98 (0.91 to 1.06) | |
| Any mental health condition (except dementia) | 1.31 (1.18 to 1.46) | 1.23 (1.15 to 1.33) | 1.28 (1.21 to 1.36) | |
| Factor | Value | All patients, HF | All patients, non-HF | ||
|---|---|---|---|---|---|
| OR (95% CI) | p-value | OR (95% CI) | p-value | ||
| Age group (years) | 18–44 | 1.10 (0.80 to 1.52) | 0.546 | 1.11 (0.90 to 1.36) | 0.340 |
| 45–49 | 0.97 (0.67 to 1.39) | 0.856 | 1.15 (0.93 to 1.44) | 0.203 | |
| 50–54 | 0.92 (0.69 to 1.23) | 0.566 | 0.97 (0.80 to 1.16) | 0.718 | |
| 55–59 | 1.05 (0.84 to 1.32) | 0.646 | 0.88 (0.75 to 1.03) | 0.101 | |
| 60–64 | 1.03 (0.85 to 1.25) | 0.753 | 0.94 (0.82 to 1.06) | 0.303 | |
| 65–69 | 1 | 1 | |||
| 70–74 | 1.12 (0.96 to 1.30) | 0.147 | 1.00 (0.90 to 1.11) | 0.967 | |
| 75–79 | 1.13 (0.98 to 1.30) | 0.101 | 1.14 (1.03 to 1.25) | 0.008 | |
| 80–84 | 1.05 (0.91 to 1.21) | 0.497 | 1.12 (1.02 to 1.24) | 0.015 | |
| 85–89 | 1.17 (1.01 to 1.35) | 0.038 | 1.20 (1.09 to 1.32) | < 0.001 | |
| 90+ | 1.21 (1.03 to 1.42) | 0.018 | 1.20 (1.08 to 1.33) | 0.001 | |
| Sex | Males | 1.09 (1.02 to 1.16) | 0.014 | 0.97 (0.92 to 1.01) | 0.134 |
| Emergency admission | Yes | 1.87 (1.52 to 2.31) | < 0.001 | 1.52 (1.33 to 1.73) | < 0.001 |
| Deprivation quintile (1 is least deprived) | 1 | 1 | 1 | ||
| 2 | 1.06 (0.94 to 1.19) | 0.345 | 1.00 (0.93 to 1.08) | 0.987 | |
| 3 | 1.12 (1.00 to 1.26) | 0.045 | 1.03 (0.95 to 1.10) | 0.513 | |
| 4 | 1.13 (1.01 to 1.26) | 0.036 | 1.03 (0.96 to 1.11) | 0.445 | |
| 5 | 1.17 (1.04 to 1.30) | 0.008 | 1.09 (1.01 to 1.17) | 0.024 | |
| CABG in year before or during index HF admission | 0.79 (0.57 to 1.09) | 0.151 | 0.77 (0.62 to 0.96) | 0.023 | |
| PTCA in year before or during index HF admission | 1.22 (0.99 to 1.50) | 0.059 | 1.16 (1.00 to 1.34) | 0.052 | |
| Pacemaker (not CRT) inserted in year before or during index HF admission | 1.09 (0.89 to 1.33) | 0.406 | 0.94 (0.81 to 1.08) | 0.381 | |
| CRT inserted in year before or during index HF admission | 0.54 (0.32 to 0.90) | 0.019 | 0.78 (0.59 to 1.03) | 0.085 | |
| OPD appointments missed in year before index HF admission | Per appointment | 1.04 (1.00 to 1.08) | 0.057 | 1.10 (1.07 to 1.12) | < 0.001 |
| OPD appointments attended in year before index HF admission | Per appointment | 1.01 (0.99 to 1.03) | 0.202 | 1.03 (1.01 to 1.04) | < 0.001 |
| LOS in nights of index HF admission (nights) | 0 | 1 | 1 | ||
| 1 | 0.85 (0.72 to 0.99) | 0.042 | 1.03 (0.91 to 1.15) | 0.655 | |
| 2 | 0.70 (0.58 to 0.83) | < 0.001 | 0.98 (0.86 to 1.11) | 0.750 | |
| 3+ | 0.71 (0.62 to 0.81) | < 0.001 | 1.03 (0.94 to 1.13) | 0.522 | |
| Stroke | 0.98 (0.76 to 1.27) | 0.900 | 1.31 (1.12 to 1.52) | 0.001 | |
| Pneumonia | 1.07 (0.96 to 1.19) | 0.236 | 1.21 (1.13 to 1.30) | < 0.001 | |
| Ischaemic heart disease | 1.23 (1.15 to 1.31) | < 0.001 | 1.16 (1.10 to 1.21) | < 0.001 | |
| Dementia | 0.94 (0.79 to 1.11) | 0.461 | 1.28 (1.16 to 1.42) | < 0.001 | |
| Arrhythmias | 1.15 (1.07 to 1.23) | < 0.001 | 0.99 (0.95 to 1.04) | 0.698 | |
| Heart valve disorders | 1.13 (1.05 to 1.23) | 0.002 | 1.03 (0.97 to 1.08) | 0.334 | |
| Peripheral vascular disease | 1.09 (0.98 to 1.22) | 0.123 | 1.14 (1.06 to 1.23) | 0.001 | |
| Hypertension | 0.96 (0.90 to 1.03) | 0.299 | 1.00 (0.96 to 1.05) | 0.982 | |
| Chronic lung diseases | 1.13 (1.05 to 1.22) | 0.001 | 1.27 (1.21 to 1.33) | < 0.001 | |
| Diabetes | 1.13 (1.05 to 1.21) | 0.001 | 1.06 (1.01 to 1.11) | 0.020 | |
| Renal disease | 1.42 (1.32 to 1.53) | < 0.001 | 1.18 (1.12 to 1.25) | < 0.001 | |
| Obesity | 0.83 (0.70 to 0.99) | 0.040 | 0.91 (0.81 to 1.02) | 0.110 | |
| Any mental health condition (except dementia) | 1.10 (0.97 to 1.25) | 0.124 | 1.25 (1.16 to 1.36) | < 0.001 | |
Length of stay was seen to have a bigger association within 7 days than within 30 or more days and was more important for HF. LOS was truncated at 3+ days for presentation, as analysis using a highest band of 14+ days did not alter the conclusions.
Readmission rates varied widely by hospital for each cause. For this analysis, we combined 4 years of index HF admissions (2009/10 to 2012/13) and included only emergency admissions in order to be more contemporaneous with the National HF Audit, which published figures by hospital for the first time for 2011. Thirty-day rates for HF ranged from 1.5% to 9.0% (median 5.4%), while 30-day rates for non-HF ranged from 7.6% to 17.6% (median 13.6%). Rates showed statistically significant but modest negative correlations (rho from –0.18 to –0.24, p < 0.05) with all six publicly available quality of care measures from the National HF Audit88 for readmissions for HF within 7 days but only three of them for readmissions for HF within 30 days; there were no significant correlations between these measures and non-HF readmission rates.
Finally, we applied a range of models to try to predict not just the next unplanned readmission but future unplanned inpatient activity within the year after discharge: readmissions (all-cause and HF-specific) and bed-days (all-cause and HF-specific). Activity was also divided into ‘buckets’ and models fitted to predict which patient would go on to be in the highest resource-use categories. Around half the patients had no further emergency admissions in the year after discharge; the Poisson model therefore fitted the data poorly, particularly for bed-days. When they converged, all other model specifications performed well for readmissions and bed-days. The NBH model performed best, though convergence was hard to achieve for readmissions for HF only, so the ZINB was used for that outcome. The best-performing model for the number of readmissions was a NBH model. Convergence problems prevented the ZINB model from being fitted.
To simplify, we present the results for all-cause readmissions only. Figures 4 and 5 compare the actual with the predicted number of bed-days and readmissions under various model assumptions.
FIGURE 4.
Actual versus predicted number of all-cause emergency readmissions within a year of discharge using different models (ZINB did not converge). NB, negative binomial; P, Poisson; PH, Poisson hurdle; ZIP, zero-inflated Poisson.
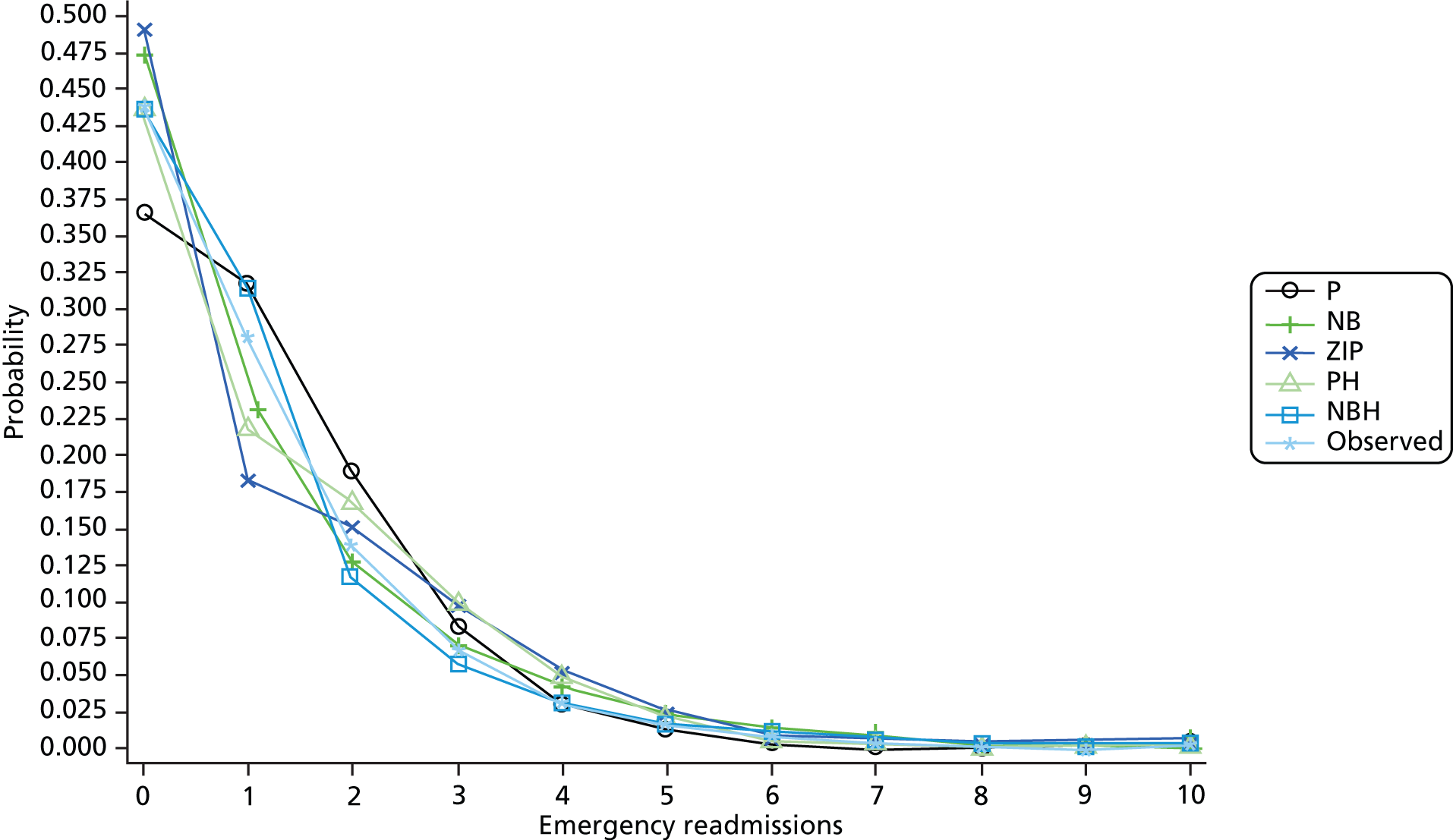
FIGURE 5.
Actual versus predicted all-cause emergency bed-days (capped at 12 for presentation) within a year of discharge using different models. NB, negative binomial; P, Poisson; PH, Poisson hurdle; ZIP, zero-inflated Poisson.
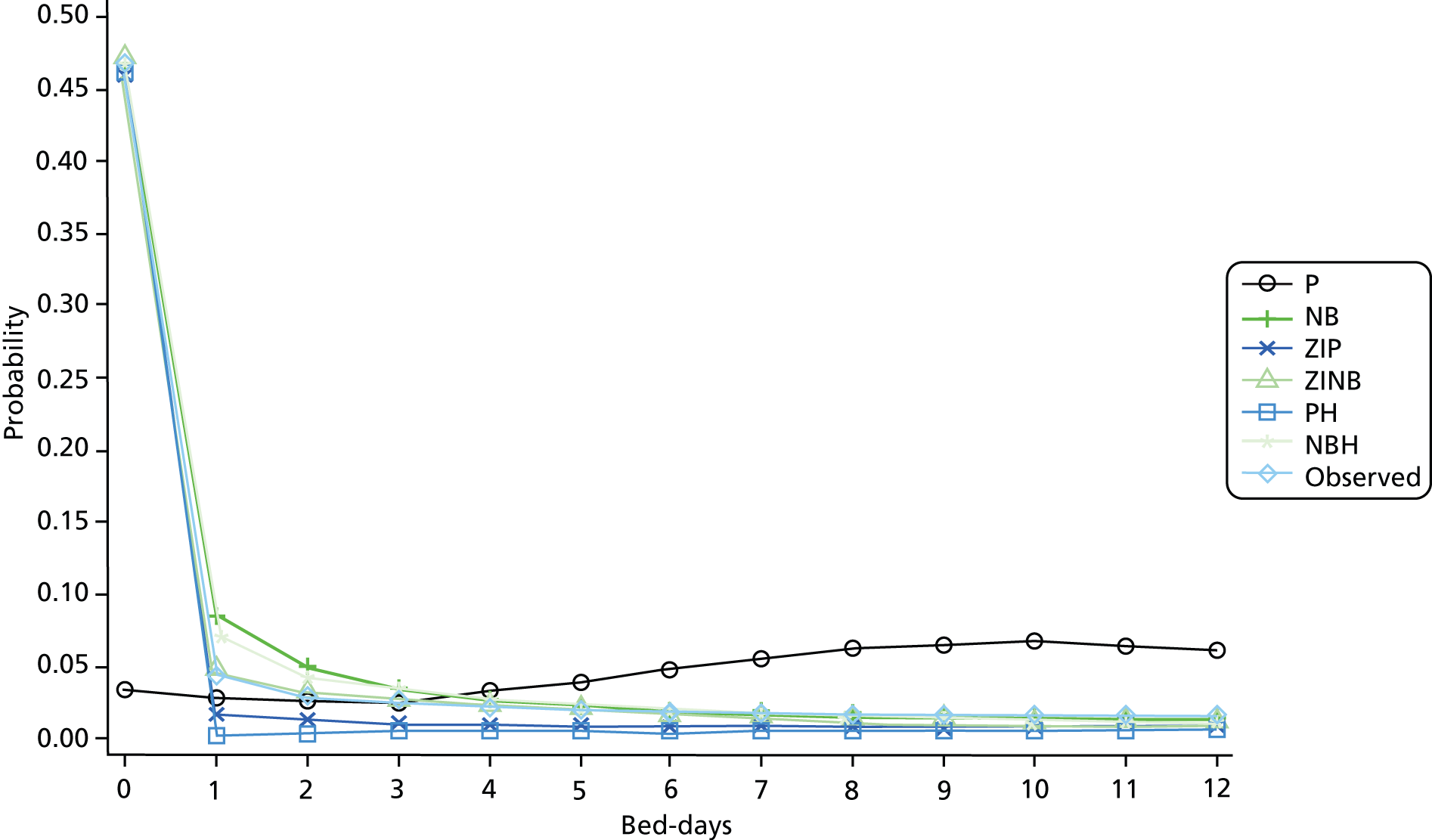
Defining buckets using bed-days, the significant predictors for membership of the highest resource-use bucket (fifth) were almost all the same for those for the two highest resource-use buckets. Predictors for the highest resource use were similar to those for the first readmission within 30 days given above, with the exceptions of gender (females had raised odds only for the bucket), very old age (raised odds only for readmission), defibrillator implantation (raised odds only for readmission) and LOS (raised odds for any stays of a week or more compared with 1–6 days for the bucket, whereas only stays of a month or more had raised odds for readmission).
Comparing results for the count models is more complicated because the best-fitting models yielded a separate set of coefficients for zero from that for non-zero bed-days or readmissions. Table 14 gives the incident rate ratios from the hurdle models alongside the ORs from the 365-day readmission model, with all-cause hospitalisations in each case. Many results were consistent. Deprivation, previous OPD non-attendance and living alone were all associated with higher odds of one or more readmissions, a greater number of readmissions and more bed-days; previous selection for CABG showed reduced risk of all three. Older age was associated with higher odds of readmission and lower odds of no readmissions or bed-days. In the hurdle models for patients with at least some future inpatient activity, however, older age did not predict extra admissions but did predict more bed-days. This may be interpreted as older patients having longer stays when they are admitted but not being admitted more often than those aged in their 60s.
| All-cause readmission with 365 days | Number of all-cause readmissions | Number of all-cause bed-days | ||||
|---|---|---|---|---|---|---|
| Probability of no readmissions | Number of readmissions | Probability of no bed-days | Number of bed-days | |||
| Factor | Value | OR (95% CI) | IRR (95% CI) | |||
| Females | 1.03 (1.00 to 1.06) | 0.94 (0.92 to 0.97) | 0.96 (0.93 to 0.99) | 0.96 (0.93 to 0.99) | 0.98 (0.96 to 1.00) | |
| Age (years) (compared with 65–69) | 70–74 | 1.10 (1.04 to 1.17) | 0.92 (0.86 to 0.97) | 1.00 (0.94 to 1.06) | 0.88 (0.81 to 0.95) | 1.09 (1.03 to 1.15) |
| 75–79 | 1.20 (1.14 to 1.27) | 0.86 (0.81 to 0.91) | 0.99 (0.94 to 1.05) | 0.84 (0.78 to 0.90) | 1.24 (1.17 to 1.30) | |
| 80–84 | 1.34 (1.27 to 1.42) | 0.80 (0.75 to 0.84) | 0.99 (0.94 to 1.05) | 0.74 (0.69 to 0.79) | 1.30 (1.23 to 1.37) | |
| 85–89 | 1.50 (1.42 to 1.58) | 0.75 (0.71 to 0.80) | 0.99 (0.93 to 1.05) | 0.64 (0.60 to 0.69) | 1.42 (1.35 to 1.50) | |
| 90+ | 1.50 (1.41 to 1.59) | 0.80 (0.75 to 0.85) | 0.97 (0.91 to 1.03) | 0.63 (0.58 to 0.68) | 1.41 (1.33 to 1.49) | |
| Most deprived quintile compared with least | Most deprived | 1.28 (1.23 to 1.34) | 0.76 (0.72 to 0.79) | 1.28 (1.22 to 1.34) | 0.76 (0.72 to 0.80) | 1.06 (1.02 to 1.10) |
| IHD | 1.29 (1.26 to 1.32) | 0.78 (0.76 to 0.80) | 1.24 (1.21 to 1.28) | 0.74 (0.71 to 0.76) | 1.01 (0.99 to 1.04) | |
| Mental health | 1.18 (1.13 to 1.24) | 0.83 (0.80 to 0.87) | 1.22 (1.17 to 1.27) | 0.80 (0.75 to 0.85) | 1.06 (1.02 to 1.10) | |
| Diabetes mellitus | 1.22 (1.18 to 1.25) | 0.81 (0.79 to 0.84) | 1.06 (1.03 to 1.09) | 0.78 (0.75 to 0.81) | 1.03 (1.00 to 1.06) | |
| PVD | 1.23 (1.18 to 1.29) | 0.83 (0.79 to 0.87) | 1.13 (1.09 to 1.18) | 0.77 (0.72 to 0.82) | 1.09 (1.05 to 1.14) | |
| Chronic pulmonary disease | 1.35 (1.31 to 1.39) | 0.74 (0.72 to 0.77) | 1.27 (1.24 to 1.31) | 0.69 (0.67 to 0.72) | 1.08 (1.05 to 1.11) | |
| Renal disease | 1.27 (1.23 to 1.31) | 0.85 (0.82 to 0.88) | 1.13 (1.09 to 1.16) | 0.76 (0.73 to 0.80) | 1.19 (1.16 to 1.23) | |
| Number of OPD not attended | 1.09 (1.08 to 1.11) | 0.92 (0.90 to 0.93) | 1.07 (1.06 to 1.09) | 0.89 (0.87 to 0.91) | 1.04 (1.02 to 1.05) | |
| Index LOS (nights) compared with 1–6 | 0 | 0.99 (0.94 to 1.04) | 1.00 (0.95 to 1.06) | 1.03 (0.97 to 1.09) | 1.07 (1.00 to 1.15) | 0.94 (0.89 to 0.99) |
| 7–13 | 1.01 (0.98 to 1.04) | 1.03 (1.00 to 1.06) | 0.97 (0.94 to 1.00) | 0.99 (0.96 to 1.03) | 1.20 (1.17 to 1.23) | |
| 28+ | 0.77 (0.73 to 0.81) | 1.74 (1.65 to 1.83) | 0.89 (0.84 to 0.94) | 1.32 (1.23 to 1.41) | 1.61 (1.54 to 1.68) | |
| Live alone | 1.09 (1.04 to 1.15) | 0.96 (0.91 to 1.01) | 1.13 (1.07 to 1.18) | 0.93 (0.87 to 0.99) | 1.15 (1.10 to 1.20) | |
Several factors showed a stronger association with the readmissions outcomes than with future bed-days. These included previous defibrillator implantation, ischaemic heart disease, mental health conditions, diabetes, peripheral vascular disease and chronic lung diseases. Long LOS was associated with more bed-days but not readmission; indeed, a very long index LOS was associated with lower odds of readmission.
Chapter 4 Discussion of methods and findings
We set out to derive robust casemix adjustment models for a set of common outcomes for different patient groups using the NHS’s national hospital administrative database, HES, adjusting for available covariates such as comorbidity. For OPD non-attendance, we aimed to derive risk-prediction models and assess the influence of the interval between hospital inpatient discharge and first follow-up appointment. We had the following overarching questions in mind:
-
How well do such models perform for various outcomes?
-
How should one adjust for comorbidity?
-
When predicting future inpatient activity, how much information is lost when using the standard 30-day all-cause readmission measure?
-
Is the extra difficulty involved in implementing and understanding machine learning methods such as ANNs worthwhile with these data?
We now discuss each of these in turn. We then note the main limitations to our analyses and suggest further work.
How well do such models perform for various outcomes?
The best-performing models were for mortality for the procedure groups considered. In general, discrimination (c-statistic) was high for mortality, low for first readmission and RTT and intermediate for other readmission measures and missed OPD appointments. Poor discrimination can be caused by risk adjustment that lacks key variables and by data noise, but it can also be due to variations in quality of care. Calibration was often a problem, particularly for the diagnosis groups, mainly because of overprediction for low-risk patients. Recalibration is advisable for a number of patient groups (see the section on machine learning methods in Chapter 4). HES lacks some important physiological variables to give as accurate prediction for individual patients as more detailed clinical databases, though previous work has found that augmentation with just a few items, such as creatinine, can be sufficient. 89 In risk-adjustment modelling for benchmarking units, the impact of miscalibration on standardised mortality ratios is modest for a typical hospital, as we showed for ACS admissions,67 though it will vary by hospital.
A key difference between risk prediction for an individual patient and risk adjustment for comparing units is that much greater accuracy in the prediction is in general required for the former than for the latter. Some of the differences in casemix can be expected to ‘average out’ when aggregating to unit level. Also, if the casemix does not vary by unit, then risk adjustment will not be necessary. For prediction when used for bedside clinical management, discrimination is generally more important than calibration, whereas the reverse is true for risk adjustment. One reason for this is that a low c-statistic has three principal causes: poor data quality, the lack of key patient factors in the database and variations in the quality and delivery of care. Whereas data quality can be assessed, there is no easy way of distinguishing between the other two. Readmission models, as we and many others have found, often have c-statistics in the region of just 0.60, whereas for mortality they can exceed 0.8 or even 0.9. Patient factors that explain a fair proportion of the variation in mortality can be less important or even insignificant in readmission models, where factors such as health-seeking behaviour that are not captured routinely in databases contribute more. We suspect that a fair amount of the unexplained variation for readmission is nonetheless due to differences in the delivery of care both before and after discharge, but it is not possible to quantify these using HES.
How should one adjust for comorbidity?
Our systematic review revealed the importance of calibrating the comorbidity weights or scores to the database used rather than relying on published weights from another country. Our analysis using HES suggested that the Elixhauser set plus dementia with our amended codes performed best. Consideration should be given to including interaction terms with age because this improves the fit. We also tried using polynomials to incorporate the time between previous admissions and the index one for HF patients, a group with high use of NHS services. This approach worked better than simply counting the number of previous unplanned admissions, though the impact was far from spectacular.
When predicting future inpatient activity, is the 30-day all-cause readmission measure sufficient?
As others have found, the predictive power of readmission models is generally low with administrative data, within both 7 and 30 days of discharge. Our analysis of the HF cohort using follow-up periods of between 7 and 365 days suggests that 30 days is as good a time point as any in terms of model performance and which patient factors are important predictors of the outcome (with the exception of index LOS). Hospital-level variation as estimated from the hierarchical models was also similar for 7, 30 and 365 days. Comorbidity is common in patients admitted for HF or COPD. This is reflected in the primary diagnosis of their subsequent readmissions; for HF patients, for example, only a third of their readmissions within a year of index discharge were for HF. We found that a number of factors predicted HF but non-HF readmissions and vice versa. More importantly, hospital-level readmission rates for HF did not correlate with rates for non-HF, and national audit process measures correlated with only the former. This suggests that the use of all-cause readmissions is of limited use in quality improvement, though it remains the more relevant measure for patients and for benchmarking.
Our count and bucket models of subsequent inpatient activity for the HF cohort were harder and took longer to fit and, as many predictors were common across outcomes, only added some extra useful information. For instance, it was notable that a number of the predictors of the fact of readmission, including a number of comorbidities, showed weaker associations with the number of future bed-days.
What do machine learning methods offer in this context that logistic regression does not?
The machine learning methods that we tried here are popular but did not offer noticeably better prediction or adjustment with these data and outcomes than LR as measured by discrimination (c-statistics). They were more difficult to implement and took longer to run, particularly the SVMs. The advantage of ANNs lay in their superior calibration, with the standard logistic link function used in regression often found to be a fairly poor fit. However, we also improved the calibration of LR using an extra step, which would be useful for risk adjustment at the cost of interpretable ORs for each factor included in the model.
Study strengths and limitations
This project has benefited from the use of rich, national data by a team experienced in using them, a selection of advanced statistical methods as well as the standard LR, and a variety of patient outcomes including, but also going beyond the common ones of, death and readmission. We focused on common patient groups and outcomes that are of interest to patients, the NHS and policy-makers.
We considered a large number of patient groups as defined by their primary diagnosis or procedure, but for reasons of brevity and interpretation we have limited the results in Chapter 3 to some illustrative examples. Our analyses could be extended in various ways given in the next section, particularly by repeating our HF and RTT analyses on other patient groups. RTT needs to be derived separately for each index procedure, in consultation with surgical and coding experts following empirical analysis, and is therefore quite a time-consuming process.
We considered only a few of the growing number of machine learning methods, restricting ourselves to those that were likely to be the most appropriate for the administrative data set we were using. Methods such as boosted trees may be worth trying on richer data. For comorbidity adjustment, we focused on the two most widely used and validated indices, Charlson and Elixhauser. The newer but so far much less adopted Holman index is promising, but we were unable to test it to the same degree as the two better-established measures. This is still a developing field, and we have recently heard of a superior German index that has not yet been published.
For prediction of future hospital use in HF patients, we considered a range of count models, but the list was not exhaustive. We did not use the Healthcare Resource Group tariff information, which would give an indication of the financial burden, though some imputation is needed for missing values. These tariffs do not in any case represent actual costs.
With a large number of models to fit, we have focused on the c-statistic and HL test to describe the model fit, together with calibration plots. We have generally split the data into a training and a testing set, though our experience in this project and previous work has found this to be unnecessary with LR. 90 However, we have not assessed such goodness of fit measures such as influential points and outliers. In general, we did not test for or include covariate interactions except between age and comorbidity index in some cases. Such interactions are unlikely to add anything of real value to the models but could be tried.
We have found that discrimination is higher if coding levels are higher,11 but for this project we used all hospitals combined rather than split by coding levels. It would be worth repeating our modelling on US data, for example, as their recording of secondary diagnoses is notably higher, and CMS data have present on admission information in order to exclude complication codes. Likewise, it would be possible to include those hospitals with high levels of coverage and completeness for their A&E records as we did in a separate project for birth records,91 though the effect on the results in terms of reduced sample size and potential bias would need to be assessed.
Finally, in this project we have focused on the quality of HES data, the performance of the risk models and the definition of the outcome measures. There are several other criteria that characterise a good indicator beyond model performance. These include high frequency; variation across providers; consistency over time unless changes in apparent performance are due to changes in quality of care; correct attribution of outcome to provider (a particular issue when patients are transferred between hospitals or, especially for readmission, discharged to community services); and actionability. If the information on performance is not presented in a way that users understand, for example, then the users are unlikely to pay much attention.
Recommendations for future research
There is growing interest in reinventions, and our approach to defining RTT could be applied to other index procedures and specialties. Similarly, it would be interesting to know whether the count models are as useful for other chronic conditions such as diabetes as we found them to be for HF. For readmissions, we considered the first and also the total number, but more sophisticated approaches such as multistate analysis or cluster analysis to look for patterns of activity could be usefully employed.
We have used time-to-event methods only for modelling readmission and investigating patient-level predictors. The methods could be also applied to determining to what extent variation in hospital-level performance is explained by differences in the timing of outcomes. For example, when do the ‘excess’ deaths or readmissions occur at hospitals with high rates compared with those with low rates? Some recent evidence for HF patients suggests that the timing of readmissions within the standard 30-day follow-up period does not vary in Medicare patients,92 but this is not well established with other populations, patient groups or outcomes.
If the A&E records improve in quality, then they could potentially be used both in risk-adjustment models and also for outcome measures. Post-discharge attendances not resulting in admission should be considered alongside those that do. As well as inpatient activity, attendances (and OPD appointments) could be used much more in economic modelling. Reattendance rates could be calculated and explored as an indicator rather than relying on costly casenote reviews.
Dissemination activity
Up to September 2014, we have disseminated various findings from this project as:
-
Systematic review of studies comparing two or more comorbidity indices: paper published by Medical Care in 2012. 20
-
Provider profiling models for ACS mortality using administrative data: paper published by the International Journal of Cardiology online first in 2012 and in print in 2013. 67
-
Project overview and early results of the comparison of methods: invited oral presentation at the International Society of Clinical Biostatistics conference in Bergen, August 2012.
-
Comparison of methods and calibration issues: two oral presentations at the IMA (The Institute of Mathematics and its Applications) Modelling in Healthcare conference in London, March 2013.
-
Oral presentation of results of HF readmission modelling to the Institute of Electrical and Electronics Engineers (IEEE) meeting in Philadelphia, September 2013, with publication in conference proceedings.
-
Poster and short oral presentation of HF readmissions modelling and hospital-level rates at the International Society for Quality in Health Care (ISQua) conference in Edinburgh, October 2013.
-
Classifier calibration using splined empirical probabilities in clinical risk prediction: paper published online first by Health Care Management Science in its special conference issue in February 2014. 50
-
Poster on count models for HF accepted for the Cambridge biostatistics meeting, March 2014.
-
Effect of the readmission primary diagnosis and time interval in HF patients: analysis of English administrative data: paper published by the European Journal of Heart Failure online in July 2014. 93
-
Return to theatre for elective hip and knee replacements: what is the relative importance of patient factors, surgeon and hospital? Paper in press at the Bone and Joint Journal. 94
One more paper has been submitted to journals and is under review.
We are working with relevant charities to decide the best way to publicise our work relating to HF.
Chapter 5 Conclusions
Robust risk-adjustment models can be derived from HES for mortality, though c-statistics are lower for readmissions, RTT and OPD non-attendance than for mortality. Overprediction of low risk was a common explanation for the often poor calibration, which was a bigger problem for diagnosis than for procedure groups. The remaining variation in hospital-level outcomes will be due to data quality, care and missing casemix information, but it is not possible to distinguish between them. MLM suggests there is much variation at surgeon and hospital level for RTT but a lot less for other outcomes.
Hospital Episode Statistics OPD data add some useful information to the risk models for readmission and future hospital activity, but they are currently limited to the fact and number of prior appointments and non-attendances, as diagnostic information is still usually absent. A&E records are too patchy to be used nationally, but analysis might be confined to those trusts with good data for the years 2009/10 onwards.
In terms of adjustment for comorbidity, our review and results suggest using a combination of the Elixhauser set of comorbidities plus dementia with our extra codes. Using prior admissions to get extra comorbidity information does not appear to be worthwhile in general, though for multimorbid groups such as patients with HF a one-year lookback period gave a useful boost to the prevalence of some conditions. The timing of these previous admissions, however, adds only a little to the prediction of readmission.
We considered a range of outcome measures. RTT is readily definable in HES, shows wide variation by surgeon and hospital, but needs tailoring to the index procedure with specialist surgical and coding input. Of the readmission measures, the standard 28- or 30-day window seems in general as good as any other from 7 to 365 days in the HF group. Combining all causes, as is typically done, however, loses key information. Cause-specific versions are likely to be more useful for HF and COPD patients in quality improvement projects.
Prediction of OPD non-attendance is moderate rather than good or poor in HES. An interval of 3–6 weeks between inpatient discharge and first follow-up appointment was associated with around 10% significantly lower odds of non-attendance. Even after adjusting for available confounders, we find that non-attenders go on to have more OPD and unplanned NHS contacts and higher death rates than attenders.
Finally, we conclude with some remarks about statistical methods. We believe that commonly used machine learning methods are not worthwhile with administrative (or at least HES) data, though calibration for LR could and perhaps should be improved, for instance using the extra step we suggested for risk-adjustment models when simple coefficient interpretation is not important. For readmission-type outcomes, we also applied a number of count models to the HF cohort and found the NBH or zero-inflated models to perform best despite sometimes having difficulty converging. These models yielded some – rather than a large amount of – useful extra information beyond that provided by the simpler and quicker fact-of-readmission LR models.
Implications for practice and translation of findings
The use of risk prediction and risk stratification models is well established in medical decision-making. Some risk scores are simple enough to be calculated by hand, whereas others need a calculator, smartphone app or other electronic device. Risk-adjusted outcomes at the unit level can be displayed graphically or in tabular form using similar technology, and there are a growing number of websites that allow a prospective patient to choose a hospital this way. Many private companies offer interactive information tools that allow drill-down and stratified analyses, for example to see if a hospital has a higher mortality at the weekend than during the week or if the uptake of services by demographic subgroup matches the demographic distribution of the surrounding population that it serves.
As well as some methodological lessons regarding risk adjustment and prediction, this project has produced some findings that relate to clinical practice. Our analyses of OPD non-attendance and readmission showed clear variations by factors such as age, sex and deprivation that other researchers had previously identified but also the strong association with the number of previously missed OPD appointments for both outcomes. We found that patients who miss appointments go on to have poorer outcomes a year later that are unlikely to be explained wholly by disease status or comorbidity. This suggests that repeat non-attendance be considered a warning sign that closer monitoring is needed.
The second finding relating to non-attendance is that we found that the lowest non-attendance rate at the first appointment following discharge from an emergency admission for one of several acute conditions occurred 6 weeks after discharge. The highest rate occurred within a week or more than 12 weeks after. While we were unable from the data to identify reliably whether or not this first post-discharge appointment had been planned before the admission, the finding does suggest scheduling more follow-up slots for around 6 weeks after discharge in order to reduce non-attendance.
Finally, the fact that we found no significant correlation between HF and non-HF readmission rates and that performance on the national audit process measures correlated mostly with just the HF readmission rates suggests that more focus should be put on these patients’ comorbidities. Good performance and/or low rates of readmission for HF often did not translate into low rates of readmission for other conditions. For quality improvement, we recommend splitting the readmission outcome and monitoring its diagnosis-specific components.
Acknowledgements
We are grateful to Christine Sweeting, a freelance clinical coding expert, for her valuable input regarding comorbidity and RTT codes. We thank Mark Loeffler, consultant orthopaedic surgeon at Colchester General Hospital, for his help in defining the RTT metric for hip and knee replacements and for providing associated clinical input. We thank Sherry Morris for her key contribution to the smooth administration of the project and for creating and maintaining the project website. We are of course indebted to our database manager, Hima Daby, for maintaining our HES databases.
Contributions of authors
Alex Bottle (Senior Lecturer in Medical Statistics) oversaw the project, prepared the HES data extracts, oversaw and contributed to the analysis, and contributed to writing the report.
Rene Gaudoin (Research Associate) performed the ANN, SVM and polynomial analysis and contributed to writing the report.
Rosalind Goudie (Research Assistant) performed much of the HF analysis and contributed to writing the report.
Simon Jones (Professor of Healthcare Management and Policy) performed the random forests analysis and contributed to writing the report.
Paul Aylin (Professor of Epidemiology and Consultant in Public Health) contributed to the management of the project and to the writing of the report.
Publications
Sharabiani MTA, Aylin P, Bottle A. Systematic review of comorbidity indices for administrative data. Med Care 2012;50:1109–18.
Bottle A, Sanders RD, Mozid A, Aylin P. Provider profiling models for acute coronary syndrome mortality using administrative data. Int J Cardiol 2013;168:338–43.
Gaudoin R, Montana G, Jones S, Aylin P, Bottle A. Classifier calibration using splined empirical probabilities in clinical risk prediction. [epub ahead of print 21 February 2014]. Health Care Manag Sci 2014.
Bottle A, Aylin P, Bell D. Effect of the readmission primary diagnosis and time interval in heart failure patients: analysis of English administrative data. Eur J Heart Fail 2014;16:846–53.
Bottle A, Aylin P, Loeffler M. Return to theatre for elective hip and knee replacements: what is the relative importance of patient factors, surgeon and hospital? Bone Joint J 2014; in press.
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the HS&DR programme or the Department of Health. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the HS&DR programme or the Department of Health.
References
- Charlson ME, Pompei P, Ales KL, MacKenzie CR. A new method of classifying prognostic comorbidity in longitudinal studies: development and validation. J Chronic Dis 1987;40:373-83. http://dx.doi.org/10.1016/0021-9681(87)90171-8.
- Bottle A, Aylin P. Intelligent information: a national system for monitoring clinical performance. Health Serv Res 2008;43:10-31.
- Carstairs V, Morris R. Deprivation and Health in Scotland. Aberdeen: Aberdeen University Press; 1991.
- Hansell A, Bottle A, Shurlock L, Aylin P. Accessing and using hospital activity data. J Public Health Med 2001;23:51-6. http://dx.doi.org/10.1093/pubmed/23.1.51.
- Audit Commission . Data Assurance Framework n.d. www.audit-commission.gov.uk/information-and-analysis/data-assurance-framework/ (accessed March 2014).
- Burns EM, Rigby E, Mamidanna R, Bottle A, Aylin P, Ziprin P, et al. Systematic review of discharge coding accuracy. J Public Health (Oxf) 2012;34:138-48. http://dx.doi.org/10.1093/pubmed/fdr054.
- Mayer EK, Bottle A, Aylin P, Darzi AW, Athanasiou T, Vale JA. The volume–outcome relationship for radical cystectomy in England: an analysis of outcomes other than mortality. BJU Int 2011;108:E258-65. http://dx.doi.org/10.1111/j.1464-410X.2010.10010.x.
- Elixhauser A, Steiner C, Harris DR, Coffey RM. Comorbidity measures for use with administrative data. Med Care 1998;36:8-27. http://dx.doi.org/10.1097/00005650-199801000-00004.
- Sullivan LM, Massaro JM, D’Agostino RB. Presentation of multivariate data for clinical use: the Framingham Study risk score functions. Stat Med 2004;23:1631-60. http://dx.doi.org/10.1002/sim.1742.
- Sundararajan V, Henderson T, Perry C, Muggivan A, Quan H, Ghali WA. New ICD-10 version of the Charlson comorbidity index predicted in-hospital mortality. J Clin Epidemiol 2004;57:1288-94. http://dx.doi.org/10.1016/j.jclinepi.2004.03.012.
- Bottle A, Aylin P. Comorbidity scores for administrative data benefited from adaptation to local coding and diagnostic practices. J Clin Epidemiol 2011;64:1426-33. http://dx.doi.org/10.1016/j.jclinepi.2011.04.004.
- van Walraven C, Austin PC, Jennings A, Quan H, Forster AJ. A modification of the Elixhauser comorbidity measures into a point system for hospital death using administrative data. Med Care 2009;47:626-33. http://dx.doi.org/10.1097/MLR.0b013e31819432e5.
- Normand SL, Morris CN, Fung KS, McNeil BJ, Epstein AM. Development and validation of a claims based index for adjusting for risk of mortality: the case of acute myocardial infarction. J Clin Epidemiol 1995;48:229-43. http://dx.doi.org/10.1016/0895-4356(94)00126-B.
- Desai MM, Bogardus ST, Williams CS, Vitagliano G, Inouye SK. Development and validation of a risk-adjustment index for older patients: the High-Risk Diagnoses for the Elderly Scale. J Am Geriatr Soc 2002;50:474-81. http://dx.doi.org/10.1046/j.1532-5415.2002.50113.x.
- Fleming ST, Pearce KA, McDavid K, Pavlov D. The development and validation of a comorbidity index for prostate cancer among black men. J Clin Epidemiol 2003;56:1064-75. http://dx.doi.org/10.1016/S0895-4356(03)00213-0.
- Ash AS, Ellis RP, Pope GC, Ayanian JZ, Bates DW, Burstin H, et al. Using diagnoses to describe populations and predict costs. Health Care Financ Rev 2000;21:7-28.
- Holman CDAJ, Preen DB, Baynham NJ, Finn JC, Semmens JB. A multipurpose comorbidity scoring system performed better than the Charlson index. J Clin Epidemiol 2005;58:1006-14. http://dx.doi.org/10.1016/j.jclinepi.2005.01.020.
- Gagne JJ, Glynn RJ, Avorn J, Levin R, Schneeweiss S. A combined comorbidity score predicted mortality in elderly patients better than existing scores. J Clin Epidemiol 2011;64:749-59. http://dx.doi.org/10.1016/j.jclinepi.2010.10.004.
- Thombs BD, Singh VA, Halonen J, Diallo A, Milner SM. The effects of pre-existing medical comorbidities on mortality and length of hospital stay in acute burn injury: evidence from a national sample of 31,338 adult patients. Ann Surg 2007;245:629-34. http://dx.doi.org/10.1097/01.sla.0000250422.36168.67.
- Sharabiani MTA, Aylin P, Bottle A. Systematic review of comorbidity indices for administrative data. Med Care 2012;50:1109-18. http://dx.doi.org/10.1097/MLR.0b013e31825f64d0.
- de Groot V, Beckerman H, Lankhorst GJ, Bouter LM. How to measure comorbidity: a critical review of available methods. J Clin Epidemiol 2003;56:221-9. http://dx.doi.org/10.1016/S0895-4356(02)00585-1.
- Extermann M. Measuring comorbidity in older cancer patients. Eur J Cancer 2000;36:453-71. http://dx.doi.org/10.1016/S0959-8049(99)00319-6.
- Hall WH, Jani AB, Ryu JK, Narayan S, Vijayakumar S. The impact of age and comorbidity on survival outcomes and treatment patterns in prostate cancer. Prostate Cancer Prostatic Dis 2005;8:22-30. http://dx.doi.org/10.1038/sj.pcan.4500772.
- Leal JR, Laupland KB. Validity of ascertainment of co-morbid illness using administrative databases: a systematic review. Clin Microbiol Infect 2010;16:715-21. http://dx.doi.org/10.1111/j.1469-0691.2009.02867.x.
- Needham DM, Scales DC, Laupacis A, Pronovost PJ. A systematic review of the Charlson comorbidity index using Canadian administrative databases: a perspective on risk adjustment in critical care research. J Crit Care 2005;20:12-9. http://dx.doi.org/10.1016/j.jcrc.2004.09.007.
- Kohl P. Importance of risk stratification models in cardiac surgery. Eur Heart J 2006;27:768-9. http://dx.doi.org/10.1093/eurheartj/ehi792.
- Cohen ME, Dimick JB, Bilimoria KY, Ko CY, Richards K, Hall BL. Risk adjustment in the American College of Surgeons National Surgical Quality Improvement Program: a comparison of logistic versus hierarchical modeling. J Am Coll Surg 2009;209:687-93. http://dx.doi.org/10.1016/j.jamcollsurg.2009.08.020.
- Glance LG, Dick A, Osler TM, Li Y, Mukamel DB. Impact of changing the statistical methodology on hospital and surgeon ranking: the case of the New York State cardiac surgery report card. Med Care 2006;44:311-19. http://dx.doi.org/10.1097/01.mlr.0000204106.64619.2a.
- The Centre for Medicare and Medicaid Services . Statistical Issues in Assessing Hospital Performance n.d. www.cms.gov/Medicare/Quality-Initiatives-Patient-Assessment-Instruments/HospitalQualityInits/Downloads/Statistical-Issues-in-Assessing-Hospital-Performance.pdf (accessed March 2014).
- Mohammed MA, Manktelow BN, Hofer TP. Comparison of four methods for deriving hospital standardised mortality ratios from a single hierarchical logistic regression model. Stat Methods Med Res 2012. http://dx.doi.org/10.1177/0962280212465165.
- Austin PC, Alter DA, Tu JV. The use of fixed- and random-effects models for classifying hospitals as mortality outliers: a Monte Carlo assessment. Med Decis Making 2003;23:526-39. http://dx.doi.org/10.1177/0272989X03258443.
- Austin P. A comparison of Bayesian methods for profiling hospital performance. Med Decis Making 2002;22:163-72. http://dx.doi.org/10.1177/0272989X0202200213.
- Snijders TAB, Bosker RJ. Multilevel Analysis: an Introduction to Basic and Advanced Multilevel Modeling. London: Sage Publications; 1999.
- Green M, Björk J, Forberg J, Ekelund U, Edenbrandt L, Ohlsson M. Comparison between neural networks and multiple logistic regression to predict acute coronary syndrome in the emergency room. Artif Intell Med 2006;38:305-18. http://dx.doi.org/10.1016/j.artmed.2006.07.006.
- Bottaci L, Drew PJ. Artificial neural networks applied to outcome prediction for colorectal cancer patients in separate institutions. Lancet 1997;350:469-73. http://dx.doi.org/10.1016/S0140-6736(96)11196-X.
- Nilsson J, Ohlsson M, Thulin L, Höglund P, Nashef SA, Brandt J. Risk factor identification and mortality prediction in cardiac surgery using artificial neural networks. J Thorac Cardiovasc Surg 2006;132:12-9. http://dx.doi.org/10.1016/j.jtcvs.2005.12.055.
- Song X, Mitnitski A, Cox J, Rockwood K. Comparison of machine learning techniques with classical statistical methods in predicting health outcomes. Medinfo 2004;107:736-40.
- Camps-Valls G, Rodrigo-Gonzalez A, Muoz-Mari J, Gomez-Chova L, Calpe-Maravilla J. Hyperspectral image classification with Mahalanobis relevance vector machines. Proceedings of IGARSS, 2007 Geoscience and Remote Sensing Symposium, IEEE n.d.:3802-5.
- Joachims T, Schölkopf B, Burges C, Smola A. Advances in Kernel Methods: Support Vector Learning. Cambridge, MA: MIT Press; 1999.
- Hertz J, Krogh A, Palmer RG. An Introduction to the Theory of Neural Computation. Redwood City, CA: Addison-Wesley; 1991.
- Bengio Y. Learning deep architectures for AI. Found Trends Machine Learn 2009;2:1-127. http://dx.doi.org/10.1561/2200000006.
- Breiman L. Bagging predictors. Machine Learn 1996;24:123-40. http://dx.doi.org/10.1007/BF00058655.
- Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. New York, NY: Chapman & Hall; 1984.
- Genuer R, Poggi J-M, Tuleau C. Random Forests: Some Methodological Insights 2014. http://arxiv.org/abs/0811.3619.
- Breiman L. Consistency for a Simple Model of Random Forests. Berkeley, CA: UC Berkeley; 2004.
- Cook N. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation 2007;115:928-35. http://dx.doi.org/10.1161/CIRCULATIONAHA.106.672402.
- Hosmer DW, Hosmer T, Le Cessie S, Lemeshow S. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med 1997;16:965-80. http://dx.doi.org/10.1002/(SICI)1097-0258(19970515)16:9<965::AID-SIM509>3.0.CO;2-O.
- Boström H. Calibrating Random Forests n.d.:121-6.
- Zadrozny B, Elkan C. Proceedings of the 8th International Conference on Knowledge Discovery and Data Mining. Edmonton, AB: ACM Press; 2002.
- Gaudoin R, Montana G, Jones S, Aylin P, Bottle A. Classifier calibration using splined empirical probabilities in clinical risk prediction [published online ahead of print 21 February 2014]. Health Care Manag Sci 2014. http://dx.doi.org/10.1007/s10729-014-9267-1.
- Lau B, Cole SR, Gange SJ. Competing risk regression models for epidemiologic data. Am J Epidemiol 2009;170:244-56. http://dx.doi.org/10.1093/aje/kwp107.
- Haller B, Schmidt G, Ulm K. Applying competing risks regression models: an overview. Lifetime Data Anal 2013;19:33-58. http://dx.doi.org/10.1007/s10985-012-9230-8.
- Kohl M, Heinze G. PSHREG: A SAS Macro for Proportional and Nonproportional Subdistribution Hazards Regression with Competing Risk Data. Vienna: Medical University of Vienna; 2012.
- Au AG, McAlister FA, Bakal JA, Ezekowitz J, Kaul P, van Walraven C. Predicting the risk of unplanned readmission or death within 30 days of discharge after a heart failure hospitalization. Am Heart J 2012;164:365-72. http://dx.doi.org/10.1016/j.ahj.2012.06.010.
- Amarasingham R, Patel PC, Toto K, Nelson LL, Swanson TS, Moore BJ, et al. Allocating scarce resources in real-time to reduce heart failure readmissions: a prospective, controlled study. BMJ Qual Saf 2013;22:998-1005. http://dx.doi.org/10.1136/bmjqs-2013-001901.
- Muzzarelli S, Leibundgut G, Maeder MT, Rickli H, Handschin R, Gutmann M, et al. TIME-CHF Investigators. Predictors of early readmission or death in elderly patients with heart failure. Am Heart J 2010;160:308-14. http://dx.doi.org/10.1016/j.ahj.2010.05.007.
- Damen NLM, Pelle AJM, Szabó BM, Pedersen SS. Symptoms of anxiety and cardiac hospitalizations at 12 months in patients with heart failure. J Gen Intern Med 2012;27:345-50. http://dx.doi.org/10.1007/s11606-011-1843-1.
- Braunstein JB, Anderson GF, Gerstenblith G, Weller W, Niefeld M, Herbert R, et al. Noncardiac comorbidity increases preventable hospitalizations and mortality among Medicare beneficiaries with chronic heart failure. J Am Coll Cardiol 2003;42:1226-33. http://dx.doi.org/10.1016/S0735-1097(03)00947-1.
- Billings J, Dixon J, Mijanovich T, Wennberg D. Case finding for patients at risk of readmission to hospital: development of algorithm to identify high risk patients. BMJ 2006;333. http://dx.doi.org/10.1136/bmj.38870.657917.AE.
- Bottle A, Aylin P, Majeed A. Identifying patients at high risk of emergency hospital admissions: a logistic regression analysis. J R Soc Med 2006;99:406-14. http://dx.doi.org/10.1258/jrsm.99.8.406.
- Johnson TJ, Basu S, Pisani BA, Avery EF, Mendez JC, Calvin JE, et al. Depression predicts repeated heart failure hospitalizations. J Cardiac Fail 2012;18:246-52. http://dx.doi.org/10.1016/j.cardfail.2011.12.005.
- Chun S, Tu JV, Wijeysundera HC, Austin PC, Wang X, Levy D, et al. Lifetime analysis of hospitalizations and survival of patients newly admitted with heart failure. Circulation 2012;5:414-21. http://dx.doi.org/10.1161/CIRCHEARTFAILURE.111.964791.
- Hu M-C, Pavlicova M, Nunes EV. Zero-inflated and hurdle models of count data with extra zeros: examples from an HIV-risk reduction intervention trial. Am J Drug Alcohol Abuse 2011;37:367-75. http://dx.doi.org/10.3109/00952990.2011.597280.
- Vuong QH. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989;57:307-33. http://dx.doi.org/10.2307/1912557.
- Clarke KA. A simple distribution-free test for nonnested model selection. Political Anal 2007;15:347-63. http://dx.doi.org/10.1093/pan/mpm004.
- Cameron AC, Trivedi PK. Regression Analysis of Count Data. Cambridge: Cambridge University Press; 2013.
- Bottle A, Sanders RD, Mozid A, Aylin P. Provider profiling models for acute coronary syndrome mortality using administrative data. Int J Cardiol 2013;168:338-43. http://dx.doi.org/10.1016/j.ijcard.2012.09.048.
- Burns EM, Bottle A, Aylin P, Darzi A, Nicholls RJ, Faiz O. Variation in reoperation after colorectal surgery in England as an indicator of surgical performance: retrospective analysis of Hospital Episode Statistics. BMJ 2011;343. http://dx.doi.org/10.1136/bmj.d4836.
- Mitchell AJ, Selmes T. Why don’t patients attend their appointments? Maintaining engagement with psychiatric services. Adv Psych Treat 2007;13:423-34. http://dx.doi.org/10.1192/apt.bp.106.003202.
- Hamilton W, Round A, Sharp D. Patient, hospital and general practitioner characteristics associated with non-attendance: a cohort study. Br J Gen Pract 2002;52:317-19.
- Lloyd M, Bradford C, Webb S. Non-attendance at outpatient clinics: is it related to the referral process?. Fam Pract 1993;10:111-17. http://dx.doi.org/10.1093/fampra/10.2.111.
- Dockery F, Rajkumar C, Chapman C, Bulpitt C, Nicholl C. The effect of reminder calls in reducing non-attendance rates at care of the elderly clinics. Postgrad Med J 2001;77:37-9. http://dx.doi.org/10.1136/pmj.77.903.37.
- Stone CA, Palmer JH, Saxby PJ, Devaraj VS. Reducing non-attendance in outpatient clinics. J R Soc Med 1999;92:114-18.
- Carlsen KH, Carlsen KM, Serup J. Non-attendance rate in a Danish university clinic of dermatology. J Eur Acad Dermatol Venereol 2001;25:1269-74. http://dx.doi.org/10.1111/j.1468-3083.2010.03962.x.
- Bateson MC. Non-attendance at clinic: cycles of audit of a consultant based gastroenterology outpatient department. Postgrad Med J 2004;80:615-16. http://dx.doi.org/10.1136/pgmj.2003.013797.
- Humphreys L, Hunter A, Zimak A, O’Brien A, Korneluk Y, Cappelli M. Why patients do not attend for their appointments at a genetics clinic. J Med Genet 2000;37:810-15. http://dx.doi.org/10.1136/jmg.37.10.810.
- Andrews R, Morgan JD, Addy DP, McNeish AS. Non-attendance at outpatient clinics: is it related to the referral process?. Arch Dis Child 1990;65:192-5. http://dx.doi.org/10.1136/adc.65.2.192.
- Collins J, Santamaria N, Clayton L. Why outpatients fail to attend their scheduled appointments: a prospective comparison of differences between attenders and non-attenders. Aust Health Rev 2003;26:52-63. http://dx.doi.org/10.1071/AH030052.
- Frankel S, Farrow A, West R. Non-attendance or non-invitation? A case–control study of failed outpatient appointments. BMJ 1989;298:1343-5. http://dx.doi.org/10.1136/bmj.298.6684.1343.
- King A, David D, Jones HS, O’Brien C. Factors affecting non-attendance in an ophthalmic outpatient department. J R Soc Med 1995;88:88-90.
- Dyer PH, Lloyd CE, Lancashire RJ, Bain SC, Barnett AH. Factors associated with clinic non-attendance in adults with type 1 diabetes mellitus. Diabetic Med 1998;115:339-43. http://dx.doi.org/10.1002/(SICI)1096-9136(199804)15:4<339::AID-DIA577>3.0.CO;2-E.
- Kosmider S, Shedda S, Jones IT, McLaughlin S, Gibbs P. Predictors of clinic non-attendance: opportunities to improve patient outcomes in colorectal cancer. Int Med J 2010;40:757-63. http://dx.doi.org/10.1111/j.1445-5994.2009.01986.x.
- Cooper NA, Lynch MA. Lost to follow up: a study of nonattendance at a general paediatric outpatient clinic. Arch Dis Child 1979;54:765-9. http://dx.doi.org/10.1136/adc.54.10.765.
- Waller J, Hodgkin P. Defaulters in general practice, who are they and what can be done about them. Fam Pract 2000;17:252-3. http://dx.doi.org/10.1093/fampra/17.3.252.
- Gatrad AR. A completed audit to reduce hospital outpatients non-attendance rates. Arch Dis Child 2000;82:59-61. http://dx.doi.org/10.1136/adc.82.1.59.
- Sharp DJ, Hamilton W. Non-attendance at general practices and outpatient clinics. BMJ 2001;323:1081-2. http://dx.doi.org/10.1136/bmj.323.7321.1081.
- Dickey W, Morrow JI. Can outpatient non-attendance be predicted from the referral letter? An audit of default at neurology clinics. J R Soc Med 1991;84:662-3.
- Cleland J, Dargie H, Hardman S, McDonagh T, Mitchell P. National Heart Failure Audit April 2011–March 2012 n.d. www.hqip.org.uk/heart-failure-audit-2011-12/ (accessed September 2014).
- Pine M, Jordan HS, Elixhauser A, Fry DE, Hoaglin DC, Jones B, et al. Modifying ICD-9-CM coding of secondary diagnoses to improve risk-adjustment of inpatient mortality rates. Med Decis Making 2009;29:69-81. http://dx.doi.org/10.1177/0272989X08323297.
- Aylin P, Bottle A, Majeed A. Use of administrative data or clinical databases as predictors of risk of death in hospital: comparison of models. BMJ 2007;334. http://dx.doi.org/10.1136/bmj.39168.496366.55.
- Murray J, Saxena S, Modi N, Majeed A, Aylin P, Bottle A. Medicines for Neonates Investigator Group. Quality of routine hospital birth records and the feasibility of their use for creating birth cohorts. J Public Health (Oxf) 2013;35:298-307. http://dx.doi.org/10.1093/pubmed/fds077.
- Dharmarajan K, Hsieh AF, Lin Z, Bueno H, Ross JS, Horwitz LI, et al. Hospital readmission performance and patterns of readmission: retrospective cohort study of Medicare admissions. BMJ 2013;347. http://dx.doi.org/10.1136/bmj.f6571.
- Bottle A, Aylin P, Bell D. Effect of the readmission primary diagnosis and time interval in heart failure patients: analysis of English administrative data. Eur J Heart Fail 2014;16:846-53. http://dx.doi.org/10.1002/ejhf.129.
- Bottle A, Aylin P, Loeffler M. Return to theatre for elective hip and knee replacements: what is the relative importance of patient factors, surgeon and hospital?. Bone Joint J 2014.
Glossary
- Artificial neural networks
- Well-established, flexible type of machine learning method.
- c-statistic
- Also known as the area under the receiver operating characteristic curve, this measures the discrimination of a model, i.e. the ability of the model to give a higher probability of the outcome (such as death) occurring to people who in fact have the outcome (die) than those who do not (survive).
- Calibration
- The ability of the model to give an accurate probability of the outcome. Typically assessed using the Hosmer–Lemeshow statistic and/or plots.
- Casemix
- Patient factors that are often associated with the outcome of interest, such as age and comorbidity, and that therefore need to be accounted for when comparing performance by hospital.
- Clinical Classification System
- Algorithm developed by the Agency for Healthcare Research and Quality in the USA to group the thousands of International Classification of Diseases codes into 259 clinically meaningful diagnosis groups for use in health services research.
- Discrimination
- See c-statistic.
- Hierarchical modelling
- Widely used approach for dealing with the problem of dependence between observations. This occurred in this project, as patients admitted to the same hospital or treated by the same surgeon are expected to have more similar outcomes than those admitted to different hospitals (they are ‘clustered’ by hospital and/or by surgeon).
- Hospital Episode Statistics
- Administrative database covering the main types of patient-level NHS hospital activity.
- Machine learning methods
- General term covering many different types of algorithm that learn their way to modelling the data. We considered artificial neural networks, support vector machines and random forests in this project.
- Outcome, or outcome measure
- What happened to the patient during or after their admission, for example death, readmission. These are commonly distinguished from process measures, which describe the actions of health-care professionals, for example prescribing medication, following protocols.
- Overfitting
- A common problem with machine learning methods in particular, when the algorithm learns the (training) data set too well, so that its results generalise poorly to other data sets (e.g. the test set).
- Random forests
- Type of machine learning method used in classification problems.
- Relative risk
- In this project, this refers specifically to the ratio of observed (actual) to predicted (model-based) outcomes at hospital level.
- Return to theatre
- Some complications following an operation require another operation or procedure: these are unplanned returns to theatre.
- Secondary Uses Service
- A data warehouse designed to provide patient-based data for purposes other than direct clinical care, such as health-care planning, commissioning and research.
- Support vector machines
- Type of machine learning method used in classification problems.
List of abbreviations
- A&E
- accident and emergency
- ACS
- acute coronary syndrome
- ACSC
- ambulatory care-sensitive condition
- AHRQ
- Agency for Healthcare Research and Quality
- AIC
- Akaike information criterion
- AMI
- acute myocardial infarction
- ANN
- artificial neural network
- CABG
- coronary artery bypass graft
- CCS
- Clinical Classification System
- CMS
- Center for Medicare and Medicaid Services
- COPD
- chronic obstructive pulmonary disease
- HES
- Hospital Episode Statistics
- HF
- heart failure
- HIV
- human immunodeficiency virus
- HL
- Hosmer–Lemeshow
- HR
- hip replacement
- ICC
- intraclass correlation coefficient
- ICD-9
- International Classification of Diseases, Ninth Edition
- ICD-10
- International Classification of Diseases, Tenth Edition
- KR
- knee replacement
- LOS
- length of stay
- LR
- logistic regression
- NBH
- negative binomial hurdle
- OPD
- outpatients department
- OR
- odds ratio
- PAV
- pool adjacent violator
- QMAE
- Accident and Emergency Quarterly Monitoring Data Set
- RR
- relative risk
- RTT
- (unplanned) return to theatre
- SMR
- standardised mortality ratio
- SUS
- Secondary Uses Service
- SVM
- support vector machine
- ZINB
- zero-inflated negative binomial