Notes
Article history
The research reported in this issue of the journal was funded by the HS&DR programme or one of its preceding programmes as project number 09/2000/65. The contractual start date was in July 2011. The final report began editorial review in February 2015 and was accepted for publication in June 2015. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HS&DR editors and production house have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the final report document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
none
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2015. This work was produced by Harrison et al. under the terms of a commissioning contract issued by the Secretary of State for Health. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
Chapter 1 Introduction
The provision of high-quality care is a fundamental objective of the NHS. 1 The most widely used framework for assessing the quality of health care is that proposed by Donabedian. 2 He describes three distinct domains from which inferences about the quality of care can be made: structure, process and outcome. Structure describes the attributes of the setting within which care occurs. Process denotes what is actually done in giving and receiving care. Outcome is defined as the effects of care on the health status of patients and populations.
The domains of structure and process can be assessed within an individual health-care provider. Indicators of structure are assessed against professional standards, regulations and recommendations. They relate to the provider rather than the patient and, therefore, require only periodic assessment. Indicators of process are assessed against national or international clinical guidelines, based ideally on high-quality evidence. The gold standard is 100% adherence to the guidelines and there is no need to compare performance with other health-care providers.
Assessing outcomes for a single health-care provider requires comparison against other providers (comparative audit) to put the outcome of the particular health-care provider in context and to enable benchmarking. However, the quality of care is only one of many factors that will contribute to a patient’s outcome and, if crude outcomes were to be compared between health-care providers, then any effect of quality would probably be overwhelmed by variation in the patient demographics, underlying health status, acute conditions and severity of the acute illness (factors collectively termed ‘case mix’). When comparing outcomes between health-care providers, it is therefore essential to take the differing case mix of patients treated by the providers into account in order to be able to make fair comparisons.
National clinical audit has a key role to play in ensuring high-quality care,3,4 particularly in areas of health care, such as emergency and critical care, where patient choice does not, and cannot, play a significant part. Sophisticated and accurate risk prediction models, developed using high-quality clinical data, are key in underpinning fair comparisons among health-care providers. 5 They can also enable risk-adjusted observational research and risk stratification in randomised controlled trials.
The Intensive Care National Audit & Research Centre (ICNARC) is an independent charitable organisation that runs national clinical audit programmes to monitor and improve care for the critically ill. ICNARC co-ordinates two national clinical audits: the Case Mix Programme (CMP), a national clinical audit for adult critical care; and the National Cardiac Arrest Audit (NCAA), a national clinical audit for in-hospital cardiac arrest, co-ordinated jointly with the Resuscitation Council (UK). Both national clinical audits are listed for inclusion in the Department of Health’s NHS Quality Accounts,6 and both are underpinned by the need and ability to report accurate risk-adjusted outcomes.
The Case Mix Programme
The CMP is the national clinical audit for adult critical care, with a remit for England, Wales and Northern Ireland. Participation of adult, general critical care units delivering level 3 or combined level 2/3 care (intensive care units and combined high-dependency/intensive care units) is approaching 100%, but participation of other critical care units, such as specialist units (e.g. neurocritical care units and cardiothoracic critical care units) and stand-alone level 2 (high-dependency) units, is lower. For all participating units, data on consecutive admissions are recorded prospectively and abstracted from the medical records by trained data collectors in accordance with precise rules and definitions. The data collected include raw physiological and diagnostic data from the first 24 hours following admission to the critical care unit, together with demographic, outcome and activity data. The data undergo extensive validation, both locally and centrally, before being pooled into the central CMP database. Details of data collection and validation have been reported previously, and the CMP database has been independently assessed to be of high quality. 7
Risk prediction models for adult, general critical care are well established, but ongoing improvement work is essential to further improve accuracy. 8 In 2006, ICNARC published a validation of four existing models [the Acute Physiology and Chronic Health Evaluation (APACHE) model versions II and III,9,10 the Simplified Acute Physiology Score (SAPS) version II11 and the Mortality Probability Models (MPM) version II12] and concluded that there was little difference in performance among the models, but that there was scope for further improvement. 13 While retaining the APACHE II model for the purpose of international comparisons, ICNARC developed and validated the ICNARC model,14,15 which underpins the risk-adjusted outcomes reported for the CMP. However, a number of areas were identified where we have the potential to improve our modelling.
The National Cardiac Arrest Audit
The NCAA is the national clinical audit of patients, aged greater than 28 days, in acute hospitals in the UK who receive cardiopulmonary resuscitation (CPR) and are attended by the hospital-based resuscitation team (or equivalent) in response to a 2222 call (2222 is the emergency telephone number used to summon a resuscitation team in UK hospitals). CPR is defined in the NCAA as chest compressions and/or defibrillation. Standardised data are collected at the time of the cardiac arrest and from the medical records in accordance with precise rules and definitions. Staff members at participating hospitals enter data onto a dedicated secure online data entry system. Data are validated, both at the point of entry and centrally, for completeness, illogicalities and inconsistencies. Details of data collection and validation have been reported previously. 16
Prior to this project, there was no validated risk prediction model for predicting outcomes following in-hospital cardiac arrest. Initial comparative reporting for the NCAA was based on stratifying patients according to single risk factors.
Governance
Both the CMP and NCAA have approval from the Confidentiality Advisory Group of the Health Research Authority for the collection and use of patient-identifiable data without consent under Section 251 of the NHS Act 200617 [approval numbers PIAG 2-10(f)/2005 and ECC 2-06(n)/2009].
The project was overseen by an Expert Advisory Group (see Acknowledgements), which included a member who had previous experience as a patient in a critical care unit. The Expert Advisory Group met five times during the project, reviewed its progress against each of the objectives and gave advice on the future directions for the project. Individual members of the Expert Advisory Group were also contacted between meetings and asked to provide input in their particular areas of expertise.
Aim and objectives
The aim of the current project was to improve risk prediction models to underpin quality improvement programmes for the critically ill (patients receiving general or specialist adult critical care or experiencing an in-hospital cardiac arrest).
We set out to address this aim through the following objectives:
-
To improve current risk prediction models for critically ill patients, to include:
-
external validation of current models in critical care units in Scotland
-
introduction of new important variables
-
improved modelling of interactions between physiological parameters
-
improved handling of missing data and
-
improved modelling of reasons for admission to/diagnosis on admission to critical care.
-
-
To develop and validate new risk prediction models for critically ill patients, to include:
-
models for cardiothoracic critical care
-
models for patients experiencing an in-hospital cardiac arrest and
-
models for critical care units admitting lower-risk patients.
-
-
Immediate translation of improved risk prediction models into practice, through:
-
adoption into routine comparative outcome reporting for national clinical audits and
-
communication of research output to providers, managers, commissioners, policy-makers and academics in critical care.
-
Following early advice from the Expert Advisory Group, objective 2iii was incorporated into objective 1 by aiming to improve risk prediction at the patient level to the extent that a separate model for critical care units admitting lower-risk patients was no longer required.
Chapter 2 reports the external validation of the current ICNARC model in critical care units in Scotland (objective 1i). Chapter 3 reports the development and validation of a preliminary risk prediction model for admissions to specialist cardiothoracic critical care units (objective 2i). Chapter 4 reports the development and validation of a new, improved risk prediction model for admissions to all adult (general and specialist) critical care units (objectives 1ii–v). Chapter 5 reports the development and validation of risk prediction models for outcomes following in-hospital cardiac arrest (objective 2ii). Chapter 6 reports the translation and dissemination work conducted to date (objective 3). Chapter 7 draws conclusions from the project as a whole, including implications for practice, and makes recommendations for further research in this field.
Chapter 2 External validation of the current Intensive Care National Audit & Research Centre model in Scottish critical care units
Introduction
Risk prediction models require validation before they can be used with confidence. 18 Ideally, external validation should be conducted using independently collected data from a different source to that used to develop the original model. 19 The ICNARC model was developed and validated using data from the CMP from adult, general critical care units in England, Wales and Northern Ireland. 14 It has subsequently been validated using further data from the CMP, including external validation among critical care units that joined the programme after the development of the model,15 but it has never undergone validation using independently collected data.
Scotland, as a devolved nation within the UK, has a very similar health-care system to the rest of the UK. However, it has a separate, independent, national clinical audit for adult critical care, co-ordinated by the Scottish Intensive Care Society Audit Group (SICSAG) through the Information Services Division of NHS National Services Scotland. Consequently, this is the ideal setting in which to externally validate the ICNARC model using independently collected data. This chapter reports the validation of the ICNARC risk prediction model using data from adult, general critical care units in Scotland.
Methods
The current Intensive Care National Audit & Research Centre model
Risk predictions in the ICNARC model are calculated for each admission based on the following predictors:
-
age in years at admission to the critical care unit
-
location prior to admission to the critical care unit (emergency department, ward, theatre, other critical care unit, other acute hospital or not in hospital) and, for admissions directly from theatre, urgency of surgery (either elective/scheduled or emergency/urgent)
-
CPR within the 24 hours prior to admission to the critical care unit
-
the ICNARC Physiology Score – an integer score between 0 and 100 based on derangement in 12 physiological parameters during the first 24 hours following admission to the critical care unit
-
primary reason for admission to the critical care unit
-
some interactions between the ICNARC Physiology Score and primary reason for admission.
The ICNARC model is regularly recalibrated using CMP data to ensure ongoing fit.
The Scottish Intensive Care Society Audit Group database
The SICSAG has maintained a national database of patients admitted to adult critical care units in Scotland since 1995. Initially, only adult, general intensive care and combined high-dependency/intensive care units (critical care) units participated in the audit. More recently, specialist critical care units have joined the audit, with the result that, as of 2014, all adult, general and specialist critical care units in Scotland participate voluntarily in the audit. Data are collected prospectively using a dedicated software system. Annual data extracts are pooled centrally onto servers at the Information Services Division and validation queries relating to discharges, outcomes, ages and missing treatment information are then issued and fed back to individual units for checking by local and regional audit coordinators.
Use of the SICSAG database for this study was approved by the Privacy Advisory Committee, NHS National Services Scotland (application number 53/10).
Inclusion and exclusion criteria
Data were extracted from the SICSAG database for all admissions to all 24 adult general critical care units in Scotland between 1 January 2007 and 31 December 2009. During this study period, specialist cardiothoracic critical care units were not participating in the national audit; admissions to one specialist neurocritical care unit were not included in the data extract. The following admissions were excluded from the analysis: admissions flagged in the database as ‘exclude from severity of illness scoring’; readmissions of the same patient within the same acute hospital stay; admissions missing the outcome of status at discharge from acute hospital; admissions missing age, location prior to admission or primary reason for admission to the critical care unit; and admissions for whom the primary reason for admission was unable to be mapped onto the ICNARC coding method (see Primary reason for admission).
Application of the Intensive Care National Audit & Research Centre model to the Scottish Intensive Care Society Audit Group database
The most appropriate recalibration of the ICNARC model was selected based on the time period of the data included in the analysis – this was a recalibration undertaken in 2009 using CMP data from 194,892 admissions to 187 critical care units between 1 January 2006 and 31 December 2008.
In order to apply the ICNARC model to data from the SICSAG database, certain assumptions and recoding were required. These are detailed in the following subsections: Location prior to admission, Systolic blood pressure, Arterial pH, Neurological status and Primary reason for admission. After applying this recoding, the predicted risk of acute hospital mortality from the ICNARC model was calculated for each admission using standard algorithms developed for the CMP.
Location prior to admission
In the ICNARC model, for admissions to the critical care unit from an imaging department and from the recovery area (when used as a temporary critical care area rather than for postoperative purposes), the previous location is used. For admissions collected to version 0 of the SICSAG data set (phased out from June 2008 to May 2009), only a single location immediately prior to admission to the critical care unit was recorded and, therefore, the weighting for location prior to admission for these admissions was assigned based on the most common previous location in both the SICSAG version 203 data (introduced from June 2008) and CMP data. Admissions from an imaging department were assumed to have previously been in an emergency department and admissions from the recovery area were assumed to have previously been on a general ward.
Systolic blood pressure
In the ICNARC Physiology Score, weighting of systolic blood pressure (SBP) is based on the lowest value during the first 24 hours following admission to the critical care unit. For the SICSAG data (all versions), only the highest SBP values with paired diastolic blood pressure (DBP) values and the lowest DBP values with paired SBP values were recorded. The lowest SBP value was therefore imputed using a regression model fitted to 574,864 admissions to 181 critical care units in the CMP between 1995 and 2008 with all these parameters recorded. The resulting imputation equation was:
Arterial pH
In the ICNARC Physiology Score, weighting of arterial pH is based on the lowest pH value during the first 24 hours following admission to the critical care unit. For the SICSAG data (all versions), only the pH from the arterial blood gas with the lowest partial pressure of oxygen (PaO2) was recorded. The lowest pH was therefore imputed using a regression model fitted to 1,011,217 admissions to 224 critical care units in the CMP between 1995 and 2013 with both pH measurements recorded. The resulting equation was:
Neurological status
In the ICNARC Physiology Score, weighting of neurological status is based on either the lowest total Glasgow Coma Scale (GCS) score during the first 24 hours following admission to the critical care unit (for admissions not sedated during that period) or a separate weighting for patients who were sedated or paralysed and sedated during the first 24 hours. For admissions collected to version 203 of the SICSAG data set (introduced from June 2008), sedation was not recorded. Admissions were therefore assumed to be sedated if they had no lowest total GCS score recorded during the first 24 hours following admission to the critical care unit (this was true for 99% of such admissions in SICSAG version 0 data).
Primary reason for admission
In the ICNARC model, weighting of the primary reason for admission to the critical care unit is based on weightings for conditions/body systems from the ICNARC coding method, developed for the CMP. 20 The ICNARC coding method is a five-tier, hierarchical system for coding reasons for admission to critical care. It currently contains 795 individual conditions within a hierarchy of type (surgical or non-surgical), body system, anatomical site, pathological or physiological process and individual condition. Coding to the system tier is sufficient to be able to assign a weight for the ICNARC model, although all admissions in the CMP are coded to at least the site tier. For all the SICSAG data, the primary reason for admission to the critical care unit was collected using Scottish Intensive Care Society diagnostic coding. These diagnoses were mapped to appropriate codes within the ICNARC coding method by a consultant intensivist with extensive experience of coding data for the CMP. Of the 423 Scottish Intensive Care Society diagnoses in use, 295 (70%) were mapped to a specific condition in the ICNARC coding method, 44 (10%) were mapped to the process tier of the hierarchy, 37 (9%) to the site tier, 28 (7%) to the system tier and 19 (4%) could not be mapped (Box 1).
Disseminated malignancy.
Endoscopy.
Interventional radiology.
Interventional radiology/cardiology.
MRSA.
Massive blood loss/transfusion without shock.
Massive blood transfusion.
Multiple surgical procedures.
Other anaesthetic complication.
Other chronic physical disorder.
Other drug-related problem.
Other infection.
Other surgery.
Other trauma.
Pre-operative assessment/monitoring/optimisation.
Self-inflicted injury.
Surgical complication.
Systemic embolism.
VRE.
MRSA, meticillin-resistant Staphylococcus aureus; VRE, vancomycin-resistant Enterococcus.
The Acute Physiology And Chronic Health Evaluation II model
The APACHE II model was selected as a comparator for this study, as it was the model in use in Scotland at that time. The SICSAG database does not include all the requisite fields to enable a head-to-head comparison against other, more recent, risk prediction models. The APACHE II model was originally developed using data from 19 critical care units in 13 US hospitals,9 and has subsequently been validated and recalibrated using UK data. 13,21 Risk predictions are calculated for each admission based on the following predictors:
-
the APACHE II Score – an integer score between 0 and 71 comprising an Acute Physiology Score (0–60 points) based on derangement in 12 physiological parameters during the first 24 hours following admission to the critical care unit, age points (0–6) for age categories of ≤ 44, 45–54, 55–64, 65–74 or ≥ 75 years, and chronic health points (0–5) for very severe conditions in the patient’s medical history
-
admission to the critical care unit following emergency surgery
-
diagnostic categories based on the primary reason for admission to the critical care unit.
Values of predicted acute hospital mortality were supplied by the Information Services Division, calculated from the original published coefficients9 using the standard algorithms applied for routine reporting of the SICSAG audit results at that time.
Statistical methods
The ICNARC model was validated using measures of calibration, discrimination and overall fit, as described below. The validation was conducted in the full 3-year SICSAG database extract and for each year separately.
Discrimination was assessed by the c-index,22 which is equivalent to the area under the receiver operating characteristic curve. 23 Calibration was assessed graphically and tested using the Hosmer–Lemeshow test for perfect calibration in 10 equal-sized groups by predicted probability of survival. 24 As the Hosmer–Lemeshow test does not provide a measure of the magnitude of miscalibration and is very sensitive to sample size,25,26 calibration was also assessed using Cox’s calibration regression, which assesses the degree of linear miscalibration by fitting a logistic regression of observed survival on the predicted log-odds of survival from the risk prediction model. 27 Accuracy was assessed by the Brier score (the mean-squared error between outcome and prediction)28 and Shapiro’s R (the geometric mean of the probability assigned to the event that occurred),29 and the associated approximate R2 statistics (termed the ‘sum-of-squares’ R2 and the ‘entropy-based’ R2, respectively), which are obtained by scaling each measure relative to the value achieved from a null model. 30
The performance of the ICNARC model was compared with that of the APACHE II model. The difference in c-index between the two models was assessed using the method of DeLong et al. 31 Confidence intervals (CIs) for observed acute hospital mortality were calculated using the method of Wilson. 32
Statistical analyses were performed using Stata/SE, version 13.0 (StataCorp LP, College Station, TX, USA).
Results
Available data
Data were extracted from the SICSAG database for 29,626 admissions to 24 adult, general critical care units between 1 January 2007 and 31 December 2009. The following admissions were excluded: 3599 admissions (12.1%) flagged in the database as ‘exclude from severity of illness scoring’ (Table 1 contains the breakdown of reasons for exclusion); 1324 (4.5%) readmissions of the same patient within the same acute hospital stay; 173 (0.6%) admissions missing the outcome of acute hospital mortality; 869 (2.9%) admissions missing location prior to admission (n = 16) or primary reason for admission to the critical care unit (n = 864); and 392 (1.3%) admissions for whom the primary reason for admission was unable to be mapped. No admissions were missing age. This resulted in a cohort of 23,269 (78.5%) admissions for analysis.
| Reason for exclusion | Number (%) | Acute hospital mortality, deaths/n (%) |
|---|---|---|
| Excluded from APACHE II model | 445 (1.5) | 290/407 (71.3) |
| Death within 4 hours | 231 (0.8) | 231/231 (100) |
| Missing core physiology data | 103 (0.3) | 33/101 (32.7) |
| Age less than 16 years | 65 (0.2) | 5/30 (16.7) |
| Admission for primary burn injury | 46 (0.2) | 21/45 (46.7) |
| Low-risk patients | 2305 (7.8) | 174/2291 (7.6) |
| High-dependency unit patient | 1707 (5.8) | 116/1694 (6.8) |
| Admission for postsurgical recovery | 598 (2.0) | 58/597 (9.7) |
| Responsibility of other team | 88 (0.3) | 35/88 (39.8) |
| Awaiting transfer | 45 (0.2) | 22/45 (48.9) |
| In critical care under another team | 43 (0.1) | 13/43 (30.2) |
| Unspecified | 761 (2.6) | 232/743 (31.2) |
| ‘Unit decision not to score patient’ | 369 (1.2) | 118/360 (32.8) |
| Other (unspecified) | 298 (1.0) | 87/293 (29.7) |
| Reason missing or not documented | 94 (0.3) | 27/90 (30.0) |
| Total excluded | 3599 (12.1) | 731/3529 (20.7) |
Of the admissions flagged as ‘exclude from severity of illness scoring’, acute hospital mortality was reported for 3529 admissions (98.1%); 731 (20.7%) of these patients died before discharge from the acute hospital (see Table 1 for breakdown). It was not possible to include these patients in the analysis, even using statistical imputation methods to account for missing data, as insufficient predictor data were recorded. Owing to the large number of admissions flagged as ‘exclude from severity of illness scoring’, a post hoc analysis was undertaken to investigate the potential impact of such exclusions using CMP data (see Simulation of exclusion criteria).
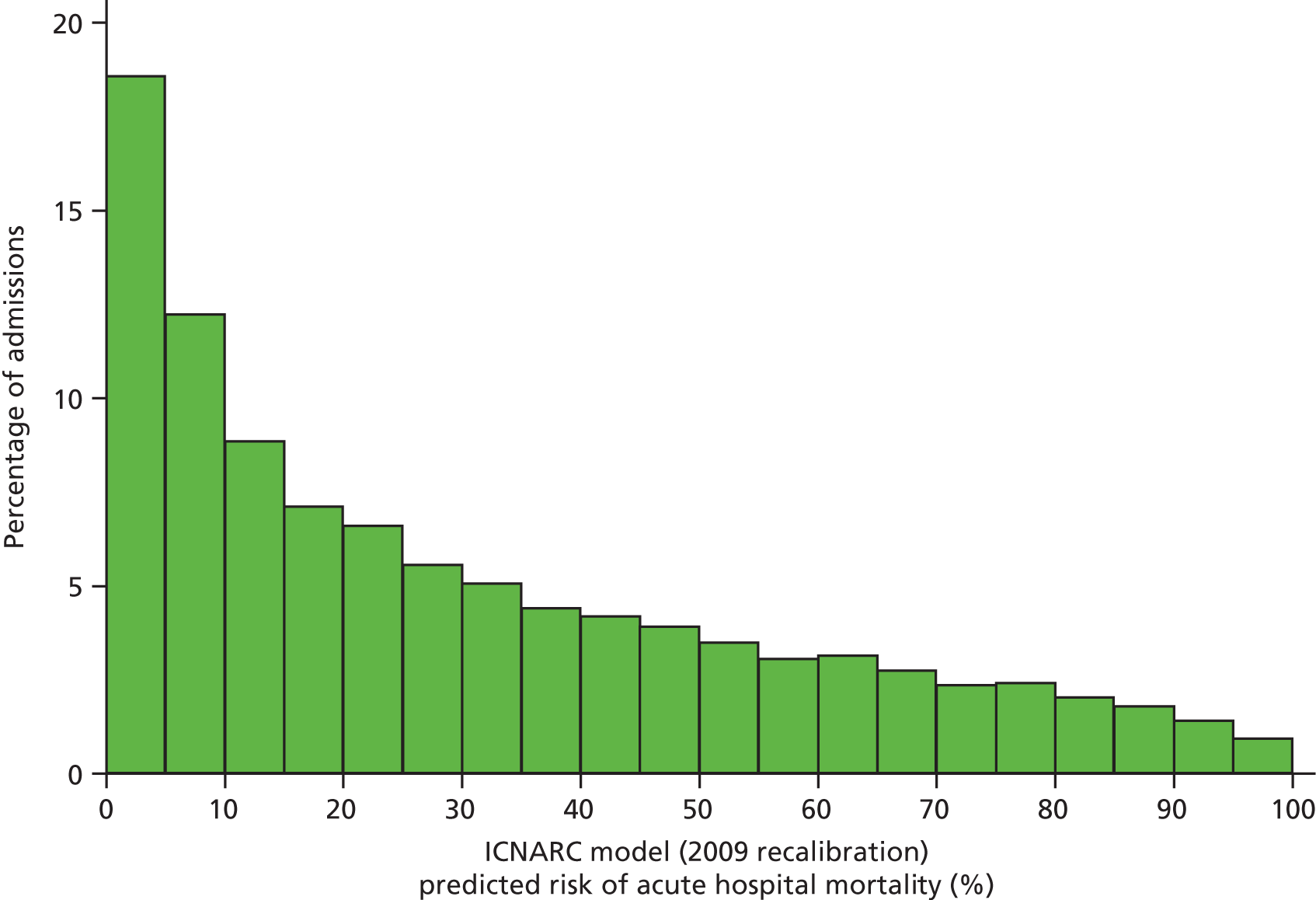
Table 2 summarises the case mix and outcomes for the included admissions, overall and for each year. The mean age of admitted patients was 57 years, 56% were male, and two-thirds of patients were admitted for non-surgical reasons. These characteristics were relatively stable over the 3-year period. The distribution of predicted risk of acute hospital death from the ICNARC model (2009 recalibration) is shown in Figure 1. The mean predicted risk of death (expected acute hospital mortality) was 30.1%, which was very close to the overall observed acute hospital mortality of 29.7%. Compared with the CMP data set used to produce the 2009 recalibration of the ICNARC model, patients admitted to Scottish critical care units were, on average, slightly younger (median 61 vs. 64 years), less likely to be admitted following elective/scheduled surgery (10.5% vs. 23.3%) and had higher acute severity of illness (mean ICNARC Physiology Score 19.6 vs. 18.0).
| Characteristic | SICSAG data | Recalibration data seta | |||
|---|---|---|---|---|---|
| Overall | 2007 | 2008 | 2009 | ||
| Number of admissions | 23,269 | 7396 | 7994 | 7879 | 194,926 |
| Age (years) | |||||
| Mean (SD) | 57.5 (18.0) | 57.6 (18.1) | 57.4 (18.2) | 57.5 (17.8) | 60.1 (18.8) |
| Median (IQR) | 61 (45–72) | 61 (45–72) | 61 (45–72) | 61 (45–71) | 64 (48–75) |
| Sex, n (%) | |||||
| Female | 10,211 (43.9) | 3218 (43.5) | 3543 (44.3) | 3450 (43.8) | 85,619 (43.9) |
| Male | 13,058 (56.1) | 4178 (56.5) | 4451 (55.7) | 4429 (56.2) | 109,307 (56.1) |
| Surgical status, n (%) | |||||
| Elective/scheduled | 2438 (10.5) | 695 (9.4) | 846 (10.6) | 897 (11.4) | 45,397 (23.3) |
| Emergency/urgent | 5196 (22.4) | 1580 (21.4) | 1851 (23.2) | 1765 (22.5) | 36,731 (18.8) |
| Non-surgical | 15,608 (67.2) | 5121 (69.2) | 5296 (66.3) | 5191 (66.1) | 112,794 (57.9) |
| ICNARC Physiology Score | |||||
| Mean (SD) | 19.6 (9.5) | 20.0 (9.5) | 19.4 (9.5) | 19.2 (9.4) | 18.0 (10.0) |
| Median (IQR) | 18 (12–25) | 18 (13–26) | 18 (12–25) | 18 (12–25) | 16 (10–24) |
| ICNARC model (2009 recalibration) predicted risk of acute hospital mortality (%) | |||||
| Mean (SD) | 30.1 (26.3) | 31.2 (26.6) | 29.7 (26.3) | 29.6 (26.0) | 27.4 (26.7) |
| Median (IQR) | 22.3 (7.3–47.9) | 24.0 (7.8–49.6) | 21.8 (7.1–47.0) | 21.4 (7.2–47.3) | 17.0 (5.1–44.3) |
| APACHE II Score | |||||
| Mean (SD) | 19.1 (8.1) | 19.2 (8.0) | 19.1 (8.2) | 18.9 (8.2) | 16.7 (7.4) |
| Median (IQR) | 18 (13–24) | 19 (13–24) | 18 (13–24) | 18 (13–24) | 16 (11–21) |
| APACHE II model predicted risk of acute hospital mortality (%) | |||||
| Mean (SD) | 33.0 (25.3) | 33.3 (25.0) | 32.9 (25.3) | 32.8 (25.5) | 25.2 (21.7) |
| Median (IQR) | 27.4 (11.3–49.7) | 28.5 (12.0–49.7) | 27.0 (11.3–49.7) | 26.6 (10.9–50.1) | 18.5 (8.5–36.4) |
| Acute hospital mortality | |||||
| Deaths (%) | 6907 (29.7) | 2296 (31.0) | 2342 (29.3) | 2269 (28.8) | 53,660 (27.5) |
| 95% CI | 29.1 to 30.3 | 30.0 to 32.1 | 28.3 to 30.3 | 27.8 to 29.8 | 27.3 to 27.7 |
FIGURE 1.
Distribution of predicted risk from the ICNARC risk prediction model (2009 recalibration) for admissions to Scottish critical care units, 2007 to 2009.
Model validation
The measures of model performance of the ICNARC model (2009 recalibration) compared to the APACHE II model are shown in Table 3. The ICNARC model outperformed the APACHE II model on all measures of model performance. The ICNARC model had substantially better discrimination (c-index 0.848 vs. 0.806; p < 0.001; Figure 2) and was also much better calibrated (Figure 3). Cox calibration regression showed an intercept and slope for the ICNARC model very close to the ideal values of 0 and 1, respectively. In contrast, the APACHE II model underpredicted both risk (intercept < 0) and variability (slope < 1). Performance of the ICNARC model remained consistent across the 3 years studied.
| Measures of model performance | Overall | 2007 | 2008 | 2009 |
|---|---|---|---|---|
| ICNARC model | n = 23,269 | n = 7396 | n = 7994 | n = 7879 |
| c-index (95% CI) | 0.848 (0.843 to 0.853) | 0.846 (0.837 to 0.855) | 0.852 (0.843 to 0.861) | 0.845 (0.836 to 0.854) |
| Hosmer–Lemeshow test | ||||
| Chi-squared (p-value) | 18.8 (0.043) | 3.5 (0.97) | 12.7 (0.24) | 10.8 (0.37) |
| Cox calibration regression | ||||
| Intercept (95% CI) | –0.02 (–0.06 to 0.02) | –0.02 (–0.07 to 0.06) | –0.01 (–0.08 to 0.06) | –0.05 (–0.12 to 0.02) |
| Slope (95% CI) | 1.02 (0.99 to 1.05) | 1.02 (0.96 to 1.07) | 1.04 (0.98 to 1.09) | 1.01 (0.96 to 1.06) |
| Chi-squared (p-value) | 5.3 (0.070) | 0.5 (0.78) | 2.9 (0.24) | 3.6 (0.17) |
| Brier score | 0.140 | 0.143 | 0.137 | 0.139 |
| Sum-of-squares R2 | 0.331 | 0.331 | 0.338 | 0.325 |
| Shapiro’s R | 0.652 | 0.646 | 0.656 | 0.653 |
| Entropy-based R2 | 0.296 | 0.295 | 0.303 | 0.290 |
| APACHE II | n = 22,700 | n = 7277 | n = 7992 | n = 7431 |
| c-index (95% CI) | 0.806 (0.800 to 0.812) | 0.793 (0.782 to 0.804) | 0.808 (0.798 to 0.818) | 0.817 (0.807 to 0.827) |
| Hosmer–Lemeshow test | ||||
| Chi-squared (p-value) | 214 (< 0.001) | 44.9 (< 0.001) | 85.1 (< 0.001) | 120 (< 0.001) |
| Cox calibration regression | ||||
| Intercept (95% CI) | –0.26 (–0.30 to –0.23) | –0.18 (–0.24 to –0.12) | –0.27 (–0.33 to –0.21) | –0.34 (–0.40 to –0.28) |
| Slope (95% CI) | 0.91 (0.89 to 0.94) | 0.88 (0.83 to 0.93) | 0.92 (0.87 to 0.97) | 0.95 (0.90 to 1.00) |
| Chi-squared (p-value) | 208 (< 0.001) | 39.2 (< 0.001) | 77.1 (< 0.001) | 117 (< 0.001) |
| Brier score | 0.157 | 0.165 | 0.156 | 0.151 |
| Sum-of-squares R2 | 0.244 | 0.234 | 0.246 | 0.250 |
| Shapiro’s R | 0.621 | 0.608 | 0.623 | 0.631 |
| Entropy-based R2 | 0.214 | 0.200 | 0.217 | 0.224 |
FIGURE 2.
Receiver operating characteristic curves for the ICNARC (2009 recalibration) and the APACHE II risk prediction models among admissions to Scottish critical care units, 2007 to 2009.
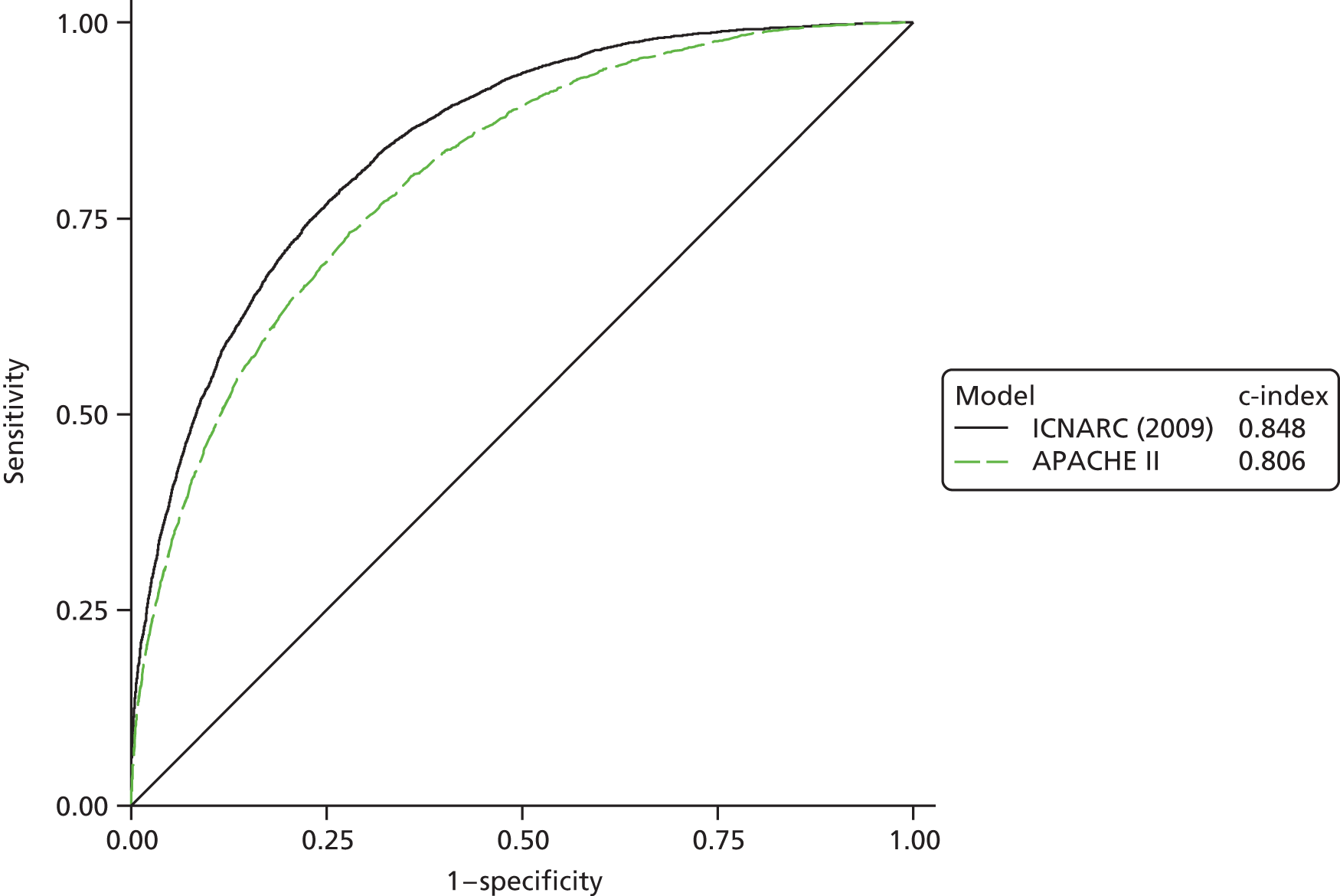
FIGURE 3.
Calibration plots showing observed against expected mortality in 10 equal-sized groups for the ICNARC (2009 recalibration) and APACHE II risk prediction models among admissions to Scottish critical care units, 2007 to 2009.

Simulation of exclusion criteria
In simulations using CMP data to reproduce the potential impact of the exclusion of patients flagged as ‘exclude from severity of illness scoring’, randomly excluding an equivalent proportion of the same types of patients resulted in the following percentage changes in measures of model performance: c-index from −0.3% to +0.02%; Brier score from −0.8% to +3.8%; and ratio of observed to expected deaths from −1.1% to +0.6% (Table 4).
| Simulated exclusions (% excluded at random in 50 repeated simulations) | Performance measure (% change) | ||
|---|---|---|---|
| c-index | Brier score | Observed/expected deaths | |
| Age < 16 years (25) | 0.8640 (–0.015) | 0.1238 (+0.11) | 0.9722 (–0.003) |
| Death within 4 hours (50) | 0.8644 (+0.023) | 0.1227 (–0.76) | 0.9619 (–1.06) |
| Admission for burns (50) | 0.8641 (–0.002) | 0.1237 (+0.009) | 0.9722 (–0.002) |
| Admission for level 2 care (25) | 0.8613 (–0.33) | 0.1283 (+3.75) | 0.9777 (+0.57) |
| All of above | 0.8614 (–0.32) | 0.1275 (+3.09) | 0.9673 (–0.51) |
Discussion
The ICNARC model demonstrated excellent performance when validated in an external sample of data collected from adult, general critical care units in Scotland. The model performance exceeded that of the APACHE II model, being used for benchmarking outcomes in Scotland at the time of this study, on all measures and was consistent over time.
The discrimination of the ICNARC model (c-index 0.848) was slightly lower than that reported previously from the original development and validation samples (0.872 and 0.870, respectively)14 and previous external validation using data from the same source but from different critical care units (0.868). 15 The finding that all measures of model performance were consistent over time was surprising, as previous studies have suggested that, although discrimination of risk prediction models is maintained, calibration deteriorates over time, necessitating regular recalibration of the models. 13,33
The main strength of this study is the large, representative data set. As these data come from a very similar health-care system to the rest of the UK, where the model was developed, but were collected, managed and validated independently, they represent the ideal setting in which to validate the ICNARC model. Independent, external validation of the ICNARC model within the rest of the UK is impossible as the CMP has almost 100% coverage, meaning that there are not sufficient critical care units outside the CMP in which this could be done.
The study does have some limitations; most notable is the number of admissions that it was necessary to exclude. One-fifth of exclusions were of multiple admissions of the same patient, which are essential to exclude as outcomes for these admissions are not independent, and follow-up was excellent, with only 0.6% of admissions excluded because of missing outcomes. However, the largest category of exclusions consists of those flagged as ‘exclude from severity of illness scoring’ (12.1% of all admissions). The main reason for these exclusions seems to have been to reduce the data collection burden for admissions that would not have been included in benchmarking using the APACHE II model and for those patients considered to have a very low risk of death. However, 761 admissions (2.6% of all admissions) were excluded without any clear reason being specified. The excluded admissions did not have sufficient data recorded to be able to reinstate them into the analysis; however, simulating similar exclusions in the CMP data demonstrated that the impact of these exclusions was likely to be small.
It was necessary to apply some assumptions and mapping of data in order to be able to apply the ICNARC model to the SICSAG data set. The simplest approach to assigning weights for lowest SBP and lowest arterial pH would have been to use the most similar available value of these parameters (the SBP associated with the lowest DBP and the pH from the arterial blood gas with the lowest PaO2); however, this would have resulted in measurements that were slightly less extreme than the true values and, therefore, would have potentially underestimated risk of death. Consequently, we used data from the CMP to develop appropriate regression imputation equations. Following a data set revision, explicit recording of sedation during the first 24 hours following admission to the critical care unit was removed from the SICSAG data set. It was therefore necessary to make the assumption that patients with no GCS score recorded were sedated. Using the earlier portion of the data set, where explicit recording of sedation was available, this assumption was demonstrated to be reasonable, with 99% of missing GCS values being due to sedation. Any impact on risk predictions will therefore have been minimal.
It was also necessary to map reasons for admission to critical care, which had been recorded using a different coding system. Although only 70% of the diagnostic categories could be mapped to a specific condition in the ICNARC coding method, the hierarchical nature of the ICNARC coding method enabled most of the remaining diagnostic categories to be mapped to a higher level in the hierarchy; only 4% of diagnostic categories were unable to be mapped, resulting in the exclusion of 1.3% of admissions. It is possible that the slightly less specific diagnostic coding, combined with the need to map these onto a different coding system, may have contributed to the slightly lower discrimination of the ICNARC model than reported from the CMP data.
Chapter 3 Development and validation of a risk prediction model for admissions to cardiothoracic critical care units
Introduction
With the development of advanced circulatory support technologies and strategies, cardiothoracic critical care has developed into its own distinct specialty. In the UK, cardiothoracic critical care units are the principal areas where both complicated surgical and medical cardiac and thoracic admissions are managed.
The traditional risk prediction models used for adult general critical care may not be applicable to cardiothoracic critical care units for the following reasons. First, the majority of admissions to cardiothoracic critical care units are cardiac surgery cases, which were predominantly excluded from earlier versions of commonly used risk prediction models. 34 Although admissions following cardiac surgery were not excluded from the development of the ICNARC model,14 the model was developed using data from adult, general critical care units only and, therefore, any cardiac surgery cases included would probably be atypical. Second, the pathophysiological mechanisms underlying organ failure in the cardiac surgery population are inherently different from those seen in the adult, general critical care population, where admissions are most commonly due to sepsis or respiratory failure. 35 As such, the physiological variables that constitute the risk scores may not be calibrated for a population consisting mainly of cardiac surgery patients.
The majority of critical care units participating in the CMP are adult general units; however, an increasing number of cardiothoracic critical care units are now joining. Although we ultimately aim to produce a single risk prediction model that performs well across all types of critical care units, we believe that a model specifically focused on this unique group of patients would complement this output. This chapter therefore reports on the development and validation of a risk prediction model to predict acute hospital mortality for admissions to cardiothoracic critical care units.
Methods
Inclusion and exclusion criteria
For the development data set, data were extracted from the CMP database for all admissions to cardiothoracic critical care units between 1 January 2010 and 31 December 2012. Patients aged less than 16 years and readmissions to the critical care unit within the same acute hospital stay were excluded.
The validation data set consisted of admissions to cardiothoracic critical care units between 1 January 2013 and 30 June 2014. The same exclusion criteria were applied.
Outcome and candidate predictors
The outcome for the risk prediction model was acute hospital mortality, defined as death before final discharge from acute hospital and including deaths after direct transfer to another acute hospital from the hospital housing the critical care unit.
Candidate predictors were chosen based on expert clinical opinion and availability in the CMP database. The candidate predictors included were as follows: age; sex; severe conditions in the past medical history; dependency prior to admission to acute hospital; CPR within 24 hours prior to admission to the critical care unit; location prior to admission to the critical care unit; highest heart rate; mean arterial pressure (from the blood pressure measurement with the lowest SBP); highest temperature (central measurement or, if none available, non-central + 0.5 °C); ratio of PaO2 to fraction of inspired oxygen (FiO2) (from the arterial blood gas with the lowest PaO2); lowest arterial pH; partial pressure of carbon dioxide in arterial blood (PaCO2) (from the arterial blood gas with the lowest pH); highest blood lactate concentration; highest urea value; highest creatinine value; lowest sodium value; highest potassium value; lowest haemoglobin value; lowest white blood cell (WBC) count; lowest platelet count; lowest total GCS score; and mechanical ventilation status.
Severe conditions in the past medical history were defined according to the APACHE II method9 and categorised as liver disease, renal disease, cardiovascular disease, respiratory disease, metastatic disease, haematological malignancy and immunocompromisation. Conditions must have been evident in the 6 months prior to admission to the critical care unit. Dependency prior to admission to acute hospital was assessed according to the ability to complete activities of daily living, categorised as the ability to live without assistance in daily activities, with some (minor or major) assistance with daily activities or with total assistance with all daily activities. Location prior to admission was categorised as theatre, ward (including intermediate care areas), other critical care unit or emergency department. Admissions from theatre were further categorised as following elective/scheduled or emergency/urgent surgery. Where indicated among candidate predictors as lowest or highest, physiological predictors were the lowest or highest value from the first 24 hours following admission to the critical care unit.
Handling of missing data
Although moderate (from 0.1% to 3.2%), missing data were imputed to address potential bias and loss of precision. Fully conditional specification (FCS)36 was used as the multiple imputation method. All the candidate predictors (with or without missing values)37 and the outcome,38 as well as auxiliary variables related to missingness,39 were entered into the imputation model. When required, simple or zero-skewness log-transformation for non-normality was used. Unless the rate of missing information is unusually high, there tends to be little or no practical benefit to using more than 10 imputations40 and so, in the following analysis, 10 repeat imputations were performed. The examination of the imputed data showed the distribution to be broadly similar to that of the observed data, indicating no obvious problems with the imputation process.
Model development
The distributions of all candidate predictors were explored in patients with and without the primary outcome.
For modelling continuous predictors, different approaches were considered, including fractional polynomials, restricted cubic splines and generalised additive models. The best functional form for each predictor was selected based on fit, plausibility, accuracy and clinical knowledge.
After appropriate functional forms were decided in the univariable setting, a full multivariable model, with all continuous and non-continuous predictors, was fitted to determine the association between the predictors and the outcome. This model was redefined by removing predictors with no significant global effect. To test predictors’ global significance and individual linearity, Wald tests (based on Wald statistics for pooled estimates) were applied. Predictors that were non-significant at a cut-off p-value of 0.1 were discarded. The model was refitted and the remaining predictors were retested. The process continued until all the predictors in the model were significant. Using the resultant model as a starting point, a parsimonious model was developed using a backward elimination strategy. At each step one predictor was dropped from the model while comparing the c-index22 and Brier score. 28 The 10 performance estimates (from the 10 multiply imputed data sets) were averaged and their variances pooled according to Rubin’s rules. 41 The least significant predictor was removed and the process continued until no predictors remained in the model. The final model was chosen to balance parsimony and model performance.
As the majority of patients were admitted to the cardiothoracic critical care unit directly from theatre following cardiac surgery, two expanded models with additional predictors and interactions were tested to improve model performance. The first expanded model included an additional predictor for the pathological or physiological process of the primary reason for admission to the critical care unit (e.g. congenital or acquired deformity, degeneration, dissection or aneurysm, obstruction) from the hierarchical ICNARC coding method among admissions following cardiac surgery. 20 The second expanded model tested interactions between the physiological predictors and cardiac surgery as the primary reason for admission. A nominal p-value of 0.001 was used to retain interaction terms in the model. The enhanced models were tested for improvements in discrimination and calibration.
In order to further evaluate the expanded models, net reclassification improvement (NRI) was determined. Reclassification has been proposed as a measure of utility or improvement in a risk prediction model. 42 The proportions of patients with and without the outcome reclassified into lower- or higher-risk categories are compared. The NRI is defined as the proportion of non-survivors moving to a higher-risk category minus the proportion moving to a lower-risk category plus the proportion of survivors moving to a lower-risk category minus the proportion moving to a higher-risk category.
The final model coefficients were estimated using Rubin’s rules, to give a single estimate and standard error.
Model validation
The risk prediction model was then further validated in the temporally distinct validation data set. The 10 performance estimates of the final model were averaged and their variances pooled according to Rubin’s rules. The predictive performance of the model was estimated by bootstrapping the c-index and Brier score. 43 Calibration was assessed by Cox calibration regression27 and graphically using calibration plots, with 20 equal-sized risk groups. Using Rubin’s rules, 10 linear predictions were calculated and averaged from the new model equation for each admission. The predicted probability of acute hospital mortality was calculated from this pooled result.
Statistical analyses were performed using Stata/SE, version 13.0.
Results
Available data
Between 1 January 2010 and 31 December 2012 there were 17,002 eligible admissions to five cardiothoracic critical care units participating in the CMP, which formed the development data set, and between 1 January 2013 and 30 June 2014 there were a further 10,238 eligible admissions to six cardiothoracic critical care units (one additional unit having joined the CMP), which formed the validation data set (Table 5).
| Characteristic | Development data set (n = 17,002) | Validation data set (n = 10,238) |
|---|---|---|
| Age (years) | ||
| Mean (SD) | 65.1 (14.1) | 65.8 (13.3) |
| Median (IQR) | 68 (58–75) | 68 (59–76) |
| Sex, n (%) | ||
| Female | 5266 (31.0) | 3120 (30.5) |
| Male | 11,736 (69.0) | 7118 (69.5) |
| Severe conditions in past medical history, n (%) | ||
| Any severe condition | 2535 (14.9) | 1015 (9.9) |
| Liver disease | 44 (0.3) | 20 (0.2) |
| Renal failure | 175 (1.0) | 89 (0.9) |
| Cardiovascular disease | 1470 (8.6) | 491 (4.8) |
| Respiratory disease | 517 (3.0) | 218 (2.1) |
| Metastatic disease | 172 (1.0) | 101 (1.0) |
| Haematological malignancy | 95 (0.6) | 58 (0.6) |
| Immunocompromise | 394 (2.3) | 174 (1.7) |
| Dependency, n (%) | ||
| No assistance with daily activities | 13,986 (82.3) | 9022 (88.1) |
| Some assistance with daily activities | 2994 (17.6) | 1198 (11.7) |
| Total assistance with daily activities | 22 (0.1) | 18 (0.2) |
| Location prior to admission, n (%) | ||
| Theatre – elective/scheduled | 11,779 (69.4) | 7138 (69.8) |
| Theatre – emergency/urgent | 1186 (7.0) | 1098 (10.7) |
| Ward or intermediate care area | 2099 (12.4) | 1025 (10.0) |
| High-dependency unit | 1242 (7.3) | 487 (4.8) |
| ED or not in hospital | 677 (4.0) | 481 (4.7) |
| Primary reason for admission, n (%) | ||
| Surgical | 12,970 (76.3) | 8237 (80.5) |
| Cardiac surgery | 11,758 (69.2) | 7651 (74.7) |
| Thoracic surgery | 635 (3.7) | 354 (3.5) |
| Transplant | 178 (1.0) | 108 (1.1) |
| Other | 399 (2.3) | 124 (1.2) |
| Non-surgical | 4032 (23.7) | 2001 (19.5) |
| Cardiovascular | 1995 (11.7) | 1116 (10.9) |
| Respiratory | 1501 (8.8) | 659 (6.4) |
| Other | 536 (3.2) | 226 (2.2) |
| Intervention, n (%) | ||
| Mechanically ventilated during first 24 hours | 13,025 (77.0) | 8513 (83.5) |
| CPR prior to admission, n (%) | 701 (4.1) | 499 (4.9) |
| ICNARC Physiology Score | ||
| Mean (SD) | 15.2 (7.7) | 14.9 (7.4) |
| Median (IQR) | 13 (10–18) | 13 (10–18) |
| Length of stay (days), median (IQR) | ||
| Critical care unit stay | 1.2 (0.9–3.4) | 1.3 (0.9–3.7) |
| Acute hospital stay | 11 (7–21) | 11 (7– 20) |
| Mortality, deaths (%) | ||
| Critical care unit mortality | 1251 (7.4) | 653 (6.4) |
| Acute hospital mortality | 1881 (11.1) | 985 (9.7) |
In the development data set, the majority of admitted patients were male (69%) with a median age of 66 years. Only 14.9% of admitted patients had any previous severe conditions in the past medical history, with the majority of those present being due to severe cardiovascular disease (8.6% of admissions). Most patients were fully functional prior to hospital admission (82.3%) and reported as needing no assistance with their activities of daily living. Over three-quarters of all admissions were surgical, of which 97% followed cardiothoracic surgery. Most surgery was elective or scheduled and most patients were ventilated during the first 24 hours following admission to the unit. The median length of critical care unit stay was 1.2 days, while the median total length of stay in acute hospital was 11 days. Critical care unit mortality was 7.4% and acute hospital mortality was 11.1%.
The validation data set had similar characteristics, although a lower proportion of admissions had one or more severe conditions in the past medical history (9.9%), particularly severe cardiovascular disease (4.8%), and a correspondingly higher proportion were fully functional prior to hospital admission (88.1%). Mortality was also lower, both in the critical care unit (6.4%) and in acute hospital (9.7%).
Model development
The best functional form for the relationship between each of the 15 continuous predictors and the outcome of acute hospital mortality was explored (see Table 6). All 15 predictors showed significant non-linearity (p < 0.001). Restricted cubic splines were chosen for the final modelling as they showed the best combination of flexibility and precision. To avoid overfitting spurious dips and unrealistic features of the curve, four knots were chosen to model the continuous predictors. When functional form was reassessed in the full multivariable model, the evidence for non-linearity in the relationship for blood lactate concentration was weak and so this predictor was finally analysed as linear. The final functional form for each predictor, including the position of the knots for restricted cubic splines, is shown in Table 6.
| Candidate predictor | Functional form | Position of knots |
|---|---|---|
| Age (years) | RCS | 37, 63, 74, 83 |
| Heart rate (beats per minute) | RCS | 75, 90, 100, 132 |
| Mean arterial pressure (mmHg) | RCS | 45, 59, 67, 82 |
| Temperature (°C) | RCS | 36.0, 36.9, 37.5, 38.5 |
| PaO2/FiO2 (mmHg) | RCS | 90, 189, 375, 411 |
| Arterial pH | RCS | 7.16, 7.29, 7.33, 7.41 |
| PaCO2 (mmHg) | RCS | 34, 43, 48, 63 |
| Blood lactate concentration (mmol/l) | Linear | – |
| Urea level (mmol/l) | RCS | 3.6, 5.7, 7.8, 19.2 |
| Creatinine level (µmol/l) | RCS | 51, 80, 106, 247 |
| Sodium level (mmol/l) | RCS | 129, 136, 139, 144 |
| Potassium level (mmol/l) | RCS | 4, 4.6, 4.9, 5.8 |
| Haemoglobin level (g/dl) | RCS | 7.4, 8.9, 10.2, 12.8 |
| WBC count (× 109/l) | RCS | 5.4, 9, 11.9, 19.5 |
| Platelet count (× 109/l) | RCS | 73, 134, 183, 337 |
The full multivariable model, including the 22 predictors, had a c-index and Brier score of 0.902 and 0.0635, respectively (Table 7). Of the initial 22 predictors, 18 were found to be associated with acute hospital mortality on multivariable analysis (p < 0.1): age; one or more severe conditions in the past medical history; dependency; CPR within 24 hours prior to admission; location prior to admission; heart rate; mean arterial pressure; temperature; PaO2/FiO2; arterial pH; PaCO2; blood lactate concentration; urea level; creatinine level; sodium level; WBC count; platelet count; and GCS score. Removal of the non-significant predictors resulted in minimal change to c-index and Brier score (see Table 7).
| Model | Number of predictors in the model | c-indexa | Brier scorea |
|---|---|---|---|
| Full model | 22 | 0.9021 | 0.06354 |
| Removing non-significant predictors | 18 | 0.9018 | 0.06356 |
| Predictors dropped | |||
| CPR | 17 | 0.9014 | 0.06365 |
| Sodium level | 16 | 0.9010 | 0.06376 |
| PaCO2 | 15 | 0.9009 | 0.06385 |
| Temperature | 14 | 0.8998 | 0.06460 |
| Previous medical history | 13 | 0.8998 | 0.06459 |
| Heart rate | 12 | 0.8994 | 0.06467 |
| PaO2/FiO2 | 11 | 0.8983 | 0.06487 |
| Urea level | 10 | 0.8950 | 0.06561 |
| Creatinine level | 9 | 0.8896 | 0.06625 |
| WBC count | 8 | 0.8876 | 0.06671 |
| Mean arterial pressure | 7 | 0.8848 | 0.06759 |
| Dependency | 6 | 0.8807 | 0.06822 |
| Platelet count | 5 | 0.8771 | 0.06915 |
| Arterial pH | 4 | 0.8715 | 0.07083 |
| Age | 3 | 0.8575 | 0.07233 |
| GCS score | 2 | 0.8412 | 0.07512 |
| Blood lactate concentration | 1 | 0.7698 | 0.08485 |
| Location | 0 | 0.5000 | 0.09929 |
| Expanded models | |||
| + reason for admission | 11 | 0.8986 | 0.06525 |
| + interaction terms | 11 | 0.8991 | 0.06491 |
The 18 significant predictors were entered into a stepwise model selection (see Table 7). The model which best balanced parsimony with precision consisted of 10 predictors: age; dependency; location prior to admission; mean arterial pressure; arterial pH; blood lactate concentration; creatinine level; WBC count; platelet count; and GCS score. The c-index and Brier score were 0.895 and 0.0656 respectively.
The first expanded model, incorporating reason for admission, performed moderately better than the baseline parsimonious model, with a c-index of 0.899 and Brier score of 0.0652 (see Table 7). The second expanded model, incorporating interactions between admission following cardiac surgery and blood lactate concentration, creatinine level and platelet count, demonstrated a c-index of 0.899 and Brier score of 0.0649 (see Table 7).
After comparing the reclassification of the two expanded models using risk categories defined by thresholds of 0%, 2%, 5%, 10%, 20% and 50% (Tables 8 and 9), the model with interaction terms was superior (Table 10). With this model, a total of 3677 (23%) admissions were reclassified and 2382 of those (65%) were placed in more appropriate categories. The total NRI for the expanded model with interaction terms was 11.1% (standard error 1.1%; p < 0.0001) compared with 6.5% (1.0%; p < 0.0001) for the expanded model with reasons for admission. The calibration regression for the expanded model with interaction terms demonstrated a slope of 0.98 and an intercept of −0.07, indicating a well-calibrated model. This was therefore taken as the final model. The coefficients for the final model are shown in Table 11.
| Risk category (parsimonious model) | Risk category (expanded model incorporating reason for admission) | |||||
|---|---|---|---|---|---|---|
| 0–1.99% | 2–4.99% | 5–9.99% | 10–19.99% | 20–49.99% | 50–100% | |
| Survivors | ||||||
| 0–1.99% | 5416 | 500 | 18 | |||
| 2–4.99% | 1055 | 2566 | 366 | 37 | ||
| 5–9.99% | 469 | 1023 | 179 | 5 | ||
| 10–19.99% | 178 | 896 | 96 | |||
| 20–49.99% | 100 | 1006 | 27 | |||
| 50–100% | 18 | 286 | ||||
| Non-survivors | ||||||
| 0–1.99% | 26 | 13 | 1 | |||
| 2–4.99% | 14 | 70 | 33 | 6 | ||
| 5–9.99% | 24 | 83 | 31 | 3 | ||
| 10–19.99% | 22 | 185 | 30 | |||
| 20–49.99% | 23 | 458 | 25 | |||
| 50–100% | 19 | 611 | ||||
| Risk category (parsimonious model) | Risk category (expanded model incorporating interaction terms) | |||||
|---|---|---|---|---|---|---|
| 0–1.99% | 2–4.99% | 5–9.99% | 10–19.99% | 20–49.99% | 50–100% | |
| Survivors | ||||||
| 0–1.99% | 5581 | 309 | 44 | |||
| 2–4.99% | 1527 | 2096 | 348 | 53 | ||
| 5–9.99% | 6 | 461 | 931 | 271 | 7 | |
| 10–19.99% | 7 | 122 | 901 | 140 | ||
| 20–49.99% | 1 | 71 | 1046 | 15 | ||
| 50–100% | 25 | 279 | ||||
| Non-survivors | ||||||
| 0–1.99% | 31 | 6 | 3 | |||
| 2–4.99% | 23 | 59 | 34 | 7 | ||
| 5–9.99% | 20 | 85 | 31 | 5 | ||
| 10–19.99% | 15 | 173 | 49 | |||
| 20–49.99% | 14 | 465 | 27 | |||
| 50–100% | 26 | 604 | ||||
| Change in classification | Expanded model incorporating reason for admission | Expanded model incorporating interaction terms | ||
|---|---|---|---|---|
| Survivors | Non-survivors | Survivors | Non-survivors | |
| Down | 1820 (12.8%) | 102 (6.1%) | 2220 (15.6%) | 98 (5.8%) |
| No change | 11,193 (78.6%) | 1433 (85.4%) | 10,834 (76.1%) | 1417 (84.5%) |
| Up | 1228 (8.6%) | 142 (8.5%) | 1187 (8.3%) | 162 (9.7%) |
| Net improvementa (SE) | +4.2% (0.4%) | +2.4% (0.9%) | +7.3% (0.4%) | +3.8% (1.0%) |
| Predictor | Coefficient (SE) | p-value |
|---|---|---|
| Age (years), spline variablesa | < 0.0001 | |
| age1 | 0.0133 (0.00602) | |
| age2 | 0.0180 (0.0114) | |
| age3 | –0.0294 (0.104) | |
| Dependency (vs. none) | < 0.0001 | |
| Some assistance | 0.543 (0.070) | |
| Total assistance | 0.199 (0.598) | |
| Location prior to admission (vs. ED or not in hospital) | < 0.0001 | |
| Theatre – elective/scheduled surgery | –0.867 (0.157) | |
| Theatre – emergency/urgent surgery | –0.438 (0.168) | |
| Ward or intermediate care area | 0.186 (0.119) | |
| High-dependency unit | 0.172 (0.128) | |
| Admission following cardiac surgery | –2.91 (0.880) | 0.001 |
| Mean arterial pressure (mmHg), spline variablesa | < 0.0001 | |
| map1 | –0.0406 (0.00760) | |
| map2 | 0.0174 (0.0259) | |
| map3 | 0.0292 (0.112) | |
| Lowest arterial pH, spline variablesa | < 0.0001 | |
| ph1 | –4.34 (0.703) | |
| ph2 | 0.856 (2.01) | |
| ph3 | 23.0 (19.9) | |
| Highest blood lactate concentration (mmol/l) | 0.0808 (0.0138) | < 0.0001 |
| Interaction between cardiac surgery and blood lactate concentration | 0.0641 (0.0193) | 0.001 |
| Highest creatinine level (µmol/l), spline variablesa | < 0.0001 | |
| creat1 | –0.0185 (0.00432) | |
| creat2 | 0.253 (0.0475) | |
| creat3 | –0.574 (0.106) | |
| Interaction between cardiac surgery and creatinine | 0.0003 | |
| creat1 | 0.0147 (0.0112) | |
| creat2 | –0.0824 (0.111) | |
| creat3 | 0.167 (0.245) | |
| Lowest WBC count (× 109/l), spline variablesa | < 0.0001 | |
| wbc1 | –0.0861 (0.0282) | |
| wbc2 | 0.550 (0.134) | |
| wbc3 | –1.43 (0.351) | |
| Lowest platelet count (× 109/l), spline variablesa | < 0.0001 | |
| plc1 | –0.0130 (0.00217) | |
| plc2 | 0.0612 (0.0125) | |
| plc3 | –0.147 (0.0322) | |
| Interaction between cardiac surgery and platelet count | 0.0003 | |
| plc1 | 0.00352 (0.00346) | |
| plc2 | –0.0488 (0.0218) | |
| plc3 | 0.147 (0.0576) | |
| GCS score (vs. 15) | < 0.0001 | |
| 9–14 | 0.433 (0.113) | |
| 3–8 | 1.83 (0.217) | |
| Sedated | 0.898 (0.0770) |
Model validation
The performance in the validation data set of 10,238 admissions from January 2013 to June 2014 was excellent: a c-index of 0.904 (95% CI 0.893 to 0.915) and Brier score of 0.055. The calibration of the model was satisfactory (Figure 4), with a calibration slope of 0.961 and a calibration intercept of –0.183.
FIGURE 4.
Calibration in the validation data set of the final risk prediction model for admissions to cardiothoracic critical care units.

Discussion
The case mix of admissions to cardiothoracic critical care units is different from that of admissions to adult general critical care units. Specific risk prediction models may aid benchmarking, performance improvement and resource allocation. Using a combination of baseline clinical and physiological predictors, collected in the first 24 hours following admission to a cardiothoracic critical care unit, a parsimonious model with good discrimination was developed and validated. The best-performing model combined age, dependency, prior location and seven physiological predictors, of which three had interactions with cardiothoracic surgery as the primary reason for admission.
There are several strengths to this study. First, this study is one of the few to examine cardiothoracic critical care units rather than isolated cohorts of cardiac or thoracic surgery admissions. Second, cardiothoracic critical care admissions were from five distinct cardiothoracic critical care units and included a large sample of admissions. To our knowledge, this is the largest study in terms of sample size from which a model has been developed. Finally, the data on risk factors are of high fidelity and the CMP database from which the data derive has been previously assessed to be of high quality. 7 The main limitation of the study is the available data. Specifically, risk factor analysis and model development were limited by the data that have already been collected for the CMP.
Previous literature on risk prediction models in the cardiothoracic critical care unit setting is limited. There is a substantial body of literature on risk prediction for patients undergoing cardiac surgery with emphasis on preoperative risk prediction. 44,45 By definition, preoperative risk prediction fails to account for intraoperative events and will therefore not necessarily be adequate for critical care risk prediction. There are also several studies examining postoperative risk factors in cardiac and thoracic surgery admissions, but these are limited in that they are mostly single-centre studies, with risk prediction models that have not been validated in a separate cohort. 46,47 Badreldin et al. evaluated the Sequential Organ Failure Assessment (SOFA) score and Cardiac Surgery Score (CASUS) in a single-centre study and found high c-indices associated with both scores, but greater with CASUS. 46 CASUS is promising in that it consistently demonstrates a high c-index, but has yet to be validated in a large multicentre cohort. Tamayo et al. developed the Post Cardiac Surgery (POCAS) score in a single-centre study which used four postoperative risk factors (mean arterial pressure, bicarbonate level, blood lactate concentration and the international normalised ratio) to model in hospital mortality and which demonstrated a c-index of 0.89. 48 Again, the main limitation of this study is the bias inherent in a single-centre study design.
Several multicentre studies have been conducted in an attempt to predict outcomes using postoperative risk factors. Becker et al. evaluated the APACHE III model in admissions to a critical care unit after coronary artery bypass surgery in a multicentre cohort study. 49 Using a model that included the acute physiology score of the APACHE III model and baseline clinical risk factors, a c-index of 0.85 was demonstrated for acute hospital mortality. Similarly, Simchen et al. 50 tested multiple models, which included pre-, intra- and postoperative risk factors, to predict 30-day mortality in patients with coronary artery bypass surgery admitted to 14 units. The best model that emerged was the one which included postoperative risk factors with a c-index of 0.92. Gomes et al. 51 developed a model in a multicentre cohort, which included PaO2/FiO2, vasopressor and inotrope use, mechanical ventilation and pre- and intraoperative risk factors, to predict acute hospital mortality in cardiac surgery admissions with a c-index of 0.84. Multiple other studies have examined the association between mortality and postoperative risk factors in multicentre cohort studies in both cardiac and thoracic surgery admissions. Significant postoperative risk factors included creatinine level, serum glucose concentration, number of blood transfusions received, low cardiac output, stroke, reoperation, intra-aortic balloon pump use, organ failure, mechanical ventilation time and serum transaminase levels. 52–58 All these studies examined postoperative risk factors in cardiac or thoracic surgery admissions. To our knowledge, this is the first study to examine postoperative risk factors in a cohort of cardiothoracic critical care admissions to multiple cardiothoracic critical care units.
In addition to using postoperative physiological predictors in our model, we attempted to augment its predictive ability by adding interaction terms to it that would account for the unique physiology of the post cardiac surgery patient. The injury in cardiac surgery is usually a result of the cardiopulmonary bypass and, in comparison with patients with sepsis, for example, it is transient and often reversible. To account for these differences we interacted physiological predictors with cardiac surgery as the primary reason for admission to the critical care unit. This expanded model was better able to predict and classify patient outcomes in cardiothoracic critical care units.
Models specifically designed for cardiothoracic critical care units may be warranted given the differences in case mix of cardiothoracic critical care units compared to that of adult, general critical care units. A parsimonious model using a combination of clinical and physiological variables collected in the first 24 hours following admission was shown to have good discrimination and calibration, and will serve as a benchmark for establishing whether or not use of a single risk prediction model across all types of adult critical care units is appropriate in these highly specialised units.
Chapter 4 Development and validation of the new ICNARC model for prediction of acute hospital mortality for admissions to adult critical care units
Introduction
Although the current ICNARC model has been shown to perform well in a head-to-head comparison with other models,14 in more recent validation data from the CMP,15 and now in external validation data from Scottish critical care units (see Chapter 2), there are still a number of areas that we have identified for potential improvements in the model.
The first potential area for improvement is the setting for model development. The current ICNARC model was developed and validated using data from adult, general critical care units. However, increasingly, specialist critical care units and stand-alone high-dependency units are participating in the CMP. The original objectives of this project included development of separate risk prediction models for cardiothoracic critical care units (Chapter 3) and units admitting low-risk patients. However, on the advice of the Expert Advisory Group, we decided to seek, instead, to develop a single risk prediction model that would work well across all types of adult critical care units.
The second potential area for improvement is the introduction of new variables. Blood lactate concentration was introduced into the CMP data set on the basis of emerging evidence that it is a strong predictor of mortality,59,60 and pupil reactivity, a common predictor in risk prediction models for acute traumatic brain injury,61 was introduced on the basis that it may provide an alternative, and more readily available, predictor of neurological status than the GCS score. Additionally, in an attempt to better summarise a patient’s underlying health status prior to the acute episode, a new variable of patient dependency, based on the ability to carry out usual daily activities, was added to the data set. Other existing predictors were further refined, for example by introducing the ability to distinguish in-hospital from community CPR, and collecting additional data on whether the critical care unit admission was planned or unplanned.
The third potential area for improvement is the handling of missing data. In the application of previous risk prediction models for adult critical care, the usual approach to missing physiological predictors has been to assume that they are ‘normal’, falling in the category of the severity score with zero weight. This assumption has been justified on the basis that physiological data are predominantly missing because a test was not requested; it is assumed that the test was not requested because it was expected to be normal. It has also been noted that this approach to handling missing data encourages complete recording, as any missing data are assumed to be in the lowest risk category, which may tend to cause an underestimation of risk. 62 This approach is, however, reliant on the presence of a ‘normal’ category, and may not generalise well to a continuous approach to handling physiological predictors (where one would instead be imputing a single ‘normal’ value). In addition, it is unclear to what extent applying such an approach during model development may bias parameter estimates from the risk prediction model when compared with alternatives, such as complete case analysis (i.e. using only patients with complete data for all predictors when developing the risk prediction model), or more advanced statistical techniques, such as multiple imputation.
The fourth potential area for improvement is the modelling of physiology. Following the original APACHE model,63 most risk prediction models for critical care, including the current ICNARC model, have been based around integer scores that capture physiological derangement through a number of categories for each physiological predictor, with weights assigned to each category. Although this approach has generally worked well, and has the added benefit of providing a measure of acute severity in the form of a severity score, it does have drawbacks. In particular, it has the tendency to define quite wide ‘normal’ ranges for each predictors, within which the risk is assumed not to change at all; once the predictor is sufficiently extreme to be in the highest or lowest risk band, again the risk is assumed to remain constant. These assumptions do not hold in practice. In general, dividing continuous predictors into categories has been shown not to be a good approach to modelling. Straightforward approaches exist to fit flexible, continuous, non-linear models to each predictor, which more closely follow the true underlying relationships between predictor and outcome, and require considerably fewer model parameters than a set of up to eight categories. Furthermore, such models can readily be extended to consider interactions both among physiological predictors and between physiological and non-physiological predictors. The current ICNARC model introduced the concept of interactions between the physiology score and reasons for admission to the critical care unit. In the new model, we take this further by considering interactions at the level of individual physiological predictors, taking into account the evidence that continues to emerge that physiological predictors do not have uniform effects across all subgroups of critically ill patients. 64
The final potential area for improvement is the modelling of the primary reason for admission to the critical care unit. Reasons for admission are recorded in the CMP using the ICNARC coding method, a five-tiered, hierarchical method specifically designed for this purpose. 20 However, in the current ICNARC model, only two of the tiers are used in assigning a weight to the reason for admission: either the specific condition (e.g. bacterial pneumonia) or the body system (e.g. respiratory). We therefore sought to use intermediate information from the hierarchy to enhance the modelling of reason for admission.
This chapter reports on the development and validation of the new ICNARC model for prediction of acute hospital mortality among admissions to adult critical care units, addressing all of the above potential areas for improvement.
Selection of data and candidate predictors
Owing to the high coverage of the CMP, high throughput of patients, high event rate, and previous work demonstrating changing model fit over time,13 while taking account of any seasonal variation,65 model development was based on a single year of data. Model development was done using all available, validated data for patients admitted to an adult critical care unit participating in the CMP between 1 January 2012 and 31 December 2012. There were a total of 155,239 eligible admissions to 232 adult critical care units included in the development data set, of which 121,573 (78.3%) had complete data for all candidate predictors (see Handling of missing physiological data in model development and validation). The characteristics of the participating critical care units are summarised in Table 12 and the included patients are described in Table 13. The model was prospectively validated in 90,017 admissions to 216 critical care units from 1 January 2013 to 30 September 2013 of whom 72,447 (80.5%) had complete data for all predictors.
| Characteristic | Development data set | Validation data set |
|---|---|---|
| Number of critical care units | 232 | 216 |
| Type of unit, n (%) | ||
| Adult, general critical care unit | 195 (84.1) | 183 (84.7) |
| Combined general and neurocritical care unit | 15 (6.5) | 13 (6.0) |
| Specialist neurocritical care unit | 5 (2.2) | 4 (1.8) |
| Specialist cardiothoracic critical care unit | 6 (2.6) | 6 (2.8) |
| Specialist liver critical care unit | 1 (0.4) | 1 (0.5) |
| Stand-alone high-dependency unit | 10 (4.3) | 9 (4.2) |
| Hospital teaching status, n (%) | ||
| University | 71 (30.6) | 65 (30.1) |
| University affiliated | 39 (16.8) | 37 (17.1) |
| Non-university | 122 (52.6) | 114 (52.8) |
| Number of beds in the unit | ||
| Mean (SD) | 11.7 (6.0) | 12.0 (6.7) |
| Median (IQR) | 10 (8–15) | 10 (8–15) |
| Characteristic | Development data set (N = 155,239) | Validation data set (N = 90,017) |
|---|---|---|
| Age (years) | ||
| Mean (SD) | 61.2 (18.0) | 61.6 (17.9) |
| Median (IQR) | 65 (50–75) | 65 (50–75) |
| Sex, n (%) | ||
| Female | 68,131 (43.9) | 39,366 (43.7) |
| Male | 87,108 (56.1) | 50,651 (56.3) |
| Ethnicity, n (%) | ||
| White | 140,075 (90.2) | 81,792 (90.9) |
| Mixed | 828 (0.5) | 464 (0.5) |
| Asian or Asian British | 5268 (3.4) | 2823 (3.1) |
| Black or black British | 3537 (2.3) | 1906 (2.1) |
| Other | 2129 (1.4) | 1302 (1.4) |
| Not stated | 3402 (2.2) | 1730 (1.9) |
| BMI (kg/m2) | ||
| Mean (SD) | 27.0 (7.2) | 27.1 (7.5) |
| Median (IQR) | 25.8 (22.9–29.7) | 25.9 (22.9–29.9) |
| Quintile of deprivation, n (%) | ||
| 1 (least deprived) | 26,168 (17.1) | 15,668 (17.2) |
| 2 | 28,585 (18.7) | 16,441 (18.5) |
| 3 | 30,611 (20.0) | 17,585 (19.8) |
| 4 | 31,934 (20.9) | 18,672 (21.1) |
| 5 (most deprived) | 35,385 (23.2) | 20,711 (23.4) |
| Severe conditions in past medical history, n (%) | ||
| Liver disease | 4156 (2.7) | 2253 (2.5) |
| Renal failure | 2787 (1.8) | 1776 (2.0) |
| Cardiovascular disease | 2643 (1.7) | 1460 (1.6) |
| Respiratory disease | 3760 (2.4) | 2225 (2.5) |
| Metastatic disease | 4950 (3.2) | 2641 (2.9) |
| Haematological malignancy | 2881 (1.9) | 1642 (1.8) |
| Immunocompromise | 10,805 (7.0) | 6044 (6.7) |
| Dependency, n (%) | ||
| No assistance with daily activities | 119,779 (77.2) | 67,668 (75.2) |
| Minor assistance with some daily activities | 27,228 (17.5) | 17,211 (19.1) |
| Major assistance with majority of/all daily activities | 6750 (4.3) | 4279 (4.8) |
| Total assistance with all daily activities | 1485 (1.0) | 859 (1.0) |
| CPR within 24 hours prior to admission, n (%) | ||
| Community CPR | 3714 (2.4) | 2420 (2.7) |
| In-hospital CPR | 4520 (2.9) | 2839 (3.2) |
| No CPR | 147,005 (94.7) | 84,758 (94.2) |
| Location prior to admission, n (%) | ||
| Emergency department or not in hospital | 34,549 (22.3) | 21,101 (23.4) |
| Other hospital (not critical care) | 2100 (1.4) | 1327 (1.5) |
| Other critical care unit | 8460 (5.4) | 4867 (5.4) |
| Theatre – elective/scheduled surgery | 42,346 (27.3) | 22,951 (25.5) |
| Theatre – emergency/urgent surgery | 25,880 (16.7) | 15,398 (17.1) |
| Ward or intermediate care area | 41,904 (27.0) | 24,373 (27.1) |
| Surgical status, n (%) | ||
| Surgical | 68,226 (43.9) | 38,349 (42.6) |
| Non-surgical | 87,013 (56.1) | 51,668 (57.3) |
| Urgency of admission, n (%) | ||
| Planned | 45,926 (29.6) | 25,465 (28.3) |
| Unplanned | 109,313 (70.4) | 64,552 (71.7) |
| ICNARC Physiology Score | ||
| Mean (SD) | 15.2 (8.7) | 16.9 (9.3) |
| Median (IQR) | 13 (9–20) | 15 (10–22) |
| ICNARC model (2013 recalibration) predicted risk of acute hospital mortality (%) | ||
| Mean (SD) | 18.5 (22.7) | 21.3 (24.7) |
| Median (IQR) | 8.1 (2.4–27.0) | 10.0 (2.8–32.5) |
| APACHE II Score | ||
| Mean (SD) | 15.4 (6.9) | 15.7 (6.9) |
| Median (IQR) | 15 (11–19) | 15 (11–20) |
| APACHE II (2013 recalibration) predicted risk of acute hospital mortality (%) | ||
| Mean (SD) | 19.8 (20.9) | 20.7 (21.3) |
| Median (IQR) | 11.7 (4.0–28.8) | 12.6 (4.1–30.8) |
| Critical care unit mortality | ||
| Deaths (%) | 21,254 (13.7) | 12,942 (14.4) |
| 95% CI | 13.5 to 13.9 | 14.1 to 14.6 |
| Acute hospital mortality | ||
| Deaths (%) | 32,064 (20.7) | 19,333 (21.5) |
| 95% CI | 20.5 to 20.9 | 21.2 to 21.7 |
The outcome, as for the previous ICNARC model, was acute hospital mortality, defined as death before ultimate discharge from acute hospital: that is, patients transferred from the hospital housing the critical care unit to another acute hospital were followed up until final discharge from acute hospital.
A set of 20 physiological and 18 non-physiological candidate predictors of acute hospital mortality was specified a priori based on the previous ICNARC model, recent research evidence and clinical input from clinicians on the Expert Advisory Group. A description of the candidate predictors is given in Table 14.
| Candidate predictor | Definition | Categories | Rationale |
|---|---|---|---|
| Physiological | |||
| Highest heart rate | Highest heart rate during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Lowest SBP | Lowest SBP during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Highest temperature | Highest central temperature during the first 24 hours following admission to the critical care unit. (If no central temperatures are recorded, the highest non-central temperature + 0.5 °C is substituted) | Continuous | Included in the current ICNARC model |
| Lowest respiratory rate | Lowest respiratory rate (either ventilated or non-ventilated) during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| PaO2/FiO2 | Ratio of PaO2 to FiO2 from the arterial blood gas with the lowest PaO2 from blood sampled during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Lowest arterial pH | Lowest arterial pH from blood sampled during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| PaCO2 | PaCO2 from the arterial blood gas with the lowest pH | Continuous | Reconsidered because of potential for interaction with pH |
| Highest blood lactate concentration | Highest blood lactate concentration during the first 24 hours following admission to the critical care unit | Continuous | New – added to CMP data set based on evidence as a risk factor59,60 |
| Urine output | Total urine output during the first 24 hours following admission to the critical care unit. (For admissions with a critical care unit length of stay less than 24 hours, the total urine output over the entire stay is recorded and scaled to represent a 24-hour equivalent) | Continuous | Included in the current ICNARC model |
| Highest urea level | Highest serum urea concentration during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Highest creatinine level | Highest serum creatinine concentration during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Highest sodium level | Highest serum sodium concentration during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Highest potassium level | Highest serum potassium concentration during the first 24 hours following admission to the critical care unit | Continuous | Reconsidered because of inclusion in other risk prediction models |
| Lowest glucose level | Lowest blood glucose concentration during the first 24 hours following admission to the critical care unit | Continuous | Reconsidered because of potential impact of glycaemic control |
| Lowest haemoglobin level | Lowest haemoglobin level during the first 24 hours following admission to the critical care unit | Continuous | Reconsidered because of inclusion in other risk prediction models |
| Lowest WBC count | Lowest WBC count during the first 24 hours following admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Neutrophil count | Neutrophil count associated with the lowest WBC count during the first 24 hours following admission to the critical care unit | Continuous | New – added to CMP data set because of potential impact of neutropenic sepsis66 |
| Lowest platelet count | Lowest platelet count during the first 24 hours following admission to the critical care unit | Continuous | Reconsidered because of inclusion in other risk prediction models |
| Sedated/paralysed/GCS score | Lowest total GCS score during the first 24 hours following admission to the critical care unit. The GCS must be assessed when the patient is determined to be free of the effects of sedation. (Separate categories are included for patients who are either sedated or paralysed and sedated for the entirety of the first 24 hours following admission) | 15; 14; 7–13; 6; 5; 4; 3; sedated; paralysed and sedated | Included in the current ICNARC model |
| Pupil reactivity | Recorded as the reactivity (reactive/unreactive/unable to assess) of each pupil and categorised as both reactive, one reactive or neither reactive. (Admissions for whom only one pupil could be assessed were categorised as either ‘both reactive’ or ‘neither reactive’ according to the reactivity of the one pupil that could be assessed) | Both reactive; one reactive; neither reactive | New – added to CMP data set because of potential as an alternative method to assess neurological status, which may be more valid among admissions for whom the GCS cannot be assessed because of sedation |
| Non-physiological | |||
| Age | The age of the patient in whole years at admission to the critical care unit | Continuous | Included in the current ICNARC model |
| Sex | The genotypical sex of the patient | Female; male | Reconsidered because of potential for interaction with physiology, e.g. response to infection67 |
| Ethnicity | Ethnic group, collected using NHS ethnic codes and categorised as white (white-British, white-Irish or white-any other), mixed (mixed-white and black Caribbean, mixed-white and black African, mixed-white and Asian or mixed-any other), Asian or Asian British (Asian or Asian British-Indian, Asian or Asian British-Pakistani, Asian or Asian British-Bangladeshi or Asian or Asian British-any other), black or black British (black or black British-Caribbean, black or black British-African or black or black British-any other), other ethnic group (other ethnic group-Chinese or any other ethnic group) or not stated | White; mixed; Asian or Asian British; black or black British; other ethnic group; not stated | New – added to CMP data set because of potential for interaction with physiology, e.g. renal function68 |
| BMI | Calculated from the weight (either measured or estimated) and height (either measured or estimated) of the patient as weight in kilograms divided by height in metres squared | Continuous | New – added to CMP data set because of research evidence suggesting relationship with mortality69 |
| Residence prior to admission | The patient’s permanent or semi-permanent place of residence prior to admission to acute hospital | Home; nursing home; health-related institution; non-health-related institution; residential place of work or education; hospice or equivalent; no fixed abode or temporary abode | New – added to CMP data set as a potential alternative indicator of dependency prior to the acute episode |
| Deprivation | Quintiles of deprivation, assigned from the patient’s usual residential postcode according to the Index of Multiple Deprivation 2010 for England, Welsh Index of Multiple Deprivation 2008 or Northern Ireland Multiple Deprivation Measure 2010 | Quintile 1 (least deprived); 2; 3; 4; 5 (most deprived) | New – previous research from the CMP indicates association with mortality70 |
| Severe conditions in the past medical history | Defined according to the APACHE II method.9 Must have been evident in the 6 months prior to admission to the critical care unit and documented prior to or on admission to the unit | Seven binary variables (see below) | Reconsidered as rejection may have been owing in part to poor data quality and because of potential for interactions with physiology |
| Liver disease | Biopsy-proven cirrhosis, portal hypertension or hepatic encephalopathy | Yes; no | |
| Respiratory disease | Permanent shortness of breath with light activity because of pulmonary disease or a requirement for home ventilation | Yes; no | |
| Renal disease | Current requirement for chronic renal replacement therapy for irreversible renal disease | Yes; no | |
| Cardiovascular disease | Fatigue, claudication, dyspnoea or angina at rest (New York Heart Association Functional Class IV) | Yes; no | |
| Metastatic disease | Distant metastases documented by surgery, imaging or biopsy | Yes; no | |
| Haematological malignancy | Acute or chronic myelogenous leukaemia, acute or chronic lymphocytic leukaemia, multiple myeloma or lymphoma | Yes; no | |
| Immunocompromise | AIDS (HIV positive and AIDS-defining illness), congenital immunohumoral or cellular immune deficiency state, chemotherapy, radiotherapy or daily high-dose steroid treatment (≥ 0.3 mg/kg prednisolone or equivalent) | Yes; no | |
| Dependency prior to admission | Dependency prior to admission to acute hospital, assessed as the best description for the dependency of the patient in the 2 weeks prior to admission to acute hospital and prior to the onset of the acute illness based on the level of assistance required with daily activities. (Daily activities include bathing, dressing, going to the toilet, moving in/out of bed/chair, continence and eating) | Able to live without assistance in daily activities; minor assistance with some daily activities; major assistance with majority of/all daily activities; total assistance with all daily activities | New – added to CMP data set as a potential alternative indicator of dependency prior to the acute episode |
| CPR prior to admission | CPR (internal or external cardiac massage) received within 24 hours prior to admission to the critical care unit, categorised as either in-hospital CPR (administered by an in-hospital resuscitation team or equivalent) or community CPR (not administered by an in-hospital resuscitation team or equivalent). Where a patient received CPR both in the community and in-hospital, this is recorded as community CPR | In-hospital CPR; community CPR; no CPR | Included in the current ICNARC model – expanded to consider potential different effect for in-hospital and community CPR |
| Source of admission/urgency of surgery/planned admission | The location of the patient immediately prior to admission to the critical care unit, combined with the urgency of surgery (for patients admitted direct from theatre) assigned according to the definitions of the National Confidential Enquiry into Patient Outcome and Death, and whether admission to the critical care unit was planned or unplanned. [For patients whose location immediately prior to admission was a transient location of clinic, imaging department, recovery (used as a temporary critical care area) or specialist treatment area, their last non-transient location is used] |
ED or not in hospital (unplanned admission); ED or not in hospital (planned admission); other acute hospital (not critical care); other critical care unit (repatriation); other critical care unit (planned or unplanned transfer); theatre (planned admission following elective or scheduled surgery); theatre (unplanned admission following elective or scheduled surgery); theatre (admission following emergency or urgent surgery); ward or intermediate care area | Included in the current ICNARC model – expanded to incorporate additional information on planned vs. unplanned admission |
| Primary reason for admission | The primary reason for admission to the critical care unit, coded using the ICNARC coding method20 | Five-tiered, hierarchical code | Included in the current ICNARC model |
| Mechanical ventilation | Mechanical ventilation at any time during the first 24 hours following admission to the critical care unit, identified by recording of a ventilated respiratory rate | Yes; no | Included in the current ICNARC model (interaction with PaO2/FiO2) |
Handling of missing physiological data in model development and validation
The percentage of physiological predictors with missing values in the development data set ranged from 0.6% for highest heart rate to 16.2% for pupil reactivity (Table 15). Because of the high level of missing data for the new field of pupil reactivity, it was decided not to further consider imputation for this predictor. The potential impact of pupil reactivity, therefore, was subsequently assessed in separate models within the subset of patients for which it was recorded. Overall, complete data for all physiological predictors, excluding pupil reactivity, were available for 77.9% (121,603) of admissions (Table 16). In the case of laboratory measurements, an available option was to record the last measured value up to 4 hours prior to admission to the critical care unit if no values were available from the first 24 hours following admission. After reviewing the available data in the pre-admission fields, it was decided that it was not appropriate to use these as a direct substitute for first-24-hour values as their use made minimal impact on the number of missing values and different relationships were found between physiology and outcome for the pre-admission and first-24-hour values. Although the proportion of admissions with missing data was moderate (< 25%), we explored whether it was better to impute or to use only the observed values in the development of the new ICNARC model. The multiple imputation method was chosen to address the potential bias and loss of precision of a complete case analysis.
| Predictora | Number of missing values | Percentage missing |
|---|---|---|
| Highest heart rate | 993 | 0.6 |
| Lowest SBP | 1019 | 0.7 |
| Highest temperature | 1388 | 0.9 |
| Lowest respiratory rate | 1111 | 0.7 |
| Mechanical ventilationa | 1106 | 0.7 |
| PaO2/FiO2b | 21,662 | 13.9 |
| Lowest pHb | 21,662 | 13.9 |
| PaCO2b | 21,665 | 13.9 |
| Highest blood lactate concentrationb | 21,727 | 13.9 |
| Urine output | 4786 | 3.1 |
| Highest urea level | 8397 | 5.4 |
| Highest creatinine level | 7768 | 5.0 |
| Highest sodium level | 6311 | 4.0 |
| Highest potassium level | 6546 | 4.2 |
| Lowest glucose level | 16,526 | 10.6 |
| Lowest haemoglobin level | 6736 | 4.3 |
| Lowest WBC count | 7722 | 4.9 |
| Neutrophil count | 8966 | 5.7 |
| Lowest platelet count | 7738 | 5.0 |
| Sedated/paralysed/GCS score | 5515 | 3.5 |
| Pupil reactivity | 25,287 | 16.2 |
| Missing predictors | Number with pattern | Percentage with patterna |
|---|---|---|
| All physiology | 606 | 0.39 |
| ABG + blood lactate concentration + laboratoryb + urine output | 786 | 0.50 |
| ABG + blood lactate concentration + laboratoryb | 2550 | 1.63 |
| ABG + blood lactate concentration + urine output | 693 | 0.44 |
| ABG + blood lactate concentration | 11,579 | 7.41 |
| ABG | 3154 | 2.02 |
| Blood lactate concentration only | 2975 | 1.90 |
| Laboratoryb + urine output | 789 | 0.51 |
| Laboratoryb | 775 | 0.50 |
| Urine output only | 1376 | 0.88 |
| Sedated/paralysed/GCS score only | 3772 | 2.42 |
| None | 121,603 | 77.86 |
Missing data mechanism
Before missing values were imputed, we studied the missing data mechanism40 by creating indicator variables for missing values for each predictor and fitting logistic regression models with the indicator variable as the outcome and the other predictors as covariates.
Findings suggested that it was not plausible to assume that data were missing completely at random (MCAR) so it was assumed that data were missing at random (MAR), conditional on observed data; the plausibility of the MAR assumption holding was improved by conditioning on auxiliary variables that were found to be predictive of missingness in the imputation model. Furthermore, some methodologists have argued that routine departures from MAR may not be large enough to cause serious bias in the resulting estimates. 71
Imputation of missing data
We imputed missing data using FCS. 36 This method provides a practical and flexible approach to generating imputations based on a set of imputation models, one for each variable with missing values, allowing one to specify the regression equation for the imputation; this is usually linear regression for continuous variables and logistic regression (binary, ordinal, or unordered multinomial) for categorical variables. In addition, under logistic imputation, imputed values for categorical variables will also be categorical, so rounding to plausible values is not necessary. In large data sets (such as the CMP database), it is common for missing values to occur in several variables, both continuous and categorical, so this approach was chosen because of its ability to impute both continuous and categorical variables appropriately, permitting a great deal of flexibility.
The imputation model and analysis model should be compatible; that is, any relationship in the analysis model should also be part of the imputation model. All the potential predictors that will be considered in the analysis, with or without missing values, should therefore be included in the imputation model. 37 The response variable38 and auxiliary variables related to missingness39 were entered into the imputation model as well.
When required, transforming for non-normality gave better imputed values,72 so logarithmic transformation was used. Urine output had a particularly unusual distribution, with a proportion of values equal to zero and a continuous, but heavily skewed, distribution among the remaining values. A semi-continuous approach to imputation is recommended for this situation. 73 This involves separately imputing a binary variable that indicates whether a value is zero or positive, and then a continuous variable for the value if positive. However, this approach did not work well in the case of urine output, as it overestimated the proportion of zero values; finally, the shifted log-transformation f(z) = ln(± z − a) was chosen for this predictor. Different approaches were considered for imputing sedated/paralysed/GCS score (ordinal, multinomial or predictive mean matching). All produced similar results, so finally the ordinal approach based on logistic regression was used.
As well as including all variables planned to be included in the analysis model, the imputation model must also include them in an appropriate way, that is, in the correct functional form and with any interactions that are required. However, when imputing data, one does not necessarily know what terms will be required in a sequence of analyses, and allowing for all possible terms might make the imputation model impractically large. On the other hand, the simplest approach of passive imputation (i.e. using simple linear and logistic regression models and ignoring interactions and non-linearity that are in the analysis model) could result in biased terms in the analysis model. 74 To assess the impact of omitting interactions, we produced a provisional and relatively simple imputation model, including non-linear terms and any interactions of key scientific/clinical interest. The imputed data were then used to build and check an analysis model, investigating the need for non-linear terms in the imputation model as well as the best way to impute them. The following approaches for imputing non-linear terms were explored: the traditional, passive (‘impute then transform’) method;75 ‘just another variable’ (JAV; also termed ‘transform then impute’);75,76 and substantive model compatible FCS (SMC-FCS). 77 SMC-FCS is a modification of the FCS approach to multiple imputation which ensures that each of the imputation models is compatible with the assumed substantive model. 77
In our imputation process, most of the relationships of the physiology variables followed the same pattern, so a more general model was specified for the candidate predictors with missing data.
Simulation studies have shown that the required number of repeated imputations (m) can be as low as 3 for data with 20% of entries missing. 41 We used a more conservative choice of m = 5.
Validation of imputed data
Graphical assessment and differences in means and proportions were used to compare the distributions of the imputed and observed data. Examination of the imputed data showed that the distribution was broadly similar to that for the observed data, indicating no obvious problems with the imputation process. A few imputed values were placed outside of the distribution of observed data; however, these were too few to be considered important, and some differences are to be expected if the data are not MCAR.
Simulation study
Imputing missing data, especially multiple imputation, is becoming standard in risk prediction modelling. 78 However, it is often implemented without adequate consideration of whether or not it offers any advantage over complete case analysis for the research question of interest. Multiple imputation is not always better than complete case analysis for missing covariate problems. 79 Recovering information in estimating the coefficient could be a potential gain, but previous studies have demonstrated that, although it may be important to use multiple imputation to recover information when there are missing data in covariates required for adjustment, multiple imputation has substantially less value when there are missing data (even when MAR) in the exposure of interest. 80
We explored the impact of missing data in the planned analysis using a simulation study under two different scenarios by creating data sets with MCAR and MAR missing values from 300,000 complete data values (a random sample drawn from the original complete case data: see Appendix 1). To test the consistency of the finding in these scenarios, logistic regression models were estimated on the original data set with no missing values (used as a reference) and the complete case data set after creation of missing values, as well as on multiply imputed data sets using FCS. Results were compared in terms of coefficients, standard errors and p-values.
If we impute from a model that does not allow for a potential non-linear association with outcome, we would expect to obtain inconsistent parameter estimates;74 therefore, in a secondary analysis we also investigated, under our these two scenarios of MCAR and MAR, the non-linearity effect on the risk prediction model estimation and the reliability of the prediction using the different approaches as mentioned above.
Results and conclusions
It was expected that multiple imputation would raise the risk estimates in comparison with the complete case analysis, but only slight differences in estimates were found, even among non-response mechanisms (Table 17). The increase in precision of risk estimates under MAR is therefore minimal at best, and the risk estimates hardly change.
| Predictor | Reference (n = 300,000) | MCAR | MAR | ||
|---|---|---|---|---|---|
| Complete case (n = 235,572) | MI (n = 300,000) | Complete case (n = 238,013) | MI (n = 300,000) | ||
| Coefficients | |||||
| Highest heart rate | 0.01084 | 0.01073 | 0.01082 | 0.01032 | 0.01084 |
| Lowest SBP | –0.01220 | –0.01213 | –0.01224 | –0.009965 | –0.01089 |
| Highest temperature | –0.2191 | –0.2193 | –0.2193 | –0.2112 | –0.2222 |
| Lowest respiratory ratea | 0.06052 | 0.06110 | 0.06079 | 0.05239 | 0.06022 |
| PaO2/FiO2a | –0.003147 | –0.003212 | –0.003144 | –0.002728 | –0.003153 |
| Lowest pH | –1.703 | –1.749 | –1.739 | –1.585 | –1.678 |
| Highest ureaa | 0.04444 | 0.04410 | 0.04434 | 0.04078 | 0.04560 |
| Highest creatininea | –0.0009818 | –0.0009792 | –0.0009940 | –0.001091 | –0.001128 |
| Highest sodium | –0.006443 | –0.007170 | –0.006432 | –0.004121 | –0.004722 |
| Lowest WBC counta | 0.01094 | 0.01086 | 0.01080 | 0.009977 | 0.009837 |
| Urine outputa | –0.0001942 | –0.0001846 | –0.0001960 | –0.0002042 | –0.0002270 |
| S/P/GCS | –0.08710 | –0.08689 | –0.08676 | –0.08389 | –0.08718 |
| Constant | 21.01 | 21.44 | 21.28 | 19.48 | 20.64 |
| Standard errors | |||||
| Highest heart rate | 0.0002193 | 0.0002478 | 0.0002220 | 0.0002320 | 0.0002190 |
| Lowest SBP | 0.0002826 | 0.0003195 | 0.0002880 | 0.0003035 | 0.0002840 |
| Highest temperature | 0.004766 | 0.005391 | 0.004820 | 0.004982 | 0.004825 |
| Lowest resp ratea | 0.001186 | 0.001340 | 0.001217 | 0.001301 | 0.001257 |
| PaO2/FiO2a | 0.0000477 | 0.0000540 | 0.0000500 | 0.0000518 | 0.0000510 |
| Lowest pH | 0.04610 | 0.05206 | 0.04775 | 0.04808 | 0.04633 |
| Highest ureaa | 0.0006850 | 0.0007729 | 0.0006880 | 0.0007339 | 0.0007220 |
| Highest creatininea | 0.0000451 | 0.0000508 | 0.0000460 | 0.0000481 | 0.0000470 |
| Highest sodium | 0.0008847 | 0.0009989 | 0.0008930 | 0.0009210 | 0.0008890 |
| Lowest WBC counta | 0.0005765 | 0.0006512 | 0.0005780 | 0.0005965 | 0.0005720 |
| Urine outputa | 0.0000042 | 0.0000048 | 0.0000043 | 0.0000046 | 0.0000049 |
| S/P/GCS | 0.0008381 | 0.0009471 | 0.0008610 | 0.0008665 | 0.0008390 |
| Constant | 0.3829 | 0.4325 | 0.3951 | 0.3982 | 0.3861 |
Under our scenarios of missing data that with either MCAR or MAR, both complete case analysis and multiple imputation had negligible bias compared to the reference results based on the data set prior to the creation of missing values. The results indicated that a multiple imputation-based method (FCS) produced similar estimates to the complete case analysis; therefore, little information was gained regarding the coefficients for the predictors with missing values when we imputed those missing values, regardless of the number of missing data (at the levels observed within our data sets). Similar findings of inconsistent benefits of multiple imputation were observed in the coefficients for the predictors with no missing values. No differences in the inference were found. The different approaches to imputation of non-linear terms gave similar results (Table 18), including the passive (‘impute then transform’) approach, JAV (‘transform then impute’) and SMC-FCS, although SMC-FCS gave slightly smaller standard errors. These findings could indicate that, in our scenarios, including non-linear terms into the imputation model is not necessary.
| Predictor | Reference | Complete case | Multiple imputation | ||
|---|---|---|---|---|---|
| Passive | JAV | SMC-FCS | |||
| Coefficients | |||||
| Highest heart rate | 2.060 | 2.102 | 2.101 | 2.183 | 2.119 |
| Highest heart rate squared | –5.671 | –5.832 | –5.830 | –6.002 | –5.929 |
| Lowest Hb | –0.3377 | –0.3075 | –0.3077 | –0.3086 | –0.3119 |
| Lowest Hb squared | 0.000834 | 0.000755 | 0.000756 | 0.000752 | 0.000735 |
| Urine output | –0.7693 | –0.8142 | –0.8149 | –0.8291 | –0.8059 |
| Neutrophil count | 0.09299 | 0.08998 | 0.09015 | 0.09298 | 0.09944 |
| PaO2/FiO2 | –0.00380 | –0.00398 | –0.00398 | –0.00395 | –0.00395 |
| Lowest SBP | –0.00698 | –0.00694 | –0.00696 | –0.00708 | –0.00745 |
| Highest blood lactate | 0.1343 | 0.1391 | 0.1391 | 0.1446 | 0.1355 |
| Age | 0.03203 | 0.03283 | 0.03284 | 0.03251 | 0.03411 |
| CPR | 1.065 | 1.139 | 1.139 | 1.160 | 1.158 |
| Constant | 4.179 | 4.061 | 4.063 | 4.208 | 4.077 |
| Standard errors | |||||
| Highest heart rate | 0.089819 | 0.1082 | 0.1082 | 0.1023 | 0.1011 |
| Highest heart rate squared | 0.1917 | 0.2313 | 0.2313 | 0.2196 | 0.2171 |
| Lowest Hb | 0.01274 | 0.01570 | 0.01570 | 0.01523 | 0.01504 |
| Lowest Hb squared | 0.000036 | 0.000044 | 0.000045 | 0.000044 | 0.000042 |
| Urine output | 0.01496 | 0.01828 | 0.01828 | 0.01762 | 0.01750 |
| Neutrophil count | 0.004160 | 0.005063 | 0.005061 | 0.004973 | 0.004876 |
| PaO2/FiO2 | 0.000064 | 0.000079 | 0.000079 | 0.000077 | 0.000078 |
| Lowest SBP | 0.000381 | 0.000468 | 0.000468 | 0.000451 | 0.000447 |
| Highest blood lactate | 0.002541 | 0.003066 | 0.003066 | 0.002973 | 0.003072 |
| Age | 0.000452 | 0.000560 | 0.000560 | 0.000537 | 0.000532 |
| CPR | 0.02510 | 0.03025 | 0.03025 | 0.02968 | 0.02988 |
| Constant | 0.1379 | 0.1693 | 0.1693 | 0.1625 | 0.1612 |
In conclusion, coefficient estimates appear to be insensitive to the missing data and the various models used to deal with them. The benefits of using multiple imputation in developing our risk prediction model are likely to be minimal.
However, there are some factors contributing to the apparent stability of the estimates, such as the moderate number of missing data, the large sample size and the fact that the differences in mortality between complete and incomplete are too small to exert a serious impact on the estimates. Another factor might be that imputations do not contain important information or that the covariates are missing not at random; in this circumstance multiple imputation may be biased while complete case analysis may not be.
Finally, we decided that the model building and analysis process would be done with non-imputed (complete case) data and that a parallel analysis would be done at the same time on the multiply imputed data set in order to test the consistency of the results.
Development of the new Intensive Care National Audit & Research Centre model
Functional form
Linearity of the association between continuous predictors and the outcome should not automatically be assumed because this could lead to incorrect interpretation of the effect and inaccurate predictions when the model is applied to new individuals. 81 In addition, the use of the appropriate functional form for a continuous variable is crucial for valid predictions because the expected value of the outcome can be different for the same value of a continuous variable with different functional form. As many of the physiological predictors are known to have non-linear (often U-shaped) relationships with outcome, they have typically previously been modelled using categorical approaches and combined into a severity score. 9–11,14,82 One aim of the current project was to model the physiological predictors separately as continuous variables, so how to deal with non-linearity was carefully considered.
The predictor–outcome relationship was explored by expanding the variable into multiple terms and testing pooled and individual non-linearity. The shape of the relationship of continuous predictors with the outcome was also studied, by plotting with a smoothed curve (running line smoother) as a reference. The traditional use of a categorical approach failed to detect the continued increase or decrease in risk for subjects at higher/lower levels of risk, making the implausible assumption that the risk does not vary at the extremes. Moreover, ignoring intracategory variation means throwing away information, tends to reduce a study’s power to detect an association and may lead to inaccurate estimates. 83,84 After the hypothesis of linearity was rejected, two different approaches for modelling continuous predictors were considered: non-linear functions such as second-order fractional polynomials85 and restricted cubic splines. 84
Spline fits could be sensitive to the number of knots so, to avoid overfitting, spurious dips and inflection points, as well as unrealistic features of the curve, three, four or five knots were considered. With large numbers of observations, three or four knots may work better, and more than five knots are usually not necessary unless the response to the predictor is extremely complicated. Knot positions were selected according to the recommendations of Harrell. 84 Right-restricted cubic splines (i.e. with the linearity restriction applied only at the right-hand end of the curve) were used when appropriate to allow more flexibility.
For optimal power fractional polynomials, we selected the family of second order because this offers considerable flexibility and a very rich set of possible functions, including U- and J-shaped relationships (an order higher than 2 is rarely required in practice86).
In order to judge the plausibility and accuracy of the fitted curves, we plotted observed log-odds against the alternative modelling approaches and used a running line smoother as a reference. The Akaike information criterion (AIC) and Bayesian information criterion (BIC) were calculated to compare the fit of the strategies for modelling continuous variables, taking three-knot-restricted cubic splines as a reference point, to assess whether or not the increased complexity of the model that resulted from including more knots was worthwhile.
The best functional form for each predictor was selected based on fitting, plausibility, accuracy and prior knowledge about the predictor.
Finally, we explored collapsing extreme points to determine whether or not the shape of the curves could be affected by outlying values. Additional analysis using imputed data was done in parallel to provide reassurance about the results.
Modelling of interactions
Improved modelling of interactions between physiological predictors was one of the main project objectives. The assumption that all predictors act independently on outcome is physiologically untrue and, although most of the significant past medical history–physiology, intervention–physiology and physiology–physiology interactions were not expected to make an important contribution to the model, these interactions could reflect important dependencies as well as intrinsic prognostic features of the data. Clinical members of the Expert Advisory Group, together with additional clinicians with relevant experience of risk prediction models in clinical epidemiology, identified and prioritised key, potential interactions between predictors. These pre-defined past medical history–physiology, intervention–physiology and physiology–physiology interactions were tested and checked graphically for any spurious interactions as a result of mis-modelling the main terms in the model. We tested each interaction’s importance in predicting the outcome using the BIC in order to reduce the chance of overfitting. Only significant interactions were considered in the model-building process.
In addition, the relationship between physiology and outcome may depend on primary reason for admission to the critical care unit, and a model incorporating interactions could take into account these differences. In the current ICNARC model, patients have a different coefficient for their ICNARC Physiology Score depending on primary reason for admission but, in the new model, these interactions were addressed for each individual physiological predictor.
Reason for admission
Reasons for admission to critical care are recorded in the CMP using the ICNARC coding method: a five-tiered (type – surgical or non-surgical/body system/anatomical site/physiological or pathological process/condition) coding system specifically developed for this purpose. 20 Currently, coefficients for the ICNARC model are applied at only two levels of the hierarchical code (either at tier 5, the individual condition, or at tier 2, the body system), but we aimed to improve the overall performance by incorporating intermediate levels of information and, in that way, to allow for variation in the effect on mortality between different physiological or pathological processes (e.g. infection or trauma).
The following steps were taken in modelling primary reason for admission:
-
If a process did not have the required sample size (number of events < 20):
-
it was added to a related process or
-
it was combined with other similar processes to create a new group.
-
-
Indicators were created for each combination of process and system.
-
If a process/system combination did not have the required sample size (number of events < 20):
-
it was added to a related process/system combination or
-
it was combined with other similar process/system combinations to create a new group or
-
it was combined with the same process across all systems as a single process category.
-
-
When a process/system combination either was non-significant after adjusting for process or did not make an important contribution to the model:
-
it was added to the process category.
-
-
The resulting set of categories was redefined to make a grouping with clinical sense.
-
Finally, the set of categories was refined by adding specific conditions:
-
Process/system categories were split into individual conditions which had sufficient sample size (number of events ≥ 20).
-
Each individual condition was retained as a new category if it was significant after adjusting for process/system and made an important contribution to the model.
-
Individual conditions were combined with other individual conditions within each process/system category if the difference in risk was not significant.
-
Model building process
The model building process consisted of a number of stages (Figure 5).
FIGURE 5.
Stages in the model building process for the risk prediction model for adult critical care units.

Development of a parsimonious physiology model
After appropriate functional forms were selected in the univariable setting, a multivariable full physiology model was fitted. Wald tests were applied to test the global significance of the predictors and their linearity. The linearity Wald test is of special interest here because it tests whether or not the restricted cubic spline model can be reduced to a model in which the predicted log-odds are linear in the predictor. A low p-value means we should reject the hypothesis of linearity. The full physiology model was refined by removing any predictors with a non-significant global effect and the expanded (cubic spline) terms for any predictors with a non-significant linearity test. The model was refitted and the functional form was tested. The process continued until all the factors in the model were significant.
One caveat in model building is that new candidate predictors selected solely on consideration of small p-values can be misleading. 78,84 An often disappointing result of multivariable risk prediction models combining new physiological predictors with established ones is that the proposed new predictors may seem statistically significant (i.e. have small p-values) in the adjusted model, but then may not increase the prognostic ability of the model overall. 78,87–89 Following the previous physiology model, a parsimonious model was developed using a backward elimination strategy that considered the influence of the individual predictors and their contribution to the model performance. At each step, one predictor was dropped and the c-index and Brier score of the model without that predictor were compared. The least significant predictor was removed and the process continued until no predictors remained in the model. To correct for potential overfitting, a bootstrap analysis was performed. 43,81,84 At each step, the estimates of c-index and Brier score were adjusted for overfitting based on 500 bootstrap samples.
Development of a parsimonious main-terms model
Starting from this simplified physiology model, a full multivariable model adding the rest of the current predictors, as well as all potential new predictors, was fitted. From this preliminary main-terms model, the variable selection was done in a two-step process:
Step 1. Deleting, refitting and verifying process. To test the global significance of the predictors and linearity of continuous predictors, Wald and likelihood ratio tests were applied to each predictor in the model. The model was redefined by dropping predictors with non-significant global effects and/or data reduction (e.g. dropping non-linear terms, combining categories) where appropriate. After refitting, the remaining predictors were tested. The process continued until all the predictors in the model were significant.
Step 2. Model simplification. When a large sample size is used in model building, significance tests are usually less relevant than summary measures of predictive power because p-values go quickly to zero, so small effects can become strongly statistically significant but with a weak contribution to model fit. 90 Therefore, to get a more parsimonious model, only the predictors that made an important contribution were retained in the model, using BIC and coefficients close to one on the odds ratio scale as criteria. This process was repeated until all predictors included in the model were making an important contribution.
Selection of interactions
The selection of interaction terms was carried out in a three-step process:
Step 1. Interaction terms between primary reason for admission and physiological predictors were added one at a time into the model containing all the main effects and significance was assessed using the likelihood ratio test. A p-value of < 0.05 was used as the selection criterion.
Step 2. All the interaction terms found to be significant in step 1 were added, simultaneously, to the main effects model and evaluated, adjusting for the other interaction terms. An interaction was retained if it had a nominal p-value of < 0.001. This lower level was used to control for overfitting, complexity and incremental predictive accuracy.
Step 3. Pre-defined interactions between past medical history and physiology, between interventions and physiology and between physiological predictors were added one by one to the previous model and retained if they had a nominal p-value of < 0.001.
A final process of deleting, refitting and verifying was performed to ensure that all included predictors were significant and were making an important contribution to the model.
Results
The predicted risk from continuous approaches to modelling physiology was a much better approximation of the true risk function than the previous categorical approach (Figure 6), especially if the factor distribution was skewed and, in particular, for relationships with a single turning point, such as for SBP, heart rate, arterial pH, WBC count, potassium level and haemoglobin level.
FIGURE 6.
Alternative approaches to modelling continuous physiological predictors. FP, fractional polynomial; RCS, restricted cubic spline; RRCS, right-restricted cubic spline.
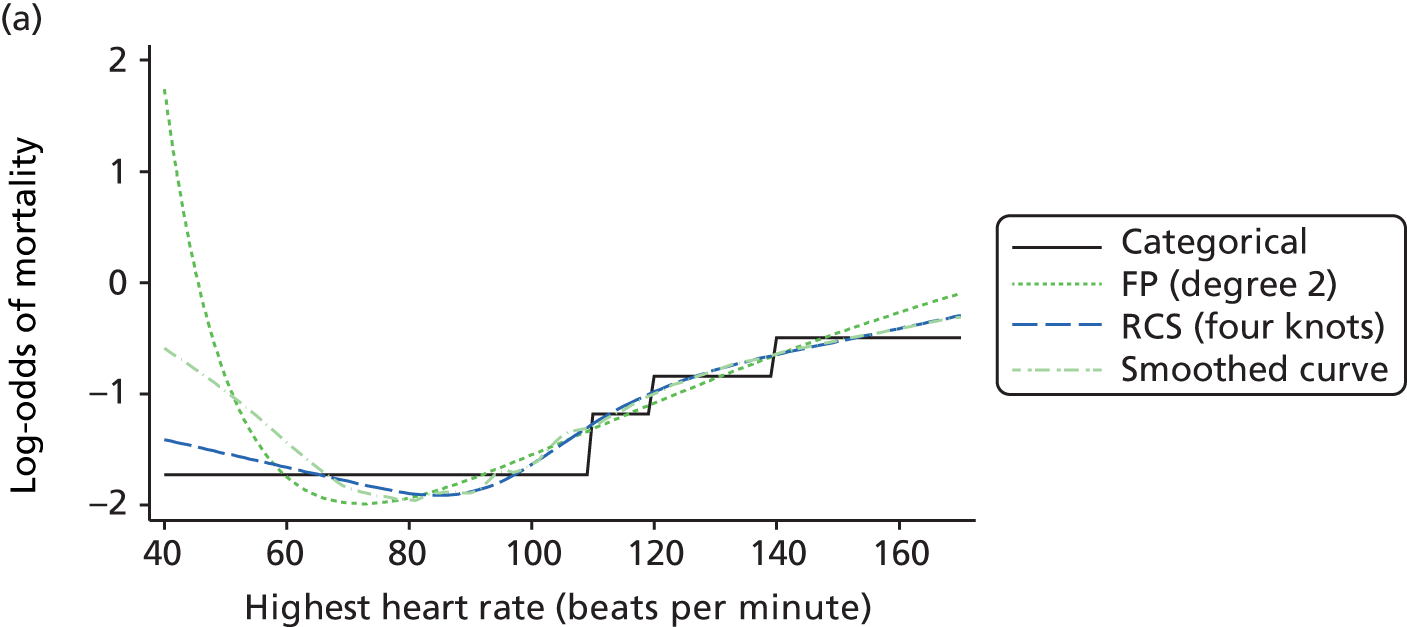
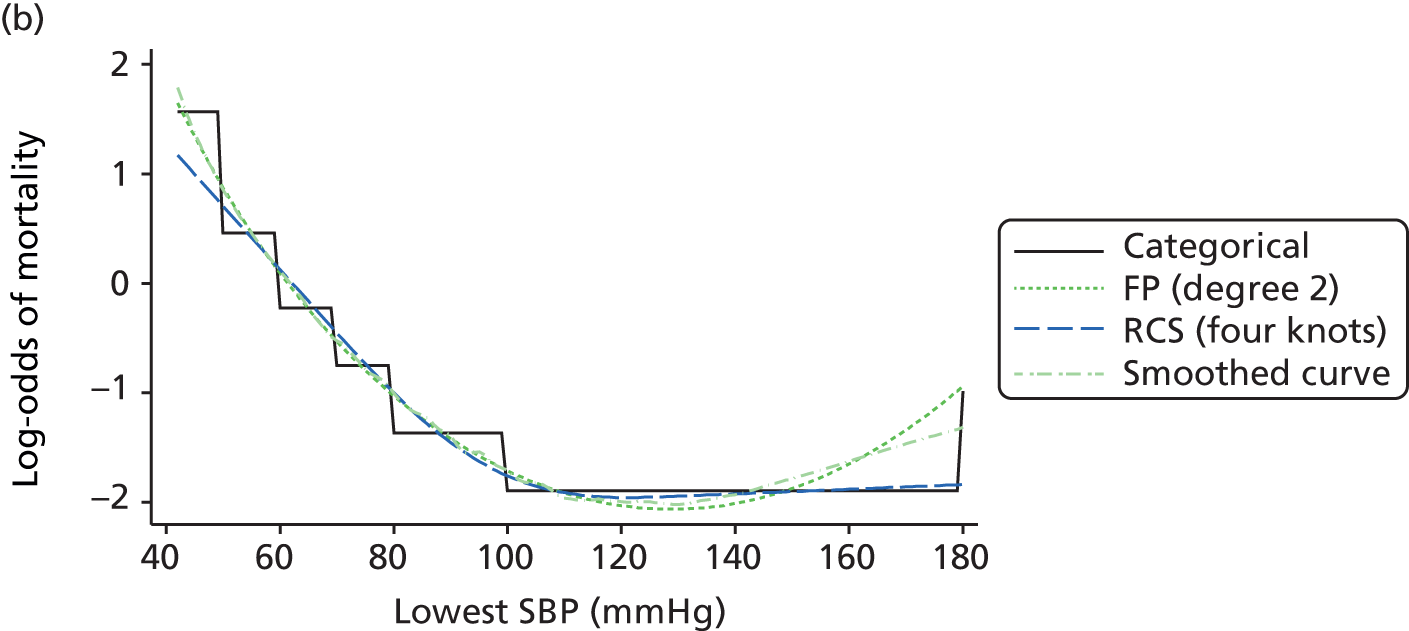
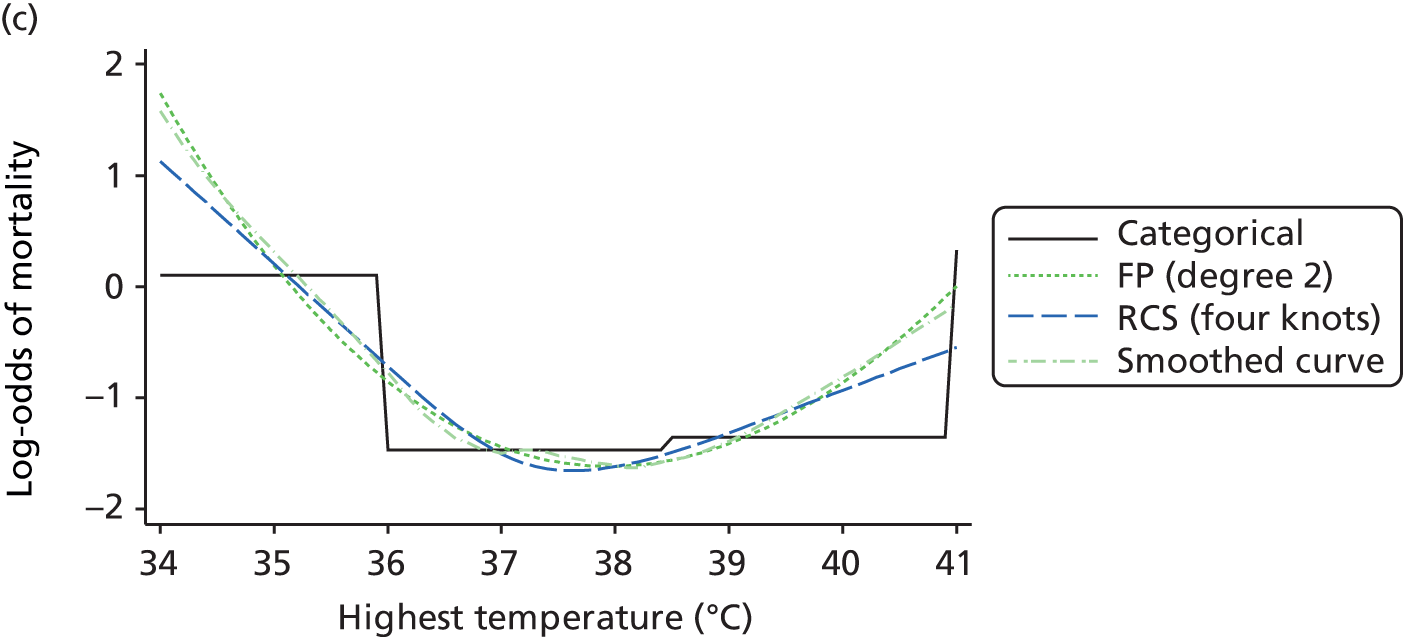

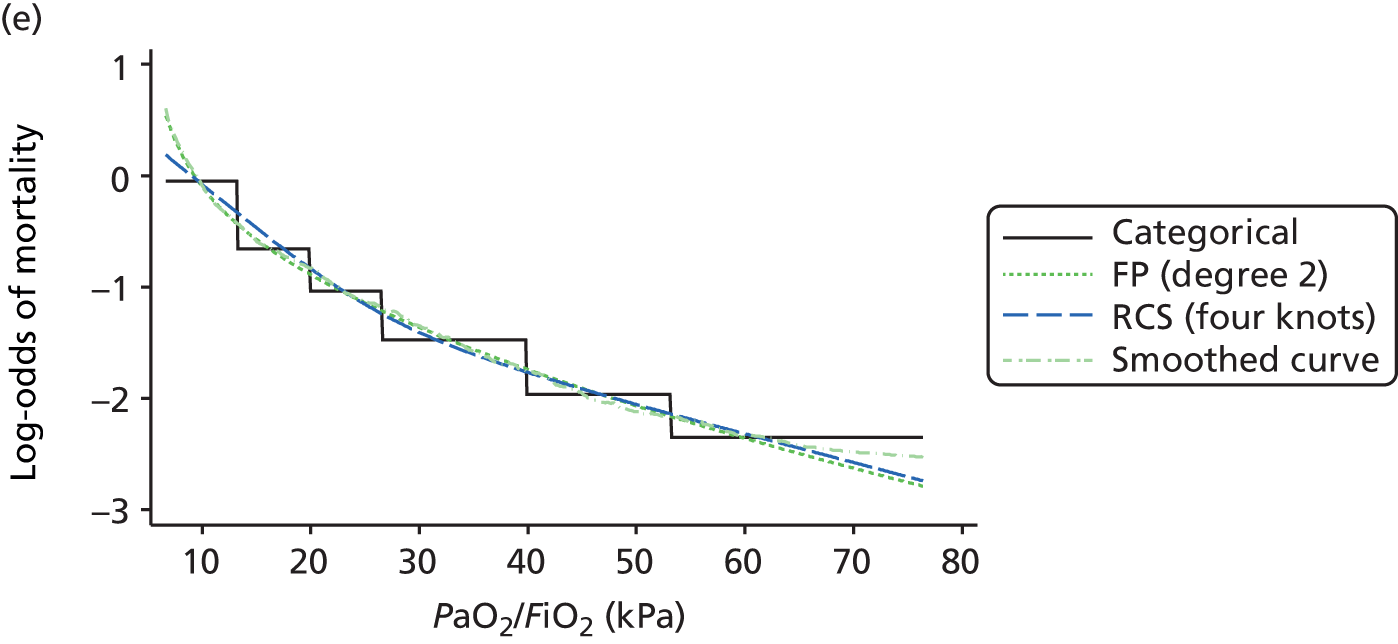
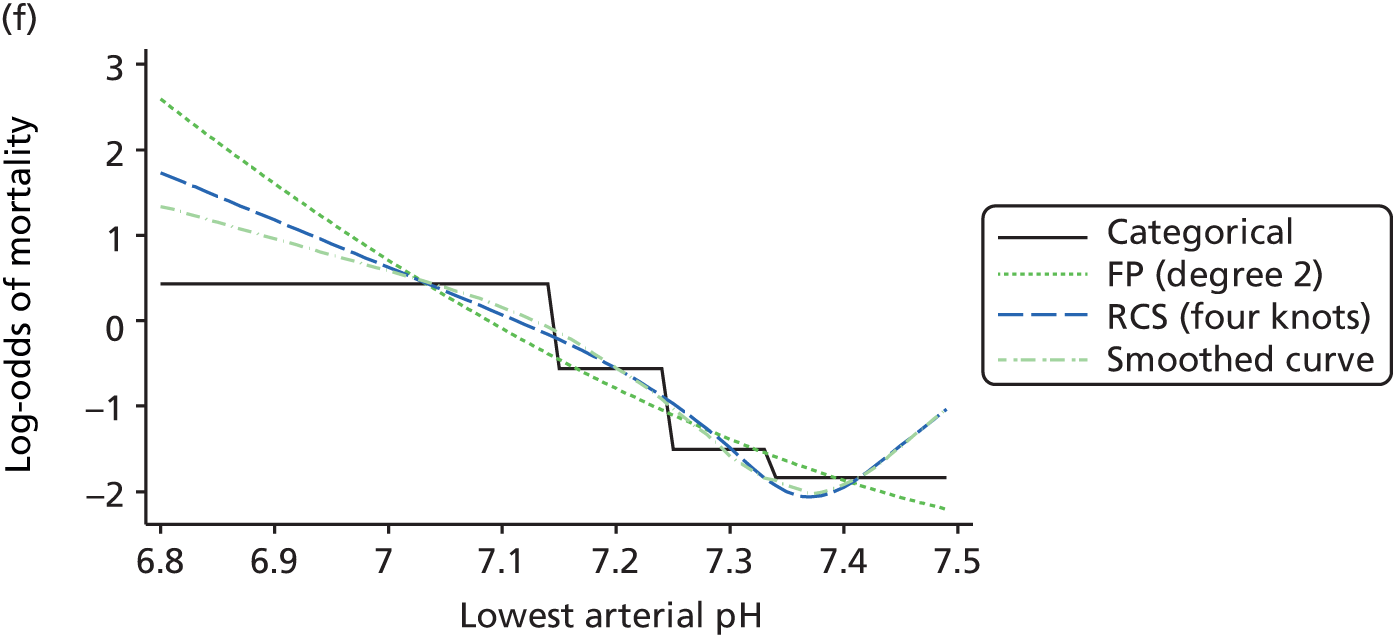


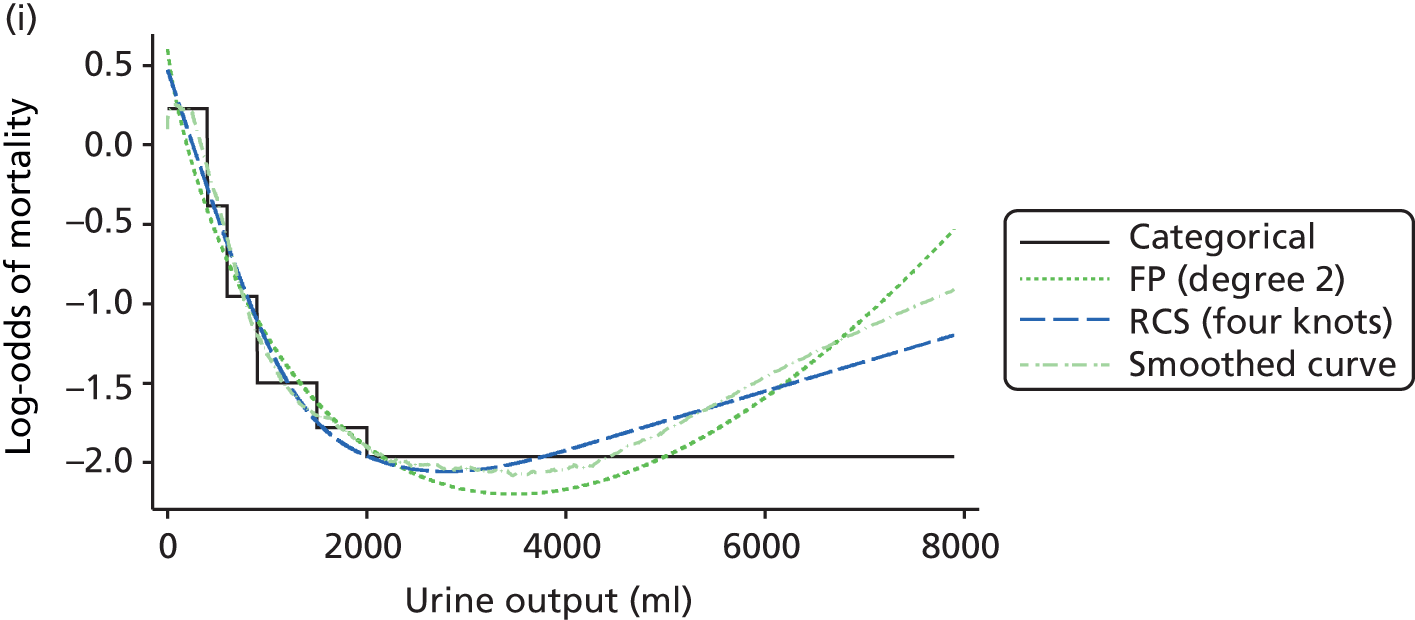
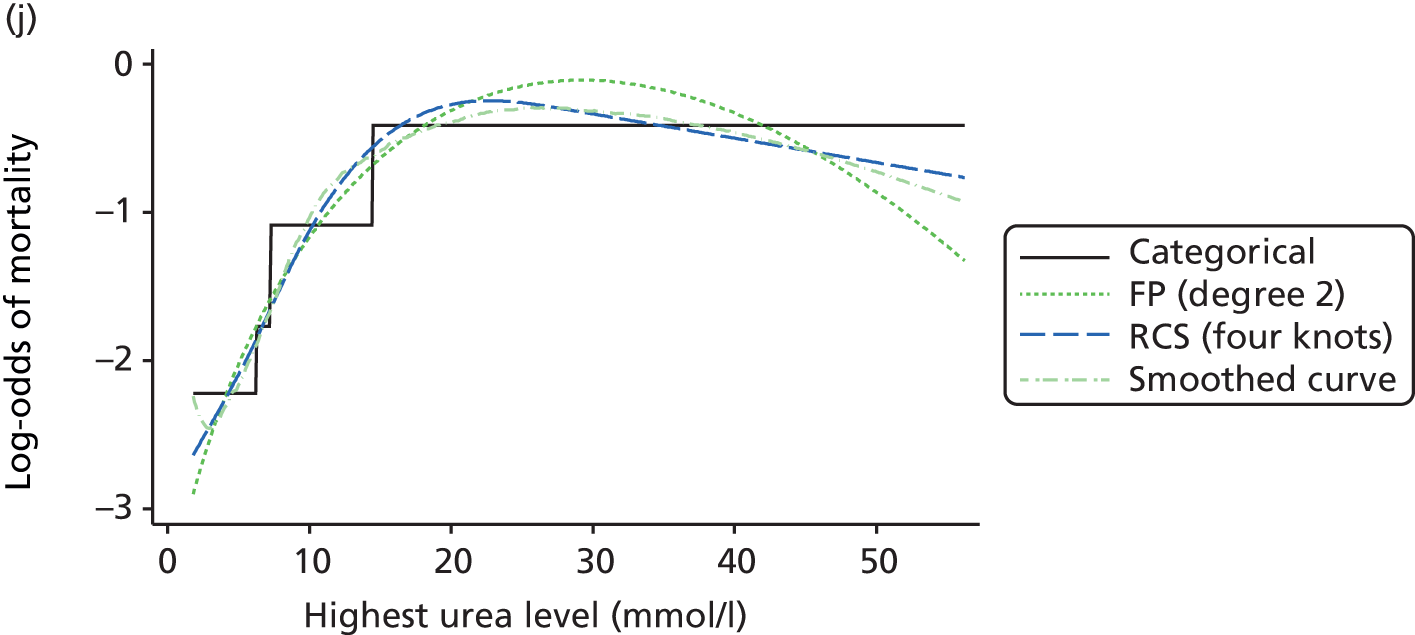
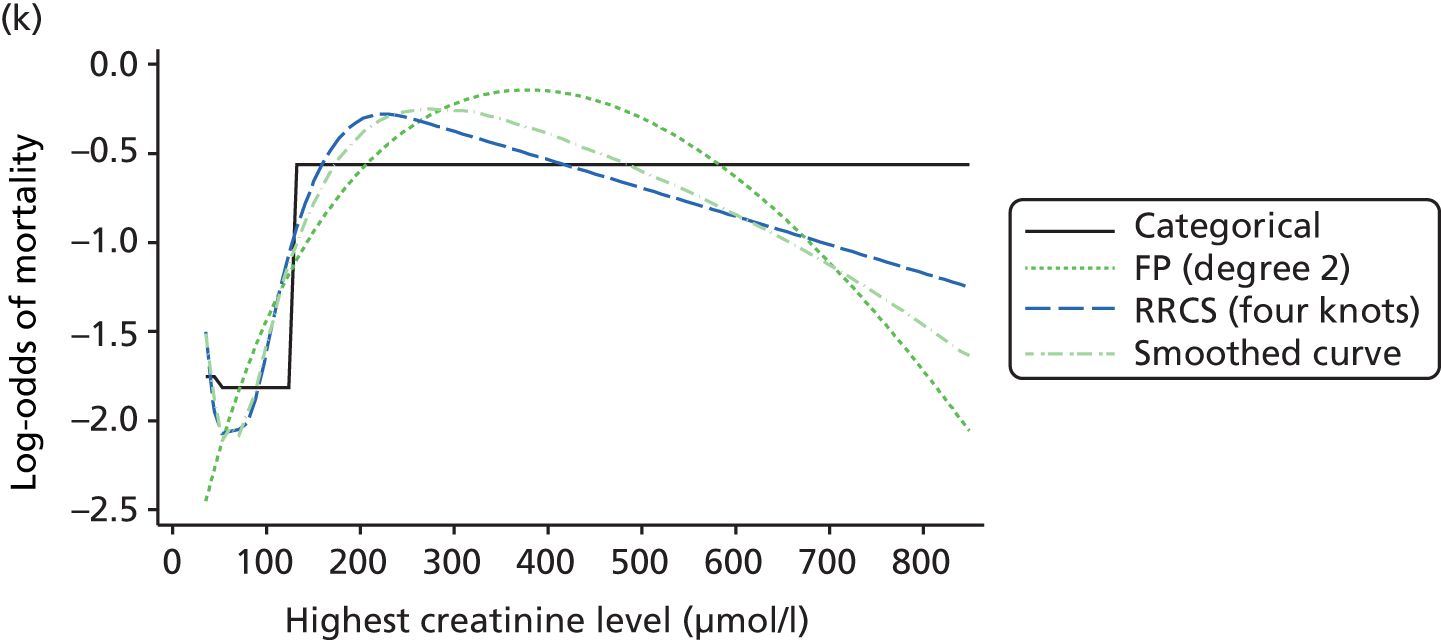
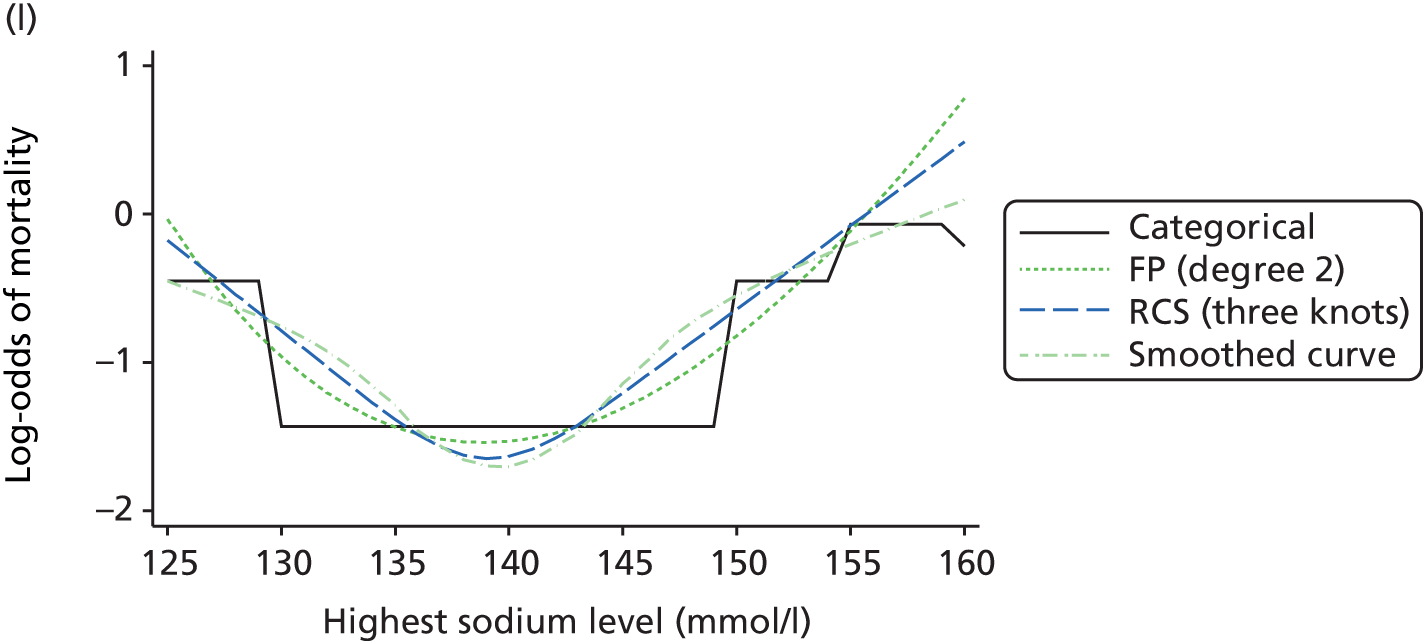
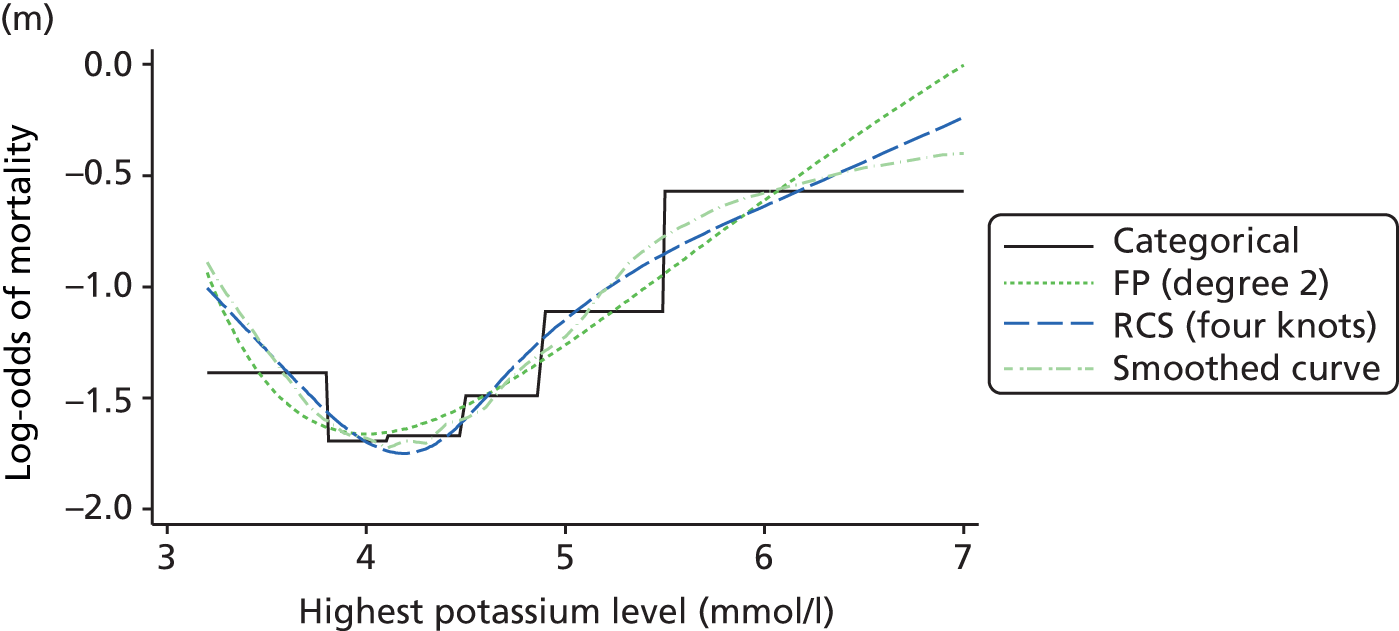
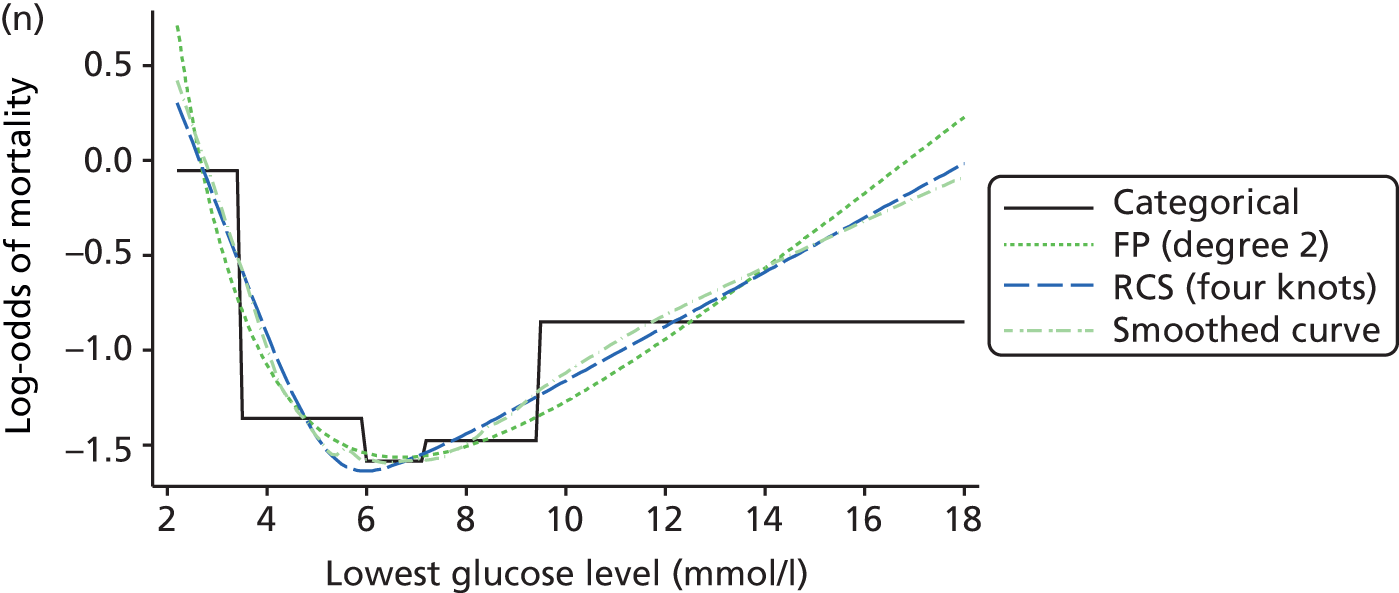
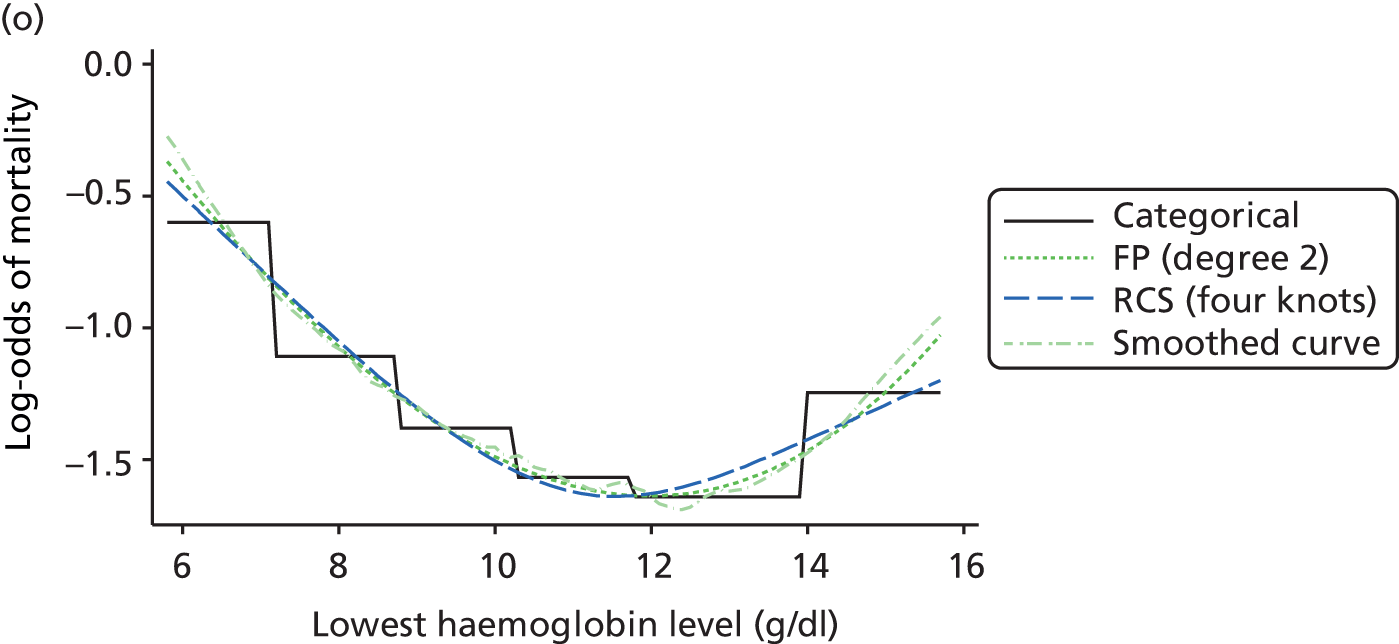

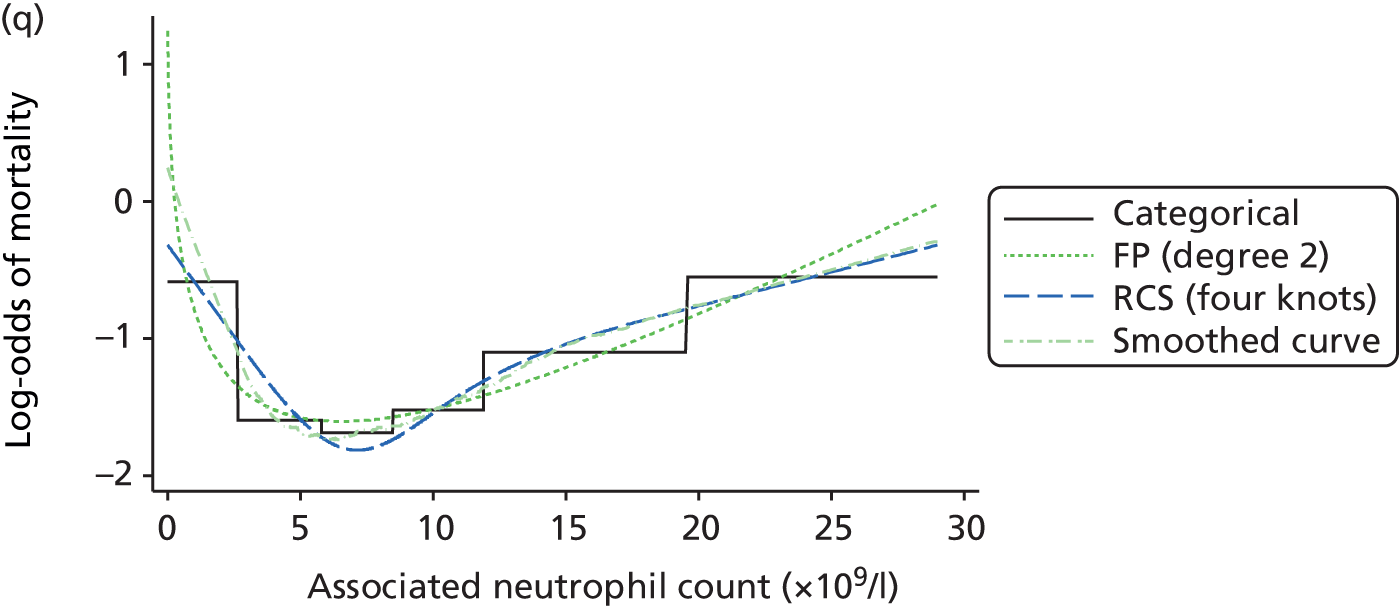
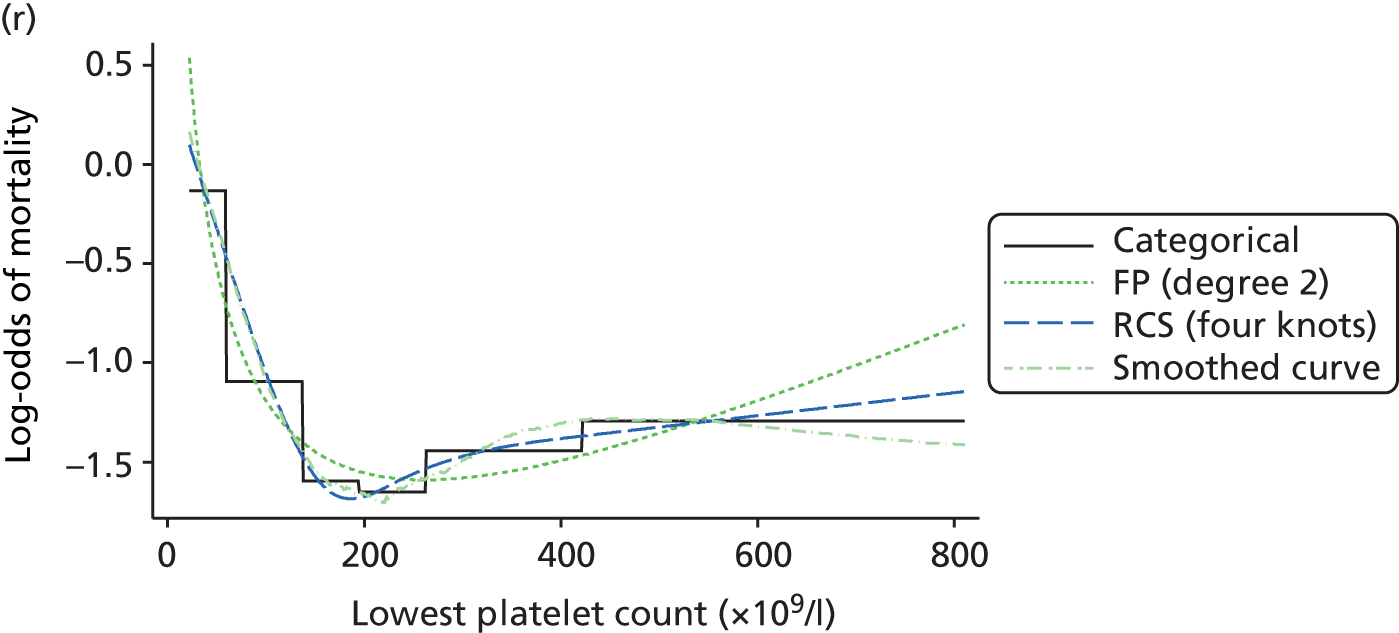
In general, both methods for continuous modelling (fractional polynomial models and restricted cubic splines) agreed closely, but variation between the two approaches occurred in the regions with sparsest data. Although the data contain little information on mortality, the fractional polynomial fit was poorer at extreme predictor values where a strong non-monotonic relationship was suggested (e.g. arterial pH and creatinine level), whereas restricted cubic splines accommodated a more realistic final trend at the ends of the curve. In addition, the SBP, heart rate and neutrophil fitted curves were more sensitive to extreme values using fractional polynomials, while the ensured linearity in the tails by restricted cubic splines avoided this unrealistic end effect and seemed not to be affected by the collapsed values. We decided to use restricted cubic splines because they showed the flexibility of fractional polynomials, but with better behaviour in the tails, they captured the most prominent features of the relationship between predictors and outcomes and because the fit was more plausible than that of the previous categorical approach.
The optimal functional form selected to model the continuous physiological predictors (Table 19) was four knots for heart rate, SBP, temperature, PaO2/FiO2, arterial pH, blood lactate concentration, urine output, urea level, potassium level, glucose level, haemoglobin level, WBC count, neutrophil count and platelet count because this accommodated the trend of decreasing/increasing mortality in a non-monotonic way, as well as capturing the behaviour at extremes. For PaCO2 and sodium level, a simplification using three knots was enough to accommodate the non-linear behaviour and had better AIC and BIC than four knots. Respiratory rate and creatinine level were modelled using right-restricted cubic splines. This was necessary to capture the initial decrease in mortality and ‘spoon’ behaviour (Figure 6). This approach had better fit than five knots and was more plausible than four. Finally, the stability of the fitted curves and the knots was assessed in each of the 10 imputed data sets, showing similar results.
| Candidate predictor | Approach to modelling |
|---|---|
| Physiological | |
| Highest (beats per minute) | RCS (71, 93, 110, 146) |
| Lowest SBP (mmHg) | RCS (66, 89, 102, 130) |
| Highest temperature (°C) | RCS (36.0, 37.2, 38.0, 39.2) |
| Lowest respiratory rate (breaths per minute) | RRCS (8, 12, 13, 15) |
| PaO2/FiO2 (kPa) | RCS (9.7, 26.0, 39.7, 61.4) |
| Lowest arterial pH | RCS (7.08, 7.30, 7.36, 7.44) |
| PaCO2 (kPa) | RCS (3.9, 5.2, 7.0) |
| Highest blood lactate (mmol/l) | RCS (0.7, 1.5, 2.5, 8.2) |
| Urine output (ml) | RCS (164, 1215, 2020, 4255) |
| Highest urea level (mmol/l) | RCS (2.8, 5.6, 9.3, 28.1) |
| Highest creatinine level (µmol/l) | RRCS (53, 80, 106, 168) |
| Highest sodium level (mmol/l) | RCS (133, 139, 145) |
| Highest potassium level (mmol/l) | RCS (3.6, 4.3, 4.7, 6.0) |
| Lowest glucose level (mmol/l) | RCS (3.5,5.4,6.6,9.5) |
| Lowest haemoglobin level (g/dl) | RCS (0.7,1.5,2.5, 8.2) |
| Lowest WBC count (× 109/l) | RCS (3.7, 8.7, 12.3, 22.5) |
| Neutrophil count (× 109/l) | RCS (2.6, 6.9, 10.3, 19.6) |
| Lowest platelet count (× 109/l) | RCS (60, 162, 232, 422) |
| Sedated/paralysed/GCS score | Categorical (nine levels) |
| Pupil reactivity | Categorical (three levels) |
| Non-physiological | |
| Age | Linear |
| Sex | Categorical (two levels) |
| Ethnicity | Categorical (six levels) |
| BMI | RCS (20.6, 25.8, 34.9) |
| Residence prior to admission | Categorical (seven levels) |
| Deprivation | Categorical (two levels – quintiles 1, 2 and 3 combined; 4 and 5 combined) |
| Severe conditions in the past medical history | Seven binary indicators |
| Dependency prior to admission | Categorical (three levels) |
| CPR prior to admission | Categorical (three levels) |
| Source of admission/urgency of surgery | Categorical (nine levels) |
| Primary reason for admission | Categorical (combinations of process/system or process or individual conditions) |
Consistency with both optimal functional form and global significance of the predictors was found after fitting a model adjusted for all physiological predictors from the current ICNARC model.
A more parsimonious physiology model was then developed using a backward process in order to balance parsimony and model performance (Table 20). All candidate physiological predictors, including those not incorporated in the current ICNARC model, were entered into a full model, which was then simplified. Three new candidate physiological predictors (PaCO2, blood lactate concentration and platelet count) were retained, as well as all physiological predictors from the current ICNARC model.
| Model | c-index | BS bias-corrected 95% CI | Brier score | BS bias-corrected 95% CI |
|---|---|---|---|---|
| Full model | 0.8539 | 0.8511 to 0.8559 | 0.1166 | 0.1155 to 0.1176 |
| Predictors dropped | ||||
| Neutrophil count | 0.8541 | 0.8508 to 0.8560 | 0.1167 | 0.1154 to 0.1179 |
| Highest potassium | 0.8539 | 0.8506 to 0.8561 | 0.1168 | 0.1158 to 0.1177 |
| Lowest glucose | 0.8538 | 0.8507 to 0.8559 | 0.1170 | 0.1160 to 0.1180 |
| Lowest haemoglobin | 0.8533 | 0.8513 to 0.8561 | 0.1171 | 0.1160 to 0.1182 |
| Lowest WBC count | 0.8529 | 0.8500 to 0.8557 | 0.1173 | 0.1160 to 0.1185 |
| Lowest pH | 0.8522 | 0.8493 to 0.8540 | 0.1176 | 0.1164 to 0.1188 |
| Lowest SBP | 0.8511 | 0.8481 to 0.8532 | 0.1183 | 0.1171 to 0.1194 |
| Highest heart rate | 0.8494 | 0.8467 to 0.8515 | 0.1188 | 0.1176 to 0.1200 |
| Lowest platelet count | 0.8478 | 0.8453 to 0.8505 | 0.1192 | 0.1180 to 0.1203 |
| Highest temperature | 0.8458 | 0.8431 to 0.8485 | 0.1203 | 0.1190 to 0.1216 |
| PaCO2 | 0.8434 | 0.8408 to 0.8454 | 0.1209 | 0.1198 to 0.1219 |
| Highest urea | 0.8322 | 0.8288 to 0.8344 | 0.1237 | 0.1225 to 0.1248 |
| Highest sodium | 0.8278 | 0.8252 to 0.8311 | 0.1248 | 0.1237 to 0.1259 |
| Highest creatinine | 0.8231 | 0.8207 to 0.8252 | 0.1259 | 0.1247 to 0.1270 |
| Highest blood lactate | 0.8154 | 0.8119 to 0.8175 | 0.1299 | 0.1287 to 0.1309 |
| Lowest respiratory rate | 0.8055 | 0.8030 to 0.8083 | 0.1315 | 0.1304 to 0.1325 |
| PaO2/FiO2 | 0.7709 | 0.7691 to 0.7745 | 0.1322 | 0.1308 to 0.1334 |
| Urine output | 0.7038 | 0.7000 to 0.7064 | 0.1439 | 0.1427 to 0.1451 |
| Sedated/paralysed/GCS | 0.5000 | 0.1699 | ||
Changes were made to a number of the current non-physiological predictors, in particular CPR within 24 hours prior to admission, which was expanded to three categories (in-hospital CPR, community CPR and no CPR), and source of admission, which was expanded into nine categories combining information from admission type. After exploring the relationship with outcome, deprivation was collapsed into two categories (quintiles 1–3 and quintiles 4 and 5) and dependency prior to hospital admission was collapsed into three categories [no dependency, partial dependency (combining either minor or major assistance with activities of daily living) or total dependency]. After adjusting for current and new potential predictors, deprivation and body mass index (BMI) were not retained in the main-terms model because of their lower contribution to the model fit. The new predictor of dependency prior to hospital admission was retained. Severe conditions in the past medical history were added into the model, but the only conditions ultimately retained were severe liver disease, owing to its interaction with physiology, and metastatic disease and haematological malignancy, because of their significant effect. Ventilation was also retained because it is the main term in several interactions. This main-terms model had a c-index of 0.8779 and a Brier score of 0.1098 (Table 21).
| Model | c-index (95% CI) | Brier score |
|---|---|---|
| Main-terms model | 0.8779 (0.8756 to 0.8800) | 0.1098 |
| Main-terms model with reason for admission | 0.8881 (0.8859 to 0.8901) | 0.1041 |
| Main-terms model with reason for admission plus interactions with physiology | 0.8898 (0.8877 to 0.8919) | 0.1033 |
| Final model | 0.8906 (0.8885 to 0.8926) | 0.1028 |
A total of 56 process/system combinations and 16 individual conditions from the ICNARC coding method form the new reason for admission categories (Table 22). These were selected after the modelling process described above and accounted for 93.6% and 6.4% of admissions respectively.
| Reason for admission new categorical variable | Frequency | Percentage |
|---|---|---|
| Combinations of process and system | ||
| Accidental intoxication or poisoning (endocrinea) | 531 | 0.34 |
| Acidaemia (endocrine) | 519 | 0.33 |
| Burns or hyperthermia (dermatological) | 167 | 0.11 |
| Collapse (respiratory) | 862 | 0.55 |
| Coma or encephalopathy (neurological) | 727 | 0.47 |
| Congenital or acquired deformity or abnormality (cardiovascular) | 773 | 0.50 |
| Congenital or acquired deformity or abnormality (musculoskeletal) | 3012 | 1.93 |
| Congenital or acquired deformity or abnormality (neurological) | 1176 | 0.75 |
| Congenital or acquired deformity or abnormality (respiratory) | 859 | 0.55 |
| Congenital or acquired deformity or abnormality (endocrine; gastrointestinal; genitourinary; haematological/immunological) | 2184 | 1.40 |
| Degeneration (cardiovascular) | 1903 | 1.22 |
| Degeneration (neurological) | 89 | 0.06 |
| Diabetes mellitus (endocrine) | 1844 | 1.18 |
| Dissection or aneurysm (cardiovascular) | 4456 | 2.85 |
| Failure (cardiovascular) | 1546 | 0.99 |
| Failure (genitourinary) | 5861 | 3.75 |
| Haemorrhage (cardiovascular) | 197 | 0.13 |
| Haemorrhage (gastrointestinal) | 3776 | 2.42 |
| Haemorrhage (genitourinary) | 1066 | 0.68 |
| Haemorrhage (neurological) | 2229 | 1.43 |
| Haemorrhage (respiratory) | 322 | 0.21 |
| Hyperkalaemia (endocrine) | 388 | 0.25 |
| Hypertension (cardiovascular) or over- or under-activity (cardiovascular; genitourinary) | 3514 | 2.25 |
| Hypokalaemia (endocrine) | 184 | 0.12 |
| Hyponatraemia (endocrine) | 262 | 0.17 |
| Hypoplasia or dysplasia (haematological/immunological) | 101 | 0.06 |
| Hypothermia (endocrine) | 146 | 0.09 |
| Infection (cardiovascular) | 610 | 0.39 |
| Infection (genitourinary) | 1935 | 1.24 |
| Infection (respiratory) | 16,413 | 10.51 |
| Infection (dermatological; gastrointestinal; haematological/immunological; musculoskeletal; neurological) | 7306 | 4.68 |
| Inflammation (gastrointestinal) | 4148 | 2.66 |
| Inflammation (neurological) | 350 | 0.22 |
| Inflammation (respiratory) | 3393 | 2.17 |
| Inflammation (cardiovascular; dermatological; genitourinary; musculoskeletal) | 501 | 0.32 |
| Obstruction (cardiovascular) | 7604 | 4.87 |
| Obstruction (gastrointestinal) | 5938 | 3.80 |
| Obstruction (genitourinary) | 712 | 0.46 |
| Obstruction (respiratory) | 4405 | 2.82 |
| Other endocrine processesb (endocrine) | 693 | 0.44 |
| Seizures (neurological) | 3558 | 2.28 |
| Self intoxication or self poisoning (endocrine) | 4412 | 2.83 |
| Shock and hypotension (cardiovascular) | 4401 | 2.82 |
| Transplant or related (gastrointestinal) | 626 | 0.40 |
| Transplant or related (cardiovascular; endocrine; genitourinary; haematological/immunological; respiratory) | 282 | 0.18 |
| Trauma, perforation or rupture (cardiovascular) | 389 | 0.25 |
| Trauma, perforation or rupture (gastrointestinal) | 6490 | 4.16 |
| Trauma, perforation or rupture (neurological) | 3070 | 1.97 |
| Trauma, perforation or rupture (dermatological; genitourinary; musculoskeletal; respiratory) | 4736 | 3.03 |
| Tumour or malignancy (genitourinary) | 4510 | 2.89 |
| Tumour or malignancy (haematological/immunological) | 377 | 0.24 |
| Tumour or malignancy (neurological) | 3067 | 1.96 |
| Tumour or malignancy (cardiovascular; dermatological; endocrine; gastrointestinal; musculoskeletal; respiratory) | 14,263 | 9.14 |
| Vascular (cardiovascular) | 766 | 0.49 |
| Vascular (gastrointestinal) | 1379 | 0.88 |
| Vascular (neurological) | 1040 | 0.67 |
| Specific conditions | ||
| Acute alcoholic hepatitis/alcoholic cirrhosis | 529 | 0.34 |
| Anaphylaxis | 484 | 0.31 |
| Anoxic or ischaemic coma or encephalopathy | 983 | 0.63 |
| Asthma attack in new or known asthmatic | 1600 | 1.02 |
| Enteroenteric or enterocutaneous fistula | 132 | 0.08 |
| Fractured ribs | 252 | 0.16 |
| Fungal or yeast pneumonia | 210 | 0.13 |
| Haemolysis or thrombocytopenia | 166 | 0.11 |
| Hanging or strangulation | 192 | 0.12 |
| Intracerebral haemorrhage | 1524 | 0.98 |
| Leaking large bowel anastomosis/perforated biliary tree or gall bladder | 884 | 0.57 |
| Lower limb artery stenosis or occlusion | 1239 | 0.79 |
| Pulmonary fibrosis or fibrosing alveoli | 200 | 0.13 |
| Secondary hydrocephalus | 235 | 0.15 |
| Thrombo-occlusive disease of brain | 864 | 0.55 |
| Toxic or drug-induced coma or encephalopathy | 549 | 0.35 |
The incorporation of primary reason for admission categories, plus interactions with physiology (n = 19), in the risk prediction model produced better fit (see Table 21) and, therefore, could reduce bias when applied across different settings with differing case mix. 15 One of the pre-defined past medical history–physiology interactions, six of the pre-defined intervention–physiology interactions and three of the pre-defined physiology–physiology interactions were retained after adjusting for the main term model plus significant primary reason for admission–physiology interactions. Apart from ventilation with arterial blood gas results, most of the significant interactions added did not make an important contribution to the model (Table 23); however, these interactions could reflect important dependencies as well as intrinsic prognostic features of the data.
| Predictor | p-value for non-linearity | p-value for global effect | Difference in BICa | c-indexa | Brier scorea |
|---|---|---|---|---|---|
| Physiological | |||||
| Highest heart rate | < 0.0001 | < 0.0001 | 260.286 | 0.8896 | 0.1031 |
| Lowest SBP | 0.0004 | < 0.0001 | –12.862 | 0.8906 | 0.1028 |
| Highest temperature | 0.0008 | < 0.0001 | –11.374 | 0.8906 | 0.1028 |
| Lowest respiratory rate | < 0.0001 | < 0.0001 | 222.766 | 0.8898 | 0.1032 |
| PaO2/FiO2 | < 0.0001 | < 0.0001 | 300.785 | 0.8896 | 0.1033 |
| Lowest arterial pH | 0.0001 | < 0.0001 | 1.898 | 0.8905 | 0.1028 |
| PaCO2 | 0.0003 | < 0.0001 | 15.800 | 0.8905 | 0.1028 |
| Highest blood lactate concentration | 0.0010 | 0.0022 | –20.535 | 0.8906 | 0.1028 |
| Urine output | < 0.0001 | < 0.0001 | 345.397 | 0.8895 | 0.1033 |
| Highest urea level | < 0.0001 | < 0.0001 | 76.738 | 0.8903 | 0.1030 |
| Highest creatinine level | < 0.0001 | < 0.0001 | 338.498 | 0.8895 | 0.1034 |
| Highest sodium level | < 0.0001 | < 0.0001 | 223.715 | 0.8899 | 0.1031 |
| Lowest WBC count | < 0.0001 | < 0.0001 | 36.504 | 0.8904 | 0.1029 |
| Lowest platelet count | < 0.0001 | < 0.0001 | 234.304 | 0.8897 | 0.1032 |
| Sedated/paralysed/GCS score | – | < 0.0001 | 3478.910 | 0.8875 | 0.1042 |
| Non-physiological | |||||
| Age | – | < 0.0001 | 2806.928 | 0.8813 | 0.1065 |
| Severe liver disease in past medical history | – | 0.0847 | –8.555 | 0.8906 | 0.1028 |
| Metastatic disease | – | < 0.0001 | 122.263 | 0.8902 | 0.1030 |
| Haematological malignancy | – | < 0.0001 | 119.012 | 0.8902 | 0.1030 |
| Dependency prior to admission | – | < 0.0001 | 573.037 | 0.8886 | 0.1035 |
| CPR prior to admission | – | 0.0078 | –13.554 | 0.8906 | 0.1028 |
| Source of admission/urgency of surgery | – | < 0.0001 | 889.910 | 0.8875 | 0.1040 |
| Primary reason for admission | – | < 0.0001 | 374.353 | 0.8865 | 0.1043 |
| Ventilation | – | 0.1102 | –9.148 | 0.8906 | 0.1028 |
| Interactions | |||||
| Arterial pH × PaCO2 | – | < 0.0001 | 12.177 | 0.8905 | 0.1028 |
| Arterial pH × blood lactate concentration | – | < 0.0001 | –24.330 | 0.8905 | 0.1028 |
| Urine output × urea level | – | < 0.0001 | –20.355 | 0.8905 | 0.1028 |
| Liver disease × temperature | – | < 0.0001 | –11.362 | 0.8906 | 0.1028 |
| CPR × temperature | – | < 0.0001 | –41.720 | 0.8906 | 0.1028 |
| CPR × SBP | – | < 0.0001 | –44.717 | 0.8906 | 0.1028 |
| Collapse (respiratory) × platelet count | – | < 0.0001 | –16.203 | 0.8906 | 0.1028 |
| Congenital (neurological) × urine output | – | < 0.0001 | –19.459 | 0.8906 | 0.1028 |
| Diabetes mellitus (endocrine) × heart rate | – | < 0.0001 | –17.168 | 0.8906 | 0.1028 |
| Haemorrhage (gastrological) × sodium level | – | < 0.0001 | –4.124 | 0.8906 | 0.1028 |
| Haemorrhage (neurological) × urine output | – | < 0.0001 | 2.495 | 0.8906 | 0.1028 |
| Haemorrhage (neurological) × blood lactate concentration | < 0.0001 | 14.506 | 0.8905 | 0.1029 | |
| Infection (respiratory) × heart rate | – | < 0.0001 | –19.264 | 0.8906 | 0.1028 |
| Infection (respiratory) × PaO2/FiO2 | – | < 0.0001 | 1.315 | 0.8905 | 0.1028 |
| Self-poisoning (endocrine) × creatinine level | – | < 0.0001 | –30.209 | 0.8905 | 0.1028 |
| Self-poisoning (endocrine) × blood lactate concentration | – | < 0.0001 | –7.324 | 0.8905 | 0.1028 |
| Trauma (neurological) × sodium level | – | < 0.0001 | –4.254 | 0.8906 | 0.1028 |
| Trauma (neurological) × WBC count | – | < 0.0001 | 2.779 | 0.8905 | 0.1028 |
| Trauma (neurological) × urine output | – | < 0.0001 | 11.672 | 0.8905 | 0.1028 |
| Trauma (neurological) × platelet count | – | < 0.0001 | –6.734 | 0.8905 | 0.1028 |
| Tumour (haematological/immunological) × WBC count | – | < 0.0001 | –19.998 | 0.8906 | 0.1028 |
| Tumour (neurological) × urine output | – | < 0.0001 | –18.574 | 0.8906 | 0.1028 |
| Tumour (other) × sodium level | – | < 0.0001 | –4.767 | 0.8906 | 0.1028 |
| Alcoholic hepatitis/cirrhosis × urea level | – | 0.001 | –19.033 | 0.8906 | 0.1028 |
| Anoxic/ischaemic coma × SBP | – | < 0.0001 | 4.567 | 0.8905 | 0.1028 |
| Intracerebral haemorrhage × temperature | – | < 0.0001 | –16.786 | 0.8906 | 0.1028 |
| Intracerebral haemorrhage × urine output | – | < 0.0001 | 17.770 | 0.8905 | 0.1029 |
| Secondary hydrocephalus × creatinine level | – | 0.001 | 9.691 | 0.8906 | 0.1028 |
| Ventilation × heart rate | – | < 0.0001 | –5.314 | 0.8905 | 0.1028 |
| Ventilation × respiratory rate | – | < 0.0001 | –27.440 | 0.8905 | 0.1028 |
| Ventilation × PaO2/FiO2 | – | < 0.0001 | 17.936 | 0.8905 | 0.1029 |
| Ventilation × PaCO2 | – | < 0.0001 | 31.996 | 0.8904 | 0.1029 |
The addition of non-physiological predictors and interactions did not affect the functional form of the physiological predictors.
The estimates for the model parameters obtained using data from the multiply imputed data set were similar to values estimated from the development data set and, therefore, the bias that could arise from using only the available information was considered to be very small.
Following the development process described above, the significance and importance of the predictors in the final model are shown in Table 23. Full coefficients for the final model [i.e. the new ICNARC model for acute hospital mortality (ICNARCH-2014)] are presented in Appendix 2. The distribution of predicted acute hospital mortality from the new model is shown in Figure 7.
FIGURE 7.
Distribution of predicted acute hospital mortality from the new ICNARC model in the development data set.
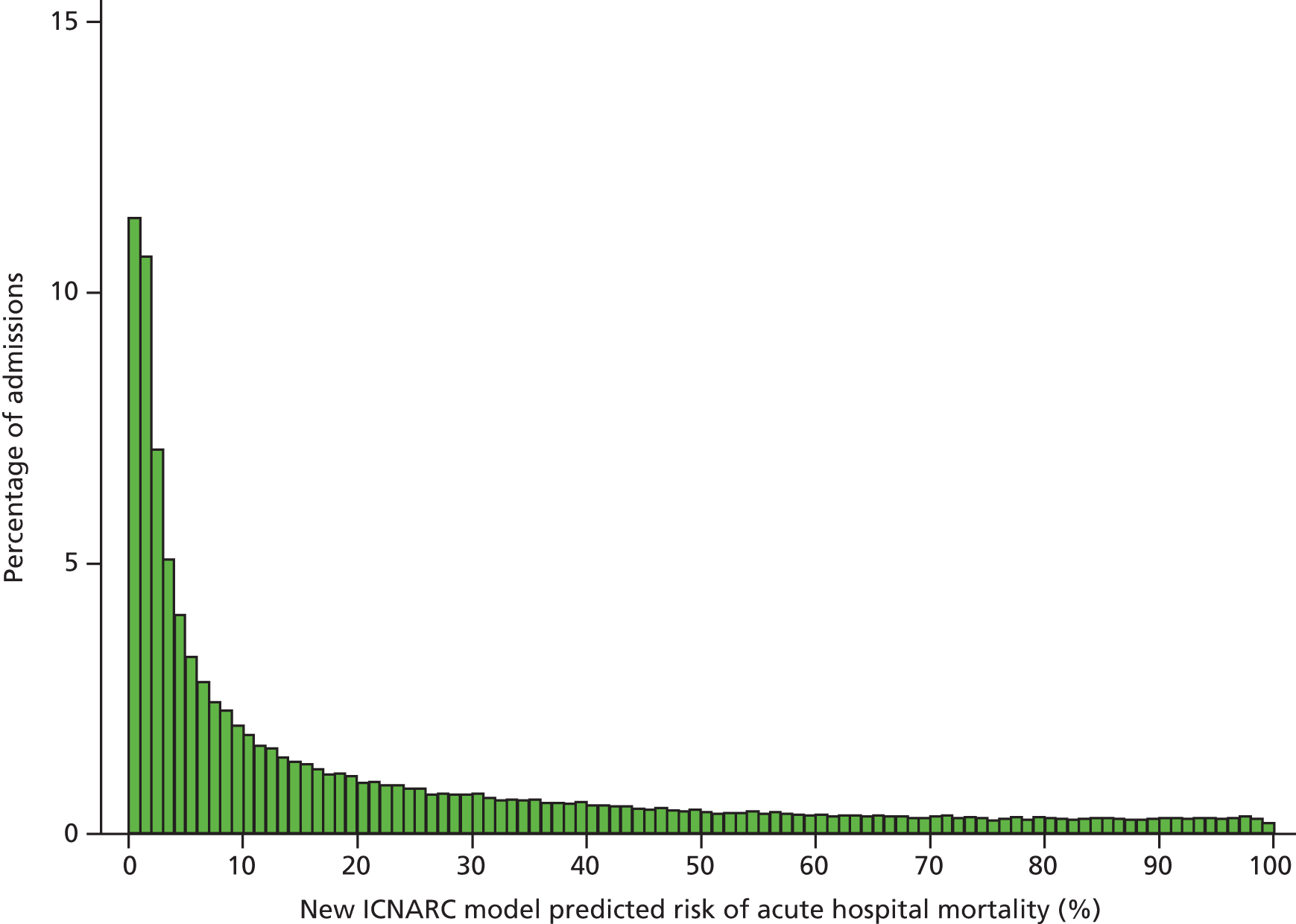
Among the subset of patients with pupil reactivity recorded (n = 104,063), a model using pupil reactivity in place of the sedated/paralysed/GCS score predictor had very similar discrimination (c-index 0.8883 vs. 0.8887).
Validation of the new Intensive Care National Audit & Research Centre model
Assessing the predictive performance
Discrimination, calibration and accuracy are key aspects of the predictive performance of prediction models. Discrimination is the ability of a model to distinguish individuals who experienced the outcome from those who remained event free, and calibration is the agreement between the probability of developing the outcome of interest as estimated by the model and the observed outcome frequencies. Accuracy refers to the difference between predictions and observed outcomes at the level of individuals.
The discrimination of the model was estimated by the c-index22 (equivalent to the area under the receiver operating characteristic curve23) and accuracy was assessed by the Brier score (mean-square error between outcome and prediction). 28 We assessed calibration graphically with predicted probability on the x-axis and the observed outcomes on the y-axis in 10 equal-sized risk groups (calibration plot) and by Cox’s calibration regression (linear recalibration of the predicted log-odds). 27
The use of calibration plots and parameters from Cox calibration regression (intercept and calibration slope) to assess the calibration of the model, and not the Hosmer–Lemeshow c-statistic,24 is because the last statistic reflects the statistical significance of miscalibration and not its magnitude and hence, in general, models validated in a large sample and/or with the ability to provide very low mortality risk predictions will tend to have a worse Hosmer–Lemeshow c-statistic than models validated in a small sample size and/or providing a smaller range of mortality risks. 25,26
Some researchers have proposed reclassification level as a measure of added utility or improvement. Cook recommends producing a ‘reclassification table’ to show how many subjects are reclassified by adding a marker to a model. 91 Pencina et al. extended the reclassification idea by conditioning on the outcome; therefore, reclassification of subjects with and without the outcome should be considered separately. 42 Any ‘upwards’ movement in categories for subjects with the outcome implies improved classification, and any ‘downwards’ movement indicates worse classification. The interpretation is opposite for subjects without the outcome. The improvement in classification was quantified as the sum of differences in proportions of individuals moving up minus the proportion moving down for those with the outcome, and the proportion of individuals moving down minus the proportion moving up for those without the outcome (NRI).
Internal validation
Validation of predictive models, either internally to adjust for optimism and overfitting or externally to assess generalisability, is essential in terms of understanding the reliability of both the choice of variables and the values of coefficients for each variable. The performance of a predictive model could be overestimated when simply determined on the sample of subjects that was used to construct the model; several internal validation methods are available that aim to provide a more accurate estimate of model performance in new subjects and to estimate the potential for optimism and overfitting in model performance. Bootstrapping is now widely regarded as a better approach to validation than data splitting18,43,88 and the c-index is often used to indicate optimism if the value decreases substantially in an independent data set. Harrell et al. 88 presented an algorithm for estimating the optimism or overfitting in predictive models. Their method is based on using bootstrapping to derive the expected bias-corrected c-index, which is referred to as the optimism-corrected c-index.
When a predictive model is based on a very large sample size, as in this project, and relevant variables are included in the final model, reasonable estimates of the coefficient values for each variable are likely. 92 Optimism is small and so the apparent estimates of model performance (c-index and Brier score in the development data set) are attractive because of their stability. 43 However, to assess optimistic performance, the percentage of overfitting was estimated by the optimism-corrected c-index.
External validation
External validation is an important issue because the performance of most developed and internally validated prediction models, when applied to new individuals, is poorer than the performance seen in the sample from which it was developed. Internal validation does not make use of data other than the development data and, therefore, will not provide the degree of heterogeneity that will be encountered in real-life application of the model.
External validation of any type consists of taking the original model, with its predictors and assigned weights estimated from the development data set, and applying it to a different data set, obtaining the measured predictor and outcome values in the new individuals and quantifying the model’s predictive performance. In this project, external validation was done for a different period of time and in different specialist units. We used the validation data set (January to September 2013) to compare the predictive accuracy of the new model with that of the current ICNARC model, both overall as well as across different types of admissions (surgical vs. non-surgical and planned vs. unplanned). An objective of this project was to develop a single, general risk prediction model that could be applied across all adult critical care units, including specialist cardiothoracic and neurocritical care units and stand-alone high-dependency units. However, it is possible that a single, general model may under- or overestimate mortality in selected admission subpopulations or different unit types and so could show worse performance than specifically designed or calibrated models. Therefore, in addition, we used the validation data set to evaluate the use of a general model in specialist units by comparing it to versions of the current ICNARC model specifically recalibrated to each unit type.
Results
The final model showed good performance (c-index 0.8909 and Brier score 0.1027) and internal calibration of the model was satisfactory (see Table 21 and Figure 8). Overfitting was of limited relevance because of the very large data set and, as expected, model optimism was negligible (0.16% estimated overfitting).
FIGURE 8.
Calibration of the new ICNARC model in the development data set.
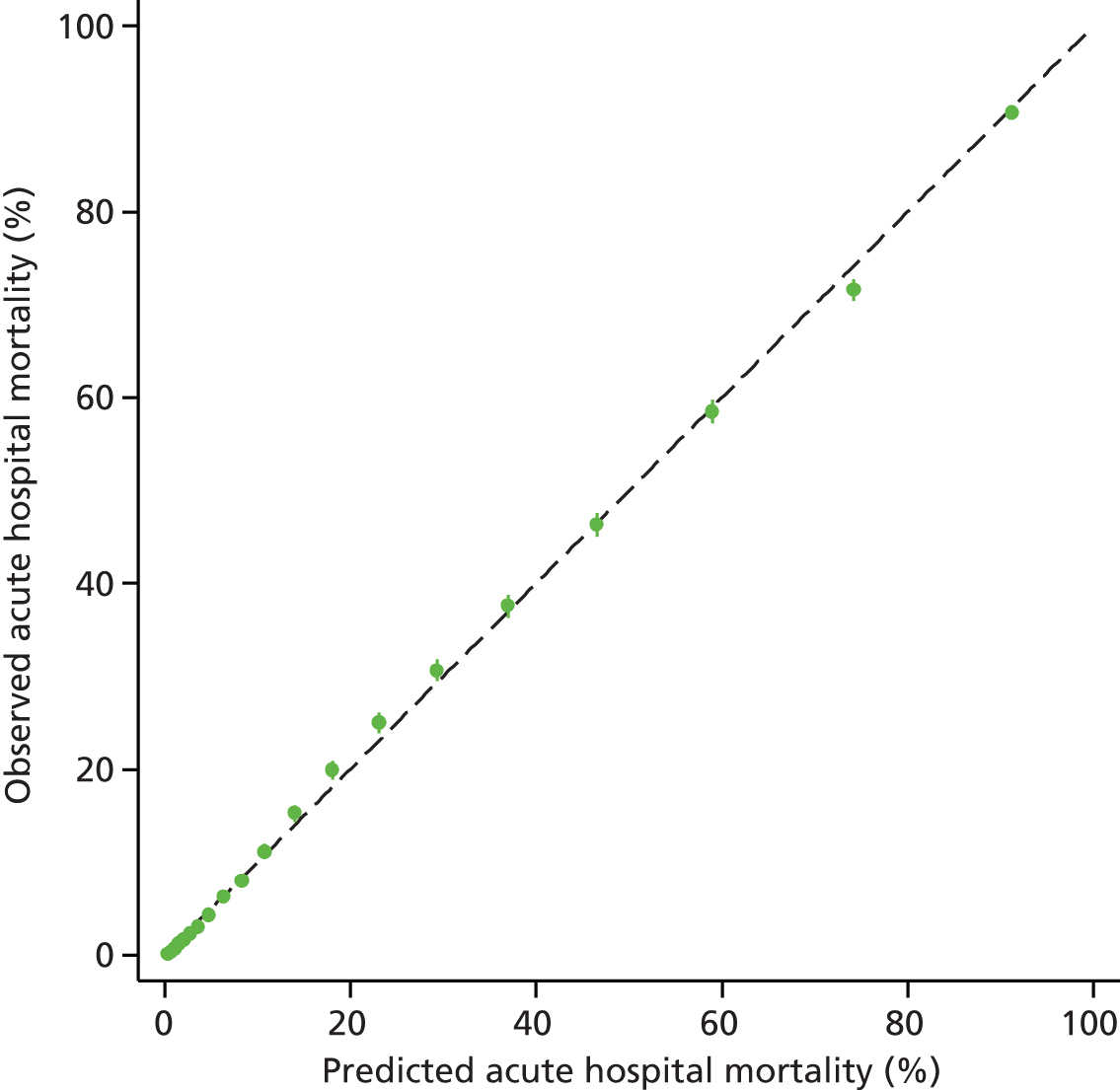
The performance in the validation data set (January to September 2013) is presented in Table 24 and Figure 9. Compared with the current ICNARC model, the new model demonstrated small improvements in discrimination and accuracy (c-index 0.8853 vs. 0.8693, Brier score 0.1076 vs. 0.1146). The current ICNARC model tended to slightly overestimate overall mortality; observed and mean predicted mortality were 22.6% and 23.2%, respectively, for a standardised mortality ratio (SMR, defined as observed divided by predicted mortality) of 0.97 (95% CI 0.96 to 0.99). A total of 30,739 (42.8%) of the admissions were reclassified by the new model (31.4% of survivors and 17.2% of non-survivors; Tables 25 and 26) and 20,252 of those (65.8%) were placed into more appropriate categories. The total NRI for the new model was 19.9 (p < 0.0001) and the new model showed a better risk classification, allocating more admissions in the extremes (Table 27).
| Model | c-index (95% CI) | Brier score | Predicted mortality (%) | Observed mortality (%) | SMR (95% CI) |
|---|---|---|---|---|---|
| Currenta | 0.8693 (0.8663 to 0.8722) | 0.1146 | 23.23 | 22.62 | 0.97 (0.96 to 0.99) |
| Newb | 0.8853 (0.8825 to 0.8880) | 0.1076 | 22.94 | 0.99 (0.97 to 1.00) |
FIGURE 9.
Calibration of the new ICNARC model compared with the current ICNARC model (2013 recalibration) in the external validation data set. a, 2013 recalibration; and b, developed in this project.
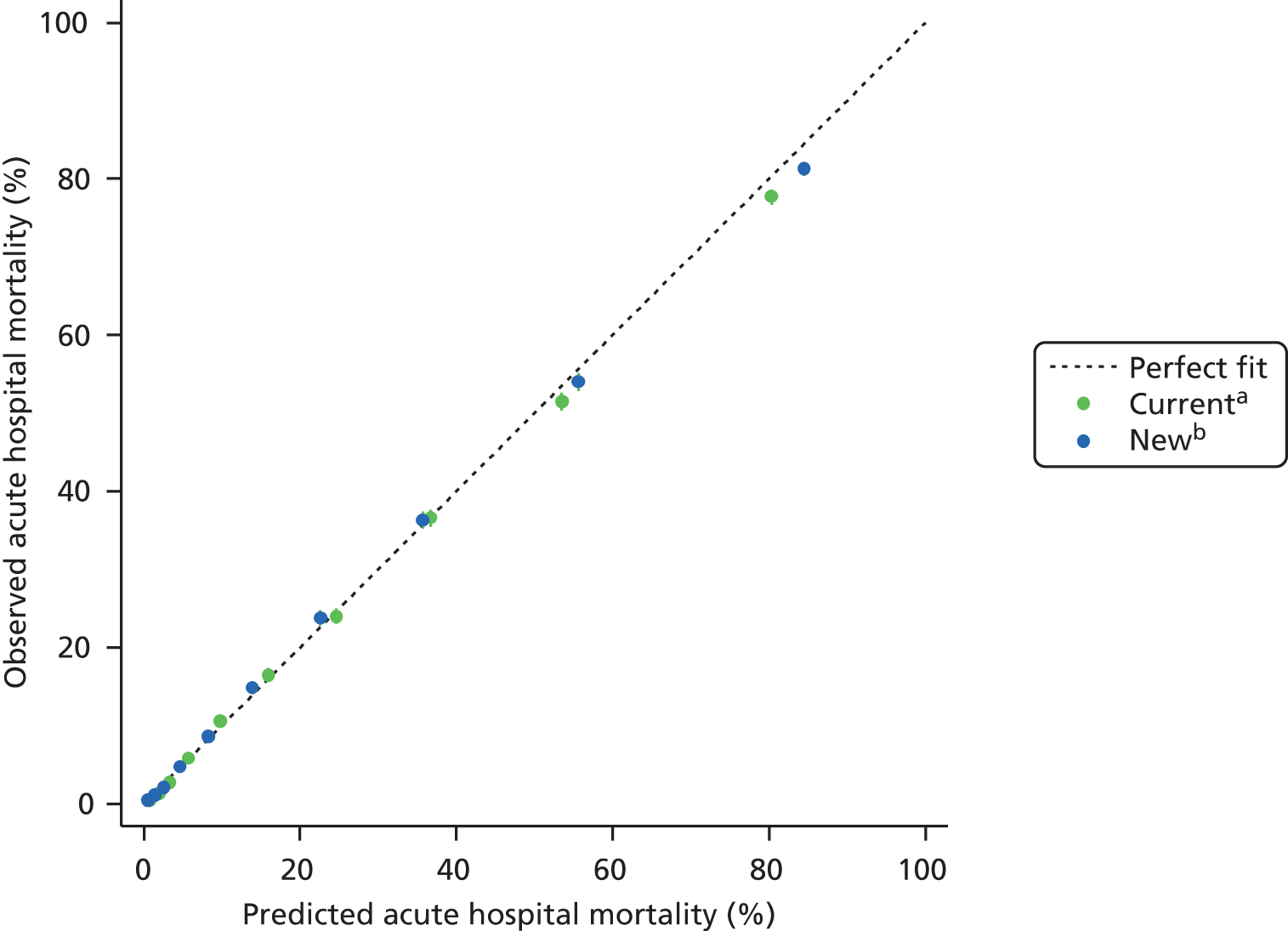
| Risk category (currenta) | Risk category (newb) | |||||
|---|---|---|---|---|---|---|
| 0–1.99% | 2–4.99% | 5–9.99% | 10–19.99% | 20–49.99% | 50–100% | |
| Survivors | ||||||
| 0–1.99% | 9530 | 1370 | 199 | 37 | 10 | 1 |
| 2–4.99% | 4518 | 5356 | 1553 | 358 | 65 | 4 |
| 5–9.99% | 552 | 3289 | 3096 | 1398 | 356 | 24 |
| 10–19.99% | 105 | 836 | 2815 | 3398 | 1625 | 109 |
| 20–49.99% | 23 | 113 | 679 | 3108 | 6193 | 1120 |
| 50–100% | 1 | 3 | 7 | 59 | 1327 | 2281 |
| Non-survivors | ||||||
| 0–1.99% | 40 | 21 | 5 | 1 | 1 | |
| 2–4.99% | 43 | 133 | 93 | 45 | 17 | 1 |
| 5–9.99% | 11 | 124 | 239 | 230 | 111 | 12 |
| 10–19.99% | 4 | 42 | 254 | 574 | 597 | 95 |
| 20–49.99% | 2 | 9 | 87 | 621 | 3077 | 1575 |
| 50–100% | 10 | 8 | 26 | 1032 | 7098 | |
| Change | Survivors | Non-survivors |
|---|---|---|
| Down, n (%) | 17,435 (31.4) | 2272 (14.0) |
| No change, n (%) | 29,854 (53.8) | 11,161 (68.7) |
| Up, n (%) | 8229 (14.8) | 2805 (17.3) |
| Net improvementa (SE) | 16.6% (0.3%) | 3.3% (0.4%) |
| Risk category | Number of admissions | Predicted mortality (%) | Observed mortality (%) |
|---|---|---|---|
| Current ICNARC model (2013 recalibration) | |||
| 0–1.99% | 11,215 | 1.1 | 0.6 |
| 2–4.99% | 12,186 | 3.3 | 2.7 |
| 5–9.99% | 9442 | 7.2 | 7.7 |
| 10–19.99% | 10,454 | 14.6 | 15.0 |
| 20–49.99% | 16,608 | 33.2 | 32.3 |
| 50–100% | 11,851 | 71.1 | 69.0 |
| New ICNARC model (developed in this project) | |||
| 0–1.99% | 14,879 | 1.0 | 0.7 |
| 2–4.99% | 11,358 | 3.3 | 2.9 |
| 5–9.99% | 9126 | 7.2 | 7.6 |
| 10–19.99% | 9979 | 14.5 | 15.2 |
| 20–49.99% | 14,654 | 32.9 | 33.6 |
| 50–100% | 12,451 | 73.9 | 71.2 |
When compared across different types of admissions (surgical vs. non-surgical and planned vs. unplanned), the new model improved discrimination (Table 28) and calibration (Figure 10) compared with the current ICNARC model. For surgical admissions, the new model showed excellent discrimination and calibration (c-index 0.8905, SMR 1.00) and for all other subgroups, good discrimination and SMRs close to 1, which indicated good calibration among these subgroups.
| Model | c-index (95% CI) | Brier score | Predicted mortality (%) | Observed mortality (%) | SMR (95% CI) |
|---|---|---|---|---|---|
| Surgical (n = 30,282) | |||||
| Currenta | 0.8716 (0.8651 to 0.8781) | 0.0663 | 10.07 | 10.30 | 1.02 (0.99 to 1.06) |
| Newb | 0.8905 (0.8845 to 0.8963) | 0.0624 | 10.33 | 1.00 (0.96 to 1.03) | |
| Non-surgical (n = 41,474) | |||||
| Currenta | 0.8330 (0.8290 to 0.8370) | 0.1499 | 32.84 | 31.63 | 0.96 (0.95 to 0.98) |
| Newb | 0.8538 (0.8500 to 0.8575) | 0.1407 | 32.14 | 0.98 (0.97 to 1.00) | |
| Planned (n = 19,237) | |||||
| Currenta | 0.8747 (0.8651 to 0.8844) | 0.0520 | 8.37 | 7.62 | 0.92 (0.88 to 0.97) |
| Newb | 0.8900 (0.8811 to 0.8989) | 0.0499 | 7.92 | 0.96 (0.91 to 1.01) | |
| Unplanned (n = 52,519) | |||||
| Currenta | 0.8444 (0.8409 to 0.8479) | 0.1376 | 28.71 | 28.12 | 0.98 (0.97 to 0.99) |
| Newb | 0.8646 (0.8612 to 0.8678) | 0.1288 | 28.28 | 0.99 (0.98 to 1.00) | |
FIGURE 10.
Calibration of the new ICNARC model compared with the current ICNARC model (2013 recalibration) on patient subgroups. (a) Surgical; (b) non-surgical; (c) planned; and (d) unplanned. a, 2013 recalibration; b, developed in this project.
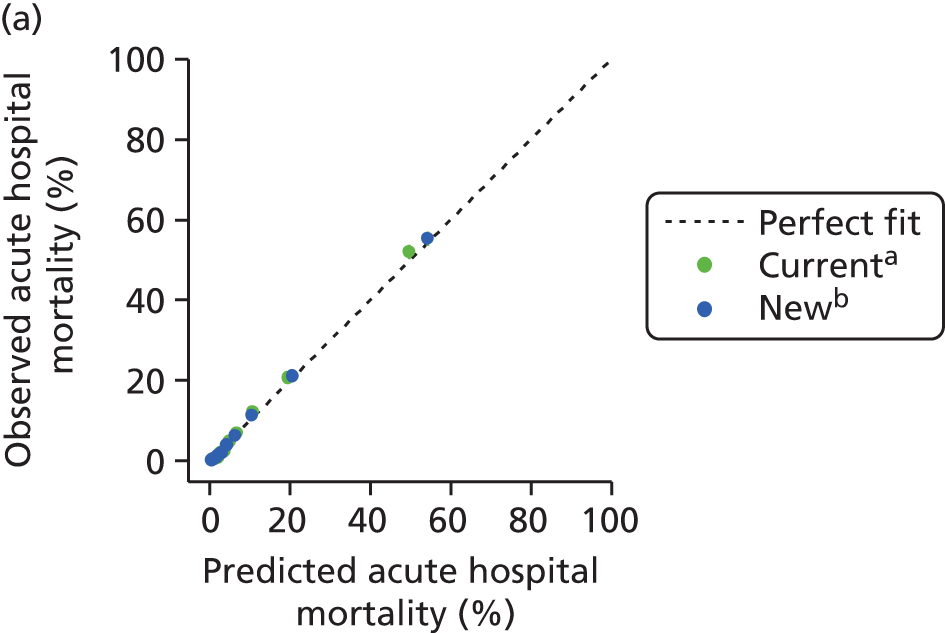
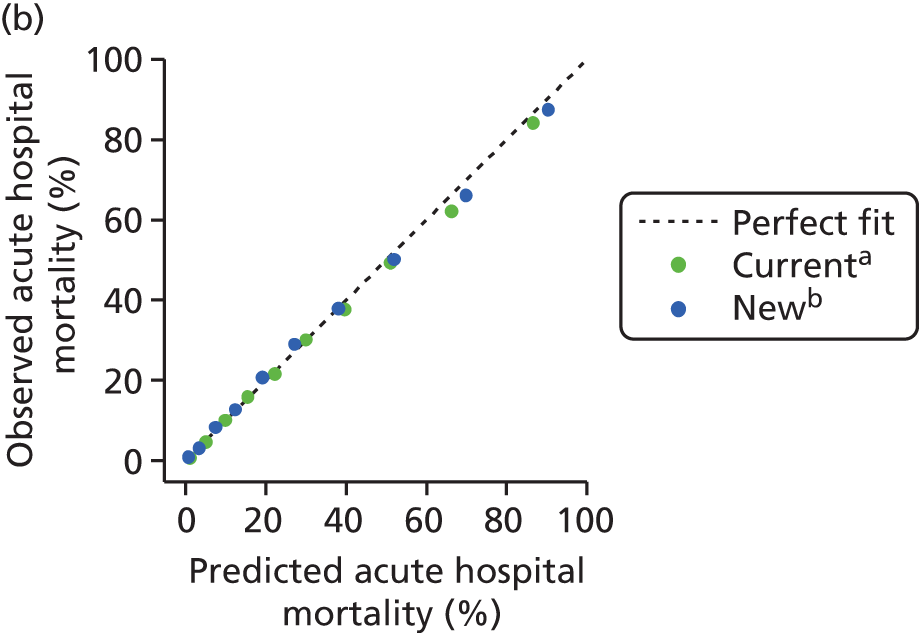
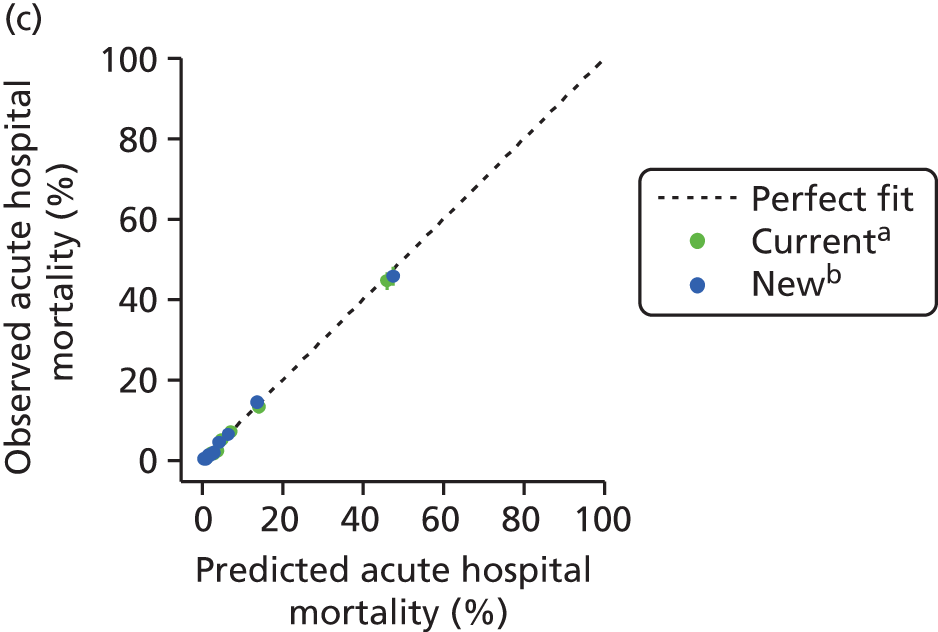
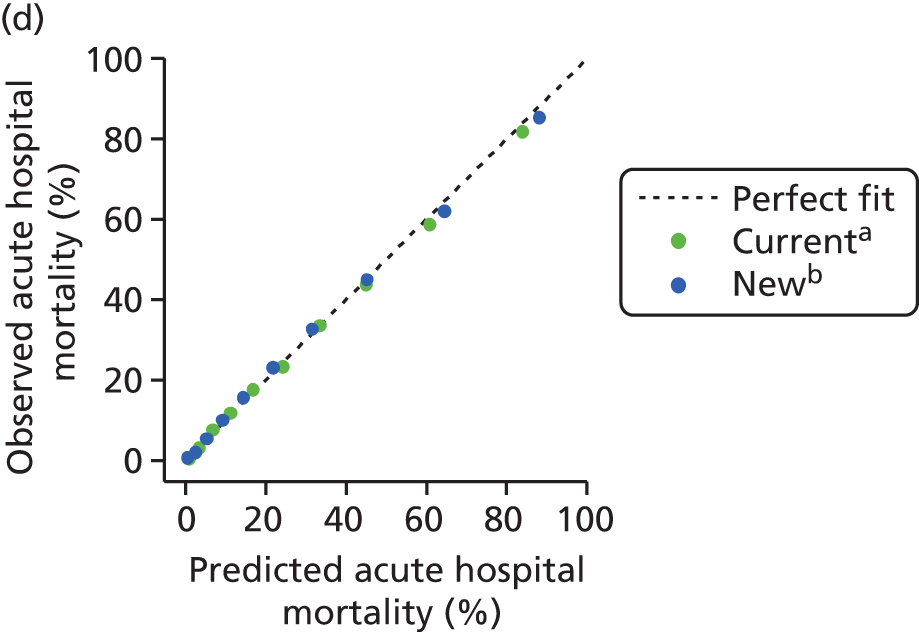
To evaluate the performance of the new ICNARC model in specialist units, it was tested in each type of unit using the January–September 2013 validation data set and was compared with specific, recalibrated versions of the current ICNARC model for these units and, for cardiothoracic critical care units only, the new specific model developed in Chapter 3 of this report (Table 29). The new model showed, in general, a better performance than the specific, recalibrated models. Overall performance improved: the Brier score decreased and discriminative ability showed an increase compared with the specific risk prediction models, except for in the case of cardiothoracic units, where discrimination was similar but calibration was very good (Figure 11). The observed mortality was uniformly lower than the predicted mortality (SMR < 1) in both new and specific recalibrated risk prediction models, except for the new risk model for cardiothoracic critical care units, which gave slightly lower predicted mortality (SMR 1.04), and the new ICNARC model when applied to neurocritical care units, which showed excellent calibration (SMR 1.00). Across all types of unit, the group of admissions with the highest observed mortality had higher predicted risk according to the new model than according to the specific recalibrated models, corresponding to more extreme predictions and a greater spread of predicted risk (Figure 11).
| Model | c-index (95% CI) | Brier score | Predicted mortality (%) | Observed mortality (%) | SMR (95% CI) |
|---|---|---|---|---|---|
| Cardiothoracic critical care units (n = 3200) | |||||
| Currenta | 0.8895 (0.8701 to 0.9088) | 0.0620 | 10.16 | 9.87 | 0.97 (0.87 to 1.07) |
| Specificb | 0.8898 (0.8718 to 0.9079) | 0.0637 | 9.45 | 1.04 (0.94 to 1.15) | |
| Newc | 0.8899 (0.8709 to 0.9088) | 0.0614 | 10.69 | 0.92 (0.83 to 1.02) | |
| Neurocritical care units (n = 9439) | |||||
| Currenta | 0.8453 (0.8363 to 0.8543) | 0.1223 | 24.53 | 22.44 | 0.92 (0.88 to 0.95) |
| Newc | 0.8644 (0.8559 to 0.8728) | 0.1147 | 22.36 | 1.00 (0.97 to 1.04) | |
| Stand-alone high-dependency units (n = 2350) | |||||
| Currenta | 0.8749 (0.8576 to 0.8920) | 0.0957 | 17.84 | 16.59 | 0.93 (0.85 to 1.01) |
| Newc | 0.8986 (0.8830 to 0.9140) | 0.0860 | 17.65 | 0.96 (0.87 to 1.05) | |
FIGURE 11.
Calibration of the new ICNARC model compared with recalibrations of the current ICNARC model in different types of critical care unit. (a) Cardiothoracic critical care units; (b) neurocritical care units; and (c) high-dependency units. a, 2013 recalibration (specific to unit type); b, developed in this project (single model for all unit types).
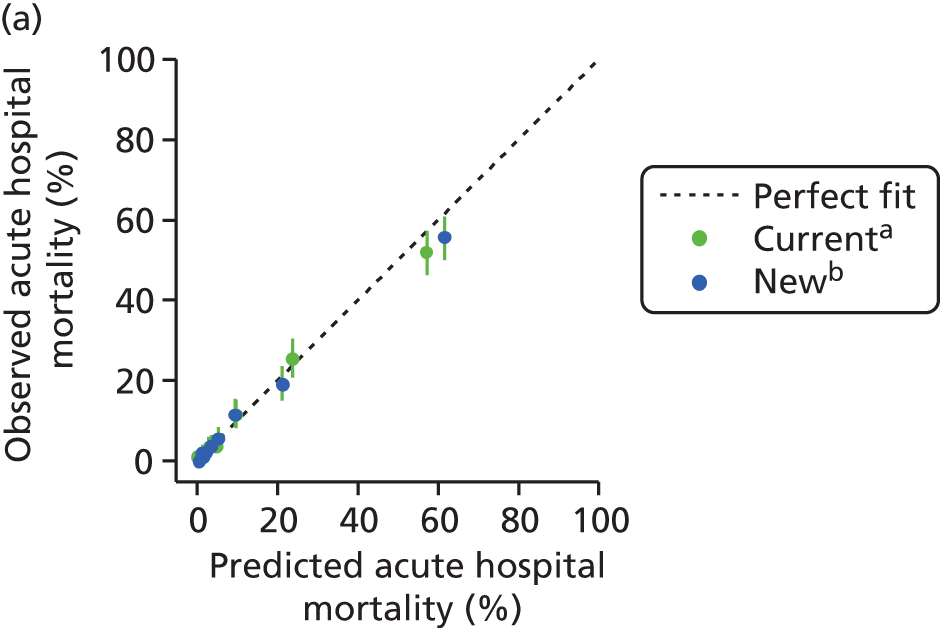
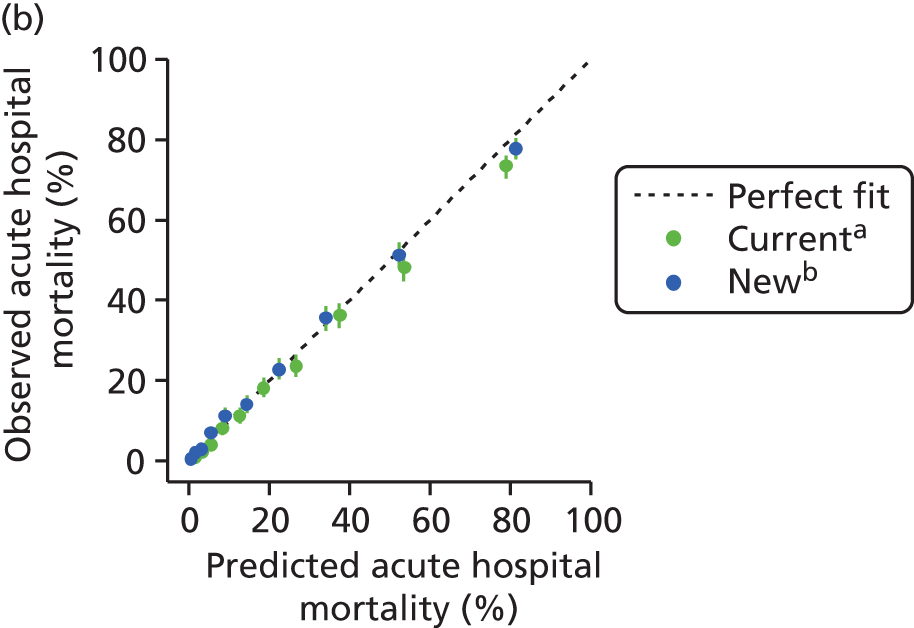
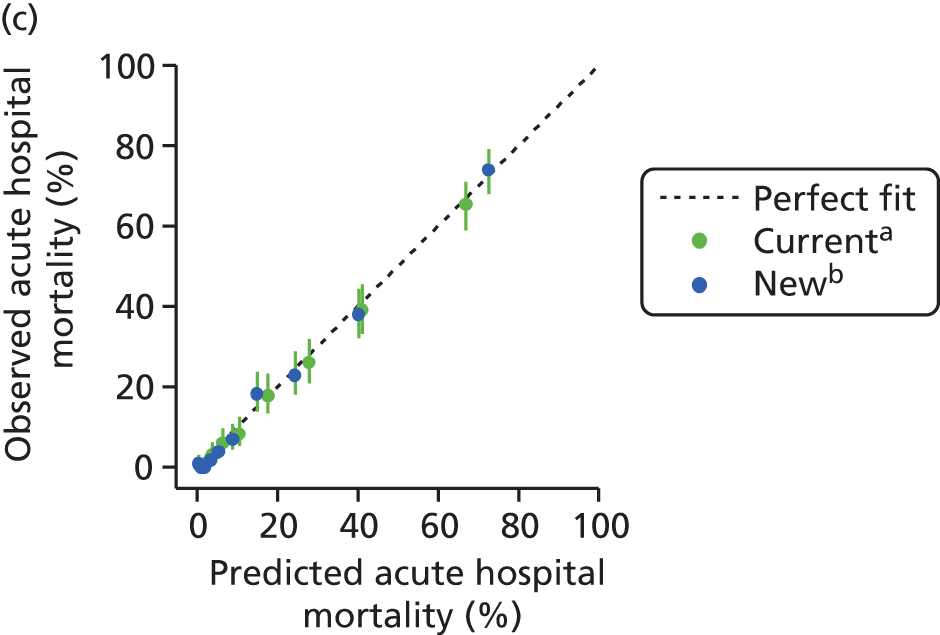
Conclusions
The new ICNARC model showed good discrimination and calibration and had good performance when externally validated using data from a different time period. In addition, it improved the discrimination and reclassification compared with the current model. When validated on specialist units, both discrimination and calibration were close to that of specific recalibrated versions of the current ICNARC model; therefore, use of this single model, which works across general and specialist units, is recommended.
Missing data: risk prediction model application in routine practice
As shown in Table 15, data for all predictors in the model may not be measured and so it is necessary for missing predictor values to be dealt with in order to apply the model to new admissions. Missing values for physiological variables in the current ICNARC model are assumed to be normal on the assumption that, most likely, the test was not required, as the treating clinician expected that the result would be normal. Although this approach is easily applicable in routine practice, it is likely to be biased and only works for categories. In addition, in the CMP there are not standard patterns of missing data (see Table 16) and it is likely that neither are there standard mechanisms for the missingness, so no simple recipe for handling missingness could fit because the appropriate approach may depend on the proportion of missing values, the number of missing predictors and whether or not the predictor with missing values is a strong predictor.
In this section, we compare different approaches for handling missing data across the main missing data patterns in order to evaluate which method of imputation of missing values leads to the most accurate model predictions in the CMP when a risk prediction model is applied to individual patients. As the SMR is used to evaluate the performance of a critical care unit we also explore the impact of handling missing physiological predictors on the SMR and the impact of the location of critical care units on the funnel plot.
Methods
Influence of imputation on model performance
We compared five different, alternative approaches that could be used to deal with missing values in future application of the new ICNARC risk prediction model:
-
multiple imputation by FCS
-
single imputation
-
regression imputation
-
normal/mean imputation
-
submodels for specific patterns.
For the multiple imputation approach, we imputed five values of the missing predictors for each admission. We then calculated five linear predictions from the new ICNARC model for each admission and averaged them using Rubin’s rules. We obtained the predicted probability of acute hospital mortality from this pooled result. This procedure is better than transforming each linear prediction to probability and averaging these five probabilities because the risk is not normally distributed.
Single imputation applied the same technique as the multiple imputation but with only one repetition instead of the five used for multiple imputation and, this time, without the outcome in the imputation model.
For regression imputation, a regression model was built to predict the missing values based on admissions with complete data. The predictor with missing values was considered to be the outcome variable, with all other available data for an admission used as the predictor variables. One of the pitfalls of this approach is the low correlation between predictors, as well as the fact that that predictors were missing simultaneously in related physiological predictors, such as arterial blood gas, blood lactate concentration and laboratory measurements, therefore we needed to use additional variables correlated with the missing physiology in the regression imputation. To avoid the increase of uncertainty, this approach was only considered in the case of isolated missing predictor patterns (blood lactate concentration, urine output and sedated/paralysed/GCS score).
For normal/mean imputation, the missing predictor value was imputed with the mean value of the predictor, estimated from the development data set or the established ‘normal’ value (e.g. score of 15 for GCS).
Unlike the previous four strategies, which impute the missing values in such a way that the original prediction model can be applied, the last strategy (submodels for specific patterns) does not fill in missing values but uses a modified prediction model; that is, a submodel without the unobserved predictors, derived from the development data set. In these submodels, the intercept and regression coefficients of the remaining (observed) predictors are adjusted for the exclusion of the unobserved predictors. This approach was applied to patterns of missingness (all physiology missing, arterial blood gas and laboratory missing, and arterial blood gas missing).
The application data set consisted of the 71,756 admissions in the validation data set with all information available. This data set did not contain any missing predictor values and served as the reference. We then identified the most prevalent missing data patterns in the development data set and used the application data set to create randomly generated missing data using their relative prevalence and the probabilities of having each pattern to mimic the missingness scenarios observed in the development data set.
We estimated the accuracy of the five approaches to handling missing data by quantifying the discrimination and calibration, as well as the overall predicted probability, and both overall and individual units’ SMRs in the admissions with imputed values. For each scenario of missing patterns, we compared the different approaches with the reference situation (as the observed values are known).
Influence of imputation on benchmarking
The predicted risk of mortality for each patient was determined from the new ICNARC model equation. The impact of addressing the missing data on the SMR of the included critical care units (benchmarking) was assessed by calculating the SMRs for each unit and visualising the differences in their locations in a funnel plot of SMR against number of admissions93 according to control limits. Differences were evaluated in terms of the percentage change relative to the reference SMR, as well as differences in the proportion of negative and positive alerts/alarms (i.e. the proportions of critical care units outside the control limits). Imputation strategies of multiple imputation, single imputation and normal/mean imputation were compared with complete case data.
Results
Influence of imputation on model performance
The results of the approaches considered over the different situations are summarised in Tables 30 and 31.
| Approach to missing data | c-index (95% CI) | Brier score | Cox calibration regression | |
|---|---|---|---|---|
| β | α | |||
| All admissions (n = 71,756) | ||||
| Referencea | 0.885 (0.882 to 0.888) | 0.1076 | 0.9499 | –0.0685 |
| Single imputation | 0.884 (0.881 to 0.886) | 0.1082 | 0.9459 | –0.0737 |
| Multiple imputation | 0.885 (0.883 to 0.888) | 0.1075 | 0.9647 | –0.0531 |
| Normal/mean imputation | 0.884 (0.881 to 0.886) | 0.1081 | 0.9526 | –0.0486 |
| Any physiology missing (n = 15,039) | ||||
| Referencea | 0.886 (0.880 to 0.892) | 0.1069 | 0.9614 | –0.0701 |
| Single imputation | 0.880 (0.874 to 0.886) | 0.1092 | 0.9474 | –0.1135 |
| Multiple imputation | 0.888 (0.882 to 0.894) | 0.1062 | 1.0384 | –0.0204 |
| Normal/mean imputation | 0.881 (0.874 to 0.887) | 0.1091 | 0.9751 | –0.0012 |
| All physiology missing (n = 287) | ||||
| Referencea | 0.903 (0.865 to 0.940) | 0.0980 | 0.8839 | –0.3122 |
| Submodel | 0.829 (0.777 to 0.880) | 0.1261 | 0.9615 | –0.1334 |
| Single imputation | 0.888 (0.835 to 0.924) | 0.1048 | 1.0459 | –0.4227 |
| Multiple imputation | 0.908 (0.873 to 0.943) | 0.0988 | 1.3720 | –0.0378 |
| Normal/mean imputation | 0.873 (0.829 to 0.916) | 0.1099 | 1.1193 | 0.2511 |
| Arterial blood gas, blood lactate concentration and laboratory values missing with or without urine output (n = 1584) | ||||
| Referencea | 0.886 (0.867 to 0.903) | 0.1091 | 0.9618 | –0.0492 |
| Submodel | 0.854 (0.833 to 0.874) | 0.1215 | 0.9468 | –0.0642 |
| Single imputation | 0.861 (0.840 to 0.882) | 0.1171 | 0.8799 | –0.2043 |
| Multiple imputation | 0.885 (0.867 to 0.903) | 0.1074 | 1.0871 | 0.0313 |
| Normal/mean imputation | 0.868 (0.847 to 0.889) | 0.1134 | 0.9478 | –0.1240 |
| Arterial blood gas values missing with or without blood lactate concentration (n = 7577) | ||||
| Referencea | 0.883 (0.874 to 0.891) | 0.1070 | 0.9512 | –0.0912 |
| Submodel | 0.866 (0.856 to 0.874) | 0.1160 | 0.9481 | –0.0927 |
| Single imputation | 0.880 (0.871 to 0.889) | 0.1087 | 0.9607 | –0.0774 |
| Multiple imputation | 0.886 (0.877 to 0.894) | 0.1060 | 1.0061 | –0.0308 |
| Normal/mean imputation | 0.881 (0.872 to 0.889) | 0.1083 | 0.9658 | –0.0689 |
| Isolated missing values: blood lactate concentration (n = 742) | ||||
| Referencea | 0.899 (0.868 to 0.910) | 0.1021 | 1.0182 | –0.0984 |
| Regression imputation | 0.894 (0.868 to 0.920) | 0.1031 | 1.0092 | –0.1194 |
| Single imputation | 0.900 (0.868 to 0.910) | 0.1045 | 1.0396 | –0.0375 |
| Multiple imputation | 0.900 (0.870 to 0.911) | 0.1011 | 1.0443 | –0.0450 |
| Normal/mean imputation | 0.900 (0.868 to 0.910) | 0.1013 | 1.0395 | –0.0375 |
| Isolated missing values: urine output (n = 435) | ||||
| Referencea | 0.917 (0.885 to 0.931) | 0.0999 | 1.0919 | 0.1773 |
| Regression imputation | 0.915 (0.885 to 0.943) | 0.1046 | 1.1337 | 0.4590 |
| Single imputation | 0.902 (0.863 to 0.915) | 0.1090 | 0.9105 | –0.1039 |
| Multiple imputation | 0.926 (0.891 to 0.937) | 0.0939 | 1.2090 | 0.1818 |
| Normal/mean imputation | 0.926 (0.888 to 0.934) | 0.0948 | 1.1848 | 0.1571 |
| Isolated missing values: sedated/paralysed/GCS (n = 1131) | ||||
| Referencea | 0.870 (0.859 to 0.894) | 0.1236 | 0.8961 | 0.0340 |
| Regression imputation | 0.864 (0.841 to 0.886) | 0.1265 | 0.8792 | –0.0755 |
| Single imputation | 0.870 (0.855 to 0.893) | 0.1218 | 0.8876 | –0.0584 |
| Multiple imputation | 0.870 (0.860 to 0.894) | 0.1248 | 1.0148 | 0.0379 |
| Normal/mean imputation | 0.859 (0.849 to 0.885) | 0.1325 | 0.9158 | 0.3912 |
| Approach to missing data | Predicted mortality (%) | Observed mortality (%) | SMR (95% CI) |
|---|---|---|---|
| Any physiology missing (n = 15,039) | |||
| Referencea | 23.01 | 22.58 | 0.98 (0.95 to 1.01) |
| Single imputation | 23.62 | 0.98 (0.95 to 1.01) | |
| Multiple imputation | 23.12 | 0.98 (0.95 to 1.01) | |
| Normal/mean imputation | 22.37 | 1.01 (0.98 to 1.04) | |
| All physiology missing (n = 287) | |||
| Referencea | 21.87 | 19.86 | 0.91 (0.70 to 1.12) |
| Submodel | 21.07 | 0.94 (0.72 to 1.16) | |
| Single imputation | 23.44 | 0.85 (0.65 to 1.05) | |
| Multiple imputation | 23.17 | 0.86 (0.66 to 1.06) | |
| Normal/mean imputation | 18.50 | 1.07 (0.82 to 1.32) | |
| Arterial blood gas, blood lactate concentration and laboratory values missing with or without urine output (n = 1584) | |||
| Referencea | 22.94 | 22.73 | 0.99 (0.90 to 1.08) |
| Submodel | 22.98 | 0.99 (0.90 to 1.08) | |
| Single imputation | 24.04 | 0.95 (0.86 to 1.03) | |
| Multiple imputation | 23.13 | 0.98 (0.89 to 1.07) | |
| Normal/mean imputation | 23.68 | 0.96 (0.87 to 1.05) | |
| Arterial blood gas values missing with or without blood lactate concentration (n = 7577) | |||
| Referencea | 22.61 | 22.05 | 0.98 (0.93 to 1.02) |
| Submodel | 22.65 | 0.97 (0.93 to 1.01) | |
| Single imputation | 22.55 | 0.98 (0.94 to 1.02) | |
| Multiple imputation | 22.44 | 0.98 (0.94 to 1.02) | |
| Normal/mean imputation | 22.50 | 0.98 (0.94 to 1.02) | |
| Isolated missing values: blood lactate concentration (n = 742) | |||
| Referencea | 23.79 | 22.64 | 0.95 (0.82 to 1.08) |
| Regression imputation | 23.95 | 0.95 (0.82 to 1.07) | |
| Single imputation | 23.34 | 0.97 (0.87 to 1.07) | |
| Multiple imputation | 23.45 | 0.97 (0.84 to 1.09) | |
| Normal/mean imputation | 23.34 | 0.97 (0.84 to 1.10) | |
| Isolated missing values: urine output (n = 435) | |||
| Referencea | 24.65 | 25.75 | 1.04 (0.88 to 1.21) |
| Regression imputation | 22.31 | 1.15 (1.01 to 1.30) | |
| Single imputation | 26.22 | 0.98 (0.82 to 1.14) | |
| Multiple imputation | 25.34 | 1.02 (0.85 to 1.18) | |
| Normal/mean imputation | 25.42 | 1.01 (0.85 to 1.18) | |
| Isolated missing values: sedated/paralysed/GCS score (n = 1131) | |||
| Referencea | 24.22 | 25.55 | 1.06 (0.95 to 1.16) |
| Regression imputation | 25.44 | 1.00 (0.90 to 1.10) | |
| Single imputation | 23.42 | 1.08 (0.97 to 1.19) | |
| Multiple imputation | 20.02 | 1.01 (0.91 to 1.11) | |
| Normal/mean imputation | 19.86 | 1.28 (1.15 to 1.40) | |
To evaluate a global scenario (admissions that had missing values in any physiology), we compared the three approaches that simultaneously address different patterns of missing data: multiple imputation, single imputation and normal/mean imputation. All approaches were similarly accurate methods for imputation. The c-index for each method was close to the reference, as were the calibration slope and intercept. Correlation between probabilities with imputed and observed data was high (0.96 for multiple imputation, 0.94 for single imputation and 0.94 for normal/mean imputation) and the difference in the means of the predicted probabilities to the reference was minimal and did not affect the overall SMRs. Only normal/mean imputation increased the overall SMR (Table 31).
The strategies were then evaluated across our different missing data scenarios. The proportion of admissions with all physiology missing was small (0.39%) and only two main frequent patterns of missing data were observed: arterial blood gas (PaO2/FiO2, pH, PaCO2), blood lactate concentration and laboratory measurements (urea level, creatinine level, sodium level, WBC count, platelet count) missing with or without urine output (2.13%); and arterial blood gas missing with or without blood lactate concentration (9.43%). Isolated predictors with a relatively high proportion of missing values were blood lactate concentration (1.90%), urine output (0.88%) and sedated/paralysed/GCS score (2.42%).
All physiology missing
A submodel in which no physiological predictors were considered was compared with imputation methods of multiple imputation, single imputation and normal/mean imputation.
All the approaches produced values of the c-index close to the reference value except the submodel without physiology, which gave a lower c-index of 0.82. Only this method had a calibration slope < 1, indicating too optimistic predictions. However, none of the methods resulted in a calibration slope similar to the reference. Except for multiple imputation (calibration intercept 0.03), all the approaches showed insufficient calibration in the large.
The correlation between the predicted probability from the imputed data and from the observed data was lower for single imputation (0.70) and normal/mean imputation (0.67) than for multiple imputation. The means of the predicted probabilities were higher than the reference value for both multiple imputation and single imputation, and therefore the overall SMRs were lower. The opposite was true for normal/mean imputation, which underestimated the risks and therefore increased the SMR.
Arterial blood gas, blood lactate concentration and laboratory values missing with or without urine output
A submodel without arterial blood gas measurements, blood lactate concentration, laboratory measurements and urine output was compared to imputation methods of multiple imputation, single imputation and normal/mean imputation.
The results showed that all methods led to lower c-indices than the reference, but least so with multiple imputation (0.88). Although the submodel had a lower c-index (0.85), it had good calibration in the large (calibration intercept −0.06). Single imputation gave too optimistic predictions (calibration slope 0.88) and was the least well correlated, with predicted probability from the reference values (0.87). Both single imputation and normal/mean imputation overestimated the risk, with a calibration intercept of −0.20 and −0.12 respectively. In addition, both gave mean predicted probabilities higher than the reference and, therefore, lower overall SMRs.
Arterial blood gas missing with or without blood lactate concentration
A submodel without arterial blood gas measurements and blood lactate concentration was compared with imputation methods of multiple imputation, single imputation and normal/mean imputation.
The c-index was close to the reference value in all strategies, but least so for the submodel. The calibration slopes and intercepts were similar, but the best calibrated was multiple imputation. All approaches had a strong correlation with the predicted probability from the reference data, but single imputation had the lowest correlation (0.88) and multiple imputation the highest (0.93). All methods gave a mean predicted probability and overall SMRs close to the reference.
Isolated predictors missing
To deal with isolated missing physiological predictors, we considered using a regression imputation for the three parameters that presented a high proportion of missing values.
-
Blood lactate concentration.
The prediction model applied to blood lactate values imputed from a regression was compared with multiple imputation, single imputation and normal/mean imputation.
The differences in c-index relative to the reference were minimal. All methods led to a good calibration, but the regression approach, on average, overestimated the risk (calibration intercept −0.12), although there was no impact on overall SMR. The overall SMR increased in the rest of the approaches, but the change was negligible. All approaches resulted in an excellent correlation with the reference predicted probabilities.
-
Urine output.
The prediction model applied to urine output values imputed from a regression model was compared with multiple imputation, single imputation and normal/mean imputation.
The four methods showed good discrimination, with a c-index close to the reference, but the regression imputation, on average, underestimated the risk (calibration intercept 0.46) and so increased the overall SMR. Apart from single imputation, the approaches were too optimistic, but the impact on overall SMR was minimal, whereas single imputation decreased the SMR to 0.98.
-
Sedated/paralysed/GCS score.
The prediction model applied to the values of the neurological predictor (indicating whether the patient was sedated or paralysed and sedated for the entirety of the first 24 hours in the critical care unit or, if not, their lowest total GCS score) imputed from a regression model was compared with multiple imputation, single imputation and normal/mean imputation.
While multiple imputation and single imputation led to values of the c-index close to the reference value, regression imputation and mean/normal imputation decreased the c-index to 0.864 and 0.859 respectively. All methods showed good calibration except normal/mean imputation, which underestimated the overall risk (calibration intercept 0.39) and increased the overall SMR to 1.28. Regression imputation and multiple imputation decreased the SMR.
Influence of imputation on benchmarking
When different approaches (single imputation, multiple imputation and normal/mean imputation) were compared, there was no significant difference in overall SMR between the approaches (0.99, 95% CI 0.97 to 1.00; 0.99, 95% CI 0.98 to 1.00; and 0.99, 95% CI 0.98 to 1.00 respectively) or with complete case analysis (0.99, 95% CI 0.97 to 1.00) compared with the reference value (0.99, 95% CI 0.97 to 1.00).
Table 32 and Figure 12 present the critical care unit performance according to original, complete case and imputation approaches. The proportion of critical care units performing above and below expectation, according to 95% control limits, is higher after the imputation approaches but close to the reference, varying from 13 (6.0%), with single and multiple imputation, to 14 (6.5%) with normal/mean imputation. Distribution of the SMRs under each performance category was similar to the reference for all imputation approaches with a high agreement (kappa 0.927, 0.963 and 0.927 for single imputation, multiple imputation and normal imputation respectively). On the other hand, complete case analysis led to a substantially higher number of critical care units performing ‘in control’ [193 (90%) vs. 186 (86.5%) for the reference]. Most of these critical care units shifted from in control (based on complete case) to positive alert after imputation, although complete case still showed a good agreement with the reference (kappa 0.724). No positive alarms were found in the data.
| Approach to missing data | Location of critical care units relative to funnel plot lines, n (%) | ||||
|---|---|---|---|---|---|
| Negative alarm | Negative alert | In control | Positive alert | Positive alarm | |
| Reference | 5 (2.4) | 12 (5.6) | 186 (86.5) | 12 (5.6) | 0 (0) |
| Complete case | 7 (3.0) | 8 (3.7) | 193 (90.0) | 7 (3.0) | 0 (0) |
| Single imputation | 6 (2.8) | 13 (6.0) | 183 (85.6) | 13 (6.0) | 0 (0) |
| Multiple imputation | 5 (2.4) | 13 (6.0) | 184 (85.6) | 13 (6.0) | 0 (0) |
| Normal/mean imputation | 4 (2.0) | 14 (6.5) | 183 (85.0) | 14 (6.5) | 0 (0) |
FIGURE 12.
Funnel plots for alternative approaches to handling missing data in the simulation study for application of the new ICNARC model. (a) Complete case; (b) multiple imputation; (c) single imputation; and (d) normal/mean imputation.
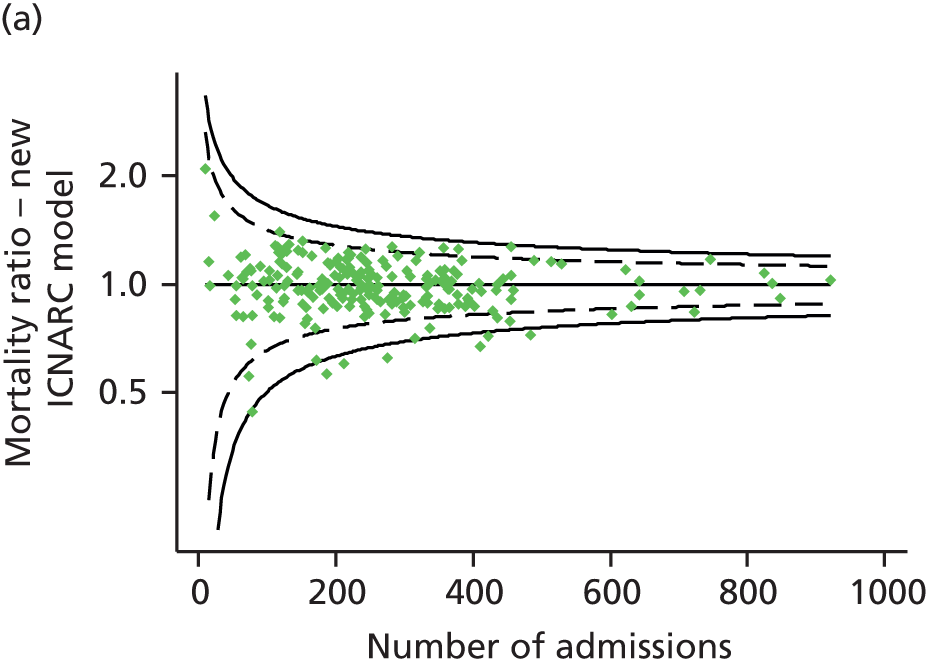
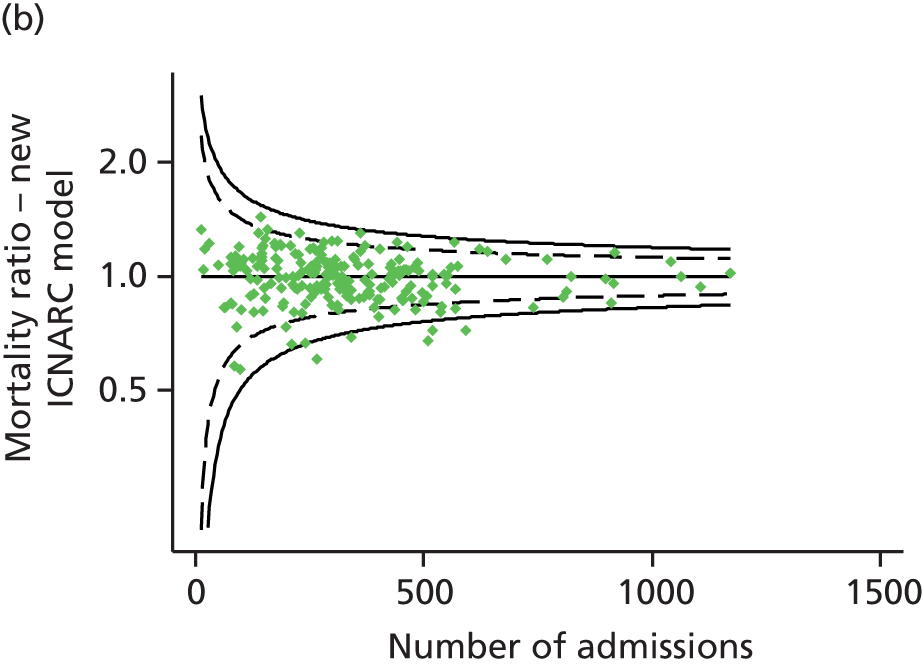
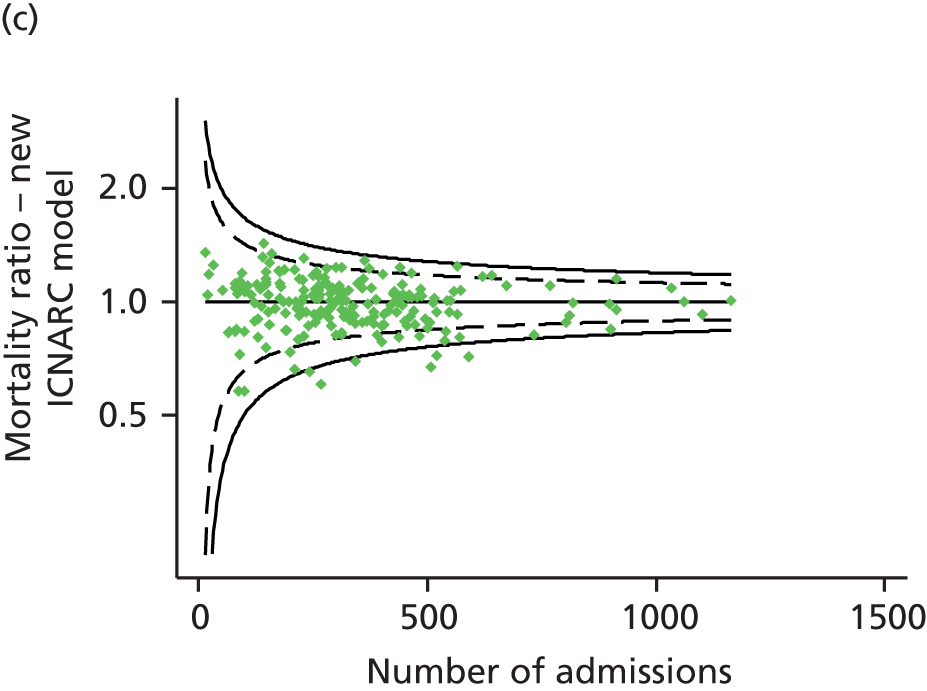
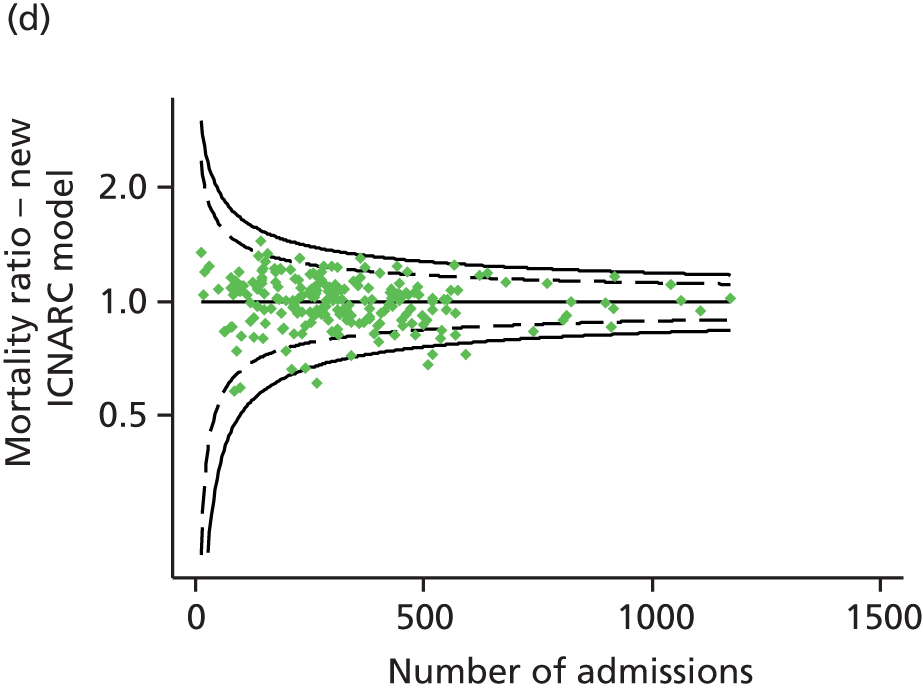
Evaluation with real missing values
Table 33 shows the results when the different approaches (multiple imputation, single imputation, normal/mean imputation and complete case) were applied to the full data set, including missing values. Using the normal/mean imputation strategy, the model showed a c-index of 0.892 (95% CI 0.890 to 0.895) and a calibration slope of 0.980 with a calibration intercept of –0.021. For the single and multiple imputation strategies, the c-index was slightly higher (0.894, 95% CI 0.892 to 0.896, and 0.895, 95% CI 0.892 to 0.898 respectively) with a similar calibration slope (0.979 and 0.988 respectively) and small difference in calibration intercept (−0.061 and −0.051 respectively). Under our ‘real’ scenario, the imputation of missing predictors prevented a drop of 0.01 in the c-index compared to a complete case approach (0.885, 95% CI 0.882 to 0.888). This 0.01 drop in the c-index may be considered to be a relevant decrease in the accuracy of predicted risks of individual patients because the c-index is relatively insensitive.
| Approach to missing data | c-index (95% CI) | Brier score | Cox calibration regression | Predicted mortality (%) | Observed mortality (%) | SMR (95% CI) | |
|---|---|---|---|---|---|---|---|
| β | α | ||||||
| Complete case (n = 71,756) | 0.885 (0.882 to 0.887) | 0.107 | 0.949 | –0.068 | 22.94 | 22.63 | 0.99 (0.97 to 1.00) |
| Single imputation (n = 90,107) | 0.894 (0.891 to 0.896) | 0.100 | 0.979 | –0.061 | 21.92 | 21.48 | 0.98 (0.97 to 0.99) |
| Multiple imputation (n = 90,107) | 0.895 (0.892 to 0.897) | 0.100 | 0.988 | –0.051 | 21.89 | 0.98 (0.97 to 0.99) | |
| Normal/mean imputation (n = 90,107) | 0.893 (0.890 to 0.895) | 0.101 | 0.980 | –0.021 | 21.52 | 1.00 (0.99 to 1.01) | |
Observed acute hospital mortality was 22.6% for the complete case admissions, in contrast to the predicted mortality of 22.9%, giving an SMR of 0.99 (95% CI 0.97 to 1.00). With the imputation approaches (single, multiple and normal/mean imputation), observed mortality was 21.48%, with predicted mortality 21.92%, 21.89% and 21.52%, respectively, for SMRs of 0.98 (95% CI 0.97 to 0.99), 0.98 (95% CI 0.97 to 0.99) and 1.00 (95% CI 0.99 to 1.01 respectively).
Table 34 and Figure 13 show the critical care unit performance relative to control limits for the complete case and imputation approaches in order to evaluate their impact on benchmarking when applied to the ‘real’ scenario. The proportions of critical care units with SMRs below 1 according to 95% and 99.8% control limits were similar for all approaches, including complete case. In contrast to what the simulation results showed, the proportion of critical care units with positive alert was higher based on complete case and normal/mean imputation and lower after single and multiple imputation approaches. Most of the shifts were from positive alert (based on complete case) to in control after imputation, although three critical care units remained as positive alert after normal/mean imputation. No positive alarms were found in the data.
| Approach to missing data | Location of critical care units relative to funnel plot lines, n (%) | ||||
|---|---|---|---|---|---|
| Negative alarm | Negative alert | In control | Positive alert | Positive alarm | |
| Complete case (n = 71,756) | 5 (2.3) | 12 (5.6) | 186 (86.5) | 12 (5.6) | 0 (0) |
| Single imputation (n = 90,107) | 6 (2.8) | 11 (5.1) | 193 (90) | 6 (2.8) | 0 (0) |
| Multiple imputation (n = 90,107) | 5 (2.3) | 12 (5.6) | 192 (89.3) | 6 (2.8) | 0 (0) |
| Normal/mean imputation (n = 90,107) | 5 (2.3) | 11 (5.1) | 189 (87.9) | 10 (4.7) | 0 (0) |
FIGURE 13.
Funnel plots for alternative approaches to handling real missing data in the application of the new ICNARC model. (a) Complete case; (b) multiple imputation; (c) single imputation; and (d) normal/mean imputation.
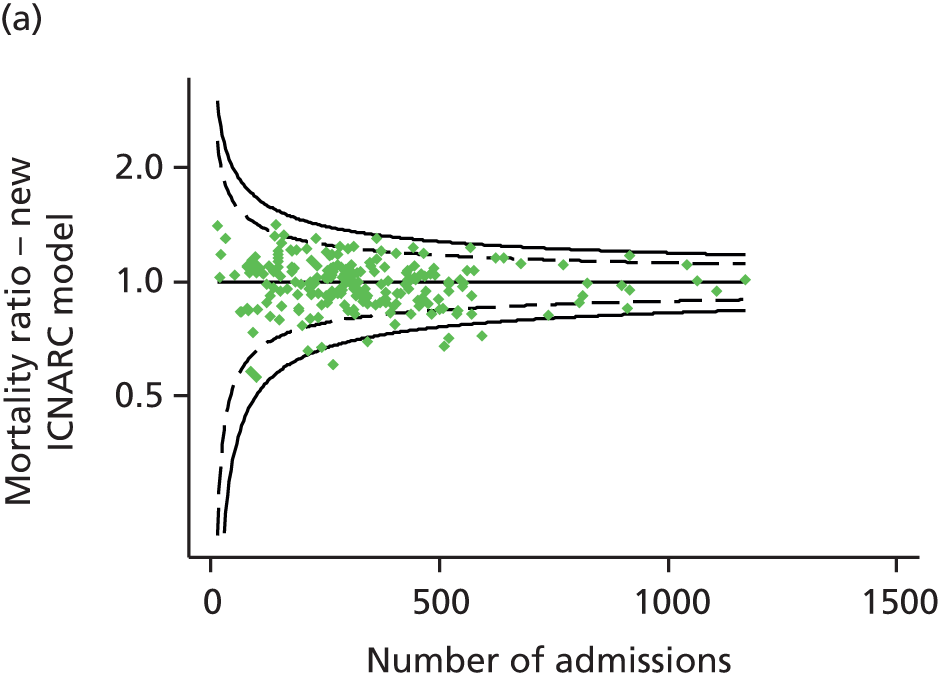

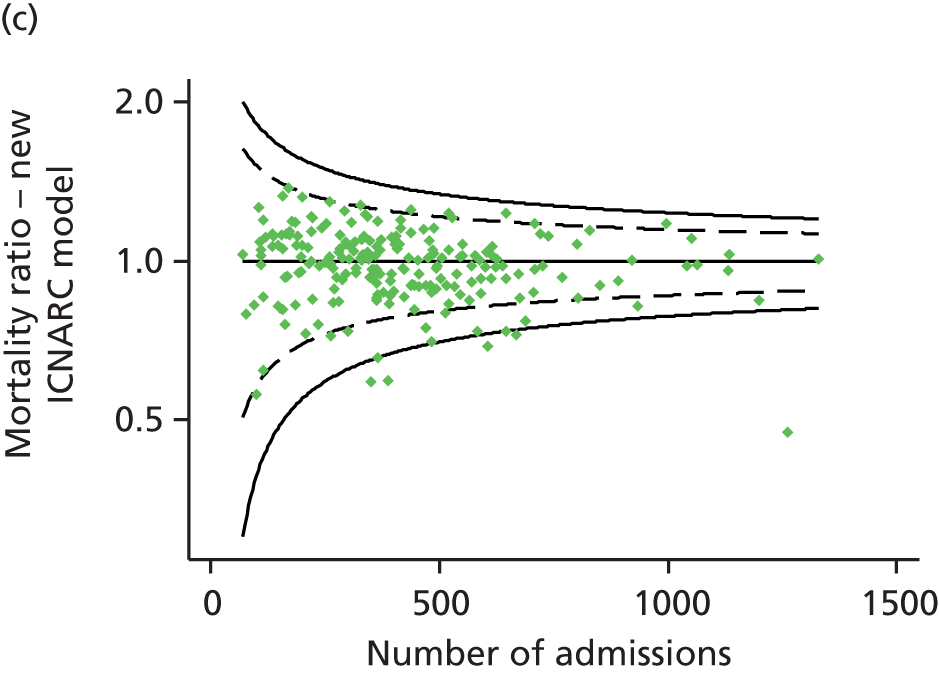
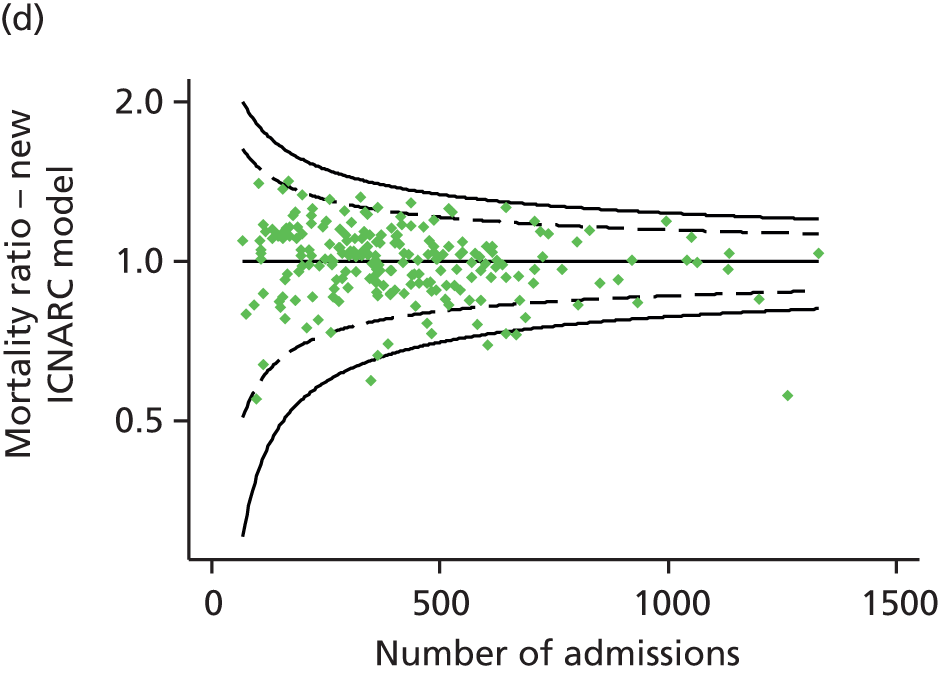
Conclusions
The similarity of multiple imputation, single imputation and normal/mean imputation on the global results suggests a low impact of missing data on the overall outcomes. The differences in the means of the predicted probabilities to the reference were also minimal so will not affect the overall SMR in a large data set. The difference in performance between multiple imputation and single imputation suggests that repetition is an important component if the approach is to use imputed values; we therefore reject any further consideration of single imputation.
The multiple imputation approach was usually the most accurate method of imputation. However, imputation of normal/mean values demonstrated comparable accuracy in addressing isolated missing physiological predictors, except when imputing sedated/paralysed/GCS score, for which multiple imputation was the best approach. Regression methods for imputing isolated missing values were not the best approach and actually normal/mean imputation performed better in that situation.
When the number of missing predictors was high, the quality of the imputed values was not as good and the imputed values required careful evaluation. If the missing values were in strong predictors, multiple imputation resulted in a c-index that was close to the reference value, whereas all other methods, including a specific submodel, led to an underestimated c-index. In theory, using submodels derived from the development data set that contain only the available predictors could give better discrimination than imputing missing values; however, this is less likely if a strong predictors is missing, because any submodel without the predictor loses discriminative ability. In addition, if those risk-increasing predictors are ignored, then all the predicted risks are lower.
Differences between imputation methods depend not only on the number of missing values but also on the number of predictors missing and their importance in the model. Apparently the discriminative ability of the model was based on one particularly strong predictor (sedated/paralysed/GCS score) and the physiology and that is why when we have fewer missing values in these factors we recover information and improve the accuracy.
The lack of consistency of the approaches under different situations is an important finding, suggesting that there is no standard missing-value mechanism and thus no simple method for handing missing values when a model is applied.
For missing data at the point of model application, we could conclude that multiple imputation is the best approach for addressing patterns of missing predictors (i.e. when missing values occur simultaneously in multiple predictors) and normal/mean imputation for isolated missing predictors. Regression-based approaches showed the worst results and submodels lost discriminative ability and accuracy because of the importance of the missing factors in the risk prediction model. In order to be able to apply the model to a new single admission (or small number of admissions) with missing data, in which case multiple imputation is not feasible, normal/mean imputation is likely to be the best approach.
In a simulation study, we found that complete case analysis led to a substantially lower number of providers performing statistically above or below the national average. This may indicate that complete case analysis fails to detect statistically significant outliers (negative and positive alerts), increasing the proportion identified as ‘in control’.
Missing physiological values may lead to underestimation of predicted mortality; therefore, the number and type of missing variables should be taken into consideration when assessing the performance of a critical care unit. However, when represented using funnel plots, the impact of missing data was no longer evident. In a large data set, the impact of missing data could be minimal and not affect the SMR.
Discussion
We have developed a new ICNARC model that outperforms the most recent recalibration of the current ICNARC model on measures of discrimination, calibration and overall fit. Furthermore, the new ICNARC model works well across all different types of critical care units participating in the CMP, performing as well as, or better than, specific versions of the current ICNARC model recalibrated according to type of unit.
We have demonstrated that in this setting, development of the risk prediction model using complete case data produces equivalent estimates of model coefficients to those from multiply imputed data. For application of the model to future data, we recommend that multiple imputation provides the most reliable estimates of critical care unit performance. However, under most circumstances single imputation of mean/normal values produced similar results and is likely to be the most appropriate method to allow the model to be applied to smaller cohorts of patients where multiple imputation is not feasible.
For modelling continuous physiological predictors, we found that the best approach was restricted cubic splines. For most predictors, four knots were sufficient to adequately model the predictor–outcome relationship; this is equivalent to a model with only four categories in terms of model parameters, but offers a much more flexible approach and better fit to the data. The improved discrimination of the new model compared with the previous ICNARC model may be due, in part, to the use of continuous non-linear modelling of the physiological predictors. This observation further highlights the importance of appropriate functional forms for continuous variables when developing risk prediction models. Harrell84 and Steyerberg et al. 43 describe approaches for selecting the optimal functional form; we, however, propose a more flexible approach by using a smoothed curve (running line smoother) to establish the reference curve, comparing restricted cubic spline, fractional polynomial and simple parametric forms to approximate the reference curve and using the model fit information (AIC, BIC) to select the best functional form, continuing to recheck and, if necessary, to refine the functional form at each step of the multivariable regression modelling process. The reason for these extensions is that non-linear approaches may not represent the underlying shape of the relationship between a continuous predictor and the outcome in certain situations, and so we should avoid blindly using them without checking the appropriate reference curves.
Another key finding from the present work is that the incorporation of new variables contributed to the model performance. No previous model has included lactate level among the assessed predictors, despite published information about its independent prognostic impact. 59,60 Dependency prior to admission was found to be an important predictor, and we continue to adjust for the prognostic impact of the patient’s location prior to admission to the critical care unit while now additionally combining information on admission type (to distinguish, for example, planned from unplanned admissions following elective surgery). This significant combination of information suggests that source and type of admission have a simultaneous effect on mortality. It is interesting to note that we did not observe improved model performance when including deprivation, despite a previously reported association with mortality for admissions to UK critical care units. 70 Similarly, although BMI has been shown to be related to outcome in critically ill patients,69 we found that, while statistically significant, it did not contribute substantively to the model’s predictive performance.
Although pupil reactivity was found to be a potentially important predictor, it had considerably more missing values than the predictor currently used to assess neurological status (16.2% and 3.5%, respectively), so we decided not to incorporate it into the model. However, we recommend a focus on improving the availability and recording of this predictor in order to reassess its inclusion in future.
The reason for admission to the critical care unit is an important variable in predicting mortality, even when previous health status and the degree of acute physiological dysfunction are similar. 94 By utilising the hierarchical nature of the diagnostic coding within the data set, we have developed a categorisation of reasons for admission based on the body system and pathological/physiological process that provides similar prognostic information with fewer model coefficients than in the previous ICNARC model, reducing the risk of overfitting. As with any risk prediction model designed to work across the heterogeneous case mix of patients admitted to critical care, there will inevitably be individual conditions where this categorisation does not work well. Where sufficient data on an individual condition were available to demonstrate significantly different outcomes than for the system/process category, a separate coefficient was assigned. However, other conditions that clinical experience dictates are associated with higher or lower mortality will remain within the broader categories. With regard to these, it should be emphasised that the goal of the modelling was to develop a model that works well across cohorts of critically ill patients and not for individual prognostication.
We found that the relationship between physiology and mortality is different in some chronic conditions than others, suggesting that the untoward effects of physiological derangement are greater in certain underlying medical conditions. In addition, the finding that the physiology–mortality relationship varied with reason for admission indicates that the same is true of acute conditions.
A key advantage of the new modelling approach is that it considered the physiological predictors separately from a combined risk score. This feature allowed us to analyse not only individual physiology–mortality relationships, but also the interactions between these and other covariates. In the previous ICNARC model, the use of interactions between the physiology score and diagnostic category produced better fit within individual diagnostic groups and answered the question of whether physiological conditions contribute equally to mortality in all critically ill patients or whether specific individuals or groups are disproportionately affected. 14 In the present work, however, the question regarded whether these physiological abnormalities just reflect the severity of the illness or contribute independently to mortality. The ability to analyse this relationship independently of a common score allowed us to identify which physiological predictors are the most relevant for outcome for different underlying conditions or reasons for admission.
We also investigated the potential for interactions between age and physiological predictors, but these were not found to improve the model’s performance compared with simpler model formulations. In other words, the increased risk of death associated with older age is more strongly associated with age itself than with age-related factors specific to individual physiological abnormalities. Nevertheless, a potential factor that may be taken into account for improvements in model performance is the presence of comorbid conditions that are more likely to be observed in older than younger patients.
There is a consensus that all of the many suggested model-building strategies have weaknesses,95 but opinions on the relative advantages and disadvantages of particular strategies differ considerably. We consider one of the strengths of the presented model to be the rigor of variable selection and the statistical methods applied to avoid overfitting the models to the study population. In this study, different statistical approaches were explored and compared in order to derive the best prediction model. Instead of basing the variable selection on univariable analyses or automated model-selection procedures, we employed a method combining clinical experience and judgement with computer-based statistics. We designed an approach to select the set of well-established predictors that were making an important contribution to the model with subsequent addition of interaction terms with physiological variables, while controlling for overfitting, complexity and incremental predictive accuracy. Because the physiological and non-physiological predictors, underlying conditions and the potential interactions play different roles in both model structure and contribution to the model, we propose a multistage process with particular decisions and evaluations instead of selection based on a single standard criterion. There are many theoretical reasons why an automatic process may perform poorly in selecting predictors. 96 In this case some subjective influence over which variables are selected may be preferred. Because of multiplicity, many spurious interactions may be identified by any modelling approach; therefore, selecting from pre-specified interactions is recommended. Interactions should also be checked for consistency with subject matter knowledge, where available. Relevance of a specific factor must, however, be evaluated with regards to its relationship to the goal of developing an accurate risk prediction model; this requires the selection of a relevant subset of predictors while ignoring those predictors that do not improve model performance. Although predictive models may be used to provide insight into causality of pathophysiology of the outcome, causality is neither a primary aim nor a requirement for variable inclusion. Our purpose was to derive the best risk model for prediction using the available information rather than to identify individual predictors with clinical relevance to the outcome, and so internal and external model validation rather than inspection of features for clinical plausibility was the appropriate approach for evaluating our results.
One limitation of our approach is that the use of continuous non-linear modelling of physiology and interaction terms no longer has the user-friendly by-product of a simple severity of illness score. Because our goal was to develop an improved and updated risk model to predict acute hospital mortality, we favoured superior discrimination and calibration over simplicity of calculation. As a consequence, the model is relatively complex to calculate, and we would certainly not recommend calculation by hand; however, the calculations can be easily implemented in software and only 28 raw data fields are required for the new ICNARC model. With developments in computing technology, risk predictions are more likely to be calculated automatically by clinical information systems or using stand-alone applications on mobile technology, and methods should no longer be constrained by a need for calculation to be possible using pencil and paper. Existing scores, such as the ICNARC Physiology Score14 or APACHE III Acute Physiology Score,10 continue to be useful summary measures of severity of illness and a further such measure is not required.
True external validation of the model using independently collected data is extremely difficult within the UK because of the extremely high coverage of the CMP. Our primary purpose has always been to underpin the risk-adjusted outcomes reported for the CMP. If the model is to be used in other settings, we recommend first validating the model and then recalibrating it if necessary before more widespread adoption. It is also worth noting that, while the new model outperformed the previous ICNARC model when temporally validated, it has not been directly compared against the latest versions of other risk prediction models such as the APACHE IV,97 SAPS 382 and MPM0-III models. 98
Chapter 5 Development and validation of risk prediction models to predict outcomes following in-hospital cardiac arrest
Introduction
The NCAA was established in 2009 as the national clinical audit for in-hospital cardiac arrest, a joint initiative between the Resuscitation Council (UK) and ICNARC. The aims of the audit are to improve patient outcomes, decrease the incidence of avoidable cardiac arrests, decrease the incidence of inappropriate resuscitation and promote adoption and compliance with evidence-based practice. The key patient outcomes monitored by the audit are return of spontaneous circulation (ROSC) sustained for more than 20 minutes and survival to hospital discharge (hospital survival). However, prior to this project, no validated risk prediction models existed for predicting these outcomes following in-hospital cardiac arrest.
This chapter reports the development and validation of risk prediction models to predict these outcomes following in-hospital cardiac arrests attended by a hospital-based resuscitation team in NHS hospitals. These risk prediction models will underpin comparative reporting for the NCAA, to promote consistent delivery of high-quality resuscitation and best outcomes for patients following cardiac arrest in NHS hospitals across the UK.
Methods
Inclusion and exclusion criteria
For the NCAA, data are collected for all individuals (excluding neonates) receiving chest compressions and/or defibrillation and attended by a hospital-based resuscitation team (or equivalent) in response to a 2222 call (2222 is the telephone number used to summon a resuscitation team in UK NHS hospitals). 16
For development of the risk prediction models, data were extracted for all individuals meeting the scope of the NCAA with a date of 2222 call between 1 April 2011 and 30 September 2012. Data for individual hospitals were included if the hospital had commenced participation in the NCAA prior to April 2012 and had validated data for at least 6 months. Individual team visit records meeting any of the following criteria were considered ineligible for inclusion in the risk prediction models: the arrest occurred before the patient’s arrival at hospital (even if the patient was subsequently attended by a hospital-based resuscitation team, usually in the emergency department, and, therefore, met the scope of the NCAA); second and subsequent visits to the same patient during the same hospital stay; a ‘do not attempt cardiopulmonary resuscitation’ (DNACPR) was already documented in the patient’s notes. The following exclusion criteria were applied to individual team visit records: the patient’s last known status was still in hospital; either of the outcomes of ROSC > 20 minutes or hospital survival was missing; and data for the candidate predictors were missing.
For validation of the risk prediction models, data were extracted for all individuals in hospitals that contributed data to the development data set with a date of 2222 call between 1 October 2012 and 31 March 2013, and for all individuals in hospitals that commenced participation in the NCAA between April and September 2012 (and therefore did not contribute data to the development data set), with a date of 2222 call between 1 April 2012 and 31 March 2013. The same eligibility and exclusion criteria were applied at the individual team visit level as for the development data set.
Outcomes and candidate predictors
Risk prediction models were developed for two outcomes: ROSC > 20 minutes and hospital survival. Patients were followed up to discharge from the original acute hospital and any patients transferred to another acute hospital were reported as hospital survivors.
A list of candidate predictors was established from the data set developed and collected for the NCAA. A valid predictor was considered to be any variable collected either prior to or at the time of the arrival of the hospital-based resuscitation team and not related to the quality of care (e.g. whether or not the appropriate resuscitation was delivered). If factors related to the quality of care were included within the risk prediction model, then the expected number of events would be adjusted to account for these factors. Consequently, a poorly performing provider would not be identified as an outlier and these discrepancies in the quality of care would not be recognised.
The full list of candidate predictors is presented in Table 35. Location of arrest was not considered to be a predictor for patients with a reason for admission to/attendance at/visit to hospital of ‘staff’ or ‘visitor’. Prior to any modelling, candidate predictors were examined for data completeness and distribution. Where categories with very few patients were identified, combining with other categories eliminated these. Multicollinearity between candidate predictors was assessed using variance inflation factors.
| Candidate predictor | Approach to modelling |
|---|---|
| Age | Restricted cubic splines with five knots |
| Sex | Categorical (male; female) |
| Length of stay in hospital prior to 2222 call | Categorical (0 days; 1 day; 2–7 days; 8–30 days; > 30 days) |
| Reason for admission to/attendance at/visit to hospital | Categorical (patient – medical; patient – trauma; patient – elective surgery; patient – emergency surgery; patient – obstetric; outpatient; staff; visitor) |
| Location of arrest | Categorical (ED; EAU; ward; obstetric area; intermediate care area; CCU; HDU; ICU or ICU/HDU; PHDU; PICU; specialist treatment area; imaging department; cardiac catheter laboratory; theatre and recovery; other inpatient location; clinic; non-clinical area) |
| Patient deteriorating (not yet arrested) at team arrival | Binary (yes; no) |
| Presenting/first documented rhythm | Categorical (VF; VT; shockable – unknown rhythm; asystole; PEA; bradycardia; non-shockable – unknown rhythm; unknown) |
Age was modelled as a continuous, non-linear relationship using restricted cubic splines with five knots. All other candidate predictors were modelled as categorical variables. After examining plots of the distribution and the association with the outcomes, the continuous predictor length of stay in hospital prior to 2222 call was categorised as 0 days (i.e. cardiac arrest on the same calendar day as admission to/attendance at/visit to hospital), 1 day, 2–7 days, 8–30 days and > 30 days.
Model development
An initial, full model for each outcome was fitted, including all candidate predictors, using multilevel logistic regression with random effects of hospital. The basis for using multilevel models is that, as with the majority of health outcomes, there is ‘clustering’ at the level of health-care providers; that is, outcomes for patients within the same hospital will be, on average, more similar than outcomes for patients in different hospitals. If clustering is ignored, then the resulting model estimates will have standard errors that are too small, contributing to the potential for misleading conclusions.
These models were then simplified in three stages: first, by testing for non-linearity in the relationship for age; second, by testing for differences between pre-specified combinations of categories of predictors to reduce the numbers of categories; and, third, by stepwise reduction of the models to reduce the number of predictors. Combining categories of predictors was conducted in such a way as to ensure the same categories were used in the models for both outcomes. This was achieved by combining categories if the difference in outcome between the categories (adjusted for all other predictors) was non-significant (p > 0.1) for both outcomes. The combinations considered were:
-
Prior length of stay: adjacent categories.
-
Location of arrest:
-
adjacent categories from: emergency department; emergency admissions unit; ward, obstetric area or other inpatient location; intermediate care area; coronary care unit; high-dependency unit or paediatric high-dependency unit; intensive care unit, combined high-dependency/intensive care unit or paediatric intensive care unit
-
any combination of categories from: specialist treatment area; imaging department; cardiac catheter laboratory; and, if no difference was found between any of the three previous categories, theatre and recovery
-
categories for clinic and non-clinical area.
-
Stepwise reduction was conducted separately for the two outcomes, allowing the models for ROSC > 20 minutes and hospital survival to include different combinations of predictors. At each step, the least significant predictor was removed and the reduced model assessed for discrimination (c-index22), calibration (Hosmer–Lemeshow test24), accuracy (Brier score28 and Shapiro’s R29) and model fit (AIC99). Stepwise reduction was continued until all predictors had been removed and a model was selected to balance simplicity against model performance.
Finally, the models were further enhanced by the consideration of interactions between predictors. The interactions considered were pre-specified following presentation of an initial model with no interaction terms and a request for input from the NCAA Steering Group, representatives from hospitals participating in the NCAA, and the Expert Advisory Group. The interactions considered were:
-
age with sex
-
age with reason for attendance
-
age with presenting rhythm (non-shockable rhythms compared with shockable or unknown)
-
location of arrest with presenting rhythm.
Interaction terms were added to the full model and retained if significant at p < 0.01. For the interaction of location of arrest with presenting rhythm, in order to reduce the potentially large number of interaction terms, combining interaction terms for similar groups of categories of both presenting rhythm (e.g. all shockable arrests, all non-shockable arrests) and location of arrest (e.g. emergency department and emergency admissions unit, emergency admissions unit and ward, coronary care unit and cardiac catheter laboratory) was considered.
Comparisons of models (for testing linearity, combining categories, stepwise reduction and adding interactions) were performed with likelihood ratio tests.
Model validation
The resulting models were validated for discrimination, calibration and accuracy in (1) the development data set; (2) the full validation data set; and (3) the validation data from hospitals that commenced participation in the NCAA from April 2012 onwards not included in the development data set (providing true external validation in a smaller sample of hospitals). To reduce overfitting, model estimates were shrunk using the uniform (heuristic) shrinkage method of Van Houwelingen and Le Cessie. 100
Discrimination was assessed by the c-index. 22 Calibration was assessed graphically and tested using the Hosmer–Lemeshow test for perfect calibration in 10 equal-sized groups by predicted probability of survival. 24 As the Hosmer–Lemeshow test does not provide a measure of the degree of miscalibration and is very sensitive to sample size,25,26 calibration was also assessed using Cox’s calibration regression. 27 Accuracy was assessed by the Brier score28 and Shapiro’s R,29 and the associated approximate R2 statistics. 30 Measures of model performance were calculated using the marginal predicted probabilities from the risk prediction model (i.e. without taking into account hospital-level effects) to represent the predicted probability of survival for a patient with the given characteristics in an ‘average’ hospital.
The final risk prediction models were refitted to all data (development and validation data sets combined) to maximise precision and generalisability, with shrinkage applied to reported coefficients.
Statistical analyses were performed using Stata/SE, version 10.1 (StataCorp LP, College Station, TX, USA).
Results
Available data
Between 1 April 2011 and 31 March 2013, 148 hospitals participated in the NCAA. During this time there were a total of 28,987 resuscitation team visits following 2222 calls for cardiac arrest reported to the NCAA. After excluding data that were still undergoing central validation (at the level of calendar months within hospitals) and hospitals with less than 6 months’ data, 27,998 team visits in 143 hospitals were included (Figure 14). After removing records that were ineligible for risk predictions (pre-hospital arrests, second and subsequent visits to the same patient and patients with a documented DNACPR decision) and those excluded for missing data, a total of 22,479 team visits in 143 hospitals were included: 14,688 (65.3%) in the development data set and 7791 (34.7%) in the validation data set. Rates of missing data were very low, with only 0.1% of patients excluded from the development data set (0.1% from the validation data set) because of missing predictor variables and 0.1% (0.8% from the validation data set) because of missing outcomes, and it was therefore not necessary to consider more complex statistical methods for handling missing data. The breakdown of exclusions in the development data set, the validation data set and the external validation data set (the subset of the validation data set from hospitals not included in the development data set) are shown in Table 36, and characteristics and outcomes are summarised in Table 37.
FIGURE 14.
Participation of hospitals in the NCAA, 1 April 2011 to 31 March 2013.

| Characteristic | Development | Validation | External validation |
|---|---|---|---|
| Number of hospitals | 122 | 143 | 21 |
| Total number of resuscitation team visits following 2222 calls for cardiac arrest | 18,304 | 9694 | 1819 |
| Excluded (ineligible), n (% of table) | 3580 (19.6%) | 1840 (19.0%) | 124 (6.8%) |
| Pre-hospital arrests | 2666 (14.6%) | 1283 (13.2%) | 33 (1.8%) |
| Second and subsequent visits to the same patient | 533 (2.9%) | 315 (3.2%) | 58 (3.2%) |
| Documented DNACPR decision | 381 (2.1%) | 242 (2.5%) | 33 (1.8%) |
| Eligible patients | 14,724 | 7854 | 1695 |
| Excluded (missing data), n (% of eligible) | 36 (0.2%) | 63 (0.8%) | 38 (2.2%) |
| Last known status still in hospital | 7 (< 0.1%) | 1 (< 0.1%) | 0 (0%) |
| Missing ROSC > 20 minutes | 5 (< 0.1%) | 58 (0.7%) | 37 (2.2%) |
| Missing hospital outcome | 2 (< 0.1%) | 0 (0%) | 0 (0%) |
| Missing predictorsa | 22 (0.1%) | 4 (0.1%) | 1 (0.1%) |
| Included, n (% of eligible) | 14,688 (99.8%) | 7791 (99.2%) | 1657 (97.8%) |
| Characteristic | Development (N = 14,688) | Validation (N = 7791) | External validation (N = 1657) |
|---|---|---|---|
| Age, mean (SD) | 72.6 (16.4) | 72.9 (16.3) | 72.8 (16.3) |
| Sex male, n (%) | 8422 (57.3) | 4467 (57.3) | 970 (58.5) |
| Length of stay in hospital prior to 2222 call, median (IQR) | 2 (0–7) | 2 (0–7) | 3 (1–8) |
| Reason for admission to/attendance at/visit to hospital, n (%) | |||
| Patient – medical | 11,837 (80.6) | 6307 (81.0) | 1277 (77.1) |
| Patient – trauma | 604 (4.1) | 250 (3.2) | 56 (3.4) |
| Patient – elective surgery | 981 (6.7) | 480 (6.2) | 102 (6.2) |
| Patient – emergency surgery | 1043 (7.1) | 663 (8.5) | 198 (11.9) |
| Patient – obstetric | 40 (0.3) | 7 (0.1) | 2 (0.1) |
| Outpatient | 149 (1.0) | 69 (0.9) | 18 (1.1) |
| Staff | 10 (0.1) | 1 (< 0.1) | 1 (0.1) |
| Visitor | 24 (0.2) | 14 (0.2) | 3 (0.2) |
| Location of arrest, n (%) | |||
| Emergency department | 1655 (11.3) | 702 (9.0) | 41 (2.5) |
| Emergency admissions unit | 1211 (8.2) | 719 (9.2) | 190 (11.5) |
| Ward | 8242 (56.1) | 4582 (58.8) | 1052 (63.5) |
| Obstetric area | 29 (0.2) | 6 (0.1) | 2 (0.1) |
| Intermediate care area | 46 (0.3) | 9 (0.1) | 0 (0) |
| Coronary care unit | 1390 (9.5) | 668 (8.6) | 140 (8.4) |
| HDU | 259 (1.8) | 128 (1.6) | 19 (1.1) |
| ICU or ICU/HDU | 680 (4.6) | 348 (4.5) | 61 (3.7) |
| Paediatric HDU | 15 (0.1) | 11 (0.1) | 1 (0.1) |
| Paediatric ICU | 19 (0.1) | 20 (0.3) | 6 (0.4) |
| Specialist treatment area | 182 (1.2) | 89 (1.1) | 20 (1.2) |
| Imaging department | 205 (1.4) | 89 (1.1) | 20 (1.2) |
| Cardiac catheter laboratory | 431 (2.9) | 263 (3.4) | 71 (4.3) |
| Theatre and recovery | 189 (1.3) | 87 (1.1) | 15 (0.9) |
| Other inpatient location | 4 (< 0.1) | 5 (0.1) | 2 (0.1) |
| Clinic | 46 (0.3) | 32 (0.4) | 10 (0.6) |
| Non-clinical area | 85 (0.6) | 33 (0.4) | 7 (0.4) |
| Patient deteriorating (not yet arrested) at team arrival, n (%) | 728 (5.0) | 365 (4.7) | 39 (2.4) |
| Presenting/first documented rhythm, n (%) | |||
| Ventricular fibrillation | 1695 (11.5) | 817 (10.5) | 194 (11.7) |
| Ventricular tachycardia | 707 (4.8) | 370 (4.7) | 73 (4.4) |
| Shockable – unknown rhythm | 94 (0.6) | 39 (0.5) | 7 (0.4) |
| Asystole | 3572 (24.3) | 1882 (24.2) | 391 (23.6) |
| Pulseless electrical activity | 7176 (48.9) | 3900 (50.1) | 797 (48.1) |
| Bradycardia | 102 (0.7) | 54 (0.7) | 9 (0.5) |
| Non-shockable – unknown rhythm | 314 (2.1) | 178 (2.3) | 45 (2.7) |
| Unknown | 1028 (7.0) | 551 (7.1) | 141 (8.5) |
| ROSC > 20 minutes, n (%) | 6605 (45.0) | 3509 (45.0) | 767 (46.3) |
| Hospital survival, n (%) | 2926 (19.9) | 1437 (18.4) | 316 (19.1) |
Model development
Prior to modelling, the following categories of predictors were combined to remove small categories. For reason for admission to/attendance at/visit to hospital, the categories of staff and visitor were combined. For location of arrest, the following categories were combined: ward, obstetric area and other inpatient location (noting that obstetric patients are distinguished by the separate reason for attendance field); high-dependency unit and paediatric high-dependency unit; and intensive care unit or combined high-dependency/intensive care unit and paediatric intensive care unit (noting that paediatric patients are distinguished by age).
The initial, full model, including the main effects of all candidate predictors (see Table 35), had a c-index of 0.727 for a ROSC > 20 minutes and 0.804 for hospital survival (Table 38). There was no evidence of multicollinearity (all variance inflation factors less than 2). Age was significantly non-linear in both models (p < 0.001 for a ROSC > 20 minutes and p = 0.007 for hospital survival).
| Risk prediction model | df | LL | AIC | c-index | HLa | Brier score | R |
|---|---|---|---|---|---|---|---|
| ROSC > 20 minutes | |||||||
| Full model | 37 | –8830 | 17,733 | 0.727 | 64.7 | 0.208 | 0.547 |
| After combining categories | 32 | –8832 | 17,727 | 0.727 | 70.7 | 0.209 | 0.547 |
| Variables removed (p-value) | |||||||
| Deteriorating (0.33) | 31 | –8832 | 17,726 | 0.727 | 72.3 | 0.209 | 0.547 |
| Sex (0.001) | 30 | –8837 | 17,735 | 0.726 | 63.9 | 0.209 | 0.546 |
| Prior LOS (< 0.001) | 27 | –8849 | 17,753 | 0.725 | 57.0 | 0.209 | 0.546 |
| Reason (< 0.001) | 21 | –8886 | 17,813 | 0.722 | 47.7 | 0.210 | 0.544 |
| Age (< 0.001) | 17 | –8951 | 17,935 | 0.711 | – | 0.212 | 0.542 |
| Location (< 0.001) | 9 | –9142 | 18,302 | 0.678 | – | 0.219 | 0.533 |
| Rhythm (< 0.001) | 2 | –9985 | 19,975 | 0.500 | – | 0.248 | 0.503 |
| After adding interactionsb | 46 | –8741 | 17,574 | 0.733 | 24.6 | 0.206 | 0.550 |
| Hospital survival | |||||||
| Full model | 37 | –5768 | 11,610 | 0.804 | 23.1 | 0.123 | 0.674 |
| After combining categories | 32 | –5770 | 11,603 | 0.804 | 21.3 | 0.123 | 0.674 |
| Variables removed (p-value) | |||||||
| Deteriorating (0.76) | 31 | –5770 | 11,601 | 0.804 | 23.0 | 0.123 | 0.674 |
| Sex (0.47) | 30 | –5770 | 11,600 | 0.804 | 18.8 | 0.123 | 0.674 |
| Prior LOS (< 0.001) | 27 | –5797 | 11,649 | 0.802 | 14.9 | 0.124 | 0.672 |
| Reason (< 0.001) | 21 | –5878 | 11,799 | 0.794 | 25.0 | 0.126 | 0.668 |
| Age (< 0.001) | 17 | –6040 | 12,114 | 0.776 | – | 0.130 | 0.660 |
| Location (< 0.001) | 9 | –6308 | 12,634 | 0.721 | – | 0.137 | 0.647 |
| Rhythm (< 0.001) | 2 | –7188 | 14,379 | 0.500 | – | 0.160 | 0.607 |
| After adding interactionsb | 45 | –5677 | 11,444 | 0.811 | 10.6 | 0.121 | 0.678 |
After following the pre-specified process for combining categories of predictors, the following categories were combined:
-
Prior length of stay: 8–30 days with > 30 days (p = 0.21 for a ROSC > 20 minutes and p = 0.73 for hospital survival).
-
Location of arrest:
-
ward, obstetric area or other inpatient location with intermediate care area (p = 0.56, p = 0.47 respectively)
-
high-dependency unit or paediatric high-dependency unit with intensive care unit, combined high-dependency/intensive care unit or paediatric high-dependency unit (p = 0.16, p = 0.40 respectively)
-
specialist treatment area with imaging department (p = 0.82, p = 0.34 respectively)
-
clinic with non-clinical area (p = 0.69, p = 0.39 respectively).
-
Combining categories had a minimal effect on the measures of model performance and resulted in an improvement (decrease) in the AIC (see Table 38).
The stepwise reduction of the models is shown in Table 38. The predictor ‘patient deteriorating (not yet arrested) at team arrival’ was removed from both models and sex was removed from the model for hospital survival. All other predictors were highly statistically significant.
After testing the pre-specified interactions, a significant interaction (p < 0.001) was found between location of arrest and presenting rhythm in both models; therefore, alternative categorisations for interactions between location of arrest and presenting rhythm were considered. All other interaction terms were non-significant.
The non-linear relationships between age and outcome are illustrated in Figure 15. For ROSC > 20 minutes, the relationship with age was flat up to around age 60 years, with a rapid decrease in the odds of ROSC > 20 minutes at older ages. Hospital survival decreased across the full age range, although this relationship was steeper at older ages.
FIGURE 15.
Relationship between age and ROSC > 20 minutes (a) and hospital survival following in-hospital cardiac arrest; and (b) odds ratios presented relative to age 70 years.
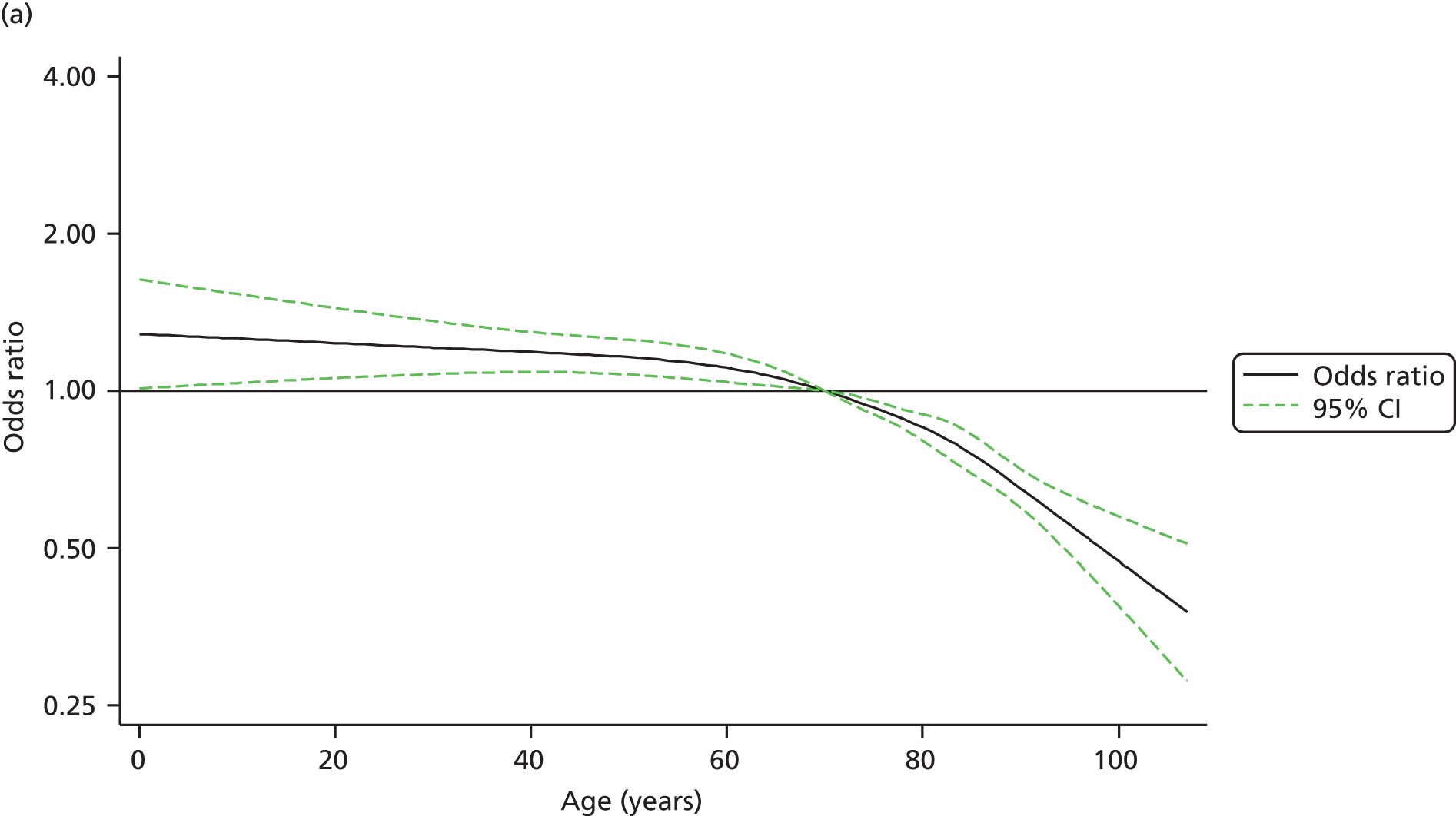
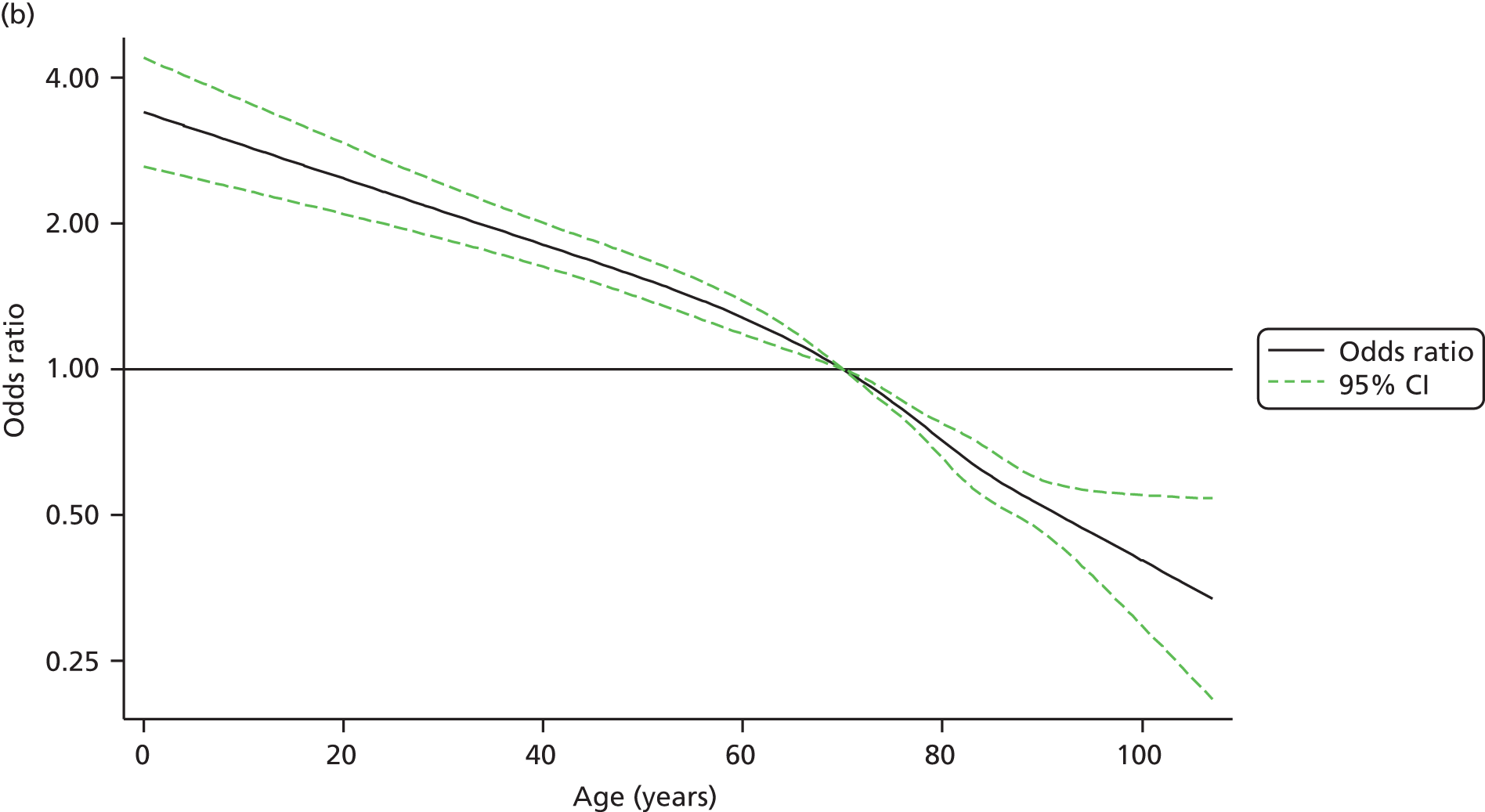
Model validation
The results of the model validation, based on models fitted in the development data set, are shown in Table 39. Discrimination and accuracy were better for hospital survival (c-index ≈ 0.81, R2 = 0.21–0.24) than for ROSC > 20 minutes (c-index ≈ 0.73, R2 = 0.11–0.17). Calibration was generally good, supported visually by calibration plots (Figure 16), although there was some evidence of worse calibration for ROSC > 20 minutes in the validation data set. Model performance was generally well preserved in the validation data sets compared with the development data set, particularly for hospital survival. Model accuracy was also compared across age groups (Figure 17). Although there was some variation in outcomes (consistent with chance) in the age groups with smaller sample sizes, overall the model fit was good across all age groups. Interactions between age and other predictors were considered but were found to be unnecessary.
| Measures of model performancea | Development (n = 14,688) | Validation (n = 7791) | External validation (n = 1657) |
|---|---|---|---|
| ROSC > 20 minutes | |||
| c-index (95% CI) | 0.733 (0.725 to 0.741) | 0.720 (0.709 to 0.732) | 0.725 (0.701 to 0.750) |
| Hosmer–Lemeshow test | |||
| Chi-squared (p-value) | 24.6 (0.002) | 15.0 (0.13) | 10.4 (0.41) |
| Cox calibration regression | |||
| Intercept (95% CI) | 0.021 (–0.016 to 0.058) | 0.015 (–0.034 to 0.066) | 0.038 (–0.070 to 0.146) |
| Slope (95% CI) | 1.000 (0.957 to 1.043) | 0.989 (0.928 to 1.051) | 1.003 (0.870 to 1.136) |
| Chi-squared (p-value) | 1.3 (0.52) | 0.6 (0.73) | 0.5 (0.78) |
| Brier score | 0.206 | 0.211 | 0.210 |
| Sum-of-squares R2 | 0.168 | 0.150 | 0.156 |
| Shapiro’s R | 0.550 | 0.544 | 0.545 |
| Entropy-based R2 | 0.131 | 0.115 | 0.120 |
| Hospital survival | |||
| c-index (95% CI) | 0.811 (0.802 to 0.820) | 0.811 (0.799 to 0.824) | 0.804 (0.776 to 0.832) |
| Hosmer–Lemeshow test | |||
| Chi-squared (p-value) | 10.6 (0.23) | 23.2 (0.010) | 6.9 (0.73) |
| Cox calibration regression | |||
| Intercept (95% CI) | 0.036 (–0.029 to 0.101) | –0.043 (–0.134 to 0.048) | –0.091 (–0.280 to 0.098) |
| Slope (95% CI) | 1.001 (0.961 to 1.041) | 1.047 (0.989 to 1.106) | 1.014 (0.891 to 1.137) |
| Chi-squared (p-value) | 2.1 (0.34) | 10.8 (0.004) | 2.3 (0.32) |
| Brier score | 0.121 | 0.115 | 0.119 |
| Sum-of-squares R2 | 0.240 | 0.234 | 0.232 |
| Shapiro’s R | 0.678 | 0.688 | 0.681 |
| Entropy-based R2 | 0.221 | 0.219 | 0.211 |
FIGURE 16.
Calibration plots for ROSC > 20 minutes (a–c) and hospital survival (d–f) following in-hospital cardiac arrest. Observed outcome (with 95% CI) plotted against predicted outcome in 10 equal-sized groups, based on models using coefficients fitted in the development data set.

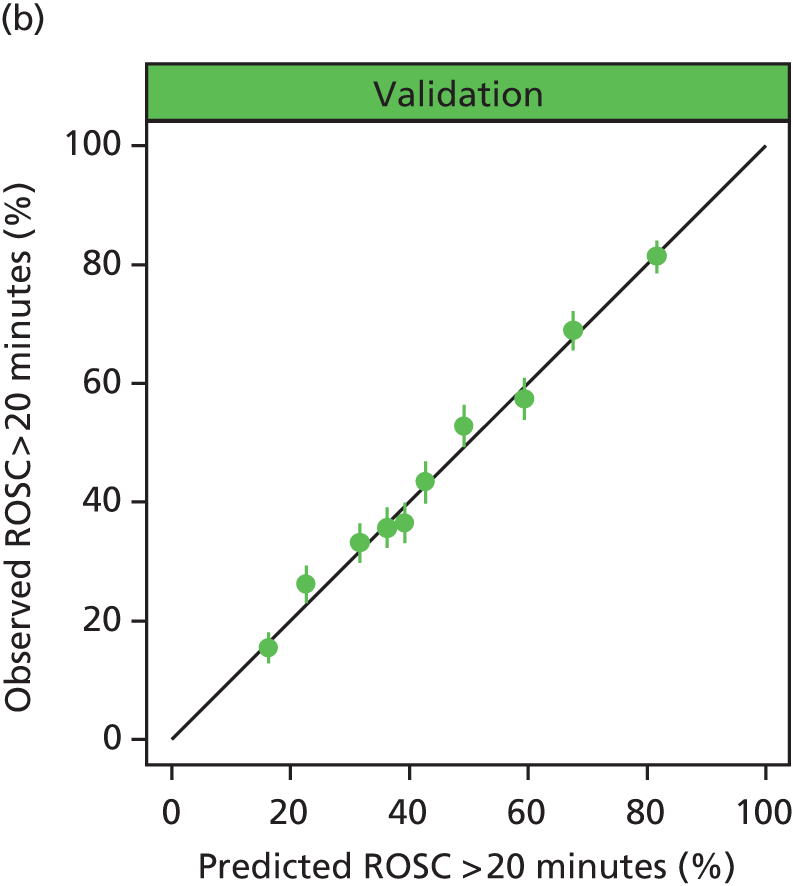
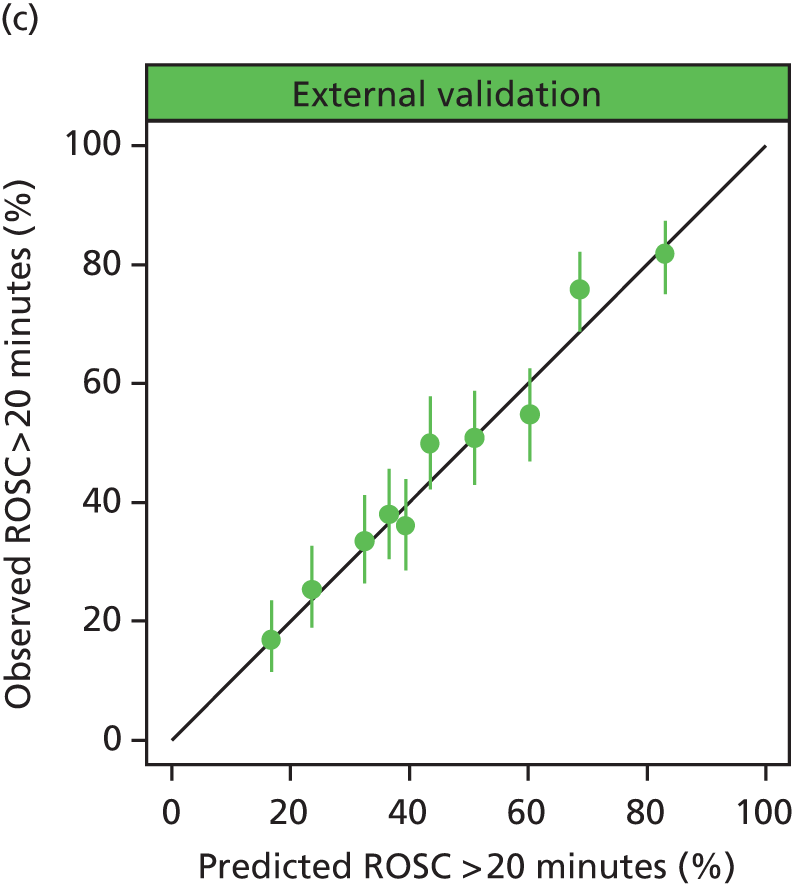


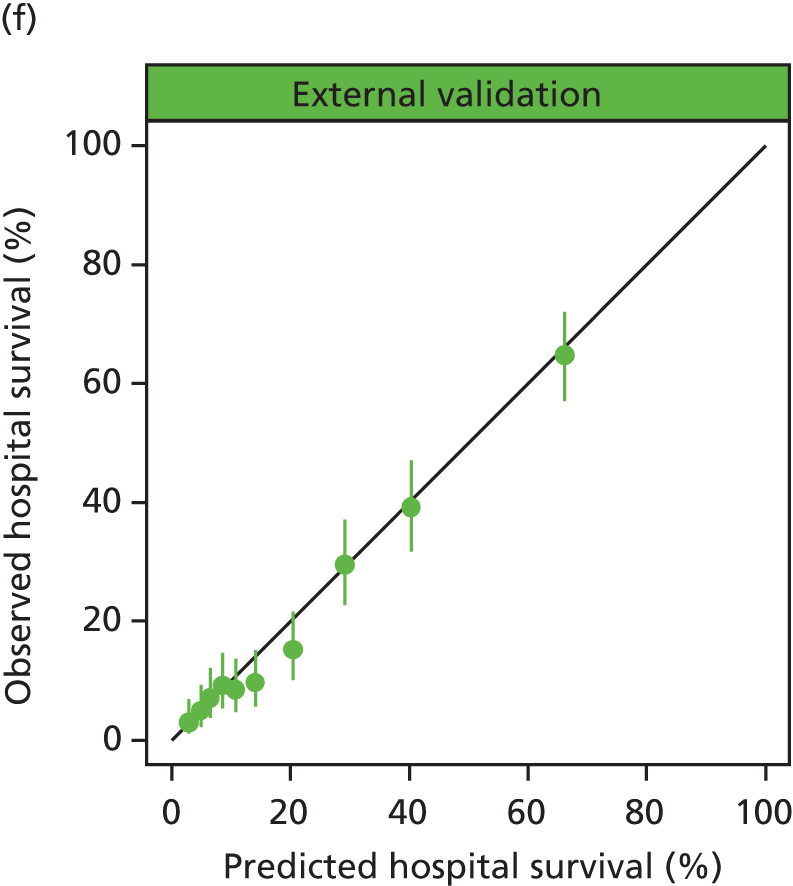
FIGURE 17.
Numbers of in-hospital cardiac arrests and observed and predicted outcomes by age in 5-year bands. (a) Development data set; and (b) validation data set.
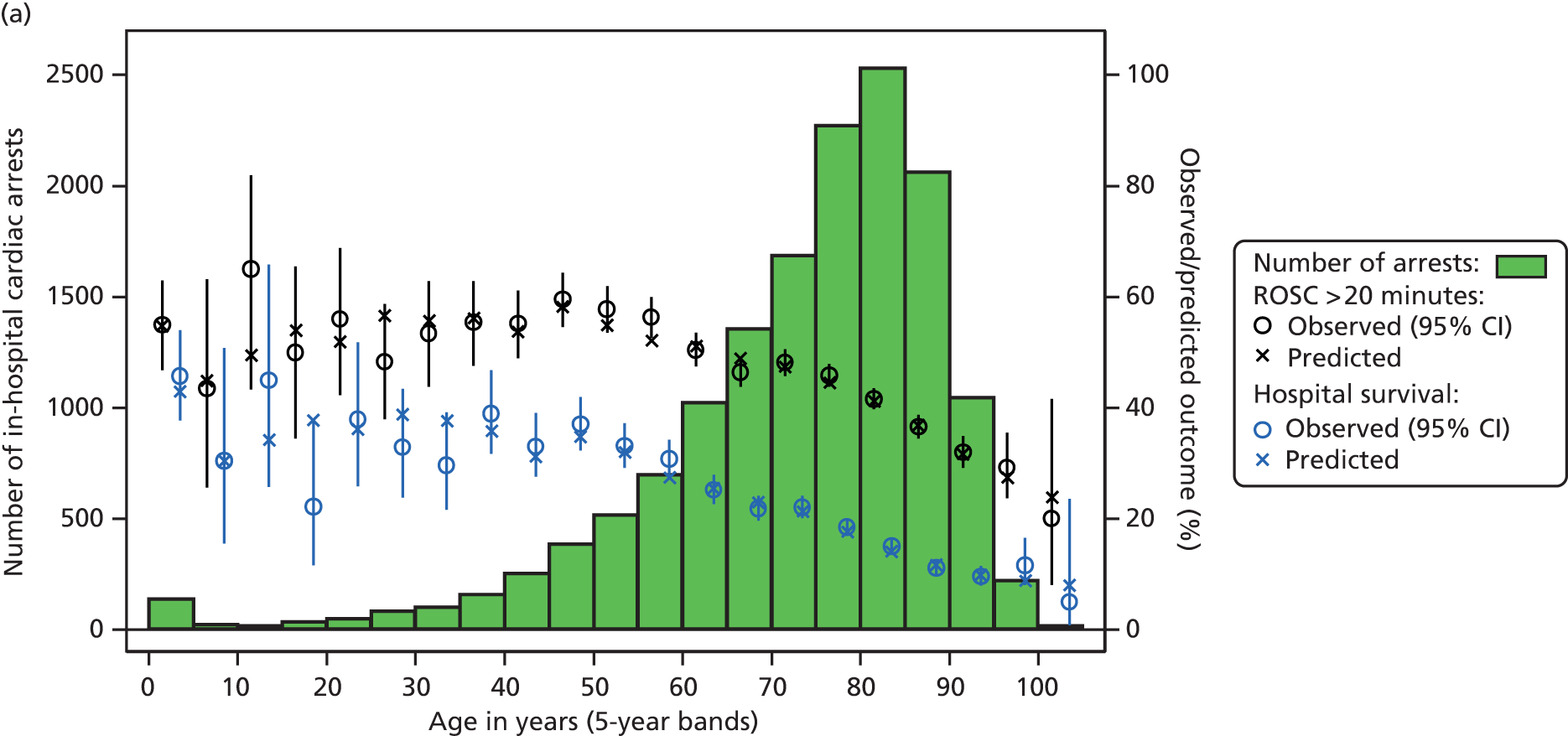
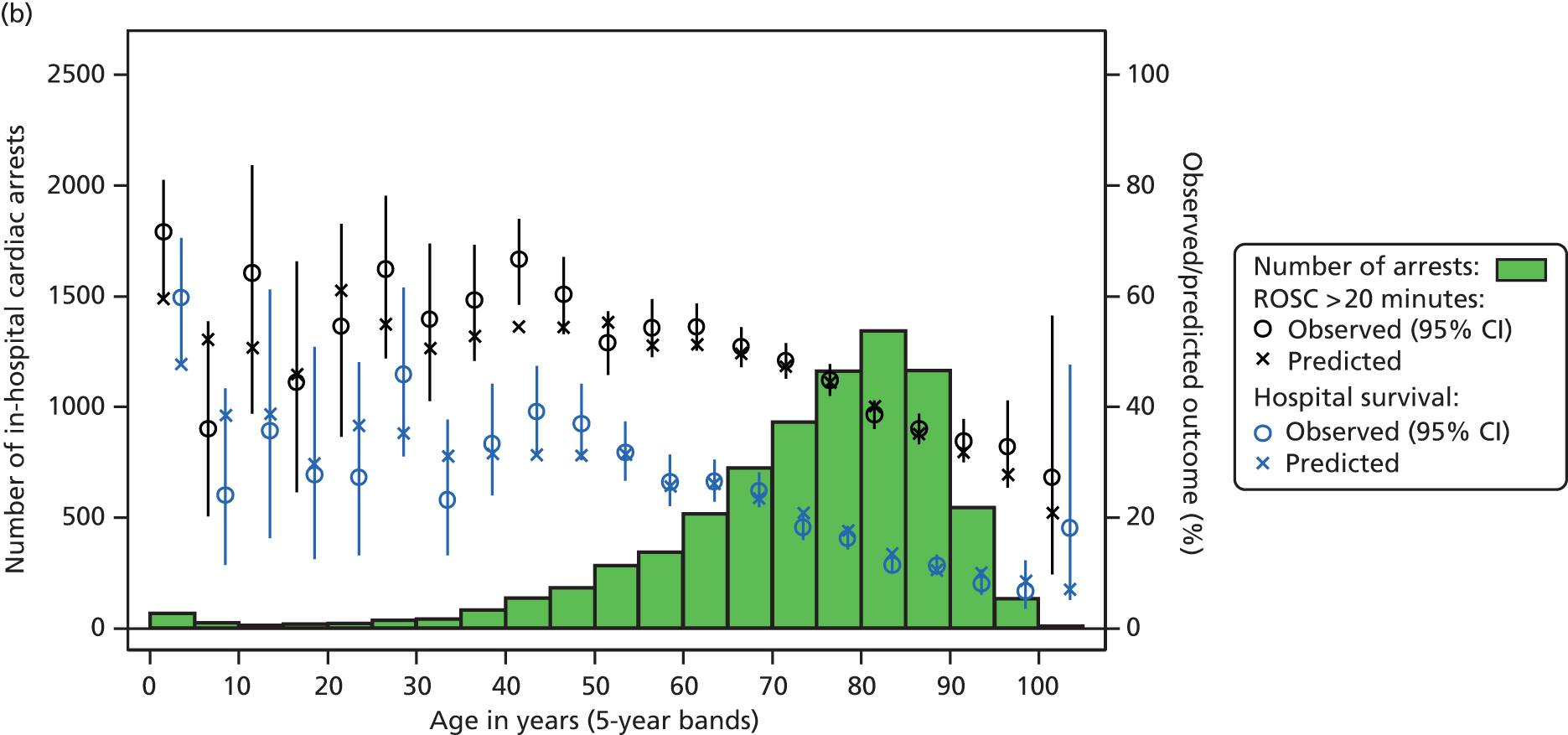
The final models for ROSC > 20 minutes and hospital survival, refitted to the full data set, are shown in Tables 40 and 41 respectively. The shrinkage factors were 0.964 and 0.970, respectively, indicating very little overfitting.
| Predictor | Patients, n (N = 22,479) |
ROSC > 20 minutes, n (%) (N = 10,114) |
Coefficient (95% CI) |
|---|---|---|---|
| Age (spline base variablesa) | |||
| age1 | – | – | –0.0019 (–0.0066 to 0.0027) |
| age2 | – | – | –0.0118 (–0.0259 to 0.0024) |
| age3 | – | – | 0.0315 (–0.1772 to 0.2403) |
| age4 | – | – | –0.1120 (–0.7397 to 0.5157) |
| Sex | |||
| Female | 9590 | 4289 (44.7) | 0 |
| Male | 12,889 | 5825 (45.2) | –0.1167 (–0.1762 to –0.0573) |
| Prior length of stay | |||
| 0 days | 6276 | 3334 (53.1) | 0 |
| 1 day | 3804 | 1758 (46.2) | –0.1060 (–0.2075 to –0.0045) |
| 2–7 days | 7136 | 2859 (40.1) | –0.2350 (–0.3313 to –0.1388) |
| 8 or more days | 5263 | 2163 (41.1) | –0.1753 (–0.2785 to –0.0722) |
| Reason for attendance | |||
| Patient – medical | 18,144 | 7923 (43.7) | 0 |
| Patient – trauma | 854 | 319 (37.4) | 0.0173 (–0.1383 to 0.1729) |
| Patient – elective surgery | 1461 | 872 (59.7) | 0.4920 (0.3671 to 0.6170) |
| Patient – emergency surgery | 1706 | 770 (45.1) | –0.0529 (–0.1666 to 0.0609) |
| Patient – obstetric | 47 | 38 (80.9) | 1.4674 (0.7045 to 2.2303) |
| Outpatient | 218 | 158 (72.5) | 0.4281 (0.0365 to 0.8197) |
| Staff or visitor | 49 | 34 (69.4) | 0.2874 (–0.3605 to 0.9353) |
| Location of arrest | |||
| Emergency department | 2357 | 1039 (44.1) | –0.1061 (–0.3518 to 0.1396) |
| Emergency admissions unit | 1929 | 846 (43.9) | 0.1853 (0.0708 to 0.2998) |
| Ward, obstetric area, intermediate care area or other inpatient location | 12,912 | 4822 (37.3) | 0 |
| Coronary care unit | 2057 | 1263 (61.4) | 0.9226 (0.7112 to 1.1340) |
| Critical care unit | 1480 | 952 (64.3) | 0.1712 (–0.1322 to 0.4746) |
| Imaging department or specialist treatment area | 565 | 347 (61.4) | 0.6062 (0.0574 to 1.1549) |
| Cardiac catheter laboratory | 694 | 507 (73.1) | 1.0379 (0.7755 to 1.3003) |
| Theatre and recovery | 276 | 193 (69.9) | 0.3557 (–0.4972 to 1.2085) |
| Clinic or non-clinical area | 160 | 111 (69.4) | 0.4783 (0.0423 to 0.9143) |
| Presenting/first documented rhythm | |||
| Ventricular fibrillation | 2512 | 1821 (72.5) | 0 |
| Ventricular tachycardia | 1077 | 857 (79.6) | 0.2960 (0.1158 to 0.4763) |
| Shockable – unknown rhythm | 133 | 75 (56.4) | –0.4064 (–0.7771 to –0.0357) |
| Asystole | 5454 | 1431 (26.2) | –2.0035 (–2.1427 to –1.8644) |
| Pulseless electrical activity | 11,076 | 4534 (40.9) | –1.0853 (–1.2085 to –0.9621) |
| Bradycardia | 156 | 110 (70.5) | –0.0973 (–0.4974 to 0.3029) |
| Non-shockable – unknown rhythm | 492 | 247 (50.2) | –0.6084 (–0.8318 to –0.3850) |
| Unknown | 1579 | 1039 (65.8) | –0.0137 (–0.1767 to –0.1493) |
| Interaction between asystole and location of arrest | |||
| Emergency department | – | – | 0.4118 (0.0851 to 0.7385) |
| EAU, ward, obstetric area, intermediate care area or other inpatient location | – | – | 0 |
| CCU or cardiac catheter lab | – | – | 0.7700 (0.4761 to 1.0639) |
| Critical care unit | – | – | 1.4013 (1.0245 to 1.7781) |
| Imaging department or specialist treatment area | – | – | 0.1224 (–0.5778 to 0.8225) |
| Theatre and recovery | – | – | 1.4432 (0.3919 to 2.4946) |
| Interaction between PEA and location of arrest | |||
| Emergency department | – | – | 0.0079 (–0.2537 to 0.2695) |
| EAU, ward, obstetric area, intermediate care area or other inpatient location | – | – | 0 |
| CCU or cardiac catheter lab | – | – | –0.8256 (–1.0672 to –0.5840) |
| Critical care unit | – | – | 0.4604 (0.1205 to 0.8004) |
| Imaging department or specialist treatment area | – | – | –0.0692 (–0.6623 to 0.5239) |
| Theatre and recovery | – | – | 0.4798 (–0.4350 to 1.3945) |
| Interaction between other non-shockable/unknown rhythms and location of arrest | |||
| Emergency department | – | – | –0.0748 (–0.4751 to 0.3255) |
| EAU, ward, obstetric area, intermediate care area or other inpatient location | – | – | 0 |
| CCU or cardiac catheter lab | – | – | –0.2823 (–0.7227 to 0.1581) |
| Critical care unit | – | – | 0.3021 (–0.2682 to 0.8724) |
| Imaging department or specialist treatment area | – | – | 0.2937 (–0.5486 to 1.1360) |
| Theatre and recovery | – | – | 0.6059 (–0.7864 to 1.9982) |
| Constant | – | – | 1.1309 (0.8574 to 1.4043) |
| SD of random effect | – | – | 0.3016 (0.2501 to 0.3636) |
| ICC | – | – | 0.0269 (0.0187 to 0.0386) |
| Predictor | Patients, n (N = 22,479) |
Hospital survival, n (%) (N = 4363) |
Coefficient (95% CI) |
|---|---|---|---|
| Age (spline base variablesa) | |||
| age1 | – | – | –0.0153 (–0.0203 to –0.0102) |
| age2 | – | – | –0.0125 (–0.0295 to 0.0044) |
| age3 | – | – | –0.0133 (–0.2848 to 0.2582) |
| age4 | – | – | 0.2135 (–0.6492 to 1.0762) |
| Prior length of stay | |||
| 0 days | 6276 | 1809 (28.8) | 0 |
| 1 day | 3804 | 741 (19.5) | –0.2339 (–0.3598 to –0.1080) |
| 2–7 days | 7136 | 1061 (14.9) | –0.4342 (–0.5535 to –0.3149) |
| 8 or more days | 5263 | 752 (14.3) | –0.4593 (–0.5897 to –0.3289) |
| Reason for attendance | |||
| Patient – medical | 18,144 | 3276 (18.1) | 0 |
| Patient – trauma | 854 | 84 (9.8) | –0.2790 (–0.5307 to –0.0274) |
| Patient – elective surgery | 1461 | 491 (33.6) | 0.8545 (0.7136 to 0.9955) |
| Patient – emergency surgery | 1706 | 325 (19.1) | –0.0916 (–0.2437 to 0.0604) |
| Patient – obstetric | 47 | 35 (74.5) | 2.2917 (1.5873 to 2.9961) |
| Outpatient | 218 | 124 (56.9) | 0.8693 (0.4831 to 1.2555) |
| Staff or visitor | 49 | 28 (57.1) | 0.8531 (0.2298 to 1.4765) |
| Location of arrest | |||
| Emergency department | 2357 | 457 (19.4) | 0.2175 (–0.0267 to 0.4618) |
| Emergency admissions unit | 1929 | 291 (15.1) | 0.1055 (–0.0534 to 0.2644) |
| Ward, obstetric area, intermediate care area or other inpatient location | 12,912 | 1596 (12.4) | 0 |
| Coronary care unit | 2057 | 802 (39.0) | 1.2194 (1.0355 to 1.4033) |
| Critical care unit | 1480 | 408 (27.6) | –0.0865 (–0.3600 to 0.1869) |
| Imaging department or specialist treatment area | 565 | 188 (33.3) | 0.2111 (–0.2413 to 0.6634) |
| Cardiac catheter laboratory | 694 | 386 (55.6) | 1.3527 (1.1132 to 1.5923) |
| Theatre and recovery | 276 | 124 (44.9) | 0.3853 (–0.3438 to 1.1145) |
| Clinic or non-clinical area | 160 | 83 (51.9) | 0.6961 (0.2544 to 1.1378) |
| Presenting rhythm | |||
| Ventricular fibrillation | 2512 | 1200 (47.8) | 0 |
| Ventricular tachycardia | 1077 | 573 (53.2) | 0.1576 (–0.0009 to 0.3161) |
| Shockable – unknown rhythm | 133 | 36 (27.1) | –0.4498 (–0.8724 to –0.0273) |
| Asystole | 5454 | 501 (9.2) | –2.4155 (–2.6145 to –2.2165) |
| Pulseless electrical activity | 11,076 | 1316 (11.9) | –1.5656 (–1.7048 to –1.4264) |
| Bradycardia | 156 | 74 (47.4) | –0.0027 (–0.4024 to 0.3970) |
| Non-shockable – unknown rhythm | 492 | 110 (22.4) | –0.6150 (–0.8771 to –0.3529) |
| Unknown | 1579 | 553 (35.0) | –0.0119 (–0.1804 to 0.1567) |
| Interaction between asystole and location of arrest | |||
| Emergency department | – | – | 0.3481 (–0.0661 to 0.7623) |
| EAU, ward, obstetric area, intermediate care area or other inpatient location | – | – | 0 |
| CCU or cardiac catheter lab | – | – | 1.3103 (0.9978 to 1.6228) |
| Critical care unit | – | – | 1.6794 (1.2840 to 2.0748) |
| Imaging department or specialist treatment area | – | – | 0.7625 (0.0042 to 1.5208) |
| Theatre and recovery | – | – | 2.0083 (1.0440 to 2.9725) |
| Interaction between PEA and location of arrest | |||
| Emergency department | – | – | –0.4057 (–0.7026 to –0.1087) |
| EAU, ward, obstetric area, intermediate care area or other inpatient location | – | – | 0 |
| CCU or cardiac catheter lab | – | – | –0.6241 (–0.8736 to –0.3745) |
| Critical care unit | – | – | 0.5458 (0.2082 to 0.8833) |
| Imaging department or specialist treatment area | – | – | 0.5060 (–0.0204 to 1.0324) |
| Theatre and recovery | – | – | 0.8750 (0.0694 to 1.6806) |
| Interaction between other non-shockable/unknown rhythms and location of arrest | |||
| Emergency department | – | – | –0.5479 (–0.9610 to –0.1348) |
| EAU, ward, obstetric area, intermediate care area or other inpatient location | – | – | 0 |
| CCU or cardiac catheter lab | – | – | –0.7431 (–1.1414 to –0.3448) |
| Critical care unit | – | – | 0.0329 (–0.5010 to 0.5668) |
| Imaging department or specialist treatment area | – | – | 0.9988 (0.2978 to 1.6998) |
| Theatre and recovery | – | – | 0.1470 (–0.9878 to 1.2817) |
| Constant | – | – | 0.8737 (0.5825 to 1.1650) |
| SD of random effect | – | – | 0.2850 (0.2285 to 0.3556) |
| ICC | – | – | 0.0241 (0.0156 to 0.0370) |
Discussion
Based on a relatively simple data set, we have developed a risk prediction model with good discrimination (c-index greater than 0.8) for predicting hospital survival following an in-hospital cardiac arrest attended by the hospital-based resuscitation team. This model validated well in subsequent data, including external validation in data from 21 hospitals not included in the development data set. A risk prediction model for ROSC > 20 minutes performed less well, being potentially more sensitive to inter-hospital variation in the organisation and delivery of resuscitation practice, but still demonstrated acceptable discrimination (c-index greater than 0.7). Although there were statistically significant departures from perfect calibration, the Hosmer–Lemeshow test is highly sensitive to sample size25,26 and graphical plots demonstrated that overall calibration was generally good in both the development and validation data sets.
The main strengths of the study are the large, representative, high-quality clinical data set, with coverage approaching 50% of UK acute hospitals; high levels of data completeness, with only 0.3% of patients excluded because of missing data; and robust statistical modelling techniques, including using multilevel random-effects models to account for clustering of outcomes within hospitals, using restricted cubic splines to model non-linear relationships between age and outcome and considering important interactions between predictors.
There are, however, some limitations. The available predictors and outcomes were limited to those recorded in the NCAA data set, which were in turn driven by the need to ensure that data could be collected accurately in all participating hospitals on all eligible patients. Consequently, data were not available for some variables that have been found to be significant predictors of outcome in other studies of in-hospital cardiac arrest, such as pre-arrest comorbidities and interventions. In addition, patients were followed up to discharge from the original acute hospital only, with any patients transferred to another acute hospital recorded as survivors. Finally, the risk prediction models developed predict only survival and not quality of survival.
Although several audits and registries of in-hospital cardiac arrest have been established [most notably the American Heart Association’s ‘Get With The Guidelines®-Resuscitation’ (GWTG-R) registry (formerly the National Registry of Cardiopulmonary Resuscitation), established in 2000101], the first validated risk prediction model for outcome following in-hospital cardiac arrest (developed contemporaneously with those presented here) was only published in 2013. 102 Furthermore, this risk prediction model, based on data from the USA, may not transfer well to different health-care systems. 13,103,104 There are several differences between our models and the GWTG-R model for hospital survival in terms of inclusion criteria and available predictors; however, there are also many similarities. The GWTG-R is a registry of all in-hospital cardiac arrests, whereas the NCAA is a national clinical audit monitoring outcomes for hospital-based resuscitation teams. Consequently, although the majority of arrests in the GWTG-R registry occurred in monitored areas, many of the arrests in these areas are managed by staff in the monitored area and would not result in an emergency call to the resuscitation team and, therefore, would not meet the scope of the NCAA. In terms of predictors included in the models, the GWTG-R registry model includes pre-arrest comorbidities and interventions, which are not currently available in the NCAA data set. However, other predictors included in their model were similar. The discrimination of the NCAA model for hospital survival (c-index 0.811) exceeded that of the GWTG-R registry model (0.734) and also of a previous, more complex, model from the same database (0.780). 105
The findings of our research are consistent with the recognised benefits of the patient being monitored before an arrest; the arrest being witnessed; staff members with advanced life-support skills being available in the immediate vicinity of the arrest; and equipment and drugs necessary to treat the arrest being immediately available. These are all more likely to exist when the arrest occurs in a critical care unit or coronary care unit. We found that both asystole and pulseless electrical activity were always less likely to result in ROSC and hospital survival than ventricular fibrillation. It is well recognised that for asystole and pulseless electrical activity the specific treatment necessary may be unclear, whereas for ventricular fibrillation the essential therapy (defibrillation) is readily available in most clinical areas of hospitals. Further, asystole may occur following ventricular fibrillation and is recognised to be a ‘less survivable’ rhythm. Both ROSC > 20 minutes and hospital survival were more likely when asystole occurred on the critical care unit or coronary care unit than on the ward (odds ratios 4.82 and 5.43 for ROSC > 20 minutes, and 4.92 and 12.55 for hospital survival in the critical care unit and coronary care unit, respectively). Similarly, ROSC > 20 minutes was also more likely when ventricular fibrillation occurred in the critical care unit or coronary care unit than the ward (odds ratios 1.22 and 2.46, respectively). However, although hospital survival was more likely when ventricular fibrillation occurred in the coronary care unit than the ward (odds ratio 3.32), this was not the case for ventricular fibrillation occurring in a critical care unit (odds ratio 0.90), which probably reflects the underlying severity of illness of patients on the critical care unit.
Chapter 6 Translation of the risk models into routine practice
Introduction
A key strength of this project was the nesting of the model development within ongoing national clinical audits, enabling the rapid translation of the risk models into routine use within these audits. This chapter reports the adoption of the risk models into routine comparative outcome reporting for the CMP and NCAA and the wider ongoing dissemination work to communicate the research output to providers, managers, commissioners, policy-makers and academics in critical care.
Adult critical care: the Case Mix Programme
In 2011, ICNARC became the first critical care audit internationally to publicly report critical care units’ outcomes when it introduced the Annual Quality Report (AQR), a publicly accessible report on potential quality indicators for adult critical care, including risk-adjusted acute hospital mortality, for critical care units participating in the CMP. 106 For the first 2 years, the report was only for adult, general critical care units. In 2013, ICNARC introduced separate reports for high-dependency units, specialist neurocritical care units and cardiothoracic critical care units. As the original ICNARC model was only developed using data from adult, general critical care units, it was necessary to recalibrate the model using data from these different unit types in order to produce these separate reports. With the new ICNARC model, which has been demonstrated to perform well across all unit types, the 2014–15 AQR will now be able to be a single report encompassing all adult critical care units, regardless of type.
Following consultation with stakeholders, the new ICNARC model is also being incorporated into a new product for regular routine reporting of results to the adult critical care units participating in the CMP: the Quarterly Quality Report (QQR). The QQR will be distributed to participating critical care units quarterly, building up cumulatively to the AQR that is made available to the public. Using the new ICNARC model, it will incorporate risk-adjusted acute hospital mortality, together with other potential quality indicators, and will present the indicators in the form of funnel plots, mapped against other critical care units, and as trends over time within the unit. The purpose of the QQR is to enable timely identification of potential areas for local quality improvement work and monitoring of trends and changes in the potential quality indicators.
In-hospital cardiac arrest: the National Cardiac Arrest Audit
Prior to the development of the risk prediction models for in-hospital cardiac arrest in this project, routine comparative reports to hospitals participating in the NCAA included only crude, unadjusted outcomes and outcomes stratified by individual risk factors (age, presenting/first documented rhythm and location of arrest). Following the development of the risk prediction models, these reports now incorporate risk-adjusted rates for ROSC > 20 minutes and hospital survival presented in the form of funnel plots. These reports are produced quarterly, 6-monthly or annually, depending on a hospital’s throughput of eligible arrests.
In addition, now that staff members in the participating hospitals are becoming familiar with the reporting of risk-adjusted outcomes, the availability of the risk prediction models will enable the NCAA to move towards public reporting of results, based on the template of the CMP AQR.
Wider dissemination
During the course of the research, the risk-adjusted outputs of the national clinical audits have greatly increased in prominence. Clinical Reference Groups have been established for the commissioning of specialist services within the NHS and we have worked closely with the Clinical Reference Group for Adult Critical Care in their definition of key service outcomes, which include standardised case-mix-adjusted mortality using the latest risk prediction models. These key service outcomes are included in quarterly data submissions from the CMP to underpin the Adult Critical Care Quality Dashboard. 107 In addition, the Care Quality Commission (CQC) has identified critical care as a core service for CQC inspections of NHS acute hospitals, with both the CMP and NCAA serving as important sources of information for the inspection teams. 108 We are working with the CQC to streamline the provision of data in advance of inspections. Further dissemination of the results of this project to the wider clinical and academic community is ongoing through preparation of articles for publication in peer-reviewed journals.
Chapter 7 Conclusions and recommendations
Summary of findings
We have established that the current ICNARC model14 demonstrates similar performance to that reported from previous (internal and external) validation within the CMP when externally validated using independently collected, but similar, data from critical care units in Scotland. Nevertheless, we identified a number of areas where the current risk prediction model could be improved. The first of these related to its performance in specialist critical care units. The ICNARC model was developed using data from adult, general critical care units and the probable performance of a single risk prediction model across various types of critical care unit was unknown. This is of particular relevance to cardiothoracic critical care units. The majority of admissions to such units present with considerable derangement to physiology, owing to the major insult of cardiac surgery, but this insult is transient and usually reversible and, consequently, mortality is low. We developed a specific risk prediction model for admissions to cardiothoracic critical care units, which had excellent performance (c-index 0.904 in the validation data set). As well as being specifically tailored to the unique case mix of these units, this model also served as a baseline for assessing the performance of a new ICNARC model in cardiothoracic critical care units, acting as a comparator for the ability of a generic model to work across different types of units.
In developing the new ICNARC model we also addressed further areas for improvement, including the handling of missing data (both in the development and validation data sets and in the application of the risk prediction model), continuous non-linear modelling of physiological predictors and making better use of available data from the hierarchical coding of reasons for admission to the critical care unit. The resulting risk prediction model performed well not only in the full validation data set (c-index 0.885) but also when evaluated in specific patient subgroups and specific types of critical care unit.
Finally, using data from the NCAA, we developed risk prediction models to predict two important outcomes following in-hospital cardiac arrest: the immediate outcome of ROSC sustained for more than 20 minutes and the slightly longer-term outcome of survival to hospital discharge. Based on only a small number of predictors, the model for hospital survival had good discrimination (c-index 0.811) and validated well, including among 21 hospitals that did not contribute to the development data set (c-index 0.804). The performance of the model for ROSC > 20 minutes was less good, possibly reflecting inter-hospital variation in resuscitation practice, but it still achieved a c-index of 0.725 in the external validation data set.
Discussion
Although the main aim of the project was pragmatic (to improve risk prediction models to underpin quality improvement programmes for the critically ill), this study provides a number of insights into prognostic modelling more generally, and modelling of risk-adjusted hospital mortality in particular.
In Chapters 3 and 4, we explored the effect of missing data when modelling under certain situations and addressed issues to which little attention has been devoted in the literature, such as the impact of strategies for handling missing data on the application of risk prediction models in routine practice and on benchmarking.
In Chapters 3–5, we illustrated a practical approach to obtaining the appropriate functional form for continuous predictors. We described the methods used to specify, estimate and simplify the full models in order to derive the best risk prediction model, as well as the performance criteria we used. We also offer some guidance for avoiding overfitting and mis-specification, as well as about the problems that arise when modelling with very large samples (see Chapter 4). We have shown that with a large sample size, stepwise reduction procedures perform better than a literature-based assessment would suggest and indicate that careful pre-selection of a set of candidate predictors and interactions based on subject knowledge, combining judgement with computer-based statistics instead of basing the variable selection on univariable analyses, remains key to good modelling.
Because the aim of this project was prediction rather explanation, it was more appropriate to seek predictive accuracy than interpretation of regression coefficients, and a model with superior discrimination and calibration was preferable to one that gave a better explanation of the physiological processes. However, because the data set was large and comprehensive, there was also interest in the prognostic models themselves: which factors were predictive of outcome and, in particular, was their effect mediated through other factors?
This project concentrated solely on predictive accuracy and we did not consider statistical inference in our evaluations; for example, CI coverage and estimation of effects for individual variables. If learning about the most important prognostic relationships is the focus of a study, inference issues need more attention in model development, therefore the methods, conclusions and recommendations for modelling of the present project should be considered in a risk prediction context.
The project was overseen by an Expert Advisory Group, comprising clinicians, statisticians, health services researchers, NHS managers and a service user representative (see Acknowledgements), which met five times during the course of the project. Discussions with the Expert Advisory Group contributed to key decisions regarding the direction of the project. An early, important decision, guided by the Expert Advisory Group, was to widen the focus of objective 1 from adult, general critical care units (the setting for the previous ICNARC model) to encompass all adult critical care units, removing the need for objective 2iii to consider separately units admitting low-risk patients. The resulting model showed good performance across all types of units, validating the group’s recommendation and contributing to the project’s overall aim of making fairer comparisons across providers. Other discussions with the Expert Advisory Group concerned alternative approaches for multiple imputation of missing data; the potential to use pre-admission physiology data for admissions with no data available from the first 24 hours following admission to the critical care unit; how to handle physiological predictors for patients who stayed less than 24 hours in the critical care unit; pros and cons of the alternative methods for modelling continuous predictors; the need for pre-specification of potentially important interaction terms; and how to structure the categorisation of reasons for admission to the critical care unit.
Implications for health care
The newly developed risk prediction models either have been or are being introduced into routine national clinical audit comparative reporting for both the CMP and NCAA. For the CMP, this will enable fairer comparison across critical care units, including, for the first time, across different types of critical care units, underpinning annual public reporting of critical care unit outcomes. 106 For the NCAA, the models permit, for the first time, genuine risk-adjusted comparisons across hospitals and will enable the NCAA to progress towards public reporting of results.
Recommendations for research
Recommendation 1: further research should be conducted by linking with death registrations to evaluate mortality at fixed time points and using time to event analyses
To date, the main outcome for national clinical audits, including the CMP and NCAA, has been mortality at acute hospital discharge, an event-based outcome. Time-based outcomes, for example, mortality at 30 or 90 days following admission or duration of survival, would be less prone to bias arising from variation in provision of community health- and social care services, which may impact the timing of patients being discharged from acute hospital. Research from the Netherlands has suggested that comparison of risk-adjusted mortality across critical care units using mortality at 30 or 90 days, rather than at hospital discharge, results in less heterogeneity. 109 Acute hospital mortality has predominantly been selected because of its convenience to record and collect, as follow-up of patients beyond acute hospital discharge has not been seen as practicable. However, with the increased availability of electronic data sets and the establishment of the NHS Number as a national unique identifier, the vast majority of patients admitted to UK critical care units will now be able to be followed up for mortality following discharge from acute hospital by using data linkage with death registrations maintained by the Office for National Statistics. Furthermore, to enable reporting in a useful timeframe for quality improvement, the main outcomes for national clinical audit are necessarily relatively short term in nature. However, recovery from critical illness can be a slow process, with studies reporting substantial ongoing burden of mortality several years after discharge from hospital. 110,111 Data linkage with death registrations would also permit follow-up of longer-term mortality, enabling us to better understand the time course of recovery from critical illness and which risk factors impact on longer-term mortality.
Recommendation 2: further research in this field should make better use of data linkage across national clinical audits
Although mortality is clearly an important and patient-centred outcome, the impact and consequences of critical care go beyond mortality. As data on longer-term, health-related quality of life for survivors of critical care are currently not routinely collected, national clinical audits of chronic health conditions provide an ideal opportunity to better understand the impact and consequences of critical illness on these specific chronic health conditions, gaining some insight into the wider impact of critical care on patients’ subsequent health status. Critical illness-related hyperglycaemia, for example, has previously been linked with subsequent development of type 2 diabetes,112,113 and acute kidney injury, common among critically ill patients, has been strongly linked with subsequent end-stage renal disease. 114 Both these conditions have well-established national clinical audits (the National Diabetes Audit and the UK Renal Registry), and data linkage across these audits would permit a better understanding of the specific consequences of critical illness. In addition, the risk prediction models developed in this report were limited to the available predictors within the CMP and NCAA data sets which, in turn, are limited by what it is feasible to expect providers to routinely collect for the purpose of national clinical audit. Data linkage across national clinical audits would also enhance the available pool of candidate predictors on which risk prediction models could be developed, potentially allowing for improved prediction with no additional data collection burden. For example, existing literature on predictors of mortality for post cardiac surgery patients suggests that outcomes are best predicted by a combination of pre-, intra- and postoperative risk factors. 51 The CMP data set is a reliable source of postoperative information, but has limited pre- or intraoperative data. Data linkage with the National Adult Cardiac Surgery Audit would greatly increase the available pre- and intraoperative data to improve risk prediction among this patient group.
Recommendation 3: further research in this field should make better use of other routinely collected data sets
Making better use of other routinely collected data sets, such as Hospital Episode Statistics (HES), would also potentially expand the available predictors and outcomes. For example, the recently developed US risk prediction model for hospital survival following in-hospital cardiac arrest includes information on pre-arrest comorbidities and interventions. Collection of comorbidities was considered for the NCAA, but it was decided that this would add a considerable data collection burden. Data linkage with HES would permit evaluation of comorbidities and interventions through use of diagnostic and procedural codes. If these factors improve the fit of the model, then options to either undertake this data linkage routinely or to incorporate specific additional fields into the NCAA data set could be explored. In terms of expanding available outcomes, survivors of critical care experience significant morbidity with substantial resultant health-care resource use and costs. 115 Data linkage with HES would enable the cost of subsequent hospitalisations, and its association with severity and/or duration of critical illness and other risk factors, to be estimated
Recommendation 4: future research should consider the necessity for specific data collection to support national clinical audit compared with benchmarking providers using routinely collected data alone
National clinical audits rely on a separate, specific collection of clinical data in addition to the routine data, such as HES, that are collected in the course of a patient’s journey through the health-care system. It has generally been held that these detailed clinical data are essential for reliable benchmarking of specific clinical services. However, national clinical audit is relatively expensive and consideration should therefore be given to whether or not clinical services, such as critical care, can be benchmarked using routinely collected data alone. Considerations would include data capture, that is, whether or not the same patients can be identified from both national clinical audit data and routine data (both in terms of the completeness of data capture for national clinical audit and also whether the users of a specific service can reliably be identified from routine data), and also the performance of risk prediction models based on routinely collected data, compared with those based on detailed clinical data, for identifying providers with potentially outlying performance.
Acknowledgements
We wish to thank all the staff at critical care units participating in the CMP (www.icnarc.org/Our-Audit/Audits/Cmp/About/Participation) and hospitals participating in the NCAA (www.icnarc.org/Our-Audit/Audits/Ncaa/About/Participation).
Nazir Lone, Catriona Haddow, Moranne MacGillivray, Angela Khan and Brian Cook contributed to the external validation of the ICNARC model in Scottish critical care units.
Sarah Power and Stephen Webb contributed to the development and validation of a risk prediction model for cardiothoracic critical care units.
Ben Creagh-Brown, Ari Ercole, Mike Gillies, Steve Harris, Rupert Pearse, Manu Shankar-Hari, Alasdair Short, Marius Terblanche and Duncan Young contributed to the development and validation of the new ICNARC model for adult critical care units.
Krishna Patel, Edel Nixon, Jasmeet Soar, Gary Smith, Carl Gwinnutt and Jerry Nolan contributed to the development and validation of risk prediction models for outcomes following in-hospital cardiac arrest.
Contribution of authors
Dr David A Harrison (Senior Statistician) conceived and designed the study, conducted the validation of the ICNARC model in Scottish critical care units, oversaw the risk prediction modelling work, and drafted and critically revised the manuscript.
Paloma Ferrando-Vivas (Statistician/Risk prediction modeller) conducted the risk prediction modelling for cardiothoracic critical care units and adult critical care units and drafted the manuscript.
Dr Jason Shahin (Assistant Professor, Respiratory and Critical Care Medicine) contributed to the risk prediction modelling work for cardiothoracic critical care units and drafted the manuscript.
Professor Kathryn M Rowan (Director of Scientific & Strategic Development and Honorary Professor of Health Services Research) conceived and designed the study and critically revised the manuscript.
Expert Advisory Group
Professor Doug Altman (Professor of Statistics in Medicine, University of Oxford); Professor Nick Black (Professor of Health Services Research, London School of Hygiene and Tropical Medicine); Professor James Carpenter (Professor of Medical Statistics, London School of Hygiene and Tropical Medicine); Dr Gary Collins (Associate Professor and Head of Prognosis Methodology, University of Oxford); Maureen Dalziel (service user representative); Professor Mike Grocott (Professor of Anaesthesia and Critical Care Medicine, University of Southampton); Dr Steve Harris (Clinical Lecturer in Anaesthesia and Critical Care, University College London); Professor Jon Nicholl (Professor of Health Services Research, University of Sheffield); Dr Andrew Padkin (Consultant in Intensive Care Medicine, Royal United Hospital Bath NHS Trust); and Graham Ramsay (former Chief Executive, Mid Essex Hospital Services NHS Trust).
Publications
Harrison DA, Lone NI, Haddow C, MacGillivray M, Khan A, Cook B, et al. External validation of the Intensive Care National Audit & Research Centre (ICNARC) risk prediction model in critical care units in Scotland. BMC Anesthesiol 2014;14:116. http://dx.doi.org/10.1186/1471-2253-14-116
Harrison DA, Patel K, Nixon E, Soar J, Smith GB, Gwinnutt C, et al. Development and validation of risk models to predict outcomes following in-hospital cardiac arrest attended by a hospital-based resuscitation team. Resuscitation 2014;85:993–1000. http://dx.doi.org/10.1016/j.resuscitation.2014.05.004
Data sharing statement
Data from the CMP and the NCAA can be obtained from ICNARC (see www.icnarc.org/Our-Audit/Audits/Cmp/Reports/Access-Our-Data and www.icnarc.org/Our-Audit/Audits/Ncaa/Reports/Access-Our-Data).
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the HS&DR programme or the Department of Health. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the HS&DR programme or the Department of Health.
References
- High Quality Care For All. NHS Next Stage Review. London: Department of Health; 2008.
- Donabedian A. The quality of care. How can it be assessed?. JAMA 1988;260:1743-8. http://dx.doi.org/10.1001/jama.1988.03410120089033.
- Black N. Assessing the quality of hospitals. BMJ 2010;340. http://dx.doi.org/10.1136/bmj.c2066.
- Black N. Time for a new approach to assessing the quality of hospitals in England. BMJ 2013;347. http://dx.doi.org/10.1136/bmj.f4421.
- Higgins TL. Quantifying risk and benchmarking performance in the adult intensive care unit. J Intensive Care Med 2007;22:141-56. http://dx.doi.org/10.1177/0885066607299520.
- Healthcare Quality Improvement Partnership . National Clinical Audits for Inclusion in Quality Accounts n.d. www.hqip.org.uk/national-clinical-audits-for-inclusion-in-quality-accounts (accessed January 2015).
- Harrison DA, Brady AR, Rowan K. Case mix, outcome and length of stay for admissions to adult, general critical care units in England, Wales and Northern Ireland: the Intensive Care National Audit & Research Centre Case Mix Programme Database. Crit Care 2004;8:R99-111. http://dx.doi.org/10.1186/cc2834.
- Moreno RP. Outcome prediction in intensive care: why we need to reinvent the wheel. Curr Opin Crit Care 2008;14:483-4. http://dx.doi.org/10.1097/MCC.0b013e328310dc7d.
- Knaus WA, Draper EA, Wagner DP, Zimmerman JE. APACHE II: a severity of disease classification system. Crit Care Med 1985;13:818-29. http://dx.doi.org/10.1097/00003246-198510000-00009.
- Knaus WA, Wagner DP, Draper EA, Zimmerman JE, Bergner M, Bastos PG, et al. The APACHE III prognostic system. Risk prediction of hospital mortality for critically ill hospitalized adults. Chest 1991;100:1619-36. http://dx.doi.org/10.1378/chest.100.6.1619.
- Le Gall JR, Lemeshow S, Saulnier F. A new Simplified Acute Physiology Score (SAPS II) based on a European/North American multicenter study. JAMA 1993;270:2957-63. http://dx.doi.org/10.1001/jama.1993.03510240069035.
- Lemeshow S, Teres D, Klar J, Avrunin JS, Gehlbach SH, Rapoport J. Mortality Probability Models (MPM II) based on an international cohort of intensive care unit patients. JAMA 1993;270:2478-86. http://dx.doi.org/10.1001/jama.1993.03510200084037.
- Harrison DA, Brady AR, Parry GJ, Carpenter JR, Rowan K. Recalibration of risk prediction models in a large multicenter cohort of admissions to adult, general critical care units in the United Kingdom. Crit Care Med 2006;34:1378-88. http://dx.doi.org/10.1097/01.CCM.0000216702.94014.75.
- Harrison DA, Parry GJ, Carpenter JR, Short A, Rowan K. A new risk prediction model for critical care: the Intensive Care National Audit & Research Centre (ICNARC) model. Crit Care Med 2007;35:1091-8. http://dx.doi.org/10.1097/01.CCM.0000259468.24532.44.
- Harrison DA, Rowan KM. Outcome prediction in critical care: the ICNARC model. Curr Opin Crit Care 2008;14:506-12. http://dx.doi.org/10.1097/MCC.0b013e328310165a.
- Nolan JP, Soar J, Smith GB, Gwinnutt C, Parrott F, Power S, et al. Incidence and outcome of in-hospital cardiac arrest in the United Kingdom National Cardiac Arrest Audit. Resuscitation 2014;85:987-92. http://dx.doi.org/10.1016/j.resuscitation.2014.04.002.
- National Health Service Act 2006. London: The Stationery Office; 2006.
- Altman DG, Royston P. What do we mean by validating a prognostic model?. Stat Med 2000;19:453-73. http://dx.doi.org/10.1002/(SICI)1097-0258(20000229)19:4<453::AID-SIM350>3.0.CO;2-5.
- Altman DG, Vergouwe Y, Royston P, Moons KG. Prognosis and prognostic research: validating a prognostic model. BMJ 2009;338. http://dx.doi.org/10.1136/bmj.b605.
- Young JD, Goldfrad C, Rowan K. Development and testing of a hierarchical method to code the reason for admission to intensive care units: the ICNARC coding method. Intensive Care National Audit & Research Centre. Br J Anaesth 2001;87:543-8. http://dx.doi.org/10.1093/bja/87.4.543.
- Rowan KM, Kerr JH, Major E, McPherson K, Short A, Vessey MP. Intensive Care Society’s APACHE II study in Britain and Ireland – II: Outcome comparisons of intensive care units after adjustment for case mix by the American APACHE II method. BMJ 1993;307:977-81. http://dx.doi.org/10.1136/bmj.307.6910.977.
- Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. JAMA 1982;247:2543-6. http://dx.doi.org/10.1001/jama.1982.03320430047030.
- Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982;143:29-36. http://dx.doi.org/10.1148/radiology.143.1.7063747.
- Hosmer DW, Lemeshow S. Goodness-of-fit tests for the multiple logistic regression model. Commun Stat 1980;A9:1043-69. http://dx.doi.org/10.1080/03610928008827941.
- Kramer AA, Zimmerman JE. Assessing the calibration of mortality benchmarks in critical care: The Hosmer–Lemeshow test revisited. Crit Care Med 2007;35:2052-6. http://dx.doi.org/10.1097/01.CCM.0000275267.64078.B0.
- Peek N, Arts DG, Bosman RJ, van der Voort PH, de Keizer NF. External validation of prognostic models for critically ill patients required substantial sample sizes. J Clin Epidemiol 2007;60:491-50. http://dx.doi.org/10.1016/j.jclinepi.2006.08.011.
- Cox DR. Two further applications of a model for binary regression. Biometrika 1958;45:562-5. http://dx.doi.org/10.1093/biomet/45.3-4.562.
- Brier GW. Verification of forecasts expressed in terms of probability. Mon Wea Rev 1950;75:1-3. http://dx.doi.org/10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2.
- Shapiro AR. The evaluation of clinical predictions. A method and initial application. N Engl J Med 1977;296:1509-14. http://dx.doi.org/10.1056/NEJM197706302962607.
- Mittlbock M, Schemper M. Explained variation for logistic regression. Stat Med 1996;15:1987-97. http://dx.doi.org/10.1002/(SICI)1097-0258(19961015)15:19<1987::AID-SIM318>3.0.CO;2-9.
- DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 1988;44:837-45. http://dx.doi.org/10.2307/2531595.
- Wilson EB. Probable inference, the law of succession, and statistical inference. J Am Stat Assoc 1927;22:209-12. http://dx.doi.org/10.1080/01621459.1927.10502953.
- Minne L, Eslami S, de Keizer N, de Jonge E, de Rooij SE, Abu-Hanna A. Effect of changes over time in the performance of a customized SAPS-II model on the quality of care assessment. Intensive Care Med 2012;38:40-6. http://dx.doi.org/10.1007/s00134-011-2390-2.
- Wunsch H, Brady AR, Rowan K. Impact of exclusion criteria on case mix, outcome, and length of stay for the severity of disease scoring methods in common use in critical care. J Crit Care 2004;19:67-74. http://dx.doi.org/10.1016/j.jcrc.2004.04.008.
- Turner JS, Mudaliar YM, Chang RW, Morgan CJ. Acute physiology and chronic health evaluation (APACHE II) scoring in a cardiothoracic intensive care unit. Crit Care Med 1991;19:1266-9. http://dx.doi.org/10.1097/00003246-199110000-00008.
- van Buuren S. Multiple imputation of discrete and continuous data by fully conditional specification. Stat Methods Med Res 2007;16:219-42. http://dx.doi.org/10.1177/0962280206074463.
- Schafer JL. Analysis of Incomplete Multivariate Data. London: Chapman & Hall; 1997.
- Moons KG, Donders RA, Stijnen T, Harrell FE. Using the outcome for imputation of missing predictor values was preferred. J Clin Epidemiol 2006;59:1092-101. http://dx.doi.org/10.1016/j.jclinepi.2006.01.009.
- van Buuren S, Boshuizen HC, Knook DL. Multiple imputation of missing blood pressure covariates in survival analysis. Stat Med 1999;18:681-94. http://dx.doi.org/10.1002/(SICI)1097-0258(19990330)18:6<681::AID-SIM71>3.0.CO;2-R.
- Schafer JL. Multiple imputation: a primer. Stat Methods Med Res 1999;8:3-15. http://dx.doi.org/10.1191/096228099671525676.
- Rubin DB. Multiple Imputation for Nonresponse in Surveys. New York, NY: J Wiley & Sons; 1987.
- Pencina MJ, D’Agostino RB, D’Agostino RB, Vasan RS. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med 2008;27:157-72. http://dx.doi.org/10.1002/sim.2929.
- Steyerberg EW, Harrell FE, Borsboom GJ, Eijkemans MJ, Vergouwe Y, Habbema JD. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol 2001;54:774-81. http://dx.doi.org/10.1016/S0895-4356(01)00341-9.
- Parolari A, Pesce LL, Trezzi M, Cavallotti L, Kassem S, Loardi C, et al. EuroSCORE performance in valve surgery: a meta-analysis. Ann Thorac Surg 2010;89:787-93. http://dx.doi.org/10.1016/j.athoracsur.2009.11.032.
- Siregar S, Groenwold RH, de Heer F, Bots ML, van der Graaf Y, van Herwerden LA. Performance of the original EuroSCORE. Eur J Cardiothorac Surg 2012;41:746-54. http://dx.doi.org/10.1093/ejcts/ezr285.
- Badreldin AM, Doerr F, Ismail MM, Heldwein MB, Lehmann T, Bayer O, et al. Comparison between Sequential Organ Failure Assessment score (SOFA) and Cardiac Surgery Score (CASUS) for mortality prediction after cardiac surgery. Thorac Cardiovasc Surg 2012;60:35-42. http://dx.doi.org/10.1055/s-0030-1270943.
- Doerr F, Badreldin AM, Heldwein MB, Bossert T, Richter M, Lehmann T, et al. A comparative study of four intensive care outcome prediction models in cardiac surgery patients. J Cardiothorac Surg 2011;6. http://dx.doi.org/10.1186/1749-8090-6-21.
- Tamayo E, Fierro I, Bustamante-Munguira J, Heredia-Rodriguez M, Jorge-Monjas P, Maroto L, et al. Development of the Post Cardiac Surgery (POCAS) prognostic score. Crit Care 2013;17. http://dx.doi.org/10.1186/cc13017.
- Becker RB, Zimmerman JE, Knaus WA, Wagner DP, Seneff MG, Draper EA, et al. The use of APACHE III to evaluate ICU length of stay, resource use, and mortality after coronary artery by-pass surgery. J Cardiovasc Surg 1995;36:1-11.
- Simchen E, Galai N, Zitser-Gurevich Y, Braun D, Mozes B. Sequential logistic models for 30 days mortality after CABG: pre-operative, intra-operative and post-operative experience – the Israeli CABG study (ISCAB). Three models for early mortality after CABG. Eur J Epidemiol 2000;16:543-55. http://dx.doi.org/10.1023/A:1007658719671.
- Gomes RV, Tura B, Mendonca Filho HT, Almeida Campos LA, Rouge A, Matos Nogueira PM, et al. A first postoperative day predictive score of mortality for cardiac surgery. Ann Thorac Cardiovasc Surg 2007;13:159-64.
- Brandrup-Wognsen G, Haglid M, Karlsson T, Berggren H, Herlitz J. Mortality during the two years after coronary artery bypass grafting in relation to perioperative factors and urgency of operation. Eur J Cardiothorac Surg 1995;9:685-91. http://dx.doi.org/10.1016/S1010-7940(05)80126-5.
- Brown JR, Cochran RP, Dacey LJ, Ross CS, Kunzelman KS, Dunton RF, et al. Perioperative increases in serum creatinine are predictive of increased 90-day mortality after coronary artery bypass graft surgery. Circulation 2006;114:I409-13. http://dx.doi.org/10.1161/CIRCULATIONAHA.105.000596.
- Chan V, Jamieson WR, Chan F, Germann E. Valve replacement surgery complicated by acute renal failure – predictors of early mortality. J Card Surg 2006;21:139-43. http://dx.doi.org/10.1111/j.1540-8191.2006.00194.x.
- Glance LG, Osler TM, Mukamel DB, Dick AW. Effect of complications on mortality after coronary artery bypass grafting surgery: evidence from New York State. J Thorac Cardiovasc Surg 2007;134:53-8. http://dx.doi.org/10.1016/j.jtcvs.2007.02.037.
- He GW, Acuff TE, Ryan WH, He YH, Mack MJ. Determinants of operative mortality in reoperative coronary artery bypass grafting. J Thorac Cardiovasc Surg 1995;110:971-8. http://dx.doi.org/10.1016/S0022-5223(05)80164-3.
- Jones KW, Cain AS, Mitchell JH, Millar RC, Rimmasch HL, French TK, et al. Hyperglycemia predicts mortality after CABG: postoperative hyperglycemia predicts dramatic increases in mortality after coronary artery bypass graft surgery. J Diabetes Complications 2008;22:365-70. http://dx.doi.org/10.1016/j.jdiacomp.2007.05.006.
- Mohnle P, Snyder-Ramos SA, Miao Y, Kulier A, Bottiger BW, Levin J, et al. Postoperative red blood cell transfusion and morbid outcome in uncomplicated cardiac surgery patients. Intensive Care Med 2011;37:97-109. http://dx.doi.org/10.1007/s00134-010-2017-z.
- Khosravani H, Shahpori R, Stelfox HT, Kirkpatrick AW, Laupland KB. Occurrence and adverse effect on outcome of hyperlactatemia in the critically ill. Crit Care 2009;13. http://dx.doi.org/10.1186/cc7918.
- Nichol AD, Egi M, Pettila V, Bellomo R, French C, Hart G, et al. Relative hyperlactatemia and hospital mortality in critically ill patients: a retrospective multi-centre study. Crit Care 2010;14. http://dx.doi.org/10.1186/cc8888.
- Harrison DA, Prabhu G, Grieve R, Harvey SE, Sadique MZ, Gomes M, et al. Risk Adjustment In Neurocritical care (RAIN) – prospective validation of risk prediction models for adult patients with acute traumatic brain injury to use to evaluate the optimum location and comparative costs of neurocritical care: a cohort study. Health Technol Assess 2013;17. http://dx.doi.org/10.3310/hta17230.
- Bridgewater B, Hickey GL, Cooper G, Deanfield J, Roxburgh J. Publishing cardiac surgery mortality rates: lessons for other specialties. BMJ 2013;346. http://dx.doi.org/10.1136/bmj.f1139.
- Knaus WA, Zimmerman JE, Wagner DP, Draper EA, Lawrence DE. APACHE-acute physiology and chronic health evaluation: a physiologically based classification system. Crit Care Med 1981;9:591-7. http://dx.doi.org/10.1097/00003246-198108000-00008.
- Young PJ, Saxena M, Beasley R, Bellomo R, Bailey M, Pilcher D, et al. Early peak temperature and mortality in critically ill patients with or without infection. Intensive Care Med 2012. http://dx.doi.org/10.1007/s00134-012-2478-3.
- Harrison DA, Lertsithichai P, Brady AR, Carpenter JR, Rowan K. Winter excess mortality in intensive care in the UK: an analysis of outcome adjusted for patient case mix and unit workload. Intensive Care Med 2004;30:1900-7. http://dx.doi.org/10.1007/s00134-004-2390-6.
- Weinkove R, Bailey M, Bellomo R, Saxena MK, Tam CS, Pilcher DV, et al. Association between early peak temperature and mortality in neutropenic sepsis. Ann Hematol 2015;94:857-64. http://dx.doi.org/10.1007/s00277-014-2273-z.
- Sakr Y, Elia C, Mascia L, Barberis B, Cardellino S, Livigni S, et al. The influence of gender on the epidemiology of and outcome from severe sepsis. Crit Care 2013;17. http://dx.doi.org/10.1186/cc12570.
- Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D. A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group. Ann Intern Med 1999;130:461-70. http://dx.doi.org/10.7326/0003-4819-130-6-199903160-00002.
- Oliveros H, Villamor E. Obesity and mortality in critically ill adults: a systematic review and meta-analysis. Obesity 2008;16:515-21. http://dx.doi.org/10.1038/oby.2007.102.
- Welch CA, Harrison DA, Hutchings A, Rowan K. The association between deprivation and hospital mortality for admissions to critical care units in England. J Crit Care 2010;25:382-90. http://dx.doi.org/10.1016/j.jcrc.2009.11.003.
- Schafer JL, Graham JW. Missing data: our view of the state of the art. Psychol Methods 2002;7:147-77. http://dx.doi.org/10.1037/1082-989X.7.2.147.
- Royston P, Sauerbrei W. Building multivariable regression models with continuous covariates in clinical epidemiology – with an emphasis on fractional polynomials. Methods Inf Med 2005;44:561-71.
- Schafer JL, Olsen MK. Modeling and Imputation of Semicontinuous Survey Variables, Technical Report No. 00–39. State College, PA: The Pennsylvania State University; 1999.
- Seaman SR, Bartlett JW, White IR. Multiple imputation of missing covariates with non-linear effects and interactions: an evaluation of statistical methods. BMC Med Res Methodol 2012;12. http://dx.doi.org/10.1186/1471-2288-12-46.
- von Hippel PT. How to impute interactions, squares, and other transformed variables. Sociol Methodol 2009;39:265-91. http://dx.doi.org/10.1111/j.1467-9531.2009.01215.x.
- White IR, Royston P, Wood AM. Multiple imputation using chained equations: Issues and guidance for practice. Stat Med 2011;30:377-99. http://dx.doi.org/10.1002/sim.4067.
- Bartlett JW, Seaman SR, White IR, Carpenter JR. Multiple imputation of covariates by fully conditional specification: accommodating the substantive model. Stat Methods Med Res 2014.
- Moons KG, Kengne AP, Woodward M, Royston P, Vergouwe Y, Altman DG, et al. Risk prediction models: I. Development, internal validation, and assessing the incremental value of a new (bio)marker. Heart 2012;98:683-90. http://dx.doi.org/10.1136/heartjnl-2011-301246.
- White IR, Carlin JB. Bias and efficiency of multiple imputation compared with complete-case analysis for missing covariate values. Stat Med 2010;29:2920-31. http://dx.doi.org/10.1002/sim.3944.
- Lee KJ, Carlin JB. Recovery of information from multiple imputation: a simulation study. Emerg Themes Epidemiol 2012;9. http://dx.doi.org/10.1186/1742-7622-9-3.
- Royston P, Moons KG, Altman DG, Vergouwe Y. Prognosis and prognostic research: developing a prognostic model. BMJ 2009;338. http://dx.doi.org/10.1136/bmj.b604.
- Moreno RP, Metnitz PG, Almeida E, Jordan B, Bauer P, Campos RA, et al. SAPS 3 – From evaluation of the patient to evaluation of the intensive care unit. Part 2: development of a prognostic model for hospital mortality at ICU admission. Intensive Care Med 2005;31:1345-55. http://dx.doi.org/10.1007/s00134-005-2763-5.
- Altman DG. Categorising continuous variables. Br J Cancer 1991;64. http://dx.doi.org/10.1038/bjc.1991.441.
- Harrell FE. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. New York, NY: Springer; 2001.
- Royston P, Ambler G, Sauerbrei W. The use of fractional polynomials to model continuous risk variables in epidemiology. Int J Epidemiol 1999;28:964-74. http://dx.doi.org/10.1093/ije/28.5.964.
- Royston P. A strategy for modelling the effect of a continuous covariate in medicine and epidemiology. Stat Med 2000;19:1831-47. http://dx.doi.org/10.1002/1097-0258(20000730)19:14<1831::AID-SIM502>3.0.CO;2-1.
- Cook NR. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation 2007;115:928-35. http://dx.doi.org/10.1161/CIRCULATIONAHA.106.672402.
- Harrell FE, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 1996;15:361-87. http://dx.doi.org/10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4.
- Taylor JM, Ankerst DP, Andridge RR. Validation of biomarker-based risk prediction models. Clin Cancer Res 2008;14:5977-83. http://dx.doi.org/10.1158/1078-0432.CCR-07-4534.
- Lewis-Beck MS, Bryman AE, Futing Liao T. The SAGE Encyclopedia of Social Science Research Methods. New York, NY: SAGE Publications; 2003.
- Cook NR. Statistical evaluation of prognostic versus diagnostic models: beyond the ROC curve. Clin Chem 2008;54:17-23. http://dx.doi.org/10.1373/clinchem.2007.096529.
- Mallett S, Royston P, Dutton S, Waters R, Altman DG. Reporting methods in studies developing prognostic models in cancer: a review. BMC Med 2010;8. http://dx.doi.org/10.1186/1741-7015-8-20.
- Spiegelhalter DJ. Funnel plots for comparing institutional performance. Stat Med 2005;24:1185-202. http://dx.doi.org/10.1002/sim.1970.
- Vincent JL, Moreno R. Clinical review: scoring systems in the critically ill. Crit Care 2010;14. http://dx.doi.org/10.1186/cc8204.
- Miller A. Subset Selection in Regression. 2nd edn. Boca Raton, FL: Chapman & Hall; 2002.
- Ratner B. Variable selection methods in regression: ignorable problem, outing notable solution. Journal of Targeting, Measurement and Analysis for Marketing 2010;18:65-7. http://dx.doi.org/10.1057/jt.2009.26.
- Zimmerman JE, Kramer AA, McNair DS, Malila FM. Acute Physiology and Chronic Health Evaluation (APACHE) IV: hospital mortality assessment for today’s critically ill patients. Crit Care Med 2006;34:1297-310. http://dx.doi.org/10.1097/01.CCM.0000215112.84523.F0.
- Higgins TL, Teres D, Copes WS, Nathanson BH, Stark M, Kramer AA. Assessing contemporary intensive care unit outcome: an updated Mortality Probability Admission Model (MPM0-III). Crit Care Med 2007;35:827-35. http://dx.doi.org/10.1097/01.CCM.0000257337.63529.9F.
- Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr 1974;19:716-23. http://dx.doi.org/10.1109/TAC.1974.1100705.
- Van Houwelingen JC, Le Cessie S. Predictive value of statistical models. Stat Med 1990;9:1303-25. http://dx.doi.org/10.1002/sim.4780091109.
- Peberdy MA, Kaye W, Ornato JP, Larkin GL, Nadkarni V, Mancini ME, et al. Cardiopulmonary resuscitation of adults in the hospital: a report of 14720 cardiac arrests from the National Registry of Cardiopulmonary Resuscitation. Resuscitation 2003;58:297-308. http://dx.doi.org/10.1016/S0300-9572(03)00215-6.
- Chan PS, Berg RA, Spertus JA, Schwamm LH, Bhatt DL, Fonarow GC, et al. Risk-standardizing survival for in-hospital cardiac arrest to facilitate hospital comparisons. J Am Coll Cardiol 2013;62:601-9. http://dx.doi.org/10.1016/j.jacc.2013.05.051.
- Ronning PA, Pedersen T, Skaga NO, Helseth E, Langmoen IA, Stavem K. External validation of a prognostic model for early mortality after traumatic brain injury. J Trauma 2011;70:E56-61. http://dx.doi.org/10.1097/TA.0b013e3181e80f0a.
- Yap CH, Reid C, Yii M, Rowland MA, Mohajeri M, Skillington PD, et al. Validation of the EuroSCORE model in Australia. Eur J Cardiothorac Surg 2006;29:441-6. http://dx.doi.org/10.1016/j.ejcts.2005.12.046.
- Larkin GL, Copes WS, Nathanson BH, Kaye W. Pre-resuscitation factors associated with mortality in 49,130 cases of in-hospital cardiac arrest: a report from the National Registry for Cardiopulmonary Resuscitation. Resuscitation 2010;81:302-11. http://dx.doi.org/10.1016/j.resuscitation.2009.11.021.
- Intensive Care National Audit & Research Centre . Public Reporting Website n.d. https://onlinereports.icnarc.org (accessed February 2015).
- NHS Commissioning . Specialised Services Quality Dashboards n.d. www.england.nhs.uk/commissioning/spec-services/npc-crg/spec-dashboards/ (accessed June 2015).
- Care Quality Commission . Inspection Framework: NHS Acute Hospitals. Core Service: Critical Care n.d. www.cqc.org.uk/content/inspection-frameworks-nhs-acute-hospital-core-services (accessed August 2015).
- Brinkman S, Abu-Hanna A, de Jonge E, de Keizer NF. Prediction of long-term mortality in ICU patients: model validation and assessing the effect of using in-hospital versus long-term mortality on benchmarking. Intensive Care Med 2013;39:1925-31. http://dx.doi.org/10.1007/s00134-013-3042-5.
- Lone NI, Walsh TS. Impact of intensive care unit organ failures on mortality during the five years after a critical illness. Am J Respir Crit Care Med 2012;186:640-7. http://dx.doi.org/10.1164/rccm.201201-0059OC.
- Williams TA, Dobb GJ, Finn JC, Knuiman MW, Geelhoed E, Lee KY, et al. Determinants of long-term survival after intensive care. Crit Care Med 2008;36:1523-30. http://dx.doi.org/10.1097/CCM.0b013e318170a405.
- Gornik I, Vujaklija A, Lukic E, Madzarac G, Gasparovic V. Hyperglycaemia in critical illness is a risk factor for later development of type II diabetes mellitus. Acta Diabetol 2010;47:29-33. http://dx.doi.org/10.1007/s00592-009-0115-6.
- Gornik I, Vujaklija-Brajkovic A, Renar IP, Gasparovic V. A prospective observational study of the relationship of critical illness associated hyperglycaemia in medical ICU patients and subsequent development of type 2 diabetes. Crit Care 2010;14. http://dx.doi.org/10.1186/cc9101.
- Chawla LS, Amdur RL, Amodeo S, Kimmel PL, Palant CE. The severity of acute kidney injury predicts progression to chronic kidney disease. Kidney Int 2011;79:1361-9. http://dx.doi.org/10.1038/ki.2011.42.
- Lone NI, Seretny M, Wild SH, Rowan KM, Murray GD, Walsh TS. Surviving intensive care: a systematic review of healthcare resource use after hospital discharge. Crit Care Med 2013;41:1832-43. http://dx.doi.org/10.1097/CCM.0b013e31828a409c.
Appendix 1 Simulation study of missing values
Appendix 2 The new Intensive Care National Audit & Research Centre model: ICNARCH-2014
The raw data fields required for calculation of the new ICNARC model for predicting acute hospital mortality, ICNARCH-2014, are shown in Table 42 and the final model coefficients are provided in Table 43. For continuous predictors, coefficients are provided for the cubic spline base variables, calculated for each predictor as follows.
| Predictor (units of measurement) | Field type (range) | Definition/categories |
|---|---|---|
| Highest heart rate (beats per minute) | Integer (0–450) | Highest heart rate from the first 24 hours following admission to the critical care unit |
| Lowest SBP (mmHg) | Integer (0–400) | Lowest SBP from the first 24 hours following admission to the critical care unit |
| Highest temperature (°C) | Real (0.0–46.0) | Highest central temperature from the first 24 hours following admission to the critical care unit. If no central temperature recorded, use highest non-central temperature + 0.5 °C |
| Lowest respiratory rate (breaths per minute) | Integer (0–100) | Lowest rate (either ventilated or non-ventilated) from the first 24 hours following admission to the critical care unit |
| Lowest PaO2 (kPa) | Real (1.0–100.0) | Lowest PaO2 from an arterial blood gas using blood sampled during the first 24 hours following admission to the critical care unit |
| Associated FiO2 | Real (0.21–1.00) | FiO2 associated with the arterial blood gas with the lowest PaO2 |
| Lowest arterial pH | Real (6.10–9.00) | Lowest arterial pH from blood sampled during the first 24 hours following admission to the critical care unit |
| Associated PaCO2 (kPa) | Real (0.0–50.0) | PaCO2 from the arterial blood gas with the lowest arterial pH |
| Highest blood lactate concentration (mmol/l) | Real (0.1–35.0) | Highest blood lactate concentration from the first 24 hours following admission to the critical care unit |
| Total urine output (ml) | Integer (0–99999) | Total urine output from the first 24 hours following admission to the critical care unit. For admissions with a length of stay less than 24 hours, the total over the entire stay is recorded and scaled to represent a 24-hour equivalent |
| Highest urea level (mmol/l) | Real (0.0–300.0) | Highest serum urea concentration from the first 24 hours following admission to the critical care unit |
| Highest creatinine level (µmol/l) | Integer (9–5000) | Highest serum creatinine concentration from the first 24 hours following admission to the critical care unit |
| Highest sodium level (mmol/l) | Integer (40, 260) | Highest serum sodium concentration from the first 24 hours following admission to the critical care unit |
| Lowest WBC count (× 109/l) | Real (0.0–9999.9) | Lowest WBC count from the first 24 hours following admission to the critical care unit |
| Lowest platelet count (× 109/l) | Integer (0–9999) | Lowest platelet count from the first 24 hours following admission to the critical care unit |
| Sedation/paralysis | Categorical | Sedation/paralysis during the first 24 hours following admission to the critical care unit, categorised as: sedated for the entire of the first 24 hours; paralysed and sedated for the entire of the first 24 hours; or neither sedated nor paralysed and sedated for the entire of the first 24 hours |
| Lowest total GCS score | Integer (3–15) | Lowest total GCS score from the first 24 hours following admission to the critical care unit if neither sedated nor paralysed and sedated |
| Age (years) | Integer (0–125) | Age in whole years at admission to the critical care unit |
| Severe liver disease in past medical history | Boolean (yes/no) | Biopsy-proven cirrhosis, portal hypertension or hepatic encephalopathy, evident during the 6 months prior to admission to the critical care unit and documented prior to or at admission to the unit |
| Metastatic disease | Boolean (yes/no) | Distant metastases documented by surgery, imaging or biopsy, evident during the 6 months prior to admission to the critical care unit and documented prior to or at admission to the unit |
| Haematological malignancy | Boolean (yes/no) | Acute or chronic myelogenous leukaemia, acute or chronic lymphocytic leukaemia, multiple myeloma or lymphoma, evident during the 6 months prior to admission to the critical care unit and documented prior to or at admission to the unit |
| Dependency prior to admission | Categorical | Dependency prior to admission to acute hospital, assessed as the best description for the dependency of the patient in the two weeks prior to admission to acute hospital and prior to the onset of the acute illness Categorised as: able to live without assistance in daily activities; some (minor or major) assistance with daily activities; or total assistance with all daily activities. Daily activities include bathing, dressing, going to the toilet, moving in/out of bed/chair, continence and eating |
| CPR prior to admission | Categorical | CPR (internal or external cardiac massage) received within 24 hours prior to admission to the critical care unit, categorised as: in-hospital CPR (administered by an in-hospital resuscitation team or equivalent); community CPR (not administered by an in-hospital resuscitation team or equivalent); or no CPR. Where a patient received CPR both in the community and in-hospital, this is recorded as community CPR |
| Source of admission | Categorical | The location of the patient immediately prior to admission to the critical care unit, categorised as: emergency department or not in hospital; other acute hospital; Other critical care unit; theatre; or ward or intermediate care area. For patients whose location immediately prior to admission was a transient location of clinic, imaging department, recovery (used as a temporary critical care area) or specialist treatment area, their last non-transient location is recorded |
| Urgency of surgery | Categorical | For patients whose location immediately prior to admission was theatre, the urgency of surgery, categorised as: elective/scheduled; or emergency/urgent (according to the classification of the National Confidential Enquiry into Patient Outcome and Death) |
| Planned admission to the critical care unit | Categorical | Planned admission to the critical care unit, categorised as: planned; unplanned; or, for transfers from another critical care unit only, repatriation. For admissions from theatre, planned admission is defined as acceptance by the critical care unit prior to induction of anaesthesia. For medical admissions, a planned admission is a pre-arranged admission for a planned investigation or high-risk medical treatment. For transfers from another health-care provider, a planned admission is a pre-arranged admission after treatment or initial stabilisation but requiring specialist or higher-level critical care that cannot be provided at the source. Repatriation is defined as a planned transfer because the patient either originated from that critical care unit (i.e. returning after specialist treatment elsewhere) or from that hospital or local area |
| Primary reason for admission | String (13) | Primary reason for admission to the critical care unit, coded using the ICNARC coding method (www.icnarc.org/Our-Audit/Audits/Cmp/Resources/Icm-Icnarc-Coding-Method) |
| Mechanical ventilation | Boolean (yes/no) | Mechanical ventilation at any time during the first 24 hours following admission to the critical care unit |
| Predictor | Coefficient (SE) |
|---|---|
| Constant | 19.093 (6.635) |
| Physiological predictors | |
| Highest heart rate (beats per minute) – RCS (71, 93, 110, 146) [106] | |
| hr1 | –0.00005 (0.00325) |
| hr2 | 0.05999 (0.01205) |
| hr3 | –0.1927 (0.0350) |
| Lowest SBP (mmHg) – RCS (66, 89, 102, 130) [95] | |
| sbp1 | –0.03310 (0.00735) |
| sbp2 | 0.10080 (0.02765) |
| sbp3 | –0.3907 (0.1272) |
| Highest temperature (°C) – RCS (36.0, 37.2, 38.0, 39.2) [37.6] | |
| temp1 | –0.1530 (0.0548) |
| temp2 | –0.1349 (0.3290) |
| temp3 | 1.939 (1.495) |
| Lowest respiratory rate (breaths per minute) – RRCS (8, 12, 13, 15) [13] | |
| rr1 | –0.07682 (0.00690) |
| rr2 | 0.00772 (0.01019) |
| rr3 | –0.01448 (0.01426) |
| rr4 | 0.00698 (0.00797) |
| rr5 | 0.00024 (0.00014) |
| PaO2/ FiO2 (kPa) – RCS (9.7, 26.0, 39.7, 61.4) [33.0] | |
| pf1 | –0.04360 (0.00438) |
| pf2 | 0.07204 (0.01510) |
| pf3 | –0.17258 (0.04498) |
| Lowest arterial pH – RCS (7.08, 7.30, 7.36, 7.44) [7.31] | |
| ph1 | –0.6547 (0.8709) |
| ph2 | –4.2092 (1.3490) |
| ph3 | 29.727 (22.008) |
| PaCO2 (kPa) – RCS (3.9, 5.2, 7.0) [5.4] | |
| pc1 | 2.89904 (0.64885) |
| pc2 | 0.47630 (0.13307) |
| Highest blood lactate concentration (mmol/l) – RCS (0.7, 1.5, 2.5, 8.2) [2.8] | |
| bl1 | –11.0662 (3.2726) |
| bl2 | 188.9267 (51.7254) |
| bl3 | –351.1491 (95.6690) |
| Urine output (ml) – RCS (164, 1215, 2020, 4255) [1800] | |
| up1 | –0.00136 (0.00009) |
| up2 | 0.002416 (0.00035) |
| up3 | –0.00466 (0.00097) |
| Highest urea level (mmol/l) – RCS (2.8, 5.6, 9.3, 28.1) [10.5] | |
| ur1 | –0.07858 (0.02591) |
| ur2 | 1.8777 (0.36564) |
| ur3 | –3.4724 (0.6610) |
| Highest creatinine level (µmol/l) – RRCS (53, 80, 106, 168) [141] | |
| cr1 | 0.00213 (0.00012) |
| cr2 | 0.29314 (0.12838) |
| cr3 | –0.11159 (0.05119) |
| cr4 | 0.02867 (0.00790) |
| cr5 | –0.00035 (0.00006) |
| Highest sodium level (mmol/l) – RCS (133, 139, 145) [139] | |
| na1 | –0.05476 (0.00357) |
| na2 | 0.05908 (0.00386) |
| Lowest WBC count (× 109/l) – RCS (3.7, 8.7, 12.3, 22.5) [12.0] | |
| wbc1 | –0.03935 (0.00759) |
| wbc2 | 0.21809 (0.03518) |
| wbc3 | –0.60698 (0.10216) |
| Lowest platelet count (× 109/l) – RCS (60, 162, 232, 422) [211] | |
| plc1 | –0.00646 (0.00041) |
| plc2 | 0.02136 (0.00171) |
| plc3 | –0.05719 (0.00520) |
| Sedated/paralysed/GCS score [15] | |
| 15 | 0 |
| 14 | 0.277 (0.0320) |
| 7–13 | 0.533 (0.0294) |
| Sedated | 0.745 (0.0295) |
| 6 | 0.849 (0.0914) |
| 5 or paralysed and sedated | 0.928 (0.0582) |
| 4 | 1.273 (0.1142) |
| 3 | 1.751 (0.0596) |
| Non-physiological predictors | |
| Age (years) | 0.03723 (0.00073) |
| Severe liver disease in past medical history | 11.224 (6.501) |
| Metastatic disease | 0.621 (0.0524) |
| Haematological malignancy | 0.673 (0.0583) |
| Dependency prior to admission | |
| No assistance with daily activities | 0 |
| Some assistance with daily activities | 0.474 (0.0205) |
| Total assistance with daily activities | 0.890 (0.0870) |
| CPR prior to admission | |
| Community CPR | 0 |
| In-hospital CPR | 10.892 (3.500) |
| No CPR | 3.732 (2.449) |
| Source of admission/urgency of surgery | |
| ED or not in hospital (unplanned admission) | 0 |
| ED or not in hospital (planned admission) | 0.022 (0.1169) |
| Other acute hospital (not critical care) | 0.369 (0.0838) |
| Other critical care unit (repatriation) | 0.593 (0.1131) |
| Other critical care unit (planned or unplanned transfer) | 0.257 (0.0430) |
| Theatre (planned admission following elective or scheduled surgery) | –0.934 (0.0518) |
| Theatre (unplanned admission following elective or scheduled surgery) | –0.455 (0.0694) |
| Theatre (admission following emergency or urgent surgery) | –0.223 (0.0359) |
| Ward or intermediate care area | 0.405 (0.0264) |
| Primary reason for admission | |
| Accidental intoxication or poisoning (endocrinea) | –0.080 (0.2578) |
| Acidaemia (endocrine) | –0.117 (0.2274) |
| Burns or hyperthermia (dermatological) | 1.004 (0.3180) |
| Collapse (respiratory) | 2.157 (0.6381) |
| Coma or encephalopathy (neurological) | 0.463 (0.2030) |
| Congenital or acquired deformity or abnormality (cardiovascular) | 0 |
| Congenital or acquired deformity or abnormality (musculoskeletal) | –0.196 (0.2330) |
| Congenital or acquired deformity or abnormality (neurological) | –2.853 (1.3406) |
| Congenital or acquired deformity or abnormality (respiratory) | 0.940 (0.2046) |
| Congenital or acquired deformity or abnormality (endocrine; gastrointestinal; genitourinary; or haematological/immunological) | 0.040 (0.2081) |
| Degeneration (cardiovascular) | –0.194 (0.2209) |
| Degeneration (neurological) | 1.837 (0.3511) |
| Diabetes mellitus (endocrine) | –0.494 (2.8285) |
| Dissection or aneurysm (cardiovascular) | 0.246 (0.1817) |
| Failure (cardiovascular) | 0.574 (0.1848) |
| Failure (genitourinary) | 0.257 (0.1774) |
| Haemorrhage (cardiovascular) | –0.366 (0.3263) |
| Haemorrhage (gastrointestinal) | 8.352 (2.8243) |
| Haemorrhage (genitourinary) | –0.574 (0.2988) |
| Haemorrhage (neurological) | 0.370 (0.6378) |
| Haemorrhage (respiratory) | 0.214 (0.2583) |
| Hyperkalaemia (endocrine) | 0.011 (0.2464) |
| Hypertension (cardiovascular) or over- or under-activity (cardiovascular; genitourinary) | 0.198 (0.1800) |
| Hypokalaemia (endocrine) | –0.494 (0.4010) |
| Hyponatraemia (endocrine) | –0.268 (0.2864) |
| Hypoplasia or dysplasia (haematological/immunological) | 0.651 (0.3303) |
| Hypothermia (endocrine) | 0.190 (0.2953) |
| Infection (cardiovascular) | 0.775 (0.2100) |
| Infection (genitourinary) | –0.140 (0.1885) |
| Infection (respiratory) | 2.116 (0.5798) |
| Infection (dermatological; gastrointestinal; haematological/immunological; musculoskeletal; or neurological) | 0.372 (0.1758) |
| Inflammation (gastrointestinal) | 0.486 (0.1799) |
| Inflammation (neurological) | –0.191 (0.2739) |
| Inflammation (respiratory) | 0.377 (0.1785) |
| Inflammation (cardiovascular; dermatological; genitourinary; musculoskeletal) | –0.017 (0.2435) |
| Obstruction (cardiovascular) | 0.220 (0.1776) |
| Obstruction (gastrointestinal) | 0.437 (0.1783) |
| Obstruction (genitourinary) | –0.420 (0.2600) |
| Obstruction (respiratory) | 0.158 (0.1792) |
| Other endocrine processesa (endocrine) | –0.1557 (0.2333) |
| Seizures (neurological) | –0.138 (0.1872) |
| Self intoxication or self poisoning (endocrine) | 0.513 (1.0021) |
| Shock and hypotension (cardiovascular) | 0.410 (0.1770) |
| Transplant or related (gastrointestinal) | –1.125 (0.2922) |
| Transplant or related (cardiovascular; endocrine; genitourinary; haematological/immunological; respiratory) | 0.153 (0.3162) |
| Trauma, perforation or rupture (cardiovascular) | 0.128 (0.2558) |
| Trauma, perforation or rupture (gastrointestinal) | 0.398 (0.1771) |
| Trauma, perforation or rupture (neurological) | –0.475 (3.8994) |
| Trauma, perforation or rupture (dermatological; genitourinary; musculoskeletal; respiratory) | 0.260 (0.1827) |
| Tumour or malignancy (genitourinary) | 0.052 (0.2007) |
| Tumour or malignancy (haematological/immunological) | 0.116 (0.2997) |
| Tumour or malignancy (neurological) | 0.590 (0.6974) |
| Tumour or malignancy (cardiovascular; dermatological; endocrine; gastrointestinal; musculoskeletal; respiratory) | 11.442 (2.581) |
| Vascular (cardiovascular) | 0.593 (0.1989) |
| Vascular (gastrointestinal) | 0.654 (0.1897) |
| Vascular (neurological) | 1.294 (0.2195) |
| Acute alcoholic hepatitis/alcoholic cirrhosis | 0.670 (0.8356) |
| Anaphylaxis | –0.950 (0.3475) |
| Anoxic or ischaemic coma or encephalopathy | 0.687 (1.3371) |
| Asthma attack in new or known asthmatic | –1.132 (0.2533) |
| Enteroenteric or enterocutaneous fistula | 1.667 (0.3242) |
| Fractured ribs | 0.249 (0.2571) |
| Fungal or yeast pneumonia | 1.255 (0.2413) |
| Haemolysis or thrombocytopenia | –0.027 (0.3676) |
| Hanging or strangulation | 1.790 (0.2644) |
| Intracerebral haemorrhage | 32.963 (14.5399) |
| Leaking large bowel anastomosis/perforated biliary tree or gall bladder | 0.670 (0.8356) |
| Lower limb artery stenosis or occlusion | 1.009 (0.2054) |
| Pulmonary fibrosis or fibrosing alveoli | 2.919 (0.2727) |
| Secondary hydrocephalus | –2.218 (6.1830) |
| Thrombo-occlusive disease of brain | 1.899 (0.2010) |
| Toxic or drug-induced coma or encephalopathy | 0.129 (0.2480) |
| Mechanical ventilation | 0.7160 (0.4495) |
| Interactions | |
| Arterial pH × PaCO2 | |
| ph1 × pc1 | –0.42784 (0.09097) |
| ph1 × pc2 | –0.03535 (0.01712) |
| ph2 × pc1 | 0.58168 (0.21846) |
| ph3 × pc1 | –1.14392 (3.91387) |
| Arterial pH × blood lactate concentration | |
| ph1 × bl1 | 1.563 (0.4481) |
| ph1 × bl2 | –26.37 (7.0874) |
| ph1 × bl3 | 49.00 (13.111) |
| ph2 × bl1 | –0.1573 (0.12837) |
| ph3 × bl1 | 7.797 (2.4084) |
| Urine output × urea | |
| up1 × ur1 | 0.00005 (0.00001) |
| up1 × ur2 | –0.00065 (0.00015) |
| up1 × ur3 | 0.00116 (0.00027) |
| up2 × ur1 | –0.00002 (0.00002) |
| up3 × ur1 | 0.00005 (0.00005) |
| Liver disease × temperature | |
| temp1 | –0.2845 (0.17794) |
| temp2 | 0.9400 (0.49252) |
| temp3 | –4.648 (1.8547) |
| CPR × SBP | |
| In-hospital CPR × sbp1 | 0.00043 (0.00940) |
| In-hospital CPR × sbp2 | 0.01370 (0.03616) |
| In-hospital CPR × sbp3 | –0.03798 (0.16478) |
| No CPR × sbp1 | 0.01281 (0.00753) |
| No CPR × sbp2 | –0.07066 (0.02817) |
| No CPR × sbp3 | 0.31309 (0.12912) |
| CPR × temperature | |
| In-hospital CPR × temp1 | –0.3232 (0.09522) |
| In-hospital CPR × temp2 | 0.8444 (0.45897) |
| In-hospital CPR × temp3 | –3.230 (2.0050) |
| No CPR × temp1 | –0.1547 (0.06646) |
| No CPR × temp2 | 0.2818 (0.34462) |
| No CPR × temp3 | –1.556 (1.5416) |
| Collapse (respiratory) × platelet count | |
| plc1 | –0.01305 (0.00547) |
| plc2 | 0.02428 (0.02238) |
| plc3 | –0.04071 (0.06688) |
| Congenital (neurological) × urine output | |
| up1 | 0.00324 (0.00150) |
| up2 | –0.01064 (0.00576) |
| up3 | 0.02702 (0.01488) |
| Diabetes mellitus (endocrine) × heart rate | |
| hr1 | 0.00544 (0.03384) |
| hr2 | –0.1944 (0.11643) |
| hr3 | 0.7147 (0.32881) |
| Haemorrhage (gastrological) × sodium level | |
| na1 | –0.05819 (0.02074) |
| na2 | 0.02272 (0.02189) |
| Haemorrhage (neurological) × urine output | |
| up1 | –0.00010 (0.00050) |
| up2 | 0.00080 (0.00188) |
| up3 | –0.00157 (0.00484) |
| Haemorrhage (neurological) × blood lactate concentration | |
| bl1 | 0.8467 (0.34277) |
| bl2 | –6.623 (5.9342) |
| bl3 | 11.09 (11.197) |
| Infection (respiratory) × heart rate | |
| hr1 | –0.01412 (0.00655) |
| hr2 | 0.03690 (0.02251) |
| hr3 | –0.1021 (0.06348) |
| Infection (respiratory) × PaO2/FiO2 | |
| pf1 | –0.01559 (0.00611) |
| pf2 | –0.01082 (0.02796) |
| pf3 | 0.13753 (0.09825) |
| Self poisoning (endocrine) × creatinine level | |
| cr1 | –0.00098 (0.00174) |
| cr2 | –0.94067 (2.33612) |
| cr3 | 0.44148 (0.70236) |
| cr4 | –0.13545 (0.09162) |
| cr5 | 0.00024 (0.00073) |
| Self poisoning (endocrine) × blood lactate concentration | |
| bl1 | –1.347 (0.6578) |
| bl2 | 29.70 (10.375) |
| bl3 | –56.39 (19.128) |
| Trauma (neurological) × sodium level | |
| na1 | –0.00217 (0.02855) |
| na2 | 0.04362 (0.02519) |
| Trauma (neurological) × WBC count | |
| wbc1 | 0.07408 (0.07799) |
| wbc2 | –0.04864 (0.31443) |
| wbc3 | 0.23081 (0.88934) |
| Trauma (neurological) × urine output | |
| up1 | 0.0004 (0.00047) |
| up2 | –0.00050 (0.00180) |
| up3 | 0.00118 (0.00462) |
| Trauma (neurological) × platelet count | |
| plc1 | 0.00290 (0.00327) |
| plc2 | –0.02458 (0.01346) |
| plc3 | 0.06889 (0.04086) |
| Tumour (haematological/immunological) × WBC count | |
| wbc1 | 0.06610 (0.06833) |
| wbc2 | 0.5778 (0.51906) |
| wbc3 | –2.313 (1.6231) |
| Tumour (neurological) × urine output | |
| up1 | 0.00007 (0.00075) |
| up2 | 0.00033 (0.00282) |
| up3 | –0.00053 (0.00722) |
| Tumour (other) × sodium level | |
| na1 | –0.08002 (0.01897) |
| na2 | 0.06770 (0.02276) |
| Acute alcoholic hepatitis/alcoholic cirrhosis × urea level | |
| ur1 | 0.02320 (0.17484) |
| ur2 | 2.009 (2.6257) |
| ur3 | –4.264 (4.7798) |
| Anoxic/ischaemic coma × SBP | |
| sbp1 | 0.00209 (0.01739) |
| sbp2 | 0.08982 (0.05797) |
| sbp3 | –0.3009 (0.24374) |
| Intracerebral haemorrhage × temperature | |
| temp1 | –0.8292 (0.39703) |
| temp2 | 0.6162 (0.94252) |
| temp3 | 0.1163 (3.23562) |
| Intracerebral haemorrhage × urine output | |
| up1 | –0.00026 (0.00055) |
| up2 | 0.00181 (0.00212) |
| up3 | –0.00401 (0.00551) |
| Secondary hydrocephalus × creatinine level | |
| cr1 | –0.02572 (0.03126) |
| cr2 | –0.53674 (2.02834) |
| cr3 | –0.30353 (1.05165) |
| cr4 | 0.06243 (0.23562) |
| cr5 | 0.00220 (0.00542) |
| Mechanical ventilation × heart rate | |
| hr1 | 0.00386 (0.00416) |
| hr2 | –0.04434 (0.01538) |
| hr3 | 0.1481 (0.04462) |
| Mechanical ventilation × respiratory rate | |
| rr1 | 0.03380 (0.01191) |
| rr2 | –0.01425 (0.01245) |
| rr3 | 0.03415 (0.01803) |
| rr4 | –0.01939 (0.01019) |
| rr5 | –0.00004 (0.00020) |
| Mechanical ventilation × PaO2/FiO2 | |
| pf1 | 0.02427 (0.00523) |
| pf2 | –0.05202 (0.001912) |
| pf3 | 0.14406 (0.05891) |
| Mechanical ventilation × PaCO2 | |
| pc1 | –0.1153 (0.03488) |
| pc2 | 0.02085 (0.03791) |
Restricted cubic splines with j knots (positioned at k1,. . .,kj) require (j − 1) base variables x1 to xj − 1 calculated from the continuous predictor x as:
Right-restricted cubic splines with j knots (positioned at k1,. . ., kj) require (j + 1) base variables x1 to xj+ 1 calculated from the continuous predictor x as:
The predicted log-odds of acute hospital mortality for patient i, li, are calculated by multiplying each coefficient from the preceding table by the value of the corresponding predictor variable and summing. The predicted risk of acute hospital mortality, pi, is calculated from the predicted log-odds by the inverse logit function:
where exp() denotes the exponential function.
Glossary
- Accuracy
- Closeness of computations or estimates to the exact or true values that the statistics were intended to measure. An accurate risk prediction model would give predictions close to 1 for individuals who experience the event (e.g. death) and predictions close to 0 for those who do not.
- Bias
- A systematic difference between an estimated value and the true value that the statistic was intended to measure. Bias occurs when a particular design or analysis is likely to favour a particular outcome and would, therefore, make those results unreliable.
- Brier score
- A measure of the accuracy of a risk prediction model defined as the mean-squared error between the outcome and the prediction. If the predictions are perfect (i.e. all individuals who experience the event have a predicted risk of 1 and all individuals who do not experience the event have a predicted risk of 0), Brier score is 0; if all individuals have a constant predicted risk of 0.5, Brier score is 0.25.
- c-index
- The concordance or agreement between an outcome and a prediction. If two individuals are selected at random, the c-index is the probability that the individual with the higher value of the outcome will also have the higher prediction. For an outcome with only two values (e.g. dead or alive), this is equivalent to the area under the receiver operating characteristic curve. It is a measure of the discrimination of a risk prediction model. If all individuals who experience the event (e.g. death) have higher predictions than all those who do not, the c-index is 1; if predictions are no better than chance, the c-index is 0.5.
- Calibration
- The ability of a risk prediction model to give an accurate prediction of the average outcome either overall (calibration in the large) or across groups of individuals.
- Calibration plot
- A plot of observed (actual) against expected (predicted) outcomes used to show the calibration of a risk prediction model. Individuals are ordered according to predicted risk of the outcome and split into a number of equal-sized groups (typically 5, 10 or 20). The proportion of individuals within each group who experienced the event is then plotted against the overall predicted risk for the group (the average of the predictions for each individual in the group). If the model is well calibrated, then the points will lie along the diagonal line of observed = expected.
- Case mix
- A combination of patient factors that may be associated with the outcome of interest, such as age, comorbidity and severity of illness. These factors need to be accounted for when comparing the outcomes achieved by different health-care providers; risk prediction models can therefore also be called case mix adjustment models.
- Complete case analysis
- An analysis that includes only individuals for whom information on all predictors and the outcome is complete (i.e. there are no missing data).
- Confidence interval
- An interval that has a specified chance (e.g. 95%) of containing the true value of a parameter.
- Confidentiality Advisory Group
- A group that provides independent expert advice to the Health Research Authority (for research applications) and the Secretary of State for Health (for non-research applications) on whether applications to access patient information without consent should or should not be approved under Section 251 of the NHS Act (Great Britain. National Health Service Act 2006. London: The Stationery Office; 2006).
- Discrimination
- The ability of a risk prediction model to separate individuals who experience an event from those who do not, for example to give a higher predicted risk of death to patients who die than to those who survive.
- External validation
- An assessment of the performance of a risk prediction model (typically its discrimination, calibration and accuracy) in a different population of patients from those used to develop the model. This assesses the validity of claims for ‘plausibly related’ populations (the ‘generalisability’ or ‘transportability’ of the model). It may use patients who were treated more recently (temporal validation), from other locations (geographic validation), or in fully different settings (strong external validation).
- Fractional polynomials
- Smooth curved functions consisting of a combination of polynomial transformations, including regular polynomials (e.g. x, x2, x3), negative powers (e.g. x−2 = 1/x2), fractional powers (e.g. x0.5 = √x), the natural logarithm [ln(x), denoted by power 0] and repeated powers [where the repeated power is the original power multiplied by ln(x)]. A combination of up to two powers from the set (−2, −1, −0.5, 0, 0.5, 1, 2, 3) is sufficient to model most non-linear shapes.
- Funnel plot
- A plot of an unadjusted or adjusted outcome of interest (e.g. standardised mortality ratio) against a measure of the precision of the estimate (typically the number of eligible individuals) across a number of groups (e.g. health-care providers). As precision increases, the uncertainty of the estimates reduces, resulting in a funnel shape of points around the overall value of the outcome. Funnel-shaped control limits (at 2 and 3 standard deviations) indicate that, as sample size decreases, observations must be further from average to be considered significantly different.
- Glasgow Coma Scale
- A neurological scale that aims to give a reliable, objective way of recording the consciousness state of a person for initial as well as subsequent assessment.
- Goodness of fit
- A general term for how close the agreement is between an observed set of values (e.g. the outcome) and a second set which are derived wholly or partly on a hypothetical basis, that is, from the ‘fitting’ of a model to the data.
- Hierarchical modelling
- A widely used statistical approach for dealing with data that have a natural hierarchy or nesting of observations (e.g. patients within hospitals). This is necessary as patients admitted to the same hospital are likely to have outcomes that are more similar than the outcomes of those admitted to different hospitals (they are said to be ‘clustered’ by hospital). This results in observations that are not independent.
- Imputation
- A procedure for filling in a value for a specific data item when the value is missing or unusable.
- Insult
- The acute event that caused a patient to be critically ill. This may be an injury or trauma, acute illness or major surgery.
- Intensive Care National Audit & Research Centre coding method
- A way of recording the reason a patient was admitted to the critical care unit through the use of a tiered numeric coding system. It avoids the need for data collectors to enter the full name of the condition in free-text format or having to select from a full list of all possible conditions.
- Internal validation
- An assessment of the performance of a risk prediction model (typically its discrimination, calibration and accuracy) in the same population of patients that was used to develop the model. This assesses the validity of claims for the underlying population from which the data originated (‘reproducibility’).
- Multiple imputation
- A process of repeatedly filling in missing values multiple times to produce complete data sets that can be analysed and the results of these analyses combined to allow for the uncertainty in the missing values.
- Outcome (or outcome measure)
- A change in the health of an individual that may be attributable to the care he or she received. For risk prediction models, this is usually in the form of an event that happened to the patient during or after their admission (e.g. death or readmission). Outcome measures are commonly distinguished from process measures, which describe the actions of health-care professionals (e.g. prescribing medication, following protocols).
- Overfitting
- A problem that occurs when a statistical model’s complexity is such that it describes the relationships within the data set used to develop it too precisely and its results are poorly generalisable to other data sets.
- Parsimonious
- Reduced to the fewest components; a parsimonious model is the simplest one that serves the required purpose.
- Predictor
- A variable that can be used to predict the value of another variable.
- Restricted cubic splines
- Smooth curved functions that take the form of cubic polynomials (ax3 + bx2 + cx + d) between pre-specified ‘knot’ positions with linear (straight line) tails below the lowest knot and above the highest knot.
- Risk prediction model
- A statistical model that uses data available at a given point in time to make a prediction of the likelihood of a future outcome.
- Routinely collected data
- Data collected as part of the day-to-day running of a health service.
- Standardised mortality ratio
- The observed number of deaths in a population divided by the expected (or predicted) number of deaths (calculated as the sum of the predicted risk for each patient from a risk prediction model).
- Stepwise selection
- A procedure to select which candidate predictors to include in a risk prediction model by either adding predictors to the model one by one (forward stepwise selection) or removing predictors one by one (backward stepwise selection).
List of abbreviations
- AIC
- Akaike information criterion
- APACHE
- Acute Physiology And Chronic Health Evaluation
- AQR
- Annual Quality Report
- BIC
- Bayesian information criterion
- BMI
- body mass index
- CASUS
- Cardiac Surgery Score
- CI
- confidence interval
- CMP
- Case Mix Programme
- CPR
- cardiopulmonary resuscitation
- CQC
- Care Quality Commission
- DBP
- diastolic blood pressure
- DNACPR
- Do Not Attempt Cardiopulmonary Resuscitation
- FCS
- fully conditional specification
- FiO2
- fraction of inspired oxygen
- GCS
- Glasgow Coma Scale
- GWTG-R
- Get With The Guidelines®-Resuscitation
- HES
- Hospital Episode Statistics
- ICNARC
- Intensive Care National Audit & Research Centre
- JAV
- just another variable
- MAR
- missing at random
- MCAR
- missing completely at random
- MPM
- Mortality Probability Model
- NCAA
- National Cardiac Arrest Audit
- NRI
- net reclassification improvement
- PaCO2
- arterial carbon dioxide pressure
- PaO2
- arterial oxygen pressure
- POCAS
- Post Cardiac Surgery
- QQR
- Quarterly Quality Report
- ROSC
- return of spontaneous circulation
- SAPS
- Simplified Acute Physiology Score
- SBP
- systolic blood pressure
- SICSAG
- Scottish Intensive Care Society Audit Group
- SMC-FCS
- substantive model compatible fully conditional specification
- SMR
- standardised mortality ratio
- SOFA
- Sequential Organ Failure Assessment
- WBC
- white blood cell