Notes
Article history
The research reported in this issue of the journal was funded by the HS&DR programme or one of its preceding programmes as project number 11/1022/19. The contractual start date was in January 2013. The final report began editorial review in January 2016 and was accepted for publication in August 2016. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HS&DR editors and production house have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the final report document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
Maria Jose Aragon reports grants from the National Institute for Health Research (NIHR) during the conduct of the study, grants from the Department of Health, grants from the Department of Health via Economics of Social and Health Care Research Unit (ESCHCRU), grants from the Wellcome Trust via the Centre for Chronic Diseases and Disorders (C2D2) and grants from NHS England outside the submitted work. Martin Chalkley reports grants from NIHR during the conduct of the study, grants from the Department of Health, grants from ESCHCRU, grants from C2D2 and grants from NHS England outside the submitted work.
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2017. This work was produced by Chalkley et al. under the terms of a commissioning contract issued by the Secretary of State for Health. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
Chapter 1 Background and research objectives
There has been considerable growth in the number of planned care episodes – between 2001/2 and 2011/12, admissions increased by 35.4% – but such growth during a period of financial pressure would create substantial fiscal and hospital management problems. The causes of this rise in activity are poorly understood and, consequently, the likely path of planned care growth is also poorly understood. There are useful databases available both to model demand and, if required, to moderate it with least impact on patients [e.g. Hospital Episode Statistics (HES), patient-reported outcome measures (PROMs), referral numbers from Choose and Book by general practitioner (GP), practice, specialty and hospital], but these raw data are of limited value in both strategic and patient-level decisions. We aim to add to the literature by interrogating some of these data sets and producing analyses that will help commissioners to make appropriate decisions.
The overall aim of this project is to contribute to a better understanding of how to moderate activity growth in ways that minimise the loss of patient health, by exploring hypotheses that would extend the literature by deepening understanding of local health economies and providing evidence for commissioners to minimise the health loss that may accompany diminished budgets, and to support GPs both as commissioners and in terms of their clinical performance. This is done in a collection of related but independent studies that look at differing aspects of planned care, considering national health policies, more local interventions in primary and secondary care, and the provision of benchmarking information for Clinical Commissioning Groups (CCGs), using similar ideas to those in the NHS Atlases. 1
Both system reform and population ageing are possible drivers of admissions growth and provide barriers to readily introducing measures to manage growth. We ask how important these two issues are in explaining rapid admissions growth. Chapter 2 presents estimates of the separate influences of system reform and capacity growth in explaining the post-2002 increase in elective care at local levels. This is intended to examine how far the rise in planned admissions has been prompted by system reform rather than by increases in capacity using the Scottish health-care system, which did not undergo the same reforms, as a control.
One specific piece of reform, namely the introduction of a tariff system [Payment by Results (PbR)] to replace a block grant funding model in some service areas has influenced provision and may have contributed to changing activity patterns. Chapter 3 examines the effect of such system reform on the extent of variation across the NHS. This study complements others that have examined the influence of reform on the rates of admission. 2
The ageing population has also been regarded as a key driver of elective admissions growth (e.g. see Reinhardt3) and we examine this in Chapter 4. Using an age–period–cohort (APC) analysis of elective admissions and bed-days per 1000 population, we separate the roles of age, year of admission and year of birth on the rates of admission and the rates of bed-days used. Thus, we partition the increase in elective activity from 1997/8 to 2014/15 into an age effect (factors associated with the patient’s age, A), a period effect (the year of the patient’s admission, P) and a cohort effect (the patient’s year of birth, C). This allows the impact of ageing to be assessed while also allowing the likelihood of entering, or continuing in, hospital to vary with the year of birth of the individual. In particular, we study whether or not later generations are less likely to enter hospital at a given age. We also apply APC analysis to selected groups of procedures to test consistency across different conditions.
In Chapters 5 and 6, we provide an analysis of two policies that commissioners have considered, and that some have adopted, to ameliorate admissions: (1) an increase in the provision of GPs and (2) a constraint or target imposed on GP referrals. To study whether or not an increase in the density of GP provision would lead to reduced admissions, we begin by providing a model of GP referrals that is consistent with NHS objectives to maximise patient welfare. We discuss how a single-payer health system is better incentivised than a competitive insurance system to train and monitor GPs to maximise patient welfare, and how NHS GPs may act as gatekeepers when making referrals. This builds on Mariñoso and Jelovac,4 one of the few theoretical studies of the relative benefits of gatekeeping. In Mariñoso and Jelovac’s4 model, gatekeeping arises because GP treatments are cheaper; our model does not make this assumption. The provision of more GPs reduces the patient load and changes referral behaviour. We carry out an empirical investigation to gauge the effect that these density variables have on admissions, and then to assess how far a policy of reducing referrals may lead to a reduction in treatment. We also consider the impact of practice size by full-time equivalent (FTE) GP. This study provides information on the effectiveness of a policy that works by increasing GP treatment in primary care and reducing referrals, rather than by acting on hospital incentives to reduce activity.
One concern is that growth in elective care has reduced referral thresholds (e.g. see Keenan et al. ,5 which looks at time trends and geographical variation in cataract surgery rates), and some CCGs have introduced policies to require GPs to refer fewer patients. Commissioners are also likely to value evidence on how far changing thresholds for pre-operative conditions for patients reflect the decisions of GP referrals or those of consultants. Chapter 6 uses a panel of GP practice data to study (1) the rate of first referral per 1000 patients and (2) the rate of hospital admission for those given a first referral. We examine the cross-sectional relationship between referral rates and treatment rates to see if it is broadly consistent with the view that patients in certain local areas are healthier than others and will experience lower referrals and lower admissions. We also explore the impact of specific exogenous influences on referrals, such as GP experience and sex and patient and practice characteristics. The rate of treatments following first referral at a practice is then modelled as a function of the referral rate and exogenous influences, allowing for local practice-level unobserved health effects to impact on both referrals and admissions. These models of treatment and referral enable us to trace the impact of reduced referrals on the level of treatment when practices have sharply different referral rates.
Devlin and Appleby6 note the potential value of PROMs data for commissioning, but, to date, PROMs data have been used only to analyse providers’ services (e.g. Street et al. 7) and patient benefits. The studies in Chapters 7 and 8 use PROMs data to focus on ways to (1) minimise the consequences of reduced hospital activity, by identifying pre-operative characteristics of patients who gain least from intervention and (2) uncover whether or not variation in patient heath gain across CCGs, adjusted for case mix, is attributable to the CCGs themselves, the providers they commission and the surgical teams the providers employ.
Finally, we consider whether or not any attempts to manage demand for elective care will have undesired consequences for the demand of emergency care, using an extensive data set and the natural experiment provided by the introduction of independent sector treatment centres (ISTCs) in the past decade. Many studies have looked at elective and emergency activity levels separately. 8–10 However, work studying the interaction between emergency and elective care has been limited. Equally, there have been several studies of ISTCs (e.g. Cooper et al. 11) but little work on their effect on emergency activity.
This is a challenging time for the NHS and novel and imaginative solutions are required to ensure that the NHS can continue to treat patients in the best way possible. We hope that the work that follows in this report will help to inform the debate and improve understanding of how commissioners and providers can continue to provide the level of performance expected by their patients while operating under budgetary pressures.
Chapter 2 Demand management for elective care: system reform and other drivers of growth – an examination of the factors affecting the growth of elective hospital activity in England from 1998 to 2012 and the implications of these for managing demand for elective activity
Summary
Introduction
The volume of admitted patient care in England has grown considerably over the period 1998–2012. The focus of this report is on the part of admitted patient care that is termed elective or planned. A substantial part of the growth in elective care appears to coincide with the reforms of the NHS in England that included the adoption of PbR and greater emphasis on patient choice. Under PbR, hospitals are paid for the care they provide to patients, taking account of the complexity of each case.
The current financial environment places increasing constraints on the NHS, and responsibility for ensuring that health care continues to meet the health needs of England’s population while working within these constraints falls upon CCGs. In managing elective care, an understanding of the trend rates of growth, what determines these trends and whether or not their own populations exhibit deviations from the overall trends observed in England will help CCGs. The purpose of the investigation we report in this paper is to provide that understanding; a particular focus is the impact that system reform has had, and may continue to have, in setting the extent of the challenge that managing elective care presents.
The study reported here is a part of a larger project on elective (planned) hospital activity and the influence that policies have had on that activity and its growth. Our findings set a context for understanding growth in England by comparing it with the growth observed in Scotland, which despite having had a similar expansion in resources for health care, has not been subject to the same, or as extensive, system reform.
Background
Hospital and Community Health Services (HCHS) constitute around 65% of NHS expenditure in England (2010 data), admitted patient care (inpatient and day cases) represents approximately one-third of total HCHS expenditure and elective care accounts for almost half of the admitted care expenditure. The starting point for our investigation is the observed pattern of growth in elective care in England over the past 15 years. There are a number of ways of measuring the extent of elective treatments, and Figure 1 shows one such measure – the number of continuous inpatient stays (CIPSs) – as well as the population-adjusted change in activity from 2000 to 2009. In Figure 1, as elsewhere in this report, we scale the measure of CIPSs per 1000 population. We consider the definition of different measures of activity in Data and empirical methods.
FIGURE 1.
Continuous inpatient stays per 1000 population in England.
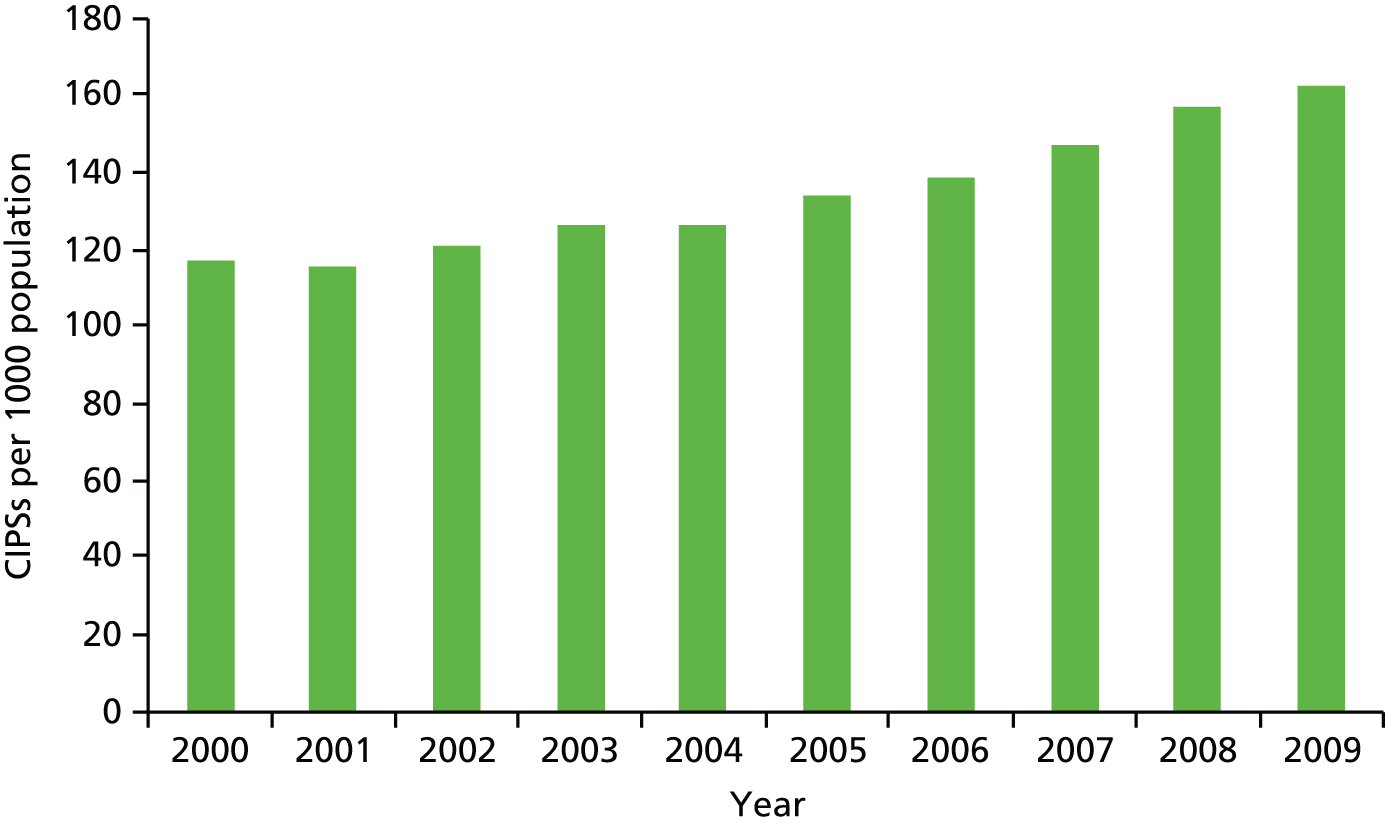
Figure 1 appears to show a sharp increase in activity commencing in the middle of the decade and continuing until the end. The middle years of the decade correspond to a period of substantial reform in the organisation and, in particular, the financing of hospital care in England; one potential inference from the figure is that it is system reform that led to the increase in activity.
The main component of the system reform introduced in England was an activity-based payment system, known as PbR. 12 Such a payment system has been argued to provide incentives to reduce costs, by, for example, reducing length of stay (LOS), and to increase in the levels of activity, therefore reducing waiting times. 13 How strongly these incentives will affect the outcomes of hospitals will depend on how much of their revenue relates directly to their activity levels; in England it accounts for around 60% of hospitals’ revenue. 14 In terms of elective activity, there is evidence that PbR has increased activity levels and the proportion of activity performed as day cases and reduced LOS. 2,12 However, there have been concerns regarding the lack of efficiency-improving incentives in block contracts not linked to activity or its quality and the proportion of hospitals’ revenue being negotiated locally rather than by using the PbR system. 15 It has been argued that, given the incentives to increase activity and its efficiency, PbR is more appropriate for elective activity. 16 For more results on the effects of PbR, see reports by The King’s Fund16 and the Nuffield Trust. 17 PbR constitutes what is termed a form of prospective payment system, whereby the price of treatment is determined before treatment actually occurs and according to the patient’s medical condition or treatment requirements. The grouping of patients under PbR is by Healthcare Resource Groups (HRGs), which share a number of features with what are termed Diagnosis Related Groups (DRGs) in other jurisdictions; this terminology was established by the reform of the US Medicare Program in 1983. 18 Systems based on DRGs have proliferated around the world, especially in Europe. 19 Their introduction has been accompanied by extensive investigation of their impact, which has usually focused on hospital efficiency and quality of care,20 but there has been little focus in these other contexts on the impact on activity, which is our focus. The findings we present in this chapter form a contribution to the evidence concerning the impact of PbR (a ‘DRG-like’ prospective payment system) on hospital performance, but we do not attempt to separate out this effect from the general package of coinciding reforms that occurred with its introduction.
Other changes taking place in the NHS in England during the 2000s were patient choice21,22 and increases in the budget. 23 The key focus of investigations of the impact of patient choice has been on the impact for quality of care, usually proxied by hospital mortality (see Cooper et al. 24 and the references therein) and, as far as we can determine, there has been no investigation of the impact of patient choice on observed hospital activity. Previous analysis of the relationship between NHS expenditure and activity has focused on describing trends,25 whereas we utilise regression analysis to decompose those trends into their component drivers.
The current financial climate and pressures on public funding indicate a need to manage growth in activity going forwards and this task is one of the key responsibilities of the recently established purchasers of health care, namely CCGs. In this context, knowing more about what drives elective activity, whether or not the apparent trend in activity can be explained by factors that are controllable or endemic in the system and whether or not any impetus to growth given by system reform is likely to continue are questions of concern to CCGs.
Given that a CCG has responsibility for its constituent population, it will be especially concerned with the local position, whereas Figure 1 illustrates the overall picture for England. Hence, in addition to the broad questions outlined in this section, we anticipate that CCGs will wish to understand growth in elective care in their own regional context.
Therefore, the purpose of our investigation is to inform some answers to these questions with a view to offering CCGs a better understanding of the environment in which they operate and the constraints that they are likely to face in seeking to manage elective activity.
Modelling growth in elective activity: the role of another jurisdiction
The challenge to isolating the effect of any one influence on the growth of elective activity requires the identification of appropriate controls against which to assess the impact of a given treatment factor. Thus, for example, if we wish to isolate the effect of an ageing population it is most helpful to observe what happens to elective care in an area where there is population ageing and to compare that with (ideally) an otherwise identical area where there is no such ageing. Such ideal comparisons do not exist in practice and, as is standard, our approach is to look for variations across locations and across time that will reflect many influences and to isolate the effect of any one influence using multiple regression methods.
A key focus of our study is to understand whether or not (and if so, how) system reform in England might have impacted on growth in elective care, because, as noted above, such reform sets an important part of the context in which CCGs operate. Given that reform was enacted across all of England, we are limited in regard to variation that can be used to isolate its effect. There is some useful variation in the timing of the introduction of reform across different HRGs, but this is limited. We therefore make use of another jurisdiction of the UK, namely Scotland, as a comparator and control, because the NHS in Scotland is similar to, but independent of, the NHS in England and policy in regard to it is a reserved matter for the Scottish Government. In our analysis we control for variations in the number and composition of the populations of Scotland and England but note that they have evolved in a similar manner over the period under investigation. The respective populations of England and Scotland are shown in Figure 2 and the age composition of these populations is depicted in Figure 3 for Scotland and Figure 4 for England.
FIGURE 2.
Population 1998–2011 (thousands) in England and Scotland.
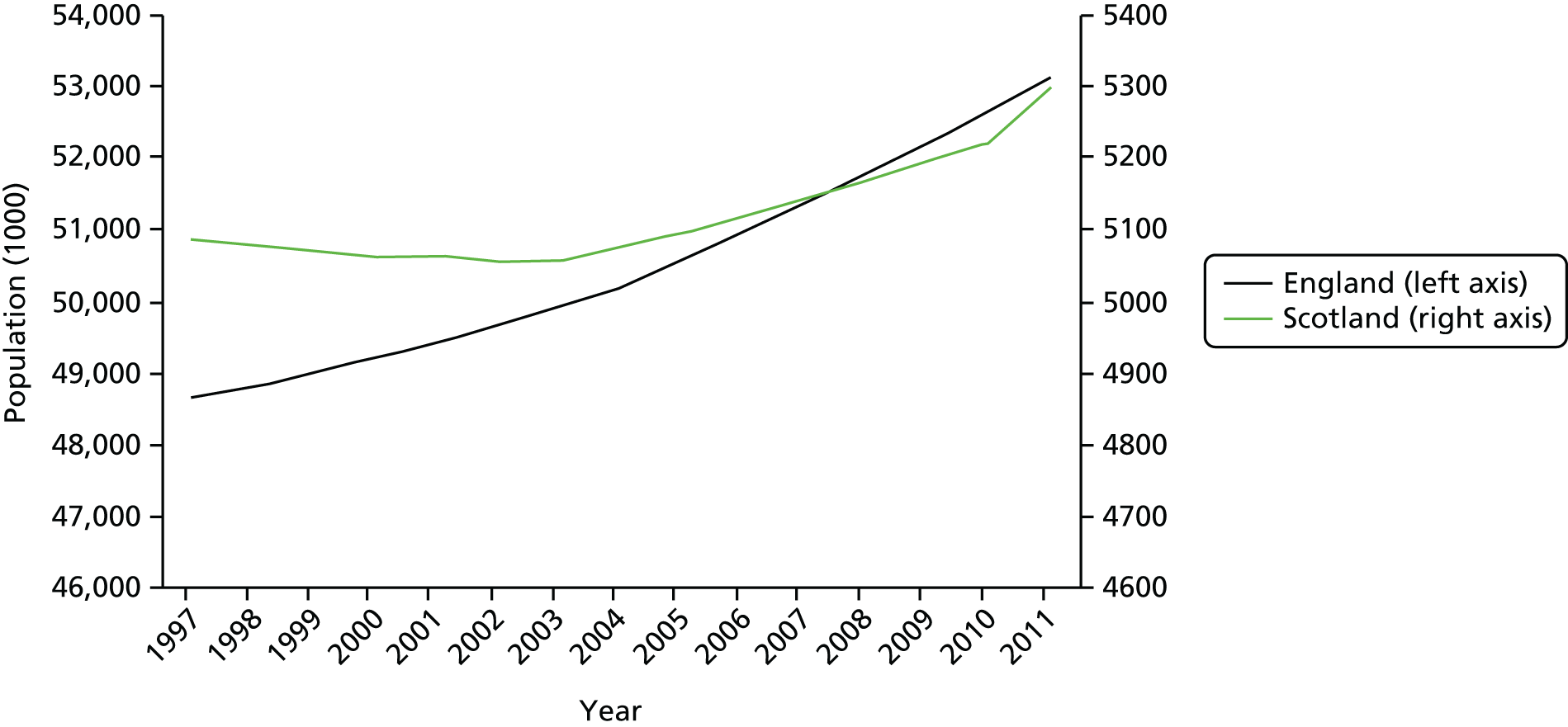
FIGURE 3.
Age composition in Scotland 1998–2011.

FIGURE 4.
Age composition in England 1998–2011.

Importantly for our study, Scotland and England have had a similar expansion in the funding of their health services, as illustrated in Figure 5. However, the NHS in Scotland did not undergo the reorganisation of financing of hospital care that was undertaken in England.
FIGURE 5.
Expenditure per capita in 2011/12 prices.
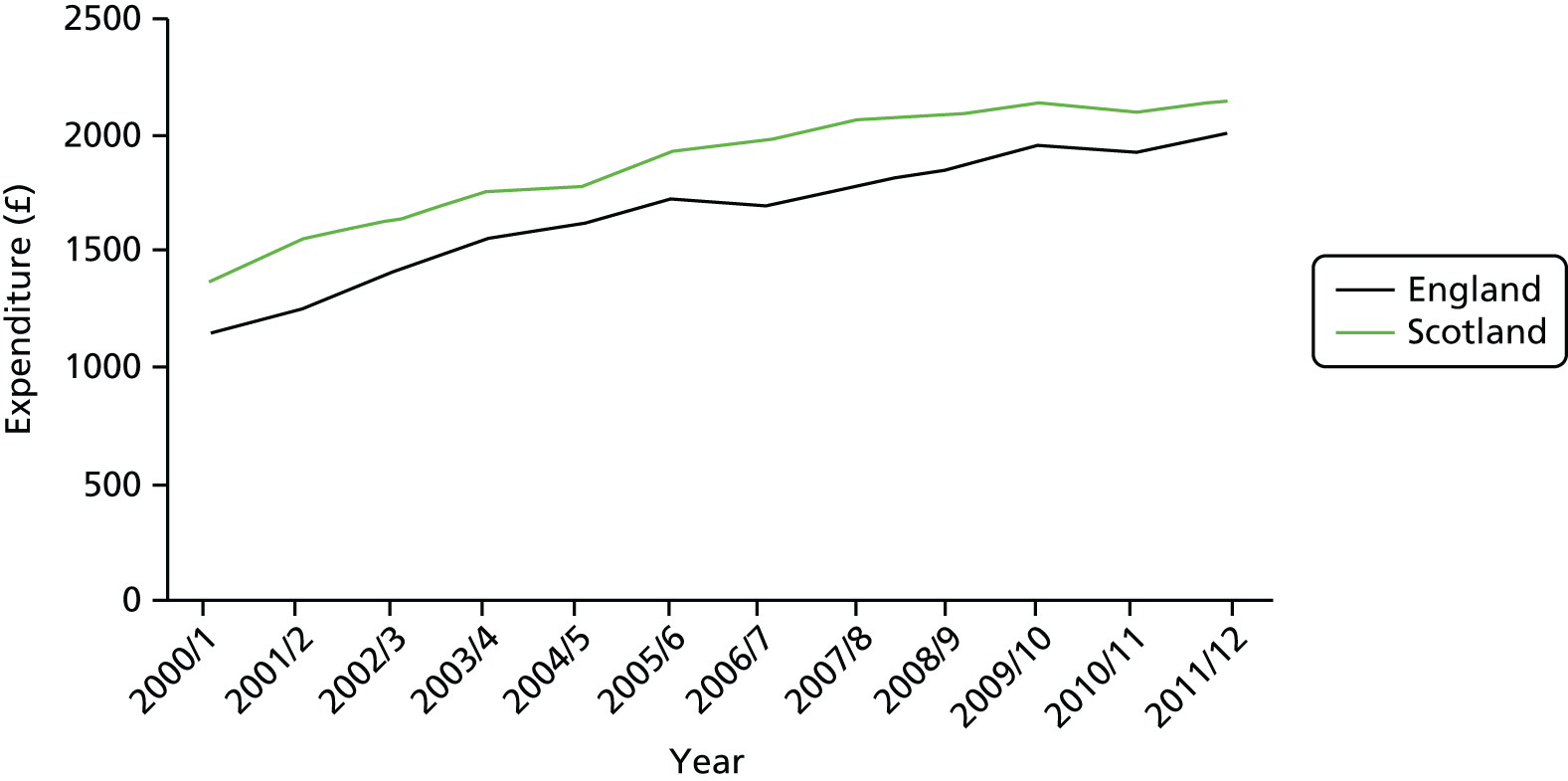
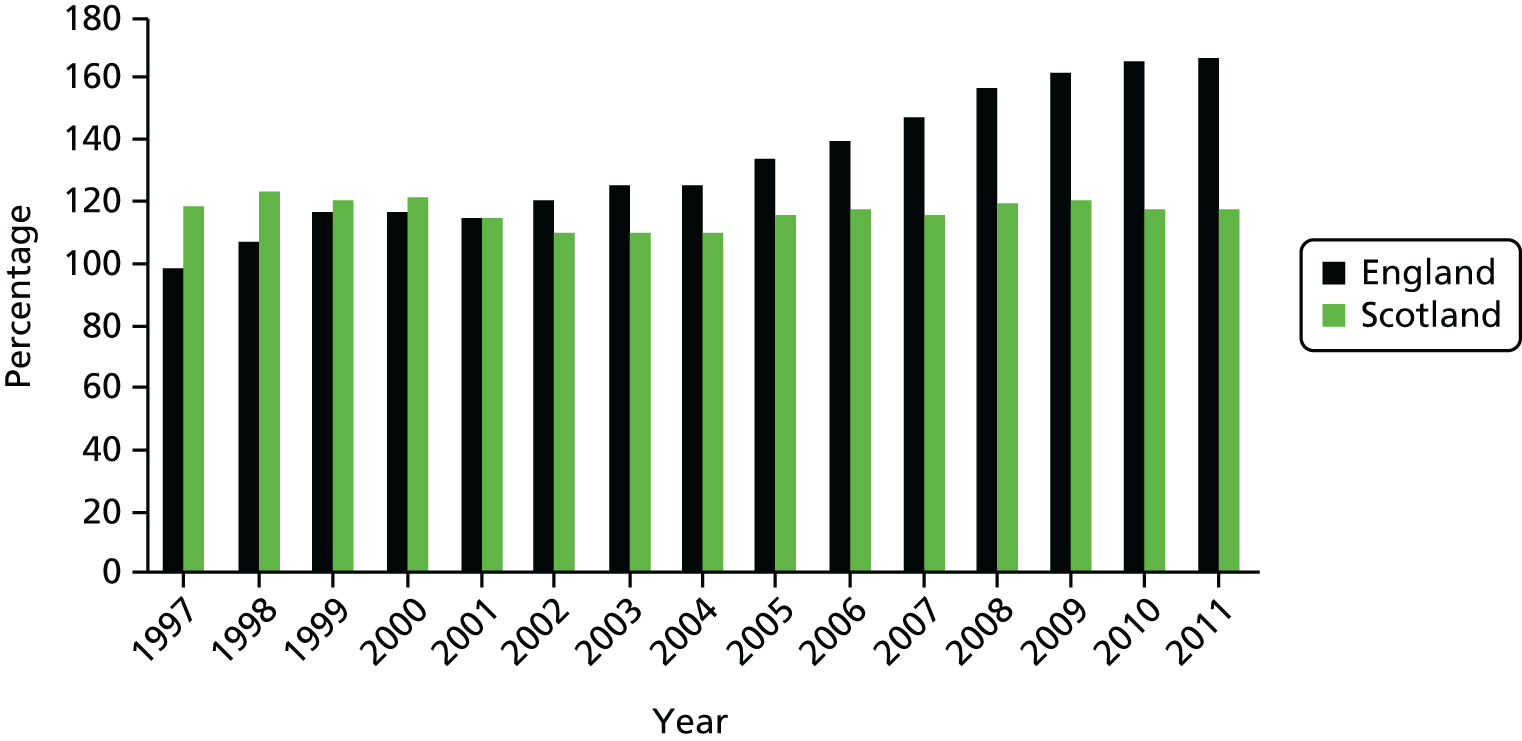
Figure 6 illustrates how having such a comparator may be potentially useful in assessing the growth in elective activity. The measure of activity is once again CIPSs per 1000 population, and the scale has been extended to cover the period 1997 to 2011. As can be seen, compared with what appears to be substantial growth in elective activity in England, activity in Scotland seems flat, which particularly applies to the period 2002–5, the period of most active system reform in England. Our empirical strategy is thus to make use of Scotland as a comparator for assessing the impact of changes that have taken place in England.
FIGURE 6.
Continuous inpatient stays per 1000 population in England and Scotland.
The information presented in Figure 6 can also usefully be summarised using regression methods and, because these are the methods that we use the most, a regression corresponding to Figure 6 is helpful. This is provided in Table 1.
| Regression model | ||
|---|---|---|
| (1) | (2) | |
| Time trend, t (standard error) | 0.007** (0.002) | 0.005** (0.002) |
| t × England (standard error) | 0.022*** (0.002) | 0.016*** (0.004) |
| System reform | No | Yes |
| n | 30 | 30 |
| R 2 | 0.8593 | 0.8826 |
Table 1 reports the results of a regression of the natural logarithm of elective CIPSs per 1000 population against a linear time trend and that trend interacted with a dummy variable for England. It is included here simply to aid subsequent interpretation of regression estimates. Focusing first on regression model 1, the regression indicates that the annual growth in elective activity in Scotland is 0.7%, because the logarithm scale enables the interpretation of regression estimates in percentage terms. The annual growth rate for England is 2.2% higher than that (i.e. it is 2.9% per annum). Hence, the regression confirms and quantifies what is shown in Figure 6, namely that growth in elective activity has been substantially lower in Scotland than in England. Regression model 2 adds a variable capturing the occurrence of system reform in England to the regression. This potentially addresses the question of whether or not the differential trend that we see is coincident with the implementation of system reform. The details of our methods and the extension of this approach to account for numerous potential drivers of elective care are set out in Data and empirical methods and Results below, but here we simply note that the inclusion of system reform does not appear to change the underlying view that elective care grows faster in England than in Scotland. In regression model 2 we see that the growth rate in elective care in Scotland is estimated to be 0.5% and in England is 2.1%. We can tentatively conclude that system reform is important – its inclusion changes our estimates – but is a long way from being the complete story.
Different perspectives on activity
The current system of financing hospital activity in accordance with the National Tariff Payment System (NTPS), which sets a fixed price for each patient receiving an elective treatment within a defined HRG, naturally suggests measuring activity in terms of the number of treatments. The expenditure of a CCG depends on the number of inpatient spells that it has to fund and spells are closely related to CIPSs. Thus, from a CCG perspective, the measure of activity that must be managed is CIPS. More details of the definitions of spells and CIPSs and the reasons why we use the latter are set out in Data and empirical methods.
Although the number of CIPSs (weighted by the HRGs in which they occur) is a good proxy for the financial resources devoted to elective care by CCGs, from a broader societal perspective it fails to account for the real resources that are consumed in that activity. Over time it can be expected that the price per CIPS set under the national tariff will adjust to reflect changes in resource use within CIPSs and, thus, it is useful to have a perspective on at least some aspects of changing resource use in CIPSs.
The total resources devoted to elective activity comprise the combination of hospital capital, staffing and medical equipment and supplies. One possible proxy for these resources is the total number of hospital days that are devoted to elective care. Figure 7 shows the evolution of bed-days in England and Scotland from 1997 to 2011. There is a substantial decline in total elective bed-days in England, despite the rapid increase in elective CIPSs, but a less marked reduction in Scotland. Thus, even at an aggregate level, care must be taken before concluding that elective activity has increased substantially in England relative to Scotland; on one measure it has but on another it has not. Figure 7 can be further understood by noting that the average stay in hospital associated with an elective admission – the LOS – has declined rapidly, more so in England than in Scotland. Figure 8 shows the LOS in both countries over time.
FIGURE 7.
Total bed-days per 1000 population England and Scotland.
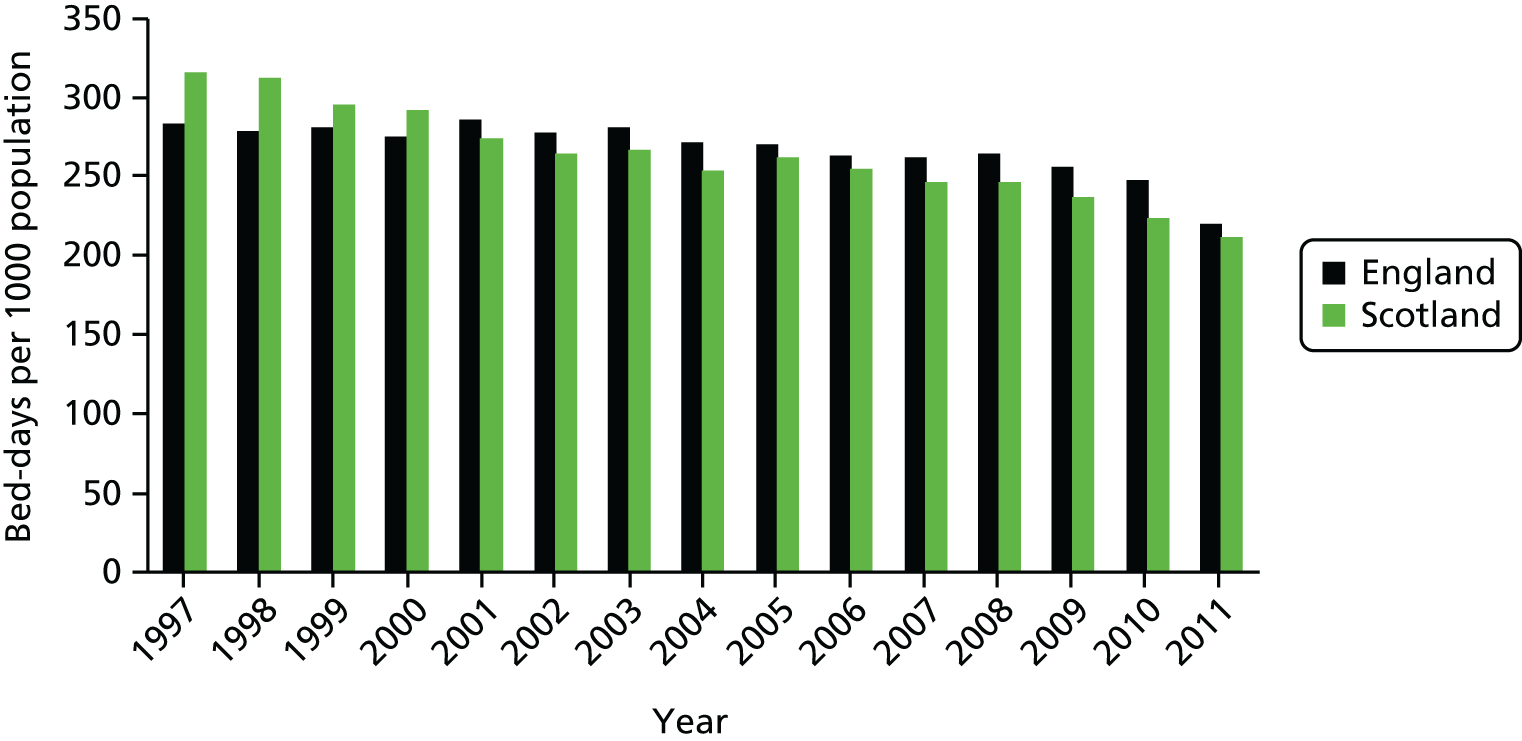
FIGURE 8.
Average LOS in England and Scotland.
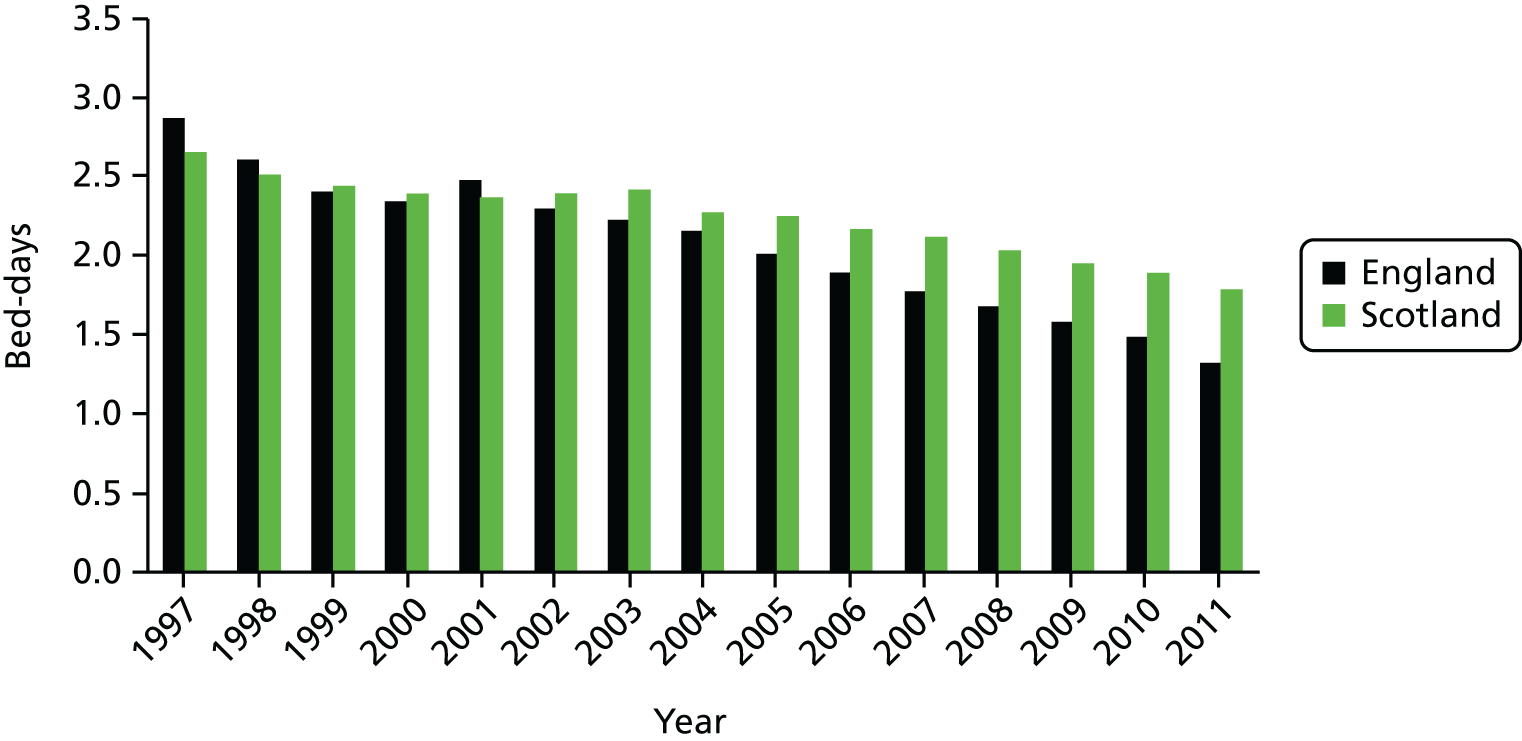
The trend reduction in LOS has previously been noted, although as far as we can establish it has not been documented over such a long period as depicted in Figure 8. There have been previous studies concerned with the question of whether or not a shorter-term reduction can be attributed to system reform. 2 The relationship between growth in CIPSs, falling LOS and system reform is therefore of direct relevance to our main topic of enquiry.
A regression model again confirms and quantifies the changes depicted in Figures 7 and 8. The regression estimates presented in Table 2 follow the same pattern as those presented in Table 1 but focus on the LOS measure. Omitting the control for system reform, the rate of decline is estimated to be 2.8% per year in Scotland and 4.5% per year in England. Including system reform, the rates are 2.7% and 3.8%, respectively.
| Regression model | ||
|---|---|---|
| (1) | (2) | |
| Time trend, t (standard error) | –0.028*** (0.002) | –0.027*** (0.002) |
| t × England (standard error) | –0.017*** (0.002) | –0.011*** (0.003) |
| System reform | No | Yes |
| n | 30 | 30 |
| R 2 | 0.9444 | 0.9537 |
The importance of differential trends
If we combine the information in Figures 1–7 and Tables 1 and 2, the picture that emerges is one of substantial differences between Scotland and England with regard to changes in elective care in terms of both volume (CIPSs) and resource-intensity (LOS) over time. Volume has grown faster in England, whereas resource-intensity appears to have fallen more quickly.
These differences in trends are potentially valuable for the purposes of understanding drivers of elective care. Although Scotland and England have different populations with possibly different underlying disease patterns, they share many trends in their population characteristics. This suggests that it is simple to explain a different level of activity or intensity, but less straightforward to explain differential trends. Put simply, the differential trends would appear to be driven by factors other than the (common trend) changes in population or any other common trend changes, such as the growth in funding illustrated in Figure 5. Because both countries have experienced a similar trend in terms of the overall resources devoted to health care, resources or ‘capacity to treat’ in this broad sense also cannot be an explanation of the diverging trends in elective care.
The issues involved in unpicking exactly how these differential trends can be explained are complex, and a substantial part of our investigation can be seen as an attempt to address an important question: ‘treating Scotland as the benchmark, how and why has the volume and intensity of elective care in England displayed a different evolution; and what are the lessons of this for managing growth in the future?’.
Our approach with regard to this question can be understood in terms of seeking to account for intuitively important factors, such as differences in case mix, idiosyncratic regional influences, residual differential trends in population structure (age, sex, deprivation), and then considering what the unexplained residual difference in trends amounts to.
A framework for understanding elective activity and its growth
Observed activity is the outcome of a complex interaction of decisions, by GPs, their patients, commissioners, NHS trusts and the Department for Health. We cannot expect to unravel all of these disparate influences, but it is nevertheless useful to distinguish between factors that influence the needs of the population, which might be termed the demand side of elective care, and factors that reflect the capacity of the health-care system and decisions to treat, which might be termed the supply side. Various influences can be categorised as either demand- or supply-side focused.
Factors such as population ageing, age-specific morbidity and social and economic factors can all be expected to influence the demand for elective activity, and so we factor in any differences in the trends in these factors to account for demand-side differences between Scotland and England.
Two key elements of the supply-side impetus to elective activity are (1) funding, and the impact of that funding on capacity to deliver health care, and (2) policy interventions. Having controlled for demand-side factors, we use a comparison between Scotland and England to begin to establish the role of these supply-side factors. Scotland and England have exhibited very similar paths of resourcing expansion of their health-care systems over the period we study. Therefore, the residual trend in elective activity in Scotland, having controlled for demand-side factors, can be expected to give an indication of the role of expanding capacity on elective activity.
If the trend in elective activity in England, again adjusted for demand-side factors, deviates from this adjusted trend in Scotland, it is attributable to the different policies pursued, differences in the inherent functioning of the health-care systems, or differences in the demand side that have not been captured fully by our demand-side variables. To isolate the first of these influences, we make adjustments for policy interventions in England considering the fact that these are concentrated towards the middle of the period we study and hence can be expected to have a differential effect (in England alone) over time. If differences in trend persist after all of these adjustments, we are driven to conclude that it is residual systemic differences in either, or both, of the supply and demand sides between the two nations that are at work.
The management challenge
Managing growth in elective activity can be defined in terms of identifying mechanisms for moderating future growth. CCGs have no ability to regulate the age, sex or deprivation profiles or their populations; they are thus reliant on funding allocations to reflect these factors. Our analysis takes these factors as exogenous and establishes the extent of the remaining growth in England.
We can attribute some of this growth to the expansion in resources from which the NHS in England has benefited over the last 15 years. Because that expansion has largely been matched in Scotland, the common trend growth in elective activity in Scotland and England gives a measure of this resource effect. The extent to which extra resources finance increases in activity is something that primary care trusts (PCTs), which were at the time responsible, and the CCGs that followed them, can be expected to manage by conventional means.
Clinical Commissioning Groups operate in a national context in which their financing of elective activity and the incentives to which the financing mechanism gives rise are outside their control. Hence, the consequences of the (external to CCGs) system reforms represent one element of management challenge. If it is found that those reforms created additional growth in activity which has persisted beyond their introduction, then there may be a rationale and imperative for those overseeing the system to consider adapting it so as to moderate these influences; CCGs have little power to act unilaterally on this. Although local variation from the NTPS is envisaged, this is not expected to impact on the fundamentals of the system or on the incentives to engage in activity that it encourages.
Any residual growth in activity after we have accounted for demand-side drivers, resourcing and system reform constitutes the real management challenge that CCGs face and have responsibility for. Being a ‘residual’, our model, despite quantifying the growth to be managed, cannot attribute a causal mechanism to it. We view our role here as one of information provision. As detailed below (see Summary of findings and Results), we find that the residual growth in elective activity is substantial. We also find that residual growth is not evenly distributed across England and, thus, the challenges faced by some CCGs are inherently greater than those faced by others. We therefore devote some attention to identifying those CCGs (located within former PCT clusters) for which the challenges appear greatest. We leave it to others to consider whether or not the evidence for the inherently greater challenge facing some CCGs justifies their being offered greater resources or assistance.
There are many other dimensions in which the extent of growth in elective activity could be measured. Our approach is to take overall elective activity and to account for variations in case mix across time, jurisdictions and regions. An alternative is to consider specific areas of elective activity, for example, specific HRGs or the treatments provided to specific age groups. Thus, we could narrow down further and specify where the management challenge is greatest within a CCG. There are other strands in the broader project of which our work is a part that are pursuing these issues and so we do not consider them here. However, the framework that we have developed is capable of development and extension with regard to these issues and we provide some illustrations of how such work might be progressed.
Summary of findings
The details of the data that we use and our empirical methods are set out in Data and empirical methods and the detailed results of our regression analysis can be found in Results. In the remainder of this section we summarise and interpret our key findings.
Growth in elective activity in England has been rapid and faster than in Scotland
Our analysis confirms that there has been a rapid expansion in per capita elective activity in England over the period 1997–2011 and that this expansion cannot be attributed to changes in population structure or in changes in case mix.
Using Scotland as a comparator reveals that the growth is specific to England; whereas there has been some expansion in Scotland, expansion in England has been much faster. Placing this growth in context, we estimate overall increases in elective CIPSs at the rate of 4.3% in England per annum, which results in a doubling of per capita activity over a period of (just over) 16 years. The comparable rate for Scotland is, in effect, zero, despite the fact that the NHS in Scotland has had a similar expansion in resources over the period.
Thus, the picture that emerges is of a national context in which expectations of rapidly expanding activity has become established. This sets the environment in which future growth will need to be managed.
England has also exhibited a relatively rapid decline in lengths of stay
To understand the evolution of elective care, the expansion in the volume of activity and the associated long-term trend towards shorter hospital stays for elective treatments must be considered. This trend has previously been noted over shorter time periods but our analysis confirms it over the longer run, and confirms that it is not a consequence of changing population structure or changes in case mix proxied by HRGs.
The changes that have taken place in England are again more rapid than those that have occurred in Scotland, but the differences are not so marked. Against the benchmark reduction of 3% per annum in Scotland, the reduction in England is 3.4% per annum. Thus, although the greater reduction in LOS moderates the pressure on capacity to treat that has resulted from the expansion in the volume of activity in England, it does not negate it.
The system of financing hospital care under the NTPS does not immediately reflect any savings that result from shorter stays in hospital in the form of lower costs for those financing elective care, that is, the CCGs. Hence, this process of rapidly expanding volume, accompanied by less rapidly contracting lengths of stay, will have generated pressures on purchaser’s budgets, and, if the process continues, so too will the pressure.
The faster growth in continuous inpatients stays in England cannot be explained in terms of either capacity or system reform
Having established that the overall picture is one of rapidly expanding volumes of elective care and declining LOSs, our empirical approach is designed to establish whether or not these changes can be attributed to the expansion of resources in the English NHS, or to the substantial reforms in the financing of hospital care that it has undergone.
We find little evidence of a substantial role for either. For the former, we rely on the observation that the NHS in Scotland has also had increased resources over the period studied. Thus, if resources were driving growth we should expect this to be reflected by a common trend. As indicated above, all of the growth in elective activity in England has been in excess of that in Scotland. To assess the latter, we model system reform through both the timing of its introduction and its differential introduction in England and its lack of adoption in Scotland.
We can establish that system reform is associated with changes in both elective activity and LOSs. We estimate that the combined effects of reforms such as PbR (leading to the NTPS) and patient choice are associated with a 7.7% reduction in elective activity. However, this is an effect on the level of activity, not on its growth rates. When we estimate regressions to allow for both a shift and growth effect of system reform, we find that the latter is very small.
Similar observations regarding system reform apply to the shortening durations of treatments
Previous literature has focused on the potential impact of system reform on lengths of stay. 13 This has been based on a conceptual framework that gives rise to an expectation that the switch to fixed prices would lead to reductions in LOSs. We find that system reform is associated with a 5.6% reduction. This figure is consistent with a range of estimates previously published and establishes further evidence in this regard.
However, as with our finding in relation to the volume of activity, this effect is on the level, and not the growth, of hospital stays, and when we include a term to capture a growth effect, the estimated coefficient is small and not statistically significant different from zero.
There is evidence of considerable diversity across Healthcare Resource Groups
The assignment of elective treatments to HRGs provides a natural way of considering different types of treatments and of examining whether or not the pattern of growth observed overall is repeated for different HRGs. There are many different possible subgroups of HRGs to consider, and a comprehensive analysis of subgroups is beyond the scope of this report. However, we consider two groups of HRGs by way of examples of what subgroup analysis might reveal. Both groups are defined in terms of high expenditure, the first in terms of overall high elective inpatient expenditure on that HRG and the second in terms of expenditure on day cases.
For high elective inpatient expenditure HRGs we find a substantially different pattern of growth. For these HRGs growth is faster overall but only moderately so, at 4.8% versus 4.3% per annum. However, for these HRGs almost all of the growth is common across Scotland and England. This suggests that the drivers of growth for these HRGs are also different. We cannot exclude resource growth as a potentially important driver, because the growth exhibits a common trend with growth in Scotland. It is thus possible that this group of HRGs, along with others that further analysis might identify, are susceptible to being managed through tighter budget constraints.
The pattern of growth is different again for those HRGs that represent high expenditure among day cases. For this group we find that growth rates are very high (8.2% per annum), and differentially so, compared with growth in Scotland (which is 2.5% per annum). This therefore suggests a different management scenario to the all-elective high expenditure HRGs. The large differential trend suggests a process of growth in England that is pervasive and not closely related to the past expansion of resources.
Our general modelling approach permits the analysis of other subgroups of HRGs that might be of specific interest to purchasers as and when those are identified.
For both subgroups there are corresponding differences in the pattern of decline in lengths of stay. These are described in detail in Subgroup analysis: high-expenditure Healthcare Resource Groups.
There is considerable diversity of experience across groupings of Clinical Commissioning Groups
Our modelling approach facilitates the analysis of growth rates separately for groupings of CCGs, with the grouping based on historic PCT clusters. The research questions here are whether or not, and, if so, how, growth in elective activity varies between clusters. The clusters concerned are largely defined geographically and we include a listing of CCGs and their associated cluster.
We find a large variety of experiences about all-HRG elective activity growth. Whereas some PCT clusters exhibit only moderate growth in activity, those at the top end of the range of experiences have very high growth rates, which implies a doubling of activity in around 8 years. These rates are all estimated per capita and adjusted for population changes and thus represent very substantial increases. We identify the growth rates of all 49 clusters and so every CCG can find its local growth rate from our model.
Whereas CCGs may be most concerned with the volume of activity, its intensity in terms of LOS sets the context in which activity is to be managed, and we repeat our cluster-level analysis for this measure. It also shows very large variations across PCT cluster (see Examining the effects across primary care trust clusters for details, where we summarise and explain the PCT cluster-specific growth rates).
Overall, the context in which Clinical Commissioning Groups have to manage elective care is a very challenging one
Taken together, our findings suggest an environment in which elective activity in some clinical areas and in some regions of England has exhibited rapid growth.
We do not find that this growth can be attributed to system reform, which implies that CCGs cannot rely on a period of sustained systemic stability to moderate growth.
We find only weak evidence of growth being exclusively related to growth in resources; our comparator jurisdiction, Scotland, exhibits similar resource growth but much lower growth in activity.
It is therefore possible that growth in elective activity in England is entrenched and may thus be very difficult to manage downwards.
In a more positive vein, elective activity in England has also seen a continuous process of reductions in the length of hospital stays. If those reductions reflect real resource savings, and if the process by which they are generated is sustainable, those savings may be reflected in the NTPS and give CCGs more real purchasing power for their limited budgets.
The tools that we have developed can be extended and adapted
An important observation is that experiences across different elements of elective care and across different areas of England are very diverse. This implies that management challenges will vary between CCGs. We have set up our model to facilitate a targeted analysis of elective activity in both the HRG and CCG dimensions.
Hence, we can take a specific subgroup of HRGs and produce a bespoke analysis of elective activity growth for that subgroup. Moreover, depending on how narrowly the HRG subgroup is defined, we can produce a PCT cluster analysis of growth in elective activity and bed-days for that subgroup.
Data and empirical methods
Data
The basis of our study is episode-level data on in-hospital elective care. This activity is reported in the admitted patient data set of the HES in England and the Scottish Morbidity Record 01 for Scotland. 26 These data sets include both elective and emergency admissions, including day cases, and, unlike HES, SMR01 does not include maternity. We therefore exclude maternity admissions from HES. We consider the period covering the financial years 1997/98 to 2011/12. Central to our investigation is the designation of hospital activity between emergency and elective care. There are important differences between HES and SMR01 in this regard. In HES, all episodes that have an elective (emergency) admission as their origin are classified as elective (emergency) episodes, whereas in SMR01 transfers are recorded as planned regardless of whether they originate from an elective or an emergency admission. We therefore classify complete stays in hospital in SMR01 according to the admission route for the first episode.
Hospital Episode Statistics consists of individual records on each episode of hospital care, with each corresponding to a ‘single period of care under one consultant’. 27 These episodes can be grouped into two types of spells: (1) hospital-specific spells and (2) spells that allow for transfers, namely provider spells (‘time that a patient stays in one hospital’) and CIPS (‘continuous period of care within the NHS, regardless of any transfers which may take place. It can therefore be made up of one or more provider spells’). 27 The extract of SMR01 that is available to us also consists of episodes for which it is possible to identify CIPSs but not provider spells. Thus, our analysis will consider CIPSs to avoid any spurious differences that arise from different reporting practices in England and Scotland.
There remains one further difference in the definition of CIPSs used in England and Scotland. Although in England the Health and Social Care Information Centre (HSCIC) methodology27 allows for a gap between the end of one provider-spell and the beginning of the next of up to 2 days, in Scotland a CIPS is defined as an unbroken inpatient period. 28 To make the two measures comparable, we modified the procedure to obtain CIPSs in HES so as not to allow for gaps within a CIPS; hence, in both countries we shall be using unbroken hospital stays (including transfers between hospitals).
Continuous inpatient stays in HES are constructed using the algorithm (based on the HSCIC methodology) developed by the Centre for Health Economics at the University of York for that purpose,27 which first groups together consecutive episodes of care within the same hospital (provider spell) and then groups together consecutive provider spells that end and/or begin as transfers (CIPSs). In SMR01, CIPS are constructed using an individual identifier and a CIPS marker.
The first episode on each CIPS will provide the following information for that CIPS: date of admission, elective/emergency classification and HRG (version 4, 2009/10). 29 The duration of the CIPS is calculated using the dates on which a CIPS started and ended.
Our unit of analysis is the total number of CIPSs or the average LOS within a geographical area (see Variables for details). In England we consider PCT clusters as geographical areas; these clusters were created as part of the transition from PCTs to CCGs, which ended in March 2013 with the abolition of PCTs and the introduction of CCGs. 30,31 A list of clusters32 and a map33 are available online. We use PCT clusters in place of CCGs because CCGs did not exist before April 2013 and cannot be identified in the historical data; it is assumed that all PCTs within a cluster will have the same growth characteristics. For Scotland, we consider the country as a whole, without making any distinction between its Health Boards, because our framework requires only one control group (i.e. a place where the system reform was not implemented).
The analysis also includes characteristics of the PCT clusters, including population composition (sex and age groups) and deprivation, which are derived from the characteristics of the PCTs that form each of them. All these variables are expressed as percentages, and their construction is described in detail in Variables.
Table 3 presents a complete list of PCT cluster population and activity in England and Scotland for the last year in our data (2011/12). We observe that the size of the PCT clusters varies across England (the biggest cluster is five times the size of the smallest cluster) and that they are all smaller than Scotland. In terms of activity, CIPSs per 1000 population show a higher variation than LOSs among the PCT clusters in England, and both measures of activity are higher than in Scotland.
| Country or PCT cluster | Population | CIPSs per 1000 population | Average LOS (days) |
|---|---|---|---|
| Country | |||
| Scotland | 5,299,900 | 118.22 | 1.78 |
| England | 53,107,169 | 167.26 | 1.31 |
| PCT cluster | |||
| Airedale, Bradford and Leeds | 1,273,798 | 153.51 | 1.38 |
| Arden | 863,469 | 143.86 | 1.28 |
| Bath and North East Somerset, Wiltshire | 649,857 | 166.33 | 1.35 |
| Bedfordshire and Luton | 617,125 | 131.57 | 1.39 |
| Berkshire West and Berkshire East | 875,865 | 149.44 | 1.22 |
| Birmingham and Solihull | 1,281,139 | 179.06 | 1.20 |
| Black Country | 1,141,679 | 184.12 | 1.14 |
| Bournemouth and Poole, Dorset | 745,338 | 241.92 | 1.25 |
| Bristol, North Somerset, South Gloucestershire | 894,582 | 191.28 | 1.24 |
| Calderdale, Kirklees and Wakefield | 953,573 | 152.19 | 1.34 |
| Cambridgeshire and Peterborough | 806,769 | 165.53 | 1.20 |
| Cheshire | 1,222,808 | 169.60 | 1.28 |
| Cornwall and Isles of Scilly | 535,984 | 208.03 | 1.38 |
| Cumbria | 499,817 | 211.69 | 1.25 |
| Derbyshire | 986,304 | 152.29 | 1.34 |
| Devon, Plymouth, Torbay | 1,135,491 | 188.33 | 1.34 |
| Gloucestershire, Swindon | 813,192 | 185.31 | 1.30 |
| Greater Manchester | 2,718,713 | 184.31 | 1.20 |
| Hertfordshire | 1,119,824 | 135.17 | 1.44 |
| Humber | 915,521 | 166.89 | 1.36 |
| Kent and Medway | 1,731,351 | 150.17 | 1.38 |
| Leicestershire | 1,018,387 | 124.56 | 1.36 |
| Lincolnshire | 717,294 | 178.66 | 1.25 |
| Merseyside | 1,186,655 | 191.16 | 1.24 |
| County Durham and Darlington | 618,578 | 179.08 | 1.45 |
| Norfolk and Waveney | 974,782 | 233.82 | 1.12 |
| North Central London | 1,353,385 | 197.91 | 1.29 |
| North East London and The City | 1,787,159 | 131.68 | 1.39 |
| North West London | 1,982,762 | 135.66 | 1.44 |
| North of Tyne | 796,576 | 189.82 | 1.31 |
| South East London | 1,668,947 | 187.87 | 1.33 |
| South West London | 1,412,154 | 147.57 | 1.42 |
| South of Tyne and Wear | 623,843 | 204.68 | 1.29 |
| Tees | 557,444 | 172.50 | 1.37 |
| North Essex | 976,490 | 149.00 | 1.54 |
| North Yorkshire and York | 798,989 | 157.12 | 1.34 |
| Northamptonshire and Milton Keynes | 949,311 | 144.77 | 1.31 |
| Nottinghamshire | 977,692 | 138.76 | 1.51 |
| Oxfordshire and Buckinghamshire | 1,150,698 | 145.69 | 1.20 |
| Pan Lancashire | 1,461,295 | 240.75 | 1.11 |
| Somerset | 531,581 | 175.18 | 1.24 |
| South Essex | 752,651 | 169.21 | 1.21 |
| South Yorkshire and Bassetlaw | 1,456,808 | 163.76 | 1.35 |
| Southampton, Hampshire, Isle of Wight and Portsmouth | 1,901,813 | 143.03 | 1.46 |
| Staffordshire | 1,098,265 | 174.88 | 1.38 |
| Suffolk | 614,777 | 163.43 | 1.34 |
| Surrey | 1,123,439 | 141.78 | 1.41 |
| Sussex | 1,609,080 | 143.81 | 1.33 |
| West Mercia | 1,224,115 | 164.16 | 1.35 |
Empirical methods
We are interested in the growth of activity, measured as the number of CIPSs or bed-days, in different geographical areas across time, but we also need to consider that this activity is classified, according to its diagnoses and treatments, into HRGs. We use regression methods to examine interdependencies in order to simultaneously account for multiple influences on elective activity. Of these influences, the identification and inclusion of different treatments via HRGs is a powerful and important element in our approach because it adjusts for changing case mix over time. In the absence of this adjustment, an observed reduction in, for example, bed-days, might simply be a consequence of a changing pattern of treatments towards less time-intensive interventions.
To take into account the time-constant unobserved heterogeneity arising from location (e.g. country or PCT cluster) and HRG that might be correlated with observed characteristics, a fixed-effect regression framework might seem most useful. However, the high number of HRGs and PCT clusters makes it computationally demanding, in terms of both computing memory and time.
We chose as a regression method the Stata® (StataCorp LP, College Station, TX, USA) command ‘felsdvreg’, which was developed to reduce the computing memory needed to fit a fixed-effects model with two high-dimensional fixed effects. 34 In this case, the fixed effects will be the HRGs (around 1200) and the PCT clusters (around 50). Our choice of PCT clusters as geographical areas has the advantage of reducing the dimensionality of the fixed effects that need to be estimated compared with using the PCTs (approximately 50 vs. 150).
We examined a number of different regression formulations but focus in this report on a log-linear approach, which facilitates an interpretation of regression coefficients in terms of percentages and thereby established changes in growth rates. The general form of the model we estimate is the following:
The dependent variable, A, is a measure of activity corresponding to HRG, h, in location, l, in the year, y, expressed in logs. We consider two measures of activity: CIPS adjusted by the population size of the cluster in which they are observed, and the average LOS for each HRG–cluster–year combination. The use of population adjusted CIPSs means that all of our results can be scaled to relate to per capita quantities and, in particular, mean that when we refer to growth henceforth, we are considering growth in per capita activity.
The explanatory variables include: t, a time trend measured as the difference with the initial period; l, dummy variable(s) that indicate the location (country or PCT cluster); SR, a dummy variable which represents the system reform introduced in England in the mid-2000s; Xy, the characteristics of the PCT cluster [i.e. population composition and deprivation (considering Scotland as another cluster)]; αh, the HRG fixed effect; αcl, the PCT cluster effect; and µ, the error. Whether or not the coefficients of interest, namely β1 and β2, change if the controls for population composition and deprivation are not included in the model is considered below (see Results excluding additional controls).
The numbers attached to the underbraces correspond to columns in the tables of regression results.
Using this formulation, the coefficient β1 provides an estimate of the growth trend in activity in Scotland, whereas β2 provides an estimate of the extent to which growth in England is different from growth in Scotland. These coefficients are central to understanding the issue of ‘managing demand’. If we regard Scotland as the control, given that it has not followed the kinds of proactive system reform undertaken in England, then β1 is the inherent capacity-driven growth in demand for elective care. Growth that differs from this in England is either attributable to system reform, or idiosyncratic to a particular cluster, or has other causes that are common to England but not present Scotland. In all cases it represents elements of growth that any one CCG might attempt to influence or control.
Modelling system reform
A key element of the Scotland–England comparative study is to determine the effect (if any) of system reform on planned care growth in England and to establish whether or not any such effect is persistent.
System reform includes a large raft of policies and interventions that were pursued in England in the mid-2000s. The usual focus of attention is PbR, which was rolled out for elective care throughout 2004 and 2005. This policy explicitly introduced financial incentives and was supported or augmented by a number of other initiatives such as empowering patient choice (in 2006). This suite of changes is our particular focus when examining system reform.
In order to establish empirical evidence of the effect of these policies, we require both a treatment and a control group. Given that policies are usually rolled out nationally and simultaneously, the scope for policy evaluation using data on one country alone is rather limited, although, in the case of PbR, it is possible to exploit the differential introduction for different HRGs and/or providers. We, however, have data for Scotland and can use Scotland as a control group against the system reform treatment of England. The standard methodology is difference-in-differences, in which markers (dummy variable or variables) are constructed for the introduction of system reform and for region or other units of observation. Regression analyses include these dummy variables and their interactions, and coefficient estimates of the interaction terms identify the effect of system reform.
Because the nature of system reform is complex, our regressions adopt a number of different specifications, but we focus on the most parsimonious in reporting results. The most general specifications allow for both the phasing in of system reform in England and the absence of system reform in Scotland to identify the impact of policy. To operationalise this we construct dummy variables that are directly an interaction of the introduction of policy and the domain in which that policy is introduced. Specifically, we adopt this approach for PbR, for which specific HRGs and particular providers function as the relevant domains so that HRGs, providers and jurisdictions in which the policy does not apply function as controls (see Alternative models of system reform for results using this approach).
Because the exact timing of system reform is often not clear, and to allow for the fact that the impact of any policy may be affected by lags, we adopt a flexible approach to specifying some of our policy dummy variables. Thus, for example, a generic system reform dummy variable is formulated so as to allow for the raft of policies to come into effect in 2005 (a 2005-on-in England variable) or 2006 (a 2006-on-in England variable), and we run regressions with the former of these alternative specifications to assess robustness (see Alternative models of system reform for results).
Although general specifications have the merit of not imposing restrictive assumptions, the resulting regressions are more difficult to interpret. We have, therefore, engaged in a specification comparison to seek a simple, yet robust, framework for reporting and interpreting results. Our investigation of this issue has produced what we believe to be important insights. In essence, we find that the impact of system reform can be captured rather simply. Our regression estimates of primary interest (the rate of growth of elective activity, across HRGs and PCT clusters) are largely invariant to the precise way in which reform is incorporated. So, although models with complex policy dummy variables capture more variation in the data, they do not affect the relevant conclusions regarding growth in elective activity. We have thus focused on reporting results for a simple, parsimonious model in which the effect of system reform is captured by a single (2006 onwards) policy variable. The results of interest to our study are invariant to the precise choice of this. We note in passing that it was never the intention of the study to attempt to unpick the effects of the component elements of system reform (something that our more general specifications might facilitate in the future) but rather to understand their effect in totality. In this regard we conclude that the total effect of system reform can be established using a simple empirical characterisation of that reform.
Previous studies of policy evaluation have typically considered only short time periods prior and subsequent to policy intervention. A unique and powerful element of our study is that we have assembled what we believe to be the largest (in terms of constituent elements) and longest (covering 15 years, 6 of which are prior to the onset of system reform, in 2003/04) data set to be used to address these issues. In addition to giving us much better estimates of underlying trends in activity (against which the impact of policy can be gauged), this permits us to consider the potential effect of system reform on those trends. To operationalise this aspect of our study we generalise the standard difference-in-differences method, which considers the levels of an observed variable (e.g. spells of care or average LOSs) and allows for policy interventions to impact on the estimated trend rate of growth of such variables; we do this by allowing interactions between policy dummy variables and time trends in the regressions (see Estimating the impact of system reform).
Variables
The data with which we estimate Equation 1 do not comprise individual observations, but rather aggregations of CIPSs within a HRG–cluster–year combination. Thus, individual observations were collapsed into HRG–cluster–year totals and will be used for the regressions reported in the next section. The data can also be aggregated at country level; this aggregation was used, for example, to create the activity plots (see Introduction). The definition of clusters is described above. For the assignment of HRGs we classified data for all years in HES and SMR01 according to HRG4, 2009/10, using the relevant Reference Costs Grouper. 29
There are 1486 HRGs, of which approximately 1200 are populated with data and therefore controlled for using fixed effects in our regressions. Owing to dimensionality issues we do not include these directly as dummy variables or include their interactions with time trends. Hence, HRGs are modelled in effect as shift dummy variables but differenced out of the regressions. HRGs can be grouped according to the subchapter in which they are defined. Our inclusion of HRG fixed effects is to control for case-mix variation (over time, between PCT clusters and across jurisdictions) and one dimension of this variation is shown in Table 4, in which it can be seen there are substantial differences in elective activity (measured as CIPSs per 1000 population) between England and Scotland in respect of some HRG subchapters. Failing to account for such variation would risk misattributing variation in activity to factors that are correlated with HRG case mix. We leave for future consideration the question of whether or not some of the differences between Scotland and England require greater scrutiny. The most extreme example is subchapter LA (Renal Procedures and Disorders) which constitutes 10.5% of elective CIPSs in England, but < 1% of elective CIPSs in Scotland. These figures do not seem to be consistent with the data describing the same treatment interventions. The specific HRG that gives rise to this discrepancy is LA08E and we ran regressions with and without data relating to this HRG; our results are not affected up to the second significant figure.
| Subchapter | Description | HRGs | CIPSs per 1000 population, 2011/12 | |
|---|---|---|---|---|
| England | Scotland | |||
| AA | Nervous system procedures and disorders | 31 | 2.21 | 1.79 |
| AB | Pain management | 6 | 4.14 | 1.26 |
| BZ | Eyes and periorbital procedures and disorders | 33 | 11.08 | 8.82 |
| CZ | Mouth, head, neck and ears procedures and disorders | 93 | 10.27 | 8.43 |
| DZ | Thoracic procedures and disorders | 98 | 2.66 | 2.35 |
| EA | Cardiac procedures | 35 | 4.06 | 3.11 |
| EB | Cardiac disorders | 14 | 0.80 | 0.62 |
| FZ | Digestive system procedures | 122 | 27.64 | 23.83 |
| GA | Hepatobiliary and pancreatic system surgery | 21 | 1.21 | 1.21 |
| GB | Hepatobiliary and pancreatic system endoscopies, etc. | 16 | 0.82 | 0.78 |
| GC | Hepatobiliary and pancreatic system disorders | 28 | 0.26 | 0.35 |
| HA | Orthopaedic trauma procedures | 64 | 0.95 | 0.66 |
| HB | Orthopaedic non-trauma procedures | 64 | 12.49 | 9.84 |
| HC | Spinal surgery and disorders | 33 | 1.38 | 0.97 |
| HD | Musculoskeletal disorders | 21 | 2.56 | 2.04 |
| HR | Orthopaedic reconstruction procedures | 9 | 0.38 | 0.30 |
| JA | Breast procedures and disorders | 19 | 2.50 | 2.03 |
| JB | Burns procedures and disorders | 11 | 0.04 | 0.01 |
| JC | Skin surgery | 36 | 5.23 | 3.75 |
| JD | Skin disorders | 17 | 0.39 | 0.41 |
| KA | Endocrine system disorders | 11 | 0.52 | 0.32 |
| KB | Diabetic medicine | 10 | 0.06 | 0.03 |
| KC | Metabolic disorders | 7 | 1.11 | 1.51 |
| LA | Renal procedures and disorders | 32 | 17.66 | 0.55 |
| LB | Urological and male reproductive system procedures | 83 | 14.02 | 10.84 |
| LC | Renal dialysis | 8 | – | – |
| MA | Female reproductive system procedures | 26 | 6.48 | 6.12 |
| MB | Female reproductive system disorders | 12 | 0.34 | 0.57 |
| MC | Assisted reproduction medicine | 9 | 0.01 | 0.04 |
| NZ | Obstetric medicine | 28 | 0.34 | 0.01 |
| PA | Paediatric medicine | 112 | 3.05 | 2.11 |
| PB | Neonatal disorders | 3 | 0.07 | 0.01 |
| QZ | Vascular procedures and disorders | 34 | 3.45 | 2.54 |
| RA | Diagnostic imaging procedures | 35 | – | – |
| SA | Haematological procedures and disorders | 55 | 7.22 | 6.60 |
| SB | Chemotherapy | 18 | 11.42 | 9.72 |
| SC | Radiotherapy | 29 | – | – |
| SD | Specialist palliative care | 10 | – | – |
| UZ | Undefined groups | 1 | 4.44 | 3.58 |
| VA | Undefined groups | 8 | 0.01 | 0.02 |
| VB | Emergency medicine | 11 | – | – |
| VC | Rehabilitation | 23 | – | – |
| WA | Immunology, infectious diseases, poisoning, shock, etc. | 56 | 5.48 | 0.93 |
| WD | Treatment of mental health patients by non-mental health providers | 3 | 0.48 | 0.07 |
| WF | Non-admitted consultations | 8 | 0.00 | 0.08 |
| XA | Neonatal critical care | 6 | – | – |
| XB | Paediatric critical care | 8 | – | – |
| XC | Adult critical care | 7 | – | – |
| XD | High-cost drugs | 44 | – | – |
| Total | 1468 | 167.27 | 118.22 | |
We use two dependent variables: CIPS and average LOS. CIPSs correspond to the number of CIPSs per 1000 population in a given HRG–cluster–year combination. Average LOSs are calculated using the total number of bed-days and total number of CIPSs in a given HRG–cluster–year combination; the total number of bed-days is calculated including CIPSs with zero bed-days (day cases) but assigning them a positive number (0.7) to reflect that, even though there is no overnight stay, there are still resources assigned to these admissions. We use this adjustment to ensure that day cases are reflected in our regression analysis. The figure of 0.7 was chosen following the method of Farrar35 and we checked the robustness of our finding against an alternative value of 0.2. All results that we report are unchanged up to the second significant figure.
As can be seen in Equation 1, the main explanatory variables include a time trend, a location indicator and a policy dummy variable. The time trend is calculated as the difference between the observation’s financial year and the initial period (1997/8). The location indicator will vary depending on the geographical unit considered, when using country data there will be only one variable, which will take a value of one for England and zero for Scotland; when using PCT clusters each will be represented by a dummy variable and Scotland will be considered as the reference cluster (i.e. there is no dummy variable for Scotland).
A policy dummy variable captures the system changes introduced in England that were not implemented in Scotland. The alternative formulations for this variable are discussed in Modelling system reform. The results reported (see Results) are based on the definition of that variable as zero for Scotland in all years and switching from zero to one in 2006 in England. We report results based on alternative and more sophisticated formulations and discuss any differences that arise (see Checks on the sensitivity of main results).
In addition, we control for PCT cluster characteristics including population and deprivation, which are the aggregation of the characteristics of the PCTs that form the cluster. The population data for England were collected from the HSCIC Indicator Portal;36 some PCTs did not have population data for some years as their borders did not match local authority borders. In such cases the population of the local authority which was assigned to more than one PCT was divided equally among the PCTs to which it belonged. The population data for Scotland come from the Population Estimates Time Series Data in the National Records of Scotland. 37 The data for deprivation correspond to the English Index of Multiple Deprivation (IMD). 38 The data were at lower-layer super output area (LSOA) level, and were grouped into local authorities and then into PCTs using the same mapping as for population; the percentages in each quintiles were then calculated using the number of LSOAs in each decile and the total number of LSOAs in a PCT. For Scotland, because we consider the whole country, there would be no variation and each quintile would have one-fifth of the population by definition; to avoid this lack of variation over time, we used the deprivation decile reported for patients in SMR for each year to calculate the percentage of patients in each quintile.
Results
Regression estimates of our generic model set out in Equation 1 are central to our results. As noted previously, we consider two measures of activity. Tables 5 and 6 show the regression estimates for the number of CIPSs and average LOS, respectively.
| Regression model | ||
|---|---|---|
| (1) | (2) | |
| Time trend, t (standard error) | 0.005** (0.002) | –0.001 (0.002) |
| t × England (standard error) | 0.038*** (0.002) | 0.044*** (0.002) |
| System reform | No | Yes |
| Sex | Yes | Yes |
| Age groups | Yes | Yes |
| Deprivation | Yes | Yes |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 755,170 | 755,170 |
| R 2 | 0.8214 | 0.8214 |
| F-test HRG and PCT cluster FE | 2633.96 | 2634.55 |
| F-test HRG FE | 2723.71 | 2724.28 |
| F-test PCT cluster FE | 348.76 | 350.23 |
| Regression model | ||
|---|---|---|
| (1) | (2) | |
| Time trend, t (standard error) | –0.026*** (0.002) | –0.030*** (0.002) |
| t × England (standard error) | –0.008*** (0.001) | –0.004*** (0.001) |
| System reform | No | Yes |
| Sex | Yes | Yes |
| Age groups | Yes | Yes |
| Deprivation | Yes | Yes |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 755,170 | 755,170 |
| R 2 | 0.7263 | 0.7263 |
| F-test HRG and PCT cluster FE | 1494.00 | 1494.22 |
| F-test HRG FE | 1548.28 | 1548.50 |
| F-test PCT cluster FE | 348.76 | 68.74 |
In the first columns of Tables 5 and 6 the regression includes the common time trend, the differential time trend for England, controls for population characteristics that are expected to influence demand for elective care and the fixed effects for PCT clusters and HRGs. In the second columns the regressions additionally include a variable capturing system reform. The full details of the construction and rationale for this variable are set out in Modelling system reform. The results reported in this section adopt the most straightforward formulation, with results for alternative formulations being set out with commentary below (see Checks on the sensitivity of main results). All of the results we report here are robust to the choice of formulation.
There are a large number of coefficient estimates underlying the tables, most of which, for reasons of parsimony, we do not report. Thus, for example, there are 17 age category dummy variables, four deprivation category variables, 49 dummy variables associated with PCT clusters, 49 variables arising from allowing for cluster-specific growth effects and > 1200 implicit dummy variables capturing case-mix variation using HRGs. Under the computation method, which is described in detail in Empirical methods, these last estimates are not directly available but could be recovered if desired. We note simply that the majority of the dummy variables that are not reported here are significant at the 1% level and where there may be value or interest in establishing and reporting their values, we are able to do so. As evidenced by the F-test results reported in Tables 5 and 6 the different levels of fixed effects are jointly and separately significant at the 1% level. Overall, therefore, our model as specified in Equation 1 incorporates variables that are important in accounting for variation in elective activity.
Growth in continuous inpatient stays
Table 5 shows the results for CIPSs adjusted by population. The first coefficient (time trend) establishes the common trend rate of growth in this measure of elective activity in England and Scotland. It is important to note that in both columns the coefficient is small, and in the second column it is not statistically significantly different from zero. The estimate in column 1 implies a rate of growth of 0.5% per annum and in column 2 (not significant) of –0.1%. This is in contrast to the estimates from the simple time-series regression reported above (see Modelling growth in elective activity: the role of another jurisdiction), which suggested common growth rates of 1% and 0.7%. Given that our variable for system reform is significant, its omission will bias the estimates of other parameters in the regression; we should therefore focus on the column-2 value.
We can therefore conclude that including the combination of population controls and fixed effects is important for drawing inferences regarding the underlying rate of growth in elective activity. Omitting these factors leads to the erroneous conclusion that there is underlying growth, whereas including them suggests that this is not the case.
When these controls are included, we use the common trend between England and Scotland as a means of establishing the effect of factors that are common between them on the growth in elective activity. We conclude that these common factors, which include the growth in resources that both England and Scotland have exhibited over the period are not associated with any underlying growth in elective activity. The second coefficient in Table 5 captures the trend growth in England that is additional to any common trend. The estimates in column 2 imply (summing with the first row estimates) a growth rate in elective activity in England of 4.3% per annum in both cases. A comparison with Table 1 is useful here, in which the respective figures are 2.9% per annum (column 1) and 2.1% per annum (column 2). Hence, omitting the additional controls for population, case mix and locality downwards biases the estimate of growth in elective activity in England. A figure of 4.3% growth per annum is substantial. It implies a doubling in activity in approximately 16 years, whereby activity is measured in per capita terms. Simply as a matter of magnitude, our estimates indicate that managing growth in elective activity is a substantial challenge.
Comparing across columns 1 and 2 in Table 5, the only difference in the regressions reported is the inclusion of the system reform dummy variable. If system reform had been instrumental in causing much greater growth in elective activity in England, we should expect its inclusion as a variable to substantially change the estimates of both common trend (time trend) and differential trend (t × England). In fact, this is not the case and we can conclude that system reform in the sense of the changes associated with the adoption of PbR and patient choice is not a key driver of the growth in elective activity in England. That is not to say that system reform is not an important element in the pattern and evolution of activity – as we shall see later in this chapter, it is – but rather it does not account for the very substantial trend growth in activity seen in England over this period.
Given that the estimates reported in Table 5 suggest rapid expansion in elective activity, which is not attributable per se to the expansion of resources or to system reform or driven by population changes, what this growth is attributable to remains a key question. We return to this question of interpretation later in this chapter but, first, we report the alternative perspective on elective activity offered by the average bed-day measure.
Decline in average length of stay
Results relating to LOSs are reported in Table 6 in the same format as for CIPSs. Although not reported in detail, the estimated coefficients on the additional controls (with the exception of four of the 18 age categories and one deprivation category) are all statistically significantly different from zero, and the HRG and PCT cluster effects are jointly and separately significant.
With regard to column 1, there is confirmation of the observation made above (see Summary) of a negative trend in lengths of elective stays. The common trend reduction is 2.6% per annum, which indicates (allowing for compounding) a reduction of two-thirds over 20 years. The decline in England is greater than this, at 3.4% per annum (the sum of the first two row estimates). In comparison with the estimates that are not adjusted for population, case-mix or area-level effects (i.e. the estimates set out in Table 2), these results suggest that the additional decline in England is less substantial, because in Table 2 the estimated decline in England is 4.5%.
When the effect of system reform is included in the regression (column 2) the estimated additional rate of decline in England is reduced further but the estimate of the common trend increases (indicating that column 1 figures are biased owing to the omission of the system reform variable). The overall trend rate of reduction for England becomes 3.4% compared with a common trend reduction of 3%. The specific effect that system reform has had on the decline in lengths of stay is reported in the next section.
Estimating the impact of system reform
As noted earlier in this chapter, the inclusion of system reform as a variable does not substantially change the estimates of underlying trends in elective activity in England or Scotland. Thus, in terms of headline growth, the impact of system reform is modest. In order to better understand the impact that system reform has had, we extend our model to include both a shift effect, as included in Tables 5 and 6, and an interaction with the time trend. This latter component enables us to examine whether, and, if so, to what extent, system reform directly changed the growth rate of elective activity in England. The relevant regression results are reported in Table 7 for CIPSs and in Table 8 for LOS.
| Regression model | |||
|---|---|---|---|
| (1) | (2) | (3) | |
| Time trend, t (standard error) | 0.005** (0.002) | –0.001 (0.002) | 0.000 (0.002) |
| t × England (standard error) | 0.038*** (0.002) | 0.044*** (0.002) | 0.047*** (0.002) |
| System reform (standard error) | –0.077*** (0.006) | –0.020 (0.038) | |
| t × system reform (standard error) | –0.007 (0.004) | ||
| Sex | Yes | Yes | Yes |
| Age groups | Yes | Yes | Yes |
| Deprivation | Yes | Yes | Yes |
| PCT cluster FE | Yes | Yes | Yes |
| HRG4 FE | Yes | Yes | Yes |
| n | 755,170 | 755,170 | 755,170 |
| R 2 | 0.8214 | 0.8214 | 0.8214 |
| F-test HRG and PCT cluster FE | 2633.96 | 2634.55 | 2634.53 |
| F-test HRG FE | 2723.71 | 2724.28 | 2724.28 |
| F-test PCT cluster FE | 348.76 | 350.23 | 350.28 |
| Regression model | |||
|---|---|---|---|
| (1) | (2) | (3) | |
| Time trend, t (standard error) | –0.026*** (0.002) | –0.030*** (0.002) | –0.030*** (0.002) |
| t × England (standard error) | –0.008*** (0.002) | –0.004*** (0.002) | –0.002 (0.002) |
| System reform (standard error) | –0.056*** (0.005) | –0.024 (0.029) | |
| t × system reform (standard error) | –0.004 (0.003) | ||
| Sex | Yes | Yes | Yes |
| Age groups | Yes | Yes | Yes |
| Deprivation | Yes | Yes | Yes |
| PCT cluster FE | Yes | Yes | Yes |
| HRG4 FE | Yes | Yes | Yes |
| n | 755,170 | 755,170 | 755,170 |
| R 2 | 0.7263 | 0.7263 | 0.7263 |
| F-test HRG and PCT cluster FE | 1494.00 | 1494.22 | 1494.17 |
| F-test HRG FE | 1548.28 | 1548.50 | 1548.50 |
| F-test PCT cluster FE | 348.76 | 68.74 | 68.07 |
In Table 7 the first column omits system reform and thus replicates the results shown in Table 5. The second column also replicates the earlier results but also indicates the estimated impact of system reform. The coefficient in the third row indicates that system reform is associated with a 7.7% reduction in CIPSs. Thus, the regression estimates suggest that system reform moderated elective activity with regard to CIPSs. In terms of the estimated underlying growth in elective activity, the downwards shift associated with system reform equates to just < 2 years’ growth. In the third column we report results from allowing both a shift and a growth effect of system reform. The estimates here suggest that system reform is associated both with a reduction in activity (of 2%) and a moderation of growth of activity of 0.7% per annum.
One tentative hypothesis is that system reform, having established stronger incentives for hospitals to expand activity, might be associated with an increase in growth. This hypothesis is not supported by our estimates; in respect of CIPSs, system reform is associated with a moderating influence on growth, but the effect has been small. There is, therefore, no evidence to support the view that once system reform has become fully established there will be a substantial change in growth either up or down.
In Table 8 the regression results for LOS again indicate that the impact of system reform is negative. The estimated effect [in the third row of column (2)] is to reduce average bed-days by 5.6%. We note that this figure is consistent with other research that has evaluated the effect of PbR. 2 Our estimates benefit from a longer time period and suggest a moderately greater impact than previously estimated. This finding also has support from the theoretical models of prospective payment systems, of which PbR is one example. The theory suggests that making hospitals residual claimants over cost savings that they achieve through efficiency increases their effort to pursue efficiency savings, and this view is supported by the negative coefficient attached to system reform. The results in column (3) suggest that we cannot separately identify a shift and a trend effect. The coefficients on system reform and its interaction with the time trend are both negative but have large standard errors and are not, therefore, significantly different from zero. The magnitude of the trend effect is also small (< 0.5%). We can conclude that system reform exerted a negative influence on LOSs but any effect on trend is likely to be negligible.
Interpreting growth in elective activity in England
We note a potential tension under the NTPS between CCGs, which are concerned with the number of hospital treatments not their duration, and the overall management of the NHS, which might be more focused on resource use and, hence, bed-days. This potential tension is reflected in the different results for CIPSs and LOS, one of which displays growth and the other decline. This could imply that the reduction in resource use achieved by reducing the average LOS does not necessarily translate into savings for CCGs. Nevertheless, the two measures of changing activity are important to understanding the evolution of elective care.
Although the experience in England differs from that in Scotland on both measures, the larger magnitudes relate to growth in CIPSs. England has displayed substantially faster growth in CIPSs and only moderately faster decline in average bed-days.
Subgroup analysis: high-expenditure Healthcare Resource Groups
The formulation of our empirical model makes it possible to consider subgroups for analysis. Thus, subject to data limitations and the resulting number of observations, we can consider specific groups of patients or cases within a HRG or specific HRGs and consider whether or not, and, if so, how, growth in elective activity for these groups differs from that for England as a whole. There are too many such subgroups to present results for all of them. However, here, to illustrate the potential for such exercises, we consider a subgroup of HRGs corresponding to higher expenditure elective procedures and then consider HRGs in which there is high expenditure on day cases. We use the term expenditure here to avoid confusion with unit cost. The HRGs that we consider have high overall cost to the NHS, which is defined in terms of their overall cost evaluated at reference costs. These reference costs determine the national tariff and, in this sense, high-cost HRGs create high expenditure for CCGs.
The regression estimates for the first subset of HRGs are reported in Table 9, which contains results for both CIPSs and average LOS but is restricted to regressions that include a variable for system reform [thus being comparable to columns (2) in Tables 5 and 6]. The overall growth rate for CIPSs in England implied by these estimates is 4.8% per annum, which is very similar to the figure (4.3%) from Table 5, which applies across all HRGs. However, in the case of high-expenditure HRGs, this growth rates is common across England and Scotland, whereas when considering all HRGs the greater part of growth was specific to England.
| CIPSs per 1000 population | Average LOS | |
|---|---|---|
| Time trend, t (standard error) | 0.048*** (0.017) | –0.044*** (0.006) |
| t × England (standard error) | –0.002 (0.014) | –0.009** (0.004) |
| Earlier system reform | Yes | Yes |
| Sex | Yes | Yes |
| Age groups | Yes | Yes |
| Deprivation | Yes | Yes |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 6318 | 6318 |
| R 2 | 0.8590 | 0.9082 |
| F-test HRG and PCT cluster FE | 625.99 | 743.89 |
| F-test HRG FE | 4441.95 | 5264.38 |
| F-test PCT cluster FE | 3.05 | 5.87 |
The HRGs we consider are those listed for NHS trusts in table 2.7 of the Office of Health Economics Guide to UK Health and Health Care Statistics 2013. 39 The HRGs are:
-
HB21C – major knee procedures for non-trauma, category 2, without complications
-
HB12C – major hip procedures for non-trauma, category 1, without complications
-
MA07D – major open upper genital tract procedures without major complications
-
HB21B – major knee procedures for non-trauma, category 2, with complications
-
HR05Z – reconstruction procedures, category 2
-
EA14Z – coronary artery bypass graft (first time)
-
HC04C – extradural spine intermediate 1 without complications
-
HB11C – major hip procedures for non-trauma, category 2, without complications
-
GA10D – laparoscopic cholecystectomy, 19 years and over, with length of stay 1 day or more, without complications.
One possible interpretation of these results is that expansion in resources, which has been broadly the same in England and Scotland, is more instrumental in explaining growth in elective activity for high-expenditure HRGs. More generally, these results suggest that there may be important differences in the explanation of activity growth in different areas of elective activity. Hence, the methods of managing growth may need to be tailored to the particular HRGs or groups of HRGs under consideration. In the case of high-expenditure HRGs, these may be amenable to conventional budgeting controls, expanding when resources were expanding and being liable to contract or undergo limited expansion in a climate of greater financial constraint.
In respect of LOS, the pattern of decline, which comprises a large common trend and a marginally higher overall trend in England and which is seen in Table 5 for all HRGs, is repeated and slightly increased for high-expenditure HRGs. Over all HRGs we have estimated a common trend reduction of 3% per annum and a rate of 3.4% per annum in England. The respective figures for high-expenditure HRGs are 4.4% and 5.3%. It is worth noting that the resources applied per treatment in these high expenditure areas of activity are declining faster than for all areas of activity taken together. Thus, to some extent, the management challenge for CCGs is exacerbated by a greater trend reduction in resource use. The broader challenge for the health-care system is to ensure that any real savings in resources are reflected in the prices set under the NTPS in order that CCGs benefit from these.
As noted earlier in this section, our focus on high expenditure HRGs is an example of subgroup analysis that our framework permits. As a further illustration of this method and as an example of the possible extent of variation across different HRGs, we consider an alternative definition of high-expenditure HRGs and present results according to that alternative definition. One characteristic of elective activity that has already been a focus of our analysis is the reduction in LOS in hospital; this is evidenced by the decline in average bed-days. One aspect of this reduction is a move towards treating a greater proportion of patients as day cases. We therefore focus on those HRGs for which expenditure on day cases has been highest. 13 These HRGs still represent a mixture of day cases and longer stays in hospital, but constitute a different mix of HRGs to those reported in Table 9. The results for this set of HRGs are provided Table 10.
| CIPSs per 1000 population | Average LOS | |
|---|---|---|
| Time trend, t (standard error) | 0.024** (0.012) | –0.016*** (0.003) |
| t × England (standard error) | 0.057*** (0.010) | 0.004* (0.002) |
| System reform | Yes | Yes |
| Sex | Yes | Yes |
| Age groups | Yes | Yes |
| Deprivation | Yes | Yes |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 6750 | 6750 |
| R 2 | 0.7138 | 0.8207 |
| F-test HRG and PCT cluster FE | 236.97 | 515.65 |
| F-test HRG FE | 1573.66 | 3652.99 |
| F-test PCT cluster FE | 18.73 | 3.43 |
This set of HRGs provides an interesting comparison with the high-expenditure HRGs considered previously. First, we note that growth in activity for this group has been higher than that for either all high-expenditure or all other HRGs. The common trend growth rate is estimated to be 2.5% per annum. The differential growth in England has been substantially higher, at 5.7%, giving an overall growth rate in England of 8.1%. As before, this is a rate per 1000 population and has been adjusted for population age and socioeconomic changes. This rate of growth leads to a doubling of adjusted activity in approximately 9 years. Furthermore, the differential trend element is large, suggesting that this is growth that cannot be explained simply in terms of expanding resources. If our conclusion that growth in other high-expenditure HRGs might be easily moderated by financial restraint is correct, then this group of HRGs for which we cannot so easily rationalise such a mechanism might constitute a major challenge for CCGs.
It is, furthermore, notable that the decline in average LOS has been more limited in this set of HRGs and there is no evidence that the decline has been faster in England than in Scotland. The common trend reduction is 1.6% per annum compared with 3% across all HRGs. The differential trend for England is small but positive, which suggests that the overall decline in LOS for this subgroup is only 1.2% per annum in England. Hence, in terms of both activity growth and an absence of mitigating real resource savings, the HRGs reported in Table 10 would appear to be particularly challenging to CCGs.
Examining the effects across primary care trust clusters
Our results have hitherto been reported in terms of a comparison between Scotland and England, both for all HRGs and for subsets of HRGs. Our regressions allow for regional effects, which are captured as dummy variables defined according for each PCT cluster. Hence, PCT cluster might hitherto be interpreted as a potential confounding factor, which, if omitted, might bias the estimated growth in activity or decline in bed-days.
The empirical methodology that we have adopted allows us to focus greater attention on the potential disparities that arise across PCT clusters and we next turn to reporting on this level of analysis. The regressions reported above assume that a PCT cluster can have a higher or lower level of activity or average number of bed-days. This captures the idea that there are differences across different areas of the country that we do not observe but that nevertheless impact on elective activity. The PCT cluster-level effect is estimated alongside other parameters in the regression, and it would be possible to report this as an indicator of whether or not a particular PCT cluster starts the period of analysis with a higher- or lower-than-average level of activity.
A generalisation of this approach is to allow a PCT cluster to affect not only the level but also the growth rate of activity. We implement this approach empirically by adding variables that are formed by interacting the PCT cluster in which a treatment occurs with a time trend variable. To use this approach we must omit England as a separate time trend, because the complete set of PCT clusters span England. Thus, we replace the single England time-trend interaction with 49 PCT cluster time-trend interactions. Each estimated coefficient represents the differential growth in elective activity in that PCT cluster, over and above the benchmark trend growth which we express as the average growth across PCT clusters. This average is 5.6%, which is different from the 4.4% reported across England, because the average is taken across PCT clusters and some smaller PCT clusters have high growth rates. The same method can be applied to LOS, thus giving a PCT cluster-specific rate of decline for hospital LOSs, and can be applied to subgroups of HRGs, although we do not present subgroup results in this report.
The proliferation of regression coefficient estimates places constraints on reporting. Although we can estimate a growth rate for each of two outcomes (CIPSs and average bed-days) for each of 49 PCT clusters, we present results only in terms of ranking or graphically.
The results at PCT cluster level for CIPSs are reported in Figure 9 as a simple ranking illustrating the mean rate of growth for each PCT cluster. Recall that zero constitutes the average growth of CIPSs across PCT clusters. The lowest ranked PCT cluster, closest to the origin in the figure has a growth rate in CIPSs of approximately 8% below the average, which implies that it experienced decline in elective activity over the period. This one PCT cluster (and thus its associated CCGs) is an outlier and may therefore need further investigation. As we move to the right in the diagram we observe PCT clusters with higher growth rates. Towards the right hand limit of the figure, there are PCT Clusters with growth more than 5% above the average and hence they experience double-digit growth rates. CCGs in these clusters therefore are operating in local environments where growth in CIPSs is doubling in less than 8 years. This growth is per capita and after adjustment for changes in population age structure or deprivation. The figure immediately suggests that some CCGs face a very substantially greater challenge than others in regard to managing growth in elective activity. Referring back to the discussion above (see Growth in continuous inpatient stays) growth is not readily explained in terms of expansion in resources and so it is not clear that it is readily controlled by budgetary constraints.
FIGURE 9.
Deviation from average growth (%) in CIPSs per 1000 population.

For reasons of legibility Figure 9 is presented without labels for the names of PCT clusters. These are set out in the order in which the clusters appear on the horizontal axis, in Box 1.
Cumbria.
Somerset.
North Yorkshire and York.
Cheshire.
South of Tyne and Wear.
Suffolk.
North of Tyne.
Lincolnshire.
West Mercia.
Norfolk and Waveney.
Derbyshire.
County Durham and Darlington.
Calderdale, Kirklees and Wakefield.
Leicestershire.
Gloucestershire, Swindon.
Cambridgeshire and Peterborough.
Merseyside.
Greater Manchester.
Cornwall and Isles of Scilly.
Bedfordshire and Luton.
Humber.
South Yorkshire and Bassetlaw.
Pan Lancashire.
Staffordshire.
Southampton, Hampshire, Isle of Wight and Portsmouth.
North Essex.
Bristol, North Somerset, South Gloucestershire.
Devon, Plymouth, Torbay.
Bath and North East Somerset, Wiltshire.
Kent and Medway.
South Essex.
Arden.
Surrey.
Hertfordshire.
Tees.
Bournemouth and Poole, Dorset.
Sussex.
Airedale, Bradford and Leeds.
Northamptonshire & Milton Keynes.
Black Country.
Nottinghamshire.
North Central London.
North West London.
Birmingham and Solihull.
Oxfordshire and Buckinghamshire.
South West London.
Berkshire West and Berkshire East.
South East London.
North East London and The City.
The disparities in growth depicted in Figure 9 may be a consequence of initial disparities in elective activity, whereby PCT clusters that have very low initial activity may have grown fast in a process of catching up. Our model permits us to examine this hypothesis by recovering the PCT cluster fixed effects and comparing these with growth rates. This is shown in Figure 10, in which a cluster’s growth rate (on the y-axis) is plotted against its initial (corrected for other variables) level of elective activity. If the catching-up hypothesis is correct, we would expect to see a well-determined negative trend in Figure 10, with high growth associated with a low initial level. Figure 10 also includes a regression trend line between the two variables that does exhibit negative slope. However, the relationship is weak with many clusters located well away from the trend and the trend line explaining < 1% of the variation depicted.
FIGURE 10.
Continuous inpatient stays per 1000 population.
We therefore conclude that there are substantial differences between PCT clusters in respect of growth of elective CIPSs and that these differences cannot be accounted for by initial discrepancies in activity.
The results set out in Figures 11 and 12 and in the associated labels (Box 2) show the same variation across PCT clusters with regard to average LOS decline. A low ranking is associated with large negative ‘growth’ rates of average LOS and the highest rankings correspond to the small number of PCT clusters to have experienced increasing average LOS. We again see that variations in the decline in LOSs have little correspondence to the initial circumstances of the PCT cluster.
FIGURE 11.
Deviation from average growth (%) in average LOSs.
FIGURE 12.
Average LOSs.

Black Country.
Suffolk.
Norfolk and Waveney.
Arden.
North West London.
Cornwall and Isles of Scilly.
Bristol, North Somerset, South Gloucestershire.
Southampton, Hampshire, Isle of Wight and Portsmouth.
South Yorkshire and Bassetlaw.
Pan Lancashire.
North Essex.
Kent and Medway.
Bath and North East Somerset, Wiltshire.
Surrey.
South West London.
North Central London.
Oxfordshire and Buckinghamshire.
Cambridgeshire and Peterborough.
Birmingham and Solihull.
Somerset.
Cheshire.
Devon, Plymouth, Torbay.
Airedale, Bradford and Leeds.
Gloucestershire, Swindon.
Berkshire West and Berkshire East.
Greater Manchester.
Derbyshire.
Lincolnshire.
West Mercia.
South of Tyne and Wear.
South Essex.
Merseyside.
Bournemouth and Poole, Dorset.
Bedfordshire and Luton.
Cumbria.
Calderdale, Kirklees and Wakefield.
Nottinghamshire.
North Yorkshire and York.
Hertfordshire.
Leicestershire.
North of Tyne.
North East London and The City.
County Durham and Darlington.
Sussex.
Humber.
Staffordshire.
Northamptonshire and Milton Keynes.
Tees.
South East London.
Overall, these results give a different perspective on the organisation of hospital services in an area. CCGs in PCT clusters in the higher rankings operate in areas where bed capacity is more likely to be a constraint on growing activity.
Checks on the sensitivity of the main results
Results excluding additional controls
Earlier in this section, we report regressions that include controls for changing population age structure and deprivation. An indication that these controls do not exert a great influence on our results is given by examining the simple time-series regressions (reported in Tables 1 and 2) with the main regression results reported in Tables 5 and 6. However, the former regressions omit controls for case mix (HRGs) or regional effects (PCT clusters). Therefore, to establish that our choice of population controls is not strongly influencing our results, we ran regressions in the same form as those reported in Tables 5 and 6 but omitted these additional controls.
The results are reported in Table 11. Although some coefficients are slightly smaller in absolute value than those reported in Results, both the overall patterns and magnitudes are similar. This indicates that our results are not overly sensitive to the precise choice of controls. This is also further evidence for the relative similarity of trends in population between Scotland and England.
| CIPSs per 1000 population | Average LOS | |
|---|---|---|
| Time trend, t (standard error) | 0.001 (0.001) | –0.022*** (0.001) |
| t × England (standard error) | 0.036*** (0.001) | 0.006*** (0.001) |
| System reform | Yes | Yes |
| Sex | No | No |
| Age groups | No | No |
| Deprivation | No | No |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 755,170 | 755,170 |
| R 2 | 0.8207 | 0.7257 |
| F-test HRG and PCT cluster FE | 2635.66 | 1492.95 |
| F-test HRG FE | 2712.34 | 1545.31 |
| F-test PCT cluster FE | 606.29 | 100.71 |
Alternative models of system reform
Phased introduction
We define system reform as a dummy variable that is always zero for Scotland and changes from zero to one in 2006 for England (see Results). A more general specification is to allow the phasing in of system reform in England. To operationalise this we constructed a dummy variable, which is an interaction between the jurisdiction of policy (England) and the circumstances of the treatment being observed. We focus this approach on the adoption of PbR. This policy was phased in for different HRGs and different providers. 12 We can thereby construct a dummy variable, which takes a value of 1 if the HRG, provider and year combination for that CIPS indicates that it would be subject to PbR, and takes the value of zero otherwise. All CIPSs in Scotland are assigned the value zero.
Relative to the simpler formulation used in Results, this approach identifies the effect of policy through both its jurisdiction and its timing. If the simpler approach omits timing effects applying to different treatments that are important in determining the impact of policy, we can expect our results to be biased. Hence to check the robustness of our findings we run comparable regressions to those reported in Tables 5 and 6 using the more sophisticated system reform approach. The results are set out in Table 12.
| CIPSs per 1000 population | Average LOS | |
|---|---|---|
| Time trend, t (standard error) | –0.002 (0.002) | –0.025*** (0.002) |
| t × England (standard error) | 0.046*** (0.002) | –0.010*** (0.001) |
| Phased system reform | Yes | Yes |
| Sex | Yes | Yes |
| Age groups | Yes | Yes |
| Deprivation | Yes | Yes |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 755,170 | 755,170 |
| R 2 | 0.8215 | 0.7263 |
| F-test HRG and PCT cluster FE | 2635.49 | 1490.97 |
| F-test HRG FE | 2725.29 | 1544.99 |
| F-test PCT cluster FE | 349.03 | 68.30 |
The coefficients in Table 12 are very similar to those in Table 5 and 6 and thus we conclude that our findings are not sensitive to omitting the difference in the introduction of policy for different HRGs or providers.
Earlier introduction of system reform
As a further robustness check, we changed the definition of the system reform variable, keeping it as zero for all Scottish observations and making the change from zero to one in England in 2005 instead of 2006.
As before, we report the relevant coefficients, the estimate of the growth trend in activity in Scotland and the estimate of the extent to which growth in England is different from that in Scotland, for CIPSs and average bed-days.
The regressions reported in Table 13 correspond to those in column 2 in Tables 5 and 6. For both CIPSs and average bed-days, the results are again similar.
| CIPSs per 1000 population | Average LOS | |
|---|---|---|
| Time trend, t (standard error) | 0.003 (0.002) | –0.028*** (0.002) |
| t × England (standard error) | 0.040*** (0.002) | 0.007*** (0.001) |
| Earlier system reform | Yes | Yes |
| Sex | Yes | Yes |
| Age groups | Yes | Yes |
| Deprivation | Yes | Yes |
| PCT cluster FE | Yes | Yes |
| HRG4 FE | Yes | Yes |
| n | 755,170 | 755,170 |
| R 2 | 0.8214 | 0.7263 |
| F-test HRG and PCT cluster FE | 2634.01 | 1494.02 |
| F-test HRG FE | 2723.76 | 1548.31 |
| F-test PCT cluster FE | 348.63 | 68.40 |
Information for commissioning
In this section, we indicate a method by which the model we have developed might be used to provide commissioners with specific information regarding the growth of elective care in their area, defined in terms of the PCT cluster to which they belong. This information is intended to assist the process of planning services and alerting commissioners to the challenges they face with regard to managing elective activity.
Our model contains a number of dimensions by which growth may be decomposed. It is neither possible nor useful to consider every possible permutation of PCT cluster, time frame, HRG grouping and elective activity. However, the model can be deployed in responsive mode and provide relevant estimates for any given desired configuration in these dimensions.
One way of conceptualising this process is through the generation of commissioner-specific reports. We indicate here two possibilities, each of which is illustrated with a report template.
A generic primary care trust cluster report
It is straightforward to supply some summary information based on our model at PCT cluster level. The format of this information could take the form of a PCT cluster generic report, adopting the following template (Table 14). In the current formulation of the model there would be 49 such reports.
| PCT cluster in which this CCG resides | Cluster name |
| How does elective activity (the number of CIPSs per 1000 population) in this cluster compare with the national picture? | |
| At what rate has elective activity grown in this cluster over the past 15 years? | |
| How does this growth compare with the national average? | |
| How does this cluster compare with the national average in terms of LOSs in hospital? | |
| How quickly have LOSs declined over the past 15 years? | |
| How does this decline compare with the national average? |
A bespoke Clinical Commissioning Group report
We can envisage that some commissioners may be interested in more detailed and tailored information, perhaps relating specifically to experience over a specific time period, or relating to specific HRGs, or specific population age groups. A report addressing these specific requirements would necessarily be more bespoke, but the broad structure that it might follow is set out in the following template (Table 15).
| PCT cluster in which this CCG resides | Cluster name |
| For which period has this report been prepared? | |
| For which HRG chapters is the information requested? | |
| For which age groups is the information required? | |
| A detailed report would follow here using the same headings as in the generic report but providing details for each of the subgroups identified above |
Chapter 3 Declining variation in English hospital bed-use and Payment by Results
Introduction
It has long been known that changes to the way hospital payments are made can influence the levels of activity and quality of treatment. Coulam and Gaumer40 and Hodgkin and McGuire41 consider the consequences of the prospective payment system introduced in US medical care during the 1980s and find that it led to generally shorter lengths of stay and fewer admissions, whereas McClellan42 explains how quality of health care can be affected by payment systems. There is also extensive research examining how prospective payment schemes affect LOS by, among others, Farrar et al. ,13 Theurl and Winner43 and Newhouse and Byrne. 44 In addition, Appleby et al. 16 consider the effect of payment schemes on quality in English hospitals, and it is one factor analysed in Chapter 2 of this research as a possible driver for growth of elective care.
This report focuses on the effects of payment reform, and the introduction of tariffs in particular, on the variation of care, specifically in terms of hospital admission rates and LOSs across PCTs. We first examine whether or not there were reductions in the variation of NHS hospital bed-use, rather than its level, during the period of system reform (2003–9). Second, we explore the hypothesis that the introduction of a prospective payment tariff in England (PbR) may have reduced certain variation in patient treatment and resource use across English hospitals from 2002/3 to 2008/9, thereby reducing the ‘post-code lottery’ in the provision of treatments.
Many policies are assumed in statistical analysis to bear evenly on the affected hospitals, patients and clinicians, increasing volume or, perhaps, quality uniformly across the relevant population. However, some policies may increase or reduce the variation in the affected variables. This has been of particular interest for patient selection and quality of patient care. For example, Shen45 tests the hypothesis that performance-based contracting may encourage providers to treat patients with less severe symptoms at the expense of more severely affected patients. Dranove et al. 46 showed that prospective payment might encourage ‘cream-skimming’ of more profitable patients. These unintended effects of policy and more familiar unidentified ‘post-code lottery’ effects are examples of unwarranted variation.
As Skinner47 explains, some variation in health-care use can justifiably be explained as a consequence of different ‘prices, illness or income’. However, the residual variation not described by these factors is undesirable and suggests that some providers may be operating inefficiently. As such, policies that reduce the inequality of patient treatments and outcomes may increase overall efficiency and are recognised to be of potentially considerable social value. For example, a policy of regulating minimum quality thresholds is likely to have impacted most on the quality of lesser performing hospitals and their patient outcomes, and more so than on those that were performing well before policy innovation. In this case, the increase in patient value is a direct consequence of policy to reduce variance.
During the 6 years from 2002/3 to 2008/9, major changes to the NHS were introduced. In addition to considerable technological progress, changing the patterns of health-care demand across diseases and patient groups was actively encouraged. Reform, such as the introduction of a prospective payment model and waiting time targets, introduced a common set of economic incentives for managers that rewarded improved performance in a way that was likely to increase quality of care levels, as shown by Miraldo et al. 48 and Propper et al. 49
Prior to the tariff, health-care providers in England were reimbursed on a block grant basis, which gave physicians and managers considerable individual influence over the allocation of hospital resources, without sanction for low rates of treatment. The introduction of the tariff created different incentives for medical professionals, which may have altered behaviour towards that required to sustain hospital revenues and thereby jobs. The tariff may also have made internal political hospital problems of reallocating resources more tractable. Tariff policies are likely to have placed greater financial pressure on hospitals that offered long LOSs and low admission rates, and to have contributed to a narrowing of variation in activity levels and LOSs across England as scope for locally developed policies reduced.
This report examines whether or not variation has decreased by studying the system-wide pattern of hospital bed use, by investigating whether or not the frequency and lengths of admissions became more similar across PCTs, and, in particular, investigating whether or not the introduction of a tariff-based payment system may have shaped these changes.
In order to separate the consequences of tariff reform from other developments, this work exploits the fact that reform was not introduced uniformly across specialties. Whereas a reduction in the variation of LOS between 2002/3 and 2008/9 is found in emergency and, to a lesser extent, elective care, this pattern was not reproduced in mental health, a specialty that has yet to see a full introduction of the tariff. The next section studies variation across PCTs, with particular emphasis on LOS, which is likely to have been most affected by the introduction of the tariff. The tariff and variation in hospital bed-use applies similar methods to mental health data. An alternative explanation: the changing geography of resource allocation and bed-use considers the impact of funding patterns on variation, in particular whether the changing model of resource allocation to local areas, to capture need, provides an alternative explanation to system reform for the reductions in heterogeneity between 2002/3 and 2008/9. The relationship between efficiency gain and initial mean length of stay explores how LOSs have converged across the distribution, showing that areas with higher LOSs in 2002/3 have experienced greater decreases in LOS.
The changes in variation of hospital bed-use across primary care trusts, 2002/3–2008/9
This section discusses the evidence concerning particular bed use across English PCTs and how far patients’ usage became more similar.
The data come from HES, a database of ‘all admissions, appointments and attendances at NHS hospitals in England’. 50 Two financial years (2002/3 and 2008/9) are considered to see how resource use and variation across space altered during this time. These years are selected to capture the time period across which the tariff was introduced in the NHS. The measures considered are total bed-days, total admissions (finished consultant episodes) and average LOS, which is calculated by dividing the total bed-days by the total number of admissions.
Episodes are aggregated by the PCT of patient residence, so that there are 152 observations for each measure for each year. This is not the same as investigating treatment at hospitals. If hospitals were the unit of investigation, then this research would be a direct study of policy on hospital activity, but, by considering these alternative measures, it becomes more about how geographic groups of patients are affected by policy and its impact on hospital incentives.
The distributions are presented graphically as Kernel density plots in Figure 13.
FIGURE 13.
The distributions of emergency and elective admissions and LOS. (a) Emergency bed-days per 1000 population; (b) emergency admissions per 1000 population; (c) emergency LOS; (d) elective bed-days per 1000 population; (e) elective admissions per 1000 population; and (f) elective LOS.
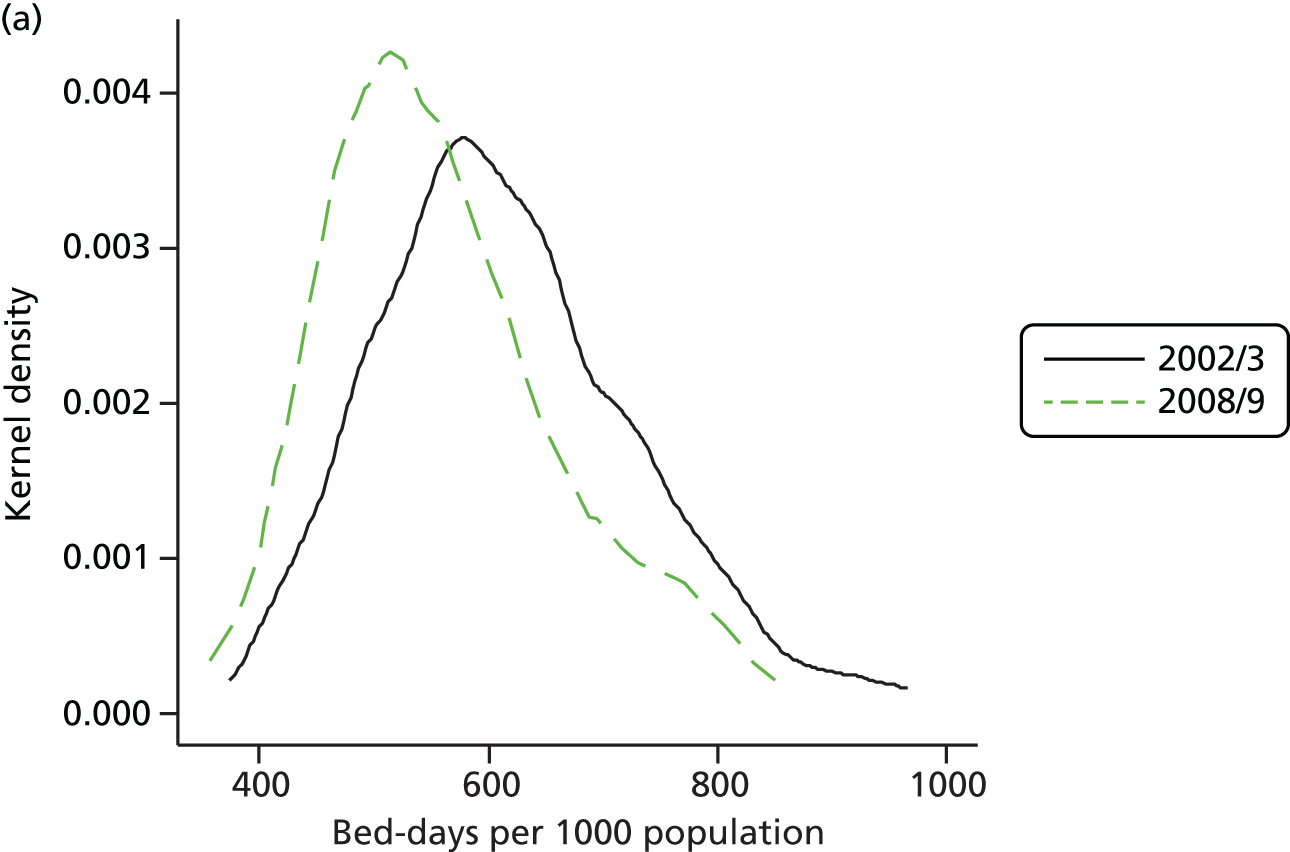
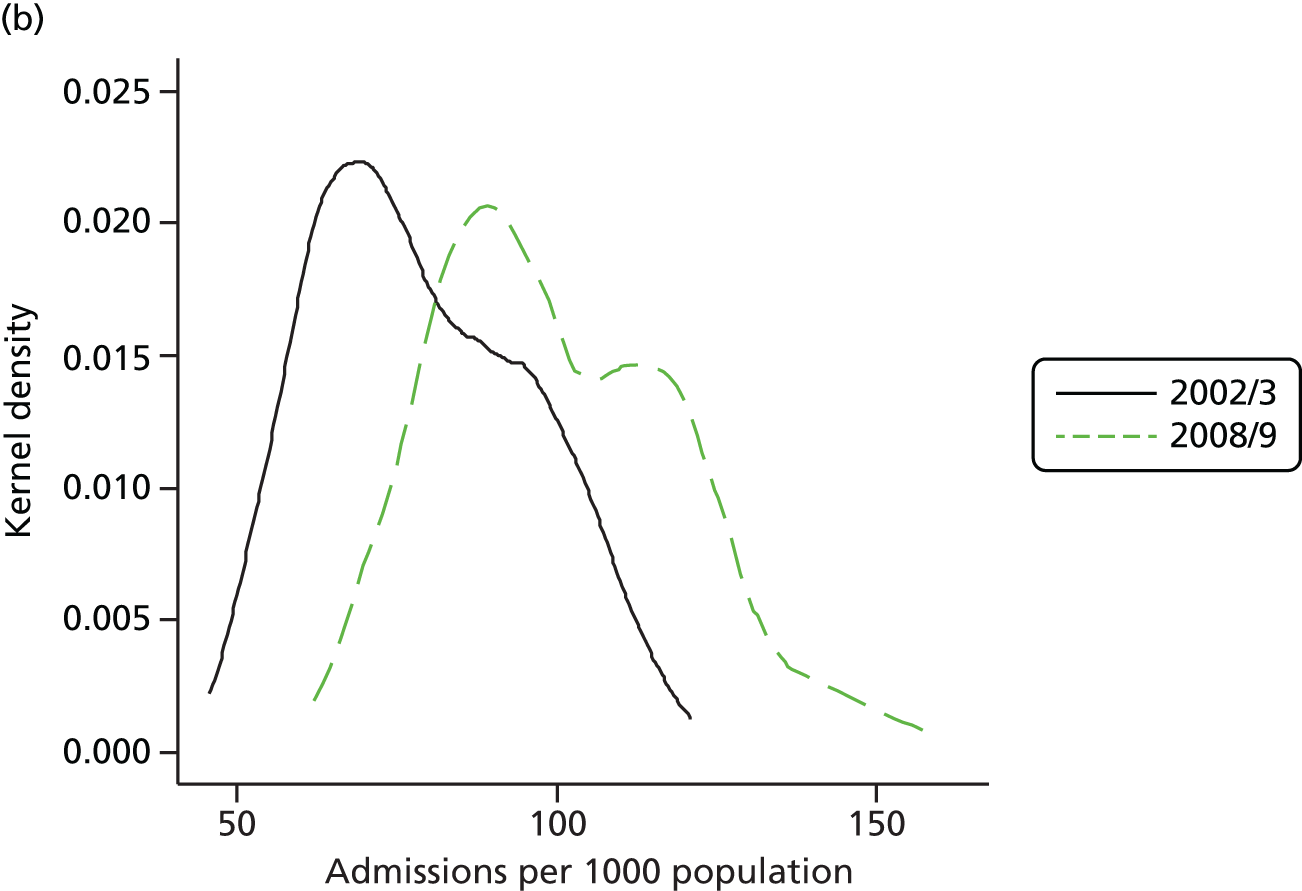
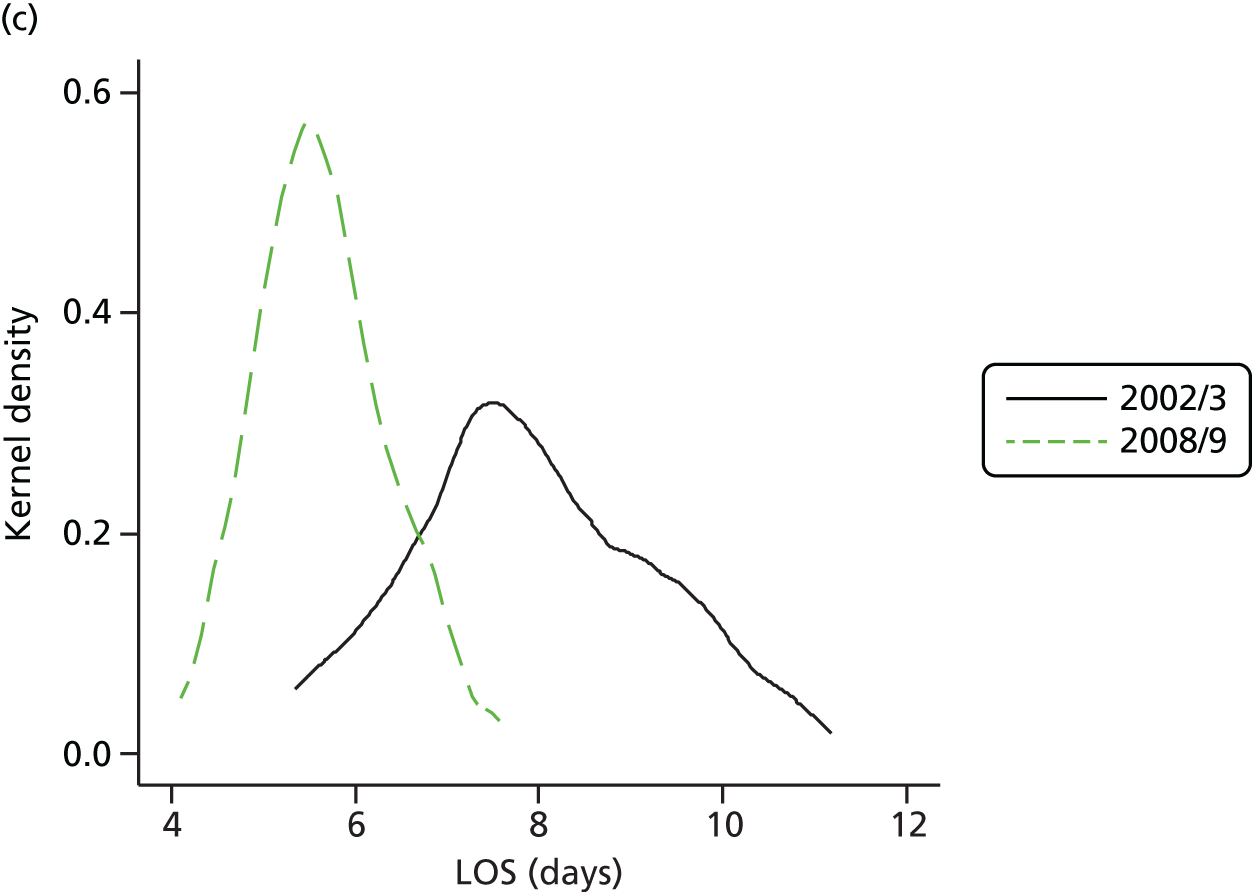
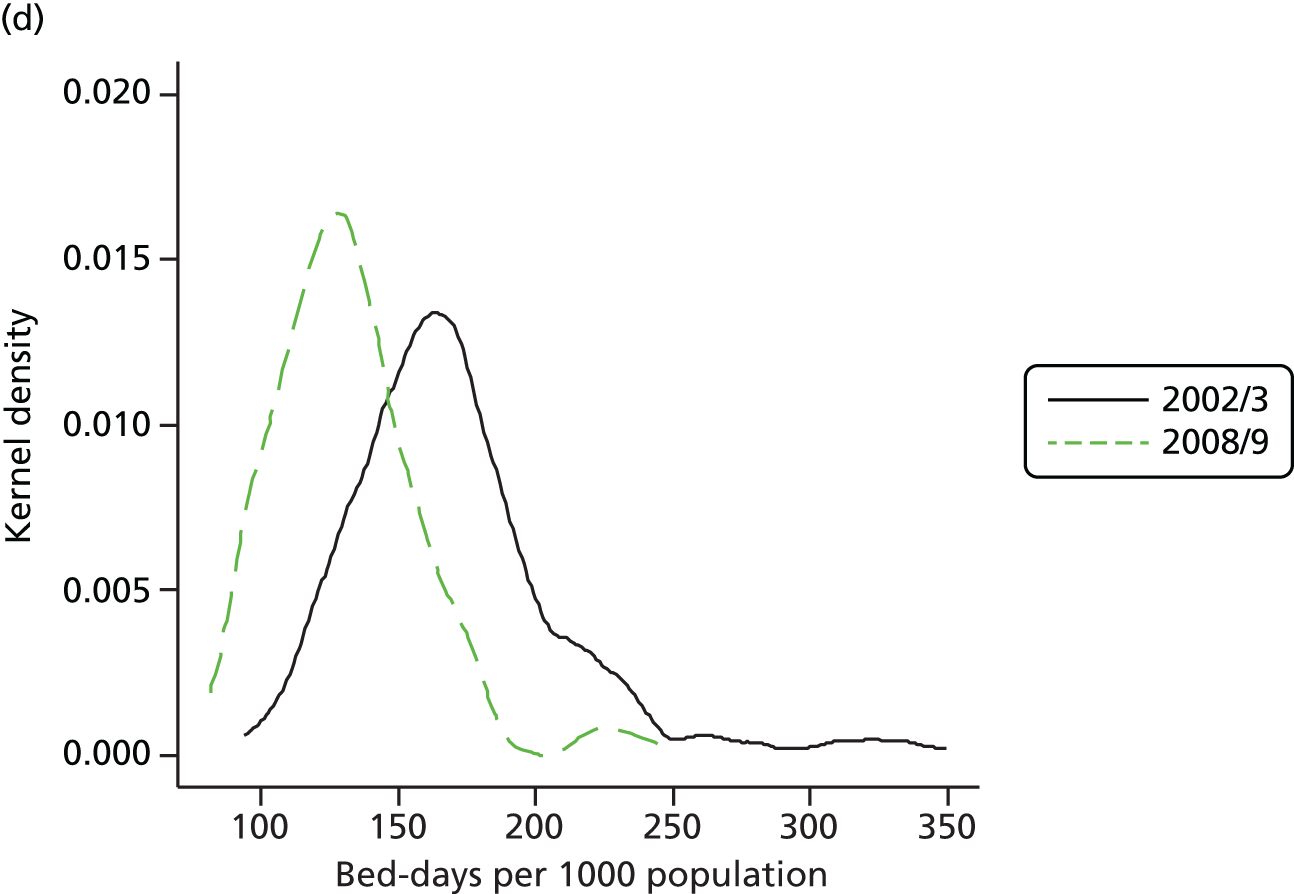
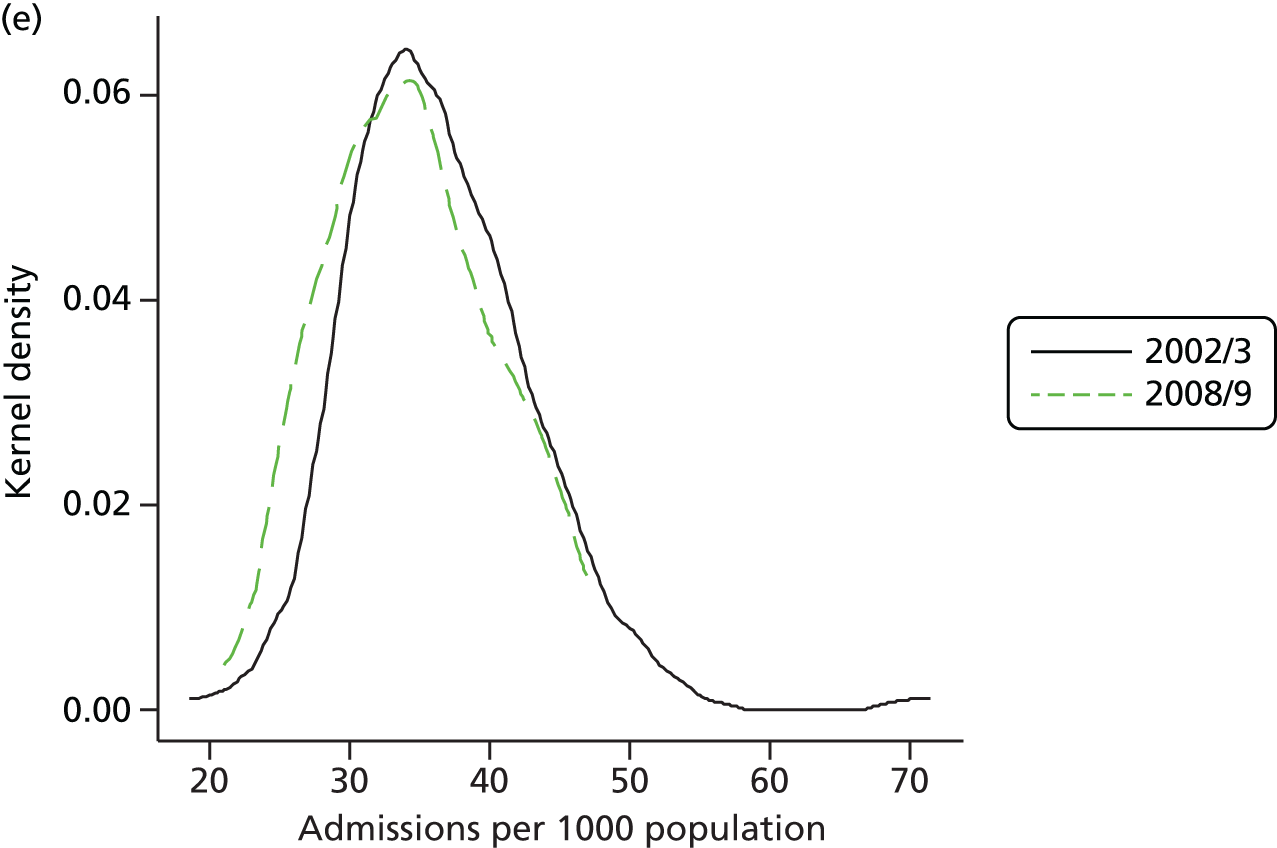

The distribution of emergency bed-days has shifted slightly to the left between these 2 years and become more concentrated. This shows that average bed-days per PCT has fallen slightly, with a significant reduction in the variance across PCTs.
The distribution of admissions has seen different changes to the bed-days distribution, with the 2008/9 plot flatter than the 2002/3 plot and shifted to the right. This indicates an increase in the average rate of admissions and a higher variation in the admission rate across English PCTs.
Owing to the fall in emergency bed-days and an increase in the number of admissions, the average LOS has decreased significantly. Variation has also decreased markedly.
Elective data in Figure 13d–f show that bed-days have declined and that there is less variation. There has been a marginal decrease in total admissions and the variance has also fallen, but these changes are small and the distribution has a similar shape in both years. As a consequence of the changes in bed-days and admissions, the average LOS and its variance decreased between 2002/3 and 2008/9. Tables 16–18 show some descriptive statistics.
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency | Elective | |||||
| Total bed-days | Total admissions | Average LOS | Total bed-days | Total admissions | Average LOS | |
| 2002/3 | 30,071,461 | 3,837,953 | 7.84 | 8,583,478 | 1,789,705 | 4.80 |
| 2008/9 | 28,316,363 | 5,014,784 | 5.65 | 6,852,104 | 1,759,853 | 3.89 |
| Change (%) | –5.84 | 30.66 | –27.93 | –20.17 | –1.67 | –18.96 |
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency (152 PCTs) | Elective (150 PCTs) | |||||
| Bed-days | Admissions | Average LOS | Bed-days | Admissions | Average LOS | |
| 2002/3 | 616.85 | 79.03 | 7.95 | 170.80 | 36.45 | 4.71 |
| 2008/9 | 559.90 | 100.33 | 5.64 | 131.66 | 34.39 | 3.86 |
| Change (%) | –9.23*** | 26.96*** | –29.14*** | –22.92*** | –5.66*** | –18.01*** |
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency (152 PCTs) | Elective (150 PCTs) | |||||
| Bed-days | Admissions | Average LOS | Bed-days | Admissions | Average LOS | |
| 2002/3 | 113.36 | 16.60 | 1.30 | 40.46 | 6.67 | 0.81 |
| 2008/9 | 101.30 | 19.30 | 0.70 | 27.65 | 5.91 | 0.69 |
| Change (%) | –10.64* | 16.28* | –45.85*** | –31.66** | –11.40* | –14.69* |
In 2002/3, 30.1 million emergency bed-days were used in England to support approximately 3.8 million admissions (excluding day cases), indicating an average LOS of 7.8 days. Elective treatment was on a smaller scale, with 8.5 million bed-days and 1.8 million admissions at an average of 4.8 bed-days. Over the following 6 years, emergency bed-days fell by 6%, even though admissions increased by 30%. Consequently, the mean length of emergency stay fell by 28% to 5.6 days. There were 152 PCTs in England in 2008/9 but early analysis suggested that North Staffordshire and Stoke on Trent were outliers and were omitted from work carried out on the elective care data set. Elective admissions declined by 1.7%. There was a 20% reduction in bed-days and a similar decrease in average LOS, from 4.8 days to 3.9 days. This was at a time when a significant amount of hospital beds closed, with the number of available beds falling from 183,826 in 2002/3 to 160,254 in 2008/9.
Table 18 shows standard deviations (SDs) of rates per 1000 population for the PCTs in England. The SD for emergency bed-days fell by 4.7%. This was due to a large reduction in average LOS variation, which fell by 45%, whereas admission variation increased. Variation in elective admissions and average LOS remained fairly constant, but total bed-day variation decreased by 25%.
It is worth noting the increasing proportion of patients who are treated as day cases rather than overnight admissions. Methods such as key-hole surgery allow treatment to be less invasive and patients are regularly sent home after procedures that might have previously required significant recovery time in a hospital bed. The data used in this research include all patients who were expected to have an overnight stay and do not include day cases. By omitting day cases – a growing proportion of hospital treatment for which there is, by definition, minimal variation in treatment length – the results presented here are likely to underestimate the reduction in variation that has occurred.
These results suggest that variation in hospital resource use has declined, mainly as a consequence of shorter and less varied LOSs. Admissions have either remained fairly constant (in elective care) or increased (in emergency care), but patients are being discharged much more quickly on average and this appears to be the main reason for decreased variation. This fits with the patterns predicted above (see Introduction) in that clinicians appear to have become more similar in their behaviour.
The next section attempts to determine whether or not this decline in variation was due to the change from a block grant funding system to a prospective payment system.
The tariff and variation in hospital bed-use
Beginning in 2003/4 with 15 HRGs and a select group of providers, the block grant system of funding was replaced by a prospective payment tariff model that reimburses hospitals for treatments and procedures on a fixed unit-price basis. 51 This process continued until 2008/9, by which time all acute trusts were paid according to a tariff measure for 546 HRGs in elective, non-elective accident and emergency (A&E) and outpatient care, with mental health one of the few specialties still paid for with block grants. In this new framework there are strong incentives for hospitals to operate more efficiently to ensure that costs do not exceed tariff revenues. One way of achieving this is to reduce the LOS for patients in order both to reduce costs and to release capacity that might support additional admissions. Hospitals providing activity at costs above tariff have been increasingly pressed to reduce costs in order to avoid deficits. Given that bed use is a major source of cost, more homogeneous bed use appears to be a probable consequence of the tariff. In addition, it is predicted that admissions would increase in PCTs that had long lengths of stay before the introduction of the tariff, causing LOS variation to decrease. The impact on bed-days variation is less clear-cut, as this is likely to depend on demographic factors. The process of introducing the tariff had started sooner in elective than in emergency care, so it is expected that this had already had some impact on variation and that the consequences would be felt more strongly in emergency care.
Although there has been significant reform in most parts of the NHS, one of the least affected areas has been mental health, which has retained a block grant system instead of adopting the prospective payment policy. If mental health experienced similar patterns of change to the hospital system as a whole, it would cast doubt on the theory that system reform, at least the introduction of the tariff system, is responsible for reducing variation.
Distributions of emergency and elective resource use for mental health patients are presented in Figure 14.
FIGURE 14.
The distributions of emergency and elective admissions and LOS in mental health. (a) Emergency bed-days per 1000 population; (b) emergency admissions per 1000 population; (c) emergency LOS; (d) elective bed-days per 1000 population; (e) elective admissions per 1000 population; and (f) elective LOS.
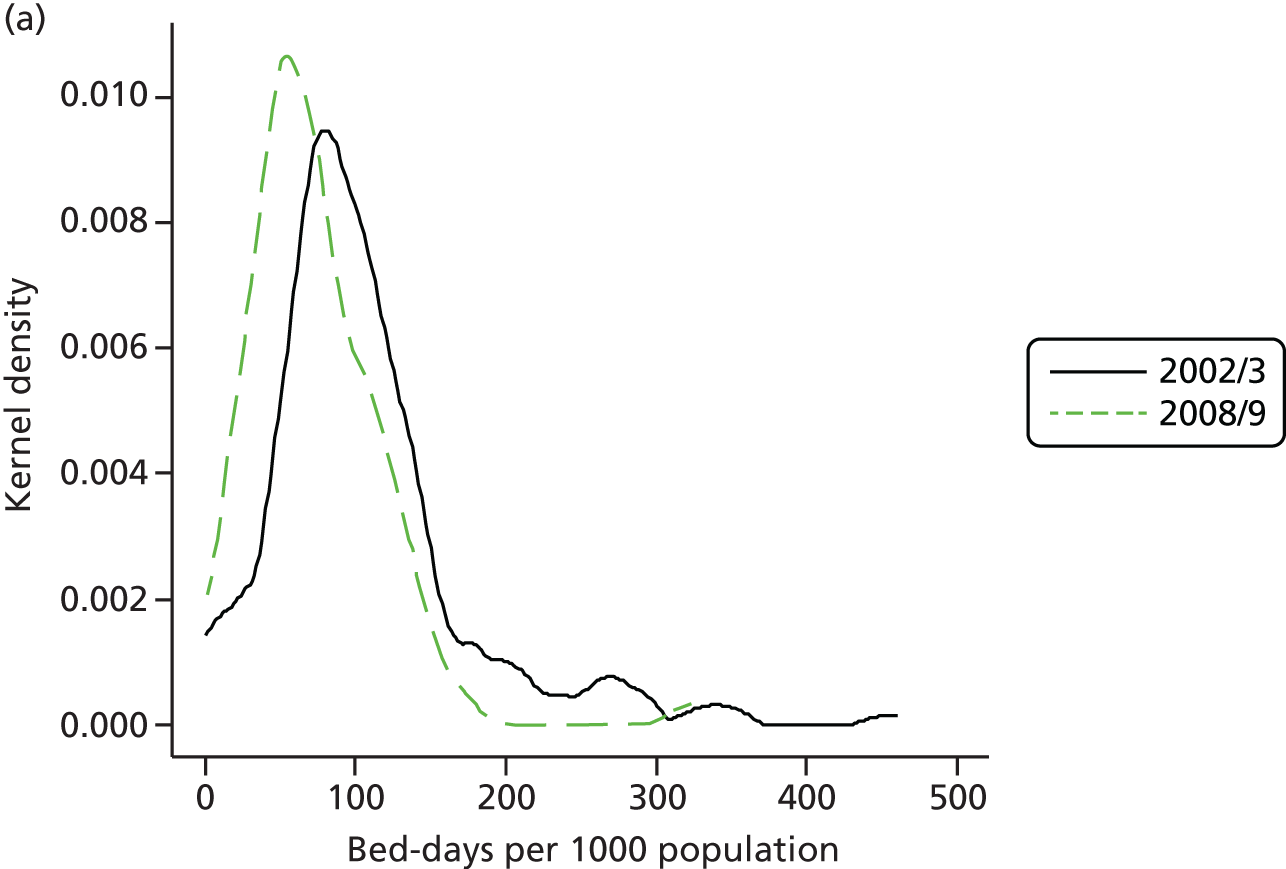
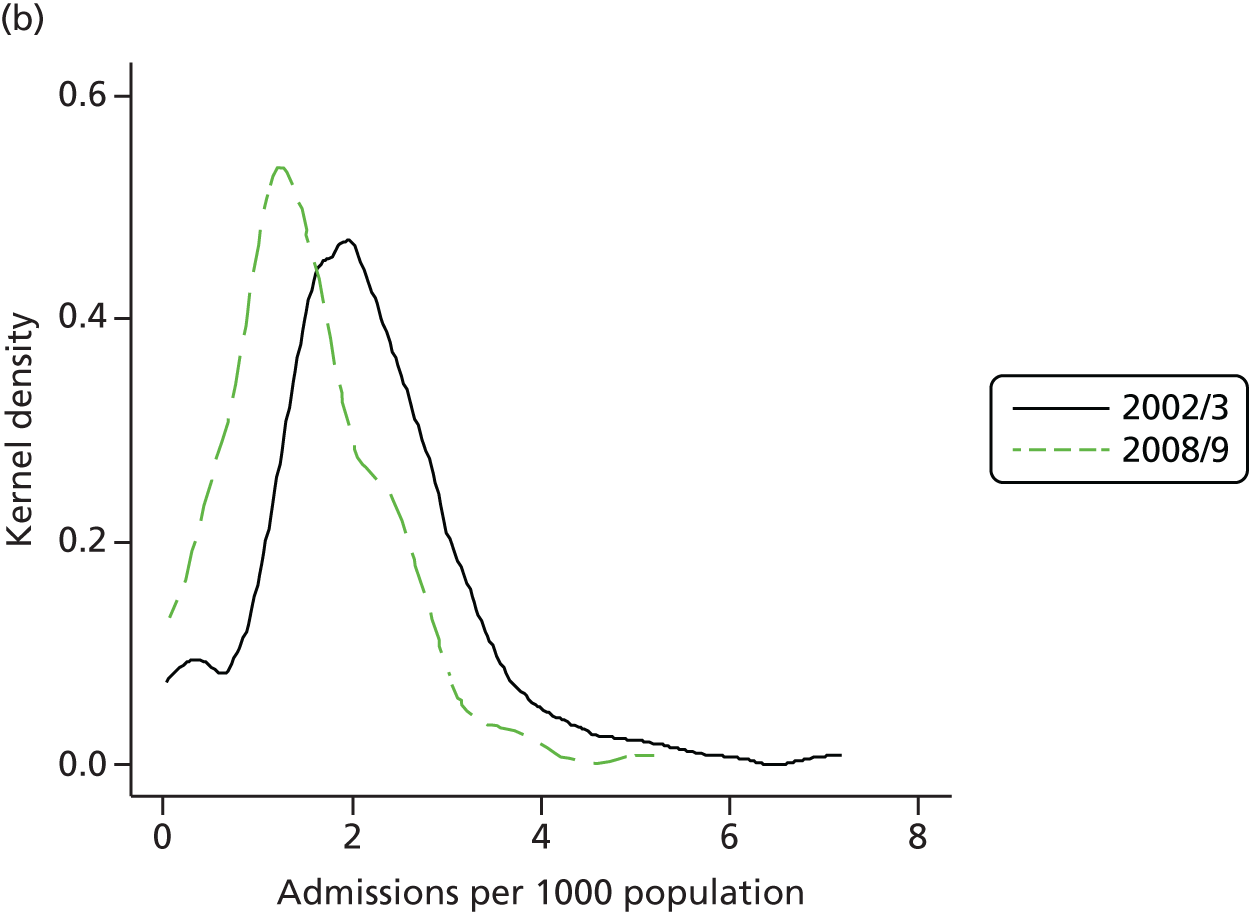
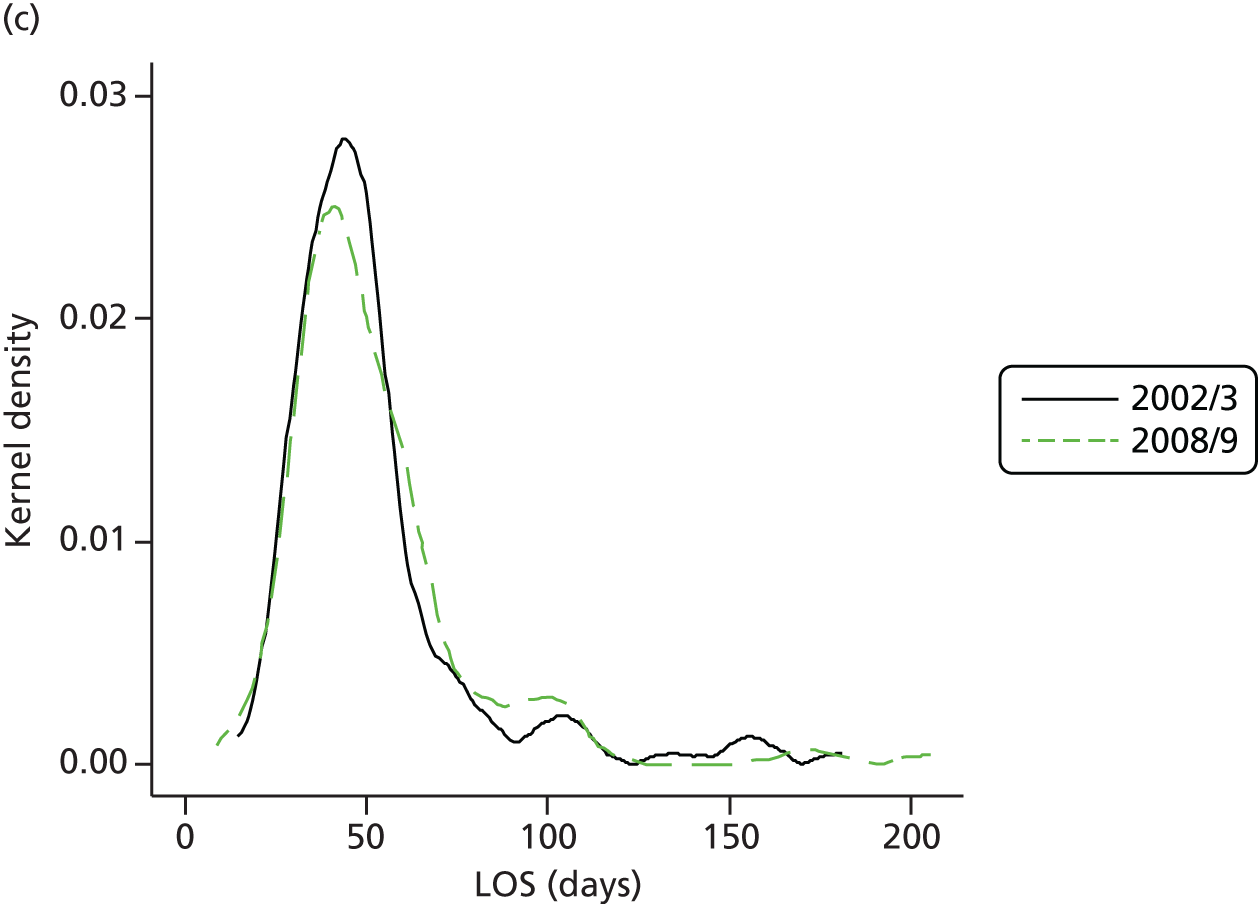
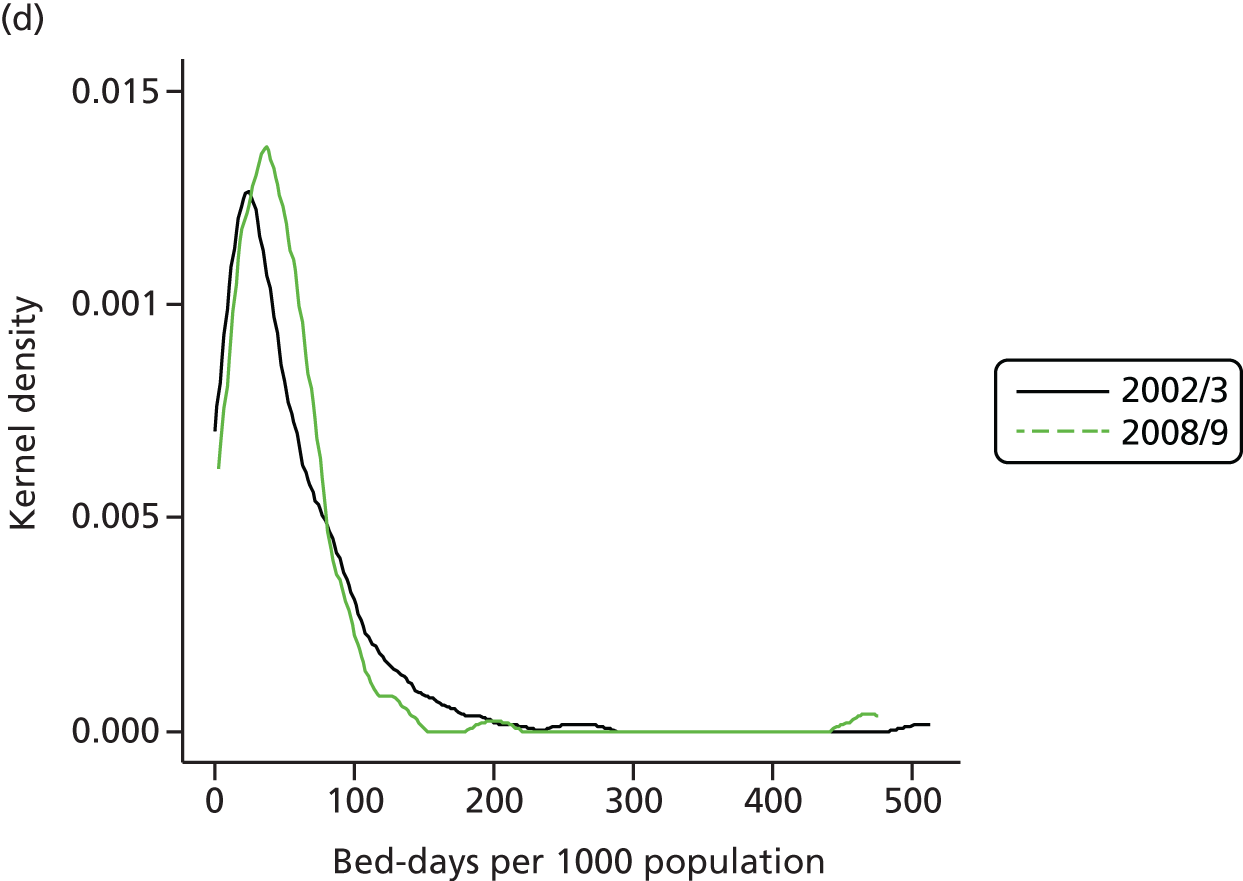
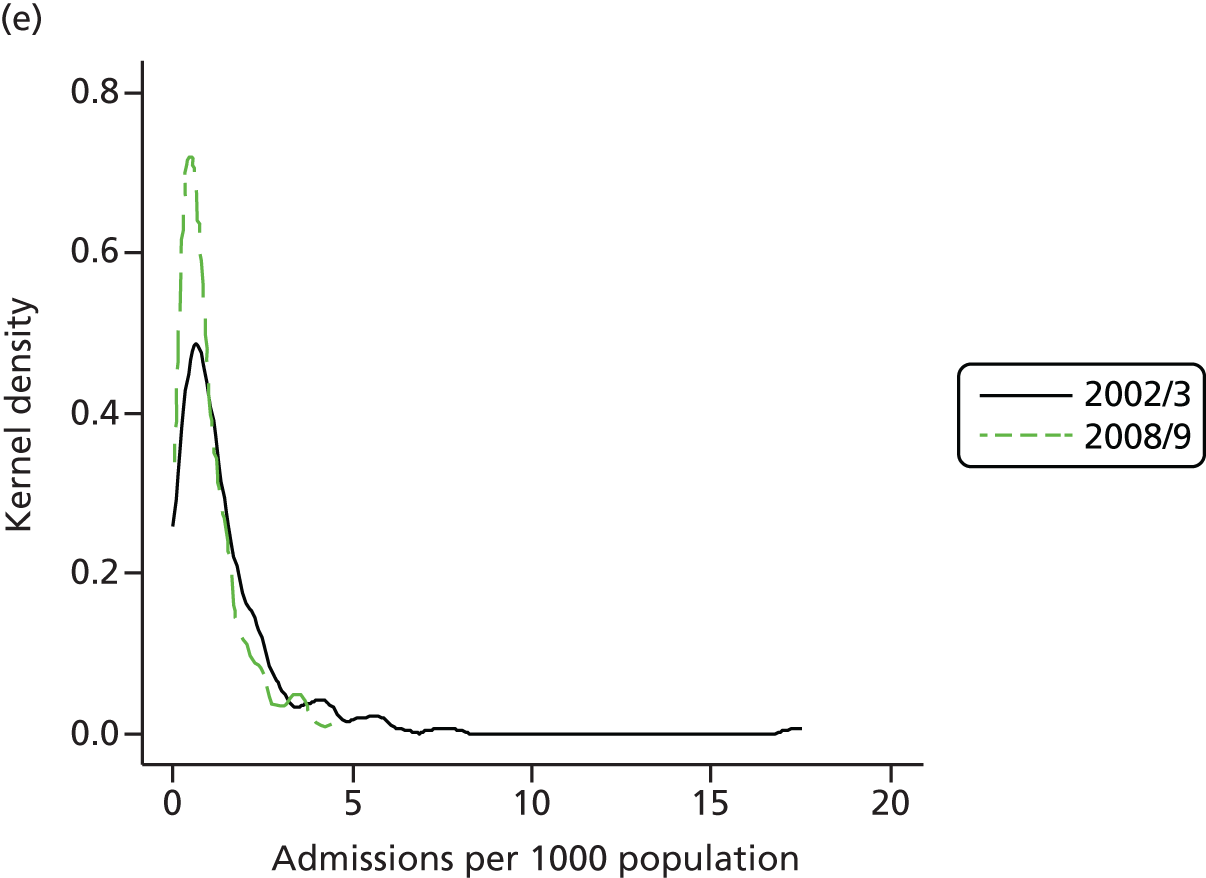

A comparison of Figures 13 and 14, which uses all admission data, shows that the mental health sector has experienced different changes to hospitals in general. The biggest changes in all-admission data were a significant decreases in LOS variation for both elective and emergency admissions, but this did not occur in mental health. Looking solely at mental health, the emergency LOS distributions are similar in the 2 years and elective LOSs have become more dispersed across English PCTs. This suggests that incentives and clinician behaviour were affected in different ways by the policies adopted in different specialties of health care and highlights the role of the tariff introduction.
Tables 19–22 show descriptive statistics for mental health, where a mental health admission was defined as one in which the HES ‘tretspef’ variable was one of the following: 700 – Learning Disability; 710 – Adult Mental Illness; 711 – Child and Adolescent Psychiatry; 712 – Forensic Psychiatry; 713 – Psychotherapy; 715 – Old age Psychiatry; 720 – Eating Disorders; 721 – Addiction Services; 722 – Liaison Psychiatry; 723 – Psychiatric Intensive Care; or 724 – Perinatal Psychiatry.
| Year | Admissions | |||
|---|---|---|---|---|
| Emergency | Elective | |||
| Total bed-days | Total admissions | Total bed-days | Total admissions | |
| 2002/3 (%) | 17.6 | 2.7 | 33.5 | 4.1 |
| 2008/9 (%) | 12.0 | 1.4 | 35.0 | 2.8 |
| Change (%) | –32.03 | –49.41 | 4.43 | –32.32 |
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency | Elective | |||||
| Total bed-days | Total FCEs | Average LOS | Total bed-days | Total FCEs | Average LOS | |
| 2002/3 | 5,293,291 | 103,977 | 50.91 | 2,873,516 | 73,115 | 39.30 |
| 2008/9 | 3,388,093 | 68,737 | 49.29 | 2,395,595 | 48,659 | 49.23 |
| Change (%) | –35.99 | –33.89 | –3.18 | –16.63 | –33.45 | 25.27 |
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency (152 PCTs) | Elective (151 PCTs) | |||||
| Bed-days | FCEs | Average LOS | Bed-days | FCEs | Average LOS | |
| 2002/3 | 105.44 | 2.13 | 51.41 | 52.40 | 1.46 | 54.14 |
| 2008/9 | 72.95 | 1.50 | 52.62 | 51.73 | 0.97 | 77.47 |
| Change (%) | –30.81*** | –29.58*** | 2.35 | –1.28 | –33.56** | 43.09*** |
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency (152 PCTs) | Elective (151 PCTs) | |||||
| Bed-days | FCEs | Average LOS | Bed-days | FCEs | Average LOS | |
| 2002/3 | 68.32 | 1.09 | 26.19 | 57.63 | 1.86 | 53.11 |
| 2008/9 | 47.19 | 0.86 | 27.10 | 57.22 | 0.84 | 78.86 |
| Change (%) | –30.93*** | –21.10*** | 3.47 | –0.69 | –54.84*** | 48.48*** |
Table 20 shows overall levels of resource use in the mental health sector. Between 2002/3 and 2008/9, emergency admissions fell from 103,977 to 68,737 per annum, and bed-days decreased by 36% to 3.4 million. The average LOS went down from 50.91 to 49.29, but this is not a statistically significant change. These values show that hospital stays have remained similar in terms of lengths for patients who are admitted but that fewer people receive care in this setting.
Figure 14d–f suggests that West Kent PCT is an outlier. This PCT is therefore dropped from the calculations of sample means and SDs for the elective data series. For the remaining PCTs, bed-days and admissions in mental health elective care have experienced declines, but with admissions falling much more than bed-days (33.5% vs. 1.3%, respectively), average LOSs have increased significantly. These changes do not reflect those discovered in the complete data set. Using aggregate values or average rates of sample PCT means (see Table 21) makes no difference to the conclusion that mental health has not changed in the same way as overall health care.
Table 22 presents SDs to show how variation in mental health admissions and bed-days across England has changed. In emergency mental health, bed-day and admissions variation decreased by 31% and 21%, respectively, and there has been no significant change in average LOS variation, with a small increase of only 3.5%. In mental health elective care, bed-day variation has fallen by an insignificant 0.7%, whereas the other two series have seen much larger changes in variation; admission variation fell by nearly 55% to 0.84, whereas average LOSs have become much more variable across PCTs, with the SD increasing by 48% to nearly 79 days.
New central policies are perhaps the most likely cause of changing patterns of variation but there are other potential contributing factors. Distinguishing between the effects of all relevant factors would be a complex task and is beyond the scope of this report. However, the evidence here suggests that policy had a major role.
An alternative explanation: the changing geography of resource allocation and bed-use
The analysis thus far has uncovered significant changes in the geographic distributions of resource use in both elective and emergency care settings, with a tendency for variation to decrease. One explanation for these changes, beyond policy or other endogenous factors, is a changing pattern of need and the associated flows of finance: PCTs could have become more similar if funding levels incentivised them to do so. For example, a narrowing in the distribution of funding owing to a compression in centrally assessed need could reduce the variance of behaviour, as hospital managers will be working with increasingly similar budgets.
To see if this is a likely explanation, this section looks at the relationship between the data series and a variable that captures different levels of need across PCTs, namely a ‘need index’, which is taken from the Department of Health ‘revenue resource limits’ publications. 51 This is a ratio of the actual population to a need-corrected population base and is used in the resource allocation framework.
There has been significant convergence in the need distribution. The average level has declined slightly, but a more noticeable difference between the two series is that the range has decreased and the variance has fallen.
Thus far, the investigation has used raw data on emergency and elective admissions. To accommodate changes in the distribution of need, it is necessary to needs-adjust these raw data. It is then possible to examine whether or not the distribution of data adjusted for need declines over the time period on a scale as great as the decrease noted in the distribution of unadjusted data.
Need has a large role in explaining emergency care, as the regressions in Tables 23 and 24 show. The coefficients all increase in absolute terms over the 6 years, with a statistically significant increase in the effect of need on admission rates and bed-days. This has been tested by running a stacked regression of both years data, with the t-statistic derived from the coefficient on a variable, which is zero if a 2002/3 observation and the need value if a 2008/9 observation.
| Variables | 2002/3 | 2008/9 | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Admission rates | Bed-day rates | LOS | Admission rates | Bed-day rates | LOS | |
| Need (2004/5) | 64.68*** (6.60) | 357.58*** (49.77) | –1.86*** (0.64) | – | – | – |
| Need (2008/9) | – | – | – | 137.15*** (10.61) | 532.42*** (68.29) | –2.31*** (0.53) |
| Intercept | 12.07* (6.91) | 246.71*** (52.13) | 9.88*** (0.67) | –39.95*** (10.90) | 15.32 (70.19) | 7.99*** (0.54) |
| F-statistic | 96.18 | 51.61 | 8.34 | 167.19 | 60.79 | 18.99 |
| R 2 | 0.39 | 0.25 | 0.05 | 0.53 | 0.288 | 0.11 |
| Observations | 152 | 152 | 152 | 152 | 152 | 152 |
| t-test: has coefficient changed over time? | – | – | – | 5.83*** | 2.01** | –0.47 |
| Variables | 2002/3 | 2008/9 | ||||
|---|---|---|---|---|---|---|
| 7 | 8 | 9 | 10 | 11 | 12 | |
| Admission rates | Bed-day rates | LOS | Admission rates | Bed-day rates | LOS | |
| Need (2004/5) | 11.12*** (3.29) | 9.87 (20.66) | –1.11*** (0.40) | – | – | – |
| Need (2008/9) | – | – | – | 11.48** (4.66) | 5.82 (22.21) | –1.12** (0.54) |
| Intercept | 24.94*** (3.44) | 160.60*** (21.63) | 5.85*** (0.42) | 22.66*** (4.78) | 125.72*** (22.81) | 5.01*** (0.56) |
| F-statistic | 11.46 | 0.23 | 7.58 | 6.08 | 0.07 | 4.26 |
| R 2 | 0.07 | 0.00 | 0.05 | 0.01 | 0.00 | 0.04 |
| Observations | 150 | 150 | 150 | 150 | 150 | 150 |
| t-test: has coefficient changed over time? | – | – | – | 0.06 | –0.12 | –0.03 |
The relationship between elective care and need is not well defined, with R-squared values never exceeding 0.07. The coefficients on need in equations explaining admissions and bed-day rates are positive, whereas those in the LOS regressions are negative, but none changes significantly between 2002/3 and 2008/9 and it is hard to draw strong conclusions given the lack of explanatory power in these regressions.
Need does not appear to make a significant difference to the patterns discovered earlier. The standard errors in Table 25, which take need into account, are all lower in absolute terms than the SDs for the emergency series, as would be expected, but the SD of bed-days fell by a similar magnitude to the standard error over these years and it was similar to LOS. The standard errors and SDs in the admission series both experienced slight increases.
| Year | Admissions | |||||
|---|---|---|---|---|---|---|
| Emergency (152 PCTs) | Elective (150 PCTs) | |||||
| Bed-days | Admissions | Average LOS | Bed-days | Admissions | Average LOS | |
| 2002/3 | 98.11 | 13.00 | 1.27 | 40.57 | 6.45 | 0.79 |
| 2008/9 | 85.74 | 13.32 | 0.66 | 27.74 | 5.81 | 0.68 |
| Change (%) | –12.6 | 2.5 | –48.0 | –31.6 | –9.9 | –13.9 |
Given that there is minimal correlation between need and the elective series, it is not surprising that the standard errors in the need-controlled distributions are very close to the SDs calculated using the unadjusted data.
These results appear to confirm the view that a changing pattern of need is not the main driver for the reduction in variation and that structural change, whether as a result of changing policies or other factors that cannot be separately identified, are responsible.
The relationship between efficiency gain and initial mean length of stay
The pattern by which LOSs have converged across England deserves further attention. It is likely that those PCTs starting with longest mean LOS had the greatest scope to gain from reducing LOS without damaging patient care. Regressions were performed to test this prediction. English PCTs were collected into five approximately equal groups, ranked from those with the longest LOS in 2002/3 (quintile 1) to the shortest (quintile 5). Dummy variables for these groups (omitting quintile 5) were then used, in addition to change in need, to predict the change in LOS from 2002/3 to 2008/9.
The regression equation estimated is:
In this specification, the coefficient on the constant term shows the change in average LOS for the 20% of PCTs that had the lowest average levels in 2002/3, with the coefficient on each quintile’s dummy variable showing the difference between the average change in the lowest 20% and the average change in the corresponding quintile. Therefore, a coefficient would be statistically significant when the given quintile has a change in average LOS that is significantly different from that in the 20% of PCTs that had the lowest LOSs in 2002/3. Results for elective and emergency care, in hospitals as a whole and using just mental health data, are presented in Table 26.
| Variables | Admissions | |||
|---|---|---|---|---|
| All | Mental health | |||
| Emergency | Elective | Emergency | Elective | |
| 2002/3 LOS quintile 1 | –2.92*** (0.19) | –1.24*** (0.18) | –30.44*** (7.66) | –78.30*** (22.51) |
| 2002/3 LOS quintile 2 | –1.67*** (0.18) | –0.74*** (0.17) | –1.68 (7.65) | –11.50 (22.45) |
| 2002/3 LOS quintile 3 | –1.12*** (0.18) | –0.15 (0.17) | –3.72 (7.71) | 10.81 (2.76) |
| 2002/3 LOS quintile 4 | –0.81*** (0.18) | –0.16 (0.17) | –4.90 (7.79) | 6.67 (22.67) |
| Change in need (2008/9–2004/5) | 2.48*** (0.91) | 0.65 (0.89) | 18.48 (37.29) | –131.75 (110.40) |
| Intercept | –0.96*** (0.13) | –0.38*** (0.13) | 9.92* (5.49) | 36.62** (16.18) |
| Average LOS 2002–3 | 7.95 | 4.71 | 51.41 | 54.14 |
| Average of dependent variable | –2.32 | –0.85 | 1.21 | 23.33 |
| F-statistic | 55.78 | 13.85 | 4.40 | 4.40 |
| R 2 | 0.66 | 0.32 | 0.13 | 0.13 |
| Observations | 152 | 150 | 152 | 151 |
In all four data sets, the PCTs with the longest 2002/3 LOSs experienced greater declines than the PCTs with the shortest LOSs. This pattern was most apparent in the all-admission emergency data, which had significantly larger falls in quintiles 1–4 than in quintile 5, with increasingly greater coefficients from quintile 4 to quintile 1. These results suggest that the 20% of PCTs with the longest LOSs in 2002/3 reduced their LOSs by nearly 3 days more, on average, than those with short emergency stays. There was a similar pattern in the all-admission elective data (omitting North Staffordshire and Stoke on Trent, which previous analysis suggested were outliers), although only the top two groups of PCTs had significantly larger decreases than the bottom 20%. The coefficients for each quintile were smaller than the corresponding values from the emergency data. This supports earlier results, which suggested that the introduction of the tariff affected emergency care more than elective care.
As discussed above (see The tariff and variation in hospital bed-use), the tariff was not introduced in mental health care during this time period, so data from this sector can function as a useful control. The 20% of PCTs with the longest average LOSs in 2002/3 for both emergency and elective mental health admissions had significantly greater reductions, as was also found in the all-admissions data. However, the coefficient on the quintile 1 variable is the only quintile variable coefficient that is statistically different from zero. The lack of a consistent pattern in the size of the coefficients across the quintiles – in contrast to the steadily falling series of coefficients in the all admissions regressions – shows that care in a specialty that was excluded from the tariff changed differently to care across the whole system. The fact that data from PCTs in quintile 1 would be most at risk from the effects of ‘outlier’ observations, whether as a result of incorrect recording or patients who remained in hospital for a particularly long time, is a possible non-policy reason to expect these PCTs to tend to the mean over time.
Conclusions
The evidence here shows that variation in emergency admissions LOSs across English PCTs declined sharply between 2002/3 and 2008/9, and variation in LOSs for elective treatment also reduced. The variation in admission rates per thousand heads of population declines only slightly.
An analysis of the ways in which the system has changed suggests that the introduction of the tariff may have been responsible. The various influences on hospital behaviour in this period make it difficult to be certain, but evidence from the mental health sector and adjusting for changing need produces findings that are consistent with those expected if the introduction of the tariff was a major cause.
Nevertheless, it is apparent that PCTs have responded to a changing environment in different ways, with those that had the longest LOSs in 2002/3 reducing their stay lengths by more than others. Health-care managers across England are facing challenges going forwards and when reviewing policies, analysts need to ensure that they are using models that are sufficiently rich to assess the full impact.
Chapter 4 Trends in elective admissions: an age–period–cohort analysis
Introduction
The total number of elective admissions rose by 50% between 1999/2000 and 2014/15, from 5.50 million in 1999/2000 to 8.26 million 2014/15, an average rise of 2.7% per year. The age-standardised admission rate per 1000 population rose from 112.2 in 1999/2000 to 146.3 in 2014/15, an average increase of 1.8% per year. If admission rates by age and sex had remained constant, the number of elective admissions would have risen by only around 13% rather than by 50% over this 15-year period.
An understanding of the factors driving this substantial rise in elective admissions is important in the context of this study. We need to consider whether or not the pressures responsible for the upwards trend are likely to persist and what they mean for the prospects of controlling future growth in numbers of elective admissions.
In an earlier study, we conducted APC analyses of trends in elective and emergency admissions and bed-days. 52 The aim was to examine how far the trends in hospital admissions can be explained by the effects of the age distribution of the population, together with rising numbers of older people, by cohort effects, that is, effects attributable to differing admission rates of people born in different years (different birth cohorts) and by period effects, that is, admissions effects relating to a specific year, which cannot be explained by either age or cohort effects.
Age–period–cohort analysis is a form of multivariate regression analysis. The dependent variable is emergency admission rates by age and year, using single years and single year age bands (but with a top band of ≥ 85 years). The independent variables are dummies for each age, year of birth and year of admission.
The findings of our APC analysis in respect of total elective admissions (including day cases) are reported in Wittenberg et al. 52 Annex A of that report explains the methodology. We found that a favourable cohort effect (the more recent the cohort, the lower the admission rate given the age) broadly offset the age effect (the older the age group, the higher the admission rate, given the cohort) and the impact of rising numbers of older people. The rate of elective admissions, averaged across all ages, fell for successive cohorts, after controlling for period effects. We also found a substantial positive period effect.
Although the age and cohort effects are likely to reflect demographic and epidemiological change, the period effects capture admissions that could not have been anticipated given evidence concerning the changing age structure and years of birth of the population: these period effects would reflect both changes in supply-side willingness to admit, perhaps as a result of policy or technological innovations, and any increases to admission demand unconnected to age and cohort.
The trends in elective admissions were not due to a substantial shift in the balance between elective and emergency admissions. The number of emergency admissions also rose rapidly, by 2.1% per year between 1997/8 and 2014/15. The age and cohort effects did not differ significantly between the two types of admissions, but the period effect was not quite as high for emergency as for elective admissions. 52
We have investigated trends in elective admissions for four selected groups of procedures to examine variation between procedures in the pattern of APC effects. The purpose of looking at the four groups of procedures is to check whether or not the forces identified for electives as a whole also apply at a disaggregated level. For example, evidence of a weaker upwards age effect, or a stronger negative cohort effect, or a weaker or negative period effect for these procedures may suggest that the growth that we have seen in the overall number of elective admissions may not inevitably continue.
The four sets of procedures that we have examined are:
-
diagnostic procedures, the numbers of which rose somewhat more slowly than total elective admissions
-
hip and knee replacements, the numbers of which rose especially rapidly
-
coronary circulation procedures, the numbers of which fell
-
menorrhagia procedures, the numbers of which also fell.
These four sets of procedures account for 26% of total elective admissions in 1999/2000 and 21% of total elective admissions in 2014/15.
Our analyses use HES for England for each year from 1999/2000 to 2014/15. Although our earlier analysis of total elective admissions related to the 17-year period from 1997/98 to 2014/15, in our analyses of these four groups of procedures we considered the 15-year period 1999/2000 to 2014/15. The reason is concern about the accuracy of the coding of procedures in the early years of the HES data for 1997/98 and 1998/99.
The following sections of this chapter set out the findings of our APC analyses for the four sets of procedures. We present the findings in two ways for each of the APC effects. We first describe how the coefficients on the APC variables in the regression vary with changes in age, period and cohort, respectively. We then present an example of the ratio between the admission rates at different ages holding the cohort and period constant (and similarly for the other two effects). This form of presentation is intended to illustrate the varying effects of APC in a helpful way but it should be considered illustrative. This is mainly because the ratios vary with the values of the two factors that are held constant (e.g. with the cohort and period in the case of the ratio of admission rates between different ages).
Diagnostic procedures admissions
The total number of elective admissions for a range of diagnostic procedures (Box 3) rose from 1.08 million in 1999/2000 to 1.49 million in 2014/15 (Figure 15). This is an increase of 38.5% over the full 15-year period and an average annual increase of 2.2%. This compares with an annual average increase of 2.7% for all elective admissions (including day cases) over this period.
A18 Diagnostic endoscopic examination of ventricle of brain.
A55 Diagnostic spinal puncture.
E25 Diagnostic endoscopic examination of pharynx.
E36 Diagnostic endoscopic examination of larynx.
E49 Diagnostic fibre optic endoscopic examination of lower respiratory tract.
E51 Diagnostic endoscopic examination of lower respiratory tract using rigid bronchoscope.
E63 Diagnostic endoscopic examination of mediastinum.
G16 Diagnostic fibre optic endoscopic examination of oesophagus.
G19 Diagnostic endoscopic examination of oesophagus using rigid oesophagoscope.
G45 Diagnostic fibre optic endoscopic examination of upper gastrointestinal tract.
G55 Diagnostic endoscopic examination of duodenum.
G65 Diagnostic endoscopic examination of jejunum.
G80 Diagnostic endoscopic examination of ileum.
H22 Diagnostic endoscopic examination of colon.
H25 Diagnostic endoscopic examination of lower bowel using fibre optic sigmoidoscope.
H28 Diagnostic endoscopic examination of sigmoid colon using rigid sigmoidoscope.
J09 Diagnostic endoscopic examination of liver using laparoscope.
J13 Diagnostic percutaneous operations on liver.
J25 Diagnostic percutaneous operations on gall bladder.
J43 Diagnostic endoscopic retrograde examination of bile duct and pancreatic duct.
J44 Diagnostic endoscopic retrograde examination of bile duct.
J45 Diagnostic endoscopic retrograde examination of pancreatic duct.
J67 Diagnostic percutaneous operations on pancreas.
K51 Diagnostic transluminal operations on coronary artery.
K58 Diagnostic transluminal operations on heart.
L72 Diagnostic transluminal operations on other artery.
L95 Diagnostic transluminal operations on vein.
M11 Diagnostic endoscopic examination of kidney.
M30 Diagnostic endoscopic examination of ureter.
M45 Diagnostic endoscopic examination of bladder.
M77 Diagnostic endoscopic examination of urethra.
Q18 Diagnostic endoscopic examination of uterus.
Q39 Diagnostic endoscopic examination of fallopian tube.
Q50 Diagnostic endoscopic examination of ovary.
R02 Diagnostic endoscopic examination of foetus.
R05 Diagnostic percutaneous examination of foetus.
T11 Diagnostic endoscopic examination of pleura.
T43 Diagnostic endoscopic examination of peritoneum.
W36 Diagnostic puncture of bone.
W87 Diagnostic endoscopic examination of knee joint.
W88 Diagnostic endoscopic examination of other joint.
FIGURE 15.
Diagnostic procedures: admissions by broad age band, England, 1999/2000–2014/15.
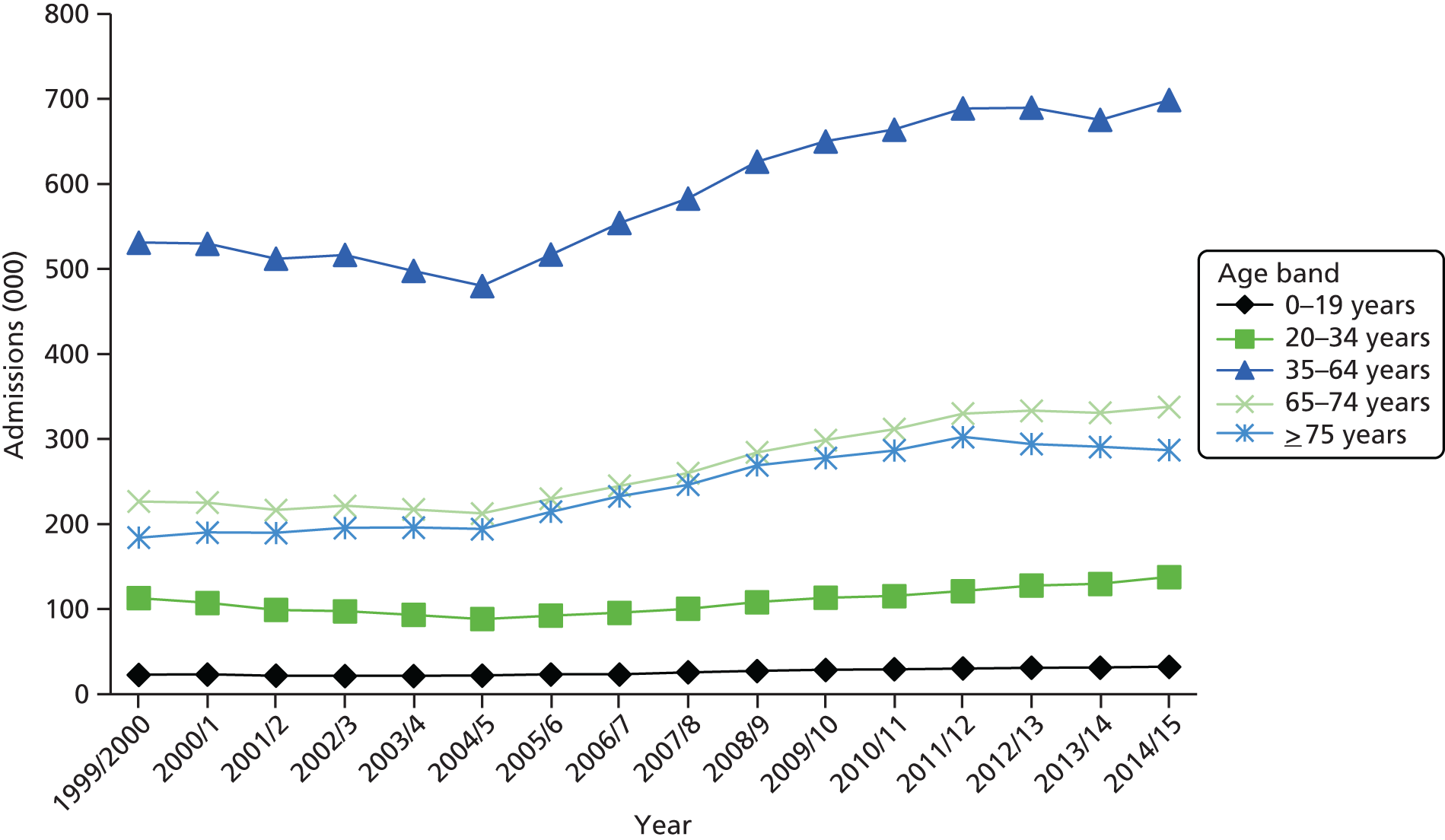
The numbers of elective admissions for diagnostic procedures rose for all age groups, but, in the case of the 20–34 years, 35–64 years and 65–74 years age groups, the rise followed a decline in the years 1999/2000 to 2004/5.
The overall admission rate for these procedures per 1000 population first fell slightly from 22 in 1999/2000 to 20 in 2005/6 and then rose to 27 in 2014/15, which amounts to a rise of 25% between 1999/2000 and 2014/15. The age-standardised rate rose by 19%, from 22 in 1999/2000 to 26 in 2014/15, an annual average increase of around 1.2% (Figure 16). This compares with an annual average increase, on the same basis, of 1.8% for total elective admissions over this period.
FIGURE 16.
Diagnostic procedures indexed age-standardised admission rates by age band in England, 1999/2000–2014/15.
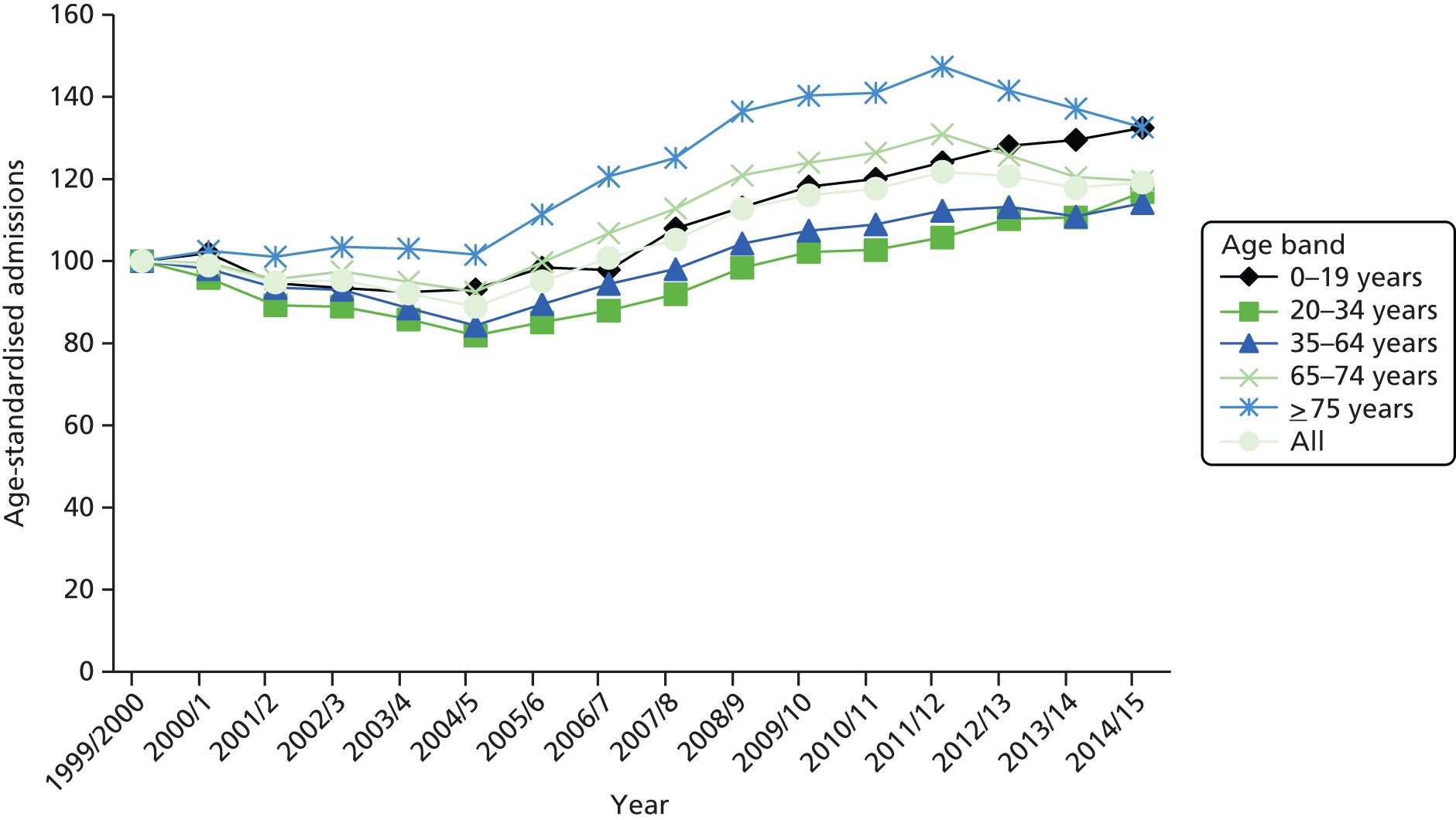
The age-standardised admission rate for diagnostic procedures rose most rapidly for children and young people aged < 20 years (by 35%) and least rapidly for the 20–34 years age group (by 14%).
If the admission rates for these procedures by age band had remained constant at their 1999/2000 levels, the number of admissions would have reached 1.25 million in 2014/15 rather than 1.49 million, an increase since 1999/2000 of 16% rather than of 39%.
The age effect findings show that, after controlling for cohort and period effects, the elective admission rate for diagnostic procedures rises with age from 9 years to 74 years. It falls with age up to 9 years and from ≥ 74 years. The admission rate at 75 years of age is over twice the rate at 25 years of age and around 35% higher than the rate at 50 years of age. This is on the basis of constant 2010 period effect and 1970 cohort effect (Figure 17).
FIGURE 17.
Diagnostic procedures: predicted admissions by age, for fixed cohort and period.

The cohort effect findings are that each successive cohort from the cohort born since 1915 onward has experienced a lower elective admission rate for diagnostic procedures at a given age than the preceding cohorts, after controlling for period as well as age effects. This is subject to minimal change for cohorts born between 1985 and 1995. The admission rate for those born in 1960 is around one-third lower than for those born in 1940 and half that of those born in 1920. This is at 50 years of age and a constant 2010 period effect (Figure 18).
FIGURE 18.
Diagnostic procedures: predicted admissions by cohort, for fixed age and period.

The period effect fell slightly between 1999/2000 and 2004/5 and then rose sharply almost every year to 2014/15, after controlling for age and cohort effects. The elective admission rate in 2014/15 is around 60% higher than the rate in 1999/2000, for the 1970 cohort and age 50 (Figure 19).
FIGURE 19.
Diagnostic procedures: predicted admissions by period, for fixed age and cohort.
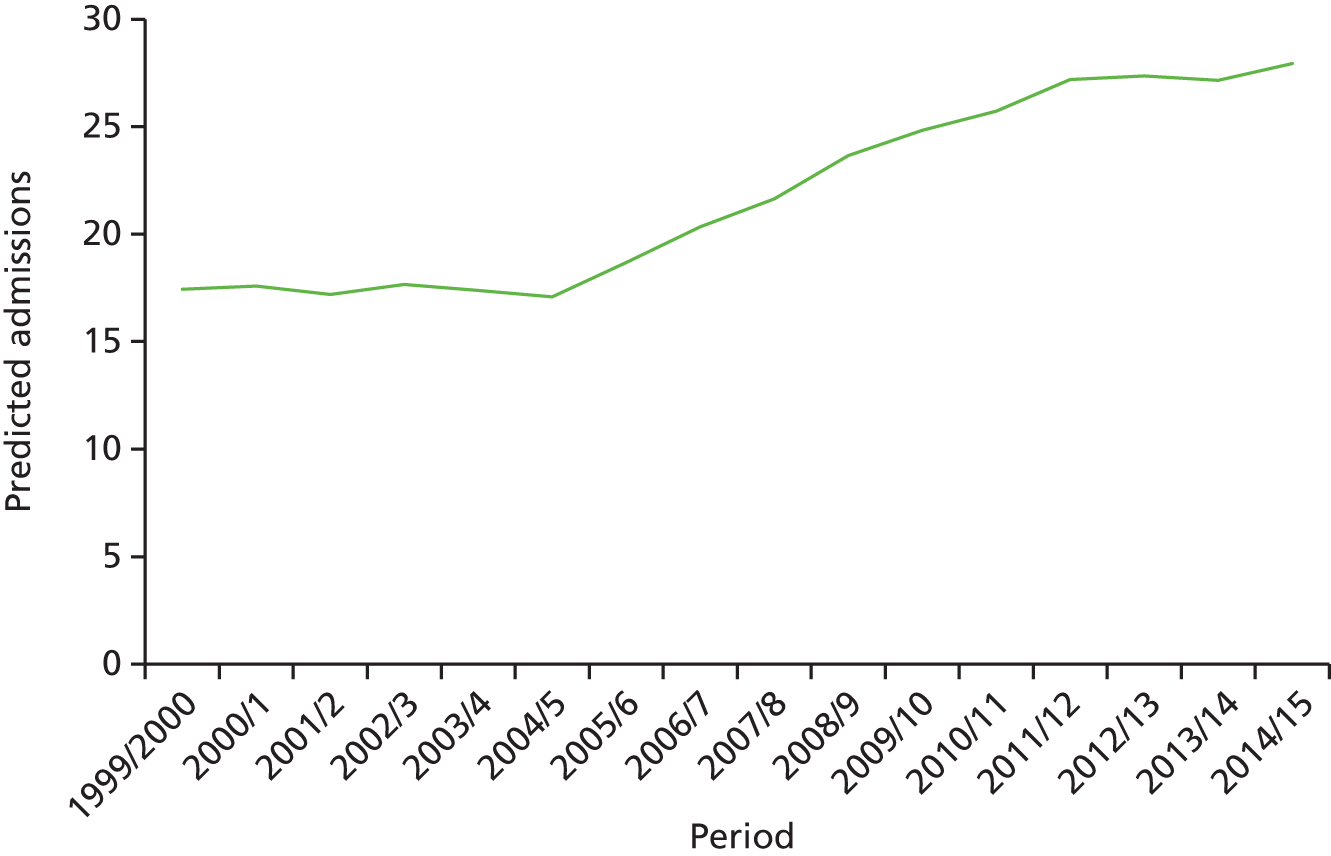
If there had been no period effect, the annual number of elective admissions for diagnostic procedures would have fallen between 1999/2000 and 2014/15 to around 925,000 in 2014/15 (Table 27). This indicates that the downwards cohort effect has more than offset the age effect over the period 1999/2000 to 2014/15.
| Description of component | Value |
|---|---|
| 1999/2000 actual level | 1.08 million |
| 2014/15 actual level | 1.49 million |
| 2014/15, constant 1999/2000 rates | 1.25 million |
| 2014/15, no period effects | 0.92 million |
| Decomposition of the % rise in levels, 1999/2000–2014/15: impact of ageing (1.25/1.08) | 16% |
| Impact of cohort effect (0.92/1.25) | –26% |
| Impact of period effect (1.49/0.92) | 61% |
| Total admissions increase, 1999/2000–2014/15 (1.49/1.08 = 1.16 × 0.74 × 1.61) | 38% |
Hip and knee replacement procedures
The total number of elective admissions for the prosthetic replacement of hip or knee joint (procedures codes W37 to W42) rose from 76.99 thousand in 1999/2000 to 157.46 thousand in 2014/15 (Figure 20). This is an increase of 104.5% over the full 15-year period and an average annual increase of 4.9%. This compares with an annual average increase of 2.7% for all elective admissions (including day cases) over this period.
FIGURE 20.
Hip and knee replacements: admissions by broad age band, England, 1999/2000–2014/15.
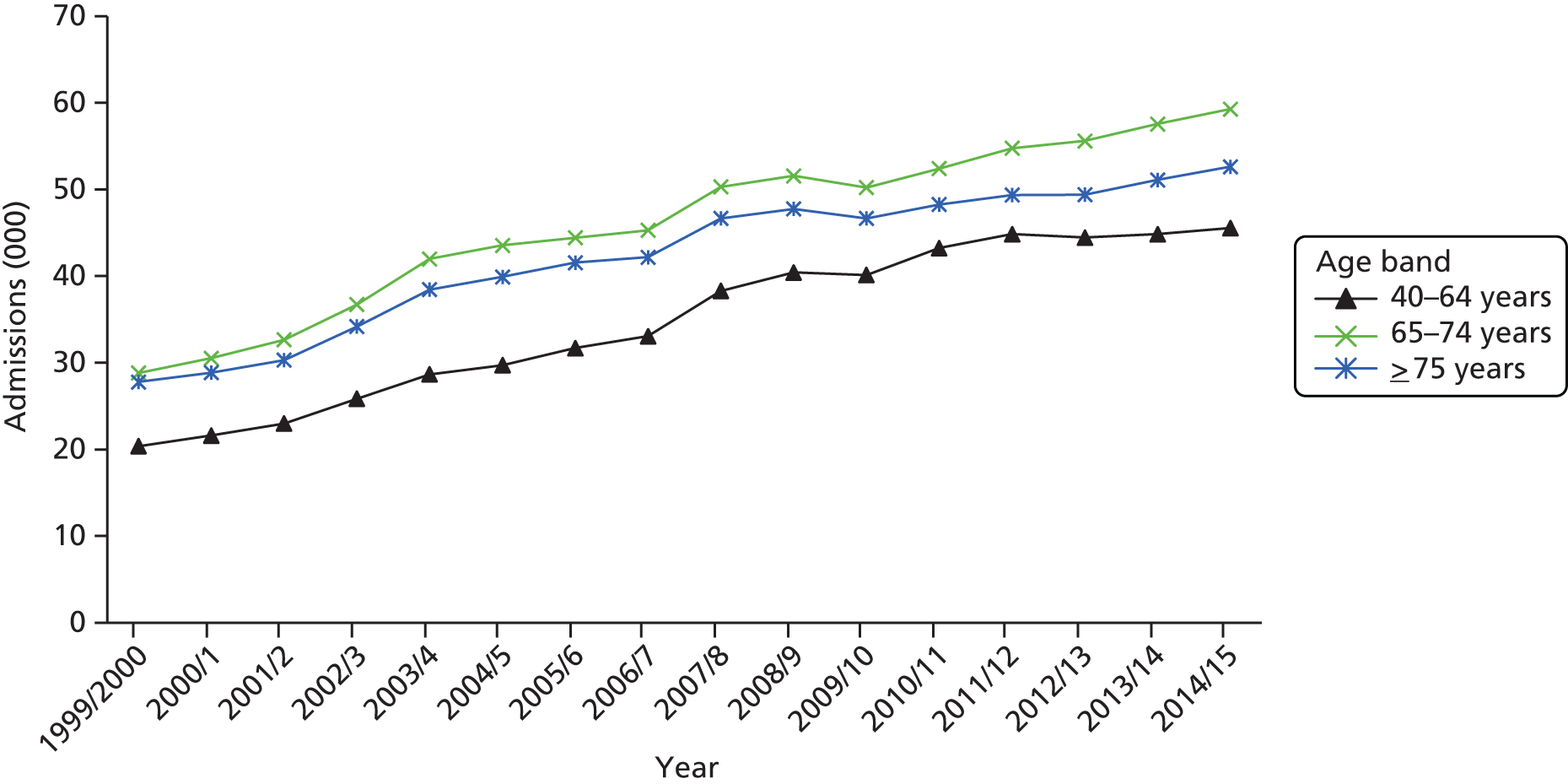
The numbers of elective admissions for these procedures rose in each year except 2009/10, with the fastest rise in the period 2000/1 to 2003/4. The numbers rose for each of three age groups (40–64 years, 65–74 years and ≥ 75 years). Younger age groups are not included in the analysis because joint replacements are rare below the age of 40 years.
The overall admission rate for these procedures per 1000 population rose from around 3.4 in 1999/2000 to 5.8 in 2014/15, which amounts to a rise of 71%. The rate rose most rapidly for the 40–64 years age group and least rapidly for the ≥ 75 years age group. The age-standardised rate rose slightly more slowly, by 70%, over the period 1999/2000 to 2014/15, an annual average increase of around 3.6% (Figure 21). This compares with an annual average increase, on the same basis, of 1.8% for total elective admissions over this period.
FIGURE 21.
Hip and knee replacements: indexed age-standardised admission rates by broad age band, England, 1999/2000–2014/15.

If the admission rates for these procedures by age band had remained constant at their 1999/2000 levels, the number of admissions would have reached 93.5 thousand in 2014/15 rather than 157.5 thousand, an increase since 1999/2000 of 22% rather than of 105%.
The age effect findings show that, after controlling for cohort and period effects, the elective admission rate for hip and knee joint replacement procedures rises with age from 40 to 73 years and then falls with age. This pattern would be expected because need is lower at lower ages and rises with age, but in late old age the risks of joint replacement are higher and the benefits may be lower. The rate at 75 years of age is around 65% higher than the rate at 60 years, 65% higher than the rate at 83 years and around 3.5 times higher than the rate at 50 years of age. This is on the basis of constant 2010 period effect and 1970 cohort effect (Figure 22).
FIGURE 22.
Hip and knee replacements: predicted admissions by age, for fixed cohort and period.

The cohort effect findings are that each successive cohort from the cohort born in 1915 onwards has experienced a lower elective admission rate for hip and knee joint replacement procedures at a given age than the preceding cohorts, after controlling for period, as well as age, effects. This is subject to a few single year rises and to minimal change for cohorts born between 1950 and 1958. The rate for those born in 1960 is around two-thirds that of the rate for those born in 1940 and slightly over one-third that of the rate for those born in 1920. This is at 50 years of age and constant 2010 period effect (Figure 23).
FIGURE 23.
Hip and knee replacements: predicted admissions by cohort, for fixed age and period.
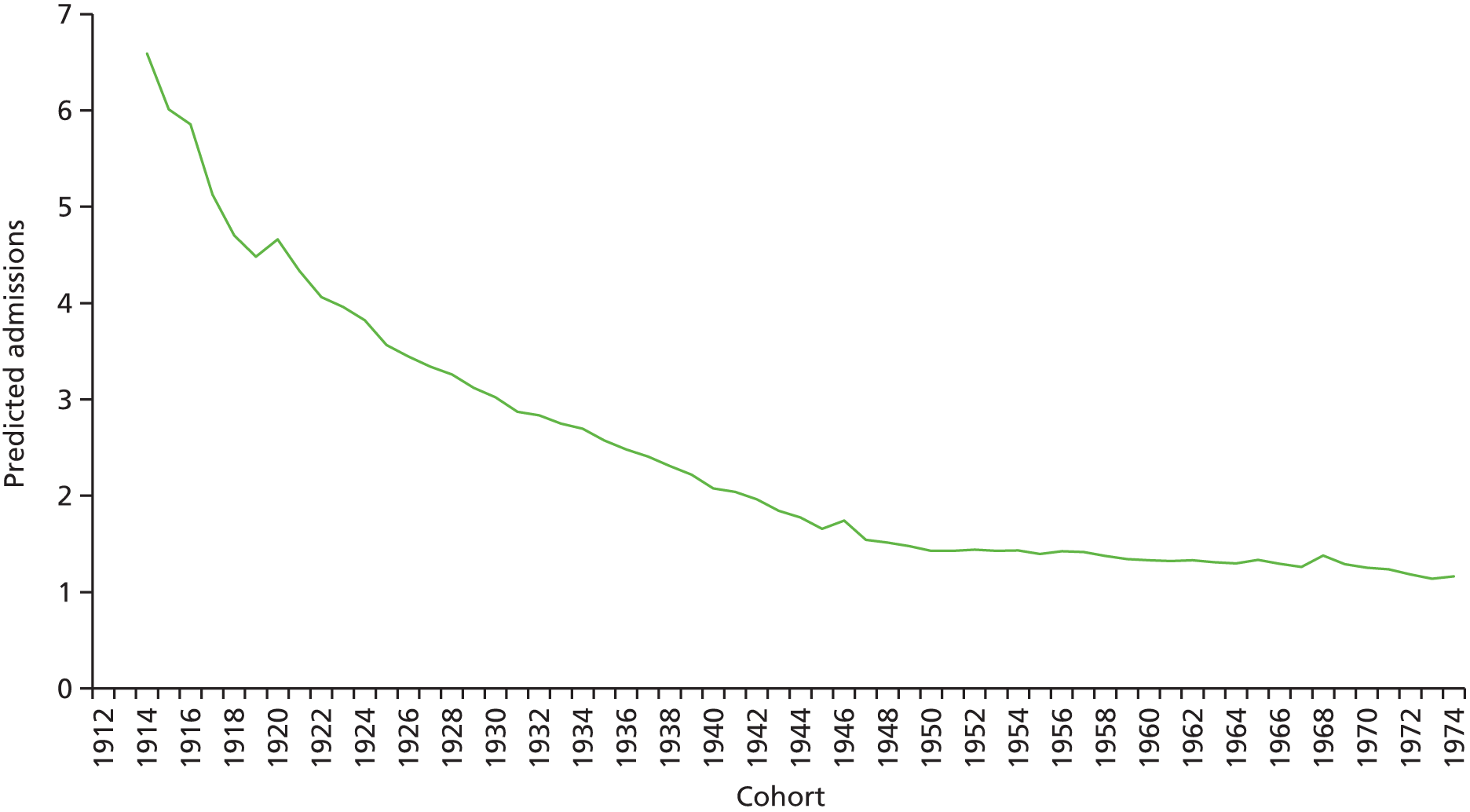
The period effect rose each year between 1999/2000 and 2014/15 except 2009/10. The elective admission rate for hip and knee joint replacement procedures in 2014/15 is around three times the rate in 1999/2000, for the 1970 cohort and at 50 years of age (Figure 24).
FIGURE 24.
Hip and knee replacements: predicted admissions by period, for fixed age and cohort.

If there had been no period effect, the annual number of elective admissions for hip and knee joint replacement procedures would have fallen between 1999/2000 and 2014/15 to around 54,100 in 2014/15 (Table 28). This indicates that the downwards cohort effect has more than offset the age effect over the period 1999/2000 to 2014/15.
| Description of component | Value |
|---|---|
| 1999/2000 actual level | 76,990 |
| 2014/15 actual level | 157,460 |
| 2014/15, constant 1999/2000 rates | 93,540 |
| 2014/15, no period effects | 54,160 |
| Decomposition of the % rise in levels,1999/2000–2014/15: impact of ageing | 21% |
| Impact of cohort effect | –42% |
| Impact of period effect | 191% |
| Total admissions increase, 1999/2000–2014/15 | 105% |
Coronary circulation admissions
The total number of elective admissions for coronary circulation procedures (K40–K46 – replacement or bypass of coronary artery, and K49–K51, K75 – transluminal operations on coronary artery) among people aged ≥ 35 years first rose from 37,580 in 1999/2000 to peak at around 64,750 in 2005/6 and then fell back to 51,210 in 2014/15 (Figure 25). This is an increase of 38.1% over the full 15-year period and an average annual increase of 2.2%. This compares with an annual average increase of 2.7% for all elective admissions (including day cases) over this period.
FIGURE 25.
Coronary circulation admissions: admissions by broad age band, England, 1999/2000–2014/15.

The numbers of elective admissions for these procedures for those aged 35–64 years and 65–74 years peaked in 2005/6 and then declined, with levels remaining fairly static since 2009. The ≥ 75 years age group experienced more steady growth, with the number of admissions increasing from 3718 in 1999/2000 to 12,854 in 2014/15.
The overall admission rate for these procedures per 1000 population first rose from 1.43 in 1999/2000 to 2.30 in 2005/6 and fell to 1.71 in 2014/15, which amounts to an increase of 20% between 1999/2000 and 2014/15. The age-standardised rate increased by 14%, from 1.43 in 1999/2000 to 1.63 in 2014/15, an annual average increase of 0.9% (Figure 26). This compares with an annual average increase, on the same basis, of 1.8% for total elective admissions over the period 1999/2000 to 2014/15.
FIGURE 26.
Coronary circulation admissions: indexed age-standardised admission rates by broad age band, England, 1999/2000–2014/15.

The age-standardised admission rate for these procedures fell (by 13%) for the 35–64 years age group, but it rose considerably (by 213%) for the ≥ 75 years age group (see Figure 26). Although the rate for the ≥ 75 years age group was three times the rate for the 65–74 years age group in 1999/2000, the rates for both groups are now similar.
If the admission rates for these procedures by age band had remained constant at their 1999/2000 levels, the number of admissions would have reached 44,140 in 2014/15 rather than 51,910, an increase since 1999/2000 of 17% rather than of 38%.
The age effect findings show that, after controlling for cohort and period effects, the elective admission rate for coronary circulation procedures rises with age to 62 years and then falls, especially after the age of 73 years. This is for constant 2010 period effect and 1970 cohort effect (Figure 27).
FIGURE 27.
Coronary circulation admissions: predicted admissions by age, for fixed cohort and period.

The cohort effect findings are that each successive cohort from the cohort born in 1932 onward has experienced a lower elective admission rate for coronary circulation procedures at a given age, after controlling for period as well as age effects, subject only to a rise for the 1946 cohort and some minor deviations in the late 1970s. Prior to 1932, the rate rose for cohorts born between 1915 and 1932. The admission rate for those born in 1950 is around 51% lower than for those born in 1932 but similar to the admission rate for those born in 1922. This is at 50 years of age and constant 2010 period effect (Figure 28).
FIGURE 28.
Coronary circulation admissions: predicted admissions by cohort, for fixed age and period.
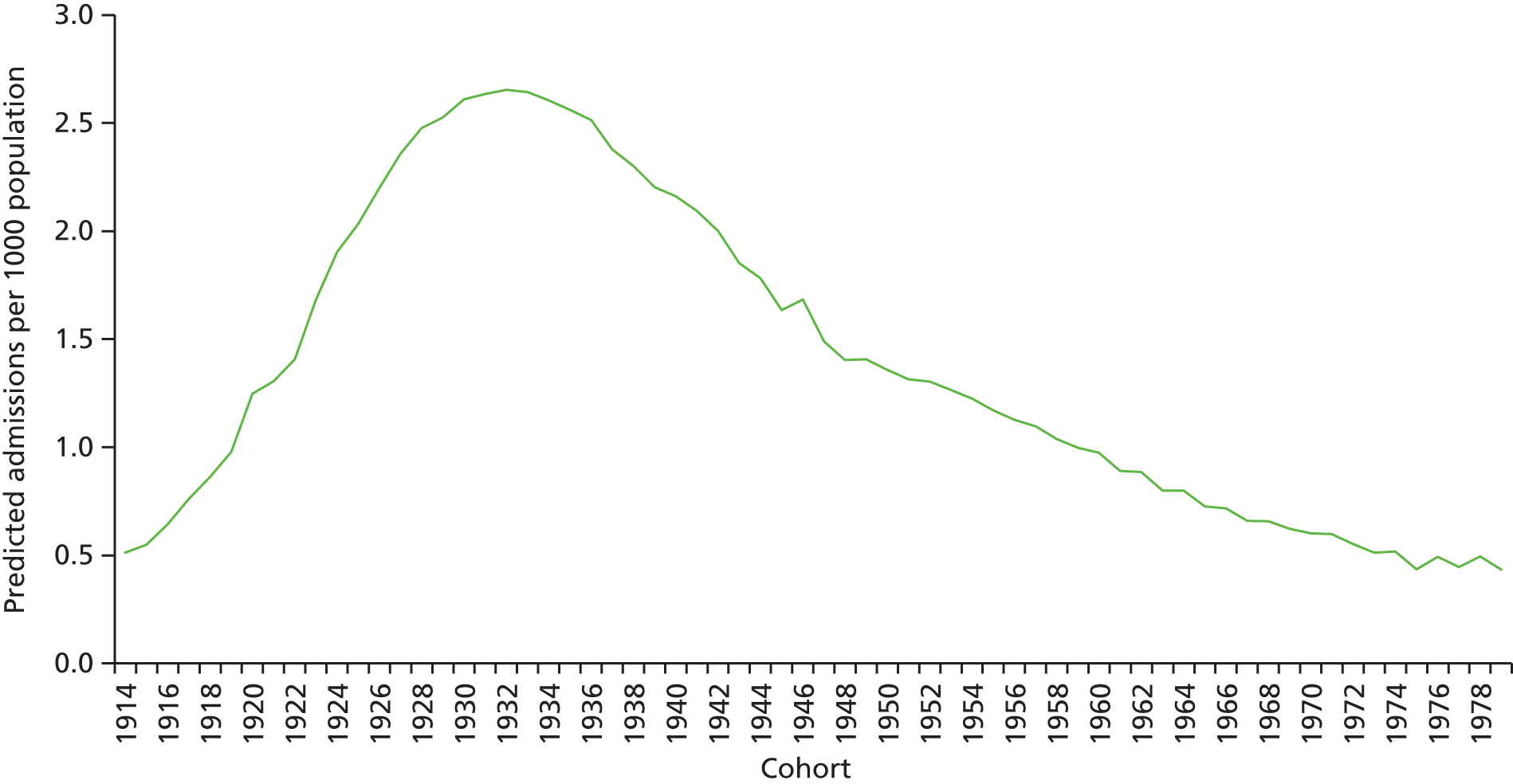
The period effect rose every year from 1999/2000 to 2005/6, fell rapidly in 2006/7 and was then fairly constant with a small upwards trend between 2007/8 and 2014/15, after controlling for age and cohort effects (Figure 29).
FIGURE 29.
Coronary circulation admissions: predicted admissions by period, for fixed age and cohort.
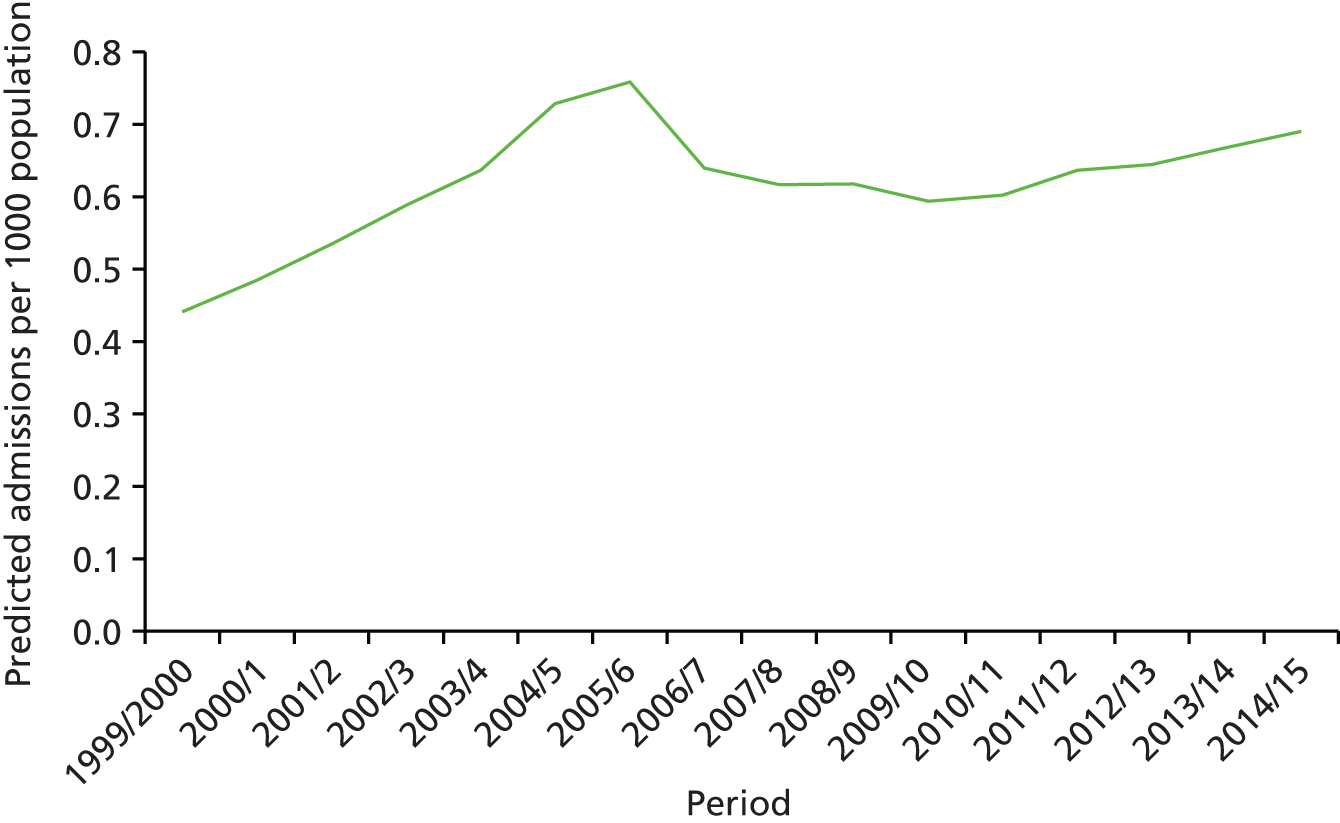
If there had been no period effect, the annual number of elective admissions for coronary circulation procedures would have remained constant from 1999/2000 to 2005/6 and then fallen slightly to around 33,070 in 2014/15 (see Figure 29). Table 29 illustrates further evidence of the importance of the period effect, which has caused a rise of 57% in the levels of admissions.
| Description of component | Value |
|---|---|
| 1999/2000 actual level | 37,576 |
| 2014/15 actual level | 51,911 |
| 2014/15, constant 1999/2000 rates | 44,142 |
| 2014/15, no period effects | 33,067 |
| Decomposition of the % rise in levels, 1999/2000–2014/15: impact of ageing | 17% |
| Impact of cohort effect | –25% |
| Impact of period effect | 57% |
| Total admissions increase, 1999/2000–2014/15 | 38% |
Menorrhagia procedure admissions
The total number of elective admissions for menorrhagia procedures (codes Q07–Q10 and Q16) fell from 106,620 in 1999/2000 to 66,740 in 2014/15 (Figure 30 and Table 30). This is a decrease of 37.4% over the full 15-year period and an average annual decrease of 3.1%. The most likely reason for this decrease is increased use of the Mirena® coil (Bayer, Whippany, NJ, USA), which is very effective for the treatment of menorrhagia. The decrease of 3.1% per year contrasts with an annual average increase of 2.7% for all elective admissions (including day cases), over this period.
FIGURE 30.
Menorrhagia procedures: admissions by broad age band, England, 1999/2000–2014/15.
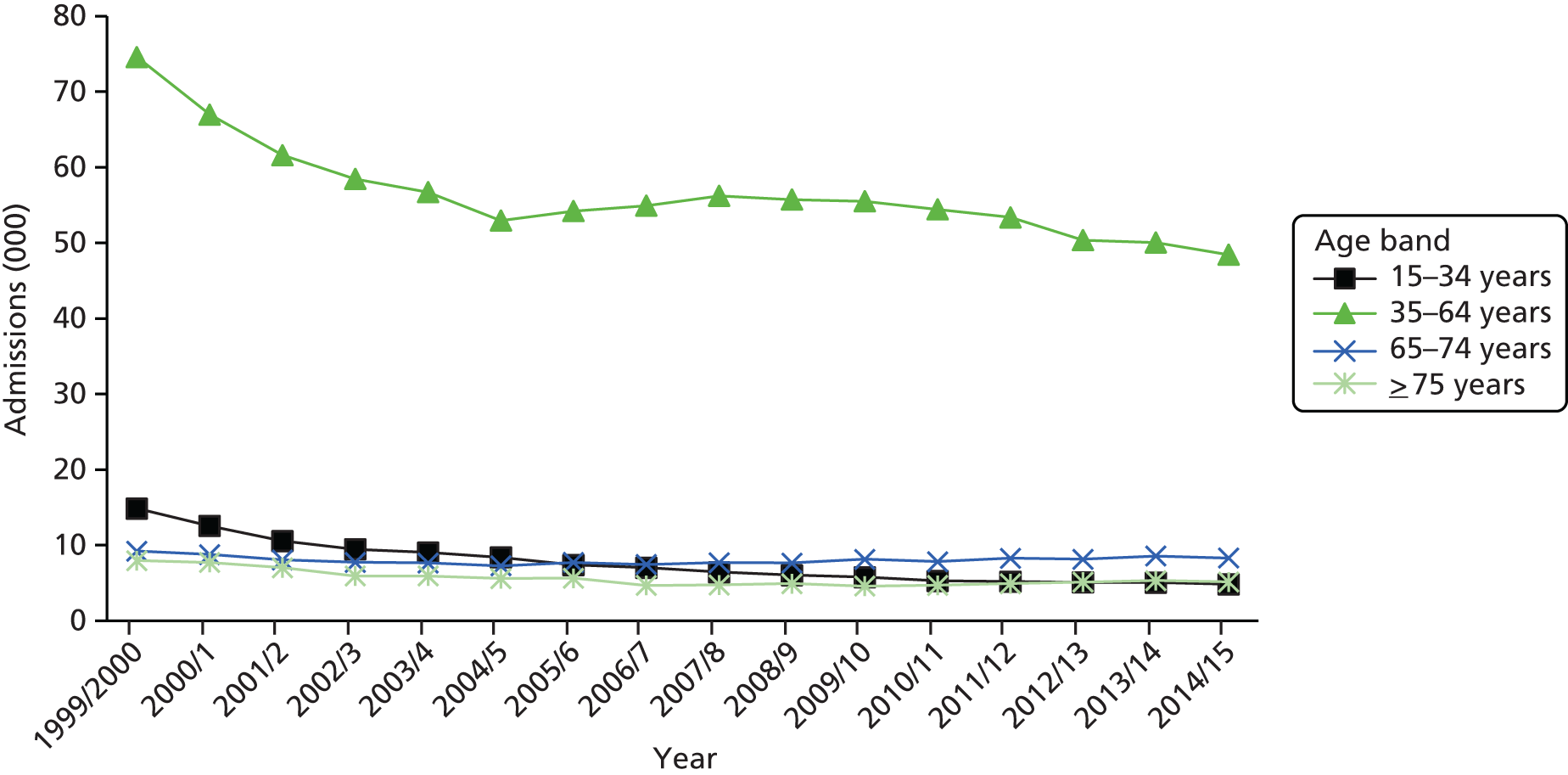
| Description of component | Value |
|---|---|
| 1999/2000 actual level | 106,620 |
| 2014/15 actual level | 66,740 |
| 2014/15, constant 1999/2000 rates | 119,690 |
| 2014/15, no period effects | 120,400 |
| Decomposition of the % rise in levels,1999/2000–2014/15: impact of ageing | 12% |
| Impact of cohort effect | 1% |
| Impact of period effect | –45% |
| Total admissions increase, 1999/2000–2014/15 | –37% |
The number of elective admissions for these procedures fell sharply between 1999/2000 and 2004/5, rose slightly between 2004/5 and 2007/8 and then fell slowly to 2014/15. More than 70% of these admissions are of women aged 35–64 years.
The overall admission rate for these procedures per 1000 women fell from 5.19 in 1999/2000 to 2.91 in 2014/15, which amounts to a fall of 44% between 1999/2000 and 2014/15. The rate fell most rapidly for the 15–34 years age group and least rapidly for the 65–74 years age group. The age-standardised rate also fell by 44% over the period 1999/2000 to 2014/15, an annual average decrease of around 5.3% (Figure 31). This contrasts with an annual average increase, on the same basis, of 1.8% for total elective admissions over this period.
FIGURE 31.
Menorrhagia procedures: age-standardised indexed admission rates by broad age band, England, 1999/2000–2014/15.
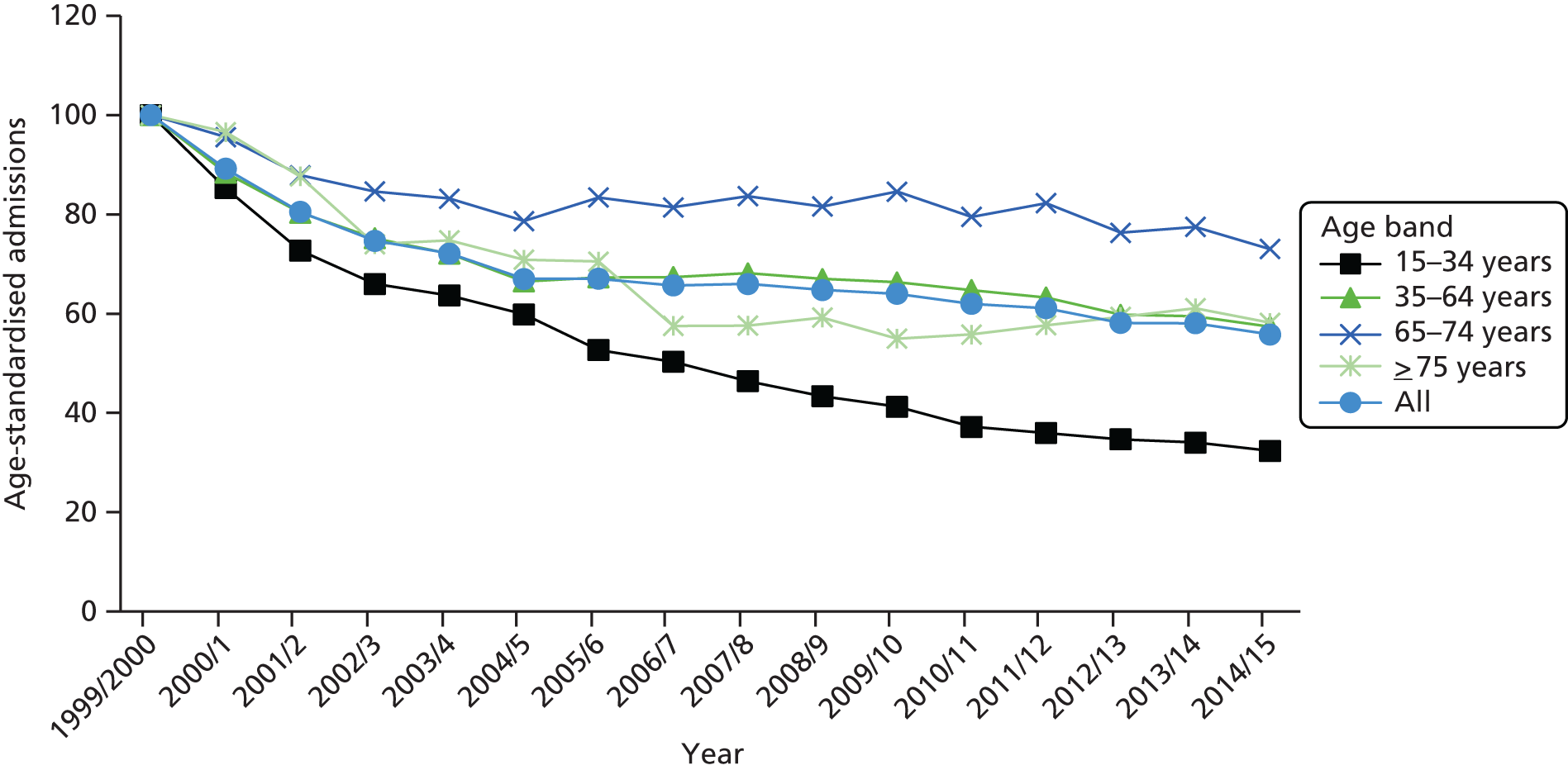
If admission rates for these procedures by age band had remained constant at their 1999/2000 level, the number of admissions would have reached 119,700 in 2014/15 rather than fallen to 66,700, an increase since 1999/2000 of 12% rather than a decline of 37%.
The age effect findings show that, after controlling for cohort and period effects, the elective admission rate for menorrhagia procedures rises with age from 15 years to around 45 years, then falls with age to around 60 years and then remains constant from 60 years to around 75 years of age. The rate at 45 years of age is more than twice the rate at 35 years of age. This is on the basis of constant 2010 period effect and 1970 cohort effect (Figure 32).
FIGURE 32.
Menorrhagia procedures: predicted admissions by age, for fixed cohort and period.

The cohort effect findings are that each successive cohort from the cohort born in 1968 onwards has experienced a lower elective admission rate for menorrhagia procedures at a given age than the preceding cohorts, after controlling for period as well as age effects. Prior to the 1968 cohort, each successive cohort from 1920 to around 1945 experienced a higher admission rate for these procedures. The rate then fell for cohorts born between 1945 and 1953 before rising to reach a peak for the cohort born in 1968. The rate for those born in 1965 is around 20% higher than the rate for the 1955 cohort and 20% higher than for the 1975 cohort. This is at 50 years of age and constant 2010 period effect (Figure 33).
FIGURE 33.
Menorrhagia procedures: predicted admissions by cohort, for fixed age and period.
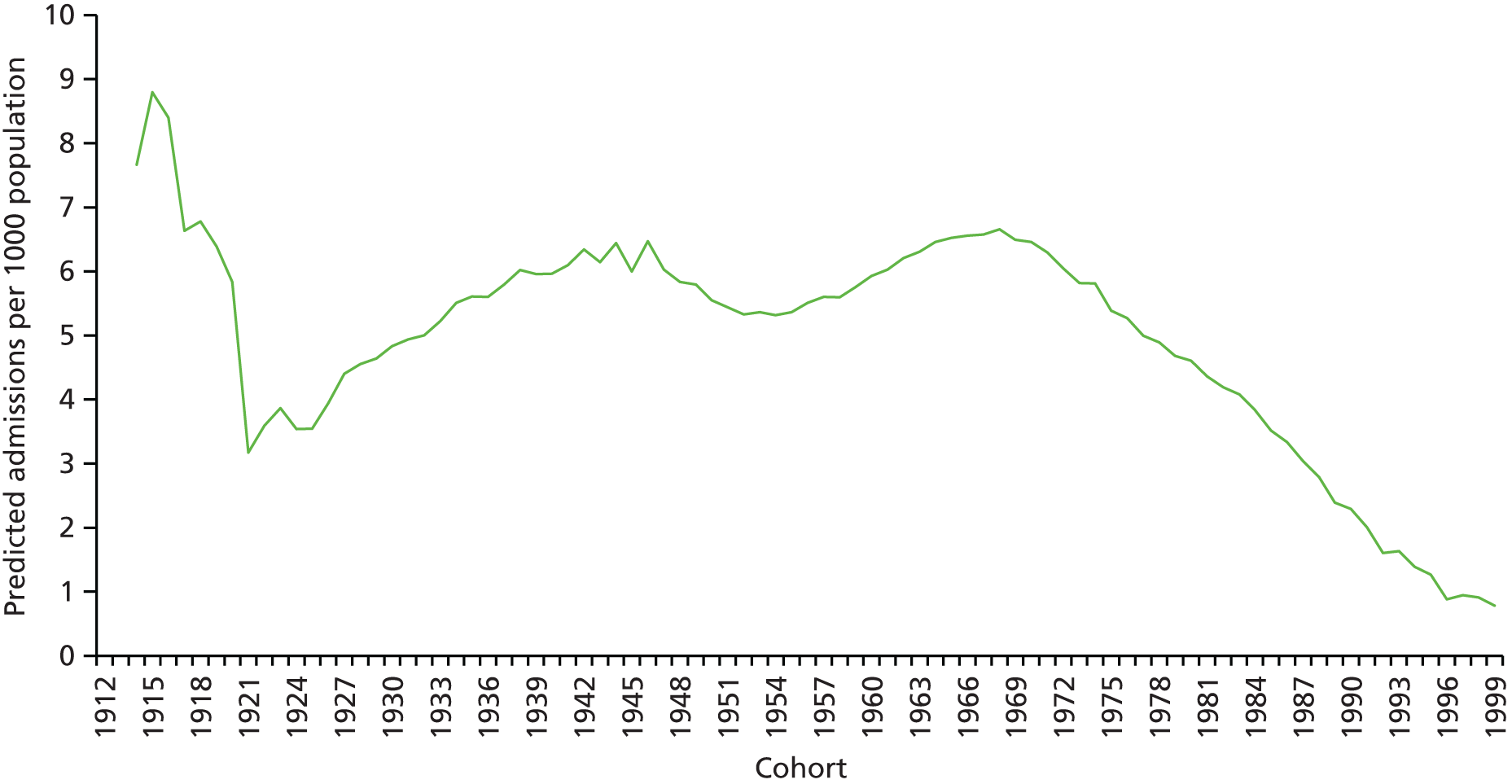
The period effect fell each year between 1999/2000 and 2014/15. The elective admission rate for menorrhagia procedures in 2014/15 is only around 60% of the rate in 1999/2000, for the 1970 cohort and 50 years of age (Figure 34). As indicated above, the most likely reason for declining period effect is increased use of the Mirena coil.
FIGURE 34.
Menorrhagia procedures: predicted admissions by period, for fixed age and cohort.

If there had been no period effect, the annual number of elective admissions for menorrhagia procedures would have risen between 1999/2000 and 2014/15 to around 120.4 thousand. This indicates that the cohort effect has marginally more than offset the age effect over the period 1999/2000 to 2014/15.
Conclusions
We have explored in this chapter how far the considerable increase in the number of elective hospital admissions over the 15-year period from 1999/2000 to 2014/15 is due to the ageing population, how far to cohort effects and how far to period effects. We have considered in our APC analyses the trends in total elective admissions (including day cases) and trends in elective admissions for four sets of procedures. These four sets of procedures accounted for 26% of all elective admissions in 1999/2000 and 21% in 2014/15.
Total elective admissions rose by 2.7% per year over this 15-year period. Elective admissions for diagnostic procedures rose somewhat more slowly (2.2% per year) and admissions for hip or knee replacements rather more rapidly (4.9% per year). In contrast, coronary circulation procedures and procedures for menorrhagia both fell (by 4.4% and 3.1% per year, respectively) over this period.
The age effects are fairly similar across all the procedures we considered (Table 31). They are, not surprisingly, a little higher than average for joint replacements, which are concentrated on older ages, and a little lower for menorrhagia procedures, which are concentrated on younger women.
| Description | Diagnostic procedures | Coronary circulation | Hip and knee replacements | Menorrhagia procedures | All elective admissions |
|---|---|---|---|---|---|
| 1999/2000 actual (000) | 1080 | 37.6 | 77.0 | 106.6 | 5070 |
| 2014/15 actual (000) | 1490 | 51.9 | 157.5 | 66.7 | 8260 |
| 2014/15, constant 1999/2000 rates (000) | 1250 | 44.1 | 93.5 | 119.7 | 5840 |
| 2014/15, no period effects (000) | 925 | 33.1 | 54.2 | 120.4 | 5330 |
| Decomposition of the % rise in levels, 1999/2000–2014/15 (%) | |||||
| Impact of ageing | 16 | 17 | 21 | 12 | 15 |
| Impact of cohort effect | –26 | –25 | –42 | 1 | –9 |
| Impact of period effect | 61 | 57 | 191 | –45 | 55 |
| Total increase over 15 years | 38 | 38 | 105 | –37 | 63 |
| % change | 38 | 38 | 105 | –37 | 63 |
| Annual % change | 2.2 | 2.2 | 4.9 | –3.1 | 2.9 |
The cohort effects are more strongly negative for three of the sets of procedures than for electives in general (see Table 31). There has been an especially large downwards cohort effect for hip and knee replacements and substantial downwards cohort effects for coronary circulation procedures and diagnostic procedures. A potential explanation is that health at a given age has improved more than average for coronary artery disease and for arthritis of the hips and knees. For menorrhagia, however, there has been no significant cohort effect.
The variation in period effects for the different procedures is of considerable interest (see Table 31). Period effects relate to factors that cannot be explained by age or cohort effects: they may include demand effects such as shifts in demand at a particular time period, as well as supply factors such as uptake of new technologies.
For menorrhagia procedures, the large downwards period effect is likely to be due to the introduction of the Mirena coil, which has proved to be an effective treatment for the condition. For coronary artery disease, new technology may also be an explanation for the downwards period effect. The upwards period effect for diagnostic procedures is higher, albeit not much higher, than the period effect for all elective admissions. It may be that the scope for diagnostic procedures has risen greatly, even faster than the scope for other valuable elective procedures.
For three of the groups of procedures the negative cohort effect outweighs the positive age effect, and for one of these three (hip and knee replacements), the cohort effect is strongly negative. We would therefore conclude that demographic/epidemiological effects (in so far as the balance of age and cohort effects captures them) do not inevitably generate increases in the number of elective admissions.
The period effects are positive for the two sets of procedures for which new technologies have offered improved prospects of benefit (diagnostic procedures and hip and knee replacements) and negative for the two sets of procedures for which new technologies have provided alternatives to surgery (coronary circulation procedures and menorrhagia procedures). A positive period effect is not inevitable. To reduce elective admissions, the best approach may be to promote research to find less invasive alternatives to surgery.
Chapter 5 Will increasing the supply of gatekeeper general practitioners reduce referrals and hospital admissions?
Introduction
In the decade to 2011/12, hospital admissions in England increased by 35.4%. 53 Policy reforms, including a new GP contract, and increased numbers of GPs, were introduced to reduce admissions growth by strengthening less costly and more accessible primary care. Several explanations have been proposed for the growth in hospital admissions. They include an increase in illness and frailty linked to the ageing population (see, e.g., Blatchford and Capewell54 and Gillam55); increased ability to detect and treat illness (e.g. Hobbs56); the effects of incentives in the tariff model of paying hospitals (e.g. Farrar et al. 13 and Health and Social Care Information Centre57); and ‘targets’ to reduce waiting for both elective and emergency care. The working practice of GPs has also changed, notably the new ‘out-of-hours’ (OOH) services (Coast et al. ;58 Bunn and Kendall;59 Sibley et al. 60), and this may also have contributed to admissions. For example, Dusheiko et al. 61 find that since GP contract changes, primary care performance has been associated with lower hospital costs in stroke care only. However, there is a substantial body of literature that argues that primary care physicians provide high-quality care at a lower cost than specialists (Chernew et al. ,62 Franks and Fiscella63 and Macinko et al. 64). This may be the case particularly in situations in which primary care physicians operate as gatekeepers (Forrest and Starfield65). The primary intention of the new contract was to incentivise several patient management interventions to improve patient access and increase cost-effectiveness by moving treatment for chronic care out of hospitals. Austerity funding has heightened interest in understanding how increasing GP services might reduce both referrals and elective admissions, as well as emergency care, with the two main UK political parties in the 2015 general election both proposing an increase in GP supply. This report addresses these issues in two ways: (1) a model of GP referrals is developed, which examines the interaction between GP and specialist, but does not assume that gatekeeping arises because GP treatments are cheaper, as do, for example, Mariñoso and Jelovac,4 in the first of the few theoretical studies of the relative benefits of gatekeeping. Instead, gatekeeping (i.e. limiting access) enables greater efficiency in supplying diagnostic information and, hence, in maximising health gain net of cost. (2) The chapter reports estimates of the influence on referrals and admissions of increasing (1) GP supply and (2) mean GP practice size. The changing supply of NHS GPs to areas across England in the period 2004–11 is used to construct panel data estimates of their effects on referrals and admissions, which allow for the endogeneity of GP location choice.
Theoretical studies of gatekeeping by GPs have been particularly concerned with the implications of alternative payment schemes on GPs’ effort to diagnose accurately, and for the incentive to refer or treat efficiently (see, e.g., Malcomson,66 Mariñoso and Jelovac4, Gonzáles67 and Allard et al. 68). The schemes most often analysed are fee for service, fundholding and capitation, which is the UK arrangement during the period we analyse and commonplace in Health Maintenance Organisations (HMOs). We study a model in which GPs are paid by capitation and there is a competitive specialist sector. We use a characterisation of disease drawn from these models to study the consequences for referrals and admissions of an increased market supply of GPs.
Given that NHS GPs are paid by capitation on registered patients, and that their use of time is not observed, it is necessary to decide how to model how GPs are constrained from pursuing their own utility rather than patient health. There are three approaches in the literature: (1) a physician’s objective function reflects his or her imperfect role as agent to the patient (principal) and includes both his or her own utility and, for altruistic or professional reasons, her patients’ health. This approach is widely adopted, for example, in Iversen and Ma69 and Gaynor et al. ,70 and was studied by Ellis and McGuire71 and, recently, by Chandra et al. ;72 (2) clinical decisions reflect a bargain between the treating clinician and patient, as discussed by Ellis and McGuire73 and Ma and Riordan;74 and (3) GP referrals are constrained towards efficient levels by patient access to a second opinion, an idea that is analysed by Malcomson. 66
A difficulty with using the familiar ‘altruistic clinician’ model to explain NHS GP referral behaviour is that, because GPs are paid by capitation, a GP offered the choice either to refer or to increase effort and treat a sick patient will refer to a specialist because it serves the interests of both the patient and the GP; hence, as Malcomson66 argues, gatekeeping cannot be explained. The puzzle of why GPs paid by capitation may nevertheless limit specialist access and provide treatments is resolved here by exploring the nature of patient ‘agency’, and by introducing a GP objective suited to the aims of GPs employed in single-payer insurance systems and insurer organisations including HMOs that employ GPs. In single-payer and managed-care contexts, the insurer influences the GP, and the principal may be regarded as the insurer and not the patient as in the ‘altruistic clinician’ model. However, the insurer has imperfect information about a GP’s decisions, and the GP can be an imperfect agent of the insurer. Unless the GP is constrained to efficient behaviour by ethics or a second opinion, moral hazard problems arise, as they do in a different form in the ‘altruistic clinician’ model.
In the model the first best captures the intuition that if specialists can treat at no higher cost than GPs and can provide low-cost patient insight before costly diagnostics, an efficient solution would be to refer all patients and for a specialist to decide diagnostic expenditure and treatment. We show, however, that limiting patient access to specialists can increase efficency in a health system with information failures and insurance. We discuss why a single-payer insurer is more likely to address these failures by encouraging gatekeeping. In this system we study the effects of more GPs, and a more elastic demand for GP registration, on referrals and specialist treatment.
A single information constraint underpins the argument in the model that a health authority (HA) will regard gatekeeping as in the patient’s interest: the HA imperfectly observes the evidence used by specialists to choose diagnostics. This creates a moral hazard, with a higher than optimal level of diagnostic expenditure by consultants who compete to attract patients by maximising health gain. Efficient equilibria in which GP patient information is used by a specialist to refuse an exact diagnostic test are not selected by the specialist, and such equilibria can be obtained only if a GP limits access to specialists. However, a competitive GP is not incentivised to limit access. If a GP is trained to refer in the interests of the insured, then a perfect agent can fully correct the distortion of excess diagnostics, whereas an imperfect agent can reduce the distortionary costs.
This report discusses why GPs in single-payer systems and those employed by insurance companies may behave differently from GPs in a devolved primary care system, as is found across much of the USA, and why a single-payer insurer is more incentivised than a competitive insurer to invest in GP training to represent the interests of the insured. Nevertheless, GPs who value their leisure and income are likely to be imperfect agents of the HA. Their incentive is to set higher referral rates than insurers prefer to secure more patient revenue and personal leisure. If a specialist can order diagnostics without HA oversight then competition to maximise health gain leads to using the best diagnostics.
We model a GP whose intrinsic concerns are his/her own utility and the objective of the insurer, which wishes to maximise the social welfare of those insured, as in Malcomson. 66 This approach may be viewed as being professionally underpinned by the ‘population health’ dimension of ethical medical practice. GPs learn to be aware of the opportunity cost of their decisions for other insured patients by following ‘value for money’ guidelines. The NHS reinforces this by requiring GPs to lead budget-holding organisations and monitor referrals, which holds GPs decisions to account and subject to peer pressure (see Department of Health75). We discuss how this supports GPs voluntarily limiting access to specialists, even if this is not in the interests of their patient, or themselves, and why this is efficient. Unlike a competitive insurer, this investment is incentivised because the HA is a single payer and receives all the benefits from the training investment, which it may view as ‘firm-specific’ rather than ‘general’. Even if GPs in competitive primary care systems wish to maximise the expected utility of insurees, information on the patient value of alternative treatments is costly, and clinicians have little incentive to invest in cost-effectiveness information if their decisions are imperfectly observed by the insurer. Instead, to compete for patients, the clinician selects the treatment offering the greatest benefit.
Individuals may become mildly or severely ill. A ‘single-payer’ HA funds treatments by GPs and specialists. However, the evidence on which a specialist decides whether or not to use a costly diagnostic test, and GP effort to treat, is unobserved by the HA. In view of the specialist tendency to purchase excess diagnostics in order to compete in providing patient gross health gain, the HA trains the GP to refer to maximise the expected utility of registered patients. The GP gathers patient information to estimate severity and uses it to decide on referrals, recognising also the distortion in specialist behaviour. If, for some patients, GP information is valuable to economise on diagnostic spending, this is possible only if a patient is not referred. We discuss assumptions under which there exists an interior solution, in which a GP acting as an imperfect agent of the insurer treats some ill patients and refers the others. We discuss the consequence of increasing the supply of GPs, and reducing their local monopoly power, for patient welfare, referrals and costs/taxes.
Increasing the market supply of GPs results in fewer patients per GP. This reduces the loss of utility from complying to a welfare-maximising professional norm that requires that GPs treat more patients to refer a smaller proportion. It thereby increases the expected health gain of insurees, while reducing the demand for specialists. In contrast, GPs who are ‘altruistic clinicians’ will, given the absence of fees for most NHS GP services, refer all patients to specialists regardless of GP supply. In this model, GP referrals are unaffected by offering patients a second GP opinion, if the second opinion is obtained from a new GP provider and not an adjudicator without the responsibilty to treat.
‘Gatekeeping’ is a feature of primary care systems in various countries, including Scandinavian countries and the UK, and, as Glied76 explains, in US HMOs, there is little evidence of the effect of the impact of gatekeeping or increasing the supply of GPs. Gulliford,77 in a cross-sectional study of 99 UK HAs, finds that an increased supply of GPs is associated with lower hospital admissions for both chronic and acute conditions. Harris et al. ,78 in a cross-sectional study of 68 English practices, find little evidence that GP supply influences emergency admissions. Baicker and Chandra79 and Chernew et al. 62 find that US Medicare reimbursement is lower in markets with a higher percentage of primary care physicians. Wright and Ricketts80 show that inpatient admissions are lower in those US areas with a higher density of GPs. There is evidence that financial incentives may influence GP referrals and admissions, as with GP fundholding, for example, in Dusheiko et al. 81 The recent literature (e.g. de Bruin et al. ,82 Carroll and Dowling83) focuses on the impact of primary care disease management programmes on health-care expenditure, finding that the cost saving is small. Improved primary care may not necessarily result in fewer admissions; indeed, more GPs may improve patient screening or access and thereby increase elective care (see Blustein et al. 84). Iversen and Ma69 present a model of how the degree of competition for patients may influence GP rate sof referral and, using Norwegian data, find no evidence that more GPs and competition reduces referrals to specialists. Fang and Rizzo85 show that the empirical influence of an increased supply of GPs on referrals is sensitive to whether or not GPs are self-employed or working in a HMO, in which an increased supply of GPs is found to reduce referrals.
Using panel data from the NHS in 2004/11, and instrumental variable (IV) methods to correct for the possible endogenous choice of location by GPs, we are able to estimate the effect of GP supply and the density of GP practices on hospital admissions. Using a method to address the problem of endogenous variables, proposed by Chernozhukov and Hansen,86 the effects of these variables at different points along distribution of hospital admissions is estimated by quantile regression. Panel data estimates suggest that increases in the local supply of GPs helps to explain the pattern of referrals and admissions in a way consistent with the hypothesis developed below (see A model of general practitioner gatekeeping, diagnosis and referrals).
The next section describes the model and hypotheses. The empirical strategy, data and results are then presented (see Economic strategy, Clinical data and Results). Robustness checks, including whether or not the findings are similar in less and more deprived areas, and quantile regression estimates of the effect of GP supply, are then discussed (see Robustness checks) and conclusions are then outlined.
Model of general practitoner gatekeeping, diagnosis and referrals
The economy has two sectors, a consumption good sector and a health-care sector. Labour is the only input. There is a population of n, all of whom are equally vulnerable to illness and equally productive in three jobs: hospital specialists, GPs and craftsmen. Hours of work are fixed except for GPs, who work the hours required to treat their patients, which they choose. Individual utility is an additive separable in income, leisure and health. Health care is produced using GPs and specialists, who produce an economic surplus in the form of a patient health gain net of cost. This has a value that depends on the match between the patient’s severity of illness and the treatment. The surplus from each illness–treatment pair is known with certainty, but the patient’s initial illness is uncertain. This uncertainty may be reduced by a diagnosis, which is exact and costs c if made by a specialist, and is inexact and free if made by a GP. A single-payer HA financed by a lump sum tax, t, funds services and chooses GP numbers and a GP capitation fee. Specialist and craftsmen employment is endogenous. Patients first contact a GP, who refers all or only a fraction of patients to a specialist.
Illness, treatment, utility and registration
Each period, otherwise identical persons become ill with probability θ. Illness is severe with probability q, and otherwise mild. Individuals do not recognise severity. Ill patients, and some well patients, contact their GP. There are two treatments with certain costs and gains: treatment 1 gives a large gain, net of treatment costs, z, to severely ill patients, and a small or negative net gain, z˜, to others; treatment 2 gives a small net gain, g, to all ill patients. The cost is the doctor’s fee.
General practitioners estimate patient severity, s, where a higher value of s denotes patients estimated to have a higher probability of severe illness. The estimate, s, has the probability density and distribution functions, f(s) and F(s), and support s ϵ (0,1) at all practices. GPs refer by forwarding this estimate to a specialist, if s exceeds a threshold, s*, where s* is a level of estimated severity, chosen by the GP. The unwell 0 < s < s* receive treatment 2 from their GP. Specialists treat only referred patients and know how to give an exact diagnostic test, as well as treatments 1 and 2. Specialists and GPs are equally productive in giving treatment 2. Test information is verifiable, and the specialist treats optimally: treatment 1 to those with severe illness and treatment 2 to those with mild illness. The information used by a specialist to decide to test a patient includes both GP and specialist views about the patient and is not verifiable. The markets for specialist diagnostic and treatment services are competitive, with prices reflecting specialist wages. To compete for patients, specialists maximise patient health gain, and so all referred partients are tested.
If a GP uses a threshold, s*, the probability that a patient is treated by the GP is F(s*); if s* = 0, all are referred, F(0) = 0; and, similarly, F(1) = 1. GPs choose s* to maximise their objective function and are assumed to know treatment costs and benefits and specialist behaviour. s* is not observable for each GP but it can be calculated from anonymous surveys. GPs know p(s), the probability that a patient with estimated severity s will be found to be severely ill following a diagnostic test. Assuming that GP estimates are not perverse, the probability that a patient is diagnosed as severe after testing is non-decreasing in s, dp(s)/ds ≥ 0. If the GP’s estimate, s, is uninformative about severity, then p(s)=q,for all s. The variables s and p are positively correlated.
Single-period individual utility, U, is a linear function of exogenous wage income net of a lump sum tax, x – t, and expected health, net of a personal cost of using the health system, T, comprising time to register with a GP, and, if ill, acquire care. Hence:
where β denotes the monetary value of a unit increase in a health index. H0 is the exogenous pre-treatment level of health, and absolute health gain, G¯, depends positively on H0, and negatively on s*, the severity threshold at which GPs refer to specialists. This is because health care gives a larger gain to those most ill, and the more restrictive a GP is in referring patients, the lower the expected absolute gain, G¯. Individuals differ in terms of H0 and T. Uncertainty arises in initial health, H0. The costs and benefits of treatments conditional upon severity are certain.
The value of T differs between individuals. Those with a higher cost are less likely to register and to have low utility for one period if they become ill. Because everyone is insured, registration increases with the expected gross gain from health care, G¯: patients with a cost of registration less than G¯ register. Let T(N) be the total cost of system use for the N patients in an area, with least cost. The marginal cost of a registration for the Nth least costly is T′(N) (> 0), and T′> 0, because those with a higher cost register if the number registered, N, increases. Individuals register if:
which implies βG¯(H0,s*)≥T′(N), that is, the health gain offered locally is at least as large as the marginal registrant’s cost of use. The number registering, N, is given by T′−1{βG¯(s*)}, where s* is the GP threshold referral rate. Given that G′¯(s*)<0 (fewer referrals reduces gross health gain), and T′> 0, patient registration declines with a higher threshold, s*: dN/ds*< 0.
N = N(s*) where
General practitioners recognise that the number of registrants increases with their utility offer to ill patients, u(s*), which falls in value with increases in their referral threshold, s*.
Occupational mobility and the general practitioners per capita fee
Individuals live in one of many identical areas, each of which has one GP practice and an identical number of GPs. General practitioners are partners and each practice is a local monopoly. HAs pay practices a capitation fee of r per registered patient.
General practitioners have λN(s*) registered patients, where λ is a parameter to capture shifts in the market supply of GPs and is inversely proportional to the supply of GPs. Each period, θλN of each GP’s patients become ill; of these, θλN(s*)F(s*) are treated by the GP, and each treatment 2 takes a fixed number, k, of units of time. Hence, total GP leisure time, L, is, T – kθλN(s*)F(s*), where T is total time available each period. GP income, y, is r, per listed patient, £rλN(s*). We assume that GP utility, V, is linear in income and leisure; thus, V = rλN + β(T – λNkθs). If workers do not earn a surplus in employment, w = β, and to simplify the discussion of economic surplus in this economy, we make this assumption. If workers are substitutable between, and indifferent to, occupation, then we may write utility in other jobs as wT. The HA chooses the payment per registrant, r, such that,
The capitation fee increases with the proportion of patients that the GP treats, F(s*), the wage elsewhere, w, and the time supplied per patient, k. If s is uniformly distributed, f(s) = 1, and F(s*) = s*, in which case r = kwθs*. This is proportionately less than kw, the specialist payment for treatment 2 by θs*, which is the proportion of registrants who become ill and are treated by the GP. This reflects the assumption that GPs and specialists are equally productive in giving treatment 2.
Expected net health gain and the referral threshold
A crucial feature of this problem is that the net health gain from each illness–treatment pair is constant and known, and efficiency is determined by how well the GP’s choice of referral threshold, s*, gives an efficient choice of diagnostic matching of illness to treatment. The expected health gain net of cost for a registered patient of a GP who uses referral threshold s* is G(s*), where:
where g is the gross health benefit of treatment 2. Because the only work of the GP is the cost of giving treatment 2, the per capita cost r is equal to the costs of giving treatment 2. This may be written as:
The cost of treatment 2, if provided by a specialist, is (g¯−g) and
Given that, from Equation 6, rθ–1 = kwF(s), these terms cancel and the expression for θ–1G simplifies to:
where g, c and z are exogenous, and GC< 0, Gg > 0, GZ > 0. The term (z – g) is the incremental net health gain for severely ill patients from treatment 1 compared to treatment 2.
From Equation 11, net health gain G(s*) has three parts: (1) a minimum health gain of (g – c) for mildly ill patients who are given treatment 2 by the specialist after a diagnostic test; (2) the saved diagnostic costs, cF(s*), from those given treatment 2 by the GP; and (3) the extra expected health gain for patients who are referred, found to be severely ill and given treatment 1 by the specialist,
Increasing s* has two effects on G(s*): lower diagnostic costs and fewer severely ill patients receiving the greater benefits of treatment 1.
If no patients are referred, then s* = 1 and F(1) = 1. Hence, from Equation 6, G(s* = 1) = g. If all are referred then s* = 0, F(s* = 0) = 0 and G(s* = 0) = (g – c) + (z – g)q. Thus, if q(z – g) > c, a policy to ‘refer all’ followed by specialist diagnosis increases health gain more than one of ‘no referrals’. This requires that the expected health gain from referral exceeds the diagnostic cost. This is more likely the greater the probability of severe illness, and the greater the relative benefit of treatment 1, and the lower are specialty diagnostic costs. Diagnosis of those referred gives greater patient gain than treating all with treatment 1 if c<(g−z˜)(1−q)/(1+q). For this condition to hold, we assume that the severe form of the disease is sufficiently rare.
The change in expected health gain from a marginal increase in the referral threshold s*, thereby reducing referrals, is given by differentiating G(s*) in Equation 11:
Because f(s) is positive, sign (dG/ds*) is given by sign [c –(z – g)p(s*)]. This sign is independent of s* if p(s*), the probability that a ‘marginal’ referred patient is tested to be severely ill, is independent of the threshold, s*. This occurs if GPs cannot prioritise the severely ill and p(s*) = q, ∀s*, and reducing referrals will not increase the mean severity of those referred. In this case, to maximise health gain, either c < (z – g)q, in which case all are referred, or c > (z – g)q and all are treated by the GP. Thus, if p(s*) = q, s* = 1 or 0.
Proposition 1
-
A necessary condition for an internal (gatekeeping) equilibrium, at which some, but not all, ill patients are referred to a specialist, 0 < s* < 1, is that GPs are able to identify patients with a higher probability of being severely ill (p is increasing in s) and thereby refer a greater fraction of severely ill patients than q.
-
If GPs are able to prioritise the severely ill (dp(s)/ds > 0), and if f(s) (patient severity) is uniformly distributed, then from Equation 13 Sign(d2G/ds*2) = Sign[–(z – g)dp/ds*] < 0 so that G(s*) is concave. G(s*) has a maximum when the health maximising referral threshold, s* satisfies p(s*) = c/(z – g), so that the referral threshold is s* = p–1(c/(z – g)). Registered patient health is maximised if the GP refers if s > p–1[c/(z – g)], and treats otherwise.
The health-maximising share of patients referred, s*, diminishes with diagnostic cost, c, and increases with, z – g, the incremental benefit of specialist treatment relative to a generic treatment, for the severely ill.
Result (1) above illlustrates how obtaining efficiency gains from limiting some patients access requires the GP to be able to assess the likelihood of patient severity; and (2) provides assumptions under which health gain is concave in the referral rate. The intuition for concavity is straightforward; at low values of s*, only those with low probabilities of severe illness are referred and, if referrals are reduced, these have the least loss of expected health gain from not being exactly tested. At higher values of s*, the forgone expected health gain, if s* increases, concerns those with higher probabilities of being severely ill, so that any gain from limiting access will be smaller. From Equation 13, a sufficient condition for gatekeeping to offer higher welfare is that p(0) = 0, in which case, (dG/ds*) > 0, at s* = 0.
Patient utility
Expected utility for a registered patient, E(U), is given by:
Health is measured with 1 denoting full health, a*(< 1) health when mildly ill pre treatment, and a(< a*) is health when severely ill pre treatment; g is health gain for those given treatment 2, and g1 is health gain if given treatment 1 when severely ill. From the expression for E(U), all mildly ill patients receive treatment 2, and referral affects the utility only of those who are severely ill.
The public budget constraint is that nt = vN. The lump sum tax, t, is of equal value to the funding cost per registrant, multiplied by the fraction of population registered. Hence, the lump sum tax = v(s*)N(s*)/n, where v(s*) = Wθ[k1 + q(1 – s*)(k2 – k1) + c0(1 – s*)] and dv/ds* < 0.
The lump sum tax t decreases with s*, because N and v are both negative functions of s*.
Social welfare optimium
Social welfare, W, is the sum of the welfare of N registered and (n – N) non-registered patients, constrained by the production of health gain net of GP and specialist cost, G, and the supply of patients, N. At a welfare optimum, the population are partitioned to maximise economic surplus – production of net health gain – into (1) those registered with a GP, N, and (2) the proportion of those registered and ill who are referred to a specialist, s*. This determines GP and specialist employment and, implicitly, craftsmen employment.
Thus:
If we (1) use the relationship βE(G¯)=βG+v, where v is the cost of health inputs per registrant, and (2) the public budget constraint nt = Nv, in the maximand, this simplifies to:
The economic surplus produced by the economy is the expected health gain net of registered patients net of clinician costs, G, and net of patients’ cost of using the health system, T.
This implies:
Because β, H0 and N are positive, this implies that at a social optimum:
Equations 18 and 20 determine the optimal referral threshold, se*, and the number of patients who register with GPs, Ne. From Equation 20, se* is chosen to maximise the expected health gain net of costs. The optimal level of registrations, Ne, is that at which the cost of using health care for the marginal registrant is equal to the maximum expected health gain asociated with se*. If GPs set a threshold for referrals below or above se*, this reduces expected health gain and thereby also reduces GP registrations. If there is free registration, then too many patients register because insurance is costless.
Equilibrium referrals with gatekeeping in a single-payer system
Now suppose that GPs in a single-payer system are trained by the HA to maximise the health gain of the representative registered patient, E(U), but remain imperfect agents. In both cases, the GP must have some degree of monoply power, otherwise solely meeting the objectives of sick patients would be necessary to retain patients. To do this the HA invests in (1) influencing the preferences of the GP towards population health, rather than the immediate patient, and (2) GP knowledge of cost-effectiveness. We first consider the GP maximisation problem for a given supply of GPs, before discussing the HA problem to select the optimal level of GPs.
The timing of events in each period is as follows. The HA chooses the market supply of GPs, where λ is the inverse of that supply, a registrant fee, r, and a lump sum tax, t. GPs choose a minimum level of severity, s*, above which they refer. Patients choose whether or not to register. The GP costlessly diagnoses the well. Of those who are ill, the GP either treats or refers. The number of patients diagnosed or treated by the individual GP is not verifiable, but survey data can give economy-level estimates for policy design.
The choice of the referral threshold, s*
General practitioners’ objectives are (1) their own utility, V, which is a function of their income and leisure; and (2) the expected health gain of the representative registrant, G. A GP is assumed to choose the referral threshold, s*, to maximise V¯, where the arguments of V encompass both gatekeepers (α > 0, Ψ = 0) and ‘altruistic clinicians’, who care about the health gain of their ill patients and their own utility (α = 0, Ψ > 0):
where α, β, ψ ≥ 0, dN(s*)/ds* ≤ 0, dG(s*)/ds*≶ 0, du(s*)/ds* < 0.
The inverse of the number of GPs, λ, and a registrant fee, r, are chosen by the HA. A higher referral threshold, s*, (1) reduces N(s*), and hence income from registrants, and (2) has an ambiguous effect on GP leisure by reducing the number of patients but increasing the share of patients treated by the GP. An increase in s* increases the value of the maximand by increasing representative patient health, G(s*), while reducing u(s*), the utility of ill patients.
We can show that the value of s* chosen by the GP is less than the health gain-maximising referral level, p–1(c/b). From the GP’s maximisation problem (Equation 21), the first-order condition for s* is given by:
If a GP maximises a weighted sum of his or her personal utility and the expected health gain of the representative patient (Ψ = 0 and α > 0), then rearranging Equation 21 gives,
Equation 23 describes the trade-off that determines s*, the GP’s referral rate, where the LHS gives the GP’s value of an increase in patient health gain attributable to a marginal reduction in the referral rate. The first term on the RHS of Equation 23 gives the forgone utility of leisure following an increase in the referral threshold, s*, so that referrals are reduced and GPs work longer work hours treating patients. The second term is the change in GP personal utility attributable to a smaller patient list, caused by an increase in s*. This second term is zero if the fee per patient is adjusted by the HA to ensure that GPs are paid as well as specialists, r = βkθF(s*). In this case, the GP is indifferent to changes in the patient list. Hence, G’ is determined by the value placed by the GP on the leisure forgone as a result of performing more treatments (making fewer referrals), which is positive. Hence, at the gatekeeping equilibrium, G’(s*) > 0. This implies, given concavity of G, that s* < se*, the social optimum, so that referrals exceed the social optimum and too few patients are treated in primary care. Thus, we have proposition 2, below.
Proposition 2
The gatekeeping general practitioner referral threshold, s*, is less than se*, the threshold that maximises expected health gain
Why are fewer patients treated in primary care than the number that maximises expected health gain? The GP is an imperfect agent of the HA, and, although willing to treat some patients who wish to be referred, also enjoys the leisure from not treating at less than the socially optimal level. Because s* is less than se*, expected health gain is also lower, so that registration is lower than the socially optimal level.
If specialist moral hazard to diagnose as precisely as possible were absent, the undersupply of effort to treat by the GP does not constrain the equilibrium: the HA would train GPs not to gatekeep, but rather to pass on relevant information to the specialist, who acts in the insuree’s interest, so that the information constrained social optimum is obtained.
The laissez-faire benchmark
The laissez-faire (LF) outcome is characterised by (1) the absence of a HA, so that GPs are not trained to regard the insured as their principal; and (2) a market determined number of GPs. Informational imperfections are as in the single-payer model.
Training to gatekeep is unlikely in a LF economy with competing insurance companies and GPs. Small insurance companies are not incentivised to supply training because each GP works for patients funded by many insurance companies, so that the returns to an insurance company from training are minimal. GPs whose decisions are not closely monitored and rewarded by insurance companies are not incentivised to buy such training. Working as an imperfect agent of the patient leads to all patients being referred, so that s* = 0. Treatment activity by GPs ceases and their work is replaced by a signpost to a specialist. GP income and employment is zero; there are more specialists in a system that provides a larger gross health gain but at a higher cost, and less health gain net of cost. We have given assumptions under which expected insuree health gain is lower if s* = 0, and GPs are replaced with signposts to specialists. A sufficient condition for a gatekeeper to offer higher welfare is that p(0) = 0.
Comparative statics and the welfare economics of general practitioner employment
An increase in the supply of general practitioners
In this model the HA chooses the supply of GPs. Additional GPs are allocated to existing practices, which share patients between a larger number of GPs. This reduces registered patients per GP, λN(s), and is captured by a reduction in λ. The comparative static results of increasing both GP supply and the elasticity of practice demand for registrations can be found from Equation 21. If the GP refers as a gatekeeper, maximising health gain for the representative patient Ψ = 0 and α > 0), then assuming GP choice of s* is a maximum (Vss < 0), it follows from totally differentiating Equation 21 that:
-
This result implies that an increase in the supply of GPs which reduces patient load, (λ) will increase the referral threshold, s*, thereby reducing referrals and increasing GP treatments. Given fewer referrals, the number of patients diagnosed by specialists to be severely ill, and given treatment 1, will also be reduced, as will the demand for specialists. However, the welfare of registered patients increases as the GP list falls, because s*e > s*. The policy to increase the expected utility of registered patients is therefore in tension with the contemperaneous interest of ill patients. This is because the costs of health care are shared, but the benefits are received without charge by those sick at a point in time.
-
Insofar as a GP’s per capita fee is adjusted to hold constant GP utility at the level of specialists, a greater elasticity of patient supply has no effect on referrals or welfare.
Discussion
What is the intuitive reason that an increase in the supply of GPs, and hence fewer patients per GP, increases s*, and reduces referrals? Essentially, having fewer patients reduces the loss of utility that follows if s* is increased towards the referral rate that maximises health gain. Maximising health gain for the representative patient requires that a GP limits specialist access and treats more patients than if income and leisure were his or her only concern. This requires that he or she accepts less income and leisure than at maximum GP utility. A GP with fewer patients has a smaller loss of capita income and leisure when treating a larger fraction of his or her patients than is utility maximising; and, because the cost of more closely conforming to his or her professional ethic of a ‘health maximising GP’ is lower, he or she is willing to treat a higher proportion of patients. By increasing the referral threshold, s*, a GP reduces patients’ gross health gain, because more referrals always add to health gain, but increases health gain net of costs, and insuree utility. In this model it is optimal for GPs to have a minimal list of patients, and this may be constrained at a plausible level by a requirement for a minimum daily income or leisure hours, at a social optimum. The effect of reducing λ on GP income is ambiguous.
Why does a more elastic demand for registration have no effect on s* and patient welfare?
Insofar as changes to s* lead to larger changes in employment hours if there is a greater elasticity, it might be thought that greater elasticity of patient demand makes following the professional ethic to be concerned with the utility of the representative registrant more costly for the GP. However, the constraint that the capita fee is adjusted so that GPs are always offered a level of utility equal to the exogenous utility level of specialists ensures that GPs are indifferent to the changes in hours and are thus unaffected by larger variations in patient demand when choosing s* with an elastic supply of patients.
General practitioner practice density
Consider now whether or not having fewer GP practices, holding constant the system supply of GPs, will influence hospital admissions. In the model of GP choice we assume that per capita revenues are paid to the GP. This is necessarily the case for practices with one GP, but it is commonplace to pay partners by sharing practice revenue net of costs. In this case the marginal revenue of an extra patient for an individual GP in choosing his or her threshold, s*, and thus his or her referrals, in a practice of J GPs, is r/J. The GP’s leisure cost of treatment is unchanged. We can readily show in (Equation 23) that if we substitute r/J for r, then the referral threshold falls with increases in r, (ds*/dJ > 0). Thus, GPs at larger practices (higher J) choose an increased s*, closer to the social optimum. This reduces referrals and increases patient welfare. Intuitively, why do larger practices refer at lower, more efficient levels? A GP in a large practice has a smaller loss of registrants and expected personal income if he or she reduces referrals to comply with his or her professional ethic. This is because falls in GP per capita income from reducing referrals are shared. Given lower personal costs of reducing referrals towards the social optimum, GPs in larger practices refer less.
Econometric strategy
Our empirical strategy is to estimate a fixed-effects panel data model for three classes of hospital referrals/admissions (outpatients, elective and emergency) at LSOA level, controlling for a group of area-specific characteristics, and primary care variables. The model is the following:
where Fjt represents the number of outpatient referrals or hospital admissions (elective or emergency) per 1000 population resident at each LSOA (j) in each year. Xjt is a vector of socioeconomic characteristics that are time-varying at LSOA j in time t. It includes percentage of sex, age and ethnicity, and β is a vector of the slope effects of these variables.
The key explanatory variables that capture the supply of GP services in each year t, are a measure of both the number of GPs employed and FTE GP employment. Although the latter may be a more representative measure of local labour supply, unfortunately, FTE information is available only for GPs working in traditional practices. The term αGPjt represents this effect of the density of GPs for each 1000 population of the LSOA j in the PCT (p) in time t, or the GP FTE supply in PCT p in time t. Instead, ρGRjt represents the density of GP practices at time t in PCT p per 1000 of population. Both of these effects (αGPjt and ρGRjt) are estimated in models with LSOA fixed effects, so that each captures the influence of changes in the variable over time within a LSOA.
In addition, in some models we also control for certain other new models of delivering primary care services, namely walk in centres (WICs) and OOH services, that are labelled ‘other cost prescribing centres’. In each case we calculate density by dividing the number of each of type of provider by the local PCT population in 1000s. Because the geographic area of PCTs does not change over time the fixed LSOA effects control for large and small area PCTs, allowing the density variables to capture the average effects of within-LSOA changes in density of traditional practices, or WICs.
The terms zjt and djt capture measures of the urban and deprivation local area dummy variables. Finally, we control for time (µt) with year effects, disease prevalence (ωjp) and LSOA (σj) fixed effects. To avoid any possibility of the endogenous recording of conditions following hospital admission, we use the prevalence data for the year prior to that for the year of study for hospital admissions. The inclusion of these effects allows us to identify the impact of variations in primary care supply on the hospital admission at the LSOA area level. Our principal objective in this report is to measure how variations in the scale and concentration of GP services affects hospital admissions. εjt is a random error term, which is assumed to be normally distributed.
Identification and instrumental variables
There are several issues to address in the estimation of the model. The stock of headcount GPs and FTE GPs in each PCT may not be exogenous and may be correlated with unobserved positive demand shocks for health care. Thus, an increased supply of GPs may be correlated with unobserved demand factors that increase hospital admissions, even after controlling for the time-constant differences between areas and for socioeconomic factors.
However, there may be a negative bias to the estimates of the GP effects. GP location decisions are also affected by the GP remuneration system, and some types of payment are related to the mix of types of patient, the composition of which varies across areas. For example, payments are related to the age of patients and their deprivation levels, fee per item payments for such things as night visits for high risk groups, and payments for meeting quality targets. Thus, it is possible that there may be higher rewards per patient in areas with different health status. Hence, it is possible that GP supply could be positively or negatively associated with hospital admission and whether or not GP supply has an impact on it.
To control for this potential endogeneity we build two instruments for each of the two GP supply variables, capturing headcount numbers and FTE. For the headcount GPs we follow the methodology proposed in 1991 by Altonji and Card,87 which recognises the salience of immigrant enclaves and uses instruments for recent flows of country-specific immigration with the current national flow of migrants to the USA and the distribution of country-specific destinations of past migrants. The approach relies on the empirical observation that immigrants tend to cluster in cities where prior immigrants from their country of origin have already settled. Thus, the ‘network’ instrument achieves identification, in part, by leveraging city-specific factors that pull immigrants to particular locations. Altonji and Card,87 Card88 and Card and Lewis89 have used this instrument to estimate a causal effect of immigration on the labour market outcomes of US natives.
This approach typically relies on an IV that assigns different numbers of immigrants to each city in each year without influencing labour market outcomes in the city through any channel other than its impact on immigration flows. In this context we assume that we can use the same instrument for our variable headcount GPs. The number of GPs located in a PCT over time are instrumented by the share of GPs located in this area in 1980 multiplied by the total number of GPs in year t. Specifically, let GPpt be the total population of GPs resident in the PCT p in year t, and SGPp1980 the share of that GPs resident in PCT p in year 1980. The share of GPs in 1980 in area p is calculated as:
We then construct the imputed stock of GP supply in PCT p in year t as follows:
We use this to forecast the supply of GPs in PCT p in year t as the instrument for the explanatory variable GPjt in the hospital admissions equations. For the FTE GPs we use as instruments the shares of male and female GPs per 1000 of population in PCT p in time t. We observe that the percentage of time allocation by sex is different: women prefer to work fewer hours than men. This instrument is correlated with the hours of work but is not correlated with the number of hospital admissions.
Our analysis is performed with a two-stage least squares model (2SLS), in which we correct the standard errors in order to control for heteroscedasticity. Evidence for GP supply using both headcount and FTE data is provided in order to give a comprehensive account.
Data
Clinical data
The HES provides information concerning all inpatients and outpatients admitted to NHS hospitals from 1989 to 1990 onwards. It includes private patients treated in NHS hospitals, patients resident outside England and care delivered by treatment centres (TCs) (including those in the independent sector) funded by the NHS. Each patient record contains detailed information, including clinical information, patient characteristics, such as age and sex, and administrative and location information, such as method of admission and the geography of treatment and residence. Given that our focus is on GP influence upon admissions, our analysis concerns only the ‘first admission’ to the hospital, which the GP is most likely to influence, rather than admissions for continuing treatments.
To explain referrals and admissions, it is important to control for prevalence. The Quality and Outcomes Framework (QOF) provides valuable clinical information concerning prevalence for 22 specific diseases in 2013, which influenced the demand for hospital admissions. QOF is a system to remunerate general practices for providing good-quality care to their patients, and to help fund work to further improve the quality of health care delivered. Prevalence data are used within QOF to calculate points and payments within each of the clinical domain areas and provide a snapshot of the number of ill patients on the practice register, as a proportion of the total number of patients registered at the practice. In this study we consider just 11 clinical conditions, which are the clinical domains created for the year 2004. The QOF prevalence used in our analysis is the raw prevalence rates for 11 conditions, which means no account is taken of differences between populations in terms of their age or sex profiles or other factors that influence the prevalence of health conditions. The specific conditions used are coronary heart disease, left ventricular dysfunction, stroke and transient ischaemic attack, hypertension, diabetes mellitus, chronic obstructive pulmonary disease, epilepsy, hypothyroidism, cancer, mental health and asthma. The data on prevalence of the clinical conditions are grouped at PCT level. The data cover almost all GP practices in England and are extracted from disease registers submitted to the national Quality Management and Analysis System (QMAS). The prevalence of all illnesses increased during the refereed period, except for epilepsy and asthma. However, at any given time, many of those who have a disease have not received a diagnosis. By the end of the period, illness prevalence is representative of that at England level and, by that time point, 90% of the population is registered with a GP. However, there could be under-reporting bias, especially in the early years.
Lower-layer super output area and deprivation controls
Anonymous patient records were extracted by financial year (1 April to 31 March) and aggregated at LSOA. LSOAs are geographic areas developed by the Office for National Statistics (ONS). LSOAs on average (mean) contain a population of 1500 persons and 650 households. In 2011 there were 32,482 LSOAs in England. We use ONS mid-year population estimates to calculate LSOA populations, and these data are linked to those of individual characteristics at LSOA level, such as the percentage by sex, ethnicity and age. Small areas are mapped to 151 PCTs locked at 2011 boundary configurations. From 1 October 2006, 303 PCTs merged into 151 PCTs and then later into CCGs. Socioeconomic status at LSOA level is measured using the deprivation domain of the English Indices of Deprivation (see Noble et al. 90) The index of deprivation combines information regarding the proportion of individuals living in low-income households with indices of crime, education, employment rates, health status and environmental quality. We exclude the health component of the deprivation index to avoid potential endogeneity, but use controls for 10 levels of the adjusted index of deprivation.
The supply of general practitioners, the size of practices and hospital admissions
It is critical for this study to measure carefully the supply of GP services. To do this, HES data are linked with the ‘General Medical Practices Exeter Payments’ data and the ‘Practitioners of NHS Connecting for Health’ data for the period 2004/11. The Exeter data concern current GPs in traditional GP practices and give both headcount and FTE information. The NHS Connecting for Health data include all prescribing GPs, including employees of non-traditional providers such as WICs, but give only headcount and not hours worked (FTE) information (there is not currently a collection that provides FTE information on all GP providers). To address these data issues, the study combines the use of both FTE and headcount data to check the robustness of the results to alternative data sources.
To recognise both traditional and new primary care delivery models, practice density at PCT level is measured using two variables: (1) the number of traditional GP practices per 1000 population (density of practices); and (2) the total number of WICs and OOH services per 1000 population. The data for both of these series are supplied by the Information Centre as part of the information on Prescribing Centres.
There are about 10,100 general practices in UK, and patients wishing to receive NHS primary care must register with a single practice. In 2011 there were approximately 50 GP practices in a typical PCT of 300,000 persons, with PCTs on average having 4.3 FTE GPs per practice. The mean number of GPs per practice varies considerably between PCTs, with some as low as 3 and others as high as 7. Each practice is contracted to provide care for patients between 08.30 and 18.30 from Monday to Friday. GPs may be partners who share ownership of a practice, or salaried in receipt of a wage for a specified number of sessions/hours. The payments from the NHS to GPs are made to the practice and not to the individual. The funding is a formula based on population need characteristics of the patients on the GP’s list and is independent of the number of elective or emergency admissions that patients incur, or the treatments given by GPs. Average income before tax for contractor GPs in 2010/11 was about £99,000. Since 2004, GPs may choose whether to provide 24-hour care or to transfer responsibility for OOH services to PCTs, now CCGs. The OOH service operates from 18.30 to 08.00 on weekdays and all day at weekends.
We have shown that referrals and elective admissions may decline with GP supply but have not discussed emergency care. A practice will aim to arrange patient care using as little as possible emergency care, whereas the increased use of elective care may be a consequence of the overall objective of providing high-quality care. However, patients may still require some unscheduled care. A greater supply of GPs may increase patient access to and use of primary care, including that use of OOH services, rather than emergency care. Nevertheless, it is unclear how far more GPs reduce emergency care use if the organisation of primary care is not directed towards OOH provision. For completeness, we discuss the empirical findings below for this case, as well as for referrals and elective care. Table 32 contains descriptions and sources of the data used in the following analysis.
| Name of variable | Description | Data source |
|---|---|---|
| Emergency | Total first admissions per 1000 population at LSOA level in the financial year: emergency | HES |
| Elective | Total first admissions per 1000 population at LSOA level in the financial year: inpatients | HES |
| Outpatients | Total first admissions per 1000 population at LSOA level in the financial year: outpatients | HES |
| Female population (%) | Percentage of female population at LSOA level | ONS |
| Female population aged ≥ 60 years (%) | Percentage of female population aged ≥ 60 years at LSOA level | ONS |
| Male population aged ≥ 65 years (%) | Percentage of male population aged ≥ 65 years at LSOA level | ONS |
| Black ethnicity (%) | Percentage of black ethnicity at PCT level | ONS |
| Asian ethnicity (%) | Percentage of Asian population at PCT level | ONS |
| Headcount GPs density at PCT per 1000 population | Number of GPs per 1000 population at PCT level | HSCIC |
| Ratio of practices at PCT per 1000 population | Number of GP practices at PCT per 1000 population | HSCIC |
| FTE GPs density at PCT per 1000 population | Number of GPs FTE per 1000 population at PCT level | HSCIC |
| GP practice density at PCT per 1000 population | Number of GP practices per 1000 population at PCT level | HSCIC |
| WIC and OOH density at PCT per 1000 population | WIC and OOH centres per 1000 population at PCT level | HSCIC |
| Revenue per head | HS expenditure per capita at PCT level | DH |
| Deprivation areas | Index of deprivation at LSOAs in 10 deciles | ONS |
| Prevalence diseases | Prevalence of specific diseases per 1000 population at PCT level from QOF | HSCIC |
Summary statistics
Table 33 provides a summary description of the variables used to study the period 2004/11. The three categories of hospital service (outpatient referrals, elective admissions and emergency admissions) all increase over time, with outpatient referrals increasing most rapidly. The mean proportion of the elderly in local populations increases slightly for both males and females over time. The mean PCT density of GPs per head increases by about 27% between 2004 and 2011; the mean PCT density of GP FTEs increases by about 11% between 2001 and 2009 but then declines by 3% in the period 2009/11. The mean number of traditional GP practices per 1000 population is unchanged at one practice per 5000 persons. Mean age and ethnic population proportions have also experienced increases. The WICs and OOH services are primary care services that were started around 2005/7 and, as reported by Exeter data, remain few in number.
| Variable | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | Total |
|---|---|---|---|---|---|---|---|---|---|
| Elective per 1000 population (SD) | 114.92 (35.36) | 120.23 (36.70) | 124.02 (38.03) | 130.64 (37.99) | 138.78 (39.75) | 142.34 (40.13) | 145.19 (40.26) | 147.93 (43.36) | 133.01 (40.69) |
| Emergency per 1000 population (SD) | 116.33 (44.20) | 122.70 (45.66) | 123.18 (46.92) | 124.16 (48.17) | 132.20 (49.41) | 138.33 (51.59) | 141.30 (52.73) | 140.47 (52.04) | 129.83 (49.73) |
| Outpatients per 1000 population (SD) | 261.65 (79.27) | 294.42 (86.01) | 298.29 (93.87) | 321.53 (101.38) | 362.30 (132.89) | 400.18 (182.78) | 405.76 (239.71) | 411.86 (312.76) | 344.50 (181.26) |
| Female population, % (SD) | 51.04 (2.30) | 51.01 (2.31) | 50.98 (2.36) | 50.95 (2.48) | 50.92 (2.67) | 50.90 (2.85) | 50.87 (3.11) | 50.97 (2.28) | 50.96 (2.56) |
| Female population aged ≥ 60 years, % (SD) | 11.78 (4.59) | 11.83 (4.61) | 11.90 (4.65) | 12.10 (4.73) | 12.28 (4.82) | 12.43 (4.88) | 12.38 (4.82) | 12.56 (4.94) | 12.16 (4.77) |
| Male population aged ≥ 65 years, % (SD) | 6.87 (2.71) | 6.92 (2.75) | 6.96 (2.80) | 7.02 (2.86) | 7.14 (2.94) | 7.28 (3.04) | 7.42 (3.15) | 7.27 (3.06) | 7.11 (2.92) |
| Black ethnicity, % (SD) | 2.60 (4.40) | 2.67 (4.26) | 2.72 (4.12) | 2.78 (3.99) | 2.84 (3.87) | 2.88 (3.75) | 2.93 (3.64) | 2.91 (3.29) | 2.79 (3.93) |
| Asian ethnicity, % (SD) | 5.65 (6.89) | 5.88 (6.80) | 6.11 (6.71) | 6.37 (6.66) | 6.58 (6.57) | 6.78 (6.50) | 7.01 (6.46) | 7.12 (6.08) | 6.44 (6.61) |
| Revenue per head (SD) | 1.00 (0.69) | 1.00 (0.69) | 1.00 (0.68) | 1.00 (0.68) | 1.00 (0.13) | 0.99 (0.13) | 1.00 (0.14) | 1.00 (0.14) | 1.00 (0.49) |
| Headcount GPs density at PCT per 1000 population (SD) | 0.83 (0.10) | 0.87 (0.10) | 0.89 (0.11) | 0.93 (0.12) | 0.96 (0.13) | 1.00 (0.13) | 1.04 (0.17) | 1.06 (0.18) | 0.95 (0.15) |
| FTE GPs density at PCT per 1000 population (SD) | 0.61 (0.07) | 0.62 (0.07) | 0.65 (0.08) | 0.64 (0.08) | 0.66 (0.08) | 0.68 (0.08) | 0.68 (0.10) | 0.67 (0.09) | 0.65 (0.09) |
| General practices density at PCT per 1000 population (SD)a | 0.17 (0.04) | 0.17 (0.04) | 0.16 (0.04) | 0.16 (0.04) | 0.16 (0.04) | 0.16 (0.04) | 0.16 (0.04) | 0.16 (0.04) | 0.16 (0.04) |
| WIC and OOH density at PCT per 1000 population (SD)b | 0.00 (0.01) | 0.01 (0.01) | 0.01 (0.01) | 0.01 (0.01) | 0.01 (0.01) | 0.01 (0.01) | 0.01 (0.01) | 0.01 (0.01) | 0.01 (0.01) |
| n | 32,482 | 32,482 | 32,482 | 32,482 | 32,482 | 32,482 | 32,482 | 32,482 | 259,856 |
Figure 35 describes the distribution of mean GP practice size by PCT in 2004 and 2011. This highlights both the wide variation of mean PCT practice size and the increasing mean PCT practice size over this period. The additional GPs in traditional practices have mostly joined existing general practices, which has increased their mean size. The number of single-handed GPs is falling as older GPs retire, and is down by 28% since 2004. 91
FIGURE 35.
Distribution of mean GP practice size by PCT in 2004 and 2011.
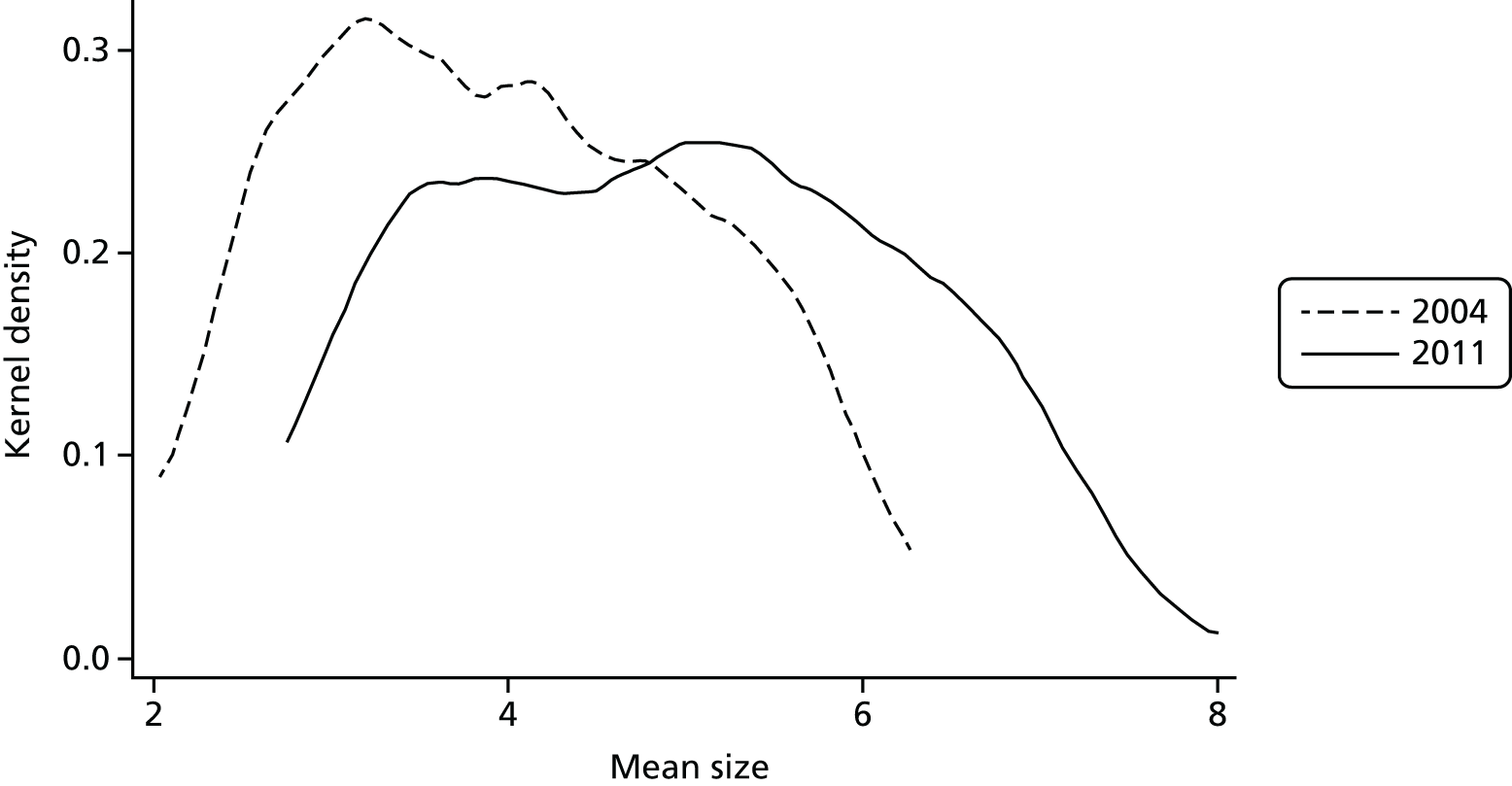
Figure 36 gives a regional breakdown of the change in admissions by PCT in the period 2004/11 per 1000 population with the south-west, East Anglia and the north-west having smaller increases.
FIGURE 36.
Change in hospital admissions between 2004 and 2011 by PCT per 1000 population. Contains OS data © Crown copyright and database right 2016.
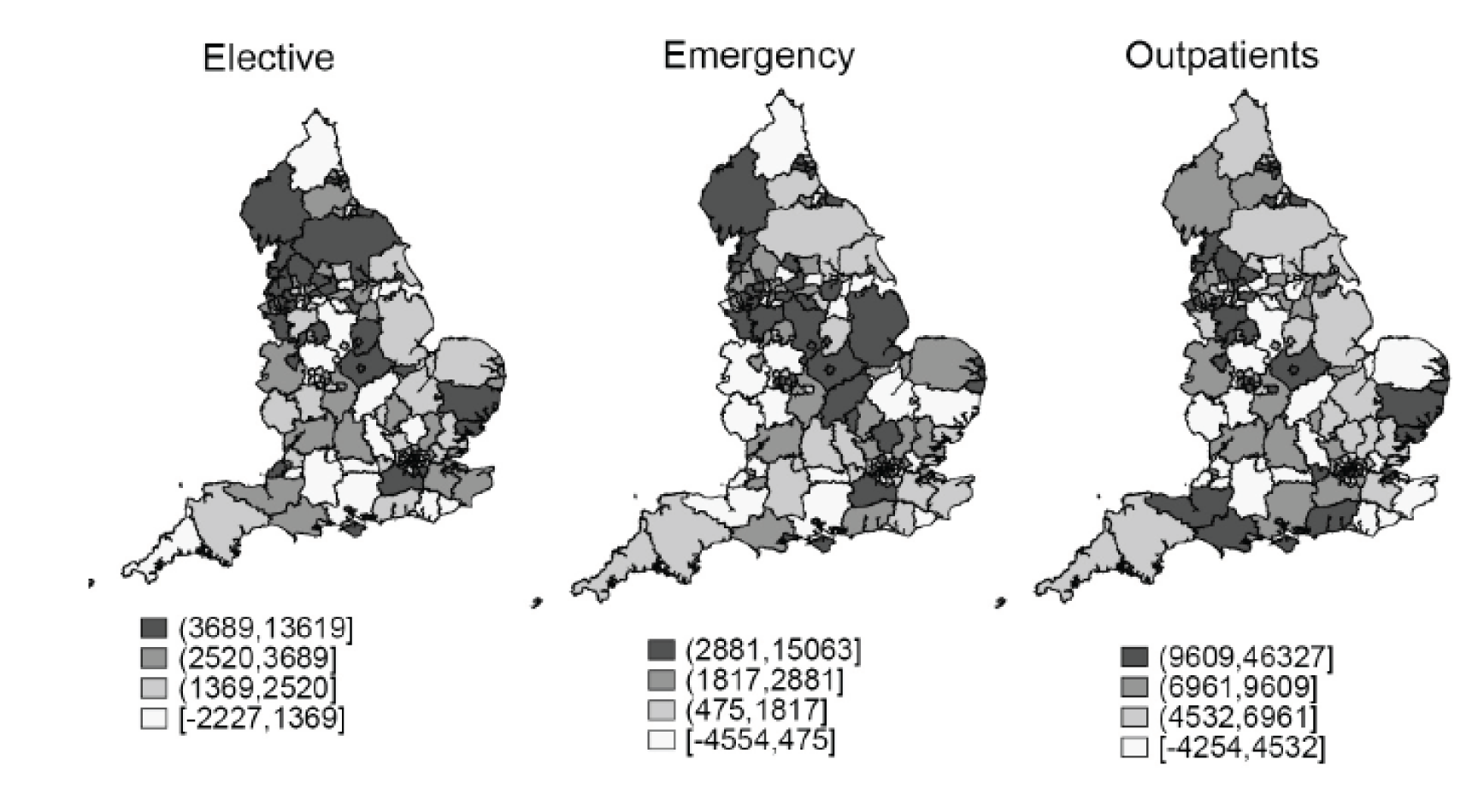
Results
For each type of hospital admission (outpatient referral, elective and emergency), two sets of results are presented corresponding to the two GP supply variables per head of PCT population: (1) total GP headcount; and (2) FTE (hours) data. Each set of results also estimates the influence of the density of places of provision, which is measured using the number of GP traditional practices per head of population, and also the density of other ‘prescribing cost centres’, which includes the recent innovations of WICs and OOH service centres. Estimates for both ordinary least sqaures (OLS) and 2SLS are given, the latter of which allow GP density to be endogenous and estimated using IV methods, as described above (see Identification and instrumental variables).
Outpatient and elective admissions
Tables 34 and 35 show the results for the estimation of referrals and elective admissions, respectively. The influence of an increase in GP density on elective admissions is consistently negative across the models for both headcount and FTE data. This consistency is robust to alternative specifications for the prevalence of local area disease. Overall, allowing for the endogenous choice of GP location increases this measured effect, but it also holds in OLS estimates. The parameter is larger in the headcount data than in the FTE data, but significant in both. Consider a GP with a patient list of 1200 and who can expect, on average, 177 elective admissions each year, including day cases but not maternity admissions. The 2SLS FTE results estimate that adding an extra 0.2 FTE GP to the practice may reduce this by in the order of 2–3 elective admissions per annum. Thus, although statistically significant, the effect by itself could not justify a 0.2 FTE GP appointment. Nevertheless, because GPs provide services in addition to reducing elective admissions, this cost saving contributes to the overall case to make such an appointment.
| Variable, coefficient (SE) | GPs | |||||||
|---|---|---|---|---|---|---|---|---|
| Headcounts | FTE | |||||||
| OLS | 2SLS | OLS | 2SLS | |||||
| Female population (%) | 2.398*** (0.731) | 2.421*** (0.738) | 2.339*** (0.7) | 2.360*** (0.689) | 2.408*** (0.717) | 2.423*** (0.726) | 2.421*** (0.72) | 2.439*** (0.728) |
| Female population aged ≥ 60 years (%) | 2.011*** (0.648) | 1.947*** (0.625) | 1.954*** (0.673) | 1.946*** (0.628) | 2.017*** (0.659) | 1.959*** (0.626) | 2.068*** (0.643) | 1.996*** (0.616) |
| Male population aged ≥ 65 years (%) | 8.098* (4.571) | 8.013* (4.557) | 8.111* (4.569) | 8.087* (4.643) | 8.097* (4.577) | 8.001* (4.581) | 8.086* (4.567) | 7.951* (4.559) |
| Black ethnicity (%) | –4.406*** (1.265) | –5.493*** (1.242) | –3.384* (2.045) | –4.028 (2.855) | –4.617*** (1.208) | –5.401*** (1.168) | –4.452*** (1.223) | –5.367*** (1.172) |
| Asian ethnicity (%) | 3.229** (1.361) | 1.915 (1.203) | 1.309 (2.099) | 0.655 (2.161) | 3.545*** (1.21) | 1.922* (1.061) | 4.090*** (1.255) | 2.149** (1.063) |
| Revenue per head | –1.694 (5.411) | –1.763 (5.228) | –0.661 (4.673) | –0.206 (3.575) | –1.89 (5.342) | –1.747 (5.156) | –1.9 (5.287) | –1.956 (5.157) |
| GPs density PCT per 1000 population | 11.63 (21.521) | –3.762 (20.977) | 72.335 (71.025) | 64.501 (105.226) | 3.799 (29.373) | –18.808 (32.947) | –35.766 (31.222) | –74.863** (36.48) |
| General practice density PCT per 1000 population | 299.142*** (108.423) | 82.005 (335.012) | 329.321** (143.107) | 454.936*** (125.128) | ||||
| WIC–OOH density PCT per 1000 population | 1151.910* (683.615) | 1206.622 (764.381) | 1163.573* (683.954) | 1189.345* (693.532) | ||||
| n | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 |
| Year dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Prevalence diseases (QOF) | Y | Y | Y | Y | Y | Y | Y | Y |
| Urban dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Deprivation dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Variable, coefficient (SE) | GPs | |||||||
|---|---|---|---|---|---|---|---|---|
| Headcounts | FTE | |||||||
| OLS | 2SLS | OLS | 2SLS | |||||
| Female population (%) | 0.345*** (0.083) | 0.348*** (0.083) | 0.330*** (0.082) | 0.334*** (0.08) | 0.324*** (0.084) | 0.325*** (0.084) | 0.326*** (0.084) | 0.328*** (0.084) |
| Female population aged ≥ 60 years (%) | 2.608*** (0.103) | 2.589*** (0.104) | 2.594*** (0.103) | 2.589*** (0.104) | 2.589*** (0.104) | 2.589*** (0.104) | 2.598*** (0.104) | 2.595*** (0.104) |
| Male population aged ≥ 65 years (%) | 3.289*** (0.174) | 3.265*** (0.172) | 3.292*** (0.174) | 3.282*** (0.17) | 3.293*** (0.176) | 3.293*** (0.173) | 3.291*** (0.175) | 3.285*** (0.172) |
| Black ethnicity (%) | –0.486* (0.259) | –0.717*** (0.269) | –0.234 (0.278) | –0.38 (0.357) | –0.121 (0.271) | –0.158 (0.271) | –0.09 (0.271) | –0.153 (0.274) |
| Asian ethnicity (%) | 1.966*** (0.413) | 1.713*** (0.471) | 1.493*** (0.43) | 1.423*** (0.433) | 1.293** (0.508) | 1.237** (0.567) | 1.394*** (0.498) | 1.273** (0.561) |
| Revenue per head | –2.008*** (0.679) | –2.170*** (0.661) | –1.753*** (0.674) | –1.812*** (0.633) | –1.641** (0.717) | –1.580** (0.705) | –1.643** (0.71) | –1.614** (0.701) |
| GP density PCT per 1000 population | –21.556*** (4.194) | –26.023*** (3.829) | –6.598 (4.724) | –10.317 (10.026) | –0.625 (3.752) | –0.99 (4.206) | –7.985** (3.766) | –9.980** (4.598) |
| General practice density PCT per 1000 population | 83.178*** (28.5) | 33.218 (53.421) | 2.621 (27.519) | 22.765 (30.416) | ||||
| WIC–OOH density PCT per 1000 population | 87.711 (57.892) | 100.299 (63.092) | 109.023* (65.746) | 113.156* (63.939) | ||||
| n | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 |
| Year dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Prevalence diseases (QOF) | Y | Y | Y | Y | Y | Y | Y | Y |
| Urban dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Deprivation dummy | Y | Y | Y | Y | Y | Y | Y | Y |
It is instructive to consider the estimates for first outpatient referrals to confirm whether or not an increase in the supply of GPs also reduces referrals, as would be expected given that an increase in GPs has been shown to reduce elective care. Estimates using the FTE data give a highly significant relationship, in which increased GP supply reduces outpatient referrals. The slope effect is substantial. In contrast, using the headcount data, the estimates that allow for GP endogeneity are not significantly different from zero, and those that do not allow for endogeneity are positive. The FTE data imply that the small practice with a patient list of 1200 would expect, on average, about 493 first outpatient appointments each year, and a 0.2 FTE increase in GP services may reduce this level of outpatient referrals by about 16 per annum or a little over one per month. Thus, the FTE data suggest that, overall, an extra 0.2 FTE GPs may reduce referrals by 16 per annum and ensuing elective admissions by 2–3 per annum.
Tables 34 and 35 also give the effects of practice density on referrals and admissions. In both the NHS headcount and FTE data, increasing the number of practices, all things being equal, has a consistently positive effect on both first outpatient referrals and elective admissions: a reduction in mean practice size is associated with a significant increase in both of these hospital activities. This effect holds consistently in both data sets and estimation methods. This may be interpreted as gatekeeping being less of a constraint on patient demand in areas with many smaller practices, and in which there may be less clinical access if there are economies of scale at practice level, and perhaps greater competitive pressures from patients.
The effects of a larger share of elderly males and females are positive as expected and, interestingly, are somewhat larger for elective admissions than for emergency care.
Considering the ethnic variables, the most notable effect is that of a much lower first outpatient appointment rate for LSOAs with a larger share of people of black ethnicity. The empirical size of this effect is large: a 10% increase in the share of the local black population (10% reduction in the white population) results in a reduction in outpatient referrals by 45 per 1000 or about 11% of outpatient appointments. In the headcount data we also see that people of black ethnicity experience lower rates of elective care, but this is not the case in the FTE data for traditional practices. Thus, setting these results in the context of the notably higher black admission rates for emergency care that are discussed below, it appears that the patient–doctor relationship is unlikely to be leading to appropriate use of outpatient consultations, and, possibly, elective care. The more marginal effect of black population shares on elective care is likely to reflect the fact that specialists are treating a higher proportion of black patient referrals. As part of the attempt to moderate the use of emergency care, while increasing planned patient care, it appears important to consider initiatives to examine and develop the patient–doctor relationship for black families in primary care.
In contrast to the results for black households, the Asian ethnic population effects are positive, suggesting, all else being equal, that LSOAs with higher shares of Asian households have higher rates of outpatient referral and elective admissions than areas with higher white populations.
The provision of relatively higher PCT funding, all things being equal, has a generally insignificant effect on outpatient referrals, but is associated with a lower level of elective treatments.
Emergency admissions
Table 36 reports the effects of GP supply on emergency admissions. Using the FTE data, the effect of GP supply on emergency admissions is very small and insignificant if the model allows for endogenous GP supply. In the headcount data the effect is negative using OLS estimation but becomes insignificant when the estimation allows for endogenous GP supply. Overall, the estimated effect is sensitive to the model context, and in all of the models the effect of GP density on emergency admissions does not imply a noteworthy economic effect. In the models using GP FTE data, the effect of more GPs is always insignificant in models allowing for endogeneity of GP supply. The effect is also insignificant in models that do not allow for endogeneity, if PCT fixed effects are included. Overall, the evidence suggests that areas with more GP FTEs, all else being equal, do not have different emergency admissions to areas with fewer GPs. This is consistent with Harris et al. ,78 who show, in a cross-sectional study of a small number of practices, that primary care access would not appear to influence emergency department attendance.
| Variable, coefficient (SE) | GPs | |||||||
|---|---|---|---|---|---|---|---|---|
| Headcounts | FTE | |||||||
| OLS | 2SLS | OLS | 2SLS | |||||
| Female population (%) | 0.483*** (0.083) | 0.483*** (0.084) | 0.455*** (0.081) | 0.454*** (0.081) | 0.465*** (0.081) | 0.465*** (0.082) | 0.467*** (0.081) | 0.466*** (0.082) |
| Female population aged ≥ 60 years (%) | 1.792*** (0.12) | 1.770*** (0.12) | 1.769*** (0.118) | 1.770*** (0.12) | 1.778*** (0.122) | 1.770*** (0.121) | 1.782*** (0.122) | 1.774*** (0.121) |
| Male population aged ≥ 65 years (%) | 1.858*** (0.171) | 1.836*** (0.174) | 1.870*** (0.174) | 1.871*** (0.179) | 1.868*** (0.174) | 1.858*** (0.174) | 1.867*** (0.173) | 1.854*** (0.173) |
| Black ethnicity (%) | 1.101*** (0.335) | 0.909*** (0.34) | 1.576*** (0.296) | 1.602*** (0.333) | 1.378*** (0.286) | 1.350*** (0.282) | 1.392*** (0.286) | 1.353*** (0.28) |
| Asian ethnicity (%) | 1.313*** (0.351) | 1.039*** (0.388) | 0.417 (0.416) | 0.441 (0.429) | 0.753* (0.442) | 0.66 (0.457) | 0.800* (0.436) | 0.68 (0.455) |
| Revenue per head | –0.41 (0.62) | –0.696 (0.604) | 0.055 (0.658) | 0.041 (0.696) | –0.138 (0.648) | –0.228 (0.629) | –0.139 (0.645) | –0.246 (0.623) |
| GPs density PCT per 1000 population | –15.264*** (4.271) | –20.588*** (4.396) | 11.360** (5.071) | 11.746 (7.356) | 1.685 (4.04) | –0.344 (4.626) | –1.682 (4.608) | –5.363 (5.067) |
| General practices density PCT per 1000 population | 99.005*** (27.016) | –3.845 (36.739) | 34.288 (28.479) | 45.535* (27.552) | ||||
| WIC/OOH density PCT per 1000 population | –69.66 (80.991) | –43.745 (83.957) | –53.001 (82.86) | –50.693 (82.201) | ||||
| n | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 | 298,801 |
| Year dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Prevalence diseases (QOF) | Y | Y | Y | Y | Y | Y | Y | Y |
| Urban dummy | Y | Y | Y | Y | Y | Y | Y | Y |
| Deprivation dummy | Y | Y | Y | Y | Y | Y | Y | Y |
The influence of a PCT allocating the given supply of GPs to more practices, and thus having more GP practices per head of population, is to increase emergency admissions: LSOAs in PCTs with on average smaller practices tend, all else being equal, to have more admissions. This may reflect the fact that a small practice is unlikely to offer as much immediate clinical access as larger practices, and thus patients require greater use of emergency care.
Of the other variables, the share of females in the local population does not have a significant effect on emergency admissions, whereas the shares of elderly males and females both have the expected positive effect. The emergency admission rate increases significantly with the shares of the black and Asian populations in the LSOA, although to a lesser extent for Asian populations. An increase of 10% in the percentage share of the black population results in approximately a 10.7% increase in emergency admissions; an increase of 10% in the percentage share of the Asian population results in an increase of 7.8% in emergency admissions. The PCTs with higher relative resource revenue tend to have either an insignificantly different rate of admissions or, in the models that do not allow for endogeneity of GP supply, one that is lower. This may reflect the fact that higher PCT funding is used to increase various primary care services rather than hospital admissions.
Robustness checks
The aim of these robustness checks is to explore potential differences between LSOAs that may have been overlooked by the modelling thus far. One motivation is that the supply of health-care services may be different across LSOAs in a way that alters how demand is presented and how admissions are determined. Our particular concern is with potential differences between deprived and more prosperous areas of the country. To better understand how the influence of GP supply may differ across LSOAs with quite different levels of admissions, we first compare two groups of LSOAs: the 20% most deprived LSOAs compared with the 20% least deprived LSOAs, using the Index of Deprivation by decile.
Consider Figures 37 and 38. Figure 37a gives the density of practices and prescribing cost centres in the population for deprived and least deprived LSOA areas, 2004–11; Figure 37b gives the density of headcount and FTE GPs in the population for the least and most deprived LSOA areas, for the same years. The structure of primary care is both different and in an important sense changing in a more problematic way in the most deprived areas than in less deprived areas. The deprived areas have about twice the number of practices per head and on average smaller practices, but although GP headcount increases steadily in all areas, the GP FTE falls after 2007 in both the least and most deprived areas. This decline in FTE also steadily narrows the difference in FTE GP supply between the most and least deprived areas.
FIGURE 37.
Density of general practices and prescribing cost centres in the population for most deprived and least deprived areas, 2004–11. (a) Density of practices and prescribing cost centres in the population for most deprived and least deprived LSOA areas; and (b) density of headcount and FTE GPs in the population for the least and most deprived LSOA areas.

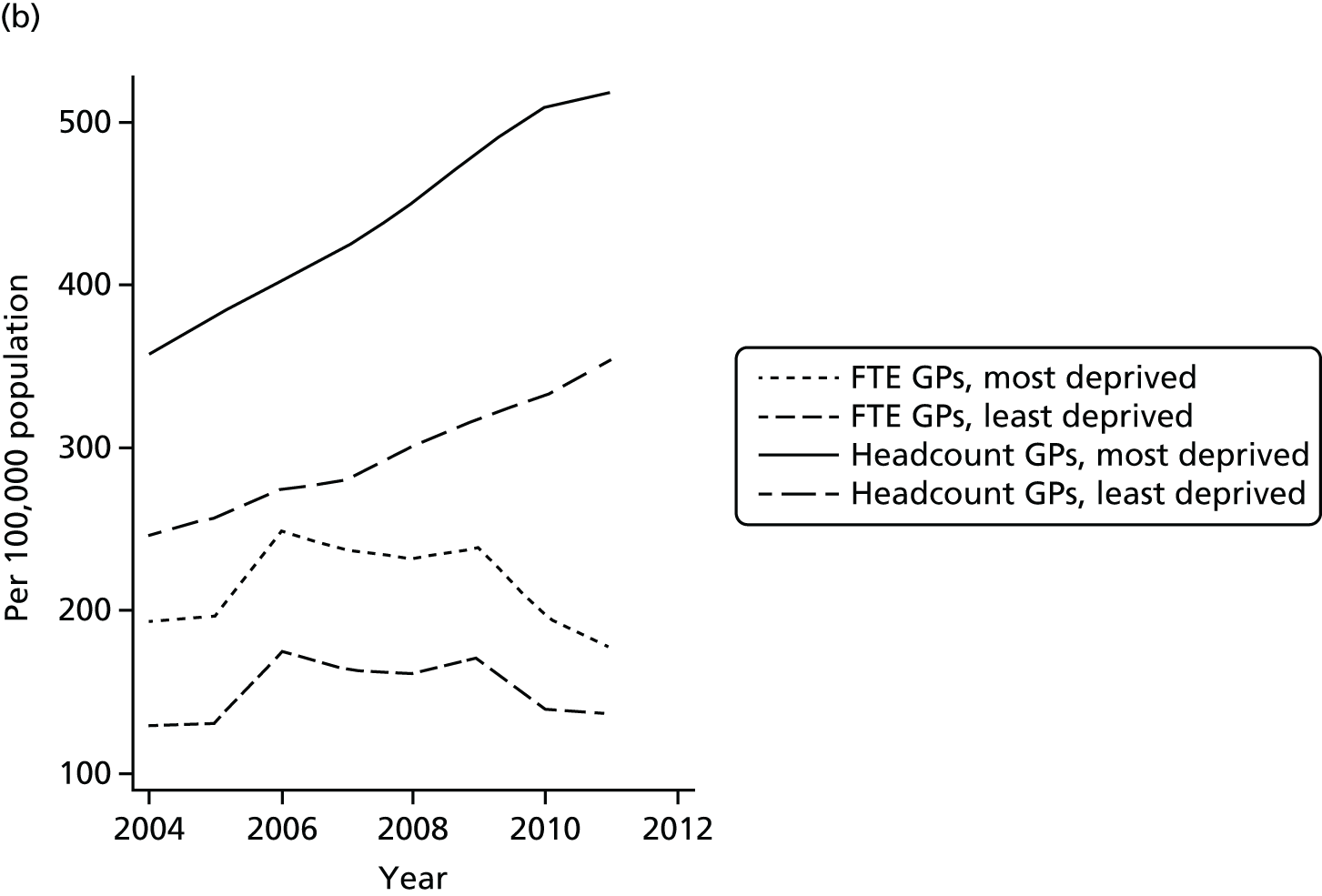
FIGURE 38.
Hospital referrals and emergency admissions for the least and most deprived areas, 2004–11. (a) Average emergency admission rates for the most/least deprived 10% of areas; (b) average elective admission rates for the most/least deprived 10% of areas; and (c) average outpatient rates for the most/least deprived 10% of areas.

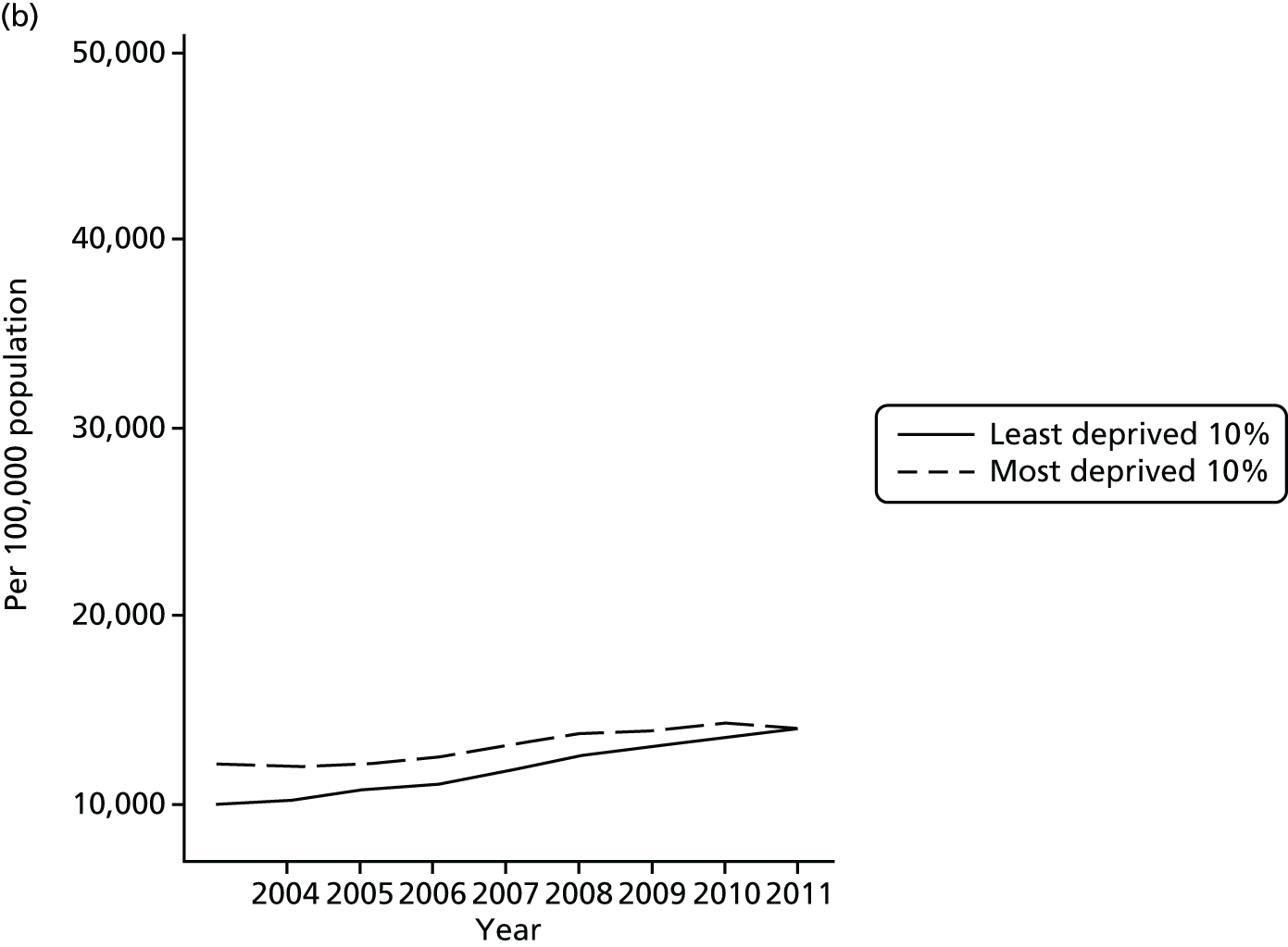
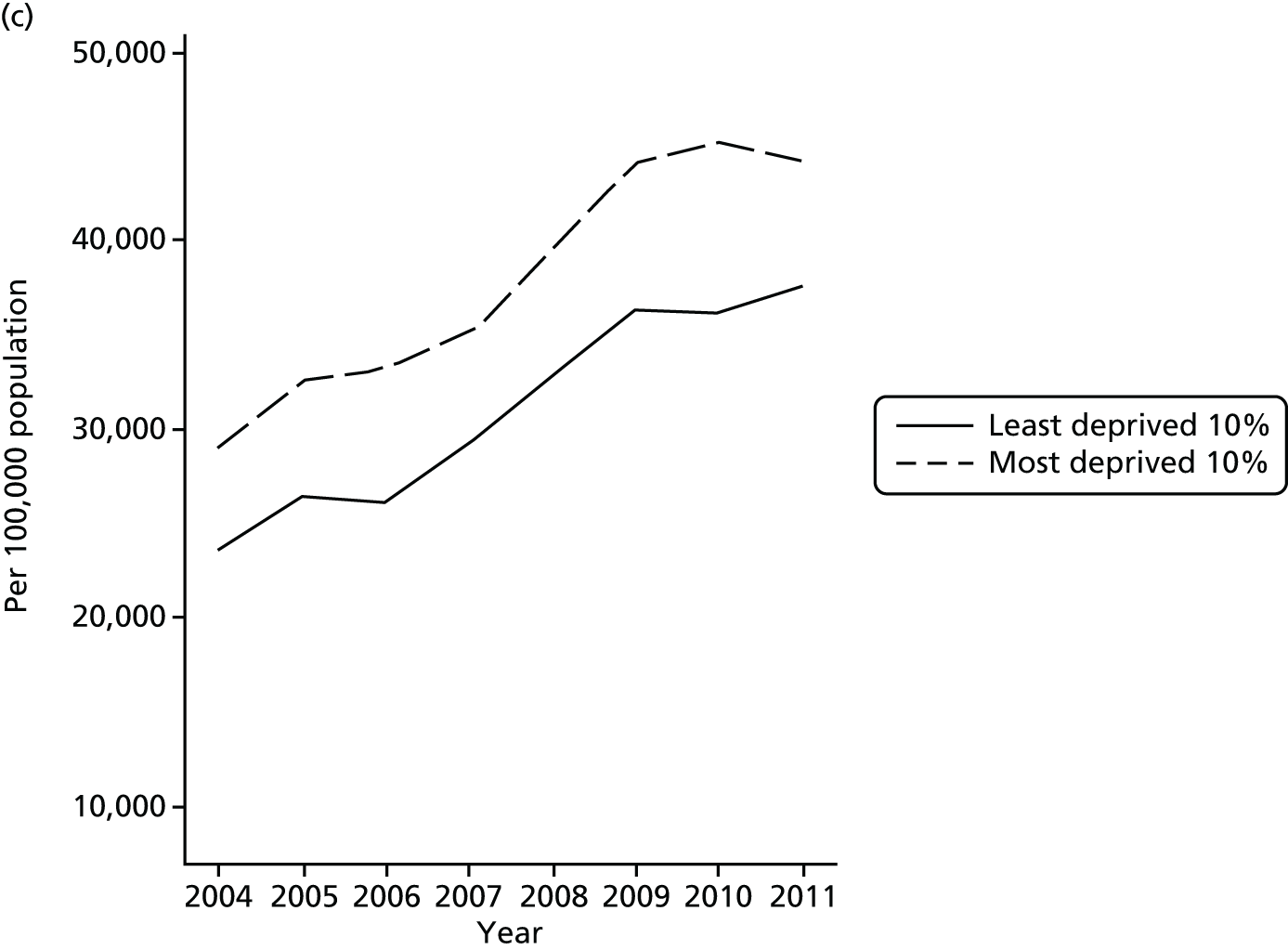
Figure 38 shows how specialist referrals and emergency admissions are relatively high for the most deprived areas, although admissions for elective care in the least deprived areas have increased relative to those in the most deprived areas. Given that the levels of admissions are quite different across these deprived and non-deprived LSOAs, it appears important to examine whether the effects of GP supply on admissions should be robust to whether the LSOA has high or low expected levels of each type of admission/referral.
In Table 37 we report the 2SLS model for each of the two groups of LSOAs, applying the same estimation methods described above (see Identification and instrumental variables) to models of hospital admissions (outpatients, elective and emergency). These estimates suggest that increasing GP supply significantly decreases hospital admissions in deprived areas, but does not do so in the least deprived areas. The influence of more practices, holding GP supply constant, has a positive and significant effect on admissions in both types of area. The influence of age follows the same pattern for both areas: it has a positive and significant influence on admissions. Ethnicity has different effects in deprived and less deprived areas. Black ethnicity has a positive influence on referrals and both types of hospital admission in deprived areas but has no effect in the least deprived areas. The influence of Asian populations on hospital admissions has a positive influence in deprived areas but, in the non-deprived areas, has a negative effect. We may conclude that the influence on admissions of individual characteristics, and GP variables, are different in these two types of areas, as well as the levels of admission also often being quite different.
| Variables, coefficient (SE) | Deprived areas | Not deprived areas | ||||
|---|---|---|---|---|---|---|
| Outpatients | Elective | Emergency | Outpatients | Elective | Emergency | |
| Female population (%) | 2.807*** (0.561) | 0.219* (0.122) | 0.764*** (0.169) | 2.221*** (0.418) | 0.347*** (0.122) | 0.617*** (0.125) |
| Female population aged ≥ 60 years (%) | 2.921*** (0.637) | 2.658*** (0.186) | 2.107*** (0.213) | 2.395*** (0.504) | 1.986*** (0.172) | 1.576*** (0.155) |
| Male population aged ≥ 65 years (%) | 5.356*** (0.976) | 3.633*** (0.269) | 2.705*** (0.268) | 3.748*** (0.643) | 2.826*** (0.23) | 1.547*** (0.187) |
| Black ethnicity (%) | –3.977*** (1.178) | –0.629* (0.362) | 1.962*** (0.385) | 0.966 (3.747) | 0.017 (1.519) | 0.056 (1.721) |
| Asian ethnicity (%) | 4.526** (2.025) | 1.773*** (0.591) | 1.039 (0.654) | –10.291*** (2.539) | –3.936*** (0.764) | –1.885*** (0.575) |
| Revenue per head | 2.221 (3.556) | –2.035*** (0.708) | –0.093 (0.75) | 1.965 (4.004) | –0.783 (0.99) | –0.761 (0.719) |
| GPs density PCT per 1000 population | –128.532*** (47.594) | –14.817** (5.781) | –12.812* (7.24) | 11.93 (19.299) | –2.685 (5.219) | 3.663 (4.614) |
| General practice density PCT per 1000 population | 573.063*** (133.52) | 62.235* (33.586) | 68.401* (39.995) | 173.468 (122.371) | 86.525*** (29.399) | –8.965 (21.764) |
| WIC–OOH density PCT per 1000 population | 896.028*** (246.33) | 169.826* (88.887) | –29.104 (94.613) | 278.29 (377.914) | 175.192** (84.743) | 113.502 (82.917) |
| N | 89,762 | 89,762 | 89,762 | 86,530 | 86,530 | 86,530 |
| Year dummy | Y | Y | Y | Y | Y | Y |
| Prevalence diseases (QOF) | Y | Y | Y | Y | Y | Y |
| Urban dummy | Y | Y | Y | Y | Y | Y |
To address this heterogeneity across LSOAs, and, in particular, whether or not the impact of GPs is similar for both low and high admission areas, we estimate a quantile regression model accounting for the endogeneity of GP supply. Quantile regression is a widely used tool for estimating conditional quantile models (see, for example, Koenker and Bassett92 and Koenker. 93 Quantile regression modelling gives estimates of quantile-specific effects that describe the impact of covariates not only on average, but also on the tails of the conditional outcome distribution. Although central effects, such as the mean effect obtained through conditional mean regression, provide useful summary statistics of the impact of a covariate, they fail to describe the distribution of the impact. Standard linear regression techniques summarise the average relationship between a set of regressors and the outcome variable based on the conditional mean function E(y ∣ x). This provides only a partial view of the relationship, as we might be interested in describing the relationship at different points in the conditional distribution of y. Quantile regression provides that information. Analogous to the conditional mean function of linear regression, we may consider the relationship between the regressors and outcome using the conditional median function Qq(y ∣ x), where the median is the 50th percentile, or quantile q, of the empirical distribution. The quantile q∈(0,1) is that y, which splits the data into proportions q below and 1 – q above: F(yq) = q and yq = F – 1(q): for the median, q = 0.5.
In many studies, the variables of interest (education, health or prices) are endogenous. Endogeneity of covariates renders the conventional quantile regression inconsistent for estimating the causal effects of covariates on the quantiles of economic outcomes, just as with the conventional linear model. To study the relation between GP supply across the conditional distribution of hospital admissions (outpatient, elective and emergency) we use a new quantile instrumental variable (QIV) panel estimator, developed by Chernozhukov and Hansen. 86 The principal identifying assumption of the model is the imposition of conditions that restrict how rank variables (structural errors) may vary across treatment states. These conditions allow the use of IVs to overcome the endogeneity problem and hence recover the true quantile treatment effects (QTEs). This framework also ties naturally to simultaneous equations models, corresponding to a structural simultaneous equation model with non-additive errors. Estimation and inference procedures for linear quantile models have been developed by Chernozhukov and Hansen,86 Chernozhukov et al. 94 and Chernozhukov et al. 95
The QIV estimator allows us to obtain estimates of the influence of GP supply that vary across the conditional LSOAs hospital admissions distribution. Unlike estimators of the conditional mean, which can be very sensitive to values in the tail of the distribution, conditional quantile estimators are inherently more robust to extreme values, which is particularly advantageous. In addition, the QIV estimator allows us to address the endogeneity described in the previous section with an IV identification strategy. To estimate the quantile regression we use the same variables as used above to estimate the 2SLS of the hospital admissions, except that Strategic Health Authority (SHA) fixed effects are included instead of LSOA fixed effects owing to the problem of the incidental parameter giving inconsistent estimates using individual fixed effects in a quantile regression (see Kato et al. 96).
Table 38 reports the quantile regression accounting for the endogeneity of GP FTE density, and the intervals of confidence for outpatient appointments, elective admissions and emergency admissions. The major variation across the distribution is observed in the outpatient referral equation. This implies that an increase in FTE GPs of the same amount will have a larger effect on outpatient referrals in a LSOA with low rate of referrals per head than one with a high rate of referrals. Figures 39 and 40 show the quantile estimation for the influence of four independent variables: the number per head of population of (1) FTE GPs, (2) general practices, (3) Asian populations and (4) black populations.
| Admissions | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Outpatients | Elective | Emergency | |||||||||||||
| 10 | 25 | 50 | 75 | 95 | 10 | 25 | 50 | 75 | 95 | 10 | 25 | 50 | 75 | 95 | |
| GP density PCT per 1000 population (95% CI) | 48.81 (44.99 to 52.46) | 53.86 (50.69 to 56.50) | 88.92 (82.86 to 93.30) | 144.33 (134.24 to 144.74) | 188.04 (179.08 to 186.71) | –8.08 (–9.00 to –4.55) | –17.11 (–18.54 to –15.36) | –25.61 (–26.93 to –24.86) | –27.15 (–28.51 to –26.76) | –13.98 (–16.96 to –9.65) | 8.43 (5.83 to 9.94) | 9.62 (6.10 to 10.56) | 13.61 (11.30 to 15.74) | 18.22 (16.35 to 20.60) | 26.07 (25.76 to 30.45) |
| Female population, % (95% CI) | 1.83 (1.75 to 1.92) | 1.94 (1.84 to 2.15) | 2.12 (2.02 to 2.26) | 2.24 (2.13 to 2.36) | 2.76 (2.58 to 2.95) | 0.55 (0.52 to 0.58) | 0.73 (0.69 to 0.75) | 0.74 (0.70 to 0.76) | 0.66 (0.63 to 0.75) | 0.67 (0.54 to 0.80) | 0.33 (0.29 to 0.36) | 0.40 (0.31 to 0.40) | 0.37 (0.31 to 0.41) | 0.28 (0.23 to 0.33) | 0.31 (0.21 to 0.33) |
| Female population aged ≥ 60 years, % (95% CI) | 2.35 (2.21 to 2.49) | 2.14 (1.91 to 2.23) | 2.08 (1.99 to 2.26) | 2.56 (2.48 to 2.74) | 3.35 (2.87 to 3.61) | 1.58 (1.48 to 1.64) | 1.65 (1.61 to 1.70) | 1.91 (1.80 to 2.00) | 2.07 (1.92 to 2.08) | 2.61 (2.48 to 2.86) | 4.14 (4.08 to 4.30) | 4.69 (4.68 to 4.78) | 5.47 (5.41 to 5.55) | 6.53 (6.53 to 6.60) | 8.15 (8.19 to 8.32) |
| Male population aged ≥ 65 years, % (95% CI) | 4.50 (4.32 to 4.80) | 4.29 (4.16 to 4.63) | 4.52 (4.17 to 4.66) | 4.57 (4.31 to 4.85) | 4.75 (4.38 to 5.72) | 3.51 (3.47 to 3.64) | 3.89 (3.81 to 3.96) | 4.12 (3.97 to 4.25) | 4.56 (4.49 to 4.76) | 4.93 (4.51 to 5.10) | –1.25 (0–1.53 to –1.15) | –1.48 (–1.63 to –1.43) | –1.85 (–1.98 to –1.74) | –2.55 (–2.66 to –2.52) | –3.60 (–3.92 to –3.68) |
| Black ethnicity, % (95% CI) | 2.58 (2.38 to 2.61) | 2.71 (2.57 to 2.76) | 2.45 (2.37 to 2.52) | 2.40 (2.23 to 2.45) | 2.63 (2.04 to 3.19) | 0.76 (0.70 to 0.75) | 0.74 (0.73 to 0.78) | 0.71 (0.68 to 0.76) | 0.72 (0.72 to 0.77) | 0.78 (0.70 to 0.82) | –0.11 (–0.17 to –0.04) | –0.38 (–0.42 to –0.35) | –0.72 (–0.78 to –0.68) | –1.05 (–1.09 to –1.00) | –1.50 (–1.53 to –1.36) |
| Asian ethnicity, % (95% CI) | –1.86 (–1.98 to –1.83) | –1.06 (–1.12 to –1.03) | –0.43 (–0.47 to –0.39) | 0.65 (0.51 to 0.74) | 2.52 (2.13 to 2.53) | –0.32 (–0.40 to –0.28) | –0.21 (–0.24 to –0.18) | –0.10 (–0.13 to –0.08) | –0.06 (–0.09 to –0.05) | –0.02 (–0.15 to 0.09) | 0.16 (0.13 to 0.18) | 0.16 (0.10 to 0.15) | 0.09 (0.03 to 0.09) | 0.09 (0.03 to 0.12) | 0.18 (0.09 to 0.28) |
| General practice density PCT per 1000 population (95% CI) | 60.81 (51.90 to 69.85) | 81.44 (81.01 to 90.58) | 70.12 (75.01 to 78.74) | 16.48 (7.80 to 33.56) | –98.09 (–106.65 to –59.88) | 23.08 (20.40 to 29.02) | 28.68 (26.08 to 30.15) | 22.91 (21.42 to 26.14) | 11.91 (9.05 to 17.23) | –5.27 (–15.11 to 0.58) | –48.43 (–55.05 to –42.48) | –46.03 (–47.81 to –41.42) | –57.18 (–59.28 to –54.04) | –71.24 (–73.18 to –69.25) | –82.33 (–94.59 to –76.18) |
| Revenue per head (95% CI) | 4.21 (3.24 to 5.20) | 4.12 (3.80 to 4.47) | 5.91 (5.63 to 6.05) | 10.42 (9.75 to 10.61) | 14.34 (14.36 to 16.77) | –2.81 (–3.01 to –2.29) | –2.48 (–2.82 to –2.09) | –2.58 (–2.68 to –2.45) | –4.00 (–4.30 to –3.70) | –6.39 (–7.29 to –5.52) | –1.54 (–1.88 to –1.24) | –1.24 (–1.45 to –1.05) | –1.03 (–1.37 to –0.70) | –0.79 (–1.32 to –0.48) | –0.07 (–1.13 to 0.30) |
| n | 259,856 | 259,856 | 259,856 | ||||||||||||
FIGURE 39.
Quantile regression for hospital admissions: estimated coefficients for independent variables. (a) FTE GPs density per 1000 population; and (b) GPs density per 1000 population.
FIGURE 40.
Quantile regression for hospital admissions: estimated coefficients for independent variables. (a) Percentage black ethnicity; and (b) percentage Asian ethnicity.

We find that the influence of GP supply is unchanged across the distribution for elective and emergency admissions, whereas its influence on referrals is positive and larger in the LSOAs with high levels of referrals. In contrast, the influence of the density of general practice is positive and larger in the middle of outpatients distribution, whereas along the tails it decreases until it becomes negative at the top of the distribution. Again, the influence of practice density is constant along the distributions of elective and emergency. The same flat pattern is found for the impact of ethnicity (black and Asian population shares) for the elective, outpatients and emergency distributions. The sole exception is that the coefficient of Asian ethnicity is negative in LSOAs with few outpatients admissions and positive in the LSOAs with more outpatients admissions. This is consistent with the estimates discussed above in this section for deprived and non-deprived areas. This estimate gives insight into how the influence of GP supply is greater for outpatient referrals to hospital in areas with high referrals, which are the more deprived areas. This is consistent with the findings concerning the relative responsiveness to increases in GP supply given for deprived areas in Table 38. In contrast, the levels of elective and emergency admissions respond in a similar way at all levels of admission rates to changes in GP supply.
Conclusions
This report discusses a model of GP referrals in which a GP, in order to increase efficiency, may not refer certain patients despite this not being in the interests of either the patient or the GP. It explores in this model the hypothesis that adding GPs to a given patient population will reduce the demand for elective hospital services. It gives assumptions under which a shorter list of registered patients will lead a GP to reduce specialist referrals and to treat a larger share of his or her patients in primary care. These assumptions include that a GP acts as an imperfect agent of the insurer, maximising an objective function of his or her own utility and the expected health gain of a representative patient in the health system. Although the GP and his or her patients both benefit from referring all ill patients, the GP’s professional ethic prompts GP treatments for patients that he or she believes to be only mildly ill. Increasing the number of GPs is found to lead each GP to treat a larger share of their shorter patient list and to make fewer specialist referrals. This increase brings referrals closer to the level that maximises expected health gain, because, as long as GPs consider their own welfare, as well as that of patients, referrals are below that level.
We find that both the local supply of GPs and whether or not GPs are concentrated into larger practices help to explain hospital admissions, but only in deprived areas; an increased density of GPs tends to reduce both outpatient referrals and elective, but not emergency, admissions. In more prosperous areas these effects are either not present or weaker. This may be because in the more prosperous areas patient choice predominates and the gatekeeping role of the GP is de-emphasised. PCTs with a large number of small practices, but the same density of GPs, tend to have more outpatient referrals and elective and emergency admissions. Various robustness checks also suggest that the structural relationships between GP and practice density and admissions differ between deprived and non-deprived areas, with additional GPs in the more deprived areas reducing both referrals and elective admissions. However, even in deprived areas, the value of these savings does not by itself meet the cost of additional GPs.
Chapter 6 The determinants of general practitioner referrals and elective hospital admissions: a practice-level study
Introduction
In 20011/12, first referrals by GPs to specialists reached a level of 11.2 million, with referrals to orthopaedic and general surgeons, ophthalmologists and gynaecologists being particularly significant, and in the preceding eight years, both first referrals and total elective care grew by about one-third. Referrals are usually intended to initiate treatment by specialists (see Donohoe et al. 97) and thus cause a large part of NHS expenditures, even though GPs do not refer all patients seeking a specialist consultation. This amelioration of referrals is usually thought of as reflecting NHS and GP concerns to limit the impact of insurance on patient demand for care, so that care is consumed to the point at which the patient’s marginal benefit equals the marginal social, and not private, cost. With austerity-driven cost-saving programmes currently in place across government, it is unsurprising that policy to reduce the growth of elective admissions has included the consideration of whether or not GP ‘gatekeepers’ might support this constraint on unaffordable growth by reducing referrals. For example, Lambeth CCG has incentivised GPs to refer at mean practice rates, whereas Lincolnshire CCG has incentivised GPs to refer at a rate similar to the low referral practices. Such policies implicitly assume that fewer referrals might play a decisive part in reducing admissions. However, this overlooks the role of specialists, who determine thresholds of illness below which a patient is not admitted. Following changes in referral policy, the mix of patients eligible for a specialist’s threshold might be increased if patients with lower priority for treatment are no longer referred. The literature, usefully summarised by O’Donnell,98 discusses the socioeconomic determinants of GP referrals and variation in referral rates between practices. The samples used are usually quite small. In contrast, partly owing to obstacles in obtaining appropriate data and the difficulty of linking/measuring the hospital admissions of the patients of specific practices, there are very few studies about the variation of treatment rates between practices, and none has linked the analysis of these two critical building blocks of the relationship between GP and specialist.
The aims of this chapter are, first, to contribute to a small body of literature on understanding the determinants of large variations in ‘first’ referral rates across practices and, second, to examine the determinants of treatment rates by practice following first referrals and how far a reduction in GP referrals at practice level will reduce specialist treatments. We wish to answer the following questions and, in part, to illuminate the benefits of alternative policies to increase GP supply: what are the GP and patient characteristics that explain high rates of GP referrals? Are certain groups of GPs more likely to refer patients who induce particularly productive work by the specialist, insofar as they refer a higher proportion of patients who are either subsequently treated or not discharged without follow-up by the specialist? How should we think of the relationship across NHS GP practices between a practice’s rate of patient referral and the rate of elective treatment following first referral of patients at that practice? An intuitive supposition would be that practice variation in both referral and treatment is driven by patient health, and that practices with less healthy patient populations will have both higher referrals and admissions. This suggests that practice admissions per registered patient will broadly increase with practice referrals. We shall explore this relationship, and also explore hypotheses regarding referrals that shed light on the appropriateness of referrals for various socioeconomic groups, by age for both very young and very old patients, and by the level of prosperity in the patients’ local area. This may also indicate whether or not savings can be made to the health economy by caring for patients in primary care rather than by referring them to specialists (see Foot et al. 99). The absence of experimental data leads us to use observational data comparing the level of treatments received by patients of practices with observationally similar practice, local area and patient characteristics, but with differing referral rates. This requires that we estimate the joint roles of (1) practice referral rates, (2) patient and GP practice characteristics and (3) local socioeconomic and health system characteristics to explain the likelihood that a patient is referred and that a referred patient is admitted for treatment. To do this, we have created a rich data set that combines practice-, hospital- and area-level data for all English GP practices, for the period 2004–12, together with the characteristics of their clinicians and the morbidities and socioeconomic characteristics of their patients. The sample size of practices declines from about 8400 practices in 2004 to 7950 in 2012. One feature of the data is that we have created an index of deprivation for each practice based on the socioeconomic groups of the LSOA in which their patients reside.
We shall examine the implications of the recent changing structure of GP practices for first referrals. There is a growing dependence on salaried GPs and locums within GP practices; there has also been an increase in part-time working by GPs and a growth of average practice size. Another GP characteristic that may influence the referral rate is the sex of the GP, as other studies have found that female GPs are more likely to refer, all else being equal. 100
O’Donnell98 summarises the literature concerning variations in the referral rate among GPs, discussing how the variation of referral rate among GPs remains largely unexplained in the literature. In an early contribution, Coulter et al. 101 examined the variation in rates of admission to hospital among general practices to determine the relationship between referral rates and admission rates. Analysing 19 general practices in three districts in the Oxford Regional Health Authority, the authors found that patients referred to surgical specialties were more likely than those referred to medical specialties to be admitted after an outpatient referral, and they report only modest increases of patient treatment rates at practices with higher levels of referral rates – a ‘flattening’ of the treatment/referral relationship at higher referral levels. Hippisley-Cox and Jumbu102 describe the trend increase in consultation in general practices, from 3.9 per patient per year in 1995 to 5.4 per patient per year in 2007. Consultation rates vary markedly by age, with the highest rates for the elderly. Consultation rates for females are generally higher than for males, although the consultation rates at the extremes of age (i.e. the very young and the very elderly) were similar for males and females.
There has been considerable interest in whether or not use of NHS services differs by socioeconomic group. Recent evidence from studies showing the distribution of use of different levels of service find that use of GPs is broadly equitable but that specialist treatment favours the more affluent. Recent microstudies of cardiac surgery, elective surgery, cancer care, preventative care and chronic care support the findings of an earlier review that use of services was higher relative to need among higher socioeconomic groups (Dixon et al. 103). We explore these issues below.
In cities, health services are more widely available than in the countryside, where GPs are often the only providers of care. With highly mobile populations and a plentiful supply of doctors in cities, the prevailing regulations for access and use of services are more difficult to maintain. It is also more difficult to control access and, thus, opportunities for inappropriate use are greater, as reported by Boerma et al. 104 The implications of this for referrals are ambiguous: first referrals may fall if patients approach emergency care more often in cities, but GPs in cities may feel under more pressure to refer if their patients can more readily seek emergency care or move to another practice. Hospital characteristics, such as unoccupied hospital beds in a particular area and consultant-to-consultant referrals restrictions, are shown to register an increase in GPs referrals to hospitals in some areas. 105
Ringberg et al. 100 show that in Norway, male GPs and specialists in family medicine refer significantly less frequently to secondary care, but that the latter refer more frequently to radiological examination. They conclude that high referral rates to secondary care by GPs are associated with GPs’ sex and specialist qualifications in family medicine. Evans et al. 106 examine how peer review with consultant engagement may influence GPs and improve the quality of referrals. van Dijk et al. 107 looked at the variation in the referral rate in primary care and if more provision of services can influence referral rate. They found that practice-level services were not associated with the referral rate. Noone et al. 108 studied the variation in referral rates among practices after a new hospital opened in the Oxford region in order to analyse how referral rates may increase after a positive shock to the supply.
Madeley et al. 109 found no difference in referral rates between single-handed GPs and those in partnerships in Lincolnshire. However, in a multivariate study, Christensen et al. 110 found a significant association between single-handed practices and high referral rates in Nottinghamshire. Srirangalingam et al. 111 surveyed GPs to determine whether or not implementation of the General Medical Services (GMS) contract has led to changes in referrals to a secondary care diabetes mellitus clinic and found no significant change in numbers of referrals received pre and post contract. We shall return to both of these issues below.
There is a broad literature on variation in referral rates between practices, although the samples used are usually quite small. In contrast, there are very few studies about the variation of treatment rates between practices on a national basis, and none has linked the analysis of these critical building blocks of the relationship between GP and specialist. This is partly due to obstacles in obtaining appropriate data and also to the difficulty of linking/measuring the hospital admissions of the patients of specific practices.
The remainder of the chapter is structured as follows. The next section describes the data. The empirical strategy and results are presented in Empirical strategy and hypotheses and Results, respectively. A conclusion then follows.
Data
We use three blocks of data that come from different sources referring to practices, patients and hospital admissions, for the period 2004–12. The GP data are primarily from the HSCIC, under its previous guise as ‘NHS Connecting for Health’, and relate to current GPs, including the practice at which they work, and the start and end dates of employment from 2004 to 2011. These data refer to all GPs in work, not only in a general practice, but also employees of a PCT, SHA or an OOH service/WIC. Unfortunately, these data do not provide information beyond headcount about the hours of work for each GP, and, specifically, the FTE labour supply. However, data from the NHS Annual Work Force Census of NHS employees provide practice-level information about work hours.
Additionally collected data provide a rich information base for each practice: the size of the patient list, the total FTE GP hours, the total number of GPs, the sex of GPs, if they have studied outside the UK, their years of qualification and birth, and the their type of contract [salaried, provider (partner) or in training]. There is further information regarding the practice, including the practice location, whether or not it is single handed and the type of contract [GMS or Personal Medical Services (PMS)] agreed with the PCT. For each practice, we also link individual-level patient information. In the UK, each individual must be registered with only one general practice. Patients’ information at each practice includes their age structure (divided in three groups: 0–34 years, 35–59 years, ≥ 60 years), sex mix and the number of patients resident in each LSOA.
As we know the residential location of the patients, we can calculate indices of deprivation and rurality for each practice. Socioeconomic status level is measured using the deprivation domains of the English Indices of Deprivation. 90 The general practice IMD is estimated by taking a weighted average of the IMD scores for each LSOA in which a given practice has registrations. We have done the same to calculate the index of rurality for each practice.
Patient demand for admissions is likely to be shaped by patient illnesses. Clinical information concerning the prevalence of specific diseases for the patients registered with the practice, and quality care of practice, is provided by the QOF database. The data cover almost all GP practices in England and are extracted from disease registers submitted to the national QMAS. The prevalence of all illnesses except epilepsy and asthma increased during the study period. By the end of the period, 90% of the population was registered with a GP, and the observed illness prevalence is quite representative at the England level. However, there could be some under-reporting bias, especially in the early years. In addition, for each practice there is a score from 100 to 1000 about the quality of care. The QOF, which was introduced in 2004, requires that some patients with conditions such as chronic kidney disease and angina are routinely referred for specialist review, which will inevitably generate a higher number of referrals from primary care. However, these will be appropriate referrals that reflect adherence to agreed protocols and/or best practice. For example, one study has shown an increase in referrals for poor glycaemic control after implementation of the new GMS contract to a secondary care diabetes mellitus clinic; see Srirangalingam et al. 111
To estimate the models of GP referrals and specialist treatments, we have used data from the HES database. These data provide information concerning all inpatients and outpatients admitted to the English NHS, as well as A&E attendances. It includes private patients treated in NHS hospitals, patients resident outside England and care delivered by TCs (including those in the independent sector) funded by the NHS. Admitted patient care data are available for every financial year from 1989–90 onwards. Each HES record contains information about individuals admitted to NHS hospitals, including clinical information about diagnoses and operations; patient characteristic information, such as age group, sex, ethnicity, registered practice; administrative information, such as time waited, dates and methods of admission; and geographical discharge information, such as where patients are treated and area of residence. Because the focus is on GP influence upon admissions, our analysis concerns only the ‘first admission’ to the hospital, which the GP is most likely to influence, rather than subsequent admissions for continuing treatments. Moreover, we focus on only those referrals made by GPs and we link these referrals with treatment data (inpatients).
In 2011/12 there were 91.0 million outpatient appointments, of which 72.6 million (79.8%) were attended. Although the total number of appointments has increased year on year, the percentage that are attended (79.8%) has remained relatively stable since 2007–8, decreasing by 1.8 percentage points. First appointments accounted for 21.8 million attendances (30.1% of all attendances), of which 11.3 million (51.5%) were referred from a GP. London SHA had the greatest number of appointments, at 18.5 million appointments, compared with the North East SHA which had the lowest number of appointments (4.9 million). London SHA also had the highest rate of appointments (by population), with an average of 2.25 per person, and South Central SHA had the lowest at 1.34 per person. The main consultant specialties with the most attendances were Trauma & Orthopaedics (7.1 million; 9.8%), Allied Health Professional Episodes (6.5 million; 9.0%), Ophthalmology (6.3 million; 8.6%) and General Surgery (4.1 million; 5.7%), which together made up one-third (33.1%) of all attendances.
Three stylised facts
A description of the distributions of the rates of (1) first referrals and (2) planned hospital admission rates following first GP referrals for English GP practices in 2011 is given in Figure 41. The referrals rate has a mean of 201 per 1000 registered patients, and the planned admission rate from these referrals is 72 per 1000 registered patients. There are also planned admissions following referrals by hospital specialists, in the case of emergency attendance, and nurses at medical centres, which are excluded from this study.
FIGURE 41.
Admission vs. referral rates (per 1000 patients) across practices, 2011.

Fact 1: we confirm, for the first time in a national sample, that the variation in referral rates is considerable, and that using the SD of referral rates as the metric of variation suggests that variation has risen since 2004. The practice referral rate had a SD of 40.4 in 2004 and 54.4 in 2012. However, the mean referral rate also rose during this period so that the coefficient of variation remained unchanged at 0.27.
Fact 2: although referral rates vary considerably by practice, following a GP first referral at practice level, the number of planned hospital admissions per 1000 patients exhibits considerably more variation. Moreover, the practice admission rate shows increased variation since 2004. The coefficient of variation in 2012 was 0.27 for referrals, and 0.59 for elective admissions following GP first referral, having increased from 0.45 in 2004.
Fact 3: the joint distribution of practice first referral rates and subsequent hospital admission rates has a bimodal structure. There is a concentration of practices around 200 referrals per 1000 patients and 50 admissions per 1000 patients, and a weaker second concentration around a slightly lower referral rate, but with a considerably higher admission rate that is slightly > 100 per 1000 patients. The differences in the health of patient populations between practices readily explains why both referrals and treatments should be higher at some practices, and we should expect random variation in both variables. However, it is far from clear why at some practices, admissions are so much lower, given their referral levels, or, put differently, why referral rates are similar when the practice treatment rates are so different. If it is correct to assume that the practices with less healthy patient populations have higher treatment rates, we can ask why many practices with these unhealthy populations have low patient referral rates.
There are two contrasting explanations for the bimodal relationship found in Figure 41. First, the demand for admissions may present itself differently across practices. GP referral behaviour may follow guidelines/protocols which result in a narrow referral range despite quite different patient populations, or patients in different areas may seek GP advice at different stages of disease. This may inhibit referrals in some areas until patients’ illnesses are more advanced and treatment is more likely. Second, it may be that supply differs between areas and that providers vary in treatment thresholds despite referral patterns being otherwise quite similar.
Figure 41 also suggests that a careful model of factors explaining elective treatment rates across practices, other than GP first referrals, is crucial if the relationship between referral and treatment rates is to be estimated accurately. Figure 42 gives the same cross-sectional portrait as Figure 41 but without the indication of point density and is a reminder of the difficulty of using scatterplots with very large samples.
FIGURE 42.
Admission vs. referral rates (per 1000 patients) across practices, 2011.
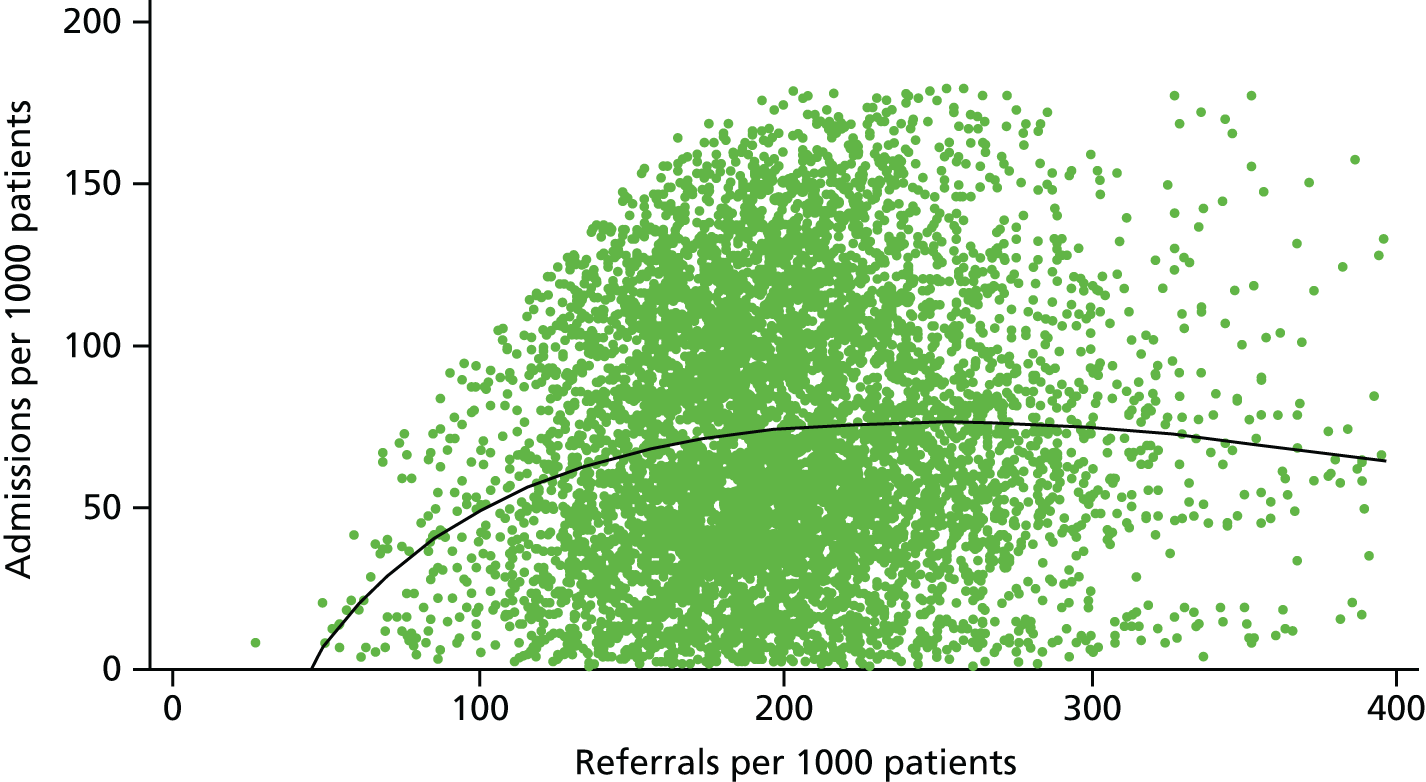
Figure 43 gives the distributions of practice referral rates, distinguishing between referrals for which the patient is given a second appointment and those that are ended after one appointment. About two-thirds of referrals are followed up by specialists with further appointments. Although this is not to argue that only those followed up are of high value, it is probable that those followed up are, on average, more likely to be the referrals that lead to larger patient health gains net of cost being provided by the secondary sector. The distribution of referrals that are discharged is less variable, but there is a long tail of practices with non-followed up referral rates in excess of twice the national mean rate of about 50 per 1000 patients.
FIGURE 43.
Outcome of referrals (1000 per registered patients) by practice: discharge rates vs. follow-up rates.

In Table 39 we report the descriptive statistics by year of the variables that we include in our estimated models. The time trend of the first referrals made by GP practices shows steady growth, and the resulting treatments from first referrals increased until 2008 and subsequently declined until flattening out after 2010. There is considerable variation across general practices in referrals and treatments, as we can see from the SD and Figure 41. However, although the coefficient of variation scarcely changes for referrals, the coefficient of variation for treatments increased from 0.45 to 0.59 in only 8 years and most of this happened after 2006 when system reforms, including the new GP contract, initiated change.
| Variables description | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|---|
| First referrals per 1000 patients by GPS (SD) | 153.61 (40.8) | 162.4 (41.15) | 156.89 (39.35) | 164.07 (41.33) | 183.31 (45.52) | 196.74 (50.61) | 200.7 (51.86) | 200.88 (51.39) | 205.05 (55.76) |
| Related treatments per 1000 patients (SD) | 75.16 (33.57) | 75.82 (34.58) | 75.13 (34.67) | 72 (34.27) | 75.04 (38.87) | 74.42 (39.64) | 71.98 (40.53) | 71.92 (41.94) | 71.93 (42.38) |
| Proportion of beds occupied at PCT | 0.8 | 0.81 | 0.82 | 0.81 | 0.81 | 0.82 | 0.82 | 0.79 | 0.8 |
| Proportion of patients aged 0–34 years | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 |
| Proportion of patients aged 35–59 years | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 |
| Proportion of patients aged ≥ 60 years | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 |
| Proportion of female patients | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 |
| Index deprivation by practice | 23.47 | 23.4 | 23.42 | 23.33 | 23.35 | 23.37 | 23.2 | 23.25 | 23.23 |
| Rural indicator per practice | 5.33 | 5.34 | 5.33 | 5.32 | 5.33 | 5.32 | 5.34 | 5.33 | 5.35 |
| Ln QOF points | 6.88 | 6.92 | 6.87 | 6.88 | 6.86 | 6.85 | 6.86 | 6.88 | 6.87 |
| Mean patient list per practice | 6664 | 6720 | 6794 | 6871 | 6918 | 6992 | 7042 | 7095 | 7193 |
| Total FTE hours per practice | 3.29 | 3.38 | 3.76 | 3.88 | 3.91 | 4.02 | 3.91 | 3.92 | 3.91 |
| Proportion of single-handed practice | 0.20 | 0.20 | 0.18 | 0.16 | 0.14 | 0.13 | 0.12 | 0.12 | 0.12 |
| Mean age of GPs (years) | 48.36 | 48.84 | 48.75 | 48.79 | 48.77 | 48.88 | 49.01 | 49.07 | 49.22 |
| Proportion of FTE female GPs | 0.3 | 0.31 | 0.34 | 0.35 | 0.36 | 0.37 | 0.37 | 0.38 | 0.39 |
| Proportion of FTE immigrant GPs | 0.29 | 0.3 | 0.31 | 0.3 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 |
| Proportion of GPs working FTE ≥ 1 | 0.82 | 0.82 | 0.88 | 0.84 | 0.8 | 0.78 | 0.7 | 0.67 | 0.67 |
| Proportion of GPs working 0.6 ≤ FTE < 1 | 0.18 | 0.18 | 0.06 | 0.08 | 0.09 | 0.12 | 0.16 | 0.16 | 0.18 |
| Proportion of GPs working FTE< 0.6 | 0.00 | 0.00 | 0.06 | 0.08 | 0.11 | 0.11 | 0.14 | 0.16 | 0.15 |
| Years of education of GPs | 18.86 | 18.86 | 18.86 | 18.85 | 18.83 | 18.82 | 18.81 | 18.8 | 18.79 |
| Proportion of GPs provider | 0.92 | 0.93 | 0.91 | 0.87 | 0.84 | 0.83 | 0.82 | 0.83 | 0.83 |
| GMS contract | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.58 | 0.58 | 0.58 |
| Total observations | 8364 | 8355 | 8259 | 8216 | 8167 | 8125 | 8241 | 8174 | 7951 |
We also observe that registered patients per practice increased by about 8% over the period 2004–12 and the share of single-handed practices decreased from 20% in 2004 to 12% in 2012. The percentage of female GPs has increased from 30% to 39% and this has consequences for the average hours worked: the percentage of full-time GPs had declined from 82% to 67%. The percentage of partner GPs has decreased from 92% to 83% in the period 2004–12, whereas the mean age of GPs has increased by almost 1 year during this period.
Empirical strategy and hypotheses
This work aims to improve understanding of how policy might influence the level of hospital admissions by studying two central and inter-related aspects of the relationship between GPs and specialists: first, we study the determinants of the rate of practice first referrals; and, second, we study the determinants of the probability that a patient given a first GP referral is admitted for hospital treatment, which can be affected by exogenous influences that are linked to policy as well as the total rate of first referrals from the referring practice. By studying these two decisions separately, we are able to decompose the effect of a variable of interest on the likelihood that a registered patient is admitted for hospital treatment into a part arising from its influence on the probability of a referral, which is decided by the GP, and a second part influencing the probability that the specialist decides to admit the referred patient. Thus, for example, we give further insight into why patients from deprived areas may receive too little secondary care relative to need.
Our empirical strategy consists of two steps: first, we estimate a model of how the characteristics of general practices, GPs and their patients influence the rate of referrals. This is the first paper to provide this evidence for a comprehensive set of controls, for almost all of the practices in England and for a panel data set covering a long period.
We estimate a model of the form:
where lnRit represents the logarithm of the number of first referrals at each practice i in each year t per 1000 patients. Referrals made by others (specialists, nurses, etc.) are excluded to ensure that we capture the effects of various primary care characteristics on GP referral decisions and the subsequent hospital admissions. GPXit is a vector of GP and practice characteristics that are time-varying at practice i in time t. The GP characteristics include the proportion of female GPs, mean practice GP age, ethnicity of GPs, type of GP contract (provider/partner vs. salaried) and practice characteristics (single-handed practice, QOF score and GMS/PMS contract), and θ is a vector of the slope effects of these variables.
The term Patit represents a vector of patients’ characteristics at practice i in year t (the share of patients in each of several age categories, sex share, rural practice and the deprivation index). The terms zit capture the proportions of patients registered at each practice with each of several chronic diseases indexed i (asthma, cancer, chronic obstructive pulmonary disease, coronary heart disease, diabetes mellitus, epilepsy, hypertension, hypothyroidism, left ventricular failure, mental health and stroke). Finally, we control for time (µt) with year effects, HA (λi) and practices (σi) with fixed effects. We use panel data fixed effects to estimate our model. In panel data, individuals (cities, firms, etc.) are observed at several time points (e.g. days, years, etc.). Panel data are most useful when we suspect that the outcome variable depends on explanatory variables which are not observable but correlated with the observed explanatory variables. If such omitted variables are constant over time, panel data estimators allow the consistent estimation of the effect of observed explanatory variables. The main advantage of working with panel data is that we are able to control for practice-specific, time-invariant, unobserved heterogeneity, the presence of which could lead to bias in standard estimators such as OLS. The fixed-effect component, σi, captures unobserved heterogeneity across practices, which is fixed over time. In addition, we correct the standard errors in order to control for heteroscedasticity. In practice, the idiosyncratic errors, ξit, are often serially correlated when T > 2. Bertrand et al. 112 show that the usual standard errors of the fixed-effects estimator are drastically understated in the presence of serial correlation. It is therefore advisable to always use cluster-robust standard errors for the fixed-effects estimator. However, cluster-robust standard errors have no impact on the estimated coefficients but do have an effect on standard errors. Therefore, potential bias in the estimated coefficients remains.
We also estimate a practice-level model of the probability of elective admissions of first referral patients. To specify this model, we begin by assuming that the probability of a referred patient from practice i being admitted is determined by the various (patient, practice and GP) characteristics associated with the practice, as well as by the practice rate of referrals. An increase in the practice referral rate is hypothesised to reduce the probability of admissions if the practices with higher referral rates refer at the margin those patients whose expected health value of treatment is lower. In this case, if the proportion of referred patients who are admitted from practice i in year t is git, and the practice referral rate per registered patient is Rit, then the treatment rate per registered patient Tit may be estimated in the following model:
where zit, Pit and GPXit are exogenous influences on the proportion of referrals being admitted. If the proportion being treated, git, declines with increases in the practice referral rate, in a multiplicative separable relationship, then we have:
We assume a semi-log specification for γ, so that a unit change in R gives β% reduction in γ, the probability of admission. Thus, γ = R-β and hence in Equation 29,
If we cannot reject the hypothesis that β = 0, the likelihood of treatment for patients from practices with higher rates of referrals, all else being equal, is not significantly different from patients referred from smaller practices. The greater β is, the greater the fall in the probability of treatment for patients from practices with higher levels of referrals. If we assume that g is an exponential function of its determinants, then in Equation 30, the expression for admissions takes the form:
To examine whether, and to what extent, the treatment rate is declining with the referral rate, we test whether or not β is significantly greater than zero and interpret the size of β. Using this formulation, we estimate a model of the elective admissions that follow a GP referral, using IV panel data estimation at practice level, and controlling for the level of referrals, and a group of GP- and patient-specific characteristics as described above, which may influence g, the probability that a referral is treated. The estimated model is:
where lnTit represents the logarithm of the number of elective hospital admissions following a GP referral, per 1000 patients at each practice i in each year t. The term in the logarithm of the referrals captures the expected influence of referrals by the GPs of practice i on the rate of hospital admissions. We exclude from the treatment data – as we did with referral data – those admissions resulting from referrals by others (specialists, nurses) in order to focus on the effects of GP referral decisions on subsequent treatments. It would be valuable to study the joint determination of the various strands of referrals and admissions, but this is beyond the scope of this report. The rest of the control variables in this model are explained above.
A problem with estimating the model in Equations 28 and 33 is that the referrals made by GPs, rather than being exogenous, may be correlated with unobserved determinants of admissions, even after controlling for the time-constant differences between practices and socioeconomic factors. For example, a contagious local illness may increase both referrals and the error term in the treatment equation, leading to biased and inconsistent estimates. We therefore use IV estimation and the first lag of the referrals in practice i in time t as an instrument for referrals to control for the endogeneity (we have also used 2-year lag and the results are similar). The referrals made at t – 1 may not be correlated with the hospital treatment decisions on current year, but could influence the decision of GPs to refer this year, as referrals are partly based on past experience. Finally, we correct the standard errors in order to control for heteroscedasticity.
Hypotheses and model
To organise our hypotheses and motivate the interpretation of the estimates, we use the following model of GP referrals and specialist admissions. We assume that GPs are concerned with maximising social welfare and that all sick patients are given either primary or secondary care. GPs therefore provide the fall-back provision of treatment. GPs costlessly recognise an ill patient, and their decision to refer is based on the expected additional benefits from secondary care minus the additional extra costs. GPs are gatekeepers who limit access to specialists because specialists, unless constrained by regulation, have a tendency to compete for patients by aiming to deliver the greatest health gains for patients, rather than the greatest level of utility for all those insured. If unconstrained in the choice of diagnostics by the insurer (in this setting, the NHS), specialists will tend to overspend on diagnostics to enable them to maximise health gain. GPs do not refer all patients and allow specialists to choose who to treat, because the expected cost of fully diagnosing patients who have a low probability of benefiting from specialist treatment is greater than the expected health benefit from secondary care, above that of primary care.
At each practice we assume that a GP forms an unbiased estimate for each of their patients, indexed h, of the value of added health, vh, given by a secondary sector intervention net of costs. These interventions are assumed to require hospital treatment. If symptoms indicating the probability of benefiting from secondary care differ between patients, then GPs may order patients by the expected value of vh. To decide whether or not to refer patient h, GPs compare the expected value of vh with the expected benefit of primary care provision, net of cost ph. The GP refers if vh > ph, where the optimal level of referrals R* is such that the incremental net health gain from secondary treatment is equal to the incremental net health gain from primary treatment. This gives the socially optimal level of referrals and the threshold value of vh, above which GPs refer, vt. Crucially for the theory, in determining vh and, thus, vt, the GP considers the tendency of specialists to overspend on diagnostics. The ‘demand’ for secondary treatment is given by ψD(vh) in Figure 44, which gives the number of patients at a practice whose net benefit from secondary care is greater than the height of the curve at that point, and where ψ is a parameter that changes the demand for care. Viewed by the GP maximising social welfare as an agent for the NHS, the opportunity cost of secondary treatment for the ill patient is the health benefit of primary care net of cost. We shall assume that the gross benefit of primary care treatment is constant for all sick patients and that the cost of primary care may rise with primary care supply for all patients, owing to the increasing opportunity cost of GP non-work time as hours of work increase. Under these assumptions, beyond some level of treatments, the net benefit of primary care ΩB(ph) is upwards sloping and where Ω is a parameter that changes the supply of care. It is socially optimal to refer patients for whom D > B so that the optimal level of referrals is R*.
FIGURE 44.
Determining the optimal level of referrals.
The level of referrals will increase if the number of patients for whom the benefit of secondary care, net of its costs, increases. This is captured by an increase in ψ and shifting D upwards and to the right, or by the benefits of primary care increasing, or the costs declining, both of which increase Ω and shift ΩB upwards and to the left. An increase in ψ will increase referrals, whereas an increase in Ω, and an upwards shift of B, will reduce referrals. The various effects that we shall study can be grouped into those that shift either ψ or Ω.
We may think of several factors that might increase the demand for secondary care and increase the referrals per patient at a practice. First, the social characteristics of patients differ across practices, and we may expect that older patients and, possibly, female patients, given the various issues arising from childbirth, may benefit more from a higher referral rate. Patients living in rural areas may be discouraged by distance to surgery to maintain a close GP relationship, and may be less likely to be referred. If patients from deprived areas, after controlling for morbidities, are more distracted by life problems from forming strong GP relationships or less informed to present early, then this effect might independently influence the practice demand for referrals or the treatment consequences. If female or immigrant GPs form stronger relationships with (at least some) patients, or are more risk averse, this may also increase the rate of demand for referrals from these GPs.
Certain groups of GPs, for example, more experienced older GPs, may be more discerning in identifying patients who will be treated and alter the demand curve to become more inelastic – with more referrals of seriously ill patients, and fewer unlikely to receive specialist treatment. They may also be less likely to refer for advice. Certain patient groups that we might characterise as the ‘worried well’ may press for referrals, thereby increasing demand for referrals by these patients who have lower values of vh, but not altering demand among those very ill who expect to be referred. The ‘worried well’ can increase their rate of referral but would not necessarily seek to increase their treatment level beyond what the specialist would normally use following diagnosis and hence would be unlikely to be treated (thus, ψ is increased for vh below a critical level, v*, which increases referrals for this group of marginal referrals, and has little effect on referrals for those with high probability of requiring admission). This influence of the ‘worried well’ on the demand for referral is shown as ψ2D(v) in Figure 44.
The cost of secondary care may be regarded by GPs as higher if there is a high proportion of local hospital beds occupied and therefore may reduce their demand for referrals. Specialists may also reduce admissions, conditional upon referrals, in this circumstance. Partners at practices may have longer time horizons for planning and have more concern for the reputation of their practices with specialists, which may lead to a lower demand for referrals. The willingness to restrict access to specialists may be lower for some practices/GPs, who therefore refer more patients even though their patients are not perceived to be more ill. Patients from these practices/GPs patients will have a high probability of being referred, but a lower probability of treatment given referral.
Results
The model of referrals
In Table 40 we give the parameter estimates of the influence of patient, practice, and GP characteristics in a model of GP practice referrals per 1000 patients for the years 2004–12. In model 1 we consider only practice variables, and in models 2 and 3 add sequentially the influence of sets of patient and GP variables. Adding incremental sets of variables only marginally increases the goodness of fit, which is largely determined by the chronic disease, year, practice and SHA region fixed effects, although a few of the variables of interest turn out to be highly statistically significant. The variation of referral rates among practices is largely unexplained by the literature (see O’Donnell98). This is also broadly the implication of our estimation, where we can observe that only a few variables have an effect on GP referrals.
| Characteristic | OLS | ||
|---|---|---|---|
| Model 1 | Model 2 | Model 3 | |
| Practice characteristics (SE) | |||
| Ln QoF points | –0.03 (0.02) | –0.027 (0.02) | –0.036* (0.02) |
| Single-handed practice | –0.010* (0.006) | –0.010* (0.006) | 0.013** (0.007) |
| Rural indicator of practice | –0.021 (0.013) | –0.02 (0.013) | –0.016 (0.013) |
| GMS contract | 0.001 (0.001) | 0.001 (0.001) | 0.001 (0.001) |
| Index deprivation of practice patients | –0.002** (0.001) | –0.002** (0.001) | –0.001 (0.001) |
| % beds occupied at hospitals in PCT | –0.008 (0.007) | –0.009 (0.007) | –0.009 (0.007) |
| Patients’ characteristics | |||
| Proportion of patients aged 35–59 years | 0.282* (0.167) | 0.291* (0.167) | |
| Proportion of patients aged ≥ 60 years | 0.290** (0.118) | 0.298** (0.118) | |
| Proportion of female patients | 1.010*** (0.218) | 0.951*** (0.217) | |
| GPs’ characteristics | |||
| Total FTE GPs at practice | –0.002 (0.002) | ||
| Mean age of GPs (years) | –0.001*** (0.000) | ||
| Proportion of FTE female GPs at practice | 0.051*** (0.010) | ||
| Proportion of FTE immigrant GPs at practice | –0.036*** (0.011) | ||
| GPs working full-time: proportion FTE ≥ 1 | 0.010 (0.008) | ||
| GPs working with 0.6 ≤ proportion FTE < 1 | 0.013 (0.009) | ||
| Years of education of GPs | 0.001 (0.002) | ||
| Proportion of GPs who are partners | –0.016** (0.008) | ||
| Number of observations | 65,818 | 65,818 | 65,818 |
| R 2 | 0.375 | 0.376 | 0.379 |
From Table 40 model 3, which gives estimates with all variables included, we find that practices with larger proportions of patients aged ≥ 60 years have higher referral rates than those with larger proportions of under 35-year-olds, as expected, but also that those aged 35–59 years are as likely to be referred to a specialist as patients aged ≥ 60 years, which is not expected. This, and the large gap between the referral rates for under 35-year-olds and the middle-aged, deserves further analysis. Practices with larger proportions of female patients also have higher referrals, all else being equal.
Considering practice and area characteristics, single-handed practices are estimated to have higher referral rates but only when other characteristics are being controlled, and the effect is of marginal statistical significance. We find that neither rural practices, nor those with GMS contracts rather than PMS, have referral rates that are significantly different from other practices. The various concerns that elements of the QOF might raise referrals are not found to be warranted, with the evidence suggesting that high QOF-rated practices have slightly lower referrals. We find no evidence that GPs in areas where hospital beds are more fully occupied allow this to inhibit their referrals. We are unable to detect any incremental effect of living in a deprived area on referral rates, provided patient and GP variables are included as specified in Table 40, model 3.
Various recent studies have focused on inequalities in health and the use of the health system between different social groups (e.g. Dixon et al). 103 In our study we have calculated for the first time the index of deprivation at practice level for each of the years of the study. If we think of the index of deprivation in the referral equation as capturing unmeasured health problems that are not captured by the listed exogenous variables and patient morbidities, then we might expect it to have a positive effect on referrals. If these unmeasured effects are disproportionately serious health concerns requiring admission, then deprivation may also increase the probability of treatment conditional upon referral. We find that referrals are higher if patients are living in deprived areas, all else being equal. One reason why this variable is not positive may be that people living in deprived areas usually tend to use more A&E, as found by McCormick et al. 113
Turning to GP characteristics, the statistically significant results are that female GPs make more referrals, immigrant GPs make fewer referrals, and that older/more experienced GPs make fewer referrals, all else being equal. We also find that practice size, as measured by the total FTE number of GPs employed in the practice, has little impact on referrals, once single-handed GPs are controlled separately. We shall look further at these findings after discussing their effects in the treatment equation. However, we note that the finding that female GPs have a positive and significant effect on the rate of referrals confirms that of other studies, such as Ringberg et al. ,100 who found that male GPs and specialists in family medicine referred significantly less frequently to secondary care.
The model of hospital admissions following first referral
Table 41 presents model 3 from Table 40, together with estimates of our preferred model of admissions conditional on referral, based on Equation 33. The model of admissions is estimated using 2SLS to allow for the possible correlation between practice referrals and the error term in the practice admissions equation. The parameter estimates for each model are placed adjacent to each other to facilitate comparison.
| Variable, coefficient (SE) | Ln referrals per 1000 patients (Equation 28) | Ln elective admissions per 1000 patients (Equation 33) |
|---|---|---|
| OLS | 2SLS | |
| Ln referrals per 1000 patients | 0.621*** (0.045) | |
| Practice and area characteristics | ||
| Ln QoF points | –0.036* (0.02) | 0.001 (0.053) |
| Single-handed practice | 0.013** (0.007) | –0.054*** (0.014) |
| Rural indicator of practice | –0.016 (0.013) | 0.000 (0.002) |
| GMS contract | 0.001 (0.001) | –0.009 (0.03) |
| Index deprivation of practice patients | –0.001 (0.001) | 0.020*** (0.002) |
| Beds occupied at hospitals in PCT (%) | –0.009 (0.007) | 0.007 (0.013) |
| Patients’ characteristics | ||
| Proportion of patients aged 35–59 years | 0.316* (0.167) | –1.731*** (0.404) |
| Proportion of patients aged ≥ 60 years | 0.319*** (0.118) | 2.813*** (0.329) |
| Proportion of female patients | 0.958*** (0.218) | –0.346 (0.43) |
| GPs’ characteristics | ||
| Total FTE GPs at practice | –0.002 (0.002) | –0.010** (0.004) |
| Mean age of GPs (years) | –0.001*** (0.000) | 0.005*** (0.001) |
| Proportion of FTE female GPs at practice | 0.051*** (0.01) | 0.023 (0.021) |
| Proportion of FTE immigrant GPs at practice | –0.036*** (0.011) | 0.004 (0.023) |
| GPs working full-time: proportion FTE ≥ 1 | 0.01 (0.008) | 0.026 (0.02) |
| GPs working with 0.6 ≤ proportion FTE < 1 | 0.013 (0.009) | –0.051** (0.022) |
| Years of education of GPs | 0.001 (0.002) | –0.005 (0.003) |
| Proportion of GPs who are partners | –0.016** (0.008) | 0.037* (0.02) |
| Number of observations | 65818 | 57762 |
| R 2 | 0.379 | 0.061 |
The parameter on Ln referrals has an estimated value of 0.621, and is significant at the 1% level of significance. Our estimate of β in Equation 33 is 0.38. This suggests that a 10% increase in referrals will, on average, lead to a 6.2% increase in admissions, all else being equal. We show in Table 42 the much smaller parameter estimates – and correspondingly larger values of β – when OLS is used, indicating the importance of allowing for the endogeneity of referrals in modelling treatment.
| Variable | Not including practice, GP or patient characteristics | Including practice, GP and patient characteristics | ||
|---|---|---|---|---|
| OLS | 2SLS | OLS | 2SLS | |
| Ln referrals | 0.286*** | 0.617*** | 0.247*** | 0.621*** |
| Per 1000 patients | 0.025 | 0.041 | 0.026 | 0.045 |
| Year fixed effects | Yes | Yes | Yes | Yes |
| HA fixed effects | Yes | Yes | Yes | Yes |
| Practices’ characteristics | No | No | Yes | Yes |
| GPs’ characteristics | No | No | Yes | Yes |
| Patients’ characteristics | No | No | Yes | Yes |
| n | 65,825 | 57,769 | 65,818 | 57,762 |
| R 2 | 0.05 | 0.026 | 0.087 | 0.061 |
In Table 43 we use the model to simulate the effects of a policy to reduce referrals by 50 persons per practice on the levels of treatment at practices with high, low and mean rates of referrals. Row 1 gives the referral rate at three quantile points. Row 2 gives the forecast treatment rate at each quantile. Row 4 gives the referral rate at each quantile if referrals are reduced by 50, and row 5 gives the estimated admission rate conditional upon the lower referral rate. The treatment rate falls by 8 (11%) at high referral rate practices, by 9 (16%) at the mean, and by 10 (23%) at low referral rate practices. If treatments are to be equally protected at all practices then it is not optimal to require all practices to equally reduce referrals, and the policy will require reductions to increase with the practice referral rate. Implementation of policy would require a standardisation of practice referral rates by scale of morbidities and other factors, such as deprivation, that are indicative of poor health.
| Variable | Ln admissions per 1000 patients | ||
|---|---|---|---|
| 2SLS | |||
| Ln referrals per 1000 patients | 0.621*** (0.045) | ||
| Quantile on referral rate | 90Q | 50Q | 10Q |
| 1. Average referral rate (per 1000 patients) at each quantile | 243 | 175 | 122 |
| 2. Estimated treatment rate (per 1000 patients) at each quantile | 75 | 57 | 44 |
| 3. Reducing by 50 the referral rate (per 1000 patients) | |||
| 4. Average referral rate (per 1000 patients) at each quantile after reduction (estimate from row 1 minus 50) | 193 | 125 | 72 |
| 5. Estimated treatment rate (per 1000 patients) at each quantile after reduction (as for row 2 except row 4 referrals) | 67 | 48 | 34 |
| Absolute (%) reduction | 8 (11) | 9 (16) | 10 (23) |
Turning to consider the effects of the various influences on admissions, we find that the sex of patients matters more for the GP referral rates than admissions conditional upon referrals. Thus, the positive effects of sex on referrals appears warranted by the criterion that women referred are admitted to hospital with equal probability as their male counterparts. The results for age are less encouraging. Recall that both old and middle-aged patients are equally likely to be referred, and more so than those aged < 35 years; however, middle-aged patients are not only significantly less likely to be admitted than patients aged ≥ 60 years, but, more disconcerting, are also significantly less likely to be admitted than those aged < 35 years of age who are referred. The model of the worried well appears to fit the ‘middle aged’ who may manage ‘low need’ demand better than other age groups, and benefit at the expense of more specialist attention to the needs of those aged < 35 years.
Among the practice characteristics, patients referred from single-handed practices are significantly less likely to be admitted, whereas patients from deprived areas, all else being equal, are more likely to be admitted, if referred. Other effects are insignificant.
Of the GP characteristics, four effects are significant:
-
Referrals from larger practices have somewhat lower probabilities of admission, but this is smaller in magnitude than single-handed practices. This suggests a non-linear – possibly U-shaped – relationship between practice size and admission conditional upon referral, with mid-size practices having the highest probabilities.
-
Older GPs are found to have significantly higher probabilities of referrals being admitted. Combined with their lower probability of referral this suggests a picture consistent with the model of experience bringing an understanding of those patients who will benefit from admission, or who are less likely to require, and be referred for, specialist advice.
-
Practices with a high share of partners in their GPs are also more likely to have referrals admitted.
-
Finally, there is some evidence that referred patients from practices with a large share of part-time GPs are less likely to be admitted.
Explaining the variation in hospital admission rates between practices
The striking bimodality in Figure 41, in which one group of practices has a referral rate of 200 per 1000 patients, and a hospital treatment rate of about 50 per 1000 patients, and another group has a similar referral rate but a treatment rate that is twice as high, can now be explained using evidence from the treatment equation. We may ask: what characteristics are associated with a practice that has a high rate of patient hospital treatments, but a low level of referrals? In Table 44 we examine the consequence for the two endogenous variables of a 1-SD change in significant explanatory variables. Two variables stand out as critical to explaining large variations in hospital treatment rates following referral, at given levels of referrals: (1) the measure of deprivation in the residential areas occupied by the patients of the practice; and (2) the proportion of practice patients aged > 60 years. A 1-SD change in both of these variables will increase the hospital treatment rate at a given level of referrals by about 35 patients admitted, which may be compared with the mean annual planned admission rate following first referral of 74 per 1000 registered patients in the middle of our sample period. It would appear desirable to exclude practices with high shares of the elderly, and high shares of deprived area patients, from any policy to uniformly reduce referrals.
| Variable | Referrals (mean referral 180) | Admissions (mean admissions 74) | ||||
|---|---|---|---|---|---|---|
| Beta | SD | Implied change | Beta | SD | Implied change | |
| Single-handed practice | 0.013 | 0.3230 | 0.224 | –0.053 | 0.3230 | –1.55 |
| Index deprivation | a | a | 0.02 | 11.9910 | 19.67 | |
| Proportion of patients aged 35–59 years | a | a | –1.731 | 0.0351 | –4.64 | |
| Proportion of patients aged ≥ 60 years | 0.319 | 0.0690 | 3.463 | 2.813 | 0.0690 | 15.49 |
| Proportion of female patients | 0.958 | 0.0238 | 3.608 | a | a | |
| Total FTE hours | a | a | –0.01 | 2.5300 | –2.14 | |
| Age of GPs | –0.001 | 7.0700 | –1.796 | 0.005 | 7.0700 | 2.35 |
| Proportion of FTE female GPs | 0.051 | 0.2570 | 1.836 | a | a | |
| Proportion of FTE immigrant GPs | –0.036 | 0.3670 | –2.887 | a | a | |
| Proportion of GPs working FTE < 1 and ≥ 0.6 | a | a | –0.05 | 0.2338 | –1.16 | |
| Proportion of provider GPs (partners) | –0.016 | 0.2168 | –1.153 | a | a | a |
Considering the referral equation, variation between practices with shares of patients over 60 years, and female patients, appear the most important influences on variation of practice referral rates, once morbidities are controlled. An increase of 1 SD of the proportion of female patients increases the referral rate per 1000 patients by approximately four. These results are in line with the literature; Hippisley-Cox and Jumbu102 found that consultation rates varied markedly by age and sex, with highest rates for the elderly.
Robustness checks
Quantile regression
To study better heterogeneity across practices and how the relationship between referral and admission rates may not be linear, we estimate a quantile regression model that also accounts for the endogeneity of referrals. Quantile regression is a widely used tool for estimating conditional quantile models; see for example, Koenker and Bassett92 and Koenker. 93 Quantile regression modelling gives estimates of quantile-specific effects that describe the impact of covariates not only on average, but also on the tails of the conditional outcome distribution. Although central effects, such as the mean effect obtained through conditional mean regression, provide useful summary statistics of the impact of a covariate, they fail to describe the distribution of the impact. Standard linear regression techniques summarise the average relationship between a set of regressors and the outcome variable based on the conditional mean function. In many studies, the variables of interest (education, health or prices) are endogenous. Endogeneity of covariates renders the conventional quantile regression inconsistent for estimating the causal effects of covariates on the quantiles of economic outcomes, just as with the conventional linear model. To study the relation between referrals and hospital admissions at practice level we use the QIV panel estimator, developed by Chernozhukov and Hansen. 86 The principal identifying assumption of the model is the imposition of conditions that restrict how rank variables (structural errors) may vary across treatment states. These conditions allow the use of IVs to overcome the endogeneity problem and hence recover the true QTEs. This framework also ties naturally to simultaneous equations models, corresponding to a structural simultaneous equation model with non-additive errors. Estimation and inference procedures for linear quantile models have been developed by Chernozhukov et al. 86,95,114
The QIV estimator allows us to obtain estimates of the influence of referral rates at practice level that vary across the conditional hospital admissions distribution that have been made by GPs. We use the same variables used above to estimate the 2SLS model of the hospital admissions to estimate the quantile regression.
Table 45 reports the quantile regression that allows for the endogeneity of referral rates and the implications for confidence intervals. The most notable variation of parameter estimates across the distribution is observed in the referrals coefficient. This coefficient increases quite sharply in the first two quantiles and becomes flat and similar across the median quantiles, increasing again in the highest quantiles of treatment. The estimation is in line with the previous results and emphasises the non-linearity of the effect of referrals on treatments, which the specification in the previous regressions may have oversimplified. The explanation may well reflect the heterogeneity of practices which in those with highest treatment levels may experience relatively high levels of treatment for additional referrals given the unmeasured health problems of the patients in these practices. The rest of the variables do not change across the distribution, with the exception of the proportion of GP partners, which has a strong and positive effect on the first two quantiles.
| Treatments per 1000 patients by GPs | Quartile | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| Ln referrals per 1000 patients | |||||||||
| Estimated coefficient | 0.64 | 0.61 | 0.45 | 0.30 | 0.23 | 0.24 | 0.27 | 0.31 | 0.37 |
| Lower | 0.53 | 0.55 | 0.42 | 0.28 | 0.20 | 0.22 | 0.25 | 0.28 | 0.33 |
| Upper | 0.74 | 0.66 | 0.49 | 0.34 | 0.26 | 0.28 | 0.32 | 0.33 | 0.37 |
| Ln QOF points | |||||||||
| Estimated coefficient | –0.13 | –0.14 | –0.20 | –0.27 | –0.33 | –0.38 | –0.34 | –0.29 | –0.24 |
| Lower | –0.31 | –0.32 | –0.26 | –0.48 | –0.57 | –0.57 | –0.57 | –0.50 | –0.36 |
| Upper | 0.57 | 0.21 | 0.09 | –0.06 | –0.14 | –0.27 | –0.24 | –0.22 | –0.14 |
| Proportion of FTE female GPs | |||||||||
| Estimated coefficient | –0.04 | –0.06 | –0.06 | –0.07 | –0.07 | –0.06 | –0.07 | –0.07 | –0.07 |
| Lower | –0.15 | –0.09 | –0.09 | –0.08 | –0.06 | –0.07 | –0.07 | –0.07 | –0.08 |
| Upper | 0.01 | 0.01 | –0.01 | –0.03 | –0.02 | –0.03 | –0.03 | –0.04 | –0.04 |
| Total FTE hours | |||||||||
| Estimated coefficient | –0.02 | –0.01 | –0.01 | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Lower | –0.02 | –0.02 | –0.01 | –0.01 | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| Upper | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 |
| Single-handed practice | |||||||||
| Estimated coefficient | –0.03 | 0.01 | –0.01 | –0.03 | –0.03 | –0.02 | 0.00 | –0.01 | 0.00 |
| Lower | –0.05 | 0.00 | –0.02 | –0.04 | –0.05 | –0.04 | –0.02 | –0.02 | –0.02 |
| Upper | 0.09 | 0.07 | 0.02 | –0.01 | –0.01 | –0.01 | 0.01 | 0.01 | 0.02 |
| Mean age of GPs | |||||||||
| Estimated coefficient | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Lower | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Upper | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Rural indicator per practice | |||||||||
| Estimated coefficient | 0.02 | 0.00 | –0.01 | –0.01 | –0.01 | –0.01 | –0.01 | –0.01 | 0.00 |
| Lower | 0.01 | –0.01 | –0.01 | –0.01 | –0.01 | –0.02 | –0.02 | –0.01 | –0.01 |
| Upper | 0.03 | 0.01 | 0.00 | 0.00 | 0.00 | –0.01 | 0.00 | 0.00 | 0.00 |
| Proportion of beds occupied at PCT | |||||||||
| Estimated coefficient | 0.15 | 0.18 | 0.15 | 0.03 | –0.08 | –0.11 | –0.12 | –0.12 | –0.11 |
| Lower | 0.12 | 0.11 | 0.09 | 0.01 | –0.10 | –0.15 | –0.14 | –0.13 | –0.13 |
| Upper | 0.23 | 0.26 | 0.21 | 0.11 | –0.04 | –0.07 | –0.09 | –0.10 | –0.09 |
| Proportion of FTE immigrant GPs | |||||||||
| Estimated coefficient | 0.02 | 0.04 | 0.07 | 0.07 | 0.07 | 0.07 | 0.05 | 0.04 | 0.03 |
| Lower | –0.09 | 0.01 | 0.02 | 0.04 | 0.04 | 0.06 | 0.04 | 0.02 | 0.01 |
| Upper | 0.07 | 0.08 | 0.09 | 0.10 | 0.09 | 0.10 | 0.08 | 0.06 | 0.05 |
| Proportion of GPs working FTE ≥ 1 | |||||||||
| Estimated coefficient | 0.05 | 0.08 | 0.08 | 0.09 | 0.09 | 0.07 | 0.06 | 0.04 | 0.01 |
| Lower | –0.14 | 0.00 | 0.03 | 0.06 | 0.06 | 0.02 | 0.04 | 0.02 | –0.02 |
| Upper | 0.11 | 0.16 | 0.14 | 0.16 | 0.14 | 0.11 | 0.09 | 0.09 | 0.05 |
| Proportion of GPs working 0.6 ≤ FTE < 1 | |||||||||
| Estimated coefficient | –0.19 | –0.10 | –0.03 | –0.01 | 0.01 | 0.00 | 0.01 | 0.02 | 0.01 |
| Lower | –0.32 | –0.16 | –0.10 | –0.06 | –0.05 | –0.06 | –0.02 | –0.03 | –0.03 |
| Upper | 0.00 | 0.00 | 0.03 | 0.10 | 0.13 | 0.09 | 0.08 | 0.08 | 0.06 |
| Proportion of patients aged 35–59 years | |||||||||
| Estimated coefficient | 0.17 | 0.75 | 1.11 | 1.19 | 1.45 | 1.48 | 1.46 | 1.25 | 1.05 |
| Lower | –0.71 | –0.03 | 0.39 | 0.85 | 1.23 | 1.19 | 1.24 | 1.10 | 0.86 |
| Upper | 0.36 | 0.82 | 1.03 | 1.26 | 1.50 | 1.61 | 1.63 | 1.46 | 1.28 |
| Proportion of patients aged 60+ years | |||||||||
| Estimated coefficient | 2.58 | 2.06 | 1.64 | 1.27 | 1.14 | 1.06 | 1.03 | 1.07 | 0.99 |
| Lower | 1.95 | 1.68 | 1.31 | 0.83 | 0.69 | 0.75 | 0.74 | 0.91 | 0.96 |
| Upper | 3.06 | 2.29 | 1.78 | 1.36 | 1.24 | 1.08 | 1.13 | 1.20 | 1.30 |
| Proportion of female patients | |||||||||
| Estimated coefficient | –0.17 | 0.63 | 1.17 | 1.63 | 1.70 | 1.60 | 1.44 | 1.15 | 0.72 |
| Lower | –1.52 | 0.03 | 0.56 | 1.10 | 1.12 | 1.04 | 0.93 | 0.83 | 0.41 |
| Upper | –0.15 | 0.78 | 1.28 | 2.21 | 2.30 | 2.05 | 1.84 | 1.46 | 0.98 |
| Years of education of GPs | |||||||||
| Estimated coefficient | –0.02 | –0.02 | –0.01 | –0.01 | –0.01 | –0.01 | –0.01 | –0.01 | 0.00 |
| Lower | –0.03 | –0.02 | –0.02 | –0.01 | –0.01 | –0.01 | –0.01 | –0.01 | 0.00 |
| Upper | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | –0.01 | 0.00 | 0.00 | 0.00 |
| Proportion of provider GPs | |||||||||
| Estimated coefficient | 0.28 | 0.26 | 0.19 | 0.16 | 0.13 | 0.10 | 0.07 | 0.07 | 0.06 |
| Lower | 0.20 | 0.17 | 0.13 | 0.14 | 0.10 | 0.06 | 0.04 | 0.03 | 0.05 |
| Upper | 0.36 | 0.35 | 0.26 | 0.24 | 0.18 | 0.14 | 0.10 | 0.09 | 0.09 |
| GMS contract | |||||||||
| Estimated coefficient | –0.04 | –0.03 | –0.03 | –0.02 | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| Lower | –0.05 | –0.04 | –0.04 | –0.04 | –0.02 | –0.01 | 0.00 | 0.00 | 0.00 |
| Upper | 0.01 | –0.01 | –0.01 | –0.01 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 |
| Index deprivation by practice | |||||||||
| Estimated coefficient | –0.01 | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Lower | –0.02 | –0.01 | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Upper | –0.01 | –0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Conclusions
We have studied certain aspects of the experience of NHS patients at their GP practices using a panel data set for the years 2004–12, to better understand the relationship between referrals and hospital treatments. The referral and treatment of NHS patients is based on their GP and the relationships created between themselves and the practice GPs, so it is perhaps unsurprising that practice referrals and treatment rates are far from uniform. Although the observation that practices have, on average, the equivalent of about four full-time GPs and approaching 8000 patients might suggest that professional peer pressure and the law of large numbers would considerably ameliorate heterogeneity between practices, striking differences remain even when observed patient morbidities are controlled. Some of these differences reflect the comparative needs of patients and practice locations or various external constraints on practice capacities. As such, some differences may be not simply benign but rather symptomatic of high performance. Other findings are less easy to understand or justify.
For example, the evidence that the middle aged are much more likely to be referred than those under 35 years, despite it being much less likely that the referral will lead to a high value hospital treatment, appears difficult to reconcile with efficient behaviour. Instead it raises the concern that the health ‘model’ as a whole (and the responsibility may not be with individual practice decisions) gives insufficient attention to anticipating the health problems of the young, and it may be that the ‘middle aged’ are, in comparison, the ‘worried well’. In contrast, although the growth of participation among female GPs has almost certainly helped to explain a small part of the rise in referrals in the past decade, the appropriateness of these referrals is supported with as high a specialist treatment rate for this larger body of referrals per FTE as for male GP referrals.
We have found that variation between practices first referrals and ensuing hospital treatments is not consistent with a simple model in which the registered patients at some practices are less healthy and, as a result, have higher rates of both referrals and hospital admissions. Instead, practices with high rates of hospital admissions tend to have similar referral rates to low admission rate practices. This may reflect that practices with largely healthy patients refer too much, or that practices with comparatively ill patients refer too little, or perhaps neither of these. However, the fact of this non-relationship needs further explanation.
Finally, we have discussed how a policy to reduce referrals by a uniform amount may reduce hospital treatments by as much as 20% of the absolute reduction in referrals and disproportionately reduce treatments at practices that make few referrals. We also suggest that practices in deprived areas, and with high proportions of persons over 60 years of age, should be excluded from these policies on the grounds that the referral levels from these practices are low relative to the incipient clinical need as determined by hospital admission rates following first referral.
Chapter 7 Prioritising patients for elective surgery: the efficiency of alternative selection criteria
Introduction
In 2012 the English NHS set up CCGs to commission health-care services for patients within designated geographical areas. CCGs broadly aim to maximise the health gain from treatment while keeping within a budget, based on indicators of local need. To achieve this, many have issued ‘treatment and referral guidelines’ to GPs. The guidelines are generally intended to discourage GPs from referring patients with less to gain from treatment. Sometimes, particularly for joint replacements, thresholds are specified in terms of condition-specific scores such as the Oxford Hip Score (OHS) or the Oxford Knee Score (OKS). 115 Referral management centres, which many CCGs have inherited from the PCTs they have supplanted, offer a method for screening GP referrals to reduce activity. These centres were set up in the expectation that they would reduce the number of outpatient attendances. Not all have done so. 116 As another means of limiting volume, the NHS locally has sometimes set thresholds for treatment for specific elective procedures. NHS managers, frustrated by an inability to control expenditure, and limited by ‘austerity’ funding, may yet resort to volume capping. The growing use of eligibility criteria, additional hurdles on the patient pathway and thresholds imposed by management, raises questions as to the effectiveness of alternative criteria for choosing patients with most to gain. This chapter evaluates criteria such as the OHS and other condition-specific metrics, a generic measure of baseline health, the patient’s quality-adjusted life-year (QALY), and a predictive score combining these factors along with comorbidities, age and social deprivation.
Only a few studies have tested the effectiveness of selection criteria, or thresholds, that are designed to identify those patients with most to gain. An early instance is a study of 341 patients observed in the New Zealand Clinical Priority Assessment Criteria initiative. 117 The study considers QALY change – the EuroQol-5 Dimensions (EQ-5D) variant – measured before and after surgery as its leading indicator of health gain. A key conclusion is that a patient’s baseline health status weakly explains the magnitude of benefit following surgery. In contrast, a similar Dutch study of 114 hip patients found that a range of baseline measures strongly predicts outcome. 118 A more recent study in the NHS with 3307 observations concludes that baseline OKS or OHS have no value in predicting one specific outcome (patient satisfaction) of hip or knee replacement surgery and, consequently, should not be used to select patients. 119 A study of 1991 patients in London found that < 20% of the variability in a binary outcome variable based on the OKS is explained by a carefully selected set of baseline characteristics. 120 An analysis of a specific eligibility criterion imposed by some NHS commissioners for a specific elective procedure – knee replacement (2131 patients) – shows that treatment would be cost-effective if offered to those patients deemed ineligible by the criterion. 121 The authors conclude that that ‘the rationing methods proposed . . . are not supported by evidence on health outcomes or cost effectiveness’ and that the use of baseline characteristics as eligibility criteria has been misguided. A study of PROMs procedures that shows no evidence of a diminishing of reported patient gains to higher local volumes leads the authors to conclude that ‘policies by commissioners to reduce surgical rates in the English NHS cannot be justified on the grounds of avoiding inappropriate operations or increasing cost-utility.’122
Using different samples and methodologies, these studies suggest that for NHS patients whom clinicians have accepted as suitable for treatment, it is unclear that criteria exist to identify those patients whose subsequent treatment will not prove cost-effective. In this paper, we first show how PROMs data allow the finding discussed by Dakin et al. 121 to be generalised in several ways – to apply to a large national sample, a wide range of threshold OKS scores, and beyond knees to hips and varicose veins, using the OHS and the score from the Aberdeen Varicose Vein Questionnaire (AVVQ). Second, we consider how far selection criteria other than a condition specific score may identify ex ante those patients who are currently chosen by NHS clinicians for treatment, but whose treatment would not be cost-effective. We first examine the use of pre-operative health status as measured by EQ-5D as a criterion, and, second, estimate a model of QALY gain drawing upon patients’ pre-operative characteristics. The model is estimated on 3 years of PROMs data, and applied to identify the treated patients in a post-sample period who are not forecast to be cost-effective, and thus whom the model would not indicate treatment. We then consider the actual QALY gain for these patients to determine whether their treatment was in retrospect cost-effective. For our measure of health gain we follow Dakin et al. 121 in choosing the change in QALY, specifically the change in EQ-5D status combined with an estimate of the persistence of the change.
The PROMs data set used in this study is much larger than hitherto available and offers an opportunity to assess selection criteria on a sample of 100,000 with complete data for hip replacements. 123 Every NHS patient treated with the procedures in question over a period of 4 years has the opportunity to complete a questionnaire before and after surgery. In addition to pre- and post-operative EQ-5D status [EuroQol-5 Dimensions three-level questionnaire (EQ-5D-3L) variant with the UK time trade-off value set, the UK standard] the questions provide a range of baseline data.
The thresholds specified by CCGs for hip and knee scores (OHS/OKS) range from 20 to 30, in which lower scores indicate more severe symptoms. In the PROMs database, about 10% of currently treated patients record baseline scores of 30 or more, whereas 36–40% exceed scores of 20. Consequently, although CCGs do not specify a volume cap, the thresholds selected would have the effect of reducing volume and, indeed, that is their intention. The PROMs data set can be used to compare different selection criteria in terms of their ability to identify patients who will benefit from treatment. CCGs may find these results helpful to refine the referral and treatment guidance they give to clinicians or otherwise to inform expenditure control policy.
The next section (see Summary statistics) gives summary statistics for each of the PROMs conditions, concerning the distribution of benefits and cost-effectiveness of treatment across patients. Simple eligibility criteria: Oxford Hip Score and Oxford Knee Score uses the PROMs data set to estimate (1) the proportion of knee replacement patients who would be ineligible under various levels of the OKS criterion and (2) the cost-effectiveness of their treatment. We then determine the OKS corresponding to a cost per QALY benchmark of £30,000 and the potential savings from the adoption of this criterion. Simple eligibility criteria: baseline quality-adjusted life-year explores the effectiveness of using the patient’s baseline QALY as a selection criterion instead of the baseline OKS. Finally, as a comparator, we consider similar evidence for hip replacements.
Selection criteria using a range of baseline data develops a model of patient QALY gain in an attempt to identify a higher proportion of patients whose treatment is not cost-effective. The model has three versions. The full version draws on a number of pre-operative patient characteristics. Two restricted versions are developed that might be aligned to political constraints on patient selection. In the first, potentially controversial variables such as age, sex and social class are omitted. In the second, only baseline QALY and baseline condition-specific score are included. We extend the analysis to consider the other two PROMs procedures – groin hernia and varicose veins – to test how far the results for major joint replacements generalise to other procedures.
Results: Comparing the patient selection criteria brings the results together and presents estimates of the savings in resources and the sacrifice of health gain from using the different criteria to identify patients whose treatment would not be cost-effective.
Summary statistics
Patient-reported EQ-5D scores may be used to indicate the change in patient health status following their operation. Table 46 shows the distribution across categories of change in health status, for each of the four procedures. A substantial minority of hip patients are restored to full health (36%), a small proportion derive no benefit (6%) or actually get worse (6%), the majority derive benefit but do not reach full health (52%) and a small proportion die (0.7%). A slightly larger proportion of knee patients either receive no benefit (10%) or get worse (11%). In the case of groin hernia and varicose veins, larger proportions of patients experience no benefit (31%) or get worse (15–18%).
| Change in health status | Procedure (%) | |||
|---|---|---|---|---|
| Hip | Knee | Varicose vein | Groin hernia | |
| Loss | 6 | 11 | 15 | 18 |
| No change | 6 | 10 | 31 | 31 |
| Gain | 88 | 79 | 54 | 51 |
| Total | 100 | 100 | 100 | 100 |
| Mean gain in EQ-5D scorea | 0.452 | 0.330 | 0.120 | 0.105 |
Despite notable proportions of patients who do not benefit, these procedures all score highly in cost-effectiveness for the average patient. The mean cost per QALY associated with these gains can be found by combining this information with estimates of the unit cost of treatment and the duration for which the QALY change persists. The unit cost of knee replacements and the duration of the QALY gain or loss are taken from Dakin et al. 121 These estimates are also assumed to apply to hip replacements, based on very similar unit costs for the two procedures reported in a PCT presentation. 124 For varicose vein and groin procedures, the unit cost is estimated from the weighted average of HRG data, codes QZ21–2 and FZ18, respectively. 125 For consistency with the hip and knee replacement estimates, these estimates are deflated back to 2007–8 levels using the HCHS pay and prices index. 126 The unit costs are hip or knee replacement, £7500; varicose vein procedure, £1063; groin hernia procedure, £1518. For varicose vein and groin hernia procedures, the QALY benefit or loss reported by the patient is assumed to persist for 5 years, again in line with Dakin et al. 121
The mean cost per QALY for the patients undergoing different procedures is given in Table 47.
| Procedure | Mean cost (£) |
|---|---|
| Hip replacements | 3500 |
| Knee replacements | 4500 |
| Varicose vein procedures | 1800 |
| Groin hernia procedures | 2900 |
These values compare favourably with the ‘passmark’ of £30,000 per QALY, which NICE is widely believed to apply in health technology assessments and which we shall illustrate throughout this chapter. Although the average cost per QALY is far below £30,000, not all patients’ cost per QALY is < £30,000.
We now determine the proportion of patients whose treatment does not meet the £30,000 per QALY threshold. Using unit cost and duration of benefit data it is possible to infer for each of the four procedures the QALY gain required to achieve the £30,000 cost per QALY benchmark. If C is the unit cost of each procedure, Q is the QALY change as measured by the post-operative EQ-5D score minus the pre-operative EQ-5D score and P is duration of the effect in years, then the change in EQ-5D score corresponding to £30,000 per QALY is Q = C/(30P). For hips and knees this figure is 0.05, for varicose veins it is 0.007 and for groin hernias it is 0.011. In 2012 the percentages of patients not achieving these levels of benefit, and thereby having a cost per QALY > £30,000, were in the case of hip replacements 13.7%, knee replacements 22.9%, varicose vein procedures, 45.8% and groin hernia procedures, 48.2%. These proportions are substantial and it is well worth attempting to predict which patients will fall into this category.
Simple eligibility criteria: Oxford Hip Score and Oxford Knee Score
We now consider predicting those patients whose treatment does not prove cost-effective, first using pre-operative OHS or OKS scores. The method is to note the mean QALY gain associated with each value of the OKS or OHS score in the PROMs data set. For singleton baseline metrics such as OKS and OHS, a single value covers a number of respondents with a range of values for QALY gain. In these cases each baseline OKS/OHS value is assigned the mean QALY change for that value. It is then straightforward to identify patients who would be ineligible under the different baseline scores, to uncover their mean QALY gain and to convert this into a cost per QALY.
Table 48 gives the percentage of patients whose OKS/OHS scores exceed successively more restrictive OKS/OHS thresholds and the corresponding cost per QALY. It shows that at each threshold it is cost-effective to treat those with scores above the threshold. PROMs data confirm that no realistic OKS/OHS threshold would identify a substantial proportion of patients whose treatment is not cost-effective. Even under the least demanding threshold (< 40), it would be cost-effective to treat those above it (£16,000 vs. £30,000 for knee replacements).
| OKS/OHS threshold | Percentage | Mean cost per QALY (£) | ||
|---|---|---|---|---|
| Knee replacement | Hip replacement | Knee replacement | Hip replacement | |
| < 25 | 23.4 | 21.7 | 7800 | 6900 |
| < 30 | 9.4 | 9.3 | 8600 | 8100 |
| < 35 | 2.5 | 3.4 | 10,900 | 10,400 |
| < 40 | 0.4 | 0.9 | 16,000 | 19,000 |
The pre-operative threshold scores that would identify patients with a cost per QALY of £30,000 or over is 43 for knee replacements and 45 for hip replacements, which identify only 0.1% of knee-replacement patients and 0.2% of hip-replacement patients. Because we know that 22.9% of knee-replacement patients and 13.7% of hip-replacement patients in this data set do not achieve a cost per QALY of £30,000, some of whom are worse off (see Table 46), there is room for improvement in the selection of patients for treatment compared with an OKS/OHS criterion.
Of the other two PROMs procedures, only varicose vein procedures have a condition-specific score [Aberdeen Varicose Vein Score (AVVS)] comparable to OKS and OHS. Their performance is similar – they would identify 0.2% patients as ineligible.
We have shown that we can extend the result reported in Dakin et al. ,121 namely that it is in fact cost-effective to treat those whose treatment would be ineligible under thresholds put forward by commissioners, to different levels of the threshold, to a national survey of knee-replacement patients, and to surveys of hip replacement and varicose vein procedure patients. However, 22.9% of knee patients and 13.7% of hip patients receive treatment that is not cost-effective. The condition-specific scores do not identify patients with low QALY gain. We now consider how far the patients’ pre-operative level of health as measured by their QALY (EQ-5D) is helpful in guiding patient selection.
Simple eligibility criteria: baseline quality-adjusted life-year
The measure of health gain that we are adopting is reported QALY change, which may be related to the level of QALY the patient reports prior to the operation. The extensive awareness of the concept of QALY, and its increase as an aim of policy, may help to increase its acceptability as a criterion that might be used to help identify cost-effective patients among those selected by physicians together with, or instead of, baseline OKS. However, there are objections to using the QALY gain as an instrument in resource allocation. These include its generic nature, insensitivity to small changes in patient condition and equity issues. Insofar as it is used only as a supplement to clinical decisions, the key issue appears to be equity considerations in determining patient gain, in particular, a possible ageist ‘bias’ because patients with lower life expectancy have fewer years of benefit, and a ‘bias’ against patients with poorer health. This latter concern arises because of the nature of the QALY tariff in which a patient with a serious comorbidity is assigned a lower QALY gain from a given procedure, all other things being equal. Moreover, there are sources of health gain or costs of care not taken into account in the cost per QALY measure, for example when treatment may relieve the burden on the patient’s carer or when the patient is enabled to care for someone else. However, we are concerned here to consider the value of patient QALY measured at a point in time to support ongoing patient decisions, rather than to assess the benefit of outcomes. To assess the potential contribution of the QALY, we now explain the method used.
For hip and knee replacements, choosing patients to be treated by baseline QALY, from among those presently treated, performs only a little better than OKS/OHS, identifying a very small proportion of patients (0.8% of knee patients and 0.6% of hip patients) for whom treatment would not be cost-effective in the sense of meeting the standard cost per QALY passmark of £30,000.
For the other two procedures, however, a threshold in which only patients with a pre-operative QALY of < 0.850 would be treated identifies a substantial proportion of patients whose treatment would not be cost-effective. For varicose veins, this proportion is 22.3% of the treated population, about half of those patients whose treatment is not cost-effective. For groin hernia the proportion is 29.1%, a large proportion of both patients currently treated and those patients whose treatment is not cost-effective.
Selection criteria using a range of baseline data
We now consider a simple model of patient QALY gain using variables known prior to the operation, and how it may be used to identify patients whose treatments prove not to be cost-effective. We draw on various determinants of QALY benefit that have been included in studies predicting the outcomes of joint replacement, such as age, sex, comorbidities, body mass index (BMI), deprivation, social circumstances, treatment history and duration of symptoms. 117–121 Both the QALY and the condition-specific scores are summary measures covering a range of dimensions of health status. However, it is possible that factors not fully captured in these metrics, or omitted from them, could have an influence on the benefit that a patient derives from surgery. Their inclusion alongside the singleton baseline metrics may strengthen the prediction of change in health. The explanatory variables are drawn from the pre-operative patient characteristics in the PROMs data: OHS; QALY (EQ-5D) score; age; sex; presence of each of several comorbidities; duration of symptoms; previous surgery; previous hip replacement (i.e. revision vs. primary); and ethnicity.
Based on patient area of residence, we consider area deprivation status as given by the IMD in a patient’s LSOA; BMI as proxied by mean BMI in a patient’s middle layer super output area; the efficiency of the CCG as proxied by the annual volume of hip operations, age and sex-adjusted, per 1000 population, 2011–12; and year of admission, to take account of efficiency improvements, with 2009 = 1, 2010 = 2 and so on.
Summary statistics
The mean and distribution of these variables are set out in Table 49. What follows focuses on hip replacement, with brief comments on the other procedures when different. The mean baseline QALY for hip replacement patients is 0.331 and the mean change is 0.411 (knee replacement: baseline 0.385, change 0.320; varicose vein procedures: baseline 0.742, change 0.119; groin hernia procedures: baseline 0.776, change 0.103). Although the hip replacement patients are pre-operatively slightly less well than knee replacement patients, they have somewhat fewer comorbidities. The sample is very large, with 200,000 observations for hip replacement. About half of the observations have a full set of the candidate pre-operative variables.
| Variable | Hip replacement | Knee replacement | Varicose vein procedures | Groin hernia procedures |
|---|---|---|---|---|
| Health status, mean (SD) | ||||
| EQ-5D | 0.331 (0.327) | 0.385 (0.319) | 0.742 (0.234) | 0.776 (0.213) |
| OHS, OKS or AVVS | 17.6 (8.5) | 18.4 (8.0) | 20.0 (11.0) | NA |
| Comorbidities (% prevalence) | ||||
| Heart disease | 10 | 11 | 4 | 9 |
| Hypertension | 39 | 45 | 17 | 26 |
| Stroke | 2 | 2 | 1 | 2 |
| Circulatory disease | 7 | 9 | 18 | 5 |
| Lung disease | 7 | 8 | 5 | 7 |
| Diabetes mellitus | 9 | 13 | 4 | 6 |
| Kidney disease | 2 | 2 | 1 | 1 |
| Nervous system | 1 | 1 | 1 | 1 |
| Liver disease | 1 | 1 | 1 | 1 |
| Cancer | 5 | 4 | 2 | 4 |
| Depression | 8 | 9 | 8 | 6 |
| Arthritis | 71 | 76 | 17 | 17 |
| Other | ||||
| IMD rank [1 (most deprived)–32,482], mean (SD) | 18,179 (6775) | 17,233 (8932) | 15,791 (9124) | 17,569 (9038) |
| Revision (%) | 5 | 5 | Not applicable | Not applicable |
| Age (years) | 67.8 (11.3) | 69.2 (9.4) | 50.6 (14.7) | 58.7 (16.3) |
| Sex (% male) | 41 | 44 | 38 | 89 |
| BMI (kg/m2) | 24.5 (4.0) | 24.8 (4.0) | NA | NA |
| Duration of symptoms, years (1, 2, 3, 4)a | 2.1 (0.8) | 2.6 (0.9) | 3.2 (0.9) | NA |
| Previous surgery (%) | 11 | 8 | 39 | NA |
| Adjusted CCG procedure rate | 1.07 (0.21) | 1.02 (0.19) | 1.36 (0.82) | 1.02 (0.13) |
| Breakdown by year of surgery (%) | ||||
| 2008 | 1 | 1 | 0 | 0 |
| 2009 | 18 | 17 | 22 | 18 |
| 2010 | 26 | 27 | 31 | 26 |
| 2011 | 27 | 29 | 27 | 28 |
| 2012 | 26 | 27 | 20 | 26 |
We discuss above how some variables are not socially acceptable as a basis to limit care. Three models are estimated and presented below (Table 50). Each reflects different views of the acceptability of alternative criteria:
-
model 1 – with a wide range of pre-operative variables
-
model 2 – as model 1 but with controversial variables such as age, sex and social class omitted
-
model 3 – only baseline QALY, OHS and the year of admission are included
| Variable | Replacement surgery | |||||
|---|---|---|---|---|---|---|
| Hip | Knee | |||||
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | |
| Baseline scores | ||||||
| OHS/OKS | 0.005*** | 0.005*** | 0.006*** | 0.008*** | 0.008*** | 0.009*** |
| EQ-5D score | –0.744*** | –0.722*** | –0.656*** | –0.664*** | –0.645*** | –0.573*** |
| EQ-5D score2 | –0.228*** | –0.252*** | –0.313*** | –0.315*** | –0.332*** | –0.401*** |
| Age | 0.009*** | 0.017*** | ||||
| Age2 | –6.68 × 10–5*** | –1.07 × 10–4*** | ||||
| Comorbidities | ||||||
| Heart disease | –0.025*** | –0.030*** | –0.025*** | –0.020*** | ||
| Hypertension | –0.005*** | –0.004*** | ||||
| Stroke | –0.046*** | –0.046*** | –0.036*** | –0.030*** | ||
| Circulatory disease | –0.082*** | –0.091*** | –0.065*** | –0.063*** | ||
| Lung disease | –0.035*** | –0.036*** | –0.026*** | –0.025*** | ||
| Diabetes mellitus | –0.030*** | –0.031*** | –0.025*** | –0.025*** | ||
| Kidney disease | –0.020*** | –0.027*** | –0.014** | –0.013** | ||
| Nervous system disease | –0.065*** | –0.064*** | –0.080*** | –0.075*** | ||
| Liver disease | –0.025*** | –0.025*** | ||||
| Cancer | –0.013*** | –0.008*** | ||||
| Depression | –0.132*** | –0.141*** | –0.118*** | –0.130*** | ||
| Arthritis | –0.034*** | –0.031*** | –0.018*** | –0.014*** | ||
| IMD rank | 2.08 × 10–6*** | 2.08 × 10–6*** | ||||
| Revision | –0.055*** | –0.074*** | ||||
| Sex | –0.008*** | 0.011*** | ||||
| Year of admission | 0.004*** | 0.001 | 0.001 | 0.002** | 0.002** | 0.002 |
| Relative age- and sex-adjusted CCG procedure rate | 0.033*** | |||||
| BMI | –0.001*** | |||||
| Symptom duration | –0.014*** | |||||
| Previous surgery | –0.078*** | –0.036*** | ||||
| Constant | 0.408 | 0.669 | 0.600 | –0.183 | 0.517 | 0.463 |
| Adjusted R2 | 0.54 | 0.52 | 0.50 | 0.49 | 0.48 | 0.46 |
| F-statistic | 4,001 | 6,988 | 25,462 | 4,682 | 6,522 | 19,741 |
| Observations | 84,757 | 102.219 | 102.219 | 92,792 | 93,431 | 93,431 |
The models provide a score of expected QALY gain from treatment and may be used to identify patients with higher expected gain from among those whom clinicians have already accepted as suitable for treatment. The models are estimated using 2008–11 data. The estimated model is then applied to 2012 patients’ characteristics to predict their QALY gains. This prediction may then be contrasted with actual patient QALY gain. For groin hernia and varicose vein procedures only model 1 was estimated (Table 51).
| Variable | Procedure | |
|---|---|---|
| Varicose vein | Groin hernia | |
| AVVS | –0.002** | |
| EQ-5D score | –0.633** | –0.674** |
| Age | 0.002** | |
| Age2 | –1.4 × 10–5** | |
| Heart disease | –0.031** | –0.019** |
| Hypertension | –0.009** | |
| Stroke | –0.021** | |
| Circulatory disease | –0.053** | –0.092** |
| Diabetes mellitus | –0.032** | –0.009** |
| Lung disease | –0.027** | |
| Liver disease | –0.058** | 0.073** |
| Nervous system disease | 0.091** | –0.091** |
| Cancer | –0.010** | |
| Depression | –0.097** | –0.103** |
| Arthritis | –0.060** | –0.073** |
| IMD rank | 1.50 × 10–6** | 1.37 × 10–6** |
| Previous surgery | –0.017** | |
| Relative age- and sex-adjusted CCG procedure rate | 0.012* | |
| Sex | –0.019** | |
| Year of admission | –0.006** | |
| Constant | 0.626 | 0.551 |
| Adjusted R2 | 0.32 | 0.37 |
| F-statistic | 728 | 2014 |
| Observations | 19,870 | 54,765 |
Most of the variables considered in Table 49 are statistically significant at the 1% level. Apart from the condition-specific (OHS/OKS) variable, the coefficients have the expected sign. The negative sign on baseline OKS/OHS is anomalous; we would expect patients in a worse initial state to have more to gain. One possibility may be that for a given baseline general health status, those with less serious hip disease appear to do (slightly) better – the variance inflation factor sanctions the inclusion of both the baseline QALY score and the baseline hip score.
Clinicians have already selected these patients, but it is not clear how far the criteria they use can explain these findings. Hips and knees show a broadly similar pattern, with similar values for the coefficients. The one clear difference is the sign on sex, but the value of the coefficient is small in both models. The equations for varicose veins and groin hernia are available from the authors. The models explain about half of the variation in patient benefit.
The fitted equations incorporate a time trend to take account of trend improvements in QALY gain, based on the accumulation of experience. However, the equations, based on years 2008–11 underpredict the QALY gain in the test year 2012. Accordingly, the threshold values require adjustment to ensure that the mean potential QALY loss per patient identified is 0.05 or less. For example, it is sometimes necessary to use a lower threshold, such as 0.045, to ensure that those identified are not cost-effective, that is, they experience a change in EQ-5D < 0.05.
Box 4 reviews the influence of the different explanatory variables from the full equation for hips, model 1. In qualitative terms, the findings for knees are very similar.
OHS. Patients with a higher baseline OHS score experience a slightly greater health gain; this amounts to 0.09 of a QALY if OHS is 1-SD greater.
QALY. Baseline QALY has a large and significant negative impact on expected patient benefit. Patients with a baseline QALY 1-SD above the mean of patients treated experience a QALY gain that is, on average, 0.32 QALYS smaller.
Comorbidities. Patients with comorbidities, holding constant baseline QALY, experience lower health gain from treatment, with each additional comorbidity adding to the disadvantage. However, these patients also have a lower pre-operative QALY, which mitigates the effect of the comorbidity on predicted health gain.
Age. The benefit differs little by age. The purpose of the quadratic form of the equation is to allow for non-linearity in the effect. The age of maximum benefit can be calculated and is (coincidentally) the same as the mean age, 68 years. Those 1-SD younger or older carry a slightly smaller health gain of 0.008 of a QALY.
Sex. The benefit is slightly less for women.
Previous intervention. Those undergoing a revision incur a penalty of 0.05, rather more than 10% of the mean. Those who have undergone previous surgery carry a slightly greater penalty of 0.07, nearly 20% of the mean.
Symptom duration. Symptom duration has four categories. Those who have suffered symptoms for the longest period incur a penalty of about 10% of the mean QALY change compared with those whose symptoms are most recent.
Deprivation. Patient area of location IMD rank: the difference between the expected benefit in the least and most deprived LSOA is 0.07 of a QALY, nearly 20% of the mean.
Time trend. The mean QALY gain rises over time, at a rate of roughly 0.0035 of a QALY a year, 1% of the mean, perhaps an effect of learning by doing.
BMI. The BMI variable is not specific to the patient but the mean for the patient’s Middle Layer Super Output Area of residence. The QALY penalty for a patient having a BMI of 1-SD above the mean is 0.004, 1% of the mean QALY change.
CCG procedure rate. The relative age- and sex-adjusted CCG procedure rate is included to capture economies of scale. The range is 0.34 to 1.6 so that the range in benefit is 0.04, or 10% of the sample mean.
In the data, patient QALY benefit varies little with the number of comorbidities. However, the number of comorbidities does affect pre-operative QALY: the more comorbidities, the lower the pre-operative QALY level. The pre-operative QALY is the strongest predictor of QALY gain: the lower the pre-operative level, the higher the QALY gain. Accordingly, the role of the comorbidity variables, which appear in the regression with a negative sign, is to avoid overpredicting health gain for patients with comorbidities. Comorbidities do not influence QALY gain and, despite appearances, the forecasting equations do not discriminate against people with comorbidities.
Results: comparing the patient selection criteria
We have identified five criteria that might be used to identify patients whose treatment would not satisfy a cost per QALY threshold of £30,000 for the procedure that they have been selected to undergo: baseline QALY, baseline condition-specific score such as OKS/OHS, and three variants of model-based predicting QALY change: one using as explanatory variables baseline QALY and OKS/OHS only, one with comorbidities as well, and a third with other socioeconomic variables as well. In this section, each criterion is implemented by using PROMs data to determine a threshold value of each criterion for each procedure, which indicates whether or not a patient is expected to achieve a QALY gain at a price of > £30,000 per QALY. As we saw above (see Summary statistics), the values of EQ-5D change corresponding to £30,000 per QALY are 0.05 for hip and knee replacements, 0.007 for varicose vein procedures and 0.011 for groin hernia procedures.
The predicted QALY gain scores for the three models in Table 50 are derived for each procedure using data from 2009/11. We then apply the models to support patient selection in the post-sample year, 2012. The predicted value of QALY change is compared with the actual gain found for that patient in the post-sample year, 2012. Those patients whose mean QALY gain is predicted to fall below the threshold gain required to justify the procedure can be identified. The mean QALY loss or gain, for these patients, together with their proportion of the sample, is readily calculated.
For the condition-specific scores and the baseline QALY, the procedure for identifying those whose treatment will not be cost-effective is as follows. The mean actual QALY gain in 2012 was calculated for each level of the criterion. The QALY gain is lower for higher values of the patients’ baseline QALY. The baseline QALY at which the mean actual QALY gain was < 0.05 was chosen as the threshold. The number that would be ineligible for treatment, and their mean QALY gain forgone, could now be determined. This is possible because for each criterion the mean QALY gain monotonically increases with the value of the criterion, so that only one threshold that indicates £30,000 per QALY is available for each criterion (Table 52).
| Site of operation | Selection criteria | Threshold (1) | Percentage identified (%) (2) | Mean QALY loss (3) | Expenditure reduction (£M per annum) (4) |
|---|---|---|---|---|---|
| Hips | OHS | 45 | 0.2 | 0.004 | 1 |
| QALY | 0.848 | 0.6 | –0.020 | 3 | |
| Predictive score | |||||
| Model 3 | 0.050 | 1.1 | 0.050 | 6 | |
| Model 2 | 0.040 | 1.8 | 0.042 | 9 | |
| Model 1 | 0.045 | 2.4 | 0.048 | 12 | |
| Knees | OKS | 43 | 0.1 | –0.045 | 1 |
| QALY | 0.812 | 0.8 | –0.027 | 4 | |
| Predictive score | |||||
| Model 3 | 0.025 | 5.5 | 0.049 | 30 | |
| Model 2 | 0.040 | 7.9 | 0.049 | 44 | |
| Model 1 | 0.050 | 10.4 | 0.047 | 58 | |
| Varicose veins | AVVS | 78 | 0.2 | –0.215 | - |
| QALY | 0.850 | 22.3 | –0.039 | 6 | |
| Predictive score | 0.007 | 25.5 | –0.025 | 7 | |
| Groin hernia | QALY | 0.850 | 29.1 | –0.048 | 33 |
| Predictive score | 0.011 | 30.7 | –0.043 | 35 | |
For each of the selection criteria Table 52 shows (1) the threshold value of the criterion that corresponds to a cost per QALY of £30,000; (2) the percentage of patients identified whose treatment is not cost-effective; (3) the actual mean QALY loss of those patients predicted not to be cost-effective [a figure < 0.05 (hip and knee replacements) implies a cost per QALY in excess of £30,000]; and (4) the annual expenditure reduction corresponding to the proportion of patients identified in column (2).
Thus, the results show, for example, that in hip replacement model 1 – with a full list of pre-operative variables – a predicted patient gain of 0.045 QALY identifies 2.4% of the sample as having a cost per QALY exceeding £30,000. Their mean QALY change is 0.048, corresponding to a cost per QALY of £31,250. They therefore forgo some health gain if they do not undergo the operation.
The results for varicose vein and groin hernia procedures are more straightforward. The predictive score does not materially improve on baseline QALY as a selection criterion. The proportion not meeting the cost per QALY threshold is much higher, and they actually make a net gain from not receiving the operation – the negative values in column (3).
The predictive scores based on a restricted set of variables to reflect reservations about incorporating sociodemographic and comorbidity variables among the selection criteria show results that fall between those of the singleton criteria and the full model, as expected. However, in view of the underprediction of these models it would be necessary to set the threshold below the value corresponding to £30,000 per QALY, as shown in Table 52. The effect is to introduce uncertainty and reduce the proportion identified.
On these results, none of the single value selection criterion can identify, ex ante, more than a small proportion of hip and knee patients as not satisfying the cost per QALY benchmark. The score predicting QALY gain can identify a proportion of such knee-replacement patients. However, both QALY and predictive score can identify a substantial proportion of such groin hernia and varicose vein patients. The expenditure savings achievable are noteworthy, while at the same time, for varicose vein and groin hernia procedures, delivering a gain in QALYs. There are few such instances when the NHS could expect to improve health while reducing expenditure.
Discussion
The findings above show that for some procedures it is possible to identify ex ante those patients who are unlikely to benefit sufficiently from treatment, as measured by ‘before and after’ change in EQ-5D QALY. The more refined criteria, which nevertheless use no more information than available in PROMs and impose no extra burden on respondents or clinicians, generally perform better than baseline QALY or baseline condition-specific score in choosing patients to be treated. For example, in hip replacements, baseline QALY identifies 0.6% of patients for whom treatment would not be cost-effective. The full model identifies 2.4%. However, this outperformance is material only for knee replacements.
Questions arise as to the feasibility of the criteria in routine practice. CCGs address their referral and treatment guidelines to GPs. Clinicians carrying out procedures for which PROMs data are routinely collected could readily derive the predictive scores based on the results reported above. GPs would find it more difficult as they would have to replicate much of the PROMs questionnaire. The referral and treatment guidelines presuppose that GPs have ready access to patients’ hip and knee scores.
If any of these criteria were to come into use, patients might be tempted to exaggerate their symptoms. However, a study of an online patient-completed AVVQ found that ‘there was no apparent over-estimation of symptoms when compared with clinical scores’. 127 The authors conclude that an online questionnaire is acceptable to patients and correlates with clinical findings, and a threshold value could be used by health-care commissioners to guide varicose vein referrals. The more complicated predictive score developed above might then also prove feasible in a similar setting.
The follow-up period used above to gauge benefit is short, whereas the health benefits of these four interventions typically persist for many years. The assumption here, based on Dakin et al. ,121 is that the gain or loss patients report in the PROMs questionnaires persists for 5 years. However, cumulative results from worldwide joint register data sets record revision rates of about 6% after 5 years and 12% after 10 years for both total hip and knee replacement. 128 The effect of adjusting would be to reduce the estimates of the proportion of patients in whom treatment would not be cost-effective.
The high proportion of varicose vein and groin hernia patients reporting no benefit may owe something to the insensitivity of the QALY to register the smaller gains from what are comparatively minor procedures.
The use of a £30,000 cost per QALY benchmark may overstate the marginal cost of QALYs in the NHS generally. There are alternative estimates of £13,000. 129 If this threshold were to be applied, a higher proportion of patients would become ineligible. Under the full model for hip and knee replacements, the proportions would be 7.7% and 26.4%, respectively (compared with 2.4% and 10.4%, respectively, at £30,000 per QALY).
This analysis has adopted QALY change as the measure of health gain, mainly to make comparisons across procedures. However, a before and after generic measure of this kind reflects changes in health other than from the operation. Arguably, a better metric would be the before and after change in condition-specific score such as the OHS. Condition-specific scores showed more improvement than did EQ-5D for both hip and knee replacement (Table 53).
| Outcome of procedure | Replacement surgery (%) | Procedure (%) | ||
|---|---|---|---|---|
| Hip | Knee | Varicose vein | Groin hernia | |
| Loss | 4 | 7 | 20 | – |
| No change | 1 | 1 | 0 | – |
| Gain | 96 | 92 | 80 | – |
| Total | 100 | 100 | 100 | – |
It may be possible to get the best of both worlds by mapping condition-specific instruments into generic health outcomes. 130 Despite the difficulties,131 a mapping of the OHS into the EQ-5D QALY suggests that each point in the OHS is worth 0.0222 of a QALY. 132 A change of 20 points in the OHS, the mean value in the PROMs 2008–12 data set, would then correspond to 0.444 of a QALY (compare the actual QALY change of 0.411). This approach would abstract from extraneous health changes between the before and after questionnaires, while preserving the advantages of the QALY metric.
It is worth considering how far the findings from the four PROMs procedures apply to other elective procedures. Four is too small a number of procedures from which to draw general conclusions. In any case, the OHS/OKS, the AVVS and the predictive scores apply only to a particular procedure. However, a generic metric such as the QALY may be more widely applicable. It is worth noting that baseline EQ-5D values in the range 0.80–0.85 are associated with a cost per QALY of £30,000.
The results of the full model, including comorbidities, throw into relief certain controversies surrounding the use of QALYs, which may be at odds with society’s values in some respects. In a review of the way society values health benefits across different groups of people, Nord133 observes that (1) the worse off an individual would be without a specific intervention, the more highly society tends to value that intervention, and (2) for groups with the same severity of illness, society does not wish to give strong priority to those with greater capacity to benefit over those with lesser capacity to benefit, as long as the benefit is substantial in both groups. In model 1 set out in Table 50, patients with comorbidities are predicted, all other things being equal, to achieve lower QALY gain and the greater the number of comorbidities the greater this penalty. This problem is not unique to the QALY. Use of the OHS or OKS raises exactly the same issues, as those with comorbidities are predicted to achieve lower changes in score. However, other things are not equal. Those with depression, for example, have a much lower initial QALY, which outweighs the penalty attaching to depression, with the result that they are no more likely to be ineligible than those without depression. In this instance at least, there is no tension between QALYs and social values.
Nord’s133 second point above highlights an issue with the use of baseline QALY level in a selection criterion. Patients with higher pre-operative QALY level but the same degree of joint disorder (OHS) experience a lower QALY gain, but if surgeons select on the basis of OHS, then they will treat this group equally and confer an inefficient QALY gain on more patients who are in good health. There may be reasons connected with trust that lead clinicians to wish to use condition-specific scores and not to wish to discriminate by pre-operative QALY, but the patients in question might not accept treatment if informed of the probable poor outcome associated with their condition. Other clinicians may wish to take account of pre-operative QALYs in their selection criteria. Changing to use of the pre-operative QALY may nevertheless raise ethical issues that deserve further exploration.
Conclusions
This chapter uses PROMs data to provide results that may improve patient selection to achieve health gain. First, the analysis shows that using pre-operative condition-specific scores such as OKS, OHS, AVVS, it is not possible to identify a significant proportion of patients whose benefit from treatment is not sufficient to justify the cost. This generalises a result from Dakin et al. 121 concerning knee replacements to a larger data set, to different levels of the score and to hip replacements and varicose vein procedures as well as to knee replacements. Using the pre-operative QALY level of 0.85 to reduce the number of patients who were chosen by clinicians does only a little better, except for varicose veins and groin hernias, for which it identifies more than one in five patients.
However, more effective selection criteria can be found using multivariate analysis of a range of pre-operative characteristics to forecast the gain. The proportion of patients selected whose treatment they can identify as not cost-effective is: 2.4% for hip replacements, 10.4% for knee replacements, 25.5% for varicose vein procedures and 31% for groin hernia procedures. Hence, for the minor procedures in particular these criteria might usefully support current clinician decision-making.
These findings illustrate the value of patient-reported outcomes in identifying ex ante patients whose treatment is unlikely to prove cost-effective, and in some cases may be detrimental to the patient. They indicate a potential for saving health-care resources within current cost-effectiveness guidelines.
Chapter 8 Clinical Commissioning Groups’ performance in delivering health gain: elective procedures
Introduction
As background to this project, we analysed the variation in the rates of a selected number of elective procedures across CCGs. 134 We believe that in managing planned care, CCGs will be interested to compare their rates for different elective procedures with the national average and with each other. The purpose of the benchmarking study was to show CCGs’ procedure rates after adjustment for need based on local age, sex and demographic factors, and after allowing for random variation.
Highest variation procedures are varicose vein procedures, tooth extraction, elective caesarean section and coronary angioplasty. The procedures with low levels of variation are colorectal cancer treatment, groin hernia procedures and breast cancer. Population age is significantly associated with admission rates for all of the procedures except varicose vein procedures, coronary angioplasty and tooth extraction treatment. Deprivation was found to be positively associated with admission rates for knee replacement, varicose vein procedures, cataract procedures, coronary artery bypass grafting, tonsillectomy, tooth extraction and hysterectomy, such that admission rates increase for these procedures as deprivation increases. Sex has a significant impact (negative association) on hospital utilisation rates for surgical procedures for pacemaker implantation, tonsillectomy and colorectal cancer treatment, such that admission rates for these procedures decrease as the proportion of male residents in the local population increases.
We now compare CCGs in terms of the health gain experienced by their patients to identify the sources of variation. With the advent of PROMs in the NHS in England, it is possible to make such comparisons for four elective procedures across not only CCGs but also providers and surgical teams. In order to identify the source of variation reliably, it is important to take account of the ‘nested hierarchical’ structure of care, whereby a patient is treated by a surgical team hosted by a hospital, which in turn receives a commission from a CCG. In comparing CCGs, therefore, it is important to control both for case mix and for the health gain achieved by the units at the lower levels in the hierarchy.
Tranmer et al. 135 highlight the importance of appropriate controls in such a multilevel hierarchy, showing that the result of omitting a level is to distribute its effect spuriously between the level above and the level below. If the lowest level is omitted its effect will be attributed to the lowest level included and similarly if the highest level is omitted.
A study using CCGs alone would be liable to reflect the effects of providers, not just the specific performance of the CCG.
In the multilevel modelling that this situation demands, it is usual to assume fixed effects at the level of the individual patient or pupil and random effects for the second and higher levels, the school or the hospital. This is not the only approach but for our enquiry it has advantages in comparing units at the same level. Snijders136 sets out the following criteria for deciding between fixed effects (F) and random effects (R) for the higher levels:
-
If groups are unique entities and inference should focus on these groups: F.
This often is the case with a small number of groups.
-
If groups are regarded as a sample from a (perhaps hypothetical) population and inference should focus on this population, then R.
This is often the case with a large number of groups.
-
If level 2 effects are to be tested, then R.
-
If group sizes are small and there are many groups, and it is reasonable to assume exchangeability of group-level residuals, then R makes better use of the data.
-
If the researcher is interested only in within-group effects and is suspicious of the model for between-group differences, then F is more robust.
-
If group effects are not nearly normally distributed, R is risky.
For hip replacements there are 211 CCGs, 344 providers and 1683 surgical teams. Numbers of observations per unit are variable, although often large (range 1–702, with a mean of 61 for surgical teams). We are interested in effects between CCGs, between providers and between surgical teams, and it is reasonable to assume that these units represent random drawings from a larger population. These factors favour the use of random effects.
However, there is a trade-off. In a study of hospitals in terms of patient outcome, Austin et al. 137 use Monte Carlo analysis and show that F has higher sensitivity, whereas R has greater specificity. When the aim is to identify units performing below the mean, it may be more important to avoid false positives so that, on that score, the greater specificity of R makes it preferable.
It is worth identifying underperforming units for their potential for improvement. Improvement can come about through remedial action within the unit or by a CCG commissioning from the better performing providers. These opportunities require appraisal in a cost-effectiveness framework. The value of improvement in situ depends on the availability of remedial measures, their cost and their quantified effectiveness. The mere threat of losing referrals, or indeed of being branded as below par, may galvanise an underperforming provider. Reallocating patients raises questions as to the escapability of the cost of treatment at the provider losing referrals and the extra cost of treatment in the receiving provider, which is already likely to be working at full capacity. Sharp increases in volume over a short period may also jeopardise quality. Without information as regards these costs and benefits, the value of identifying underperforming units is less clear.
The National Clinical Audit Advisory Group offers guidance as to action that can be taken to improve underperformers. 138 The advice relates to processes, not particular interventions, and does not offer estimates of implementation costs. It focuses on pinpointing the problem and the individual responsible for putting it right, but it does not provide guidance on how to achieve a specific improvement. It predates the availability of PROMs data. There is no guidance specifically on methods for improving health gain as measured by change in a generic metric of health status such as EQ-5D. Nevertheless, the information we seek to provide, which links underperformance to the precise combination of provider and surgical team for each procedure, should be of some value. For example, a provider may find that it is underperforming on hip procedures but that the surgical teams carrying out the procedures are not underperforming. Or it may find there is an underperforming team but the hospital itself is not underperforming. Or it may find that the underperformance is in both hip and knee procedures. These detailed findings could facilitate more focused and effective performance management and could stimulate guidance focusing on improving the lower ranges of health gain, that is, change in EQ-5D score.
There is no published source of data on CCG performance in delivering health gain. The Yorkshire Health Observatory of the NHS publishes data on provider performance,139 and a spreadsheet (the PROMs tool PROMT) is available for assessing health gain by PCT. 140 The case-mix adjustment developed by Northgate Information Solutions141 for the Department of Health implicitly uses fixed effects at provider level, although it applies an adjustment to counteract the ‘overdispersion’ arising from limitations in risk adjustment and in data quality. 142,143 This procedure has a similar effect to ‘shrinkage’ in the random-effects model,144 although there is some suggestion that it is an expedient for limiting the proportion of units differing from the mean. Because the Department of Health method does not control for variation at the level of the surgical team, or the PCT for that matter, it remains possible that some of the variation attributed to providers is actually due to the surgical team, or indeed the PCT.
A number of studies have applied multilevel modelling to PROMs data as a means of assessing the performance of providers or surgical teams, although not CCGs. A study of varicose veins finds that a small but significant proportion of the variance is attributable to the provider, after controlling for patient variation using a fixed-effects regression of patient characteristics. 145 No difference was found between public and private providers. This study omits the surgical team level, so that it is possible that some of the variation attributed to providers is actually due to the surgical team. It does not identify the underperforming providers. A study of the performance of hospitals for three of the PROMs procedures after case-mix adjustment found a high proportion of providers above or below the mean. 146 The list of outlying providers identified differs from metric to metric for the two major procedures. This analysis implicitly applies fixed effects to the provider level and does not control for variation in outcome among surgical teams. A study of the performance of surgical teams using multilevel modelling, for three PROMs procedures – hip, knee and groin hernia procedures – finds that, after controlling for known patient characteristics, consultants and providers contribute little towards variation in patient outcomes. 147 For the EQ-5D measure only small numbers of consultants (< 12) were below the mean. For the condition-specific scores (OHS and OKS), the numbers were a little higher for knee procedures. As the focus was on surgical teams, the performance of providers was not reported. This study had a number of exclusions: NHS patients treated by private providers, providers with fewer than 40 patients over the previous 3 years, and consultants responsible for fewer than 10 procedures. As a result, for hip procedures the number of providers was 183 (compared with 344, of which 267 treated > 40 patients, over the period 2008–12) and the number of consultant teams was 948 (compared with 1766 for the period 2008–12). These restrictions are open to question. In multilevel modelling there is every reason to use all the data even from units with very small numbers, as they contribute information as to the distribution of the population.
The possibility that providers, or, more probably, surgical teams, specialise in particular types of case or that patients choose, or are allocated to, particular providers or teams on various criteria has received little attention. The evidence suggests that patients at least are rather insensitive to quality in choice of provider. 148 We do not pursue the issue of choice here.
Patient-reported outcome measures are prone to missing data, which may not be ‘missing at random’. Gomes et al. 149 explore the consequences of alternative assumptions about these data and propose a strategy for addressing them. Although we acknowledge the importance of missing data, we use complete-case analysis here.
The purpose of bringing to light underperforming units is to show scope for improvement. However, it is important to allow for any trade-off between cost and quality. Gutacker et al. 150 show that there is no such trade-off. Low performance does not go hand in hand with low cost. This finding simplifies matters, as there is then some confidence that the underperforming units that we shall identify genuinely are such.
Objectives
We are primarily interested in variation in health gain across CCGs, but this requires attention to the providers that they commission and so on down the line. If there is a great deal of variation between units at any given level, there is more scope for improvement from levelling up. We partition the variance to gauge how far the degree of variation lies between groups. We quantify the variation in outcome attributable to each of the levels – CCG, provider, surgical team, patient – controlling for the other levels. We use all the available data with no exclusions. We identify the CCGs, providers and surgical teams that are below or above the mean. We also consider the performances of different kinds of providers (NHS vs. private), notably TCs versus other providers. We examine the consistency of the results between generic (EQ-5D) and condition-specific scores such as the OHS, the OKS and the AVVS. We also examine the consistency of the findings across procedures – are there providers that appear as outliers for more than one procedure? Most of the literature has aimed to identify underperforming hospitals or consultants but not both. We seek to assess performance at each level, controlling for the performance of the others. By identifying units with above-average performance, we can calculate the benefits for patients and the increase in mean gain in EQ-5D if the underperformers were to match the outperformers, and if the mean were to match the outperformers.
Method
We use the data for the four PROMs procedures for the years 2008–12. The dependent variable is the change in the patient’s health status after the operation compared with before. We use a standard multilevel modelling approach based on the Stata command ‘xtmixed’, using a fixed-effects regression at the patient level for case-mix control with patient pre-operative characteristics as the explanatory variables (see Tables 50 and 51). The importance of each additional level is assessed using a likelihood ratio test.
The residuals and standard errors for each of the providers and surgical teams are derived by ‘postestimation’, following guidance from the Learning Environment for Multilevel Methods and Applications (LEMMA). 151 We can then identify, for example, the underperformers among the providers, that is, those for which the 95% upper confidence limit of their residual is negative. These estimates control for case mix and variation among surgical teams. Similarly, the estimates identifying outliers among the teams control for case mix and variation among providers. We test the importance of these controls by identifying the number of outliers among providers if the team level is omitted and vice versa.
Hip and knee replacements have a good deal in common. They share the variables explaining patient health gain. Nearly all teams and virtually all providers carry out both forms of joint replacement (93% of hip-replacement teams also carry out knee-replacement operations; 85% of knee-replacement teams also carry out hip-replacement operations). By combining hip and knee replacements, the number of observations for any unit is increased and in this way has the potential to identify additional underperforming units. The difference in mean health gain for hip and knee replacements is allowed for by a dummy variable for knee replacements in the fixed-effects regression.
Background data
The primary focus is on the variation in health gain across CCGs.
The variation across CCGs in terms of their mean health gain, the initial health state of patients treated and the treatment threshold, judged by the 95th percentile of the distribution of initial health state, is shown in Table 54.
| Variable | Replacement surgery | Procedure | ||
|---|---|---|---|---|
| Hip | Knee | Varicose vein | Groin | |
| Change in EQ-5D score | 0.073 | 0.086 | 0.421 | 0.186 |
| Initial health state | 0.155 | 0.141 | 0.063 | 0.032 |
| Threshold | 0.037 | 0.029 | 0.026 | 0.000 |
Clinical Commissioning Groups vary little in treatment thresholds. For hip and knee procedures they differ little in health gain. CCGs with high health gain for one procedure tend to have high health gain for others (Table 55).
| Replacement surgery | Varicose vein procedures | ||
|---|---|---|---|
| Hip | Knee | ||
| Knee replacements | 0.44*** | ||
| Varicose vein procedures | 0.01 | –0.01 | |
| Groin procedures | 0.15** | 0.06 | 0.18*** |
The CCGs that have high adjusted volumes for one PROMs procedure tend to have high rates for the others. The rank correlation for the age and sex adjusted procedure rate is generally positive (Table 56).
| Replacement surgery | Varicose vein procedures | ||
|---|---|---|---|
| Hip | Knee | ||
| Knee replacements | 0.51*** | ||
| Varicose vein procedures | –0.03 | 0.15** | |
| Groin procedures | 0.36*** | 0.23*** | 0.27*** |
If patients who have most to gain from treatment are receiving priority, we would expect CCGs with high needs-adjusted volumes to have less demanding treatment thresholds. Only for hip procedures is there a clear relationship in the expected direction between the needs-adjusted procedure rate on the one hand and (1) the mean initial health state and (2) the threshold, on the other (Table 57).
| Variable | Replacement surgery | Procedure | ||
|---|---|---|---|---|
| Hip | Knee | Varicose vein | Groin | |
| Change in EQ-5D score | – | – | – | – |
| Initial health state EQ-5D score | +*** | – | – | +** |
| Threshold | +*** | – | – | – |
Results
In explaining the variation in health gain, the initial focus is on CCGs, but they play little direct part. The key finding is that the great majority of the variation in outcome is between patients. The other levels play little part (Table 58).
| Replacement surgery (%) | Procedure (%) | |||
|---|---|---|---|---|
| Hip | Knee | Varicose vein | Groin | |
| CCG | 0.2 | 0.1 | 0.4 | 0.0 |
| Provider | 0.4 | 0.4 | 0.1 | 0.4 |
| Surgical team | 0.8 | 0.4 | 0.2 | 0.0 |
| Patient | 98.7 | 99.0 | 99.3 | 99.6 |
| Total | 100 | 100 | 100 | 100 |
After controlling for fixed effects, the percentages for CCG, provider and surgical team are very slightly greater.
On a likelihood ratio test in the multilevel modelling, the CCG level does not justify inclusion for any of the procedures. For varicose vein and groin hernia procedures only the provider level justifies inclusion. For hip and knee procedures we then have a three-level model: patient, surgical team and provider.
Although the CCG does not directly influence patient outcome, it can do so through its discretion as regards the choice of provider. Accordingly, commissioners will value information on the efficiency of the providers and the surgical teams that they are using. The number of providers and surgical teams delivering below mean health gain is shown in Table 59, with numbers above the mean also shown.
| Procedure | Providersa | Surgical teamsa | ||||
|---|---|---|---|---|---|---|
| Number | Below mean | Above mean | Number | Below mean | Above mean | |
| Hip replacements | 342 | 17 (26) | 9 (16) | 1674 | 10 (31) | 4 (18) |
| Knee replacements | 345 | 21 (31) | 16 (27) | 1854 | 3 (10) | 2 (9) |
| Varicose vein procedures | 228 | 5 (14) | 2 (7) | 597 | 0 (0) | 0 (0) |
| Groin procedures | 367 | 2 | 2 | 2278 | 0 | 0 |
The condition-specific scores appear more sensitive than the generic metric of health status EQ-5D.
The outperformers are predominantly TCs or private hospitals (hip procedures). However, analysis of the subsample of private providers identifies two underperforming providers and six underperforming surgical teams. One of these providers but none of these surgical teams appears on the list above (knee procedures – no providers and two teams, one of which is on the list above).
Appropriate controls are important in a hierarchical data structure such as this. Controlling for the other levels in the hierarchy when studying a particular level makes a material difference to the number of outliers identified. In hip procedures, failure to control for surgical team performance identifies 33 underperforming providers (vs. 17 when the correct controls are implemented), whereas failure to control for provider performance identifies 27 surgical teams (vs. 10 when the correct controls are implemented).
There is more interest in underperformance than outperformance. To judge from the results using EQ-5D, the following conclusions emerge. For varicose vein and groin hernia procedures, there are very few outliers among providers and none among surgical teams. For hip and knee procedures, there are very few outliers among surgical teams and a small proportion of providers (about 5% of the total for hip replacements, and 6% of the total for knee replacements). However, statistical significance reflects sample size. The providers that emerge as underperforming tend to have high volumes. They account for 8% of hip patients and 10% of knee patients.
Discussion
These results may suggest that it is hardly worth identifying underperformers, because the potential for improvement must be limited. Judging health gain by change in EQ-5D status, if all identified underperformers were to be levelled up to the current mean, the health gain for hip replacement as a percentage of total health gain from hip replacement would be 0.6% for providers and 0.1% for teams. There are some 50,000 hip operations per annum in PROMs, although only half have full data. The mean gain is 0.412. If we assume, conservatively, that benefit persists for 5 years, the annual QALY gain is just over 100,000. Assuming a QALY is worth £30,000 in line with the NICE threshold, the value of this annual output of QALYs is £3B. This estimate provides a point of reference for the potential gains attributable to teams and providers, discussed below.
Surgical teams
The annual benefit if all teams identified as underperforming were to be brought up to the current mean would be about £3M in terms of QALY gain valued at £30,000 per QALY, a substantial benefit. If they were to be brought up only to the level at which they would no longer qualify as underperforming, the benefit would be much lower – about £0.4M. However, as we noted above, there is as yet no ready way of achieving this gain and no estimate of the cost of achieving it.
Although the overall impact of underperforming teams may be minor, there remain pockets of inequality. Some patients experience comparatively poor outcomes because they are treated by underperforming teams in underperforming hospitals. Most underperforming teams are not operating in underperforming hospitals. But there is one provider that hosts two underperforming teams. Because of the controls in multilevel modelling, these two sources of estimated deficit are additive. There are 440 patients who experience a deficit of 0.04 as a result of treatment by an underperforming team and a further deficit of 0.03 attributable to the underperforming provider, making a disadvantage 0.07, against a mean of 0.412.
Underperformance in surgical teams is not a simple matter. Most teams operate predominantly with a single provider, although a proportion operate with more than one. Because of the workings of multilevel modelling, the results for teams relate to combinations of team and provider. In hip procedures there are 2746 such combinations, whereas there are 1674 teams. Multilevel modelling can accommodate multimembership structures of this kind and in this way provide a single estimate for each team. But the team–provider combinations studied here are informative. Some teams underperforming with one provider do much better with another; indeed, no team underperforms with more than one provider, with the result that the team would be unlikely to emerge as underperforming on a single estimate. Consequently, the information as to underperformance with a particular provider would be masked.
An example will illustrate the complexity of making inferences from these findings. One of the teams emerges as underperforming with a provider designated as a specialist centre. The apparent underperformance of the team may then be due to a challenging case mix that is inadequately controlled for in the fixed-effects patient level. However, taken together, the many other teams working with this provider deliver outcomes that lie above the mean. The possibility remains that this team specialises in the most difficult cases attracted by this provider.
Providers
In terms of QALYs forgone by underperformance, providers are six times more important than teams (for hip procedures). Providers are identifiable but we do not list them here. In addition, there are nine outperformers to serve as exemplars for the 17 underperformers. A total of 158 and 177 CCGs commission from a hospital on the hip and knee procedures lists of underperformers, respectively.
The underperformers are predominantly NHS providers located in less prosperous areas of the country, whereas the outperformers are predominantly TCs or private hospitals. These findings may suggest, for the underperformers, inadequate case-mix control. For the outperformers, there may be reporting bias against less successful outcomes. Gutacker et al. 152 highlight missing values as a potential source of bias. This may particularly affect private providers. One of the codes associated with the outperformers applies to the Care UK Head Office, which is listed in HES 2010–11 Month 81 Inpatient Data Quality Note153 among a list of organisations with coverage shortfalls, together with a warning to use the data with caution.
The OHS/OKS metrics mainly identify all the providers identified using EQ-5D along with a few more.
Comparison with other studies
These findings differ a little from those of El-Sheikha145 in identifying two underperforming providers as opposed to none (for varicose veins). They differ materially from those of Varagunam et al. 147 Using the same data set and applying the same exclusions, the method used above identifies seven underperforming providers and seven underperforming teams for hip replacement (seven underperforming providers and two underperforming teams for knee replacement) compared with the none identified by Varagunam et al. 147
Conclusions
Underperforming units can be identified with some confidence using multilevel modelling. Such underperformance as exists is predominantly attributable to the provider, not the surgical team. The CCG plays no direct part. The scale of underperformance is sufficiently large to be worth further investigation.
There are currently no methods for remedying the specific deficits identified. It is possible to assess the potential benefit from selected improvements but there is no information as regards the cost or effectiveness of bringing about the changes.
To enable performance management to be treated as a health technology assessment, research is required to develop methods for improving measurable health gain delivered by specific providers and for estimating cost.
Chapter 9 Does changing the local supply of elective care have any impact on the consumption of emergency care?
Introduction
Government-funded health-care spending has, on the whole, been protected from recent austerity measures, but the NHS is under pressure to improve efficiency and to avoid overspending, as the NHS planning document Everyone Counts: Planning for Patients 2013/14154 explains. This efficiency drive could have an impact on treatment levels, particularly elective procedures which are not life-threatening and can be delayed or perhaps withheld entirely, as the NHS may redeploy resources to more urgent settings. This study attempts to find a way to identify the potential consequences on levels of emergency treatment if planned care is managed downwards; the concern is that if emergency care increases when planned care is reduced, cost-savings achieved by the NHS might not be as significant as policy intends.
Many studies have looked at elective and emergency activity levels separately. The Nuffield Trust has been very active in this area, with recent work on emergency admissions,8 emergency bed use9 and trends. 10 However, work studying the interaction between emergency and elective care has been limited. One major reason for this is that most shocks that affect demand and supply in health care are likely to impact on both emergency and elective care simultaneously, making it difficult to identify the causal relationship between these two types of hospital care. However, we have identified a policy designed to increase the provision of elective care, namely the introduction of ISTCs, which can be used to assess what happens to emergency care when elective provision changes.
This policy, developed in 2003, was designed to help ease waiting lists in the NHS by allowing independent firms to perform specific elective procedures and diagnostic tests. As such, the introduction of ISTCs can be considered a shock that affected just elective activity and should have had no direct impact on emergency activity. Patients in some areas will have benefited from the extra capacity that these centres provided, but those living away from the newly created ISTCs would have remained unaffected. This provides a natural experiment that we can exploit to see what happens to emergency treatment levels when a positive shock to the supply of elective care occurs, and, under specific assumptions, this can be used to give an indication of the likely impact of a reduction in elective provision on emergency activity.
Using HES data and data on factors that have been found to affect the supply and demand for health care in other research, we create a panel data set covering English PCTs for the years 2004–12 that can be interrogated to see how the introduction of ISTCs has affected the levels of emergency treatment.
We find that this positive supply shock to the provision of elective care has increased the levels of emergency treatment. This is good news at a time when the NHS may be forced to limit elective activity, as it suggests that the two types of care function as complements and not substitutes. However, it is possible that positive and negative supply shocks have different effects, so we advise that further research be undertaken before strong conclusions can be drawn.
The rest of the chapter is structured as follows. Hospital and patient behaviour explains possible ways in which hospitals and patients could behave when there is a positive supply-side shock to elective care and the ways this may impact on the markets for emergency care. Independent sector treatment centres and literature presents further information about ISTCs and previous literature. Data details the data set, then Empirical strategy explains the econometric analysis approach. Results are then given and Discussion and conclusion discusses the policy implications and concludes.
Hospital and patient behaviour
This chapter looks at the impact of an elective supply change on emergency activity. In this section we consider how this process may occur and if it could affect (1) the demand for emergency care from patients or (2) the supply of emergency care by hospitals, or a combination of both.
Demand
There are two opposing ways in which demand for emergency treatment may be affected by an increase in elective activity. First, the two types of hospital activity may be substitutes. In particular, not performing an elective procedure may cause the patient’s condition to deteriorate to the stage at which emergency treatment is required. If this is the case, increasing elective provision would mean extra capacity for patients to be treated in a planned setting and need less emergency treatment. Second, emergency and elective activity could be complements. This may be true if elective procedures caused complications for patients that later required further treatment in an emergency setting. Depending on which of these effects dominates, demand for emergency could go up or down as a consequence of increased elective provision.
Supply
NHS hospitals are now paid for the amount of activity that they provide rather than receiving lump-sum income on a per capita basis. In this setting, extra elective capacity via new ISTCs will provide more beds in which patients may be treated. It is likely in this case that the thresholds for both emergency and elective admissions will be relaxed, with beds that would previously have been used for elective procedures being made available for emergency admissions. This would mean that emergency and elective activity levels move in opposite directions as hospitals attempt to balance their finances.
Independent sector treatment centres and literature
Independent sector treatment centres were originally conceived in the NHS Plan 2000 to help reduce pressure on waiting times in PCTs by offering additional capacity for elective procedures in private sector providers, paid for by the NHS. There has been a great deal of debate about the merits of the scheme, the costs incurred and its achievements. Work by The King’s Fund155 and Chard et al. 156 addresses these issues. Regardless of their other consequences, ISTCs treated patients who would otherwise have joined waiting lists at existing providers, and their introduction can therefore be seen as a positive shock to the supply of elective health care.
The first ISTC opened in 2003 and was followed by 24 other fixed-site centres, plus two additional mobile facilities as ‘wave 1′ of the ISTC project. There were a further nine centres created in ‘wave 2’ (2005–6), which included multiple site providers and had a wider range of roles. Here, we focus our attentions on the effects of wave 1 ISTCs. Wave 1 ISTCs performed a discrete role in specific types of procedures, namely hip, knee, cataract and varicose veins procedures, and these contracts have now finished. We do not consider wave 2, which had wider scope and is still in operation.
Figure 45 shows the number of procedures carried out by ISTCs. Levels increased dramatically between 2005 and 2006, peaked in 2008 and then started to decline as contracts expired and ISTCs closed.
FIGURE 45.
Elective admissions in ISTCs per 1000 population, 2004–11.
A map showing PCTs in which new ISTCs were located is presented in Figure 46. With only 25 ISTCs, obviously the vast majority of PCTs did not receive one of these new facilities. However, the ISTCs were spread widely across England, located from Bodmin (Cornwall) and Portsmouth on the south coast to Tyne and Wear in the north. The ISTC closest to central London was in Ilford (Essex), but London was well served by existing NHS hospitals.
FIGURE 46.
Map: location of ISTCs (http://geoportal.statistics.gov.uk). Contains OS data © Crown copyright and database right 2016.
Many other studies have studied the introduction of ISTCs and their effects. Arguably the most relevant piece of previous research is by Cooper et al. 11 This looks at the effect of ISTCs on neighbouring NHS hospitals and finds that introducing an ISTC resulted in local hospitals becoming more efficient but having to take sicker and more complex patients, which ISTCs were able to reject for admission, and this harmed the performance of hospitals overall.
Cooper et al. 157 were also involved in a study of equity and waiting times, which concluded that the NHS reforms from 1997 to 2007, including the additional provision of elective treatments in private sector organisations such as ISTCs, did not negatively impact on patients in three surgical procedures, namely knee replacement, hip replacement and cataract repair.
There is also significant research on the effects of patient choice, which ISTCs were expected to facilitate. Cooper et al. 24 concluded that mortality rates for AMI fell relatively more for patients in more competitive markets, Bloom et al. 158 found that increased competition leads to improved hospital management and performance, and Gaynor et al. 159 discovered that quality improved but treatment expenditure did not.
Another branch of research looks at the effects of supply shocks on hospital activity. The introduction of a 4-hour waiting-time limit in NHS A&E departments was the subject of analysis by Kelman and Friedman,160 who found that it resulted in patients being treated quicker without causing any undesirable problems for hospital managers.
A similar effort to reduce waiting times for consultations after referral (18 weeks) has been studied by, among others, Harrison and Appleby161 who look at how the policy was implemented, identifying the relative importance of different aspects in achieving the goals. They found that introducing private sector capacity did not play a major part.
Another source of supply shocks that have been studied is changing quantities of labour. For example, Patterson162 looks at some of the issues around nurse to patient ratios and concludes that increasing the number of nurses should lead to better outcomes.
Data
This study attempts to investigate how an elective supply shock, in the form of the introduction of ISTCs, impacts on the levels of emergency activity. To do this, emergency activity at PCT level is modelled as a function of several demographic and supply-side factors, using panel data covering the years in which the first wave of ISTCs were open (2004/12).
The main source of data is HES, which provides information concerning all inpatients and outpatients admitted to NHS hospitals from 1989–90 onwards. In addition, it includes private patients treated in NHS hospitals, patients resident outside England and care delivered by TCs (including those in the independent sector). Each patient record contains detailed information about the treatment experienced, as well as clinical issues and additional administrative data, plus patient characteristics such as age, location and sex. As our main dependent variable we use the emergency admissions at PCT level per 1000 population. Anonymous patient records are extracted by financial year (1 April to 31 March) and aggregated at PCT level. For the years considered (2004/12), there were 151 PCTs in England. We use ONS mid-year population estimates to calculate PCT populations, and these data are linked to demographic characteristics at PCT level, such as the percentage of different sexes, ethnicities and ages.
Emergency and elective admissions are likely to depend on population morbidity, so it is important to control for the prevalence of specific conditions. The QOF provides valuable clinical information concerning prevalence for 22 specific diseases in 2013. Of these, we consider eight clinical conditions that influence the demand for hospital admissions. We also control for some measures that characterise the supply of NHS services such as number of specialists per 1000 population and the number of hospitals at PCT level.
Table 60 provides a summary description of the variables used to study the period 2004–11.
| Descriptive statistics | Year | |||||||
|---|---|---|---|---|---|---|---|---|
| 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | |
| Activity data | ||||||||
| Emergency admissions per 1000 population | 101.48 | 106.87 | 96.4 | 108.41 | 108.26 | 123.83 | 128.78 | 124.91 |
| Elective ISTC per 1000 population | 0.00 | 0.28 | 1.04 | 1.14 | 1.35 | 0.97 | 0.78 | 0.70 |
| Demographic data | ||||||||
| Female population (%) | 50.96 | 50.93 | 50.88 | 50.83 | 50.78 | 50.73 | 50.78 | 50.45 |
| Male population aged > 65 years (%) | 6.64 | 6.67 | 6.69 | 6.74 | 6.82 | 6.92 | 7.06 | 6.85 |
| Female population aged > 60 years (%) | 11.42 | 11.43 | 11.46 | 11.63 | 11.77 | 11.87 | 11.81 | 11.88 |
| Asian ethnicity (%) | 6.53 | 6.76 | 6.97 | 7.22 | 7.42 | 7.61 | 7.84 | 7.90 |
| Black ethnicity (%) | 3.16 | 3.21 | 3.25 | 3.29 | 3.33 | 3.37 | 3.40 | 3.34 |
| Supply variables | ||||||||
| Specialists per 1000 population | 0.68 | 0.72 | 0.76 | 0.77 | 0.84 | 0.90 | 0.96 | 1.00 |
| Average number of hospitals per PCT | 2.36 | 2.39 | 2.21 | 2.70 | 2.80 | 3.08 | 3.21 | 3.48 |
| Disease prevalence | ||||||||
| Heart problem per 1000 population | 58.02 | 58.81 | 67.61 | 67.60 | 67.94 | 68.42 | 68.90 | 68.71 |
| Stroke per 1000 population | 15.44 | 16.32 | 16.81 | 17.07 | 17.31 | 17.59 | 17.91 | 18.01 |
| Coronary per 1000 population | 37.96 | 37.86 | 37.62 | 37.25 | 36.84 | 36.58 | 36.27 | 35.62 |
| Pulmonary obstruction per 1000 population | 14.80 | 14.99 | 15.60 | 16.19 | 16.78 | 17.23 | 17.90 | 18.42 |
| Epilepsy per 1000 population | 6.28 | 6.48 | 6.40 | 6.42 | 6.44 | 6.50 | 6.56 | 6.54 |
| Mental health per 1000 population | 6.04 | 6.58 | 7.87 | 8.11 | 8.29 | 8.62 | 8.85 | 8.95 |
| Asthma per 1000 population | 60.93 | 60.73 | 60.83 | 60.50 | 61.87 | 62.64 | 62.71 | 62.05 |
| Ventricular 1000 population | 4.62 | 4.63 | 13.18 | 13.29 | 13.78 | 14.24 | 14.71 | 15.08 |
Table 60 is broken into four sections: activity data, demographic data, variables identifying supply and the prevalence of specific diseases. Activity data show how the dependent variable (emergency activity) and our main explanatory variable (elective activity carried out by ISTCs) have changed over the time period studied. Emergency admissions were fairly constant in 2004–8, and also 2009–11, but there was a big leap between 2008 and 2009. This series is illustrated in Figure 47.
FIGURE 47.
Emergency admissions, per 1000 population, 2004–11.
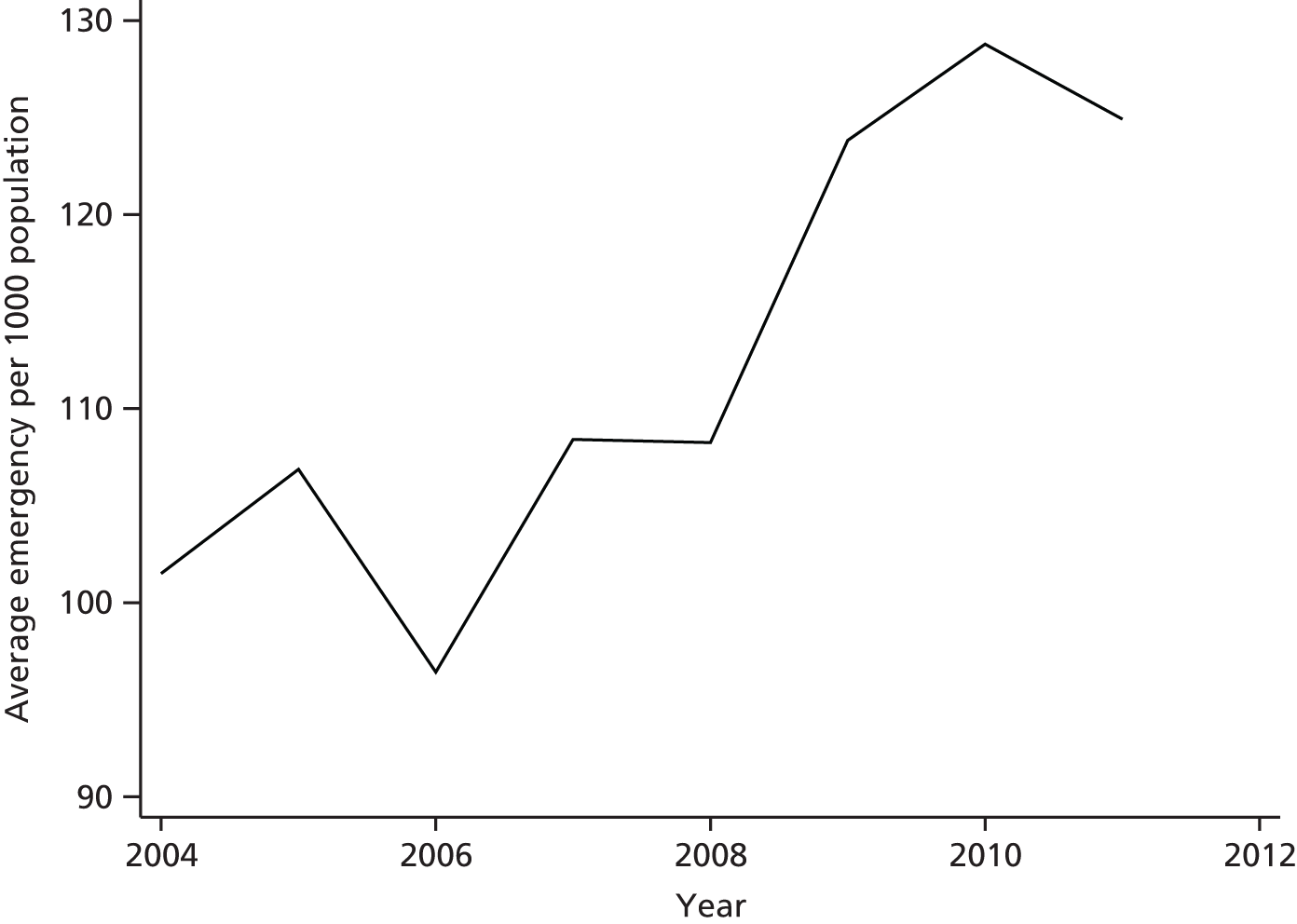
Figure 48 looks at just the PCTs in which ISTCs were introduced. These saw increases in the average number of emergency admissions that were greater than those experienced in England as a whole. This growth also carried on later than the increases seen generally across England.
FIGURE 48.
Emergency admissions in PCTs with ISTCs, per 1000 population, 2004–11.
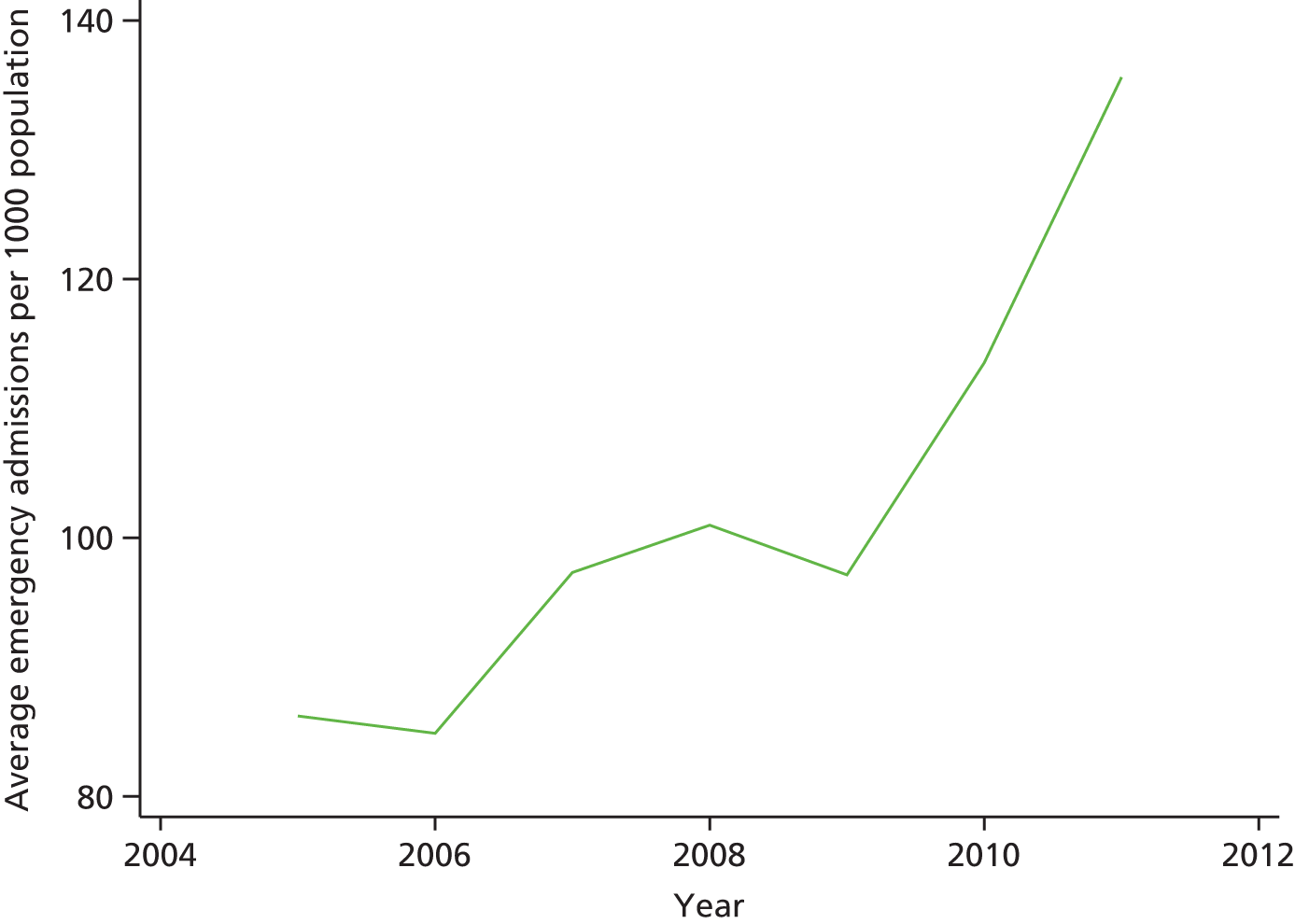
The demographic characteristics remain similar across this time period, with the major change being an increase in the average percentage of patients of Asian ethnicity per PCT, from 6.53% in 2004 to 7.90% in 2011.
The variables included to capture supply in the NHS have seen positive changes, with the number of specialists per head of population and the average number of hospitals increasing. This is unsurprising, as the time period under investigation was one of significant investment in the NHS.
Prevalence of diseases has increased for nearly all of the conditions included, with coronary heart disease the only exception. However, the nature of the QOF, and the incentives it provides for GPs, means that it is possible that these variables capture the identification of patients with these conditions and not necessarily an increase in the prevalence of the conditions themselves.
Figure 49 presents a correlation of emergency and elective activity rates for every year included in this study. These charts, which control for the different sized populations in PCTs, suggest that the two series are positively correlated, and that areas that experienced higher elective admission rates also had higher emergency admission rates. Appendix 1 presents further cross-sectional analysis of hospital data relating to different specialties and provides evidence that elective and emergency activity, in terms of both levels and change, is on the whole, positively correlated across geographical areas.
FIGURE 49.
Correlation plot of emergency and elective activity by year. (a) 2004; (b) 2005; (c) 2006; (d) 2007; (e) 2008; (f) 2009; (g) 2010; and (h) 2011.

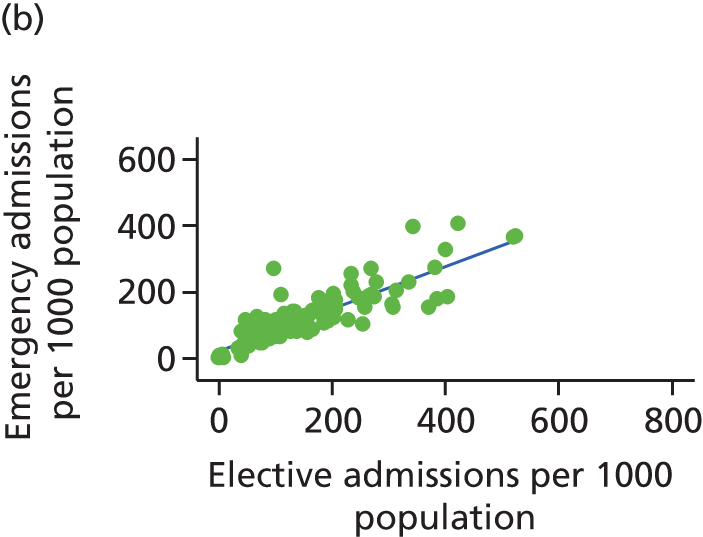
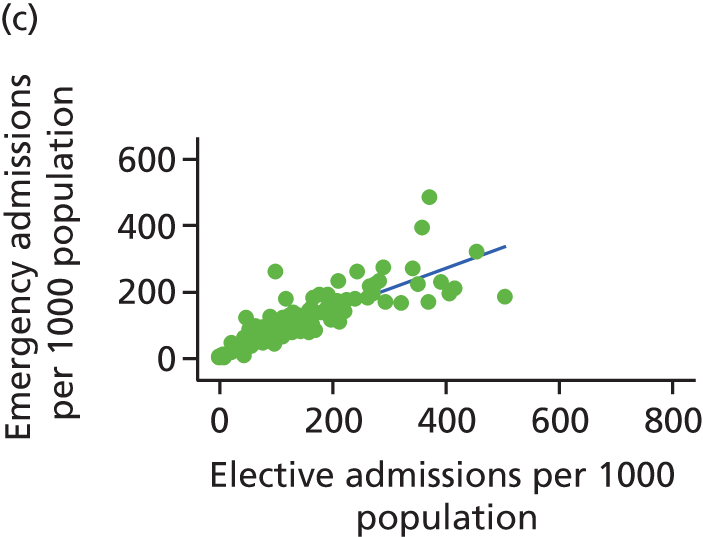
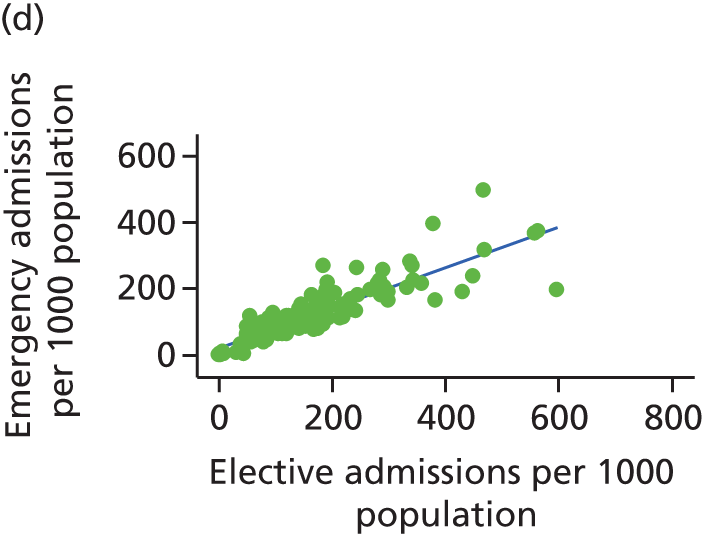
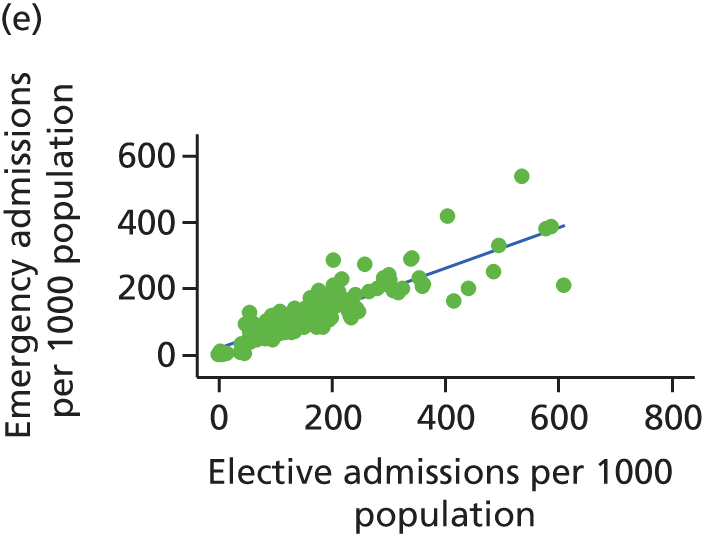
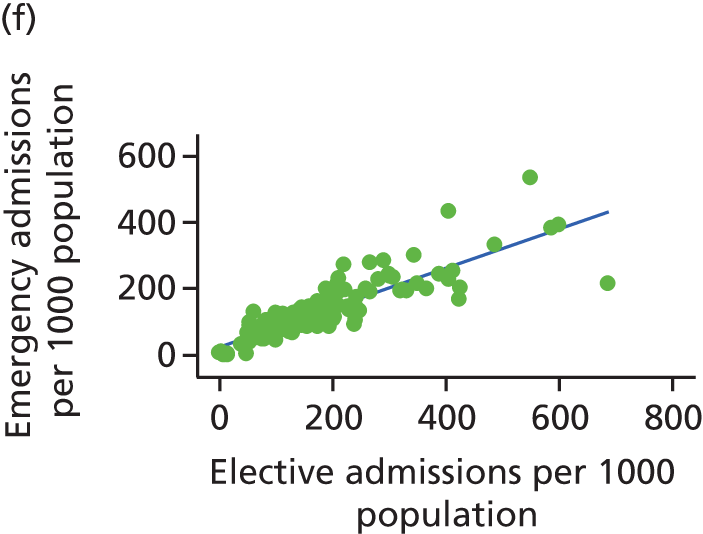
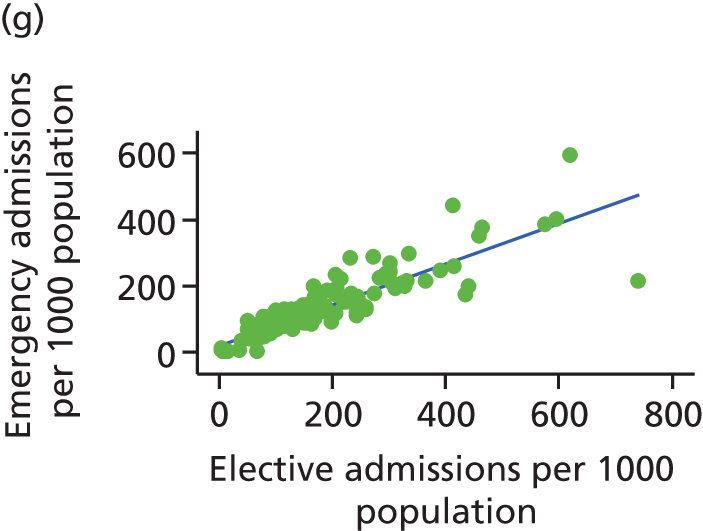

This could be caused by a number of factors, for example the demographic characteristics of the local population, and so we now turn to a more thorough model that tries to control for these issues and that can identify the specific role of elective shocks on emergency admission rates.
Empirical strategy
Our empirical strategy is to estimate a fixed-effects panel data model for emergency admissions at PCT level, controlling for a group of area-specific characteristics and other secondary care variables, plus a selection of variables intended to show the influence of ISTCs. This will produce a reduced form version of the model of hospital activity because it is not possible to estimate supply and demand separately.
We estimate two versions of the model. First:
where Ejt represents the number of emergency admissions per 1000 population resident at each PCTj in each year t. The key vector of explanatory variables that capture elective admissions of ISTCs in each year t is EListcjt, which represents elective admissions at ISTCs for each 1000 population of the PCTj in time t. Xjt is a vector of socioeconomic characteristics that are time-varying at PCTj in time, including the local population percentages of sexes, ages, diseases and ethnicities. To avoid the possibility of the endogenous recording of conditions following hospital admission, we use prevalence data for the year prior to that of the year of study for hospital admissions. β is a vector of the slope effects of these variables. Suppjt is a matrix of variables that characterise supply-side aspects of health care. Finally, we control for time with year effects (µt) and PCT with fixed effects (σj). εjt is a random-error term, which is assumed to be normally distributed.
We also estimate a similar version:
In this specification, we use the same explanatory variables but instead of treatment levels by ISTCs in individual PCT, we include a dummy variable ELdummyjt, which equals 1 if PCT j had any patients treated by an ISTC in year t and 0 if the PCT had no patients treated in an ISTC that year.
As a robustness check we also run versions of the regression detailed above in which we include values of total elective provision in year t – 1.
The results are presented in the next section.
Results
Table 61 presents the first set of regressions, as described in Equation 34. Specification (a) explains emergency admission rates using elective treatment rates and year fixed effects. In this model, the coefficient of ISTC treatment rates in positive but not statistically significant. Columns (b)–(d) add further control variables: PCT fixed effects, population characteristics, supply variables and disease prevalence rates. In regressions (a)–(d), more elective treatment in ISTCs is associated with higher emergency admissions, and the difference is statistically significant at the 5% level with all control variables, and at the 1% level in regressions (b) and (c), which have fewer explanatory variables.
| Variable | Dependent variable: emergency admissions per 1000 population | |||
|---|---|---|---|---|
| Model (a) | Model (b) | Model (c) | Model (d) | |
| Elective ISTC per 1000 population (SE) | 0.600 (0.654) | 0.862*** (0.153) | 0.909*** (0.169) | 0.733** (0.234) |
| PCT fixed effects | No | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes |
| Population control variables | No | No | Yes | Yes |
| NHS supply variables | No | No | No | Yes |
| Disease prevalence variables | No | No | Yes | Yes |
| Number of observations | 1001 | 1001 | 1001 | 992 |
Table 62 shows various versions of regressions using equation 35, with dummy variables used to identify PCTs that were affected by the introduction of ISTCs. In all but the most simplistic regression (e), the coefficient is positive but this variable has less explanatory power, with no statistically significant effect in any of the different specifications. These results should, however, be treated with caution owing to the small number of PCTs that benefited from having patients treated in ISTCs.
| Variable | Dependent variable: emergency admissions per 1000 population | |||
|---|---|---|---|---|
| Model (e) | Model (f) | Model (g) | Model (h) | |
| Elective ISTC dummy variable SE | –13.195 (15.779) | 12.326 (7.300) | 12.414 (7.429) | 5.429 (6.112) |
| PCT fixed effects | No | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes |
| Population control variables | No | No | Yes | Yes |
| NHS supply variables | No | No | No | Yes |
| Disease prevalence variables | No | No | Yes | Yes |
| Number of observations | 1001 | 1001 | 1001 | 992 |
Tables 63 and 64 include elective treatment rates from the previous year as a further explanatory variable. This variable is always positive and statistically significant at the 5% level and for some of the equations with fewer control variables, at the 1% level. Adding this variable does not alter the result from Table 55 indicating that increasing ISTC activity is associated with higher emergency admissions. Equally, the elective ISTC dummy variable remains generally positive but never statistically significant.
| Variable | Dependent variable: emergency admissions per 1000 population | |||
|---|---|---|---|---|
| Model (i) | Model (j) | Model (k) | Model (l) | |
| Elective per 1000 population at t – 1 (SE) | 0.560*** (0.062) | 0.311*** (0.089) | 0.311** (0.092) | 0.191** (0.067) |
| Elective ISTC per 1000 population (SE) | 0.663* (0.265) | 0.791*** (0.054) | 0.808*** (0.080) | 0.756*** (0.125) |
| PCT fixed effects | No | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes |
| Population control variables | No | No | Yes | Yes |
| NHS supply variables | No | No | No | Yes |
| Disease prevalence variables | No | No | Yes | Yes |
| Number of observations | 846 | 846 | 846 | 846 |
| Variable | Dependent variable: emergency admissions per 1000 population | |||
|---|---|---|---|---|
| Model (m) | Model (n) | Model (o) | Model (p) | |
| Elective per 1000 population at t – 1 (SE) | 0.559*** (0.062) | 0.313*** (0.089) | 0.312*** (0.092) | 0.192** (0.067) |
| Elective ISTC dummy variable (SE) | –0.075 (0.041) | 0.07 (0.036) | 0.071 (0.037) | 0.042 (0.032) |
| PCT fixed effects | No | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes |
| Population control variables | No | No | Yes | Yes |
| NHS supply variables | No | No | No | Yes |
| Disease prevalence variables | No | No | Yes | Yes |
| Number of observations | 846 | 846 | 846 | 846 |
In summary, these regressions suggest that there is likely to be a positive relationship between emergency and elective activity rates in English hospitals. There are specifications in which the coefficient of elective rates on emergency activity are negative, but in these rare situations the coefficients are not statistically significant.
Discussion and conclusion
The analysis presented here shows that PCTs in which an ISTC was located experienced greater rises in emergency activity, even when controlling for other factors, than areas that did not benefit from the introduction of ISTCs. This suggests that a positive supply shock to the provision of elective care at newly introduced ISTCs is correlated with an increase in the levels of emergency treatment at hospitals. We are unable to identify the exact cause of this positive correlation, but one of the more plausible explanations is that doctors working in emergency departments have been allowed to admit patients with less severe conditions in order to utilise the extra resources released by a fall in elective demand relative to capacity, as ISTCS are capable of treating only elective patients.
There are several caveats. If the impact of supply shocks in hospital care is symmetric, and the two types of care move in the same direction when there is a negative shock as well as when there is a positive one, then a policy that manages downwards elective care will have the desired impact and will have cost-saving effects, as the amount of emergency treatment could also fall.
However, it is possible that positive and negative supply shocks have different effects. For example, work stemming from that of Evans163 has suggested that health care tends to experience a large amount of supply-induced demand, where the demand for treatment tends to fill the available capacity. In addition, although clinicians may have been willing to relax admission criteria for emergency conditions as a consequence of increased elective capacity, it may be politically harder for them to tighten admission criteria if elective capacity is reduced.
Moreover, this work looks at a supply shock that affects just a small part of elective activity (i.e. the procedures that ISTCs were allowed to undertake). This extra capacity was important but its impact on overall emergency activity may not have the same impact as an increase in general elective capacity. It may be illuminating to focus on medical conditions that are directly influenced by procedures performed by ISTCs, for example how activity emergency hip fractures have changed as a consequence of additional elective joint replacements. This would require careful identification and assistance from medical experts.
In conclusion, this work does not provide sufficient evidence to fully refute several issues. As such, it would be wise to perform analyses looking at the impact of negative supply shocks that have previously occurred in order to better identify the effects of managing down demand for elective care.
Chapter 10 Conclusions
In recent years there has been a significant upwards trend in demand for elective hospital treatment: between 2001/2 and 2011/12, admissions increased by 35.4%. This project has attempted to determine some of the major causes of the increasing demand for elective treatment and to develop information and metrics that will help commissioners and providers to bring such demand under control during a time of austerity.
The hypothesis that the substantial elective admissions growth since 2002 is largely driven by either recent system reform or ageing presents a considerable challenge to health policy in that neither of these potential drivers of change is readily amenable by health policy managers. The reforms of the 2000s are presently politically non-controversial and ageing must be regarded as a given. Our first major conclusions concern the significance of these two factors and thus the capacity to ameliorate admissions growth safely.
The recent period of growth in elective care in England coincided with a growth in resources and the rolling introduction of system reform. When carefully measured on a comparable basis, elective care is found to grow more slowly in Scotland, suggesting that English system reform led to growth in elective care above the effect of increased resources. However, system reform is found to lead to a once and for all reduction of 7.7% in elective volume, without a continuing effect. Similarly, it led to a once and for all reduction of 5.6% in LOS, with no continuing effect. Thus, comparative Scottish data suggest that system reform, far from explaining higher relative growth of elective care in England, may have increased the relative growth that other factors need to explain. The trend towards higher relative admissions growth in England appears to pre-date system reform to the beginning of our study period in 1997.
We find that the additional growth in expenditure on elective care in England was partly offset by a greater reduction in LOS, and system reform may be responsible for this.
The geographic distribution of the trends was uneven across CCGs. This, combined with growth pressure, which system reform does not explain, challenges some CCGs more than others. We offer a framework whereby CCGs can gauge the extent of the challenge.
The ageing population features strongly in public debate about pressures on the NHS. An APC analysis shows that age accounts for only a small proportion of the growth in elective care, and this is nearly counterbalanced by a cohort effect, whereby successive birth cohorts have lower rates of elective care at a given age. The main driver of elective admissions is the period effect, that is, over time, a trend towards higher rates of elective care, all other things being equal.
The overall conclusion is that neither the ageing population nor system reform is a major driver of elective admissions growth. The trend captured by the ‘period effect’ may reflect a number of phenomena, including improved technical capacity for procedures to improve patient health, a greater awareness among GPs and patients of unmet need, and a higher level of expectation regarding patient health.
Our work suggests that one part of system reform – the tariff – may have reduced the variation of LOSs across PCTs for a range of elective procedures, and that this reflects the largest reductions among PCTs with the longest LOSs initially.
We find that increasing the number of GPs would reduce elective referrals and admissions in deprived, but not prosperous, areas. However, these savings by themselves would not be sufficiently large to fund the cost of extra GPs. We estimate that increasing the supply of GPs has no effect on emergency admissions.
There is some evidence that single-handed practices refer at higher rates than other practices but little evidence that this leads to higher admissions.
Striking differences in practice referral rates remain even when observed patient morbidities are taken into account. Some of these differences reflect the comparative needs of patients and practice locations or external constraints on practice capacities, but other findings are less easy to understand or justify. For example, we find that those under 35 years of age are less likely than the middle aged to be referred but that referred young patients are more likely to be admitted. We find that variation between practices rates of first referrals and ensuing hospital treatments is not consistent with an explanatory model in which the registered patients at some practices are less healthy: practices with high rates of elective treatment do not have higher referral rates. A policy to reduce practice referrals may reduce related hospital treatments by as much as 20% of the absolute reduction in referrals but may disproportionately reduce treatments at practices that make few referrals.
A selection criterion is developed to forecast patient health gain using PROMs data, and this can help to identify patients who receive procedures that are not cost-effective. Savings to the NHS could be substantial if these treatments were avoided, and, therefore, these criteria may usefully support clinician decision-making.
Using PROMs data, it is possible to compare CCGs in terms of the health gain they achieve for patients, and the data show that CCGs do not differ a great deal. There is considerable variation in procedure rates but not in any systematic way.
In assessing variation in performance in producing health gain, it is important to take account of the hierarchical structure of health care, and we discover that some providers underperform their peers. The scale of underperformance is sufficiently large to be worth further investigation, but there are currently no methods for remedying the specific deficits identified. It is possible to assess the potential benefit from selected improvements but there is no information as regards the cost or effectiveness of bringing about the changes.
If planned care is managed downwards, a concern is that cost-savings for the NHS might be minimal, as patients could require emergency admission for conditions not treated electively. Cross-sectional analysis shows that small areas with low rates of elective care, both at the aggregate level and for a range of specialties, do not have a higher rate of emergency admissions. This conclusion is confirmed by an analysis of a supply shock, the temporary introduction of additional elective capacity in a few areas – both geographical and conditions – at ISTCs.
There was a patient and public involvement representative on our advisory committee, who advised on all aspects of the project. Our patient and public involvement representative was recruited from a group of lay members who advise on the research of the Department of Health Policy Research Programme Research Unit, Quality and Outcomes of Person centred Care. This committee met annually during the project and was encouraged to give feedback on the issues studied. During the early stages of this project, we also approached several organisations that represent patient interests in the hope of engaging them in the project. This was a time-consuming process and ultimately proved unsuccessful.
This research relies entirely on secondary data sources. This allows important issues to be studied using large data sets and robust empirical methods, but it does not easily facilitate the important input of clinical experts or service users. We felt that the benchmarking information was important for CCGs, so gave NHS England (the CCG Commissioning Development Group) the opportunity to distribute the report, and subsequently mailed all CCG clinical leads with a brief summary of the findings and a signpost to the report on the Centre for Health Service Economics and Organisation website,134 together with an invitation to comment, but none responded.
It would be beneficial if other research methods could be utilised in future research now that we have uncovered important questions in this subject area. There are several areas that could benefit from further research. The benchmarking work shows that CCGs perform at different levels of activity. It is important to uncover the reasons why this might be; for example, are the high-volume CCGs eliminating unmet need?
There is also significant variation in the referral rates of GP practices. It would be interesting to investigate why GPs refer at different rates, even after controlling for patient characteristics. This work also shows significantly different referral rates for patients from different backgrounds, suggesting that ethnic groups vary in the way they access health care.
The APC analysis suggests that the period effect is dominant, dwarfing the impact of age or the birth cohort. It would be beneficial to determine what has been changing over recent years, so that this source of growth can be controlled appropriately. Investigating these topics would potentially involve surveying patients and health-care providers.
One area that would benefit from further theoretical modelling and empirical research using secondary data is the relationship between emergency and elective treatments, from the viewpoint of patient demand and hospital supply.
Acknowledgements
We would like to thank the co-applicants, namely Professor Ray Fitzpatrick, Professor Michael Goldacre, Dr Nicholas Hicks, Dr Daniel Lasserson, Professor Andrew Price and Dr Jose M Valderas, all of whom contributed to the design of the project and attended meetings at which they provided helpful guidance, feedback and direction for the research. In addition, Professor Ray Fitzpatrick reviewed Chapter 7; Professor Michael Goldacre commented on Chapter 4 and advised with the construction of data sets for Chapters 4 and 5; and Dr Jose M Valderas commented on analysis of spending by procedure for the benchmarking analysis.
We would also like to thank Mr Paul Streets, Mr Jeremy Hurst, Dr Fiona Adshead and Mr Matthew Baker who took part in advisory committee meetings throughout the course of this project.
The Hospital Episode Statistics are copyright © 1997/98–2014/15, re-used with the permission of The Health & Social Care Information Centre. All rights reserved.
The Scottish Morbidity Record data were provided by the Information and Statistics Division Scotland (ISD).
Contributions of authors
Professor Martin Chalkley contributed to the conception of the project; supervised the analysis and drafted Chapter 2.
Professor Barry McCormick led the conception and design of the project; provided oversight throughout; drafted Chapter 1; supervised Chapters 3, 7 and 9; produced the models and drafted the findings in Chapters 5 and 6; and finalised the draft report.
Mr Robert Anderson contributed to the design of the project, produced Chapters 7 and 8; and drafted the report.
Dr Maria Jose Aragon performed the analysis in Chapter 2.
Ms Nazma Nessa performed the benchmarking analysis.
Dr Catia Nicodemo performed the analysis and assisted with the drafting of Chapters 4–6 and Chapter 9.
Dr Stuart Redding assisted with the design of the project; assisted with the analysis in Chapter 4; produced Chapter 9, performed the analysis and drafted Chapter 3; assisted with the draft report and provided administrative support throughout.
Mr Raphael Wittenberg drafted Chapter 4.
Data sharing statement
All available data can be obtained from the corresponding author.
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the HS&DR programme or the Department of Health. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the HS&DR programme or the Department of Health.
References
- NHS England . NHS Atlases n.d. www.england.nhs.uk/rightcare/intel/cfv/atlas/ (accessed September 2015).
- The Right Result? Payment by Results 2003–7. London: Audit Commission; 2008.
- Reinhardt UE. Does the aging of the population really drive the demand for health care?. Health Aff 2003;22:27-39. https://doi.org/10.1377/hlthaff.22.6.27.
- Mariñoso BG, Jelovac I. GPs’ payment contracts and their referral practice. J Health Econ 2003;22:617-35. https://doi.org/10.1016/S0167-6296(03)00008-0.
- Keenan T, Rosen P, Yeates D, Goldacre M. Time trends and geographical variation in cataract surgery rates in England: study of surgical workload. Br J Ophthalmol 2007;91:901-4. http://dx.doi.org/10.1136/bjo.2006.108977.
- Devlin NJ, Appleby J. Getting the Most out of PROMS. London: The King’s Fund; 2010.
- Street AD, Gutacker N, Bojke C, Devlin N, Daidone S. Measuring Patient Reported Outcomes and Costs of Hospital Procedures and Identifying Variation Across Providers. Southampton: NIHR Journals Library; 2012.
- Blunt I, Bardsley M, Dixon J. Trends in Emergency Admissions in England 2004–2009: Is Greater Efficiency Breeding Inefficiency?. London: The Nuffield Trust; 2010.
- Poteliakhoff E, Thompson J. Emergency Bed Use: What the Numbers Tell Us. London: The King’s Fund; 2011.
- Smith P, McKeon A, Blunt I, Edwards N. NHS Hospitals Under Pressure: Trends in Acute Activity up to 2022. London: The Nuffield Trust; 2014.
- Cooper Z, Gibbons S, Skellern M. Independent Sector Treatment Centres in the English NHS: Effects on Neighbouring NHS Hospitals. London: Department of Social Policy and Centre for Economic Performance; 2015.
- A Simple Guide to Payment by Results. London: Department of Health; 2012.
- Farrar S, Yi D, Sutton M, Chalkley M, Sussex J, Scott A. Has payment by results affected the way that English hospitals provide care? Difference-in-differences analysis. BMJ 2009;339. http://dx.doi.org/10.1136/bmj.b3047.
- Cots F, Chiarello P, Salvador X, Castells X, Quentin W, Busse R, et al. Diagnosis-Related Groups in Europe – Moving Towards Transparency, Efficiency and Quality in Hospitals. Maidenhead: Open University Press and McGraw-Hill Education; 2011.
- An Evaluation of the Reimbursement System for NHS Funded Care. London: PriceWaterhouseCoopers; 2012.
- Appleby J, Harrison T, Hawkins L, Dixon A. Payment by Results: How Can Payment Systems Help to Deliver Better Care?. London: The King’s Fund; 2012.
- Charlesworth A, Hawkins L, Marshall L. NHS Payment Reform: Lessons from the Past and Directions for the Future. London: Nuffield Trust; 2014.
- Mayes R. The origins, development, and passage of Medicare’s revolutionary prospective payment system. J Hist Med Allied Sci 2007;62:21-55. http://dx.doi.org/10.1093/jhmas/jrj038.
- Busse R, Geissler A, Quentin W, Wiley M. Diagnosis-Related Groups in Europe – Moving Towards Transparency, Efficiency and Quality in Hospitals. Maidenhead: Open University Press and McGraw-Hill Education; 2011.
- Street A, O’Reilly J, Ward P, Mason A, Busse R, Geissler A, et al. Diagnosis-Related Groups in Europe – Moving Towards Transparency, Efficiency and Quality in Hospitals. Maidenhead: Open University Press and McGraw-Hill Education; 2011.
- Gregory S, Thorlby R. Free Choice at the Point of Referral. London: The King’s Fund; 2008.
- Kelly E, Tetlow G. Choosing the Place of Care: The Effect of Patient Choice on Treatment Location in England, 2003–2011. London: The Nuffield Trust; 2012.
- Bevan G, Karanikolos M, Exley J, Nolte E, Connolly S, Mays N. The Four Health Systems of the United Kingdom: How Do They Compare?. London: The Nuffield Trust; 2014.
- Cooper Z, Gibbons S, Jones S, McGuire A. Does hospital competition save lives? Evidence from the English NHS patient choice reforms. Econ J 2011;121:F228-60. http://dx.doi.org/10.1111/j.1468-0297.2011.02449.x.
- Lafond S, Arora S, Charlesworth A, McKeon A. Into the Red? The State of NHS Finances. London: The Nuffield Trust; 2014.
- Hospital Episode Statistics. n.d.
- The Health and Social Care Information Centre . Methodology to Create Provider and CIP Spells from HES APC Data 2014. www.hscic.gov.uk/media/11859/Provider-Spells-Methodology/pdf/Spells_Methodology.pdf (accessed 7 June 2016).
- Information Services Division, NHS National Services . Data Dictionary 2015. www.ndc.scot.nhs.uk/Dictionary-A-Z/ (accessed 28 January 2015).
- Health and Social Care Information Centre . HRG4 2009 10 Reference Costs Grouper Documentation 2012. www.hscic.gov.uk/article/2319/HRG4-200910-Reference-Costs-Grouper-Documentation (accessed 23 February 2015).
- NHS England . CCG Directory 2013. www.england.nhs.uk/resources/ccg-directory/ (accessed 2 December 2014).
- Department of Health, Improvement and Efficiency Directorate . PCT Cluster Implementation Guidance 2011. www.gov.uk/government/publications/pct-clusterimplementation-guidance (accessed 13 January 2015).
- NHS England . List of Proposed CCGs n.d. www.england.nhs.uk/wp-content/uploads/2012/07/list-of-proposed-ccgs-pcts-rcas.xls (accessed 20 February 2015).
- NHS England . CCG Maps n.d. www.england.nhs.uk/resources/ccg-maps/ (accessed 20 February 2015).
- Cornelissen T. The Stata command felsdvreg to fit a linear model with two high dimensional fixed effects. Stata J 2008;8:170-89. www.stata-journal.com/article.html?article=st0143 (accessed 2 December 2014).
- Farrar S, Sussex J, Yi D, Sutton M, Chalkley M, Scott A, et al. A National Evaluation of Payment by Results. York: Health Economics Research Unit, University of York; 2007.
- Health and Social Care Information Centre . Indicator Portal n.d. https://indicators.ic.nhs.uk/webview (accessed 8 January 2015).
- National Records of Scotland . Population Estimates. Time Series Data 2015. www.nrscotland.gov.uk/statistics-and-data/statistics/statistics-by-theme/population/population-estimates/mid-year-population-estimates/population-estimates-time-series-data (accessed 30 January 2015).
- Department of Communities and Local Government . English Indices of Deprivation 2015. www.gov.uk/government/collections/english-indices-of-deprivation (accessed 8 January 2015).
- Hawe E, Cockcroft L. OHE Guide to UK Health and Health Care Statistics. London: Office of Health Economics; 2013.
- Coulam RF, Gaumer GL. Medicare’s prospective payment system: a critical appraisal. Health Care Financ Rev Annu 1991:45-77.
- Hodgkin D, McGuire TG. Payment levels and hospital response to prospective payment. J Health Econ 1994;13:1-29. https://doi.org/10.1016/0167-6296(94)90002-7.
- McClellan M. Reforming payments to healthcare providers: the key to slowing healthcare cost growth while improving quality?. J Econ Perspect 2011;25:69-92. https://doi.org/10.1257/jep.25.2.69.
- Theurl E, Winner H. The impact of hospital financing on the length of stay: evidence from Austria. Health Policy 2007;82:375-89. http://dx.doi.org/10.1016/j.healthpol.2006.11.001.
- Newhouse JP, Byrne DJ. Did Medicare’s prospective payment system cause length of stay to fall?. J Health Econ 1988;7:413-6. https://doi.org/10.1016/0167-6296(88)90023-9.
- Shen Y. Selection incentives in a performance-based contracting system. Health Serv Res 2003;38:535-52. https://doi.org/10.1111/1475-6773.00132.
- Dranove D, Kessler D, McClellan M, Satterthwaite M. Is more information better? The effects of report cards on health care providers. J Polit Econ 2003;111:555-88. https://doi.org/10.1086/374180.
- Skinner J, Pauly M, McGuire TG, Barros PP. Handbook of Health Economics. Philadelphia, PA: Elsevier BV; 2011.
- Miraldo M, Goddard M, Smith PC. The Incentive Effects of Payment by Results. York: Centre for Health Economics, University of York; 2006.
- Propper C, Sutton M, Whitnall C, Windmeijer F. Incentives and targets in hospital care: evidence from a natural experiment. J Public Econ 2010;94:318-35. https://doi.org/10.1016/j.jpubeco.2010.01.002.
- Hospital Episode Statistics. n.d.
- Unified Exposition Book: 2003/04, 2004/05 & 2005/06 PCT Revenue Resource Limits. London: Department of Health; 2007.
- Wittenberg R, Redding S, Nicodemo C, McCormick B. Analysis of Trends in Emergency and Elective Hospital Admissions and Hospital Bed Days 1997/98 to 2014/15. Oxford: Centre for Health Service Economics and Organisation; 2015.
- Hospital Episode Statistics. Admitted Patient Care – England, 2011–12. Leeds: Health and Social Care Information Centre; 2012.
- Blatchford O, Capewell S. Emergency medical admissions: taking stock and planning for winter. BMJ 1997;315:1322-3. https://doi.org/10.1136/bmj.315.7119.1322.
- Gillam S. Rising hospital admissions. BMJ 2010;340. http://dx.doi.org/10.1136/bmj.c636.
- Hobbs R. Rising emergency admissions. BMJ 1995;310:207-8. https://doi.org/10.1136/bmj.310.6974.207.
- Health and Social Care Information Centre . Measuring Growth in the Volume of Input for General Practice Services 2009.
- Coast J, Inglis A, Frankel S, Gray S, Peters T. Is hospital the right place?. J Public Health Med 1995;17:239-40.
- Bunn F, Kendall S. Has Health Visiting Research Influenced Health Policy Relating to Children and Families in the UK? n.d.
- Sibley LM, Sipe TA, Brown CM, Diallo MM, McNatt K, Habarta N. Traditional birth attendant training for improving health behaviours and pregnancy outcomes. Cochrane Database Syst Rev 2007;3. https://doi.org/10.1002/14651858.cd005460.pub2.
- Dusheiko M, Gravelle H, Martin S, Rice N, Smith PC. Does better disease management in primary care reduce hospital costs? Evidence from English primary care. J Health Econ 2011;30:919-32. http://dx.doi.org/10.1016/j.jhealeco.2011.08.001.
- Chernew ME, Sabik L, Chandra A, Newhouse JP. Would having more primary care doctors cut health spending growth?. Health Aff 2009;28:1327-35. http://dx.doi.org/10.1377/hlthaff.28.5.1327.
- Franks P, Fiscella K. Primary care physicians and specialists as personal physicians. Health care expenditures and mortality experience. J Fam Pract 1998;47:105-9.
- Macinko J, Starfield B, Shi L. The contribution of primary care systems to health outcomes within Organization for Economic Cooperation and Development (OECD) countries, 1970-1998. Health Serv Res 2003;38:831-65. https://doi.org/10.1111/1475-6773.00149.
- Forrest CB, Starfield B. The effect of first-contact care with primary care clinicians on ambulatory health care expenditures. J Fam Pract 1996;43:40-8.
- Malcomson JM. Health service gatekeepers. RAND J Econ 2004;35:401-21. https://doi.org/10.2307/1593698.
- González P. The Gatekeeping Role of General Practitioners. Does Patients’ Information Matter?. Seville: Universidad Pablo de Olavide; 2006.
- Allard M, Jelovac I, Léger PT. Treatment and referral decisions under different physician payment mechanisms. J Health Econ 2011;30:880-93. http://dx.doi.org/10.1016/j.jhealeco.2011.05.016.
- Iversen T, Ma CT. Market conditions and general practitioners’ referrals. Int J Health Care Finance Econ 2011;11:245-65. http://dx.doi.org/10.1007/s10754-011-9101-y.
- Gaynor M, Rebitzer JB, Taylor LJ. Physician incentives in health maintenance organizations. J Polit Econ 2004;112:915-31. https://doi.org/10.1086/421172.
- Ellis RP, McGuire TG. Provider behavior under prospective reimbursement. Cost sharing and supply. J Health Econ 1986;5:129-51. https://doi.org/10.1016/0167-6296(86)90002-0.
- Chandra A, Cutler D, Song Z, Pauly MV, McGuire TG, Barros PP. Handbook of Health Economics. Philadelphia, PA: Elsevier BV; 2011.
- Ellis RP, McGuire TG. Optimal payment systems for health services. J Health Econ 1990;9:375-96. https://doi.org/10.1016/0167-6296(90)90001-J.
- Ma CT, Riordan MH. Health insurance, moral hazard, and managed care. J Econ Manag Strategy 2002;11:81-107. https://doi.org/10.1162/105864002317247587.
- Delivering High Quality, Effective, Compassionate Care: Developing the Right People with the Right Skills and the Right Values. London: Department of Health; 2013.
- Glied SA, Culyer AJ, Newhouse JP. Handbook of Health Economics. Amsterdam: Elsevier Science B.V.; 2002.
- Gulliford MC. Availability of primary care doctors and population health in England: is there an association?. J Public Health Med 2002;24:252-4. https://doi.org/10.1093/pubmed/24.4.252.
- Harris MJ, Patel B, Bowen S. Primary care access and its relationship with emergency department utilisation: an observational, cross-sectional, ecological study. Br J Gen Pract 2011;61:e787-93. http://dx.doi.org/10.3399/bjgp11X613124.
- Baicker K, Chandra A. The productivity of physician specialization: evidence from the Medicare program. Am Econ Rev 2004;94:357-61. https://doi.org/10.1257/0002828041301461.
- Wright DB, Ricketts TC. The road to efficiency? Re-examining the impact of the primary care physician workforce on health care utilization rates. Soc Sci Med 2010;70:2006-10. http://dx.doi.org/10.1016/j.socscimed.2010.02.043.
- Dusheiko M, Gravelle H, Jacobs R, Smith P. The effect of financial incentives on gatekeeping doctors: evidence from a natural experiment. J Health Econ 2006;25:449-78. http://dx.doi.org/10.1016/j.jhealeco.2005.08.001.
- de Bruin SR, Heijink R, Lemmens LC, Struijs JN, Baan CA. Impact of disease management programs on healthcare expenditures for patients with diabetes, depression, heart failure or chronic obstructive pulmonary disease: a systematic review of the literature. Health Policy 2011;101:105-21. http://dx.doi.org/10.1016/j.healthpol.2011.03.006.
- Carroll A, Dowling M. Discharge planning: communication, education and patient participation. Br J Nurs 2007;16:882-6. http://dx.doi.org/10.12968/bjon.2007.16.14.24328.
- Blustein J, Hanson K, Shea S. Preventable hospitalizations and socioeconomic status. Health Aff 1998;17:177-89. https://doi.org/10.1377/hlthaff.17.2.177.
- Fang H, Rizzo JA. Competition and physician-enabled demand: the role of managed care. J Econ Behav Organ 2009;72:463-74. https://doi.org/10.1016/j.jebo.2009.05.012.
- Chernozhukov V, Hansen C. An IV model of quantile treatment effects. Econometrica 2005;73:245-61. https://doi.org/10.1111/j.1468-0262.2005.00570.x.
- Altonji JG, Card D, Abowd JM, Freeman RB. Immigration, Trade, and the Labor Market. Chicago, IL: National Bureau of Economic Research, University of Chicago Press; 1991.
- Card D. Immigrant inflows, native outflows, and the local market impacts of higher immigration. J Labor Econ 2001;19:22-64. https://doi.org/10.1086/209979.
- Card D, Lewis EG, Borjas G. Mexican Immigration. Chicago, IL: University of Chicago Press; 2007.
- Noble M, McLennan D, Wilkinson K, Whitworth A, Barnes H, Dibben C. The English Indices of Deprivation 2007. London: Department for Communities and Local Government; 2008.
- Chandler MS, Malek I. Measuring Growth in the Volume of Input for General Practice Services. Newport: Office for National Statistics, UK Centre for the Measurement of Government Activity; 2009.
- Koenker RW, Bassett G. Regression quantiles. Econometrica 1978;46:33-50. https://doi.org/10.2307/1913643.
- Koenker R. Quantile Regression. Cambridge: Cambridge University Press; 2005.
- Chernozhukov V, Hansen C, Jansson M. Admissible tests for instrumental regression. Econometric Theory 2009;25:806-18. https://doi.org/10.1017/S0266466608090312.
- Chernozhukov V, Hansen C, Jansson M. Finite sample inference for quantile regression models. J Econometrics 2009;152:93-103. https://doi.org/10.1016/j.jeconom.2009.01.004.
- Kato K, Galvao AF, Montes-Rojas GV. Asymptotics for panel quantile regression models with individual effects. J Econometrics 2012;170:76-91. https://doi.org/10.1016/j.jeconom.2012.02.007.
- Donohoe MT, Kravitz RL, Wheeler DB, Chandra R, Chen A, Humphries N. Reasons for outpatient referrals from generalists to specialists. J Gen Intern Med 1999;14:281-6. https://doi.org/10.1046/j.1525-1497.1999.00324.x.
- O’Donnell CA. Variation in GP referral rates: what can we learn from the literature?. Fam Pract 2000;17:462-71. https://doi.org/10.1093/fampra/17.6.462.
- Foot C, Naylor C, Imison C. The Quality of GP Diagnosis and Referrals. London: The King’s Fund; 2010.
- Ringberg U, Fleten N, Deraas TS, Hasvold T, Førde O. High referral rates to secondary care by general practitioners in Norway are associated with GPs’ gender and specialist qualifications in family medicine, a study of 4350 consultations. BMC Health Serv Res 2013;13. http://dx.doi.org/10.1186/1472-6963-13-147.
- Coulter A, Seagroatt V, McPherson K. Relation between general practices’ outpatient referral rates and rates of elective admission to hospital. BMJ 1990;301:273-6. https://doi.org/10.1136/bmj.301.6746.273.
- Hippisley-Cox J, Jumbu G. Trends in Consultation Rates in General Practice 1995 to 2007: Analysis of the QRESEARCH Database. London: The NHS Information Centre; 2008.
- Dixon A, Le Grand J, Henderson J, Murray R, Poteliakhoff E. Is the British National Health Service equitable? The evidence on socioeconomic differences in utilization. J Health Serv Res Policy 2007;12:104-9. https://doi.org/10.1258/135581907780279549.
- Boerma WG, Groenewegen PP, Van der Zee J. General practice in urban and rural Europe: the range of curative services. Soc Sci Med 1998;47:445-53. https://doi.org/10.1016/S0277-9536(98)00074-4.
- Brown LJ, Barnett JR. Influence of bed supply and health care organization on regional and local patterns of diabetes related hospitalization. Soc Sci Med 1992;35:1157-70. https://doi.org/10.1016/0277-9536(92)90228-I.
- Evans E, Aiking H, Edwards A. Reducing variation in general practitioner referral rates through clinical engagement and peer review of referrals: a service improvement project. Qual Prim Care 2011;19:263-72.
- van Dijk CE, Korevaar JC, Koopmans B, de Jong JD, de Bakker DH. The primary-secondary care interface: does provision of more services in primary care reduce referrals to medical specialists?. Health Policy 2014;118:48-55. http://dx.doi.org/10.1016/j.healthpol.2014.04.001.
- Noone A, Goldacre M, Coulter A, Seagroatt V. Do referral rates vary widely between practices and does supply of services affect demand? A study in Milton Keynes and the Oxford region. J R Coll Gen Pract 1989;39:404-7.
- Madeley RJ, Evans JR, Muir B. The use of routine referral data in the development of clinical audit and management in North Lincolnshire. J Public Health Med 1990;12:22-7.
- Christensen B, Sørensen HT, Mabeck CE. Differences in referral rates from general practice. Fam Pract 1989;6:19-22. https://doi.org/10.1093/fampra/6.1.19.
- Srirangalingam U, Sahathevan SK, Lasker SS, Chowdhury TA. Changing pattern of referral to a diabetes clinic following implementation of the new UK GP contract. Br J Gen Pract 2006;56:624-6.
- Bertrand M, Duflo E, Mullainathan SD. How much should we trust differences-in-differences estimates?. Q J Economics 2004;119. https://doi.org/10.1162/003355304772839588.
- McCormick B, Hill P-S, Poteliakoff E. Are Hospital Services Used Differently in Deprived Areas? Evidence to Identify Commissioning Challenges. Oxford: Centre for Health Service Economics and Organisation; 2012.
- Chernozhukov V, Hansen C. Instrumental variable quantile regression: a robust inference approach. J Econometrics 2008;142:379-98. https://doi.org/10.1016/j.jeconom.2007.06.005.
- Bassetlaw Clinical Commissioning Group . Orthopaedics Referral and Treatment Guidelines 2015. www.bassetlawccg.nhs.uk/referral-treatment-guidelines/categories/79 (accessed 7 June 2016).
- Cox JM, Steel N, Clark AB, Kumaravel B, Bachmann MO. Do referral-management schemes reduce hospital outpatient attendances? Time-series evaluation of primary care referral management. Br J Gen Pract 2013;63:e386-92. http://dx.doi.org/10.3399/bjgp13X668177.
- Derrett S, Devlin N, Hansen P, Herbison P. Prioritizing patients for elective surgery: a prospective study of clinical priority assessment criteria in New Zealand. Int J Technol Assess Health Care 2003;19:91-105. https://doi.org/10.1017/S0266462303000096.
- Ostendorf M, van Stel HF, Buskens E, Schrijvers AJ, Marting LN, Verbout AJ, et al. Patient-reported outcome in total hip replacement. A comparison of five instruments of health status. J Bone Joint Surg Br 2004;86:801-8. https://doi.org/10.1302/0301-620X.86B6.14950.
- Judge A, Arden NK, Price A, Glyn-Jones S, Beard D, Carr AJ, et al. Assessing patients for joint replacement: can pre-operative Oxford hip and knee scores be used to predict patient satisfaction following joint replacement surgery and to guide patient selection?. J Bone Joint Surg Br 2011;93:1660-4. http://dx.doi.org/10.1302/0301-620X.93B12.27046.
- Judge A, Arden NK, Cooper C, Kassim Javaid M, Carr AJ, Field RE, et al. Predictors of outcomes of total knee replacement surgery. Rheumatology 2012;51:1804-13. http://dx.doi.org/10.1093/rheumatology/kes075.
- Dakin H, Gray A, Fitzpatrick R, Maclennan G, Murray D. KAT Trial Group . Rationing of total knee replacement: a cost-effectiveness analysis on a large trial data set. BMJ Open 2012;2. http://dx.doi.org/10.1136/bmjopen-2011-000332.
- Black N, Varagunam M, Hutchings A. Influence of surgical rate on patients’ reported clinical need and outcomes in English NHS. J Pub Health 2014;36:497-503. http://dx.doi.org/10.1093/pubmed/fdt088.
- Health and Social Care Information Centre . Provisional Monthly Patient Reported Outcome Measures (PROMs) in England. A Guide to PROMs Methodology 2013. www.hscic.gov.uk/media/1537/A-Guide-to-PROMs-Methodology/pdf/PROMS_Guide_v5.pdf (accessed 18 June 2014).
- Bishop S, Daniel T, Cavill S, Tyler J. NHS Spending Priorities. Leicester City NHS 2014. www.leicestercity.nhs.uk/library/spendingpriorities.ppt (accessed 3 November 2014).
- Department of Health . National Schedule of Reference Costs 2011–12 for NHS Trusts and NHS Foundation Trusts n.d. www.gov.uk/government/uploads/system/uploads/. /NSRC02-2011-12.xls (accessed 23 June 2016).
- Curtis L. Unit Costs of Health and Social Care 2013. Canterbury: Personal and Social Services Research Unit, University of Kent; 2014.
- Ward A, Abisi S, Braithwaite BD. An online patient completed Aberdeen Varicose Vein Questionnaire can help to guide primary care referrals. Eur J Vasc Endovasc Surg 2013;45:178-82. https://doi.org/10.1016/j.ejvs.2012.11.016.
- Labek G, Thaler M, Janda W, Agreiter M, Stöckl B. Revision rates after total joint replacement: cumulative results from worldwide joint register datasets. J Bone Joint Surg Br 2011;93:293-7. http://dx.doi.org/10.1302/0301-620X.93B3.25467.
- Claxton K, Martin S, Soares M, Rice N, Spackman E, Hinde S, et al. Methods for the Estimation of the NICE Cost Effectiveness Threshold. York: Centre for Health Economics, University of York; 2013.
- Rivero-Arias O, Ouellet M, Gray A, Wolstenholme J, Rothwell PM, Luengo-Fernandez R. Mapping the modified Rankin scale (mRS) measurement into the generic EuroQol (EQ-5D) health outcome. Med Decis Making 2010;30:341-54. http://dx.doi.org/10.1177/0272989X09349961.
- Oppe M, Devlin N, Black N. Comparison of the underlying constructs of the EQ-5D and Oxford Hip Score: implications for mapping. Value Health 2011;14:884-91. http://dx.doi.org/10.1016/j.jval.2011.03.003.
- Pinedo-Villanueva RA, Turner D, Judge A, Raftery JP, Arden NK. Mapping the Oxford hip score onto the EQ-5D utility index. Qual Life Res 2013;22:665-75. http://dx.doi.org/10.1007/s11136-012-0174-y.
- Nord E. Some ethical corrections to valuing health programs in terms of quality-adjusted life years (QALYs). Virtual Mentor 2005;7. http://dx.doi.org/10.1001/virtualmentor.2005.7.2.pfor3-0502.
- Nessa N, Anderson R. Demand Management for Planned Care: Benchmarking. Oxford: Centre for Health Service Economics and Organisation; 2014.
- Tranmer M, Steel DG. Ignoring a level in a multilevel model: evidence from UK census data. Environment and Planning A 2001;33:941-8. https://doi.org/10.1068/a3317.
- Snijders TAB. Multilevel Analysis. Oxford: Department of Statistics; 2012.
- Austin PC, Alter DA, Tu JV. The use of fixed- and random-effects models for classifying hospitals as mortality outliers: a Monte Carlo assessment. Med Decis Making 2003;23:526-39. http://dx.doi.org/10.1177/0272989X03258443.
- Detection and Management of Outliers. London: Department of Health/Healthcare Quality Improvement Partnership; 2011.
- Yorkshire and Humberside Quality Observatory . Quarterly PROMS Report 2013. www.yhpho.org.uk/resource/view.aspx?RID=166786 (accessed 7 June 2016).
- The Health Investment Network . QIPP Right Care n.d. www.networks.nhs.uk/nhs-networks/health-investment-network/news/patient-reported-outcome-measures-proms-for-commissioners (accessed 7 June 2016).
- Northgate Information Solutions . PROMs Risk Adjustment Methodology Guide for General Surgery and Orthopaedic Procedures 2010. www.england.nhs.uk/statistics/wp-content/uploads/sites/2/2013/07/proms-ris-adjmeth-sur-orth.pdf (accessed 13 May 2015).
- Patient Reported Outcome Measures (PROMs) in England (2012). The Case-mix Adjustment Methodology. London: Department of Health; 2012.
- Nuttall D, Parkin D, Devlin N. Inter-provider comparison of patient-reported outcomes: developing an adjustment to account for differences in patient case mix. Health Econ 2015;24:41-54. http://dx.doi.org/10.1002/hec.2999.
- Spiegelhalter DJ. Handling over-dispersion of performance indicators. Qual Saf Health Care 2005;14:347-51. http://dx.doi.org/10.1136/qshc.2005.013755.
- El-Sheikha J. A multilevel regression of patient-reported outcome measures after varicose vein treatment in England. Phlebology 2016;31:421-9. https://doi.org/10.1177/0268355515580233.
- Neuburger J, Hutchings A, van der Meulen J, Black N. Using patient-reported outcomes (PROs) to compare the providers of surgery: does the choice of measure matter?. Med Care 2013;51:517-23. http://dx.doi.org/10.1097/MLR.0b013e31828d4cde.
- Varagunam M, Hutchings A, Black N. Do patient-reported outcomes offer a more sensitive method for comparing the outcomes of consultants than mortality? A multilevel analysis of routine data. BMJ Qual Saf 2015;24:195-202. http://dx.doi.org/10.1136/bmjqs-2014-003551.
- Gutacker N, Siciliani L, Moscelli G, Gravelle H. Do patients choose hospitals that improve their health? Centre for Health Economics Research Paper No 111. York: Centre for Health Economics, University of York; 2015.
- Gomes M, Gutacker N, Bojke C, Street A. Addressing missing data in patient reported outcome measures (PROMS): Implications for the use of PROMS for comparing provider performance. Health Econ 2016;25:515-28. http://dx.doi.org/10.1002/hec.3173.
- Gutacker N, Bojke C, Daidone S, Devlin NJ, Parkin D, Street A. Truly inefficient or providing better quality of care? Analysing the relationship between risk-adjusted hospital costs and patients’ health outcomes. Health Econ 2013;22:931-47. http://dx.doi.org/10.1002/hec.2871.
- Leckie G. Three-Level Multilevel Models 2013. www.bristol.ac.uk/cmm/learning/course.html (accessed 7 June 2016).
- Gutacker N, Street A, Gomes M, Bojke C. Should English healthcare providers be penalised for failing to collect patient-reported outcome measures? A retrospective analysis. J R Soc Med 2015;108:304-16. http://dx.doi.org/10.1177/0141076815576700.
- Health & Social Care Information Centre . HES 2010-11 Month 81 Inpatient Data Quality Note 2011. www.hscic.gov.uk/catalogue/PUB04973/prov-mont-hes-2010-11-m8-feb-09-11-inp-qual.pdf (accessed 7 June 2016).
- NHS England . Everyone Counts: Planning for Patients 2013 14 n.d. www.england.nhs.uk/everyonecounts/ (accessed 7 June 2016).
- Naylor C, Gregory S. Briefing: Independent Sector Treatment Centres. London: The King’s Fund; 2009.
- Chard J, Kuczawski M, Black N, van der Meulen J. POiS Audit Steering Committee . Outcomes of elective surgery undertaken in independent sector treatment centres and NHS providers in England: audit of patient outcomes in surgery. BMJ 2011;343. http://dx.doi.org/10.1136/bmj.d6404.
- Cooper ZN, McGuire A, Jones S, Le Grand J. Equity, waiting times, and NHS reforms: retrospective study. BMJ 2009;339. http://dx.doi.org/10.1136/bmj.b3264.
- Bloom N, Propper C, Seiler S, Van Reenen J. The impact of competition on management quality: Evidence from public hospitals. Rev Econ Stud 2015;82:457-89. https://doi.org/10.1093/restud/rdu045.
- Gaynor M, Moreno-Serra R, Propper C. Death by market power: reform, competition, and patient outcomes in the National Health Service. Am Econ J 2013;5:134-66. https://doi.org/10.1257/pol.5.4.134.
- Kelman S, Friedman JN. Performance improvement and performance dysfunction: an empirical examination of distortionary impacts of the emergency room wait-time target in the English National Health Service. J Public Adm Res Theory 2009;19:917-46. https://doi.org/10.1093/jopart/mun028.
- Harrison A, Appleby J. Reducing waiting times for hospital treatment: lessons from the English NHS. J Health Serv Res Policy 2009;14:168-73. http://dx.doi.org/10.1258/jhsrp.2008.008118.
- Patterson J. The effects of nurse to patient ratios. Nurs Times 2011;107:22-5.
- Evans RG, Pearlman H. The Economics of Health and Medical Care. London: Macmillan; 1974.
- Emergency Admissions to Hospital: Managing the Demand. London: National Audit Office; 2013.
Appendix 1 Correlation between emergency and elective activity in the English NHS
The over-riding question of this research project is to consider possible ways of managing demand for planned care. However, patients can access procedures in elective settings and emergency settings, which means that the effects of change to the supply or demand of one type of hospital care could spill over into the other setting. This appendix presents plots of data relating to a number of different sections of health care to see if there are any simple relationships between emergency and elective care. There are other factors that could perhaps be included in further work using more sophisticated regression analysis, but the information presented here will give an indication of what type of relationship, if any, there is between levels of emergency and elective care in a number of different settings.
The main source of data is HES admitted patient care (i.e. inpatients), using number of first admission episodes (FAEs) as an indicator for the two types of care. This should be a good proxy for emergency/elective data, even though it is not all hospital treatment. The inclusion of outpatient data and A&E data was considered, but it was felt that this would create unnecessary complexity without improving the analysis.
Figure 50 uses data for total FAE rates at LSOA level in 1 year. The year 2011/12 was chosen because this was the last year in which the ONS produced age-specific population data for the geographical boundaries used in HES. There appears to be a positive relationship between the two data series (line of best fit has a slope of 0.31, R2 of 0.15). However, these data omit valuable information about the different populations faced by individual providers. Therefore, data were plotted for age- and sex-adjusted values at PCT level (it was not possible to use LSOAs owing to data inconsistencies). Figure 51 shows that this did not materially change the relationship between emergency and elective activity. Figures 52 and 53 control for need (using the need index from the allocation formula) and resources (again using information from the allocation formula regarding resources per head). These figures also suggest a positive relationship between emergency and elective care at PCT level.
FIGURE 50.
Emergency and elective admission rates at LSOA level, 2011–12.

FIGURE 51.
Age- and sex-adjusted rates of emergency and elective admissions at PCT level.

FIGURE 52.
Needs-adjusted rates of emergency and elective admissions at PCT level.

FIGURE 53.
Needs-adjusted rates of emergency and elective admissions at PCT level, adjusted by total resources.

Up to this point, analysis has concentrated on aggregate measures of activity. Although this has not highlighted any obvious substitutability between emergency and elective care, it is possible that at a more granular level this type of relationship could still become apparent. Therefore, the next stage is to consider the data at specialty level. The very small medical specialties have been excluded from the analysis, leaving 23 to be considered. To maintain a reliable sample size, the unit of investigation in this analysis is middle layer super output area, of which there are 6781 in England. The plots in Figure 54 show that breaking the data down into separate specialities fails to identify significant substitution between the two types of care.
FIGURE 54.
Emergency and elective admission rates for particular specialties. (a) General surgery; (b) trauma and orthopaedics; (c) ear, nose and throat; (d) ophthalmology; (e) urology; (f) oral surgery; (g) plastic surgery; (h) A&E; (i) anaesthetics; (j) general medicine; (k) gastroenterology; (l) clinical haemotology; (m) cardiology; (n) dermatology; (o) respiratory medicine (also known as thoracic medicine); (p) medical oncology; (q) medical oncology; (r) paediatrics; (s) geriatric medicine; (t) gynaecology; and (u) clinical oncology (previously radiotherapy).
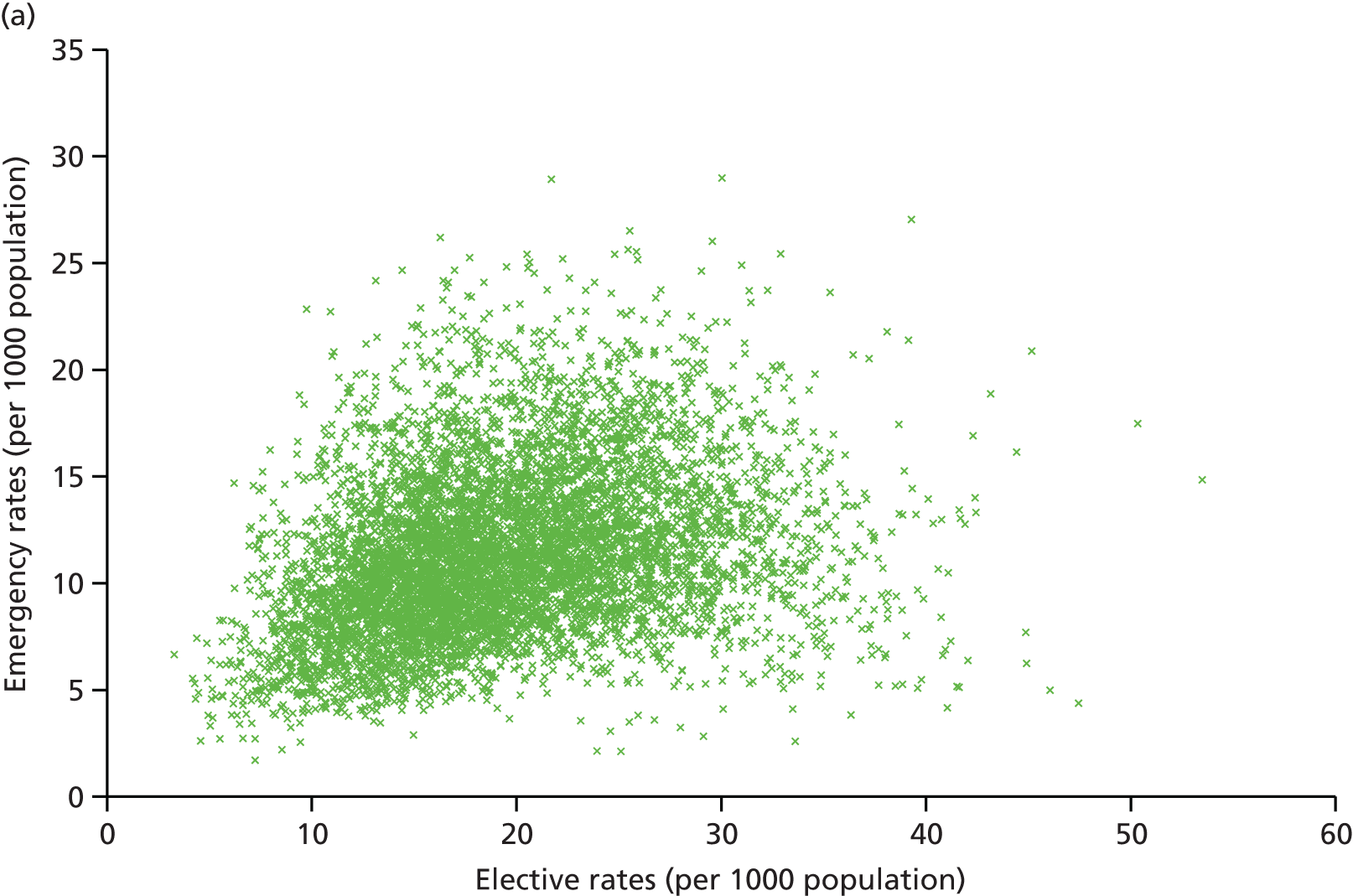
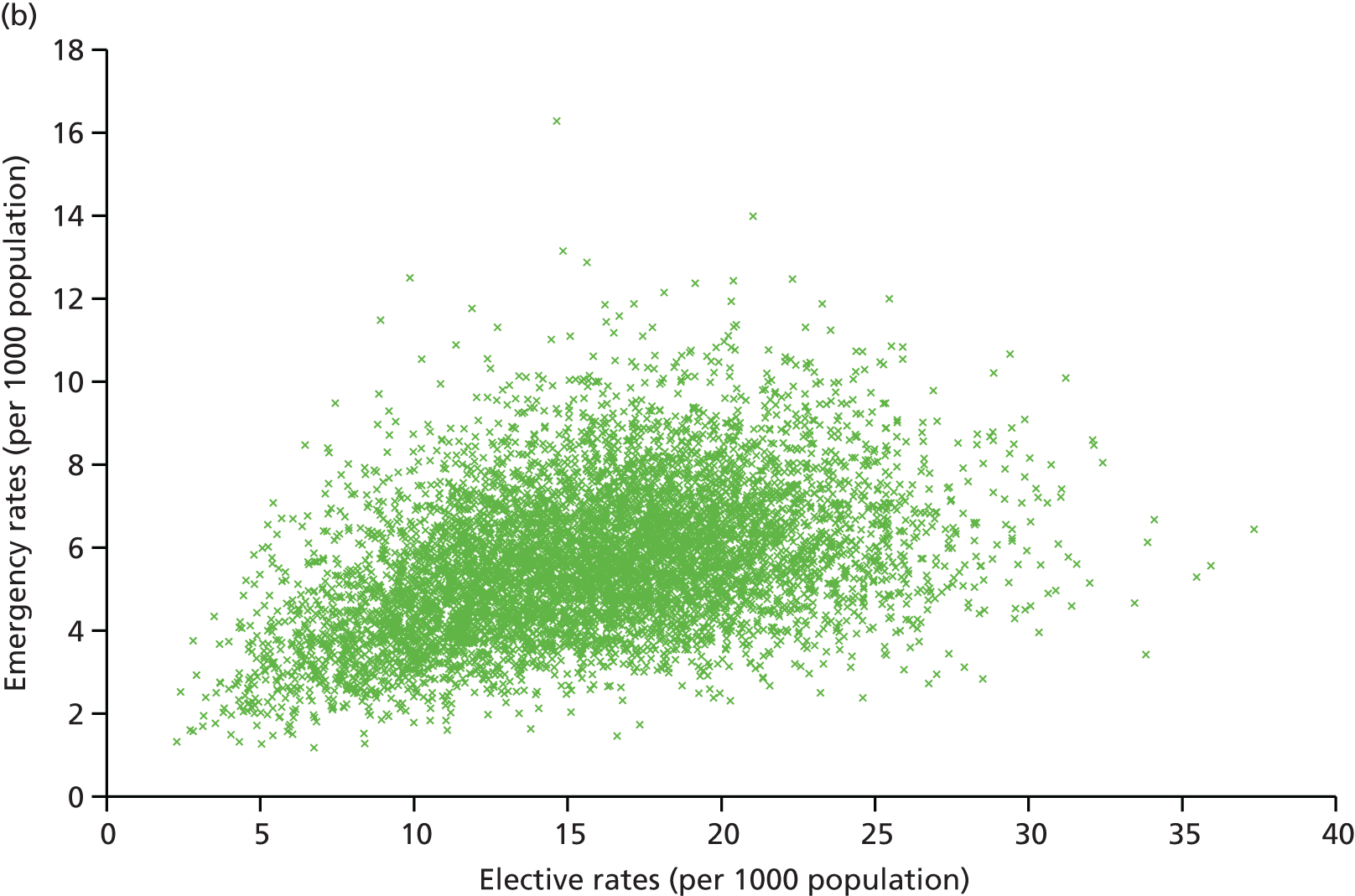

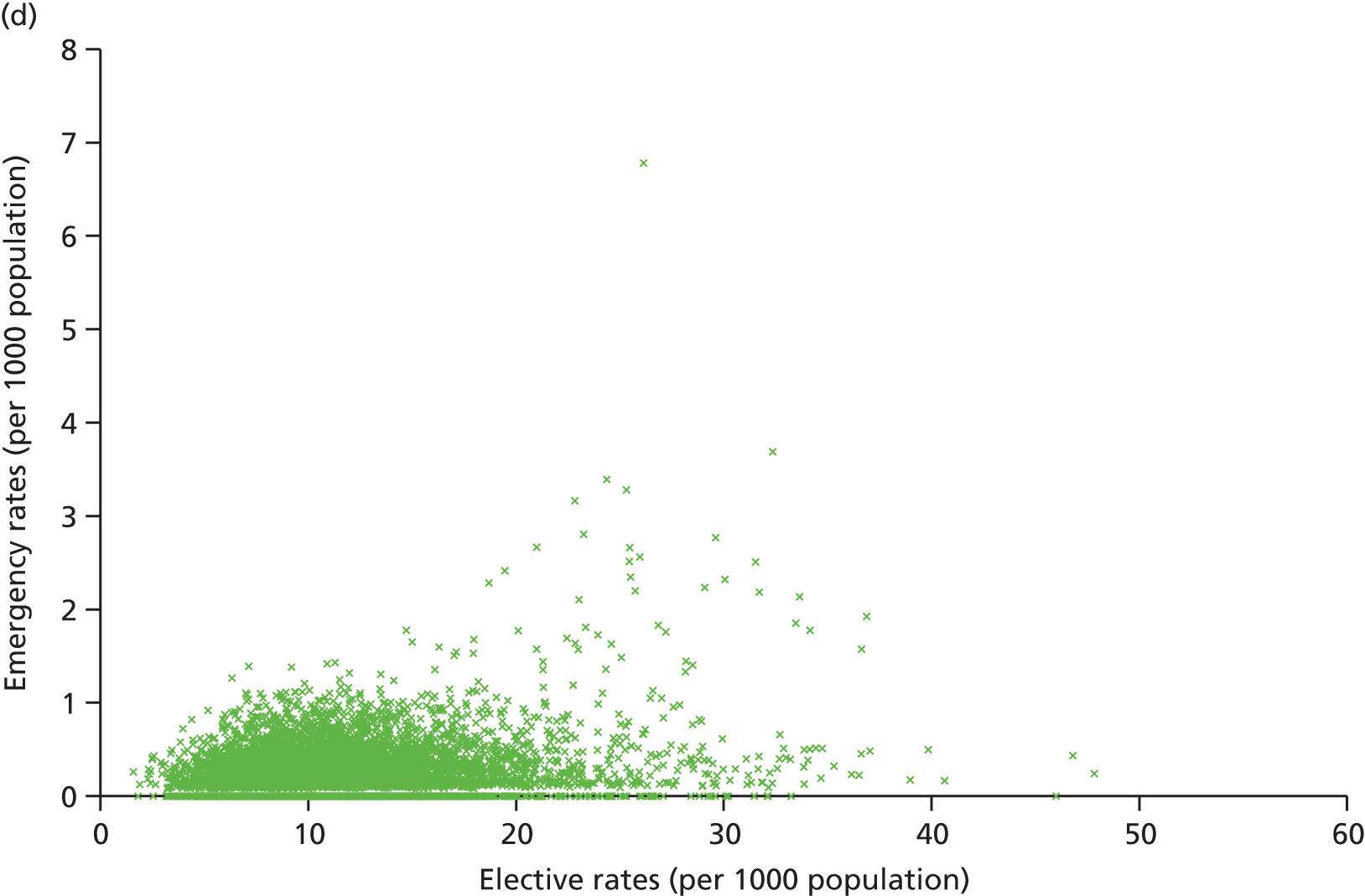
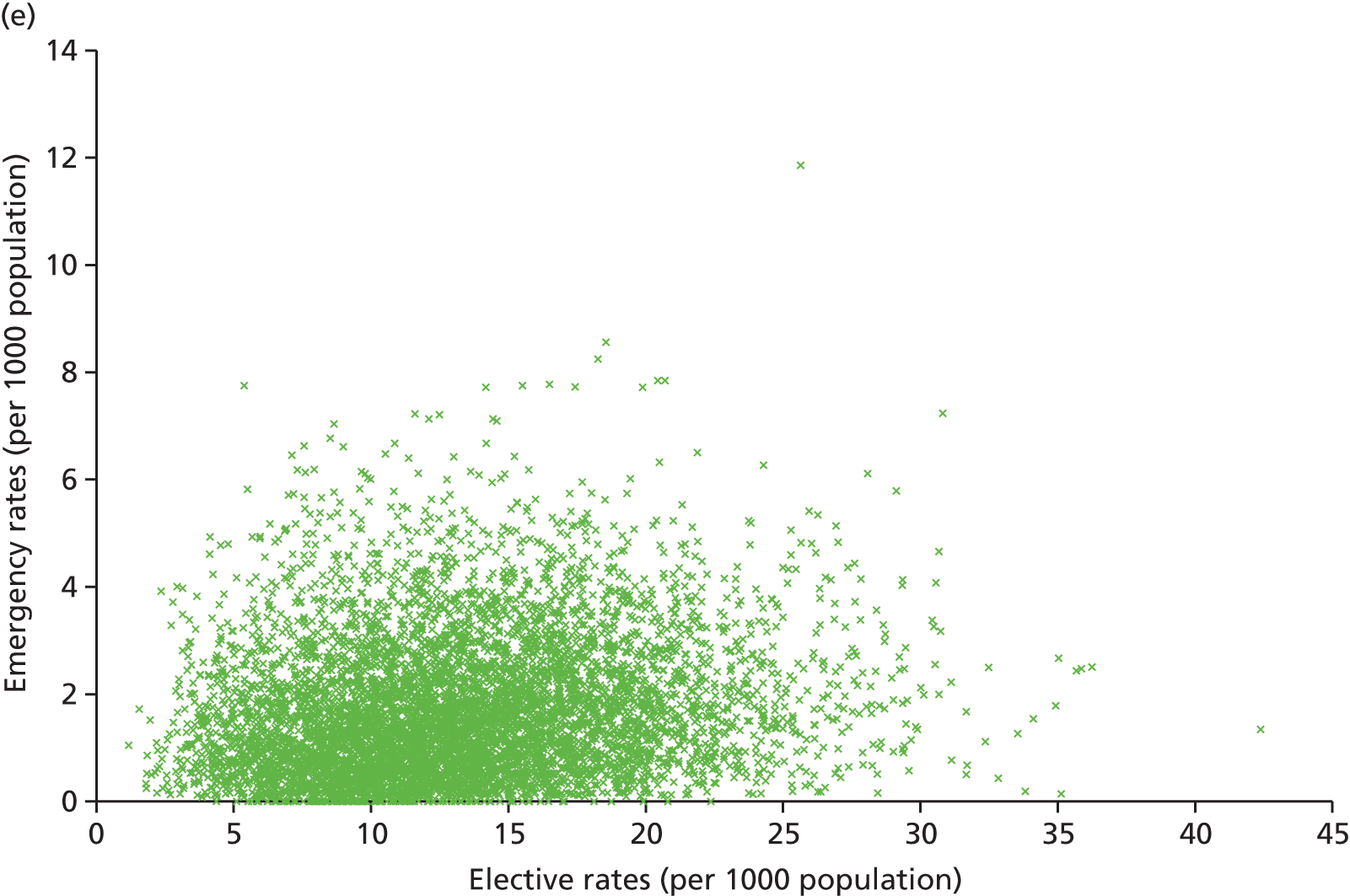
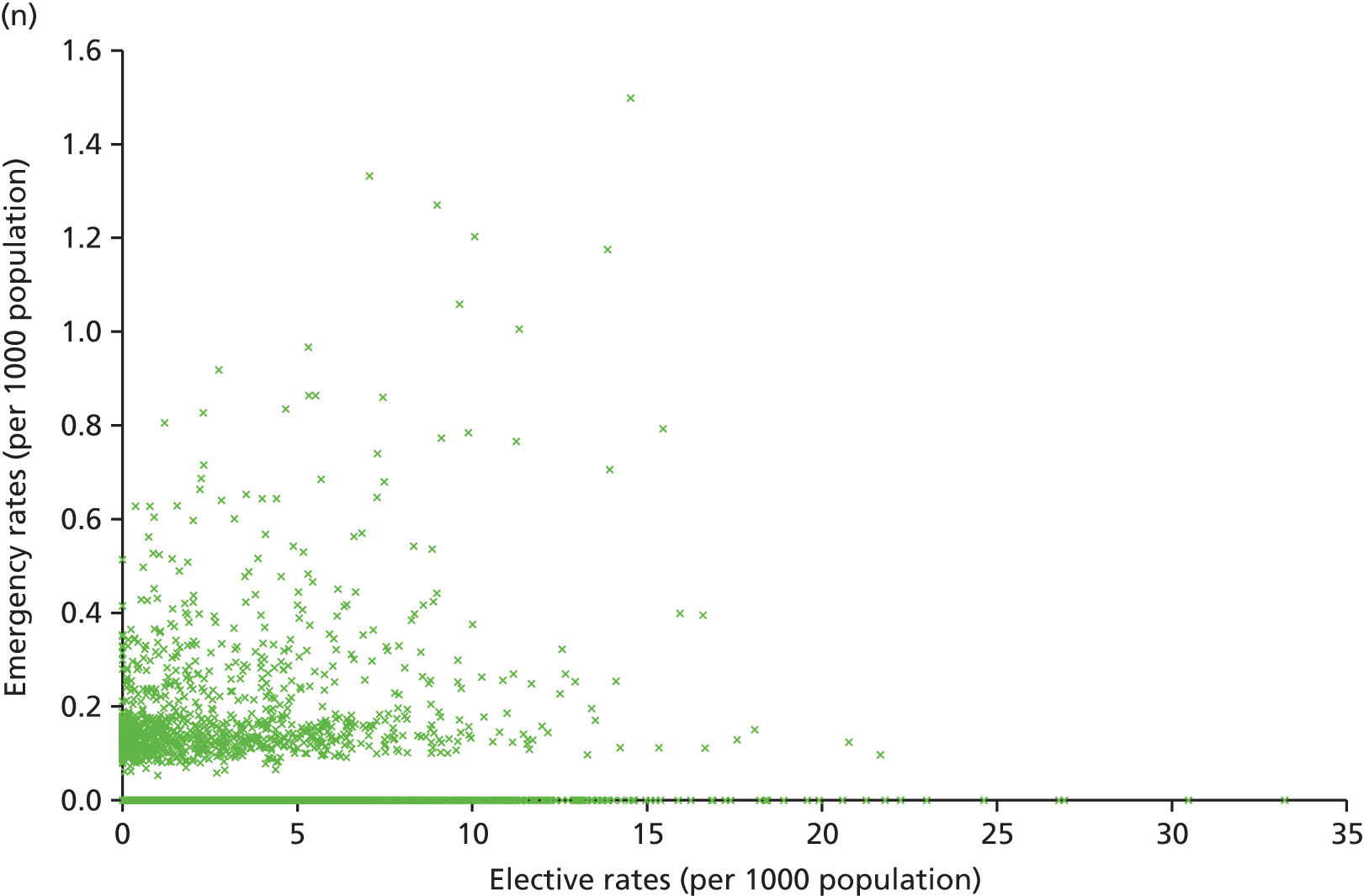
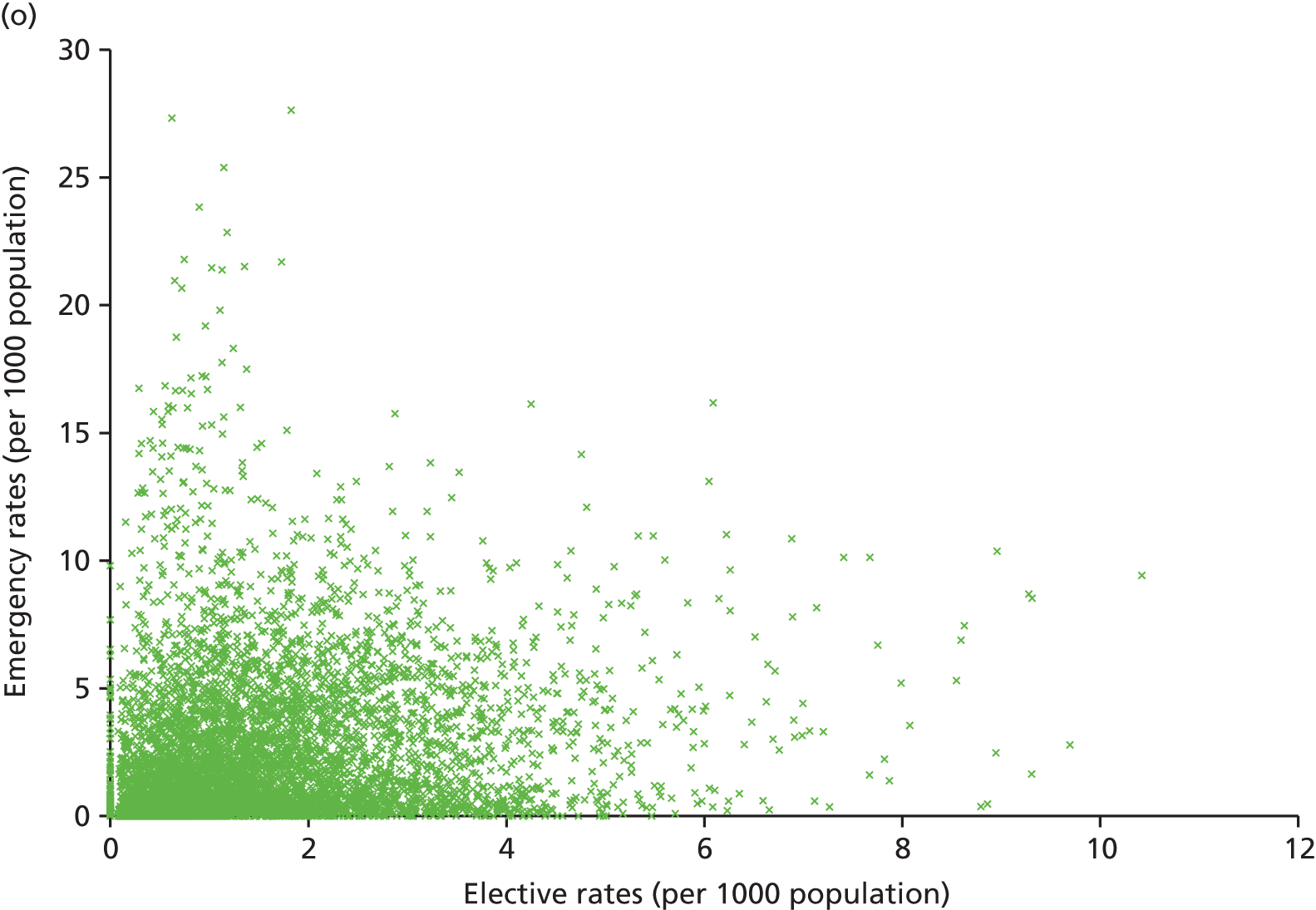
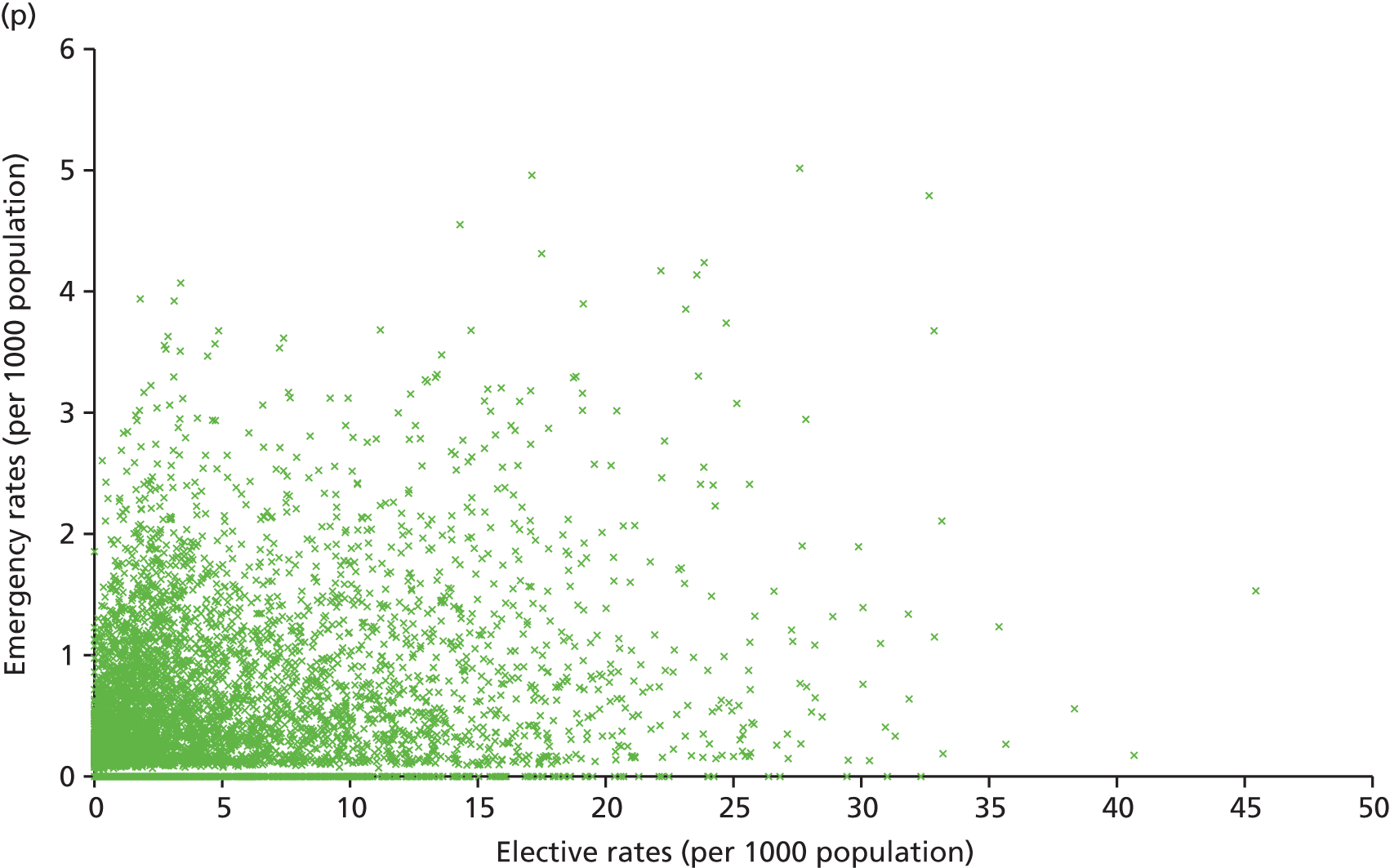
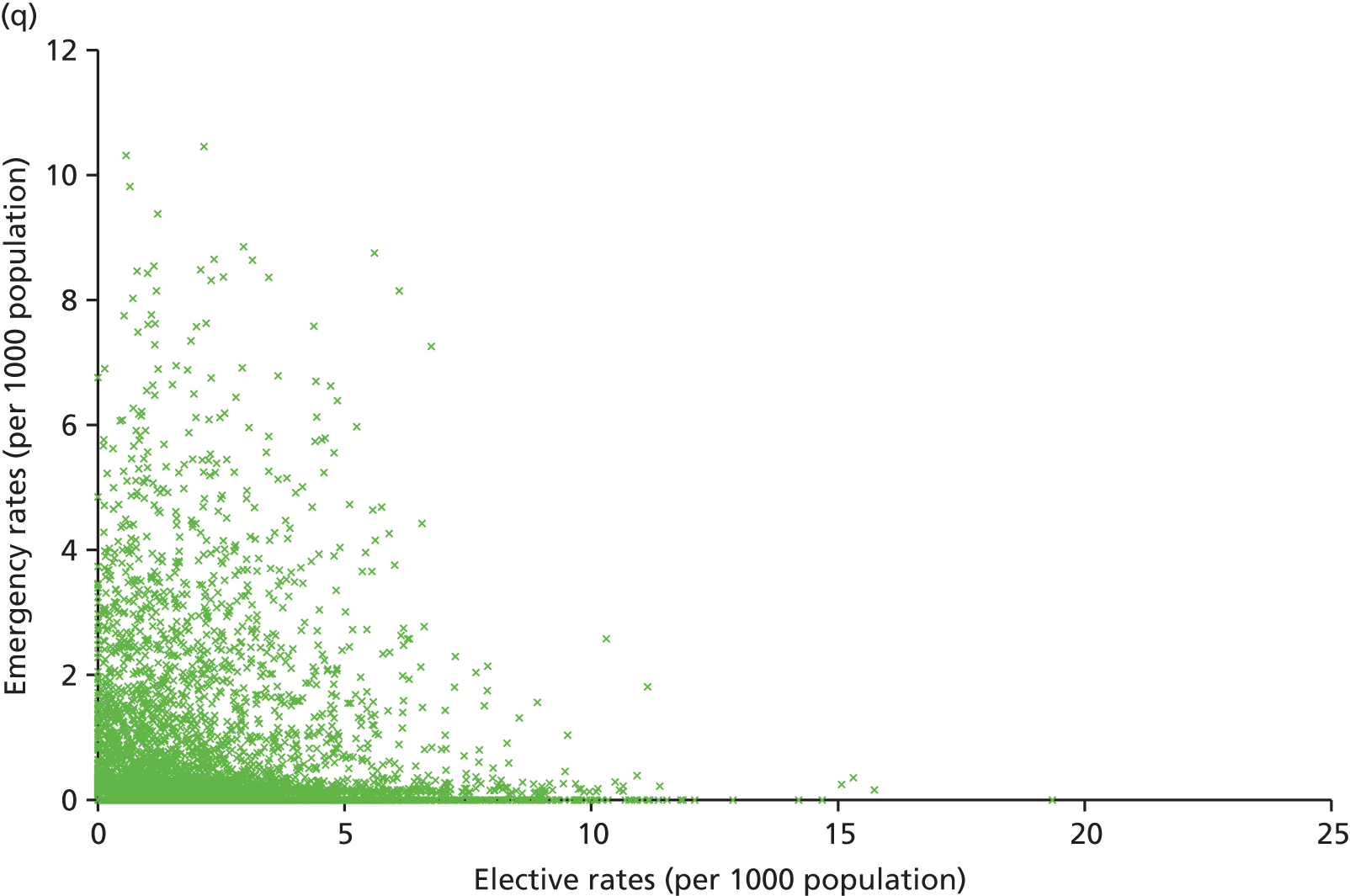
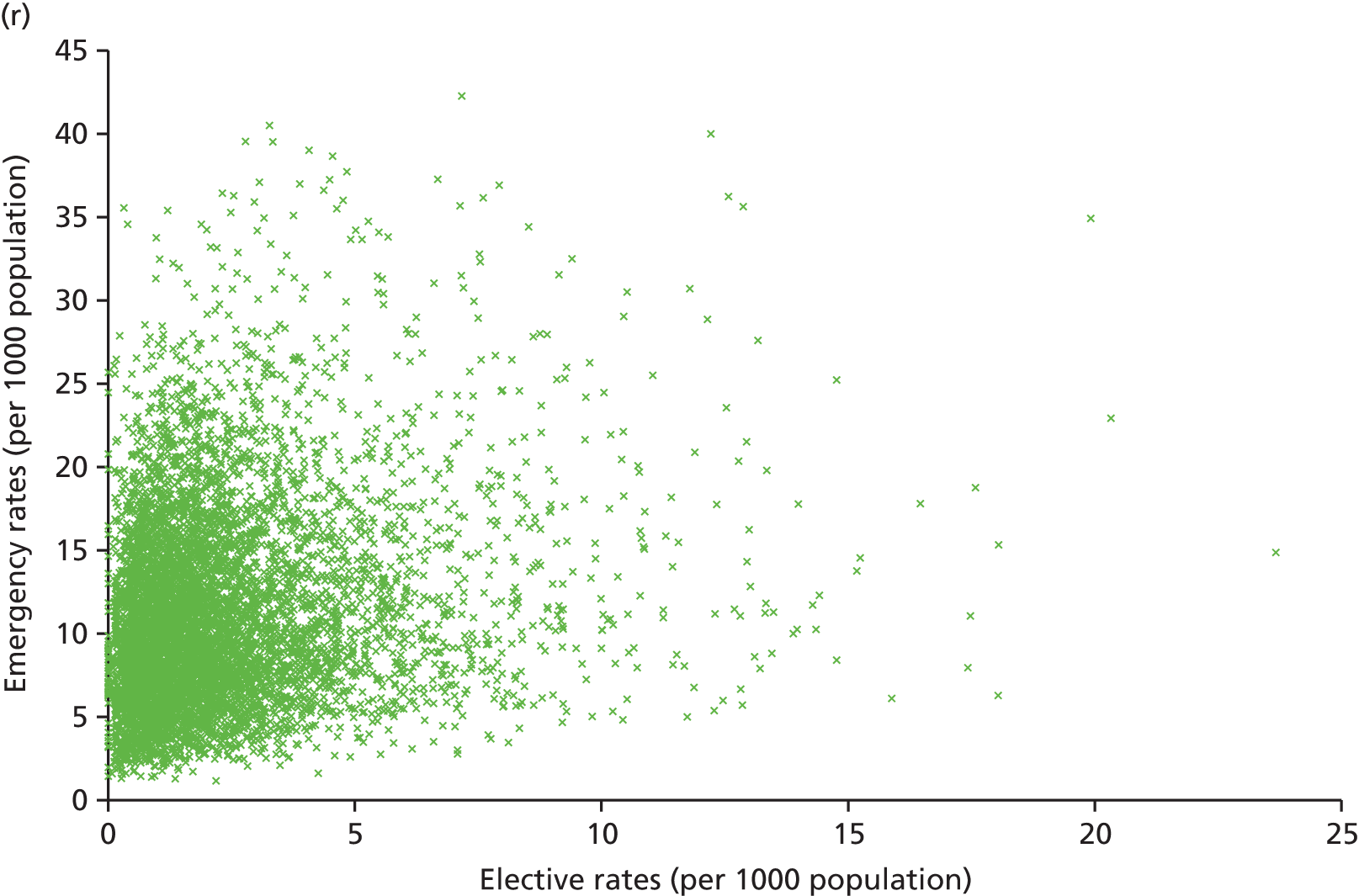

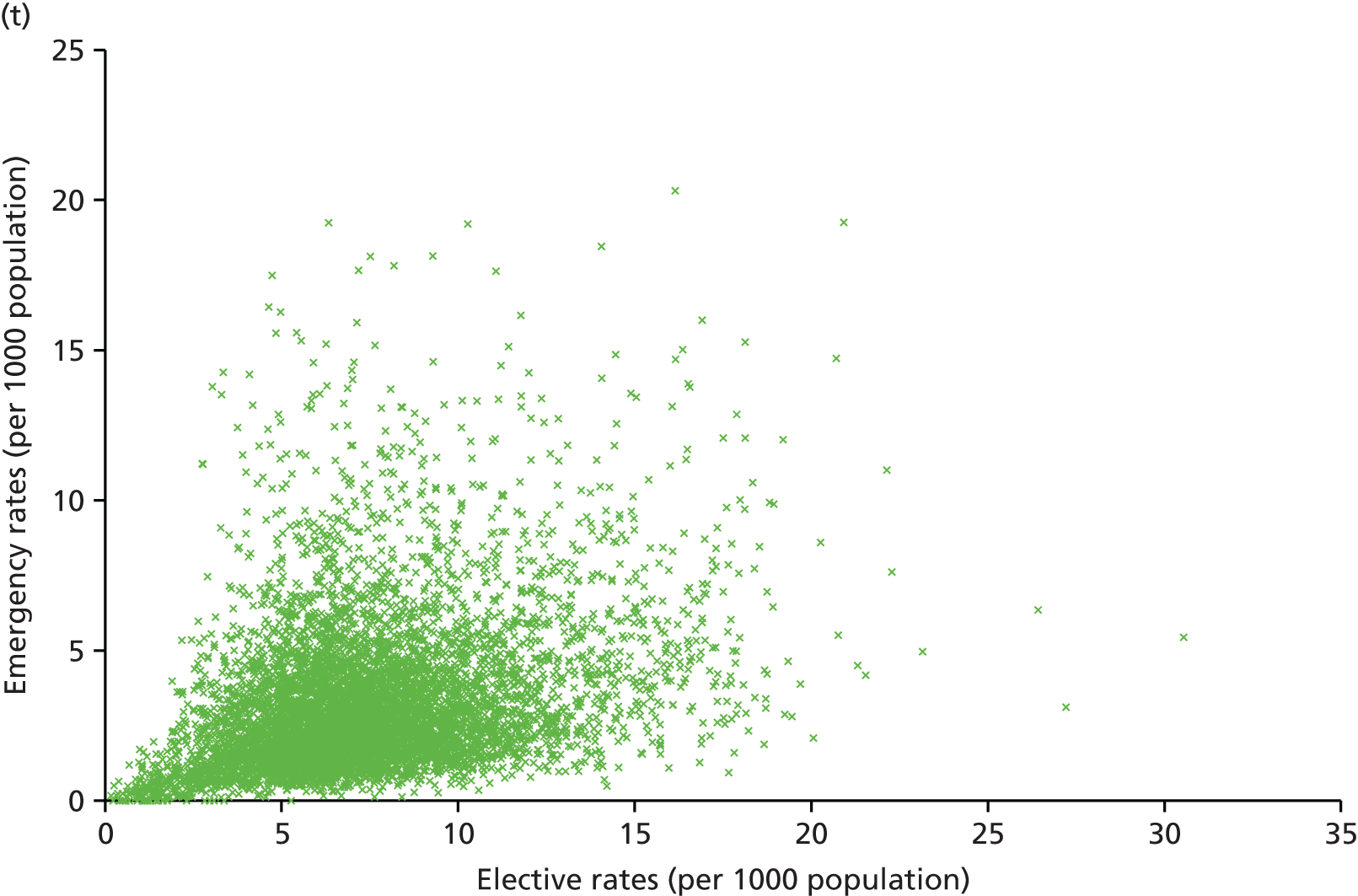

Up to this point, analysis has used single-year cross-sectional data. However, it is possible that there is an intertemporal relationship between the two types of health care, so Figure 55 shows how annual changes in elective care at LSOA level are correlated with annual changes in emergency care for the years 2008/9 to 2009/10, 2009/10 to 2010/11 and 2010/11 to 2011/12.
FIGURE 55.
Changes in elective rates plotted against changes in emergency rates. (a) 2008/9–2009/10; (b) 2009/10–2010/11; and (c) 2010/11–2011/12.
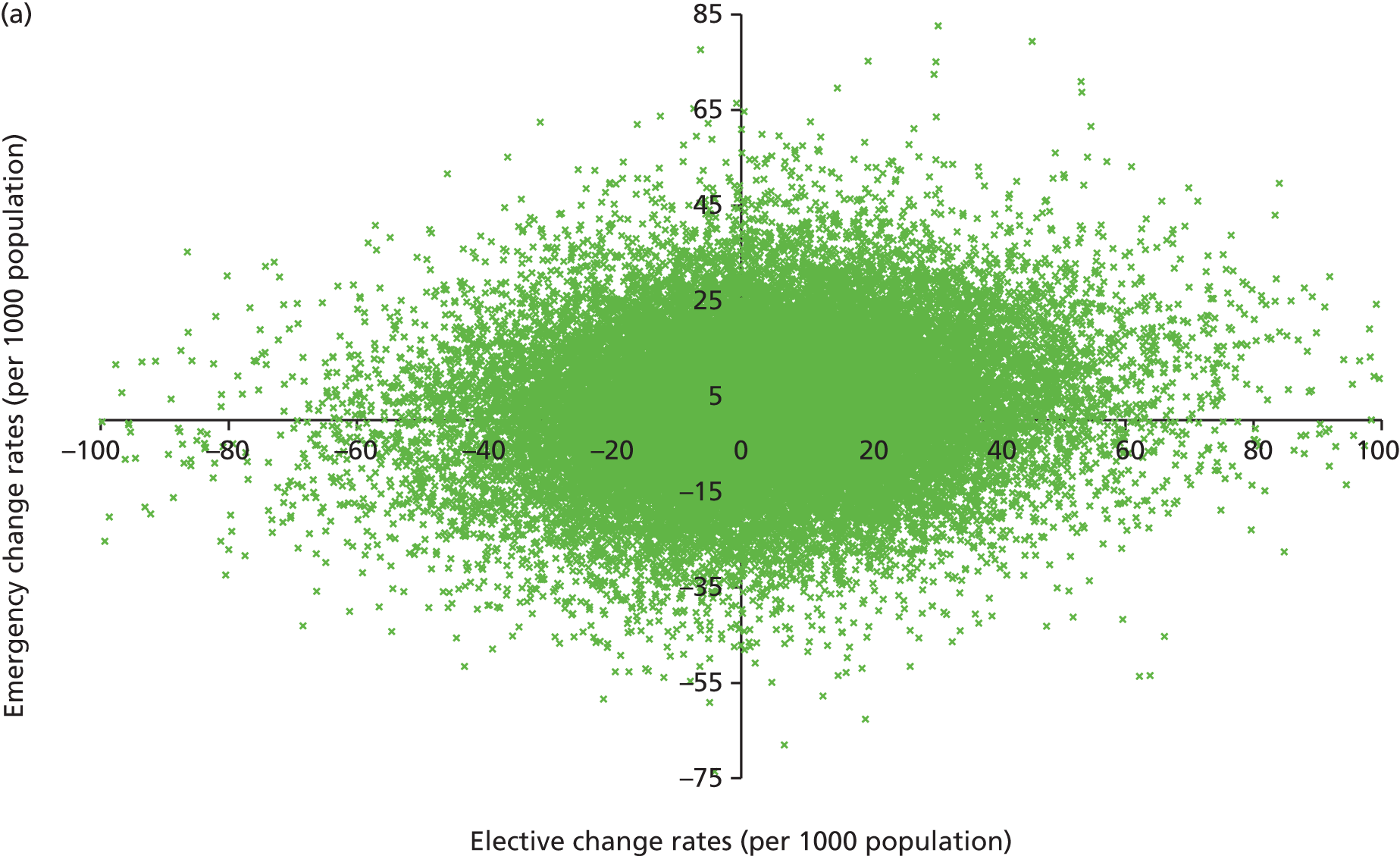

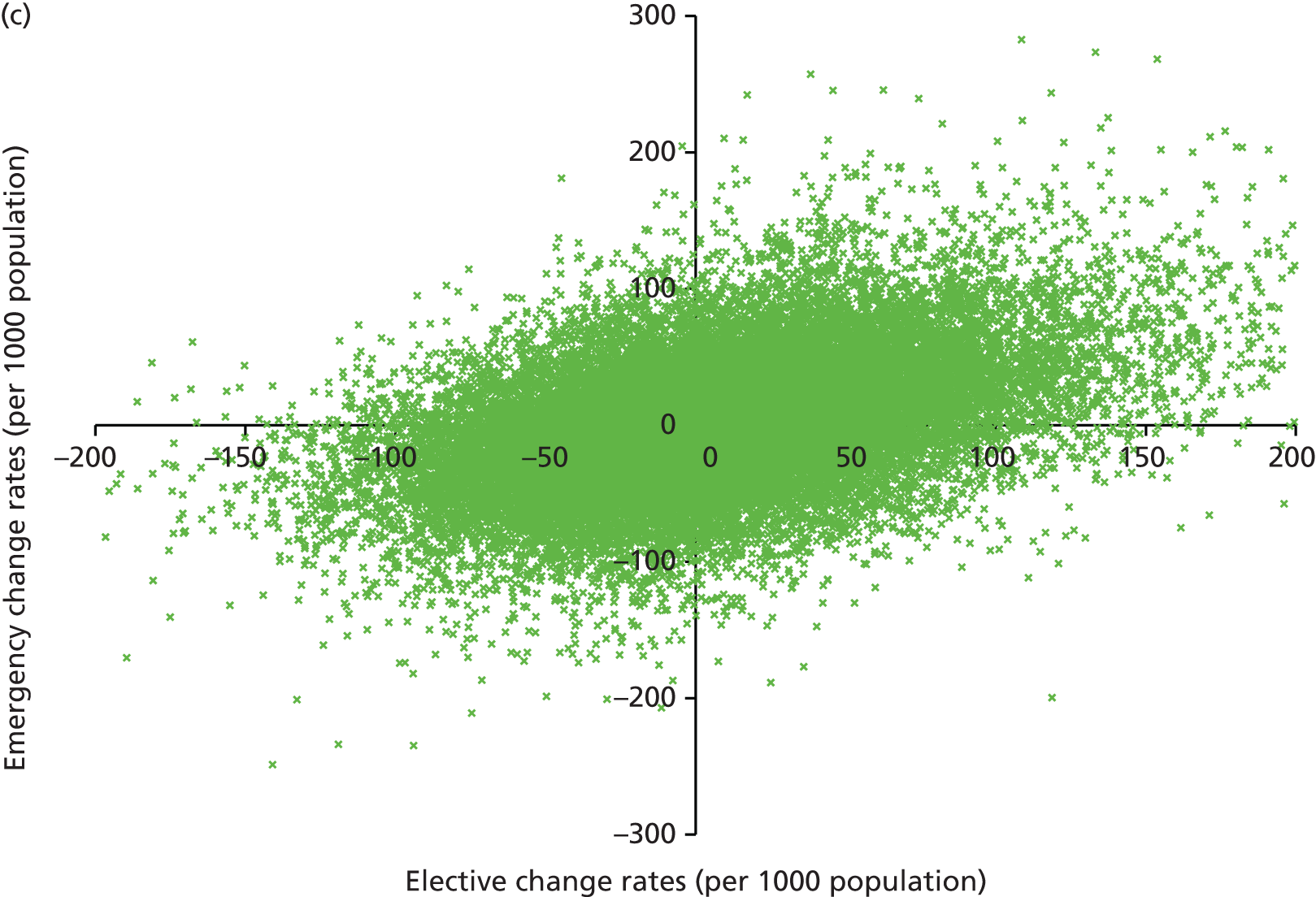
None of these plots suggests a great correlation between changes in emergency and elective care. The slope of the line of best fit for 2008/9–2009/10 and 2009/10–2010/11 is positive but small, with an R2 that is very close to zero. In 2009/10–2011/12 there appears to be a positive relationship between the changes in the type of care, with the line of best fit, suggesting an LSOA that experienced an increase of elective admissions by 10 can also expect about four extra emergency admissions.
This finding is supported by the National Audit Office in its analysis of emergency admissions. 164 It noted that an increase in the number of elective admissions carried out as day cases had caused the number of emergency admissions to go up because of an increase in complications that require in-hospital treatment. They found that this accounted for approximately 10% of the increase in emergency admissions.
This report shows some simple correlations between elective and emergency activity within hospitals and suggests that the two types are, on the whole, positively correlated across geographical areas. Although this is a useful finding, there are several areas of further work that could be performed to shed further light on the subject. In particular, it would be beneficial to study:
-
whether or not elective changes in 1 year are correlated with emergency changes in later years
-
how elective change has impacted on emergency levels
-
specific conditions in which there are direct substitute treatments in elective and emergency care. Identifying these situations will require the input of clinicians.
List of abbreviations
- 2SLS
- two-stage least squares
- A&E
- accident and emergency
- APC
- age–period–cohort
- AVVQ
- Aberdeen Varicose Vein Questionnaire
- AVVS
- Aberdeen Varicose Vein Score
- BMI
- body mass index
- CCG
- Clinical Commissioning Group
- CIPS
- continuous inpatient stay
- DRG
- Diagnosis Related Group
- EQ-5D
- EuroQol-5 Dimensions
- EQ-5D-3L
- EuroQol-5 Dimensions three-level questionnaire
- FAE
- first admission episode
- FTE
- full-time equivalent
- GMS
- General Medical Services
- GP
- general practitioner
- HA
- health authority
- HCHS
- Hospital and Community Health Services
- HES
- Hospital Episode Statistics
- HMO
- Health Maintenance Organisation
- HRG
- Healthcare Resource Group
- HSCIC
- Health and Social Care Information Centre
- IMD
- Index of Multiple Deprivation
- ISTC
- independent sector treatment centre
- IV
- instrumental variable
- LF
- laissez-faire
- LOS
- length of stay
- LSOA
- lower-layer super output area
- NTPS
- National Tariff Payment System
- OHS
- Oxford Hip Score
- OKS
- Oxford Knee Score
- OLS
- ordinary least squares
- ONS
- Office for National Statistics
- OOH
- out of hours
- PbR
- Payment by Results
- PCT
- primary care trust
- PMS
- Personal Medical Services
- PROM
- patient-reported outcome measure
- QALY
- quality-adjusted life-year
- QIV
- quantile instrumental variable
- QMAS
- Quality Management and Analysis System
- QOF
- Quality and Outcomes Framework
- QTE
- quantile treatment effect
- SD
- standard deviation
- SHA
- Strategic Health Authority
- TC
- treatment centre
- WIC
- walk in centre