Notes
Article history
The research reported in this issue of the journal was funded by the HSDR programme or one of its preceding programmes as project number 15/12/22. The contractual start date was in September 2015. The final report began editorial review in February 2022 and was accepted for publication in June 2022. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HSDR editors and production house have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the final report document. However, they do not accept liability for damages or losses arising from material published in this report.
Permissions
Copyright statement
Copyright © 2024 Guthrie et al. This work was produced by Guthrie et al. under the terms of a commissioning contract issued by the Secretary of State for Health and Social Care. This is an Open Access publication distributed under the terms of the Creative Commons Attribution CC BY 4.0 licence, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. See: https://creativecommons.org/licenses/by/4.0/. For attribution the title, original author(s), the publication source – NIHR Journals Library, and the DOI of the publication must be cited.
2024 Guthrie et al.
Chapter 1 Background to the project
Clinical guidelines are an important mechanism for defining and disseminating best practice, but are typically created for single conditions and based on evidence from trials that often exclude people with multimorbidity. 1–3 However, the majority of people with long-term conditions have multiple conditions, and the application of single-disease guidelines to people with multimorbidity can be problematic. 1,4–8 A common situation in which this is the case is the use of medicines to prevent future disease, whereby treatment is usually long term, often lifelong. The net expected benefit from such preventative treatments is often relatively small over the period examined in trials, and targeting treatment to those with the most to gain is important. Although trials are almost always done in highly selected populations,9 the standard assumption is that the relative risk reduction as a result of treatment is constant across the whole clinical population. If this assumption is true, then a major determinant of an individual’s expected benefit is their baseline risk of the outcome being prevented. Therefore, guidelines increasingly make risk-stratified treatment recommendations, whereby a risk prediction tool is recommended to estimate the risk of the outcome of choice, and preventative treatment is recommended for those above a particular risk threshold. The choice of risk threshold by the guideline development group is commonly informed by model-based cost-effectiveness analyses (CEAs), which examine cost-effectiveness for different levels of baseline risk. Risk prediction modelling and model-based CEAs are therefore increasingly important in the creation of guidelines that recommend long-term preventative medicines.
Risk prediction models, competing mortality risk and multimorbidity
Cardiovascular disease (CVD) and osteoporotic fracture are two contexts in which the National Institute for Health and Care Excellence (NICE) recommend the use of risk prediction tools to inform decisions about who should receive preventative drug treatment. 10–13 For the primary prevention of CVD using statins, NICE currently recommends the QRISK®2 risk prediction tool10 (ClinRisk Ltd, Leeds, UK), although it is considering lifetime risk prediction tools for the next guideline update. 13 The original QRISK® (ClinRisk Ltd) and QRISK2 risk prediction tools have been externally validated in UK data by the original developers14 and by independent teams,15–17 and have been shown to have good discrimination and calibration, but QRISK®3 (ClinRisk Ltd) has not been externally validated in a UK population, which is a requirement for widespread implementation. For the prevention of osteoporotic fracture using bisphosphonates, NICE recommends using either QFracture-2012 (ClinRisk Ltd) or FRAX® (Centre for Metabolic Bone Diseases, University of Sheffield, Sheffield, UK). 12 The first version of QFracture-201217 has been externally validated in UK data by independent teams,18 and the 2012 version has been externally validated by the original developers,19 again finding good discrimination and calibration. In contrast, even though it is recommended by NICE, FRAX has never been externally validated to current standards20,21 because the risk prediction algorithm is not publicly available (the external validation published by the original developers does not report discrimination in the conventional way, or calibration22).
Based on a model-based CEA, the NICE lipid modification guidelines recommend that clinicians offer statins to all people for whom predicted risk over 10 years is > 10%. 10 However, age is the strongest determinant of CVD risk, and a large majority of people in the UK will cross this threshold by age 65 years, irrespective of the presence of other CVD risk factors included in the model. Therefore, the guideline effectively recommends that all older people without CVD should be offered lifelong treatment with a statin. Similar issues apply to fracture risk prediction, where age dominates risk. NICE recommends risk assessment using a risk prediction tool for older people and for younger people with clinical risk factors for fracture, and concludes that bisphosphonates are cost-effective for those with a 1% risk of major osteoporotic fracture (MOF) over 10 years,12 but without clearly specifying that this is a threshold at which clinicians should offer treatment, and the NICE aid to patient decision-making shows data only for much higher thresholds of risk. 23
Competing mortality risk and multimorbidity
Most risk prediction tools do not account for competing mortality risk. Competing mortality risks occur when someone is at risk of death from an unrelated condition to the one being studied (e.g. death from Parkinson’s disease in a study of ischaemic heart disease). Competing mortality risk is more common among people with multimorbidity than those with single conditions, and more common among older people than younger people. 24 Risk prediction models can be designed to account for competing mortality risk, but most do not. In the context of this study, QRISK325 and QFracture-201226 do not account for competing mortality risk. QRISK®-Lifetime (ClinRisk Ltd) does account for competing mortality risk,27 as does FRAX22,28 (but FRAX cannot be externally validated because the risk prediction algorithm is not publicly available).
Competing risk is a well-recognised problem in survival analysis. 29–33 In essence, conventional survival analysis and risk prediction tool development treats death from unrelated conditions as a censoring event equivalent to loss to follow-up for other reasons. The underlying assumption is that censored individuals have the same risk of the outcome being examined as those remaining in the study. Although this may be reasonable for ordinary loss to follow-up, this is clearly not true for people who have died. The consequence is that prediction models that do not account for competing risk in their development overestimate the risk of the outcome among those with competing risks. 29,31,32
Studies comparing conventional models with models that are adjusted for competing risk have shown that conventional models, on average, overpredict CVD risk,27,34–36 but the effect of competing risks has not been systematically examined in the context of fracture risk prediction (although the NICE bisphosphonate guidance23 acknowledges that QFracture-2012 and FRAX risk predictions are difficult to compare as a result). Of note is that conventional external validation of risk prediction tools such as QRISK3 and QFracture-2012 also does not account for competing mortality risk, so the excellent observed calibration in external validation is in the context of making the same assumptions about competing mortality risk as prediction tool derivation. 16,18,19
Therefore, the risk prediction modelling element of this project is concerned, first, with external validation of existing risk prediction tools recommended by NICE (QFracture-2012) or being considered by NICE (QRISK3), accounting for competing mortality risks and examining performance in important subgroups [objective 1, whereby examination of the subgroups of people with diabetes and chronic kidney disease (CKD) was funded by the costed extension to the original grant], and, second, with the derivation and internal validation of new risk prediction tools that account for competing mortality risk in derivation (objective 2). In addition, funded by the costed extension to the original grant, we have completed an external validation of the QRISK-Lifetime tool (objective 3).
Model-based cost-effectiveness analysis
Model-based CEAs are a key source of evidence in the development of clinical guidelines by NICE and some other guideline developers. If preventative interventions are to be offered, we need robust, population-level evidence that the technologies in question provide net benefit when compared with other possible options, including no treatment. However, the single-disease approach for creating guidelines is increasingly recognised as problematic by NICE, other guideline developers and guideline users. 37,38 Most people with any long-term condition and most people aged ≥ 65 years have multimorbidity,4 and there is a demand for guidance that accommodates the needs of these more complex populations. 1 Failing to account for people with multimorbidity means that guidelines may be less useful, and risks recommendations (rightly or wrongly) not being adhered to. There is emerging evidence that taking account of multimorbidity will affect the total net benefit estimated for interventions, which, in turn, will influence whether or not to recommend the intervention for use in clinical practice. This evidence has indicated the need to account for important subgroups of the total patient population and the role of heterogeneity in the evidence base for different types of patients. 39 Evidence from the ‘Better Guidelines’ project has shown that accounting for plausible levels of competing mortality risks associated with multimorbidity and of direct treatment disutility (DTD) (the impact on health status of taking a long-term preventative medicine irrespective of specific adverse effects of the actual drug) could also influence if, and when, overall net benefit is achieved. 2,40,41 Consequently, the methods used to structure and populate model-based CEAs need to be reconsidered to examine the impact of better accounting for multimorbidity.
Models used in CEAs do account for competing mortality risks in that they typically simulate both population age-specific total mortality and cause-specific mortality related to the condition the guideline is addressing. However, treatments that are cost-effective on average may be less cost-effective (or judged not to be cost-effective) in important subgroups, such as people with life-limiting conditions for whom population-average mortality underestimates true mortality, and therefore likely overestimates treatment benefit. 39,42 In the ‘Better Guidelines’ project, we explored the impact of varying competing risks of death using the NICE lipid modification cost-effectiveness model; we found that plausible increases in competing risks significantly affected expected lifetime quality-adjusted life-year (QALY) gain, and, therefore, potentially cost-effectiveness, at different baseline risk thresholds for initiating statin treatment. 2,41 However, we could not find any published data on the distribution of competing risks across the population, which meant that it was not possible to properly explore the implications of this for cost-effectiveness. Of note is that people with greater risk of CVD or fracture will typically also have greater competing risk of non-CVD or non-fracture death. This is because, for example, smoking causes both CVD and fatal respiratory disease of various kinds, and increasing age and nursing home residence are associated with both fracture risk and risk of death from many causes.
A second way in which cost-effectiveness models may be misleading is if they do not include all harms. In the ‘Better Guidelines’ project, we examined the impact of accounting for one type of harm that is currently ignored by existing models: DTD. We define DTD as being the collective set of individuals’ strengths of preference for not taking a medicine long term, which may arise for a number of reasons. Patients are likely to value negatively the inconvenience of obtaining prescriptions from general practitioners (GPs) and collecting medicines from pharmacies; of taking medicines regularly; of having to attend for monitoring of various kinds; and of needing to modify their lifestyle to take the medicines, as is the case for bisphosphonates, for example. For some patients, taking a regular medicine or other intervention for life is an unpalatable prospect in its own right in addition to the specific hassles of being on treatment. The concept of DTD is over and above the disbenefit (i.e. harm) captured by attaching a disutility (i.e. negative impact on health status) associated with adverse drug events (ADEs) or the financial (out-of-pocket) costs for a patient. Recent studies with statins, for example, show that most or nearly all muscle aching associated with statins is a nocebo effect, as participants experience the same increase in muscle aching, compared with no tablet-taking, irrespective of whether the tablet taken contains a statin or is a placebo. 43 However, in practical terms, such individuals will experience a quality-of-life decrement if they take a statin (it is just that that decrement is not an ADE, as such). The disutility of ADEs is usually included in decision models to some extent. However, the negative impact of taking a medicine long term or for life irrespective of ADEs, especially a preventative medicine with no obvious immediate benefits, is currently ignored in model-based CEA.
In the ‘Better Guidelines’ project, we found that even very low plausible levels of DTD could significantly reduce, or even reverse, expected lifetime QALY gain in the context of statin treatment at the NICE treatment threshold of 10% CVD risk at 10 years, where treatment had a slowly accruing and relatively modest lifetime net benefit. 2,41 There is a small published body of literature in this field, with the cost-effectiveness of several primary preventative treatments shown to be sensitive to even small levels of DTD or treatment burden,44–46 but there is a need to better quantify DTD because DTD values have been elicited in only a small number of studies and there is uncertainty as to their magnitude and distribution. 47,48 DTD may also vary by treatment. For example, statins to prevent CVD have to be taken daily, compared with weekly bisphosphonates to prevent fracture, but the routine for taking bisphosphonates is much more complicated (taken on an empty stomach with a significant quantity of water and with a requirement to stay upright for at least 30 minutes and not eat or drink for 30–60 minutes after ingestion).
Therefore, this study elicits DTD values for taking lifelong statins and bisphosphonates from both general population and treated patient samples (objective 4), and uses these DTD values and data from the competing risk-adjusted prediction models to examine how expected lifetime QALY gain and cost-effectiveness of statins for primary prevention of CVD and bisphosphonates for fracture prevention vary in the presence of different levels of DTD and competing risk (objective 5).
As a subsidiary element of objective 5 (carried out as part of the costed extension to the original grant), we also sought to make the outputs of the statins model fit for present-day purposes by updating various inputs (health-related quality of life at baseline and following cardiovascular events; costs associated with interventions and cardiovascular events; type of first cardiovascular event conditional on some event having occurred). We did this because, during the development of the project, NICE announced an intention to update its guidance on CVD risk assessment and reduction, including lipid modification. 13 We did not perform similar updates for the osteoporosis model, as NICE has no similar plans to update its guidance on bisphosphonates in the foreseeable future.
Aims and objectives
The overall aim was to improve the evidence generated from risk prediction models and model-based CEAs to better inform decision-making for selecting primary prevention treatments for CVD and selecting prevention treatments for osteoporotic fracture.
The objectives were those proposed in the original grant and those included in the costed extension granted by the National Institute for Health and Care Research (NIHR):
-
objective 1 – to externally validate the recommended risk prediction tools for primary prevention of CVD (QRISK3), including performance in important subgroups, and of osteoporotic fracture (QFracture-2012)
-
objective 2 – to derive and internally validate new-incident CVD and osteoporotic fracture risk prediction models accounting for competing risks of death, and compare performance with existing risk prediction models
-
objective 3 – to externally validate the QRISK-Lifetime risk prediction tool for primary prevention of CVD
-
objective 4 – to quantify the magnitude, variation and distribution of DTD (the disutility incurred by taking a regular, long-term treatment irrespective of drug-specific side effects) in the general and statin- or bisphosphonate-treated populations
-
objective 5 – to examine the effect of accounting for competing risks and DTD on clinical effectiveness and relative cost-effectiveness in the context of the use of statins and bisphosphonates for the primary prevention of CVD and osteoporotic fracture, respectively.
Project management and public involvement
The methods used for each of these objectives are described in subsequent chapters. Although all co-applicants and collaborators contributed to all aspects of the project:
-
objectives 1–3 were predominantly the responsibility of the University of Dundee
-
objectives 4 and 5 were predominantly the responsibility of The University of Manchester.
The literature elements of the study did not require ethics review. The prediction modelling used Clinical Practice Research Datalink (CPRD) data, and the protocol was approved by the CPRD Independent Scientific Advisory Committee (reference 16_248). The DTD elicitation study was reviewed the Health Research Authority (Integrated Research Application System project number: 220,492) and granted ethics approval (Research Ethics Committee reference 17/NW/0124).
Chapter 2 reports the external validation of QRISK3, including performance in important subgroups, and the derivation and internal validation of a new competing mortality risk model (CRISK) (objectives 1 and 2 for CVD risk prediction). Chapter 3 reports the external validation of QRISK-Lifetime (objective 3). 49 Chapter 4 reports the external validation of QFracture-2012, and the derivation and internal validation of a new CRISK (i.e. CFracture) (objectives 1 and 2 for fracture risk prediction). 50,51 Chapter 5 reports the DTD elicitation (objective 4). For statins for primary prevention of CVD and bisphosphonates for prevention of fracture, Chapters 6 and 7, respectively, report the new model-based CEAs accounting for competing mortality risk more accurately and accounting for DTD (objective 5). Chapter 8 summarises the findings and their implications.
Patient and public involvement
The original research proposal was informed by qualitative analysis of patient data from eight focus groups with 48 participants and nine individual interviews about prescribing and prescribing decision-making that we did as part of our Data-driven Quality Improvement in Primary care (DQIP) prescribing safety improvement programme, which finished at the end of 2014. 52 We also carried out a group discussion with eight members of an NHS Patient and Public Participation Group, and our two public partners contributed to the development of the proposal through discussion and through their membership of our previous NIHR-funded ‘Better Guidelines’ project reference group. 2 Unsurprisingly, across these groups, there was strong support for the idea that treatment decisions for individual conditions should take account of other conditions, other treatments and the context of the individual as a whole person, and for work examining whether such accounting could improve the quality of evidence that underpinned treatment decisions. This was significantly driven by a general perception that the number of drugs people were taking regularly was increasing, and some unease about whether the benefits of this always outweighed the harms. The conceptualisation of DTD and its existence was informed by input from patient expert members of the advisory group for the ‘Better Guidelines’ project. During the conduct of this project, two patient experts took active roles in the project advisory group: Alison Allen and Graham Bell. Both contributed to the development of the grant (because they were both involved in the prior project too) and were in the study advisory group, and, most specifically, contributed to the development of the DTD elicitation questionnaire, providing extensive comments on the survey design. We were sadly informed that Graham Bell passed away in late 2020, and we have been unable to re-establish contact with Alison Allen. Therefore, we have not been able to ask our patient experts for their input on the results of this project.
Chapter 2 Cardiovascular disease risk prediction: external validation of QRISK3 and derivation and internal validation of a new competing risk model (CRISK)
Background
Although the age-specific incidence of CVD has fallen steadily in most developed countries for several decades, ageing populations mean that CVD remains a major cause of morbidity and mortality worldwide. UK guidelines for the primary prevention of CVD recommend that clinicians use a risk prediction tool to target treatment with statins at people whose predicted risk exceeds a specified threshold. The recommended threshold has been progressively reduced, with NICE changing its recommendation for England and Wales from a 10-year CVD risk of > 20% to > 10% in 2014. 10 US guidelines recommend a 7.5% threshold, although the included events are not identical. 53 Risk thresholds have been reduced because of increasing evidence of statin effectiveness for primary prevention, and the increasing cost-effectiveness of statins at lower thresholds of baseline risk because statin prices have fallen as they come off patent.
Such risk-stratified guideline recommendations are reliant on the availability of prediction tools for CVD risk. The risk prediction tools recommended in different countries and guidelines vary, reflecting variation in CVD risk factors and incidence, and reflecting that locally derived and validated tools are more likely to be appropriate to local contexts. NICE recommends the use of QRISK2 to predict CVD risk. 10 QRISK2 has been externally validated in UK primary-care data sets, and has excellent discrimination and calibration at whole-population level when evaluated on its own terms (ignoring competing mortality risk). 16 QRISK3 is a new version of the same tool that includes additional morbidities in prediction. QRISK3 has been derived and internally validated using the same methodology as for QRISK2,25 and in internal validation has excellent model discrimination in the overall population and among younger people, but only good discrimination among older people (defined as those aged ≥ 60 years). 25 External validation is required before recommending any prediction tool for routine use. 20,21,54,55
However, as with its predecessors, QRISK3 does not account for competing mortality risk in its derivation. The effects of competing mortality risk are obvious in the extreme: taking a statin is clearly futile for someone receiving end-of-life care for terminal cancer. However, across a 10-year prediction time horizon, less dramatic levels of competing mortality risk can lead to systematic and clinically significant overprediction of CVD risk among people at higher risk of dying from another cause, which will particularly apply to older people and those with multimorbidity. 34,35
In addition, because age dominates CVD risk, a risk prediction tool that covers a wide range of ages (25–84 years in the case of QRISK3) will always have good discrimination at overall population level. However, discrimination and calibration in subgroups may be poor. This is observed in reported discrimination for QRISK3 in internal validation, where, for example, discrimination is better among younger than older people, and is better among those with type 1 diabetes than those with type 2 diabetes (see the supplementary appendix of the derivation and internal validation paper25), although calibration in different groups is not reported.
In terms of NICE’s surveillance review of the lipid modification guideline, two particular subgroups of interest are people with type 1 diabetes and people with CKD. 13 There is some evidence that models derived in people with diabetes have somewhat better discrimination in diabetic populations than models derived in the general population, although the evidence is primarily for people with type 2 diabetes. 56 Discrimination of CVD risk prediction models in people with type 2 diabetes is generally poor,57 particularly in older adults. 58 QRISK3 does include a type 1 diabetes variable and so, in principle, provides a type 1 diabetes-specific prediction in a model derived from a whole population,25 and the Steno Type 1 Risk Engine (Steno Diabetes Center, Copenhagen, Denmark) provides an alternative derived from a population of people with type 1 diabetes;59 however, at the time this study was carried out, neither tool had been externally validated (an external validation60 published after we completed this element of the study is discussed in Summary). In people with CKD, CVD risk prediction tools that do not account for CKD substantially underpredict CVD risk,61–63 although adding a detailed indicator of estimated glomerular filtration rate (eGFR) and albuminuria to models calibrated to the CKD population leads to only small improvements in discrimination. 64
This study, therefore, externally evaluates the performance of QRISK3 both in its own terms (ignoring competing mortality risk) and accounting for competing risk, and examines model performance in subgroups of the population defined by age and by levels of comorbidity [a modified Charlson Comorbidity Index65 (mCCI)], for whom competing mortality risk is likely to vary, and in people with type 1 diabetes and CKD.
We then derive a new CVD prediction model based on QRISK3 that accounts for competing mortality risks (i.e. the CRISK), internally validate the model in the same data set and examine reclassification from using CRISK compared with using QRISK3 to identify people with predicted 10-year CVD risk of > 10%.
This chapter reports methods and findings for CVD risk prediction models in relation to objectives 1 and 2, as follows:
-
To externally validate the recommended risk prediction tools for primary prevention of CVD (QRISK3), including performance in important subgroups, and for osteoporotic fracture (QFracture-2012).
-
To derive and internally validate new-incident CVD (and osteoporotic fracture) risk prediction models, accounting for competing risks of death, and compare performance with existing risk prediction models.
Methods
Data sources
Data used in this study were taken from CPRD GOLD,66 which derives data from general practices using INPS Vision electronic health records and is distinct from the derivation data set, which is derived from practices using the EMIS system. Identical to QRISK3 derivation and internal validation, patients were eligible for inclusion if they:
-
were permanently registered with a general practice, contributing up-to-standard data for at least 1 year and with consent to link GP data to hospital discharge (Hospital Episodes Statistics Admitted Patient Care) and mortality [Office for National Statistics (ONS) mortality registration] data
-
were aged ≥ 25 years and < 85 years
-
had no prior history of any CVD
-
had no prior history of statin prescription.
Cohort entry was defined as the latest date of an individual’s date of registration plus 1 year, the individual’s 25th birthday or 1 January 2004. Cohort exit was defined as the earliest of:
-
the first non-fatal or fatal cardiovascular event
-
receipt of a statin prescription
-
deregistration from their participating general practice
-
date of last data collection from their participating general practice
-
end-of-study follow-up on 31 March 2016.
Of note, the QRISK3 derivation and internal validation did not censor on statin prescription, but we chose to, as the primary purpose of the tool is to inform decisions on statin initiation.
Sample size
The sample size is fixed by the size of the CPRD GOLD data set. Therefore, no formal power calculation was carried out, as it could not alter study design and the available sample size was considered sufficient for the purpose. 54
Outcome definition
The outcome was the first CVD event experienced by an individual, defined as the earliest GP, hospital or mortality record of non-fatal coronary heart disease, ischaemic stroke or transient ischaemic attack (TIA). Outcomes were defined using Read codes (for GP data) and International Statistical Classification of Diseases and Related Health Problems, Tenth Revision (ICD-10) codes (for hospital discharge and mortality data). ICD-10 codes are those listed in the published QRISK3 derivation paper;25 however, there are no published Read codesets available. We, therefore, derived our own Read codeset, and this and the ICD-10 codes are listed in appendices to the published paper67 reporting our external validation of QRISK3.
Other variable definitions
At the time the analysis was done, there were no published Read codesets for other variables included in the QRISK3 model, which we defined using Read codes in GP data which we created for this study and values [e.g. systolic blood pressure (SBP), cholesterol] in GP data (listed in our published paper). 67 There were several data-handling variations compared with the original QRISK3 derivation:
-
We chose a later cohort entry date (1 January 2004 vs. 1 January 1998).
-
Where no cholesterol value was available at baseline, then QRISK3 allowed cholesterol values after the cohort entry date to be used provided that they were before any CVD event. In contrast, we used values from before the cohort entry date only to avoid using future information in prediction.
-
CPRD makes only group Townsend deprivation scores available as vigintile (equal 20th) of Townsend score. Therefore, we estimated the median Townsend score of national vigintiles and used that in prediction.
In addition, we calculated a mCCI based on Read codes in the GP data, using a published codeset. 65 The mCCI was modified in that the original Charlson Comorbidity Index (CCI) includes several CVDs that are, by definition, excluded at baseline in this study because participants are CVD free at baseline. The mCCI was not used in prediction but was used to examine discrimination and calibration in subgroup analysis (categorised as 0, 1, 2 and ≥ 3), along with age group (categorised as 25–44 years, 45–64 years, 65–74 years and 75–84 years).
Missing data
Missing data handling and the proportion of each variable with missing data are shown in Appendix 1, Table 24. As with QRISK3 derivation, patients were excluded if the Townsend deprivation score was missing, patients with missing data on ethnicity were assumed to be white and patients with no record of a condition were assumed not to have the condition. For continuous variables [i.e. body mass index (BMI), total cholesterol : high-density lipoprotein ratio (TC : HDL), SBP, SBP variability] and for smoking status, multivariate imputation via chained equations68 was used to generate five imputed data sets. Analyses of these imputed data sets were combined using Rubin’s rules to account for the uncertainty association with imputation. 69
Analytical methods: external validation
The published QRISK3 2017 prediction model was implemented (under GNU Lesser General Public Licence v3), and the predicted 10-year risk of experiencing a CVD event was calculated for each patient without recalibration of baseline risk. Model performance was evaluated by examining discrimination and calibration.
Discrimination evaluates how well the risk score differentiates between patients who experience a CVD event (or more generally, the event of interest) during the study and patients who do not. We primarily examined discrimination using the truncated version of Harrell’s c-statistic to include only pairs where the earliest survival time was no later than 10 years after entry. A c-statistic of 0.5 indicates that the risk score performs no better than chance, whereas a c-statistic of 1 indicates perfect discrimination. Evaluating how good discrimination is for values between 0.5 and 1 is arbitrary and involves judgement. We considered c-statistic values of 0.5–0.599 poor, values of 0.6–0.699 moderate, values of 0.7–0.799 good and values > 0.8 excellent.
Two additional measures of discrimination were calculated. First, we calculated Royston and Sauerbrei’s D-statistic (based on the separation in event-free survival between patients with predicted risk scores above and below the median, where higher values indicate greater discrimination and a difference of ≥ 0.1 is suggested as indicating a meaningful difference in discrimination). 70 Second, we calculated a related R2-statistic designed for estimating explained variation in censored survival data. 71
Models may have good discrimination but imperfectly predict risk, for example by systematically overpredicting or underpredicting. Examination of calibration is, therefore, important, particularly where predicted risk is used to determine offers of treatment, as it is for primary prevention of CVD. 10 Calibration refers to how closely the predicted and observed probabilities agree at group level, and for this purpose participants were grouped into 10 equal-sized groups (deciles) of predicted risk. Calibration of the risk score predictions was assessed by plotting observed proportions against predicted probabilities. For both men and women separately, plots were generated for all patients and for prespecified subgroups of age, mCCI, diabetes type and CKD, based on summary statistics pooled across the imputed data sets. Subgroups were defined to ensure that there were enough events in each subgroup to ensure stable estimates of observed risk (and for diabetes and CKD, analysis was, therefore, in the whole subgroup without further stratification for age group or mCCI). CKD was defined in two ways: (1) only using Read codes,67 as per QRISK3 derivation25 and (2) using the same set of Read codes or the last recorded eGFR or eGFR based on last recorded serum creatinine, where an eGFR < 60 ml per minute defined CKD.
The following summary statistics and their standard errors (SEs) were obtained by decile of predicted risk score and for each imputed data set, in turn: non-parametric measures of observed risk or proportions of patients with a CVD event, the Kaplan–Meier estimator (the conventional measure ignoring competing risks), the Aalen–Johansen estimator (an extension to allow for competing events, non-CVD death in this case)16 and the mean predicted risk score. All models were fitted in R 4.0.0 (The R Foundation for Statistical Computing, Vienna, Austria) and Stata® 11.2 (StataCorp LP, College Station, TX, USA).
Analytical methods: competing risk model derivation and internal validation
Competing risk model derivation and internal validation was carried out in the same data set as QRISK3 external validation. For this purpose, participants were randomly allocated to distinct derivation and test data sets in a 2 : 1 ratio, with allocation balanced in terms of age and final event status. The derivation data set was used to derive CRISK, that is a Fine–Gray model to predict the 10-year risk of experiencing a CVD event, accounting for the competing risk of non-CVD death. Separate models were estimated for men and women. Reflecting the overall aim of the project, where we wished to explicitly compare prediction in models accounting for competing risk compared with ignoring competing risk, we included all of the same main effects (i.e. predictors) and age interactions as QRISK3, modified as follows. First, we accounted for non-CVD death as a second (competing) outcome using the Fine–Gray model, and we re-estimated fractional polynomial terms for continuous variables, including in QRISK3, selecting terms based on those performing best (as measured by the c-statistic) in balanced 10-fold cross-validation and showing consistency of model fit [i.e. Akaike information criterion (AIC)] across folds of the derivation data set (this model is called CRISK). Second, as QRISK3 predictors are focused on CVD events, we derived a further model [i.e. the competing mortality risk model with Charlson Comorbidity Index (CRISK-CCI)], which additionally included the mCCI score in the model (categorised as 0, 1, 2, ≥ 3), as CCI is a well-validated predictor of total mortality. 12 Fine–Gray models allow the cumulative incidence function or probability of a CVD event occurring over time to be directly predicted; however, the subdistribution hazard ratios (HRs) in the Fine–Gray models do not have a straightforward interpretation, as they describe the direction but not the magnitude of the effect of predictors on the cumulative incidence function. The use of fractional polynomials and the inclusion of complex interactions with age further complicate direct interpretation of model coefficients. Model coefficients are, therefore, not straightforwardly interpretable, but the derived model is provided in Appendix 1, Tables 25 and 26, to allow replication.
The performance of all three models (i.e. CRISK, CRISK-CCI and QRISK3) was evaluated in the independent validation data set by examining discrimination and calibration, as described above. R 4.0.0 was used for all analyses.
Results 1: external validation of QRISK3 in the whole population
The external validation data set had 1,648,746 women aged 25–84 years with linkage to Hospital Episode Statistics (HES) and ONS. Of these women, 164,129 (10.0%) were excluded because of missing deprivation score (0.2%), prior CVD (4.7%) or prior statin prescribing (5.1%). The external validation data set had 1,621,535 men aged 25–84 years with linkage HES and ONS. Of these men, 201,359 (12.4%) were excluded because of missing deprivation score (0.2%), prior CVD (6.9%) or prior statin prescribing (5.3%). Therefore, analysis used data for 1,484,597 women and 1,420,176 men.
The baseline characteristics of participants compared with the QRISK3 internal validation cohort25 are shown in Appendix 1, Table 27. The two cohorts were similar, although there was a higher prevalence of treated hypertension in this study, and a lower recorded prevalence of family history of premature CVD. Appendix 1, Table 24, shows that ethnicity data were less frequently missing in this study, but that TC : HDL, SBP variability and smoking status were more commonly missing (which may reflect the use of data after study entry date in QRISK3 derivation).
In women, during 8,594,620 years of follow-up, there were 42,451 incident cases of CVD observed {4.94 [95% confidence interval (CI) 4.89 to 4.99] per 1000 person-years}. In men, during 7,896,704 years of follow-up, there were 53,066 incident cases [6.72 (95% CI 6.66 to 6.78) per 1000 person-years]. Incidence progressively rose with age, from 0.3 cases per 1000 person-years in both men and women aged 25–29 years, to 44.1 cases in women aged 80–84 years and to 52.6 cases in men aged 80–84 years. CVD incidence was moderately lower than that observed in QRISK3 derivation (see Appendix 1, Table 28). 4
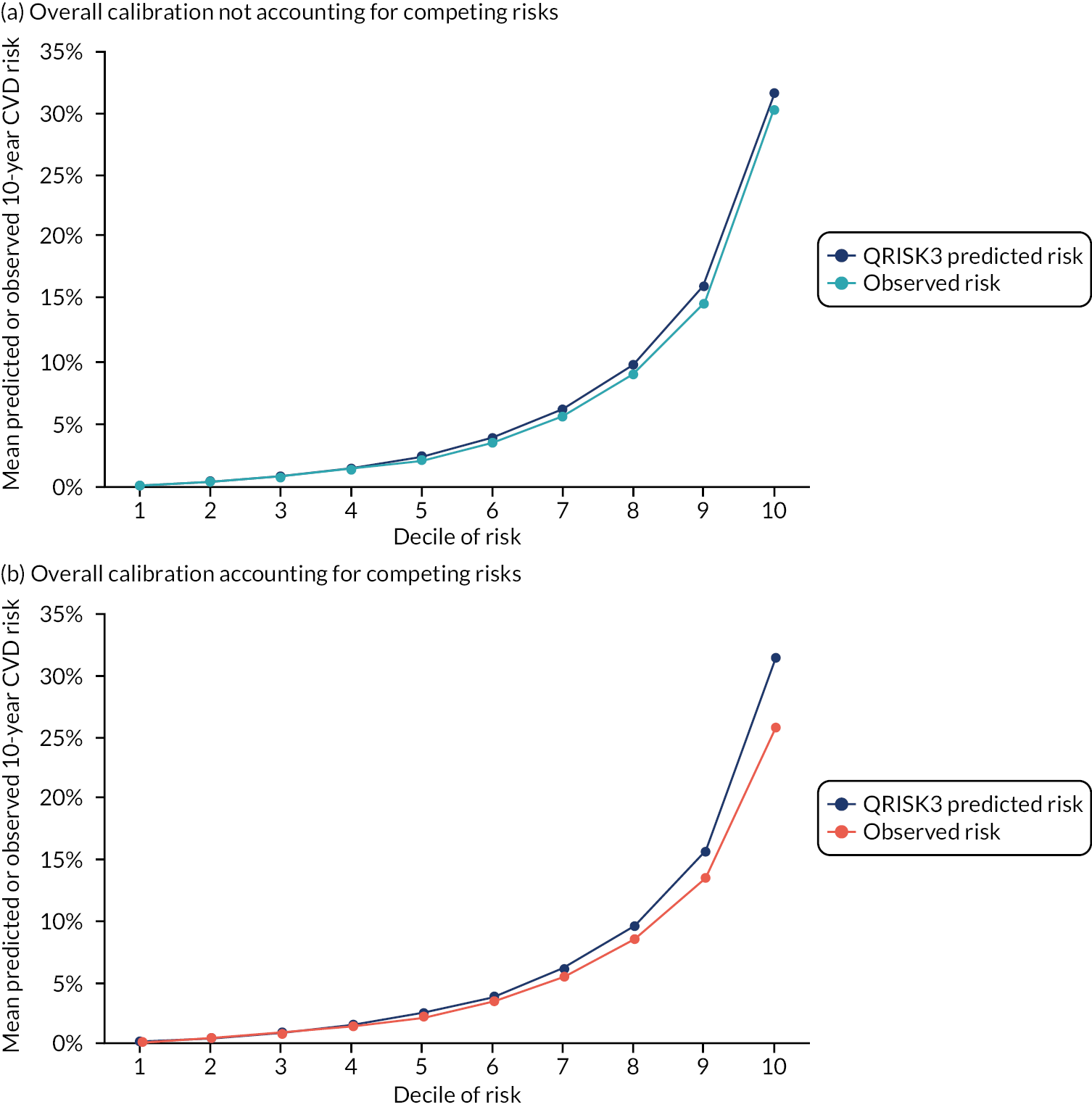
In the whole population, discrimination was excellent in both women (Harrell’s c-statistic 0.865, 95% CI 0.861 to 0.868) and men (Harrell’s c-statistic 0.834, 95% CI 0.831 to 0.837), and very similar to QRISK3 internal validation (women, Harrell’s c-statistic 0.880; men, Harrell’s c-statistic 0.858)25 (Table 1). The D-statistic was 2.43 in women (similar to the internal validation study’s D-statistic of 2.49) and 2.10 in men (somewhat lower than the internal validation study’s D-statistic of 2.26). Explained variation (R2) was 58.5% in women and 51.3% in men, compared with 59.6% and 55.0%, respectively, in the internal validation study. In all strata of age group, discrimination was worse in both men and women, varying from good in younger people (age 25–44 years Harrell’s c-statistic: women, 0.865; men, 0.757) to poor to moderate in older people (age 75–84 years Harrell’s c-statistic: women, 0.611; men, 0.585), with low levels of explained variation in older people (age 75–84 years R2: women, 8.1%; men, 4.9%). Stratified by mCCI, discrimination was excellent in people with low comorbidity, but progressively less good in people with higher comorbidity, but with less change than for age group (mCCI ≥ 3 Harrell’s c-statistic: women, 0.744; men, 0.695).
| Population subgroups | Women | Men | ||||
|---|---|---|---|---|---|---|
| Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | |
| All patients | 0.865 (0.861 to 0.868) | 2.43 (2.41 to 2.45) | 58.5 (58.1 to 58.8) | 0.834 (0.831 to 0.837) | 2.10 (2.08 to 2.12) | 51.3 (50.8 to 51.7) |
| Age group (years) | ||||||
| 25–44 | 0.758 (0.747 to 0.769) | 1.69 (1.63 to 1.76) | 40.7 (38.8 to 42.5) | 0.757 (0.749 to 0.764) | 1.57 (1.52 to 1.61) | 36.9 (35.6 to 38.2) |
| 45–64 | 0.707 (0.702 to 0.713) | 1.25 (1.22 to 1.28) | 27.2 (26.1 to 28.3) | 0.681 (0.677 to 0.685) | 1.04 (1.02 to 1.07) | 20.6 (19.8 to 21.4) |
| 65–74 | 0.641 (0.635 to 0.647) | 0.82 (0.77 to 0.86) | 13.7 (12.4 to 15.1) | 0.612 (0.606 to 0.617) | 0.63 (0.59 to 0.66) | 8.6 (7.7 to 9.5) |
| 75–84 | 0.611 (0.605 to 0.616) | 0.61 (0.56 to 0.66) | 8.1 (6.9 to 9.3) | 0.585 (0.579 to 0.591) | 0.46 (0.42 to 0.51) | 4.9 (4.1 to 5.8) |
| mCCI | ||||||
| 0 | 0.863 (0.859 to 0.867) | 2.40 (2.38 to 2.43) | 57.9 (57.4 to 58.4) | 0.827 (0.824 to 0.831) | 2.02 (2.00 to 2.04) | 49.4 (48.9 to 49.8) |
| 1 | 0.846 (0.840 to 0.852) | 2.20 (2.17 to 2.24) | 53.6 (52.8 to 54.4) | 0.829 (0.823 to 0.835) | 2.00 (1.96 to 2.03) | 48.7 (47.8 to 49.6) |
| 2 | 0.789 (0.778 to 0.799) | 1.73 (1.67 to 1.78) | 41.6 (39.9 to 43.2) | 0.728 (0.717 to 0.739) | 1.28 (1.22 to 1.34) | 28.1 (26.2 to 29.9) |
| ≥ 3 | 0.744 (0.728 to 0.760) | 1.40 (1.32 to 1.48) | 31.8 (29.2 to 34.4) | 0.695 (0.678 to 0.712) | 1.13 (1.04 to 1.21) | 23.2 (20.5 to 26.0) |
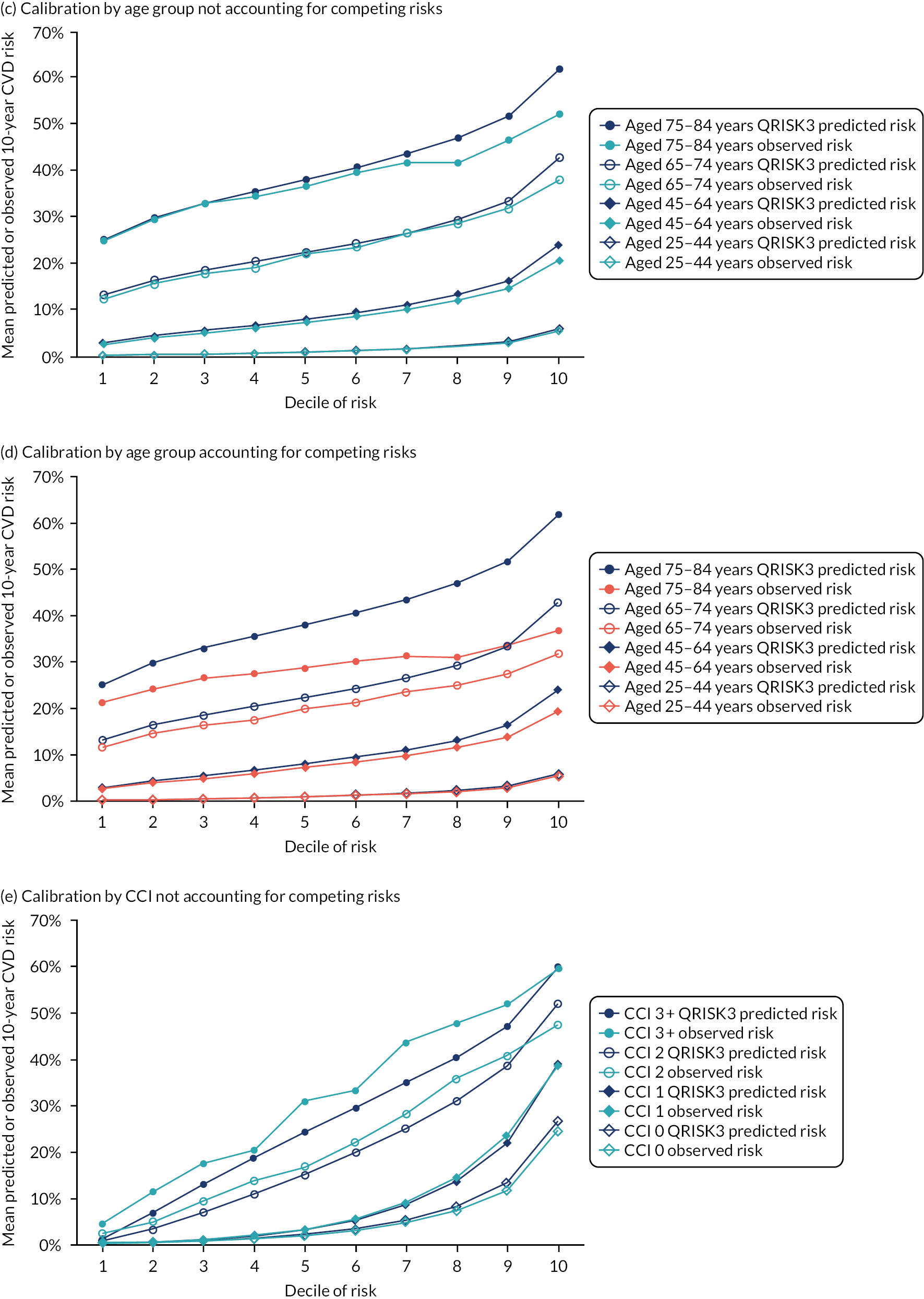
Ignoring competing mortality risk in the estimation of observed risk (Figures 1 and 2, parts a, c and e), calibration in the whole population was very good, with only minor overprediction in people at higher predicted risk (see Figures 1 and 2, part a). Stratified by age, overprediction was larger in older people (see Figures 1 and 2, part b). Stratified by mCCI, there was some overprediction in people with no baseline comorbidity, but underprediction in those with comorbidity (see Figures 1 and 2, part c). Accounting for competing mortality risk in the estimation of observed risk (see Figures 1 and 2, parts b, d and f), overprediction was larger in the whole population and in all age groups apart from the youngest (i.e. people aged 25–44 years) (see Figures 1 and 2, parts d and e). Stratified by mCCI, underprediction was still observed in people with higher comorbidity at lower levels of predicted risk, but there was large overprediction in people with higher comorbidity at higher levels of predicted risk (see Figures 1 and 2, part f).
FIGURE 1.
Calibration in women without accounting for competing risks and accounting for competing risks. (a) Overall calibration not accounting for competing risks;a (b) overall calibration accounting for competing risks;b (c) calibration by age group not accounting for competing risks;a (d) calibration by age group accounting for competing risks;b (e) calibration by CCI not accounting for competing risks;a and (f) calibration by CCI accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.
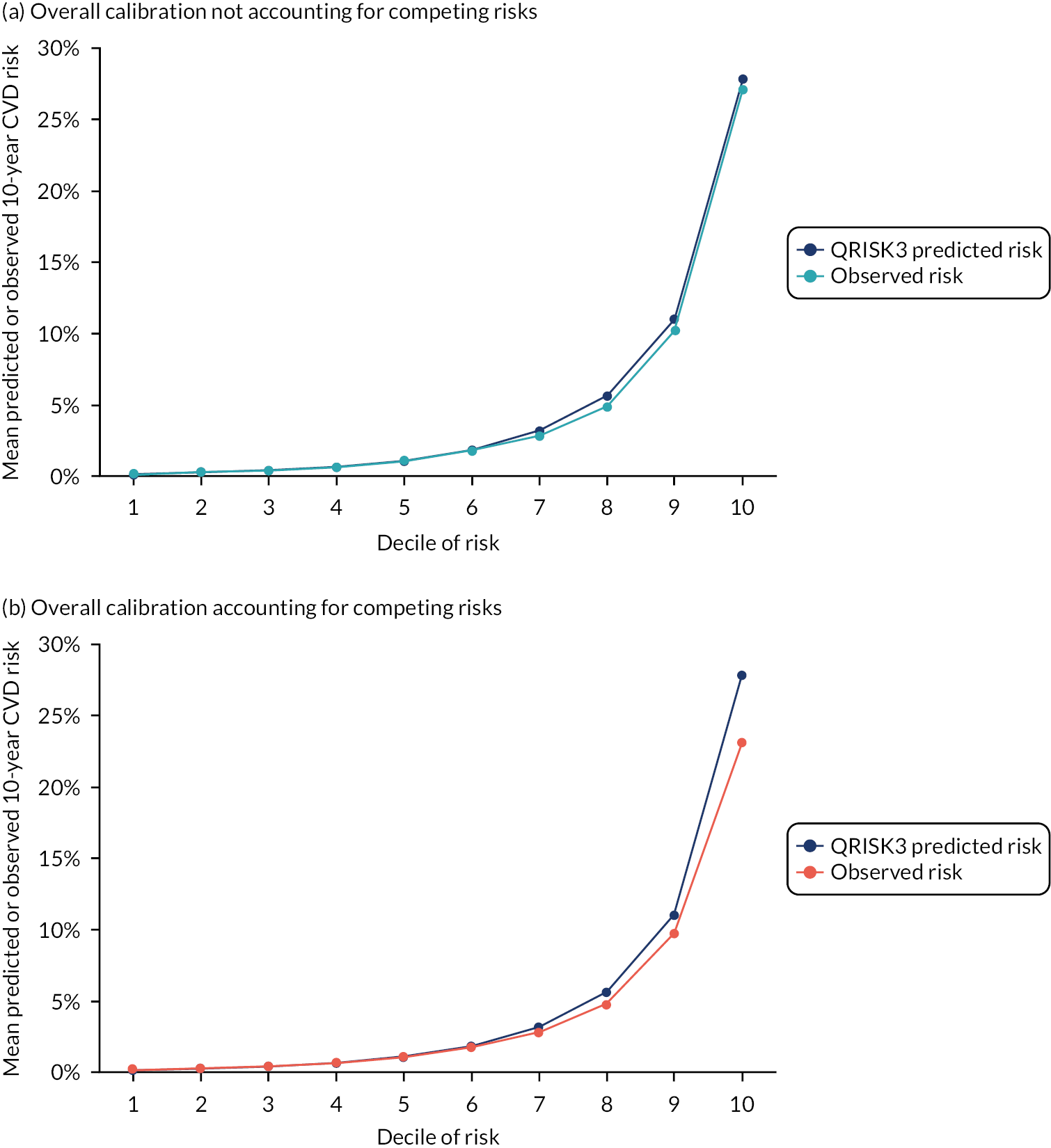
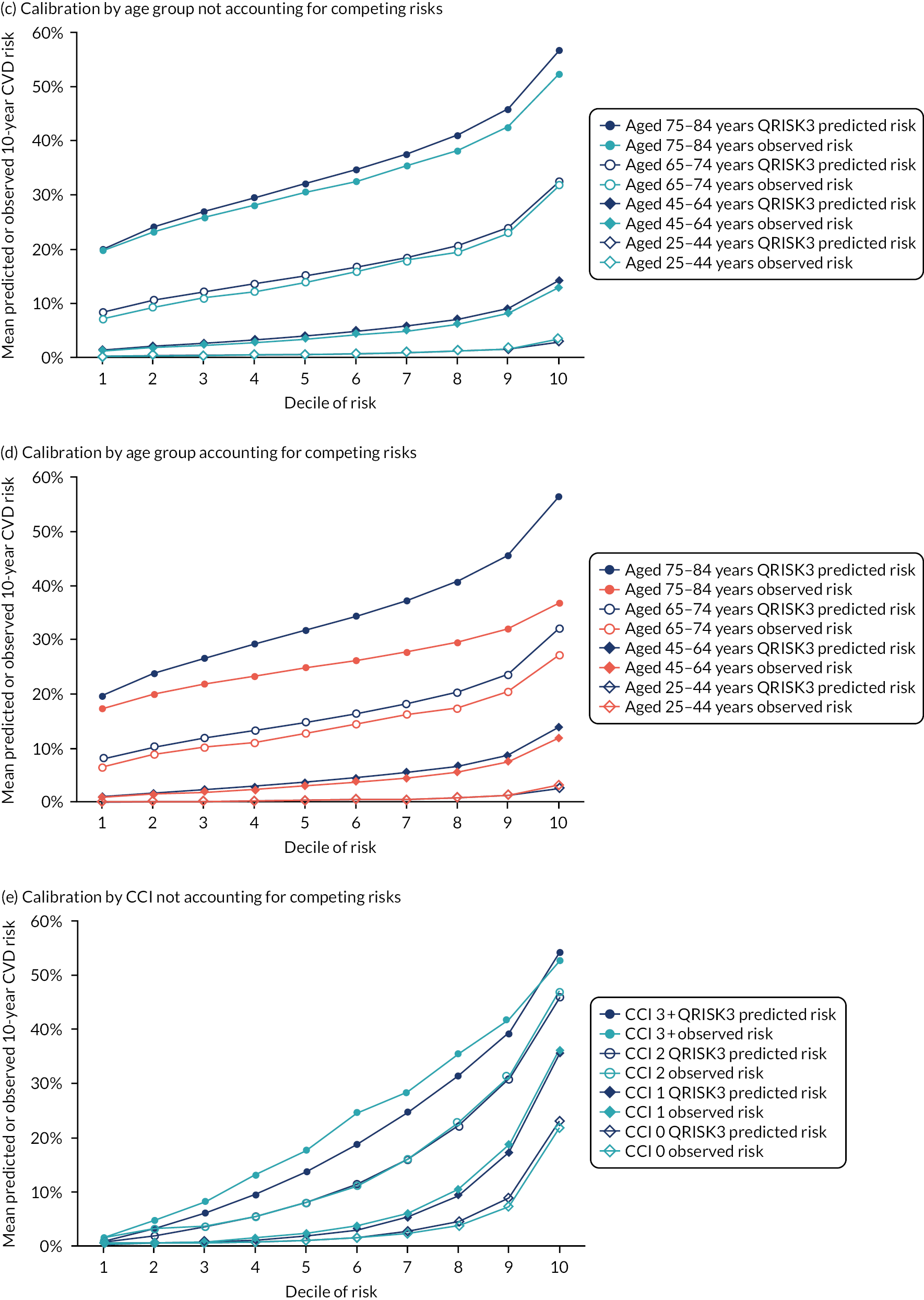
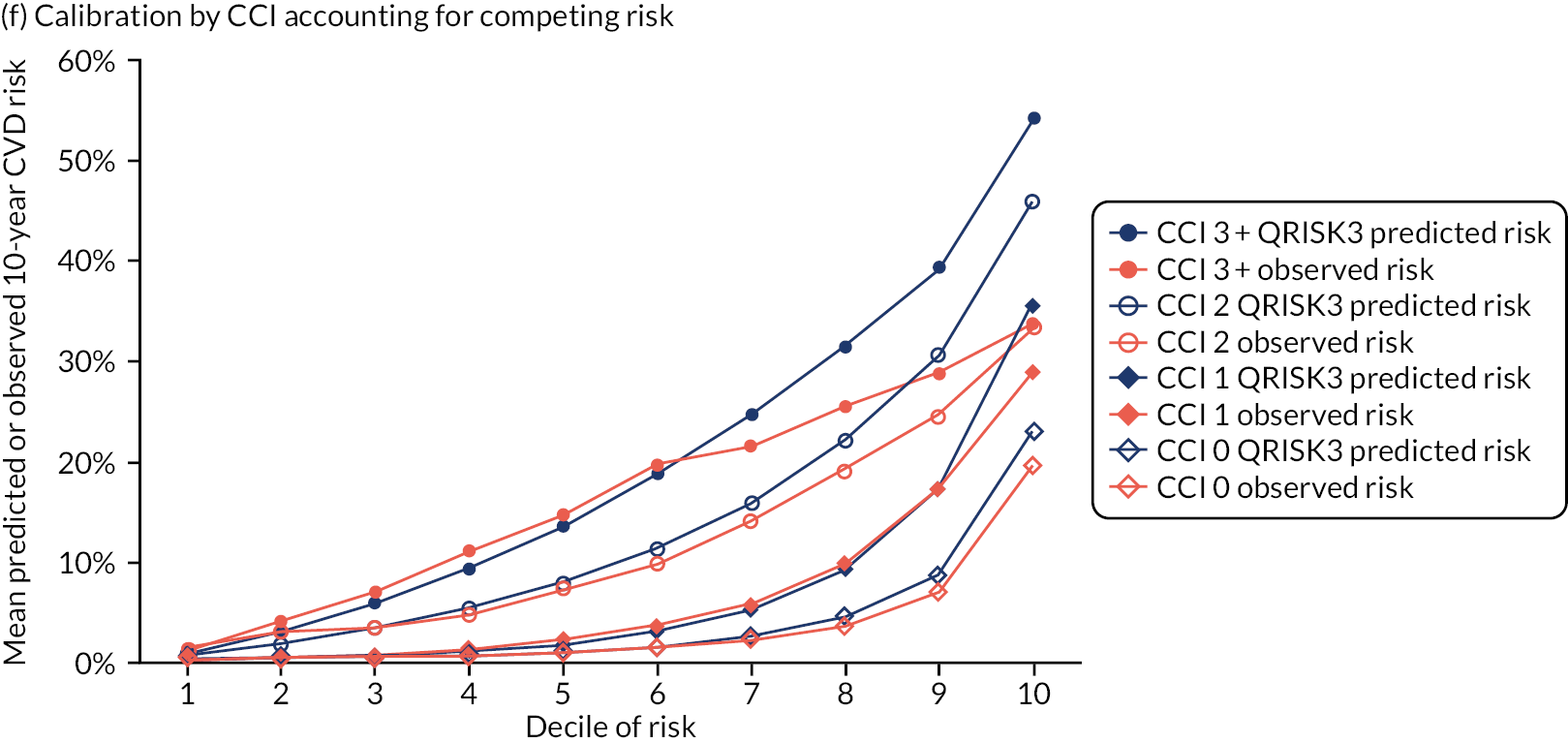
FIGURE 2.
Calibration in men without accounting for competing risks and accounting for competing risks. (a) Overall calibration not accounting for competing risks;a (b) overall calibration accounting for competing risks;b (c) calibration by age group not accounting for competing risks;a (d) calibration by age group accounting for competing risks;b (e) calibration by CCI not accounting for competing risks;a and (f) calibration by CCI accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.
Results 2: external validation of QRISK3 in people with diabetes
Type 1 diabetes
There were 6025 women with type 1 diabetes potentially eligible for inclusion, of whom 646 (10.7%) and 1627 (27.0%) were excluded because of prior CVD or prior statin prescribing for primary prevention, respectively. There were 8260 men with type 1 diabetes potentially eligible for inclusion, of whom 953 (11.5%) and 2464 (40.9%) were excluded because of prior CVD or prior statin prescribing for primary prevention, respectively. Therefore, 3752 women (62.3% of potentially eligible women with type 1 diabetes) and 4843 men (48.6% of potentially eligible men with type 1 diabetes) were included in analysis of type 1 diabetes.
During follow-up of the type 1 diabetes cohort, there were 108 CVD events in 13,098 person-years’ follow-up in women [8.25 (95% CI 6.83 to 9.94) events per 1000 person-years] and 172 CVD events in 15,824 person-years’ follow-up in men [10.90 (95% CI 9.40 to 12.60) events per 1000 person-years].
Discrimination in people with type 1 diabetes was excellent [Harrell’s c-statistic: women, 0.830 [95% CI 0.768 to 0.891; men, 0.853 (95% CI 0.803 to 0.902)] and explained variance in the model was 51.6% in women and 48.0% in men (see Appendix 1, Table 29).
Ignoring competing risks (see Appendix 1, Figure 28, parts a and c), calibration in women with type 1 diabetes was good (allowing for small number of events and, therefore, a relatively noisy plot), but there was some overprediction in men at higher predicted risk. Accounting for competing risks (see Appendix 1, Figure 28, parts b and d), there was overprediction in women at higher predicted risk and greater overprediction in men at higher predicted risk.
Type 2 diabetes
There were 53,284 women with type 2 diabetes potentially eligible for inclusion, of whom 12,068 (22.6%) and 24,194 (45.4%) were excluded because of prior CVD or prior statin prescribing for primary prevention, respectively. There were 68,236 men with type 2 diabetes potentially eligible for inclusion, of whom 19,777 (28.9%) and 27,382 (40.1%) were excluded because of prior statin prescribing for primary prevention, respectively. Therefore, 24,194 women (i.e. 31.9% of the potentially eligible women with type 2 diabetes) and 21,077 men (i.e. 30.9% of the potentially eligible men with type 2 diabetes) were, therefore, included in analysis of type 2 diabetes.
During follow-up of the type 2 diabetes cohort, there were 1167 CVD events in 44,678 person-years’ follow-up in women [26.12 (95% CI 24.68 to 27.64) events per 1000 person-years] and 1682 CVD events in 57,160 person-years’ follow-up in men [29.40 (95% CI 28.10 to 30.80) events per 1000 person-years].
Discrimination in people with type 2 diabetes was moderate to good [Harrell’s c-statistic: women, 0.741 (95% CI 0.722 to 0.760); men, 0.695 (95% CI 0.679 to 0.712)] and explained variance in the model was lower than for type 1 diabetes (i.e. 29.2% in women and 22.0% in men) (see Appendix 1, Table 29).
Ignoring competing risks (see Appendix 1, Figure 29, parts a and c), calibration in women with type 2 diabetes was good, but there was some overprediction in men at the highest predicted risk. Accounting for competing risks (see Appendix 1, Figure 29, parts b and d), there was progressively increasing overprediction in women with moderate to high predicted risk and in men in all but the lowest deciles of predicted.
Results 3: external validation of QRISK3 in people with chronic kidney disease
Chronic kidney disease defined by Read code alone
There were 16,048 women with CKD defined by Read code alone potentially eligible for inclusion, of whom 4223 (26.3%) and 4897 (30.5%) were excluded because of prior CVD or prior statin prescribing for primary prevention, respectively. There were 15,784 men with CKD defined by Read code alone potentially eligible for inclusion, of whom 5645 (35.7%) and 3850 (24.4%) were excluded because of prior CVD or prior statin prescribing for primary prevention, respectively. Therefore, 6918 women (i.e. 43.1% of the potentially eligible women with CKD defined by Read code alone) and 5659 men (i.e. 35.9% of the potentially eligible men with CKD defined by Read code alone) were, therefore, included in analysis of CKD defined by Read code alone. The mean age of women was 63.0 years and mean age of men was 59.2 years.
During follow-up of the CKD defined by Read code alone cohort, there were 541 CVD events in 25,544 person-years’ follow-up in women [21.18 (95% CI 19.48 to 23.02) events per 1000 person-years] and 569 CVD events in 21,459 person-years’ follow-up in men [26.50 (95% CI 24.40 to 28.80) events per 1000 person-years].
Discrimination in people with CKD defined by Read code alone was good [Harrell’s c-statistic: women, 0.755 (95% CI 0.728 to 0.782); men, 0.734 (95% CI 0.708 to 0.760)] and explained variance in the model was 34.2% in women and 29.7% in men (see Table 30).
Ignoring competing risks (see Appendix 1, Figure 30, parts a and c), calibration in women with CKD defined by Read code alone was reasonable (allowing for small number of events and, therefore, a relatively noisy plot) and good for men (with some underprediction for both at higher predicted risk). Accounting for competing risks (see Appendix 1, Figure 30, parts b and d), there was overprediction in women at moderate and higher predicted risk and overprediction in men at higher predicted risk.
Chronic kidney disease defined by Read code and estimated glomerular filtration rate
Laboratory values were extracted for only people included in the CVD study cohort and so it is not possible to calculate the proportions excluded because of prior CVD or prior statin prescribing. There were 71,094 women and 33,699 men with CKD defined by Read code or eGFR included in analysis, with an older mean age than the cohort with CKD defined by Read code alone (mean age: women, 70.1 years; men, 69.1 years).
During follow-up of the CKD defined by Read code or eGFR cohort, there were 8877 CVD events in 348,982 person-years’ follow-up in women [25.44 (95% CI 24.92 to 25.96) events per 1000 person-years] and 5273 CVD events in 146,730 person-years’ follow-up in men [35.90 (95% CI 35.00 to 36.90) events per 1000 person-years].
Discrimination in people with CKD defined by Read code or eGFR was somewhat worse than for people with CKD defined by Read code alone. Discrimination was moderate to good [Harrell’s c-statistic: women, 0.705 (95% CI 0.699 to 0.712); men, 0.671 (95% CI 0.663 to 0.680)] and explained variance in the model was somewhat lower than for CKD defined by Read code alone (i.e. 24.9% in women and 17.4% in men) (see Table 30).
Ignoring competing risks (see Appendix 1, Figure 31, parts a and c), calibration in women with CKD defined by Read code or eGFR was excellent, but there was some underprediction in men. Accounting for competing risks (see Appendix 1, Figure 31, parts b and d), there was progressively increasing overprediction in women and men with moderate to high predicted risk.
Results 4: derivation and internal validation of CRISK
There were 989,732 women and 946,784 men aged 25–84 years in the derivation cohort, and 494,865 women and 473,392 men in the validation cohort, with similar distribution of baseline characteristics in each. There were 14,150 incident CVD events in 2,865,660 years of follow-up in women [4.9 (95% CI 4.89 to 4.99) events per 1000 person-years] and 17,689 incident CVD events in 2,632,804 years of follow-up in men [6.7 (95% CI 6.66 to 6.78) events per 1000 person-years].
Two new models were created: (1) CRISK that is a near replication of QRISK3, which accounts for competing risk and (2) CRISK-CCI, which additionally includes the mCCI as a predictor of competing mortality.
In the whole population, discrimination of CRISK and CRISK-CCI was excellent in women and very similar to QRISK3 (CRISK Harrell’s c-statistic: women, 0.863; men, 0.833; CRISK-CCI Harrell’s c-statistic: women, 0.864; men, 0.819) (Table 2). For both new models, discrimination showed similar patterns to QRISK3 in terms of being worse in all age groups (and progressively worse with increasing age) and, to a lesser extent, worse with increasing comorbidity measured by the mCCI (see Table 2).
| Patient group | Harrell’s c-statistic (95% CI) | |||||
|---|---|---|---|---|---|---|
| Women | Men | |||||
| CRISK-CCI | CRISK | QRISK3 | CRISK-CCI | CRISK | QRISK3 | |
| All patients | 0.864 (0.859 to 0.869) | 0.863 (0.858 to 0.869) | 0.863 (0.858 to 0.868) | 0.819 (0.815 to 0.824) | 0.833 (0.828 to 0.837) | 0.832 (0.827 to 0.836) |
| Age group (years) | ||||||
| 25–44 | 0.763 (0.745 to 0.781) | 0.761 (0.743 to 0.779) | 0.765 (0.747 to 0.783) | 0.733 (0.720 to 0.746) | 0.744 (0.731 to 0.757) | 0.740 (0.727 to 0.753) |
| 45–64 | 0.713 (0.703 to 0.722) | 0.710 (0.701 to 0.720) | 0.708 (0.698 to 0.717) | 0.661 (0.654 to 0.668) | 0.683 (0.676 to 0.690) | 0.679 (0.672 to 0.686) |
| 65–74 | 0.647 (0.637 to 0.658) | 0.645 (0.634 to 0.655) | 0.641 (0.631 to 0.652) | 0.591 (0.581 to 0.600) | 0.610 (0.600 to 0.619) | 0.606 (0.596 to 0.615) |
| 75–84 | 0.616 (0.607 to 0.624) | 0.614 (0.605 to 0.622) | 0.613 (0.604 to 0.622) | 0.570 (0.559 to 0.580) | 0.594 (0.583 to 0.604) | 0.590 (0.580 to 0.601) |
| mCCI | ||||||
| 0 | 0.862 (0.855 to 0.868) | 0.862 (0.855 to 0.868) | 0.861 (0.855 to 0.868) | 0.812 (0.806 to 0.817) | 0.825 (0.820 to 0.831) | 0.824 (0.818 to 0.829) |
| 1 | 0.843 (0.833 to 0.854) | 0.843 (0.833 to 0.854) | 0.843 (0.833 to 0.854) | 0.815 (0.805 to 0.826) | 0.830 (0.820 to 0.841) | 0.830 (0.819 to 0.840) |
| 2 | 0.787 (0.770 to 0.805) | 0.788 (0.771 to 0.806) | 0.789 (0.771 to 0.806) | 0.704 (0.685 to 0.722) | 0.729 (0.710 to 0.747) | 0.728 (0.709 to 0.747) |
| ≥ 3 | 0.753 (0.725 to 0.781) | 0.754 (0.726 to 0.782) | 0.754 (0.726 to 0.782) | 0.666 (0.636 to 0.695) | 0.698 (0.668 to 0.727) | 0.695 (0.665 to 0.724) |
In terms of calibration (evaluated using only the Aalen–Johansen estimator, which accounts for competing mortality risk in estimated observed risk), QRISK3 overpredicted in both men and women in the whole population, with progressively worse overprediction at higher predicted risk (see Results 1: external validation of QRISK3 in the whole population).
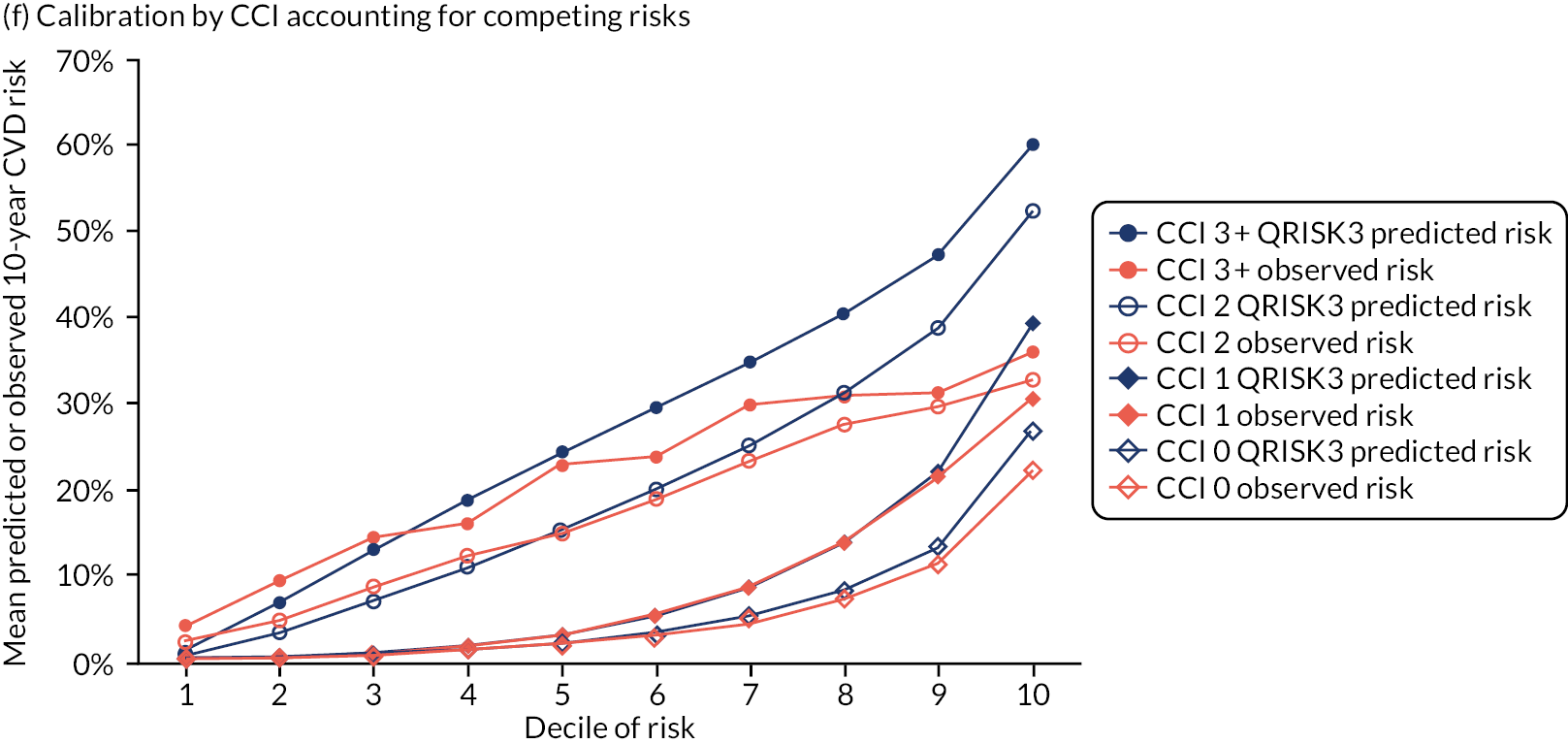
In the whole population of women, there was some overprediction with CRISK at higher levels of predicted risk, but CRISK was better calibrated than QRISK3. Calibration in women with CRISK-CCI was excellent (Figure 3). In younger women, there was some underprediction with all three prediction tools, which were similar, although CRISK was the best calibrated (Figure 4). QRISK3 and CRISK both showed overprediction in middle-aged and older women. CRISK-CCI was well calibrated in women aged 45–64 years and 65–74 years and had some overprediction at higher risk in women aged 75–84 years (but was the best calibrated model). In all CCI categories, there was some overprediction with each model at higher levels of predicted risk, which was greatest with QRISK3 and least with CRISK-CCI, although calibration of all models was broadly the same for mCCI ≥ 3 (Figure 5).
FIGURE 3.
Whole-population calibration of the competing risk model with the CCI (orange), the competing risk model without the CCI (light blue) and QRISK3 (dark blue) in (a) women; and (b) men. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.
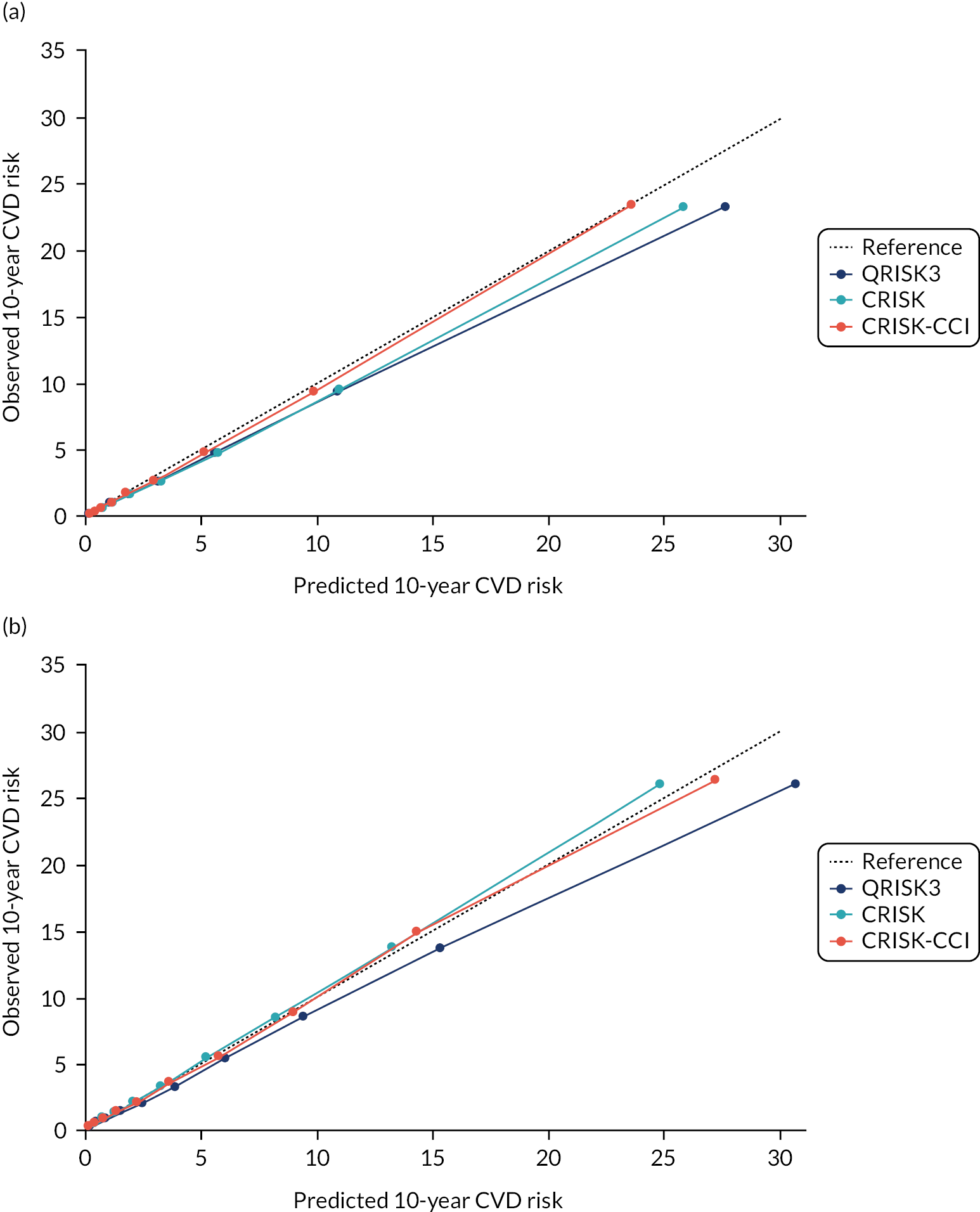
FIGURE 4.
Calibration of CRISK-CCI, CRISK and QRISK3 by age group. (a) Women aged 25–44 years; (b) men aged 25–44 years; (c) women aged 45–64 years; (d) men aged 45–64 years; (e) women aged 65–74 years; (f) men aged 65–74 years; (g) women aged 75–84 years; and (h) men aged 75–84 years. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Ideal calibration lies on the reference line, below the line is overprediction and above the line is underprediction.
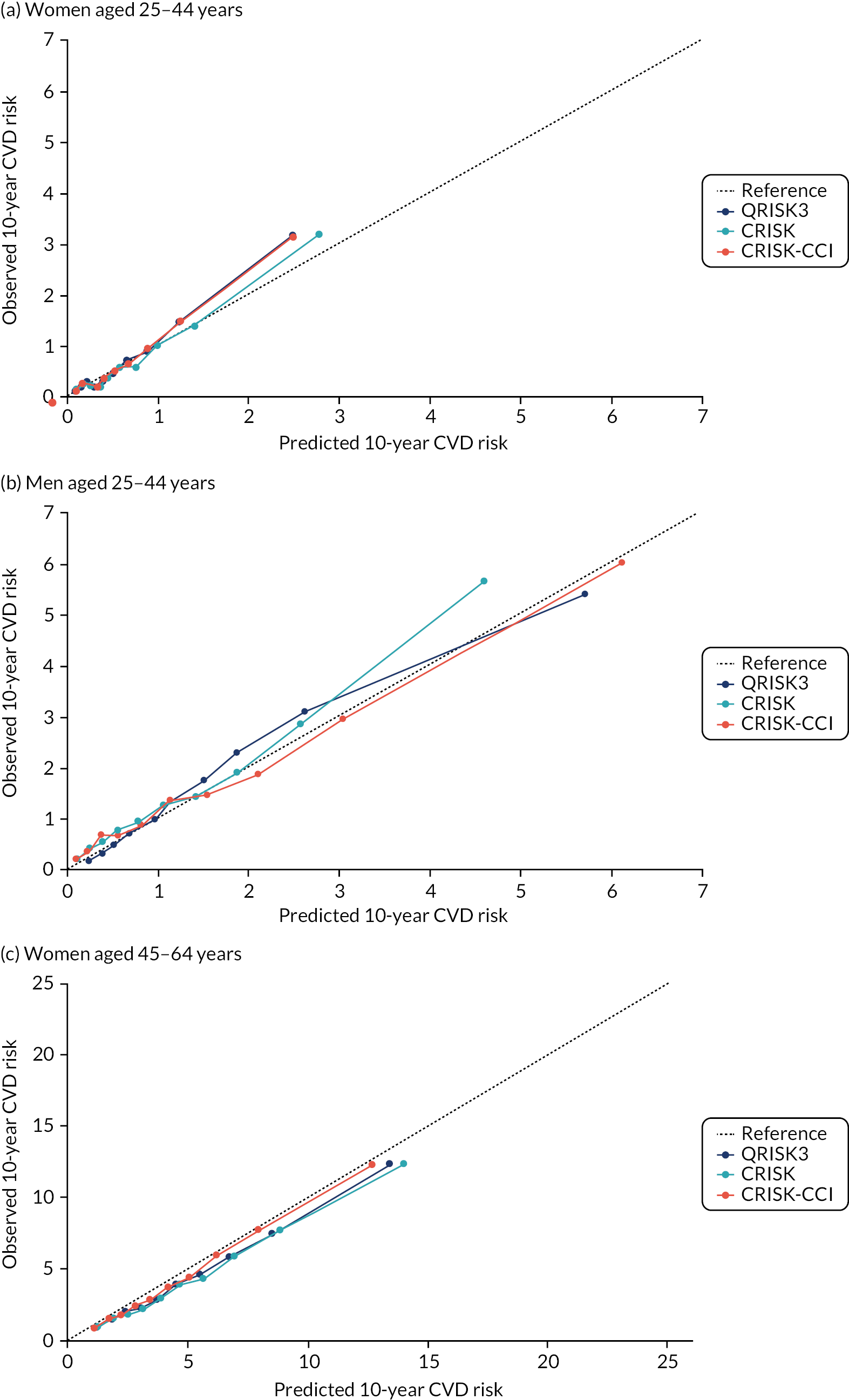
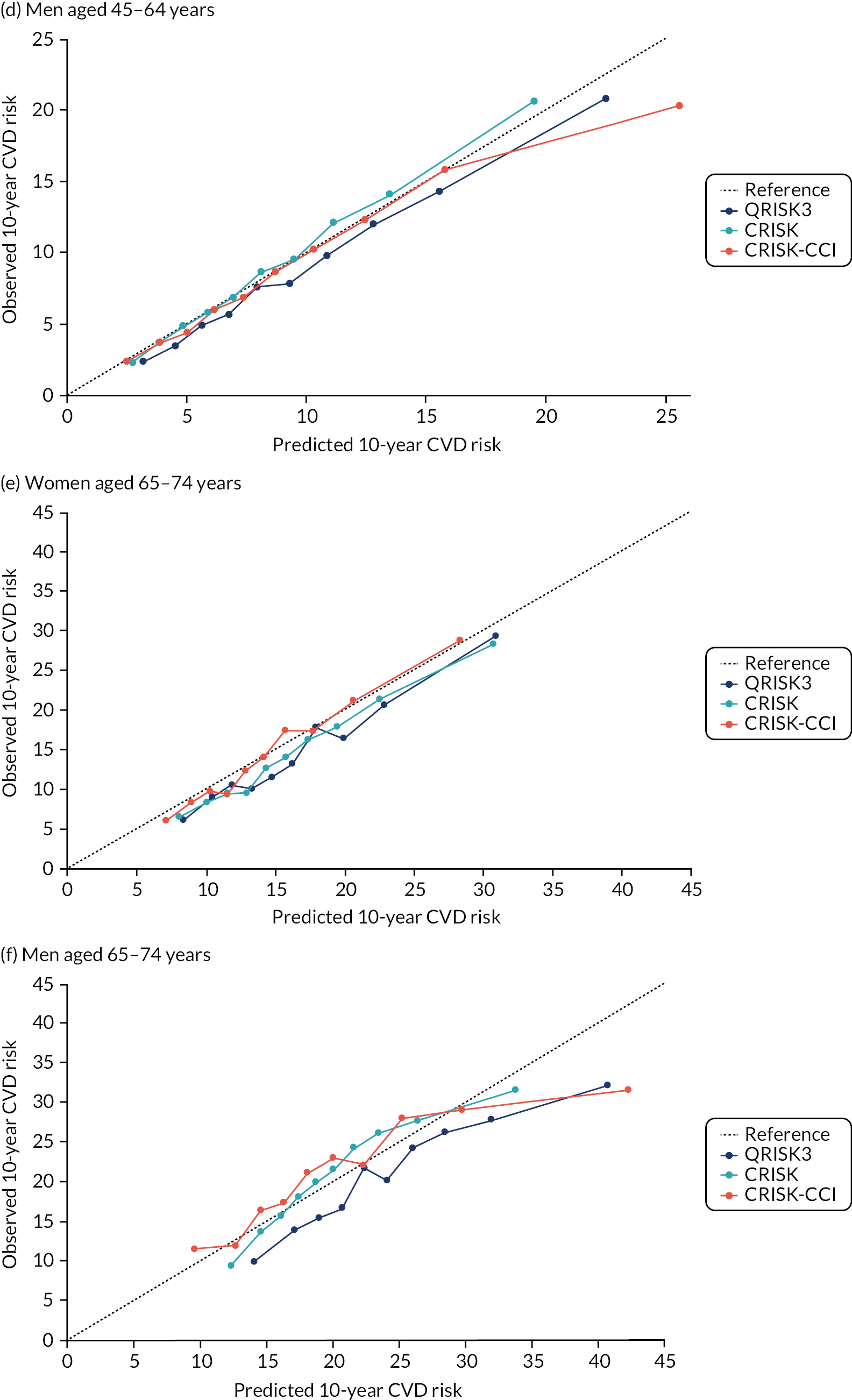
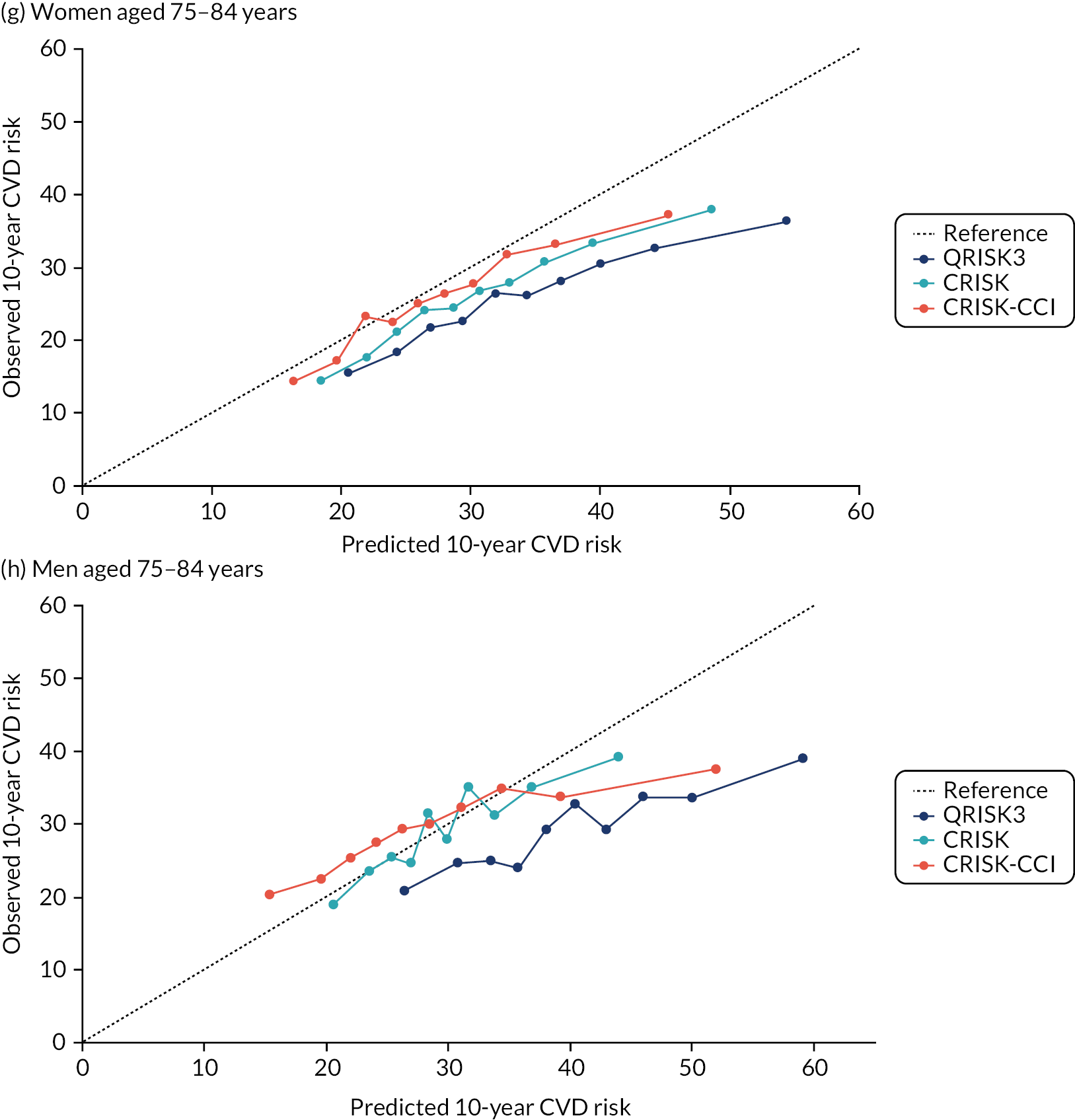
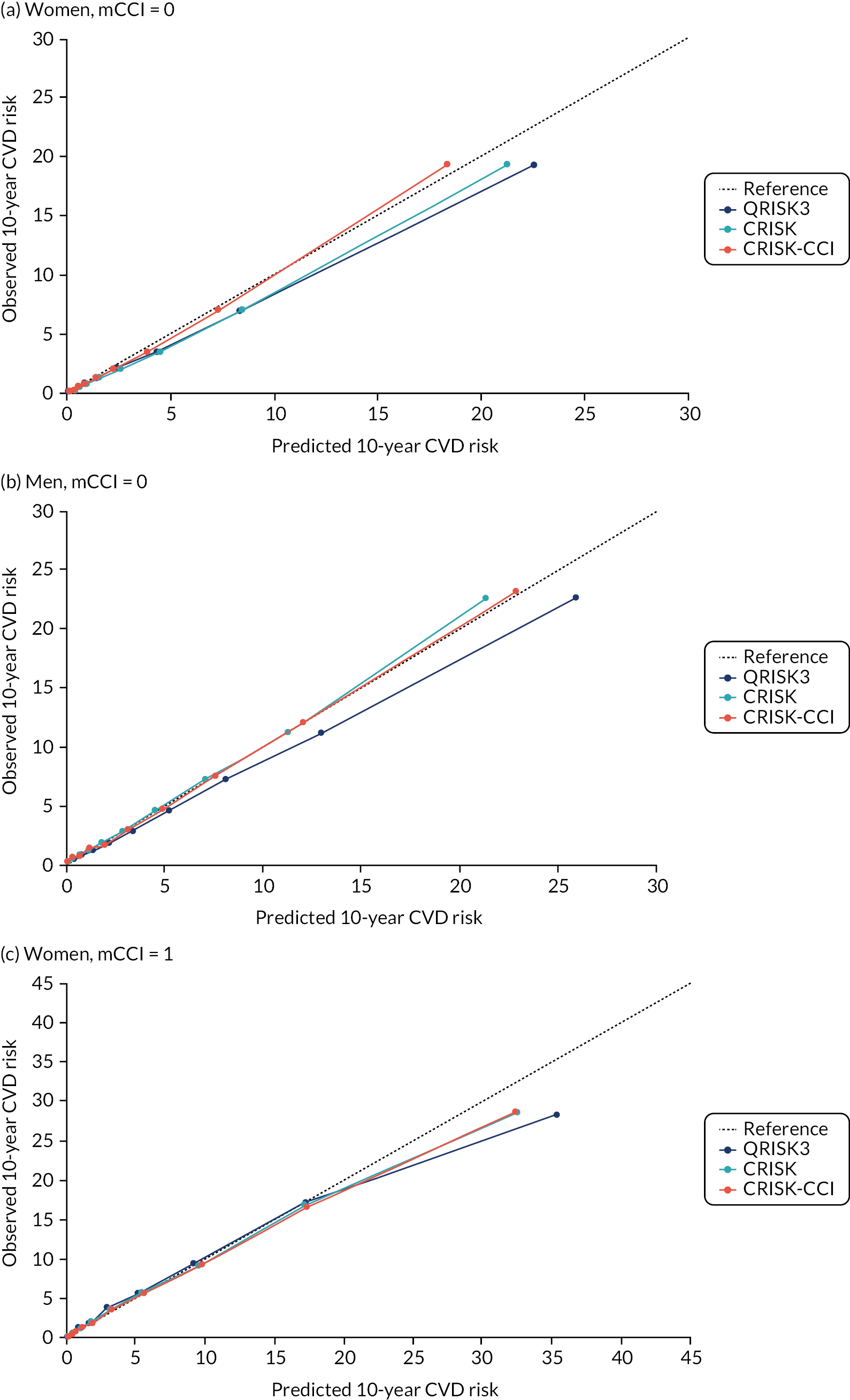
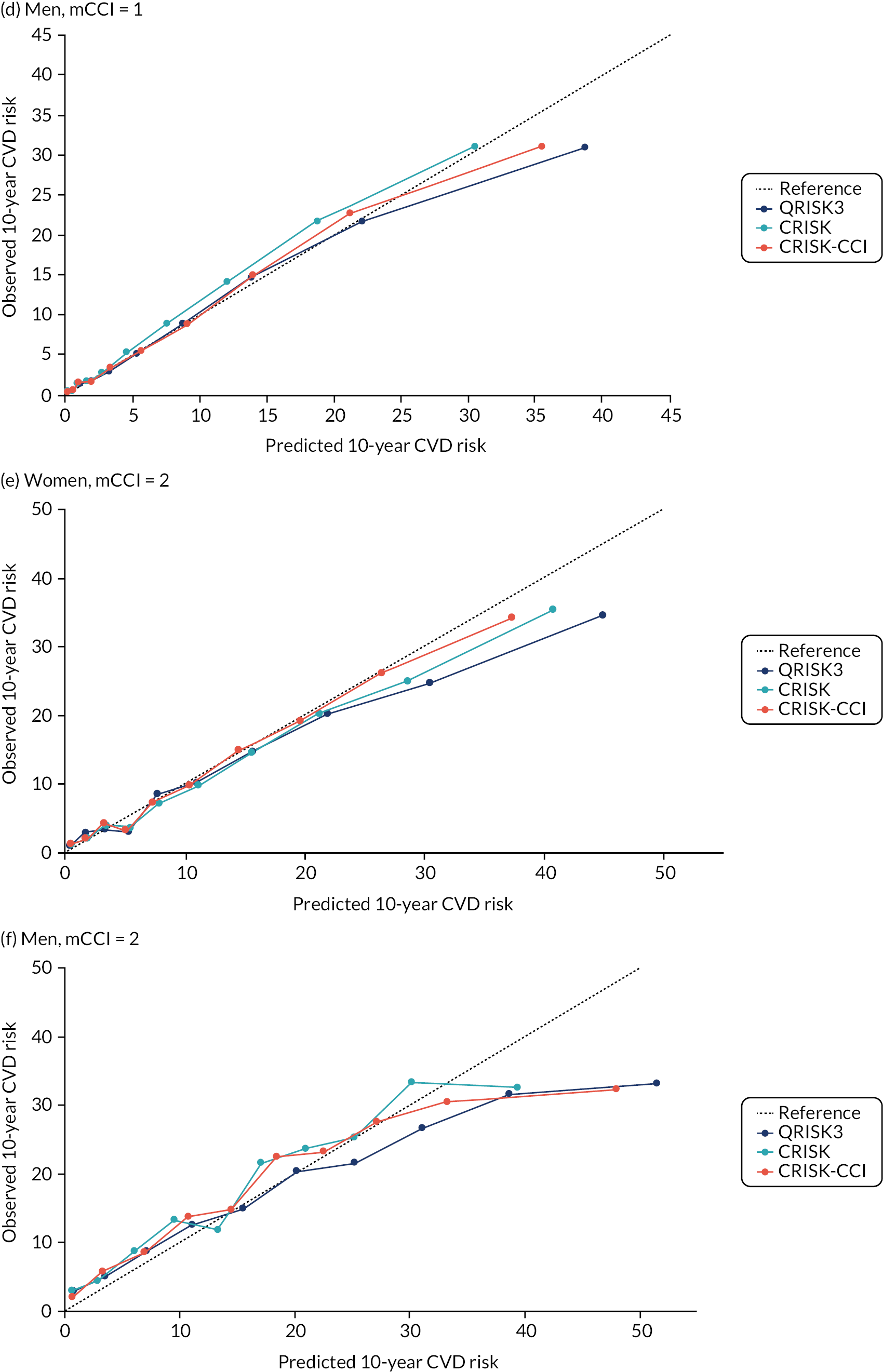
FIGURE 5.
Calibration of CRISK-CCI, CRISK and QRISK3 by mCCI group. (a) Women, mCCI = 0; (b) men, mCCI = 0; (c) women, mCCI = 1; (d) men, mCCI = 1; (e) women, mCCI = 2; (f) men, mCCI = 2; (g) women, mCCI ≥ 3; and (h) men, mCCI ≥ 3. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Ideal calibration lies on the reference line, below the line is overprediction and above the line is underprediction.
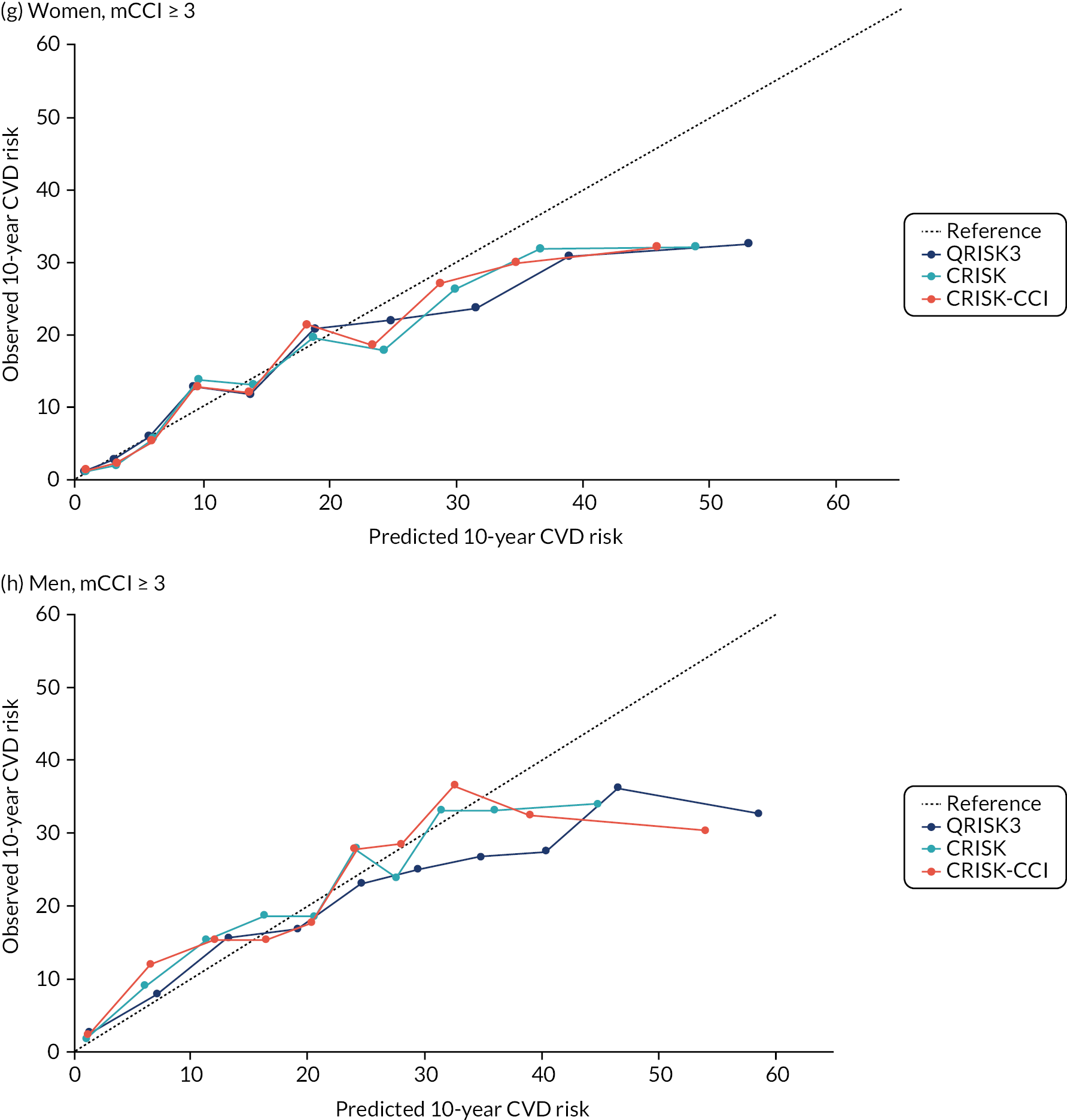
In the whole population of men, calibration using CRISK-CCI was better than calibration using CRISK, which showed some underprediction, whereas QRISK3 somewhat overpredicted CVD risk (see Figure 3). In younger men aged 25–44 years, there was some underprediction with CRISK and QRISK3, but calibration with CRISK-CCI was very good (see Figure 4). In middle-aged and older men, QRISK3 systematically overpredicted. CRISK-CCI was better calibrated in men aged 45–64 years, although CRISK-CCI was overpredicted at the highest decile of predicted risk. CRISK and CRISK-CCI had similar calibration in older men, although CRISK-CCI had greater overprediction at higher levels of predicted risk. In men with increasing CCI, QRISK3 was the least well calibrated, with overprediction in all strata. CRISK-CCI was best calibrated in people with low comorbidity (i.e. mCCI = 0 and mCCI = 1), but had greater overprediction at higher levels of predicted risk than CRISK (see Figure 5).
Summary
QRISK3 external validation
At the whole-population level, QRISK3 has excellent discrimination (which is the ability of the model to distinguish people at higher or lower risk). However, as is expected when examining discrimination in subsets of the modelled population defined by strong predictors of the outcome,72 discrimination was poor to moderate when stratified by age and additionally worse when stratified by level of comorbidity (which was not a predictor in the model). Calibration is the extent to which predicted and observed event rates are similar, and it was excellent in the whole population when ignoring competing mortality risks; however, there was systematic underprediction after competing risks were accounted for. Calibration was considerably worse in older people and in people with higher levels of comorbidity, where QRISK3 systematically overpredicted risk, particularly after competing mortality risks were accounted for.
In people with diabetes, discrimination was excellent in type 1 diabetes and moderate to good in type 2 diabetes. Similar to the whole population, calibration was good, with some overprediction when ignoring competing risks, but there was more consistent overprediction once competing risks were accounted for. Similar findings were found for people with CKD, but it is important to recognise that the populations studied exclude people with prior statin prescribing, which excludes substantial numbers of people with either condition (based on statin prescribing in the primary prevention population, 27.0% of women and 49.9% of men with type 1 diabetes, 45.4% of women and 40.1% of men with type 2 diabetes, and 30.5% of women and 24.4% of men with CKD defined by Read code were excluded).
The published external validation of QRISK2 found excellent discrimination and calibration at the whole-population level when ignoring competing mortality risk (i.e. answering the question ‘what is the risk of CVD assuming this person does not die of anything else in the next 10 years?’). 15 This study found similar, but additionally found overprediction and poor calibration in people aged 75–84 years, and moderate calibration in people aged 65–74 years and in people with the highest levels of comorbidity (mCCI = 3).
Once competing mortality risk was accounted for (i.e. answering the question ‘what is the risk of CVD allowing for the risk of death from something else first?’), then there was greater overprediction at the whole-population level, and particularly in older people and in people with more comorbidity. These findings are consistent with other studies examining the impact of competing risks on estimated CVD risk in people without CVD34,73,74 and with established CVD. 75
QRISK2 has also been shown to systematically overpredict CVD risk in a contemporary population of people with type 2 diabetes, with increasingly poor discrimination with increasing age76 and underprediction in a contemporary population of people with type 1 diabetes. 60 This highlights that good performance at the whole-population level does not necessarily mean good performance in important subgroups,72 and also that models derived in populations excluding prior statin prescribing are likely to be increasingly unrepresentative as statin prescribing increases.
CRISK and CRISK-CCI derivation and internal validation
The two new competing risk models derived (i.e. CRISK and CRISK-CCI) has similar excellent discrimination for CVD events as QRISK3. CRISK was better calibrated than QRISK3 (after accounting for competing mortality in derivation, but without adding any new predictors to the model) and CRISK-CCI was better calibrated again (after adding the mCCI as an additional predictor).
Two studies74,77 in people aged ≥ 65 years have examined the impact of competing mortality risk on CVD prediction. Like this study, the two studies74,77 also found only moderate discrimination of whole-population CVD risk prediction tools in older adults, and that newly derived competing risks models were generally better calibrated than models derived using standard Cox regression. 77 In a UK study35 evaluating a new competing risk model against the QRISK2, differences between predicted and observed CVD risk were greatest among people with highest predicted risk, as was found in this study.
Limitations
Limitations of this study are largely those that are found in all studies using routine GP data, including the original QRISK3 derivation. 20 First, there is considerable missing data for key predictors. As with QRISK3 derivation, we used multiple imputation for missing data, but the assumption that data are missing at random is a strong one because risk factors are likely to be better recorded in people at higher CVD risk. 35 This weakness is balanced against the use of more representative population data than is found in individually recruited research cohorts where data are more complete. Second, we used a more recent index date (1 January 2014) than QRISK3 (1 January 1998), which likely means that we exclude more people with prior statin prescribing. Deriving clinical prediction tools on increasingly historical data is likely biased because CVD incidence is falling,73 but using more recent data with greater rates of exclusion because of prior statin initiation may also be biased.
Chapter 3 External validation of QRISK-Lifetime
Background
Most cardiovascular risk prediction models use a medium-term time frame, most commonly 10 years. However, as age dominates cardiovascular risk, a potential problem of basing treatment on 10-year predicted risk is that younger people with very unfavourable risk factor profiles may not have high enough 10-year risk to be recommended for preventative treatment, even though in the longer-term their risk is very high. 27,78–80 International guidelines recommend consideration of lifetime risk in younger people alongside 10-year risk, although NICE does not. 10 The QRISK-Lifetime prediction tool was created in the same data set as QRISK2, and can be used as a standalone web-based tool81 as well as being the risk engine underlying the Joint British Societies’ risk calculator (JBS3)79 and Heart Age82 tools. Although lifetime tools are not currently recommended for CVD risk stratification by NICE,10 lifetime tools have been identified as a topic to examine further in a future guideline update. 13
Unlike QRISK2 and QRISK3, QRISK-Lifetime does account for competing mortality risk, which is further potential advantage. However, lifetime models are difficult to validate, as observational data sets only very rarely observe events over a lifetime (e.g. some analyses using the Framingham study have almost 40 years of follow-up83). The QRISK-Lifetime model, therefore, uses information about older people in the data set to predict what will happen to younger people in the future. There is, therefore, an assumption that observed risk in older people now will apply to younger people in several decades time, and this is a very strong assumption given the large declines in age-standardised incidence of CVD in high-income countries since the 1970s, and the unknown effect of changing risk factors more recently (with declines in smoking in high-income countries, but increases in obesity, type 2 diabetes and sedentary behaviour). Similar issues (e.g. very long follow-up) apply to data sets like the Framingham study, as, by definition, patients enter the cohort in the distant past. Given available UK data, external validation is, therefore, in practice only possible over shorter time horizons. For example, internal validation of QRISK-Lifetime in the original derivation study examined predictive performance over a 10-year time horizon and compared with QRISK2, which predicts over the same time horizon. 27 However, if tool performance is poorly calibrated in different age groups, then it is possible to infer performance over a lifetime. Although there have been studies of reclassification using QRISK-Lifetime-predicted lifetime risk compared with QRISK3 10-year predicted risk,78 to our knowledge there has not been an independent external validation.
This chapter reports findings in relation to objective 3 (i.e. to externally validate the QRISK-Lifetime risk prediction tool for primary prevention of CVD), examining discrimination and calibration over a 10-year time horizon and the characteristics of those reclassified as high risk using QRISK-Lifetime rather than QRISK3.
Methods
Data sources, outcome definition, other variable definitions and missing data
The same data set used for QRISK3 external validation was used (see Chapter 2, Methods), with the same variation in methods applying (i.e. a cohort entry date of 1 January 2004 vs. 1 January 1998 for QRISK-Lifetime, our implementation did not allow the use of future cholesterol values and Townsend deprivation scores were fitted as the median of vigintiles of Townsend score).
Analytical methods
The lifetime (i.e. to age 95 years) and 10-year risk of experiencing a cardiovascular event was calculated for each patient using publicly available QRISK-Lifetime 2011 software (under GNU Lesser General Public Licence version 3) without recalibration. As lifetime risk is not observed in the validation data set, the performance of the risk score was assessed by examining discrimination and calibration of the model using the same methods as for QRISK3 external validation (see Chapter 2, Methods) over a 10-year time horizon, as was carried out in the original derivation and internal validation study. 27 For both men and women, calibration was evaluated in the whole population and in prespecified subgroups of age and mCCI. Calibration refers to how closely predicted risk and observed probabilities agree at group level. As QRISK-Lifetime accounts for competing mortality risk, we evaluated calibration using only the Aalen–Johansen estimator of observed risk in censored survival data (i.e. an extension of the Kaplan–Meier estimator, which allows for competing events, non-CVD death in this case). 84
Clinical guideline recommendations for primary preventative treatment of CVD classify patients in relation to thresholds of predicted risk. In England and Wales, NICE-recommend treatment if 10-year predicted CVD risk is ≥ 10%. Consistent with the validation of QRISK-Lifetime over a 10-year time horizon, we examined changes in which patients were recommended for treatment based on either a QRISK3 or QRISK-Lifetime 10-year predicted risk of ≥ 10%.
However, there is no recommended threshold of lifetime risk at which to offer treatment,10 although NICE has signalled that consideration of lifetime risk models is of interest in any future guideline update. 13 Therefore, we additionally calculated the proportion of men and women recommended for treatment by QRISK3 at the 10% threshold, and used a cut-off point of QRISK-Lifetime-predicted lifetime risk above which exactly the same proportion of participants lay.
For both comparisons (i.e. QRISK3 and QRISK-Lifetime 10-year prediction > 10%; and QRISK3 prediction > 10% and matched number of participants with the highest lifetime predicted risk), we examined the characteristics of patients recommended for treatment, the observed risk of CVD at 10 years, and the number needed to treat (NNT) to prevent one new CVD event assuming all people recommended for treatment actually took a statin and with a relative risk reduction of 25% for new CVD events. All models were fitted in R and Stata.
Results 1: external validation of QRISK-Lifetime
There were 1,260,329 women and 1,223,265 men aged 30–84 years in the external validation data set, with a mean age of 49.3 years for women and 47.6 years for men (see Appendix 2, Table 31). Baseline characteristics were similar to QRISK-Lifetime internal validation, with the exception of the external validation data set having somewhat fewer people with a recorded family history of premature CVD and somewhat more people with treated hypertension and CKD.
Evaluated at 10 years’ follow-up, QRISK-Lifetime had excellent discrimination in the whole population of both women (Harrell’s c-statistic 0.844, 95% CI 0.841 to 0.847) and men (Harrell’s c-statistic 0.808, 95% CI 0.806 to 0.811), similar to the QRISK-Lifetime internal validation [area under the receiver operating curve (AUROC): women, 0.842; men, 0.828] (Table 3). 27 Explained variation in women was 53.3% compared with 45.5% in men. Stratified by age, discrimination varied from good in people aged 30–44 years (Harrell’s c-statistic: women, 0.714; men, 0.714) to poor in people aged 75–84 years (Harrell’s c-statistic: women, 0.578; men, 0.556), and explained variation progressively declined with age. Stratified by comorbidity, discrimination varied from excellent in people with low comorbidity (mCCI = 0 Harrell’s c-statistic: women, 0.844; men, 0.803) to moderate to good in people with high comorbidity (mCCI ≥ 3 Harrell’s c-statistic: women, 0.724; men, 0.656).
| Patient group | Women | Men | ||||
|---|---|---|---|---|---|---|
| Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | |
| All patients | 0.844 (0.841 to 0.847) | 2.19 (2.17 to 2.21) | 53.3 (52.9 to 53.7) | 0.808 (0.806 to 0.811) | 1.87 (1.85 to 1.89) | 45.5 (45.1 to 46.0) |
| Age group (years) | ||||||
| 30–44 | 0.714 (0.703 to 0.725) | 1.33 (1.26 to 1.39) | 29.6 (27.6 to 31.7) | 0.714 (0.706 to 0.722) | 1.24 (1.20 to 1.29) | 26.9 (25.6 to 28.3) |
| 45–64 | 0.692 (0.687 to 0.698) | 1.14 (1.10 to 1.17) | 23.5 (22.5 to 24.6) | 0.671 (0.667 to 0.675) | 0.97 (0.94 to 0.99) | 18.2 (17.4 to 19.1) |
| 65–74 | 0.631 (0.625 to 0.637) | 0.75 (0.71 to 0.79) | 11.8 (10.6 to 13.0) | 0.597 (0.591 to 0.603) | 0.54 (0.51 to 0.58) | 6.6 (5.8 to 7.3) |
| 75–84 | 0.578 (0.573 to 0.583) | 0.44 (0.40 to 0.49) | 4.5 (3.6 to 5.5) | 0.556 (0.549 to 0.562) | 0.32 (0.28 to 0.36) | 2.4 (1.9 to 3.0) |
| mCCI | ||||||
| 0 | 0.844 (0.840 to 0.848) | 2.19 (2.17 to 2.21) | 53.4 (52.8 to 53.9) | 0.803 (0.800 to 0.806) | 1.82 (1.80 to 1.84) | 44.1 (43.6 to 44.6) |
| 1 | 0.820 (0.814 to 0.826) | 1.95 (1.92 to 1.99) | 47.6 (46.7 to 48.5) | 0.798 (0.792 to 0.804) | 1.76 (1.72 to 1.80) | 42.4 (41.3 to 43.5) |
| 2 | 0.768 (0.758 to 0.779) | 1.54 (1.49 to 1.60) | 36.3 (34.6 to 37.9) | 0.701 (0.690 to 0.711) | 1.13 (1.07 to 1.19) | 23.4 (21.5 to 25.3) |
| ≥ 3 | 0.724 (0.708 to 0.740) | 1.29 (1.21 to 1.38) | 28.5 (25.8 to 31.2) | 0.656 (0.639 to 0.673) | 0.91 (0.82 to 0.99) | 16.4 (13.8 to 19.1) |
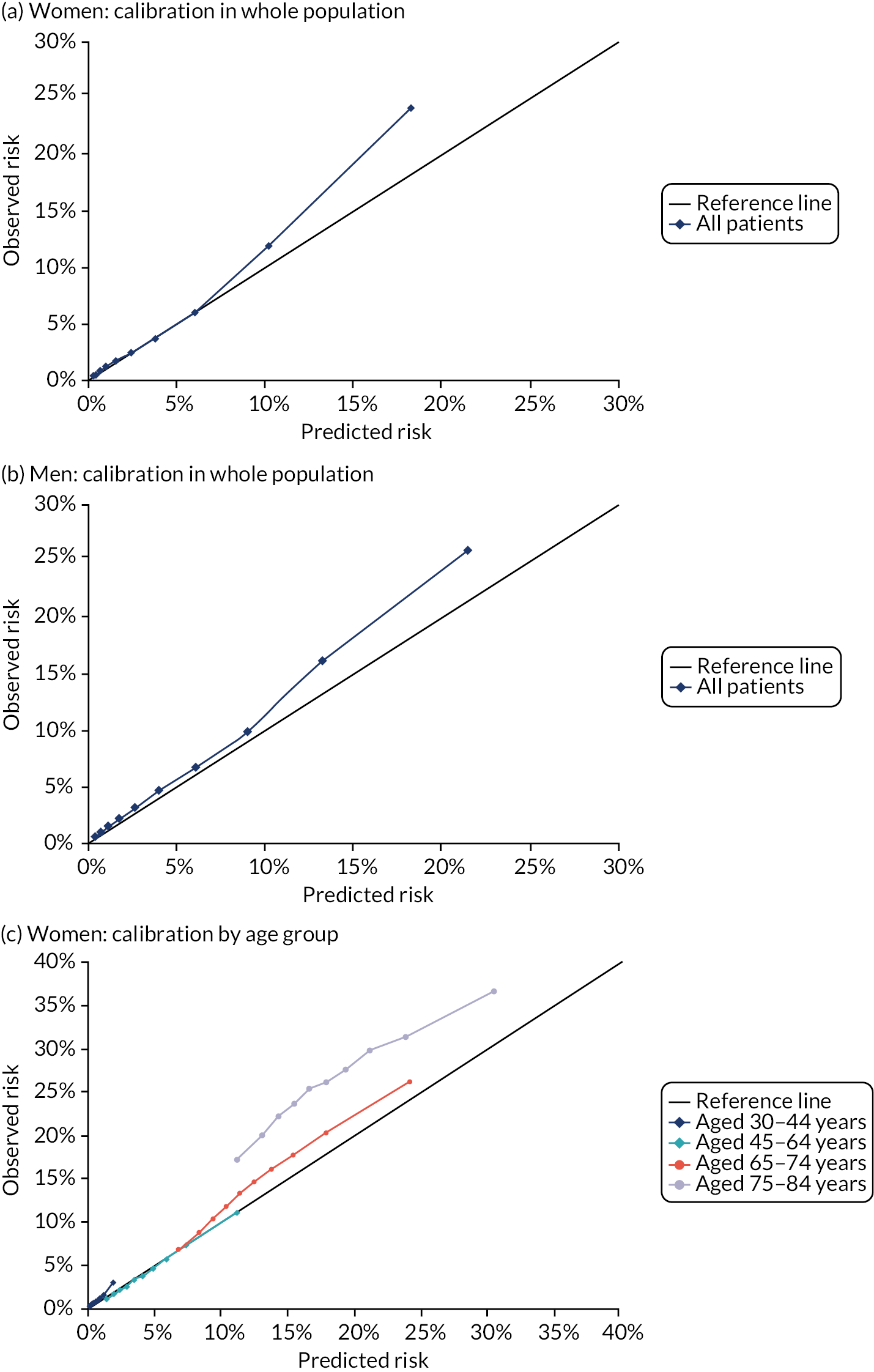
In the whole population, calibration was reasonable at lower levels of predicted risk for both men and women, but there was considerable overprediction at higher levels of predicted risk (Figure 6). Stratified by age, in both men and women, there was some underprediction in people aged 30–44 years, calibration was good in people aged 45–64 years and there was considerable underprediction in older people (see Figure 6). Stratified by comorbidity, in both men and women, there was underprediction at higher levels of predicted risk in people with low comorbidity (mCCI = 0) and consistent underprediction in people with higher comorbidity (see Figure 6).
FIGURE 6.
Calibration of QRISK-Lifetime in women and men (evaluated at 10 years): whole population and stratified by age group and CCI score. (a) Women: calibration in whole population; (b) men: calibration in whole population; (c) women: calibration by age group; (d) men: calibration by age group; (e) women: calibration by CCI; and (f) men: calibration by CCI. A prediction point/line above the reference line means that the risk score underpredicts and a predicted point/line below the reference line means that the risk score overpredicts. Source: Livingstone et al. 49

Results 2: reclassification of study participants by QRISK-Lifetime compared with QRISK3
Reclassification using QRISK-Lifetime constrained to 10-year versus QRISK3 10-year prediction
In the first reclassification analysis examining people with 10-year predicted CVD risk > 10% using QRISK-Lifetime and QRISK3, QRISK-Lifetime classified fewer people as eligible to be offered a statin than QRISK3 (Table 4). QRISK-Lifetime classified 194,411 (15.4%) women as high risk, compared with 239,396 (19.0%) women classified as high risk by QRISK3. QRISK-Lifetime classified 276,369 (22.6%) men as high risk, compared with 341,962 (28.0%) men classified as high risk by QRISK3. For women, 15.1% were classified as high risk by both tools, 3.9% were classified as high risk by QRISK3 only and 0.3% were classified as high risk by QRISK-Lifetime only, over 10 years. For men, 21.9% were classified as high risk by both tools, 6.1% were classified as high risk by QRISK3 only and 0.7% were classified as high risk by QRISK-Lifetime only, over 10 years.
| Women | Men | |||
|---|---|---|---|---|
| QRISK-Lifetime < 10% at 10 years | QRISK-Lifetime ≥ 10% at 10 years | QRISK-Lifetime < 10% at 10 years | QRISK-Lifetime ≥ 10% at 10 years | |
| QRISK-Lifetime < 32.9%a | QRISK-Lifetime ≥ 32.9%a | QRISK-Lifetime < 39.6%a | QRISK-Lifetime ≥ 39.6%a | |
| Based on 10-year risk prediction for both | ||||
| QRISK3 < 10% | 1,017,314 (80.7) | 3619 (0.3) | 872,474 (71.3) | 8829 (0.7) |
| QRISK3 ≥ 10% | 48,604 (3.9) | 190,792 (15.1) | 74,422 (6.1) | 267,540 (21.9) |
| Based on QRISK3 10-year risk prediction and QRISK-Lifetime lifetime risk (matched numbers of patients with QRISK3) | ||||
| QRISK3 < 10% | 847,786 (67.3) | 173,147 (13.7) | 647,949 (53.0) | 233,354 (19.1) |
| QRISK3 ≥ 10% | 173,147 (13.7) | 66,249 (5.3) | 233,354 (19.1) | 108,608 (8.9) |
Based on 10-year risk prediction, the characteristics of people classified as high risk by each tool were similar (Table 5). Fewer people were recommended for treatment by QRISK-Lifetime and there were fewer observed events in people recommended for treatment by QRISK-Lifetime (women, 25,461 vs. 28,373; men, 33,450 vs. 37,026), but the percentage of people experiencing an event was higher (women, 13.2% vs. 11.9%; men, 12.1% vs. 10.8%). Among people recommended for treatment with a statin, the estimated NNT from statin prescription to prevent one event was 30 and 34 in women, and 33 and 37 in men, for QRISK-Lifetime and QRISK3, respectively (see Table 5).
| Patient group | Number (%) recommended for treatment | Number (%) with a CVD event | NNTa | Mean (SD) age | Mean (SD) TC : HDL | Mean (SD) SBP (mmHg) | Mean (SD) BMI (kg/m2) | Treated HT, % (95% CI) | Current smoker, % (95% CI) | Family history of premature CVD, % (95% CI) | Minority ethnic background, % (95% CI) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Women | |||||||||||
| QRISK3 ≥ 10% predicted risk at 10 years | 239,396 (19.0) | 28,373 (11.9) | 34 | 71.3 (8.2) | 3.8 (0.8) | 143.9 (17.0) | 26.8 (4.5) | 31.9 (31.7 to 32.1) | 18.1 (17.9 to 18.2) | 6.3 (6.2 to 6.4) | 3.0 (2.9 to 3.1) |
| QRISK-Lifetime ≥ 10% predicted risk at 10 years | 194,411 (15.4) | 25,641 (13.2) | 30 | 73.3 (7.0) | 3.8 (0.8) | 145.0 (17.0) | 26.8 (4.4) | 36.2 (36.0 to 36.4) | 15.9 (15.7 to 16.0) | 7.8 (7.7 to 7.9) | 3.2 (3.1 to 3.2) |
| QRISK-Lifetime ≥ 32.9% predicted lifetime riskb | 239,396 (19.0) | 9652 (4.0) | 99 | 50.5 (12.6) | 4.0 (1.1) | 134.9 (20.0) | 28.9 (5.6) | 29.4 (29.2 to 29.6) | 21.3 (21.2 to 21.5) | 36.3 (36.2 to 36.5) | 20.8 (20.6 to 20.9) |
| Men | |||||||||||
| QRISK3 ≥ 10% predicted risk at 10 years | 341,962 (28.0) | 37,026 (10.8) | 37 | 63.8 (9.6) | 4.3 (0.9) | 140.2 (15.5) | 27.1 (3.7) | 19.6 (19.5 to 19.8) | 26.1 (26.0 to 26.2) | 7.2 (7.1 to 7.2) | 3.2 (3.1 to 3.2) |
| QRISK-Lifetime ≥ 10% predicted risk at 10 years | 276,369 (22.6) | 33,450 (12.1) | 33 | 66.2 (8.5) | 4.3 (0.9) | 140.8 (15.6) | 27.1 (3.7) | 22.3 (22.2 to 22.5) | 23.4 (23.2 to 23.6) | 8.3 (8.2 to 8.4) | 3.3 (3.3 to 3.4) |
| QRISK-Lifetime ≥ 32.9% predicted lifetime riskb | 341,962 (28.0) | 14,725 (4.3) | 100 | 46.3 (10.4) | 4.9 (0.9) | 135.7 (15.2) | 29.1 (4.1) | 15.0 (14.9 to 15.2) | 26.4 (26.2 to 26.5) | 20.0 (19.9 to 20.2) | 13.1 (13.0 to 13.2) |
Reclassification using QRISK-Lifetime lifetime risk versus QRISK3 10-year prediction
By design, the comparison with QRISK-Lifetime predicting to age 95 years (i.e. lifetime risk) was constrained to include 19.0% of women and 28.0% of men at the highest predicted lifetime risk (i.e. the same proportion of people identified as high risk based on QRISK3 10-year prediction) (see Table 4). Only 5.3% of women were identified as high risk by both QRISK3 and QRISK-Lifetime predicting to age 95 years, with a different 13.7% of women identified as high risk by one or other of the prediction tools. For men, 8.9% were identified as high risk by both prediction tools and a different 19.1% of men by one or other of the tools.
Compared with people identified as high risk by QRISK3 10-year prediction, people with the highest predicted lifetime risk were much younger, had a lower mean SBP and had a somewhat higher mean TC : HDL and BMI. In addition, a lower proportion of people with the highest predicted lifetime risk had treated hypertension and a much higher proportion had a family history of premature CVD and were from a minority ethnic background (see Table 5). Compared with people recommended for treatment based on 10-year predicted risk, there were fewer CVD events observed in people at the highest predicted lifetime risk [women, 9652 (4.0%) vs. 28,373 (11.9%); men, 14,725 (4.3%) vs. 37,026 (10.8%)]. For QRISK-Lifetime predicting to age 95 years, the estimated NNT to prevent one CVD event from statin treatment was 99 and 100 in women and men, respectively, compared with 34 and 37 in women and men, respectively, among those with > 10% 10-year QRISK3-predicted risk (see Table 5).
Summary
QRISK-Lifetime external validation
It is essentially impossible to validate lifetime risk models because lifetime follow-up of observed events either is not available or would be so historical that it would be a poor guide to performance of the model in a contemporary population. 60,85 Similar to the original internal validation,27 we evaluated QRISK-Lifetime over a 10-year prediction horizon. Within this constraint, QRISK-Lifetime had excellent discrimination in the whole population; however, as with QRISK3, discrimination was poor to moderate within the age strata, and moderate within the comorbidity strata. Calibration plots showed some underprediction in the whole population, with large underprediction in older people and people with multimorbidity at higher levels of predicted risk.
Comparing people recommended for treatment at a 10-year 10% risk threshold, QRISK-Lifetime (predicting over 10 years) recommended fewer people for statin treatment (i.e. 15.4% of women and 22.6% of men) than QRISK3 (i.e. 19.0% of women and 28.0% of men), although the people recommended experienced slightly more CVD events and the estimated NNT to prevent one CVD event was slightly lower for QRISK-Lifetime. Characteristics of people recommended for treatment over a 10-year prediction horizon were broadly similar.
Comparing people recommended for treatment by QRISK3-predicted 10-year risk ≥ 10% compared with the same proportion at highest estimated lifetime risk by QRISK-Lifetime, there was only a small overlap between the populations at highest predicted risk by the different tools. By design, each tool ‘recommended’ 19.0% of women and 28.0% of men for treatment. Only 5.3% of women and 8.9% of men were recommended for treatment by both tools, and the people recommended for treatment were considerably different, as other studies have found. 27,78 People with highest predicted lifetime risk were considerably younger, were more likely to have a family history of premature CVD and were more likely to be from a minority ethnic background. Over 10 years, people with highest predicted lifetime risk experienced many fewer CVD events (as expected given age differences), with people at highest predicted lifetime risk having an estimated NNT (with a statin to prevent one CVD event) approximately three times larger than for people recommended for treatment by QRISK3 (in women, QRISK-Lifetime highest risk NNT = 99 vs. QRISK3 risk > 10% NNT = 34; in men, QRISK-Lifetime highest risk NNT = 100 vs. QRISK3 risk > 10% NNT = 37). There is, therefore, a considerable leap of faith involved in treating based on lifetime risk, as the medium-term (10-year) benefit is considerably lower.
Limitations
This study has the same limitations as those already described in Chapter 2, Limitations, for any routine data study, but two particular limitations specifically apply. First, as with previous studies,35,67 we used multiple imputation, but the assumption that data are missing at random may be incorrect, and this is probably more likely to apply in younger people (i.e. the key target population for lifetime CVD risk prediction), as CVD risk assessment (particularly measurement of cholesterol) is likely to be carried out in people who are already suspected to be high risk. 35 Second, evaluating lifetime risk in a study with relatively short follow-up is intrinsically problematic. In this study, median follow-up of study participants was 5.7 years (interquartile range 2.2–10.2) years in women and 5.2 (interquartile range 2.0–9.3) years in men. The QRISK-Lifetime derivation paper does not state follow-up time,27 but follow-up time in this study is similar to follow-up in QRISK2 derivation, which uses a similar data set to QRISK-Lifetime. 86 Lifetime risk is, therefore, being estimated and evaluated from relatively short periods of observation. However, lifetime risk is estimated by assuming that future risk beyond the period of observation will be the same as that observed for older people during the period of observation. As QRISK-Lifetime systematically underpredicts CVD risk over the period of observation, then lifetime estimates must also underpredict. More generally, however, it is a very strong assumption that age-specific CVD incidence will be stable over the next few decades, given falling CVD incidence over the last few decades and large increases in obesity, sedentary behaviour and diabetes in the last two decades.
Chapter 4 Fracture risk prediction: external validation of QFracture-2012 and derivation and internal validation of a new competing risk model (CFracture)
Background
In older people, fragility or low-impact fractures are a common cause of morbidity, disability and (for fractured neck of femur) death. Osteoporosis and osteopenia are an important driver of this fracture risk, and guidelines internationally recommend treatment with bisphosphonates for people at high risk of fracture. 12,87–89 In the UK, guidelines recommend using a fracture risk prediction tool in older people and in middle-aged people who have risk factors for fracture, with bone mineral density measurement reserved for further risk stratification in people at intermediate risk. 87,89 In the USA, guidelines recommend similar risk stratification for middle-aged people, but additional routine use of bone mineral density measurement in older people. 90
There have been a number of fracture risk prediction tools created, and three tools (i.e. QFracture-2012, FRAX and the Garvan Fracture Risk Calculator) have been subject to substantial external validation,91,92 although for FRAX this is limited by the prediction equation not being published. 93 The first version of QFracture-201217 was externally validated by the developers19 and independently externally validated in a different UK GP data set,18 and it was found to have excellent discrimination and calibration. The QFracture-2012 algorithm has been externally validated in an Israeli data set,92 which found excellent discrimination but poor calibration with systematic underprediction of fracture risk. At the time the research was done, the QFracture-2016 algorithm had not been published, and it has not yet been externally validated in a general primary care population94 FRAX has been more extensively validated; however, the underlying algorithm has never been published and so most validation is by the developers. Across all studies, FRAX discrimination appears good, but calibration is rarely assessed. 22,91 FRAX was validated in the same Israeli study92 that examined QFracture-2012 performance, but using relatively crude categorisation of FRAX predicted risk, which was all that could be estimated given lack of access to the underlying full algorithm. Like QFracture-2012, this study92 found evidence of considerable underprediction of risk by FRAX. One reason for the difference in calibration observed between the UK and Israeli external validations may be in the definition of fracture, with QFracture-2012 derivation and the UK external validation being based on fractures recorded in GP electronic health record and death certificate data, whereas the Israeli study also included fractures recorded in hospital data (and is, therefore, more likely to be complete).
In the UK, NICE recommends the use of either QFracture-2012 or FRAX, but acknowledges that the two tools can give very different estimates for individuals,12,87 with FRAX overpredicting fracture risk when fracture ascertainment used the same method as QFracture-2012 derivation. 17,87,95 Two possible reasons for the differences are (1) FRAX accounting for competing mortality risk, whereas QFracture-2012 does not (therefore, QFracture-2012 would be expected to have generally higher predicted risk than FRAX as a result) and (2) differences in how fractures were measured in the derivation of each prediction tool (QFracture-2012 fractures are ascertained using codes in GP records and mortality data,26 whereas FRAX fractures are ascertained by self-report and hospital records28).
Overestimation of fracture risk by not accounting for competing risk is, in principle, more likely for QFracture-2012 than for QRISK3 because QFracture-2012 predictions are made for people aged up to 99 years, compared with 84 years for QRISK3, and because fracture is a much less common cause of death than CVD (and, therefore, a larger number of deaths are a competing risk rather than a predicted event). 67,96,97 This chapter reports findings for fracture risk prediction models in relation to objectives 1 and 2, as follows:
-
To externally validate the recommended risk prediction tools for primary prevention of CVD (QRISK3), including performance in important subgroups, and for osteoporotic fracture (QFracture-2012).
-
To derive and internally validate new-incident CVD (and osteoporotic fracture) risk prediction models, accounting for competing risks of death, and compare performance with existing risk prediction models.
Methods
Data sources
We used the same data from CPRD GOLD as for the CVD risk modelling. 66 These data are similar to data in the QFracture-2012 derivation data set in terms of their inclusion of linked primary care and mortality data, but the CPRD GOLD data used also has linked hospital admission data, which we used for fracture ascertainment.
Identical to QRISK3 derivation and internal validation, patients were eligible for inclusion if they:
-
were permanently registered with a general practice, contributing up-to-standard data for at least 1 year and with consent to link GP data to hospital discharge (HES admitted patient care) and mortality (ONS mortality registration) data
-
were aged ≥ 30 years and < 100 years.
Cohort entry was defined as the latest date of an individual’s date of registration plus 1 year, the individual’s 30th birthday or 1 January 2004. Cohort exit was defined as the earliest of:
-
the first MOF or first hip fracture (two distinct outcomes are modelled)
-
deregistration from their participating general practice
-
date of last data collection from their participating general practice
-
end-of-study follow-up on 31 March 2016.
All outcomes and predictors are recorded blind to the study hypothesis because they are recorded as part of routine clinical care.
Sample size
The sample size is fixed by the size of the CPRD GOLD data set. No formal power calculation was, therefore, carried out, as the calculation could not alter study design and the available sample size was considered more than sufficient for the purpose. 54
Outcome definition
QFracture-2012 has separate models to predict two outcomes (i.e. MOF and hip fracture)26 and both models were validated. In this study, MOF was defined as hip, vertebral, wrist, proximal humeral or osteoporotic fractures leading to hospital admission ascertained from codes in the GP electronic health record (using Read codes), HES discharge diagnoses (ICD-10 codes) or ONS death registration (ICD-10 codes). QFracture-2012 does not publish lists of Read codes used to define these outcomes and, therefore, we used published codesets where available98 and otherwise derived our own (see Appendix 3, Tables 32 and 33).
Other variable definitions
We implemented the published QFracture-2012 risk model (under GNU Lesser General Public Licence version 3) and calculated QFracture-2012-predicted 10-year risk of a MOF and the risk of a hip fracture for all patients in our cohort. As with fracture outcomes, we derived codesets for each predictor (see Appendix 3, Tables 34–36), which were based on published codesets where available. 98
There were two differences in our implementation from QFracture-2012 derivation. First, in our data set, Townsend deprivation score was available as vigintiles (twentieths) only, rather than as raw values (to minimise disclosure), and so for this variable we fitted the median Townsend score of each vigintile (as with the CVD models described previously). Second, QFracture-2012 allowed values such as BMI recorded after the date of study entry but before any fracture outcome to be used in prediction, whereas in this analysis we restricted predictor values to those recorded before study entry to avoid using future information in prediction.
In addition to QFracture-2012, we calculated the CCI for each patient at baseline based on primary care Read codes. As with the CVD models, CCI was used only to stratify the analysis of discrimination and calibration by level of comorbidity (i.e. CCI score grouped into 0, 1, 2 and ≥ 3).
Missing data
The extent and management of missing data are detailed in Appendix 4, Table 37. As with QFracture-2012 derivation, patients with missing Townsend deprivation score were excluded from the cohort and patients with missing ethnicity were assumed to be white. For missing BMI, smoking status and alcohol status, multivariate imputation via chained equations68 was used to generate five imputed data sets. These data sets were then combined using Rubin’s rules69 to give summary point estimates, with confidence limits reflecting the uncertainty associated with imputing missing values. Reflecting that morbidity and prescribing recording in CPRD is generally good, and consistent with QFracture-2012 derivation, morbidities and prescribing variables used in the prediction score were assumed to be absent if not recorded. 66,99
Analytical methods: external validation
The performance of the QFracture-2012 risk score was assessed by examining discrimination and calibration in the same way as for the QRISK3 external validation (see Chapter 2, Methods). Discrimination was primarily evaluated using the truncated version of Harrell’s c-statistic to include only pairs where the earliest survival time is no later than 10 years after entry. A c-statistic of 0.5 indicates discrimination no better than chance, whereas a c-statistic of 1 indicates perfect discrimination. Evaluating how good discrimination is for values between 0.5 and 1 is arbitrary and involves judgement. We considered c-statistic values of 0.5–0.599 poor, values of 0.6–0.699 moderate, values of 0.7–0.799 good and values ≥ 0.8 excellent. In addition, we calculated the D-statistic of Royston and Sauerbrei (where higher values indicate better discrimination, and a difference of ≥ 0.1 is suggested as indicating meaningfully different discrimination)70 and a related R2-statistic appropriate for estimating explained variation for censored survival data. 71 Calibration was assessed for 10 equal-sized groups (deciles) of participants ranked by predicted risk, by plotting observed proportions versus predicted probabilities. Plots were generated separately by sex for all patients and for subgroups of age and CCI based on summary statistics pooled across the imputed data sets. When examining calibration, we estimated observed risk for censored data in two ways: (1) using the standard Kaplan–Meier estimator (which is consistent with the assumptions made in QFracture-2012 derivation in that it ignores competing risks) and (2) using the Aalen–Johansen estimator (an extension to allow for competing events, non-fracture death in this case). 84 All models were fitted in R and Stata.
Analytical methods: competing risk model derivation and internal validation
Competing risk model derivation and internal validation was carried out in the same data set as QFracture-2012 external validation. For this purpose, participants were randomly allocated to distinct derivation and test data sets in a 2 : 1 ratio, with allocation balanced in terms of age and final event status. The derivation data set was used to derive CFracture, a Fine–Gray model to predict the 10-year risk of experiencing a CVD event, accounting for the competing risk of non-CVD death. Separate models were estimated for men and women. Reflecting the overall aim of the project where we wished to explicitly compare prediction in models accounting for competing risk compared with ignoring competing risk, we included all the same main effects (predictors) and age interactions as QFracture-2012 modified, as follows. we accounted for non-fracture death as a second (competing) outcome using the Fine–Gray model and we additionally included the CCI score in the model (categorised as 0, 1, 2 or ≥ 3), as CCI is a well-validated predictor of total mortality. 12 Fine–Gray models allow the cumulative incidence function or probability of a CVD event occurring over time to be directly predicted, but the subdistribution HRs in the Fine–Gray models do not have a straightforward interpretation, as they describe the direction but not the magnitude of the effect of predictors on the cumulative incidence function. The use of fractional polynomials and the inclusion of complex interactions with age further complicate direct interpretation of model coefficients. Model coefficients are, therefore, not straightforwardly interpretable, but the derived model is provided in Appendix 4, Tables 38–41, to allow replication.
The performance of CFracture and QFracture-2012 was evaluated in the independent validation data set by examining discrimination and calibration, as described above. R 4.0.0 was used for all analyses.
Results 1: external validation of QFracture-2012 for major osteoporotic fracture
There were 2,747,409 women and 2,684,730 men included in the external validation data set, with a mean age of 50.7 years in women and 48.5 years in men (vs. 50 years in the QFracture-2012 internal validation cohort26) (see Appendix 4, Table 42). Compared with the QFracture-2012 internal validation cohort, there were more people with a history of MOF at baseline (5.5% of women and 4.2% of men, vs. 1.8% of all participants in QFracture-2012), type 2 diabetes (3.0% of women and 3.7% of men vs. 2.7% of all participants in QFracture-2012), history of falls (5.6% of women and 2.8% of men vs. 1.1% of all participants in QFracture-2012), cancer (3.4% of women and 2.5% of men vs. 1.8% of all participants in QFracture-2012), asthma or chronic obstructive pulmonary disease (12.9% of women and 11.3% of men vs. 7.1% of all participants in QFracture-2012) and chronic renal disease (1.2% of women and 0.9% of men vs. 0.2% of all participants in QFracture-2012). Compared with the QFracture-2012 internal validation cohort, there was a higher proportion of missing data for BMI and smoking status, but fewer missing data for ethnicity. Fracture rates rose steadily with age; however, competing mortality rates rose faster, and in patients aged 90–99 years mortality rates were between five (women) and 10 (men) times the MOF rate (see Appendix 4, Figure 32).
In women, during 15,624,543 years of follow-up, there were 95,598 incident cases of MOF observed [6.12 (95% CI 6.08 to 6.16) cases per 1000 person-years]. In men, during 15,179,623 years of follow-up, there were 34,321 incident cases of MOF [2.26 (95% CI 2.24 to 2.29) cases per 1000 person-years]. Compared with the previous QFracture-2012 external validation,18 our observed crude incidence of MOF was substantially higher (women, 6.12/1000 person-years vs. 2.93; men, 2.26/1000 person-years vs. 0.98) (see Appendix 4, Table 43). However, the previous study was restricted to patients aged 30–84 years, and differences were smaller but still substantial. Restricting incidence estimation in this study to this population resulted in 5.33 cases per 1000 person-years for women (vs. 2.08) and 226 cases per 1000 person-years for men (vs. 0.98).
To explore the effect of including hospital ascertainment of fracture using HES admitted patient care, we also estimated fracture rates using only GP and mortality data (as was carried out in QFracture-2012 derivation and validation),18,26 and this accounted for only a minority of the additional observed MOFs in this study (see Appendix 4, Figure 33).
Discrimination of QFracture-2012 for MOF in the whole external validation population was excellent in women (with a Harrell’s c-statistic of 0.813 vs. an AUROC of 0.790 in QFracture-2012 internal validation) and good in men (with a Harrell’s c-statistic of 0.738 vs. an AUROC of 0.711 in QFracture-2012 internal validation) (Table 6). The D-statistic was 2.25 in women and 1.76 in men, similar but somewhat better than in QFracture-2012 internal validation (2.13 and 1.61, respectively). The model explained 54.8% of variation in outcome in women and 42.4% of variation in outcome in men, compared with 51.9% and 38.2%, respectively, in QFracture-2012 internal validation. Stratified by age, discrimination in women was good (Harrell’s c-statistic 0.756 for women aged 85–99 years) to moderate (Harrell’s c-statistic 0.709 for women aged 30–64 years), and moderate in all ages in men. Explained variation was lower in all strata and low in those aged 85–99 years (women, 3.4%; men, 9.6%). Stratified by CCI, discrimination was good at all levels of comorbidity.
| Patient group | Women | Men | ||||
|---|---|---|---|---|---|---|
| Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | |
| All patients | 0.813 (0.811 to 0.815) | 2.25 (2.24 to 2.27) | 54.8 (54.5 to 55.1) | 0.738 (0.735 to 0.741) | 1.76 (1.74 to 1.78) | 42.4 (41.9 to 43.0) |
| Age group (years) | ||||||
| 30–64 | 0.709 (0.706 to 0.712) | 1.30 (1.28 to 1.32) | 28.8 (28.2 to 29.4) | 0.625 (0.621 to 0.630) | 0.84 (0.81 to 0.86) | 14.4 (13.6 to 15.1) |
| 65–74 | 0.616 (0.612 to 0.620) | 0.71 (0.69 to 0.73) | 10.7 (10.1 to 11.4) | 0.660 (0.653 to 0.668) | 1.00 (0.95 to 1.04) | 19.2 (17.9 to 20.6) |
| 75–84 | 0.615 (0.612 to 0.619) | 0.67 (0.65 to 0.69) | 9.6 (9.1 to 10.2) | 0.652 (0.645 to 0.659) | 0.91 (0.87 to 0.95) | 16.4 (15.2 to 17.6) |
| 85–99 | 0.576 (0.570 to 0.581) | 0.38 (0.35 to 0.42) | 3.4 (2.9 to 4.0) | 0.624 (0.613 to 0.636) | 0.67 (0.60 to 0.73) | 9.6 (8.0 to 11.3) |
| mCCI | ||||||
| 0 | 0.795 (0.793 to 0.798) | 2.08 (2.06 to 2.10) | 50.8 (50.4 to 51.2) | 0.668 (0.664 to 0.673) | 1.22 (1.20 to 1.25) | 26.3 (25.4 to 27.1) |
| 1 | 0.801 (0.797 to 0.805) | 2.08 (2.05 to 2.10) | 50.7 (50.1 to 51.4) | 0.730 (0.723 to 0.737) | 1.64 (1.59 to 1.68) | 39.0 (37.7 to 40.2) |
| 2 | 0.747 (0.742 to 0.753) | 1.60 (1.56 to 1.63) | 37.8 (36.9 to 38.8) | 0.727 (0.719 to 0.736) | 1.54 (1.49 to 1.60) | 36.3 (34.6 to 37.9) |
| ≥ 3 | 0.712 (0.706 to 0.718) | 1.30 (1.26 to 1.33) | 28.7 (27.5 to 29.8) | 0.724 (0.715 to 0.733) | 1.46 (1.40 to 1.51) | 33.7 (32.0 to 35.4) |
Ignoring competing mortality risk in the estimation of observed risk of MOF (Figures 7 and 8, parts a, c and e), there was underprediction at all levels of predicted risk for both men and women, which was larger at higher levels of predicted risk (see Figures 7 and 8, part a). Stratified by age, there was underprediction in all age groups. Underprediction was larger in older people, although there was overprediction in 85- to 99-year-olds at highest levels of predicted risk (see Figures 7 and 8, part b). Stratified by CCI, there was underprediction at all levels of comorbidity. Underprediction was largest in people with a CCI score ≥ 3, although there was overprediction at the highest levels of predicted risk (see Figures 7 and 8, part c).
FIGURE 7.
Calibration for MOF in women without accounting for competing risks and accounting for competing risks. (a) Overall calibration not accounting for competing risks;a (b) overall calibration accounting for competing risks;b (c) calibration by age group not accounting for competing risks;a (d) calibration by age group accounting for competing risks;b (e) calibration by CCI not accounting for competing risks;a and (f) calibration by CCI accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. A coloured line (i.e. observed risk) above the matching black line (i.e. predicted risk) indicates underprediction. A coloured line (i.e. observed risk) below the matching black line (i.e. predicted risk) indicates overprediction. Source: Livingstone et al. 50
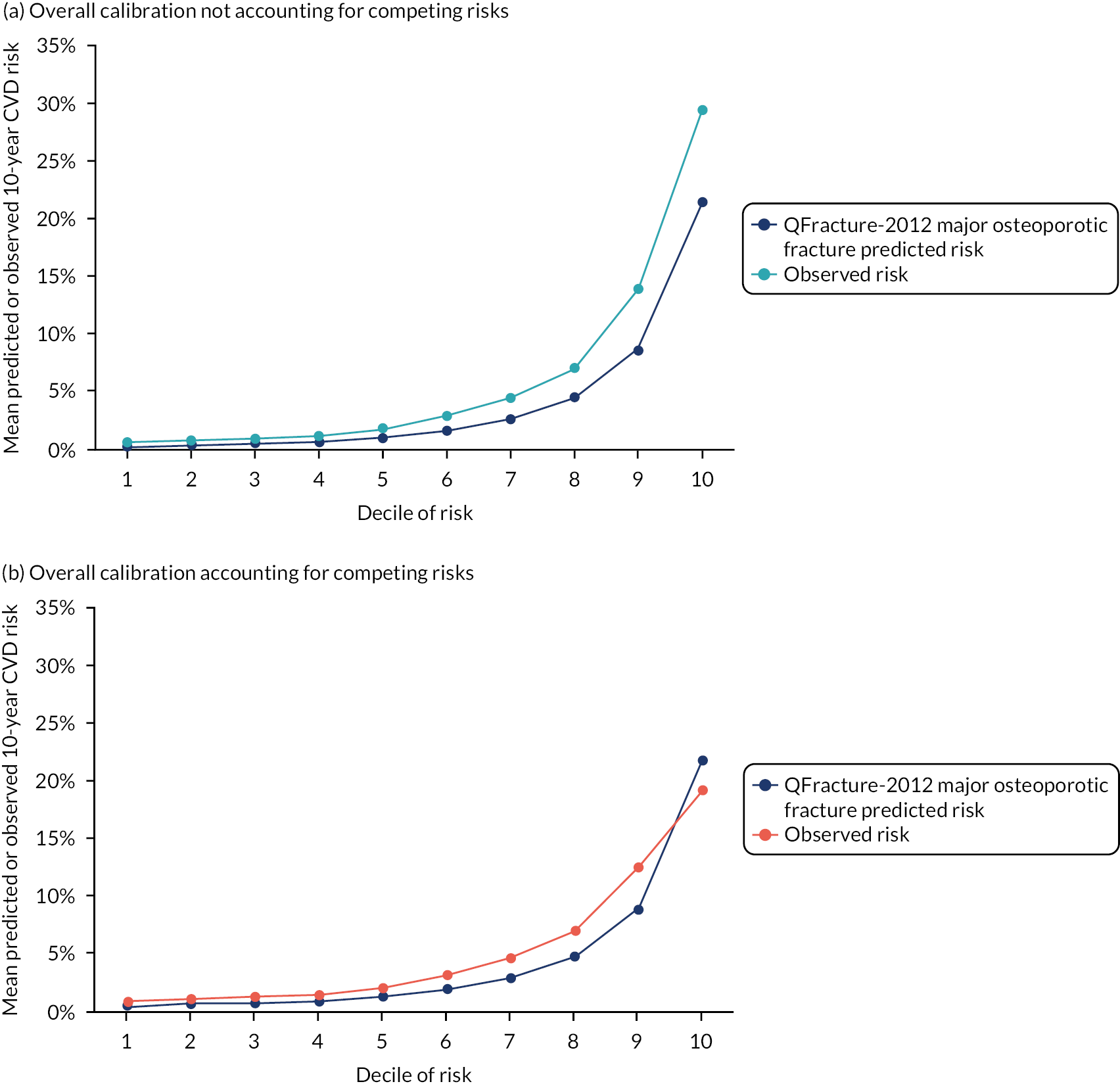
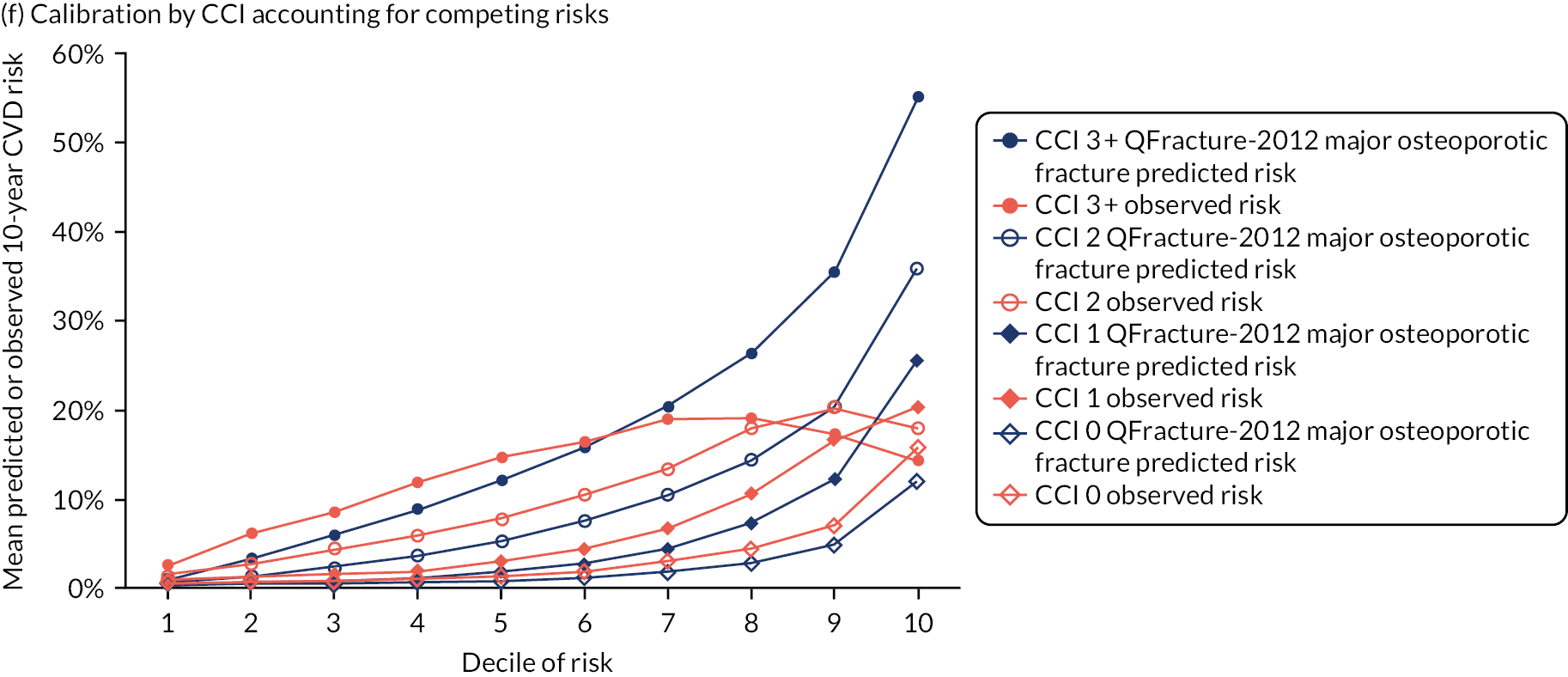
FIGURE 8.
Calibration for MOF in men without accounting for competing risks and accounting for competing risks. (a) Overall calibration not accounting for competing risks;a (b) overall calibration accounting for competing risks;b (c) calibration by age group not accounting for competing risks;a (d) calibration by age group accounting for competing risks;b (e) calibration by CCI not accounting for competing risks;a and (f) calibration by CCI accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. A coloured line (i.e. observed risk) below the matching black line (i.e. predicted risk) indicates overprediction. Source: Livingstone et al. 50
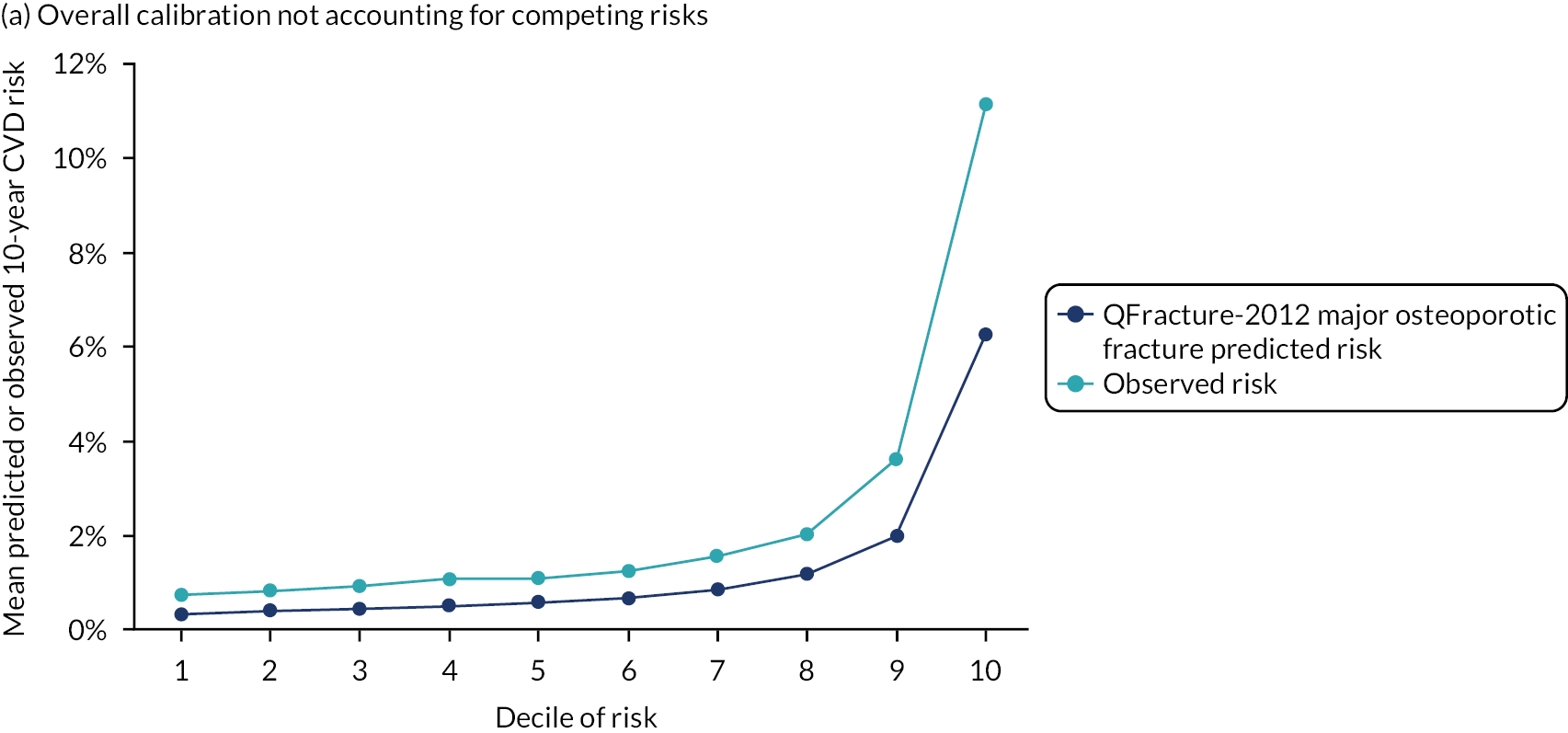
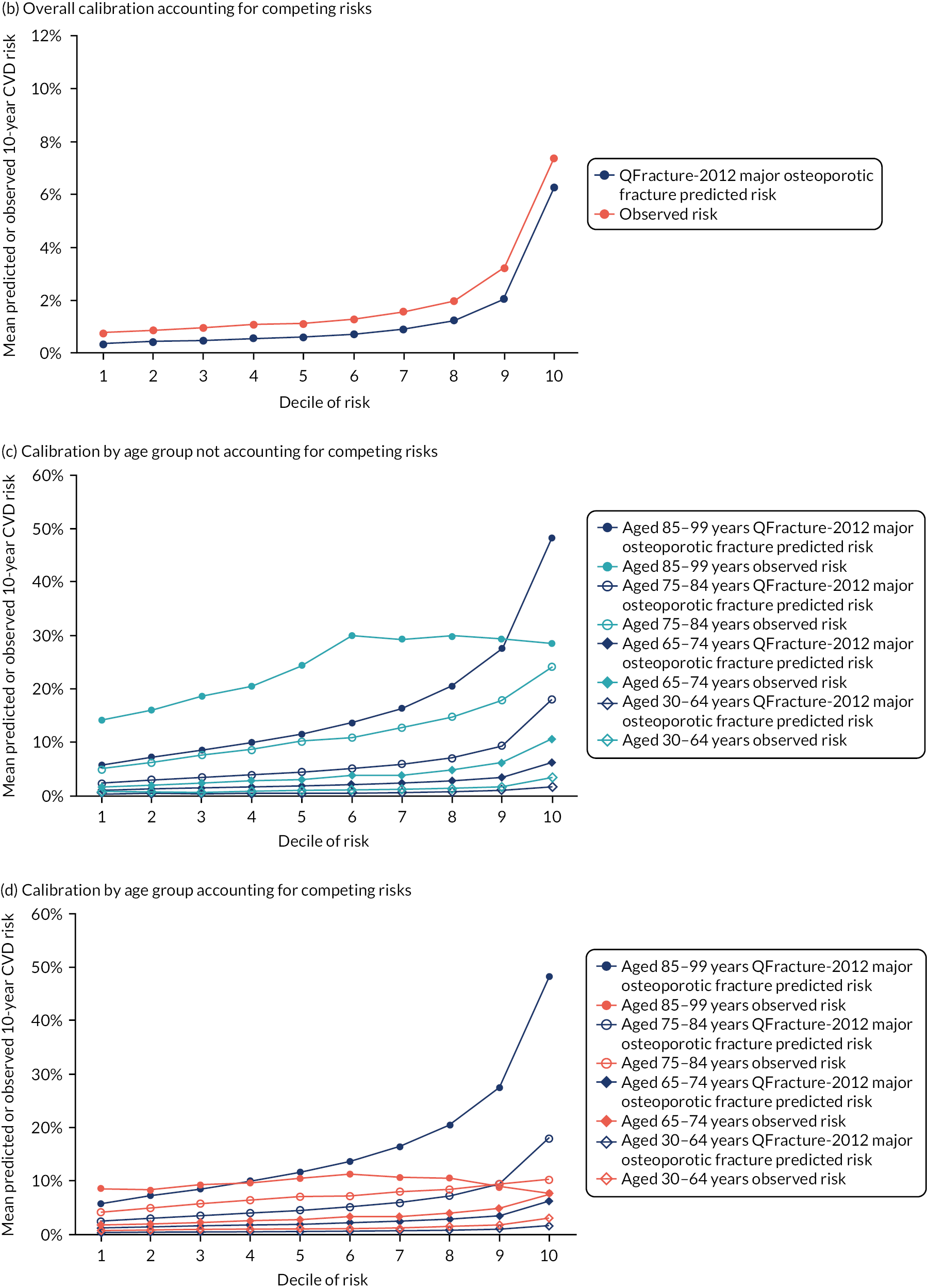
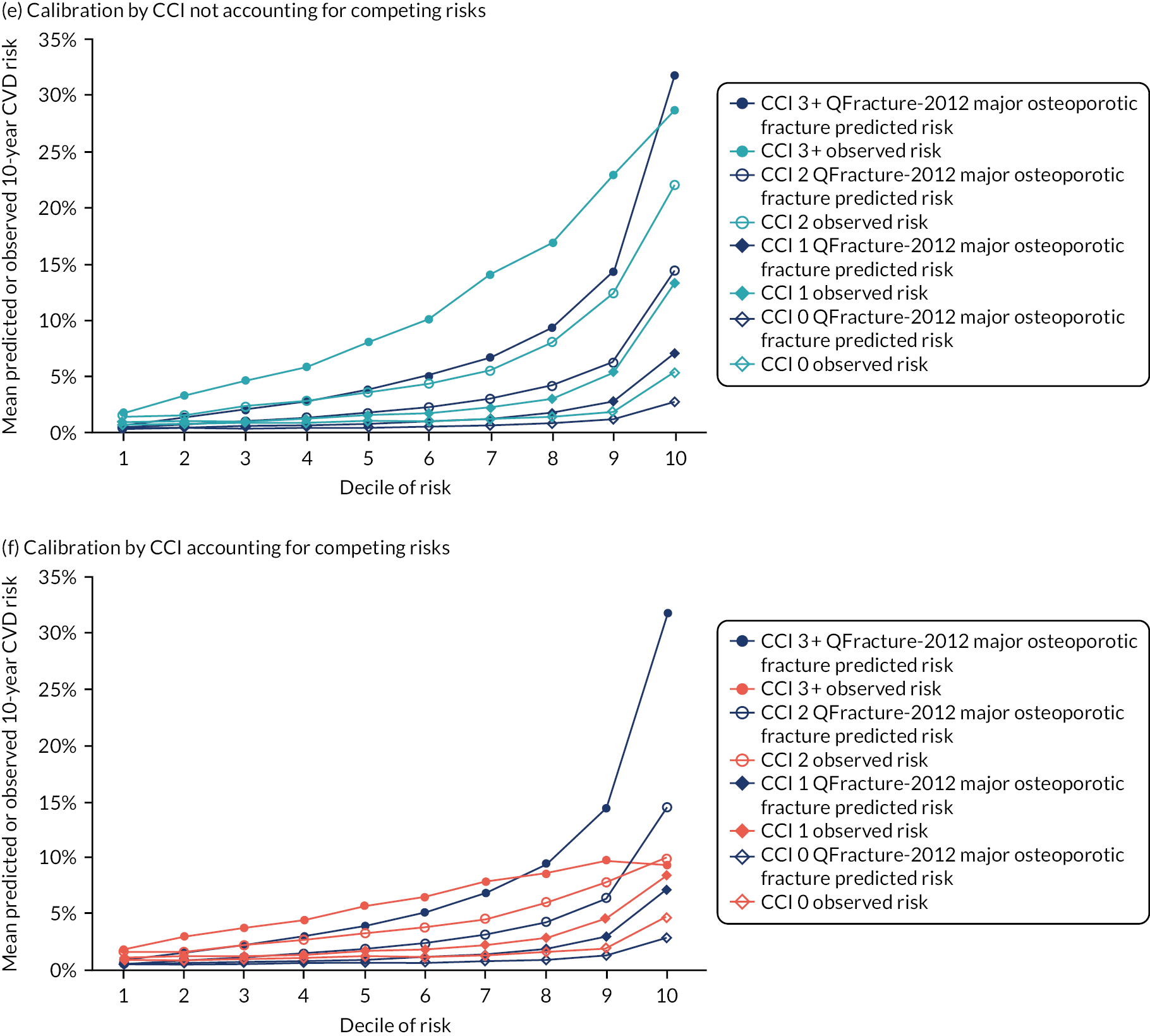
Accounting for competing mortality risk in the estimation of observed risk of MOF (see Figures 7 and 8, parts b, d and f), there was still underprediction in the whole population, but less than observed when ignoring competing mortality. Stratified by age, there was underprediction in both men and women aged 30–64 years and 65–74 years (see Figures 7 and 8, parts d and e). In the older-age groups, there was underprediction at lower levels of predicted risk, but overprediction at higher levels of predicted risk. Notably, in both women and men aged 85–99 years, observed risk accounting for competing mortality declined across the 10 deciles of increasing predicted risk. Similar patterns were observed stratified by CCI, with underprediction in people with low comorbidity, but large overprediction in people with a CCI score ≥ 3 at higher levels of predicted risk (see Figures 7 and 8, part f).
Results 2: external validation of QFracture-2012 for hip fracture
In women, during 15,842,775 years of follow-up, there were 36,400 incident cases of hip fracture observed [2.30 (95% CI 2.27 to 2.32) cases per 1000 person-years]. In men, during 15,253,462 years of follow-up, there were 13,379 incident cases of hip fracture [0.88 (95% CI 0.86 to 0.89) cases per 1000 person-years]. Compared with the previous QFracture-2012 external validation,18 observed crude incidence of hip fracture was substantially higher (women, 2.30/1000 person-years vs. 1.37; men, 0.88/1000 person-years vs. 0.47). However, the previous study was restricted to people aged 30–84 years, and differences were smaller but still substantial. Restricting incidence estimation in this study to this population resulted in 1.73 cases per 1000 person-years for women (vs. 1.37) 0.74 cases per 1000 person-years for men (vs. 0.47). Ignoring hip fractures ascertained in hospital coding accounted for all the difference in incidence in women, and for most of the difference in men (see Appendix 4, Figure 33).
Discrimination of QFracture-2012 for hip fracture in the whole external validation population was excellent in women (with a Harrell’s c-statistic of 0.918 vs. an AUROC of 0.893 in QFracture-2012 internal validation) and good in men (with a Harrell’s c-statistic of 0.888 vs. an AUROC of 0.875 in QFracture-2012 internal validation) (Table 7). The D-statistic was 3.26 in women and 3.19 in men, which is very similar to QFracture-2012 internal validation (3.26 and 3.15, respectively). The model explained 71.7% of variation in outcome in women and 70.9% of variation in outcome in men, which is very similar to QFracture-2012 internal validation (71.7% and 70.4%, respectively). Stratified by age, discrimination in women was moderate (Harrell’s c-statistic 0.601 for women aged 85–99 years) to excellent (Harrell’s c-statistic 0.832 for women aged 30–64 years), and moderate (Harrell’s c-statistic 0.637 for men aged 85–99 years) to good (Harrell’s c-statistic 0.765 for men aged 30–64 years) in men. Explained variation was lower in all strata and low in those people aged 85–99 years (women, 5.8%; men, 11.8%). Stratified by CCI, discrimination was good to excellent at all levels of comorbidity.
| Patient group | Women | Men | ||||
|---|---|---|---|---|---|---|
| Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) | |
| All patients | 0.918 (0.915 to 0.921) | 3.26 (3.24 to 3.28) | 71.7 (71.4 to 71.9) | 0.888 (0.882 to 0.893) | 3.19 (3.16 to 3.23) | 70.9 (70.4 to 71.3) |
| Age group (years) | ||||||
| 30–64 | 0.832 (0.823 to 0.841) | 2.24 (2.19 to 2.30) | 54.6 (53.4 to 55.8) | 0.765 (0.755 to 0.776) | 1.88 (1.82 to 1.94) | 45.8 (44.1 to 47.4) |
| 65–74 | 0.694 (0.687 to 0.701) | 1.20 (1.16 to 1.24) | 25.7 (24.4 to 27.0) | 0.705 (0.694 to 0.716) | 1.29 (1.23 to 1.36) | 28.5 (26.5 to 30.5) |
| 75–84 | 0.664 (0.659 to 0.669) | 0.95 (0.92 to 0.98) | 17.7 (16.8 to 18.5) | 0.679 (0.670 to 0.687) | 1.08 (1.03 to 1.13) | 21.7 (20.1 to 23.3) |
| 85–99 | 0.601 (0.595 to 0.608) | 0.51 (0.47 to 0.55) | 5.8 (5.0 to 6.7) | 0.637 (0.623 to 0.651) | 0.75 (0.67 to 0.82) | 11.8 (9.8 to 13.9) |
| CCI | ||||||
| 0 | 0.924 (0.919 to 0.929) | 3.36 (3.33 to 3.39) | 72.9 (72.6 to 73.3) | 0.852 (0.844 to 0.860) | 2.84 (2.79 to 2.89) | 65.8 (64.9 to 66.6) |
| 1 | 0.899 (0.893 to 0.905) | 2.92 (2.88 to 2.96) | 67.1 (66.4 to 67.7) | 0.872 (0.861 to 0.882) | 2.89 (2.82 to 2.96) | 66.7 (65.6 to 67.7) |
| 2 | 0.839 (0.831 to 0.846) | 2.24 (2.19 to 2.29) | 54.5 (53.4 to 55.5) | 0.808 (0.796 to 0.821) | 2.17 (2.09 to 2.25) | 53.0 (51.1 to 54.7) |
| ≥ 3 | 0.783 (0.775 to 0.792) | 1.75 (1.70 to 1.80) | 42.2 (40.8 to 43.5) | 0.782 (0.770 to 0.794) | 1.90 (1.83 to 1.97) | 46.4 (44.5 to 48.2) |
Ignoring competing mortality risk in the estimation of observed risk of hip fracture (Figures 9 and 10, parts a, c and e), there was underprediction at all levels of predicted risk for both men and women, which was larger at higher levels of predicted risk (see Figures 9 and 10, part a) and larger than for MOF. Stratified by age, there was underprediction in all age groups. Underprediction was larger in older people, although there was overprediction in 85- to 99-year-olds at highest levels of predicted risk (see Figures 9 and 10, part b). Stratified by CCI, there was underprediction at all levels of comorbidity. Underprediction was largest in people with a CCI score ≥ 3, although there was overprediction at the highest levels of predicted risk (see Figures 9 and 10, part c).
FIGURE 9.
Calibration for hip fracture in women without accounting for competing risks and accounting for competing risks. (a) Overall calibration not accounting for competing risks;a (b) overall calibration accounting for competing risks;b (c) calibration by age group not accounting for competing risks;a (d) calibration by age group accounting for competing risks;b (e) calibration by CCI not accounting for competing risks;a and (f) calibration by CCI accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. A coloured line (i.e. observed risk) above the matching black line (i.e. predicted risk) indicates underprediction. A coloured line (i.e. observed risk) below the matching black line (i.e. predicted risk) indicates overprediction. Source: Livingstone et al. 50

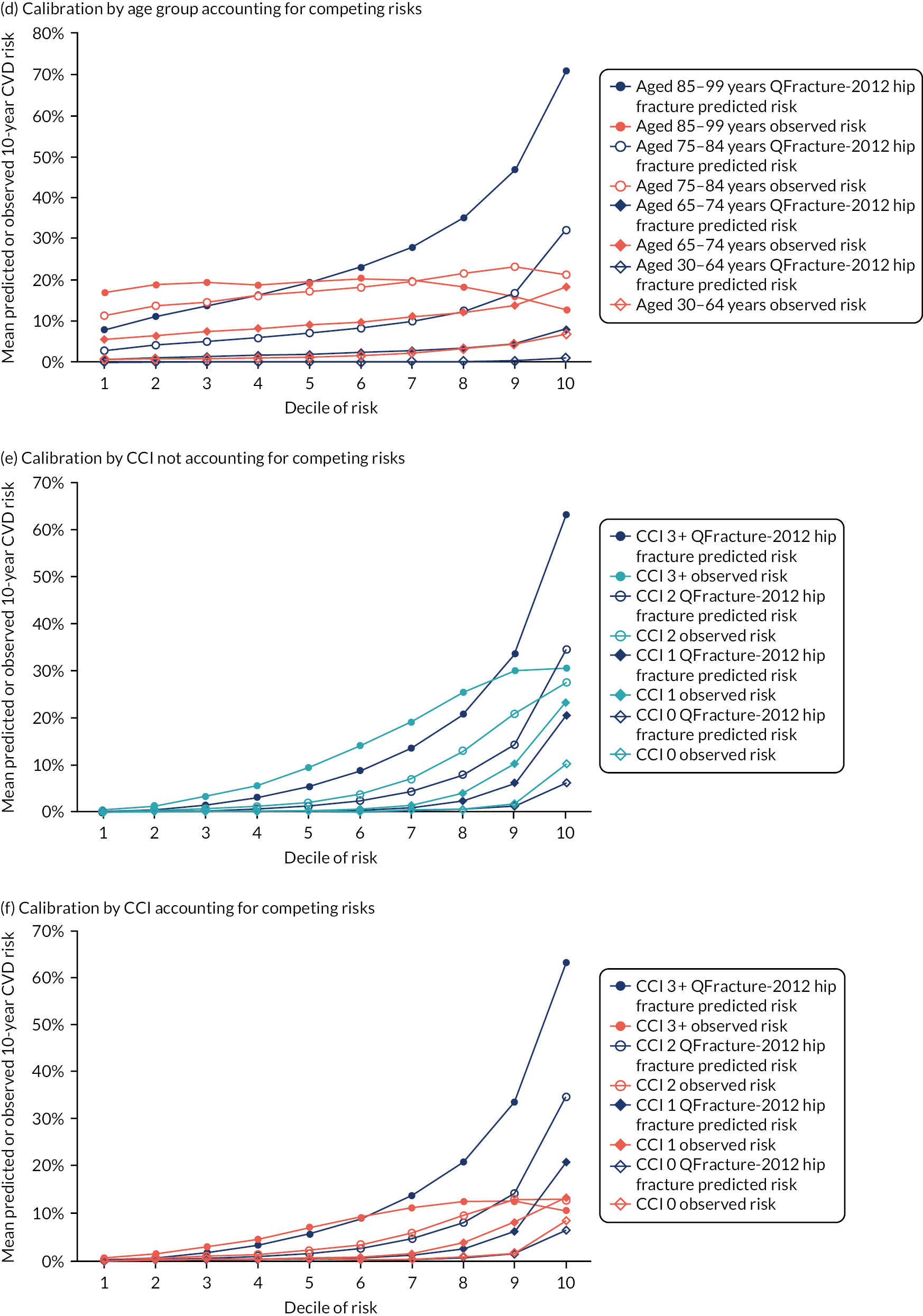
FIGURE 10.
Calibration for hip fracture in men without accounting for competing risks and accounting for competing risks. (a) Overall calibration not accounting for competing risks;a (b) overall calibration accounting for competing risks;b (c) calibration by age group not accounting for competing risks;a (d) calibration by age group accounting for competing risks;b (e) calibration by CCI not accounting for competing risks;a and (f) calibration by CCI accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. A coloured line (i.e. observed risk) above the matching black line (i.e. predicted risk) indicates underprediction. A coloured line (i.e. observed risk) below the matching black line (i.e. predicted risk) indicates overprediction. Source: Livingstone et al. 50
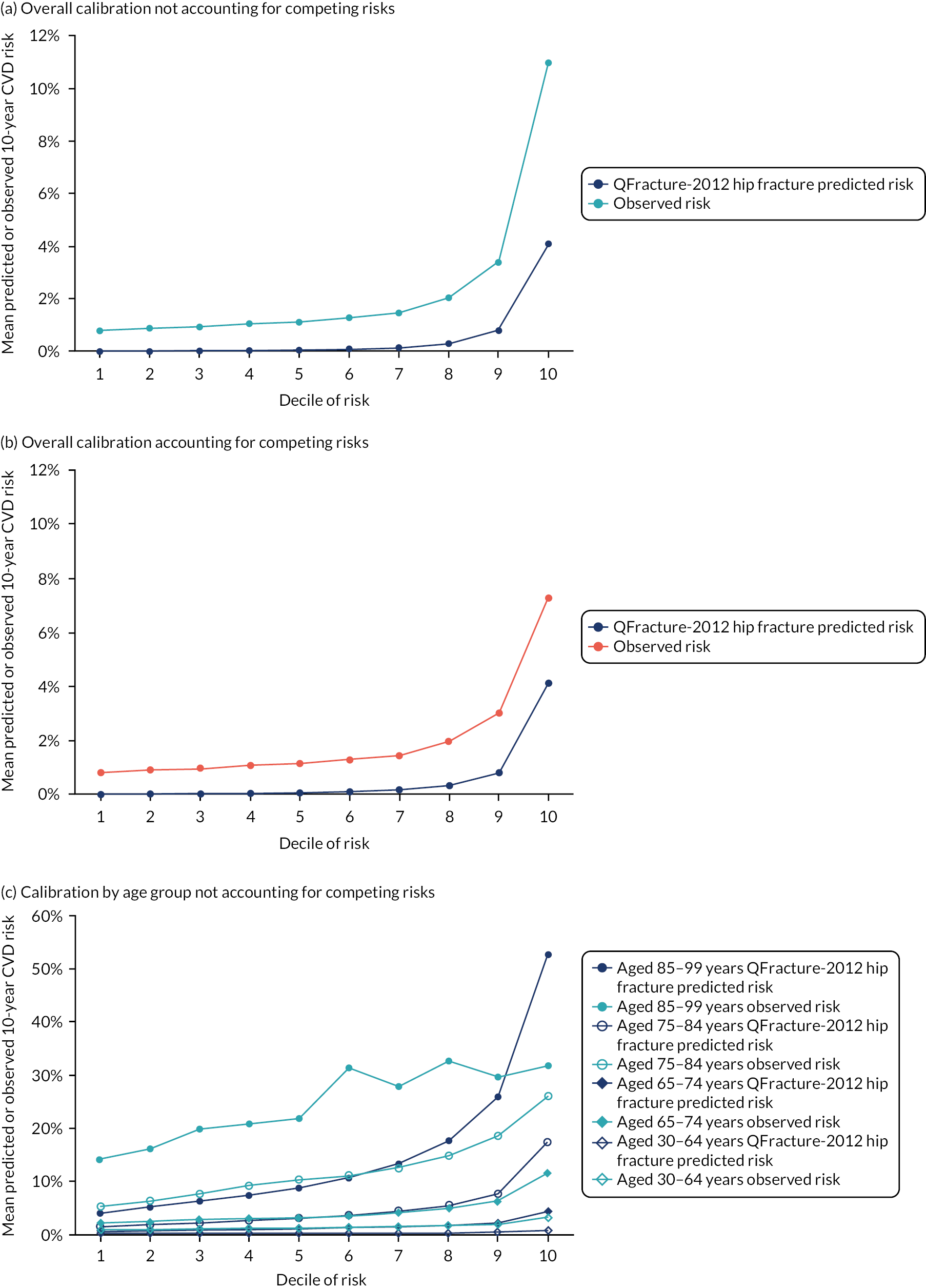

Accounting for competing mortality risk in the estimation of observed risk of hip fracture (see Figures 9 and 10, parts b, d and f), there was still underprediction in the whole population, but less than observed when ignoring competing mortality. Stratified by age, there was underprediction in all deciles of predicted risk in women aged 30–64 years and men aged 30–64 years and 65–74 years (see Figures 9 and 10, parts d and e). In the older age groups, there was underprediction at lower levels of predicted risk, but overprediction at higher levels of predicted risk. Notably, in both women and men aged 74–85 years and 85–99 years, observed risk accounting for competing mortality was flat or declined slightly across the 10 deciles of increasing predicted risk. Similar patterns were observed when stratified by CCI, with underprediction in people with low comorbidity, but large overprediction in people with a CCI score ≥ 3 at higher levels of predicted risk (see Figures 9 and 10, part f).
Results 3: derivation and internal validation of CFracture
There were 1,831,606 women and 1,789,820 men aged 30–99 years in the derivation cohort, and 915,803 and 894,910, respectively, in the validation cohort, with similar distribution of baseline characteristics in each. Two new CFracture models were created for MOF and for hip fracture, both using the same variables as QFracture-2012 but accounting for competing mortality risk in derivation and including baseline CCI in prediction.
Performance of CFracture for predicting major osteoporotic fracture
In the internal validation cohort, discrimination of CFracture for MOF in the whole population was excellent in women (Harrell’s c-statistic 0.813, 95% CI 0.810 to 0.816) and good in men (Harrell’s c-statistic 0.738, 95% CI 0.732 to 0.743), which is similar to QFracture-2012 for MOF in the same cohort (Table 8). Stratified by age, discrimination of both CFracture and QFracture-2012 was lower in all age groups and declined with age in women, although was similar in all age groups in men. Stratified by comorbidity, discrimination in the strata was somewhat worse than in the whole population, but there was no clear pattern of change with increasing comorbidity.
| Patient group | Women | Men | ||
|---|---|---|---|---|
| CFracture, Harrell’s c-statistic (95% CI) | QFracture-2012, Harrell’s c-statistic (95% CI) | CFracture, Harrell’s c-statistic (95% CI) | QFracture-2012, Harrell’s c-statistic (95% CI) | |
| All patients | 0.813 (0.810 to 0.816) | 0.813 (0.810 to 0.817) | 0.738 (0.732 to 0.743) | 0.736 (0.730 to 0.741) |
| Age group (years) | ||||
| 30–64 | 0.711 (0.705 to 0.717) | 0.709 (0.703 to 0.715) | 0.623 (0.615 to 0.631) | 0.619 (0.611 to 0.627) |
| 65–74 | 0.620 (0.613 to 0.627) | 0.614 (0.607 to 0.621) | 0.653 (0.640 to 0.666) | 0.653 (0.641 to 0.666) |
| 75–84 | 0.610 (0.604 to 0.617) | 0.617 (0.610 to 0.623) | 0.640 (0.629 to 0.652) | 0.646 (0.635 to 0.658) |
| 85–99 | 0.564 (0.555 to 0.574) | 0.568 (0.558 to 0.577) | 0.618 (0.598 to 0.639) | 0.623 (0.602 to 0.643) |
| CCI | ||||
| 0 | 0.797 (0.792 to 0.801) | 0.795 (0.791 to 0.800) | 0.665 (0.657 to 0.673) | 0.665 (0.657 to 0.673) |
| 1 | 0.801 (0.794 to 0.808) | 0.802 (0.796 to 0.809) | 0.725 (0.714 to 0.737) | 0.725 (0.714 to 0.737) |
| 2 | 0.754 (0.745 to 0.763) | 0.753 (0.744 to 0.762) | 0.730 (0.714 to 0.745) | 0.730 (0.714 to 0.745) |
| ≥ 3 | 0.701 (0.690 to 0.711) | 0.711 (0.701 to 0.721) | 0.714 (0.698 to 0.730) | 0.714 (0.698 to 0.730) |
Calibration of CFracture for MOF was better than for QFracture-2012 in the whole population. In women, there was some underprediction at higher levels of predicted risk and a in men there was a similar calibration, but with some overprediction in the middle range of predicted risk (Figure 11). Stratified by age, calibration was good in women aged 30–64 years, with some underprediction in women aged 65–74 years and 75–84 years (Figure 12). In men, there was some overprediction a higher levels of predicted risk in those aged 30–64 years and 75–84 years, and some overprediction in those aged 65–74 years. In both men and women aged 85–99 years, calibration was poor, although considerably better than QFracture-2012 in this age group, as well as all others. Stratified by CCI, calibration in women was good, although with some underprediction in women with a CCI score of 0 and some overprediction in women with a CCI score ≥ 3 in the highest decile of predicted risk (Figure 13). Calibration in men stratified by CCI was more variable in those with a CCI score of 0 or 1 but was good in those with a CCI score of 2 and in those with a CCI score ≥ 3, for whom it was good apart from some overprediction in the decile of highest predicted risk.
FIGURE 11.
Whole-population calibration of CFracture and QFracture-2012 for MOF in the internal validation data set in the whole population. (a) Women; and (b) men. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Source: Livingstone et al. 51
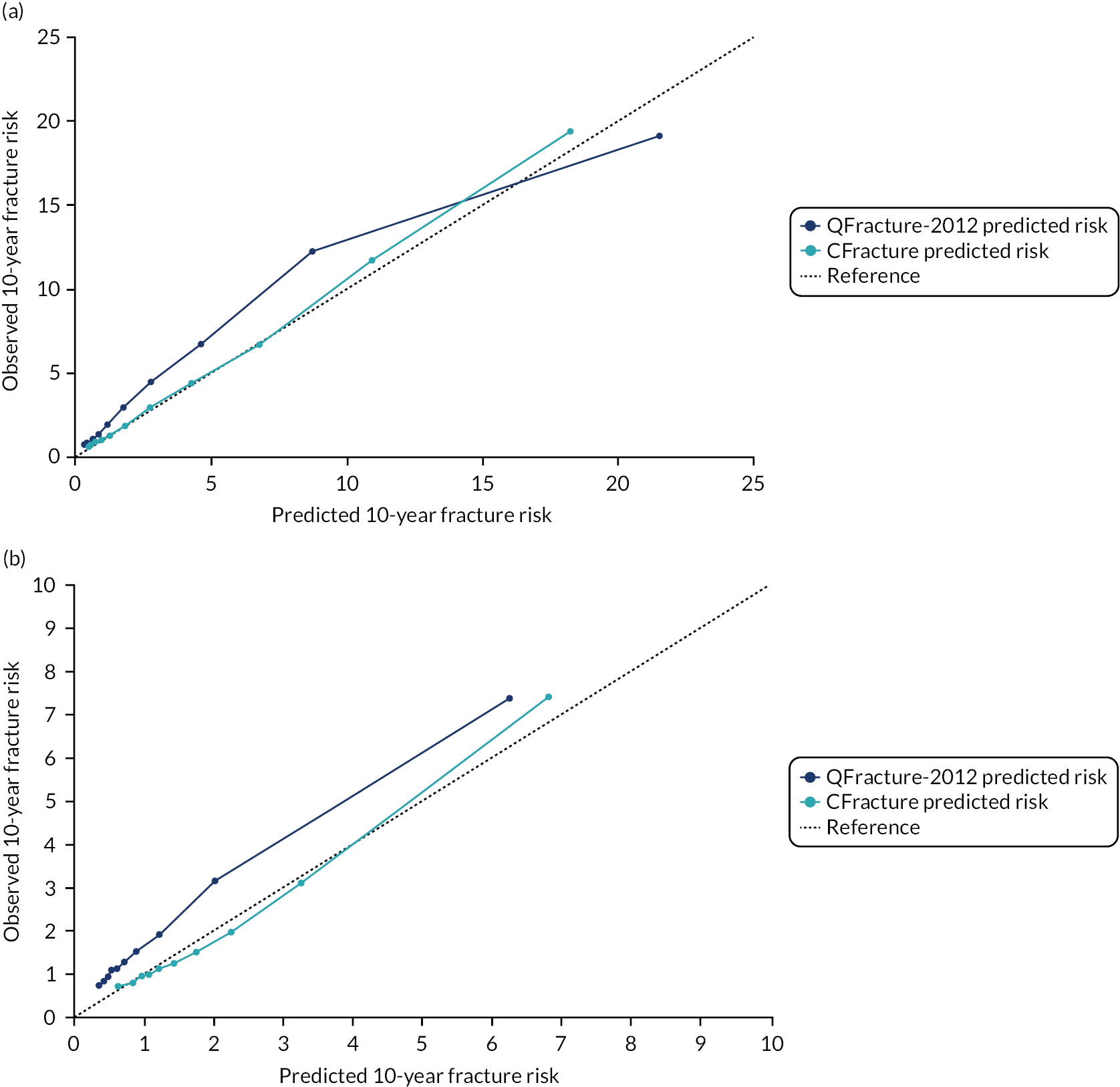
FIGURE 12.
Calibration of CFracture and QFracture-2012 for MOF in the internal validation data set stratified by age group. (a) Women aged 30–64 years; (b) men aged 30–64 years; (c) women aged 65–74 years; (d) men aged 65–74 years; (e) women aged 75–84 years; (f) men aged 75–84 years; (g) women aged 85–99 years; and (h) men aged 85–99 years. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Ideal calibration lies on the reference line. Below the reference line is overprediction and above the reference line is underprediction. Source: Livingstone et al. 51
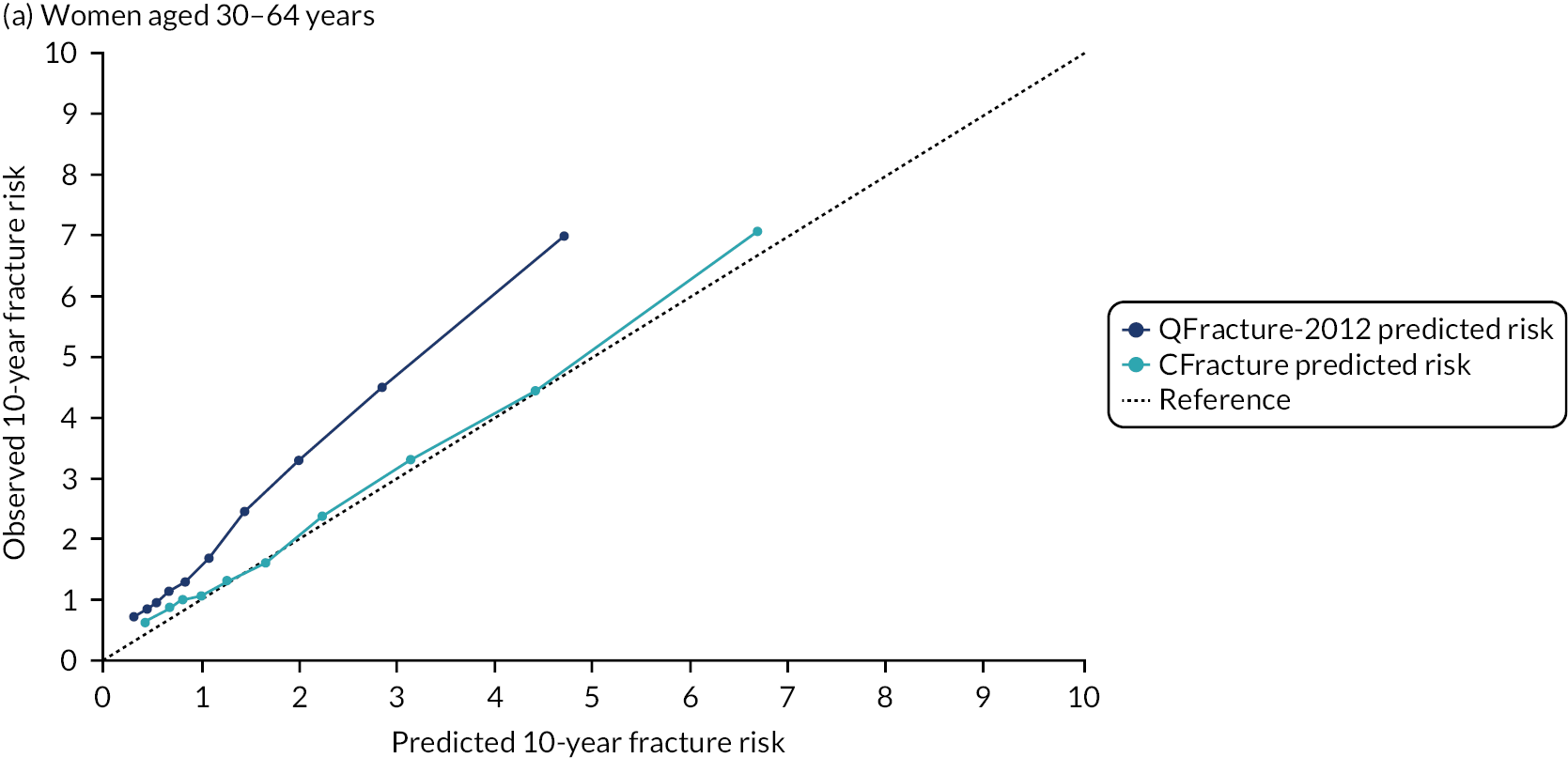
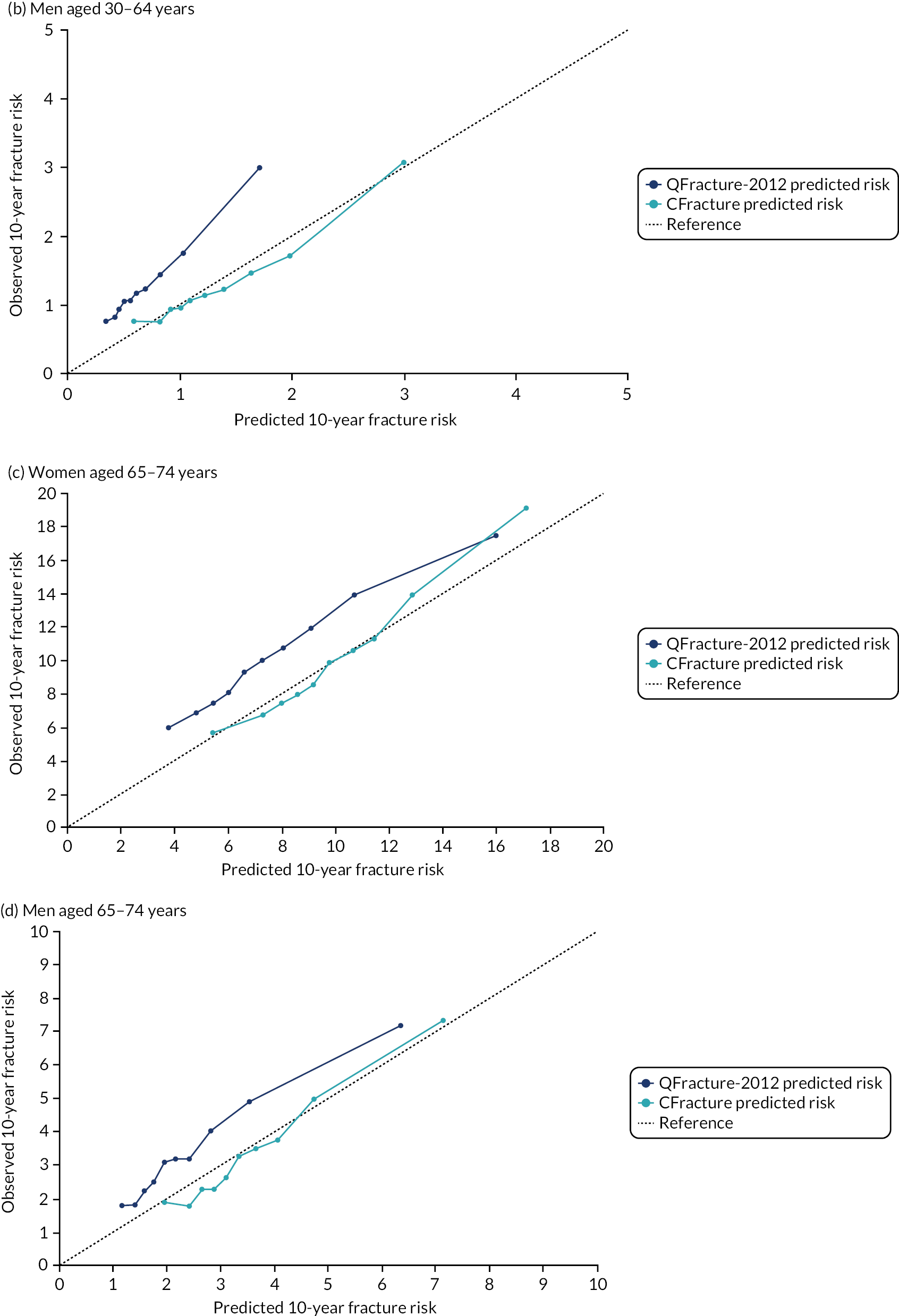

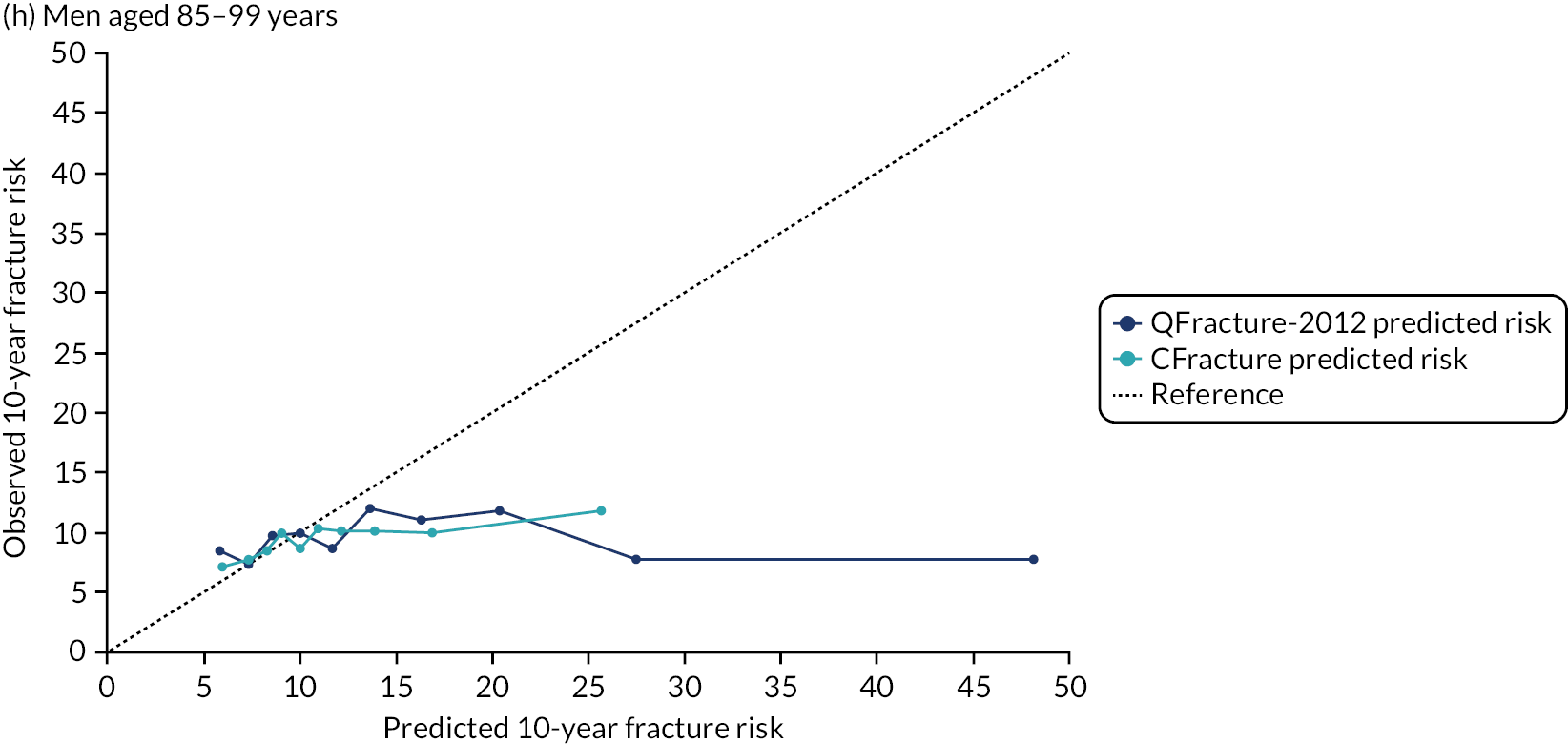
FIGURE 13.
Calibration of CFracture and QFracture-2012 for MOF in the internal validation data set stratified by mCCI. (a) Women, mCCI = 0; (b) men, mCCI = 0; (c) women mCCI = 1; (d) men, mCCI = 1; (e) women, mCCI = 2; (f) men, mCCI = 2; (g) women, mCCI ≥ 3; and (h) men, mCCI ≥ 3. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Ideal calibration lies on the reference line. Below the reference line is overprediction and above the reference line is underprediction. Source: Livingstone et al. 51

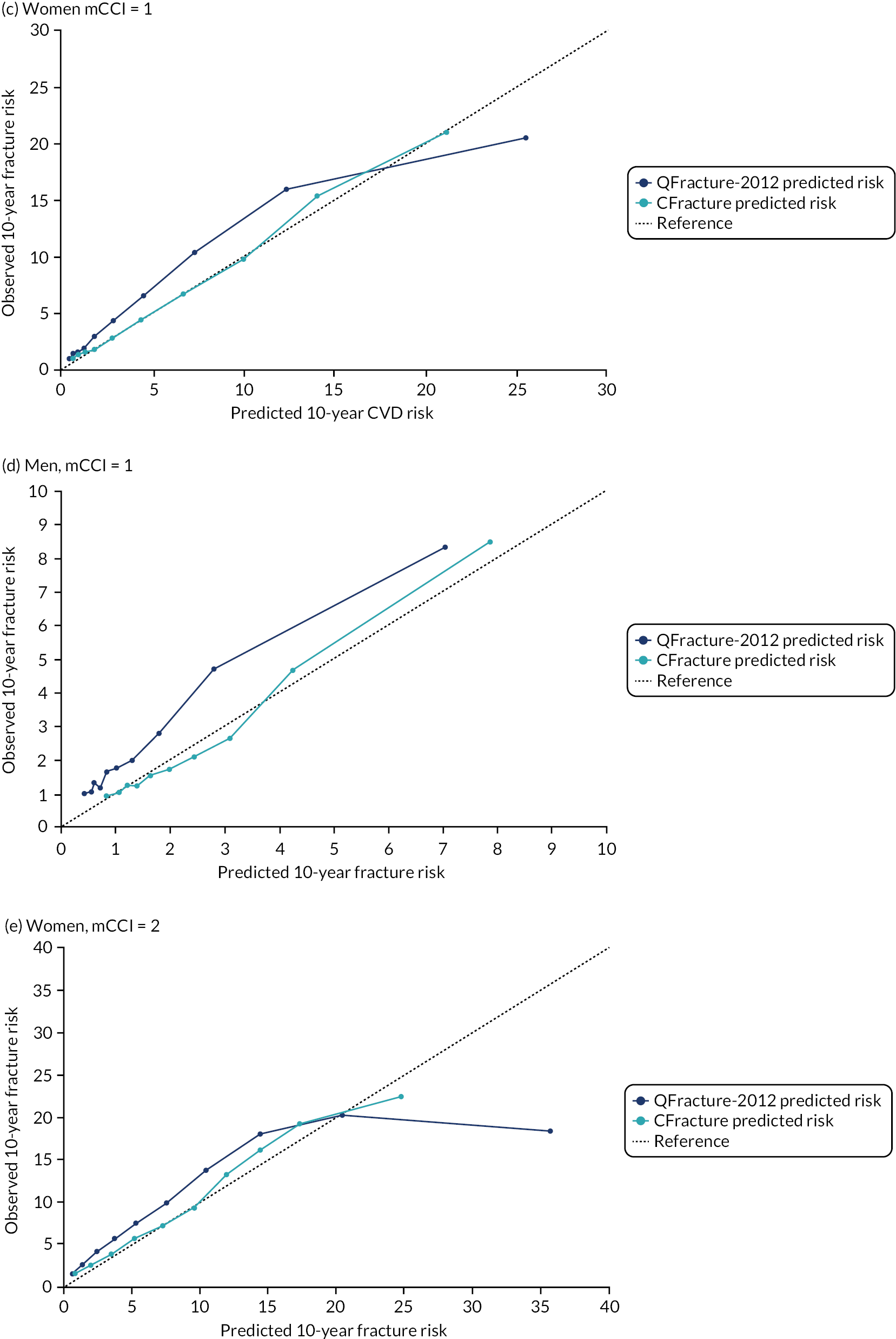
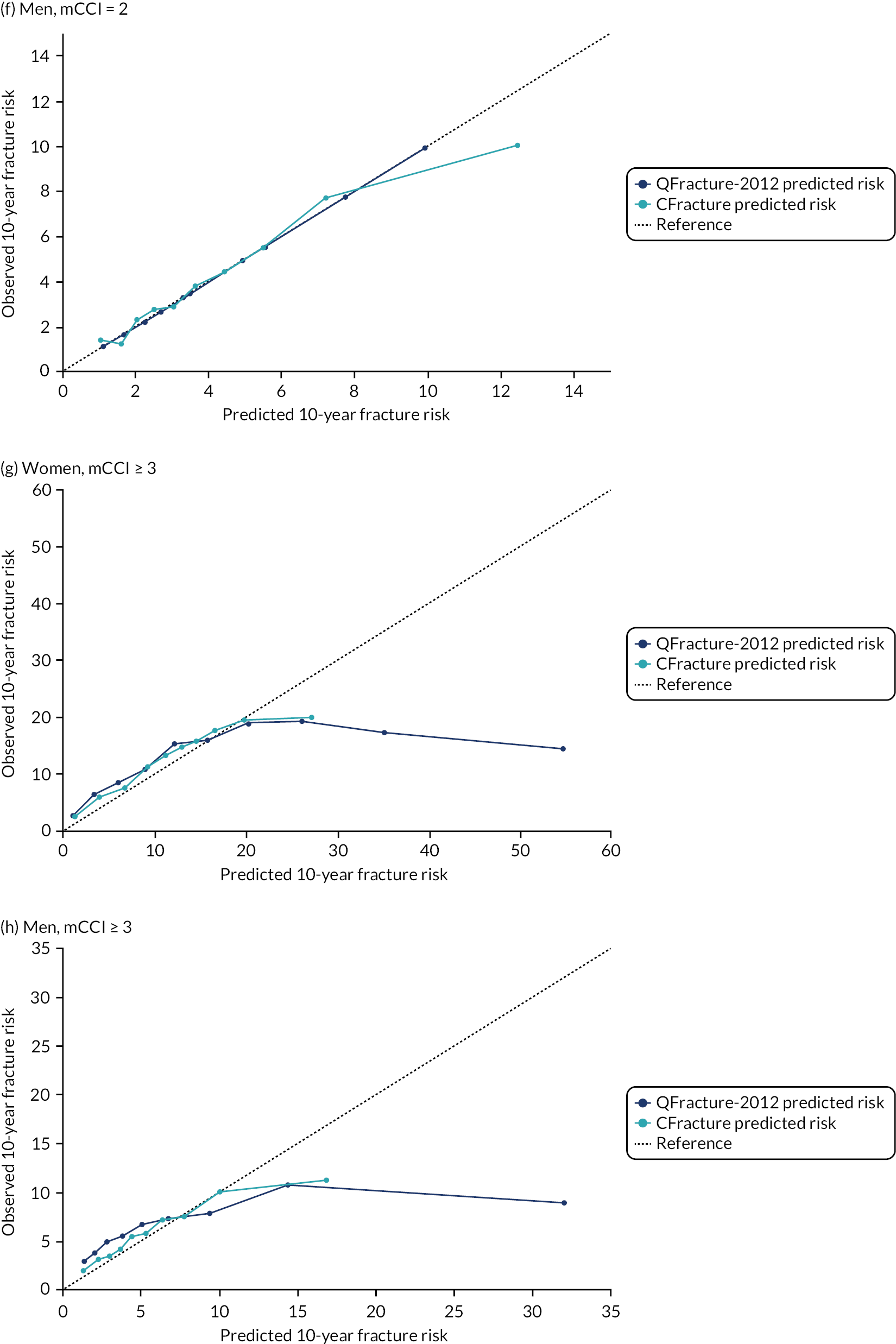
Performance of CFracture for predicting hip fracture
In the internal validation cohort, discrimination of CFracture for hip fracture in the whole population was excellent in both women (Harrell’s c-statistic 0.914, 95% CI 0.908 to 0.883) and men (Harrell’s c-statistic 0.886, 95% CI 0.877 to 0.895), similar to QFracture-2012 for hip fracture in the same cohort (Table 9). Stratified by age, discrimination of both CFracture and QFracture-2012 was lower in all age groups and declined with age in both men and women. Stratified by comorbidity, discrimination was good to excellent in all strata, although declined with increasing comorbidity.
| Patient group | Women | Men | ||
|---|---|---|---|---|
| CFracture, Harrell’s c-statistic (95% CI) | QFracture-2012, Harrell’s c-statistic (95% CI) | CFracture, Harrell’s c-statistic (95% CI) | QFracture-2012, Harrell’s c-statistic (95% CI) | |
| All patients | 0.914 (0.908 to 0.919) | 0.917 (0.912 to 0.923) | 0.886 (0.877 to 0.895) | 0.888 (0.879 to 0.897) |
| Age group (years) | ||||
| 30–64 | 0.821 (0.805 to 0.837) | 0.835 (0.819 to 0.851) | 0.769 (0.751 to 0.787) | 0.773 (0.754 to 0.791) |
| 65–74 | 0.683 (0.671 to 0.695) | 0.695 (0.683 to 0.707) | 0.695 (0.676 to 0.714) | 0.696 (0.677 to 0.715) |
| 75–84 | 0.644 (0.636 to 0.653) | 0.658 (0.649 to 0.666) | 0.681 (0.666 to 0.695) | 0.688 (0.673 to 0.702) |
| 85–99 | 0.579 (0.567 to 0.590) | 0.601 (0.589 to 0.612) | 0.616 (0.591 to 0.640) | 0.633 (0.608 to 0.657) |
| CCI | ||||
| 0 | 0.922 (0.913 to 0.930) | 0.924 (0.915 to 0.932) | 0.847 (0.832 to 0.862) | 0.850 (0.835 to 0.865) |
| 1 | 0.893 (0.882 to 0.903) | 0.897 (0.886 to 0.907) | 0.866 (0.848 to 0.884) | 0.872 (0.854 to 0.890) |
| 2 | 0.833 (0.820 to 0.847) | 0.841 (0.828 to 0.854) | 0.794 (0.773 to 0.814) | 0.806 (0.785 to 0.827) |
| ≥ 3 | 0.767 (0.753 to 0.782) | 0.783 (0.769 to 0.797) | 0.770 (0.749 to 0.790) | 0.780 (0.760 to 0.801) |
Calibration of CFracture for hip fracture was better than for QFracture-2012 in the whole population. Calibration was good in women across all levels of predicted risk. Calibration was good in men, except in the highest decile of predicted risk where there was underprediction (Figure 14). Stratified by age, calibration was good in women aged 30–64 years and 75–84 years, with some overprediction in women aged 65–74 years (Figure 15). In men, calibration was reasonable in those aged 30–64 years, 65–74 years and 75–84 years, with some underprediction at the highest level of predicted risk. In both men and women aged 85–99 years, calibration was poor, with overprediction at most levels of predicted risk, although was considerably better than QFracture-2012 in this age group, as well as all others.
FIGURE 14.
Whole-population calibration of CFracture and QFracture-2012 for hip fracture in the internal validation data set in the whole population. (a) Women; and (b) men. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Source: Livingstone et al. 51
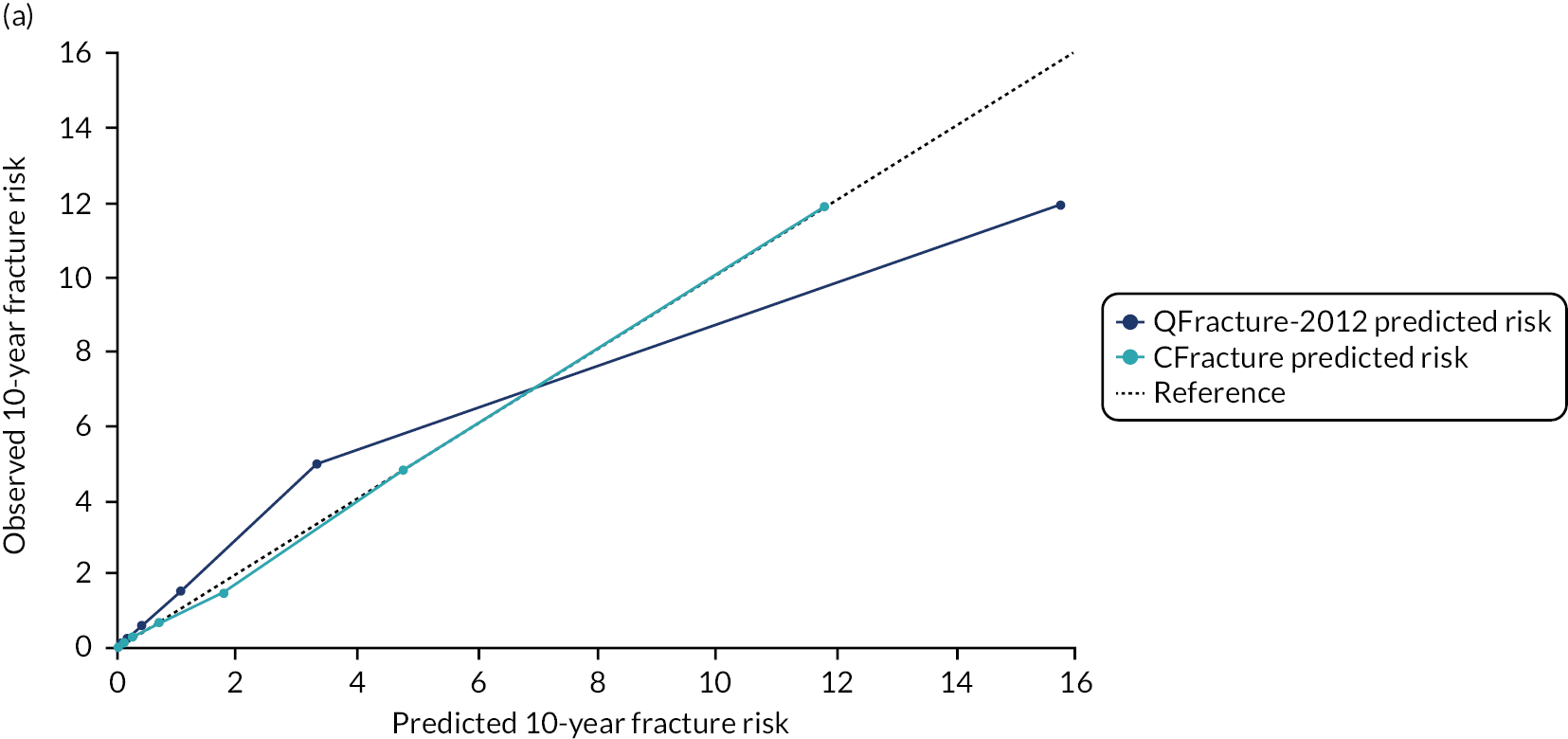
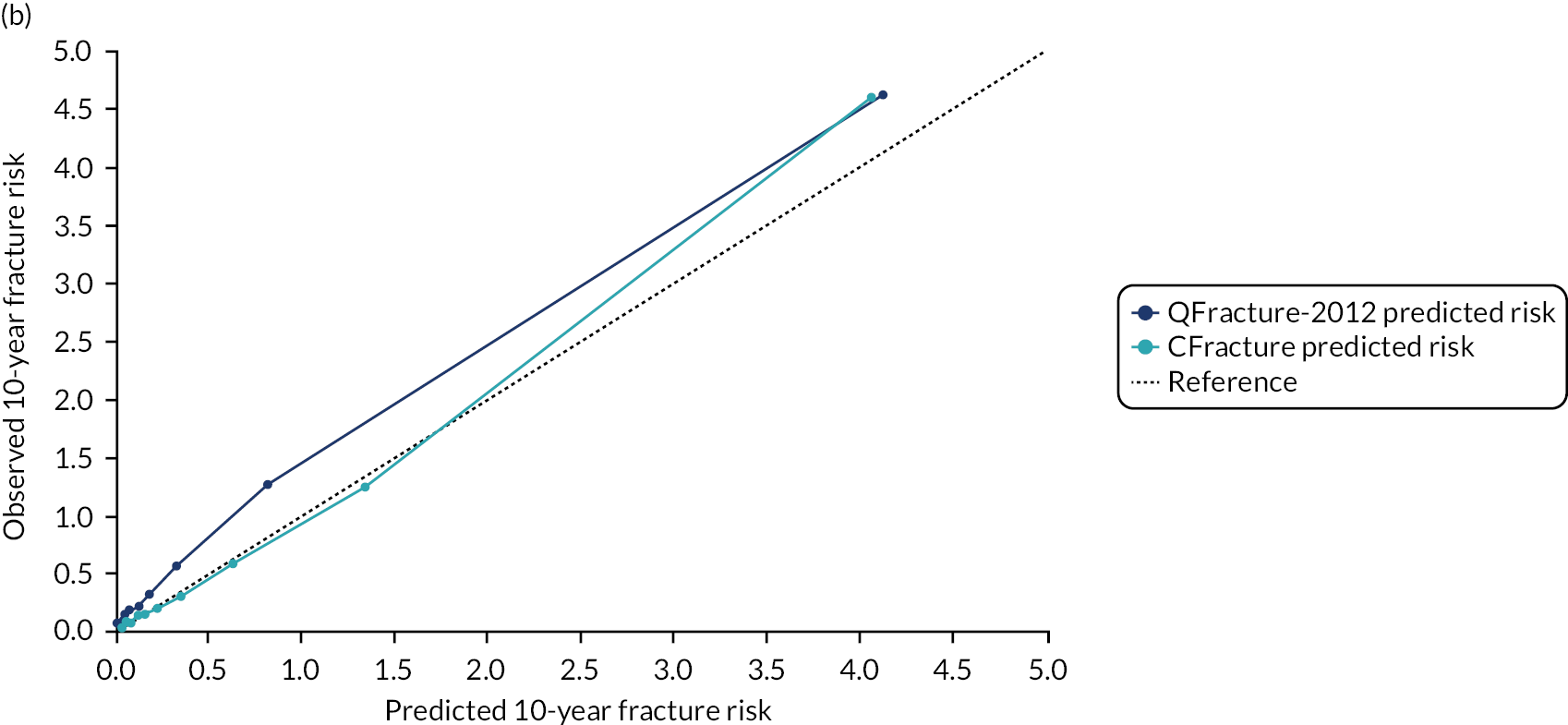
FIGURE 15.
Calibration of CFracture and QFracture-2012 for hip fracture in the internal validation data set stratified by age group. (a) Women aged 30–64 years; (b) men aged 30–64 years; (c) women aged 65–74 years; (d) men aged 65–74 years; (e) women aged 75–84 years; (f) men aged 75–84 years; (g) women aged 85–99 years; and (h) men aged 85–99 years. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Ideal calibration lies on the reference line. Below the reference line is overprediction and above the reference line is underprediction. Source: Livingstone et al. 51

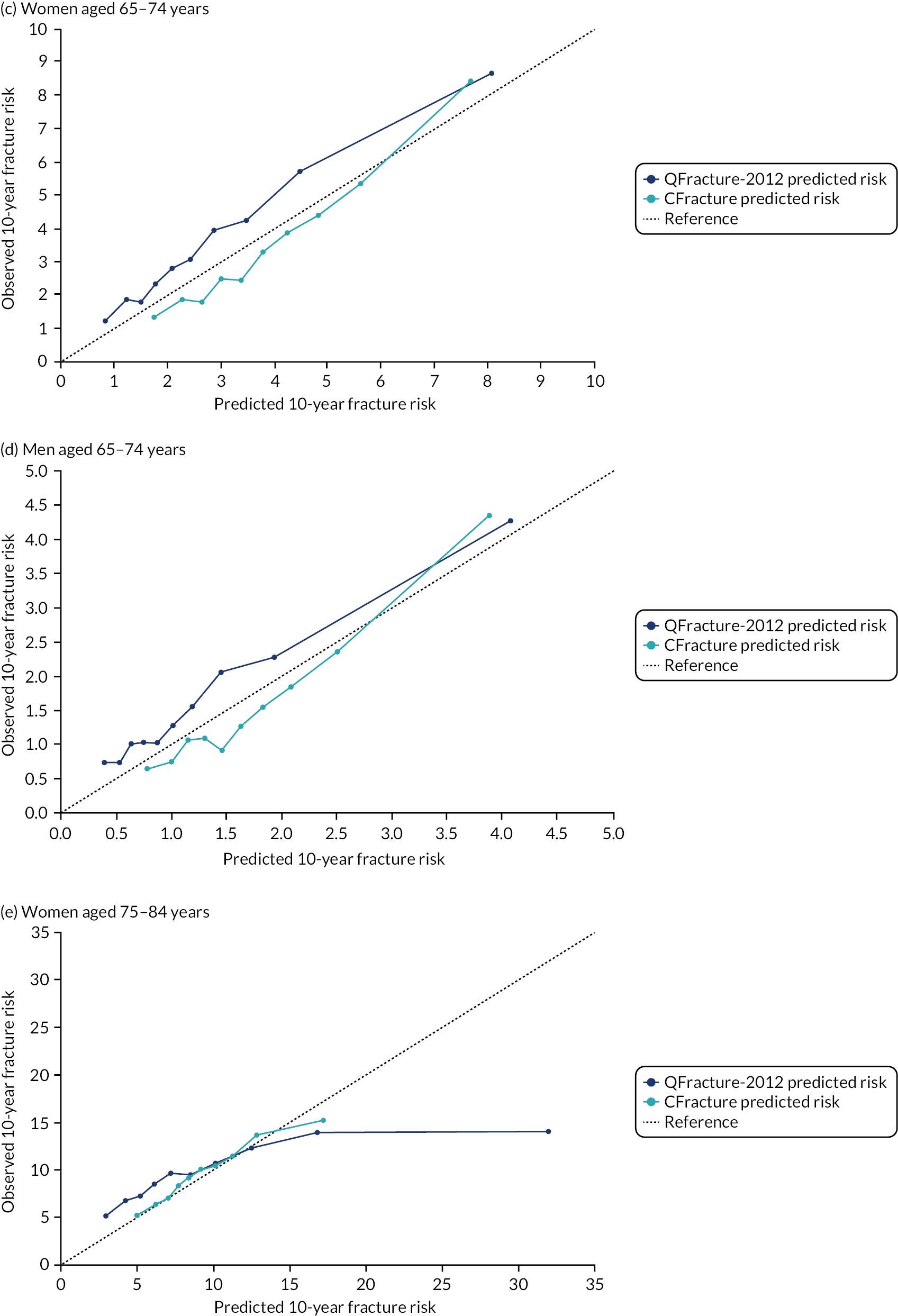
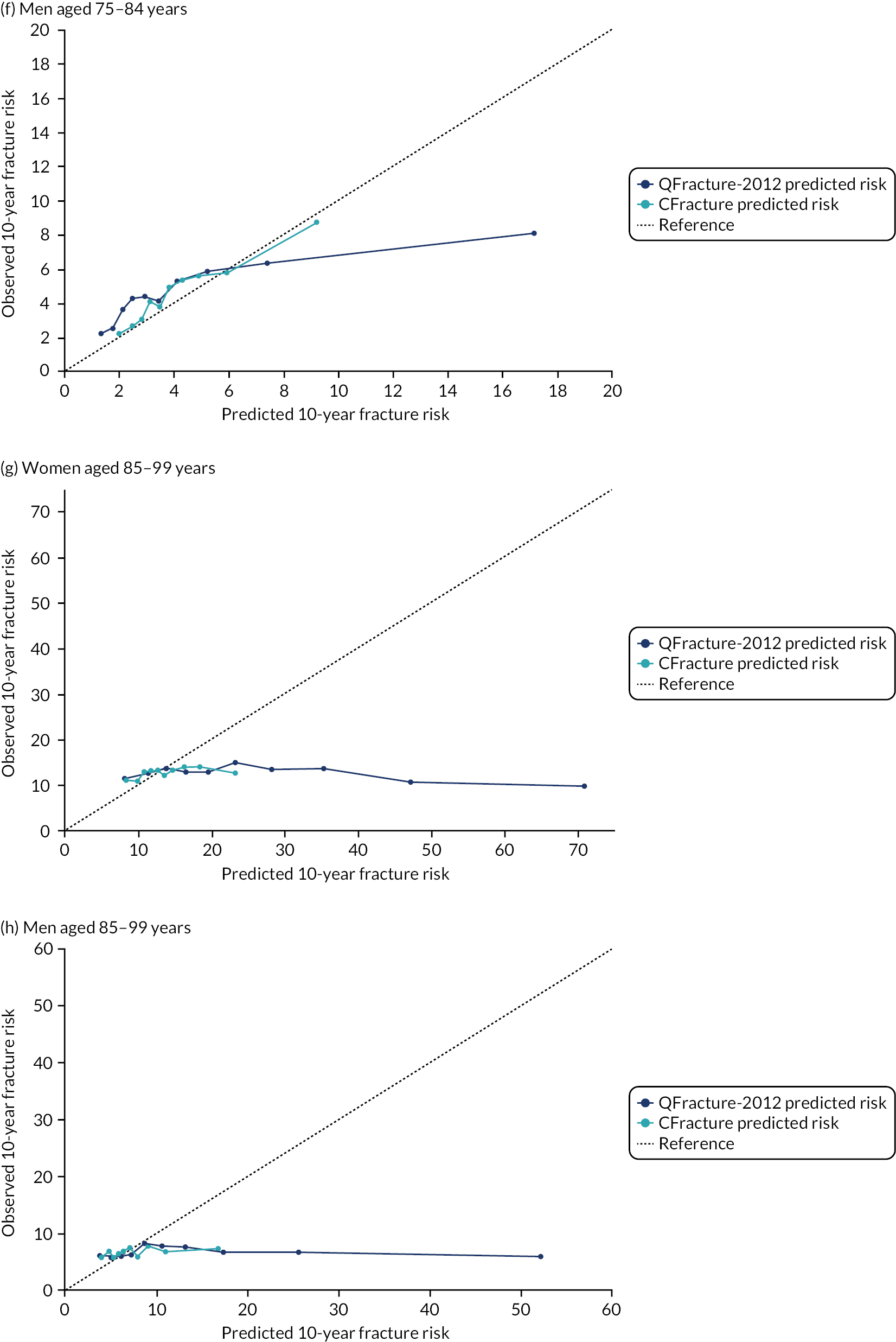
Stratified by CCI, calibration in women was good, except in the highest decile of predicted risk where there was some overprediction in CCI scores 1, 2 and ≥ 3 (Figure 16). Calibration in men stratified by CCI was good, apart from underprediction in the highest decile of predicted risk for CCI scores 0 and 1, underprediction in the middle of the predicted risk range for CCI score 2 and some overprediction in the highest decile of predicted risk for CCI score ≥ 3.
FIGURE 16.
Calibration of CFracture and QFracture-2012 for hip fracture in the internal validation data set stratified by CCI. (a) Women, CCI = 0; (b) men, CCI = 0; (c) women, CCI = 1; (d) men, CCI = 1; (e) women, CCI = 2; (f) men, CCI = 2; (g) women, CCI ≥ 3; and (h) men, CCI ≥ 3. Observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk. Ideal calibration lies on the reference line. Below the reference line is overprediction and above the reference line is underprediction. Source: Livingstone et al. 51
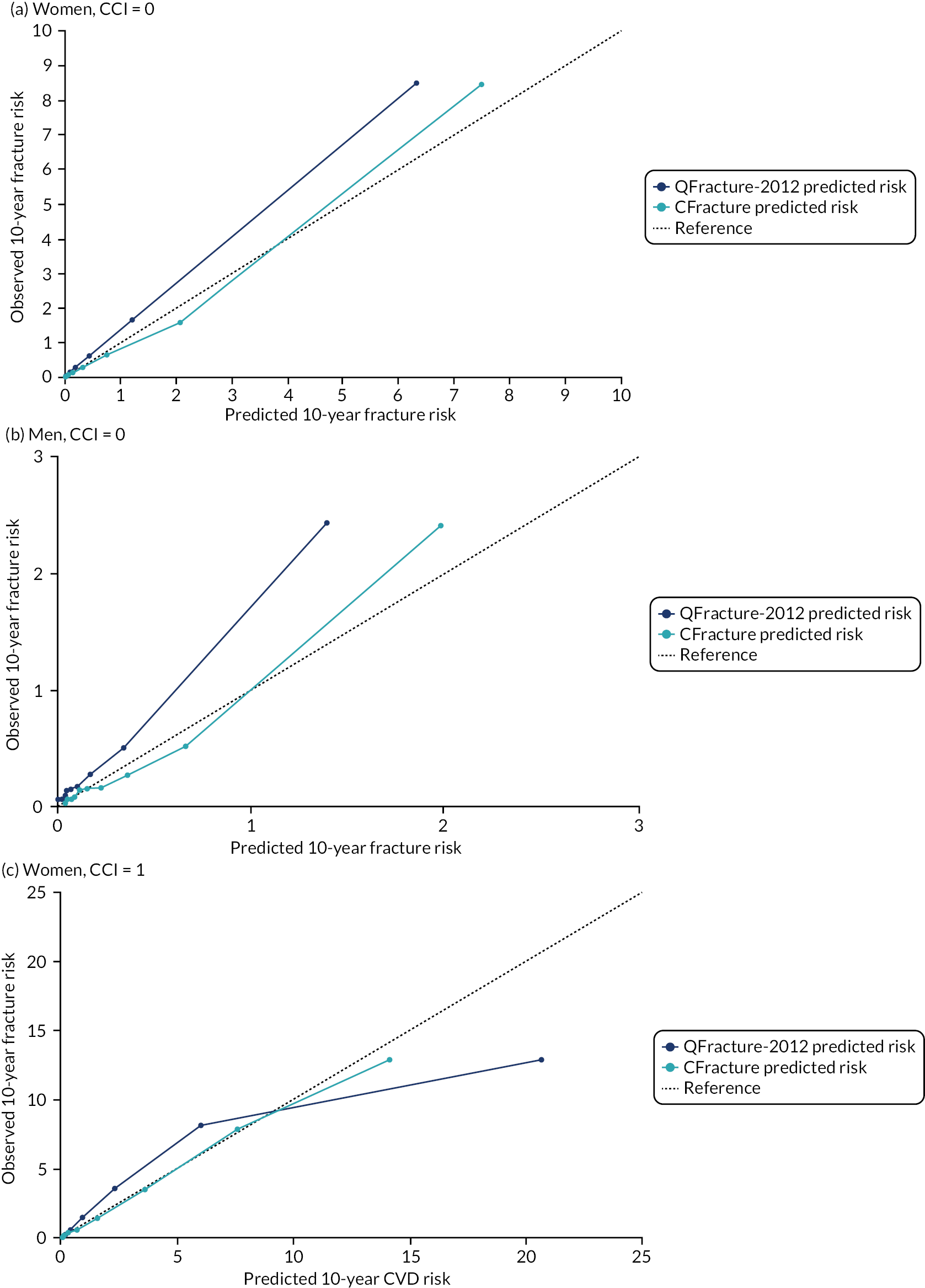

Summary
QFracture-2012 external validation
QFracture-2012 was found to have very good to excellent discrimination in the total population, with higher discrimination observed in the hip fracture model than in the MOF model. However, discrimination was typically only poor to moderate in important subgroups, including older patients (as expected given that age is such a strong predictor of risk72,100) and moderate to good those with higher levels of multimorbidity. However, calibration was very poor, irrespective of how evaluated. When evaluated in its own terms (ignoring competing risk), QFracture-2012 showed consistent underprediction for both MOF and hip fracture. The most likely explanation for this underprediction is that fracture ascertainment in this study is more complete, as it includes fractures recorded during hospital admission in addition to fractures recorded in GP electronic health records and mortality registration data. For hip fracture, the inclusion of hospital data for fracture ascertainment likely explained much of the observed difference in hip fracture incidence, but less than half of observed differences in MOF incidence. Other reasons for higher observed incidence are the use of different index dates for first study entry (1 January 2004 in this study vs. 1 January 1998 in QFracture-2012), as recording of fractures in GP data is likely to have improved over time, as well as the use of different codesets to identify fracture (although QFracture-2012 does not have a published list of Read codes for predictors and so direct comparison is not possible).
When evaluated against observed fractures estimated accounting for competing risk, in general, underprediction reduced (i.e. failing to account for competing risk causes overprediction); however, there was very large overprediction at higher levels of predicted risk in older people and in people with more complex multimorbidity. Notably, in people aged 85–99 years and with CCI score ≥ 3, calibration was extremely poor, with observed risk flat or even declining across deciles of increasing predicted risk. Therefore, in summary, QFracture-2012 has two causes of poor calibration that operate in different directions. First, QFracture-2012 considerably underpredicts in all patients because derivation is based on incomplete ascertainment of fracture. Second, QFracture-2012 considerably overpredicts in people with high competing risk of death (primarily older people and in people with more complex multimorbidity).
CFracture derivation and internal validation
In the internal validation cohort, discrimination of CFracture for MOF and hip fracture in the whole population was good to excellent for MOF and excellent for hip fracture, and was similar to QFracture-2012 performance in the same data set. Stratified by age, CFracture discrimination was less good in all age groups, with worse discrimination with increasing age, except in men with MOF, for whom there was no obvious relationship with age. Stratified by CCI, discrimination for MOF was somewhat worse in all strata than in the whole population, but there was no clear pattern with age. Stratified by CCI, discrimination for hip fracture was similar to the whole population for a CCI score of 0, but discrimination declined somewhat with increasing comorbidity (although was good to excellent in all strata).
CFracture was better calibrated than QFracture-2012 in the whole population and in every strata, although was better calibrated in women than men and was better calibrated for hip fracture than for MOF. Strikingly, however, CFracture was poorly calibrated in women and men aged 85–99 years (although much less so than QFracture-2012).
These findings are somewhat different from previous external validations. 18,19 The first version of QFracture-201217 was independently, externally validated in The Health Improvement Network data set, which is a similar (and partially overlapping) set of practices to CPRD. This study found QFracture-2012 to have excellent discrimination and calibration in the whole population. 18 The updated QFracture-2012 (as evaluated in this study)26 was externally validated in CPRD by the QFracture-2012 derivation team, and this study, again, found excellent discrimination and calibration in the whole population. 19 This study differs from both previous external validations in two ways. First, we also identified fractures recorded during hospital admission, whereas the two previous studies identified fractures recorded in GP records and mortality registration data only. Better ascertainment of fractures would be expected to lead to underprediction of risk, as observed in this study. An Israeli external validation using both community and hospital data for ascertainment also observed considerable underprediction by QFracture-2012, consistent with our findings. 92 Second, this study examined calibration against observed outcomes estimated in the same way as previous external validations (using the Kaplan–Meier estimator, which ignores competing risk) and additionally accounting for competing risk (using the Aalen–Johansen estimator). As not accounting for competing risk leads to overprediction of fractures, this partially, but not completely, compensated for the observed underprediction in the whole population. However, as expected,96,97,100 accounting for competing risks led to large changes in observed risk in older people and in people with more multimorbidity, consistent with systematic overprediction by QFracture-2012 in groups with high competing mortality (despite systematic underprediction due to incomplete fracture ascertainment in QFracture-2012 derivation).
Limitations
This study has the same limitations as any routine data study (see Chapter 2, Limitations), but several particular limitations specifically apply. First, the observed incidence of fracture is higher in this study than in QFracture-2012 derivation and the two previous external validations. 18,19,26 There are three possible reasons for this. First, this study used hospital data to identify fractures (which accounts for most of the difference for hip fracture and some of the difference for MOF). Second, this study has an earliest study entry date of 1 January 2004 compared with the original QFracture-2012 external validation date of 27 June 1994 and the updated version external validation date of 1 January 1998, and recording of fracture outcomes in GP data are likely to have improved over time. Third, the codes used to identify fractures in GP data may be different; however, because none of the previous studies published their codesets we cannot explore this further. Within our own data, one issue is that humeral fractures were most commonly recorded in the GP data without specifying whether proximal or more distal. Therefore, we included non-site-specific humeral fractures as ‘proximal humerus’ fractures, which may lead to some misclassification (i.e. some false positives). However, registry data show that ≈ 80% of humeral fractures are proximal (and > 80% of non-proximal fractures are also low energy)101 and only including humeral fractures specified as proximal would lead to larger misclassification (i.e. a larger number of false negatives).
Second, although we explicitly accounted for censoring due to death in this study, the analysis still assumes that people who deregister from a CPRD practice have the same fracture risk as people who do not. This assumption is likely to be strong in older people for whom deregistration due to moving into extra-care housing or a care home is likely to be associated with higher falls and fracture risk.
Chapter 5 Quantifying direct treatment disutility associated with preventative treatments
Background
There is a growing evidence base that taking a specific treatment, particularly one requiring long-term use for a chronic condition, can cause inconvenience or ‘disutility’ to a patient that is distinct from the unwanted harms, adverse outcomes or specific effects of the treatment. DTD is a type of process disutility102 related to the inconvenience of obtaining prescriptions and medicines, needing to modify lifestyles to take medicines and attending healthcare visits for monitoring treatment. 40 DTD may have particular relevance for long-term medication use, such as statins for the primary prevention of CVD and bisphosphonates for osteoporosis, as the benefits of treatment are typically small and accrue over long periods, while any inconvenience, however small, is likely to start with treatment initiation and may be persistent.
Existing empirical studies have estimated a range of values of DTD, with the general size of the disutility being around 0.01 on average, which is equivalent to a loss of ≈ 3.6 days of perfect health over 1 year. 47,48,103 With these sorts of DTD values, several primary preventative treatments for CVD have switched from meeting acceptable levels of cost-effectiveness to not being cost-effective. 2,44,46,104–109 The mechanism underpinning this change is a simple one, whereby the DTD value is much larger than the expected health benefits of the medicine over the longer term. However, DTD input values have been elicited empirically in only a few studies, several of which have either adopted small study sizes47 or sampling frames which are not representative of either patients48 or the general population. 103 Consequently, there is considerable uncertainty as to the actual size and distribution of DTD values, whether or not DTD changes with the experience of taking medicines and, consequently, whether or not these values could, and should, be used to inform decision-making.
Aim and objectives
The study reported in this chapter addresses objective 4:
-
To quantify the magnitude, variation and distribution of DTD (i.e. the disutility incurred by taking a regular, long-term treatment irrespective of drug-specific side effects) in the general and statin- or bisphosphonate-treated populations.
This study had two specific objectives:
-
To elicit values for DTD for two exemplars of medicines using time trade-off (TTO).
-
To elicit values for DTD for two exemplars of medicines using best–worst scaling (BWS).
Methods
This study used two types of preference elicitation methods: (1) TTO and (2) BWS.
Selection of exemplar medicines
We quantified the DTD of statins for the primary prevention of heart disease and bisphosphonates for the primary prevention of fractures using two medicine-taking case studies. Statins were chosen as an example of a class of medicines that are perceived by professionals to be benign, but which some people perceive as harmful. Bisphosphonates were selected because they are medicines we thought had an obvious influence on daily life (i.e. people who take a bisphosphonate are required to drink a large glass of water before taking the medication, remain upright for 30 minutes after taking it and avoid food and drink for 2 hours thereafter).
Selection of elicitation methods
We sought to get an accurate description of the medicine-taking health states within our survey so that our respondents could appropriately value them. In addition, we wanted to check that the methods we adopted were appropriate and robust enough to estimate small disutilities associated with the ongoing use of a medicine. Therefore, we reviewed methods from previous studies47,48,103 that had attempted to estimate DTD values and integrated those methods with the experience and views of our clinical research team, as well as our two patient representatives who were members of the research team. This review suggested that TTO should be the predominant method, but that there is emerging interest in using BWS to elicit DTD.
The context
The elicitation surveys were designed to take account of the specific context in which a respondent is taking a medicine for primary prevention. Two distinct surveys for each method (i.e. TTO and BWS) were designed to focus on each of the two exemplars of statins and bisphosphonates.
For each exemplar, respondents were asked to consider taking medicine A, which was a ‘one-off pill’ assumed to have no ongoing inconvenience, or medicine B, which was a daily pill for 10 years. In the TTO exercise, we also decided to include four scenarios to understand whether or not DTD values differed based on how the benefits and harms of the medication were framed. Therefore, we asked our respondents to consider medicines A and B in the context of the pills having (1) no side effects, (2) minor side effects (MSEs), (3) severe side effects (SSEs) and (4) reduced effectiveness. Finally, we also wanted to explore if there was any systematic difference between how different groups might value DTDs. In particular, we wanted to understand whether or not patients with experience of taking pills valued DTD differently from people with little or no experience. In addition, we thought it was important to explore other factors, such as age and sex.
Time trade-off exercise
The first method we selected to value the disutility of medicine-taking health states was the TTO method. TTOs are a widely used approach for eliciting utility values and were used to generate the valuations for the EuroQol-5 Dimensions, three-level version (EQ-5D-3L) health states, which are part of the current NICE reference case. In general, the TTO method involves asking respondents to consider the relative amounts of time (e.g. number of life-years) they would be willing to sacrifice to avoid a poorer health state. 110 In this study, the TTO method followed the approach taken by Hutchins et al. 48,103 and asked respondents the maximum amount of time they are willing to give up at the end of their life to avoid having to take a medicine. Per respondent, for each of the four questions, the estimated utility was calculated as the ratio x/t, where x is the final selected time period for the medicine A option (i.e. one pill taken once) and t is the full life-years assumed for the medicine B option (i.e. a pill taken every day for 10 years). 111
Best–worst scaling experiment
Best–worst scaling experiments are an extension of discrete choice experiments. 112 There are three types of BWS: case 1 (object case), case two (profile case) and case three (multiprofile case). 113 This study used a case 2 (profile case) BWS experiment. A profile case BWS experiments ask respondents to select their most preferred and least preferred items (defined by attributes and levels) in a question.
An argued advantage of profile case BWS over standard discrete choice experiments is that the choices made reveal more information about the relative strength of people’s preferences for each attribute in the design, using fewer questions, which could, in turn, reduce the response error. Importantly, using a BWS allows a rank ordering of the attributes in the experiment together with utility weights to be estimated. In this study, the BWS experiment was framed around the choice question ‘we want you to indicate which of the listed features of medicine A you think are the most and least likely to make you want to avoid taking the tablet’. The BWS experiment contained three attributes: (1) inconvenience (levels: no inconvenience and inconvenience), (2) probability of a MSE (levels: 1%, 5%, 9% and 13%) and (3) probability of a SSE (levels: 0.1%, 0.3%, 0.5% and 0.7%). Rapid reviews of the relevant published literature and input from the research team, including patient involvement, were used to generate a list of potential attributes and assigned levels. The BWS exercise was created using a full factorial design of 32 choice sets, which were split into four randomised blocks. Each respondent was assigned to one of the four blocks, comprising eight choice sets, with each choice set displaying three features of medicine A (i.e. inconvenience, MSE and SSE). The levels for these three features varied across choice sets.
Design of training materials
Consistent with emerging good practice in the design of a stated-preference study, training materials, that introduced the background for each case study (i.e. statin or bisphosphonate) and the attributes and levels used in the BWS exercise were created using a storyboard approach. 114 The same training materials were used for the TTO and BWS experiment. In addition, we used visual arrays to communicate absolute risk consistent with best practice. 115
Survey format and content
Online surveys were designed for each method (i.e. TTO and BWS), using the same approach and format for each exemplar medicine (i.e. statins and bisphosphonates). The surveys were formatted and administered online using Sawtooth software (Sawtooth Software, Inc., Provo, UT, USA). Respondents were sent a secure link to complete one of the surveys (no reminders were used). There were three parts to each survey. The first part of the survey consisted of the EQ-5D-3L questions, training materials and questions about the respondent’s attitude towards taking a medicine for the first time. The second part of the survey consisted of the main elicitation exercise (i.e. TTO or BWS). The third part of the survey included questions about whether respondents were currently taking or had ever taken one of the branded bisphosphonates (or statins), respondents’ perceived benefits and harms of bisphosphonates (or statins), whether or not respondents had experienced any side effects from bisphosphonates (or statins) and whether or not respondents found it inconvenient to take the medicine. Participants were also asked about their opinion on taking the medicine (i.e. whether they mind/dislike taking it), whether or not they took any other medicines, the number of medicines taken on a regular basis, the number of times medicines are taken daily and sociodemographic questions, such as age, gender, qualifications, employment status, ethnicity and religion. There were also non-compulsory probability questions to understand the respondents’ understanding of risk. Feedback questions towards the end of the survey included asking respondents about their confidence in making similar choices in real life, their perceived difficulty in making choices between alternatives and in understanding the survey, as well as general feedback comments to improve the clarity of the survey.
Piloting of experiments
Two pilot phases were conducted for the design of each experiment. For the TTO and BWS surveys, early piloting involved ‘think-aloud’ interviews with a sample of 19 patients recruited from a general practice in Greater Manchester. The intention of the early pilot was to understand whether or not the draft surveys, training materials and valuation exercises were sufficiently clear for respondents. We also wanted to understand how our respondents were interacting with the material presented. Following on from this, a few minor changes were made to the training materials and valuation exercise. The survey was then tested again in quantitative pilot studies involving members of the public to assess whether or not the data could be analysed from the survey design. No changes were made following the quantitative pilot study. The final elicitation studies were then launched and involved a sample of members of the public and a sample of people with experience of taking a statin or bisphosphonate.
Data samples
People with experience of taking a statin or bisphosphonate were recruited from general practices via the NHS Research Scotland Primary Care Network and the Scottish Health Research Register (SHARE which is a register of people living in Scotland, allowing recruitment after a search of their medical records). To be included, patients needed to have been prescribed a statin or bisphosphonate in the previous year, needed to be aged ≥ 30 years and should not have been diagnosed for dementia or be taking a drug for dementia. Members of the public for the valuation study were recruited online using the panel company Dynata (Shelton, CT, USA). Within this sample, we also identified members of the public with experience of taking a statin or bisphosphonate. Respondents to the online survey needed to be aged over ≥ 30 years, but otherwise the sample should be a demographically balanced representation of the general public willing to take an online survey.
Results
The results are presented in two distinct sections for the TTO and BWS experiments.
Time trade-off
Analysis characteristics for respondents to the TTO for statins (n = 514) and respondents to the TTO for bisphosphonates (n = 365) are reported in Table 10. Statin patients tended to report marginally higher mean TTO values than public respondents [difference 0.007 (SE 0.003); i.e. the amount of life expectancy respondents were willing to sacrifice to avoid taking statins was 0.7 percentage points greater in the public respondents than in people with experience of statins], although this finding was not statistically significant. Bisphosphonate patients reported much higher TTO values – indicating less DTD – than public respondents [difference 0.024 (SE 0.006)], with this difference being statistically significant. For both statins and bisphosphonates, changing the question context did not alter the mean TTO scores by more than 0.01. Irrespective of the type of question or respondent, there was a clear difference between statins and bisphosphonates survey results (Figure 17). Mean TTO values for the entire statin sample (0.967) were higher than TTO scores for the bisphosphonate sample (0.933), meaning that the average respondent was willing to trade twice as much life expectancy to avoid bisphosphonates as they would to avoid statins [0.033 vs. 0.067; absolute difference 0.034 (SE 0.004)] (Table 11). Respondents who had experience of taking medications more than three times a day provided a much lower DTD value than respondents who had no experience of daily medicine use. None of the other explanatory variables had a statistically significant association with DTD size, including the number of pills taken per day.
| Characteristic | Statin survey | Bisphosphonate survey | Total (n = 879) | ||||
|---|---|---|---|---|---|---|---|
| Patienta (n = 227) | Publicb (n = 287) | Total (n = 514) | Patienta (n = 86) | Publicb (n = 279) | Total (n = 365) | ||
| Age (years), n (%) | |||||||
| < 35 | 1 (0.7) | 14 (6.1) | 15 (4.0) | 0 (0.0) | 18 (7.9) | 18 (6.8) | 33 (5.2) |
| 35–44 | 4 (2.8) | 44 (19.1) | 48 (12.9) | 1 (2.7) | 42 (18.5) | 43 (16.3) | 91 (14.3) |
| 45–54 | 6 (4.2) | 46 (20.0) | 52 (14.0) | 2 (5.4) | 32 (14.1) | 34 (12.9) | 86 (13.5) |
| 55–64 | 43 (30.3) | 63 (27.4) | 106 (28.5) | 10 (27.0) | 45 (19.8) | 55 (20.8) | 161 (25.3) |
| 65–74 | 66 (46.5) | 60 (26.1) | 126 (33.9) | 15 (40.5) | 80 (35.2) | 95 (36.0) | 221 (34.7) |
| ≥ 75 | 22 (15.5) | 3 (1.3) | 25 (6.7) | 9 (24.3) | 10 (4.4) | 19 (7.2) | 44 (6.9) |
| Missing | 85 | 57 | 142 | 49 | 52 | 101 | 243 |
| Sex, n (%) | |||||||
| Female | 49 (34.5) | 115 (50.0) | 164 (44.1) | 33 (89.2) | 141 (62.4) | 174 (66.2) | 338 (53.2) |
| Male | 93 (65.5) | 115 (50.0) | 208 (55.9) | 4 (10.8) | 85 (37.6) | 89 (33.8) | 297 (46.8) |
| Missing | 85 | 57 | 142 | 49 | 53 | 102 | 244 |
| Ethnicity, n (%) | |||||||
| White British/Irish | 133 (93.7) | 211 (91.7) | 344 (92.5) | 36 (97.3) | 203 (89.4) | 239 (90.5) | 583 (91.7) |
| White other | 3 (2.1) | 10 (4.3) | 13 (3.5) | 1 (2.7) | 8 (3.5) | 9 (3.4) | 22 (3.5) |
| Mixed/multiple ethnic origins | 0 (0.0) | 1 (0.4) | 1 (0.3) | 0 (0.0) | 5 (2.2) | 5 (1.9) | 6 (0.9) |
| Black/African/Caribbean/Black British | 0 (0.0) | 3 (1.3) | 3 (0.8) | 0 (0.0) | 2 (0.9) | 2 (0.8) | 5 (0.8) |
| Asian/Asian British | 0 (0.0) | 4 (1.7) | 4 (1.1) | 0 (0.0) | 7 (3.1) | 7 (2.7) | 11 (1.7) |
| Chinese | 0 (0.0) | 1 (0.4) | 1 (0.3) | 0 (0.0) | 2 (0.9) | 2 (0.8) | 3 (0.5) |
| Other ethnicity | 6 (4.2) | 0 (0.0) | 6 (1.6) | 0 (0) | 0 (0) | 0 (0) | 6 (0.9) |
| Missing | 85 | 57 | 142 | 49 | 52 | 101 | 243 |
| Number of pills taken daily, n (%) | |||||||
| 0 | 0 (0.0) | 91 (39.6) | 91 (24.5) | 0 (0.0) | 77 (33.9) | 77 (29.2) | 168 (26.4) |
| 1 | 4 (2.8) | 52 (22.6) | 56 (15.1) | 4 (10.8) | 38 (16.7) | 42 (15.9) | 98 (15.4) |
| 2–5 | 104 (73.2) | 69 (30.0) | 173 (46.5) | 23 (62.2) | 86 (37.9) | 109 (41.3) | 282 (44.3) |
| 6–10 | 31 (21.8) | 14 (6.1) | 45 (12.1) | 5 (13.5) | 16 (7.0) | 21 (8.0) | 66 (10.4) |
| > 10 | 3 (2.1) | 4 (1.7) | 7 (1.9) | 5 (13.5) | 10 (4.4) | 15 (5.7) | 22 (3.5) |
| Missing | 85 | 57 | 142 | 49 | 52 | 101 | 243 |
| Number of different times pill taken per day, n (%) | |||||||
| None | 3 (2.1) | 94 (40.9) | 97 (26.1) | 0 (0.0) | 75 (33.0) | 75 (28.4) | 172 (27.0) |
| Once per day | 33 (23.2) | 74 (32.2) | 107 (28.8) | 18 (48.6) | 75 (33.0) | 93 (35.2) | 200 (31.4) |
| Two times a day | 87 (61.3) | 48 (20.9) | 135 (36.3) | 12 (32.4) | 54 (23.8) | 66 (25.0) | 201 (31.6) |
| Three times a day | 17 (12.0) | 11 (4.8) | 28 (7.5) | 5 (13.5) | 19 (8.4) | 24 (9.1) | 52 (8.2) |
| More than three times a day | 2 (1.4) | 3 (1.3) | 5 (1.3) | 2 (5.4) | 4 (1.8) | 6 (2.3) | 11 (1.7) |
| Missing | 85 | 57 | 142 | 49 | 52 | 101 | 243 |
| EQ-5D-3L utility mean (SD)c | 0.827 (0.2) | 0.818 (0.2) | 0.822 (0.2) | 0.770 (0.2) | 0.786 (0.2) | 0.783 (0.2) | 0.806 (0.2) |
| Missing | 56 | 41 | 97 | 35 | 33 | 68 | 165 |
FIGURE 17.
Kernel density plots showing distribution of TTO responses stratified by medicine, question context and respondent type. (a) Statin questions 1–4 utility values in patients; (b) statin questions 1–4 utility values in the public; (c) bisphosphonates questions 1–4 utility values in patients; and (d) bisphosphonates questions 1–4 utility values in the public.

| Medicine | Respondent | Question context | Mean | SD | Count | Skewness | Kurtosis | P1a | P25a | P50a | P75a | P90a | Proportion reporting disutility |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Statins | Public | No side effects | 0.965 | 0.057 | 237 | −2.936 | 13.152 | 0.942 | 0.950 | 0.983 | 1.000 | 1 | 0.746 |
| Statins | Public | Some MSEs | 0.964 | 0.063 | 233 | −3.344 | 17.003 | 0.942 | 0.950 | 0.995 | 1.000 | 1 | 0.721 |
| Statins | Public | Some SSEs | 0.964 | 0.060 | 232 | −2.682 | 10.207 | 0.942 | 0.950 | 0.988 | 1.000 | 1 | 0.725 |
| Statins | Public | Reduced effectiveness | 0.964 | 0.063 | 232 | −3.173 | 15.041 | 0.942 | 0.950 | 0.983 | 1.000 | 1 | 0.735 |
| Statins in the public | 0.964 | 0.061 | 934 | −3.063 | 14.217 | 0.942 | 0.950 | 0.992 | 1.000 | 1 | 0.731 | ||
| Statins | Patients | No side effects | 0.974 | 0.054 | 161 | −4.885 | 34.521 | 0.942 | 0.967 | 0.996 | 1.000 | 1 | 0.718 |
| Statins | Patients | Some MSEs | 0.972 | 0.056 | 156 | −4.407 | 30.351 | 0.942 | 0.958 | 0.996 | 1.000 | 1 | 0.718 |
| Statins | Patients | Some SSEs | 0.968 | 0.060 | 150 | −3.754 | 22.775 | 0.942 | 0.950 | 0.997 | 1.000 | 1 | 0.718 |
| Statins | Patients | Reduced effectiveness | 0.970 | 0.055 | 148 | −2.768 | 10.985 | 0.942 | 0.950 | 0.997 | 1.000 | 1 | 0.714 |
| Statins in patients | 0.971 | 0.056 | 615 | −3.971 | 24.829 | 0.942 | 0.967 | 0.997 | 1.000 | 1 | 0.717 | ||
| Statins all respondents | 0.967 | 0.059 | 1549 | −3.379 | 17.681 | 0.942 | 0.950 | 0.995 | 1.000 | 1 | 0.725 | ||
| Bisphosphonates | Public | No side effects | 0.925 | 0.081 | 219 | −1.312 | 4.800 | 0.833 | 0.850 | 0.967 | 0.989 | 1 | 0.860 |
| Bisphosphonates | Public | Some MSEs | 0.930 | 0.076 | 216 | −1.213 | 3.825 | 0.833 | 0.883 | 0.967 | 0.992 | 1 | 0.846 |
| Bisphosphonates | Public | Some SSEs | 0.932 | 0.076 | 214 | −1.319 | 4.205 | 0.833 | 0.883 | 0.967 | 0.996 | 1 | 0.846 |
| Bisphosphonates | Public | Reduced effectiveness | 0.933 | 0.078 | 216 | −1.436 | 4.475 | 0.833 | 0.883 | 0.967 | 0.996 | 1 | 0.842 |
| Bisphosphonates in the public | 0.930 | 0.078 | 865 | −1.325 | 4.382 | 0.833 | 0.883 | 0.967 | 0.995 | 1 | 0.849 | ||
| Bisphosphonates | Patients | No side effects | 0.949 | 0.069 | 42 | −1.136 | 2.792 | 0.833 | 0.900 | 0.983 | 1.000 | 1 | 0.814 |
| Bisphosphonates | Patients | Some MSEs | 0.955 | 0.055 | 40 | −0.977 | 2.551 | 0.867 | 0.917 | 0.967 | 1.000 | 1 | 0.826 |
| Bisphosphonates | Patients | Some SSEs | 0.958 | 0.060 | 40 | −1.695 | 5.311 | 0.867 | 0.950 | 0.975 | 1.000 | 1 | 0.802 |
| Bisphosphonates | Patients | Reduced effectiveness | 0.956 | 0.065 | 39 | −2.059 | 7.568 | 0.850 | 0.933 | 0.967 | 1.000 | 1 | 0.802 |
| Bisphosphonates in patients | 0.954 | 0.062 | 161 | −1.506 | 4.694 | 0.850 | 0.933 | 0.967 | 1.000 | 1 | 0.811 | ||
| Bisphosphonates all respondents | 0.934 | 0.076 | 1026 | −1.369 | 4.532 | 0.833 | 0.883 | 0.967 | 0.998 | 1 | 0.840 | ||
| All statins and bisphosphonates | 0.954 | 0.068 | 2575 | −2.243 | 8.926 | 0.833 | 0.942 | 0.975 | 1.000 | 1 | 0.773 | ||
Best–worst scaling experiment
Analysis characteristics for respondents completing the BWS for statins (n = 319) and respondents completing the BWS for bisphosphonates (n = 312) are reported in Table 12. Appendix 5, Table 46, shows the count data [normalised based on the number of levels for each attribute: in/convenience (two levels), MSEs (four levels), SSEs (four levels)] for the number of times a respondent chose the attribute level as ‘best’ and ‘worst’, and the difference between ‘best and worst’. Appendix 5, Figures 34 and 35, show the distribution of the count data for statins and bisphosphonates, respectively.
| Characteristic | Statin surveya | Bisphosphonate surveya | Total (n = 631) | ||||
|---|---|---|---|---|---|---|---|
| Experience of taking statin (n = 105) | No experience of taking statin (n = 214) | Total (n = 319) | Experience of taking bisphosphonate (n = 83) | No experience of taking bisphosphonate (n = 229) | Total (n = 312) | ||
| Age (years), n (%) | |||||||
| < 35 | 4 (3.81) | 19 (8.88) | 23 (7.21) | 7 (8.43) | 19 (8.3) | 26 (8.33) | 49 (7.8) |
| 35–44 | 17 (16.19) | 54 (25.23) | 71 (22.26) | 10 (12.05) | 36 (15.72) | 46 (14.74) | 117 (18.5) |
| 45–54 | 13 (12.38) | 39 (18.22) | 52 (16.3) | 6 (7.23) | 34 (14.85) | 40 (12.82) | 92 (14.6) |
| 55–64 | 24 (22.86) | 67 (31.31) | 91 (28.53) | 23 (27.71) | 44 (19.21) | 67 (21.47) | 158 (25.0) |
| 65–74 | 38 (36.19) | 29 (13.55) | 67 (21) | 23 (27.71) | 76 (33.19) | 99 (31.73) | 166 (26.3) |
| ≥ 75 | 9 (8.57) | 6 (2.8) | 15 (4.7) | 14 (16.87) | 20 (8.73) | 34 (10.9) | 49 (7.8) |
| Sex, n (%) | |||||||
| Female | 48 (45.71) | 153 (71.5) | 201 (63.01) | 71 (85.54) | 186 (81.22) | 257 (82.37) | 458 (72.6) |
| Male | 57 (54.29) | 61 (28.50) | 118 (37.0) | 12 (14.46) | 43 (18.78) | 55 (17.63) | 173 (27.4) |
| Ethnicity, n (%) | |||||||
| White British/Irish | 100 (95.24) | 183 (85.51) | 283 (88.71) | 78 (93.98) | 203 (88.65) | 281 (90.06) | 564 (89.4) |
| White other | 0 (0.00) | 13 (6.07) | 13 (4.08) | 3 (3.61) | 11 (4.8) | 14 (4.49) | 27 (4.3) |
| Mixed/multiple ethnic origins | 0 (0.00) | 1 (0.47) | 1 (0.31) | 0 (0.00) | 2 (0.87) | 2 (0.64) | 3 (0.5) |
| Black/African/Caribbean/Black British | 0 (0.00) | 4 (1.87) | 4 (1.25) | 0 (0.00) | 2 (0.87) | 2 (0.64) | 6 (1.0) |
| Asian/Asian British | 3 (2.86) | 10 (4.67) | 13 (4.08) | 1 (1.2) | 8 (3.49) | 9 (2.88) | 22 (3.5) |
| Other ethnicity | 2 (1.9) | 3 (1.4) | 5 (1.57) | 1 (1.2) | 3 (1.31) | 4 (1.28) | 9 (1.4) |
| Number of pills taken daily, n (%) | |||||||
| 0 | 6 (5.71) | 104 (48.6) | 110 (34.48) | 7 (8.43) | 86 (37.55) | 93 (29.81) | 203 (32.2) |
| 1 | 21 (20) | 52 (24.3) | 73 (22.88) | 14 (16.87) | 30 (13.1) | 44 (14.1) | 117 (18.5) |
| 2–5 | 54 (51.43) | 50 (23.36) | 104 (32.6) | 40 (48.19) | 85 (37.12) | 125 (40.06) | 229 (36.3) |
| 6–10 | 18 (17.14) | 6 (2.8) | 24 (7.52) | 19 (22.89) | 21 (9.17) | 40 (12.82) | 64 (10.1) |
| > 10 | 6 (5.71) | 2 (0.93) | 8 (2.51) | 3 (3.61) | 7 (3.06) | 10 (3.21) | 18 (2.9) |
| Number of different times pill taken per day, n (%) | |||||||
| None | 6 (5.71) | 109 (50.93) | 115 (36.05) | 7 (8.43) | 86 (37.55) | 93 (29.81) | 208 (33.0) |
| Once per day | 38 (36.19) | 64 (29.91) | 102 (31.97) | 23 (27.71) | 62 (27.07) | 85 (27.24) | 187 (29.6) |
| Two times a day | 41 (39.05) | 26 (12.15) | 67 (21) | 35 (42.17) | 59 (25.76) | 94 (30.13) | 161 (25.5) |
| Three times a day | 12 (11.43) | 7 (3.27) | 19 (5.96) | 16 (19.28) | 15 (6.55) | 31 (9.94) | 50 (7.9) |
| More than three times a day | 8 (7.62) | 8 (3.74) | 16 (5.02) | 2 (2.41) | 7 (3.06) | 9 (2.88) | 25 (4.0) |
| Mean (SD) EQ-5D-3L utilityb | 0.73 (0.34) | 0.80 (0.24) | 0.78 (0.28) | 0.72 (0.26) | 0.79 (0.24) | 0.77 (0.25) | 0.78 (0.23) |
The data show that all the respondents had the strongest preference for taking a medicine with no inconvenience, which is the result expected a priori. This result was consistent between respondents with and without previous experience of taking a statin or bisphosphonate. The results from the pooled sample indicated that respondents had a strong dislike for experiencing the highest level of risk of a SSE. Overall, the respondents with experience of taking a statin or bisphosphonate indicated a greater dislike for a SSE and stronger preference for no inconvenience.
There was significant preference heterogeneity in the results. A fully correlated mixed logit model was, therefore, used to estimate preference weights for each attribute level relative to the reference level of 0.7% risk of a SSE (Table 13). The signs for all estimated coefficients in the fully correlated mixed logit model were consistent with a priori expectations based on the normalised best–worst scores. The estimated coefficients from the fully correlated mixed logit model were ‘re-scaled’ by setting no inconvenience at a value of 1 and 0.7% risk of SSEs at zero to calculate an indicative utility score for no inconvenience. Using this approach, the DTD for a statin was 0.2 and 0.46 for a statin and bisphosphonate, respectively (i.e. compared with a life free of the medications, life lived with medications should be seen as 80% or 54% as desirable, respectively).
| Attribute level | Bisphosphonates | Statins | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| With experience | Without experience | Pooled | With experience | Without experience | Pooled | |||||||
| Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE | |
| No inconvenience | 5.232** | 0.50 | 4.445** | 0.30 | 3.675** | 0.22 | 1.907** | 0.29 | 2.700** | 0.24 | 2.850** | 0.22 |
| Inconvenience | 2.814** | 0.36 | 2.515** | 0.23 | 1.950** | 0.20 | 1.457** | 0.30 | 2.037** | 0.22 | 2.064** | 0.18 |
| MSE | ||||||||||||
| 1% | 1.383** | 0.29 | 1.898** | 0.22 | 1.411** | 0.16 | 1.147** | 0.28 | 1.236** | 0.17 | 1.498** | 0.17 |
| 5% | 1.208** | 0.29 | 1.113** | 0.23 | 0.707** | 0.17 | 0.385 | 0.29 | 0.606** | 0.17 | 0.865** | 0.18 |
| 9% | 0.921* | 0.29 | 0.695* | 0.24 | 0.275 | 0.18 | 0.246 | 0.29 | 0.037 | 0.19 | 0.546* | 0.19 |
| 13% | 0.871* | 0.30 | 0.130 | 0.24 | −0.094 | 0.19 | 0.152 | 0.30 | −0.185 | 0.19 | 0.310 | 0.19 |
| SSE | ||||||||||||
| 0.1% | −0.359 | 0.41 | 0.540* | 0.20 | 0.176 | 0.16 | 0.561 | 0.30 | 0.824** | 0.21 | 0.777** | 0.17 |
| 0.3% | −1.553* | 0.50 | 0.265 | 0.24 | 0.019 | 0.17 | −0.134 | 0.31 | 0.155 | 0.19 | 0.264 | 0.16 |
| 0.5% | −1.713* | 0.55 | 0.181 | 0.22 | −0.103 | 0.17 | −0.372 | 0.30 | −0.137 | 0.20 | 0.012 | 0.16 |
| 0.7% | 3.625 | N/A | −0.986 | N/A | −0.092 | N/A | −0.055 | N/A | −0.843 | N/A | −1.052 | N/A |
| Number of observations | 3320 | 9160 | 12,480 | 4200 | 8560 | 12,760 | ||||||
| Log-likelihood | −655.22 | −2035.81 | −2698.81 | −926.252 | −2001.62 | −2985.87 | ||||||
| BIC | 1748.26 | 4564.23 | 5906.94 | 2303.017 | 4492.20 | 6482.264 | ||||||
Discussion
In this study, using the TTO method, we find that long-term statin use is associated with a DTD of 0.034 among people willing to take statins. We find that bisphosphonate use is associated with a DTD of 0.067 among people willing to take bisphosphonates. These values imply that, even if medicines have no specific adverse effects, the act of taking medicines can have a non-trivial effect on people’s quality of life. We found no difference between patient and public disutilities for statins, but we did find that bisphosphonate patients generated smaller disutility values than the values coming from the general public.
Although we find that DTD values do not tend to differ based on the reported characteristics of the respondents in our survey, we do still find large variations across individuals. In line with previous empirical studies,47,48,103 we find strong evidence for three different groups or types of respondent: (1) some never trading, suggesting zero disutility associated with treatments, (2) some always selecting the lowest possible value, suggesting that they would be unlikely to initiate treatment and (3) some willing to trade length of life for no ongoing treatment, suggesting a DTD. In our survey, the groups willing to trade and generate a DTD made up the majority of respondents surveyed, with approximately 72% and 84% for statins and bisphosphonates respondents, respectively.
The findings from the BWS experiment had face validity in that no inconvenience was the most preferred attribute. Inconvenience was a stronger driver of what to avoid when taking a medicine, but avoiding side effects were more important. The estimated values for DTD did not, however, have face validity. The DTD values were very large. This result is probably because the design of a BWS experiment that includes only the attributes of interest would tend to inflate the importance of inconvenience. Further analysis is planned to explore the effect of adjusting the observed DTD from the BWS with results from a TTO experiment that was embedded in the BWS survey.
Our research shows that people will trade life expectancy to avoid treatment characteristics in exactly the same way they will trade like expectancy to avoid undesirable health states. However, even though the preferences can be measured on the same scale, whether or not these two types of preferences should be treated as tradeable with each other is a normative question (i.e. should the NHS be paying for patients’ convenience?) In England, at least, NICE appears to answer that question in the affirmative, stating that ‘If characteristics of healthcare technologies have a value to people independent of any direct effect on health, the nature of these characteristics should be clearly explained and if possible the value of the additional benefit should be quantified. These characteristics may include convenience and the level of information available for patients’ (emphasis added in bold; © NICE 2013 Guide to the Methods of Technology Appraisal 2013. Available from http://web.archive.org/web/20230117104032/https://www.nice.org.uk/process/pmg9/chapter/the-reference-case. All rights reserved. Subject to Notice of rights). 117 As far as we are aware, NICE has taken account of such factors only when it helps to differentiate one mode of treatment from another. For example, NICE Technology Appraisal 606,118 considered subcutaneous compared with intravenous administration of medicines for hereditary angioedema, and the economic modelling in NICE Guideline 17119 incorporated the benefit of continuous blood glucose monitoring compared with fingerprick tests. In both cases, the evidence relied on used methods that are comparable with our approach (i.e. TTO in members of the UK general population). 120,121 We see no reason why the process characteristics of some treatment compared with none should not be considered in the same way.
Nevertheless, the implications of our findings for future cost–utility analyses evaluating treatment pathways featuring statins or bisphosphonates (and potentially other oral medicines) are not straightforward. On the one hand, CEAs should ideally capture the impact of all relevant costs and consequences associated with alternative forms of treatment,122 and so it must be relevant that we have demonstrated that the average person anticipates the act of taking statins or bisphosphonates will have a non-trivial impact on their quality of life. Accounting for this disutility is likely to reduce the desirability of treatments that are currently considered very cost-effective, and estimates of cost-effectiveness for long-term preventative interventions have been shown to be particularly sensitive to the inclusion of DTD. 40,44,47,48,103,107,108,123,124 Indeed, we have previously shown that for some people for whom guidelines currently recommend statins (e.g. people at a 10% risk of a cardiovascular event over 10 years), a DTD that appears moderate in the light of the current study (0.015) would result in treatment doing more harm than good. 41
On the other hand, the apparent existence of distinct preference groups among our respondents requires careful consideration. A substantial minority of participants repeatedly indicated that they would be unwilling to trade any life expectancy to avoid taking these medicines, suggesting that participants consider any inconvenience with which they are associated negligible. It would be difficult to deny access to a treatment on the grounds that the average person would be bothered by its process characteristics, which is a danger if population-level cost-effectiveness estimates routinely incorporate average DTD.
In view of these conflicting considerations, we recommend that decision-makers review scenarios with and without DTD. If evidence suggests that including DTD would materially alter the balance of benefits, harms and costs associated with treatment, then this should be highlighted in population-level guidance, enabling prescribers at an individual level to engage in shared decision-making that gives appropriate weight to the person’s preferences for avoiding the treatment’s process characteristics. Such an approach fits well with the guideline development methods for NICE,125 which encourage the explicit identification of ‘preference-sensitive decision points’, taking the practicalities of possible treatments into account.
An alternative approach – broadly reflecting current practice – is to prescribe regardless of DTD and allow each person’s emergent level of inconvenience define whether or not they adhere to the therapy. We believe that incorporating anticipated preferences in prospective shared decision-making is a superior approach, as it allows for an informed discussion of pros and cons and enables prescribers to tailor the strength of their advice accordingly. This should have the consequence that people whose expected benefits easily outweigh their short-term inconvenience will be less likely to discontinue treatments, whereas others who can expect only marginal gain will be less likely slavishly to adhere to a course of action that impairs their quality of life just because their doctor appeared to recommend it. Similarly, given that the emphasis of treatment decision-making now emphasises ‘concordance’ (i.e. agreement) rather than ‘compliance’ by the patient with clinical recommendations, better understanding that an individual’s preferences around medicine-taking can influence whether or not net benefit is expected may lead to less potential conflict between prescribers and patients.
Limitations
There are some limitations to our study that need to be considered. Although we endeavoured to communicate complex concepts clearly within the study, this had a set of clear trade-offs for participants. The length of the survey, the cognitive burden and the time required to complete the survey were noted as challenges. Some of our respondents reported that they had difficulty understanding the TTO methods, whereas others provided inconsistent values across the survey questions. In addition, participants who took part in our survey ultimately self-selected and this could be related to their ability to complete the survey, as well as their self-reported health. Applicability for a different patient or general population should be made based on a careful judgement of the self-reported characteristics summarised for this study cohort.
It is not immediately clear which values elicited for DTD should be used. In terms of face validity, the DTD elicited from the TTO seemed ‘better’. For the decision-analytic modelling reported in Chapters 6 and 7, we used the DTD values from the TTO study. This decision was made because the TTO method is consistent with how utility values are typically elicited to attach to health states in CEA. 117
Conclusion
This study indicated that DTD does exist. It is not clear whether or not the DTD elicited from the TTO or BWS should be used; however, using face validity would suggest that the TTO method produced more realistic DTD values. We suggest that DTD should be included in model-based CEA of long-term preventative medicines, and Chapters 6 and 7 explore the impact of using the elicited DTD values from the TTO method.
Chapter 6 Cost-effectiveness analysis accounting for competing risks and direct treatment disutility: statins for the primary prevention of cardiovascular disease
Background
Preventative treatments are different from interventions for acute conditions. Preventative treatments may have both immediate and persistent harms, but their benefits are deferred. It follows that shared decision-making between the patient and clinician about whether or not to start a preventative treatment should focus on whether or not the (potential) long-term health benefits are sufficient to justify the (certain) immediate burden and (possible) immediate or delayed harms. Clinical practice guidelines may provide recommendations, indicating whether or not this trade-off is positive for an average person. In England, at least, the developers of such guidelines are often informed by a quantitative analysis exploring the benefits, harms and costs of treatments compared with each other or with no treatment. This usually takes the form of a decision-analytic model that quantifies the net effects of competing approaches in terms of QALYs, encompassing expected benefits and harms, and compares these with net costs. Interventions will typically receive positive recommendations only if the guideline developers are confident that offering the treatment in question will result in population-level QALY gain (without imposing opportunity costs that imply even greater QALY loss in the wider health system). Therefore, prescribers may assume that, all things being equal, the preventative treatments that are recommended in trustworthy guidelines provide net benefit, and this seems like helpful information until one acknowledges that, in practice, all things never are equal.
Two particular dimensions in which any given person will diverge from population average are their clinical characteristics – especially with regard to long-term conditions other than the one of interest – and their preferences – in terms of whether or not they perceive a treatment is worth taking. Clinical guidelines often neglect to consider these factors, except in nebulous terms (e.g. encouraging prescribers to consider individualised risks and benefits, without providing any objective basis on which to introduce them to an options talk).
In the cost-effectiveness sections of this project, reported in this chapter and in Chapter 7, we aim to address this gap. We explore how accounting for clinical characteristics and preferences (accounted for using DTD) could alter the balance of benefits, harms and costs of preventative interventions. By adapting current methods used to populate model-based CEA of preventative medicines, we can better reflect the potential for subgroups of the patient populations to accrue different degrees of net benefit.
Our first objective is to tailor estimates according to competing mortality risk. As explored in Chapters 2–4, all people at risk of a given health condition are also at risk of other events that preclude the incidence of the condition of interest (unrelated death is an obvious example in almost all cases). We will see that, unlike epidemiological risk prediction models, decision-analytic economic models usually have some structural way of accounting for such competing events. However, decision modellers seldom pay close attention to how the likelihood of competing events is parameterised. Often, for example, decision modellers use an unadjusted estimate of general population mortality to reflect deaths that are not related to the condition of primary interest. We wanted to assess how much a failure to handle competing risks robustly might bias model outputs. This chapter explores an example using a cohort-level state-transition model (i.e. statins for the primary prevention of CVD) and Chapter 7 looks at a patient-level discrete-event simulation (i.e. bisphosphonates for the primary prevention of osteoporotic fragility fracture). In both cases, we build on the models that were used to underpin national guidance from NICE. In the case of statins, we use the model developed for Clinical Guideline 181 (CG181). 10 For bisphosphonates, we start from the model for Technology Appraisal 464 (TA464). 12 We do not necessarily assert that these are the best possible models in each decision space, and our choice to adopt and adapt the models arises from our interest in the extent to which existing population-level guidance might be affected by the issues under consideration.
Our second objective is to incorporate the evidence regarding DTD generated in Chapter 5, using the TTO method into modelled estimates of the cost-effectiveness of statins and bisphosphonates. Having found that a majority of people would be prepared to trade some of their life expectancy to avoid the inconvenience of taking statins or bisphosphonates, it is an obvious next step to ask whether or not the benefits of the interventions are sufficient to counterbalance this level of disutility. By integrating existing evidence with our new findings, we can derive QALY estimates for preventative medicines, compared with no intervention, that help us weigh up the overall balance of options for people with different levels of preference to avoid medicines.
Modifying existing methods in these ways allows us to define cost-effective subgroups of people who reflect different levels of competing risk (defined by specified levels of competing risk at different levels of baseline risk) and different degrees of DTD (defined by specified levels/durations of DTD).
Methods
We used a cohort-based decision-analytic model to address the stated decision problem (Table 14).
| Decision-analytic model | Criterion |
|---|---|
| Decision problem | What is the impact of including competing risk in a risk prediction algorithm to inform whether or not to start a statin in a population at risk of events as a result of CVD? |
| Intervention | Statins at three different intensities: low (simvastatin 10 mg/day), medium (simvastatin 20 mg/day) and high (atorvastatin 20 mg/day) |
| Comparators | No treatment |
| Model type | State-transition Markov model |
| Population | Men and women of any age potentially eligible for a statin based on QRISK3 10-year predicted risk of incident CVD |
| Setting | Primary care services in NHS England |
| Time horizon | 40 years |
| Study perspective | NHS in England |
| Costs | Statins |
| Treating subsequent CVD-related events | |
| Measured using GBP (£) at 2019–20 prices | |
| Consequences | Impact on health status (± DTD) measured using QALYs |
| Discounting | 3.5% for costs and consequences |
| Cost-effectiveness threshold | NICE-recommended threshold of £20,000 per QALY gained |
Selection of the statins case study
The decision-analytic model we adopted and developed for this decision problem takes a cohort-level state-transition (Markov) approach to predicting events of interest and estimating costs and effects. 10
Decision-analytic models of this type account for competing risks by design. For example, consider a Markov model with the three states of (1) well, (2) myocardial infarction (MI) and (3) dead (for our purposes, we will define the latter two as absorbing states from which further transitions are not of interest) and let per-cycle transition probabilities pwell→MI and pwell→dead both be 0.1. Assuming the whole cohort starts in the well state, after one cycle of the model 10% of people will be in the dead state and 10% will be in the MI state, leaving 80% in the well state. Note that, via the transition to death, 10% of the people who were initially at risk of a MI have been taken out of the at-risk state before cycle 2 without experiencing a MI. After the second cycle, we will have 18% of the cohort in the MI state (1 × 0.1 + 0.8 × 0.1); however, if we had a two-state well MI model with no competing risk of death, then it would have been 19% (1 × 0.1 + 0.9 × 0.1). If we run the model on for 10 cycles, and we find that 44.6% of people have had a MI, then without the competing transition to death the number would be 65.1%.
This simple example demonstrates that a competing risk structure is hardwired into the kind of state-transition models that are very commonly used to assess the cost-effectiveness of healthcare interventions. The example also shows that, to parameterise any given transition within such a structure, it is appropriate to rely on evidence that censors for competing events. Were we to base our inputs on time-to-event models that, themselves, adjust for competing risks (e.g. models explored in Chapters 2 and 3), our model would underestimate the probability of events of interest, as we would be effectively double counting the competing risks.
Clearly, however, it is important that the time-to-event evidence on which a decision model relies should be valid for the population to which the decision problem pertains. It should be clear from the above that if we have an inappropriate estimate of any one of our transitions, then it is not only with respect to that outcome that our model will be biased, as it will also compromise our estimate of any events with which it competes.
In an epidemiological risk prediction model, failing to account for competing risks will result in an overestimate of event rates for the whole cohort. In a state-transition decision model, the danger is that we will fail to account accurately for competing risks, which will lead to overprediction of events in people with higher-than-average competing risk and underprediction of events in people with lower-than-average competing risks.
Model overview
Table 14 summarises the decision problem and scope of the analysis for the model-based CEA. The model from which we started directly replicates the model developed to inform decision-making about primary prevention of CVD in CG181. 10 The published guideline provides a detailed description of methods. 10
In summary, the model takes a cohort-level state-transition (Markov) approach. The model has a 1-year cycle length and a 40-year time horizon. Figure 18 illustrates the model structure. As the decision problem relates to primary prevention, the whole cohort starts in the ‘no known CVD’ state. As time progresses in the model, the model simulates a proportion of people experiencing one or more of seven distinct non-fatal cardiovascular events [i.e. stable angina (SA), unstable angina (UA), MI, stroke, TIA, peripheral arterial disease (PAD) and heart failure]. The model also accounts for cardiovascular death and other-cause mortality. For each of the non-fatal cardiovascular events, an initial 1-year cycle reflects an acute event or diagnosis and a post-event state reflects people living with a history of the event in subsequent years. Repeat acute events are possible for MI and stroke. Where evidence was available to the CG181 modellers, other secondary events occur from most acute and post-event states. However, in the base case, no further events are allowed from PAD and heart failure (as these events are associated with the highest probability of cardiovascular death, meaning that additional events would unrealistically confer an improvement in prognosis).
FIGURE 18.
Structure of state-transition model assessing statins for primary prevention of CVD. HF, heart failure.
However, in the base case, no further events are allowed from PAD and heart failure (as these events are associated with the highest probability of cardiovascular death, meaning that additional events would unrealistically confer an improvement in prognosis).
The model simulates a cohort comprising men and/or women of a specified age and a baseline 10-year risk of a first cardiovascular event (i.e. events counted by QRISK3: SA, UA, MI, stroke, TIA and cardiovascular death). (Note that the model handles heart failure and PAD separately on the assumption that their incidence is proportional to that of the QRISK3 events.) Calculations are based on true baseline risk, that is, absent competing events, 20% of people with a 20% 10-year risk will experience a first cardiovascular event in the first 10 years of the model.
The ways in which we have adapted the model fall into two broad categories. First, there were ‘general model updates’ that reflect steps we took to bring the CG181 model up to date and improve the parameterisation and/or implementation of existing functionality. Second, we introduced new features to explore the issues of interest for this project (i.e. accounting for competing risk and the incorporating DTD).
General model updates
Except where otherwise described, our version of the model retains the inputs used for the CG181 analysis (see guideline documentation for full details10).
Natural history: mortality statistics
The CG181 model relied on ONS lifetables for England for 2010–2. We configured the model to simulate present-day life expectancy using ONS lifetables for 2017–9. 126 While we were in the latter stages of preparing this report, ONS lifetables for 2018–20 became available; however, we did not update the model to use these data, as the data include substantial excess mortality owing to the COVID-19 pandemic that began in 2020.
The model also needs an estimate of the proportion of deaths that are caused by CVD. For this estimate, the CG181 model used ONS death registration statistics for England and Wales from 2012, selecting all deaths recorded under ICD-10 codes I00–I99. For this study we did exactly the same, using data for 2019 that are now available through an ONS Application Programming Interface. 127
Type of first cardiovascular event
In the CG181 model,10 as preserved in our update, a cohort’s cardiovascular risk is defined by its specified 10-year QRISK3 predicted risk. The model treats this value as deterministically exact, that is, absent competing risks, 20% of a cohort with a 20% 10-year cardiovascular risk will experience a first qualifying event in the first 10 years of the model.
The model subdivides the proportion of people experiencing a first event into eight event-specific states. Six events were covered by QRISK3 (i.e. SA, UA, MI, stroke, TIA and cardiovascular death) plus two additional events (i.e. heart failure and PAD) (see Figure 18). In CG181, the evidence used to define the split came from the original NICE technology appraisal on statins,128 which took data from a variety of sources. 129–131 This evidence is 25–40 years old and it does not account for underlying level of risk (i.e. it is plausible that people at low risk of cardiovascular events experience a different distribution of first events from people at high risk). Moreover, it is suboptimal to derive a subdivision like this using disparate sources of evidence. Therefore, we used the CPRD data set generated for the cardiovascular element of this project (see Chapter 2) to develop a new estimate of type of first cardiovascular event, conditional on some event having occurred. We fitted a multinomial logistic regression model to estimate the relative probabilities of a cardiovascular event being of each type, according to sex, age at event and baseline QRISK3 predicted risk. Appendix 6 provides full methods, including a worked example calculation and resulting inputs for the decision-analytic model.
Increasing cardiovascular risk over time
The CG181 model incorporates a year-on-year linear increase in cardiovascular risk (0.3% per year for men and 0.08% per year for women), based on a regression undertaken for the original NICE technology appraisal on statins. 128 The model applies this yearly increment in the initial 10-year period, over which the user specifies baseline risk (centring the risk around the middle of the period so that the cumulative risk over the 10 years is very close to the specified level) and then extends the same linear increase beyond to the model’s time horizon.
We retained the assumption that the increase is linear over the initial 10 years. However, beyond the period of fixed risk, we made use of evidence from the QRISK3 derivation study,25 that is increase in cardiovascular risk accelerates as people get older. We configured the model to use the age coefficients from QRISK3 to estimate HRs for people as they age. For men, QRISK3 estimates age-related risk in terms of (age/10)−1 and (age/10)3, for which the log-HRs are −17.84 and 0.0023, respectively. For women, the parameters are (age/10)−2 and (age/10) and the log-HRs are −8.14 and 0.797, respectively. We verified that our implementation of these data exactly matches the ‘HRs by age’ depicted in supplementary material for the QRISK3 derivation paper. 25 Using this approach, our model calculates HRs for people as they age, compared with their risk at the end of the initial 10-year period, and applies the HRs to calculate yearly risk increases.
When performing this update, our study also identified an error in the CG181 model in how increasing baseline risk interacts with treatment effect,10 as this leads to anomalous results where statins – despite being notionally subject to a constant relative risk indicating benefit – are associated with raised risk of some events (i.e. stroke and cardiovascular death) in later cycles of the model. A negative effect of statins also develops for heart failure, even though, in its base case, the CG181 model10 and ours assume a relative risk of 1 (i.e. no benefit) for this outcome. We corrected this error in our implementation of the model.
Treatment effectiveness
We have not updated any estimates of the effectiveness of statins in preventing CVD and, therefore, these estimates remain as in CG181. 10 For high-intensity regimens, this means relative risks of 0.46 (95% CI 0.37 to 0.59) for MI, 0.80 (95% CI 0.70 to 0.91) for stroke and 0.73 (95% CI 0.61 to 0.88) for cardiovascular death. As in CG181,10 we assume that statins’ effect in reducing MI also applies to SA, UA and PAD, and that the effect for stroke applies to TIA. We do not model a benefit for statins in reducing incidence of heart failure.
The base-case model presented in CG18110 included a benefit for statins in reducing non-cardiovascular mortality. The evidence supporting this assumption was weak in 2014, and we are not aware of any stronger data since the guideline was published. Therefore, we have removed this assumption from our base case (i.e. we do not model any non-cardiovascular benefit for statins).
Health-related quality of life: underlying
The developers of the model that informed the original NICE technology appraisal for statins128 undertook a linear regression on patient-level data from the study reported by Kind et al. 132 to estimate baseline quality of life. This analysis, which the CG181 model subsequently adopted, uses data from the general population and defined utility as a function of age, without accounting for sex or any non-linear effects. We considered that it could be important to account for these factors in a more flexible way and so we undertook a new regression, using a pooled sample of respondents from the Health Survey for England (HSE)133 (see Appendix 6 for full details).
Health-related quality of life: cardiovascular events
To quality-adjust expected survival for cost–utility analysis of a state-transition model, we require estimates of the quality of life associated with each of the model states. We performed a systematic literature review to update the health state utility values from the CG181 model. 10 To identify estimates for each model state, we adopted a pragmatic approach, following recommendations in the NICE Decision Support Unit’s technical support document for utility values. 134 Appendix 6 provides details of the values we selected for the updated model and the process by which we identified and selected them. Appendix 6, Table 51, provides full details of the final inputs.
Adverse drug events
The CG181 model accounted for one adverse effect of statins, based on evidence appearing to show hastened onset of type 2 diabetes at the time. 10 However, a recent systematic review found no association between randomisation to statins and incidence of diabetes [odds ratio (OR) 1.01, 95% CI 0.88 to 1.16]. 135 Therefore, we removed this feature from our version of the model.
The adverse event with which people most commonly believe statins are associated is muscle pain. However, it is hard to find objective evidence confirming a harm of meaningful magnitude in this domain. A recent comprehensive systematic review summarising the experience of over 65,000 trial participants found that statins are significantly associated with an increase in muscle symptoms, but the effect is extremely small, with 15 (95% CI 1 to 29) extra events per 10,000 patient-years. 135 Two UK-based randomised crossover trials that postdate the review found no difference in muscle symptoms between the phases when participants took statins and phases when participants received placebo. 43,136,137
The meta-analysis also found very small increased risks of liver, kidney and eye problems with statins compared with controls, with increased incidences of 8, 12 and 14 events per 10,000 patient-years, respectively. 135 These events are all mild and, in the case of liver and kidney reports, largely based on laboratory findings rather than clinically overt symptoms.
Even if we were to assume that all these events were serious, their incidence is increased so little that including the events in a cost–utility analysis would make no material difference to results. For example, if we ascribe the substantial disutilities that have been reported for people living with chronic complaints affecting the same body parts [−0.212 for ‘Other problems of bones/joints/muscles’, −0.102 for ‘Other digestive complaints’ (including liver), −0.176 for ‘Kidney complaints’ and −0.114 for ‘Cataract/poor eye sight/blindness’138] and assume each adverse event lasts for 1 month (except for eye problems, which we extend to a mean of 5 years to reflect the possibility of long-term harm), the net expected health loss across all these categories would total 0.0008 QALYs, which is equivalent to less than one-third of a day in perfect health. As this is a negligible amount, and almost certainly a substantial overestimate (as reported events are nowhere near as serious as those from which we obtained the utility decrements), we concluded that there would be no benefit in configuring our model to simulate adverse events.
Nevertheless, the fact that many people believe that statins cause harms is, in itself, a harm associated with statins. A recent crossover trial by Howard et al. 43 also included no-treatment periods along with statin and placebo phases. Although there was no difference between statin and placebo periods, the level of self-reported muscle symptoms was significantly higher when participants took either pill than it was for the no-treatment phases, and this strongly suggests that statins have ‘nocebo’ effects. Howard et al. 43 conclude that ‘It is clear that this cohort were indeed intolerant of statin tablets, but also that the source of the intolerance was primarily the tablet, not the statin’. We will argue below that our exploration of DTD provides a useful paradigm in which to conceptualise nocebo effects as an authentic harm of treatment.
Resource use and costs: acquisition of statins
We updated the acquisition costs of statins to present-day levels, using data from the NHS Drug Tariff (November 2021). 139 The new prices (per pack of 28 tablets) were £0.92 for simvastatin 10 mg (i.e. low intensity), £0.96 for simvastatin 20 mg (i.e. medium intensity), £1.10 for atorvastatin 20 mg (i.e. high intensity) and £1.68 for atorvastatin 80 mg (i.e. high intensity and secondary prevention).
Resource use and costs: cardiovascular events
In addition to the costs of the interventions modelled, the model requires annual per-person costs of NHS and Personal Social Services care associated with each state (in GBP and for the relevant price year) to calculate lifetime costs of CVD in each cohort. We updated all model inputs in this area on the basis of a rapid review we undertook using a pearl-growing approach based on two previously known sources (one for stroke/TIA140 and one for cardiovascular events141). Appendix 6 details our methods and shows the resulting model inputs.
New model features specific to this project
Accounting for competing risk of non-cardiovascular death
The CG181 model10 accounts for background non-cardiovascular mortality using general population lifetables. A key motivation of this project (see Background) was to improve on this by ensuring that, for any modelled cohort, the competing risk of non-cardiovascular death reflects the life expectancy of people with the specified level of cardiovascular risk. Official lifetables stratify by age and sex; however, the lifetables do not tell us how all-cause mortality might be associated with cause-specific factors, such as cardiovascular risk. Therefore, we needed a method that will enable us, in effect, to estimate cardiovascular risk-specific non-cardiovascular lifetables.
To do this, we fitted a relative survival model to the cardiovascular CPRD data set used in the cardiovascular element of this project (see Chapter 2), using the multiplicative method of Andersen et al. 142 This approach is a variant of a Cox proportional hazards model that uses the life expectancy of a reference group (in this case, non-cardiovascular survival in the general population) as a time-varying covariate. For a formal definition of the model, see Appendix 6.
Our rationale for using a relative survival model is threefold. First, we needed some way of not only characterising observed survival in the CPRD data set (which has a median follow-up of 5 years), but also extrapolating to the lifetime horizon of the decision model. Decision-analytic economic models commonly use parametric models to accomplish this type of task; however, such models invariably characterise a discrete cohort of which we can plausibly assume that the members share a survival distribution (e.g. people with newly diagnosed cancer of a given type). In this case, we want to simulate heterogeneous groups of people (e.g. 40-year-old women with a 10-year cardiovascular risk of 2%; 80-year-old men with a 10-year cardiovascular risk of 40%) and it is implausible to assume that we can describe the expected survival of all such groups with a common parametric foundation. With a relative survival model, we do not need to define a functional form, we simply have to estimate a model that we can apply to a baseline drawn from empirical lifetable data, as this will naturally produce survival curves that vary in shape and scale, even though the relative difference between the general population and the modelled cohort is a constant function of the covariates. Second, we wanted an approach we could use to estimate the life expectancy of cohorts for whom the decision to initiate statins takes place in the present day. Characterising the relative relationship between observed survival and expected population survival from contemporaneous lifetables provides us with a model we can then apply to present-day lifetables. In doing this, we make the assumption that, although absolute life expectancy may have changed over time, the extent to which factors of interest affect it generalise across time with minimal bias. Third, relative survival models provide a parsimonious way of summarising complex data. If, as discussed above, we relied on parametric models to extrapolate to lifetime expectation, then we would inevitably need to fit multiple models to discrete subsets of the data; however, if we had chosen too few, then we would have inappropriately lumped people with heterogeneous expectations together, and if we had chosen too many, then we would have generated high-variance estimates with a tendency to overfit to artefacts in uncertain data. In contrast, the relative survival approach enables us to make use of all available data while adjusting for the things that might define groups with different expectations. Another reasonable approach would have been to fit a multistate model to the CPRD data; however, this would not solve the problem of extrapolation beyond the observed evidence and may have given us less flexibility in simulating cohorts with different baseline characteristics and risk profiles.
The output of the relative survival model is the multiplicative difference in time to event (in our case, non-cardiovascular death) between a person in a specific population and someone of the same age and sex in the general population. The coefficients show how this difference varies with each covariate.
For our models, the critical covariate is ΔQ, which we define as the difference between an individual’s predicted 10-year QRISK3 score and the average score for a person of the same age and sex. Because QRISK3 predicted risk is a probability it is bounded between 0 and 1 and, therefore, it becomes mathematically convenient to transform the estimates to a log-odds scale and so we work with Δlogit(Q). Because population lifetables do not provide information on QRISK3 scores we estimated average 10-year risks by age and sex using a regression on the CPRD data set (see Appendix 6, Table 54 and Figure 39). Owing to computational constraints, we were unable to fit a single relative survival model to the whole CPRD extract and, therefore, we developed separate models for men and women.
To begin with, we fitted relative survival models with a single coefficient [i.e. Δlogit(Q)].
As lifetables are already stratified by age, it is theoretically not necessary to include a term for it in a relative survival model. However, it is plausible that the effect of other covariates – in this case, Δlogit(Q) – varies with age. Therefore, we also fitted a more complicated model including age and its interaction with Δlogit(Q). At the same time, we explored introducing polynomial terms to account for non-linearity of effect. We found that using quadratic terms for both Δlogit(Q) and age improved the fit of the model (reducing AIC by several hundred points); however, the inclusion of higher-order polynomials provided diminishing returns. Therefore, the linear component of our more complex model takes the form:
Table 15 shows the results of simple and polynomial models fitted for men and women separately.
| Parameter | Simple model, HR (95% CI) | Polynomial model, HR (95% CI) |
|---|---|---|
| Men | ||
| Δlogit(Q) | 1.9314 (1.8747 to 1.9898) | 2.7540 (2.5997 to 2.9174) |
| Δlogit(Q)2 | – | 0.8787 (0.8336 to 0.9262) |
| Age | – | 1.0111 (1.0090 to 1.0133) |
| Age2 | – | 0.9998 (0.9998 to 0.9999) |
| Δlogit(Q) × age | – | 1.0229 (1.0183 to 1.0275) |
| Δlogit(Q)2 × age | – | 0.9858 (0.9833 to 0.9883) |
| Δlogit(Q) × age2 | – | 0.9989 (0.9987 to 0.9990) |
| Δlogit(Q)2 × age2 | – | 1.0001 (1.0000 to 1.0003) |
| AIC | 518,564 | 517,989 |
| Women | ||
| Δlogit(Q) | 1.7061 (1.6789 to 1.7338) | 2.2100 (2.0959 to 2.3304) |
| Δlogit(Q)2 | – | 0.9809 (0.9473 to 1.0158) |
| Age | – | 0.9978 (0.9954 to 1.0001) |
| Age2 | – | 1.0002 (1.0001 to 1.0002) |
| Δlogit(Q) × age | – | 1.0235 (1.0190 to 1.0281) |
| Δlogit(Q)2 × age | – | 0.9918 (0.9899 to 0.9938) |
| Δlogit(Q) × age2 | – | 0.9994 (0.9992 to 0.9995) |
| Δlogit(Q)2 × age2 | – | 0.9999 (0.9998 to 1.0000) |
| AIC | 536,994 | 536,427 |
To give a worked example, consider a 60-year-old man with a 10-year QRISK3 predicted CVD risk of 20%. First, using Appendix 6, Table 54, we calculate the average logit(QRISK3) for a person with those characteristics:
On a probability scale, this is a 10-year risk of 14% (i.e. our hypothetical man is subject to higher-than-average risk). Next, we calculate Δlogit(Q), that is the difference between observed and expected risk, and in this case it is logit(0.2) minus −1.815 = 0.429. Plugging this value into our polynomial model gives:
(Note that for summation we use the natural logarithm of the coefficients given in Table 15 and age is centred around the population mean of 45.43. Therefore, in this case, 60 – 45.43 = 14.57.)
When exponentiated, this value provides a HR of 1.72. Therefore, we estimate that a 60-year-old man with a 10-year QRISK3-predicted CVD risk of 20% is, alongside his raised cardiovascular risk, subject to a hazard of non-cardiovascular death that is more than two-thirds higher than that of an average person of that age and sex. This is the value that we apply to general population lifetables (adjusted to remove cardiovascular deaths) when we simulate the non-cardiovascular life expectancy of a cohort with those characteristics.
Figure 19 shows estimates of non-cardiovascular mortality generated in the way described above, compared with empirical data across different categories of cardiovascular risk and age. The empirical Kaplan–Meier curves represent observed non-cardiovascular mortality (censored for cardiovascular death) in the CPRD extract for people of the stated age, with baseline QRISK3 predictions in the specified brackets. For our modelled estimates, we start from ONS 3-year lifetables for England and Wales (for this illustration we use 2009–11 tables, as this is in the middle of the period covered by the CPRD data). We adjust these data to remove cardiovascular deaths, estimated using proportions recorded under ICD-10 codes I00–I99 in ONS’s ‘Deaths registered in England and Wales’ series. For each combination of risk and age bracket, we calculate HRs, as described above (for comparability, we fit at the mean QRISK3 prediction and age observed within that category in the CPRD data), and apply the HRs to the ONS curves, and this produces the adjusted curves shown in Figure 19.
FIGURE 19.
Fitted relative survival models for non-cardiovascular mortality compared with empirical data. (a) Men; and (b) women.
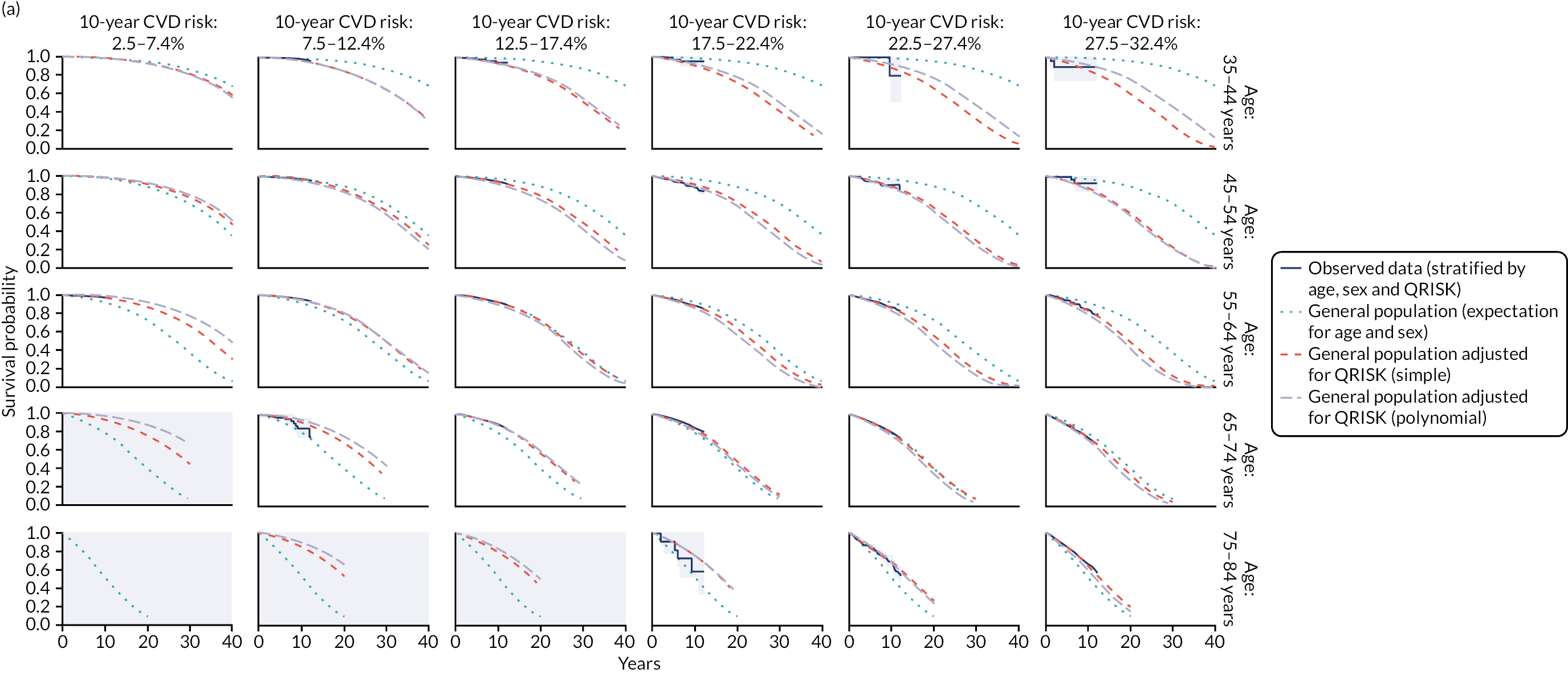

This exercise shows that the approach produces an excellent fit to the observed data. Even though the simple models (i.e. short dash) depend on a single variable, the simple models capture most of the observed variability in non-cardiovascular death. The polynomial models with age interactions (i.e. long dash) improve this fit somewhat further, at least falling within the 95% confidence limits of the observed survival functions in almost all cases. (One exception is 45- to 54-year-old women with a 10-year QRISK3 CVD prediction of 25% ± 2.5%, as these women appear to have better survival than women of the same age with lower cardiovascular risk; however, we consider this an implausible artefact of the relatively small sample of women in the category.)
Note that within each age bracket the unadjusted general population estimate (see Figure 19) remains the same across cardiovascular risk categories. Estimating competing-cause mortality on the basis of age and sex alone, without accounting for the way in which it correlates with the risk of interest, is the approach the CG181 model takes,10 but this analysis shows that such an approach can misestimate competing mortality risk to a potentially substantial degree.
For example, for women aged 65–74 years the unadjusted general population estimate suggests that women of this age have around an 84% chance of surviving 10 years without experiencing non-cardiovascular death. However, if a woman in this category had a predicted cardiovascular risk between 7.5% and 12.4%, then she would be uncommonly healthy and so her true 10-year non-cardiovascular survival would be around 91%. Conversely, if a woman had a high QRISK3-predicted risk of the order 27.5%–32.4%, then she would have below-average health and her 10-year non-cardiovascular survival probability would be around only 70%. In the former case, a model relying on unadjusted competing-cause mortality estimates would underestimate likely survival by a non-trivial amount. In the latter case, the bias is reversed. Note that in both cases the unadjusted population expectation is not within the confidence limits of the observed Kaplan–Meier estimate, whereas our adjusted estimates pass closely through them.
Incorporating direct treatment disutility
The TTO exercise we conducted as part of this project (see Chapter 5) established that most respondents would be prepared to sacrifice an amount of life expectancy to avoid the inconvenience of taking statins to prevent CVD. Across all participants, the average estimated utility was 0.966 (95% CI 0.961 to 0.971). Note that, as explained in Chapter 5, we exclude participants who would trade 50% of their life expectancy to avoid taking statins, as we take the view that people with such marked preferences are not relevant to the decision problem of whether or not to offer statins for primary prevention of CVD because they would always decline.
We explore the effect of including DTD at this level on the outputs of our model in four scenarios:
-
No DTD (i.e. as per CG18110).
-
Permanent DTD (i.e. disutility of the specified level throughout the time simulated patients are taking statins for primary prevention of CVD).
-
Time-limited DTD (i.e. disutility of the specified level for a given number of model cycles and we start by assuming that DTD lasts for 10 years, although we explore this value further).
-
Diminishing DTD (i.e. a linear decline in disutility from the specified level to zero over a given number of cycles and, again, we start from 10 years and explore further).
In our base-case analyses, we apply DTD multiplicatively (e.g. a multiplier of 0.966) and we test the model’s sensitivity to this assumption in additional scenarios in which we assume an absolute effect (e.g. a decrement of 0.034).
We do not apply DTD to states representing cardiovascular events and post-event life. Although the model assumes that people will take statins in these states and includes a cost for them, our elicitation exercise was explicitly focused on the use of statins for primary prevention in people with no cardiovascular history, and it is not clear that people would make similar trade-offs when it comes to statins for secondary prevention. It would also be difficult to apply any time-dependent DTD for secondary prevention in our model, as it has a ‘memoryless’ Markov structure, with a proportion of people experiencing first cardiovascular events at every cycle.
Model verification
Before making any updates or amendments, we verified that our version of the model exactly reproduced reported results from CG181. 10 We also performed technical verification to confirm that the model results changed in the expected direction when extreme values were used for specific model inputs.
Base-case analysis
Clinical Guideline 18110 presented cost–utility results for no preventative treatment and for statins at three levels of intensity (i.e. low, medium and high). All of the statin arms assumed class-level effects and used the acquisition costs of a single representative drug (i.e. simvastatin 10 mg/day, simvastatin 20 mg/day and atorvastatin 20 mg/day for low-, medium- and high-intensity therapy, respectively). An additional arm used identical effects to the high-intensity arm, but adopted the costs of atorvastatin 80 mg/day. Therefore, there were five arms in total.
Our model retains these five arms, and full incremental results are presented in Appendices 7 and 8. However, to simplify interpretation, the main analyses presented below focus on a pairwise comparison between high-intensity therapy with atorvastatin 20 mg/day and no treatment, as this is the approach the guideline ultimately recommended.
Sensitivity analyses
We use three types of sensitivity analyses (i.e. probabilistic sensitivity analysis based on 1000 iterations per output set, deterministic one-way sensitivity analysis and scenario analyses) to look at the impact of different assumptions about DTD.
Results
General model updates
Before accounting for competing risks or DTD, in Table 16 we break down the independent and cumulative impact of each of the steps detailed in General model updates (above). The updates with the largest impact serve to improve the estimated cost-effectiveness of statins. Correcting the miscalculation by which statins were erroneously associated with increased incidence of some cardiovascular effects has the largest effect and, unsurprisingly, this increases the incremental QALYs conferred by statins and reduces their net costs. Updating costs relating to cardiovascular events also has a large effect. Because we now use higher estimates of cost across most categories (substantially so in some cases), the value of statins in preventing events increases. For both men and women, the net effect of the updates is to increase incremental QALYs and decrease incremental costs, although this does not lead to large changes in estimated cost-effectiveness.
| Scenario | 60-year-old men with a 10% 10-year CVD risk | 60-year-old women with a 10% 10-year CVD risk | ||||
|---|---|---|---|---|---|---|
| Incremental cost (£) | Incremental QALY | ICER (£) | Incremental cost (£) | Incremental QALY | ICER (£) | |
| CG18110 base case | 1248 | 0.299 | 4177 | 1290 | 0.340 | 3795 |
| 1. Correct error in annual risk increase in CG18110 | 961 | 0.359 | 2674 | 1080 | 0.384 | 2811 |
| 2. Scenario 1 and 2021 statin costs | 938 | 0.359 | 2610 | 1056 | 0.384 | 2748 |
| 3. Scenario 1 and 2017–19 lifetables | 961 | 0.359 | 2681 | 1077 | 0.380 | 2838 |
| 4. Scenario 1 and remove non-cardiovascular death benefit | 925 | 0.289 | 3198 | 1050 | 0.324 | 3245 |
| 5. Scenario 1 and remove type 2 diabetes adverse event costs | 950 | 0.359 | 2644 | 1069 | 0.384 | 2783 |
| 6. Scenarios 1–5 (all routine updates and corrections) | 893 | 0.290 | 3079 | 1014 | 0.320 | 3172 |
| 7. Scenario 6 and new baseline utility model using HSE data | 893 | 0.314 | 2841 | 1014 | 0.333 | 3048 |
| 8. Scenario 6 and new CVD event HSUVs from review | 893 | 0.288 | 3101 | 1014 | 0.313 | 3239 |
| 9. Scenarios 6–8 (new utilities) | 893 | 0.312 | 2863 | 1014 | 0.326 | 3113 |
| 10. Scenario 6 and new CVD event costs from review | 385 | 0.290 | 1329 | 364 | 0.320 | 1138 |
| 11. Scenario 10 and apply costs for all deaths | 426 | 0.290 | 1468 | 403 | 0.320 | 1262 |
| 12. Scenarios 6–8, 10 and 11 (new utilities and costs) | 426 | 0.312 | 1365 | 403 | 0.326 | 1238 |
| 13. Scenario 6 and new model for first cardiovascular event | 816 | 0.278 | 2935 | 823 | 0.321 | 2560 |
| 14. Scenarios 6–8, 10, 11 and 13 (all new data) | 431 | 0.299 | 1441 | 409 | 0.333 | 1228 |
Appendix 7 provides full results for all five simulated strategies at varying levels of cardiovascular risks, as well as a range of deterministic and probabilistic sensitivity analyses.
Accounting for competing risk
Before examining the impact that introducing adjustment for competing risks has on the cost-effectiveness of statins, it is useful to understand how it affects the modelled natural history of people at risk of CVD without accounting for any treatment effect. Appendix 8, Figure 47, provides model state occupancy graphs in two untreated cohorts with and without adjustment for competing risk of non-cardiovascular mortality. From these examples (see Appendix 8, Figure 47), we can see that the impact of adjusting for competing risk depends on a person’s cardiovascular risk compared with an average person of their sex and age:
-
A 60-year-old woman with a 10-year QRISK3-predicted risk of 10% has above-average risk. In Figure 19, we can see that people in this category have slightly shorter non-cardiovascular life expectancy than people of the same age and sex in the general population. Consequently, when we include this adjustment in the cost-effectiveness model, the cohort experiences somewhat diminished life expectancy. The unadjusted lifetables tell us that a woman of this age has around a 35% chance of surviving until her 90th birthday. However, once we adjust for the raised risk of non-cardiovascular death that is associated with a 10-year cardiovascular risk of 10%, that figure drops to around 25%. A direct corollary of this is that the average woman with these characteristics will spend somewhat less time at risk of cardiovascular events, and we can see that the areas reflecting fatal and non-fatal cardiovascular history in the state occupancy graph (see Appendix 8, Figure 47) shrink between the unadjusted and adjusted versions.
-
Conversely, a 60-year-old man with a 10-year QRISK3-predicted risk of 10% has below-average risk (note that in Figure 19 empirical and modelled data show a slightly longer non-cardiovascular life expectancy than would be expected for an average person of that age and sex). Now we have the opposite result, that is the man spends longer alive in the model than the unadjusted lifetable would suggest. The man’s chance of reaching 90 years of age rises from around 28% to around 38%. In addition, the man spends longer at risk of cardiovascular events and so the relevant areas grow instead of shrinking.
When we layer treatments effects, costs and QALYs on these dynamics, we derive cost-effectiveness results with similar characteristics (Table 17). When estimating the cost-effectiveness of statins, the impact of adjusting for competing risk depends on the cohort’s cardiovascular risk compared with an average person of their sex and age:
-
For the 60-year-old women with a 10-year QRISK3-predicted risk of 10%, expected QALYs in both intervention and control arms decrease by around 0.65, reflecting the cohort’s below-average health. This means that a proportion of the cohort will die before they accrue all of the benefits of statins previously predicted for them. Consequently, health gains associated with high-intensity therapy (i.e. atorvastatin 20 mg/day), compared with no treatment, reduce by around 0.04 QALYs compared with the unadjusted model.
-
Our 60-year-old men with a 10-year QRISK3-predicted risk of 10% were more healthy than their average contemporaries and so our cohort accrues around 0.6 QALYs per person more in both arms when adjusting for competing risk. This additional life expectancy potentially increases each man’s capacity to benefit from statins. Therefore, we see the incremental benefits of high-intensity therapy (i.e. atorvastatin 20 mg/day), compared with no treatment, rise by a little under 0.04 QALYs per person compared with the unadjusted model.
| Strategy | Absolute | Incremental | NHB at £20,000/QALY | |||
|---|---|---|---|---|---|---|
| Cost (£) | Effect (QALY) | Cost (£) | Effect (QALY) | ICER (£/QALY) | ||
| 60-year-old men with a 10-year cardiovascular risk of 10% | ||||||
| Unadjusted updated model | ||||||
| No statins | 6343 | 12.805 | 12.488 | |||
| High-intensity statins | 6774 | 13.104 | 431 | 0.299 | 1441 | 12.766 |
| Adjusting for competing risk | ||||||
| No statins | 6943 | 13.460 | 13.113 | |||
| High-intensity statins | 7353 | 13.797 | 410 | 0.337 | 1217 | 13.429 |
| 60-year-old women with a 10-year cardiovascular risk of 10% | ||||||
| Unadjusted updated model | ||||||
| No statins | 6567 | 12.730 | 12.402 | |||
| High-intensity statins | 6976 | 13.063 | 409 | 0.333 | 1228 | 12.714 |
| Adjusting for competing risk | ||||||
| No statins | 6013 | 12.057 | 11.112 | |||
| High-intensity statins | 6443 | 12.350 | 430 | 0.292 | 1469 | 11.365 |
However, these adjustments affect treatment and non-treatment arms to a fairly similar degree. As a result, the cost-effectiveness of statins is not materially changed. The incremental cost-effectiveness ratio (ICER) for 60-year-old men with a 10-year QRISK3-predicted risk of 10% goes down by around £500 per QALY. For women with the same age and risk, the ICER goes up by a similar amount. In all cases, ICERs remain far below conventional thresholds representing an effective use of NHS resources.
Appendix 8, Figure 54, illustrates the same comparisons when analysed probabilistically. The same features are evident as in the deterministic results. For 60-year-olds with a 10% 10-year cardiovascular risk, adjusting for competing risk of non-cardiovascular death increases QALYs for men and decreases QALYs for women, although resulting cost-effectiveness estimates are not materially altered.
In Appendix 8, Figure 48, we depict the cost-effectiveness of statins for people of different ages and cardiovascular risks, and how adjusting for competing risk of non-cardiovascular death affects these results. Even before adopting this adjustment, the model suggests that statins represent a good use of resources for almost everyone. It is only for people aged ≥ 60 years with the lowest cardiovascular risk that statins represent poor value for money. However, adjusting for competing risk of non-cardiovascular death removes even this small subgroup. In practice, the distinction is moot if QRISK3 is used to predict cardiovascular risk, as it is essentially impossible for people in those age brackets to have 10-year risks low enough to enter the cost-ineffective zone. If such people did exist, then they would have extraordinary life expectancy, which is why the adjusted model concludes that it would still be good value to offer them statins, as there is every chance that even the oldest people would live to realise their benefit.
Appendix 8 provides full results from the updated model, adjusted for competing risk for all five simulated strategies at varying levels of cardiovascular risks, as well as a range of deterministic and probabilistic sensitivity analyses.
Incorporating direct treatment disutility
Introducing DTD to the analysis has a substantial impact on the results. Table 18 shows cost-effectiveness results for 60-year-old men and women under our four DTD scenarios. For the permanent scenario (with a utility multiplier of 0.966), DTD throughout the period people are taking statins for primary prevention is enough to render the statins net harmful. Although the intervention provides around 0.3 QALYs, the small day-to-day disutility of taking the tablets amounts to more than 0.4 discounted QALYs over a lifetime, and so the tablets end up doing more harm than good. Assuming that DTD lasts for no more than 10 years (with either constant or diminishing detriment over that period) attenuates but does not eradicate the benefits of statins in these cohorts, and so the statins remain reasonable value for money, assuming that QALYs are valued at conventional levels.
| Strategy | Absolute | Incremental | NHB at £20,000/QALY | |||
|---|---|---|---|---|---|---|
| Cost (£) | Effect (QALY) | Cost (£) | Effect (QALY) | ICER (£/QALY) | ||
| 60-year-old men with a 10-year cardiovascular risk of 10% | ||||||
| No DTD | ||||||
| No statins | 6943 | 13.460 | 13.113 | |||
| High-intensity statins | 7353 | 13.797 | 410 | 0.337 | 1217 | 13.429 |
| Permanent DTD | ||||||
| No statins | 6943 | 13.460 | 13.113 | |||
| High-intensity statins | 7353 | 13.370 | 410 | −0.090 | Dominated | 13.002 |
| Time-limited DTD | ||||||
| No statins | 6943 | 13.460 | 13.113 | |||
| High-intensity statins | 7353 | 13.558 | 410 | 0.098 | 4183 | 13.190 |
| Diminishing DTD | ||||||
| No statins | 6943 | 13.460 | 13.113 | |||
| High-intensity statins | 7353 | 13.655 | 410 | 0.196 | 2097 | 13.288 |
| 60-year-old women with a 10-year cardiovascular risk of 10% | ||||||
| No DTD | ||||||
| No statins | 6013 | 12.057 | 11.757 | |||
| High-intensity statins | 6443 | 12.350 | 430 | 0.292 | 1469 | 12.028 |
| Permanent DTD | ||||||
| No statins | 6013 | 12.057 | 11.757 | |||
| High-intensity statins | 6443 | 11.963 | 430 | –0.094 | Dominated | 11.641 |
| Time-limited DTD | ||||||
| No statins | 6013 | 12.057 | 11.757 | |||
| High-intensity statins | 6443 | 12.125 | 430 | 0.068 | 6323 | 11.803 |
| Diminishing DTD | ||||||
| No statins | 6013 | 12.057 | 11.757 | |||
| High-intensity statins | 6443 | 12.216 | 430 | 0.159 | 2708 | 11.894 |
We see the effect of differing DTD assumptions on the cost-effectiveness of statins across a range of ages and baseline cardiovascular event risks in Appendix 8, Figure 50.
Even though a lifetime’s unremitting DTD represents a substantial decrement to expected quality of life, statins remain an effective use of resources for younger people with higher levels of risk. This is not only because people with high levels of risk stand to gain more from taking preventative statins (as they are more likely to have an event to prevent), but also because they spend less long in the primary prevention state (as they move to the event states more swiftly and they are also, now we adjust for competing risk of non-cardiovascular mortality, more likely to die of other causes). In contrast, people with lower levels of risk may need to take statins for a long time before realising benefits, and this becomes a poor trade-off when DTD is permanent. Older people, too, experience net harm from statins if they cannot get used to taking them, and this is because the lower life expectancy of older people gives them limited time in which to experience potential benefits of the intervention, while its harms are unavoidable.
For time-limited (10-year) DTD, the age–risk threshold at which statins become cost-effective is very close to the mean QRISK3-predicted risk observed in the population. Under this scenario, anyone with above-average risk stands to gain from treatment, whereas the model suggests that anyone with below-average risk will experience net harm.
If we can assume that DTD declines over time, then statins remain good value for everyone except people with a theoretically possible – although practically unlikely – profile reflecting extraordinarily good health for their age.
We show probabilistic versions of these calculations for a representative range of age–risk profiles in Appendix 8, Figure 58. In Appendix 8, Figure 58, the ‘clouds’ converge as age and risk rises, showing that DTD has less of an absolute effect on model outputs (owing to shorter time on preventative treatment with lesser life expectancy and higher event rates). However, net value for money remains relatively unaffected. In the cost-effectiveness acceptability curves, statins are always associated with less than 20% chance of cost-effectiveness when we assume permanent DTD (assuming we value QALYs at ≥ £20,000). Conversely, without DTD, statins are certain to be cost-effective as long as we value QALYs at ≥ £6000. The temporary DTD scenarios also result in a high probability of cost-effectiveness, with the exception of 10-year DTD in 80-year-olds with a 30% risk of cardiovascular event. Under this scenario, there is around a 50 : 50 chance that statins are worth paying for, and this is fairly invariant to the value we place on QALYs.
The interaction between life expectancy, level of risk and duration of DTD discussed above begins to suggest another way of conceptualising benefit–harm trade-offs. We have previously argued that the ‘pay-off time’, that is the minimum time until people can expect net benefit from a course of action with up-front harms and long-term benefits, may provide a useful heuristic for thinking about these issues in shared decision-making. 41 Appendix 8, Figure 59, shows cumulative incremental QALYs over time for four example profiles across our four DTD scenarios (we do not discount outcomes in this instance, as we take the view that it would be impossible for a patient to arrive at their own conception of the interaction between benefit and time while mentally adjusting for the fact that an interaction of that type is hardwired into the calculation).
Under the permanent DTD scenario, for a 50-year-old with a 10-year CVD risk of 5%, a decision to take statins would confer net QALY gains only after 48 years of treatment. For 60-year-olds at 10% risk, 70-year-olds at 20% risk and 80-year-olds at 30% risk, the expected pay-off times are 36 years, 25 years and 22 years, respectively. When we assume temporary DTD of one form or another, the expected pay-off times are typically in the range of 10–20 years.
Interaction of competing risk and direct treatment disutility
Bringing the analyses above together, we can look at the combined effect of competing risk of non-cardiovascular death and DTD on the effectiveness and cost-effectiveness of statins for the primary prevention of CVD.
To do this, we present a 4 × 4 cross-categorisation of scenarios, within each of which we derive results for people at different ages and different levels of baseline risk. For competing risk calculations, we present two additional scenarios in which we halve and double the cohort’s hazard of non-cardiovascular death. These scenarios are representative of a decision problem in which people are atypically healthy or atypically well to a degree over and above what we would expect by adjusting for their cardiovascular risk alone.
Figure 20a visualises the expected incremental QALY gains associated with high-intensity statins compared with none in each of these scenarios. Without DTD, statins are associated with very little disutility in the model and, therefore, statins generate some degree of QALY benefit for people at any age and any level of cardiovascular and competing risk (see first column Figure 20a). However, when we introduce DTD, the threshold at which treatment confers net QALY gains begins to depend on age. For someone who is persistently averse to pill-taking (implying lifelong DTD; see last column of Figure 20a), many combinations of age and risk result in statins doing more harm than good (see black area in Figure 20a). For example, people with such preferences in their mid-70s and older would need a 10-year QRISK3-predicted risk of over 30% before statins would be net beneficial. If people had additional long-term conditions leading to a doubled risk of non-cardiovascular death, then that threshold would rise to 40%. Even if we assume taking pills is something people get used to (i.e. time-limited DTD), it is easy to find combinations of age and risk where statins’ DTD outweighs their cardiovascular benefits.
FIGURE 20.
Clinical effectiveness and cost-effectiveness of high-intensity statins, as a function of age and cardiovascular risk, with different levels of DTD and competing risk of non-cardiovascular death. (a) Effectiveness (incremental QALYs); and (b) cost-effectiveness (when QALYs are valued at £20,000–30,000).
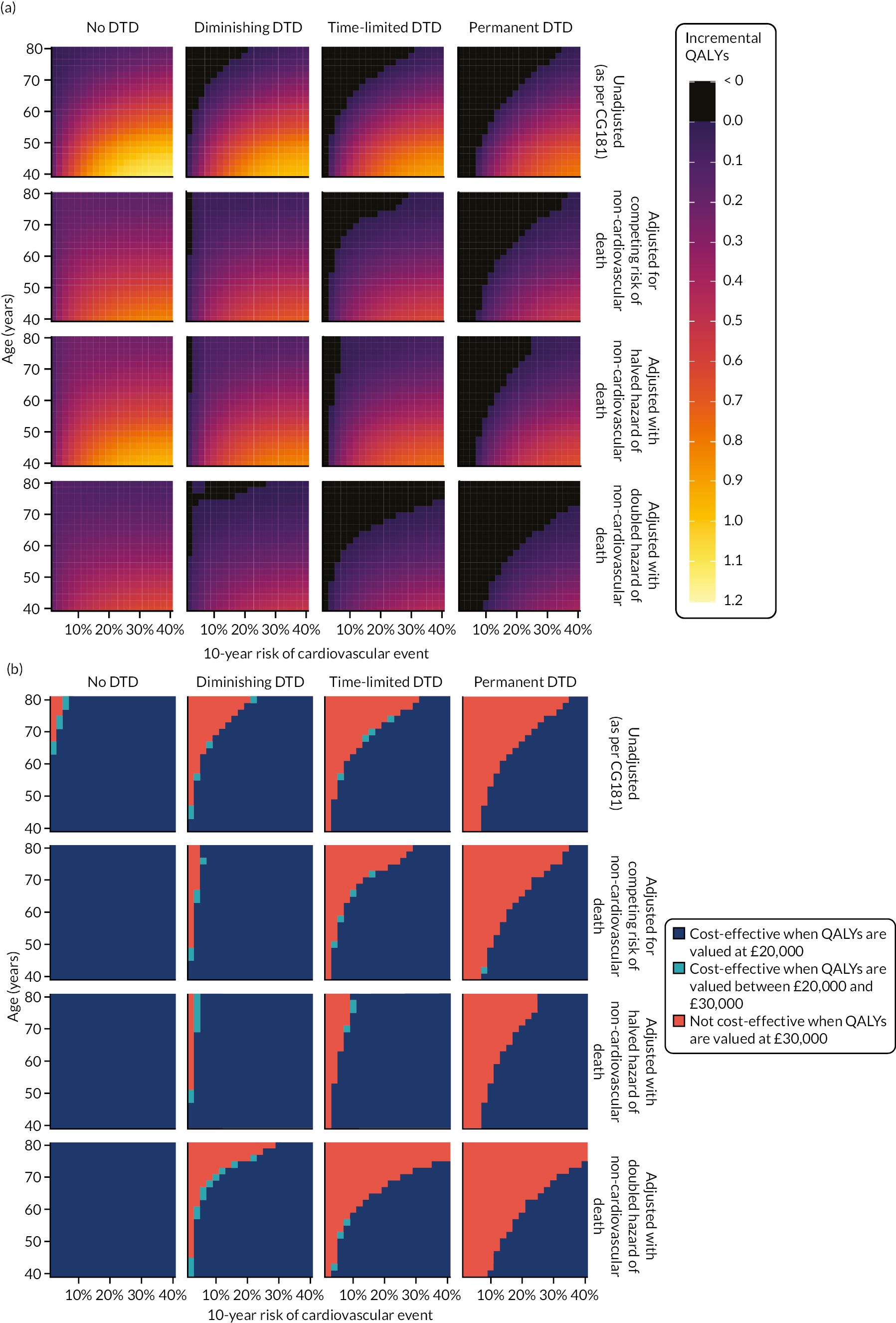
Figure 20b provides a similar analysis but introduces expected costs to the equation to establish the circumstances in which statins would be judged to provide an effective use of NHS resources (when QALYs are valued at NICE-recommended levels of £20,000–30,000). The combinations of characteristics for which statins do not provide good value for money are similar to characteristics for which they generate QALY loss (except under unusual circumstances, a technology will not be cost-effective if it is not associated with QALY gains). However, there are a small number of combinations where, although the model predicts positive QALY gains for statins, the positive QALY gains are so small that the cost of the drugs outweighs the gains (e.g. under the permanent DTD scenario, 50-year-olds with a 10% risk of cardiovascular event and an adjusted but unaltered hazard of non-cardiovascular death, as such people expect a tiny lifetime benefit of 0.006 QALYs, but at a cost that equates to an ICER of around £44,000 per QALY).
As a scenario analysis, we also explored applying DTD as an absolute decrement rather than a relative multiplier, and this results in a slightly greater impact for DTD. For example, for 80-year-olds under time-limited and permanent DTD scenarios, statins do more harm than good at all levels of risk we analyse (see Appendix 8, Figure 60).
Discussion
Main findings
When it comes to state-transition decision models, the question is not whether or not to account for competing risks, but how to do so. Our analysis shows that, where competing risks are handled in a naive manner (e.g. assuming population lifetables for all-cause death), analyses overestimate the clinical effectiveness and cost-effectiveness of preventative interventions in people with above-average risk and underestimate the clinical effectiveness and cost-effectiveness in people with below-average risk. In the case of statins for the primary prevention of CVD, the intervention appears to be almost universally cost-effective in a way that renders these biases of limited impact. However, we have shown that the potential for meaningful differences exists. Indeed, one only has to imagine high-intensity statins cost £18 per pack instead of £1.10, and appropriate adjustment for competing risk of non-cardiovascular death would make the difference between the intervention meeting and not meeting conventional thresholds of cost-effectiveness for some people, for example 75-year-old men with a 10-year cardiovascular risk of 15% (unadjusted ICER compared with no treatment, £25,700/QALY; adjusted ICER, £18,100/QALY).
Incorporating DTD has a more immediately obvious effect on the cost-effectiveness outputs of the model. However, although we see no reason for decision models not to include the most robust estimates of competing risks possible in their base cases, we would hesitate to recommend that modellers should include population-average DTD in their base-case cost–utility results, as this would result in statins being recommended for only people who appear in the dark blue areas in the bottom-right of Figure 20b for whichever DTD scenario decision-makers prefer. In Chapter 5, we argued that, rather than assuming blanket disutility, we should provide decision-makers with evidence of circumstances under which, and people for whom, DTD might tip the balance of benefits and harms (if any). In turn, decision-makers should use this information to provide guidance to prescribers that can inform shared decision-making. This case study illustrates the point well.
To return to our example of a 75-year-old man with a 10-year cardiovascular risk of 15%, without accounting for DTD, we would expect the man to achieve net QALY gains from statins (i.e. an expected value of 0.19 QALYs, which is equivalent to over 2 months in perfect health). However, once we introduce DTD, that expectation reduces. Under the diminishing DTD scenario, the man can expect fewer than 0.06 QALYs, whereas the time-limited and permanent DTD scenarios predict net QALY loss.
Nevertheless, even if we think the permanent DTD scenario is the best way to capture population-level average disutility, we would not argue in favour of adjusting everyone’s expectation to account for it (which would have the effect of rendering statins poor value for money in people with these characteristics). This is because – as clearly shown in Chapter 5 – some people anticipate negligible disutility from taking statins and, indeed, some people may even anticipate benefit over and above the directly clinical effects (i.e. ‘peace of mind’). To deny such people access to an effective treatment would clearly not maximise societal welfare, even if the average person would not feel the same. Therefore, we suggest that the appropriate way to make use of this information is as an objective basis on which decision-makers can identify what NICE refers to as ‘preference-sensitive decision-points’. 125 In this paradigm, guidelines should help prescribers to summarise benefits and harms of possible options for people for whom they are indicated, and this should include the process characteristics underlying DTD.
Precisely how such information makes it into shared decision-making is an unanswered question. It is theoretically possible to envisage ex ante preference elicitation, along similar lines as our experiment, which could be integrated into a personalised QALY-maximising analysis to provide recommendations for individual patients, and, unquestionably, this would be practically onerous, but, arguably, it would be unnecessarily prescriptive. However, we think it is useful to augment prescribers’ understanding of the strength of preference for avoiding a technology that would be necessary to outweigh its expected benefits, and our findings give an example of how this might be possible.
Since CG181, there have been two CEAs143,144 of statins for the primary prevention of CVD that predicted cardiovascular events and non-cardiovascular death based on a common set of risk factors. To do this, the analyses used either separate models144 or cause-specific survival models. 143 Like our relative survival model, these approaches should accurately predict time spent living with CVD and, therefore, QALYs because they capture the crucial correlation between cardiovascular risk and competing risk of non-cardiovascular death. However, neither analysis tested whether or not its results were sensitive to this competing risk adjustment, that is neither analysis modelled scenarios where risk of non-cardiovascular death was assumed to be independent of cardiovascular risk factors for comparison. In addition, one of these analyses found that cost-effectiveness was sensitive to DTD in the form of an additive decrement ascribed to ‘pill burden’, which was applied to each QALY. 144 Another primary prevention model124 has also reported that the cost-effectiveness of statins is sensitive to an arbitrary disutility for DTD.
There is recent, compelling evidence that many self-reported muscle symptoms in people taking statins can be explained as ‘nocebo’ effects. 43 Although this finding may represent a fascinating psychological insight, it is of limited practical value to prescribers, as few people experiencing pain when taking a statin will easily accept that their symptoms are ‘all in the mind’. However, we argue that DTD provides a helpful way to conceptualise and quantify the authentic and predictable harm that such people experience. Authors usually cite process and inconvenience factors to explain why people ascribe disutility to taking a preventative medicine they have been assured is benign. 40 However, it is also likely that part of the internal calculus reflects (1) a degree of mistrust that the substance truly has no adverse effects and (2) a reluctance to become ‘a patient’ who – among other inconveniences – will henceforth be on-guard for unpleasant symptoms. 145 Although few people would describe it in such terms, no one wants to volunteer for a nocebo effect. Therefore, by quantifying the things that people ex ante want to avoid from preventative treatment, we believe that we capture some or all of the subtler harms that people taking them report ex post. As explored in this chapter, this enables us to balance these harms against the expected benefits and costs of treatment to estimate whether or not we expect net benefit overall.
Limitations
First, we have not been able, as originally intended, to take account of the extent to which specific co-existing long-term conditions might complicate the issues explored in this chapter. In particular, we wanted to look at type 1 diabetes and CKD, as NICE identified these conditions as areas of interest in the surveillance proposal in which it announced its intention to update CG181. 13 However, we found that including additional binary covariates for one or both of these factors did not improve the fit of our relative survival models. Therefore, this implies that the impact of type 1 diabetes and CKD on cardiovascular risk is well captured by the QRISK3 algorithm, and the factors do not differentially confound the relationship between cardiovascular risk and non-cardiovascular mortality. We also found that type 1 diabetes and CKD had no meaningful effect on the type of first cardiovascular event people experience. Having found no clear point of differentiation, it would not have been meaningful to stratify our analyses. Of course, it would also be possible to tailor other model inputs (e.g. baseline utility, event disutility, cost of events) to represent people with particular long-term conditions, and this might affect outputs in non-trivial ways.
Second, our relative survival models use predicted cardiovascular risk (i.e. QRISK3 10-year predicted risk) as an overarching indicator of non-cardiovascular life expectancy. We believe that we achieved a very good fit to observed data in this way (see Figure 19). Nevertheless, it would be possible to construct a more sophisticated model that, instead of using a summary risk prediction measure, estimates relative survival as a function of each of the individual covariates on which the prediction itself relies. For example, an 80-year-old non-smoking man with type 2 diabetes and SBP of 140 mmHg has an identical 10-year QRISK3-predicted CVD risk to an 80-year-old moderate-smoking man with no diabetes and SBP of 166 mmHg. If the factors that distinguish these two individuals affect their non-cardiovascular life expectancy differentially, then our relative survival model will fail to capture this. By accounting for these factors, it might be possible to achieve an even more accurate prediction of life expectancy. However, as noted above, we found that including terms for type 1 diabetes and/or CKD did not improve the fit of our relative survival models. Nevertheless, we cannot rule out the possibility that other variables would explain some residual heterogeneity between observed and modelled survival expectation.
Third, because secondary prevention of CVD is beyond the scope of our project, we did not review any evidence about the natural and treated history of people who have had a cardiovascular event. For all secondary transitions, the model relies on the same inputs that the developers identified for CG181. 10 Although this part of the pathway is outside our decision problem, it has an important impact on our estimates of lifetime costs and effects, as it defines some of the value that an intervention provides by preventing first events. We suggest that any future updates to the model should review evidence in this area, even if secondary prevention is not the analysts’ focus.
Fourth, we do not make any adjustments to the model’s effectiveness inputs to account for imperfect patient adherence to statins, and this means we effectively assume adherence is identical to that observed in the intention-to-treat trials that underpin the effect estimates. If adherence in practice is worse than in trials, then the model is likely to overestimate, to some degree, the clinical effectiveness and cost-effectiveness of statins.
Finally, the model compares all-or-nothing strategies. In reality, the counterfactual to offering statins to a given cohort is not never offering them statins, it is not offering statins for the time being, with the option of revisiting the decision later. To simulate this decision problem, we would require detailed longitudinal data with which to project the development of risk factors over time. It would also probably necessitate moving away from a cohort model to a stochastically evaluated individual patient simulation. However, we would argue that this analysis highlights some of the major advantages of analytically evaluated cohort models. The kind of many-way scenario analyses we have been able to generate would be computationally intractable and muddied by Monte Carlo error in a patient-level simulation, and we feel sure that the kind of analytical flexibility from which our analysis benefits outweighs the flexibility in representing the pathway that would come with a patient-level simulation.
Conclusion
This analysis has shown that updating the CG181 model with newer model inputs did not materially change the conclusion that statins are an effective use of healthcare resources. In the case of statins for the primary prevention of CVD, the intervention appeared to be almost universally cost-effective in a way that renders the impact of including competing risk inconsequential. However, we argue that failure to account for competing risk in CEAs of primary prevention strategies will produce biased results and the impact of this omission is likely to become more apparent for interventions with relatively higher costs compared with their health benefits. Incorporating DTD had a more immediately obvious effect on the cost-effectiveness of statins. We advise that the impact of including DTD in sensitivity analyses on the outputs of a decision-analytic model should be an integral component of CEAs of primary prevention strategies.
Chapter 7 Cost-effectiveness analysis accounting for competing risks and direct treatment disutility: bisphosphonates for the primary prevention of osteoporotic fragility fracture
Background
Selection of the case study
The decision to offer oral bisphosphonates for the primary prevention of osteoporotic fragility fracture is a second potentially illuminating case study for examining the impact of competing risks and DTD on CEAs. The risk factors for fragility fracture include many behavioural (e.g. smoking) and pathological (e.g. type 1 diabetes) factors that are also associated with shorter life expectancy. Failing to account for these factors could lead to inflated estimates of the value of medicines that reduce the risk of fracture. Furthermore, although there is little doubt that oral bisphosphonates are effective in reducing incidence of fragility fracture, bisphosphonates are inconvenient to take, and this raises the possibility that DTD may attenuate or even outweigh the gains that previous CEAs have estimated.
NICE initially recommended two oral bisphosphonates (i.e. alendronic acid and risedronate sodium) in in its Technology Appraisal 160 in 2008. 146 A subsequent appraisal (i.e. TA46412) confirmed this decision and added a third oral medicine in the class (i.e. ibandronic acid) to the recommended options. The evidence available to the decision-making committee for TA46412 included a CEA, synthesising evidence on the benefits, harms and costs of preventative treatments, including oral bisphosphonates. The analysis concluded that oral bisphosphonates are likely to represent an effective use of NHS resources for anyone whose 10-year risk of MOF exceeds 1.5%. 147
The same authors updated their model as part of a further health technology assessment (HTA) for a subsequent NICE appraisal, and this focused on antiosteoporosis medicines other than bisphosphonates, but included bisphosphonates as comparators, although NICE subsequently chose to suspend the appraisal. 148 The updated model found that a somewhat higher level of risk, than in TA464,12 would be necessary for oral bisphosphonates to provide reasonable value for money, although the precise threshold is not quantified. 149
The model underpinning these analyses was a discrete-event simulation. Unlike the cohort model explored in Chapter 6, discrete-event simulations work by generating a virtual population of people and simulating their lives one by one. Discrete-event simulations handle competing events by randomly generating next-event times for all outcomes of interest, processing the event that will occur first and then, depending on event type and model structure, moving on to the next event or recalculating some or all next-event times to reflect the simulated person’s updated history. The simulation may also terminate (e.g. if the event is death).
Given adequate data and implementation, discrete-event simulation is an appropriate way of accounting for competing events and, because the model handles them simultaneously, it is appropriate to parameterise each event distribution using time-to-event methods that censor for competing events. This is because, in a patient-level simulation as in clinical reality, events compete naturally, and the occurrence of some events will preclude the occurrence of others. In the case in hand, some simulated people will experience hip fracture before death; however, some people will experience death first, thereby precluding a fracture event (although the model ‘knows’ when that person was destined to experience a fracture had death not intervened).
Therefore, in contrast to the situation where we want to estimate the probability that a single event in isolation will occur (as in the epidemiological analyses in Chapters 2 and 3), modellers developing simulations with multiple events need inputs for each that censor for intervening events. In the case in hand, we actively want our estimates of time to hip fracture to reflect a world in which death is not possible (e.g. relying on a Kaplan–Meier estimator censoring for death), as the model will simultaneously and independently apply an estimate of time to death. So long as both inputs represent valid estimates for the modelled population, the incidence of hip fracture observed in the model will replicate the Aalen–Johansen estimator in a real population.
However, as with a cohort model, if the estimate for any one of our competing events is biased, then we will have biased results for all outcomes. Again, a commonly overlooked question is whether or not unadjusted general population lifetables represent an appropriate estimate of life expectancy for the people the model simulates. In a patient-level model, we have information about some characteristics for each person simulated. It is common to use the age and sex of the simuland to inform the distribution from which the model draws the time to all-cause death. However, other characteristics may also be associated with greater or lesser life expectancy. In the case in hand, we are particularly interested in predicted fracture risk. If people with high fracture risk also have an increased risk of other-cause death and we fail to account for this, then we will overestimate the number of fractures that occur and this, in turn, will overstate the clinical effectiveness and cost-effectiveness of any intervention that has the potential to reduce fracture incidence.
Previous models have estimated that the benefits of bisphosphonates for the average person are, in absolute terms, small. TA46412 found that, when compared with no treatment, alendronate is associated with an average health gain no greater than 0.00247 QALYs, even in the highest-risk tenth of people. 12 The 2020 HTA149 introduced a little more benefit for oral bisphosphonates, but alendronate still conferred only mean gains in the range of 0.0001–0.0058 QALYs (equivalent to up to 2 quality-adjusted days of life in perfect health), depending on baseline risk.
These small benefits should not be casually dismissed, given the low cost of the intervention and the large population who could expect, on average, to gain. Nevertheless, it is clear that it would not take much to offset the expected gains. Both TA46412 and the 2020 HTA149 incorporate an estimate of QALY loss owing to adverse gastrointestinal effects for a proportion of people taking oral alendronate. However, these analyses do not reflect the fact that, even when well tolerated, oral bisphosphonates are inconvenient to take. As we have seen (see Chapter 5), even when taken weekly, oral bisphosphonates are associated with non-trivial DTD (significantly greater than for daily statins). Therefore, it is plausible that the routine downsides of taking bisphosphonates might attenuate or outweigh their benefits in preventing fractures, although this trade-off has not previously been explored.
Our aim was to explore the impact that better accounting for competing risk of death and incorporation of DTD might have on the estimated cost-effectiveness of bisphosphonates. TA46412 stipulates that prescribers should offer bisphosphonate treatment ‘when [it] is appropriate, taking into account [the person’s] risk of fracture, their risk of adverse effects from bisphosphonates, and their clinical circumstances and preferences’ (© NICE 2017 Bisphosphonates for Treating Osteoporosis. Available from www.nice.org.uk/guidance/ta464. All rights reserved. Subject to Notice of rights). Although fracture risk and adverse events are central to previous analyses of the cost-effectiveness of bisphosphonates, there has been little formal consideration of how decision-making might be affected by people’s clinical circumstances and preferences. The methods introduced in this project enable us to explore these dimensions and weigh them against the benefits and harms that existing models estimate.
Methods
The CEA reported here adopts and adapts the model developed for TA464 to address the decision problem (Table 19). Full details of the modelling approach can be found in Davis et al. 149,150 We did not make any modifications to this model, with the exception of how the model implements the impact of persistence (see below).
| Decision-analytic model | Criterion |
|---|---|
| Decision problem | To assess the cost-effectiveness of oral alendronate compared with no treatment at varying levels of absolute fracture risk, as defined by the QFracture-2012 risk assessment tool |
| Intervention | Oral alendronate |
| Comparators | No treatment |
| Model type | Patient-level discrete-event simulation |
| Population | People (men and women) eligible for risk assessment under NICE CG14688 |
| Setting | Primary care services in NHS England |
| Time horizon | Lifetime |
| Study perspective | NHS and Personal Social Services in England |
| Costs |
|
| Measured using GBP (£) at 2019–20 prices | |
| Consequences | Impact on health status |
| DTD | |
| Measured using QALYs | |
| Discounting | 3.5% for costs and consequences |
| Cost-effectiveness threshold | NICE-recommended threshold of £20,000 per QALY gained |
Model overview
The model is a patient-level discrete-event simulation. Figure 21 illustrates the structure of the model and Table 19 summarises key design criteria. Where state-transition models define a healthcare pathway in terms of states, discrete-event models proceed by way of events. The events that are possible in the TA464 model12 are fractures (divided into four categories of hip, vertebral, proximal humerus and wrist), admission to full-time care and death (fracture related and other cause). Simulated people who experience fractures incur costs and disutility, and their risk of additional negative events (e.g. further fractures, admission to full-time care, death) increases.
FIGURE 21.
Structure of discrete-event model: events that can occur in a simulated person’s lifetime.

Our study focused exclusively on the pairwise comparison between oral alendronate and no treatment. Our DTD elicitation exercise did not distinguish between different oral bisphosphonates, and alendronate is, by some distance, the most commonly prescribed chemical in the class, consistently accounting for over 80% of prescriptions of agents classified in British National Formulary section 6.6 (drugs affecting bone metabolism). 151
General model updates
We performed fewer general updates to the bisphosphonates model than we did for the statins analysis. Producing a revised best estimate of the cost-effectiveness of bisphosphonates is beyond the scope of this project and analysis, therefore, focuses on exploring whether or not accounting for competing risks and DTD would have materially affected the historical analyses. One exception is that we have updated how the model implements persistence with oral therapy (see below), as this not only influences the effectiveness of bisphosphonates but also has potentially important implications for DTD, which is one of our central concerns.
The 2020 bisphosphonates HTA149 introduced some other modifications to the TA464 model12 that we have adopted as detailed below.
Duration of bisphosphonate therapy
The TA464 model147 assumed that all people take oral bisphosphonates for 184 days, as this is the mean duration of treatment persistence found in a systematic review of observational cohort studies. 152 The 2020 HTA149 updated the assumed duration of treatment to 1.6 years for alendronate, using data from an analysis of UK primary care data. 153 In neither case did the models account for patient-level variation in persistence, rather the models simulated 100% of patients persisting with treatment for the fixed period specified, on the assumption that costs and benefits are linearly related to duration of treatment.
In our update of the model, we have relaxed this assumption and have incorporated an estimate of patient-level variability. We used more recent UK primary care data on persistence to osteoporosis medicines. 154 To reflect the primary prevention decision problem, we used data from people who were treatment naive. Using digitising software (Engauge 12.1), we extracted data from the Kaplan–Meier graph depicting discontinuation from oral bisphosphonates and reconstructed synthetic patient-level data using the algorithm of Guyot et al. 155 To check the accuracy of this process, we generated a Kaplan–Meier graph from the synthetic data and overlaid it on the published curve, finding an extremely close fit. To define a sampling distribution for time to discontinuation, we fitted various parametric models to the synthetic data set, and found that we could best describe the data using a log-normal distribution with a mean of 2.50 (95% CI 2.48 to 2.52) and a standard deviation of 1.74 (95% CI 1.72 to 1.75). This equates to a restricted mean treatment duration of 22.1 months (assuming no one is treated beyond the nominal maximum of 5 years). In the updated model, each simulated patient receives a random variate drawn from this distribution (capped at 5 years) as their duration of therapy with alendronate.
Health-related quality of life
As in TA464, the model estimates quality of life in the absence of fractures, using a published regression on HSE data. 156 For multipliers reflecting lost utility in the year of a fracture event and subsequently, we adopted the updated values used in the 2020 HTA,149 which mostly originate from the International Costs and Utilities Related to Osteoporotic Fractures Study (ICUROS). 157–161
Resource use and costs
The model assumes an NHS and Personal Social Services perspective (price year 2019–20).
We updated key unit costs to present-day estimates:
-
Dual-energy X-ray absorptiometry (DEXA) scan: £76.62 (average weighted according to activity of all codes from NHS Reference Costs 2019–20). 162
-
GP appointment: £39. 163
-
Alendronate pack: £0.87. 139
We also followed the updates from TA464 costings that the 2020 HTA149 introduced:
-
Accounting for monitoring costs for people on alendronate (i.e. one GP appointment per year and one DEXA scan per 5 years, annualised as 0.2 per year).
-
Estimating full-time care costs using a 50 : 50 split of residential : nursing care. When privately met contributions (36%) are deducted, this amounted to an annual cost of £23,562 in 2013–4, which we inflated, as below.
For all other costs (e.g. acute and ongoing care following fracture events, home help, residential care), we uplifted the unit costs used in TA464 to 2019–20 levels using standard inflators. 163
Treatment effectiveness
We took our estimates of the effectiveness of alendronate in preventing four categories of fragility fracture from TA464. (Note that these estimates are the outputs of the authors’ corrected network meta-analysis, see corrigendum to Davis et al. 147)
Adverse drug events
TA464 accounts for a proportion of people taking alendronate experiencing upper gastrointestinal symptoms, and we have retained this feature unchanged.
New model features specific to this project
Accounting for competing risk of non-fracture death
To estimate non-fracture death in people at risk of osteoporotic fragility fracture, we used identical methods to those we adopted for non-cardiovascular death in people at risk of CVD (see Chapter 6, Accounting for competing risk of non-cardiovascular death).
First, we fitted a model to estimate average population fracture risk as a function of age and sex (see Appendix 9, Table 57 and Figure 61). We noted that, in the CPRD data set, a relatively consistent exponential increase in risk throughout the first nine decades of life tails off somewhat in people in their nineties. We found it necessary to use a seventh-order polynomial term to capture this shape adequately. This feature is contrary to expectation, as there is no mathematical characteristic of the QFracture-2012 model that would lead to a waning of hazard. 26 Therefore, we think it is likely that selection effects in the underlying data set led to over-representation of nonagenarians with QFracture-2012 estimates that are low relative to expectation. To explore the impact of this issue, we fitted an alternative model on a restricted data set that comprised only people younger than 90 years, allowing the model to project the observed trend from people aged 30–89 years for people in their nineties, and in this case a quartic function sufficed (see Appendix 9, Table 57 and Figure 61).
As for the non-cardiovascular death model in Chapter 6, we fitted a relative survival model to estimate the multiplicative difference in time to non-fracture death between a person in the CPRD extract and someone of the same age and sex in the general population. Again, our critical covariate is Δlogit(Q), that is the difference (on a log-odds scale) between each individual’s predicted 10-year QFracture-2012 risk of major fracture and the average score for a person of the same age and sex, as estimated in the models described above.
We fitted a simple, univariable model with Δlogit(Q) as the only covariate and a more complex one with Δlogit(Q), age, polynomial terms for both and interactions between them, as per Equation 1. We tried models with Δlogit(Q) defined using each of the QFracture-2012 prediction models in Appendix 9, Table 57, and found that the relative survival model fitted better (with meaningfully lower AIC) when we used the model fitted on only people younger than 90 years. Therefore, this was the version of the relative survival model we took forward.
Table 20 shows outputs of the relative survival models for men and women.
| Parameter | Simple model, HR (95% CI) | Polynomial model, HR (95% CI) |
|---|---|---|
| Men | ||
| Δlogit(Q) | 0.7216 (0.7163 to 0.7270) | 1.7108 (1.6808 to 1.7409) |
| Δlogit(Q)2 | −0.2025 (−0.2215 to −0.1835) | |
| Age | 7.69 × 10−3 (6.87 × 10−3 to 8.51 × 10−3) | |
| Age2 | 1.17 × 10−5 (−1.03 × 10−5 to 3.36 × 10−5) | |
| Δlogit(Q) × age | −0.0218 (−0.0240 to −0.0195) | |
| Δlogit(Q)2 × age | 2.05 × 10−3 (6.65 × 10−4 to 3.44 × 10−3) | |
| Δlogit(Q) × age2 | −1.66 × 10−4 (−2.13 × 10−4 to −1.19 × 10−4) | |
| Δlogit(Q)2 × age2 | 2.93 × 10−5 (1.89 × 10−6 to 5.66 × 10−5) | |
| AIC | 5,252,183 | 5,239,595 |
| Women | ||
| Δlogit(Q) | 0.8588 (0.8507 to 0.8668) | 1.5458 (1.5081 to 1.5834) |
| Δlogit(Q)2 | 0.2280 (0.1987 to 0.2572) | |
| Age | −3.07 × 10−3 (−3.97 × 10−3 to −2.16 × 10−3) | |
| Age2 | 2.19 × 10−4 (1.97 × 10−4 to 2.41 × 10−4) | |
| Δlogit(Q) × age | −1.04 × 10−3 (−3.64 × 10−3 to 1.55 × 10−3) | |
| Δlogit(Q)2 × age | −0.0163 (−0.0184 to −0.0142) | |
| Δlogit(Q) × age2 | −5.30 × 10−4 (−5.79 × 10−4 to −4.80 × 10−4) | |
| Δlogit(Q)2 × age2 | 2.07 × 10−4 (1.66 × 10−4 to 2.48 × 10−4) | |
| AIC | 5,172,844 | 5,164,693 |
Figure 22 shows estimates of non-fracture mortality generated in the way described above, compared with empirical data across different categories of cardiovascular risk and age. The empirical Kaplan–Meier curves represent observed non-fracture mortality (censored for fracture death) in the CPRD extract for people of the stated age, with baseline QFracture-2012 predictions in the specified brackets (see Figure 22). For our modelled estimates, we start from ONS 3-year lifetables for England and Wales (we use 2009–11 tables, as this is in the middle of the period covered by the CPRD data). We adjust the data to remove fracture deaths, estimated using proportions recorded under ICD-10 code M80 in the ONS’s ‘Deaths registered in England and Wales’ series. For each combination of risk and age bracket, we calculate HRs, as described above (for comparability, we fit at the mean QFracture-2012 prediction and age observed within that category in the CPRD data), and apply the HRs to the ONS curves, and this produces the adjusted curves shown in Figure 22.
FIGURE 22.
Fitted relative survival model for non-fracture mortality compared with empirical data. (a) Men; and (b) women.
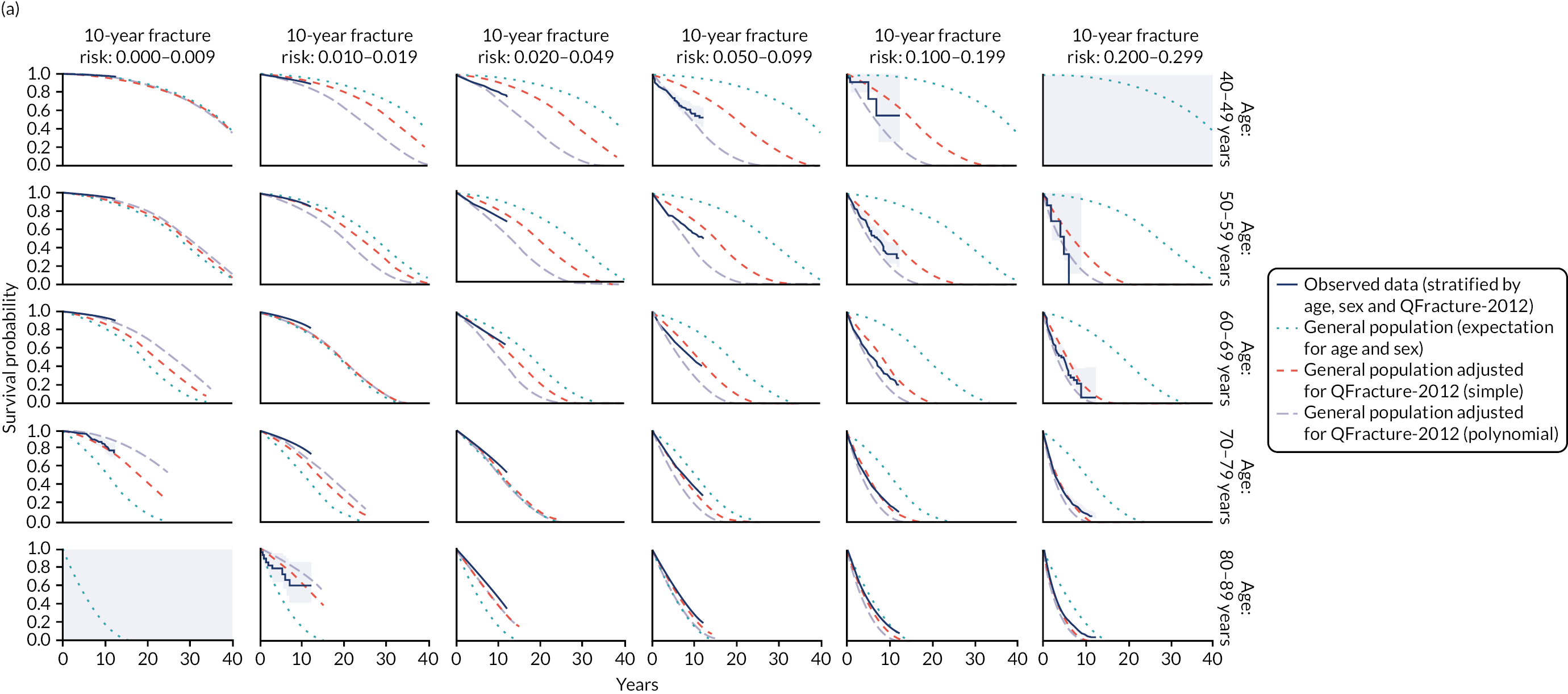
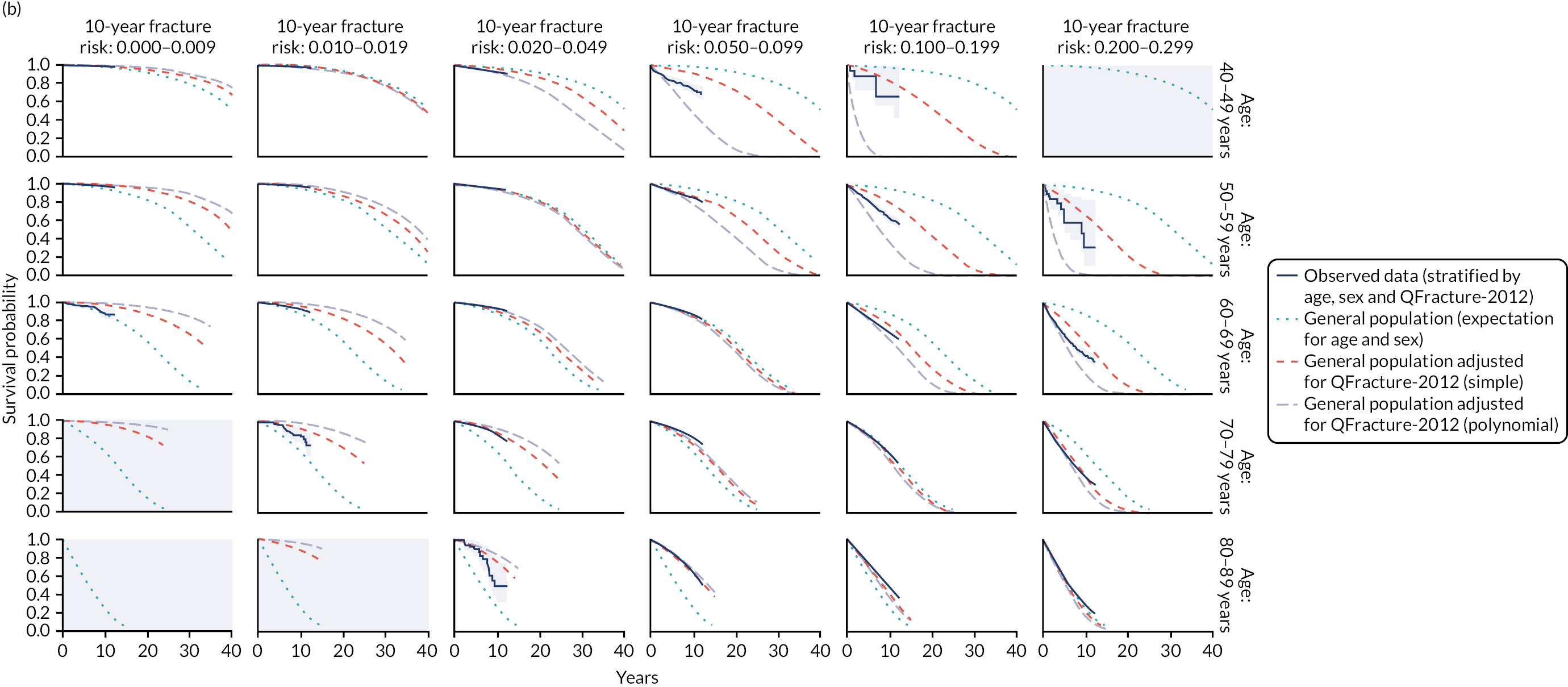
The fitted models provide a less strikingly accurate fit to the observed data than we saw with non-cardiovascular mortality, but still represent a substantial improvement over the unadjusted estimates. Larger coefficients are estimated for the polynomial terms in the more complex model, meaning that it diverges from the simple model to a somewhat greater extent than we saw for non-cardiovascular mortality.
Some instances in which the fitted models appear to depart from the empirical data seem to be due to incoherencies in the observed curves. For instance, it appears that women aged 60–69 years with a 10-year risk of less than 1% and women a decade older with a 1–2% risk have worse survival than the models predict. However, if this is true, then it means that women at this low risk have worse survival than women with higher fracture risk, which is both hard to explain and inconsistent with the patterns seen elsewhere in the data, where increasing risk is invariably associated with worse survival.
We incorporated the relative survival models into the health economic decision model by calculating a fitted HR for each sampled patient and applying it when calculating their life expectancy.
Incorporating direct treatment disutility
We explored DTD using the same four scenarios as for the statins model: (1) no DTD, (2) ‘permanent’ DTD (i.e. full DTD applies over the entire period for which the simulated person is taking the bisphosphonate), (3) ‘time-limited’ DTD (i.e. full DTD while taking the drug up to a maximum 10 years) and (4) ‘diminishing’ DTD (i.e. linear decline from full to no DTD over 10 years, applied while taking the drug). The DTD multiplier for bisphosphonates from Chapter 5 was 0.934.
Deriving results
For TA464, the modellers presented results from a single model run comprising 2 million virtual people (c. 200,000 per risk-stratified tenth), with parameter uncertainty propagated at the individual level (i.e. the model samples new parameter values from distributions reflecting uncertainty in their true value for each patient). Our preliminary investigation suggested that there is still non-trivial Monte Carlo error in the model with that many runs, but this generally appears to stabilise after around 4 million patients. Therefore, our base-case results summarise the outputs of 5 million people (c. 500,000 per tenth).
To enable us to explore results further, as in TA464, we fitted a generalised additive model (GAM) to the patient-level outputs of the discrete-event model. The response variable is incremental net monetary benefit for alendronate compared with no treatment. In its simplest version, the meta-model takes the form:
where g(.) is a link function (i.e. identity, as we assume a Gaussian distribution for INMB), f(.) is a smooth term (with a cubic regression spline basis function) that can capture non-linearities in the relationship between the predictor (i.e. baseline QFracture-2012 10-year serious fracture probability) and the response term, and Adj is a dummy variable indicating whether or not the economic model was adjusted for competing risk of non-fracture death.
We also extended the meta-modelling methods used in TA464 to provide an estimate of value for money as a function of baseline risk and age. This model takes the form:
Here, the joint effect of fracture risk and age becomes the target of the smooth term. As before, we stratify the model by adjustment condition.
As in previous iterations of the model,149,150 we found that GAM predictions become erratic above a predicted 10-year fracture risk of 30%, owing to the very small numbers of simulated patients who reach this level of risk (i.e. around 0.1% of the cohort). Therefore, we fitted the meta-model to a data set excluding the few simulated people who exceed this level of risk and present only fitted results up to this threshold.
Results
Accounting for competing risk
Table 21 summarises expected events with alendronate compared with no treatment, first in the unadjusted model and then in the version that adjusts for competing risk of non-fracture death. Table 21 presents analogous information to Table 9 in the 2020 HTA. 149 Table 37 of the analysis underpinning TA464150 has something similar, although note that this is based on an uncorrected network meta-analysis, and the corrigendum does not include an updated version of the same information. 147
| 10-year fracture risk decile (QFracture-2012) | Events prevented per 100,000 people treated with alendronate compared with no treatment | Life-years gained per patient compared with no treatment | ||||||
|---|---|---|---|---|---|---|---|---|
| Fractures | Full-time care admissions | |||||||
| Hip | Vertebral | Proximal humerus | Wrist | Fatal | Total | |||
| Unadjusted | ||||||||
| 1 (< 0.64%) | 5 | 25 | 5 | 14 | 1 | 48 | 1 | 0.0000 |
| 2 (0.64–0.85%) | 7 | 31 | 10 | 29 | 0 | 78 | 1 | 0.0001 |
| 3 (0.86–1.17%) | 13 | 43 | 13 | 43 | 1 | 112 | 2 | 0.0002 |
| 4 (1.18–1.63%) | 23 | 50 | 16 | 49 | 3 | 137 | 2 | 0.0006 |
| 5 (1.64–2.27%) | 33 | 66 | 25 | 62 | 6 | 186 | 5 | 0.0007 |
| 6 (2.28–3.20%) | 54 | 87 | 34 | 53 | 10 | 228 | 8 | 0.0010 |
| 7 (3.21–4.57%) | 84 | 123 | 50 | 87 | 15 | 344 | 16 | 0.0021 |
| 8 (4.58–6.63%) | 125 | 167 | 76 | 94 | 16 | 463 | 17 | 0.0020 |
| 9 (6.64–10.62%) | 242 | 238 | 109 | 132 | 43 | 722 | 45 | 0.0035 |
| 10 (≥ 10.63%) | 492 | 289 | 145 | 182 | 81 | 1107 | 112 | 0.0044 |
| All | 107 | 112 | 48 | 74 | 17 | 341 | 21 | 0.0014 |
| Adjusted for competing risk of non-fracture death | ||||||||
| 1 (< 0.64%) | 5 | 27 | 6 | 15 | 0 | 53 | 0 | 0.0000 |
| 2 (0.64–0.85%) | 7 | 31 | 10 | 28 | 1 | 76 | 1 | 0.0001 |
| 3 (0.86–1.17%) | 12 | 45 | 14 | 41 | 1 | 111 | 0 | 0.0002 |
| 4 (1.18–1.63%) | 22 | 49 | 17 | 49 | 3 | 137 | 3 | 0.0006 |
| 5 (1.64–2.27%) | 31 | 64 | 24 | 57 | 5 | 177 | 3 | 0.0007 |
| 6 (2.28–3.20%) | 52 | 83 | 34 | 54 | 9 | 223 | 9 | 0.0009 |
| 7 (3.21–4.57%) | 81 | 118 | 48 | 83 | 16 | 331 | 14 | 0.0019 |
| 8 (4.58–6.63%) | 124 | 163 | 72 | 94 | 18 | 452 | 17 | 0.0018 |
| 9 (6.64–10.62%) | 232 | 227 | 105 | 116 | 40 | 680 | 44 | 0.0031 |
| 10 (≥ 10.63%) | 434 | 252 | 120 | 151 | 70 | 956 | 98 | 0.0032 |
| All | 99 | 106 | 45 | 69 | 16 | 318 | 19 | 0.0012 |
Whether adjusted for competing risk or not, the updated model estimates that alendronate prevents slightly more fractures than the previous models in all categories except wrist fracture, and this is because the longer duration of treatment (and consequent extension of offset period) gives more time for the intervention to provide benefit. The reduced efficacy for wrist fracture compared with the 2020 HTA149 is probably a result of different inputs, for example the network meta-analysis developed for the 2020 HTA149 included a wider range of comparators and estimated a greater mean effect for bisphosphonates in preventing wrist fractures.
Comparing adjusted with unadjusted models reveals some relatively subtle differences. In higher-risk people (most obviously in the highest-risk tenth), the unadjusted model slightly overstates the effectiveness of alendronate. We can see this when we take account of the fact that people with high risk of fracture also experience increased risk of competing causes of death, with the result that fewer of people live to see the benefit of future fractures prevented. With a large enough sample, we would also expect to see the unadjusted model underpredicting fractures in the people with below-average risk (because their true life expectancy is longer than the unadjusted model simulates). There may be a hint of this type of effect in the lowest-risk tenth of the population; however, we would need a colossal sample size to detect the effect reliably, as events are so rare (and intervening deaths even rarer) in the few years during which the treatment effect obtains.
Table 22 shows how these dynamics translate into costs and QALYs. In absolute terms, the adjusted model generates more QALYs than the unadjusted model for people at lowest risk of fracture, and the relationship reverses as risk rises. Comparing incremental results from the unadjusted and adjusted models shows no difference in the deciles in which oral bisphosphonates represent an effective use of NHS resources. In both versions of the model, the lower-risk seven-tenths of people gain a tiny benefit from alendronate, but this benefit is insufficient to offset the additional costs associated with the intervention. Above the seventh decile, however, QALY gains get a bit larger and (because fractures cause expense to the health and care system, as well as disutility to the person) incremental costs go down, with the result that preventative treatment provides reasonable value for money (when we value QALYs at £20,000 each). In the adjusted model, the degree of net benefit expected for people at highest risk is discernibly lower than in the unadjusted version, and this is a direct result of the smaller number of fractures prevented, as discussed above. Nevertheless, both models agree about the people for whom incremental net benefit is positive.
| 10-year fracture risk decile (QFracture-2012) | No treatment | Alendronate | Incremental | INMB at £20,000/QALY | ||||
|---|---|---|---|---|---|---|---|---|
| Cost (£) | QALY | Cost (£) | QALY | Cost (£) | QALY | ICER (£) | ||
| Unadjusted | ||||||||
| 1 (< 0.64%) | 735 | 16.6161 | 847 | 16.6164 | 112 | 0.0003 | 374,536 | −106 |
| 2 (0.64–0.85%) | 1263 | 15.3859 | 1374 | 15.3864 | 111 | 0.0005 | 226,068 | −101 |
| 3 (0.86–1.17%) | 2227 | 14.0754 | 2333 | 14.0761 | 106 | 0.0007 | 147,194 | −91 |
| 4 (1.18–1.63%) | 2833 | 12.7259 | 2937 | 12.7270 | 103 | 0.0011 | 97,309 | −82 |
| 5 (1.64–2.27%) | 3056 | 11.7241 | 3153 | 11.7255 | 97 | 0.0014 | 71,532 | −70 |
| 6 (2.28–3.20%) | 3307 | 10.6404 | 3396 | 10.6422 | 89 | 0.0018 | 49,539 | −53 |
| 7 (3.21–4.57%) | 3626 | 9.5728 | 3701 | 9.5756 | 75 | 0.0028 | 27,081 | −20 |
| 8 (4.58–6.63%) | 4381 | 8.4998 | 4435 | 8.5033 | 54 | 0.0035 | 15,460 | 16 |
| 9 (6.64–10.62%) | 6842 | 6.7128 | 6856 | 6.7179 | 14 | 0.0051 | 2736 | 88 |
| 10 (≥ 10.63%) | 14,632 | 4.2055 | 14,583 | 4.2116 | −49 | 0.0061 | Dominant | 170 |
| Adjusted for competing risk of non-fracture death | ||||||||
| 1 (< 0.64%) | 993 | 17.6266 | 1105 | 17.6269 | 112 | 0.0003 | 347,850 | −106 |
| 2 (0.64–0.85%) | 1354 | 15.7936 | 1466 | 15.7941 | 111 | 0.0005 | 213,695 | −101 |
| 3 (0.86–1.17%) | 2146 | 14.0179 | 2252 | 14.0186 | 106 | 0.0007 | 144,765 | −91 |
| 4 (1.18–1.63%) | 2615 | 12.4307 | 2718 | 12.4318 | 103 | 0.0011 | 97,013 | −82 |
| 5 (1.64–2.27%) | 2781 | 11.3664 | 2879 | 11.3676 | 98 | 0.0013 | 75,730 | −72 |
| 6 (2.28–3.20%) | 2979 | 10.2520 | 3068 | 10.2537 | 89 | 0.0017 | 52,834 | −55 |
| 7 (3.21–4.57%) | 3260 | 9.1986 | 3337 | 9.2012 | 77 | 0.0026 | 29,709 | −25 |
| 8 (4.58–6.63%) | 3934 | 8.1006 | 3990 | 8.1039 | 56 | 0.0033 | 17,213 | 9 |
| 9 (6.64–10.62%) | 6117 | 6.2304 | 6137 | 6.2350 | 20 | 0.0046 | 4343 | 72 |
| 10 (≥ 10.63%) | 12,136 | 3.5817 | 12,112 | 3.5863 | −24 | 0.0046 | Dominant | 117 |
Figure 23 shows the output of the GAM meta-model (see Equation 4) fitted to patient-level output and it is directly analogous to the green line in Figure 3 in the corrigendum to the analysis that informed TA464147 (with the difference that we find it helpful to show the x-axis on a logarithmic scale; note that the first seven deciles of risk all fit into the first sixth of the natural scale graph). This is consistent with what we have seen in previous model outputs, that is the unadjusted model overestimates benefit in people at greatest risk as, once we adjust for competing risk of other-cause death, their capacity to benefit from reduced fracture risk diminishes.
FIGURE 23.
Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of risk of fracture, with different assumptions about competing risk of non-fracture death. GAM fitted to model outputs comprising 5 million simulated patients. Lines show fitted model prediction, shaded areas show 95% CI, vertical dashed bars represent deciles of risk and numbered shapes show mean values for people within each tenth of the population (where these are missing, fewer than 100 of the total 5 million simulated people fell into the group). INMB, incremental net monetary benefit.
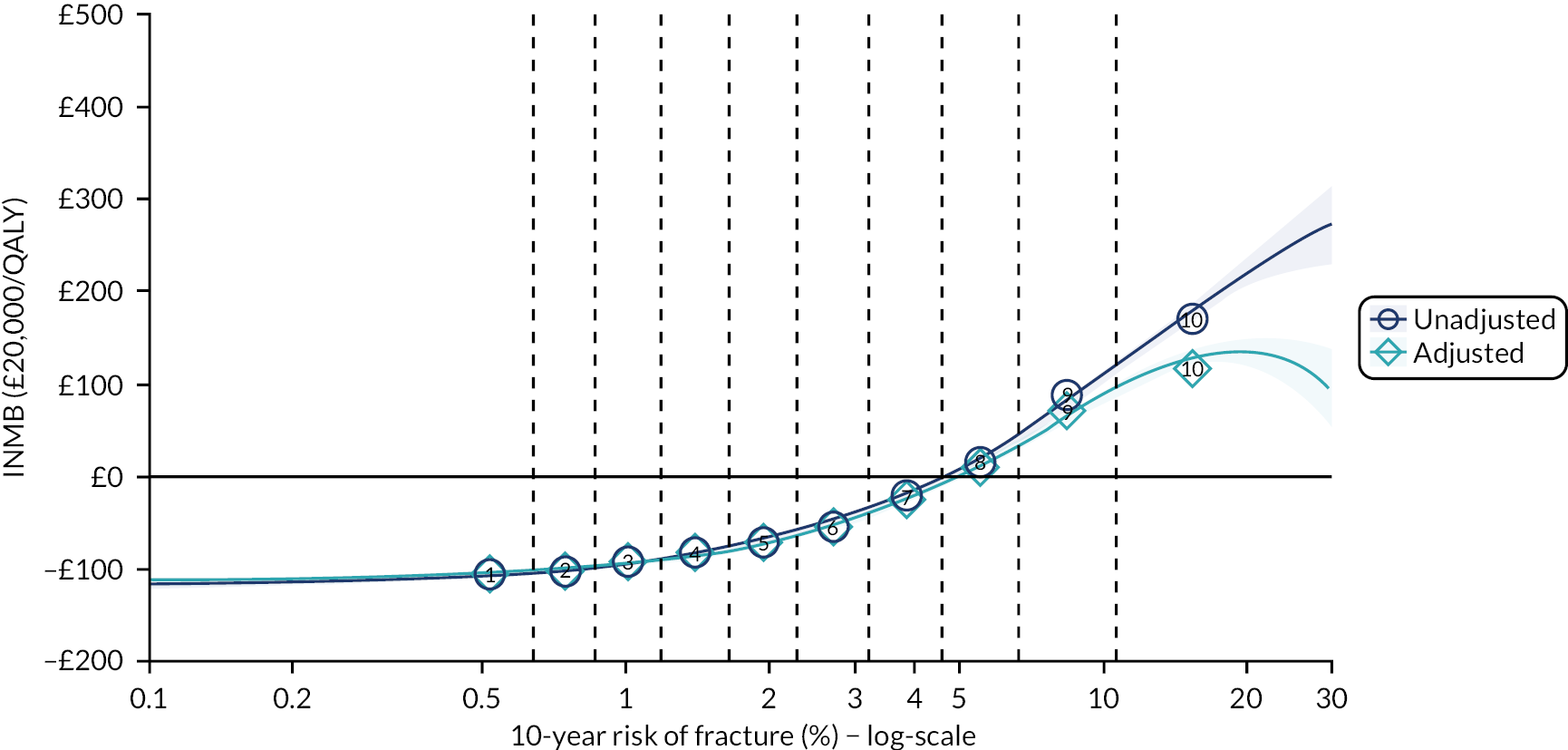
However, as seen before, the levels of risk at which this bias operates are almost exclusively above the point where – both adjusted and unadjusted models agree that – intervention provides positive net benefit. The unadjusted model suggests that the threshold at which alendronate becomes cost-effective is a 10-year MOF risk of 4.7 (95% CI 4.5 to 4.9), whereas the adjusted model estimates the same value as 5.0 (95% CI 4.8 to 5.2).
Extending the GAM meta-model to incorporate age as well as baseline risk (see Equation 5) produces outputs such as those illustrated in Figure 24 (fitted at indicative ages of 50, 60, 70 and 80 years). By and large, results replicate those in the unstratified meta-model, that is we may overestimate value for money in people at the highest risk if we do not adjust for competing risk of non-fracture death; however, this generally only affects the magnitude of expected benefit in people for whom some degree of benefit is expected. There is some indication that these expectations may diverge for the youngest people. For example, for 50-year-olds, treatment is only cost-effective in the highest-risk tenth of people once we adjust for competing risk. Note, however, that the outputs of the meta-model are much more uncertain, in this instance, as they are based on a far smaller sample size (almost all simulated people with the highest level of fracture risk are aged > 50 years).
FIGURE 24.
Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of age and risk of fracture, with different assumptions about competing risk of non-fracture death. (a) Age 50 years; (b) age 60 years; (c) age 70 years: and (d) age 80 years. GAM fitted to model outputs comprising 5 million simulated patients. Lines show fitted model prediction, shaded areas show 95% CI, vertical dashed bars represent deciles of risk and numbered shapes show mean values for people within each tenth of the population (where these are missing, fewer than 100 of the total 5 million simulated people fell into the group). INMB, incremental net monetary benefit.
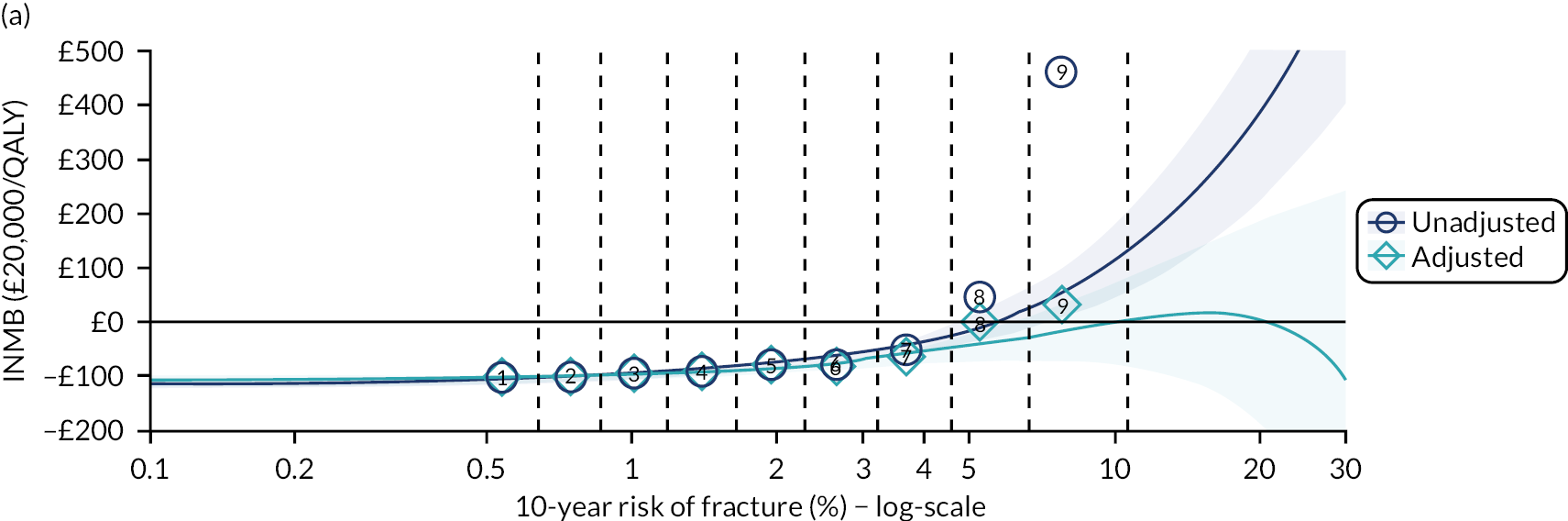

Appendix 9, Table 58, shows the threshold at which treatment becomes associated with positive net benefit according to the GAM, adjusting for age and fracture risk. Unadjusted model outputs are relatively invariant to age, whereas the adjusted model suggests that the threshold for intervention should fall as people get older (until they reach the oldest category).
As we did with the statins model, we also looked at how it would affect cost-effectiveness results if we simulated people who are fitter or less fit than average (over and above the degree that would be expected via fracture risk alone), by halving and doubling each individual’s HR for non-fracture death. Figure 25 shows results for model 2, which adjusts for fracture risk only. Figure 26 shows the same for model 2 but adjusts for age as well. Figure 27 shows a cross-categorisation of age and fracture risk, with varying assumptions about competing risk. As would be expected, we can see that the threshold at which intervention generates positive incremental net benefit is somewhat higher in people who are more likely to die of other things and somewhat lower in people whose increased life expectancy gives them every chance of surviving to realise the benefit of fractures prevented.
FIGURE 25.
Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of risk of fracture, with different assumptions about competing risk of non-fracture death. GAM fitted to model outputs comprising 5 million simulated patients. Lines show fitted model prediction, shaded areas show 95% CI, vertical dashed bars represent deciles of risk and numbered shapes show mean values for people within each tenth of the population (where these are missing, fewer than 100 of the total 5 million simulated people fell into the group). INMB, incremental net monetary benefit.

FIGURE 26.
Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of age and risk of fracture, with different assumptions about competing risk of non-fracture death. (a) Age 50 years; (b) age 60 years; (c) age 70 years; and (d) age 80 years. GAM fitted to model outputs comprising 5 million simulated patients. Lines show fitted model prediction, shaded areas show 95% CI, vertical dashed bars represent deciles of risk and numbered shapes show mean values for people within each tenth of the population (where these are missing, fewer than 100 of the total 5 million simulated people fell into the group). INMB, incremental net monetary benefit.
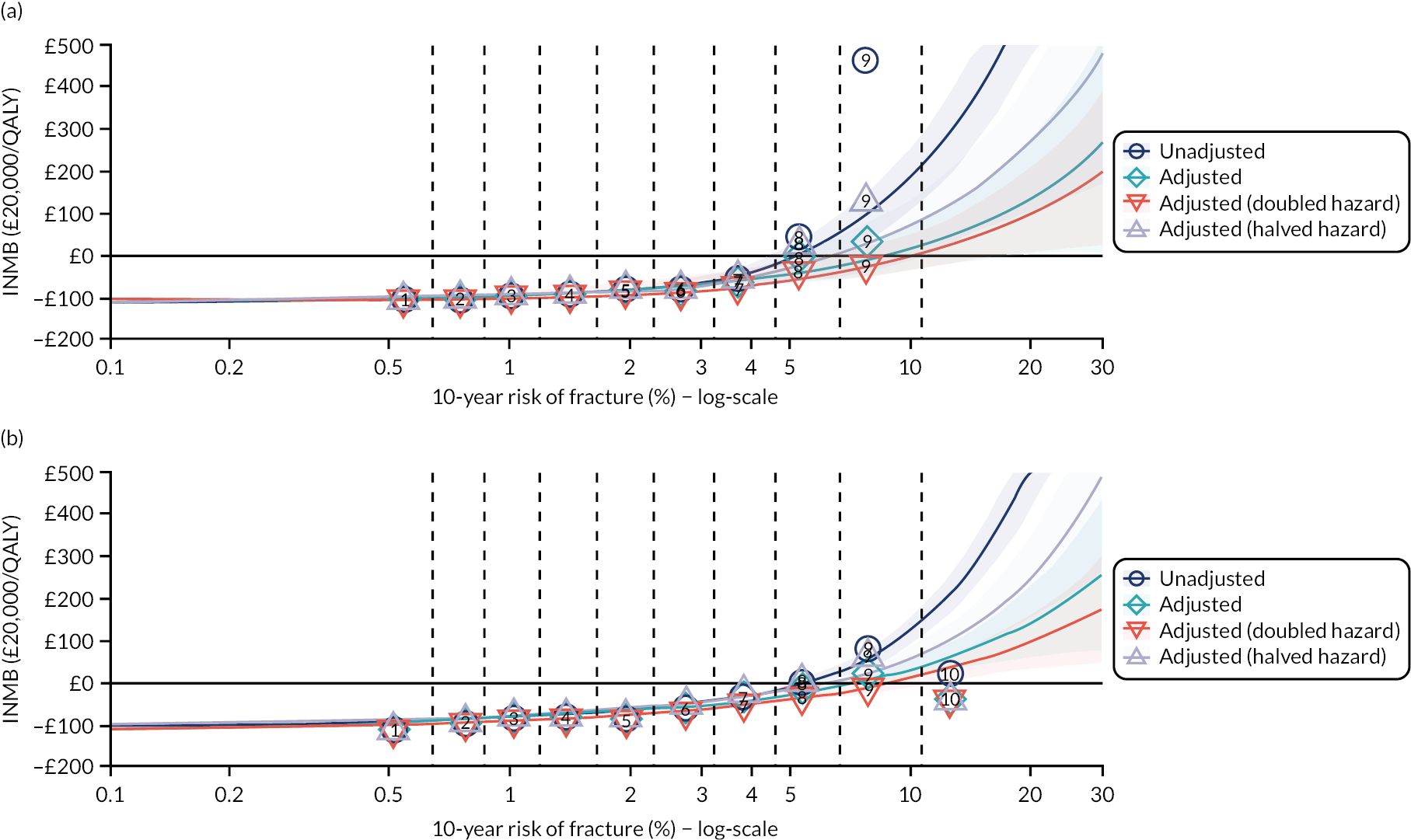
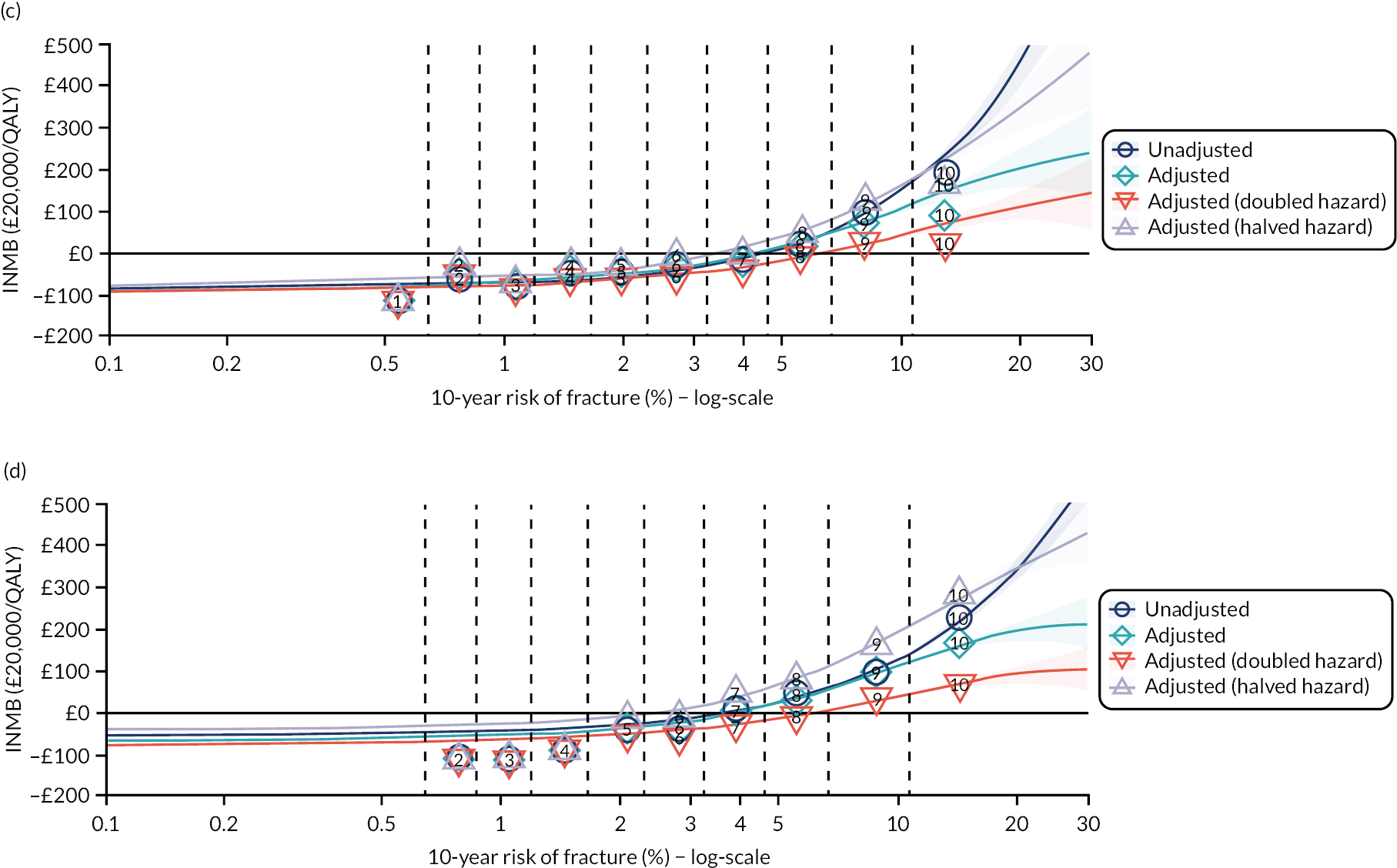
FIGURE 27.
Relationship between age, risk of fracture and cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment), with different assumptions about competing risk of non-fracture death. (a) Unadjusted (as per TA464); (b) adjusted for competing risk of non-fracture death; (c) adjusted with doubled hazard of non-fracture death; and (d) adjusted with halved hazard of non-fracture death. INMB, incremental net monetary benefit.
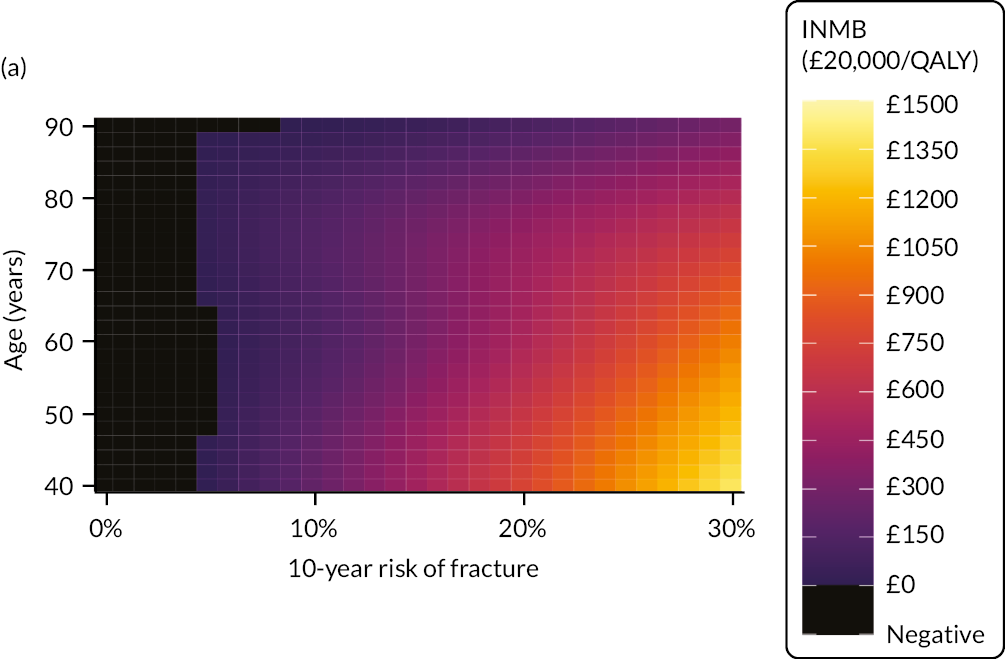
Incorporating direct treatment disutility
We show the lifetime discounted QALY losses we would expect from DTD in Table 23. Permanent and time-limited losses are identical because, in our base case, we assume that time-limited DTD lasts for 10 years and alendronate therapy is capped at 5 years. Therefore, under both scenarios, people experience full DTD for as long as they take the drug.
| 10-year fracture risk decile (QFracture-2012) | Unadjusted | Adjusted for competing risk of non-fracture death | ||||
|---|---|---|---|---|---|---|
| Permanent | Time limited | Diminishing | Permanent | Time limited | Diminishing | |
| 1 (< 0.64%) | −0.115 | −0.115 | −0.094 | −0.116 | −0.116 | −0.094 |
| 2 (0.64–0.85%) | −0.116 | −0.116 | −0.094 | −0.116 | −0.116 | −0.095 |
| 3 (0.86–1.17%) | −0.115 | −0.115 | −0.094 | −0.115 | −0.115 | −0.094 |
| 4 (1.18–1.63%) | −0.114 | −0.114 | −0.094 | −0.114 | −0.114 | −0.094 |
| 5 (1.64–2.27%) | −0.114 | −0.114 | −0.093 | −0.113 | −0.113 | −0.093 |
| 6 (2.28–3.20%) | −0.113 | −0.113 | −0.093 | −0.113 | −0.113 | −0.092 |
| 7 (3.21–4.57%) | −0.112 | −0.112 | −0.092 | −0.111 | −0.111 | −0.092 |
| 8 (4.58–6.63%) | −0.111 | −0.111 | −0.091 | −0.110 | −0.110 | −0.090 |
| 9 (6.64–10.62%) | −0.108 | −0.108 | −0.089 | −0.106 | −0.106 | −0.088 |
| 10 (≥ 10.63%) | −0.101 | −0.101 | −0.084 | −0.116 | −0.116 | −0.094 |
To give context to our estimates of DTD, we should remember that, as shown in Table 22, once we adjust for competing risk of non-fracture death, expected QALY gains associated with alendronate compared with no treatment are small (with no more than 0.005 QALYs per person), even in people at the highest risk of fracture. Even under the assumption of diminishing DTD, we estimate that people stand to lose more than 10 times as many QALYs from DTD as they stand to gain from the fracture-preventing effect of alendronate. Any version of Figure 27 that also accounted for any degree of DTD would comprise exclusively black area, as there is no combination of patient characteristics that leads to expected QALY gains that come close to justifying estimated DTD.
In the competing risk-adjusted model, fewer than 0.2% of simulated people experience QALY gains that are greater than their expected DTD (in permanent, time-limited and diminishing DTD scenarios). Even in the 10% of people at highest risk of fracture, these percentages rise to only 0.53–0.58%, depending on DTD scenario, and this suggests that if DTD is present then at least 199 out of 200 people treated with bisphosphonates would experience more harm than benefit, even if their chances of fracture are high.
Even if we assume that people get used to taking bisphosphonates over a short period of 1 year, QALY losses associated with DTD are still at least five times greater than expected QALY gains. The conclusion is inescapable: for anybody experiencing any duration of DTD of the magnitude estimated in Chapter 5, it is impossible to anticipate long-term benefits that would offset the up-front harm.
Discussion
Main findings
Although we would reiterate that our results should not be seen as a present-day best estimate of the cost-effectiveness of bisphosphonates, our results are closely comparable with the results generated in previous iterations of the same underlying model. 147,149,150 Alendronate is associated with small but positive net benefit in people with approximately the highest-third of fracture risk (i.e. anything above around 5% per year).
As with the cohort-level model explored in Chapter 6, ‘adjusting for competing risk’ in a discrete event simulation does not mean introducing a new concept that has, hitherto, been absent from such analyses. Rather, ‘adjusting for competing risk’ means taking the competing time-to-event functions the model has always simulated and ensuring that we parameterise the functions in a way that accounts for important correlations between them. We find that ‘adjusting for competing risk’ has a relatively subtle effect on model outputs, as it makes a small difference to the magnitude of expected benefit, but the people for whom adjustment makes the greatest absolute difference are people for whom adjusted and unadjusted models predict at least some degree of benefit. This is consistent with findings in our analysis of risk prediction models that miscalibration is often most obvious in people whose level of risk clearly exceeds intervention thresholds (see Chapters 2–4).
In contrast, the effects of DTD in the same decision space are anything but subtle. At the level at which we measured the effects of DTD for bisphosphonates (see Chapter 5), DTD of any duration would be enough to swamp expected benefit from fracture prevention. The low rates of persistence with oral bisphosphonates observed in practice are further evidence that people associate bisphosphonates with disutility of a magnitude that outweighs any anticipated gain, which lends some face validity to our findings. It follows that, once we factor cost into the equation, it is impossible to find any identifiable group of people for whom oral bisphosphonates represent an effective use of NHS resources if we assume population-level average DTD for everyone to whom the decision applies. In fact, there are a small number of simulated people for whom bisphosphonates would be cost-effective at conventional QALY values despite these people experiencing net harm (as this can occur when non-trivial cost savings arise from prevented fractures and associated QALY gains are marginally less than DTD-related QALY losses).
Nevertheless, in the same way we argued for statins for the primary prevention of CVD (see Chapter 6, Discussion), we would not suggest that decision-makers should advocate blanket disinvestment in bisphosphonates. On the one hand, we think it is useful information that the average person would sacrifice more quality-adjusted life expectation to avoid taking bisphosphonates than they could expect to gain from their therapeutic effect (and this is true both of people with experience of taking bisphosphonates and members of the general public). On the other hand, although our survey respondents were more eager to avoid bisphosphonates than statins, around one-sixth of the respondents still ascribed no DTD to bisphosphonates. Therefore, if adequately informed people consider the trade-off differently to the average person (and they are at sufficiently high risk of fragility fracture to justify the costs of treatment), then we would still want to offer people access to a treatment from which they could expect some benefit before any counterweighting from disadvantages they are prepared to tolerate.
Limitations
First, our epidemiological work (see Chapter 3) finds that QFracture-2012 is poorly calibrated for reasons not limited to its inability to deal with competing risks, and, on the face of it, this would seem to undermine our cost-effectiveness model that, in common with its previous iterations, predicts risk of fracture using baseline QFracture-2012 predictions. However, in the world simulated by our decision-analytic model, QFracture-2012 does not have poor predictive utility but, instead, has perfect predictive utility because the model simulates events as a direct function of each simulated person’s baseline risk (i.e. the simulated people in the model really do have the risk of fracture that QFracture-2012 would ascribe to them). Therefore, our results can be seen as assessing the cost-effectiveness of bisphosphonates in a population with accurate risk prediction. This means that our results would be valid for the more accurate risk estimates that a better risk prediction model would produce. The only areas in which QFracture-2012’s poor calibration may undermine the model are (1) the deciles of risk by which the population is subdivided bear little relation to the true risks faced in the population and (2) for TA464, the modellers derived the distributional assumptions underpinning time-to-fracture events from analysis of QFracture-2012 data (see ‘Estimating time to event from absolute fracture risk’ in Davis et al. 150). If a more accurate risk prediction model implied different functional forms and/or shape parameters, then this ought to be reflected in an updated cost-effectiveness model.
Second, as with our relative survival model for non-cardiovascular death, we acknowledge that collapsing risk to a single covariate (in this case, 10-year major fracture risk) runs the risk of lumping together people with different non-fracture survival expectations. For example, a 70-year-old woman with no long-term conditions but a family history of osteoporosis has an identical QFracture-2012 prediction to a 70-year-old woman with type 2 diabetes and CKD but no family history (as both have a 12.6% chance of major fragility fracture over 10 years). It is plausible that, although their risk of fracture is indistinguishable, these two profiles would be associated with markedly different life expectancy. Our relative survival model is blind to such dynamics, as the model uses fracture risk as a single covariate. When comparing our adjusted life expectancy estimates with observed data (see Figure 22), we acknowledge that, for some age–sex–fracture risk strata, there are larger discrepancies between modelled and observed outcomes than we saw with the cardiovascular data set. We might be able to achieve a closer fit with a more sophisticated model (i.e. instead of using a summary risk prediction measure we could estimate relative survival as a function of each of the individual covariates on which the prediction itself relies). Such an approach would theoretically be able to capture the differential effect of risk factors for fracture on life expectancy. However, this would be a very complex model to fit, and we could only validate it against ever-more stratified subsections of the empirical data, which, even when starting from a large data set, would swiftly lead to sample-size constraints. At very least, we remain confident that our simpler modelling approach results in much better estimates of life expectancy than relying on unadjusted general population data, as has been done in all previous models.
Third, our results suggest that, after one accounts for competing risk of non-fracture death, the risk threshold for intervention with bisphosphonates goes down as people get older. This is the opposite of what is recommended in NICE Quality Standard 149 (QS149),164 where intervention thresholds rise with age. The thresholds in QS149164 derive from an analysis by McCloskey et al. ,165 the predominant aim of which was to reduce the number of people in whom treatment is indicated. Our modelling suggests that a younger person with higher risk of fracture has less capacity to benefit because they are likely to be substantially less healthy than an average person of the same age and sex, with the consequence that their life expectancy leaves less room for fracture prevention. An older person with the same estimated risk will not stand out from their contemporaries in the same way and so their life expectancy will be closer to typical.
Fourth, the modelled population has a lower proportion of people with a high fracture risk than the real population because the simulation does not account for correlations between risk factors. For example, when the model generates a simuland with type 2 diabetes, then that person is no more likely than an average member of the population to have CKD or CVD, whereas, in reality, such risk factors cluster together. This has the effect that there are unrepresentatively few people with multiple risk factors and, hence, higher fracture risk in the simulated data set. This issue may have caused or compounded the problems we encountered fitting meta-models to full data sets, leading us to truncate the data to people with predicted 10-year fracture risks lower than 30% (see Deriving results).
Finally, given the computational demands of producing a probabilistic sensitivity analysis, this was not possible for this study.
Conclusion
Similar to the analysis presented in Chapter 6, this analysis has shown that including competing risk in the model-based CEA of bisphosphonates for primary prevention produced only subtle changes to the observed cost-effectiveness. However, we noted some effect and this analysis provides more evidence that competing risk should be included in CEAs of primary prevention strategies. Incorporating DTD had a dramatic effect on the cost-effectiveness of bisphosphonates. The effect was so dramatic that the observed QALY gains from taking a bisphosphonate were swamped by DTD in all scenarios. This result raises an interesting challenge to decision-makers in the context of bisphosphonates. However, rather than advise bisphosphonates should not be recommended because of the possible DTD, we advise that the impact of including DTD in sensitivity analyses on the outputs of a decision-analytic model should be an integral component of CEAs of primary prevention strategies.
Chapter 8 Summary and conclusions
Summary of findings
The overall aim was to improve the evidence generated from risk prediction models and model-based CEAs to inform decision-making for selecting primary prevention treatments for CVD and osteoporotic fracture.
In Chapter 2, we showed that QRISK3 had excellent discrimination and good calibration in the whole population of people aged 25–84 years when ignoring competing mortality risks. However, QRISK3 overpredicted somewhat in the whole population when accounting for competing risks, and had poor to moderate discrimination and calibration (with larger overprediction) in important subgroups, including older people, those with multimorbidity and people with diabetes or CKD. Overprediction was worse at higher levels of predicted CVD risk, but there was some overprediction at the 10-year 10% risk threshold currently recommended by NICE as defining who to offer statins to for primary prevention. Accounting for competing risk in derivation of new models (CRISK and CRISK-CCI) improved calibration, although discrimination was very similar to QRISK3 (which, in part, reflects that excellent discrimination in QRISK3 is primarily driven by the inclusion of a very large range of age).
Chapter 3 found that QRISK-Lifetime (evaluated with a 10-year prediction horizon) had excellent discrimination but systematic underprediction in the whole population. Discrimination was worse in all age strata, and progressively worse with increasing age and increasing comorbidity. In all age strata there was evidence of underprediction, which increased with increasing age. The systematic underprediction of 10-year risk by QRISK-Lifetime implies that lifetime risk will be underestimated. Lifetime risk prediction and QRISK3 10-year risk prediction recommended largely non-overlapping groups for treatment, with QRISK-Lifetime recommending younger people who were more likely to have a strong family history and be smokers for treatment. However, over 10 years, people recommended for statin treatment based on lifetime risk experienced considerably fewer CVD events, meaning that treatment based on lifetime risk evaluation requires a leap of faith that currently observed CVD incidence rates in older people will be maintained.
In Chapter 4, QFracture-2012 was found to have two important problems. First, QFracture-2012 underpredicted fracture risk in general, partly because its derivation used only GP and mortality data to define fracture outcomes (although other differences must reflect either better recording of fracture in more recent data and/or differences in the codesets used to ascertain fracture). Second, competing mortality risk had a much larger impact than for CVD, reflecting that osteoporotic fracture is a relatively rare cause of sudden death, and this led to overprediction in general, which was very large in older people and people with multimorbidity. Accounting for competing risk in derivation of new models (CFracture) to predict major osteoporotic and hip fracture improved calibration, although, again, discrimination was very similar to QFracture-2012. Although CFracture performed better, neither QFracture-2012 nor CFracture predicted fracture risk well in people aged 85–99 years.
The stated-preference surveys reported in Chapter 5 demonstrated that most people think the inconvenience of taking statins or bisphosphonates is not negligible. In the TTO exercise, most respondents would be prepared to forgo some life expectancy to avoid taking either pill, although it was clear that participants consider statins less bothersome than bisphosphonates. Consistent with previous studies, our findings suggest that, although most people perceive a benefit–harm trade-off, some people would avoid taking the medicines at all costs and some people foresee zero disutility. We explored the same issues in a BWS experiment, which had face validity in that inconvenience influenced preferences. However, the DTD values we have so far been able to calculate from the BWS data appear implausibly large.
As noted in Chapters 6 and 7, decision-analytic models of the type used for NICE CEAs are structurally fit to account for competing risks as a matter of course. However, the parameterisation of time to death seldom accounts for the fact that, in many cases, people who are at higher risk of condition-specific events will also be at higher risk of other-cause mortality. Our relative survival models address this problem by estimating the extent to which predicted condition-specific risk explains divergence from expected population mortality. Applying these estimates in our updated decision-analytic models has the expected effect, that is people with below-average condition-specific risk for their sex and age accrue more QALYs (because they experience lower other-cause mortality) and people with above-average condition-specific risk end up with fewer QALYs (because their other-cause life expectancy is attenuated). This phenomenon was observable in the statins model, but it had little impact on incremental cost–utility results, mostly because the model suggests that statins provide net benefit for almost everyone (and our updates made this conclusion even stronger). In the bisphosphonates model, the main impact of accurate adjustment for competing risk of non-fracture death is to attenuate expected value for money in people at highest risk of fracture. However, this generally affects the magnitude of expected net benefit in only people for whom some degree of benefit is expected. Introducing DTD to the equation has a more obvious effect in both models. For statins, if we assume that DTD applies for a prolonged period or permanently, then intervention would be net harmful for younger people at lower risk of CVD, with the risk threshold rising as people get older. However, treatment remains net beneficial for most people at higher risk of CVD. For bisphosphonates, DTD of any duration would be enough to swamp expected benefit from fracture prevention. Therefore, we are unable to find any identifiable group of people for whom oral bisphosphonates represent an effective use of NHS resources, if we assume population-level average DTD for everyone to whom the decision applies.
Implications of findings for policy and practice
A first implication is that excellent discriminative performance of clinical risk prediction tools in the entire population is not enough to conclude that a tool performs well. In this study, all risk prediction tools examined (including our own) had excellent discrimination in the whole population, but typically poor to moderate discrimination when stratified by age and moderate to good discrimination when stratified by comorbidity level. For age, this is expected because age is part of the risk equation and age is the dominant predictor of risk. 72 Put another way, however, it is relatively easy to have good discrimination when the population studied has a ≥ 60-year age range (and clinicians have little problem identifying that a 30-year-old has much lower risk of CVD or fracture than an 80-year-old). Any clinical risk prediction tool that includes such a wide age range is, therefore, likely to have good to excellent discrimination, but that does not mean that the tool will be that effective in discriminating people of similar ages. Equally, using discrimination to compare risk prediction tools that include very different age ranges will often be misleading. 100 Calibration is a better guide to prediction tool performance, but the same issue applies (i.e. good calibration in the whole population does not necessarily mean good calibration in key subgroups). Therefore, guideline developers need to carefully consider discrimination and calibration in the populations they are making recommendations for, and prediction tool developers and validators should publish age-stratified evaluations of tool performance (although we recognise that this can be limited by having too few events in some subgroups).
Second, ignoring competing mortality risks led to overprediction of risk by QRISK3 and QFracture-2012. As fractures are a rare cause of immediate death (unlike CVD where a fair proportion of CVD events are sudden death), the impact of this was much greater for QFracture-2012 than for QRISK3, with QFracture-2012 additionally predicting risk in people aged up to 99 years compared with up to 84 years for QRISK3. For QRISK3, overprediction mostly (but not entirely) happened above the NICE recommended 10-year 10% risk threshold (although overprediction would have had greater impact for the long period when NICE and others recommended a 20% threshold). For QFracture-2012, thresholds are less well defined, but overprediction was very large in older people (i.e. people aged 85–99 years) and people with high levels of comorbidity at the highest fracture risk (despite QFracture-2012 in general underpredicting).
Our new competing risk models, which are essentially adaptations of QRISK3 and QFracture-2012, were better calibrated than QRISK3 and QFracture. For the moment, clinicians should consider wider life expectancy related to other conditions when discussing long-term cardiovascular and fracture primary preventative treatment. However, when new competing risk models are externally validated (a requirement before clinical use), and assuming that the performance of the new models is good enough, they should be used to inform clinical practice. However, irrespective of which prediction model is used, clinicians need to use judgement in making treatment recommendations based on discussion and shared decision-making with the patient, including consideration of individual preferences, life expectancy and comorbidity. 166
Third, we found serious problems with the calibration of QFracture-2012, but this has since been replaced by a new version which (like this study) ascertains fractures using both GP and hospital data. 167 The observed under-ascertainment of QFracture-2012 in this study is therefore likely to be less for the current version of QFracture but we would expect competing mortality to remain a major problem.
Of note, the FRAX fracture risk prediction tool is also recommended by NICE and does account for competing mortality risk, but its calibration has not been well studied in external validation. 22,91 The same Israeli study used to externally validate QFracture-2012 also examined FRAX, finding similar levels of underprediction as was found for QFracture-2012 (although the analysis did not account for competing mortality risk). 92 However, FRAX risk prediction in Dagan et al. ’s92 study was limited to broad categorisation of FRAX-estimated risk, reflecting the failure of the FRAX developers to make the prediction algorithm publicly available and, therefore, replicable. Although FRAX does account for competing mortality risk, it remains uncertain how well calibrated a tool it is in the UK (or any other) context. Publication of the full algorithm would allow direct and fair comparison with other tools to identify the optimal tool for different contexts;92 however, for now, we do not think it can be recommended for use either. 21
Fourth, we have demonstrated that the relative survival models derived from the clinical data used in the risk prediction modelling provide an effective method of adjusting for competing risk of non-cause-specific death that modellers can easily apply in decision-analytic CEAs. Although the adjustment made relatively little difference to the estimated cost-effectiveness of preventative interventions in the examples we explored, we have shown that it could potentially be important in cases where benefits, harms and costs are more finely balanced. Therefore, we recommend that modellers consider competing risks when designing analyses of preventative treatments.
Finally, present-day policy-makers work under the assumption that, except inasmuch as they are associated with specific adverse events, people consider the act of taking oral treatments benign. Our stated-preference surveys, in conjunction with emerging evidence from elsewhere,47,48,103 show clearly that this is untrue. When incorporated in CEA, we see than DTD not only exists, but it also has the potential to alter the balance of benefits and harms for many or all people for whom preventative treatments might otherwise be indicated.
Nevertheless, as argued in Chapter 5, we do not recommend that population-level average DTD is incorporated in base-case CEAs, and this is because we have found evidence that there is clear heterogeneity in elicited DTD, with a non-trivial proportion of people unbothered by the prospect of taking pills. We believe that it would be invidious to deny such people access to treatment by assuming that they share the average person’s aversions. Therefore, we recommend that population-level decision-makers review scenarios with and without DTD and highlight the possible effects of DTD, enabling prescribers to engage in shared decision-making at an individual level that gives appropriate weight to each person’s preferences for avoiding the treatment’s process characteristics. A practical implication for prescribers is to recognise that patients with strong preferences against medicine-taking may well not realise long-term net benefit in terms of quality of life, which supports an approach to decision-making that focuses on concordance (where necessary, agreeing to disagree), rather than compliance or adherence (where there is more scope for conflict as clinicians try to persuade patients to accept the clinical recommendation). We have argued that this approach fits well with NICE’s guideline development methods, which encourage the explicit identification of ‘preference-sensitive decision-points’, taking the practicalities of possible treatments into account. 125
Implications of findings for research
There are several areas where further research would be beneficial:
-
In this study, the observed impact of competing mortality risks varied between CVD and fracture prediction tools, and it would be useful to explore the implications of accounting for competing mortality for prediction tools in other clinical contexts (although there is a strong case that all risk prediction tools intended for use in older people and people with multimorbidity should account for competing risks by default, or clearly justify why not).
-
A feature of both QRISK3 and QFracture-2012 is that they are ‘omnibus’ models predicting risk across a very wide range of ages and morbidities. It is unclear if this is a sensible approach, or whether or not subgroup models developed specifically for older adults or (in the case of CVD) people with diabetes would be a better strategy. A major disadvantage of subgroup models is that an individual might belong to multiple subgroups, for example being an older adult with diabetes and CKD; however, for diabetes at least, QRISK3 appears very poorly calibrated in external validation using diabetes registry data. 60,76 One reason for the difference between validation in registry data and the validation carried out here is that the inclusion criteria for QRISK3 derivation and validation effectively removes a large number of people with diabetes from the data set because of prior statin exposure. This has three implications for research. First, more attention needs to be paid to exactly who the derivation and validation populations are, as differences between studies will sometimes be explained by this. Second, primary prevention treatments are often very widely prescribed and so models (like QRISK3, but unlike QFracture-2012) that exclude people with prior drug exposure become increasingly unrepresentative. For blood pressure, QRISK3 fits both current SBP and a term for whether or not the person is on antihypertensive treatment, and this may be a better strategy for statin prescribing as well. Third, although it is likely that subgroup models will perform somewhat better than omnibus models, subgroup models may not perform that much better (if at all) to be worth the additional cost of developing a myriad of models for different circumstances, and relative performance is a researchable question.
-
In the fracture analysis, both QFracture-2012 and CFracture were poorly calibrated in people aged 85–99 years. In this particular case, that may be because fracture risk in younger people is more driven by characteristics associated with osteoporosis, whereas in older people it may be more driven by characteristics associated with falls risk that are not well recorded in routine data (e.g. balance, sarcopenia and frailty). More broadly, however, most risk prediction excludes the very old, and there is a need for research to examine risk prediction in the very old who are the fastest growing segment of the UK population. In this context, established risk factors may be less relevant because, for example, high cholesterol is clearly not associated with premature vascular disease in 95-year-olds without vascular disease, and where multimorbidity means that tools that predict multiple events would be ideal to inform treatment choice in the face of concerns about polypharmacy and treatment burden. 5,166 Research is needed to explore such issues, and the value of risk factor treatment in older people with comorbidity and co-prescribing who are routinely excluded from trials could be usefully clarified with targeted randomised controlled trials. 3
-
A feature of the data sets used to derive and validate QRISK3 and QFracture-2012 are that they have more limited follow-up than is generally appreciated (typically a median of 5–7 years’ follow-up). This study has examined the impact of competing risk, but other loss to follow-up due to practice deregistration is likely to create overprediction in at least some population subsets (e.g. people who deregister to move to sheltered housing or care homes are very likely to have different outcomes to those who do not). External validation in large geographical populations with less loss to follow-up (e.g. the SAIL Databank in Wales) would be valuable, as would larger-scale data federation to derive and validate new risk prediction tools for comparison with QRISK3 and other prediction models.
-
The tools examined here and most other risk prediction tools use only clinical data. In principle, polygenic risk scores using genetic data combined with key environmental exposures, like smoking, could identify people with high lifetime risk earlier than any clinical risk prediction tool. More research is needed to understand the value of such additional predictors; however, in some cases, risk prediction may be superseded or complemented by better diagnostics. In CVD, for example, lifetime risk prediction is an attempt to deal with the problem that younger people at high risk of premature CVD often do not have 10-year CVD risk that exceeds current threshold for treatment. Lowering 10-year risk thresholds might mitigate this problem, but lead to very large proportions of people being recommended for lifelong medication that most will not benefit from (and, in any case, many people will not wish to take lifelong treatment based on risk prediction alone). An alternative strategy is to screen people for asymptomatic coronary artery disease using computerised tomography coronary angiography, and to then treat the people with disease rather than people at risk of the disease. For CVD at least, early diagnosis and treatment may be an attractive strategy, given the problems of risk prediction over long periods of time. This strategy of early diagnosis and treatment has been shown to be effective in people with chest pain,168 but its value in a true primary prevention population is uncertain and needs to be established. 105,106
-
The results from the BWS method to estimate DTD should be anchored to a credible absolute estimate to generate plausible values on a utility scale that could be used in CEA. There was a TTO embedded within our BWS exercise that could perform this function, and exploring this TTO to derive results that are more directly comparable with the dedicated TTO exercise is a priority for future work.
-
We have suggested ways in which DTD can be used to augment CEA in this project. However, there is no consensus about which values are most appropriate (e.g. general population valuations vs. valuations by people with experience of the interventions) and how values should be applied in analysis (e.g. for how long should we assume effects last) and deployed in decision-making (e.g. should population-level decision-makers recommend technologies that are rendered net harmful if population-level average DTD applies?). Few of these issues are amenable to empirical research, but we would like to see consensus-building work to establish best practice.
-
Although we have substantially improved the model NICE used in CG181 to assess statins for the primary prevention of CVD [e.g. by estimating transition probabilities using the same UK data set (CPRD) used in the risk prediction modelling], it was not within our remit to update every input, and there are some respects in which it could usefully be further modified. In particular, we think it would be valuable to (1) explore stratification according to specific co-existing long-term conditions, (2) account for likely adherence to statins in practice and (3) update secondary transitions reflecting the treated history of CVD in people experiencing events.
-
Similarly, we have noted several areas in which there is room to improve future CEAs of bisphosphonates for the primary prevention of osteoporotic fragility fracture. As a priority, researchers should explore alternatives to QFracture-2012 to predict fracture risk, which, as shown in Chapter 4, suffers from under-ascertainment of events. We argue in Chapter 7 that inaccuracy of risk prediction tools does not, in itself, invalidate the results of the bisphosphonates CEA; however, it would clearly be desirable to integrate a tool with better predictive performance into such analyses. We also note that the simulated population on which the TA464 model bases its calculations is unrealistic because, when generating virtual people, the model samples each characteristic independently. Introducing evidence on correlations between risk factors would produce a more realistic cohort and may minimise the problem we (and the TA464 modellers) encountered where outputs seem unstable for people at the highest levels of risk.
Acknowledgements
Our patient and public representatives Alison Allen and Graham Bell made an indelible contribution to this project. We were saddened to hear of Graham Bell’s death in 2020.
Garima Dalal (The University of Manchester) contributed to analysis of the BWS data reported in Chapter 5.
At the University of Edinburgh, Megan McMinn contributed to the analysis of fracture data for Chapter 4, Jacques Fleuriot helped with implementation of QRISK-Lifetime C code and Chima Eke helped with implementation of QFracture-2012 C code.
Martin Harker developed the original statins cost-effectiveness model for CG181 at the National Clinical Guideline Centre. In addition, we are very grateful to David Wonderling, of the successor body, the National Guideline Centre, for providing us with an executable copy of the model to aid our replication.
We are grateful to all the survey respondents who gave us their opinions for Chapter 5.
Study Advisory Group
We would like to thank the following Study Advisory Group members for their invaluable advice and contribution to the project: Liam Smeeth (chairperson, London School of Hygiene and Tropical Medicine), Alison Allen (patient and public involvement representative), Graham Bell (patient and public involvement representative), Gerry Richardson (University of York) and Nichole Taske (NICE; for whom Joshua Pink also deputised).
Ethics
The literature elements of the study did not require ethics review. The prediction modelling used CPRD data and the protocol was approved by the CPRD Independent Scientific Advisory Committee (reference number 16_248). The DTD elicitation study was reviewed by the Health Research Authority (Integrated Research Application System project ID 220,492) and granted ethics approval (Research Ethics Committee reference 17/NW/0124).
Contributions of authors
Bruce Guthrie (https://orcid.org/0000-0003-4191-4880) (Professor of General Practice, The University of Edinburgh) was the overall chief investigator, contributed to the conceptualisation, conduct and interpretation of the study, co-ordinated the writing of the report, led the writing of Chapters 1–4 and 8, and wrote elements of Chapters 5–7.
Gabriel Rogers (https://orcid.org/0000-0001-9339-7374) (Senior Research Fellow in Health Economics, The University of Manchester) contributed to the conduct and interpretation of the study, led the writing of Chapters 6 and 7, co-wrote Chapter 4, and provided comment on and editing of the report.
Shona Livingstone (https://orcid.org/0000-0002-4621-8713) (Statistician, University of Dundee) was the employed researcher in Dundee, contributed to the conduct and interpretation of the study, and provided comment on and editing of the report.
Daniel Morales (https://orcid.org/0000-0002-0063-8069) (Wellcome Trust Clinical Research Career Development Fellow, University of Dundee) contributed to the conceptualisation, conduct and interpretation of the study, and provided comment on and editing of the report.
Peter Donnan (https://orcid.org/0000-0001-7828-0610) (Professor of Epidemiology and Biostatistics, University of Dundee) was co-chief investigator, contributed to the conceptualisation, conduct and interpretation of the study, and provided comment on and editing of the report.
Sarah Davis (https://orcid.org/0000-0002-6609-4287) (Senior Lecturer in Health Economics, The University of Sheffield) contributed to the conceptualisation, conduct and interpretation of the study, co-wrote Chapter 7, and provided comment on and editing of the report.
Ji Hee Youn (https://orcid.org/0000-0003-1382-495X) (Research Associate in Health Economics at The University of Manchester) contributed to the conduct and interpretation of the study, co-wrote Chapter 5, and provided comment on and editing of the report.
Rob Hainsworth (https://orcid.org/0000-0002-3475-800X) (Research Associate in Health Economics, The University of Manchester) contributed to the conduct and interpretation of the study, co-wrote Chapter 6, and provided comment on and editing of the report.
Alexander Thompson (https://orcid.org/0000-0003-4930-5107) (Senior Research Fellow in Health Economics, The University of Manchester) contributed to the conceptualisation, conduct and interpretation of the study, led the writing of Chapter 5, co-wrote Chapter 6, and provided comment on and editing of the report.
Katherine Payne (https://orcid.org/0000-0002-3938-4350) (Professor of Health Economics, The University of Manchester) led the health economics work, contributed to the conceptualisation, conduct and interpretation of the study, co-wrote Chapter 4, and provided comment on and editing of the report.
Publications
Livingstone S, Morales DR, Donnan PT, Payne K, Thompson AJ, Youn JH, et al. Effect of competing mortality risks on predictive performance of the QRISK3 cardiovascular risk prediction tool in older people and those with comorbidity: external validation population cohort study. Lancet Healthy Longev 2021;2:e352–61. https://doi.org/10.1016/S2666-7568(21)00088-X
Livingstone SJ, Guthrie B, Donnan PT, Thompson A, Morales DR. Predictive performance of a competing risk cardiovascular prediction tool CRISK compared to QRISK3 in older people and those with comorbidity: population cohort study. BMC Med 2022;20:152.
Livingstone S, Guthrie B, McMinn M, Eke C, Donnan P, Morales D. Predictive performance of a competing risk fracture prediction tool CFracture compared to QFracture in older people and those with comorbidity: population cohort study. Lancet Healthy Longev 2022;4:e43–e53.
Livingstone S, Morales DR, McMinn M, Eke C, Donnan PT, Guthrie B. Impact of competing mortality risks on predictive performance of the QFracture risk prediction tool for major osteoporotic fracture and hip fracture: external validation cohort study in a UK primary care population. BMJ Med 2022;1:e000316. https://doi.org/10.1136/bmjmed-2022-000316
Livingstone S, Morales DR, Fleuriot J, Donnan PT, Guthrie B. External validation of the QLifetime cardiovascular risk prediction tool: population cohort study. BMC Cardiovasc Disord 2023;23:194. https://doi.org/10.1186/s12872-023-03209-8
Data-sharing statement
The data used in the risk prediction modelling are controlled by the CPRD, and under the data licence granted the authors are not allowed to share the data. Researchers can apply to CPRD directly for access to the raw data. For the health economics modelling, the parameters of the models are all fully documented in this final report and the documents it cites, and there are no additional data to share. If you have any further queries, please contact the corresponding author.
Patient data
This work uses data provided by patients and collected by the NHS as part of their care and support. Using patient data is vital to improve health and care for everyone. There is huge potential to make better use of information from people’s patient records, to understand more about disease, develop new treatments, monitor safety and plan NHS services. Patient data should be kept safe and secure, to protect everyone’s privacy, and it is important that there are safeguards to make sure that they are stored and used responsibly. Everyone should be able to find out about how patient data are used. #datasaveslives You can find out more about the background to this citation here: https://understandingpatientdata.org.uk/data-citation.
Disclaimers
This report presents independent research funded by the National Institute for Health and Care Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, the HSDR programme or the Department of Health and Social Care. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, the HSDR programme or the Department of Health and Social Care.
References
- Guthrie B, Payne K, Alderson P, McMurdo ME, Mercer SW. Adapting clinical guidelines to take account of multimorbidity. BMJ 2012;345. https://doi.org/10.1136/bmj.e6341.
- Guthrie B, Thompson A, Dumbreck S, Flynn A, Alderson P, Nairn M, et al. Better guidelines for better care: accounting for multimorbidity in clinical guidelines structured examination of exemplar guidelines and health economic modelling. Health Serv Deliv Res 2017;5.
- He J, Morales DR, Guthrie B. Exclusion rates in randomized controlled trials of treatments for physical conditions: a systematic review. Trials 2020;21. https://doi.org/10.1186/s13063-020-4139-0.
- Barnett K, Mercer SW, Norbury M, Watt G, Wyke S, Guthrie B. Epidemiology of multimorbidity and implications for health care, research, and medical education: a cross-sectional study. Lancet 2012;380:37-43. https://doi.org/10.1016/S0140-6736(12)60240-2.
- Guthrie B, Makubate B, Hernandez-Santiago V, Dreischulte T. The rising tide of polypharmacy and drug–drug interactions: population database analysis 1995–2010. BMC Med 2015;13. https://doi.org/10.1186/s12916-015-0322-7.
- Dumbreck S, Flynn A, Nairn M, Wilson M, Treweek S, Mercer SW, et al. Drug–disease and drug–drug interactions: systematic examination of recommendations in 12 UK national clinical guidelines. BMJ 2015;350. https://doi.org/10.1136/bmj.h949.
- May C, Montori VM, Mair FS. We need minimally disruptive medicine. BMJ 2009;339. https://doi.org/10.1136/bmj.b2803.
- Hughes L, McMurdo MET, Guthrie B. Guidelines for people not for diseases: the challenges of applying UK clinical guidelines to people with multimorbidity. Age Ageing 2013;42:62-9.
- He J, Guthrie B, Morales DR. A Systematic Review of the Applicability of Clinical Trial Evidence to Real-World Patients 2016. www.crd.york.ac.uk/PROSPERO/display_record.asp?ID=CRD42016042282 (accessed 16 November 2022).
- National Institute for Health and Care Excellence (NICE) . Clinical Guideline 181: Lipid Modification: Cardiovascular Risk Assessment and the Modification of Blood Lipids for the Primary and Secondary Prevention of Cardiovascular Disease 2014. https://www.nice.org.uk/guidance/cg181/evidence/lipid-modification-update-full-guideline-pdf-243786637 (accessed 16 November 2022).
- National Institute for Health and Care Excellence (NICE) . Social Value Judgements: Principles for the Development of NICE Guidance 2008.
- National Institute for Health and Care Excellence (NICE) . Bisphosphonates for Treating Osteoporosis n.d. https://www.nice.org.uk/guidance/ta464 (accessed 24 November 2022).
- National Institute for Health and Care Excellence . Surveillance Proposal Consultation Document: Cardiovascular Disease: Risk Assessment and Reduction, Including Lipid Modification NICE Guideline CG181–4-Year Surveillance Review n.d. https://www.nice.org.uk/guidance/cg181/evidence/lipid-modification-update-full-guideline-pdf-243786637 (accessed 16 November 2022).
- Collins GS, Altman DG. An independent external validation and evaluation of QRISK cardiovascular risk prediction: a prospective open cohort study. BMJ 2009;339. https://doi.org/10.1136/bmj.b2584.
- Collins GS, Altman DG. An independent and external validation of QRISK2 cardiovascular disease risk score: a prospective open cohort study. BMJ 2010;340. https://doi.org/10.1136/bmj.c2442.
- Collins GS, Altman DG. Predicting the 10 year risk of cardiovascular disease in the United Kingdom: independent and external validation of an updated version of QRISK2. BMJ 2012;344. https://doi.org/10.1136/bmj.e4181.
- Hippisley-Cox J, Coupland C. Predicting risk of osteoporotic fracture in men and women in England and Wales: prospective derivation and validation of QFracture scores. BMJ 2009;339. https://doi.org/10.1136/bmj.b4229.
- Collins GS, Mallett S, Altman DG. Predicting risk of osteoporotic and hip fracture in the United Kingdom: prospective independent and external validation of QFracture scores. BMJ 2011;342. https://doi.org/10.1136/bmj.d3651.
- Hippisley-Cox J, Coupland C, Brindle P. The performance of seven QPrediction risk scores in an independent external sample of patients from general practice: a validation study. BMJ Open 2014;4. https://doi.org/10.1136/bmjopen-2014-005809.
- Collins GS, Reitsma JB, Altman DG, Moons KG. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. BMJ 2015;350. https://doi.org/10.1136/bmj.g7594.
- Collins GS, de Groot JA, Dutton S, Omar O, Shanyinde M, Tajar A, et al. External validation of multivariable prediction models: a systematic review of methodological conduct and reporting. BMC Med Res Methodol 2014;14. https://doi.org/10.1186/1471-2288-14-40.
- Kanis JA, Oden A, Johnell O, Johansson H, De Laet C, Brown J, et al. The use of clinical risk factors enhances the performance of BMD in the prediction of hip and osteoporotic fractures in men and women. Osteoporos Int 2007;18:1033-46. https://doi.org/10.1007/s00198-007-0343-y.
- National Institute for Health and Care Excellence (NICE) . Bisphosphonates for Treating Osteoporosis 2019.
- Berry JD, Dyer A, Cai X, Garside DB, Ning H, Thomas A, et al. Lifetime risks of cardiovascular disease. New Engl J Med 2012;366:321-9. https://doi.org/10.1056/NEJMoa1012848.
- Hippisley-Cox J, Coupland C, Brindle P. Development and validation of QRISK3 risk prediction algorithms to estimate future risk of cardiovascular disease: prospective cohort study. BMJ 2017;357. https://doi.org/10.1136/bmj.j2099.
- Hippisley-Cox J, Coupland C. Derivation and validation of updated QFracture algorithm to predict risk of osteoporotic fracture in primary care in the United Kingdom: prospective open cohort study. BMJ 2012;344. https://doi.org/10.1136/bmj.e3427.
- Hippisley-Cox J, Coupland C, Robson J, Brindle P. Derivation, validation, and evaluation of a new QRISK model to estimate lifetime risk of cardiovascular disease: cohort study using QResearch database. BMJ 2010;341. https://doi.org/10.1136/bmj.c6624.
- Kanis JA, Johnell O, Oden A, Johansson H, McCloskey E. FRAX™ and the assessment of fracture probability in men and women from the UK. Osteoporos Int 2008;19:385-97. https://doi.org/10.1007/s00198-007-0543-5.
- Koller MT, Raatz H, Steyerberg EW, Wolbers M. Competing risks and the clinical community: irrelevance or ignorance?. Stat Med 2012;31:1089-97. https://doi.org/10.1002/sim.4384.
- Wolkewitz M, Cooper BS, Bonten MJ, Barnett AG, Schumacher M. Interpreting and comparing risks in the presence of competing events. BMJ 2014;349. https://doi.org/10.1136/bmj.g5060.
- Wolbers M, Koller MT, Stel VS, Schaer B, Jager KJ, Leffondré K, et al. Competing risks analyses: objectives and approaches. Eur Heart J 2014;35:2936-41. https://doi.org/10.1093/eurheartj/ehu131.
- Pintilie M. Analysing and interpreting competing risk data. Stat Med 2007;26:1360-7. https://doi.org/10.1002/sim.2655.
- Maki E. Power and sample size considerations in clinical trials with competing risk endpoints. Pharm Stat 2006;5:159-71. https://doi.org/10.1002/pst.200.
- Wolbers M, Koller MT, Witteman JC, Steyerberg EW. Prognostic models with competing risks: methods and application to coronary risk prediction. Epidemiology 2009;20:555-61. https://doi.org/10.1097/EDE.0b013e3181a39056.
- van Staa T-P, Gulliford M, Ng ESW, Goldacre B, Smeeth L. Prediction of cardiovascular risk using Framingham, ASSIGN and QRISK2: how well do they predict individual rather than population risk?. PLOS ONE 2014;9. https://doi.org/10.1371/journal.pone.0106455.
- Ferket BS, van Kempen BJ, Heeringa J, Spronk S, Fleischmann KE, Nijhuis RL, et al. Personalized prediction of lifetime benefits with statin therapy for asymptomatic individuals: a modeling study. PLOS Med 2012;9. https://doi.org/10.1371/journal.pmed.1001361.
- House of Commons Health Committee . Managing the Care of People With Long-Term Conditions 2014.
- Rawlins M. Six Hopes and Dreams n.d.
- Sculpher M. Subgroups and heterogeneity in cost-effectiveness analysis. PharmacoEconomics 2008;26:799-806.
- Thompson A, Guthrie B, Payne K. Do pills have no ills? Capturing the impact of direct treatment disutility. PharmacoEconomics 2016;34:333-6. https://doi.org/10.1007/s40273-015-0357-9.
- Thompson A, Guthrie B, Payne K. Using the payoff time in decision-analytic models: a case study for using statins in primary prevention. Med Decis Making 2017;37:759-69. https://doi.org/10.1177/0272989X17700846.
- Espinoza MA, Manca A, Claxton K, Sculpher MJ. The value of heterogeneity for cost-effectiveness subgroup analysis: conceptual framework and application. Med Decis Making 2014;34:951-64. https://doi.org/10.1177/0272989X14538705.
- Howard JP, Wood FA, Finegold JA, Nowbar AN, Thompson DM, Arnold AD, et al. Side effect patterns in a crossover trial of statin, placebo, and no treatment. J Am Coll Cardiol 2021;78:1210-22.
- Lazar LD, Pletcher MJ, Coxson PG, Bibbins-Domingo K, Goldman L. Cost-effectiveness of statin therapy for primary prevention in a low-cost statin era. Circulation 2011;124:146-53. https://doi.org/10.1161/circulationaha.110.986349.
- Vijan S, Sussman JB, Yudkin JS, Hayward RA. Effect of patients’ risks and preferences on health gains with plasma glucose level lowering in type 2 diabetes mellitus. JAMA Intern Med 2014;174:1227-34. https://doi.org/10.1001/jamainternmed.2014.2894.
- Timbie JW, Hayward RA, Vijan S. Variation in the net benefit of aggressive cardiovascular risk factor control across the US population of patients with diabetes mellitus. Arch Intern Med 2010;170:1037-44. https://doi.org/10.1001/archinternmed.2010.150.
- Fontana M, Asaria P, Moraldo M, Finegold J, Hassanally K, Manisty CH, et al. Patient-accessible tool for shared decision making in cardiovascular primary prevention: balancing longevity benefits against medication disutility. Circulation 2014;129:2539-46. https://doi.org/10.1161/circulationaha.113.007595.
- Hutchins R, Pignone MP, Sheridan SL, Viera AJ. Quantifying the utility of taking pills for preventing adverse health outcomes: a cross-sectional survey. BMJ Open 2015;5. https://doi.org/10.1136/bmjopen-2014-006505.
- Livingstone S, Morales DR, Fleuriot J, Donnan PT, Guthrie B. External validation of the QLifetime cardiovascular risk prediction tool: population cohort study. BMC Cardiovasc Disord 2023;23. https://doi.org:10.1186/s12872-023-03209-8.
- Livingstone S, Guthrie B, McMinn M, Eke C, Donnan P, Morales D. Predictive performance of a competing risk fracture prediction tool CFracture compared to QFracture in older people and those with comorbidity: population cohort study. Lancet Healthy Longev 2022;4:e43-53.
- Livingstone S, Morales DR, McMinn M, Eke C, Donnan PT, Guthrie B. Impact of competing mortality risks on predictive performance of the QFracture risk prediction tool for major osteoporotic fracture and hip fracture: external validation cohort study in a UK primary care population. BMJ Med 2022;1. https://doi.org/10.1136/bmjmed-2022-000316.
- Dreischulte T, Donnan P, Grant A, Hapca A, McCowan C, Guthrie B. Safer P prescribing – a trial of education, informatics, and financial incentives. N Engl J Med 2016;374:1053-64.
- Stone NJ, Robinson JG, Lichtenstein AH, Merz CNB, Blum CB, Eckel RH, et al. 2013 ACC/AHA guideline on the treatment of blood cholesterol to reduce atherosclerotic cardiovascular risk in adults. Circulation 2014;129:S1-45. https://doi.org/10.1161/01.cir.0000437738.63853.7a.
- Steyerberg E. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. New York, NY: Springer; 2009.
- Royston P, Altman DG. External validation of a Cox prognostic model: principles and methods. BMC Med Res Methodol 2013;13. https://doi.org/10.1186/1471-2288-13-33.
- Echouffo-Tcheugui JB, Kengne AP. Comparative performance of diabetes-specific and general population-based cardiovascular risk assessment models in people with diabetes mellitus. Diabetes Metab 2013;39:389-96. https://doi.org/10.1016/j.diabet.2013.07.002.
- Chowdhury MZI, Yeasmin F, Rabi DM, Ronksley PE, Turin TC. Prognostic tools for cardiovascular disease in patients with type 2 diabetes: a systematic review and meta-analysis of C-statistics. J Diabetes Complications 2019;33:98-111.
- Mukamal KJ, Kizer JR, Djoussé L, Ix JH, Zieman S, Siscovick DS, et al. Prediction and classification of cardiovascular disease risk in older adults with diabetes. Diabetologia 2013;56:275-83. https://doi.org/10.1007/s00125-012-2772-1.
- Vistisen D, Andersen GS, Hansen CS, Hulman A, Henriksen JE, Bech-Nielsen H, et al. Prediction of first cardiovascular disease event in type 1 diabetes mellitus: the Steno Type 1 Risk Engine. Circulation 2016;133:1058-66. https://doi.org/10.1161/circulationaha.115.018844.
- McGurnaghan SJ, McKeigue PM, Read SH, Franzen S, Svensson AM, Colombo M, et al. Development and validation of a cardiovascular risk prediction model in type 1 diabetes. Diabetologia 2021;64:2001-11. https://doi.org/10.1007/s00125-021-05478-4.
- Weiner DE, Tighiouart H, Elsayed EF, Griffith JL, Salem DN, Levey AS, et al. The Framingham predictive instrument in chronic kidney disease. J Am Coll Cardiol 2007;50:217-24.
- Ballew SH, Matsushita K. Cardiovascular risk prediction in CKD. Semin Nephrol 2018;38:208-16. https://doi.org/10.1016/j.semnephrol.2018.02.002.
- Matsushita K, Ballew SH, Coresh J. Cardiovascular risk prediction in people with chronic kidney disease. Curr Opin Nephrol Hypertens 2016;25:518-23. https://doi.org/10.1097/MNH.0000000000000265.
- Matsushita K, Coresh J, Sang Y, Chalmers J, Fox C, Guallar E, et al. Estimated glomerular filtration rate and albuminuria for prediction of cardiovascular outcomes: a collaborative meta-analysis of individual participant data. Lancet Diabetes Endocrinol 2015;3:514-25. https://doi.org/10.1016/S2213-8587(15)00040-6.
- Khan NF, Perera R, Harper S, Rose PW. Adaptation and validation of the Charlson Index for Read/OXMIS coded databases. BMC Fam Pract 2010;11. https://doi.org/10.1186/1471-2296-11-1.
- Herrett E, Gallagher AM, Bhaskaran K, Forbes H, Mathur R, van Staa T, et al. Data resource profile: Clinical Practice Research Datalink (CPRD). Int J Epidemiol 2015;44:827-36. https://doi.org/10.1093/ije/dyv098.
- Livingstone S, Morales DR, Donnan PT, Payne K, Thompson AJ, Youn JH, et al. Effect of competing mortality risks on predictive performance of the QRISK3 cardiovascular risk prediction tool in older people and those with comorbidity: external validation population cohort study. Lancet Healthy Longev 2021;2:e352-61. https://doi.org/10.1016/S2666-7568(21)00088-X.
- van Buuren S, Groothuis-Oudshoorn K. mice: multivariate imputation by chained equations in R. J Statist Software 2011;45. https://doi.org/10.18637/jss.v045.i03.
- Rubin D. Multiple Imputation for Nonresponse in Surveys. New York, NY: John Wiley and Sons; 1987.
- Royston P, Sauerbrei W. A new measure of prognostic separation in survival data. Stat Med 2004;23:723-48. https://doi.org/10.1002/sim.1621.
- Altman DG, Vergouwe Y, Royston P, Moons KG. Prognosis and prognostic research: validating a prognostic model. BMJ 2009;338. https://doi.org/10.1136/bmj.b605.
- Cook NR. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation 2007;115:928-35.
- Nguyen QD, Odden MC, Peralta CA, Kim DH. Predicting risk of atherosclerotic cardiovascular disease using pooled cohort equations in older adults with frailty, multimorbidity, and competing risks. J Am Heart Assoc 2020;9. https://doi.org/10.1161/jaha.119.016003.
- Koller MT, Leening MJ, Wolbers M, Steyerberg EW, Hunink MG, Schoop R, et al. Development and validation of a coronary risk prediction model for older U.S. and European persons in the Cardiovascular Health Study and the Rotterdam Study. Ann Intern Med 2012;157:389-97. https://doi.org/10.7326/0003-4819-157-6-201209180-00002.
- Melberg T, Nygård OK, Kuiper KK, Nordrehaug JE. Competing risk analysis of events 10 years after revascularization. Scand Cardiovasc J 2010;44:279-88. https://doi.org/10.3109/14017431003698531.
- Read SH, van Diepen M, Colhoun HM, Halbesma N, Lindsay RS, McKnight JA, et al. Performance of cardiovascular disease risk scores in people diagnosed with type 2 diabetes: external validation using data from the National Scottish Diabetes Register. Diabetes Care 2018;41:2010-8. https://doi.org/10.2337/dc18-0578.
- Cooper H, Wells S, Mehta S. Are competing-risk models superior to standard Cox models for predicting cardiovascular risk in older adults? Analysis of a whole-of-country primary prevention cohort aged ≥ 65 years. Int J Epidemiol 2021;54:604-14. https://doi.org/10.1093/ije/dyab116.
- Brotons C, Calvo-Bonacho E, Moral I, Puig M, Garcia-Margallo MT, Cortés-Arcas MV, et al. Comparison of application of different methods to estimate lifetime cardiovascular risk. Eur J Prev Cardiol 2016;23:564-71. https://doi.org/10.1177/2047487315579616.
- JBS3 Board . Joint British Societies’ consensus recommendations for the prevention of cardiovascular disease (JBS3). Heart 2014;100:ii1-67. https://doi.org/10.1136/heartjnl-2014-305693.
- Goff DC, Lloyd-Jones DM, Bennett G, Coady S, D’Agostino RB, Gibbons R, et al. 2013 ACC/AHA guideline on the assessment of cardiovascular risk. Circulation 2014;129:S49-73. https://doi.org/10.1161/01.cir.0000437741.48606.98.
- ClinRisk . Welcome to the QRISK®-Lifetime Cardiovascular Risk Calculator n.d. www.qrisk.org/lifetime/ (accessed 11 December 2021).
- NHS Choices . What’s Your Heart Age? NHS Health Check n.d. www.nhs.uk/conditions/nhs-health-check/check-your-heart-age-tool/ (accessed 11 December 2021).
- Lloyd-Jones DM, Leip EP, Larson MG, D’Agostino RB, Beiser A, Wilson PW, et al. Prediction of lifetime risk for cardiovascular disease by risk factor burden at 50 years of age. Circulation 2006;113:791-8.
- Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: competing risks and multi-state models. Stat Med 2007;26:2389-430. https://doi.org/10.1002/sim.2712.
- Pylypchuk R, Wells S, Kerr A, Poppe K, Harwood M, Mehta S, et al. Cardiovascular risk prediction in type 2 diabetes before and after widespread screening: a derivation and validation study. Lancet 2021;397:2264-74.
- Hippisley-Cox J, Coupland C, Vinogradova Y, Robson J, Minhas R, Sheikh A, et al. Predicting cardiovascular risk in England and Wales: prospective derivation and validation of QRISK2. BMJ 2008;336:1475-82. https://doi.org/10.1136/bmj.39609.449676.25.
- National Institute for Health and Care Excellence (NICE) . Short Clinical Guideline CG146 – Osteoporosis: Fragility Fracture Risk 2012.
- National Osteoporosis Guideline Group . Osteoporosis: Clinical Guideline for Prevention and Treatment 2014.
- National Osteoporosis Guideline Group . Clinical Guideline for the Prevention and Treatment of Osteoporosis 2017.
- Cosman F, de Beur SJ, LeBoff MS, Lewiecki EM, Tanner B, Randall S, et al. Clinician’s guide to prevention and treatment of osteoporosis. Osteoporos Int 2014;25:2359-81. https://doi.org/10.1007/s00198-014-2794-2.
- Marques A, Ferreira RJ, Santos E, Loza E, Carmona L, da Silva JA. The accuracy of osteoporotic fracture risk prediction tools: a systematic review and meta-analysis. Ann Rheum Dis 2015;74:1958-67. https://doi.org/10.1136/annrheumdis-2015-207907.
- Dagan N, Cohen-Stavi C, Leventer-Roberts M, Balicer RD. External validation and comparison of three prediction tools for risk of osteoporotic fractures using data from population based electronic health records: retrospective cohort study. BMJ 2017;356. https://doi.org/10.1136/bmj.i6755.
- Damen JAAG, Hooft L, Schuit E, Debray TPA, Collins GS, Tzoulaki I, et al. Prediction models for cardiovascular disease risk in the general population: systematic review. BMJ 2016;353. https://doi.org/10.1136/bmj.i2416.
- QResearch . QFracture(c) 2016 Annual Update Information 2016. www.qresearch.org/media/qirhz3ti/qfracture-2016-annual-update-information.pdf (accessed 20 January 2023).
- Hippisley-Cox J, Coupland C. Validation of QFracture Compared with FRAX: Analysis Prepared for NICE 2011. Nottingham: University of Nottingham; 2011.
- Andersen PK, Geskus RB, de Witte T, Putter H. Competing risks in epidemiology: possibilities and pitfalls. Int J Epidemiol 2012;41:861-70. https://doi.org/10.1093/ije/dyr213.
- Leslie WD, Lix LM, Wu X. Manitoba Bone Density Program. Competing mortality and fracture risk assessment. Osteoporos Int 2013;24:681-8. https://doi.org/10.1007/s00198-012-2051-5.
- Kuan V, Denaxas S, Gonzalez-Izquierdo A, Direk K, Bhatti O, Husain S, et al. A chronological map of 308 physical and mental health conditions from 4 million individuals in the English National Health Service. Lancet Digit Health 2019;1:e63-77. https://doi.org/10.1016/S2589-7500(19)30012-3.
- Herrett E, Thomas SL, Schoonen WM, Smeeth L, Hall AJ. Validation and validity of diagnoses in the General Practice Research Database: a systematic review. Br J Clin Pharmacol 2010;69:4-14. https://doi.org/10.1111/j.1365-2125.2009.03537.x.
- Kanis JA, Oden A, Johansson H, McCloskey E. Pitfalls in the external validation of FRAX. Osteoporos Int 2012;23:423-31. https://doi.org/10.1007/s00198-011-1846-0.
- Bergh C, Wennergren D, Möller M, Brisby H. Fracture incidence in adults in relation to age and gender: a study of 27,169 fractures in the Swedish Fracture Register in a well-defined catchment area. PLOS ONE 2020;15. https://doi.org/10.1371/journal.pone.0244291.
- Brouwer WB, van Exel NJ, van den Berg B, van den Bos GA, Koopmanschap MA. Process utility from providing informal care: the benefit of caring. Health Policy 2005;74:85-99.
- Hutchins R, Viera AJ, Sheridan SL, Pignone MP. Quantifying the utility of taking pills for cardiovascular prevention. Circ Cardiovasc Qual Outcomes 2015;8:155-63. https://doi.org/10.1161/circoutcomes.114.001240.
- Augustovski FA, Cantor SB, Thach CT, Spann SJ. Aspirin for primary prevention of cardiovascular events. J Gen Intern Med 1998;13:824-35.
- British Heart Foundation . Can a CT Heart Scan Predict and Prevent Heart Attacks More Effectively Than a Risk Score? n.d. www.bhf.org.uk/research-projects/2019/04/24/12/39/computed-tomography-coronary-angiography-for-the-prevention-of-myocardial-infarction-the-scotheart-2 (accessed 11 December 2021).
- Muhlestein JB, Lappé DL, Lima JA, Rosen BD, May HT, Knight S, et al. Effect of screening for coronary artery disease using CT angiography on mortality and cardiac events in high-risk patients with diabetes: the FACTOR-64 randomized clinical trial. JAMA 2014;312:2234-43. https://doi.org/10.1001/jama.2014.15825.
- Pignone M, Earnshaw S, Tice JA, Pletcher MJ. Aspirin, statins, or both drugs for the primary prevention of coronary heart disease events in men: a cost-utility analysis. Ann Intern Med 2006;144:326-36.
- Pletcher MJ, Pignone M, Earnshaw S, McDade C, Phillips KA, Auer R, et al. Using the coronary artery calcium score to guide statin therapy: a cost-effectiveness analysis. Circ Cardiovasc Qual Outcomes 2014;7:276-84. https://doi.org/10.1161/circoutcomes.113.000799.
- Timbie JW, Hayward RA, Vijan S. Diminishing efficacy of combination therapy, response-heterogeneity, and treatment intolerance limit the attainability of tight risk factor control in patients with diabetes. Health Serv Res 2010;45:437-56. https://doi.org/10.1111/j.1475-6773.2009.01075.x.
- Torrance GW. Measurement of health state utilities for economic appraisal. J Health Econ 1986;5:1-30.
- Sackett DL, Torrance GW. The utility of different health states as perceived by the general public. J Chronic Dis 1978;31:697-704. https://doi.org/10.1016/0021-9681(78)90072-3.
- Flynn TN, Louviere JJ, Peters TJ, Coast J. Best–worst scaling: what it can do for health care research and how to do it. J Health Econ 2007;26:171-89.
- Flynn TN, Marley AAJ. Best–Worst Scaling: Theory and Methods. Cheltenham: Edward Elgar Publishing; 2014.
- Vass CM, Davison NJ, Vander Stichele G, Payne K. A picture is worth a thousand words: the role of survey training materials in stated-preference studies. Patient 2020;13:163-73. https://doi.org/10.1007/s40271-019-00391-w.
- Harrison M, Rigby D, Vass C, Flynn T, Louviere J, Payne K. Risk as an attribute in discrete choice experiments: a systematic review of the literature. Patient 2014;7:151-70. https://doi.org/10.1007/s40271-014-0048-1.
- Dolan P. Modeling valuations for EuroQol health states. Med Care 1997;35:1095-108. https://doi.org/10.1097/00005650-199711000-00002.
- National Institute for Health and Care Excellence (NICE) . Guide to the Methods of Technology Appraisal 2013 2013.
- National Institute for Health and Care Excellence . Lanadelumab for Preventing Recurrent Attacks of Hereditary Angioedema n.d. https://www.nice.org.uk/guidance/ta606 (accessed 23 November 2022).
- National Institute for Health and Care Excellence . Type 1 Diabetes in Adults: Diagnosis and Management n.d. https://web.archive.org/web/20220121052322/https://www.nice.org.uk/guidance/ta606 (accessed 23 November 2022).
- Jørgensen T, Worbes-Cerezo M, Lelli F, Lee XY, Bøgelund M, Alulis S. Preferences for route of administration, frequency and location – a time-trade-off study in the United Kingdom general population. Value Health 2017;20. https://doi.org/10.1016/j.jval.2017.08.1445.
- Matza LS, Stewart KD, Davies EW, Hellmund R, Polonsky WH, Kerr D. Health state utilities associated with glucose monitoring devices. Value Health 2017;20:507-11.
- Drummond M, Sculpher M, Torrance G, O’Brien B, Stoddart G. Methods for the Economic Evaluation of Health Care Programmes. Oxford: Oxford University Press; 2005.
- Pletcher MJ, Lazar L, Bibbins-Domingo K, Moran A, Rodondi N, Coxson P, et al. Comparing impact and cost-effectiveness of primary prevention strategies for lipid-lowering. Ann Intern Med 2009;150:243-54.
- Greving JP, Visseren FL, de Wit GA, Algra A. Statin treatment for primary prevention of vascular disease: whom to treat? Cost-effectiveness analysis. BMJ 2011;342. https://doi.org/10.1136/bmj.d1672.
- National Institute for Health and Care Excellence (NICE) . Developing NICE Guidelines: Supporting Shared Decision-Making 2018. http://www.nice.org.uk/process/pmg20/chapter/writing-the-guideline#supporting-shared-decision-making (accessed 23 November 2022).
- Office for National Statistics . National Life Tables: England 2017–19 2020.
- Odell E. nomisr: access Nomis UK labour market data. J Open Source Softw 2018;3. https://doi.org/10.21105/joss.00859.
- Ward S, Lloyd Jones M, Pandor A, Holmes M, Ara R, Ryan A, et al. A systematic review and economic evaluation of statins for the prevention of coronary events. Health Technol Assess 2007;11.
- Bamford J, Sandercock P, Dennis M, Warlow C, Jones L, McPherson K, et al. A prospective study of acute cerebrovascular disease in the community: the Oxfordshire Community Stroke Project 1981–86. 1. Methodology, demography and incident cases of first-ever stroke. J Neurol Neurosurg Psychiatry 1988;51:1373-80. https://doi.org/10.1136/jnnp.51.11.1373.
- Dennis MS, Bamford JM, Sandercock PA, Warlow CP. Incidence of transient ischemic attacks in Oxfordshire, England. Stroke 1989;20:333-9. https://doi.org/10.1161/01.str.20.3.333.
- Sutcliffe SJ, Fox KF, Wood DA, Sutcliffe A, Stock K, Wright M, et al. Incidence of coronary heart disease in a health authority in London: review of a community register. BMJ 2003;326.
- Kind P, Dolan P, Gudex C, Williams A. Variations in population health status: results from a United Kingdom national questionnaire survey. BMJ 1998;316:736-41.
- Mindell J, Biddulph J, Hirani V, Stamatakis E, Craig R, Nunn S, et al. Cohort profile: the health survey for England. Int J Epidemiol 2012;41:1585-93.
- Papaioannou D, Brazier J, Paisley S. NICE DSU Technical Support Document 9: The Identification, Review and Synthesis of Health State Utility Values from the Literature. London: NICE; 2010.
- Cai T, Abel L, Langford O, Monaghan G, Aronson JK, Stevens RJ, et al. Associations between statins and adverse events in primary prevention of cardiovascular disease: systematic review with pairwise, network, and dose–response meta-analyses. BMJ 2021;374. https://doi.org/10.1136/bmj.n1537.
- Herrett E, Williamson E, Brack K, Beaumont D, Perkins A, Thayne A, et al. Statin treatment and muscle symptoms: series of randomised, placebo controlled n-of-1 trials. BMJ 2021;372. https://doi.org/10.1136/bmj.n135.
- Herrett E, Williamson E, Brack K, Perkins A, Thayne A, Shakur-Still H, et al. The effect of statins on muscle symptoms in primary care: the StatinWISE series of 200 N-of-1 RCTs. Health Technol Assess 2021;25. https://doi.org/10.3310/hta25160.
- Ara R, Brazier JE. Using health state utility values from the general population to approximate baselines in decision analytic models when condition-specific data are not available. Value Health 2011;14:539-45.
- NHS Business Services Authority . Drug Tariff 2021.
- Xu XM, Vestesson E, Paley L, Desikan A, Wonderling D, Hoffman A, et al. The economic burden of stroke care in England, Wales and Northern Ireland: using a national stroke register to estimate and report patient-level health economic outcomes in stroke. Eur Stroke J 2018;3:82-91. https://doi.org/10.1177/2396987317746516.
- Danese MD, Gleeson M, Kutikova L, Griffiths RI, Azough A, Khunti K, et al. Estimating the economic burden of cardiovascular events in patients receiving lipid-modifying therapy in the UK. BMJ Open 2016;6. https://doi.org/10.1136/bmjopen-2016-011805.
- Andersen PK, Borch-Johnsen K, Deckert T, Green A, Hougaard P, Keiding N, et al. A Cox regression model for the relative mortality and its application to diabetes mellitus survival data. Biometrics 1985;41:921-32.
- McConnachie A, Walker A, Robertson M, Marchbank L, Peacock J, Packard CJ, et al. Longterm impact on healthcare resource utilization of statin treatment, and its cost effectiveness in the primary prevention of cardiovascular disease: a record linkage study. Eur Heart J 2014;35:290-8. https://doi.org/10.1093/eurheartj/eht232.
- Heller DJ, Coxson PG, Penko J, Pletcher MJ, Goldman L, Odden MC, et al. Evaluating the impact and cost-effectiveness of statin use guidelines for primary prevention of coronary heart disease and stroke. Circulation 2017;136:1087-98. https://doi.org/10.1161/circulationaha.117.027067.
- Sav A, Kendall E, McMillan SS, Kelly F, Whitty JA, King MA, et al. ‘You say treatment, I say hard work’: treatment burden among people with chronic illness and their carers in Australia. Health Soc Care Community 2013;21:665-74. https://doi.org/10.1111/hsc.12052.
- National Institute for Health and Care Excellence . Raloxifene for the Primary Prevention of Osteoporotic Fragility Fractures in Postmenopausal Women n.d. www.nice.org.uk/guidance/TA160 (accessed 23 November 2022).
- Davis S, Martyn-St James M, Sanderson J, Stevens J, Goka E, Rawdin A, et al. Corrigendum: a systematic review and economic evaluation of bisphosphonates for the prevention of fragility fractures. Health Technol Assess 2018;20. https://doi.org/10.3310/hta20780-c201803.
- National Institute for Health and Care Excellence . Non-Bisphosphonates for Treating Osteoporosis [ID901] n.d. www.nice.org.uk/guidance/indevelopment/gid-ta10072 (accessed 23 November 2022).
- Davis S, Simpson E, Hamilton J, James MM, Rawdin A, Wong R, et al. Denosumab, raloxifene, romosozumab and teriparatide to prevent osteoporotic fragility fractures: a systematic review and economic evaluation. Health Technol Assess 2020;24. https://doi.org/10.3310/hta24290.
- Davis S, Martyn-St James M, Sanderson J, Stevens J, Goka E, Rawdin A, et al. A systematic review and economic evaluation of bisphosphonates for the prevention of fragility fractures. Health Technol Assess 2016;20. https://doi.org/10.3310/hta20780.
- OpenPrescribing . Search GP Prescribing Data n.d. https://openprescribing.net/analyse/#org=regional_team%26numIds=0606020A0%26denomIds=6.6%26selectedTab=chart (accessed 9 January 2022).
- Imaz I, Zegarra P, González-Enríquez J, Rubio B, Alcazar R, Amate JM. Poor bisphosphonate adherence for treatment of osteoporosis increases fracture risk: systematic review and meta-analysis. Osteoporos Int 2010;21:1943-51. https://doi.org/10.1007/s00198-009-1134-4.
- Li L, Roddam A, Gitlin M, Taylor A, Shepherd S, Shearer A, et al. Persistence with osteoporosis medications among postmenopausal women in the UK General Practice Research Database. Menopause 2012;19:33-40. https://doi.org/10.1097/gme.0b013e318221bacd.
- Morley J, Moayyeri A, Ali L, Taylor A, Feudjo-Tepie M, Hamilton L, et al. Persistence and compliance with osteoporosis therapies among postmenopausal women in the UK Clinical Practice Research Datalink. Osteoporos Int 2020;31:533-45. https://doi.org/10.1007/s00198-019-05228-8.
- Guyot P, Ades AE, Ouwens MJ, Welton NJ. Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan–Meier survival curves. BMC Med Res Methodol 2012;12. https://doi.org/10.1186/1471-2288-12-9.
- Ara R, Brazier JE. Populating an economic model with health state utility values: moving toward better practice. Value Health 2010;13:509-18. https://doi.org/10.1111/j.1524-4733.2010.00700.x.
- Borgstrom F, Lekander I, Ivergard M, Strom O, Svedbom A, Alekna V, et al. The International Costs and Utilities Related to Osteoporotic Fractures Study (ICUROS) – quality of life during the first 4 months after fracture. Osteoporos Int 2013;24:811-23.
- Svedbom A, Borgstöm F, Hernlund E, Ström O, Alekna V, Bianchi ML, et al. Quality of life for up to 18 months after low-energy hip, vertebral, and distal forearm fractures-results from the ICUROS. Osteoporos Int 2018;29:557-66. https://doi.org/10.1007/s00198-017-4317-4.
- Abimanyi-Ochom J, Watts JJ, Borgström F, Nicholson GC, Shore-Lorenti C, Stuart AL, et al. Changes in quality of life associated with fragility fractures: Australian arm of the International Cost and Utility Related to Osteoporotic Fractures Study (AusICUROS). Osteoporos Int 2015;26:1781-90. https://doi.org/10.1007/s00198-015-3088-z.
- Jürisson M, Pisarev H, Kanis J, Borgström F, Svedbom A, Kallikorm R, et al. Quality of life, resource use, and costs related to hip fracture in Estonia. Osteoporos Int 2016;27:2555-66. https://doi.org/10.1007/s00198-016-3544-4.
- Svedbom A, Borgström F, Hernlund E, Ström O, Alekna V, Bianchi ML, et al. Quality of life after hip, vertebral, and distal forearm fragility fractures measured using the EQ-5D-3L, EQ-VAS, and time-trade-off: results from the ICUROS. Qual Life Res 2018;27:707-16. https://doi.org/10.1007/s11136-017-1748-5.
- Department of Health and Social Care (DHSC) . NHS Reference Costs (National Cost Collection for the NHS) 2019–20 2020. www.england.nhs.uk/publication/2019-20-national-cost-collection-data-publication/ (accessed 5 June 2023).
- Curtis LA, Burns A. Unit Costs of Health and Social Care 2020. Canterbury: PSSRU, University of Kent; 2020.
- National Institute for Health and Care Excellence . Osteoporosis. Quality Standard [QS149] n.d. https://www.nice.org.uk/guidance/qs149/ (accessed 28 November 2022).
- McCloskey E, Kanis JA, Johansson H, Harvey N, Odén A, Cooper A, et al. FRAX-based assessment and intervention thresholds – an exploration of thresholds inwomen aged 50 years and older in the UK. Osteoporos Int 2015;26:2091-9. https://doi.org/10.1007/s00198-015-3176-0.
- National Institute for Health and Care Excellence (NICE) . Multimorbidity: Clinical Assessment and Management 2016.
- ClinRisk Ltd . QFracture® 2016 Annual Update Information 2016. https://www.qresearch.org/media/qirhz3ti/qfracture-2016-annual-update-information.pdf (accessed 28 November 2022).
- The SCOT-HEART Investigators . Coronary CT angiography and 5-year risk of myocardial infarction. New Engl J Med 2018;379:924-33. https://doi.org/10.1056/NEJMoa1805971.
- Murabito JM, D’Agostino RB, Silbershatz H, Wilson PWF. Intermittent claudication. Circulation 1997;96:44-9. https://doi.org/10.1161/01.CIR.96.1.44.
- Cowie MR, Wood DA, Coats AJ, Thompson SG, Poole-Wilson PA, Suresh V, et al. Incidence and aetiology of heart failure; a population-based study. Eur Heart J 1999;20:421-8.
- Center for Reviews and Dissemination . Systematic Reviews – CRD’s Guidelines for Undertaking Reviews in Healthcare 2009.
- Hainsworth R, Payne K, Thompson A, Rogers G. Accounting for Multimorbidity, Competing Risk and Direct Treatment Disutility in Risk Prediction Tools and Model-Based Cost-Effectiveness Analysis for the Primary Prevention of Cardiovascular Disease: A Systematic Review Protocol to Identify Health State Utility Values n.d. www.crd.york.ac.uk/prospero/display_record.php?ID=CRD42021249959 (accessed 29 November 2022).
- Arber M, Garcia S, Veale T, Edwards M, Shaw A, Glanville JM. Performance of ovid MEDLINE search filters to identify health state utility studies. Int J Technol Assess Health Care 2017;33:472-80. https://doi.org/10.1017/S0266462317000897.
- Luengo-Fernandez R, Gray AM, Bull L, Welch S, Cuthbertson F, Rothwell PM. Oxford Vascular Study . Quality of life after TIA and stroke: ten-year results of the Oxford Vascular Study. Neurology 2013;81:1588-95. https://doi.org/10.1212/WNL.0b013e3182a9f45f.
- Lozano FS, González-Porras JR, March JR, Carrasco E, Lobos JM. VITAL Investigators . Differences between women and men with intermittent claudication: a cross-sectional study. J Womens Health 2014;23:834-41. https://doi.org/10.1089/jwh.2013.4653.
- Mejía A, Richardson G, Pattenden J, Cockayne S, Lewin R. Cost-effectiveness of a nurse facilitated, cognitive behavioural self-management programme compared with usual care using a CBT manual alone for patients with heart failure: secondary analysis of data from the SEMAPHFOR trial. Int J Nurs Stud 2014;51:1214-20. https://doi.org/10.1016/j.ijnurstu.2014.01.009.
- Kent S, Haynes R, Hopewell JC, Parish S, Gray A, Landray MJ, et al. Effects of vascular and nonvascular adverse events and of extended-release niacin with laropiprant on health and healthcare costs. Circ Cardiovasc Qual Outcomes 2016;9:348-54. https://doi.org/10.1161/circoutcomes.115.002592.
- Monahan M, Barton P, Taylor CJ, Roalfe AK, Hobbs FDR, Cowie M, et al. MICE or NICE? An economic evaluation of clinical decision rules in the diagnosis of heart failure in primary care. Int J Cardiol 2017;241:255-61.
- Pockett RD, McEwan P, Ray J, Tran I, Shutler S, Martin S, et al. Prospective utility study of patients with multiple cardiovascular events. J Med Econ 2018;21:616-21. https://doi.org/10.1080/13696998.2018.1454453.
- Vaidya A, Kleinegris MC, Severens JL, Ramaekers BL, Ten Cate-Hoek AJ, Ten Cate H, et al. Comparison of EQ-5D and SF-36 in untreated patients with symptoms of intermittent claudication. J Comp Eff Res 2018;7:535-48. https://doi.org/10.2217/cer-2017-0029.
- Munyombwe T, Hall M, Dondo TB, Alabas OA, Gerard O, West RM, et al. Quality of life trajectories in survivors of acute myocardial infarction: a national longitudinal study. Heart 2020;106:33-9. https://doi.org/10.1136/heartjnl-2019-315510.
- Walker S, Cox E, Rothwell B, Berry C, McCann GP, Bucciarelli-Ducci C, et al. Cost-effectiveness of cardiovascular imaging for stable coronary heart disease. Heart 2021;107:381-8. https://doi.org/10.1136/heartjnl-2020-316990.
- Luengo-Fernandez R, Silver LE, Gutnikov SA, Gray AM, Rothwell PM. Hospitalization resource use and costs before and after TIA and stroke: results from a population-based cohort study (OXVASC). Value Health 2013;16:280-7. https://doi.org/10.1016/j.jval.2012.10.013.
- Walker S, Asaria M, Manca A, Palmer S, Gale CP, Shah AD, et al. Long-term healthcare use and costs in patients with stable coronary artery disease: a population-based cohort using linked health records (CALIBER). Eur Heart J Qual Care Clin Outcomes 2016;2:125-40. https://doi.org/10.1093/ehjqcco/qcw003.
- National Institute for Health and Care Excellence . Acute Coronary Syndromes n.d. www.nice.org.uk/guidance/ng185 (accessed 29 November 2022).
- National Institute for Health and Care Excellence . Atrial Fibrillation: Diagnosis and Management n.d. www.nice.org.uk/guidance/ng196 (accessed 29 November 2022).
- National Institute for Health and Care Excellence . Heart Valve Disease Presenting in Adults: Investigation and Management n.d. https://www.nice.org.uk/guidance/ng208 (accessed 29 November 2022).
- Pohar M, Stare J. Relative survival analysis in R. Comput Methods Programs Biomed 2006;81:272-8.
Appendix 1 QRISK3 external validation, and CRISK and CRISK-CCI derivation and internal validation
| Data | How missingness was handled in analysis | Women | Men | ||
|---|---|---|---|---|---|
| External validation cohort (N = 1,484,597), n (%) missing data | QRISK3 internal validation cohort (N = 1,360,457), n (%) missing data | External validation cohort (N = 1,420,176), n (%) missing data | QRISK3 internal validation cohort (N = 1,310,841), n (%) missing data | ||
| BMI | Imputed | 409,464 (27.6) | 363,705 (26.7) | 590,513 (41.6) | 458,320 (35.0) |
| TC : HDL | Imputed | 1,260,807 (84.9) | 817,195 (60.1) | 1,207,422 (85.0) | 809,236 (61.7) |
| SBP | Imputed | 252,064 (17.0) | 214,418 (15.8) | 489,276 (34.5) | 387,874 (29.6) |
| SBP variability | Imputed | 695,935 (46.9) | 287,790 (21.2) | 1,051,621 (74.0) | 497,468 (38.0) |
| Smoking status | Imputed | 300,216 (20.2) | 191,525 (14.1) | 443,494 (31.2) | 275,416 (21.0) |
| Ethnicity | Assumed white | 309,747 (20.9) | 510,760 (37.5) | 504,698 (35.5) | 559,471 (42.7) |
| Complete data for BMI, TC : HDL, SBP, smoking status and ethnicitya | N/A | 170,056 (11.5) | 389,774 (28.7) | 153,779 (10.8) | 330,073 (25.2) |
| Age | Never missing | 0 | 0 | 0 | 0 |
| Sex | Never missing | 0 | 0 | 0 | 0 |
| Socioeconomic status | Excluded | 2796 (0.2%)b | 0.4% of all patientsc | 2671 (0.2%)b | 0.4% of all patientsc |
| Conditions and prescribing variables | Assumed to be absent if no record | N/A | N/A | N/A | N/A |
| Predictor | Subdistribution HR (95% CI) |
|---|---|
| (Age in years/10)0.5 – 2.1163 | 65.8 (51.5 to 83.9) |
| (BMI/10)2 – 7.0332 | 1.03 (1.02 to 1.05) |
| (SBP/10) – 12.5032 | 1.11 (1.06 to 1.16) |
| log(TC : HDL) – 1.2069 | 1.47 (1.28 to 1.67) |
| (Townsend score + 3.8101)0.5 – 1.620,811 | 1.31 (1.19 to 1.44) |
| Variance in SBP – 9.5910 | 1.01 (1.01 to 1.02) |
| Atrial fibrillation | 4.98 (2.52 to 9.83) |
| Atypical antipsychotics | 1.09 (0.71 to 1.68) |
| Corticosteroid use | 2.16 (1.40 to 3.26) |
| Migraine | 1.50 (1.21 to 1.86) |
| Rheumatoid arthritis | 1.31 (1.01 to 1.69) |
| CKD (stage 3, 4 or 5) | 1.79 (0.59 to 5.43) |
| Serious mental illness | 1.22 (1.06 to 1.40) |
| SLE | 1.74 (0.60 to 4.98) |
| Treated hypertension | 1.48 (1.13 to 1.94) |
| Type 1 diabetes | 2.69 (1.29 to 5.58) |
| Type 2 diabetes | 2.19 (1.30 to 3.71) |
| Family history of CHD in first-degree relative < 60 years | 1.27 (1.02 to 1.59) |
| Smoking status | |
| Non-smoker | 1 |
| Former smoker | 1.32 (1.07 to 1.63) |
| Light smoker | 2.05 (1.65 to 2.54) |
| Moderate smoker | 2.25 (1.82 to 2.79) |
| Heavy smoker | 2.62 (2.10 to 3.28) |
| Ethnicity | 1 |
| Indian, Pakistani or Bangladeshi | 1.53 (1.10 to 2.12) |
| Other Asian | 1.14 (0.47 to 2.76) |
| Black Caribbean or Black African | 0.97 (0.61 to 1.52) |
| Other | 1.07 (0.77 to 1.49) |
| CCI | |
| 0 | 1 |
| 1 | 1.22 (1.11 to 1.34) |
| 2 | 1.11 (0.96 to 1.29) |
| ≥ 3 | 1.18 (0.94 to 1.49) |
| Interactions with age term | |
| Age term – atrial fibrillation | 0.22 (0.08 to 0.63) |
| Age term – corticosteroid use | 0.38 (0.17 to 0.81) |
| Age term – migraine | 0.60 (0.35 to 1.01) |
| Age term – CKD | 0.46 (0.07 to 3.18) |
| Age term – treated hypertension | 0.73 (0.46 to 1.15) |
| Age term – type 1 diabetes | 0.61 (0.14 to 2.63) |
| Age term – type 2 diabetes | 0.43 (0.17 to 1.07) |
| Age term – family history of CHD | 0.81 (0.45 to 1.44) |
| Age term – former smoker | 0.84 (0.57 to 1.24) |
| Age term – light smoker | 0.67 (0.44 to 1.03) |
| Age term – moderate smoker | 0.55 (0.35 to 0.87) |
| Age term – heavy smoker | 0.44 (0.26 to 0.73) |
| Age term – BMI term | 0.97 (0.94 to 1.00) |
| Age term – SBP term | 0.92 (0.85 to 0.99) |
| Age term – Townsend term | 0.71 (0.59 to 0.85) |
| Age term – SLE | 0.88 (0.06 to 12.2) |
| Predictor | Subdistribution HR (95% CI) |
|---|---|
| (Age in years/10)–0.5 – 0.4888 | 7.66 × 10–10 (2.05 × 10–10 to 2.87 × 10–9) |
| (BMI/10) – 2.6514 | 1.29 (1.14 to 1.46) |
| (SBP/10) – 13.0309 | 1.12 (1.07 to 1.16) |
| log(TC : HDL) – 1.4124 | 1.54 (1.37 to 1.74) |
| (Townsend score + 3.8101)0.5 – 1.6479 | 1.20 (1.10 to 1.30) |
| (Variance in SBP + 0.0001)–0.5 – 1.6701 | 1.00 (1.00 to 1.00) |
| Atrial fibrillation | 3.92 (1.71 to 8.98) |
| Atypical antipsychotics | 1.12 (0.78 to 1.60) |
| Corticosteroid use | 1.82 (1.12 to 2.98) |
| Impotence | 1.25 (0.87 to 1.80) |
| Migraine | 1.48 (1.12 to 1.97) |
| Rheumatoid arthritis | 1.19 (0.85 to 1.68) |
| CKD (stage 3, 4 or 5) | 2.13 (1.19 to 3.80) |
| Serious mental illness | 1.22 (1.04 to 1.44) |
| SLE | 0.381 (0.05 to 3.06) |
| Treated hypertension | 1.70 (1.28 to 2.25) |
| Type 1 diabetes | 2.17 (0.71 to 6.70) |
| Type 2 diabetes | 1.87 (1.11 to 3.15) |
| Family history of CHD in first-degree relative < 60 years | 1.64 (1.32 to 2.02) |
| Smoking status | |
| Non-smoker | 1 |
| Former smoker | 1.11 (0.93 to 1.33) |
| Light smoker | 1.84 (1.48 to 2.29) |
| Moderate smoker | 2.01 (1.68 to 2.42) |
| Heavy smoker | 2.59 (2.19 to 3.06) |
| Ethnicity | 1 |
| Indian, Pakistani or Bangladeshi | 1.75 (1.30 to 2.36) |
| Other Asian | 1.58 (0.92 to 2.71) |
| Black Caribbean or Black African | 0.71 (0.46 to 1.10) |
| Other | 1.17 (0.89 to 1.53) |
| CCI | |
| 0 | 1 |
| 1 | 1.17 (1.07 to 1.28) |
| 2 | 1.19 (1.02 to 1.38) |
| ≥ 3 | 1.17 (0.93 to 1.46) |
| Interactions with age term | |
| Age term – atrial fibrillation | 2.92 (2.17 to 3.93 × 106) |
| Age term – impotence | 20.1 (0.18 to 2.21 × 103) |
| Age term – corticosteroid use | 3.71 (0.07 to 192) |
| Age term – migraine | 9.65 (0.28 to 336) |
| Age term – CKD | 259 (1.40 to 4.81 × 104) |
| Age term – treated hypertension | 21.4 (1.45 to 314) |
| Age term – type 1 diabetes | 2.77 (2.23 × 10–7 to 3.42 × 107) |
| Age term – type 2 diabetes | 31.5 (0.24 to 4.14 × 103) |
| Age term – family history of CHD | 13.7 (0.73 to 256) |
| Age term – former smoker | 1.73 (0.265 to 11.3) |
| Age term – light smoker | 17.6 (1.5 to 207) |
| Age term – moderate smoker | 44.2 (5.19 to 376) |
| Age term – heavy smoker | 120 (14.9 to 961) |
| Age term – BMI term | 3.51 (0.891 to 13.8) |
| Age term – SBP term | 1.48 (0.953 to 2.29) |
| Age term – Townsend term | 2.71 (1.1 to 6.67) |
| Data | Women | Men | ||
|---|---|---|---|---|
| External validation cohort (N = 1,484,597) | Original QRISK3 internal validation cohort (N = 1,360,457) | External validation cohort (N = 1,420,176) | Original QRISK3 internal validation (N = 1,310,841) | |
| Age (years), mean (SD) | 46.0 (15.3) | 43.3 (15.3) | 44.8 (13.9) | 42.6 (13.8) |
| BMI (kg/m2), mean (SD) | 25.9 (5.7) | 25.4 (5.1) | 26.6 (4.7) | 25.9 (4.2) |
| TC : HDL (mmol/l), mean (SD) | 3.7 (1.1) | 3.6 (1.2) | 4.4 (1.3) | 4.4 (1.3) |
| SBP (mmHg), mean (SD) | 125.4 (18.0) | 123.1 (18.1) | 131.1 (16.2) | 128.8 (16.2) |
| SBP variability (mmHg), mean (SD) | 10.0 (5.7) | 9.3 (6.1) | 10.3 (6.2) | 9.9 (6.8) |
| Ethnicity, n (%) | ||||
| White or not recorded | 1,363,146 (91.8) | 1,218,391 (89.6) | 1336,221 (94.1) | 1,171,281 (89.4) |
| Indian | 22,488 (1.5) | 23,146 (1.7) | 15,322 (1.1) | 26,479 (2.0) |
| Pakistani | 9550 (0.6) | 10,919 (0.8) | 6647 (0.5) | 14,787 (1.1) |
| Bangladeshi | 2594 (0.2) | 8738 (0.6) | 2145 (0.2) | 11,914 (0.9) |
| Other Asian | 13,697 (0.9) | 17,078 (1.3) | 9973 (0.7) | 15,966 (1.2) |
| Black Caribbean | 9505 (0.6) | 13,142 (1.0) | 6687 (0.5) | 10,642 (0.8) |
| Black African | 18,804 (1.3) | 27,678 (2.0) | 12,822 (0.9) | 25,251 (1.9) |
| Chinese | 6739 (0.5) | 8992 (0.7) | 3503 (0.2) | 6098 (0.5) |
| Other | 38,074 (2.6) | 32,373 (2.4) | 26,829 (1.9) | 28,423 (2.2) |
| Smoking status, n (% of non-missing) | ||||
| Non-smoker | 707,774 (59.8) | 706,671 (51.9) | 478,671 (49.0) | 512,252 (39.1) |
| Former smoker | 217,404 (18.4) | 194,545 (14.3) | 216,883 (22.2) | 196,459 (15.0) |
| Light smoker | 85,277 (7.2) | 154,565 (11.4) | 75,260 (7.7) | 177,693 (13.6) |
| Moderate smoker | 111,690 (9.4) | 74,933 (5.5) | 112,411 (11.5) | 84,914 (6.5) |
| Heavy smoker | 62,236 (5.3) | 38,218 (2.8) | 93,457 (9.6) | 64,107 (4.9) |
| Family history of CHD in first-degree relative aged < 60 years, n (%) | 97,624 (6.6) | 164,023 (12.1) | 75,237 (5.3) | 123,039 (9.4) |
| Type 1 diabetes, n (%) | 3752 (0.3) | 3351 (0.2) | 4843 (0.3) | 3932 (0.3) |
| Type 2 diabetes, n (%) | 17,022 (1.1) | 15,872 (1.2) | 21,077(1.5) | 19,318 (1.5) |
| Treated hypertension, n (%) | 115,944 (7.8) | 77,694 (5.7) | 82,768 (5.8) | 56,920 (4.3) |
| Rheumatoid arthritis, n (%) | 12,702 (0.9) | 15,139 (1.1) | 4724 (0.3) | 7055 (0.5) |
| Atrial fibrillation, n (%) | 8199 (0.6) | 5229 (0.4) | 10,620 (0.7) | 6874 (0.5) |
| CKD (stage 3, 4 or 5), n (%) | 6918 (0.5) | 6949 (0.5) | 5659 (0.4) | 4232 (0.3) |
| Migraine, n (%) | 117,692 (7.9) | 89,504 (6.6) | 41,471 (2.9) | 36,141 (2.8) |
| Corticosteroid use, n (%) | 20,674 (1.4) | 31,775 (2.3) | 11,824 (0.8) | 18,634 (1.4) |
| HIV/AIDS, n (%) | 289 (0.02) | 1595 (0.1) | 445 (0.03) | 2945 (0.2) |
| SLE, n (%) | 1725 (0.1) | 1349 (0.1) | 165 (0.01) | 134 (0.0) |
| Atypical antipsychotic use, n (%) | 8469 (0.6) | 6268 (0.5) | 8336 (0.6) | 6597 (0.5) |
| Severe mental illness, n (%) | 110,799 (7.5) | 94,724 (7.0) | 57,264 (4.0) | 57,830 (4.4) |
| Erectile dysfunction diagnosis or treatment, n (%) | N/A | N/A | 39,264 (2.8) | 31,136 (2.4) |
| Age group (years) | Women | Men | ||||||
|---|---|---|---|---|---|---|---|---|
| Number of incident cases | Person-years of follow-up | Rate per 1000 person-years (95% CI) | QRISK3 derivation:27 rate per 1000 person-years (95% CI)a | Number of incident cases | Person-years of follow-up | Rate per 1000 person-years (95% CI) | QRISK3 derivation:27 rate per 1000 person-years (95% CI)a | |
| 25–29 | 257 | 942,262 | 0.3 (0.2 to 0.3) | 0.3 (0.22 to 0.26) | 313 | 903,432 | 0.3 (0.3 to 0.4) | 0.4 (0.38 to 0.42) |
| 30–34 | 560 | 1,153,862 | 0.5 (0.4 to 0.5) | 0.5 (0.47 to 0.52) | 974 | 1,144,138 | 0.9 (0.8 to 0.9) | 1.0 (0.95 to 1.02) |
| 35–39 | 1098 | 1,238,221 | 0.9 (0.8 to 0.9) | 1.0 (0.99 to 1.10) | 2185 | 1,249,707 | 1.7 (1.7 to 1.8) | 2.1 (2.1 to 2.2) |
| 40–44 | 1762 | 1,136,909 | 1.5 (1.5 to 1.6) | 1.9 (1.8 to 2.0) | 3519 | 1,145,201 | 3.1 (3.0 to 3.2) | 4.0 (3.9 to 4.1) |
| 45–49 | 2221 | 939,971 | 2.4 (2.3 to 2.5) | 3.2 (3.1 to 3.3) | 4779 | 916,468 | 5.2 (5.1 to 5.4) | 6.6 (6.5 to 6.7) |
| 50–54 | 2739 | 812,590 | 3.4 (3.2 to 3.5) | 4.8 (4.7 to 4.9) | 5628 | 749,133 | 7.5 (7.3 to 7.7) | 9.9 (9.7 to 10.0) |
| 55–59 | 3776 | 754,370 | 5.0 (4.8 to 5.2) | 7.5 (7.4 to 7.6) | 6877 | 654,761 | 10.5 (10.3 to 10.8) | 14.2 (14.0 to 14.4) |
| 60–64 | 4053 | 509,885 | 7.9 (7.7 to 8.2) | 11.4 (11.2 to 11.5) | 6249 | 409,070 | 15.3 (14.9 to 15.7) | 19.7 (19.5 to 19.9) |
| 65–69 | 4864 | 387,189 | 12.6 (12.2 to 12.9) | 17.1 (16.9 to 17.4) | 6126 | 289,067 | 21.2 (20.7 to 21.7) | 26.6 (26.2 to 26.9) |
| 70–74 | 6169 | 304,427 | 20.3 (19.8 to 20.8) | 25.1 (24.8 to 25.4) | 6157 | 207,295 | 29.7 (29.0 to 30.4) | 35.5 (35.0 to 35.9) |
| 75–80 | 7117 | 237,437 | 30.0 (29.3 to 30.7) | 35.1 (34.7 to 35.5) | 5758 | 142,794 | 40.3 (39.3 to 41.4) | 45.2 (44.5 to 45.8) |
| 80–84 | 7835 | 177,496 | 44.1 (43.2 to 45.1) | 48.0 (47.4 to 48.7) | 4501 | 85,637 | 52.6 (51.1 to 54.1) | 58.3 (57.2 to 59.4) |
| Total | 42,451 | 8,594,620 | 4.94 (4.9 to 5.0) | 6.2 (6.16 to 6.22) | 53,066 | 7,896,704 | 6.72 (6.66 to 6.78) | 8.2 (8.14 to 8.21) |
| Diabetes type | Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) |
|---|---|---|---|
| Type 1 | |||
| Women | 0.830 (0.768 to 0.891) | 2.11 (1.80 to 2.43) | 51.6 (43.7 to 58.4) |
| Men | 0.853 (0.803 to 0.902) | 1.97 (1.73 to 2.20) | 48.0 (41.7 to 53.6) |
| Type 2 | |||
| Women | 0.741 (0.722 to 0.760) | 1.31 (1.22 to 1.41) | 29.2 (26.2 to 32.1) |
| Men | 0.695 (0.679 to 0.712) | 1.09 (1.00 to 1.17) | 22.0 (19.4 to 24.6) |
FIGURE 28.
Calibration in type 1 diabetes. (a) Women with type 1 diabetes not accounting for competing risks;a (b) women with type 1 diabetes accounting for competing risks;b (c) men with type 1 diabetes not accounting for competing risks;a and (d) men with type 1 diabetes accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.
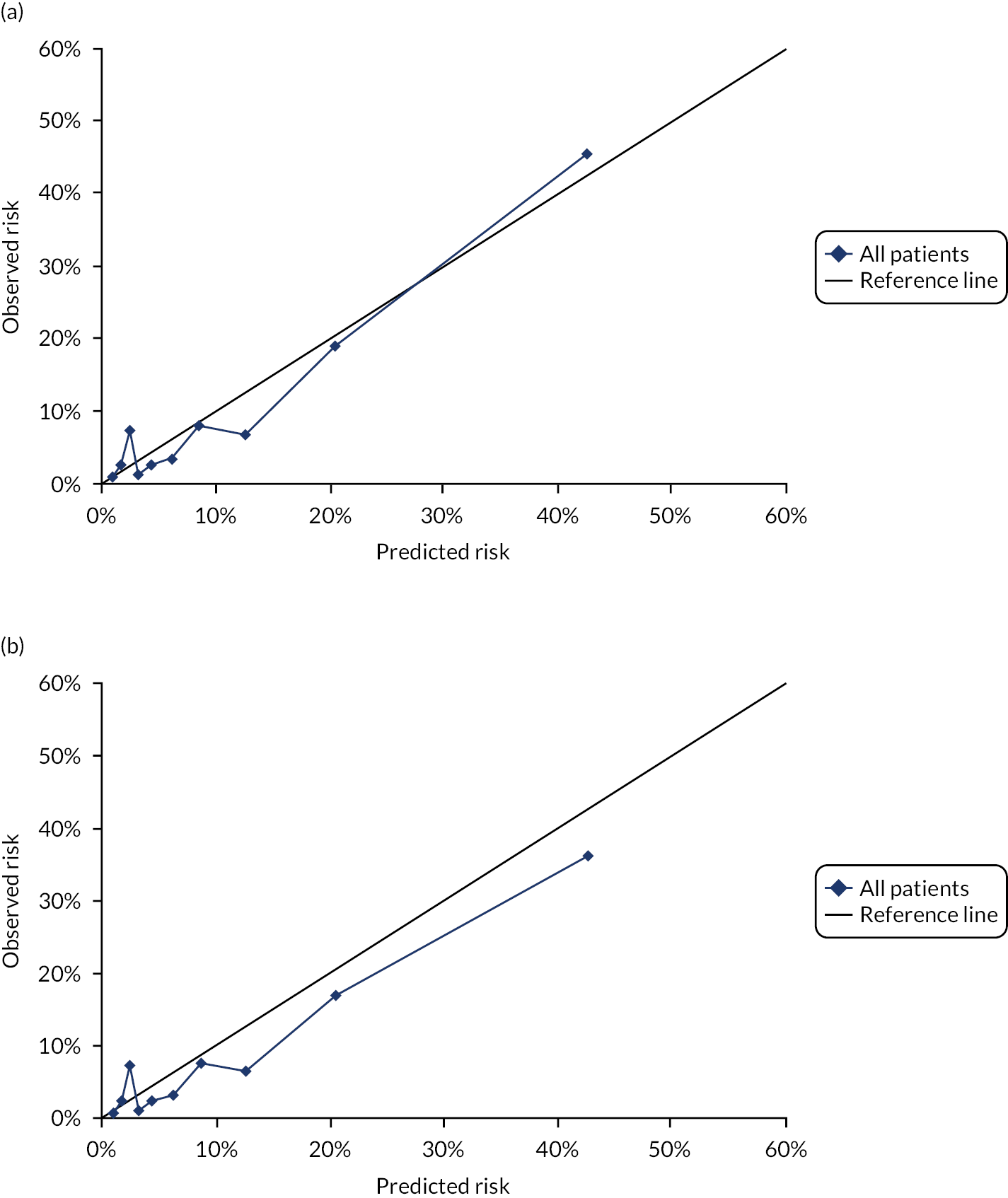
FIGURE 29.
Calibration in type 2 diabetes. (a) Women with type 2 diabetes not accounting for competing risks;a (b) women with type 2 diabetes accounting for competing risks;b (c) men with type 2 diabetes not accounting for competing risks;a and (d) men with type 2 diabetes accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.
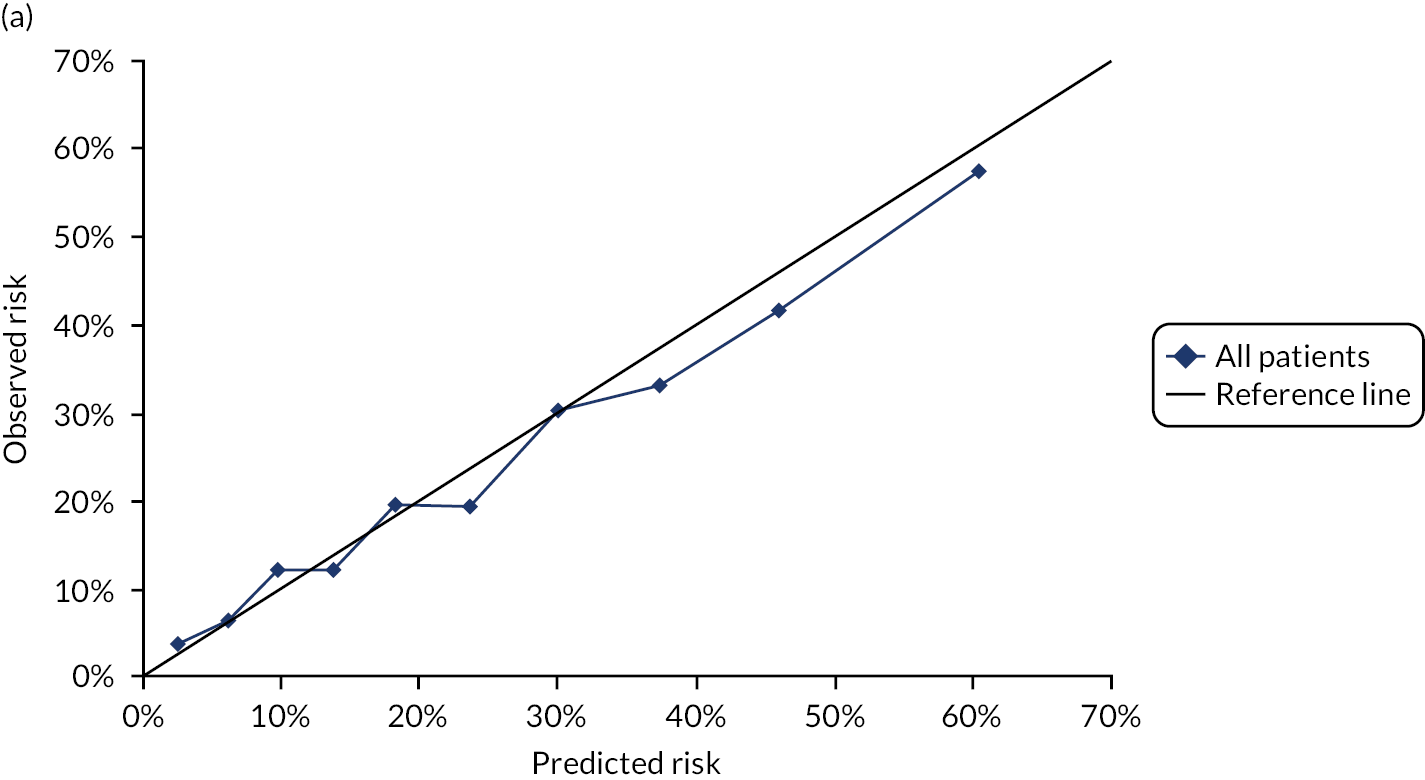
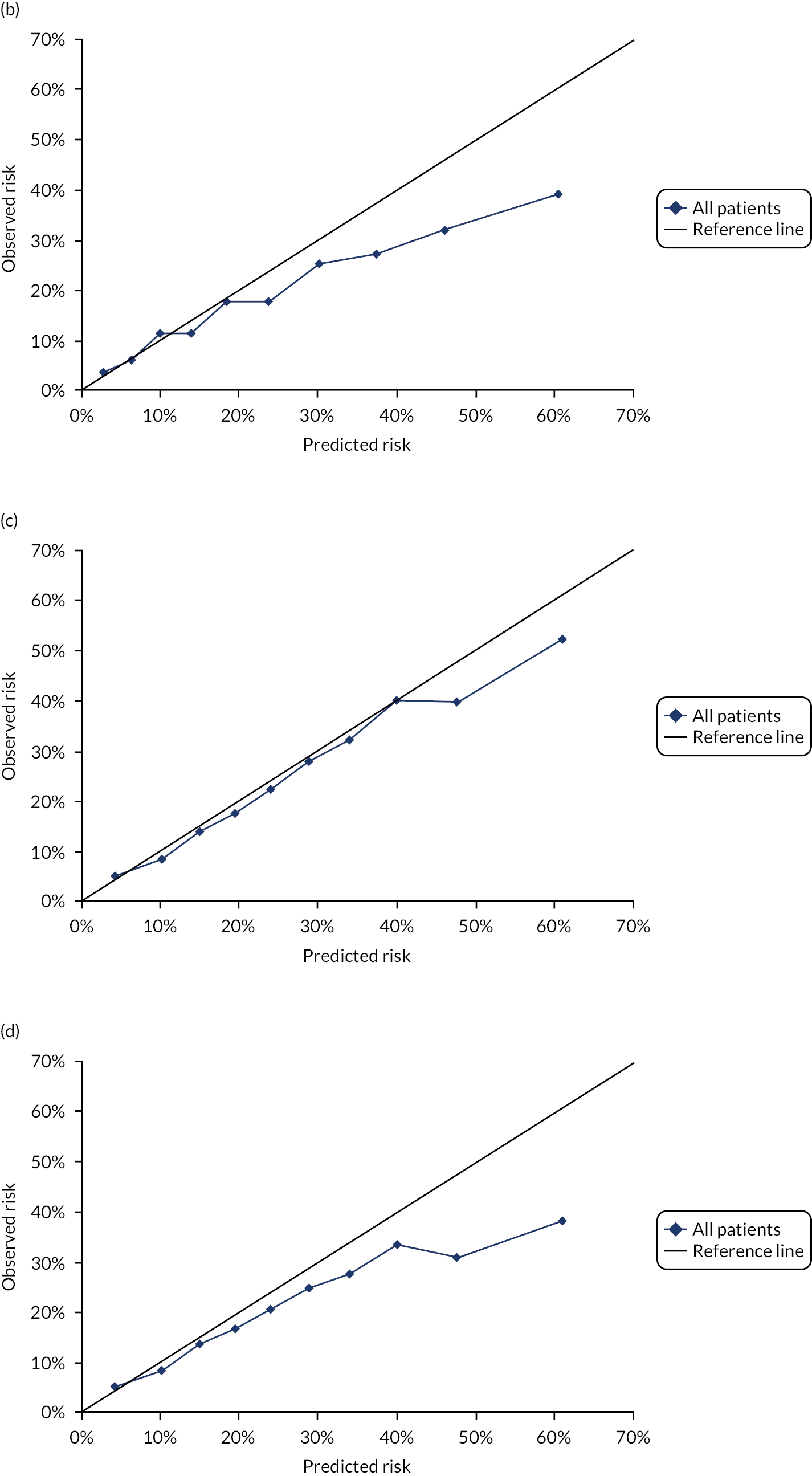
| CKD | Harrell’s c-statistic (95% CI) | D-statistic (95% CI) | R2-statistic (95% CI) |
|---|---|---|---|
| CKD Read codea | |||
| Women | 0.755 (0.728 to 0.782) | 1.47 (1.34 to 1.61) | 34.2 (29.9 to 38.3) |
| Men | 0.734 (0.708 to 0.760) | 1.33 (1.19 to 1.47) | 29.7 (25.4 to 34.0) |
| CKD Read code or eGFRb | |||
| Women | 0.705 (0.699 to 0.712) | 1.18 (1.14 to 1.22) | 24.9 (23.7 to 26.2) |
| Men | 0.671 (0.663 to 0.680) | 0.94 (0.89 to 0.99) | 17.4 (15.8 to 18.9) |
FIGURE 30.
Calibration in people with CKD defined by Read code. (a) Women with CKD defined by Read code not accounting for competing risks;a (b) women with CKD defined by Read code accounting for competing risks;b (c) men with CKD defined by Read code not accounting for competing risks;a and (d) men with CKD defined by Read code accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.
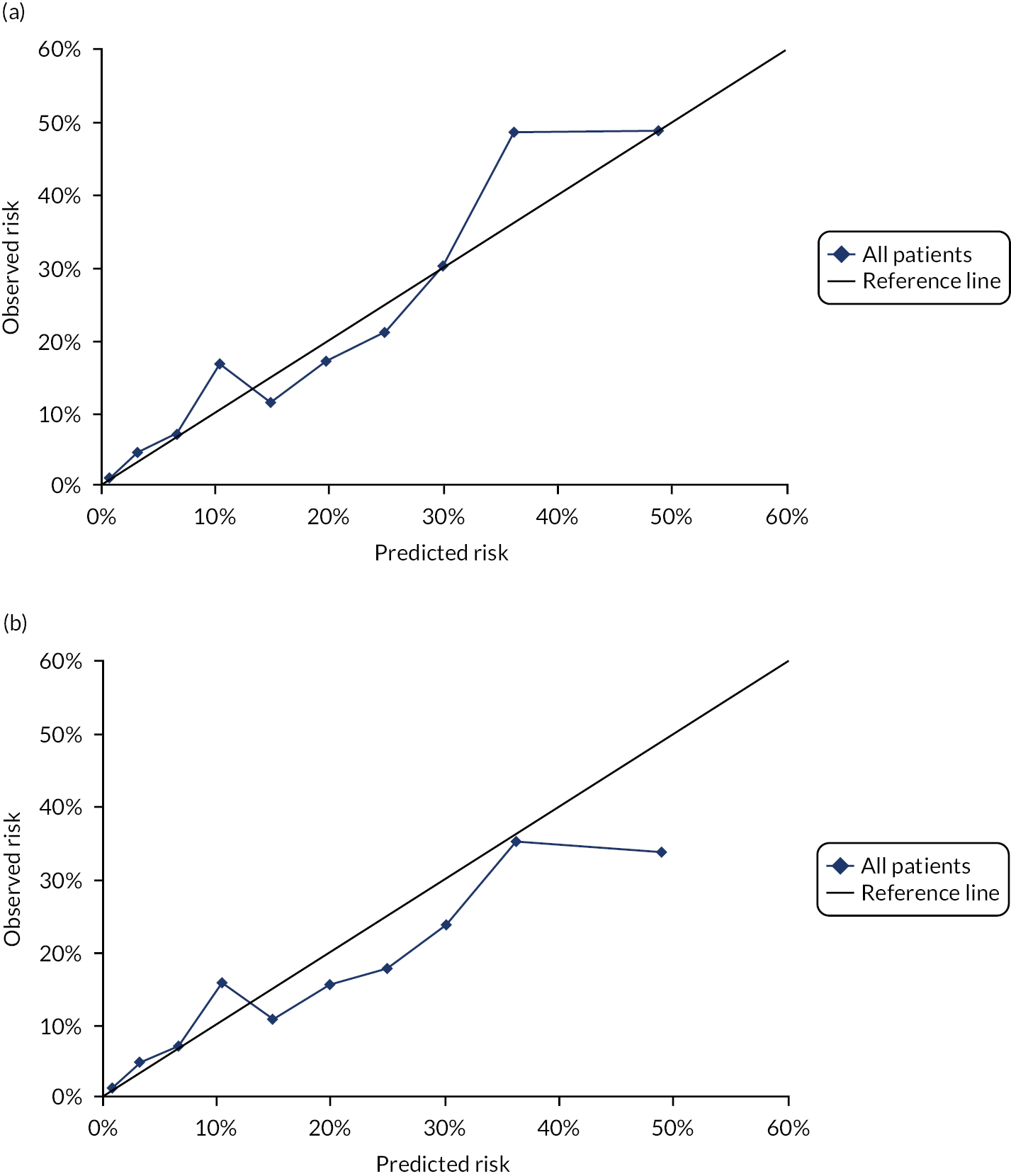
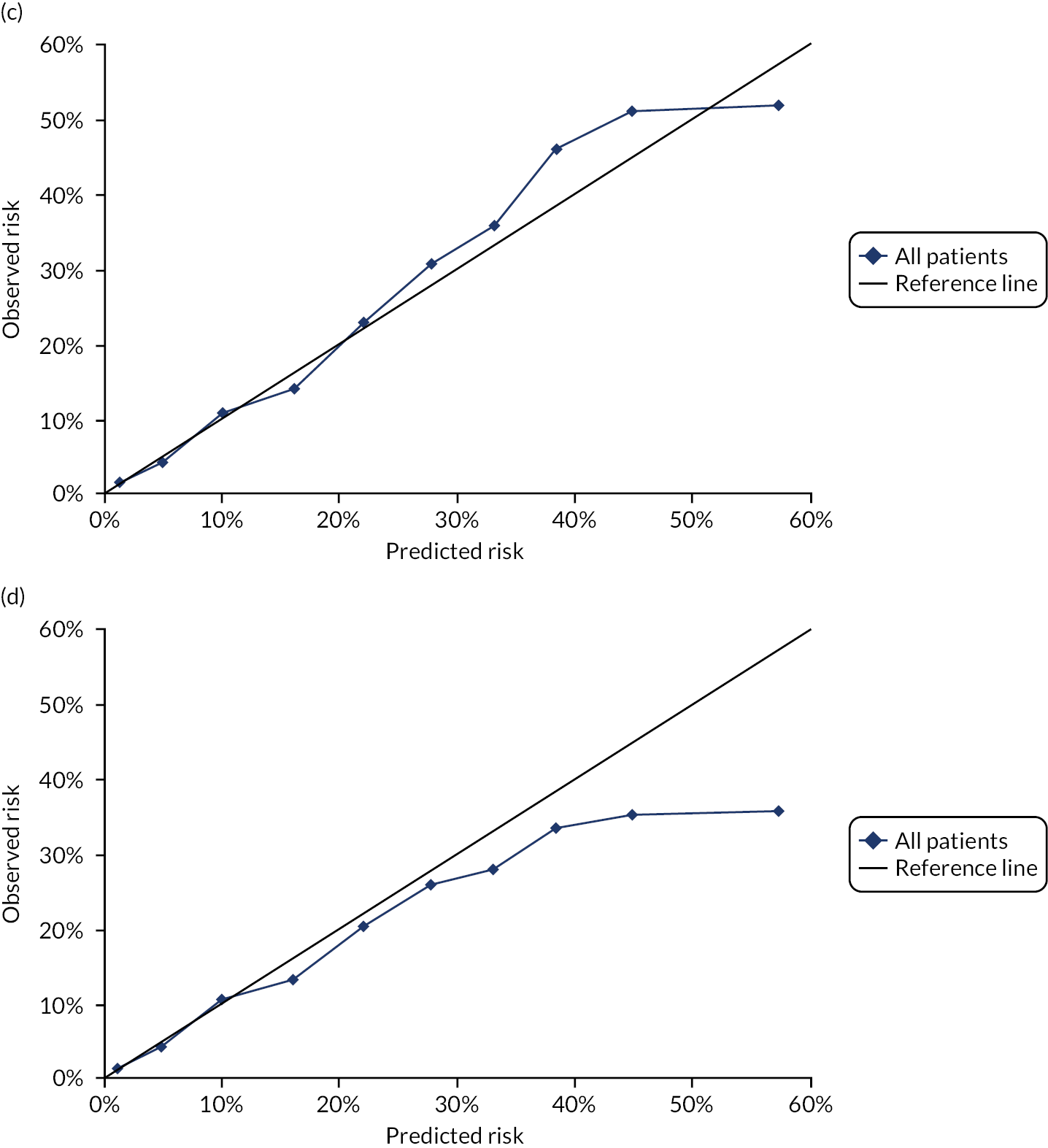
FIGURE 31.
Calibration in CKD defined by Read code and eGFR. (a) Women with CKD defined by Read code or eGFR not accounting for competing risks;a (b) women with CKD defined by Read code or eGFR accounting for competing risks;b (c) men with CKD defined by Read code or eGFR not accounting for competing risks;a and (d) men with CKD defined by Read code or eGFR accounting for competing risks. b a, Observed risk is based on the Kaplan–Meier estimator, which does not account for competing mortality risk; and b, observed risk is based on the Aalen–Johansen estimator, which accounts for competing mortality risk.


Appendix 2 QRISK-Lifetime external validation
| Data | Women external validation cohort (N = 1,260,329) | Men external validation cohort (N = 1,223,265) | All patients QRISK-Lifetime internal validation cohort (N = 1,267,159) |
|---|---|---|---|
| Age (years), mean (SD) | 49.3 (14.2) | 47.6 (13.0) | 48.0 (14.2) |
| BMI (kg/m2), mean (SD) | 26.2 (5.8) | 26.8 (4.6) | 26.1 (4.5) |
| TC : HDL (mmol/l), mean (SD) | 3.7 (1.1) | 4.4 (1.3) | 4.2 (1.3) |
| SBP (mmHg), mean (SD) | 127 (18) | 132 (16) | 131.7 (20.5) |
| Ethnicity, n (%) | |||
| White or not recorded | 1,168,417 (92.7) | 1,155,055 (94.4) | 1,219,987 (96.3) |
| Indian | 16,627 (1.3) | 12,346 (1.0) | 7577 (0.6) |
| Pakistani | 6546 (0.5) | 5031 (0.4) | 3663 (0.3) |
| Bangladeshi | 1649 (0.1) | 1604 (0.1) | 2632 (0.2) |
| Other Asian | 10,118 (0.8) | 7946 (0.6) | 5032 (0.4) |
| Black Caribbean | 8154 (0.6) | 5913 (0.5) | 4666 (0.4) |
| Black African | 14,495 (1.2) | 10,681 (0.9) | 9471 (0.8) |
| Chinese | 5135 (0.4) | 2917 (0.2) | 3068 (0.2) |
| Other | 29,188 (2.3) | 21,772 (1.8) | 11,063 (0.8) |
| Smoking status, n (%)a | |||
| Non-smoker | 585,281 (59.3) | 403,983 (48.4) | 631,545 (49.8) |
| Former smoker | 189,719 (19.2) | 198,717 (23.8) | 193,974 (15.3) |
| Light smoker | 63,592 (6.4) | 58,543 (7.0) | 71,037 (5.6) |
| Moderate smoker | 91,518 (9.3) | 90,692 (10.9) | 91,679 (7.2) |
| Heavy smoker | 56,241 (5.7) | 83,169 (10.0) | 74,056 (5.8) |
| Family history of CHD in first-degree relative aged < 60 years, n (%) | 88,164 (7.0) | 68,814 (5.6) | 143,593 (11.3) |
| Type 2 diabetes, n (%) | 16,744 (1.3) | 20,883 (1.7) | 20,868 (1.7) |
| Treated hypertension, n (%) | 115,548 (9.2) | 82,387 (6.7) | 67,986 (5.4) |
| Atrial fibrillation, n (%) | 8164 (0.6) | 10,528 (0.9) | 6589 (0.5) |
| CKD, n (%) | 6675 (0.5) | 5403 (0.4) | 1917 (0.2) |
| Rheumatoid arthritis, n (%) | 12,357 (1.0) | 4590 (0.4) | Not reported |
Appendix 3 QFracture-2012 external validation codesets
| Fracture type | CPRD Medcode | Read code | Read code description |
|---|---|---|---|
| Hip | 2225 | S30..00 | Fracture of neck of femur |
| 1994 | S30..11 | Hip fracture | |
| 38489 | S300.00 | Closed fracture proximal femur, transcervical | |
| 39984 | S300000 | Cls # prox femur, intracapsular section, unspecified | |
| 69919 | S300100 | Closed fracture proximal femur, transepiphyseal | |
| 65690 | S300200 | Closed fracture proximal femur, midcervical section | |
| 52194 | S300300 | Closed fracture proximal femur, basicervical | |
| 51861 | S300311 | Closed fracture, base of neck of femur | |
| 36391 | S300400 | Closed fracture head of femur | |
| 17019 | S300500 | Cls # prox femur, subcapital, Garden grade unspec. | |
| 34351 | S300600 | Closed fracture proximal femur, subcapital, Garden grade I | |
| 33957 | S300700 | Closed fracture proximal femur, subcapital, Garden grade II | |
| 36599 | S300800 | Closed fracture proximal femur, subcapital, Garden grade III | |
| 34078 | S300900 | Closed fracture proximal femur, subcapital, Garden grade IV | |
| 49209 | S300y00 | Closed fracture proximal femur, other transcervical | |
| 68229 | S300y11 | Closed fracture of femur, subcapital | |
| 62966 | S300z00 | Closed fracture proximal femur, transcervical, NOS | |
| 5301 | S302.00 | Closed fracture of proximal femur, pertrochanteric | |
| 19117 | S302000 | Cls # proximal femur, trochanteric section, unspecified | |
| 19387 | S302011 | Closed fracture of femur, greater trochanter | |
| 48337 | S302012 | Closed fracture of femur, lesser trochanter | |
| 45141 | S302100 | Closed fracture proximal femur, intertrochanteric, two part | |
| 29145 | S302200 | Closed fracture proximal femur, subtrochanteric | |
| 51216 | S302300 | Cls # proximal femur, intertrochanteric, comminuted | |
| 8648 | S302400 | Closed fracture of femur, intertrochanteric | |
| 44735 | S302z00 | Cls # of proximal femur, pertrochanteric section, NOS | |
| 28965 | S304.00 | Pertrochanteric fracture | |
| 8243 | S305.00 | Subtrochanteric fracture | |
| 24276 | S30w.00 | Closed fracture of unspecified proximal femur | |
| 18273 | S30y.00 | Closed fracture of neck of femur NOS | |
| 10570 | S30y.11 | Hip fracture NOS | |
| 37662 | S310000 | Closed fracture of femur, unspecified part | |
| 520 | S31z.00 | Fracture of femur, NOS | |
| Distal radius/ulna | 5951 | 7K1LM00 | Closed reduction of fracture of wrist |
| 18299 | S234.00 | Closed fracture of radius and ulna, lower end | |
| 203 | S234.11 | Wrist fracture – closed | |
| 18389 | S234000 | Closed fracture of forearm, lower end, unspecified | |
| 343 | S234100 | Closed Colles’ fracture | |
| 52389 | S234111 | Smith’s fracture – closed | |
| 1742 | S234200 | Closed fracture of the distal radius, unspecified | |
| 28708 | S234600 | Closed fracture radius and ulna, distal | |
| 2862 | S234700 | Closed Smith’s fracture | |
| 40268 | S234800 | Closed Galeazzi fracture | |
| 11066 | S234900 | Closed volar Barton’s fracture | |
| 53689 | S234911 | Closed volar Barton’s fracture-dislocation | |
| 65636 | S234912 | Closed volar Barton fracture-subluxation | |
| 50053 | S234A00 | Closed dorsal Barton’s fracture | |
| 57736 | S234A11 | Closed dorsal Barton’s fracture-dislocation | |
| 107741 | S234A12 | Closed dorsal Barton fracture-subluxation | |
| 44844 | S234C00 | Closed fracture distal radius, intra-articular, die-punch | |
| 19058 | S234D00 | Closed fracture distal radius, extra-articular, other type | |
| 28293 | S234E00 | Closed fracture distal radius, intra-articular, other type | |
| 10033 | S234F00 | Closed Barton’s fracture | |
| 102302 | S234G00 | Greenstick fracture of distal radius | |
| 27591 | S234z00 | Closed fracture of forearm, lower end, NOS | |
| 199 | S23B.00 | Fracture of lower end of radius | |
| 6213 | S23C.00 | Fracture of lower end of both ulna and radius | |
| 50654 | S23x000 | Closed fracture of forearm, unspecified | |
| 17952 | S23x100 | Closed fracture of radius (alone), unspecified | |
| 137 | S23x111 | Fracture of radius NOS | |
| 17922 | S4C0000 | Closed fracture-dislocation distal radio-ulnar joint | |
| 38408 | S4C0100 | Closed fracture-dislocation radiocarpal joint | |
| 44652 | S4C2000 | Closed fracture-subluxation, distal radio-ulnar joint | |
| 50148 | S4C2100 | Closed fracture-subluxation radiocarpal joint | |
| Proximal humerus | 6379 | 7K1LF00 | Closed reduction of fracture of humerus |
| 517 | S22..00 | Fracture of humerus | |
| 11222 | S220.00 | Closed fracture of the proximal humerus | |
| 44721 | S220000 | Closed fracture of proximal humerus, unspecified part | |
| 11313 | S220100 | Closed fracture proximal humerus, neck | |
| 33489 | S220200 | Closed fracture of proximal humerus, anatomical neck | |
| 11044 | S220300 | Closed fracture proximal humerus, greater tuberosity | |
| 28739 | S220400 | Closed fracture proximal humerus, head | |
| 52406 | S220500 | Closed fracture of humerus, upper epiphysis | |
| 40330 | S220600 | Closed fracture proximal humerus, three part | |
| 29137 | S220700 | Closed fracture proximal humerus, four part | |
| 38353 | S220z00 | Closed fracture of proximal humerus not otherwise specified | |
| 19186 | S222000 | Closed fracture of humerus NOS | |
| 2101 | S226.00 | Fracture of upper end of humerus | |
| 10382 | S22z.00 | Fracture of humerus NOS | |
| Vertebral | 16895 | N1y1.00 | Fatigue fracture of vertebra |
| 44386 | N331.14 | Osteoporotic vertebral collapse | |
| 15837 | N331011 | Collapse of thoracic vertebra | |
| 17377 | N331800 | Osteoporosis + pathological fracture lumbar vertebrae | |
| 12673 | N331900 | Osteoporosis + pathological fracture thoracic vertebrae | |
| 48772 | N331A00 | Osteoporosis + pathological fracture cervical vertebrae | |
| 9319 | N331F00 | Collapse of thoracic vertebra | |
| 45736 | N331H00 | Collapse of cervical vertebra due to osteoporosis | |
| 5841 | N331J00 | Collapse of lumbar vertebra due to osteoporosis | |
| 19048 | N331K00 | Collapse of thoracic vertebra due to osteoporosis | |
| 4013 | N331L00 | Collapse of vertebra due to osteoporosis NOS | |
| 53337 | S100H00 | Closed fracture cervical vertebra, wedge | |
| 27404 | S102.00 | Closed fracture thoracic vertebra | |
| 28524 | S102100 | Closed fracture thoracic vertebra, wedge | |
| 8266 | S104100 | Closed fracture lumbar vertebra, wedge | |
| 5381 | S15..00 | Fracture of thoracic vertebra |
| Fracture type | ICD-10 code | ICD-10 code description |
|---|---|---|
| Hip | S72.0 | Fracture of neck of femur |
| S72.1 | Pertrochanteric fracture | |
| S72.2 | Subtrochanteric fracture | |
| Distal radius/ulna | S52.5 | Fracture of lower end of radius |
| S52.6 | Fracture of lower end of both ulna and radius | |
| Proximal humerus | S42.2 | Fracture of upper end of humerus |
| Vertebral | M48.5 | Collapsed vertebra, not elsewhere classified |
| Osteoporotic | M80.0 | Postmenopausal osteoporosis with pathological fracture |
| M80.1 | Postoophorectomy osteoporosis with pathological fracture | |
| M80.3 | Postsurgical malabsorption osteoporosis with pathological fracture | |
| M80.5 | Idiopathic osteoporosis with pathological fracture | |
| M80.8 | Other osteoporosis with pathological fracture | |
| M80.9 | Unspecified osteoporosis with pathological fracture |
| Morbidity | Definition |
|---|---|
| Type 1 diabetes and type 2 diabetes | As defined for GP data in Kuan et al.98 |
| Parental history of osteoporosis/hip fracture | Bespoke codeset (see Table 35) |
| Care home resident | Bespoke codeset (see Table 35) |
| Previous fracture | As per fracture outcomes (see Table 32) plus bespoke codeset for ‘history of’ codes (see Table 35) |
| History of falls | Bespoke codeset (see Table 35) |
| Dementia | As defined for GP data in Kuan et al.98 |
| Cancer | As defined for GP data in Kuan et al.98 |
| Asthma or COPD | As defined for GP data in Kuan et al.98 |
| Heart attack, angina, stroke or TIA | CVD outcomes in GP data defined in supplementary file in Livingstone et al.67 |
| Chronic liver disease | As defined for GP data in Kuan et al.98 |
| CKD | As defined for GP data in Kuan et al.98 |
| Parkinson’s disease | As defined for GP data in Kuan et al.98 |
| Rheumatoid arthritis or SLE | As defined for GP data in Kuan et al.98 |
| Malabsorptiona | Crohn’s disease, ulcerative colitis and coeliac disease, as defined for GP data in Kuan et al.;98 malabsorption, steatorrhoea or blind loop syndrome in bespoke codeset (see Table 35) |
| Endocrine problemsb | Hyperparathyroidism as defined for GP data in Kuan et al.;98 thyrotoxicosis and Cushing syndrome in bespoke codeset (see Table 35) |
| Epilepsy | As defined for GP data in Kuan et al.98 |
| Morbidity | CPRD Medcode | Read code | Read code description |
|---|---|---|---|
| Parenteral history of osteoporosis or hip fracture | 11218 | 1268.00 | FH: osteoporosis |
| Family history of osteoporosis or hip fracture | 51427 | 12I6.00 | FH: fragility fracture |
| 37204 | 12I4.00 | FH: maternal hip fracture | |
| 42319 | 12I5.00 | FH: hip fracture in first-degree relative | |
| 43219 | 12I8.00 | FH: maternal hip fracture before age 75 | |
| Care home resident | 13359 | 13F6100 | Lives in a nursing home |
| 7653 | 9N1G.00 | Seen in nursing home | |
| 24956 | 13FK.00 | Lives in a residential home | |
| 13360 | 13F6.00 | Nursing/other home | |
| 49681 | 13FX.00 | Lives in care home | |
| 27968 | 13F7.00 | Residential institution | |
| 13361 | 13F4.11 | Lives in warden-controlled accommodation | |
| 30807 | 13F4000 | Resident in sheltered accommodation | |
| 98592 | 8Ce4.00 | Preferred place of care – nursing home | |
| 6859 | 9N1F.00 | Seen in warden sup home | |
| 93998 | 9b0i.00 | Residential home visit note | |
| 10993 | ZLG4.00 | Discharge to nursing home | |
| 101003 | 9NFR.00 | Home visit request by residential institution | |
| 28773 | ZV60700 | [V]Sheltered housing | |
| 100080 | 8Ce5.00 | Preferred place of care – residential home | |
| 7101 | 9N1F.12 | Seen in old people’s home | |
| 59653 | 6991.00 | Geriatric home admission exam | |
| 73321 | 9b1P.00 | Nursing home | |
| 102493 | 8Ht..00 | Admission to nursing home | |
| 107443 | 9NFW000 | Care home visit for initial patient assessment | |
| 35187 | 9N1D.00 | Seen in warden sup house | |
| 35172 | 9N1E.00 | Seen in warden sup flat | |
| 34794 | 13F9.11 | Living in sheltered accommodation | |
| 21280 | 13F5200 | Resident in part III accommodation | |
| 107602 | 9NFW100 | Care home visit for follow-up patient review | |
| 42191 | ZLG3.00 | Discharge to residential home | |
| 24828 | Z177F00 | Nursing home care | |
| 73083 | 9b0Y.00 | Nursing home visit note | |
| 94070 | 8O24.00 | Provision of continuing care in nursing home | |
| 107757 | 9NFW.00 | Care home visit | |
| 59548 | 13FT.00 | Lives in an old people’s home | |
| 102598 | 8Hs..00 | Discharge to nursing home | |
| 27936 | 8HE6.00 | Delayed discharge to nursing home | |
| 24816 | Z177C00 | Residential care | |
| 50792 | 9N1F.11 | Seen in Part 3 accommodation | |
| 36096 | 13F5.11 | Part 3 accommodation | |
| 6991 | 9493.00 | Patient died in nursing home | |
| 43915 | ZLG4100 | Discharge to private nursing home | |
| 49138 | ZV63212 | [V]Delayed discharge – nursing home vacancy awaited | |
| 27360 | 13F5100 | Part III accommodation arranged | |
| 98758 | 13Zo.00 | Previously lived in care home | |
| 36905 | ZLG5100 | Discharge to warden-controlled accommodation | |
| 35040 | ZLG5.00 | Discharge to sheltered housing | |
| 102230 | M270100 | Nursing home acquired pressure ulcer | |
| 48549 | ZLG3100 | Discharge to private residential home | |
| 95795 | 923O.00 | FP22 – removal from residential institute | |
| 67903 | U105100 | [X]Fall involving wheelchair occurrence residential instit’n | |
| 46642 | 9b79.00 | Other residential care homes managed by local authority | |
| 66122 | 13F5111 | Part 3 accommodation arranged | |
| 99148 | 9b7A.00 | Other residential care home man voluntary/private agents | |
| 96836 | ZK76.00 | Temporary home care service provision | |
| History of fracturea | 17936 | 14G7.00 | H/O: hip fracture |
| 18731 | 14G6.00 | H/O: fragility fracture | |
| 19235 | 14G8.00 | H/O: vertebral fracture | |
| History of falls | 384 | TC...11 | Fall – accidental |
| 6815 | TC...00 | Accidental falls | |
| 6008 | 16D..00 | Falls | |
| 4859 | R200.12 | [D] Geriatric fall | |
| 6835 | TCz..00 | Accidental falls NOS | |
| 8694 | 16D1.00 | Recurrent falls | |
| 8730 | TCy..00 | Other falls | |
| 15112 | TC5..00 | Fall on same level from slipping, tripping or stumbling | |
| 11307 | TC0..00 | Fall on or from stairs or steps | |
| 11308 | TCyz.00 | Other accidental fall NOS | |
| 17167 | TC01.00 | Fall on or from stairs | |
| 11709 | TC51.00 | Fall on same level from tripping | |
| 33887 | TC4..00 | Other fall from one level to another | |
| 17728 | TC01000 | Fall on stairs | |
| 108062 | 16D6.00 | Fall | |
| 18007 | TC50.00 | Fall on same level from slipping | |
| 21081 | TC01100 | Fall from stairs | |
| 26432 | TC42100 | Fall from bed | |
| 7948 | TC52.00 | Fall on same level from stumbling | |
| 33529 | TC5z.00 | Fall on same level from slipping | |
| 98223 | 16D5.00 | Fall onto outstretched hand | |
| 41909 | TC01z00 | Fall on or from stairs NOS | |
| 43092 | TC02000 | Fall on steps | |
| 43571 | TC3..00 | Fall into hole or other opening in surface | |
| 21306 | TC4z.00 | Fall from one level to another NOS | |
| 53082 | TC02100 | Fall from steps | |
| 44626 | TC02.00 | Fall on or from steps | |
| 38818 | TC42000 | Fall from chair | |
| 64696 | TC0z.00 | Fall on or from stairs or steps NOS | |
| 7876 | TC4yz00 | Other fall from one level to another NOS | |
| 41853 | TC4y.00 | Other fall from one level to another | |
| 69020 | TC4y200 | Fall from stationary vehicle | |
| 93574 | 8O9..00 | Provision of telecare community alarm service | |
| 53463 | TC00.00 | Fall on or from escalator | |
| 56316 | TC00000 | Fall on escalator | |
| 64722 | TC02z00 | Fall on or from steps NOS | |
| 59404 | TC42.00 | Fall from chair or bed | |
| 29568 | TC3yz00 | Fall into other hole | |
| 55743 | 67ID.00 | Falls advice – hip protectors advised | |
| 48309 | 67IE.00 | Falls advice – hip protectors supplied | |
| 44119 | 8BIG.00 | Falls caused by medication | |
| 109088 | 9Nlf.00 | Seen by community falls team | |
| 16684 | T04..00 | Fall in | |
| 58753 | T040.00 | Fall in train | |
| 94933 | T040100 | Fall in train | |
| 59911 | T041.00 | Fall on train | |
| 97335 | T04z.00 | Fall in | |
| 18097 | T170.00 | MVTA – fall down stairs of motor bus while board/alighting | |
| 41114 | T171.00 | MVTA – fall from car in street while boarding/alighting | |
| 60782 | T53..00 | Fall in | |
| 110413 | T53z.00 | Fall in | |
| 60003 | TC42z00 | Fall from chair or bed NOS | |
| 17638 | TH03.00 | Late effects of accidental fall | |
| 7970 | U10..00 | [X]Falls | |
| 21903 | U100.00 | [X]Fall on same level involving ice and snow | |
| 68559 | U100000 | [X]Fall on same level involving ice and snow occurrence home | |
| 63515 | U100200 | [X]Fall sam lvl inv ice/snw occ sch oth inst/pub admin area | |
| 43615 | U100300 | [X]Fall same levl involv ice/snow | |
| 60427 | U100400 | [X]Fall same levl inv ice and snow | |
| 93148 | U100500 | [X]Fall same levl inv ice/snow | |
| 71613 | U100z00 | [X]Fall same levl inv ice/snow | |
| 29821 | U101.00 | [X]Fall on same level from slipping | |
| 49035 | U101000 | [X]Fall same levl frm slip trip+stumb | |
| 49210 | U101100 | [X]Fall same level from slip trip+stumb occ resid instit | |
| 60424 | U101200 | [X]Fall sme levl slp trp+stmb occ sch | |
| 49100 | U101300 | [X]Fall sme levl frm slip trip+stumb | |
| 52452 | U101400 | [X]Fall same level from slip trip+stumb | |
| 68616 | U101500 | [X]Fall sme lvl frm slip trip+stumb | |
| 68895 | U101600 | [X]Fall same levl | |
| 61705 | U101700 | [X]Fall same level from slip trip+stumbling | |
| 49218 | U101y00 | [X]Fall same level | |
| 68579 | U101z00 | [X]Fall same levl frm slip trip+stumbling | |
| 111606 | U102200 | [X]Fall | |
| 66934 | U103000 | [X]Oth fall same levl | |
| 109428 | U103500 | [X]Oth fall sme levl coll/push anth pers occ trad/serv area | |
| 62109 | U103y00 | [X]Oth fall sme levl coll/push anoth per occ oth spec place | |
| 93454 | U103z00 | [X]Oth fall same levl coll/push anoth pers occ unspec place | |
| 67230 | U104.00 | [X]Fall while being carried or supported by other persons | |
| 52410 | U104000 | [X]Fall while carried/supported by other persons | |
| 51851 | U104100 | [X]Fall whle carried/supported oth persons occ resid instit | |
| 110968 | U104z00 | [X]Fall whle carr’d/supportd by oth per | |
| 21349 | U105.00 | [X]Fall involving wheelchair | |
| 98315 | U105000 | [X]Fall involving wheelchair | |
| 67903 | U105100 | [X]Fall involving wheelchair occurrence residential instit’n | |
| 85959 | U105500 | [X]Fall involving wheelchair occurrence at trade/service area | |
| 98713 | U105700 | [X]Fall involving wheelchair | |
| 109423 | U105y00 | [X]Fall involv wheelchair | |
| 52374 | U106.00 | [X]Fall involving bed | |
| 44419 | U106000 | [X]Fall involving bed | |
| 69762 | U106100 | [X]Fall involving bed occurrence in residential institution | |
| 50572 | U107.00 | [X]Fall involving chair | |
| 68600 | U107000 | [X]Fall involving chair | |
| 68617 | U107z00 | [X]Fall involving chair | |
| 55553 | U108.00 | [X]Fall involving other furniture | |
| 68591 | U108000 | [X]Fall involving other furniture | |
| 66922 | U108100 | [X]Fall involv other furniture occurrn resident institut’n | |
| 36402 | U10A.00 | [X]Fall on and from stairs and steps | |
| 52432 | U10A000 | [X]Fall on and from stairs and steps | |
| 52466 | U10A100 | [X]Fall on+from stair+step occurrence resident instit’n | |
| 111571 | U10A200 | [X]Fall on+frm stair+step occ sch oth inst/pub adm area | |
| 99385 | U10A400 | [X]Fall on+from stairs+steps occurrn on street/highway | |
| 51284 | U10A500 | [X]Fall on+from stair+step occurrn at trade/servce area | |
| 41105 | U10A511 | [X]Fall on or from escalator | |
| 68613 | U10Ay00 | [X]Fall on+from stair+step occurrn at oth specif place | |
| 64193 | U10Az00 | [X]Fall on+from stair+step occurrnce at unspecif place | |
| 50316 | U10D.00 | [X]Fall from | |
| 52380 | U10D000 | [X]Fall from out of/through building/structur occurn home | |
| 100710 | U10D100 | [X]Fall from out of/thro buildng/struct occ resid instit’n | |
| 110898 | U10D400 | [X]Fall from out/thro buildng/struct occ on street/highway | |
| 92721 | U10H.00 | [X]Other fall from one level to another | |
| 51669 | U10H000 | [X]Other fall from one level to another | |
| 68609 | U10H200 | [X]Othr fall frm one level to anothr | |
| 68562 | U10H400 | [X]Othr fall from one level to anothr occurrn street/h’way | |
| 68604 | U10H500 | [X]Other fall frm one level to anothr occ at trde/serv area | |
| 95961 | U10H600 | [X]Other fall frm one level to anoth occ indust/constr area | |
| 72468 | U10Hy00 | [X]Other fall frm one levl to anothr occ at oth specif plce | |
| 49233 | U10Hz00 | [X]Othr fall frm one level to anothr occurrn at unspec plce | |
| 48496 | U10J.00 | [X]Other fall on same level | |
| 43191 | U10J000 | [X]Other fall on same level | |
| 72474 | U10J100 | [X]Other fall on same level | |
| 100060 | U10J200 | [X]Other fall on same levl occ schl oth inst/pub admin area | |
| 101254 | U10J400 | [X]Other fall on same level | |
| 68608 | U10J600 | [X]Other fall on same levl | |
| 101523 | U10Jy00 | [X]Other fall on same level occurrn at oth specified place | |
| 98876 | U10Jz00 | [X]Other fall on same level occurrence at unspecified place | |
| 24776 | U10z.00 | [X]Unspecified fall | |
| 10419 | U10z000 | [X]Unspecified fall | |
| 46303 | U10z100 | [X]Unspecified fall | |
| 55202 | U10z300 | [X]Unspecified fall | |
| 97327 | U10z400 | [X]Unspecified fall | |
| 106900 | U10z700 | [X]Unspecified fall | |
| 96546 | U10zy00 | [X]Unspecified fall | |
| 61170 | U10zz00 | [X]Unspecified fall | |
| 6785 | ZV71B00 | [V]Examination and observation following a fall | |
| Malabsorptionb | 9355 | J69..00 | Intestinal malabsorption |
| 5088 | J69yz00 | Other gastrointestinal tract malabsorption NOS | |
| 4787 | J690.15 | Steatorrhea – idiopathic | |
| 6663 | J69y.00 | Other intestinal malabsorption | |
| 42715 | J69z.00 | Intestinal malabsorption NOS | |
| 23498 | J692.00 | Blind loop syndrome | |
| 31392 | J69y600 | Intestinal malabsorption of fat | |
| 2482 | D011100 | Vit B12 defic anaemia due to malabsorption with proteinuria | |
| 19441 | C285.00 | Adult osteomalacia due to malabsorption | |
| 37440 | J693.11 | Postsurgical malabsorption – other | |
| 49191 | J69y200 | Intestinal malabsorption of protein | |
| 55481 | D012300 | Folate-deficiency anaemia due to malabsorption | |
| 72529 | Jyu9000 | [X]Other intestinal malabsorption | |
| 57647 | J693100 | Post gastrointestinal tract surgery malnutrition | |
| 49739 | J69y300 | Intestinal malabsorption of carbohydrate | |
| 93655 | N330700 | Postsurgical malabsorption osteoporosis | |
| Endocrine problemsc | 1472 | C02..11 | Hyperthyroidism |
| 5257 | C020.12 | Graves’ disease | |
| 6245 | 1431.00 | H/O: hyperthyroidism | |
| 3857 | C052.11 | Autoimmune thyroiditis | |
| 17604 | C150.00 | Cushing syndrome | |
| 11947 | L181500 | Postpartum thyroiditis | |
| 30799 | C051.00 | Subacute thyroiditis | |
| 4898 | C050.00 | Acute thyroiditis | |
| 18382 | C150111 | Drug-induced Cushing syndrome | |
| 26362 | 212P.00 | Hyperthyroidism resolved | |
| 106640 | C025.00 | Subclinical hyperthyroidism | |
| 21747 | C051.11 | De Quervain’s thyroiditis | |
| 20275 | C150100 | Iatrogenic Cushing syndrome | |
| 60534 | C150z00 | Cushing syndrome NOS | |
| 49508 | C024.00 | Thyrotoxicosis from ectopic thyroid nodule | |
| 68626 | FyuBD00 | [X]Dysthyroid exophthalmos | |
| 42323 | C050z00 | Acute thyroiditis NOS | |
| 53682 | C150200 | Pituitary dependent Cushing syndrome | |
| 65444 | C05y.00 | Other and unspecified chronic thyroiditis | |
| 61026 | C054.00 | Iatrogenic thyroiditis | |
| 53667 | C053.11 | Riedel’s thyroiditis | |
| 65907 | C05y400 | Chronic thyroiditis with transient thyrotoxicosis | |
| 65754 | C150500 | Alcohol-induced pseudo-Cushing syndrome | |
| 67972 | C050000 | Acute nonsuppurative thyroiditis | |
| 65120 | C150300 | Ectopic ACTH secretion causing Cushing syndrome | |
| 60690 | F395100 | Myopathy due to Cushing syndrome | |
| 70967 | C150000 | Idiopathic Cushing syndrome | |
| 56270 | C024z00 | Thyrotoxicosis from ectopic thyroid nodule NOS | |
| 70773 | C050100 | Acute suppurative thyroiditis | |
| 95807 | Cyu4500 | [X]Other Cushing syndrome | |
| 64656 | C024000 | Thyrotoxicosis from ectopic thyroid nodule with no crisis |
| CPRD Prodcode | CPRD drug/substance (drug name as recorded in CPRD) | QFracture-2012 variable |
|---|---|---|
| 34916 | Amitriptyline hydrochloride | Antidepressant |
| 45242 | Amitriptyline hydrochloride | Antidepressant |
| 83 | Amitriptyline hydrochloride | Antidepressant |
| 33090 | Amitriptyline hydrochloride | Antidepressant |
| 52867 | Amitriptyline hydrochloride | Antidepressant |
| 24141 | Amitriptyline hydrochloride | Antidepressant |
| 57972 | Amitriptyline hydrochloride | Antidepressant |
| 55491 | Amitriptyline hydrochloride | Antidepressant |
| 70991 | Amitriptyline hydrochloride | Antidepressant |
| 61835 | Amitriptyline hydrochloride | Antidepressant |
| 76839 | Amitriptyline hydrochloride | Antidepressant |
| 45233 | Amitriptyline hydrochloride | Antidepressant |
| 34731 | Amitriptyline hydrochloride | Antidepressant |
| 66578 | Amitriptyline hydrochloride | Antidepressant |
| 80135 | Amitriptyline hydrochloride | Antidepressant |
| 57107 | Amitriptyline hydrochloride | Antidepressant |
| 65879 | Amitriptyline hydrochloride | Antidepressant |
| 24152 | Amitriptyline hydrochloride | Antidepressant |
| 59161 | Amitriptyline hydrochloride | Antidepressant |
| 34401 | Amitriptyline hydrochloride | Antidepressant |
| 46801 | Amitriptyline hydrochloride | Antidepressant |
| 64000 | Amitriptyline hydrochloride | Antidepressant |
| 79826 | Amitriptyline hydrochloride | Antidepressant |
| 70300 | Amitriptyline hydrochloride | Antidepressant |
| 76298 | Amitriptyline hydrochloride | Antidepressant |
| 46818 | Amitriptyline hydrochloride | Antidepressant |
| 76927 | Amitriptyline hydrochloride | Antidepressant |
| 487 | Amitriptyline hydrochloride | Antidepressant |
| 34197 | Amitriptyline hydrochloride | Antidepressant |
| 41729 | Amitriptyline hydrochloride | Antidepressant |
| 42394 | Amitriptyline hydrochloride | Antidepressant |
| 34474 | Amitriptyline hydrochloride | Antidepressant |
| 32439 | Amitriptyline hydrochloride | Antidepressant |
| 49 | Amitriptyline hydrochloride | Antidepressant |
| 34782 | Amitriptyline hydrochloride | Antidepressant |
| 54877 | Amitriptyline hydrochloride | Antidepressant |
| 24145 | Amitriptyline hydrochloride | Antidepressant |
| 55139 | Amitriptyline hydrochloride | Antidepressant |
| 42078 | Amitriptyline hydrochloride | Antidepressant |
| 71042 | Amitriptyline hydrochloride | Antidepressant |
| 65987 | Amitriptyline hydrochloride | Antidepressant |
| 64647 | Amitriptyline hydrochloride | Antidepressant |
| 79766 | Amitriptyline hydrochloride | Antidepressant |
| 34503 | Amitriptyline hydrochloride | Antidepressant |
| 24134 | Amitriptyline hydrochloride | Antidepressant |
| 66579 | Amitriptyline hydrochloride | Antidepressant |
| 60355 | Amitriptyline hydrochloride | Antidepressant |
| 77167 | Amitriptyline hydrochloride | Antidepressant |
| 65439 | Amitriptyline hydrochloride | Antidepressant |
| 66572 | Amitriptyline hydrochloride | Antidepressant |
| 24147 | Amitriptyline hydrochloride | Antidepressant |
| 34129 | Amitriptyline hydrochloride | Antidepressant |
| 6312 | Amitriptyline hydrochloride | Antidepressant |
| 78364 | Amitriptyline hydrochloride | Antidepressant |
| 67127 | Amitriptyline hydrochloride | Antidepressant |
| 34224 | Amitriptyline hydrochloride | Antidepressant |
| 60410 | Amitriptyline hydrochloride | Antidepressant |
| 4682 | Amitriptyline hydrochloride | Antidepressant |
| 40396 | Amitriptyline hydrochloride | Antidepressant |
| 1888 | Amitriptyline hydrochloride | Antidepressant |
| 34274 | Amitriptyline hydrochloride | Antidepressant |
| 34634 | Amitriptyline hydrochloride | Antidepressant |
| 64330 | Amitriptyline hydrochloride | Antidepressant |
| 78221 | Amitriptyline hydrochloride | Antidepressant |
| 46970 | Amitriptyline hydrochloride | Antidepressant |
| 34182 | Amitriptyline hydrochloride | Antidepressant |
| 69712 | Amitriptyline hydrochloride | Antidepressant |
| 33624 | Amitriptyline hydrochloride | Antidepressant |
| 34107 | Amitriptyline hydrochloride | Antidepressant |
| 4690 | Amitriptyline hydrochloride | Antidepressant |
| 34251 | Amitriptyline hydrochloride | Antidepressant |
| 59820 | Amitriptyline hydrochloride | Antidepressant |
| 64141 | Amitriptyline hydrochloride | Antidepressant |
| 76952 | Amitriptyline hydrochloride | Antidepressant |
| 77497 | Amitriptyline hydrochloride | Antidepressant |
| 26213 | Amitriptyline hydrochloride | Antidepressant |
| 20026 | Amitriptyline hydrochloride | Antidepressant |
| 27008 | Amitriptyline hydrochloride | Antidepressant |
| 24680 | Amitriptyline hydrochloride | Antidepressant |
| 2486 | Amitriptyline hydrochloride | Antidepressant |
| 2985 | Amitriptyline hydrochloride | Antidepressant |
| 8726 | Amitriptyline hydrochloride | Antidepressant |
| 7751 | Amitriptyline hydrochloride | Antidepressant |
| 8332 | Amitriptyline hydrochloride | Antidepressant |
| 19779 | Amitriptyline hydrochloride | Antidepressant |
| 182 | Amitriptyline hydrochloride | Antidepressant |
| 22070 | Amitriptyline hydrochloride | Antidepressant |
| 3777 | Amitriptyline hydrochloride | Antidepressant |
| 2525 | Amitriptyline hydrochloride | Antidepressant |
| 48065 | Amitriptyline hydrochloride | Antidepressant |
| 8878 | Amitriptyline hydrochloride | Antidepressant |
| 8831 | Amitriptyline hydrochloride | Antidepressant |
| 21081 | Amitriptyline hydrochloride/chlordiazepoxide | Antidepressant |
| 18342 | Amitriptyline hydrochloride/chlordiazepoxide | Antidepressant |
| 11963 | Amitriptyline hydrochloride/chlordiazepoxide | Antidepressant |
| 14534 | Amitriptyline hydrochloride/chlordiazepoxide | Antidepressant |
| 3490 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 595 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 1453 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 1208 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 38827 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 16323 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 6894 | Amitriptyline hydrochloride/perphenazine | Antidepressant |
| 3652 | Amoxapine | Antidepressant |
| 4411 | Amoxapine | Antidepressant |
| 17319 | Amoxapine | Antidepressant |
| 3351 | Amoxapine | Antidepressant |
| 21357 | Amoxapine | Antidepressant |
| 24723 | Amoxapine | Antidepressant |
| 15380 | Amoxapine | Antidepressant |
| 14398 | Amoxapine | Antidepressant |
| 55289 | Amoxapine | Antidepressant |
| 12227 | Butriptyline hydrochloride | Antidepressant |
| 32457 | Butriptyline hydrochloride | Antidepressant |
| 18932 | Butriptyline hydrochloride | Antidepressant |
| 3195 | Clomipramine | Antidepressant |
| 30375 | Clomipramine hydrochloride | Antidepressant |
| 26513 | Clomipramine hydrochloride | Antidepressant |
| 7515 | Clomipramine hydrochloride | Antidepressant |
| 3657 | Clomipramine hydrochloride | Antidepressant |
| 8719 | Clomipramine hydrochloride | Antidepressant |
| 7693 | Clomipramine hydrochloride | Antidepressant |
| 7894 | Clomipramine hydrochloride | Antidepressant |
| 3194 | Clomipramine hydrochloride | Antidepressant |
| 34866 | Clomipramine hydrochloride | Antidepressant |
| 68665 | Clomipramine hydrochloride | Antidepressant |
| 41628 | Clomipramine hydrochloride | Antidepressant |
| 62620 | Clomipramine hydrochloride | Antidepressant |
| 43561 | Clomipramine hydrochloride | Antidepressant |
| 3670 | Clomipramine hydrochloride | Antidepressant |
| 34245 | Clomipramine hydrochloride | Antidepressant |
| 41563 | Clomipramine hydrochloride | Antidepressant |
| 45350 | Clomipramine hydrochloride | Antidepressant |
| 65762 | Clomipramine hydrochloride | Antidepressant |
| 8720 | Clomipramine hydrochloride | Antidepressant |
| 64458 | Clomipramine hydrochloride | Antidepressant |
| 3925 | Clomipramine hydrochloride | Antidepressant |
| 45318 | Clomipramine hydrochloride | Antidepressant |
| 41597 | Clomipramine hydrochloride | Antidepressant |
| 53187 | Clomipramine hydrochloride | Antidepressant |
| 78324 | Clomipramine hydrochloride | Antidepressant |
| 65804 | Clomipramine hydrochloride | Antidepressant |
| 53161 | Clomipramine hydrochloride | Antidepressant |
| 38274 | Clomipramine hydrochloride | Antidepressant |
| 78057 | Clomipramine hydrochloride | Antidepressant |
| 8661 | Clomipramine hydrochloride | Antidepressant |
| 7981 | Desipramine | Antidepressant |
| 7979 | Desipramine | Antidepressant |
| 43024 | Dosulepin hydrochloride | Antidepressant |
| 77130 | Dosulepin hydrochloride | Antidepressant |
| 70838 | Dosulepin hydrochloride | Antidepressant |
| 84 | Dosulepin hydrochloride | Antidepressant |
| 23426 | Dosulepin hydrochloride | Antidepressant |
| 34745 | Dosulepin hydrochloride | Antidepressant |
| 34643 | Dosulepin hydrochloride | Antidepressant |
| 31824 | Dosulepin hydrochloride | Antidepressant |
| 44853 | Dosulepin hydrochloride | Antidepressant |
| 29875 | Dosulepin hydrochloride | Antidepressant |
| 33164 | Dosulepin hydrochloride | Antidepressant |
| 34641 | Dosulepin hydrochloride | Antidepressant |
| 76317 | Dosulepin hydrochloride | Antidepressant |
| 34223 | Dosulepin hydrochloride | Antidepressant |
| 50722 | Dosulepin hydrochloride | Antidepressant |
| 71023 | Dosulepin hydrochloride | Antidepressant |
| 70593 | Dosulepin hydrochloride | Antidepressant |
| 74 | Dosulepin hydrochloride | Antidepressant |
| 32121 | Dosulepin hydrochloride | Antidepressant |
| 19186 | Dosulepin hydrochloride | Antidepressant |
| 67728 | Dosulepin hydrochloride | Antidepressant |
| 42734 | Dosulepin hydrochloride | Antidepressant |
| 31826 | Dosulepin hydrochloride | Antidepressant |
| 34525 | Dosulepin hydrochloride | Antidepressant |
| 62681 | Dosulepin hydrochloride | Antidepressant |
| 71059 | Dosulepin hydrochloride | Antidepressant |
| 34058 | Dosulepin hydrochloride | Antidepressant |
| 57926 | Dosulepin hydrochloride | Antidepressant |
| 1940 | Dosulepin hydrochloride | Antidepressant |
| 15632 | Dosulepin hydrochloride | Antidepressant |
| 21820 | Dosulepin hydrochloride | Antidepressant |
| 21819 | Dosulepin hydrochloride | Antidepressant |
| 67990 | Dosulepin hydrochloride | Antidepressant |
| 51758 | Dosulepin hydrochloride | Antidepressant |
| 1169 | Dosulepin hydrochloride | Antidepressant |
| 2320 | Dosulepin hydrochloride | Antidepressant |
| 30376 | Dosulepin hydrochloride | Antidepressant |
| 21157 | Dosulepin hydrochloride | Antidepressant |
| 19168 | Dosulepin hydrochloride | Antidepressant |
| 45737 | Dosulepin hydrochloride | Antidepressant |
| 6054 | Dosulepin hydrochloride | Antidepressant |
| 10948 | Dosulepin hydrochloride | Antidepressant |
| 5190 | Doxepin hydrochloride | Antidepressant |
| 9558 | Doxepin hydrochloride | Antidepressant |
| 15975 | Doxepin hydrochloride | Antidepressant |
| 3842 | Doxepin hydrochloride | Antidepressant |
| 3554 | Doxepin hydrochloride | Antidepressant |
| 5073 | Doxepin hydrochloride | Antidepressant |
| 73363 | Doxepin hydrochloride | Antidepressant |
| 7059 | Doxepin hydrochloride | Antidepressant |
| 35258 | Doxepin hydrochloride | Antidepressant |
| 35493 | Doxepin hydrochloride | Antidepressant |
| 10413 | Doxepin hydrochloride | Antidepressant |
| 12129 | Doxepin hydrochloride | Antidepressant |
| 12125 | Doxepin hydrochloride | Antidepressant |
| 14519 | Doxepin hydrochloride | Antidepressant |
| 40777 | Doxepin Hydrochloride | Antidepressant |
| 2936 | Fluphenazine hydrochloride/nortriptyline hydrochloride | Antidepressant |
| 7780 | Fluphenazine hydrochloride/nortriptyline hydrochloride | Antidepressant |
| 1310 | Imipramine hydrochloride | Antidepressant |
| 41681 | Imipramine hydrochloride | Antidepressant |
| 34222 | Imipramine hydrochloride | Antidepressant |
| 67935 | Imipramine hydrochloride | Antidepressant |
| 71253 | Imipramine hydrochloride | Antidepressant |
| 70287 | Imipramine hydrochloride | Antidepressant |
| 32863 | Imipramine hydrochloride | Antidepressant |
| 34872 | Imipramine hydrochloride | Antidepressant |
| 1809 | Imipramine hydrochloride | Antidepressant |
| 34813 | Imipramine hydrochloride | Antidepressant |
| 34355 | Imipramine hydrochloride | Antidepressant |
| 41408 | Imipramine hydrochloride | Antidepressant |
| 8055 | Imipramine hydrochloride | Antidepressant |
| 42247 | Imipramine hydrochloride | Antidepressant |
| 33074 | Imipramine hydrochloride | Antidepressant |
| 2579 | Imipramine hydrochloride | Antidepressant |
| 56501 | Imipramine hydrochloride | Antidepressant |
| 7910 | Imipramine hydrochloride | Antidepressant |
| 4404 | Imipramine hydrochloride | Antidepressant |
| 27476 | Iprindole | Antidepressant |
| 27733 | Iprindole | Antidepressant |
| 24700 | Iprindole | Antidepressant |
| 31672 | Iprindole | Antidepressant |
| 79397 | Lofepramine | Antidepressant |
| 58450 | Lofepramine hydrochloride | Antidepressant |
| 2093 | Lofepramine hydrochloride | Antidepressant |
| 41627 | Lofepramine hydrochloride | Antidepressant |
| 114 | Lofepramine hydrochloride | Antidepressant |
| 34046 | Lofepramine hydrochloride | Antidepressant |
| 34950 | Lofepramine hydrochloride | Antidepressant |
| 71067 | Lofepramine hydrochloride | Antidepressant |
| 74586 | Lofepramine hydrochloride | Antidepressant |
| 66100 | Lofepramine hydrochloride | Antidepressant |
| 34578 | Lofepramine hydrochloride | Antidepressant |
| 68657 | Lofepramine hydrochloride | Antidepressant |
| 67742 | Lofepramine hydrochloride | Antidepressant |
| 56703 | Lofepramine hydrochloride | Antidepressant |
| 34672 | Lofepramine hydrochloride | Antidepressant |
| 60591 | Lofepramine hydrochloride | Antidepressant |
| 56229 | Lofepramine hydrochloride | Antidepressant |
| 43534 | Lofepramine hydrochloride | Antidepressant |
| 4218 | Lofepramine hydrochloride | Antidepressant |
| 77717 | Lofepramine hydrochloride | Antidepressant |
| 25444 | Lofepramine hydrochloride | Antidepressant |
| 7468 | Mianserin hydrochloride | Antidepressant |
| 8144 | Mianserin hydrochloride | Antidepressant |
| 8585 | Mianserin hydrochloride | Antidepressant |
| 3083 | Mianserin hydrochloride | Antidepressant |
| 47363 | Mianserin hydrochloride | Antidepressant |
| 4329 | Mianserin hydrochloride | Antidepressant |
| 6255 | Mianserin hydrochloride | Antidepressant |
| 12368 | Mianserin hydrochloride | Antidepressant |
| 11956 | Mianserin hydrochloride | Antidepressant |
| 12192 | Mianserin hydrochloride | Antidepressant |
| 7677 | Nortriptyline hydrochloride | Antidepressant |
| 8640 | Nortriptyline hydrochloride | Antidepressant |
| 3183 | Nortriptyline hydrochloride | Antidepressant |
| 65237 | Nortriptyline hydrochloride | Antidepressant |
| 55970 | Nortriptyline hydrochloride | Antidepressant |
| 72626 | Nortriptyline hydrochloride | Antidepressant |
| 68228 | Nortriptyline hydrochloride | Antidepressant |
| 3903 | Nortriptyline hydrochloride | Antidepressant |
| 48216 | Nortriptyline hydrochloride | Antidepressant |
| 63276 | Nortriptyline hydrochloride | Antidepressant |
| 66201 | Nortriptyline hydrochloride | Antidepressant |
| 78224 | Nortriptyline hydrochloride | Antidepressant |
| 69317 | Nortriptyline hydrochloride | Antidepressant |
| 17183 | Nortriptyline hydrochloride | Antidepressant |
| 12549 | Nortriptyline hydrochloride | Antidepressant |
| 12353 | Nortriptyline hydrochloride | Antidepressant |
| 4118 | Nortriptyline hydrochloride | Antidepressant |
| 39145 | Nortriptyline hydrochloride | Antidepressant |
| 7678 | Nortriptyline hydrochloride | Antidepressant |
| 8493 | Nortriptyline hydrochloride/fluphenazine hydrochloride | Antidepressant |
| 14578 | Nortriptyline hydrochloride/fluphenazine hydrochloride | Antidepressant |
| 20571 | Nortriptyline hydrochloride/fluphenazine hydrochloride | Antidepressant |
| 60929 | Protriptyline hydrochloride | Antidepressant |
| 7755 | Protriptyline hydrochloride | Antidepressant |
| 7816 | Protriptyline hydrochloride | Antidepressant |
| 11187 | Protriptyline hydrochloride | Antidepressant |
| 7756 | Protriptyline hydrochloride | Antidepressant |
| 4194 | Trazodone hydrochloride | Antidepressant |
| 4003 | Trazodone hydrochloride | Antidepressant |
| 4874 | Trazodone hydrochloride | Antidepressant |
| 8174 | Trazodone hydrochloride | Antidepressant |
| 13621 | Trazodone hydrochloride | Antidepressant |
| 1730 | Trazodone hydrochloride | Antidepressant |
| 34580 | Trazodone hydrochloride | Antidepressant |
| 73639 | Trazodone hydrochloride | Antidepressant |
| 19181 | Trazodone hydrochloride | Antidepressant |
| 41709 | Trazodone hydrochloride | Antidepressant |
| 41710 | Trazodone hydrochloride | Antidepressant |
| 65152 | Trazodone hydrochloride | Antidepressant |
| 72291 | Trazodone hydrochloride | Antidepressant |
| 66749 | Trazodone hydrochloride | Antidepressant |
| 12710 | Trazodone hydrochloride | Antidepressant |
| 4020 | Trazodone hydrochloride | Antidepressant |
| 73419 | Trazodone hydrochloride | Antidepressant |
| 77915 | Trazodone hydrochloride | Antidepressant |
| 73636 | Trazodone hydrochloride | Antidepressant |
| 76480 | Trazodone hydrochloride | Antidepressant |
| 30983 | Trazodone hydrochloride | Antidepressant |
| 29857 | Trazodone hydrochloride | Antidepressant |
| 34470 | Trazodone hydrochloride | Antidepressant |
| 55137 | Trazodone hydrochloride | Antidepressant |
| 55138 | Trazodone hydrochloride | Antidepressant |
| 57226 | Trazodone hydrochloride | Antidepressant |
| 3355 | Trazodone hydrochloride | Antidepressant |
| 34003 | Trazodone hydrochloride | Antidepressant |
| 71031 | Trazodone hydrochloride | Antidepressant |
| 29339 | Trazodone hydrochloride | Antidepressant |
| 41609 | Trazodone hydrochloride | Antidepressant |
| 34421 | Trazodone hydrochloride | Antidepressant |
| 61842 | Trazodone hydrochloride | Antidepressant |
| 6442 | Trazodone hydrochloride | Antidepressant |
| 59931 | Trazodone hydrochloride | Antidepressant |
| 70521 | Trazodone hydrochloride | Antidepressant |
| 77474 | Trazodone hydrochloride | Antidepressant |
| 61657 | Trazodone hydrochloride | Antidepressant |
| 69355 | Trazodone hydrochloride | Antidepressant |
| 8928 | Trimipramine maleate | Antidepressant |
| 2532 | Trimipramine maleate | Antidepressant |
| 2531 | Trimipramine maleate | Antidepressant |
| 4310 | Trimipramine maleate | Antidepressant |
| 42228 | Trimipramine maleate | Antidepressant |
| 53808 | Trimipramine maleate | Antidepressant |
| 2039 | Trimipramine maleate | Antidepressant |
| 45226 | Trimipramine maleate | Antidepressant |
| 57978 | Trimipramine maleate | Antidepressant |
| 66493 | Trimipramine maleate | Antidepressant |
| 3196 | Trimipramine maleate | Antidepressant |
| 65445 | Trimipramine maleate | Antidepressant |
| 66919 | Trimipramine maleate | Antidepressant |
| 65213 | Trimipramine maleate | Antidepressant |
| 12309 | Viloxazine hydrochloride | Antidepressant |
| 12111 | Viloxazine hydrochloride | Antidepressant |
| 3861 | Citalopram hydrobromide | Antidepressant |
| 79784 | Citalopram hydrobromide | Antidepressant |
| 63953 | Citalopram hydrobromide | Antidepressant |
| 1712 | Citalopram hydrobromide | Antidepressant |
| 2408 | Citalopram hydrobromide | Antidepressant |
| 34498 | Citalopram hydrobromide | Antidepressant |
| 476 | Citalopram hydrobromide | Antidepressant |
| 34586 | Citalopram hydrobromide | Antidepressant |
| 64423 | Citalopram hydrobromide | Antidepressant |
| 32848 | Citalopram hydrobromide | Antidepressant |
| 49165 | Citalopram hydrobromide | Antidepressant |
| 42660 | Citalopram hydrobromide | Antidepressant |
| 52100 | Citalopram hydrobromide | Antidepressant |
| 59650 | Citalopram hydrobromide | Antidepressant |
| 53787 | Citalopram hydrobromide | Antidepressant |
| 71005 | Citalopram hydrobromide | Antidepressant |
| 33720 | Citalopram hydrobromide | Antidepressant |
| 52408 | Citalopram hydrobromide | Antidepressant |
| 34436 | Citalopram hydrobromide | Antidepressant |
| 45286 | Citalopram hydrobromide | Antidepressant |
| 75697 | Citalopram hydrobromide | Antidepressant |
| 52824 | Citalopram hydrobromide | Antidepressant |
| 59193 | Citalopram hydrobromide | Antidepressant |
| 63441 | Citalopram hydrobromide | Antidepressant |
| 34499 | Citalopram hydrobromide | Antidepressant |
| 60888 | Citalopram hydrobromide | Antidepressant |
| 41528 | Citalopram hydrobromide | Antidepressant |
| 56355 | Citalopram hydrobromide | Antidepressant |
| 34413 | Citalopram hydrobromide | Antidepressant |
| 54827 | Citalopram hydrobromide | Antidepressant |
| 34722 | Citalopram hydrobromide | Antidepressant |
| 67 | Citalopram hydrobromide | Antidepressant |
| 34356 | Citalopram hydrobromide | Antidepressant |
| 67097 | Citalopram hydrobromide | Antidepressant |
| 34871 | Citalopram hydrobromide | Antidepressant |
| 53394 | Citalopram hydrobromide | Antidepressant |
| 48026 | Citalopram hydrobromide | Antidepressant |
| 56009 | Citalopram hydrobromide | Antidepressant |
| 58476 | Citalopram hydrobromide | Antidepressant |
| 52607 | Citalopram hydrobromide | Antidepressant |
| 52354 | Citalopram hydrobromide | Antidepressant |
| 34415 | Citalopram hydrobromide | Antidepressant |
| 34970 | Citalopram hydrobromide | Antidepressant |
| 73417 | Citalopram hydrobromide | Antidepressant |
| 72373 | Citalopram hydrobromide | Antidepressant |
| 26016 | Citalopram hydrobromide | Antidepressant |
| 34966 | Citalopram hydrobromide | Antidepressant |
| 60568 | Citalopram hydrobromide | Antidepressant |
| 34822 | Citalopram hydrobromide | Antidepressant |
| 71848 | Citalopram hydrobromide | Antidepressant |
| 43519 | Citalopram hydrobromide | Antidepressant |
| 4770 | Citalopram hydrobromide | Antidepressant |
| 36746 | Citalopram hydrobromide | Antidepressant |
| 69571 | Citalopram hydrobromide | Antidepressant |
| 46977 | Citalopram hydrobromide | Antidepressant |
| 75075 | Citalopram hydrobromide | Antidepressant |
| 60839 | Citalopram hydrobromide | Antidepressant |
| 70790 | Citalopram hydrobromide | Antidepressant |
| 55033 | Citalopram hydrobromide | Antidepressant |
| 75702 | Citalopram hydrobromide | Antidepressant |
| 34603 | Citalopram hydrobromide | Antidepressant |
| 45223 | Citalopram hydrobromide | Antidepressant |
| 34466 | Citalopram hydrobromide | Antidepressant |
| 45304 | Citalopram hydrobromide | Antidepressant |
| 46926 | Citalopram hydrobromide | Antidepressant |
| 32546 | Citalopram hydrobromide | Antidepressant |
| 29756 | Citalopram hydrobromide | Antidepressant |
| 74753 | Citalopram hydrobromide | Antidepressant |
| 815 | Citalopram hydrochloride | Antidepressant |
| 513 | Citalopram hydrochloride | Antidepressant |
| 57936 | Citalopram hydrochloride | Antidepressant |
| 56292 | Citalopram hydrochloride | Antidepressant |
| 72124 | Citalopram hydrochloride | Antidepressant |
| 74785 | Escitalopram oxalate | Antidepressant |
| 648 | Escitalopram oxalate | Antidepressant |
| 74858 | Escitalopram oxalate | Antidepressant |
| 26056 | Escitalopram oxalate | Antidepressant |
| 6360 | Escitalopram oxalate | Antidepressant |
| 41062 | Escitalopram oxalate | Antidepressant |
| 785 | Escitalopram oxalate | Antidepressant |
| 603 | Escitalopram oxalate | Antidepressant |
| 63916 | Escitalopram oxalate | Antidepressant |
| 74993 | Escitalopram oxalate | Antidepressant |
| 20152 | Escitalopram oxalate | Antidepressant |
| 6218 | Escitalopram oxalate | Antidepressant |
| 72773 | Escitalopram oxalate | Antidepressant |
| 40726 | Escitalopram oxalate | Antidepressant |
| 6405 | Escitalopram oxalate | Antidepressant |
| 33071 | Fluoxetine hydrochloride | Antidepressant |
| 67431 | Fluoxetine hydrochloride | Antidepressant |
| 69941 | Fluoxetine hydrochloride | Antidepressant |
| 77881 | Fluoxetine hydrochloride | Antidepressant |
| 42499 | Fluoxetine hydrochloride | Antidepressant |
| 75645 | Fluoxetine hydrochloride | Antidepressant |
| 38890 | Fluoxetine hydrochloride | Antidepressant |
| 22 | Fluoxetine hydrochloride | Antidepressant |
| 19183 | Fluoxetine hydrochloride | Antidepressant |
| 71852 | Fluoxetine hydrochloride | Antidepressant |
| 45329 | Fluoxetine hydrochloride | Antidepressant |
| 60962 | Fluoxetine hydrochloride | Antidepressant |
| 75799 | Fluoxetine hydrochloride | Antidepressant |
| 67736 | Fluoxetine hydrochloride | Antidepressant |
| 45247 | Fluoxetine hydrochloride | Antidepressant |
| 75688 | Fluoxetine hydrochloride | Antidepressant |
| 34202 | Fluoxetine hydrochloride | Antidepressant |
| 34294 | Fluoxetine hydrochloride | Antidepressant |
| 69525 | Fluoxetine hydrochloride | Antidepressant |
| 59358 | Fluoxetine hydrochloride | Antidepressant |
| 66744 | Fluoxetine hydrochloride | Antidepressant |
| 34288 | Fluoxetine hydrochloride | Antidepressant |
| 42107 | Fluoxetine hydrochloride | Antidepressant |
| 62155 | Fluoxetine hydrochloride | Antidepressant |
| 19470 | Fluoxetine hydrochloride | Antidepressant |
| 45224 | Fluoxetine hydrochloride | Antidepressant |
| 67769 | Fluoxetine hydrochloride | Antidepressant |
| 34456 | Fluoxetine hydrochloride | Antidepressant |
| 34849 | Fluoxetine hydrochloride | Antidepressant |
| 67092 | Fluoxetine hydrochloride | Antidepressant |
| 45316 | Fluoxetine hydrochloride | Antidepressant |
| 33410 | Fluoxetine hydrochloride | Antidepressant |
| 60534 | Fluoxetine hydrochloride | Antidepressant |
| 60138 | Fluoxetine hydrochloride | Antidepressant |
| 2548 | Fluoxetine hydrochloride | Antidepressant |
| 34216 | Fluoxetine hydrochloride | Antidepressant |
| 42803 | Fluoxetine hydrochloride | Antidepressant |
| 60619 | Fluoxetine hydrochloride | Antidepressant |
| 73414 | Fluoxetine hydrochloride | Antidepressant |
| 30258 | Fluoxetine hydrochloride | Antidepressant |
| 36893 | Fluoxetine hydrochloride | Antidepressant |
| 68266 | Fluoxetine hydrochloride | Antidepressant |
| 69685 | Fluoxetine hydrochloride | Antidepressant |
| 74886 | Fluoxetine hydrochloride | Antidepressant |
| 67496 | Fluoxetine hydrochloride | Antidepressant |
| 79590 | Fluoxetine hydrochloride | Antidepressant |
| 67562 | Fluoxetine hydrochloride | Antidepressant |
| 75068 | Fluoxetine hydrochloride | Antidepressant |
| 78889 | Fluoxetine hydrochloride | Antidepressant |
| 4075 | Fluoxetine hydrochloride | Antidepressant |
| 75247 | Fluoxetine hydrochloride | Antidepressant |
| 67888 | Fluoxetine hydrochloride | Antidepressant |
| 34856 | Fluoxetine hydrochloride | Antidepressant |
| 62335 | Fluoxetine hydrochloride | Antidepressant |
| 14740 | Fluoxetine hydrochloride | Antidepressant |
| 67758 | Fluoxetine hydrochloride | Antidepressant |
| 77381 | Fluoxetine hydrochloride | Antidepressant |
| 418 | Fluoxetine hydrochloride | Antidepressant |
| 48220 | Fluoxetine hydrochloride | Antidepressant |
| 61335 | Fluoxetine hydrochloride | Antidepressant |
| 69542 | Fluoxetine hydrochloride | Antidepressant |
| 57532 | Fluoxetine hydrochloride | Antidepressant |
| 252 | Fluoxetine hydrochloride | Antidepressant |
| 75943 | Fluoxetine hydrochloride | Antidepressant |
| 4907 | Fluoxetine hydrochloride | Antidepressant |
| 37256 | Fluoxetine hydrochloride | Antidepressant |
| 33779 | Fluoxetine hydrochloride | Antidepressant |
| 29786 | Fluoxetine hydrochloride | Antidepressant |
| 12123 | Fluvoxamine maleate | Antidepressant |
| 2897 | Fluvoxamine maleate | Antidepressant |
| 2290 | Fluvoxamine maleate | Antidepressant |
| 48045 | Fluvoxamine maleate | Antidepressant |
| 44861 | Fluvoxamine maleate | Antidepressant |
| 43518 | Fluvoxamine maleate | Antidepressant |
| 2880 | Fluvoxamine maleate | Antidepressant |
| 3391 | Nefazodone hydrochloride | Antidepressant |
| 4297 | Nefazodone hydrochloride | Antidepressant |
| 63827 | Nefazodone hydrochloride | Antidepressant |
| 4554 | Nefazodone hydrochloride | Antidepressant |
| 4011 | Nefazodone hydrochloride | Antidepressant |
| 67757 | Nefazodone hydrochloride | Antidepressant |
| 35021 | Paroxetine hydrochloride | Antidepressant |
| 76946 | Paroxetine hydrochloride | Antidepressant |
| 59288 | Paroxetine hydrochloride | Antidepressant |
| 67259 | Paroxetine hydrochloride | Antidepressant |
| 527 | Paroxetine hydrochloride | Antidepressant |
| 50 | Paroxetine hydrochloride | Antidepressant |
| 34419 | Paroxetine hydrochloride | Antidepressant |
| 32899 | Paroxetine hydrochloride | Antidepressant |
| 73668 | Paroxetine hydrochloride | Antidepressant |
| 40892 | Paroxetine hydrochloride | Antidepressant |
| 34351 | Paroxetine hydrochloride | Antidepressant |
| 55023 | Paroxetine hydrochloride | Antidepressant |
| 33978 | Paroxetine hydrochloride | Antidepressant |
| 1397 | Paroxetine hydrochloride | Antidepressant |
| 34587 | Paroxetine hydrochloride | Antidepressant |
| 40165 | Paroxetine hydrochloride | Antidepressant |
| 64785 | Paroxetine hydrochloride | Antidepressant |
| 78843 | Paroxetine hydrochloride | Antidepressant |
| 68325 | Paroxetine hydrochloride | Antidepressant |
| 35112 | Paroxetine hydrochloride | Antidepressant |
| 66292 | Paroxetine hydrochloride | Antidepressant |
| 74588 | Paroxetine hydrochloride | Antidepressant |
| 841 | Paroxetine hydrochloride | Antidepressant |
| 73589 | Paroxetine hydrochloride | Antidepressant |
| 77650 | Paroxetine hydrochloride | Antidepressant |
| 3601 | Paroxetine hydrochloride | Antidepressant |
| 1575 | Paroxetine hydrochloride | Antidepressant |
| 55537 | Paroxetine hydrochloride | Antidepressant |
| 76772 | Paroxetine hydrochloride | Antidepressant |
| 79383 | Paroxetine hydrochloride | Antidepressant |
| 79381 | Paroxetine hydrochloride | Antidepressant |
| 75054 | Paroxetine hydrochloride | Antidepressant |
| 65771 | Sertraline | Antidepressant |
| 4352 | Sertraline hydrochloride | Antidepressant |
| 77385 | Sertraline hydrochloride | Antidepressant |
| 1612 | Sertraline hydrochloride | Antidepressant |
| 727 | Sertraline hydrochloride | Antidepressant |
| 55146 | Sertraline hydrochloride | Antidepressant |
| 62950 | Sertraline hydrochloride | Antidepressant |
| 61503 | Sertraline hydrochloride | Antidepressant |
| 59600 | Sertraline hydrochloride | Antidepressant |
| 62692 | Sertraline hydrochloride | Antidepressant |
| 69726 | Sertraline hydrochloride | Antidepressant |
| 67928 | Sertraline hydrochloride | Antidepressant |
| 66560 | Sertraline hydrochloride | Antidepressant |
| 54933 | Sertraline hydrochloride | Antidepressant |
| 66413 | Sertraline hydrochloride | Antidepressant |
| 68756 | Sertraline hydrochloride | Antidepressant |
| 44944 | Sertraline hydrochloride | Antidepressant |
| 73962 | Sertraline hydrochloride | Antidepressant |
| 49519 | Sertraline hydrochloride | Antidepressant |
| 77607 | Sertraline hydrochloride | Antidepressant |
| 78278 | Sertraline hydrochloride | Antidepressant |
| 62819 | Sertraline hydrochloride | Antidepressant |
| 54826 | Sertraline hydrochloride | Antidepressant |
| 78626 | Sertraline hydrochloride | Antidepressant |
| 73759 | Sertraline hydrochloride | Antidepressant |
| 54081 | Sertraline hydrochloride | Antidepressant |
| 488 | Sertraline hydrochloride | Antidepressant |
| 32401 | Sertraline hydrochloride | Antidepressant |
| 58723 | Sertraline hydrochloride | Antidepressant |
| 42387 | Sertraline hydrochloride | Antidepressant |
| 45915 | Sertraline hydrochloride | Antidepressant |
| 62693 | Sertraline hydrochloride | Antidepressant |
| 69725 | Sertraline hydrochloride | Antidepressant |
| 63481 | Sertraline hydrochloride | Antidepressant |
| 58664 | Sertraline hydrochloride | Antidepressant |
| 67730 | Sertraline hydrochloride | Antidepressant |
| 69898 | Sertraline hydrochloride | Antidepressant |
| 55488 | Sertraline hydrochloride | Antidepressant |
| 75952 | Sertraline hydrochloride | Antidepressant |
| 62927 | Sertraline hydrochloride | Antidepressant |
| 75405 | Sertraline hydrochloride | Antidepressant |
| 7328 | Sertraline hydrochloride | Antidepressant |
| 77538 | Sertraline hydrochloride | Antidepressant |
| 77707 | Sertraline hydrochloride | Antidepressant |
| 40494 | Agomelatine | Antidepressant |
| 40295 | Agomelatine | Antidepressant |
| 74774 | Duloxetine hydrochloride | Antidepressant |
| 7122 | Duloxetine hydrochloride | Antidepressant |
| 13151 | Duloxetine hydrochloride | Antidepressant |
| 62688 | Duloxetine hydrochloride | Antidepressant |
| 63370 | Duloxetine hydrochloride | Antidepressant |
| 65618 | Duloxetine hydrochloride | Antidepressant |
| 65809 | Duloxetine hydrochloride | Antidepressant |
| 66412 | Duloxetine hydrochloride | Antidepressant |
| 70405 | Duloxetine hydrochloride | Antidepressant |
| 70728 | Duloxetine hydrochloride | Antidepressant |
| 73298 | Duloxetine hydrochloride | Antidepressant |
| 74907 | Duloxetine hydrochloride | Antidepressant |
| 79628 | Duloxetine hydrochloride | Antidepressant |
| 6895 | Duloxetine hydrochloride | Antidepressant |
| 14849 | Duloxetine hydrochloride | Antidepressant |
| 51383 | Duloxetine hydrochloride | Antidepressant |
| 63216 | Duloxetine hydrochloride | Antidepressant |
| 63763 | Duloxetine hydrochloride | Antidepressant |
| 64442 | Duloxetine hydrochloride | Antidepressant |
| 65888 | Duloxetine hydrochloride | Antidepressant |
| 65892 | Duloxetine hydrochloride | Antidepressant |
| 66405 | Duloxetine hydrochloride | Antidepressant |
| 68096 | Duloxetine hydrochloride | Antidepressant |
| 69428 | Duloxetine hydrochloride | Antidepressant |
| 69752 | Duloxetine hydrochloride | Antidepressant |
| 69965 | Duloxetine hydrochloride | Antidepressant |
| 72211 | Duloxetine hydrochloride | Antidepressant |
| 73540 | Duloxetine hydrochloride | Antidepressant |
| 73868 | Duloxetine hydrochloride | Antidepressant |
| 74190 | Duloxetine hydrochloride | Antidepressant |
| 78777 | Duloxetine hydrochloride | Antidepressant |
| 76857 | Duloxetine hydrochloride | Antidepressant |
| 6421 | Mirtazapine | Antidepressant |
| 43253 | Mirtazapine | Antidepressant |
| 64101 | Mirtazapine | Antidepressant |
| 43241 | Mirtazapine | Antidepressant |
| 66580 | Mirtazapine | Antidepressant |
| 61856 | Mirtazapine | Antidepressant |
| 43248 | Mirtazapine | Antidepressant |
| 43246 | Mirtazapine | Antidepressant |
| 68680 | Mirtazapine | Antidepressant |
| 55482 | Mirtazapine | Antidepressant |
| 58291 | Mirtazapine | Antidepressant |
| 77865 | Mirtazapine | Antidepressant |
| 65555 | Mirtazapine | Antidepressant |
| 43237 | Mirtazapine | Antidepressant |
| 48698 | Mirtazapine | Antidepressant |
| 54012 | Mirtazapine | Antidepressant |
| 6795 | Mirtazapine | Antidepressant |
| 43239 | Mirtazapine | Antidepressant |
| 53699 | Mirtazapine | Antidepressant |
| 66183 | Mirtazapine | Antidepressant |
| 59953 | Mirtazapine | Antidepressant |
| 46668 | Mirtazapine | Antidepressant |
| 66752 | Mirtazapine | Antidepressant |
| 43242 | Mirtazapine | Antidepressant |
| 54342 | Mirtazapine | Antidepressant |
| 54644 | Mirtazapine | Antidepressant |
| 74557 | Mirtazapine | Antidepressant |
| 43257 | Mirtazapine | Antidepressant |
| 16154 | Mirtazapine | Antidepressant |
| 53321 | Mirtazapine | Antidepressant |
| 61547 | Mirtazapine | Antidepressant |
| 47966 | Mirtazapine | Antidepressant |
| 68544 | Mirtazapine | Antidepressant |
| 6488 | Mirtazapine | Antidepressant |
| 43250 | Mirtazapine | Antidepressant |
| 53648 | Mirtazapine | Antidepressant |
| 48185 | Mirtazapine | Antidepressant |
| 68052 | Mirtazapine | Antidepressant |
| 69420 | Mirtazapine | Antidepressant |
| 76187 | Mirtazapine | Antidepressant |
| 59694 | Mirtazapine | Antidepressant |
| 742 | Mirtazapine | Antidepressant |
| 47945 | Mirtazapine | Antidepressant |
| 40160 | Mirtazapine | Antidepressant |
| 54792 | Mirtazapine | Antidepressant |
| 69005 | Mirtazapine | Antidepressant |
| 77488 | Mirtazapine | Antidepressant |
| 78654 | Mirtazapine | Antidepressant |
| 60538 | Mirtazapine | Antidepressant |
| 56209 | Mirtazapine | Antidepressant |
| 68933 | Mirtazapine | Antidepressant |
| 71543 | Mirtazapine | Antidepressant |
| 63403 | Mirtazapine | Antidepressant |
| 6481 | Mirtazapine | Antidepressant |
| 43235 | Mirtazapine | Antidepressant |
| 43236 | Mirtazapine | Antidepressant |
| 43256 | Mirtazapine | Antidepressant |
| 43247 | Mirtazapine | Antidepressant |
| 64139 | Mirtazapine | Antidepressant |
| 43234 | Mirtazapine | Antidepressant |
| 49820 | Mirtazapine | Antidepressant |
| 6854 | Mirtazapine | Antidepressant |
| 33337 | Mirtazapine | Antidepressant |
| 58625 | Mirtazapine | Antidepressant |
| 59954 | Mirtazapine | Antidepressant |
| 64223 | Mirtazapine | Antidepressant |
| 77377 | Mirtazapine | Antidepressant |
| 4726 | Mirtazapine | Antidepressant |
| 67272 | Mirtazapine | Antidepressant |
| 60370 | Mirtazapine | Antidepressant |
| 6846 | Mirtazapine | Antidepressant |
| 50892 | Mirtazapine | Antidepressant |
| 10083 | Mirtazapine | Antidepressant |
| 53543 | Mirtazapine | Antidepressant |
| 15268 | Mirtazapine | Antidepressant |
| 9534 | Nefazodone hydrochloride | Antidepressant |
| 15163 | Reboxetine mesilate | Antidepressant |
| 2356 | Reboxetine mesilate | Antidepressant |
| 54747 | Tryptophan | Antidepressant |
| 5611 | Tryptophan | Antidepressant |
| 20504 | Tryptophan | Antidepressant |
| 12221 | Tryptophan | Antidepressant |
| 54686 | Tryptophan | Antidepressant |
| 4422 | Tryptophan | Antidepressant |
| 52516 | Venlafaxine hydrochloride | Antidepressant |
| 52074 | Venlafaxine hydrochloride | Antidepressant |
| 71806 | Venlafaxine hydrochloride | Antidepressant |
| 61236 | Venlafaxine hydrochloride | Antidepressant |
| 45664 | Venlafaxine hydrochloride | Antidepressant |
| 45959 | Venlafaxine hydrochloride | Antidepressant |
| 65738 | Venlafaxine hydrochloride | Antidepressant |
| 67271 | Venlafaxine hydrochloride | Antidepressant |
| 623 | Venlafaxine hydrochloride | Antidepressant |
| 6274 | Venlafaxine hydrochloride | Antidepressant |
| 67288 | Venlafaxine hydrochloride | Antidepressant |
| 77089 | Venlafaxine hydrochloride | Antidepressant |
| 9182 | Venlafaxine hydrochloride | Antidepressant |
| 74010 | Venlafaxine hydrochloride | Antidepressant |
| 5710 | Venlafaxine hydrochloride | Antidepressant |
| 51280 | Venlafaxine hydrochloride | Antidepressant |
| 65899 | Venlafaxine hydrochloride | Antidepressant |
| 74011 | Venlafaxine hydrochloride | Antidepressant |
| 75894 | Venlafaxine hydrochloride | Antidepressant |
| 1474 | Venlafaxine hydrochloride | Antidepressant |
| 76771 | Venlafaxine hydrochloride | Antidepressant |
| 43968 | Venlafaxine hydrochloride | Antidepressant |
| 43673 | Venlafaxine hydrochloride | Antidepressant |
| 41299 | Venlafaxine hydrochloride | Antidepressant |
| 48199 | Venlafaxine hydrochloride | Antidepressant |
| 41314 | Venlafaxine hydrochloride | Antidepressant |
| 41033 | Venlafaxine hydrochloride | Antidepressant |
| 59753 | Venlafaxine hydrochloride | Antidepressant |
| 60843 | Venlafaxine hydrochloride | Antidepressant |
| 40817 | Venlafaxine hydrochloride | Antidepressant |
| 40815 | Venlafaxine hydrochloride | Antidepressant |
| 39809 | Venlafaxine hydrochloride | Antidepressant |
| 39770 | Venlafaxine hydrochloride | Antidepressant |
| 57751 | Venlafaxine hydrochloride | Antidepressant |
| 52716 | Venlafaxine hydrochloride | Antidepressant |
| 40514 | Venlafaxine hydrochloride | Antidepressant |
| 40515 | Venlafaxine hydrochloride | Antidepressant |
| 70420 | Venlafaxine hydrochloride | Antidepressant |
| 70495 | Venlafaxine hydrochloride | Antidepressant |
| 69819 | Venlafaxine hydrochloride | Antidepressant |
| 70315 | Venlafaxine hydrochloride | Antidepressant |
| 50081 | Venlafaxine hydrochloride | Antidepressant |
| 59035 | Venlafaxine hydrochloride | Antidepressant |
| 49511 | Venlafaxine hydrochloride | Antidepressant |
| 58726 | Venlafaxine hydrochloride | Antidepressant |
| 74516 | Venlafaxine hydrochloride | Antidepressant |
| 58681 | Venlafaxine hydrochloride | Antidepressant |
| 55501 | Venlafaxine hydrochloride | Antidepressant |
| 2654 | Venlafaxine hydrochloride | Antidepressant |
| 70806 | Venlafaxine hydrochloride | Antidepressant |
| 60549 | Venlafaxine hydrochloride | Antidepressant |
| 71782 | Venlafaxine hydrochloride | Antidepressant |
| 43334 | Venlafaxine hydrochloride | Antidepressant |
| 39360 | Venlafaxine hydrochloride | Antidepressant |
| 50934 | Venlafaxine hydrochloride | Antidepressant |
| 62734 | Venlafaxine hydrochloride | Antidepressant |
| 65666 | Venlafaxine hydrochloride | Antidepressant |
| 40054 | Venlafaxine hydrochloride | Antidepressant |
| 58837 | Venlafaxine hydrochloride | Antidepressant |
| 45806 | Venlafaxine hydrochloride | Antidepressant |
| 301 | Venlafaxine hydrochloride | Antidepressant |
| 56662 | Venlafaxine hydrochloride | Antidepressant |
| 73667 | Venlafaxine hydrochloride | Antidepressant |
| 68050 | Venlafaxine hydrochloride | Antidepressant |
| 75525 | Venlafaxine hydrochloride | Antidepressant |
| 59923 | Venlafaxine hydrochloride | Antidepressant |
| 70353 | Venlafaxine hydrochloride | Antidepressant |
| 51361 | Venlafaxine hydrochloride | Antidepressant |
| 60895 | Venlafaxine hydrochloride | Antidepressant |
| 51699 | Venlafaxine hydrochloride | Antidepressant |
| 13237 | Venlafaxine hydrochloride | Antidepressant |
| 2617 | Venlafaxine hydrochloride | Antidepressant |
| 470 | Venlafaxine hydrochloride | Antidepressant |
| 71257 | Venlafaxine hydrochloride | Antidepressant |
| 59563 | Venlafaxine hydrochloride | Antidepressant |
| 68876 | Venlafaxine hydrochloride | Antidepressant |
| 43203 | Venlafaxine hydrochloride | Antidepressant |
| 39359 | Venlafaxine hydrochloride | Antidepressant |
| 1222 | Venlafaxine hydrochloride | Antidepressant |
| 60449 | Venlafaxine hydrochloride | Antidepressant |
| 73658 | Venlafaxine hydrochloride | Antidepressant |
| 66437 | Venlafaxine hydrochloride | Antidepressant |
| 56457 | Venlafaxine hydrochloride | Antidepressant |
| 63859 | Venlafaxine hydrochloride | Antidepressant |
| 53326 | Venlafaxine hydrochloride | Antidepressant |
| 63268 | Venlafaxine hydrochloride | Antidepressant |
| 40062 | Venlafaxine hydrochloride | Antidepressant |
| 40407 | Venlafaxine hydrochloride | Antidepressant |
| 45818 | Venlafaxine hydrochloride | Antidepressant |
| 40059 | Venlafaxine hydrochloride | Antidepressant |
| 44936 | Venlafaxine hydrochloride | Antidepressant |
| 44937 | Venlafaxine hydrochloride | Antidepressant |
| 71932 | Venlafaxine hydrochloride | Antidepressant |
| 70931 | Venlafaxine hydrochloride | Antidepressant |
| 40092 | Venlafaxine hydrochloride | Antidepressant |
| 67563 | Venlafaxine hydrochloride | Antidepressant |
| 40277 | Venlafaxine hydrochloride | Antidepressant |
| 76727 | Venlafaxine hydrochloride | Antidepressant |
| 75263 | Venlafaxine hydrochloride | Antidepressant |
| 40517 | Venlafaxine hydrochloride | Antidepressant |
| 42600 | Venlafaxine hydrochloride | Antidepressant |
| 40764 | Venlafaxine hydrochloride | Antidepressant |
| 40917 | Venlafaxine hydrochloride | Antidepressant |
| 40049 | Venlafaxine hydrochloride | Antidepressant |
| 78585 | Venlafaxine hydrochloride | Antidepressant |
| 40048 | Venlafaxine hydrochloride | Antidepressant |
| 75848 | Venlafaxine hydrochloride | Antidepressant |
| 55424 | Venlafaxine hydrochloride | Antidepressant |
| 67874 | Vortioxetine hydrobromide | Antidepressant |
| 69991 | Vortioxetine hydrobromide | Antidepressant |
| 69992 | Vortioxetine hydrobromide | Antidepressant |
| 65483 | Vortioxetine hydrobromide | Antidepressant |
| 66890 | Vortioxetine hydrobromide | Antidepressant |
| 65482 | Vortioxetine hydrobromide | Antidepressant |
| 25945 | Iproniazide | Antidepressant |
| 18290 | Iproniazide | Antidepressant |
| 41731 | Isocarboxazid | Antidepressant |
| 12207 | Isocarboxazid | Antidepressant |
| 12503 | Isocarboxazid | Antidepressant |
| 9206 | Moclobemide | Antidepressant |
| 5832 | Moclobemide | Antidepressant |
| 2883 | Moclobemide | Antidepressant |
| 67305 | Moclobemide | Antidepressant |
| 41747 | Moclobemide | Antidepressant |
| 5187 | Moclobemide | Antidepressant |
| 3349 | Phenelzine sulfate | Antidepressant |
| 4321 | Phenelzine sulfate | Antidepressant |
| 10787 | Tranylcypromine sulfate | Antidepressant |
| 3783 | Tranylcypromine sulfate | Antidepressant |
| 41654 | Tranylcypromine sulfate | Antidepressant |
| 3356 | Trifluoperazine hydrochloride/tranylcypromine sulphate | Antidepressant |
| 3955 | Trifluoperazine hydrochloride/tranylcypromine sulphate | Antidepressant |
| 24890 | Trifluoperazine hydrochloride/tranylcypromine sulphate | Antidepressant |
| 28215 | Dexamethasone sodium phosphate | Corticosteroid |
| 37500 | Dexamethasone sodium phosphate | Corticosteroid |
| 14906 | Dexamethasone sodium phosphate | Corticosteroid |
| 61316 | Dexamethasone sodium phosphate | Corticosteroid |
| 53173 | Dexamethasone sodium phosphate | Corticosteroid |
| 19259 | Dexamethasone sodium phosphate | Corticosteroid |
| 47598 | Dexamethasone sodium phosphate | Corticosteroid |
| 61958 | Dexamethasone sodium phosphate | Corticosteroid |
| 56940 | Dexamethasone sodium phosphate | Corticosteroid |
| 35453 | Dexamethasone sodium phosphate | Corticosteroid |
| 10657 | Dexamethasone sodium phosphate | Corticosteroid |
| 13972 | Dexamethasone sodium phosphate | Corticosteroid |
| 26299 | Dexamethasone sodium phosphate | Corticosteroid |
| 13952 | Dexamethasone sodium phosphate | Corticosteroid |
| 26454 | Dexamethasone sodium phosphate | Corticosteroid |
| 31948 | Dexamethasone sodium phosphate | Corticosteroid |
| 34083 | Dexamethasone sodium phosphate | Corticosteroid |
| 4233 | Dexamethasone sodium phosphate | Corticosteroid |
| 8108 | Hydrocortisone acetate | Corticosteroid |
| 1893 | Hydrocortisone acetate | Corticosteroid |
| 925 | Lidocaine hydrochloride/methylprednisolone acetate | Corticosteroid |
| 48800 | Methylprednisolone acetate | Corticosteroid |
| 48748 | Methylprednisolone acetate | Corticosteroid |
| 48746 | Methylprednisolone acetate | Corticosteroid |
| 14982 | Methylprednisolone acetate | Corticosteroid |
| 71106 | Methylprednisolone acetate | Corticosteroid |
| 27413 | Methylprednisolone acetate | Corticosteroid |
| 33132 | Methylprednisolone acetate | Corticosteroid |
| 35349 | Methylprednisolone acetate | Corticosteroid |
| 35040 | Methylprednisolone acetate | Corticosteroid |
| 35688 | Methylprednisolone acetate | Corticosteroid |
| 1133 | Methylprednisolone acetate | Corticosteroid |
| 5493 | Methylprednisolone acetate | Corticosteroid |
| 20157 | Methylprednisolone acetate/lidocaine hydrochloride | Corticosteroid |
| 50253 | Methylprednisolone acetate/lidocaine hydrochloride | Corticosteroid |
| 49076 | Methylprednisolone acetate/lidocaine hydrochloride | Corticosteroid |
| 50734 | Methylprednisolone acetate/lidocaine hydrochloride | Corticosteroid |
| 7405 | Methylprednisolone acetate/lidocaine hydrochloride | Corticosteroid |
| 35156 | Methylprednisolone acetate/lidocaine hydrochloride | Corticosteroid |
| 18266 | Methylprednisolone sodium succinate | Corticosteroid |
| 13397 | Methylprednisolone sodium succinate | Corticosteroid |
| 12405 | Methylprednisolone sodium succinate | Corticosteroid |
| 18765 | Methylprednisolone sodium succinate | Corticosteroid |
| 14188 | Methylprednisolone sodium succinate | Corticosteroid |
| 25226 | Methylprednisolone sodium succinate | Corticosteroid |
| 25839 | Methylprednisolone sodium succinate | Corticosteroid |
| 23511 | Methylprednisolone sodium succinate | Corticosteroid |
| 21540 | Methylprednisolone sodium succinate | Corticosteroid |
| 14962 | Triamcinolone acetonide | Corticosteroid |
| 35578 | Triamcinolone acetonide | Corticosteroid |
| 14335 | Triamcinolone acetonide | Corticosteroid |
| 14958 | Triamcinolone acetonide | Corticosteroid |
| 50216 | Triamcinolone acetonide | Corticosteroid |
| 22047 | Triamcinolone acetonide | Corticosteroid |
| 50026 | Triamcinolone acetonide | Corticosteroid |
| 33131 | Triamcinolone acetonide | Corticosteroid |
| 16583 | Triamcinolone acetonide | Corticosteroid |
| 48406 | Triamcinolone acetonide | Corticosteroid |
| 9368 | Triamcinolone acetonide | Corticosteroid |
| 11123 | Triamcinolone acetonide | Corticosteroid |
| 4488 | Triamcinolone acetonide | Corticosteroid |
| 30244 | Triamcinolone acetonide | Corticosteroid |
| 4125 | Triamcinolone acetonide | Corticosteroid |
| 4123 | Triamcinolone acetonide | Corticosteroid |
| 8864 | Triamcinolone acetonide | Corticosteroid |
| 13981 | Triamcinolone acetonide | Corticosteroid |
| 768 | Triamcinolone acetonide | Corticosteroid |
| 37737 | Triamcinolone acetonide | Corticosteroid |
| 3703 | Triamcinolone acetonide | Corticosteroid |
| 16582 | Triamcinolone acetonide | Corticosteroid |
| 50854 | Triamcinolone hexacetonide | Corticosteroid |
| 50853 | Triamcinolone hexacetonide | Corticosteroid |
| 57856 | Triamcinolone hexacetonide | Corticosteroid |
| 66867 | Triamcinolone hexacetonide | Corticosteroid |
| 15016 | Triamcinolone hexacetonide | Corticosteroid |
| 7992 | Triamcinolone hexacetonide | Corticosteroid |
| 10864 | Betamethasone | Corticosteroid |
| 11149 | Betamethasone | Corticosteroid |
| 7286 | Betamethasone sodium phosphate | Corticosteroid |
| 64235 | Betamethasone sodium phosphate | Corticosteroid |
| 68306 | Betamethasone sodium phosphate | Corticosteroid |
| 1971 | Betamethasone sodium phosphate | Corticosteroid |
| 50225 | Betamethasone sodium phosphate | Corticosteroid |
| 12398 | Cortisone acetate | Corticosteroid |
| 229 | Cortisone acetate | Corticosteroid |
| 53143 | Cortisone acetate | Corticosteroid |
| 7548 | Cortisone acetate | Corticosteroid |
| 53705 | Cortisone acetate | Corticosteroid |
| 18637 | Cortisone acetate | Corticosteroid |
| 12400 | Cortisone acetate | Corticosteroid |
| 10574 | Cortisone acetate | Corticosteroid |
| 23210 | Cortisone acetate | Corticosteroid |
| 22555 | Deflazacort | Corticosteroid |
| 29112 | Deflazacort | Corticosteroid |
| 20577 | Deflazacort | Corticosteroid |
| 41335 | Deflazacort | Corticosteroid |
| 9375 | Deflazacort | Corticosteroid |
| 78839 | Deflazacort | Corticosteroid |
| 17410 | Deflazacort | Corticosteroid |
| 3992 | Deflazacort | Corticosteroid |
| 53207 | Dexamethasone | Corticosteroid |
| 9994 | Dexamethasone | Corticosteroid |
| 34801 | Dexamethasone | Corticosteroid |
| 71926 | Dexamethasone | Corticosteroid |
| 78335 | Dexamethasone | Corticosteroid |
| 45234 | Dexamethasone | Corticosteroid |
| 66724 | Dexamethasone | Corticosteroid |
| 56443 | Dexamethasone | Corticosteroid |
| 76339 | Dexamethasone | Corticosteroid |
| 77085 | Dexamethasone | Corticosteroid |
| 52396 | Dexamethasone | Corticosteroid |
| 77849 | Dexamethasone | Corticosteroid |
| 74156 | Dexamethasone | Corticosteroid |
| 74157 | Dexamethasone | Corticosteroid |
| 36055 | Dexamethasone | Corticosteroid |
| 1280 | Dexamethasone | Corticosteroid |
| 62909 | Dexamethasone | Corticosteroid |
| 60120 | Dexamethasone | Corticosteroid |
| 34880 | Dexamethasone | Corticosteroid |
| 68182 | Dexamethasone | Corticosteroid |
| 64747 | Dexamethasone | Corticosteroid |
| 5157 | Dexamethasone | Corticosteroid |
| 54793 | Dexamethasone | Corticosteroid |
| 70611 | Dexamethasone | Corticosteroid |
| 78214 | Dexamethasone | Corticosteroid |
| 70893 | Dexamethasone | Corticosteroid |
| 68489 | Dexamethasone | Corticosteroid |
| 72537 | Dexamethasone | Corticosteroid |
| 69572 | Dexamethasone | Corticosteroid |
| 4779 | Dexamethasone | Corticosteroid |
| 55401 | Dexamethasone | Corticosteroid |
| 34915 | Dexamethasone | Corticosteroid |
| 186 | Dexamethasone | Corticosteroid |
| 74436 | Dexamethasone | Corticosteroid |
| 56347 | Dexamethasone | Corticosteroid |
| 68593 | Dexamethasone | Corticosteroid |
| 73216 | Dexamethasone | Corticosteroid |
| 21903 | Dexamethasone | Corticosteroid |
| 60064 | Dexamethasone sodium phosphate | Corticosteroid |
| 64766 | Dexamethasone sodium phosphate | Corticosteroid |
| 66200 | Dexamethasone sodium phosphate | Corticosteroid |
| 68103 | Dexamethasone sodium phosphate | Corticosteroid |
| 4943 | Dexamethasone sodium phosphate | Corticosteroid |
| 58474 | Dexamethasone sodium phosphate | Corticosteroid |
| 71404 | Dexamethasone sodium phosphate | Corticosteroid |
| 77483 | Dexamethasone sodium phosphate | Corticosteroid |
| 66524 | Dexamethasone sodium phosphate | Corticosteroid |
| 66287 | Dexamethasone sodium phosphate | Corticosteroid |
| 68860 | Dexamethasone sodium phosphate | Corticosteroid |
| 21218 | Dexamethasone sodium phosphate | Corticosteroid |
| 72848 | Dexamethasone sodium phosphate | Corticosteroid |
| 79684 | Dexamethasone sodium phosphate | Corticosteroid |
| 64050 | Dexamethasone sodium phosphate | Corticosteroid |
| 78307 | Dexamethasone sodium phosphate | Corticosteroid |
| 21668 | Dexamethasone sodium phosphate | Corticosteroid |
| 26300 | Dexamethasone sodium phosphate | Corticosteroid |
| 11334 | Dexamethasone sodium phosphate | Corticosteroid |
| 75064 | Hydrocortisone | Corticosteroid |
| 74502 | Hydrocortisone | Corticosteroid |
| 75065 | Hydrocortisone | Corticosteroid |
| 76671 | Hydrocortisone | Corticosteroid |
| 3418 | Hydrocortisone | Corticosteroid |
| 65984 | Hydrocortisone | Corticosteroid |
| 64787 | Hydrocortisone | Corticosteroid |
| 66666 | Hydrocortisone | Corticosteroid |
| 38022 | Hydrocortisone | Corticosteroid |
| 75019 | Hydrocortisone | Corticosteroid |
| 51849 | Hydrocortisone | Corticosteroid |
| 51872 | Hydrocortisone | Corticosteroid |
| 64059 | Hydrocortisone | Corticosteroid |
| 54794 | Hydrocortisone | Corticosteroid |
| 4535 | Hydrocortisone | Corticosteroid |
| 66327 | Hydrocortisone | Corticosteroid |
| 57931 | Hydrocortisone | Corticosteroid |
| 75384 | Hydrocortisone | Corticosteroid |
| 77646 | Hydrocortisone | Corticosteroid |
| 51871 | Hydrocortisone | Corticosteroid |
| 75937 | Hydrocortisone | Corticosteroid |
| 52053 | Hydrocortisone | Corticosteroid |
| 75020 | Hydrocortisone | Corticosteroid |
| 53953 | Hydrocortisone | Corticosteroid |
| 63138 | Hydrocortisone | Corticosteroid |
| 14076 | Hydrocortisone | Corticosteroid |
| 51722 | Hydrocortisone | Corticosteroid |
| 51824 | Hydrocortisone | Corticosteroid |
| 75729 | Hydrocortisone | Corticosteroid |
| 74497 | Hydrocortisone | Corticosteroid |
| 71620 | Hydrocortisone | Corticosteroid |
| 38054 | Hydrocortisone | Corticosteroid |
| 10754 | Hydrocortisone | Corticosteroid |
| 6098 | Hydrocortisone | Corticosteroid |
| 13043 | Hydrocortisone | Corticosteroid |
| 77994 | Hydrocortisone | Corticosteroid |
| 58592 | Hydrocortisone | Corticosteroid |
| 59418 | Hydrocortisone | Corticosteroid |
| 35172 | Hydrocortisone sodium phosphate | Corticosteroid |
| 35175 | Hydrocortisone sodium phosphate | Corticosteroid |
| 71905 | Hydrocortisone sodium phosphate | Corticosteroid |
| 37638 | Hydrocortisone sodium phosphate | Corticosteroid |
| 43355 | Hydrocortisone sodium phosphate | Corticosteroid |
| 77821 | Hydrocortisone sodium phosphate | Corticosteroid |
| 9574 | Hydrocortisone sodium phosphate | Corticosteroid |
| 2615 | Hydrocortisone sodium phosphate | Corticosteroid |
| 49707 | Hydrocortisone sodium succinate | Corticosteroid |
| 49498 | Hydrocortisone sodium succinate | Corticosteroid |
| 51167 | Hydrocortisone sodium succinate | Corticosteroid |
| 54715 | Hydrocortisone sodium succinate | Corticosteroid |
| 34166 | Hydrocortisone sodium succinate | Corticosteroid |
| 13350 | Hydrocortisone sodium succinate | Corticosteroid |
| 3754 | Hydrocortisone sodium succinate | Corticosteroid |
| 3651 | Hydrocortisone sodium succinate | Corticosteroid |
| 18042 | Methylprednisolone | Corticosteroid |
| 8261 | Methylprednisolone | Corticosteroid |
| 10683 | Methylprednisolone | Corticosteroid |
| 15555 | Methylprednisolone | Corticosteroid |
| 14172 | Methylprednisolone | Corticosteroid |
| 10552 | Methylprednisolone | Corticosteroid |
| 76923 | Methylprednisolone | Corticosteroid |
| 10684 | Methylprednisolone | Corticosteroid |
| 2130 | Methylprednisolone | Corticosteroid |
| 78546 | Prednisolone | Corticosteroid |
| 27962 | Prednisolone | Corticosteroid |
| 28859 | Prednisolone | Corticosteroid |
| 25272 | Prednisolone | Corticosteroid |
| 23512 | Prednisolone | Corticosteroid |
| 20095 | Prednisolone | Corticosteroid |
| 34914 | Prednisolone | Corticosteroid |
| 5913 | Prednisolone | Corticosteroid |
| 5490 | Prednisolone | Corticosteroid |
| 59283 | Prednisolone | Corticosteroid |
| 34631 | Prednisolone | Corticosteroid |
| 66645 | Prednisolone | Corticosteroid |
| 66015 | Prednisolone | Corticosteroid |
| 80110 | Prednisolone | Corticosteroid |
| 59229 | Prednisolone | Corticosteroid |
| 69568 | Prednisolone | Corticosteroid |
| 78129 | Prednisolone | Corticosteroid |
| 64007 | Prednisolone | Corticosteroid |
| 64008 | Prednisolone | Corticosteroid |
| 64009 | Prednisolone | Corticosteroid |
| 69686 | Prednisolone | Corticosteroid |
| 64128 | Prednisolone | Corticosteroid |
| 63172 | Prednisolone | Corticosteroid |
| 58234 | Prednisolone | Corticosteroid |
| 65626 | Prednisolone | Corticosteroid |
| 34109 | Prednisolone | Corticosteroid |
| 9727 | Prednisolone | Corticosteroid |
| 33691 | Prednisolone | Corticosteroid |
| 64416 | Prednisolone | Corticosteroid |
| 74239 | Prednisolone | Corticosteroid |
| 66914 | Prednisolone | Corticosteroid |
| 72421 | Prednisolone | Corticosteroid |
| 80050 | Prednisolone | Corticosteroid |
| 578 | Prednisolone | Corticosteroid |
| 34452 | Prednisolone | Corticosteroid |
| 34404 | Prednisolone | Corticosteroid |
| 73553 | Prednisolone | Corticosteroid |
| 58384 | Prednisolone | Corticosteroid |
| 63549 | Prednisolone | Corticosteroid |
| 28376 | Prednisolone | Corticosteroid |
| 2368 | Prednisolone | Corticosteroid |
| 38407 | Prednisolone | Corticosteroid |
| 61132 | Prednisolone | Corticosteroid |
| 75001 | Prednisolone | Corticosteroid |
| 34660 | Prednisolone | Corticosteroid |
| 51753 | Prednisolone | Corticosteroid |
| 34748 | Prednisolone | Corticosteroid |
| 56891 | Prednisolone | Corticosteroid |
| 34978 | Prednisolone | Corticosteroid |
| 59338 | Prednisolone | Corticosteroid |
| 557 | Prednisolone | Corticosteroid |
| 28375 | Prednisolone | Corticosteroid |
| 34461 | Prednisolone | Corticosteroid |
| 76020 | Prednisolone | Corticosteroid |
| 55480 | Prednisolone | Corticosteroid |
| 79930 | Prednisolone | Corticosteroid |
| 68497 | Prednisolone | Corticosteroid |
| 63066 | Prednisolone | Corticosteroid |
| 73294 | Prednisolone | Corticosteroid |
| 54434 | Prednisolone | Corticosteroid |
| 63082 | Prednisolone | Corticosteroid |
| 67076 | Prednisolone | Corticosteroid |
| 53313 | Prednisolone | Corticosteroid |
| 2704 | Prednisolone | Corticosteroid |
| 53336 | Prednisolone | Corticosteroid |
| 78144 | Prednisolone | Corticosteroid |
| 41745 | Prednisolone | Corticosteroid |
| 65020 | Prednisolone | Corticosteroid |
| 54118 | Prednisolone | Corticosteroid |
| 67507 | Prednisolone | Corticosteroid |
| 69811 | Prednisolone | Corticosteroid |
| 44 | Prednisolone | Corticosteroid |
| 31532 | Prednisolone | Corticosteroid |
| 32803 | Prednisolone | Corticosteroid |
| 66550 | Prednisolone | Corticosteroid |
| 67107 | Prednisolone | Corticosteroid |
| 73678 | Prednisolone | Corticosteroid |
| 58987 | Prednisolone | Corticosteroid |
| 34393 | Prednisolone | Corticosteroid |
| 59912 | Prednisolone | Corticosteroid |
| 45302 | Prednisolone | Corticosteroid |
| 75763 | Prednisolone | Corticosteroid |
| 33988 | Prednisolone | Corticosteroid |
| 33990 | Prednisolone | Corticosteroid |
| 95 | Prednisolone | Corticosteroid |
| 21417 | Prednisolone | Corticosteroid |
| 29333 | Prednisolone | Corticosteroid |
| 58000 | Prednisolone | Corticosteroid |
| 58369 | Prednisolone | Corticosteroid |
| 34781 | Prednisolone | Corticosteroid |
| 60421 | Prednisolone | Corticosteroid |
| 41515 | Prednisolone | Corticosteroid |
| 55024 | Prednisolone | Corticosteroid |
| 63791 | Prednisolone | Corticosteroid |
| 67559 | Prednisolone | Corticosteroid |
| 61162 | Prednisolone | Corticosteroid |
| 32835 | Prednisolone | Corticosteroid |
| 64221 | Prednisolone | Corticosteroid |
| 1063 | Prednisolone sodium phosphate | Corticosteroid |
| 47142 | Prednisolone sodium phosphate | Corticosteroid |
| 955 | Prednisolone sodium phosphate | Corticosteroid |
| 61689 | Prednisolone sodium phosphate | Corticosteroid |
| 74493 | Prednisolone sodium phosphate | Corticosteroid |
| 63214 | Prednisolone sodium phosphate | Corticosteroid |
| 19141 | Prednisolone sodium phosphate | Corticosteroid |
| 78789 | Prednisolone sodium phosphate | Corticosteroid |
| 70603 | Prednisolone sodium phosphate | Corticosteroid |
| 77760 | Prednisolone sodium phosphate | Corticosteroid |
| 24224 | Prednisolone sodium phosphate | Corticosteroid |
| 31327 | Prednisolone steaglate | Corticosteroid |
| 3345 | Prednisolone steaglate | Corticosteroid |
| 21833 | Prednisone | Corticosteroid |
| 54432 | Prednisone | Corticosteroid |
| 44803 | Prednisone | Corticosteroid |
| 44802 | Prednisone | Corticosteroid |
| 44380 | Prednisone | Corticosteroid |
| 3557 | Prednisone | Corticosteroid |
| 46711 | Prednisone | Corticosteroid |
| 58061 | Prednisone | Corticosteroid |
| 44723 | Prednisone | Corticosteroid |
| 62656 | Prednisone | Corticosteroid |
| 43544 | Prednisone | Corticosteroid |
| 2949 | Prednisone | Corticosteroid |
| 24014 | Triamcinolone acetonide | Corticosteroid |
| 15617 | Triamcinolone acetonide | Corticosteroid |
| 19908 | Triamcinolone acetonide | Corticosteroid |
| 23111 | Triamcinolone acetonide | Corticosteroid |
Appendix 4 QFracture-2012 external validation, and CFracture derivation and internal validation
| Missing data | How missingness was handled in analysis | External validation cohort | All patients original QFracture-2012 internal validation cohort (N = 1,583,373), n (%) missing data | |
|---|---|---|---|---|
| Women, n (%) missing da | Men, n (%) missing data | |||
| Age | Never missing | 0 | 0 | 0 |
| Sex | Never missing | 0 | 0 | 0 |
| Socioeconomic status | Excluded from cohort | 0 | 0 | 0 |
| BMI | Imputed | 932,720 (34.0) | 1,233,196 (45.9) | 418,478 (26.4) |
| Smoking status | Imputed | 780,226 (28.4) | 963,580 (35.9) | 258,144 (16.3) |
| Alcohol status | Imputed | 698,902 (25.4) | 866,622 (32.3) | 461,740 (29.2) |
| Ethnicity | Assumed to be white | 1,278,931 (46.6) | 1,494,450 (55.7) | 855,485 (54.0) |
| Conditions and prescribing variables | Assumed to be absent if no record | N/A | N/A | N/A |
| Predictor | Subdistribution HR | 95% CI |
|---|---|---|
| (Age in years/10)2 – 28.7076 | 1.1861 | 1.1821 to 1.1902 |
| (Age in years/10)3 – 179.3379 | 0.9872 | 0.9869 to 0.9876 |
| (BMI/10)–1 – 0.3914 | 5.6848 | 5.0121 to 6.4478 |
| Ethnicity | ||
| South Asian | 0.4235 | 0.3781 to 0.4745 |
| Black African/Caribbean | 0.2185 | 0.1974 to 0.2420 |
| Other | 0.3728 | 0.3251 to 0.4276 |
| Alcohol intake | ||
| Trivial (< 1 unit/day) | 0.9953 | 0.9764 to 1.0145 |
| Light (1–2 units/day) | 1.0407 | 1.0116 to 1.0706 |
| Moderate (3–6 units/day) | 1.1315 | 1.0713 to 1.1951 |
| Heavy (7–9 units/day) | 1.3272 | 1.1514 to 1.5299 |
| Very heavy (> 9 units/day) | 1.2479 | 1.0818 to 1.4395 |
| Smoking status | ||
| Ex-smoker | 1.0653 | 1.0444 to 1.0866 |
| Light smoker | 1.1055 | 1.0647 to 1.1479 |
| Moderate smoker | 1.1755 | 1.1350 to 1.2174 |
| Heavy smoker | 1.2051 | 1.1508 to 1.2619 |
| Asthma or chronic obstructive airways disease | 1.0710 | 1.0447 to 1.0981 |
| Cancer | 0.9753 | 0.9405 to 1.0114 |
| CVD | 0.9566 | 0.9340 to 0.9797 |
| Dementia | 0.7548 | 0.7195 to 0.7919 |
| Epilepsy diagnosis or prescribed anti-convulsant | 1.3021 | 1.2492 to 1.3572 |
| History of falls | 1.2502 | 1.2211 to 1.2800 |
| Chronic liver disease | 1.2872 | 1.1532 to 1.4368 |
| Parkinson’s disease | 1.0518 | 0.9677 to 1.1431 |
| Rheumatoid arthritis or SLE | 1.1598 | 1.1045 to 1.2178 |
| Chronic renal disease | 0.8661 | 0.8179 to 0.9172 |
| Type 1 diabetes | 1.6056 | 1.4349 to 1.7966 |
| Type 2 diabetes | 1.0902 | 1.0532 to 1.1286 |
| Prior fracture | 1.6713 | 1.6347 to 1.7087 |
| Endocrine disorders | 0.9878 | 0.9252 to 1.0546 |
| Malabsorption | 1.1261 | 1.0644 to 1.1914 |
| Parental history of osteoporosis or hip fracture | 1.1306 | 1.0216 to 1.2512 |
| Antidepressants | 1.1875 | 1.1616 to 1.2140 |
| Corticosteroids | 1.1273 | 1.0794 to 1.1773 |
| Oestrogen-only HRT | 0.7642 | 0.7124 to 0.8198 |
| CCI | ||
| 1 | 1.1160 | 1.0915 to 1.1410 |
| 2 | 1.1027 | 1.0712 to 1.1351 |
| ≥ 3 | 1.0528 | 1.0118 to 1.0955 |
| Predictor | Subdistribution HR | 95% CI |
|---|---|---|
| (Age in years/10)0.5 – 2.410e-14 | 8.318e-03 | 5.184e-03 to 1.335e-02 |
| (Age in years/10) – 6.376e-15 | 4.075 | 3.688 to 4.502 |
| (BMI/10)–1 + 6.372e-15 | 2.346e+08 | 1.584e+06 to 3.474e+10 |
| (BMI/10)0.5 – 2.303e-14 | 1.325e-09 | 2.706e-12 to 6.486e-07 |
| Ethnicity | ||
| South Asian | 0.581 | 0.502 to 0.674 |
| Black African/Caribbean | 0.329 | 0.305 to 0.355 |
| Other | 0.357 | 0.296 to 0.431 |
| Alcohol intake | ||
| Trivial (< 1 unit/day) | 0.956 | 0.910 to 1.003 |
| Light (1–2 units/day) | 0.964 | 0.925 to 1.004 |
| Moderate (3–6 units/day) | 1.008 | 0.951 to 1.069 |
| Heavy (7–9 units/day) | 1.282 | 1.149 to 1.431 |
| Very heavy (> 9 units/day) | 1.991 | 1.783 to 2.223 |
| Smoking status | ||
| Ex-smoker | 1.063 | 1.026 to 1.101 |
| Light smoker | 1.226 | 1.127 to 1.333 |
| Moderate smoker | 1.284 | 1.221 to 1.349 |
| Heavy smoker | 1.286 | 1.227 to 1.347 |
| Asthma or chronic obstructive airways disease | 1.010 | 0.968 to 1.053 |
| Cancer | 1.010 | 0.952 to 1.070 |
| CVD | 0.938 | 0.903 to 0.975 |
| Dementia | 0.814 | 0.734 to 0.902 |
| Epilepsy diagnosis or prescribed anti-convulsant | 1.631 | 1.534 to 1.735 |
| History of falls | 1.438 | 1.367 to 1.512 |
| Chronic liver disease | 1.129 | 0.953 to 1.337 |
| Parkinson’s disease | 1.415 | 1.268 to 1.580 |
| Rheumatoid arthritis or SLE | 1.354 | 1.212 to 1.512 |
| Chronic renal disease | 0.951 | 0.867 to 1.043 |
| Type 1 diabetes | 1.737 | 1.512 to 1.996 |
| Type 2 diabetes | 1.050 | 0.996 to 1.107 |
| Prior fracture | 2.126 | 2.035 to 2.221 |
| Malabsorption | 1.196 | 1.082 to 1.321 |
| Care home resident | 0.563 | 0.484 to 0.660 |
| Parental history of osteoporosis | 1.808 | 1.439 to 2.271 |
| Antidepressants | 1.305 | 1.246 to 1.366 |
| Corticosteroids | 1.116 | 1.023 to 1.217 |
| CCI | ||
| 1 | 1.221 | 1.176 to 1.268 |
| 2 | 1.314 | 1.251 to 1.380 |
| ≥ 3 | 1.336 | 1.255 to 1.423 |
| Predictor | Subdistribution HR | 95% CI |
|---|---|---|
| (Age in years/10)2 + 4.237e-13 | 1.4043 | 1.3913 to 1.4174 |
| (Age in years/10)3 + 4.225e-12 | 0.9750 | 0.9742 to 0.9758 |
| (BMI/10)2 – 5.803e-16 | 26.7979 | 20.0393 to 35.8359 |
| Ethnicity | ||
| South Asian | 0.5776 | 0.4632 to 0.7201 |
| Black African/Caribbean | 0.3060 | 0.1929 to 0.4855 |
| Other | 0.5367 | 0.4172 to 0.6904 |
| Alcohol intake | ||
| Trivial (< 1 unit/day) | 0.9424 | 0.9129 to 0.9728 |
| Light (1–2 units/day) | 0.9775 | 0.9423 to 1.0141 |
| Moderate (3–6 units/day) | 1.0302 | 0.9354 to 1.1345 |
| Heavy (7–9 units/day) | 1.1886 | 0.9149 to 1.5441 |
| Very heavy (> 9 units/day) | 1.3425 | 1.0004 to 1.8015 |
| Smoking status | ||
| Ex-smoker | 1.0350 | 1.0027 to 1.0684 |
| Light smoker | 1.1938 | 1.1150 to 1.2781 |
| Moderate smoker | 1.2787 | 1.2004 to 1.3620 |
| Heavy smoker | 1.4071 | 1.3133 to 1.5075 |
| Asthma or chronic obstructive airways disease | 1.0419 | 1.0022 to 1.0831 |
| Cancer | 0.9496 | 0.9008 to 1.0011 |
| CVD | 0.9763 | 0.9444 to 1.0092 |
| Dementia | 0.9237 | 0.8721 to 0.9783 |
| Epilepsy diagnosis or prescribed anti-convulsant | 1.2616 | 1.1828 to 1.3458 |
| History of falls | 1.2174 | 1.1772 to 1.2590 |
| Chronic liver disease | 1.3347 | 1.1199 to 1.5908 |
| Parkinson’s disease | 1.2782 | 1.1540 to 1.4157 |
| Rheumatoid arthritis or SLE | 1.3488 | 1.2583 to 1.4459 |
| Chronic renal disease | 0.8515 | 0.7886 to 0.9195 |
| Type 1 diabetes | 2.2159 | 1.8568 to 2.6444 |
| Type 2 diabetes | 1.1742 | 1.1170 to 1.2343 |
| Prior fracture | 1.4615 | 1.4148 to 1.5098 |
| Endocrine disorders | 1.1495 | 1.0467 to 1.2623 |
| Antidepressants | 1.1790 | 1.1392 to 1.2202 |
| Corticosteroids | 1.0418 | 0.9762 to 1.1118 |
| Oestrogen-only HRT | 0.7794 | 0.6784 to 0.8955 |
| CCI | ||
| 1 | 1.1250 | 1.0869 to 1.1644 |
| 2 | 1.1160 | 1.0691 to 1.1650 |
| ≥ 3 | 1.0739 | 1.0140 to 1.1373 |
| Predictor | Subdistribution HR | 95% CI |
|---|---|---|
| (Age in years/10)3 + 3.047e-12 | 1.0489 | 1.0464 to 1.0515 |
| (Age in years/10)3 × log(Age in years/10) + 3.317e-12 | 0.9818 | 0.9808 to 0.9829 |
| (BMI/10)2 – 1.723e-15 | 187.7101 | 106.6578 to 330.3562 |
| Ethnicity | ||
| South Asian | 0.4936 | 0.3661 to 0.6656 |
| Black African/Caribbean | 0.2640 | 0.1318 to 0.5287 |
| Other | 0.5366 | 0.3806 to 0.7565 |
| Alcohol intake | ||
| Trivial (< 1 unit/day) | 0.9275 | 0.8706 to 0.9882 |
| Light (1–2 units/day) | 0.8902 | 0.8348 to 0.9492 |
| Moderate (3–6 units/day) | 0.9585 | 0.8847 to 1.0386 |
| Heavy (7–9 units/day) | 1.2728 | 1.1157 to 1.4520 |
| Very heavy (> 9 units/day) | 1.7853 | 1.4829 to 2.1494 |
| Smoking status | ||
| Ex-smoker | 1.0666 | 1.0106 to 1.1257 |
| Light smoker | 1.3543 | 1.2301 to 1.4909 |
| Moderate smoker | 1.4657 | 1.3361 to 1.6078 |
| Heavy smoker | 1.5036 | 1.3826 to 1.6351 |
| Asthma or chronic obstructive airways disease | 0.9623 | 0.9040 to 1.0243 |
| Cancer | 0.9402 | 0.8699 to 1.0163 |
| CVD | 0.9100 | 0.8637 to 0.9589 |
| Dementia | 1.1374 | 1.0107 to 1.2799 |
| Epilepsy diagnosis or prescribed anti-convulsant | 1.7134 | 1.5641 to 1.8770 |
| History of falls | 1.4025 | 1.3083 to 1.5034 |
| Chronic liver disease | 1.2790 | 0.9728 to 1.6816 |
| Parkinson’s disease | 1.7864 | 1.5671 to 2.0363 |
| Rheumatoid arthritis or SLE | 1.4296 | 1.2268 to 1.6660 |
| Chronic renal disease | 1.1160 | 0.9951 to 1.2514 |
| Type 1 diabetes | 2.4706 | 2.0042 to 3.0455 |
| Type 2 diabetes | 1.0826 | 1.0064 to 1.1644 |
| Prior fracture | 1.9079 | 1.7758 to 2.0498 |
| Care home resident | 0.7210 | 0.5987 to 0.8682 |
| Parental history of osteoporosis or hip fracture | 1.0542 | 0.6810 to 1.6320 |
| Antidepressants | 1.2116 | 1.1276 to 1.3018 |
| Corticosteroids | 0.9206 | 0.8105 to 1.0457 |
| CCI | ||
| 1 | 1.2446 | 1.1741 to 1.3193 |
| 2 | 1.3116 | 1.2226 to 1.4070 |
| ≥ 3 | 1.3630 | 1.2479 to 1.4887 |
| Data | External validation cohort | All patients QFracture-2012 internal validation (N = 1,583,373) | |
|---|---|---|---|
| Women external validation cohort (N = 2,747,409; 50.6%) | Men (N = 2,684,730; 49.4%) | ||
| Age (years), mean (SD) | 50.7 (17.4) | 48.5 (15.6) | 50 (1.6) |
| BMI (kg/m2), mean (SD) | 26.6 (6.0) | 27.1 (4.8) | 26.1 (4.6) |
| Women, n (%) | 2,747,409 (50.6) | 804,563 (50.8) | |
| Ethnicity, n (%) | |||
| White or not recorded | 2,614,423 (95.2) | 2,556,923 (95.2) | 1,493,455 (94.3) |
| Indian | 25,420 (0.9) | 27,087 (1.0) | 17,670 (1.1) |
| Pakistani | 11,121 (0.4) | 12,316 (0.5) | 6489 (0.4) |
| Bangladeshi | 3473 (0.1) | 4972 (0.2) | 4191 (0.3) |
| Other Asian | 18,896 (0.7) | 17,758 (0.7) | 10,779 (0.7) |
| Black Caribbean | 4780 (0.2) | 4030 (0.2) | 10,144 (0.6) |
| Black African | 22,736 (0.8) | 20,776 (0.8) | 17,367 (1.1) |
| Chinese | 7358 (0.3) | 5517 (0.2) | 5206 (0.3) |
| Other ethnic group | 39,202 (1.4) | 35,351 (1.3) | 18,072 (1.1) |
| Smoking status, n (%) | |||
| Non-smoker | 1,146,025 (58.3) | 807,294 (46.9) | 773,198 (48.8) |
| Ex-smoker | 390,520 (19.9) | 439,503 (25.5) | 257,087 (16.2) |
| Light (< 10 cigarettes/day) | 135,272 (6.9) | 125,229 (7.3) | 94,400 (6.0) |
| Moderate (10–19 cigarettes/day) | 188,078 (9.6) | 190,990 (11.1) | 113,757 (7.2) |
| Heavy (20 + cigarettes/day) | 107,288 (5.5) | 158,134 (9.2) | 86,787 (5.5) |
| Current smoking amount not recorded | 43,957 (11.5) | 78,372 (23.3) | 65,106 (4.1) |
| Not recorded | 780,226 (28.4) | 963,580 (35.9) | 193,038 (12.2) |
| Alcohol status | |||
| None | 570,900 (27.9) | 317,208 (17.4) | 330,695 (20.9) |
| < 1 unit/day | 854,476 (41.7) | 548,761 (30.2) | 402,847 (25.4) |
| 1–2 units/day | 561,603 (27.4) | 669,776 (36.8) | 287,441 (18.2) |
| 3–6 units/day | 52,785 (2.6) | 224,507 (12.3) | 84,478 (5.3) |
| 7–9 units/day | 5750 (0.3) | 38,273 (2.1) | 8743 (0.6) |
| > 9 units/day | 2993 (0.1) | 9583 (1.1) | 7429 (0.5) |
| Not recorded | 698,902 (25.4) | 866,622 (32.3) | 461,740 (29.2) |
| Previous MOF | 152,417 (5.5) | 113,520 (4.2) | 27,907 (1.8) |
| Parental history of osteoporosis or hip fracture | 10,561 (0.4) | 1077 (0.04) | 4227 (0.3) |
| Nursing or care home resident | 16,819 (0.6) | 7455 (0.3) | 1535 (0.1) |
| Condition or prescription | |||
| Type 1 diabetes | 8747 (0.3) | 12,008 (0.4) | 4322 (0.3) |
| Type 2 diabetes | 81,715 (3.0) | 100,009 (3.7) | 43,437 (2.7) |
| History of falls | 153,841 (5.6) | 74,368 (2.8) | 17,382 (1.1) |
| Dementia | 34,892 (1.3) | 15,036 (0.6) | 7791 (0.5) |
| Cancer | 94,090 (3.4) | 67,380 (2.5) | 28,203 (1.8) |
| Asthma or COPD | 355,014 (12.9) | 303,541 (11.3) | 113,175 (7.1) |
| CVD | 156,577 (5.7) | 195,378 (7.3) | 77,824 (4.9) |
| Chronic liver disease | 6093 (0.2) | 6753 (0.3) | 3216 (0.2) |
| Chronic renal disease | 33,274 (1.2) | 24,395 (0.9) | 3413 (0.2) |
| Parkinson’s disease | 7585 (0.3) | 8348 (0.3) | 3650 (0.2) |
| Rheumatoid arthritis or SLE | 11,970 (0.4) | 32,950 (1.2) | 10,091 (0.6) |
| Malabsorption | 34,884 (1.3) | 27,122 (1.0) | 8026 (0.5) |
| Endocrine disorders | 25,089 (0.9) | 5866 (0.2) | 7882 (0.5) |
| Epilepsy or prescribed anticonvulsants | 66,145 (2.4) | 59,214 (2.2) | 26,271 (1.7) |
| Prescribed antidepressants | 66,145 (2.4) | 59,214 (2.2) | 111,229 (7.0) |
| Prescribed corticosteroid | 37,169 (1.4) | 22,632 (0.8) | 30,998 (2.0) |
| Prescribed oestrogen-only HRT | 33,679 (1.2) | 127 (0.0) | 14,988 (0.9) |
| Age range (years) | Women | Men | ||||
|---|---|---|---|---|---|---|
| Incident MOF | Total follow-up (years) | Rate per 1000 person-year (95% CI) | Incident MOF | Total follow-up (years) | Rate per 1000 person-years (95% CI) | |
| 30–34 | 2603 | 2,741,657 | 0.95 (0.91 to 0.99) | 2828 | 2,784,175 | 1.02 (0.98 to 1.05) |
| 35–39 | 2025 | 1,870,595 | 1.08 (1.04 to 1.13) | 2121 | 1,927,589 | 1.10 (1.05 to 1.15) |
| 40–44 | 2698 | 1,833,507 | 1.47 (1.42 to 1.53) | 2222 | 1,917,796 | 1.16 (1.11 to 1.21) |
| 45–49 | 3633 | 1,595,805 | 2.28 (2.20 to 2.35) | 2239 | 1,681,808 | 1.33 (1.28 to 1.39) |
| 50–54 | 5292 | 1,449,369 | 3.65 (3.55 to 3.75) | 2248 | 1,497,499 | 1.50 (1.44 to 1.56) |
| 55–59 | 7422 | 1,490,080 | 4.98 (4.87 to 5.10) | 2644 | 1,505,675 | 1.76 (1.69 to 1.82) |
| 60–64 | 7762 | 1,210,157 | 6.41 (6.27 to 6.56) | 2743 | 1,191,801 | 2.30 (2.22 to 2.39) |
| 65–69 | 9455 | 1,024,227 | 9.23 (9.05 to 9.42) | 2859 | 960,815 | 2.98 (2.87 to 3.09) |
| 70–74 | 11,757 | 861,260 | 13.65 (13.41 to 13.90) | 3456 | 748,844 | 4.62 (4.46 to 4.77) |
| 75–80 | 14,148 | 688,855 | 20.54 (20.21 to 20.88) | 4068 | 516,507 | 7.88 (7.64 to 8.12) |
| 80–84 | 14,653 | 508,415 | 28.82 (28.36 to 29.28) | 3891 | 304,005 | 12.80 (12.41 to 13.20) |
| 85–90 | 9017 | 237,728 | 37.93 (37.17 to 38.71) | 2080 | 107,018 | 19.44 (18.63 to 20.28) |
| 90–99 | 5133 | 112,888 | 45.47 (44.27 to 46.70) | 922 | 36,093 | 25.55 (23.97 to 27.22) |
| Total | 95,598 | 15,624,543 | 6.12 (6.08 to 6.16) | 34,321 | 15,179,623 | 2.26 (2.24 to 2.29) |
| Women | Men | |||||
|---|---|---|---|---|---|---|
| Age range (years) | Incident hip fractures | Total follow-up (years) | Rate per 1000 person-years (95% CI) | Incident hip fractures | Total follow-up (years) | Rate per 1000 person-years (95% CI) |
| 30–34 | 93 | 2,750,441 | 0.03 (0.03 to 0.04) | 214 | 2,793,615 | 0.08 (0.07 to 0.09) |
| 35–39 | 109 | 1,878,222 | 0.06 (0.05 to 0.07) | 223 | 1,935,329 | 0.12 (0.10 to 0.13) |
| 40–44 | 183 | 1,842,965 | 0.10 (0.09 to 0.11) | 307 | 1,925,573 | 0.16 (0.14 to 0.18) |
| 45–49 | 374 | 1,607,632 | 0.23 (0.21 to 0.26) | 377 | 1,689,307 | 0.22 (0.20 to 0.25) |
| 50–54 | 599 | 1,467,062 | 0.41 (0.38 to 0.44) | 442 | 1,504,825 | 0.29 (0.27 to 0.32) |
| 55–59 | 1149 | 1,515,268 | 0.76 (0.72 to 0.80) | 701 | 1,513,119 | 0.46 (0.43 to 0.50) |
| 60–64 | 1554 | 1,234,523 | 1.26 (1.20 to 1.32) | 948 | 1,197,990 | 0.79 (0.74 to 0.84) |
| 65–69 | 2614 | 1,051,678 | 2.49 (2.39 to 2.58) | 1217 | 966,352 | 1.26 (1.19 to 1.33) |
| 70–74 | 4460 | 889,669 | 5.01 (4.87 to 5.16) | 1709 | 754,325 | 2.27 (2.16 to 2.38) |
| 75–80 | 6905 | 715,572 | 9.65 (9.43 to 9.88) | 2432 | 521,184 | 4.67 (4.48 to 4.86) |
| 80–84 | 8752 | 527,816 | 16.58 (16.24 to 16.93) | 2640 | 307,196 | 8.59 (8.27 to 8.93) |
| 85–90 | 5968 | 246,247 | 24.24 (23.64 to 24.85) | 1469 | 108,226 | 13.57 (12.90 to 14.28) |
| 90–99 | 3640 | 115,681 | 31.47 (30.48 to 32.49) | 700 | 36,423 | 19.22 (17.86 to 20.68) |
| Total | 36,400 | 15,842,775 | 2.30 (2.27 to 2.32) | 13,379 | 15,253,462 | 0.88 (0.86 to 0.89) |
| Age range (years) | Women | Men | ||||
|---|---|---|---|---|---|---|
| Incident non-fracture death | Total follow-up (years) | Rate per 1000 person-years (95% CI) | Incident non-fracture death | Total follow-up (years) | Rate per 1000 person-years (95% CI) | |
| 30–34 | 1348 | 2,741,657 | 0.49 (0.47 to 0.52) | 2346 | 2,784,175 | 0.84 (0.81 to 0.88) |
| 35–39 | 1677 | 1,870,595 | 0.90 (0.85 to 0.94) | 2411 | 1,927,589 | 1.25 (1.20 to 1.30) |
| 40–44 | 2534 | 1,833,507 | 1.38 (1.33 to 1.44) | 3605 | 1,917,796 | 1.88 (1.82 to 1.94) |
| 45–49 | 3714 | 1,595,805 | 2.33 (2.25 to 2.40) | 5094 | 1,681,808 | 3.03 (2.95 to 3.11) |
| 50–54 | 4991 | 1,449,369 | 3.44 (3.35 to 3.54) | 7398 | 1,497,499 | 4.94 (4.83 to 5.05) |
| 55–59 | 7996 | 1,490,080 | 5.37 (5.25 to 5.48) | 12,167 | 1,505,675 | 8.08 (7.94 to 8.23) |
| 60–64 | 10,378 | 1,210,157 | 8.58 (8.41 to 8.74) | 15,427 | 1,191,801 | 12.94 (12.74 to 13.15) |
| 65–69 | 14,216 | 1,024,227 | 13.88 (13.65 to 14.11) | 20,779 | 960,815 | 21.63 (21.34 to 21.92) |
| 70–74 | 19,734 | 861,260 | 22.91 (22.60 to 23.23) | 26,842 | 748,844 | 35.84 (35.43 to 36.27) |
| 75–80 | 27,874 | 688,855 | 40.46 (40.00 to 40.93) | 31,087 | 516,507 | 60.19 (59.54 to 60.84) |
| 80–84 | 36,030 | 508,415 | 70.87 (70.17 to 71.58) | 30,228 | 304,005 | 99.43 (98.37 to 100.50) |
| 85–89 | 29,415 | 237,728 | 123.73 (122.42 to 125.06) | 16,832 | 107,018 | 157.28 (155.11 to 159.48) |
| 90–99 | 23,799 | 112,888 | 210.82 (208.45 to 213.21) | 8865 | 36,093 | 245.62 (241.20 to 250.09) |
| Total | 183,706 | 15,624,543 | 11.76 (11.70 to 11.81) | 183,081 | 15,179,623 | 12.06 (12.01 to 12.12) |
FIGURE 32.
Major osteoporotic fracture, hip fracture and non-fracture death incidence in (a) women; and (b) men. Source: Livingstone et al. 50
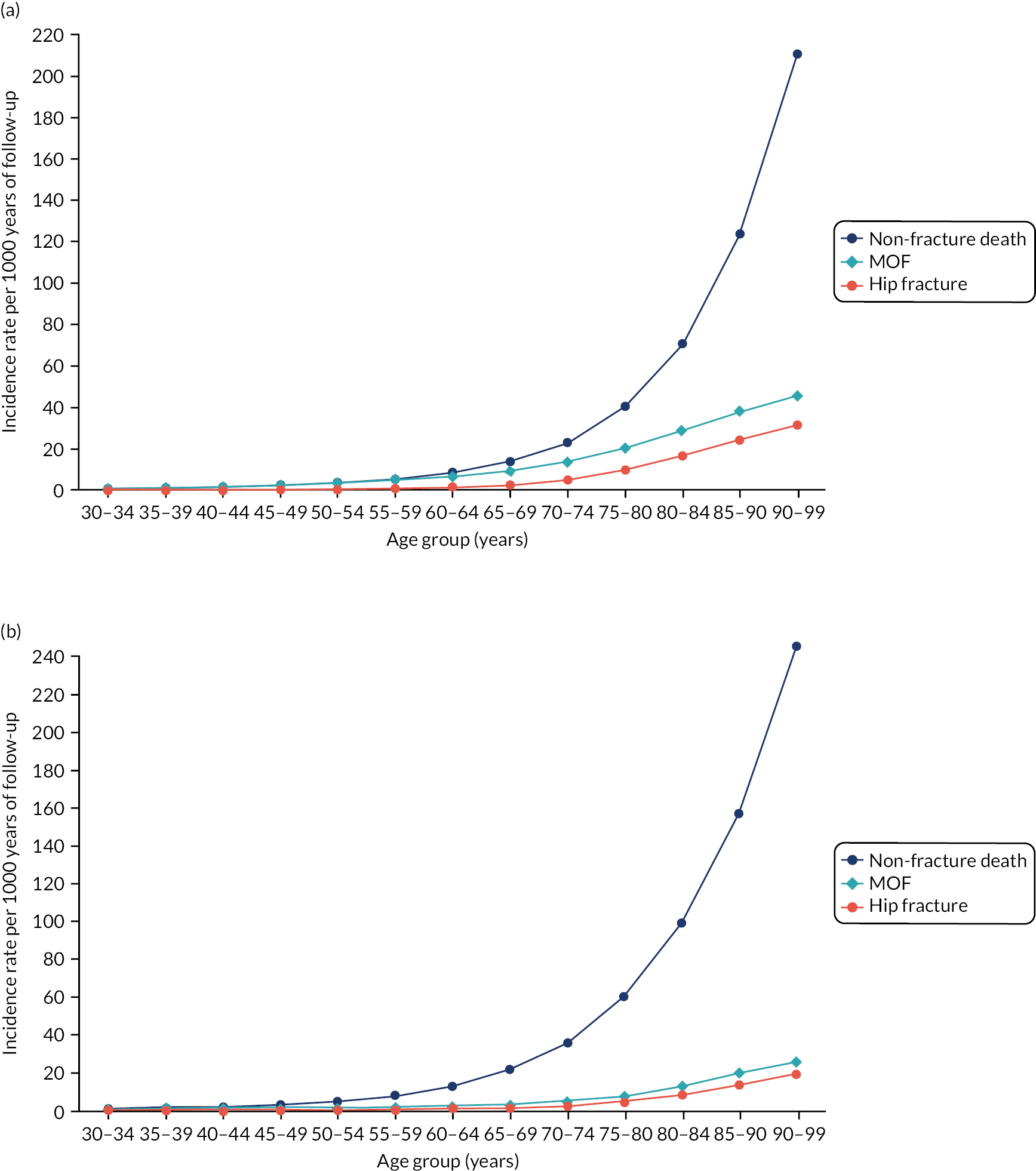
FIGURE 33.
Comparison of fracture incidence in this study (using GP, mortality and hospital admission data), previous external validation (using GP and ONS data, but maximum age 85 years) and this study matched to previous external validation ascertainment (using GP and ONS data). (a) Women: MOFs; (b) women: hip fractures; (c) men: MOFs; and (d) men: hip fractures. Source: Livingstone et al. 50
Appendix 5 Direct treatment disutility elicitation: supplementary results
| Attribute level | Bisphosphonates | Statins | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experience of taking bisphosphonates (n = 83) | No experience of taking bisphosphonates (n = 229) | Pooled (n = 312) | Experience of taking statins (n = 105) | No experience of taking statins (n = 214) | Pooled (n = 319) | |||||||||||||
| Best | Worst | Best–worst | Best | Worst | Best–worst | Best | Worst | Best–worst | Best | Worst | Best–worst | Best | Worst | Best–worst | Best | Worst | Best–worst | |
| No inconvenience | 0.76 | 0.11 | 0.65 | 0.62 | 0.15 | 0.47 | 0.65 | 0.15 | 0.50 | 0.62 | 0.15 | 0.47 | 0.65 | 0.15 | 0.50 | 0.64 | 0.15 | 0.49 |
| Inconvenience | 0.62 | 0.22 | 0.40 | 0.61 | 0.17 | 0.45 | 0.56 | 0.19 | 0.37 | 0.61 | 0.17 | 0.45 | 0.56 | 0.19 | 0.37 | 0.58 | 0.18 | 0.39 |
| MSE | ||||||||||||||||||
| 1% | 0.15 | 0.17 | −0.02 | 0.24 | 0.23 | 0.00 | 0.23 | 0.25 | −0.02 | 0.24 | 0.23 | 0.00 | 0.23 | 0.25 | −0.02 | 0.23 | 0.25 | −0.01 |
| 5% | 0.16 | 0.22 | −0.05 | 0.20 | 0.36 | −0.16 | 0.17 | 0.37 | −0.20 | 0.20 | 0.36 | −0.16 | 0.17 | 0.37 | −0.20 | 0.18 | 0.37 | −0.19 |
| 9% | 0.16 | 0.28 | −0.12 | 0.20 | 0.38 | −0.19 | 0.16 | 0.46 | −0.29 | 0.20 | 0.38 | −0.19 | 0.16 | 0.46 | −0.29 | 0.17 | 0.43 | −0.26 |
| 13% | 0.14 | 0.28 | −0.13 | 0.19 | 0.43 | −0.24 | 0.18 | 0.49 | −0.32 | 0.19 | 0.43 | −0.24 | 0.18 | 0.49 | −0.32 | 0.18 | 0.47 | −0.29 |
| SSE | ||||||||||||||||||
| 0.1% | 0.14 | 0.58 | −0.44 | 0.20 | 0.46 | −0.27 | 0.28 | 0.37 | −0.09 | 0.20 | 0.46 | −0.27 | 0.28 | 0.37 | −0.09 | 0.25 | 0.40 | −0.15 |
| 0.3% | 0.17 | 0.60 | −0.42 | 0.16 | 0.49 | −0.32 | 0.21 | 0.43 | −0.22 | 0.16 | 0.49 | −0.32 | 0.21 | 0.43 | −0.22 | 0.19 | 0.45 | −0.25 |
| 0.5% | 0.16 | 0.61 | −0.45 | 0.17 | 0.50 | −0.34 | 0.17 | 0.46 | −0.29 | 0.17 | 0.50 | −0.34 | 0.17 | 0.46 | −0.29 | 0.17 | 0.47 | −0.31 |
| 0.7% | 0.14 | 0.60 | −0.46 | 0.19 | 0.50 | −0.31 | 0.18 | 0.49 | −0.31 | 0.19 | 0.50 | −0.31 | 0.18 | 0.49 | −0.31 | 0.19 | 0.50 | −0.31 |
FIGURE 34.
Kernel density plots showing distribution of BWS responses stratified by question context and respondent type: statins. (a) No inconvenience; (b) inconvenience; (c) MSE 1%; (d) MSE 5%; (e) MSE 9%; (f) MSE 13%; (g) SSE 0.1%; (h) SSE 0.3%; (i) SSE 0.5%; and (j) SSE 0.7%.

FIGURE 35.
Kernel density plots showing distribution of BWS responses stratified by question context and respondent type: bisphosphonates. (a) No inconvenience; (b) inconvenience; (c) MSE 1%; (d) MSE 5%; (e) MSE 9%; (f) MSE 13%; (g) SSE 0.1%; (h) SSE 0.3%; (i) SSE 0.5%; and (j) SSE 0.7%.
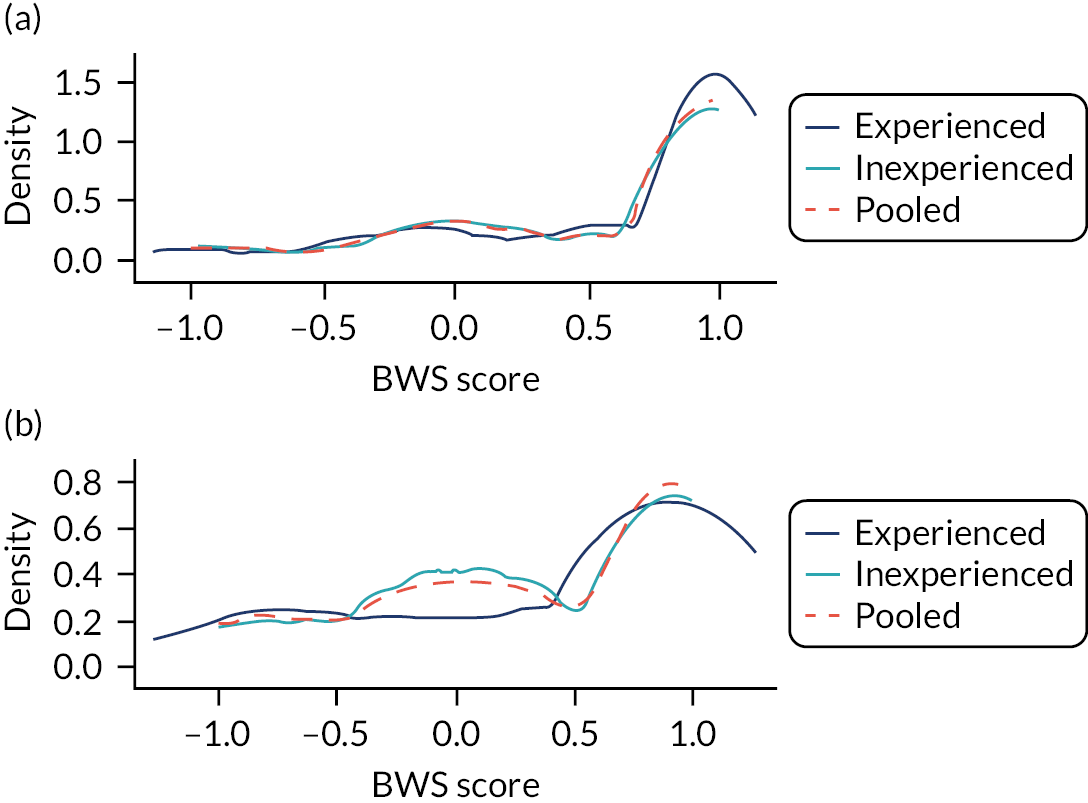
Appendix 6 Supplementary methods for model assessing cost-effectiveness of statins for the primary prevention of cardiovascular disease
Type of first cardiovascular event
We fitted a multinomial logistic regression model to the CPRD data set (which excluded people who have previously experienced cardiovascular events or received statins) to estimate the relative probabilities of a cardiovascular event being of each type, according to sex, age at event and baseline QRISK3-predicted risk. Multinomial logistic regression provides a way of predicting the likelihood of each of a number of possible events in a single statistical model. In logistic regression, the probabilities of each event are output as log-transformed odds of the events against a reference event. Accordingly, for each included risk factor, the model estimates a separate coefficient for each event, which can be interpreted as a log-transformed OR. Exponentiating these coefficients gives the ratios by which a unit change of the corresponding risk factors changes the odds of the event against the reference.
Table 47 shows the output from the multinomial regression model that we constructed, for which cardiovascular death was the reference event. Applying the coefficient values for an event type to a set of covariate values reflecting a cohort’s risk factors gives the log-odds between that event and cardiovascular death for the cohort.
| Parameter | MI | SA | Stroke | TIA | UA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | 95% CI | Estimate | 95% CI | Estimate | 95% CI | Estimate | 95% CI | Estimate | 95% CI | |
| Intercept | 4.28826 | 4.28812 to 4.28840 | −0.08864 | −0.08877 to −0.08851 | −3.91704 | −3.91717 to −3.91692 | −5.49010 | −5.49024 to −5.48996 | 5.85206 | 5.85192 to 5.85219 |
| Male | −0.27917 | −0.27934 to −0.27900 | −0.97014 | −0.97029 to −0.96998 | −0.42471 | −0.42488 to −0.42454 | 0.53725 | 0.53707 to 0.53744 | −2.19771 | −2.19781 to −2.19761 |
| Logit(QRISK3) | 1.30783 | 1.30769 to 1.30798 | 0.63785 | 0.63772 to 0.63799 | −0.64463 | −0.64479 to −0.64447 | −0.48442 | −0.48459 to −0.48426 | 1.74833 | 1.74819 to 1.74846 |
| Age | −0.10524 | −0.11121 to −0.09927 | 0.04209 | 0.03676 to 0.04742 | 0.08843 | 0.08285 to 0.09401 | 0.12395 | 0.11794 to 0.12996 | −0.17737 | −0.18239 to −0.17234 |
| Age2 | 0.00057 | 0.00049 to 0.00064 | −0.00052 | −0.00059 to −0.00045 | −0.00050 | −0.00057 to −0.00043 | −0.00079 | −0.00087 to −0.00072 | 0.00100 | 0.00094 to 0.00106 |
| Male × logit (QRISK3) | −0.29154 | −0.29170 to −0.29138 | −0.82318 | −0.82332 to −0.82303 | −0.39047 | −0.39064 to −0.39030 | −0.27136 | −0.27154 to −0.27119 | −1.17876 | −1.17890 to −1.17861 |
| Age × male | 0.03327 | 0.02666 to 0.03987 | 0.02899 | 0.02288 to 0.03510 | 0.02439 | 0.01767 to 0.03112 | −0.00780 | −0.01514 to −0.00046 | 0.07193 | 0.06816 to 0.07569 |
| Age2 × male | −0.00033 | −0.00042 to −0.00025 | −0.00019 | −0.00027 to −0.00012 | −0.00025 | −0.00033 to −0.00017 | 0.00001 | −0.00008 to 0.00010 | −0.00054 | −0.00059 to −0.00048 |
| Age × logit (QRISK3) | −0.04975 | −0.05214 to −0.04736 | −0.03331 | −0.03553 to −0.03108 | −0.00323 | −0.00546 to −0.00099 | −0.01097 | −0.01328 to −0.00867 | −0.06871 | −0.07124 to −0.06618 |
| Age2 × logit (QRISK3) | 0.00034 | 0.00030 to 0.00038 | 0.00024 | 0.00020 to 0.00028 | 0.00006 | 0.00003 to 0.00010 | 0.00011 | 0.00007 to 0.00014 | 0.00050 | 0.00045 to 0.00054 |
| Age × male × logit (QRISK3) | 0.01713 | 0.01425 to 0.02002 | 0.03821 | 0.03544 to 0.04098 | 0.02679 | 0.02392 to 0.02966 | 0.02588 | 0.02281 to 0.02894 | 0.04828 | 0.04513 to 0.05143 |
| Age2 × male × logit (QRISK3) | −0.00016 | −0.00021 to −0.00011 | −0.00034 | −0.00039 to −0.00030 | −0.00027 | −0.00032 to −0.00022 | −0.00027 | −0.00033 to −0.00022 | −0.00040 | −0.00046 to −0.00034 |
To give a worked example, consider 50-year-old women with a 10-year QRISK3-predicted CVD risk of 10%. For women in this subgroup who experience a cardiovascular event, we can calculate the log-odds that this event will be a MI compared with cardiovascular death as follows. For each unit of age, one unit of the corresponding coefficient for MI (set at its mean value) is added (not multiplied because, before exponentiation, we are working on a logarithmic scale) to the intercept: 4.2883 + 50 × −0.1052. For women, we do not apply the ‘male’ coefficient. The transformations and interactions described in Table 47 must be applied to age, sex and QRISK3-predicted risk before applying all other coefficients in the same way. Let I be the set of cohort characteristics (i.e. women, 50 years old, 10% QRISK3). Therefore, the final equation is:
We exponentiate to give the odds of MI against non-cardiovascular death for covariates I:
Once we have calculated the odds of each event against the reference, we may calculate the absolute probabilities of each event as follows. First, we express the absolute probability of the event being a MI as a multiple of the absolute probability of the event being cardiovascular death:
Repeating steps 1–3 for each other event gives:
People who had a cardiovascular event recorded in the CPRD data set must have had one of these types of events or be classified as a cardiovascular death. Therefore, the sum of these absolute probabilities, along with that of cardiovascular death, must equal 1:
Now, we can substitute the values from Equation 7 into Equation 8 and use the result to calculate the probability of the reference event: cardiovascular death:
Finally, we compute the absolute probabilities of each event from Equation 7 using the value we calculated for P(CV death)I:
Figure 36 illustrates the results of the model for men and women at a range of ages and underlying levels of cardiovascular risk. For comparison, Figure 36 also shows the raw distribution of first events in the CPRD data to which we fitted the model. Strokes and cardiovascular deaths become more common first events as people get older. In contrast, the probability that the first sign of CVD will be an acute coronary event (MI or UA) is highest in younger people. Predicted cardiovascular risk at baseline and sex have relatively little influence on the distribution of events.
FIGURE 36.
First CVD event stratified by age, sex and CVD risk: predictions from multinomial model compared with observed data from CPRD.
The events available in the CPRD data set comprise only events used by QRISK3 as predictors (i.e. SA, UA, MI, stroke, TIA and cardiovascular death). Therefore, we had to replicate the approach used in CG181 of combining predicted events within each cohort with external evidence estimating age- and sex-specific rates of PAD169 and heart failure. 170
To extend our example of a 50-year-old woman, this evidence suggests that, for women in the age bracket of 45–55 years, there are 6.3% as many cases of heart failure and 62.5% as many cases of PAD as QRISK3 events. This means that the QRISK3 events accounted for: 1/[P(PAD)I + P(HF)I + 1] = 0.593. Multiplying this number by our calculations from Equation 10 we arrive at our final proportions:
Health-related quality of life: underlying
We created the data set we used from a pooled sample of respondents from the HSE. 133 The HSE is a nationally representative cross-sectional sample of people residing privately in England. Each year, respondents complete a set of core questions about their general health (including the EQ-5D-3L), their lifestyle choices and behaviour, as well as their personal characteristics. From year to year, additional modules are integrated within the HSE and respondents are asked detailed questions about particular topics. We pooled HSE data sets from 2003, 2006 and 2011, as these surveys focused on CVD, with respondents being asked whether or not they had ever been specifically diagnosed with CVD by a doctor. After pooling the data, we dropped individuals with missing data for age and EQ-5D-3L. The remaining sample (n = 26,400) included only people who reported having no doctor-diagnosed CVD.
To account for non-linearity in the relationship between age and quality of life, we explored a range of polynomial forms. We introduced sex as a covariate and tested various degrees of interaction with the age terms. The model that best described the data (i.e. the most parsimonious model with AIC within 3 points of the lowest observed) had a quintic form with full interaction with sex (equivalent to fitting separate models for men and women). Table 48 details the final model.
| Parameter | EQ-5D-3L (95% CI) |
|---|---|
| Constant | 1.0800 (0.8332 to 1.3268) |
| Male | 0.2198 (−0.1610 to 0.6006) |
| Age | −0.0181 (−0.0496 to 0.0135) |
| Age2 | 9.59 × 10−4 (−5.37 × 10−4 to 2.46 × 10−3) |
| Age3 | −2.57 × 10−5 (−5.89 × 10−5 to 7.60 × 10−6) |
| Age4 | 3.11 × 10−7 (−3.81 × 10−8 to 6.60 × 10−7) |
| Age5 | −1.41 × 10−9 (−2.81 × 10−9 to −1.29 × 10−11) |
| Male × age | −0.0270 (−0.0759 to 0.0220) |
| Male × age2 | 1.28 × 10−3 (−1.06 × 10−3 to 3.61 × 10−3) |
| Male × age3 | −2.85 × 10−5 (−8.07 × 10−5 to 2.37 × 10−5) |
| Male × age4 | 3.07 × 10−7 (−2.45 × 10−7 to 8.59 × 10−7) |
| Male × age5 | −1.27 × 10−9 (−3.49 × 10−9 to 9.55 × 10−10) |
For people aged 90–100 years, we did not use modelled quality-of-life estimates and, instead, we relied on a simple average of values for men and women in that age group. We did this because data for nonagenarians are very scanty in the HSE data set (with only 52 women and 26 men represented) and, although it is clear that quality of life in the 10th decade is lower than in preceding years, there is no indication of a within-decade decline in this subpopulation of people with no cardiovascular history. Contrary to this, a continuous function fitted to all ages results in a dramatic drop-off in quality of life between 90 and 100 years (as the continuous function extrapolates the decline that is seen in the more plentiful data for previous decades). This can be solved by incorporating higher-order polynomial terms for age, but this results in implausible tail effects, where quality of life suddenly and markedly improves among the oldest people. We concluded that there are simply not enough data to assume any trends in within-decade quality of life for nonagenarians, and used a simple average instead (Table 49).
| Parameter | n | EQ-5D-3L (95% CI) |
|---|---|---|
| Women | 52 | 0.638 (0.568 to 0.705) |
| Men | 26 | 0.531 (0.381 to 0.679) |
Figure 37 provides a visualisation of the new fitted model and alternative approaches compared with the underlying data. It is clear that the linear decline assumed in CG181 provides a poor approximation, as it overestimates quality of life in the oldest and youngest people and underestimates it for people aged 40–85 years. The quadratic function suggested by Ara and Brazier156 provides a better fit, especially for women; however, it is less well suited to men, overestimating quality of life in the first three decades of adulthood and underestimating quality of life from age 60 to 90 years.
FIGURE 37.
Underlying quality of life of people with no history of CVD: new polynomial model compared with linear assumption from CG181 and quadratic model from Ara and Brazier. 156 (a) Women; and (b) men.

For similar reasons, for women up until age 85 years, our new quintic model mirrors Ara and Brazier’s156 quadratic model fairly closely, but differences are more apparent in men. In particular, the raw data suggest that – in this subgroup of men with no cardiovascular history (which will become an increasingly atypical group as age rises) – quality of life is fairly well preserved throughout middle age, and only begins to tail off appreciably in their 80s and 90s. This suggests that a good proportion of the expected decline in the quality of life of men as they age can be attributed to CVD itself (or other morbidities that are strongly correlated with cardiovascular events). The remaining men with no cardiovascular history – the population of interest for our primary prevention decision problem – appear to escape without much deterioration in their underlying utility, and our new model captures this where other alternatives do not.
Health-related quality of life: cardiovascular events
To quality adjust expected survival for cost–utility analysis of a state-transition models, we require estimates of the quality of life associated with each of the model states. We updated the health state utility values from the CG181 model using a systematic review and in accordance with the Centre for Reviews and Dissemination guidelines. 171 To identify estimates for each model state, we adopted a pragmatic approach following recommendations in the NICE Decision Support Unit’s technical support document for utility values. 134
Table 50 reports the focus [i.e. population, intervention, comparator, outcome, study type (PICOS)] of this review. Two reviewers screened titles and abstracts for inclusion, resolving conflicts by consensus. Following this, one reviewer screened full texts for inclusion. A second reviewer checked a sample of full texts. One reviewer extracted data from the included studies. The protocol was published (PROSPERO CRD42021249959). 172
| Characteristic | Description |
|---|---|
| Population | Adult (aged ≥ 18 years) with one of the prespecified conditions of interest |
| Intervention | Experiencing a prespecified health state or condition: |
|
|
| Comparator | Utility value for an adult population without the specified health states or conditions of interest |
| Outcome | Mean utility score with measure of dispersion |
| Study type | Empirical study using direct or indirect measurement methods to produce utility values |
We searched MEDLINE and EMBASE databases via Ovid. The search strategy combined cardiovascular terms from CG181 with the York precision-maximising filter for utility values. 173 We excluded studies if they were unavailable in English or used only condition-specific measures of quality of life.
The search returned 5080 distinct studies, of which 4132 were excluded on abstract screening (Figure 38). A further 526 studies were excluded on full-text screening for the following reasons: 165 studies had no primary data; 128 studies did not consider any of our specified health states; 32 studies considered unrepresentative subgroups of specified states only; 2 studies collected only condition-specific measures of health-related quality of life; 157 studies did not report overall health-related quality-of-life estimate; and 44 studies were unavailable to download or were unavailable in English.
FIGURE 38.
A PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) flow chart for systematic review of health state utility values.
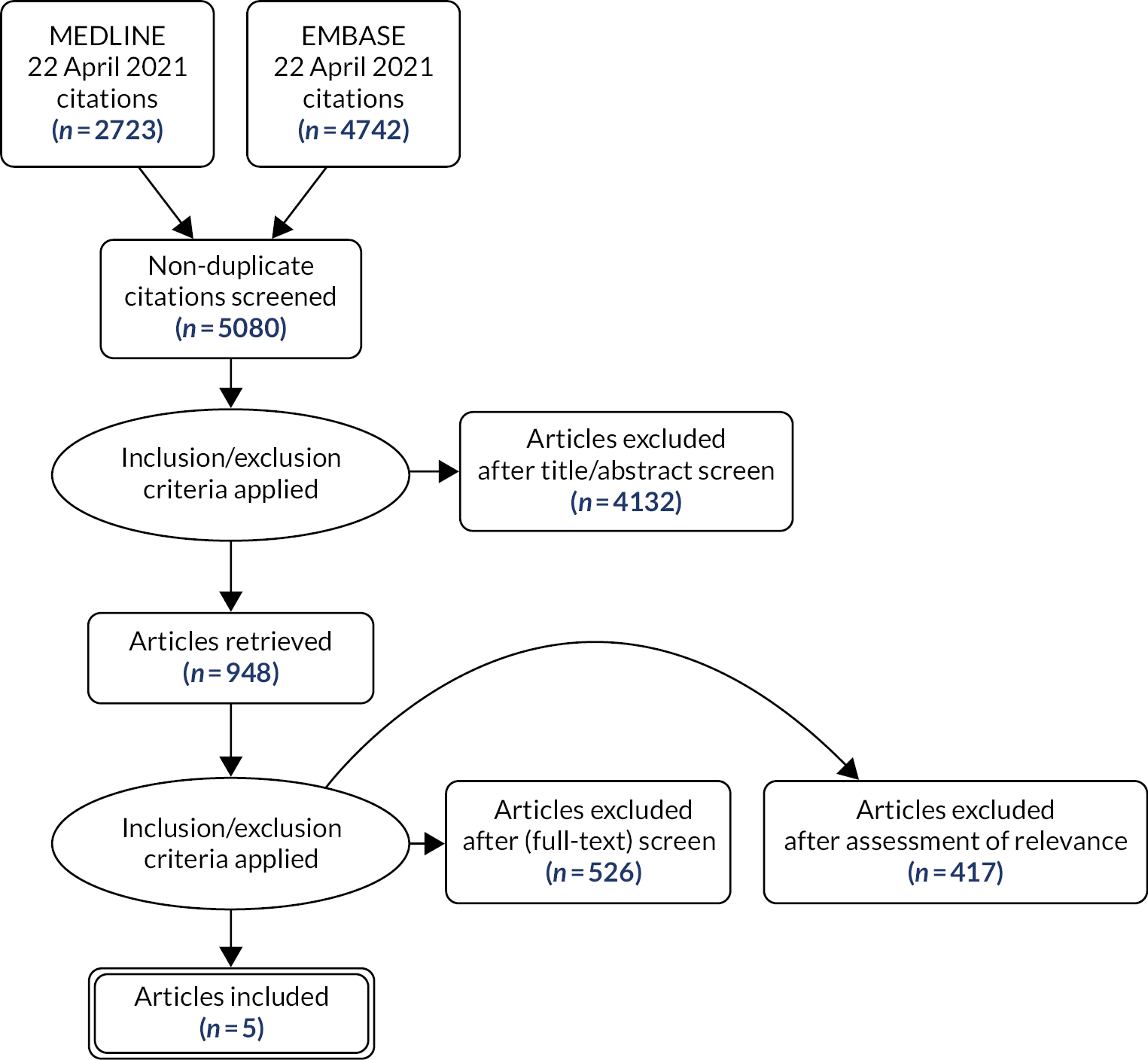
The review results included studies that collected EQ-5D-3L responses from British populations with each of the specified conditions, with the exception of PAD. Estimates based on European EQ-5D-3L responses, evaluated according to the British tariff, were available for PAD. For each of the events that had an associated post-event state, it was possible to source HSUVs for post-event states from the same source as first year.
We filtered the results of the review to show studies that evaluated the EQ-5D-3L responses of British, or similar, populations according to a UK tariff. We assessed the relevance of these studies to our purposes using high-level characteristics, such as sample size and the number of conditions of interest considered. We identified the studies judged to be most suitable as candidates from which to source disutility multipliers for the model. We used a self-developed quality assessment tool to compare candidate studies according to risk of bias and applicability. There were nine candidate studies in total. 174–182
A set of disutilities for the health states of interest was chosen according to their critical appraisal performance and clinical face validity when compared with one another. Two clinicians assessed the face validity of the chosen set of disutilities. The two clinicians confirmed that each estimate, as well as the rank order between them, was plausible.
We selected a study recruiting people experiencing their first TIA (n = 314) or stroke (n = 445) across five general practices. 174 Heart failure estimates were sourced from cases (n = 260) detected from clinics/acute care/GPs at two UK sites in 2006–8. 176 For SA, we pooled results across three management strategies for people aged ≥ 30 years with suspected SA who were suitable for revascularisation. 182 For PAD, we used data from 204 consecutive cases of PAD diagnosed by ankle-brachial index of ≤ 0.9 in the Netherlands, evaluated using UK tariff. 180
If we were to choose our preferred sources for each individual state independently, there is a risk that we would be left with an implausible ranking of multipliers. For MI, it appeared that a study covering all UK cases in a 5-year period181 was the best source based on critical appraisal and recruitment policy. However, when chosen together with our preferred source for SA,182 the study suggested that angina decreases health-related quality of life to a greater extent than MI. To avoid an implausible ordering of these states, we chose a third study (which considered multiple states of interest, but considered only three sites rather than the whole UK) for both UA (n = 898) and MI (n = 1176). 179 People who were aged ≥ 18 years and who had not been revascularised or received a coronary artery bypass graft within the previous 6 months were eligible for inclusion in this study. We did not use separate values for any comorbidities of the conditions modelled. We did not use three of the candidate studies175,177,178 identified by the review.
Three of the source studies174,179,182 had the advantage of being longitudinal. We calculated average annual utility from the time points given using the AUROC approach. Otherwise, the single estimates provided were used. 176,180 The studies used for stroke, TIA and MI provided estimates of quality of life 1 month after the event in question, but did not give a baseline value. 174,179 For stroke and TIA, our area under the curve calculations assumed that baseline values were equal to those at 1 month. For MI, we applied the ratio of baseline to 1-month estimates from an alternative source181 to the 1-month estimates from the study used to derive a baseline estimate.
We applied utility values to baseline quality of life using a multiplicative approach. For stroke and TIA, the study reported health-related quality of life of controls without CVD174 and so we used this directly to estimate the relative impact of the events. For other states, we calculated disutility multipliers by comparing reported EQ-5D-3L values with our prediction of baseline utility for people with the same mean age and proportion of men and women but no CVD (see above). The model multiplies the age-and sex-specific baseline utility by the relevant disutility multiplier to adjust people’s quality of life accordingly (Table 51).
| Health state | EQ-5D-3L disutility multiplier (95% CI)a | Risk of bias | Relevance | Source | CG18115 |
|---|---|---|---|---|---|
| SA | 0.865 (0.852 to 0.876) | Minor | Direct | Walker et al.182 | 0.808 |
| Post SA | 0.869 (0.854 to 0.883) | ||||
| UA | 0.740 (0.719 to 0.762) | Minor | Direct | Pockett et al.179 | 0.770 |
| Post UA | 0.731 (0.711 to 0.752) | 0.880 | |||
| MI | 0.816 (0.800 to 0.833) | Minor | Direct | Pockett et al.179 | 0.760 |
| Post MI | 0.818 (0.800 to 0.837) | 0.880 | |||
| TIA | 0.899 (0.871 to 0.927) | Minor | Direct | Luengo-Fernandez et al.174 | 0.900 |
| Post TIA | 0.892 (0.862 to 0.924) | ||||
| Stroke | 0.808 (0.784 to 0.834) | Minor | Direct | Luengo-Fernandez et al.174 | 0.628 |
| Post stroke | 0.788 (0.757 to 0.819) | ||||
| Heart failure | 0.714 (0.671 to 0.754) | Minor | Direct | Mejía et al.176 | 0.683 |
| Post heart failure | |||||
| PAD | 0.756 (0.722 to 0.792) | Minor | Partial | Vaidya et al.180 | 0.808 |
| Post PAD | |||||
Resource use and costs: cardiovascular events
We performed a rapid review using pearl-growing from two previously known sources: one for stroke/TIA140 and one for cardiovascular events. 141 Table 52 reports the focus (PICOS) of this review. One researcher conducted the pearl-growing and checked citations of included studies. For the rapid review, the researcher used the medical subject heading terms for the original pearl papers to find similar papers in both MEDLINE and EMBASE using Ovid Online. These papers were combined with the papers found using the ‘Find Similar’ tool within Ovid Online. Finally, all references within the pearls were extracted and combined with any papers citing the pearls. The researcher then removed duplicates and screened titles and abstracts of studies identified for inclusion based on PICOS. Following this, two researchers screened full texts for inclusion based on PICOS. One researcher extracted data from the included studies and a second researcher checked the extraction.
| Characteristic | Description |
|---|---|
| Population | Adult (≥ 18 years) with one of the prespecified conditions of interest |
| Intervention | Experiencing a prespecified health state or condition: |
|
|
| Comparator | NHS costs for an adult population without the specified health states or conditions of interest |
| Outcome | Mean cost with measure of dispersion |
| Study type | Empirical study or review reporting cost data |
We included five studies140,141,182–184 and used the studies to select a set of base-case values (Table 53).
| Health state | Cost (£), mean (95% CI)a | Source | Original cost-year | Note | CG18110 cost (£) | |
|---|---|---|---|---|---|---|
| Original | Inflated | |||||
| SA | 1592 (1445 to 1734) | Walker et al.182 | 2016–7 | Pooled across trial arms | 7736 | 8700 |
| Post SA | 130 (105 to 158) | 240 | 270 | |||
| UA | 2591 (2473 to 2717) | Danese et al.141 | 2013–4 | 3314 | 3727 | |
| Post UA | 363 (227 to 501) | 385 | 433 | |||
| MI | 5238 (4951 to 5511) | Danese et al.141 | 2013–4 | 3337 | 3753 | |
| Post MI | 1020 (667 to 1365) | 788 | 886 | |||
| TIA | 2089 (1882 to 2305) | Danese et al.141 | 2013–4 | 578 | 650 | |
| Post TIA | 779 (481 to 1092) | 124 | 139 | |||
| Stroke | 17,528 (16,639 to 18,494) | Xu et al.140 | 2015–6 | Ischaemic stroke only; assumes that 50% of social care costs are met by the individual | 4092 | 4602 |
| Post stroke | 3459 (3058 to 3824) | 155 | 175 | |||
| HF | 3171 (2842 to 3507) | Danese et al.141 | 2013–4 | 2297 | 2583 | |
| Post HF | 937 (391 to 1489) | 2597 | 2921 | |||
| PAD | 1888 (1739 to 2040) | Walker et al.184 | 2011–2 | CVD costs only; estimate for ‘history of PAD’ assumed for in-year and post-PAD | 952 | 1070 |
| Post PAD | 529 | 595 | ||||
| CV death | 2306 (2250 to 2362) | Walker et al.184 | 2011–2 | All healthcare costs | 1174 | 1320 |
| Non CV death | 2572 (2528 to 2615) | 0 | 0 | |||
We required annual costs in both the year of the event and following years (i.e. post event). When possible, we chose studies reporting values in a format that most closely reflected first-year and post-event costs for the base case. We sought to source the post-event costs from the same studies as the year 1 costs.
Furthermore, we required incremental costs compared with healthcare costs for somebody in the primary prevention population and, therefore, we chose studies reporting incremental costs for the base case where possible. When we deemed estimates to be equally relevant, we chose those with more recent cost-years for the base case. All cost-years were projected to 2019–20, which was the year for which the most recent inflators163 and Personal Social Services Research Unit costs of health and social care159 were available at the time of analysis.
We discounted estimated social care costs of stroke and post-stroke by 50% to reflect the proportion of this cost that we assume is paid out-of-pocket by individuals (this assumption has precedent in NICE guidelines185–187). In the source study,140 disaggregated health and social care costs were available for only all strokes and not for ischaemic stroke, which we preferred for our decision context. Therefore, we approximated the required numbers by applying the ratio of overall ischaemic stroke costs to overall all stroke costs to disaggregated health and social care costs for all strokes.
One study184 reported a regression model to calculate costs depending on characteristics, such as age and sex. Therefore, we adjusted costs from this study for start age and sex of each cohort modelled. The average cost reported in each other study was applied to all cohorts.
Two studies141,184 included reported estimates for multiple model states. In the base case, we prioritised choosing the most relevant estimates for each state over consistently sourcing from the same paper, and this meant that we used a combination of estimates from the two studies. 141,184 We did, however, model scenarios that relied on each of the two studies wherever possible and used base-case values otherwise. In one of these scenarios, reported model coefficients were applied to costs for SA to calculate costs for other states because people with SA were the reference population for the source study. 184 In a final two scenarios, we used the values from CG181 in its original cost-year and then inflated to 2019–20.
Formal specification of relative survival model
We used the multiplicative version of the relative survival model from formula 6 of Andersen et al. 142 to predict the effect of cardiovascular risk on time of non-cardiovascular death. Let the adjusted hazard of non-cardiovascular death be given by λunadj. Therefore, as in Equation 12 of Pohar and Stare,188 the adjusted hazard, λadj., for covariate values [x1,..., xk]d and coefficients [β0, β1,..., βk], is given by:
We can express λunadj. as the exponent of its own natural logarithm. Therefore, the above is equivalent to:
Then, applying the laws of multiplication for exponents, we obtain:
This can be interpreted in the same way as a Cox model with a log-transformed unadjusted hazard of survival included as a covariate and with coefficient βf fixed at 1:
Accounting for competing risk of non-cardiovascular death
As explained in the main text, the critical covariate for our relative survival models is Δlogit(Q), that is the difference between an individual’s predicted 10-year QRISK3 score and the average score for a person of the same age and sex. We estimate the latter using a regression on the CPRD data set. Table 54 shows the model coefficients and Figure 39 shows the model fitted for men and women as a function of age. We found that the relationship between age and logit(QRISK3) was best described by a quintic function. Although still-higher-order polynomials reduced measures of model fit (AIC) further, we observed that their introduction caused artefacts at high ages (e.g. a sudden reduction in expected risk) that strongly suggested overfitting. Therefore, we preferred the quintic model.
| Parameter | Estimate (95% CI) |
|---|---|
| Intercept | −12.90 (−13.21 to −12.58) |
| Age | 0.353 (0.319 to 0.387) |
| Age2 | −5.60 × 10−3 (−6.99 × 10−3 to −4.21 × 10−3) |
| Age3 | 6.31 × 10−5 (3.54 × 10−5 to 9.08 × 10−5) |
| Age4 | −4.18 × 10−7 (−6.85 × 10−7 to −1.51 × 10−7) |
| Age5 | 1.42 × 10−9 (4.29 × 10−10 to 2.42 × 10−9) |
| Male | −11.02 (−11.48 to −10.55) |
| Male × age | 0.986 (0.936 to 1.036) |
| Male × age2 | 0.0320 (−0.0341 to −0.0300) |
| Male × age3 | 5.20 × 10−4 (4.79 × 10−4 to 5.61 × 10−4) |
| Male × age4 | −4.28 × 10−6 (−4.68 × 10−6 to −3.88 × 10−6) |
| Male × age5 | 1.41 × 10−8 (1.26 × 10−8 to 1.56 × 10−8) |
FIGURE 39.
Average 10-year risk of cardiovascular event (QRISK3) in people with no history of CVD as a function of age and sex.
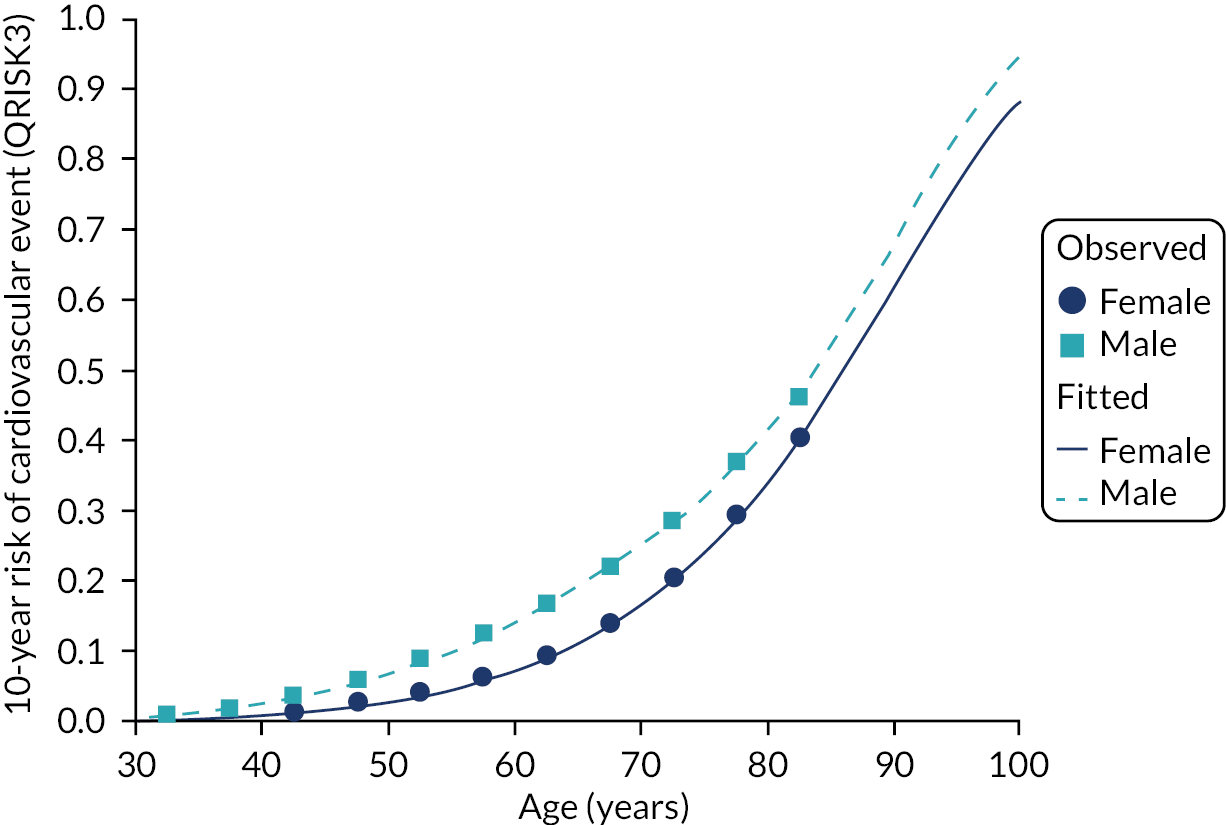
Appendix 7 Full results from updated cost–utility model assessing statins for the primary prevention of cardiovascular disease before accounting for competing risk and direct treatment disutility
This appendix contains cost–utility results from the statins model following the updates described in Chapter 6, General model updates, that is the model includes all the steps we took to update and enhance the CG181 model but does not account for competing risk or DTD.
Base case
Deterministic incremental cost–utility results
Table 55 replicates the structure of Table 97 in appendix L of CG181,10 showing estimated costs and QALYs for each statin strategy and no treatment. Figure 40 shows the option with greatest net benefit (when we value QALYs at £20,000 each) for men and women across a range of ages and levels of cardiovascular risk. Table 55 also gives net health benefit (NHB) for each arm (valuing QALYs at £20,000 each).
| Strategy | 60-year-old men | 60-year-old women | ||||
|---|---|---|---|---|---|---|
| Cost (£) | QALY | NHB | Cost (£) | QALY | NHB | |
| 10-year cardiovascular risk = 30% | ||||||
| No statins | 11,198 | 11.360 | 10.800 | 11,845 | 11.158 | 10.566 |
| Low-intensity statin (S10) | 11,423 | 11.622 | 11.051 | 12,052 | 11.438 | 10.836 |
| Medium-intensity statin (S20) | 10,653 | 11.796 | 11.263 | 11,248 | 11.628 | 11.065 |
| High-intensity statin (A20) | 10,686 | 11.949 | 11.415 | 11,291 | 11.796 | 11.231 |
| High-intensity statin (A80) | 10,772 | 11.949 | 11.410 | 11,379 | 11.796 | 11.227 |
| 10-year cardiovascular risk = 25% | ||||||
| No statins | 10,269 | 11.684 | 11.171 | 10,873 | 11.501 | 10.958 |
| Low-intensity statin (S10) | 10,606 | 11.927 | 11.396 | 11,191 | 11.763 | 11.203 |
| Medium-intensity statin (S20) | 9875 | 12.089 | 11.596 | 10,420 | 11.942 | 11.421 |
| High-intensity statin (A20) | 9892 | 12.226 | 11.731 | 10,443 | 12.092 | 11.570 |
| High-intensity statin (A80) | 9984 | 12.226 | 11.726 | 10,537 | 12.092 | 11.565 |
| 10-year cardiovascular risk = 20% | ||||||
| No statins | 9183 | 12.030 | 11.571 | 9715 | 11.873 | 11.388 |
| Low-intensity statin (S10) | 9664 | 12.247 | 11.763 | 10,180 | 12.109 | 11.600 |
| Medium-intensity statin (S20) | 8989 | 12.393 | 11.944 | 9460 | 12.272 | 11.799 |
| High-intensity statin (A20) | 8994 | 12.509 | 12.060 | 9466 | 12.401 | 11.928 |
| High-intensity statin (A80) | 9091 | 12.509 | 12.055 | 9567 | 12.401 | 11.923 |
| 10-year cardiovascular risk = 15% | ||||||
| No statins | 7897 | 12.403 | 12.008 | 8311 | 12.280 | 11.865 |
| Low-intensity statin (S10) | 8564 | 12.585 | 12.157 | 8972 | 12.481 | 12.032 |
| Medium-intensity statin (S20) | 7967 | 12.709 | 12.311 | 8332 | 12.620 | 12.204 |
| High-intensity statin (A20) | 7966 | 12.802 | 12.404 | 8327 | 12.724 | 12.307 |
| High-intensity statin (A80) | 8069 | 12.802 | 12.398 | 8435 | 12.724 | 12.302 |
| 10-year cardiovascular risk = 10% | ||||||
| No statins | 6343 | 12.805 | 12.488 | 6567 | 12.730 | 12.402 |
| Low-intensity statin (S10) | 7258 | 12.944 | 12.581 | 7501 | 12.883 | 12.508 |
| Medium-intensity statin (S20) | 6773 | 13.039 | 12.700 | 6982 | 12.989 | 12.640 |
| High-intensity statin (A20) | 6774 | 13.104 | 12.766 | 6976 | 13.063 | 12.714 |
| High-intensity statin (A80) | 6883 | 13.104 | 12.760 | 7090 | 13.063 | 12.709 |
| 10-year cardiovascular risk = 9% | ||||||
| No statins | 5992 | 12.890 | 12.591 | 6165 | 12.826 | 12.518 |
| Low-intensity statin (S10) | 6965 | 13.018 | 12.670 | 7166 | 12.967 | 12.609 |
| Medium-intensity statin (S20) | 6509 | 13.107 | 12.781 | 6679 | 13.066 | 12.732 |
| High-intensity statin (A20) | 6511 | 13.166 | 12.841 | 6674 | 13.133 | 12.799 |
| High-intensity statin (A80) | 6622 | 13.166 | 12.835 | 6790 | 13.133 | 12.794 |
| 10-year cardiovascular risk = 8% | ||||||
| No statins | 5624 | 12.976 | 12.695 | 5742 | 12.924 | 12.637 |
| Low-intensity statin (S10) | 6661 | 13.093 | 12.760 | 6816 | 13.053 | 12.712 |
| Medium-intensity statin (S20) | 6236 | 13.175 | 12.863 | 6363 | 13.144 | 12.825 |
| High-intensity statin (A20) | 6240 | 13.228 | 12.916 | 6360 | 13.204 | 12.886 |
| High-intensity statin (A80) | 6352 | 13.228 | 12.911 | 6478 | 13.204 | 12.880 |
| 10-year cardiovascular risk = 7% | ||||||
| No statins | 5240 | 13.064 | 12.802 | 5296 | 13.024 | 12.759 |
| Low-intensity statin (S10) | 6345 | 13.170 | 12.852 | 6449 | 13.140 | 12.818 |
| Medium-intensity statin (S20) | 5952 | 13.243 | 12.946 | 6033 | 13.222 | 12.920 |
| High-intensity statin (A20) | 5958 | 13.291 | 12.993 | 6033 | 13.275 | 12.974 |
| High-intensity statin (A80) | 6072 | 13.291 | 12.987 | 6152 | 13.275 | 12.968 |
| 10-year cardiovascular risk = 6% | ||||||
| No statins | 4837 | 13.153 | 12.911 | 4825 | 13.126 | 12.885 |
| Low-intensity statin (S10) | 6015 | 13.247 | 12.946 | 6063 | 13.229 | 12.926 |
| Medium-intensity statin (S20) | 5657 | 13.313 | 13.030 | 5689 | 13.301 | 13.017 |
| High-intensity statin (A20) | 5667 | 13.354 | 13.071 | 5692 | 13.347 | 13.063 |
| High-intensity statin (A80) | 5781 | 13.354 | 13.065 | 5813 | 13.347 | 13.057 |
| 10-year cardiovascular risk = 5% | ||||||
| No statins | 4415 | 13.243 | 13.023 | 4327 | 13.230 | 13.014 |
| Low-intensity statin (S10) | 5670 | 13.325 | 13.042 | 5657 | 13.319 | 13.036 |
| Medium-intensity statin (S20) | 5350 | 13.382 | 13.115 | 5329 | 13.382 | 13.115 |
| High-intensity statin (A20) | 5364 | 13.417 | 13.149 | 5335 | 13.420 | 13.154 |
| High-intensity statin (A80) | 5480 | 13.417 | 13.143 | 5458 | 13.420 | 13.147 |
FIGURE 40.
Updated CG181 model10 (not accounting for competing risk or DTD): relationship between age and risk of non-cardiovascular death: cost-effectiveness of statins. (a) Men; and (b) women. Coloured area identifies option with highest net benefit when we value QALYs at £20,000 each.

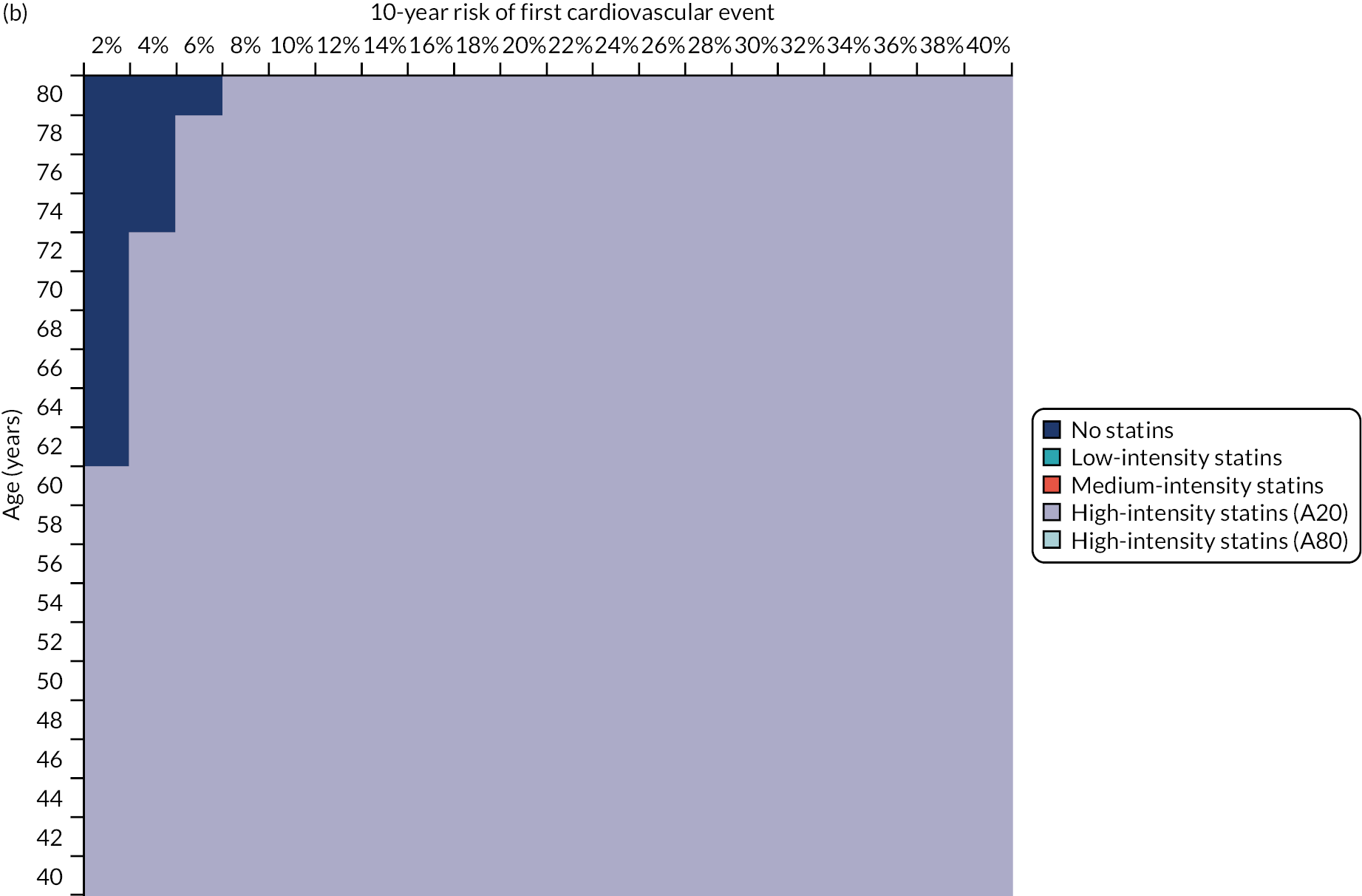
Deterministic sensitivity analysis
One-way sensitivity analysis
One-way sensitivity analyses are depicted in Figures 41–43.
FIGURE 41.
Updated CG181 model10 (not accounting for competing risk or DTD): one-way sensitivity analysis for high-intensity statins (atorvastatin 20 mg/day) compared with no treatment. Thirty most influential parameters shown. Positive incremental NHB implies that high-intensity statins is the preferred option (i.e. it would be associated with an ICER of £20,000/QALY or better vs. no treatment). CV, cardiovascular; RR, relative risk.

FIGURE 42.
Updated CG181 model10 (not accounting for competing risk or DTD): one-way sensitivity analysis for high-intensity statins (atorvastatin 20 mg/day) compared with medium-intensity statins (simvastatin 20 mg/day). Thirty most influential parameters shown. Positive incremental NHB implies that high-intensity statins is the preferred option (i.e. it would be associated with an ICER of £20,000/QALY or better vs. medium-intensity statins). CV, cardiovascular; RR, relative risk.
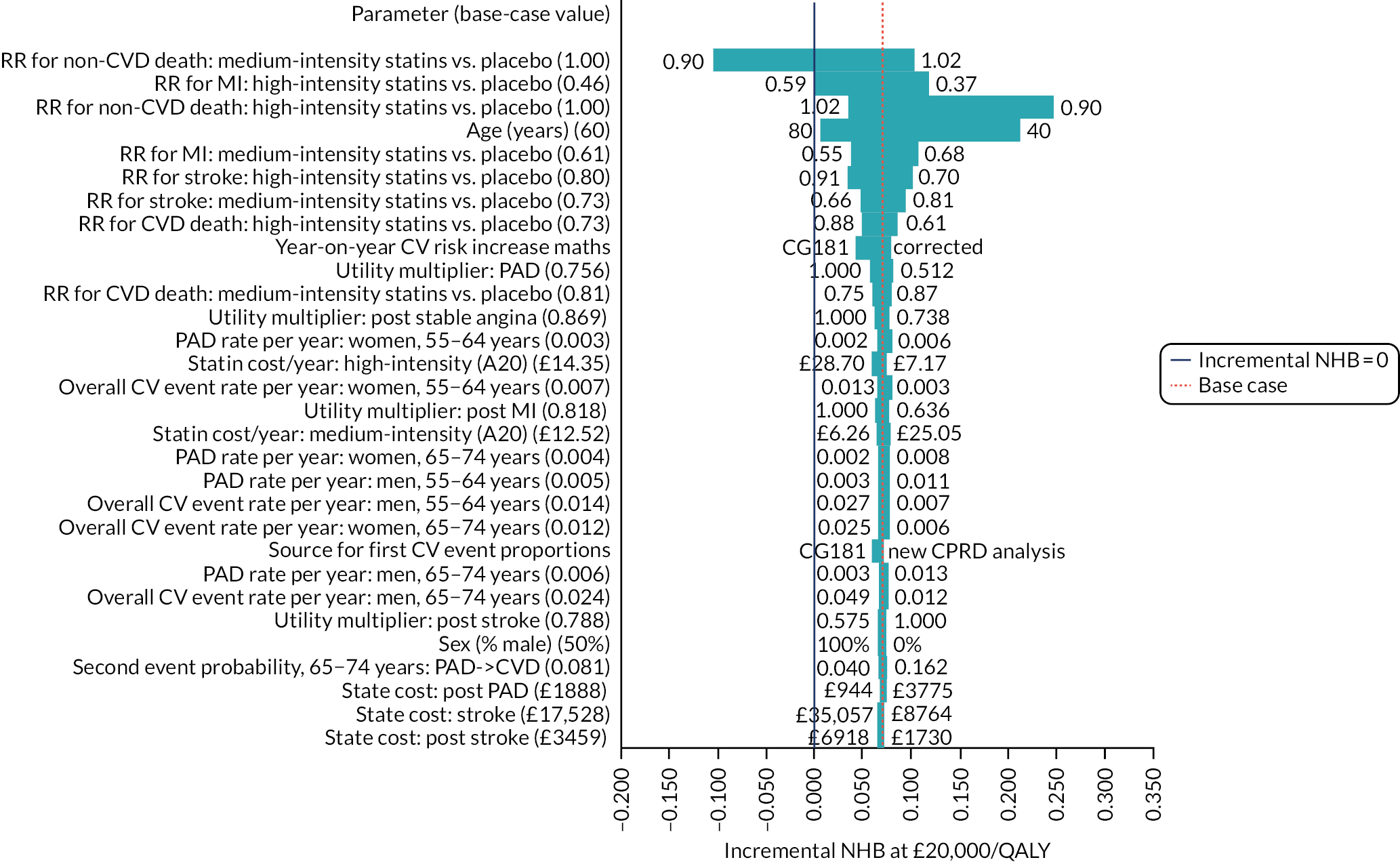
FIGURE 43.
Updated CG181 model10 (not accounting for competing risk or DTD): one-way sensitivity analysis for medium-intensity statins (simvastatin 20 mg/day) compared with low-intensity statins (simvastatin 10 mg/day). Thirty most influential parameters shown. Positive incremental NHB implies that medium-intensity statins is the preferred option (i.e. it would be associated with an ICER of £20,000/QALY or better vs. low-intensity statins). CV, cardiovascular; RR, relative risk.
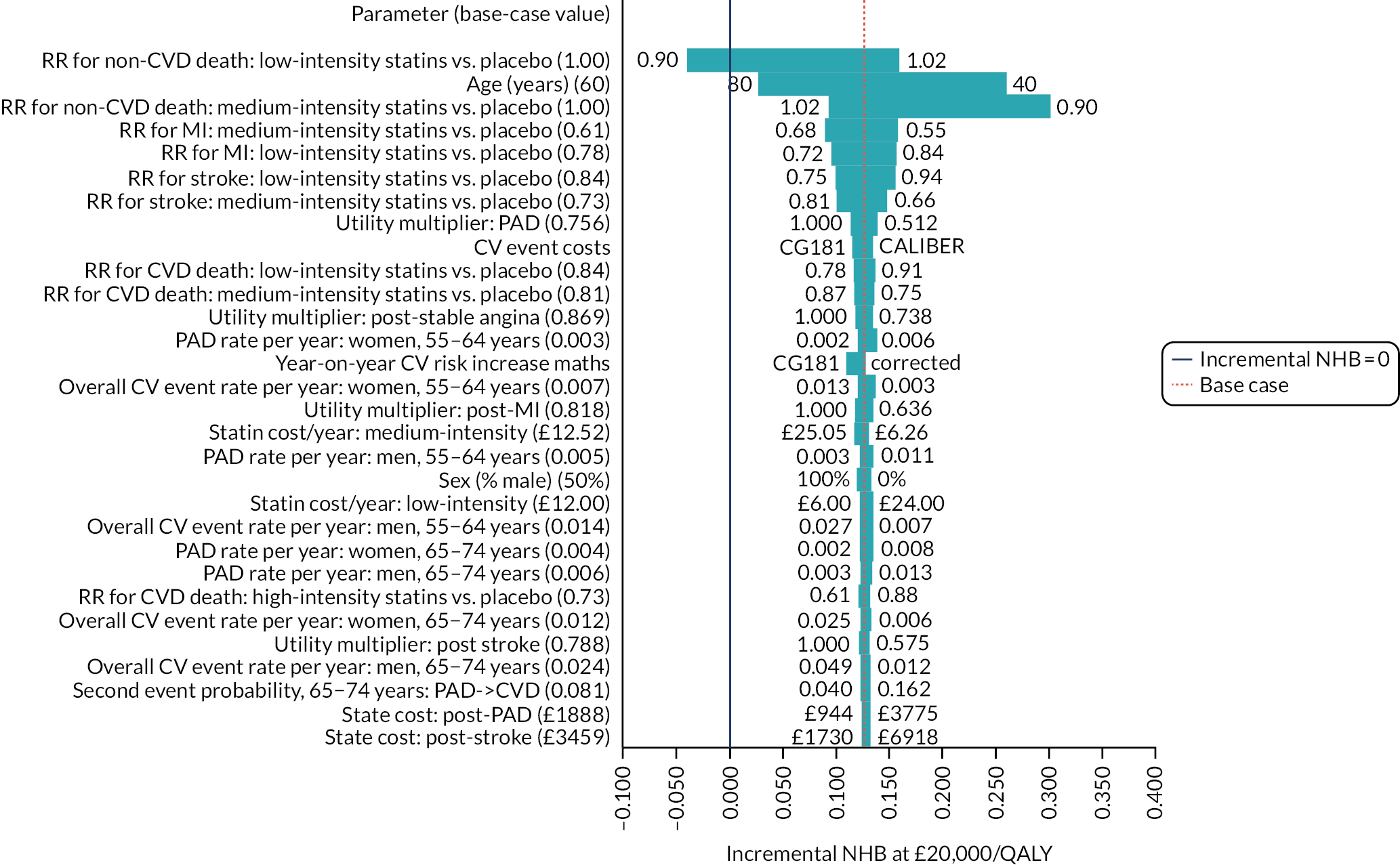
Probabilistic sensitivity analysis
Probabilistic sensitivity analyses are depicted in Figures 44–46.
FIGURE 44.
Updated CG181 model10 (not accounting for competing risk or DTD): probabilistic cost–utility scatterplot for all options (60-year-olds; 50 : 50 men : women; 10-year risk of cardiovascular event = 10%).
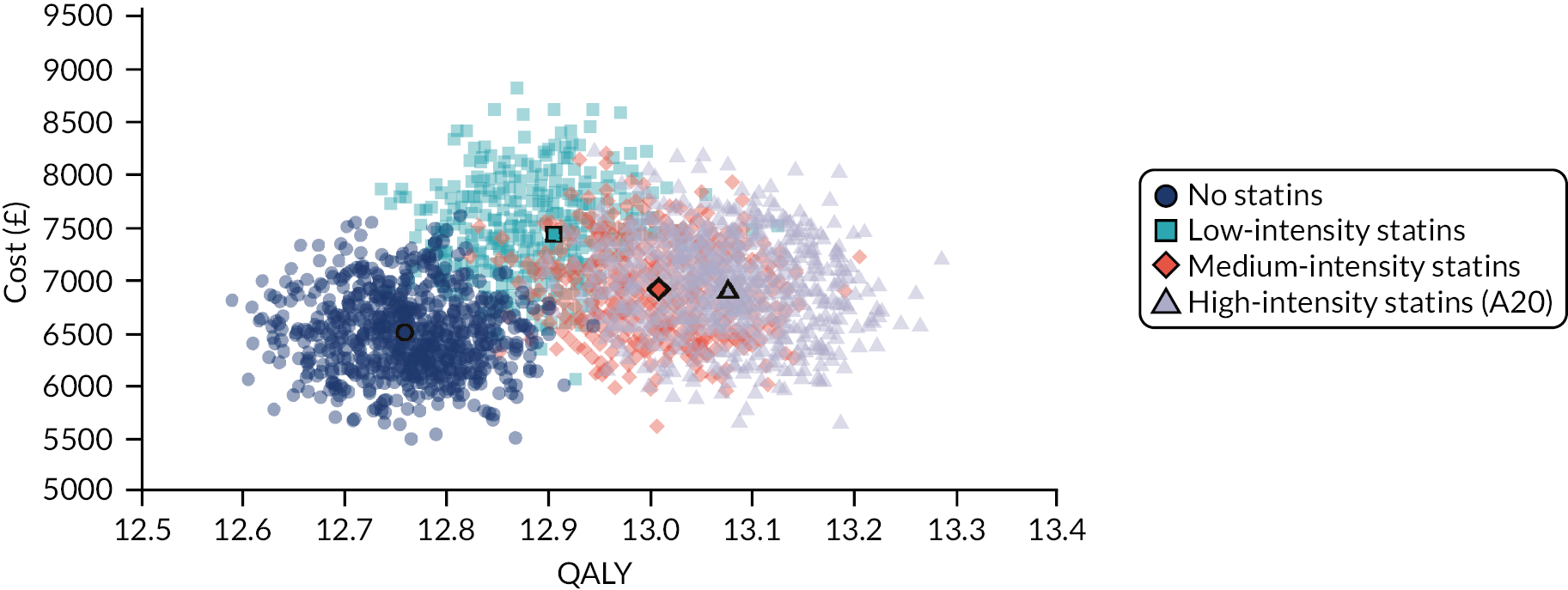
FIGURE 45.
Updated CG181 model10 (not accounting for competing risk or DTD): probabilistic incremental cost–utility scatterplot – high-intensity statins (atorvastatin 20 mg/day) compared with no treatment (60-year-olds, 50 : 50 men : women; 10-year risk of cardiovascular event = 10%).

FIGURE 46.
Updated CG181 model (not accounting for competing risk or DTD): cost-effectiveness acceptability curve (60-year-olds, 50 : 50 men : women; 10-year risk of cardiovascular event = 10%). Bold line shows cost-effectiveness acceptability frontier.
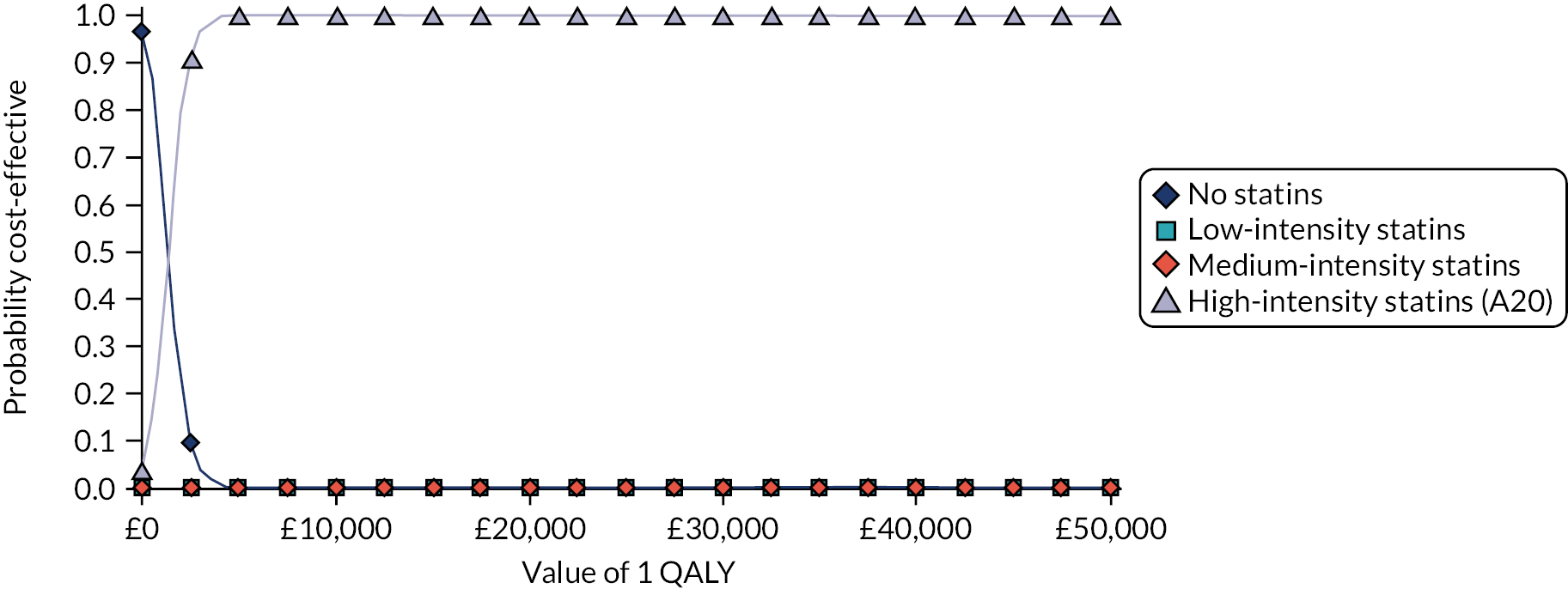
Appendix 8 Full results from cost–utility model assessing statins for the primary prevention of cardiovascular disease including adjustment for competing risk
This appendix contains cost–utility results from the statins model following the updates described in Chapter 6, General model updates, and subsequent inclusion of adjustment competing risk of non-cardiovascular death, as described in Chapter 6, New model features specific to this project.
Base case
State occupancy
Figure 47 provides model state occupancy graphs in two untreated cohorts with and without adjustment for competing risk of non-cardiovascular mortality. Both groups comprise 60-year-olds with a 10-year QRISK3-predicted risk of 10%, but one cohort is 100% male and the other cohort is 100% female.
FIGURE 47.
State occupancy (no treatment) with and without adjustment for competing risk of non-cardiovascular mortality in example cohorts. (a) 60-year-old men, 10-year cardiovascular risk=10%: unadjusted for competing risk of non-cardiovascular mortality; (b) 60-year-old women, 10-year cardiovascular risk=10%: unadjusted for competing risk of non-cardiovascular mortality; (c) 60-year-old men, 10-year cardiovascular risk=10%: adjusted for competing risk of non-cardiovascular mortality; and (d) 60-year-old women, 10-year cardiovascular risk=10%: adjusted for competing risk of non-cardiovascular mortality. CV, cardiovascular.

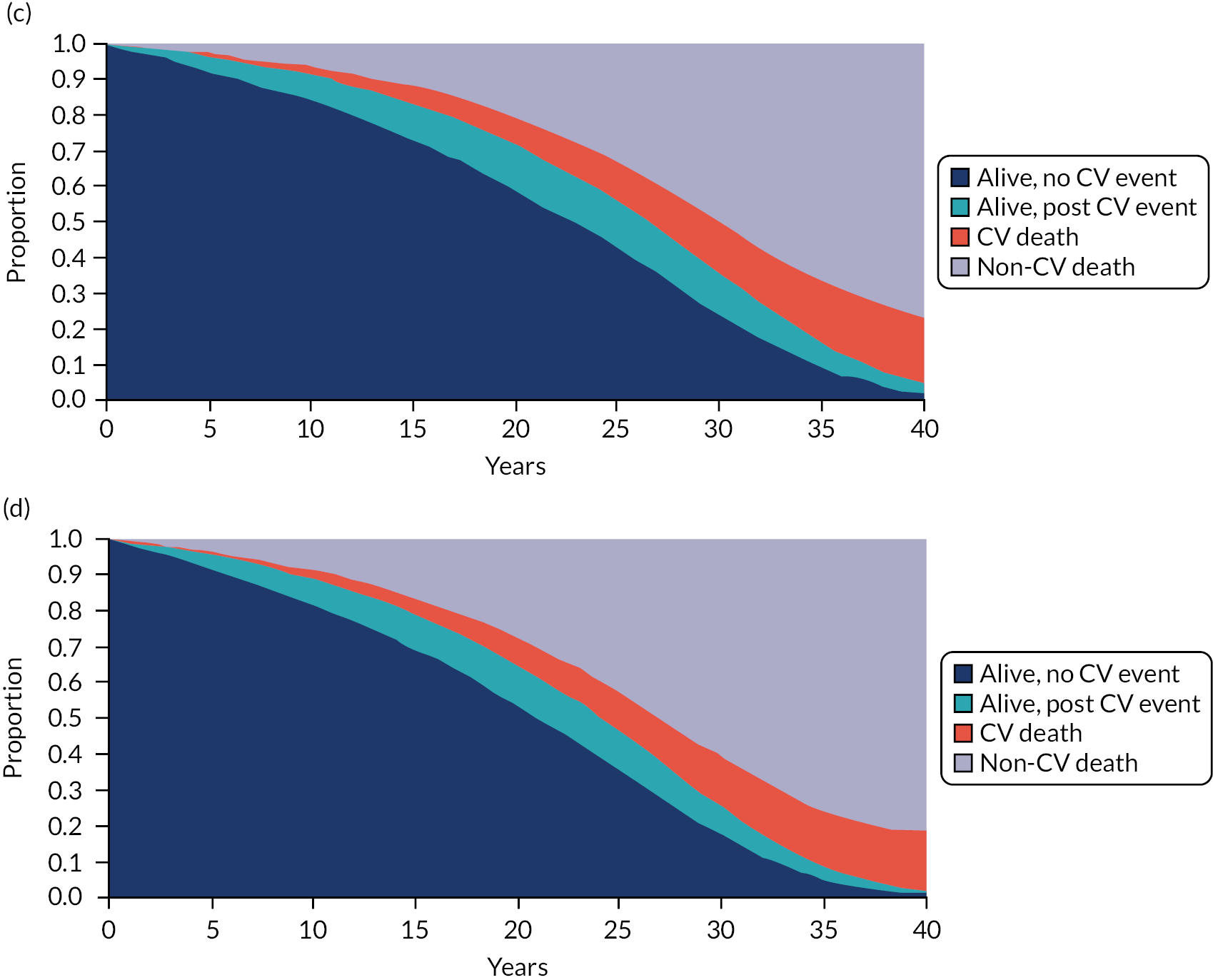
Deterministic incremental cost–utility results
Table 56 replicates Table 97 in appendix L of CG181,10 showing estimated costs and QALYs for each statin strategy and no treatment. Table 56 also gives NHB for each arm (valuing QALYs at £20,000 each).
| Strategy | 60-year-old men | 60-year-old women | ||||
|---|---|---|---|---|---|---|
| Cost (£) | QALY | NHB | Cost (£) | QALY | NHB | |
| 10-year cardiovascular risk = 30% | ||||||
| No statins | 8590 | 9.410 | 8.981 | 8328 | 8.630 | 8.214 |
| Low-intensity statin (S10) | 8811 | 9.598 | 9.157 | 8528 | 8.807 | 8.380 |
| Medium-intensity statin (S20) | 8176 | 9.721 | 9.313 | 7904 | 8.925 | 8.530 |
| High-intensity statin (A20) | 8114 | 9.831 | 9.425 | 7818 | 9.031 | 8.640 |
| High-intensity statin (A80) | 8189 | 9.831 | 9.422 | 7890 | 9.031 | 8.636 |
| 10-year cardiovascular risk = 25% | ||||||
| No statins | 8272 | 10.099 | 9.685 | 7935 | 9.229 | 8.832 |
| Low-intensity statin (S10) | 8604 | 10.283 | 9.852 | 8246 | 9.400 | 8.988 |
| Medium-intensity statin (S20) | 7985 | 10.405 | 10.006 | 7642 | 9.517 | 9.134 |
| High-intensity statin (A20) | 7934 | 10.509 | 10.112 | 7565 | 9.616 | 9.238 |
| High-intensity statin (A80) | 8015 | 10.509 | 10.108 | 7644 | 9.616 | 9.234 |
| 10-year cardiovascular risk = 20% | ||||||
| No statins | 7914 | 10.946 | 10.550 | 7451 | 9.946 | 9.573 |
| Low-intensity statin (S10) | 8388 | 11.125 | 10.705 | 7906 | 10.110 | 9.715 |
| Medium-intensity statin (S20) | 7791 | 11.245 | 10.856 | 7332 | 10.222 | 9.856 |
| High-intensity statin (A20) | 7755 | 11.342 | 10.954 | 7268 | 10.313 | 9.950 |
| High-intensity statin (A80) | 7845 | 11.342 | 10.950 | 7354 | 10.313 | 9.946 |
| 10-year cardiovascular risk = 15% | ||||||
| No statins | 7495 | 12.025 | 11.650 | 6839 | 10.846 | 10.504 |
| Low-intensity statin (S10) | 8158 | 12.195 | 11.787 | 7486 | 10.998 | 10.623 |
| Medium-intensity statin (S20) | 7589 | 12.311 | 11.932 | 6954 | 11.103 | 10.755 |
| High-intensity statin (A20) | 7576 | 12.398 | 12.020 | 6908 | 11.183 | 10.837 |
| High-intensity statin (A80) | 7676 | 12.398 | 12.015 | 7004 | 11.183 | 10.833 |
| 10-year cardiovascular risk = 10% | ||||||
| No statins | 6943 | 13.460 | 13.113 | 6013 | 12.057 | 11.757 |
| Low-intensity statin (S10) | 7868 | 13.616 | 13.222 | 6933 | 12.191 | 11.844 |
| Medium-intensity statin (S20) | 7336 | 13.724 | 13.357 | 6463 | 12.284 | 11.961 |
| High-intensity statin (A20) | 7353 | 13.797 | 13.429 | 6443 | 12.350 | 12.028 |
| High-intensity statin (A80) | 7468 | 13.797 | 13.423 | 6552 | 12.350 | 12.022 |
| 10-year cardiovascular risk = 9% | ||||||
| No statins | 6794 | 13.805 | 13.466 | 5806 | 12.360 | 12.069 |
| Low-intensity statin (S10) | 7784 | 13.957 | 13.568 | 6796 | 12.488 | 12.149 |
| Medium-intensity statin (S20) | 7261 | 14.062 | 13.699 | 6341 | 12.578 | 12.261 |
| High-intensity statin (A20) | 7286 | 14.132 | 13.768 | 6327 | 12.640 | 12.324 |
| High-intensity statin (A80) | 7404 | 14.132 | 13.762 | 6439 | 12.640 | 12.318 |
| 10-year cardiovascular risk = 8% | ||||||
| No statins | 6620 | 14.174 | 13.843 | 5576 | 12.690 | 12.411 |
| Low-intensity statin (S10) | 7681 | 14.321 | 13.937 | 6643 | 12.813 | 12.481 |
| Medium-intensity statin (S20) | 7168 | 14.423 | 14.065 | 6206 | 12.900 | 12.590 |
| High-intensity statin (A20) | 7199 | 14.489 | 14.129 | 6199 | 12.958 | 12.648 |
| High-intensity statin (A80) | 7322 | 14.489 | 14.123 | 6314 | 12.958 | 12.642 |
| 10-year cardiovascular risk = 7% | ||||||
| No statins | 6409 | 14.567 | 14.246 | 5316 | 13.055 | 12.789 |
| Low-intensity statin (S10) | 7549 | 14.708 | 14.330 | 6470 | 13.172 | 12.848 |
| Medium-intensity statin (S20) | 7046 | 14.806 | 14.454 | 6052 | 13.254 | 12.952 |
| High-intensity statin (A20) | 7085 | 14.867 | 14.513 | 6052 | 13.308 | 13.005 |
| High-intensity statin (A80) | 7212 | 14.867 | 14.507 | 6172 | 13.308 | 12.999 |
| 10-year cardiovascular risk = 6% | ||||||
| No statins | 6147 | 14.983 | 14.676 | 5017 | 13.460 | 13.209 |
| Low-intensity statin (S10) | 7374 | 15.117 | 14.748 | 6268 | 13.570 | 13.257 |
| Medium-intensity statin (S20) | 6885 | 15.211 | 14.867 | 5872 | 13.648 | 13.354 |
| High-intensity statin (A20) | 6932 | 15.267 | 14.920 | 5880 | 13.696 | 13.402 |
| High-intensity statin (A80) | 7063 | 15.267 | 14.914 | 6004 | 13.696 | 13.396 |
| 10-year cardiovascular risk = 5% | ||||||
| No statins | 5814 | 15.421 | 15.131 | 4662 | 13.915 | 13.682 |
| Low-intensity statin (S10) | 7139 | 15.546 | 15.189 | 6025 | 14.017 | 13.716 |
| Medium-intensity statin (S20) | 6668 | 15.634 | 15.301 | 5655 | 14.089 | 13.806 |
| High-intensity statin (A20) | 6722 | 15.684 | 15.348 | 5671 | 14.132 | 13.849 |
| High-intensity statin (A80) | 6858 | 15.684 | 15.341 | 5800 | 14.132 | 13.842 |
In Figures 48 and 49, we depict the cost-effectiveness of statins for people of different ages and cardiovascular risks, and how adjusting for competing risk of non-cardiovascular death affects these results. Even before adopting this adjustment, the model suggests that statins represent a good use of resources for almost everyone. It is only for people aged > 60 years with the lowest cardiovascular risk that statins represent poor value for money. However, adjusting for competing risk of non-cardiovascular death removes even this small subgroup. In practice, the distinction is moot if QRISK3 is used to predict cardiovascular risk, as it is essentially impossible for people in those age brackets to have 10-year risks low enough to enter the cost-ineffective zone. If such people did exist, then they would have extraordinary life expectancy, which is why the adjusted model concludes that it would still be good value to offer them statins, as there is every chance that even the oldest people would live to realise their benefit.
FIGURE 48.
Cost-effectiveness of high-intensity statins (atorvastatin 20 mg/day) compared with no treatment, as a function of age and cardiovascular risk. (a) Unadjusted (as per CG181); and (b) adjusted for competing risk of non-cardiovascular death.
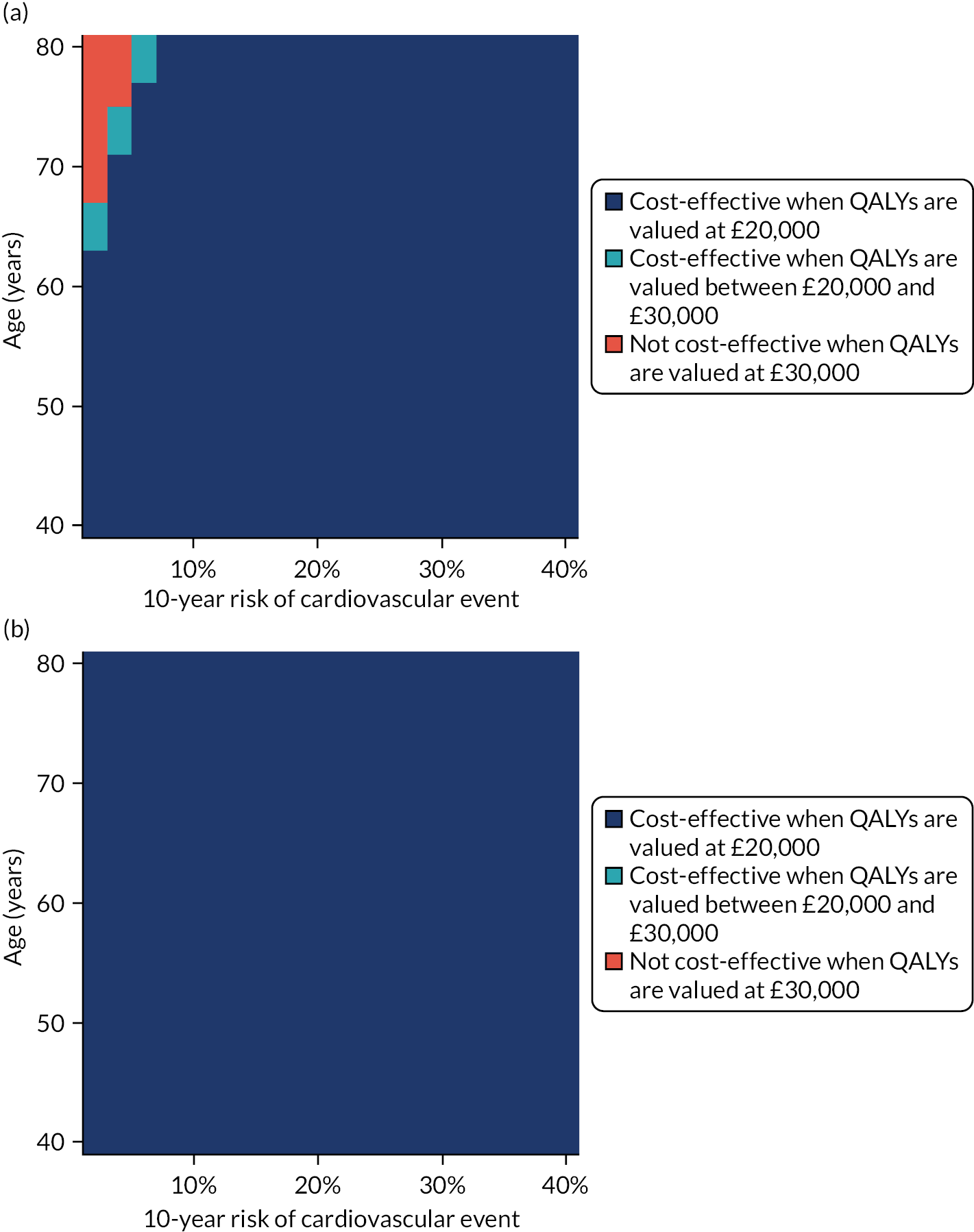
FIGURE 49.
Updated CG181 model (not accounting for competing risk or DTD): relationship between age and risk of non-cardiovascular death: cost-effectiveness of statins. (a) Men; and (b) women. Coloured area identifies option with highest net benefit when we value QALYs at £20,000 each.
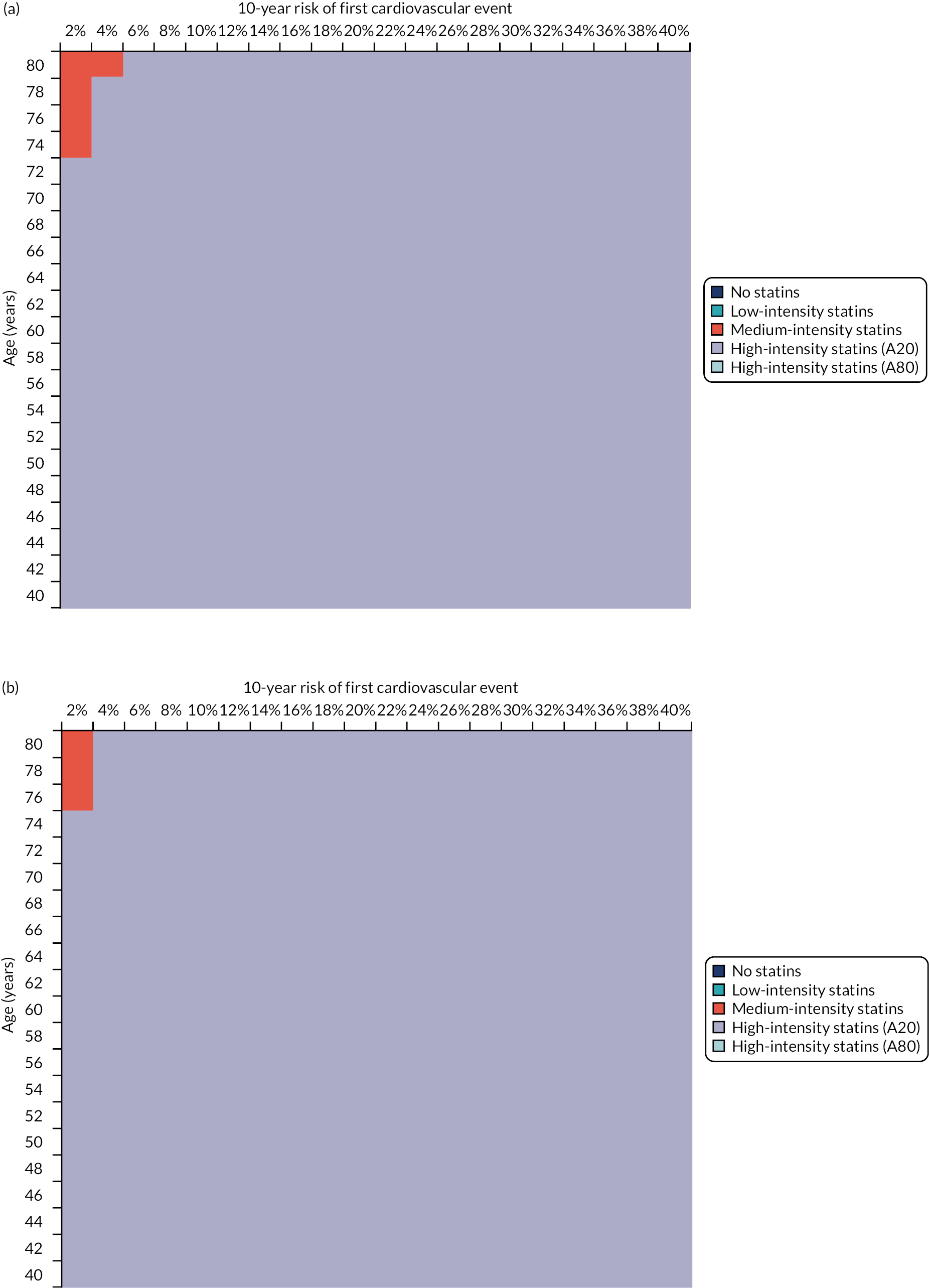
With direct treatment disutility
We see the effect of differing DTD assumptions on the cost-effectiveness of statins across a range of ages and baseline cardiovascular event risks in Figure 50.
FIGURE 50.
Cost-effectiveness of high-intensity statins (atorvastatin 20 mg/day) compared with no treatment, as a function of age, cardiovascular risk and DTD. (a) No DTD; (b) diminishing DTD; (c) time-limited DTD; and (d) permanent DTD. 50 : 50 men : women. All analyses include general model updates and adjustment for non-cardiovascular competing risk.
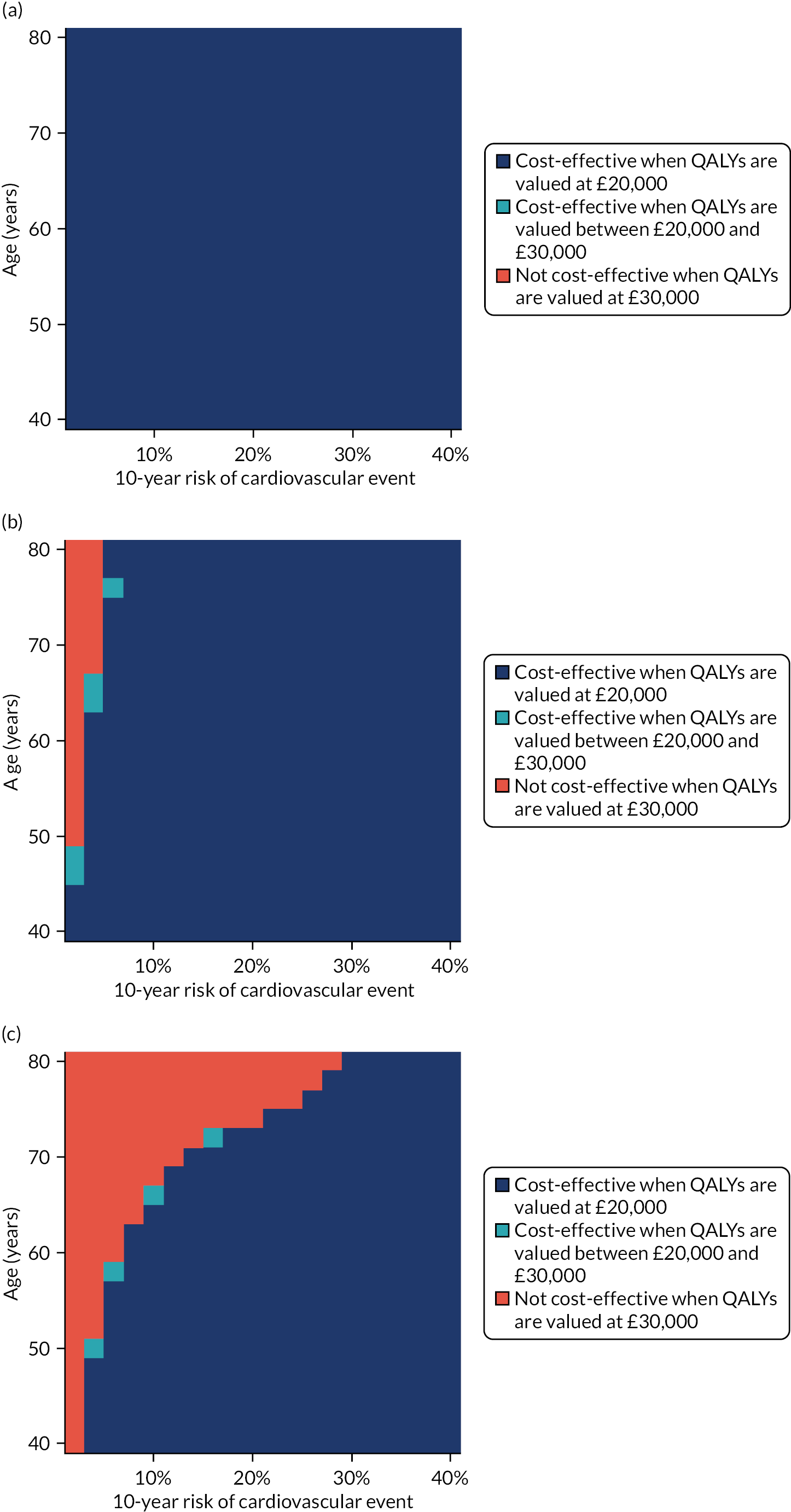
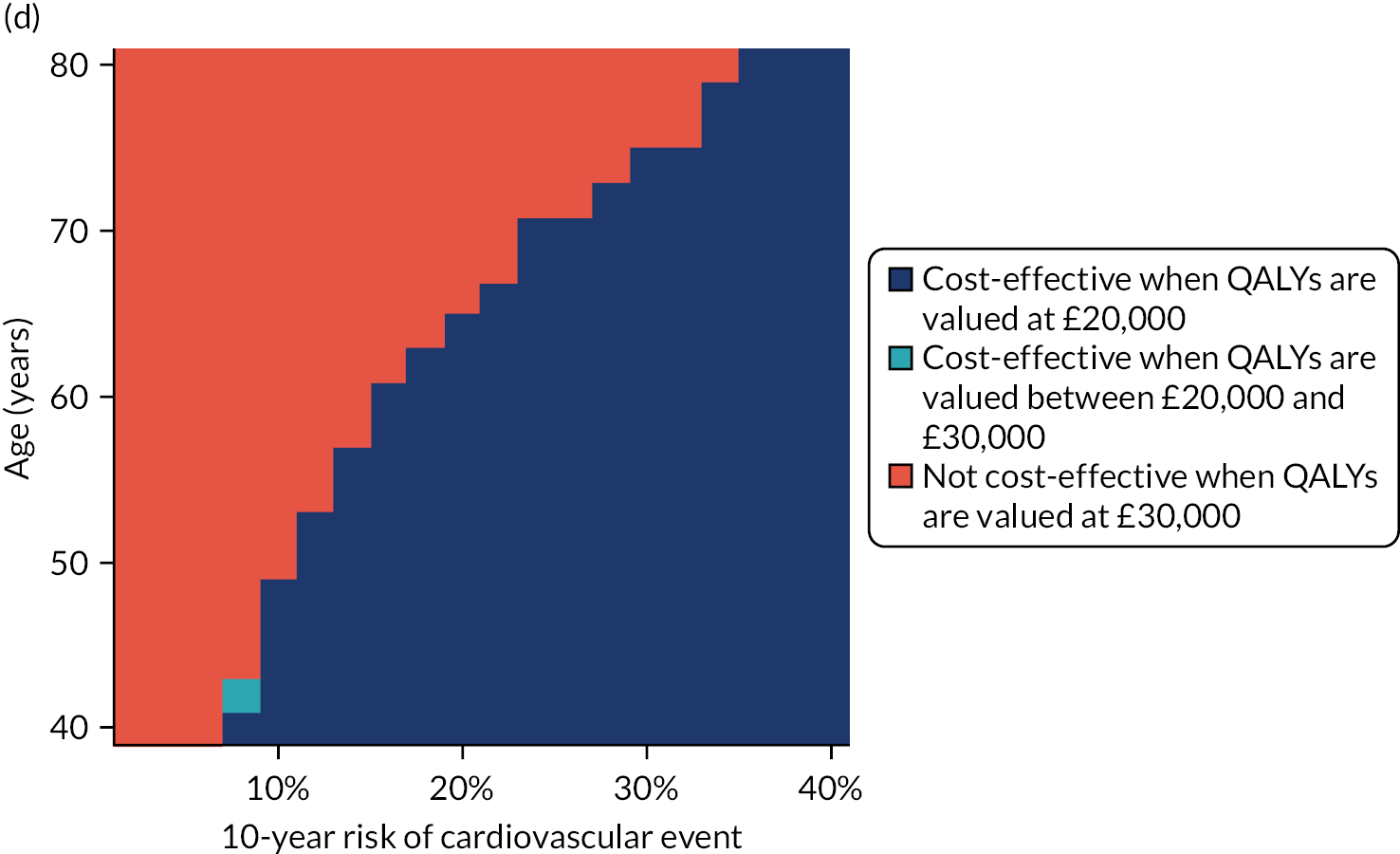
Deterministic sensitivity analysis
One-way sensitivity analysis
One-way sensitivity analyses are depicted in Figures 51–53.
FIGURE 51.
Updated model, including adjustment for competing risk of non-cardiovascular death: one-way sensitivity analysis for high-intensity statins (atorvastatin 20 mg/day) compared with no treatment (60-year-olds, 50 : 50 men : women, 10% 10-year cardiovascular event risk). Thirty most influential parameters shown. Positive incremental NHB implies that high-intensity statins is the preferred option (i.e. it would be associated with an ICER of £20,000/QALY or better vs. no treatment). CV, cardiovascular; RR, relative risk.
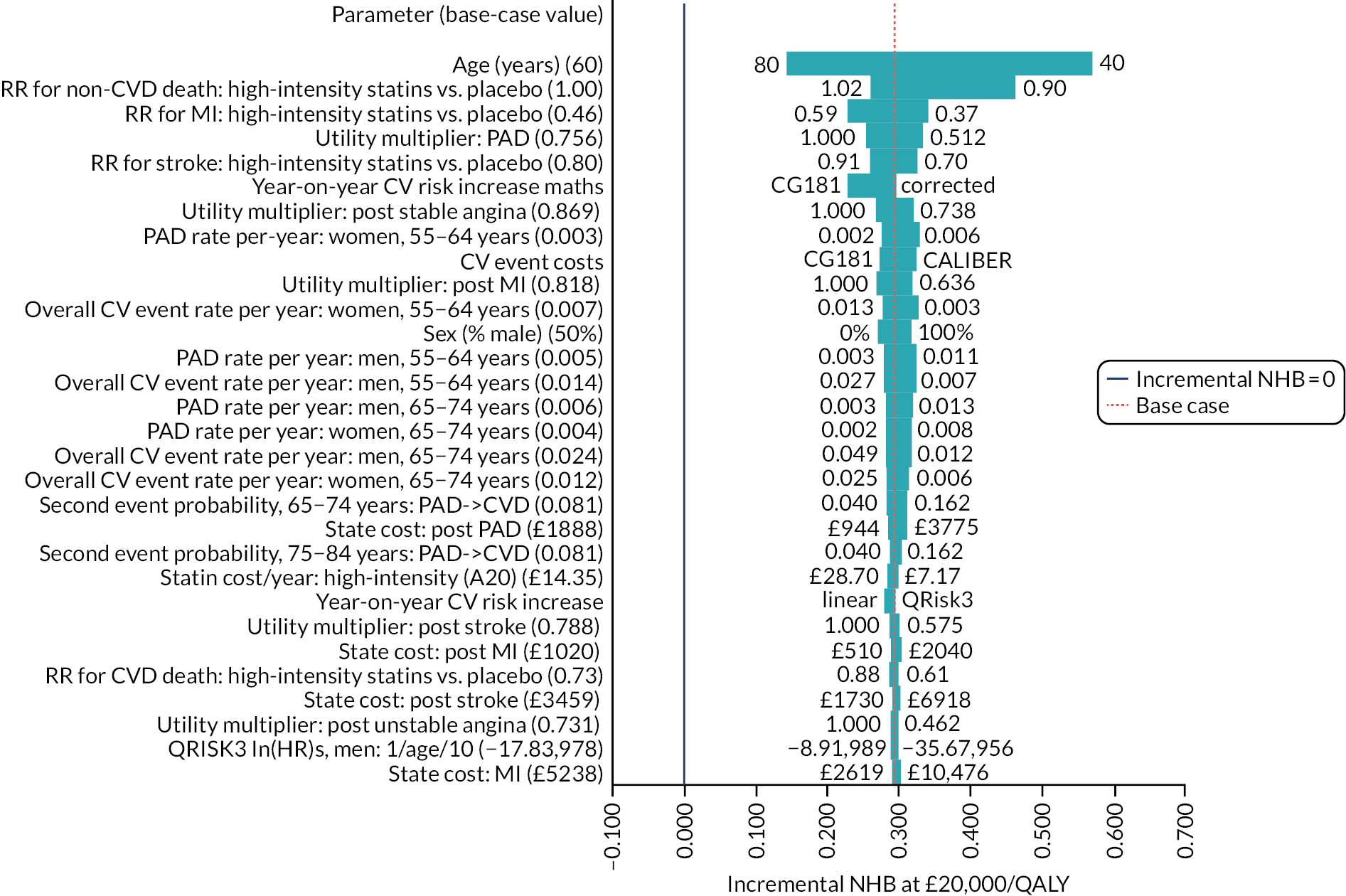
FIGURE 52.
Updated model, including adjustment for competing risk of non-cardiovascular death: one-way sensitivity analysis for high-intensity statins (atorvastatin 20 mg/day) compared with medium-intensity statins (simvastatin 20 mg/day) (60-year-olds, 50 : 50 men : women, 10% 10-year cardiovascular event risk). Thirty most influential parameters shown. Positive incremental NHB implies that high-intensity statins is the preferred option (i.e. it would be associated with an ICER of £20,000/QALY or better vs. no treatment). CV, cardiovascular; RR, relative risk.

FIGURE 53.
Updated model, including adjustment for competing risk of non-cardiovascular death: one-way sensitivity analysis for medium-intensity statins (simvastatin 20 mg/day) compared with low-intensity statins (simvastatin 10 mg/day) (60-year-olds, 50 : 50 men : women, 10% 10-year cardiovascular event risk). Thirty most influential parameters shown. Positive incremental NHB implies that high-intensity statins is the preferred option (i.e. it would be associated with an ICER of £20,000/QALY or better vs. no treatment). CV, cardiovascular; RR, relative risk.
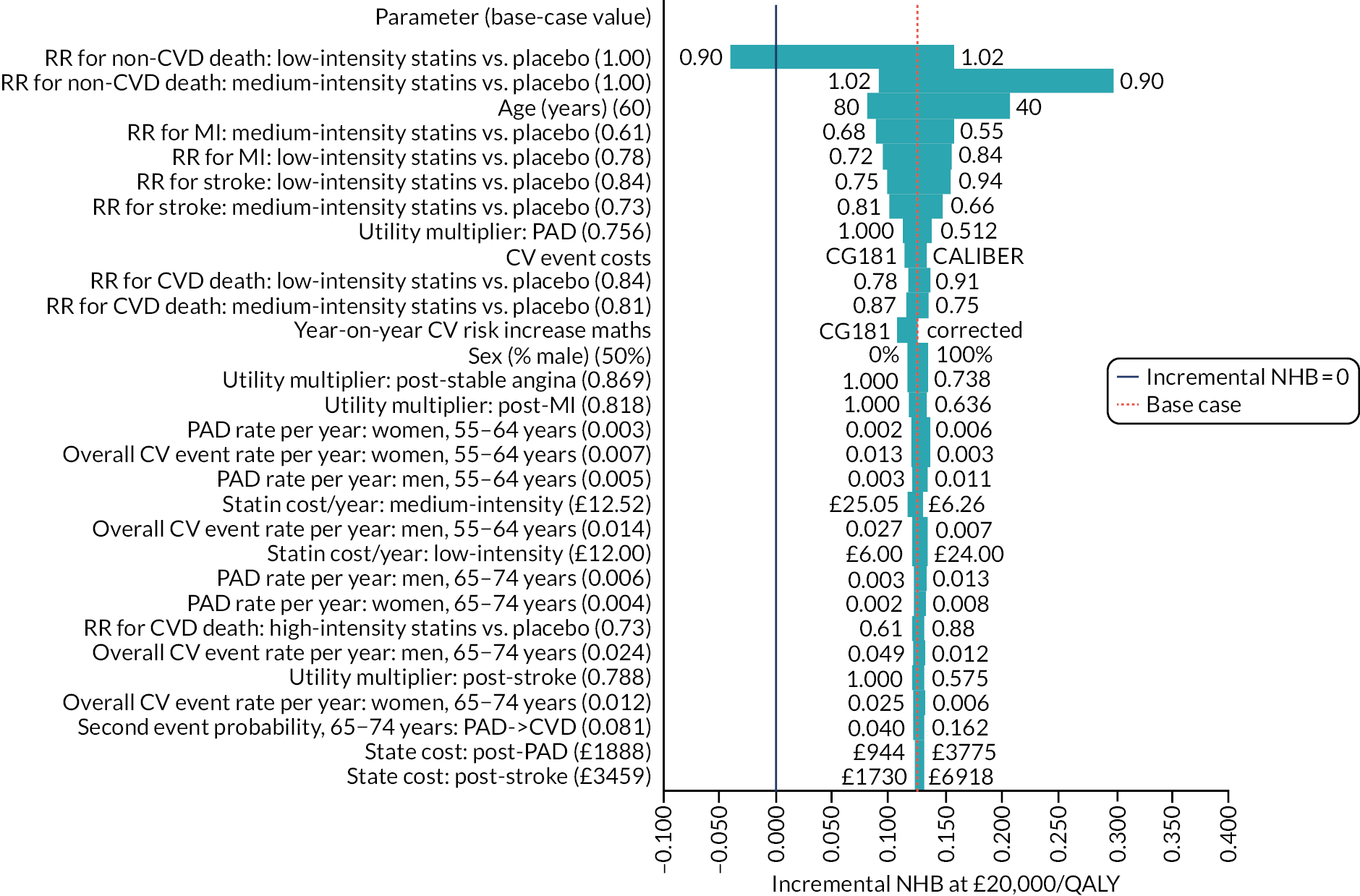
Probabilistic sensitivity analysis
Figures 54–57 illustrate the pairwise comparison between high-intensity statins (atorvastatin 20 mg/day) and no treatment with and without adjustment for competing risk of non-cardiovascular death when analysed probabilistically.
FIGURE 54.
Probabilistic sensitivity analysis for high-intensity statins (atorvastatin 20 mg/day vs. no treatment) with and without adjustment for competing risk of non-cardiovascular death in example cohorts. (a) cost–utility scatterplot for 60-year-old men, 10-year cardiovascular risk = 10%; (b) cost–utility scatterplot for 60-year-old women, 10-year cardiovascular risk = 10%; (c) cost-effectiveness acceptability curves for 60-year-old men, 10-year cardiovascular risk = 10%; and (d) cost-effectiveness acceptability curves for 60-year-old women, 10-year cardiovascular risk = 10%.
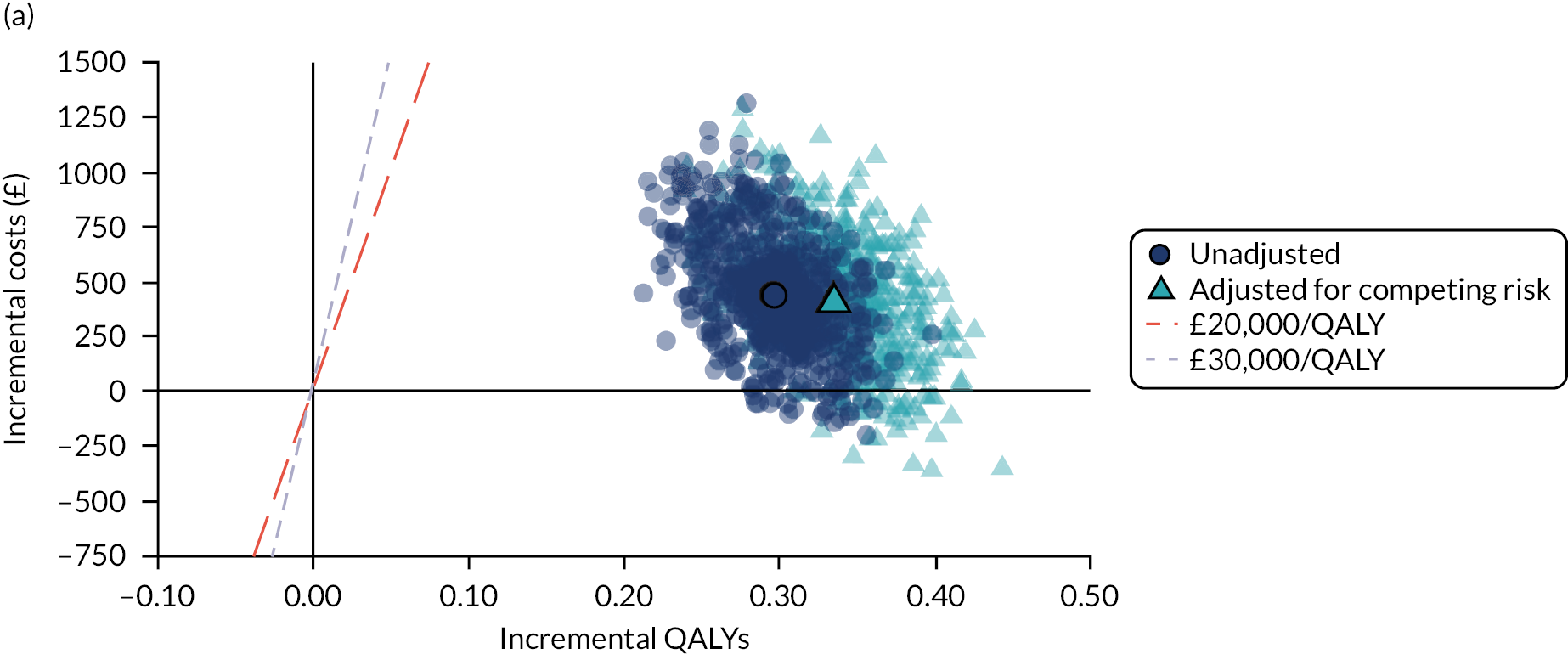

FIGURE 55.
Updated model, including adjustment for competing risk of non-cardiovascular death: probabilistic cost–utility scatterplot for all options (60-year-olds, 50 : 50 men : women, 10% 10-year cardiovascular event risk).
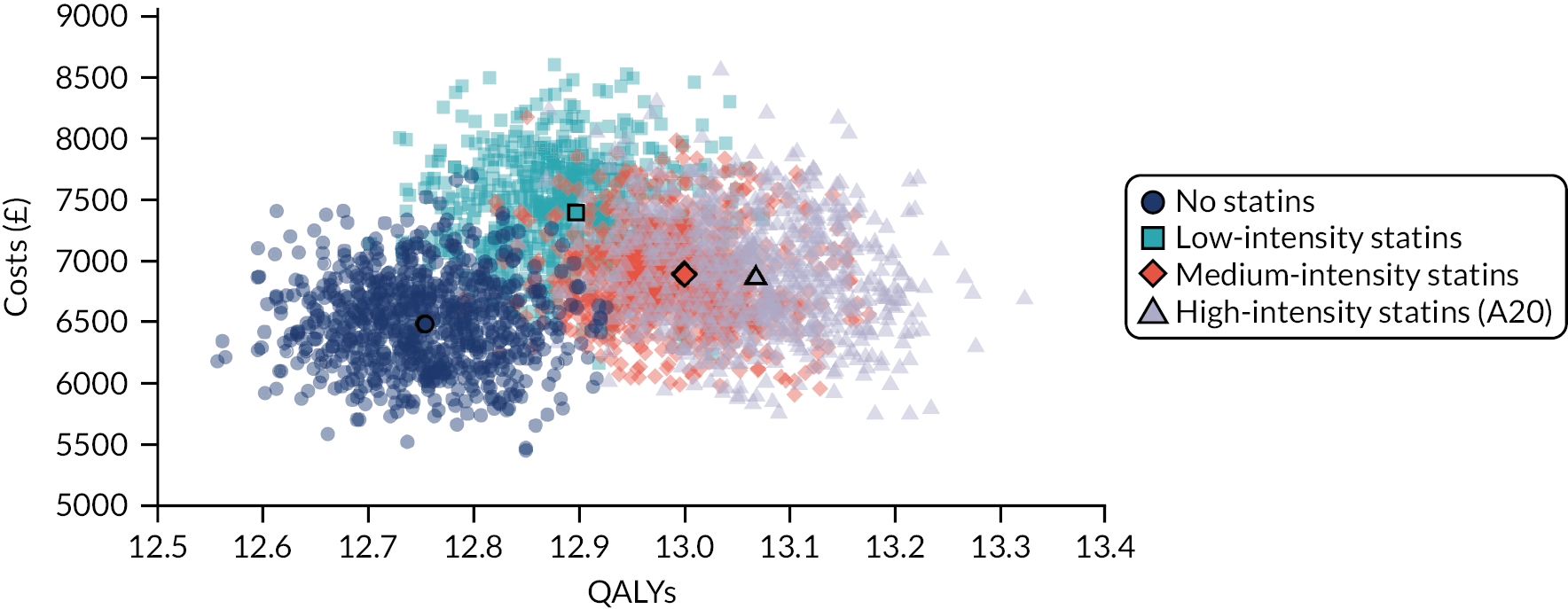
FIGURE 56.
Updated model, including adjustment for competing risk of non-cardiovascular death: cost-effectiveness acceptability curve (60-year-olds, 50 : 50 men : women, 10% 10-year cardiovascular event risk). Bold line shows cost-effectiveness acceptability frontier.

FIGURE 57.
Updated model, including adjustment for competing risk of non-cardiovascular death: probabilistic incremental cost–utility scatterplot – high-intensity statins (atorvastatin 20 mg/day) compared with no treatment (60-year-olds, 50 : 50 men : women, 10% 10-year cardiovascular event risk).

With direct treatment disutility
In Figure 58, we show probabilistic versions of the pairwise comparison between high-intensity statins (atorvastatin 20 mg/day) and no treatment under varying DTD scenarios for a representative range of age risk profiles.
FIGURE 58.
Probabilistic sensitivity analysis for high-intensity statins (atorvastatin 20 mg/day vs. no treatment) under varying DTD scenarios for example cohorts. (a) Cost–utility scatterplot for 50-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 5%; (b) cost-effectiveness acceptability curves for 50-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 5%; (c) cost–utility scatterplot for 60-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 10%; and (d) cost-effectiveness acceptability curves for 60-year-olds, 50 : 50 men women, 10-year cardiovascular risk = 10%; (e) cost–utility scatterplot for 70-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 20%; (f) cost-effectiveness acceptability curves for 70-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 20%; (g) cost–utility scatterplot for 80-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 30%; and (h) cost-effectiveness acceptability curves for 80-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 30%.
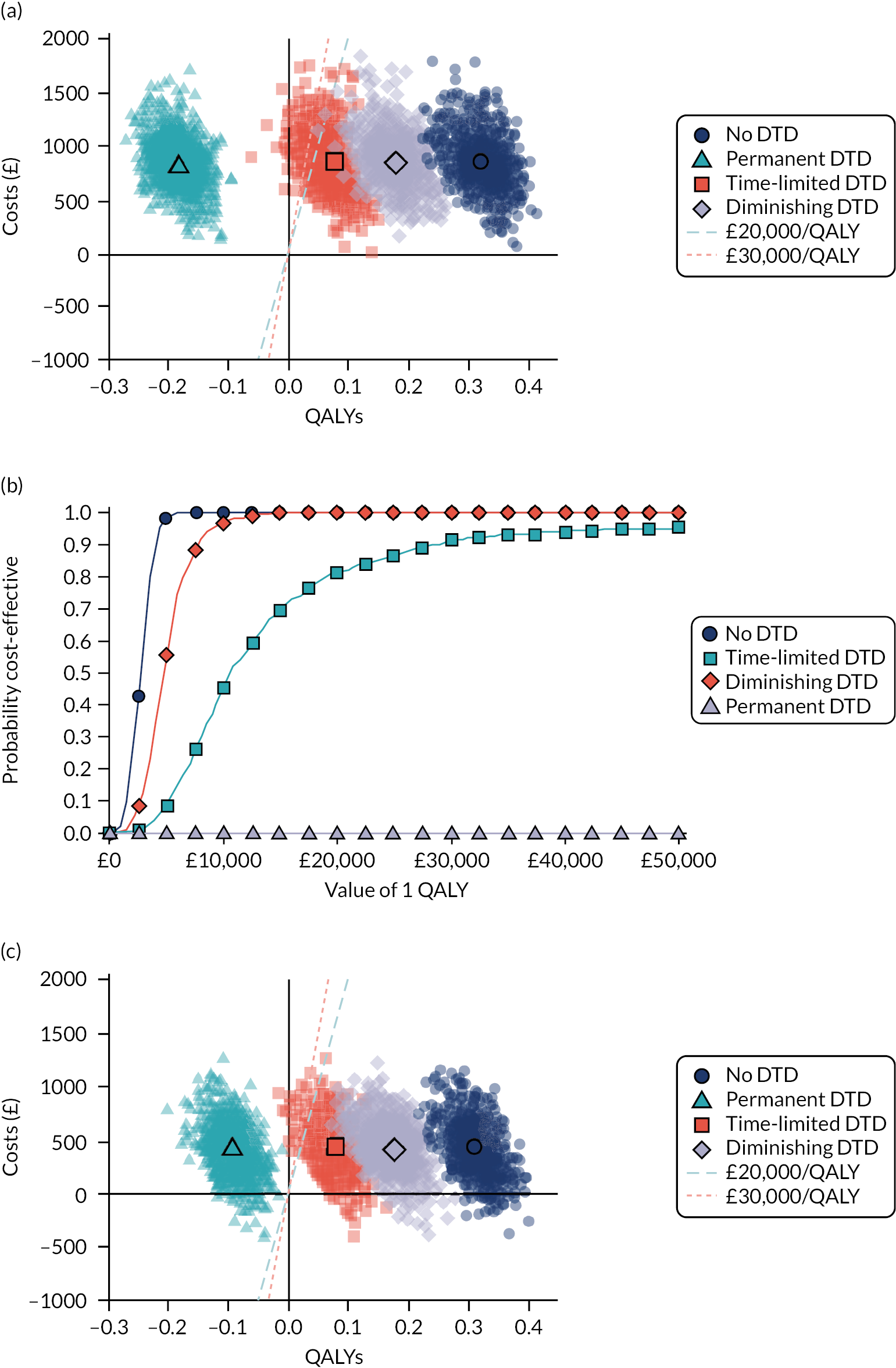
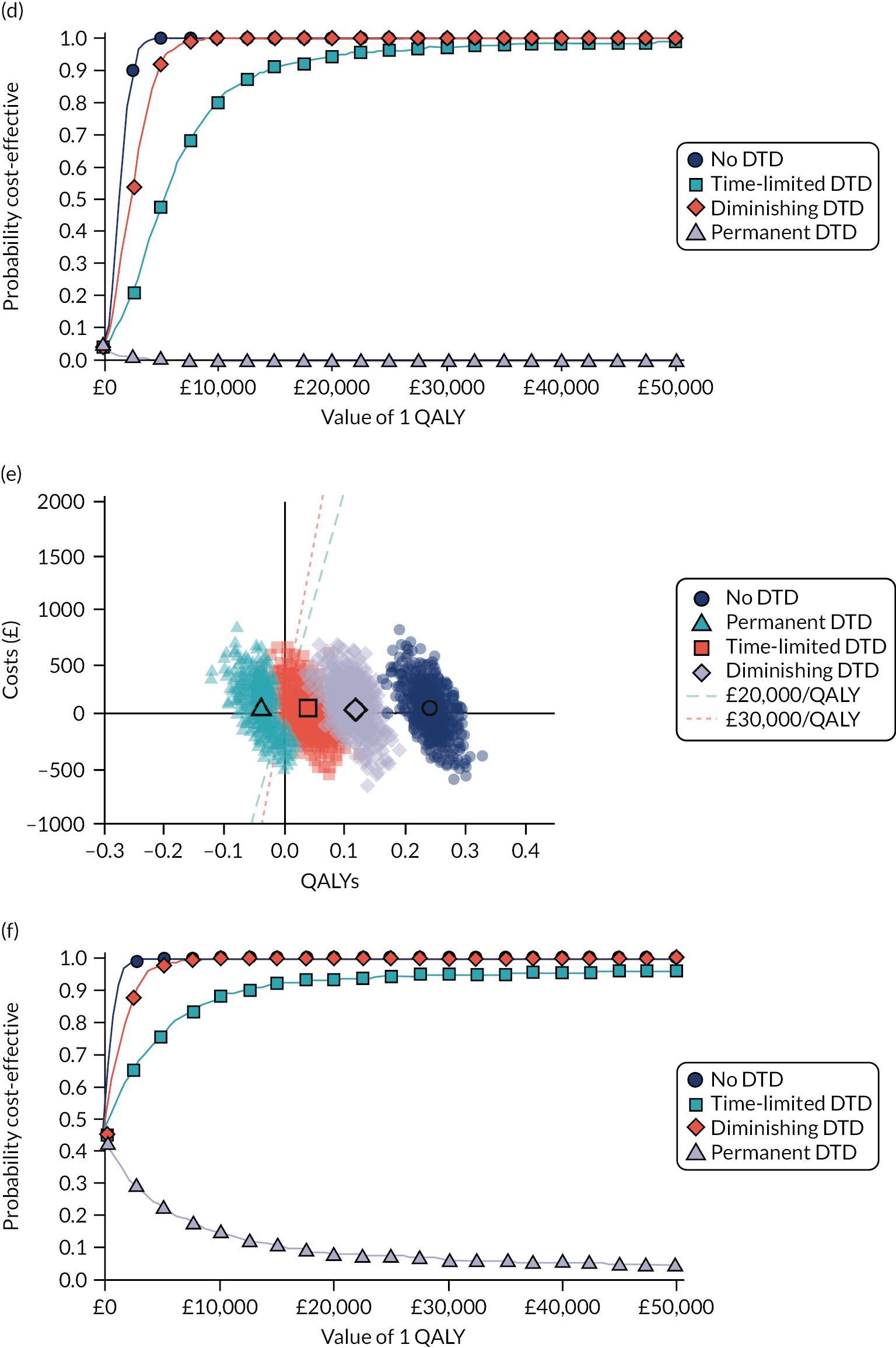

Scenario analysis
Pay-off time under varying direct treatment disutility assumptions
Figures 59 and 60 show cumulative incremental QALYs over time for four example profiles across our four DTD scenarios.
FIGURE 59.
Payoff time for high-intensity statins (atorvastatin 20 mg/day) compared with no treatment, for different example populations under different DTD scenarios. (a) Undiscounted cumulative incremental QALYs for 50-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 5%; (b) undiscounted cumulative incremental NHB for 50-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 5%; (c) undiscounted cumulative incremental QALYs for 60-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 10%; and (d) undiscounted cumulative incremental NHB for 60-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 10%; (e) undiscounted cumulative incremental QALYs for 70-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 20%; (f) undiscounted cumulative incremental NHB for 70-year-olds, 50 : 50 men : women, 10-year cardiovascular risk= 20%; (g) undiscounted cumulative incremental QALYs for 80-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 30%; and (h) undiscounted cumulative incremental NHB for 80-year-olds, 50 : 50 men : women, 10-year cardiovascular risk = 30%.

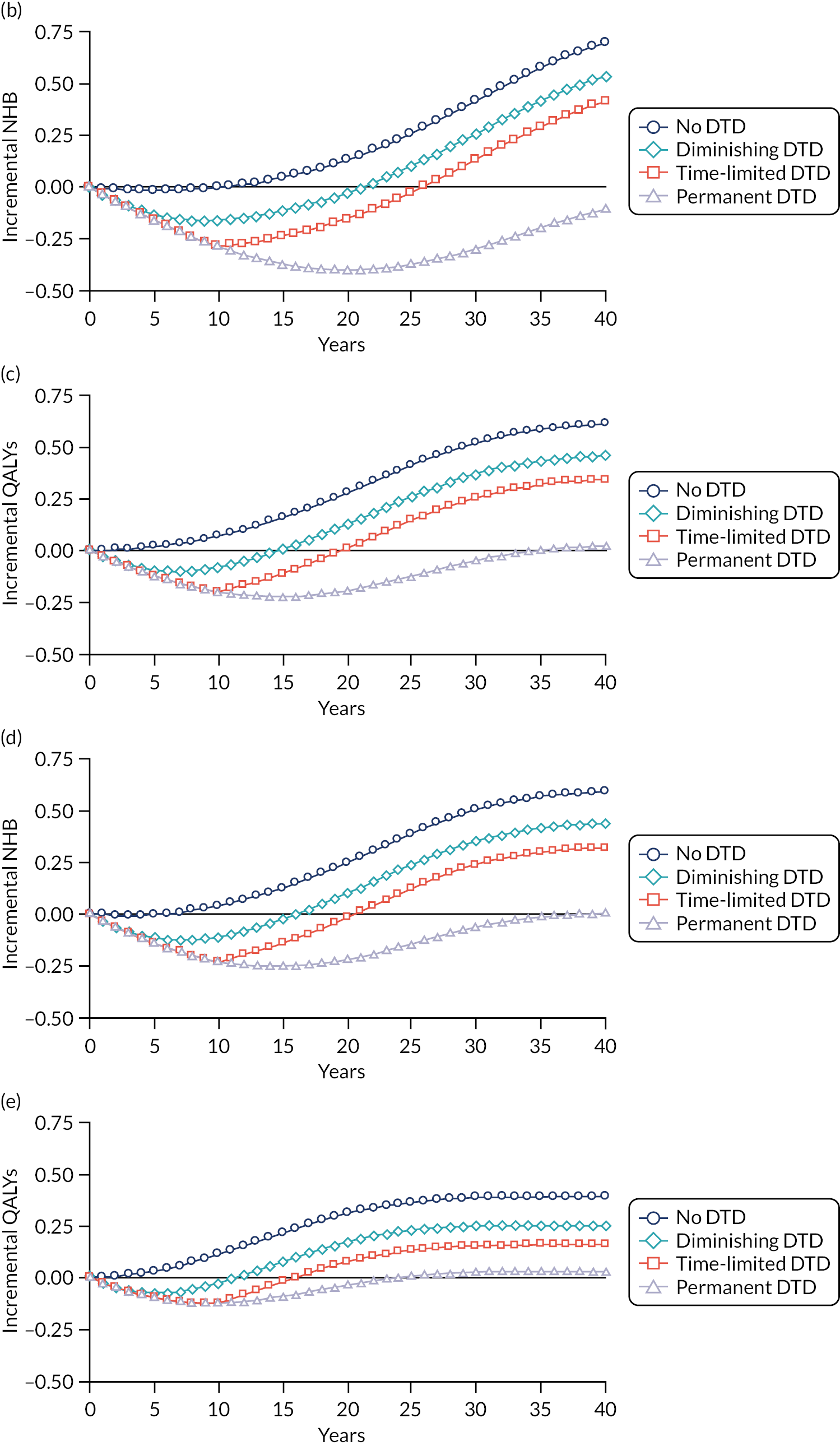
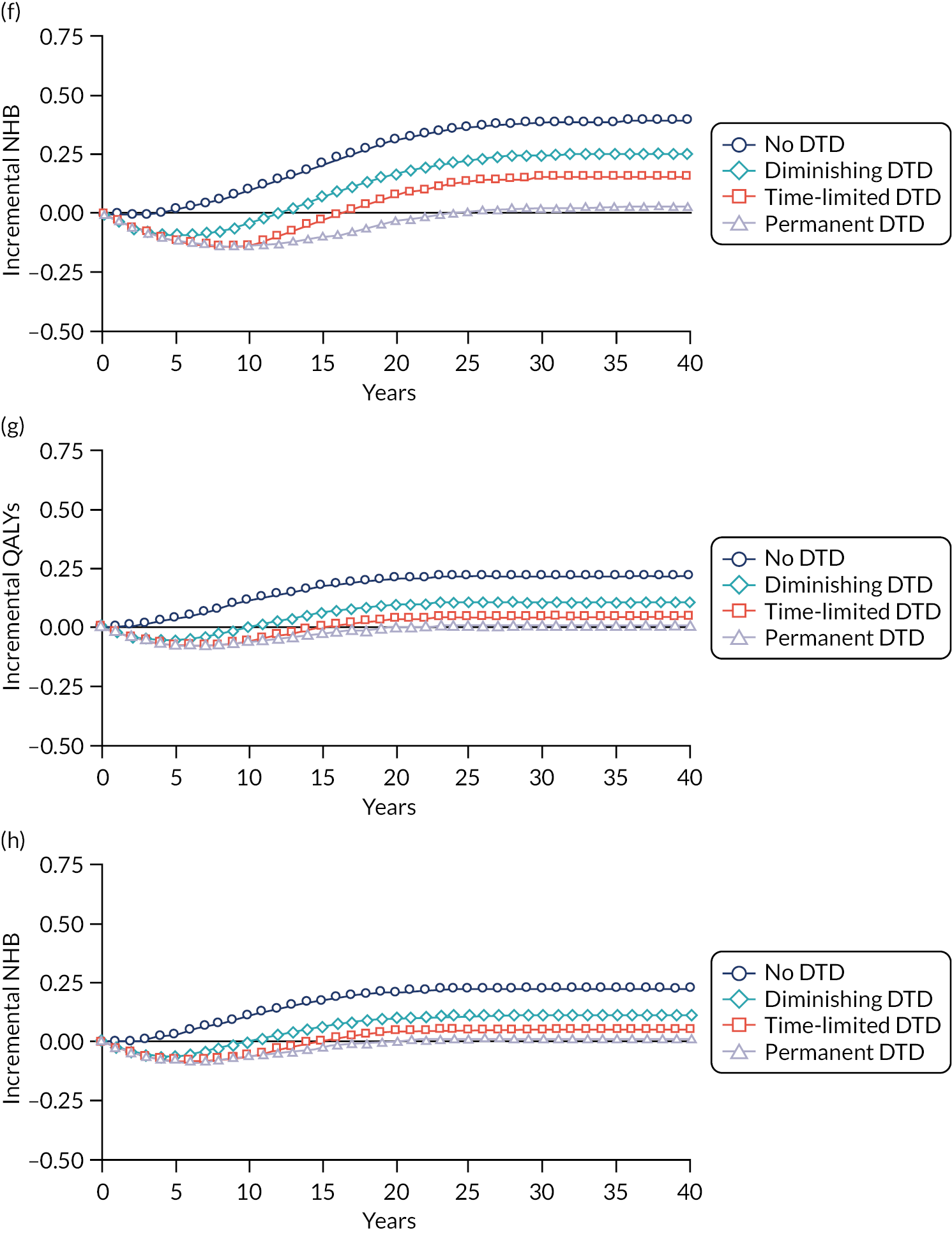
FIGURE 60.
Clinical effectiveness and cost-effectiveness of high-intensity statins, as a function of age and cardiovascular risk, with different levels of DTD (as absolute decrement) and competing risk of non-cardiovascular death. (a) Effectiveness (incremental QALYs); and (b) cost-effectiveness (when QALYs are valued at £20,000–30,000).
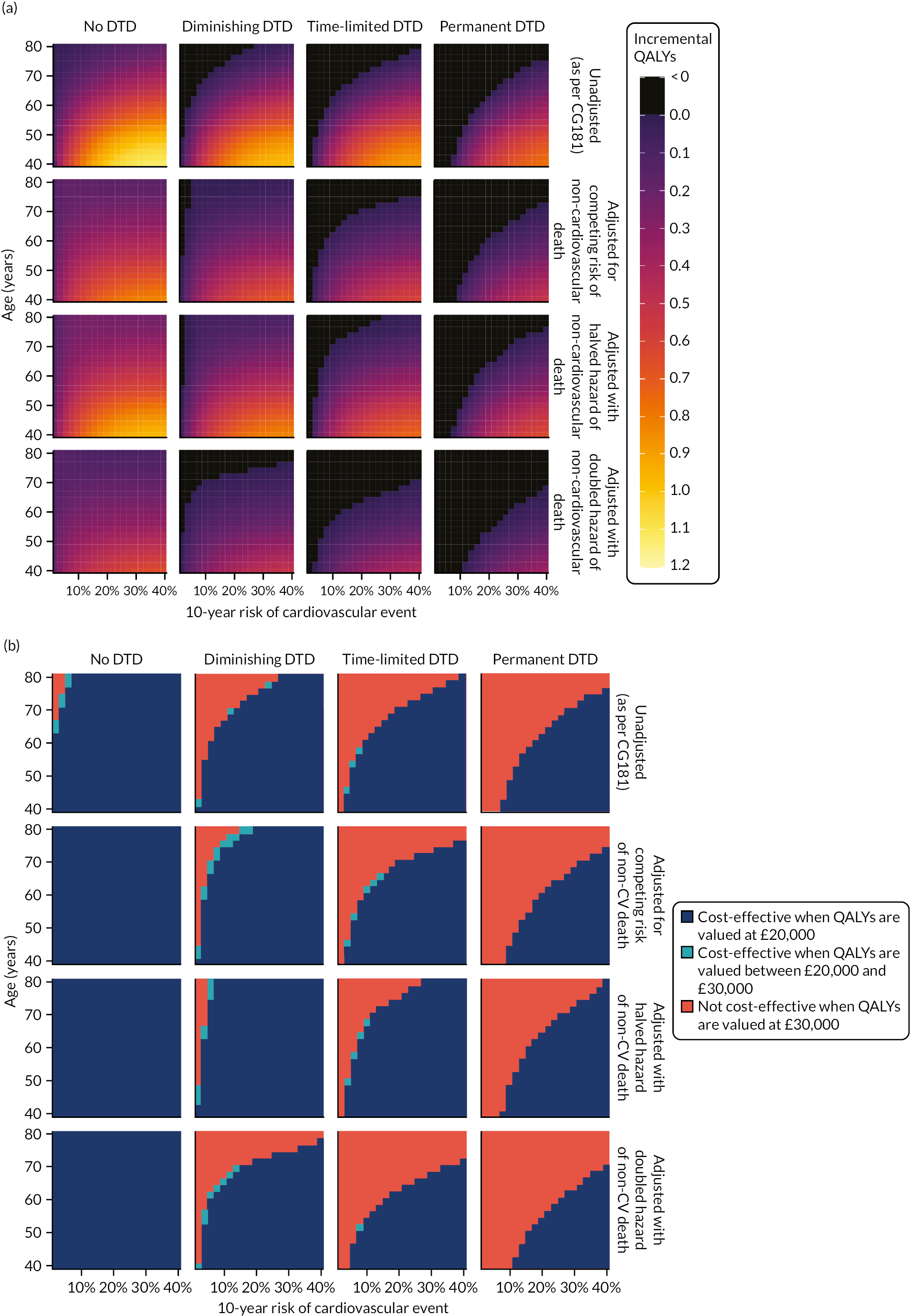
Appendix 9 Supplementary methods and results for model assessing cost-effectiveness of bisphosphonates for the primary prevention of osteoporotic fragility fracture
Supplementary methods
Accounting for competing risk of non-cardiovascular death
As explained in the main text (see Accounting for competing risk of non-cardiovascular death, p.91), the critical covariate for our relative survival models is Δlogit(Q), that is the difference between an individual’s predicted 10-year QFracture-2012 score and the average score for a person of the same age and sex. We estimate the latter using a regression on the CPRD data set. Table 57 shows the model coefficients and Figure 61 shows the model fitted for men and women as a function of age.
| Parameter | Fitted to all ages, estimate (95% CI) | Fitted to people aged < 90 years only, estimate (95% CI) |
|---|---|---|
| Intercept | −2.27 (−4.47 to −0.06) | −5.70 (−5.77 to −5.63) |
| Age | −0.509 (−0.797 to −0.220) | −0.065 (−0.070 to −0.059) |
| Age2 | 2.82 × 10−2 (1.24 × 10−2 to 4.39 × 10−2) | 3.45 × 10−3 (3.30 × 10−3 to 3.60 × 10−3) |
| Age3 | −8.09 × 10−4 (−1.27 × 10−3 to −3.44 × 10−4) | −3.75 × 10−5 (−3.92 × 10−5 to −3.57 × 10−5) |
| Age4 | 1.48 × 10−5 (6.74 × 10−6 to 2.28 × 10−5) | 1.53 × 10−7 (1.45 × 10−7 to 1.61 × 10−7) |
| Age5 | −1.68 × 10−7 (−2.49 × 10−7 to −8.66 × 10−8) | |
| Age6 | 1.07 × 10−9 (6.27 × 10−10 to 1.52 × 10−9) | |
| Age7 | −2.93 × 10−12 (−3.97 × 10−12 to −1.90 × 10−12) | |
| Male | 18.48 (15.18 to 21.79) | 4.63 (4.53 to 4.73) |
| Male × age | −2.053 (−2.488 to −1.619) | −0.232 (−0.240 to −0.224) |
| Male × age2 | 1.03 × 10−1 (7.93 × 10−2 to 1.27 × 10−1) | 3.57 × 10−3 (3.36 × 10−3 to 3.79 × 10−3) |
| Male × age3 | −2.97 × 10−3 (−3.68 × 10−3 to −2.26 × 10−3) | −2.91 × 10−5 (−3.17 × 10−5 to −2.65 × 10−5) |
| Male × age4 | 5.06 × 10−5 (3.83 × 10−5 to 6.30 × 10−5) | 1.20 × 10−7 (1.08 × 10−7 to 1.31 × 10−7) |
| Male × age5 | −5.07 × 10−7 (−6.33 × 10−7 to −3.81 × 10−7) | |
| Male × age6 | 2.76 × 10−9 (2.06 × 10−9 to 3.46 × 10−9) | |
| Male × age7 | −6.27 × 10−12 (−7.90 × 10−12 to −4.64 × 10−12) |
FIGURE 61.
Average 10-year risk of MOF (QFracture-2012) as a function of age and sex.
Supplementary results
Threshold at which treatment becomes associated with positive net benefit according to the generalised additive model adjusting for age and fracture risk
The threshold at which treatment becomes associated with positive net benefit according to the GAM and adjusting for age and fracture risk is shown in Table 58.
| Age (years) | Unadjusted threshold (95% CI) | Adjusted for competing risk of non-fracture death threshold (95% CI) |
|---|---|---|
| 40 | 4.9 (4 to 6.7) | 8.5 (5.5 to infa) |
| 50 | 5.1 (4.5 to 6.4) | 8.5 (6.1 to 17) |
| 60 | 5.5 (5 to 6.1) | 7.4 (6.2 to 9.4) |
| 70 | 4.6 (4.2 to 4.9) | 4.6 (4.2 to 4.9) |
| 80 | 4.1 (3.4 to 4.6) | 4.2 (3.7 to 4.7) |
| 90 | 8.8 (0 to 12) | 8.3 (0 to 12) |
Cost-effectiveness of bisphosphonates for the primary prevention of osteoporotic fragility fracture: meta-model accounting for age, sex and baseline fracture risk
The meta-model takes the form:
Figure 62 shows the fitted model for men and women at indicative ages of 50, 60, 70 and 80 years, and Table 59 tabulates the threshold at which net benefit becomes positive (assuming that decision-makers value QALYs at £20,000 each).
FIGURE 62.
Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of age, sex and risk of fracture, with different assumptions about competing risk of non-fracture death. (a) Men aged 50 years; (b) women aged 50 years; (c) men aged 60 years; (d) women aged 60 years; (e) men aged 70 years; (f) women aged 70 years; (g) men aged 80 years; and (h) women aged 80 years. GAM fitted to model outputs comprising 5 million simulated patients. Lines show fitted model prediction, shaded areas show 95% CI, vertical dashed bars represent deciles of risk and numbered shapes show mean values for people within each tenth of the population (where these are missing, fewer than 100 of the total 5 million simulated people fell into the group).


| Age (Years) | Unadjusted | Adjusted | ||||||
|---|---|---|---|---|---|---|---|---|
| Men | Women | Men | Women | |||||
| Threshold | 95% CI | Threshold | 95% CI | Threshold | 95% CI | Threshold | 95% CI | |
| 40 | 5.1 | 3.6 to infa | 4.6 | 3.5 to 7.2 | infa | 5.5 to infa | 7.6 | 4.3 to infa |
| 50 | 4.3 | 3.5 to 6.1 | 5 | 4.3 to 6.4 | infa | 5.5 to infa | 7.7 | 5.2 to infa |
| 60 | 4 | 3.4 to 4.7 | 5.4 | 5 to 6.1 | 9.2 | 5.4 to infa | 7.8 | 6.2 to 16 |
| 70 | 3.8 | 3.4 to 4.3 | 5.1 | 4.7 to 5.4 | 8.8 | 5.2 to infa | 4.5 | 3.9 to 5 |
| 80 | 4 | 3.4 to 4.6 | 5.2 | 0 to 5.9 | 6.6 | 3.6 to infa | 3.5 | 0 to 4.6 |
| 90 | 5.8 | 0 to 8.7 | 12 | 0 to 14 | 3.5 | 0 to 13 | 0.1 | 0 to 11 |
List of abbreviations
- ADE
- adverse drug event
- AIC
- Akaike information criterion
- AUROC
- area under the receiver operating curve
- BMI
- body mass index
- BWS
- best–worst scaling
- CCI
- Charlson Comorbidity Index
- CEA
- cost-effectiveness analysis
- CG181
- Clinical Guideline 181
- CI
- confidence interval
- CKD
- chronic kidney disease
- CPRD
- Clinical Practice Research Datalink
- CRISK
- competing mortality risk model
- CRISK-CCI
- competing mortality risk model with Charlson Comorbidity Index
- CVD
- cardiovascular disease
- DTD
- direct treatment disutility
- eGFR
- estimated glomerular filtration rate
- EQ-5D-3L
- EuroQol-5 Dimensions, three-level version
- GAM
- generalised additive model
- GP
- general practitioner
- HES
- Hospital Episode Statistics
- HR
- hazard ratio
- HSE
- Health Survey for England
- HTA
- Health Technology Assessment
- ICD-10
- International Statistical Classification of Diseases and Related Health Problems, Tenth Revision
- ICER
- incremental cost-effectiveness ratio
- mCCI
- modified Charlson Comorbidity Index
- MI
- myocardial infarction
- MOF
- major osteoporotic fracture
- MSE
- minor side effect
- NHB
- net health benefit
- NICE
- National Institute for Health and Care Excellence
- NIHR
- National Institute for Health and Care Research
- NNT
- number needed to treat
- ONS
- Office for National Statistics
- OR
- odds ratio
- PAD
- peripheral arterial disease
- PICOS
- population, intervention, comparator, outcome, study type
- QALY
- quality-adjusted life-year
- QS149
- Quality Standard 149
- SA
- stable angina
- SBP
- systolic blood pressure
- SE
- standard error
- SHARE
- Scottish Health Research Register
- SSE
- severe side effect
- TA464
- Technology Appraisal 464
- TC : HDL
- total cholesterol: high-density lipoprotein ratio
- TIA
- transient ischaemic attack
- TTO
- time trade-off
- UA
- unstable angina
