Notes
Article history
The research reported in this issue of the journal was funded by the HTA programme as project number 09/91/39. The contractual start date was in May 2011. The draft report began editorial review in May 2014 and was accepted for publication in August 2014. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HTA editors and publisher have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the draft document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
none
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2015. This work was produced by Grant et al. under the terms of a commissioning contract issued by the Secretary of State for Health. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
Chapter 1 Background
Abdominal aortic aneurysm
An aneurysm is defined as a dilatation of a blood vessel by more than 50% of its original diameter. Although aneurysms can affect any blood vessel, the abdominal aorta is most commonly affected. The normal diameter of the abdominal aorta is not usually greater than 2 cm; therefore, an abdominal aortic aneurysm (AAA) is defined as a dilatation of the abdominal aorta to a diameter of greater than 3 cm.
Abdominal aortic aneurysms can be grouped into:
-
those that develop as a result of connective tissue disorders
-
infective or inflammatory AAAs
-
late-onset AAAs.
Late-onset AAAs are by far the most common, affecting 5–8% of men over the age of 65 years. 1–4 The prevalence of AAA has been shown to be influenced by increasing age,2,5,6 male sex,2,5,7 a history of smoking8,9 and a family history of AAA. 5,10
Abdominal aortic aneurysm growth and rupture
Once an AAA develops, the initial dilatation of the aorta leads to an increase in tension of the vessel wall and further growth (law of Laplace). 11 AAA growth rates increase as the AAA gets larger. 12–14 Growth rates have also been shown to be higher in smokers15–18 and lower in patients taking beta blockers,19 angiotensin-converting enzyme inhibitors or statins20,21 and lower in patients with diabetes. 16,18,22,23
Most AAAs continue to grow until the aneurysm ruptures or is repaired or the patient dies of other causes. Rupture with significant haemorrhage is the most common and devastating complication of AAA. Most patients who suffer AAA rupture die immediately and, even in those who reach hospital and are able to undergo emergency surgery, the operative mortality approaches 50%. 24 AAA rupture causes roughly 7000 deaths/year in the UK, approximately 2.5% of all deaths in men over the age of 65 years. 1 The most significant risk factor for AAA growth and rupture is maximum aneurysm diameter. 25,26
Detection of abdominal aortic aneurysm
As AAA rupture has such a poor outcome, it is important to identify and repair AAA early. Most patients with AAA experience no symptoms and in the past were identified incidentally on abdominal imaging by ultrasound or computed tomography for other reasons. Ultrasound is non-invasive, pain free and entirely reliable in the detection of AAA. 27 It has been extensively studied as a method of population screening for early detection of AAA. There have been four large randomised controlled trials (RCTs) evaluating screening for AAA;1–4 a review of these trials concluded that screening was associated with significant reductions in AAA-related mortality in men and a decreased incidence of ruptured aneurysm. 28 The National AAA Screening Programme (NAAASP) was introduced throughout the UK during 2010–13.
Repair of abdominal aortic aneurysm
The primary aim in the management of AAA is to prevent premature death due to AAA rupture. Currently, approximately 4000 elective AAA repairs are performed each year in the UK,29 a number that is thought to be rising. 30 In patients with symptoms attributable to their AAA, repair should be performed urgently, as these symptoms may represent impending rupture. However, the vast majority of patients are asymptomatic and the clinical decisions are (1) when should the AAA repair be performed? and (2) what method should be used to repair the AAA?
Open or endovascular repair
Open AAA repair is major surgery involving laparotomy, displacing the abdominal viscera, cross-clamping the aorta for at least 40–60 minutes and replacing the aneurysmal aorta with a synthetic graft. Laparoscopic AAA repair is similar in principle to open AAA repair but performed using laparoscopy rather than a laparotomy; it has not been widely adopted because of the difficulty and frequency of complications. 31 Although there are inevitable variations,32 the mortality following open elective AAA repair is generally accepted as being approximately 5% with some evidence that the 30-day mortality rate is falling. 33,34 In addition to this mortality risk, there is a significant risk of major medical morbidity and laparotomy-related complications. 35
Endovascular aneurysm repair (EVAR) is performed by catheterising the common femoral arteries on both sides and deploying a stent–graft across the aneurysmal segment of the aorta. The stent–graft then expands, engaging the aortic wall with the blood flow confined within the graft rather than throughout the aneurysmal segment of the aorta. The advantage of EVAR over open AAA repair is that it is considerably less invasive and associated with a lower initial mortality rate and morbidity rates. 35–37 The main disadvantage of EVAR is that the repair is less stable with a substantially higher rate of late AAA-related complications including endoleak, graft displacement, stent fracture and even AAA rupture. 35,38
There have been a number of comparative studies between open AAA repair and EVAR. The randomised EVAR 1 trial demonstrated that perioperative mortalities were lower in patients who underwent EVAR39 but found no difference in mid-term or long-term all-cause mortality. 38 EVAR was, however, associated with a more frequent need for AAA-related reinterventions and late AAA ruptures. An additional RCT reported similar perioperative mortality rates to the EVAR 1 trial35 but again demonstrated no difference in cumulative survival between open surgery and EVAR beyond 2 years. 40 Similar findings have also been reported in a large propensity-matched registry study. 41 There is, therefore, strong evidence that procedure-related mortality may be lower in patients who undergo EVAR, but overall survival is similar from 2 years onwards.
The current indication to repair abdominal aortic aneurysm
The decision on when to perform AAA repair is a balance between the risks of repair and the risk of death due to rupture. It has generally being accepted for many years that patients with large AAAs (> 5.5 cm in men and > 5.0 cm in women) or those with back ache, abdominal loin or groin pain that might be attributed to the AAAs should undergo early or urgent repair.
The current indication for surgery for small asymptomatic AAAs (between 4.0 and 5.5 cm in diameter) is based on two RCTs, the UK Small Aneurysm Trial (UKSAT) and the Aneurysm Detection and Management (ADAM) trial. 42,43 Both trials randomised patients with AAAs between 4.0 and 5.5 cm in diameter to either early AAA repair or ultrasound surveillance with AAA repair when indicated.
Although mortality was initially higher in the immediate repair group, there was no significant difference in mortality between the two groups at 2, 4, 6 and 12 years following randomisation in the UKSAT. 44 In the ADAM trial, the results were similar but follow-up was for a mean of only 4.9 years. 43 A pooled analysis of the two trials confirmed no benefit for early surgery over ultrasound surveillance in AAAs between 4.0 and 5.5 cm. 45 As a result, the established indication was to offer repair of asymptomatic AAAs when the AAA diameter reached 5.5 cm in men. As there is good evidence that women have a greater risk of rupture for a given size of AAA than men,18 it has become normal practice to repair AAAs in women when diameter reaches 5.0 cm. It is possible that this is a consequence of the generally greater ratio of AAA diameter to normal size in women, as women have smaller aortas.
Can a population-based indication be applied to individuals?
Although the current indication for elective AAA repair is based on well-conducted randomised trials, we question whether or not these population-based findings are applicable to individual patients with AAAs. In the UKSAT, all patients aged 60–76 years were included with the ADAM trial including patients aged 50–79 years. These trials were not designed to determine whether or not the indication for younger patients might be different for that in older patients. Furthermore, although these trials convincingly demonstrate that, within this age, there is no benefit in early surgery for aneurysms in the size range 4.0–5.5 cm, an alternative interpretation of this data is that the true indication for AAA repair in the individual patient might be anywhere within this size range. The timing of repair for a 5.0 cm or 5.5 cm AAA to optimise survival may not be the same for a 60-year-old healthy man and an 80-year-old man with multiple comorbidities. The trials focused on aneurysm size, whereas other factors, such as age, fitness and presence of other comorbidities influence perioperative mortality and long-term survival. There is evidence to support this argument from the subgroup analysis of the UKSAT, as shown in Table 1.
| Factor | Surveillance | Early surgery | Hazard ratioa | p-valueb |
|---|---|---|---|---|
| Age (years) | ||||
| 60–66 | 5.8 | 4.7 | 0.76 | 0.10 |
| 67–71 | 8.9 | 6.8 | 0.80 | |
| 72–76 | 7.6 | 9.5 | 1.25 | |
| AAA diameter (cm) | ||||
| 4.0–4.4 | 6.5 | 7.4 | 1.14 | 0.26 |
| 4.5–4.8 | 6.8 | 6.3 | 0.88 | |
| 4.9 –5.5 | 9.5 | 7.4 | 0.79 | |
This subgroup analysis shows that the number of deaths per 100 person-years following early surgery was highest in the elderly and much lower in those aged 60–66 years. Although this measure of mortality increases with age at surveillance, these findings suggest that across the size range 4.0–5.5 cm there is a mean advantage to patients aged 60–66 years from undergoing early surgery but a disadvantage in patients aged 72–76 years. This is entirely what would be expected and completely compatible with the final conclusion of this study based on all patients aged 60–76 years.
Similar results are reported with respect to AAA diameter. For smaller AAAs in the size range 4.0–4.4 cm, the risk of mortality is clearly lower with surveillance than it is with early surgery. However, for larger aneurysms in the size range 4.9–5.5 cm there is a lower risk of death in those patients randomised to early surgery, even though this population included patients aged over 72 years. An alternative conclusion from this study is clearly that in patients aged 60–76 years the optimal indication for AAA repair is somewhere between 4.5 and 4.8 cm and that this indication to repair changes with advancing age.
The current indications for AAA repair based on AAA diameter alone also ignore the following important variables which may influence survival: (1) the patient’s life expectancy, (2) factors that influence AAA growth and risk of rupture, (3) factors that influence perioperative mortality and (4) factors that influence long-term survival following elective AAA repair.
Overall aim of the project
This project was designed to gather evidence and explore the potential for the Aneurysm Repair Decision Aid (ARDA) to formalise and improve the current clinical decision processes by calculating the timing of elective AAA repair to optimise survival in individual patients with AAA. The aim of the economic analysis was to explore whether or not adopting the ARDA in place of the existing indications for elective AAA repair would be cost-effective. Although this work is focused on the UK and has implications for the NHS and the NAAASP, this work could be adapted using data from other regions to be similarly relevant to the management of patients with AAA worldwide.
Chapter 2 Research objectives
Aims and objectives
The overall objective was to develop an algorithm (ARDA) to calculate the optimum timing of elective AAA repair to maximise survival in individual patients with AAA.
To develop this algorithm we have undertaken the following steps:
-
development and validation of models to predict the risk of perioperative mortality in elective AAA repair
-
development of a model that predicts long-term survival following elective AAA repair
-
development of an algorithm that calculates the expected AAA growth rate and risk of rupture for each individual patient based on RESCAN data18
-
comparison of the clinical effectiveness and cost-effectiveness of decisions based on the ARDA with the current indications for elective AAA repair.
Structure of the report
The data sources used for this research are presented in Chapter 3. Patient and public involvement (PPI) in the research is discussed in Chapter 4. Chapter 5 describes the development and validation of models for the prediction of perioperative mortality. Chapter 6 describes the development of a survival model for elective AAA repair. Chapter 7 describes the development of the discrete event simulation (DES) model used in the ARDA and provides example patient clinical scenarios (vignettes), which illustrate the information provided by the ARDA. Chapter 8 describes the methods used to assess the cost-effectiveness of decisions based on the ARDA, with the results of this analysis presented in Chapter 9. Chapter 10 provides a discussion of the strengths and limitations of all of the component studies. Conclusions and research priorities are reported in Chapter 11. A list of published papers arising from this work is provided in Acknowledgements.
Chapter 3 Data sources
Background
The statistical models and algorithms developed in this project rely on good-quality data. The individual patient data (IPD) used in the development process were made available by the Vascular Governance North West (VGNW) database and the National Vascular Database (NVD). Where appropriate, previously published information was gathered from peer-reviewed papers. The IPD utilised for this project are summarised in Figure 1.
FIGURE 1.
Individual patient data used in this project. a, Reduced number of records available because of in-hospital mortality and missing date of discharge information.

The Vascular Governance North West programme
The VGNW database was established as a registry of all vascular procedures in the North West region. The need to implement the quality agenda in specialist surgery was clearly identified following the Bristol inquiry. 46 In April 1999, vascular surgeons in the North West (50 surgeons in 24 units) set up a peer-led clinical governance initiative. Prospective data collection began in February 2000, with surgeons also able to submit retrospective records. The main function of the project was to collect and analyse procedure-specific surgical data. These include open AAA repair (from 1999) and EVAR (from 2006). Fifty-six consultants from the North West region currently participate in this regional audit programme. A full list of all surgeons who have contributed to the VGNW database is given in Appendix 1.
At present, data are collected at each hospital: on paper forms, on Microsoft Excel 2010 spreadsheets (version 14.0.6129.5000, Microsoft Corporation, Redmond, WA, USA), or using the web-based data entry tool of the NVD, which has recently evolved into the National Vascular Registry (NVR). Data are transferred to the VGNW audit office at the University Hospital of South Manchester, where it is anonymised and stored in a secure Microsoft Access 2010 database (version 14.0.6129.5000, Microsoft Corporation, Redmond, WA, USA). All the data received directly are submitted to the NVR, with VGNW member surgeons providing nearly 30% of the NVD/NVR data. This VGNW project has also supplied carotid data to the nationwide UK carotid endarterectomy audit and the Greater Manchester Abdominal Aortic Aneurysm Quality Improvement Programme (AAA QIP).
Vascular Governance North West data quality is checked annually by local members of each clinical team to confirm the accuracy and completeness of the data held. Each surgeon is given a summary report of his or her cases and outcomes for cross-checking. Inconsistencies are followed up and resolved by the local VGNW team. Owing to the number of data, 100% checks of individual patient characteristics are not feasible, meaning that inaccuracies in patient risk factor data may be present.
The VGNW programme has been granted ethical approval to provide data sets for research purposes. The steering committee of the VGNW approved use of the data for this National Institute for Health Research (NIHR) Health Technology Assessment (HTA) project. These data have been used in the development of models to predict perioperative mortality (see Chapter 5) and survival models (see Chapter 6). The data fields collected by the VGNW programme for patients undergoing AAA repair are shown in Appendix 2, Table 43. At the start of the project, VGNW had preoperative data on over 3600 patients undergoing AAA repair (with 240 who died postoperatively in hospital). Data completeness was variable across all sites, as shown in Figure 2.
FIGURE 2.
Vascular Governance North West data completeness levels at the beginning (2011) and end (2014) of the project by hospital.

Owing to the number of hospitals involved and the quality of the data required for the modelling work, the VGNW team sought support from the comprehensive local research network to improve AAA data quality. The comprehensive local research network teams, assisting the local surgical and audit teams, were instrumental in the completion of over 5000 missing data points and of an additional 1700 new patient records. There are now 5333 elective AAA operations recorded in the VGNW database. The number of missing points of data has fallen from 30% to 10%, with improvements in data completeness achieved at all contributing centres. Current data completeness compared with the start of the project is illustrated in Figure 2.
Patient mortality status and date of death were also necessary to perform survival analysis. Our PPI group advised against contacting patients directly to gather this information. This decision was taken to avoid upsetting bereaved family members, particularly as the average age at operation of a VGNW patient is 76 years. Survival data were originally for patients who died within 30 days of the operation. To gather long-term follow-up data, an ethical amendment to the VGNW protocol was submitted to the North West regional ethics committee. Section 251 approval was gained from the National Information Governance Board to merge mortality information from the demographic batch service with the VGNW clinical database. This was done using patient NHS numbers and allowed the long-term follow-up mortality status of over 4000 patients to be determined.
The National Vascular Database
The NVD was established in 1997 by the Vascular Society of Great Britain and Ireland, which has a long history of promoting scientific research and clinical excellence in vascular surgery. The NVD was managed by a project co-ordinator, who assisted surgeons, nurses and administrators who input data to the NVD. Contributing surgeons could view activity and outcome reports online to allow local performance to be mapped against national activity in real time. Submission to the NVD was voluntary. Governance of the NVD was the responsibility of the Vascular Society of Great Britain and Ireland. Data were collected on three index procedures: AAA repair, infra-inguinal bypass and amputations. Data collected included patient demographics, comorbidity data, preoperative investigations, intraoperative details and postoperative outcomes. The NVD had a defined minimum data set, and case submission was regularly validated against Hospital Episode Statistics data. No formal validation of clinical data was carried out. For this programme of research; only data on elective AAA repairs were analysed. These data were used in the development of models for perioperative mortality (see Chapter 5). The data fields collected by the NVD for AAA surgery along with the minimum data set required for data submission are shown in Appendix 2, Table 44. The NVD has subsequently been replaced by the NVR.
Aneurysm growth and risk of rupture
Information on AAA growth and risk of rupture was taken from the previously published NIHR HTA programme-funded RESCAN project. 18,47 The aim of the RESCAN project was to inform the evidence base for choice of appropriate surveillance intervals for small AAAs. Information on AAA growth and risk of rupture was obtained from an analysis of IPD from existing surveillance programmes. IPD were obtained on 15,475 patients under surveillance for small AAA in 18 studies (Appendix 3). The data were harmonised with individual AAA diameters in each study analysed using a random-effects model that allowed for between-patient variability in size and growth rates. Rupture rates were analysed by joint proportional hazards regression to incorporate the modelled AAA diameter as a time-varying covariate. Predictions of the risks of AAA exceeding 5.5 cm in diameter, and of rupture, within given time intervals were estimated and pooled across studies in a second stage using random-effects meta-analysis.
The influence of covariates (including demographics and medical and drug history) on aneurysm growth and rupture rates was investigated in each IPD surveillance data set. Growth rates were analysed using longitudinal random-effects modelling, and rupture rates were analysed by Cox proportional hazards regression with adjustment for aneurysm diameter. The effects of covariates were combined across studies in a second stage using random-effects meta-analysis.
The specific data extracted from the RESCAN project are detailed in Chapter 7. For AAA diameters outside that included in the RESCAN project, information on AAA growth and risk of rupture was taken from other previously published studies. 47–50
Chapter 4 Patient and public involvement
Introduction
The NIHR HTA programme encourages the involvement of service users in research. 51 A PPI group was established to ensure the aims of this research met patient needs, to monitor and direct progress and to review outcomes from the project. This chapter reviews the contributions our PPI group made to the project.
The group and setting
The group was established at the inception of the NIHR HTA project and contributed to the design of this research and to our NIHR-HTA grant application. It included 12 AAA patients and three patient relatives supported by appropriate medical staff including the AAA surveillance nurse. It met quarterly at the University Hospital of South Manchester Education and Research Centre.
The membership consists of a consultant vascular surgeon and anaesthetist, two vascular research fellows, a vascular specialist nurse, a research assistant, five patients who have undergone EVAR, three who have undergone open repair (in one case for a ruptured aneurysm), four patients under surveillance who will possibly need repair in the future and three family members of patients (Appendix 4). This group met quarterly during the NIHR-HTA project with one of its cochairmen attending the research project’s management committee.
The group was initiated by Professor McCollum using the University Hospital of South Manchester AAA surveillance nurse (Helen O’Donnell), to identify interested patients from local AAA preoperative and follow-up clinics. A member of the research team contacted the patients by letter and then by phone to give background information and arrange the first meeting.
Group impact
The involvement of patients in research has been immensely beneficial to the project from its inception. The main purpose of the group was to harness the unique patient perspective of the NHS AAA care pathway to advise on the form taken and content produced by the risk prediction algorithm. Other contributions were review of patient information leaflets (Appendix 5), review of research progress reports given during meetings and feedback on the direction of the project, advice on future research agenda and contributions to the management committee by the attendance of the group’s chairman.
Important recommendations that the group made included changing the focus of our risk prediction algorithm to produce 5- and 10-year survival rather than median life expectancy, changing the way that the outputs from the algorithm will be communicated with patients, calculating the chance that an operation will be necessary in one’s lifetime, pursuing the possibility of presenting an operation window, developing questionnaires for patients in the surveillance programme, reviewing patient information sheets and advising pursuit of section 251 approval to avoid upset of bereaved relatives when gathering long-term follow-up data. The last recommendation was vital to the survival analysis in our project and an unforeseen necessary ethical application highlighted by the patient group. They have also encouraged further work to incorporate the prediction of complications following repair into the ARDA and to produce quality-of-life information (sexual health and mobility).
Chapter 5 Predicting perioperative mortality following elective abdominal aortic aneurysm repair
Background
The risk of short-term mortality following elective AAA repair is dependent on both patient and operative characteristics. The risk of in-hospital mortality following a surgical procedure is commonly estimated using a risk prediction model. A risk prediction model is a mathematical formula that utilises risk factor information to estimate the probability of a patient developing an outcome. Several risk prediction models have been developed and validated for predicting outcomes following AAA repair. A systematic review published in 2008 found that, out of the available risk predication models, the Glasgow Aneurysm Score (GAS) was the most useful model but none was entirely satisfactory. 52,53
Objective
The aim of the study was to develop and externally validate a suitable risk prediction model for short-term mortality following elective AAA repair. This is used as an input to the ARDA.
Development of a regional model: methods
Data from the VGNW programme on 2765 consecutive AAA repairs carried out between September 1999 and October 2009 were utilised. These data were selected because at the start of the project the VGNW database represented the most reliable large clinical registry data available for elective AAA repairs in the UK. Although including AAA repairs over a wide time period would introduce inevitable temporal effects, this was necessary to provide an adequate sample size for model development and validation.
All variables missing for more than 15% of subjects were excluded from analyses. Missing dichotomous risk factor data were assumed to represent absence of the risk factor and the sample median was substituted for continuous or categorical variables. This imputation approach was adopted for both the perioperative and survival modelling performed on clinical registry data in this project. Although multiple imputation was considered, an understanding of the data collection process identified that multiple imputation would be inappropriate, as the data were known to be missing not at random. Discussions with surgeons and administrators responsible for inputting data indicated that they were likely to leave a field blank if a risk factor was not present.
Patient characteristics for the regional model development cohort are shown in Table 2. The outcome for the model was 30-day mortality, defined as death within 30 days following elective AAA repair regardless of cause. Outcome data for patients who died in hospital within 30 days of AAA repair were collected by the VGNW programme; deaths occurring after discharge but within 30 days of AAA repair were captured using the National Strategic Tracing service.
| Characteristic | Patients, n (%) | 30-day mortality (%) | Odds ratio (95% CI) | p-value | |
|---|---|---|---|---|---|
| Age (years) | < 75 | 1313 (67.8) | 52 (4.0) | Reference | 0.001 |
| ≥ 75 | 623 (32.2) | 46 (7.4) | 1.93 (1.28 to 2.91) | ||
| Sex | Male | 1593 (82.3) | 68 (4.3) | Reference | < 0.001 |
| Female | 343 (17.7) | 30 (8.8) | 2.16 (1.38 to 3.37) | ||
| Ischaemic heart disease | No | 1175 (60.7) | 55 (4.7) | Reference | 0.336 |
| Yes | 761 (39.3) | 43 (5.7) | 1.22 (0.81 to 1.84) | ||
| History of myocardial infarction | No | 1531 (79.1) | 68 (4.4) | Reference | 0.015 |
| Yes | 405 (20.9) | 30 (7.4) | 1.73 (1.11 to 2.69) | ||
| Diabetes | No | 1764 (91.1) | 83 (4.7) | Reference | 0.023 |
| Yes | 172 (8.9) | 15 (8.7) | 1.92 (1.08 to 3.41) | ||
| Respiratory disease | No | 1390 (71.8) | 56 (4.0) | Reference | < 0.001 |
| Yes | 546 (28.2) | 42 (7.7) | 1.99 (1.32 to 3.01) | ||
| Obesity | No | 1818 (93.9) | 86 (4.7) | Reference | 0.009 |
| Yes | 118 (6.1) | 12 (10.2) | 2.28 (1.21 to 4.29) | ||
| Antiplatelet medication | No | 950 (49.1) | 29 (3.1) | Reference | < 0.001 |
| Yes | 986 (50.9) | 69 (7.0) | 2.39 (1.54 to 3.73) | ||
| Antianginal medication | No | 1640 (84.7) | 74 (4.5) | Reference | 0.009 |
| Yes | 296 (15.3) | 24 (8.1) | 1.86 (1.15 to 2.99) | ||
| Antihypertensive medication | No | 1005 (51.9) | 33 (3.3) | Reference | < 0.001 |
| Yes | 931 (48.1) | 65 (7.0) | 2.21 (1.44 to 3.39) | ||
| Statin medication | No | 1058 (54.6) | 51 (4.8) | Reference | 0.602 |
| Yes | 878 (45.4) | 47 (5.4) | 1.11 (0.74 to 1.67) | ||
| Creatinine (µmol/l) | ≤ 120 | 1557 (80.4) | 68 (4.4) | Reference | 0.005 |
| > 120 | 379 (19.6) | 30 (7.9) | 1.88 (1.21 to 2.94) | ||
| WCC (× 109/l) | ≤ 11 | 1816 (93.8) | 91 (5.0) | Reference | 0.674 |
| > 11 | 120 (6.2) | 7 (5.8) | 1.19 (0.54 to 2.62) | ||
| Urea (mmol/l) | ≤ 9 | 1680 (86.8) | 78 (4.6) | Reference | 0.031 |
| > 9 | 256 (13.2) | 20 (7.8) | 1.74 (1.05 to 2.89) | ||
| Haemoglobin (g/dl) | ≤ 13 | 563 (29.1) | 46 (8.2) | Reference | < 0.001 |
| > 13 | 1373 (70.9) | 52 (3.8) | 0.44 (0.29 to 0.67) | ||
| Systolic blood pressure (mmHg) | ≤ 140 | 1334 (68.9) | 57 (4.3) | Reference | 0.018 |
| > 140 | 602 (31.1) | 41 (6.8) | 1.64 (1.08 to 2.47) | ||
| Abnormal ECG | No | 1324 (68.4) | 62 (4.7) | Reference | 0.258 |
| Yes | 612 (31.6) | 36 (5.9) | 1.28 (0.84 to 1.95) | ||
| Symptomatic aneurysm | No | 1176 (60.7) | 49 (4.2) | Reference | 0.025 |
| Yes | 760 (39.3) | 49 (6.4) | 1.59 (1.06 to 2.38) | ||
| Maximum aneurysm diameter (cm) | ≤ 6 | 712 (36.8) | 38 (5.3) | Reference | 0.674 |
| > 6 | 1224 (63.2) | 60 (4.9) | 0.91 (0.60 to 1.39) | ||
| Level of aneurysm | Infrarenal | 1752 (90.5) | 84 (4.8) | Reference | 0.038 |
| Juxta/suprarenal | 184 (9.5) | 14 (7.6) | 1.88 (1.02 to 3.46) | ||
| Type of surgery | EVAR | 366 (18.9) | 6 (1.6) | Reference | < 0.001 |
| Open | 1570 (81.1) | 92 (5.9) | 3.72 (1.62 to 8.57) | ||
Standard statistical tests were used to calculate odds ratios and 95% confidence intervals (CIs). The data were split randomly, using a simple random sample method without replacement, into a development data set (n = 1936, 70.0%) and a validation data set (n = 829, 30.0%). A logistic regression analysis was undertaken on the development data set, using the forward stepwise technique, to develop a risk prediction model for 30-day mortality. 54 Candidate variables with p < 0.100 were entered into the model and retained if the p-value achieved was below 0.050.
Model performance in the development data set was evaluated by calculating the area under the receiver operating characteristic (ROC) curve55 and the Hosmer–Lemeshow goodness-of-fit statistic to assess the discrimination and calibration of the model respectively. An area under the ROC curve statistic of 0.5 suggests no discrimination and an area under the curve (AUC) of 1 indicates perfect discrimination. The relative contribution of each variable to the prediction of 30-day mortality was also calculated. To further assess the model’s calibration, the cohort was split into low-risk (bottom half of cohort), medium-risk (third quarter of cohort) and high-risk (fourth quarter) groups, based on their predicted probability of 30-day mortality.
The model performance was then tested on the validation data set. Observed and expected rates of 30-day mortality in the development and the validation data set were compared and the ROC curve and the Hosmer–Lemeshow goodness-of-fit statistic were calculated. All statistical analysis was performed with SAS for Windows® version 8.2 (SAS Institute Inc., Cary, NC, USA) and, for all analyses, p < 0.050 was considered significant.
The Vascular Governance North West risk prediction model for mortality following elective abdominal aortic aneurysm repair: results
Of the 1936 patients undergoing elective AAA repair in the development data set, 98 (5.1%) died within 30 days. EVAR was performed in 366 patients (18.9%) and open repair in 1570 (81.1%), with 30-day mortality rates of 1.6% and 5.9% respectively. Most procedures (n = 1752, 90.5%) were for infrarenal AAA. The majority of patients were men (82.3%) and the median age was 73 years (interquartile range 68–77 years). Increasing age, female sex, history of myocardial infarction (MI), diabetes, obesity, respiratory disease, symptomatic aneurysm, raised serum creatinine concentration, raised urea level, low haemoglobin level and preoperative systolic blood pressure exceeding 140 mmHg, preoperative antiplatelet, antianginal and antihypertensive medications along with the type of aneurysm and whether or not EVAR or open repair was performed were all associated with mortality on univariate analysis, as shown in Table 2. These variables were, therefore, included in the logistic regression analysis.
The risk prediction model developed included the following independent risk factors for 30-day mortality: increasing age, female sex, diabetes, raised serum creatinine level, respiratory disease, antiplatelet medication and open surgery (Table 3).
| Model | Coefficient | Odds ratio (95% CI) | p-value |
|---|---|---|---|
| Age (continuous in years) | 0.0486 | 1.05 (1.02 to 1.09) | 0.005 |
| Female sex | 0.7322 | 2.08 (1.31 to 3.31) | 0.002 |
| Diabetes | 0.6620 | 1.94 (1.07 to 3.51) | 0.029 |
| Creatinine (continuous in µmol/l)a | 0.0073 | 1.01 (1.00 to 1.01) | 0.006 |
| Respiratory disease | 0.4718 | 1.61 (1.05 to 2.46) | 0.031 |
| Antiplatelet medication | 0.7762 | 2.17 (1.38 to 3.43) | < 0.001 |
| Open surgery | 1.3130 | 3.72 (1.59 to 8.66) | 0.002 |
| Intercept | –9.3431 |
Vascular Governance North West model performance
The area under the ROC curve for the multivariable prediction model was 0.73 in the development data set. The Hosmer–Lemeshow goodness-of-fit statistic across groups of risk was not statistically significant (p = 0.118) demonstrating good model calibration (Figure 3). Low-, medium- and high-risk groups were created based on the predicted risk of 30-day mortality. Low-risk patients had a maximum risk of death within 30 days of 3.5%, medium-risk patients had a risk greater than 3.5% but no more than 6.5% and high-risk patients had a risk exceeding 6.5%. Of the 98 observed deaths, 59 (60.2%) occurred in the group predicted to be at high risk. After stratifying the patients into risk groups, the observed versus expected 30-day mortality rates were 2.4% versus 2.0% in low-risk patients (p = 0.523), 3.2% versus 4.8% in medium-risk patients (p = 0.214) and 12.1% versus 11.1% (p = 0.617) in high-risk patients, demonstrating that the model has good calibration in different risk groups.
FIGURE 3.
Observed and expected 30-day mortality compared for 10 groups of increasing risk in (a) the development data set (p = 0.118); and (b) the validation data set (p = 0.853). (Hosmer–Lemeshow goodness-of-fit test.)


In the validation data set, 50 patients (6.0%) died within 30 days of intervention. The AUC was 0.70 and the model was well calibrated with a non-significant Hosmer–Lemeshow test (p = 0.853), as demonstrated in Figure 3. The expected 30-day mortality rate in the validation data set was 5.1%, which did not differ significantly from the 6.0% observed 30-day mortality rate, giving an observed to expected (O : E) ratio of 1.18 (p = 0.391). Observed versus expected 30-day mortality rates were 3.2% versus 2.0% in low-risk patients (O : E ratio 1.60; p = 0.272), 6.1% versus 5.1% in the medium-risk group (O : E ratio 1.20; p = 0.671) and 11.1% versus 10.7% in high-risk patients (O : E ratio 1.04; p = 0.879), demonstrating good calibration in clinical subgroups.
The VGNW model incorporates the type of repair (open or EVAR) and six readily available preoperative patient characteristics. The model demonstrates acceptable discriminatory ability on split-data validation with no significant deviation from perfect fit and good calibration.
External validation of the Vascular Governance North West model using the National Vascular Database
External validation is the gold standard for risk prediction model assessment and is used to confirm that the model performs as expected in new but similar patients. 56 An external validation involves assessing a model’s calibration, discrimination and clinical validity in a cohort of patients that is different from the cohort used for model development in either location or time. 57 Before a model can be deemed clinically useful it is important that it is externally validated to ensure that there is no overfitting and that adequate discrimination and calibration are retained. Therefore, the VGNW model was validated using data from the NVD and its performance was compared with a number of other risk prediction models for AAA repair.
Data on all elective AAA repairs performed between 1 January 2008 and 31 December 2010 from the NVD were included. Records from hospitals in the North West region of England and Wales were excluded, so that there was no overlap with the VGNW model development data set. If these data were included, this might have resulted in an overoptimistic estimation of VGNW model performance. All variables with significant missing data were excluded from the analysis. For retained variables, imputation of missing data was performed as for development of the VGNW model. As 30-day mortality is not collected in the NVD, the primary outcome for the study was in-hospital mortality, defined as any death regardless of cause during the hospital admission for elective AAA repair.
In addition to the VGNW model, other models validated included the Medicare model, the Vascular Physiological and Operative Severity Score for enUmeration of Mortality (V-POSSUM) model, the Vascular Biochemistry and Haematology Outcome Model (VBHOM) and the GAS. 53 The equations used to calculate all of the validated models are included in Appendix 6.
As the NVD database was not designed to collect risk factor information necessary for calculation of all the models except the VBHOM, a number of risk factor assumptions were necessary. For the GAS, shock was assumed to be absent in all patients, as only elective cases were included. Myocardial disease included any history of ischaemic heart disease or congestive cardiac failure. Patients were defined as having cerebrovascular disease if they were taking antiplatelet medication (because cerebrovascular disease was not recorded in the NVD) and renal disease was defined as a serum creatinine level exceeding 160 µmol/l. For V-POSSUM, all patients with a history of congestive cardiac failure or ischaemic heart disease in the NVD were assigned a score of 2 for the cardiac component of the physiology score. Respiratory disease was not available in the NVD and was therefore assumed to be absent for all patients. All patients were assumed to have a Glasgow Coma Scale score of 15. For the Medicare model, chronic renal insufficiency was defined as a serum creatinine level exceeding 160 µmol/l, and end-stage renal disease was defined by the need for dialysis. Congestive heart failure included patients who also had any ischaemic heart disease, as these risk factors were not separated out in the NVD. Vascular disease was defined by the need to take antiplatelet medication. For the VGNW model, respiratory disease was assumed to be absent for all patients, as this was not recorded in the NVD.
The ROC curve was calculated to assess the discrimination of each model, with calibration measured by comparing the observed with the expected mortality for equally sized quintiles of ranked predicted risk and by performing a chi-squared test.
Model performance in the National Vascular Database
The validation cohort included 10,891 patients who underwent elective AAA repair. EVAR was performed in 5938 patients (54.5%) and open repair in 4953 (45.5%), with in-hospital mortality rates of 1.3% and 4.7% respectively (overall 2.9%). The patient characteristics of the cohort are shown in Table 4. The majority (67.3%) of NVD records were complete for all available and required variables, with only 11.8% of the records missing more than four of the variables required for the analysis. Both the VGNW (AUC 0.71, 95% CI 0.68 to 0.74) and Medicare models (AUC 0.71, 95% CI 0.69 to 0.74) demonstrated fair discrimination, as shown in Table 5. 54 The GAS, VBHOM and V-POSSUM all demonstrated lower discrimination with ROC curve values of 0.60 (95% CI 0.56 to 0.63), 0.61 (95% CI 0.58 to 0.64) and 0.62 (95% CI 0.59 to 0.65) respectively.
| Patient characteristic | Number of patients (n = 10,891) (%) |
|---|---|
| Age > 75 years | 4701 (43.2) |
| Age > 80 years | 2010 (18.5) |
| Women | 1388 (12.7) |
| Diabetes | 1209 (11.1) |
| Cardiac diseasea | 4368 (40.1) |
| Antiplatelet medication | 6725 (61.7) |
| Statin | 7021 (64.5) |
| Abnormal ECGb | 2974 (27.3) |
| Renal dialysis | 60 (0.6) |
| Current smoker | 1999 (18.4) |
| Haemoglobin (g/dl) | |
| 13.0–16.0 | 7203 (66.1) |
| 11.5–12.9 or 16.1–17.0 | 2529 (23.2) |
| < 11.5 or > 17.0 | 1159 (10.6) |
| WCC (× 109/l) | |
| 4.0–10.0 | 9505 (87.3) |
| 10.1–20.0 or 3.1–3.9 | 1328 (12.2) |
| < 3.0 or > 20.0 | 58 (0.5) |
| Urea (mmol/l) | |
| < 7.6 | 7897 (72.5) |
| 7.6–10.0 | 2003 (18.4) |
| > 10.0 | 991 (9.1) |
| Sodium (mmol/l) | |
| > 135 | 9733 (89.4) |
| 131–135 | 991 (9.1) |
| < 131 | 167 (1.5) |
| Potassium (mmol/l) | |
| 3.5–5.0 | 10,227 (93.9) |
| 3.2–3.4 or 5.1–5.3 | 454 (4.2) |
| < 3.2 or > 5.3 | 210 (1.9) |
| Creatinine (µmol/l) | |
| ≤ 120 | 8896 (81.7) |
| 121–160 | 1431 (13.1) |
| > 160 | 564 (5.2) |
| EVAR | 5938 (54.5) |
| Risk model | Area under ROC curve (95% CI) |
|---|---|
| GAS | 0.60 (0.56 to 0.63) |
| VBHOM | 0.61 (0.58 to 0.64) |
| V-POSSUM | 0.62 (0.59 to 0.65) |
| Medicare | 0.71 (0.69 to 0.74) |
| VGNW | 0.71 (0.68 to 0.74) |
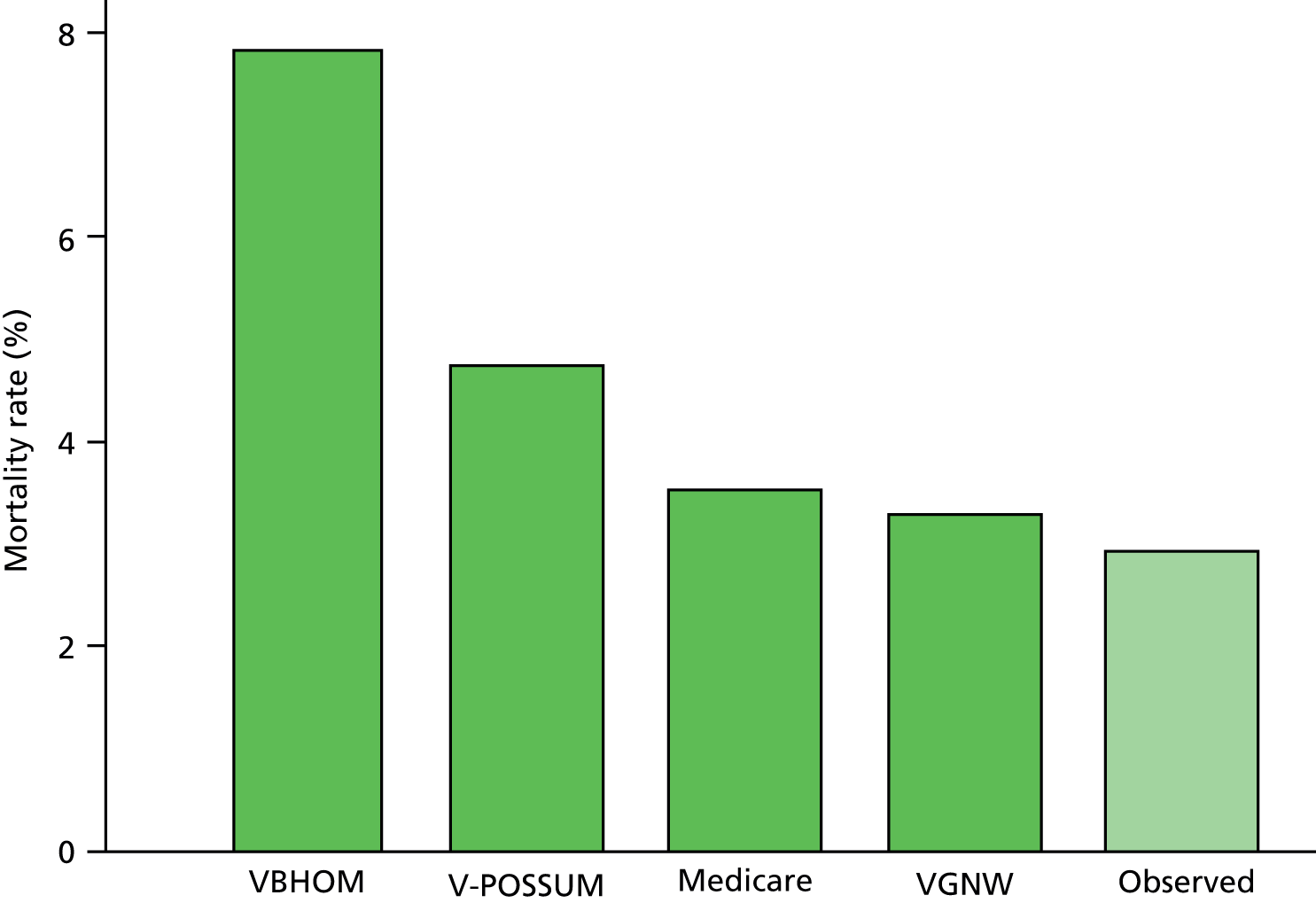
The VGNW model was the only logistic model that accurately predicted the overall mortality rate in the cohort (p = 0.066). The Medicare (p = 0.006), V-POSSUM (p < 0.001) and VBHOM (p < 0.001) all significantly overpredicted the overall mortality rate in the cohort, as shown in Figure 4.
FIGURE 4.
Observed and expected in-hospital mortality rates for the VBHOM, V-POSSUM, Medicare and VGNW model for elective AAA repair in the NVD. Dark green, expected; light green, observed.
As the VGNW and Medicare models were the only models to demonstrate acceptable discrimination, these models were selected to generate the quintiles for further assessment of calibration (Tables 6 and 7). The VGNW model demonstrated the best calibration for both data splits, accurately predicting mortality rates in four quintiles. The Medicare model accurately predicted risk in three quintiles for both splits. The V-POSSUM model predicted risk accurately in two quintiles when the data were split using the VGNW model and one quintile when they were split using the Medicare model. The VBHOM did not predict risk accurately in any quintile for either analysis. As the GAS is not a logistic model its calibration could not be assessed.
| Quintile | Number of patients | Predicted mortality (%) | Observed mortality (%) | |||
|---|---|---|---|---|---|---|
| VBHOM | V-POSSUM | Medicare | VGNW | |||
| First | 2179 | 6.2a | 3.6a | 1.2 | 0.7 | 1.2 |
| Second | 2175 | 7.3a | 4.3a | 2.0a | 1.4 | 1.0 |
| Third | 2180 | 8.3a | 4.8a | 3.0a | 2.3 | 2.0 |
| Fourth | 2178 | 8.0a | 5.0 | 4.2 | 3.7 | 3.9 |
| Fifth | 2179 | 9.2a | 6.1 | 7.4 | 8.5a | 6.4 |
| Quintile | Number of patients | Predicted mortality (%) | Observed mortality (%) | |||
|---|---|---|---|---|---|---|
| VBHOM | V-POSSUM | Medicare | VGNW | |||
| First | 2188 | 6.1a | 3.5a | 1.0 | 0.9 | 1.1 |
| Second | 2186 | 6.9a | 4.2a | 1.8a | 1.5 | 1.0 |
| Third | 2098 | 7.8a | 4.3a | 2.7 | 2.7 | 2.2 |
| Fourth | 2237 | 8.2a | 5.1a | 4.1a | 3.9a | 2.7 |
| Fifth | 2182 | 10.1a | 6.7 | 8.1 | 7.5 | 7.3 |
These results demonstrate that both the VGNW and Medicare models are potentially useful for risk prediction in elective AAA repair in the UK. The other three models assessed (V-POSSUM, VBHOM and GAS) performed poorly in comparison and are therefore not recommended for contemporary risk prediction in elective AAA repair in the UK.
A national risk prediction model for mortality following elective abdominal aortic aneurysm repair
Both the VGNW model and Medicare model demonstrated potential suitability for predicting mortality following elective AAA repair. The risk factors in both models were similar, suggesting clinical validity; however, both models only just demonstrated acceptable discrimination. In addition, the compatibility of the models with national vascular practice is potentially limited, as both models contained risk factors not collected by the NVD. Therefore, a decision was made by the research team to explore the development of a model using NVD data.
Prospectively collected data on all elective AAA repairs performed between 1 April 2008 and 31 March 2011 were extracted from the NVD for analysis. The data were cleaned by resolving transcriptional discrepancies and clinical conflicts, removing or transforming aberrant and extreme values and validating procedure type using available Office of Population Censuses and Surveys (OPCS) codes. Records in which the hospital identifier was missing were removed from the study; otherwise all other records were used for model development.
All NVD database variables with 15% or more missing data were excluded from the analysis. For the remaining variables, any missing patient factor was assumed to be absent for categorical variables or replaced with the median value for continuous variables and the mode for ordinal variables. The primary outcome for the study was in-hospital mortality. Continuous variables were dichotomised into abnormal and normal ranges, with the following measurements defined as abnormal: serum > 120 µmol/l; haemoglobin < 11 g/dl for women, < 13 g/dl for men; white cell count (WCC) < 3.0 × 109/l or > 11.0 × 109/l; serum urea > 7.5 mmol/l; serum sodium < 135 mmol/l or > 145 mmol/l; serum potassium < 3.5 mmol/l or > 5.5 mmol/l; systolic blood pressure < 90 mmHg or > 140 mmHg; and highest preoperative heart rate > 80 beats/minute. Cardiac disease included a history of ischaemic heart disease, heart failure or both.
A multiple logistic regression model was fitted including all variables deemed clinically relevant. Backwards model selection using the Akaike information criterion (AIC) was applied. 58 Age and AAA diameter were retained as continuous variables and the linearity assumption was checked using standard diagnostics. 54 Model performance was assessed using bootstrap methodology to sample repeatedly from the complete data set and refit the final multiple logistic regression model 40 times.
Model performance summary statistics were calculated at each stage and averaged over all bootstrapped samples. Model calibration was evaluated using the Hosmer–Lemeshow test (not based on bootstrapped data)54 and a calibration plot and by dividing the cohort into three groups based on their ranked predicted risk of in-hospital death with goodness of fit between the observed and expected outcomes evaluated using a chi-squared test on 1 degree of freedom. In addition, calibration was also assessed by fitting a logistic regression model between the predicted and observed outcomes, and model discrimination was evaluated using the AUC. 55 Bias associated with the AUC was calculated using bootstrapping,59 and DeLong’s method for calculating AUC variance was used to calculate the 95% CI for the AUC. 60
Model performance was also assessed separately for open AAA repair and EVAR subgroup with only within-data diagnostic statistics reported. A p-value < 0.05 was considered significant. All statistical analyses were carried out using R software version 2.14.2 (R Foundation for Statistical Computing, Vienna, Austria). Model selection was done using the MASS package (R Foundation for Statistical Computing, Vienna, Austria),61 and internal model validation was assessed using the rms package (R Foundation for Statistical Computing, Vienna, Austria). 62
The British Aneurysm Repair Score
In total, 11,423 records were included in the analysis for model development. The level of missing data in each of the variables included in the final analysis varied between 0% (operation type) and 14.6% (highest preoperative pulse). Overall, there were 6314 records (55.3%) without any missing risk factor data. A summary of patient characteristics is shown in Table 8. There were 312 in-hospital deaths after AAA repair, giving an in-hospital mortality rate of 2.7% (95% CI 2.4% to 3.0%).
| Characteristic | Frequency/mean | Percentage/SD | |
|---|---|---|---|
| Age | ≤ 75 years | 6450 | 56.5 |
| > 75 years | 4973 | 43.5 | |
| Continuous | 73.8 | 7.5 | |
| Sex | Male | 9926 | 86.9 |
| Female | 1497 | 13.1 | |
| Diabetes | No | 10,052 | 88.0 |
| Yes | 1371 | 12.0 | |
| Antiplatelet agent | No | 3896 | 34.1 |
| Yes | 7527 | 65.9 | |
| Cardiac disease | No | 6682 | 58.5 |
| Yes | 4741 | 41.5 | |
| Current smoker | No | 9222 | 80.7 |
| Yes | 2201 | 19.3 | |
| Abnormal ECG | No | 8181 | 71.6 |
| Yes | 3242 | 28.4 | |
| Beta blocker | No | 7888 | 69.1 |
| Yes | 3535 | 30.9 | |
| Statin | No | 3519 | 30.8 |
| Yes | 7904 | 69.2 | |
| Systolic BP (mmHg) | 90–140 | 8230 | 72.0 |
| < 90 or > 140 | 3193 | 28.0 | |
| Continuous | 131.5 | 20.0 | |
| Pulse (bpm) | ≤ 80 | 8727 | 76.4 |
| > 80 | 2696 | 23.6 | |
| Continuous | 74.5 | 12.6 | |
| Haemoglobin | ≥ 11 (female) or ≥ 13 (male) | 8729 | 76.4 |
| < 11 (female) or < 13 (male) | 2694 | 23.6 | |
| Continuous | 13.5 | 1.6 | |
| Previous aortic surgery/stent | No | 11,089 | 97.1 |
| Yes | 334 | 2.9 | |
| WCC (× 109) | 3–11 | 10,618 | 93.0 |
| < 3 or > 11 | 805 | 7.0 | |
| Continuous | 8 | 3.5 | |
| Urea (mg/dl) | ≤ 7.5 | 8099 | 70.9 |
| > 7.5 | 3324 | 29.1 | |
| Continuous | 7.2 | 4.7 | |
| Serum creatinine (µmol/l) | ≤ 120 | 9281 | 81.2 |
| > 120 | 2142 | 18.8 | |
| Continuous | 103.6 | 43.3 | |
| Sodium (mmol/l) | 135–145 | 10,410 | 91.1 |
| < 135 or > 145 | 1013 | 8.9 | |
| Continuous | 139.6 | 3.2 | |
| Potassium (mmol/l) | 3.5–5.5 | 11,130 | 97.4 |
| < 3.5 or > 5.5 | 293 | 2.6 | |
| Continuous | 4.3 | 0.4 | |
| AAA diameter (cm) | > 6.5 | 7876 | 68.9 |
| ≤ 6.5 | 3547 | 31.1 | |
| Continuous | 6.3 | 1.1 | |
| ASA grade | 1 | 375 | 3.3 |
| 2 | 3857 | 33.8 | |
| 3 | 6788 | 59.9 | |
| 4 | 403 | 3.5 | |
| Repair type | EVAR | 6483 | 56.8 |
| Open | 4940 | 43.2 | |
The final risk prediction model with estimated model coefficients, standard errors, Wald z-values, corresponding p-values, approximate 95% CI and model equation is shown in Table 9. Open AAA repair, age (continuous), female sex, cardiac disease, American Society of Anesthesiologists (ASA) grade and previous aortic surgery or stent were all included. Preoperative investigations included were raised serum creatinine concentration, abnormal WCC, abnormal sodium level and abnormal electrocardiogram (ECG). AAA diameter was also included in the model as a continuous variable.
| Model | Coefficient | Odds ratio (95% CI) | p-value |
|---|---|---|---|
| Open AAA repair | 1.54192 | 4.67 (3.6 to 6.13) | < 0.001 |
| Age (years) | 0.05396 | 1.06 (1.04 to 1.07) | < 0.001 |
| Female | 0.72735 | 2.07 (1.56 to 2.72) | < 0.001 |
| Creatinine > 120 µmol/l | 0.59902 | 1.82 (1.40 to 2.35) | < 0.001 |
| Cardiac disease | 0.34204 | 1.41 (1.10 to 1.80) | 0.006 |
| Abnormal ECG | 0.32107 | 1.38 (1.07 to 1.77) | 0.011 |
| Previous aortic surgery or stent | 0.84174 | 2.32 (1.33 to 3.80) | 0.002 |
| Abnormal WCC | 0.36911 | 1.45 (0.95 to 2.13) | 0.072 |
| Abnormal sodium | 0.31338 | 1.37 (0.96 to 1.91) | 0.076 |
| AAA diameter (cm) | 0.13677 | 1.15 (1.04 to 1.25) | 0.003 |
| ASA grade | |||
| Grade 2 | 0.25229 | 1.29 (0.56 to 3.72) | 0.593 |
| Grade 3 | 0.74919 | 2.12 (0.95 to 6.02) | 0.104 |
| Grade 4 | 1.66830 | 5.3 (2.19 to 15.85) | < 0.001 |
| Intercept | –10.71810 | ||
The Hosmer–Lemeshow chi-squared test did not provide sufficient evidence to reject any assumption of good calibration (χ2 = 2.477, p = 0.963). For the calibration plot displayed in Figure 5, the points represent the mean predicted and observed mortality proportion for deciles of predicted probabilities, and error bars represent 95% CIs for the observed mortality. A locally weighted scatterplot smoothing curve (apparent) indicating the general predictive trend, a bias-corrected calibration curve and the line of equality (perfect calibration) are also shown. The bias-corrected calibration curve started to deviate noticeably from the optimal calibration line only for predictions greater than 15%. The bootstrapped intercept and slope of the logistic regression model fitted to the transformed prediction values; observed outcomes were −0.100 and 0.966 respectively, suggesting a minor degree of overfitting.
FIGURE 5.
Calibration plot comparing observed and predicted in-hospital mortality, which demonstrates good calibration for the British Aneurysm Repair score.

For the risk group assessment, patients were classified as low risk if their predicted mortality was ≤ 1.5% (5712 patients), medium risk if their predicted mortality was between 1.5% and 3.3% (2856 patients) and high risk if their predicted mortality was greater than 3.3% (2855 patients) (Table 10). After risk stratification, the observed versus expected in-hospital mortality rates were 0.84% versus 0.83% in low-risk patients (p = 0.970), 2.2% versus 2.3% in the medium-risk group (p = 0.821) and 7.0% versus 6.9% (p = 0.938) in the high-risk group.
| Risk group | Total records | Open records | EVAR records | BAR range | Observed mortality | Predicted mortality | p-valuea |
|---|---|---|---|---|---|---|---|
| Low | 5712 | 918 | 4794 | < 1.5% | 0.84 | 0.83 | 0.970 |
| Medium | 2855 | 1677 | 1178 | 1.5% ≥ BAR ≤ 3.3% | 2.2 | 2.3 | 0.821 |
| High | 2856 | 2443 | 413 | > 3.3% | 7.0 | 6.9 | 0.938 |
The AUC applied to the data set was 0.781 (95% CI 0.756 to 0.806), which represents good discrimination. Bias-corrected AUC based on the bootstrap method was 0.774; this was 0.007 smaller than the discriminatory ability in the complete data set.
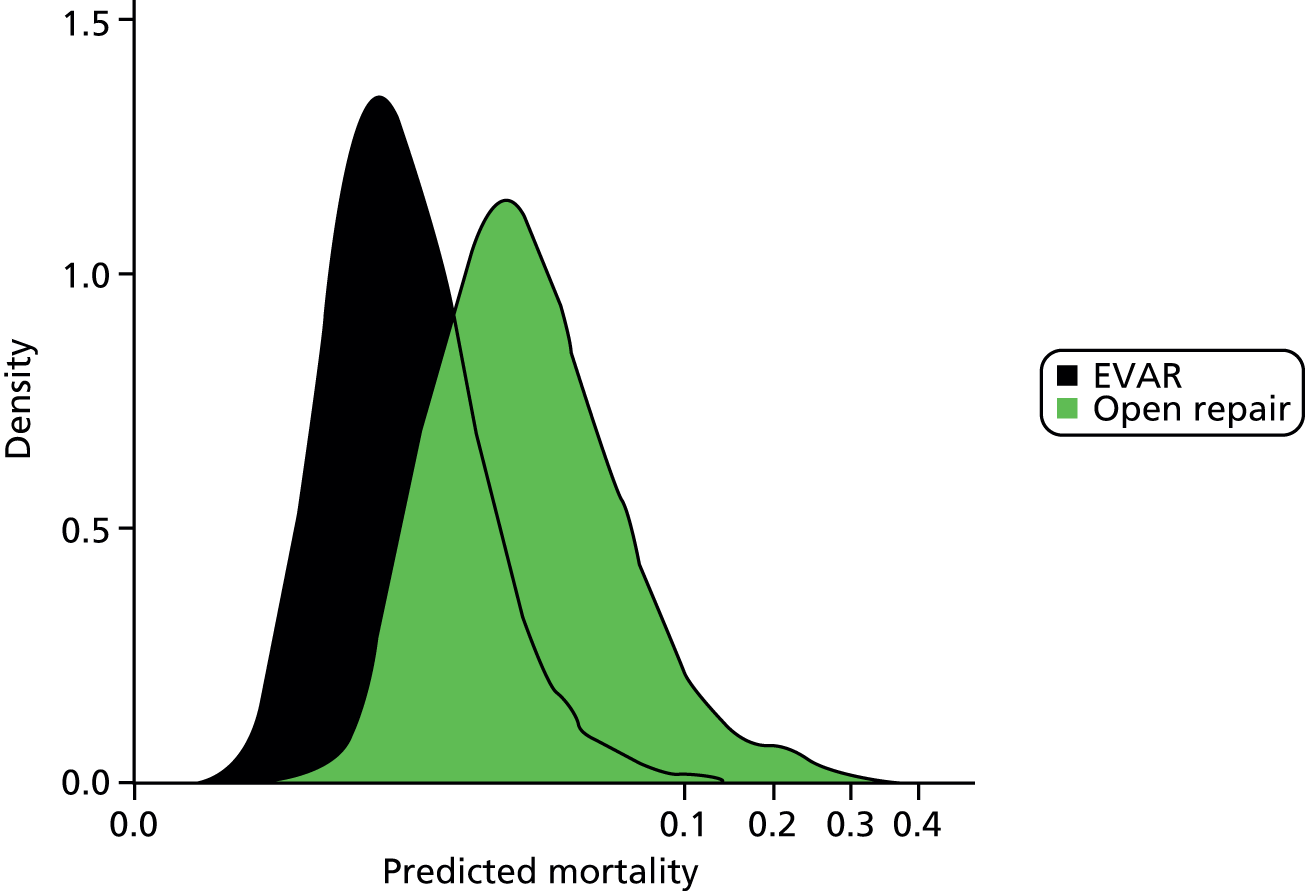
The overall cohort included 4940 open AAA repairs (43.2%) and 6483 EVARs (56.8%). There were 230 in-hospital deaths following open AAA repair (4.7%; 95% CI 4.1% to 5.3%) and 82 deaths following EVAR (1.3%; 95% CI 1.0% to 1.6%). The distributions of the British Aneurysm Repair (BAR) score-predicted mortality risks for open AAA repair and EVAR are shown as density plots in Figure 6. Distributions of predicted risks for open AAA repair and EVAR were different, but there was substantial overlap between the subgroups. The model calibration in each group was good, as assessed using the Hosmer–Lemeshow test (open AAA repair: p = 0.971, χ2 = 2.293; EVAR: p = 0.321, χ2 = 9.256). The discrimination in the open AAA repair group was 0.723 (95% CI 0.690 to 0.757) and that in the EVAR group was 0.749 (95% CI 0.698 to 0.800).
FIGURE 6.
British Aneurysm Repair score-predicted mortality density plots for open AAA repair and EVAR subgroups. The horizontal axis has been transformed for better visualisation.
The BAR score is made up of 11 preoperative risk factors that are collected easily as part of routine clinical practice. The model demonstrates good calibration and discrimination for all patients undergoing elective AAA repair. The model also demonstrated good performance in open AAA repair and EVAR subgroups. External validation of model performance is required before it can be recommended above other models for the prediction of perioperative mortality.
External validation of the British Aneurysm Repair score
To validate the BAR score externally, data were analysed for consecutive elective AAA repairs performed between April 2011 and March 2013 in the VGNW programme. This time period was selected to ensure that no data used for development of either the VGNW model or BAR score were included in the data set.
The data were cleaned by removing duplicate records, correcting transcriptional discrepancies and resolving any clinical or temporal conflicts. Missing data were imputed with the sample median for continuous or ordinal variables and the mode for dichotomous variables. The primary outcome measure used was in-hospital mortality. In addition to the BAR score, the VGNW model and the Medicare model were also validated. Model performance was assessed using measures of calibration and discrimination in the overall cohort and separately in both procedural and sex subgroups.
Discrimination was evaluated by determining the AUC, with AUC variance used for the calculation of AUC 95% CIs. In the overall cohort and procedural subgroups, model calibration has been summarised by calculating the O : E ratio and performing a goodness-of-fit chi-squared test on 1 degree of freedom. Model calibration was further assessed in the overall cohort by dividing the cohort into low-risk (bottom 50%), medium-risk (middle 25%) and high-risk (top 25%) approximate groups based on the model’s predicted mortality. Calibration plots for each model based on these groups were produced showing the mean predicted probability of outcome against the observed proportion of outcomes. Approximate 95% CIs for the observed mortality proportions are shown as error bars. The calibration intercepts and slope parameters were also calculated for each model in the overall cohort. All statistical analyses were performed using R version 3.0.2 (R Foundation for Statistical Computing, Vienna, Austria).
Data were available on 1124 elective AAA repairs. The mean age of the population was 74.4 years [standard deviation (SD) 7.7 years] and 193 (17.2%) of patients were female. The majority of patients (n = 759, 67.5%) underwent EVAR and most patients (n = 1037, 92.3%) were asymptomatic. Additional patient characteristic information for this cohort is shown in Table 11. There were 32 in-hospital deaths in the cohort, giving an in-hospital mortality of 2.8%. In this cohort of patients, no deaths occurred following discharge but within 30 days of the procedure.
| Risk factor | Frequency (%) | Missing data (%) |
|---|---|---|
| Age (years)a | 74.4 (7.7) | 0.2 |
| Female | 193 (17.2) | 0.0 |
| AAA diameter (cm)a | 6.3 (1.2) | 6.0 |
| Previous aortic surgery/stent | 67 (6.0) | 1.3 |
| AAA symptoms | 87 (7.7) | 6.1 |
| Ischaemic heart disease | 357 (31.8) | 8.5 |
| Previous MI | 163 (14.5) | 8.5 |
| Cardiac failure | 27 (2.4) | 9.2 |
| Respiratory disease | 199 (17.7) | 14.5 |
| Diabetes | 162 (14.4) | 3.2 |
| Antiplatelet medication | 716 (63.7) | 0.5 |
| Antihypertensive medication | 371 (33.0) | 0.5 |
| Statin therapy | 778 (69.2) | 0.4 |
| Smoking status | – | 12.2 |
| Ex-smoker | 298 (26.5) | – |
| Current smoker | 246 (21.9) | – |
| Abnormal ECG | 359 (31.9) | 5.7 |
| Abnormal sodium | 105 (9.3) | 11.0 |
| Abnormal potassium | 36 (3.2) | 10.4 |
| Abnormal urea | 308 (27.4) | 10.4 |
| Creatinine > 120 µmol/l | 186 (16.5) | 10.1 |
| Creatinine > 200 µmol/l | 21 (1.9) | 10.1 |
| Abnormal WCC | 82 (7.3) | 9.0 |
| Abnormal haemoglobin | 296 (26.3) | 9.0 |
| ASA grade | – | 11.4 |
| 1 | 56 (5.0) | – |
| 2 | 434 (38.6) | – |
| 3 | 604 (53.7) | – |
| 4 | 30 (2.7) | – |
| Open repair | 365 (32.5) | 0.0 |
The BAR score-predicted mortality was 2.4%, giving an O : E ratio of 1.2 (p = 0.509). The other validated models also demonstrated good overall calibration (VGNW-predicted mortality 3.2%, O : E ratio 0.9; p = 0.622; Medicare-predicted mortality 2.8%, O : E ratio 1.0; p = 0.904). The calibration plots for the three models are shown in Figure 7. The calibration intercept and slope also demonstrated good calibration for all three models, with each unreliability statistic being non-significant (Medicare p = 0.332, VGNW p = 0.756, BAR p = 0.581).
FIGURE 7.
Calibration plots for low-, medium- and high-risk groups for the BAR, Medicare and VGNW risk models. The black dashed line is the line of equality that represents perfect calibration. Vertical lines represent 95% binomial CIs of the observed mortality proportion.

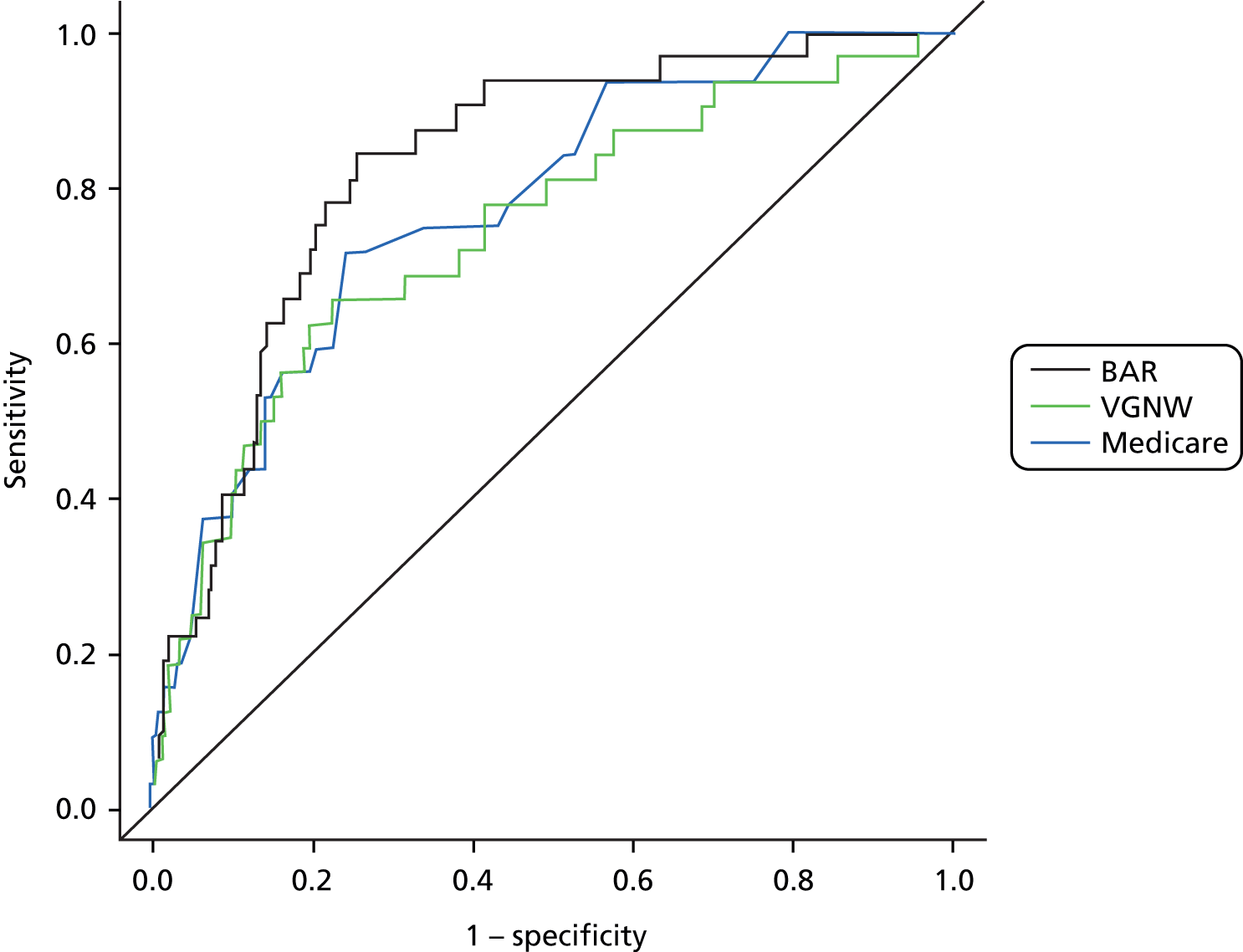
The BAR score demonstrated excellent discrimination in the overall cohort, with an AUC of 0.83 (95% CI 0.76 to 0.89). The discriminative ability of the Medicare and VGNW models was acceptable, with AUCs of 0.78 (95% CI 0.70 to 0.86) and 0.75 (95% CI 0.65 to 0.84) respectively. The ROC curves for the models in the overall cohort are shown in Figure 8.
FIGURE 8.
Receiver operating characteristic curves for the BAR, Medicare and VGNW risk models in the overall cohort. The diagonal line represents the line of equality.
To further check the clinical validity of the modes, performance was assessed in separate procedural and sex subgroups. The in-hospital mortality rates for open AAA repair and EVAR were 6.8% and 0.9% respectively. The predicted mortality in the open AAA repair group was 4.4% (O : E ratio 1.5; p = 0.148), 5.4% (O : E ratio 1.3; p = 0.442) and 4.9% (O : E ratio 1.4; p = 0.271) for the Medicare, VGNW and BAR scores respectively. In the EVAR group the predicted mortality was 2.0% (O : E ratio 0.5; p = 0.086), 2.1% (O : E ratio 0.4; p = 0.059) and 1.2% (O : E ratio 0.8; p = 0.615) for the Medicare, VGNW and BAR scores respectively. In the open AAA repair subgroup, again, only the BAR score demonstrated acceptable discrimination, with an AUC of 0.70 (95% CI 0.61 to 0.78). Both the Medicare and VGNW models demonstrated unacceptable discrimination, with AUCs of 0.68 (95% CI 0.58 to 0.78) and 0.64 (95% CI 0.53 to 0.75). In the EVAR subgroup, only the BAR score demonstrated acceptable discrimination, with an AUC of 0.75 (95% CI 0.55 to 0.95). Both the Medicare and VGNW models demonstrated unacceptable discrimination, with AUCs of 0.66 (95% CI 0.47 to 0.85) and 0.56 (95% CI 0.31 to 0.81) respectively.
The in-hospital mortality for men was 2.8%, and for women it was 3.1%. The predicted mortality for men was 2.4% (O : E ratio 0.9; p = 0.559), 2.6% (O : E ratio 0.9; p = 0.774) and 1.9% (O : E ratio 0.7%; p = 0.222) for the Medicare, VGNW and BAR scores respectively. For women the predicted mortality was 4.5% (O : E ratio 1.5; p = 0.429), 6.2% (O : E ratio 2.0; p = 0.148) and 4.8% (O : E ratio 1.5; p = 0.429) for the Medicare, VGNW and BAR scores respectively. For men the BAR score demonstrated excellent discriminatory ability, with an AUC of 0.85 (95% CI 0.78 to 0.92). Both the Medicare and VGNW models demonstrated acceptable discrimination, with AUCs of 0.78 (95% CI 0.69 to 0.86) and 0.76 (95% CI 0.65 to 0.86) respectively. For women the Medicare model demonstrated excellent discriminatory ability, with an AUC of 0.88 (95% CI 0.77 to 0.99). The BAR score and VGNW model both demonstrated acceptable discrimination, with AUCs of 0.79 (95% CI 0.67 to 0.91) and 0.76 (95% CI 0.55 to 0.98) respectively.
Summary
Two models (one regional and one national) have been developed for the prediction of perioperative mortality following elective AAA repair. Both models have demonstrated satisfactory performance on external validation. A number of current models have been found to be inadequate for contemporary elective AAA repair. As the BAR score is based on national UK data, demonstrated excellent discriminatory ability overall and retained discriminatory ability in procedural subgroups, this model has been chosen to estimate the risk of in-hospital mortality for the overall algorithm.
Chapter 6 Predicting survival following elective abdominal aortic aneurysm repair
Background
Historically, surgeons have emphasised the in-hospital or 30-day mortality rate after elective AAA repair, and there is a considerable amount of literature published on the topic. 63–66 As the incidence of AAA repair increases with age, with most patients in their eighth decade, often with significant comorbidity,28 understanding long-term survival is increasingly important. As most patients with AAA are asymptomatic, the principal indication of repair is to prevent rupture and increase survival.
Objective
To identify preoperative risk factors that predict long-term survival following elective AAA repair.
Modelling survival following elective abdominal aortic aneurysm repair: methods
Data from the VGNW programme for all patients who underwent elective AAA repair from January 2000 to April 2013 were included in this analysis. Over this study period there were 87 contributing surgeons across 24 hospitals. Emergency repairs for AAA rupture or repairs of thoracoabdominal aneurysms were excluded. The demographic batch service was used to determine mortality status for all patients up to and including 31 May 2013.
The data were cleaned by first resolving transcriptional discrepancies and clinical conflicts. Aberrant and extreme values were removed or transformed if the cause was inconsistent measurement units. Database variables with significant missing data (15%) were excluded from the analysis. For the remaining variables, any missing patient factor was imputed to the median value for continuous variables and assumed to be absent for categorical variables. The following preoperative measurements were defined as abnormal: serum creatinine concentration > 120 µmol/l; haemoglobin level < 11 g/dl for women and < 13 g/dl for men; WCC < 3.0 × 109/l or > 11.0 × 109/l; serum urea concentration > 7.5 mmol/l; serum sodium level < 135 mmol/l or > 145 mmol/l; potassium level < 3.5 mmol/l or > 5.5 mmol/l. Ischaemic heart disease included a history of previous MI, angina or both. All analyses and cleaning were performed using R version 3.0.1 (R Foundation for Statistical Computing, Vienna, Austria).
Survival analyses were performed using the Kaplan–Meier method, and differences in survival were compared using the log-rank test. 67,68 Age and AAA diameter were retained as continuous variables as they did not violate the linearity assumption (checked using standard diagnostics). 54 Individual Cox proportional hazards models were used for univariate analysis of preoperative variables. Variables of clinical significance and those with a p-value < 0.2 by univariate analysis were included in a multivariate Cox proportional hazards model to identify significant preoperative prognostic indicators of long-term survival. Backward stepwise selection using AIC was used to optimise this model. Scaled Schoenfield residuals were analysed to ensure the proportional hazards assumptions were not violated for variables associated with long-term survival. 69,70
Modelling survival following elective abdominal aortic aneurysm repair: results
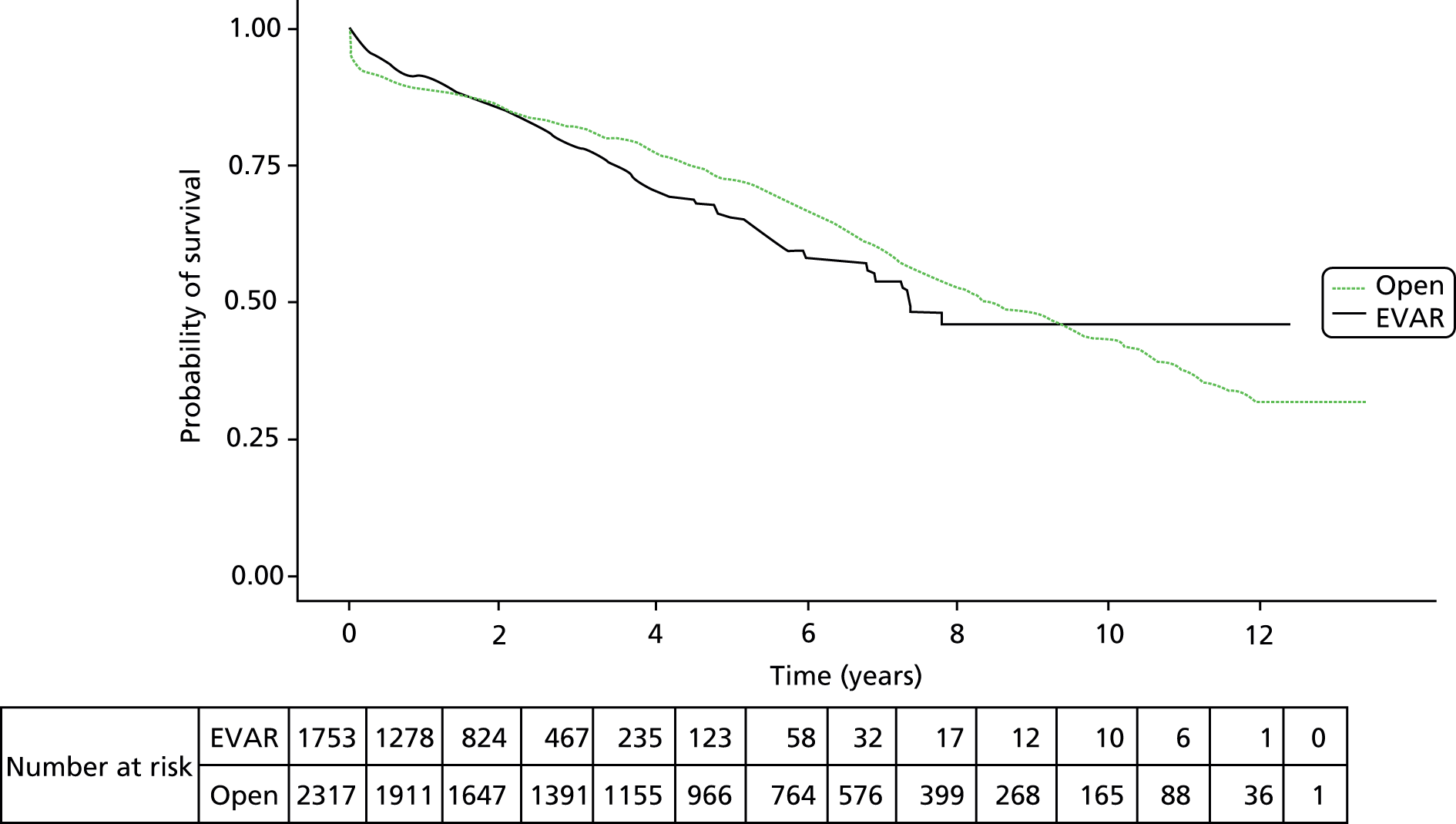
In the 13-year period, 4070 patients underwent AAA repair in the North West region. Of these, 2317 (57%) were by open surgical repair and 1753 (43%) were by EVAR. The mean age was 73.5 years and the majority of patients, 3398 (84%), were men. Patient characteristics are shown in Table 12. Overall cohort survival was 70.2% at 5 years and 41% at 10 years, with a median survival of 8.1 years (Figure 9). The in-hospital mortality was 5.2% overall, which improved over the study period to a mean of 3.0% during the last 5 years (2009–13). For those patients that survived the perioperative period following open surgical repair or EVAR, the apparent early benefit of EVAR (1-year survival of 88.3% and 91.2% respectively; Figure 10) was lost by year 2 of follow-up and at 5 years, 71.3% of patients following open repair were alive compared with 65.4% following EVAR. Table 12 shows that the main reason for this improved survival following open surgery may be the younger age and lower comorbidities in patients selected for open surgery by the surgeon.
| Patient characteristic | All patients (n = 4070) | Open repair (n = 2317) | EVAR (n = 1753) | p-valuea |
|---|---|---|---|---|
| Mean (SD) age (years) | 73.5 (7.3) | 72.1 (7.1) | 75.4 (7.1) | < 0.001 |
| Female (%) | 16.5 | 19.5 | 12.6 | < 0.001 |
| Ischaemic heart disease (%) | 41.0 | 35.2 | 49.2 | < 0.001 |
| Diabetes (%) | 12.3 | 10.8 | 14.5 | < 0.001 |
| Previous aortic surgery/stent (%) | 5.5 | 3.4 | 8.9 | < 0.001 |
| Antiplatelet medication (%) | 56.4 | 53.5 | 60.2 | < 0.001 |
| Statin therapy (%) | 56.1 | 50.6 | 63.4 | < 0.001 |
| Antihypertensive medication (%) | 40.3 | 44.0 | 35.3 | < 0.001 |
| Abnormal ECG (%) | 31.9 | 29.0 | 36.2 | < 0.001 |
| WCC (× 109/l), < 3 or > 11 | 6.0 | 6.5 | 5.4 | 0.2 |
| Haemoglobin (g/dl), < 11 (female) or < 13 (male) | 24.3 | 20.9 | 28.8 | < 0.001 |
| Sodium (mmol/l), < 135 or > 145 | 10.3 | 10.4 | 10.2 | 0.9 |
| Potassium (mmol/l), < 3.5 or > 5.5 | 3.5 | 3.7 | 3.2 | 0.48 |
| Serum creatinine (µmol/l), > 120 | 21.4 | 22.9 | 20.1 | 0.05 |
| Urea (mg/dl), > 7.5 | 30.8 | 30.0 | 31.8 | 0.26 |
| Aneurysm diameter (cm), (SD) | 6.5 (1.2) | 6.6 (1.3) | 6.3 (1.1) | < 0.001 |
| Aneurysm level, infrarenal | 92.2 | 89.2 | 96.3 | – |
| Aneurysm level, juxta/suprarenal | 7.8 | 10.8 | 3.7 | < 0.001 |
| Symptomatic aneurysm | 24.7 | 34.1 | 11.8 | < 0.001 |
| Aneurysm type, standard | 94.5 | 91.2 | 99.1 | – |
| Aneurysm type, inflammatory | 5.5 | 8.8 | 0.9 | < 0.001 |
FIGURE 9.
Overall survival following AAA repair of the cohort from day of operation using Kaplan–Meier.
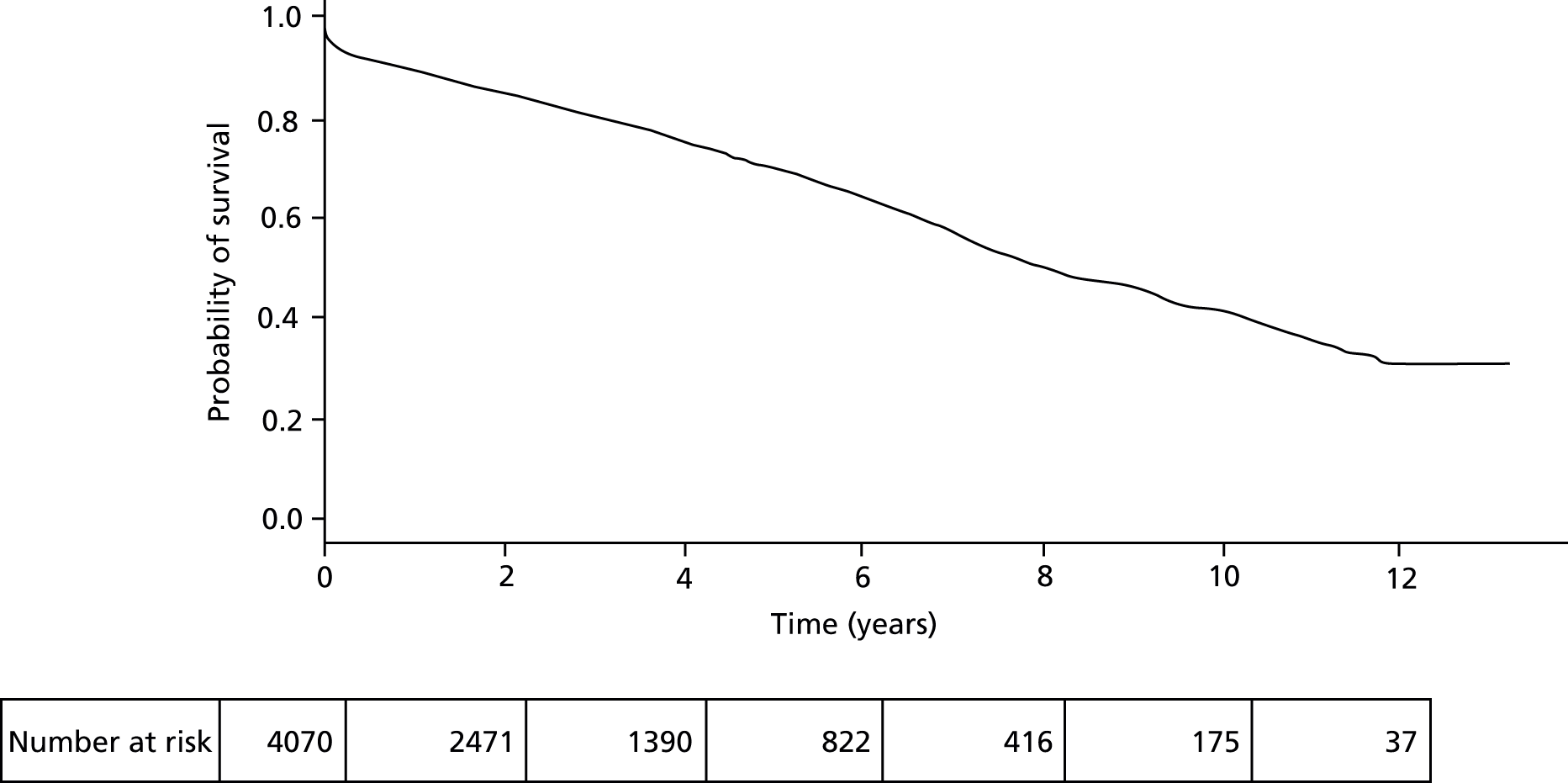
FIGURE 10.
Overall survival in patients undergoing open repair or EVAR from date of operation using Kaplan–Meier. No significant survival advantage was noted between the groups (p = 0.441).
On univariate analysis, increasing patient age, female sex and ischaemic heart disease were all significantly associated with reduced survival. Preoperative investigations associated with reduced survival included abnormal ECG, raised serum concentrations of creatinine and urea, an abnormal serum sodium and anaemia. Larger AAA diameter was also a risk factor for poor survival following repair. Preoperative statin therapy was associated with improved survival long term.
Multivariate Cox proportional hazards model of prognostic factors for overall survival following AAA repair are shown in Table 13. This model was stratified on repair type because of the violation of the proportional hazards assumption demonstrated in Figure 10. The patient characteristics significantly associated with reduced survival included increasing age [hazard ratio (HR) 1.05, 95% CI 1.04 to 1.06], female sex (HR 1.32, 95% CI 1.14 to 1.53) and ischaemic heart disease (HR 1.16, 95% CI 1.02 to 1.32). Preoperative statin therapy was associated with improved survival (HR 0.76, 95% CI 0.67 to 0.87). Antiplatelet therapy and diabetes, although included in the model, were not statistically significant predictors of survival (p = 0.11 and p = 0.09 respectively).
| Patient characteristic | HR (95% CI) | p-value |
|---|---|---|
| Female sex | 1.32 (1.14 to 1.53) | < 0.001 |
| Age (years) | 1.05 (1.04 to 1.06) | < 0.001 |
| Ischaemic heart disease | 1.16 (1.02 to 1.32) | 0.03 |
| Diabetes | 1.17 (0.97 to 1.41) | 0.09 |
| Antiplatelet use | 0.90 (0.79 to 1.03) | 0.11 |
| Statin use | 0.76 (0.67 to 0.87) | < 0.001 |
| Abnormal ECG | 1.19 (1.05 to 1.36) | < 0.001 |
| Abnormal sodium | 1.40 (1.17 to 1.67) | < 0.001 |
| Serum creatinine > 120 µmol/l | 1.28 (1.12 to 1.47) | < 0.001 |
| Anaemia | 1.30 (1.15 to 1.48) | < 0.001 |
As a sensitivity analysis, multivariate Cox proportional hazard models were prepared on open repair and EVAR patient cohorts separately. These models are shown in Tables 14 and 15. Both models include female sex, age, ischaemic heart disease, diabetes, serum creatinine > 120 µmol/l and anaemia. Statin use and abnormal sodium are included in the open repair model while inflammatory aneurysm, antiplatelet use and antihypertensive use are included in the EVAR model. All significant patient characteristics from the separate models are included in the combined model apart from inflammatory aneurysm type, which occurred in very low frequency (0.9% of patients) in the EVAR patient cohort.
| Patient characteristic | HR (95% CI) | p-value |
|---|---|---|
| Female sex | 1.28 (1.08 to 1.52) | 0.004 |
| Age (years) | 1.05 (1.04 to 1.07) | < 0.001 |
| Ischaemic heart disease | 1.15 (0.99 to 1.34) | 0.062 |
| Diabetes | 1.23 (0.98 to 1.54) | 0.069 |
| Statin use | 0.75 (0.65 to 0.87) | < 0.001 |
| Abnormal sodium | 1.51 (1.22 to 1.86) | < 0.001 |
| Serum creatinine > 120 µmol/l | 1.23 (1.05 to 1.45) | 0.010 |
| Anaemia | 1.21 (1.03 to 1.42) | 0.021 |
| Patient characteristic | HR (95% CI) | p-value |
|---|---|---|
| Female sex | 1.48 (1.08 to 2.02) | 0.014 |
| Age (years) | 1.05 (1.03 to 1.07) | < 0.001 |
| Ischaemic heart disease | 1.29 (1.03 to 1.61) | 0.027 |
| Diabetes | 1.01 (1.00 to 1.02) | 0.015 |
| Inflammatory aneurysm | 2.58 (1.13 to 5.86) | 0.024 |
| Antiplatelet use | 0.71 (0.57 to 0.88) | 0.002 |
| Antihypertensive use | 0.79 (0.62 to 1.00) | 0.051 |
| Serum creatinine > 120 µmol/l | 1.32 (1.03 to 1.71) | 0.031 |
| Anaemia | 1.63 (1.30 to 2.05) | < 0.001 |
To address the possibility that specific preoperative factors may influence perioperative mortality more than long-term survival and given the extensive analyses already performed on perioperative mortality, a further Cox proportional hazards analysis from the date of discharge from hospital following AAA repair was performed.
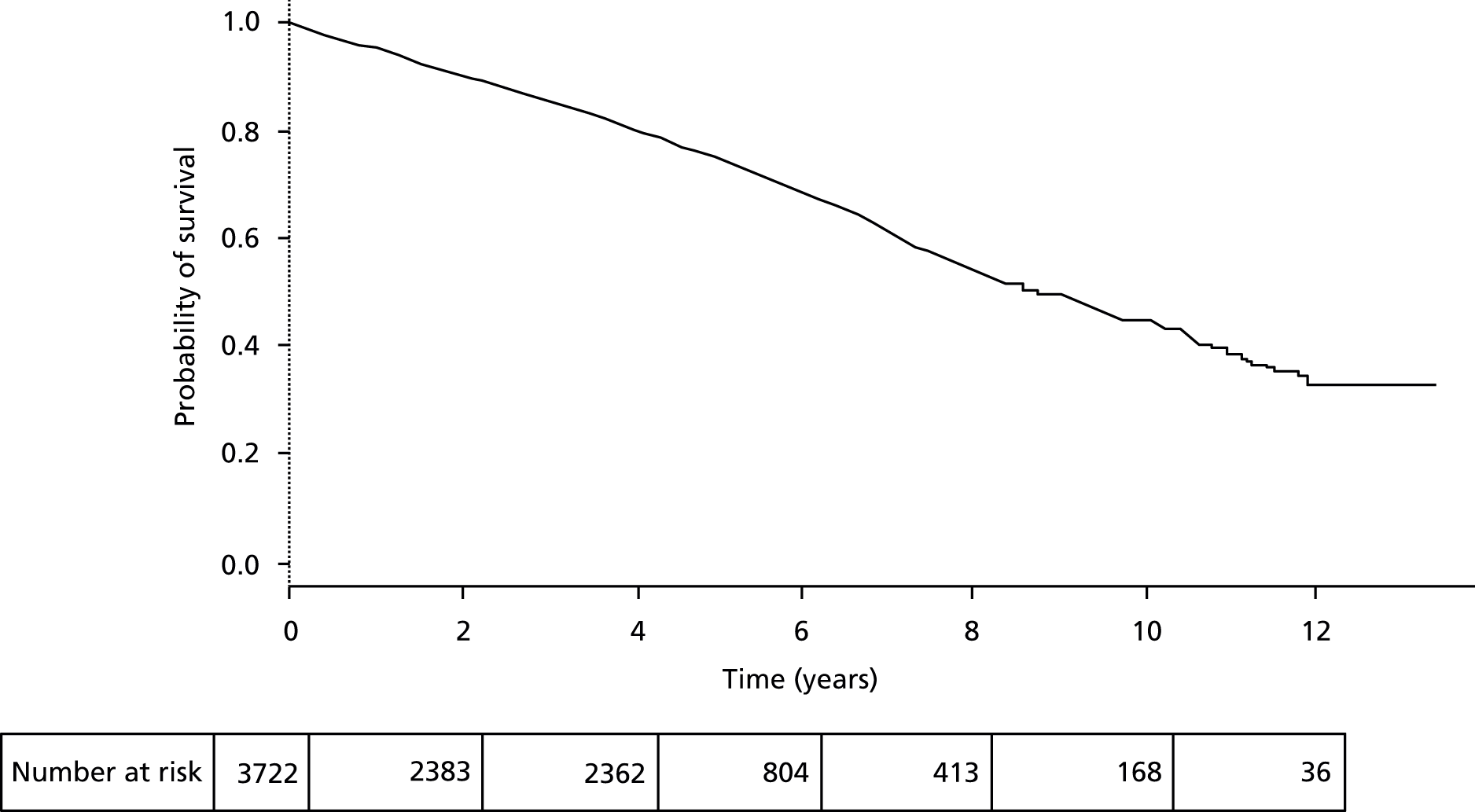
In patients surviving to discharge, the median subsequent survival time improved to 8.7 years with 75.0% 5-year survival (Figure 11). Multivariate Cox proportional hazards model of prognostic factors for survival following discharge from hospital are shown in Table 16. This model did not require stratification on repair type, as the proportional hazards assumption was not violated (Figure 12). Interaction terms for type of repair (open versus EVAR) and year of operation were assessed against the variables in this model as EVAR became increasingly used in the later years of this study. In all cases p < 0.05 was considered statistically significant.
FIGURE 11.
Overall survival of the cohort from date of discharge using Kaplan–Meier.
| Patient characteristic | HR (95% CI) | p-value |
|---|---|---|
| Open repair | 0.70 (0.60 to 0.82) | < 0.001 |
| Female sex | 1.21 (1.02 to 1.44) | 0.03 |
| Age (years) | 1.05 (1.04 to 1.06) | < 0.001 |
| Antiplatelet use | 0.85 (0.73 to 0.98) | 0.02 |
| Statin use | 0.80 (0.69 to 0.92) | < 0.001 |
| Abnormal ECG | 1.18 (1.02 to 1.36) | < 0.001 |
| Abnormal sodium | 1.37 (1.11 to 1.67) | 0.003 |
| Serum creatinine > 120 µmol/l | 1.30 (1.12 to 1.51) | < 0.001 |
| Anaemia | 1.35 (1.17 to 1.56) | < 0.001 |
FIGURE 12.
Overall survival in patients undergoing open repair or EVAR from date of discharge using Kaplan–Meier. A significant survival advantage was noted for the open repair group (p < 0.0001).

Increasing age (HR 1.05, 95% CI 1.04 to 1.06), female sex (HR 1.21, 95% CI 1.02 to 1.44), abnormal ECG (HR 1.18, 95% CI 1.02 to 1.36), abnormal sodium (HR 1.37, 95% CI 1.11 to 1.67), creatinine (HR 1.30, 95% CI 1.12 to 1.51) and anaemia (HR 1.35, 95% CI 1.17 to 1.56) were predictive of poor long-term survival. Open repair (HR 0.70, 95% CI 0.60 to 0.82), statin therapy (HR 0.80, 95% CI 0.69 to 0.92) and antiplatelet therapy (HR 0.85, 95% CI 0.73 to 0.98) were predictive of improved long-term survival in patients that survived AAA repair.
In order to include individual patient predicted survival in the DES model, a survival model with a baseline hazard function was required. A Weibull survival model was developed including risk factors identified as in the previous Cox proportional hazards survival models. Backward stepwise AIC model selection was again used to optimise the model.
The Weibull model of prognostic factors for survival following discharge from hospital is shown in Table 17. This model did not require stratification on repair type. Female sex (HR 1.02, 95% CI 1.00 to 1.04), abnormal ECG (HR 1.02, 95% CI 1.01 to 1.04), abnormal sodium (HR 1.03, 95% CI 1.01 to 1.05), creatinine (HR 1.03, 95% CI 1.01 to 1.05) and anaemia (HR 1.03, 95% CI 1.01 to 1.05) were predictive of poor long-term survival. Open repair (HR 0.97, 95% CI 0.96 to 0.99), increasing age (HR 0.99, 95% CI 0.99 to 1.00), previous aortic surgery or stent (HR 0.95, 95% CI 0.91 to 1.00), statin therapy (HR 0.97, 95% CI 0.96 to 0.99) and antiplatelet therapy (HR 0.98, 95% CI 0.97 to 1.00) were predictive of improved survival in those patients that survived to discharge following AAA repair.
| Patient characteristic | HR (95% CI) | p-value |
|---|---|---|
| Open repair | 0.97 (0.96 to 0.99) | < 0.001 |
| Female sex | 1.02 (1.00 to 1.04) | 0.047 |
| Age (years) | 0.99 (0.99 to 1.00) | < 0.001 |
| Previous aortic surgery or stent | 0.95 (0.91 to 1.00) | 0.040 |
| Antiplatelet use | 0.98 (0.97 to 1.00) | 0.032 |
| Statin use | 0.97 (0.96 to 0.99) | 0.002 |
| Abnormal ECG | 1.02 (1.01 to 1.04) | 0.009 |
| Abnormal sodium | 1.03 (1.01 to 1.05) | 0.009 |
| Serum creatinine > 120 µmol/l | 1.03 (1.01 to 1.05) | 0.002 |
| Anaemia | 1.03 (1.01 to 1.05) | 0.001 |
Patient age is seen to be protective in this model, but this is accounted for, as the baseline hazard function is monotonically increasing with time which captures the increasing risk of death with increasing age. This increase in risk with time is effectively the patient ageing. Age in this model may represent the healthy-old-person effect where only the healthiest elderly people undergo repair. Alternatively, developing an AAA at an earlier age may indicate more aggressive disease and therefore a poor long-term prognosis.
Summary
Our model has identified preoperative factors such as advancing age, female sex, ischaemic heart disease, abnormal ECG, anaemia, abnormal serum sodium and creatinine as being associated with worse long-term survival following AAA repair. Statin and antiplatelet therapy confer improved survival. This survival model will be incorporated into the final decision aid calculating individual patient indications for AAA repair, as it represents the principal reason for repairing an AAA.
Chapter 7 The Aneurysm Repair Decision Aid
Background
The patient pathway from AAA diagnosis through scheduled surveillance to a decision on repair and ultimately survival following the repair cannot be modelled using standard statistical techniques because the pathway is too complex. In the earlier chapters we illustrated how various components of this pathway can be modelled (AAA growth and rupture rates, perioperative mortality and long-term survival). Each of these elements separately does not allow us to derive optimal intervention strategies for individual patients. This is because the elements interact with each other in a complex manner (for example, once an aneurysm is operated on, it no longer continues to grow nor has a risk of rupture; on the other hand, there is the perioperative and longer-term survival to consider following an intervention).
A DES approach was used as the basis for the ARDA. This approach was chosen as, unlike other approaches, it combines the modelling approaches for each component of the patient pathway into one system. It is a microsimulation approach, that is, a patient with particular baseline demographics is simulated forward in time. A key advantage is that outputs are patient-specific (different outputs would be observed for a patient with different baseline demographics). The system is simulated under different intervention rules (an intervention rule is defined as carrying out AAA repair at a particular aneurysm size). The output of the DES can therefore be used to compare the merits (in terms of a range of outcomes) of the various intervention rules, and hence guide treatment decisions.
Discrete event simulation development and structure
Model development
The DES model was developed in a top-down approach. First, the entire patient journey at a high level was described and discussed by experts. The final description was agreed and coded. Individual modules that described individual components of the model in detail were developed and coded (a module for evaluating AAA growth and a module for calculating the BAR score). Each module was internally assessed for face validity and, where possible, compared with existing implementations (for example, BAR scores were validated against the BAR score web application). The entire DES was then checked for face validity. Further development of the DES code was then undertaken so that cost and health-related quality-of-life outcomes could be simulated in parallel with survival and other clinical data.
Model structure
The code base of the DES algorithm was developed in R. The model is based on an underlying decision rule to consider AAA repair once the AAA has reached a given size. For current practice this rule is to repair when the AAA reaches 5.0 cm diameter for women and 5.5 cm diameter for men. The model was developed to explore the full range of AAA sizes and the potential intervention rules for each size. This includes, as the extreme cases, repairing immediately and not repairing at all. The DES model structure is designed to estimate the consequences of each of these options to reflect the need for management that is tailored to the characteristics and needs of each patient. The DES model informs the decision of when to repair using either open surgery or EVAR but not the decision about which method of repair. This latter decision should be made by the vascular surgeon and patient, not by the ARDA.
The DES uses baseline information about each patient, including age, sex, AAA diameter, comorbidities and blood results. Then, for each patient, the life course of the patient is simulated 100,000 times, starting from their current age and AAA diameter, to construct a distribution of the outcomes that the patient could experience. Figure 13 gives an overview of the structure of the model.
FIGURE 13.
Overview of DES model structure.
The DES model starts with a patient with a specified initial age, AAA diameter, clinical and demographic characteristics. Unless a decision is made to repair the AAA immediately, the patient and AAA growth are then monitored through a surveillance programme (in the UK this is generally every 12 months for aneurysms less than 4.4 cm in diameter, after which surveillance is every 3 months). Between surveillance visits, the following events are included in the DES model:
-
The patient gets older.
-
The AAA grows.
-
A rupture of the AAA may occur.
-
The patient may die of other causes and exit the model.
The model loops to update the between surveillance events on a 3-monthly basis. At the next surveillance visit the size of the aneurysm may pass the threshold diameter for repair, when immediate repair is indicated.
For those people who have a ruptured AAA, a proportion will die before emergency treatment can be initiated or during emergency repair and will exit the model. Those people who survive emergency repair will then move to the post-surgery survival part of the model.
If the AAA is below the threshold diameter for repair at the surveillance visit, then the patient continues with regular surveillance. If the AAA is at or above the threshold diameter for repair at the surveillance visit, then elective surgery for AAA repair is indicated. Whether surgery is open or EVAR is a decision for the surgeon and patient and is not considered in the DES model of clinical effectiveness. For those patients having elective repair, there is a chance of dying during the inpatient admission. If a patient survives elective surgery and is discharged alive, they move into the post-surgery stage of the model. The patient then remains alive until their date of death (generated from the survival model described in Chapter 6) is reached.
Data sources and variable estimation
The DES model is based on the English surveillance programme of an outpatient visit and scan every 12 months until the aneurysm grows to 4.5 cm or more, after which surveillance is every 3 months. This schedule could be optimised,47 and indeed the ARDA can incorporate different surveillance schedules. While the aneurysm is growing the patient remains under surveillance until a threshold diameter is reached.
The aneurysm grows at a random rate generated from the distributions reported by the RESCAN growth model for AAAs. 18 The growth rate used in the DES model is adjusted for patient characteristics such as smoking, diabetes and sex. Specifically, the growth rate is assumed to follow a normal distribution with a mean and SD derived from the 95% prediction intervals reported in the RESCAN studies and meta analysis. 18 This growth rate is recalculated annually. Annual growth rates are assumed to be independent. The RESCAN analysis47 includes only growth rates up to an AAA diameter of 5.0 cm. Beyond this, growth rates in this DES model are extrapolated up to 6.0 cm and assumed constant beyond that. For the DES model the annual growth rates are calculated from Table 18 as follows:
| AAA diameter (cm) | Men | Women | ||
|---|---|---|---|---|
| Mean growth rate (cm) | SD | Mean growth rate (cm) | SD | |
| 3.0 | 1.28 | 0.569 | 1.46 | 0.73 |
| 3.5 | 1.86 | 0.518 | 1.98 | 0.63 |
| 4 | 2.44 | 0.487 | 2.51 | 0.533 |
| 4.5 | 3.02 | 0.513 | 3.06 | 0.452 |
| 5 | 3.61 | 0.592 | 3.62 | 0.423 |
| 5.5a | 4.21a | 0.592a | 4.22a | 0.423a |
| 6a | 4.81a | 0.592a | 4.82a | 0.423a |
-
At the beginning of each year, find the row in the table corresponding to the largest size that has yet been reached (e.g. current diameter = 3.3 cm, use row 3.0 cm; current diameter = 5.5 cm, use row 5.5 cm, current diameter = 6.5 cm, use row 6.0 cm).
-
Generate total growth for the year as N [µ, σ2 (mean and variance respectively)] with means and SDs derived from the table.
-
Share this annual growth equally between the 12 months (as the algorithm updates in 3-month time steps).
While the aneurysm is growing, there is a risk of rupture. Rupture probability is also generated from the RESCAN model. 18 Following rupture it is assumed that the probability of mortality is 0.8, otherwise the patient survives emergency repair. 48 Information for rupture rates for small aneurysms comes from the RESCAN data,18 which was then extrapolated for larger aneurysms. Rupture rates up to 5.0 cm come from table 1 of the RESCAN meta-analysis. 47 Extrapolation assumes rupture probability doubles every 0.5 cm size increase up to 6.5 cm, then switches to the given values for 7.0 cm and 8.0 cm. 49,50 The current data we use are shown in Table 19.
| AAA diameter (cm) | Male rupture probability | Female rupture probability |
|---|---|---|
| 0 | 0.0005 | 0.0022 |
| 3.5 | 0.0009 | 0.0045 |
| 4 | 0.0017 | 0.0079 |
| 4.5 | 0.0032 | 0.0147 |
| 5 | 0.0064 | 0.0297 |
| 5.5a | 0.0128a | 0.0594a |
| 6a | 0.0256a | 0.1188a |
| 6.5a | 0.0512a | 0.2376a |
| 7 | 0.2 | 0.4 |
| 8 | 0.5 | 0.5 |
While the patient is managed by scheduled surveillance there is also the chance of death from other causes. This was estimated from the age of the patient while in surveillance. The age at ‘other cause of death’ was generated from the survival models detailed in Chapter 6. In this simulation, a patient is assumed to die at that age if he or she reaches that age before another terminal event.
When an AAA grows to a size that it should be repaired using the current intervention rule, and has been observed at that size in scheduled surveillance, the patient is assumed to undergo repair. Following repair, the probability of a perioperative death is calculated from the BAR score,71 which is influenced by that patient’s individual risk factors.
A patient who survives repair remains alive until he or she reaches the age determined by our survival model (see Chapter 6).
In some patients, the AAA may never reach the size at which surgery is indicated. In this case, the patient simply dies at the time calculated from the survival model, without undergoing any procedure.
Summary of key assumptions
-
The growth of AAA is assumed to rise by 0.6 cm per year for aneurysms of 5.5–6.0 cm; the SD is assumed to the same as that for an AAA of 5.0 cm diameter. Aneurysm growth rates are assumed to be constant beyond 6.0 cm diameter.
-
The annual growth rate is assumed to be independent within a patient between years (given current size). For example, the growth rate in year 2 depends on the aneurysm size in year 2 but not the growth rate in year 1.
-
To estimate the risk of rupture, it was assumed that reported HRs approximate relative risks, that there is negligible uncertainty in rupture rates and that rupture rate doubles for each subsequent 0.5 cm AAA size beyond 5.0 cm.
-
It was assumed that the patient would have immediate surgery when the threshold AAA diameter is detected.
-
Two-year survival is assumed to be identical for both open surgery and EVAR. The simulations account for this by assuming that the additional perioperative mortality of open surgery is an ‘acceleration’ of a death that would have happened in the following 2 years had surgery not been undertaken.
-
It was assumed that death from other causes is independent of the AAA and its risk factors.
-
The estimates of in-hospital mortality derived from the BAR score model are accurate. Uncertainty in the parameters in the score was not factored into the DES model.
-
Long-term survival was assumed to be identical regardless of whether or not surgery has been undertaken. There is additional hazard of mortality pre surgery because of the risk of rupture and additional hazard of mortality per surgery driven by the BAR score.
-
It was assumed that a patient’s specific risk factors do not change over time. This may not accurately reflect what would occur in routine practice. Operating on patients when they are younger, and thus healthier, may be a large source of benefit of early intervention. The ARDA could also be rerun when a patient’s risk factors change.
-
The probability of rupture is calculated annually. At the end of each year, the aneurysm ruptures with the probability derived from the appropriate row of Table 19.
-
Growth rates per year are assumed to be normally distributed. Independence between years is currently assumed (e.g. faster than average growth this year does not mean faster than average growth next year) (see Table 18).
Results
The results of the DES model and the ARDA are summarised below for each of the eight vignettes evaluated, to allow the reader to assess the value of these outputs in clinical decision-making. The full output definitions are listed in Appendix 7. For each vignette a series of patient characteristics were selected. The outputs displayed from the ARDA for each vignette include a plot of median life expectancy based on the AAA size at intervention and a table showing all the outputs calculated by the ARDA. We then show an abbreviated table of outputs, likely to be most useful to surgeons and their patients.
Vignette A
Table 20 reports the patient demographic and clinical characteristics used in vignette A. In this vignette the DES model outputs are reported for two examples. The first is a person with an aneurysm of 4 cm diameter. The second is a person with the same characteristics but an aneurysm of 6.8 cm diameter.
| Risk factor | Status |
|---|---|
| Initial age (years) | 65 |
| Initial AAA diameter (cm) | 4.0/6.8 |
| Sex | Male |
| Type of repair | Open |
| Cardiac disease | No |
| Abnormal ECG | No |
| Previous aortic surgery or stent | No |
| Smoker | No |
| Diabetes | No |
| BMI (kg/m2) | 30 |
| Antiplatelet medication use | Yes |
| Statin use | Yes |
| Anaemia | No |
| WCC | Normal |
| Serum sodium | Normal |
| Serum creatinine | Normal |
| ASA grade | 2 |
In this 65-year-old man with an AAA of 4 cm diameter, repair would not be indicated using the current guidelines based on size alone. Based on the AAA growth rate predicted from RESCAN data, it would take a mean of 5.5 years for this individual’s aneurysm to reach the current threshold for intervention, with a risk of death due to rupture during that period of just 1% (Table 21 and Figure 14). The patient’s life expectancy remains largely unchanged if the repair is carried out at any size between 4.0 and 5.5 cm. The predicted risk of in-hospital death at the time of repair is 1% at both 4 and 5.5 cm but rises to 3% if surgery is delayed by a mean of 8 years until the aneurysm reaches 6.5 cm. The probabilities of survival to 1, 2, 5 and 10 years are all almost identical for repair at 4 cm and 5.5 cm.
| Output | Repair at | No elective repair | |||||
|---|---|---|---|---|---|---|---|
| 4.0 cm | 4.5 cm | 5.0 cm | 5.5 cm | 6.0 cm | 6.5 cm | ||
| Median life expectancy (years) | 76.92 | 76.95 | 76.87 | 76.83 | 76.81 | 76.68 | 75.50 |
| 1-year survival | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 |
| 2-year survival | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 |
| 5-year survival | 0.83 | 0.83 | 0.82 | 0.83 | 0.83 | 0.83 | 0.83 |
| 10-year survival | 0.60 | 0.60 | 0.60 | 0.60 | 0.59 | 0.58 | 0.51 |
| Other cause of death (prior to repair) | 0.00 | 0.08 | 0.13 | 0.19 | 0.24 | 0.29 | 0.53 |
| Death due to rupture | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.02 | 0.38 |
| Rupture survival | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.10 |
| Postoperative survival | 0.99 | 0.91 | 0.86 | 0.79 | 0.73 | 0.67 | NA |
| Growth rate at size | 0.24 | 0.30 | 0.36 | 0.42 | 0.48 | 0.48 | NA |
| 1-year rupture probability at intervention | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | NA |
| Probability of repair | 1.00 | 0.92 | 0.87 | 0.81 | 0.75 | 0.69 | NA |
| In-hospital mortality on repair | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.03 | NA |
| 5-year postoperative survival | 0.84 | 0.79 | 0.76 | 0.72 | 0.69 | 0.65 | NA |
| 10-year postoperative survival | 0.61 | 0.51 | 0.45 | 0.40 | 0.34 | 0.30 | NA |
| Median age at repair (years) | 65.00 | 68.00 | 69.00 | 70.50 | 71.75 | 73.00 | NA |
| Median years to reach size | 0.00 | 3.00 | 4.00 | 5.50 | 6.75 | 8.00 | NA |
FIGURE 14.
Median life expectancy: the ARDA outputs for vignette A with initial AAA diameter of 4.0 cm.
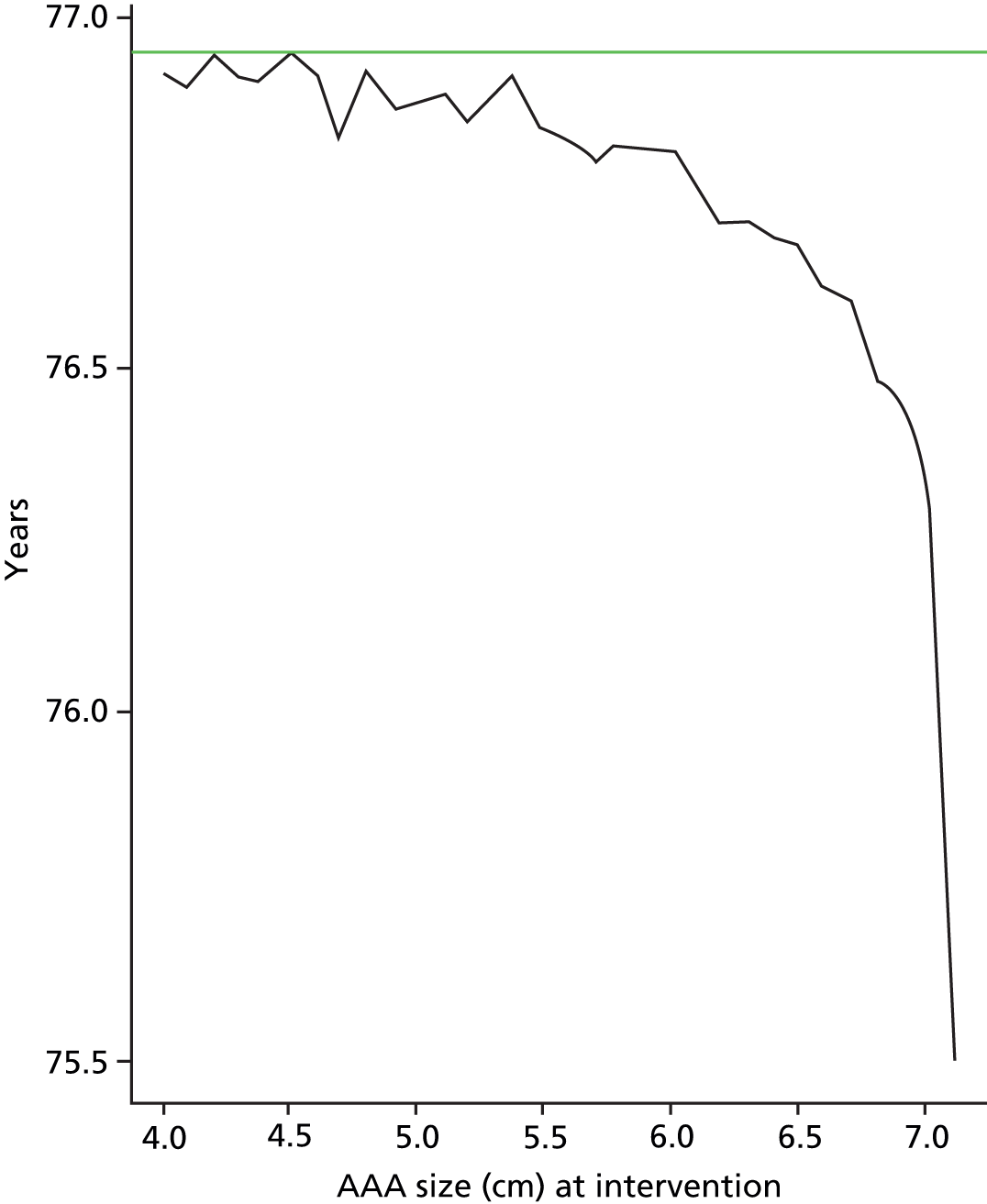
Table 22 is based on the same reasonably fit but marginally overweight 65-year-old man but now assumes that his AAA at presentation was 6.8 cm.
| Output | Repair at 6.8 cm | No elective repair |
|---|---|---|
| Median life expectancy (years) | 76.95 | 69.75 |
| 1-year survival | 0.97 | 0.92 |
| 2-year survival | 0.94 | 0.84 |
| 5-year survival | 0.83 | 0.47 |
| 10-year survival | 0.60 | 0.18 |
| Other cause of death (prior to repair) | 0.00 | 0.20 |
| Death due to rupture | 0.00 | 0.64 |
| Rupture survival | 0.00 | 0.16 |
| Postoperative survival | 0.99 | NA |
| Growth rate at size | 0.48 | NA |
| 1-year rupture probability at intervention | 0.02 | NA |
| Probability of repair | 1.00 | NA |
| In-hospital mortality on repair | 0.01 | NA |
| 5-year postoperative survival | 0.84 | NA |
| 10-year postoperative survival | 0.61 | NA |
| Median age at repair (years) | 65.00 | NA |
| Median years to reach size | 0.00 | NA |
Quite clearly, the patient’s life expectancy is substantially enhanced if the AAA is repaired immediately compared with no repair, as are his probabilities of surviving for 1, 2, 5 and 10 years. If no repair is undertaken, there is a 64% chance that he will die as a result of aneurysm rupture. As he is young and fit, the risk of perioperative death is only 1%; this result is entirely supportive of our current clinical practice.
Vignette B
Table 23 reports the patient demographic and clinical characteristics used in vignette B. In this vignette the DES model outputs are reported for two examples. The first is for a person with an aneurysm of 4 cm diameter. The second is for a person with the same characteristics but an aneurysm of 7.0 cm diameter.
| Risk factor | Status |
|---|---|
| Initial age (years) | 86 |
| Initial AAA diameter (cm) | 4.0/7.0 |
| Sex | Male |
| Type of repair | EVAR |
| Cardiac disease | Yes |
| Abnormal ECG | Yes |
| Previous aortic surgery or stent | No |
| Smoker | No |
| Diabetes | No |
| BMI (kg/m2) | 25 |
| Antiplatelet medication use | Yes |
| Statin use | No |
| Anaemia | No |
| WCC | Normal |
| Serum sodium | Normal |
| Serum creatinine | Abnormal |
| ASA grade | 4 |
This very different patient, aged 86 years, has an aneurysm that can be repaired by EVAR, but he also has a number of important comorbidities including a history of cardiac disease and a raised serum creatinine. As a result, his ASA grade is 4 and the ARDA predicts a risk of perioperative death of 7% in the case of immediate repair, but rising to 11% if we wait until his AAA reaches 5.5 cm. The outputs of the ARDA (Table 24) suggest that there is no benefit in elective repair compared with no elective repair at any aneurysm size.
| Output | Repair at | No elective repair | |||||
|---|---|---|---|---|---|---|---|
| 4.0 cm | 4.5 cm | 5.0 cm | 5.5 cm | 6.0 cm | 6.5 cm | ||
| Median life expectancy (years) | 88.74 | 88.95 | 89.00 | 89.00 | 89.00 | 89.00 | 89.00 |
| 1-year survival | 0.75 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 |
| 2-year survival | 0.60 | 0.62 | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 |
| 5-year survival | 0.26 | 0.25 | 0.25 | 0.27 | 0.27 | 0.27 | 0.27 |
| 10-year survival | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 |
| Other cause of death (prior to repair) | 0.00 | 0.44 | 0.62 | 0.76 | 0.84 | 0.89 | 0.94 |
| Death due to rupture | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.05 |
| Rupture survival | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 |
| Postoperative survival | 0.93 | 0.51 | 0.34 | 0.21 | 0.12 | 0.08 | NA |
| Growth rate at size | 0.24 | 0.30 | 0.36 | 0.42 | 0.48 | 0.48 | NA |
| 1-year rupture probability at intervention | 0.00 | 0.00 | 0.01 | 0.01 | 0.03 | 0.06 | NA |
| Probability of repair | 1.00 | 0.59 | 0.44 | 0.31 | 0.25 | 0.22 | NA |
| In-hospital mortality on repair | 0.07 | 0.09 | 0.10 | 0.11 | 0.13 | 0.14 | NA |
| 5-year postoperative survival | 0.28 | 0.20 | 0.16 | 0.12 | 0.10 | 0.07 | NA |
| 10-year postoperative survival | 0.04 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | NA |
| Median age at repair (years) | 86.00 | 89.00 | 90.00 | 91.50 | 92.75 | 93.75 | NA |
| Median years to reach size | 0.00 | 3.00 | 4.00 | 5.50 | 6.75 | 7.75 | NA |
The results shown in Table 25 refer to the same 86-year-old man outlined in vignette B, but this time assuming that he has presented with an aneurysm 7.0 cm in diameter. As seen in Table 25, his probabilities of surviving 1 year and 2 years are higher if he does undergo repair even though repair is associated with a 10% risk of mortality. In this vignette, the risk of rupture within 12 months is calculated at 22%, which is clearly greater than the risk associated with EVAR. However, even following repair, his life expectancy is only an average of 2.6 years. Quite clearly, an 86-year-old man may decide that he does not want to undergo aneurysm repair.
| Output | Repair at 7.0 cm | No elective repair |
|---|---|---|
| Median life expectancy (years) | 88.62 | 87.75 |
| 1-year survival | 0.73 | 0.66 |
| 2-year survival | 0.58 | 0.43 |
| 5-year survival | 0.25 | 0.06 |
| 10-year survival | 0.03 | 0.01 |
| Other cause of death (prior to repair) | 0.00 | 0.37 |
| Death due to rupture | 0.00 | 0.51 |
| Rupture survival | 0.00 | 0.13 |
| Postoperative survival | 0.90 | NA |
| Growth rate at size | 0.48 | NA |
| 1-year rupture probability at intervention | 0.22 | NA |
| Probability of repair | 1.00 | NA |
| In-hospital mortality on repair | 0.10 | NA |
| 5-year postoperative survival | 0.28 | NA |
| 10-year postoperative survival | 0.04 | NA |
| Median age at repair (years) | 86.00 | NA |
| Median years to reach size | 0.00 | NA |
Vignette C
Table 26 reports the patient demographic and clinical characteristics used in vignette C. In this vignette the DES model outputs are reported for two examples. The first is for a person with an aneurysm of 3.8 cm diameter. The second is for a person with the same characteristics but an aneurysm of 5.2 cm diameter.
| Risk factor | Status |
|---|---|
| Initial age (years) | 70 |
| Initial AAA diameter (cm) | 3.8/5.2 |
| Sex | Female |
| Type of repair | Open |
| Cardiac disease | No |
| Abnormal ECG | Yes |
| Previous aortic surgery or stent | No |
| Smoker | No |
| Diabetes | No |
| BMI (kg/m2) | 35 |
| Antiplatelet medication use | Yes |
| Statin use | Yes |
| Anaemia | No |
| WCC | Normal |
| Serum sodium | Abnormal |
| Serum creatinine | Normal |
| ASA grade | 3 |
This vignette assumes a woman aged 70 years. She has an abnormal ECG and is obese with a body mass index (BMI) of 35 kg/m2. She takes both platelet inhibitory therapy and a statin and has normal full blood count and abnormal serum sodium. The risk of rupture is only 1% if repair is delayed until AAA diameter reaches 4.5 cm. As her risk of in-hospital death is estimated to be 7–8% at the age of 70 or 71 years, but rises to 11% at the age of 74 years, her life expectancy is marginally increased (by approximately 4 months) by repairing this AAA before it reaches 4.5 cm (Table 27). As she is obese, her surgeon may advise her to take regular exercise and to diet with a view to losing as much weight as possible in the year before her AAA reaches 4 cm in diameter. Her risk of perioperative death would drop substantially if she were fitter and reduced her weight such that her BMI is below 30 kg/m2.
| Output | Repair at | No elective repair | ||||||
|---|---|---|---|---|---|---|---|---|
| 3.8 cm | 4.0 cm | 4.5 cm | 5.0 cm | 5.5 cm | 6.0 cm | 6.5 cm | ||
| Median life expectancy (years) | 77.28 | 77.22 | 77.16 | 76.92 | 76.50 | 77.00 | 77.25 | 77.25 |
| 1-year survival | 0.90 | 0.90 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 |
| 2-year survival | 0.86 | 0.81 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 |
| 5-year survival | 0.66 | 0.65 | 0.62 | 0.61 | 0.65 | 0.65 | 0.65 | 0.66 |
| 10-year survival | 0.32 | 0.32 | 0.32 | 0.32 | 0.31 | 0.30 | 0.24 | 0.26 |
| Other cause of death (prior to repair) | 0.00 | 0.10 | 0.24 | 0.34 | 0.44 | 0.53 | 0.60 | 0.76 |
| Death due to rupture | 0.00 | 0.00 | 0.01 | 0.01 | 0.02 | 0.03 | 0.05 | 0.19 |
| Rupture survival | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.05 |
| Postoperative survival | 0.93 | 0.83 | 0.66 | 0.55 | 0.43 | 0.32 | 0.23 | NA |
| Growth rate at size | 0.20 | 0.25 | 0.31 | 0.36 | 0.42 | 0.48 | 0.48 | NA |
| 1-year rupture probability at intervention | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | 0.03 | 0.07 | NA |
| Probability of repair | 1.00 | 0.91 | 0.78 | 0.70 | 0.62 | 0.57 | 0.55 | NA |
| In-hospital mortality on repair | 0.07 | 0.08 | 0.11 | 0.14 | 0.19 | 0.25 | 0.32 | NA |
| 5-year postoperative survival | 0.70 | 0.66 | 0.60 | 0.57 | 0.52 | 0.51 | 0.49 | NA |
| 10-year postoperative survival | 0.35 | 0.29 | 0.21 | 0.17 | 0.13 | 0.11 | 0.09 | NA |
| Median age at repair (years) | 70.00 | 71.00 | 74.00 | 75.00 | 76.50 | 77.75 | 79.00 | NA |
| Median years to reach size | 0.00 | 1.00 | 4.00 | 5.00 | 6.50 | 7.75 | 9.00 | NA |
Table 28 and Figure 15 assume the same woman aged 70 years in vignette C, but her aneurysm is now 5.2 cm. As might be expected, the ARDA calculates her optimal life expectancy if the repair is undertaken immediately, with the probabilities of surviving to 1, 2 and 5 years all higher than if repair is delayed or if the no elective repair decision is taken. In this case, her predicted risk of perioperative death would be 8%. She and her surgeon would have a difficult decision over whether or not it was appropriate and safe to delay surgery for 3–4 months while she pursues a diet and exercise programme with a view to weight loss. Her risk of perioperative death could be reduced if she were able to decrease her weight, although obviously this would be a challenge in only 3 months. However, as the annual risk of rupture is only 1%, a well-motivated 70-year-old woman may decide to pursue an exercise programme and to diet with a view to weight reduction.
| Output | Repair at | No elective repair | |||
|---|---|---|---|---|---|
| 5.2 cm | 5.5 cm | 6.0 cm | 6.5 cm | ||
| Median life expectancy (years) | 77.28 | 77.20 | 77.03 | 76.77 | 75.50 |
| 1-year survival | 0.89 | 0.85 | 0.93 | 0.93 | 0.93 |
| 2-year survival | 0.86 | 0.82 | 0.84 | 0.85 | 0.85 |
| 5-year survival | 0.66 | 0.65 | 0.64 | 0.60 | 0.53 |
| 10-year survival | 0.32 | 0.32 | 0.31 | 0.30 | 0.13 |
| Other cause of death (prior to repair) | 0.00 | 0.06 | 0.14 | 0.22 | 0.51 |
| Death due to rupture | 0.00 | 0.01 | 0.02 | 0.05 | 0.39 |
| Rupture survival | 0.00 | 0.00 | 0.01 | 0.01 | 0.10 |
| Postoperative survival | 0.92 | 0.85 | 0.74 | 0.62 | NA |
| Growth rate at size | 0.36 | 0.42 | 0.48 | 0.48 | NA |
| 1-year rupture probability at intervention | 0.01 | 0.02 | 0.03 | 0.07 | NA |
| Probability of repair | 1.00 | 0.94 | 0.85 | 0.76 | NA |
| In-hospital mortality on repair | 0.08 | 0.09 | 0.11 | 0.14 | NA |
| 5-year postoperative survival | 0.71 | 0.69 | 0.65 | 0.63 | NA |
| 10-year postoperative survival | 0.35 | 0.31 | 0.26 | 0.23 | NA |
| Median age at repair (years) | 70.00 | 71.00 | 72.25 | 73.50 | NA |
| Median years to reach size | 0.00 | 1.00 | 2.25 | 3.50 | NA |
FIGURE 15.
Median life expectancy: the ARDA model outputs for vignette C with initial AAA diameter of 5.2 cm.
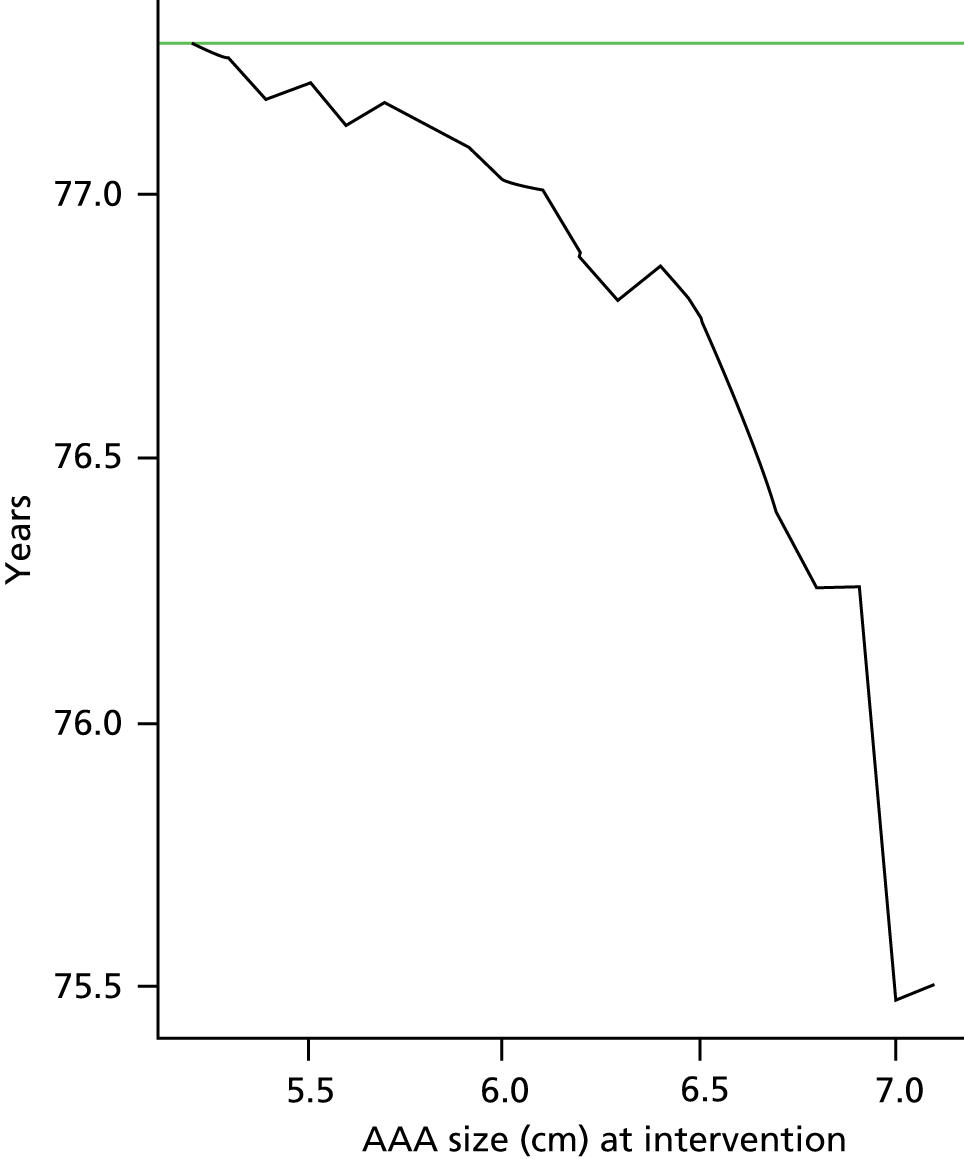
Vignette D
Table 29 reports the patient demographic and clinical characteristics used in vignette D. In this vignette the DES model outputs are reported for two examples. The first is for a person with an aneurysm of 4.8 cm diameter. The second is for a person with the same characteristics but an aneurysm of 6.5 cm diameter.
| Risk factor | Status |
|---|---|
| Initial age (years) | 80 |
| Initial AAA diameter (cm) | 4.8/6.5 |
| Sex | Male |
| Type of repair | EVAR |
| Cardiac disease | No |
| Abnormal ECG | No |
| Previous aortic surgery or stent | No |
| Smoker | No |
| Diabetes | No |
| BMI (kg/m2) | 30 |
| Antiplatelet medication use | Yes |
| Statin use | Yes |
| Anaemia | No |
| WCC | Normal |
| Serum sodium | Normal |
| Serum creatinine | Normal |
| ASA grade | 2 |
This vignette assumes an 80-year-old man who is fit in every way with the single exception of being a little overweight, with a BMI of 30 kg/m2. He is ASA grade 2 and his risk of in-hospital death is predicted to be 0.4%. Under these circumstances, his life expectancy is optimised by repairing this AAA early, although there is no important difference in life expectancy if the repair is delayed until the diameter of his aneurysm is 5.5 cm or more (Table 30 and Figure 16). The probabilities of the patient surviving for 1, 2, 5 and 10 years are all identical in both cases, with only a small deterioration if repair is delayed until the AAA reaches 5.5 cm. Again, this patient and his surgeon may conclude that repair could be delayed until a time convenient for them both. There is the opportunity to improve his general fitness although any improvement in his fitness would have only a marginal effect on perioperative risk.
| Output | Repair at | No elective repair | ||||
|---|---|---|---|---|---|---|
| 4.8 cm | 5.0 cm | 5.5 cm | 6.0 cm | 6.5 cm | ||
| Median life expectancy (years) | 86.65 | 86.62 | 86.56 | 86.48 | 86.34 | 85.75 |
| 1-year survival | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 |
| 2-year survival | 0.85 | 0.84 | 0.84 | 0.85 | 0.85 | 0.85 |
| 5-year survival | 0.62 | 0.62 | 0.61 | 0.61 | 0.59 | 0.59 |
| 10-year survival | 0.29 | 0.29 | 0.28 | 0.28 | 0.27 | 0.09 |
| Other cause of death (prior to repair) | 0.00 | 0.06 | 0.18 | 0.27 | 0.36 | 0.58 |
| Death due to rupture | 0.00 | 0.00 | 0.01 | 0.02 | 0.03 | 0.33 |
| Rupture survival | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.09 |
| Postoperative survival | 1.00 | 0.93 | 0.81 | 0.71 | 0.60 | NA |
| Growth rate at size | 0.30 | 0.36 | 0.42 | 0.48 | 0.48 | NA |
| 1-year rupture probability at intervention | 0.00 | 0.00 | 0.01 | 0.02 | 0.03 | NA |
| Probability of repair | 1.00 | 0.94 | 0.82 | 0.71 | 0.61 | NA |
| In-hospital mortality on repair | 0.004 | 0.004 | 0.005 | 0.006 | 0.007 | NA |
| 5-year postoperative survival | 0.62 | 0.60 | 0.55 | 0.51 | 0.47 | NA |
| 10-year postoperative survival | 0.29 | 0.26 | 0.21 | 0.17 | 0.14 | NA |
| Median age at repair (years) | 80.00 | 80.75 | 82.25 | 83.50 | 84.75 | NA |
| Median years to reach size | 0.00 | 0.75 | 2.25 | 3.50 | 4.75 | NA |
FIGURE 16.
Median life expectancy: the ARDA model outputs for vignette D with initial AAA diameter of 4.8 cm.
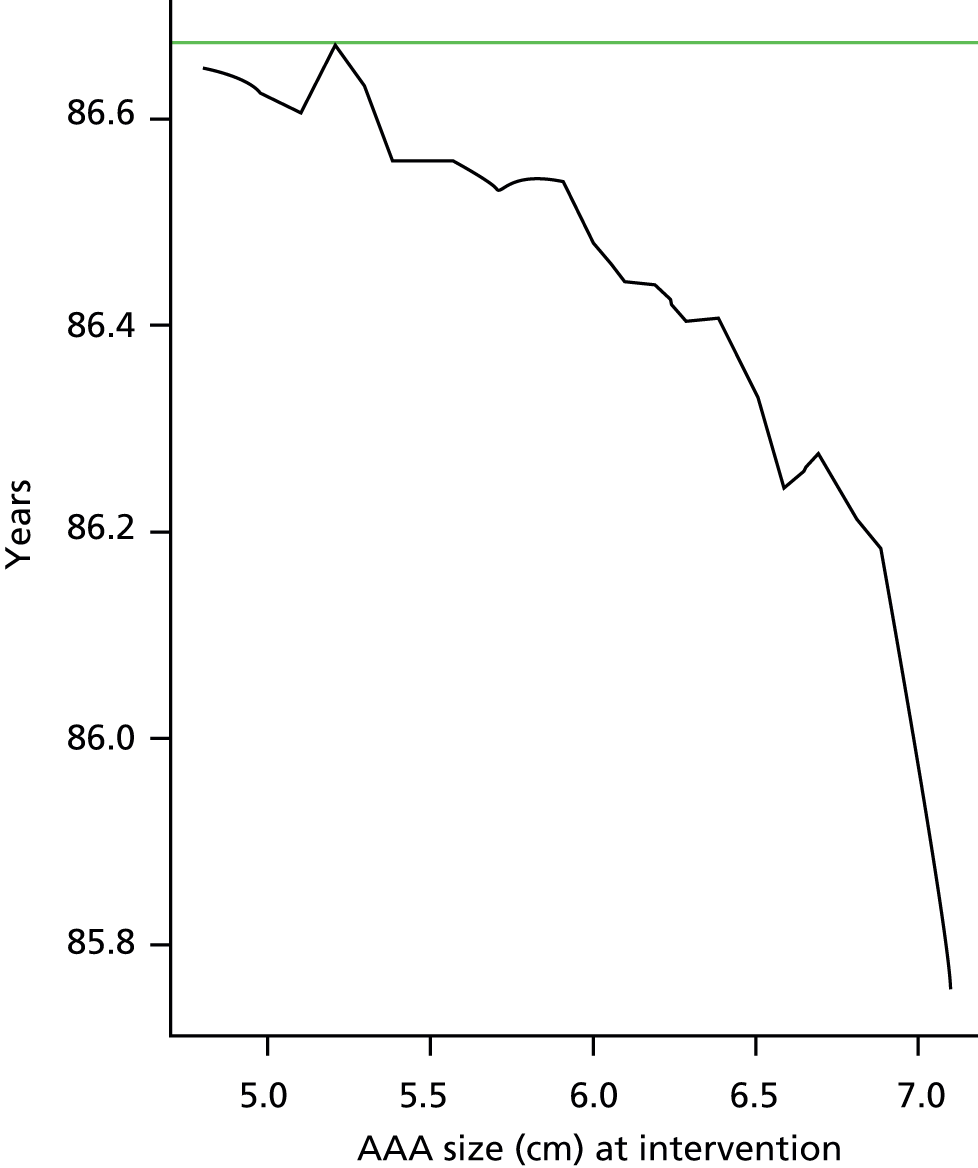
This final example again refers to the 80-year-old man in vignette D but now assumes that the initial AAA diameter was 6.5 cm. Under these circumstances, the patient’s optimal life expectancy is achieved by immediate repair, with the probabilities of surviving for 1, 2, 5 and 10 years all better than would be achieved by no repair (Table 31). The anticipated risk of perioperative death is only 0.5%. This verifies our current indication for repair of an AAA at 5.5 cm in diameter for a man of this age.
| Output | Repair at 6.5 cm | No operation |
|---|---|---|
| Median life expectancy | 86.65 | 83.75 |
| 1-year survival | 0.92 | 0.90 |
| 2-year survival | 0.85 | 0.74 |
| 5-year survival | 0.62 | 0.27 |
| 10-year survival | 0.29 | 0.06 |
| Other cause of death (prior to repair) | 0.00 | 0.31 |
| Death due to rupture | 0.00 | 0.55 |
| Rupture survival | 0.00 | 0.14 |
| Postoperative survival | 1.00 | NA |
| Growth rate at size | 0.48 | NA |
| 1-year rupture probability at intervention | 0.03 | NA |
| Probability of repair | 1.00 | NA |
| In-hospital mortality on repair | 0.005 | NA |
| 5-year postoperative survival | 0.62 | NA |
| 10-year postoperative survival | 0.29 | NA |
| Median age at repair (years) | 80.00 | NA |
| Median years to reach size | 0.00 | NA |
Summary
The ARDA allows individualised evaluation of the relative benefits of undergoing surgery for AAA at various intervention points. The main strength of this algorithm is that it incorporates information from all stages of the clinical pathway from the growth of the AAA, through to repair, and long-term survival following the intervention. The simulation approach means that CI and other uncertainty measures can be incorporated into the decision being made by patients and their surgeons.
The particular strength of the ARDA is that it is designed to be used at each surveillance stage. Where the ARDA shows that there is no need to repair an AAA, it is not necessary for the patient or the surgeon to decide at what size this AAA should be repaired. The surgeon can advise on an approximate time that the patient may require surveillance, but does not need to indicate the aneurysm size at which a repair should be undertaken. It would not be appropriate to assume that the patient characteristics will be the same in 6 or 12 months. A patient may gain weight, lose weight, suffer a MI, develop angina or develop diabetes in the intervening period. The surgeon and patient merely need to conclude that surveillance should be undertaken in 3, 6 or 12 months as appropriate and to rerun the ARDA at that time. Repair can be scheduled when the ARDA indicates that it is appropriate. A particular advantage of the ARDA is that it provides a wealth of information that can be only vaguely estimated when surgeons talk their patients. The summary ARDA output allows the surgeon to discuss the probability of 1-, 5- and 10-year survival with and without repair. We can indicate the risk of rupture if a repair is not undertaken and can tell a patient how likely it is that a repair would be necessary in any event (at the standard current indication). Finally, the BAR score allows the surgeon to discuss perioperative mortality with greater accuracy than previously.
As the ARDA calculates that only marginal benefit results from repairing smaller AAAs when compared with repair at the current indication (5.5 cm in men and 5.0 cm in women), the patient and surgeon may conclude that taking time to optimise fitness and to reduce the risk of perioperative mortality might be the ideal strategy. Patients also have the choice to delay surgery during this interval, when the AAA is still smaller than the current indication, for reasons of convenience such as holiday or work commitments. On the other hand, a patient may decide that they wish to undergo repair sooner rather than wait until the AAA diameter reaches the current threshold for intervention to reduce anxiety associated with having an AAA. The ARDA provides a range of information to support the patient and their surgeon in making this important decision and optimising care.
Chapter 8 Economic evaluation: methods
Approach
An economic model was used to synthesise clinical and economic data to estimate the incremental cost per unit of outcome of undertaking elective repair at the indication identified by the ARDA. The comparator was the current guideline to repair when the aneurysm reaches 5.0 cm (women) or 5.5 cm (men) diameter. Standard practice also includes informal consideration by the surgeon of other factors such as age and fitness/readiness for surgery. The perspective taken was that of the NHS and social care providers and patients. This viewpoint reflects that recommended by the National Institute for Health and Care Excellence (NICE)72 and comprises the key components of a societal perspective.
The measure of health benefit for the primary analysis was the quality-adjusted life-year (QALY). Using life-years gained (LYGs) as the measure, health benefit was included in two of the sensitivity analyses.
For the primary analysis, the model estimated the incremental cost-effectiveness ratio (ICER) associated with intervening at the aneurysm size identified by the ARDA as maximising QALYs gained. Sensitivity analysis assessed the ICER if the algorithm was used to minimise costs and whether or not this would change the recommended timing of surgery. Additional sensitivity analyses assessed the impact on the ICER using a number of cost sources including the minimum and maximum costs reported in the NHS reference costs. 73 The time horizon for the model is lifetime from identification of the AAA to death from any cause. The lifetime impact was discounted at 3.5% as recommended by NICE. 72
Economic model
Population
The population for the model is people with a confirmed AAA, the size of which is below current thresholds for surgery or who present with an AAA at or above the current thresholds for surgery. As with the clinical effectiveness analysis, this population is characterised by eight vignettes that describe typical patients eligible for elective surgical repair (see Chapter 7).
Model structure
The DES model developed for the clinical effectiveness analysis (see Chapter 7) was used as the basis for the analysis of the relative cost-effectiveness of repair at the indication recommended by the ARDA. The overall model structure and processes were not changed. The cost and utility values associated with events in the model were added to estimate net costs and QALYs. Figure 17 shows the points at which cost and utility data were added to the model structure.
FIGURE 17.
Abdominal aortic aneurysm DES model structure adapted for health economic analysis. Dashed border, queue; solid border, activity; solid green boxes, start point/end point.
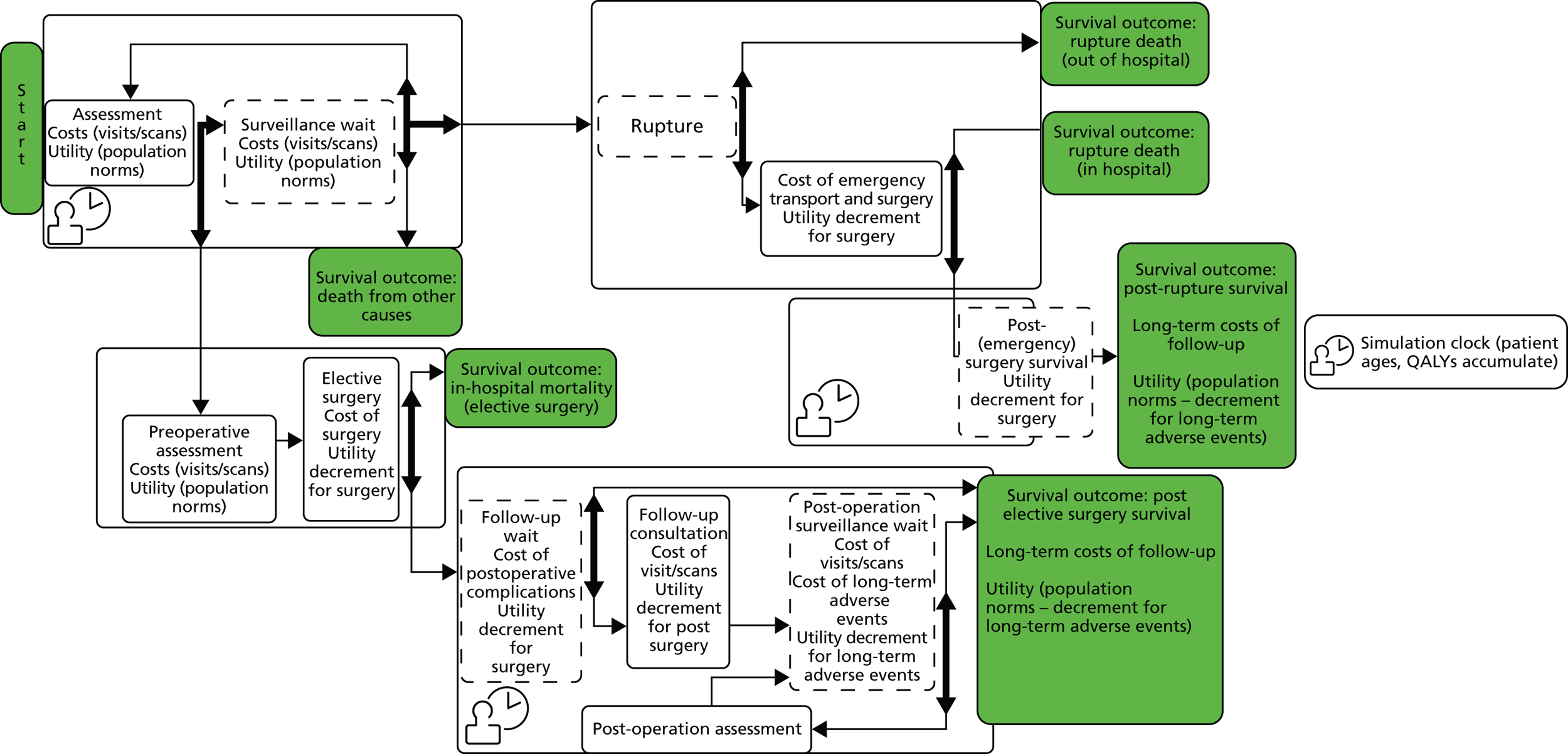
Embedded within the cost calculations are a number of decision trees. Figure 18 indicates the pathway for cost estimation for those people whose AAA ruptures and who die at some point between the rupture and postoperative follow-up. Figure 19 indicates the pathway for estimation of the costs of adverse events (complications and reinterventions) following elective or emergency surgery. The total number of reinterventions and the discount year that applies to each reintervention are calculated by running a once-monthly check for whether or not a reintervention has occurred for the first 6 months after surgery and an annual check thereafter. These checks continue until death. The total number of possible reinterventions is not capped.
FIGURE 18.
Pathway following AAA rupture for those who die following rupture.
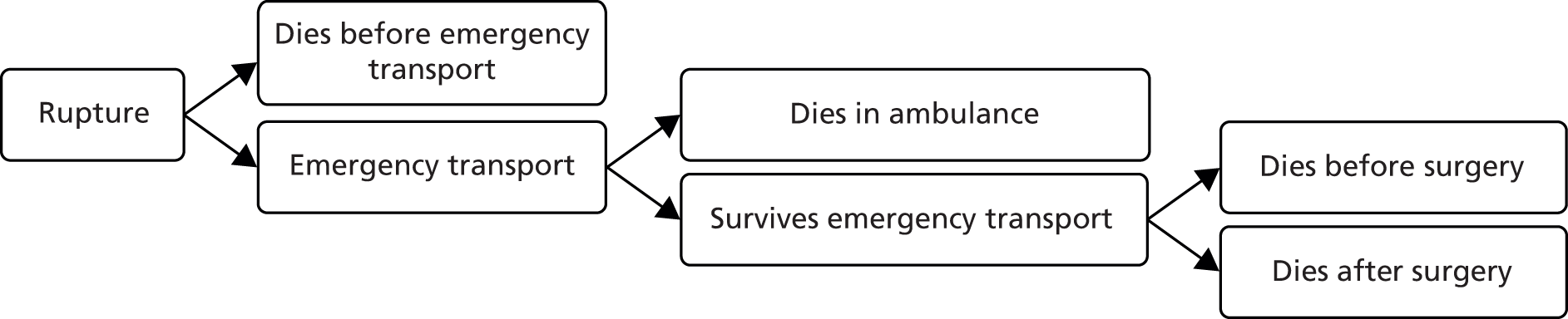
FIGURE 19.
Complications and reinterventions following surgery.
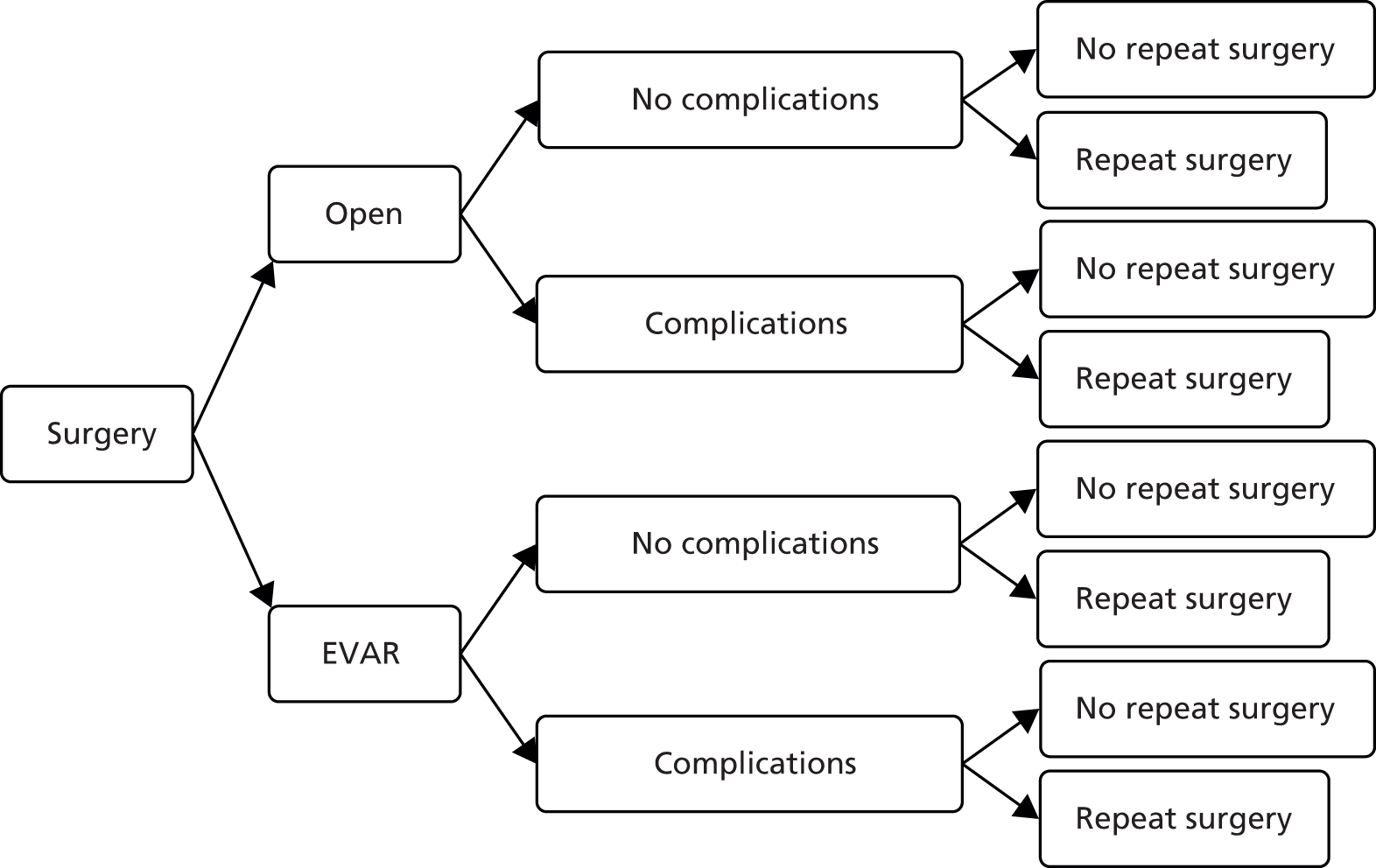
Data inputs
The clinical and probability data for the DES model to estimate LYGs are described in Chapter 7. AAAs can be treated by open surgical repair or EVAR, and in routine practice the surgeon/patient decision to intervene is made when the risk of repair is considered to be less than the risk of rupture. 74 RCTs have been conducted to compare treatment methods for AAA, with mixed results. 75–78 Cost, utility and cost-effectiveness data have been published for RCTs of AAA repair. 79–81 A number of studies have also explored the costs and outcomes of preoperative surveillance. 82,83 However, less is known about the costs and utilities associated with preoperative assessments and postoperative care. In addition, the existing evidence is primarily from trial settings and patient samples, which may be atypical of those in routine care, collected over a limited follow-up period. These factors mean that the results may not reflect the longer-term costs and outcomes found in routine care.
The clinical algorithm developed and assessed for this project is intended for use in a range of settings. For this reason it is important to assess the costs associated with AAA surveillance and repair in standard care settings. Cost and utility data for the economic model were identified from a focused systematic review of published economic evaluations and population norms for utility values, review of the NHS reference cost data set and a prospective study of patient records held in the VGNW programme.
Systematic review
A focused electronic search was conducted in the Centre for Reviews and Dissemination NHS Economic Evaluations Database (EED) to identify studies that reported service use and/or costs related to AAA surveillance, assessment, repair and postoperative follow-up and utility values associated with these events. This database uses a robust, sensitive search of published literature to identify studies that report economic data84 and is updated weekly. 85 Given the detailed searches used to identify studies for the NHS EED database, a simple search strategy was used to identify relevant studies for this part of the project. The terms ‘aneurysm’ and ‘aortic’ were combined using ‘AND’. An initial search indicated that key journal papers already identified for the clinical evaluation and/or known to the authors were identified. However, two reports and monographs published by HTA agencies that were known to the research team were not identified. Accordingly, the search was extended to include the Centre for Reviews and Dissemination HTA database. In addition, the following sources were searched to identify costs and/or utilities of relevant events: published UK data sets (NHS national schedule of reference costs;73 Personal Social Services Research Unit costs),86 the EuroQOL website (http://www.euroqol.org/home.html) and NICE technology appraisals.
The technologies for AAA surveillance and repair have evolved in recent years, at the same time as changes to the organisation and provision of health-care services. To take these changes into account and identify data relevant to current practice, the search was restricted to studies published between January 2004 and April 2014. The search was conducted in October 2012 and rerun between February and April 2014. The identified titles and abstracts were reviewed by two researchers (DN and LMD). Predefined inclusion and exclusion criteria were used to select studies for service use and cost data extraction. The inclusion criteria were as follows:
-
The study was focused on the surveillance, repair or assessment of AAA.
-
The study included any of the following economic data for use in the economic model: details of patient service use or costs; utility values.
-
The study was based on primary data collection or systematic review of observational studies.
-
The study included data other than charge data used and/or reported resource use or costs relevant to the UK setting.
-
Sufficient detail was reported to extract costs and utility values relevant to short- and long-term events related to AAA to populate the economic model.
The data were extracted on pre-defined forms by one researcher (see Appendix 8). Descriptive statistics (mean, SD, 95% CI) were used to summarise the data and to derive average values and distributions for the events in the economic model.
Vascular Governance North West programme
The VGNW database is approved by the National Research Ethics Service (09/H1010/2) to gather clinical and service use data about vascular procedures including AAA repair for the purposes of research. The VGNW covers secondary and tertiary care services in the north-west of England and Wales and is part of the NVD. The VGNW team collect data prospectively and check for completeness retrospectively by reviewing patient notes and hospital administrative systems.
A review was done of 118 VGNW patients who received elective treatment for AAA in the north-west of England between January 2009 and April 2012 to gather additional service use information. Pilot data were collected to assess the availability and influence of costing data identified in a systematic review of the cost-effectiveness of AAA repair. 87 After review of initial pilot data, a standard proforma (see Appendix 9) was designed to capture preoperative, perioperative and postoperative appointments, scans, and procedures clinically associated with the AAA repair. Data were collected from a mix of district general and university hospitals by the VGNW team. This cohort is demographically representative of patients in the VGNW database. There was no statistical difference between the age (73.5 years vs. 72.3 years) and proportion of female patients (16.5% vs. 17.8%) in the two populations. The period of interest is from diagnosis of AAA to December 2012. The service use for each patient was multiplied by the relevant unit cost to estimate the costs of events. The unit costs of services were derived from the NHS national schedule of reference costs (2012–13). 73
The costs of preoperative assessment and preparation for AAA repair and the costs of postoperative follow-up included inpatient admissions, scans and outpatient clinic visits. The costs of scans and outpatient clinic visits were estimated by multiplying the number of visits for scans and assessment appointments by the relevant unit cost. Admissions to hospital for procedures in preparation for AAA repair or needed following AAA repair were estimated in two stages. First, for admissions with a similar length of stay (LOS) to that reported in the NHS reference costs,73 the observed patient LOS was multiplied by the average unit cost per day. Second, for stays longer than the mean LOS, excess bed-day costs associated with the procedure were applied. The total preoperative and postoperative follow-up cost for each patient was estimated.
Each patient admission for an AAA repair was matched with an associated NHS national schedule of reference cost procedure. This involved classification of open procedures as with or without complication and EVAR procedures by graft type. The admission was costed in the same way as preoperative and postoperative admissions.
Descriptive statistics (mean, SD, 95% CI) were used to summarise the data and to derive average values and distributions for the events in the economic model. The data from VGNW were used to derive costs for preoperative assessment and postoperative follow-up events, to supplement data from the systematic review for the primary analysis. In addition, the VGNW average cost of elective EVAR or open repair was used in the sensitivity analysis.
Analysis of economic model
A probabilistic sensitivity analysis was conducted for the primary analysis and each of the sensitivity analyses. This approach takes into account the uncertainty inherent in each of the estimates of the probability, cost and outcomes associated with the model events and pathways. DES with 100,000 iterations was used to estimate the (expected) costs and outcomes for the probabilistic sensitivity analyses. As described in Chapter 7, the DES samples random pathways and the distribution of possible values for each parameter in the decision model. This means that mean costs and outcomes, and measures of variance (standard deviation and 95% CIs) can be estimated to assess the uncertainty inherent in the data used for the model.
These simulated data were used for a cost-effectiveness acceptability analysis. The cost-effectiveness acceptability analysis estimated the probability that undertaking repair at the aneurysm size identified by the ARDA as maximising QALYs gained was cost-effective compared with the current guidelines. This is an approach recommended by NICE for health technology appraisals. 72 The approach revalues effects or outcomes in monetary terms. However, in the UK there is no universally agreed monetary value for the types of outcome measures used in cost-effectiveness analyses. An approach used in health care is to ask the question: what is the maximum amount decision-makers are willing to pay to gain 1 unit of outcome? An analysis of decisions made by NICE suggests a range of implicit values between £15,000 and £30,000 for the amount a decision-maker is prepared to pay to gain 1 QALY. 88
For this analysis, the outcomes were revalued using a range of maximum willingness-to-pay values from £1 to £50,000 to gain 1 QALY or 1 life-year (LY). These reflect a range of hypothetical willingness-to-pay thresholds (WTPTs) from decision-makers being willing to pay £1 to gain 1 QALY or 1 LY to them being willing to pay £50,000 to gain 1 QALY or 1 LY. The data for the cost-effectiveness acceptability curve (CEAC) are derived by first revaluing each of the 100,000 net outcomes from the simulation by a single WTPT. This is repeated for each WTPT. A net benefit (NB) statistic for each pair of simulated net costs and net outcomes for each WTPT can then be calculated as
where O = net outcome score and C = net cost. This calculation was repeated for each WTPT. CEACs plot the proportion of simulations in which the NB of an intervention is greater than zero for each WTPT. 89–92
Sensitivity analysis and key assumptions
One-way and multiple-way sensitivity analyses, varying the measure of health benefit, cost and utility estimates were used to identify whether or not changes would affect the conclusions of the primary analysis. The costs, effects, ICERs and CEACs were re-estimated for each sensitivity analysis. Probabilistic sensitivity analysis was used to assess parameter uncertainty for each of the sensitivity analyses.
A number of simplifying assumptions were used for the primary analysis and these were explored in the sensitivity analyses. It was assumed that the new clinical algorithm would change the timing of surgery but not affect the long-term likelihood of stroke and other disabling events that occur after the postoperative period. This is similar to the approach used in recent UK economic models of the long-term costs of EVAR repair,79,80 although earlier economic models did include the cost and utility impact of non-fatal stroke and MI. 93 The impact of excluding long-term incidence of disability was explored in the sensitivity analyses by increasing the long-term follow-up costs and adding a decrement to utility. Published population norms and trial data for utility values are available for age bands, rather than by year of age. In addition, the published utility data are not sufficiently detailed to derive utility values for each vignette that are specific to characteristics other than age band and sex. Accordingly, the model assumes that the published utility data for age band and sex adequately reflect the likely utility value for the patients’ underlying health status in each vignette. In addition, it is assumed that the average decrements due to surgery are applicable to each of the vignettes. Again, this assumption was tested by varying utility values for each vignette to assess whether or not changes affected the probability that the new clinical algorithm was cost-effective.
Chapter 9 Economic evaluation: data inputs and results
Data inputs
Systematic review
The number of economic studies identified by the search of Centre for Reviews and Dissemination NHS EED, screened and excluded is shown in Figure 20. Three additional sources of utility data were identified from the reference lists of papers found by the electronic search. 76,94,95 Costs of hospital visits and admissions were extracted from the NHS reference cost database for 2012/13. 73 Full references of identified papers and a summary of included papers and data extracted are reported in Appendices 8 and 10. The derived parameter estimates of utility and cost values are reported in Table 32.
FIGURE 20.
Flow diagram of economic studies identified by search of Centre for Reviews and Dissemination NHS EED (excluding duplicate records).
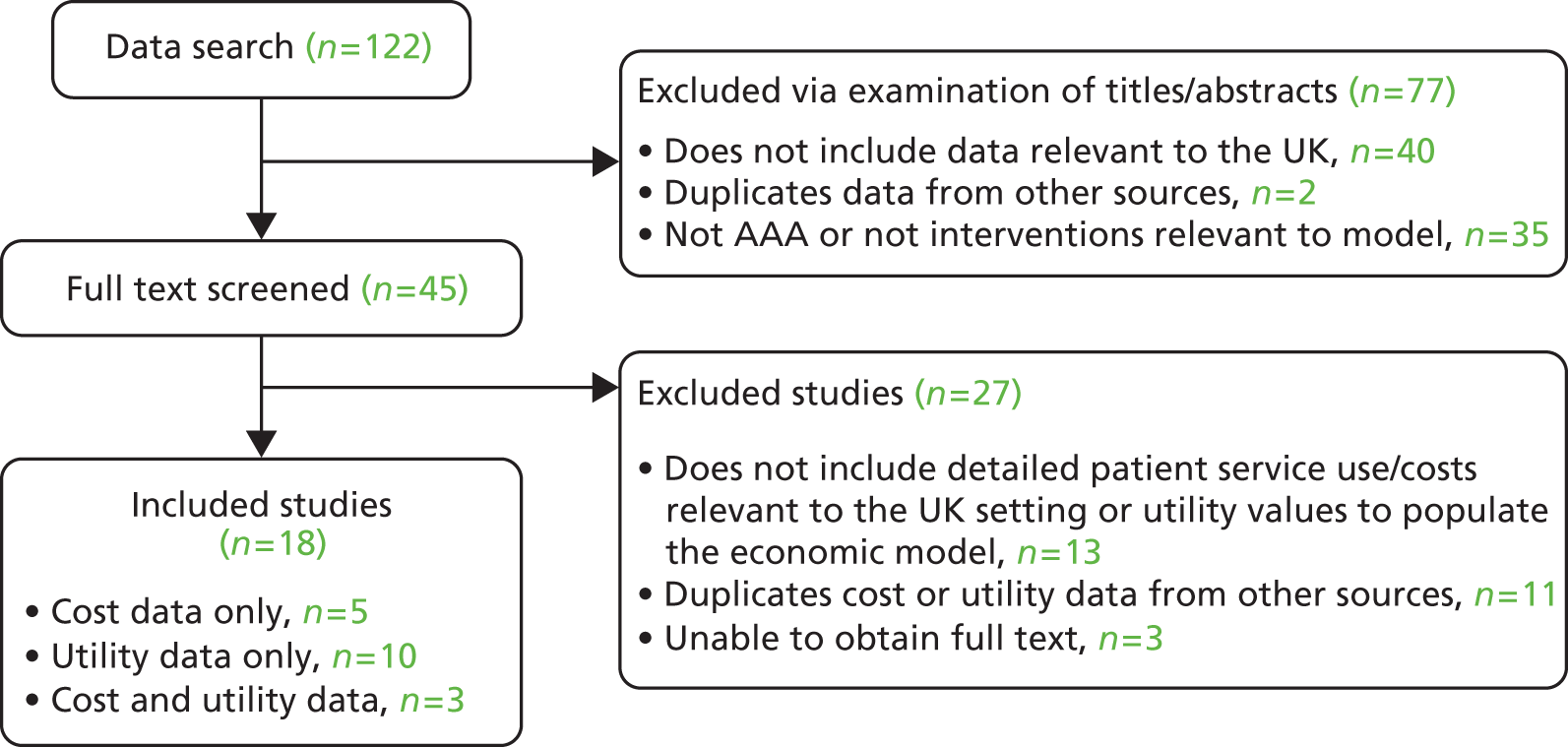
| LOS and costs | EVAR | Open | All patients | |||
|---|---|---|---|---|---|---|
| n | Mean (SD) | n | Mean (SD) | n | Mean (SD) | |
| VGNW LOS (days) | 57 | 5.95 (4.63) | 61 | 13.16 (9.59) | 118 | 9.68 (8.40) |
| National LOS (days)a | 57 | 3.77 (NA) | 61 | 9.26 (NA) | 118 | 6.61 (NA) |
| VGNW perioperative costs (£) | 57 | 12,440 (2751) | 61 | 13,380 (4820) | 118 | 12,930 (3970) |
| National perioperative costs (£)a | 57 | 11,856 (NR) | 61 | 9365 (NR) | 118 | 10,569 (NR) |
| VGNW total preoperative, perioperative and postoperative costs (£) | 57 | 15,580 (4367) | 61 | 15,640 (5336) | 118 | 15,610 (4871) |
Vascular Governance North West
The service use and cost data collected from the VGNW are summarised in Figures 21 and 22. Appendix 11 gives details of service use and costs for preoperative and postoperative visits over the follow-up period. Overall, the average cost of preoperative visits was similar for EVAR and open repair. EVAR was associated with higher costs postoperatively, reflecting a higher number of follow-up visits per year and additional procedures to manage complications.
FIGURE 21.
Average costs of pre- and postoperative hospital visits and procedures, 2012–13.

FIGURE 22.
Length of inpatient stay for AAA repair.

Overall, the LOS (see Figure 22) and associated cost per admission was higher for open repair than for EVAR, which is similar to findings from published trials and to the LOS and costs reported in the NHS references costs. 73 However, Table 33 illustrates that the average LOS and cost of admissions was higher for people in the VGNW than for those reported in national NHS reference cost data and lower than those reported in the EVAR 1 trial for patients undergoing EVAR but higher for patients undergoing open repair. 73,77
| Primary analysis | Value | Source |
|---|---|---|
| Starting value for model: non-smoker, male | ||
| 65–74 years, mean (SD) | 0.79 (0.27) | Kind et al. 199994 |
| > 75 years, mean (SD) | 0.75 (0.29) | Kind et al. 199994 |
| Starting value for model: non-smoker, female | ||
| 65–74 years, mean (SD) | 0.78 (0.25) | Kind et al. 199994 |
| > 75 years, mean (SD) | 0.71 (0.27) | Kind et al. 199994 |
| Elective and emergency postoperative utility decrements (% decrease applied to population norm)a | ||
| EVAR 1-month postoperative utility | 2.67 | Brown et al. 201279 |
| EVAR 3-month postoperative utility | 5.33 | Brown et al. 201279 |
| EVAR 12-month postoperative utility | 1.33 | Brown et al. 201279 |
| Open 1-month postoperative utility | 9.46 | Brown et al. 201279 |
| Open 3-month postoperative utility | 1.35 | Brown et al. 201279 |
| Open 12-month postoperative utility | 0.00 | Brown et al. 201279 |
| Sensitivity analysis | ||
| Decrement for 80 > years (% decrease applied to population norm)b | 8.75 | Kind et al. 1999;94 Montreuil et al. 2008;96 Henriksson et al. 200597 |
| Starting value for model, minimum (range) | 0.67 (0.67–0.90) | Ehlers et al. 2009;98 Szende et al. 201499 |
| Starting value for model, maximum (range) | 0.90 (0.67–0.90) | Ehlers et al. 2009;98 Szende et al. 201499 |
| Elective and emergency 1-month postoperative utility decrements (% decrease applied to population norm)c | ||
| EVAR, maximum (range) | 0.9 (0.9–8.1) | Brown et al. 2012;79 Epstein et al. 200893 |
| EVAR, maximum (range) | 8.1 (0.9–8.1) | Brown et al. 2012;79 Epstein et al. 200893 |
| Open, maximum (range) | 8.7 (8.7–17.3) | Brown et al. 2012;79 Epstein et al. 200893 |
| Open, maximum (range) | 17.3 (8.7–17.3) | Brown et al. 2012;79 Epstein et al. 200893 |
Cost and utility parameter estimates for the economic model
Table 34 details the utility parameter estimates used for the model, for the primary economic analysis and the sensitivity analyses. The asymptomatic nature of AAA suggests that the condition will have no direct impact on health status and utility. This means that population norms are likely to reflect health status during the surveillance or active monitoring phase. In addition, available evidence suggests that the health of people having AAA repair returns to preoperative levels in the first year after surgery. Comparison of the UK population norm utility data with those from other European and Scandinavian countries indicates differences in underlying health and utility weights. 99 The values for the UK population are at the lower end of the range of population norm utility estimates (UK = 0.773 for 64–75 years, range = 0.773–0.904). 99 However, the UK population norm utility values for non-smokers94 lie within the ranges reported at baseline in clinical trials, which are between 0.72 and 0.81 for participants in evaluations of surveillance or surgical repair. 76,78,79,100,101 Economic models that use age-specific population norms report values in the range 0.72–0.87. 80,95–98,102,103 In all but one study96 the values were derived from the European Quality of Life-5 Dimensions (EQ-5D).
| Description | Point estimate | Source |
|---|---|---|
| Death from rupture before emergency transport | 0.40 | Expert opinion |
| Death during emergency transport | 0.25 | Expert opinion |
| Death of ruptured patients before emergency surgery | 0.33 | Expert opinion |
| Death following emergency surgery | 0.34 | Thompson et al. 201383 |
| EVAR emergency – no or mild complications | 0.67 | NHS reference costs73 |
| EVAR emergency – moderate to severe complications | 0.33 | |
| Open emergency – no or mild complications | 0.69 | |
| Open emergency – moderate to severe complications | 0.31 | |
| EVAR elective – no or mild complications | 0.95 | |
| EVAR elective – moderate to severe complications | 0.05 | |
| Open elective – no or mild complications | 0.83 | |
| Open elective – moderate to severe complications | 0.17 | |
| EVAR reintervention probability (0–6 months) | 0.02 | Brown et al. 201279 |
| Open reintervention probability (0–6 months) | 0.01 | |
| EVAR reintervention probability (6 months–4 years) | 0.03 | |
| Open reintervention probability (6 months–4 years) | 0.003 |
Table 34 reports the probability data used to estimate weighted average costs for those patients with a ruptured AAA and for the perioperative and postoperative costs of elective AAA repair and Tables 57 and 58 in Appendix 12 report the cost of events used in the economic model for the primary and sensitivity analyses.
The main source of cost data for elective or emergency surgical repair and reintervention procedures was the NHS reference costs,73 to represent the likely national costs that would apply in UK practice. As noted above, the reference cost data indicate lower average costs than those found in the VGNW. The LOS and cost of admissions for primary repair procedures in the VGNW and estimated from the NHS reference cost database (EVAR: mean = 3.5 days, SD = 3.5; open: mean = 5 days, SD = 3.7) were lower than those reported in the UK-based trial of EVAR 1 (EVAR: mean = 10.3 days, SD = 17.8; open: mean = 15.7 days, SD = 16.9). 73,77 The data for the EVAR trial were collected between 1999 and 2004, so may reflect the influence of changes in the organisation and funding of care tending to reduce length of inpatient stay, as well as possible differences in the case mix of patients and patient socio-demographic characteristics. In addition, the shorter stays associated with EVAR may be a result of increased experience and use of the technique during and following the EVAR 1 trial. 79 Accordingly, the NHS reference costs73 were used as the key source of cost estimates for EVAR and open repair and reinterventions, for both the primary and most of the sensitivity analyses.
Results
Vignette A, male, 65 years, aneurysm 4.0 cm or 6.8 cm, open repair
Tables 35 and 36 report the costs and QALYs found in the primary and sensitivity analyses, with the threshold aneurysm size for surgery. Figures 23 and 24 present the cost-effectiveness plane and CEAC for the primary analysis. The primary analysis assesses the net costs and QALYs of the ARDA to maximise QALYs compared with standard guidelines (5.5 cm). Appendix 13 reports the mean costs and QALYs for the primary and sensitivity analyses and the cost-effectiveness planes and CEACs for the sensitivity analyses.
| Economic model outputs | Initial aneurysm size = 4 cm | Initial aneurysm size = 6.8 cm |
|---|---|---|
| Threshold size to maximise QALYs | 4.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | –172 (–11,644 to 18,275) | 162 (–13,823 to 13,793) |
| Net QALY (95% CIs) | 0.047 (–8.962 to 9.055) | 0.025 (–9.121 to 9.073) |
| ICER (£) | NA | 6583 |
| Probability cost-effectivea | 0.50 | 0.51 |
| NB (95% CIs) (£)a | –1105 (–173,946 to 168,320) | 331 (–176,462 to 176,034) |
| Economic model outputs | Initial aneurysm size = 4 cm | Initial aneurysm size = 6.8 cm |
|---|---|---|
| Sensitivity analysis: outcome is LYGs | ||
| Threshold size to maximise LYGs | 4.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | –172 (–11,644 to 18,275) | 162 (–13,823 to 13,793) |
| Net LYGs (95% CIs) | 0.079 (–18.079 to 18.122) | 0.045 (–18.020 to 18.212) |
| ICER (£) | NA | 3622 |
| Probability cost-effectivea | 0.50 | 0.50 |
| NB (95% CIs) (£)a | –463 (–356,444 to 350,835) | 711 (–6976 to 7968) |
| Sensitivity analysis: decision rule is minimise costs | ||
| Threshold size to minimise costs | 7.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | –172 (–17,585 to 16,938) | –162 (–13,793 to 13,822) |
| Net QALY (95% CIs) | –0.144 (–8.946 to 8.946) | 0.025 (–9.121 to 9.073) |
| ICER (£) | NA | 6583 |
| Probability cost-effectiveb | 0.50 | 0.50 |
| NB (95% CIs) (£)b | –1946 (–164,807 to 162,508) | 331 (–176,462 to 176,034) |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Threshold size to maximise QALYs | 5.1 cm | 7.0 cm |
| Net cost (95% CIs) (£) | –242 (–16,631 to 16,900) | 185 (–14,288 to 13,767) |
| Net QALY (95% CIs) | 0.021 (–11.264 to 11.316) | 0.107 (0 to 12.853) |
| ICER (£) | NA | 1733 |
| Probability cost-effectiveb | 0.50 | 0.812 |
| NB (95% CIs) (£)b | 288 (–212,734 to 213,471) | 7231 (–7894 to 25,512) |
| Sensitivity analysis: VGNW costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | –224 (–11,510 to 19,889) | 95 (–14,471 to 14,129) |
| Net QALY (95% CIs) | 0.047 (–8.962 to 9.055) | 0.025 (–9.121 to 9.073) |
| ICER (£) | NA | 3858 |
| Probability cost-effectiveb | 0.50 | 0.50 |
| NB (95% CIs) (£)b | 329 (21,322 to 21,134) | 398 (–182,551 to 182,055) |
| Sensitivity analysis: EVAR 1 costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | –368 (–6966 to 20,323) | 94 (–13,870 to 10,679) |
| Net QALY (95% CIs) | 0.047 (–8.962 to 9.055) | 0.025 (–9.121 to 9.073) |
| ICER (£) | NA | 3843 |
| Probability cost-effectiveb | 0.49 | 0.50 |
| NB (95% CIs) (£)b | –2574 (–183,909 to 178,683) | 399 (–182,930 to 182,008) |
| Sensitivity analysis: high assessment and follow-up costs, low surgery costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | 59 (–8659 to 14,475) | 239 (–9019 to 9234) |
| Net QALY (95% CIs) | 0.047 (–8.962 to 9.055) | 0.025 (–9.121 to 9.073) |
| ICER (£) | 1279 | 9664 |
| Probability cost-effectiveb | 0.50 | 0.50 |
| NB (95% CIs) (£)b | –181 (180,785 to 180,689) | –995 (–456,396 to 453,777) |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 6.9 cm |
| Net cost (95% CIs) (£) | –300 (–15,794 to 23,284) | 98 (–19,518 to 19,326) |
| Net QALY (95% CIs) | 0.047 (–8.962 to 9.055) | 0.025 (–9.121 to 9.073) |
| ICER (£) | NA | 3979 |
| Probability cost-effectiveb | 0.50 | 0.50 |
| NB (95% CIs) (£)b | –1657 (–183,320 to 179,728) | –395 (–182,602 to 182,865) |
FIGURE 23.
Cost-effectiveness plane and CEAC for vignette A at 4.0 cm. (a) Cost-effectiveness plane; and (b) CEAC.


FIGURE 24.
Cost-effectiveness plane and CEAC for vignette A at 6.8 cm. (a) Cost-effectiveness plane; and (b) CEAC.


The primary analysis indicates repair of the AAA at a lower size (4 cm) than current guidelines, based on a decision rule of maximising QALYs. Repair at 4 cm is associated with a net saving and gain of QALYs. However, as the 95% CIs and cost-effectiveness plane indicate, there is wide variation in the net costs and QALYs, with the 95% CIs crossing zero. The CEAC in Figure 23 indicates that if decision-makers are willing to pay £5000 or more to gain 1 QALY, the ARDA will be cost-effective in around 50% of cases. The probability that decisions based on the ARDA are cost-effective was similar in all the sensitivity analyses.
The sensitivity analyses of alternative estimates of the cost parameters and use of LYGs as the outcome measure indicate similar threshold repair sizes to the primary analysis and are associated with high variation in the net costs, net QALYs and NB estimates. If alternative estimates of the utility parameters are used or the decision rule is to choose a threshold that minimises costs, then the threshold size of the AAA at which repair is indicated changes. However, net costs, QALYs and NB estimates are again characterised by high variation and uncertainty.
For an initial aneurysm size of 6.8 cm, the primary analysis indicates repair of the AAA at a similar size (6.9 cm), based on a decision rule of maximising QALYs. This is associated with a net cost and gain of QALYs. However, as the 95% CIs and cost-effectiveness plane indicate, there is wide variation in the net costs and QALYs, with the 95% CIs crossing zero. The CEAC in Figure 24 indicates that if decision-makers are willing to pay £5000 or more to gain 1 QALY, decisions based on the ARDA information will be cost-effective in around 50% of cases. The probability that the ARDA is cost-effective was similar in all the sensitivity analyses.
Vignette B, male, 86 years, aneurysm 4 cm or 7 cm, endovascular aneurysm repair
Tables 37 and 38 report the costs and QALYs found in the primary and sensitivity analyses, with the threshold aneurysm size for surgery. Figure 25 presents the cost-effectiveness plane and CEAC for the primary analysis for an initial aneurysm size of 4 cm. For an initial aneurysm size of 7.0 cm, no comparator threshold is available, as the ARDA-recommended threshold equals the current practice threshold. The reported cost and QALY data are mean and not net costs and QALYs.
| Economic model outputs | Initial aneurysm size = 4.0 cm | Initial aneurysm size = 7.0 cma |
|---|---|---|
| Threshold size to maximise QALYs | 6.0 cm | 7.0 cm |
| Net cost (95% CIs) (£) | –405 (–17,655 to 13,576) | 8591 (699 to 37,110) |
| Net QALY (95% CIs) | 0.017 (–4.940 to 4.926) | 2.309 (0 to 6.788) |
| ICER (£) | NA | NA |
| Probability cost-effectiveb | 0.51 | NA |
| NB (95% CIs) (£)b | 2338 (–5110 to 12,425) | NA |
| Economic model outputs | Initial aneurysm size = 4.0 cm | Initial aneurysm size = 7.0 cma |
|---|---|---|
| Sensitivity analysis: decision rule is maximise LYGs | ||
| Threshold size to maximise LYGs | 7.0 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –1465 (–21,774 to 7929) | 8591 (699 to 37,110) |
| Net LYGs (95% CIs) | 0.086 (–8.009 to 7.847) | 3.295 (0 to 10.538) |
| ICER (£) | NA | NA |
| Probability cost-effectiveb | 0.52 | NA |
| NB (95% CIs) (£)b | 3186 (–151,866 to 149,092) | NA |
| Sensitivity analysis: decision rule is minimise costs | ||
| Threshold size to minimise costs | 7.0 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –815 (–17,653 to 8036) | 8591 (699 to 37,110) |
| Net LYGs (95% CIs) | 0.017 (–4.972 to 4.888) | 3.295 (0 to 10.538) |
| ICER (£) | NA | NA |
| Probability cost-effectiveb | 0.52 | NA |
| NB (95% CIs) (£)b | 1147 (–90,143 to 89,875) | NA |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Threshold size to maximise QALYs | 6.8 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –729 (–17,595 to 9192) | 8522 (693 to 36,910) |
| Net QALY (95% CIs) | 0.050 (–6.160 to 6.31) | 2.750 (0 to 8.381) |
| ICER (£) | NA | 3471 |
| Probability cost-effectivec | 0.51 | NA |
| NB (95% CIs) (£)c | 1727 (–113,666 to 117,455) | NA |
| Sensitivity analysis: VGNW costs | ||
| Threshold size to maximise QALYs | 6.0 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –781 (–17,010 to 15,253) | 12,849 (5979 to 27,032) |
| Net QALY (95% CIs) | 0.017 (–4.940 to 4.926) | 2.309 (0 to 6.788) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.51 | NA |
| NB (95% CIs) (£)c | 1113 (–98,826 to 100,490) | NA |
| Sensitivity analysis: EVAR 1 costs | ||
| Threshold size to maximise QALYs | 6.0 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –1023 (–17,074 to 17,073) | 16,876 (14,475 to 33,306) |
| Net QALY (95% CIs) | 0.017 (–4.940 to 4.926) | 2.309 (0 to 6.788) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.51 | NA |
| NB (95% CIs) (£)c | 1356 (–99,341 to 101,205) | NA |
| Sensitivity analysis: high assessment and follow-up costs, low surgery costs | ||
| Threshold size to maximise QALYs | 6.0 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –133 (–10,983 to 10,665) | 5849 (1271 to 15,782) |
| Net QALY (95% CIs) | 0.017 (–4.940 to 4.926) | 2.309 (0 to 6.788) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.50 | NA |
| NB (95% CIs) (£)c | 465 (–99,398 to 98,972) | NA |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Threshold size to maximise QALYs | 6.0 cm | 7.0 cma |
| Net cost (95% CIs) (£) | –589 (–18,448 to 14,340) | 9739 (788 to 35,574) |
| Net QALY (95% CIs) | 0.017 (–4.940 to 4.926) | 2.309 (0 to 6.788) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.51 | NA |
| NB (95% CIs) (£)c | 678 (–98,972 to 100,273) | NA |
FIGURE 25.
Cost-effectiveness plane and CEACs for vignette B at 4.0 cm. (a) Cost-effectiveness plane; and (b) CEAC.


The primary analysis assesses the net costs and QALYs of the ARDA to maximise QALYs compared with standard guidelines (5.5 cm). Appendix 13 reports the mean costs and QALYs for the primary and sensitivity analyses and the cost-effectiveness planes and CEACs for the sensitivity analyses.
For an initial aneurysm size of 4.0 cm, the primary analysis indicates repair of the AAA at a higher size (6.0 cm) than current guidelines (5.0 cm), based on a decision rule of maximising QALYs. Repair at 6.0 cm is associated with a net saving and gain of QALYs. However, as the 95% CIs and cost-effectiveness plane indicate, there is wide variation in the net costs and QALYs, with the 95% CIs crossing zero. The CEAC in Figure 25 indicates that if decision-makers are willing to pay £5000 or more to gain 1 QALY, the ARDA will be cost-effective in around 50% of cases. The probability that the ARDA is cost-effective was similar in all the sensitivity analyses.
The sensitivity analyses of alternative estimates of the cost parameters indicate similar threshold repair sizes to the primary analysis and are associated with high variation in the net costs, net QALYs and NB estimates. If alternative estimates of the utility parameters are used, LYGs is used as the outcome measure or the decision rule is to choose a threshold that minimises costs, then the threshold size of the AAA at which repair is indicated increases to 6–7 cm. However, net costs, QALYs and NB estimates are again characterised by high variation and uncertainty.
Vignette C, female, 70 years, aneurysm 3.8 cm or 5.2 cm, open repair
Tables 39 and 40 report the costs and QALYs found in the primary and sensitivity analyses, with the threshold aneurysm size for surgery. Figure 26 presents the cost-effectiveness plane and CEAC for the primary analysis for an initial aneurysm size of 3.8 cm. The primary analysis assesses the net costs and QALYs of the ARDA to maximise QALYs compared with standard guidelines (5.0 cm). Appendix 13 reports the mean costs and QALYs for the primary and sensitivity analyses and the cost-effectiveness planes and CEACs for the sensitivity analyses.
| Economic model outputs | Initial aneurysm size = 3.8 cm | Initial aneurysm size = 5.2 cma |
|---|---|---|
| Threshold size to maximise QALYs | 4.0 cm | 5.2 cm |
| Net cost (95% CIs) (£) | 2716 (–13,650 to 22,552) | 12,790 (5644 to 23,859) |
| Net QALY (95% CIs) | 0.044 (–7.901 to 7.825) | 4.962 (0 to 10.756) |
| ICER (£) | 63,361 | NA |
| Probability cost-effectiveb | 0.49 | NA |
| NB (95% CIs) (£)b | –1831 (–150,921 to 144,164) | NA |
| Economic model outputs | Initial aneurysm size = 3.8 cm | Initial aneurysm size = 5.2 cma |
|---|---|---|
| Sensitivity analysis: outcome is LYGs | ||
| Threshold size to maximise LYGs | 4.0 cm | 5.2 cma |
| Net cost (95% CIs) (£) | 2716 (–13,650 to 22,552) | 12,790 (5644 to 23,859) |
| Net LYGs (95% CIs) | 0.043 (–14.162 to 14.006) | 7.772 (0 to 18.782) |
| ICER (£) | 63,610 | NA |
| Probability cost-effectiveb | 0.49 | NA |
| NB (95% CIs) (£)b | –1862 (–276,819 to 268,676) | NA |
| Sensitivity analysis: decision rule is minimise costs | ||
| Threshold size to minimise costs | 7.0 cm | 7.0 cm |
| Net cost (95% CIs) (£) | –2322 (–16,948 to 18,669) | –2394 (–17,881 to 22,943) |
| Net QALY (95% CIs) | –0.13 (–7.72 to 7.36) | –0.37 (–8.11 to 7.84) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.51 | 0.47 |
| NB (95% CIs)c | –11 (–141,334 to 135,314) | –4953 (–150,793 to 150,597) |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Threshold size to maximise QALYs | 5.4 cm | 5.3 cm |
| Net cost (95% CIs) (£) | –514 (–16,590 to 20,082) | 63 (–14,051 to 24,204) |
| Net QALY (95% CIs) | 0.03 (–9.48 to 9.57) | 0.14 (–9.9 to 10.22) |
| ICER (£) | NA | 444 |
| Probability cost-effectivec | 0.51 | 0.51 |
| NB (95% CIs) (£)c | 1121 (–177,022 to 178,786) | 2757 (–191,975 to 198,960) |
| Sensitivity analysis: high assessment and follow-up costs, low surgery costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.2 cma |
| Net cost (95% CIs) (£) | 1942 (–11,252 to 17,168) | 11,071 (6242 to 18,141) |
| Net QALY (95% CIs) | 0.04 (–7.90 to 7.83) | 4.962 (0 to 10.756) |
| ICER (£) | 43,865 | NA |
| Probability cost-effectivec | 0.49 | NA |
| NB (95% CIs) (£)c | –1056 (–160,547 to 155,234) | NA |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.2 cma |
| Net cost (95% CIs) (£) | 3314 (–17,165 to 28,626) | 14,365 (5285 to 30,600) |
| Net QALY (95% CIs) | 0.044 (–7.901 to 7.825) | 4.962 (0 to 10.756) |
| ICER (£) | 74,858 | NA |
| Probability cost-effectivec | 0.49 | NA |
| NB (95% CIs) (£)c | –1831 (–150,921 to 144,164) | NA |
| Sensitivity analysis: EVAR 1 costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.2 cma |
| Net cost (95% CIs) (£) | 4097 (–16,317 to 23,615) | 17,332 (13,221 to 25,740) |
| Net QALY (95% CIs) | 0.044 (–7.901 to 7.825) | 4.962 (0 to 10.756) |
| ICER (£) | 92,549 | NA |
| Probability cost-effectivec | 0.49 | NA |
| NB (95% CIs) (£)c | –3312 (–163,320 to 153,662) | NA |
| Sensitivity analysis: VGNW costs | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.2 cma |
| Net cost (95% CIs) (£) | 3173 (–14,649 to 24,475) | 14,367 (7320 to 26,022) |
| Net QALY (95% CIs) | 0.044 (–7.901 to 7.825) | 4.962 (0 to 10.756) |
| ICER (£) | 71,675 | NA |
| Probability cost-effectivec | 0.49 | NA |
| NB (95% CIs) (£)c | –2288 (–162,109 to 154,481) | NA |
FIGURE 26.
Cost-effectiveness plane and CEAC for vignette C at 3.8 cm. (a) Cost-effectiveness plane; and (b) CEAC.


For an initial aneurysm size of 3.8 cm, the primary analysis indicates repair of the AAA at a lower size (4.0 cm) than current guidelines (5.0 cm), based on a decision rule of maximising QALYs. Repair at 4.0 cm is associated with a net cost and gain of QALYs. However, as the 95% CIs and cost-effectiveness plane indicate, there is wide variation in the net costs and QALYs, with the 95% CIs crossing zero. The CEAC in Figure 26 indicates that if decision-makers are willing to pay £5000 or more to gain 1 QALY, the ARDA will be cost-effective in around 50% of cases. The probability that the ARDA is cost-effective was similar in all the sensitivity analyses.
The sensitivity analysis of using LYGs as the outcome measure indicates the same threshold repair size to the primary analysis and sensitivity analyses relating to costs recommend a minor adjustment to a 3.8 cm threshold size – all are associated with high variation in the net costs, net QALYs and NB estimates. If alternative estimates of the utility parameters are used or the decision rule is to choose a threshold that minimises costs, then the threshold size of the AAA at which repair is indicated increases from 4.0 cm (suggested by the primary analysis) to 5.4 cm or 7.0 cm. However, net costs, QALYs and NB estimates are again characterised by high variation and uncertainty.
For an initial aneurysm size of 5.2 cm in the primary analysis, the ARDA recommended 5.2 cm as the threshold for maximising QALYs.
Vignette D, male, 80 years, aneurysm 4.8 cm or 6.5 cm, endovascular aneurysm repair
Tables 41 and 42 report the costs and QALYs found in the primary and sensitivity analyses, with the threshold aneurysm size for surgery. Figures 27 and 28 present the cost-effectiveness plane and CEAC for the primary analysis. The primary analysis assesses the net costs and QALYs of the ARDA to maximise QALYs compared with standard guidelines (5.5 cm). Appendix 13 reports the mean costs and QALYs for the primary and sensitivity analyses and the cost-effectiveness planes and CEACs for the sensitivity analyses.
| Economic model outputs | Initial aneurysm size = 4.8 cm | Initial aneurysm size = 6.5 cm |
|---|---|---|
| Threshold size to maximise QALYs | 4.9 cm | 6.6 cm |
| Net cost (95% CIs) (£) | 218 (–29,623 to 39,303) | 143 (–32,285 to 39,933) |
| Net QALY (95% CIs) | 0.033 (–7.478 to 7.504) | 0.006 (–7.516 to 7.510) |
| ICER (£) | 5799 | 23,155 |
| Probability cost-effectivea | 0.50 | 0.50 |
| NB (95% CIs) (£)a | 535 (–143,900 to 143,655) | –20 (–148,886 to 149,026) |
| Economic model outputs | Initial aneurysm size = 4.8 cm | Initial aneurysm size = 6.5 cma |
|---|---|---|
| Sensitivity analysis: decision rule is to maximise LYGs | ||
| Threshold size to maximise LYGs | 4.9 cm | 6.7 cm |
| Net cost (95% CIs) (£) | 45 (–31,632 to 39,303) | 171 (–32,335 to 39,627) |
| Net LYGs (95% CIs) | 0.039 (–13.735 to 13.841) | 0.014 (–13.741 to 13.807) |
| ICER (£) | 1137 | 12,554 |
| Probability cost-effectiveb | 0.50 | 0.50 |
| NB (95% CIs) (£)b | 743 (–270,789 to 272,419) | 101 (–272,234 to 272,681) |
| Sensitivity analysis: decision rule is minimise costs | ||
| Threshold size to minimise costs | 7.0 cm | 7.0 cm |
| Net cost (95% CIs) (£) | –1047 (–29,946 to 30,834) | –214 (–32,546 to 38,088) |
| Net QALYs (95% CIs) | –0.18 (–7.51 to 7.347) | –0.117 (–7.692 to 7.42) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.49 | 0.49 |
| NB (95% CIs) (£)c | –2579 (–141,491 to 139,155) | –2133 (–150,309 to 146,578) |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Threshold size to maximise QALYs | 4.9 cm | 6.7 cm |
| Net cost (95% CIs) (£) | 242 (–29,717 to 39,216) | 74 (–32,999 to 39,564) |
| Net QALY (95% CIs) | 0.08 (–9.57 to 9.65) | 0.14 (–9.53 to 9.76) |
| ICER (£) | 3162 | 517 |
| Probability cost-effectivec | 0.50 | 0.51 |
| NB (95% CIs) (£)c | 1289 (–187,079 to 187,361) | 2796 (–187,752 to 192,291) |
| Sensitivity analysis: high assessment and follow-up costs, low surgery costs | ||
| Threshold size to maximise QALYs | 4.9 cm | 6.6 cm |
| Net cost (95% CIs) (£) | –770 (–13,163 to 18,156) | 178 (–12,247 to 17,906) |
| Net QALY (95% CIs) | 0.038 (–7.365 to 7.445) | 0.006 (–7.516 to 7.510) |
| ICER (£) | NA | NA |
| Probability cost-effectivec | 0.51 | 0.50 |
| NB (95% CIs) (£)c | 1523 (–147,487 to 150,066) | –54 (–150,872 to 150,478) |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Threshold size to maximise QALYs | 4.9 cm | 6.6 cm |
| Net cost (95% CIs) (£) | 785 (–27,275 to 37,503) | –38 (–30,074 to 37,698) |
| Net QALY (95% CIs) | 0.038 (–7.365 to 7.445) | 0.006 (–7.516 to 7.510) |
| ICER (£) | 20,834 | NA |
| Probability cost-effectivec | 0.50 | 0.50 |
| NB (95% CIs) (£)c | –31 (150,731 to 150,870) | 162 (–153,477 to 153,086) |
| Sensitivity analysis: EVAR 1 costs | ||
| Threshold size to maximise QALYs | 4.9 cm | 6.6 cm |
| Net cost (95% CIs) (£) | 2080 (–19,998 to 39,895) | –200 (–24,223 to 39,703) |
| Net QALY (95% CIs) | 0.038 (–7.365 to 7.445) | 0.006 (–7.516 to 7.510) |
| ICER (£) | 55,225 | NA |
| Probability cost-effectivec | 0.49 | 0.50 |
| NB (95% CIs) (£)c | –1372 (–151,705 to 148,506) | 324 (–151,764 to 152,098) |
| Sensitivity analysis: VGNW costs | ||
| Threshold size to maximise QALYs | 4.9 cm | 6.6 cm |
| Net cost (95% CIs) (£) | 1214 (–18,471 to 30,461) | –116 (–19,231 to 30,706) |
| Net QALY (95% CIs) | 0.038 (–7.365 to 7.445) | 0.006 (–7.516 to 7.510) |
| ICER (£) | 32,235 | NA |
| Probability cost-effectivec | 0.50 | 0.50 |
| NB (95% CIs) (£)c | –461 (–150,157 to 149,287) | 240 (–151,215 to 151,759) |
FIGURE 27.
Cost-effectiveness plane and CEAC for vignette D at 4.8 cm. (a) Cost-effectiveness plane; and (b) CEAC.


FIGURE 28.
Cost-effectiveness plane and CEAC for vignette D at 6.5 cm. (a) Cost-effectiveness plane; and (b) CEAC.
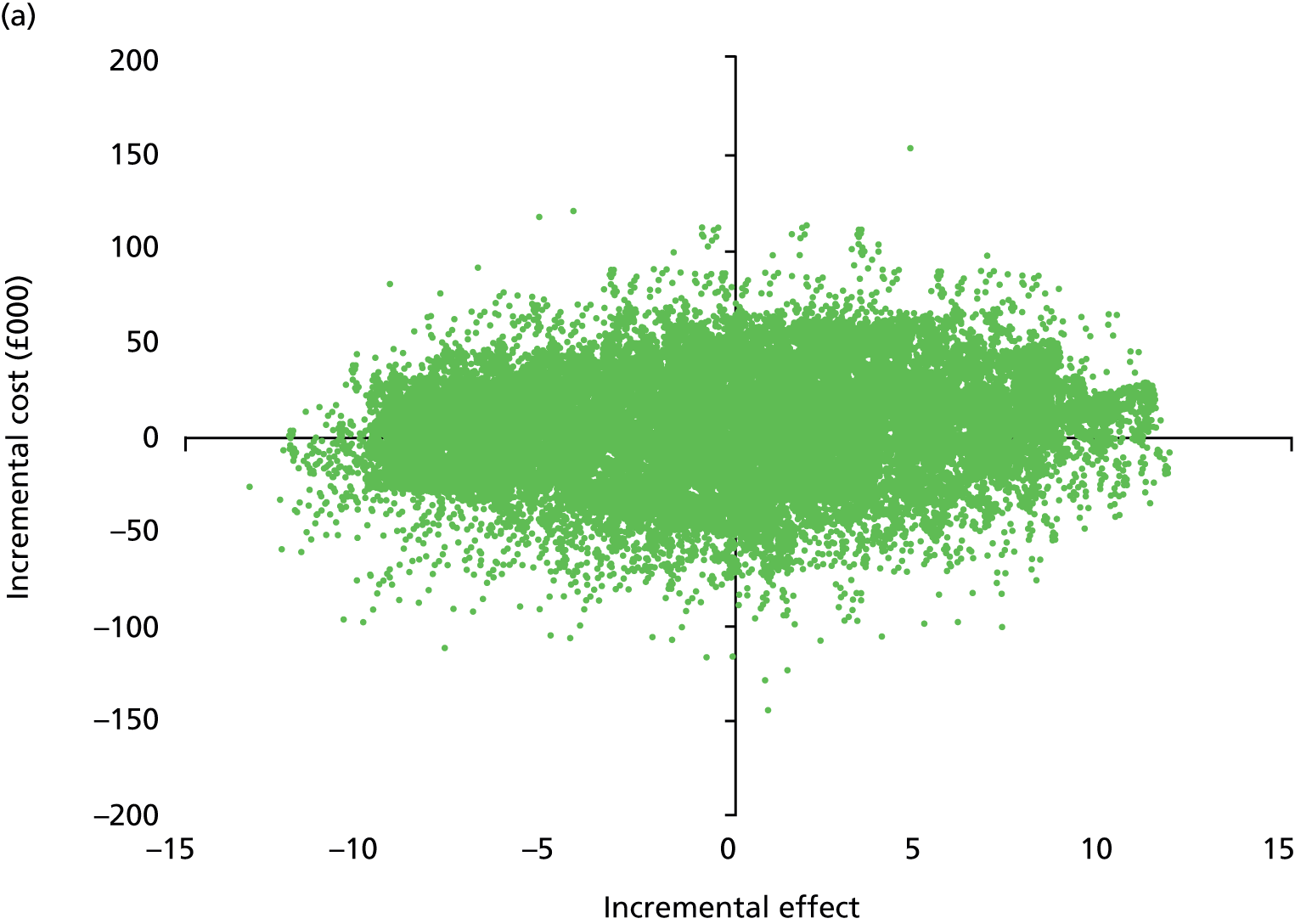

For an initial aneurysm size of 4.8 cm, the primary analysis indicates repair of the AAA at 4.9 cm, which is slightly lower than standard guidelines (5.5 cm), based on a decision rule of maximising QALYs. Repair at 4.9 cm is associated with net costs and a gain of QALYs. However, as the 95% CIs and cost-effectiveness plane indicate, there is wide variation in the net costs and QALYs, with the 95% CIs crossing zero. The CEAC in Figure 27 indicates that if decision-makers are willing to pay £5000 or more to gain 1 QALY, the ARDA will be cost-effective in around 50% of cases. The probability that the ARDA is cost-effective was similar in all the sensitivity analyses.
For an initial aneurysm size of 6.5 cm, the primary analysis indicates repair of the AAA at a similar size (6.6 cm), based on a decision rule of maximising QALYs. This is associated with a net cost and gain of QALYs. However, as the 95% CIs and cost-effectiveness plane indicate, there is wide variation in the net costs and QALYs, with the 95% CIs crossing zero. The CEAC in Figure 28 indicates that if decision-makers are willing to pay £5000 or more to gain 1 QALY, the ARDA will be cost-effective in around 50% of cases.
The sensitivity analyses indicated similar results to the primary analyses for initial aneurysm sizes of 4.8 cm and 6.5 cm, with the exception that making cost minimisation the decision criterion delays recommended intervention until 7.0 cm.
Summary
Overall, the economic model indicates no clear difference in the mean expected costs or QALYs between the ARDA, which formally combines aneurysm size and other factors, and the current thresholds for surgery based on the size of the aneurysm alone. In the primary analysis, the net costs of decisions based on the ARDA information ranged between a saving of £405 (95% CI –£17,655 to £13,576) to a net cost of £2716 (95% CI –£13,650 to £22,552). All the vignettes and aneurysm sizes were associated with a net QALY gain, which ranged between 0.006 (95% CI –7.516 to 7.510) and 0.047 (95% CI –8.962 to 9.055). The net costs and QALYs were characterised by wide 95% CIs, which crossed zero. This is similar to the results found for the analysis of cost-effectiveness and LYGs. The probability that the ARDA-based decisions about timing of repair were cost-effective was around 50% for all of the primary analyses, with a NB that ranged between –£1831 (95% CI –£150,921 to £144,164) and £2338 (95% CI –£5110 to £12,425) for vignettes. Again the 95% CIs are wide and cross zero.
Overall, the results suggest that there is high uncertainty. The wide CIs around the net QALYs gained and net costs generated by this economic analysis reflect the uncertainty in the data and underline the need for reliable data to inform decision aids of this type. As a result of the high level of uncertainty, it was not possible to confidently identify whether the repair indication recommended by the ARDA is likely to be more cost-effective than current guidelines. The sensitivity analysis to explore the impact of using LYGs, alternative costs and utility estimates did not change this result.
Chapter 10 Discussion
Prediction of perioperative mortality
The work on developing models to predict perioperative mortality following elective AAA repair is presented in Chapter 5. Prior to this programme of work, several risk prediction models were developed to predict outcomes following AAA repair. A systematic review of risk prediction models for AAA repair published in 2008 found the GAS to be the most useful and consistently validated model. 52 The GAS is a simplified model constructed in 1994 using 500 patients who underwent AAA repair for either intact or ruptured AAA and includes age, shock, myocardial disease, cerebrovascular disease and renal disease. 53 The GAS has since been validated in a number of cohorts,104–109 but the GAS includes emergency as well as elective AAA repair. As a result, this may mean that it achieves useful discrimination only in populations which include patients undergoing emergency repair. Other models assessed as part of this study include V-POSSUM which was developed using data from 1313 patients who had a range of arterial surgery,110 the VBHOM which was derived from an earlier cohort of patients in the NVD111 and the Medicare model which was developed on 45,660 patients who had elective AAA repair between 2001 to 2004 in the USA. 112 Both the V-POSSUM and VBHOM were previously validated. 109,113,114
In our validation, performed using 10,891 elective AAA repairs, the Medicare model was the only external model to demonstrate fair discrimination, with AUCs > 0.70;54 the GAS, V-POSSUM and VBHOM were developed from elective and emergency data, and all achieved lower discrimination, with AUCs of 0.60–0.65, which is considered to be poor. 54 The calibration of the V-POSSUM and VBHOM was also poor, indicating that they are not suitable for contemporary elective AAA repair, which is a key finding of this project.
To address the known limitations of existing models, VGNW data were initially used for developing a perioperative risk prediction model, as it contained risk factor data not found in the NVD, such as respiratory disease, and it was thought that the available risk factor data were more accurate. The VGNW model included the following risk factors: age, female sex, diabetes, raised serum creatinine level, respiratory disease, antiplatelet medication and open surgery. The AUC was 0.70 on validation with acceptable calibration. On external validation using the NVD, the VGNW model demonstrated good discrimination with an AUC of 0.71 and acceptable calibration.
Although the VGNW model demonstrated potential for predicting perioperative mortality risk following elective AAA repair, there are a number of limitations. First, the validation data set was relatively small, with only 50 deaths, which may be insufficient for assessing model accuracy. 115 Second, the model was built using regional data. Regional differences in patient populations with regards to health and social deprivation may mean that the model’s applicability to other areas in the UK is limited. Third, the model was developed using data collected over a 10-year period during which EVAR was not widely adopted, and outcomes following AAA repair have improved considerably. Case-mix in elective AAA repair has changed significantly over the past 10 years, as can be seen by comparing the patient characteristics of the cohort of patients used to develop the VGNW model and to validate this model using the NVD data (Tables 2 and 11). The most significant change was in the procedure type, with over two-thirds of patients undergoing EVAR in the more contemporary cohort, compared with just 18.9% in the earlier cohort used to develop the VGNW model.
To try and improve the generalisability and statistical performance of the perioperative prediction model, the BAR score was developed using NVD data. The BAR score was developed using more efficient statistical methodology and a larger cohort of patients who underwent elective AAA repair over a shorter period of time. The BAR model included the following risk factors: open repair, age, female sex, serum creatinine over 120 µmol/l, cardiac disease, abnormal ECG, previous aortic surgery or stent, abnormal WCC, abnormal serum sodium, AAA diameter and ASA grade. The AUC (bias-corrected) was 0.77 with good calibration.
Although the BAR score demonstrated improved statistical performance on internal validation compared with the VGNW model, a limitation of the BAR score is that it does not include a history of respiratory disease, as this was not collected in the NVD. Respiratory disease is included in the VGNW model and is viewed as an important predictor of outcomes by the majority of surgeons. Patients with significant respiratory disease will be identified by the ASA grade, which is included in the BAR score, but future models will almost certainly need to include this risk factor. On the final external validation of the VGNW model and BAR score, the BAR score demonstrated improved discriminatory ability on both internal and external validation compared with the VGNW model and demonstrated adequate discrimination in procedural subgroups.
General limitations of the development of the perioperative risk prediction models include potential incomplete case ascertainment. However, data submission to the NVD is improving, and coverage has reached 84%, which compares favourably with administrative data sets such as Hospital Episode Statistics data. 116 Although data cleaning was performed in both the VGNW and NVD databases, inaccuracies were likely to persist. Missing data were more of a problem with NVD. A number of potential risk factors had to be removed prior to any analysis because of significant missing data. For dichotomous risk factors with lower levels of missing data, a single imputation approach was adopted. Based on our in-depth understanding of the data collection process with regards to surgical clinical registries achieved through discussions with database managers and submitting clinicians and administrators, it was decided that missing data were much more likely to reflect absence of the risk factor than to be truly missing. As a result of this, data are therefore unlikely to be missing at random, meaning that other approaches to handling missing data, such as multiple imputation, would be inappropriate. For continuous or ordinal risk factors, either the median or the mean was imputed.
There is a difference in the outcomes the models were designed to predict. The BAR score was developed to predict in-hospital mortality, whereas the VGNW model was designed to predict 30-day mortality. A combined outcome of in-hospital mortality and 30-day mortality is potentially the most appropriate. However, no deaths occurred following discharge but within 30 days of the procedure in the most contemporary cohort of VGNW data. This suggests that the use of in-hospital mortality for perioperative predictive models in this setting is appropriate. Another potential limitation is that centre variation in perioperative mortality is not corrected for in the models we have considered. The issue of how to appropriately combine population-level and centre-level outcome data is an important area of current and future research in risk prediction modelling. Since publication, both the VGNW model and the BAR score have performed well in external validations conducted by other groups. 64,117 The first of these external validations used single-centre data from the UK (VGNW model only) with the second study using data from the Dutch Randomised Endovascular Aneurysm Management (DREAM) trial. 117
Survival modelling
The work on developing models to predict survival following elective AAA repair is presented in Chapter 6. The presented data demonstrate good long-term survival following elective AAA repair in the north-west of England and Wales compared with other historical series. 118,119 This could be as a result of improved standards of care and improved population survival in general. As with all modelling studies using secondary data, there were challenges in terms of the data available, which were collected for other purposes, as they did not include all relevant variables, used uncontrolled designs that may introduce bias and reflected historical rather than current practice. These drawbacks limit the generalisability of this model to other settings and further research is required to validate the model externally.
The NVD did not record long-term outcome, which meant that the survival model used regional data for the north-west of England and Wales (VGNW). There are known geographical differences in population health that could influence survival independently of the method of AAA repair. At present the extent to which the survival model and outputs are generalisable within the UK and internationally is uncertain. The applicability of the survival model to current clinical practice is also uncertain because of the significant changes in clinical practice that have occurred since the early part of the data set with the increase use of EVAR being the most significant change. However, this will continue to be a limitation of studies assessing long-term outcomes until clinical practices stabilise.
Our survival model demonstrates a significant survival benefit at 5 years for patients who underwent open surgery compared with those undergoing EVAR. This contrasts with the published randomised trials in which survival following open repair and EVAR is similar. 38,76,120 This could be a result of differences in the patients selected for EVAR or open repair. Unlike earlier clinical trials, surgeons now undertake EVAR in most patients with suitable anatomy that are unfit for open repair. As more complex EVAR repairs are introduced, the trend for surgeons to reserve open surgery for the fittest patients only is likely to persist.
When modelling survival from the date of discharge, a history of ischaemic heart disease was not included in the model; abnormal preoperative ECG, however, was still a significant risk factor and included in the final survival model. This was presumably a consequence of patients with more significant underlying ischaemic heart disease dying in the early postoperative period. 118,119,121,122 Our finding that statins and antiplatelet therapy improve long-term survival emphasises the importance of these medications in the prevention of late cardiovascular events. 123 That statin use is associated with improved long-term survival is in keeping with previously published reports. 124,125
The Aneurysm Repair Decision Aid
The DES model represents a novel approach to clinical decision-making in patients with AAA. It allows individualised evaluation of the relative benefits of continued surveillance or repair when patients attend surveillance. This approach contrasts with the current indication for elective AAA repair: a blanket AAA diameter threshold (5.5 cm in men and 5.0 cm in women) for all patients irrespective of individuals’ characteristics. The ARDA now includes information from all stages of the clinical pathway: from predicted AAA growth through to repair and finally long-term survival following intervention. This project has demonstrated that it is possible to construct a model that represents and makes explicit a complex decision-making process, using secondary data sources. As the DES model underpinning the ARDA is refined and adapted for use in practice, future simulation can calculate CIs and other uncertainty measures to provide the surgeon and patient with additional information. The DES approach used by the ARDA can and should be updated when new data become available for any parts of the patient pathway. This means that the model can potentially be adapted for other geographical areas or refined as more accurate modelling for AAA growth or risk of rupture becomes available. Even if the patient pathway is altered, the ARDA can be adapted easily.
The model relies on the estimates of perioperative mortality and long-term survival produced by the regression models developed for the project. This means that the limitations of these models also apply to the DES model and the ARDA.
A number of additional assumptions were required to implement the DES/ARDA model. Most of these related to making best use of the data available. There were no data about the growth of AAAs of 5.5 cm and above, and the annual growth rate was assumed to independent from previous years. It was also assumed that death from other causes is independent of the AAA and its risk factors. It is not clear whether or not these assumptions would under- or overestimate life expectancy or the optimal repair size.
To make the model tractable at this development stage, it was assumed that the patient would have immediate surgery when the threshold AAA diameter is detected and that a patient’s specific risk factors do not change over time. These assumptions may not accurately reflect what would occur in routine practice. For example, operating on younger and healthier patients may be a benefit of early intervention, which is not accounted for by the model. If there are delays between the decision to repair and the repair taking place, there is a risk of rupture or other adverse events that are not accounted for by the model. It was also assumed that 2-year survival is identical for both open surgery and EVAR. This implies that the additional perioperative mortality of open surgery is an acceleration of a death that would have happened in the following 2 years had surgery not been undertaken.
A limitation of the ARDA is that no information of the risk of reintervention following AAA repair is included in the clinical effectiveness analysis. Reintervention following EVAR and to some extent open AAA repair is an important outcome for both patients and health-care providers. Reintervention following EVAR is thought to be due mainly to AAA morphology and these data were not included in the available data sets used for the clinical effectiveness analysis. In the absence of data to the contrary, it was assumed that reintervention would occur soon after the initial repair. It was also assumed that the impact of reintervention on longer-term survival would be incorporated in the data used to estimate life expectancy. The probability and cost and QALY consequences of reintervention were included in the economic evaluation. However, this was based on published data from clinical trials. As discussed previously, this may not reflect current practice.
Much of the modelling behind the ARDA is based on observational real-world data. This strategy has strengths and limitations. A strength is that effect size estimates are based on the same population of patients that the ARDA will be applied to, whereas randomised trials tend to be conducted in highly selected populations. Effect size estimates are also based on realistic, rather than ideal, conditions. A weakness is that the data are prone to selection bias and confounding by indication. This means that any new clinical decision taken by the ARDA may not have the consequences that the DES modelling indicates.
There are also parts of the pathway where the data are limited. For example, long-term survival is measured following repair. There is no reliable survival information for patients who do not undergo repair. AAA growth rates are currently recalculated annually based on AAA diameter and are assumed to be independent of previous growth rates, an assumption that may not be true as long-term growth trajectories are not yet available.
The outcomes and decision thresholds predicted by the model and reported in Chapter 7 demonstrate the potential for the model to help support surgeon and patient decision-making. However, the analysis did not include an assessment of uncertainty in the clinical data inputs and outcomes. Further validation of the model structure is required. The economic analysis did include a probabilistic assessment of uncertainty. This illustrated the high level of uncertainty associated with the data currently available.
There are computational limitations. Simulating each individual 100,000 times requires computing power and takes time. The code we use has yet to be optimised and was developed in R, a statistical package, rather than a fast, low-level programming language. We plan software development to address this.
The algorithm is intended to be used at surveillance consultations for patients with AAAs > 4.0 cm in diameter as a decision support tool for patients and clinicians. It is not intended to replace clinical decision-making. It is also not intended to be used to calculate whether open repair or EVAR should be performed. The information provided will help the patient and clinician to make a joint and informed decision on the timing and appropriateness of repair. The algorithm is designed to help the clinician and patient to reach an informed joint decision on whether to operate now, continue surveillance or even discontinue surveillance. As the AAA grows and the patient gets older or acquires new comorbidities, the information available to the algorithm updates; therefore, the algorithm should be rerun at each clinical encounter.
Economic analysis
The economic model used robust, but focused, methods to identify and extract data about the costs and utility associated with decisions on AAA repair. Focusing the electronic search on one database of published economic evaluations may have meant that other relevant papers and data were missed. However, the electronic search strategy, supplemented by hand searching of bibliographies to identify clinical trial reports, identified all the key papers reporting clinical and economic evaluations known to the research team.
The objective of the ARDA was to improve decision-making in the management of patients with AAA. Accordingly, the economic model used costs and utility values derived from national databases where possible. For the primary analysis, the costs of initial elective repair, revision surgery and emergency surgery (the key short-term costs) were estimated from the English NHS reference cost data set73 to reflect the costs of EVAR and open surgery repair in routine practice. While these are relevant to routine practice in England, they may limit the generalisability of the data to other settings. However, the sensitivity analyses, which incorporated the range of cost estimates found for other settings, suggested that the results were robust.
In the absence of any reliable data from other sources, local data from VGNW were used to estimate NHS resources used in patient care during surveillance and long-term follow-up. However, comparison of the costs of AAA repair between VGNW, the NHS reference costs73 and those previously published77 indicate real differences. It is not clear whether or not this would also apply to the costs of surveillance and long-term follow-up. Again the results of the sensitivity analyses suggest that the results of the economic model were robust and the main conclusions were unaffected by different cost estimates.
Published data about population norms were used to estimate the starting utility values for people with AAA to estimate QALYs. Decrements were then applied to account for increasing age and the impact of AAA repair. The strength of this approach is that it may better reflect the values likely to be found in routine practice rather than clinical trials. As most patients with AAA are asymptomatic, AAA may have no direct impact on health status and utility until repair or rupture. Additionally, the UK population norm utility values for non-smokers94 lie within the ranges reported at baseline in clinical trials on AAA surveillance or surgical repair. 76,78,79,100,101 The approach used in this evaluation is similar to that used in evaluations of the cost-effectiveness of screening and surveillance programmes for AAA. 80,95–98,102,103
However, there are a number of limitations. The first is that published population norms aggregated utility values for age ranges, rather than by year of age. This means that the starting values for each vignette are approximated to the age specified for that person, which changes over time, as the ageing process is modelled in a stepwise rather than continuous fashion. The UK population norms report utility values for people aged > 75 years, which may overestimate the longer-term benefits if people survive to old age. Published population norms for other settings suggest that the utility values for people aged >80 years are in the region of 9% lower than those in the age range 70–79 years. Sensitivity analyses to explore the impact of alternative utility values indicated that the results of the economic model are robust to changes in the population norm values and decrements applied for ageing and the effects of AAA repair on health status.
Age, sex and smoking status were the only patient attributes used to estimate health-related utility values. As the ARDA is intended to provide information that can inform decisions for individual patients, it should be noted that current estimates of QALYs may be misleading for patients with significant comorbidities.
Comparison of the UK population norm utility data with those from other European and Scandinavian countries indicates differences in underlying health and utility weights. 99 The values for the UK population are at the lower end of the range of population norm utility estimates (UK = 0.773 for 64–75 years, range = 0.773–0.904). 99 Estimates of resource use and costs also appear to vary between countries and between routine practice and published research on screening, surveillance and AAA repair. This may reduce the generalisability of the results from this economic evaluation to other settings. However, the sensitivity analyses, which incorporated the range of utility values found for other settings, suggested the results were robust to changes in these estimates.
The economic model does not include the long-term costs and utility of non-fatal stroke and other disabling events in the estimation of net costs and QALYs. The impact of these events on life expectancy was incorporated in the survival data used in the model. The exclusion of the costs and utilities of non-fatal adverse events was based on several factors. First, trials of EVAR and open repair indicate no significant difference in the occurrence of these events. Second, the main objective of the algorithm is to determine the timing of AAA repair and to prevent rupture and the need for emergency surgery. Only a higher rate of non-fatal stroke and other disabling events associated with rupture and emergency surgery than the rate of events associated with elective surgery would impact on the value of the algorithm.
Chapter 11 Conclusions and recommendations
Conclusions
The ARDA is a DES algorithm that allows an individualised evaluation of the relative benefits of continued surveillance or repair for patients with AAA. Although it is impossible to report the results for all the possible permutations, AAA repair at 5.0 cm and 5.5 cm for women and men respectively appears to be supported by the algorithm. Young patients at low risk of perioperative mortality would not be harmed but could potentially benefit from earlier repair than the current threshold. Elderly patients with high operative mortalities may benefit from delaying repair beyond the current threshold or not undertaking repair at all.
To inform the DES model, two models for perioperative mortality following elective AAA repair were developed. The regional model (VGNW) included age, female sex, diabetes, renal dysfunction, respiratory disease, open surgery and antiplatelet medication (a surrogate marker for vascular disease) as predictors. The national model (BAR) included 11 risk factors: open repair, age, female sex, creatinine > 120 µmol/l, cardiac disease, abnormal ECG, previous aortic surgery or stent, abnormal WCC, abnormal sodium, AAA diameter and ASA grade. On subsequent external validation, the BAR score outperformed both the VGNW and Medicare models demonstrating excellent discrimination overall and good discrimination in procedural subgroups. This suggests that the BAR score should be adopted for the prediction of perioperative mortality following elective AAA repair; this model was used for the ARDA.
Survival modelling using only preoperative risk factors identified age, female sex, ischaemic heart disease, abnormal ECG, anaemia, abnormal serum sodium and creatinine > 120 µmol/l as predictors of poorer long-term survival following AAA repair with statin and antiplatelet therapy associated with improved survival. These patient-related factors are available and should be considered when making clinical decisions regarding elective AAA repair.
The overall results of the economic evaluation comparing the ARDA to the current indication for elective AAA repair suggest little difference in overall cost, although mean costs may be marginally lower if the ARDA is adopted. The sensitivity analysis to explore the impact of using LYGs, alternative cost and utility estimates did not change this result.
Although the blanket indication for elective AAA repair at 5.0 cm in women and 5.5 cm in men is still applicable to many patients, the ARDA provides surgeons and their patients with the key information they need to make an explicit and informed decision. For younger, fit patients, particularly if AAA repair during their lifetime is almost inevitable, earlier repair improves QALYs and may even be less expensive. For older or unfit patients, repair may be delayed until the AAA diameter increases, or may not be undertaken at all. The ARDA should not be used to influence the decision between open surgery and EVAR repair, as it assumes that this decision is made by the surgeon.
Future research
The discussion in Chapter 10 identified a number of key limitations in the data that were available to structure and populate the predictive models of perioperative mortality, survival and DES that underpin the ARDA. Assumptions were required to make the DES tractable in this development stage. Further work is required to develop the model for implementation into routine practice, to assess the feasibility and acceptability of the ARDA, to address the data limitations and to develop the processes needed to update the model structure and data as practice changes. Evaluation of the feasibility and acceptability of the ARDA is required followed by rigorous analysis of its clinical effectiveness and cost-effectiveness in routine care.
The ARDA can be characterised as a complex intervention. It reflects and makes explicit a multifactorial decision-making process and synthesises a number of mechanisms (e.g. underlying patient health and demographic characteristics, surveillance, aneurysm growth and rupture, choice of AAA repair procedure and associated mortality and survival). Each component has an independent effect on patient outcomes. In addition, there is the potential for one or more components to mediate or modify the impact of other components on outcome. For example, a patient’s underlying health and demographic characteristics may mediate or moderate the rate of aneurysm growth, choice of repair (EVAR or open) and costs and outcomes of AAA repair. There are a range of important and inter-related outcomes that are relevant at differing levels to participants, service providers and policy-makers. The work reported here has developed the ARDA using best evidence and theory. This reflects the first stage of the Medical Research Council guidance for the development and evaluation of complex interventions. The next steps to move towards implementation of the ARDA into routine practice include:
-
development work to refine and adapt the ARDA for use in routine practice and improve the evidence base with which to populate the underpinning models
-
phased evaluation of the intervention starting with studies to test the acceptability and feasibility of implementing the ARDA, to assess the acceptability and feasibility of alternative evaluation designs and procedures, to develop and assess methods of recruitment and retention of participants, and to estimate sample size. These are required prior to exploratory and definitive trials of clinical effectiveness and cost-effectiveness
-
implementation, monitoring and surveillance of the intervention.
Development of the Aneurysm Repair Decision Aid and data inputs
The discussion highlighted a number of assumptions made in the model structure to implement this first phase of the work. In addition, the structure and methods used for the underpinning regression models and DES model require rigorous internal and external validation. This is to ensure that the models reflect routine practice and patient populations, to ensure that bias is minimised and to optimise the accuracy of the outputs. There are also limitations in terms of computing power and time. The ARDA needs to be accessible to both clinicians and patients in terms of the user interface and in computation.
Research priority 1
Further development work is needed to statistically validate the ARDA and underpinning model structures in different settings and populations. Work is also needed to translate the DES model structure from the R statistical package to a fast, low-level programming language that optimises the simulation processes for use in routine practice. A user interface is required to ensure the ARDA is accessible to all those involved in clinical decisions and policy.
Research priority 2
Further systematic review and qualitative work with surgeons, patients and policy-makers is required. This is needed to expand and validate the DES model structure; ensure that it captures all the events that are important to each of these actors; and to develop and test the user interface. For example, it is essential that information that predicts the risk of reintervention or complications following repair (particularly AAA morphology for EVAR) are incorporated into the algorithm as this has important clinical, quality-of-life and cost implications. Processes to routinely identify changes in practice to update the structure of the models incorporated in the ARDA (AAA growth and rupture risk, BAR score and survival models). Perioperative risk models will lose calibration over time. 126 The interval for validating and updating the different models is not known and work is needed to identify this. For the future, the ARDA may need to include new variables and factors that may predict AAA growth, risk of rupture or outcome following repair. Potential risk factors include biomarkers,127 assessments of functional capacity128 and genetic analysis. 129 Cardiopulmonary exercise testing assesses individual patient functional capacity and identifies patients at increased risk of perioperative death. 128,130–133 Cardiopulmonary exercise test data may be incorporated into the ARDA in the future if it becomes widely implemented in routine practice.
The outcomes and decision thresholds predicted by the model and reported in Chapter 7 demonstrate the potential for the model to help support surgeon and patient decision-making. The economic analysis included a probabilistic assessment of uncertainty for the estimates of cost, QALYs and LYGs. This illustrated the high level of uncertainty associated with using the data currently available. As noted in the discussion in Chapter 10, the underpinning models for the ARDA use data collected for other purposes. Key issues are that the data are incomplete (owing to missing observations in available data sets and to lack of any data for specific variables), may be inaccurate or biased and may relate to previous rather than current practice and patient populations. To be of use in clinical practice, the data used in the models will need to be updated to reflect changes in patient selection and health as well as changes in repair techniques.
Research priority 3
Research is needed to develop existing databases and registries that use routinely recorded data. This includes methods to extend the scope of the NVD and other relevant data sets, to include key variables required for the ARDA models and to better inform clinical practice in the absence of the ARDA. These include key clinical, service use and cost and patient health status data to reduce uncertainty in the estimates of clinical effectiveness and cost-effectiveness of the ARDA-based decisions. It is also necessary that there is work to identify methods to increase the accuracy and minimise bias in existing data, which can be implemented in the NHS and used in routine data collection. Work to explore the feasibility and acceptability of implementing processes to link the data sets with the ARDA is required, to facilitate the timely and routine updating of the data used by the models.
The economic evaluation conducted in this project assessed the relative cost-effectiveness of decisions to repair AAA based on the ARDA recommendations or current guidelines. It was outside the scope of this research to assess the cost-effectiveness of implementing the ARDA into routine practice. There are likely to be additional costs incurred in the routine use and maintenance of the ARDA. These could be offset by increases in patient health benefit that may also reduce future service costs.
Research priority 4
As the ARDA models are developed and the feasibility and acceptability of implementing them into routine practice are evaluated, the model used for the economic evaluation needs to be extended to explore the potential for the ARDA to be cost-effective.
Phased evaluation of the intervention
This project has established that it is possible to construct a complex decision aid that provides useful information to support patient and surgeon decision-making about the timing of AAA repair. The service user group for the project has had an active role in defining the scope and outputs of the ARDA. However, little is known at this stage about the acceptability and feasibility of implementing the ARDA and associated data requirements in routine practice.
Research priority 5
Mixed-method evaluations are required to qualitatively and quantitatively assess the feasibility of implementing the ARDA and methods to collect and update the data required for the decision tool; barriers and facilitators to implementation; likely adherence with the recommendations of the ARDA; and the acceptability of the tool and its recommendations to patients, surgeons and policy-makers.
If the ARDA and associated data collection and updating processes is demonstrated to be feasible and acceptable, then prospectively collected evidence is required about the long- and short-term clinical effectiveness and cost-effectiveness. While a RCT is seen as the gold standard design to minimise bias and impact of confounding factors, there are also limitations in terms of length, costs and feasibility. The prospective evaluation design needs to be sufficiently robust to identify potentially small but important and relevant effects of the ARDA that may take some time to occur following implementation into practice and use in any individual patient–surgeon decision. In addition, there are likely to be important effects of selection, allocation and unobservable biases.
Research priority 6a
Mixed-methods research is needed to qualitatively and quantitatively assess the feasibility and acceptability of a RCT, or other prospective study design, to all stakeholders. The research should also identify key confounders and biases and barriers to evaluation and any barriers and facilitators to the recruitment and retention of study centres, staff and participants. A comparison of the specific strengths and weaknesses of alternative designs to evaluate the ARDA and data collection processes in the UK setting is an important component of this stage. A major aim of this research would be to inform the design of the full RCT/controlled non-randomised evaluation of clinical effectiveness and cost-effectiveness.
Research priority 6b
Pilot and/or small exploratory trials are required to test the study design for a full, definitive trial. The main objectives of these trials include assessment of methods to recruit and retain study centres, staff and participants; documentation of likely drop-out rates; exploration of reasons for non-compliance with the study protocol and/or interventions; the feasibility and acceptability of data collection methods and instruments to measure outcomes and service use.
Research priority 6c
Full definitive RCTs/controlled, integrated clinical effectiveness and cost-effectiveness evaluations are needed in the UK setting. The target population and participant sample, intervention and comparator, outcomes and measures need to be clearly described and analysed. The design of the evaluation needs to be evidence based and informed by the work identified in research priorities 1–5. The length of follow-up needs to be sufficient to identify the impact of the ARDA on the decision to repair the AAA and the longer-term impact on survival, service use and costs and patient health benefit.
Acknowledgements
The authors are grateful to NIHR for funding this work, the VGNW team for assisting with data collection, the Vascular Society for allowing access to the NVD data, the PPI group members who advised us and the RESCAN team.
Other individuals who contributed substantially to this work are Dr Graeme Hickey, Mr Anthony Grayson, Ms Debasree Purkayastha, Mr David Mitchell, Professor Johnathon Michaels, Professor Andrew Bradbury, Ms Anne Worthington and Ms Sue Williams.
Contribution of authors
Stuart W Grant (Honorary Senior Lecturer) managed the project and led on the development of models for perioperative mortality. He provided guidance for survival modelling, DES model development and health economic analyses and led the drafting of the resulting manuscripts and this report.
Matthew Sperrin (Lecturer, Health Data Science) developed the DES model and drafted the corresponding chapter in this report.
Eric Carlson (Research Assistant, Cardiovascular Surgery) co-ordinated the project and final report, drafted sections of this report, conducted the survival and regional health economic analysis and organised the patient group.
Natasha Chinai (Clinical Research Fellow) advised on the clinical aspects of the survival analysis, drafted the corresponding chapter in this report and provided clinical input for the DES model development.
Dionysios Ntais (Research Associate, Health Economics) conducted the systematic review to inform the economic evaluation (with Matthew Hamilton and Linda Davies), codeveloped the health economic components of the DES, undertook the cost-effectiveness analyses and provided comments and critical input during the drafting of the report.
Matthew Hamilton (Research Associate, Health Economics) conducted the systematic review to inform the economic evaluation (with Dionysios Ntais and Linda Davies), codeveloped the health economic components of the DES, undertook the cost-effectiveness analyses and provided comments and critical input during the drafting of the report.
Graham Dunn (Professor, Biostatistics) provided statistical guidance on the overall project.
Iain Buchan (Clinical Professor, Public Health Informatics) provided statistical guidance on the overall project and public health implications and edited the report.
Linda Davies (Professor, Health Economics) supervised the health economic modelling work, and (with Dionysios Ntais, Matthew Hamilton and Eric Carlson) wrote the economic evaluation chapters. Linda Davies also had a substantive, critical input to the discussion, conclusion and recommendations for research sections as well as critically reviewing the report overall.
Charles N McCollum (Professor, Surgery) was principal investigator of the project, provided overall direction and supervision for all aspects of the project and edited this report.
Publications
Grant SW, Grayson AD, Purkayastha D, Wilson SD, McCollum C. Logistic risk model for mortality following elective abdominal aortic aneurysm repair. Br J Surg 2011;98:652–8.
Grant SW, Grayson AD, Mitchell DC, McCollum CN. Evaluation of five risk prediction models for elective abdominal aortic aneurysm repair using the UK National Vascular Database. Br J Surg 2012;99:673–9.
Grant SW, Hickey GL, Grayson AD, Mitchell DC, McCollum CN. National risk prediction model for elective abdominal aortic aneurysm repair. Br J Surg 2013;100:645–53.
Grant SW, Hickey GL, Carlson ED, McCollum CN. Comparison of Three Contemporary Risk Scores for Mortality Following Elective Abdominal Aortic Aneurysm Repair. Eur J Vasc Endovasc Surg 2014;48:38–44.
Sweeting MJ, Thompson SG, Brown LC, Powell JT. Meta-analysis of individual patient data to examine factors affecting growth and rupture of small abdominal aortic aneurysms. Br J Surg 2012;99:655–65.
Powell JT, Sweeting MJ, Brown LC, Gotensparre SM, Fowkes FG, Thompson SG. Systematic review and meta-analysis of growth rates of small abdominal aortic aneurysms. Br J Surg 2011;98:609–18.
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the HTA programme or the Department of Health. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the HTA programme or the Department of Health.
References
- Ashton HA, Buxton MJ, Day NE, Kim LG, Marteau TM, Scott RAP, et al. The Multicentre Aneurysm Screening Study (MASS) into the effect of abdominal aortic aneurysm screening on mortality in men: a randomised controlled trial. Lancet 2002;360:1531-9. http://dx.doi.org/10.1016/S0140-6736(02)11522-4.
- Scott RAP, Wilson NM, Ashton HA, Kay DN. Influence of screening on the incidence of ruptured abdominal aortic-aneurysm – 5-year results of a randomized controlled-study. Br J Surg 1995;82:1066-70. http://dx.doi.org/10.1002/bjs.1800820821.
- Jamrozik K, Norman PE, Spencer CA, Parsons RW, Tuohy R, Lawrence-Brown MM, et al. Screening for abdominal aortic aneurysm: lessons from a population-based study. Med J Aust 2000;173:345-50.
- Lindholt JS, Juul S, Fasting H, Henneberg EW. Screening for abdominal aortic aneurysms: single centre randomised controlled trial. BMJ 2005;330.
- Lederle FA, Johnson GR, Wilson SE, Chute EP, Hye RJ, Makaroun MS, et al. The aneurysm detection and management study screening program – validation cohort and final results. Arch Intern Med 2000;160:1425-30. http://dx.doi.org/10.1001/archinte.160.10.1425.
- Singh K, Bonaa KH, Jacobsen BK, Bjork L, Solberg S. Prevalence of and risk factors for abdominal aortic aneurysms in a population-based study – the Tromso study. Am J Epidemiol 2001;154:236-44. http://dx.doi.org/10.1093/aje/154.3.236.
- Scott RAP, Bridgewater SG, Ashton HA. Randomized clinical trial of screening for abdominal aortic aneurysm in women. Br J Surg 2002;89:283-5. http://dx.doi.org/10.1046/j.0007-1323.2001.02014.x.
- Lederle FA, Johnson GR, Wilson SE, Chute EP, Littooy FN, Bandyk D, et al. Prevalence and associations of abdominal aortic aneurysm detected through screening. Ann Intern Med 1997;126:441-9. http://dx.doi.org/10.7326/0003-4819-126-6-199703150-00004.
- Vardulaki KA, Walker NM, Day NE, Duffy SW, Ashton HA, Scott RAP. Quantifying the risks of hypertension, age, sex and smoking in patients with abdominal aortic aneurysm. Br J Surg 2000;87:195-200. http://dx.doi.org/10.1046/j.1365-2168.2000.01353.x.
- Hirsch AT, Haskal ZJ, Hertzer NR, Bakal CW, Creager MA, Halperin JL, et al. American College of Cardiology/American Heart Association 2005 practice guidelines for the management of patients with peripheral arterial disease (lower extremity, renal, mesenteric, and abdominal aortic) – a collaborative report from the American Association for Vascular Surgery/Society for Vascular Surgery,* Society for Cardiovascular Angiography and Interventions, Society for Vascular Medicine and Biology, Society of Interventional Radiology, and the ACC/AHA Task Force on Practice Guidelines (Writing Committee to Develop Guidelines for the Management of Patients with Peripheral Arterial Disease). Circulation 2006;113:E463-654.
- Hall AJ, Busse EFG, McCarville DJ, Burgess JJ. Aortic wall tension as a predictive factor for abdominal aortic aneurysm rupture: improving the selection of patients for abdominal aortic aneurysm repair. Ann Vasc Surg 2000;14:152-7. http://dx.doi.org/10.1007/s100169910027.
- Bengtsson H, Nilsson P, Bergqvist D. Natural-history of abdominal aortic-aneurysm detected by screening. Br J Surg 1993;80:718-20. http://dx.doi.org/10.1002/bjs.1800800613.
- Bown MJ, Sweeting MJ, Brown LC, Powell JT, Thompson SG. RESCAN collaborators . Surveillance intervals for small abdominal aortic aneurysms a meta-analysis. JAMA 2013;309:806-13. http://dx.doi.org/10.1001/jama.2013.950.
- Vardulaki KA, Prevost TC, Walker NM, Day NE, Wilmink ABM, Quick CRG, et al. Growth rates and risk of rupture of abdominal aortic aneurysms. Br J Surg 1998;85:1674-80. http://dx.doi.org/10.1046/j.1365-2168.1998.00946.x.
- Macsweeney STR, Ellis M, Worrell PC, Greenhalgh RM, Powell JT. Smoking and growth-rate of small abdominal aortic-aneurysms. Lancet 1994;344:651-2. http://dx.doi.org/10.1016/S0140-6736(94)92087-7.
- Thompson AR, Cooper JA, Ashton HA, Hafez H. Growth rates of small abdominal aortic aneurysms correlate with clinical events. Br J Surg 2010;97:37-44. http://dx.doi.org/10.1002/bjs.6779.
- Brady AR, Thompson SG, Fowkes FGR, Greenhalgh RM, Powell JT. Abdominal aortic aneurysm expansion – risk factors and time intervals for surveillance. Circulation 2004;110:16-21. http://dx.doi.org/10.1161/01.CIR.0000133279.07468.9F.
- Sweeting MJ, Thompson SG, Brown LC, Powell JT. RESCAN collaborators . Meta-analysis of individual patient data to examine factors affecting growth and rupture of small abdominal aortic aneurysms. Br J Surg 2012;99:655-65. http://dx.doi.org/10.1002/bjs.8707.
- Englund R, Hudson P, Hanel K, Stanton A. Expansion rates of small abdominal aortic aneurysms. Aust N Z J Surg 1998;68:21-4. http://dx.doi.org/10.1111/j.1445-2197.1998.tb04630.x.
- Hackam DG, Thiruchelvam D, Redelmeier DA. Angiotensin-converting enzyme inhibitors and aortic rupture: a population-based case–control study. Lancet 2006;368:659-65. http://dx.doi.org/10.1016/S0140-6736(06)69250-7.
- Schouten O, van Laanen JHH, Boersma E, Vidakovic R, Feringa HHH, Dunkelgrun M, et al. Statins are associated with a reduced infrarenal abdominal aortic aneurysm growth. Eur J Vasc Endovasc Surg 2006;32:21-6. http://dx.doi.org/10.1016/j.ejvs.2005.12.024.
- Santilli SM, Littooy FN, Cambria RA, Rapp JH, Tretinyak AS, d’Audiffret AC, et al. Expansion rates and outcomes for the 3.0-cm to the 3.9-cm infrarenal abdominal aortic aneurysm. J Vasc Surg 2002;35:666-71. http://dx.doi.org/10.1067/mva.2002.121572.
- de Ceniga MV, Gomez R, Estallo L, Rodriguez L, Baquer M, Barba A. Growth rate and associated factors in small abdominal aortic aneurysms. Eur J Vasc Endovasc Surg 2006;31:231-6. http://dx.doi.org/10.1016/j.ejvs.2005.10.007.
- Bown MJ, Sutton AJ, Bell PRF, Sayers RD. A meta-analysis of 50 years of ruptured abdominal aortic aneurysm repair. Br J Surg 2002;89:714-30. http://dx.doi.org/10.1046/j.1365-2168.2002.02122.x.
- McCarthy RJ, Shaw E, Whyman MR, Earnshaw JJ, Poskitt KR, Heather BP. Recommendations for screening intervals for small aortic aneurysms. Br J Surg 2003;90:821-6. http://dx.doi.org/10.1002/bjs.4216.
- Brown PM, Zelt DT, Sobolev B. The risk of rupture in untreated aneurysms: the impact of size, gender, and expansion rate. J Vasc Surg 2003;37:280-3. http://dx.doi.org/10.1067/mva.2003.119.
- Lindholt JS, Vammen S, Juul S, Henneberg EW, Fasting H. The validity of ultrasonographic scanning as screening method for abdominal aortic aneurysm. Eur J Vasc Endovasc Surg 1999;17:472-5. http://dx.doi.org/10.1053/ejvs.1999.0835.
- Cosford PA, Leng GC. Screening for abdominal aortic aneurysm. Cochrane Database Syst Rev 2007;2.
- Lees T, Stansby G, Baker S, Mitchell D, Holt P, Taylor P, et al. The National Vascular Database Report. London: The Audit and Research Committee of the Vascular Society of Great Britain and Ireland; 2009.
- Anjum A, von Allmen R, Greenhalgh R, Powell JT. Explaining the decrease in mortality from abdominal aortic aneurysm rupture. Br J Surg 2012;99:637-45. http://dx.doi.org/10.1002/bjs.8698.
- Coggia M, Javerliat I, Di Centa I, Colacchio G, Cerceau P, Kitzis M, et al. Total laparoscopic infrarenal aortic aneurysm repair: preliminary results. J Vasc Surg 2004;40:448-54. http://dx.doi.org/10.1016/j.jvs.2004.06.037.
- Hallin A, Bergqvist D, Holmberg L. Literature review of surgical management of abdominal aortic aneurysm. Eur J Vasc Endovasc Surg 2001;22:197-204. http://dx.doi.org/10.1053/ejvs.2001.1422.
- Wanhainen A, Bylund N, Bjorck M. Outcome after abdominal aortic aneurysm repair in Sweden 1994–2005. Br J Surg 2008;95:564-70. http://dx.doi.org/10.1002/bjs.6109.
- Cowan JA, Dimick JB, Henke PK, Rectenwald J, Stanley JC, Upchurch GR. Epidemiology of Aortic Aneurysm Repair in the United States from 1993 to 2003. Abdominal Aortic Aneurysm: Genetics, Pathophysiology and Molecular Biology. Oxford: Blackwell Publishing; 2006.
- Schermerhorn ML, O’Malley AJ, Jhaveri A, Cotterill P, Pomposelli F, Landon BE. Endovascular vs. open repair of abdominal aortic aneurysms in the medicare population. N Engl J Med 2008;358:464-74. http://dx.doi.org/10.1056/NEJMoa0707348.
- Livesay JJ, Messner GN, Vaughn WK. Milestones in the treatment of aortic aneurysm. Tex Heart Inst J 2005;32:130-4.
- Elkouri S, Gloviczki P, McKusick MA, Panneton JM, Andrews J, Bower TC, et al. Perioperative complications and early outcome after endovascular and open surgical repair of abdominal aortic aneurysms. J Vasc Surg 2004;39:497-505. http://dx.doi.org/10.1016/j.jvs.2003.10.018.
- Greenhalgh RM, Brown LC, Powell JT, Thompson SG, Epstein D, Sculpher MJ, et al. Endovascular versus open repair of abdominal aortic aneurysm. N Engl J Med 2010;362:1863-71. http://dx.doi.org/10.1056/NEJMoa0909305.
- Greenhalgh RM, Brown LC, Kwong GPS, Powell JT, Thompson SG. Comparison of endovascular aneurysm repair with open repair in patients with abdominal aortic aneurysm (EVAR trial 1), 30-day operative mortality results: randomised controlled trial. Lancet 2004;364:843-8. http://dx.doi.org/10.1016/S0140-6736(04)16979-1.
- Blankensteijn JD, de Jong S, Prinssen M, van der Ham AC, Buth J, van Sterkenburg SMM, et al. Two-year outcomes after conventional or endovascular repair of abdominal aortic aneurysms. N Engl J Med 2005;352:2398-405. http://dx.doi.org/10.1056/NEJMoa051255.
- Prinssen M, Verhoeven ELG, Buth J, Cuypers PWM, van Sambeek M, Balm R, et al. A randomized trial comparing conventional and endovascular repair of abdominal aortic aneurysms. N Engl J Med 2004;351:1607-18. http://dx.doi.org/10.1056/NEJMoa042002.
- Powell JT, Brady AR, Brown LC, Forbes JF, Fowkes FGR, Greenhalgh RM, et al. Mortality results for randomised controlled trial of early elective surgery or ultrasonographic surveillance for small abdominal aortic aneurysms. Lancet 1998;352:1649-55. http://dx.doi.org/10.1016/S0140-6736(98)10137-X.
- Lederle FA, Wilson SE, Johnson GR, Reinke DB, Littooy FN, Acher CW, et al. Immediate repair compared with surveillance of small abdominal aortic aneurysms. N Engl J Med 2002;346:1437-44. http://dx.doi.org/10.1056/NEJMoa012573.
- Powell JT, Brown LC, Forbes JF, Fowkes FGR, Greenhalgh RM, Ruckley CV, et al. Final 12-year follow-up of surgery versus surveillance in the UK Small Aneurysm Trial. Br J Surg 2007;94:702-8. http://dx.doi.org/10.1002/bjs.5778.
- Ballard DJ, Filardo G, Fowkes G, Powell JT. Surgery for small asymptomatic abdominal aortic aneurysms. Cochrane Database Syst Rev 2008;4. http://dx.doi.org/10.1002/14651858.CD001835.pub2.
- Kennedy I. Learning from Bristol: The Report of the Public Inquiry into Children’s Heart Surgery at the Bristol Royal Infirmary 1984–1995 2001. http://webarchive.nationalarchives.gov.uk/20090811143745/http://www.bristol-inquiry.org.uk/final_report/index.htm (accessed 2 January 2014).
- Bown MJ, Sweeting MJ, Brown LC, Powell JT, Thompson SG. RESCAN collaborators . Surveillance intervals for small abdominal aortic aneurysms: a meta-analysis. JAMA 2013;309:806-13. http://dx.doi.org/10.1001/jama.2013.950.
- Basnyat PS, Biffin AH, Moseley LG, Hedges AR, Lewis MH. Mortality from ruptured abdominal aortic aneurysm in Wales. Br J Surg 1999;86:765-70. http://dx.doi.org/10.1046/j.1365-2168.1999.01170.x.
- Brewster DC, Cronenwett JL, Hallett JW, Johnston KW, Krupski WC, Matsumura JS, et al. Guidelines for the treatment of abdominal aortic aneurysms. Report of a subcommittee of the Joint Council of the American Association for Vascular Surgery and Society for Vascular Surgery. J Vasc Surg 2003;37:1106-17. http://dx.doi.org/10.1067/mva.2003.363.
- Lederle FA, Johnson GR, Wilson SE, Ballard DJ, Jordan WD, Blebea J, et al. Rupture rate of large abdominal aortic aneurysms in patients refusing or unfit for elective repair. JAMA 2002;287:2968-72. http://dx.doi.org/10.1001/jama.287.22.2968.
- Oliver S, Clarke-Jones L, Rees R, Milne R, Buchanan P, Gabbay J, et al. Involving consumers in research and development agenda setting for the NHS: developing an evidence-based approach. Health Technol Assess 2004;8.
- Patterson BO, Holt PJE, Hinchliffe R, Loftus IM, Thompson MM. Predicting risk in elective abdominal aortic aneurysm repair: a systematic review of current evidence. Eur J Vasc Endovasc Surg 2008;36:637-45. http://dx.doi.org/10.1016/j.ejvs.2008.08.016.
- Samy AK, Murray G, MacBain G. Glasgow aneurysm score. Cardiovasc Surg 1994;2:41-4.
- Hosmer D, Lemeshow S. Applied Logistic Regression. New York, NY: John Wiley & Sons Inc.; 1989.
- Hanley JA, McNeil BJ. The meaning and use of the area under a Receiver Operating Characteristic (ROC) curve. Radiology 1982;143:29-36. http://dx.doi.org/10.1148/radiology.143.1.7063747.
- Altman DG, Royston P. What do we mean by validating a prognostic model?. Stat Med 2000;19:453-73.
- Altman DG, Vergouwe Y, Royston P, Moons KGM. Prognosis and prognostic research: validating a prognostic model. BMJ 2009;338. http://dx.doi.org/10.1136/bmj.b605.
- Akaike H. New look at statistical-model identification. IEEE Trans Automat Control 1974;19:716-23. http://dx.doi.org/10.1109/TAC.1974.1100705.
- Harrell FJ. Regression Modeling Strategies. New York, NY: Springer; 2001.
- DeLong ER, DeLong DM, Clarke-Pearson DI. Comparing the areas under 2 or more correlated receiver operating characteristic curves – a nonparametric approach. Biometrics 1988;44:837-45.
- Venables WN, Ripley BD. Modern Applied Statistics with S. New York, NY: Springer; 2002.
- Harrell FJ. RMS: Regression Modeling Strategies 2012. http://CRAN.R-project.org/package=rms (accessed 30 August 2012).
- Stonebridge PA, Callam MJ, Bradbury AW, Murie JA, Jenkins AM, Ruckley CV. Comparison of long-term survival after successful repair of ruptured and non-ruptured abdominal aortic aneurysm. Br J Surg 1993;80:585-6. http://dx.doi.org/10.1002/bjs.1800800511.
- Choke E, Lee K, McCarthy M, Nasim A, Naylor AR, Bown M, et al. Risk models for mortality following elective open and endovascular abdominal aortic aneurysm repair: a single institution experience. Eur J Vasc Endovasc Surg 2012;44:549-54. http://dx.doi.org/10.1016/j.ejvs.2012.08.011.
- Lindholt JS, Norman PE. Meta-analysis of postoperative mortality after elective repair of abdominal aortic aneurysms detected by screening. Br J Surg 2011;98:619-22. http://dx.doi.org/10.1002/bjs.7464.
- Ramanan B, Gupta PK, Sundaram A, Gupta H, Johanning JM, Lynch TG, et al. Development of a risk index for prediction of mortality after open aortic aneurysm repair. J Vasc Surg 2013;58:871-8. http://dx.doi.org/10.1016/j.jvs.2013.03.024.
- Hosmer DW, Lemeshow S, May S. Applied Survival Analysis: Regression Modeling of Time-to-event Data. New York, NY: John Wiley & Sons Inc.; 2008.
- Clark TG, Bradburn MJ, Love SB, Altman DG. Survival analysis Part I: basic concepts and first analyses. Br J Cancer 2003;89:232-8. http://dx.doi.org/10.1038/sj.bjc.6601118.
- Bradburn MJ, Clark TG, Love SB, Altman DG. Survival analysis Part III: multivariate data analysis – choosing a model and assessing its adequacy and fit. Br J Cancer 2003;89:605-11. http://dx.doi.org/10.1038/sj.bjc.6601120.
- Royston P. Estimating a Smooth Baseline Hazard Function for the Cox Model. London: Medical Research Council Clinical Trials Unit and University College of London; 2011.
- Grant SW, Hickey GL, Grayson AD, Mitchell DC, McCollum CN. National risk prediction model for elective abdominal aortic aneurysm repair. Br J Surg 2013;100:645-53. http://dx.doi.org/10.1002/bjs.9047.
- Guide to the Methods of Technology Appraisal. London: NICE; 2008.
- Department of Health . National Schedules of Reference Costs: 2012–2013 2013. www.gov.uk/government/publications/nhs-reference-costs-2012-to-2013 (accessed 3 January 2014).
- Filardo G, Powell JT, Martinez MA, Ballard DJ. Surgery for small asymptomatic abdominal aortic aneurysms. Cochrane Database Syst Rev 2012;3.
- Becquemin JP, Pillet JC, Lescalie F, Sapoval M, Goueffic Y, Lermusiaux P, et al. A randomized controlled trial of endovascular aneurysm repair versus open surgery for abdominal aortic aneurysms in low- to moderate-risk patients. J Vasc Surg 2011;53:1167-73.e1. http://dx.doi.org/10.1016/j.jvs.2010.10.124.
- Lederle FA, Freischlag JA, Kyriakides TC, Padberg FT, Matsumura JS, Kohler TR, et al. Outcomes following endovascular vs open repair of abdominal aortic aneurysm: a randomized trial. JAMA 2009;302:1535-42. http://dx.doi.org/10.1001/jama.2009.1426.
- Evar trial participants . Endovascular aneurysm repair versus open repair in patients with abdominal aortic aneurysm (EVAR trial 1): randomised controlled trial. Lancet 2005;365:2179-86. http://dx.doi.org/10.1016/S0140-6736(05)66627-5.
- Prinssen M, Buskens E, Blankensteijn JD. The Dutch Randomised Endovascular Aneurysm Management (DREAM) trial. Background, design and methods. J Cardiovasc Surg 2002;43:379-84.
- Brown LC, Powell JT, Thompson SG, Epstein DM, Sculpher MJ, Greenhalgh RM. The UK EndoVascular Aneurysm Repair (EVAR) trials: randomised trials of EVAR versus standard therapy. Health Technol Assess 2012;16. http://dx.doi.org/10.3310/hta16090.
- Chambers D, Epstein D, Walker S, Fayter D, Paton F, Wright K, et al. Endovascular stents for abdominal aortic aneurysms: a systematic review and economic model. Health Technol Asssess 2009;13. http://dx.doi.org/10.3310/hta13480.
- Stroupe KT, Lederle FA, Matsumura JS, Kyriakides TC, Jonk YC, Ge L, et al. Cost-effectiveness of open versus endovascular repair of abdominal aortic aneurysm in the OVER trial. J Vasc Surg 2012;56:901-9.e2. http://dx.doi.org/10.1016/j.jvs.2012.01.086.
- Kim LG, RA PS, Ashton HA, Thompson SG. Multicentre Aneurysm Screening Study G . A sustained mortality benefit from screening for abdominal aortic aneurysm. Ann Intern Med 2007;146:699-706. http://dx.doi.org/10.7326/0003-4819-146-10-200705150-00003.
- Thompson SG, Brown LC, Sweeting MJ, Bown MJ, Kim LG, Glover MJ, et al. Systematic review and meta-analysis of the growth and rupture rates of small abdominal aortic aneurysms: implications for surveillance intervals and their cost-effectiveness. Health Technol Assess 2013;17. http://dx.doi.org/10.3310/hta17410.
- Glanville J, Kaunelis D, Mensinkai S. How well do search filters perform in identifying economic evaluations in MEDLINE and EMBASE. Int J Technol Assess 2009;25:522-9. http://dx.doi.org/10.1017/S0266462309990523.
- Centre for Reviews and Dissemination . About the CRD Databases 2014. www.crd.york.ac.uk/CRDWeb/AboutPage.asp (accessed 02 April 2014).
- Curtis L. Unit Costs of Health and Social Care 2013. Kent: Personal Social Services Research Unit, University of Kent; 2013.
- Jonk YC, Kane RL, Lederle FA, MacDonald R, Cutting AH, Wilt TJ. Cost-effectiveness of abdominal aortic aneurysm repair: a systematic review. Int J Technol Assess Health Care 2007;23:205-15. http://dx.doi.org/10.1017/S0266462307070316.
- Rawlins MD, Culyer AJ. National Institute for Clinical Excellence and its value judgments. BMJ 2004;329:224-7. http://dx.doi.org/10.1136/bmj.329.7459.224.
- Briggs AH, O’Brien BJ, Blackhouse G. Thinking outside the box: recent advances in the analysis and presentation of uncertainty in cost-effectiveness studies. Ann Rev Public Health 2002;23:377-401. http://dx.doi.org/10.1146/annurev.publhealth.23.100901.140534.
- Fenwick E, Claxton K, Sculpher M. Representing uncertainty: the role of cost-effectiveness acceptability curves. Health Econ 2001;10:779-87. http://dx.doi.org/10.1002/hec.635.
- Hoch JS, Briggs AH, Willan AR. Something old, something new, something borrowed, something blue: a framework for the marriage of health econometrics and cost-effectiveness analysis. Health Econ 2002;11:415-30. http://dx.doi.org/10.1002/hec.678.
- Sendi PP, Briggs AH. Affordability and cost-effectiveness: decision-making on the cost-effectiveness plane. Health Econ 2001;10:675-80. http://dx.doi.org/10.1002/hec.639.
- Epstein DM, Sculpher MJ, Manca A, Michaels J, Thompson SG, Brown LC, et al. Modelling the long-term cost-effectiveness of endovascular or open repair for abdominal aortic aneurysm. Br J Surg 2008;95:183-90. http://dx.doi.org/10.1002/bjs.5911.
- Kind P, Hardman G, Macran S. UK Population Norms for EQ-5D. York, University of York: Centre for Health Economics; 1999.
- Sorensen J, Davidsen M, Gudex C, Pedersen KM, Bronnum-Hansen H. Danish EQ-5D population norms. Scand J Public Health 2009;37:467-74. http://dx.doi.org/10.1177/1403494809105286.
- Montreuil B, Brophy J. Screening for abdominal aortic aneurysms in men: a Canadian perspective using Monte Carlo-based estimates. Can J Surg 2008;51:23-34.
- Henriksson M, Lundgren F. Decision-analytical model with lifetime estimation of costs and health outcomes for one-time screening for abdominal aortic aneurysm in 65-year-old men. Br J Surg 2005;92:976-83. http://dx.doi.org/10.1002/bjs.5122.
- Ehlers L, Overvad K, Sorensen J, Christensen S, Bech M, Kjolby M. Analysis of cost effectiveness of screening Danish men aged 65 for abdominal aortic aneurysm. BMJ 2009;338. http://dx.doi.org/10.1136/bmj.b2243.
- Szende A, Janssen B, Cabasés J. Self-Reported Population Health: An International Perspective Based on EQ-5D. The Netherlands: Springer Open; 2014.
- Bowen J DRG, Hopkins R, Novick T, Blackhouse G, Tarride J-E, . Systematic Review and Cost-effectiveness Analysis of Elective Endovascular Repair Compared to Open Surgical Repair of Abdominal Aortic Aneurysms – Interim Report. Toronto: Program for Assessment of Technology in Health (PATH) at McMaster University and London Health Sciences Centre, on behalf of the Medical Advisory Secretariat (MAS); 2005.
- Eisenstein EL, Davidson-Ray L, Edwards R, Anstrom KJ, Ouriel K. Economic analysis of endovascular repair versus surveillance for patients with small abdominal aortic aneurysms. J Vasc Surg 2013;58:302-10. http://dx.doi.org/10.1016/j.jvs.2013.01.038.
- Lindholt JS, Sorensen J, Sogaard R, Henneberg EW. Long-term benefit and cost-effectiveness analysis of screening for abdominal aortic aneurysms from a randomized controlled trial. Br J Surg 2010;97:826-34. http://dx.doi.org/10.1002/bjs.7001.
- Spronk S, van Kempen BJ, Boll AP, Jorgensen JJ, Hunink MG, Kristiansen IS. Cost-effectiveness of screening for abdominal aortic aneurysm in the Netherlands and Norway. Br J Surg 2011;98:1546-55. http://dx.doi.org/10.1002/bjs.7620.
- Samy AK, Murray G, MacBain G. Prospective evaluation of the Glasgow Aneurysm Score. J R Coll Surg Edinb 1996;41:105-7.
- Biancari F, Leo E, Ylonen K, Vaarala MH, Rainio P, Juvonen T. Value of the Glasgow Aneurysm Score in predicting the immediate and long-term outcome after elective open repair of infrarenal abdominal aortic aneurysm. Br J Surg 2003;90:838-44. http://dx.doi.org/10.1002/bjs.4130.
- Biancari F, Heikkinen M, Lepantalo M, Salenius JP. Glasgow Aneurysm Score in patients undergoing elective open repair of abdominal aortic aneurysm: a Finnvasc study. Eur J Vasc Endovasc Surg 2003;26:612-17. http://dx.doi.org/10.1016/S1078-5884(03)00348-4.
- Hirzalla O, Emous M, Ubbink DT, Legemate D. External validation of the Glasgow Aneurysm Score to predict outcome in elective open abdominal aortic aneurysm repair. J Vasc Surg 2006;44:712-16. http://dx.doi.org/10.1016/j.jvs.2006.06.009.
- Nesi F, Leo E, Biancari F, Bartolucci R, Rainio P, Satta J, et al. Preoperative risk stratification in patients undergoing elective infrarenal aortic aneurysm surgery: Evaluation of five risk scoring methods. Eur J Vasc Endovasc Surg 2004;28:52-8. http://dx.doi.org/10.1016/j.ejvs.2004.02.010.
- Tang TY, Walsh SR, Fanshawe TR, Seppi V, Sadat U, Hayes PD, et al. Comparison of risk-scoring methods in predicting the immediate outcome after elective open abdominal aortic aneurysm surgery. Eur J Vasc Endovasc Surg 2007;34:505-13. http://dx.doi.org/10.1016/j.ejvs.2007.07.019.
- Prytherch DR, Ridler BMF, Beard JD, Earnshaw JJ. A model for national outcome audit in vascular surgery. Eur J Vasc Endovasc Surg 2001;21:477-83. http://dx.doi.org/10.1053/ejvs.2001.1369.
- Tang T, Walsh SR, Prytherch DR, Lees T, Varty K, Boyle JR. VBHOM, a data economic model for predicting the outcome after open abdominal aortic aneurysm surgery. Br J Surg 2007;94:717-21. http://dx.doi.org/10.1002/bjs.5808.
- Giles KA, Schermerhorn ML, O’Malley AJ, Cotterill P, Jhaveri A, Pomposelli FB, et al. Risk prediction for perioperative mortality of endovascular vs open repair of abdominal aortic aneurysms using the Medicare population. J Vasc Surg 2009;50:256-62. http://dx.doi.org/10.1016/j.jvs.2009.01.044.
- Prytherch DR, Sutton GL, Boyle JR. Portsmouth POSSUM models for abdominal aortic aneurysm surgery. Br J Surg 2001;88:958-63. http://dx.doi.org/10.1046/j.0007-1323.2001.01820.x.
- Tang TY, Walsh SR, Prytherch DR, Wijewardena C, Gaunt ME, Varty K, et al. POSSUM models in open abdominal aortic aneurysm surgery. Eur J Vasc Endovasc Surg 2007;34:499-504. http://dx.doi.org/10.1016/j.ejvs.2007.04.007.
- Vergouwe Y, Steyerberg EW, Eijkemans MJC, Habbema JDF. Substantial effective sample sizes were required for external validation studies of predictive logistic regression models. J Clin Epidemiol 2005;58:475-83. http://dx.doi.org/10.1016/j.jclinepi.2004.06.017.
- Donders ART, van der Heijden G, Stijnen T, Moons KGM. Review: a gentle introduction to imputation of missing values. J Clin Epidemiol 2006;59:1087-91. http://dx.doi.org/10.1016/j.jclinepi.2006.01.014.
- van Beek SC, Blankensteijn JD, Balm R. Validation of three models predicting in-hospital death in patients with an abdominal aortic aneurysm eligible for both endovascular and open repair. J Vasc Surg 2013;58:1452-7.e1. http://dx.doi.org/10.1016/j.jvs.2013.05.104.
- Crawford ES, Saleh SA, Babb JW, Glaeser DH, Vaccaro PS, Silvers A. Infrarenal abdominal aortic aneurysm: factors influencing survival after operation performed over a 25-year period. Ann Surg 1981;193:699-70. http://dx.doi.org/10.1097/00000658-198106000-00005.
- Koskas F, Kieffer E. Long-term survival after elective repair of infrarenal abdominal aortic aneurysm: results of a prospective multicentric study. Association for Academic Research in Vascular Surgery (AURC). Ann Vasc Surg 1997;11:473-81. http://dx.doi.org/10.1007/s100169900078.
- De Bruin JL, Baas AF, Buth J, Prinssen M, Verhoeven EL, Cuypers PW, et al. Long-term outcome of open or endovascular repair of abdominal aortic aneurysm. N Engl J Med 2010;362:1881-9. http://dx.doi.org/10.1056/NEJMoa0909499.
- Aune S, Amundsen SR, Evjensvold J, Trippestad A. Operative mortality and long-term relative survival of patients operated on for asymptomatic abdominal aortic aneurysm. Eur J Vasc Endovasc Surgery 1995;9:293-8. http://dx.doi.org/10.1016/S1078-5884(05)80133-9.
- Bernstein EF, Dilley RB, Randolph HF. The improving long-term outlook for patients over 70 years of age with abdominal aortic aneurysms. Ann Surg 1988;207:318-22. http://dx.doi.org/10.1097/00000658-198803000-00016.
- Eldrup N, Budtz-Lilly J, Laustsen J, Bibby BM, Paaske WP. Long-term incidence of myocardial infarct, stroke, and mortality in patients operated on for abdominal aortic aneurysms. J Vasc Surg 2012;55:311-17. http://dx.doi.org/10.1016/j.jvs.2011.08.046.
- Diehm N, Becker G, Katzen B, Benenati J, Kovacs M, Dick F. Statins are associated with decreased mortality in abdominal, but not in thoracic aortic aneurysm patients undergoing endovascular repair: propensity score-adjusted analysis. VASA Zeitschrift Fur Gefasskrankheiten 2008;37:241-9. http://dx.doi.org/10.1024/0301-1526.37.3.241.
- Twine CP, Williams IM. Systematic review and meta-analysis of the effects of statin therapy on abdominal aortic aneurysms. Br J Surg 2011;98:346-53. http://dx.doi.org/10.1002/bjs.7343.
- Hickey GL, Grant SW, Murphy GJ, Bhabra M, Pagano D, McAllister K, et al. Dynamic trends in cardiac surgery: why the logistic EuroSCORE is no longer suitable for contemporary cardiac surgery and implications for future risk models. Eur J Cardiothorac Surg 2013;43:1146-52. http://dx.doi.org/10.1093/ejcts/ezs584.
- Bryce GJ, Payne CJ, Gibson SC, Byrne DS, Delles C, McClure J, et al. B-type natriuretic peptide predicts postoperative cardiac events and mortality after elective open abdominal aortic aneurysm repair. J Vasc Surg 2013;57:345-53. http://dx.doi.org/10.1016/j.jvs.2012.07.053.
- Carlisle J, Swart M. Mid-term survival after abdominal aortic aneurysm surgery predicted by cardiopulmonary exercise testing. Br J Surg 2007;94:966-9. http://dx.doi.org/10.1002/bjs.5734.
- Bown MJ, Horsburgh T, Nicholson ML, Bell PRF, Sayers RD. Cytokines, their genetic polymorphisms, and outcome after abdominal aortic aneurysm repair. Eur J Vasc Endovasc Surg 2004;28:274-80. http://dx.doi.org/10.1016/j.ejvs.2004.05.008.
- Nugent AM, Riley M, Megarry J, O’Reilly MJG, MacMahon J, Lowry R. Cardiopulmonary exercise testing in the preoperative assessment of patients for repair of abdominal aortic aneurysm. Irish J Med Sci 1998;167:238-41. http://dx.doi.org/10.1007/BF02937421.
- Thompson AR, Peters N, Lovegrove RE, Ledwidge S, Kitching A, Magee TR, et al. Cardiopulmonary exercise testing provides a predictive tool for early and late outcomes in abdominal aortic aneurysm patients. Ann R Coll Surg Engl 2011;93:474-81. http://dx.doi.org/10.1308/003588411X587235.
- Hennis PJ, Meale PM, Grocott MP. Cardiopulmonary exercise testing for the evaluation of perioperative risk in non-cardiopulmonary surgery. Postgrad Med J 2011;87:550-7. http://dx.doi.org/10.1136/pgmj.2010.107185.
- Hartley RA, Pichel AC, Grant SW, Hickey GL, Lancaster PS, Wisely NA, et al. Preoperative cardiopulmonary exercise testing and risk of early mortality following abdominal aortic aneurysm repair. Br J Surg 2012;99:1539-46. http://dx.doi.org/10.1002/bjs.8896.
- Prinssen M, Buskens E, de Jong SE, Buth J, Mackaay AJ, Sambeek MR, et al. Cost-effectiveness of conventional and endovascular repair of abdominal aortic aneurysms: results of a randomized trial. J Vasc Surg 2007;46:883-90. http://dx.doi.org/10.1016/j.jvs.2007.07.033.
- Young KC, Awad NA, Johansson M, Gillespie D, Singh MJ, Illig KA. Cost-effectiveness of abdominal aortic aneurysm repair based on aneurysm size. J Vasc Surg 2010;51:27-32. http://dx.doi.org/10.1016/j.jvs.2009.08.004.
- Burström K, Johannesson M, Diderichsen F. Swedish population health-related quality of life results using the EQ-5D. Qual Life Res 2001;10:621-35. http://dx.doi.org/10.1023/A:1013171831202.
- Sørensen J, Davidsen M, Gudex C, Pedersen KM, Brønnum-Hansen H. Danish EQ-5D population norms. Scand J Public Health 2009;37:467-74. http://dx.doi.org/10.1177/1403494809105286.
Appendix 1 Vascular Governance North West contributing surgeons
Surgeons who contributed to the Vascular Governance North West database
| John Abraham | Maher Hamish | Srinivasa Rao Vallabhaneni |
| Haytham Al-Khaffaf | Madgi Hanafy | David Reilly |
| Nile Allaf | Simon Hardy | Steve Richardson |
| Mohamed Baguneid | Neil Hulton | Graham Riding |
| Arun Balakrishnan | Riza Ibrahim | Yousef Rouhani |
| Stephen Blair | Mohideen Jameel | Robert Salaman |
| John Brennan | David Jones | Mark Scriven |
| Moatasiem Bukhari | Jos Joseph | James Scurr |
| John Calvey | Ursula Kirkpatrick | Ferdinand Serracino-Inglott |
| Colin Chan | Otto Klimach | Raashid Shahbazi |
| Ramasubramanyan Chandrasekar | Manmohan Madan | Ramanathan Shivalingham |
| Antonio da Silva | Barun Majumder | Jonathan Smout |
| Linda De Cossart | Frank Mason | Vince Smyth |
| Sameh Dimitri | Charles McCollum | William Tait |
| Susan Drinkwater | Paul Moody | Rashid Tawqeer |
| Paul Edwards | John Mosley | Nee Beng Teo |
| Ansy Egun | David Murray | George Thomson |
| Graeme Ferguson | Jag Naik | Mark Tomlinson |
| Robert Fisher | Simon Neequaye | Francesco Torella |
| Jonathan Ghosh | Tom Nicholas | Richard Ward |
| Martin Greaney | Deji Olojugba | Mark Welch |
| Andrew Guy | Madu Onwudike | Leith Williams |
| Mathew Hadfield | Taohid Oshodi | Gerard Williams |
| Hisham Osman | Paul Wilson | |
| Vittorio Perricone | Leszek Wolowczyk | |
| Chowdary Pratap | Anthony Woodyer | |
| Asad Rahi | Iraj Zeynali |
Appendix 2 Individual patient data
| Data field | Data type |
|---|---|
| Demographic data | |
| Hospital | Free text |
| Surgeon | Free text |
| Anaesthetist | Free text |
| Radiologist | Free text |
| Surname | Free text |
| First name | Free text |
| NHS number | Free text |
| Postcode | Free text |
| Date of birth | Free text |
| Sex | List |
| AAA specific data | |
| Symptoms | Yes/no |
| Level | List |
| Diameter | Free text |
| Type | List |
| Comorbidity data | |
| Ischaemic heart disease | Yes/no |
| Previous MI | Yes/no |
| Cardiac failure | Yes/no |
| Chronic respiratory disease | Yes/no |
| Dyspnoea | Yes/no |
| Previous stroke/TIA | Yes/no |
| Peripheral vascular disease | Yes/no |
| Diabetes | Yes/no |
| Antiplatelet medication | Yes/no |
| Antihypertensive medication | Yes/no |
| Statin medication | Yes/no |
| Smoker | List |
| Preoperative investigations | |
| Abnormal ECG | Free text |
| Sodium | Free text |
| Potassium | Free text |
| Urea | Free text |
| Creatinine | Free text |
| eGFR | Free text |
| Haemoglobin | Free text |
| WCC | Free text |
| Platelets | Free text |
| Data field | Data type |
| Operative details | |
| Admission date | Free text |
| Procedure date | Free text |
| Procedure urgency | List |
| Procedure type | List |
| Previous aortic surgery/stent | Yes/no |
| Open surgery details | |
| Type of repair | List |
| Clamp level | List |
| Intraoperative blood loss | Free text |
| Blood transfusion | Free text |
| EVAR details | |
| Graft type | List |
| Fenestrations | Yes/no |
| Branched | Yes/no |
| Scallops | Yes/no |
| Chimney | Yes/no |
| Access | List |
| Adjunct procedure | Yes/no |
| Intraoperative blood loss | Free text |
| Blood transfusion | Free text |
| Contrast volume | Free text |
| Conversion to open | Yes/no |
| Endoleak on completion | Yes/no |
| Device name | Free text |
| Outcomes | |
| Return to theatre | Yes/no |
| Graft limb occlusion | Yes/no |
| Limb ischaemia | Yes/no |
| Wound infection | Yes/no |
| MI | Yes/no |
| Stroke | Yes/no |
| Respiratory failure | Yes/no |
| Renal failure | Yes/no |
| In-hospital mortality | Yes/no |
| Discharge date | Free text |
| Additional comments | Free text |
| Data field | Data type |
|---|---|
| Preoperative data | |
| Patient date of birtha | Date |
| Local patient identifiera | Free text |
| Sexa | List |
| OPCS procedure codea | List |
| Admission datea | Date |
| Admission modea | List |
| Transfer | Yes/no |
| Diabetes | Yes/no |
| Cardiac history | Yes/no |
| Current smoker | Yes/no |
| Renal dialysis | Yes/no |
| Renal transplant | Yes/no |
| Glasgow Coma Scale | List |
| Loss of consciousness | Yes/no |
| Symptomatic aneurysm | Yes/no |
| Maximum AAA diameter | Free text |
| AAA screening programme | Yes/no |
| Surveillance programme | Yes/no |
| Suitable for EVAR | Yes/no |
| Fit for open surgery | Yes/no |
| ECG | List |
| Other abnormal rhythm | Free text |
| Antiplatelet agent | Yes/no |
| Beta-blocker | Yes/no |
| Statin | Yes/no |
| Lowest preoperative SBP | Free text |
| Highest preoperative pulse | Free text |
| Haemoglobin | Free text |
| WCC | Free text |
| Urea | Free text |
| Creatinine | Free text |
| Sodium | Free text |
| Potassium | Free text |
| Albumin | Free text |
| INR | Free text |
| MRSA positive | List |
| Operative data | |
| Operation datea | Date |
| ASA grade | List |
| Operation start timea | Date/time |
| Operation finish timea | Date/time |
| Grade of senior surgeon | List |
| Timing of surgery | List |
| Previous aortic surgery/stent | Yes/no |
| Data field | Data type |
| AAA surgery | List |
| EVAR | Yes/no |
| Type of graft | List |
| Type of graft other | Free text |
| Laparoscopic AAA repair | List |
| Anaesthetic | Check |
| Grade of anaesthetist | List |
| Aortic findings | Multilist |
| Intraoperative blood loss | List |
| Volume of cell salvage transfused | Text |
| Open area of necrosis | Yes/no |
| Wound class | List |
| Graft used | List |
| Lowest intraoperative systolic blood pressure | Text |
| Highest intraoperative pulse | Text |
| Postoperative data | |
| AAA reoperation | Yes/no |
| Any complications | Yes/no |
| Limb ischaemia | List |
| Anastomotic complications | Radio |
| Haemorrhage | Radio |
| Infection | Multilist |
| Diagnosis date | Date |
| Surgical site infection | List |
| Organism | Free text |
| Postoperative positive for MRSA | Yes/no |
| Developed MRSA bacteraemia | Yes/no |
| Developed Clostridium difficile diarrhoea | Yes/no |
| Wound dehiscence | List |
| Venous thromboembolism | List |
| Postoperative stroke | List |
| Postoperative MI | Yes/no |
| Postoperative cardiac failure | Yes/no |
| Postoperative impaired renal function | Yes/no |
| Need for haemofiltration/dialysis | Yes/no |
| Postoperative hypotension | Yes/no |
| Postoperative respiratory failure | Yes/no |
| Postoperative ischaemic bowel | Yes/no |
| Other complication | Free text |
| Destination after operation | List |
| Return to theatre within 30 days | Yes/no |
| Discharge statusa | List |
| Discharge datea | Date |
| Death datea | Date |
| Death causea | Free text |
Appendix 3 Studies used in the RESCAN analysis of abdominal aortic aneurysm growth and rupture
| Study | Number of patients |
|---|---|
| Western Australia | 685 |
| Bournemouth, UK | 677 |
| Chichester, UK | 1504 |
| Edinburgh, UK | 1052 |
| Gloucestershire, UK | 1981 |
| Huntingdon, UK | 629 |
| Leeds, UK | 267 |
| Leicester, UK | 899 |
| Manchester, UK | 1095 |
| MASS, UK | 1122 |
| Tromsó, Norway | 224 |
| PIVOTAL, USA | 715 |
| Propranolol, Canada | 548 |
| Galdakao, Spain | 926 |
| Stirling, UK | 457 |
| Gävle, Sweden | 243 |
| UKSAT, UK | 2227 |
| Viborg, Denmark | 224 |
Appendix 4 Patient and public involvement group membership
| Name | Group position |
|---|---|
| Helen O’Donnell | Vascular specialist nurse |
| Nick Wisely | Consultant anaesthetist |
| Anthony Echersley | Patient |
| Max Ramsey | Patient |
| Wendy Ramsey | Patient relative |
| Ann Pollard | Patient |
| Doug Claydon | Patient (cochairman) |
| David Vaughan | Patient |
| Janet Vaughan | Patient relative |
| Robert Rolfe | Patient |
| Malcolm Pythian | Patient |
| Pat Pythian | Patient relative |
| Colin Sadler | Patient |
| Lionel Nuttall | Patient |
| John Hatton | Patient |
| David Smith | Patient (cochairman) |
| Peter Gardiner | Patient |
Appendix 5 Patient and surgeon information
Appendix 6 Risk prediction scores in abdominal aortic aneurysm repair
Glasgow Aneurysm Score
Vascular Biochemistry and Haematology Outcome Model
Vascular Physiological and Operative Severity Score for enUmeration of Mortality
A physiology score calculator is available (http://www.riskprediction.org.uk). The score can be calculated using table 1 in the POSSUM scoring system manuscript. 114
Medicare model
Vascular Governance North West model
Appendix 7 Discrete event simulation model output definitions
| Output | Definition |
|---|---|
| Median life expectancy | Median age at death of all patient simulations |
| 1-year survival | Per cent of all patient simulations still alive at 1 year following initiation of the simulation |
| 2-year survival | Per cent of all patient simulations still alive at 2 years following initiation of the simulation |
| 5-year survival | Per cent of all patient simulations still alive at 5 years following initiation of the simulation |
| 10-year survival | Per cent of all patient simulations still alive at 10 years following initiation of the simulation |
| Other cause of death (prior to repair) | Per cent of all non-AAA patient simulation deaths prior to AAA repair |
| Death due to rupture | Per cent of all patient simulations with death due to rupture of AAA |
| Rupture survival | Per cent of all patient simulations with rupture of AAA and discharge from hospital following AAA repair |
| Postoperative survival | Per cent of all patient simulations that undergo AAA repair and also survive until discharge |
| Growth rate at size | Mean growth rate (cm/year) of AAA of all patient simulations at designated repair threshold |
| 1-year rupture probability at intervention | Per cent of all patient simulations that would rupture within 1 year following the designated repair threshold |
| Probability of repair | Per cent of all patients simulations that reach the designated repair threshold |
| In-hospital mortality on repair | Per cent of all patients simulations that reach the designated repair threshold that die in hospital following elective repair |
| 5-year postoperative survival | Per cent of all patient simulations that reach the designated repair threshold that also are still alive at 5 years following elective repair |
| 10-year postoperative survival | Per cent of all patient simulations that reach the designated repair threshold that also are still alive at 10 years following elective repair |
| Median age at repair (years) | Median age of all patient simulations that reach the designated repair threshold |
| Median years to reach size | Median time (years) to reach the designated repair threshold |
Appendix 8 Excluded and included economic studies
| Reference | Reason for exclusion |
|---|---|
| Abbotts J, McIntosh H. Is There a Difference in Operative Mortality Between Endovascular Aneurysm Repair and Open Surgery in Elective Abdominal Aortic Aneurysm? Glasgow: NHS Quality Improvement Scotland (NHS QIS); 2012 | 1 |
| Abularrage CJ, Sheridan MJ, Mukherjee D. Endovascular versus ‘fast-track’ abdominal aortic aneurysm repair. Vasc Endovascular Surg 2005;39:229–36 | 1 |
| Arnaoutakis GJ, Hundt JA, Shah AS, Cameron DE, Black JH. Comparative analysis of hospital costs of open and endovascular thoracic aortic repair. Vasc Endovascular Surg 2011;45:39–45 | 1 |
| Aune S, Laxdal E, Pedersen G, Dregelid E. Lifetime gain related to cost of repair of ruptured abdominal aortic aneurysm in octogenarians. Eur J Vasc Endovascular Surg 2004;27:299–304 | 1 |
| Ballard JL, Abou-Zamzam AM, Teruya TH, Bianchi C, Petersen FF, Quinones W, et al. Quality of life before and after endovascular and retroperitoneal abdominal aortic aneurysm repair. J Vasc Surg 2004;39:797–803 | 1 |
| Beeman BR, Doctor LM, Doerr K, McAfee-Bennett S, Dougherty MJ, Calligaro KD. Duplex ultrasound imaging alone is sufficient for midterm endovascular aneurysm repair surveillance: a cost analysis study and prospective comparison with computed tomography scan. J Vasc Surg 2009;50:1019–24 | 3 |
| Beinfeld MT, Wittenberg E, Gazelle GS. Cost-effectiveness of whole-body CT screening. Radiology 2005;234:415–22 | 1, 2 |
| Bisdas T, Wilhelmi M, Haverich A, Teebken OE. Cryopreserved arterial homografts vs silver-coated Dacron grafts for abdominal aortic infections with intraoperative evidence of microorganisms. J Vasc Surg 2011;53:1274–81 | 3 |
| BlueCross BlueShield Association. Special Report: Critical Appraisal of CT Colonography Cost-effectiveness Analyses. Chicago, IL: BCBS; 2009 | 3 |
| Brooke BS, Goodney PP, Powell RJ, Fillinger MF, Travis LL, Goodman DC, et al. Early discharge does not increase readmission or mortality after high-risk vascular surgery. J Vasc Surg 2013;57:734–40 | 3 |
| Canadian Agency for Drugs and Technologies in Health. Endovascular Therapy for Elective and Ruptured Abdominal Aortic Aneurysm Procedures: A description of Utilization Trends across Canada. Ottawa, ON: CADTH; 2013 | 1 |
| Chandra V, Greenberg JI, Al-Khatib WK, Harris EJ, Dalman RL, Lee JT. Cost impact of extension cuff utilization during endovascular aneurysm repair. Ann Vasc Surg 2012;26:86–92 | 1 |
| Chen S, Husereau D, Noorani H, Tran K, Boudreau R, Lentle B, et al. Portable ultrasound devices in emergency departments. Ottawa, ON: Canadian Coordinating Office for Health Technology Assessment (CCOHTA); 2006 | 3 |
| Chisci E, Setacci F, Iacoponi F, De Donato G, Cappelli A, Setacci C. Surveillance imaging modality does not affect detection rate of asymptomatic secondary interventions following EVAR. Eur J Vasc Endovasc Surg 2012;43:276–81 | 3 |
| Cote B, Lance JM, LeBrun M. Population Ultrasound Screening for Abdominal Aortic Aneurysms. Montreal, QC: Agence d’Evaluation des Technologies et des Modes d’Intervention en Sante (AETMIS); 2010 | 1 |
| Dachman AH, Flicker MS, Tsoukas AT, Hazra A. Economic impact of extracolonic findings at computed tomographic colonography. J Comput Assist Tomo 2008;32:497–503 | 3 |
| del Mar Polo de Santos M, Matos SL, Navarro BM, Alcazar RA. Systematic Review of the Effectiveness and Safety of Endovascular Treatment of Thoracic Aortic Diseases. Madrid: Agencia de Evaluacion de Tecnologias Sanitarias (AETS); 2005 | 3 |
| Duriseti RS, Brandeau ML. Cost-effectiveness of strategies for diagnosing pulmonary embolism among emergency department patients presenting with undifferentiated symptoms. Ann Emerg Med 2010;56:321–32 | 3 |
| Fleisher LA, Corbett W, Berry C, Poldermans D. Cost-effectiveness of differing perioperative beta-blockade strategies in vascular surgery patients. J Cardiothorac Vasc Anesth 2004;18:7–13 | 3 |
| Fleming C, Whitlock E, Beil T, Lederle F. Primary Care Screening for Abdominal Aortic Aneurysm. Rockville, MD: Agency for Healthcare Research and Quality (AHRQ); 2005 | 1 |
| Galician Agency for Health Technology Assessment (AVALIA-T). Efficacy and Effectiveness of Screening for Abdominal Aortic Aneurysm in a Population at Risk. Cost-effectiveness Analysis. Applicability inside the National Healthcare System. Santiago de ComPostela: Galician Agency for Health Technology Assessment (AVALIA-T); 2008 | 1 |
| Gazoni LM, Speir AM, Kron IL, Fonner E, Crosby IK. Elective thoracic aortic aneurysm surgery: better outcomes from high-volume centers. J Am Coll Surg 2010;210:855–60 | 3 |
| Giles KA, Hamdan AD, Pomposelli FB, Wyers MC, Dahlberg SE, Schermerhorn ML. Population-based outcomes following endovascular and open repair of ruptured abdominal aortic aneurysms. J Endovasc Ther 2009;16:554–64 | 1 |
| Goodyear SJ, Yow H, Saedon M, Shakespeare J, Hill CE, Watson D, et al. Risk stratification by preoperative cardiopulmonary exercise testing improves outcomes following elective abdominal aortic aneurysm surgery: a cohort study. Periop Med 2013;2 | 3 |
| Guirguis-Blake JM, Beil TL, Sun X, Senger CA, Whitlock EP. Primary Care Screening for Abdominal Aortic Aneurysm: A Systematic Evidence Review for the U.S. Preventative Services Task Force. Rockville, MD: Agency for Healthcare Research and Quality (AHRQ); 2014 | 1 |
| Ha CD, Calcagno D. Amplatzer Vascular Plug to occlude the internal iliac arteries in patients undergoing aortoiliac aneurysm repair. J Vasc Surg 2005;42:1058–62 | 3 |
| Hassan C, Pickhardt P, Laghi A, Kim D, Zullo A, Iafrate F, et al. Computed tomographic colonography to screen for colorectal cancer, extracolonic cancer, and aortic aneurysm: model simulation with cost-effectiveness analysis. Arch Intern Med 2008;168:696–705 | 1, 3 |
| Haute Autorite de Sante/French National Authority for Health (drafted by the former National Agency for Accreditation and Evaluation in Healthcare). Stent-grafts in the Treatment of Thoracic Aortic Aneurysm and Dissection. Paris: Haute Autorite de Sante (French National Authority for Health) (HAS); 2006 | 3 |
| HAYES, Inc. Endovascular Repair, Abdominal Aortic Aneurysms. Lansdale, PA: HAYES, Inc.; 2007 | 1 |
| HAYES, Inc. Endovascular Repair of Thoracic Aortic Aneurysms and Dissections. Lansdale, PA: HAYES, Inc.; 2007 | 3 |
| HAYES, Inc. Endovascular Repair of Abdominal Aortic Aneurysms. Lansdale, PA: HAYES, Inc.; 2009 | 1 |
| HAYES, Inc. Thoracic Aortic Aneurysms and Dissections (TAAD). Lansdale, PA: HAYES, Inc.; 2011 | 3 |
| HAYES, Inc. Endovascular Repair of Abdominal Aortic Aneurysms. Lansdale, PA: HAYES, Inc.; 2013 | 1 |
| Institut fuer Qualitaet und Wirtschaftlichkeit im Gesundheitswesen (IQWiG). Production of an Evidence Report on the Relationship Between the Quantity of Operations Performed in Patients Undergoing Elective Surgery of an Abdominal Aortic Aneurysm and the Quality of Outcome. Cologne: Institut fuer Qualitaet und Wirtschaftlichkeit im Gesundheitswesen (IQWiG); 2006 | 1 |
| Jean-Baptiste E, Hassen-Khodja R, Haudebourg P, Bouillanne PJ, Declemy S, Batt M. Percutaneous closure devices for endovascular repair of infrarenal abdominal aortic aneurysms: a prospective, non-randomized comparative study. Euro J Vasc Endovasc Surg 2008;35:422–8 | 3 |
| Kalko Y, Ugurlucan M, Basaran M, Nargileci E, Kafa U, Kosker T, Yerebakan C, Yasar T. Standard open repair versus minilaparotomy approach for abdominal aortic aneurysms: what is the best approach in patients with ischemic heart disease? Minerva Chir 2008;63:269–76 | 1 |
| Karmy-Jones R, Bloch R, Nicholls S. A comparison of endovascular repair versus open repair of abdominal aortic aneurysms in a community setting. Innovations 2009;4:261–4 | 1 |
| Lachat ML, Pecoraro F, Mayer D, Guillet C, Glenck M, Rancic Z, et al. Outpatient endovascular aortic aneurysm repair: experience in 100 consecutive patients. Ann Surg 2013;258:754–9 | 1 |
| Lee WA, Brown MP, Nelson PR, Huber TS. Total percutaneous access for endovascular aortic aneurysm repair (‘Preclose’ technique). J Vasc Surg 2007;45:1095–101 | 1 |
| Luengo S, del Mar Polo M. Monitored Use of Endovascular Treatment of Abdominal Aortic Aneurysms Using Endovascular Grafts IPE-05/44 (Public report). Madrid: Agencia de Evaluacion de Tecnologias Sanitarias (AETS); 2005 | 1 |
| Mani K, Alund M, Bjorck M, Lundkvist J, Wanhainen A. Screening for abdominal aortic aneurysm among patients referred to the vascular laboratory is cost-effective. Eur J Vasc Endovasc Surg 2010;39:208–16 | 1, 2 |
| Mani K, Wanhainen A, Lundkvist J, Lindstrom D. Cost-effectiveness of intensive smoking cessation therapy among patients with small abdominal aortic aneurysms. J Vasc Surg 2011;54:628–36 | 3 |
| Mantha S, Foss J, Ellis JE, Roizen MF. Intense cardiac troponin surveillance for long-term benefits is cost-effective in patients undergoing open abdominal aortic surgery: a decision analysis model. Anesth Analg 2007;105:1346–56 | 1 |
| Markovic M, Davidovic L, Savic N, Sindjelic R, Ille T, Dragas M. Intraoperative cell salvage versus allogeneic transfusion during abdominal aortic surgery: clinical and financial outcomes. Vascular 2009;17:83–92 | 3 |
| McCutcheon BA, Talamini MA, Chang DC, Rose JA, Bandyk DF, Wilson SE. The comparative effectiveness of surgeons over interventionalists in endovascular repairs of abdominal aortic aneurysm. Ann Surg 2013;258:476–82 | 3 |
| McIntosh H. What is the Published Evidence of an Association Between Hospital Volume and Operative Mortality for Surgical Repair (Open and Endovascular) of Unruptured and Ruptured Abdominal Aortic Aneurysms? Glasgow: NHS Quality Improvement Scotland (NHS QIS); 2012 | 3 |
| McNally MM, Agle SC, Parker FM, Bogey WM, Powell CS, Stoner MC. Preoperative statin therapy is associated with improved outcomes and resource utilization in patients undergoing aortic aneurysm repair. J Vasc Surg 2010;51:1390–6 | 3 |
| Medical Advisory Secretariat. Fenestrated endovascular grafts for the repair of juxtarenal aortic aneurysms: an evidence-based analysis. Ont Health Technol Assess Ser 2009;9:1–51 | 3 |
| Medical Advisory Secretariat. Endovascular repair of abdominal aortic aneurysms in low surgical risk patients. Ont Health Technol Assess Ser 2009;10(Suppl. 1):1–15 | 1 |
| Medical Advisory Secretariat. Endovascular repair of descending thoracic aortic aneurysm: an evidence-based analysis. Ont Health Technol Assess Ser 2005;5:1–59 | 3 |
| Medical Advisory Secretariat. Ultrasound screening for abdominal aortic aneurysm: an evidence-based analysis. Ont Health Technol Assess Ser 2006;6:1–67 | 1, 3 |
| Min SI, Min SK, Ahn S, Kim SM, Park D, Park T, et al. Comparison of costs of endovascular repair versus open surgical repair for abdominal aortic aneurysm in Korea. J Korean Med Sci 2012;27:416–22 | 1 |
| Morimae H, Maekawa T, Tamai H, Takahashi N, Ihara T, Hori A, et al. Cost disparity between open repair and endovascular aneurysm repair for abdominal aortic aneurysm: a single-institute experience in Japan. Surg Today 2012;42:121–6 | 1 |
| Moysidis T, Lohmann M, Lutkewitz S, Kemmeries G, Kroger K. Cost associated with D-Dimer screening for acute aortic dissection. Adv Ther 2011;28:1038–44 | 3 |
| Murphy EH, Beck AW, Clagett GP, DiMaio JM, Jessen ME, Arko FR. Combined aortic debranching and thoracic endovascular aneurysm repair (TEVAR) effective but at a cost. Arch Surg 2009;144:222–7 | 3 |
| National Institute for Clinical Excellence (NICE). Endovascular Stent-Graft Placement in Thoracic Aortic Aneurysms and Dissections. London: NICE; 2005 | 3 |
| National Institute for Health and Care Excellence (NICE). Stent-Graft Placement in Abdominal Aortic Aneurysm. London: NICE; 2006 | 2 |
| Narayan P, Wong A, Davies I, Angelini GD, Bryan AJ, Wilde P, et al. Thoracic endovascular repair versus open surgical repair: which is the more cost-effective intervention for descending thoracic aortic pathologies? Eur J Cardiothorac Surg 2011;40:869–74 | 3 |
| Ni ZH, Luo JF, Huang WH, Liu Y, Xue L, Fan RX, et al. Totally percutaneous thoracic endovascular aortic repair with the preclosing technique: a case–control study. Chin Med J 2011;124:851–5 | 3 |
| Noll RE, Tonnessen BH, Kim J, Money SR, Sternbergh WC. Long-term postplacement cost comparison of AneuRx and Zenith Endografts. Ann Vasc Surg 2008;22:710–15 | 3 |
| Ohrlander T, Nessvi S, Gottsater A, Dencker M, Acosta S. Influence of preoperative medical assessment prior to elective endovascular aneurysm repair for abdominal aortic aneurysm. Int Angiol 2012;31:368–75 | 1 |
| Ontario Ministry of Health and Long-Term Care. Endovascular Repair of Abdominal Aortic Aneurysms in Low Surgical Risk Patients: rapid review. Toronto, ON: Medical Advisory Secretariat (MAS); 2010 | 2 |
| Pellerin O, Caruba T, Kandounakis Y, Novelli L, Pineau J, Prognon P, et al. Embolization of the internal iliac artery: cost-effectiveness of two different techniques. Cardiovasc Interv Radiol 2008;31:1088–93 | 3 |
| Pichon Riviere A, Augustovski F, Cernadas C, Ferrante D, Regueiro A, Garcia Marti S. Elective endovascular repair for aortic abdominal aneurysm. Ciudad de Buenos Aires: Institute for Clinical Effectiveness and Health Policy (IECS); 2007 | 1 |
| Pickhardt PJ, Hassan C, Laghi A, Zullo A, Kim DH, Iafrate F, et al. Small and diminutive polyps detected at screening CT colonography: a decision analysis for referral to colonoscopy. Am J Roentgenol 2008;190:136–44 | 3 |
| Pickhardt PJ, Hassan C, Laghi A, Kim DH. CT colonography to screen for colorectal cancer and aortic aneurysm in the Medicare population: cost-effectiveness analysis. Am J Roentgenol 2009;192:1332–40 | 1 |
| Roos H, Falkenberg M, Zachrisson K, Wingren U, Samuelsson O, Jivegard L, et al. Fenestrated aortic repair of aortic aneurysm. Gothenburg: The Regional Health Technology Assessment Centre (HTA-centrum), Region Vastra Gotaland; 2010 | 1 |
| Ryer EJ, Garvin RP, Webb TP, Franklin DP, Elmore JR. Comparison of outcomes with coils versus vascular plug embolization of the internal iliac artery for endovascular aortoiliac aneurysm repair. J Vasc Surg 2012;56:1239–45 | 3 |
| Tatsuishi W, Kohri T, Kodera K, Asano R, Kataoka G, Kubota S, et al. Usefulness of an enhanced recovery after surgery protocol for perioperative management following open repair of an abdominal aortic aneurysm. Surg Today 2012;42:1195–200 | 1 |
| Tawfick WA, O’Connor M, Hynes N, Sultan S. Implementation of the Continuous AutoTransfusion System (C.A.T.S) in open abdominal aortic aneurysm repair: an observational comparative cohort study. Vasc Endovasc Surg 2008;42:32–9 | 3 |
| Vogel TR, Nackman GB, Brevetti LS, Crowley JG, Bueno MM, Banavage A, et al. Resource utilization and outcomes: effect of transfer on patients with ruptured abdominal aortic aneurysms. Ann Vasc Surg 2005;19:149–53 | 1 |
| Vogel TR, Dombrovskiy VY, Haser PB, Graham AM. Has the implementation of EVAR for ruptured AAA improved outcomes? Vasc Endovasc Surg 2009;43:252–7 | 1 |
| Vogel TR, Dombrovskiy VY, Graham AM, Lowry SF. The impact of hospital volume on the development of infectious complications after elective abdominal aortic surgery in the Medicare population. Vasc Endovasc Surg 2011;45:317–24 | 3 |
| Wanhainen A, Lundkvist J, Bergqvist D, Bjorck M. Cost-effectiveness of screening women for abdominal aortic aneurysm. J Vasc Surg 2006;43:908–14 | 1 |
| Warmuth M. Endovascular repair of aortic aneurysms. Vienna: Ludwig Boltzmann Institut fuer Health Technology Assessment (LBIHTA); 2013 | 1 |
| Williams TK, Schneider EB, Black JH, Lum YW, Freischlag JA, Perler BA, et al. Disparities in outcomes for Hispanic patients undergoing endovascular and open abdominal aortic aneurysm repair. Ann Vasc Surg 2013;27:29–37 | 1 |
| Reference | Reason for exclusion |
|---|---|
| Badger SA, Jones C, Murray A, Lau LL, Young IS. Implications of attendance patterns in Northern Ireland for abdominal aortic aneurysm screening. Eur J Vasc Endovasc Surg 2011;42:434–9 | 1 |
| Blackhouse G, Hopkins R, Bowen JM, De Rose G, Novick T, Tarride JE, et al. A cost-effectiveness model comparing endovascular repair to open surgical repair of abdominal aortic aneurysms in Canada. Value Health 2009;12:245–52 | 2 |
| Bonneux L, Cleemput I, Vrijens F, Vanoverloop J, Galloo P, Ramaekers D. Elective Endovascular Treatment of the Abdominal Aortic Aneurysm (AAA). Brussels: Belgian Health Care Knowledge Centre (KCE); 2005 | 4 |
| Center for Medical Technology Assessment. Screening for Abdominal Aortic Aneurysm – A Health Economic Assessment. Linkoping: Center for Medical Technology Assessment (CMT); 2004 | 4 |
| Flynn K. Guidance for Screening for Abdominal Aortic Aneurysms in Veterans Health Administration. Boston, MA: VA Technology Assessment Program (VATAP); 2005 | 4 |
| Fotis T, Tsoumakidou G, Katostaras T, Kalokairinou A, Konstantinou E, Kiki V, et al. Cost and effectiveness comparison of endovascular aneurysm repair versus open surgical repair of abdominal aortic aneurysm: a single-center experience. J Vasc Nurs 2008;26:15–21 | 1 |
| Giardina S, Pane B, Spinella G, Cafueri G, Corbo M, Brasseur P, et al. An economic evaluation of an abdominal aortic aneurysm screening program in Italy. J Vasc Surg. 2011;54:938–46 | 1 |
| Health Care Insurance Board/College voor zorgverzekeringen. Dutch Randomized Endovascular Aneurysm Management Dream-trial-primary research. Diemen: Health Care Insurance Board/College voor Zorgverzekeringen (CVZ); 2005 | 2 |
| Henriksson M, Lundgren F. Decision-analytical model with lifetime estimation of costs and health outcomes for one-time screening for abdominal aortic aneurysm in 65-year-old men. Br J Surg 2005;92:976–83 | 2 |
| Henriksson M, Lundgren F, Carlsson P. Informing the efficient use of health care and health care research resources: the case of screening for abdominal aortic aneurysm in Sweden. Health Econ 2006;15:1311–22 | 2 |
| Hynes N, Sultan S. A prospective clinical, economic, and quality-of-life analysis comparing endovascular aneurysm repair (EVAR), open repair, and best medical treatment in high-risk patients with abdominal aortic aneurysms suitable for EVAR: the Irish patient trial. J Endovasc Ther 2007;14:763–76 | 1 |
| Kapma MR, Groen H, Oranen BI, Van Der Hilst CS, Tielliu IF, Zeebregts CJ, et al. Emergency abdominal aortic aneurysm repair with a preferential endovascular strategy: mortality and cost-effectiveness analysis. J Endovasc Ther 2007;14:777–84 | 1 |
| Kim LG, Scott AP, Ashton HA, Thompson SG. A sustained mortality benefit from screening for abdominal aortic aneurysm. Ann Intern Med 2007;146:699–706 | 2 |
| Kim LG, Thompson SG, Briggs AH, Buxton MJ, Campbell HE. How cost-effective is screening for abdominal aortic aneurysms? J Med Screen 2007;14:46–52 | 2 |
| Lederle FA, Stroupe KT. Cost-effectiveness at two years in the VA open versus endovascular repair trial. Eur J Vasc Endovasc Surg 2012;44:543–8 | 1 |
| Maceira Rozas MC, Atienza Merino G, Sampedro Morandeira JL. Efficacy and Effectiveness of Screening for Abdominal Aortic Aneurysm in a High Risk Population. Cost-effectiveness Analysis. Applicability in the National Health Care Service. Santiago de ComPostela: Galician Agency for Health Technology Assessment (AVALIA-T); 2007 | 1 |
| Michaels JA, Drury D, Thomas SM. Cost-effectiveness of endovascular abdominal aortic aneurysm repair. Br J Surg 2005;92:960–7 | 2 |
| Mundy L, Hiller JE. Targeted screening for abdominal aortic aneurysm. Adelaide, SA: Adelaide Health Technology Assessment (AHTA); 2008 | 2 |
| National Institute for Health and Care Excellence (NICE). Endovascular Stent-Grafts for the Treatment of Abdominal Aortic Aneurysms. London: NICE; 2009 | 2 |
| Perras C, Ho C, Spry C, Argaez C, Fitzsimmons H. Elective endovascular Abdominal Aortic Aneurysm Repair Versus Open Surgery: A review of the Clinical and Cost-effectiveness. Ottawa, ON: Canadian Agency for Drugs and Technologies in Health (CADTH); 2009 | 2 |
| Shahidi S, Schroeder TV, Carstensen M, Sillesen H. Outcome and survival of patients aged 75 years and older compared to younger patients after ruptured abdominal aortic aneurysm repair: do the results justify the effort? Ann Vasc Surg 2009;23:469–77 | 1 |
| Sogaard R, Laustsen J, Lindholt JS. Cost-effectiveness of abdominal aortic aneurysm screening and rescreening in men in a modern context: evaluation of a hypothetical cohort using a decision analytical model. BMJ 2012;345:e4276 | 1 |
| Stroupe KT, Lederle FA, Matsumura JS, Kyriakides TC, Jonk YC, Ge L, et al. Cost-effectiveness of open versus endovascular repair of abdominal aortic aneurysm in the OVER trial. J Vasc Surg 2012;56:901–9 | 1 |
| Sultan S, Hynes N. Clinical efficacy and cost per quality-adjusted life-years of pararenal endovascular aortic aneurysm repair compared with open surgical repair. J Endovasc Ther 2011;18:181–96 | 1 |
| Swedish Council on Technology Assessment in Health Care. Screening for Abdominal Aortic Aneurysm. Stockholm: Swedish Council on Technology Assessment in Health Care (SBU); 2008 | 1 |
| Tarride JE, Blackhouse G, De Rose G, Novick T, Bowen JM, et al. Cost-effectiveness analysis of elective endovascular repair compared with open surgical repair of abdominal aortic aneurysms for patients at a high surgical risk: a 1-year patient-level analysis conducted in Ontario, Canada. J Vasc Surg 2008;48:779–87 | 2 |
| Wilt TJ, Lederle FA, MacDonald R, Jonk YC, Rector TS, Kane RL. Comparison of Endovascular and Open Surgical Repairs for Abdominal Aortic Aneurysm. Rockville, MD: Agency for Healthcare Research and Quality (AHRQ); 2006 | 1 |
| Reference | Type of intervention | Planned or emergency surgery | Type of data extracted |
|---|---|---|---|
| Bowen J, De Rose G, Hopkins R, Novick T, Blackhouse G, Tarride J-E, et al. Systematic Review and Cost-effectiveness Analysis of Elective Endovascular Repair Compared to Open Surgical Repair of Abdominal Aortic Aneurysms – Interim report. Toronto, ON: Program for Assessment of Technology in Health (PATH) at McMaster University on behalf of the Medical Advisory Secretariat (MAS); 2005 | Surgical repair | Planned | Utility data |
| Brown LC, Powell JT, Thompson SG, Epstein DM, Sculpher MJ, Greenhalgh RM. The UK EndoVascular Aneurysm Repair (EVAR) trials: randomised trials of EVAR versus standard therapy. Health Technol Assess 2012;16(9) | Surgical repair | Planned | Utility and cost data |
| Chambers D, Woolacott N, Fayter D, Paton F, Wright K. Endovascular stents for abdominal aortic aneurysms. Health Technol Assess 2009;13(48) | Surgical repair | Planned | Utility and cost data |
| Ehlers L, Overvad K, Sorensen J, Christensen S, Bech M, Kjolby M. Analysis of cost-effectiveness of screening Danish men aged 65 for abdominal aortic aneurysm. BMJ 2009;338:b2243 | Screening | NA | Utility data |
| Eisenstein EL, Davidson-Ray L, Edwards R, Anstrom KJ, Ouriel K. Economic analysis of endovascular repair versus surveillance for patients with small abdominal aortic aneurysms. J Vasc Surg 2013;58:302–10 | Surgical repair | Planned | Utility data |
| Epstein DM, Sculpher MJ, Manca A, Michaels J, Thompson SG, Brown LC, et al. Modelling the long-term cost-effectiveness of endovascular or open repair for abdominal aortic aneurysm. Br J Surg 2008;95:183–90 | Surgical repair | Planned | Utility data |
| Hayes PD, Sadat U, Walsh SR, Noorani A, Tang TY, Bowden DJ, et al. Cost-effectiveness analysis of endovascular versus open surgical repair of acute abdominal aortic aneurysms based on worldwide experience. J Endovasc Ther 2010;17:174–82 | Surgical repair | Emergency | Cost data |
| Henriksson M, Lundgren F. One-time Screening for Abdominal Aortic Aneurysm in 65-year-old men: a Decision-Analytic Model with Lifetime Estimation of Costs and Health Outcomes. Linkoping: Center for Medical Technology Assessment (CMT); 2005 | Screening | NA | Utility data |
| IMPROVE Trial Investigators. Endovascular or open repair strategy for ruptured abdominal aortic aneurysm: 30 day outcomes from IMPROVE randomised trial. BMJ 2014;348:f7661 | Surgical repair | Emergency | Cost data |
| Kapma MR, Dijksman LM, Reimerink JJ, de Groof AJ, Zeebregts CJ, Wisselink W, et al. Cost-effectiveness and cost-utility of endovascular versus open repair of ruptured abdominal aortic aneurysm in the Amsterdam Acute Aneurysm Trial. Br J Surg 2014;101:208–15 | Surgical repair | Emergency | Utility data |
| Lindholt JS, Sorensen J, Sogaard R, Henneberg EW. Long-term benefit and cost-effectiveness analysis of screening for abdominal aortic aneurysms from a randomized controlled trial. Br J Surg 2010;97:826–34 | Screening | NA | Utility data |
| Montreuil B, Brophy J. Screening for abdominal aortic aneurysms in men: a Canadian perspective using Monte Carlo-based estimates. Can J Surg 2008;51:23–34 | Screening | NA | Utility data |
| Prinssen M, Buskens E, de Jong SE, Buth J, Mackaay AJ, Sambeek MR, et al. Cost-effectiveness of conventional and endovascular repair of abdominal aortic aneurysms: results of a randomized trial. J Vasc Surg 2007;46:883–90 | Surgical repair | Planned | Utility data |
| Rollins KE, Shak J, Ambler GK, Tang TY, Hayes PD, Boyle JR. Mid-term cost-effectiveness analysis of open and endovascular repair for ruptured abdominal aortic aneurysm. Br J Surg 2014;101:225–31 | Surgical repair | Emergency | Cost data |
| Spronk S, van Kempen BJ, Boll AP, Jorgensen JJ, Hunink MG, Kristiansen IS. Cost-effectiveness of screening for abdominal aortic aneurysm in the Netherlands and Norway. Br J Surg 2011;98:1546–55 | Screening | NA | Utility data |
| Thompson S, Brown L, Sweeting M, Bown M, Kim L, Glover M, et al. Systematic review and meta-analysis of the growth and rupture rates of small abdominal aortic aneurysms: implications for surveillance intervals and their cost-effectiveness. Health Technol Assess 2013;17(41) | Surveillance | NA | Cost data |
| Thompson SG, Ashton HA, Gao L, Scott RA, the Multicentre Aneurysm Screening Study Group. Screening men for abdominal aortic aneurysm: 10 year mortality and cost-effectiveness results from the randomised Multicentre Aneurysm Screening Study. BMJ 2009;338:b2307 | Screening | NA | Cost data |
| Young KC, Awad NA, Johansson M, Gillespie D, Singh MJ, Illig KA. Cost-effectiveness of abdominal aortic aneurysm repair based on aneurysm size. J Vasc Surg 2010;51:27–32 | Surveillance | NA | Utility data |
Appendix 9 Vascular Governance North West health economic data collection proforma
Appendix 10 Utility values for economic evaluation
| Lead author; year | Source of utility data | Intervention | n | Mean age (years) (SD) | Utility measure | Baseline | 30 days | 90 days | 180 days | 1 year |
|---|---|---|---|---|---|---|---|---|---|---|
| Primary evaluations of planned AAA repair | ||||||||||
| Bowen; 2006100 | Prospective cohort | EVAR | 140 | 76 | EQ-5D (mean) | 0.77a,b | 0.66a,b | 0.76a,b | 0.79a,b | 0.75a,b |
| Prospective cohort | Open repair (high risk) | 52 | 74 | EQ-5D (mean) | 0.76a,b | 0.66a,b | 0.75a,b | 0.89a,b | 0.91a,b | |
| Prospective cohort | Open repair (low risk) | 143 | 72 | EQ-5D (mean) | 0.80a,c | 0.7a,c | 0.87a,c | 0.90a,c | 0.91a,c | |
| Brown; 201279 | EVAR 1 RCT | EVAR | 541 | 74 | EQ-5D (mean, SD) | 0.75 (0.22)c | 0.73 (0.21)c | 0.71 (0.25)c | NR | 0.74 (0.24)c |
| EVAR 1 RCT | Open | 531 | 74 | EQ-5D (mean, SD) | 0.74 (0.23)c | 0.67 (0.25)c | 0.73 (0.23)c | NR | 0.75 (0.25)c | |
| EVAR 2 RCT | EVAR | 166 | 77 | EQ-5D (mean, SD) | 0.58 (0.31)c | 0.57 (0.28)c | 0.64 (0.28)c | NR | 0.65 (0.24)c | |
| EVAR 2 RCT | No repair | 172 | 76 | EQ-5D (mean, SD) | 0.63 (0.28)c | 0.56 (0.29)c | 0.60 (0.26)c | NR | 0.60 (0.30)c | |
| Lederle; 200976 | RCT | EVAR | 444 | 69.6 (7.8) | EQ-5D (mean, SD) | 0.79 (0.16) | Change from baseline: 1 year = –0.02 (0.16); 2 years = –0.01 (0.19) | |||
| RCT | Open | 437 | 70.5 (7.8) | EQ-5D (mean, SD) | 0.79 (0.16) | Change from baseline: 1 year = –0.00 (0.17); 2 years = –0.02 (0.16) | ||||
| Prinssen; 2007134 | RCT | EVAR | 170 | 64–77 (range) | EQ-5D (mean, 95% CI) | 0.76 (0.68 to 0.85)a | 0.64 (0.56 to 0.72)a,d | 0.75 (0.68 to 0.82)a | 0.75 (0.68 to 0.82)a | 0.77 (0.70 to 0.84)a |
| RCT | Open | 170 | 63–76 (range) | EQ-5D (mean, 95% CI) | 0.72 (0.64 to 0.80)a | 0.57 (0.46 to 0.68)a,c | 0.78 (0.72 to 0.84)a | 0.80 (0.72 to 0.88)a | 0.82 (0.75 to 0.88)a | |
| Lead author; year | Intervention | Utility value or decrement |
|---|---|---|
| Chambers; 200980 | EVAR | Decrement for 6 months after EVAR = 0.027a |
| Open | Decrement for 6 months after surgery = 0.077a | |
| Preoperation | Population norms (UK); see Kind,94 Table 54 | |
| Epstein; 200893 | EVAR | Decrement for 1 month after surgery = 0.027 (95% CI 0.007 to 0.061)b |
| Open and reintervention | Decrement for one month after surgery = 0.094 (95% CI 0.065 to 0.128)b | |
| Preoperation | Population norms (UK); see Kind,94 Table 54 | |
| Young; 2010135 | EVAR | 12 months postsurgery mean = 0.70 (minimum 0.3, maximum 1) |
| Observation | Mean = 0.75 (minimum 0.5, maximum 1) | |
| Open | 12 months postsurgery mean = 0.71 (minimum 0.3, maximum 1) |
| Lead author; year | Utility value or decrement |
|---|---|
| Henriksson; 200597 | Decrement for diagnosis of AAA used in sensitivity analysis only = 0.071, gamma distribution (12.6, 0.01) |
| Decrement for postoperative state used in sensitivity analysis only = 0.10, gamma distribution (16, 0.01) | |
| Baseline health state assumed equal to population norms (Sweden); see Burström,136 Table 54 | |
| Lindholt; 2010102 | Elective surgery (assumed decrement for 6 months) = 0.05 |
| Emergency surgery – no rupture (assumed decrement for 6 months) = 0.1 | |
| Emergency surgery – rupture (assumed decrement for 6 months) = 0.15 | |
| No screen and screen states: population norms (Denmark); see Sørenson,137 Table 54 | |
| aMontreuil; 200896 | Decrement for dialysis = 0.1 |
| Decrement for MI = 0.07 | |
| Decrement for stroke = 0.25 | |
| Baseline health for age 65–69 years = 0.82 | |
| Baseline health for age 70–79 years = 0.79 | |
| Baseline health for age > 80 years = 0.72 | |
| Spronk; 2011103 | Assumed decrement for two or more operations = 0.1 (0.052 to 0.147) |
| Assumed decrement for irreversible adverse event = 0.15 (0.102 to 0.197) | |
| Baseline health state assumed equal to population norms, derived from Lindholt 2010102 and reported in Burström136 (see Table 54) |
| Lead author; year | Source of utility data | n | Age (years) | Utility measure | Utility value |
|---|---|---|---|---|---|
| Burström; 2001136 | Population survey | 387 | 60–69 | EQ-5D (mean, SE) | All: 0.80 (0.010); male: 0.83 (0.012); female: 0.78 (0.015) |
| Population survey | 318 | 70–79 | EQ-5D (mean, SE) | All: 0.79 (0.012); male: 0.81 (0.018); female: 0.78 (0.017) | |
| Population survey | 122 | 80–88 | EQ-5D (mean, SE) | All: 0.74 (0.021); male: 0.74 (0.037); female: 0.74 (0.026) | |
| Kind; 199994 | Population survey | 484 | 55–64 | EQ-5D (mean, SD) | All: 0.80 (0.26); male: 0.78 (0.28); female: 0.81 (0.26) |
| Population survey | 488 | 65–74 | EQ-5D (mean, SD) | All: 0.78 (0.26); male: 0.78 (0.28); female: 0.78 (0.25) | |
| Population survey | 314 | > 75 | EQ-5D (mean, SD) | All: 0.73 (0.27); male: 0.75 (0.28); female: 0.71 (0.27) | |
| Sørenson; 2009137 | Population survey | 2121 | 60–69 | EQ-5D (mean, SD) | Male: 0.883 (0.153); female: 0.839 (0.177) |
| Population survey | 1408 | 70–79 | EQ-5D (mean, SD) | Male: 0.847 (0.183); female: 0.818 (0.198) |
Appendix 11 Economic data from Vascular Governance North West
| Length of time | Open | EVAR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | Number of visits | Cost of visits (£) | n | Number of visits | Cost of visits (£) | |||||
| Mean (SD) | Minimum–maximum | Mean (SD) | Minimum–maximum | Mean (SD) | Minimum–maximum | Mean (SD) | Minimum–maximum | |||
| > 3 years pre operation | 61 | 0.30 (0.78) | 0–4 | 53 (144) | 0–681 | 57 | 0.39 (1.31) | 0–8 | 60 (212) | 0–1362 |
| 2–3 years pre operation | 61 | 0.66 (1.11) | 0–4 | 107 (191) | 0–763 | 57 | 0.51 (0.95) | 0–4 | 120 (425) | 0–3124 |
| 1–2 years pre operation | 61 | 1.05 (1.73) | 0–8 | 196 (487) | 0–3470 | 57 | 1.28 (1.56) | 0–5 | 195 (273) | 0–1509 |
| 0–1 year pre operation | 61 | 5.00 (2.29) | 1–11 | 1249 (841) | 164–4707 | 57 | 5.05 (2.10) | 1–10 | 1085 (628) | 119–3582 |
| Average visits/costs before AAA repair | 61 | 7.18 (4.48) | 1–16 | 1640 (1158) | 170–6207 | 57 | 7.30 (4.32) | 1–17 | 1473 (987) | 119–5988 |
| 0–1 year post operation | 61 | 1.10 (0.89) | 0–3 | 227 (340) | 0–2481 | 57 | 2.65 (1.49) | 0–7 | 682 (1248) | 0–9564 |
| 1–2 years post operation | 53 | 0.25 (0.65) | 0–3 | 42 (120) | 0–640 | 49 | 0.96 (1.08) | 0–5 | 426 (1794) | 0–12,650 |
| 2–3 years post operation | 44 | 0.16 (0.75) | 0–4 | 27 (131) | 0–740 | 37 | 0.59 (0.86) | 0–3 | 81 (123) | 0–468 |
| > 3 years post operation | 44 | 0.14 (0.63) | 0–4 | 85 (511) | 0–3390 | 37 | 0.38 (0.68) | 0–3 | 552 (3114) | 0–18,970 |
| Average visits/costs after AAA repair | 61 | 1.62 (1.84) | 0–10 | 617 (701) | 86–4774 | 57 | 4.2 (2.17) | 0–9 | 1671 (3135) | 86–19,290 |
Appendix 12 Cost parameter estimates for economic models
| Description | Mean | SD | Source |
|---|---|---|---|
| EVAR active monitoring and surveillance, cost per visit per patient (£) | 75 | 36 | NHS reference costs,73 weighted average of procedure codesa |
| EVAR active monitoring diagnostic tests, cost per test per patient (£) | 209 | 144 | NHS reference costs,73 weighted average of procedure codesa |
| Open active monitoring and surveillance, cost per visit per patient (£) | 85 | 45 | NHS reference costs,73 weighted average of procedure codesa |
| Open active monitoring diagnostic tests, cost per test per patient (£) | 200 | 145 | NHS reference costs,73 weighted average of procedure codesa |
| EVAR preoperative assessment, cost per visit per patient (£) | 107 | 113 | NHS reference costs,73 weighted average of procedure codesa |
| EVAR preoperative diagnostic tests, cost per test per patient (£) | 104 | 151 | NHS reference costs,73 weighted average of procedure codesa |
| Open preoperative assessment, cost per visit per patient (£) | 84 | 63 | NHS reference costs,73 weighted average of procedure codesa |
| Open preoperative diagnostic tests, cost per test per patient (£) | 61 | 81 | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative assessment, cost per visit per patient (£) | 85 | 34 | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative assessment diagnostic tests, cost per test per patient (£) | 155 | 110 | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative assessment, cost per visit per patient (£) | 95 | 20 | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative assessment diagnostic tests, cost per test per patient (£) | 320 | 232 | NHS reference cost,73 weighted average of procedure codesa |
| EVAR postoperative monitoring, cost per visit per patient (£) | 56 | 33 | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative monitoring diagnostic tests, cost per test per patient (£) | 129 | 212 | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative monitoring, cost per visit per patient (£) | 94 | 29 | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative monitoring diagnostic tests, cost per test per patient (£) | 346 | 192 | NHS reference costs,73 weighted average of procedure codesa |
| Transport costs for emergency surgery/rupture, cost per visit per patient (£) | 201 | 0 | NHS reference costs,73 weighted average of procedure codesa |
| Elective surgery and reintervention surgery cost per finished consultant episode | |||
| EVAR no complications (£) | 5608 | 5188 | NHS reference costs,73 weighted average of procedure codes QZ15G–QZ15J, RC12A–RC13E plus emergency transport costs73 |
| EVAR complications (£) | 10,675 | 7475 | NHS reference costs,73 weighted average of procedure codes QZ15D–QZ15F, RC11A–RC11E plus emergency transport costs73 |
| Open no complications (£) | 8305 | 1610 | NHS reference costs,73 weighted average of procedure codes QZ01E-QZ01F plus emergency transport costs73 |
| Open complications (£) | 12,836 | 2308 | NHS reference costs73, weighted average of procedure codes QZ01C and QZ01D plus emergency transport costs73 |
| Emergency surgery cost per finished consultant episode | |||
| EVAR no complications (£) | 5934 | 8947 | NHS reference costs,73 weighted average of procedure codes QZ15G–QZ15J, RC12A–RC13E plus emergency transport costs73 |
| EVAR complications (£) | 8630 | 3864 | NHS reference costs 73, weighted average of procedure codes QZ15D–QZ15F, RC11A–RC11E plus emergency transport costs73 |
| Open no complications (£) | 7493 | 1946 | NHS reference costs,73 weighted average of procedure codes QZ01E and QZ01F plus emergency transport costs73 |
| Open complications (£) | 12,558 | 4848 | NHS reference costs,73 weighted average of procedure codes QZ01C and QZ01D plus emergency transport costs73 |
| Description | Minimum (SD) | Maximum (SD) | Source |
|---|---|---|---|
| EVAR active monitoring and surveillance, cost per visit per patient (£) | 63 (17) | 123 (51) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR active monitoring diagnostic tests, cost per test per patient (£) | 168 (164) | 224 (179) | NHS reference costs,73 weighted average of procedure codesa |
| Open active monitoring and surveillance, cost per visit per patient (£) | 59 (16) | 121 (57) | NHS reference costs,73 weighted average of procedure codesa |
| Open active monitoring diagnostic tests, cost per test per patient (£) | 162 (162) | 214 (178) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR preoperative assessment, cost per visit per patient (£) | 100 (118) | 171 (123) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR preoperative diagnostic tests, cost per test per patient (£) | 94 (152) | 114 (179) | NHS reference costs,73 weighted average of procedure codes a |
| Open preoperative assessment, cost per visit per patient (£) | 72 (63) | 134 (75) | NHS reference costs,73 weighted average of procedure codesa |
| Open preoperative diagnostic tests, cost per test per patient (£) | 50 (71) | 63 (90) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative assessment, cost per visit (£) | 46 (20) | 122 (74) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative assessment diagnostic tests, cost per test per patient (£) | 82 (27) | 162 (133) | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative assessment, cost per visit per patient (£) | 52 (13) | £129 (70) | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative assessment diagnostic tests, cost per test per patient (£) | 77 (27) | 371 (287) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative monitoring, cost per visit per patient (£) | 29 (23) | 76 (65) | NHS reference costs,73 weighted average of procedure codesa |
| EVAR postoperative monitoring diagnostic tests, cost per test per patient (£) | 115 (321) | 152 (324) | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative monitoring, cost per visit per patient (£) | 53 (14) | 134 (70) | NHS reference costs,73 weighted average of procedure codesa |
| Open postoperative monitoring diagnostic tests, cost per test per patient (£) | 94 (17) | 397 (245) | NHS reference costs,73 weighted average of procedure codesa |
| Transport costs for emergency surgery/rupture per finished consultant episode (£) | 201 (0) | 201 (0) | NHS reference costs,73 weighted average of procedure codesa |
| Elective surgery and reintervention surgery cost per finished consultant episode | |||
| EVAR no complications, mean (SD) (£) | 3429 (2919) | 7254 (8329) | NHS reference costs,73 weighted average of procedure codes QZ15G–QZ15J, RC12A–RC13E plus emergency transport costs73 |
| EVAR complications, mean (SD) (£) | 6446 (4426) | 13,062 (12,849) | NHS reference costs,73 weighted average of procedure codes QZ15D–QZ15F, RC11A–RC11E plus emergency transport costs73 |
| Open no complications, mean (SD) (£) | 5895 (299) | 9080 (2244) | NHS reference costs,73 weighted average of procedure codes QZ01E and QZ01F plus emergency transport costs73 |
| Open complications, mean (SD) (£) | 6562 (795) | 14,964 (7096) | NHS reference costs,73 weighted average of procedure codes QZ01C and QZ01D plus emergency transport costs73 |
| VGNW elective surgery cost | |||
| EVAR, mean (SD) (£) | 12,440 (2751) | VGNW | |
| Open, mean (SD) (£) | 13,380 (4820) | VGNW | |
| EVAR 1 Trial primary procedure cost, inflated to 2012–2013 prices | |||
| EVAR, mean (£) | 13,019 | Brown et al. 201279 | |
| Open, mean (£) | 11,842 | Brown et al. 201279 | |
| EVAR 1 Trial reintervention procedure cost, inflated to 2012–2013 prices | |||
| Reintervention, mean (SD) (£) | 7536 (10,679) | Brown et al. 201279 | |
| Emergency surgery cost per finished consultant episode | |||
| EVAR no complications, mean (SD) (£) | 4052 (9683) | 7144 (9735) | NHS reference costs,73 weighted average of procedure codes QZ15G–QZ15J, RC12A–RC13E plus emergency transport costs73 |
| EVAR complications, mean (SD) (£) | 5788 (3797) | 11,092 (4675) | NHS reference costs, 73 weighted average of procedure codes QZ15D–QZ15F, RC11A–RC11E plus emergency transport costs73 |
| Open no complications, mean (SD) (£) | 5405 (2228) | 8703 (1857) | NHS reference costs, 73 weighted average of procedure codes QZ01E–QZ01F plus emergency transport costs73 |
| Open complications, mean (SD) (£) | 7962 (4141) | 16,390 (6699) | NHS reference costs, 73 weighted average of procedure codes QZ01C and QZ01D plus emergency transport costs73 |
Appendix 13 Mean cost and quality-adjusted life-year results
| Analysis | Algorithm | Standard practice |
|---|---|---|
| Primary analysis | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 12,068 (6722 to 25,541) | 12,240 (413 to 23,450) |
| Mean QALY (95% CIs) | 7.111 (0.706 to 13.012) | 7.064 (0.745 to 12.786) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 14,419 (6569 to 25,764) | 14,256 (6689 to 25,757) |
| Mean QALY (95% CIs) | 7.093 (0.691 to 12.801) | 7.069 (0.691 to 12.801) |
| Sensitivity analysis: outcome is LYGs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 12,068 (6722 to 25,541) | 12,240 (413 to 23,450) |
| Mean LYGs (95% CIs) | 12.152 (0.708 to 25.298) | 12.073 (1 to 25.190) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 14,419 (6569 to 25,764) | 14,256 (6689 to 25,757) |
| Mean LYGs (95% CIs) | 12.113 (0.50 to 25.29) | 12.068 (0.50 to 25.290) |
| Sensitivity analysis: maximise LYGs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size maximise LYGs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 12,068 (6722 to 25,541) | 12,240 (413 to 23,450) |
| Mean LYGs (95% CIs) | 12.152 (0.708 to 25.298) | 12.073 (1 to 25.190) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size maximise LYGs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 14,419 (6569 to 25,764) | 14,256 (6689 to 25,757) |
| Mean LYGs (95% CIs) | 12.113 (0.50 to 25.29) | 12.068 (0.50 to 25.29) |
| Sensitivity analysis: decision rule is minimise costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to minimise costs | 7.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 12,068 (407 to 23,030) | 12,240 (413 to 23,450) |
| Mean QALY (95% CIs) | 6.920 (0.743 to 12.674) | 7.064 (0.745 to 12.728) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to minimise costs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 14,419 (6569 to 25,764) | 14,256 (6689 to 25,757) |
| Mean QALY (95% CIs) | 7.093 (0.691 to 12.801) | 7.069 (0.691 to 12.801) |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 5.1 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 12,090 (403 to 23,497) | 12,225 (401 to 23,399) |
| Mean QALY (95% CIs) | 8.924 (0.982 to 16.109) | 8.903 (0.986 to 16.055) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 7.0 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 14,455 (5743 to 25,878) | 14,270 (6752 to 25,703) |
| Mean QALY (95% CIs) | 8.901 (0.767 to 16.088) | 8.794 (0.249 to 11.573) |
| Sensitivity analysis: VGNW costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 13,091 (8377 to 27,845) | 13,314 (402 to 25,053) |
| Mean QALY (95% CIs) | 7.111 (0.706 to 13.012) | 7.064 (0.745 to 12.786) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 15,988 (8180 to 27,987) | 15,893 (8358 to 27,970) |
| Mean QALY (95% CIs) | 7.093 (0.691 to 12.801) | 7.069 (0.691 to 12.801) |
| Sensitivity analysis: EVAR 1 costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 14,942 (14,066 to 28,958) | 15,309 (419 to 24,257) |
| Mean QALY (95% CIs) | 7.111 (0.706 to 13.012) | 7.064 (0.745 to 12.786) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 18,898 (14,009 to 28,690) | 18,804 (13,965 to 28,897) |
| Mean QALY (95% CIs) | 7.093 (0.691 to 12.801) | 7.069 (0.691 to 12.801) |
| Sensitivity analysis: high assessment and follow-up costs low surgery costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 11,703 (7285 to 20,036) | 11,646 (474 to 19,524) |
| Mean QALY (95% CIs) | 7.111 (0.706 to 13.012) | 7.064 (0.745 to 12.786) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 12,984 (7279 to 20,294) | 12,745 (7181 to 20,006) |
| Mean QALY (95% CIs) | 7.093 (0.691 to 12.801) | 7.069 (0.691 to 12.801) |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 12,077 (5679 to 31,596) | 12,376 (285 to 27,696) |
| Mean QALY (95% CIs) | 7.111 (0.706 to 13.012) | 7.064 (0.745 to 12.786) |
| Initial aneurysm size: 6.8 cm | ||
| Threshold size to maximise QALYs | 6.9 cm | 6.8 cm |
| Mean cost (95% CIs) (£) | 15,068 (5612 to 31,736) | 14,970 (5700 to 31,661) |
| Mean QALY (95% CIs) | 7.093 (0.691 to 12.801) | 7.069 (0.691 to 12.801) |
| Analysis | Algorithm | Standard practice |
|---|---|---|
| Primary analysis | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 3071 (152 to 16,000) | 3476 (151 to 19,975) |
| Mean QALY (95% CIs) | 2.446 (0.196 to 6.539) | 2.450 (0.192 to 6.603) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 8591 (699 to 37,110) | NA |
| Mean QALY (95% CIs) | 2.309 (0 to 6.788) | NA |
| Sensitivity analysis: outcome is LYGs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 3071 (152 to 16,000) | 3476 (151 to 19,975) |
| Mean LYGs (95% CIs) | 3.704 (0.250 to 10.422) | 3.662 (0.250 to 10.501) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean costs (95% CIs) (£) | 8591 (699 to 37,110) | NA |
| Mean LYGs (95% CIs) | 2.309 (0 to 6.788) | NA |
| Sensitivity analysis: maximise LYGs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise LYGs | 7.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 2660 (152 to 9911) | 3476 (151 to 19,975) |
| Mean LYGs (95% CIs) | 3.721 (0.250 to 10.050) | 3.662 (0.250 to 10.5018) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise LYGs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 8591 (699 to 37,110) | NA |
| Mean LYGs (95% CIs) | 3.295 (0 to 10.538) | NA |
| Sensitivity analysis: decision rule is minimise costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to minimise costs | 7.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 2660 (152 to 9911) | 3476 (151 to 19,975) |
| Mean QALY (95% CIs) | 2.466 (0.196 to 6.382) | 2.450 (0.192 to 6.603) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to minimise costs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 8591 (699 to 37,110) | NA |
| Mean QALY (95% CIs) | 2.309 (0 to 6.788) | NA |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.8 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 2723 (151 to 11,265) | 3452 (151 to 11,265) |
| Mean QALY (95% CIs) | 3.241 (0.25 to 8.217) | 3.191 (0.250 to 8.350) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 8522 (693 to 36,910) | NA |
| Mean QALY (95% CIs) | 2.750 (0 to 8.381) | NA |
| Sensitivity analysis: VGNW costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 3059 (149 to 17,377) | 4290 (151 to 19,029) |
| Mean QALY (95% CIs) | 2.446 (0.196 to 6.539) | 2.450 (0.192 to 6.603) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 12,849 (5979 to 27,032) | NA |
| Mean QALY (95% CIs) | 2.31 (0 to 6.775) | NA |
| Sensitivity analysis: EVAR 1 costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 4026 (152 to 18,162) | 5049 (149 to 18,142) |
| Mean QALY (95% CIs) | 2.446 (0.196 to 6.539) | 2.450 (0.192 to 6.603) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 16,876 (14,475 to 33,306) | NA |
| Mean QALY (95% CIs) | 2.304 (0 to 6.756) | NA |
| Sensitivity analysis: high assessment and follow-up costs low surgery costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 3246 (186 to 12,724) | 3378 (184 to 13,094) |
| Mean QALY (95% CIs) | 2.446 (0.196 to 6.539) | 2.450 (0.192 to 6.603) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 5849 (1271 to 15,782) | NA |
| Mean QALY (95% CIs) | 2.304 (0 to 6.756) | NA |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Initial aneurysm size: 4.0 cm | ||
| Threshold size to maximise QALYs | 6.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 2777 (96 to 16,485) | 3367 (96 to 20,432) |
| Mean QALY (95% CIs) | 2.446 (0.196 to 6.539) | 2.450 (0.192 to 6.603) |
| Initial aneurysm size: 7.0 cm | ||
| Threshold size to maximise QALYs | 7.0 cma | NA |
| Mean cost (95% CIs) (£) | 9739 (788 to 35,574) | NA |
| Mean QALY (95% CIs) | 2.307 (0 to 6.802) | NA |
| Analysis | Algorithm | Standard practice |
|---|---|---|
| Primary analysis | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 11,184 (254 to 22,552) | 8468 (247 to 20,345) |
| Mean QALY (95% CIs) | 4.967 (0.378 to 10.715) | 4.923 (0.38 to 10.565) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.2 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 12,790 (5644 to 23,859) | 12,790 (5644 to 23,859) |
| Mean QALY (95% CIs) | 4.962 (0 to 10.756) | 4.962 (0 to 10.756) |
| Sensitivity analysis: outcome is LYGs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 4.0 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 11,184 (254 to 22,552) | 8468 (247 to 20,345) |
| Mean LYGs (95% CIs) | 7.778 (0.5 to 18.804) | 7.735 (0.5 to 18.695) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.2 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 11,184 (254 to 22,552) | 8468 (247 to 20,345) |
| Mean LYGs (95% CIs) | 7.772 (0 to 18.782) | 7.772 (0 to 18.782) |
| Sensitivity analysis: maximise LYGs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size maximise LYGs | 4.0 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 11,184 (254 to 22,552) | 8468 (247 to 20,345) |
| Mean LYGs (95% CIs) | 7.778 (0.5 to 18.804) | 7.735 (0.5 to 18.695) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size maximise LYGs | 5.2 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 11,184 (254 to 22,552) | 8468 (247 to 20,345) |
| Mean LYGs (95% CIs) | 7.772 (0 to 18.782) | 7.772 (0 to 18.782) |
| Sensitivity analysis: decision rule is minimise costs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to minimise costs | 7.0 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 6146 (252 to 18,669) | 8468 (247 to 20,345) |
| Mean QALY (95% CIs) | 4.791 (0.394 to 10.306) | 4.923 (0.38 to 10.565) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to minimise costs | 7.0 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 10,396 (829 to 22,943) | 12,790 (5644 to 23,859) |
| Mean QALY (95% CIs) | 4.595 (0.381 to 10.463) | 4.962 (0 to 10.756) |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 5.4 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 11,182 (258 to 22,457) | 8493 (245 to 20,324) |
| Mean QALY (95% CIs) | 6.046 (0.5 to 13.077) | 6.128 (0.5 to 13.132) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.3 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 12,823 (5628 to 23,954) | 12,823 (5628 to 23,954) |
| Mean QALY (95% CIs) | 6.007 (0 to 13,113) | 6.007 (0 to 13,113) |
| Sensitivity analysis: VGNW costs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 3.8 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 11,184 (254 to 22,552) | 8468 (247 to 20,345) |
| Mean QALY (95% CIs) | 4.967 (0.378 to 10.715) | 4.923 (0.38 to 10.565) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.3 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 14,367 (7320 to 26,022) | 14,367 (7320 to 26,022) |
| Mean QALY (95% CIs) | 4.944 (0 to 10.74) | 4.944 (0 to 10.74) |
| Sensitivity analysis: EVAR 1 costs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 3.8 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 15,090 (254 to 23,615) | 10,993 (248 to 19,890) |
| Mean QALY (95% CIs) | 4.97 (0.393 to 10.723) | 4.932 (0.405 to 10.561) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.2 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 17,332 (13,221 to 25,740) | 17,332 (13,221 to 25,740) |
| Mean QALY (95% CIs) | 4.95 (0 to 10.739) | 4.95 (0 to 10.739) |
| Sensitivity analysis: high assessment and follow-up costs, low surgery costs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 3.8 cm | 5.0 cm |
| Mean cost (95% CIs) (£) | 9707 (294 to 17,168) | 7765 (286 to 16,294) |
| Mean QALY (95% CIs) | 4.954 (0.391 to 10.703) | 4.916 (0.393 to 10.559) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.2 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 11,071 (6242 to 18,141) | 11,071 (6242 to 18,141) |
| Mean QALY (95% CIs) | 4.95 (0 to 10.745) | 4.95 (0 to 10.745) |
| Sensitivity analysis: low assessment and follow-up costs, high surgery costs | ||
| Initial aneurysm size: 3.8 cm | ||
| Threshold size to maximise QALYs | 3.8 cm | 5 cm |
| Mean cost (95% CIs) (£) | 12,547 (167 to 28,626) | 9234 (166 to 25,308) |
| Mean QALY (95% CIs) | 4.967 (0.398 to 10.747) | 4.940 (0.411 to 10.559) |
| Initial aneurysm size: 5.2 cm | ||
| Threshold size to maximise QALYs | 5.2 cm | 5.2 cm |
| Mean cost (95% CIs) (£) | 14,365 (5285 to 30,600) | 14,365 (5285 to 30,600) |
| Mean QALY (95% CIs) | 4.945 (0 to 10.766) | 4.945 (0 to 10.766) |
| Analysis | Algorithm | Standard practice |
|---|---|---|
| Primary analysis | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise QALYs | 4.9 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 9995 (819 to 39,303) | 9776 (766 to 31,854) |
| Mean QALY (95% CIs) | 4.617 (0.301 to 10.111) | 4.579 (0.295 to 7.446) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise QALYs | 6.6 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 9991 (986 to 39,933) | 9847 (1040 to 39,567) |
| Mean QALY (95% CIs) | 4.606 (0.376 to 10.124) | 4.6 (0.441 to 10.27) |
| Sensitivity analysis: outcome is LYGs | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise QALYs | 4.9 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 9995 (819 to 39,303) | 9776 (766 to 31,854) |
| Mean LYGs (95% CIs) | 7.363 (0.5 to 18.444) | 7.323 (0.5 to 13.841) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise QALYs | 6.6 cm | 6.5 cm |
| Mean costs (95% CIs) (£) | 9991 (986 to 39,933) | 9847 (1040 to 39567) |
| Mean LYGs (95% CIs) | 7.329 (0.294 to 18.436) | 4.6 (0.441 to 10.27) |
| Sensitivity analysis: maximise LYGs | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise LYGs | 4.9 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 9995 (819 to 39,303) | 9776 (766 to 31,854) |
| Mean LYGs (95% CIs) | 7.363 (0.5 to 18.444) | 7.323 (0.5 to 13.841) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise LYGs | 6.7 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 10,018 (802 to 39,627) | 9847 (1040 to 39,567) |
| Mean LYGs (95% CIs) | 7.334 (0.5 to 18.428) | 7.32 (0.283 to 18.485) |
| Sensitivity analysis: decision rule is minimise costs | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to minimise costs | 7.0 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 8730 (767 to 30,384) | 9776 (766 to 31,854) |
| Mean QALY (95% CIs) | 4.398 (0.299 to 9.984) | 4.579 (0.295 to 7.446) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to minimise costs | 7.0 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 9633 (753 to 38,088) | 9847 (1040 to 39,567) |
| Mean QALY (95% CIs) | 4.483 (0.283 to 10.101) | 4.6 (0.441 to 10.27) |
| Sensitivity analysis: low starting utility values and high post-repair decrements | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise QALYs | 4.8 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 10,005 (802 to 39,216) | 9763 (769 to 31,672) |
| Mean QALY (95% CIs) | 5.887 (0.5 to 13.073) | 5.81 (0.498 to 9.651) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise QALYs | 6.7 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 9952 (990 to 39,696) | 9929 (1052 to 40,103) |
| Mean QALY (95% CIs) | 5.8 (0.5 to 13.018) | 5.719 (0.505 to 12.917) |
| Sensitivity analysis: VGNW costs | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise QALYs | 4.8 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 14,495 (836 to 30,461) | 13,281 (767 to 21,885) |
| Mean QALY (95% CIs) | 4.602 (0.3 to 10.073) | 4.587 (0.299 to 7.453) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise QALYs | 6.5 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 14,536 (5636 to 30,706) | 14,652 (6620 to 30,927) |
| Mean QALY (95% CIs) | 4.595 (0.344 to 10.121) | 4.605 (0.441 to 10.255) |
| Sensitivity analysis: EVAR 1 costs | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise QALYs | 4.8 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 18,235 (816 to 39,895) | 16,155 (777 to 26,754) |
| Mean QALY (95% CIs) | 4.602 (0.286 to 10.064) | 4.562 (0.294 to 7.446) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise QALYs | 6.5 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 18,280 (14,766 to 39,703) | 18,480 (14,767 to 41,008) |
| Mean QALY (95% CIs) | 4.588 (0.322 to 10.124) | 4.615 (0.45 to 10.249) |
| Sensitivity analysis: high assessment and follow-up costs, low surgery costs | ||
| Initial aneurysm size: 4.8 cm | ||
| Threshold size to maximise QALYs | 4.8 cm | 5.5 cm |
| Mean cost (95% CIs) (£) | 7400 (1021 to 18,156) | 8,170 (957 to 12,078) |
| Mean QALY (95% CIs) | 4.594 (0.303 to 10.082) | 4.588 (0.312 to 7.4) |
| Initial aneurysm size: 6.5 cm | ||
| Threshold size to maximise QALYs | 6.6 cm | 6.5 cm |
| Mean cost (95% CIs) (£) | 7217 (1474 to 17,906) | 7040 (1739 to 17,871) |
| Mean QALY (95% CIs) | 4.599 (0.33 to 10.12) | 4.591 (0.440 to 10.242) |
Appendix 14 Meeting dates of study committees
Steering Committee
3 February 2012.
16 October 2012.
21 May 2013.
3 September 2013.
27 November 2013.
Management Committee
24 May 2011.
19 December 2011.
24 May 2012.
2 August 2012.
16 October 2012.
21 May 2013.
11 June 2013.
17 June 2013.
25 June 2013.
8 July 2013.
3 September 2013.
7 November 2013.
Patient and public involvement group
20 September 2011.
19 December 2011.
23 July 2012.
26 October 2012.
25 January 2013.
31 May 2013.
13 September 2013.
10 January 2014.
List of abbreviations
- AAA
- abdominal aortic aneurysm
- ADAM
- aneurysm detection and management
- AIC
- Akaike information criterion
- ARDA
- Aneurysm Repair Decision Aid
- ASA
- American Society of Anesthesiologists
- AUC
- area under the curve
- BAR
- British Aneurysm Repair
- BMI
- body mass index
- CEAC
- cost-effectiveness acceptability curve
- CI
- confidence interval
- DES
- discrete event simulation
- ECG
- electrocardiogram
- EED
- Economic Evaluations Database
- EQ-5D
- European Quality of Life-5 Dimensions
- EVAR
- endovascular aneurysm repair
- GAS
- Glasgow Aneurysm Score
- HR
- hazard ratio
- HTA
- Health Technology Assessment
- ICER
- incremental cost-effectiveness ratio
- IPD
- individual patient data
- LOS
- length of stay
- LY
- life-year
- LYG
- life-year gained
- MI
- myocardial infarction
- NAAASP
- National AAA Screening Programme
- NB
- net benefit
- NICE
- National Institute for Health and Care Excellence
- NIHR
- National Institute for Health Research
- NVD
- National Vascular Database
- NVR
- National Vascular Registry
- O : E
- observed to expected
- OPCS
- Office of Population Censuses and Surveys
- PPI
- patient and public involvement
- QALY
- quality-adjusted life-year
- RCT
- randomised controlled trial
- ROC
- receiver operating characteristic
- SD
- standard deviation
- UKSAT
- UK Small Aneurysm Trial
- VBHOM
- Vascular Biochemistry and Haematology Outcome Model
- VGNW
- Vascular Governance North West
- V-POSSUM
- Vascular Physiological and Operative Severity Score for enUmeration of Mortality
- WCC
- white cell count
- WTPT
- willingness-to-pay threshold