Notes
Article history
This issue of the Health Technology Assessment journal series contains a project commissioned/managed by the Methodology research programme (MRP). The Medical Research Council (MRC) is working with NIHR to deliver the single joint health strategy and the MRP was launched in 2008 as part of the delivery model. MRC is lead funding partner for MRP and part of this programme is the joint MRC–NIHR funding panel ‘The Methodology Research Programme Panel’.
To strengthen the evidence base for health research, the MRP oversees and implements the evolving strategy for high-quality methodological research. In addition to the MRC and NIHR funding partners, the MRP takes into account the needs of other stakeholders including the devolved administrations, industry R&D, and regulatory/advisory agencies and other public bodies. The MRP funds investigator-led and needs-led research proposals from across the UK. In addition to the standard MRC and RCUK terms and conditions, projects commissioned/managed by the MRP are expected to provide a detailed report on the research findings and may publish the findings in the HTA journal, if supported by NIHR funds.
The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HTA editors and publisher have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the draft document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
Dr Emsley reports grants from the UK Medical Research Council (MRC) during the conduct of the study. Professor Landau reports grants from the National Institute for Health Research (NIHR) during the conduct of the study. Professor Pickles reports grants from the MRC and from the NIHR during the conduct of the study and royalties from Western Psychological Services outside the submitted work.
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2015. This work was produced by Dunn et al. under the terms of a commissioning contract issued by the Secretary of State for Health. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
Chapter 1 Efficacy and mechanism evaluation
Background
The development of the capability and capacity to implement high-quality clinical research, including the evaluation of complex interventions through randomised trials, is a key priority of the NHS, the National Institute for Health Research (NIHR) and the Medical Research Council (MRC). 1 The evaluation of complex treatment programmes for mental illness [e.g. cognitive–behavioural therapy (CBT) for depression or psychosis] not only is a vital component of this research in its own right but also provides a well-established model for the evaluation of complex interventions in other clinical areas. It is recognised, however, that randomised trials of psychological treatments need to be implemented on a larger scale than has typically been the case hitherto, and the NIHR Mental Health Research Network (MHRN) was established to foster and support developments in this area. The parallel development of research methodology for the optimal design, implementation and interpretation of the results of such trials is an essential component of these developments. In particular, there is a need for robust methods to make valid causal inferences for explanatory analyses of the mechanisms of treatment-induced change in clinical and economic outcomes in randomised clinical trials. This has been recognised by the MHRN in the formation of a MHRN Methodology Research Group, of which all investigators are members and which is led by the principal investigator in the current project. The MHRN Methodology Research Group is an initiative to bring key scientists in the field together, to develop resources and training programmes, and to foster the development and evaluation of relevant methodologies.
Broadly speaking, the research presented in this report aims to answer four questions about complex interventions/treatments:
-
Does it work?
-
How does it work?
-
Whom does it work for?
-
What factors make it work better?
In particular, the present project was aimed at strengthening the methodological underpinnings of psychological treatment trials: to develop, evaluate and disseminate statistical and econometric methods for the explanatory analysis of trials of psychological treatment programmes involving complex interventions and multivariate responses.
By explanatory analysis, we mean a secondary analysis in which one tries to explain how a given therapeutic effect has been achieved or, alternatively, why the therapy is apparently ineffective. This is scientifically useful because it can allow investigators to tailor treatments more effectively or to identify different mechanisms. An explanatory trial is one that is designed to answer these questions.
We use psychological treatment trials as an exemplar of complex interventions, but the methodology and associated problems are more generic and can be readily applied to other clinical areas (although this is beyond the scope of this report).
Hand in hand with the development of the methods of analysis there was consideration of more effective designs for these trials, particularly in the choice of social and psychological markers as potential prognostic factors, predictors (moderators) and mediators or candidate surrogate outcomes of clinical treatment effects. We will define these formally later in the chapter; however, in summary, a prognostic variable indicates the long-term treatment-free outcome for patients and a predictive variable interacts with treatment to identify if the treatment effect varies depending on the level of the predictive variable. All of these have direct relevance to the development and evaluation of personalised therapies (stratified medicine).
Much of the methodological work in this area is mirrored by wider interests in statistical methods for biomarker validation2 and the evaluation of their role as putative surrogate outcomes. 3 The aim is to add significantly to our understanding of biological and behavioural processes [see the NIHR Efficacy and Mechanism Evaluation (EME) programme – www.eme.ac.uk]. Part of the rationale for the present project was to integrate statistical work on surrogate outcome and other biomarker validation with that on the evaluation of mediation in the social and behavioural sciences. We refer to the term ‘marker’ to emphasise this common ground.
The present project was focused on the use of social and psychological markers to assess both treatment effect mediation and treatment effect modification by therapeutic process measures (‘therapeutic mechanisms evaluation’) in the presence of measurement errors, hidden confounding (selection effects) and missing data. The proposed programme of work had three integrated components: (1) the extension of instrumental variable (IV) methods to latent growth curve models and growth mixture models (GMMs) for repeated-measures data; (2) the development of designs and meta-analytic/metaregression methods for parallel trials (and/or strata within trials); and (3) the evaluation of the sensitivity/robustness of findings to the assumptions necessary for model identifiability. A core feature of the programme was the development of trial designs, involving alternative randomisations to different interventions, specifically aimed at solving the identifiability problems. Incidentally, the programme also led to the development of easy-to-use software commands for the evaluation of mediational mechanisms.
The role of the present report is not simply to summarise our research findings (although it will do this) but primarily to disseminate them in a relatively non-technical way in which the philosophy and technical approaches described in the modern causal inference literature can be applied to the design and analysis of rigorous randomised clinical trials for the evaluation of both treatment efficacy and treatment effect mechanisms. These are known as EME trials. This type of trial usually tests if an intervention works in a well-defined group of patients, and also tests the underlying treatment mechanisms, which may lead to improvements in future iterations of the intervention. One particularly promising area of application of this methodological work is in the development of EME trials for personalised therapies (or, more generally, the whole field of personalised or stratified medicine). Our aim here is to promote the full integration of marker information in EME trials in personalised (stratified) therapy.
Treatment efficacy
Let us start with the question ‘Does it work?’, which underpins the concept of treatment efficacy. We begin by describing some of the fundamental ideas of causal inference: the role of potential outcomes (counterfactuals) in the evaluation of treatment effects; average treatment effects (ATEs) and the challenges of confounding and treatment effect heterogeneity; and the challenges and pitfalls of mechanisms evaluation.
What is the effect of therapy?
Alice has suffered from depressive episodes, on and off, for several years. Six months ago a family friend advised her to ask for a course of CBT. She accepted the advice, asked her doctor for a referral to a clinical psychology service and has had several of what she believes to be helpful sessions with the therapist. She is now feeling considerably less miserable. Let us assume that her Beck Depression Inventory (BDI)4 score is now 10, having been 20 6 months ago. What proportion of the drop in the BDI score from 20 to 10 points might be attributed to the receipt of therapy? Has the treatment worked? We ask whether Alice’s depression has improved ‘because of the treatment, despite the treatment, or regardless of the treatment’. 5 What would the outcome have been if she had not received a course of CBT? The effect of the therapy is a comparison of what is and what might have been. It is counterfactual. We wish to estimate the difference between Alice’s observed outcome (i.e. after the sessions of CBT) and the outcome that would have been observed if, contrary to fact, she had carried on with treatment (if any) as usual. 6 Without the possibility of comparison, the treatment effect is not defined. Prior to the decision to treat (treatment allocation in the context of an RCT), we can think of two potential outcomes:
BDI following 6 months of therapy: BDI(T).
BDI following 6 months in the control condition: BDI(C).
The effect of therapy is the difference (Δ): Δ = BDI(T) – BDI(C).
This is called the individual treatment effect, which, since the BDI is a continuous score, is the difference between BDI(T) and BDI(C). The problem, however, is that this effect can never be observed. Any given individual receives treatment and we observe BDI(T), or the person receives the control condition and we observe BDI(C). We never observe both: we know the outcome of psychotherapy for Alice but the outcome that we might have seen had she not received therapy remains an unobserved counterfactual.
Efficacy: the average treatment effect
For a given individual, the effect of therapy is the difference Δ = BDI(T) – BDI(C) and, over a relevant population of individuals, the ATE is Ave[BDI(T) – BDI(C)]. Here we use ‘Ave[]’ instead of the mathematical statisticians’ customary expectation operator ‘E[]’ in order to make the discussion a little easier for the non-mathematically trained reader to follow (but later in the report we will use ‘E[]’ because of the need for both clarity and precision). Therefore, the efficacy of the therapy is the average of the individual treatment effects. How do we estimate efficacy? The ideal is through a well-designed and well-implemented randomised controlled trial (RCT).
Confounding and the role of randomisation
Note the simple mathematical equality:
If the selection of treatment options is purely random (as in a perfect RCT in which all participants are exposed to the treatment to which they have been allocated) then immediately it follows from the random allocation of treatment that:
Here ‘Ave[BDI|Treatment]’ means ‘the average of the BDI scores in the treated group’.
If treatment is randomly allocated, then efficacy is the difference between the average of the outcomes after treatment and the average of the outcomes under the control condition. It is estimated by simply comparing the corresponding averages resulting from the implemented trial. This straightforward and simple approach to the data analysis arises from the fact that treatment allocation and outcome do not have any common causes (the only influence on treatment allocation is the randomisation procedure) and therefore the effect of treatment receipt on clinical outcome is not subject to confounding.
Readers should note at this stage that this simple situation applies only if there is perfect adherence to (or compliance with) the randomly allocated treatments. If there are departures from the allocated treatments then the familiar intention-to-treat (ITT) estimator (i.e. compare outcomes as randomised) does not provide us with an unbiased estimator of efficacy. It provides an estimate of the effect of offer of treatment (effectiveness) and not the effect of actually receiving it (but is still not subject to confounding, as it is just estimating something subtly different from treatment efficacy). Common alternatives are the so-called per-protocol analysis (restricting the analyses to the outcomes for only those participants who have complied with their treatment application) and as-treated analysis (ignoring randomisation altogether). Both of these are potentially flawed. Both are likely to be subject to confounding by treatment-free prognosis: patients withdrawing from treatment, or being withdrawn by their clinician, may have quite a different prognosis from those who remain on therapy. In general, using a more general notation of Y for an outcome variable rather than BDI, we introduce potential outcomes Y(T) and Y(C). It is important to remember that generally:
Accordingly, how do we approach the problem of estimating efficacy (rather than effectiveness) in the presence of non-compliance? We will describe this below; however, first we introduce the problem (challenge) of treatment effect heterogeneity.
Treatment effect heterogeneity
Returning to our therapeutic intervention to improve levels of depression, there is no reason to believe that the individual treatment effect, Δ = BDI(T) – BDI(C), is constant from one individual to another. It is very likely to be variable, and we would like to evaluate how it might depend on potential moderators (‘predictive markers’ in the jargon of stratified or personalised medicine) and process measures such as the strength of the therapeutic alliance. Indeed, it is an article of faith among the personalised therapy community that there will be high levels of treatment effect heterogeneity among the general population and, given our ability to find markers that will be good predictors of treatment effect differences, these markers should then be very useful in the selection of therapies that might be optimal for patients with a given set of characteristics. This will form the basis of later discussions, but here we will illustrate the implications of treatment effect heterogeneity for efficacy estimation in RCTs for which there is a substantial amount of non-compliance with allocated treatment (compliance assumed for simplicity to be either all or none).
Staying with our relatively simple RCT in which we allocate participants to a treatment or a control condition, we can envisage situations in which those allocated to treatment fail to turn up for any of their therapy. There may also be participants who were allocated to the control condition but who, for whatever reason, actually received a course of therapy. Here the decision concerning the actual receipt of treatment is not determined by the trial investigators and, in particular, it is certainly not solely determined by the randomisation (although we would hope that, compared with the control participants, a considerably higher proportion of those allocated to the treatment condition would actually receive the therapy). An obvious question now is ‘What is the effect of treatment in the treated participants?’. Similarly, we might ask what the effect of treatment might have been in those who did not receive it. These two treatment effects are the average effect of treatment in the treated and the average effect of treatment in the untreated. If treatment effects were homogeneous (i.e. the same for everyone in the trial or equivalent target population) then these two ATEs would be identical and therefore the same as the ATE. If there is treatment effect heterogeneity, however, and actual receipt of treatment is in some way associated with treatment efficacy, then life becomes considerably more complicated. Frequently, we cannot estimate without bias the average effect of treatment in the people treated under these circumstances, but we can still define a group of participants for which we might be able to infer a treatment effect progress using randomisation (together with some additional assumptions). We refer to this group as the compliers and the average effect of treatment in the compliers as the complier-average causal effect (CACE). 7
The complier-average causal effect
Barnard et al. 8 have described a RCT in which there is non-compliance with allocated treatment together with subsequent loss to follow-up as ‘broken’. Our aim is to make sense of the outcome data from a broken trial. Can the broken trial be ‘mended’? Yes, but subject to the validity of a few assumptions. Before proceeding with this topic, however, we stress that, in a randomised trial, non-adherence or non-compliance with an allocated therapy or other intervention is neither an indicator of a trial’s failure (or lack of quality) nor a judgement on the trial participants. Especially in mental health, non-compliance can arise from patients making the wisest choice as they gather more information; for example, there may have been an adverse event which appeared to be linked to the therapy and, in this case, the patient’s doctor may have been involved in the decision to withdraw from treatment. The analysis of data from trials with a significant amount of non-compliance does need careful thought, however, particularly if non-compliance increases the risk of there being no follow-up data on outcome. Returning to our hypothetical trial with two types of non-compliance with allocated treatment (failure to turn up if you are in the therapy group, obtaining therapy if you are a control), we start by following Angrist et al. 7 and postulate that a trial comprises up to four types or classes of patient:
-
those who will always receive therapy irrespective of their allocation (always treated)
-
those who will never receive therapy irrespective of their allocation (never treated)
-
those who receive therapy if and only if they are allocated to the treatment arm (compliers)
-
those who receive therapy if and only if they are allocated to the control arm (defiers).
It is reasonable to assume that under most circumstances there are no defiers7 (the so-called monotonicity assumption), leaving us with three classes (the always treated, the never treated and compliers). However, we cannot always identify which class a particular participant should belong to; a patient who is allocated to the treatment group who then receives therapy is either always treated or a complier, and a participant who is allocated to the control group and who actually experiences the control condition is either never treated or a complier. However, a participant who is allocated to treatment and fails to receive therapy must be a member of the never treated. Similarly, a participant who is allocated to the control group and in fact receives therapy must be a member of the always treated.
The CACE is defined as the average effect of treatment in the compliers. This is the average effect that we hope we can estimate. However, first we have to make two additional assumptions:
-
As a direct result of randomisation the proportions of the three classes are (on average) the same in the two arms of the trial.
-
The effects of random allocation (i.e. the ITT effects) on outcome in the always treated and the never treated are both zero (the so-called exclusion restrictions). Note that this is not the same as saying that the ATEs (if they could be estimated) would be zero.
Following assumption 1 we can immediately estimate the proportion of the always treated from the proportion receiving therapy in the control group. Similarly, the proportion of the never treated follows from the proportion in the treatment group who fail to turn up for their therapy. The proportion of compliers is then what is left. Representing these three proportions as PAT, PNT and PC, respectively, and the associated ITT effects in the three classes as ITTAT, ITTNT and ITTC, then it should be clear that the overall ITT effect is the weighted sum of these class-specific effects:
The CACE is estimated by ITTC, and the other two ITT effects on the right-hand side of the equation (ITTAT and ITTNT) have both been assumed to be zero. It follows immediately that the CACE can be estimated by dividing the overall ITT effect by the estimated proportion of compliers (which, itself, is actually the ITT effect on the receipt of therapy: the arithmetic difference between the proportion receiving therapy in the treatment arm and the proportion receiving therapy in the control arm).
In the absence of treatment effect heterogeneity, the CACE estimate provides us with an estimate of the ATE. If this is actually the case, then it is clear that the overall ITT effect is a biased estimator of the ATE (it is attenuated, shrunk towards the null hypothesis of a zero treatment effect, the shrinkage being the proportion of compliers, PC). If, however, we are convinced that there is a possibility of treatment effect heterogeneity, then all we can say is that the CACE estimate is simply the estimated treatment effects for the compliers in this particular trial. It tells us nothing about the ATE in the always treated and never treated, and it follows that we have only limited information about the ATE (bounds can be determined for the ATE9,10 but this is beyond the scope of the present report). If, in a subsequent trial (or trials), the conditions are such that different participants are induced to be compliers, then the CACE will shift accordingly. It is a challenge to use one particular CACE estimate to generalise or predict what the ATE in the compliers will be under different circumstances.
Here, we have introduced the CACE to illustrate how treatment effect heterogeneity can complicate and threaten the validity of apparently straightforward estimators of ATEs (efficacy). Although treatment effect heterogeneity holds out great promise for the development of personalised therapies, it is also a potential nuisance and trap for the unwary. Exposure to the concept of the CACE, however, is also motivated by other considerations. Treatment receipt provides a simple introduction to mediation. Random allocation encourages participants to take part in therapy (or not, if they are in the control arm), which in turn influences clinical outcomes. The exclusion restrictions (random allocation has no effect on outcome in the always treated and the never treated) are equivalent to the assumptions that there is no direct effect of randomisation on outcome but that the effect of randomisation is completely mediated by treatment received. Randomisation, here, is an example of an IV (see Chapter 3) and the above expression for the CACE estimate is an example of what is known as an IV estimator. 7 Finally, the four latent classes of Angrist et al. 7 (always treated, never treated, compliers and defiers) also provide a relatively simple and straightforward example of principal stratification,11 an idea which will be described in some detail in Chapters 2 and 3.
Therapeutic mechanisms
We have discussed the rationale of efficacy estimation in some detail. What about the second component of EME: the challenge of evaluating mechanisms? ‘How does the treatment/complex intervention work?’. We will illustrate this with a description of a trial currently funded by the NIHR EME programme, the Worry Intervention Trial (WIT). 12 Here, we summarise the trial protocol.
The approach taken by the WIT was to improve the treatment by focusing on key individual symptoms and to develop interventions that are designed to target the mechanisms that are thought to maintain them. In the investigators’ earlier work, worry had been found to be an important factor in the development and maintenance of persecutory delusions. Worry brings implausible ideas to mind, keeps them in mind and makes the ideas distressing. The aim of the trial was to test the effect of a cognitive–behavioural intervention to reduce worry in patients with persecutory delusions and, very relevant to the context of the present report, determine how the worry treatment might reduce delusions. WIT involved randomising 150 patients with persecutory delusions either to the worry intervention in addition to standard care or to standard care alone. The principal hypotheses to be evaluated by the trial results are that a worry intervention will reduce levels of worry and that it will also reduce the persecutory delusions.
The key features of WIT are to establish that (1) the worry intervention reduces levels of worry, (2) the worry intervention reduces the severity of persecutory delusions and (3) the reduction in levels of worry leads to a reduction in persecutory delusions [i.e. that worry is a mediator of the effect of the intervention on the important clinical outcome (persecutory delusions)]. It is reasonably straightforward to establish the efficacy of the intervention in terms of its influence on worry (the intermediate outcome) and on persecutory delusions (the ‘final’ outcome). It is also straightforward to show whether or not levels of worry are associated or correlated with levels of persecutory delusions. However, this association could arise from three sources (not necessarily mutually exclusive): worry may have a causal influence on delusions; delusions may have a causal influence on worry; and there may be common causes of both (some or all of them neither measured nor even suspected to exist). As the randomised intervention is very clearly targeting worry, it seems reasonable to assume that worry is the intermediate outcome (mediator) leading to persecutory delusions, and not vice versa. Ruling out or making adjustments for common causes (confounding) is much more of a challenge. Another challenge is measurement error in the intermediate outcome (mediator). Finally, we have to deal with missing data (missing values for the mediator, missing values for the final outcome or both). Methods for tackling these problems will be discussed in detail in Chapter 2.
The evaluation of mediation is a key component of mechanisms evaluation for complex interventions. A second important aspect of mechanisms evaluation is the role of psychotherapeutic processes as a possible explanation of treatment effect heterogeneity. This answers the question ‘What factors make the treatment work better?’. For example, how might the treatment effect be influenced by characteristics of the therapeutic process such as the amount of therapy received (sessions attended), adherence to treatment protocols (the fidelity/validity of the treatment received13) or the strength of the therapeutic alliance between therapist and patient?14 Although they are modifiers of the effects of treatment, such process measures are integral to the therapy (they do not precede the therapy) and cannot be regarded as predictive markers or treatment moderators. One major hurdle in the evaluation of the role of these process measures is that they are not measured (or even defined) in the absence of therapy; they cannot be measured in the control participants. One cannot measure the strength of the therapeutic alliance in the absence of therapy. Second, the potential effect modifiers are likely to be measured with a considerable amount of measurement error (number of sessions attended, for example, is only a proxy for the ‘dose’ of therapy; rating scales for strength of the therapeutic alliance will have only modest reliability). Third, there are also likely to be hidden selection effects (hidden confounding). A participant may, for example, have a good prognosis under the control condition (no treatment). If that same person were to receive treatment, however, the factors that predict good outcome in the absence of treatment would also be likely to predict good compliance with the therapy (e.g. number of sessions attended or strength of the therapeutic alliance). Severity of symptoms or level of insight, measured at the time of randomisation, for example, is likely to be a predictor of both treatment compliance and treatment outcome. They are potential confounders. If we were to take a naive look at the associations between measures of treatment compliance and outcomes in the treated group, then we would most likely be misled. These associations would reflect an inseparable mix of selection and treatment effects (i.e. the inferred treatment effects would be confounded). We can allow for confounders in our analyses, if they have been measured, but there will always be some residual confounding that we cannot account for. The fourth and final challenge to be considered here arises from missing outcome data. Data are unlikely to be missing purely by chance. Prognosis, compliance with allocated treatment and the treatment outcome itself are all potentially related to loss to follow-up, which, in turn, leads to potentially biased estimates of treatment effects, their mediated parts and estimates of the influences of treatment effect modifiers. These methodological issues will be discussed in detail in Chapter 3.
Personalised therapy
The explicit notion of the heterogeneity of the causal effect of treatment on outcome, and the search for patient characteristics (i.e. markers) that will explain this heterogeneity and will be useful in subsequent treatment choice, is at the very core of what we label as personalised therapy. This answers our question ‘Whom does the treatment work for?’.
Other names that have been used for this activity in the wider context of medical and health-care research are ‘personalised medicine’, ‘stratified medicine’ (stratification implying classifying patients in terms of their probable response to treatment), ‘predictive medicine’, ‘genomic medicine’ and ‘pharmacogenomics’. None of these names, on its own, is fully satisfactory, but taken together they convey most of the essential information. We start by assuming that there is treatment effect heterogeneity: a given treatment will be more beneficial for some patients than for others. If we have a second competing treatment available for the same condition, then we also assume that it too will display varying efficacy but, with luck, it will be (most) beneficial for the patients for whom the first treatment seems to offer little promise (a distinct possibility if the second treatment has a completely different mechanism of action). A related approach might be motivated by reduction in the incidence of unpleasant or life-threatening side effects (possibly more relevant to drug treatment than psychotherapies but they should always be borne in mind). None of this knowledge is of any practical value, however, unless we can identify (in advance of treatment allocation) which patients might gain most benefit from each of the treatment options. We need access to pre-treatment characteristics (markers, often biological or biomarkers, but also including social, demographic and clinical indicators) that singly or jointly predict (i.e. are correlated or associated with) treatment effect heterogeneity. These so-called predictive markers (more familiarly known as treatment moderators in the psychological literature) can be identified through prior biological or psychological (cognitive) theory concerning treatment mechanisms or through statistical searches but, before they can be incorporated into a large clinical trial to validate their use, the preliminary evidence for their predictive role needs to be pretty convincing. If the predictive biomarker passes this preliminary hurdle, our contention is that a large trial of efficacy, designed to evaluate both treatment effect heterogeneity and corresponding mediational mechanisms, will provide a richer and more robust foundation for personalised or stratified therapy. We will return to these thoughts in detail in Chapter 5.
Markers and their potential roles
We start with the rather confusing terminology and with definitions provided by Simon:15 ‘a “prognostic biomarker” is a biological measurement made before treatment to indicate long-term outcome for patients either untreated or receiving standard treatment’ and ‘a “predictive biomarker” is a biological measurement made before treatment to identify which patient is likely or unlikely to benefit from a particular treatment’. In our view, both definitions need to be clarified and expanded in the context of a given evaluative RCT (we will interpret ‘biological marker’ here as meaning any type of useful biological, psychological, social or clinical information). Let us assume that we are planning to run a controlled psychotherapy trial: supposedly active therapy [plus treatment as usual (TAU)] versus TAU alone. Here, a purely prognostic marker would be a marker for which the effect on patient outcome is identical in the two arms of the trial (i.e. we would need to include no interactions between marker and treatment but only the independent effects of marker and randomised treatment in, for example, a generalised linear model to describe the treatment outcomes). Equivalently, the treatment’s effect on outcome does not vary with (is independent of) the value of a prognostic marker. On the other hand, the treatment’s effect is dependent on (predicted by) the value of a predictive marker (i.e. there would be a need to include, and estimate, the size of interactions between marker and treatment in the model to describe the treatment outcomes). In the extensive literature in the behavioural and social sciences (and mental health trials) a predictive marker would be called a treatment moderator;16,17 the baseline marker moderates or modifies the effect of the subsequent treatment. Our prognostic marker is usually referred to as a predictor or predictive variable. To add to the confusion, these definitions imply not that a predictive marker has no prognostic value but simply that its prognostic value is different in the two arms of the trial (another interpretation of the marker by treatment interaction). Graphical representations of the effects of prognostic and predictive biomarkers are illustrated in Figure 1.
FIGURE 1.
Graphical representations of the effects of (a) prognostic and (b) predictive markers. Black arrows indicate causal effects (the heavy lines being the ones of particular interest); the green arrow indicates moderation of the effect of treatment on outcome.
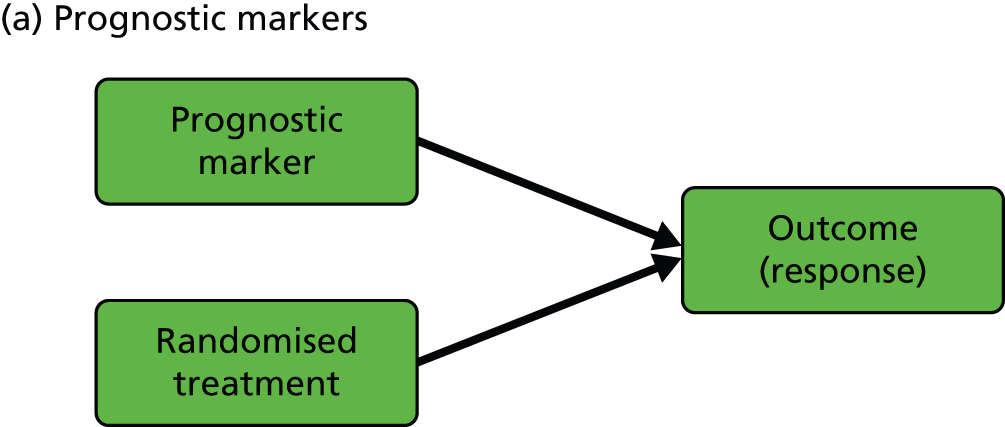
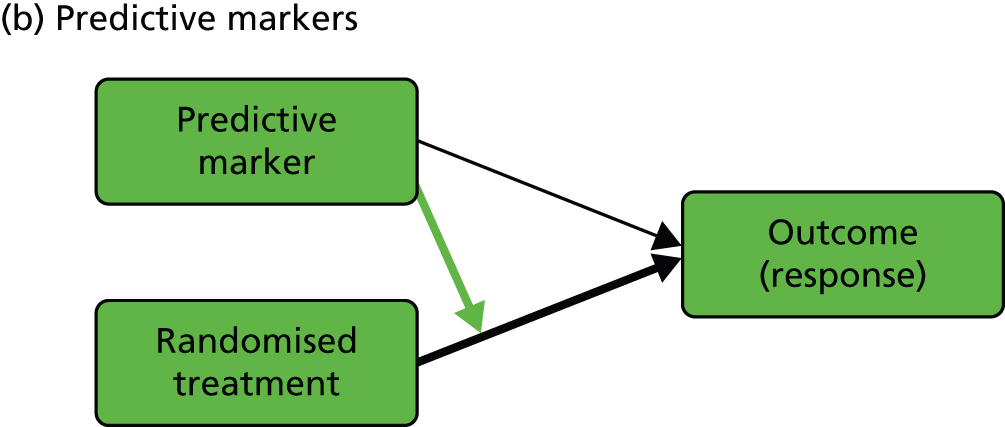
In the present report, we are primarily concerned with the distinction between prognostic and predictive markers, but of course we also discuss markers of mediational mechanisms and therapeutic processes. We use the terms ‘prognostic marker’ and ‘predictive marker’ to indicate measurements made prior to treatment allocation (i.e. a subset of the more general profile of potential baseline covariates in a conventional randomised trial, genetic markers being particularly prominent). Returning to measurements made after the onset of treatment, the third type of biomarker that would be potentially very useful is a marker of the function targeted by the treatment (i.e. the putative mediator). In some situations, investigators might wish to evaluate and promote the putative treatment effect mediator as a surrogate outcome; however, the evaluation of surrogate outcomes is not a topic that we wish to pursue here.
The rest of the report: where do we go from here?
In the next chapter we discuss the statistical evaluation of treatment effect mediation in some detail, starting with long-established strategies from the psychological literature,17–19 with the possibility of using prognostic markers for confounder adjustment, introducing definitions of direct and indirect effects based on potential outcomes (counterfactuals) (together with appropriate methods for their estimation), and then moving on to methods allowing for the possibility of hidden confounding between mediator and final outcome. In Chapter 3 we start by criticising the usual naive approach to evaluating the modifying effects of process measures (correlating their values with clinical outcomes in the treated group, with no reference to the controls) and then describe modern methods developed from the use of IVs14 and principal stratification. 7,11 Chapter 4 extends the ideas from these two chapters to cover trials involving longitudinal data structures (repeated measures of the putative mediators and/or process variables, as well as of clinical outcomes). Chapter 5 considers the challenge of trial design in the context of the use of IV methods and principal stratification. A considerable proportion of the discussion within this chapter will focus on EME trials for personalised therapy. Many of the statistical methods for mechanisms evaluation in EME trials (in fact all of them) require assumptions that are not testable using the data at hand. We will discuss sensible strategies for the reporting and interpretation of a given set of trial results (Appendices 5 and 6 summarise the results of a series of Monte Carlo simulations to assess the sensitivity of the results to departures from these assumptions). In Chapter 6, we finish with a general overview of our results and discussion of possibilities for future research but, perhaps more importantly, we provide a practical guideline for the design and analysis of EME trials with accompanying software scripts to help readers implement their own analysis strategies.
Chapter 2 Treatment effect mediation
Putative mediators
We have already briefly described the rationale for the MRC/NIHR WIT. Here, the mediational hypothesis is that the therapeutic intervention will lower the levels of worry, which, in turn, will lead to lowering of the levels of persecutory delusions. Worry is the proposed mediator: the treatment effect mechanism.
The MRC COMMAND trial was a multicentre RCT of cognitive therapy to prevent harmful compliance with command hallucinations. 20 Here, the cognitive therapy was aimed at reducing the perceived power of the auditory hallucinations (voices), which, in turn, would lead to lowering of the risk of the patient complying with voices telling him or her to harm him- or herself or others. The putative mediator is the perceived power of the voices.
Another example comes from the MRC Motivational Interviewing for Drug and Alcohol misuse in Schizophrenia (MIDAS) trial. 21 The intervention being evaluated was a combination of motivational interviewing and cognitive therapy to improve psychotic symptoms in dual-diagnosis patients (a combination of psychosis and substance abuse). In cannabis users, for example, the aim was to test whether or not the intervention reduced cannabis use, which, in turn, would lead to reduction in psychotic symptoms. The level of substance misuse was the putative mediator.
The MRC Pre-school Autism Communication Trial (PACT) was a two-arm RCT of about 150 children with core autism aged 2 years to 4 years 11 months. 22 Its aim was to evaluate a parent-mediated communication-focused treatment in in these children. After an initial orientation meeting, families attended twice-weekly clinic sessions for 6 months followed by a 6-month period of monthly booster sessions. Families were asked to undertake 30 minutes’ daily home practice between sessions. The primary outcome of the trial was the Autism Diagnostic Observation Schedule-Generic social communication algorithm score,23 which is a measure of the severity of the autism symptoms. Secondary outcomes included a measure of parent–child interaction, which was assessed through video ratings. Previous analysis of PACT data has shown that children and parents assigned to the PACT intervention showed some reduction of a modified Autism Diagnostic Observation Schedule-Generic algorithm score compared with those assigned to TAU, although the effect size was not statistically significant. 22 However, the between-group effect size for the secondary outcomes of parental synchronous acts (as a proportion of total parent communication acts) and child initiations (as a proportion of total child acts) were substantial and statistically significant. In the evaluation of treatment effect mechanisms the goal is to understand the two-step mechanism by which the intervention influences the child behavioural outcome with the parent and then, in turn, generalises to behaviour with the external Autism Diagnostic Observation Schedule-Generic assessor.
In summary, in the above trials the aim was to evaluate and estimate the size of the indirect effect of the intervention (i.e. that explained by changes in the proposed mediator). The direct effect (that explained by a mechanism or mechanisms not involving the proposed mediator), although important, was not the main focus of interest.
In some cases, however, the reverse scenario is true. For example, Prevention of Suicide in Primary Care Elderly: Collaborative Trial (PROSPECT) was a prospective, randomised trial designed to evaluate the impact of a primary care-based intervention on the reduction of major risk factors (including depression) for suicide in later life. 24 The trial was intended to evaluate an intervention based on treatment guidelines tailored for the elderly with care management compared with TAU. Bruce et al. 24 reported an ITT analysis for a cohort of participants recognised as being depressed at the time of randomisation. Data from this trial have also been analysed in detail in a series of papers25–28 developing and illustrating the estimation of direct and indirect treatment effects in RCTs in the presence of possible hidden confounding between the intermediate and the final outcome. An intermediate outcome (putative mediator) in PROSPECT was whether or not the trial participant adhered to antidepressant medication during the period following allocation of the intervention. The question here is whether or not changes in medication adherence following the intervention might explain some or all of the observed (ITT) effects on clinical outcome. The focus is on the estimation of direct effects of the intervention, that is the effects of CBT that are not explained by changes in medication. We call these intermediate variables ‘nuisance mediators’, as the intervention is not hypothesised to work directly through them, and we seek to estimate direct effects as our primary focus, the indirect effect being considered of secondary importance.
A brief description of mediation and moderation
We start with a trial in which there are no measured baseline covariates. Consider the simple directed or causal inference graph (causal graph) given in Figure 2a. In such a graph, each arrow represents an assumed causal influence of one variable on another. Randomised treatment allocation (Z) has an effect on an intermediate outcome (M), which, in turn, has an effect on the final outcome, Y. There is also a direct effect of Z on Y. The part of the influence of Z on Y that is explained by the effect of Z on M is an indirect or mediated effect. The intermediate variable, M, is a treatment effect mediator. The key thing to remember is that Figure 2a is representing structural or causal relationships, not merely patterns of association. The effect of Z on M is the effect of manipulating Z, that is, setting Z to equal a particular value z. Similarly, the effect of M on Y is the effect of manipulating M on the outcome Y. It is not necessarily the same as the observed association between M and Y given an observed value of the mediator that has not been manipulated by the investigator.
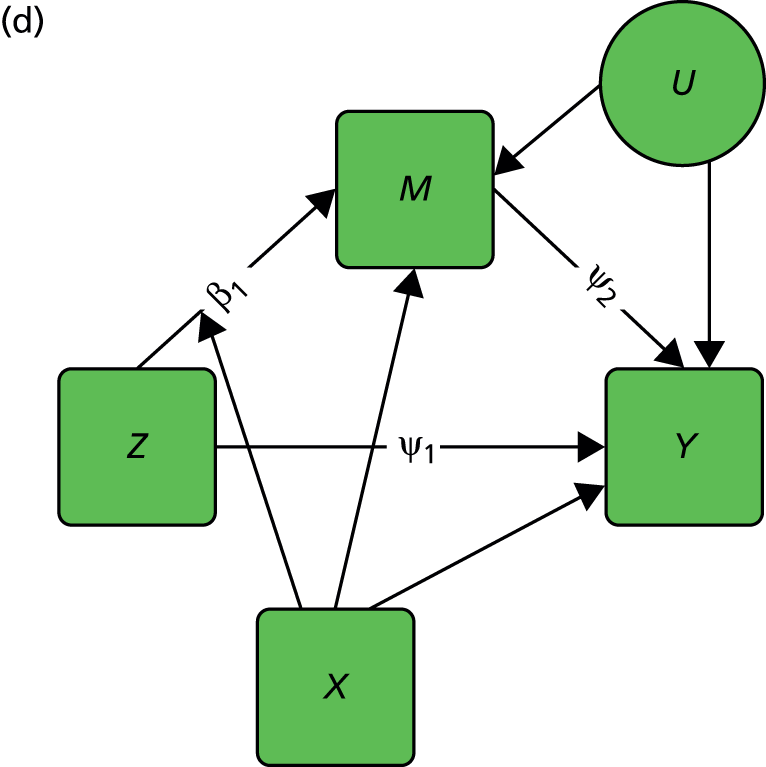
FIGURE 2.
Causal path diagrams relating randomised treatment allocation (Z) to an intermediate outcome (M) and a final outcome (Y). (a) Diagram showing mediation of Z on Y through M; (b) mediation with unmeasured confounding U between mediator and outcome; (c) mediation with measurement error in M, where M* is the error-prone measure; (d) mediation with the interaction between X and Z as a valid instrumental variable; and (e) mediation with moderation of all effects by X.


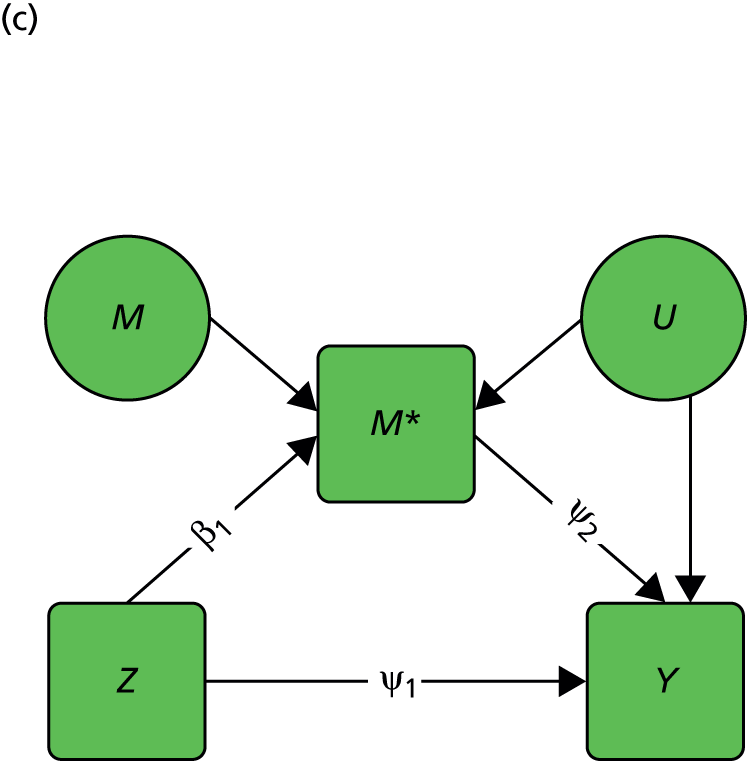

The important skill that an investigator needs in interpreting directed graphs such as Figure 2a, is to think automatically ‘What vital component might be missing?’ or ‘What’s not in the graph?’. In our experimental set-up (the RCT), we are able to manipulate Z through random allocation (so we can assume that there are no confounders of the effects of Z on either M or Y). However, typically, we have no control over either M or Y (they are both, in fact, outcomes of randomisation). Therefore, there may be unobserved variables, other than treatment (Z), that influence both M and Y. Let these unobserved influences be represented by the variable U. The directed graph for this situation is shown in Figure 2b. Let us further suppose that we cannot measure M directly (i.e. without error), but we have an error-prone proxy, M*. The corresponding graph is now Figure 2c.
Let us assume that a data analyst uses simple (multiple) linear regression or structural equation modelling (SEM) approaches to estimate the size of the effects illustrated by Figure 2a. Can one interpret the resulting regression coefficients as causal effects? Yes, if and only if the model represented by Figure 2a is the correct one. However, if either Figure 2b or c, or a more complex model, is correct then a naive analysis based on Figure 2a will lead to invalid results.
Let us finally assume that we have measured an important baseline covariate, X. Suppose the effect of Z on M is influenced by the value of X. The covariate X is said to be a moderator of the effect of Z on M. In addition, X itself is assumed to influence the values of M and to directly influence the values of Y, but we assume here that there are no interactions between covariate and treatment for these components of the model. The resulting graph (assuming M is measured without error) is given in Figure 2d. By convention, a causal graph or diagram with multiple arrows pointing at a single variable implicitly allows for interactions between the causal variables. 5 To explicitly reflect the absence/presence of interactions in our models, we depart from this convention and indicate the interaction between X and Z on M (i.e. the moderation of the effect of Z on M by X) by a single-headed arrow from X to the causal pathway from Z to M. This approach is the one commonly taken in the path analysis/SEM literature in the psychological and social sciences. Again, when interpreting Figure 2d we should be carefully considering what components are missing (the two additional arrows for the interactions that may have incorrectly been assumed to be absent, for example the green arrows in Figure 2e, as well as the ones that are drawn). The missing paths are indicative of some of the vital assumptions on which any valid analysis might be made.
Brief historical survey
At present the field comprises two distinct traditions. The older and more popular approach, particularly in the social and behavioural sciences, is concerned with the estimation of direct and indirect effects through the use of path analysis (and associated regression models) and SEM. More recently, the ‘causal inference’ approach is being developed by statisticians, econometricians and others interested in explicitly defining the assumptions needed for valid inferences concerning the causal effects of treatments/interventions.
One key difference between the two approaches is in the degree of care taken in the specification of the statistical models so that parameter estimates can be legitimately interpreted as causal effects. In the former approach, the assumptions are sometimes implicit (and users are frequently unaware of what they are or of their implications). In the newer approach, every attempt is made to make the assumptions explicit (and open to challenge). We will refer to the latter as ‘causal mediation analysis’, keeping in mind that no mediation analysis makes sense in the absence of any attempt to infer causality.
As we shall discuss in more detail in the following sections, we summarise that the traditional approach has four main differences from the casual mediation analysis methods:
-
It assumes no unmeasured confounding between mediator and outcome.
-
It assumes that there are no interactions between exposure and mediator on outcome.
-
It does not easily extend to non-linear models.
-
It assumes that all the statistical models are correctly specified.
Traditional methods: the Baron and Kenny approach
The traditional methods of statistical mediation analysis are discussed in detail by the psychologist David MacKinnon,19 whose methodological work has been very influential in this area (e.g. MacKinnon and Dwyer29). Papers by Judd and Kenny,18 and particularly by Baron and Kenny (B&K),16 have also been extremely influential. We introduce some notation whereby the subscript i denotes an individual i, Yi represents the observed outcome, Mi represents the observed value for the mediator, Zi represents treatment – for example, for simplicity, an intervention (Zi = 1) or control (Zi = 0) – and Xi represents a vector of baseline covariates.
In their 1986 paper, B&K16 set out three steps in the evaluation of mediation through the use of appropriate linear regression models: (1) demonstrate that treatment, Z, has an effect on the outcome, Y; (2) demonstrate that treatment, Z, has an effect on the putative mediator, M; and (3) demonstrate that the mediator, M, has an effect on the outcome, Y, after controlling for treatment, Z.
Many authors, including MacKinnon,19 have argued that the first step is not necessary. It implies that the evaluation of mediation is of value only when we have a statistically significant total treatment effect on the final clinical outcome. However, analysis of mediation might also tell us why a trial result is negative. Is it because the intervention has failed to shift the mediator or could it be that the mediator failed to influence the outcome? Or is there a harmful direct effect of the intervention that counterbalances the benefits attained via the mediator?
The B&K procedure for statistical mediation analysis16 uses two regression models:
The first is a model for the mediator conditional on treatment and the set of covariates (note that the original B&K procedure did not explicitly include covariates). The second model is the expectation of the outcome conditional on the mediator, covariates and treatment. From these, the direct effect of treatment on outcome would be ψ1 and the indirect effect of treatment acting through the mediator would be β1 × ψ2.
The validity of this approach is dependent on three key assumptions, which were introduced in Figure 2:
-
BK1: there are no other common causes of M and Y, that is there is no unmeasured confounding between mediator and the outcomes.
-
BK2: there is no interaction between M and Z on Y.
-
BK3: there is no error in the measurements of M.
Assumption BK3 also applies to Z, of course, but, in the case of a RCT, we assume that random allocation is known and that we are working with ITT effects; however, non-compliance with randomised treatment would complicate the issue if we were concentrating on the effects of actually receiving treatment.
It is clear that, if Figure 2a is the true underlying data-generating model, then we can obtain unbiased estimates of ψ1, β1 and ψ2. However, if Figure 2b or c is the true model, then using the regression model for the outcome outlined previously we can no longer obtain an unbiased estimate for ψ2 or ψ1, so the resulting estimates of the direct and indirect effect are biased.
Assumption BK1 can be made more plausible by the inclusion of measured confounders (such as X in the models above), but the presence of unmeasured variables cannot be unequivocally ruled out, so the results of the mediation analysis should be considered with this caveat in mind. Alternative IV methods have been proposed (see Structural mean models), which allow for valid estimation in the presence of unmeasured confounding by proposing alternative assumptions. 14,30,31
Assumption BK2 rules out the presence of treatment–mediator interactions in the outcome model. If such an interaction were to be included, the second model would become:
This model has an additional parameter, ψ3, and it becomes unclear how this parameter should be incorporated into the definition of direct and indirect effects proposed by the B&K procedure, as, for example, the direct effect ψ1 now also depends on the value of m.
Causal mediation analysis: formal definitions of direct and indirect effects
Alternative parameters for mediation analysis have been proposed in the causal inference literature, which uses the counterfactual framework for defining causal effects. The first rigorous description of the problems arising in the estimation of direct and indirect effects appears to be that provided by Robins and Greenland. 32 A thorough exposition has also been provided by Pearl and his colleagues. 5,33,34 We now review the essence of these proposals, and demonstrate when they are equivalent to the definitions provided previously.
We define the following counterfactual outcomes:
-
Mi(z) represents the mediator with treatment level Zi = z.
-
Yi(z,m) represents the outcome with treatment level Zi = z and mediator level Mi = m.
-
Yi(0) = Yi(0,Mi(0)) represents the outcome if randomised to usual care with mediator Mi(0).
-
Yi(1) = Yi(1,Mi(1)) represents the outcome if randomised to treatment with mediator Mi(1).
Note that these counterfactual outcomes differ from the observed outcomes. In the usual-care arm where Z = 0, Yi = Yi(0) and Mi = Mi(0), so that Mi(0) and Yi(0) are the observed values and Mi(1) and Yi(1) are unobserved. Similarly in the treatment arm where Z = 1, Mi(0) and Yi(0) are unobserved and Yi = Yi(1) and Mi = Mi(1) are observed.
Using the counterfactual definitions, we can define the following causal parameters:5,33
Natural direct effect:
Natural indirect effect:
Controlled direct effect at mediator level m:
The natural direct effect is the direct effect of treatment on outcome, given the ‘natural’ level of the mediator Mi (0), that is the level that the mediator would be at under the usual care condition. The natural indirect effect is the effect of the change in mediator on outcome if receiving treatment (i.e. Z = 1), that is the direct effect of treatment on outcome remains constant but alters the mediator. The controlled direct effect is the direct effect of treatment on outcome at mediator level m. It can easily be shown, as below, that the total effect is the sum of the natural direct effect and the natural indirect effect. 5 When there is no interaction between treatment and mediator, the controlled direct effect is constant at all levels of M and is equal to the natural direct effect. In many of the analyses presented in the present report, we will be assuming the absence of this interaction.
The total effect of randomisation (Z) on outcome (Y) for the ith subject is:
-
Yi(1,Mi(1))−Yi(0,Mi(0)).
Similarly, the effect of Z on the intermediate outcome or mediator (M) is:
-
Mi(1) − Mi(0).
Taking expectations (averaging) over i, and reverting to the usual mathematical notation of E[], we define the ATE on the outcome as:
and the ATE on the mediator as:
Here, the first component of this decomposition is the direct effect of randomisation given M(0) and the second component is the effect of the change in mediator if randomised to receive treatment (i.e. Z = 1). The first of these is the natural direct effect, and the second is the natural indirect effect, as we defined previously.
We define the direct effect of treatment assignment on outcome at mediator level m as Yi (1, m) − Yi (0, m) (i.e. the controlled direct effect, as defined above) and if we are prepared to assume that this does not depend on m then for any m and m′:
This enables us to define the mean direct effect as:
Now, if we define the effect of M on Y via:
where we acknowledge lack of homogeneity of treatment effects (σε2 > 0; E(εi) = 0) but we assume that Cov(εi, (Mi(1) − Mi(0))) = 0 (i.e. that there is no essential heterogeneity as defined in the econometrics literature35). It follows from equations 13 and 15 that:
This is the decomposition from a traditional path analysis model as we observed previously.
It is no coincidence that the decomposition of the causal mediation parameters leads to the same decomposition as from the traditional model. When there is no interaction between treatment and mediator, and the outcome and mediator are continuous so that we have linear models for the expectations, this result will hold. The coefficient for randomisation ψ1 in the model for the outcome Y estimates the controlled direct effect and (equivalently) the natural direct effect, and the β1 × *ψ2 term estimates the natural indirect effect. However, this result only holds under linear models without interaction terms, as we discuss in Estimation and assumptions.
Estimation and assumptions
No hidden confounding or measurement error in the putative mediator
When we have no hidden confounding or any measurement error in the mediator, then the B&K approach yields results that can safely be interpreted as causal. Work on identification and estimation of the natural direct and indirect effects, and controlled direct effects using parametric regression models has been developed by VanderWeele and Vansteelandt. 36,37 Informally this extends the B&K procedure to allow for interactions between mediator and treatment on outcome (we will not pursue the details here). It allows for confounding by observed covariates. It also extends the models to include binary mediators and/or binary or count outcomes; this requires the parameters from the parametric regression models to be combined through the mediation formula to generate the causally defined mediation parameters. In the context of the present project, Emsley et al. 38 have produced the paramed command to implement these estimation procedures in Stata (StataCorp LP, College Station, TX, USA) (see Appendix 1).
Problems arising through omitted common causes (hidden confounding)
Let us briefly consider complete mediation, where there is no direct effect of treatment on outcome. In the absence of any hidden confounding (i.e. no unmeasured common causes of M and Y) we have conditional independence between treatment and outcome: Z╨Y |M, X (here we use the symbol ‘╨’ to mean ‘is statistically independent of’). Now, if we have a source of hidden confounding, U, complete mediation implies Z╨Y |M, X, U. Note that in the presence of U it is not true that Z╨Y |M, X. Examination of partial correlations or the equivalent partial regression coefficients, ignoring U, will lead us astray. Similarly, hidden confounding caused by U will lead investigators astray in using regression or SEM to assess incomplete mediation. Their estimated regression coefficients will be biased. The probable presence of hidden confounding, U, is the reason why the standard SEM approach has doubtful validity.
In a RCT, the mediator and the final clinical outcome are both outcomes of randomisation. The standard regression/SEM approach involves controlling for the mediator (the intermediate outcome) when evaluating the direct effects of randomisation on the final outcome. The potential pitfalls of controlling for post-randomisation variables have been recognised for many years (e.g. Herting39). In the context of the estimation and testing of direct and indirect effects, there are several powerful critiques of the standard methods. 32,40–44 But it is worth noting at this point that it is not SEM as a general technique that is necessarily at fault but that the users of the methodology are frequently fitting the wrong (i.e. mispecified) models. 45 Subject to solving the problems of identification, it is possible to use SEM methodology in an appropriate way (see Coping with hidden confounding).
Coping with hidden confounding
One way around the hidden confounding problem is to assume a priori that there is no direct effect of treatment (i.e. complete mediation). This leads to the use of IV methods with randomisation as the instrument. Briefly, in a standard regression model, if an explanatory variable is correlated with the error term (known as endogeneity) its coefficient cannot be estimated unbiasedly. An IV is a variable that does not appear in the model, is uncorrelated with the model’s error term and is correlated with the endogenous explanatory variable; randomisation, where available, often satisfies these criteria. A two-stage least squares (2SLS) procedure can then be applied to estimate the coefficient. At its simplest, the first stage involves using a simple linear regression of the endogenous variable on the instrument and saving the predicted values. In the second stage the outcome is then regressed on the predicted values, with the latter regression coefficient being the required estimate of the coefficient. This procedure is routinely used by econometricians and further details including the derivation of the standard errors (SEs) are found in standard econometric texts such as Wooldridge. 46
The main concern of this report is evaluating both direct and indirect effects in the presence of hidden confounding between mediator and outcome. IVs provide one method of estimating these effects, although the identification of valid instruments is a major challenge. Of related interest is the pioneering work of Gennetian et al. 47,48 on the use of IV methods to look at the joint effects of two or more putative mediators, where, again, identification of the causal parameters is the major challenge. 49 Here the authors propose to use as instruments baseline covariates that are good predictors of an assumed heterogeneous effect of treatment allocation (i.e. randomisation) on levels of the mediator (i.e. moderators of the effect of treatment on the putative mediator).
Ten Have et al. 25 have recently used G-estimation methods to solve the problem of valid estimation of direct and indirect effects (see also Bellamy et al. 26 and Lynch et al. 27). In this approach we observe treatment-free outcomes in those randomised to the control group and, if we can deduct the effect of treatment from each of the participants allocated to the treatment group to obtain their treatment-free outcomes, then we would expect treatment-free outcome to be independent of randomisation. In essence, G-estimation is a means of finding a treatment effect estimate that makes the treatment-free outcome independent of randomisation. Methods based on 2SLS and extensions of the G-estimation algorithms of Fischer-Lapp and Goetghebeur50 have been described by Dunn and Bentall14 (and been shown, in the case of the appropriate linear models, to be exactly equivalent). Albert51 also used 2SLS estimation. Recent reviews of these methods are provided by Emsley et al. 30 and by Ten Have and Joffe. 52
Measurement errors
In the context of epidemiological and psychological/sociological modelling, measurement and misclassification errors in explanatory variables (putative risk factors as well as confounders) are a well-known threat to the validity of causal inference,53–55 although the problems are not so well appreciated among the applied clinical research community as one might hope. An implicit assumption in our models of mediation has been that the mediator is measured without error. It is highly likely that this assumption is invalid (or not even approximately true in the case of many psychological markers). Although it is difficult, if not impossible, to verify, measurement and misclassification errors might be a greater problem in this area than unmeasured confounders. How might one cope with this threat? One possibility is replication (either independent repeated measurements of the mediator in question or the use of a panel of distinct instruments to measure it) and to explicitly use latent variable models. 55 We will not pursue this option here but instead will discuss a similar approach using PACT later in this chapter. Another possibility is to use IV (2SLS) procedures, even when there is no hidden confounding suspected. The use of IV methods is a well-known tool for coping with biases caused by random measurement errors in explanatory variables,55–57 although their explicit use in allowing for measurement errors in putative mediators and process variables seems to be quite rare. 14,58,59 So some of the changes in inference about mediation that might arise from a comparison of naive B&K analyses with IV-based analyses might arise from this source rather than from unobserved confounders. Moreover, in a typical trial we commonly have additional information about the reliability of measurement of the mediator, and further information about other possible mediators. In simple single-mediator problems, failure to account for measurement error in the mediator results in systematic underestimation of the mediated path. 14,60 In the multiple mediators case, biases in either direction are possible. This suggests that sources of information on measurement error can be exploited to provide adjusted estimates of mediation without the cost of the much increased uncertainty of the IV method.
Structural mean models
A structural mean model is a model relating the potential outcomes Yi (z, m) to one another or to Yi (0, 0). If we assume a linear model for the potential outcome Yi (0, 0) in terms of a set of measured baseline covariates, Xi (including a vector of 1s), then as Lynch et al. ,27 we could write:
for all values of z and m, with ε being independent of Z but not of X and M, that is E[εi|Z = z] = 0.
However, it is unnecessary to model counterfactuals that would not have been observed under either randomisation. Instead, we can write this as follows, where the aim is to estimate the causal parameters ψ1 and ψ2:
where E[ei] = 0 and σe2 > 0. This term allows for treatment effect heterogeneity, but assuming that Cov(ei, (Mi(1) – Mi (0))) = 0 (no essential heterogeneity as previously35).
At the same time we have a model for M(z), which for quantitative M(z) might be:
Again, there is a random departure term, ωi (z), with zero expectation. The valid estimation of β1 and the effects of the baseline covariates on M (i.e. the θ) is very straightforward by linear regression. Unfortunately, the estimation of ψ1 and ψ2 is much more problematic. In the presence of hidden confounding between M and Y, these two parameters are not identified. Often, however, we can improve our ability to identify and estimate ψ1 and ψ2 by finding a moderator of the effect of Z on M (i.e. a predictive marker) and introducing the moderator by randomisation interaction into the model for M(z).
Model identification and parameter estimation: utilisation of baseline covariate (moderator) by randomisation interactions
Consider a binary pre-randomisation covariate, X. This covariate is assumed (or has been shown) to be a moderator of the effect of treatment (i.e. it is a predictive marker) on outcome (Y). We make the crucial assumption that X influences the total treatment effect (τ) through its effect on the level of mediation (β1) but that X does not moderate (modify) either the direct effect of the intervention (ψ1) or the effect of the mediator on the outcome (ψ2), as illustrated in Figure 2d.
For level 1 of the moderator (X = 1), we have a level specific total effect of Z on Y:
Similarly, for level 2 of the moderator (X = 2):
(being careful to distinguish the meaning of the new parameter, ψ3, from the earlier use of ψ3 to describe a randomisation by mediator interaction on the outcome).
Clearly, τ1 – τ2 = (ψ2 – ψ3)β1, and it immediately follows that β1 = (τ1 – τ2)/(ψ2 – ψ3). Recall that τ1, τ2 (the level-specific effects of randomisation on outcome), ψ2 and ψ3 (the level-specific effects of randomisation on the mediator) may all be estimated by regressing Y and M on Z separately at each level X = 1,2 (possibly adjusting for other covariates). Therefore, β1 is now identified, as is ψ1 (by substitution back into either of the above equations).
Thus, we have managed to allow for hidden confounding. Note, too, that, apart from possible lack of precision, the effects of the treatment on the mediator (ψ2 and ψ3) will not be affected by random measurement error in the mediator (they will be consistent). So, we have also dealt with imprecision in the mediator measurements. But the Achilles heel of this solution is finding convincing treatment moderators, particularly when their influence on the effects of treatment on outcomes is expected to be fully explained by the moderation of the treatment effects on the putative mediator (see Chapter 5).
If instead the baseline covariate, X, has many levels then, in general, τx = ψ1 + ψ(x + 1)β1 and so β1 and ψ1 are, respectively, the slope and intercept of the straight line relating the ATE (τ) at each level of X to the average effect of treatment on the mediator (ψx+ 1) at that level of X. This approach has much in common with the meta-analytic regression techniques for the evaluation of surrogate outcomes. 3,61–63 We note, again, that if a proxy for the mediator (M*) is simply the true mediator subject to random measurement error, then using M* rather than M itself will still yield valid causal effect estimates, as will the IV methods. 59,61
As the baseline covariate is influencing the size of the effect of treatment on the mediator, we have an X by Z interaction in the structural model for M(z). There is no interaction in the model for Y(z,m), and therefore the interaction is an IV (its only influence on outcome is through the mediator, as stated in our previous definition). So, if we have baseline covariates (e.g. X1 and X2), then at an individual level we can fit an equivalent IV model through the use of 2SLS. 14,51 In Stata, for example, we could use the following ivregress command:
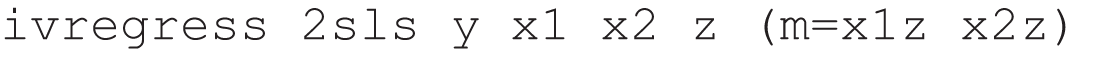
where x1z and x2z are the products of x1 or of x2 and randomisation, respectively. For a binary mediator, we might wish to use a control function approach; these are an additional function which when added to the standard regression equation removes the endogeneity because they account for the correlation between the error term and the unobserved part of the outcome. 64 A typical Stata command would be:

Binary mediators: an alternative two-stage least-squares estimation procedure
Elsewhere (Emsley et al. 65), we demonstrate both mathematically and through Monte Carlo simulation studies that the G-estimation procedure as described by Ten Have et al. 25 is identical to an IVs 2SLS estimation procedure using a function of the subject’s compliance score as an IV for M. Assuming that a set of covariates, X, contain the required moderators of the treatment effect on the mediator, this procedure can by fitted using standard statistical software, for example using the following procedure:
-
Fit a model for the probability that Mi = 1 given the covariates, Xi, for those in the intervention group (i.e. Pr[Mi = 1|Xi, Zi = 1]) using a logistic regression, and predict this probability for everyone in the trial.
-
Fit a model for the probability that Mi = 1 given the covariates, Xi, for those in the control group (i.e. Pr[Mi = 1|Xi, Zi = 0]) using a logistic regression, and, again, predict this probability for everyone in the trial.
-
Calculate cscore = (Zi – q){Pr[Mi = 1|Xi, Zi = 1] – Pr[Mi = 1|Xi, Zi = 0]} for each subject in the whole sample (where q is the proportion of the subjects randomised to receive treatment and the difference between the probabilities predicted by steps 1 and 2, Pr[Mi = 1|Xi, Zi = 1] – Pr[Mi = 1|Xi, Zi = 0], is the subject’s compliance score, denoted cscore).
-
Use a 2SLS procedure with cscore as the instrument for Mi (allowing for covariates, Xi, in both stages of the estimation).
Application of the alternative two-stage least squares algorithm
Although we do not believe that the present report is the right place to formally describe the mathematical and statistical equivalence of our 2SLS procedure and the G-estimation algorithm described by Ten Have et al. ,25 readers may find it useful to see an empirical demonstration of their equivalence. We do this by analysing the data from PROSPECT.
Data from this trial are available on the Biometrics website (www.biometrics.tibs.org/datasets/060225CF_biomweb.zip) as supplementary material to the paper by Ten Have et al. 25 Table 1 summarises these data and comprises information on the 297 depressed elderly trial participants with complete outcome data (here the Hamilton Depression Rating Scale66 score at 4 months after randomisation, the variable hamda). Here we use variable labels as provided in the Biometrics file. The baseline covariates are site (used in our analyses as the categorical factor site or as two dummy variables s1 and s2), previous use of medication (scr01), use of antidepressants at the time of the baseline assessment (cad1, scored from 0 to 5), a dichotomised measure of suicidal ideation at baseline (ssix01), based on the Scale for Suicidal Ideation67 and the Hamilton Depression Rating Scale total at baseline (hamda1). Medication adherence following treatment allocation (interven) is recorded by the binary variable amedx.
| Variable | Site 1 | Site 2 | Site 3 | |||
|---|---|---|---|---|---|---|
| Control (N = 53) | Intervention (N = 53) | Control (N = 57) | Intervention (N = 54) | Control (N = 4) | Intervention (N = 38) | |
| Baseline characteristics: n (%) | ||||||
| Antidepressant use, cad1 | 22 (41.5) | 18 (34.0) | 25 (43.9) | 25 (46.3) | 25 (59.5) | 21 (55.3) |
| Previous medication, scr01a | 27 (50.9) | 24 (45.3) | 25 (43.9) | 28 (51.9) | 29 (69.1) | 20 (52.6) |
| Suicidal ideation, ssix01 | 9 (17.0) | 13 (24.5) | 12 (21.1) | 18 (33.3) | 13 (31.0) | 16 (42.1) |
| Post-randomisation adherence to antidepressant medication: n (%) | ||||||
| Amedx | 20 (37.7) | 44 (83.0) | 19 (33.3) | 45 (83.3) | 30 (71.4) | 34 (89.5) |
| Hamilton depression scores: mean (SD) | ||||||
| At baseline, hamda1 | 16.48 (5.33) | 18.11 (6.15) | 17.25 (5.26) | 19.87 (6.40) | 18.62 (6.32) | 18.74 (5.85) |
| At 4 months, hamda | 13.42 (8.12) | 11.98 (7.75) | 14.10 (8.55) | 12.12 (7.29) | 12.98 (8.53) | 9.97 (6.92) |
There appears to be a beneficial effect of the intervention on the 4-month Hamilton Depression Rating Scale score, but there is also a clear effect of intervention on adherence to antidepressant medication. Could this be explaining the observed ITT effect on outcome? In our analyses, reported in Table 2, similar to previous authors, we make no attempt to allow for the clustering of the data within primary care practices.
| Estimation method | Estimate | SE | 95% CI |
|---|---|---|---|
| ITT effect | –3.15 | 0.82 | –4.76 to –1.53 |
| Effect of mediator on outcome (ψ2) | |||
| G-estimation | –1.975 | 2.313 | –6.509 to 2.560 |
| 2SLS using function of compliance score as IV | –1.975 | 2.401 | –6.680 to 2.730 |
| 2SLS using interactions as IVs | –1.953 | 2.714 | –7.294 to 3.388 |
| Regression as in B&K | –1.244 | 1.092 | –3.394 to 0.906 |
| Direct effect of the intervention on outcome (ψ1) | |||
| G-estimation | –2.367 | 1.274 | –4.864 to 0.130 |
| 2SLS using function of compliance score as IV | –2.367 | 1.316 | –4.946 to 0.212 |
| 2SLS using interactions as IVs | –2.376 | 1.350 | –5.032 to 0.281 |
| Regression as in B&K | –2.656 | 0.926 | –4.479 to –0.832 |
Ten Have et al. ’s original analysis split the baseline covariates into two sets. 25 One set is used in the logistic model to calculate the compliance score. The other set is used in the linear outcome model. We used all the baseline covariates in both steps (analogous to the standard 2SLS procedures). We compared the results of using this G-estimation procedure with those using the standard B&K regression, those from a conventional 2SLS run using baseline covariate by intervention interactions as instruments and, finally, using our modified 2SLS procedure using the compliance score as the IV.
First, we translated the Ten Have et al. 25 SAS G-estimation programs (available in the ZIP file from the Biometrics website) into Stata do files. We do not provide any details here (these available from the authors on request). We simply present the results.
The B&K regression is as follows:
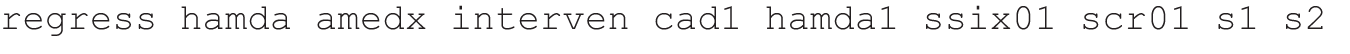
The standard 2SLS regression, using intervention by covariate interactions (the products icad1 ihamda1 issix01 iscr01 is1 is2) as instruments, is:
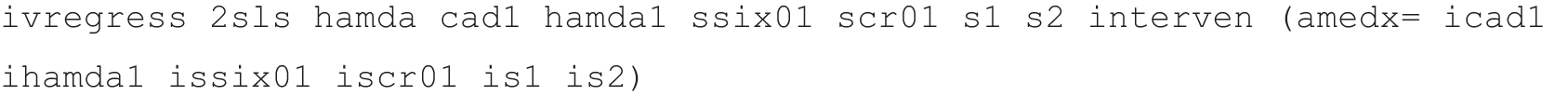
The modified 2SLS algorithm, using the compliance score as instrument, was operationalised as follows:
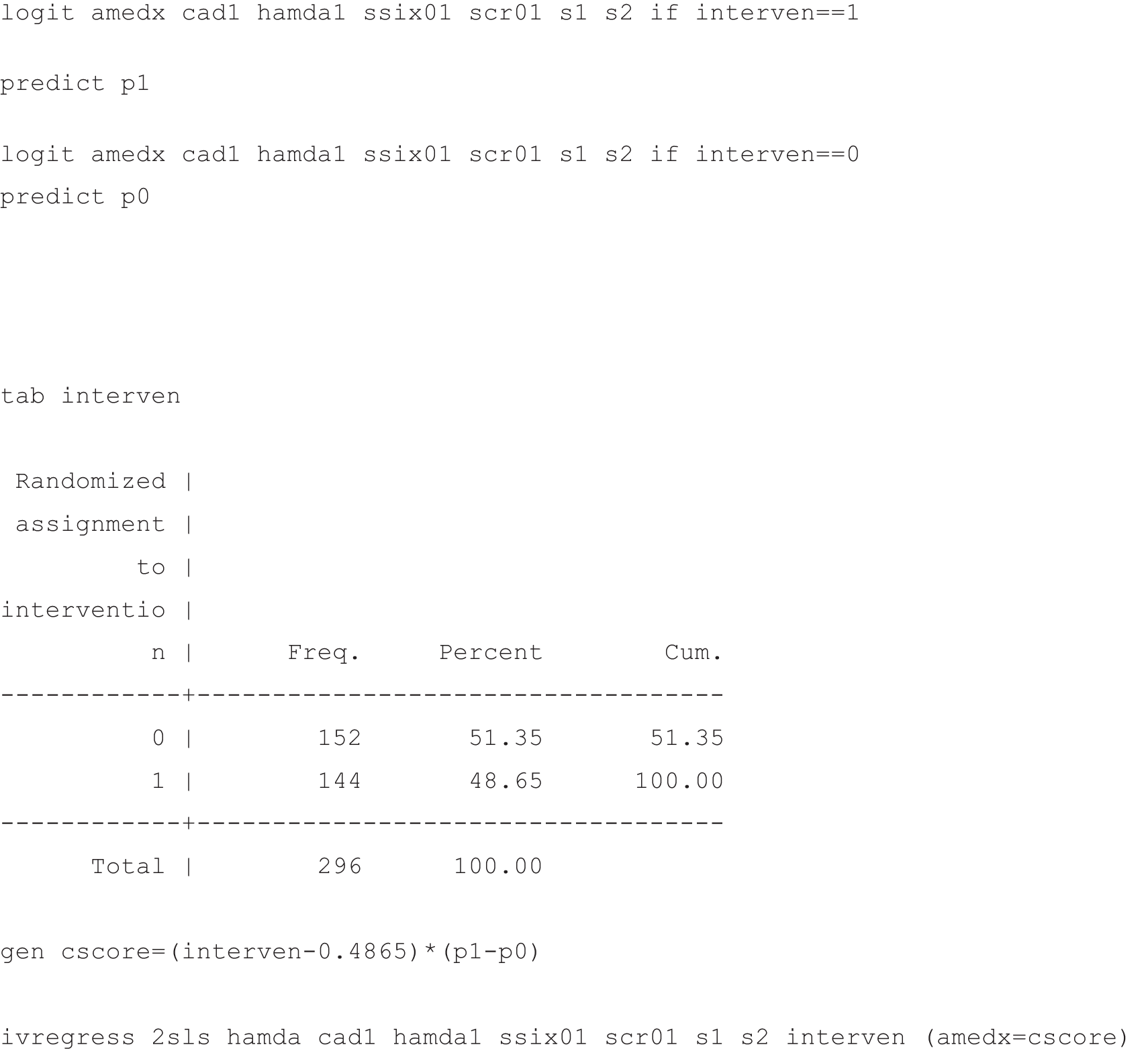
The results are shown in Table 2. They speak for themselves; the effect estimates from G-estimation and the modified 2SLS estimates are identical (their SEs are slightly different, however, because they are based on different procedures). The standard 2SLS estimates are also very close. As expected, the B&K estimates are out on a limb (possibly biased, but much more precise). Our conclusion is that practising EME triallists need not bother with the computationally intensive G-estimation algorithm but should instead use the modified 2SLS procedure, or even the standard 2SLS approach.
PACT: accounting for error in the measurements of the mediator
Although we focus on extensions to longitudinal data in Chapter 4, with repeated measurement of the mediator we have the scope for constructing a classical measurement error model that partitions the variance in the mediator into true variation and measurement error and illustrate this here. Figure 3 shows such a model where we assume a latent autoregressive model for the mediator, with some restriction on the measurement errors, for example that they are independent and have a constant variance. The mediator [the child behavioural outcome with the parent, which is the proportion of parent synchronous acts (PSAs)] was measured at baseline (M0), at 7-month midpoint (M1) and again at 13-month follow-up (M2). The outcome for this analysis (Y), the proportion of child initiation acts, was assessed at 13-month follow-up.
FIGURE 3.
PACT: accounting for error in the measurements of the mediator (M) using repeated measures.
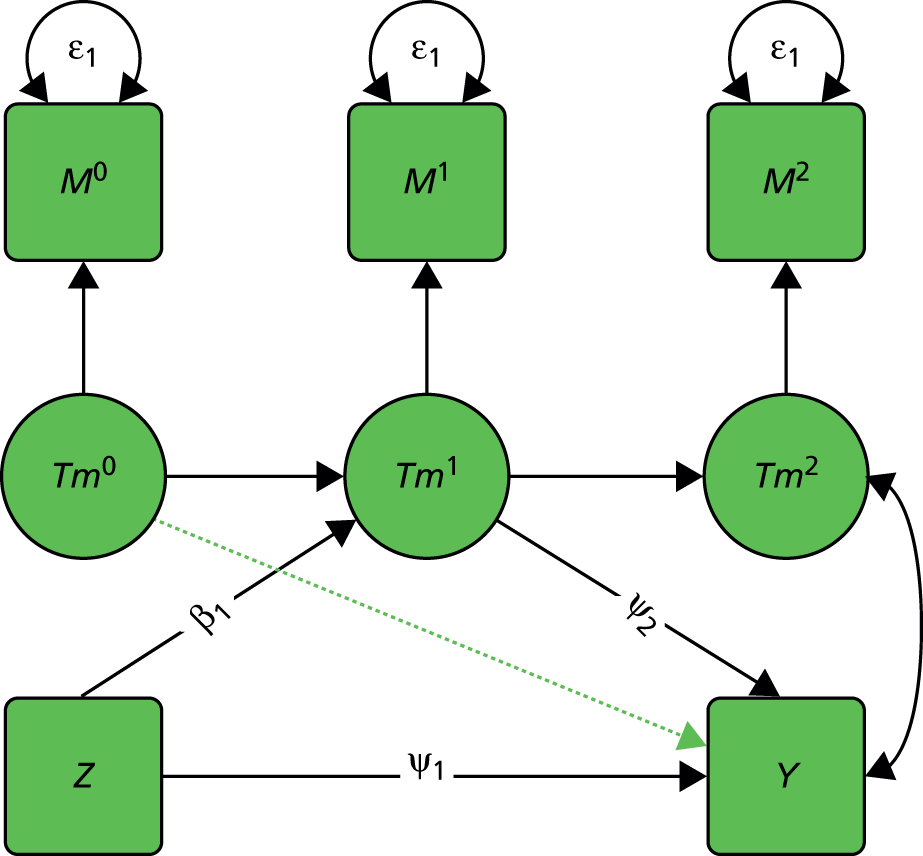
While the structural model remains concerned with estimating the effect of the midpoint mediator on the end point outcome, a correlation between the end point mediator and outcome must be allowed. The dashed green arrow represents the possibility of accounting for the effects of baseline mediator on the outcome. This is perhaps one of the most obvious variables that might act as a confounder of the M1 to Y relationship.
We begin by examining how parent behaviour mediates the effect of treatment on the behaviour of the child with that parent. As shown in Table 3, under the naive mediation model the estimated indirect effect of treatment group via parent synchronicity (the product β1 × ψ2) is 0.281 (p = 0.005). The direct effect, given by path ψ1, is estimated as 0.188 (p = 0.320). These results imply that approximately 60% of the effect of treatment is mediated via parent behaviour, and that 40% of the effect of the treatment remains identified as direct. As the baseline mediator is a plausible confounder of the midpoint mediator to outcome path, we added the baseline mediator to the model with paths to both mid-point mediator and outcome. This reduced the estimated proportion mediated to 50%.
| Model | Estimate | 95% CI | p-value | % of treatment effect |
|---|---|---|---|---|
| Naive model | ||||
| Indirect | 0.281 | 0.086 to 0.475 | 0.005 | 59.9 |
| Direct | 0.188 | –0.183 to 0.559 | 0.320 | 40.1 |
| Naive model, controlling for baseline mediator | ||||
| Indirect | 0.231 | 0.034 to 0.428 | 0.022 | 50.6 |
| Direct | 0.225 | –0.150 to 0.600 | 0.240 | 49.3 |
| Repeated measurement error model, controlling for baseline mediator (see Figure 3) | ||||
| Indirect | 0.361 | 0.053 to 0.669 | 0.022 | 79.2 |
| Direct | 0.095 | –0.343 to 0.533 | 0.670 | 20.8 |
Fitting the latent autoregressive model of Figure 3 in Mplus (version 7.1, Muthén & Muthén, Los Angeles, CA, USA) gave an estimate of intraclass reliability (r2) of the mediator M1 of 0.78. This model gave an estimated indirect effect of 0.361 (p = 0.022) and a direct effect of 0.095 (p = 0.670), giving the estimated proportion of treatment effect mediated via PSAs as 79%. As expected, accounting for attenuation due to measurement error of the regression coefficient of the mediator on the outcome substantially increases the estimated proportion mediated. Models of this kind can be extended to multiple mediators68 by the inclusion of correlated latent autoregressive measurement models.
Reflections
Let us go back to basics. What do we need to produce a credible claim for a mediational mechanism in an EME trial? Following the sequence suggested by B&K,16 we need to demonstrate:
-
an effect of the intervention (treatment) on the clinical outcome of the trial
-
an effect of the intervention on the putative mediator
-
that the effect of the intervention on the mediator provides at least some of the explanation of its effect on the outcome.
Demonstrating (a) and (b) are relatively easy as both are based on ITT analyses. Task (c) is much more difficult and will probably never be accomplished with certainty. Clinical triallists, who, in general, have no experience of evaluating mediational mechanisms (traditionally focusing only on ITT effects), either reject the challenge out of hand or simply make do with correlating outcome and mediator. Mental health researchers and other behavioural and social scientists have a long tradition of exposure to work on mediation and their analytical methods are more sophisticated. They tend to base their analyses on the B&K regression models (or the equivalent approach to simultaneous SEM, path analysis). Frequently, however, they are aware neither of the implicit assumptions they are making (e.g. no measurement errors in their mediators, no unmeasured variables i.e. no hidden confounders) nor of the implications of the failure of these assumptions to hold. Their assumptions may be true but we do not know. Many triallists fail to realise the importance of confounding and accordingly do not think to record potential confounders and condition on them in their B&K regression models. Clearly, if much more attention were paid to pre-randomisation confounders (prognostic markers), then this would be an important indicator of progress. There remains the measurement error problem and also confounders (such as adverse life events, etc.) that arise after the onset of treatment. Although IVs are not a panacea,68 they do offer a very promising way forward. Perhaps the most convincing aspect of their use (and that of modern causal inference methods, in general) is that it encourages the investigator to focus on the explicit assumptions behind their valid use. Questioning the validity of a proposed instrument (and possibly finding alternatives) is an intellectually sobering activity.
In the end, we can use different analytical strategies and see if we can find consistent results. If B&K estimates are not too dissimilar from those obtained by using IV methods then perhaps we can be fairly confident in our qualitative conclusions (even if not entirely confident concerning the precise quantitative implications).
Chapter 3 Therapeutic process evaluation
Introduction
Here we are concerned not with mediational mechanism but with characteristics of a therapeutic intervention (process variables) that might influence or be associated with the efficacy of the intervention. The assumption is that there exists treatment effect heterogeneity and that some of this heterogeneity might be explained by these process measures. The process measures are post-randomisation treatment effect modifiers; they are not, strictly speaking, treatment effect moderators, as these are assumed to be measured (or measurable, in principle) before allocation to or onset of therapy. Examples include the strength of the therapeutic alliance, fidelity to a given treatment manual (whether or not CBT, for example, includes pre-specified components such as problem formulation and the setting of homework between sessions).
What are the technical challenges?
First, the potential intervention effect modifier might be a process measure that is ascertained only in those participants who receive treatment. In other words, it is a variable that describes the characteristics of patients when receiving treatment and thus these values are missing for those in an untreated control group (fidelity of a patient’s therapy to a CBT protocol or strength of the therapeutic alliance are obvious examples). Second, it is likely that the process measures would be measured with a considerable amount of measurement error (rating scales for strength of the therapeutic alliance, for example, will have only modest reliability). Third, there are also likely to be hidden selection effects (hidden confounding). A participant may, for example, have a good prognosis under the control condition (no treatment). If that same person were to receive treatment, however, the factors that predict good outcome in the absence of treatment would also be likely to predict good compliance with the therapy (e.g. strength of the therapeutic alliance). Severity of symptoms, or level of insight, measured at the time of randomisation, for example, are likely to be predictors of both treatment compliance and treatment outcome. They are potential confounders. If we were to take a naive look at the associations between measures of treatment compliance and outcomes in the treated group we would most likely be misled. These associations would reflect an inseparable mix of selection and treatment effects (i.e. the inferred treatment effects would be confounded); we would not know whether those who did well did so because they responded well to the treatment or if they would have done well anyway. We can allow for confounders in our analyses, if they have been measured, but there will always be some residual confounding that we cannot account for. The fourth and final challenge to be considered here arises from missing data, not just missing outcomes but also missing process measures for at least some of patients receiving therapy; this is different from the missing process information for the control patients. In the latter, the information does not exist (therapeutic processes do not exist in the absence of therapy) but in the former it exists but is not measured or recorded. These data are unlikely to be missing purely by chance. Prognosis, compliance with allocated treatment and the treatment outcome itself are all potentially related to loss of data, which, in turn, leads to potentially biased estimates of treatment effects and estimates of the influences of treatment effect modifiers.
Notation
We randomise participants to receive treatment (e.g. psychotherapy plus routine care) or to be in the control condition (routine care alone). As an example, we will consider the therapeutic alliance (A) as the process variable under investigation. Dropping the subject-specific subscript for simplicity, for each subject we have a potential (possibly not observed) or observed measure of the following:
-
Z, treatment group – the outcome of randomisation (1 for treatment, 0 for control)
-
Y, observed outcome
-
Y(0), potential outcome under the control condition (no access to therapy)
-
Y(1,a), potential outcome under the treatment condition with resulting strength of alliance, a
-
X′ = X1, X2 . . . Xp, baseline covariates
-
X1Z, X2Z, . . . XpZ, baseline covariate by randomised treatment group interactions (products)
-
A, the strength of the therapeutic alliance (only observed in the treated group), with observed level a.
All baseline covariates are assumed to be available for every participant in the trial (irrespective of randomisation).
For the time being we assume that we have a complete data set (there are no missing values, other than the counterfactuals determined by the design, i.e. those in the treatment-free control group).
How not to do it: correlate process measure (A) with outcome (Y) in the treated arm (and completely ignore the control arm)
For the participants in the treatment arm, the individual treatment effect, Δ, is the difference Y(1,a) – Y(0). It follows that the outcome of treatment is given by
If we correlate Y(1,a) with background variables (e.g. with putative predictive markers) or with process measures recorded during treatment, thinking that this is examining explanations for treatment effect heterogeneity, then our thinking is flawed. Take the strength of the therapeutic alliance, for example. A trial participant receiving CBT may or may not be able to form a strong working relationship with his or her therapist. It is highly likely that a participant who is able to develop such a relationship is also likely to have had the better treatment-free outcome, Y(0). If this is the case, then we would see a correlation between outcome Y(0) and alliance, A, even when the treatment effect, Δ, is zero for all participants. It is therefore possible to demonstrate a strong relationship between treatment outcome Y(1,a) and alliance even when the intervention is ineffective. A similar example from the field of vaccine development is illustrated by Follmann. 68 From the results of a randomised human immunodeficiency virus (HIV) vaccine trial, Follmann restricts his analysis to the treated arm and illustrates a strong relationship between the immune response to vaccination (the process variable) and subsequent resistance to HIV infection. He then points out that the ITT analysis of the data from both arms had demonstrated that the HIV vaccine was not effective. One plausible explanation is that the immune response (a correlate of protection) is related to the trial participant’s innate immunity (i.e. in the absence of vaccination), that is the treatment-free (vaccine-free) outcome. In trials of both vaccination and psychotherapy, correlations between treatment outcome and the treatment process measure are not robust indicators of the influence of the process measures on subsequent causal treatment effects. They are confounded by the unobserved (hidden) treatment-free outcome. Therefore, we need a different approach.
The causal (structural) model
The vital component of all our models is randomisation, which ensures that, conditional on observed baseline covariates, X, both counterfactual outcomes, Y(0) and Y(1,a), are independent of treatment allocation (Y(0), Y(1,a) ┴ Z|X):
We assume that randomisation (treatment allocation) has an effect on treatment received (if received and how much) and, in particular, that participants in the control arm do not get access to any treatment.
What is the treatment effect for the individual subject (Δ) in terms of their potential therapeutic alliance status, A? Here A is the strength of the therapeutic alliance that is measured on the receipt of treatment. What is the relationship between Δ and A? We consider a simple linear ‘dose’–response model:
where ε is an individual-specific contribution to the treatment effect (or gain) not explained by the model. We assume ε is uncorrelated with the therapeutic alliance and therefore that:
Note that there is an intercept term (the ATE is not necessarily zero at zero alliance). Note that, for a treated individual, Δ|(A = a, X = x) = Y(1,a) – Y(0) and therefore:
Given randomisation:
Similarly:
It follows from these equalities that, if we were prepared to assume that βz = 0 (an exclusion restriction), then we could simply estimate the remaining parameter, βa, by dividing the effect of randomised treatment on outcome by the average alliance score in the treated. This is the classic IV estimator described in Chapter 1 (see Chapter 1, The complier-average causal effect). However, unfortunately, we are not in a position to safely assume that βz = 0 (the therapy may well have an effect at zero alliance) and we therefore have to recognise that we have an underidentified model (we have too many parameters to estimate given the availability of only two treatment means). We need information on potential predictors of the therapeutic alliance in order to proceed. This will be the focus of attention in Instrumental variable methods.
Before moving on, however, we should acknowledge explicitly that, unlike a more straightforward measure of compliance with treatment allocation, the number of sessions attended, for example the therapeutic alliance, is not a ratio-level measurement. A scale value of zero is arbitrary; it does not indicate zero alliance. Recognising this, it might make our parameters more interpretable if we were first to rescale our alliance measures. Scores on the anglicised and simplified version of the California Therapeutic Alliance Scales (CALPAS),69 as used in Dunn and Bentall,14 for example, range from a minimum of 0 to a maximum of 7. Dunn and Bentall transformed these scores so that they ranged from a minimum of –7 to a maximum of 0. Accordingly, the parameter βz is now a measure of the average therapeutic effect in those participants with an optimal alliance with their therapist. The value and interpretation of the second parameter, βa, is unaffected by this simple change of scale (a shift of location only).
Instrumental variable methods
We have stated that we need (good) predictors of the therapeutic alliance in order to make progress (i.e. to attain identifiability). We illustrate this using a simple form of G-estimation, as described by Fischer-Lapp and Goetghebeur. 50 First we regress the alliance (A) on baseline covariates, X, some of which are known (or hoped) to be predictors of the alliance. This regression model is then used to predict the alliance for everyone in the trial (both treated and the control patients). Second, we regress outcome in the treated group on the baseline covariates, X, and the outcome under treatment [Y(1,a)] is predicted from this model, again for everyone in the trial. Similarly, we regress outcome in the control group on the same baseline covariates, X, and the outcome under control conditions [Y(0)] is again predicted for everyone in the trial. The individual treatment effects, Δ, are then calculated from the difference in the predicted treatment outcomes and predicted control outcomes and, finally, the predicted Δ is regressed on the predicted alliance. The slope provides us with an estimate of βa and the intercept is an estimate of βz. In this last regression we are estimating the effect of the randomised therapy [i.e. Y(1,a) – Y(0)] conditional on the level of the therapeutic alliance predicted by the baseline covariates. There are no baseline covariates in this last model; we are assuming that all of the moderating influences of the baseline covariates are acting through their influence on the therapeutic alliance. Valid SEs, confidence intervals (CIs) and associated p-values can be obtained by bootstrapping the whole multistage procedure.
An alternative approach is to use IV methods and, in particular, the familiar 2SLS procedure. First, we assign an arbitrary value to the level of the missing therapeutic alliance in the control group. Here we assign a value of zero for everyone. The first-stage regression then involves the prediction of the therapeutic alliance from randomisation (i.e. treatment group), baseline covariates, X and all interactions between randomisation and each of the baseline covariates. As the measured level of alliance has been fixed at a constant value (zero) for everyone in the control group, there will be no effect of any of the covariates on alliance in this group. However, the effects of the covariates on alliance will be free to be estimated in the treated participants (exactly as at the corresponding stage of the G-estimation algorithm). The second-stage regression then simply involves the prediction of outcome by randomised treatment, the predicted level of alliance and the baseline covariates (there are no treatment by baseline interactions). The treatment by baseline covariates in the first-stage model are IVs (assumed to have an effect on alliance but no effect on outcome that is not explained by their effect on the alliance). Theoretical details are provided by Dunn and Bentall. 14 If there are no missing data, except missing process measures in the control group (i.e. every case is complete), this 2SLS procedure will give identical estimates to those provided by the above G-estimation algorithm. 14
Although conceptually very different, the practicalities of use of 2SLS methods are the same for the investigation of therapeutic processes (the effects of post-randomisation effect modifiers) as those described in the previous chapter to investigate treatment effect mediation. In some cases this conceptual distinction is just a reflection of different ways of thinking about the problem. On the one hand, dose of therapy (number of sessions attended), for example, can be thought of as a mediator of the offer of treatment (and, with an assumed exclusion restriction, no therapeutic effect when no sessions attended and complete mediation of the offer of treatment on outcome). On the other hand, dose of therapy can be considered as a post-randomisation modifier of the ITT effect: the ITT effect increasing with increasing dose. Comparison of 2SLS approaches and principal stratification for the estimation of the CACE also illustrate this point.
Binary process measures: principal stratification
It is possible, and quite straightforward, to use 2SLS estimation methods when the process measure is binary (high vs. low alliance; problem formulation vs. no formulation; homework vs. no homework). The validity of the method is not dependent on the process measure being normally distributed, for example, or actually a quantitative variable. The alternative IV estimator described in Chapter 2, based on the use of the compliance score as an instrument, would be equally applicable. Here, however, we approach the problem through latent class models: principal stratification. We are concerned with the natural extension of the use of latent classes in CACE estimation (compliers vs. non-compliers) through simply relaxing the exclusion restriction on the stratum equivalent to the non-compliers (e.g. low therapeutic alliance). In summary, we assume that we have two partially observed strata (low and high alliance); we can observe alliance status in the treated group and assume that there are, on average, the same proportions of the two classes in the control arm. We are concerned with the estimation of two ITT effects: that in the low-alliance stratum and that in the high-alliance stratum. The overall ITT effect is a weighted average of these two stratum-specific ITT effects. Staying with high versus low therapeutic alliance, we have:
where PH is the proportion of the high-alliance stratum. It should be immediately clear from this equation that, again, this simple model is underidentified. We cannot estimate ITThigh and ITTlow from a knowledge (estimate) of PH and ITToverall. In CACE estimation we assume that one of the stratum-specific ITT effects is zero. This is not justified here. Instead, we attain identifiability by using baseline covariates that are (good) predictors of principal stratum membership (i.e. predictors of observed stratum membership in treated participants). This is entirely analogous to the search for effective covariate by treatment interactions to use as instruments in 2SLS; we additionally assume that there are no covariate-by-treatment interactions in the model predicting outcome within each of the two strata. 70,71
In principle, principal stratification can easily be extended to cope with categorical process measures with three or more unordered categories. Dunn et al. ,13 for example, considered non-compliers (those who never turned up for CBT), participants who attended (or would have attended) their CBT sessions but did not receive the CBT as intended (being more akin to supportive listening) and participants who received (or would have received) CBT as intended. Here it was thought to be legitimate to introduce the exclusion restriction for the non-compliers but the model was still underidentified. Once again, identifiability was achieved by being able to predict stratum membership using baseline covariates. These authors also allowed for missing process measurements in the treated (CBT) arm by extending the latent class modelling to allow for the process measure to be latent in both arms of the trial. We will not pursue these technical details but stay with the simpler binary process measure, assumed to be available for everyone in the treated group.
Missing outcome data
All psychotherapy trials have some missing outcome data, some quite a lot. In the Outcome of Depression International Network (ODIN) trial of psychotherapy for depression, for example, only 74% of the randomised participants provided outcome measures at 6-month follow-up. Even more striking was the dependence of the follow-up rates on the compliance (process measure) status of the participants: 73% for the control participants, 92% for the compliers in the treatment arm and only 55% for the non-compliers in the treatment arm (the non-compliers representing 46% of those allocated to receive treatment). 71,72 It is highly likely that levels of missing outcome data will depend on other process measures such as the strength of the observed therapeutic alliance in the treated group and/or the potential therapeutic alliance in the controls (i.e. that alliance that would be observed had the control participant received treatment). Principal stratification using latent class models fitted by maximum likelihood will automatically allow for missing data patterns that are determined by observed alliance in the treated arm. Simultaneously fitting the two stages of the conventional IV model using maximum likelihood will also allow for this contingency; both are allowing for missing outcomes to be missing at random (MAR, in the terminology of Little and Rubin73). In the context of principal stratification it is also straightforward to allow for a non-ignorable missing data mechanism, missingness being determined by principal stratum membership, called ‘latent Ignorability’ by Frangakis and Rubin. 74 This will be illustrated in our case study in the next section.
What about the conventional use of 2SLS? If a 2SLS command is used, the analysis is based on only those participants with complete data (the so-called complete-case analysis). To allow for loss to follow-up that is dependent on the observed process measure (compliance with treatment allocation, strength of the therapeutic alliance and so on) we need to carry out the two stages of the two-stage estimation separately. The first (prediction of the process measure) uses everyone randomised and involves saving the predicted values of the process variable. The second involves only those with non-missing outcomes but models these using the predicted process measures obtained from the complete first stage. Bootstrapping of the whole two-stage procedure provides valid SEs, CIs and corresponding p-values. An alternative (and more or less equivalent) approach would be to stick with the complete-case procedure but supplement the command by declaring inverse probability weights determined by modelling loss to follow-up using baseline covariates and the observed process measures.
What about missing process measurements? In many trials (to date) collection of data on process measurements has not been seen as a vitally important aspect of their implementation. Often, collection of process data has been part of a supplementary ‘add-on’ project. So, in practice, there is quite a lot of missing process information. How should this affect our approach to analysis? One solution is to simply ignore the participants for which the process measurements are missing, that is drop them from the data file. Dunn and Bentall14 took this approach in order to simplify the analysis strategy (the aim of the paper being to explain and illustrate methodological developments and not to make any substantive claims concerning the role of the process measure, the therapeutic alliance in this case). Clearly, a more principled approach needs to be taken in an analysis undertaken to yield valid substantive conclusions. A detailed examination of approaches that might be taken (including multiple imputation) is currently being carried out by Lucy Goldsmith, a PhD student at the University of Manchester. The results of these investigations will be published elsewhere. Here we illustrate a simple solution, but not necessarily the optimal one, based on principal stratification. Principal strata are partially observed latent classes; in our example above, class membership is known for the treated group (e.g. high or low alliance) but latent in the control group. Following Dunn et al. ,13 we include those from the treated group with missing alliance data but acknowledge that their stratum status is hidden, just as for the control group (assuming that conditional on the baseline covariates, the distribution of alliance status is not dependent on whether or not it is observed). We illustrate the details in the following section.
Case study
Here, we consider the Study of Cognitive Realignment Therapy in Early Schizophrenia (SoCRATES) trial, which was designed to evaluate the effects of CBT and supportive counselling (SC) on the outcomes of an early episode of schizophrenia. Participants were allocated to three conditions: CBT in addition to TAU, SC and TAU, or TAU alone. Recruitment and randomisation was within three catchment areas (treatment centres): Liverpool (centre 1), Manchester (centre 2) and Nottinghamshire (centre 3). In summary, 101 participants were allocated to CBT + TAU, 106 to SC + TAU and 102 to TAU alone. Of these, 225 participants (75% of those randomised) were interviewed at 18 months’ follow-up: 75 in the CBT + TAU arm, 79 in the SC + TAU arm and 71 in the TAU alone arm. The remaining participants died during the follow-up period (n = 7), withdrew consent (n = 4) or were lost (n = 73). Further details can be found elsewhere. 75,76
The post-randomisation variable that has a potential explanatory role in the analysis of treatment effect heterogeneity is the measure of the quality or strength of the therapeutic alliance at the fourth session of therapy. Therapeutic alliance is a general term for a variety of therapist–client interactional and relational factors which operate in the delivery of treatment. It was measured at the fourth session of therapy because it was early in the time course of the intervention, but not too early to assess the development of the relationship between therapist and patient. (The alliance was also assessed at the tenth session, but we will not pursue this added complication here.) The strength of the therapeutic alliance was measured in SoCRATES using two different methods, but here we report the results from an anglicised and simplified version of the short 12-item patient-completed version of the CALPAS. 69 Total CALPAS scores (ranging from zero, indicating low alliance, to 7, indicating high alliance) have been used in our previous analyses,14,31,32 but here we follow Emsley et al. 30 by creating a binary alliance indicator (one if CALPAS score greater than or equal to 5, otherwise zero) and illustrate an analysis based on principal stratification.
The primary outcome measure in the trial was the Positive and Negative Syndromes Schedule77 (PANSS). The PANSS was administered at baseline, once a week over the first 6 weeks and then at 3 months, 9 months and 18 months. For the present purposes, only the initial (baseline) and 18-month PANSS total scores are considered. The initial PANSS score is considered as a baseline covariate in all analyses reported here. Other baseline covariates used in the analyses reported here are centre membership (binary dummy variables, C1 and C2), the logarithm of the duration of untreated psychosis (logDUP) and years of education.
Further details and the trial outcomes have been reported elsewhere. 75,76 Briefly, from an ITT analysis, there was no evidence of an effect on speed of recovery over the first 6 weeks of treatment. However, at the 18-month follow-up, both psychological treatment groups had a superior outcome in terms of symptoms (as measured using the PANSS) compared with the control group, although there was no effect on relapse rates. There were no differences in the effects of CBT compared with SC, but there was a strong centre effect, with outcomes for the psychological therapies at one of the centres (Liverpool) being significantly better than at the remaining two.
For illustrative purposes, we here ignore the distinction between CBT and SC. Note that, as indicated above, not everyone in the treated groups provided data on the strength of their therapeutic alliance. In fact, 45% of the participants who were expected to provide CALPAS measures at the fourth session of therapy failed to do so. Table 4 provides a detailed summary of the results of the trial that are relevant to the present discussion. Results are shown separately for each of the three centres (Liverpool, Manchester and Nottinghamshire) and within each of these centres according to their treatment status: control group, treated group with observed low-alliance, treated group with observed high alliance and treated group with an unknown (missing) alliance. The proportion of participants with missing alliance measures varies with centre, as does the proportion of those observed with a high alliance. Ignoring missing data, Liverpool has the highest proportion of participants with a high alliance (74%), consistent with treatment being more effective in this centre.
| Variable | Observations | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|---|
| Liverpool | |||||
| Control | |||||
| Years of education | 39 | 11.31 | 1.78 | 9 | 16 |
| logDUP | 39 | 1.08 | 0.53 | 0 | 2.72 |
| PANSS, baseline | 39 | 80.05 | 12.36 | 56 | 102 |
| PANSS, 18 months | 23 (59%) | 69.52 | 13.55 | 41 | 91 |
| Therapy, low alliance | |||||
| Years of education | 10 | 11.00 | 2.26 | 9 | 17 |
| logDUP | 10 | 1.27 | 0.51 | 0.60 | 2.18 |
| PANSS, baseline | 10 | 82.90 | 11.30 | 67 | 105 |
| PANSS, 18 month | 7 (70%) | 56.71 | 14.10 | 42 | 83 |
| Therapy, high alliance (74% of those with known alliance) | |||||
| Years of education | 28 | 11.43 | 2.52 | 9 | 20 |
| logDUP | 28 | 1.24 | 0.54 | 0.60 | 2.78 |
| PANSS, baseline | 28 | 76.75 | 15.21 | 54 | 106 |
| PANSS, 18 months | 23 (82%) | 49.35 | 11.67 | 31 | 80 |
| Therapy, unknown alliance (i.e. 47% missing) | |||||
| Years of education | 34 | 11.56 | 2.40 | 9 | 20 |
| logDUP | 34 | 0.98 | 0.43 | 0 | 1.72 |
| PANSS, baseline | 34 | 85.29 | 17.28 | 49 | 128 |
| PANSS, 18 months | 18 (53%) | 55.78 | 14.78 | 31 | 79 |
| Manchester | |||||
| Control | |||||
| Years of education | 35 | 12.71 | 2.40 | 9 | 18 |
| logDUP | 35 | 1.42 | 0.59 | 0.60 | 2.30 |
| PANSS, baseline | 35 | 97.9 | 16.60 | 69 | 141 |
| PANSS, 18 months | 25 (71%) | 73.20 | 22.36 | 44 | 115 |
| Therapy, low alliance | |||||
| Years of education | 19 | 11.63 | 2.36 | 9 | 17 |
| logDUP | 19 | 1.51 | 0.57 | 0.60 | 2.48 |
| PANSS, baseline | 19 | 98.95 | 17.66 | 66 | 131 |
| PANSS, 18 months | 15 (79%) | 82.53 | 15.65 | 56 | 108 |
| Therapy, high alliance (61% of those with known alliance) | |||||
| Years of education | 30 | 11.73 | 1.82 | 10 | 17 |
| logDUP | 30 | 1.35 | 0.66 | 0.30 | 2.76 |
| PANSS, baseline | 30 | 101.53 | 15.52 | 76 | 126 |
| PANSS, 18 months | 24 (80%) | 69.25 | 21.00 | 33 | 112 |
| Therapy, unknown alliance (i.e. 35% missing) | |||||
| Years of education | 26 | 11.04 | 1.51 | 8 | 15 |
| logDUP | 26 | 1.37 | 0.64 | 0.48 | 2.80 |
| PANSS, baseline | 26 | 101.08 | 15.43 | 77 | 129 |
| PANSS, 18 months | 16 (62%) | 73.69 | 17.99 | 51 | 107 |
| Nottinghamshire | |||||
| Control | |||||
| Years of education | 26 | 11.69 | 2.98 | 7 | 21 |
| logDUP | 26 | 0.81 | 0.41 | 0 | 1.41 |
| PANSS, baseline | 26 | 84.92 | 14.91 | 52 | 106 |
| PANSS, 18 months | 21 (81%) | 54.52 | 10.07 | 41 | 82 |
| Therapy, low alliance | |||||
| Years of education | 10 | 10.10 | 2.77 | 5 | 14 |
| logDUP | 10 | 0.82 | 0.29 | 0.48 | 1.48 |
| PANSS, baseline | 10 | 84.20 | 11.95 | 69 | 109 |
| PANSS, 18 months | 9 (90%) | 46.22 | 5.54 | 37 | 55 |
| Therapy, high alliance (58% of those with known alliance) | |||||
| Years of education | 14 | 11.14 | 2.74 | 9 | 16 |
| logDUP | 14 | 0.86 | 0.43 | 0.30 | 1.56 |
| PANSS, baseline | 14 | 82.64 | 9.96 | 67 | 99 |
| PANSS, 18 months | 14 (100%) | 50.86 | 7.57 | 38 | 63 |
| Therapy, unknown alliance (i.e. 56% missing) | |||||
| Years of education | 30 | 12.03 | 2.58 | 8 | 16 |
| logDUP | 30 | 0.82 | 0.51 | 0.30 | 1.86 |
| PANSS, baseline | 30 | 79.30 | 19.21 | 0a | 115 |
| PANSS, 18 months | 25 (83%) | 54.00 | 9.40 | 40 | 72 |
Here we illustrate the use of principal stratification to answer the question ‘is the treatment effect in the high-alliance class better than that for those in the low-alliance class?’. We estimate the SEs of our treatment effect estimates using asymptotic likelihood-based methods and through the use of the simple bootstrap78 (1000 replications). We assume that either outcome data are MAR or, alternatively, missing outcomes are latently ignorable (LI). Finally, we use two options for dealing with treatment participants with missing alliance data; by either restricting the analysis to those with non-missing alliance or including everyone in the analysis by coding missing class membership as unknown (as is the case for the control group, that is conditional on the relevant baseline covariates we are assuming that the distribution of strata is the same in the treated with observed alliance as in the treated with missing alliance, and, in turn, the same as that in the control group). Under each of these options, we examine whether or not it is reasonable to assume that the treatment effect in the low-alliance group is zero (i.e. introduce the exclusion restriction as the result of empirical findings rather than as an a priori assumption).
In all of these analyses we use Mplus version 7. 79 The input file for the case when missing outcomes are assumed to be latently ignorable is given in Appendix 2 (we do not expect readers who are unfamiliar with Mplus to be able to follow the content of this file but include it as an exact record of what Mplus was instructed to carry out). We will now explain what the analysis entails. We specify that we have two latent classes (principal strata: high and low alliance) and that their distribution is to be estimated through a finite mixture model. Class membership is predicted by a logistic regression with baseline total PANSS score, years of education, logarithm of duration of untreated illness and centre membership (two binary dummy variables, c1 and c2) as covariates. These covariates were selected informally using the analyst’s judgement. A detailed examination of approaches that might be taken (including familiar forward or backward selection methods and the use of the various penalised alternatives) is currently being carried out by Clare Flach, a PhD student at the University of Manchester. The results of these investigations will be published elsewhere. To carry out this finite mixture modelling, observed data on the therapeutic alliance (the so-called training set) are coded by two binary dummy variables, a1 and a2. Low alliance is indicated when a1 = 1 and a2 = 0; high alliance when a1 = 0 and a2 = 1. If alliance is unknown (as in the control or treated participants with missing alliance ratings) then Mplus expects the coding a1 = 1 and a2 = 1. Simultaneously, the effect of randomised treatment allocation (i.e. the ITT effect) is estimated within each of the two classes using an analysis of covariance model in which the effects of the covariates (the same as those included in the model to predict stratum membership) are constrained to be equal for the two strata (i.e. ensuring no covariate by alliance interaction). If the input program makes no reference to the missing outcome data [i.e. a variable here called ‘resp’ (short for ‘response’); with resp = 1 if outcome is observed, 0 otherwise] then we are assuming that outcome is MAR, that is conditional on covariates, the probability of being missing may differ between the high- and low-alliance groups in the treatment arm, but is assumed to be homogeneous in the control group. Under the LI assumption we introduce logistic regression models to predict response by randomised treatment allocation and the other covariates within each of the two strata separately (again constraining the covariate effects other than treatment to be the same within the two strata). So, here, the probability of having a missing outcome is dependent upon latent class (principal stratum) membership rather than just observed treatment status as in MAR; hence the term ‘latent ignorability’.
We carry out a sequence of model fitting. First we use the data from the control group and only those of the treated participants who have a recorded alliance measure. All included participants may or may not have missing 18-month outcome (PANSS) data. We estimate the within-stratum treatment effects together with their SEs in Mplus using an expectation and maximisation (EM)–maximum likelihood algorithm. We then repeat the same analysis but estimate the SEs using the bootstrap. Next, we carry out a third run having constrained the treatment effect in the low alliance stratum to be zero (again using the bootstrap to estimate the SE of the treatment effect in the high alliance stratum). All three runs are carried out twice: once assuming that outcomes are MAR and again assuming that they are LI. The six sets of results are presented in the Excluding participants with missing alliance values section of Table 5. We now repeat the whole exercise including the treatment group participants with missing alliance data. The second six sets of results are presented in the Using all data: including treated participants with missing alliance values section of Table 5.
| Missing data assumptions | Low alliance | High alliance |
|---|---|---|
| Excluding participants with missing alliance values | ||
| Missing data ignorable (MAR) | + 7.58 (5.00) | –15.97 (3.36) |
| Missing data ignorable (MAR), bootstrapped | + 7.58 (9.51) | –15.97 (5.23) |
| Missing data ignorable (MAR), bootstrapped | 0 (constraint) | –13.34 (4.85) |
| Missing data latently ignorable (LI) | + 5.64 (4.42) | –17.52 (3.99) |
| Missing data latently ignorable (LI), bootstrapped | + 5.64 (8.81) | –17.52 (7.39) |
| Missing data latently ignorable (LI), bootstrapped | 0 (constraint) | –13.18 (7.79) |
| Using all data: including treated participants with missing alliance values | ||
| Missing data ignorable (MAR) | + 9.27 (3.62) | –16.58 (3.45) |
| Missing data ignorable (MAR) – bootstrapped | + 9.27 (6.31) | –16.58 (5.07) |
| Missing data ignorable (MAR) – bootstrapped | 0 (constraint) | –12.74 (5.63) |
| Missing data latently ignorable (LI) | + 8.75 (3.67) | –17.18 (4.08) |
| Missing data latently ignorable (LI), bootstrapped | + 8.75 (7.48) | –17.18 (6.23) |
| Missing data ignorable (LI), bootstrapped | 0 (constraint) | –15.72 (7.07) |
What can we conclude from these results? We conclude that:
-
All treatment effect estimates are imprecise.
-
We gain a little more precision by including treatment participants with missing alliance status.
-
It makes little difference whether we are assuming that missing outcome data are MAR or LI.
-
The conventional likelihood-based SE estimates appear to be too optimistic. It is much safer to use non-parametric bootstrapping.
-
There is a beneficial effect of treatment in the high-alliance stratum but not in the low-alliance stratum. In fact, there is a suggestion that treatment might be detrimental in the latter (but the effect is not statistically significant).
-
We have not yet established that the treatment effects differ in the two strata, that is that there is evidence of effect modification. This we now proceed to do.
We now look at contrasts between the estimated treatment effects for the two principal strata. Considering the results after excluding trial participants with missing alliance data, the estimated difference between the treatment effect estimates for the two strata is –15.97 – 7.58 = –23.55 with a bootstrapped SE of 13.25 (p = 0.076) when assuming that missing outcomes are MAR. The difference is –17.52 – 5.64 = – 23.15 with a bootstrapped SE of 13.97 (p = 0.097) when assuming that missing outcomes are LI. If we analyse the full data set (including treatment participants with missing alliance measures), the corresponding estimates after assuming either MAR or LI are, respectively, –16.58 – 9.27 = –25.85 with a bootstrapped SE of 9.71 (p = 0.008) and –17.18 – 8.75 = –25.93 with a bootstrapped SE of 11.69 (p = 0.027). The gain in precision attained by including all of the participants now appears to be considerable. We cautiously conclude that the therapeutic alliance does modify treatment efficacy.
Reflections
It appears that what we need is a baseline variable that is a powerful predictor of the therapeutic process indicator in the treatment group (adherence to prescribed number of sessions of therapy, strength of the therapeutic alliance, fidelity to a CBT treatment manual, etc.). This is to predict the level of the process indicator for those in the control group; without one or more good predictors we cannot do this accurately and would effectively be predicting random values.
How do we design a trial in which we can use this predictor? Design issues are dealt with mainly in Chapter 5 but we here briefly consider two possible options. In a different context, Follmann68 was concerned with what he termed ‘augmented’ designs to assess immune response in vaccine trials (the immune response only being observed in the participants receiving the vaccine). He suggested two designs.
Follmann’s first design involved vaccinating, prior to randomisation, all of the participants recruited to the trial with an irrelevant vaccine (e.g. against rabies) and measuring the immune response to this vaccine. This response is assumed to be highly correlated to the subsequent immune response to HIV vaccination in those participants who then go on in the actual trial to receive the HIV vaccine. The implication is also that the response to the rabies vaccine is a strong predictor of the missing HIV response in the control participants (i.e. the immune response that would have been produced in the control participants had they (contrary to fact) been allocated to receive the HIV vaccine. In the context of our psychotherapy trials, an equivalent two-stage design might involve measurement of the strength of the therapeutic alliance (or quality of the more general working relationship) with, for example, the participant’s case manager prior to randomisation in the trial itself. With luck, the case manager alliance by treatment interaction would provide a powerful IV in the adjustment for hidden confounding of the effect of the intervention’s therapeutic alliance in the trial itself.
Follmann’s second design involved the use of what psychologists refer to as a waiting-list control group. The randomised HIV vaccine trial is a carried out as a standard parallel-group study (the immune response being measured in the vaccinated participants, and outcome assessed in everyone). At the end of a specified follow-up period, the control participants are given the vaccine against HIV and their immune response measured. Further follow-up is unnecessary. The immune response in the control participants at follow-up is used to predict the immune response that would have been observed had they been vaccinated at the beginning of the trial. In principle, this waiting-list controlled design might be feasible in a psychotherapy trial, but only if we can be confident that the majority of the control participants would not recover in the absence of therapy. This is quite a stringent condition that would not hold in many cases.
In Chapter 2, we have indicated that measurement error in the intermediate variable might be of more significance than hidden confounding. Clearly, process measures such as the strength of the therapeutic alliance will be subject to considerable error (no one would ever claim that they are infallible). Although IV methods adequately adjust for random measurement error, as well as for hidden confounding,14,59,70 the use of multiple indicators of the therapeutic alliance, for example, will help to improve the precision of the required causal parameter estimates58,60,80 (see the example using the PACT data at the end of the previous chapter). Similar use of multiple indicators would help to refine the definition of stratum membership for principal stratification; clearly, as it is used above, there will be misclassification errors and these will dilute (attenuate) differences between the ITT effects within strata.
Chapter 4 Extension to longitudinal data structures
Introduction
In Chapter 2 we discussed how to model mediational mechanisms and in Chapter 3 discussed a separate approach for analysing the effect-modifying role of post-randomisation process variables. However, in both settings we considered the situation only with a single measure of the outcome and, in general, this is unlikely to be reflective of the data available in a randomised trial. Outcome measures are usually collected at multiple time points during the follow-up period, often at the end of the treatment phase, and at least one later measurement occasion to assess longer-term effects of the intervention.
In addition, when considering mediation modelling there are often repeated measures of the putative mediator collected which could all be during the treatment phase or could extend into the follow-up phase. For example, in the MRC MIDAS trial,21 the putative mediator was substance misuse, and this was measured at baseline and at 6, 12, 18 and 24 months after baseline. The corresponding outcome measures of psychotic symptoms were collected at baseline and at 12 and 24 months. The mediation analysis described in Chapter 2 would consider these time points only as single measures, and does not exploit the longitudinal design of the trial or assess whether or not changes in these mediators lead to changes in the outcome.
Similarly, we can collect repeated measures of process variables, and typically these would occur during the treatment phase of the intervention. For example, in the Prevention of Relapse in Psychosis (PRP) trial,81 a measure of therapist and client empathy was completed at each session of therapy attended. Rather than picking a single session measure of empathy to consider as the post-randomisation effect modifier, using all the measures could provide additional information to more accurately model the underlying process.
This chapter will extend the methods previously described in Chapters 2 and 3 to these longitudinal data structures. We begin by considering a setting with repeated measures of a mediator and outcome, and then demonstrate how to examine mediation using growth curve models. We will redefine the B&K steps outlined in Chapter 2 for this longitudinal context. This is just one possible approach, and we describe the potential use of several other methods. Then we change focus to the analysis of process measures and first consider a single process measure (such as therapeutic alliance at a single session, as given in the SoCRATES example) with repeated measures of the outcome. Finally, we consider how to model repeated measures of the process variables (therapist empathy at each session) and consider these as post-randomisation effect modifiers of treatment effects in an extension of the principal stratification approach, which are called principal trajectories.
Extensions to repeated measures of mediators and outcomes
One of the difficulties in extending mediation analysis to longitudinal settings is that it becomes more complicated to define the question of interest, to identify which mediation parameters are of interest and to account for time-varying confounding (i.e. the confounders of the M and Y could be time-invariant or time-varying). For example, patients will enter a trial with a certain level of the mediator variable, for example substance use, which is independent of the random allocation and instead influenced by a set of other characteristics. Owing to the randomisation assumption, we assume that the mean level of substance use is the same in both arms of the trial. We hope that the intervention will lead to a greater reduction in substance use in the intervention arm than in the control arm, and that this in turn leads to a better outcome in the intervention arm. Implicitly, we are interested in the change in substance use from baseline, but at which time point? If we only have two repeated measures of the mediator, then we could continue using the methods outlined in Chapter 2 by adjusting for the baseline mediator as a potential confounder (as was illustrated in Figure 3, analogous to an analysis of covariance model). If we have several repeated measures of the mediator, we could explicitly calculate change at each of these, but this then allows for multiple mediation pathways which may complicate the interpretation of the results. Alternatively, we could consider a single change over the whole of the repeated measures using a more complicated modelling approach.
Let us consider an example with three measures of both the mediator and the outcomes and, although it is not necessary for these to be measured at the same occasion, for simplicity we denote these as occurring at the same time points. Our first step involves deciding on a suitable model for the univariate mediator measures (and likewise the univariate outcome measures), before combining these in a bivariate model with randomisation as an explanatory variable and defining the mediation pathways. MacKinnon19 (see Chapter 8) extensively discusses estimation of this three-time-point model; here we model this with a set of latent growth factors for the mediator and outcome separately, using parallel processes, and estimate the structural parameters explaining relationships between them.
For example, in Figure 4, Mt(t = 0,1,2) represents the observed mediator at time points t = 0 (baseline), t = 1 and t = 2. We are interested in modelling the relationship over time between these mediators. The univariate model is driven by the baseline levels (the random intercept, Im) and the linear change (the random slope, Sm). In Figure 4:
-
The errors ε1, ε2 and ε3 are independent.
-
The observed scores are explained by Im and Sm.
-
The means and variances of Im and Sm are freely estimated.
-
The covariance between Im and Sm is freely estimated.
FIGURE 4.
A univariate growth process for the repeated measures of the mediator M. Unlabelled paths are fixed to be equal to 1.
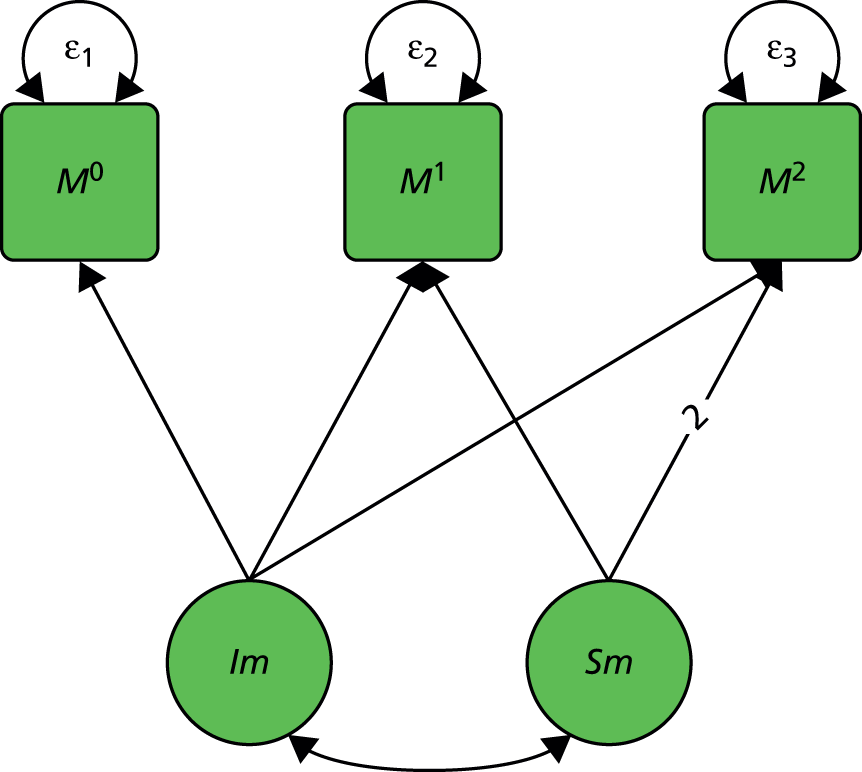
The next stage is to model the observed outcome in a similar way, essentially replacing Mt by Yt in Figure 4. While it is not necessary to assume that the outcome growth process will be the same as the mediator growth process, for illustrative purposes we will make this assumption. These models are then combined in a bivariate growth model, and the treatment variable Z included as a cause of the random slope of the mediator Sm and the random slope of the outcome Sy. As Z is randomly assigned and Im represents the baseline values, we can assume that there is no covariance between Z and Im. The aim is to assess whether or not the intervention affects the growth trajectory of the mediating variable, which in turn affects the growth trajectory of the outcome variable. 82
This is represented in Figure 5. Here, the coefficients β1, ψ2 and ψ1 refer to:
-
β1, the effect of the intervention on the slope of the mediator process
-
ψ2, the effect of the mediator process slope on the slope of the outcome process
-
ψ1, the direct effect of intervention on slope of the outcome process.
FIGURE 5.
A bivariate growth process with randomised group included in the model.
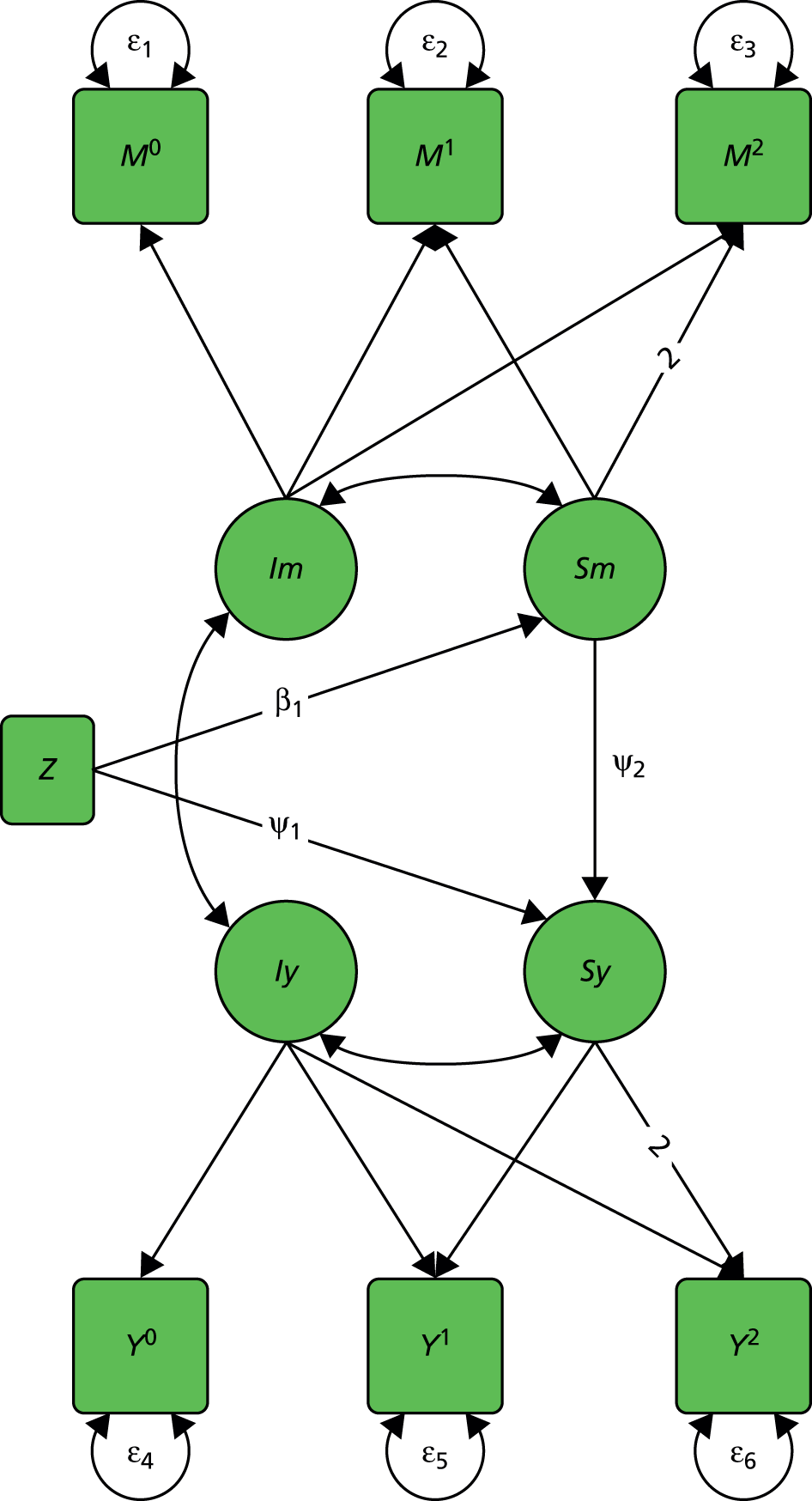
Logically, these follow the same interpretation as the standard direct and indirect effects from the single-mediator/outcome approach described in Chapter 2. Since the growth factors are normally distributed latent variables, we can interpret the coefficients as being from linear models and redefine the B&K16 steps as follows:
-
Demonstrate that treatment, Z, has an effect on the slope of the outcome Sy.
-
Demonstrate that treatment, Z, has an effect on the slope of the putative mediator Sm.
-
Demonstrate that the slope of the mediator Sm has an effect on the slope of the outcome Sy after controlling for treatment Z.
As previously described, the lack of a significant total effect on the outcome in step 1 might not necessarily preclude a meaningful mediation analysis from being undertaken, if it helps to explain why a treatment was not effective. The essential criterion is step 2 because, if it cannot be shown that the treatment has influenced the putative mediator, then this cannot be on the causal pathway from treatment to outcome. As treatment is assumed to be randomised, this is an ITT analysis and so can be assessed without bias.
While this approach offers a more realistic model for the data collected in a trial and the underlying process, it suffers from the same problem as the B&K approach, namely that there could be unmeasured confounders affecting both Sm and Sy.
We demonstrated at the end of Chapter 2, in PACT, that repeated measures of the mediator can be used to avoid attenuation bias due to measurement error in a single mediator. We expect the same to apply here. The estimator of the mediation parameter ψ2 should not be subject to attenuation bias due to measurement error in the repeated measures Mt (t = 0,1,2). Our growth model for the mediator represents a measurement model. We could make this more explicit in Figures 4 and 5 by specifying a latent true score loading onto each of these observed variables, which would be denoted as Tm0, Tm1 and Tm2, respectively. The growth factors would then be defined on these latent true scores. This is the focus of ongoing work and will be reported separately elsewhere.
To account for unmeasured confounding between Sm and Sy, which if present would lead to biased estimates of ψ1 and ψ2, one solution is, as before, allowing for correlated errors between the random slopes. This model is not identified, as we are also interested in estimating the directed arrow from Sm to Sy in order to infer mediation; however, we can take the IV approach as used previously and apply it to this model. The instruments, which could be randomisation by baseline covariate interactions as described in Chapter 2, would be assumed to influence the growth in the mediator Sm but have no direct effect on the growth in the outcome Sy. Again, this is the focus of ongoing work and will be reported separately elsewhere.
Finally, we stated that the first step in our approach to modelling repeated measures of the mediators and outcomes was identifying a suitable univariate model to describe the growth process in each of these. We demonstrated this with a linear growth curve model, but there are other possibilities too. These include piecewise growth models, change score models and autoregressive models. Many of these are discussed in MacKinnon,19 Muthén and Khoo,83 and McArdle. 84 They follow the same procedure as described with the growth curve model but produce different measures of ‘change’, and so they lead to different driving variables and different interpretations of which aspect of the mediator is changing which aspect of the outcome. We will not explore these models in more detail here, but instead now consider alternative longitudinal extensions.
Extensions to repeated measures of outcomes with a single-process measure
In Chapter 3, we introduced principal stratification for assessing how treatment effects vary depending on the latent principal stratum. This treated the process measure, such as therapeutic alliance, as a post-randomisation effect modifier. Recall that the strata are partially observed, remaining hidden in the control group but identifiable in the treatment group where the process measure is observed; our approach relies on having good predictors X of the strata membership. In our previous SoCRATES example, we considered only a single outcome measure, the PANSS score at 18 months; now we consider the situation where we have repeated outcome measures.
In the previous section we introduced the latent growth curve model (see Figure 4). Here, we demonstrate how GMMs can be applied to account for repeated measures of the outcome. We will use a finite mixture model approach to estimate the proportion of patients in the latent classes (principal stratum). Then we fit separate random coefficient models to the outcome data within each principal stratum using maximum likelihood estimation, to assess if the effect of random allocation on the slope of the outcome varies by latent class. The question of interest within these models is ‘how is the effect of treatment on the growth parameters influenced by the different latent classes or principal strata?’.
We simultaneously fit the following models using maximum likelihood with the EM algorithm:
-
Fit a latent class model (the latent classes being the principal stratum) using the single measure of the process variable and baseline covariates to predict class membership.
-
Within each of the above latent classes (principal strata), fit a growth curve for the repeated measures of the outcome.
-
Evaluate the effects of the intervention on the growth parameter (slope) within each class.
We can test whether or not the effects of the intervention on the slope parameters are the same within each stratum by introducing and evaluating the introduction of between-stratum using constraints. The combined model is an example of a GMM.
The model is shown in Figure 6. Here, since A is a categorical latent variable, the interpretation of this GMM is not the same as for a continuous latent variable. The arrows from A to the growth factors indicate that both the intercepts and slopes vary with A (i.e. A has a prognostic effect on outcome), as well as being influenced by the baseline covariates X. In addition, the arrow from A to that of the effect of randomisation (Z) on the slope factor indicates that A is a treatment effect modifier.
FIGURE 6.
Growth mixture model for repeated outcomes within principal strata.
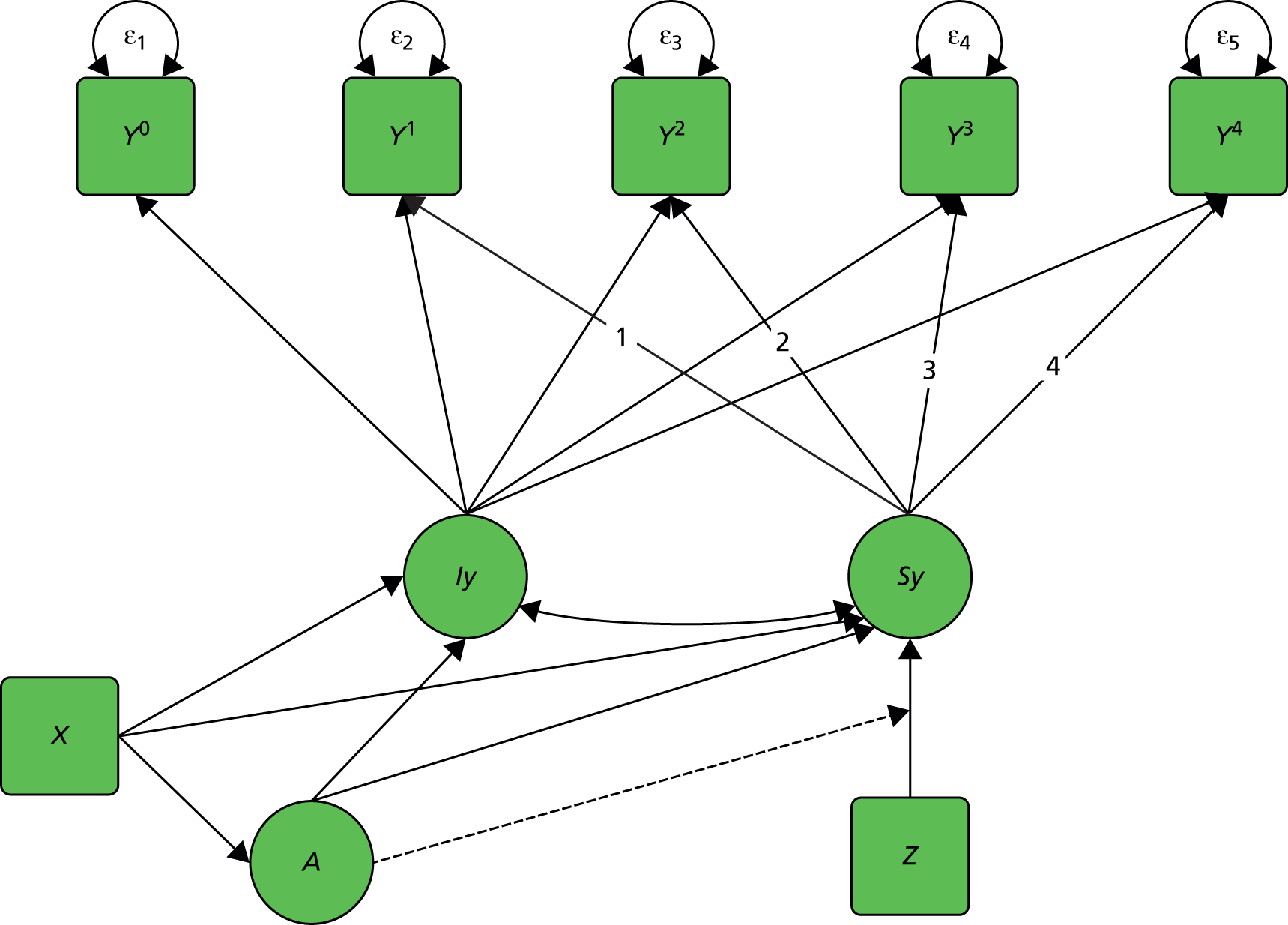
In the context of CACE estimation (as described in Chapter 1), Muthén and Brown85 have investigated the use of latent growth curve or trajectory models for repeated measures of outcomes with a single measure of compliance; it is this approach we extend using alternative process measures rather than compliance.
Recently it has been pointed out that such a one-step approach ‘can be flawed because the secondary model for the outcome may affect the latent class formation and the latent class variable may lose its meaning as the latent variable measured by the indicator variables’. 86 The authors describe an alternative three-step approach, in which the latent class model is estimated in the first step based on the latent class indicator variables only, independently of the outcome variables and its model. This has some appeal in our current context, as we would want to form latent classes based on the process variables which do not change with the outcome being analysed; however, this three-step approach has only recently been incorporated into Mplus, and further work is needed to compare with the one-step approach in our work.
SoCRATES example
Following the analysis of the SoCRATES trial presented in Chapter 3, in which we considered the therapeutic alliance at the fourth session of therapy as our process variable, we can postulate the existence of two principal strata:
-
High-alliance participants: those observed to have a high alliance in the therapy group together with those in the control group who would have had a high alliance had they been allocated to receive therapy.
-
Low-alliance participants: those observed to have a low alliance in the therapy group together with those in the control group who would have had a low alliance had they been allocated to receive therapy.
Rather than estimate the treatment effect on the outcome measured only at 18 months, we acknowledge that we have five repeated measures of PANSS outcomes in SoCRATES. These were measured at baseline (time score 0), 6 weeks (time score 1.94591), 3 months (time score 2.5649493), 9 months (time score 3.6109178) and 18 months (time score 4.3694477). In the analyses we log transformed the time scale as measured in weeks, which is shown in parenthesis above.
We simultaneously fit the following models using maximum likelihood with the EM algorithm:
-
principal stratum membership on the baseline covariates: logDUP, centre, years of education
-
linear growth model within each class, allowing all the random-effect means and variances to vary between high- and low-alliance classes
-
effect of randomisation on the slope within each class.
The procedure was bootstrapped to obtain valid SE estimates, and the method allows for missing data under a MAR assumption. Figure 7 shows the observed trajectories and the estimated mean PANSS score at each time point for the 63 subjects assigned low-alliance class. Figure 8 shows the observed trajectories and estimated mean PANSS score for the 138 subjects in the high-alliance class.
FIGURE 7.
SoCRATES: estimated mean and the observed trajectories for low-alliance class (n = 63).
FIGURE 8.
SoCRATES: estimated means and observed trajectories for high-alliance class (n = 138).

The results for the effect of randomisation on slope by principal stratum are as in Table 6.
| Strata/class | Coefficient | SE | p-value |
|---|---|---|---|
| Low alliance | 1.808 | 1.644 | 0.271 |
| High alliance | –2.843 | 1.136 | 0.012 |
We reach similar conclusions to those found in the analysis in Chapter 3: in the high-alliance class there appears to be a beneficial effect of the treatment but in the low-alliance class there is a non-significant but detrimental effect of treatment compared with control.
Extensions to repeated measures of process measure: principal trajectories
In Chapter 3, we demonstrated how the principal stratification approach can be used to analyse process measures with a single time point. However, in many of our randomised trials, we collect the process measures at each session of treatment. For example, in the PRP trial of CBT, the patients rated their empathy with the therapist at each session of CBT they attended. The control group received TAU so there was no corresponding measure of empathy that could be observed in the control group. To use the principal stratification approach, we would have to select a session of therapy and use the empathy value from the treatment group at that session; this is clearly not making the most efficient use of all the available data.
Here we propose a new extension to principal stratification, termed principal trajectories, that makes efficient use of the repeated measures of process variables and can also allow for participants with missing data or who drop out of the intervention. In summary, we estimate general GMMs on the repeated measures of the process variables in the intervention group using maximum likelihood, assigning participants to hypothesised latent trajectory classes by estimated posterior probabilities. Using baseline covariates which predict class membership, we assign which class the control group participants would have been in, had they been randomised to intervention. We then examine the effect of random allocation on outcome within each class. If required, an exclusion restriction of no treatment effect within one of the latent classes can be imposed to aid identification.
To illustrate this approach, first we consider the simpler scenario of repeated measures of only one variable, for example the mediator or outcome, and reintroduce the idea of the latent trajectory model. In this form, the random part of the model is represented by discrete trajectory classes Ac with probability of class membership πA and by a separate intercept and slope estimated in each class. This scenario is shown hypothetically in Figure 9; the left-hand panel shows individual trajectories of empathy over therapy sessions and the right-hand panel shows these trajectories have been grouped into distinct latent classes (in this case, two classes).
FIGURE 9.
Individual trajectories grouped into latent classes (principal trajectories).
However, these trajectories and classes can be produced only for the treatment group, as there is no measure of empathy in the control group. We need to make an inference about the empathy trajectory of members of the control group had they been randomised to the treatment group. We could either infer the trajectories themselves or assign an empathy class membership to the patients in the control group, based on the observed trajectory classes from the treatment group. This latter approach relies on there being good baseline predictors of class membership, as with the principal stratification approach.
There are two options for proceeding when we have calculated the potential trajectories for each subject:
-
Within classes, separate models can be fit investigating the relationship between randomisation and outcome. This can be either a straightforward ITT effect based on a regression model or more complicated models allowing for repeated measures in the outcome variables as well. The differences in the coefficients for randomisation between the classes can be interpreted as providing evidence for different between class treatment effects.
-
Rather than forming the latent classes on just the mediator trajectories, we could combine these with outcome trajectories, and form latent classes based on both the mediator and outcome trajectory patterns (involving estimating shared growth parameters).
Figure 10 shows a latent variable model illustrating the first of these scenarios: Ac represents a categorical latent variable which determines the growth terms Iy and Sy; Ac is predicted by baseline covariates X, and the effect of randomisation Z on Y is modified by Ac.
FIGURE 10.
A latent variable model illustrating the principal trajectories approach.
A latent variable model illustrating the principal trajectories approach.
The full principal trajectories estimating procedure is outlined as follows:
-
For the repeated process measures in the treatment group, examine the pattern of the observed trajectories and assess variation between participants.
-
Fit GMMs using maximum likelihood to find principal stratum (latent trajectory classes).
-
Assign participants in the intervention group to the most likely principal stratum (latent class) using estimated posterior probabilities.
-
Use an appropriate regression model to examine baseline predictors of stratum/class membership.
-
Use the estimated parameters from this regression model to assign the control group participants to the stratum (latent class) they would have been in, had they been randomised to the treatment group.
-
Examine the effect of treatment (i.e. randomisation) on outcome within each stratum/class separately. An exclusion restriction can be imposed here in order to aid identification.
Example: the Prevention of Relapse in Psychosis trial
The primary analysis of the PRP trial showed that neither the CBT nor the Family Intervention groups had an effect on remission, relapse or days in hospital compared with TAU but that CBT had a beneficial effect on depression scores (BDI) at 24 months compared with TAU alone. 81 The CBT intervention and family intervention for psychosis focused on relapse prevention for 20 sessions of therapy over 9 months, with the therapist–client empathy measured by the client at each session (where a high score is better). For this analysis, we compare the CBT + TAU group with the TAU alone group. We applied the principal trajectories steps outlined above using Mplus version 7.11, with the one-step maximum likelihood estimation procedure. This led to the following results:
-
a linear mixed model (random slope and intercept) fits the observed shape of trajectories in the CBT group
-
two distinct latent classes found (class 1, always high empathy; and class 2, improving empathy)
-
76 CBT clients were assigned to class 1 and 16 were assigned to class 2
-
baseline predictors were carer involved in treatment (yes/no), centre, depression outcome (BDI), gender, outpatient status (yes/no)
-
total of 176 clients assigned to class 1, 46 assigned to class 2 (entropy = 0.71)
-
compare BDI scores at 12 and 24 months between CBT versus TAU.
Our model found two classes, which subjectively we call an ‘always high’ class, and an ‘improving’ class. Figure 11 shows the observed mean scores and the model predicted mean scores for the empathy measure at each session, by latent class. The estimated ITT effects within classes for CBT compared with TAU on BDI scores common at 12 and 24 months are shown in Table 7, where a negative effect indicates CBT improves BDI.
FIGURE 11.
Example of principal trajectories in the PRP trial, with two latent classes.

| Strata/class | Coefficient | SE | 95% CI |
|---|---|---|---|
| Always high | 1.71 | 1.74 | –1.70 to 5.13 |
| Improving | –10.12 | 5.84 | –21.57 to 1.33 |
Although the results are not conclusive and do not achieve statistical significance, it suggests that in the ‘improving’ class the treatment effect is larger and in the expected direction of CBT being superior, whereas in the ‘always high’ class the CBT does not appear to be superior to TAU. One could construct a post-hoc justification for this; that those clients in the always-high group might have characteristics that suggests their outcome will be good regardless of their treatment allocation, and so the CBT does not have an effect. This suggests that empathy may have a causal role in explaining treatment effect heterogeneity; however, further, ongoing work is needed to verify these findings and so these should be interpreted with caution. At present, they serve as a real illustration of our proposed new method.
Conclusions
We have presented linked but distinct extensions for longitudinal settings in three scenarios:
-
repeated measures of both mediators and outcomes
-
single process measures with repeated outcome measures
-
repeated process measures with a single outcome.
The methods proposed have highlighted some of the advantages of collecting additional data during the course of the trials, in that they allow for different, and arguably more realistic, modelling of the true underlying process of how interventions influence outcomes. However, it has also raised some additional issues and highlighted the assumptions that underpin these methods.
Chief among these is the requirement for ‘good’ baseline covariates which are predictive of latent classes, for the principal stratification or the principal trajectories method. What constitutes ‘good’? This is still an open question, but we can use measures such as the entropy to judge how well our model separates participants into the latent classes. Pre-specifying an analysis of this form would give more belief in the findings, as it could be considered an inappropriate subgroup analysis, and also gives triallists the opportunity to design and collect the baseline measures that predict class membership.
Finally, we note that this work is still an area of active research, and the focus of our current MRC methodology research grant (Landau S, Pickels A, White I, Emsley R, Dunn G, Clark P, et al. , Developing methods for understanding mechanism in complex interventions, King’s College London, London, 2013–16; grant number MR/K006185/1).
Chapter 5 Trial design for efficacy and mechanism evaluation
Yes, but what’s the mechanism? (Don’t expect an easy answer).
Bullock et al. 87
Introduction
The application of many, if not all, of the IV methods described in the earlier chapters of this report has relied on archived trial data together with post-hoc observations on treatment heterogeneity (treatment effect moderation). Here the use of the treatment by moderator interaction as an IV is open to several important criticisms. The role of these post-hoc moderators (e.g. treatment centre) has no strong theoretical underpinning and, in many cases, it is unlikely that the treatment effect moderation observed would provide us with a strong enough instrument. We are typically faced with a so-called ‘weak instrument’ problem. 88,89 If we have weak instruments the treatment effect estimates are very imprecise and, worse than that, they are inconsistent; estimators can be biased even with large sample sizes88,89 and, in these instances, might have worse statistical properties than an ordinary least squares (OLS) estimator. Another problem is that the treatment effect heterogeneity induced by recruitment and treatment within the different centres, for example, is unlikely to be restricted to the effects of a complex intervention (psychotherapy) on just a single putative mediator. If our analysis is concentrating on a single putative mediator (as is often the case), then this will imply moderation by the prognostic marker (treatment centre) on the so-called ‘direct effect’ of treatment (i.e. the effect not explained by our selected mediator). For these analytical methods to develop increasing credibility in practice, we need to find convincing theoretically justified and well-measured predictive markers. That is, we need baseline markers with a strong theoretically justified moderating effect on a targeted intervention (TI) specifically designed to influence a theoretically justified putative mediator. If the targeting is good enough and the theoretical justification of its proposed effects on the mediator are scientifically valid, then heterogeneity of the direct effects of the TI should not now be a major problem. These are major challenges and there are unlikely to be any short routes to success. We also have to realise that the models underlying our estimation procedures will never be better than reasonably good approximations to reality. Results will always need to be interpreted with extreme caution.
Despite this apparent pessimism and associated ‘health warnings’, we now consider various options for the improvement in the design of EME trials.
Using predictors (prognostic markers) for confounder adjustment
Baseline (pre-randomisation) predictors (prognostic markers) are variables that are predictors of outcome, regardless of treatment received. A mediator is an intermediate outcome (a mechanistic marker) of a treatment or other intervention, and a prognostic marker may have, and it is likely to have, an effect on both the intermediate and clinical outcomes. If so, then the prognostic marker is a confounder. If we measure and record the value of the predictor variable (prognostic marker), then we are in a position to allow for its effects in our analyses (as in analyses of covariance, for example); ideally, we should have measurements on several such predictors (baseline covariates thought to have prognostic value). In a two-stage analysis (as in B&K), we first estimate the effect of treatment on the mediator, adjusting for all of our additional measurements (baseline covariates/predictors), and then we look at the joint effects of mediator and treatment on outcome, again adjusting for all of our measured confounders (baseline covariates/predictors). This two-stage procedure will be valid if, and only if, we have accounted for all of the common causes of the mediator (M) and outcome (Y). Otherwise the effects we are attempting to estimate will suffer from hidden or residual confounding (residual biases). But, of course, allowing for the predictors will have reduced the bias in the estimates of the causal effects being modelled and is likely also to have increased their precision (certainly in the case of quantitative outcomes). However, there may be important baseline markers that we might have measured but have not. We may be unaware of their existence for example, and there are likely to be events (common causes) influencing the participant once treatment has been initiated (post-randomisation confounders: infections, bereavements, accidents and other life events, comorbid illness, additional medications, etc.). We can never be sure. Merely adjusting for measured predictors of outcome is unlikely to be entirely satisfactory. Even when we do manage to get measurements for all or, at least most, of the prognostic markers, many of them will be subject to measurement errors and it is likely that there will still be some residual confounding arising from this. 54
Using predictors of outcome (prognostic markers) as instrumental variables (Mendelian randomisation)
What if we have prior biological or psychological knowledge which makes it highly plausible that a particular prognostic marker has an effect on the mediator and, although it is related to clinical outcome, it has no direct effect on the clinical outcome? If this were the case, and the marker was also uncorrelated with the omitted common causes, then such a prognostic marker would be an IV. If the prognostic biomarker were a genetic variant, then this IV technique is an example of what has been called Mendelian randomisation. 90,91 It is labelled ‘Mendelian’ because we are dealing with genetic variation and ‘randomisation’ because of the random assortment of alleles during gamete formation.
As we have seen earlier in this report, if our assumptions concerning the use of IV methods are credible, we will obtain consistent (asymptotically unbiased) estimators of the causal parameters of interest (direct and indirect effects) but with lower precision. Assuming that we are prepared to exchange lower precision for lack of bias, why should we not decide that we now have the solution? What are the limitations of Mendelian randomisation or the similar use of other prognostic variables as instruments in the context of randomised trials for mechanisms evaluation? The first is that, in order to be of real practical value, the instrument has to have a strong effect on the putative mediator. In the context of a randomised trial specifically focusing on an intervention targeting the proposed mediator, genes are to explain very little of the within-treatment variability of the mediator (i.e. the ‘weak instrument’ problem referred to above). Another potential problem is that the assumption of no direct effect of the prognostic variable on clinical outcome may be untenable (there may be problems arising from linkage disequilibrium, pleiotropy, genetic heterogeneity and population stratification; see Didelez and Sheehan92 for a discussion of these and other problems). We want to be fairly confident that our identifying assumptions (those needed to allow us to estimate the relevant treatment effect parameters without bias) are not obviously open to challenge. In this context, it will be practically impossible to verify them using the data at hand.
Using moderators of treatment effects (predictive markers) to generate instrumental variables
A treatment moderator or predictive marker is a baseline (pre-randomisation) measurement that predicts the effects of the treatment or comparable intervention. Although it may predict outcome within the different randomised treatment groups (i.e. function as a prognostic variable and also as a potential confounder), its key characteristic is that it is a treatment effect moderator. 16,17 The predictive marker itself will not be a valid instrument but, in the context of an appropriate statistical model, the treatment by marker interaction (the moderating effect of the marker) may be. Taking a much wider context than just the application in randomised trials of complex psychological interventions, the very essence of predictive (stratified) medicine is that there is very strong moderation by the predictive marker of the treatment effect on a supposedly known target mechanism (mediator) and that the moderating effect of the predictive marker on the clinical (distal) outcome is explained by treatment-induced changes in the mediator. Accepting these conditions (assumptions) is equivalent to stating that the treatment by predictive marker interaction is an IV. This is a strong assumption, always open to challenge.
This is a very attractive model. First, however, we need to find a convincing treatment effect moderator. Despite the optimism in the recent stratified medicine field and the long-held views of psychologists and others that personality traits and clinical/life history, for example, should be powerful moderators of treatment effects, this is easier said than done. Second, we need to have established that we can measure this prognostic marker with sufficient accuracy (reliability and validity). Again, this might be a challenge. Third, we need a credible candidate for the marker of the mechanism of effect of a TI (i.e. a credible mediator). And, again, this is quite a challenge. In the case of a complex intervention, we also need to be convinced that there will be no (or, perhaps more realistically) very little moderation by the predictive marker on the effects of treatment on other mediators not included in our model (i.e. that, in the context of our statistical model, the direct effects of treatment are not dependent on predictive marker status). We will return to these challenges later. Here we describe the appropriate statistical model.
Let the binary treatment be represented by the variable treat. Anticipating our simulated EME trial [see A suggested biomarker (moderator)-stratified efficacy and mechanism evaluation trial and associated analysis strategy], let a binary predictive marker be X10 and the product of treat and X10 be X11 (we will explain the choice of the labels X10 and X11 when we introduce our full Monte Carlo simulations). The two causal (structural) models are:
where εm and εy are the random deviations (‘errors’) associated with each of the two models, respectively. We assume that these errors are correlated, that is cov(εm, εy) ≠ 0, acknowledging the fact that there are missing common causes of M and Y. β2 is the effect of treatment on the mediator (M) when X10 = 0. β3 is a measure of the strength of the effect on the mediator of the interaction between treatment and predictive biomarker. The effect of the treatment on the mediator when X10 = 1 is the sum of β2 and β3. The direct effect of treatment on outcome (Y) is the parameter ψ2 and the effect of the mediator on outcome (irrespective of the levels of treatment and X10) is ψ3. β1 and ψ1 are of no intrinsic interest but are included to allow for the confounding explained by the predictive marker, X10.
The total effect of treatment on outcome when X10 = 0 is simply β2ψ3 + ψ2, and the proportion explained by its effect on the mediator is β2ψ3/(β2ψ3 + ψ2). Similarly, the total effect of treatment when X10 = 1 is (β2 + β3)ψ3 + ψ2, and the proportion explained by its effect on the mediator is (β2 + β3)ψ3/((β2 + β3)ψ3 + ψ2). Note that we have assumed homogeneity of treatment effects within the strata defined by the marker X10.
Is our assumption that the interaction X11 is a valid IV justified? This depends on the strength of the biological, psychological or social theory and the supporting evidence for considering X10 to be a good predictive marker. Is it likely that the interaction (X11) is a weak instrument? No. If it were a weak instrument (i.e. a weak moderator) then we would suggest that it would have already been discarded as a potentially useful stratifying marker. For a predictive biomarker to have met the necessary development milestones implies that it is confidently assumed to be a powerful moderator of the effect of the treatment on the proposed mediator (these developmental milestones are well beyond the scope of the present report).
Taking equations 30 and 31 to represent the core feature of an EME trial for a personalised treatment, we later integrate all of our potential biomarker measurements to suggest a viable trial design and associated data analysis strategy. First, however, we briefly describe other design options.
Simple multiarm trials focusing on a single mediator or process measure
A key component of the Garety et al. 93 cognitive model for psychosis is that reasoning biases contribute to the development and persistence of delusions by influencing the appraisal of disturbing anomalous experiences and adverse events. It now is well established that people with psychosis ‘jump to conclusions’, a bias towards gathering fewer data than control participants to reach a decision. 94,95 One of the putative mediators of the effects generic cognitive–behavioural therapy for psychosis (CBTp) is a reduction in these reasoning biases. Here we will not be concerned with the other potential mediators of CBTp, but simply combine their unmeasured effects into the causal parameter measuring the direct effect of therapy [i.e. the therapeutic effect that is not explained by changes in jumping to conclusions (JTC)]. We will not, here, be concerned with the practicalities of measuring JTC, but simply represent its measure by M1. The strength of delusional conviction is the clinical outcome (Y) that we would like to reduce by our therapeutic interventions. Consider a three-arm randomised trial to compare the outcomes (strength of delusional conviction) after:
-
routine care
-
routine care plus generic CBTp
-
routine care plus generic CBTp plus a TI.
The TI might be a highly focused reasoning training delivered by computer. What might we be justified in assuming from the structure of this trial and the nature of the interventions? We might be justified in believing (assuming) the following:
-
The effect of CBTp is the same in arms (b) and (c), that is its efficacy is not influenced by the addition of TI.
-
Assuming that both CBTp and TI influence the strength of delusional conviction, then the outcome in (b) will be better than in (a) and outcome in (c) better than in (b).
-
There is no direct effect of TI on delusional conviction, that is its effect is wholly explained by its action on the mediator, JTC. This is a very strong assumption, of course, and dependent on how convincing the claimed specificity of the targeting. There would need to be quite a lot of developmental work to generate convincing evidence that this assumption is, at least approximately, valid.
In addition to M1 and Y being JTC and strength of conviction, respectively, let the randomised binary indicator Z1 indicate the presence of CBTp [Z1 is 0 for arm (a) and 1 for arms (b) and (c)]. Let the randomised binary indicator, Z2, indicate the presence of TI [Z2 is 0 for arms (a) and (b), and 1 for arm (a)]. The combined structural model that is consistent with our three assumptions is the following:
with cov(εm1, εy) ≠ 0.
The TI indicator (Z2) is assumed to be an IV, or instrument, for the mediator, M1. Estimation of the parameters for this structural model is very straightforward using 2SLS. Extra precision might be obtained by the inclusion of baseline prognostic markers (baseline covariates such as the baseline levels of JTC and strength of delusional conviction).
A similar design might also apply to process evaluation. The TI arm might be allocation to a component of therapy specifically targeted at improving adherence to homework assignments, for example.
Returning to mediational mechanism evaluation, if we have a second putative mediator, M2, (e.g. level of anxiety) and an intervention precisely targeted on M2 then it is possible to extend the design to four arms (and so on, as extra mediators are added to the system). The model would now be:
with non-zero covariances among the three error terms. We assume that M1 has no effect on M2, and vice versa.
Z1 and Z2 are now the combined instruments for M1 and M2 and the use of 2SLS follows, accordingly.
If we consider trials in which we may wish to evaluate the treatment effect modifying influences of specific components of therapy (e.g. setting homework), then it is also fairly straightforward to envisage similar designs in which the specific component is ‘boosted’ by a specific TI.
What’s the catch? The validity of the above approach is dependent on the validity of our assumption that the TI only affects the targeted mediator. We have already explained the need for developmental work to generate a body of evidence that this is actually the case. If the TI has an effect on a mediator other than M, then the method is flawed. How flawed and how much it matters, of course, depend on the strength of the alternative pathway(s). It is likely that expert judgement is very useful here. If the putative mediator, M, is the main pathway to recovery and the TI changes M considerably more than the more generic CBT, then we would consider abandoning the generic CBT in favour of targeting, regardless of our assumptions concerning the absence of direct effects of the TI.
Using data from parallel trials
Here we consider a similar situation where we might have two separate randomised trials, (1) TAU versus generic CBT and (2) TAU versus a TI. One possible advantage (or disadvantage, depending on the circumstances) is that these two trials need not be run concurrently, although we would hope that the populations from which participants were recruited would be similar. The pursuit of parallel trials would not always be productive but there are some circumstances in which they might be useful. Returning to PROSPECT introduced in Chapter 2, the intermediate outcome (putative mediator) was whether or not the trial participant adhered to antidepressant medication during the period following allocation of the intervention. The question here is whether or not changes in medication adherence following the intervention might explain some or all of the observed (ITT) effects of the primary-care intervention on clinical outcome. Ignoring the complication of the variation in types of antidepressant prescribed in PROSPECT, in principle it would be straightforward to have designed a placebo-controlled antidepressant trial to run in parallel with PROSPECT (if evaluating the efficacy of antidepressant medication was also an unanswered research question at the time). Presumably, some participants would not have complied with their antidepressant prescription in this second trial, so we would be concerned with CACE estimation to evaluate the effect of medication in the subset of compliers. Representing antidepressant use by the mediator, M, if we were to analyse the data from the two parallel trials, our structural models would be as follows.
For PROSPECT:
with cov(εm1, εy1) ≠ 0.
Here Z1 is indicator of the random allocation to either the control or the primary-care intervention.
For the parallel supplementary antidepressant trial:
with cov(εm2, εy2) ≠ 0.
Here Z2 is the indicator of randomisation to receive antidepressant medication, assumed to be a strong instrument for medication (it has a powerful effect on medication use but no direct effect on outcome). Clearly, the effects of the two interventions on the mediator (i.e. β1 and β2) will differ (the equivalent of a trial by randomisation interaction in the IV set-up as described in Chapter 2). We can easily estimate ψ2*, the average effect of medication on outcome in the supplementary antidepressant trial using standard IV/CACE methods. Now, if we are prepared to believe that the average effect of medication is the same in the two trials (i.e. ψ2 = ψ2*) we can then plug in our estimate of ψ2* into the analysis of the PROSPECT data, so achieving the identification of the average direct effect of psychotherapy, ψ1. Of course, a better approach would to be to use simultaneous SEM software to jointly analyse the data from the two trials, subject to the constraint ψ2 = ψ2*.
Again, this is equivalent to the standard IV set-up as described in Chapter 2, the effect of the mediator being assumed to be homogeneous, that is there is no M by trial interaction in the model for outcome.
Problem solved? Possibly, but probably not. The remaining issue is common to all of our mediation/process evaluations, but is specifically highlighted by our use of CACE methodology in the present example. In our introduction to CACE estimation in Chapter 1 we emphasised that, in the presence of highly likely treatment effect heterogeneity, we were not justified in inferring that the average effects of treatment in the non-compliers would be the same as that estimated for the compliers. Similarly, in the presence of this treatment effect heterogeneity, if we were to have a series of randomised trials in which different proportions of participants were induced to comply with their treatment allocation, then an implication of this would be that the CACEs (not just the CACE estimates) would change from one trial to another. Returning to our present pair of trials (PROSPECT and its hypothetical supplementary antidepressant trial) we have already firmly concluded that the effects of random allocation on medication use (i.e. β1 and β2) differ between the two trials. Even if the effects were similar, we would have no way of knowing whether or not the compliers in the two trials were similar. If there is significant treatment (antidepressant) effect heterogeneity, then the implication is that ψ2 ≠ ψ2*, and therefore neither ψ2 nor ψ1 is estimable.
Should this IV approach be abandoned? No, of course not. We just need to be aware of all of the potential pitfalls. 87 One potential approach that might be very informative is in a sensitivity analysis similar to that proposed by Emsley and VanderWeele96 (see also VanderWeele97), which is essentially plugging in external estimates of causal parameters (such as one for ψ2*), or we could investigate the potential impact of effect heterogeneity. We could carry out an evaluation of mediation in a trial such as PROSPECT, for example, using either the newer IV methods or the traditional B&K approach (or both). We may then be able to obtain an estimate of the effect of medication on outcome (ψ2*) in a comparable population of patients from a systematic review of the relevant trials literature, acknowledging that the estimate will not be ideal; it is likely to be based on ITT analysis, for example, not on the potentially more valid CACE analysis (but we might decide that the estimate is good enough or use these arguments in favour of running the two parallel trials). If we decide that the estimate is good enough, we could then plug in this estimate and see what effect it has on the other relevant structural parameter estimate (ψ1, the average direct effect of psychotherapy). We could even use the estimate of ψ2* as the basis for an informative prior distribution in a Bayesian approach to the analysis. The stability (or lack of stability) of our estimates of ψ1 will have (or should have) a powerful effect on our confidence concerning our conclusions.
Note that psychologists have also suggested similar experimental procedures, involving direct manipulation of the putative mediator,98,99 and some of the practical and conceptual obstacles to this approach are discussed in detail by Bullock et al. 87
Parallel trials for parallel mediators
Here, for example, we consider three parallel randomised trials, each evaluating a separate intervention, Z1, Z2 and Z3, specifically targeted on putative mediators, M1, M2 and M3, respectively (the mediators are assumed to be working in parallel and, importantly, are assumed not to be influencing each other). We have a common clinical outcome, Y.
Trial 1
with possibility of correlation between the error terms for the mediators and that of the outcome.
Trial 2
again, with possibility of correlation between the error terms for the mediators and that of the outcome.
Trial 3
again, with the possibility of correlation between the error terms for the mediators and that of the outcome.
This system of models is clearly not identified. How might we proceed? Inevitably, we have to start by assuming treatment effect homogeneity (but see warning in the previous sections) and make the following three sets of assumptions:
One possibility (in addition to effect heterogeneity) is the introduction of exclusion restrictions (we assume that there are no mediators other than M1, M2 and M3), that is ψ11 = ψ21 = ψ31 = 0. The models are now identified. We now have a set of three instruments (Z1, Z2 and Z3, equivalent to the trial by randomisation interactions in our original IV set-up in Chapter 2) and three confounded effects to be estimated (ψ2, ψ3 and ψ4). It is unlikely that these exclusion restrictions hold; however, they could be true if we had a good enough theory to cover the spectrum of possible mediation paths. Again, this stresses the importance of prior developmental work to justify the use of any given trial design.
What else can we do? Perhaps we really are precisely targeting each of the three mediators in turn. That is perhaps β20 = β30 = 0, β′10 = β′30 = 0, and β′10 = β′20 = 0 (in addition to the exclusion restrictions). If so, we would, again, have identifiability. Unlike the other assumptions, these constraints can be tested empirically (i.e. is there an effect of each intervention on each of the mediators?) but only if we are prepared to accept the exclusion restrictions (no direct effects).
If treatments are not crossed, then running multiple parallel trials is really the same scenario as a single multiarm design but with a bigger control group (and a possible trial effect). Either would be more informative than the single two-arm trials we have at present but, similar to the present situation, we still might have to strengthen our analyses through the use of within-trial covariate by treatment interactions as additional IVs. Further work is being carried out as a major component of our current MRC Methodology Programme grant (Landau S, Pickles A, White I, Emsley R, Dunn G, Clark P, et al. , Developing methods for understanding mechanism in complex interventions, King's College London, London, 2013–16; grant number MR/K006185/1). Here, we change direction and take a more detailed look at the implications of the evaluation of mediational mechanisms for personalised therapies (stratified medicine).
A suggested biomarker (moderator)-stratified Efficacy and Mechanism Evaluation trial and associated analysis strategy
Here we return to the development of the ideas presented in Chapter 2 on the use of predictive marker (treatment effect moderator) by randomisation interactions as IVs for the estimation of unconfounded effects of a putative mediator (treatment effect mechanisms) on clinical outcome. In the predictive marker by treatment interaction design, we stratify patients according to predictive marker status and randomise to treatments within each marker stratum. 100 An alternative phrase to describe this design is ‘biomarker-stratified design’. 15,101 We are concerned with evaluating whether or not the treatment effects are the same in the different strata. In the present context, our stratifying marker (treatment moderator) is the binary variable, X10, as described in Using moderators of treatment effects (predictive markers) to generate instrumental variables. Here, we assume that we are planning a new trial but, of course, the same principles might be applied to a retrospective analysis of archived trial data (or the meta-analysis of individual patient data from several trials), although we would be pleasantly surprised if a rich enough data set were available for such an analysis. The essential feature is not stratification prior to randomisation but the ability to stratify during the analysis.
Taking the moderator (predictive marker) stratified design, we supplement the baseline information (i.e. X10 status) by measuring all previously validated predictive variables (prognostic markers, e.g. X1 to X9) together with other baseline covariates (demographic information; clinical and treatment history; co-morbidity; social, psychological and cultural variables; etc.) also thought to have prognostic value. One obvious covariate is the baseline measurement of the putative mediator. Another might be a baseline value for the final outcome measurement. The rationale for all of these measurements is (1) to allow for as much confounding of the effects of the mediator on final outcome as is feasible, (2) to assess sensitivity of the results to assumptions concerning residual hidden confounding and, perhaps more importantly, (3) to increase the precision of the estimates of the important causal parameters. This is the biomarker-stratified EME (BS-EME) trial. 102 Perhaps psychologists would prefer the description ‘moderator-stratified efficacy and mechanism evaluation’.
The graphical representation of the causal influences to be estimated from data arising from our proposed design is shown in Figure 12. The black pathways correspond to those treatment effects that we wish to evaluate. The blue pathway illustrates the moderating effect of the predictive marker (assumed to act only through the effect of the treatment on the mediator). The dotted green lines represent the effects of both observed and hidden confounders.
FIGURE 12.
The BS-EME trial. Using the predictive marker by treatment interaction as an IV with all available information.
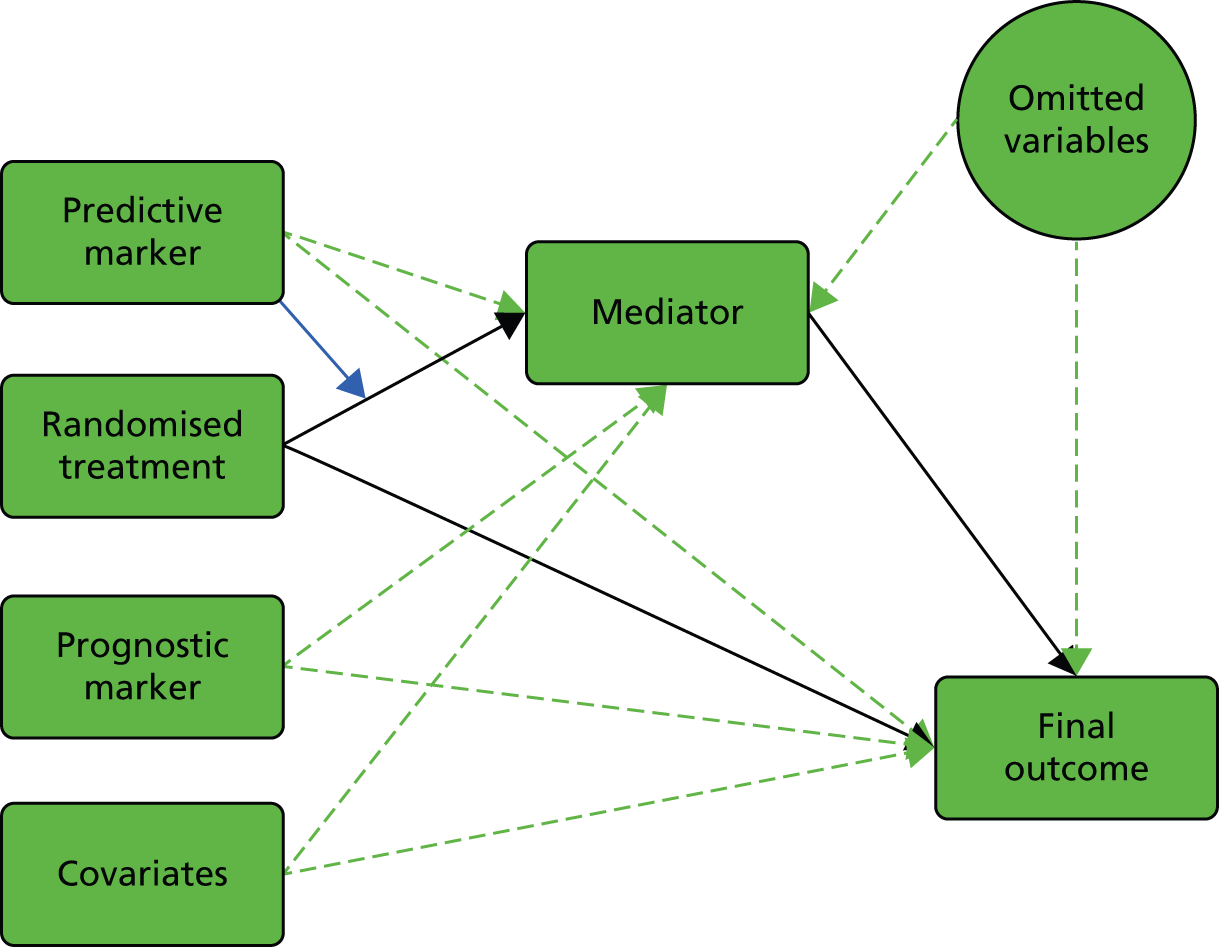
The two main components of the model are (1) that for the combined effects of treatment, markers and covariates on the mediator (including the treatment by predictive marker interaction) and (2) that for the combined effects of treatment, mediator, markers and covariates on the final outcome (but with no treatment by predictive biomarker interaction). Again, we bear in mind the hidden confounding. These two regression models can be fitted simultaneously with ease using 2SLS.
Illustration: Monte Carlo simulation of biomarker-stratified Efficacy and Mechanism Evaluation trials
At this point, it would be nice to be able to illustrate our ideas by reference to the analysis of data from a real trial. Unfortunately, we are not aware of the existence of any trial providing data along the lines advocated here, and we do not have access to any archived trial data that might be used as a suitable illustration.
We simulated a series of trials with 100, 250 or 500 participants randomly allocated to each of two arms (i.e. total trial size 200, 500 and 100, respectively), with varying prevalence of a binary predictive marker and a range of values for the relevant causal (structural) effects to be estimated. For each combination of characteristics and parameter values we carried out 10,000 simulations and summarised the results accordingly. We have baseline (pre-randomisation) measurements of nine binary prognostic markers (X1–X9) on all participants: genetic, demographic, psychological or social markers (variables). Here these variables are binary covariates with varying response frequencies (details are provided in Appendix 4). We postulate a normally distributed quantitative mediator (M) and, similarly, a normally distributed indicator of final outcome (Y). The presence of each of the prognostic markers coded as 1 increases both the mediator and the outcome by five units (i.e. these prognostic markers are all confounders of the effect of M on Y). We now introduce the randomised treatment (Z), together with a binary (0 or 1) predictive biomarker, X10, with the prevalence of the variant coded as 1 fixed at three possible levels, 10%, 50% or 90%, again measured prior to randomisation. As before, the product of X10 and Z, X11, is the statistical interaction that measures the strength of the moderation of the treatment effect by X10. The marker X10 itself has a prognostic effect on both M and Y (i.e. it too is a confounder). If we allow appropriately for X1 to X11 in our statistical analyses of the resulting data, there will be no hidden confounding (no omitted variables effects).
Therefore, the statistical (causal) models used to generate the data are:
Here, because we have accounted for all confounding (the effects of X1–X9), cov(εm, εy) = 0.
Full details are given in Appendix 4. Here, all we need to know are the true values of β2 and β3, and of ψ2 and ψ3. Those for β2, ψ2 and ψ3 are fixed at 5, 10 and 2, respectively. For β3 we chose three alternatives: 5, 10 and 20. A value of 20 for β3 may appear to be unusually high but for a predictive biomarker to have met the necessary development milestones implies that is a powerful moderator of the effect of the treatment on the proposed mediator.
Finally, we also introduced the possibility of misclassification error in the recorded (i.e. as used in the analysis) binary predictive biomarker; 20% of the predictive marker positives were actually recorded as being negative and 20% of the marker negatives were incorrectly recorded as being positive (i.e. the specificity and sensitivity of the recorded marker classification are both set to be 80%). The resulting error-prone indicators that were then used in the analyses were X10m and X11m.
In summary, we used trials of sizes 200, 500 and 1000, with a predictive marker prevalence of 10%, 50% or 90%, with or without 10% misclassification of the predictive marker status, and with the strength of the moderating effect of the predictive marker being 5, 10 or 20. This provides 54 combinations in total. For each of the 10,000 simulated data sets corresponding to these 54 combinations nine different estimations were carried out: six using OLS and three using IV regression (2SLS). The first three OLS regressions modelled the effects of treatment (Z), the mediator (M) and the predictive marker (X10) on outcome (Y), first allowing for none of the other prognostic markers, then allowing for four of them (X1–X4) and finally allowing for all nine (X1–X9). The second set of three OLS regressions included the interaction (X11) in addition to those above. Finally, we carried out three instrumental regressions, modelling the effects of Z, M and X10 on Y, using the interaction X11 as the instrument for M. The first made no allowance for any of the prognostic variables, the second included X1–X4 as covariates and the third used all nine prognostic markers (X1–X9) as covariates. Note that our current simulations are generating prognostic marker, covariate and mediator data that are not subject to measurement error; allowing for this would make the argument we make below in favour of using IV methods even more convincing.
The Stata commands used for these analyses were the following:

When there is misclassification of the predictive marker, x10 and x11 are replaced in the above commands by x10m and x11m, respectively.
Rather than risking overwhelming the reader with data, we start in Table 8 with summary statistics from just two of the trial simulations: with and without misclassification of the predictive marker in trials of 1000 participants, at 10% prevalence of the predictive marker and with the size of the interaction (the effect of X11) being set at 20. The main feature to note is the large dilution of the treatment effect when there is misclassification of the predictive marker, X10 [comparing the treatment effects when X10 = 1 with those when X10m = 1, the latter being attenuated by many marker-negative participants (X10 = 0) being incorrectly classified as marker positive (X10m = 1)]. We then present a selection from the main simulations in Table 9. The full summary of the simulation studies can be found in Appendix 5.
| Variable | Observations | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|---|
| No misclassification of X10 | |||||
| X10 = 0, treat = 0 | |||||
| M | 445 | 72.51 | 8.06 | 48.49 | 99.27 |
| Y | 445 | 167.83 | 22.02 | 105.55 | 242.57 |
| X10 = 0, treat = 1 | |||||
| M | 450 | 77.43 | 8.35 | 50.63 | 103.17 |
| Y | 450 | 187.62 | 22.52 | 106.04 | 258.17 |
| X10 = 1, treat = 0 | |||||
| M | 55 | 78.11 | 7.85 | 59.78 | 93.21 |
| Y | 55 | 185.10 | 21.63 | 141.52 | 228.77 |
| X10 = 1, treat = 1 | |||||
| M | 50 | 103.41 | 7.45 | 86.43 | 119.53 |
| Y | 50 | 243.86 | 21.87 | 194.54 | 290.88 |
| Misclassification of X10 (20) | |||||
| X10m = 0, treat = 0 | |||||
| M | 374 | 72.59 | 8.43 | 48.11 | 98.43 |
| Y | 374 | 167.88 | 23.22 | 102.27 | 237.91 |
| X10m = 0, treat = 1 | |||||
| M | 362 | 77.86 | 9.13 | 54.19 | 112.56 |
| Y | 362 | 188.94 | 23.81 | 130.92 | 269.40 |
| X10m = 1, treat = 0 | |||||
| M | 126 | 73.82 | 8.48 | 54.60 | 93.08 |
| Y | 126 | 171.84 | 23.58 | 115.42 | 226.80 |
| X10m = 1, treat = 1 | |||||
| M | 138 | 85.14 | 15.63 | 50.72 | 127.38 |
| Y | 138 | 204.18 | 37.87 | 102.64 | 313.30 |
| Estimation method | ψ2 (true value 10) | ψ3 (true value 2) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | MSE | % | Mean | SD | MSE | % | |
| No misclassification of X10 | ||||||||
| OLS | 6.17 | 0.44 | 14.89 | 0.00 | 2.55 | 0.02 | 0.30 | 0.00 |
| OLS, including X1–X4 | 7.12 | 0.43 | 8.47 | 0.00 | 2.41 | 0.03 | 0.17 | 0.00 |
| OLS, including X1–X9 | 10.00 | 0.37 | 0.14 | 95.17 | 2.00 | 0.03 | 0.00 | 94.84 |
| OLS, including X11 | 6.89 | 0.44 | 9.89 | 0.00 | 2.62 | 0.02 | 0.39 | 0.00 |
| OLS, including X11 and X1–X4 | 7.56 | 0.43 | 6.12 | 0.01 | 2.49 | 0.03 | 0.24 | 0.00 |
| OLS, including X11 and X1–X9 | 10.00 | 0.37 | 0.14 | 95.23 | 2.00 | 0.03 | 0.00 | 94.92 |
| 2SLS | 10.03 | 0.80 | 0.65 | 95.01 | 1.99 | 0.09 | 0.01 | 95.03 |
| 2SLS, including X1–X4 | 10.02 | 0.69 | 0.47 | 94.81 | 2.00 | 0.08 | 0.01 | 94.76 |
| 2SLS, including X1–X9 | 10.00 | 0.49 | 0.24 | 95.07 | 2.00 | 0.05 | 0.00 | 94.94 |
| Misclassification of X10 (20) | ||||||||
| OLS | 6.44 | 0.44 | 12.85 | 0.00 | 2.51 | 0.02 | 0.26 | 0.00 |
| OLS, including X1–X4 | 7.25 | 0.42 | 7.74 | 0.00 | 2.39 | 0.02 | 0.16 | 0.00 |
| OLS, including X1–X9 | 9.23 | 0.36 | 0.73 | 43.90 | 2.11 | 0.02 | 0.01 | 9.33 |
| OLS, including X11m | 7.13 | 0.49 | 8.47 | 0.00 | 2.52 | 0.02 | 0.27 | 0.00 |
| OLS, including X11m and X1–X4 | 7.78 | 0.47 | 5.17 | 0.38 | 2.40 | 0.02 | 0.16 | 0.00 |
| OLS, including X11m and X1–X9 | 9.37 | 0.40 | 0.55 | 64.93 | 2.11 | 0.02 | 0.01 | 0.18 |
| 2SLS | 10.30 | 2.28 | 5.27 | 94.98 | 1.95 | 0.33 | 0.11 | 94.63 |
| 2SLS, including X1–X4 | 10.20 | 1.65 | 2.77 | 95.32 | 1.97 | 0.23 | 0.06 | 95.32 |
| 2SLS, including X1–X9 | 10.05 | 1.11 | 1.23 | 95.86 | 1.99 | 0.16 | 0.02 | 95.24 |
The results of the various methods of estimation of the causal parameters ψ2 and ψ3 using these two combinations of trial statistics are summarised in Table 9. We ignore the estimation β2 and β3 here (it being much more straightforward) but note that their estimates will inevitably be biased (attenuated) by misclassification of the marker X10 (and this will be a problem common to all of the analytical methods). This would have important implications if we were to try to estimate the proportion of the treatment effect explained by the mediator in each of the two predictive strata but is not the particular focus of the present investigation. Dunn et al. 102 provide a description of methods to estimate the relative contributions of the direct and indirect pathways using this stratified trial design.
What do we learn from the results concerning mechanisms evaluation (mediation)? In the case that the predictive marker is recorded without error, Table 9 clearly illustrates the greater bias but also greater precision of the OLS estimates compared with the 2SLS IV-based methods. The bias in the OLS estimates reduces as more observed confounders are included in the regression models, and disappears completely when all of the confounders (X1–X9) are included. The 2SLS estimates are unbiased and the effect of including the observed confounders into the analyses is to increase precision. The simulated trials here have 1000 participants, a size greater than the vast majority of psychological intervention trials to date. If we need to reduce the size of these trials, then the recording and inclusion of baseline confounders might make the difference between a trial that is likely to be viable and one that is clearly not.
Table 9 illustrates the effect of introducing misclassification error into the recording of the predictive marker. It has little effect on the precision of the OLS estimates, but they remain biased even when all of the confounding variables are allowed for in the analysis. On the other hand, the 2SLS estimates reveal little or no bias, but their precision is markedly reduced. The misclassified predictive marker by randomisation interaction is still a valid IV, but it is considerably weaker than the equivalent IV generated using the correct marker status (i.e. it is a weaker predictor of the mediator). This, too, might make all the difference between a feasible and a hopeless trial. We stress that a vital component of the development work leading to a proposal of a BS-EME trial is to establish the high validity and high precision of the predictive marker (moderator).
Moving on, Table 10 shows clearly that, as the prevalence of the ‘positive’ stratum of the predictive marker moves away from 50%, the precision of the estimates is decreased (but not dramatically). As the size of the treatment by marker interaction is reduced, so also is the precision of the estimates. Perhaps the most important finding, however, is again, the dramatic impact of measurement error on the precision of the 2SLS estimates. This more than reinforces the conclusion arising from the results in Table 9.
| Simulation scenario | X10 | True β3 | Est. ψ2 | Est. ψ3 | ||
|---|---|---|---|---|---|---|
| Mean | SE | Mean | SE | |||
| No error in X10 | 10 | 5 | 10.35 | 2.56 | 1.93 | 0.45 |
| X10 misclassified | 10 | 5 | 10.21 | 60.72 | 1.96 | 11.04 |
| No error | 10 | 10 | 10.07 | 1.04 | 1.99 | 0.16 |
| X10 misclassified | 10 | 10 | 11.22 | 22.7 | 1.81 | 3.87 |
| No error | 10 | 20 | 10.02 | 0.69 | 2.00 | 0.08 |
| X10 misclassified | 10 | 20 | 10.20 | 1.65 | 1.97 | 0.23 |
| No error in X10 | 50 | 5 | 10.09 | 1.51 | 1.99 | 0.19 |
| X10 misclassified | 50 | 5 | 10.94 | 23.4 | 1.88 | 3.1 |
| No error | 50 | 10 | 10.01 | 1.01 | 2.00 | 0.09 |
| X10 misclassified | 50 | 10 | 10.16 | 1.77 | 1.98 | 0.17 |
| No error | 50 | 20 | 9.99 | 0.80 | 2.00 | 0.05 |
| X10 misclassified | 50 | 20 | 10.06 | 1.29 | 2.00 | 0.08 |
| No error | 90 | 5 | 10.61 | 5.80 | 1.94 | 0.6 |
| X10 misclassified | 90 | 5 | 9.00 | 125.66 | 2.10 | 13.18 |
| No error | 90 | 10 | 10.18 | 2.25 | 1.99 | 0.16 |
| X10 misclassified | 90 | 10 | 13.63 | 91.9 | 1.74 | 6.49 |
| No error | 90 | 20 | 10.18 | 1.80 | 2.00 | 0.08 |
| X10 misclassified | 90 | 20 | 10.85 | 5.64 | 1.96 | 0.24 |
Reflections
Designing the perfect EME trial is difficult, if not impossible. Investigators will always be in a position of having to make unverifiable assumptions. Perhaps no single trial or experiment will ever be able to produce results that are not open to challenge. 87 There will always be a possibility of unmeasured confounding, but recording as many confounders as possible and allowing for them in the subsequent statistical analyses (whether OLS based or 2SLS) will always help. Recent work by Imai et al. 103,104 has focused on the design of experiments to establish patterns of mediation, but it is difficult to see how their designs can be applied to controlled clinical trials.
The key to successful mediation evaluation seems to be a treatment that is specifically targeted on the putative mediator, together with a treatment effect moderator (predictive marker) justified by psychological, biological and social theory (not just ad hoc subgroup analysis) linking it to the proposed mechanism of action of the targeted therapy on the mediator. And, of course, it is vital that the moderator is measured and recorded with little or no error.
Personalised (stratified) medicine (the development and evaluation of targeted therapies) and treatment effect mechanisms evaluation are inextricably linked. Stratification without corresponding mechanisms evaluation lacks credibility. In the presence of the almost certain presence of mediator–outcome confounding, mechanisms evaluation is dependent on treatment effect heterogeneity (stratification) for its validity. Both stratification and treatment effect mediation can be evaluated using a treatment effect moderator (predictive marker) stratified trial design together with detailed baseline measurement of all known prognostic markers/covariates. Direct and indirect (mediated) effects should be estimated through the use of IV methods (the IV being the predictive marker by treatment interaction) together with adjustments for all known prognostic markers (confounders), the latter adjustments contributing to increased precision (as in a conventional analysis of treatment effects) rather than bias reduction.
Chapter 6 Conclusions and recommendations for research
This report describes the development, evaluation and dissemination of statistical and econometric methods for the design of explanatory trials of psychological treatments and the explanatory analysis of the clinical end points arising from these trials. We have been concerned with making valid causal inferences about the mediational mechanisms of treatment-induced change in these clinical outcomes. In Chapter 1, we identified four questions about complex interventions/treatments. We present these questions again, and relate these to the methods we have discussed in this report.
Does it work?
In Chapter 1, we described the fundamental concepts of causal inference and how this provides estimators of treatment efficacy (the ATE) which underpin randomised trials. In the presence of non-compliance, or departures from randomised treatments, we identified an alternative estimator, the CACE, and described the necessary assumptions to identify the CACE.
How does it work?
In Chapter 2, we discussed the statistical evaluation of treatment effect mechanisms through mediation analysis in some detail, starting with long-established strategies from the psychological literature, with the possibility of using prognostic markers for confounder adjustment. We introduced definitions of direct and indirect effects based on potential outcomes (counterfactuals), together with some appropriate methods for their estimation, and then introduced IV methods to allow for the possibility of hidden confounding between mediator and final outcome. In Chapter 4 we extended the ideas to cover trials involving longitudinal data structures (repeated measures of the putative mediators as well as of clinical outcomes).
What factors make it work better?
In Chapter 3, we outlined the usual naive approach to evaluating the modifying effects of process measures (correlating their values with clinical outcomes in the treated group with no reference to the control group) and then describe modern methods developed from the use of IVs and principal stratification. These methods evaluate the modifying effect of the process variable on the treatment effect, rather than the prognostic effect on the outcome as the naive methods estimate. In Chapter 4 we extended the ideas to cover trials involving longitudinal data structures (repeated measures of the process measures as well as of clinical outcomes).
In Chapter 5, we considered the challenge of trial design in the context of the use of IV methods and principal stratification to answer the questions about treatment effect mechanisms and process measures. These designs included using predictors of outcome as instruments, using moderators of treatment effects to generate instruments, using simple multiarm trials and using data from parallel trials with single or parallel mediators.
Who does it work for?
During the programme of research, we focused increasingly on the question of who treatments work best for and the idea of targeting the right treatment to the right patient at the right time. This concept has been elucidated throughout the report. For example, the use of moderators as instruments essentially involves identifying subgroups of individuals for whom the treatment is thought to be most efficacious, exploiting treatment effect heterogeneity in the data. We considered the role of targeted therapies, multiarm trials and the use of parallel trials to help elucidate the evaluation of mediators working in parallel. We gave particular attention to the role of stratification (based on treatment effect moderators or predictive markers) in the evaluation of treatment effect mechanisms motivating the development of personalised therapies. In Chapter 5, we introduced our new proposed BS-EME trial design as one contribution to the stratified medicine literature, although uniquely with a focus on testing the underpinning mechanism of the stratification.
Examples
We have primarily used psychological or psychosocial treatment trials as our motivating examples throughout the report. We make no apologies for focusing on mental health, because the challenges provided in this area are considerable and in many cases led directly to the methodological research presented. This is especially true for issues of obtaining reliable measurements of mediators (and outcomes), of confounding between the mediator and outcome, and of measurement error in the mediator.
However, it is worth noting that the problems identified with measurement (e.g. of process variables or of potential mediators) are not exclusive to mental health and are both shared and common to other areas of health research. We would argue that most, if not all, self-reported measures of health-related variables (such as pain intensity, diet, sleep, fatigue, etc.), are similarly problematic and even biological markers or clinically observed variables such as blood pressure and cholesterol are not immune to measurement problems. We do not imply that all the problems and challenges identified with trials of complex interventions are associated only with psychological interventions: rather, these are generic problems, and mental health is one discipline that has paid considerable attention to these issues.
Concluding tips for Efficacy and Mechanism Evaluation triallists
In order to demonstrate both efficacy and mechanism, you need to:
-
demonstrate a treatment effect on the primary (clinical) outcome
-
demonstrate a treatment effect on the putative mediator (mechanism).
These two steps are necessary but not sufficient to demonstrate a causal pathway from treatment to mediator to outcome. You might proceed to:
-
Evaluate the correlation between mediator and outcome (possibly conditioning on treatment arm). But beware, the correlation can arise from (1) the effect of mediator on outcome; (2) the effect of outcome on the mediator (perhaps unlikely if the treatment is primarily targeted on the mediator; or (3) a common cause other than treatment (confounding). The effects are not, of course, mutually exclusive. We may, for example, have both (1) and (3). In this case, our aim is to evaluate (1) in the presence of (3).
The common causes of the mediator and outcome may be characteristics of the trial participant prior to treatment (i.e. potential covariates or prognostic markers that could, in principle, be measured prior to randomisation). There could also be common causes (such as comorbidity, life events, etc.) that arise after the onset of treatment. The latter are much more difficult to handle. Instead of simply correlating mediator and outcome, you would be better using a regression model to predict outcome by both levels of mediator and treatment arm (as in B&K16). This would be preferable to a correlational analysis if the mediator is binary rather than quantitative. The natural extension to this would then be:
-
Regress outcome on mediator and treatment, allowing for all measured baseline covariates that may possibly be of prognostic value (do not bother about the statistical significance of their effects, include them regardless).
You will very rarely, if ever, be in a position to confidently claim that you have allowed for all common causes. Some may be impossible to measure and others you may not even have thought of. Many of the covariates in your regression model will be subject to measurement error. Your model will be an improvement on a simple correlation or linear regression of outcome on mediator and treatment (without covariate adjustment) but it will not lead to a complete elimination of biases.
Now is the time to try allowing for unmeasured common causes (hidden confounders) through:
-
An IV model (e.g. using 2SLS). The instrument is assumed to be strongly related to the mediator but statistically independent of outcome conditional on both the mediator and the common causes. Allowing for the measured confounders (baseline covariates) in both stages of the two-stage IV procedure will improve the precision of the causal effect estimates. But beware, convincing instruments are difficult to find.
The key to finding useful and convincing instruments appears to be treatment effect heterogeneity. Here we have access to treatment effect moderators, the effects of which can be observed in terms of their influence of treatment effects on both the proposed mediator and the final outcome (if these effects are not observed in our trial then this approach is not going to be fruitful). But we need, in addition to this, an assumption that the moderation of the treatment effect on outcome is wholly explained by the moderation of the treatment effect on the mediator (treatment effect mechanism). This depends on convincing prior biological or psychological theory (and possibly evidence from earlier experimental investigations) concerning the targeted nature of the intervention and convincing theory justifying the role of the moderator (predictive marker) in the construction of a valid instrument. Careful design is essential. Here we pursue a line of thought that is different to, but fully consistent with, the development of the argument above.
The role of efficacy and mechanism evaluation in the development of personalised therapies (stratified medicine)
We conclude with a series of simple statements102 aimed at encouraging triallists to seriously consider the role of markers that enable the simultaneous evaluation of the utility of a putative predictive biomarker and the treatment effect mechanisms motivating its use.
-
Personalised therapy (stratified medicine) and treatment effect mechanisms evaluation are inextricably linked.
-
Stratification without corresponding mechanisms evaluation lacks credibility.
-
In the almost certain presence of mediator–outcome confounding, mechanisms evaluation is dependent on stratification for its validity.
-
Both stratification and treatment effect mediation can be evaluated using a biomarker-stratified trial design together with detailed baseline measurement of all known prognostic biomarkers and other prognostic covariates.
-
Direct and indirect (mediated) effects should be estimated through the use of IV methods (the IV being the predictive marker by treatment interaction) together with adjustments for all known prognostic markers (confounders), the latter adjustments contributing to increased precision (as in a conventional analysis of treatment effects) rather than bias reduction.
Role of therapeutic process evaluation
In many ways this faces the same conceptual and technical problems as the evaluation of mediation. Both are concerned with the investigation of therapeutic mechanisms. Both mediators and indicators of the therapeutic process are subject to measurement errors and it is very likely that their effects are subject to confounding. Both might be the focus of personalised therapies. The difference is that the process variables are not measured (not defined) in the absence of therapy. One solution, in addition to use of the more familiar IV methods, is to introduce the use of principal stratification. Do not just look at associations between process and outcome in the treated participants. This is flawed logic.
Recommendations for research
We end with some recommendations about future research in this area, building on the methods described in this report. It is important to note that this is a growing field which is developing rapidly, particularly in the context of personalised therapies and causal mediation analysis, and these recommendations do not include every aspect of these fields.
Linking efficacy and mechanism evaluation explicitly
In Chapter 1, we focused on treatment efficacy before moving on to consider treatment effect mechanisms and process variables separately. However, in practice, these are strongly linked. For example, if a client does not attend any sessions of therapy, how would we expect his or her mediator to change as a result of the random allocation alone? If the client does not attend therapy, how can we measure a therapeutic alliance? Conversely, perhaps the therapeutic alliance is low and this leads to poor attendance at therapy? It seems logical that, if our aim is to conduct a thorough explanatory analysis of these trials, we need to consider models with non-compliance and mediation jointly. We plan to explore this by considering compliance and the mechanism as causally ordered mediators in the framework of Daniel et al. 105
Design of trials for efficacy and mechanism evaluation and implications for sample size
Are the sample sizes derived from powering a trial for the primary ITT analysis sufficient to permit the use of the methods described in this report? We have not explicitly researched the implications for sample size and so cannot give a definitive answer. For example, we have shown that IV procedures decrease the precision of the estimates relative to standard regression approaches. This is the usual trade-off between bias and precision. Further research could investigate the power to detect mediation effects of a specific magnitude using IV procedures.
In our BS-EME simulations, we noted the role of prognostic markers in increasing the precision of the estimates (i.e. lowering the SEs). It is known from the ITT analysis of randomised trials that including pre-specified prognostic variables in the outcome regression model gains precision of the treatment effect estimate. What is interesting in the context of mediation is that this gain is with respect to all the parameters of interest. This implies that, given a fixed sample size, the reduction in statistical power for mediation effects from using an IV approach will be lessened by inclusion of prognostic covariates.
Similar issues arise in the analysis of process variables using the principal stratification. While the key identifying aspect is the availability of strong baseline predictors of class membership in the treatment group, the sample size must be large enough to accommodate this modelling approach.
We identified a number of approaches to improving the design of EME trials, but the next stage is the adoption of these in applications. Designing the perfect EME trial is difficult, if not impossible, as investigators will always be in a position of having to make unverifiable assumptions. However, while there will always be a possibility of unmeasured confounding, recording as many confounders as possible and allowing for them in the subsequent statistical analyses will always help. Considering the recent work by Imai et al. 103,104 on the design of experiments for mediation analysis, being able to apply their designs to controlled clinical trials would be a major step forward.
Measurement of mediators (reliability and measurement error)
As we have highlighted, measurement is the key issue in many areas of clinical research, not just psychology and mental health. Likewise, obtaining reliable, reproducible and valid measures without systematic measurement error can be a challenge, but one which any mechanisms evaluation ultimately relies on. As we described in Chapter 2, Pickles et al. 80 proposed a solution to account for measurement error in the mediator by making use of the repeated measures of the mediator in the UK PACT. Valeri et al. 106 have proposed an alternative approach when the mediator is continuous for any outcome under a generalised linear model. More research is needed into the impact of measurement error in the mediator and solutions for this problem.
Other forms of outcome variable
Many of the methods we have introduced in this report are based on linear models. On one hand, this is natural, as continuous measurement scales are common in mental health and psychology, and this is the discipline our examples are drawn from. On the other hand, the generalisability of the methods to other clinical areas may therefore be limited. For example, there is little literature on mediation analysis with survival outcomes107 and particularly with IVs estimation for survival outcomes. Future research should seek to generalise the methods to alternative forms of outcomes.
Sensitivity analysis
VanderWeele108 and VanderWeele and Arah109 have proposed general methods estimating bias formulas for sensitivity analysis for unmeasured confounding for direct and indirect effects. Given that we have identified unmeasured confounding as a key limitation in both the more traditional approaches to mechanisms evaluation and some of the more advanced approaches, the application of these and other proposed sensitivity analysis techniques to our clinical examples and motivating questions should be investigated.
Acknowledgements
This programme of work presents independent research funded under the MRC–NIHR Methodology Research Programme (grant ref. G0900678) building on foundations laid by a previous methodology project (grant ref. 0600555). Richard Emsley also held a MRC Career Development Award in Biostatistics (ref. G0802418). Sabine Landau and Andrew Pickles are also supported through the NIHR Mental Health Biomedical Research Centre at the South London and Maudsley NHS Foundation Trust and King’s College London. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.
Graham Dunn, Richard Emsley, Sabine Landau, Ian White and Andrew Pickles are all members of the NIHR MHRN Methodology Research Group.
This work would not have been possible without the active collaboration of others. First, we would like to acknowledge the input of our methodological collaborators: Professors Paul Clark, Linda Davies, Chris Roberts and Frank Windmeijer. Graham Dunn’s PhD students, Clare Flach and Lucy Goldsmith, are also thanked for their stimulating input to many methodological discussions. Last, but not least, we would like to thank our many clinical collaborators: Professors Christine Barrowclough, Richard Bentall, Max Birchwood, Shôn Lewis, Tony Morrison and Alison Wearden. In particular, Graham Dunn would like to acknowledge his long-standing and very productive collaboration with members of the PRP trial: Professor Paul Bebbington, Professor David Fowler, Professor Daniel Freeman, Professor Philippa Garety and Professor Elizabeth Kuipers.
Contribution of authors
Graham Dunn (statistician), Professor of Biomedical Statistics, co-led the programme of research, planned the report, carried out some of the statistical analyses and wrote initial drafts of all chapters except Chapter 4.
Richard Emsley (statistician), Senior Lecturer in Biostatistics, co-led the project, carried out some of the statistical analyses, wrote the draft of Chapter 4 and was responsible for revisions and submission of the report.
Hanhua Liu (quantitative researcher/programmer), Research Associate, wrote the statistical software (Paramed, etc.), carried out much of the statistical analyses and all of the work on Monte Carlo simulations, and wrote much of the material on these in the appendices.
Sabine Landau (statistician), Professor of Biostatistics, provided advice on the structure of the report.
Jonathan Green (child psychiatrist), Professor of Child Psychiatry, provided advice on the structure of the report.
Ian White (statistician) provided advice on the structure of the report.
Andrew Pickles (statistician), Professor of Biostatistics and Psychological Methods, contributed to the analysis and description of PACT in Chapter 2, and provided advice on the structure of the report.
All authors commented on and contributed to the revision of the initial drafts, and are responsible for its final form.
Publications
Much of the development of ideas pursued in the present report has also appeared in our previous publications.
Dunn G, Bentall R. Modelling treatment-effect heterogeneity in randomized controlled trials of complex interventions (psychological treatments). Stat Med 2007;26:4719–45.
Emsley R, Dunn G, White IR. Mediation and moderation of treatment effects in randomised controlled trials of complex interventions. Stat Methods Med Res 2010;19:237–70.
Dunn G, Fowler D, Rollinson R, Freeman D, Kuipers E, Smith B, et al. Effective elements of cognitive behaviour therapy for psychosis: results of a novel type of subgroup analysis based on principal stratification. Psychol Med 2012;42:1057–68.
Emsley R, Dunn G. Evaluation of Potential Mediators in Randomized Trials of Complex Interventions (Psychotherapies). In Berzuini C, Dawid P, Bernardinelli L, editors. Causality: Statistical Perspectives and Applications. Chichester: Wiley; 2012.
Dunn G, Emsley R, Liu H, Landau S. Integrating biomarker information within trials to evaluate treatment mechanisms and efficacy for personalised medicine. Clin Trials 2013;10:712–22.
Emsley R, Dunn G. Process Evaluation Using Latent Variables: Applications and Extensions of Finite Mixture Models. In Brentari E, Carpita M, editors. Advances in Latent Variables. Milan: Vita e Pensiero; 2013.
We will also be submitting further articles for publication which detail the theoretical work in this report. Planned publications are below.
Emsley RA, VanderWeele TJ. Mediation and sensitivity analysis using two or more trials. 2015; in preparation.
Emsley R, Liu H, Dunn G, Valeri L, VanderWeele TJ. Paramed: A command to perform causal mediation analysis using parametric models. 2015; in preparation.
Emsley R, Dunn G, Liu H, Clarke P, White IR, Windmeijer F. Estimating rank preserving models using instrumental variables for causal mediation analysis. 2015; in preparation.
Emsley R, Pickles A, Dunn G. Mediation analysis with growth mixture modelling. 2015; in preparation.
Emsley R, Dunn G. Principal trajectories: extending principal stratification for repeated measures. 2015; in preparation.
Landau S, Emsley R, Dunn G, White I. Trial designs for the evaluation of complex interventions. 2015; in preparation.
Data sharing statement
No data analysed in this report have been collected for the purposes of the research presented and all the analysis reported comprises secondary analysis of the data.
Disclaimers
This report presents independent research funded under a MRC–NIHR partnership. The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, the MRC, NETSCC, the HTA programme or the Department of Health. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, the MRC, NETSCC, the HTA programme or the Department of Health.
References
- MRC . Developing and Evaluating Complex Interventions: New Guidance 2008. www.mrc.ac.uk/complexinterventionsguidance (accessed 3 June 2015).
- Buyse M. Towards validation of statistically reliable biomarkers. Eur J Cancer 2007;5:89-95. http://dx.doi.org/10.1016/S1359-6349(07)70028-9.
- Joffe MM, Greene T. Related causal frameworks for surrogate outcomes. Biometrics 2009;65:530-8. http://dx.doi.org/10.1111/j.1541-0420.2008.01106.x.
- Beck A, Ward C, Mendelson M, Mock J, Erbaugh J. An inventory for measuring depression. Arch Gen Psychiatry 1961;4:561-71. http://dx.doi.org/10.1001/archpsyc.1961.01710120031004.
- Pearl J. Causality. New York, NY: Cambridge University Press; 2009.
- Rubin DB. Estimating causal effects of treatment in randomized and non-randomized studies. J Educ Psychol 1974;66:688-701. http://dx.doi.org/10.1037/h0037350.
- Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. J Am Stat Assoc 1996;91:444-55. http://dx.doi.org/10.1080/01621459.1996.10476902.
- Barnard J, Frangakis CE, Hill JL, Rubin DB. Principal stratification approach to broken randomized experiments: a case study of school choice vouchers in New York City. J Am Stat Assoc 2003;98:299-311. http://dx.doi.org/10.1198/016214503000071.
- Manski CF. Nonparametric bounds on treatment effects. Am Econ Rev 1990;80:319-23.
- Balke A, Pearl J. Bounds on treatment effects from studies with imperfect compliance. J Am Stat Assoc 1997;92:1172-6. http://dx.doi.org/10.1080/01621459.1997.10474074.
- Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics 2002;58:21-9. http://dx.doi.org/10.1111/j.0006-341X.2002.00021.x.
- Freeman D, Dunn G, Startup H, Kingdon D. The effects of reducing worry in patients with persecutory delusions: study protocol for a randomized controlled trial. Trials 2012;13. http://dx.doi.org/10.1186/1745-6215-13-223.
- Dunn G, Fowler D, Rollinson R, Freeman D, Kuipers E, Smith B, et al. Effective elements of cognitive behaviour therapy for psychosis: results of a novel type of subgroup analysis based on principal stratification. Psychol Med 2012;42:1057-68. http://dx.doi.org/10.1017/S0033291711001954.
- Dunn G, Bentall R. Modelling treatment-effect heterogeneity in randomized controlled trials of complex interventions (psychological treatments). Stat Med 2007;26:4719-45. http://dx.doi.org/10.1002/sim.2891.
- Simon R. Clinical trials for predictive medicine: new challenges and paradigms. Clin Trials 2010;7:516-24. http://dx.doi.org/10.1177/1740774510366454.
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol 1986;51:1173-82. http://dx.doi.org/10.1037/0022-3514.51.6.1173.
- Kraemer HC, Fairburn CG, Agras WS. Mediators and moderators of treatment effects in randomized clinical trials. Arch Gen Psychiatry 2002;59:877-83. http://dx.doi.org/10.1001/archpsyc.59.10.877.
- Judd CM, Kenny DA. Process analysis – estimating mediation in treatment evaluations. Eval Rev 1981;5:602-19. http://dx.doi.org/10.1177/0193841X8100500502.
- MacKinnon DP. Introduction to Statistical Mediation Analysis. New York, NY: Taylor & Francis Group; 2008.
- Birchwood M, Peters E, Tarrier N, Dunn G, Lewis S, Wykes T, et al. A multi-centre, randomised controlled trial of cognitive therapy to prevent harmful compliance with command hallucinations. BMC Psychiatry 2011;11. http://dx.doi.org/10.1186/1471-244X-11-155.
- Barrowclough C, Haddock G, Wykes T, Beardmore R, Conrod P, Craig T, et al. Integrated motivational interviewing and cognitive behavioural therapy for people with psychosis and comorbid substance misuse: randomised controlled trial. BMJ 2010;341. http://dx.doi.org/10.1136/bmj.c6325.
- Gallop R, Small DS, Lin JY, Elliot MR, Joffe MM, Ten Have TR. Mediation analysis with principal stratification. Stat Med 2009;28:1108-30. http://dx.doi.org/10.1002/sim.3533.
- Green J, Charman T, McConachie H, Aldred C, Slonims V, Howlin H, et al. Parent-mediated communication-focused treatment in children with autism (PACT): a randomised controlled trial. Lancet 2010;375:2152-60. http://dx.doi.org/10.1016/S0140-6736(10)60587-9.
- Bruce ML, Ten Have TR, Reynolds CF, Katz II, Schulberg HC, Mulsant BH, et al. Reducing suicidal ideation and depressive symptoms in depressed older primary care patients – a randomized controlled trial. JAMA 2004;291:1081-91. http://dx.doi.org/10.1001/jama.291.9.1081.
- Ten Have TR, Joffe MM, Lynch KG, Brown GK, Maisto SA, Beck AT. Causal mediation analysis with rank preserving models. Biometrics 2007;63:926-34. http://dx.doi.org/10.1111/j.1541-0420.2007.00766.x.
- Bellamy SL, Lin JY, Ten Have TR. An introduction to causal modelling in clinical trials. Clin Trials 2007;4:58-73. http://dx.doi.org/10.1177/1740774506075549.
- Lynch K, Cary M, Gallop R, Ten Have TR. Causal mediation analyses for randomized trials. Health Serv Outcomes Res Methodol 2008;8:57-76. http://dx.doi.org/10.1007/s10742-008-0028-9.
- Lord C, Risi S, Lambrecht L, Cook EH, Leventhal BL, DiLavore PC, et al. The autism diagnostic observation schedule-generic: a standard measure of social and communication deficits associated with the spectrum of autism. J Autism Dev Disord 2000;30:205-23. http://dx.doi.org/10.1023/A:1005592401947.
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Eval Rev 1993;17:144-58. http://dx.doi.org/10.1177/0193841X9301700202.
- Emsley R, Dunn G, White IR. Mediation and moderation of treatment effects in randomised controlled trials of complex interventions. Stat Methods Med Res 2010;19:237-70. http://dx.doi.org/10.1177/0962280209105014.
- Emsley R, Dunn G, Berzuini C, Dawid P, Bernardinelli L. Causality: Statistical Perspectives and Applications. Chichester: Wiley; 2012.
- Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology 1992;3:143-55. http://dx.doi.org/10.1097/00001648-199203000-00013.
- Pearl J, Breese J, Koller D. Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann: San Francisco, CA; 2011.
- Cai ZH, Kuroki M, Pearl J, Tian J. Bounds on direct effects in the presence of confounded intermediate variables. Biometrics 2008;64:695-701. http://dx.doi.org/10.1111/j.1541-0420.2007.00949.x.
- Wooldridge JM. Econometric Analysis of Cross Section and Panel Data. Cambridge, MA: MIT Press; 2002.
- VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, interventions and composition. Stat Interface 2009;2:457-68. http://dx.doi.org/10.4310/SII.2009.v2.n4.a7.
- VanderWeele TJ, Vansteelandt S. Odds ratios for mediation analysis for a dichotomous outcome. Am J Epidemiol 2010;172:1339-48. http://dx.doi.org/10.1093/aje/kwq332.
- Emsley R, Liu H, Dunn G, Valeri L, VanderWeele TJ. Paramed: A Command to Perform Causal Mediation Analysis Using Parametric Models 2015.
- Herting JR. Evaluating and rejecting true mediation models: a cautionary note. Prevent Sci 2002;3:285-9. http://dx.doi.org/10.1023/A:1020828709115.
- Holland PW. Causal inference, path analysis and recursive structural equation models (with discussion). Sociol Methodol 1988;18:449-84. http://dx.doi.org/10.2307/271055.
- Kaufman JS, MacLehose R, Kaufman S. A further critique of the analytic strategy of adjusting for covariates to identify biologic mediation. Epidemiol Perspect Innovations 2004;1.
- Kaufman S, Kaufman JS, MacLehose RF, Greenland S, Poole C. Improved estimation of controlled direct effects in the presence of unmeasured confounding of intermediate variables. Stat Med 2005;24:1683-702. http://dx.doi.org/10.1002/sim.2057.
- Tritchler D. Explanatory analyses of randomised studies. Biometrics 1996;52:1450-6. http://dx.doi.org/10.2307/2532858.
- Tritchler D. Reasoning about data with directed graphs. Stat Med 1999;18:2067-76. http://dx.doi.org/10.1002/(SICI)1097-0258(19990830)18:16<2067::AID-SIM182>3.0.CO;2-2.
- McDonald RP. Haldane’s lungs: a case study in path analysis. Mul Behav Res 1997;32:1-38. http://dx.doi.org/10.1207/s15327906mbr3201_1.
- Wooldridge JM. Introductory Econometrics: A Modern Approach. Ohio, OH: Thompson Learning; 2003.
- Gennetian LA, Morris PA, Bos JM, Bloom HS, Bloom HS. Learning More From Social Experiments: Evolving Analytic Approaches. New York, NY: Russell Sage Foundation; 2005.
- Gennetian LA, Magnuson K, Morris PA. From statistical associations to causation: what developmentalists can learn from instrumental variables techniques coupled with experimental data. Develop Psychol 2008;44:381-94. http://dx.doi.org/10.1037/0012-1649.44.2.381.
- Sobel ME. Identification of causal parameters in randomised studies with mediating variables. J Educ Behav Stat 2008;33:230-51. http://dx.doi.org/10.3102/1076998607307239.
- Fischer-Lapp K, Goetghebeur E. Practical properties of some structural mean analyses of the effect of compliance in randomized trials. Control Clin Trials 1999;20:531-46. http://dx.doi.org/10.1016/S0197-2456(99)00027-6.
- Albert JM. Mediation analysis via potential outcomes models. Stat Med 2008;27:1282-304. http://dx.doi.org/10.1002/sim.3016.
- Ten Have TR, Joffe M. A review of causal estimation of effects in mediation analyses. Stat Methods Med Res 2012;21:77-107. http://dx.doi.org/10.1177/0962280210391076.
- Fuller WA. Measurement Error Models. New York, NY: Wiley; 1987.
- Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu CM. Measurement Error in Non-Linear Models. London: Chapman & Hall; 2006.
- Bollen K. Structural Equations with Latent Variables. New York, NY: John Wiley & Sons, Inc; 1989.
- Dunn G. Statistical Evaluation of Measurement Errors. London: Arnold; 2004.
- Dunn G. Regression models for method comparison data. J Biopharm Stat 2007;17:739-56. http://dx.doi.org/10.1080/10543400701329513.
- Dunn G. The problem of measurement error in modelling the effect of compliance in a randomised trial. Stat Med 1999;18:2863-77. http://dx.doi.org/10.1002/(SICI)1097-0258(19991115)18:21<2863::AID-SIM238>3.0.CO;2-I.
- Goetghebeur E, Vansteelandt S. Structural mean models for compliance analysis in randomised clinical trials and the impact of errors in exposure. Stat Methods Med Res 2005;14:397-415. http://dx.doi.org/10.1191/0962280205sm407oa.
- Dunn G, Everitt BS, Pickles A. Modelling Covariances and Latent Variables in EQS. London: Chapman & Hall; 1993.
- Weir CJ, Walley RJ. Statistical evaluation of biomarkers as surrogate endpoints: literature review. Stat Med 2006;25:183-20. http://dx.doi.org/10.1002/sim.2319.
- Daniels MJ, Hughes MD. Meta-analysis for the evaluation of potential surrogate markers. Stat Med 1997;16:1965-82. http://dx.doi.org/10.1002/(SICI)1097-0258(19970915)16:17<1965::AID-SIM630>3.0.CO;2-M.
- Burzykowski T, Molenberghs G, Buyse M. The Evaluation of Surrogate Endpoints. New York, NY: Springer; 2006.
- Florens JP, Heckman JJ, Meghir C, Vytlacil E. Identification of treatment effects using control functions in models with continuous, endogenous treatment and heterogeneous effects. Econometrica 2008;76:1191-206. http://dx.doi.org/10.3982/ECTA5317.
- Emsley RA, Dunn G, Liu H, Clarke P, White IR, Windmeijer F. Estimating Rank Preserving Models Using Instrumental Variables for Causal Mediation Analysis 2015.
- Hamilton M. A rating scale for depression. J Neurol Neurosurg Psychiatry 1960;23:56-62. http://dx.doi.org/10.1136/jnnp.23.1.56.
- Beck AT, Brown GK, Steer RA. Psychometric characteristics of the scale for suicide ideation with psychiatric outpatients. Behav Res Ther 1997;35:1039-46. http://dx.doi.org/10.1016/S0005-7967(97)00073-9.
- Follmann D. Augmented designs to assess immune response in vaccine trials. Biometrics 2006;62:1161-9. http://dx.doi.org/10.1111/j.1541-0420.2006.00569.x.
- Gunderson JG, Frank AF, Katz HM, Vannicelli ML, Frosch JP, Knapp PH. Effects of psychotherapy in schizophrenia: II. Comparative outcome of two forms of treatment. Schizophr Bull 1984;10:564-98. http://dx.doi.org/10.1093/schbul/10.4.564.
- Jo B. Estimation of intervention effects with noncompliance: alternative model specifications. J Educ Behav Stat 2002;27:385-409. http://dx.doi.org/10.3102/10769986027004385.
- Dunn G, Maracy M, Tomenson B. Estimating treatment effects from randomized clinical trials with noncompliance and loss to follow-up: the role of instrumental variable methods. Stat Method Med Res 2005;14:369-95. http://dx.doi.org/10.1191/0962280205sm403oa.
- Dunn G, Maracy M, Dowrick C, Ayuso-Mateos JL, Dalgard OS, Page H, et al. Estimating psychological treatment effects from an RCT with both non-compliance and loss to follow-up. Br J Psychiatry 2013;183:323-31. http://dx.doi.org/10.1192/bjp.183.4.323.
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. Hoboken, NJ: Wiley; 2002.
- Frangakis CE, Rubin DB. Addressing complications of intention-to-treat analysis in the combined presence of all-or-none treatment-noncompliance and subsequent missing outcomes. Biometrika 1999;86:365-79. http://dx.doi.org/10.1093/biomet/86.2.365.
- Lewis S, Tarrier N, Haddock G, Bentall R, Kinderman P, Kingdon D, et al. Randomised controlled trial of cognitive–behavioural therapy in early schizophrenia: acute-phase outcomes. Br J Psychiatry 2002;181:S91-7. http://dx.doi.org/10.1192/bjp.181.43.s91.
- Tarrier N, Lewis S, Haddock G, Bentall R, Drake R, Kinderman P, et al. Cognitive–behavioural therapy in first-episode and early schizophrenia – 18-month follow-up of a randomised controlled trial. Br J Psychiatry 2004;184:231-9. http://dx.doi.org/10.1192/bjp.184.3.231.
- Kay SR, Fiszbein A, Opler LA. The positive and negative syndrome scale (PANSS) for schizophrenia. Schiz Bull 1987;13:261-76. http://dx.doi.org/10.1093/schbul/13.2.261.
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. London: Chapman & Hall; 1993.
- Muthén LK, Muthén BO. Mplus User’s Guide. Los Angeles, CA: Muthén & Muthén; 2012.
- Pickles A, Green J. PACT consortium . Therapeutic mechanism in the MRC Pre-school Autism Communication Trial: implications for study design and parent focussed therapy for children. J Child Psychol Psychiatry 2015;56:162-70. http://dx.doi.org/10.1111/jcpp.12291.
- Garety P, Fowler D, Freeman D, Bebbington P, Dunn G, Kuipers E. Cognitive–behavioural therapy and family intervention for relapse prevention and symptom reduction in psychosis: randomised controlled trial. Br J Psychiatry 2008;192:412-23. http://dx.doi.org/10.1192/bjp.bp.107.043570.
- Cheong J, MacKinnon D, Khoo ST. Investigation of mediational processes using parallel process latent growth curve modeling. Struct Equation Modeling 2003;10. http://dx.doi.org/10.1207/S15328007SEM1002_5.
- Muthén B, Khoo ST. Longitudinal studies of achievement growth using latent variable modeling. Learn Individ Differences 1998;10:73-101. http://dx.doi.org/10.1016/S1041-6080(99)80135-6.
- McArdle JJ. Latent variable modeling of differences and changes with longitudinal data. Ann Rev Psychol 2009;60:577-605. http://dx.doi.org/10.1146/annurev.psych.60.110707.163612.
- Muthén B, Brown H. Estimating drug effects in the presence of placebo response: Causal inference using growth mixture modeling. Stat Med 2009;28:3363-85. http://dx.doi.org/10.1002/sim.3721.
- Asparouhov T, Muthén B. Auxiliary Variables in Mixture Modeling: 3-Step Approaches Using Mplus 2014.
- Bullock JG, Green DP, Ha SE. Yes, but what’s the mechanism? (Don’t expect an easy answer). J Personality Soc Psychol 2010;98:550-8. http://dx.doi.org/10.1037/a0018933.
- Burgess S, Thompson SG. Avoiding bias from weak instruments in Mendelian randomisation studies. Int J Epidemiol 2011;40:755-64. http://dx.doi.org/10.1093/ije/dyr036.
- Burgess S, Thompson SG. Bias in causal estimates from Mendelian randomisation studies with weak instruments. Stat Med 2011;30:1312-23. http://dx.doi.org/10.1002/sim.4197.
- Davey Smith G, Ebrahim S. ‘Mendelian randomisation’: can genetic epidemiology contribute to understanding environmental determinants of disease?. Int J Epidemiology 2003;32:1-22. http://dx.doi.org/10.1093/ije/dyg070.
- Lawlor DA, Harbord RM, Sterne JAC, Timpson N, Davey Smith G. Mendelian randomisation: using genes as instruments for making causal inferences in epidemiology. Stat Med 2008;27:1133-63. http://dx.doi.org/10.1002/sim.3034.
- Didelez V, Sheehan NA. Mendeleian randomisation as an instrumental variable approach to causal inference. Stat Methods Med Res 2007;16:309-30. http://dx.doi.org/10.1177/0962280206077743.
- Garety PA, Kuipers E, Fowler D, Freeman D, Bebbington PE. A cognitive model of the positive symptoms of psychosis. Psychol Med 2001;31:189-95. http://dx.doi.org/10.1017/S0033291701003312.
- Garety P, Freeman D. Cognitive approaches to delusions: a critical review of theories and evidence. Br J Clin Psychol 1999;38:113-54. http://dx.doi.org/10.1348/014466599162700.
- Freeman D. Suspicious minds: the psychology of persecutory delusions. Clin Psychol Rev 2007;27:425-57. http://dx.doi.org/10.1016/j.cpr.2006.10.004.
- Emsley RA, VanderWeele TJ. Mediation and Sensitivity Analysis Using Two or More Trials 2015.
- VanderWeele TJ. Explanation in Causal Analysis: Methods for Mediation and Interaction. New York, NY: Oxford University Press; 2015.
- Spencer SJ, Zanna MP, Fong GT. Establishing a causal chain: why experiments are often more effective than mediational analyses in examining psychological processes. J Pers Soc Psychol 2005;89:845-51. http://dx.doi.org/10.1037/0022-3514.89.6.845.
- Stone-Romero EF, Rosopa PJ. The relative validity of inferences about mediation as a function of research design characteristics. Org Res Methods 2008;11:326-52. http://dx.doi.org/10.1177/1094428107300342.
- Young KY, Laird A, Zhou ZX. The efficiency of clinical trial designs for predictive biomarker validation. Clin Trials 2010;7:557-66. http://dx.doi.org/10.1177/1740774510370497.
- Freidlin B, McShane LM, Korn EL. Randomized clinical trials with biomarkers: design issues. J Nat Cancer Inst 2010;102:152-60. http://dx.doi.org/10.1093/jnci/djp477.
- Dunn G, Emsley R, Liu H, Landau S. Integrating biomarker information within trials to evaluate treatment mechanisms and efficacy for personalised medicine. Clin Trials 2013;10:712-22. http://dx.doi.org/10.1177/1740774513499651.
- Imai K, Tingley D, Yamamoto T. Experimental designs for identifying causal mechanisms. J R Stat Soc A 2013;76:5-51. http://dx.doi.org/10.1111/j.1467-985X.2012.01032.x.
- Imai K, Keele L, Tingley, D, Yamamoto T. Unpacking the black box of causality: learning about causal mechanisms from experimental and observational studies. Am Political Sci Rev 2011;105:765-89. http://dx.doi.org/10.1017/S0003055411000414.
- Daniel RM, De Stavola BL, Cousens SN, Vansteelandt S. Causal mediation analysis with multiple mediators. Biometrics 2015;71:1-14.
- Valeri L, Lin X, VanderWeele TJ. Mediation analysis when a continuous mediator is measured with error and the outcome follows a generalized linear model. Stat Med 2014;33:4875-90. http://dx.doi.org/10.1002/sim.6295.
- VanderWeele TJ. Causal mediation analysis with survival data. Epidemiology 2011;22:582-5. http://dx.doi.org/10.1097/EDE.0b013e31821db37e.
- VanderWeele TJ. Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology 2010;21:540-51. http://dx.doi.org/10.1097/EDE.0b013e3181df191c.
- VanderWeele TJ, Arah OA. Bias formulas for sensitivity analysis of unmeasured confounding for general outcomes, treatments, and confounders. Epidemiology 2011;22:42-5. http://dx.doi.org/10.1097/EDE.0b013e3181f74493.
Appendix 1 The Stata paramed command
Appendix 2 Mplus input file illustrating principal stratification (process evaluation)
Appendix 3 Mplus input file for longitudinal analyses
Appendix 4 Stata do file for simulation of biomarker-stratified Efficacy and Mechanism Evaluation trials
Appendix 5 Detailed results summary of simulated biomarker-stratified Efficacy and Mechanism Evaluation trials
Predictive marker recorded without error: true predictive marker prevalence 10%
Summary
-
For these simulations, the focus is on the 10% predictive marker prevalence, that is 10% of participants are predictive marker positive.
-
The simulations examine the performance of the standard regressions when excluding the interaction term of treatment and predictive biomarker, that is the IV X11, when including X11, and when including the IV estimator.
-
The performance of varying instrument strengths (X11) are examined: first with 20 × X11, then 10 × X11 and then reduced to 5 × X11.
-
The simulations also examine different sample sizes: 200, 500 and 1000.
-
For all analyses, 10,000 data sets are simulated from the EME model described in Appendix 4.
Results
The results are as follows:
-
In the standard regressions when excluding X11, smaller interactions lead to less bias and better precision for all three parameters: X10, the predictive biomarker, treat, the randomisation term, and M, the mediator.
-
In the standard regressions including X11, smaller interactions lead to unchanged results for the X10, treat and M parameters. Smaller interactions leads to less bias and better precision for the X11 parameter.
-
In the IV method, weaker IVs lead to increased bias and reduced precision for all three parameters X10, treat and M.
-
When there are hidden confounders, the IV method is less biased than the standard regressions but IV is less precise than the standard regressions. The standard regressions have very poor coverage. The IV method has very good coverage (approximately 95%).
-
When all confounders (i.e. X1–X9) are adjusted for the standard regressions and the IV estimator are unbiased, but in all cases the IV estimator is less precise.
-
Larger sample size leads to better precision in all cases.
Comparing these simulations with 10% predictive marker prevalence to those with 50% predictive marker prevalence, that is the balanced predictive marker prevalence (see Chapter 5)
-
When using IV and the standard regressions excluding X11, bias has increased while precision has reduced in the parameters X10 and M. Bias has reduced while precision has increased in the parameter treat.
-
Using standard regressions including X11, bias remains similar while precision has reduced in the parameters X10 and X11. Bias stays similar but precision has increased in the parameter treat. Bias and precision remain unchanged in the parameter M.
Predictive marker recorded without error: true predictive marker prevalence 50%
Summary
-
For these simulations, the focus is on the 50% predictive marker prevalence, that is 50% of participants are predictive marker positive.
-
The simulations examine the performance of the standard regressions when excluding the interaction term of treatment and predictive biomarker, that is the IV and X11, when including X11, and when including the IV estimator.
-
The performance of varying instrument strengths (X11) are examined: first with 20 × X11, then 10 × X11, then reduced to 5 × X11.
-
The simulations also examine different sample sizes: 200, 500 and 1000.
-
For all analyses, 10,000 data sets are simulated from the EME model described in Appendix 4.
Results
The results are as follows:
-
In the standard regressions excluding X11, smaller interactions lead to less bias and better precision for all three parameters: X10, the predictive biomarker, treat, the randomisation term, and M, the mediator.
-
In the standard regressions including X11, smaller interactions lead to unchanged results for the X10, treat and M parameters. Smaller interactions lead to less bias and better precision for the X11 parameter.
-
In the IV method, weaker IVs leads to increased bias and reduced precision for all three parameters X10, treat and M.
-
When there are hidden confounders, the IV method is less biased than the standard regressions but IV is less precise than the standard regressions. The standard regressions have very poor coverage. The IV method has very good coverage (approximately 95%).
-
When all confounders (i.e. X1–X9) are adjusted for, the standard regressions and the IV estimator are unbiased but in all cases the IV estimator is less precise.
-
Larger sample size leads to better precision in all cases.
Predictive marker recorded without error: true predictive marker prevalence 90%
Summary
-
For these simulations, the focus is on the 90% predictive marker prevalence, that is 90% of the participants are predictive marker positive.
-
The simulations examine the performance of the standard regressions when excluding the interaction term of treatment and predictive biomarker, that is the IV X11, and when including X11, and the IV estimator.
-
The performance of varying instrument strengths (X11) are examined: first with 20 × X11, then 10 × X11 and then reduced to 5 × X11.
-
The simulations also examine different sample sizes: 200, 500 and 1000.
-
For all analyses, 10,000 data sets are simulated from the EME model described in Appendix 4.
Results
The results are as follows:
-
In the standard regressions excluding X11, smaller interactions lead to less bias and better precision for all three parameters: X10, the predictive biomarker; treat, the randomisation term; and M, the mediator.
-
In the standard regressions including X11, smaller interactions lead to unchanged results for the X10, treat and M parameters. Smaller interactions lead to less bias and better precision for the X11 parameter.
-
In the IV method, weaker IVs lead to increased bias and reduced precision for all three parameters X10, treat and M.
-
Where there are hidden confounders the IV method is less biased than the standard regressions but IV is less precise than the standard regressions. The standard regressions have very poor coverage. The IV method has very good coverage (approximately 95%).
-
When all confounders (i.e. X1–X9) are adjusted for, the standard regressions and the IV estimator are unbiased, but in all cases the IV estimator is less precise.
-
Larger sample size leads to better precision in all cases.
Comparing these simulations with 90% predictive marker prevalence to those with 50% predictive marker prevalence, i.e. the balanced predictive marker prevalence
-
When using IV and the standard regressions excluding X11, bias has increased while precision has reduced in all of the three parameters X10, treat and M.
-
Using standard regressions including X11, bias remains similar while precision has reduced in the parameters X10, treat and X11. Bias and precision remain unchanged in the parameter M.
Misclassifications in the predictive marker: true predictive marker prevalence 50%
With misclassifications in the 50% predictive marker prevalence, the results are as follows:
-
In the standard regressions excluding X11mc, smaller interactions lead to slightly less bias and better precision for the parameters X10mc and treat but slightly more bias and less precision for M.
-
In the standard regressions including X11mc, smaller interactions lead to reduced bias and increased precision for X11mc.
-
In the IV method, weaker IVs lead to largely reduced precision in X10mc, treat and M. The adjustment for confounders does not affect bias considerably, but it makes the estimates more precise.
-
When there are hidden confounders, the IV method is less biased than the standard regressions but IV is less precise than the standard regressions. The standard regressions have poorer coverage than the IV method.
-
When all confounders (X1–X9) are adjusted for, the IV estimator is less biased but less precise than the standard regressions.
-
Larger sample size leads to better precision in all cases.
Comparing these simulations with misclassifications in the 50% predictive marker prevalence to those with NO misclassification in the 50% predictive marker prevalence
-
With misclassification, the IV regressions have increased bias and reduced precision, but the adjustment for confounders does not eliminate bias.
Misclassifications in the predictive marker: true predictive marker prevalence 90%
With misclassifications in the 90% predictive marker prevalence, the results are as follows:
-
In the standard regressions excluding X11mc, smaller interactions lead to slightly less bias and better precision for the parameters X10mc and treat but slightly more bias and less precision for M.
-
In the standard regressions including X11mc, smaller interactions lead to reduced bias and increased precision for X11mc.
-
In the IV method, weaker IVs lead to largely reduced precision in all: X10mc, treat and M. The adjustment for confounders does not affect bias considerably but it makes the estimates more precise.
-
When there are hidden confounders, the IV method is less biased than the standard regressions but IV is less precise than the standard regressions. The standard regressions have poorer coverage than the IV method.
-
When ALL confounders (X1–X9) are adjusted for, the IV estimator is less biased but less precise than the standard regressions.
-
Larger sample size leads to better precision in all cases.
Comparing these simulations with misclassifications in the 90% predictive marker prevalence to those of NO misclassification in the 90% predictive marker prevalence
-
With misclassification, the IV regressions have increased bias and reduced precision but the adjustment for confounders does not eliminate bias.
Appendix 6 Analysis of sensitivity to assumptions for instrumental variables estimation: a simulation study
Introduction
Instrumental variable methods provide unbiased estimates at the expense of precision, but model identification using more informative and more realistic models requires potentially invalid assumptions. In particular, aside from imposing parametric structure, they require moderation of treatment effects on markers by covariates but no moderation of the direct effect of treatment on outcome, equivalent to using covariate by treatment interactions as IVs; no moderation of effects of marker on outcome by covariates; and no marker by treatment interactions on the direct effect of treatment on outcome. Further, considering the unmeasured confounder as a post-randomisation rather than baseline variable we consider the effect on estimation procedures if the confounder is directly influenced by treatment.
We perform Monte Carlo simulation studies under a variety of scenarios involving selection effects, measurement error and imperfect prediction of markers. We weaken these identifying assumptions in turn and allow treatment to predict the post-randomisation confounder in two ways: by a mean change between the treatment groups and by independently introducing heteroskedasticity. Using these results we provide recommendations concerning informative designs and on corresponding sample size requirements for marker evaluation in complex intervention trials. We illustrate how the methods can be implemented using a randomised trial of CBT in psychosis.
Dunn and Bentall14 examined social and psychological markers as potential mediators (effect moderator) of treatment effects of psychological interventions in RCTs. They evaluated two such mediators, namely the number of therapeutic sessions actually attended (compliance with therapy) and the strength of the therapeutic alliance between therapist and patient (the quality of therapy). These two variables were considered as characteristics of the therapeutic process and were post-randomisation variables rather than variables measured at baseline. They performed Monte Carlo simulation studies using these two post-randomisation variables to assess treatment effect mediation in the presence of selection effects (i.e. unmeasured or hidden confounding between the mediators and outcome), measurement errors in and imperfect prediction of the proposed mediator (in their case, the strength of the therapeutic alliance).
Dunn and Bentall14 defined the causal effect of treatment in terms of the counterfactual or potential outcomes approach of Rubin6 (for notation see Chapter 3). We define the effect of treatment received by an individual i as a comparison of the outcome under treatment with the corresponding treatment-free outcome, typically the arithmetic difference:
There is no reason to assume that Δ remains the same from one participant to another and, in particular, we might be interested in investigating how Δ might be jointly influenced by the number and quality of sessions of treatment attended. How might we model these influences?
With a quantitative effect modifier, A, and a set of baseline covariates, X, the linear model we deal with here has the form:
Note that this regression model does not contain an intercept term (i.e E(Δi|Si = 0) = 0).
This is the causal (structural) model that we refer to as the ‘S + S × A model’. They considered various permutations in the estimation of the S + S × A model. The key estimation procedures being considered were G-estimation for structural mean models [SMM(G)] and IVs [using the 2SLS estimation, IV(2SLS)], in comparison with a standard regression approach, the OLS focusing on treatment received, OLS(TR). If there is hidden confounding between sessions attended and outcome, and also between the product of sessions and alliance and outcome, then our OLS estimates of βs and βsa will be biased. We need instruments for S and SA so that we can obtain unbiased estimates using, for example, 2SLS. We can assume that one of these instruments can clearly be the randomisation indicator (Z); it has a strong influence of sessions attended and there is no effect of randomisation on outcome other than receipt of therapy. However, one instrument is enough in this model with two endogenous process measures (S and SA). Let us assume, for example, that we have measurements on two baseline covariates (X′ = X1, X2) that jointly predict S and SA in the treatment arm, and they have no effect in the control arm, as both are constrained to be zero. That is the products of the covariates and randomised treatment (the treatment by covariate interaction) jointly predict the process measures, S and SA. If we can also assume that these interactions have no direct effect on outcome (i.e. their moderating effect on outcome is wholly explained by their effects on the intermediate process measures) then they can be used as IVs. A typical Stata command line would be:
where x1z and x2z are the products of each of the covariates and the binary randomisation indicator (z), respectively. Results obtained through this command are referred to as the IV(2SLS) estimates. The corresponding OLS regression is implemented using the command:
The results of using the latter command are referred to as the OLS(TR) estimates.
Dunn and Bentall’s simulations showed that the estimates provided by the IV(2SLS) and SMM(G) were identical (see Dunn and Bentall14 for further details). In the following we will only use IV(2SLS). The OLS(TR) procedure produced results that were quite different from the IV(2SLS) estimates in all cases except when there were no selection effects (i.e. no unmeasured confounding between the mediators and outcome) and there were no measurement errors in therapeutic alliance. Their studies showed that in all situations the precision of the OLS(TR) estimates was considerably better than that from the use of the IV(2SLS) method. Their results indicated that the introduction of random measurement errors into therapeutic alliance had no impact on the IV estimates, but these procedures yielded estimates with higher precision in the presence of selection effects (unmeasured confounding) between mediators (in their case, therapeutic alliance) and outcome than when they were absent. Their results demonstrated the importance of being able to predict post-randomisation markers (in their case, therapeutic alliance) from baseline or pre-randomisation covariates. So they drew the more general conclusion that, if they were unable to predict the post-randomisation markers or, equivalently, obtain good estimates of the compliance score, then their causal models are not identified. If they had poor prediction they would have only weakly identified models and very imprecise estimates of the required treatment effects.
Conditional on valid assumptions, IV methods provide unbiased estimates at the cost of decreased precision, but model identification using more informative and more realistic models requires potentially invalid assumptions. In particular, four assumptions are required. The first three assumptions are from the definition: (1) the association between instrument and mediator; (2) no direct effect of the instrument on outcome; and (3) no unmeasured confounding for the instrument and outcome. There are a wide variety of fourth assumptions, and different assumptions result in the estimation of different causal effects. In particular, aside from imposing parametric structure, they require moderation of treatment effects on mediator by covariates but no moderation of the direct effect of treatment on outcome, equivalent to using covariate by treatment interactions as IVs; no moderation of mediator effects on outcome by covariates; and no mediator by treatment interactions on the direct effect of treatment on outcome.
The Monte Carlo simulation work presented here follows on from the simulations of Dunn and Bentall14 but restricting the attention to the case where there is hidden confounding. Focusing on the same post-randomisation variables, that is the number of therapeutic sessions actually attended (compliance with therapy) and the strength of the therapeutic alliance between therapist and patient (the quality of therapy), we run simulations under a variety of scenarios of the S + S × A model, involving selection effects (unmeasured confounding between the mediator and outcome), measurement errors in and imperfect prediction of therapeutic alliance. In particular, we are interested in testing the sensitivity of some of the key assumptions underpinning the IV method using the 2SLS estimation, IV(2SLS). We consider this by (1) weakening these identifying assumptions in turn, and allowing treatment to predict the unmeasured post-randomisation confounder (in this case, selection effects) between mediators and outcome; and (2) independently introducing unmeasured confounding (selection effects) into the S +S × A model through its relationships with the post-randomisation variables (i.e. compliance with therapy and the quality of therapy) and the response outcome.
First we describe the details of the Dunn and Bentall data generation model. Then we replicate the IV(2SLS) and OLS(TR) parts of the Dunn and Bentall simulation studies presented in table II(a) of their paper, which will be referred to when looking at the results of the present simulations. We also set out what results are presented and how they are calculated in the tables presented in this report.
Then we present three sets of simulation studies. First, we weaken the key identifying assumptions underpinning IV(2SLS) in two ways: by a mean change between the treatment groups and by independently introducing heteroskedasticity. Second, we weaken the key identifying assumptions underpinning IV(2SLS) by allowing treatment to influence the unmeasured confounder. Third, we examine the influence of hidden confounding in three ways: introduce hidden confounding through its relationship with the control response alone; introduce hidden confounding through its relationships with the control response and the latent therapeutic alliance simultaneously; and introduce hidden confounding through its relationships with the latent compliance with therapy and the latent therapeutic alliance simultaneously. Key findings from our current simulations are summarised at the end of each section.
Monte Carlo simulation: the Dunn and Bentall data generation model
Following Dunn and Bentall,14 the trial data generation model is specified as follows: one-half of participants are assigned to the control group (Z = 0) and the other half to the treatment group (Z = 1).
X1, X2 and X3 are three baseline covariates available for all participants. X1 and X2 are independent normal variates with means 100 and 10, and standard deviations (SDs) 10 and 3, respectively. The characteristics of X3, also normally distributed, are described once we have define the measure of therapeutic alliance. The control response, Y0 [the potential outcome Y(0), is given by Y0 = X1 + e1, where e1 is an independent normal variate with mean 0 and SD 10]. e1 is the origin of the selection effect (hidden confounding between mediators and final outcome).
The latent compliance with treatment, C, is given by C = 0.6 + ((X2 – 10)/10) + 0.01 × e1 + e2, where e1 is as defined as given above and e2 is an independent normal variate with mean 0 and SD 0.1. e2 is an error term. Any values of C less than 0 are set to 0 and any above 1 are set to 1 (C = 0 if C < 0; C = 1 if C > 1). The number of therapeutic sessions actually attended (compliance with treatment), S, is equal to the corresponding C in the treated group and is 0 in the control group (S = C when Z = 1; S = 0 when Z = 0).
The latent strength of therapeutic alliance, A1, is given by A1 = e3 + 0.05 × e1, where e1 is as defined as given above, and e3 is an independent normal variate with mean 3 and SD 1. e3 is an error term. The measured strength of therapeutic alliance, A, is given by A = A1 + e4 in the treated group, where e4 is an independent normal variate with mean 0 and SD 1. e4 is the measurement error in the measured therapeutic alliance. A is set as missing in the control group but its product with S, that is S × A is set at 0 in the control group.
The third baseline covariate, X3, is given by X3 = A1 + e5, where e5 is an independent normal variate with mean 0 and SD 1. e5 is responsible for the imperfect prediction by X3 of the latent therapeutic alliance.
The treatment response, Y1 [i.e. the potential outcome Y(sa)], is given by Y1 = Y0 + 0.5 × C × (1 – 6 × A1) + e6, where e6 is an independent variate with mean 0 and SD 2. e6 is an error term. The final outcome (the response variable) is given by outcome = Y1 × Z + Y0 × (1 – Z). Referring to the parameters of our causal (structural model), the expression for Y1 above implies that βs = +0.5 and βsa = –3.0. The characteristics of the various estimates of these two parameters are the focus of our simulation studies.
So, in the general model, the number of therapeutic sessions actually attended, S, is measured without error and is mainly predicted by the baseline covariate X2. The measured level of therapeutic alliance, A, is measured by a variable subject to measurement errors (A = A1 + e4) and is predicted by the baseline covariate X3. The control response is determined by X1.
Three modifications to the above model are considered, giving four possibilities in total. The first is to assume that we are able to measure therapeutic alliance without error (i.e. A = A1). The second is to assume that we are able to predict the latent therapeutic alliance perfectly from the baseline covariate X3 (i.e. A1 = X3). The third is to assume both the absence of measurement errors in the measured therapeutic alliance, A, and perfect prediction of the latent therapeutic alliance, A. For each condition, 1000 simulated data sets are generated and analysed.
In summary, we generate data sets with and without hidden confounding (selection effects) for both therapeutic sessions actually attended, S, and therapeutic alliance, A. We also illustrate the effects of adding measurement errors to A (note that S is always assumed to be measured without measurement errors) and varying our ability to predict the latent therapeutic alliance, A1, from a baseline covariate, X3, measured in both groups. The causal parameters of interest are βs and βsa. In all cases, βs is the effect of S (compliance with therapy) when A = 0, and has a true value of + 0.50. βs is the causal effect of S × A (compliance with therapy by quality of therapy) and has a true value of –3.00. The key estimation procedure being considered is the IV method using the 2SLS estimation, IV(2SLS), in comparison with the OLS procedure based on treatment received, OLS(TR). The base program (a Stata do file) is given in Appendix 1.
Replication of the Dunn and Bentall simulations
Dunn and Bentall used different seeds in the simulations of various permutations in the estimation of the S + S × A model. Here we replicate the IV(2SLS) and OLS(TR) parts of their simulations using a common seed (1951) for all of the simulations.
The replications are presented in Table 11, which will be referred to when discussing the results of the new simulations (the ones of interest here). Looking at the four rows of the table, we are distinguishing the true model characteristics (scenarios) as follows:
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | 0.30 | 4.00 | –0.20 | 16.06 | 96.0 | –5.39 | 1.71 | –5.89 | 37.55 | 7.0 |
| βsa | –3.00 | –2.94 | 1.25 | 0.06 | 1.56 | 96.5 | –0.04 | 0.46 | 2.96 | 8.96 | 0.0 | |
| SL + IP | βs | +0.50 | 0.33 | 4.06 | –0.17 | 16.52 | 94.5 | –5.28 | 2.29 | –5.78 | 38.65 | 26.9 |
| βsa | –3.00 | –2.95 | 1.26 | 0.05 | 1.58 | 95.2 | –0.07 | 0.65 | 2.93 | 9.00 | 0.6 | |
| SL + ME + PP | βs | +0.50 | 0.37 | 3.00 | –0.13 | 9.00 | 94.7 | –1.45 | 1.73 | –1.95 | 6.82 | 79.0 |
| βsa | –3.00 | –2.96 | 0.91 | 0.04 | 0.83 | 94.5 | –1.39 | 0.47 | 1.61 | 2.82 | 7.2 | |
| SL + PP | βs | +0.50 | 0.39 | 2.95 | –0.11 | 8.70 | 93.9 | 4.35 | 2.41 | 3.85 | 20.6 | 62.4 |
| βsa | –3.00 | –2.96 | 0.89 | 0.04 | 0.79 | 94.1 | –3.24 | 0.72 | –0.24 | 0.58 | 93.1 | |
-
‘SL’ indicates the existence of selection effects (i.e. hidden confounding, determined by e1); this is common to all four rows (scenarios).
-
‘ME’ indicates that there are measurement errors in the measured therapeutic alliance, A.
-
‘IP’ indicates imperfect prediction of the latent therapeutic alliance.
-
‘PP’ indicates perfect prediction of the latent therapeutic alliance by variable X3.
So, for example, the first row ‘SL + ME + IP’ indicates that we are simulating the (1) introduction of random selection effects between mediators and outcome, (2) random measurement errors in the measured therapeutic alliance and (3) imperfect prediction of the latent therapeutic alliance.
Table 11 presents the summaries for 1000 simulations under each of the scenarios. We report the mean of the 1000 estimates of each of the two structural parameters, the SD of the estimates, bias, mean square error (MSE) and per cent coverage (calculated as the percentage of simulations whose 95% CIs contain the true values). What are our overall conclusions? IV methods achieve coverage very close to the nominal 95%, whereas OLS regressions do not. IV estimates are unbiased but much less precise than the OLS estimates.
New simulation studies
The three sets of simulations are described as follows:
Weakening the key identifying assumptions underpinning IV (2SLS)
Change the standard deviation of e1, e2 and e6
In the simulations reported in Tables 12–14, we change the SD of e1, e2 and e6, in turn.
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | + 0.50 | 0.50 | 1.01 | 0.00 | 1.02 | 95.3 | –4.53 | 0.45 | –5.03 | 25.55 | 0.0 |
| βsa | –3.00 | –3.00 | 0.33 | 0.00 | 0.11 | 95.6 | –1.31 | 0.14 | 1.69 | 2.87 | 0.0 | |
| SL + IP | βs | + 0.50 | 0.49 | 0.82 | –0.01 | 0.67 | 94.9 | 0.41 | 0.53 | –0.09 | 0.29 | 89.2 |
| βsa | –3.00 | –3.00 | 0.26 | 0.00 | 0.07 | 95.0 | –2.96 | 0.16 | 0.04 | 0.03 | 88.1 | |
| SL + ME + PP | βs | + 0.50 | 0.47 | 0.77 | –0.03 | 0.59 | 94.5 | –5.11 | 0.45 | –5.61 | 31.63 | 0.0 |
| βsa | –3.00 | –2.99 | 0.24 | 0.01 | 0.06 | 95.0 | –1.12 | 0.13 | 1.88 | 3.55 | 0.0 | |
| SL + PP | βs | + 0.50 | 0.49 | 0.59 | –0.01 | 0.35 | 95.2 | 0.51 | 0.53 | 0.01 | 0.28 | 93.3 |
| βsa | –3.00 | –3.00 | 0.19 | 0.00 | 0.04 | 94.5 | –2.99 | 0.17 | 0.01 | 0.03 | 92.2 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | + 0.50 | 0.30 | 4.61 | –0.20 | 21.29 | 95.7 | –7.01 | 1.45 | –7.51 | 58.46 | 0.0 |
| βsa | –3.00 | –2.93 | 1.47 | 0.07 | 2.16 | 96.0 | –0.46 | 0.42 | 2.54 | 6.62 | 0.0 | |
| SL + IP | βs | + 0.50 | 0.31 | 4.64 | –0.19 | 21.54 | 94.4 | –5.72 | 1.83 | –6.22 | 42.04 | 8.4 |
| βsa | –3.00 | –2.94 | 1.46 | 0.06 | 2.15 | 95.9 | –0.91 | 0.55 | 2.09 | 4.69 | 4.7 | |
| SL + ME + PP | βs | + 0.50 | 0.34 | 3.40 | –0.16 | 11.57 | 95.0 | –4.10 | 1.44 | –4.60 | 23.19 | 11.0 |
| βsa | –3.00 | –2.95 | 1.06 | 0.05 | 1.12 | 95.5 | –1.45 | 0.41 | 1.55 | 2.57 | 4.7 | |
| SL + PP | βs | + 0.50 | 0.38 | 3.36 | –0.12 | 11.31 | 93.9 | 0.55 | 1.93 | 0.05 | 3.74 | 93.8 |
| βsa | –3.00 | –2.95 | 1.04 | 0.05 | 1.08 | 94.0 | –2.97 | 0.61 | 0.03 | 0.37 | 94.9 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | + 0.50 | 0.26 | 4.86 | –0.24 | 23.70 | 95.9 | –5.42 | 2.31 | –5.92 | 40.32 | 20.2 |
| βsa | –3.00 | –2.94 | 1.52 | 0.06 | 2.31 | 97.1 | –0.04 | 0.64 | 2.96 | 9.18 | 0.4 | |
| SL + IP | βs | + 0.50 | 0.37 | 4.93 | –0.13 | 24.33 | 94.3 | –5.24 | 3.11 | –5.74 | 42.54 | 44.4 |
| βsa | –3.00 | –2.97 | 1.53 | 0.03 | 2.35 | 95.0 | –0.09 | 0.90 | 2.91 | 9.27 | 8.4 | |
| SL + ME + PP | βs | + 0.50 | 0.39 | 3.71 | –0.11 | 13.79 | 95.7 | –1.42 | 2.30 | –1.92 | 8.98 | 84.1 |
| βsa | –3.00 | –2.97 | 1.13 | 0.03 | 1.27 | 95.2 | –1.41 | 0.64 | 1.59 | 2.95 | 24.1 | |
| SL + PP | βs | + 0.50 | 0.39 | 3.71 | –0.11 | 13.73 | 95.0 | 4.29 | 3.13 | 3.79 | 24.15 | 73.0 |
| βsa | –3.00 | –2.96 | 1.13 | 0.04 | 1.28 | 95.4 | –3.22 | 0.96 | –0.22 | 0.96 | 92.6 | |
In Table 12 we reduce the SD of e1 from 10 (as in Table 11) to 1 (with mean = 0, as before). e1 is random-selection effects and is defined as hidden confounding or the unmeasured confounder. e1 enters the model through its relationships with the control response, Y0, the latent compliance with therapy, C, and the latent therapeutic alliance, A1. Reducing the variability of e1 implies a lowering of the selection effects (hidden confounding).
In Table 13 we increase the SD of e2 from 0.1 (as in Table 11) to 10 (with mean = 0, as before). e2 is the random error in the latent compliance with treatment, C. Increasing the SD of e2 means increases the variance of the unexplained variation in C.
In Table 14 we increase the SD of e6 from 2 (as in Table 11) to 10 (with mean = 0, as before). e6 are random errors in the treatment response, Y1. Increasing the SD of e6 increases the unexplained variation in Y1.
Summary of Tables 12–14
-
Reducing the SD of e1 (see Table 12) leads to estimates being closer to their true values (less biased) with considerably improved precision.
-
Increasing the SD of e2 (see Table 13) only affects the estimates and hence bias slightly but leads to loss of precision.
-
Increasing the SD of e6 (see Table 14) affects bias only very slightly but leads to lower precision.
Change the mean of e1, e2 and e6
In the simulations reported in Tables 15–17 we change the mean of e1, e2 and e6, in turn.
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | + 0.50 | 0.30 | 4.03 | –0.20 | 16.27 | 96.0 | –7.38 | 1.71 | –7.88 | 65.02 | 0.4 |
| βsa | –3.00 | –2.94 | 1.09 | 0.06 | 1.20 | 96.2 | –0.09 | 0.42 | 2.91 | 8.62 | 0.0 | |
| SL + IP | βs | + 0.50 | 0.33 | 4.08 | –0.17 | 16.69 | 94.9 | –7.06 | 2.33 | –7.56 | 62.64 | 9.3 |
| βsa | –3.00 | –2.95 | 1.10 | 0.05 | 1.21 | 95.2 | –0.18 | 0.59 | 2.82 | 8.30 | 0.4 | |
| SL + ME + PP | βs | + 0.50 | 0.37 | 3.00 | –0.13 | 9.02 | 94.6 | –3.12 | 1.75 | –3.62 | 16.14 | 45.7 |
| βsa | –3.00 | –2.97 | 0.80 | 0.03 | 0.63 | 94.4 | –1.34 | 0.43 | 1.66 | 2.95 | 3.0 | |
| SL + PP | βs | + 0.50 | 0.39 | 2.95 | –0.11 | 8.68 | 93.5 | 3.60 | 2.52 | 3.10 | 15.95 | 75.4 |
| βsa | –3.00 | –2.96 | 0.78 | 0.04 | 0.61 | 94.0 | –3.20 | 0.67 | –0.20 | 0.48 | 93.6 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | + 0.50 | 0.40 | 2.30 | –0.10 | 5.29 | 95.4 | –7.76 | 1.09 | –8.26 | 69.44 | 0.0 |
| βsa | –3.00 | –2.96 | 0.74 | 0.04 | 0.54 | 96.3 | –0.25 | 0.31 | 2.75 | 7.67 | 0.0 | |
| SL + IP | βs | + 0.50 | 0.41 | 2.32 | –0.09 | 5.37 | 94.6 | 0.42 | 1.73 | –0.08 | 2.99 | 6.4 |
| βsa | –3.00 | –2.97 | 0.73 | 0.03 | 0.54 | 95.3 | –2.98 | 0.54 | 0.02 | 0.29 | 6.3 | |
| SL + ME + PP | βs | + 0.50 | 0.42 | 1.73 | –0.08 | 2.99 | 95.1 | –5.04 | 1.15 | –5.54 | 32.05 | 0.3 |
| βsa | –3.00 | –2.98 | 0.54 | 0.02 | 0.29 | 94.6 | –1.15 | 0.33 | 1.85 | 3.52 | 0.1 | |
| SL + PP | βs | + 0.50 | 0.44 | 1.67 | –0.06 | 2.80 | 93.6 | 0.44 | 1.67 | –0.06 | 2.80 | 93.6 |
| βsa | –3.00 | –2.97 | 0.52 | 0.03 | 0.27 | 94.1 | –2.97 | 0.52 | 0.03 | 0.27 | 94.1 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | + 0.50 | 16.11 | 4.28 | 15.61 | 262 | 2.3 | 8.45 | 1.63 | 7.95 | 66 | 0.2 |
| βsa | –3.00 | –3.42 | 1.33 | –0.42 | 1.94 | 92.7 | –0.24 | 0.44 | 2.76 | 7.79 | 0.0 | |
| SL + IP | βs | + 0.50 | 16.13 | 4.13 | 15.63 | 261 | 2.3 | 9.19 | 2.19 | 8.69 | 80 | 2.4 |
| βsa | –3.00 | –3.43 | 1.28 | –0.43 | 1.83 | 93.0 | –0.48 | 0.62 | 2.52 | 6.75 | 2.4 | |
| SL + ME + PP | βs | + 0.50 | 16.71 | 3.09 | 16.21 | 272 | 0.0 | 12.16 | 1.67 | 11.66 | 139 | 0.0 |
| βsa | –3.00 | –3.62 | 0.93 | –0.62 | 1.25 | 88.7 | –1.52 | 0.45 | 1.48 | 2.40 | 10.8 | |
| SL + PP | βs | + 0.50 | 16.64 | 2.90 | 16.14 | 269 | 0.2 | 18.43 | 2.33 | 17.93 | 327 | 0.0 |
| βsa | –3.00 | –3.59 | 0.88 | –0.59 | 1.12 | 89.6 | –3.52 | 0.70 | –0.52 | 0.77 | 88.3 | |
In Table 15 we change the mean of e1 from 0 (as in Table 11) to 10 (with its SD unchanged). This increases the mean of hidden confounding (selection effects) introduced through the control response, Y0, the latent compliance with therapy, C, and the latent therapeutic alliance, A1, at the same time.
In Table 16, we change the mean of e2 from 0 (as in Table 11) to 10 (leaving its SD unchanged). This introduces systematic (as opposed to random) error in the latent compliance measure, C.
In Table 17, we change the mean of e6 from 0 (as in Table 11) to 10 (leaving its SD unchanged). This increases the treatment response, Y1 by 10 units on average, representing, for example, assessor bias.
Summary of Tables 15–17
-
Increasing the mean of e1 (see Table 15) does not affect the estimates overall. Bias is unaffected, while there is a slight gain in precision of estimates.
-
Increasing the mean of e2 (see Table 16) leads to estimates closer to their true values, that is less bias and greater precision.
-
Increasing the mean of e6 (see Table 17) leads to estimates of βs enormously biased but with lowered precision. Changes in bias of the estimates of βsa are in the same direction as in βs but far less marked.
Allowing unmeasured confounding to be influenced by treatment
In our simulations described above (see Tables 11–17), the unmeasured confounder (selection effects), denoted e1, enters the model through its effect on the control response, Y0 = X1 + e1; the latent compliance with therapy, C = 0.6 + ((X2 – 10)/10) + 0.01 × e1 + e2; and the latent therapeutic alliance, A1 = e3 + 0.05 × e1.
Here, we run simulations in which we allow for the unmeasured confounder to be directly influenced by treatment. In particular, we are interested in examining the effect on the estimation procedures of allowing the unmeasured confounder to be a function of randomisation.
We create the selection effects predicted by randomisation variable, e1z, which is given by e1z = z × e1 + (1 – Z) × e7, where e7 is a new independent normal variable with mean 0 and SD 10 (the same as e1) and Z is randomisation (Z = 0 for the control group; Z = 1 for the treatment group).
The newly created variable, e1z, consists of either e1 or e7 (depending on treatment allocation). Values and settings for the remaining variables are kept unchanged apart from being affected and thus changed by e1z. Now the control response, Y0, is given by Y0 = X1 + e1z; the latent compliance with therapy, C, is given by C = 0.6 + ((X2–10)/10) + 0.01 × e1z + e2 (which is dependent upon randomisation); and the latent therapeutic alliance, A1, is given by A1 = e3 + 0.05 × e1z (also dependent upon randomisation). So far, however, this will not have any practical implications: e1 and e2 are identically distributed. But we can now proceed to change this situation by either allowing their SD to differ, or their means to differ, so allowing for hidden confounding to depend on treatment allocation.
Summary of simulations (Tables 18–24)
-
In Table 18 we introduce new condition e1z, keeping the mean and SD of both e1 and e7 the same. As expected, Tables 11 and 18 are practically identical.
-
In Table 19, we keep the value of e1 unchanged but reduce the SD of e7 from 10 (as in Table 18) to 1 (with the means of both remaining unchanged at 0). Compared with Table 18, we see estimates are increasingly biased and the signs of both βs and βsa have reversed in all rows with SL (selection effects or hidden confounding).
-
In Table 20, we still keep the value of e1 unchanged but increase the SD of e7 from 10 (as in Table 18) to 15 (with mean unchanged). Again, we see again estimates that are increasingly biased but the signs of both βs and βsa remain the same as those in Table 18.
-
In Table 21, we keep the SD and mean of e7 unchanged but reduce the SD of e1 from 10 to 1 (with mean unchanged). The results are consistent with those in Table 20.
-
In Table 22, when we still keep the mean and SD of e7 unchanged, but increase the SD of e1 from 10 to 15 (with the mean unchanged). As expected, the results are consistent with those in Table 19.
-
In Table 23, we keep the mean and SD of e1 unchanged but increase the mean of e7 from mean = 0 (as in Table 18) to 10 (with SD unchanged). We see the estimates of βs are increasingly biased; in fact, the signs for βs have reversed from those of Table 18. Interestingly, there is very little bias in the estimates of the moderating effect of the alliance, A (i.e. in the estimates of βsa).
-
In Table 24, we keep the mean and SD of e7 unchanged but increase the mean of e1 from 0 to 10 (leaving its SD unchanged). We see that the signs of the estimates are the same as those in Table 18 but estimates of both βs and βsa are more biased than those of Table 23.
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | 0.31 | 3.96 | –0.19 | 15.72 | 95.6 | –5.40 | 1.65 | –5.90 | 37.53 | 6.2 |
| βsa | –3.00 | –2.96 | 1.24 | 0.04 | 1.54 | 95.8 | –0.04 | 0.44 | 2.96 | 8.93 | 0.0 | |
| SL + IP | βs | +0.50 | 0.47 | 3.87 | –0.03 | 14.99 | 96.1 | –5.13 | 2.17 | –5.63 | 36.38 | 26.5 |
| βsa | –3.00 | –2.99 | 1.19 | 0.01 | 1.42 | 96.3 | –0.12 | 0.64 | 2.88 | 8.69 | 0.5 | |
| SL + ME + PP | βs | +0.50 | 0.54 | 2.91 | 0.04 | 8.48 | 96.1 | –1.50 | 1.71 | –2.00 | 6.92 | 76.6 |
| βsa | –3.00 | –3.03 | 0.88 | –0.03 | 0.77 | 95.8 | –1.38 | 0.46 | 1.62 | 2.83 | 7.2 | |
| SL + PP | βs | +0.50 | 0.41 | 2.80 | –0.09 | 7.87 | 95.7 | 4.32 | 2.30 | 3.82 | 19.90 | 64.1 |
| βsa | –3.00 | –2.97 | 0.86 | 0.03 | 0.73 | 95.9 | –3.24 | 0.70 | –0.24 | 0.55 | 94.2 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | –20.2 | 2.99 | –20.7 | 436.4 | 0.00 | –8.06 | 1.49 | –8.56 | 75.53 | 0.0 |
| βsa | –3.00 | 3.75 | 0.92 | 6.75 | 46.37 | 0.00 | 0.88 | 0.42 | 3.88 | 15.22 | 0.0 | |
| SL + IP | βs | +0.50 | –20.2 | 2.92 | –20.7 | 438.3 | 0.0 | –10.9 | 1.96 | –11.4 | 134.1 | 0.0 |
| βsa | –3.00 | 3.77 | 0.88 | 6.77 | 46.66 | 0.0 | 1.79 | 0.59 | 4.79 | 23.32 | 0.0 | |
| SL + ME + PP | βs | +0.50 | –20.1 | 2.36 | –20.6 | 431.8 | 0.0 | –6.84 | 1.57 | –7.34 | 56.28 | 0.2 |
| βsa | –3.00 | 3.75 | 0.71 | 6.75 | 46.05 | 0.0 | 0.46 | 0.43 | 3.46 | 12.15 | 0.0 | |
| SL + PP | βs | +0.50 | –20.2 | 2.25 | –20.7 | 433.8 | 0.0 | –8.79 | 2.050 | –9.29 | 90.6 | 0.4 |
| βsa | –3.00 | 3.77 | 0.67 | 6.77 | 46.32 | 0.0 | 1.10 | 0.62 | 4.10 | 17.21 | 0.0 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | 20.65 | 5.19 | 20.15 | 432.9 | 1.4 | –2.46 | 1.85 | –2.96 | 12.19 | 73.3 |
| βsa | –3.00 | –9.61 | 1.63 | –6.61 | 46.40 | 0.8 | –1.06 | 0.47 | 1.94 | 3.99 | 4.4 | |
| SL + IP | βs | +0.50 | 20.86 | 4.80 | 20.36 | 437.6 | 0.6 | 1.09 | 2.41 | 0.59 | 6.17 | 97.3 |
| βsa | –3.00 | –9.66 | 1.48 | –6.66 | 46.57 | 0.5 | –2.18 | 0.70 | 0.82 | 1.16 | 86.1 | |
| SL + ME + PP | βs | +0.50 | 17.30 | 3.52 | 16.80 | 294.5 | 0.1 | 3.56 | 1.88 | 3.06 | 12.9 | 68.8 |
| βsa | –3.00 | –8.51 | 1.06 | –5.51 | 31.53 | 0.0 | –3.12 | 0.50 | –0.12 | 0.26 | 96.6 | |
| SL + PP | βs | +0.50 | 17.16 | 3.18 | 16.66 | 287.6 | 0.0 | 15.77 | 2.52 | 15.27 | 239.6 | 0.0 |
| βsa | –3.00 | –8.45 | 0.97 | –5.45 | 30.67 | 0.0 | –7.04 | 0.75 | –4.04 | 16.87 | 0.0 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | 22.7 | 4.03 | 22.18 | 508.00 | 0.0 | –1.86 | 0.94 | –2.36 | 6.45 | 55.9 |
| βsa | –3.00 | –10.4 | 1.31 | –7.39 | 56.38 | 0.0 | –2.21 | 0.21 | 0.79 | 0.67 | 36.3 | |
| SL + IP | βs | +0.50 | 22.9 | 3.20 | 22.41 | 512.26 | 0.0 | 6.40 | 1.15 | 5.90 | 36.13 | 1.2 |
| βsa | –3.00 | –10.5 | 1.03 | –7.47 | 56.82 | 0.0 | –4.96 | 0.32 | –1.96 | 3.92 | 0.1 | |
| SL + ME + PP | βs | +0.50 | 20.7 | 2.64 | 20.21 | 415.26 | 0.0 | 0.60 | 1.05 | 0.10 | 1.10 | 98.3 |
| βsa | –3.00 | –9.8 | 0.84 | –6.75 | 46.28 | 0.0 | –3.03 | 0.27 | –0.03 | 0.08 | 99.7 | |
| SL + PP | βs | +0.50 | 20.6 | 2.19 | 20.12 | 409.69 | 0.0 | 14.85 | 1.61 | 14.35 | 208.5 | 0.0 |
| βsa | –3.00 | –9.7 | 0.69 | –6.71 | 45.50 | 0.0 | –7.77 | 0.49 | –4.77 | 23.03 | 0.0 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | –19.00 | 4.39 | –19.50 | 399.84 | 0.6 | –8.09 | 2.08 | –8.59 | 78.15 | 1.9 |
| βsa | –3.00 | 3.21 | 1.31 | 6.21 | 40.27 | 0.1 | 1.71 | 0.54 | 4.71 | 22.49 | 0.0 | |
| SL + IP | βs | +0.50 | –18.80 | 4.37 | –19.30 | 391.28 | 0.9 | –12.8 | 2.63 | –13.3.0 | 184.90 | 0.2 |
| βsa | –3.00 | 3.16 | 1.28 | 6.16 | 39.59 | 0.4 | 3.18 | 0.74 | 6.18 | 38.68 | 0.0 | |
| SL + ME + PP | βs | +0.50 | –16.80 | 3.48 | –17.30 | 311.33 | 0.0 | –2.76 | 2.11 | –3.26 | 15.07 | 61.0 |
| βsa | –3.00 | 2.52 | 1.0 | 5.52 | 31.49 | 0.0 | –0.16 | 0.55 | 2.84 | 8.34 | 0.0 | |
| SL + PP | βs | +0.50 | –17.00 | 3.42 | –17.50 | 316.76 | 0.0 | –2.06 | 2.78 | –2.56 | 14.27 | 83.3 |
| βsa | –3.00 | 2.58 | 0.99 | 5.58 | 32.14 | 0.0 | –0.37 | 0.81 | 2.63 | 7.59 | 10.0 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | –12.00 | 4.46 | –12.50 | 176.90 | 22.8 | –17.30 | 1.81 | –17.80 | 318.7.0 | 0.0 |
| βsa | –3.00 | –3.05 | 1.37 | –0.05 | 1.87 | 95.3 | –0.06 | 0.47 | 2.94 | 8.88 | 0.0 | |
| SL + IP | βs | +0.50 | –12.00 | 4.34 | –12.50 | 173.70 | 19.3 | –17.00 | 2.41 | –17.50 | 310.30 | 0.0 |
| βsa | –3.00 | –3.05 | 1.31 | –0.05 | 1.71 | 96.3 | –0.14 | 0.69 | 2.86 | 8.64 | 1.8 | |
| SL + ME + PP | βs | +0.50 | –10.90 | 3.31 | –11.40 | 140.80 | 7.4 | –11.30 | 1.90 | –11.80 | 143.40 | 0.0 |
| βsa | –3.00 | –2.97 | 0.95 | 0.03 | 0.91 | 95.4 | –1.63 | 0.49 | 1.37 | 2.12 | 21.7 | |
| SL + PP | βs | +0.50 | –11.10 | 3.17 | –11.60 | 143.9 | 5.4 | –4.10 | 2.59 | –4.60 | 27.40 | 60.0 |
| βsa | –3.00 | –2.90 | 0.91 | 0.10 | 0.84 | 95.5 | –3.82 | 0.74 | –0.82 | 1.22 | 81.4 | |
| Simulation scenario | Parameter | True value | IV(2SLS) | OLS(TR) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Bias | MSE | Coverage (%) | Mean | SD | Bias | MSE | Coverage (%) | |||
| SL + ME + IP | βs | +0.50 | 14.30 | 3.98 | 13.80 | 206.30 | 4.7 | 4.52 | 1.57 | 4.02 | 18.62 | 31.7 |
| βsa | –3.00 | –3.59 | 1.11 | –0.59 | 1.59 | 91.8 | –0.24 | 0.38 | 2.76 | 7.78 | 0.0 | |
| SL + IP | βs | +0.50 | 14.50 | 3.73 | 14.00 | 209.80 | 3.1 | 5.52 | 2.08 | 5.02 | 29.51 | 34.3 |
| βsa | –3.00 | –3.64 | 1.03 | –0.64 | 1.48 | 92.2 | –0.52 | 0.56 | 2.48 | 6.47 | 0.8 | |
| SL + ME + PP | βs | +0.50 | 13.39 | 2.75 | 12.89 | 173.70 | 0.4 | 7.46 | 1.62 | 6.96 | 51.06 | 0.9 |
| βsa | –3.00 | –3.68 | 0.76 | –0.68 | 1.05 | 87.0 | –1.40 | 0.41 | 1.60 | 2.74 | 3.1 | |
| SL + PP | βs | +0.50 | 13.30 | 2.54 | 12.80 | 170.30 | 0.1 | 14.07 | 2.21 | 13.57 | 189.00 | 0.0 |
| βsa | –3.00 | –3.65 | 0.72 | –0.65 | 0.94 | 87.1 | –3.34 | 0.62 | –0.34 | 0.50 | 92.6 | |
The results presented in Tables 19–24 show that when e1 and e7 have different distributions (i.e. when either their SDs or their means differ) the estimates for our S + S × A model are hugely biased.
Stata do file
The following base program (in Stata) for these simulations is based on that of Dunn and Bentall. 14
Glossary
- Assumptions
- The a priori beliefs about the data or experimental set-up that are a prerequisite for valid statistical testing and therapeutic-effect estimation.
- Average treatment effect
- The average (mean) of the individual treatment effects for all of the clients recruited to a given clinical trial (or from everyone in the population from which one wishes to infer effects of the therapeutic intervention).
- Average treatment effect for the treated
- The average (mean) of the individual treatment effects for all of the clients recruited to a given clinical trial who actually received the treatment. There is no reason to believe that this average will be the same as the average treatment effect in the untreated population. Clients who turn up and adhere to their therapy, for example, might do so because they correctly believe that it will work. Those who drop out may know that, for them, it is unlikely to be beneficial.
- Baseline variables (covariates)
- Information such as initial values for subsequent outcome measures or demographic information (e.g. age, gender, etc.) collected and recorded on a client at the time of the recruitment to the trial (ideally just before randomisation). The data are frequently collected because they have prognostic value and can be incorporated into an analysis in order to increase the precision of the therapeutic effect estimates. They may also be useful to examine which type of client might benefit most from the therapy (see Moderation) or non-compliance with allocated therapy, and so on. Common examples include the client’s age, gender, education, family circumstances and clinical history, and the baseline values of variables that are going to be used to measure the outcome of therapy (severity of depression and other symptoms).
- Clustering
- The lack of independence of participants’ outcomes. This between-participant correlation is induced either by the method of treatment allocation (such as in a cluster randomised trial) or by the method of delivery of the therapy (individual therapists being responsible for the treatment of several clients; therapy being delivered in groups).
- Complier-average causal effect
- The average treatment effect in those clients (in a given trial) who comply with their actual treatment allocation and would have complied had they been allocated to any of the other treatment conditions. The intention-to-treat estimate is an unbiased estimate of the effect of treatment allocation (effectiveness) but is typically a biased (attenuated) estimate of the effect of actually receiving treatment (efficacy). This attenuation is increased as the amount of non-compliance increases. One way of adjusting for non-compliance in a simple two-arm trial (therapy vs. control) is to divide the intention-to-treat estimate of the effect of allocation on outcome by the corresponding intention-to-treat effect of allocation on the receipt of treatment (i.e. the difference between the proportions receiving therapy in the two randomised groups).
- Confounding
- The ability to attribute an apparent effect of an intervention (e.g. therapy) to an omitted common cause. When a client decides to seek counselling or psychotherapy the decision may be in some way related to treatment-free prognosis. A general practitioner may refer a depressed patient to cognitive–behavioural therapy because he or she appears to have particular chronic problems and are not responding to antidepressants. Clients receiving counselling or psychotherapy might or might not have had a worse treatment-free outcome. If we wish to estimate and/or test the causal effect of therapy (treatment effect), then we need to eliminate confounding. It is possible that we can measure some of these omitted common causes and allow for them in our statistical analyses, but the only sure way of being confident that their effects have been eliminated is to randomise treatment allocation, as done in a randomised controlled trial. The great advantage of randomisation is that it ensures (on average, at least) that we have accounted for all confounders (omitted causes) even if we have not measured them or are not even aware of their existence.
- Correlation and causation
- The relation between two variables and whether or not a change in one is the reason for a change in the other. If we observe a correlation then something must have caused it. The big problem is to decide what. If we observe, for example, that the strength of the therapeutic alliance during therapy is positively correlated with improvement in clinical outcome, it is very tempting to infer that it is the good alliance that has led to the better outcomes. However, it is not as simple as that. It could be that very early improvements in clinical outcome enabled the client to develop a strong therapeutic relationship, that is the causal influence is actually the other way round. The timing of the measurements may go some way to solve this problem (temporal precedence is important for inferences concerning causality) but very rarely in a fully satisfactory way. The third possibility (and it may even be a combination of all three) is that there is confounding. Clients with a good treatment-free prognosis (their clinical improvement will be relatively better even if they do not receive therapy) may be the ones who are able to develop a strong therapeutic alliance. For the same reason, it is likely that they will have a better outcome under treatment. The common procedure of taking a cohort of treated clients (either a case series or those in the therapy arm of a clinical trial), simply correlating the outcome of therapy with the strength of the therapeutic alliance and then inferring that there is a causal influence of alliance on outcome is fundamentally flawed. This procedure, in particular, cannot distinguish the phenomenon we are looking for (the relationship of the alliance with a treatment effect) from that resulting from an omitted common cause (therapy-free prognosis).
- Dose–response relationship
- The way in which a treatment effect changes with the dose of treatment, for example the concentration of drug in the blood. In a psychotherapy trial, we may be interested in the effect of the number of sessions attended or perhaps the overall duration of therapy. The different doses of drugs or psychotherapies may be determined by the random allocation procedure or may be simply a reflection of the level of patience adherence to the prescribed medication or psychotherapeutic intervention. In the latter case (the level of patience adherence to the prescribed medication or psychotherapeutic intervention), the estimation of a dose–response relationship is by no means straightforward (it may be subject to confounding). Dose–response relationships in a psychotherapy trial are much less straightforward. It is not always clear how dose of therapy might be measured; it may be a function of the prescribed (allocated) number of sessions, the number of therapy sessions actually attended, or the quality or intensity of the therapeutic process (quality of the therapeutic alliance or fidelity of the sessions to a given therapeutic model). This is an extremely challenging area; none of these characteristics can be measured without error and their effects on outcome are almost certainly subject to hidden confounding. It is usually best to assume that virtually all simple, naive analyses will be invalid and the corresponding conclusions unfounded.
- Effectiveness
- The effect of being offered (allocated to) treatment.
- Efficacy
- The effect of receiving treatment.
- Explanatory analysis
- Usually a secondary analysis (in addition to the primary intention-to-treat analyses, not instead of them) in which one tries to explain how a given therapeutic effect has been achieved or, alternatively, why the therapy is apparently ineffective. Such analyses may aim to evaluate treatment effect by client characteristic interactions (such as a subgroup analysis or treatment effect moderation), estimation of efficacy and dose–response relationships (particularly the effects of non-compliance), and the intervening effects of process measures such as the therapeutic alliance and treatment fidelity. It will frequently also involve the evaluation of the role of putative mediators. All these areas are fraught with difficulties. Subgroup analyses might easily find differences arising by chance (particularly if they are the result of a so-called ‘fishing expedition’). Process variables (including mediators) are subject to considerable measurement error and their effects on outcome subject to hidden confounding. It is usually best to assume that virtually all simple, naive analyses will be invalid and the corresponding conclusions unfounded.
- Group-based therapies
- Therapies that are delivered to groups of clients rather than to individuals. Outcomes for clients within these groups are likely to be correlated (i.e. not statistically independent). The behaviour or outcome of one client may influence that of another in the group, particularly if the group contains unco-operative or disruptive individuals), so violating one of the assumptions underlying the use of the simpler traditional significance tests and estimation procedures. Technically, the problems may be a little more difficult than in a traditional cluster-randomised trial because we may be comparing a group therapy (clustered) with treatment as usual (not clustered) or even a therapy (potentially the same one) delivered to individuals (again, not clustered).
- Hidden confounding
- Confounding in which we have not measured all of the relevant confounders (or even been aware of their existence) and therefore cannot allow for them in our statistical analyses.
- Individual treatment effect
- The comparison of a particular individual’s outcome after receiving therapy with the outcome for that same individual had he or she received the control condition. Without a comparison a treatment effect is not defined. Of course, an individual treatment effect can never be observed or measured. Our only hope is to use statistical methods to estimate what it might be in groups of similar individuals.
- Intention-to-treat analysis
- Analysis of participants as randomised, that is an analysis that estimates and tests the effect of the treatment assignment as determined by random allocation and not by the effect of the treatment that was actually received. It estimates the effect of the offer of treatment (effectiveness) as opposed to the receipt of treatment (efficacy). This is the gold standard for the analysis of the results of clinical trials, primarily because it answers the pragmatic question: is there convincing evidence that it is worth offering this intervention in clinical practice? It is also an estimation procedure that is dependent upon the fewest unverifiable assumptions (concerning lack of confounding), is open to fewest abuses during the analysis phase of trials and, accordingly, is the one preferred by regulatory authorities. In practice, it is not always straightforward to implement, as there will almost always be trial participants in whom outcome data cannot be obtained, but the aim should be that the analysed population is as close as possible to the intention-to-treat population.
- Mediation
- An intermediate outcome of therapy (a process variable) that, in turn, leads to changes in the clinical outcome. A cognitive therapist, for example, may have a strong a priori conceptual model that states that if the therapy is able to change a client’s beliefs (attributions) concerning his or her depression, for example, then changes in these beliefs will lead to improvements in the client’s symptoms of depression. Similarly, changes in levels of worry may lead to lower levels of psychotic symptoms in patients suffering from delusions. In these two examples, the putative mediators are attributions and levels of worry, respectively. The effect of the therapy on the clinical outcomes (depression or severity of delusions, respectively) is said to be mediated by the effects of the more immediate outcomes of the intervention (attributions or worry). A third example arises in a situation in which mediation, itself, is not the prime interest. In randomised trials of cognitive therapy for depression, for example, we might observe that it is likely that clients will adhere better to their antidepressant medication (such medication is not usually prohibited by the trials protocol, particularly in a pragmatic trial) or even ask to be prescribed medication by their doctor. The obvious question that then follows is ‘How much of the therapeutic effect of the cognitive therapy is explained by the changes in medication?’. Is there a direct effect of therapy on outcome (depression) that is not explained by the increased levels of medication? Despite the vast literature on mediation in psychology, there is very little valid evidence concerning meditational mechanisms in psychotherapy (or elsewhere, for that matter) because naive investigators consistently fail to distinguish inferences concerning association (correlation) from implications concerning causality. The putative mediator and the final clinical outcome are both therapeutic outcomes that are not under the control of the investigator. It is very likely that there are (hidden) common causes other than the therapy itself and therefore the effect of mediator on clinical outcome will be subject to (hidden) confounding. Standard potentially flawed methods of analysis of mediation are based on the almost universally unstated (and unappreciated) assumption that the effects of the supposed mediator are not subject to hidden confounding.
- Moderation
- Modification of a treatment effect by a stable patient characteristic measured prior to treatment allocation (or, if not, a characteristic that is convincingly not influenced by treatment allocation), that is, a source of treatment effect heterogeneity. What works for whom? It is usually demonstrated by a statistically significant treatment by patient characteristic interaction. Such a finding is much more convincing; it is one of very few such moderating effects specified in a prior data analysis plan. Post-hoc searches for moderators are notoriously unreliable and very rarely reveal anything other than the play of chance. What variables might be important moderators? Candidates include a history of child abuse, length of untreated illness, chronicity of the illness, and so on. Moderation is the foundation of so-called stratified medicine (personalised therapy) in which a patient’s or client’s characteristics predict his or her optimal therapy. Some patients might respond well to pharmacotherapy, for example, and others to a psychological intervention or counselling. Biological psychiatrists are convinced that the most important moderators (stratifying factors) will be genetic/genomic characteristics but, so far, there is little valid evidence to convince us that this is the case.
- Non-compliance (non-adherence)
- The situation in which a client receives a therapy or other form of intervention not exactly as intended by the trial’s allocation procedure. She or he may not turn up for the allocated therapy, for example, or may turn up for one or two sessions and then drop out of the trial. There should not necessarily be any inference concerning ‘delinquency’ on behalf of the client; the decision to drop or to switch treatments may be made by the client’s clinician in the interests of the client’s safety or health (she or he may be prescribed some sort of rescue medication, for example, or admitted to an inpatient unit if she or he has become suicidal or is a danger to others). Accordingly, ‘adherence’ is thought by many to be better than ‘compliance’ (it is a more ‘politically correct’ description). Consider a trial to compare inpatient admission and the use of outpatient care in patients who are newly diagnosed with severe psychotic symptoms. Many of the patients will receive the care to which they have been allocated. Several allocated to inpatient admission may never actually be admitted to hospital (because there are not enough available beds) and several of those allocated to outpatient day care may, in the end, have to be admitted because they have become severely disturbed and have become a danger to either themselves or others.
- Per-protocol analysis
- An analysis of a trial’s outcomes restricted to those participants who have been seen to adhere to the original protocol (received the intervention to which they were allocated). Frequently, randomised participants do not receive the treatment or therapy that they were allocated to (see Non-compliance). Those who do receive their allocated intervention have adhered to the trial’s protocol (i.e. per protocol). The results are potentially biased, as lack of adherence does not occur simply by chance and therefore this is very likely to be confounding.
- Potential outcomes
- The outcomes of all potential courses of action. Consider a depressed patient deciding whether or not to seek counselling or psychotherapy. Prior to the decision and seeking help (or not) there are two potential courses of action and associated outcomes. She or he can seek help (therapy), and the severity of her or his depression (e.g. Beck Depression Inventory score) can be measured after a given follow-up period (let us label this ‘Beck Depression Inventory after therapy’). The other potential course of action is not to seek therapy (let us call it the control condition) and, again, the severity of the patient’s depression can be measured after the same period of follow-up (‘Beck Depression Inventory after control’). Once a decision has been made (e.g. the patient receives therapy) then only one of these outcomes is observed (Beck Depression Inventory after therapy) and the other one becomes a counterfactual (what might have been). Although it is impossible to observe both of these potential outcomes for any individual, they do provide us with a very powerful way of defining individual treatment effects and associated average treatment effects.
- Predictive marker
- A biological measurement made before treatment to identify which patient is likely or unlikely to benefit from a particular treatment.
- Prognostic marker
- A biological measurement made before treatment to indicate long-term outcome for patients either untreated or receiving standard treatment.
- Regression to the mean
- The phenomenon whereby clients, particularly when they have been recruited into a trial at a time of crisis, will improve even without any intervention (i.e. drift back to their own typical state). For this reason it is unwise to assess a therapeutic intervention by simply observing a cohort (case series) of clients who have all received the same treatment. The data from such a study cannot distinguish regression to the mean from an effect of the therapeutic intervention.
- Statistical interaction
- Tests for statistical interactions that involve a comparison of the average treatment effect in, say, one subgroup of participants, with the average treatment effect in another. They are used in subgroup analysis and in the evaluation of moderation of treatment effects.
- Stratified medicine
- The identification and development of treatments that are effective for particular groups or subgroups of patients with distinct mechanisms of disease, or particular responses to treatments. It aims to ensure that the right patient gets the right treatment at the right time. The key underlying concept is treatment effect heterogeneity, and the search for patient characteristics (predictive markers identified through a statistical interaction) that will explain this heterogeneity and will be useful in subsequent treatment choice. Stratified medicine is also commonly referred to as personalised therapy, personalised medicine, predictive medicine, genomic medicine and pharmacogenomics, and, more recently, precision medicine.
- Structural equation modelling
- Statistical models used to evaluate whether or not theoretical models are plausible when compared with observed data. Structural equation models are very general, and include common methods such as confirmatory factor analysis, path analysis and latent growth modelling.
- Therapeutic alliance
- A measure of the strength of the working partnership between therapist and client. It is claimed to be a vital ingredient of all successful therapy, irrespective of the theoretical underpinnings of any given therapeutic approach.
- Therapist effect
- Differences in the ability of therapists to successfully treat clients all other things being equal. This might be (and is) of interest in its own right but it will also have possible implications for the design and analysis of a trial in which they deliver therapy.
- Treatment effect estimate
- The comparison between the average outcomes under one treatment condition and the average outcomes under another, conditional on the belief that allocation of participants to the alternative treatment conditions is not confounded, that is, that treatment allocation is essentially random. Comparison of the outcomes under different conditions is the vital ingredient; a treatment effect cannot be estimated validly by simply observing the outcome of a single cohort (case series) of clients receiving a given therapy.
- Treatment effect heterogeneity
- Variation in treatment effects from one individual to another or from one group of similar individuals to another. The treatment effect may differ between those who choose to seek treatment and those who do not, or between participants who comply with their allocated treatment in a randomised trial and those who do not. This is the basis for the increasingly important area (in cancer treatment development, for example, but equally in psychotherapy and counselling) of personalised or stratified medicine, that is investigating what treatments work for whom.
- Treatment fidelity
- The extent to which therapy, as delivered, is the same as that prescribed, for example in the treatment manual. How closely, for example, does therapy conform to the procedures specified by a given form of cognitive–behavioural therapy? It is frequently assessed within a therapy trial by audio- or video-taping a sample of therapy sessions.
- Treatment received analysis
- In a trial in which there has been treatment switching or non-adherence to the allocated treatments, analysis of the results in terms of the treatment(s) actually received rather than those to which the client was allocated. The method is potentially flawed (subject to confounding) and the results potentially biased. It is sometimes referred to as an as-treated analysis.
List of abbreviations
- 2SLS
- two-stage least squares
- ATE
- average treatment effect
- B&K
- Baron and Kenny
- BDI
- Beck Depression Inventory
- BS-EME
- biomarker-stratified Efficacy and Mechanism Evaluation
- CACE
- complier-average causal effect
- CALPAS
- California Therapeutic Alliance Scales
- CBT
- cognitive–behavioural therapy
- CBTp
- cognitive–behavioural therapy for psychosis
- CI
- confidence interval
- EM
- expectation and maximisation
- EME
- Efficacy and Mechanism Evaluation
- GMM
- growth mixture model
- HIV
- human immunodeficiency virus
- ITT
- intention to treat
- IV
- instrumental variable
- JTC
- jumping to conclusions
- LI
- latently ignorable
- logDUP
- logarithm of the duration of untreated psychosis
- MAR
- missing at random
- MHRN
- Mental Health Research Network
- MIDAS
- Motivational Interviewing for Drug and Alcohol misuse in Schizophrenia
- MRC
- Medical Research Council
- MSE
- mean square error
- NIHR
- National Institute for Health Research
- OLS
- ordinary least squares
- PACT
- Pre-school Autism Communication Trial
- PANSS
- Positive and Negative Syndromes Schedule
- PROSPECT
- Prevention of Suicide in Primary Care Elderly: Collaborative Trial
- PRP
- Prevention of Relapse in Psychosis
- PSA
- parent synchronous act
- RCT
- randomised controlled trial
- SC
- supportive counselling
- SE
- standard error
- SEM
- structural equation modelling
- SoCRATES
- Study of Cognitive Realignment Therapy in Early Schizophrenia
- SMM(G)
- G-estimation for structural mean models
- TAU
- treatment as usual
- TI
- targeted intervention
- WIT
- Worry Intervention Trial