Notes
Article history
The research reported in this issue of the journal was funded by the HTA programme as project number 10/55/01. The contractual start date was in August 2011. The draft report began editorial review in August 2015 and was accepted for publication in May 2016. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HTA editors and publisher have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the draft document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
Kate Tilling has received non-financial support from the Multiple Sclerosis (MS) Trust during the conduct of the study, and had her expenses paid by the MS Trust to attend meetings of the UK MS risk-sharing scheme (RSS) scientific advisory group in order to outline the plan for these analyses. Michael Lawton has had his expenses paid by the MS Trust to attend meetings of the UK MS RSS scientific advisory group in order to outline the plan for these analyses, and also his travel and accommodation expenses for visiting Vancouver to analyse the British Columbia MS data set. Neil Robertson has received travel grants and honoraria from Biogen, Novartis, Serono, Sanofi, Genzyme and Bayer and holds grants for unrelated work from Genzyme and Novartis. Helen Tremlett is funded by the MS Society of Canada (Don Paty Career Development Award), Michael Smith Foundation for Health Research and is the Canada Research Chair for Neuroepidemiology and MS. She has received research support from the National MS Society, the Canadian Institutes of Health Research and the UK MS Trust; and speaker honoraria and/or travel expenses to attend conferences from the Consortium of MS Centres (2013), the National MS Society (2012, 2014), Bayer Pharmaceuticals (2010), Teva Pharmaceuticals (2011), European Committee for Treatment and Research in MS (2011, 2012, 2013 and 2014), UK MS Trust (2011), the Chesapeake Health Education Program, US Veterans Affairs (2012), Novartis Canada (2012), Biogen Idec (2014) and the American Academy of Neurology (2013, 2014 and 2015). Unless otherwise stated, all speaker honoraria are either donated to a MS charity or to an unrestricted grant for use by her research group. Yoav Ben-Shlomo has had his expenses paid by the MS Trust to attend meetings of the UK MS RSS Scientific Advisory Group in order to outline the plan for these analyses, and has a relative with MS who is currently on treatment for the disease. He is a member of the UK MS RSS Scientific Advisory Group.
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2016. This work was produced by Tilling et al. under the terms of a commissioning contract issued by the Secretary of State for Health. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
Chapter 1 Background
Multiple sclerosis (MS) is a chronic inflammatory and neurodegenerative disorder in which clinical features, including presentation, disease course and rates of accumulation of neurological disability, demonstrate high degrees of individual variation. Consequently, predicting progression in MS and providing a realistic prognosis to patients, and those affected by MS, is challenging. Better prognostic indicators or models are needed to facilitate this process. The majority of patients (≈85%) will present with a relapsing–remitting (RR) disease course, typified by acute relapses (‘attacks’) followed by periods of remission (recovery). 1 Over time, relapsing–remitting multiple sclerosis (RRMS) can convert to secondary-progressive multiple sclerosis (SPMS), which is associated with a progressive course (gradual worsening) with or without superimposed relapses. 1 Currently, there is no known cure for MS, although disease-modifying therapies (DMTs) have shown partial efficacy in relatively short-term clinical trials (typically with 2 years’ follow-up);2–5 however, the impact of these drugs on longer-term outcomes, such as accrual of disability, is unknown. Patients with MS develop increasing functional limitations and reduced quality of life, although the overly pessimistic prognosis, initially based on selected earlier series, is being increasingly challenged by well-validated longitudinal studies with representative samples. 6,7 Further details on the London, Ontario, cohort, which represents one of these earlier selected series, are outlined below (see MS treatment). In addition, details on two well-validated longitudinal studies that constitute our natural history cohorts used here [The University of Wales Multiple Sclerosis (UoWMS) cohort and the British Columbia Multiple Sclerosis (BCMS) cohort] are outlined in Chapter 3, Sections University of Wales Multiple Sclerosis cohort and British Columbia Multiple Sclerosis cohort.
Multiple sclerosis treatment
There is no cure for MS, but treatments are available and generally fall into four categories, with currently the first two categories being available only to those with RR onset MS:
-
drugs that aim to modify the disease process (DMTs)
-
corticosteroids to accelerate recovery from a relapse
-
symptomatic drug treatment, to help ease symptoms of MS
-
other non-pharmacological therapies and general support to minimise the impact of disability.
The DMTs are also known as ‘immunomodulatory agents’ and are currently licensed only for patients with relapsing-onset MS (RR or SPMS). In 2002, there were four licensed DMTs: two forms of interferon beta-1a [Avonex® (Biogen Idec Ltd) and Rebif® (Merck Serono Ltd), with high- and low-dose formulations available, 44 µg and 22 µg, respectively], one form of interferon beta-1b [Betaferon® (Bayer Plc)] and glatiramer acetate [Copaxone® (Teva UK Ltd)] (first generation of this drug). At that time, the UK’s National Institute for Health and Care Excellence appraised the evidence for cost-effectiveness of these DMTs and concluded that these drugs were not cost-effective over a 10- or 15-year period. 8 However, it also concluded that, because the relevant clinical trials were based on only short-term outcomes, there was not enough information to assess the longer-term implications of these DMTs. To try to address these concerns, the UK MS risk-sharing scheme (UK MS RSS) was established in 2002. 9,10 Under the scheme, the UK’s Department of Health agreed to pay for the DMTs (see UK multiple sclerosis risk-sharing scheme cohort), conditional on treated patients being included in a 10-year monitoring study aiming to assess progression of the disease. The monitoring study aimed to compare progression of MS within this treated group of patients with progression in an untreated cohort. Initially, a cohort of untreated patients from London, Ontario, Canada, were selected [a subset of 314 patients judged to have fulfilled the Association of British Neurologists (ABN) criteria, from the London, Ontario, cohort of 1043 patients recruited between 1972 and 1984]. The first report from the UK MS RSS, based on the 2-year follow-up data, was unable to find evidence for the effectiveness of DMTs, but the authors were hesitant in drawing any firm conclusions because of methodological limitations. 9 The main concerns raised related to the use of the London, Ontario, cohort, which only permitted patients to have stable or deteriorated disability scores; this is not what is observed in actual clinical practice, in which scores naturally fluctuate and can also improve. 11 This use of the London, Ontario, cohort forced a complex algorithm to be used in the analysis, creating an artificial ‘no-improvement’ rule. This caused multiple problems, resulting in uncertainty in the findings, with the sensitivity analysis revealing qualitatively different results from the main analysis (suggesting that the DMTs might actually have a beneficial effect). In addition, there were concerns about missing data and a simple best-case/worst-case approach was taken so that either disability scores were assumed to be unchanged at follow-up or a simple linear extrapolation was done. The authors highlighted these problems9 and suggested that future analyses should seek a different, more powerful cohort in which raw (observed) rather than smoothed and adjusted disability scores could be used. They also highlighted the possibility of exploring other analytical models to complement the Markov model that was used for that analysis. In addition, they noted that, given potential secular trends in the natural history of MS (e.g. an improvement in prognosis over calendar time, as a result of other treatments for MS being made available or better overall management of the disease), a more contemporary cohort would be preferable. However, there is little evidence of change in disability progression between 1975 and 1995,12 indicating that a historical cohort could potentially be used.
Outcomes in multiple sclerosis clinical trials and observational studies
Commonly used outcomes in MS studies include measures of relapse rate, magnetic resonance imaging metrics and disability measures, such as the Expanded Disability Status Scale (EDSS). 13 Relapses are typically defined as periods of worsening of neurological symptoms in terms of severity or duration (e.g. present for at least 24 hours), in the absence of fever or infection. Relapses can be subject to recall bias and have been shown to be sensitive to the placebo effect. 13 Disability is usually measured by a disease-specific scale, with the most commonly used being the EDSS,14 although others have been developed, such as the MS Functional Composite. 15 The EDSS score can range from 0 (normal neurological exam) to 10 (death due to MS), and the scale is shown in Table 1. The scale is ordinal, and was not designed for use as a cardinal scale; thus, changes of 1 point at lower levels on the scale do not equate to 1-point changes at higher scores. The MS Functional Composite15 was developed to overcome some of these problems, being a metric (rather than ordinal) scale, and includes a measure of cognitive function that is not directly captured by the EDSS. 16 However, it is more complex to administer than the EDSS, may not be any more sensitive to change, and is highly affected by visual/speech deficits and learning effects. 16 Therefore, the EDSS continues to be the tool of choice for measuring outcome in many MS clinical trials and observational studies, and was used in the original pivotal clinical trials of the DMTs; it is also the only outcome-measuring tool available for the UK MS RSS.
| Score | Description |
|---|---|
| 0 | No disability |
| 1 | No disability, minimal signs in one FS |
| 1.5 | No disability, minimal signs in more than one FS |
| 2 | Minimal disability in one FS |
| 2.5 | Mild disability in one FS or minimal disability in two FSs |
| 3 | Moderate disability in one FS, or mild disability in three or four FSs. No impairment to walking |
| 3.5 | Moderate disability in one FS and more than minimal disability in several others. No impairment to walking |
| 4 | Significant disability but self-sufficient and up and about some 12 hours a day. Able to walk without aid or rest for 500 m |
| 4.5 | Significant disability but up and about much of the day, able to work a full day, may otherwise have some limitation of full activity or require minimal assistance. Able to walk without aid or rest for 300 m |
| 5 | Disability severe enough to impair full daily activities and ability to work a full day without special provisions. Able to walk without aid or rest for 200 m |
| 5.5 | Disability severe enough to preclude full daily activities. Able to walk without aid or rest for 100 m |
| 6 | Requires a walking aid – cane, crutch, etc. – to walk about 100 m with or without resting |
| 6.5 | Requires two walking aids – pair of canes, crutches, etc. – to walk about 20 m without resting |
| 7 | Unable to walk beyond approximately 5 m, even with aid. Essentially restricted to wheelchair, although wheels self in standard wheelchair and transfers alone. Up and about in wheelchair some 12 hours a day |
| 7.5 | Unable to take more than a few steps. Restricted to wheelchair and may need aid in transferring. Can wheel self but cannot carry on in standard wheelchair for a full day and may require a motorised wheelchair |
| 8 | Essentially restricted to bed or chair or pushed in wheelchair. May be out of bed itself much of the day. Retains many self-care functions. Generally has effective use of arms |
| 8.5 | Essentially restricted to bed much of day. Has some effective use of arms retains some self-care functions |
| 9 | Confined to bed. Can still communicate and eat |
| 9.5 | Confined to bed and totally dependent. Unable to communicate effectively or eat/swallow |
| 10 | Death due to MS |
Methods in multiple sclerosis observational studies assessing disability progression
Studies of progression in MS tend to use survival analysis techniques to model outcomes over time, for example, examining time to a sustained and a confirmed EDSS score of 6 points (often chosen as it represents a ‘hard’ outcome and a turning point in the MS disease course, indicating that the individual can no longer walk without an aid, such as a cane or crutch) or age at which an EDSS score of 6 points is reached. 17 Such analyses have several disadvantages:
-
Outcome data are usually available only at discrete intervals (e.g. annually) and thus the exact time to the outcome may not be known.
-
The analysis cannot take into account further deterioration (or improvement) once the outcome is achieved.
-
The analysis cannot take into account the actual disability either before or after the outcome is achieved: a person with annual EDSS scores of 4, 4, 4 and 6 points would contribute the same information to the analysis as someone with annual EDSS scores of 1, 3, 5, 7 and 9 points, and yet clearly the progression of disease is very different in these two cases.
-
The method for dealing with missing data is unclear: for example, given a patient with annual scores of 1, 3, missing and 7 points or 6, 6, 7, 8 and 9 points (i.e. who had already reached the outcome of interest by their first assessment), in both cases the exact time to the outcome would be uncertain.
Alternatives have been suggested, including discrete Markov models18 and the construction of percentile charts. 19,20 Discrete Markov models can relate the probabilities of transitions between disease states to covariates, including baseline characteristics and time. Such models have been applied to the UK MS RSS cohort,9 but, at least in the 2-year analysis, which used the London, Ontario, comparator cohort, the models showed such sensitivity to missing data and model assumptions that firm conclusions could not be drawn. 9 One disadvantage of these discrete models is that the repeated measures need to be at similar (discrete) time intervals on all patients for common transition probabilities to be estimable. There are more complex ‘continuous’ Markov models, which can overcome this disadvantage. Percentile charts have been constructed for the development of EDSS score over time since diagnosis. 19,20 However, these were essentially cross-sectional in nature, being either empirical or smooth functions of the percentiles of EDSS score at each year post onset or post diagnosis, and thus do not always reflect how a given individual changes over time. For this method also, all patients are required to be assessed at the same, discrete time intervals. In addition, the relationship between these centiles and patient characteristics cannot easily be modelled.
Predictors of progression in multiple sclerosis
There is wide variation in disease trajectory between MS patients, with limited consensus over the factors affecting progression. 17 A systematic review of studies of MS disability progression (carried out in 2004–5) identified 27 published studies related to RRMS. 21 The prognostic factors identified were male sex (evidence mixed, but a suggestion of poorer prognosis for males), age at onset (all but one study related poorer prognosis to older age at onset), type of symptoms at onset (little evidence for any of the symptoms examined except for bowel/bladder involvement, which was associated with poorer prognosis), incomplete recovery from the first attack (consistently associated with poorer prognosis) and shorter interval between first and second attacks (consistently associated with poorer prognosis). 21 An examination of time to SPMS in the BCMS cohort also identified poorer prognosis for males and those with an older age at onset, and found no evidence of associations between onset symptoms and progression. 22
Summary
In the case of a disease whose median duration may be as long as 30–40 years from onset,23,24 with outcomes that vary greatly and are largely unpredictable, ranging from so-called ‘benign’ to ‘malignant’ disease, it is of considerable importance to be able to better predict long-term outcomes. This could potentially facilitate the prognosis given to patients as well as informing therapeutic and management choices made by clinicians and patients. This is particularly relevant when recent developments in therapeutics may allow significant impact on natural history but with costs in terms of associated adverse events. Patients and their carers increasingly request access to relevant prognostic information to help plan both professional and family life decisions, although this information is often not readily available.
Chapter 2 Objectives
The aims of this study were to explore the applicability of advanced multilevel models to longitudinal data on disease progression in patients with relapsing-onset MS, and to use such models to compare outcomes in cohorts of untreated and treated patients. The ultimate goal is to be able to better predict disease progression in relapsing-onset MS and to assess the impact of the current disease-modifying drugs for MS on progression.
Objectives
-
To develop and apply multilevel models to repeated measures (longitudinal) data on disease progression in patients with relapsing-onset MS (RR and secondary progressive) in the UoWMS and BCMS cohorts. This will allow us to determine average progression trajectory, individual deviations from the average and accuracy of prediction of individual trajectories.
-
To examine the impact of informative censoring using joint modelling of the EDSS trajectory and time to dropout and, if necessary, use multiple imputation methods as part of a sensitivity analysis.
-
To apply the multilevel model developed above to data from the UK MS RSS to estimate average progression trajectory, individual deviations from the average, difference between individual progression trajectories in the UK MS RSS and progression predicted by the BCMS model; and, thus, estimate the effect of the MS drugs on disability progression.
-
To apply patient-derived utilities to the differences in EDSS score as a result of DMTs and, thus, obtain an estimate of the value put on EDSS score-related progression associated with DMT by patients.
Chapter 3 Methods
The work in this chapter is reproduced under the Open Government Licence from Lawton et al. 25
Data sets
In this study, we have used data from two cohorts of patients with relapsing-onset MS to develop and validate models for the prediction of EDSS score. These cohorts are the UoWMS cohort and the BCMS cohort. We used data from a third cohort, the UK MS RSS, to examine the ability of the model for EDSS score to identify changes in progression in a treated (rather than natural history) cohort.
Data from the BCMS cohort can be analysed only in Canada. Therefore, we used the UoWMS cohort for initial exploratory analysis, before travelling to Canada to analyse the BCMS cohort and develop a natural history model independently using this large cohort. This BCMS model was validated on the UoWMS cohort (which is smaller). The BCMS model was then used as an untreated comparison arm for the UK MS RSS.
Patient eligibility and selection of the analysis data sets are presented below under each cohort heading, and in Eligibility.
University of Wales Multiple Sclerosis cohort
The University Hospital of Wales is the major tertiary referral centre for neurology in Wales, serving a local population of 1.2 million, and provides a network of MS clinics across south-east Wales. Approximately 1000 patient contacts are documented annually, and clinical data, including EDSS scores, are collected routinely at each clinic visit. The database currently has around 2000 registered MS patients, and has repeated EDSS score data on a large proportion of these patients. For example, at least two EDSS scores are available for 1283 patients and at least four EDSS scores are available for 809 patients. Sociodemographic and clinical features at disease onset are recorded in a standardised fashion, including degree of recovery and initial inter-relapse interval. Only patients with a valid onset date and a valid diagnosis date (i.e. both dates recorded in the database, and compatible with date of birth and date of first observation) were included in this analysis. In addition, if data for any patient were clearly inconsistent, for example any observations were dated before the date of disease onset, the patient was excluded from the analysis. This left 404 patients for analysis.
British Columbia Multiple Sclerosis cohort
The BCMS research group’s database7 is one of the world’s largest geographical and population-based natural history MS databases, capturing 80% of the BCMS population in the pre-MS drug era. British Columbia is a province on the west coast of Canada, with a population of around 4 million. As of 2009, the database contained records for over 5900 MS patients spanning 28 years (> 25,000 cumulative years) of prospective follow-up, from all four MS clinics in British Columbia. Strengths of the BCMS database included regular follow-up of patients, and consistent care provided by the same four core neurologists, who had treated over 85% of the patients considered for this study. The EDSS scores are recorded after a face-to-face consultation with an MS specialist neurologist. The BCMS database has already been used extensively in relation to research about the natural history of MS. 6,12,22,23 The BCMS database is housed in the Brain Research Centre, University of British Columbia, Vancouver, British Columbia, Canada; data analyses were conducted onsite for this study. Only patients with definite MS and a minimum of two EDSS scores recorded, at least 9 months apart were included in this analysis, giving a sample of 978 patients.
UK Multiple Sclerosis Risk-Sharing Scheme cohort
The UK MS RSS ensured that people who met the 2001 ABN criteria for treatment could be prescribed one of the four DMTs for MS (Avonex®, Betaferon®, Copaxone® or Rebif®) and included in a long-term monitoring study. 9 Between 2002 and 2005, 5583 patients were recruited to the scheme within 73 specialist centres across the UK. Data collected included each patient’s initial and then annual EDSS score.
Eligibility
In all cohorts, all patients with primary-progressive MS were excluded, as were any EDSS score observations before the age of 18 years. In the UK MS RSS cohort, only patients who had RRMS at baseline were included in this analysis, whereas in the BCMS and UoWMS cohorts, patients who had RRMS or SPMS at baseline were included.
Because the aim of the ‘natural history’ model is to act as a control for a DMT-treated population, we are interested only in patients who become eligible for treatment. Patients in both natural history cohorts (UoWMS and BCMS) were included in the modelling data sets if they ever became eligible for DMT according to the ABN criteria. Here, we defined a patient as satisfying the ABN criteria at the first point at which they were aged at least 18 years, had an EDSS score of ≤ 6.5 and had ≥ 2 relapses during the previous 2 years. 26 All EDSS score observations prior to ABN eligibility were removed from the data set, so we modelled the EDSS trajectory only post ABN eligibility. The EDSS score at ABN eligibility was thus considered the baseline measure for the purpose of this study.
Censoring
In the BCMS cohort, data on all patients were censored at the end of 1995, as this represented the last full year before DMTs were widely available in British Columbia (i.e. the DMTs were covered by the provincial government’s reimbursement scheme starting in 1996). However, 45 patients initiated DMT before the end of 1995, and their data were censored at the time of DMT initiation. In the UoWMS cohort, patients were censored at the first time point at which use of a DMT was recorded.
Patient characteristics
Characteristics considered for inclusion in our models were sex, age at symptom onset, MS disease course at ABN eligibility (RR vs. SPMS), initial symptoms, disease duration and number of relapses in the 2 years prior to ABN eligibility. At least two relapses in 2 years were required to satisfy the ABN eligibility criteria, so the number of relapses more than two (in the 2 years prior to ABN eligibility) was used when this variable was included as a covariate.
Relapses
A relapse was defined as worsening neurological symptoms lasting > 24 hours, in the absence of fever or infection. The starting date of each relapse was recorded by a MS specialist neurologist. Our focus was to model true accumulation of disability over time, and not to model the short-term disability that presents itself within a relapse. Consequently, all EDSS score assessments made within 1 month post relapse were removed from the BCMS and UoWMS cohorts. There is evidence that some patients may continue to improve in physical disability beyond the 1-month post-relapse window, although the majority of improvement in physical ability has been shown to occur by 2 months post relapse. 27 Nonetheless, we carried out sensitivity analyses by also removing all observations within 3 and 6 months of a documented relapse.
Modelling the natural history of multiple sclerosis in the Welsh and British Columbia cohorts
The EDSS scores on the same person measured over time are likely to be correlated. Therefore, we used multilevel models with two levels: measurement occasion (level 1) clustered within person (level 2). 28 These longitudinal methods have several advantages over approaches previously used: they take into account the correlation of observations within an individual; they use all available data (i.e. all available EDSS scores); time can be modelled continuously and thus all patients do not need to have measures at rigidly fixed intervals (which mimics well-patient visits in clinical practice) and important covariates can be included, such as age at disease onset and disease duration. In addition, patients with missing data should not bias the analysis, provided that data are missing at random. Furthermore, the impact of any data which are not missing at random (e.g. informative censoring) can be examined using extensions to this method (see objective 2). Although the usual multilevel models treat the EDSS score as a continuous variable, extensions to these methods could also consider transformations of the EDSS score, or model it as an ordinal outcome, if there was evidence of poor model fit.
We modelled the EDSS scores of individuals using repeated measure multilevel models. Our model had two levels: the level 2 unit was the individual and the level 1 unit was the observation. A simple multilevel repeated measure model is a linear random intercept and random slope model. This ‘random intercept, random slope’ model assumes that there is a linear change in the outcome (y) for the population, and the population average change is described by Equation 1. However, the model does not assume that every individual will follow that pattern of change exactly. Instead, each individual is allowed their own intercept (the ‘random intercept’), for which the individual intercepts are normally distributed around the population average. Similarly, each individual is allowed their own slope (the ‘random slope’), for which the individual slopes are normally distributed about the population average slope. In addition, the individual intercepts and slopes are allowed to be correlated, for example if people who have a lower intercept then progress faster, the model would allow a negative correlation between individual intercept and individual slope.
The random intercept, random slope model is detailed below:
where yij is the EDSS score for the ith individual on the jth time point and tij is the time variable for the ith individual’s jth time point.
where N2(0, D) is a multivariate normal distribution with degree 2, mean 0 and covariance matrix D, and N(0, σ2) is a univariate normal distribution, with mean 0 and variance σ2.
The uki (the ‘random intercept’ and ‘random slope’) are often referred to as the level 2 (individual-level) random effects and the eij as the level 1 (observation-level) random effects.
For all the following multilevel repeated measure models the following assumptions were made:
-
Individual-level random effects are correlated with each other (with freely estimated covariances), as are observation-level random effects.
-
The observation-level and individual-level random effects are uncorrelated with each other.
We explored different time axes (e.g. age, time since onset, time since ABN eligibility, etc.), using Akaike information criterion (AIC)29 and the variation of the differences between fitted and observed EDSS scores to identify the best-fitting model.
Individuals were (right) censored when a DMT was initiated to avoid a potential treatment-effect bias, although we recognised this was at the cost of introducing a potential indication bias [whereby DMT initiation may be triggered by changes (i.e. worsening) in disability (EDSS score)]. 30 We tested the model assumption that the patient-level and individual-level residuals are normally distributed, and if necessary would allow for non-normal random effects. 31
Average trajectory of Expanded Disability Status Scale score with time
We used fractional polynomials to identify the best-fitting trajectory of the EDSS scores – with the time variable identified as providing the best fit. This method compares fit among a family of flexible polynomial functions;32 we have used these methods to model nonlinear growth in multilevel models. 33,34
A fractional polynomial of degree n contains n different powers of the time variable. For notational purposes the power zero denotes the logarithmic transformation and a combination of two identical powers is interpreted as the product of the power and the logarithmic transformation. Hence a fractional polynomial in t (time) of degree 2 with powers = (1, 1) would include t and tlogt. In order to fit fractional polynomials, the time variable must be strictly positive (as it is impossible to take the logarithm of zero or a negative number). We also added 1 year to each time variable considered (i.e. recalibrated time such that the minimum value was 1) as in the range of 0 to 1 some of the fractional polynomials (in particular log and negative powers) can exhibit behaviour unlikely to fit data well.
Models with different degrees of fractional polynomials of time are compared using likelihood ratio tests. 35 The powers of time we will consider for comparing the fractional polynomials are –2, –1, –0.5, 0, 0.5, 1, 2 and 3. As well as considering likelihood ratio tests as a marker of model fit, we also looked at the root-mean-square error (RMSE) for the difference between predictions and observed values and also the proportion of predictions within ± 0.5 EDSS score points of the observed EDSS score.
In the model, for ease of interpretation, the same powers of time were used for the fixed effects and the patient-level random effects. Hence the following multilevel repeated measure model was considered:
where yij is the EDSS score for the ith individual on the jth time point and n is the degree of fractional polynomial. In addition, when k = 0, then r10 = 0; hence β0 is the mean intercept across individuals and u0i is the ith individual’s difference between their personal intercept and the mean intercept. The individual differences between their personal value for each polynomial function (including the intercept) and the average value (the uki) are normally distributed:
The occasion-level error terms (eij) are also normally distributed, and independent from the uki. To check whether or not outlying values were having an undue influence on choice of function of time, we carried out a sensitivity analysis on two restricted data sets. First, we restricted the data set by removing observations made at a time since onset of 30 years or more and, second, by removing observations made at a time since onset of 15 years or more.
Examining non-linearity of the Expanded Disability Status Scale
Having identified the best-fitting trajectory of the EDSS score with time, we examined the residuals from this model to see whether or not transformation of the EDSS scores was necessary. Linear multilevel models have been used to model the Barthel Score (for Activities of Daily Living) after stroke, and were robust to the non-normality and the discrete nature of this 20-point scale. 33,34 However, for some outcomes, transformation has been necessary: for example, prostate-specific antigen was log-transformed in order to normalise residuals. 36,37 Our a priori criterion for concluding that there was no need to transform the EDSS score or to consider alternative distributions for the residuals or alternative models (e.g. ordinal models) was that the residuals should be approximately normally distributed.
Including patient characteristics in the model
Characteristics initially considered were sex, age at symptom onset, disease duration at ABN eligibility and number of relapses in the 2 years prior to ABN eligibility. We related EDSS score and rate of EDSS score change to these characteristics (thus identifying characteristics that affected the rate of change and those that had a constant effect on the EDSS scores).
Complex measurement error
As with virtually any measurement scale, assessor variability or ‘measurement error’ can occur. It is possible that the measurement error in the EDSS will change across the scale, as it is thought that there is greater inter- and intrarater variability for EDSS score measurements at the lower end of the spectrum. 38,39 This would lead to a decrease in measurement error over time, and was checked empirically by plotting the level 1 residuals against time. If there was evidence of complex measurement error after choosing the best time axis and powers of time for the fixed effects and patient-level random effects the model was developed further by considering a more complex model for the level 1 random effects using fractional polynomials as described in the previous section. Powers of time used for the observation-level random effects (l) were allowed to differ from those used for the fixed effects and patient-level random effects (k). Thus, we considered the following model:
where:
and r20 = 0 (allowing for a constant level 1 variance), and the degree of fractional polynomial considered is m.
Thus, as before, the individual-level and occasion-level residuals are normally distributed and independent from each other.
Autocorrelation
Autocorrelation is when measures close in time on the same individual are correlated more than would be implied by the overall within-individual correlation. If present, this would invalidate the assumption that observation residuals within an individual are independent and identically distributed. We investigated autocorrelation by plotting each residual against the next residual in time within the same individual. A large correlation coefficient for the points in this plot can indicate a high level of autocorrelation.
The standard method for analysing whether or not autocorrelation is present would be to fit a model with and without autocorrelated level 1 residuals and then carry out a likelihood ratio test. However, with unbalanced data there is no simple method to fit a model with autocorrelation because the number of observations per person and the time between successive observations is not constant.
To remove any autocorrelation, we divided each individual’s time axis into quarter-year intervals. If there was more than one observation within that interval, a new observation was created by taking the median time and the median EDSS score of all the observations within that interval. This would remove observations that are close together in time.
Relapses
All EDSS score observations made within 1 month post relapse were removed from the BCMS and UoWMS cohorts (see Data sets, Relapses). Given that the exact duration of a relapse is difficult to measure, this 1-month window was explored via sensitivity analyses, whereby all EDSS score observations made within 3 or 6 months post onset of a relapse were removed (see Data sets, Relapses). We fitted a model to these data sets using the same functional form that was developed for our chosen model. The resulting two models were compared with the original model by looking at each parameter and its 95% confidence interval (CI). We considered the models similar if each parameter’s 95% CI overlapped with the original model’s parameter’s 95% CI. If the models were similar, we would consider the average disability (EDSS score) accumulation to be unaffected by our original decision to remove EDSS scores 1 month post relapse.
Censoring
Informative censoring can occur when the reason for a patient leaving the study is related to the EDSS score at the time of leaving the study. This could occur in several situations, for example when a patient was stable with mild disability and did not wish to attend, or alternatively, was unwell and found it difficult to physically attend the clinic. Censoring such observations can introduce bias into the prognostic models. Informative censoring was unlikely to be an issue with the BCMS cohort, as this was truncated at 1995 precisely in order to avoid this problem (see Data sets, Censoring). For the UoWMS cohort, informative censoring was investigated using joint modelling of the EDSS trajectory and time to dropout. 40 When convergence issues meant that such joint models were unable to be used, a binary indicator variable for whether or not the patient remained uncensored to the end of the study was included instead as a covariate in the model. This allowed investigation of whether or not patterns of EDSS score over time were different for those remaining in the study and those leaving it.
Missing data
The multilevel models are robust to data that are missing at random, that is when the reasons for the data being missing are contained in observed variables. 41 For example, if people who have a lower EDSS score at the 1-year follow-up are less likely to turn up to the 2-year follow-up, this would be missing at random, and would not bias the multilevel model. However, if those with a lower EDSS score at the time of the scheduled 2-year follow-up decide not to attend, this would be missing not at random, and would bias the models. The procedure described in Censoring (for censoring) will model this bias if patients drop out of the study altogether, but not if they just miss the 2-year follow-up but return for their 3-year follow-up, perhaps because their EDSS score has increased and they want to seek medical opinion.
Missing data in covariates could also bias the models, if the data were more likely to be missing for those with higher/lower EDSS scores; however, this seems unlikely, given that the data on baseline covariates were collected before the repeated EDSS scores. If data were missing based only on the model covariates (e.g. men were more likely to drop out than women), this would not bias the multilevel models. Imputation of baseline covariates in a multilevel model has to be done using specialist software,42 and, given that we had few missing data among the covariates and did not expect this to cause any bias, we carried out complete-case analyses.
Predicting Expanded Disability Status Scale for an individual
Once an EDSS trajectory model was fitted, we used previously developed multilevel methodology to predict future trajectory based on one or more observed EDSS scores (further details given below). 34,43 These methods have been applied to predicting outcome after stroke33 and to predicting longitudinal changes in prostate-specific antigen37 and prostate volume. 44 A major advantage of these methods is that only the model coefficients are needed to predict outcome for a different data set under that model. Thus, the model developed for the natural history of MS (using the BCMS cohort) can be applied to the UoWMS cohort, and the final model (developed using the BCMS cohort) can be applied to the UK MS RSS cohort, without data from the three cohorts ever having to be shared or merged.
Suppose that the chosen model includes two powers of time:
where yij is the EDSS score for the ith individual at the jth time point and tij is the time/age for the ith individual at the jth time point.
The between-individual variation of this growth curve at time t is given by:
The within-individual variation (i.e. the variation of an individual’s observed EDSS score about their individual predicted curve) at time t is given by:
If there is complex level 1 variation (see Complex measurement error), then the equation for the level 1 variation will be modified accordingly.
The variance of the individual curve from the predicted curve at t is given by:
where Vbt and Vwt are the between- and within-individual variances defined above.
The covariance between the predicted value for an individual at t1 and that at t2 is given by:
Suppose that we wish to predict outcome yit2 at any time point t2 given a previous observation of outcome yit1 measured at time t1. Let the predicted outcome (from the fixed part of the model) be fit1 and fit2 at times t1 and t2, respectively.
The regression coefficient for (yit2 – fit2) on (yit1 – fit1) is given by:
Thus, given observed outcome yit1 measured at time t1, and the values predicted (from the fixed coefficients) at times t1 and t2, the predicted outcome at time t2 can be predicted using only the random coefficients.
The standard error of the prediction is given by:
Model comparisons
The initial model developmental work used the UoWMS cohort to select the best time axis and the best-fitting function of that time axis. These models and findings then needed to be explored in an independent data set with greater power. 45 We repeated the above multilevel analysis in the BCMS cohort to validate the best-fitting model found in the UoWMS cohort.
Comparisons made between the BCMS and the UoWMS models were:
-
the powers of time selected
-
any transformations needed for the EDSS score
-
the functional form of the multilevel model, including the coefficients for the fixed and random effects
-
the predictive ability of the BCMS model to predict EDSS score values in the UoWMS cohort.
Confidence intervals
Confidence intervals were derived for the estimates of all analyses. The standard error of the predicted EDSS score was calculated using standard regression results (see Predicting Expanded Disability Status Scale for an individual).
Modelling the impact of disease-modifying therapy on disease progression in the UK Multiple Sclerosis Risk-Sharing Scheme
Multilevel modelling
A multilevel model, identical in form to that derived from the BCMS cohort, was fitted to the UK MS RSS data (including all data up to the 6-year data lock). This model includes all data from all eligible patients (even those with missing EDSS score data at the 6-year follow-up).
Estimating the Expanded Disability Status Scale score under the natural history model
The primary population consisted of all UK MS RSS participants with RRMS at baseline and at least one valid EDSS score value post baseline. The model for EDSS score developed using the BCMS natural history cohort (objectives 1 and 2) was applied to these data from the UK MS RSS cohort, to predict EDSS scores for these individuals under the assumption of no treatment. The predicted EDSS scores were then compared with their actual EDSS scores. An overall mean difference in EDSS score between observed and predicted EDSS score (together with its 95% CI, using bootstrap methods) was obtained and used to summarise the overall difference between EDSS score predicted under natural history and EDSS score observed in a treated cohort.
To apply patient-derived utilities to the Expanded Disability Status Scale score
Utility is a measure of society’s perception of the quality of life of a patient in a given state of health. A utility of 1 represents perfect health; a utility of 0.5 implies that on average people would regard 12 months of life in that health state as equally preferable to 6 months of life in perfect health. We derived our utility measures from EDSS scores using previous data that reported European Quality of Life-5 Dimensions scores for different EDSS states, on the advice of the MS Scientific Advisory Group. 46 We predicted the utility for the UK MS RSS cohort under the natural history assumption, by relating each predicted EDSS score to the appropriate utility (Table 2). We therefore calculated a difference between each individual’s utility on treatment (the utility derived from the observed EDSS score) and that assumed if that individual had not been treated (the utility derived from the EDSS score predicted from the natural history model). We calculated bootstrap-derived CIs (which do not assume normality) for the difference in EDSS scores and in utilities.
| EDSS score | Utility |
|---|---|
| 0 | 0.9248 |
| 1 or 1.5 | 0.7614 |
| 2 or 2.5 | 0.6741 |
| 3 or 3.5 | 0.5643 |
| 4 or 4.5 | 0.5643 |
| 5 or 5.5 | 0.4906 |
| 6 or 6.5 | 0.4453 |
| 7 or 7.5 | 0.2686 |
| 8 or 8.5 | 0.0076 |
| 9 or 9.5 | –0.2304 |
| 10 | 0 |
Statistical software
All computations were carried out using Stata software (StataCorp LP, College Station, TX, USA), and all multilevel models estimated using the runmlwin command.
Chapter 4 Results: modelling the natural history of multiple sclerosis
The work in this chapter is reproduced under the Open Government Licence from Lawton et al. 25
The natural history data sets
Table 3 shows the patient characteristics for the Welsh (UoWMS) and British Columbia (BCMS) natural history cohorts.
| Characteristic | Cohort | |
|---|---|---|
| BCMS (1980–95) | UoWMS (1976–2011) | |
| N | 978 | 404 |
| Females, n (%) | 728 (74.4) | 306 (75.7) |
| Age (years) at MS symptom onset, mean (SD); range | 29.1 (8.6); 3.4–61.1 | 31.1 (8.7); 13.4–60.0 |
| Age (years) at ABN eligibility, mean (SD); range | 37.3 (9.3); 18.1–70.0 | 38.6 (9.1); 18.8–80.1 |
| Disease duration (years from MS symptom onset) at ABN eligibility, mean (SD); range | 8.2 (6.9); 0.2–38.9 | 7.4 (7.1); 0.5–43.8 |
| SPMS at ABN eligibility, n (%) | 150 (15.3) | 83 (20.5) |
| Reached SPMS during study period, n (%) | 563 (57.6) | 139 (34.4) |
| Relapses in the 2 years prior to ABN eligibility, mean (SD); range | 2.85 (1.2); 2–9 | 3.45 (0.9); 2–9 |
| EDSS score at ABN eligibility, median (quartiles); range | 2 (1, 3.5); 0–6.5 | 3.5 (2, 4.5); 0–6.5 |
| Year of ABN eligible EDSS score, range | 1980–95 | 1976–2011 |
| Year of last EDSS score, range | 1981–95 | 1984–2011 |
| Number of EDSS scorea assessments, total; (mean per person); range | 7335 (7.5); 1–73 | 2290 (5.7); 1–72 |
| Prospective follow-up time (years), mean (SD); range | 5.8 (3.8); 0–15 | 2.88 (3.86); 0–29.3 |
| Prospectively followed, ≥ 5 years, n (%) | 560 (57.3) | 92 (22.8) |
| Prospectively followed, ≥ 10 years, n (%) | 159 (16.3) | 16 (4.0) |
| Ever prescribed a DMT, n (%) | 232 (23.7) | 109 (27.0) |
The BCMS cohort contained information on more than twice as many individuals as the UoWMS cohort, and had a larger number of observations (EDSS scores) per person. However, the patient characteristics were remarkably similar for sex, age at ABN eligibility, age at MS symptoms onset, disease duration at ABN eligibility and the proportion of patients with SPMS at ABN eligibility. The age at onset was 2 years lower in the BCMS cohort than in the UoWMS cohort, although the longer disease duration at ABN eligibility meant that the average age at ABN eligibility in the BCMS cohort was only 1.3 years lower than in the UoWMS cohort. A higher proportion of the BCMS cohort reached secondary-progressive disease during follow-up and this is probably related to the longer duration of follow-up in this cohort. There were slightly more relapses in the 2 years prior to, and a moderately higher EDSS score at, ABN eligibility in the UoWMS cohort than in the BCMS cohort.
Model development using the University of Wales Multiple Sclerosis cohort
Choice of time axis
When considering the different time axes, we compared the models with different powers of time for the fixed effects and patient-level random effects. When age was considered in a model, an age of 18 years was considered as ‘time zero,’ in the time axis, because the youngest age that an individual could have met the ABN eligibility criteria (see Eligibility) was aged 18 years. Table 4 indicates that the linear random slope and intercept model with time since onset as the time axis had a lower AIC (by 53.26 units) than the same model using age at EDSS score measurement as the time axis. The model with time since onset as the time axis also had a lower RMSE and a higher proportion of observations within ± 0.5 of observed EDSS score for both sets of predictions. This indicates that time since onset may be a preferable time axis to age.
| Time axis | AIC | Fixed effects only | Fixed effects plus individual-level residuals | ||
|---|---|---|---|---|---|
| RMSE fixed | % within ± 0.5 EDSS score (n/N) | RMSE | % within ± 0.5 EDSS score (n/N) | ||
| Linear age | 6256.66 | 2.11 | 15.9 (365/2290) | 0.59 | 69.7 (1595/2290) |
| Linear time since onset | 6203.40 | 2.00 | 17.9 (409/2290) | 0.58 | 70.7 (1619/2290) |
Choice of powers of time
We next identified the shape of the trajectory. We looked at the best degree 3 polynomial for the entire data set, but there was no significant increase in model fit compared with the best model with degree 2 polynomials (chi-squared test, p = 0.09).
We found the best polynomial of degree 2 had significantly better fit than the best polynomial of degree 1 (p < 0.001). Table 5 shows the best-fitting powers of time for both age and time since onset. The models in Table 5 all have the same number of parameters, so the difference in AIC is the same as the difference in the –2 × log-likelihoods. It is clear to see that the best models with time since onset have an AIC lower by over 100 units. A difference in AIC of 10 units is said to be strong evidence of a significant difference in the model fit.
| Powers of time for fixed and level 2 random effects with age as time axis (AIC) | Powers of time for fixed and level 2 random effects with time since onset as time axis (AIC) |
|---|---|
| t2,1t (6177.79) | t, log t (6063.25) |
| t3,1t2 (6238.95) | t, log t (6066.72) |
| t,(t×log t) (6252.38) | t2,t (6073.26) |
| log t,(log t×log t) (6254.55) | t, t2 (6073.89) |
| t,1t (6264.65) | t,1t (6076.75) |
The evidence strongly suggested that using time since onset as the time axis gave a model with a better fit to the data.
To investigate the influence of outliers on the time axis, we created two subsets of the UoWMS cohort in which we restricted the observations to be within 0–30 years since onset or 0–15 years since onset. Table 6 shows that linear and log-time, or square root and log-time, were consistently among the models with the smallest magnitude of –2 × log-likelihood or, equivalently, AIC. However, these two models tended to have very similar AICs (maximum difference = 4.15 units). Comparing the RMSE of these two models showed that the model with linear and log-time tended to have fitted values which were closer to the observed EDSS scores (with a RMSE of 0.54, compared with 0.57 for the model with the square root and log-time) and more observations within ± 0.5 EDSS score of the individual specific mean lines (72.4% compared with 70.2%). Therefore, the best powers of time since onset to include in the fixed effects and patient-level random effects were linear and log-time.
| Entire data set | Time from 0 to 30 years since onset | Time from 0 to 15 years since onset |
|---|---|---|
| t, log t (6063.25) | t, log t (5954.79) | log t, (log t)2 (4695.39) |
| t, log t (6066.72) | t, log t (5959.78) | t, log t (4696.63) |
| t2, t (6073.26) | t2, t (5963.89) | t, 1t (4697.93) |
| t, t2 (6073.89) | t, t2 (5964.08) | t,1t (4698.92) |
| t, 1t (6076.75) | t2, log t (5973.41) | t, log t (4700.42) |
Complex measurement error
In order to assess the distribution of the measurement error, we plotted the level 1 residuals from the best-fitting model (time since onset, including time and the log of time since onset) against time since onset (Figure 1).
FIGURE 1.
Level 1 residuals plotted over time since MS symptom onset. Source: adapted under the Open Government Licence from Lawton et al. 25
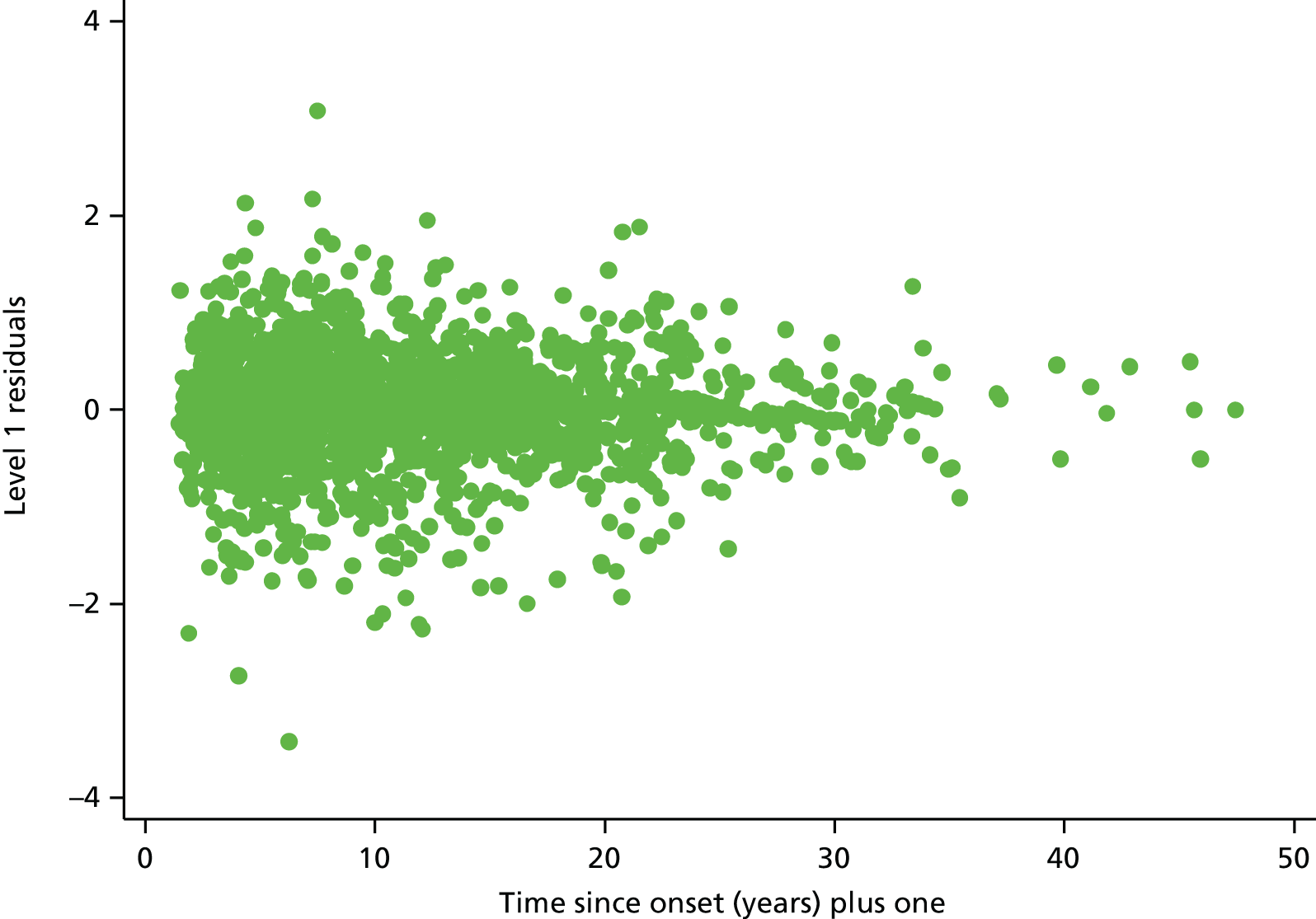
Figure 1 shows some evidence that the variance of the level 1 residuals in the chosen model are decreasing over time.
Fractional polynomials of degree 2 in the level 1 random effects did not significantly improve the fit of the model compared with fractional polynomials of degree 1 (p = 0.08). Adding a linear time term to the level 1 random effects resulted in a clear improvement in the model fit (p < 0.001). This was not the best level 1 random effect of time, as including the square root of time gave a better fit than the model with linear time. However, the difference between the model with linear time and square root of time as a level 1 random effect was not large (difference in AIC = 1.1 units). The model with linear time as a level 1 random effect was chosen for ease of convergence of the model and also for parsimony of not including different powers of time in the level 1 random effects compared with those in level 2 random effects and fixed effects.
We adjusted the level 1 time variance term to be equal to zero, as its 95% CI included zero. Hence we allowed only the covariance term between the constant and level 1 time term to be freely estimated. This constraint did not affect the model fit considerably (difference in AIC = 5.39).
Autocorrelation
In the UoWMS cohort some individuals presented with up to 72 EDSS score observations, with as many as 21 observations within 1 year.
Therefore, we created a new data set with only one observation per individual per quarter-year interval. When an individual had more than one EDSS score observed in a given quarter-year interval, we used the median EDSS score and the median time of observation within that quarter-year interval. This avoided autocorrelation, without removing too many data, as this might have created an unrealistic representation of an individual’s fluctuating disability measurements. Using quarter-year intervals reduced our UoWMS cohort from 2290 to 1876 observations (total), with the maximum number of observations for a single individual decreasing from 72 to 26.
As we were considering complex level 1 variation, to examine autocorrelation in the observations we needed to look at the observations about the patient-specific curve. We fitted the model described in the previous subsection (i.e. the model with complex measurement error) and calculated the difference between the patient’s observations and the fitted patient-specific curve. We then took this ‘residual’ and compared it with the next ‘residual’, as ordered by time. Table 7 showed that when we considered individuals with fewer observations there was far less evidence of autocorrelation. When the number of observations per person increased, the lagged ‘residual’ correlation increased to show some evidence of persistence. In the data set when we deleted observations the correlation tended to be lower in each case, with far less evidence of persistence.
| Number of observations per person included | Lagged ‘residual’ correlation for the complete data set | Lagged ‘residual’ correlation for the data set with concatenated observations |
|---|---|---|
| Entire data set | 0.169 | –0.011 |
| 3 or more | 0.197 | 0.021 |
| 4 or more | 0.222 | 0.049 |
| 5 or more | 0.128 | 0.077 |
| 6 or more | 0.162 | 0.105 |
| 7 or more | 0.182 | 0.134 |
| 8 or more | 0.206 | 0.143 |
| 9 or more | 0.224 | 0.158 |
| 10 or more | 0.248 | 0.183 |
Relapses
The best-fitting model to the UoWMS data thus included time since onset and the log of time since onset, allowed these to vary between individuals, and also allowed measurement error to vary with time. We then considered the effect of allowing EDSS score observations at different times post relapse (Table 8).
| Parameter | 1 month post relapse | 3 months post relapse (chosen model) | 6 months post relapse |
|---|---|---|---|
| Fixed effects | |||
| Intercept | 2.63 (2.09 to 3.17) | 2.63 (2.00 to 3.27) | 2.53 (1.85 to 3.21) |
| Time since onset | 0.16 (0.10 to 0.21) | 0.16 (0.10 to 0.22) | 0.14 (0.08 to 0.20) |
| Log-time since onset | –0.15 (–0.63 to 0.34) | –0.15 (–0.70 to 0.40) | 0.03 (–0.51 to 0.57) |
| Level 2 random effects | |||
| Var(intercept) | 6.81 (3.97 to 9.65) | 8.67 (5.05 to 12.29) | 7.11 (3.48 to 10.75) |
| Cov(intercept, time since onset) | 0.04 (–0.26 to 0.34) | 0.09 (–0.23 to 0.40) | –0.17 (–0.38 to 0.03) |
| Var(time since onset) | 0.07 (0.04 to 0.11) | 0.08 (0.05 to 0.12) | 0.05 (0.03 to 0.08) |
| Cov(intercept, log-time since onset) | –4.05 (–6.71 to –1.39) | –5.38 (–8.57 to –2.19) | –3.04 (–5.69 to –0.39) |
| Cov(time since onset, log-time since onset) | –0.51 (–0.81 to –0.22) | –0.60 (–0.92 to –0.28) | –0.31 (–0.53 to –0.09) |
| Var(log-time since onset) | 5.86 (3.14 to 8.58) | 7.13 (4.01 to 10.27) | 4.41 (2.04 to 6.79) |
| Level 1 random effects | |||
| Var(intercept) | 0.51 (0.46 to 0.56) | 0.40 (0.35 to 0.45) | 0.38 (0.33 to 0.43) |
| Cov(intercept, time since onset) | –0.004 (–0.006 to –0.003) | –0.003 (–0.005 to –0.002) | –0.003 (–0.005 to –0.002) |
| Var(time since onset) | Set equal to zero | Set equal to zero | Set equal to zero |
The first column (observations removed at 1 month post relapse) shows that the average EDSS score at disease onset was 2.63 points. This increases at a rate of 0.16 points per year, but also has a negative relationship with the log of years since disease onset (decreasing at 0.15 points per log-year). The level 2 random effects show the between-individual variance in EDSS score at disease onset, and how this varies over time; however, the association with time since disease onset is a function of time and the log of time, and cannot easily be interpreted. The level 1 random effects show the within-individual variance in EDSS score, and show that this decreases (slightly) with time since disease onset.
Comparing the models shows little difference in the fixed-effect estimates, with all the 95% CIs overlapping. The 95% CIs for the level 2 random effects overlapped and the mean estimates were very similar. However, when we consider the level 1 random effects, there was evidence suggesting that the variance of the constant term was lower in the model using only observations at least 6 months post relapse than in the model excluding observations within 1 month of relapse, whilst the model excluding observations within 3 months of relapse seemed similar to both the 1- and 6-month models in the level 1 random effects. Therefore, we decided to exclude all EDSS score observations taken within 3 months of a documented relapse. This restricted data set forms the basis for the final natural history model for the UoWMS cohort and also for making predictions from the BCMS models.
Censoring
Informative censoring was not considered an issue with the BCMS cohort, as this was truncated at 1995 in order to avoid this problem (see Data sets, Censoring), although 45 patients initiated DMT before the end of 1995 and their data were censored at this point. For the UoWMS cohort, informative censoring was investigated using joint modelling of the EDSS trajectory and time to dropout. 40 However, there were relatively few patients starting on drug treatment or dying and, therefore, many missing data on time to censoring for those remaining alive and untreated. This meant that many of the joint models failed to converge. We then investigated the possibility of informative censoring by including starting medication as a binary covariate (in which an individual’s value for this covariate was coded as one if they ever started medication, and zero otherwise). Those who eventually were censored as a result of starting medication tended to have a lower EDSS score at eligibility and slightly slower progression over time than those who remained uncensored (Table 9). However, the differences are small when considered univariately, and smaller but with wider CIs when the association with the entire trajectory is considered in one model. Hence, we can conclude there was little evidence of any informative censoring within the UoWMS model.
| Ever censored compared with never censored | Univariate (95% CI) | Mutually adjusted (95% CI) |
|---|---|---|
| Intercept | –0.31 (–0.77 to 0.16) | 0.14 (–1.61 to 1.89) |
| Time since onset | –0.04 (–0.09 to 0.007) | –0.02 (–0.23 to 0.18) |
| Log-time since onset | –0.20 (–0.44 to 0.04) | –0.16 (–1.87 to 1.56) |
Model for natural history of multiple sclerosis using the University of Wales Multiple Sclerosis cohort
The best-fitting model to the UoWMS data included time since onset and the log of time since onset, allowed these to vary randomly between individuals, and also allowed measurement error to vary with time. The model included only observations taken at least 3 months after a relapse. The coefficients for this model are shown in Table 10.
| Parameter | Estimate (95% CI) |
|---|---|
| Fixed effects | |
| Intercept (EDSS score at onset) | 2.63 (2.00 to 3.27) |
| Time since onset | 0.16 (0.10 to 0.22) |
| Log-time since onset | –0.15 (–0.70 to 0.40) |
| Level 2 random effects | |
| Var(intercept) | 8.67 (5.05 to 12.29) |
| Cov(intercept, time since onset) | 0.09 (–0.23 to 0.40) |
| Var(time since onset) | 0.08 (0.05 to 0.12) |
| Cov(intercept, log-time since onset) | –5.38 (–8.57 to –2.19) |
| Cov(time since onset, log-time since onset) | –0.60 (–0.92 to –0.28) |
| Var(log-time since onset) | 7.13 (4.01 to 10.27) |
| Level 1 random effects | |
| Var(intercept) | 0.40 (0.35 to 0.45) |
| Cov(intercept, time since onset) | –0.003 (–0.005 to –0.002) |
| Var(time since onset) | Set equal to zero |
Assessing model fit
The main assumption of the multilevel models was that the level 1 and level 2 residuals were normally distributed. This was tested using quantile–quantile (Q–Q) plots of the level 1 and level 2 residuals for our chosen model. The Q–Q plots are shown in Figure 2 and were close to normality.
FIGURE 2.
The Q–Q plots for all residuals from the final UoWMS model. (a) Level 1 (constant); (b) level 1 (time); (c) level 2 (constant); (d) level 2 (time); and (e) level 2 (log-time). Source: adapted under the Open Government Licence from Lawton et al. 25

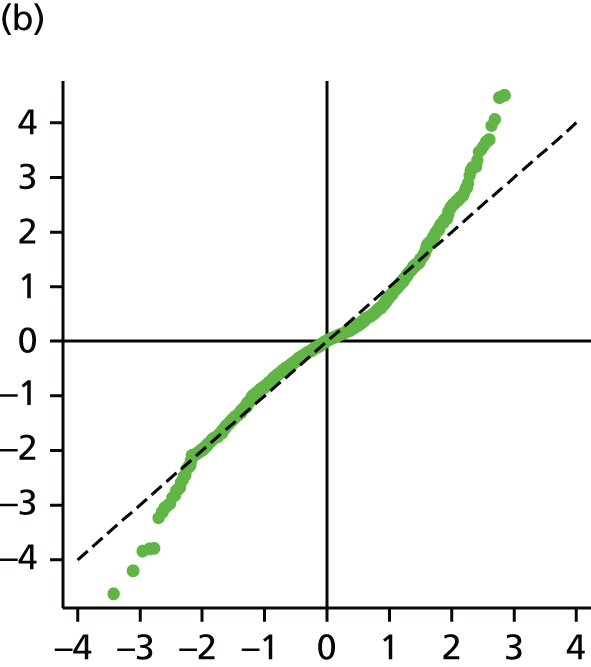
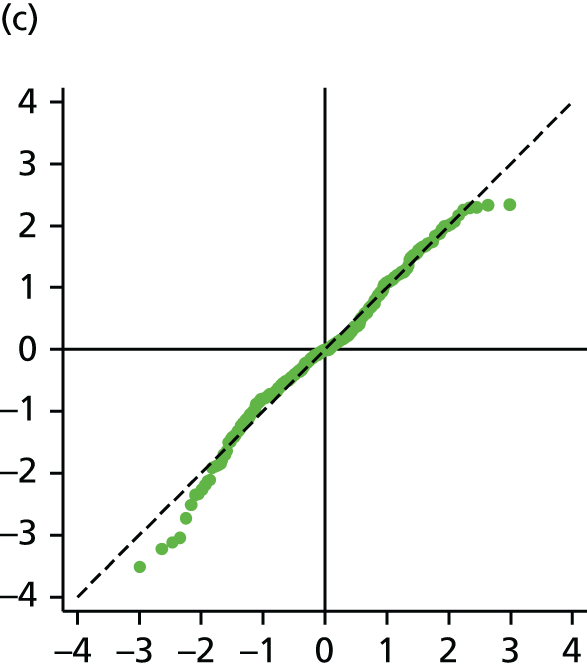

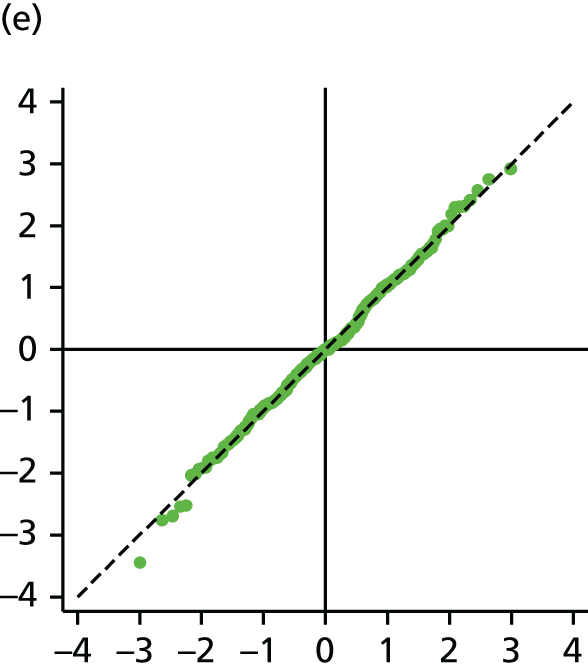
Model development with the British Columbia Multiple Sclerosis cohort
Model development using the BCMS data gave very similar results. First, time since onset was found to be a better time axis than age. Second, linear and log-time for the individual trajectories gave a good fit to the data and fractional polynomials of degree 3 showed little improvement. The AICs for the top three models are shown in Appendix 1 (see Table 20). Third, adding complex measurement error (i.e. a linear time term to the observation-level random effects) gave a model with better fit, and fractional polynomials of degree 2 for the measurement error term showed little improvement over this.
The only difference from the UoWMS model was that minimal changes were observed in the model when the 1-, 3- and 6-month post-relapse windows were explored. Hence we choose to use the BCMS model, which included only observations taken at least 1 month after a relapse.
The two models in Table 11 showed a significant difference only in the level 1 constant random effect and the constant fixed effect. A difference in the constant fixed effect was expected, given that, from the patients’ characteristics (see Table 3), the first ‘ABN eligible’ EDSS score was, on average, higher in the UoWMS cohort. The difference in the level 1 constant random effect shows that there was less variation around the initial EDSS score for the UoWMS cohort than for the BCMS cohort. This could be partly because of the lower estimated EDSS score at onset in the BCMS cohort, if measurement error is higher when assessing lower EDSS scores. Model fit was assessed by examining the distributions of the residuals. Figure 8 (see Appendix 1) indicates that these were reasonably normally distributed.
| Parameter | UoWMS (95% CI) | BCMS (95% CI) |
|---|---|---|
| Fixed effects | ||
| Intercept (EDSS score at onset) | 2.63 (2.00 to 3.27) | 1.05 (0.79 to 1.31) |
| Time since onset | 0.16 (0.10 to 0.22) | 0.22 (0.19 to 0.26) |
| Log-time since onset | –0.15 (–0.70 to 0.40) | –0.13 (–0.39 to 0.14) |
| Level 2 random effects | ||
| Var(intercept) | 8.67 (5.05 to 12.29) | 2.80 (1.87 to 3.73) |
| Cov(intercept, time since onset) | 0.09 (–0.23 to 0.40) | 0.09 (–0.05 to 0.24) |
| Var(time since onset) | 0.08 (0.05 to 0.12) | 0.10 (0.08 to 0.12) |
| Cov(intercept, log-time since onset) | –5.38 (–8.57 to –2.19) | –2.73 (–3.82 to –1.63) |
| Cov(time since onset, log-time since onset) | –0.60 (–0.92 to –0.28) | –0.65 (–0.81 to –0.48) |
| Var(log-time since onset) | 7.13 (4.01 to 10.27) | 6.14 (4.78 to 7.49) |
| Level 1 random effects | ||
| Var(intercept) | 0.40 (0.35 to 0.45) | 0.76 (0.70 to 0.82) |
| Cov(intercept, time since onset) | –0.003 (–0.005 to –0.002) | –0.004 (–0.005 to –0.002) |
| Var(time since onset) | Set equal to zero | Set equal to zero |
Chapter 5 Examining the disease-modifying therapy treated history of multiple sclerosis
In order to examine treated history of MS using the UK MS RSS cohort, we fitted models with the same form as in Table 11 to the BCMS and UoWMS data sets, using time since ABN eligibility (rather than time since onset) as the time axis. We fitted two models to each data set: one including all covariates (Table 12) and one including no covariates (see Appendix 1, Table 21 and Figure 9).
| Parameter | UoWMS model (95% CI) | BCMS model (95% CI) |
|---|---|---|
| Fixed effects | ||
| Intercept (EDSS score at ABN eligibility) | 1.91 (1.00 to 2.83) | 1.10 (0.66 to 1.55) |
| Time since eligibility | 0.36 (–0.06 to 0.77) | 0.12 (–0.05 to 0.29) |
| Log-time since eligibility | –0.68 (–2.12 to 0.76) | 0.37 (–0.22 to 0.96) |
| Age at eligibility | 0.018 (–0.003 to 0.038) | 0.024 (0.013 to 0.035) |
| Time since eligibility × age at eligibility | –0.006 (–0.016 to 0.005) | 0.001 (–0.003 to 0.006) |
| Log-time since eligibility × age at eligibility | 0.024 (–0.012 to 0.060) | –0.000 (–0.016 to 0.015) |
| SP compared with RR | 2.11 (1.73 to 2.49) | 2.39 (2.13 to 2.64) |
| Number of relapses in 2 years prior to ABN eligibility | 0.19 (0.026 to 0.343) | 0.033 (–0.417 to 0.108) |
| Female (compared with male) | –0.092 (–0.436 to 0.251) | –0.20 (–0.40 to 0.01) |
| Level 2 random effects | ||
| Var(intercept) | 2.21 (1.80 to 2.62) | 1.86 (1.65 to 2.07) |
| Cov(intercept, time since ABN eligibility) | –0.18 (–0.32 to –0.04) | –0.25 (–0.32 to –0.19) |
| Var(time since ABN eligibility) | 0.16 (0.09 to 0.23) | 0.15 (0.12 to 0.18) |
| Cov(intercept, log-time since ABN eligibility) | 0.12 (–0.38 to 0.61) | 0.82 (0.60 to 1.04) |
| Cov(time since ABN eligibility, log-time since ABN eligibility) | –0.63 (–0.90 to –0.35) | –0.47 (–0.57 to –0.37) |
| Var(log-time since ABN eligibility) | 3.05 (1.97 to 4.14) | 2.26 (1.85 to 2.67) |
| Level 1 random effects | ||
| Var(intercept) | 0.35 (0.29 to 0.40) | 0.61 (0.56 to 0.66) |
| Cov(intercept, time since ABN eligibility) | –0.009 (–0.013 to –0.004) | –0.005 (–0.009 to –0.002) |
The associations between covariates and progression were similar across both cohorts (see Table 12). All covariates except age were related only to average EDSS score. Those with SPMS had a higher average EDSS score [by 2.11 (UoWMS)/2.39 (BCMS) points] than those with RRMS. Women had a slightly lower average EDSS score [by 0.092 (UoWMS)/0.20 (BCMS) points] than men. Those who experienced more relapses in the year prior to ABN eligibility tended to have a higher average EDSS score [by 0.19 (UoWMS)/0.033 (BCMS) points] per relapse. Those who were older at onset of MS tended to have a higher average EDSS score [by 0.018 (UoWMS)/0.024 (BCMS) points per year older at MS onset], with some evidence (in the UoWMS cohort) of also having a more rapid increase in EDSS score over time.
Final model relating Expanded Disability Status Scale to time since Association of British Neurologists eligibility, and including age at onset
For comparison with the Markov modelling approach to the UK MS RSS cohort,46 we then fitted a model including only one covariate: the binary indicator of whether or not the age at onset was above or below the median age of 27.9 years (Table 13). There was not a strong association between the binary indicator for age at onset and EDSS trajectory, with some indication that those younger at onset had higher EDSS scores [by 0.14 (UoWMS)/0.096 (BCMS) points].
| Parameter | UoWMS model (95% CI) | BCMS model (95% CI) |
|---|---|---|
| Fixed effects | ||
| Intercept (EDSS score at ABN eligibility) | 3.17 (2.84 to 3.49) | 2.19 (2.03 to 2.35) |
| Time since eligibility | 0.19 (0.07 to 0.32) | 0.17 (0.11 to 0.22) |
| Log-time since eligibility | 0.15 (–0.32 to 0.62) | 0.37 (0.17 to 0.56) |
| Age onset binary (≥ 27.9 years) | 0.14 (–0.27 to 0.55) | 0.096 (–0.13 to 0.33) |
| Age onset binary × time | –0.062 (–0.220 to 0.095) | 0.015 (–0.065 to 0.096) |
| Age onset binary × log-time | 0.17 (–0.43 to 0.77) | –0.019 (–0.30 to 0.26) |
| Level 2 random effects | ||
| Var(intercept) | 3.11 (2.58 to 3.64) | 2.82 (2.52 to 3.11) |
| Cov(intercept, time since ABN eligibility) | –0.21 (–0.35 to –0.07) | –0.28 (–0.36 to –0.21) |
| Var(time since ABN eligibility) | 0.12 (0.07 to 0.17) | 0.15 (0.12 to 0.18) |
| Cov(intercept, log-time since ABN eligibility) | 0.27 (–0.26 to 0.81) | 0.97 (0.71 to 1.23) |
| Cov(time since ABN eligibility, log-time since ABN eligibility) | –0.49 (–0.70 to –0.27) | –0.46 (–0.56 to –0.36) |
| Var(log-time since ABN eligibility) | 2.68 (1.76 to 3.59) | 2.24 (1.83 to 2.65) |
| Level 1 random effects | ||
| Var(intercept) | 0.32 (0.29 to 0.35) | 0.62 (0.57 to 0.67) |
| Cov(intercept, time since ABN eligibility) | –0.005 (–0.006 to –0.004) | –0.006 (–0.009 to –0.002) |
Validation of the British Columbia Multiple Sclerosis model relating Expanded Disability Status Scale to time since Association of British Neurologists eligibility, using the University of Wales multiple sclerosis cohort
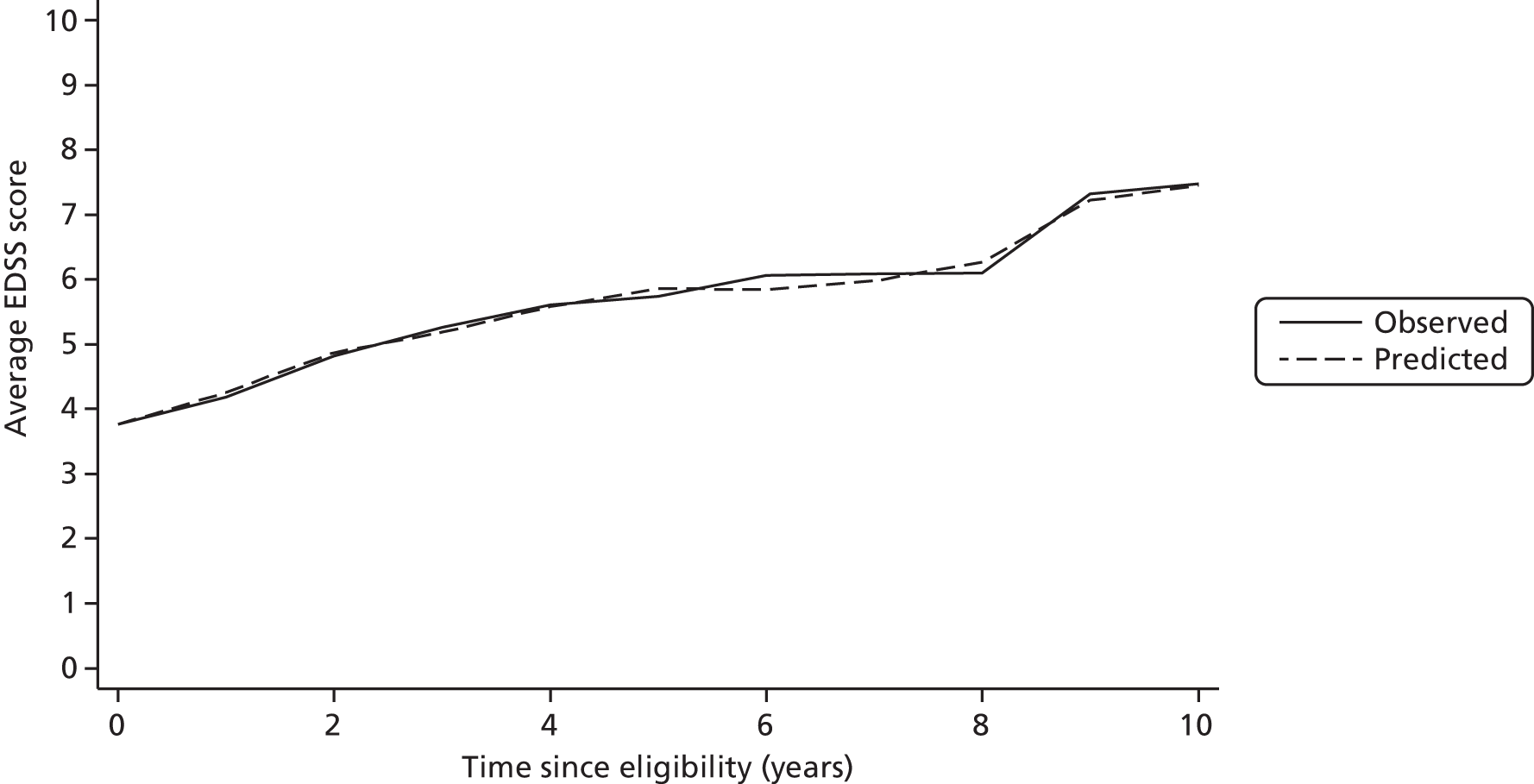
We examined portability of the model between populations by using the BCMS model to predict EDSS score for individuals in the UoWMS cohort (when the UoWMS cohort included only observations taken at least 3 months after a relapse). Table 14 is based on 253 individuals who have at least two EDSS scores, and shows the differences between observed EDSS score in the UoWMS cohort and EDSS score predicted by the BCMS model (conditional on the first observed EDSS score, i.e. using the first observed EDSS score as the baseline). The average EDSS score over time and the average predicted by the BCMS model are shown in Figure 3. There is reasonable evidence that the BCMS model can be used to predict EDSS scores in the UoWMS cohort. There does appear to be slight evidence of a pattern, in that differences early in follow-up are positive (the model overpredicts) and those later in follow-up tend to be negative (the model underpredicts). However, the average differences are small in magnitude, compared with the spread of the differences, the measurement error and variation of EDSS score.
| Time since eligibility (years) | EDSS score | ||||||
|---|---|---|---|---|---|---|---|
| Observed in the UoWMS | Predicted using the BCMS model | Predicted – UoWMS observed | |||||
| Number of observations (number of individuals) | Mean | SD | Mean | SD | Mean | SD | |
| 0–0.5 | 88 (72) | 3.76 | 1.71 | 3.77 | 1.63 | 0.01 | 0.99 |
| 0.5–1.5 | 292 (153) | 4.18 | 2.02 | 4.26 | 1.81 | 0.08 | 1.14 |
| 1.5–2.5 | 265 (118) | 4.82 | 1.78 | 4.87 | 1.59 | 0.05 | 1.14 |
| 2.5–3.5 | 202 (101) | 5.27 | 1.61 | 5.19 | 1.62 | –0.08 | 1.32 |
| 3.5–4.5 | 182 (92) | 5.61 | 1.77 | 5.58 | 1.67 | –0.03 | 1.53 |
| 4.5–5.5 | 142 (72) | 5.74 | 1.73 | 5.86 | 1.42 | 0.12 | 1.46 |
| 5.5–6.5 | 138 (54) | 6.07 | 1.77 | 5.85 | 1.35 | –0.22 | 1.57 |
| 6.5–7.5 | 75 (39) | 6.09 | 1.79 | 5.98 | 1.38 | –0.11 | 1.68 |
| 7.5–8.5 | 52 (30) | 6.10 | 1.92 | 6.27 | 1.38 | 0.17 | 1.69 |
| 8.5–9.5 | 29 (14) | 7.33 | 1.22 | 7.22 | 1.67 | –0.10 | 1.48 |
| 9.5–10.5 | 30 (10) | 7.48 | 1.16 | 7.45 | 1.80 | –0.03 | 1.49 |
| Total | 1495 (253) | 5.20 | 1.97 | 5.20 | 1.80 | –0.001 | 1.35 |
FIGURE 3.
Observed and predicted EDSS score in the UoWMS cohort using the model relating EDSS score to time since ABN eligibility and including age at onset as a binary covariate.
Validation of the British Columbia Multiple Sclerosis model to predict utility in the University of Wales Multiple Sclerosis cohort
Table 15 is again based on 253 individuals who have at least two EDSS scores, and shows the ability of the BCMS model to predict utility scores related to disease progression in the UoWMS population. Here we predicted EDSS score using our model (conditional on first observed EDSS score) and then converted both predicted and observed EDSS score to 1 – primary utility. The overall difference between predicted and observed (predicted – observed) utility related to disease progression for all non-baseline observations between eligibility and a time of 10.5 years (n = 1495) has a mean (standard deviation) of –0.00 (0.16) and hence a 95% CI of –0.01 to 0.00 for the mean difference. The RMSE of the difference is 0.16. The average observed and predicted utility related to disease progression over time are shown in Figure 4. Again, it appears that the BCMS model can be used to predict utility related to disease progression in the UoWMS cohort. There does appear to be slight evidence of a pattern, in that differences early in follow-up are positive (the model overpredicts) and those later in follow-up are negative (the model underpredicts). However, the average differences are small in magnitude compared with the spread of the differences (and the potential measurement error and variation of the EDSS score).
| Time since eligibility (years) | UoWMS observed 1 – utility | 1 – utility predicted using the BCMS model | Predicted – observed | ||||
|---|---|---|---|---|---|---|---|
| Number of observations (number of individuals) | Mean | SD | Mean | SD | Mean | SD | |
| 0–0.5 | 88 (72) | 0.420 | 0.10 | 0.429 | 0.12 | 0.008 | 0.09 |
| 0.5–1.5 | 292 (153) | 0.448 | 0.15 | 0.458 | 0.14 | 0.010 | 0.12 |
| 1.5–2.5 | 265 (118) | 0.490 | 0.13 | 0.493 | 0.11 | 0.003 | 0.10 |
| 2.5–3.5 | 202 (101) | 0.527 | 0.13 | 0.535 | 0.15 | 0.008 | 0.13 |
| 3.5–4.5 | 182 (92) | 0.567 | 0.19 | 0.576 | 0.18 | 0.009 | 0.16 |
| 4.5–5.5 | 142 (72) | 0.579 | 0.18 | 0.590 | 0.17 | 0.012 | 0.17 |
| 5.5–6.5 | 138 (54) | 0.656 | 0.24 | 0.582 | 0.17 | –0.074 | 0.23 |
| 6.5–7.5 | 75 (39) | 0.648 | 0.22 | 0.607 | 0.17 | –0.041 | 0.23 |
| 7.5–8.5 | 52 (30) | 0.639 | 0.22 | 0.649 | 0.22 | 0.010 | 0.23 |
| 8.5–9.5 | 29 (14) | 0.843 | 0.21 | 0.754 | 0.24 | –0.088 | 0.23 |
| 9.5–10.5 | 30 (10) | 0.830 | 0.22 | 0.790 | 0.29 | –0.041 | 0.25 |
| Total | 1495 (253) | 0.543 | 0.19 | 0.538 | 0.18 | –0.005 | 0.16 |
FIGURE 4.
Observed and predicted 1 – utility in the UoWMS cohort using the BCMS model relating EDSS score to time since ABN eligibility and including age at onset as a binary covariate.

Model fit
The models have been assessed for goodness of fit (see Appendix 1, Figures 10 and 11). The normality assumptions of the residuals appear to be fairly well satisfied, meaning that there is no need to transform the EDSS score.
Summary of natural history modelling
We developed models using two independent data sets, and found evidence of a non-linear pattern of progression, and also that time since disease milestones (onset, ABN eligibility) provided a better fit to the data than modelling EDSS score progression as a function of age.
As shown in Figures 5 and 6, the predictions (conditional on the first observed EDSS scores) fit the actual data well, with time since eligibility providing a closer fit to the data than time since onset. The model coefficients from the BCMS cohort (based on a larger sample size with longer follow-up) are a better predictor of the UoWMS data than the coefficients derived from the UoWMS cohort itself. When using the BCMS model coefficients to predict observations in the UoWMS cohort there is a slight underestimate to begin with, owing to differences in EDSS score at ABN eligibility between the two data sets. However, at 4 years post eligibility, there is no material difference between observed and expected EDSS score. These figures support for the idea of using a model developed in British Columbia as a non-randomised comparison group for natural history of MS in the UK.
FIGURE 5.
Fit of the UoWMS models (not including covariates) to the UoWMS cohort EDSS score data.
FIGURE 6.
Fit of the BCMS models (not including covariates) to the UoWMS cohort EDSS score data.

Chapter 6 Application of multilevel models to the UK multiple sclerosis risk-sharing scheme cohort
A total of 4304 patients with RRMS were eligible and treated at baseline for the UK MS RSS cohort, with 4137 of these having at least one valid EDSS score at 1 year post baseline or later. The summary statistics for the UK MS RSS cohort are given in Table 16, and can be compared with those for the BCMS and the UoWMS cohorts (see Table 3). Those included in the primary analysis (i.e. those with an EDSS score at the 6-year follow-up) are comparable to the full UK MS RSS cohort. The UK MS RSS cohort has a slightly higher median age at onset than the BCMS cohort; the average EDSS score at baseline in the UK MS RSS is also slightly higher than the average EDSS score at ABN eligibility in the BCMS cohort (see Table 3). However, ‘baseline’ for the UK MS RSS is defined by entry to the study, so this difference could be (partly) because some time passed between ABN eligibility and entry to the study.
| Characteristic | UK MS RSS cohort (n = 4304) | UK MS RSS cohort: patients included in the primary analysis (n = 4137) |
|---|---|---|
| Female: n (%) | 3233 (75.1) | 3124 (75.5) |
| Age (years) at onset, mean (SD); median (range) | 30.5 (8.39); 30 (24–36) | 30.5 (8.37); 30 (24–36) |
| Years since symptom onset, mean (SD); median (range) | 7.7 (6.6); 5.7 (2.6–11.0) | 7.7 (6.6); 5.7 (2.6–11.1) |
| EDSS score at baseline, mean (SD); median (range) | 3.08 (1.52); 3 (2–4) | 3.06 (1.52); 3 (2–4) |
Table 17 shows the EDSS score at last follow-up by year of last follow-up, showing that most patients have an EDSS score at 6 years, and that there is little difference in last EDSS score between those who do and those who do not have an EDSS score at 6 years.
| Year of last follow-up | n (%) | Mean EDSS score (SD) |
|---|---|---|
| 6 | 2968 (72) | 4.03 (2.1) |
| 5 | 568 (14) | 3.90 (2.1) |
| 4 | 238 (6) | 4.20 (2.3) |
| 3 | 154 (4) | 4.00 (2.4) |
| 2 | 106 (3) | 3.58 (2.0) |
| 1 | 103 (2) | 3.88 (2.1) |
Age onset binary models for time since eligibility
Table 18 compares the models with age at onset as a binary variable in the BCMS, UoWMS and UK MS RSS cohorts. The estimated average EDSS score is lowest in the BCMS cohort and highest in the UoWMS cohort, and the association between age at onset and average EDSS score is similar across cohorts.
| Parameter | Model | ||
|---|---|---|---|
| UoWMS (95% CI) | BCMS (95% CI) | UK MS RSS (95% CI) | |
| Fixed effects | |||
| Intercept (EDSS score at ABN eligibility) | 3.17 (2.84 to 3.49) | 2.19 (2.03 to 2.35) | 2.78 (2.70 to 2.86) |
| Time since eligibility | 0.19 (0.07 to 0.32) | 0.17 (0.11 to 0.22) | 0.21 (0.18 to 0.24) |
| Log-time since eligibility | 0.15 (–0.32 to 0.62) | 0.37 (0.17 to 0.56) | –0.13 (–0.22 to –0.04) |
| Age onset binary (≥ 27.9 years) | 0.14 (–0.27 to 0.55) | 0.096 (–0.13 to 0.33) | 0.10 (0.004 to 0.20) |
| Age onset binary × time | –0.062 (–0.220 to 0.095) | 0.015 (–0.065 to 0.096) | 0.002 (–0.032 to 0.036) |
| Age onset binary × log-time | 0.17 (–0.43 to 0.77) | –0.02 (–0.30 to 0.26) | 0.02 (–0.095 to 0.14) |
| Level 2 random effects | |||
| Var(intercept) | 3.11 (2.58 to 3.64) | 2.82 (2.52 to 3.11) | 2.18 (2.07 to 2.29) |
| Cov(intercept, time since ABN eligibility) | –0.21 (–0.35 to –0.07) | –0.28 (–0.36 to –0.21) | –0.23 (–0.26 to –0.20) |
| Var(time since ABN eligibility) | 0.12 (0.07 to 0.17) | 0.15 (0.12 to 0.18) | 0.16 (0.15 to 0.17) |
| Cov(intercept, log-time since ABN eligibility) | 0.27 (–0.26 to 0.81) | 0.97 (0.71 to 1.23) | 0.63 (0.53 to 0.72) |
| Cov(time since ABN eligibility, log-time since ABN eligibility) | –0.49 (–0.70 to –0.27) | –0.46 (–0.56 to –0.36) | –0.45 (–0.49 to –0.41) |
| Var(log-time since ABN eligibility) | 2.68 (1.76 to 3.59) | 2.24 (1.83 to 2.65) | 1.86 (1.70 to 2.01) |
| Level 1 random effects | |||
| Var(intercept) | 0.32 (0.29 to 0.35) | 0.62 (0.57 to 0.67) | 0.52 (0.50 to 0.55) |
| Cov(intercept, time since ABN eligibility) | –0.005 (–0.006 to –0.004) | –0.006 (–0.009 to –0.002) | –0.007 (–0.009 to –0.005) |
Figure 7 shows the predicted average EDSS score from ABN eligibility for the BCMS and UoWMS cohorts, and from baseline for the UK MS RSS cohort. Increase in the EDSS score seems to be slightly slower in the UK MS RSS cohort than in the two natural history cohorts. In particular, the UoWMS and UK MS RSS cohorts have similar baseline EDSS values, but quite different trajectories over time. This could be for many reasons, including chance, the different settings and calendar time of the cohorts, confounder distribution, but also possibly because of an effect of DMT treatment on EDSS score progression.
FIGURE 7.
Predicted average EDSS score across time since ABN eligibility for the models from the UoWMS, BCMS and UK MS RSS cohorts.
Using the natural history model to predict progression in UK multiple sclerosis risk-sharing scheme
Table 19 shows the observed progression (EDSS score at up to 6 years minus EDSS score at baseline) for the UK MS RSS cohort, together with progression predicted under the natural history model. Observed progression in the treated UK MS RSS cohort was 0.6 points lower than predicted by the BCMS model (95% CI 0.5 to 0.6 points lower). This translated to a difference in the utility related to disease progression of –0.04 (95% CI –0.05 to –0.04). Thus, the increase in disability (as measured by the EDSS) was slightly less in the DMT-treated UK MS RSS cohort than would have been predicted by the natural history model. There was a corresponding small decrease in utility related to disease progression in the DMT-treated UK MS RSS cohort than would have been predicted by the natural history model.
| Analysis | Observed (95% CI) | Predicted without treatment (95% CI) | Observed progression (follow-up minus baseline) (95% CI) | Predicted progression without treatment (95% CI) | Difference (observed – predicted) (95% CI) |
|---|---|---|---|---|---|
| EDSS | 4.01 (3.94 to 4.07) | 4.59 (4.55 to 4.64) | 0.94 (0.89 to 1.00) | 1.53 (1.52 to 1.55) | –0.59 (–0.64 to –0.54) |
| Utility | 0.44 (0.44 to 0.45) | 0.48 (0.48 to 0.49) | 0.06 (0.06 to 0.07) | 0.10 (0.10 to 0.11) | –0.04 (–0.05 to –0.04) |
Chapter 7 Discussion
This study aimed to use multilevel models to examine the trajectory of EDSS score in untreated MS patients, and to investigate whether or not two populations of MS patients showed similar trajectories. The secondary aim of this study was to then use these natural history cohorts as non-randomised comparison groups to examine the effects of treatments for MS.
Key findings
-
Our main study finding was the remarkably similar disability trajectories (EDSS score) over time in the two geographically distinct cohorts of MS patients. Whether the time axis was time since onset or time since ABN eligibility, the Welsh and British Columbia cohorts gave rise to very similar models (aims 1 and 2).
-
The coefficients from the models based on one cohort could be used to predict EDSS score for patients from the second cohort, by conditioning on the first EDSS score observed for an individual. However, the accuracy of these predictions will always be limited by any measurement error in the EDSS score. Thus, when using the BCMS model to predict EDSS scores for individual patients in the UoWMS cohort, conditional on their first two EDSS score observations, 90% of the predictions lay within –2 to 2 points of the observed EDSS score. This compared with an estimated intrarater reliability of 1 point or an inter-rater reliability of 1.5 points, for those scores between 1 and 3.5 points on the EDSS. 39
-
Although the accuracy of these predictions may not be sufficiently good for predicting at an individual level for clinical purposes, these results provide strong evidence of the ability to use one of these cohorts of MS patients as a non-randomised comparison group for another. The overall mean difference between EDSS scores for the UoWMS cohort and those predicted by the BCMS model was –0.001 points, with a standard deviation of 1.35 points, thus giving a 95% CI for the difference of –0.07 to 0.07 points. This was a narrow CI, and thus would be of utility in comparing average effects between two cohorts.
-
We identified several covariates as either being related to the average EDSS score, or to the rate of change in disability (EDSS score) over time. The estimates of these associations were consistent between the two cohorts. Most were consistent with either observations from previously published natural history studies17,21 or with clinical expectations. For instance, consistent with the wider literature,47 those who were older at MS onset tended to have greater disability (higher EDSS scores) and worsened somewhat more rapidly over time. Consistent with clinical expectations, those with SP disease had a higher EDSS score at ABN eligibility. However, of interest was the absence of any obvious difference in subsequent progression compared with those who remained RR. Patients with more relapses in the 2 years prior to ABN eligibility tended to have higher EDSS scores at ABN eligibility. Women had lower EDSS scores, on average, than men but again there were no obvious differences in EDSS score trajectory compared with men.
-
Our study suggests that EDSS trajectories can be modelled using multilevel models. In all models, there was no strong evidence of non-normality of residuals and, therefore, no need to consider further transformations of EDSS. As previously suggested, there was evidence that intra individual variability in the EDSS score and this variability was greater for lower EDSS scores. 39 Our models treat the EDSS as a continuous outcome (rather than ordinal) and we found no evidence that this gave rise to poor prediction or poor fit of the model to the observed data.
-
Finally, our results suggest that progression (as measured by the EDSS) may be slower in a cohort treated with DMT than that predicted by natural history models, with an estimated difference in EDSS score of –0.59 (95% CI –0.64 to –0.54) points at up to 6 years post treatment (aim 3). This translated to a difference in the utility related to disease progression of –0.04 points (95% CI –0.05 to –0.04 points) (aim 4). This is a very small mean difference, particularly when set against the variation in EDSS score both within and between individuals.
Strengths and weaknesses
A major strength of our study was the ability to develop models using one cohort (the BCMS cohort) and to validate their predictive power on a cohort, which was distinct in both time and geography (the UoWMS cohort). The remarkable similarity between the models for these two cohorts indicates that these models may be useful for comparing EDSS score between different populations.
The multilevel model approach meant that coefficients from a model developed on one cohort could be used to predict EDSS score for an individual from a different cohort, and that this prediction could be improved by conditioning on the first (or first two) observed EDSS scores.
Both cohorts contained a reasonably large number of individuals, assessed by MS specialist neurologists at several points over the course of disease. Moreover, many of these data were collected before the DMTs were either widely used or licensed for MS, meaning that most patients were largely unexposed to any drug treatment known to modify the MS disease course. These types of data sets are incredibly valuable and cannot be recreated given the ubiquitous use of DMTs for MS in clinical practice today. However, one limitation is that, for this project, DMTs were considered as a single class, and no attempt was made to model progression differently for different drugs. Another potential source of bias is that only a small proportion of the available data from each cohort was used; the eligibility criteria mean that only those individuals with definite SPMS or RRMS were included, and of those, only those who were ABN eligible, and who had at least two EDSS score measures. These restrictions may have led to selection bias, if underlying progression was related to the chance of being selected for these analyses.
A potential weakness of our study was the inability to capture physician-level information, as we were unable to adjust for the capture of EDSS scores by different physicians. In the BCMS cohort, four core neurologists assessed > 85% of the EDSS scores considered in this current study, thus minimising differences between neurologists. Nonetheless, given the documented variation between measures taken by different raters on the same individual,39 this could limit the precision with which EDSS score can be predicted.
A further issue is that our models treat the EDSS score as a continuous measure. Although the EDSS score is an ordinal measure, and was not designed for use as a continuous outcome, all the models showed good fit to the observed data. Examination of the residuals from the models also showed no evidence of lack of fit of these models. Models treating the EDSS as a continuous outcome are much simpler to fit and interpret than models treating the EDSS as an ordinal scale, and this advantage may outweigh the disadvantage of lack of fit with the original design of the EDSS. We have used only the EDSS (which has a particular focus on walking abilities) as an outcome measure, so have not taken into account other domains of life that are affected by MS (including quality of life).
A further weakness was the censoring of patients after first exposure to a DMT in the UoWMS cohort. In the BCMS cohort, this was largely overcome by limiting the entire cohort to a time period when the DMTs were largely not available (1980–95). If the decision to initiate a DMT was based on one or more of the observed variables which are in the model (e.g. EDSS history after ABN eligibility or relapse rate at ABN eligibility), then this should not have biased the models, and the similarity between the BCMS and UoWMS models would indicate that this was the case.
Our definition of ABN eligibility included the number of relapses in the 2 years prior to a given EDSS score measure. This variable was also one of the covariates in our models. However, a patient in whom data were available for < 2 years since onset, but who had experienced more than two documented relapses in that time, would have satisfied the ABN eligibility criteria, although the number of relapses in the previous 2 years would be based on an observation period of < 2 years. An alternative would have been to calculate an annualised relapse rate for each patient at ABN eligibility; however, we felt that this might give too much weight to an individual who had two relapses in a fairly short time (e.g. two relapses within 6 months would give an annualised relapse rate of four, but this individual is perhaps unlikely to have had another two relapses in the next 6 months). This potential measurement error in our definition of the number of relapses in the 2 years prior to ABN eligibility may have caused overestimation of the association between relapses at ABN eligibility and EDSS score at eligibility.
Another weakness is that patients with SPMS at the time of ABN eligibility were included in the derivation of the natural history models (for both BCMS and UoWMS cohorts), whereas patients with SPMS at baseline were excluded from the UK MS RSS analyses presented here. This could result in the UK MS RSS cohort having lower initial EDSS scores than those from the natural history cohorts; however, given that that natural history models did not identify any association of SPMS with EDSS trajectory, this should not bias our results. Sensitivity analyses presented elsewhere46 confirm that including patients with SPMS at baseline in the UK MS RSS analyses resulted in a tiny attenuation of the difference between UK MS RSS and natural history-predicted values of EDSS score. A similar issue is that in deriving our natural history models, we removed all observations made within 1 month (BCMS cohort) or 3 months (UoWMS cohort) of a relapse. In the UK MS RSS, the clinicians were instructed not to take EDSS score measures during a relapse. Measures made close to (but not during) a relapse in the UK MS RSS could have been higher than usual and thus we could have underestimated the difference between natural history and treated cohorts.
We applied the natural history model to all patients from the UK MS RSS with EDSS score data at 6 years post treatment, and assumed that a difference between observed EDSS score and that predicted by the natural history model could be because of DMT. Patients not remaining on DMT for 6 years in the UK MS RSS may have higher EDSS score values at 6 years than if they had been treated throughout, meaning that we have a conservative estimate of the effect of treatment. We have factored in potential bias because of missing data at 6 years, and this seems unlikely to account for the observed ‘treatment effect’.
The key potential source of bias in this study is that this is a purely observational study, and there could also be other differences between the cohorts that could account for the observed lower EDSS score in the UK MS RSS cohort, rather than this difference being as a result of treatment. Our examination of the portability of the natural history models between the BCMS and UoWMS cohorts gives some confidence that the model from one population can be used as non-randomised comparison group for progression in a different population. However, the difference in EDSS scores is small (–0.6 points) and could at least partially be accounted for by unmeasured differences between the BCMS and UK MS RSS cohorts. For example, if in the UK only those with physician-reported better prognosis, or those who were generally healthier (e.g. with fewer comorbidities), were recruited to the UK MS RSS, this could lead to an apparent better progression in this group than predicted. Similarly, if other improvements in MS care have taken place in the time between the BCMS cohort and the UK MS RSS cohort, this could be responsible for the apparent difference in EDSS score (rather than it being a result of DMT treatment). The agreement between the BCMS model (data for this study collected 1980–95) and the UoWMS model (data for this study collected 1976–2011) might suggest that there has not been a time-dependent improvement in EDSS score; however, with the comparison of only two cohorts, strong conclusions cannot be drawn.
Future research
Our model development opens up several important areas of future research. First, although these models have been developed and validated using two valuable natural history data sets, further validation in other MS cohorts would be useful, the caveats being the relative dearth of suitable data sets and the financial constraints, which may limit long-term follow-up. The ability of these models to predict disability (EDSS score) for the individual (rather than the population average), conditional on their first observed EDSS score and characteristics such as age at onset, needs further investigation and validation. This could include examination of different modelling strategies (such as Markov transition models or different parameterisations of time).
Such research would need to be accompanied by qualitative research into the needs of patients, their families, and clinicians, and to provide evidence around the best way to present prognostic models to these groups. In addition, qualitative research could examine the value put upon the small mean difference in EDSS score by patients, their carers and families, and how this balances against the prospects of long-term treatment. Utilities (as used here) are a relatively crude measure to examine this, and utility may change over time or depending on the treatment regime used. Multivariate models could be used to jointly model outcomes of relevance to patients, in addition to EDSS score, for example modelling EDSS score progression jointly with the occurrence of relapses or a quality-of-life score.
Second, these models were developed in patients who became ABN eligible and, therefore, represent a subset of MS patients. Although these individuals are highly relevant to the UK MS RSS (as these patients represent the only individuals likely to receive these drugs), applying these models to other cohorts with broader prescribing ability might be limited. Similar modelling strategies could be used to model natural history of MS in all patients with RRMS, rather than restricting to this subgroup. The models could also be expanded to look at prognosis in those with SPMS. Focusing follow-up on those who may be likely to progress more quickly (e.g. those with a high EDSS score at baseline and RRMS) would also enable more accurate modelling of factors affecting prognosis for those individuals.
A third key area is to what degree the uncertainty around individual predictions could help decide management decisions around different therapeutic options. Newer agents for MS, such as natalizumab,48 fingolimod or alemtuzumab,49 appear to have greater benefits in terms of reductions in relapse rates, but their impact on longer-term gains in terms of disease progression is uncertain, and any gains are at a higher burden of side effects and toxicity. Thus, careful patient selection for these drugs is important. Further research should examine how incorporation of formal prognostic models may or may not enhance shared clinical decision-making between clinicians and patients.
The same approach as used here could also be applied to assessing the associations of newer DMTs and other potential treatments for MS with progression, to aid in health-care decision-making. While, this approach (using a natural history non-randomised comparison group) remains inferior to randomised controlled trials, it may represent a compromise in terms of the ethical and financial constraints on future funding of randomised controlled trials. Recent developments in network meta-analysis also allow better use of randomised controlled trial data to infer different comparisons among treatments. 50
Here, we used natural history models as a non-randomised comparison group for a treated population, in order to estimate the long-term effect of treatment. More robust estimates of this long-term effect would be provided if it were feasible (ethically, logistically and financially) to conduct long-term randomised controlled trials, and by bringing all available evidence together using systematic review and (when appropriate) meta-analysis. It would also be useful to examine whether or not any treatment effect remains constant over time, and whether or not there are any subgroups of patients (e.g. those with lower baseline EDSS score, those with longer duration of disease) who benefit more or less from DMT treatment.
Chapter 8 Conclusions
The main conclusion from this study is that the trajectory of the EDSS score over time was very similar in two different cohorts of largely untreated MS patients (i.e. not exposed to any MS-specific drugs). Whether the time axis was time since onset or time since ABN eligibility, the Welsh and British Columbia cohorts gave rise to very similar models. The trajectory of the EDSS score over time in a third DMT treated cohort (the UK MS RSS) was slightly different, with marginally slower progression over time.
The coefficients from one of the two natural history models could be used to predict EDSS score for individuals from the other natural history cohort. Although the accuracy of these predictions may not be sufficiently good for predicting at an individual level for clinical purposes, these results provide strong evidence of the ability to use one cohort of MS patients as a non-randomised comparison group for another.
We identified several covariates as being related either to average EDSS score, or to rate of change of EDSS score over time. Those who were older at MS onset tended to have higher EDSS scores and slightly greater increases over time. Those with SP disease had a higher EDSS score at ABN eligibility (although no obvious difference in progression), as did those with more relapses in the 2 years prior to ABN eligibility. Women had lower EDSS scores on average than men, but again with no obvious differences in EDSS score trajectory. The estimates of these associations were again consistent between the two cohorts.
Using the natural history models to predict what the EDSS score would have been if a treated cohort (the UK MS RSS) had not been treated leads to the conclusion that EDSS score is slightly lower in the DMT-treated UK MS RSS (by 0.59 points, 95% CI 0.54 to 0.64 points) at up to 6 years post treatment. However, as this is a purely observational study, we cannot conclude that DMT treatment causes this difference.
Acknowledgements
Other acknowledgements
We would like to thank:
Professor Alasdair Coles, Professor Mark Gilthorpe and Professor Andrew Pickles, who formed the Advisory Group for this project and provided helpful input to the model development.
Dr Jackie Palace, Dr Charles Dobson and Dr Martin Duddy, who led the UK MS RSS, and who provided guidance on clinical interpretation and implications.
Thomas Bregenzer (Paraexcel), who provided the data from the UK MS RSS cohort, and also comparison analyses using Markov models.
Professor Richard Lilford (chairperson) and Professor Richard Gray and Dr Pelham Barton, of the UK MS RSS Scientific Advisory Group, who developed the statistical analysis plan for the main RSS analysis.
The MS Trust, which provided access to the data from the UK MS RSS and sponsored Mr Michael Lawton in applying this work to further analyses of the UK MS RSS data set, in particular Nicola Russell, who facilitated access to the data.
BCMS cohort, we thank all the MS patients for participating in these studies. We gratefully acknowledge the BCMS clinic neurologists who contributed to the study through patient examination and data collection (current members listed here by primary clinic):
University of British Columbia MS Clinic: A Traboulsee (University of British Columbia Hospital MS Clinic Director and Head of the UBC MS Programmes); A-L Sayao; V Devonshire; S Hashimoto (University of British Columbia and Victoria MS Clinics); J Hooge (University of British Columbia and Prince George MS Clinic); L Kastrukoff (University of British Columbia and Prince George MS Clinic); and J Oger.
Kelowna MS Clinic: D Adams; D Craig; and S Meckling.
Prince George MS Clinic: L Daly.
Victoria MS Clinic: O Hrebicek; D Parton; and K Atwell-Pope.
UoWMS cohort: we thank all the MS patients for participating in these studies. We gratefully acknowledge the neurologists who contributed to the study through patient examination and data collection (current members listed here in alphabetical order): M Cossburn; C Hirst; G Ingram; S Luppe; T Pickersgill; and also M Wardle, who wrote the MS database.
Contributions of authors
Kate Tilling (Professor of Medical Statistics, University of Bristol) helped design and obtain funding for the project. She also oversaw the project including all the statistical analyses, and drafted and revised the manuscript.
Michael Lawton (Research Assistant, Medical Statistics, University of Bristol) performed all the statistical analyses, generated the data sets from the UoWMS cohort based on the selection criteria, and assisted in writing and revising the manuscript.
Neil Robertson (Professor of Neurology, Institute of Psychological Medicine and Clinical Neuroscience, Cardiff University) collected and collated clinical data for the UoWMS cohort, gave feedback on the analysis and revised the manuscript.
Helen Tremlett (Professor and Canada Research Chair in Neuroepidemiology and MS, Faculty Medicine, Division of Neurology, University of British Columbia) facilitated and supervised patient selection and data extraction for the BCMS cohort, gave feedback on the analysis and revised the manuscript.
Feng Zhu (Statistician, Department of Medicine, Division of Neurology, University of British Columbia) generated the data sets from the BCMS cohort based on the selection criteria and revised the manuscript.
Katharine Harding (Clinical Lecturer in Neurology, Institute of Psychological Medicine and Neurology, Cardiff University) collected and collated clinical data for the UoWMS cohort, gave feedback on the analysis and revised the manuscript.
Joel Oger (Professor, University of British Columbia) was one of the neurologists entering patients in the BCMS database for over 30 years and has financed the database for over 10 years. He ensured that when new clinics were created in British Columbia they reported to the main database, and negotiated with the local neurologists for the participation of the BCMS database in the UK MS RSS. He has reviewed a draft of the manuscript.
Yoav Ben-Shlomo (Professor of Clinical Epidemiology, University of Bristol) helped design and obtain funding for the project. He was also involved in setting up the collaborations with the UoWMS and BCMS data sets, discussing the analysis plans, commenting on initial results, and reviewing and commenting on the draft and final report.
Publications
Lawton M, Tilling K, Robertson N, Tremlett H, Zhu F, Harding K, et al. A longitudinal model for disease progression was developed and applied to multiple sclerosis. J Clin Epidemiol 2015:68;1355–65.
Palace J, Duddy M, Bregenzer T, Lawton M, Zhu F, Boggild M, et al. Effectiveness and cost-effectiveness of interferon beta and glatiramer acetate in the UK Multiple Sclerosis Risk Sharing Scheme at 6 years: a clinical cohort study with natural history comparator. Lancet Neurol 2015;14:497–505.
Data sharing statement
Requests for access to the natural history data should be addressed to Helen Tremlett (BCMS cohort) or Neil Robertson (UoWMS cohort). Requests for access to the UK MS RSS data should be addressed to Nicola Russell at the Multiple Sclerosis Trust, Spirella Building, Letchworth SG6 4ET, UK.
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the HTA programme or the Department of Health. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the HTA programme or the Department of Health.
References
- Lublin FD, Reingold SC. Defining the clinical course of multiple sclerosis: results of an international survey. National Multiple Sclerosis Society (USA) Advisory Committee on Clinical Trials of New Agents in Multiple Sclerosis. Neurology 1996;46:907-11. http://dx.doi.org/10.1212/WNL.46.4.907.
- Comi G, Filippi M, Wolinsky JS. European/Canadian multicenter, double-blind, randomized, placebo-controlled study of the effects of glatiramer acetate on magnetic resonance imaging – measured disease activity and burden in patients with relapsing multiple sclerosis. European/Canadian Glatiramer Acetate Study Group. Ann Neurol 2001;49:290-7. http://dx.doi.org/10.1002/ana.64.
- PRISMS (Prevention of Relapses and Disability by Interferon beta-1a Subcutaneously in Multiple Sclerosis) Study Group . Randomised double-blind placebo-controlled study of interferon beta-1a in relapsing/remitting multiple sclerosis. Lancet 1998;352:1498-504. http://dx.doi.org/10.1016/S0140-6736(98)03334-0.
- Jacobs LD, Cookfair DL, Rudick RA, Herndon RM, Richert JR, Salazar AM, et al. Intramuscular interferon beta-1a for disease progression in relapsing multiple sclerosis. The Multiple Sclerosis Collaborative Research Group (MSCRG). Ann Neurol 1996;39:285-94. http://dx.doi.org/10.1002/ana.410390304.
- The IFNB Multiple Sclerosis Study Group . Interferon beta-1b is effective in relapsing-remitting multiple sclerosis. I. Clinical results of a multicenter, randomized, double-blind, placebo-controlled trial. Neurology 1993;43:655-61. http://dx.doi.org/10.1212/WNL.43.4.655.
- Tremlett H, Paty D, Devonshire V. The natural history of primary progressive MS in British Columbia, Canada. Neurology 2005;65:1919-23. http://dx.doi.org/10.1212/01.wnl.0000188880.17038.1d.
- Tremlett H, Paty D, Devonshire V. Disability progression in multiple sclerosis is slower than previously reported. Neurology 2006;66:172-7. http://dx.doi.org/10.1212/01.wnl.0000194259.90286.fe.
- Beta Interferon and Glatiramer Acetate for the Treatment of Multiple Sclerosis. London: NICE; 2002.
- Boggild M, Palace J, Barton P, Ben-Shlomo Y, Bregenzer T, Dobson C, et al. Multiple sclerosis risk sharing scheme: two year results of clinical cohort study with historical comparator. BMJ 2009;339. http://dx.doi.org/10.1136/bmj.b4677.
- Pickin M, Cooper CL, Chater T, O’Hagan A, Abrams KR, Cooper NJ, et al. The Multiple Sclerosis Risk Sharing Scheme Monitoring Study – early results and lessons for the future. BMC Neurol 2009;9. http://dx.doi.org/10.1186/1471-2377-9-1.
- Tremlett H, Zhu F, Petkau J, Oger J, Zhao Y, BC MS. Clinic Neurologists. Natural, innate improvements in multiple sclerosis disability. Mult Scler 2012;18:1412-21. http://dx.doi.org/10.1177/1352458512439119.
- Shirani A, Zhao Y, Kingwell E, Rieckmann P, Tremlett H. Temporal trends of disability progression in multiple sclerosis: findings from British Columbia, Canada (1975–2009). Mult Scler 2012;18:442-50. http://dx.doi.org/10.1177/1352458511422097.
- D’Souza M, Kappos L, Czaplinski A. Reconsidering clinical outcomes in multiple sclerosis: relapses, impairment, disability and beyond. J Neurol Sci 2008;274:76-9. http://dx.doi.org/10.1016/j.jns.2008.08.023.
- Kurtzke JF. Rating neurologic impairment in multiple sclerosis: an expanded disability status scale (EDSS). Neurology 1983;33:1444-52. http://dx.doi.org/10.1212/WNL.33.11.1444.
- Cutter GR, Baier ML, Rudick RA, Cookfair DL, Fischer JS, Petkau J, et al. Development of a multiple sclerosis functional composite as a clinical trial outcome measure. Brain 1999;122:871-82. http://dx.doi.org/10.1093/brain/122.5.871.
- Zajicek J. Diagnosis and disease modifying treatments in multiple sclerosis. Postgrad Med J 2005;81:556-61. http://dx.doi.org/10.1136/pgmj.2004.031294.
- Tremlett H, Zhao Y, Rieckmann P, Hutchinson M. New perspectives in the natural history of multiple sclerosis. Neurology 2010;74:2004-15. http://dx.doi.org/10.1212/WNL.0b013e3181e3973f.
- Gauthier SA, Mandel M, Guttmann CR, Glanz BI, Khoury SJ, Betensky RA, et al. Predicting short-term disability in multiple sclerosis. Neurology 2007;68:2059-65. http://dx.doi.org/10.1212/01.wnl.0000264890.97479.b1.
- Achiron A, Barak Y, Rotstein Z. Longitudinal disability curves for predicting the course of relapsing-remitting multiple sclerosis. Mult Scler 2003;9:486-91. http://dx.doi.org/10.1191/1352458503ms945oa.
- Achiron A. Predicting the course of relapsing-remitting MS using longitudinal disability curves. J Neurol 2004;251:v65-8. http://dx.doi.org/10.1007/s00415-004-1510-0.
- Langer-Gould A, Popat RA, Huang SM, Cobb K, Fontoura P, Gould MK, et al. Clinical and demographic predictors of long-term disability in patients with relapsing-remitting multiple sclerosis: a systematic review. Arch Neurol 2006;63:1686-91. http://dx.doi.org/10.1001/archneur.63.12.1686.
- Tremlett H, Yinshan Z, Devonshire V. Natural history of secondary-progressive multiple sclerosis. Mult Scler 2008;14:314-24. http://dx.doi.org/10.1177/1352458507084264.
- Kingwell E, van der Kop M, Zhao Y, Shirani A, Zhu F, Oger J, et al. Relative mortality and survival in multiple sclerosis: findings from British Columbia, Canada. J Neurol Neurosurg Psychiatr 2012;83:61-6. http://dx.doi.org/10.1136/jnnp-2011-300616.
- Hirst C, Swingler R, Compston DA, Ben-Shlomo Y, Robertson NP. Survival and cause of death in multiple sclerosis: a prospective population-based study. J Neurol Neurosurg Psychiatr 2008;79:1016-21. http://dx.doi.org/10.1136/jnnp.2007.127332.
- Lawton M, Tilling K, Robertson N, Tremlett H, Zhu F, Harding K. A longitudinal model for disease progression was developed and applied to multiple sclerosis. J Clin Epidemiol n.d.;68:1355-65. http://dx.doi.org/10.1016/j.jclinepi.2015.05.003.
- Association of British Neurologists . Revised (2009) Association of British Neurologists’ Guidelines for Prescribing in Multiple Sclerosis 2009. www.theabn.org/media/docs/ABN%20publications/ABN_MS_Guidelines_2009_Final(1).pdf (accessed 27 June 2016).
- Hirst CL, Ingram G, Pickersgill TP, Robertson NP. Temporal evolution of remission following multiple sclerosis relapse and predictors of outcome. Mult Scler 2012;18:1152-8. http://dx.doi.org/10.1177/1352458511433919.
- Goldstein H. Multilevel Statistical Models. London: Edward Arnold Publishers Ltd; 1995.
- Fang Y. Asymptotic equivalence between cross-validations and Akaike information criteria in mixed-effects models. J Data Sci 2011;9:15-21.
- Law NJ, Taylor JM, Sandler H. The joint modeling of a longitudinal disease progression marker and the failure time process in the presence of cure. Biostatistics 2002;3:547-63. http://dx.doi.org/10.1093/biostatistics/3.4.547.
- Subtil F, Rabilloud M. Robust non-linear mixed modelling of longitudinal PSA levels after prostate cancer treatment. Stat Med 2010;29:573-87.
- Royston P, Sauerbrei W. Stability of multivariable fractional polynomial models with selection of variables and transformations: a bootstrap investigation. Stat Med 2003;22:639-59. http://dx.doi.org/10.1002/sim.1310.
- Tilling K, Sterne JA, Rudd AG, Glass TA, Wityk RJ, Wolfe CD. A new method for predicting recovery after stroke. Stroke 2001;32:2867-73. http://dx.doi.org/10.1161/hs1201.099413.
- Tilling K, Sterne JA, Wolfe CD. Multilevel growth curve models with covariate effects: application to recovery after stroke. Stat Med 2001;20:685-704. http://dx.doi.org/10.1002/sim.697.
- Royston P, Altman DG. Regression using fractional polynomials of continuous covariates – parsimonious parametric modeling. J R Stat Soc Ser C Appl Stat 1994;43:429-67.
- Bosch JL, Tilling K, Bohnen AM, Donovan JL. Krimpen Study. Establishing normal reference ranges for PSA change with age in a population-based study: the Krimpen study. Prostate 2006;66:335-43. http://dx.doi.org/10.1002/pros.20293.
- Tilling K, Garmo H, Metcalfe C, Holmberg L, Hamdy FC, Neal DE, et al. Development of a new method for monitoring prostate-specific antigen changes in men with localised prostate cancer: a comparison of observational cohorts. Eur Urol 2010;57:446-52. http://dx.doi.org/10.1016/j.eururo.2009.03.023.
- Hughes S, Spelman T, Trojano M, Lugaresi A, Izquierdo G, Grand’Maison F, et al. The Kurtzke EDSS rank stability increases 4 years after the onset of multiple sclerosis: results from the MSBase registry. J Neurol Neurosurg Psychiatr 2012;83:305-10. http://dx.doi.org/10.1136/jnnp-2011-301051.
- Goodkin DE, Cookfair D, Wende K, Bourdette D, Pullicino P, Scherokman B, et al. Inter- and intrarater scoring agreement using grades 1.0 to 3.5 of the Kurtzke Expanded Disability Status Scale (EDSS). Multiple Sclerosis Collaborative Research Group. Neurology 1992;42:859-63. http://dx.doi.org/10.1212/WNL.42.4.859.
- Taffé P, May M, Swiss HIV. Cohort Study. A joint back calculation model for the imputation of the date of HIV infection in a prevalent cohort. Stat Med 2008;27:4835-53. http://dx.doi.org/10.1002/sim.3294.
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. Hoboken, NJ: Wiley; 2002.
- Carpenter JR, Goldstein H, Kenward MG. REALCOM-IMPUTE software for multilevel multiple imputation with mixed response types. J Stat Softw 2011;45:1-14. http://dx.doi.org/10.18637/jss.v045.i05.
- Pan H, Goldstein H. Multi-level models for longitudinal growth norms. Stat Med 1997;16:2665-78. http://dx.doi.org/10.1002/(SICI)1097-0258(19971215)16:23<2665::AID-SIM711>3.0.CO;2-V.
- Bosch JL, Tilling K, Bohnen AM, Bangma CH, Donovan JL. Establishing normal reference ranges for prostate volume change with age in the population-based Krimpen-study: prediction of future prostate volume in individual men. Prostate 2007;67:1816-24. http://dx.doi.org/10.1002/pros.20663.
- Altman DG, Vergouwe Y, Royston P, Moons KG. Prognosis and prognostic research: validating a prognostic model. BMJ 2009;338. http://dx.doi.org/10.1136/bmj.b605.
- Palace J, Duddy M, Bregenzer T, Lawton M, Zhu F, Boggild M, et al. Effectiveness and cost-effectiveness of interferon beta and glatiramer acetate in the UK Multiple Sclerosis Risk Sharing Scheme at 6 years: a clinical cohort study with natural history comparator. Lancet Neurol 2015;14:497-505. http://dx.doi.org/10.1016/S1474-4422(15)00018-6.
- Bergamaschi R, Berzuini C, Romani A, Cosi V. Predicting secondary progression in relapsing-remitting multiple sclerosis: a Bayesian analysis. J Neurol Sci 2001;189:13-21. http://dx.doi.org/10.1016/S0022-510X(01)00572-X.
- Polman CH, O’Connor PW, Havrdova E, Hutchinson M, Kappos L, Miller DH, et al. A randomized, placebo-controlled trial of natalizumab for relapsing multiple sclerosis. N Engl J Med 2006;354:899-910. http://dx.doi.org/10.1056/NEJMoa044397.
- Coles AJ, Fox E, Vladic A, Gazda SK, Brinar V, Selmaj KW, et al. Alemtuzumab versus interferon β-1a in early relapsing-remitting multiple sclerosis: post-hoc and subset analyses of clinical efficacy outcomes. Lancet Neurol 2011;10:338-48. http://dx.doi.org/10.1016/S1474-4422(11)70020-5.
- Filippini G, Del Giovane C, Vacchi L, D’Amico R, Di Pietrantonj C, Beecher D, et al. Immunomodulators and immunosuppressants for multiple sclerosis: a network meta-analysis. Cochrane Database Syst Rev 2013;6. http://dx.doi.org/10.1002/14651858.CD008933.pub2.
Appendix 1 Supplementary results
| Powers of time for the fixed and level 2 random effects | AIC |
|---|---|
| t, t | 22,634.22 |
| t, log t | 22,698.89 |
| log t, t | 22,711.81 |
FIGURE 8.
Q–Q plots for all residuals from the best-fitting model based on the BCMS cohort with time since onset as the time axis. (a) Level 2 residuals (constant); (b) level 2 residuals (time); (c) level 2 residuals (log-time); (d) level 1 residuals (constant); and (e) level 1 residuals (time).

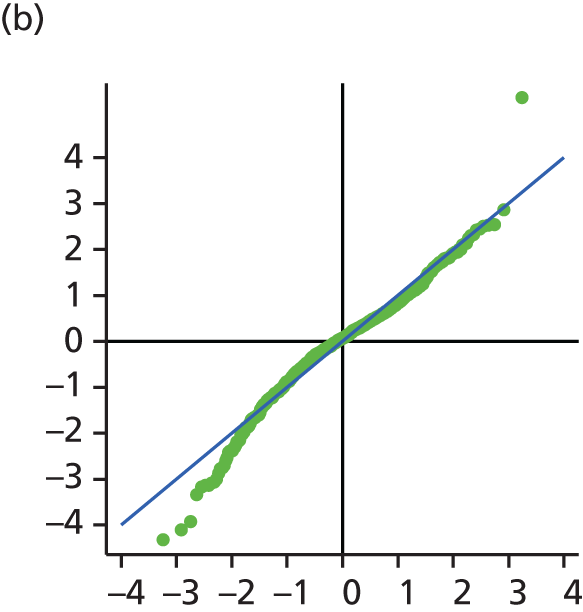
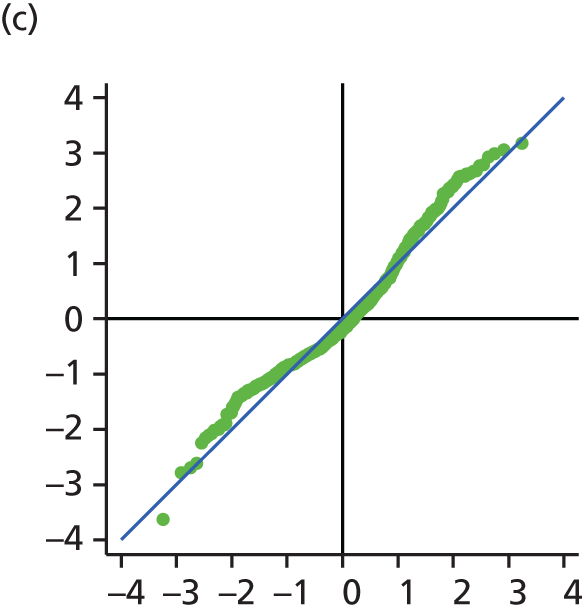

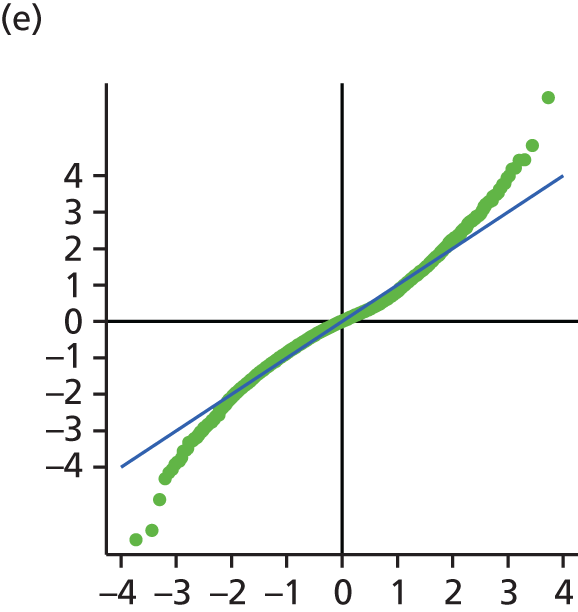
| Effects | Model | |
|---|---|---|
| Fixed effects | UoWMS cohort (95% CI) | BCMS cohort (95% CI) |
| Intercept (EDSS score at ABN eligibility) | 3.25 (3.05 to 3.45) | 2.24 (2.13 to 2.35) |
| Time since eligibility | 0.16 (0.07 to 0.25) | 0.17 (0.13 to 0.21) |
| Log-time since eligibility | 0.22 (–0.10 to 0.54) | 0.36 (0.22 to 0.50) |
| Level 2 random effects | ||
| Var(intercept) | 3.11 (2.57 to 3.65) | 2.82 (2.52 to 3.12) |
| Cov(intercept, time since ABN eligibility) | –0.22 (–0.39 to –0.05) | –0.28 (–0.36 to –0.21) |
| Var(time since ABN eligibility) | 0.15 (0.08 to 0.23) | 0.15 (0.12 to 0.18) |
| Cov(intercept, log-time since ABN eligibility) | 0.29 (–0.29 to 0.87) | 0.97 (0.71 to 1.23) |
| Cov(time since ABN eligibility, log-time since ABN eligibility) | –0.60 (–0.87 to –0.33) | –0.46 (–0.56 to 0.36) |
| Var(log-time since ABN eligibility) | 2.99 (1.92 to 4.07) | 2.24 (1.83 to 2.65) |
| Level 1 random effects | ||
| Var(intercept) | 0.34 (0.29 to 0.40) | 0.62 (0.57 to 0.67) |
| Cov(intercept, time since ABN eligibility) | –0.0082 (–0.0129 to –0.0036) | –0.0056 (–0.0094 to –0.0018) |
FIGURE 9.
Mean and 95% CIs for the 11 parameters in the time since eligibility models without covariates. (a) Constant FE; (b) time FE; (c) log-time FE; (d) level 2 RE var(constant); (e) level 2 RE cov(constant, time); (f) level 2 RE var(time); (g) level 2 RE cov(constant, log-time); (h) level 2 RE cov(time, log-time); (i) level 2 RE var(log-time); (j) level 1 RE var(constant); and (k) level 1 RE cov(constant, log-time). FE, fixed effect; RE, random effect.


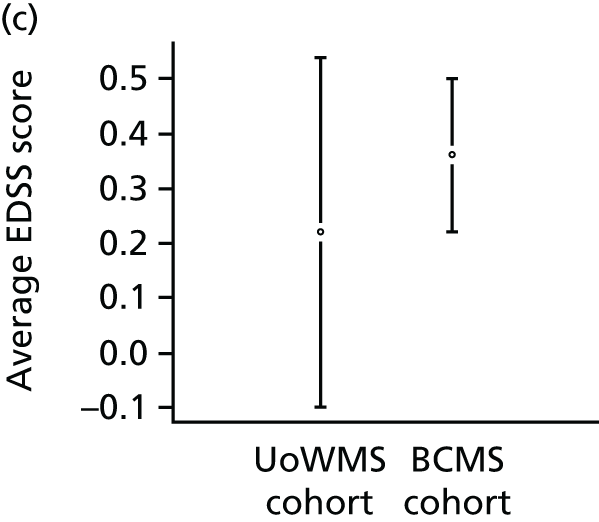



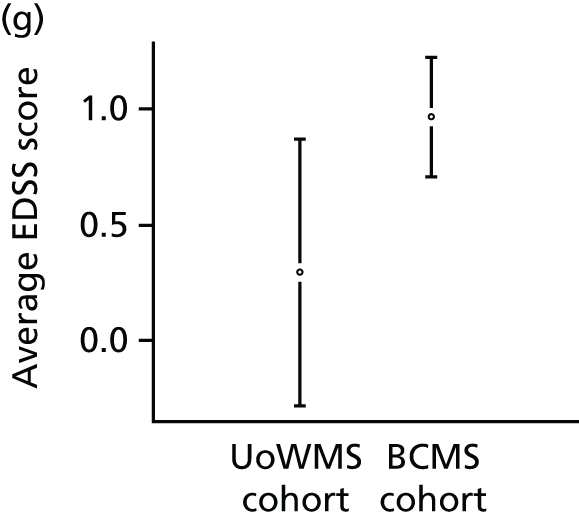


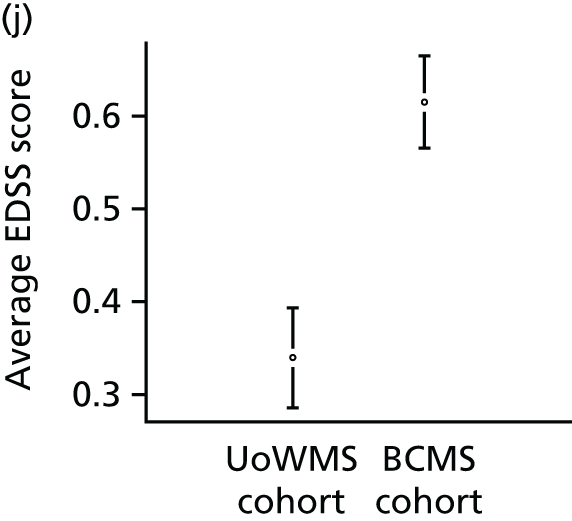
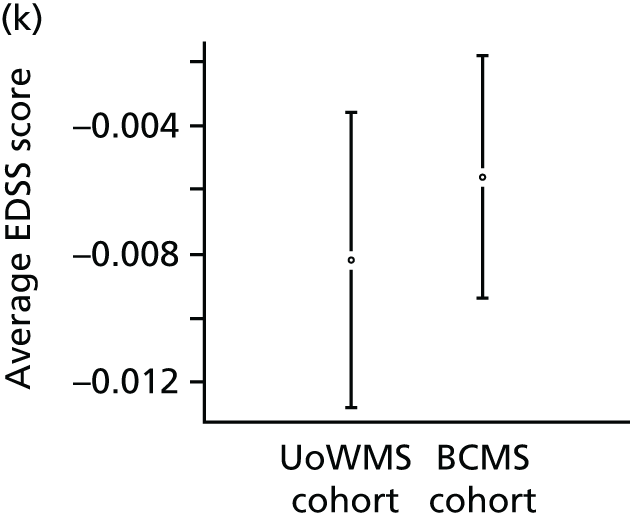
FIGURE 10.
The Q–Q plots for all residuals for the BCMS model with time since ABN eligibility and no covariates. (a) Level 1 residuals (constant); (b) level 1 residuals (time); (c) level 2 residuals (constant); (d) level 2 residuals (time); and (e) level 2 residuals (log-time).
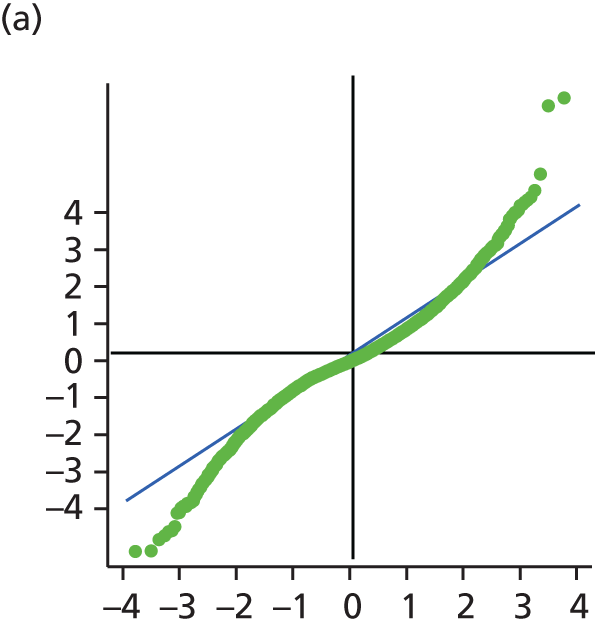
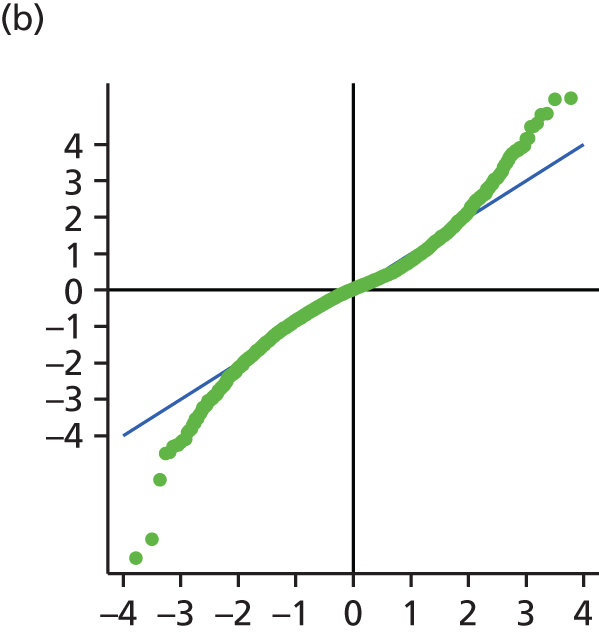
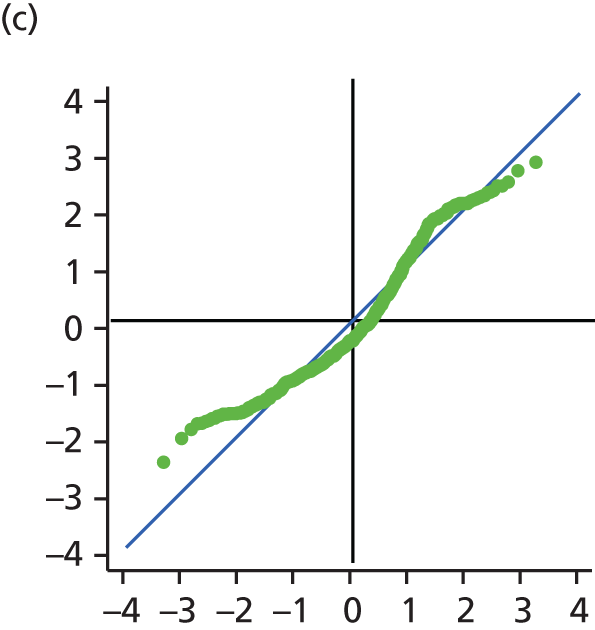
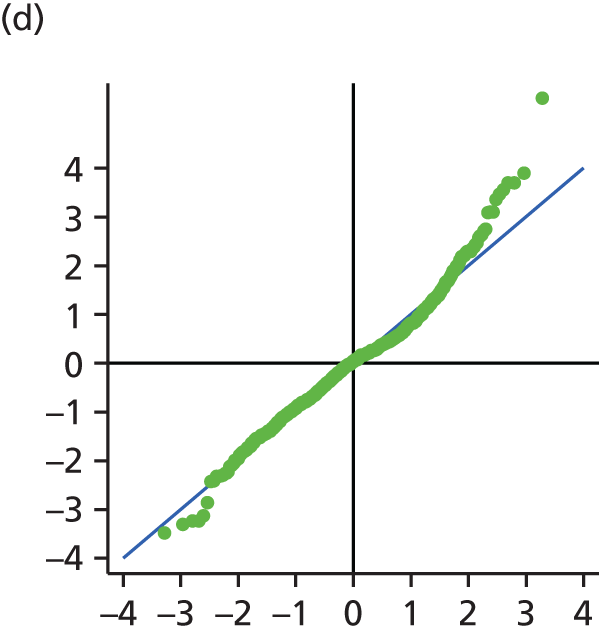
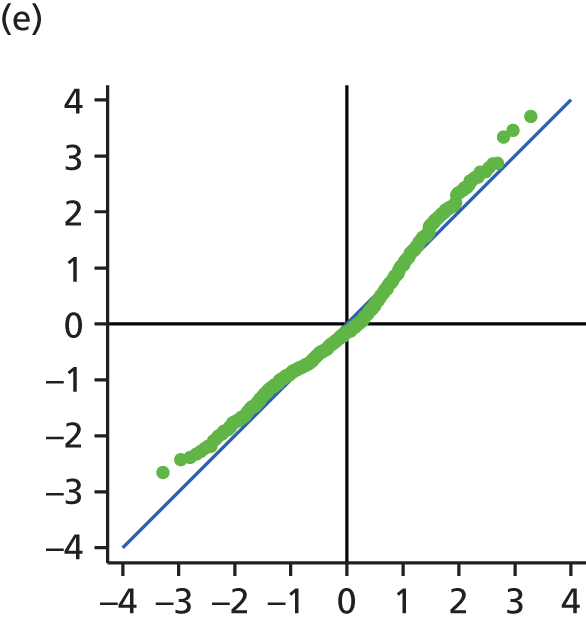
FIGURE 11.
The Q–Q plots for all residuals for the UoWMS model, with time since ABN eligibility and no covariates. (a) Level 1 (constant); (b) level 1 (time); (c) level 2 (constant); (d) level 2 (time); and (e) level 2 (log-time).



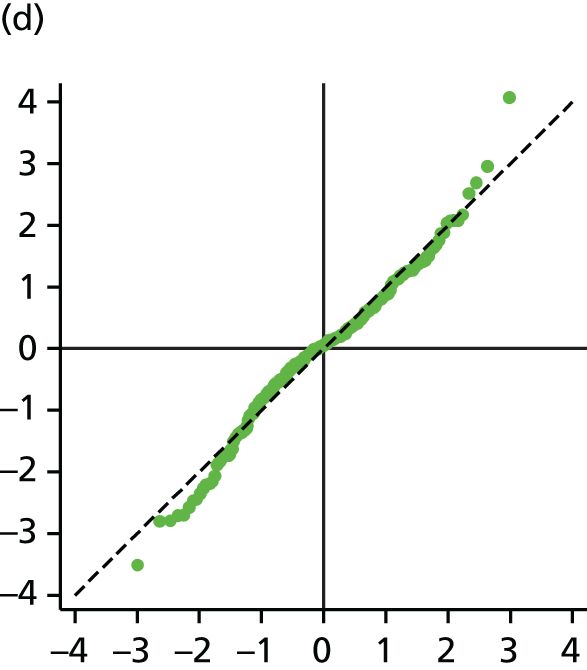

List of abbreviations
- ABN
- Association of British Neurologists
- AIC
- Akaike information criterion
- BCMS
- British Columbia Multiple Sclerosis
- CI
- confidence interval
- DMT
- disease-modifying therapy
- EDSS
- Expanded Disability Status Scale
- MS
- multiple sclerosis
- Q–Q
- quantile–quantile
- RMSE
- root-mean-square error
- RR
- relapsing–remitting
- RRMS
- relapsing–remitting multiple sclerosis
- RSS
- risk-sharing scheme
- SPMS
- secondary-progressive multiple sclerosis
- UoWMS
- University of Wales Multiple Sclerosis