Notes
Article history
The research reported in this issue of the journal was funded by the HTA programme as award number 11/103/01. The contractual start date was in August 2013. The draft manuscript began editorial review in August 2022 and was accepted for publication in August 2023. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HTA editors and publisher have tried to ensure the accuracy of the authors’ manuscript and would like to thank the reviewers for their constructive comments on the draft document. However, they do not accept liability for damages or losses arising from material published in this article.
Permissions
Copyright statement
Copyright © 2024 Lamb et al. This work was produced by Lamb et al. under the terms of a commissioning contract issued by the Secretary of State for Health and Social Care. This is an Open Access publication distributed under the terms of the Creative Commons Attribution CC BY 4.0 licence, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. See: https://creativecommons.org/licenses/by/4.0/. For attribution the title, original author(s), the publication source – NIHR Journals Library, and the DOI of the publication must be cited.
2024 Lamb et al.
Chapter 1 Introduction
Background and rationale
Globally, the overall prevalence of all stages of chronic kidney disease (CKD) is estimated to be 9%. In the UK a model developed using data from the Health Survey for England– 2009 and 2010 and the 2011 Census predicted the prevalence of CKD stages 3–5 [glomerular filtration rate (GFR) < 60 ml/minute/1.73 m2] in people aged 16 years and older to be 6.1% (2.6 million people). 1 The prevalence was higher in women than in men (7.4% vs. 4.7%) and there was a clear association between increasing age and prevalence. Overall, prevalence increased from 0.1% in people aged 16–34 years to 32.7% in those aged 75 years and over. Based on the projected population increase and assuming no change in the age-specific prevalence of CKD stages 3–5 and no improvement in the prevention and management of CKD stages 3–5, estimates of CKD prevalence are expected to increase to 8.3% of the population by 2036, representing roughly 4.2 million people.
The progression of CKD to kidney failure requiring consideration of kidney replacement therapy (dialysis and/or transplantation) is associated with a huge physical and mental health burden for individuals affected, including premature morbidity and mortality. There are also significant social and economic burdens for those individuals, their families and communities and the NHS. Data from the latest report from the UK Renal Registry suggest that the current rates of kidney replacement treatment are between 110 and 150 per million population per year. 2 Department of Health estimates of the annual cost of kidney failure treatment in England were approximately £1.5 billion in 2012 and were predicted to rise to £3.2 billion by 2027. 3 A secondary analysis of 7246 patients (2498 on dialysis) with moderate-to-severe CKD contributing 28,261 years of patient data from the Study of Heart and Renal Protection randomised trial has also been used to model costs. 4 Inclusion of non-fatal cardiovascular events, deaths, all hospital admissions, routine dialysis treatments and recorded outpatient/day-case attendances in UK 2011 prices led to estimates that those on maintenance dialysis incurred annual hospital costs of £18,986 in the year of initiation and £23,326 annually thereafter. Patients with a functioning kidney transplant incurred hospital care costs of £24,602 in the year of transplantation and £1148 annually thereafter. Non-fatal major vascular events increased annual costs in the year of the event by £6133 for patients on dialysis and by £4350 for patients not on dialysis.
Research has demonstrated that increasing severity of CKD is associated with greater risk for adverse outcomes which include cardiovascular disease, acute kidney injury (AKI), mortality (both all-cause and cardiovascular) as well as progression of CKD to kidney failure. 5–8 The increased risk for CKD progression in adults is driven by common, potentially modifiable risk factors, such as hypertension, diabetes and obesity as well as less modifiable genetic risk factors such as renin–angiotensin–aldosterone system (RAAS) genes. 9 Earlier recognition of CKD and improved identification of those at risk of adverse outcomes would enable earlier intervention, improved outcomes and avoidance of unnecessary costs. Blood pressure (BP) control and treatment with angiotensin-converting enzyme (ACE) inhibitors and angiotensin 2 receptor blockers (A2RBs) have renoprotective benefits in people with CKD, particularly in those with diabetes and albuminuria10–12 but also in non-diabetic nephropathy. 13 A subsequent cost-effectiveness study suggested that ramipril delayed progression to kidney failure and prolonged patient survival by 1.5–2.2 and 1.2–1.4 years, respectively, and saved US$16,605–23,894 lifetime and US$2422–4203 annually direct costs per patient. 14
More recently, a number of large placebo-controlled randomised controlled trials have shown that treatment with sodium-glucose cotransporter-2 (SGLT2) inhibitors in people with CKD not only substantially reduces the risk of kidney failure, AKI and hospitalisation for heart failure, but also moderately reduces the risk of cardiovascular death and myocardial infarction (MI). 15–19 Data on lifetime benefits for people with CKD suggest that treatment with a combination of ACE inhibitors/A2RBs and SGLT2 inhibitors in patients with albuminuric CKD without diabetes is expected to substantially increase kidney failure-free survival. 20 For a 50-year-old patient until the age of 75 years, the estimated survival free from kidney failure or death was 17.0 [95% confidence interval (CI), 12.4 to 19.6] years with the combination therapy and 9.6 (95% CI, 8.4 to 10.7) years with no treatment with any of these agents.
Chronic kidney disease is commonly identified using estimation of GFR and/or detection of protein in the urine (albuminuria/proteinuria). GFR is accepted as the best overall measure of kidney function and is central to diagnosis, staging and management of CKD. Ideally, GFR is measured using reference procedures which follow the clearance of an infused exogenous substance [e.g. inulin, 125I-iothalamate, 51Cr-ethylenediaminetetraacetic acid (EDTA) or iohexol] which is neither reabsorbed from nor secreted into the renal tubule. 21 However, these methods are cumbersome and impractical for general kidney disease detection, monitoring and management. Estimation of GFR [estimated glomerular filtration rate (eGFR)] using equations based on serum creatinine with adjustments for age, gender and, until recently, black ethnicity has been widely used as surrogate measures of GFR. In England, the National Institute for Health and Care Excellence (NICE) have made recommendations regarding which individuals should be tested for the presence of CKD (e.g. those with diabetes or hypertension) and have stated that GFR should be estimated 6-monthly in people with stage 3 CKD (GFR 30–59 ml/minute/1.73 m2),22 comprising approximately 6–7% of the overall UK population. 23,24 (Note that the International CKD staging system actually requires knowledge of both GFR and albuminuria to define stage. In this report, stage 3 CKD refers to all individuals with a GFR of 30–59 ml/minute/1.73 m2 irrespective of albuminuria status.) The aim of disease detection is to identify and manage individuals at increased risk of progression to kidney failure (GFR < 15 ml/minute/1.73 m2) and/or increased risk of morbidity and mortality compared to individuals without CKD. In addition to the accurate identification of CKD, the ability of tests to identify which individuals with CKD have higher risk of progressive or mortal disease is a crucial issue. Many people with stage 3 CKD are not at increased risk of progressive disease and there are concerns that CKD detection using creatinine-based approaches may be identifying some individuals who are at low risk and unlikely to benefit from active management. 25
Creatinine has many limitations as a marker of kidney function, including its relationship to muscle mass and age, and susceptibility of its measurement to analytical, drug and dietary interferences. An alternative marker of GFR, cystatin C, is less susceptible to the problems affecting creatinine measurement and interpretation of creatinine results. Early studies demonstrated the superiority of cystatin C measurement compared with creatinine for the detection of kidney disease. 26 Equations utilising serum cystatin C instead of, or in addition to, creatinine have been studied. Generally, such equations have demonstrated modest improvement in accuracy for estimating GFR compared to creatinine-only equations. 27,28 Furthermore, accumulating evidence suggests that cystatin C gives improved risk prediction for death and kidney failure compared to creatinine. 29,30 However, there have been no large, prospective studies of the value of cystatin C to identify and track changes in kidney function in a representative population of NHS patients. Given the higher costs of cystatin C compared to creatinine (approximately £3.80/test compared to £0.43/test for creatinine) and the scale of testing across the NHS, it is critical that its diagnostic accuracy and prognostic ability are carefully validated ahead of widespread introduction into the NHS.
Measuring glomerular filtration rate
Standard clearance of inulin, including urine collection, remains the ‘gold-standard’ method for GFR measurement but few studies use this. Most evaluations of GFR equations have used radiolabelled plasma clearance methods which are assumed to be closely related to inulin clearance. Radiolabelled iothalamate plasma clearance was the method used for developing estimating equations that are the standard of care in routine clinical practice, the Modification of Diet in Renal Disease (MDRD) study31 and Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI)32 GFR-estimating equations (see below), while the CKD-EPI equation validation data set used a variety of reference GFR methods including iohexol. 32 Although regarded as the reference approach for assessment of kidney function, it is increasingly appreciated that non-inulin plasma clearance methods are not all equivalent. 33 Furthermore, as with any physiological measurement, GFR has an intrinsic biological variability, an understanding of which is critical to appreciation of disease-related change. Using a variety of reference markers, values (coefficient of variation, CV%) ranging between 5.5% and 11.6% have been reported for the biological variation of GFR. 34 However, most of these estimates were from older studies that did not conform to recommended processes for deriving and reporting biological variation estimates. 35,36
Estimating glomerular filtration rate
A variety of equations have been developed to estimate GFR (Table 1). The MDRD Study equation, which estimates GFR adjusted for body surface area (BSA), was originally developed in 1999. 31 A simplified (‘4-variable’) version of the equation which requires knowledge only of serum creatinine concentration, age, gender and race (black or other) was later published and subsequently re-expressed for use with a standardised serum creatinine assay. 37,38 Generally, the MDRD equation has been seen to perform better, and offer practical advantages, over other GFR equations that had been used previously. Its use has been endorsed by national professional healthcare organisations including in the UK. 39,40 However, accuracy of the equation is suboptimal. In the CKD field, accuracy of GFR-estimating equations is commonly expressed as the P30, the percentage of eGFR values within 30% of ‘true’ GFR. This metric captures aspects of both imprecision (measurement error) and bias (systematic over- and/or underestimation). Reported P30 values for the MDRD equation typically range between 73% and 93%. 41 The MDRD equation has also been criticised on the basis that it significantly underestimates GFR (particularly in individuals with GFR > 60 ml/minute/1.73 m2) and has poor precision. 32
| Abbreviation | GFR equation expressed as a single equation |
|---|---|
| MDRD38 | GFR (ml/minute/1.73 m2) = 175 × (SCr × 0.01131)–1.154 × (age)–0.203 × (1.212 if patient is black) × (0.742 if patient is female) |
| CKD-EPIcreatinine32 | GFR (ml/minute/1.73 m2) = 141 × min(SCr × 0.01131/κ, 1)α × max(SCr × 0.01131/κ, 1)–1.209 × 0.993age × 1.018 (if female) × 1.159 (if black), where SCr is serum creatinine, κ is 0.7 for females and 0.9 for males, α is −0.329 for females and −0.411 for males, min indicates the minimum of SCr/κ or 1, and max indicates the maximum of SCr/κ or 1 |
| CKD-EPIcystatin28 | GFR (ml/minute/1.73 m2) = 133 × min(SCys/0.8, 1)–0.499 × max(SCys/0.8, 1)–1.328 × 0.996Age × 0.932 (if female), where min indicates the minimum of SCys/κ or 1, and max indicates the maximum of SCys/κ or 1 |
| CKD-EPIcreatinine-cystatin28 | GFR (ml/minute/1.73 m2) = 135 × min(SCr × 0.01131/κ, 1)α × max(SCr × 0.01131/κ, 1)–0.601 × min(SCys/0.8, 1)–0.375 × max(SCys/0.8, 1)–0.711 × 0.995Age × 0.969 (if female) × 1.08 (if black), where SCr is serum creatinine, SCys is serum cystatin C, κ is 0.7 for females and 0.9 for males, α is −0.248 for females and −0.207 for males, min indicates the minimum of SCr/κ or 1, and max indicates the maximum of SCr/κ or 1 |
| BIS1creatinine42 | GFR (ml/minute/1.73 m2) = 3736 × (SCr × 0.01131)–0.87 × age–0.95 × 0.82 (if female) |
| BIS2creatinine-cystatin42 | GFR (ml/minute/1.73 m2) = 767 × SCys–0.61 × (SCr × 0.01131)–0.40 × age–0.57 × 0.87 (if female) |
| CAPAcystatin43 | GFR (ml/minute/1.73 m2) = 130 × SCys–1.069 × age–0.117 −7 |
| FAScreatinine44 | GFR (ml/minute/1.73 m2) = 107.3/(SCr/Q) for 2 ≤ age ≤ 40 GFR (ml/minute/1.73 m2) = [107.3/(SCr/Q)] × 0.988(age–40) for age > 40 where Q values are the mean or median serum creatinine concentration for age-/sex-specific healthy reference populations |
| FAScreatinine-cystatin45 | FAScombi=107.3α×ScrQcrea+(1−α)×ScysCQcysC×[ 0.988(Age-40)whenage40years ]. where Q values are the mean or median serum creatinine or cystatin C concentration for age-/sex-specific healthy reference populations. When α = 0.5, the denominator is equal to the weighted average of the two normalised biomarkers |
| LMRcreatinine46 | eX − 0.0158 × age + 0.438 × ln(age), where X varies by gender and serum creatinine concentration (refer to paper) |
| EKFCcreatinine47 | GFR (ml/minute/1.73 m2) = 107.3 × (SCr/Q)−0.322 for age 2–40 and SCr/Q < 1 GFR (ml/minute/1.73 m2) = 107.3 × (SCr/Q)−1.132 for age 2–40 and SCr/Q ≥ 1 GFR (ml/minute/1.73 m2) = 107.3 × (SCr/Q)−0.322 × 0.990(Age − 40) for age > 40 and SCr/Q < 1 GFR (ml/minute/1.73 m2) = 107.3 × (SCr/Q)−1.132 × 0.990(Age − 40) for age > 40 and SCr/Q ≥ 1 where Q values are the mean or median serum creatinine concentration for age-/gender-specific healthy reference populations |
| CKD-EPI(2021)creatinine48 | GFR (ml/minute/1.73 m2) = 142 × min(Scr/κ,1)α × max(Scr/κ,1)–1.200 0.9938age × 1.012 (if female), where Scr is serum creatinine, κ is 0.7 for females and 0.9 males, α is −0.241 for females and −0.302 for males, min indicates the minimum of Scr/κ or 1, max indicates the maximum of Scr/κ or 1 |
| CKD-EPI(2021)creatinine-cystatin48 | GFR (ml/minute/1.73 m2) = 135 × min(Scr/κ,1)α × max(Scr/κ,1)–0.544 × min(Scys/0.8,1)–0.323 × max(Scys/0.8,1)–0.778 × 0.9961age × 0.963 (if female), where Scr is serum creatinine Scys is serum cystatin C, κ is 0.7 for females and 0.9 males, α is −0.219 for females and −0.144 for males, min indicates the minimum of Scr/κ or 1, max indicates the maximum of Scr/κ or 1 |
An alternative equation, the CKD-EPIcreatinine equation, was published in 2009 and is claimed to partially address this issue, producing less biased estimates of GFR at higher levels of kidney function,32 although reportedly less accurate estimates as GFR falls below 60 ml/minute/1.73 m2. 41 P30 values for the CKD-EPIcreatinine equation are slightly superior to those of the MDRD equation in studies that have undertaken a head-to-head comparison. 41 The NICE CKD guidance first published in 2008 recommended the MDRD equation for routine clinical care. The guidance was updated in 2014 and this recommendation was changed to the CKD-EPI equation, a recommendation that was continued in the 2021 CKD guideline. However, currently many laboratories in England continue to report eGFR using the MDRD equation.
Cystatin C, a small-molecular-weight protein, has been proposed as an improved marker of GFR compared to creatinine. 49,50 In 2010 an international standard for cystatin C became available which paved the way for the development of generalisable cystatin C-based GFR-estimating equations, either alone or in conjunction with creatinine. 51 Following publication of the original CKD-EPIcreatinine equation, the CKD-EPI Collaboration published two further CKD-EPI equations: one based on cystatin C (CKD-EPIcystatin) and one using both cystatin C and creatinine (CKD-EPIcreatinine-cystatin). 28 Members of the current study group have independently validated the latter equations in older people in the UK. 52
During the period of the current study, further equations have been published and validated, including the Berlin Initiative Study (BIS) equations BIS1 (creatinine-based) and BIS2 (creatinine and cystatin C based),42 the Lund–Malmö revised (LMR) equation,53 the Caucasian, Asian, Pediatric and Adult (CAPA) equation,43 the full age spectrum creatinine (FAScreatinine)44 and FAScreatinine-cystatin equations,45 the European Kidney Function Consortium (EKFC) equation,47 and recently in 2021 revised versions of the CKD-EPI equations [CKD-EPI(2021)creatinine and CKD-EPI(2021)creatinine-cystatin]. 48 These equations are described in further detail later.
Estimating glomerular filtration rate in British ethnic minority populations
People from South Asian and African-Caribbean backgrounds are at a three- to fivefold increased risk of developing established kidney failure requiring transplantation or dialysis compared to Caucasians. However, the proportion of the population from South Asian and African-Caribbean backgrounds with an eGFR of < 60 ml/minute/1.73 m2 is not similarly over-represented at a population level. 54 There is debate regarding whether individuals of South Asian and African-Caribbean ethnic backgrounds are at higher risk of CKD progression compared to Caucasians. 55–58 People of South Asian and African-Caribbean ethnicity are also less likely to undergo kidney transplantation when they reach established kidney failure and are at greater risk of complications from diabetes and high BP than the rest of the population.
The black race adjustment factors in the CKD-EPI and MDRD equations were founded on the premise that the relationship between serum creatinine concentration and kidney function is different amongst people of black ethnicity. Creatinine concentration is positively related to muscle mass and the historical assumption has been that individuals of black ethnicity will have a higher serum creatinine concentration at any given level of GFR due to increased muscle mass. Hence, two inflationary adjustment factors have been included: 1.212 in the MDRD equation and 1.159 in the CKD-EPIcreatinine equation (Table 1). In the development of these equations, predominantly in North American cohorts, use of these adjustment factors improved the agreement between mGFR (‘true’) and eGFR.
When widespread use of GFR estimation was first introduced into the UK (and other countries), it was recommended that the same adjustment factors for people of black ethnicity should be applied to African-Caribbean individuals in the UK, although the lack of UK evidence supporting this was acknowledged. NICE have recently reviewed the evidence in this area. 59 While GFR-estimating equations have been validated in African-Caribbean communities from North America60 and endemic Asian populations,61–66 there remains no independent validation in British South Asian or African-Caribbean populations. 59 There is increasing concern, both in the UK and elsewhere,67 that GFR adjustment may have contributed to falsely high GFR estimations amongst people of black ethnicity, potentially exacerbating pre-existing inequalities in access to health care in some individuals (e.g. access to certain drugs that are prescribed based on GFR level, access to advanced kidney care planning).
Adjusting GFR estimations for black ethnicity/race assumes that all individuals self-identifying as black share the same ancestry. There is increasing concern that the adjustment for ethnicity does not reflect the wide diversity within individuals of black ethnicity, with the adjustment based on outdated and unfounded biological assumptions for differences between ethnic groups at the expense of better understanding of social (e.g. dietary), environmental and ancestral (e.g. accuracy of self-reported ethnicity amongst individuals of mixed race) determinants. For some individuals of black ethnicity, such adjustment could lead to an overestimation of their GFR levels, and potential inequality in delivery of care. In the 2021 NICE CKD guideline the recommendation to adjust for ethnicity, present in earlier versions, was removed on the basis that adjusting for ethnicity when estimating GFR may not be valid or accurate. 59 The guideline committee recommended further research to establish, in adults, children and young people from black, Asian and other minority ethnic groups with CKD living in the UK, which existing GFR estimations are the most accurate. 59
Progression of kidney disease
There is no consistent definition of what constitutes progression of kidney disease. Many studies have used a doubling of serum creatinine, corresponding to an approximate halving of GFR, as an end-point defining progression, but this is insufficiently sensitive to be useful in clinical practice. Kidney Disease Improving Global Outcomes (KDIGO) have defined progression as a move to a higher disease category [e.g. stage 3A (GFR 45–59 ml/minute/1.73 m2) to stage 3B (GFR 30–44 ml/minute/1.73 m2)] accompanied by a fall in GFR of ≥ 25% (e.g. a decline from 50 to 35 ml/minute/1.73 m2) or an increase in albuminuria. 27 They defined rapid progression as a sustained decline in GFR of > 5 ml/minute/1.73 m2/year (e.g. a decline from 60 to < 54 ml/minute/1.73 m2 in 1 year). 27 NICE originally defined progression as a decline in GFR of more than 5 ml/minute/1.73 m2/year, or more than 10 ml/minute/1.73 m2/5 years. 40 More recently, NICE have defined accelerated progression as a sustained decrease in GFR of 25% or more and a change in GFR category within 12 months, or a sustained decrease in GFR of 15 ml/minute/1.73 m2 per year. 59
Progression is not necessarily common even amongst people with known CKD, for example amongst people with stage 3 CKD only 1.3% progressed to stage 5 CKD (established kidney failure, typically requiring dialysis or transplantation) over 5 years. 68 Amongst community-dwelling older (> 65 years) adults with stage 3 CKD, Hemmelgarn et al. reported mean decline of GFR of 3.6 and 2.8 ml/minute/1.73 m2/year, respectively, in male and female subjects with diabetes and somewhat lower values amongst subjects without diabetes (1.9 and 1.1 ml/minute/1.73 m2/year amongst males and females, respectively). 69 In the Ramipril Efficacy in Nephropathy study proteinuric (> 1 g/24 hours) non-diabetic subjects with GFRs in the approximate range 30–50 ml/minute/1.73 m2 showed a decline of GFR of 7.0 ml/minute/1.73 m2/year with slightly lower values being observed in those receiving RAAS blockade. 70
There are some data, mainly restricted to small studies in people with diabetes, describing disease progression in terms of decline in reference GFR measurements. 71,72 Generally, disease progression in people with diabetes has been described as following a broadly linear decline, being influenced by BP and albuminuria and ameliorated by antihypertensive medication/RAAS blockade. 71,73,74 A similar pattern has been observed using estimated rather than measured glomerular filtration rate (mGFR). 75
Identifying and predicting progressive kidney disease and clinical risk
A significant problem is the ability of GFR-estimating equations to identify progression of kidney disease against background change in GFR (i.e. that due to ‘normal’ ageing; commonly cited as approximately 1 ml/minute/1.73 m2/year) given the biological and measurement variability of both reference and eGFR. The intraindividual variation (CVI) of the main determinant (serum creatinine) of eGFR has been reported as 4.3%76 to which should be added analytical variation (CVA) of approximately 3.0%. 39 These data can be used to calculate the critical difference or reference change value (RCV) for serum creatinine using the equation:35
where Z is the number of standard deviations (SDs) appropriate to the probability.
For 95% probability (Z = 1.96), the derived RCV for serum creatinine is approximately 14.5% (i.e. this is the difference that can be considered ‘real’ with 95% probability). Substituting this level of variation into change in eGFR, it can be calculated that an individual with a GFR of 60 ml/minute/1.73 m2 will need to fall below approximately 50 ml/minute/1.73 m2 before the change can be considered a significant decrease. Some,77,78 although not the majority,79–82 of data suggest that the biological variation of serum cystatin C is greater than that of creatinine. If this were the case, then it would clearly impact on the ability of cystatin C-based GFR-estimating equations to detect changes in true GFR vis-à-vis serum creatinine.
Glomerular filtration rate changes of this order exceed the limit that most nephrologists would consider clinically significant. However, there is little prospective longitudinal data assessing the relative abilities of GFR-estimating equations to detect change in underlying ‘true’ GFR. In a 1-year prospective study of 71 patients with autosomal dominant polycystic kidney disease, the MDRD and CKD-EPIcreatinine equations underestimated the change in iohexol mGFR (mean change 8.4 ml/minute/1.73 m2) by > 50%. 83 A retrospective but larger (3532 participants with CKD followed for a mean of 2.6 years) study also addressed the accuracy of GFR-estimating equations compared to 125I-iothalamate mGFR over time in people with kidney disease. 84 The authors concluded that GFR-estimating equations accurately reflected changes in mGFR over time. Neither of these studies included eGFR data derived using cystatin C. Observational data suggest that for identification of progressive CKD the combination of eGFR using cystatin C and albumin-to-creatinine ratio (ACR) ranks highest, followed by eGFR using cystatin C alone, then the combination of ACR and eGFR using creatinine, and finally eGFR using creatinine alone. 85 The combined use of cystatin C and creatinine in a GFR-estimating equation, which is claimed to be less influenced by ethnicity, has not been tested as a predictor of progression.
In addition to identifying change in kidney function, there is evidence to suggest that baseline GFR estimates using cystatin C may be better able to predict patients likely to have progressive decline in kidney function, and increased risk of other outcomes including mortality, than equations based upon creatinine. 30,85 This closer relation to clinical risk was one of the justifications for inclusion of cystatin C GFR estimation in certain patients, as an adjunct to creatinine-based GFR estimations, in the 2014 NICE CKD guidance. 22
Evidence explaining why this study was needed and remains relevant
Chronic kidney disease is common, with an estimated population prevalence in England in 2016 of 13.9%. 86 Most commonly, it is detected using eGFR and/or albuminuria. Estimation of GFR on every blood creatinine request received by laboratories is recommended by NICE. 59 Circa 50 million GFR estimates are produced by UK NHS laboratories every year. As discussed earlier, NICE have recently removed the recommendation to adjust GFR estimates for individuals of black ethnicity. Of note, the guideline committee also recently expressed doubts that P30 accuracy was a good enough measure to make a recommendation on the use of one GFR-estimating equation over another because P30 covers a wide range compared to P15, which would be preferred if there were enough data. 22,59
The NICE guideline group originally also included cystatin C measurement, as a confirmatory test, in their guidance on CKD detection and diagnosis, in agreement with that from KDIGO. 22,27 However, this recommendation has been withdrawn, on the basis of an absence of good evidence for the accuracy of cystatin C-containing GFR equations and concerns that, although such equations may reduce false-positive (FP) tests for CKD, they may also increase false-negative (FN) results. 59 Conversely, a task force from the National Kidney Foundation and American Society of Nephrology have recommended increased, routine and timely use of cystatin C, especially to confirm creatinine-based eGFR in adults for clinical decision-making. 67 While the clinical utility of cystatin C remains uncertain, the increasing availability of cystatin C assays on large, automated laboratory test platforms may increase the pressure on NHS laboratories to introduce this test, which is significantly more expensive than creatinine testing.
The NICE guidelines have made a research recommendation for a large study to establish the diagnostic accuracy of cystatin C-based equations to estimate GFR as a measurement of kidney function in adults, children and young people in the UK. 59 There is also a further research recommendation to determine which biomarkers or factors, other than ethnicity, improve the diagnostic accuracy of GFR estimations in adults, children and young people from black, Asian and other minority ethnic groups with CKD living in the UK. 59 While introduction of routine GFR estimations is generally deemed to have brought significant health advantages,87 there is also concern that individuals without CKD may be inappropriately identified as having CKD. 25 Further, the ability of tests to identify which individuals with CKD will have high-risk (i.e. progressive disease and/or increased mortality risk) disease is seen as a crucial issue. A significant problem has been the ability of GFR-estimating equations to identify progression of kidney disease given the biological variability of its main determinant (serum creatinine). There are few prospective studies of the ability of GFR-estimating equations to monitor progression and no studies at all in adults of the monitoring ability of GFR-estimating equations incorporating cystatin C; there have been no prospective validations of GFR-estimating equations in British ethnic minority populations. The present study addresses these important issues.
The study
While there is significant published literature describing the accuracy of creatinine-based GFR estimation against reference methods, there are few data addressing the ability of GFR-estimating equations, including those incorporating cystatin C, to detect change in GFR. Furthermore, there are no data addressing the accuracy of these equations in British ethnic minority populations. The study protocol was published in 2014. 88 The study assessed whether eGFR using either creatinine or cystatin C or a combination of both was superior at detecting changes in GFR as measured by a reference GFR method. The utility of baseline eGFR and urinary ACR to predict who were more likely to show progressive kidney disease was also tested. We chose plasma iohexol clearance as the reference measure of GFR for our study because it is equivalent to inulin clearance, is widely used in clinical and research practice, is not radioactive, can be measured accurately and precisely, and is relatively cheap. 89–91 We chose to study the CKD-EPI and MDRD equations because they are internationally accepted GFR-estimating equations anchored to both creatinine and cystatin C reference methodology and therefore likely to generate data that will be valid in perpetuity. During the study several other GFR-estimating equations have been published and gained credence: these have also been evaluated here.
The study population was a large cohort of people with stage 3 CKD including people of South Asian and African-Caribbean ethnicity and participants with diabetes and albuminuria. A substudy modelled disease progression in a smaller cohort. The study built on the findings of previous research but used a prospective design with regular reference GFR measurements: the impact of medication on disease progression was estimated and included in the model. We also used a classical study design to establish the intraindividual biological variability of both mGFR and eGFR: this information was used as one of the tools in defining progression and assessing the ability of GFR-estimating equations to detect it. A cost analysis exploring the impact of including cystatin C in GFR-estimating equations in a monitoring context was undertaken.
To address these issues, a study in three parts was undertaken to provide the required portfolio of evidence to identify the optimal estimate of GFR to use in clinical practice:88
-
Main study. A large 3-year prospective longitudinal cohort study using 6-monthly estimates of GFR and baseline and final reference GFR values was undertaken to assess and compare the accuracy and precision of each estimate of GFR and change in GFR. The study included adults (n = 1229) with stage 3 CKD (GFR 30–59 ml/minute/1.73 m2) recruited across six centres. The cohort was enriched for participants more likely to have progressive kidney disease (i.e. those with albuminuria and/or diabetes) and those from South Asian and African-Caribbean ethnic groups.
-
Substudy of disease progression. We modelled predictors of progression of GFR in a subset of the cohort (n = 278) who received annual mGFR tests, in addition to 6-monthly GFR estimates and urinary ACR measurements, assessing risk factors and over time.
-
Substudy of biological variation. We undertook a substudy in 20 participants investigating sources of variability to estimate the components of measurement error in each measure and estimate of GFR.
We used the results from the comparative accuracy study to inform a measurement model analysis. In this, the trajectory of participants’ mGFR and eGFR over 10 years was used to estimate the proportion meeting the NICE threshold of accelerated progression (see Progression of kidney disease), assuming an annual testing schedule, and the number of participants expected to be incorrectly managed at each of the evaluated monitoring time points using the different estimating equations. Based on the findings, the comparative costs of monitoring with GFR-estimating equations were estimated.
Specific objectives
Primary objectives
The study evaluated the comparative performance of GFR-estimating equations, including those incorporating cystatin C, in assessing and monitoring GFR in people with stage 3 CKD. The data were analysed to assess the impact of ethnicity, albuminuria, diabetes and other characteristics on equation performance. The aims of the study were:
-
to estimate and compare the accuracy of GFR-estimating equations at baseline based on the MDRD equation and three CKD-EPI equations using either creatinine or cystatin C or a combination of both in individuals with stage 3 CKD
-
to estimate the accuracy of the GFR-estimating equations according to ethnic group (particularly Caucasian, South Asian and African-Caribbean), and baseline diabetes, albuminuria, age, gender, BMI and mGFR level
-
to evaluate and compare how accurately these GFR-estimating equations track mGFR and detect change in mGFR over 3 years
-
to estimate the biological variability of mGFR and eGFR
-
to establish which GFR-estimating equation, together with urinary ACR, or ACR alone, most accurately predicts mortality and those individuals that have progressive loss of kidney function (CKD progression)
-
to estimate and model disease progression (decline in GFR or increase in ACR) and differences in progression between ethnic groups (Caucasian, South Asian and African-Caribbean), baseline diabetes and albuminuria status and other potential risk factors
-
to explore the comparative cost effectiveness of monitoring strategies for identifying people who have progressive loss of kidney function (CKD progression) utilising different GFR-estimating equations.
Secondary objectives
-
To estimate and compare the accuracy of more recent GFR-estimating equations that have been published while the study has been ongoing including BIS1 and BIS2 equations, CAPA equation, LMR equation, FAScreatinine equation, FAScreatinine-cystatin equation, EKFC equation and the 2021 revisions of the CKD-EPI equations (Table 1).
-
To evaluate and compare how accurately these newer GFR-estimating equations reflect and detect change in GFR over 3 years.
-
To estimate and compare the performance of the MDRD equation and CKD-EPI equations using the Haycock equation92 for BSA adjustment instead of the Du Bois equation. 93
-
To assess the impact of cystatin C calibration on the performance of the CKD-EPI equations.
-
To assess the impact of creatinine methodology [enzymatic vs. isotope dilution mass spectrometry (ID-MS)] on the performance of the MDRD equation and creatinine-based CKD-EPI equations.
Chapter 2 Methods
Main study: prospective longitudinal cohort study
The main study comprised a prospective longitudinal test evaluation cohort study in which adults (≥ 18 years) with stage 3 CKD (GFR 30–59 ml/minute/1.73 m2) had baseline investigations of kidney function (mGFR and eGFR and albuminuria) and were then followed for 3 years, with 6-monthly estimates of GFR and a repeat reference mGFR at the end of the study (Figure 1). 88
FIGURE 1.
Outline of study.
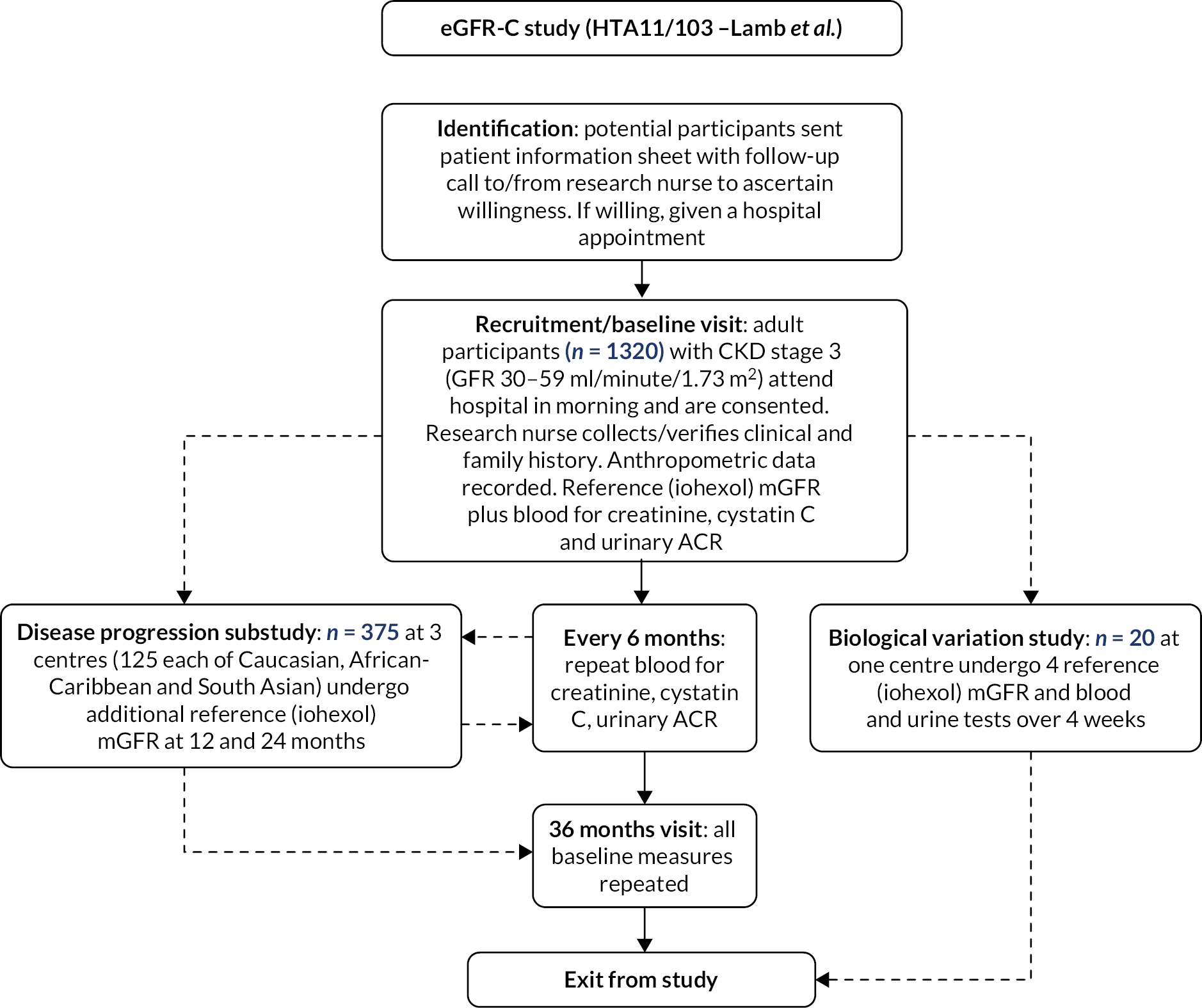
Recruitment
Adults with stage 3 CKD were recruited to the study at six centres, with a target case mix as follows:
-
Birmingham – 50% Caucasian, 25% South Asian, 25% African-Caribbean from secondary care
-
Canterbury – predominantly Caucasian cohort from secondary care
-
Derby – predominantly Caucasian cohort from primary care
-
Leicester – 50% Caucasian, 50% South Asian, from primary and secondary care
-
Salford – predominantly Caucasian cohort from secondary care
-
London – Kings College Hospital – 50% Caucasian, 50% African-Caribbean from secondary care.
Participants were recruited from both primary and secondary/tertiary care. Recruitment in secondary/tertiary care was primarily from CKD clinics. Potential participants were identified by the research nurse/co-investigator at each of the recruiting centres from the individual renal unit databases. Recruitment from primary care utilised the following approaches. In Leicester, letters were sent to general practitioners (GPs) inviting them to participate. Research active practices were approached by the Clinical Research Network and consenting practices were given instructions to help identify eligible people from the CKD register, for example using READ code searches. MIQUEST (Morbidity Information QUery and Export SynTax) software was used to extract an up-to-date data set. The practices sent invitation letters with a stamped envelope to eligible people. The invitation was sent out with the patient information sheet. Potential recruits were given a dedicated study phone line to use to indicate willingness to participate and the research assistant then telephoned willing participants to further discuss the study and schedule hospital attendance. Signed informed consent was obtained upon hospital attendance for the reference GFR test (see below). In Derbyshire, a similar process was followed except that eligible participants were identified from a database of participants from the Renal Risk in Derby study,94 a cohort study of persons with CKD in primary care.
Inclusions
Individuals aged 18 years and older having stage 3 CKD (eGFR measurements between 30 and 59 ml/minute/1.73 m2 inclusive sustained over at least 3 months prior to recruitment) were included. Recruitment was targeted such that approximately 20% would have severely increased albuminuria (ACR > 30 mg/mmol) and a similar proportion would have diabetes, since such prevalences are fairly typical of the CKD population being studied, at least in secondary care. Albuminuria and diabetes prevalence were monitored during the course of the study to ensure reasonable representation.
Exclusions
History of untoward reactions to iodinated contrast media or allergy to topical iodine, pregnant or breastfeeding, known current alcohol or drug abuse, kidney transplant recipient, people whose life expectancy would make study completion unlikely,95 inability to consent, for example due to cognitive impairment, inability to comply with study schedule and follow-up, amputation of whole or part limb, recent (last 6 months) episode of AKI, as defined by the Acute Kidney Injury Network criteria96 and sickle cell disease.
Sampling and data collection
Baseline visit: Participants were asked to attend hospital in the morning after having been advised to consume a light breakfast (no meat or fish). A clinical and drug history was recorded using a standardised questionnaire taken by research nurses on the day of hospital attendance. Vascular disease was defined as the presence of MI (including ST-elevation myocardial infarction and non-ST elevation myocardial infarction), angina, congestive cardiac failure (heart failure) or a requirement for coronary intervention (angioplasty, coronary artery bypass graft or pacemaker), cerebrovascular or peripheral vascular disease. Information on ethnicity was gathered using a modified version of the 2011 UK Census Questionnaire, with ethnicity being mapped to the following codes:
Caucasian 31, 32, 33, 34; South Asian 39, 40, 41; African-Caribbean 44, 45, 46.
Height was measured to the nearest 0.1 cm with a rigid stadiometer. Body weight was measured in light indoor clothing to the nearest 0.1 kg. Waist circumference was recorded to the nearest 0.1 cm at the mid-point between the lower costal margin and the level of the anterior superior iliac crest. Brachial BP was measured as recommended by the British and Irish Hypertension Society [https://bihsoc.org/resources/bp-measurement/measure-blood-pressure/ (accessed 26 July 2023)] three times in the sitting position using standardised Omron M7 digital sphygmomanometers (Omron Healthcare, Milton Keynes, UK). The average of the second and third BP readings was recorded.
Baseline blood was taken for serum creatinine and cystatin C, and a urine sample was collected for ACR. Blood samples were also taken for haemoglobin and glycated haemoglobin (only if known to have diabetes) measurement. Further aliquots of serum and urine were stored for potential analysis of future markers of GFR or disease progression. Blood samples were collected using standard venepuncture and phlebotomy procedures including the use of a tourniquet. Blood was collected in appropriate Greiner VacuetteTM tubes [www.gbo.com (accessed 26 July 2023)] following the manufacturer’s recommended order of draw. The urine sample was taken into a plain Sterilin pot. Samples were transported to the local laboratory, where plasma/serum was separated within 4–6 hours of venepuncture by centrifuging at 2000 g for 10 minutes. Aliquots of serum/plasma and urine were then stored at −80 °C pending transportation to the central laboratories [St. Thomas’s (iohexol, ID-MS creatinine) or Canterbury (enzymatic creatinine, cystatin C, ACR) depending on analyte] and analysis.
Glomerular filtration rate was measured using an iohexol clearance method. 97 A 5 ml bolus of Omnipaque 240 (518 g/l iohexol corresponding to 240 g/l of iodine, GE Healthcare [www.gehealthcare.co.uk/ (accessed 12 April 2023)] followed by 10 ml of normal saline was injected into the antecubital vein. Blood samples were collected at 5, 120, 180 and 240 minutes after injection. Exact time of the samples in relation to the bolus injection was accurately recorded. Participants were allowed free access to fluids during the collection procedure but were asked to refrain from protein intake (i.e. biscuits/toast would be permitted) and to refrain from excessive exercise. Samples were stored at −80 °C prior to analysis. Iohexol was determined using an ID-MS method (see below) and GFR calculated. 98
Glomerular filtration rate was estimated using published GFR-estimating equations: the simplified ID-MS traceable version of the MDRD equation and the three CKD-EPI equations (CKD-EPIcreatinine, CKD-EPIcystatin and CKD-EPIcreatinine-cystatin) for the primary study objectives. For the secondary study objectives, the BIS1 and BIS2, CAPA, LMR, FAScreatinine, FAScreatinine-cystatin, EKFC and the 2021 revisions of the CKD-EPI equations were studied (Table 1).
Follow-up: Participants were followed for 3 years. All the above measurements and the clinical history were repeated at 36 months. At each 6-month interval, blood samples of all participants were taken for serum creatinine, according to standard care,40 in addition to cystatin C and a urine sample was collected for ACR: GFR was estimated as above. All measurements were undertaken in accordance with standard operating procedures by trained staff. Nursing staff familiar with these procedures at the Canterbury centre cascade trained other recruiting centres. Clinicians and others involved in patient care were blinded to the reference measured (iohexol) GFR and cystatin C-based eGFR results for the duration of the study. During the course of the study, participants were given advice regarding the management of their CKD according to standard evidence-based practice. 40
Laboratory analyses
Iohexol was measured using electrospray isotope dilution tandem mass spectrometry on an ABSCIEX API6500 Q-trap (ABSCIEX, Warrington, UK) mass spectrometer. 97 Iohexol stock standard, 10 mmol/l, was prepared by diluting Omnipaque 300 solution (647 g/l) in deionised water and stored in 1 ml aliquots at −80 °C. Aqueous iohexol calibrators (0, 10, 100 and 500 µmol/l) were prepared from the stock iohexol standard by dilution and stored in 0.5 ml aliquots at −80 °C. Iohexol stable isotope, d5-iohexol (Toronto Research Chemicals Inc., Toronto, ON, Canada), was obtained from 2BScientific Ltd, Upper Heyford, UK, dissolved in deionised water at circa 10 mmol/l, and stored at −80 °C. Plasma control samples were prepared by spiking a plasma pool with iohexol stock standard at 10, 100 and 400 µmol/l. Calibrators, controls, patient samples and stable isotope stock solutions were thawed from frozen on a roller mixer at room temperature for no more than 60 minutes, and then centrifuged for 4 minutes at 1500 g at 4 °C (Eppendorf 5810R centrifuge, VWR International Ltd, Lutterworth, UK). Working iohexol stable isotope was prepared by diluting the circa 10 mmol/l solution 1 : 200 with deionised water. Calibrators, controls and samples were pipetted (20 µl) into 2 ml microcentrifuge tubes [000-MICR-200, Elkay Laboratory Products (UK) Ltd, Basingstoke, UK] and 50 µl working iohexol stable isotope, followed by 200 µl acetonitrile (Rathburn Chemicals Ltd, Walkerburn, UK) were added to each tube. Samples were capped, vortex-mixed for 5 seconds and centrifuged for 5 minutes at 20,800 g at 4 °C (Eppendorf 5417R centrifuge, VWR International Ltd, Lutterworth, UK). Supernatants (200 µl) were then transferred into a 96 deep well plate and loaded onto the autosampler. The sample (2 µl) was automatically injected into a mobile phase stream of acetonitrile : water (1: 1) with 0.025% formic acid using a Hewlett-Packard 1100 Series autosampler and pump (Applied Biosystems, Warrington, UK) at 250 µl/minute. Chromatography was performed on a Chirobiotic T 100 × 2.1 mm column with a 2 cm × 4.0 mm guard column (Sigma-Aldrich Company Ltd, Poole, UK).
Tandem mass spectrometry was performed in positive ion multiple reaction monitoring mode: iohexol 821.849/602.8, d5-iohexol 826.849/607.8. Data acquisition time was 6 minutes with a pause time of 5.0070 milliseconds between transitions and a scan speed of 10 Da/s. Iohexol concentrations were calculated in Analyst 1.6 (ABSCIEX, Warrington, UK) using the ratio of sample peak area to stable isotope peak area. Between-day imprecision (CV, %) was 1.0%, 0.8% and 1.5% at 10, 100 and 400 μmol/l, respectively. The laboratory participated in an international proficiency testing scheme [EQUALIS, https://equalis.se/en/ (accessed 5 April 2023)] for iohexol measurement with good performance.
Iohexol concentrations were log-transformed (natural log) and plotted as a function of time. GFR was calculated from the slope-intercept method using a single compartment model:99,100
To ensure integrity of the iohexol procedure (dose administration, sample collection, sample labelling, and iohexol analysis), the iohexol data were rigorously reviewed for every mGFR. The 5-minute sample enabled identification of procedures where the iohexol was given subcutaneously in error, or where saline flushing of the infusion line was suboptimal, as demonstrated by low and high iohexol concentrations respectively. In addition, all procedures where the iohexol concentration versus time correlation coefficient (r) was < 0.98 (< 6% of total procedures) were re-analysed to check for any within-assay sample transposition.
Glomerular filtration rate was adjusted for BSA using the Du Bois equation93 and corrected for the fast exponential. 98 In a separate analysis, GFR was adjusted for BSA using an alternative approach (Haycock equation92) to assess the impact of these adjustments on the accuracy of GFR estimation.
Serum creatinine was measured using an enzymatic assay on an Abbott Architect analyser [Abbott Diagnostics Ltd, www.abbott.co.uk/ (accessed 12 April 2023)] standardised to the reference material, NIST SRM 967 and 914. Between-day imprecision (CV, %) was 0.8%, 0.3% and 0.4% at concentrations of 75, 176 and 760 μmol/l, respectively. The laboratory participated in an international proficiency testing scheme [UKNEQAS, https://birminghamquality.org.uk/ (accessed 5 April 2023)] for creatinine measurement and GFR estimation with satisfactory performance. Additionally, serum creatinine was measured using ID-MS on an ABSCIEX API6500 Q-trap mass spectrometer.
Cystatin C was measured by a turbidimetric immunoassay on an Abbott Architect analyser. Between-day imprecision was 2.3% and 1.6% at concentrations of 0.9 and 4.0 mg/l, respectively. The laboratory participated in an international proficiency testing scheme (EQUALIS) for cystatin C measurement and GFR estimation with good performance.
During the course of the study, we became aware of published data describing a significant positive bias of the Abbott cystatin C assay. 101 This was supported by information from the EQUALIS proficiency testing scheme and our own re-analysis of historical stored samples (data not presented here). To investigate this, a recovery study was undertaken in which lyophilised human serum cystatin C ERM-DA471/IFCC [Sigma-Aldrich Chemical Co., www.sigmaaldrich.com (accessed 5 April 2023)] was added to pooled non-uraemic serum to give samples with a range of expected concentrations covering 1.47–3.41 mg/l. These samples were analysed and the mean recovery calculated.
To further explore this bias, in a subset of samples (n = 106) covering a representative range of concentrations cystatin C was also measured by a particle-enhanced nephelometric immunoassay according to the manufacturer’s instructions on a Siemens BN Prospec analyser [www.siemens.com (accessed 12 April 2023)]. Between-batch imprecision (n = 38) for the Siemens assay was 3.5% at 0.87 mg/l and 3.6% at 4.64 mg/l. Both Abbott and Siemens assays were calibrated against the internationally certified reference material ERM-DA471/IFCC for cystatin C. 51
Prior to analysis, samples were thawed at room temperature, mixed by inversion and centrifuged prior to measurement. For the biological variation study, all samples from each individual subject were measured in duplicate in random order in a single assay. Each of the biomarker analyses was undertaken by a single operator blinded to participant data using a single instrument. Creatinine and cystatin C measurements were undertaken in an accredited laboratory by scientists registered with the Health and Care Professions Council.
Substudy of disease progression
Participants in the substudy underwent additional testing to that described in the main study, with a reference mGFR each year over the 3-year study period (i.e. four reference GFR measures in total) (Figure 1). Serum creatinine and cystatin C measurements to inform the eGFR equations and ACR measurements were taken every 6 months. Four eGFR equations were investigated [MDRD, CKD-EPIcreatinine, CKD-EPIcystatin and CKD-EPIcreatinine-cystatin (Table 1)]. CKD-EPIcreatinine is the NICE-recommended equation and was the primary result to compare to mGFR.
It was planned to recruit at least 375 participants in the substudy enriched to include equal numbers of South Asian, African-Caribbean and Caucasian participants, and approximately equal numbers with and without diabetes and/or albuminuria (high and low risk).
The majority of participants in the substudy were recruited from the Birmingham, Leicester and London centres. An additional two centres (Canterbury and Salford) were later added to increase recruitment to the substudy.
The aim was to develop a model of disease progression based on reference GFR measurement and to estimate differences in progression for risk factors. The target number of subjects for inclusion was considered to provide a range of values over the main factors considered to influence disease progression and allow assessment of covariates in the statistical model. Inclusions/exclusions and laboratory methods for this substudy were as described above.
Further assessment of covariates was performed by combining the data from the disease progression substudy with the main study, and fitting the final covariate models for the substudy to the full data set. The evaluable population included those participants from the main study or substudy with paired mGFR and eGFR at two time points or more.
Substudy of intraindividual biological variability
At one centre (Canterbury) a study was undertaken to define the normal biological variability of a reference GFR test in addition to the eGFR tests. Participants with stage 3 CKD (n = 20) underwent four iohexol reference measures of GFR over 4 successive weeks, with standardisation for time of day (morning after a light breakfast) and day of week. Inclusions/exclusions and laboratory methods for this substudy were as above (see Recruitment). Individuals participating in this substudy were eligible for inclusion in the main study and the substudy of disease progression if they were happy to do so.
Sample size calculations
Main study: prospective longitudinal cohort study
The sample size calculation for the main study focused on the ability to detect differences in accuracy of measurement between the MDRD equation and the CKD-EPIcystatin equation. We also made secondary comparisons with the other equations. While it is relatively easy to estimate the relationship between each equation and the reference standard in smaller samples, a relatively large sample is required to have adequate statistical power to make the comparison in accuracy. Similarly, while it is possible to show a relationship between eGFR and progression within a cohort, to show that one equation predicts progression better than another is more challenging.
The measure of accuracy we used was the P30, the percentage of eGFR values within 30% of ‘true’ GFR. Describing percentiles of the distribution of the differences between estimated and mGFR was endorsed as a useful measure of accuracy by the National Kidney Foundation – Kidney Disease Outcomes Quality Initiative (NKF-KDOQI) in 2002 and has been widely used subsequently in the GFR field. 102 The approach captures aspects of both imprecision (measurement error) and bias (systematic over- and/or underestimation). NKF-KDOQI suggested that GFR equations should achieve a P30 value in excess of 90%. Having undertaken initial algebraic sample size calculations based on comparing variance estimates of measurement error, we defined our final sample size based on a simulation study to estimate differences in P30 and estimates of rate of change which are not amenable to algebraic solution. Our simulations modelled the full structure of the study including random variability, and computed statistical power through noting the percentage of simulations yielding statistically significant results for analysis of each outcome. Power estimates were based on 1000 simulations.
Values of P30 for the alternative eGFR equations have previously been estimated to range between 73% and 95% across the literature. 41 The original MDRD validation cohort achieved a P30 of 91%,31 whereas in the CKD-EPI cohort, this fell to 81%, compared to 84% for the CKD-EPI equation itself. 32 In the external validation data sets of Inker et al. 28 the CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations achieved P30 values of 86% and 92%, respectively. In our recent study of GFR-estimating equation performance in older people, the MDRD equation achieved a P30 of 81% compared to 86% for the CKD-EPIcreatinine-cystatin equation. 52
We evaluated the ability of the present study to detect a difference of 5% in P30, between 81% and 86%, which is of a magnitude considered clinically important and likely to occur with the expected scale of differences in imprecision between the equations. With 1000 evaluable subjects our simulations showed 87% power for detecting a difference at the 5% level. We thus aimed to recruit 1300 people, which, allowing for 15–20% dropout, would deliver over 90% power. This calculation was conservative in that it only took imprecision into account. In the presence of systematic bias (a reasonable assumption) the power was estimated to be greater than this. In relation to estimating equation performance amongst the ethnic groups, the proposed sample size of these subgroups allowed P30 estimates to be reported with 95% CIs of 10%.
The annual rate of change over 3 years can be estimated by the observed difference between follow-up and baseline measurements or by using regression techniques for estimated and mGFR. Padala et al. proposed two cut-points for estimating accuracy of rates of change comparing estimated to mGFR: > 3 ml/minute/1.73 m2/year error and > 5% error. 84 Our simulations predicted that with the magnitude of measurement error that corresponds with P30 measures of 81% and 86% the study would have over 90% power to detect differences in the proportions with > 3 ml/minute/1.73 m2/year error and over 80% power to detect differences in proportions with > 5% error.
Ideally, we would like to have been able to detect differences in progression to stage 4 CKD between estimating equations. While it is possible to estimate a relationship with progression for each equation, a study would need to have 10,000 participants to be able to have 90% power to detect a difference in predictive abilities to stage 4 CKD between equations. Therefore, our study did not have power to evaluate this as an outcome, but it was considered in the model-based analysis.
Substudy of disease progression
A target sample size of 375 was chosen based on practical considerations to allow investigation of 12 covariates of interest (gender, age, diabetes, duration of diabetes, ethnicity, albuminuria, baseline GFR, BP, BMI, waist circumference, smoking status and presence of vascular disease) in addition to variables for time, drug effects and random effects. Another consideration was to include a reasonable number of subjects in each of the ethnic groups and high- and low-risk subgroups. General sample size formulae103 for multiple regression models indicate that a sample of 300 individuals, with 15–20% attrition, will provide 90% power to detect a change in R2 of 0.11 (medium-to-small effect size103) attributed to 20 independent variables, 6 controlled independent variables and a significance level of 0.05.
Study of intraindividual biological variation
Sample sizes in biological variation studies are somewhat dictated by the practical limitations and costs of handling the large numbers of analyses generated while minimising the effects of pre-analytical and analytical variation. However, biological variation studies are known to be robust to the effects of sample size. For example, using 4 samples on 10 subjects, Gowans et al. estimated a CVI for creatinine of 4.1%,76 whereas Keevil et al. using 10 samples from 12 subjects obtained a CVI of 4.9%. 77
The sample size was based on the precision of CVI, which was estimated to be 10%. With 20 participants recruited, tested on 4 occasions and assayed in duplicate and assuming data are log-normally distributed, an approximate 95% CI for CVI has limits ± 2% (absolute).
Statistical methods
Main study: prospective longitudinal cohort study
Data were analysed to address three main questions.
Which of the glomerular filtration rate-estimating equations is the most accurate assessment of measured glomerular filtration rate?
The baseline creatinine or cystatin C result obtained using the baseline sample from the iohexol-mGFR procedure was used to estimate GFR. Measured GFR was accepted as the reference measure of GFR against which each GFR-estimating equation was compared. The performance of the GFR-estimating equations was evaluated as proposed by NKF-KDOQI102 by assessing accuracy, bias and precision. Accuracy was assessed by establishing the proportion of GFR estimates within 30% (P30) of iohexol-mGFR and also as root mean square error (RMSE). For the primary objectives, we compared P30 values between GFR-estimating equations using McNemar’s test for paired data. We also reported P15 (the proportion of GFR estimates within 15% of iohexol mGFR) values for each estimating equation, but the study was not powered to detect differences in P15 values between equations. The mean difference between estimated and mGFR provided a measure of bias. The median difference provided a second measure of bias that was valid and less influenced by outliers. Data were also visually examined using bias plots (eGFR minus mGFR against mGFR) with lowess (locally weighted scatterplot smoothing). Precision was assessed as the interquartile range (IQR) of the differences between mGFR and eGFR. Exploratory analyses of GFR accuracy were also undertaken in which data were stratified by age (< 50, 50–59, 60–69, 70–79 and ≥ 80 years), gender (male/female), diabetes (diabetic or not diabetic as recorded in medical history), albuminuria (< 3.0, 3.0–29.9 or ≥ 30.0 mg/mmol, corresponding to normal, moderately and severely increased albuminuria in the international classification of CKD),27 BMI (< 30 or ≥ 30 kg/m2, corresponding to healthy/overweight and obese/severely obese)104 and level of kidney function (mGFR < 45 or ≥ 45 ml/minute/1.73 m2). Accuracy was also studied by race (Caucasian, South Asian, African-Caribbean, with ethnicity being self-reported and classified as described in Sampling and data collection).
Which glomerular filtration rate-estimating equation most accurately tracks glomerular filtration rate over time?
For each individual, the difference between baseline and 3-year follow-up eGFR was calculated and the change per year was derived by averaging change over the time between baseline and 3-year follow-up. Similarly, the difference between baseline and 3-year follow-up mGFR was calculated and the change per year was derived by averaging change over the time between baseline and 3-year follow-up. The outcome of interest was error, the difference between the annual change in mGFR and eGFR. Large error was accepted as ≥ 3 ml/minute/1.73 m2/year, or > 5%/year difference in slope between mGFR and eGFR. Differences in the slopes of estimated and mGFR were therefore considered present when the slope for eGFR exceeded ± 3 ml/minute/1.73 m2/year or ± 5%/year of the mGFR slope. The primary analysis used observed eGFR compared to observed mGFR, both calculated as absolute change per year calculated from difference between 3-year and baseline measurements. The rate of change was calculated using actual calendar sampling date rather than nominal date in cases where follow-up period was not exactly 3 years.
Different approaches were explored in two sensitivity analyses: in the first, as described by Padala et al. ,84 (1) change in eGFR values derived from a linear regression model (change per year calculated from a linear regression model fitted per person using all available measurements, i.e. up to seven measurements per individual) was compared to observed mGFR (calculated as per the primary analysis); and in the second (2) change in eGFR values derived from linear regression models, as above in (1), was compared to estimated change in mGFR from a mixed-effects linear regression model (coefficient from a single mixed-effects model obtained using all available measures for all individuals, i.e. up to four measurements per individual including additional mGFRs from the substudy).
The percentage of participants demonstrating large error when comparing change over time between the eGFR and mGFR values, for each GFR-estimating equation for the primary objectives, was compared. The numbers meeting the two criteria were compared with McNemar’s test.
Which glomerular filtration rate-estimating equation most accurately detects change in glomerular filtration rate?
We also calculated, for each participant, whether their change in mGFR (reference test) and eGFRs (index tests) was ≥ 10 ml/minute/1.73 m2 over the 3 years and compared these to calculate the sensitivity (i.e. percentage of patients with a change in mGFR ≥ 10 ml/minute/1.73 m2 over the 3 years in whom a change ≥ 10 ml/minute/1.73 m2 was also observed in the GFR estimate), specificity (i.e. percentage of patients without a change in mGFR ≥ 10 ml/minute/1.73 m2 over the 3 years in whom a change ≥ 10 ml/minute/1.73 m2 was also not observed in the GFR estimate), positive predictive value (PPV) and negative predictive value (NPV) for each of the eGFRs. The 10 ml/minute/1.73 m2 cut-point was chosen as it was felt by clinical members of the study group to be a useful metric in practice, representing significant loss of renal function, and mapping to the original 2008 NICE definition of progression (albeit defined over 5 years, not 3 years). 40 A further analysis was undertaken based on whether participants showed a change of > 25% in mGFR and eGFR over the 3 years,59 and separately a change of > 25% in combination with a change in disease category. 27 The sensitivity, specificity, positive and NPVs for the four eGFRs of interest to the primary outcome were calculated using standard approaches. A separate analysis was undertaken based on the biological variation of mGFR, as defined in the substudy (see Study of intraindividual biological variation). A true change in GFR was assumed to be a value that exceeded or equalled the RCV derived for the reference (measured) GFR test. The above analyses were all repeated looking only at declines in mGFR and eGFR rather than changes in either direction, for example a decline of > 10 ml/minute/1.73 m2/year, > 25%/year or greater than the RCV.
Which glomerular filtration rate-estimating equation, together with albumin-to-creatinine ratio, or albumin-to-creatinine ratio alone, most accurately predicts mortality and those people who have progressive loss of kidney function (chronic kidney disease progression)?
An analysis was undertaken to identify factors associated with loss of kidney function (defined in terms of decline in mGFR but also in terms of an increase in albuminuria category, as defined by KDIGO). Baseline eGFR, ACR and other relevant baseline variables (age, gender, ethnicity) were investigated as potential factors associated with progression. Baseline ACR was categorised into the three clinical ACR stages: < 3.0, 3.0–29.9 and ≥ 30.0 mg/mmol. We used logistic regression to model the relationship between the baseline factors and loss of kidney function, separately for each of the eGFRs. Logistic and Cox regression models were also used to study the relationship between these baseline variables and death within the study and time to death, respectively, as outcomes.
Substudy of disease progression
Analysis was undertaken using Stata/IC version 16.1.
The rate of decline (ml/minute/1.73 m2/year) in mGFR and the difference between mGFRs and eGFRs (bias), assessed every 12 months, were modelled over time using a longitudinal linear random coefficients regression model, to estimate average and variability in disease progression and bias. 84 The random coefficients model included random effects for intercept and slope, allowing a different intercept and slope for each individual within the model. Rates of change in mGFR and bias were estimated from the slopes of the regression model, and reported with 95% CIs. Participants were included in the analysis if they had measurements recorded on more than one occasion during the study. Measured GFR was modelled on the natural and log-transformed scales. Parameters of the model for mGFR and bias were estimated using maximum likelihood. Between- and within-patient variability in the rate of decline of mGFR was also estimated.
Diagnostic plots of residuals, fitted values and marginal predictors for intercept and slope were assessed for normal distribution and constant variance assumptions and goodness of fit. The final models for mGFR and eGFRs on the natural scale indicated that normal distribution assumptions and goodness of fit were acceptable; for ACR, the diagnostic plots of log-transformed data were acceptable, and there was evidence of non-normality on the natural scale.
Covariates explored in the disease progression model for mGFR were as described earlier (see Substudy of disease progression). The time-varying covariates in the model were BMI, waist circumference, systolic BP and diastolic BP, the mean of the second and third BP measurements at each time was used for systolic and diastolic BP.
The effect of covariates on the population average intercept and longitudinal time effect (progression) was assessed. The method of backward elimination was used to remove covariates that were not significant from the model. As this was an exploratory analysis and the sample size was relatively small, parameters were retained in the model if the p-value was < 0.20. This enabled detection of possible associations which may be more significant in a larger sample. Where there was evidence of an interaction with time, indicating a difference in progression between categories defined by the covariate (e.g. between males and females), a factor was included in the model to estimate separate intercepts for categories of the covariate as well as separate slopes. Similarly, for continuous covariates in the model, if there was evidence that progression changed with different values of the covariate, an estimate of the change in intercept for the covariate was also included in the model.
The effect of drug class on the rate of progression was explored for drug classes where at least 10 participants in the substudy were taking medication within that class. Drug classes included in the analysis were thiazide diuretics, loop diuretics, beta-blockers, calcium channel blockers (CCBs), ACE inhibitors, A2RBs, alpha-blockers, statins, xanthine oxidase inhibitors (allopurinol) and antiplatelet agents.
It was originally planned to use the population Fisher information matrix optimal design algorithms (R open source software) to calculate the D-optimal105 sampling times from the disease progression model based on reference GFR for people with diabetes and/or albuminuria, and for those with neither of these conditions. We intended to select optimal monitoring strategies from a set of designs with sampling every 6 months and compare monitoring strategies with a number of sampling points (between two and six). However, the mGFR disease progression model was linear and therefore these methods were not needed, as the optimal design solution is simplified for linear models, intuitively the slope is estimated optimally by the two design points with the greatest spread. 105 More frequent monitoring will increase accuracy of estimation.
Additional disease progression modelling was performed on eGFR (CKD-EPIcreatinine and CKD-EPIcystatin) and ACR measured every 6 months. The covariates and drug classes explored in the mGFR analysis were also explored in the eGFRs and ACR models. Parameter estimates, 95% CIs and estimates of within- and between-patient variability were compared to those for mGFR.
While our longitudinal cohort did not have adequate power to detect differences in progression, our data on mGFR and eGFR over time (study 1), patterns and determinants of progression (study 2), and intraindividual biological variation (study 3) were combined in a measurement model to evaluate the impact of alternative monitoring strategies on detection of NICE’s combined progression criteria (see Clinical guidelines) and/or progression to stage 4 CKD. True GFR values were modelled over time for representative cohorts of people, and the comparative performance of alternative monitoring strategies in detecting progression (varying in choice of eGFR equation) was simulated utilising estimates of measurement error and accuracy. Outcome variables that were assessed included FP progression rates, and the sensitivity and delays in detecting progression.
Further assessment of covariates was performed by combining the data from the disease progression substudy with the main study and fitting the final covariate models for the substudy to the full data set. The main purpose of this was to check the inferences are consistent across the two data sets, as the full data set had more participants and hence more covariate information, while the substudy has more time points so progression is better defined.
Study of intraindividual biological variation
Data were log-transformed and normality tests were performed using the Shapiro–Wilk test. Outliers between duplicate measurements and of within-subject variance were excluded using Cochran’s test and outliers amongst mean values of subjects were excluded using Reed’s test. 35 Sensitivity analyses were also performed without exclusion of identified outliers. Log transformation was used to simplify calculation and because it improved the normality of the data as assessed by an increase in Shapiro–Wilk W statistic and visual examination of the distributions.
Terminology used was as proposed by Simundic et al. 106 Analytical (CVA), individual (CVI) and between-subject (CVG) components of variation were calculated using standard approaches35 of linear random-effects modelling with restricted maximum likelihood estimation (allowing for the clustering of observations within time points and repeated observations per patient) (Stata version 15). Exact geometric CVs [(exp(S2)−1)×100]107,108 were calculated. CIs for SDs and CVs were estimated as described by Burdick and Graybill. 109 Differences in measures of CV, comparing the eGFR measures to mGFR, were investigated using multilevel models accounting for the clustering of test observations within individuals, using unstructured covariance matrices, in addition to the clustering of test results (multiple results per person, observation points and assessments). The critical difference (RCV) for significant changes in serial results with 95% probability was calculated using the approach for log-normal data giving a negative and positive limit. 110 The derived RCV for the reference GFR was used to test the ability of eGFR equations to detect a true change in GFR. The number of specimens (n) required to produce a precise estimate of the homeostatic set-point with 95% confidence within ± 10% was calculated as:
For each biomarker, the index of individuality (II) was calculated as:
To confirm kidney function was stable across the study period, the iohexol GFR measures were modelled to identify trend with time using a multilevel linear regression model (allowing for clustering of assessments within time points and observations within individuals).
Secondary objectives
Secondary analyses covered a range of more recently published equations and modified versions of the equations evaluated in the primary analysis.
To estimate and compare the accuracy of more recent GFR-estimating equations that have been published while the study has been ongoing (BIS1 and BIS2 equations, CAPA equation, LMR equation, FAS creatinine equation, FAS creatinine-cystatin equation, EKFC equation and the 2021 revisions of the CKD-EPI equations, Table 1)
The P30 statistic was calculated to enable comparison of each of these equations to the reference mGFR, as in the primary analysis.
To evaluate and compare how accurately these newer GFR-estimating equations reflect and detect change in GFR over 3 years
Equations were subjected to the same analysis as described above (see Which glomerular filtration rate-estimating equation most accurately tracks glomerular filtration rate over time? and Which glomerular filtration rate-estimating equation most accurately detects change in glomerular filtration rate?).
To estimate and compare the performance of the MDRD and CKD-EPI equations using the Haycock equation for body surface area adjustment instead of the Du Bois equation
For the equations specified in the primary analysis, we calculated the P30 for the baseline measurements (comparing mGFR to eGFRs) using the Haycock equation for BSA adjustment rather than the more widely used Du Bois equation.
To assess the impact of cystatin C calibration on the performance of the cystatin C GFR-estimating equations
Samples (n = 106) covering a representative range of concentrations were measured by both methods (i.e. Abbott and Siemens). These observations were analysed using both Deming regression and linear regression analyses to generate an equation to adjust the Abbott results in the entire baseline study cohort to mimic Siemens results. These adjusted results were then used to estimate GFR in equations incorporating cystatin C and generated comparisons with mGFR for baseline and follow-up measurements, as per main study.
To assess the impact of creatinine methodology (enzymatic vs. isotope dilution mass spectrometry) on the performance of the MDRD equation and creatinine-based CKD-EPI equations
P30 for the baseline eGFR data was calculated using the ID-MS creatinine method and compared to that obtained with the enzymatic creatinine assay. We also undertook direct comparison of the ID-MS and enzymatic creatinine assays using regression and bias plot analyses.
Clinical accuracy and health economic analysis of monitoring with different estimated glomerular filtration rate equations
If cystatin C-based eGFR was found to be an improved approach to monitoring progression of CKD, then this would have cost implications for the healthcare sector. Cystatin C is more expensive than creatinine (£3.80 vs. £0.43); however, prompt identification of worsening kidney disease function may reduce additional treatment costs, offsetting the additional cost of testing. Furthermore, more accurate identification of individuals at high risk using cystatin C may reduce costs due to overdiagnosis and provide better management of low-risk individuals. 25,85
A systematic review was conducted to identify previous studies that have assessed the cost-effectiveness of test-based strategies for CKD using a decision-analytic model. This review was conducted and published at the beginning of the project and then updated in the last year of the project (full details and results can be found in Appendix 2). A key objective was to examine how existing models have captured the clinical impact of monitoring kidney function over time, given that we only have accuracy data available from this study.
To better understand definitions around kidney disease progression and triggers for clinical action (which have been updated since the initiation of this study), we then summarised the latest key clinical guidelines (see Clinical guidelines). We then used the data and results from this study to compare the accuracy of the different estimating equations for predicting CKD progression (using the definitions warranting clinical action based on the latest clinical guidelines) – we describe this as ‘clinical accuracy’ [see Comparative accuracy of estimated glomerular filtration rate equations for predicting accelerated progression (measurement model analysis)]. This analysis is based on a simulated measurement model, which considers a 10-year horizon of annual GFR monitoring, with GFR estimation error simulated onto mGFR values based on the bias profile information derived from the current study.
A cost–utility analysis was planned to estimate the health and economic consequences of implementing cystatin C-based eGFR or a combination of both cystatin C and creatinine-based eGFR for monitoring subjects who are initially stage 3 CKD compared to MDRD (creatinine-based) eGFR alone. In the absence of an accuracy improvement, a comparative cost analysis was reported to demonstrate the economic implications of implementing cystatin C based equations for monitoring those who are initially stage 3 CKD (see Comparative cost of monitoring with different estimated glomerular filtration rate equations).
Serious adverse events
The only study-related safety risk to participants involved the administration of iohexol (contrast medium) required for the reference GFR measure, which does not form part of routine clinical practice and takes approximately 5 hours to complete. The associated risks may include risk from venepuncture and vein cannulation, idiosyncratic reaction to iohexol and a theoretical risk of deteriorating kidney function with injection of iohexol.
These risks are in all cases extremely low. The following adverse events (AEs) that could be reasonably ‘expected’ for this group of patients during the course of the study were:
-
nausea
-
mild urticaria, with or without pruritus
-
transient sensation of mild warmth
-
haematomas and ecchymoses around injection site
-
bronchospasm.
These represent minimal risk to participants, so for the purposes of this study these AEs did not require reporting to the eGFR-C Study Office. Serious adverse events (SAEs) occurring within 24 hours of iohexol administration (and not listed as ‘expected’ as defined above) were reportable to the eGFR-C Study Office on an SAE form. The assessment of relatedness and expectedness to the administration of iohexol is a clinical decision based on all available information at the time. SAEs outside of this time frame could also be reported if it was the opinion of the investigator that there was a possible causal relationship to another aspect of the study. An independent clinical assessment of relatedness and expectedness would also be undertaken.
Study oversight and ethical approval
All co-investigators were members of the project management group. Annual face-to-face meetings were held at the Birmingham Clinical Trials Unit (BCTU) with approximately bimonthly teleconferences. The project management group reviewed issues including recruitment against target, data management, nursing aspects, training issues (e.g. with the reference GFR technique), laboratory issues and statistical interpretation.
There was an independent study steering committee (Trial Steering Committee equivalent). This comprised an independent chairperson (Dr Charlie Tomson, Consultant Nephrologist and Immediate Past-President of the Renal Association), one other independent nephrologist (Professor Hugh Gallagher), a patient representative, the study statistician, an independent statistician (Professor Rafael Perera, Director of MaDOX, University of Oxford), the chief investigator, the study lead research nurse and one co-applicant. This group met at the beginning of the study and thereafter up to 6-monthly intervals depending on progress.
The study budget was managed by East Kent Hospitals University NHS Foundation Trust with subcontracts being arranged with the other participating organisations.
The Health Technology Assessment (HTA) grant award commenced on 1 August 2013. Approval from the National Research Ethics Service was obtained (reference 13/LO/1349, approved 9 October 2013). Written informed consent was obtained from all participants. Participant information leaflets were prepared in collaboration with the patient representative on the study group [Mrs Fiona Loud, Director of the former Kidney Alliance and now Policy Director of Kidney Care UK (www.kidneycareuk.org/, accessed 12 April 2023)] and were circulated for comment to patient groups at the recruiting units and to the Research Design Service south-east public patient involvement group. Recruitment and retention strategies were adjusted to meet the needs of the specific ethnic minority groups including the production of translated material and use of translators where required for non-English speakers.
Data from this study were handled by the BCTU, a full-time research facility dedicated to, and with substantial experience in, the design and conduct of clinical research. Data were collected, analysed and reported using secure data collection procedures and anonymisation was used.
Chapter 3 Results
Recruitment and flow of participants through the study
The aim of the study was to recruit 1320 individuals in total, including 300 who would participate in the substudy of disease progression and 20 who would participate in the biological variation substudy. 88 The first participant was recruited in April 2014 (see Appendix 1, Table 36) but not all centres opened to recruitment at the same time. It was anticipated that with 6 recruiting centres a recruitment rate of approximately 72 participants per month was realistic, but this rate was difficult to achieve. Recruitment to the substudy of disease progression was particularly difficult, possibly due to its more intensive testing regime. Recruitment of Asian and African-Caribbean individuals was also more difficult than expected, and target population sizes had to be modified accordingly. Recruitment and retention were reviewed and discussed regularly at study management group meetings. Various changes to the study were made to improve recruitment, including extending primary care recruitment beyond the two centres originally envisaged, modifying and translating participant information sheets. Retention in the study was encouraged through newsletters and sending final appointment reminder letters. In January 2017 revised sample size/power calculations indicated that under the proposed analysis method for the primary outcomes, with 1167 evaluable subjects the study had > 87% power to detect a 5% difference in P30 between equations at baseline, and with 875 evaluable subjects at study end had > 85% power to compare proportions of equations with a more than 3 ml/minute/1.73 m2/year error over 3 years. Following discussion between the study management group, the independent study steering committee and the funder, recruitment was terminated due to low ongoing recruitment rates.
Main study: prospective longitudinal cohort study
In total, 29,845 people were screened for potential suitability for study inclusion: 15,340 were deemed unsuitable at an early stage from informatics and clinic lists due to not having CKD stage 3. Other identified reasons for unsuitability included that they were too unwell, had recently had AKI, were unable to consent, were known alcohol or drug abusers, had had a previous reaction to iodine, were amputees, were under 18 years of age or were pregnant or breastfeeding. People considered suitable for study inclusion (n = 6209) were approached in person and/or sent participant information sheets. A further 4000 individuals were contacted through their primary care provider. Reasons for declining to participate were recorded in 928 cases. The major reasons for declining were that the participants were not interested in research; that they had too many medical appointments; that the 5-hour appointment time was too long; that too much travel was involved; that they were already in other research studies; and that the study involved too many injections.
A total of 1229 participants were recruited to the main study between April 2014 and January 2017, representing 95% of the target recruitment number. Recruitment was primarily from secondary/tertiary care, with 72 patients being recruited from primary care. Details of cumulative recruitment per month and recruitment by site and withdrawal by site may be found in Appendix 1 (see Appendix 1, Tables 37 and 38). Figure 2 shows the flow of participants through the study, using the format recommended by the Consolidated Standards of Reporting of Trials. 111
FIGURE 2.
Consolidated Standards of Reporting Trials flow diagram illustrating recruitment and follow-up in the prospective longitudinal cohort study.
Of the 1229 participants recruited to the study, 1205 and 1180 respectively had evaluable estimated and mGFRs at baseline, with 1167 (95.0%) having both eGFRs and mGFRs recorded. At 36 months 976 participants remained in the study, of whom 875 (71.2%) had evaluable estimated and mGFRs at both baseline and 36 months. The last patient visit occurred in January 2020. Following laboratory analyses and data queries, the study database was locked on 30 April 2021 (see Appendix 1, Table 36).
Overall, 253 (20.6%) participants withdrew from the study. Consent was withdrawn by 112 (9.1%), 79 (6.4%) were lost to follow-up (LTFU) and there were 62 (5.0%) deaths. Causes of death were cancer (16), cardiovascular disease (14), respiratory disease (11), kidney disease (4), cerebrovascular (1), liver disease (1), other (6) and unknown (9). In addition to death and loss to follow-up, reasons for withdrawing from the study included illness (60), commencement of kidney replacement therapy (12), inability to complete sampling (9), suspected reaction to iohexol (5), loss from area (3), carer commitment (2), other reasons (7) and no reason given (14). A further 25 participants were unable to complete their 36-month mGFR test, increasing the total effective dropout rate to 22.6%. Study dropout appears to escalate at the final time point of the study: this reflects closure of records of participants that the research teams had been trying to retain in the study up to this point (e.g. the participant was no longer contactable).
Substudy of disease progression
Fewer participants were recruited to the substudy than planned. In addition, due to difficulties in recruiting participants from some ethnic groups, more than the planned number of Caucasian participants and fewer South Asian and African-Caribbean participants were recruited. A total of 278 participants were recruited to the substudy of patterns of disease progression between April 2014 and December 2016, representing 93% of the target recruitment number. Of these, 128 (46%) had diabetes and/or albuminuria. There were 196 Caucasian (70%), 47 African-Caribbean (17%) and 35 South Asian participants (13%) in the substudy.
Figure 3 shows the flow of participants through the substudy. Of the 278 participants recruited to the study, 269 and 273 respectively had evaluable mGFRs and at least one eGFR recorded at baseline, with 265 (95%) having both estimated and mGFRs recorded. Attrition was 22.7% for the substudy, with 215 participants remaining in the study at the end of year 3. Of these, 214 and 198 respectively had evaluable estimated and mGFRs, with 197 (71%) having both mGFRs and at least one eGFR recorded. The last patient visit occurred in December 2019.
FIGURE 3.
Consolidated Standards of Reporting Trials flow diagram illustrating recruitment and follow-up in the substudy of disease progression.

Overall, 63 (22.7%) participants dropped out of the study. Consent was withdrawn by 31, 22 were LTFU and there were 10 deaths. Of those who were LTFU, 50% were African-Caribbean. Causes of death were cancer (2), cardiovascular disease (4), respiratory disease (2) and unknown (2). In addition to death and loss to follow-up, reasons for withdrawing from the study included illness (20), suspected reaction to iohexol (1), loss from the area (1), other reasons (1) and no reason given (8). A further 17 participants were unable to complete their 36-month mGFR test, increasing the total effective dropout rate to 28.8%. Seventeen participants crossed over from the substudy to the main study (i.e. withdrawing from additional iohexol-mGFR tests). One patient crossed over to the main study at one time point but subsequently returned to the substudy. Patients have been included in the substudy analysis if data were collected at more than one time point.
The number of participants recruited was sufficient to perform the planned analysis and investigate the 12 covariates of interest. There were only three participants with type I diabetes; therefore type of diabetes was not included in the analysis model. Smoking status changed very little during the study and the number of current smokers was small so only baseline smoking status was used in the analysis. Similarly, most participants with diabetes were diagnosed before the study began and baseline diabetes status was used in the analysis model and the duration of diabetes was calculated at baseline. Vascular disease was defined as described above (see Sampling and data collection). Due to the low numbers of South Asian and African-Caribbean participants, separate variance parameters were not included in the analysis models for these ethnic groups. It was assumed that variability is similar across ethnic groups. Differences between ethnic groups were explored, and estimates and CIs were calculated. Inferences drawn from the substudy analysis results should be interpreted more cautiously due to the limited number of South Asian and African-Caribbean participants.
Study of intraindividual biological variation
Participants (n = 20) were recruited to the study between August 2014 and July 2015. 97 Figure 4 shows the flow of participants through the study. All 20 patients attended all four iohexol-mGFR procedures except one patient who missed their final appointment. Results from five iohexol clearances (five separate patients) were excluded before analysis, as the dose given was not fully administered or it was given subcutaneously. Medications were held constant during the 4 weeks of the study, except that two patients received a 1-week course of amoxicillin (500 mg tds) due to chest infection. Sixteen of the participants subsequently entered the main study, with their first iohexol-mGFR being used as their baseline test.
FIGURE 4.
Consolidated Standards of Reporting Trials flow diagram illustrating recruitment and follow-up in the study of intraindividual biological variation.

Baseline characteristics of the study subjects
Main study: prospective longitudinal cohort study
Characteristics of the study subjects are shown in Table 2. The median age of participants was 67.5 years; 714 (58%) were male and 1066 (87%) were Caucasian. Diabetes was a pre-existing diagnosis in 28.3% of participants. The median mGFR at baseline was 46.8 ml/minute/1.73 m2 and 56.8% had albuminuria (ACR ≥ 3 mg/mmol). There were 71 people in the baseline cohort with mGFR below 30 ml/minute/1.73 m2 and 211 people with mGFR ≥ 60 ml/minute/1.73 m2, with a total range of values from 11.9 to 103.7 ml/minute/1.73 m2.
| Characteristics | All participants recruited | All participants with mGFR and eGFR at baselinea | All participants with mGFR and eGFR at baseline and 3-year follow-upb |
|---|---|---|---|
| n | 1229 | 1167 | 875 |
| Age, years | 67.5 (58.2–74.5) | 67.5 (58.3–74.5) | 67.1 (58.1–73.6) |
| M : F, n | 714 : 515 | 680 : 487 | 505 : 370 |
| Ethnicity | |||
| Caucasian, n (%) | 1066 (86.7) | 1014 (86.9) | 773 (88.3) |
| African-Caribbean, n (%) | 68 (5.5) | 60 (5.1) | 36 (4.1) |
| South Asian, n (%) | 67 (5.5) | 66 (5.7) | 46 (5.3) |
| Other, n (%)c | 28 (2.3) | 27 (2.3) | 20 (2.3) |
| Height, cm | 170 (162–176) | 170 (162–176) | 170 (163–176) |
| Weight, kg | 84.6 (72.6–97.7) | 84.1 (72.5–97.3) | 84.7 (73–97.2) |
| Du Bois BSA, m2 | 1.96 (1.80–2.11) | 1.96 (1.80–2.10) | 1.96 (1.81–2.11) |
| Haycock BSA, m2 | 2.02 (1.84–2.20) | 2.02 (1.84–2.19) | 2.02 (1.86–2.19) |
| BMI, kg/m2 | 29.0 (25.8–33.5) | 29.0 (25.8–33.3) | 29.0 (25.7–33.4) |
| Medication recorded (n, %) | Thiazide diuretic (128, 10.4), loop diuretic (193, 15.7), potassium-sparing diuretic (27, 2.2), beta-blocker (326, 26.5), CCB (394, 32.1), ACE inhibitor (435, 35.4), A2RB (362, 29.5), alpha-blocker (160, 13.0), HMG CoA reductase inhibitor (668, 54.4), allopurinol (143, 11.6), antiplatelet drugs (387, 31.5) | Thiazide diuretic (123, 10.5), loop diuretic (180, 15.4), potassium-sparing diuretic (26, 2.2), beta-blocker (314, 26.9), CCB (376, 30.6), ACE inhibitor (411, 35.2), A2RB (348, 29.8), alpha-blocker (153, 13.1), HMG CoA reductase inhibitor (635, 54.4), allopurinol (137, 11.7), antiplatelet drugs (367, 31.4) | Thiazide diuretic (94, 10.7), loop diuretic (114, 13.0), potassium-sparing diuretic (18, 2.1), beta-blocker (223, 25.5), CCB (273, 31.2), ACE inhibitor (317, 36.2), A2RB (267, 30.5), alpha-blocker (111, 12.7), HMG CoA reductase inhibitor (463, 52.9), allopurinol (105, 12.0), antiplatelet drugs (258, 29.5) |
| Comorbidity recorded (n, %)d | Diabetes mellitus (348, 28.3), ischaemic heart disease (189, 15.4), angina (91, 7.4), heart failure (57, 4.6), cerebrovascular disease (92, 7.5), TIA (51, 4.1), stroke (42, 3.4), HBV (20, 1.6), malignancy (203, 16.5) | Diabetes mellitus (324, 27.8), ischaemic heart disease (177, 15.2), angina (88, 7.5), heart failure (55, 4.7), cerebrovascular disease (85, 7.3), TIA (48, 4.1), stroke (37, 3.2), HBV (18, 1.5), malignancy (191, 16.4) |
Diabetes mellitus (220, 25.1), ischaemic heart disease (120, 13.7), angina (60, 6.9), heart failure (30, 3.4), cerebrovascular disease (56, 6.4), TIA (29, 3.3), stroke (26, 3.0), HBV (14, 1.6), malignancy (134, 15.3) |
| Smoking status | |||
| Non-smoker, n (%) | 612 (49.8) | 590 (50.6) | 453 (51.8) |
| Current smoker, n (%) | 110 (9.0) | 101 (8.7) | 63 (7.2) |
| Former smoker, n (%) | 502 (40.9) | 474 (40.6) | 357 (40.8) |
| Unknown, n (%) | 5 (0.4) | 2 (0.2) | 2 (0.2) |
| Urine albumin concentration | |||
| < 3 mg/mmol, n (%) | 498 (40.5) | 483 (41.4) | 375 (42.9) |
| 3–30 mg/mmol, n (%) | 421 (34.3) | 396 (33.9) | 295 (33.7) |
| > 30 mg/mmol, n (%) | 277 (22.5) | 269 (23.1) | 195 (22.3) |
| Missing, n (%) | 33 (2.7) | 19 (1.6) | 10 (1.1) |
| Serum creatinine, µmol/l | 129 (108–153) n = 1209 |
129 (107–154) n = 1167 |
132 (109–162) n = 875 |
| Serum cystatin C, mg/l (Siemens) | 1.53 (1.28–1.81) n = 1209 |
1.53 (1.28–1.81) n = 1167 |
1.55 (1.26–1.84) n = 875 |
| Serum cystatin C, mg/l (Abbott) | 1.71 (1.45–2.01) n = 1209 |
1.71 (1.45–2.01) n = 1167 |
1.73 (1.43–2.04) n = 875 |
| CKD GFR category (‘stage’) at baseline based on mGFR, n (%) | |||
| 1 n (%) | 7 (0.6) | 7 (0.6) | 5 (0.6) |
| 2, n (%) | 204 (17.3) | 204 (17.5) | 163 (18.6) |
| 3A, n (%) | 458 (38.8) | 452 (38.7) | 366 (41.8) |
| 3B, n (%) | 440 (37.3) | 434 (37.2) | 303 (34.6) |
| 4, n (%) | 69 (5.8) | 68 (5.8) | 38 (4.3) |
| 5, n (%) | 2 (0.2) | 2 (0.2) | 0 (0) |
| Measured GFR, ml/minute/1.73 m2 | 46.8 (38.7–56.3) n = 1180 |
47.0 (38.7–56.4) n = 1167 |
48.1 (40.2–57.2) n = 875 |
| MDRD, ml/minute/1.73 m2 | 44.1 (36.2–52.0) n = 1205 |
44.0 (36.2–52.0) n = 1167 |
44.6 (37.1–52.4) n = 875 |
| CKD-EPIcreatinine, ml/minute/1.73 m2 | 44.8 (36.9–53.8) n = 1205 |
44.8 (36.7–53.8) n = 1167 |
45.7 (37.7–54.2) n = 875 |
| CKD-EPIcystatin, ml/minute/1.73 m2 (Siemens) | 42.1 (33.7–53.4) n = 1205 |
42.3 (33.8–53.4) n = 1167 |
43.6 (35.0–54.3) n = 875 |
| CKD-EPIcystatin, ml/minute/1.73 m2 (Abbott) | 36.3 (29.3–45.3) n = 1205 |
36.4 (29.4–45.5) n = 1167 |
37.5 (30.4–46.3) n = 875 |
| CKD-EPIcreatinine-cystatin, ml/minute/1.73 m2 (Siemens) | 42.6 (34.7–52.2) n = 1205 |
42.7 (34.6–52.4) n = 1167 |
43.4 (35.9–53.3) n = 875 |
| CKD-EPIcreatinine-cystatin, ml/minute/1.73 m2 (Abbott) | 39.3 (32.2–48.1) n = 1205 |
39.4 (32.2–48.1) n = 1167 |
40.2 (33.3–48.9) n = 875 |
Substudy of disease progression
Characteristics of the study participants are shown in Table 3. The characteristics of those who remained in the study at the end of year 3 were similar to those at baseline. The proportion of participants in the substudy who were current smokers was low. There were very few missing values for the participant characteristics and continuous covariates at baseline. Analysis was performed on observed data and missing values were not estimated.
| Characteristics | All participants recruited | All participants with paired mGFR and eGFR on at least two occasions |
|---|---|---|
| n | 278 | 239 |
| Age, years | 65.0 (56.0–74.0) | 65.0 (57.0–73.0) |
| M : F, n | 180 : 98 | 161 : 78 |
| Ethnicity | ||
| Caucasian, n (%) | 196 (70.5) | 174 (72.8) |
| African-Caribbean, n (%) | 47 (16.9) | 35 (14.6) |
| South Asian, n (%) | 35 (12.6) | 30 (12.6) |
| Height, cm | 170 (163–177) | 170 (164–178) |
| Weight, kg | 85.5 (72.8–98.0) | 85.1 (72.0–97.3) |
| BSA, m2 | 1.98 (1.79–2.12) | 1.98 (1.79–2.12) |
| BMI, kg/m2 | 29.3 (25.6–33.3) | 28.7 (25.3–33.2) |
| Medication record (n, %)a | Thiazide diuretic (28, 10.1), loop diuretic (56, 20.1), beta-blocker (80, 28.8), CCB (111, 39.9), ACE inhibitor (111, 39.9), A2RB (79, 28.4), alpha-blocker (49, 17.6), HMG CoA reductase inhibitor (148, 53.2), allopurinol (33, 11.9), antiplatelet drugs (86, 30.9) | Thiazide diuretic (26, 10.9), loop diuretic (45, 18.8), beta-blocker (65, 27.2), CCB (94, 39.3), ACE inhibitor (92, 38.5), A2RB (68, 28.4), alpha-blocker (40, 16.7), HMG CoA reductase inhibitor (126, 52.7), allopurinol (32, 13.4), antiplatelet drugs (71, 29.7) |
| Comorbidity (n, %)a | Diabetes mellitus (73, 26.6), ischaemic heart disease (33, 12.0), heart failure (15, 4.4), cerebrovascular disease (22, 8.0), TIA (12, 4.4), stroke (10, 3.6), angina (15, 5.5), malignancy (40, 14.6) | Diabetes mellitus (60, 25.1), ischaemic heart disease (28, 11.8), heart failure (10, 4.2), cerebrovascular disease (19, 8.0), TIA (11, 4.6), angina (12, 5.0), malignancy (36, 15.1) |
| Smoking status | ||
| Non-smoker, n (%) | 156 (56.5) | 132 (55.2) |
| Current smoker, n (%) | 27 (9.8) | 23 (9.6) |
| Former smoker, n (%) | 93 (33.7) | 84 (35.2) |
| Urine albumin concentration < 3 mg/mmol, n (%) | 100 (36.0) | 92 (38.5) |
| Urine albumin concentration 3–30 mg/mmol, n (%) | 102 (36.7) | 86 (36.0) |
| Urine albumin concentration > 30 mg/mmol, n (%) | 76 (27.3) | 61 (25.5) |
| Serum creatinine, µmol/l | 135 (114–167) n = 276 |
135 (115–170) n = 238 |
| Serum cystatin C, mg/l (Siemens) | 1.56 (1.29–1.80) n = 276 |
1.57 (1.27–1.81) n = 238 |
| Measured GFR, ml/minute/1.73 m2 | 47.2 (38.2–57.9) n = 269 |
47.2 (38.4–58.2) n = 235 |
| MDRD, ml/minute/1.73 m2 | 42.8 (35.2–52.5) n = 273 |
43.2 (34.8–52.8) n = 236 |
| CKD-EPIcreatinine, ml/minute/1.73 m2 | 43.6 (36.2–53.4) n = 273 |
44.6 (35.4–53.6) n = 236 |
| CKD-EPIcystatin, ml/minute/1.73 m2 | 42.1 (34.8–54.0) n = 273 |
42.1 (34.9–54.5) n = 236 |
| CKD-EPIcreatinine-cystatin, ml/minute/1.73 m2 | 42.1 (35.1–52.8) n = 273 |
42.1 (35.2–54.4) n = 236 |
The evaluable population for disease progression modelling included those participants with paired mGFR and eGFR at two or more time points. We included individuals with at least two times so the data for each individual could contribute to the random intercept and slope terms in the model, and by including those with both mGFR and eGFR at two time points comparisons of mGFR and eGFR models were based on the same samples.
Study of intraindividual biological variation
Characteristics of the study subjects are shown in Table 4. Application of Cochran and Reed’s tests led to the exclusion of between one and three duplicate measurements for mGFR or eGFR and to the exclusion of one outlying within-subject measurement for iohexol clearance. Overall, no patient was completely excluded and all calculations of biological variation for mGFRs and eGFRs were based on a minimum of 3 weeks’ data in all individuals.
| Characteristic | |
|---|---|
| n | 20 |
| Age, years | 71 (50–80) |
| M : F | 10 : 10 |
| Caucasian (n) | 20 |
| Height, cm | 170.5 (154–194) |
| Weight, kg | 79.5 (47.1–118.1) |
| BSA, m2 | 1.99 (1.42–2.47) |
| BMI, kg/m2 | 28.2 (19.6–40.9) |
| Medication record (n) | Thiazide diuretic (3), loop diuretic (3), potassium sparing diuretic (2), beta-blocker (7), CCB (4), ACE inhibitor (8), A2RB (6), alpha-blocker (1), isosorbide mononitrate (1), HMG CoA reductase inhibitor (13), allopurinol (4), antiplatelet drugs (7) |
| Comorbidity (n) | Type 2 diabetes mellitus (3), ischaemic heart disease (7), angina (1), heart failure (2) |
| Smoking status – current/former (n) | 1/10 |
| Urine albumin concentration < 3 mg/mmol (n) | 9 |
| Urine albumin concentration 3–30 mg/mmol (n) | 7 |
| Urine albumin concentration > 30 mg/mmol (n) | 4 |
| Serum creatinine, µmol/l | 124 (79–182) |
| Serum cystatin C, mg/l (Abbott) | 1.67 (1.01–2.30) |
| Measured GFR, ml/minute/1.73 m2 | 49.0 (30.8–71.6)a |
| MDRD, ml/minute/1.73 m2 | 42.2 (31.5–61.4) |
| CKD-EPIcreatinine, ml/minute/1.73 m2 | 43.0 (30.8–62.8) |
| CKD-EPIcystatin, ml/minute/1.73 m2 | 36.8 (23.5–67.1) |
| CKD-EPIcreatinine-cystatin, ml/minute/1.73 m2 | 38.2 (27.2–65.4) |
Primary study: objectives and results
Accuracy of Glomerular Filtration Rate-estimating equations including the Modification of Diet in Renal Disease equation and three Chronic Kidney Disease-Epidemiology Consortium equations using either creatinine or cystatin C or a combination of both in people with stage 3 chronic kidney disease: baseline analysis
During the course of the study, we became aware of significant published concerns regarding bias of the Abbott cystatin C assay. Re-analysis of some historical stored samples suggested to us that the Abbott assay had undergone a significant change in standardisation around the time when the present study commenced (data not shown). In a laboratory analytical recovery study, the Abbott cystatin C assay was found to over-recover added international reference preparation cystatin C by an average of 109.1%. Given the potential negative impact of this on cystatin C eGFR, this was further explored by comparing cystatin C values with those obtained with an alternative assay (Siemens). Cystatin C results obtained using the Siemens method were lower than those using the Abbott assay, the relationship between the two methods being described by the linear regression equation Siemens = −0.08 + 0.94(Abbott). CIs for the intercept and slope were −0.12, −0.03 and 0.92, 0.96, respectively (see Appendix 1, Figure 14). Deming regression produced a similar equation (see Appendix 1, Table 39).
Glomerular Filtration rate estimates of cystatin C containing CKD-EPI equations were recalculated using a recalibration of cystatin C values based on this regression equation. The rationale for this recalibration is considered further in the Discussion section of this report. In this section (Accuracy of glomerular filtration rate-estimating equations including the Modification of Diet in Renal Disease equation and three Chronic Kidney Disease-Epidemiology Consortium equations using either creatinine or cystatin C or a combination of both in people with stage 3 chronic kidney disease: baseline analysis), results for both the initial (Abbott) cystatin C equations and the recalibrated (Siemens) cystatin C containing equations are shown to illustrate the impact of calibration. In subsequent sections of the results chapter, only the recalibrated cystatin C-containing equations are shown.
All estimates of GFR relating to the primary study objectives were negatively biased overall compared to mGFR (see Table 5 and Figure 5). As would be predicted, recalibration of the cystatin C-containing equations with Siemens results improved the negative bias. There was no difference in bias overall against mGFR between the MDRD, CKD-EPIcreatinine, CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations. However, both the MDRD and CKD-EPIcreatinine equations demonstrated positive bias at lower levels of GFR and increasing negative bias at higher levels of GFR: this effect was largely attenuated when the CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations were used (Figure 6). CKD-EPI equations incorporating recalibrated cystatin C values showed an improvement in performance (P30, 95% CI) compared to the same equations using Abbott cystatin C results (Table 5); for example, CKD-EPIcystatin 72.5 (69.8 to 75.0) versus 89.5 (87.6 to 91.2) when adjusted values were used. Accuracy (P30) of the recalibrated CKD-EPIcystatin equation did not differ from that of the MDRD and CKD-EPIcreatinine equations (Table 6), while accuracy of the recalibrated CKD-EPIcreatinine-cystatin equation was superior to that of all of these equations (94.9% CI 93.5 to 96.1) (see Table 6 and Figure 5). In general, P15 values followed a similar rank order between equations to P30 values but were significantly lower.
| Equation | Bias (eGFR minus mGFR), mean difference (SD) (95% CI), ml/minute/1.73 m2 | Bias (eGFR minus mGFR), median difference (IQR), ml/minute/1.73 m2 | Accuracy, percentage of estimates within 30% of mGFR (P30) (95% CI) | Accuracy, percentage of estimates within 15% of mGFR (P15) (95% CI) | Accuracy, RMSE, ml/minute/1.73 m2 |
|---|---|---|---|---|---|
| MDRD | −3.8 (9.2) (−4.3 to −3.3) | −3.7 (−9.7 to 2.4) | 89.5 (87.6 to 91.2) | 52.0 (49.1 to 54.9) | 9.09 |
| MDRD (no race adjustment) | −4.2 (9.3) (−4.7 to −3.7) | −4.0 (−10.1 to 2.0) | 88.4 (86.5 to 90.2) | 51.0 (48.1 to 53.9) | 9.25 |
| CKD-EPIcreatinine | −2.5 (9.1) (−3.0 to −1.9) | −2.8 (−8.2 to 3.5) | 90.2 (88.4 to 91.9) | 56.0 (53.1 to 58.8) | 8.83 |
| CKD-EPIcreatinine (no race adjustment) | −2.8 (9.2) (−3.3 to −2.3) | −2.9 (−8.6 to 3.4) | 89.6 (87.7 to 91.3) | 55.4 (52.5 to 58.2) | 8.97 |
| CKD-EPIcystatin |
−3.4 (9.1) (−3.9 to −2.9)
−9.9 (7.9) (−10.3 to −9.4) |
−4.1 (−9.3 to 1.5)
−9.8 (−14.9 to −5.3) |
89.5 (87.6 to 91.2)
72.5 (69.8 to 75.0) |
52.4 (49.5 to 55.3)
30.6 (28.0 to 33.3) |
7.58
7.60 |
| CKD-EPIcreatinine-cystatin |
−3.7 (7.3) (−4.1 to −3.3)
−7.2 (7.1) (−7.6 to −6.8) |
−3.9 (−8.4 to 1.1)
−7.2 (−11.7 to −2.4) |
94.9 (93.5 to 96.1)
90.4 (88.6 to 92.0) |
60.4 (57.5 to 63.2)
45.7 (42.8 to 48.6) |
7.07
7.08 |
| CKD-EPIcreatinine-cystatin (no race adjustment) | −3.9 (7.3) (−4.3 to −3.4) −7.3 (7.1) (−7.8 to −6.9) |
−4.0 (−8.5 to 0.9) −7.4 (−11.9 to −2.6) |
94.7 (93.2 to 95.9) 89.9 (88.0 to 91.6) |
60.1 (57.2 to 62.9) 45.2 (42.3 to 48.1) |
7.09 7.10 |
| CKD-EPI(2021)creatinine | 0.0 (9.3) (−0.6 to 0.5) | −0.4 (−6.0 to 6.1) | 88.0 (86.0 to 89.8) | 57.5 (54.6 to 60.4) | 8.99 |
| CKD-EPI(2021)creatinine-cystatin | −1.1 (7.6) (−1.5 to −0.6) −5.2 (7.2) (−5.6 to −4.8) |
−1.3 (−6.1 to 3.7) −5.3 (−9.9 to −0.4) |
94.9 (93.4 to 96.1) 94.2 (92.7 to 95.4) |
66.1 (63.3 to 68.8) 55.2 (52.3 to 58.1) |
7.06 7.07 |
| BIS1creatinine | 1.0 (12.9) (0.2 to 1.7) | −0.6 (−6.5 to 6.6) | 85.9 (83.7 to 87.8) | 53.2 (50.3 to 56.1) | 10.94 |
| BIS2creatinine-cystatin | −1.8 (8.6) (−2.3 to −1.3) −5.0 (8.4) (−5.5 to −4.5) |
−2.2 (−7.0 to 2.5) −5.1 (−10.2 to −0.7) |
93.2 (91.6 to 94.6) 93.1 (91.5 to 94.5) |
65.0 (62.1 to 67.7) 52.6 (49.7 to 55.5) |
8.31 8.38 |
| CAPAcystatin | −2.2 (9.0) (−2.7 to −1.7) −8.5 (8.0) (−9.0 to −8.1) |
−2.8 (−7.9 to 3.0) −8.6 (−13.6 to −3.3) |
91.0 (89.2 to 92.6) 78.6 (76.1 to 80.9) |
56.6 (53.7 to 59.4) 37.4 (34.7 to 40.3) |
7.82 7.79 |
| FAScreatinine | −3.5 (9.2) (−4.1 to −3.0) | −3.7 (−9.3 to 2.5) | 89.4 (87.5 to 91.1) | 54.2 (51.2 to 57.0) | 9.10 |
| FAScreatinine-cystatin | −2.9 (7.9) (−3.3 to −2.4) −5.5 (7.9) (−5.9 to −5.0) |
−3.0 (−7.9 to 2.0) −5.4 (−10.6 to −0.6) |
94.4 (93.0 to 95.7) 92.6 (91.0 to 94.1) |
61.0 (58.1 to 63.8) 53.0 (50.1 to 55.9) |
7.89 7.92 |
| LMRcreatinine | −6.2 (9.1) (−6.7 to −5.6) | −6.4 (−11.9 to −0.2) | 84.2 (82.0 to 86.2) | 45.3 (42.4 to 48.2) | 8.93 |
| EKFCcreatinine | −4.4 (9.0) (−4.9 to −3.8) | −4.4 (−10.0 to 1.3) | 89.4 (87.5 to 91.1) | 52.5 (49.6 to 55.4) | 8.87 |
FIGURE 5.
Bias of GFR-estimating equations compared to mGFR shown as box and whisker plots. The box shows the median and the first (Q1) and third quartiles (Q3). The whiskers span all data points within 1.5 IQR of the nearer quartile, with Tukey outliers outside of this range (< Q1–1.5 IQR or > Q3 + 1.5 IQR). The CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations are shown both before and after recalibration against the Siemens assay.
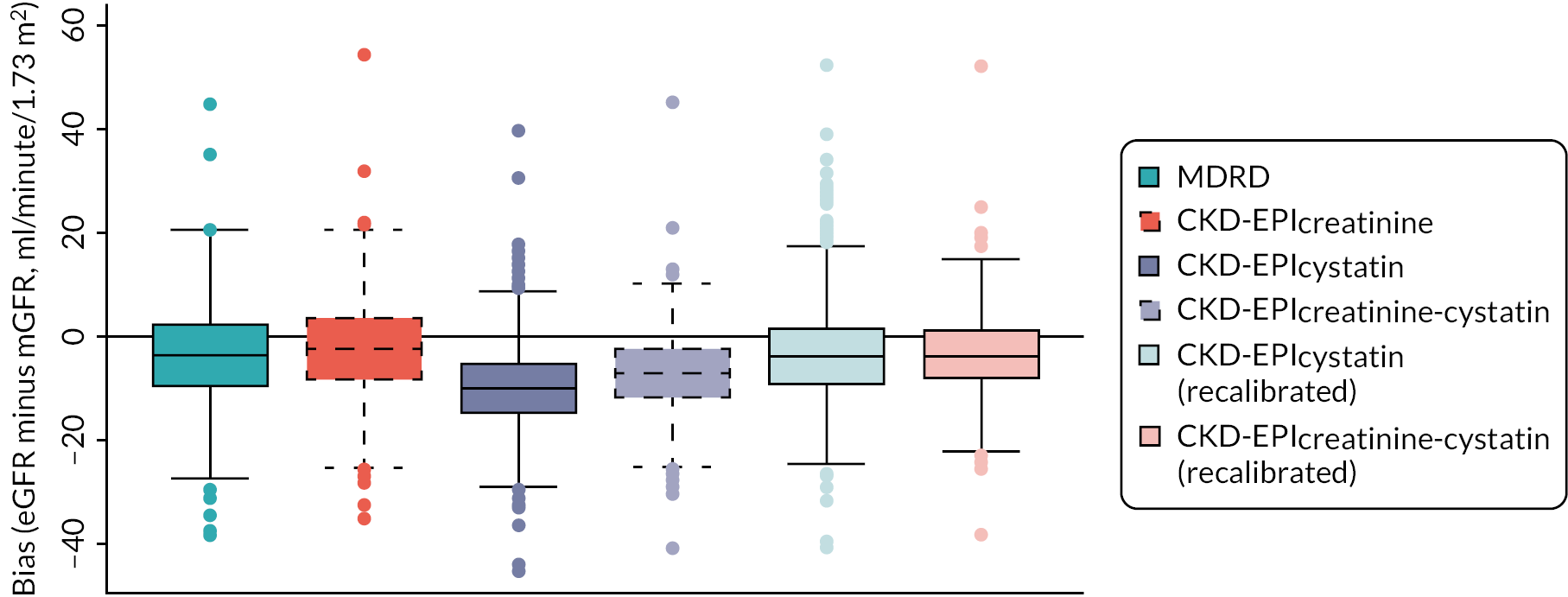
FIGURE 6.
Bias of GFR-estimating equations compared to mGFR shown as lowess plots. Bias plots for the baseline cohort (n = 1167) are shown with lowess (locally weighted scatterplot smoothing) function (red solid line). The solid black line shows zero bias, and the dashed red line shows mean bias. The CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations are shown both after (c, d) and before (e, f) recalibration against the Siemens assay. (a) MDRD eGFR vs. mGFR; (b) CKD-EPIcreatinine eGFR vs. mGFR; (c) CKD-EPIcystatin eGFR vs. mGFR (Siemens); (d) CKD-EPIcreatinine-cystatin eGFR vs. mGFR (Siemens); (e) CKD-EPIcystatin eGFR vs. mGFR (Abbott); and (f) CKD-EPIcreatinine-cystatin eGFR vs. mGFR (Abbott).
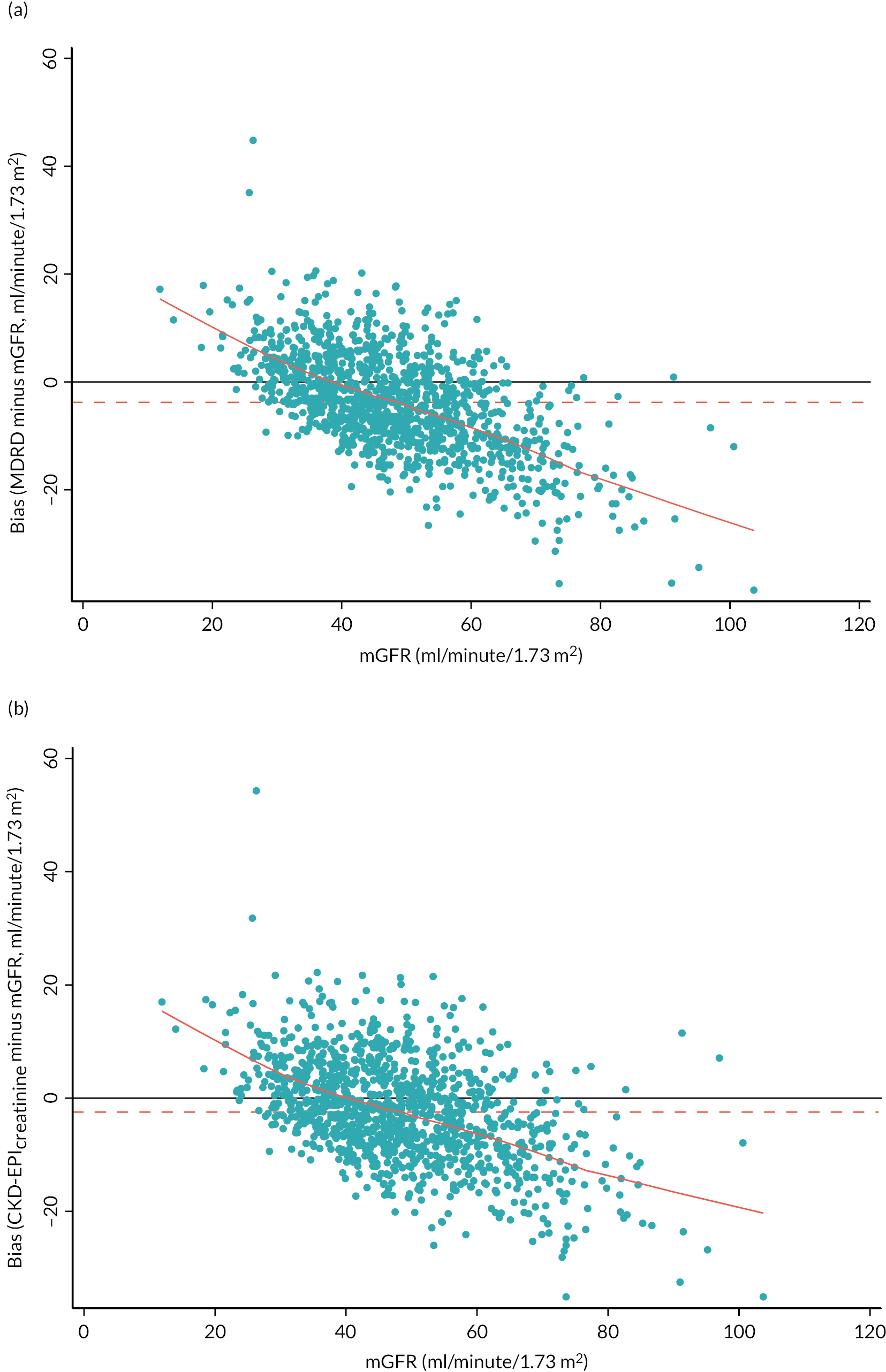

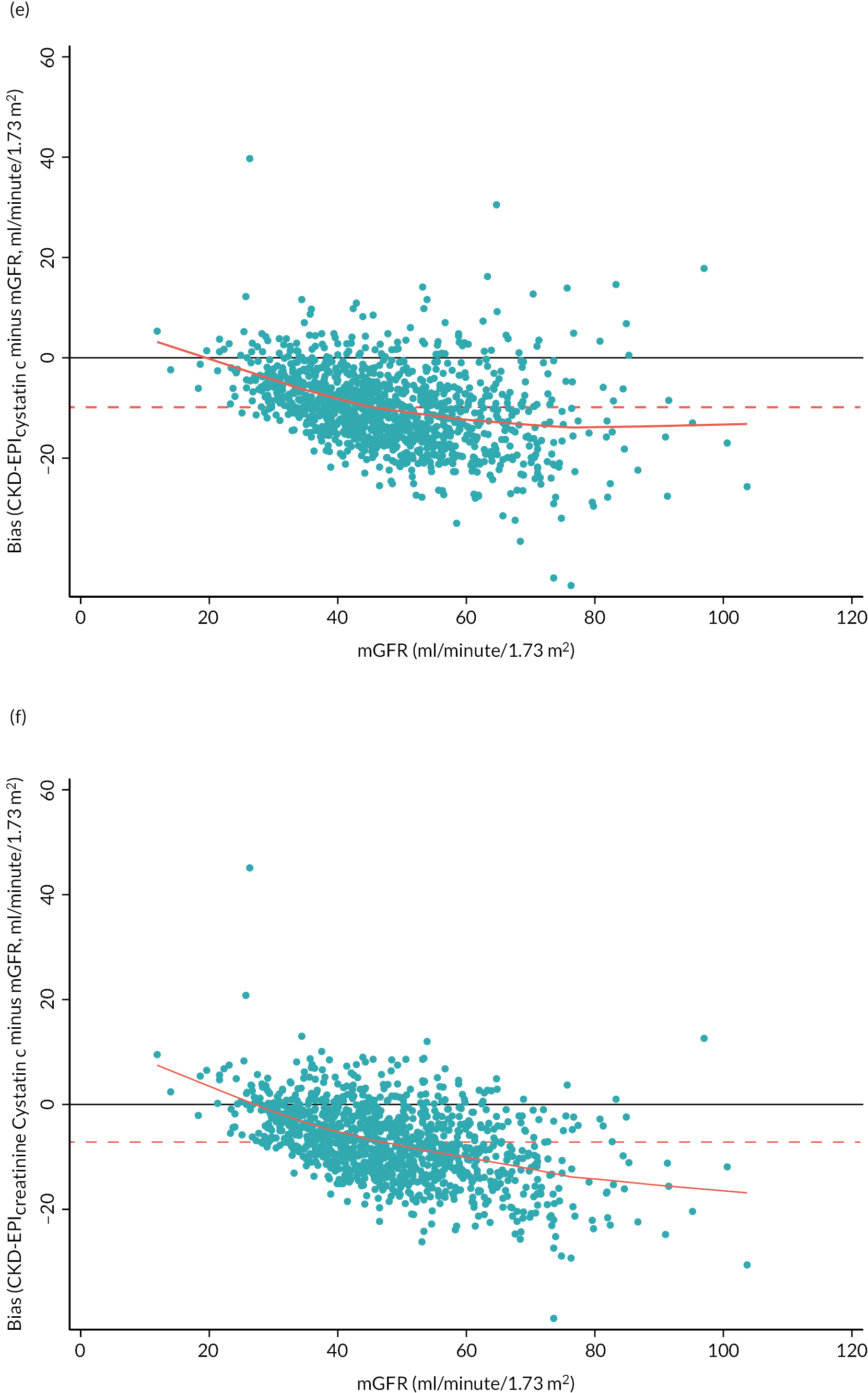
| Test B | Test A | ||
|---|---|---|---|
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | |
| MDRD | |||
| CKD-EPIcreatinine | 0.8 (−0.5 to 2.0) p = 0.2529 | ||
| CKD-EPIcystatin | 0.0 (−2.5 to 2.5) p > 0.999 −17.0 (−20.2 to −13.8) p < 0.001 |
−0.8 (−3.3 to 1.7) p = 0.5783 −17.7 (−20.9 to −14.6) p < 0.001 |
|
| CKD-EPIcreatinine-cystatin | 5.5 (3.6 to 7.4) p < 0.001 0.9 (−1.2 to 3.0) p = 0.4031 |
4.7 (2.9 to 6.5) p < 0.001 0.2 (−1.9 to 2.2) p = 0.9322 |
5.5 (3.8 to 7.2) p < 0.001 17.9 (15.5 to 20.4) p < 0.001 |
Accuracy of glomerular filtration rate-estimating equations according to age, gender, diabetes, albuminuria, body mass index, measured glomerular filtration rate level and ethnic group (particularly Caucasian, South Asian and African-Caribbean)
Performance (P30) of GFR-estimating equations was examined by categories of age, gender, diabetes, albuminuria, BMI, level of GFR (Table 7) and ethnic group (particularly Caucasians, South Asian and African-Caribbean) (Table 8). For each characteristic, data for equations incorporating cystatin C utilised cystatin C values obtained following assay recalibration (see Accuracy of glomerular filtration rate-estimating equations including the Modification of Diet in Renal Disease equation and three Chronic Kidney Disease-Epidemiology Consortium equations using either creatinine or cystatin C or a combination of both in people with stage 3 chronic kidney disease: baseline analysis). Although in some cases point estimates suggest differences with certain characteristics (e.g. inferior performance in people with higher BMI), for none of the equations were any of the changes significant (i.e. confidence intervals of the P30 estimates were overlapping across categories).
| Equation | Demographic/clinical category | ||||
|---|---|---|---|---|---|
| Age (years) | |||||
| < 50 ( n = 149) | 50–59 ( n = 177) | 60–69 (n = 376) | 70–79 (n = 368) | ≥ 80 ( n = 97) | |
| MDRD | 85.2 (78.5 to 90.5) | 87.0 (81.1 to 91.6) | 89.1 (85.5 to 92.1) | 92.9 (89.8 to 95.3) | 88.7 (80.6 to 94.2) |
| CKD-EPIcreatinine | 87.9 (81.6 to 92.7) | 88.7 (83.1 to 93.0) | 88.8 (85.2 to 91.8) | 92.9 (89.8 to 95.3) | 91.8 (84.4 to 96.4) |
| CKD-EPIcystatin | 90.6 (84.7 to 94.8) | 92.1 (87.1 to 95.6) | 87.0 (83.1 to 90.2) | 90.5 (87.0 to 93.3) | 88.7 (80.6 to 94.2) |
| CKD-EPIcreatinine-cystatin | 97.3 (93.2 to 99.3) | 94.4 (89.9 to 97.3) | 93.6 (90.7 to 95.9) | 95.7 (93.0 to 97.5) | 94.8 (88.4 to 98.3) |
| Gender | |||||
| Males ( n = 680) | Females ( n = 487) | ||||
| MDRD | 88.2 (85.6 to 90.6) | 91.2 (88.3 to 93.5) | |||
| CKD-EPIcreatinine | 88.5 (85.9 to 90.8) | 92.6 (89.9 to 94.8) | |||
| CKD-EPIcystatin | 90.3 (87.8 to 92.4) | 88.3 (85.1 to 91.0) | |||
| CKD-EPIcreatinine-cystatin | 94.4 (92.4 to 96.0) | 95.7 (93.5 to 97.3) | |||
| Diabetes | |||||
| Non-diabetic ( n = 843) | Diabetic ( n = 324) | ||||
| MDRD | 89.6 (87.3 to 91.5) | 89.2 (85.3 to 92.4) | |||
| CKD-EPIcreatinine | 90.7 (88.6 to 92.6) | 88.9 (85.0 to 92.1) | |||
| CKD-EPIcystatin | 89.9 (87.7 to 91.9) | 88.3 (84.4 to 91.6) | |||
| CKD-EPIcreatinine-cystatin | 95.1 (93.5 to 96.5) | 94.4 (91.4 to 96.7) | |||
| Albuminuria category | |||||
| A0 < 3 mg/mmol ( n = 483) | A1 3.0–29.9 mg/mmol (n = 396) | A2 ≥ 30 mg/mmol ( n = 269) | |||
| MDRD | 90.9 (88.0 to 93.3) | 89.6 (86.2 to 92.5) | 87.0 (82.4 to 90.8) | ||
| CKD-EPIcreatinine | 91.7 (88.9 to 94.0) | 90.4 (87.1 to 93.1) | 87.7 (83.2 to 91.4) | ||
| CKD-EPIcystatin | 91.9 (89.1 to 94.2) | 86.9 (83.1 to 90.0) | 89.2 (84.9 to 92.7) | ||
| CKD-EPIcreatinine-cystatin | 95.7 (93.4 to 97.3) | 95.5 (92.9 to 97.3) | 92.9 (89.2 to 95.7) | ||
| BMI | |||||
| < 30 kg/m2 (n = 668) | ≥ 30 kg/m2 (n = 499) | ||||
| MDRD | 90.4 (87.9 to 92.5) | 88.2 (85.0 to 90.9) | |||
| CKD-EPIcreatinine | 91.2 (88.8 to 93.2) | 89.0 (85.9 to 91.6) | |||
| CKD-EPIcystatin | 90.9 (88.4 to 92.9) | 87.6 (84.4 to 90.3) | |||
| CKD-EPIcreatinine-cystatin | 96.0 (94.2 to 97.3) | 93.6 (91.1 to 95.6) | |||
| Measured GFR (ml/minute/1.73 m2) | |||||
| GFR < 45 (n = 504) | GFR ≥ 45 (n = 663) | ||||
| MDRD | 87.7 (84.5 to 90.4) | 90.8 (88.3 to 92.9) | |||
| CKD-EPIcreatinine | 88.1 (84.9 to 90.8) | 91.9 (89.5 to 93.8) | |||
| CKD-EPIcystatin | 87.7 (84.5 to 90.4) | 90.8 (88.3 to 92.9) | |||
| CKD-EPIcreatinine-cystatin | 93.7 (91.2 to 95.6) | 95.9 (94.1 to 97.3) | |||
| Equation | Reported ethnicitya | Difference (95% CI) for African-Caribbeans with and without adjustment factor; p-values (n = 60)b | |||
|---|---|---|---|---|---|
| Caucasian (n = 1014) | South Asian (n = 66) | African-Caribbean (n = 60) | African-Caribbean, adjustment factor removed (n = 60) | ||
| MDRD | 89.8 (87.8 to 91.6) | 87.9 (77.5 to 94.6) | 83.3 (71.5 to 91.7) | 63.3 (49.9 to 75.4) | −20.0 (−35.4 to −4.6); p = 0.0118 |
| CKD-EPIcreatinine | 90.8 (88.9 to 92.5) | 86.4 (75.7 to 93.6) | 81.7 (69.6 to 90.5) | 70.0 (56.8 to 81.2) | −11.7 (−23.8 to 0.4); p = 0.0654 |
| CKD-EPIcystatin | 89.6 (87.6 to 91.5) | 86.4 (75.7 to 93.6) | 90.0 (79.5 to 96.2) | N/A | N/A |
| CKD-EPIcreatinine-cystatin | 95.0 (93.4 to 96.2) | 93.9 (85.2 to 98.3) | 95.0 (86.1 to 99.0) | 90.0 (79.5 to 96.2) | −5.0 (−12.2 to 2.2); p = 0.2500 |
| CKD-EPI(2021)creatinine | 88.9 (86.8 to 90.7) | 84.8 (73.9 to 92.5) | 75.0 (62.1 to 85.3) | N/A | N/A |
| CKD-EPI(2021)creatinine-cystatin | 95.1 (93.6 to 96.3) | 92.4 (83.2 to 97.5) | 93.3 (83.8 to 98.2) | N/A | N/A |
In the overall cohort, removal of the race adjustment factors had no impact (overlapping CIs) on the median bias or accuracy (P30) of the MDRD, CKD-EPIcreatinine and CKD-EPIcreatinine-cystatin equations (see Table 5). There was no evidence (overlapping CIs) of a difference in accuracy of any of the equations across ethnic groups (Table 8). Removal of the adjustment factor for African-Caribbean ethnicity in the MDRD, CKD-EPIcreatinine and CKD-EPIcreatinine-cystatin equations resulted in decreased point estimates of P30 for these participants, although this only achieved significance (p < 0.05) for the MDRD equation (see Table 8). The 2021 revisions of the CKD-EPI equations, which were specifically remodelled to address concerns around interethnic performance, were also included here for comparison.
Performance of glomerular filtration rate-estimating equations at detecting changes in measured glomerular filtration rate over 3 years
The median mGFR (ml/minute/1.73 m2) at baseline was 48.1 falling to 43.6 at 3-year follow-up. The equivalent changes for the eGFRs were: 44.6–41.5 (MDRD); 45.7–42.0 (CKD-EPIcreatinine); 43.6–40.4 (CKD-EPIcystatin); and 43.4–40.6 (CKD-EPIcreatinine-cystatin). Of the 875 participants with mGFR and eGFR at both baseline and 3-year follow-up, 7 (0.8%) reached kidney failure (mGFR < 15) at follow-up. Of the 875 participants over the study duration, 268 (30.6%) had a change in GFR > 10; 235 (26.8%) had a decline in GFR > 10; 272 (31.1%) had a GFR decline of > RCV; 156 (17.8%) had a GFR decline of > 25%; and 139 (15.9%) had a GFR decline of > 25% in combination with a change in disease category.
As opposed to assessments of equation accuracy at baseline (see Table 5), in the analyses shown in this section which relate to monitoring GFR over time, the ‘race adjustment factor removed’ versions of equations are not shown. This adjustment involves scaling an element of the equation in African-Caribbean individuals only by a constant factor on each occasion, so monitoring an individual over time will have no impact on the ability of an equation to reflect change over time. This was confirmed empirically, and the data have not been included to aid clarity. In all tables in this section, data for equations incorporating cystatin C utilise cystatin C values obtained following assay recalibration (see Accuracy of glomerular filtration rate-estimating equations including the Modification of Diet in Renal Disease equation and three Chronic Kidney Disease-Epidemiology Consortium equations using either creatinine or cystatin C or a combination of both in people with stage 3 chronic kidney disease: baseline analysis).
Concordance of glomerular filtration rate-estimating equations with measured glomerular filtration rate within a tolerance of 3 ml/minute/1.73 m2/year or five percentage points over 3 years
The abilities of GFR-estimating equations to track mGFR within 3 ml/minute/1.73 m2 or within five percentage points of the observed change in mGFR are summarised in Tables 9 and 10. For the three CKD-EPI equations, an exploratory analysis was undertaken to compare differences in baseline characteristics between those identified as having a change within 3 ml/minute/1.73 m2 mGFR and those in whom the eGFR was > 3 ml/minute/1.73 m2 different from the change in mGFR: no clear differences were identified (see Appendix 1, Table 40).
| Equation | Difference in change per year (eGFR – mGFR) within 3 ml/minute/1.73 m2 | Absolute difference in % change (eGFR – mGFR) within 5% | ||
|---|---|---|---|---|
| n/N | %, (95% CI) | n/N | %, (95% CI) | |
| MDRD | 660/875 | 75.4 (72.4 to 78.2) | 655/875 | 74.9 (71.8 to 77.7) |
| CKD-EPIcreatinine | 640/875 | 73.1 (70.1 to 76.1) | 627/875 | 71.7 (68.5 to 74.6) |
| CKD-EPIcystatin | 662/875 | 75.7 (72.7 to 78.5) | 646/875 | 73.8 (70.8 to 76.7) |
| CKD-EPIcreatinine-cystatin | 688/875 | 78.6 (75.8 to 81.3) | 662/875 | 75.7 (72.7 to 78.5) |
| CKD-EPI(2021)creatinine | 635/875 | 72.6 (69.5 to 75.5) | 631/875 | 72.1 (69.0 to 75.1) |
| CKD-EPI(2021)creatinine-cystatin | 683/875 | 78.1 (75.2 to 80.8) | 665/875 | 76.0 (73.0 to 78.8) |
| BIS1creatinine | 668/875 | 76.3 (73.4 to 79.1) | 718/875 | 82.1 (79.4 to 84.5) |
| BIS2creatinine-cystatin | 712/875 | 81.4 (78.6 to 83.9) | 729/875 | 83.3 (80.7 to 85.7) |
| CAPAcystatin | 664/875 | 75.9 (72.9 to 78.7) | 664/875 | 75.9 (72.9 to 78.7) |
| FAScreatinine | 681/875 | 77.8 (74.9 to 80.5) | 699/875 | 79.9 (77.1 to 82.5) |
| FAScreatinine-cystatin | 703/875 | 80.3 (77.6 to 82.9) | 728/875 | 83.2 (80.6 to 85.6) |
| LMRcreatinine | 651/875 | 74.4 (71.4 to 77.3) | 633/875 | 72.3 (69.3 to 75.3) |
| EKFCcreatinine | 669/875 | 76.5 (73.5 to 79.2) | 653/875 | 74.6 (71.6 to 77.5) |
| Test B | Test A | ||
|---|---|---|---|
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | |
| MDRD | |||
| CKD-EPIcreatinine | (a) −2.3 (−3.8 to −0.7), p = 0.0029 (b) −3.2 (−4.5 to −1.9), p < 0.0001 |
||
| CKD-EPIcystatin | (a) 0.2 (−3.1 to 3.5), p = 0.9442 (b) −1.0 (−4.2 to 2.2), p = 0.5607 |
(a) 2.5 (−0.9 to 5.9), p = 0.1567 (b) 2.2 (−1.1 to 5.4), p = 0.1973 |
|
| CKD-EPIcreatinine-cystatin | (a) 3.2 (0.6 to 5.8), p = 0.0134 (b) 0.8 (−1.7 to 3.3), p = 0.5692 |
(a) 5.5 (2.8 to 8.2), p < 0.0001 (b) 4.0 (1.6 to 6.4), p = 0.0010 |
(a) 3.0 (0.7 to 5.3), p = 0.0103 (b) 1.8 (−0.6 to 4.3), p = 0.1523 |
Sensitivity analysis for change over time
Sensitivity analyses used alternative methods to estimate the change in eGFR (using a linear regression model per person) and mGFR (multilevel model) (Table 11).
| Equation | Sensitivity analysis 1 | Sensitivity analysis 2 | ||
|---|---|---|---|---|
| n/N | % (95% CI) | n/N | % (95% CI) | |
| MDRD | 681/875 | 77.8 (74.9 to 80.5) | 723/875 | 82.6 (79.9 to 85.1) |
| CKD-EPIcreatinine | 673/875 | 76.9 (74.0 to 79.7) | 704/875 | 80.5 (77.7 to 83.0) |
| CKD-EPIcystatin | 655/875 | 74.9 (71.8 to 77.7) | 694/875 | 79.3 (76.5 to 82.0) |
| CKD-EPIcreatinine-cystatin | 685/875 | 78.3 (75.4 to 81.0) | 726/875 | 83.0 (80.3 to 85.4) |
Ability of glomerular filtration rate-estimating equations to detect a change in measured glomerular filtration rate > 10 ml/minute/1.73 m2 over 3 years
For this analysis, we were interested in the clinically meaningful results of a change in GFR > 10 ml/minute/1.73 m2 over 3 years (in either direction), which we considered a positive result and, consequently, a change in GFR ≤ 10 ml/minute/1.73 m2 over 3 years (in either direction) negative. We have also investigated the outcome of a GFR decline only of > 10 ml/minute/1.73 m2 over 3 years. Using the observed data, we calculated whether a positive or negative result was achieved for each estimated equation (index tests) and compared these to the result from mGFR (the reference standard) (Table 12).
| Change in GFR | ||||||||
|---|---|---|---|---|---|---|---|---|
| > |10| | ≤ |10| | % (95% CI) | ||||||
| Equation | TP | FN | FP | TN | Sensitivity | Specificity | PPV | NPV |
| MDRD | 104 | 164 | 104 | 503 |
38.8
(32.9 to 44.9) |
82.9
(79.6 to 85.8) |
50.0
(43.0 to 57.0) |
75.4
(72.0 to 78.6) |
| CKD-EPIcreatinine | 119 | 149 | 127 | 480 |
44.4
(38.4 to 50.6) |
79.1
(75.6 to 82.2) |
48.4
(42.0 to 54.8) |
76.3
(72.8 to 79.6) |
| CKD-EPIcystatin | 134 | 134 | 121 | 486 |
50.0
(43.9 to 56.1) |
80.1
(76.7 to 83.2) |
52.5
(46.2 to 58.8) |
78.4
(74.9 to 81.6) |
| CKD-EPIcreatinine-cystatin | 123 | 145 | 111 | 496 |
45.9
(39.8 to 52.1) |
81.7
(78.4 to 84.7) |
52.6
(46.0 to 59.1) |
77.4
(73.9 to 80.6) |
| CKD-EPI(2021)creatinine | 120 | 148 | 143 | 464 | 44.8 (38.7 to 50.9) |
76.4 (72.9 to 79.8) |
45.6 (39.5 to 51.9) |
75.8 (72.2 to 79.2) |
| CKD-EPI(2021)creatinine-cystatin | 129 | 139 | 126 | 481 | 48.1 (42.0 to 54.3) |
79.2 (75.8 to 82.4) |
50.6 (44.3 to 56.9) |
77.6 (74.1 to 80.8) |
| BIS1creatinine | 103 | 165 | 73 | 534 | 38.4 (32.6 to 44.5) |
88.0 (85.1 to 90.5) |
58.5 (50.9 to 65.9) |
76.4 (73.1 to 79.5) |
| BIS2creatinine-cystatin | 103 | 165 | 67 | 540 | 38.4 (32.6 to 44.5) |
89.0 (86.2 to 91.3) |
60.6 (52.8 to 68.0) |
76.6 (73.3 to 79.7) |
| CAPAcystatin | 126 | 142 | 121 | 486 | 47.0 (40.9 to 53.2) |
80.1 (76.7 to 83.2) |
51.0 (44.6 to 57.4) |
77.4 (73.9 to 80.6) |
| FAScreatinine | 101 | 167 | 72 | 535 | 37.7 (31.9 to 43.8) |
88.1 (85.3 to 90.6) |
58.4 (50.7 to 65.8) |
76.2 (72.9 to 79.3) |
| FAScreatinine-cystatin | 99 | 169 | 64 | 543 | 36.9 (31.1 to 43.0) |
89.5 (86.7 to 91.8) |
60.7 (52.8 to 68.3) |
76.3 (73.0 to 79.3) |
| LMRcreatinine | 112 | 156 | 107 | 500 | 41.8 (35.8 to 47.9) | 82.4 (79.1 to 85.3) | 51.1 (44.3 to 57.9) | 76.2 (72.8 to 79.4) |
| EKFCcreatinine | 108 | 160 | 95 | 512 | 40.3 (34.4 to 46.4) |
84.3 (81.2 to 87.1) |
53.2 (46.1 to 60.2) |
76.2 (72.8 to 79.4) |
| MDRD | 96 | 139 | 68 | 572 |
40.9
(34.5 to 47.4) |
89.4
(86.7 to 91.7) |
58.5
(50.6 to 66.2) |
80.5
(77.3 to 83.3) |
| CKD-EPIcreatinine | 111 | 124 | 87 | 553 |
47.2
(40.7 to 53.8) |
86.4
(83.5 to 89.0) |
56.1
(48.8 to 63.1) |
81.7
(78.6 to 84.5) |
| CKD-EPIcystatin | 109 | 126 | 81 | 559 |
46.4
(39.9 to 53.0) |
87.3
(84.5 to 89.8) |
57.4
(50.0 to 64.5) |
81.6
(78.5 to 84.4) |
| CKD-EPIcreatinine-cystatin | 107 | 128 | 79 | 561 |
45.5
(39.0 to 52.1) |
87.7
(84.9 to 90.1) |
57.5
(50.1 to 64.7) |
81.4
(78.3 to 84.3) |
| CKD-EPI(2021)creatinine | 112 | 123 | 96 | 544 | 47.7 (41.1 to 54.3) |
85.0 (82.0 to 87.7) |
53.8 (46.8 to 60.8) |
81.6 (78.4 to 84.4) |
| CKD-EPI(2021)creatinine-cystatin | 111 | 124 | 88 | 552 | 47.2 (40.7 to 53.8) |
86.3 (83.3 to 88.8) |
55.8 (48.6 to 62.8) |
81.7 (78.5 to 84.5) |
| BIS1creatinine | 99 | 136 | 65 | 575 | 42.1 (35.7 to 48.7) |
89.8 (87.2 to 92.1) |
60.4 (52.4 to 67.9) |
80.9 (77.8 to 83.7) |
| BIS2creatinine-cystatin | 92 | 143 | 57 | 583 | 39.1 (32.9 to 45.7) |
91.1 (88.6 to 93.2) |
61.7 (53.4 to 69.6) |
80.3 (77.2 to 83.1) |
| CAPAcystatin | 103 | 132 | 80 | 560 | 43.8 (37.4 to 50.4) |
87.5 (84.7 to 90.0) |
56.3 (48.8 to 63.6) |
80.9 (77.8 to 83.8) |
| FAScreatinine | 96 | 139 | 62 | 578 | 40.9 (34.5 to 47.4) |
90.3 (87.8 to 92.5) |
60.8 (52.7 to 68.4) |
80.6 (77.5 to 83.4) |
| FAScreatinine-cystatin | 89 | 146 | 54 | 586 | 37.9 (31.6 to 44.4) |
91.6 (89.1 to 93.6) |
62.2 (53.8 to 70.2) |
80.1 (77.0 to 82.9) |
| LMRcreatinine | 104 | 131 | 81 | 559 | 44.3 (37.8 to 50.9) | 87.3 (84.5 to 89.8) | 56.2 (48.7 to 63.5) | 81.0 (77.9 to 83.9) |
| EKFCcreatinine | 102 | 133 | 75 | 565 | 43.4 (37.0 to 50.0) |
88.3 (85.5 to 90.7) |
57.6 (50.0 to 65.0) |
80.9 (77.8 to 83.8) |
Ability of glomerular filtration rate-estimating equations to detect a change in measured glomerular filtration rate greater than the reference change value over 3 years
Table 13 shows the ability of GFR estimations to detect a change in mGFR exceeding the RCV. The bounds of the RCV are asymmetric, so we have a different positive and negative percentage change indicating a meaningful change and a positive result; we also consider change only in the negative direction. Of the main equations assessed, MDRD had the highest specificity for change overall (79.9%) and for detecting decline (87.4%), but CIs for all equations overlapped for specificity and sensitivity.
| Change in GFR | ||||||||
|---|---|---|---|---|---|---|---|---|
| Equation | > RCV (> 21.5% or < −17.7%) |
≤ RCV | % (95% CI) | |||||
| TP | FN | FP | TN | Sensitivity | Specificity | PPV | NPV | |
| MDRD creatinine | 170 | 144 | 113 | 448 |
54.1
(48.5 to 59.7) |
79.9
(76.3 to 83.1) |
60.1
(54.1 to 65.8) |
75.7
(72.0 to 79.1) |
| CKD-EPIcreatinine | 179 | 135 | 133 | 428 |
57.0
(51.3 to 62.6) |
76.3
(72.6 to 79.8) |
57.4
(51.7 to 62.9) |
76.0
(72.3 to 79.5) |
| CKD-EPIcystatin | 191 | 123 | 144 | 417 |
60.8
(55.2 to 66.3) |
74.3
(70.5 to 77.9) |
57.0
(51.5 to 62.4) |
77.2
(73.4 to 80.7) |
| CKD-EPIcreatinine-cystatin | 189 | 125 | 121 | 440 |
60.2
(54.5 to 65.6) |
78.4
(74.8 to 81.8) |
61.0
(55.3 to 66.4) |
77.9
(74.2 to 81.2) |
| CKD-EPI(2021)creatinine | 175 | 139 | 127 | 434 | 55.7 (50.0 to 61.3) |
77.4 (73.7 to 80.8) |
57.9 (52.2 to 63.6) |
75.7 (72.0 to 79.2) |
| CKD-EPI(2021)creatinine-cystatin | 190 | 124 | 124 | 437 | 60.5 (54.9 to 66.0) |
77.9 (74.2 to 81.3) |
60.5 (54.9 to 66.0) |
77.9 (74.2 to 81.3) |
| BIS1creatinine | 150 | 164 | 73 | 488 | 47.8 (42.1 to 53.5) |
87.0 (83.9 to 89.7) |
67.3 (60.7 to 73.4) |
74.8 (71.3 to 78.1) |
| BIS2creatinine-cystatin | 164 | 150 | 66 | 495 | 52.2 (46.5 to 57.9) |
88.2 (85.3 to 90.8) |
71.3 (65.0 to 77.1) |
76.7 (73.3 to 80.0) |
| CAPAcystatin | 183 | 131 | 128 | 433 | 58.3 (52.6 to 63.8) |
77.2 (73.5 to 80.6) |
58.8 (53.1 to 64.4) |
76.8 (73.1 to 80.2) |
| FAScreatinine | 168 | 146 | 87 | 474 | 53.5 (47.8 to 59.1) |
84.5 (81.2 to 87.4) |
65.9 (59.7 to 71.7) |
76.5 (72.9 to 79.7) |
| FAScreatinine-cystatin | 160 | 154 | 71 | 490 | 51.0 (45.3 to 56.6) |
87.3 (84.3 to 90.0) |
69.3 (62.9 to 75.1) |
76.1 (72.6 to 79.3) |
| LMRcreatinine | 186 | 128 | 143 | 418 | 59.2 (53.6 to 64.7) | 74.5 (70.7 to 78.1) | 56.5 (51.0 to 62.0) | 76.6 (72.8 to 80.0) |
| EKFCcreatinine | 176 | 138 | 116 | 445 | 56.1 (50.4 to 61.6) |
79.3 (75.7 to 82.6) |
60.3 (54.4 to 65.9) |
76.3 (72.7 to 79.7) |
| MDRD | 156 | 116 | 76 | 527 |
57.4
(51.2 to 63.3) |
87.4
(84.5 to 89.9) |
67.2
(60.8 to 73.2) |
82.0
(78.8 to 84.9) |
| CKD-EPIcreatinine | 166 | 106 | 97 | 506 |
61.0
(55.0 to 66.9) |
83.9
(80.7 to 86.8) |
63.1
(57.0 to 69.0) |
82.7
(79.4 to 85.6) |
| CKD-EPIcystatin | 168 | 104 | 102 | 501 |
61.8
(55.7 to 67.6) |
83.1
(79.8 to 86.0) |
62.2
(56.1 to 68.0) |
82.8
(79.6 to 85.7) |
| CKD-EPIcreatinine-cystatin | 170 | 102 | 85 | 518 |
62.5
(56.5 to 68.3) |
85.9
(82.9 to 88.6) |
66.7
(60.5 to 72.4) |
83.5
(80.4 to 86.4) |
| CKD-EPI(2021)creatinine | 162 | 110 | 91 | 512 | 59.6 (53.5 to 65.4) |
84.9 (81.8 to 87.7) |
64.0 (57.8 to 69.9) |
82.3 (79.1 to 85.2) |
| CKD-EPI(2021)creatinine-cystatin | 170 | 102 | 84 | 519 | 62.5 (56.3 to 68.3) |
86.1 (83.0 to 88.7) |
66.9 (60.8 to 72.7) |
83.6 (80.4 to 86.4) |
| BIS1creatinine | 145 | 127 | 64 | 539 | 53.3 (47.2 to 59.4) |
89.4 (86.6 to 91.7) |
69.4 (62.6 to 75.6) |
80.9 (77.7 to 83.8) |
| BIS2creatinine-cystatin | 149 | 123 | 58 | 545 | 54.8 (48.7 to 60.8) |
90.4 (87.7 to 92.6) |
72.0 (65.3 to 78.0) |
81.6 (78.4 to 84.5) |
| CAPAcystatin | 160 | 112 | 88 | 515 | 58.8 (52.7 to 64.7) |
85.4 (82.3 to 88.1) |
64.5 (58.2 to 70.5) |
82.1 (78.9 to 85.1) |
| FAScreatinine | 158 | 114 | 73 | 530 | 58.1 (52.0 to 64.0) |
87.9 (85.0 to 90.4) |
68.4 (62.0 to 74.3) |
82.3 (79.1 to 85.2) |
| FAScreatinine-cystatin | 147 | 125 | 56 | 547 | 54.0 (47.9 to 60.1) |
90.7 (88.1 to 92.9) |
72.4 (65.7 to 78.4) |
81.4 (78.2 to 84.3) |
| LMRcreatinine | 172 | 100 | 100 | 503 | 63.2 (57.2 to 69.0) | 83.4 (80.2 to 86.3) | 63.2 (57.2 to 69.0) | 83.4 (80.2 to 86.3) |
| EKFCcreatinine | 164 | 108 | 90 | 513 | 60.3 (54.2 to 66.2) |
85.1 (82.0 to 87.8) |
64.6 (58.3 to 70.4) |
82.6 (79.4 to 85.5) |
Ability of glomerular filtration rate-estimating equations to detect a change in measured glomerular filtration rate of > 25% over 3 years
Of the four main study equations, the sensitivity of the eGFRs to detect change in mGFR > 25% (in either direction) over 3 years was between 44.1% and 55.3%; and the specificity ranged from 84.0% to 88.4% (Table 14). The PPV (percentage of eGFR-positive participants that were mGFR-positive) ranged between 48.1% and 54.5%, whereas the NPV (percentage of eGFR-negative participants that were mGFR-negative) ranged between 85.3% and 87.7%. Sensitivity, specificity, PPV and NPV all increased when using only a reduction in GFR of > 25%, but in all cases CIs of equations overlapped.
| Change in GFR | ||||||||
|---|---|---|---|---|---|---|---|---|
| Equation | > |25%| | ≤ |25%| | % (95% CI) | |||||
| TP | FN | FP | TN | Sensitivity | Specificity | PPV | NPV | |
| MDRD | 83 | 105 | 80 | 607 |
44.1
(36.9 to 51.6) |
88.4
(85.7 to 90.7) |
50.9
(43.0 to 58.8) |
85.3
(82.4 to 87.8) |
| CKD-EPIcreatinine | 91 | 97 | 94 | 593 |
48.4
(41.1 to 55.8) |
86.3
(83.5 to 88.8) |
49.2
(41.8 to 56.6) |
85.9
(83.1 to 88.4) |
| CKD-EPIcystatin | 102 | 86 | 110 | 577 |
54.3
(46.8 to 61.5) |
84.0
(81.0 to 86.7) |
48.1
(41.2 to 55.1) |
87.0
(84.2 to 89.5) |
| CKD-EPIcreatinine-cystatin | 104 | 84 | 87 | 600 |
55.3
(47.9 to 62.6) |
87.3
(84.6 to 89.7) |
54.5
(47.1 to 61.7) |
87.7
(85.0 to 90.1) |
| CKD-EPI(2021)creatinine | 89 | 99 | 93 | 594 | 47.3 (40.0 to 54.7) |
86.5 (83.7 to 88.9) |
48.9 (41.4 to 56.4) |
85.7 (82.9 to 88.2) |
| CKD-EPI(2021)creatinine-cystatin | 103 | 85 | 94 | 593 | 54.8 (47.4 to 62.0) |
86.3 (83.5 to 88.8) |
52.3 (45.1 to 59.4) |
87.5 (84.7 to 89.9) |
| BIS1creatinine | 70 | 118 | 47 | 640 | 37.2 (30.3 to 44.6) |
93.2 (91.0 to 94.9) |
59.8 (50.4 to 68.8) |
84.4 (81.7 to 86.9) |
| BIS2creatinine-cystatin | 81 | 107 | 45 | 642 | 43.1 (35.9 to 50.5) |
93.4 (91.3 to 95.2) |
64.3 (55.3 to 72.6) |
85.7 (83.0 to 88.1) |
| CAPAcystatin | 98 | 90 | 95 | 592 | 52.1 (44.7 to 59.5) |
86.2 (83.4 to 88.7) |
50.8 (43.5 to 58.0) |
86.8 (84.0 to 89.3) |
| FAScreatinine | 77 | 111 | 62 | 625 | 41.0 (33.9 to 48.3) |
91.0 (88.6 to 93.0) |
55.4 (46.7 to 63.8) |
84.9 (82.1 to 87.4) |
| FAScreatinine-cystatin | 80 | 108 | 44 | 643 | 42.6 (35.4 to 50.0) |
93.6 (91.5 to 95.3) |
64.5 (55.4 to 72.9) |
85.6 (82.9 to 88.1) |
| LMRcreatinine | 94 | 94 | 109 | 578 | 50.0 (42.6 to 57.4) | 84.1 (81.2 to 86.8) | 46.3 (39.3 to 53.4) | 86.0 (83.2 to 88.5) |
| EKFCcreatinine | 87 | 101 | 80 | 607 | 46.3 (39.0 to 53.7) |
88.4 (85.7 to 90.7) |
52.1 (44.2 to 59.9) |
85.7 (82.9 to 88.2) |
| MDRD | 76 | 80 | 51 | 668 |
48.7
(40.6 to 56.8) |
92.9
(90.8 to 94.7) |
59.8
(50.8 to 68.4) |
89.3
(86.9 to 91.4) |
| CKD-EPIcreatinine | 84 | 72 | 65 | 654 |
53.8
(45.7 to 61.8) |
91.0
(88.6 to 93.0) |
56.4
(48.0 to 64.5) |
90.1
(87.7 to 92.2) |
| CKD-EPIcystatin | 89 | 67 | 71 | 648 |
57.1
(48.9 to 64.9) |
90.1
(87.7 to 92.2) |
55.6
(47.6 to 63.5) |
90.6
(88.3 to 92.7) |
| CKD-EPIcreatinine-cystatin | 92 | 64 | 64 | 655 |
59.0
(50.8 to 66.8) |
91.1
(88.8 to 93.1) |
59.0
(50.8 to 66.8) |
91.1
(88.8 to 93.1) |
| CKD-EPI(2021)creatinine | 82 | 74 | 64 | 655 | 52.6 (44.4 to 60.6) |
91.1 (88.8 to 93.1) |
56.2 (47.7 to 64.4) |
89.8 (87.4 to 91.9) |
| CKD-EPI(2021)creatinine-cystatin | 91 | 65 | 65 | 654 | 58.3 (50.2 to 66.2) |
91.0 (88.6 to 93.0) |
58.3 (50.2 to 66.2) |
91.0 (88.6 to 93.0) |
| BIS1creatinine | 68 | 88 | 41 | 678 | 43.6 (35.7 to 51.8) |
94.3 (92.3 to 95.9) |
62.4 (52.6 to 71.5) |
88.5 (86.0 to 90.7) |
| BIS2creatinine-cystatin | 73 | 83 | 35 | 684 | 46.8 (38.8 to 54.9) |
95.1 (93.3 to 96.6) |
67.6 (57.9 to 76.3) |
89.2 (86.8 to 91.3) |
| CAPAcystatin | 85 | 71 | 59 | 660 | 54.5 (46.3 to 62.5) |
91.8 (89.5 to 93.7) |
59.0 (50.5 to 67.1) |
90.3 (87.9 to 92.3) |
| FAScreatinine | 74 | 82 | 45 | 674 | 47.4 (39.4 to 55.6) |
93.7 (91.7 to 95.4) |
62.2 (52.8 to 70.9) |
89.2 (86.7 to 91.3) |
| FAScreatinine-cystatin | 74 | 82 | 35 | 684 | 47.4 (39.4 to 55.6) |
95.1 (93.3 to 96.6) |
67.9 (58.3 to 76.5) |
89.3 (86.9 to 91.4) |
| LMRcreatinine | 88 | 68 | 74 | 645 | 56.4 (48.2 to 64.3) | 89.7 (87.3 to 91.8) | 54.3 (46.3 to 62.2) | 90.5 (88.1 to 92.5) |
| EKFCcreatinine | 82 | 74 | 59 | 660 | 52.6 (44.4 to 60.6) |
91.8 (89.5 to 93.7) |
58.2 (49.6 to 66.4) |
89.9 (87.5 to 92.0) |
Ability of glomerular filtration rate-estimating equations to detect a change in measured glomerular filtration rate of > 25% over 3 years in combination with a change in disease stage
All main study equations had relatively poor sensitivity (< 56%) and good specificity (> 93%) at detecting change in mGFR of > 25% over 3 years (in either direction) in combination with a change in disease stage. Marker characteristics (sensitivities, specificities, PPV, NPV) improved slightly when only a decline in GFR was considered. There were no differences in performance between the main study equations (Table 15).
| Change in GFR | ||||||||
|---|---|---|---|---|---|---|---|---|
| Equation | > 25% and change in stage | ≤ 25% and no change in stage | % (95% CI) | |||||
| TP | FN | FP | TN | Sensitivity | Specificity | PPV | NPV | |
| MDRD | 76 | 94 | 32 | 673 |
44.7
(37.1 to 52.5) |
95.5
(93.7 to 96.9) |
70.4
(60.8 to 78.8) |
87.7
(85.2 to 90.0) |
| CKD-EPIcreatinine | 82 | 88 | 38 | 667 |
48.2
(40.5 to 56.0) |
94.6
(92.7 to 96.2) |
68.3
(59.2 to 76.5) |
88.3
(85.8 to 90.5) |
| CKD-EPIcystatin | 93 | 77 | 46 | 659 |
54.7
(46.9 to 62.3) |
93.5
(91.4 to 95.2) |
66.9
(58.4 to 74.6) |
89.5
(87.1 to 91.7) |
| CKD-EPIcreatinine-cystatin | 94 | 76 | 38 | 667 |
55.3
(47.5 to 62.9) |
94.6
(92.7 to 96.2) |
71.2
(62.7 to 78.8) |
89.8
(87.4 to 91.9) |
| CKD-EPI(2021)creatinine | 80 | 90 | 38 | 667 | 47.1 (39.4 to 54.9) |
94.6 (92.7 to 96.2) |
67.8 (58.6 to 76.1) |
88.1 (85.6 to 90.3) |
| CKD-EPI(2021)creatinine-cystatin | 93 | 77 | 43 | 662 | 54.7 (46.9 to 62.3) |
93.9 (91.9 to 95.6) |
68.4 (59.9 to 76.1) |
89.6 (87.1 to 91.7) |
| BIS1creatinine | 65 | 105 | 23 | 682 | 38.2 (30.9 to 46.0) |
96.7 (95.1 to 97.9) |
73.9 (63.4 to 82.7) |
86.7 (84.1 to 89.0) |
| BIS2creatinine-cystatin | 73 | 97 | 21 | 684 | 42.9 (35.4 to 50.7) |
97.0 (95.5 to 98.1) |
77.7 (67.9 to 85.6) |
87.6 (85.1 to 89.8) |
| CAPAcystatin | 90 | 80 | 43 | 662 | 52.9 (45.1 to 60.6) |
93.9 (91.9 to 95.6) |
67.7 (59.0 to 75.5) |
89.2 (86.8 to 91.4) |
| FAScreatinine | 70 | 100 | 28 | 677 | 41.2 (33.7 to 49.0) |
96.0 (94.3 to 97.3) |
71.4 (61.4 to 80.1) |
87.1 (84.6 to 89.4) |
| FAScreatinine-cystatin | 72 | 98 | 19 | 686 | 42.4 (34.8 to 50.2) |
97.3 (95.8 to 98.4) |
79.1 (69.3 to 86.9) |
87.5 (85.0 to 89.7) |
| LMRcreatinine | 84 | 86 | 45 | 660 | 49.4 (41.7 to 57.2) | 93.6 (91.6 to 95.3) | 65.1 (56.2 to 73.3) | 88.5 (86.0 to 90.7) |
| EKFCcreatinine | 78 | 92 | 36 | 669 | 45.9 (38.2 to 53.7) |
94.9 (93.0 to 96.4) |
68.4 (59.1 to 76.8) |
87.9 (85.4 to 90.1) |
| MDRD | 70 | 69 | 23 | 713 |
50.4
(41.8 to 58.9) |
96.9
(95.3 to 98.0) |
75.3
(65.2 to 83.6) |
91.2
(89.0 to 93.1) |
| CKD-EPIcreatinine | 76 | 63 | 29 | 707 |
54.7
(46.0 to 63.1) |
96.1
(94.4 to 97.3) |
72.4
(62.8 to 80.7) |
91.8
(89.7 to 93.7) |
| CKD-EPIcystatin | 80 | 59 | 29 | 707 |
57.6
(48.0 to 65.9) |
96.1
(94.4 to 97.3) |
73.4
(64.1 to 81.4) |
92.3
(90.2 to 94.1) |
| CKD-EPIcreatinine-cystatin | 83 | 56 | 29 | 707 |
59.7
(51.1 to 67.9) |
96.1
(94.4 to 97.3) |
74.1
(65.0 to 81.9) |
92.7
(90.6 to 94.4) |
| CKD-EPI(2021)creatinine | 74 | 65 | 29 | 707 | 53.2 (44.6 to 61.7) |
96.1 (94.4 to 97.3) |
71.8 (62.1 to 80.3) |
91.6 (89.4 to 93.4) |
| CKD-EPI(2021)creatinine-cystatin | 82 | 57 | 30 | 706 | 59.0 (50.3 to 67.3) |
95.9 (94.2 to 97.2) |
73.2 (64.0 to 81.1) |
92.5 (90.4 to 94.3) |
| BIS1creatinine | 64 | 75 | 18 | 718 | 46.0 (37.6 to 54.7) |
97.6 (96.2 to 98.5) |
78.0 (67.5 to 86.4) |
90.5 (88.3 to 92.5) |
| BIS2creatinine-cystatin | 66 | 73 | 16 | 720 | 47.5 (39.0 to 56.1) |
97.8 (96.5 to 98.8) |
80.5 (70.3 to 88.4) |
90.8 (88.6 to 92.7) |
| CAPAcystatin | 77 | 62 | 26 | 710 | 55.4 (46.7 to 63.8) |
96.5 (94.9 to 97.7) |
74.8 (65.2 to 82.8) |
92.0 (89.8 to 93.8) |
| FAScreatinine | 68 | 71 | 20 | 716 | 48.9 (40.4 to 57.5) |
97.3 (95.8 to 98.3) |
77.3 (67.1 to 85.5) |
91.0 (88.8 to 92.9) |
| FAScreatinine-cystatin | 67 | 72 | 14 | 722 | 48.2 (39.7 to 56.8) |
98.1 (96.8 to 99.0) |
82.7 (72.7 to 90.2) |
90.9 (88.7 to 92.8) |
| LMRcreatinine | 79 | 60 | 31 | 705 | 56.8 (48.2 to 65.2) | 95.8 (94.1 to 97.1) | 71.8 (62.4 to 80.0) | 92.2 (90.0 to 94.0) |
| EKFCcreatinine | 74 | 65 | 28 | 708 | 53.2 (44.6 to 61.7) |
96.2 (94.5 to 97.5) |
72.5 (62.8 to 80.9) |
91.6 (89.4 to 93.5) |
To estimate and model disease progression (decline in glomerular filtration rate or increase in albumin-to-creatinine ratio) and differences in progression between ethnic groups (Caucasian, South Asian and African-Caribbean), and baseline diabetes and albuminuria status and other potential risk factors
In the substudy of disease progression, 239 participants with paired mGFR and eGFR on at least 2 occasions were evaluable and included in the disease progression covariate models. There were no obvious changes in the covariates BP, BMI and waist circumference (Table 16) or mGFR or eGFR over time (Table 17), although there was a tendency towards lower GFR and higher ACR values over time (see Appendix 1, Figures 15–17).
| Characteristic | Time (years) | |||
|---|---|---|---|---|
| Baseline | 1 | 2 | 3 | |
| Systolic BP (mmHg) | 130 (118–142) 239 |
127 (117–140) 224 |
130 (118–142) 201 |
129 (116–144) 208 |
| Diastolic BP (mmHg) | 78 (72–86) 239 |
78 (71–86) 224 |
77 (71–85) 201 |
77 (69–84) 208 |
| BMI (kg/m2) | 28.7 (25.3–33.2) 239 |
28.6 (25.6–33.8) 224 |
28.8 (25.5–32.8) 200 |
28.9 (25.4–33.1) 209 |
| Waist circumference (cm) | 101 (91–111) 239 |
102 (93–111) 224 |
102 (93–113) 199 |
102 (91–113) 205 |
| Time (years) | GFR–ml/minute/1.73 m2 | Urine ACR–mg/mmol | ||||
|---|---|---|---|---|---|---|
| Measured GFR | MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | ||
| Baseline | 47.2 (38.4–58.2) 235 |
43.2 (34.8–52.8) 236 |
44.6 (35.4–53.6) 236 |
42.1 (34.9–54.5) 236 |
42.1 (35.2–54.4) 236 |
5.0 (1.6–27.4) 236 |
| 0.5 | Not applicable | 43.1 (34.8–51.8) 227 |
42.9 (35.1–53.5) 227 |
40.2 (32.4–52.4) 227 |
41.3 (33.5–50.7) 227 |
5.9 (1.7–30.4) 219 |
| 1.0 | 44.8 (35.5–55.9) 215 |
42.2 (34.1–50.9) 221 |
41.8 (34.3–51.5) 221 |
41.4 (32.3–55.5) 221 |
40.8 (33.3–54.4) 221 |
5.7 (1.6–30.1) 221 |
| 1.5 | Not applicable | 40.6 (32.0–48.5) 217 |
40.7 (31.9–49.6) 217 |
40.6 (30.1–52.2) 217 |
40.1 (30.7–51.7) 217 |
6.8 (1.6–46.2) 212 |
| 2.0 | 45.7 (34.8–56.6) 187 |
41.2 (32.0–53.1) 198 |
41.6 (31.8–54.9) 198 |
40.5 (29.6–57.9) 198 |
40.7 (29.8–54.7) 198 |
7.4 (2.0–41.0) 200 |
| 2.5 | Not applicable | 39.4 (31.7–51.2) 190 |
39.0 (30.7–53.0) 190 |
37.3 (27.9–53.3) 190 |
38.1 (28.9–53.1) 190 |
6.3 (1.7–38.8) 186 |
| 3.0 | 43.8 (32.9–54.3) 197 |
41.2 (30.8–52.7) 209 |
41.1 (30.5–53.5) 209 |
41.4 (30.4–56.7) 209 |
40.9 (30.4–55.3) 209 |
6.2 (1.8–29.8) 208 |
The difference between estimated and mGFR (bias) at each time point is summarised in Table 18. The baseline differences (bias) between estimated and mGFR in the substudy were similar to those observed in the main study, and did not change during the course of the study, although the bias at baseline was larger than observed at later time points for all eGFRs except CKD-EPIcreatinine (see also Appendix 1, Figure 17).
| Time (years) | Bias (eGFR – mGFR)– ml/minute/1.73 m2 | |||
|---|---|---|---|---|
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |
| Baseline | −4.7 (−11.0 to 2.0), 232 | −3.8 (−9.6 to 3.5), 232 | −3.5 (−9.4 to 2.6), 232 | −4.2 (−9.0 to 1.1), 232 |
| 1 | −3.4 (−9.4 to 3.1), 212 | −3.0 (−8.0 to 3.2), 212 | −1.9 (−7.3 to 4.0), 212 | −3.3 (−7.1 to 2.0), 212 |
| 2 | −3.8 (−8.2 to 2.0), 184 | −3.0 (−7.2 to 2.6), 184 | −1.1 (−6.9 to 4.7), 184 | −2.2 (−6.2 to 1.8), 184 |
| 3 | −4.0 (−9.0 to 1.0), 196 | −4.0 (−8.0 to 1.8), 196 | −1.4 (−6.3 to 4.4), 196 | −2.5 (−6.4 to 2.6), 196 |
The estimated slopes (progression) and variance estimates for mGFRs and eGFRs and bias (eGFR minus mGFR) from the random coefficients regression model without covariates are presented in Table 19.
| Outcome measure | Slope (rate of change), ml/minute/1.73 m2/year | Variance estimate | ||
|---|---|---|---|---|
| Estimate | 95% CI | Between slopes | Residual | |
| Measured GFR | −1.47 | −1.85 to −1.09 | 2.33 | 28.5 |
| MDRD | −1.33 | −1.69 to −0.967 | 4.76 | 20.1 |
| CKD-EPIcreatinine | −1.56 | −1.94 to −1.19 | 5.14 | 23.0 |
| CKD-EPIcystatin | −0.743 | −1.17 to −0.314 | 7.88 | 22.7 |
| CKD-EPIcreatinine-cystatin | −1.01 | −1.39 to −0.632 | 6.19 | 17.5 |
| Difference MDRD – mGFR | 0.325 | −0.038 to 0.688 | 0.707 | 33.1 |
| Difference CKD-EPIcreatinine – mGFR | 0.101 | −0.272 to 0.474 | 0.734 | 35.0 |
| Difference CKD-EPIcystatin – mGFR | 0.840 | 0.441 to 1.24 | 1.78 | 34.7 |
| Difference CKD-EPIcreatinine-cystatin – mGFR | 0.619 | 0.266 to 0.971 | 1.07 | 29.3 |
The rates of decline were steepest for mGFR and CKD-EPIcreatinine eGFR, and slope estimates were similar. The rates of decline were slowest for cystatin C eGFR. The model-predicted slopes for mGFR and CKD-EPIcreatinine and CKD-EPIcystatin eGFR are shown in Appendix 1, Figure 18.
The variability of slopes was larger for the eGFRs compared to mGFR and the residual variability was lower. This is likely due to the difference in the number of observations for each individual for mGFR and eGFR. In the regression model for eGFRs, more data points are included for each individual (includes 6-monthly data), resulting in less shrinkage towards the population mean slope, more variability between slopes and lower residual variability (variability between observations and individual slope fitted values).
There was little evidence of decline in bias (difference) over time based on the difference between CKD-EPIcreatinine GFR and mGFR (slope estimate 0.101, 95% CI −0.272 to 0.474). Similarly for the difference between MDRD and mGFR, the slope estimate was 0.325 and 95% CI −0.038 to 0.688. In contrast, differences of mGFR from CKD-EPIcystatin and CKD-EPIcreatinine-cystatin showed an incline in slope over time indicated by the positive slope estimates with 95% CI not overlapping zero (e.g. 0.840, CI 0.441 to 1.24 for difference between CKD-EPIcystatin GFR and mGFR), suggesting an increase in bias (i.e. eGFR minus mGFR) over time. The median bias was negative at all times for CKD-EPIcystatin and CKD-EPIcreatinine-cystatin (i.e. these estimates of GFR were always lower than the mGFR), but the median bias at later time points was closer to zero compared to the median bias at baseline (Table 18).
Prior to conducting the random coefficients regression modelling with covariates, correlations between the covariates to be included in the model were explored to identify collinearity (Table 20). Correlations were calculated using the data from baseline and from all time points for evaluable participants (i.e. those with estimated and mGFR available on at least two time points). The final covariate models for mGFR, eGFR and ACR should be interpreted bearing in mind the observed associations between covariates. Where collinearity exists, some covariates associated with the GFR measure were excluded from the final multiple regression model. A correlation of 0.3 or higher and < 0.5 was considered moderate, and correlations of 0.5 or above high. Table 20 shows the correlation coefficients for each covariate pair. The highest correlation was seen between waist circumference and BMI (0.856). Waist circumference was also moderately correlated with gender (0.337) and diabetes status (0.384). BMI and diabetes status were moderately correlated (0.383), as were systolic and diastolic BP (0.400). All other correlations were < 0.3, although there were a number of correlations between 0.2 and 0.3 which could have impacted covariate selection in the model.
| Covariate | Gender | Age (years) | Diabetes (yes/no) | Ethnicity group | Proteinuria | Systolic BP (mmHg) | Diastolic BP (mmHg) | BMI (kg/m2) | Waist circumference (cm) | Smoking status (yes/no) |
|---|---|---|---|---|---|---|---|---|---|---|
| Age (years) | 0.105 | 1.00 | ||||||||
| Diabetes (yes/no) | 0.130 | 0.120 | 1.00 | |||||||
| Ethnicity group | 0.058 | 0.249 | 0.190 | 1.00 | ||||||
| Albuminuria | 0.154 | 0.271 | 0.111 | 0.152 | 1.00 | |||||
| Systolic BP (mmHg) | 0.154 | 0.285 | −0.033 | 0.140 | 0.166 | 1.00 | ||||
| Diastolic BP (mmHg) | 0.022 | −0.287 | −0.247 | 0.074 | 0.146 | 0.400 | 1.00 | |||
| BMI (kg/m2) | 0.084 | −0.046 | 0.383 | 0.130 | 0.059 | −0.141 | −0.137 | 1.00 | ||
| Waist circumference (cm) | 0.337 | 0.135 | 0.384 | 0.144 | 0.077 | −0.077 | −0.190 | 0.856 | 1.00 | |
| Smoking status (yes/no) | 0.179 | 0.231 | 0.063 | 0.146 | 0.182 | 0.100 | 0.098 | 0.143 | 0.203 | 1.00 |
| Vascular disease (yes/no) | 0.164 | 0.215 | 0.092 | 0.127 | 0.014 | −0.002 | −0.219 | 0.092 | 0.136 | 0.123 |
Regression modelling to explore the effect of each covariate individually on the intercept and progression slope was conducted prior to modelling the combined covariates in the full models. For mGFR, the individual unadjusted covariate regression models had coefficients with a p-value of < 0.2 for the intercept term for all covariates with the exception of BMI and smoking status. Similarly, the individual regressions had coefficients with p < 0.2 for the rate of change (progression) for covariates age, diabetes status, ethnicity group, albuminuria, BMI, waist circumference and smoking status (data not shown).
Measured glomerular filtration rate random coefficients final covariate model
Estimates from the random coefficients final covariate model for mGFR for both the substudy and the combined substudy and main study data combined are shown in Table 21. All covariates were controlled for other terms in the model, that is the estimated coefficients show the additional effect of the covariate after all other variables in the model have been accounted for.
| Model term/covariate | Measured GFR (ml/minute/1.73 m2) | |
|---|---|---|
| Substudy data only | Main study and substudy data combined | |
| Intercept constant (Caucasian, no albuminuria, no CCB antagonists) | 0.202 (−4.518 to 4.922), 0.933 | 0.042 (−1.857 to 1.943), 0.965 |
| Age (years) | −0.036 (−0.081 to 0.008), 0.111 | −0.019 (−0.038 to −0.001), 0.042 |
| Baseline mGFR (ml/minute/1.73 m2) | 0.957 (0.916 to 1.000), < 0.001 | 0.984 (0.968 to 1.000), < 0.001 |
| Ethnicity group | ||
| African-Caribbean | 0.146 (−1.401 to 1.693), 0.853 | 0.096 (−0.788 to 0.979), 0.832 |
| South Asian | −0.660 (−2.308 to 0.998), 0.433 | −0.270 (−1.12 to 0.585), 0.536 |
| Albuminuria | ||
| 3–30 mg/mmol | 0.527 (−0.708 to 1.761), 0.403 | 0.123 (−0.353 to 0.600), 0.612 |
| > 30 mg/mmol | −0.069 (−1.533 to 1.395), 0.927 | −0.021 (−0.584 to 0.541), 0.941 |
| Systolic BP (mmHg) | 0.031 (0.006 to 0.056), 0.016 | 0.015 (0.004 to 0.025), 0.008 |
| Slope constant (progression rate of change) (ml/minute/1.73 m2/year) | 1.051 (−0.800 to 2.902), 0.266 | 2.121 (1.226 to 3.016), < 0.001 |
| Ethnicity group * slope | ||
| African-Caribbean | 1.014 (−0.198 to 2.226), 0.101a | 1.113 (0.171 to 2.055), 0.021 |
| South Asian | −0.655 (−1.917 to 0.606), 0.309 | −0.218 (−1.095 to 0.659) 0.625 |
| Albuminuria * slope | ||
| 3–30 mg/mmol | −0.935 (−1.758 to −0.112), 0.026 | −0.549 (−0.959 to −0.140), 0.009 |
| > 30 mg/mmol | −1.619 (−2.631 to −0.607), 0.002 | −1.521 (−2.007 to −1.036), < 0.001 |
| Baseline mGFR * slope | −0.037 (−0.069 to 0.005), 0.025 | −0.064 (−0.080 to −0.048), < 0.001 |
The coefficients for each of the categorical variates in the regression model correspond to the difference from the reference category, for example the albuminuria coefficients for the two higher categories correspond to the difference from those with no albuminuria (< 3 mg/mmol). To estimate the intercept for a particular subgroup, the regression coefficients of the constant term and each of the covariate main effect terms (not interactions) are used. As an example consider the estimated intercept from the mGFR substudy final model for a baseline mGFR of 60 ml/minute/1.73 m2, ACR of 10 mg/mmol, age 70 years, South Asian ethnicity, and systolic BP 120 mmHg: the estimate of intercept is 0.202 − (0.036 × 70) + (0.957 × 60) − 0.660 + 0.527 + (0.031 × 120), which is equal to 58.7 ml/minute/1.73 m2. Similarly, progression can be estimated using the slope constant term and the coefficients of the interactions with the slope (the terms appearing below the slope constant term in the table). For the example given above, the estimate of progression would be 1.051 – 0.655 – 0.935 – (0.037 × 60), which is equal to a rate of change of −2.76 ml/minute/1.73 m2/year.
In the substudy data, the intercept (including covariates) was the expected mean value of mGFR when the time was equal to zero (baseline). In the final model, this was derived using baseline mGFR, age (increasing age lowers the intercept) and systolic BP (higher systolic BP increases the intercept) (p < 0.2). Of these, baseline-mGFR was the main determinant. Intercept terms were also included in the model for covariates which were associated with slope. In the final model, the rate of change in mGFR over time was associated with baseline GFR, ethnicity group and albuminuria (p < 0.2). Baseline GFR increased the intercept by 0.957 ml/minute/1.73 m2 (95% CI 0.916 to 1.000) for each unit of baseline GFR, and decreased the progression slope (steeper decline) by −0.037 ml/minute/1.73 m2/year (95% CI −0.069 to 0.005) for each unit. African-Caribbean ethnicity increased the progression slope (slower decline) by 1.01 ml/minute/1.73 m2/year (95% CI −0.198 to 2.226). However, inspection of the individual data revealed one participant (ID 19877) who had much higher values of mGFR at baseline and at 3 years in the African-Caribbean ethnicity group. Sensitivity analysis excluding this participant (ID 19877) showed no evidence of effects of ethnicity on progression or intercept (p > 0.2).
The rate of decline was steeper for those with higher levels of albuminuria: the slope decreased by −0.935 ml/minute/1.73 m2/year (95% CI −1.758 to −0.112) for those with ACR between 3 and 30 mg/mmol (inclusive) and −1.619 ml/minute/1.73 m2/year (95% CI −2.631 to −0.607) for those with ACR > 30 mg/mmol.
Age and systolic BP were associated with the intercept only. There was a decrease of −0.036 ml/minute/1.73 m2 (95% CI −0.081 to −0.008) for each year of age, and an increase of 0.031 ml/minute/1.73 m2 (95% CI 0.006 to 0.056) for each unit of systolic BP (mmHg).
Plots of the fitted and observed data by participants for the final covariate model for mGFR are shown for completeness in Report Supplementary Material 1.
The parameter estimates from the model using the full data set were similar to those from the substudy for all covariates (Table 21). The association between African-Caribbean ethnicity and progression (i.e. with African-Caribbean ethnicity being associated with reduced progression) was more significant when the model was fitted to the full data set (p = 0.021). Sensitivity analysis excluding the data for one participant (ID 19877) discussed earlier made very little difference to the statistical significance of this association (p = 0.032) (see Appendix 1, Figure 19). It should be noted that the number of evaluable participants in the full data set was still quite low for African-Caribbean (n = 46) and South Asian (n = 51) ethnicity groups.
Figure 7 illustrates the changes in mGFR progression over time for albuminuria status. The median mGFR of those with albuminuria declines more steeply compared to those who do not have albuminuria. The equivalent figure for the combined main and substudy data may be found in Appendix 1, Figure 20.
FIGURE 7.
Median and IQR mGFR over time by albuminuria status (substudy data).

Creatinine estimated glomerular filtration rate random coefficients final covariate model
The individual covariate regression models for CKD-EPIcreatinine had coefficients with a p-value of < 0.2 for the intercept term for all covariates with the exception of ethnicity group and systolic BP. Similarly, the individual regressions had coefficients with p < 0.2 for the rate of change (progression) for covariates age, diabetes status, ethnicity group, albuminuria, diastolic BP, waist circumference and smoking status (data not shown).
Table 22 shows the estimates from the random coefficients regression final covariate model for CKD-EPIcreatinine for all main study and substudy data compared to the model estimates including the substudy data only.
| Model term/covariate | CKD-EPIcreatinine (ml/minute/1.73 m2) | |
|---|---|---|
| Substudy data only | Main study and substudy data combined | |
| Intercept constant (Caucasian, no diabetes, no albuminuria, no beta-blockers, no A2RB) | 7.971 (3.462 to 12.480), 0.001 | 5.125 (2.819 to 7.431), < 0.001 |
| Age (years) | −0.038 (−0.080 to −0.003), 0.069 | −0.017 (−0.039 to 0.004), 0.109 |
| Baseline CKD-EPIcreatinine (ml/minute/1.73 m2) | 0.945 (0.905 to 0.985), < 0.001 | 0.909 (0.888 to 0.930), < 0.001 |
| Diabetes (yes) | −0.094 (−1.294 to 1.106), 0.878 | −0.515 (−1.099 to 0.067), 0.083 |
| Ethnicity group | ||
| African-Caribbean | 0.786 (−0.604 to 2.177), 0.268 | 0.952 (−0.144 to 2.048), 0.089 |
| South Asian | −0.621 (−2.150 to 0.908), 0.426 | 0.174 (−0.876 to 1.224), 0.745 |
| Albuminuria | ||
| 3–30 mg/mmol | −0.180 (−1.207 to 0.847), 0.731 | 0.056 (−0.449 to 0.562), 0.828 |
| > 30 mg/mmol | 0.138 (−1.033 to 1.308), 0.818 | 0.651 (0.073 to 1.228), 0.027 |
| BMI (kg/m2) | −0.085 (−0.173 to 0.003), 0.058 | −0.0001 (−0.040 to 0.040), 0.995 |
| Beta-blocker (yes) | −0.434 (−1.460 to 0.592), 0.407 | −0.222 (−0.741 to 0.297), 0.402 |
| A2RB (yes) | −0.695 (−1.665 to 0.275), 0.160 | −0.669 (−1.160 to −0.177), 0.008 |
| Slope constant (progression rate of change) (ml/minute/1.73 m2/year) | −1.082 (−1.749 to −0.414), 0.001 | −1.197 (−1.498 to −0.895), < 0.001 |
| Diabetes * slope | 1.058 (0.153 to 1.964), 0.022 | 0.037 (−0.403 to 0.477), 0.870 |
| Ethnicity group * slope | ||
| African-Caribbean | 0.161 (−0.992 to 1.315), 0.784 | −0.046 (−0.935 to 0.842), 0.919 |
| South Asian | −1.011 (−2.249 to 0.227), 0.109 | −0.581 (−1.419 to 0.256), 0.173 |
| Albuminuria * slope | ||
| 3–30 mg/mmol | −0.251 (−0.942 to 0.440), 0.477 | 0.048 (−0.276 to 0.371), 0.772 |
| > 30 mg/mmol | −0.861 (−1.685 to −0.037), 0.040 | −0.479 (−0.858 to −0.099), 0.013 |
| Beta-blocker * slope | −0.598 (−1.348 to 0.152), 0.118 | 0.043 (−0.300 to 0.385), 0.808 |
| A2RB * slope | −0.609 (−1.335 to 0.117), 0.100 | −0.235 (−0.560 to 0.090) 0.156 |
In the substudy, intercept was associated with baseline CKD-EPIcreatinine, age, BMI and A2RB medication (p < 0.2). Intercept terms were also included in the model for covariates which were associated with slope. In the final model, the rate of change in CKD-EPIcreatinine over time is associated with ethnicity group, albuminuria and diabetes status, and beta-blocker and A2RB medication (p < 0.2).
Albuminuria decreased the progression slope (steeper decline) by −0.861 ml/minute/1.73 m2/year (95% CI −1.685 to −0.037) for those with ACR > 30 mg/mmol. South Asian ethnicity decreased the progression slope (steeper decline) by −1.011 ml/minute/1.73 m2/year (95% CI −2.249 to 0.227). Diabetes increased the slope (slower decline) by 1.058 ml/minute/1.73 m2/year (95% CI 0.153 to 1.964): this seems counterintuitive and may be partially due to the lower intercept for those with diabetes. The coefficient is the combined effect of diabetes status with all other covariates in the model and diabetes status is correlated with BMI which is also included in the model and could affect the coefficient for this covariate. The rate of decline was steeper for those prescribed beta-blocker medication, the slope decreasing by −0.598 ml/minute/1.73 m2/year (95% CI −1.348 to 0.152), and for those prescribed A2RBs, who had a decrease in slope of −0.609 ml/minute/1.73 m2/year (95% CI −1.335 to 0.117). The intercept also decreased by −0.695 ml/minute/1.73 m2 (95% CI −1.665 to 0.275) for those taking A2RBs.
Age, baseline CKD-EPIcreatinine and BMI were associated with intercept only. There was a decrease of −0.038 ml/minute/1.73 m2 (95% CI −0.080 to −0.003) for each year of age, an increase of 0.945 ml/minute/1.73 m2 (95% CI 0.905 to 0.985) for each unit of baseline CKD-EPIcreatinine and a decrease of −0.085 ml/minute/1.73 m2 (−0.173 to 0.003) for each BMI unit (kg/m2).
Using the full data set, diabetes status was associated with the intercept estimates of CKD-EPIcreatinine (p = 0.083), but not associated with progression, and the association of BMI with the intercept was no longer significant, but BMI and diabetes status were highly correlated so it is likely these effects are presenting in a different way in the model. Using the full data set, there was no longer an association between the use of beta-blocker medication and progression, but there was a statistically significant association between A2RB use and the intercept levels of CKD-EPIcreatinine. Other covariate estimates for the full data set were similar to those seen for the substudy.
Figures 8–10 illustrate CKD-EPIcreatinine progression over time in the substudy for diabetes, albuminuria and ethnicity groups, respectively. In Figure 8 the decline in the medians of those who have and those who do not have diabetes appears to be similar, the differences seen in the model could be due to the differences in the intercepts of those with and without diabetes, and the correlation between BMI and diabetes status. In Figure 9 the steeper decline over time is more obvious for those with albuminuria, compared to those who do not have albuminuria. The equivalent figure for the combined main and substudy data may be found in Appendix 1, Figure 21. Figure 10 suggests a steeper decline for people of South Asian ethnicity. The equivalent figure for the combined main and substudy data may be found in Appendix 1 (Figure 22).
FIGURE 8.
Median and IQR CKD-EPIcreatinine over time by diabetes status (substudy data).

FIGURE 9.
Median and IQR CKD-EPIcreatinine over time by albuminuria status (substudy data).
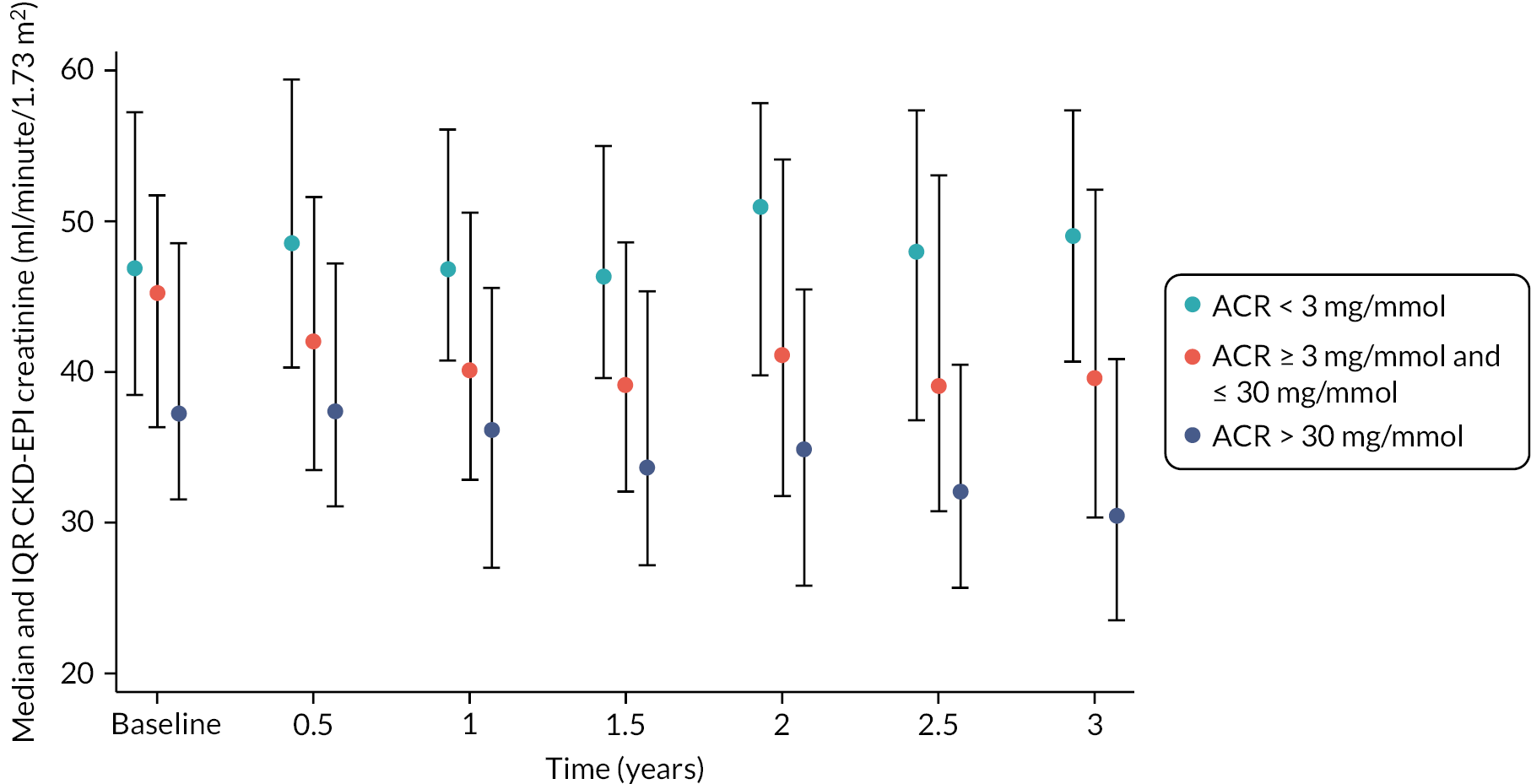
FIGURE 10.
Median and IQR CKD-EPIcreatinine over time by ethnicity group (substudy data).

Cystatin C estimated glomerular filtration rate random coefficients final covariate model
The individual covariate regression models for CKD-EPIcystatin had coefficients with a p-value of < 0.2 for the intercept term for all covariates with the exception of albuminuria and diastolic BP. The individual regressions had coefficients with p < 0.2 for the rate of change (progression) for covariates gender, baseline CKD-EPIcystatin, albuminuria, systolic and diastolic BP, BMI, waist circumference and smoking status (data not shown).
Table 23 shows the estimates from the random coefficients regression final covariate model for CKD-EPIcystatin. For the substudy, intercept was associated with baseline CKD-EPIcystatin, gender, ethnicity group, BMI, waist circumference and smoking status (p < 0.2). Intercept terms were also included in the model for covariates which were associated with slope. In the final model, the rate of change in CKD-EPIcystatin over time was associated with baseline CKD-EPIcystatin, diastolic BP, BMI and beta-blocker and A2RB medication (p < 0.2).
| Model term/covariate | CKD-EPIcystatin (ml/minute/1.73 m2) | |
|---|---|---|
| Substudy data only | Main study and substudy data combined | |
| Intercept constant (Caucasian, females, non-smoker, no beta-blockers, no A2RB) | 1.862 (−3.446 to 7.190), 0.493 | 0.914 (−1.784 to 3.612), 0.507 |
| Baseline CKD-EPIcystatin (ml/minute/1.73 m2) | 0.991 (0.957 to 1.025), < 0.001 | 0.963 (0.946 to 0.980), < 0.001 |
| Males | −0.768 (−1.895 to 0.358), 0.181 | 0.574 (0.016 to 1.132), 0.044 |
| Ethnicity group | ||
| African-Caribbean | 1.082 (−0.300 to 2.463), 0.125 | 0.975 (−0.151 to 2.101), 0.090 |
| South Asian | −0.110 (−1.603 to 1.382), 0.885 | −0.372 (−1.449 to 0.703), 0.497 |
| Diastolic BP (mmHg) | 0.008 (−0.034 to 0.050), 0.708 | 0.009 (−0.013 to 0.031), 0.429 |
| BMI (kg/m2) | −0.220 (−0.366 to −0.073), 0.003 | −0.004 (−0.078 to 0.071), 0.927 |
| Waist circumference (cm) | 0.046 (−0.011 to 0.103), 0.115 | −0.006 (−0.036 to 0.023), 0.677 |
| Smoking status | ||
| Current smoker | −1.547 (−3.203 to 0.108), 0.067 | −0.078 (−1.024 to 0.868), 0.872 |
| Ex-smoker | −0.012 (−1.077 to 1.053), 0.983 | −0.535 (−1.060 to −0.009), 0.046 |
| Beta-blockers (yes) | 0.065 (−0.982 to 1.112), 0.903 | −0.274 (−0.825 to 0.272), 0.323 |
| A2RB (yes) | 0.486 (−0.511 to 1.483), 0.339 | −0.095 (−0.609 to 0.418), 0.717 |
| Slope constant (progression rate of change) (ml/minute/1.73 m2/year) | −2.047 (−5.488 to 1.393), 0.244 | −0.142 (−1.739 to 1.455), 0.861 |
| Baseline CKD-EPIcystatin * slope | 0.031 (0.003 to 0.060), 0.031 | 0.011 (−0.003 to 0.025), 0.118 |
| Diastolic BP * slope | −0.024 (−0.052 to 0.004), 0.094 | −0.016 (−0.029 to −0.002), 0.022 |
| BMI * slope | 0.077 (0.005 to 0.148), 0.035 | 0.006 (−0.027 to 0.038), 0.727 |
| Beta-blockers * slope | −0.997 (−1.826 to −0.168), 0.018 | 0.018 (−0.354 to 0.390), 0.924 |
| A2RB * slope | −0.855 (−1.633 to −0.077), 0.031 | −0.389 (−0.739 to −0.038), 0.030 |
Baseline CKD-EPIcystatin increased the intercept by 0.991 ml/minute/1.73 m2 (95% CI 0.957 to 1.025) for each unit of baseline CKD-EPIcystatin, and increased the progression slope (slower decline) by 0.031 ml/minute/1.73 m2/year (95% CI 0.003 to 0.060) for each unit. The rate of decline was also steeper for those prescribed beta-blocker medication, the slope decreasing by −0.997 ml/minute/1.73 m2/year (95% CI −1.826 to −0.168), and for those prescribed A2RBs, who had a decrease in the slope of −0.855 ml/minute/1.73 m2/year (95% CI −1.633 to −0.077). Diastolic BP decreased the progression slope (steeper decline) by −0.024 ml/minute/1.73 m2/year (95% CI −0.052 to 0.004) for each mmHg unit of BP. BMI decreased the intercept by −0.220 ml/minute/1.73 m2 (95% CI −0.366 to −0.073) for each unit (kg/m2), and increased the progression slope (slower decline) by 0.077 ml/minute/1.73 m2/year (95% CI 0.005 to 0.148).
Gender, ethnicity group, waist circumference and smoking status were associated with the intercept only. There was an increase of 0.046 ml/minute/1.73 m2 (95% CI −0.011 to 0.103) for each unit change in waist circumference (cm), a decrease of −0.768 ml/minute/1.73 m2 (95% CI −1.895 to 0.358) for males, an increase of 1.082 ml/minute/1.73 m2 (95% CI −0.300 to 2.463) for African-Caribbean ethnicity and a decrease in intercept of −1.547 ml/minute/1.73 m2 (95% CI −3.203 to 0.108) for those who currently smoke.
Using the full data set, BMI and waist circumference were no longer associated with the intercept estimates of CKD-EPIcystatin, and BMI was no longer associated with progression. The effect of smoking status changed: using the substudy data only, there was an association between current smokers and the intercept, whereas using the full data set there was an association between ex-smokers and the intercept. This change may be due to the increased number of ex-smokers in the full data set (n = 367), compared to the number of current smokers (n = 70). Using the full data set, there was no longer an association between the use of beta-blocker medication and progression. Other estimates for the full data set were similar to those seen for the substudy data.
Figure 11 illustrates the changes in CKD-EPIcystatin progression over time by ethnicity group. Those of African-Caribbean ethnicity have a different profile over time compared to the other ethnicity groups, although there was little evidence to suggest a difference in progression over time, but the intercept was higher for African-Caribbeans in the final model. The equivalent figure for the combined main and substudy data may be found in Appendix 1, Figure 23.
FIGURE 11.
Median and IQR CKD-EPIcystatin over time by ethnicity group (substudy data).
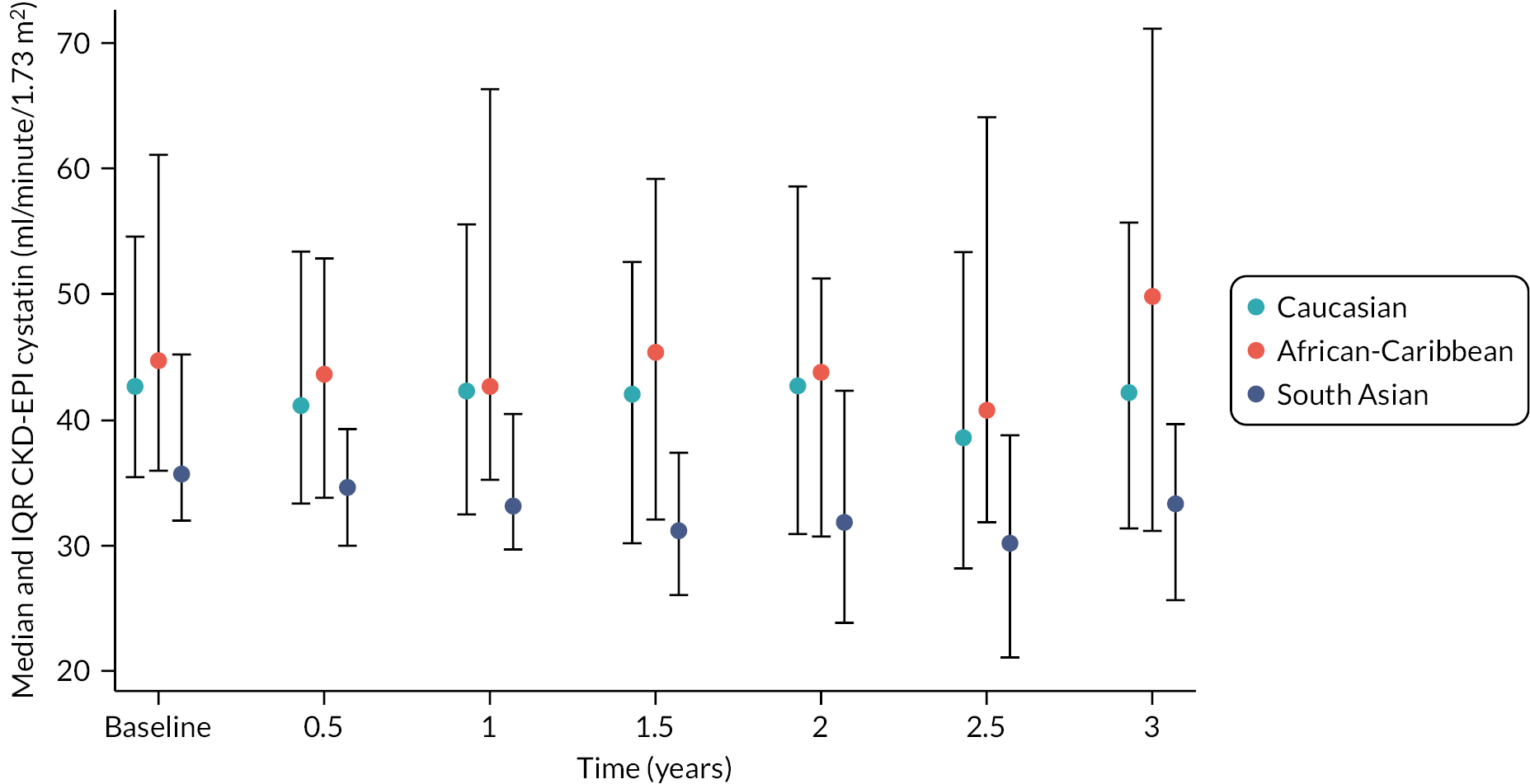
Urinary albumin-to-creatinine ratio random coefficients final covariate model
The individual covariate regression models for log-transformed urinary ACR had intercept coefficients with a p-value of < 0.2 for all covariates with the exception of diabetes, BMI, waist circumference and vascular disease. The individual regressions had coefficients with p < 0.2 for the rate of change (progression) for covariates diabetes status, ethnicity group, albuminuria, baseline log ACR, systolic and diastolic BP and waist circumference (data not shown).
Table 24 shows the estimates from the random coefficients regression final covariate model for log ACR. For the substudy, intercept was associated with baseline log ACR, albuminuria (ACR category), age, systolic BP, diabetes, smoking status and loop diuretic medication (p < 0.2). Intercept terms were also included in the model for covariates associated with slope. In the final model, the rate of change in log ACR over time was associated with baseline log ACR, diabetes status, ethnicity group, albuminuria (ACR category), diastolic BP, smoking status and loop diuretic and CCB medication (p < 0.2).
| Model term/covariate | Log-transformed ACR (mg/mmol) | |
|---|---|---|
| Substudy data only | Main study and substudy data combined | |
| Intercept (Caucasian, no diabetes, no albuminuria, non-smoker, no loop diuretics, no CCB) | −4.88% (−31.2% to 60.8%), 0.816 | 1.21% (−19.4% to 27.3%), 0.916 |
| Age (years) | −0.499% (−0.896% to 0.100%), 0.011 | −0.200% (−0.399% to 0.030%), 0.101 |
| Baseline ACR (log mg/mmol)+ | 0.605% (0.557% to 0.653%), < 0.001 | 0.533% (0.508% to 0.558%), < 0.001 |
| Diabetes (yes) | 10.1% (0.300% to 21.2%), 0.049 | 5.44% (0.300% to 10.7%), 0.038 |
| Ethnicity group | ||
| African-Caribbean | 2.02% (−13.8% to 11.4%), 0.756 | 3.15% (−7.69% to 15.1%), 0.587 |
| South Asian | −7.87% (−19.7% to 5.76%), 0.243 | −1.09% (−10.8% to 9.75%), 0.839 |
| Albuminuria | ||
| 3–30 mg/mmol | 129% (101% to 160%), < 0.001 | 178% (160% to 198%), < 0.001 |
| > 30 mg/mmol | 472% (360% to 611%), < 0.001 | 713% (625% to 812%), < 0.001 |
| Systolic BP (mmHg) | 0.300% (0.100% to 0.602%), 0.002 | 0.200% (0.100% to 0.300%), 0.001 |
| Diastolic BP (mmHg) | −0.200% (−0.598% to 0.300%), 0.470 | −0.200% (−0.399% to 0.100%), 0.133 |
| Smoking status | ||
| Current smoker | 4.39% (−10.6% to 21.9%), 0.587 | −3.82% (−12.1% to 5.34%), 0.404 |
| Ex-smoker | −4.11% (−12.9% to 5.44%), 0.387 | −4.21% (−8.88% to 0.702%), 0.092 |
| Loop diuretic (yes) | 12.5% (1.01% to 25.4%), 0.032 | 3.46% (−3.34% to 10.7%), 0.330 |
| CCB (yes) | 0.401% (−7.87% to 9.31%), 0.936 | −1.49% (−6.29% to 3.56%), 0.557 |
| Slope (progression rate of change) (% mg/mmol/year) |
−12.5% (−27.9% to 6.18%), 0.175 | −5.35% (−14.2% to 4.39%), 0.274 |
| Baseline ACR * slopea | −0.118% (−0.146% to −0.092%), < 0.001 | −0.090% (−0.103% to −0.077%), < 0.001 |
| Ethnicity group * slope | ||
| African-Caribbean | 12.0% (2.74% to 22.0%), 0.010 | 10.8% (3.87% to 18.3%), 0.002 |
| South Asian | 10.6% (1.01% to 21.0%), 0.030 | 8.98% (2.63% to 15.7%), 0.005 |
| Albuminuria * slope | ||
| 3–30 mg/mmol | 25.6% (16.6% to 35.4%), < 0.001 | 15.4% (11.2% to 19.7%), < 0.001 |
| > 30 mg/mmol | 57.6% (39.2% to 78.6%), < 0.001 | 41.8% (33.2% to 50.7%), < 0.001 |
| Diastolic BP * slope | 0.170% (−0.060% to 0.411%), 0.147 | 0.100% (−0.020% to 0.220%), 0.103 |
| Smoking status * slope | ||
| Current smoker | 12.4% (1.31% to 24.7%), 0.028 | 6.82% (1.41% to 12.6%), 0.014 |
| Ex-smoker | 7.25% (0.702% to 14.1%), 0.029 | 4.71% (1.82% to 7.79%), 0.001 |
| Loop diuretic * slope | −10.1% (−16.3% to −3.54%), 0.003 | −3.15% (−6.67% to 0.501%), 0.094 |
| CCB * slope | 4.29% (−1.19% to 10.1%), 0.129 | 3.56% (0.803% to 6.50%), 0.012 |
There was a 0.605% increase in ACR intercept (95% CI 0.557% to 0.653%) for each 1% increase in baseline ACR, and a −0.118% decrease in slope (slower incline) (95% CI −0.146% to −0.092%) for each 1% increase in baseline ACR. Albuminuria (ACR category) increases both the intercept and the slope (steeper incline), larger increases were seen for those with ACR higher than 30 mg/mmol, ACR intercept increased by 472% (95% CI 360% to 611%) and slope increased by 57.6% (95% CI 39.2% to 78.6%) for those with ACR > 30 mg/mmol. Diastolic BP increased the slope (steeper incline) by 0.170% (95% CI −0.060% to 0.411%), for each increasing unit of BP (mmHg). For current smokers, there was an increase in progression (steeper incline) of 12.4% (95% CI 1.31% to 24.7%). For ex-smokers, the slope increased (steeper incline) by 7.25% (95% CI 0.702% to 14.1%). For African-Caribbean ethnicity, there was an increase in slope of 12.0% (95% CI 2.74% to 22.0%), compared to an increase in slope of 10.6% (95% CI 1.01% to 21.0%) for those of South Asian ethnicity. The rate of incline was slower for those prescribed loop diuretic medication, the slope decreasing by −10.1% (95% CI −16.3 to −3.54%); in contrast, the rate of incline was faster for those prescribed CCB who had an increase in slope of 4.29% (95% CI −1.19% to 10.1%).
Age and systolic BP were associated with the intercept only. Age decreased the ACR intercept by −0.499% (95% CI −0.896% to 0.100%) for each increasing year of age, and there was an increase of 0.300% (95% CI 0.100% to 0.602%) for each increasing unit of systolic BP (mmHg).
The parameter estimates of covariates associated with progression from the model using the full data set were similar to those from the substudy for all covariates in the final model. The parameter estimates for covariates associated with the intercept were different for some covariates using the full data set. Diastolic BP and smoking status were associated with intercept estimates of log ACR (p < 0.2) using the full data set, and there was no significant association between loop diuretic use and intercept levels of log ACR. Smoking status showed an association between ex-smokers and the intercept, which is likely a result of having more ex-smokers in the full data set (n = 367). Other estimates for the full data set were similar to those seen for the substudy data.
Figures 12 and 13 illustrate the changes in log-transformed ACR progression over time for albuminuria status and ethnicity groups, respectively. In Figure 12 the profiles of those with albuminuria incline more steeply compared to those who do not have albuminuria, although the data show high variability. The equivalent figure for the combined main and substudy data may be found in Appendix 1, Figure 24. Figure 13 supports a steeper incline overall for those with African-Caribbean and South Asian ethnicity. The equivalent figure for the combined main and substudy data may be found in Appendix 1, Figure 25.
FIGURE 12.
Median and IQR ACR over time by albuminuria status (substudy data).

FIGURE 13.
Median and IQR ACR over time by ethnicity group (substudy data).

The biological variability of measured and estimated glomerular filtration rate
Estimates of components of biological variation are given in Table 25. 97 The geometric exact CVI value (95% CI) for mGFR was 6.7% (5.6 to 8.2). CVI values for the eGFR equations were broadly equivalent: MDRD 5.0% (4.3 to 6.1), CKD-EPIcreatinine 5.3% (4.5 to 6.4), CKD-EPIcystatin 5.3% (4.5 to 6.5), and CKD-EPIcreatinine-cystatin 5.0% (4.3 to 6.2) to each other. Modelling to investigate differences showed the CVI for MDRD and CKD-EPIcreatinine-cystatin eGFRs to be significantly (at 5% level) lower than for mGFR (difference −1.8%, p = 0.027 and difference −1.8%, p = 0.022 respectively). Using the MDRD equation, positive and negative RCVs were 15.1% and 13.1%, respectively. For example, if the baseline MDRD GFR (ml/minute/1.73 m2) in an individual is 59, significant increases or decreases would be to values > 68 or < 51, respectively.
| Estimated GFR | |||||||
|---|---|---|---|---|---|---|---|
| Measured GFR | Creatinine | Cystatin C | MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |
| Geometric exact | |||||||
| CVA (%) | 2.3 (1.9 to 2.7) | 0.7 (0.6 to 0.8) | 0.6 (0.5 to 0.7) | 0.8 (0.7 to 0.9) | 0.8 (0.7 to 1.0) | 0.7 (0.6 to 0.9) | 0.6 (0.5 to 0.7) |
| CVI (%) | 6.7 (5.6 to 8.2) | 4.4 (3.7 to 5.3) | 4.0 (3.4 to 4.9) | 5.0 (4.3 to 6.1) | 5.3 (4.5 to 6.4) | 5.3 (4.5 to 6.5) | 5.0 (4.3 to 6.2) |
| CVG (%) | 16.7 (12.5 to 24.9) | 20.0 (15.0 to 29.6) | 19.0 (14.4 to 28.2) | 17.8 (13.4 to 26.0) | 19.3 (15.5 to 29.2) | 25.2(18.9 to 37.5) | 20.2 (15.2 to 30.0) |
| Positive RCV (%) | 21.5 | 13.0 | 11.8 | 15.1 | 15.9 | 15.9 | 15.1 |
| Negative RCV (%) | −17.7 | −11.5 | −10.6 | −13.1 | −13.7 | −13.8 | −13.1 |
| Homeostatic set point | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| Index of individuality | 0.4 | 0.2 | 0.2 | 0.3 | 0.3 | 0.2 | 0.3 |
Sensitivity analyses were carried out without outlier detection and deletion. Data were similar to those obtained following outlier removal, with analyses after outlier removal estimating slightly reduced CVs.
Modelling to identify any trends over time resulted in non-significant slopes [coef = −0.005; 95% CI (−0.020 to 0.009); p = 0.488], thus providing no evidence of a change in disease state (kidney function) over the duration of the study.
Ability of glomerular filtration rate-estimating equations, together with albumin-to-creatinine ratio, or albumin-to-creatinine ratio alone, to predict those people that have progressive loss of kidney function (chronic kidney disease progression) and to predict mortality
We investigated the association between baseline factors and CKD progression. Models were developed for each of the main study equations using CKD progression defined as (1) a 25% decrease in mGFR and/or an increase in ACR category within the study period (Table 26) and (2) decrease in mGFR exceeding the RCV, and/or an increase in ACR category within the study period (Table 27). All models demonstrated an association between lower baseline eGFR and increased risk of renal progression within the study follow-up period.
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OR | 95% CI | p | OR | 95% CI | p | OR | 95% CI | p | OR | 95% CI | p | |
| Estimated GFR (ml/minute/1.73 m2) | 0.96 | (0.95 to 0.98) | < 0.001 | 0.96 | (0.95 to 0.98) | < 0.001 | 0.96 | (0.95 to 0.98) | < 0.001 | 0.96 | (0.94 to 0.97) | < 0.001 |
| Ethnicity | ||||||||||||
| African-Caribbean | 1.47 | (0.70 to 3.07) | 0.310 | 1.34 | (0.64 to 2.80) | 0.438 | 1.55 | (0.73 to 3.29) | 0.253 | 1.48 | (0.70 to 3.13) | 0.307 |
| South Asian | 1.79 | (0.95 to 3.34) | 0.070 | 1.79 | (0.96 to 3.36) | 0.069 | 1.59 | (0.84 to 2.98) | 0.152 | 1.64 | (0.87 to 3.09) | 0.124 |
| Age (years) | 1.00 | (0.98 to 1.01) | 0.701 | 0.99 | (0.98 to 1.01) | 0.238 | 0.99 | (0.97 to 1.00) | 0.059 | 0.99 | (0.97 to 1.00) | 0.093 |
| Female | 0.83 | (0.61 to 1.13) | 0.235 | 0.87 | (0.64 to 1.18) | 0.359 | 0.85 | (0.63 to 1.16) | 0.311 | 0.86 | (0.63 to 1.17) | 0.347 |
| ACR category | ||||||||||||
| 3–30 mg/mmol | 0.96 | (0.68 to 1.35) | 0.799 | 0.95 | (0.68 to 1.34) | 0.786 | 0.86 | (0.60 to 1.22) | 0.388 | 0.87 | (0.62 to 1.24) | 0.448 |
| > 30 mg/mmol | 0.80 | (0.53 to 1.21) | 0.299 | 0.80 | (0.53 to 1.21) | 0.285 | 0.68 | (0.45 to 1.04) | 0.075 | 0.70 | (0.46 to 1.06) | 0.094 |
| Vascular disease | 1.09 | (0.75 to 1.58) | 0.664 | 1.09 | (0.75 to 1.58) | 0.667 | 1.06 | (0.73 to 1.55) | 0.757 | 1.06 | (0.73 to 1.55) | 0.743 |
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OR | 95% CI | p | OR | 95% CI | p | OR | 95% CI | p | OR | 95% CI | p | |
| Estimated GFR (ml/minute/1.73 m2) | 0.96 | (0.95 to 0.98) | < 0.001 | 0.96 | (0.95 to 0.98) | < 0.001 | 0.96 | (0.95 to 0.98) | < 0.001 | 0.96 | (0.94 to 0.97) | < 0.001 |
| Ethnicity | ||||||||||||
| African-Caribbean | 1.47 | (0.70 to 3.07) | 0.310 | 1.34 | (0.64 to 2.80) | 0.438 | 1.55 | (0.73 to 3.29) | 0.253 | 1.48 | (0.70 to 3.13) | 0.307 |
| South Asian | 1.79 | (0.95 to 3.34) | 0.070 | 1.79 | (0.96 to 3.36) | 0.069 | 1.59 | (0.84 to 2.98) | 0.152 | 1.64 | (0.87 to 3.09) | 0.124 |
| Age (years) | 1.00 | (0.98 to 1.01) | 0.701 | 0.99 | (0.98 to 1.01) | 0.238 | 0.99 | (0.97 to 1.00) | 0.059 | 0.99 | (0.97 to 1.00) | 0.093 |
| Female | 0.83 | (0.61 to 1.13) | 0.235 | 0.87 | (0.64 to 1.18) | 0.359 | 0.85 | (0.63 to 1.16) | 0.311 | 0.86 | (0.63 to 1.17) | 0.347 |
| ACR category | ||||||||||||
| 3–30 mg/mmol | 0.96 | (0.68 to 1.35) | 0.799 | 0.95 | (0.68 to 1.34) | 0.786 | 0.86 | (0.60 to 1.22) | 0.388 | 0.87 | (0.62 to 1.24) | 0.448 |
| > 30 mg/mmol | 0.80 | (0.53 to 1.21) | 0.299 | 0.80 | (0.53 to 1.21) | 0.285 | 0.68 | (0.45 to 1.04) | 0.075 | 0.70 | (0.46 to 1.06) | 0.094 |
| Vascular disease | 1.09 | (0.75 to 1.58) | 0.664 | 1.09 | (0.75 to 1.58) | 0.667 | 1.06 | (0.73 to 1.55) | 0.757 | 1.06 | (0.73 to 1.55) | 0.743 |
Models including all of the GFR equations demonstrated an association between lower baseline eGFR and renal progression, defined as a decrease in GFR exceeding the RCV, and/or an increase in ACR category within the study follow-up period (see Table 27). For every 1 ml/minute/1.73 m2 higher eGFR at baseline, there was a 4% reduction in the odds of progressing.
To evaluate the outcome of death in this cohort, two regression models were fitted: a logistic model (Table 28) with death within the study as an outcome and a Cox regression model (Table 29) to evaluate time to death.
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OR | 95% CI | p | OR | 95% CI | p | OR | 95% CI | p | OR | 95% CI | p | |
| Estimated GFR (ml/minute/1.73 m2) | 0.97 | (0.94 to 1.00) | 0.042 | 0.97 | (0.94 to 1.00) | 0.040 | 0.94 | (0.91 to 0.97) | < 0.001 | 0.95 | (0.92 to 0.98) | < 0.001 |
| Ethnicity | ||||||||||||
| African-Caribbean | 0.58 | (0.08 to 4.42) | 0.600 | 0.54 | (0.07 to 4.14) | 0.556 | 0.61 | (0.08 to 4.67) | 0.631 | 0.56 | (0.07 to 4.30) | 0.578 |
| South Asian | 0.79 | (0.18 to 3.48) | 0.760 | 0.79 | (0.18 to 3.48) | 0.758 | 0.59 | (0.13 to 2.61) | 0.484 | 0.66 | (0.15 to 2.92) | 0.583 |
| Age (years) | 1.07 | (1.04 to 1.11) | < 0.001 | 1.07 | (1.03 to 1.10) | < 0.001 | 1.05 | (1.02 to 1.09) | 0.002 | 1.06 | (1.03 to 1.09) | 0.001 |
| Female | 0.53 | (0.28 to 1.00) | 0.051 | 0.55 | (0.29 to 1.04) | 0.065 | 0.53 | (0.28 to 1.00) | 0.049 | 0.54 | (0.29 to 1.02) | 0.059 |
| ACR category | ||||||||||||
| 3–30 mg/mmol | 1.21 | (0.64 to 2.27) | 0.561 | 1.21 | (0.64 to 2.27) | 0.562 | 0.94 | (0.49 to 1.80) | 0.853 | 1.03 | (0.54 to 1.96) | 0.924 |
| > 30 mg/mmol | 1.30 | (0.62 to 2.69) | 0.486 | 1.29 | (0.62 to 2.69) | 0.489 | 0.91 | (0.43 to 1.93) | 0.815 | 1.04 | (0.49 to 2.18) | 0.923 |
| Vascular disease | 1.59 | (0.89 to 2.82) | 0.114 | 1.59 | (0.89 to 2.81) | 0.115 | 1.58 | (0.89 to 2.80) | 0.120 | 1.58 | (0.89 to 2.80) | 0.119 |
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HR | 95% CI | p | HR | 95% CI | p | HR | 95% CI | p | HR | 95% CI | p | |
| Estimated GFR (ml/minute/1.73 m2) | 0.97 | (0.95 to 1.00) | 0.068 | 0.98 | (0.95 to 1.00) | 0.065 | 0.95 | (0.92 to 0.97) | < 0.001 | 0.95 | (0.93 to 0.98) | 0.001 |
| Ethnicity | ||||||||||||
| African-Caribbean | 0.56 | (0.08 to 4.13) | 0.571 | 0.53 | (0.07 to 3.91) | 0.533 | 0.64 | (0.09 to 4.67) | 0.657 | 0.57 | (0.08 to 4.22) | 0.585 |
| South Asian | 0.81 | (0.19 to 3.38) | 0.774 | 0.81 | (0.19 to 3.38) | 0.772 | 0.68 | (0.16 to 2.82) | 0.590 | 0.73 | (0.17 to 3.03) | 0.662 |
| Age (years) | 1.07 | (1.04 to 1.11) | < 0.001 | 1.07 | (1.03 to 1.10) | < 0.001 | 1.06 | (1.02 to 1.09) | 0.001 | 1.06 | (1.03 to 1.10) | < 0.001 |
| Female | 0.53 | (0.28 to 0.97) | 0.040 | 0.54 | (0.29 to 1.00) | 0.050 | 0.53 | (0.28 to 0.97) | 0.040 | 0.54 | (0.29 to 0.99) | 0.048 |
| ACR category | ||||||||||||
| 3–30 mg/mmol | 1.17 | (0.64 to 2.15) | 0.608 | 1.17 | (0.64 to 2.15) | 0.609 | 0.92 | (0.50 to 1.71) | 0.802 | 1.01 | (0.55 to 1.87) | 0.970 |
| > 30 mg/mmol | 1.19 | (0.59 to 2.42) | 0.629 | 1.19 | (0.59 to 2.41) | 0.633 | 0.84 | (0.41 to 1.73) | 0.637 | 0.95 | (0.46 to 1.95) | 0.887 |
| Vascular disease | 1.58 | (0.91 to 2.73) | 0.101 | 1.58 | (0.91 to 2.73) | 0.102 | 1.57 | (0.91 to 2.69) | 0.105 | 1.57 | (0.91 to 2.71) | 0.102 |
Secondary study objectives results
Accuracy of more recent GFR-estimating equations including BIS1 and BIS2 equations, CAPA equation, LMR equation, FAS creatinine equation, FAS creatinine–cystatin equation, EKFC equation and 2021 CKD-EPI equations: baseline analysis
Performance characteristics of the more recent GFR-estimating equations are described in Table 5. With the exception of the CKD-EPI(2021)creatinine and BIS1creatinine equations, all of the newer GFR-estimating equations were negatively biased compared to mGFR (negative median bias with non-overlapping CIs). Biases of the cystatin C containing equations, before recalibration (see Impact of cystatin C calibration on the performance of more recent cystatin C containing glomerular filtration rate-estimating equations), tended to be greater than those of the creatinine containing equations, with equations incorporating both cystatin C and creatinine having intermediate bias. Several of the equations [BIS2creatinine-cystatin, FAScreatinine-cystatin, CKD-EPI(2021)creatinine-cystatin] achieved P30 values in excess of 90%. The overall performance (P30) of the CKD-EPI(2021)creatinine-cystatin and BIS2creatinine-cystatin equations was superior to that of their respective creatinine-only equations [CKD-EPI(2021)creatinine and BIS1creatinine].
Ability of the newer glomerular filtration rate-estimating equations to reflect and detect changes in glomerular filtration rate over 3 years
The ability of the newer GFR-estimating equations to reflect and detect change in GFR over time is shown in Tables 9 and 12–15. As observed for the four primary equations, the newer equations, compared to mGFR, all estimated change in GFR within either 3 ml/minute/1.73 m2/years or difference in % observed change within 5%/years (absolute difference) for > 70% of patients (see Table 9).
The sensitivity and specificity of the newer equations to detect change in mGFR > 10 ml/minute/1.73 m2 were similar to that of the primary study equations (see Table 12). Similar observations were seen for the other change metrics investigated: GFR change in excess of the RCV, change in excess of 25% and change in excess of 25% in addition to a change in the GFR category (see Tables 13–15).
Influence of body surface area adjustment method on accuracy (P30) of glomerular filtration rate-estimating equations: Haycock equation compared to the Du Bois equation
Accuracy of the GFR equations was unaffected by the method of BSA adjustment (Table 30). Bias and precision data for these analyses may be found in Appendix 1 (see Appendix 1, Table 41).
| Equation | Du Bois BSA adjustment | Haycock BSA adjustment |
|---|---|---|
| MDRD | 89.5 (87.6 to 91.1) | 89.5 (87.6 to 91.2) |
| CKD-EPIcreatinine | 90.2 (88.4 to 91.9) | 90.1 (88.2 to 91.7) |
| CKD-EPIcystatin | 89.5 (87.6 to 91.2) | 90.7 (88.9 to 92.3) |
| CKD-EPIcreatinine-cystatin | 94.9 (93.5 to 96.2) | 95.3 (94.0 to 96.5) |
Impact of cystatin C calibration on the performance of more recent cystatin C containing glomerular filtration rate-estimating equations
As noted with the original CKD-EPI cystatin C containing equations (see Table 5), in all cases, substitution of recalibrated cystatin C values into the newer GFR-estimating equations was associated with a decrease in bias, with non-overlapping CIs, and with an increase in P30, in some cases with non-overlapping CIs compared to the equivalent non-cystatin C containing equation (e.g. BIS1 compared to BIS2). Relative improvement in performance tended to be more marked in the cystatin-only equations compared to the creatinine–cystatin equations (see Table 5).
Impact of creatinine method on accuracy of glomerular filtration rate-estimating equations: enzymatic compared to isotope dilution mass spectrometry method
There was no evidence of an effect of creatinine method on the performance of creatinine-based GFR-estimating equations; for example, CKD-EPIcreatinine using enzymatic creatinine P30 was 90.2 (88.4 to 91.9) compared to 89.0 (87.1 to 90.8) for ID-MS-creatinine (Table 31).
| Equation | Enzymatic creatinine | ID-MS creatinine | ||
|---|---|---|---|---|
| n/N | P30 (%, 95% CI) | n/N | P30 (%, 95% CI) | |
| MDRD | 1044/1167 | 89.5 (87.6 to 91.1) | 1054/1167 | 89.6 (87.7 to 91.3) |
| CKD-EPIcreatinine | 1053/1167 | 90.2 (88.4 to 91.9) | 1047/1167 | 89.0 (87.1 to 90.8) |
| CKD-EPIcreatinine-cystatin | 1108/1167 | 94.9 (93.5 to 96.1) | 1112/1167 | 95.3 (93.9 to 96.4) |
Creatinine results obtained using the enzymatic method were higher than those using the ID-MS assay, the relationship between the two methods being described by the linear regression equation; enzymatic = 3.23 + 1.01(ID-MS), R2 0.969 (see Appendix 1, Figure 26). Deming regression produced a similar equation [enzymatic = 1.20 + 1.03(ID-MS)].
Bias plot analysis demonstrated a constant mean positive bias of 4.7 μmol/l (CI 4.3 to 5.0) for the enzymatic compared to the ID-MS assays (see Appendix 1, Figure 27).
Chapter 4 Health economics: comparative clinical accuracy and cost of annual monitoring using glomerular filtration rate-estimating equations
Introduction
This chapter presents the health-economic analysis. Systematic review of economic evaluations presents a brief summary of findings from a systematic review of model-based economic evaluations, which is provided in full in Appendix 2. Clinical guidelines provides a summary of key clinical guidelines for monitoring CKD in the UK, focusing on the recommended criteria for identifying those with progressive disease. Comparative accuracy of estimated glomerular filtration rate equations for predicting accelerated progression (measurement model analysis) reports on the clinical accuracy of the different estimating equations for predicting CKD progression compared to mGFR, based on a simulated measurement model over a 10-year horizon. Comparative cost of monitoring with different estimated glomerular filtration rate equations presents the comparative costs of monitoring with GFR estimating equations, followed by a description of the implications of the results of the measurement model and the wider literature on longer-term costs and outcomes in Longer-term differences in costs and outcomes.
Systematic review of economic evaluations
A systematic review was conducted to identify previous studies that have assessed the cost-effectiveness of test-based strategies for CKD using a decision-analytic model. The objective was not to draw conclusions about the cost effectiveness of different testing strategies; rather the aim was to examine how economic models have been previously implemented in this setting. Full details of the systematic review, including Preferred Reporting Items for Systematic Reviews and Meta-Analyses diagrams and results tables, can be found in Appendix 2 (see Figures 32 and 33, Tables 42–44). Here, we provide a brief summary of the key findings.
Across the initial (February 2015)112 and updated (February 2020) literature searches, 28 studies were included in the review. All of the identified studies evaluated screening strategies in at-risk groups or general populations not currently diagnosed with CKD. No studies which assessed test-based monitoring strategies for patients with known CKD (i.e. matching the role of monitoring being considered in this HTA) were identified. The majority of studies (n = 24) evaluated proteinuria or albuminuria tests, with only six studies focusing on GFR estimation.
Eight studies did not incorporate any measure of diagnostic accuracy into the model, despite evaluating test-based strategies. Of the 20 studies that did explicitly incorporate diagnostic accuracy into their models, the majority were based on data from a single published study. In terms of modelling the impact of test inaccuracies, patients with FN results were assumed to remain in ‘untreated’ health states, and thereby could not benefit from treatment for CKD until future screening rounds, leading to higher risks of progression to later CKD stages. In the case of FP results, the most common consequence modelled was the unnecessary cost of additional/confirmatory testing. In most cases, confirmatory testing was assumed to have perfect accuracy, thus removing all FP cases at this stage. Of those studies that evaluated repeated testing scenarios and explicitly accounted for diagnostic accuracy in the model, the majority assumed that the same diagnostic accuracy values would apply over time.
The majority of studies used a cohort Markov model approach to model disease progression. [N.B. Markov models, also known as cohort transition models, track the movement of a group (i.e. cohort) of patients through mutually exclusive health states (e.g. GFR levels or CKD stages), which are each associated with state-specific health-related quality of life and cost values; the movement of patients between modelled health states occurs at fixed time points (e.g. every month, or year) and is dictated by defined transition probabilities.] Of those studies that tracked progression according to GFR levels, the stages of CKD were most often split into five GFR ‘stages’. Most studies assumed a step-by-step process of disease progression (i.e. patients could only move up one health state in the ladder of progression per model cycle), and only a minority explicitly allowed for the possibility of the reversibility in CKD severity.
The cost of testing related to screening activities captured in the included studies was typically limited to the unit cost of the screening test alone. Eight studies also included the cost of a physician/GP visit associated with the initial screening test(s) undertaken.
The most common issue apparent from the study quality assessment concerned a failure of all but four studies to discuss all of the issues relevant to users, which in this case meant that studies did not include any discussion regarding the impact of test diagnostic accuracy on the modelled outcomes, or the impact of testing from the patient perspective (e.g. costs incurred, anxiety.
Following the completion of our systematic review, Perera et al. published a highly relevant report that focused on long-term monitoring in primary care for CKD and chronic heart failure. 113 A short summary of this report is provided below. Perera et al. reported a programme of research exploring the optimal monitoring of individuals with CKD in primary care. 113 Pertinent to our research was an economic evaluation exploring the cost-effectiveness of monitoring CKD in primary care, using evidence generated for other components of the research programme. Qualitative interviews with clinicians and stakeholders highlighted that a key objective of GFR monitoring is to guide treatments to manage cardiovascular disease risk in those with CKD. However, the authors concluded that this finding was at odds with guideline recommendations at the time, as statins are recommended for all individuals with CKD and an eGFR < 60 ml/minute/1.73 m2 who are pre-dialysis, and eGFR has no impact on recommendations for antiplatelet agents for secondary prevention. 59,114
Perera et al. also conducted a systematic review to synthesise the effects of medication on the progression of stages G3 (GFR 30–59 ml/minute/1.73 m2) and G4 (GFR 15–29 ml/minute/1.73 m2) CKD. Their review focused on four classes of drugs: antihypertensives, lipid-modifying drugs, glycaemic control medications in patients with diabetes and sodium bicarbonate. Nineteen studies provided data for patients with CKD stages G3 and G4. The key conclusions were:
-
Pooled estimates showed no significant differences in renal function for those taking antihypertensive drugs compared to a control group (either placebo, no drug intervention or a comparator drug from one of the three other classes).
-
There were no significant differences in cardiovascular events or mortality in studies of antihypertensives.
-
Estimated GFR was 4% higher in those taking lipid-modifying drugs. Treatment with lipid-modifying drugs led to a significant reduction in the risk of CVD (risk ratio = 0.64, 95% CI 0.52 to 0.80) and all-cause mortality (risk ratio = 0.74, 95% CI 0.56 to 0.98).
-
Estimated GFR was 6% higher in those taking glycaemic control drugs. There were no significant differences in cardiovascular events or mortality in studies of glycaemic control medications.
-
No data were identified for the effects of sodium bicarbonate medication.
As the treatments that may slow progression are already indicated for those with G3 disease onwards, the authors concluded that there is no evidence to support the impact of monitoring GFR in those with CKD on the management of cardiovascular disease. GFR monitoring, therefore, cannot be justified on this basis.
Perera et al. did however explore whether it would be cost-effective to monitor GFR in individuals with impaired renal function (an eGFR of < 90 ml/minute/1.73 m2) but no CKD (defined as albuminuria or an eGFR of < 60 ml/minute/1.73 m2). It was estimated that the most cost-effective interval of GFR monitoring (based on a £20,000 per QALY cost-effectiveness threshold) in this group is every 3 years for individuals aged < 60 years, every 4 years for individuals aged 60–69 years, and not cost-effective in those aged 70 years and above.
One of the key conclusions of the overall research programme was ‘monitoring individuals with CKD is difficult to justify by the usual logic of treatment initiation or titration. Alternative ways of quantifying its benefit might be required’. 113
Clinical guidelines
An update of the NICE clinical guideline ‘Chronic kidney disease: assessment and management (NG203)’ was published in 2021. 59 The guideline covers the care and treatment of people with, or at risk of, CKD with the aim of preventing or delaying progression and reducing the risk of complications associated with CKD. Here we summarise the recommendations pertinent to our research question.
According to the NICE guideline, the recommended minimum frequency of monitoring those with GFR categories 3a and 3b is annual GFR estimation and ACR measurements. NICE recommend obtaining a minimum of three GFR estimations over a period of not < 90 days to identify the rate of progression of CKD. Additionally, in adults with a new finding of reduced GFR, to repeat the GFR within 2 weeks to exclude causes of acute deterioration of GFR, for example, AKI or starting RAAS therapy.
The guideline defines the exact criteria for accelerated progression of CKD in adults as either (1) a sustained decrease in GFR of 25% or more and a change in GFR category within 12 months, or (2) a sustained decrease in GFR of 15 ml/minute/1.73 m2 or more per year. Such individuals are considered at increased risk of progression to kidney failure. 59 NICE recommend that, when assessing CKD progression, the current rate of decline of GFR is extrapolated and taken into account when planning intervention strategies, particularly if it suggests that the person might need kidney replacement therapy in their lifetime.
In the original current study protocol, the main outcome of interest for the health-economic analysis was listed as progression to CKD stage G4. In light of the updated NICE clinical guidelines on identifying progression in this patient population, it was decided to instead focus the analysis on the role of GFR monitoring for identifying accelerated progression based on the NICE criteria. Progression to CKD stage G4 is reported as a secondary analysis.
Comparative accuracy of estimated glomerular filtration rate equations for predicting accelerated progression (measurement model analysis)
The aim of this analysis was to construct a measurement model describing the trajectory of patients mGFR and eGFR over 10 years, based on extrapolating mGFR and eGFR bias data from the study. This model was used to assess the proportion of patients meeting the NICE threshold of accelerated progression (see Clinical guidelines), assuming an annual testing schedule, and the number of patients expected to be incorrectly managed at each of the evaluated monitoring time points using the different estimating equations. The outcomes produced from this measurement model were used to inform the subsequent cost analysis presented in Comparative cost of monitoring with different estimated glomerular filtration rate equations.
Methods
Data
Study participants who had complete data on mGFR and eGFR at baseline and 36 months were used to inform this analysis (n = 875) (see Table 2).
Measured glomerular filtration rate trajectories
Each individual’s absolute change in mGFR over the 3-year follow-up period was calculated by a simple subtraction of the baseline mGFR from the 36-month mGFR. Assuming a linear model of GFR change over time, as suggested by the above statistical analysis (see Chapter 3), the annual change (calculated as the 3-year change divided by three) was then used to interpolate individuals’ mGFR values at the year 1 and year 2 time points. Extrapolation was similarly conducted to estimate annual GFR measurements beyond the study follow-up period, up to 10 years from baseline.
Patients’ true GFR categories over time (required for the first element of the NICE progression criteria) were classified using individuals’ longitudinal GFR measurements and according to the CKD GFR classification (all units in ml/minute/1.73 m2):
-
G1: GFR ≥ 90
-
G2: 90 > GFR ≥ 60
-
G3a: 60 > GFR ≥ 45
-
G3b: 45 > GFR ≥ 30
-
G4: 30 > GFR ≥ 15
-
G5: GFR < 15.
The primary analysis of the measurement model focused on evaluating when patients would meet NICE’s combined progression criteria (see Clinical guidelines), based on the individual's annual mGFR. A secondary outcome looking at the number of patients transitioning into CKD category G4 or higher (GFR < 30 ml/minute/1.73 m2) was also conducted.
Estimated glomerular filtration rate equations
Information on the diagnostic accuracy of the eGFR values was calculated, according to how well they were able to accurately predict the NICE progression criteria. The four primary equations included in the statistical analysis were evaluated: MDRD, CKD-EPIcreatinine, CKD-EPIcystatin and CKD-EPIcreatinine-cystatin.
The eGFR values at baseline and year 3 were based on the patients’ recorded GFR estimations at those time points. Estimated GFR values for other time points (years 1, 2 and 4–10) were estimated as a function of the underlying mGFR value (derived from the linear trajectories of mGFR previously described) plus a simulated measurement error factor representing the expected measurement error incurred with each GFR-estimating equation. The estimation of GFR values is represented by the following measurement error equation:
where mGFRi is the underlying ‘true’ GFR measurement taken from the model of mGFR trajectories described previously; biasi is the expected measurement bias associated with the given eGFR equation at the given level of mGFRi, applied within a lognormal distribution; and SDi is the expected SD of the measurement bias at the given level of mGFRi. The adopted equation above follows the standard approach used in the modelling literature, whereby error in repeated measurements is assumed to be log-normally distributed. 115
Rather than assuming a fixed level of bias for each of the eGFR equations (as reported in previous chapters), the above approach allows the expected bias associated with GFR estimations to change depending on the underlying level of mGFR. This is important since, in the laboratory context, test measurement error often varies over the measurement range: for example, being lower or higher at certain regions of the measurement range.
The individual-level bias values used in the measurement error equation were derived from bias profiles for each of the GFR equations, which show the relationship between the expected level of measurement error occurring for each GFR equation across the range of observed mGFR values (see Appendix 1, Figures 28–31). These bias profiles were obtained using available information on the difference between reported mGFR and eGFR values for each annual sampling point from the study (separate profiles are presented for baseline, year 1, year 2 and year 3), and fitting a loess regression model to the data to estimate the mean expected bias over the measurement range. [N.B. the baseline profile was not actually used in the simulation (at baseline the directly reported mGFR and eGFR values were used) but is included in the results here for interest.] Since repeated GFR estimations were not undertaken at fixed mGFR time points, we could not obtain different SD values over the measurement range – instead, the simplifying assumption was made that SD would remain fixed for each GFR equation over the measurement range, using the aggregate SD values (reported in Table 18).
In the simulation, eGFR values were based on the observed values where both mGFR and eGFR values were available for the whole cohort (i.e. at baseline and year 3). For all other years, eGFR values were simulated by applying the above bias profile and SD data within the previously reported measurement error equation.
The same approach as outlined for mGFR was undertaken with the eGFR values, to calculate the proportion of patients classified as progressing according to NICE guidelines, at each time point. The eGFR progression outcomes were then compared against those obtained using mGFR, to calculate the clinical accuracy of the GFR-estimating equations.
Analysis and outcomes
The measurement model extrapolated mGFR and eGFR values over a 10-year period. The results are based on a two-stage simulation process: an ‘inner loop’, sampling with replacement from the main study data (n = 875) to produce a bootstrap data set of 20,000 patients; followed by an ‘outer loop’, repeating the bootstrap process 1000 times with different random number sequences (to account for first-order uncertainty). Mean and 95% credible intervals were calculated from the 1000 samples, for the following outcomes:
-
the percentage of patients [out of the starting cohort (n = 20,000)] tested each year
-
the percentage of all annual test results that are positive (i.e. meet the threshold for progression)
-
the percentage of annual positive test results that are:
-
FPs
-
true positives (TPs)
-
-
the percentage of all annual test results that are negative (i.e. do not meet the threshold for progression)
-
the percentage of annual negative test results that are:
-
FNs
-
-
for FNs:
-
the average delay time (in years) patients experience between their FN result and eventually being identified (for those identified within the analysis 10-year period)
-
the percentage of patients that are not identified during the analysis period
-
-
cumulative sensitivity and specificity values (e.g. for cumulative sensitivity: up to year X, out of all the patients who experienced a true progression event, how many have been correctly identified)
-
cumulative PPV and NPV values (e.g. for cumulative PPV: up to year X, out of all positive test results, how many patients were truly progressing at that time point).
Note that in all analyses the proportion of patients tested reduces over time, according to the number of patients assumed to be removed from annual monitoring due to identified progression. Patients were assumed to be removed from the monitoring cohort once they reached one of two outcomes: (1) a TP test result, (2) a delayed positive test result – that is patients whose first point of progression was not identified, but who received a subsequent positive test result (which may or may not be a TP in that year, depending on the patient’s subsequent progression status). All other patients with FP test results were assumed to return to the standard monitoring cohort following confirmatory testing.
In addition to the primary analysis, the analysis was repeated with progression defined as anyone transitioning into CKD category G4 or above.
Assumptions
Key assumptions underpinning the simulation analysis are listed below:
-
Measured GFR represents true measurement (measurement error in the mGFR is not considered).
-
Measured GFR exhibits a linear change over time.
-
Random variability in the eGFR measurement error (i.e. SD) is constant over the measurement range.
-
Patients receiving a TP or delayed positive eGFR test result (i.e. a positive test following a previous missed progression event) are assumed to undergo a change in management and are taken out of the annual monitoring cohort.
-
All patients are assumed to comply with annual testing.
Results
Measured glomerular filtration rate outcomes
According to the study data, when considering all study participants with complete mGFR and eGFR data at baseline and year 3 (n = 875), mGFR declined by an average of −4.83 ml/minute/1.73 m2 over 3 years, equivalent to an annual decline of −1.61 ml/minute/1.73 m2. Focusing only on patients exhibiting a decline in mGFR (n = 631), the average annual drop was −2.96 ml/minute/1.73 m2, compared to an average rise of 1.89 ml/minute/1.73 m2 per year in patients who exhibited stable or increasing mGFR (n = 244).
Table 32 shows the cumulative proportion of patients meeting the NICE accelerated progression criteria according to their mGFR, as well as the numbers progressing into GFR category 4 or above, based on the 10-year measurement model of mGFR trajectories. From these results, we observe that for the study cohort, the NICE individual criteria stipulating a decrease in GFR of ≥ 15 ml/minute/1.73 m2 per year only identified one patient and therefore provides minimal utility in this context. Note however that under the criteria of an absolute drop in mGFR, when assuming a constant linear decline in GFR, any patients meeting these criteria would be identified in year 1. Thus, the utility of this criteria is also limited by the assumption of a linear decline in mGFR.
| Year | Individual NICE criteria (cumulative N, %) | NICE combined progression criteria: (1) or (2) | Progression to GFR category 4 + (GFR < 30 ml/minute/1.73 m2) | |
|---|---|---|---|---|
| (1) Decrease in GFR of ≥ 15 ml/minute/1.73 m2/year | (2) A sustained decrease in GFR ≥ 25% and a change in GFR category within 12 months | |||
| Baseline | – | – | – | – |
| Year 1 | 1 (0.1) | 0 (0) | 1 (0.1) | 23 (2.6) |
| Year 2 | 1 (0.1) | 5 (0.6) | 6 (0.7) | 40 (4.6) |
| Year 3 | 1 (0.1) | 10 (1.1) | 10 (1.1) | 88 (10.1) |
| Year 4 | 1 (0.1) | 23 (2.6) | 23 (2.6) | 141 (16.1) |
| Year 5 | 1 (0.1) | 45 (5.1) | 45 (5.1) | 194 (22.2) |
| Year 6 | 1 (0.1) | 66 (7.5) | 66 (7.5) | 244 (27.9) |
| Year 7 | 1 (0.1) | 90 (10.3) | 90 (10.3) | 276 (31.5) |
| Year 8 | 1 (0.1) | 105 (12.0) | 105 (12.0) | 312 (35.6) |
| Year 9 | 1 (0.1) | 117 (13.4) | 117 (13.4) | 348 (39.8) |
| Year 10 | 1 (< 0.1) | 125 (14.3) | 125 (14.3) | 371 (42.4) |
The second NICE progression criteria, stipulating both a decrease in GFR ≥ 25% and a change in GFR category within 12 months, return a comparatively higher number of patients: 10 (1.1%) by year 3 and 125 (14.3%) by year 10. This is therefore the major component of the NICE combined GFR progression criteria.
A higher number of patients are seen to meet the criteria of a stage shift in the GFR category (to category 4 +), compared to the NICE progression criteria. This reflects the fact that a significant proportion of patients progress into GFR category 4 (or 5) without exhibiting a significant relative or absolute decline in their GFR: typically, the average relative decline in GFR for those patients progressing into stage 4 or above was ~10–18%, with only a minority of patients, thus meeting the 25% decline requirement required by the NICE progression criteria.
Estimated glomerular filtration rate outcomes
Estimated glomerular filtration rate bias profiles
The bias profiles for each of the primary eGFR equations are provided in Appendix 1, Figures 28–31). Note that the bias profile at baseline is shown for interest only – this was not used in the simulation analysis.
Combined National Institute for Health and Care Excellence progression criteria
Full results tables and a Markov model structure for the accuracy outcomes of the primary eGFR equations (MDRD, CKD-EPIcreatinine, CKD-EPIcystatin and CKD-EPIcreatinine-cystatin, respectively) for the combined NICE progression criteria are provided in Report Supplementary Material 2. These tables provide information on the proportion of patients who test positive and negative over the 10-year analysis; the proportion of FP and FN test results; the average delay experienced for patients with FN results; and the proportion of FN results never correctly identified over the analysis period. Table 33 reports a summary of the cumulative sensitivity, specificity, PPVs and NPVs results. The reported credible intervals represent the 5th and 95th percentile of the mean simulated results [based on 1000 simulations of bootstrap (n = 20,000) analyses].
| Year | MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | ||||
|---|---|---|---|---|---|---|---|---|
| Cumulative sensitivity and specificity [mean (%) (95% credible interval)] | ||||||||
| Sensitivity | Specificity | Sensitivity | Specificity | Sensitivity | Specificity | Sensitivity | Specificity | |
| Year 1 | 21.8 (7.5 to 38.5) |
85.8 (82.9 to 88.4) |
34.1 (14.6 to 50.0) |
84.3 (81.1 to 87.0) |
98.3 (95.8 to 100) |
80.0 (77.6 to 82.5) |
90.9 (81.0 to 100) |
85.6 (83.3 to 88.1) |
| Year 2 | 47.5 (42.3 to 53.0) |
84.4 (82.6 to 85.8) |
49.0 (43.4 to 54.7) |
83.4 (81.4 to 85.1) |
40.3 (33.7 to 54.3) |
78.6 (77.3 to 80.1) |
43.1 (35.7 to 56.7) |
84.9 (83.6 to 86.5) |
| Year 3 | 50.7 (40.6 to 61.9) |
82.4 (81.2 to 83.6) |
51.8 (42.7 to 62.7) |
81.5 (80.3 to 82.7) |
45.7 (34.0 to 57.6) |
77.5 (76.3 to 78.8) |
47.4 (35.8 to 59.6) |
82.8 (81.1 to 85.0) |
| Year 4 | 50.0 (41.8 to 60.3) |
82.9 (82.1 to 83.6) |
51.1 (43.0 to 61.3) |
82.3 (81.5 to 83.1) |
44.7 (33.3 to 55.8) |
77.2 (76.4 to 78.2) |
46.4 (35.6 to 57.8) |
83.2 (82.6 to 84.2) |
| Year 5 | 50.1 (42.2 to 60.3) |
82.3 (81.5 to 83.1) |
51.1 (43.2 to 61.3) |
81.8 (80.9 to 82.7) |
44.6 (33.3 to 55.5) |
77.3 (76.6 to 78.0) |
46.3 (35.6 to 57.7) |
83.2 (82.6 to 83.9) |
| Year 6 | 45.7 (41.5 –51.7) |
82.0 (81.1 to 82.8) |
46.0 (41.8 to 52.2) |
81.6 (80.6 to 82.4) |
42.2 (36.0 to 48.7) |
77.5 (76.8 to 77.9) |
43.3 (37.3 to 50.4) |
83.2 (82.7 to 83.7) |
| Year 7 | 42.8 (39.4 to 47.1) |
82.0 (80.9 to 82.7) |
43.0 (39.5 to 47.3) |
81.6 (80.5 to 82.4) |
39.8 (35.2 to 45.0) |
77.8 (77.0 to 78.2) |
40.3 (35.7 to 45.7) |
83.5 (82.8 to 83.9) |
| Year 8 | 42.6 (39.4 to 46.8) |
81.9 (80.8 to 82.7) |
42.8 (39.5 to 47.1) |
81.6 (80.4 to 82.4) |
39.5 (35.2 to 44.6) |
78.1 (77.2 to 78.5) |
40.0 (35.7 to 45.4) |
83.6 (82.9 to 84.1) |
| Year 9 | 42.6 (39.4 to 46.8) |
81.9 (80.6 to 82.6) |
42.7 (39.5 to 47.1) |
81.5 (80.3 to 82.3) |
39.5 (35.2 to 44.5) |
78.3 (77.3 to 78.7) |
39.9 (35.7 to 45.2) |
83.7 (82.9 to 84.3) |
| Year 10 | 40.0 (37.1 to 43.3) |
81.9 (80.5 to 82.7) |
40.4 (37.6 to 43.6) |
81.6 (80.2 to 82.4) |
37.9 (34.5 to 41.8) |
78.5 (77.5 to 79.0) |
37.5 (33.9 to 41.9) |
84.0 (82.9 to 84.5) |
| PPV and NPV [mean (%) (95% credible interval)] | ||||||||
| PPV | NPV | PPV | NPV | PPV | NPV | PPV | NPV | |
| Year 1 | 0.0 (0.0 to 0.3) |
100.0 (99.8 to 100) |
0.1 (0.0 to 0.4) |
100.0 (99.8 to 100) |
0.1 (0.0 to 1.0) |
100.0 (100 to 100) |
0.2 (0.0 to 1.3) |
100.0 (100 to 100) |
| Year 2 | 3.4 (1.5 to 7.3) |
99.3 (98.4 to 99.7) |
3.3 (1.5 to 7.0) |
99.3 (98.4 to 99.7) |
2.0 (1.1 to 4.2) |
99.1 (98.0 to 99.7) |
3.1 (1.6 to 6.5) |
99.2 (98.2 to 99.8) |
| Year 3 | 2.6 (1.3 to 4.5) |
99.5 (98.9 to 99.7) |
2.5 (1.2 to 4.4) |
99.5 (98.8 to 99.7) |
1.8 (0.8 to 3.3) |
99.3 (98.7 to 99.7) |
2.5 (1.1 to 4.4) |
99.4 (98.8 to 99.7) |
| Year 4 | 2.2 (1.0 to 3.6) |
99.5 (99.2 to 99.8) |
2.1 (1.0 to 3.5) |
99.5 (99.2 to 99.8) |
1.5 (0.6 to 2.7) |
99.4 (98.9 to 99.7) |
2.1 (0.9 to 3.7) |
99.5 (99.1 to 99.8) |
| Year 5 | 1.8 (0.8 to 2.8) |
99.6 (99.3 to 99.8) |
1.8 (0.8 to 2.8) |
99.6 (99.3 to 99.8) |
1.3 (0.5 to 2.2) |
99.5 (99.2 to 99.8) |
1.8 (0.7 to 3.0) |
99.6 (99.2 to 99.8) |
| Year 6 | 3.2 (1.6 to 4.4) |
99.2 (98.9 to 99.5) |
3.1 (1.6 to 4.3) |
99.2 (98.9 to 99.5) |
2.4 (1.2 to 3.5) |
99.0 (98.7 to 99.4) |
3.2 (1.6 to 4.7) |
99.1 (98.8 to 99.5) |
| Year 7 | 3.9 (2.6 to 4.9) |
98.8 (98.5 to 99.1) |
3.8 (2.6 to 4.8) |
98.8 (98.5 to 99.1) |
3.0 (1.9 to 3.9) |
98.7 (98.4 to 99.0) |
4.0 (2.6 to 5.2) |
98.8 (98.5 to 99.1) |
| Year 8 | 3.5 (2.3 to 4.6) |
98.9 (98.5 to 99.2) |
3.4 (2.3 to 4.5) |
98.9 (98.5 to 99.2) |
2.7 (1.7 to 3.7) |
98.8 (98.4 to 99.1) |
3.6 (2.3 to 4.9) |
98.9 (98.5 to 99.2) |
| Year 9 | 3.1 (2.0 to 4.2) |
99.0 (98.6 to 99.3) |
3.1 (2.0 to 4.1) |
99.0 (98.7 to 99.3) |
2.5 (1.6 to 3.4) |
98.9 (98.6 to 99.2) |
3.3 (2.1 to 4.5) |
99.0 (98.7 to 99.3) |
| Year 10 | 4.0 (3.1 to 5.0) |
98.6 (98.3 to 98.9) |
3.9 (3.1 to 4.9) |
98.6 (98.3 to 98.9) |
3.2 (2.4 to 3.9) |
98.5 (98.1 to 98.8) |
4.1 (3.1 to 5.1) |
98.6 (98.2 to 98.9) |
Overall, clinical accuracy results when looking at annual time frames are lower than those previously reported in the statistical analysis of 3-year progression outcomes, due to the fact that it is harder to obtain (e.g.) a 25% drop over 1 year versus 3 years, as the NICE accelerated progression criteria demands. In general, no significant difference is observed between the eGFR equations in terms of the 10-year clinical accuracy results. In year 1, it appears that the cystatin-based equations have significantly higher sensitivity compared to MDRD and CKD-EPIcreatinine; however, these results should be interpreted with caution due to the very low number of true progression events that occurred in year 1. Over the remainder of the time horizon the cystatin-based equations performed consistently lower than the other equations in terms of sensitivity, and higher in terms of specificity; although for both cystatin-based equations the credible intervals overlapped with the other GFR equations.
Overall, there was no evidence to suggest that any of the estimating equations are superior for identifying progression, as defined by NICE. 59 This reflects the findings of the statistical analysis presented in Chapter 3.
Secondary analysis
Progression to glomerular filtration rate stage 4 +
The complete results tables for the secondary analysis (progression to CKD stage G4 +) are provided in Report Supplementary Material 2. Table 34 provides the summary results showing the cumulative sensitivity, specificity, PPV and NPV results for the primary eGFR equations.
| Year | MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | ||||
|---|---|---|---|---|---|---|---|---|
| Cumulative sensitivity and specificity [mean (%) (95% credible interval)] | ||||||||
| Sensitivity | Specificity | Sensitivity | Specificity | Sensitivity | Specificity | Sensitivity | Specificity | |
| Year 1 | 1.9 (0.0 to 22.6) |
91.1 (90.0 to 92.4) |
2.8 (0.0 to 27.9) |
91.4 (90.3 to 92.8) |
5.8 (0.0 to 29.8) |
89.3 (87.6 to 91.3) |
3.3 (0.0 to 34.8) |
90.9 (89.1 to 92.5) |
| Year 2 | 24.4 (11.0 to 36.2) |
91.2 (90.3 to 92.5) |
24.9 (11.1 to 37.8) |
91.5 (90.6 to 92.8) |
18.5 (7.6 to 31.6) |
88.6 (87.5 to 89.9) |
21.8 (9.3 to 35.3) |
90.7 (89.5 to 92.0) |
| Year 3 | 33.8 (27.8 to 40.6) |
90.9 (89.3 to 92.3) |
32.2 (27.0 to 37.6) |
90.9 (89.1 to 92.4) |
33.1 (29.1 to 38.3) |
86.9 (83.6 to 89.1) |
33.4 (28.9 to 37.9) |
87.7 (84.0 to 90.9) |
| Year 4 | 41.2 (34.8 to 46.3) |
91.6 (90.8 to 92.5) |
39.6 (34.1 to 44.1) |
91.6 (90.7 to 92.6) |
34.9 (26.0 to 43.2) |
87.7 (85.2 to 89.4) |
43.6 (38.2 to 48.2) |
89.0 (86.4 to 90.9) |
| Year 5 | 40.0 (34.6 to 44.1) |
91.4 (90.7 to 92.2) |
38.7 (34.0 to 43.1) |
91.5 (90.8 to 92.3) |
33.9 (26.0 to 39.4) |
88.1 (86.1 to 89.5) |
42.1 (37.9 to 46.5) |
89.4 (87.3 to 90.9) |
| Year 6 | 39.1 (34.7 to 42.6) |
91.3 (90.6 to 92.0) |
38.0 (34.3 to 41.5) |
91.4 (90.7 to 92.2) |
33.7 (27.3 to 37.8) |
88.4 (86.8 to 89.6) |
40.8 (37.4 to 44.3) |
89.7 (87.9 to 91.0) |
| Year 7 | 37.8 (34.5 to 40.4) |
91.5 (90.7 to 92.2) |
37.1 (34.3 to 39.9) |
91.6 (90.9 to 92.4) |
33.1 (28.6 to 36.3) |
88.9 (87.6 to 90.0) |
38.9 (36.5 to 41.6) |
90.1 (88.7 to 91.3) |
| Year 8 | 36.5 (33.5 to 38.9) |
91.7 (90.8 to 92.5) |
35.9 (33.4 to 38.3) |
91.9 (91.1 to 92.7) |
32.3 (28.1 to 35.5) |
89.5 (88.3 to 90.5) |
37.3 (34.8 to 39.6) |
90.7 (89.4 to 91.8) |
| Year 9 | 35.7 (32.7 to 38.2) |
92.1 (91.0 to 92.8) |
35.2 (32.6 to 37.1) |
92.2 (91.2 to 93.0) |
31.8 (27.8 to 35.2) |
90.0 (89.0 to 91.0) |
36.3 (33.7 to 38.3) |
91.2 (90.1 to 92.2) |
| Year 10 | 35.5 (32.7 to 37.8) |
92.3 (91.1 to 93.1) |
35.0 (32.5 to 36.9) |
92.5 (91.4 to 93.3) |
31.7 (27.9 to 35.0) |
90.4 (89.6 to 91.4) |
36.1 (33.7 to 38.0) |
91.6 (90.7 to 92.6) |
| PPV and NPV [mean (95% credible interval)] | ||||||||
| PPV | NPV | PPV | NPV | PPV | NPV | PPV | NPV | |
| Year 1 | 0.4 (0.0 to 3.9) |
97.1 (94.8 to 99.0) |
0.5 (0.0 to 5.0) |
97.1 (94.8 to 99.1) |
0.8 (0.0 to 4.3) |
97.1 (94.7 to 99.3) |
0.6 (0.0 to 6.4) |
97.1 (94.8 to 99.1) |
| Year 2 | 6.6 (3.1 to 12.9) |
97.8 (96.9 to 98.8) |
6.9 (3.2 to 13.2) |
97.8 (96.9 to 98.8) |
4.0 (1.8 to 6.9) |
97.6 (96.6 to 98.6) |
5.6 (2.5 to 10.8) |
97.7 (96.8 to 98.7) |
| Year 3 | 11.6 (9.1 to 14.6) |
97.3 (96.3 to 98.1) |
11.1 (8.9 to 14.2) |
97.2 (96.3 to 98.0) |
8.4 (6.3 to 10.3) |
97.1 (96.2 to 98.1) |
9.1 (6.6 to 11.8) |
97.2 (96.2 to 98.0) |
| Year 4 | 15.9 (12.3 to 18.8) |
97.3 (96.8 to 97.7) |
15.4 (12.3 to 17.9) |
97.3 (96.8 to 97.7) |
10.5 (6.6 to 13.9) |
96.9 (96.4 to 97.4) |
14.1 (9.8 to 17.2) |
97.4 (96.9 to 97.7) |
| Year 5 | 13.7 (9.9 to 17.5) |
97.5 (96.8 to 98.1) |
13.4 (9.9 to 16.4) |
97.4 (96.7 to 98.1) |
9.5 (5.5 to 13.8) |
97.2 (96.5 to 97.7) |
12.7 (8.4 to 16.8) |
97.6 (96.8 to 98.1) |
| Year 6 | 13.9 (10.3 to 17.2) |
97.3 (96.5 to 97.9) |
13.6 (10.4 to 16.4) |
97.3 (96.4 to 97.9) |
10.0 (6.3 to 13.9) |
97.1 (96.3 to 97.6) |
13.1 (9.1 to 16.9) |
97.4 (96.5 to 97.9) |
| Year 7 | 15.1 (11.8 to 17.7) |
96.9 (96.3 to 97.5) |
15.0 (11.9 to 17.4) |
96.9 (96.2 to 97.5) |
11.2 (7.8 to 14.3) |
96.7 (96.1 to 97.2) |
14.3 (10.5 to 17.2) |
97.0 (96.3 to 97.5) |
| Year 8 | 15.5 (12.6 to 17.6) |
96.7 (96.1 to 97.4) |
15.4 (12.7 to 17.3) |
96.7 (96.1 to 97.4) |
11.8 (8.6 to 14.4) |
96.5 (96.0 to 97.1) |
14.9 (11.2 to 17.3) |
96.7 (96.2 to 97.4) |
| Year 9 | 15.3 (13.3 to 17.2) |
96.7 (96.1 to 97.0) |
15.3 (13.4 to 17.4) |
96.7 (96.1 to 97.0) |
11.8 (9.4 to 13.9) |
96.5 (96.0 to 96.8) |
14.9 (12.1 to 16.9) |
96.7 (96.2 to 97.1) |
| Year 10 | 14.8 (12.6 to 16.4) |
96.8 (96.2 to 97.2) |
14.8 (12.7 to 16.4) |
96.8 (96.2 to 97.2) |
11.5 (9.0 to 13.6) |
96.7 (96.1 to 97.0) |
14.5 (11.6 to 16.4) |
96.9 (96.3 to 97.2) |
Based on these results, it appears that all of the GFR-estimating equations perform poorly in terms of identifying patients progressing into higher CKD GFR categories, with sensitivity values below 45% across the modelled timeline (and significantly lower than this at several time points for all of the tests). Excluding year 1, the CKD-EPIcystatin equation is consistently the lowest performer in terms of sensitivity and specificity, while either the MDRD or CKD-EPIcreatinine-cystatin equations tended to yield the highest levels of sensitivity, with the CKD-EPIcreatinine equation achieving the highest mean specificity values. However, as in the primary analysis evaluating the performance of the GFR equations at identifying NICE accelerated progression, in this analysis we again observe that the credible intervals of the results for all of the GFR equations overlapped. There is therefore no evidence to suggest that any of the estimating equations are superior for identifying progression into higher CKD GFR stages.
Comparative cost of monitoring with different estimated glomerular filtration rate equations
The economic analysis in this chapter focuses on the respective cost of monitoring individuals using the different GFR-estimating equations, based on the results from the measurement model analyses which estimate test accuracy for accelerated progression (defined by NICE criteria) over a 10-year period.
The analysis focuses on the cost of monitoring with eGFR and does not include the costs associated with additional testing (e.g. urine albumin) or treatment. In line with the assumptions of the measurement model analysis, monitoring costs are included up to the point that an individual receives a TP or delayed positive eGFR result when patients are assumed to undergo a change in management and are taken out of the annual monitoring cohort. Those who receive a FP or TP result are assumed to undergo an additional GFR estimation in line with clinical guidance59 and return to the annual monitoring cohort.
Appointment costs
Appointment costs were only assigned to annual monitoring visits. Based on clinical advice, repeat tests due to a FP test result were unlikely to result in an additional clinical appointment, other than an outpatient phlebotomy appointment (£4). 116
The 2019/20 NHS National Cost Collection data provide costs for consultant and non-consultant-led appointments based on whether it is an initial or follow-up appointment. 116 For the purposes of our analysis and, given that the study cohort was primarily recruited in secondary care (i.e. post referral to specialist nephrologist), we assumed that our cohort had already had an initial appointment with a nephrologist and that monitoring appointments should be costed at the slightly lower follow-up rate. We weighted the proportion of consultant-led versus non-consultant-led appointments by the total number of appointments in each category in the cost collection data (88.8% consultant-led, consultant-led follow-up appointment: £170.93, non-consultant-led follow-up appointment: £145.85). Post referral to a nephrologist, a significant proportion of individuals are referred back and monitored in primary care (estimated to be 80% in a recent NICE economic model). 59 We therefore applied this weighting to the costings for the annual monitoring appointments, applying the cost of a GP appointment instead (£33.19). 117
Test costs
The costs of the CKD-EPIcreatinine and CKD-EPIcystatin tests were calculated as part of the study, taking into account the cost of reagents, staff and overheads. The cost of a CKD-EPIcreatinine test was estimated to be £0.43 and the cost of a CKD-EPIcystatin test was £3.80. The cost of a CKD-EPIcreatinine-cystatin test was calculated as the cost of a CKD-EPIcystatin test plus the cost of a CKD-EPIcreatinine test. In some primary care settings, laboratory tests are charged at a fixed rate which is based on the annual cost of the whole service divided by the number of tests conducted each year. This tariff cost may vary by region, but it is typically more than the cost of a creatinine test and notably less than a cystatin C test. Here we have used the true estimated direct costs of the tests rather than the tariff cost, even if monitoring took place in primary care, to reflect the increased cost to the NHS overall.
Results
The breakdown and total cost of monitoring the study cohort (n = 875) over a 10-year period are presented in Table 35. As there were no notable differences in accuracy between the different GFR equations, the primary driver of the differences observed in costs is due to the higher unit cost of the cystatin C test.
| MDRD | CKD-EPIcreatinine | CKD-EPIcystatin | CKD-EPIcreatinine-cystatin | |
|---|---|---|---|---|
| Cost of annual monitoring | £508,968.22 (98.58%) |
£508,968.22 (98.55%) |
£538,054.00 (97.26%) |
£542,064.99 (97.81%) |
| Cost of repeat testing due to FP | £6829.73 (1.32%) |
£6952.89 (1.35%) |
£14,289.60 (2.58%) |
£11,256.99 (2.03%) |
| Cost of repeat testing due to TP | £515.76 (0.10%) |
£520.53 (0.10%) |
£896.03 (0.16%) |
£891.51 (0.16%) |
| Total cost ( n = 875) | £516,313.71 | £516,441.63 | £553,239.63 | £554,213.50 |
| Average per patient cost | £590.07 | £590.22 | £632.27 | £633.39 |
| Incremental per patient cost | – | £0.15 | £42.20 | £43.32 |
Longer-term differences in costs and outcomes
In an earlier-stage CKD cohort (CKD stage G3), the main clinical justification for monitoring GFR is to promptly detect disease progression and offer interventions that may prevent or delay it. It is therefore the comparative sensitivity of the different testing strategies that would drive any differences in long-term costs and outcomes. In our measurement model analysis, we simulated the comparative accuracy of the GFR equations in an annual monitoring context and found no consistent improvement in sensitivity when applying GFR equations based on or incorporating cystatin C compared to creatinine alone. These results echo the findings of the statistical analysis of the 3-year cohort data reported in Chapter 3. We therefore have no evidence to support an analysis of the longer-term cost and health consequences of implementing a cystatin-based GFR equation.
In anticipation of cystatin-based GFR equations demonstrating an improvement in sensitivity, we developed a Markov model in R to capture the impact of identifying individuals whose CKD is progressing earlier. We would like to make the code for this model structure freely available for future research and adaptation as it may be useful in two key contexts: (1) if a more sensitive means of detecting progression is identified, and (2) if a novel intervention for preventing or delaying progression in individuals with CKD stage 3a/b is found. Details about the model structure and parameterisation can be found in Report Supplementary Material 2, along with a link to the R code.
When reviewing the literature and developing the model, we struggled to find evidence which quantified the impact of GFR monitoring on the rate of CKD progression. The most recently available evidence at the time was a NIHR programme report by Perera et al. which synthesised the evidence on the impact of monitoring GFR on cardiovascular disease management in those with G3 CKD. 113 Given that statin treatment is already recommended for all those with CKD category G359 and the use of antihypertensives is based on BP and urinary ACR,59 Perera et al. concluded that monitoring eGFR in those with CKD is unlikely to be a driver of cardiovascular therapy indication. 113 Since the time of this programme, there have been a number of publications on the impact of glycaemic medications both on progression of CKD and on cardiovascular disease events in individuals with CKD. 17 This led to a new recommendation by NICE in November 2021 on the use of SGLT2 inhibitors in adults with CKD and type 2 diabetes who are taking an A2RB or an ACE inhibitor. 59 The use of this medication is dependent on ACR and eGFR threshold, and therefore may provide a means of quantifying the impact of monitoring GFR on longer-term costs and outcomes. Thus, it is important to note that if we had found that cystatin C was more sensitive than the creatinine alone equations, the health economic argument would likely be centred on the use of eGFR monitoring to trigger the use of these new hypoglycaemic medications.
Chapter 5 Discussion
Main study: prospective, longitudinal cohort study
We have studied GFR-estimating equations that were in widespread use in clinical practice at the inception of the study. We have also reported data describing the performance of equations that have been published during the progress of the study, including some recent equations specifically designed to address concerns about the use of ethnic adjustment factors in individuals of African descent. We have studied accuracy of these equations in a cross-sectional baseline analysis and also the ability of these equations to reflect and detect changes in mGFR over 3 years, in relation to several clinically relevant thresholds. We have explored possible causes for differences in the performance of some of the equations, in particular, issues related to the calibration of cystatin C. In the following discussion, comments relating to the characteristics of the cystatin C equations are based upon the use of recalibrated cystatin C data, except where calibration itself is the issue under consideration (see The impact of calibration on cystatin C and glomerular filtration rate estimation).
Which glomerular filtration rate-estimating equation is the most diagnostically accurate assessment of measured glomerular filtration rate?
Accuracy of the main study glomerular filtration rate-estimating equations
The main study estimated that GFR equations were negatively biased overall compared to mGFR. Median bias ranged from −2.8 to −4.1 ml/minute/1.73 m2, with no evidence of a difference in bias between these equations. The overall bias we have observed for these equations is of a very similar order to that observed when the equations were originally validated. 28,32 However, the creatinine-based equations (MDRD and CKD-EPIcreatinine) demonstrated a clear shift in bias depending on the level of GFR (positively biased at lower levels of GFR, approximately < 35 ml/minute/1.73 m2, and negatively biased at higher levels, approximately > 50 ml/minute/1.73 m2). Inclusion of cystatin C within the equations largely attenuated this effect. Within the target population of the present study (i.e. individuals with GFR 30–59 ml/minute/1.73 m2), the impact of this effect was less dramatic than at more extreme levels of GFR, but the data suggest that cystatin C-containing equations may perform more consistently in terms of bias across a wider range of GFR levels. This could be an important advantage in terms of disease detection. It is widely accepted that the MDRD equation displays negative bias at levels of GFR > 60 ml/minute/1.73 m2 and this was one of the drivers for its replacement with the CKD-EPIcreatinine equation in clinical practice. 32,41 The bias-GFR level effect we have observed for the CKD-EPIcreatinine equation is not consistent with other studies. Although Levey et al. observed a slight increase in negative bias at higher levels of GFR,32 in large European studies Pottel et al. observed positive bias for the CKD-EPIcreatinine equation which was fairly constant across the GFR range studied and across adult (> 30 years) age ranges,44,47 while Björk et al. report positive bias at GFR levels up to 90 ml/minute/1.73 m2. 118 Comparisons with other studies are complicated by factors including the demographics of the populations and the range of GFRs studied, and by methodological differences in reference and test methodologies.
Twenty years ago the NKF-K/DOQI suggested a P30 minimal performance target of 90% for GFR equations, a position that was later adopted by KDIGO (2012). 27,102 Many equations, particularly creatinine-based equations, have not achieved this level of performance, including in their original published descriptions. 32,44,47 While the MDRD equation achieved a P30 of 92% in the stage 3 CKD GFR range in its development cohort,38 this was not sustained in a validation data set. 32
Encouragingly, in the present study, all of the primary equations achieved P30 > 89%. In relation to the primary study question of which equation is the most accurate in this population, the MDRD, CKD-EPIcreatinine and CKD-EPIcystatin equations provide similar assessments of mGFR. The CKD-EPIcreatinine equation is the NICE-endorsed equation. We found no evidence of the superiority of this equation over the MDRD equation, which it supplanted in the NICE 2014 guideline. 22 These observations pertain only to performance in a predominantly stage 3 CKD cohort and other data would have informed the NICE decision at that time, for example the reported increasing negative bias and poorer precision of the MDRD equation at higher levels of GFR. We also observed no benefit of using cystatin C in isolation in an equation. However, the CKD-EPIcreatinine-cystatin equation demonstrated somewhat superior performance to the other three equations with a P30 point estimate of 94.9% and CI that did not overlap 90%. Performance of the CKD-EPIcreatinine-cystatin equation was also superior to that of all of the secondary study equations that did not incorporate cystatin C.
Accuracy of more recently described glomerular filtration rate-estimating equations
More recently published creatinine-based equations generally had similar slight negative bias compared to mGFR, with CIs overlapping those of the main study equations and P30 values > 89%. The exceptions to this were CKD-EPI(2021)creatinine (zero bias, P30 88.0%), the BIS1creatinine equation (slight positive bias 1.0 ml/minute/1.73 m2, P30 85.9%) and the LMRcreatinine equation, which performed poorly in this study (negative bias 6.2 ml/minute/1.73 m2, P30 84.2%). More recently published cystatin-based and combined creatinine–cystatin C-based equations were negatively biased compared to mGFR. Equations that incorporated both creatinine and cystatin C demonstrated improved performance, with the CKD-EPI(2021)creatinine-cystatin, BIS2creatinine-cystatin and FAScreatinine-cystatin equations achieving P30 values equivalent to those of the CKD-EPIcreatinine-cystatin equation. However, we found no evidence to suggest that any of the newer equations were superior to the CKD-EPIcreatinine-cystatin equation in this setting.
Our observations and conclusions are limited to a predominantly stage 3 CKD adult cohort. Furthermore, there may be good reasons for recommending other equations in specific situations and beyond the sole consideration of accuracy performance. The BIS1 (creatinine-based) and BIS2 (creatinine and cystatin C-based) equations were developed in a predominantly non-CKD community-dwelling population of older (> 70 years) adults. The blood creatinine concentration/GFR relationship is often different in older compared to younger adults, potentially leading to inaccuracies in GFR estimation when equations derived in younger adults are applied to older people. The authors observed low bias for the BIS2 equation and recommend the use of this equation, in preference to the CKD-EPI equations, in older adults. 42 The LMR equation53 is a creatinine-based equation that has also demonstrated good performance in older Caucasian adults. 46 The CAPA equation was developed in northern European and Japanese cohorts. It is solely cystatin C-based and no adjustments are required for race or gender. 43 A recognised limitation of many equations, including the CKD-EPI and BIS equations, has been their lack of applicability across all age groups and lack of continuity as individuals cross age thresholds (e.g. from adolescence to adulthood). The FAScreatinine44 and FAScreatinine-cystatin equations45 address this issue. Observed creatinine or cystatin C concentrations are utilised in these equations as ratios to the age- and gender-matched median concentrations, obtained from large reference interval studies. The EKFC equation extended this general approach but also introduced different exponential coefficients depending on whether the creatinine concentration was above or below the age and gender-related median. 47 This produced an equation with good accuracy and precision compared to earlier equations, although validation was only undertaken in Caucasian populations. As a general consideration, equations that utilise only cystatin C are likely to be less influenced by racial differences or recent ingestion of meat. 119 In 2021, amidst growing concerns about the use of race adjustment in GFR-estimating equations, new CKD-EPI equations that omitted race were developed. This issue is discussed later.
Assessing the accuracy of glomerular filtration rate estimation: P30 versus P15
The P30 is the most commonly used metric to measure the accuracy of GFR equations, yet it was defined in the absence of clinical and statistical rationale. 120 The arbitrary choice of a 30% margin is actually rather broad and can span multiple GFR categories, especially at higher GFR values. Other stricter criteria such as the P5, P10 and P15 (where 5, 10 and 15 represent the acceptable percentage margin of error between estimated and mGFR) provide an alternative to the P30 and NICE advise that the P5 and P15 are also useful for clinical decision-making. 59 Calculation of the P15 was not originally specified in the statistical analysis plan (and the sample size calculation did not consider the P15), but the decision was made to include it to reflect the current view from NICE.
The P15 values of different equations generally fell in similar rank order to P30 values with some exceptions {e.g. while both the original and 2021 revised CKD-EPIcreatinine-cystatin equations achieved P30 values of 94.9%, the P15 value of the remodelled 2021 equation was superior to that of the original equation [66.1% (63.3 to 68.8) compared to 60.4% (57.5 to 63.2)]}. All of the combined creatinine–cystatin equations achieved P15 values > 60%, whereas all of the creatinine-only equations achieved P15 values < 58%.
The benchmark value for the P30 is often quoted as 90%, but there does not appear to be any standard or published aspiration in terms of what the P15 should be. Porrini et al. however state that to be clinically meaningful, a GFR-estimating equation should achieve a P10 of 90%120 – a much stricter criterion than the same 90% threshold for the P30. The P15 values we observed were all much lower than 90% illustrating that current equations are unlikely to meet this target.
While we would agree that the P30 range is rather broad for clinical decision-making, it is questionable how much further progress can be made in improving on this situation using current approaches. In addition to issues relating to the accuracy of creatinine measurement, and those which can be compensated for in estimating equations (e.g. age, gender), there are a large number of non-glomerular influences on serum creatinine concentration including tubular secretion, extrarenal elimination, differences in skeletal muscle mass,121 dietary intake119,122 and differences in creatinine production rate which may be genetically determined. 123 Although non-glomerular influences on serum cystatin C concentration are generally considered less important than those of creatinine, cystatin C concentration has been reported to be affected by factors such as lean mass,124 glucocorticoid treatment,125 smoking status126,127 and also genetic influences. 128 Some progress may be made by the use of multimarker approaches. The addition of beta-trace protein and beta-2 microglobulin did not lead to incremental improvements in GFR estimation in one study,129 but in the future, the use of multimarker metabolite profiling may hold promise. 130 However, an issue which will affect the upper limits of accuracy of any approach is the biological and analytical variability of the reference mGFR procedure itself (see Study of intraindividual biological variation).
The impact of calibration on cystatin C and glomerular filtration rate estimation
Using the Abbott cystatin C assay we observed significant negative bias of CKD-EPIcystatin and CKD-EPIcreatinine-cystatin GFR-estimating equations. This was unexpected based on earlier data from members of the study group. 52 Cystatin C assays are calibrated against an international reference preparation (ERM-DA471/IFCC) developed with the aim of achieving improved agreement between assays from different manufacturers. 51 ERM-DA471/IFCC was originally verified as being commutable for use in the Abbott immunoassay. 51 However, during the course of this study, evidence emerged of continuing discordance between different manufacturers methods. 131 A report in 2017 described a significant positive bias of some 16–20% of the Abbott cystatin C assay, resulting in significantly negatively biased GFR estimates. 101 Re-analysis of some historical stored samples in the present study supported this report. Communication with Abbott Diagnostics confirmed that they had seen a shift in their calibration but that the assay remained within their manufacturing tolerance.
We further explored this issue through a laboratory recovery study, which confirmed an average over-recovery of 9.1% in the Abbott cystatin C assay, sufficient to cause negative bias of GFR estimates of the order we observed (see Table 5 and Figure 5). We also undertook a comparison study against the Siemens BN Prospec assay, which further supported a positive bias of the Abbott assay. In a recent study, the Siemens method on the BN Prospec analyser was the only commercially available assay achieving prespecified performance criteria in relation to bias and precision. 101 After careful consideration, we decided that our Abbott cystatin C data should be recalibrated against the Siemens BN Prospec assay, to ensure that our study data represented the performance of cystatin C-based GFR-estimating equations under internationally standardised conditions. Following recalibration, the negative bias of the CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations was significantly improved and indistinguishable from that of the MDRD and CKD-EPIcreatinine equations.
The positive bias of the Abbott cystatin C assay illustrates the difficulty when transferring reference calibrator values to field methods. The issues are particularly complex with immunoassay where the major ‘reagent’ is antibody-based. There are multiple potential sources of variation. For example, there may be subtle differences in the antigens that different manufacturers use to inoculate the antibody-producing animals. The animal species used to make the antibodies may also influence the speed and affinity of the reaction with the antigen. Consequently, antibodies used by different manufacturers may have differing selectivity, affinity and avidity for cystatin C in the sample, and they may be differentially affected by matrix effects present in human serum samples (other proteins, salt, phospholipids, complement, drugs and other substances), and possibly also by genetic variation. 128 This issue is important: there is an assumption that the introduction of the international standard for cystatin C has resulted in globally aligned assays. Although there is evidence that between-method agreement has improved following the introduction of the standard, evidence from this study and others indicates that further efforts are required to improve assay comparability in this area. 101,131 Additionally, in contrast to the situation with creatinine, there is currently no certified reference measurement procedure for cystatin C to definitively establish target values for the reference material. 132
Attention to accuracy of standardisation of cystatin C assays has important clinical and research implications. This was illustrated in a UK primary care study of older patients with stage 3 CKD, where the use of the Abbott cystatin C assay classified a greater proportion as having more advanced CKD than the use of GFRcreatinine, with associated increased monitoring costs, leading the authors to refute the recommendation of the NICE 2014 guideline in relation to use of cystatin C. 133
Influence of body surface area adjustment method on accuracy (P30) of glomerular filtration rate-estimating equations: Haycock equation compared to the Du Bois equation
To adjust GFR for differences in body size, mGFR is commonly adjusted for BSA, with a population average BSA value of 1.73 m2 being used. 134 The Du Bois equation was first reported in 1916 and enabled estimation of BSA from height and weight of an individual based on a laboratory comparison with direct measurements of BSA in a relatively small number (n = 9) of individuals. 93 The Haycock equation was developed in a larger cohort of individuals but still only included 19 adult subjects. 92 The method involved reducing the limbs and trunk to a series of cylinders, or a sphere in the case of the head, measuring the length of the cylinders and calculating and summing surface area from these measurements. The BSA equation was then derived using multiple regression analysis to solve BSA from height and weight measurements.
While many studies in this field have used the Du Bois equation to adjust their reference mGFR, including the MDRD equation,31 there is no consensus on this point. Indeed in some publications, including some of those used in the development data set of the CKD-EPI equation, the BSA adjustment method is not described. 60,135 The Haycock equation is the preferred method of the British Nuclear Medicine Society when adjusting GFR for BSA. 100 Other BSA equations have also been described. 136 Estimated GFR values are already adjusted for BSA because BSA was taken into account when the equations were originally derived using regression modelling against measured BSA-adjusted GFR.
In the present study, all eGFR equations were equally accurate in terms of P30 whether the mGFR was adjusted using the Du Bois or the Haycock equation. This accords with other reports. 136,137 The Haycock equation will give higher BSA results, and consequently lower adjusted GFR results, in individuals of higher BMI. For example, in an individual weighing 100 kg of height 1.75 m, the Haycock BSA estimate will be 3.9% higher than Du Bois. Our cohort had a median BMI of 29.0, with 43% of individuals having BMI > 30. Consequently, the Haycock BSA was slightly higher than the Du Bois estimate (2.02 vs. 1.96 m2), with slightly lower BSA-adjusted mGFR (Table 2). The impact of using Haycock-adjusted mGFR would be to reduce the negative bias of all the GFR-estimating equations by approximately 1.4 ml/minute/1.73 m2 (see Appendix 1, Table 41).
Although the validity of GFR adjustment for BSA has been questioned,134 the practice remains widespread. Our data indicate that the difference between Du Bois and Haycock BSA GFR adjustments is small. Nevertheless, the adjustment method does have an impact which is larger in individuals with higher BMI and will contribute to between-study comparisons of GFR equation performance. It would seem sensible for the scientific and clinical community to reach an agreement on the adjustment method that should be used and for authors in this field to ensure such information is available in published reports.
Impact of creatinine method on accuracy of glomerular filtration rate-estimating equations: enzymatic compared to isotope dilution mass spectrometry method
An enzymatic creatinine assay was used throughout the study. Such assays are less susceptible to interferences than older colorimetric (Jaffe) methods, although are not immune to such effects. Accuracy of the main study equations did not differ in terms of P30 irrespective of whether GFR was estimated using enzymatic or ID-MS creatinine results. However, regression and bias plot analysis demonstrated that enzymatic creatinine results were slightly higher than ID-MS results, with a mean positive bias of 4.7 μmol/l that was fairly consistent across the concentration range of the study cohort. Between-method differences are not unexpected, and even within-method differences across different laboratories. The consistency of the bias across the concentration range suggests a sample matrix interference in the enzymatic assay as opposed to a standardisation issue. The enzymatic assay demonstrated excellent performance in external quality assessment schemes throughout the study period, although it is widely appreciated that external quality assessment materials do not always reflect performance in clinical samples (i.e. the test materials are not necessarily commutable). According to recommendations of the National Kidney Disease Education Program, the low imprecision of the assay (analytical between-day imprecision < 0.9%) was consistent with optimal assay performance in relation to biological variation and the bias in relation to the reference method (ID-MS) was acceptable. 39
Nevertheless, it is clearly the case that substitution of ID-MS creatinine values for the enzymatic ones would, on average, have increased GFR estimates and reduced the negative bias we observed against mGFR. The purpose of our study was to evaluate the performance of GFR equations using analytical methods representing typical clinical laboratory conditions. We therefore chose not to use ID-MS creatinine results for our analyses. It is the case however, as with cystatin C, that the accuracy of commercial creatinine methods remains a critical issue when considering the accuracy of GFR-estimating equations.
Influence of baseline diabetes and albuminuria, age, gender, body mass index, measured glomerular filtration rate level and ethnicity (Caucasian, South Asian and African-Caribbean), on accuracy of glomerular filtration rate-estimating equations
In unadjusted analyses, accuracy of the main study equations at baseline did not change significantly across any of the characteristics studied (i.e. age, gender, BMI, kidney function, ethnic origin and in the presence and absence of diabetes). Many studies have described differences in the performance of GFR-estimating equations across different characteristics (e.g. age,138,139 gender,138 level of GFR,32,138,140,141 BMI138,139). While we did not observe any of these described effects it should be noted that our study was not powered to address these issues, we only undertook unadjusted analyses with P30 as a fairly crude overall indicator of equation performance, and our cohort was, by design, restricted to a relatively narrow level of kidney function.
The performance of GFR-estimating equations in non-Caucasian ethnic groups has always been an area of debate. As discussed earlier, this interest has heightened recently with the recommendation by the National Kidney Foundation-American Society of Nephrology67 that black race adjustment factors should no longer be used and by the publication of revised CKD-EPI equations that were remodelled without the inclusion of a black race adjustment factor. 48 Similarly, the 2021 revision of the NICE CKD guideline no longer includes a recommendation to adjust for black ethnicity. 59
One of the aims of the present study was to evaluate the performance of GFR-estimating equations in South Asian and African-Caribbean ethnic groups living in the UK. Unfortunately, the study under-recruited from these populations and any conclusions we can draw are limited by the small sample size of these groups (see Table 8). Overall, however, we found no evidence of a difference in the accuracy of the main study equations across the three ethnic groups. Simple removal of the African-Caribbean factor did not alter the performance of the MDRD, CKD-EPI creatinine or CKD-EPIcreatinine-cystatin equations in the overall cohort (see Table 5), but this is predictable given that African-Caribbean participants represented only 5.1% of the overall cohort. However, removal of the African-Caribbean adjustment factor from the MDRD and CKD-EPIcreatinine equations, as proposed by NICE,59 did lead to reduced point estimates of P30/accuracy amongst African-Caribbean individuals. This decrease only achieved significance for the MDRD equation, which is probably explained by the heavier weighting of the adjustment factor in this equation (i.e. MDRD 1.212; CKD-EPIcreatinine 1.159; CKD-EPIcreatinine-cystatin 1.08). This finding is at odds with a large (n = 1888), retrospective, UK-based study using 51Cr-EDTA mGFR as the reference test compared to MDRD and CKD-EPIcreatinine-based eGFR. 142 Amongst the black participants (n = 266), MDRD and CKD-EPIcreatinine estimates of GFR demonstrated significant positive median bias (16.0 and 20.0 ml/minute/1.73 m2, respectively), which was ameliorated by removal of the ethnic adjustment factors (bias 1.0 and 7.0 ml/minute/1.73 m2 for MDRD and CKD-EPIcreatinine, respectively). Additionally, the study also observed significant positive bias of MDRD and CKD-EPIcreatinine-based eGFR amongst the white participants (n = 1622, 12.0 and 14.0 ml/minute/1.73 m2, respectively) and poor accuracy overall in black and white participants (P30 < 78% in all cases). 142 Demographic, methodological and clinical differences between this cohort and ours make direct comparison difficult. As conceded by the authors, one potential source of this bias may have been that many participants had their GFR measured in preparation for chemotherapy as treatment for (predominantly haematological) cancer and may therefore have had lower than expected muscle mass. 143 While the removal of inflationary ethnic adjustment factors will inevitably lower estimates of GFR, further research is required to establish whether this improves or worsens overall accuracy in black people.
There are theoretical reasons why simple removal of the African-Caribbean factor from the 2009 CKD-EPI equations may be inappropriate, specifically that the equations were developed using regression modelling that included race as a factor. The CKD-EPI consortium observed a worsening of bias of eGFR amongst black individuals using the original 2009 equation as a result of racial factor removal from the CKD-EPIcreatinine equation, from a positive bias of 3.7 ml/minute/1.73 m2 to a negative bias of 7.1 ml/minute/1.73 m2. The bias was reduced using a new CKD-EPI(2021)creatinine equation developed using regression modelling that had included only age, gender and serum creatinine concentration, but not race, as variables. However, the CKD-EPI(2021)creatinine equation did not perform as well as the original equation in non-black individuals. The equation that incorporated both creatinine and cystatin C [CKD-EPI(2021)creatinine-cystatin] was less biased and more accurate amongst black individuals than the original CKD-EPIcreatinine-cystatin equation but had the reverse effects amongst non-black individuals. Overall differences in accuracy between black and non-black individuals were reduced using the CKD-EPI(2021)creatinine-cystatin equation compared to the original CKD-EPIcreatinine-cystatin equation, equations with creatinine alone and the CKD-EPIcystatin equation. 48 A report published simultaneously by the Chronic Renal Insufficiency Cohort Study investigators reached broadly similar conclusions. 144 In the present study, the CKD-EPI(2021)creatinine and CKD-EPIcreatinine-cystatin equations demonstrated equivalent performance compared to their respective original CKD-EPI equations in the overall cohort (see Table 5) and amongst Caucasians and South Asians. However, the CKD-EPI(2021)creatinine equation had a reduced point estimate of accuracy amongst African-Caribbean individuals.
Our data represent one of the first evaluations of the CKD-EPI(2021) equations in a UK population. While further evaluation across a broader spectrum of GFR values is required, the data presented here would not preclude future use of the CKD-EPI(2021) equations amongst the Caucasian UK population, but further validation in ethnic minority groups is still required. Simple removal of the racial adjustment factors from the original CKD-EPI equations, as (indirectly) proposed by NICE,59 has minimal impact on performance in the population overall, but further research is required to reassure that this does not have a deleterious effect on performance in African-Caribbean individuals.
Concordance of glomerular filtration rate-estimating equations with measured glomerular filtration rate within a tolerance of 3 ml/minute/1.73 m2/year or five percentage points over 3 years
The ability of estimating equations to track mGFR over 3 years was assessed by analysing agreement in two separate analyses (estimated change per year within 3 ml/minute/1.73 m2 of mGFR change per year and change per year for eGFR within 5 percentage points of the % change in mGFR per year). To clarify, this analysis compared the slopes of change for mGFR and eGFR and did not compare absolute values. Agreement was considered present when the eGFR slope lay within ±3 ml/minute/1.73 m2/years (or ± 5%/years) of the slope of change for mGFR. In both situations, the main study equations achieved > 70% agreement with mGFR. We observed that the CKD-EPIcreatinine-cystatin equation generally had better concordance with mGFR than the other three primary study equations. This difference was significant compared to all three other equations when considering concordance within a change of ±3 ml/minute/1.73 m2/years and compared to the CKD-EPIcreatinine equation when considering change within ± 5%/years of mGFR. However, CIs overlapped in all cases. Performance of the CKD-EPIcreatinine equation was inferior to that of the MDRD and CKD-EPIcreatinine-cystatin equations but not compared to the CKD-EPIcystatin equation.
In the above analyses, the observed changes in mGFR and eGFR per year were used (i.e. final mGFR/eGFR minus initial mGFR/eGFR to calculate change per year in either ml/minute/1.73 m2 and for percentage change using the calculated change per year in GFR and comparing this to the initial GFR measurement to generate a percentage change per year). Additional sensitivity analyses were undertaken estimating the change per year and percentage change per year using all the data points available in the study (up to three mGFR and seven eGFR time points per participant) to enable analyses using two different regression modelling approaches. The approaches were: (1) linear regression models to estimate the slope for each individual for the eGFR measurements and observed differences in mGFR and (2) linear regression models to estimate the slope for each individual for the eGFR measurements and a single multilevel model allowing individual predictions of mGFR slopes. Both these approaches, using the change in eGFR calculated from linear regression and using the change in mGFR calculated using a multilevel model, suggested the changes in eGFRs were within the specified tolerances (3 units and 5%) for more participants than when using only the observed data to calculate change over time, for all main study equations. For example, for the CKD-EPIcreatinine equation, the main analysis for tolerance within ±3 ml/minute/1.73 m2/years of change demonstrated 73.1% concordance with mGFR; in sensitivity analyses 1 and 2, this increased to 76.9% and 80.5%, respectively. In these sensitivity analyses, the CKD-EPIcreatinine-cystatin equation again consistently had the highest point estimates compared to the other equations, although CIs overlapped in most cases. While the modelling methods used in these sensitivity analyses allowed data at all time points to be used, they also removed the variability in the measurements. This would not be observable in practice, hence the apparent superior performance of all estimating equations in these analyses compared to the main analysis using just the observed changes over time. The approaches using interim data points with statistical methods to describe the change over time, as performed by Padala et al. ,84 give a more accurate estimate of the true change in estimated and mGFR over time, but this does not reflect the observed changes that would be seen in practice.
Of the more recent study equations, when considering concordance within ±3 ml/minute/1.73 m2/years or ± 5%/years of mGFR, those equations that included both creatinine and cystatin C [CKD-EPI(2021)creatinine-cystatin, BIS2creatinine-cystatin, FAScreatinine-cystatin] achieved higher point estimates of agreement than their corresponding creatinine-only equations [CKD-EPI(2021)creatinine, BIS1creatinine, FAScreatinine respectively], although CIs overlapped in all cases. Of these more recent study equations, BIS2creatinine-cystatin performed best, but with CIs overlapping with CKD-EPIcreatinine-cystatin.
The limits of ± 3 ml/minute/1.73 m2/years (or ± 5%/years) were selected based on the earlier study of Padala et al. where the authors considered that such errors would be considered large in clinical terms. 84 Padala et al. concluded that CKD-EPIcreatinine eGFR accurately reflected changes in mGFR over time, with only 15.3% of their participants having an error that exceeded ± 3 ml/minute/1.73 m2/years, similar to the results in the present study. However, given that the overall median change in mGFR in the present study was −1.5 ml/minute/1.73 m2/years (i.e. from 48.1 to 43.6 ml/minute/1.73 m2 over 3 years), with similar magnitude overall changes in eGFRs, concordance within a change of ± 3 ml/minute/1.73 m2/years (or ± 5%/years) represents a fairly wide degree of tolerance. Even given biological and analytical variability, the majority of patients would have been unlikely to show excursions of eGFR outside of these limits. Only 30.6% of the study population showed a change in GFR of > 10 ml/minute/1.73 m2 (approximately 3.3 ml/minute/1.73 m2/year) over the study period. In other words, achievement of > 70% concordance, or higher, depending on the statistical approach used, is not altogether surprising and may not represent a strenuous test of the ability of GFR-estimating equations to monitor change. Similar considerations would presumably apply to the study of Padala et al., where the average rate of change was −2.25 ml/minute/1.73 m2/year. It should also be considered, given the median baseline mGFR in our cohort was 48.1 ml/minute/1.73 m2, that tolerance limits of ± 3 ml/minute/1.73 m2/years or ± 5%/years equate very closely (and would be equivalent at a GFR of 60 ml/minute/1.73 m2). This is reflected in the similar performance of all of the equations against these two limits (e.g. 75.4% or 74.9% concordance respectively for MDRD eGFR): in retrospect, use of quantitatively similar thresholds has added little value to the data.
There have been earlier longitudinal studies of the ability of creatinine-based eGFR to track mGFR over time. 145–148 A consistent feature of all studies has been that eGFR underestimated the decline in mGFR. In a study comparable to ours in terms of duration (minimum 2.6 years), GFR range of the study cohort (25–55 ml/minute/1.73 m2) and estimating equation used (MDRD), Xie et al. observed eGFR to underestimate the slope of iothalamate mGFR decline by 28%, with 42% of individuals having an eGFR slope that differed from the mGFR slope by ≥ 2 ml/minute/1.73 m2, similar to the discordance observed in the present study. 148 The annual change in mGFR seen in the present cohort was smaller than that observed by Xie et al. (−1.5 vs. −3.9 ml/minute/1.73 m2/years), but we also observed that changes in eGFR were smaller than changes in mGFR (MDRD −1.0, CKD-EPIcreatinine −1.2, CKD-EPIcystatin −1.1, and CKD-EPIcreatinine-cystatin −0.9 ml/minute/1.73 m2/years). Possible reasons for this are discussed in Ability of glomerular filtration rate-estimating equations to detect change in measured glomerular filtration rate over 3 years. In keeping with Xie et al.,148 we found no differences in baseline characteristics that could predict whether individual eGFRs would be discordant with mGFR. The annual underestimation of change we observed was small but could potentially have significant clinical implications where eGFR measurements are being used to plan future renal care.
Most studies have focused on the value of creatinine-based GFR estimates when monitoring GFR over time. A relatively small (n = 20) early study suggested that cystatin C may have advantages over creatinine in this respect. 149 However, studies of patients with type 1 diabetes (n = 977) and of patients with human immunodeficiency virus infection (n = 184) found no additional benefit of using cystatin-containing CKD-EPI equations compared to CKD-EPIcreatinine when monitoring GFR over time. 150,151 Our data concur with these latter reports. While there was some evidence of improved concordance for the CKD-EPIcreatinine-cystatin equation within the tolerance limits studied, the underestimation of mGFR slope certainly appears no better with this equation. Indeed, slope estimates derived from random coefficients models in the substudy [see To estimate and model disease progression (decline in glomerular filtration rate or increase in albumin-to-creatinine ratio) and differences in progression between ethnic groups (Caucasian, South Asian and African-Caribbean), and baseline diabetes and albuminuria status and other potential risk factors] show reduced slope estimates (i.e. less steep decline in GFR over time) for cystatin-containing equations compared to mGFR and creatinine-based GFR estimates.
Ability of glomerular filtration rate-estimating equations to detect change in measured glomerular filtration rate over 3 years
The performance characteristics (sensitivity, specificity, NPV, PPV) of GFR-estimating equations were studied in relation to their ability to detect several different thresholds of change in mGFR over 3 years: (1) > 10 ml/minute/1.73 m2; (2) > RCV (a > 21.5% increase or a > 17.7% decrease); (3) > 25% change; and (4) > 25% change in combination with a change in disease stage. The rationale for studying these thresholds is described earlier (see Progression of kidney disease and Which glomerular filtration rate-estimating equation most accurately detects change in glomerular filtration rate?).
A change in GFR > 10 ml/minute/1.73 m2 was observed in 30.6% of the cohort. The sensitivity (% of patients with a positive result from mGFR that were also positive using the estimating equation) was ≤ 50% in all cases, whether change in GFR or decline in GFR only was being considered. The specificity (% of patients with a negative result from mGFR that were also negative using the estimating equation) exceeded 79% for all primary study equations and was improved (point estimates > 86%) when only a decline in GFR was considered.
Consequently, GFR-estimating equations have relatively poor PPVs for identifying change in GFR exceeding 10 ml/minute/1.73 m2 (TPs), but good NPVs where GFR change has not exceeded 10 ml/minute/1.73 m2 [true negatives (TNs)], particularly when only decline in GFR is being considered.
Similar equation performance in terms of sensitivity for detecting both overall change and decline only were observed when other threshold changes in mGFR were considered, either changes in excess of the RCV (> + 21.5%/−17.7%) or the larger change > 25% overall or > 25% decline only. In our cohort, changes in excess of the RCV or of 10 ml/minute/1.73 m2 are numerically similar thresholds, and this is illustrated by the similar sensitivities and specificities of these two criteria.
In all scenarios, specificity was good, particularly for the larger > 25% change in GFR studied and when considering a decline in GFR only, where point estimates in excess of 90% were observed. Combining 25% change in GFR with a change in disease category, as recommended by KDIGO when defining progression,27 made little difference to the point estimates of sensitivity, but the more stringent criteria for positivity did increase the specificity of all equations, and NPVs were in excess of 90%.
There was no clear difference in sensitivity or specificity (overlapping CIs) between the four main study equations at all thresholds studied. Sensitivity and specificity estimates of newer GFR-estimating equations had similar point estimates to the main study equations. For all equations and all metrics, there was no clear evidence of improved performance of cystatin-containing equations compared to their matched creatinine-only equation.
In relation to detection of disease progression, the performance of estimating equations is poor and may appear somewhat at odds with the high concordance noted earlier between estimated and mGFR change when considering annual change within 3 ml/minute/1.73 m2 or 5% of mGFR. The earlier analysis assessed whether the eGFR change was within a certain tolerance (± 3 ml/minute/1.73 m2/years or ± 5%/years) of the mGFR change. However, as noted above, the majority of individuals did not show large excursions of GFR from baseline. When assessing the sensitivity and specificity of GFR-estimating equations to detect change, changes in both estimated and mGFR are converted to binary measures (either positive or negative) with no tolerance (i.e. mGFR and eGFR either show the difference of the magnitude investigated or do not). Sensitivity estimates are based only on the minority (e.g. 30.6% or 21.4% for the ≥ 10 ml/minute/1.73 m2 or > 25% criteria respectively) of individuals showing a larger change in mGFR that also show a larger change in eGFR, rather than studying the whole group. Conversely, specificity estimates will be based on the majority of individuals who did not show a large change in mGFR that also did not show a large change in eGFR.
Definitions of progressive kidney disease vary (see Progression of kidney disease). It is important to consider whether, in the clinical context, estimates of GFR allow for detection of progressive kidney disease over a useful time frame. Our data, based on change detection over 3 years, suggest that reported ‘normal’ mean age-related decline in GFR of 1 ml/minute/1.73 m2/years,152 or reported rates of decline of between 2.8 and 3.6 ml/minute/1.73 m2/years in older adults with diabetes and moderate CKD69 would not be reliably detected by eGFR measurement. It is possible that reported mean GFR declines of 7.0 ml/minute/1.73 m2/year amongst proteinuric (> 1 g/24 hours) patients would be detected by a programme of annual monitoring of individual patient’s GFR. 70 NICE have recently defined accelerated progression as a sustained fall in GFR in excess of 25% and a progression in disease category [e.g. G3a (GFR 45–59 ml/minute/1.73 m2) to G3b (GFR 30–44 ml/minute/1.73 m2)] in a 12-month period, or a sustained decline in GFR of 15 ml/minute/1.73 m2 over a 12-month period. 59 Of concern, assuming our data gathered over 3 years are reflective of the ability of eGFR to detect annual change, monitoring of GFR would not reliably permit detection of accelerated progression by this definition. While the NICE accelerated progression criteria concur broadly with our biological variation estimates as being consistent with true change (see Study of intraindividual biological variation), monitoring patients with annual eGFR would detect such changes only approximately half of the time. Part of this limitation will be due to the poor accuracy of GFR equations: as noted earlier, at best, current equations only achieve a P30 of around 90%, and the P30 itself is a rather broad metric of accuracy. It should also be considered that the reference mGFR test has its own intrinsic biological and analytical variability, which is in fact greater than that of GFR-estimating equations (see Study of intraindividual biological variation).
In terms of progression, there are theoretical reasons why one might consider that creatinine-based equations will be suboptimal at detecting change, in particular decline, in GFR. Changes in tubular secretion and extrarenal elimination of creatinine will increase as renal disease progresses, potentially blunting the response of eGFR to declining kidney function. 121 Creatinine is a product of muscle creatine metabolism, being continuously formed at a rate of 1.6–1.7% of creatine mass per day. Creatine is synthesised in a two-part process. The first step, the synthesis of guanidinoacetate, occurs in the kidney, implying that as renal functional mass declines (i.e. GFR declines) the production rate of guanidinoacetate (and creatinine) will fall. 153 Furthermore, as kidney disease progresses there is a tendency for muscle mass to decrease with a high prevalence of sarcopenia, itself possibly driven, in part, by reduced synthesis of creatine and resulting in a change in the usual plasma creatinine–GFR relationship. However, given that plasma cystatin C concentration is considered to be less dependent on muscle mass, it is disappointing that equations incorporating cystatin C did not demonstrate improved sensitivity. Modelling within the substudy demonstrated a decline in progression slope over time for the CKD-EPIcystatin equation (see Substudy of disease progression) which could have countered the ability to detect change.
Substudy of disease progression
Modelling of disease progression in the substudy
Recruitment to the substudy fell short of target, probably partly due to the more intensive nature of the study design, requiring four iohexol reference GFR procedures in total. Results should be interpreted cautiously as estimates derived in small subgroups are more sensitive to influence by extreme values, in particular ethnicity group and smoking status. There were only 35 African-Caribbean participants and 30 South Asian participants, and only 23 current smokers in the evaluable population.
There was evidence of collinearity among some of the covariates, which should be considered when interpreting the results. The covariates were selected based on known or purported associations with kidney disease progression observed in previous studies (e.g. ethnicity,57,58 diabetes,69 proteinuria70). All of the unadjusted covariates were associated with GFR and/or ACR intercept or progression in single covariate regression models with the exception of vascular disease.
The final multiple regression random coefficients models showed a strong association between albuminuria status and rate of progression in mGFR and CKD-EPIcreatinine eGFR. In each case, those with albuminuria had faster progression (steeper decline), consistent with the body of evidence in this area. 70,154
Higher baseline values of mGFR were associated with a faster rate of progression for mGFR. A similar observation has been made by others. 155 This effect was not seen for CKD-EPIcreatinine eGFR. There is some evidence to support the finding of higher baseline GFR being associated with steeper GFR decline, possibly reflecting hyperfiltration in some individuals even in the presence of normal or slightly reduced overall GFR (i.e. hyperfiltration in remaining nephrons). 156 A further confounding influence here could be the nature of the primary renal disease: it is known that different primary renal diseases may progress at different rates. For example, on average, patients with autosomal dominant polycystic kidney disease progress at a significantly higher rate, as to a lesser extent do patients with diabetic nephropathy, than those with other primary causes of kidney disease. 155 Primary cause of kidney disease was not recorded in the present study. In the case of the CKD-EPIcystatin eGFR model, although there was still progression overall, higher baseline values were associated with slower progression of CKD-EPIcystatin eGFR. It is possible that this may have been influenced by the decreased progression slope, and perhaps by the reduction in bias over time compared to the mGFR, that was observed for CKD-EPIcystatin (see below).
There was some evidence of an ethnicity group association with progression for mGFR, CKD-EPIcreatinine and ACR. African-Caribbean ethnicity increased the estimate of the progression slope (slower decline) and South Asian ethnicity decreased the estimate of the progression slope (faster decline) for mGFR and CKD-EPIcreatinine GFR, respectively. For mGFR, sensitivity analysis excluding one extreme value in the African-Caribbean group reduced this association. Both South Asian and African-Caribbean ethnicity increased the estimates of progression slope (faster progression) for ACR. Overall, there was no evidence to suggest African-Caribbean ethnicity, but some evidence to suggest South Asian ethnicity, was associated with increased decline in GFR, in keeping with some,56–58 but not all 55 reports. However, as noted above, recruitment of ethnic minority participants in particular to the substudy fell short of target, thereby limiting the strength of any conclusions that can be drawn.
Diabetes status was strongly associated with progression for CKD-EPIcreatinine eGFR but not for the other measures, with those with diabetes exhibiting slower GFR decline as estimated by the CKD-EPIcreatinine equation. As discussed earlier (see Ability of glomerular filtration rate-estimating equations to detect change in measured glomerular filtration rate over 3 years), underestimation of decline in creatinine-based eGFR has been reported previously. 145–148
There were four drug types (loop diuretic, CCB, A2RB and beta-blocker) that were associated with progression, as measured by at least one of the mGFR, eGFR or ACR. The group sizes for each of these types were reasonable, the smallest subgroup was for loop diuretics with just under one-fifth of evaluable participants prescribed this medication (n = 45, 18.8%). Participants taking CCBs had faster progression based on ACR (steeper incline). There is evidence that the use of CCBs, in particular L-type CCBs (e.g. amlodipine, nifedipine, verapamil, diltiazem), may increase albuminuria due to selective vasodilation of afferent arterioles in the kidney. 157 Faster progression in eGFRs (CKD-EPIcreatinine and CKD-EPIcystatin) was seen for those prescribed beta-blockers or A2RB. It should be considered that the effect of specific types of medication on progression may be more related to the population prescribed the medication than the effect of the medicine itself, and estimates should be interpreted in this way.
Random coefficient regression models were also fitted to the differences between the eGFRs and mGFRs (bias), without covariates. These models of the bias suggested an incline in slope over time for CKD-EPIcystatin and CKD-EPIcreatinine-cystatin, eGFRs were lower than mGFR and the model suggests that the biases became smaller over time. This was not evident for the other eGFRs.
Findings from the substudy warrant external validation in a large sample to further define the predictive model.
Application of substudy models to the full data set
The full data set is larger and hence contains more covariate information compared to the substudy, although with fewer measurement times, progression is less well-defined. To check consistency of inferences across the data sets the final models from the substudy were fitted to the full data set.
The model estimates from the combined data set were very similar to the estimates from the substudy data, supporting the covariate models, with a few exceptions.
African-Caribbean ethnicity and progression for mGFR were significantly associated, with a slower decline seen in African-Caribbean as observed in the substudy. This association persisted even in a sensitivity analysis excluding an outlying participant.
An association between smoking status and CKD-EPIcystatin, but not mGFR or CKD-EPIcreatinine, was observed. Using the substudy data only current smoking lowered the intercept for CKD-EPIcystatin GFR by 1.5 ml/minute/1.73 m2; using the full study data set being an ex-smoker lowered the intercept for CKD-EPIcystatin by 0.5 ml/minute/1.73 m2. This difference may be due to the increased number of ex-smokers in the full data set (n = 367), compared to the number of current smokers (n = 70). As discussed earlier, this is consistent with earlier multivariable analyses demonstrating an association between current cigarette smoking and increased serum cystatin C concentration. 126,127
Study of intraindividual biological variation
To our knowledge, this is the first study to simultaneously establish the biological variation of mGFR and eGFR in patients with CKD. Data from this aspect of the study have previously been published. 97 We observed the within-subject biological variation of mGFR to be 6.7%, with similar, although in some cases significantly lower, biological variation of eGFR (5.0%, 5.3%, 5.3% and 5.0% for the MDRD, CKD-EPIcreatinine, CKD-EPIcystatin and CKD-EPIcreatinine-cystatin equations, respectively). Taking analytical and within-subject biological variability into account produced RCVs (%, positive/negative) of 21.5/−17.7 (mGFR), 15.1/−13.1 (MDRD), 15.9/−13.7 (CKD-EPIcreatinine), 15.9/−13.8 (CKD-EPIcystatin) and 15.1/−13.1 (CKD-EPIcreatinine-cystatin).
Although there have been several previous studies of the biological variation of GFR, few have followed the rigour of design required of a biological variation study. 35,36 Nevertheless, several of these earlier studies report biological variability of GFR of a similar magnitude to that observed here, despite a variety of techniques and study designs; 4.5%,79 5.7%,91 6.3%,158 5.5%,159 with some authors reporting higher estimates – 9.8%99 and 8.0%. 160 Some of the differences observed may reflect the underlying level of kidney function in the groups studied: both Levey et al. 158 and Brochner-Mortensen et al. 159 report higher variation estimates in individuals with GFR < 30 ml/minute/1.73 m2. Other factors including length of time between repeat procedures (10 months) and total study duration (12 years),99 inattention to hydration status, fasting and exercise before and during the test160 may also have increased the variability reported in some studies.
When considering any change in a patient’s results, healthcare practitioners need to be able to distinguish true change (‘signal’) from the ‘noise’ of variability. In clinical practice, biological variation is best considered in terms of the RCV, which takes both biological and analytical variation of mGFR into account: the positive and negative RCVs of mGFR were 21.5% and −17.7%, respectively. These values describe the change in mGFR in excess of which can be considered true with 95% certainty. For example, if the baseline mGFR in an individual is 59 ml/minute/1.73 m2, significant increases or decreases would be to values > 72 or < 48 ml/minute/1.73 m2. Given the lower CVI and CVA of eGFR, slightly lower RCVs may be applied when monitoring patients using GFR-estimating equations (e.g. if an individual’s baseline MDRD eGFR was 59, significant increases or decreases would be to values > 68 or < 51 ml/minute/1.73 m2, respectively). However, it must be remembered that our biological variation estimates were obtained under idealised conditions, over a relatively short observation period, with optimisation of preanalytical variables and precise laboratory methods. In an uncontrolled operational clinical environment, it is likely that biological and analytical variation, and hence RCVs, would increase.
The within-subject biological variation of serum creatinine we observed (4.4%) was in broad agreement with values reported in other studies in both healthy (4.1–7.6%)76–79,81,82,161–163 and diseased (5.7–9.9%)78,164–166 cohorts. Enzymatic creatinine methods are less prone to interference than Jaffe methods and the use of an enzymatic assay in the present study improves confidence in the estimate of biological variation we have reported. While calculation of CVI excludes any contribution due to CVA, it cannot account for biological variability of non-creatinine chromogens (e.g. bilirubin, glucose, ketones, protein and certain drugs) that are known to interfere in Jaffe methods of creatinine measurement. Similarly, our reported within-subject biological variation of cystatin C (4.0%) is similar to most (3.1%,167 4.1%,162 4.5%79,81 and 4.8%164) but not all (6.8%,163 8.6%78 and 13.3%77) previous estimates. As for mGFR, differences in study design and data analysis may account for differences in reported estimates of variation: for example, most of these studies did not report their approach to outlier detection; the time interval between repeat sampling was prolonged in some studies. 163
Depending on the equation used, eGFR is based on the concentration of creatinine, cystatin C or both. Therefore, eGFR will have a similar CVI to creatinine or cystatin C, mathematically inflated by the power function in the respective equation. The point estimates for CVI of the four studied equations lie between 5.0% and 5.3% and have overlapping CIs.
It is uncertain why the CVI of the eGFR should be lower than that of the mGFR. Probably the complexity of the iohexol clearance procedure, involving multiple measurements and blood samplings, contributes to a higher CVI for mGFR than eGFR. However, it is also possible that the variability of eGFR is somewhat attenuated compared to physiological fluctuations in mGFR, as noted, in an extreme example, following a renal insult in an AKI episode where there is a delay between the fall in GFR and the consequent rise in blood creatinine concentration.
These data have implications for the use of mGFR versus eGFR in clinical practice and research. Within-subject biological variation of mGFR was similar to that of eGFR, implying that significant change in kidney function should be considered to have taken place, or not taken place, with quantitatively similar temporal differences in estimated or mGFR. However, this should not be interpreted as an indication that eGFR should replace mGFR when an accurate assessment of GFR is required. As noted above (see Ability of glomerular filtration rate-estimating equations to detect change in measured glomerular filtration rate over 3 years), eGFR had poor sensitivity for detecting changes in mGFR. Reference techniques are considered more accurate than eGFR primarily because they are not influenced by the non-GFR determinants of endogenous filtration markers. Reference GFR measurements will remain important as the benchmark in clinical research studies and also to inform clinical situations in which more accurate knowledge of GFR is important. These situations include certain chemotherapies (e.g. carboplatin); the use of any drug that is nephrotoxic or renally excreted and has a narrow therapeutic margin; the assessment of potential living-related kidney donors; and the assessment of GFR in patients with muscle-wasting disorders, including spina bifida and paraplegia.
The strengths of this aspect of the overall study include that it followed a strict design to minimise pre-analytical variation and investigator bias. 36 Outliers were excluded using a formal exclusion protocol: sensitivity testing was undertaken using excluded data to confirm that the presented results were representative. Estimation of components of variation was derived using a nested analysis of variance approach, which takes into account analytical variation for estimation of within-subject biological variation. The studied patient group represents a major population in which monitoring of kidney function to detect worsening disease is regularly undertaken and which is mandated in international guidance. 22,27,59 Prescribed medication was unaltered during the study, with the exception of two patients who received a course of amoxicillin. No patient showed significant trends in GFR during the study period, confirming that the variation we have reported is physiological and not pathological in nature.
Our biological variation study had some limitations. 97 The cohort studied was recruited from a single centre and was exclusively Caucasian: biological variability estimates may not be transferable to other ethnic groups. Although the study was adequately powered to answer the primary question,168 we were unable to investigate whether variability is higher at differing levels of GFR or albuminuria. Although previous studies have observed statistically significant differences in CVI when individuals are stratified for level of GFR/albuminuria,164 such effects are unlikely to be of practical importance. 162 Our mGFR data were based on a plasma iohexol clearance procedure. While constant infusion urinary inulin clearance would be considered the reference measure of GFR, single-bolus plasma clearance of iohexol demonstrates good agreement with this technique and is widely used in clinical practice. 169 In terms of CVI, plasma clearance techniques are likely to produce lower values than urinary clearance techniques due to problems of inaccurate urine collection. We have chosen to calculate RCVs representing 95% probability, as is conventional. However, if a lower probability was considered clinically acceptable, then the RCV would be smaller. 161
Ability of glomerular filtration rate-estimating equations, together with albumin-to-creatinine ratio, or albumin-to-creatinine ratio alone, to predict people who have progressive loss of kidney function (chronic kidney disease progression) and to predict mortality
Several previous large studies have shown an association between kidney disease progression and level of GFR and albuminuria. 85,170,171 In the present study, logistic models demonstrated that lower baseline eGFR (using any of the four main study equations) predicted renal disease progression, defined as either a 25% decrease in mGFR or a decrease in mGFR exceeding the RCV and/or an increase in ACR category within the study period. There were no clear differences between the GFR equations and no impact of the ACR category on the ORs. Conversely, in the substudy of disease progression (see Substudy of disease progression), higher levels of baseline mGFR were associated with faster decline of mGFR, and albuminuria was fairly consistently associated with renal disease progression. The apparent contradiction between these two findings probably reflects the statistical approaches used. The substudy analyses used changes in actual values, whereas the logistic models studied fixed percentage changes at a point in time. Individuals with higher initial values of GFR have the biggest potential for decline in absolute terms, but this does not necessarily mean a large percentage change. The substudy analysis explored covariates associated with progression for all eligible participants, not only those who meet the criteria for renal progression. The results of the main study and substudy analyses should be interpreted differently as 30% or less of eligible participants met the criteria for renal progression in the main study analysis.
Previous studies have also identified independent associations between decreased levels of GFR,7,172,173 male gender,174,175 increasing albuminuria7,173 and mortality amongst patients with CKD. Studies have observed differences between the MDRD and CKD-EPI equations as predictors of risk (e.g. Matsushita et al. )176. Several studies have observed a stronger association between cystatin C eGFR and risk of death compared to creatinine-based eGFR. 30,177,178
In this study of 1159 individuals, we observed 62 deaths during the 3-year follow-up period. The study was not powered for hard end points. In agreement with earlier studies, regression models including each GFR-estimating equation separately and addressing both death within the study and time to death as outcomes, each demonstrated mortality within the study follow-up period was associated with lower eGFR, increasing age and male gender. An association with categorical albuminuria was not observed. As with the models addressing progression, we found no evidence of superiority of CKD-EPI equations as predictors compared to the MDRD equation, or of a strengthened association with cystatin C-containing GFR equations. Results were similar across the models showing a decrease in both odds and hazard for mortality as eGFR increased, with no clear differences between the GFR equations. Point estimates suggested a decrease in the hazard ratio and OR for the cystatin C-containing equations compared to the creatinine-based equations, but the CIs across the models overlapped.
Overall, our data are in agreement with reported associations between eGFR and both mortality risk and renal progression. However, we did not find evidence to support superiority of any equation in these contexts including of those estimating GFR using cystatin C.
Strengths and limitations of the study
We have undertaken a large, prospective, longitudinal study of the clinical performance of contemporary GFR-estimating equations in a UK population of people with moderate CKD, which included participants of South Asian and African-Caribbean ethnicity. The accuracy of GFR-estimating equations was assessed at baseline in 1167 participants, 875 of whom subsequently provided a second reference GFR measure after 3 years. A health economic analysis was included.
All analytical methods used in the study were rigorously quality-assured. The strengths of the study include the use of a reference GFR test including a three-point iohexol clearance procedure, with the final sample being taken at 4 hours post injection. This time interval has generally been considered suitable for patients with GFR > 30 ml/minute/1.73 m2, with a longer collection period being recommended for individuals with lower GFRs. 179 More recently, it has been suggested that the threshold of 30 ml/minute/1.73 m2 is too low and that patients with higher levels of GFR should also be tested using an extended clearance period. 180 The potential impact of not using an extended collection period in individuals with low GFR is that GFR will be overestimated. The use of three time points in the present study enabled confirmation of linear decline in iohexol concentration using regression analysis (r > 0.99 in the vast majority of study subjects), with no suggestion that delayed clearance in those with lower GFR was an issue. Furthermore, our data are not suggestive of this being a problem, given the relatively close alignment of eGFR and mGFR. On a pragmatic note, our study protocol was developed with patient involvement: it is our belief that prolonged test duration, beyond 240 minutes, would have adversely affected recruitment into the study. Further research is needed in this area leading to the development of a standardised protocol for GFR measurement using plasma iohexol clearance. More generally, the issue of standardisation of the reference methodology itself in GFR studies, including choice of marker (i.e. inulin, iohexol or iothalamate clearance techniques),181 whether urinary or plasma clearance is studied, the timing of sample collection, patient preparation, BSA correction method and laboratory analytical approach remains a pertinent issue, with important clinical and research practice implications;182 it must be remembered that both eGFR and mGFR have error compared to ‘true’ GFR.
Creatinine and cystatin C were measured in centralised laboratories reducing any between-laboratory variability in our data. Patients were asked to avoid meat intake on the day of the test visit. Meat is known to acutely increase blood creatinine concentration, causing suppression of eGFR. 119 While this increases the accuracy of our data, these idealised sampling conditions may be unreflective of the clinical situation.
An enzymatic creatinine method was used. These are less prone to interference than the widely used Jaffe methods and their specificity facilitates standardisation against ID-MS reference methodology. Additional assurance was provided by direct comparison of our enzymatic creatinine results against an ID-MS method with good agreement. Nevertheless, we observed some bias compared to the ID-MS method, the removal of which would have improved the performance of the estimating equations against mGFR. This represents a true field situation and illustrates that accuracy of creatinine measurement remains an issue contributing to variation in GFR estimation between laboratories.
The critical importance of laboratory method accuracy is often under-appreciated. We also explored the issue of cystatin C calibration on GFR equation performance to an extent not usually considered in such studies. An adjustment was made to address a standardisation issue with the cystatin C assay. Nevertheless, a limitation of our study is that our cystatin C recalibration was based on regression analysis using a subset of our cohort (n = 106). Ideally, we would have tested this analysis in a validation cohort. However, the sample size and measurement range used in this study met globally accepted standards for method comparison studies in laboratory medicine, and the approach to recalibration was tested using two regression approaches with relatively tight CIs. 183 Within the context of a research study, we were able to study and adjust accordingly the calibration of our commercial cystatin C method: it should be appreciated that this is not an adjustment that would be available to most clinical diagnostic laboratories.
By design, our study was limited to CKD stage 3. However, despite the inclusion criteria targeting individuals with stable stage 3 CKD as determined by MDRD eGFR, at baseline 26% of those recruited had mGFR outside 30–59 ml/minute/1.73 m2. This is to be expected given biological variation and the performance characteristics of GFR-estimating equations in terms of accuracy and precision compared to mGFR. For example, if a GFR-estimating equation has a P30 of 90%, for individuals with mGFR 59 ml/minute/1.73 m2, then the eGFR will lie within 41 and 77 ml/minute/1.73 m2 90% of the time; in 10% of cases, it will lie outside of this range. This has allowed for some general observations to be made regarding the performance of the equations outside of stage 3 CKD, but the strength of any conclusions in this respect is limited.
The primary cause of kidney disease was not recorded in our study, potentially limiting the generalisability of our data and the granular detail to which statistical models could be developed. Modelling also suggested a linear pattern of GFR decline, which is not a universal finding. 184–186
The study aimed to recruit a minimum of 20% of individuals with diabetes and 20% with albuminuria (ACR > 30 mg/mmol) and this was achieved. However, we encountered difficulties with adequate recruitment of people from South Asian and African-Caribbean backgrounds. Although there were no consistent reasons why patients from these ethnic backgrounds declined to take part in the study, the acceptance rate in these populations was lower and in keeping with previous experience. Barriers to participation in research among ethnic minority populations are complex and may include challenges with the language, mistrust of researchers, poor awareness and stigma of research, cultural factors and beliefs about research, unawareness of benefits of research and inaccessibility to research, particularly in deprived populations as well as concerns of costs of time and money. 187,188 Anecdotally, patients said they had caring responsibilities, were unhappy with being included in research and could not take time off from work. It is recognised that specific strategies can be used to increase recruitment from patients from different ethnic backgrounds and future studies should include the use of validated and culturally competent toolkits to ensure these populations are better represented. 189 During the COVID-19 pandemic and the accompanying vaccination trials, much was learnt regarding reasons for non-participation and barriers from ethnic minority groups. Mechanisms which we would take forward in future studies would include the use of ‘research buddies’ and ‘community champions’ in addition to public patient involvement strategies more focused on black and ethnic minority groups, for example the design of study materials. 190,191
Suggestions for further research
We observed no clear advantage to the use of cystatin C-containing GFR-estimating equations for the monitoring of kidney function in patients with stage 3 CKD. This does not preclude the use and investigation of cystatin C in other settings and for different purposes, including for identification of CKD and prediction of outcomes. Both the MDRD and CKD-EPIcreatinine equations demonstrated a negative bias at GFR levels > 50 ml/minute/1.73 m2, which was not apparent with cystatin C-containing equations. There would be merit in extending this observation by studying the relative specificity of cystatin C and creatinine-eGFR for CKD at such levels of GFR, including in patients with GFR correlating to stage 2 CKD (60–89 ml/minute/1.73 m2). There are other specific populations in which it is reasonable to suspect cystatin C eGFR may offer advantages over creatinine, in particular due to the relationship of the latter with muscle mass. Such populations would include children and people with unusual muscle mass (e.g. amputees, people with advanced malignancy). A growing concern is how best to estimate GFR in transgender people, where the assignment of sex for this purpose can be complex. Cystatin C equations are less influenced by gender and may offer advantages in this scenario. Further research in this population is warranted.
The use, or not, of adjustment for race when estimating GFR remains an important issue. Our data suggest that simple removal of the African-Caribbean adjustment factor from the MDRD and, to a lesser extent, the original CKD-EPIcreatinine equations may reduce accuracy in such populations. Although our African-Caribbean cohort was relatively small, we did observe that the original CKD-EPIcreatinine-cystatin and the 2021 CKD-EPIcreatinine-cystatin equations performed well in African-Caribbean people and equally well across Caucasian and South Asian ethnic groups. Further research is required to confirm this observation, which could lend stronger impetus to the use of cystatin C in routine practice.
Assessment of the accuracy of GFR-estimating equations has for many years been based upon the use of P30 values. This metric has recently been questioned, with NICE suggesting that P5, P10 and P15 values should be used instead. 59 Future research should evaluate the sensitivity of these metrics to bias effects and applicability across a range of GFR. As noted above, some of the achieved P30 value is a product of between- and within-study variation in the GFR reference method itself and there is a need for research and standardisation in this area.
While cystatin C appears to offer little benefit for monitoring GFR in the population we have studied, and only marginal benefit in terms of diagnostic accuracy, there is an increasing literature describing the advantages of cystatin C compared to creatinine in relation to prognosis. 29,30 Prospective, large-scale studies of the value of cystatin C in this respect are warranted, including in combination with other markers (e.g. albuminuria) and as a component of established risk equations (e.g. the kidney failure risk equation). 59,192
Chapter 6 Conclusions
The estimation of GFR using prediction equations is important in clinical practice for both the detection and diagnosis of CKD, and for monitoring individual patients over time. Especially in relation to detection and diagnosis, accuracy compared to a reference measured GFR test is important. Our conclusions are confined to the study of patients with predominantly stage 3 CKD. In this cohort, all of the main study equations achieved acceptable accuracy as judged by P30. There was little difference between the equations in accuracy, but the CKD-EPIcreatinine-cystatin equation had a slightly higher P30 and there was some evidence that bias across the GFR range was more consistent when cystatin C was included in the equation. Since the inception of the study, many newer GFR-estimating equations have been described. Many of these newer equations have been developed in European populations and in theory could be more applicable to a UK population, compared to the MDRD and CKD-EPI equations, which were predominantly developed in North American populations. However, while most of the newer equations demonstrated acceptable accuracy, none were superior to the CKD-EPIcreatinine-cystatin equation.
Across several important characteristics (age, gender, BMI, levels of mGFR and albuminuria) we found little difference in accuracy of GFR-estimating equations. Due to difficulties in recruitment, we were not able to fully address the accuracy of the equations in British South Asian and African-Caribbean populations. However, we found some evidence to suggest a cautious approach should be taken before advocating simple removal of the black race factor from the original CKD-EPI equations or introducing the more recently reported CKD-EPI(2021) equations.
In the longitudinal study, we observed that CKD-EPIcreatinine-cystatin displayed slightly better concordance with mGFR than the other main study equations when tracking patients, but all study equations underestimated the mGFR decline. The sensitivity of GFR equations to detect several clinically relevant threshold changes in mGFR, either overall or when considering decline in GFR only, was < 63% for all equations. This is of concern given that such thresholds, including the NICE definition of accelerated progression and the change recognised as being true as determined by biological variation data, were studied. It must be borne in mind that some of the observed changes in mGFR could represent FP signals, given the higher within-person variability of mGFR compared to eGFR (see below).
Overall, our data comparing the accuracy of different GFR-estimating equations demonstrated no notable benefit of using a cystatin or creatinine–cystatin-based estimating GFR equation in predicting CKD progression over time. The measurement model underpinning the health economic analysis focused on the comparative accuracy of the estimating equations to detect accelerated progression according to NICE’s definition or of progression to CKD G4. The analysis estimated accuracy over a longer trajectory than the main study and factored in measurement error, but also found no clear benefit of using a cystatin C-based estimating equation. There was therefore no evidence to suggest that adding a cystatin C measurement to current GFR monitoring protocols would be cost-effective.
The evidence presented in the health economics chapter highlighted the current challenge in justifying and quantifying the health impact of monitoring eGFR in those with CKD G3. It is unclear what interventional decisions would be made as a result of monitoring eGFR at this earlier stage, as the cardiovascular and renal progression therapies which currently have an evidence base for use are not changed in patients with CKD G3 based on change in GFR, but on monitoring of BP and/or ACR.
The disease progression modelling of the substudy data suggested a linear decline over time for mGFR and eGFR. There were associations between GFR or ACR and all of the covariates selected for modelling in this study, with the exception of vascular disease. The final models included those covariates where there was evidence of association, following adjustment for other covariates in the model. In particular, there was a strong association between albuminuria and mGFR and CKD-EPIcreatinine eGFR, with faster progression associated with albuminuria. There were also associations between four drug types (loop diuretic, CCB, A2RB and beta-blocker) and progression, in each case progression was faster for those taking medication, which is most likely a reflection of the characteristics of the population prescribed these medications. Fitting the final models to the full study data set confirmed the inferences found in the substudy data, with only a few exceptions; of note is the change of the association with smoking status on the intercept for CKD-EPIcystatin and ACR; data from the full study suggested an association with ex-smokers which was not evident in the substudy analysis.
We described the biological variability of mGFR and eGFR in a carefully designed study. 97 The data generated have implications for monitoring of patients with CKD and clinical ability to understand CKD progression, both in clinical practice and in clinical trials, whether using mGFR or eGFR. Within-subject biological variation of mGFR is similar to that of eGFR and, in terms of variability, suggests no real advantage to the use of mGFR when monitoring patients over time. There were no clear differences in biological variability when measured by the different GFR-estimating equations. Most importantly, the information presented provides an evidence base allowing clinicians to have meaningful discussions with their patients about the implications of changes in their GFR results.
We have found evidence that inclusion of cystatin C in GFR-estimating equations leads to marginal improvements in accuracy and more consistent bias across the range of GFR values studied. However, there were no clear advantages to the inclusion of cystatin C in terms of monitoring patients over time. Problems of standardisation of cystatin C assays remain, despite the introduction of an international standard. Cystatin C may find niche applications of benefit, for example when managing children with CKD and in adults with unusual creatinine–GFR relationships (e.g. amputees). The independence of cystatin C from racial and dietary influences offers further advantages. Cystatin C may offer advantages over creatinine in the prediction of risk and outcomes in patients with CKD. 30 However, given that the use of cystatin C increases the economic cost of CKD management with little apparent gain, our data do not support the use of cystatin C for the monitoring of GFR in people with stage 3 CKD.
Additional information
Contributions of authors
Edmund J Lamb (https://orcid.org/0000-0002-5154-7351) (Consultant Clinical Scientist in Clinical Biochemistry) was the chief investigator for the study and was involved in all aspects of the research from original proposal to submission of final report.
Jonathan Barratt (https://orcid.org/0000-0002-9063-7229) (Professor of Renal Medicine) was principal investigator for recruitment in Leicester, provided critical review of the results throughout the study and reviewing and editing the study report.
Elizabeth A Brettell (https://orcid.org/0000-0002-0669-3085) (Trial Management Team Leader) was the Clinical Trials Unit co-investigator involved in planning and developing the study and responsible for oversight of study management.
Paul Cockwell (https://orcid.org/0000-0003-1975-266X) (Consultant Nephrologist and Honorary Professor of Nephrology) was involved in development of the study protocol, principal investigator for recruitment in Birmingham, critical review of the results throughout the study and reviewing and editing the study report.
R Neil Dalton (https://orcid.org/0000-0001-9201-5266) (Professor and Consultant Clinical Scientist in Paediatrics) was a co-principal investigator involved in all aspects of the research, from original proposal to submission of final report, with primary responsibility for the iohexol measurements.
Jon J Deeks (https://orcid.org/0000-0002-8850-1971) (Professor of Biostatistics) was the senior statistician and was involved in developing the study proposal, planning the analysis, overseeing the analysis, and contributed to the final report.
Gillian Eaglestone (https://orcid.org/0000-0001-9860-8679) (Senior Research Nurse in Renal Medicine) was the lead research nurse for the study and was involved in protocol development, patient recruitment and data collection.
Tracy Pellatt-Higgins (https://orcid.org/0000-0002-2543-461X) was one of the study statisticians and was involved in planning and developing the methodology for the substudy of disease progression, analysing the substudy data, and writing and reviewing the final report.
Philip A Kalra (https://orcid.org/0000-0001-7652-1572) (Professor of Nephrology) was involved in development of the study protocol, principal investigator for recruitment in Salford, critical review of the results throughout the study and reviewing and editing the study report.
Kamlesh Khunti (https://orcid.org/0000-0003-2343-7099) (Professor of Primary Care Diabetes and Vascular Medicine) was co-principal investigator in Leicester and provided input in recruitment of diverse populations and reviewing the final report.
Fiona C Loud (https://orcid.org/0000-0001-7706-5396) (Director of Kidney Alliance at the start of this study, subsequently Policy Director of the British Kidney Patient Association, now known as Kidney Care UK) provided lay input, recommendations on patient involvement and patient representation on participation sheets and study news.
Ryan S Ottridge (https://orcid.org/0000-0002-8685-2145) (Trial Management Team Leader) was the trial manager responsible for data quality, and day-to-day management and administrative support of the study.
Aisling Potter (https://orcid.org/0000-0003-4366-1039) (Research Scientist) undertook laboratory analyses, data entry and analysis for the study and contributed to writing and reviewing the final report.
Ceri Rowe (https://orcid.org/0000-0002-6150-1816) (Clinical Scientist) undertook laboratory analyses, statistical analysis and report writing for the biological variation substudy of the project and contributed to writing and reviewing the final report.
Katie Scandrett (https://orcid.org/0000-0001-6111-2805) (Research Associate in Biostatistics) was responsible for analysing data from the main study and contributed to writing and reviewing the final report.
Alice J Sitch (https://orcid.org/0000-0001-7727-4497) (Associate Professor of Biostatistics) was the study statistician (main and biological variability study) and was involved in planning and developing the study, analysing the data, observing further analysis of the data, writing and reviewing the final report.
Paul E Stevens (https://orcid.org/0000-0001-7606-0649) (Consultant Nephrologist) was involved in the original proposal and development of the study protocol. He was principal investigator for recruitment in Canterbury, critically reviewed results throughout the study and reviewed and edited the final report.
Claire C Sharpe (https://orcid.org/0000-0003-1704-8492) (Professor in Renal Medicine) was a co-principal investigator and contributed to the original proposal, patient recruitment, discussion of data analysis and reviewing and editing the final report.
Bethany Shinkins (https://orcid.org/0000-0001-5350-1018) (Associate Professor of Health Economics) took over as lead health economist from Andrew Sutton (Andrew left his post) part-way through the project. She was involved in planning and developing the health economic statistical and economic analysis, supervising the economic evaluation systematic review update, and writing and reviewing the final report.
Alison Smith (https://orcid.org/0000-0001-7709-1869) (Lecturer in Health Economics) undertook the economic evaluation systematic review update and the health economic statistical analysis, was involved in the economic analysis, and writing and reviewing the final report.
Andrew J Sutton (https://orcid.org/0000-0001-7008-4770) (Health Economist) was the Lead health economist in the early stages of the study. He wrote the health economics section of the original research proposal, and protocol, and was responsible for planning and conducting the initial economic evaluation systematic review. He has reviewed the final report.
Maarten W Taal (https://orcid.org/0000-0002-9065-212X) (Professor of Medicine and Honorary Consultant Nephrologist) was a co-principal investigator and contributed to the grant application, protocol design, participant recruitment and discussion of data interpretation as well as review of the final report.
Acknowledgements
We acknowledge the contributions of the following people: Reshma Ali (Data Manager, Birmingham Clinical Trials Unit) who provided data management and administrative support to the study. Antoine Berckley (Senior Research Nurse, Salford Royal Hospital, Northern Care Alliance NHS Foundation Trust) undertook patient recruitment and study delivery. Joanne Carter (Clinical Scientist) undertook sample handling, laboratory analyses and data entry in the initial years of the study. Elizabeth Clarke (Clinical Research Nurse, East Kent Hospitals University NHS Foundation Trust) provided research nurse support to the study. Hugh Gallagher (Consultant Nephrologist, Epsom and St Helier Hospitals) was a member of the independent study steering committee. Kevin Harris (Consultant Nephrologist, University Hospitals of Leicester NHS Trust) was involved in the initial development of the study protocol and grant submission. Adam R Khan (Data Manager, Birmingham Clinical Trials Unit) provided data management and administrative support to the study. Sarah Knight (Clinical Research Nurse, East Kent Hospitals University NHS Foundation Trust) provided research nurse support to the study. Frances Morris (Clinical Research Nurse, East Kent Hospitals University NHS Foundation Trust) provided research nurse support to the study. Nicholas Palmer (Independent Patient Representative, British Kidney Patients Association) was a member of the independent study steering committee. Rafael Perera (Statistician, Director of MaDOX, University of Oxford) was a member of the independent study steering committee. Amelia Te (Senior Research Nurse, King’s College Hospital NHS Foundation Trust) undertook all aspects of work directly related to patient recruitment and study delivery. Charlie Tomson (Consultant Nephrologist, Freeman Hospital, Newcastle on Tyne) chaired the independent study steering committee. Stephanie Whittaker (Senior Research Nurse, Salford Royal Hospital, Northern Care Alliance NHS Foundation Trust) undertook patient recruitment and study delivery. Judy Wright (Information Specialist) ran the database searches for the economic evaluation systematic review update and provided support throughout the review update process.
Patient data statement
This work uses data provided by patients and collected by the NHS as part of their care and support. Using patient data is vital to improve health and care for everyone. There is huge potential to make better use of information from people’s patient records, to understand more about disease, develop new treatments, monitor safety and plan NHS services. Patient data should be kept safe and secure, to protect everyone’s privacy, and it is important that there are safeguards to make sure that they are stored and used responsibly. Everyone should be able to find out about how patient data are used. #datasaveslives You can find out more about the background to this citation here: https://understandingpatientdata.org.uk/data-citation.
Data-sharing statement
All data requests should be submitted to the corresponding author for consideration by the CI and the co-sponsors. Access to anonymised data may be granted following review, no earlier than 6 months after this publication.
Ethics statement
Approval for this research study was obtained from the National Research Ethics Service (NRES Committee South East Coast – Surrey, reference 13/LO/1349, approved 9 October 2013).
Information governance statement
University of Birmingham is committed to handling all personal information in line with the UK Data Protection Act (2018) and the General Data Protection Regulation (EU GDPR) 2016/679. Under the Data Protection legislation, University of Birmingham is the Data Controller, and you can find out more about how we handle personal data, including how to exercise your individual rights and the contact details for our Data Protection Officer here: https://www.birmingham.ac.uk/privacy.
Disclosure of interests
Full disclosure of interests: Completed ICMJE forms for all authors, including all related interests, are available in the toolkit on the NIHR Journals Library report publication page at https://doi.org/10.3310/HYHN1078.
Primary conflicts of interest: Paul Cockwell is President of the UK Kidney Association. R Neil Dalton is Director of SpOtOn Clinical Diagnostics Ltd. Claire Sharpe and Philip Kalra have received honoraria from pharmaceutical companies for consultancy work and lectures within the field of chronic kidney disease (CKD) but are not directly related to the present study. Philip Kalra reports grants, consulting fees, and honoraria from various organisations; and travel support from Pharmacosmos and Vifor. Kamlesh Khunti has received honoraria and grants from pharmaceutical companies within the field of CKD and diabetes but not directly related to the present study. He is also member of the Kidney Disease Improving Global Outcomes (KDIGO) CKD in Diabetes Guideline Group, the COVID-19 Reviewing Committee and the HS&DR Funding Committee. Edmund Lamb reports travel support from KDIGO CKD, and NICE CKD. Fiona Loud reports grants from AstraZeneca, Pfizer, and Novartis; speaking fees from various institutions; and travel support from Astellas. Ceri Rowe reports travel support from Association for Clinical Biochemistry and Laboratory Medicine. Claire Sharpe reports grants, consulting fees, and honoraria from various organisations. Paul Stevens reports grant from NIHR (HTA 16/31/127). All other authors declare they have no competing interests. All authors have completed the unified competing interest form at www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare (1) no financial support for the submitted work from anyone other than their employer; (2) no financial relationships with commercial entities that might have an interest in the submitted work; (3) no spouses, partners, or children with relationships to commercial entities that might have an interest in the submitted work; and (4) no non-financial interests that may be relevant to the submitted work.
Publications
Lamb EJ, Brettell EA, Cockwell P, Dalton RN, Deeks JJ, Harris K, et al. The eGFR-C Study. Accuracy of glomerular filtration rate (GFR) estimation using creatinine and cystatin C and albuminuria for monitoring disease progression in patients with stage 3 chronic kidney disease: a prospective longitudinal study in a multiethnic population. BMC Nephrol 2014;15:13. http://doi.org/10.1186/1471-2369-15-13
Sutton AJ, Breheny K, Deeks J, Khunti K, Sharpe C, Ottridge RS, et al. Methods used in economic evaluations of chronic kidney disease testing – a systematic review. PLOS ONE 2015:10:e0140063.
Rowe C, Sitch AJ, Brettell EA, Barratt J, Cockwell P, Dalton RN, et al. Biological variation of measured and estimated glomerular filtration rate in patients with chronic kidney disease. Kidney Int 2019;96:429–35.
Disclaimers
This article presents independent research funded by the National Institute for Health and Care Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, the HTA programme or the Department of Health and Social Care. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, the HTA programme or the Department of Health and Social Care.
References
- Public Health England . Chronic Kidney Disease Prevalence Model 2014. https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/612303/ChronickidneydiseaseCKDprevalencemodelbriefing.pdf (accessed 26 July 2023).
- United Kingdom Renal Registry . 24th Annual Report 2022. https://ukkidney.org/audit-research/annual-report/24th-annual-report-data-31122020 (accessed 26 July 2023).
- Kerr M, Bray B, Medcalf J, O’Donoghue DJ, Matthews B. Estimating the financial cost of chronic kidney disease to the NHS in England. Nephrol Dial Transplant 2012;27:iii73-80.
- Kent S, Schlackow I, Lozano-Kuhne J, Reith C, Emberson J, Haynes R, et al. SHARP Collaborative Group . What is the impact of chronic kidney disease stage and cardiovascular disease on the annual cost of hospital care in moderate-to-severe kidney disease?. BMC Nephrol 2015;16.
- van der Velde M, Matsushita K, Coresh J, Astor BC, Woodward M, Levey A, et al. Chronic Kidney Disease Prognosis Consortium . Lower estimated glomerular filtration rate and higher albuminuria are associated with all-cause and cardiovascular mortality. A collaborative meta-analysis of high-risk population cohorts. Kidney Int 2011;79:1341-52.
- Gansevoort RT, Matsushita K, van der Velde M, Astor BC, Woodward M, Levey AS, et al. Chronic Kidney Disease Prognosis Consortium . Lower estimated GFR and higher albuminuria are associated with adverse kidney outcomes. A collaborative meta-analysis of general and high-risk population cohorts. Kidney Int 2011;80:93-104.
- Matsushita K, van der Velde M, Astor BC, Woodward M, Levey AS, de Jong PE, et al. Chronic Kidney Disease Prognosis Consortium . Association of estimated glomerular filtration rate and albuminuria with all-cause and cardiovascular mortality in general population cohorts: a collaborative meta-analysis. Lancet 2010;375:2073-81.
- Grams ME, Sang Y, Ballew SH, Gansevoort RT, Kimm H, Kovesdy CP, et al. CKD Prognosis Consortium . A meta-analysis of the association of estimated GFR, albuminuria, age, race, and sex with acute kidney injury. Am J Kidney Dis 2015;66:591-60.
- Hannan M, Ansari S, Meza N, Anderson AH, Srivastava A, Waikar S, et al. CRIC Study Investigators . Risk factors for CKD progression: overview of findings from the CRIC study. Clin J Am Soc Nephrol 2021;16:648-59.
- Brenner BM, Cooper ME, de Zeeuw D, Keane WF, Mitch WE, Parving HH, et al. RENAAL Study Investigators . Effects of losartan on renal and cardiovascular outcomes in patients with type 2 diabetes and nephropathy. N Engl J Med 2001;345:861-9.
- Lewis EJ, Hunsicker LG, Bain RP, Rohde RD. The effect of angiotensin-converting-enzyme inhibition on diabetic nephropathy. The Collaborative Study Group. N Engl J Med 1993;329:1456-62.
- Heart Outcomes Prevention Evaluation (HOPE) Study Investigators . Effects of ramipril on cardiovascular and microvascular outcomes in people with diabetes mellitus: results of the HOPE study and MICRO-HOPE substudy. Lancet 2000;355:253-9.
- Gruppo Italiano di Studi Epidemiologici in Nefrologia . Randomised placebo-controlled trial of effect of ramipril on decline in glomerular filtration rate and risk of terminal renal failure in proteinuric, non-diabetic nephropathy. Lancet 1997;349:1857-63.
- Ruggenenti P, Pagano E, Tammuzzo L, Benini R, Garattini L, Remuzzi G. Ramipril prolongs life and is cost effective in chronic proteinuric nephropathies. Kidney Int 2001;59:286-94.
- Heerspink HJL, Stefansson BV, Correa-Rotter R, Chertow GM, Greene T, Hou FF, et al. DAPA-CKD Trial Committees and Investigators . Dapagliflozin in patients with chronic kidney disease. N Engl J Med 2020;383:1436-46.
- Nuffield Department of Population Health Renal Studies Group; SGLT2 inhibitor Meta-Analysis Cardio-Renal Trialists' Consortium . Impact of diabetes on the effects of sodium glucose co-transporter-2 inhibitors on kidney outcomes: collaborative meta-analysis of large placebo-controlled trials. Lancet 2022;400:1788-801.
- Staplin N, Roddick AJ, Emberson J, Reith C, Riding A, Wonnacott A, et al. Net effects of sodium-glucose co-transporter-2 inhibition in different patient groups: a meta-analysis of large placebo-controlled randomized trials. EClinicalMedicine 2021;41.
- Herrington WG, Staplin N, Wanner C, Green JB, Hauske SJ, Emberson JR, et al. The EMPA-KIDNEY Collaborative Group . Empagliflozin in patients with chronic kidney disease. N Engl J Med 2023;388:117-27.
- Perkovic V, Jardine MJ, Neal B, Bompoint S, Heerspink HJL, Charytan DM, et al. CREDENCE Trial Investigators . Canagliflozin and renal outcomes in type 2 diabetes and nephropathy. N Engl J Med 2019;380:2295-306.
- Vart P, Vaduganathan M, Jongs N, Remuzzi G, Wheeler DC, Hou FF, et al. Estimated lifetime benefit of combined RAAS and SGLT2 inhibitor therapy in patients with albuminuric CKD without diabetes. Clin J Am Soc Nephrol 2022;17:1754-62.
- Gaspari F, Perico N, Ruggenenti P, Mosconi L, Amuchastegui CS, Guerini E, et al. Plasma clearance of nonradioactive iohexol as a measure of glomerular filtration rate. J Am Soc Nephrol 1995;6:257-63.
- National Institute for Health and Care Excellence . Chronic Kidney Disease. Early Identification and Management of Chronic Kidney Disease in Adults in Primary and Secondary Care 2014.
- Stevens PE, O’Donoghue DJ, de Lusignan S, Van Vlymen J, Klebe B, Middleton R, et al. Chronic kidney disease management in the United Kingdom: NEOERICA project results. Kidney Int 2007;72:92-9.
- de Lusignan S, Tomson C, Harris K, van Vlymen J, Gallagher H. Creatinine fluctuation has a greater effect than the formula to estimate glomerular filtration rate on the prevalence of chronic kidney disease. Nephron Clin Pract 2011;117:c213-24.
- Moynihan R, Doust J, Henry D. Preventing overdiagnosis: how to stop harming the healthy. BMJ 2012;344.
- Kyhse-Andersen J, Schmidt C, Nordin G, Andersson B, Nilsson-Ehle P, Lindstrom V, et al. Serum cystatin C, determined by a rapid, automated particle-enhanced turbidimetric method, is a better marker than serum creatinine for glomerular filtration rate. Clin Chem 1994;40:1921-6.
- Kidney Disease Improving Global Outcomes . Clinical practice guideline for the evaluation and management of chronic kidney disease. Kidney Int 2013;3:1-150.
- Inker LA, Schmid CH, Tighiouart H, Eckfeldt JH, Feldman HI, Greene T, et al. CKD-EPI Investigators . Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med 2012;367:20-9.
- Peralta CA, Katz R, Sarnak MJ, Ix J, Fried LF, De Boer I, et al. Cystatin C identifies chronic kidney disease patients at higher risk for complications. J Am Soc Nephrol 2011;22:147-55.
- Lees JS, Welsh CE, Celis-Morales CA, Mackay D, Lewsey J, Gray SR, et al. Glomerular filtration rate by differing measures, albuminuria and prediction of cardiovascular disease, mortality and end-stage kidney disease. Nat Med 2019;25:1753-60.
- Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D. A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group. Ann Intern Med 1999;130:461-70.
- Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF, Feldman HI, et al. CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration) . A new equation to estimate glomerular filtration rate. Ann Intern Med 2009;150:604-12.
- Hsu CY, Bansal N. Measured GFR as ‘gold standard’ – all that glitters is not gold?. Clin J Am Soc Nephrol 2011;6:1813-4.
- Kwong YTD, Stevens LA, Selvin E, Zhang YL, Greene T, Van Lente F, et al. Imprecision of urinary iothalamate clearance as a gold-standard measure of GFR decreases the diagnostic accuracy of kidney function estimating equations. Am J Kidney Dis 2010;56:39-4.
- Fraser CG, Harris EK. Generation and application of data on biological variation in clinical chemistry. Crit Rev Clin Lab Sci 1989;27:409-37.
- Bartlett WA, Braga F, Carobene A, Coskun A, Prusa R, Fernandez-Calle P, et al. Biological Variation Working Group, European Federation of Clinical Chemistry and Laboratory Medicine (EFLM) . A checklist for critical appraisal of studies of biological variation. Clin Chem Lab Med 2015;53:879-85.
- Levey AS, Greene T, Kusek JW, Beck GJ. A simplified equation to predict glomerular filtration rate from serum creatinine. J Am Soc Nephrol 2000;11.
- Levey AS, Coresh J, Greene T, Stevens LA, Zhang YL, Hendriksen S, et al. Chronic Kidney Disease Epidemiology Collaboration . Using standardized serum creatinine values in the modification of diet in renal disease study equation for estimating glomerular filtration rate. Ann Intern Med 2006;145:247-54.
- Myers GL, Miller WG, Coresh J, Fleming J, Greenberg N, Greene T, et al. National Kidney Disease Education Program Laboratory Working Group . Recommendations for improving serum creatinine measurement: a report from the Laboratory Working Group of the National Kidney Disease Education Program. Clin Chem 2006;52:5-18.
- National Institute for Health and Care Excellence . Chronic Kidney Disease: National Clinical Guideline for Early Identification and Management in Adults in Primary and Secondary Care. Clinical Guideline 73 2008.
- Earley A, Miskulin D, Lamb EJ, Levey AS, Uhlig K. Estimating equations for glomerular filtration rate in the era of creatinine standardization: a systematic review. Ann Intern Med 2012;156:785-95.
- Schaeffner ES, Ebert N, Delanaye P, Frei U, Gaedeke J, Jakob O, et al. Two novel equations to estimate kidney function in persons aged 70 years or older. Ann Intern Med 2012;157:471-81.
- Grubb A, Horio M, Hansson LO, Björk J, Nyman U, Flodin M, et al. Generation of a new cystatin C-based estimating equation for glomerular filtration rate by use of 7 assays standardized to the international calibrator. Clin Chem 2014;60:974-86.
- Pottel H, Hoste L, Dubourg L, Ebert N, Schaeffner E, Eriksen BO, et al. An estimated glomerular filtration rate equation for the full age spectrum. Nephrol Dial Transplant 2016;31:798-806.
- Pottel H, Delanaye P, Schaeffner E, Dubourg L, Eriksen BO, Melsom T, et al. Estimating glomerular filtration rate for the full age spectrum from serum creatinine and cystatin C. Nephrol Dial Transplant 2017;32:497-50.
- Björk J, Bäck SE, Ebert N, Evans M, Grubb A, Hansson M, et al. GFR estimation based on standardized creatinine and cystatin C: a European multicenter analysis in older adults. Clin Chem Lab Med 2018;56:422-35.
- Pottel H, Björk J, Courbebaisse M, Couzi L, Ebert N, Eriksen BO, et al. Development and validation of a modified full age spectrum creatinine-based equation to estimate glomerular filtration rate: a cross-sectional analysis of pooled data. Ann Intern Med 2021;174:183-91.
- Inker LA, Eneanya ND, Coresh J, Tighiouart H, Wang D, Sang Y, et al. Chronic Kidney Disease Epidemiology Collaboration . New creatinine- and cystatin C-based equations to estimate GFR without race. N Engl J Med 2021;385:1737-49.
- Dharnidharka VR, Kwon C, Stevens G. Serum cystatin C is superior to serum creatinine as a marker of kidney function: a meta-analysis. Am J Kidney Dis 2002;40:221-6.
- Laterza OF, Price CP, Scott MG. Cystatin C: an improved estimator of glomerular filtration rate?. Clin Chem 2002;48:699-707.
- Grubb A, Blirup-Jensen S, Lindström V, Schmidt C, Althaus H, Zegers I. IFCC Working Group on Standardisation of Cystatin C (WG-SCC) . First certified reference material for cystatin C in human serum ERM-DA471/IFCC. Clin Chem Lab Med 2010;48:1619-21.
- Kilbride HS, Stevens PE, Eaglestone G, Knight S, Carter JL, Delaney MP, et al. Accuracy of the MDRD (Modification of Diet in Renal Disease) study and CKD-EPI (CKD Epidemiology Collaboration) equations for estimation of GFR in the elderly. Am J Kidney Dis 2013;61:57-66.
- Björk J, Grubb A, Sterner G, Nyman U. Revised equations for estimating glomerular filtration rate based on the Lund-Malmö Study cohort. Scand J Clin Lab Invest 2011;71:232-9.
- Hounkpatin HO, Fraser SDS, Honney R, Dreyer G, Brettle A, Roderick PJ. Ethnic minority disparities in progression and mortality of pre-dialysis chronic kidney disease: a systematic scoping review. BMC Nephrol 2020;21.
- Pallayova M, Rayner H, Taheri S, Dasgupta I. Is there a difference in progression of renal disease between South Asian and white European diabetic adults with moderately reduced kidney function?. J Diabetes Complications 2015;29:761-5.
- Gerber C, Cai X, Lee J, Craven T, Scialla J, Souma N, et al. Incidence and progression of chronic kidney disease in black and white individuals with type 2 diabetes. Clin J Am Soc Nephrol 2018;13:884-92.
- Mathur R, Dreyer G, Yaqoob MM, Hull SA. Ethnic differences in the progression of chronic kidney disease and risk of death in a UK diabetic population: an observational cohort study. BMJ Open 2018;8.
- Major RW, Shepherd D, Medcalf JF, Xu G, Gray LJ, Brunskill NJ. Comorbidities and outcomes in South Asian individuals with chronic kidney disease: an observational primary care cohort. Nephrol Dial Transplant 2021;37:108-14.
- National Institute for Health and Care Excellence . Chronic Kidney Disease: Assessment and Management [NG203] 2021. www.nice.org.uk/guidance/ng203 (accessed 26 July 2023).
- Lewis J, Agodoa L, Cheek D, Greene T, Middleton J, O’Connor D, et al. African-American Study of Hypertension and Kidney Disease . Comparison of cross-sectional renal function measurements in African Americans with hypertensive nephrosclerosis and of primary formulas to estimate glomerular filtration rate. Am J Kidney Dis 2001;38:744-53.
- Ma YC, Zuo L, Chen JH, Luo Q, Yu XQ, Li Y, et al. Modified glomerular filtration rate estimating equation for Chinese patients with chronic kidney disease. J Am Soc Nephrol 2006;17:2937-44.
- Matsuo S, Imai E, Horio M, Yasuda Y, Tomita K, Nitta K, et al. Collaborators developing the Japanese equation for estimated GFR . Revised equations for estimated GFR from serum creatinine in Japan. Am J Kidney Dis 2009;53:982-92.
- Horio M, Imai E, Yasuda Y, Watanabe T, Matsuo S. Modification of the CKD epidemiology collaboration (CKD-EPI) equation for Japanese: accuracy and use for population estimates. Am J Kidney Dis 2010;56:32-8.
- Teo BW, Xu H, Wang D, Li J, Sinha AK, Shuter B, et al. GFR estimating equations in a multiethnic Asian population. Am J Kidney Dis 2011;58:56-63.
- Praditpornsilpa K, Townamchai N, Chaiwatanarat T, Tiranathanagul K, Katawatin P, Susantitaphong P, et al. The need for robust validation for MDRD-based glomerular filtration rate estimation in various CKD populations. Nephrol Dial Transplant 2011;26:2780-5.
- Wang Y, Levey AS, Inker LA, Jessani S, Bux R, Samad Z, et al. Performance and determinants of serum creatinine and cystatin C-based GFR estimating equations in South Asians. Kidney Int Rep 2021;6:962-75.
- Delgado C, Baweja M, Crews DC, Eneanya ND, Gadegbeku CA, Inker LA, et al. A unifying approach for GFR estimation: recommendations of the NKF-ASN task force on reassessing the inclusion of race in diagnosing kidney disease. Am J Kidney Dis 2022;79:268-288.e1.
- Keith DS, Nichols GA, Gullion CM, Brown JB, Smith DH. Longitudinal follow-up and outcomes among a population with chronic kidney disease in a large managed care organization. Arch Intern Med 2004;164:659-63.
- Hemmelgarn BR, Zhang J, Manns BJ, Tonelli M, Larsen E, Ghali WA, et al. Progression of kidney dysfunction in the community-dwelling elderly. Kidney Int 2006;69:2155-61.
- Ruggenenti P, Perna A, Remuzzi G. ACE inhibitors to prevent end-stage renal disease: when to start and why possibly never to stop: a post hoc analysis of the REIN trial results. Ramipril Efficacy in Nephropathy. J Am Soc Nephrol 2001;12:2832-7.
- Gall MA, Nielsen FS, Smidt UM, Parving HH. The course of kidney function in type 2 (non-insulin-dependent) diabetic patients with diabetic nephropathy. Diabetologia 1993;36:1071-8.
- MacIsaac RJ, Tsalamandris C, Panagiotopoulos S, Smith TJ, McNeil KJ, Jerums G. Nonalbuminuric renal insufficiency in type 2 diabetes. Diabetes Care 2004;27:195-200.
- Parving HH, Andersen AR, Smidt UM, Hommel E, Mathiesen ER, Svendsen PA. Effect of antihypertensive treatment on kidney function in diabetic nephropathy. Br Med J (Clin Res Ed) 1987;294:1443-7.
- Björck S, Nyberg G, Mulec H, Granerus G, Herlitz H, Aurell M. Beneficial effects of angiotensin converting enzyme inhibition on renal function in patients with diabetic nephropathy. Br Med J (Clin Res Ed) 1986;293:471-4.
- Hoefield RA, Kalra PA, Baker PG, Sousa I, Diggle PJ, Gibson MJ, et al. The use of eGFR and ACR to predict decline in renal function in people with diabetes. Nephrol Dial Transplant 2011;26:887-92.
- Gowans EM, Fraser CG. Biological variation of serum and urine creatinine and creatinine clearance: ramifications for interpretation of results and patient care. Ann Clin Biochem 1988;25:259-63.
- Keevil BG, Kilpatrick ES, Nichols SP, Maylor PW. Biological variation of cystatin C: implications for the assessment of glomerular filtration rate. Clin Chem 1998;44:1535-9.
- Reinhard M, Erlandsen EJ, Randers E. Biological variation of cystatin C and creatinine. Scand J Clin Lab Invest 2009;69:831-6.
- Delanaye P, Cavalier E, Depas G, Chapelle JP, Krzesinski JM. New data on the intraindividual variation of cystatin C. Nephron Clin Pract 2008;108:c246-8.
- Andersen TB, Erlandsen EJ, Frøkiaer J, Eskild-Jensen A, Brøchner-Mortensen J. Comparison of within- and between-subject variation of serum cystatin C and serum creatinine in children aged 2–13 years. Scand J Clin Lab Invest 2010;70:54-9.
- Bandaranayake N, Ankrah-Tetteh T, Wijeratne S, Swaminathan R. Intra-individual variation in creatinine and cystatin C. Clin Chem Lab Med 2007;45:1237-9.
- Toffaletti JG, McDonnell EH. Variation of serum creatinine, cystatin C, and creatinine clearance tests in persons with normal renal function. Clin Chim Acta 2008;395:115-9.
- Ruggenenti P, Gaspari F, Cannata A, Carrara F, Cella C, Ferrari S, et al. GFR-ADPKD Study Group . Measuring and estimating GFR and treatment effect in ADPKD patients: results and implications of a longitudinal cohort study. PLOS ONE 2012;7.
- Padala S, Tighiouart H, Inker LA, Contreras G, Beck GJ, Lewis J, et al. Accuracy of a GFR estimating equation over time in people with a wide range of kidney function. Am J Kidney Dis 2012;60:217-24.
- Peralta CA, Shlipak MG, Judd S, Cushman M, McClellan W, Zakai NA, et al. Detection of chronic kidney disease with creatinine, cystatin C, and urine albumin-to-creatinine ratio and association with progression to end-stage renal disease and mortality. JAMA 2011;305:1545-52.
- Hounkpatin HO, Harris S, Fraser SDS, Day J, Mindell JS, Taal MW, et al. Prevalence of chronic kidney disease in adults in England: comparison of nationally representative cross-sectional surveys from 2003 to 2016. BMJ Open 2020;10.
- Levin A, Stevens PE. Early detection of CKD: the benefits, limitations and effects on prognosis. Nat Rev Nephrol 2011;7:446-57.
- Lamb EJ, Brettell EA, Cockwell P, Dalton N, Deeks JJ, Harris K, et al. eGFR-C study group . The eGFR-C study: accuracy of glomerular filtration rate (GFR) estimation using creatinine and cystatin C and albuminuria for monitoring disease progression in patients with stage 3 chronic kidney disease – prospective longitudinal study in a multiethnic population. BMC Nephrol 2014;15.
- Erley CM, Bader BD, Berger ED, Vochazer A, Jorzik JJ, Dietz K, et al. Plasma clearance of iodine contrast media as a measure of glomerular filtration rate in critically ill patients. Crit Care Med 2001;29:1544-50.
- Schwartz GJ, Work DF. Measurement and estimation of GFR in children and adolescents. Clin J Am Soc Nephrol 2009;4:1832-43.
- Gaspari F, Perico N, Matalone M, Signorini O, Azzollini N, Mister M, et al. Precision of plasma clearance of iohexol for estimation of GFR in patients with renal disease. J Am Soc Nephrol 1998;9:310-3.
- Haycock GB, Schwartz GJ, Wisotsky DH. Geometric method for measuring body surface area: a height-weight formula validated in infants, children, and adults. J Pediatr 1978;93:62-6.
- Du Bois D, Du Bois EF. A formula to estimate the approximate surface area if height and weight be known. Arch Intern Med 1916;17:863-71.
- Shardlow A, McIntyre NJ, Fluck RJ, McIntyre CW, Taal MW. Chronic kidney disease in primary care: outcomes after five years in a prospective cohort study. PLOS Med 2016;13.
- Turin TC, Tonelli M, Manns BJ, Ravani P, Ahmed SB, Hemmelgarn BR. Chronic kidney disease and life expectancy. Nephrol Dial Transplant 2012;27:3182-6.
- Bellomo R, Ronco C, Kellum JA, Mehta RL, Palevsky P. Acute Dialysis Quality Initiative workgroup . Acute renal failure – definition, outcome measures, animal models, fluid therapy and information technology needs: the Second International Consensus Conference of the Acute Dialysis Quality Initiative (ADQI) Group. Crit Care 2004;8:R204-12.
- Rowe C, Sitch AJ, Barratt J, Brettell EA, Cockwell P, Dalton RN, et al. eGFR-C Study Group . Biological variation of measured and estimated glomerular filtration rate in patients with chronic kidney disease. Kidney Int 2019;96:429-35.
- Bröchner-Mortensen J. A simple method for the determination of glomerular filtration rate. Scand J Clin Lab Invest 1972;30:271-4.
- Blake GM, Roe D, Lazarus CR. Long-term precision of glomerular filtration rate measurements using 51Cr-EDTA plasma clearance. Nucl Med Commun 1997;18:776-84.
- Burniston M. Clinical Guideline for the Measurement of Glomerular Filtration Rate (GFR) Using Plasma Sampling. Approved by the British Nuclear Medicine Society Professional Standards Committee; 2018.
- Bargnoux AS, Pieroni L, Cristol JP, Kuster N, Delanaye P, Carlier MC, et al. Société Française de Biologie Clinique (SFBC) . Multicenter evaluation of cystatin C measurement after assay standardization. Clin Chem 2017;63:833-41.
- National Kidney Foundation . K/DOQI clinical practice guidelines for chronic kidney disease: evaluation, classification, and stratification. Am J Kidney Dis 2002;39:S1-266.
- Cohen J. Statistical Power Analysis for the Behavioural Sciences. Hillsdale, NJ: Lawrence Erlbaum Associates; 1988.
- National Institute for Health and Care Excellence . Obesity: Identification, Assessment and Management (CG189) 2014. www.nice.org.uk/guidance/cg189 (accessed 26 July 2023).
- O’Brien TE, Funk GM. A gentle introduction to optimal design for regression models. Am Stat 2003;57:265-7.
- Simundic AM, Kackov S, Miler M, Fraser CG, Petersen PH. Terms and symbols used in studies on biological variation: the need for harmonization. Clin Chem 2015;61:438-9.
- Cole TJ. Sympercents: symmetric percentage differences on the 100 log(e) scale simplify the presentation of log transformed data. Stat Med 2000;19:3109-25.
- Koopmans LH, Owen DB, Rosenblatt JI. Confidence intervals for the coefficient of variation for the normal and log normal distributions. Biometrika 1964;51:25-32.
- Burdick RK, Graybill FA. Confidence Intervals on Variance Components. Abingdon: Taylor & Francis; 1992.
- Fokkema MR, Herrmann Z, Muskiet FA, Moecks J. Reference change values for brain natriuretic peptides revisited. Clin Chem 2006;52:1602-3.
- Schulz KF, Altman DG, Moher D. CONSORT Group . CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. PLOS Med 2010;7.
- Sutton AJ, Breheny K, Deeks J, Khunti K, Sharpe C, Ottridge RS, et al. eGFR-C study group . Methods used in economic evaluations of chronic kidney disease testing – a systematic review. PLOS ONE 2015;10.
- Perera R, Stevens R, Aronson JK, Banerjee A, Evans J, Feakins BG, et al. Long-term Monitoring in Primary Care for Chronic Kidney Disease and Chronic Heart Failure: A Multi-Method Research Programme. Southampton: Programme Grants for Applied Research; 2021.
- National Institute for Health and Care Excellence . Cardiovascular Disease: Risk Assessment and Reduction, Including Lipid Modification. Clinical Guideline [CG181] 2014. www.nice.org.uk/guidance/cg181 (accessed 26 July 2023).
- Smith AF, Shinkins B, Hall PS, Hulme CT, Messenger MP. Toward a framework for outcome-based analytical performance specifications: a methodology review of indirect methods for evaluating the impact of measurement uncertainty on clinical outcomes. Clin Chem 2019;65:1363-74.
- NHS . National Cost Collection 2019 20 Report 2020. www.england.nhs.uk/wp-content/uploads/2021/06/National-Cost-Collection-2019-20-Report-FINAL.pdf (accessed 26 July 2023).
- Jones K, Burns A. Unit Costs of Health and Social Care. Canterbury: Personal Social Services Research Unit, University of Kent; 2021.
- Björk J, Nyman U, Courbebaisse M, Couzi L, Dalton RN, Dubourg L, et al. Prospects for improved glomerular filtration rate estimation based on creatinine-results from a transnational multicentre study. Clin Kidney J 2020;13:674-83.
- Preiss DJ, Godber IM, Lamb EJ, Dalton RN, Gunn IR. The influence of a cooked-meat meal on estimated glomerular filtration rate. Ann Clin Biochem 2007;44:35-42.
- Porrini E, Ruggenenti P, Luis-Lima S, Carrara F, Jiménez A, de Vries APJ, et al. Estimated GFR: time for a critical appraisal. Nat Rev Nephrol 2019;15:177-90.
- Shemesh O, Golbetz H, Kriss JP, Myers BD. Limitations of creatinine as a filtration marker in glomerulopathic patients. Kidney Int 1985;28:830-8.
- Shah KF, Stevens PE, Lamb EJ. The influence of a cooked-fish meal on estimated glomerular filtration rate. Ann Clin Biochem 2020;57:182-5.
- Sveinbjornsson G, Mikaelsdottir E, Palsson R, Indridason OS, Holm H, Jonasdottir A, et al. Rare mutations associating with serum creatinine and chronic kidney disease. Hum Mol Genet 2014;23:6935-43.
- Macdonald J, Marcora S, Jibani M, Roberts G, Kumwenda M, Glover R, et al. GFR estimation using cystatin C is not independent of body composition. Am J Kidney Dis 2006;48:712-9.
- Wasen E, Isoaho R, Mattila K, Vahlberg T, Kivelä SL, Irjala K. Serum cystatin C in the aged: relationships with health status. Am J Kidney Dis 2003;42:36-43.
- Knight EL, Verhave JC, Spiegelman D, Hillege HL, de Zeeuw D, Curhan GC, et al. Factors influencing serum cystatin C levels other than renal function and the impact on renal function measurement. Kidney Int 2004;65:1416-21.
- Liu X, Foster MC, Tighiouart H, Anderson AH, Beck GJ, Contreras G, et al. CRIC (Chronic Renal Insufficiency Cohort) Study Investigators . Non-GFR determinants of low-molecular-weight serum protein filtration markers in CKD. Am J Kidney Dis 2016;68:892-900.
- O’Seaghdha CM, Tin A, Yang Q, Katz R, Liu Y, Harris T, et al. Association of a cystatin C gene variant with cystatin C levels, CKD, and risk of incident cardiovascular disease and mortality. Am J Kidney Dis 2014;63:16-22.
- Inker LA, Tighiouart H, Coresh J, Foster MC, Anderson AH, Beck GJ, et al. GFR estimation using β-trace protein and β2-microglobulin in CKD. Am J Kidney Dis 2016;67:40-8.
- Freed TA, Coresh J, Inker LA, Toal DR, Perichon R, Chen J, et al. Validation of a metabolite panel for a more accurate estimation of glomerular filtration rate using quantitative LC-MS/MS. Clin Chem 2019;65:406-18.
- Eckfeldt JH, Karger AB, Miller WG, Rynders GP, Inker LA. Performance in measurement of serum cystatin C by laboratories participating in the College of American Pathologists 2014 CYS survey. Arch Pathol Lab Med 2015;139:888-93.
- Karger AB, Long T, Inker LA, Eckfeldt JH. College of American Pathologists Accuracy Based Committee and Chemistry Resource Committee . Improved performance in measurement of serum cystatin C by laboratories participating in the College of American Pathologists’ 2019 CYS survey. Arch Pathol Lab Med 2022;146:1218-23.
- Shardlow A, McIntyre NJ, Fraser SDS, Roderick P, Raftery J, Fluck RJ, et al. The clinical utility and cost impact of cystatin C measurement in the diagnosis and management of chronic kidney disease: a primary care cohort study. PLOS Med 2017;14.
- Lamb EJ, Tomson CR, Roderick PJ. Clinical Sciences Reviews Committee of the Association for Clinical Biochemistry . Estimating kidney function in adults using formulae. Ann Clin Biochem 2005;42:321-45.
- Rule AD, Larson TS, Bergstralh EJ, Slezak JM, Jacobsen SJ, Cosio FG. Using serum creatinine to estimate glomerular filtration rate: accuracy in good health and in chronic kidney disease. Ann Intern Med 2004;141:929-37.
- Faisal W, Tang HM, Tiley S, Kukard C. Not all body surface area formulas are the same, but does it matter?. J Glob Oncol 2016;2:436-7.
- Blake GM, Grewal GS. An evaluation of the body surface area correction for 51Cr-EDTA measurements of glomerular filtration rate. Nucl Med Commun 2005;26:447-51.
- Froissart M, Rossert J, Jacquot C, Paillard M, Houillier P. Predictive performance of the modification of diet in renal disease and Cockcroft-Gault equations for estimating renal function. J Am Soc Nephrol 2005;16:763-73.
- Nyman U, Grubb A, Sterner G, Björk J. The CKD-EPI and MDRD equations to estimate GFR. Validation in the Swedish Lund-Malmö Study cohort. Scand J Clin Lab Invest 2011;71:129-38.
- Poggio ED, Wang X, Greene T, Van Lente F, Hall PM. Performance of the modification of diet in renal disease and Cockcroft-Gault equations in the estimation of GFR in health and in chronic kidney disease. J Am Soc Nephrol 2005;16:459-66.
- Stevens LA, Schmid CH, Greene T, Zhang YL, Beck GJ, Froissart M, et al. Comparative performance of the CKD Epidemiology Collaboration (CKD-EPI) and the Modification of Diet in Renal Disease (MDRD) Study equations for estimating GFR levels above 60 mL/min/173 m2. Am J Kidney Dis 2010;56:486-95.
- Gama RM, Clery A, Griffiths K, Heraghty N, Peters AM, Palmer K, et al. Estimated glomerular filtration rate equations in people of self-reported black ethnicity in the United Kingdom: inappropriate adjustment for ethnicity may lead to reduced access to care. PLOS ONE 2021;16.
- Fukushima T, Nakano J, Ishii S, Natsuzako A, Hirase T, Sakamoto J, et al. Characteristics of muscle function and the effect of cachexia in patients with haematological malignancy. Eur J Cancer Care (Engl) 2019;28.
- Hsu CY, Yang W, Parikh RV, Anderson AH, Chen TK, Cohen DL, et al. CRIC Study Investigators . Race, genetic ancestry, and estimating kidney function in CKD. N Engl J Med 2021;385:1750-60.
- Lewis J, Greene T, Appel L, Contreras G, Douglas J, Lash J, et al. AASK Study Group . A comparison of iothalamate-GFR and serum creatinine-based outcomes: acceleration in the rate of GFR decline in the African American Study of Kidney Disease and Hypertension. J Am Soc Nephrol 2004;15:3175-83.
- Fontseré N, Salinas I, Bonal J, Bayés B, Riba J, Torres F, et al. Are prediction equations for glomerular filtration rate useful for the long-term monitoring of type 2 diabetic patients?. Nephrol Dial Transplant 2006;21:2152-8.
- Rossing P, Rossing K, Gaede P, Pedersen O, Parving HH. Monitoring kidney function in type 2 diabetic patients with incipient and overt diabetic nephropathy. Diabetes Care 2006;29:1024-30.
- Xie D, Joffe MM, Brunelli SM, Beck G, Chertow GM, Fink JC, et al. A comparison of change in measured and estimated glomerular filtration rate in patients with nondiabetic kidney disease. Clin J Am Soc Nephrol 2008;3:1332-8.
- Perkins BA, Nelson RG, Ostrander BE, Blouch KL, Krolewski AS, Myers BD, et al. Detection of renal function decline in patients with diabetes and normal or elevated GFR by serial measurements of serum cystatin C concentration: results of a 4-year follow-up study. J Am Soc Nephrol 2005;16:1404-12.
- de Boer IH, Sun W, Cleary PA, Lachin JM, Molitch ME, Zinman B, et al. Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications Study Research Group . Longitudinal changes in estimated and measured GFR in type 1 diabetes. J Am Soc Nephrol 2014;25:810-8.
- Lucas GM, Atta MG, Zook K, Vaidya D, Tao X, Maier P, et al. Cross-sectional and longitudinal performance of creatinine- and cystatin C-based estimating equations relative to exogenously measured glomerular filtration rate in HIV-positive and HIV-negative persons. J Acquir Immune Defic Syndr 2020;85:e58-66.
- Lindeman RD, Tobin J, Shock NW. Longitudinal studies on the rate of decline in renal function with age. J Am Geriatr Soc 1985;33:278-85.
- Post A, Tsikas D, Bakker SJL. Creatine is a conditionally essential nutrient in chronic kidney disease: a hypothesis and narrative literature review. Nutrients 2019;11.
- Turin TC, James M, Ravani P, Tonelli M, Manns BJ, Quinn R, et al. Proteinuria and rate of change in kidney function in a community-based population. J Am Soc Nephrol 2013;24:1661-7.
- Hoefield RA, Kalra PA, Lane B, O’Donoghue DJ, Foley RN, Middleton RJ. Associations of baseline characteristics with evolution of eGFR in a referred chronic kidney disease cohort. QJM 2013;106:915-24.
- Melsom T, Nair V, Schei J, Mariani L, Stefansson VTN, Harder JL, et al. Correlation between baseline GFR and subsequent change in GFR in Norwegian adults without diabetes and in Pima Indians. Am J Kidney Dis 2019;73:777-85.
- Moore KH, Clemmer JS. Questioning the renoprotective role of L-type calcium channel blockers in chronic kidney disease using physiological modeling. Am J Physiol Renal Physiol 2021;321:F548-57.
- Levey AS, Greene T, Schluchter MD, Cleary PA, Teschan PE, Lorenz RA, et al. Glomerular filtration rate measurements in clinical trials. Modification of Diet in Renal Disease Study Group and the Diabetes Control and Complications Trial Research Group. J Am Soc Nephrol 1993;4:1159-71.
- Bröchner-Mortensen J, Rödbro P. Selection of routine method for determination of glomerular filtration rate in adult patients. Scand J Clin Lab Invest 1976;36:35-43.
- Wilkinson J, Fleming JS, Waller DG. Effect of food and activity on the reproducibility of isotopic GFR estimation. Nucl Med Commun 1990;11:697-700.
- Carobene A, Marino I, Coskun A, Serteser M, Unsal I, Guerra E, et al. European Biological Variation Study of the EFLM Working Group on Biological Variation . The EuBIVAS Project: within- and between-subject biological variation data for serum creatinine using enzymatic and alkaline picrate methods and implications for monitoring. Clin Chem 2017;63:1527-36.
- Waikar SS, Rebholz CM, Zheng Z, Hurwitz S, Hsu CY, Feldman HI, et al. Biological variability of estimated GFR and albuminuria in CKD. Am J Kidney Dis 2018;72:538-46.
- Selvin E, Juraschek SP, Eckfeldt J, Levey AS, Inker LA, Coresh J. Within-person variability in kidney measures. Am J Kidney Dis 2013;61:716-22.
- Carter JL, Parker CT, Stevens PE, Eaglestone G, Knight S, Farmer CK, et al. Biological variation of plasma and urinary markers of acute kidney injury in patients with chronic kidney disease. Clin Chem 2016;62:876-83.
- Podracka L, Feber J, Lepage N, Filler G. Intra-individual variation of cystatin C and creatinine in pediatric solid organ transplant recipients. Pediatr Transplant 2005;9:28-32.
- Tan GD, Lewis AV, James TJ, Altmann P, Taylor RP, Levy JC. Clinical usefulness of cystatin C for the estimation of glomerular filtration rate in type 1 diabetes: reproducibility and accuracy compared with standard measures and iohexol clearance. Diabetes Care 2002;25:2004-9.
- Hoek FJ, Kemperman FA, Krediet RT. A comparison between cystatin C, plasma creatinine and the Cockcroft and Gault formula for the estimation of glomerular filtration rate. Nephrol Dial Transplant 2003;18:2024-31.
- Røraas T, Petersen PH, Sandberg S. Confidence intervals and power calculations for within-person biological variation: effect of analytical imprecision, number of replicates, number of samples, and number of individuals. Clin Chem 2012;58:1306-13.
- Soveri I, Berg UB, Björk J, Elinder CG, Grubb A, Mejare I, et al. SBU GFR Review Group . Measuring GFR: a systematic review. Am J Kidney Dis 2014;64:411-24.
- Tangri N, Stevens LA, Griffith J, Tighiouart H, Djurdjev O, Naimark D, et al. A predictive model for progression of chronic kidney disease to kidney failure. JAMA 2011;305:1553-9.
- Hasegawa T, Sakamaki K, Koiwa F, Akizawa T, Hishida A. CKD-JAC Study Investigators . Clinical prediction models for progression of chronic kidney disease to end-stage kidney failure under pre-dialysis nephrology care: results from the Chronic Kidney Disease Japan Cohort Study. Clin Exp Nephrol 2019;23:189-98.
- Go AS, Chertow GM, Fan D, McCulloch CE, Hsu CY. Chronic kidney disease and the risks of death, cardiovascular events, and hospitalization. N Engl J Med 2004;351:1296-305.
- Astor BC, Hallan SI, Miller ER, Yeung E, Coresh J. Glomerular filtration rate, albuminuria, and risk of cardiovascular and all-cause mortality in the US population. Am J Epidemiol 2008;167:1226-34.
- Nitsch D, Grams M, Sang Y, Black C, Cirillo M, Djurdjev O, et al. Chronic Kidney Disease Prognosis Consortium . Associations of estimated glomerular filtration rate and albuminuria with mortality and renal failure by sex: a meta-analysis. BMJ 2013;346.
- Swartling O, Rydell H, Stendahl M, Segelmark M, Trolle Lagerros Y, Evans M. CKD progression and mortality among men and women: a nationwide study in Sweden. Am J Kidney Dis 2021;78:190-9.e1.
- Matsushita K, Mahmoodi BK, Woodward M, Emberson JR, Jafar TH, Jee SH, et al. Chronic Kidney Disease Prognosis Consortium . Comparison of risk prediction using the CKD-EPI equation and the MDRD study equation for estimated glomerular filtration rate. JAMA 2012;307:1941-51.
- Astor BC, Shafi T, Hoogeveen RC, Matsushita K, Ballantyne CM, Inker LA, et al. Novel markers of kidney function as predictors of ESRD, cardiovascular disease, and mortality in the general population. Am J Kidney Dis 2012;59:653-62.
- Shlipak MG, Matsushita K, Ärnlöv J, Inker LA, Katz R, Polkinghorne KR, et al. CKD Prognosis Consortium . Cystatin C versus creatinine in determining risk based on kidney function. N Engl J Med 2013;369:932-43.
- Fleming JS, Nunan TO. British Nuclear Medicine Society . The new BNMS guidelines for measurement of glomerular filtration rate. Nucl Med Commun 2004;25:755-7.
- Ebert N, Loesment A, Martus P, Jakob O, Gaedeke J, Kuhlmann M, et al. Iohexol plasma clearance measurement in older adults with chronic kidney disease-sampling time matters. Nephrol Dial Transplant 2015;30:1307-14.
- Seegmiller JC, Burns BE, Schinstock CA, Lieske JC, Larson TS. Discordance between iothalamate and iohexol urinary clearances. Am J Kidney Dis 2016;67:49-55.
- Levey AS, Inker LA. GFR as the ‘gold standard’: estimated, measured, and true. Am J Kidney Dis 2016;67:9-12.
- Method Comparison and Bias Estimation Using Patient Samples; Approved Guideline – Second Edition. NCCLS document EP9-A2 [ISBN 1-56238-472-4]. Malvern, PA: Clinical and Laboratory Standards Institute; 2002.
- Li L, Astor BC, Lewis J, Hu B, Appel LJ, Lipkowitz MS, et al. Longitudinal progression trajectory of GFR among patients with CKD. Am J Kidney Dis 2012;59:504-12.
- Ali I, Chinnadurai R, Ibrahim ST, Kalra PA. Adverse outcomes associated with rapid linear and non-linear patterns of chronic kidney disease progression. BMC Nephrol 2021;22.
- Ali I, Ibrahim ST, Chinnadurai R, Green D, Taal M, Whetton TD, et al. A paradigm to discover biomarkers associated with chronic kidney disease progression. Biomark Insights 2020;15.
- Redwood S, Gill PS. Under-representation of minority ethnic groups in research – call for action. Br J Gen Pract 2013;63:342-3.
- Smart A, Harrison E. The under-representation of minority ethnic groups in UK medical research. Ethn Health 2017;22:65-82.
- Farooqi A, Jutlla K, Raghavan R, Wilson A, Uddin MS, Akroyd C, et al. Developing a toolkit for increasing the participation of black, Asian and minority ethnic communities in health and social care research. BMC Med Res Methodol 2022;22.
- Bodicoat DH, Routen AC, Willis A, Ekezie W, Gillies C, Lawson C, et al. Promoting inclusion in clinical trials – a rapid review of the literature and recommendations for action. Trials 2021;22.
- Ekezie W, Czyznikowska BM, Rohit S, Harrison J, Miah N, Campbell-Morris P, et al. The views of ethnic minority and vulnerable communities towards participation in COVID-19 vaccine trials. J Public Health (Oxf) 2021;43:e258-60.
- Major RW, Shepherd D, Medcalf JF, Xu G, Gray LJ, Brunskill NJ. The kidney failure risk equation for prediction of end stage renal disease in UK primary care: an external validation and clinical impact projection cohort study. PLOS Med 2019;16.
- Drummond MF, Jefferson TO. Guidelines for authors and peer reviewers of economic submissions to the BMJ. The BMJ Economic Evaluation Working Party. BMJ 1996;313:275-83.
- Gonzalez-Perez JG. Developing a scoring system to quality assess economic evaluations. Eur J Health Econ 2002;3:131-6.
- Siegel JE, Krolewski AS, Warram JH, Weinstein MC. Cost-effectiveness of screening and early treatment of nephropathy in patients with insulin-dependent diabetes mellitus. J Am Soc Nephrol 1992;3:S111-9.
- Boulware LE, Jaar BG, Tarver-Carr ME, Brancati FL, Powe NR. Screening for proteinuria in US adults: a cost-effectiveness analysis. JAMA 2003;290:3101-14.
- Palmer AJ, Valentine WJ, Chen R, Mehin N, Gabriel S, Bregman B, et al. A health economic analysis of screening and optimal treatment of nephropathy in patients with type 2 diabetes and hypertension in the USA. Nephrol Dial Transplant 2008;23:1216-23.
- Howard K, White S, Salkeld G, McDonald S, Craig JC, Chadban S, et al. Cost-effectiveness of screening and optimal management for diabetes, hypertension, and chronic kidney disease: a modeled analysis. Value Health 2010;13:196-208.
- Sekhar DL, Wang L, Hollenbeak CS, Widome MD, Paul IM. A cost-effectiveness analysis of screening urine dipsticks in well-child care. Pediatrics 2010;125:660-3.
- Kondo M, Yamagata K, Hoshi SL, Saito C, Asahi K, Moriyama T, et al. Cost-effectiveness of chronic kidney disease mass screening test in Japan. Clin Exp Nephrol 2012;16:279-91.
- Srisubat A, Sriratanaban J, Ngamkiatphaisan S, Tungsanga K. Cost-effectiveness of annual microalbuminuria screening in Thai diabetics. Asian Biomed 2014;8:371-9.
- Go DS, Kim SH, Park J, Ryu DR, Lee HJ, Jo MW. Cost-utility analysis of the National Health Screening Program for chronic kidney disease in Korea. Nephrology (Carlton) 2019;24:56-64.
- Golan L, Birkmeyer JD, Welch HG. The cost-effectiveness of treating all patients with type 2 diabetes with angiotensin-converting enzyme inhibitors. Ann Intern Med 1999;131:660-7.
- Kiberd BA, Jindal KK. Should all Pima Indians with type 2 diabetes mellitus be prescribed routine angiotensin-converting enzyme inhibition therapy to prevent renal failure?. Mayo Clin Proc 1999;74:559-64.
- Boersma C, Gansevoort RT, Pechlivanoglou P, Visser ST, van Toly FF, de Jong-van den Berg LTW, et al. Prevention of Renal and Vascular End Stage Disease Study Group . Screen-and-treat strategies for albuminuria to prevent cardiovascular and renal disease: cost-effectiveness of nationwide and targeted interventions based on analysis of cohort data from the Netherlands. Clin Ther 2010;32:1103-21.
- Hoerger TJ, Wittenborn JS, Segel JE, Burrows NR, Imai K, Eggers P, et al. Centers for Disease Control and Prevention CKD Initiative . A health policy model of CKD: 1. Model construction, assumptions, and validation of health consequences. Am J Kidney Dis 2010;55:452-62.
- Hoerger TJ, Wittenborn JS, Segel JE, Burrows NR, Imai K, Eggers P, et al. Centers for Disease Control and Prevention CKD Initiative . A health policy model of CKD: 2. The cost-effectiveness of microalbuminuria screening. Am J Kidney Dis 2010;55:463-73.
- Hoerger TJ, Wittenborn JS, Zhuo X, Pavkov ME, Burrows NR, Eggers P, et al. Cost-effectiveness of screening for microalbuminuria among African Americans. J Am Soc Nephrol 2012;23:2035-41.
- Kessler R, Keusch G, Szucs TD, Wittenborn JS, Hoerger TJ, Brügger U, et al. Health economic modelling of the cost-effectiveness of microalbuminuria screening in Switzerland. Swiss Med Wkly 2012;142.
- Farmer AJ, Stevens R, Hirst J, Lung T, Oke J, Clarke P, et al. Optimal strategies for identifying kidney disease in diabetes: properties of screening tests, progression of renal dysfunction and impact of treatment – systematic review and modelling of progression and cost-effectiveness. Health Technol Assess 2014;18:1-128.
- Ferguson TW, Tangri N, Tan Z, James MT, Lavallee BDA, Chartrand CD, et al. Screening for chronic kidney disease in Canadian indigenous peoples is cost-effective. Kidney Int 2017;92:192-200.
- Wang H, Yang L, Wang F, Zhang L. Strategies and cost-effectiveness evaluation of persistent albuminuria screening among high-risk population of chronic kidney disease. BMC Nephrol 2017;18.
- Yarnoff BO, Hoerger TJ, Simpson SK, Leib A, Burrows NR, Shrestha SS, et al. Centers for Disease Control and Prevention CKD Initiative . The cost-effectiveness of using chronic kidney disease risk scores to screen for early-stage chronic kidney disease. BMC Nephrol 2017;18.
- Wu B, Zhang S, Lin H, Mou S. Prevention of renal failure in Chinese patients with newly diagnosed type 2 diabetes: a cost-effectiveness analysis. J Diabetes Investig 2018;9:152-61.
- Le Floch JP, Charles MA, Philippon C, Perlemuter L. Cost-effectiveness of screening for microalbuminuria using immunochemical dipstick tests or laboratory assays in diabetic patients. Diabet Med 1994;11:349-56.
- Kiberd BA, Jindal KK. Screening to prevent renal failure in insulin dependent diabetic patients: an economic evaluation. BMJ 1995;311:1595-9.
- Kiberd BA, Jindal KK. Routine treatment of insulin-dependent diabetic patients with ACE inhibitors to prevent renal failure: an economic evaluation. Am J Kidney Dis 1998;31:49-54.
- Adarkwah CC, Gandjour A. Cost-effectiveness of angiotensin-converting enzyme inhibitors and angiotensin II receptor blockers in newly diagnosed type 2 diabetes in Germany. Int J Technol Assess Health Care 2010;26:62-70.
- Adarkwah CC, Gandjour A, Akkerman M, Evers SM. Cost-effectiveness of angiotensin-converting enzyme inhibitors for the prevention of diabetic nephropathy in The Netherlands – a Markov model. PLOS ONE 2011;6.
- den Hartog JR, Reese PP, Cizman B, Feldman HI. The costs and benefits of automatic estimated glomerular filtration rate reporting. Clin J Am Soc Nephrol 2009;4:419-27.
- Manns B, Hemmelgarn B, Tonelli M, Au F, Chiasson TC, Dong J, et al. Alberta Kidney Disease Network . Population based screening for chronic kidney disease: cost effectiveness study. BMJ 2010;341.
- Ravaghi H, Ebrahimnia M, Farzanah A, Rostami Z, Madani M. Cost-effectiveness analysis of screening chronic kidney disease in Iran. J Clin Diagn Res 2019;13:IC01-4.
- Critselis E, Vlahou A, Stel VS, Morton RL. Cost-effectiveness of screening type 2 diabetes patients for chronic kidney disease progression with the CKD273 urinary peptide classifier as compared to urinary albumin excretion. Nephrol Dial Transplant 2018;33:441-9.
Appendix 1 Supplementary information for Chapters 2 and 3
| Date | Milestone |
|---|---|
| 13 June 2013 | eGFR-C trial launch meeting, Birmingham |
| 1 August 2013 | Grant start date |
| 9 October 2013 | REC approval |
| 15 October 2013 | NSA 1 – Addition of ISRCTN number to protocol |
| 2 December 2013 | Study steering committee meets |
| 28 February 2014 | R&D approval |
| 8 April 2014 | First participant |
| 13 May 2014 | Study steering committee meets |
| 1 June 2014 | Substantial amendment 1 – adding consent for long-term follow-up via NHS Digital |
| 17 October 2014 | REC annual progress report submitted |
| 19 November 2014 | Study steering committee meets |
| 26 November 2014 | Investigator meeting (face to face), Birmingham |
| 29 January 2015 | Trial monitoring review meeting, HTA, London |
| 2 February 2015 | Substantial amendment 2 – adding summary information sheet |
| 20 February 2015 | NSA 2 – correcting version error in substantial amendment 2 |
| 30 March 2015 | NSA 3 – adding primary care PIC site recruitment at King’s College Hospital, London |
| 14 May 2015 | Study steering committee meets |
| 15 May 2015 | Substantial amendment 3 – adding participant newsletters |
| 6 July 2015 | Variation to contract 1 agreed by funder – 12 months funded extension |
| 8 July 2015 | NSA 4 – adding primary care PIC site recruitment for all sites; notifying of 12-month extension to trial |
| 11 September 2015 | REC annual progress report submitted |
| 5 November 2015 | Study steering committee meets |
| 24 November 2015 | Investigator meeting (face to face), Birmingham |
| 1 December 2015 | Substantial amendment 4 – updating participant information sheet |
| 16 December 2015 | NSA 5 – minor update to consent form |
| 7 January 2016 | NSA 6 – seeking REC approval to send trial newsletters to potential participants |
| 20 January 2016 | NSA 7 – changes to substudy recruitment targets |
| 13 April 2016 | Substantial amendment 5 – changes to PIC site recruitment process |
| 11 May 2016 | Study steering committee meets |
| 13 May 2016 | NSA 8 – adding Derby CCGs to PIC sites for region; adding HTA logo to documents |
| 21 September 2016 | Variation to contract 2 agreed by funder – 5 months funded extension |
| 5 October 2016 | Substantial amendment 6 – adding IRAS number to documents; notifying of 5 month extension to trial |
| 11 October 2016 | REC annual progress report submitted |
| 15 November 2016 | Study steering committee meets |
| 25 January 2017 | Last participant recruited |
| 14 February 2017 | Substantial amendment 7 – updates to SAE process |
| 12 July 2017 | Study steering committee meets |
| 10 October 2017 | REC annual progress report submitted |
| 29 November 2017 | Study steering committee meets |
| 25 July 2018 | Study steering committee meets |
| 10 October 2018 | REC annual progress report submitted |
| 14 November 2018 | Study steering committee meets |
| 8 January 2019 | NSA 9 – addition of GDPR information leaflet |
| 15 May 2019 | Substantial amendment 8 – adding final appointment reminder letter |
| 10 July 2019 | Study steering committee meets |
| 8 October 2019 | REC annual progress report submitted |
| 9 January 2020 | Follow up completed |
| 27 February 2020 | Study steering committee meets |
| 9 June 2020 | Analysis of samples complete at Kent laboratory |
| 18 July 2020 | Analysis of samples complete at London laboratory |
| 21 September 2020 | Variation to contract 3 agreed by funder – 12 months unfunded extension |
| 10 October 2020 | NSA 10 – change to trial/grant end date |
| 6 November 2020 | REC annual progress report submitted |
| 30 April 2021 | Trial database closed to data entry |
| 2 June 2021 | End of trial notified to REC |
| Month | Month | Cumulative number of participants recruited | Monthly number of participants recruited |
|---|---|---|---|
| 1 | February 2014 | 0 | 0 |
| 2 | March 2014 | 0 | 0 |
| 3 | April 2014 | 1 | 1 |
| 4 | May 2014 | 10 | 9 |
| 5 | June 2014 | 26 | 16 |
| 6 | July 2014 | 51 | 25 |
| 7 | August 2014 | 83 | 32 |
| 8 | September 2014 | 124 | 41 |
| 9 | October 2014 | 173 | 49 |
| 10 | November 2014 | 231 | 58 |
| 11 | December 2014 | 263 | 32 |
| 12 | January 2015 | 325 | 62 |
| 13 | February 2015 | 378 | 53 |
| 14 | March 2015 | 440 | 62 |
| 15 | April 2015 | 509 | 69 |
| 16 | May 2015 | 555 | 46 |
| 17 | June 2015 | 598 | 43 |
| 18 | July 2015 | 639 | 41 |
| 19 | August 2015 | 677 | 38 |
| 20 | September 2015 | 716 | 39 |
| 21 | October 2015 | 763 | 47 |
| 22 | November 2015 | 799 | 36 |
| 23 | December 2015 | 826 | 27 |
| 24 | January 2016 | 863 | 37 |
| 25 | February 2016 | 903 | 40 |
| 26 | March 2016 | 946 | 43 |
| 27 | April 2016 | 986 | 40 |
| 28 | May 2016 | 1019 | 33 |
| 29 | June 2016 | 1061 | 42 |
| 30 | July 2016 | 1097 | 36 |
| 31 | August 2016 | 1126 | 29 |
| 32 | September 2016 | 1144 | 18 |
| 33 | October 2016 | 1173 | 29 |
| 34 | November 2016 | 1210 | 37 |
| 35 | December 2016 | 1236 | 26 |
| 36 | January 2017 | 1249 | 13 |
| Total participants recruited | Total dropouts | % dropouts | |
|---|---|---|---|
| Derby | 218 | 43 | 19.7 |
| East Kent | 278 | 32 | 11.5 |
| King’s | 157 | 36 | 22.9 |
| Salford | 231 | 68 | 29.4 |
| Birmingham | 165 | 25 | 15.2 |
| Leicester | 180 | 49 | 27.2 |
| Total | 1229 | 253 | 20.6 |
| Linear regression | Deming regression | |||||
|---|---|---|---|---|---|---|
| Estimate | 95% CI | p | Estimate | 95% CI | p | |
| Abbot cystatin C | 0.94 | 0.92 to 0.96 | < 0.001 | 0.95 | 0.92 to 0.97 | < 0.001 |
| Constant | −0.08 | −0.12 to −0.03 | < 0.001 | −0.09 | −0.13 to −0.06 | < 0.001 |
| CKD-EPIcreatinine | Change within 3 ml/minute/1.73 m2 of mGFR | Change ≥ 3 ml/minute/1.73 m2 of mGFR |
|---|---|---|
| n | 640/875 | 235/875 |
| Age, years | 67 (59–74) | 66 (58–73) |
| M : F, n | 371 : 269 | 134 : 101 |
| Ethnicity | ||
| Caucasian, n (%) | 568 (88.8) | 205 (87.2) |
| African-Caribbean, n (%) | 21 (3.3) | 15 (6.4) |
| South Asian, n (%) | 33 (5.2) | 13 (5.5) |
| Other (missing), n (%)a | 18 (2.8) | 2 (0.9) |
| Height, cm | 170 (163–177) | 169 (161–176) |
| Weight, kg | 84.6 (72.8–97.1) | 84.7 (73.9–97.4) |
| BMI, kg/m2 | 28.8 (25.7–33.1) | 30.0 (25.9–34.1) |
| Smoking status | ||
| Non-smoker, n (%) | 343 (53.6) | 110 (46.8) |
| Current smoker, n (%) | 42 (6.6) | 21 (8.9) |
| Former smoker, n (%) | 253 (39.5) | 104 (44.3) |
| Unknown, n (%) | 2 (0.3) | 0 (0) |
| CKD-EPIcreatinine | Change within 3 ml/minute/1.73 m2 of mGFR | Change ≥ 3 ml/minute/1.73 m2 of mGFR |
| Diabetes (yes), n (%) | 152 (23.8) | 68 (28.9) |
| Urine albumin concentration | 4.7 (1.4–26.3) | 4.0 (1.5–27.0) |
| < 3 mg/mmol, n (%) | 254 (39.7) | 99 (42.1) |
| 3–30 mg/mmol, n (%) | 219 (34.2) | 73 (31.1) |
| > 30 mg/mmol, n (%) | 145 (22.7) | 55 (23.4) |
| Missing, n (%) | 22 (3.4) | 8 (3.4) |
| Serum creatinine, µmol/l | 133.7 (112.2–162) | 129.8 (102.5–157.6) |
| Serum cystatin C, mg/l | 1.7 (1.5–2.0) | 1.7 (1.4–2.1) |
| Measured GFR, ml/minute/1.73 m2 | 45.9 (36.4–54.7) | 50.2 (43.4–58.6) |
| CKD-EPIcystatin | Change within 3 ml/minute/1.73 m2 of mGFR | Change ≥ 3 ml/minute/1.73 m2 of mGFR |
| n | 652/875 | 223/875 |
| Age, years | 67 (59–74) | 67 (56–73) |
| M : F, n | 371 : 269 | 134 : 101 |
| Ethnicity | ||
| Caucasian, n (%) | 568 (88.8) | 205 (87.2) |
| African-Caribbean, n (%) | 21 (3.3) | 15 (6.4) |
| South Asian, n (%) | 33 (5.2) | 13 (5.5) |
| Other (missing), n (%)a | 18 (2.8) | 2 (0.9) |
| Height, cm | 171 (163–177) | 168 (161–174) |
| Weight, kg | 85.6 (73.9–98.2) | 81.3 (70.9–95.0) |
| BMI, kg/m2 | 29.1 (25.8–33.5) | 28.6 (25.5–33.0) |
| Smoking status | ||
| Non-smoker, n (%) | 343 (53.6) | 110 (46.8) |
| Current smoker, n (%) | 42 (6.6) | 21 (8.9) |
| Former smoker, n (%) | 253 (39.5) | 104 (44.3) |
| Unknown, n (%) | 2 (0.3) | 0 (0) |
| Diabetes (yes), n (%) | 152 (23.8) | 68 (28.9) |
| Urine albumin concentration | 5.5 (1.5–31.6) | 3.1 (1.4–17.4) |
| < 3 mg/mmol, n (%) | 99 (42.1) | 254 (39.7) |
| 3–30 mg/mmol, n (%) | 73 (31.1) | 219 (34.2) |
| > 30 mg/mmol, n (%) | 55 (23.4) | 145 (22.7) |
| Missing, n (%) | 8 (3.4) | 22 (3.4) |
| CKD-EPIcystatin | Change within 3 ml/minute/1.73 m2 of mGFR | Change ≥ 3 ml/minute/1.73 m2 of mGFR |
| Serum creatinine, µmol/l | 135.1 (114.0–164.3) | 120.0 (99.0–144.0) |
| Serum cystatin C, mg/l | 1.8 (1.5–2.1) | 1.5 (1.3–1.9) |
| Measured GFR, ml/minute/1.73 m2 | 46.5 (37.3–54.5) | 51.1 (40.4–59.5) |
| CKD-EPIcreatinine-cystatin | Change within 3 ml/minute/1.73 m2 of mGFR | Change ≥ 3 ml/minute/1.73 m2 of mGFR |
| n | 689/875 | 186/875 |
| Age, years | 67 (58–74) | 67 (58–74) |
| M : F, n | 407 : 282 | 98 : 88 |
| Ethnicity | ||
| Caucasian, n (%) | 611 (88.7) | 162 (87.1) |
| African-Caribbean, n (%) | 25 (3.6) | 11 (5.9) |
| South Asian, n (%) | 37 (5.4) | 9 (4.8) |
| Other (missing), n (%)a | 16 (2.3) | 4 (2.2) |
| Height, cm | 170 (163–177) | 168 (161–176) |
| Weight, kg | 85.0 (73.3–97.8) | 82.7 (70.8–96.5) |
| BMI, kg/m2 | 29.0 (25.7–33.5) | 29.0 (25.6–33.1) |
| Smoking status | ||
| Non-smoker, n (%) | 362 (52.5) | 91 (48.9) |
| Current smoker, n (%) | 47 (6.8) | 16 (8.6) |
| Former smoker, n (%) | 278 (40.4) | 79 (42.5) |
| Unknown, n (%) | 2 (0.3) | 0 (0) |
| Diabetes (yes), n (%) | 170 (24.7) | 50 (26.9) |
| Urine albumin concentration | 5.4 (1.5–30.2) | 3.1 (1.2–15.0) |
| < 3 mg/mmol, n (%) | 264 (38.3) | 89 (47.9) |
| 3–30 mg/mmol, n (%) | 232 (33.7) | 60 (32.3) |
| > 30 mg/mmol, n (%) | 167 (24.2) | 33 (17.7) |
| Missing, n (%) | 26 (3.8) | 4 (2.2) |
| Serum creatinine, µmol/l | 135.0 (113.0–163.0) | 119.8 (98.3–145.2) |
| Serum cystatin C, mg/l | 1.8 (1.5–2.1) | 1.6 (1.3–2.0) |
| Measured GFR, ml/minute/1.73 m2 | 46.5 (37.0–54.9) | 50.8 (40.6–59.5) |
| Equation | Du Bois BSA adjustment | Haycock BSA adjustment | |
|---|---|---|---|
| MDRD | Mean bias (SD) | −3.8 (9.2) | −2.4 (9.0) |
| Median bias (IQR) | −3.7 (−9.7 to 2.4) | −2.3 (−8.4 to 3.5) | |
| RMSE | 9.09 | 8.90 | |
| CKD-EPIcreatinine | Mean bias (SD) | −2.5 (9.1) | −1.1 (8.9) |
| Median bias (IQR) | −2.8 (−8.2 to 3.5) | −1.2 (−6.9 to 4.8) | |
| RMSE | 8.83 | 8.66 | |
| CKD-EPIcystatin | Mean bias (SD) | −3.4 (9.1) | −2.0 (8.9) |
| Median bias (IQR) | −4.1 (−9.3 to 1.5) | −2.8 (−7.7 to 2.7) | |
| RMSE | 7.58 | 7.25 | |
| CKD-EPIcreatinine-cystatin | Mean bias (SD) | −3.7 (7.3) | −2.3 (7.1) |
| Median bias (IQR) | −3.9 (−8.4 to 1.1) | −2.6 (−6.9 to 2.3) | |
| RMSE | 7.07 | 6.82 |
FIGURE 14.
Scatter plot comparing Abbott and Siemens cystatin C measurements. The solid line shows the linear regression line of best fit and the dotted line shows the line of identity.

FIGURE 15.
Box and whisker plot of mGFR over time in the substudy of disease progression.
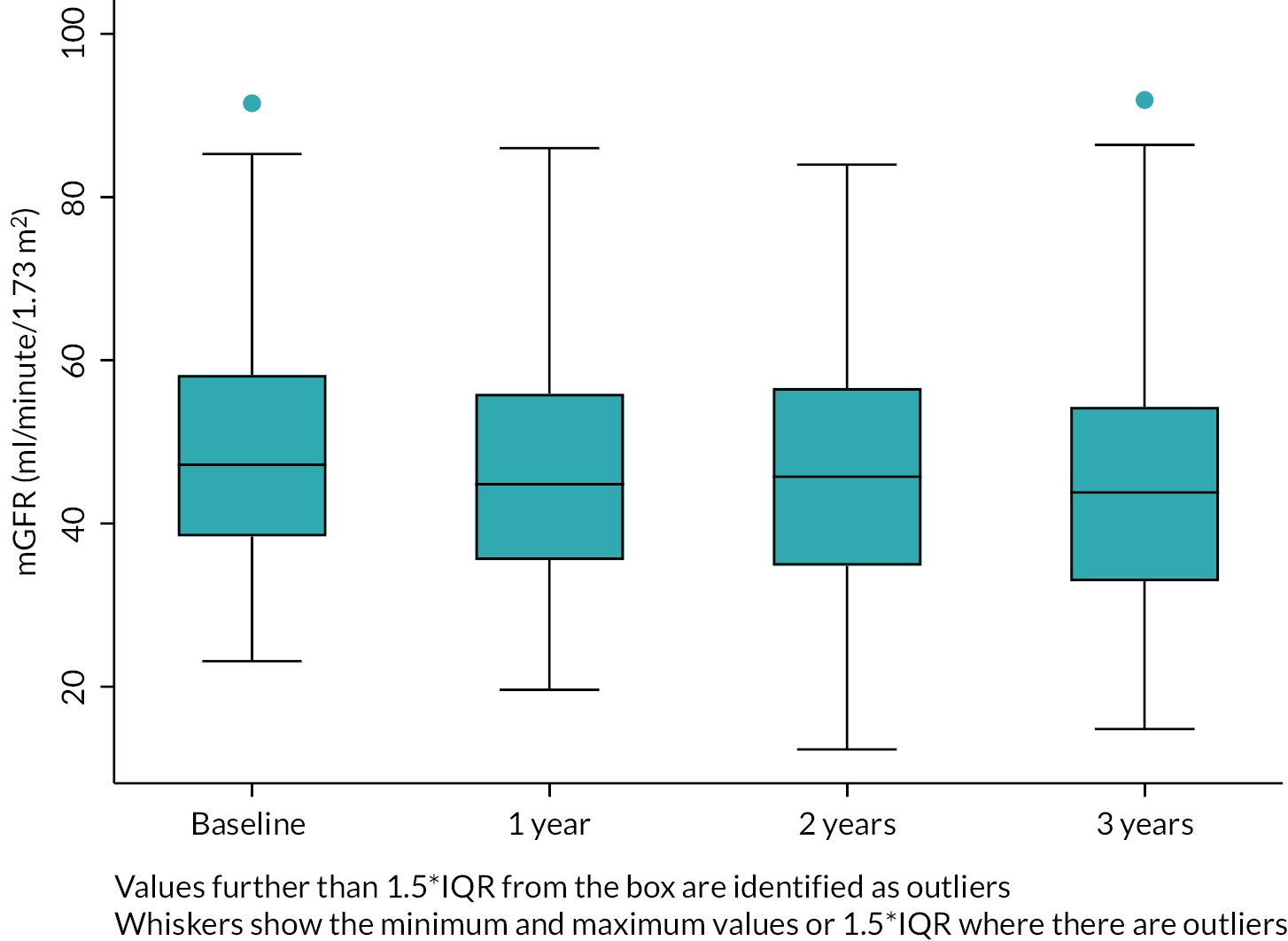
FIGURE 16.
Box and whisker plots of mGFRs and eGFRs over time in the substudy of disease progression.

FIGURE 17.
Box and whisker plots of difference (bias) between mGFRs and eGFRs in the substudy of disease progression.

FIGURE 18.
Model predicted slopes for mGFR and CKD-EPIcreatinine and CKD-EPIcystatin eGFR.
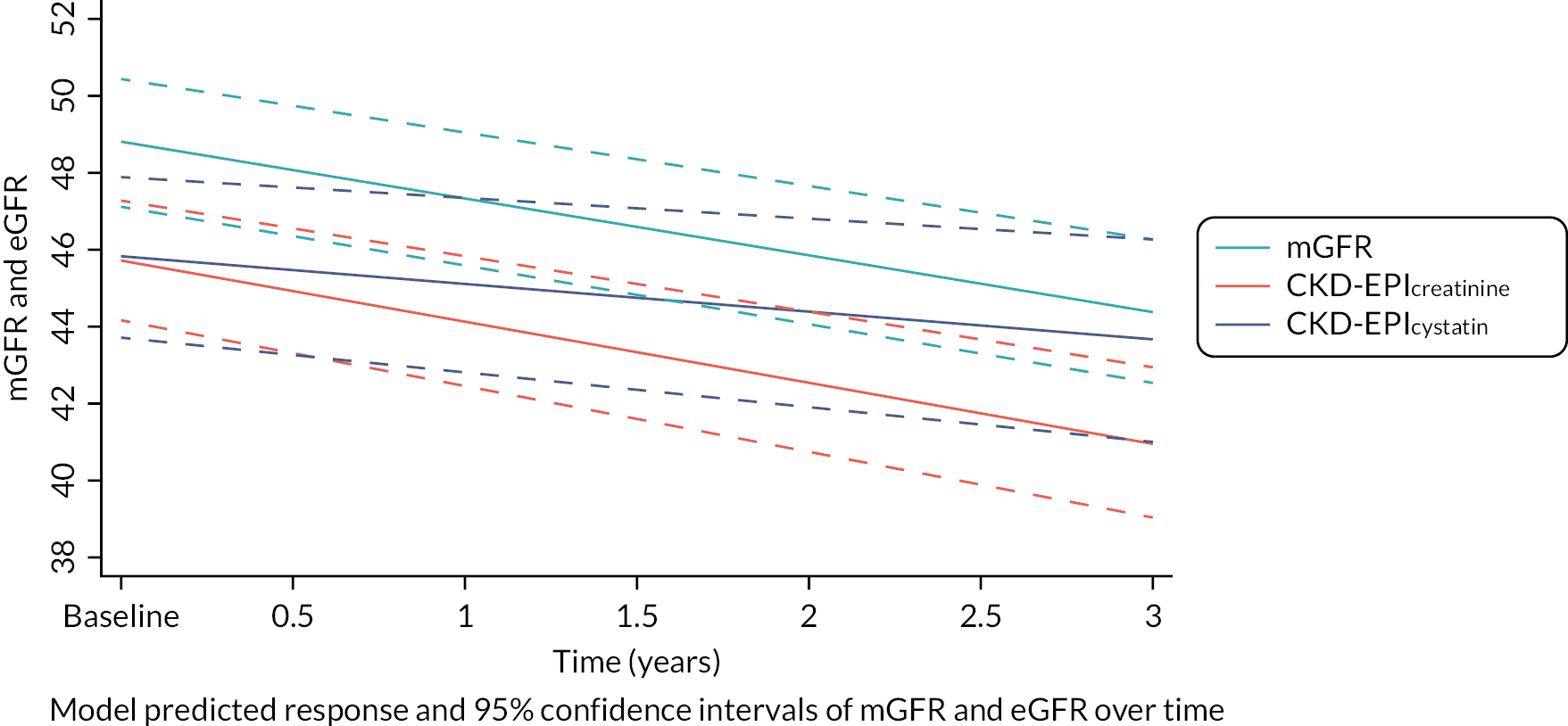
FIGURE 19.
Median and IQR mGFR over time by ethnicity group (main study and substudy data combined).
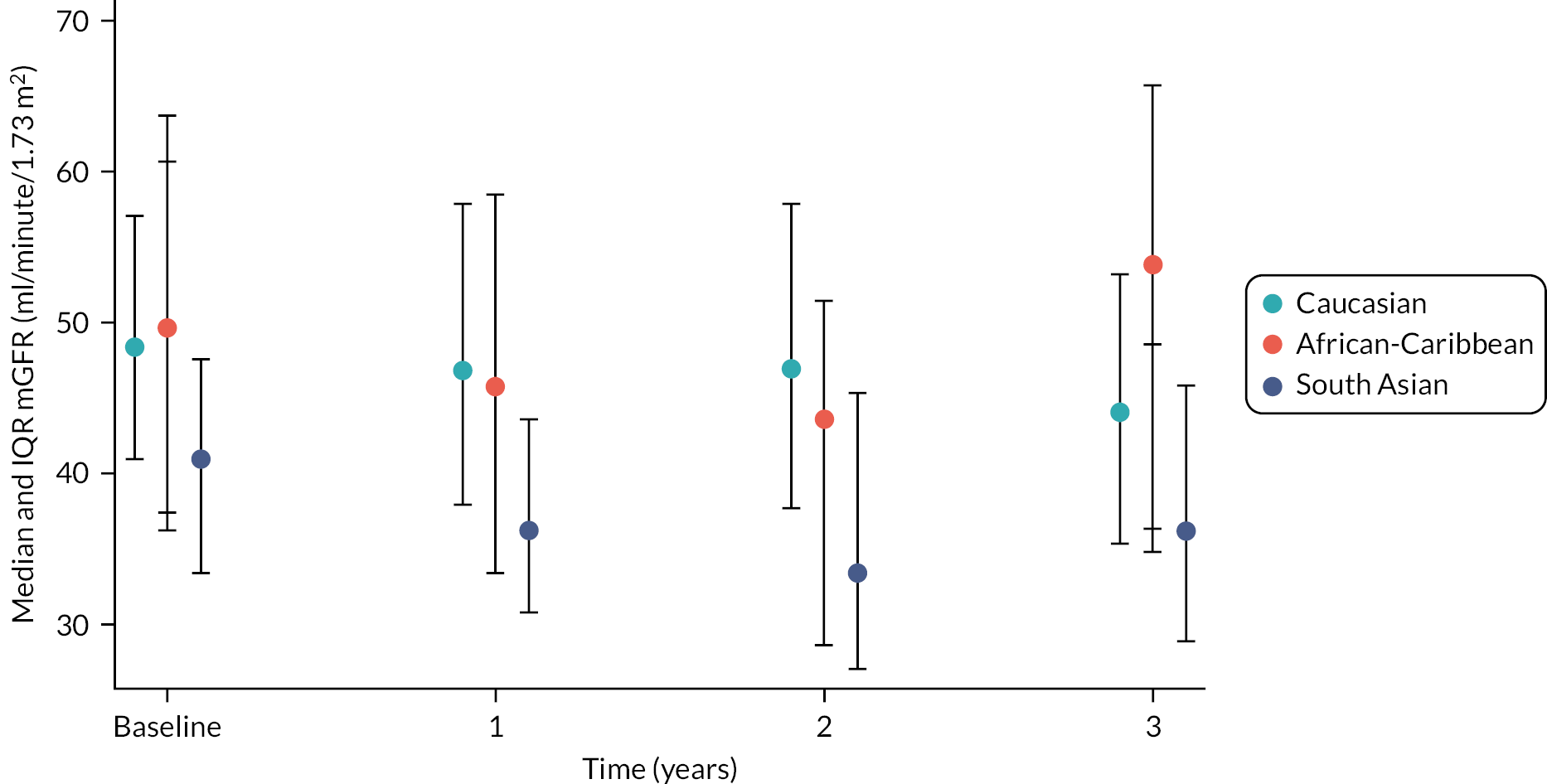
FIGURE 20.
Median and IQR mGFR over time by albuminuria status (main study and substudy data combined).

FIGURE 21.
Median and IQR CKD-EPIcreatinine over time by albuminuria status (main study and substudy data combined). The steeper decline over time is more obvious for those with albuminuria, compared to those who do not have albuminuria, particularly those with ACR > 30 mg/mmol.

FIGURE 22.
Median and IQR CKD-EPIcreatinine over time by ethnicity group (main study and substudy data combined). The data suggest a steeper decline for South Asian ethnicity.
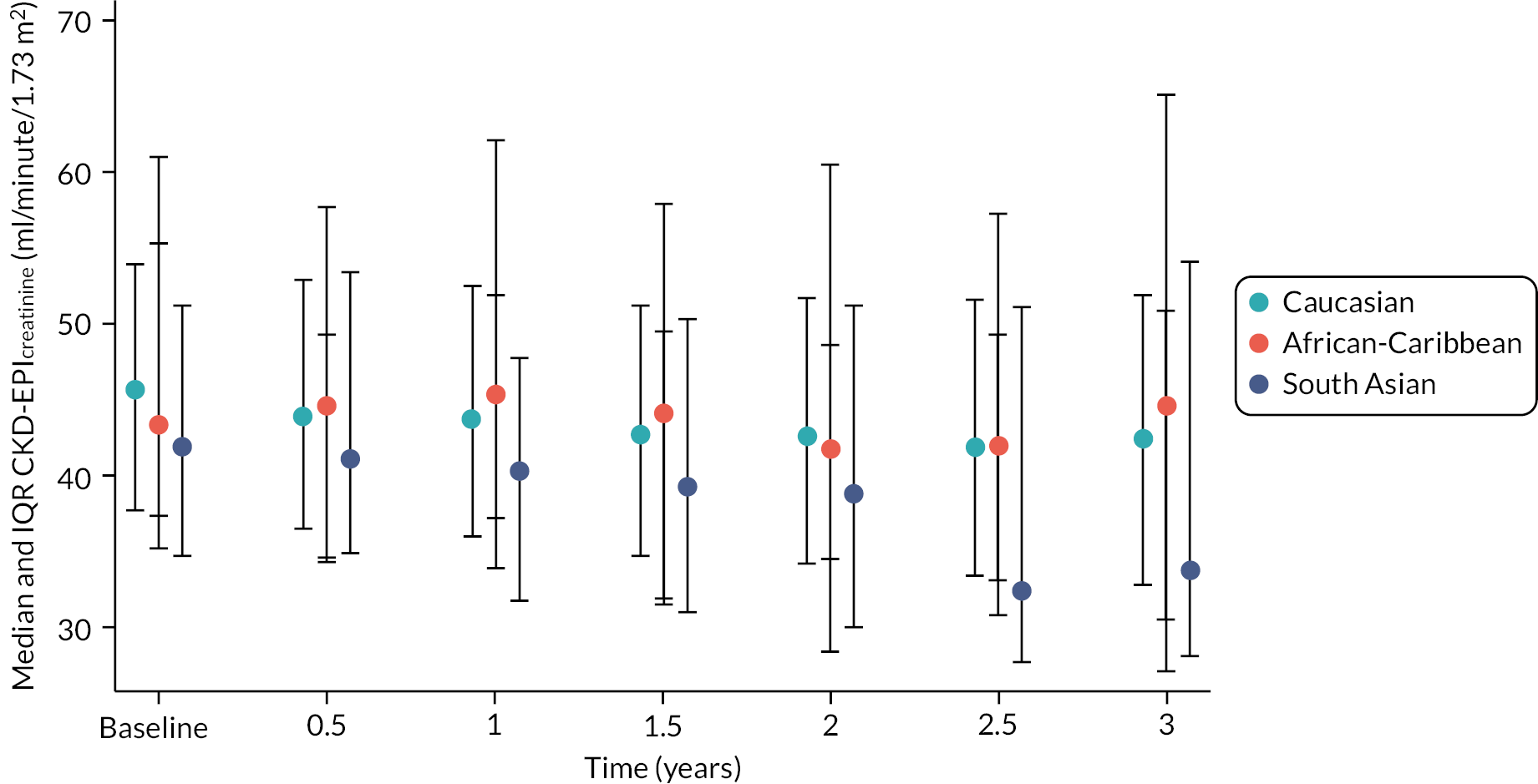
FIGURE 23.
Median and IQR CKD-EPIcystatin over time by ethnicity group (main study and substudy data combined).
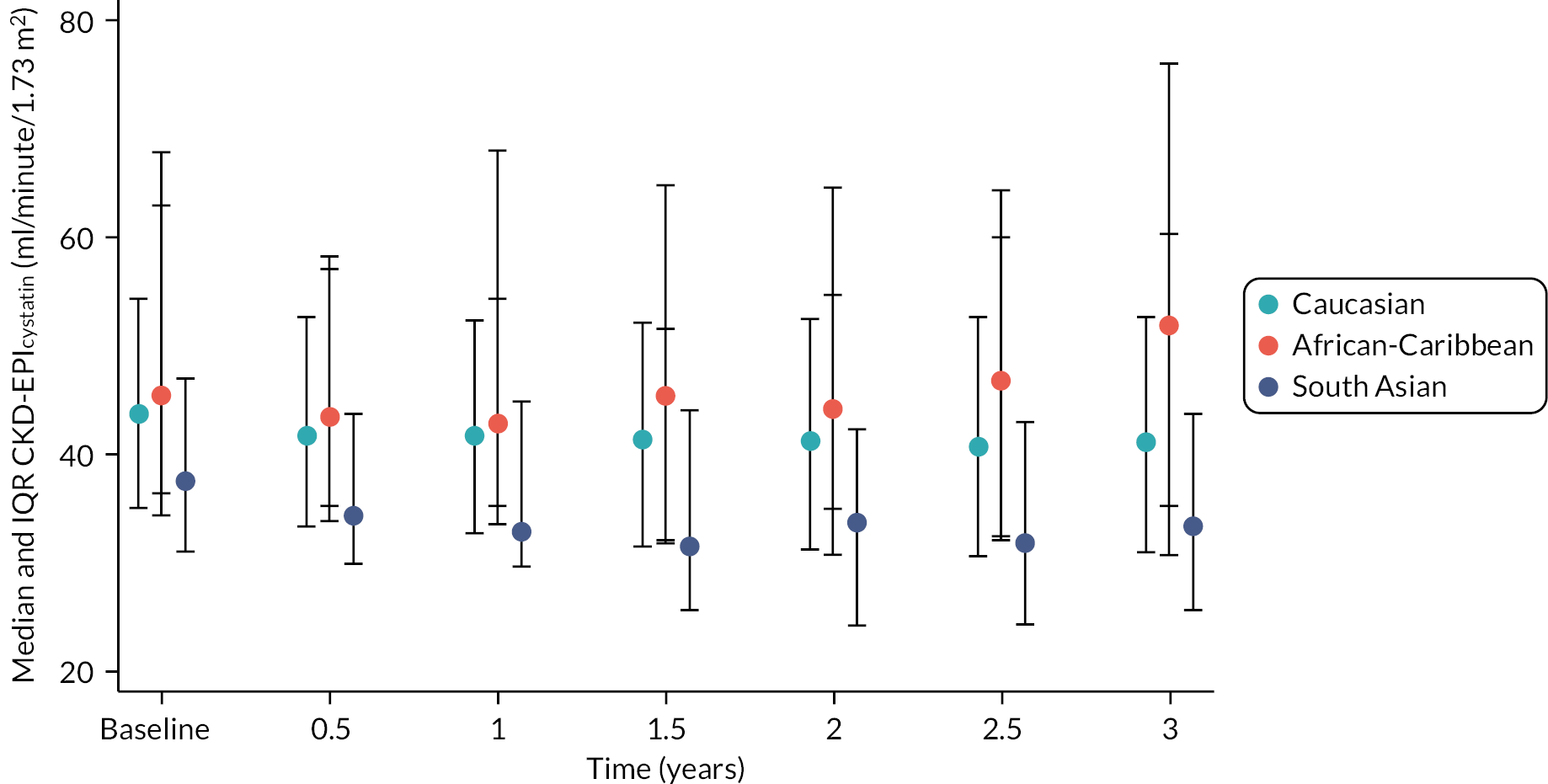
FIGURE 24.
Median and IQR ACR over time by albuminuria status (main study and substudy data combined). The model suggested that those with albuminuria incline more steeply, although this is not very apparent from examination of the median and quartiles.

FIGURE 25.
Median and IQR ACR over time by ethnicity group (main study and substudy data combined). The model suggests a steeper incline overall for those with African-Caribbean and South Asian ethnicity: plots of the median and quartiles show an incline for African-Caribbean individuals, but this is not so obvious for South Asian ethnicity.

FIGURE 26.
Linear regression analysis comparing creatinine results obtained using the enzymatic (field) and ID-MS (reference) methods. The dashed black line indicates unity and the red line shows the regression line. The relationship between the two methods was described by the linear regression equation: enzymatic = 3.23 + 1.01(ID-MS), R2 0.969.
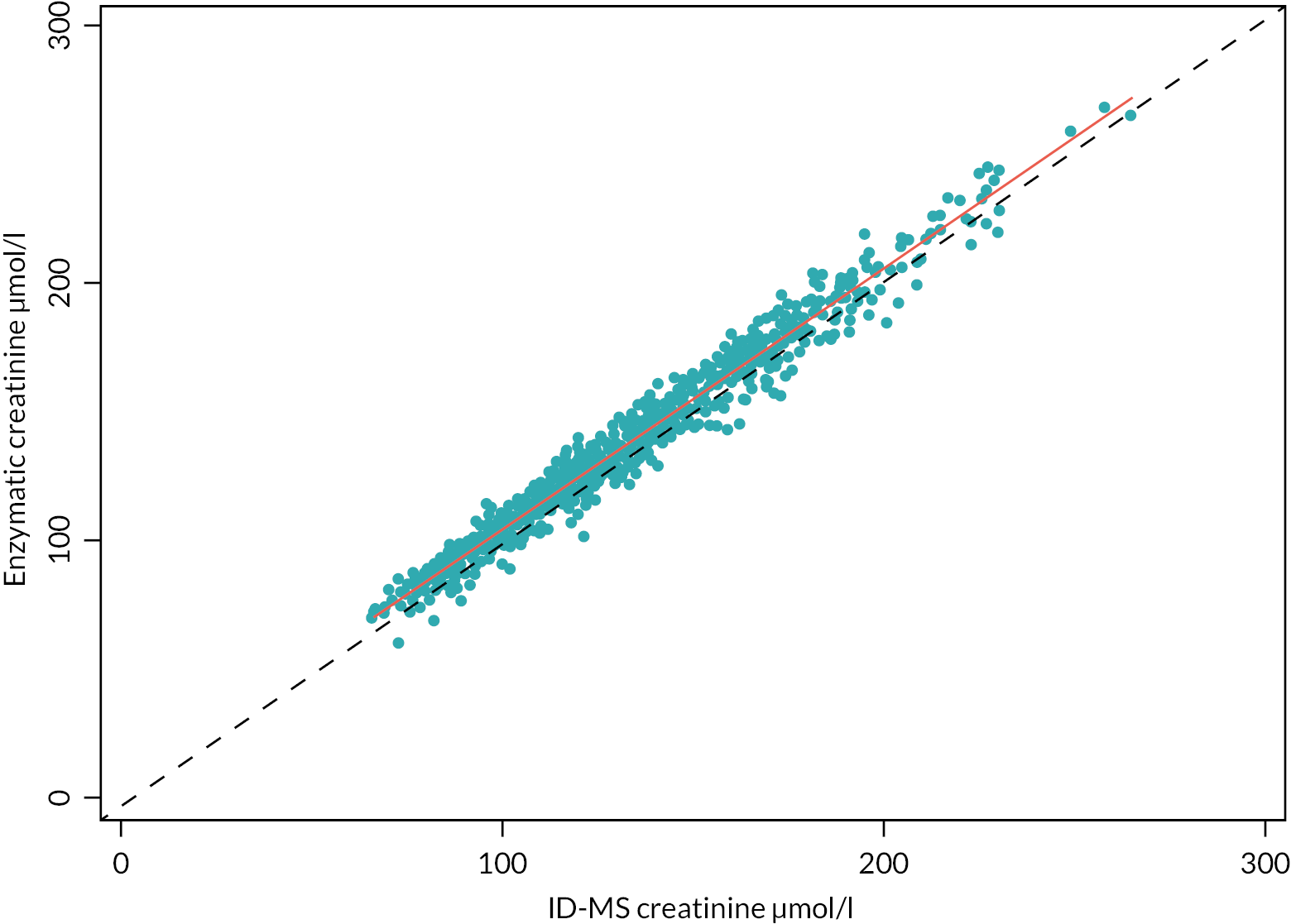
FIGURE 27.
Bias plot comparison of creatinine results obtained using the enzymatic (field) and ID-MS (reference) methods. The solid black line indicates zero bias and the dashed red line shows mean bias. A lowess (locally weighted scatterplot smoothing function) curve (red solid line) is also shown.

FIGURE 28.
Bias profiles for the MDRD equation based on annual data from the main study. The individual scatter points represent the available study data on mGFR vs. eGFR at each annual sampling point (n = 875 at baseline and year 3; n = 212 at year 1; and n = 184 at year 2); the solid blue lines representing the expected mean eGFR bias over the mGFR range, based on a fitted loess regression curve; and the red dotted line in each plot indicates the overall mean bias calculated for the given eGFR equation at each time sampling point.
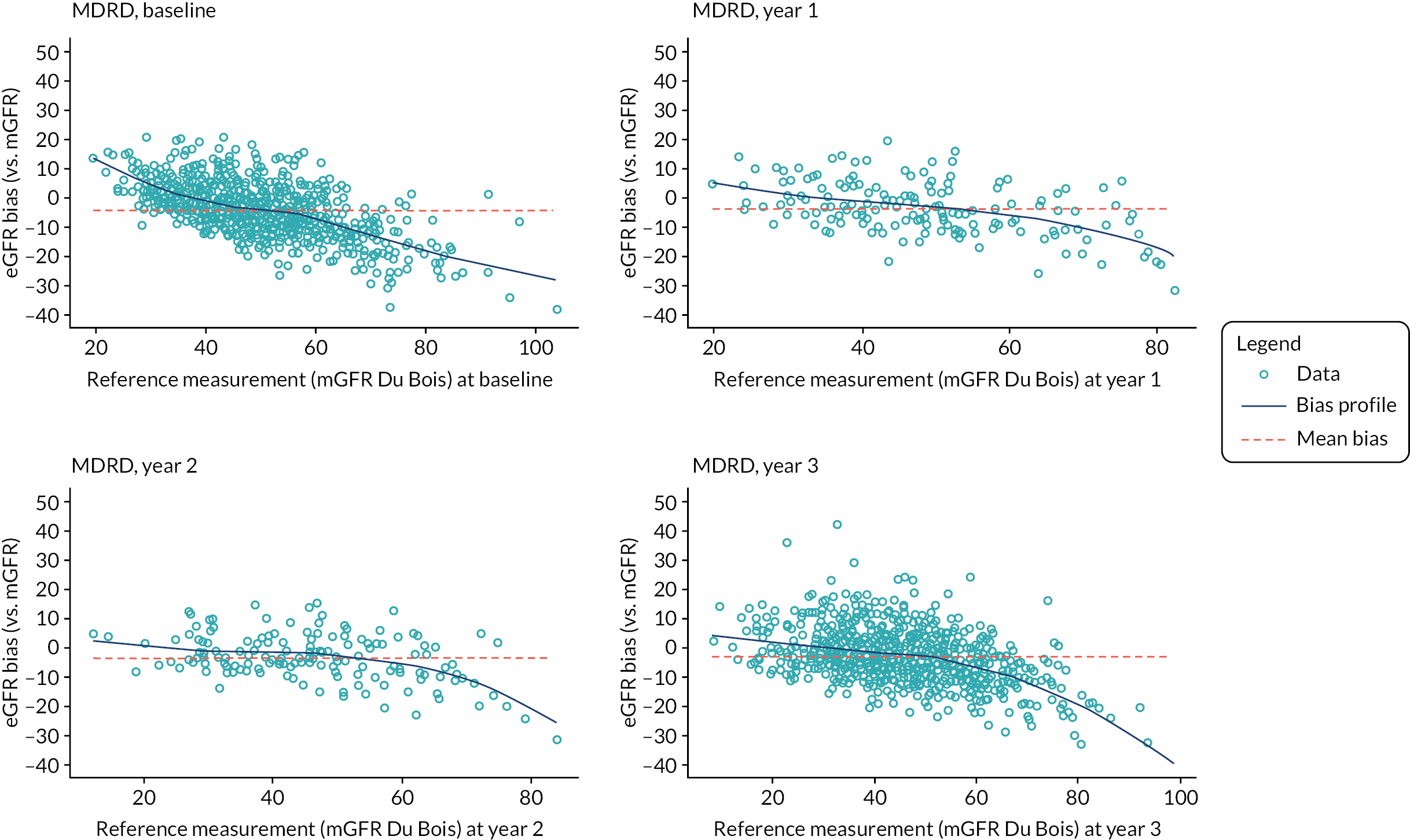
FIGURE 29.
Bias profiles for the CKD-EPIcreatinine equation based on annual data from the main study. The individual scatter points represent the available study data on mGFR vs. eGFR at each annual sampling point (n = 875 at baseline and year 3; n = 212 at year 1; and n = 184 at year 2); the solid blue lines representing the expected mean eGFR bias over the mGFR range, based on a fitted loess regression curve; and the red dotted line in each plot indicates the overall mean bias calculated for the given eGFR equation at each time sampling point.

FIGURE 30.
Bias profiles for the CKD-EPIcystatin equation based on annual data from the main study. The individual scatter points represent the available study data on mGFR vs. eGFR at each annual sampling point (n = 875 at baseline and year 3; n = 212 at year 1; and n = 184 at year 2); the solid blue lines representing the expected mean eGFR bias over the mGFR range, based on a fitted loess regression curve; and the red dotted line in each plot indicates the overall mean bias calculated for the given eGFR equation at each time sampling point.

FIGURE 31.
Bias profiles for the CKD-EPIcreatinine-cystatin equation based on annual data from the main study. The individual scatter points represent the available study data on mGFR vs. eGFR at each annual sampling point (n = 875 at baseline and year 3; n = 212 at year 1; and n = 184 at year 2); the solid blue lines representing the expected mean eGFR bias over the mGFR range, based on a fitted loess regression curve; and the red dotted line in each plot indicates the overall mean bias calculated for the given eGFR equation at each time sampling point.
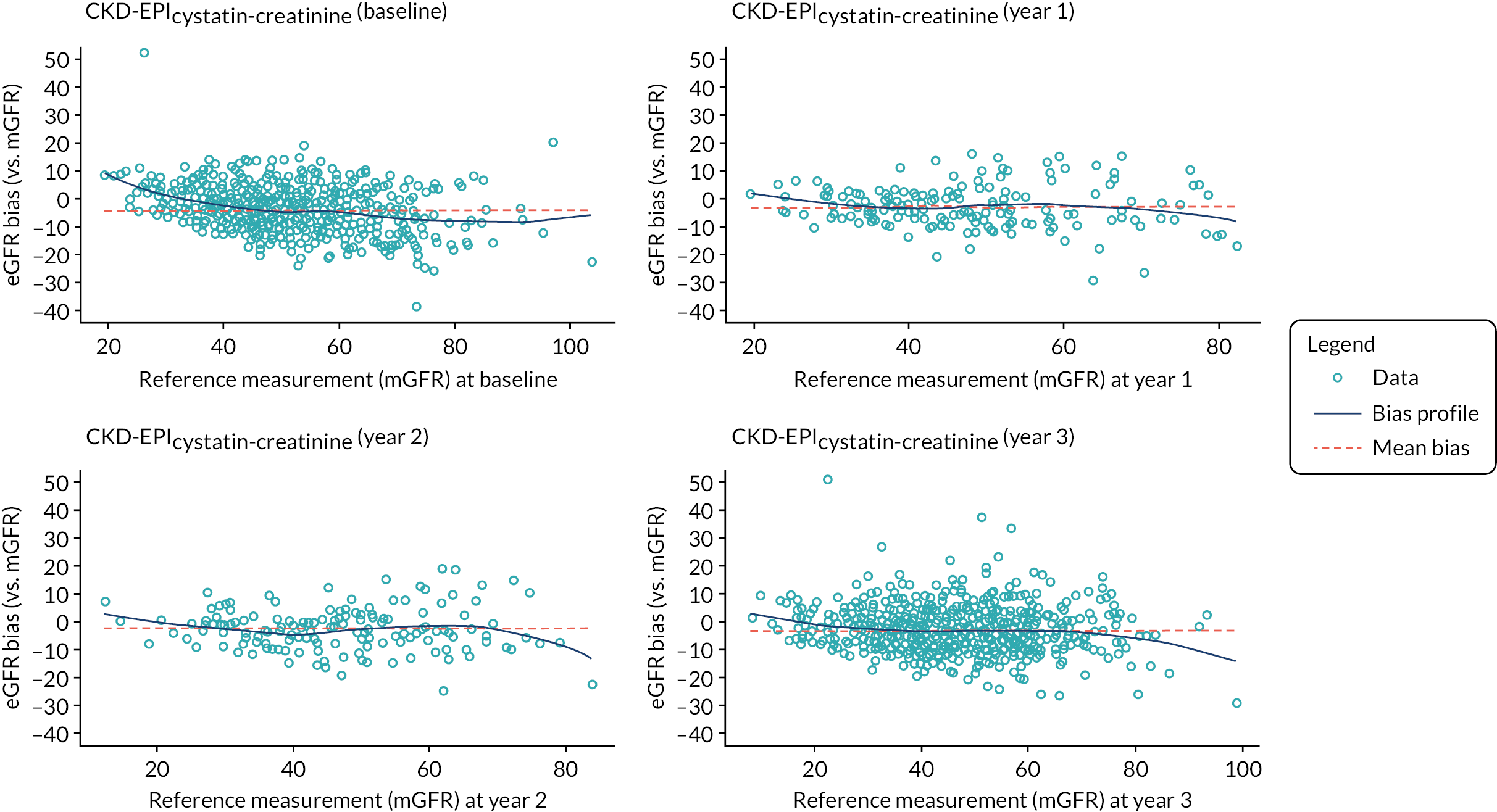
Appendix 2 Health economics systematic review
Systematic review of economic evaluations
A systematic review was conducted to identify previous studies that have assessed the cost-effectiveness of test-based strategies for CKD (including screening, diagnostic and monitoring-based strategies) using a decision-analytic model (e.g. decision tree, Markov model or microsimulation model). An original version of this review was conducted towards the beginning of the project (searches run February 2015) and published in PLOS ONE. 112 The review has since been updated for this report (searches run February 2020). The objective was not to draw conclusions about the cost-effectiveness of different testing strategies – rather the aim was to examine how economic models have been implemented in this setting to date. This section reports the methods and findings of the review.
Methods
An initial search was conducted on 17 February 2015 and published in PLOS ONE. 112 This review was subsequently updated (searches conducted on 4 February 2020) to ensure that the latest research in this area was captured before finalising the de novo economic model. As far as possible, the same methods (i.e. search strategies, screening and data extraction processes) were used in both the original and updated searches; however, it should be noted that different researchers were involved in the original and updated reviews, due to a change of research group undertaking the health economic analysis over the course of this project. Any differences in the methods employed in the original and update reviews are highlighted in the sections below.
Searches
Articles were identified through searches of electronic databases and hand-searching of the bibliographies of the included studies. In the original review (February 2015), the following databases were searched:
-
CINAHL (EBSCO) 1981–present
-
EconLit (EBSCO) 1886–present
-
EMBASE Classic + EMBASE (Ovid) 1947–present
-
Ovid MEDLINE(R) and Epub Ahead of Print, In-Process and Other Non-Indexed Citations and Daily 1946–present
-
PsycInfo (Ovid) 1806–present
-
The HTA database, accessed via the Cochrane Library (Wiley)
-
The NHS Economic Evaluation Database (EED), accessed via the Cochrane Library (Wiley).
In the updated review (February 2020), all the above databases were searched except for NHS EED, which stopped having new content added to it in January 2015. The original search of NHS EED in February 2015 would therefore have already identified any relevant records available in NHS EED for this review.
The search strategy was customised for each database and included free-text terms and medical subject headings (MeSH) terms where appropriate. The following concepts were covered: CKD, diabetes, hypertension, GFR type markers, albumin type markers and economic evaluations. For the updated review in 2020, the original search strategies from 2015 were checked for changes to subject heading such as MeSH. The strategies for CINAHL, MEDLINE and PsycInfo remained the same. Additional subject headings for CKD were found and added to the EMBASE strategies (CKD-mineral and bone disorder/and renal osteodystrophy/). The 2015 search strategy used in EconLit was a copy of the CINAHL strategy and used CINAHL headings that are not recognised in EconLit – a new search strategy was therefore devised for EconLit in the update review, based on the original search but without CINAHL subject headings applied. The HTA database stopped having new content added to it in March 2018, and in February 2020 (when the update searches were run) HTA database records were only available via searching the Centre for Reviews and Dissemination (CRD) database platform and limiting results to ‘HTA’. It was therefore not possible to replicate the original HTA search which identified records having both a relevant MeSH and a relevant text word in any field; instead, a more sensitive strategy was adopted in 2020, to search for relevant text words in any fields, without limiting results to those containing specified MeSH.
All searches were limited to English-only studies. The original February 2015 searches were not limited by date. The updated February 2020 searches were limited to studies published from 2014 onwards, to ensure that any studies from 2014 or 2015 that were added to the databases after February 2015 would be identified. For the HTA database, the updated search was run from 2014 to 31 March 2018, since new content stopped being added to that database in March 2018. The full search strategies are provided in Economic evaluation review search strategies.
The results of the database searches were stored and de-duplicated in an EndNote library. Further relevant studies were sought by hand-searching of the bibliographies of the included studies.
Inclusion criteria
The review inclusion and exclusion criteria are outlined in Table 42. Studies were included if they reported a peer-reviewed, de novo, model-based economic evaluation, which included test-based strategies (using albuminuria and/or eGFR tests), on patients with possible or confirmed CKD, and reported an incremental cost-effectiveness ratio. Studies were excluded if they: reported on non-CKD cohorts or patients with end-stage kidney disease (ESKD) only; did not report a full cost-effectiveness evaluation (e.g. focused on costs alone); did not use a decision-analytic model (e.g. clinical trial-based analyses); were not primary research (i.e. reviews or opinion pieces); or were published as a conference proceeding only (i.e. abstracts or posters).
| Component | Inclusion criteria | Exclusion criteria |
|---|---|---|
| Population | Patients at risk of, or with confirmed, CKD, including:
|
Patients with ESKD only (GFR < 15 ml/minute/1.73 m2) |
| Intervention | Albuminuria and/or eGFR-based testing | |
| Comparator | Any | |
| Outcomes | ICER | |
| Study methods/design | Model-based economic evaluation, including a CEA, CUA or CBA | Trial-based economic evaluation; or not a full economic evaluation (e.g. cost-minimisation analysis) |
| Research type | Primary research (i.e. de novo economic model) | Literature reviews, editorials, letters, opinion pieces |
| Manuscript type | Full peer-reviewed text available | Conference proceeding (abstract or poster) |
| Language | English only | Non-English language |
A two-stage screening process was undertaken to determine which studies should be included in the review. First, records were screened by title and abstract and were included if they were considered to possibly meet the above inclusion criteria. Second, the full-text reports for records were retrieved, and final inclusions were determined based on a full review of the study report. Each screening stage was undertaken in duplicate by two independent reviewers: in the original review, Andrew Sutton and Katie Breheny conducted the screening, while in the updated review, Bethany Shinkins (BS) and Alison Smith (AFS) completed the screening. Any disagreements were resolved via discussion.
Data extraction and quality assessment
For each study included in the review, data extraction was conducted by a single reviewer (AFS) to collate information on the study characteristics and methodology. The data extraction form is provided in Economic evaluation review data extraction form. In particular, data extraction focused on addressing the following research questions:
-
How was test diagnostic accuracy considered in the analysis? Was the accuracy of each test defined, justified and incorporated in the analysis? How was the accuracy of any repeated-testing scenarios characterised? Were the parameters that define the test accuracy subjected to sensitivity analysis? How did test accuracy (e.g. FP and/or FN results) impact on patient outcomes in the model?
-
What approach was used to model disease progression? What type of model was used (e.g. Markov, decision tree)? How was progression of the chronic nature of CKD described in the analysis? Were any additional clinical events, risks, or treatment side effects captured in the model?
-
Were the impacts of any delays on the testing and treatment pathway considered? Were patient outcomes in the model impacted by delays in testing, diagnosis and/or treatment? Did the analysis explore the impact of changing the timing of testing, decision-making or treatment on patient outcomes?
-
Which testing resources and costs were captured in the analyses and how? How were the testing costs derived, and what elements of resource use (e.g. test kit, laboratory personnel, GP/physician visits, confirmatory tests) were captured in the cost? Were the costs incurred by the patients (societal costs) along the testing pathway incorporated into the analysis?
Any uncertainties regarding the data extraction were discussed and checked with the second reviewer (BS). Due to the change in reviewers completing the initial versus updated review, all items in the data extraction table produced from the initial review were subsequently double checked by the primary reviewer in the updated review (AFS), to ensure consistency in the data extraction and reporting. All findings were narratively synthesised.
The methodological quality of each paper was also assessed using the 10-item checklist originally proposed by Drummond et al. 193,194 The aim of this systematic review was to examine the methods used in describing testing and diagnostic pathways in economic evaluations in this field and not to comment regarding the results and conclusions drawn from these studies. Consequently, no studies were excluded from this review due to issues regarding quality.
Results
Study selection
Figures 32 and 33 summarise the initial and update review findings respectively. For clarity, the findings of the original and updated review are shown separately.
FIGURE 32.
Preferred Reporting Items for Systematic Reviews and Meta-Analyses diagram of studies included in the initial systematic review of model-based economic evaluations.

FIGURE 33.
Preferred Reporting Items for Systematic Reviews and Meta-Analyses diagram of studies included via the updated review.

The initial search strategy of the databases conducted in February 2015 identified 2671 records, of which 908 were duplicate records. Based on title and abstract screening, 74 reports were selected for full-text review, of which 20 studies were included (reported across 21 reports). One further study was identified via citation checking, giving a total of 21 studies reported across 22 reports.
The updated search strategy conducted in February 2020 identified 1357 records, of which 342 were duplicate studies. Based on title and abstract screening, 12 reports were selected for full-text review, of which 7 studies (reported across 7 reports) were included. No studies were identified via citation checking in the update review. In total, across the initial and updated searches, 28 studies were included in the review, reported across 29 reports.
Study characteristics
A summary of the included studies is provided in Table 43. Nine studies originated from USA, four studies were from Canada, three from the Netherlands, two from China, and one each from Australia, Europe, France, Germany, Iran, Japan, Korea, UK, Switzerland and Thailand.
| Study | Population | Objective | Type and timing of testing | Testing strategies | Comparator(s) | Health outcome | Model type | Perspective | Cost-effectiveness conclusions |
|---|---|---|---|---|---|---|---|---|---|
| Adarkwah et al. (2010) Germany218 | Patients with newly diagnosed T2D, aged 50 | Assess the best time to start an ACE inhibitor (or A2RB therapy in the event of cough) | Annual screening | (1) Micro-albuminuria (HPLC; UAE > 30 mg/day); or (2) Macro-albuminuria (dipstick test; > 300 mg/day) | (1) No screening and no treatment (standard care); (2) Treat all immediately with an ACE inhibitor or A2RB | LYG/QALY | Cohort Markov model | Statutory health insurance provider | Immediately treating all patients with newly diagnosed diabetes is the most cost-effective strategy |
| Adarkwah et al. (2011) Netherlands219 | Patients with newly diagnosed T2D, aged 50 | Assess the best time to start an ACE inhibitor treatment | Annual screening | (1) Micro-albuminuria (HPLC or immune-turbidimetric; UAE > 30 mg/day); or (2) Macro-albuminuria (dipstick test; > 300 mg/day) | (1) No screening and no treatment (standard care); or (2) Treat all with an ACE inhibitor | LYG/QALY | Cohort Markov model | Statutory health insurance provider | Immediately treating all patients with newly diagnosed diabetes is the most cost-effective strategy |
| Boersma et al. (2010) Netherlands205 | General population aged 28–75 | Assess the cost-effectiveness of population screening for albuminuria | One-off screening | Micro-albuminuria (UAC ≥ 20 mg/l) with confirmatory test (24-hour UAE ≥ 30 mg/day). Treat with an ACE inhibitor | No screening and no treatment | LYG | Cohort Markov model | Healthcare provider | One-off population screening is potentially cost-effective (depends on screening age and test thresholds) |
| Boulware et al. (2003) USA196 | General population aged 50, (1) without HT or diabetes; and (2) with HT | Assess the cost-effectiveness of screening for the early detection of urine protein | Annual screening | Proteinuria (dipstick). Confirmatory ACR and eGFR testing (< 90 ml/minute/1.73 m2) (equation N/R). Treat with ACE inhibitor or A2RB therapy | No screening (but included annual opportunity for incidental testing or symptomatic presentation) | QALY | Cohort Markov model | Societal | Population screening is not cost-effective unless targeted towards at-risk groups (older or HT persons) |
| Critselis et al. (2018) Europe223 | Patients with T2D, aged 50 | Assess the cost-effectiveness of screening for CKD progression with the CKD273 classifier | Annual screening | A urinary peptide classifier (CKD273), + UAE testing (test cut-offs N/R). Treat with standard anti-HT or intensified therapy depending on albuminuria and screening status | Screen for micro-albuminuria (UEA) only (test cut-off N/R) | QALY | Cohort Markov model | European healthcare system | CKD273 screening is cost-effective in diabetic patients and high-risk patients, but not in low-risk patients |
| Den Hartog et al. (2009) USA220 | General population, aged 60 | Assess whether routine reporting of eGFR is cost-effective for identifying CKD | Annual screening | eGFR (MDRD equation) (< 60 ml/minute/1.73 m2) + serum creatinine. Treat with an ACE inhibitor and BP control | Serum creatinine (accuracy drawn from papers using a range of thresholds: 1.06–1.36 mg/dl) | QALY | Cohort Markov model | Healthcare provider | eGFR is cost-effective, but not when assuming a > 2% quality-of-life decrement for FP cases |
| Farmer et al. (2014) UK210 | Patients with: (1) T1D (mean age 27); or (2) T2D (mean age 63) | Assess the cost-effectiveness of screening for early kidney disease | Screening every 1–10 years [starting at age ≥ 12 (T1D), or from diagnosis (T2D)] | Micro-albuminuria (UACR > 2.5 mg/mmol for men and > 3.5 mg/mmol for women). Treat with ACE inhibitor or A2RB therapy | Various screening strategies evaluated, altering the screening interval from 1 to 10 years | QALY | Individual based simulation model | Healthcare provider | Annual ACR screening is cost-effective for patients with T1D and T2D compared to using longer screening intervals (supporting UK screening guidance) |
| Ferguson et al. (2017) Canada211 | Manitoba’s rural indigenous peoples, aged 18 + | Assess the cost–utility of screening for CKD in rural indigenous adults | One-off screening | (1) eGFR (≤ 30 ml/minute/1.73 m2) (CKD-EPI equation), or (2) Urine ACR (≥ 300 mg/g, or 30 mg/mmol and eGFR 30–45 mg/minute/1.73 m2). Treat with ACE inhibitor or A2RB therapy | Usual care (no screening) | QALY | Cohort Markov model | Public healthcare payer | Screening for CKD in rural indigenous adults is cost-effective, particularly in remote air access-only communities with higher risks of disease |
| Go et al. (2019) Korea202 | General population, modelled from age 20 | Estimate the cost–utility of the NHSP for CKD in Korea | Screening every 2 years, starting age 40 | Proteinuria (dipstick) and eGFR (serum creatinine; MDRD formula). Different tests, population, intervals and ages explored. Treat with ACE inhibitors | No screening | QALY | Cohort Markov model | Societal | National screening for CKD is more cost-effective for patients with diabetes or HT than the general population |
| Golan et al. (1999) USA203 | Patients with newly T2D, aged 50 | Assess the cost-effectiveness of treat all vs. screening strategies | Annual screening | (1) Micro-albuminuria (UAE 30–300 mg/day); or (2) Gross proteinuria (UAE > 300 mg/day). Treat with an ACE inhibitor | Treat all with an ACE inhibitor | LYG/QALY | Cohort Markov model | Societal | The ‘treat all’ strategy is most cost-effective, but the results depend on patients’ quality of life with treatment |
| Hoerger et al. (2010) USA206,207 | General population, aged 50 (including diabetic and HT subgroups) | Assess the cost-effectiveness of micro-albuminuria screening strategies | Screening every 1, 2. 5, or 10 years, or one-off screening | Micro-albuminuria (ACR 30–299 mg/day). Treat with ACE inhibitor or A2RB therapy | (1) No screening; (2) Usual care (including low annual screening rates for persons with diabetes and/or HT) | QALY | Micro-simulation Markov model | Healthcare provider | Screening is cost-effective for diabetic or HT patients, but not for the general pop. unless using longer intervals or as part of existing clinician visits |
| Hoerger et al. (2012) USA208 | African or non-African Americans, aged ≥ 50 (including diabetic and HT subgroups) | Assess the cost-effectiveness of micro-albuminuria screening | Screening at 1-, 2-, 5- or 10-year intervals | Micro-albuminuria (ACR 30–299 mg/g). Treat with ACE inhibitor or A2RB therapy | Usual care (including low annual screening rates for patients with diabetes and HT) | QALY | Micro-simulation Markov model | Healthcare provider | Screening African or non-African Americans with diabetes or HT at 5- or 10-year intervals respectively is cost-effective |
| Howard et al. (2010) Australia198 | Asymptomatic 50- to 69-year-olds | Assess the cost-effectiveness of strategies to prevent ESKD | Annual screening | Proteinuria (dipstick, ≥ 1 +) + confirmatory spot UPCR (> 20 mg/mg). Treat with an ACE inhibitor. Other tests used to identify diabetes and HT | Current practice, which included the opportunity for opportunistic clinical diagnosis | QALY | Cohort Markov model | Healthcare provider | Primary care screening and treatment for diabetes, HT and proteinuria are likely to be cost-effective |
| Kessler et al. (2012) Switzerland209 | General population, aged ≥ 50 (including. subgroups with diabetes or HT) | Assess the cost-effectiveness of screening in different populations | Screening every 1, 2, 5, or 10 years | Micro-albuminuria (ACR 30–299 mg/g). Treat with ACE inhibitor or A2RB therapy | (1) No screening; (2) Usual care (including low annual screening rates for patients with diabetes ± HT) | QALY | Micro-simulation Markov model | Healthcare provider | Screening is cost-effective at 2-, 5- or 10-year intervals in diabetic, HT or general populations, respectively |
| Kiberd et al. (1995) Canada216 | Patients with insulin-dependent diabetes mellitus for 5 years | Examine the conditions necessary to make screening cost-effective | Annual screening | Micro-albuminuria alone (UAE > 20 μg/minute on two out of three tests). Treat with an ACE inhibitor | Treat patients with HT and/or macro-albuminuria (dipstick > 0.3 g/l or positive Albustix confirmed with > 300 mg/day or > 200 μg/minute) | QALY | Cohort Markov model | Third party and government | Micro-albuminuria surveillance is cost-effective, but the results are sensitive to key parameters including test accuracy |
| Kiberd et al. (1998) Canada217 | Patients with insulin-dependent diabetes mellitus for 5 years | Determine how effective ACE inhibitors must be in preventing diabetic nephropathy to warrant routine administration | Annual screening | (1) Micro-albuminuria (UAE > 20 μg/minute or 30 mg ACR on two out of three tests); or (2) Treat all high-risk patients (ACE inhibitor) and screen low risk for HT and macro-albuminuria (dipstick > 0.3 g/l or positive Albustix with > 300 mg/day or 200 μg/minute proteinuria) | Treat all patients with an ACE inhibitor | LYG/QALY | Cohort Markov model | Third party and government | Routine ACE inhibitor therapy for patients with diabetes is expected to be cost-effective, especially if treatment can be targeted to high-risk individuals |
| Kiberd et al. (1999) USA204 | Pima Indians with T2D, at the point of diagnosis | Determine how effective ACE inhibitors must be to warrant early routine therapy | Annual screening | Micro-albuminuria (UACR: > 3 mg/1 mmol or > 30 mg/1 g on two of three morning urine samples), starting 1 year after diabetes diagnosis | Treat all with ACE inhibitor 1 year after diagnosis of diabetes | LYG | Cohort Markov model | Third party and government | Routine ACE inhibitor therapy in Pima Indians with T2D could be cost-effective compared micro-albuminuria screening |
| Kondo et al. (2012) Japan200 | General population, aged 40–74 | Assess the cost-effectiveness of population screening for CKD | One-off screening | (1) Proteinuria (dipstick, ≥ 1); (2) eGFR (based on serum creatinine; ≥ stage 3); or (3) Dipstick test + eGFR (≥ 1 or ≥ stage 3). Treat with ACE inhibitors | (1) Do nothing; (2) Status quo (40% receive dipstick test; 60% dipstick + serum creatinine) | QALY | Cohort Markov model | Societal | Population-based screening using the dipstick test and/or serum creatinine is cost-effective |
| Le Floch et al. (1994) France215 | Patients with T1D and T2D (mean age = 53) | Examine the cost-effectiveness of screening for albuminuria in diabetic patients | Annual screening | Semiquantitative dipstick (UAE > 20 μg/minute on ≥ 1 of two separate tests on same sample), + standard test for albuminuria for positive dipstick results. Treatments not assessed | Standard test for albuminuria using immunoturbidimetry (micro-albuminuria if > 20 μg/minute; macro-albuminuria if > 200 μg/minute) | QALY | Cohort Markov model | Healthcare provider | Dipstick pre-screening results in a cost saving of £6600 per QALY lost. The authors concluded that this may be considered cost-effective |
| Manns et al. (2010) Canada221 | General population (incl. age < 65 vs. > 65, diabetic, ± HT subgroups) | Assess the cost-effectiveness of one-off population screening for CKD | One-off screening | eGFR testing (MDRD equation) (< 60 ml/minute/1.73 m2). Treat with an ACE inhibitor or A2RB therapy | No screening | QALY | Cohort Markov model | Healthcare provider | Population screening is not cost-effective in the general public, but it is likely to be cost-effective in patients with diabetes |
| Palmer et al. (2008) USA197 | Patients with T2D and HT | Assess the cost-effectiveness of screening for nephropathy | Annual screening | Micro-albuminuria (semiquantitative urine dipsticks) (UAE 20–199 μg/minute). Treat with an A2RB + other HT agents | No screening (BP control achieved with conventional medications alone) | QALY | Cohort Markov model | US third-party health insurance payer | Micro-albuminuria screening in patients with T2D and HT is expected to be cost-effective |
| Ravaghi et al. (2019) Iran222 | General adult population (age N/R) | Explore the cost-effectiveness of screening for CKD among adults | One-off screening | eGFR (including blood creatinine + urine creatinine and volume; equation N/R), with kidney ultrasound if indicated. Treatments not specified | No screening | QALY | Cohort Markov model | Social insurance organisations | Based on the high prevalence of CKD in Iran, population-based screening is cost-effective in this setting |
| Sekhar et al. (2010) USA199 | School children aged 8–15 | Assess the cost-effectiveness of dipstick uranalysis for the detection of CKD in children | One-off screening | Proteinuria/haematuria (dipstick), + repeat test for elevated results (abnormal if: ≥ 1 proteinuria and ≥ 1 haematuria). Treatments not considered | No screening | Cases of CKD diagnosed | Decision tree | Healthcare provider | Screening for CKD using dipstick uranalysis amongst school children is not cost effective |
| Siegel et al. (1992) USA195 | Patients with newly diagnosed insulin-dependent diabetes, aged 15 | Examine the effects of screening and early ACE inhibitor treatment programs | Twice-yearly screening | (1) Proteinuria (≥ 300 μg/minute on two out of three dipstick tests); (2) Sign. micro-albuminuria (≥ 100 μg/minute in two out of three urinalyses); or (3) Micro-albuminuria (≥ 20 μg/minute in two of three tests). Treat with an ACE inhibitor | Standard therapy: annual testing for proteinuria, with ACE inhibitor treatment for HT patients only | LYG | Cohort Markov model | Healthcare provider | Early treatment with ACE inhibitors is likely to be cost-effective. Screening for micro-albuminuria and then initiation of treatment is the most cost-effective option |
| Srisubat et al. (2014) Thailand201 | 45 years old patients with T2D and normotension | Assess the cost-effectiveness of micro-albuminuria screening | Annual screening | Micro-albuminuria (urine dipstick). Treat with an ACE inhibitor | Do nothing scenario (patients receive ACE inhibitor at discovery of macro-albuminuria and ESKD) | QALY | Cohort Markov model | Societal | Micro-albuminuria screening using urine dipsticks in patients with T2D is highly cost-effective |
| Wang et al. (2017) China212 | Hospital outpatients aged 45+, with HT, diabetes or CHD, and previously elevated ACR | Identify a feasible and cost-effective strategy for the identification of persistent albuminuria | One-off screening | Micro-albuminuria (UACR > 30 mg/g creatinine); different combinations of repeated testing strategies (over 3-month period) evaluated | Different combinations of repeated testing strategies (over 3-month period) were evaluated | QALY | Decision tree + cohort Markov model | Societal | Screening using two first morning urine samples and one randomised spot urine sample over 2 consecutive days is most cost-effective |
| Wu et al. (2018) China214 | Patients with newly diagnosed T2D (mean age = 51) | Assess the cost-effectiveness of preventing CKD in patients with newly diagnosed T2D | Annual screening | Micro-albuminuria (immuno-nephelometric method) (UAE ≥ 30 mg/day). Treat with ACE inhibitor/A2RB if test positive or if patient is HT | (1) No testing and no treatment; (2) No testing and treat all (ACE inhibitor/A2RB therapy) | QALY | Decision tree + cohort Markov model | Healthcare provider | Screening for micro-albuminuria in patients with T2D is cost-effective |
| Yarnoff et al. (2017) USA213 | General population (age N/R) | Assess the cost-effectiveness of screening for early-stage CKD using published CKD risk scores | Initial screen + follow-up at 1-, 2- or 5-year intervals | Initial risk assessment (two published CKD risk scores) + albuminuria screening (ACR ≥ 30 mg/g), with follow-up screening for test negative cases. Treat with ACE inhibitors or A2RBs | No screening | QALY | Micro-simulation Markov model | Healthcare perspective (insurer payments + patient out of pocket payments) | Population screening incorporating an initial risk assessment and using a 2-year follow-up interval is cost-effective |
The majority of studies (n = 24) considered proteinuria or albuminuria tests: 8 specified the evaluated test(s) as reagent strip (or ‘dipstick’) tests;195–202 11 referred to urine albumin excretion, urine albumin concentration or urinary albumin-to-creatinine ratio tests;203–214 and 5 evaluated both dipstick and standard albuminuria tests. 215–219 Six studies meanwhile evaluated eGFR testing: two of which incorporated both dipstick and eGFR tests; and one of which incorporated both albuminuria and eGFR tests. 200,202,211,220–222 Of those studies evaluating eGFR-based strategies, four specified the equation underpinning the eGFR calculation: three used the MDRD equation, while one used the CKD-EPI equation. A final study evaluated a novel biomarker for CKD – described as a capillary electrophoresis–mass spectrometry-based urinary peptide classifier (CKD273). 223
All of the identified studies evaluated screening strategies in at-risk groups or general populations not currently diagnosed with CKD. No studies were identified which assessed test-based monitoring strategies for patients with known CKD (i.e. matching the role of monitoring being considered in this HTA). Half of the studies (n = 14) focused on screening strategies for patients with diabetes195,201,203,204,210,215–219 or patients with diabetes and/or hypertension197,212,214,223 (both known risk-factors for CKD). Note in the initial 2015 review, these screening studies (conducted in diabetic and hypertensive populations) were listed as monitoring studies. In the updated review, it was decided that for clarity these studies should be listed as screening studies. Although repeated screening within high-risk populations can be classified as a type of early-stage monitoring for disease onset, in the context of this report (where the focus is on monitoring within patients already known to have CKD), we believe it is more appropriate to identify such studies as ‘screening’ studies. This terminology also aligns with that used by the original study authors. The other half focused on screening strategies in the general population,196,198,200,202,205–209,213,220–222 with one study considering school children,199 and a further study focusing on screening within a rural indigenous population. 211 Of those studies focusing on population-based screening strategies, several also included subgroups or scenario analyses restricting screening to patients with diabetes and/or hypertension. 196,198,202,207,209,221 Testing was most often administered in primary care,195–197,199,203,205,207–210,218,219 or had no clearly-defined setting. 200,202,204,213,214,216,217,220,221,223 Less commonly explored settings included community care and secondary care settings.
The time horizons adopted in these studies were based either on the final age of the patient population or on a specific period of time. The vast majority of studies adopted long-term time horizons to capture downstream cost and health outcomes: 5 studies adopted a lifetime horizon until all the patients had died;195,202,203,210,221 10 studies ran the model analysis until the patient population had reached 90 years old or more;198,200,207–209,213,214,218,219,223 2 studies ran the analysis until the patient population had reached age 75 years;196,201 3 studies adopted a time horizon of 45–60 years;211,216,217 and 5 studies adopted a 25- to 30-year time horizon. 197,204,210,212,215 Only two studies implemented time horizons of < 20 years. 205,220 A further study did not incorporate a time horizon – this study adopted a decision tree approach and considered the cost-per-case of CKD detected for urine dipsticks targeting school-aged children. 199 One final study failed to report the time horizon. 222
Study methods
How was test diagnostic accuracy considered in the analysis?
Eight studies did not incorporate any measure of diagnostic accuracy into the model, despite evaluating test-based strategies. 195,200,203,204,211,214,221,222 Of these, most did not mention or discuss the topic of accuracy at all. Only one explicitly reported their assumptions: in their analysis of annual screening for albuminuria in patients with type 2 diabetes, Golan and colleagues explained that the evaluated test for micro-albuminuria was assumed to have perfect diagnostic sensitivity in the model (which would favour the testing arm compared to the ‘treat all’ comparator), and that the outcomes for any FP cases resulting from testing were assumed to be captured within clinical trial data used to inform subsequent CKD progression rates within the model. 203
Table 44 summarises the methods employed across the 20 studies that did explicitly incorporate diagnostic accuracy into their models. Fourteen studies incorporated the possibility of both FP and FN test results (typically using diagnostic sensitivity and specificity metrics). 196,197,201,202,207,209,210,212,213,215,220,223 Six studies meanwhile only considered the possibility of FP test results (mostly modelled using either PPV or diagnostic specificity metrics);199,205,216–219 of those, three studies explained that FN test results were not considered since the evaluated test was assumed to have perfect diagnostic sensitivity218,219 or NPV,199 without providing any justification for this assumption, while two studies did not mention or discuss the possibility of FN results. 216,217 A final study indirectly captured FPs by calculating the number of subjects needed to be screened and tested to identify and treat 1000 subjects with confirmed albuminuria. 205
| Study | Type and timing of testing | Tests evaluated | Diagnostic accuracy measures modelled | Source for diagnostic accuracy data | Consequences for FP and FN results in the model | SA conducted and key results |
|---|---|---|---|---|---|---|
| Adarkwah et al. (2010) Germany218 | Annual screening | (1) Micro-albuminuria; (2) macro-albuminuria | (1) Micro-albuminuria: assumed perfect accuracy in base case; 81% specificity applied in SA. (2) Macro-albuminuria: accuracy not discussed | Published systematic review (details N/R) | FPs: not considered. FNs: consequences unclear | Micro-albuminuria: 81% specificity applied in one-way SA. Specificity was not included in the list of parameters stated to have the greatest impact on the results |
| Adarkwah et al. (2011) The Netherlands219 | Annual screening | As above | As above | As above | As above | As above |
| Boersma et al. (2010) The Netherlands205 | One-off screening | Micro-albuminuria (UAC) + confirmatory test (UAE) | Number of subjects needed to be screened to identify 1000 subjects with albuminuria (reported 373 identified with micro-albuminuria per 10,000 screened) | PREVEND trial study data (n = 8592) | FPs: incurred cost of confirmatory testing (assumed to be perfect, thus no unnecessary treatment). FNs: not considered | Different test thresholds were explored (accuracy values N/R). Higher thresholds improved the cost-effectiveness but reduced the overall health gains achieved |
| Boulware et al. (2003) USA196 | Annual screening | Proteinuria (dipstick). Confirmatory ACR and eGFR | Proteinuria dipstick test: sensitivity (76%) and specificity (79%) | Four published studies (N/R if/how values were synthesised) | FPs: all assumed to be identified at confirmatory testing. FNs: remained in untreated states until further screening, subject to higher risk of mortality and CKD progression | In one-way SA, dipstick sensitivity and specificity values were among those parameters found to have the highest impact on the model results |
| Critselis et al. (2018) Europe223 | Annual screening | A urinary peptide classifier (CKD273) + UAE | CKD273: sensitivity (94.6%) and specificity (97.1%). UAE test: sensitivity (70%) and specificity (71%) | Two published studies | FPs: received unnecessary treatment (unclear if/when treatment would be stopped). FNs: remain untreated, and appeared to be subject to higher risk of CKD progression (full details N/R) | All variables were stated to be explored in one-way SA. No diagnostic accuracy values were included in the results (only those parameters with the highest impact were shown) |
| Den Hartog et al. (2009) USA220 | Annual screening | eGFR + serum creatinine | eGFR: sensitivity (92.4%) and specificity (83.5%). Serum creatinine: sensitivity (55.9%) and specificity (95.0%) | Averages taken across n = 2 (eGFR) and n = 3 (serum creatinine) published studies | FPs: incurred one-time cost of confirmatory testing by a nephrologist, then return to a ‘true negative’ state. FNs: remain untreated with higher risks of progression to ESKD | One-way SA showed that increasing the sensitivity of serum creatinine led to that strategy becoming superior to eGFR |
| Farmer et al. (2014) UK210 | Screening every 1–10 years | Micro-albuminuria (UACR) | FP and FN rates over time were derived from random-effects linear regression models of log-ACR, which incorporated within-patient biological variation | Regression models constructed using individual patient-level data sets (ORPS and CARDS) | FPs: lead to additional testing and unnecessary treatment. FNs: remain untreated and subject to higher risks of progression (and mortality in the case of T2D) | No SA conducted on diagnostic accuracy |
| Go et al. (2019) Korea202 | Screening every 2 years, starting age 40 | Proteinuria (urine dipstick) and eGFR | Dipstick: sensitivity (range: 31–36%) and specificity (95–98%). eGFR: sensitivity (69–74%) and specificity (88–96%). Different values listed for diabetic, HT, or ‘neither’ populations | Estimated based on NHIS claims data (2013) | FPs: unclear (not discussed). FNs: remain untreated, with higher risks of progression, CVD events and mortality | Diagnostic accuracy ranged from −20% to 1 in one-way SA. Diagnostic accuracy was not included in the list of parameters stated to have the most influential impact on the results |
| Hoerger et al. (2010), USA206,207 | Screening every 1, 2, 5 or 10 years | Micro-albuminuria (ACR) | Sensitivity (76%) and specificity (96%). | Single published study of 165 patients | FPs: receive confirmatory ACR test, with all FPs assumed to be identified at this stage. FNs: remain untreated and subject to higher risks of progression and mortality | Sensitivity of ACR test varied by ±25% in one-way SA. Compared to other parameters, the test sensitivity did not have a large impact on the results |
| Hoerger et al. (2012), USA208 | As above | As above | As above | As above | As above | No SA conducted on diagnostic accuracy |
| Howard et al. (2010) Australia198 | Annual screening | Proteinuria (urine dipstick) + confirmatory spot UPCR | Protein dipstick: sensitivity (89%) and specificity (94%) | Single published study + expert opinion | FPs: unclear (not discussed). FNs: remain untreated, with higher risks of progression, CVD events and death | No SA conducted on diagnostic accuracy |
| Kessler et al. (2012) Switzerland209 | Screening every 1, 2, 5 or 10 years | Micro-albuminuria (ACR) | As in Hoerger et al. (2010) | As in Hoerger et al. (2010) | As in Hoerger et al. (2010) | No SA conducted on diagnostic accuracy |
| Kiberd et al. (1995) Canada216 | Annual screening | (1) Micro-albuminuria (UAE); (2) macro-albuminuria (dipstick) | Micro-albuminuria: PPV (80%). Macro-albuminuria: N/R | No source provided | FPs: for micro-albuminuria screening, FPs appeared to receive unnecessary treatment (details N/R). FNs: not considered | One-way SA lowering the PPV showed that the results were sensitive to this parameter |
| Kiberd et al. (1998) Canada217 | Annual screening | (1) Micro-albuminuria (UAE); (2) macro-albuminuria (dipstick) | Micro-albuminuria: PPV (80%). Macro-albuminuria: N/R | No source provided | FPs: for micro-albuminuria screening, FPs appeared to receive unnecessary treatment (details N/R). FNs: not considered | No SA conducted on diagnostic accuracy |
| Le Floch et al. (1994) France215 | Annual screening | Semiquantitative dipstick (UAE) + standard albuminuria test for positive dipstick results | Pre-screen dipstick: sensitivity (90.8%) and specificity (80.1%) | Primary diagnostic test accuracy study (n = 506) | FPs: assumed to all be identified at confirmatory testing. FNs: days of life lost in perfect health for delays in diagnosis (1–5 years) were estimated based on an expert elicitation exercise with 30 physicians | The frequency of FN results was found to have a significant effect on the results in one-way SA |
| Palmer et al. (2008) USA197 | Annual screening | Micro-albuminuria (semiquantitative urine dipstick) (UAE) | Sensitivity (range 70–97%) and specificity (range 71–98%) reported for urine test strips | Single published study | FPs: received unnecessary treatment (unclear if/when treatment would be corrected). FNs: remain untreated and subject to higher risks of CKD progression | Test accuracy included in PSA only |
| Sekhar et al. (2010) USA199 | One-off screening | Proteinuria/haematuria (urine dipstick), + repeat test for elevated results | NPV assumed to be 100%. Reported data relating to PPV: of 8954 tested, 1264 had an initially raised result, 319 had a persistent abnormality, and 11 had a final diagnosis of CKD | Previously published study including n = 8954 children | FPs: assumed to all be identified at confirmatory testing. FNs: not considered | No SA conducted on diagnostic accuracy |
| Srisubat et al. (2014) Thailand201 | Annual screening | Micro-albuminuria (urine dipstick) | Sensitivity (95.2%) and specificity (84.7%) | Single published cost-effectiveness study | FPs: receive unnecessary treatment (unclear if/when treatment would be corrected). FNs: remain untreated and subject to higher risks of CKD progression | The PPV was found to have the largest impact on the ICER result in one-way SA |
| Wang et al. (2017) China212 | One-off screening | Micro-albuminuria (UACR) | Sensitivity (range: 93.9–100%) and specificity (46.7–81.3%) reported for different combinations of sequential testing strategies | Primary diagnostic accuracy cohort study (n = 160) | FPs: receive unnecessary treatment, with the possibility of reverting to a Negative Urine Test state. FNs: remain untreated and subject to higher risk of mortality | The FN and TP rate of different strategies were stated to have the highest impact on the cost-effectiveness results in one-way SA (full results N/R) |
| Yarnoff et al. (2017) USA213 | Initial screen + follow-up every 1, 2 or 5 years | Risk assessment + albuminuria testing (ACR) | ACR: sensitivity (73%) and specificity (96%) | Single published study | FPs: appeared to all be identified at second ACR confirmatory test. FNs: remain untreated and subject to higher risks of progression and mortality | No SA conducted on diagnostic accuracy |
In the majority of studies, diagnostic accuracy values were informed by a single published study;197–199,201,207–209,213,218,219,223 in two cases, the cited study was a systematic review. 218,219 Two studies cited multiple publications informing the diagnostic accuracy estimates,196,220 one of which reported taking averages of the published values to derive the model diagnostic accuracy parameters. 220 No studies reported conducting a formal literature review or meta-analysis to inform the model diagnostic accuracy values. Two studies derived accuracy values from a primary diagnostic accuracy study,212,215 and a further study derived values from insurance claims data. 202 One study utilised individual-level data from available data sets of repeated test values, to construct linear random-effects models of longitudinal log-ACR values (for patients with type 1 and type 2 diabetes) incorporating: (1) between-subject variation in baseline ACR (i.e. the intercept); (2) the average change in ACR over time; and (3) the difference between observed ACR and the underlying ‘true’ ACR for an individual, described as the within-person variability in ACR measurement arising from assay variability and short-term biological variability. 210 The FP and FN rates in this case were then calculated based on classification errors resulting in differences between the true and measured ACR values over different time points, based on the regression simulation models. Two final studies failed to report any source for the reported accuracy values. 216,217
In terms of modelling the impact of test inaccuracies, patients with FN results were assumed to remain in ‘untreated’ health states, and thereby could not benefit from treatment for CKD (typically corresponding to ACE inhibitor or A2RB therapy) until future screening rounds. Most often the consequence of missed treatment was modelled as higher risks of progression to later CKD stages (which in turn could be associated with higher mortality risks and lower health-related quality of life values);196–198,201,202,207–210,213,220,223 two studies also included higher risks of cardiovascular disease (CVD) events for patients with FN results. 198,202 One of the earlier studies identified quantified the impact of FN results in terms of patient lost ‘quality of life days’, based on an expert elicitation exercise conducted with 30 physicians. 215
In the case of FP results, the most common consequence modelled was the unnecessary cost of additional/confirmatory testing. 196,199,205,207–210,213,215,220 In most cases, confirmatory testing was assumed to have perfect accuracy, thus removing all FP cases at this stage (although this was typically not clearly reported). In several studies, FP cases were stated to undergo unnecessary treatment. 197,201,210,212,216,217,223 However, in general it was not clear how long patients were assumed to remain on unnecessary treatment. In two studies, the consequences for FP cases were not reported. 198,202
Of those studies that evaluated repeated testing scenarios and explicitly accounted for diagnostic accuracy in the model, the majority assumed that the same diagnostic accuracy values would apply over time. 196–198,201,202,207–209,213,215–220,223 While no study explicitly stated this assumption, it may be inferred from the fact that single values of diagnostic accuracy were reported, and that no considerations concerning accuracy over repeated tests were discussed. Two studies meanwhile did attempt to account for changes in test diagnostic accuracy that could result from sampling at different time points. 210,212 The study conducted by Wang and colleagues included a primary diagnostic accuracy study, in which the impact of within-patient biological variability and assay variability was explored by evaluating different repeated-sampling strategies over a 3-month period – consisting of different combinations of five samples taken at the first day ante meridiem of each month (labelled DAY-1, MONTH-2, MONTH-3), the second day in the first month (DAY-2) and a random spot urine sample taken in the afternoon of the first day (RANDOM-1). 212 Farmer and colleagues meanwhile constructed random-effects linear regression models to simulate the trajectory of log-ACR values over time for two separate populations (type 1 and type 2 diabetes), which accounted for errors in measured ACR values resulting from within-patient biological variation and assay imprecision. 210 Using these simulation models, the authors were able to model changing rates of FP and FN values over time.
What approach was used to model disease progression?
The majority of studies used a cohort Markov model approach to model disease progression. Four studies applied a microsimulation approach to a Markov model structure. 207–209,213 This means that the model followed patients individually as they passed through different states of the Markov model rather than monitoring the average probability of events for a representative cohort of patients. An additional study, which included two separate cost-effectiveness models (one for each of type 1 and type 2 diabetes), utilised an individual based model structure in which a series of risk equations were run within each model cycle (dependant on individual patient characteristics), to predict the timing of a series of cardiovascular and mortality events, in addition to renal failure. 210 Only one study did not model disease progression and instead used a decision tree approach to establish the cost-effectiveness of identifying cases of CKD amongst school children. 199
Amongst those studies that described the progression of CKD (prior to ESKD), this was implemented through the use of progressive albuminuria195,201,203,204,210,214–219,223 or GFR states. 202,222 In addition, four studies modelled CKD progression based on both albuminuria and GFR states:207–209,213 all of these were based on the ‘CKD Health Policy Model’, originally published by Hoerger and colleagues in 2010. 206,207 Of those studies that tracked progression via albuminuria levels, health states were typically divided into ‘normal albuminuria’, ‘microalbuminuria’ and ‘macroalbuminuria’, before progression to end-stage disease states. Of those studies that tracked progression according to GFR levels, the stages of CKD were most often split into five GFR levels. Most studies assumed a step-by-step process of disease progression (i.e. patients could only move up one health state in the ladder of progression per model cycle), and only a minority explicitly allowed for the possibility of the reversibility in CKD severity. 201,205,211
For the later stages of disease, the majority of studies included a single health state for ESKD, followed by death. Several others delineated this stage of disease, most often including states for ESKD with and without renal replacement therapy; and before and after kidney transplantation. In addition, beyond the modelled CKD health states, several studies also captured cardiovascular complications associated with CKD (including events such as ‘heart attack’, ‘stroke’, ‘cardiovascular disease’ and ‘coronary artery disease’) either in the form of separate health states or additional risks applied to CKD health states. 195,198,202,205,207–210,213,223 One study also captured additional outcomes for patients with diabetes (blindness and amputation). 210
Were the impacts of any delays on the testing and treatment pathway considered?
Since the focus of the included studies was on screening, the most common type of delay considered was in correctly identifying disease positive patients. The most frequently evaluated screening strategy involved annual screening. 196–198,201,203,204,207–210,213–220,223 Several studies also explored increasing the screening interval beyond 1 year up to a maximum of 10 years, thereby implying that a patient who becomes eligible may have to wait up to 10 years before diagnosis and treatment is offered (although several studies allowed for the possibility of clinical presentations and diagnoses, or opportunistic screening, between scheduled screening intervals). 207–210,213 Interestingly, only one study considered the possibility of a screening interval of < 1 year. 195 It is noted that among the studies included in this review, screening interventions tended to be cost-effective among patients with diabetes and/or hypertension but were typically not cost-effective within general populations unless restricted to higher-risk groups or adopting a longer screening interval.
No studies considered the possibility of a delay in receiving results following testing. While it is acknowledged that for the modern healthcare systems considered in this review, these delays will be minimal, delays in the communication of abnormal test results to patients can still occur. In addition, receiving immediate treatment following a confirmed positive test seems to have been an implicit assumption made in all of the studies where testing and treatment were considered.
Which testing costs were captured in the analyses and how?
The cost of testing related to screening activities captured in the included studies was typically limited to the unit cost of the screening test alone. 195,198,199,201–205,208,212,214–219,223 Eight studies also included the cost of a physician/GP visit associated with the initial screening test(s) undertaken. 196,197,207,209–211,213,221 One study included additional screening costs (including transportation of equipment and personnel, advertisement, human resources and dissemination) related to undertaking screening within a remote indigenous population. 211 One study provided no specific details regarding screening test costs,222 while another assumed that no screening costs would be incurred due to the fact that the tests evaluated were assumed to already be reported routinely in standard care. 220 One study applied the cost of a physician visit only, without explicitly including the cost of the screening test. 213
Of those studies that provided information on the included screening costs, the most commonly cited sources related to national costing tariffs such as the Medicare and Medicaid fee schedule or reimbursement rates in the USA,196,203,207,208,213,220 and similar costing resources across other jurisdictions. 198,212,218,221 Two studies reported that the test costs were based on a ‘recommended retail price’223 or ‘notified fee’202 but did not provide specific sources for these costs. Four studies meanwhile reported that they based screening costs on local institution (e.g. hospital)199,204,214 or national215 cost data, but failed to provide specific details. Of the remaining studies, five based the costs on previous studies including cost-effectiveness models,205,209–211,219 while one derived costs from a survey of health service providers, based on the respondents quoted prices to add the evaluated screening test to standard care (specific details about what this cost was assumed to include were not reported). 200 Five studies failed to provide a source for the included test costs,197,201,216,217,222 while one study stated that the reported test costs were based on assumed values. 195
Six studies reported adopting a societal perspective,196,200–203,212 with the remainder using a healthcare provider/insurer perspective. Of those studies stating that a societal perspective was adopted, half of them did not provide any specific details. 200,203,212 One study included societal costs relating to lost wages alone: Boulware et al. incorporated lost wages resulting from patients aged < 65 years unable to work in the ESKD health state. 196 The two remaining studies captured additional elements of societal costs. Srisubat et al. included nonmedical costs relating to food and travel expenditure in addition to lost earnings, based on a cross-sectional survey of patients with normoalbuminuria, microalbuminuria, macroalbuminuria and ESKD;201 Go and colleagues based their model health state costs on a previously published costing study, which captured productivity loss, transportation and caregiver costs associated with hospital inpatient and outpatient visits. 202 None of the identified studies specifically discussed societal costs resulting from having to attend testing (and re-testing) – rather the focus tended to be on societal costs associated with long-term treatment of disease.
Study quality
The most common issue apparent from the study quality assessment concerned a failure of all but four studies to discuss all the issues relevant to users, which in this case meant that studies did not include any discussion regarding the impact of testing diagnostic accuracy on the modelled outcomes, or the impact of testing from the patient perspective (e.g. costs incurred, anxiety, etc.).
In terms of determining the validity of the models, the most common approach was to address the cross-validity of the model results, by comparing them to results obtained from other, similar studies within the study discussion sections. 196,198–201,205,207,210,211,214,218,219,221 Seven studies took a more formal approach to model validation, and assessed the external validity of their models by comparing key model outcomes (most commonly, mortality) against external data not used in the model itself. 196,202,206,207,210,211,216,223 Only one study reported having conducted internal validation checks of the model coding. 223 Ten studies did not appear to conduct any validation exercises. 195,203,208,209,212,215–217,220,222
Economic evaluation review search strategies
All searches were conducted on 4 February 2020.
CINAHL (EBSCO) 1981–present
-
S23 S13 AND S16 AND S20 Limiters – Published Date: 20140101 150
-
S22 S13 AND S16 AND S20 Limiters – Language: English 353
-
S21 S13 AND S16 AND S20 356
-
S20 S17 OR S18 OR S19 306,573
-
S19 ((MH ‘Renal Insufficiency, Chronic’) OR (MH ‘Kidney Failure, Chronic’)) OR ‘Chronic kidney disease’ 31,469
-
S18 (MH ‘Diabetes Mellitus+’) OR ‘diabetes’ OR (MH ‘Diabetes Mellitus, Type 1+’) OR (MH ‘Diabetes Mellitus, Type 2’) 201,556
-
S17 (MH ‘Hypertension, Renal+’) OR (MH ‘Hypertension+’) OR ‘hypertension’ OR (MH ‘Masked Hypertension’) OR (MH ‘Hypertension, Renovascular’) 105,989
-
S16 S14 OR S15 32,022
-
S15 AB glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI 27,306
-
S14 TI glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI 9247
-
S13 s7 not s12 256,118
-
S12 S8 OR S9 OR S10 OR S11 711,380
-
S11 (MH ‘Animals+’) not (MH ‘Human’) 77,363
-
S10 PT commentary 264,411
-
S9 PT letter 278,709
-
S8 PT editorial 263,811
-
S7 S3 OR S4 OR S5 OR S6 274,668
-
S6 TI (cost or costs or economic* or pharmacoeconomic* or price* or pricing*) OR AB (cost or costs or economic* or pharmacoeconomic* or price* or pricing*) 206,333
-
S5 (MH ‘Health Resource Utilization’) 16,908
-
S4 (MH ‘Health Resource Allocation’) 8503
-
S3 S1 not S2 95,952
-
S2 (MH ‘Financial Management+’) OR (MH ‘Financial Support+’) OR (MH ‘Financing, Organized+’) OR (MH ‘Business+’) 766,422
-
S1 (MH ‘Economics+’) 770,281
CRD Database (University of York)
Search ALL FIELDS: (glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI)
Limit to: HTA
Limit to: 2014 TO 2020
29 records
EconLit (EBSCO) 1886–present
-
S3 S1 AND S29
-
S2 TX (kidney or renal) OR TX diabetes OR TX hypertension1030
-
S1 TX glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI3192
EMBASE Classic + EMBASE (Ovid) 1947 to 3 February 2020
-
exp chronic kidney failure/ (96540)
-
testing.mp. (877236)
-
test.mp. (3158854)
-
1 or 2 or 3 (3794963)
-
(glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI).mp. (357113)
-
health economics/ (37526)
-
exp economic evaluation/ (302308)
-
exp Health Care Cost/ (290317)
-
pharmacoeconomics/ (7284)
-
6 or 7 or 8 or 9 (537767)
-
(econom$ or cost or costs or costly or costing or price or prices or pricing or pharmacoeconomic$).ti,ab. (1057908)
-
(expenditure$ not energy).ti,ab. (40339)
-
(value adj2 money).ti,ab. (2413)
-
budget$.ti,ab. (38477)
-
11 or 12 or 13 or 14 (1094602)
-
10 or 15 [Economic Evaluations] (1323184)
-
letter.pt. (1106184)
-
editorial.pt. (642779)
-
note.pt. (792819)
-
17 or 18 or 19 (2541782)
-
16 not 20 (1219885)
-
(metabolic adj cost).ti,ab. (1523)
-
((energy or oxygen) adj cost).ti,ab. (4565)
-
((energy or oxygen) adj expenditure).ti,ab. (31751)
-
22 or 23 or 24 (36709)
-
21 not 25 (1212209)
-
animal/ (1946633)
-
exp animal experiment/ (2501074)
-
nonhuman/ (6063266)
-
(rat or rats or mouse or mice or hamster or hamsters or animal or animals or dog or dogs or cat or cats or bovine or sheep).ti,ab,sh. (6490855)
-
27 or 28 or 29 or 30 (9609463)
-
exp human/ (21886995)
-
human experiment/ (484426)
-
32 or 33 (21888608)
-
31 not (31 and 34) (7168250)
-
26 not 35 (1101886)
-
conference abstract.pt. (3694392)
-
36 not 37 [Econ Evaluations with exclusions removed] (906391)
-
4 and 5 and 38 [(Chronic Kidney Failure or test) and CKF marker and Economic Evaluation] (1671)
-
limit 39 to english language (1557)
-
limit 40 to yr=‘2014 -Current’ (727)
Ovid MEDLINE(R) and Epub Ahead of Print, In-Process and Other Non-Indexed Citations and Daily 1946 to February 03, 2020
-
chronic kidney disease.mp. or Renal Insufficiency, Chronic/ (55137)
-
Diabetes Mellitus, Type 1/ or diabetes.mp. or Diabetes Mellitus, Type 2/ or Diabetes Mellitus/ (603783)
-
Hypertension, Renal/ or Hypertension/ or hypertension.mp. (478207)
-
1 or 2 or 3 (1037198)
-
(glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI).mp. (210479)
-
Economics/ (27127)
-
exp ‘costs and cost analysis’/ (232285)
-
Economics, Dental/ (1910)
-
exp economics, hospital/ (24201)
-
Economics, Medical/ (9054)
-
Economics, Nursing/ (3996)
-
Economics, Pharmaceutical/ (2913)
-
(economic$ or cost or costs or costly or costing or price or prices or pricing or pharmacoeconomic$).ti,ab. (766016)
-
(expenditure$ not energy).ti,ab. (28921)
-
value for money.ti,ab. (1643)
-
budget$.ti,ab. (28480)
-
6 or 7 or 8 or 9 or 10 or 11 or 12 or 13 or 14 or 15 or 16 (916045)
-
((energy or oxygen) adj cost).ti,ab. (4028)
-
(metabolic adj cost).ti,ab. (1375)
-
((energy or oxygen) adj expenditure).ti,ab. (24472)
-
18 or 19 or 20 (28903)
-
17 not 21 (909395)
-
letter.pt. (1060967)
-
editorial.pt. (516776)
-
historical article.pt. (356566)
-
23 or 24 or 25 (1915078)
-
22 not 26 (873818)
-
exp animals/ not humans/ (4669954)
-
27 not 28 (818401)
-
4 and 5 and 29 (1269)
-
limit 30 to english language (1180)
-
limit 31 to yr=‘2014 -Current’ (440)
PsycInfo (Ovid) 1806 to January Week 4 2020
-
chronic kidney disease.mp. (829)
-
exp Diabetes Insipidus/ or diabetes.mp. or exp Diabetes/ or exp Diabetes Mellitus/ (30318)
-
exp Hypertension/ or exp Essential Hypertension/ or hypertension.mp. (17966)
-
1 or 2 or 3 (44050)
-
(glomerular filtration rate or gfr or egfr or microalbuminuria or macroalbuminuria or albuminuria or proteinuria or urine albumin electrolyte or UAE or albumin creatinine ratio or ACR or Modification of Diet in Renal Disease or MDRD or dipstick or serum creatinine or Cystatin C or Chronic Kidney Disease Epidemiology Collaboration equation or CKD-EPI).mp. (2044)
-
‘costs and cost analysis’/ (16418)
-
‘Cost Containment’/ (588)
-
(economic adj2 evaluation$).ti,ab. (1668)
-
(economic adj2 analy$).ti,ab. (1519)
-
(economic adj2 (study or studies)).ti,ab. (788)
-
(cost adj2 evaluation$).ti,ab. (333)
-
(cost adj2 analy$).ti,ab. (3638)
-
(cost adj2 (study or studies)).ti,ab. (862)
-
(cost adj2 effective$).ti,ab. (15030)
-
(cost adj2 benefit$).ti,ab. (3438)
-
(cost adj2 utili$).ti,ab. (1241)
-
(cost adj2 minimi$).ti,ab. (366)
-
(cost adj2 consequence$).ti,ab. (115)
-
(cost adj2 comparison$).ti,ab. (186)
-
(cost adj2 identificat$).ti,ab. (26)
-
(pharmacoeconomic$ or pharmaco-economic$).ti,ab. (314)
-
or/6-21 (34293)
-
(task adj2 cost$).ti,ab,id. (625)
-
(switch$ adj2 cost$).ti,ab,id. (1309)
-
(metabolic adj cost).ti,ab,id. (100)
-
((energy or oxygen) adj cost).ti,ab,id. (285)
-
((energy or oxygen) adj expenditure).ti,ab,id. (2686)
-
23 or 24 or 25 or 26 or 27 (4720)
-
(animal or animals or rat or rats or mouse or mice or hamster or hamsters or dog or dogs or cat or cats or bovine or sheep or ovine or pig or pigs).ab,ti,id,de. (350338)
-
editorial.dt. (43579)
-
letter.dt. (21932)
-
dissertation abstract.pt. (487548)
-
29 or 30 or 31 or 32 (881656)
-
22 not (28 or 33) (29682)
-
4 and 5 and 34 (6)
-
limit 35 to english language (6)
-
limit 36 to yr=‘2014 -Current’ (2)
Economic evaluation review data extraction form
For those papers included in this systematic review, information was extracted using the following form, copied into an Excel spreadsheet.
| Study information |
|---|
| Authors |
| Title |
| Year |
| Location |
| Study objective |
| Type of testing (e.g. monitoring/screening) |
| Timing of test (e.g. annually, one-off, etc.) |
| Testing strategies evaluated |
| Comparators evaluated |
| Specific patient group |
| Type of economic evaluation (cost-utility, cost-effectiveness etc.) |
| Source of data to parameterise model |
| Setting (e.g. primary care, secondary care) |
| Modelling methodology |
| What type of model is used (e.g. Markov model, decision tree)? |
| How is the progression of CKD described in the analysis? |
| Does the model allow for reversibility (i.e. disease regression)? |
| What model structures have been used to describe the different model states? |
| Time horizon |
| Test accuracy |
| Is test accuracy considered in the analysis? |
| How is the accuracy of repeated testing captured? |
| Is the possibility of inaccurate (e.g. TN/FP, incorrect prognosis), indeterminate or test failure considered in the analysis? |
| What was the impact of FP test results in the model? |
| What was the impact of FN test results in the model? |
| Is the test accuracy subjected to any sensitivity analysis? |
| Was confirmatory testing conducted follow test positives? |
| Patient outcomes |
| What patient outcomes are considered in the analysis (clinical events, quality of life, etc.)? |
| Can patient outcomes be influenced by time delay as a result of patients not receiving prompt treatment? |
| Can patient outcomes be influenced by the timing of testing, decision-making and treatment? |
| Economic outcomes |
| Perspective (healthcare provider, societal) |
| If societal, what societal costs are incorporated in the analysis? |
| What/how were test costs captured? |
| What/how were CKD treatment costs captured? |
| What/how were other costs captured? (e.g. cardiovascular events) |
| What was concluded from the analysis with respect to the cost-effectiveness of the tests? |
Economic evaluation review quality assessment criteria
The following criteria were used in the systematic review of model-based economic evaluations, to assess the quality of the included economic evaluations.
| Criteria for quality assessment of economic evaluations | |
|---|---|
| 1 | Was a well-defined question posed in an answerable form? |
| 2 | Was a comprehensive description of the competing alternatives given? |
| 3 | Was the effectiveness of the programmes of services established? |
| 4 | Were all the important and relevant costs and consequences for each alternative established? |
| 5 | Were costs and consequences measured accurately in appropriate physical units? |
| 6 | Were costs and consequences valued credibly? |
| 7 | Were costs and consequences adjusted for differential timing? |
| 8 | Was an incremental analysis of costs and consequences of alternatives performed? |
| 9 | Was allowance made for uncertainty in the estimates of costs and consequences? |
| 10 | Did the presentation and discussion of study results include all issues of concern to users? |
List of abbreviations
- ACE
- angiotensin-converting enzyme
- ACR
- albumin-to-creatinine ratio
- AE
- adverse event
- AKI
- acute kidney injury
- A2RB
- angiotensin 2 receptor blocker
- BCTU
- Birmingham Clinical Trials Unit
- BIS
- Berlin Initiative Study
- BMI
- body mass index
- BP
- blood pressure
- BSA
- body surface area
- CAPA
- Caucasian, Asian, paediatric and adult
- CCB
- calcium channel blocker
- CKD
- chronic kidney disease
- CKD-EPI
- Chronic Kidney Disease-Epidemiology Consortium
- CV
- coefficient of variation
- CVA
- analytical variation
- CVG
- interindividual (between-subject) variation
- CVI
- intraindividual (within-subject) variation
- EDTA
- ethylenediaminetetraacetic acid
- eGFR
- estimated glomerular filtration rate
- EKFC
- European Kidney Function Consortium
- ESKD
- end-stage kidney disease
- FAS
- full age spectrum
- FN
- false negative
- FP
- false positive
- GFR
- glomerular filtration rate
- GP
- general practitioner
- HTA
- Health Technology Assessment
- ID-MS
- isotope dilution mass spectrometry
- IQR
- interquartile range
- KDIGO
- Kidney Disease Improving Global Outcomes
- LMR
- Lund–Malmö revised
- LTFU
- lost to follow-up
- MDRD
- Modification of Diet in Renal Disease
- mGFR
- measured glomerular filtration rate
- MI
- myocardial infarction
- MIQUEST
- Morbidity Information QUery and Export SynTax
- NICE
- National Institute for Health and Care Excellence
- NIHR
- National Institute for Health and Care Research
- NKF-KDOQI
- National Kidney Foundation – Kidney Disease Outcomes Quality Initiative
- NPV
- negative predictive value
- P30
- percentage of estimated GFR results within 30% of measured GFR
- PPV
- positive predictive value
- RAAS
- renin–angiotensin–aldosterone system
- RCV
- reference change value
- RMSE
- root mean square error
- SAEs
- serious adverse events
- SGLT2
- sodium-glucose cotransporter-2 inhibitor
- TN
- true negative
- TP
- true positive
Notes
-
Measured GFR covariate model fitted and observed values shown as individual plots for each study participant
Supplementary material can be found on the NIHR Journals Library report page (https://doi.org/10.3310/HYHN1078).
Supplementary material has been provided by the authors to support the report and any files provided at submission will have been seen by peer reviewers, but not extensively reviewed. Any supplementary material provided at a later stage in the process may not have been peer reviewed.
