Notes
Article history
The research reported in this issue of the journal was funded by the PHR programme as project number 13/43/55. The contractual start date was in October 2014. The final report began editorial review in June 2017 and was accepted for publication in March 2018. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The PHR editors and production house have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the final report document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
none
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2019. This work was produced by Angelini et al. under the terms of a commissioning contract issued by the Secretary of State for Health and Social Care. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
2019 Queen’s Printer and Controller of HMSO
Chapter 1 Introduction
This project aims to provide estimates of the impact of the annual Winter Fuel Payment (WFP)1 on household temperature and health using a regression discontinuity design (RDD). 2,3 In this chapter, we provide a general overview of the relationship between temperature and health, outline the importance of labelling effects as a potential channel through which the WFP may affect the temperature and health of recipients and then provide a more detailed background to the WFP and the health indicators examined in the current study.
The relationship between temperature and health
According to the Office for National Statistics (ONS), an estimated 43,500 excess winter deaths [(EWDs) defined as the number of deaths that occurred in the winter period minus the expected number of deaths for that period based on non-winter months] occurred in England and Wales in 2014/15, and these deaths were concentrated among older people. 4 Not only is this the highest number since 1999, but it is also higher than in countries with colder winters, such as the Scandinavian countries, which suggests that many of these deaths may be preventable. EWDs therefore represent an important public health challenge, and a reduction in EWDs is one of the outcomes outlined in the Public Health Outcome Framework for England 2016–19, as part of the ‘Healthcare public health and preventing premature mortality’ domain. 5
The association between cold outdoor temperatures and health risk has long been documented in the literature. 6,7 A small body of research in epidemiology8,9 has also demonstrated that lower indoor temperature may be key for understanding EWDs, which are largely considered to be caused by fuel poverty rather than temperature itself. 10 The World Health Organization (WHO) recommends a minimum temperature of 21 °C in living rooms and 18 °C in all other rooms. 11
Cold outdoor temperatures act as an unexpected negative income shock as households need to increase fuel expenditure to keep warm. Fuel-poor households are therefore potentially faced with a ‘heat-or-eat’ trade-off, in which they have to decide whether to increase expenditure on heating and cut back on other consumption or live in cold homes. 12 Older people are particularly vulnerable to such income shocks as they are likely to be on low and/or fixed incomes, spend more time in the home and live in energy-inefficient homes. 13 Older individuals are also particularly vulnerable to cold-related health impacts. Poor physiological thermoregulation is evident in older people, even in response to mild cold stress. Circulatory (e.g. heart attack, coronary thrombosis), respiratory (e.g. respiratory tract infections) and mental health problems (e.g. depression, anxiety) are considered likely to be associated with low indoor temperatures, via mechanisms involving increased blood pressure and viscosity, inflammation, bronchoconstriction, mucus production and clearance, immune suppression, stress, discomfort and social isolation. 14
The UK government has several long-running policies (e.g. WFP, Cold Weather Payments, Warm Homes Discount Scheme) that aim to counter the adverse effects of cold temperatures, particularly among the socioeconomically disadvantaged and the elderly. In this study, we focus on the WFP, an unconditional cash transfer that was introduced in the UK in 1997 to help older people meet the costs of heating during the colder winter months. This research represents the first examination of the potential effect of the £2–3B per annum WFP government policy on biomarkers and reported health measures.
The rationale for the introduction of the WFP is reproduced here:
Winter fuel payments were introduced as part of the Government’s initiative to tackle fuel poverty among pensioners. Winter fuel payments give older people reassurance that they can afford to heat their homes in winter. They are paid in a lump sum each winter to ensure that money is available when fuel bills arrive. Older people are targeted because they are particularly vulnerable to the effects of cold weather during the winter months and older people are more likely to be on fixed incomes.
Kennedy and Parkin. 1
Although the goals of the WFP are clear, it is by no means a given that the payment will be spent as desired by the government. From the perspective of standard economic theory, the WFP is viewed as an increase in income that will be spread evenly across expenditures. A recipient of the WFP is not in any way bound to spend this cash transfer on energy or any other specific goods. Distributing the WFP across expenditures as expected by standard economic theory would lead to approximately a 3% increase in fuel consumption. 12 However, initial evidence12 suggests that > 40% of the WFP is spent on fuel, suggesting that labelling the payment as ‘winter fuel’ may be effective in increasing energy expenditure. The presence of this labelling effect is crucial to understanding our rationale for anticipating that the WFP may have a beneficial impact on household temperature and health. We therefore provide a brief description of research examining this proposed labelling mechanism.
Behavioural interventions and labelling effects
Manipulating labels can be considered a potential behavioural intervention. 15–19 By labelling an unconditional cash transfer with a particular purpose the government signals the intention that recipients spend the transfer on a particular good suggested by the label. In this way, a label can be considered a ‘nudge’ or a way of ‘influencing choice without limiting the choice set’20 and without changing economic incentives. 21 Typical examples of labelled cash transfers are child benefits and food stamps – although these transfers can be spent on anything or traded and spent on goods if necessary, their labelling tries to influence their destination. Because these payments are unconditional, they do not require expensive monitoring.
According to standard economic theory, labelling cash transfers should have no effect on how the money is spent as it should be fully fungible with other income sources. The fungibility assumption implies that individuals should treat all the money in their bank account in the same way, independently of its source. In the standard framework, the marginal propensity to consume out of all types of income and wealth should be equal. However, behavioural economists have challenged the fungibility assumption, both theoretically and empirically. According to Thaler,22 individuals have a system of mental accounts in which they group categories of income and expenditure (e.g. food, entertainment, housing). Each of these mental accounts might have a specific budget and the marginal propensity to consume can differ across them. Within this framework, individuals are particularly susceptible to sources of income labelled according to one of their mental accounts. Mental accounting, therefore, suggests that the label attached to cash transfers can affect consumption patterns. The underlying idea is that labelled cash transfers may be considered as entering the correspondingly labelled mental account and are therefore not fully fungible with other income sources.
The empirical evidence on the importance of the labelling of transfers is mixed. Kooreman23 studies how Dutch households spend the child benefits they receive from the government. He found that child benefits are much more likely to be spent on children’s clothing than other income sources are. 23 In other words, the marginal propensity to purchase children’s clothing out of child benefits is much higher than the marginal propensity to purchase children’s clothing out of other income sources. In contrast to this evidence, Blow et al. 24 found that, in the UK, child benefits lead to a significant increase in alcohol consumption and the purchase of adult clothing for both couples and single parents.
Abeler and Marklein25 analyse whether or not individuals treat different income sources as fungible using both a natural field experiment and a controlled laboratory experiment. In both experiments, the authors compare the spending patterns of a group that receives a subsidy in the form of cash with those of a group that receives the subsidy as an in-kind benefit. Their results show that individuals do not act in line with the fungibility assumption and that the effect is caused by cognitive limitations rather than preferences. Beatty and Tuttle26 study the effect of a policy that increased food stamps benefits in the USA on food-at-home expenditure. They find that the policy caused an increase in both food-at-home expenditure and the proportion of total expenditure allocated towards food at home. Benhassine et al. 27 use a large randomised experiment in Morocco to estimate the effect of an unconditional cash transfer, labelled as an education support and paid to fathers of poor children in rural communities. They show that these transfers, although not conditional on school attendance, increased school participation substantially and performed as well as more expensive conditional cash transfers.
There is also evidence to suggest that labelling the WFP as ‘winter fuel’ may have a substantial impact on how the cash transfer is spent. We provide a brief background to the WFP and detail evidence for the existence of a labelling effect.
The Winter Fuel Payment
The programme targets older people because they are considered particularly vulnerable to the effects of cold weather during the winter months. To be eligible for the WFP, the oldest member of the household needs to be aged > 60 years before the end of the qualifying week of a given year, which for winter 2015/16 was 21–27 September 2015. 1 Individuals who already receive the State Pension or any other social security benefits (95% of cases) do not need to apply; they receive the payment automatically, together with a notification by post that details the amount and timing of the payment. Individuals who do not get any benefits or a State Pension (5% of cases) need to fill in an application form the first time they become eligible (the payment then becomes automatic in subsequent years). These recipients also get a letter that indicates the level and timing of the payment.
The WFP is paid as a tax-free lump sum between November and December of each year and the rate has increased substantially since its introduction in 1997. The payment was £20 (or £50 for those in receipt of means-tested benefits) when it was first introduced in the 1997/8 winter, it increased to £100 in 1999/2000 and then to £200 in 2000/1. An additional £100 for households with a member aged ≥ 80 years was first introduced in 2003/4. In some years additional payments have also been made alongside the ‘standard’ WFP, sometimes for reasons other than to help with fuel bills. Table 1 summarises entitlements from the year in which the WFP was introduced to 2016. According to the Department for Work and Pensions,1 there are > 12 million people who benefit from the WFP and the total expenditure has been estimated to be over £2B per year, as reported in Table 2.
| Winter | Rates |
|---|---|
| 1997/8 | £20 (£50 if on certain means-tested benefits) |
| 1998/9 | £20 (£50 if on certain means-tested benefits) |
| 1999/2000 | £100 |
| 2000/1 | £200 |
| 2001/2 | £200 |
| 2002/3 | £200 |
| 2003/4 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years |
| 2004/5 | £200 for ages 60–79 years, £300 fo those aged ≥ 80 years plus a one-off £100 for households with individuals aged ≥ 70 years ‘to help with Council Tax bills’ |
| 2005/6 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years plus either a one-off ‘Council Tax Refund’ of £200 for those aged ≥ 65 years if not getting Pension Credit guarantee element or a one-off ‘living expenses’ payment of £50 if aged ≥ 70 years and getting Pension Credit guarantee element |
| 2006/7 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years |
| 2007/8 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years |
| 2008/9 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years plus either a one-off payment of £100 for those aged ≥ 80 years or a one-off payment of £50 for those aged 60–79 years |
| 2009/10 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years plus either a one-off payment of £100 for those aged ≥ 80 years or a one-off payment of £50 for those aged 60–79 years |
| 2010/11 | £200 for those aged 60–79 years, £300 for those aged ≥ 80 years plus either a one-off payment of £100 for those aged ≥ 80 years or a one-off payment of £50 for those aged < 80 years |
| 2011/12 | £200 for those aged < 80 years, £300 for those aged ≥ 80 years |
| 2012/13 | £200 for those aged < 80 years, £300 for those aged ≥ 80 years |
| 2013/14 | £200 for those aged < 80 years, £300 for those aged ≥ 80 years |
| 2014/15 | £200 for those aged < 80 years, £300 for those aged ≥ 80 years |
| 2015/16 | £200 for those aged < 80 years, £300 for those aged ≥ 80 years |
| Winter | Number of recipients (in thousands) | Expenditure in | |
|---|---|---|---|
| Nominal terms (£M) | Real terms (£M) – 2012/2013 prices | ||
| 1997/8 | 9759 | 191 | 265 |
| 1998/9 | 9953 | 194 | 266 |
| 1999/2000 | 10,084 | 759 | 1020 |
| 2000/1 | 11,106 | 1749 | 2341 |
| 2001/2 | 11,202 | 1681 | 2208 |
| 2002/3 | 11,358 | 1705 | 2183 |
| 2003/4 | 11,486 | 1916 | 2402 |
| 2004/5 | 11,430 | 1962 | 2392 |
| 2005/6 | 11,555 | 1982 | 2368 |
| 2006/7 | 11,750 | 2015 | 2330 |
| 2007/8 | 12,123 | 2070 | 2340 |
| 2008/9 | 12,421 | 2701 | 2964 |
| 2009/10 | 12,681 | 2735 | 2948 |
| 2010/11 | 12,783 | 2759 | 2896 |
| 2011/12 | 12,650 | 2146 | 2204 |
| 2012/13 | 12,522 | 2127 | 2127 |
| 2013/14 | 12,406 | 2111 | 2060 |
| 2014/15 | 12,287 | 2096 | 1995 |
| 2015/16 | 12,169 | 2084 | 1935 |
| 2016/17 | 12,039 | 2071 | 1876 |
Although this payment can be spent on any goods and services, labelling the cash transfer as payment for ‘winter fuel’ attempts to ‘nudge’ recipients towards increasing domestic heating, thereby combating fuel poverty, raising indoor temperatures and reducing EWDs. However, both the universal entitlement (contingent only on age) and the fact that it can be spent on anything has been a subject of political and academic debate.
In a report published in December 2009 by the Institute for Public Policy Research, Lawton and Stanley28 indicate that the WFP is not a well-targeted expenditure, with approximately 12% of recipients likely to be in fuel poverty. The authors suggest that the WFP could be construed as a non-means tested method for enhancing pensioner income given that take up is close to universal. If the goal of the WFP is to specifically target the fuel poor then, the authors argue, the expenditure is in need of reform.
In another report on fuel poverty in March 2010,29 the House of Commons Energy and Climate Change Committee concludes that the WFP is an unfocused and poorly targeted means of tackling fuel poverty (contains Parliamentary information licensed under the Open Parliament Licence v3.0. See www.parliament.uk/site-information/copyright-parliament/open-parliament-licence/.):1
As a means of tackling fuel poverty, the case for Winter Fuel Payments is weak. Its payment is unfocused and not targeted on people in or near fuel poverty. However, as a universal means of supplementing pensioner incomes, which is easily understood and easy to pay, the political case for the retention of Winter Fuel Payments is strong. However, it would be more intellectually honest to rename the benefit; concede that it [is] a general income supplement; and stop accounting for it as a fuel poverty measure.
Because of this criticism, in 2014 the government assessed the feasibility of a voucher scheme to pay WFP directly to energy providers. However, the feasibility study showed that there would be significant additional administrative costs to the energy providers that were likely to translate into an increase in fuel bills for all customers. 1
In the social sciences, few papers have assessed the effectiveness of the WFP in tackling fuel poverty and improving health. Using UK data from the Living Costs and Food Survey (LCF) for the years 2000–8, Beatty et al. 12 study the effect of the WFP on fuel spending. In their analysis, the authors use a RDD approach with a sharp eligibility criterion at age 60 years and a window of 15 years on either side (45–75 years). The authors found that, on average, 47% of the WFP is actually spent on fuel. This result is particularly striking given that, if the WFP were treated as cash, we would expect (based on standard economic theory) households to spend only 3% of it on fuel. The authors attribute this effect to the labelling of the transfer, based on the framework of mental accounting developed by Thaler22 and related studies discussed23–27 in Behavioural interventions and labelling effects. To reiterate, the underlying idea is that households set mental budgets for classes of expenses and labelled cash transfers are disproportionally assigned to the corresponding labelled class. Using the same methodology as Beatty et al. ,12 Lange et al. 30 also found evidence for a labelling effect. However, the authors show that the WFP has a distortionary effect, as its labelling induces households to buy fuel instead of cleaner forms of energy, thus reducing the probability of investing in renewable energy by 1.2 percentage points.
Although there is evidence to suggest that the WFP alters energy expenditure, it remains unknown whether or not this leads to warmer homes or to improved health. Iparraguirre31 found a positive correlation between the introduction of the WFP in England and Wales and the recent reduction in EWDs in the UK. However, the study is based on aggregate time-series data (as opposed to individual-based data) without comparison regions, limiting the extent to which changes in mortality can be attributed to the WFP. In the current study, we employ an approach similar to Beatty et al. ,12 capitalising on the sharp eligibility criterion for WFP eligibility to examine the impact of the payment on household temperature and both objectively recorded and self-reported health measures.
Ambient temperature and health
If the WFP is effective in raising home temperatures during cold weather, a key question is whether or not this effect is likely to improve the health of older adults. An initial aim of this study is, therefore, to identify how indoor temperature relates to a set of physiological and self-reported health measures assessed in the English Longitudinal Study of Ageing (ELSA). 32 We do this because population-representative evidence documenting the link between ambient indoor temperature and health is largely absent. It is also important to estimate these associations in the UK context given that unique country-specific factors are likely to determine indoor temperature levels and its relation to health (e.g. climate, housing efficiency/insulation level, available income, time spent indoors, body composition, clothing and comfort preferences).
There is a relatively large evidence base suggesting that exposure to cold environmental temperatures is likely to be a primary explanatory factor for increased rates of mortality and morbidity during winter seasons. 6,7 Although excess winter mortality varies between years and regions within individual countries, up to 40,000 deaths, or approximately 60 deaths per 100,000 people, occur annually in Britain as a result of low outdoor temperatures. 33,34 Peak winter mortality can exceed lowest summer rates by as much as 45%,35 with parallel increases in related morbidity largely attributable to ischaemic heart disease and stroke and respiratory disease. 36 For example, an analysis covering the years 1949–85 reported that 88% of variation in annual EWDs in England and Wales could be explained by mean temperature, number of influenza deaths and temporal trends. 33
Several lines of evidence suggest that indoor temperature may also be relevant to health outcomes. The cross-national Eurowinter survey37 of seven cities and regions calculated higher percentage increases in mortality per degree fall in winter temperature in areas with warmer, rather than colder, winter climates; greater mortality increases were associated with lower living room temperatures, limited bedroom heating and less frequent use of personal protective measures, such as wearing warm clothing or keeping active when outdoors. 38 Indoor warmth, as predicted by household and housing features, was similarly related to deaths per degree fall in outdoor temperature in time-series analyses of English mortality data. 8 These authors further reported greater seasonal fluctuations in mortality and a 20% difference in EWDs between the coldest 25% of households and the warmest 25%. In an evaluation of the Warm Front Scheme,39 which aimed to increase residential energy efficiency and reduce health effects of fuel poverty in England, households that failed to increase indoor temperatures to WHO-recommended levels post intervention experienced increased mortality with decreases in outdoor temperature (2.2% per 1 °C reduction). In contrast, households that did raise indoor temperatures did not experience an increased risk of mortality.
Cold temperatures probably induce cardiovascular responses via multiple mechanisms involving blood pressure, heart rate variability, haemodynamics, atherosclerotic plaque development and instability, and endothelial dysfunction. 40 Blood pressure increases and concentrations of inflammatory and coagulation factors that can increase the risk of thrombosis may become elevated. 41–44 For example, C-reactive protein (CRP) and fibrinogen concentrations may also increase in response to respiratory infections,45,46 which occur more frequently in cold winter weather, possibly because of the confluence of lengthened microbial survival, increased transmission with indoor crowding and individuals’ reduced immune resistance or impaired respiratory function. 47 Airway infections and resulting inflammation can further reduce lung function by aggravating or triggering acute events in people with chronic respiratory conditions, such as asthma or chronic obstructive pulmonary disease (COPD). 48,49 Inhalation of cold air can act as a direct trigger for bronchoconstriction, especially in such susceptible persons or post-exertionally. 50,51
The remainder of this section summarises epidemiological literature on associations between temperature, cardiovascular and respiratory risk factors and functional measures examined in the current study into health effects of the WFP policy, namely blood pressure, fibrinogen, CRP, lung function and mental health. Research focusing on indoor temperatures is most relevant to this investigation but, as such studies are limited in number, those measuring outdoor temperature are included. Review documents written by the Marmot Review Team14 and Public Health England52 also provide useful background, with overlap to the studies referenced.
Blood pressure
Blood pressure levels are routinely higher in winter than in summer. 45,47,53,54 Outdoor temperature appears to be an important explanatory variable for this seasonal pattern. Lower temperatures have generally been associated with higher systolic and diastolic blood pressure in both cross-sectional and longitudinal studies and across a wide range of subpopulations (i.e. age, sex, social status, region), including by hypertension and hypertensive medication status. 55–57 One study from Glasgow, Scotland, distinguished between temperature-sensitive and temperature-insensitive people with hypertension, with the former group experiencing greater cold weather-related blood pressure changes and increased mortality. 58
Effects of indoor temperature on blood pressure have also been investigated, with an inverse association observed. 59,60 After adjusting for season or outdoor conditions, effect sizes have been reported in the range of 0.2–1.3 mmHg systolic blood pressure increase per 1 °C decrease in home temperature. 45,59,61 In the elderly, indoor temperature in winter was associated with a range of absolute and diurnal variability-related blood pressure measures and with stronger effect sizes and/or improved model fit than those based on outdoor temperature. 59,62
The temperature threshold below which indoor cold begins to affect blood pressure is still uncertain. Effects have been reported with indoor temperatures as high as 18 °C in laboratory or home settings,63 but some studies have identified blood pressure risk only at lower temperatures. 43 Moreover, the discrete temperature thresholds investigated have typically been selected to correspond with existing expert guidance or allow comparisons in laboratory-based experimental settings and so may not have yet identified a universal minimum ‘healthy’ indoor temperature. Based on population-based data from the Scottish Health Survey, Shiue and Shiue60 estimated that 9% of hypertension in Scotland could be prevented by maintaining indoor residential temperatures at ≥ 18 °C.
Inflammatory biomarkers
Although seasonal variation in inflammatory biomarkers has been noted, the relationship between inflammation and ambient temperature remains unknown. Non-summer (spring and winter) peaks in CRP and fibrinogen levels have been noted in individuals in populations in Norway54 and the UK. 45,64 In the UK studies, fibrinogen levels were 23% higher in the colder 6 months compared with warmer months,64 or differed by 0.13 g/l [95% confidence interval (CI) 0.05 to 0.20 g/l]. 45
Fibrinogen and CRP concentrations have been inversely associated with body and environmental temperature measurements,64–68 although one study57 reported such an association only with ambient temperatures of < 0 °C and a positive association at higher outdoor temperatures. The temperature–fibrinogen relationship has been reported to be non-significant after adjusting for season;45 this and other research68 have been interpreted as pointing to acute respiratory infections as a mechanism linking cold weather and inflammatory changes.
In contrast, the linear association observed between higher outdoor temperatures and higher CRP levels in stable heart failure patients suggested greater adverse inflammatory effects of warmer temperatures. 69 However, this patient population may be especially vulnerable to heat effects while also spending less time outdoors in cold weather, which could explain the finding’s directionality and suggest the importance of accounting for indoor environmental conditions. Results are also variable in other studies of people with chronic health conditions. 70,71 CRP and fibrinogen concentrations were both inversely associated with outdoor temperature in a multicity European study of post-myocardial infarction patients. 70 In a small German study,71 however, effects were inconsistent in patients with coronary heart disease versus those with pulmonary disease. Although lower temperatures were associated with increased fibrinogen concentrations, the reverse was observed with CRP concentrations in people with coronary heart disease, and no association between temperature and CRP concentration was observed in those with pulmonary disease.
Lung function
The frequency and severity of respiratory exacerbations among persons with diagnosed chronic respiratory conditions increase in colder autumn and winter months. 72,73 In such non-generalisable study populations of adults and children, outdoor and indoor temperatures have been associated with lung function and symptoms. Forced expiratory volume in 1 second (FEV1) and peak expiratory flow rate were positively associated with both outdoor and indoor bedroom temperature in a small UK-based study of older patients with moderate to severe COPD identified through an outpatient clinic. 73 Peak expiratory flow was significantly lower at colder bedroom temperatures even after controlling for outdoor conditions (and not independently associated with outdoor temperature), whereas the independent relationship of FEV1 with indoor temperature was of borderline statistical significance; associations with both lung function outcomes appeared independent of effects on symptom exacerbations. Lower than recommended indoor temperatures (fewer days with ≥ 9 hours at ≥ 21 °C in living spaces and ≥ 18 °C in bedrooms) was also associated with poorer self-reported respiratory status among COPD patients, especially among smokers. 74
Among children with asthma, from low-income families, living in New Zealand, adverse short-term variation in FEV1 and peak expiratory flow was found to be most strongly associated with low bedroom temperature in the preceding 1–2 weeks. 75 In this same study population, heating system replacement was associated with increased living room and bedroom temperatures as well as reduced symptoms, health-care utilisation, sleep disturbances and missed school, but not with significant changes in objective lung function measurements. 76 An earlier and larger New Zealand intervention, in which insulation was installed in wooden houses, was also associated with self-assessed improved health and reductions in self-reported wheezing, doctor visits, and school and work absences. 77
Mental health
Potential mechanisms linking cold indoor temperatures and mental health include elevated stress resulting directly from thermal discomfort or indirectly from associated fuel poverty or perceived heating-related financial strain;35,78 decreased psychosocial benefits of the home;79,80 impaired social relationships and quality of life, including from reduced privacy and usable space and altered routines;80,81 or increased sleep onset latency (difficulty initiating sleep). 82 Support for such associations arises primarily from evaluations of housing interventions. A similar conclusion was drawn after reviewing an older, more diverse and less controlled selection of housing improvement studies. 39,76,78,81 Improvements in self-assessed mental health were noted most strongly for borderline anxiety and depression, but were both measure and study sensitive.
Interventions that were not closely targeted at individual recipients experiencing elevated risk as a result of existing medical conditions or fuel poverty were less likely to show evidence of health benefits, potentially because of ‘ceiling effects’ (where many participants may have been in good health and had sufficient income to meet their heating needs). Mental and general health effects were more significantly and consistently associated with intermediate measures of participants’ living conditions and financial security (i.e. indoor cold, draughty homes, condensation, fuel poverty, thermal comfort) that were in turn associated with receipt of home insulation or heating improvements. 78 Stress, a potentially important variable on pathways between heating-related interventions and mental health, was also strongly associated with both intermediate and health outcome measures.
We now turn to our examination of how indoor residential temperatures are associated with cardiovascular and respiratory risk factors and functional status in a representative population of older adults living in private households in England.
Chapter 2 Methodology
Objectives
This research project aims to answer four key questions:
-
What health measures are most likely to respond to changes in ambient indoor temperature (specifically examining blood pressure, CRP and fibrinogen levels, FEV, reports of chest infection and mental and physical health ratings)?
-
Does the WFP increase the household temperature in households eligible for the transfer?
-
Does the WFP improve eligible households’ health outcomes and, if so, what is the magnitude of these effects?
-
Do the household temperature and health benefits of the WFP differ based on the social position of household members (e.g. income, social class), and is there evidence that the WFP produces beneficial effects for those at risk of fuel poverty?
In this chapter, we describe the general characteristics of the data source (ELSA) and the outcome measures to be examined. We then describe the specific characteristics of the sample and study design for the temperature and health analyses (aim 1) and the core WFP analyses (aims 2–4).
Participants
We drew on data collected between 2002 and 2012 as part of the ELSA, an ongoing prospective cohort study of a nationally representative sample of community-dwelling English adults aged ≥ 50 years. The ELSA aims to understand the determinants of socioeconomic status, health and well-being of older English adults. The study began in 2002, when 11,578 households with 18,813 individuals aged ≥ 50 years who had previously participated in the Health Survey for England (HSE) between 1998 and 2001 were identified as eligible for ELSA study. Specifically, initial participants were recruited if they were born before 1 March 1952 and were then interviewed as part of the first wave in 2002/3. Of these, 12,100 individuals completed wave 1 interviews.
The ELSA sample was designed to be nationally representative of private household-dwelling persons aged ≥ 50 years. The included waves comprise nurse visits in addition to the biennial computer-assisted structured interviews and self-completion questionnaires. Data are still being collected every 2 years. The original ELSA cohort was supplemented with refresher samples of HSE respondents during ELSA waves 3, 4 and 6 in order to keep the sample representative of the ≥ 50-year-old population as members age during follow-up; refreshment cohort members ranged in age from 50 to 74 years at recruitment depending on refreshment year and lived in households in which at least one member had previously participated in HSE 2001–4, 2006 or 2009–11. Seven waves of ELSA data are currently available, through to 2015, including three waves (2, 4 and 6) that include objective health data collected during in-person nurse visits to participants’ homes. Further details of the sampling process and data collected can be found in the ELSA cohort profile. 82
Outcomes
Indoor air temperature
Ambient indoor air temperature (measured in degrees Celsius/°C) in the participant’s household was gauged prior to each blood pressure monitoring session as part of the ELSA nurse assessment in waves 2 (2004/5), 4 (2008/9) and 6 (2012/13) of the study. Temperature readings were taken as part of almost all (> 99.5%) nurse visits. Temperature was assessed using a digital thermometer placed on a surface where the measurement probe was positioned so that it did not come in contact with any object (e.g. hanging over the edge of a table). After 5 minutes, the study nurse recorded the ambient temperature correct to one decimal place. All analyses investigating the household temperature and health and WFP–temperature relationships utilised these individual-specific temperature values.
In households with multiple individuals participating in the ELSA nurse visits, up to three indoor temperature measures per nurse visit were available (56% of nurse-visited participants resided in the 39% of nurse-visited households that had more than two indoor temperature measurements). To assess the reliability and variability of the ELSA indoor temperature measure, intraclass correlation coefficients (ICCs), estimating the correlations between indoor temperature measurements from the same households over several years (i.e. between ELSA waves), across households during single visits (i.e. within single waves) and repeated within the same household and wave were calculated. The ICCs were calculated using variance components from three-level linear mixed-effects regression models with participant-specific temperature as the dependent variable, random intercepts identifying household clusters and study wave clusters within households and fixed parameters for month of nurse visit (maximum likelihood estimation and independent covariance structure). Post-split measurements were excluded when original households were identified as having separated into different households during subsequent waves. Conditional on visit month, correlation of indoor temperature measurements within households over multiple waves or study years was calculated to be statistically significant but low (ICC 0.17, 95% CI 0.15 to 0.19), with moderate and higher correlation within study year but across households (ICC 0.59, 95% 0.57 to 0.61). Together, year and household random effects were estimated to explain approximately 76% of total residual variance in indoor temperature measurements (ICC 0.76, 95% CI 0.75 to 0.77; based on 24,243 measurements in 17,548 households). This ICC of 0.76 is preferred as a reliability estimate of indoor temperature measurements taken in the same house in the same visit over a standard Pearson correlation coefficient (0.78 based on 6761 first and second temperature measurement pairs from single visits) as the repeated same-wave temperature measurements had no meaningful order and were measuring the same quantity.
Within-wave household-level indoor air temperatures (created by averaging all available measurements collected from each household at each wave) displayed similarly low correlation over the study years (ICC 0.18, 95% CI 0.16 to 0.20), as did the individual-specific temperature measurements.
Health outcomes
All analyses were conducted for the 11 health measurements summarised in Table 3. We include the variable codes used to describe outcomes succinctly in Report Supplementary Material 1. All health outcomes except recent chest infection were analysed both as continuous measures and as dichotomous variables in order to capture possible effects in the upper percentiles of the distribution at important clinical thresholds. Health outcomes were measured during nurse visits with the exception of chest infection, self-rated health and depressive symptoms, which were self-reported during the main ELSA interviews.
| Variable | Description (metric) |
|---|---|
| Sysval | Systolic blood pressure (mmHg) |
| Sysval_2 | Binary systolic blood pressure – dichotomised at 140 mmHg |
| Diaval | Diastolic blood pressure (mmHg) |
| Diaval_2 | Binary systolic blood pressure – dichotomised at 90 mmHg |
| Cfib | Fibrinogen: inflammatory marker and coagulation factor (g/l) |
| Cfib_2 | Binary fibrinogen – dichotomised at 4 g/l |
| Log_hscrp | Hs-CRP (logged): inflammatory marker (mg/l) |
| Hscrp_2 | Binary hs-CRP – dichotomised at 3 mg/l |
| FEVz | z-score-transformed FEV1 (litres) |
| FEVz_2 | Binary z-score-transformed FEV1 – dichotomised at participant-specific lower limit of normal |
| Chestinf | Chest infection: participant-reported respiratory infections in past 3 weeks |
| SRH_2 | Self-rated health: rated from 1 = excellent to 5 = poor – dichotomised health score in which those rating their health as 4/5 (fair/poor) are contrasted with those scoring 1/2/3 (excellent/very good/good) |
| CESD | Depressive symptoms experienced in the past week assessed using the eight-item CES-D |
| CESD_2 | Binary CES-D score reflecting the presence of depression – dichotomised at four or more symptoms reported |
Blood pressure
Three blood pressure readings were made on seated participants’ right arms using Omron machines (Omron Healthcare Europe BV, Hoofddorp, the Netherlands). The final two technically valid (participant had not eaten, drunk, smoked or exercised in the prior half-hour) readings were averaged to generate mean systolic and diastolic blood pressure measurements; first readings were excluded as anxiety about the clinical or measurement process may increase blood pressure to unrepresentative levels. Dichotomous systolic blood pressure was coded as 1 if systolic blood pressure was > 140 mmHg, and 0 otherwise. This definition of ‘high systolic blood pressure’ or systolic hypertension was based on the seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure from the US National Heart, Lung, and Blood Institute. 83 Dichotomous diastolic blood pressure was coded as 1 if diastolic blood pressure was > 90 mmHg.
Although diastolic blood pressure was included in our analyses of the relationship between household temperature and health, it was not included in our main WFP analyses. This was because of the inverse U-shape in diastolic blood pressure with age. Specifically, diastolic blood pressure has been found to increase from young adulthood to approximately age 60 years and to decline thereafter. 84 This non-linear relationship occurring around the age of WFP eligibility is problematic for the regression discontinuity (RD) analysis and presents a risk of identifying WFP effects in the absence of a true causal link. To avoid this possibility, we therefore elected to omit diastolic blood pressure from our WFP analyses.
Inflammation
Participants were eligible to provide blood samples unless they had a clotting or bleeding disorder, were on anticoagulant medications or had ever had an epileptic fit or a convulsion (including a convulsion associated with high fever). Fibrinogen and high-sensitivity C-reactive protein (hs-CRP) levels were measured from available blood samples. The continuous hs-CRP measure was log-transformed because of its non-normal positively skewed distribution. In addition to analysing continuous measures, fibrinogen levels were dichotomised at 4 g/l and hs-CRP at 3 mg/l to capture concentrations above reference ranges and suggestive of higher cardiovascular risk. 85
Lung function testing
The FEV1 values were based on the highest measurement recorded during three acceptable exhalations into hand-held Vitalograph microspirometers (Vitalograph Ltd, Maids Moreton, Buckingham, UK) (waves 2 and 4) or the ndd Easy On-PC spirometer (ndd Medical Technologies, Inc., MA, USA) (wave 6); a maximum of eight attempts were made per participant session to collect the three acceptable blows. In order to account for greater normal between-individual lung variability in lung function among older adults and thus avoid excessive false-positive diagnoses of lung disorders in the older study populations relevant to the WFP,86 participant-specific z-scores and lower limits of normal were calculated using the Global Lung Function Initiative all-ages reference equations87 and individual data on raw FEV1 scores and the covariates age, height, sex and race/ethnicity. In order for the reference equations to run, the following changes were made to the original ELSA data: the grouped age category of those aged > 90 years was recoded to 95 years (0.6%), all non-white race/ethnicity categories were combined (2.5%) and treated as other/mixed, and six measured FEV1 values below the minimum reference range were recoded to the minimum of 0.20 l. The resulting continuous z-score health variable provided standardised and unbiased estimates of the degree to which participants’ measured FEV1 values differed from values predicted from their individual characteristics, expressed as unitless multiples of the residual standard deviation; z-scores are negative when measured FEV1 values are below predicted and positive when above predicted. z-scores were also compared with individually calculated lower limits of normal. Values below the lower limits of normal were considered abnormally low FEV1 and coded as a dichotomous outcome variable indicating respiratory disease.
Chest infection
Information on recent chest infections was obtained from participants responding to the question ‘In the past three weeks, have you had any respiratory infections such as influenza, pneumonia, bronchitis or a severe cold?’ in the lung function module of the computer-assisted personal interview during the main ELSA visits.
Self-rated health
General self-rated health was assessed at each of the three ELSA waves examined (waves 2, 4 and 6) using the item ‘Now I would like to ask you some questions about your health. Would you say your health is . . .’ Participants’ health status was scored on a five-point scale from 1 (excellent) to 5 (poor), with a midpoint of 3 (good). This single-item measure has been shown to effectively summarise global health information. It has been shown to outpredict individual health markers derived from blood assays, physical measurements or medical histories in forecasting mortality. 88 Although this is a single-item measure, predictions of a range of outcomes including hospitalisations, health-care use and even mortality are comparable to predictions derived from multi-item self-reported health measures. 89 As self-reported general health is an ordinal variable, we dichotomise the measure so that those with values of 4 (fair) or 5 (poor) are identified as having worse general health and contrasted with those rating their current health as 1 (excellent), 2 (very good) or 3 (good).
Depressive symptoms
A validated eight-item version of the Centre for Epidemiology Studies Depression Scale (CES-D)90,91 was administered to assess depressive symptoms over the previous week. The short-form CES-D uses a yes/no response format to assess depressive symptoms in the past week including depressed affect (feeling sad, depressed), positive affect (happiness, enjoyment of life), somatic symptoms (lethargy, could not get going, sleep was restless) and interpersonal symptoms (felt lonely). Positively worded items were reverse scored and a total sum score was produced (range 0–8), with higher scores indicating the presence of a greater number of depressive symptoms. The CES-D showed high levels of reliability (Cronbach’s α = approximately 0.8). The scale was also moderately stable across study waves (r = approximately 0.5; p < 0.001).
Indoor temperature and health: study design and analysis
We examined the relationship between ambient indoor temperature levels and health measures across three waves of ELSA [wave 2 (2004/5), wave 4 (2008/9) and wave 6 (2012/13)]. This analysis yielded a maximum sample size of 12,332 and 23,908 observations in total across waves (Table 4). Multilevel random coefficient models were first used in order to include the maximum number of possible observations across the three waves and to account for non-independence among repeated observations [because of the hierarchical structure of the data with individual wave observations (t) nested within participants (i)].
| Characteristic | Wave | ||
|---|---|---|---|
| 2 (n = 7611) | 4 (n = 8312) | 6 (n = 7973) | |
| Age (years), mean (SD) | 66.53 (9.62) | 65.85 (9.57) | 67.22 (9.50) |
| Age-squared, mean (SD) | 4518.43 (1325.84) | 4427.51 (1305.10) | 4608.14 (1312.36) |
| Female (%) | 55.07 | 55.06 | 55.25 |
| White (%) | 98.20 | 97.49 | 96.94 |
| Marital status (%) | |||
| Married | 65.30 | 66.30 | 64.50 |
| Cohabiting | 3.35 | 4.70 | 5.08 |
| Neither | 31.35 | 28.97 | 30.33 |
| Retired (%) | 53.81 | 54.23 | 59.99 |
| Educational attainment (%) | |||
| No qualifications | 37.40 | 26.90 | 24.30 |
| Basic qualifications | 22.06 | 23.28 | 23.14 |
| High-school qualifications | 6.72 | 8.39 | 8.59 |
| Further qualifications | 12.25 | 15.56 | 14.22 |
| University degree/higher | 12.33 | 18.50 | 17.75 |
| Other (including foreign) | 9.21 | 7.37 | 11.99 |
| Wealth (%) | |||
| Bottom wealth quintile | 16.65 | 15.50 | 15.25 |
| Second wealth quintile | 19.28 | 17.79 | 17.75 |
| Third wealth quintile | 20.15 | 18.94 | 19.80 |
| Fourth wealth quintile | 20.87 | 19.94 | 20.75 |
| Top wealth quintile | 21.72 | 21.19 | 20.72 |
| Wealth data missing | 1.33 | 6.65 | 5.73 |
| Current smoker (%) | 14.50 | 13.27 | 11.66 |
| Long-term illness (%) | 57.45 | 54.70 | 55.20 |
| BMI (kg/m2), mean (SD) | 27.93 (4.89) | 28.26 (5.28) | 28.28 (5.27) |
| High blood pressure (%) | 33.54 | 38.68 | 39.38 |
| Blood pressure medication (%) | 14.64a | 32.49 | 34.17 |
| Region (%) | |||
| North East | 6.65 | 6.24 | 6.13 |
| North West | 12.59 | 10.74 | 10.92 |
| Yorkshire and the Humber | 10.91 | 10.80 | 10.66 |
| East Midlands | 10.41 | 10.67 | 10.64 |
| West Midlands | 10.62 | 11.14 | 10.99 |
| East | 12.10 | 12.93 | 12.76 |
| London | 8.34 | 8.34 | 8.35 |
| South East | 16.42 | 17.29 | 17.32 |
| South West | 11.88 | 11.63 | 11.92 |
| Not in England | 0.09 | 0.20 | 0.31 |
| Month of assessment (%) | |||
| January | 10.70 | 10.54 | 10.27 |
| February | 11.69 | 10.43 | 8.12 |
| March | 9.42 | 11.10 | 4.41 |
| April | 11.05 | 6.64 | 2.04 |
| May | 8.34 | 5.73 | 0.93 |
| June | 3.45 | 4.28 | 3.12 |
| July | 2.23 | 13.27 | 10.62 |
| August | 5.92 | 11.90 | 9.72 |
| September | 10.52 | 9.97 | 9.57 |
| October | 10.19 | 7.77 | 15.48 |
| November | 11.90 | 4.80 | 17.43 |
| December | 4.58 | 3.56 | 8.29 |
| Year of assessment (%) | |||
| 2004 | 44.79 | ||
| 2005 | 55.21 | ||
| 2008 | 48.08 | ||
| 2009 | 51.92 | ||
| 2012 | 73.73 | ||
| 2013 | 26.27 | ||
First, we examined the association between indoor temperature and each of the health measures (see Table 3) across the three waves examined in a model that adjusted for basic demographic factors (i.e. age, age-squared, sex and ethnicity) and included dummy variables for region of residence and the year and month of health assessment (model 1). Next, we adjusted for a broad range of additional covariates that may affect participant health and/or temperature measures examined. Specifically, marital status (married, cohabiting, neither) and employment status (retired vs. others), education [National Vocational Qualification (NVQ) level] and wealth levels (benefit unit non-pension wealth quintiles), smoking and body mass index (BMI) levels and the presence of a long-term illness were added to model 1. Blood pressure analyses were adjusted for the presence of a diagnosis of hypertension and blood pressure medication usage. In addition, in supplementary analyses of data from waves 2 and 4 it was possible to adjust for outdoor temperature levels (as described in Covariates and the regression discontinuity analysis).
Using standard nomenclature these regression models can be summarised as follows:
Next, we examined how changes in indoor temperature relate to within-person changes in health by conducting a series of fixed-effects analyses (model 2). These models were restricted to participants with two or more waves of available data. By examining within-person variation, these analyses can account for potential non-observed time-invariant confounders (e.g. factors such as sex, childhood socioeconomic background and genetic make-up that do not vary over time), essentially generating coefficients that are free from the influence of unobservable stable individual heterogeneity (α). The difference between a person’s health level in each participating wave and the person’s average level of health is represented by ‘Health measureit – Health measure¯i’:
Winter Fuel Payment intervention
Overview
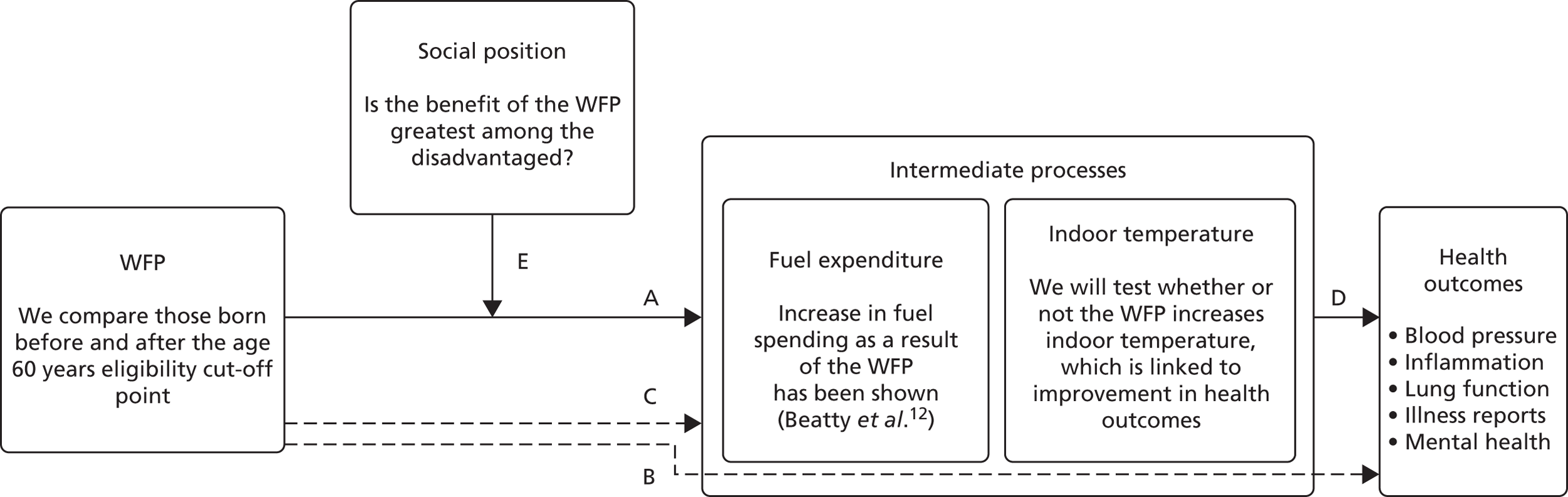
Regressions discontinuity analyses were carried out to estimate causal relationships between the WFP and a set of biomarker-based and participant-reported health outcomes. As indoor air temperature was hypothesised to be a primary intermediate factor through which such relationships could exist, separate RD analyses were conducted on the relationship between WFP receipt and indoor temperature (pathway A of the hypothesised mechanism; Figure 1) and between WFP and health outcomes (pathway B; see Figure 1). Methods and results of these analyses are described in detail here. As no significant and consistent causal effects of the WFP on indoor temperature or health were identified, two-stage RD models incorporating both stages (WFP–indoor temperature and indoor temperature–health) within the same analyses were not pursued. Our analysis rests on the assumption, supported by our empirical work, that there is a significant relationship between indoor temperature and health outcomes. Traditional random and fixed-effects regression analyses were run to formally investigate this relationship (pathway D of the hypothesised mechanism; see Figure 1), as described above. All analyses described in Figure 1 were conducted using the ELSA.
FIGURE 1.
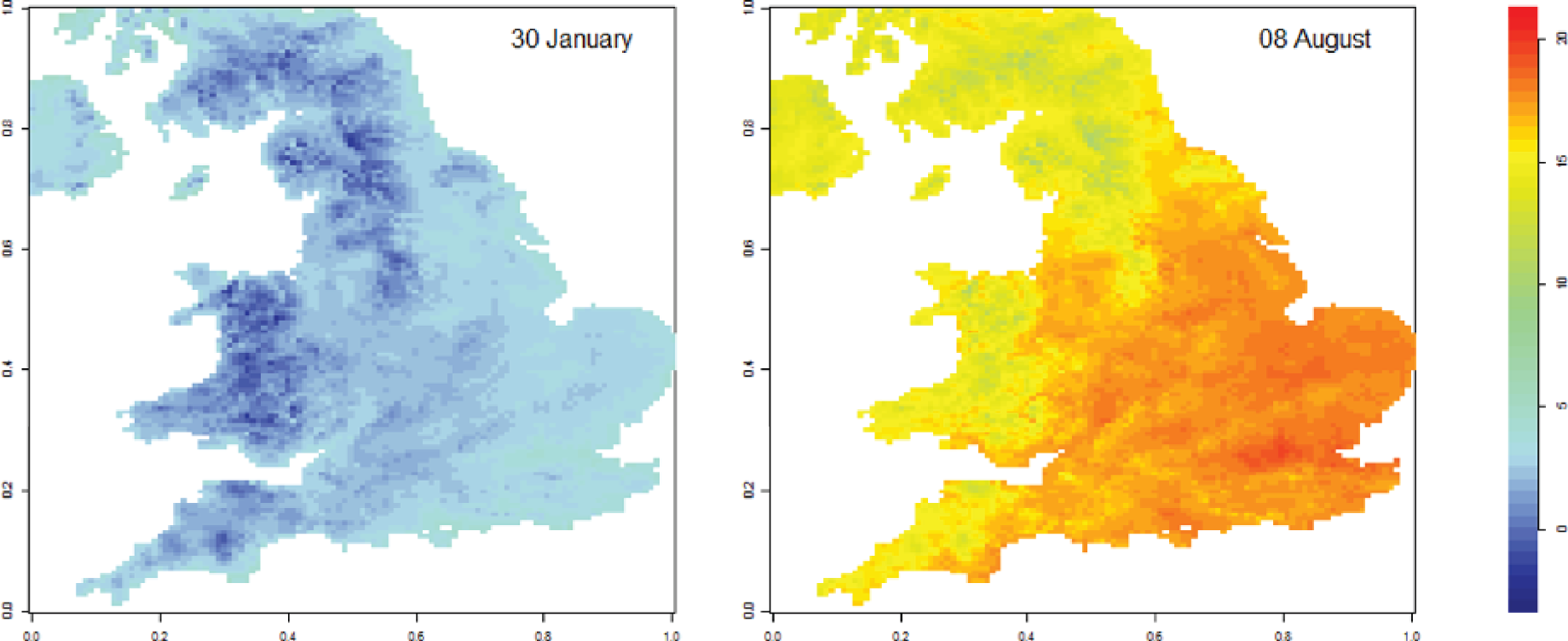
The logic model guiding the current research. Using RD analyses we examined the impact of distance from the WFP eligibility cut-off point on indoor household temperature (pathway A) and health (pathway B). This analysis considers linear and non-linear age-related trends in factors such as indoor temperature (pathway C) and health (pathway D). However, by exploiting a local randomisation and analysing observations around the age 60 years eligibility cut-off point for the WFP, it can identify ‘jumps’ or changes in the these trends attributable to the WFP. In addition, we examine the extent to which the temperature (pathway A) and health (pathway B) effects of the WFP may differ based on social position (pathway E). We anticipate that the WFP will produce larger beneficial changes in household temperature and health among low-income groups.
Regression discontinuity
Ideally, to evaluate the effects of the WFP on morbidity, one would run a randomised controlled trial in which one group is assigned to the WFP (‘treatment group’) and another one is not (‘control group’). Differences between the two groups would be randomised and a simple comparison of mean outcomes could be interpreted causally. However, some non-experimental techniques, such as the RD design, allow researchers to recover causal effects from the analysis of non-experimental observational data, under some specific conditions, which will be discussed in the following paragraphs. A growing econometric literature is developing around the RD approach, the interpretation of the RD parameter and the conditions under which said parameter can be interpreted as a causal treatment effect. The most recent contributions include those by Imbens and Lemieux92 and Lee and Lemieux. 93 What follows draws heavily from recent advances in the non-parametric estimation and inference by Calonico et al. 94–97 and Skovron and Titiunik. 98
The RD mimics a randomised experiment by exploiting features, such as sharp eligibility criteria of (social) programmes. In general, the design of the RD consists of two main features. First, applicants or eligible recipients of a programme receive something like an eligibility status based on a score (e.g. disability score or birth date), and the programme is provided to the population whose score exceeds a known cut-off point or threshold (the treatment group) and withheld from the portion of the population whose score is below such a cut-off point (the control group). The assignment mechanism (the value of such score) is decided by the body in charge of the programme and cannot be manipulated by participants. Arbitrary dates are good examples of scores. Many programmes, and even large social reforms, are based on arbitrary cut-off dates. For instance, school-leaving age has been raised a number of times in the UK since 1897 using dates as cut-off points (i.e. people born after a certain date were mandated to stay in school for an additional year whereas people born before the same date were unaffected). For instance, the 1972 compulsory education reform raised the minimum leaving age from 15 to 16 years for those English pupils born after 1 September 1957. Pupils born before that same date could leave school when aged 15 years.
The second feature that distinguishes the design of a RD is that – if one looks sufficiently close to the cut-off point – the control group must be a valid counterfactual of the treatment group. Back to our compulsory schooling reform example, it is quite innocuous to assume that people born just before an arbitrary date are statistically similar to people born just after. This means that differences in the earnings of those receiving different amount of schooling just because they are born on one side of the cut-off point (vs. the other) can be attributed to schooling (instead of unobserved ability, personality, etc.).
The WFP lends itself to be analysed using RD too. In our case, the WFP is transferred to households that include a member who is aged ≥ 60 years at the beginning of the qualifying week. The placement of the qualifying week has changed over time; however, during the years in our data, the qualifying week came in September for most of the period (see Chapter 1, The Winter Fuel Payment for a detailed background on how eligibility works). As with the case of schooling reforms, there is an arbitrary cut-off date that assigns part of the population to a treatment: the WFP cash transfer. This cut-off point is set ex ante by the government and cannot be manipulated by households as it is based on the birth date of the oldest member. It is safe to assume that households whose oldest member just missed the payment are statistically similar to households whose oldest member just received the allowance. Health differences between these households can be attributed to the WFP instead of other factors, such as ageing itself.
The RD method can be illustrated graphically. Figure 2 depicts a hypothetical situation and it has been created for illustration purposes only. It consists of two graphs, each showing the situation that might exist between a health outcome H (e.g. lung function) and age of the oldest household member (X) under different circumstances. In more technical terms, the downward-sloping line represents the regression line that measures the average health outcome at different ages. The vertical line in the centre of each graph designates the cut-off point, x0, above which households are ‘assigned’ to the treatment (i.e. receive the WFP) and below which they are ‘assigned’ to the control group. Recall that the cut-off point is based on the age of the oldest household member: he or she must be aged ≥ 60 years before the end of the qualifying week of a given year, which for winter 2015/16 was 21–27 September 2015. For simplicity we depict the situation for the oldest member of the household.
FIGURE 2.
Stylised graphical representation of the RD design (for oldest household members). (a) In the absence of the WFP → no discontinuity expected; and (b) in the presence of the WFP → discontinuity around the eligibility cut-off point indicates treatment effect.

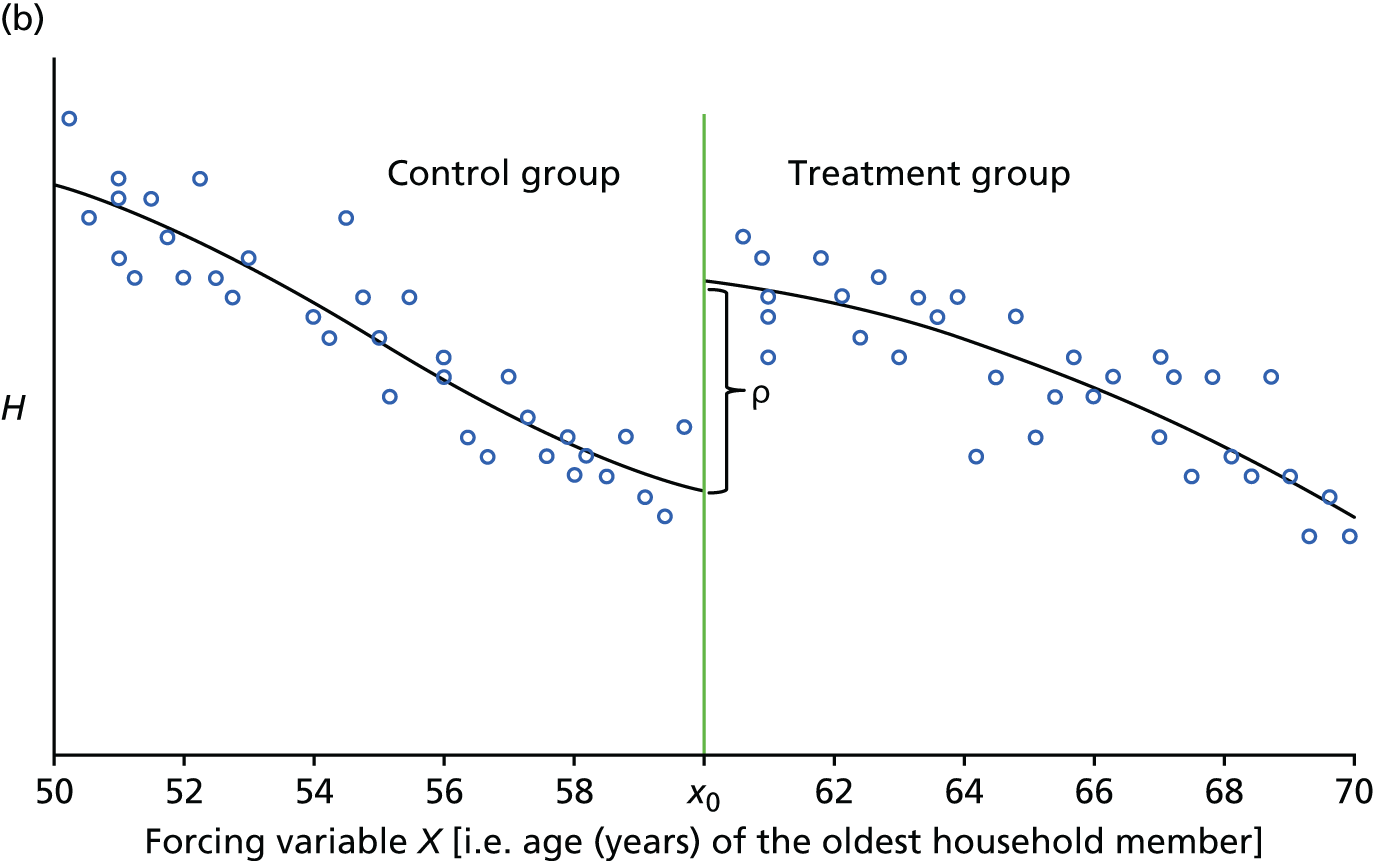
Figure 2a illustrates what one would expect in the absence of the WFP. The crucial aspect here is the smoothness of the relationship between the health outcome and age. Albeit very stylised, Figure 2a captures some essential features. The relationship is downward-sloping, implying that health (H) declines as age increases. The relationship is also continuous everywhere and around the eligibility age x0. This implies that in the absence of WFP there is no substantial difference in health outcome for households who are just above and just below the cut-off point. In other words, we can say that individuals with age right at the cut-off point x0 must be very similar (comparable) to individuals with age x0 – ε (where ε is small and positive).
Figure 2b illustrates what might occur in the presence of the WFP. Note that we can still affirm that individuals with age right at the cut-off point x0 must be very similar (comparable) to individuals with age x0 – ε (where ε is small and positive) except now the former receive the WFP (treatment group), whereas the latter do not (control group). The two regression lines represent the average health outcomes for the treatment and for the control group.
The fundamental problem of causal inference implies that we can observe only the situation depicted in Figure 2b. In the hypothetical case, there is a sharp upward jump in the relationship between health outcomes and age at the cut-off age x0. The aim of the RD analysis is to test for the presence of such jump/discontinuity around x0. Note that the overall relationship between H and age X is still negative; however, it is discontinuous right at the cut-off point.
In summary, the assignment age employed by the WFP programme is exogenous and the WFP effectively divides the population of households between a treatment group (i.e. households in which oldest member is just above x0 years of age) and a control group (i.e. households in which oldest member is just below x0 years of age). Near the cut-off age of x0, differences between these two types of households can be assumed to be random. The direction and magnitude of the jump is a direct measure of the causal effect of the WFP on health outcome H for households close to the cut-off point.
Internal validity tests
In the hypothetical case depicted in Figure 2b, there is a positive discontinuity in the relationship (the receipt of the WFP has positive effects on the health outcome): the average health outcome of the people who just received the payment is higher than that of the people who just missed the payment. Note that this can be thought of as causal if there are no other events/reasons as to why the relationship has to be discontinuous between H and X right at the WFP eligibility age. In order to ensure identification of the causal effect, one must check that no other factors except being a recipient of WFP should be discontinuous around the cut-off point. It is good practice to gather as much information as possible regarding the cut-off point to rule out other confounding explanations of potential discontinuity. We note that the WFP eligibility occurs around the same age as women’s pension eligibility. For this reason, and to avoid any confounding between WFP and female pension, our analysis is carried out both using the whole sample and restricting the sample to exclude households in which the woman is the oldest member. A more general way to rule out any potential confounding is to check for continuity of observable characteristics (and other covariates in general) that could explain a jump in the health outcome that is not related to the WFP. One could actually check if female employment is discontinuous around x0 by running a RD of the probability of being employed on x0. The absence of systematic discontinuities at the cut-off age is illustrated using RD plots for each covariate in Report Supplementary Material 1. It is also possible that the discontinuity between H and x0 is occurring just by chance and it is detected anyway by statistical tests. The best way to exclude this is to run placebo tests and show that the relationship between H and X is indeed continuous for every other value of X other than x0. However, we do not find any systematic discontinuity, so this analysis is redundant.
Formal description of models
Assignment to the WFP is determined exogenously by the age of the oldest member of the household in the arbitrary qualifying week. From this follows two important aspects. First, the entire selection into treatment is based on the observable variable age; in the RDD jargon this is referred to as ‘running (or forcing) variable X’. Second, this selection rule is exogenous – an arbitrary date established by the government every year – and cannot be manipulated by households. The continuous lines in Figure 2 represent regression functions of health outcome H of individual i on age of the oldest member (x0). Unfortunately, only the regression lines in Figure 2b are observed.
Using the potential outcome notation, the average health outcome of the treatment group 𝔼[Hi(1)|Xi] is observed only when the running variable X ≥ x0. In other words, the observed health outcome Hi is equal to the potential outcome in the presence of WFP Hi(1) for every individual i to the right of the cut-off point x0 only. Vice versa, the average health outcome of the control group is observed only for ages of the oldest member at the left of the cut-off birth date x0, when Xi < x0. In summary, the observed average health outcome H given the running variable X is:
The difference between average potential outcomes, that is, the average treatment effect 𝔼[Hi(1)|Xi] – 𝔼[Hi(0)|Xi], cannot be estimated because the regression functions do not overlap, that is, no health outcome is observed for the same value of X. This is a more formal way of representing the fundamental problem of causal inference with observational data. Hahn et al. 99 proposed a solution to this problem in the context of RDD by suggesting that outcomes very close to the cut-off point be looked at. Right at x0, we almost observe both outcomes for the same value of X. Formally, this requires the regression functions 𝔼[Hi(1)|Xi] and 𝔼[Hi(0)|Xi] to be continuous at x0 and to think in terms of differences between limits. The average treatment effect ρ can be recovered and is given by the difference between the two regression functions at the cut-off point x0:
The empirical specifications will then compare households that are immediately above and below the eligibility age of 60 years under the identifying assumption that health outcome H would have been similar in the absence of WFP receipt.
Bandwidth, functional form and weighting
As is clear from Figure 2, the regression lines need to be approximated by experimenting with different functional forms. If the functional form is not correctly specified, the estimated effects will be biased. In the worst case scenario, incorrect functional forms may confound discontinuity for nonlinearities. A further problem is that higher-order polynomials (such as cubic, quartic, etc.) tend to overfit and find discontinuity where none exist. 100 It is often the case that estimating RD implies also selecting bandwidth (BW), that is, the window of observations on either side of the cut-off point that will be used to estimate the discontinuity. This implies approximating those regression lines by using only observations whose scores are between the cut-off point x0 and a smaller width than the one presented in Figure 2 (which goes from 50 to 70). In empirical works different combinations of functional forms and BWs are used. With regard to the size of the BW, note that, as the BW becomes larger, say 10 years on either side of the cut-off points, more data are considered. However, households at either end of the spectrum are less likely to have similar (observed and unobserved) characteristics, which would result in a violation of one of the RD assumptions. Narrower BWs, on the other hand, may reduce the precision of the regression model. In their recent work, Calonico et al. 94–97 show that, for a given functional form, the precision of the regression lines approximation can depend on the BW chosen. It becomes crucial to use a data-driven algorithm to choose the optimal BW. Calonico et al. 94 propose to select the BW that minimises an approximation to the asymptotic mean squared errors (MSEs) of the RD estimator, similar to what has been suggested by Imbens and Kalyanaraman. 101 In other words, this procedure aims at reducing the bias–variance trade-off given the functional form chosen. To reduce potential overfitting problems, Skovron and Titiunik98 explain that ‘the practical recommendation is to use [. . .] a polynomial of order one’, a local linear regression.
More formally, the MSE-optimal BW estimator is:
where hopt is the optimal width around the cut-off point, V^ is the estimated variance, B^ is the estimated leading bias of the RD estimator and p is the polynomial order, in our case 1. Note that this formula contains the estimated leading bias, B^, as a factor in the denominator that is related to the difference of the estimated (p + 1) derivative of the right and left regression functions at the threshold. However, as this difference term is a factor in the denominator, if the estimated bias, B^, is (almost) 0, the denominator will be (almost) 0, leading to a very large (infinite) estimated BW. In order to counteract this tendency, Calonico et al. 94 adopt the ‘regularisation’ approach. Improving upon Imbens and Kalyanaraman,101 they introduce a term that ensures the denominator does not become too small and that the BW is optimally chosen. This leads to the regularised estimator:
where R^ is the estimated regularisation term. This term is strictly positive, and ensures that the denominator of the expression does not become too small [(V^, B^, R^) can be estimated from the data]. In practice, BWs computed without ‘regularisation’ are larger than otherwise. For the sake of robustness, and to show that our results are not sensitive to the size of the BW, we will present estimates using both formulas, the one with the regularisation term and the one without (henceforth ‘Reg’ and ‘No Reg’, respectively).
Researchers wanting to use local polynomial regressions face the choice of the type of weighting (i.e. kernel function) to apply to the observations within the BW selected. The choice that is often recommended by scholars is the use of triangular kernel function that assigns the largest weight to the observations around the cut-off point. The weight decreases to zero on either side of the cut-off point so that every observation outside the BW is given a weight equal to zero (see Skovron and Titiunik98).
Eligibility for WFP depends on an administratively determined ‘WFP qualification week’, which falls in September each year. Individuals must become age-eligible for the WFP by the last day of a year’s qualification week in order to receive a WFP for the upcoming winter (WFP payments are distributed each November or December). The qualifying age for the WFP corresponds to the State Pension age for women. Until 2010, this was 60 years. From 2010, it began to increase in line with increases in the minimum pension age for women. 1
For the present study, WFP receipt is a household-level variable because it is intended to be put towards home heating, a characteristic that affects all household occupants. Household WFP status is therefore determined by the age of the oldest household member. For RD analyses, a forcing variable identifying whether or not a household was WFP eligible at each year of ELSA data collection, and the number of years before acquiring eligibility status or since acquiring eligibility status, was created by subtracting the year’s qualifying age from the oldest household member’s age as of the most recent WFP qualifying date prior to the household’s nurse visit. Households in which the oldest member turned the WFP qualifying age just before the year’s qualifying week receive a value of zero, those whose oldest member is older than the qualifying age receive a positive value and those whose oldest member is younger receive a negative value. As mentioned earlier, the qualifying age for ELSA wave 6 participants is not the same as the standardised age for waves 2 and 4 because of changes in the WFP qualifying age beginning in 2010. Moreover, within wave 6, the choice of WFP qualifying age and thus the forcing variable depend on nurse visit date; the WFP qualifying age applied (to the nearest quarter) was 60.75 years for participants visited in mid-September 2011 through early September 2012 versus 61.25 years for participants visited in mid-September 2012 through early September 2013.
English Longitudinal Study of Ageing data on participants’ dates of birth are limited to year and quarter (January–March, April–June, July–September, October–December), so a conservative estimate of eligibility is obtained by assuming that participants are all born on the last day of the quarter in which they were born. For example, a respondent may have been born on 3 February 1952 but the ELSA data set reports only that they were born between 1 January 1952 and 31 March 1952, so their birth date is coded as 31 March 1952. This creates clustering in the forcing variable that must be taken into account when making inferences.
There are three ways in which the forcing variable is not equivalent to age at data collection minus 60 years. First, the forcing variable is based on age of the oldest household member. We have included participants who were not the oldest members of their households in some analyses, in which case the forcing variable is based not on their own age but on that of their partner. Second, the forcing variable is measured at a fixed point each year (the administratively determined annual WFP qualification week), which means that there is potentially a difference of up to 1 year between a participant’s age during his/her nurse visit and his/her age during the qualifying week; in practice, however, only visits up to the end of April (i.e. ≤ 7 months after the qualifying weeks) are used. Third, the wave 6 qualifying age (which is subtracted from the age during qualifying week) is greater than in the other two waves and also depends on when the participants were visited for data collection purposes.
Sample construction for regression discontinuity analysis
Nurse visits, during which both the indoor temperature and a range of health indicators were measured, took place only in waves 2, 4, and 6 of the ELSA. All three waves were used in all analyses and specifications.
Parallel RD analyses were carried out using two participant samples, referred to as the baseline sample and the restricted sample (‘Beatty sample’). In order to ensure that decision-making about indoor temperature and investments in heating was carried out by the study participant(s), the baseline sample was restricted to households with one adult or with two partnered adults (with or without children < 16 years); both older and younger partners in a couple were included in the baseline sample. All households with more than two adult members, multigenerational households with respondent plus his/her adult child or aged parent and households consisting of adult roommates or non-partnered relations, such as adult siblings, were excluded. Households in which one or more members lived in an institution and those for which necessary household composition data were missing (number of adults, relationships of members to head of household and whether or not the respondent’s mother or father lived in the household) were also excluded.
The restricted sample was designed to replicate Beatty et al. 12 In this sample, only those baseline sample households in which men were the oldest members were included. Households in which the oldest members were women were excluded as the age of eligibility for WFP corresponds exactly with the female State Pension age; this may cause estimates to be biased via confounding by women’s retirement. Note that although this latter sample is potentially more appropriate for identification purposes, the unrestricted baseline sample is more appropriate when evaluating the effectiveness of the WFP as a national policy.
Both samples were also restricted to those with nurse visits during the winter months, as summer indoor temperatures in the UK are determined more by outdoor temperatures than by heating. Two different definitions of ‘winter’ were used: January–March and January–April. The WFP is distributed during either November or December, so these months were not included in either definition, whereas by January the vast majority of eligible participants should have received their payment.
Four different sampling specifications were thus used in the analyses: (January–March, January–April) × (baseline, restricted). All models were estimated using each of these specifications. Table 5 shows the sample sizes for each of the four specifications and Table 6 shows the descriptive statistics for the health outcome variables utilised in the WFP analyses. Note that these are the ‘starting points’ for the RD analyses. The algorithm will balance bias and variance by identifying the optimal BW given this starting number of observations. The effective sample size for each RD will be smaller than the notional sample size (denoted by n in the results tables) and will depend on the BWs and kernel weightings used in each individual analysis. Note also that the RD tables reported here are also including covariates, so their starting sample size n may in general be slightly smaller than the one reported in Table 6 because some covariates may have missing values. As will be made clear later, we plot the full set of results in Report Supplementary Material 1.
| Wave | Time period | |||
|---|---|---|---|---|
| January–March | January–April | |||
| Unrestricted baseline sample | Restricted Beatty sample | Unrestricted baseline sample | Restricted Beatty sample | |
| 2 | 1975 | 1145 | 2702 | 2184 |
| 4 | 1484 | 1179 | 2722 | 2127 |
| 6 | 1243 | 963 | 1646 | 1284 |
| Total | 4702 | 3287 | 7070 | 5595 |
| Variable | Statistic | |||||||
|---|---|---|---|---|---|---|---|---|
| n | Mean | SD | Minimum | P25 | Median | P75 | Maximum | |
| airtemp | 6968 | 19.48 | 2.17 | 1.20 | 18.10 | 19.50 | 21.10 | 33.50 |
| sysval | 6343 | 134.75 | 18.31 | 76.50 | 122.00 | 133.50 | 145.50 | 259.00 |
| sysval_2 | 6343 | 0.34 | 0.47 | 0 | 0 | 0 | 1 | 1 |
| cfib | 5229 | 3.23 | 0.66 | 1.20 | 2.80 | 3.20 | 3.60 | 8.50 |
| cfib_2 | 5229 | 0.12 | 0.33 | 0 | 0 | 0 | 0 | 1 |
| log_hscrp | 5350 | 0.65 | 1.11 | –2.30 | –0.11 | 0.64 | 1.36 | 5.35 |
| hscrp_2 | 5350 | 0.32 | 0.47 | 0 | 0 | 0 | 0 | 1 |
| chestinf | 4068 | 0.13 | 0.34 | 0 | 0 | 0 | 1 | 1 |
| FEVz | 6016 | –0.61 | 1.26 | –5.31 | –1.35 | –0.53 | 0.23 | 8.63 |
| FEVz_2 | 6016 | 0.18 | 0.39 | 0 | 0 | 0 | 0 | 1 |
| SRH_2 | 7000 | 0.25 | 0.43 | 0 | 0 | 0 | 1 | 1 |
| CESD | 6975 | 1.40 | 1.89 | 0 | 0 | 1 | 2 | 8 |
| CESD_2 | 6975 | 0.14 | 0.34 | 0 | 0 | 0 | 0 | 1 |
Covariates and the regression discontinuity analysis
Under the assumption that any unobserved variables have a continuous distribution around the cut-off point, including or excluding covariates does not affect the consistency of RD average treatment effects. However, it is expected that the inclusion of a small number of judiciously chosen covariates might increase the precision of estimates. For this reason, the sharp RD results were estimated both with and without covariates. Including covariates that are not good predictors of outcomes, however, may be associated with a loss of precision. It is also not good practice to include covariates that interact with or are endogenous with respect to WFP receipt. It is therefore necessary to include only those covariates that have a predictive effect independent of WFP receipt. Where the results state that covariates are included, the following covariates are used: outdoor mean air temperature on the day of the nurse visit, lagged indoor air temperature on the previous nurse visit, whether or not the respondent smokes or has ever smoked, the participant’s BMI value and a flag to indicate whether or not the participant is retired.
As mentioned previously, it is also important that none of the covariates is actually driving the discontinuity. We show that none of the covariates is indeed discontinuous around the WFP eligibility age using RD plots (see Report Supplementary Material 1). Smoking and retirement status were self-reported during computer-assisted participant interviews, and BMI and lagged indoor temperatures were measured during current and previous nurse visits, respectively. Inclusion of lagged indoor temperature as a covariate was justified by indoor air temperature being the hypothesised mediator of any WFP effect, and captured auto-correlation across waves that resulted from ELSA being a longitudinal study with measurements repeated within households and individual participants;102 it is an alternative to including person-level fixed effects, which was not feasible in the present context.
The Met Office’s UKCP09 gridded observation data sets103 were used to control for outdoor temperature. These data sets provide daily mean temperatures based on weather station measurements, interpolated onto a grid at 5 km × 5 km resolution. Daily data were used to calculate lagged running mean temperatures for 7-, 30- and 90-day windows for each grid square and each day. The running means were simple lagged rolling-window means with no weighting. Mean temperatures were matched to survey interviews using participant postcodes [including Ordnance Survey (OS) northings and eastings] and the exact date of nurse visit. As a consequence of the potentially identifiable and thus confidential nature of these variables, the data were accessed and matches were made in a secure environment on NatCen Social Research premises. First, the gridded weather station measurements were uniquely identified by the northings and eastings co-ordinate of the south-west corner of each grid square and by date. Second, the northings and eastings of the ELSA participants’ postcodes were rounded down to the nearest 5000 m to identify the corresponding grid square. Finally, mean outdoor temperature data were matched to participant- and date-specific nurse visits using the rounded northings and eastings co-ordinates plus dates. Figure 3 shows the resolution available in the gridded data.
There were large numbers of missing values on outdoor temperature (24%) because data were available from 1914–2011 only, and thus do not cover the ELSA wave 6 time period. Lagged indoor temperature also included many missing values (58%) because of the delayed study entry of refreshment cohort participants, nurse visit or blood pressure module refusals, missed visits, temporary loss to follow-up, etc. Dummy covariate adjustment was used to adjust for the presence of missing values and avoid deleting cases. 104 Dummy covariate adjustment is effectively a simple imputation technique that replaces missing values with a constant (e.g. the mean of the observed values) and includes a dummy variable to indicate missingness. The method does not give consistent estimates of the covariate effects in the presence of correlation between covariates. However, as we are not interested in covariate estimation per se, and as RD estimation is robust to the specification of covariates, this does not affect the consistency of RD estimates. Descriptive statistics of covariates are presented in Table 7.
| Variable | Statistic | |||||||
|---|---|---|---|---|---|---|---|---|
| n | Mean | SD | Minimum | Quarter 1 | Median | Quarter 3 | Maximum | |
| Outdoortempa | 7070 | 6.13 | 2.86 | –4.00 | 4.60 | 6.00 | 7.90 | 14.60 |
| Indoortemp laga | 7070 | 19.35 | 1.47 | 10.20 | 19.00 | 19.00 | 19.30 | 29.30 |
| Ever smoked | 7070 | 0.51 | 0.50 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 |
| BMI | 6674 | 28.05 | 4.96 | 14.70 | 24.70 | 27.40 | 30.73 | 63.20 |
| Retired | 7070 | 0.56 | 0.50 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 |
Chapter 3 Results
Results: indoor temperature and health
The characteristics of the sample for the temperature and health analyses for each of the three waves of the ELSA examined are detailed in Table 4. On average, the sample were aged between 66 and 67 years across the three waves. Although waves 2 and 6 were 8 years apart, the age of the sample did not increase markedly because of the inclusion of younger ‘refreshment’ cohort members in waves 3, 4 and 6. Across the three waves examined, the sample was predominantly female (approximately 55%) and white (97–98%), and over half of the sample were married (65–66%), retired (ranging between 54% and 60%) and reported a long-term illness (55–57%). The number of participants included in our analyses varied depending on the outcome measure and ranged from 10,230 to 12,332.
Ambient indoor temperature
The average indoor temperature was approximately 20 °C in each of the three waves, with household temperatures ranging from 15 to 25 °C in over 97% of assessments, as illustrated in Figure 4. Indoor and outdoor temperatures were moderately correlated (r = 0.45; p < 0.001). There was large seasonal and regional variation in household temperatures, with raised temperatures in the summer months and in regions in the south-east, as shown in Table 8. Adjusting for outdoor temperature levels explained the majority of the linkages between seasonal/regional factors and indoor temperature. Household temperatures were lower in homes of participants who were not married or cohabiting and higher in households where the participant reported a long-term illness. Indoor temperatures appeared to decline with age and this decline was attenuated at older ages. Unexpectedly, wealthy and highly educated individuals tended to live in colder homes.
FIGURE 4.
Distribution of ambient indoor temperature levels in households taking part in the ELSA (waves 2, 4 and 6).
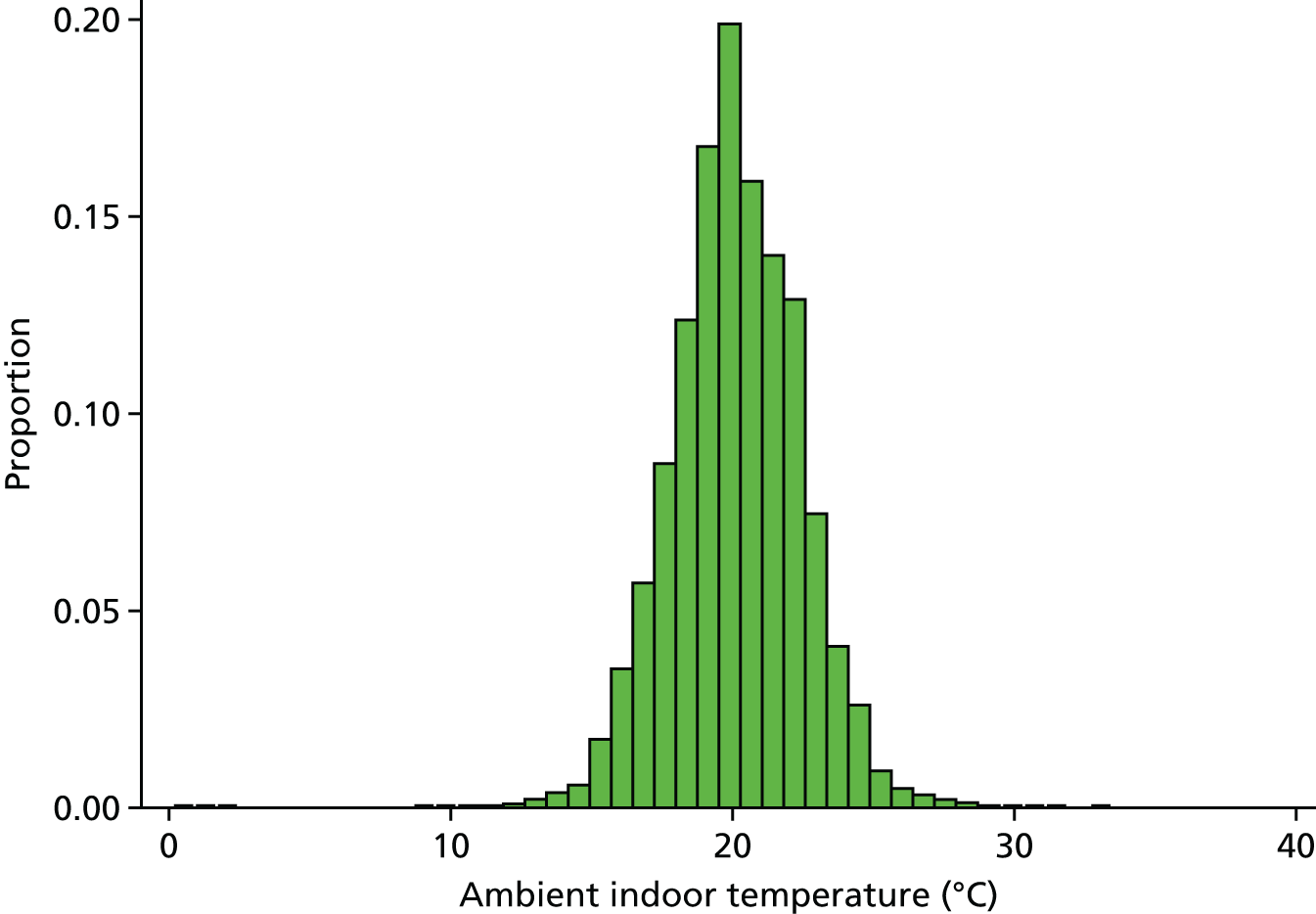
| Characteristic | β | SE | t-test | p-value | 95% CI |
|---|---|---|---|---|---|
| Age | –0.130 | 0.020 | –6.380 | 0.000 | –0.169 to –0.090 |
| Age-squared | 0.001 | 0.000 | 7.760 | 0.000 | 0.001 to 0.001 |
| Female | 0.033 | 0.030 | 1.090 | 0.277 | –0.027 to 0.093 |
| White | –0.187 | 0.096 | –1.940 | 0.053 | –0.376 to 0.002 |
| Marital status (comparison is married) | |||||
| Cohabiting | –0.063 | 0.069 | –0.920 | 0.357 | –0.199 to 0.072 |
| Neither | –0.540 | 0.036 | –14.870 | 0.000 | –0.611 to –0.469 |
| Retired | –0.052 | 0.037 | –1.410 | 0.160 | –0.124 to 0.020 |
| Educational attainment (comparison is no qualifications) | |||||
| Basic qualifications | –0.029 | 0.041 | –0.700 | 0.485 | –0.110 to 0.052 |
| High-school qualifications | –0.100 | 0.060 | –1.670 | 0.095 | –0.217 to 0.017 |
| Further qualifications | –0.122 | 0.048 | –2.530 | 0.011 | –0.217 to –0.027 |
| University degree or higher | –0.129 | 0.050 | –2.560 | 0.010 | –0.227 to –0.030 |
| Other (including foreign qualifications) | –0.034 | 0.053 | –0.650 | 0.515 | –0.137 to 0.069 |
| Wealth (comparison top quintile) | |||||
| Second quintile | –0.193 | 0.050 | –3.830 | 0.000 | –0.292 to –0.094 |
| Third quintile | –0.176 | 0.051 | –3.490 | 0.000 | –0.275 to –0.077 |
| Fourth quintile | –0.338 | 0.052 | –6.460 | 0.000 | –0.441 to –0.236 |
| Top quintile | –0.397 | 0.055 | –7.240 | 0.000 | –0.505 to –0.290 |
| Wealth data missing | –0.313 | 0.079 | –3.970 | 0.000 | –0.467 to –0.159 |
| Current smoker | –0.021 | 0.044 | –0.480 | 0.633 | –0.107 to 0.065 |
| Long-term illness | 0.126 | 0.028 | 4.420 | 0.000 | 0.070 to 0.181 |
| BMI (kg/m2) | 0.001 | 0.003 | 0.400 | 0.688 | –0.005 to 0.007 |
| Region (comparison is North East) | |||||
| North West | 0.323 | 0.070 | 4.610 | 0.000 | 0.186 to 0.460 |
| Yorkshire and the Humber | 0.114 | 0.068 | 1.690 | 0.092 | –0.018 to 0.246 |
| East Midlands | 0.092 | 0.071 | 1.310 | 0.190 | –0.046 to 0.231 |
| West Midlands | –0.162 | 0.072 | –2.250 | 0.025 | –0.302 to –0.021 |
| East | 0.047 | 0.068 | 0.690 | 0.488 | –0.086 to 0.180 |
| London | 0.514 | 0.074 | 6.940 | 0.000 | 0.369 to 0.659 |
| South East | 0.348 | 0.065 | 5.360 | 0.000 | 0.221 to 0.475 |
| South West | –0.167 | 0.067 | –2.500 | 0.012 | –0.298 to –0.036 |
| Not in England | –0.622 | 0.293 | –2.120 | 0.034 | –1.197 to –0.048 |
| Month (comparison is January) | |||||
| February | 0.090 | 0.060 | 1.500 | 0.135 | –0.028 to 0.208 |
| March | 0.231 | 0.062 | 3.720 | 0.000 | 0.109 to 0.353 |
| April | 0.555 | 0.066 | 8.410 | 0.000 | 0.425 to 0.684 |
| May | 0.964 | 0.070 | 13.780 | 0.000 | 0.827 to 1.102 |
| June | 2.257 | 0.097 | 23.310 | 0.000 | 2.067 to 2.447 |
| July | 2.634 | 0.115 | 23.000 | 0.000 | 2.410 to 2.859 |
| August | 2.638 | 0.121 | 21.870 | 0.000 | 2.402 to 2.875 |
| September | 1.415 | 0.123 | 11.500 | 0.000 | 1.174 to 1.656 |
| October | 0.785 | 0.121 | 6.500 | 0.000 | 0.548 to 1.023 |
| November | 0.538 | 0.122 | 4.400 | 0.000 | 0.298 to 0.778 |
| December | –0.034 | 0.132 | –0.260 | 0.799 | –0.292 to 0.225 |
| Year (comparison is 2004) | |||||
| 2005 | 0.032 | 0.116 | 0.280 | 0.783 | –0.195 to 0.259 |
| 2008 | –0.451 | 0.048 | –9.460 | 0.000 | –0.544 to –0.358 |
| 2009 | –0.356 | 0.113 | –3.140 | 0.002 | –0.578 to –0.134 |
| 2012 | –0.449 | 0.044 | –10.120 | 0.000 | –0.536 to –0.362 |
| 2013 | –0.227 | 0.122 | –1.870 | 0.062 | –0.466 to 0.011 |
Adjusting for outdoor temperature did not affect the associations between demographic factors and indoor temperature levels identified. In the following analyses we examine indoor temperature firstly as a continuous predictor of health and subsequently as a categorical predictor, in order to test for the potential presence of non-linearity in the association between indoor temperature and the health outcome measures examined. The categorical temperature variable was coded as follows: < 17 °C (7.7% of observations), 17–19 °C (21.4%), 19–21 °C (34.9%), 21–23 °C (26.2%) and > 23 °C (9.9%).
Health measures and indoor temperature
Blood pressure and indoor temperature
On average, across the three waves examined, systolic blood pressure levels were approaching the threshold for hypertension (ranging from 132.7 to 136.3 mmHg), as shown in Table 9. Analyses were conducted before and after adjustment for a diagnosis of high blood pressure and current use of antihypertensive medication. Over one-third of the sample reported ever having been diagnosed with high blood pressure in wave 2 (33.5%) and this rose to 39.4% by wave 6. Use of blood pressure medication ranged from 32% to 34% in waves 4 and 6, in which reports of antihypertensive medication use were included for all participants. Models which included/excluded these variables did not differ markedly. We therefore present the results of models that adjust for both diagnosis/medication variables here.
| Health outcome variable | Wave | |||||
|---|---|---|---|---|---|---|
| 2 | 4 | 6 | ||||
| n | Mean (SD)/% | n | Mean (SD)/% | n | Mean (SD)/% | |
| Ambient indoor temperature (°C) | 7614 | 20.26 (2.19) | 8312 | 20.17 (2.36) | 7976 | 20.08 (2.27) |
| Systolic blood pressure (mmHg) | 7457 | 136.32 (18.99) | 8138 | 133.41 (17.89) | 7839 | 132.70 (17.62) |
| High systolic blood pressure (> 140 mmHg) | 7457 | 38.88 | 8138 | 33.64 | 7839 | 31.42 |
| Diastolic blood pressure (mmHg) | 7457 | 75.44 (11.17) | 8137 | 74.54 (10.91) | 7839 | 73.93 (10.75) |
| High diastolic blood pressure (> 90 mmHg) | 7457 | 9.90 | 8137 | 8.04 | 7839 | 7.23 |
| CRP level (logged) | 5867 | 0.72 (1.11) | 6200 | 0.64 (1.12) | 6080 | 0.51 (1.09) |
| High CRP level (> 3 mg/l) | 5867 | 35.93 | 6200 | 33.94 | 6080 | 27.66 |
| Fibrinogen level (g/l) | 5834 | 3.23 (0.73) | 6036 | 3.37 (0.56) | 5961 | 2.96 (0.54) |
| High fibrinogen level (> 4 g/l) | 5834 | 13.94 | 6036 | 13.93 | 5961 | 4.34 |
| FEV (l) | 6982 | 2.30 (0.85) | 7466 | 2.39 (0.85) | 6972 | 2.37 (0.83) |
| Chest infection | 7449 | 9.49 | 8148 | 8.90 | 6966 | 10.71 |
| Health rated as fair/poor | 7614 | 27.11 | 8312 | 25.55 | 7976 | 26.99 |
| Depressive symptoms (CES-D score) | 7538 | 1.54 (1.92) | 8248 | 1.37 (1.89) | 7902 | 1.33 (1.88) |
| Depressed (≥ 4 CES-D symptoms) | 7538 | 14.98 | 8248 | 14.00 | 7902 | 13.09 |
Lower indoor temperatures were associated with raised systolic and diastolic blood pressure levels in random-effects models, accounting for a large set of covariates (Table 10). The increase in systolic blood pressure for each 1 °C reduction in indoor temperature was 0.44 mmHg and the reduction in was diastolic blood pressure levels 0.25 mmHg. The linkages were replicated in fixed-effects panel models, as shown in Table 10. In additional analyses (not shown here) we integrated weather station data specific to participant assessment times and areas of residence and showed that these associations were unaffected by adjustment for outdoor temperature levels.
| Indoor temperature | Blood pressure | |||||||
|---|---|---|---|---|---|---|---|---|
| Systolic | Diastolic | |||||||
| Random effects | Fixed effects | Random effects | Fixed effects | |||||
| β | SE | β | SE | β | SE | β | SE | |
| Indoor temperature (continuous) | –0.46** | 0.05 | –0.33** | 0.06 | –0.25** | 0.03 | –0.19** | 0.04 |
| Indoor temperature (categorical) | ||||||||
| < 17 °C | 4.82** | 0.55 | 3.58** | 0.67 | 2.43** | 0.32 | 1.80** | 0.39 |
| 17–19 °C | 2.86** | 0.44 | 2.49** | 0.54 | 1.72** | 0.25 | 1.33** | 0.30 |
| 19–21 °C | 2.43** | 0.40 | 2.19** | 0.48 | 1.29** | 0.23 | 1.17** | 0.28 |
| 21–23 °C | 1.95** | 0.40 | 1.99** | 0.48 | 1.08** | 0.24 | 1.05** | 0.27 |
| > 23 °C | – | – | – | – | – | – | – | – |
We also examined the association between indoor temperature and blood pressure using a categorical household temperature variable in order to assess whether this association is likely to be linear or non-linear. This analysis supported a potential linear effect of temperature on blood pressure, as detailed in the lower section of Table 10. Once again, raised systolic and diastolic blood pressure levels were associated with low household temperature levels. Specifically, those living in homes with temperature levels of < 17 °C were found to have systolic blood pressure levels over 4 points higher [β = 4.56, standard error (SE) 0.55; p < 0.001] and diastolic blood pressure levels over 2 points higher (β = 2.38, SE .32; p < 0.001) than those living in household temperatures of ≥ 23 °C. These associations were replicated in fixed-effects models, indicating that unobserved time invariant confounders had little effect on the linkages identified.
The same pattern of association was also observed in regression models examining high levels of systolic (> 140 mmHg) and diastolic (> 90 mmHg) blood pressure in multilevel mixed-effects logistic regression analyses. Each 1 °C increase in household temperature was linked to a 7% reduction in the likelihood of high systolic blood pressure and a 5% reduction in the likelihood of high diastolic blood pressure. High systolic blood pressure was almost twice as likely [odds ratio (OR) 1.95, 95% CI 1.59 to 2.37; p < 0.01] to occur at lower indoor temperatures (≤ 17 °C) than at high temperatures (≥ 23 °C). This association is particularly noteworthy considering that it was observed after adjustment for a diagnosis of hypertension and use of antihypertensive medication. Although high diastolic blood pressure was more likely to occur at low indoor temperatures (OR 1.62, 95% CI 1.18 to 2.22; p < 0.01), this association was less consistent than the robust graded link between high systolic blood pressure and temperature (Table 11). Together, these analyses lend strong support for systolic blood pressure as an indicator of cardiovascular functioning that is likely to respond to changes in indoor temperature that may occur as a result of the WFP. We also identified relatively consistent support for diastolic blood pressure as a cardiovascular measure that is likely to be affected by indoor temperature levels.
| Temperature | High systolic blood pressure | |||
|---|---|---|---|---|
| > 140 mmHg | > 90 mmHg | |||
| OR | 95% CI | OR | 95% CI | |
| Indoor temperature (continuous) | 0.93** | 0.91 to 0.95 | 0.95** | 0.92 to 0.98 |
| Indoor temperature (categorical) | ||||
| < 17 °C | 1.95** | 1.59 to 2.37 | 1.62** | 1.18 to 2.22 |
| 17–19 °C | 1.53** | 1.31 to 1.80 | 1.22 | 0.94 to 1.59 |
| 19–21 °C | 1.47** | 1.26 to 1.71 | 1.23 | 0.96 to 1.58 |
| 21–23 °C | 1.28** | 1.10 to 1.49 | 1.09 | 0.85 to 1.40 |
| > 23 °C | – | – | – | – |
Inflammation and indoor temperature
Next, we examined the relationship between ambient indoor temperature levels and CRP and fibrinogen levels. CRP levels are typically positively skewed and were therefore log-transformed in order to normalise this variable. We also tested whether or not temperature levels predicted CRP levels above the clinical cut-off point of 3 mg/l. Low indoor temperatures were weakly related to higher levels of CRP in both random- and fixed-effects models (Table 12). These associations were not replicated in our analysis using the categorical temperature variable, perhaps because of the lack of granularity in this predictor.
| Temperature | Biomarker | |||||||
|---|---|---|---|---|---|---|---|---|
| CRP (logged) | Fibrinogen | |||||||
| Random effects | Fixed effects | Random effects | Fixed effects | |||||
| β | SE | β | SE | β | SE | β | SE | |
| Indoor temperature (continuous) | –0.007* | 0.003 | –0.007† | 0.003 | –0.010** | 0.002 | –0.011** | 0.002 |
| Indoor temperature (categorical) | ||||||||
| < 17 °C | 0.033 | 0.035 | 0.015 | 0.043 | 0.067** | 0.020 | 0.079** | 0.025 |
| 17–19 °C | 0.035 | 0.028 | 0.022 | 0.034 | 0.048** | 0.016 | 0.066** | 0.020 |
| 19–21 °C | 0.030 | 0.025 | 0.005 | 0.030 | 0.038** | 0.015 | 0.048** | 0.018 |
| 21–23 °C | 0.001 | 0.025 | –0.024 | 0.030 | 0.004 | 0.014 | 0.010 | 0.018 |
| > 23 °C | – | – | – | – | – | – | – | – |
Stronger evidence was identified for a robust relationship between indoor temperature and fibrinogen levels. Low indoor temperatures were associated with raised fibrinogen levels in both random- and fixed-effects models, as outlined in Table 13. Each 1 °C reduction in indoor temperature was associated with a 0.01 g/l increase in fibrinogen levels. A similar link was observed when using a categorical temperature variable: those living in households with temperature levels of < 17 °C had fibrinogen levels that were predicted to be 0.07 g/l higher than those living in homes with temperatures of ≥ 23 °C. The categorical analyses also indicated that the relationship between ambient indoor temperature levels and fibrinogen levels is likely to be linear.
| Temperature | Biomarker | |||
|---|---|---|---|---|
| High CRP levels (> 3 mg/l) | High fibrinogen levels (> 4 g/l) | |||
| OR | 95% CI | OR | 95% CI | |
| Indoor temperature (continuous) | 0.98 | 0.96 to 1.01 | 0.93** | 0.90 to 0.96 |
| Indoor temperature (categorical) | ||||
| < 17 °C | 1.14 | 0.87 to 1.48 | 1.56** | 1.11 to 2.20 |
| 17–19 °C | 1.33** | 1.08 to 1.64 | 1.41* | 1.07 to 1.86 |
| 19–21 °C | 1.15 | 0.95 to 1.40 | 1.44** | 1.12 to 1.85 |
| 21–23 °C | 1.23* | 1.01 to 1.49 | 1.11 | 0.86 to 1.44 |
| > 23 °C | – | – | – | – |
The relationships identified in our examination of inflammation using continuous measures were broadly replicated in our models examining high levels of CRP (> 3 mg/l) and fibrinogen (> 4 g/l) in multilevel mixed-effects logistic regression analyses. In analyses using the continuous temperature predictor, each 1 °C increase in indoor temperature was associated with a 7% decreased likelihood of high fibrinogen levels and was unrelated to the likelihood of high CRP levels. High fibrinogen levels were 1.56 times more likely at low indoor temperatures (≤ 17 °C) than at high indoor temperatures (≥ 23 °C). There was also some evidence that high CRP levels may tend to occur at lower indoor temperatures (17–19 °C).
Taken together, our analyses of the link between indoor temperature levels and inflammation markers provided relatively strong support that fibrinogen levels are likely to respond to changes in indoor temperature, such that raised levels are likely to be observed at low indoor temperatures. Fibrinogen levels could therefore be considered a potential indicator for assessing the impact of the WFP on health through its effect on indoor temperature. We also identified some evidence that CRP levels may be raised when indoor temperatures are reduced. However, the inconsistencies in this association suggest that CRP may not be a strong candidate for assessing the impact of the WFP through indoor temperature.
Respiratory functioning and indoor temperature
In contrast to our predictions, indoor temperature was negatively associated with FEV1 levels in both random-effects (β = –0.006, SE 0.002; p < 0.01) and fixed-effects models (β = –0.004, SE 0.002; p < 0.05). However, these associations were weak and our analyses examining the categorical temperature variable to identify potential non-linearity in this relationship showed that FEV levels were only reduced at indoor temperature levels of ≥ 23 °C. Taken together, these analyses provide little evidence for a robust link between indoor temperature and respiratory functioning and do not support the prediction that FEV is likely to be affected by the WFP, at least through the pathway of raised indoor temperature levels.
Similarly, there was little support for a close relationship between ambient indoor temperature and participant reports of a recent chest infection. Raised indoor temperatures were linked to a reduced likelihood of chest infection as expected (OR 0.97, 95% CI 0.95 to 0.99; p < 0.05). However, an examination of the categorical temperature variable did not identify evidence of a link between chest infection and any specific temperature category. Thus, our analyses did not provide a strong empirical basis for expecting the WFP to affect respiratory functioning through the mechanisms of indoor temperature as assessed in the ELSA.
Self-rated health, depression and indoor temperature
As noted earlier, the single-item self-rated health measure (rated from 1 = excellent to 5 = poor) was dichotomised such that those rating their health as 4/5 (fair/poor) were contrasted with those scoring 1/2/3 (excellent/very good/good). We tested the association between indoor temperature and fair/poor self-rated health using a multilevel mixed-effects logistic regression model. This analysis did not yield support for a relationship between either a continuous (OR 1.01, 95% CI 0.98 to 1.03; p = 0.63) or a categorical measure (all dummies p > 0.05) of indoor temperature and fair/poor self-rated health. Similarly, the link between the continuous measure of indoor temperature levels and participant reports of depressive symptoms as assessed using the CES-D scale was not statistically significant in either random- or fixed-effects regression models. The continuous temperature measure was also unrelated to experiencing high levels of depressive symptoms (score of ≥ 4 on the CES-D). A similar pattern of results was found when indoor temperature was examined as a categorical variable. Our results therefore suggest that participant reports of their current health status and depression levels are unlikely to be related to contemporary ambient indoor temperature levels as calculated as part of the ELSA medical assessment.
Results: Winter Fuel Payment, indoor temperature and health
The main analysis employs a RD analysis to identify the impact of the WFP on a set of health outcomes using special licensed geocoded data from the ELSA matched with Met Office data. We present the results of this analysis in this chapter and in Report Supplementary Material 1.
Every table in this chapter reports the estimated average treatment effects of the WFP on the outcome of interest as measured during nurse visits or self-reported by respondents, together with clustered standard errors (in parenthesis), the size of the BW and the number of observations used to compute the latter (n).
Average treatment effects are estimated using local linear regressions with triangular kernel weights, assigning more weight to observations near the cut-off point. Every regression controls for the following covariates: outdoor mean air temperature on the day of the nurse visit, lagged indoor air temperature on the previous nurse visit, whether the respondent smokes or has ever smoked, the participant’s BMI value, and a flag to indicate whether or not the participant is retired. Standard errors are clustered at the individual level and shown in parentheses.
Every column reports estimates from different regressions. A detailed description of these methods, data and samples is found in Chapter 2, but we summarise here the salient differences:
-
First, we distinguish between observations collected by nurses during the coldest winter months, immediately after the WFP receipt, (i.e. January–March) and a broader sample that includes also March and April visits (January–April).
-
A further distinction relates to the type of households. The resulting baseline sample excludes households with more than three members as younger members may drive the decision-making at household level (in the tables below this column is denoted as ‘Baseline’). The other sample closely follows Beatty et al. 12 in that it excludes households in which the oldest member is female because the WFP eligibility age matches quite closely with female State Pension age.
-
Finally, we report coefficients from RDDs that use different methodologies of selecting optimal BWs, the aim of which is to strike a balance between bias and variance. The columns titled ‘Reg’ show estimates from regressions which BWs are computed by adding a regularisation term. The other column shows estimates computed using the algorithm without regularisation term (‘No Reg’).
For robustness purposes, and following Simonsohn et al. ,105 we display graphically the estimates from alternative specifications of this model in Report Supplementary Material 1. Each plot (or specification curve) shows every possible combination of samples and models described here, including combinations that are not presented in the following tables but were run for sensitivity purposes. We refer to Report Supplementary Material 1 for further explanations.
The previous section documented a link between indoor temperature and health, controlling for outdoor temperature. In this section, we start by asking whether or not the receipt of the WFP translates into more comfortable indoor temperatures (Table 14). Indoor temperature is the main channel via which we expect the WFP to have a positive effect on health. This is depicted in Figure 1. The estimates in every column of Table 14 present a very consistent finding. Households receiving the payment only for the first time do not experience statistically different indoor temperature from households that just miss out on the payment. The point estimates are all negative and are statistically significant in five out of eight reported estimates. It is worth noting that the specification curve in Report Supplementary Material 1 shows that for the vast majority of models the estimates are not statistically significant. Finally, most of our models predict a minimal effect on indoor temperature, ranging from –0.6 to 0.4 °C.
| BW choice method | Nurse visits | |||||||
|---|---|---|---|---|---|---|---|---|
| January–March | January–April | |||||||
| Baseline | Beatty12 | Baseline | Beatty12 | |||||
| No Reg (1) | Reg (2) | No Reg (3) | Reg (4) | No Reg (5) | Reg (6) | No Reg (7) | Reg (8) | |
| Indoor temperature (°C) | –0.077 (0.225) | –0.033 (0.294) | –0.416* (0.234) | –0.621* (0.344) | –0.272* (0.153) | –0.231 (0.229) | –0.457** (0.186) | –0.544** (0.293) |
| BW (years) | 4.527 | 2.793 | 9.475 | 4.069 | 7.265 | 3.362 | 11.578 | 4.099 |
| n | 4826 | 4826 | 2414 | 2414 | 5878 | 5878 | 2954 | 2954 |
Noting that the WFP does not seem to improve indoor temperature, we now move to show the estimate of the impact of the WFP on our set of health outcomes.
Table 15 reports the short-term effect of the WFP on two variables of systolic blood pressure. The first variable is simply the systolic blood pressure measured by the nurse (i.e. a continuous variable), whereas the second variable is an indicator that turns on when blood pressure is > 140 mmHg. The estimated average treatment effects for the continuous variable are shown in the continuous blood pressure section of Table 15. These are highly sensitive to the model and sample used and tend to vary from positive to negative.
| BW choice method | Nurse visits | |||||||
|---|---|---|---|---|---|---|---|---|
| January–March | January–April | |||||||
| All | Beatty12 | All | Beatty12 | |||||
| No Reg (1) | Reg (2) | No Reg (3) | Reg (4) | No Reg (5) | Reg (6) | No Reg (7) | Reg (8) | |
| Continuous blood pressure | ||||||||
| Blood pressure (mmHg) | 0.053 (1.434) | –1.161 (2.422) | 8.118** (3.905) | 9.680** (4.275) | 0.325 (1.229) | –0.918 (2.178) | 1.741 (2.421) | 3.162 (3.111) |
| BW (years) | 7.210 | 2.970 | 1.903 | 1.635 | 7.667 | 2.806 | 3.536 | 2.297 |
| n | 4454 | 4454 | 2242 | 2242 | 5406 | 5406 | 2738 | 2738 |
| High systolic blood pressure | ||||||||
| Binary blood pressure | 0.014 (0.036) | –0.022 (0.059) | 0.134 (0.098) | 0.197* (0.113) | 0.002 (0.036) | –0.010 (0.053) | 0.056 (0.07) | 0.097 (0.084) |
| BW (years) | 8.404 | 3.129 | 2.299 | 1.827 | 6.407 | 2.890 | 3.290 | 2.275 |
| n | 4454 | 4454 | 2242 | 2242 | 5406 | 5406 | 2738 | 2738 |
It is worth noting that when restricting our analysis to the Beatty12 sample of nurse visits in January and March, the WFP increased the blood pressure from 8.1 to 9.7 points (Table 15). The estimates from all the models using the Beatty sample, that is, excluding households where women are the oldest members, are consistently positive, as illustrated by the specification curve in Figure S2 in the Report Supplementary Material 1. Taken at face value, these estimates would suggest a negative influence of the WFP, which is contrary to our conceptual framework. This result is robust when looking at the analysis of the binary indicator in the high systolic blood pressure section of Table 15. The Beatty sample consistently shows a positive significant discontinuity for some plausible specifications (see Figure S1 in the Report Supplementary Material 1). Perhaps outliers are behind these results, but the size of the BW is so small (ranging from 1 to 3) that we are effectively comparing hundreds of people born just few months apart. We also note that this particular sample has the smallest number of observations.
The analysis of the WFP on inflammatory markers, fibrinogen and CRP, is presented in Table 16. Parts (a) and (b) focus on fibrinogen. There is no statistically significant effect estimated. The sign of the estimates is also highly dependent on the specification used. When using the binary variable, that is, when dichotomising the continuous fibrinogen measurement at 4 g/l, the point estimates change from negative to positive, whereas some of the estimated average treatment effects in panel A are positive. Standard errors are fairly large in every cell too, which is evidence of a noisy effect. Parts (c) and (d) show estimated average treatment effects on our CRP variables. When focusing on the continuous variable, the log of CRP, we can reject the presence of a statistically significant discontinuity around the WFP eligibility age. In contrast to our hypothesis, when using the binary variable as our health outcome, three estimated coefficients are positive and statistically significant at 10% (see part d of Table 16). The specification curves for fibrinogen and CRP (Figures S3–S6 in Report Supplementary Material 1) provide a bigger picture and point to the fact that these results are capturing noise because almost every specification yielded non-statistically significant discontinuities.
| BW choice method | Nurse visits | |||||||
|---|---|---|---|---|---|---|---|---|
| January–March | January–April | |||||||
| All | Beatty12 | All | Beatty12 | |||||
| No Reg | Reg | No Reg | Reg | No Reg | Reg | No Reg | Reg | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| (a) | ||||||||
| Fibrinogen (g/l) | –0.036 (0.042) | –0.013 (0.077) | 0.039 (0.078) | 0.063 (0.117) | 0.031 (0.067) | 0.074 (0.078) | 0.114 (0.088) | 0.163 (0.104) |
| BW (years) | 16.203 | 3.669 | 6.580 | 3.164 | 3.753 | 2.725 | 3.880 | 2.650 |
| n | 3717 | 3717 | 1880 | 1880 | 4523 | 4523 | 2309 | 2309 |
| (b) | ||||||||
| Binary fibrinogen | –0.011 (0.022) | –0.013 (0.04) | 0.001 (0.045) | –0.005 (0.061) | –0.014 (0.025) | 0.002 (0.037) | 0.002 (0.026) | 0.005 (0.037) |
| BW (years) | 12.542 | 3.714 | 4.310 | 2.643 | 6.159 | 2.873 | 9.785 | 4.151 |
| n | 3717 | 3717 | 1880 | 1880 | 4523 | 4523 | 2309 | 2309 |
| (c) | ||||||||
| Log of CRP (mg/l) | –0.003 (0.071) | 0.052 (0.171) | 0.134 (0.132) | 0.083 (0.261) | 0.111 (0.082) | 0.130 (0.137) | 0.001 (0.089) | 0.242 (0.19) |
| BW (years) | 24.166 | 2.670 | 6.658 | 2.351 | 7.000 | 2.856 | 16.473 | 2.656 |
| n | 3811 | 3811 | 1933 | 1933 | 4632 | 4632 | 2369 | 2369 |
| (d) | ||||||||
| Binary CRP | 0.068* (0.036) | 0.083 (0.056) | 0.134 (0.132) | 0.083 (0.261) | 0.056* (0.033) | 0.081* (0.048) | 0.000 (0.089) | 0.242 (0.19) |
| BW (years) | 8.555 | 3.712 | 6.658 | 2.351 | 8.299 | 3.819 | 16.473 | 2.656 |
| n | 3811 | 3811 | 1933 | 1933 | 4632 | 4632 | 2369 | 2369 |
Table 17 focuses on the results from RDs on the effect of the WFP on chest infection, which is a binary variable taking the value of 1 if the respondent reports having had a respiratory infection in the previous 3 weeks. Our models estimate a positive discontinuity at the eligibility WFP age, which is not statistically significant in six out of eight estimations. The full combination of WFP effects plotted in Figure S7 shows that there are few models for which the WFP would lead to positive responses to the chest infection question. Parts (b) and (c) of Table 17 extend this analysis by examining lung function. Part 9b investigates whether or not there is a statistically significant discontinuity for FEV (i.e. the z-score-transformed FEV), whereas part (c) focuses on a binary variable for FEV, which takes the value of 1 at participant-specific lower limit of normal. In part (b), the estimated discontinuity is never statistically significant and the point estimate is positive or negative depending on the specification, although it is positive and statistically significant at 10% in one case out of eight cases in part (c). Figure S9 in the Report Supplementary Material 1 shows that the average effect is really around zero.
| BW choice method | Nurse visits | |||||||
|---|---|---|---|---|---|---|---|---|
| January–March | January–April | |||||||
| All | Beatty12 | All | Beatty12 | |||||
| No Reg | Reg | No Reg | Reg | No Reg | Reg | No Reg | Reg | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| (a) | ||||||||
| Chest infection | 0.088 (0.058) | 0.097 (0.063) | 0.094 (0.084) | 0.137 (0.093) | 0.071* (0.042) | 0.093** (0.047) | 0.051 (0.058) | 0.096 (0.063) |
| BW (years) | 2.245 | 1.909 | 2.396 | 1.897 | 3.293 | 2.418 | 3.755 | 2.648 |
| n | 3138 | 3138 | 1587 | 1587 | 3629 | 3629 | 1856 | 1856 |
| (b) | ||||||||
| FEV | –0.021 (0.055) | 0.012 (0.092) | –0.122 (0.077) | –0.015 (0.154) | –0.020 (0.051) | 0.0001 (0.081) | –0.005 (0.11) | 0.014 (0.13) |
| BW (years) | 14.380 | 3.849 | 9.916 | 2.454 | 9.936 | 3.702 | 3.245 | 2.321 |
| n | 4421 | 4421 | 2225 | 2225 | 5405 | 5405 | 2733 | 2733 |
| (c) | ||||||||
| Binary FEV | 0.018 (0.03) | –0.012 (0.054) | 0.007 (0.068) | –0.025 (0.093) | 0.041 (0.026) | 0.044 (0.037) | 0.072* (0.039) | 0.052 (0.055) |
| BW (years) | 7.291 | 2.813 | 2.906 | 1.973 | 7.490 | 3.779 | 4.830 | 2.641 |
| n | 4396 | 4396 | 2217 | 2217 | 5374 | 5374 | 2723 | 2723 |
Table 18 analyses self-reported general health and depression. Whereas the first two outcomes are imprecisely estimated and the sign is not consistent, every point estimate of the binary depressive symptoms variable goes in the direction expected, and a negative sign implies a lower likelihood of having experienced depressive symptoms. The specification curves in the Report Supplementary Material 1 (Figures S10–S12) confirm that there is indeed no evidence of a discontinuity in the relationship between self-assessed health and depression around the WFP eligibility age.
| BW choice method | Nurse visits | |||||||
|---|---|---|---|---|---|---|---|---|
| January–March | January–April | |||||||
| All | Beatty12 | All | Beatty12 | |||||
| No Reg | Reg | No Reg | Reg | No Reg | Reg | No Reg | Reg | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| (a) | ||||||||
| Self-rated health | –0.087 (0.060) | –0.123* (0.067) | 0.054 (0.047) | 0.101* (0.054) | –0.017 (0.039) | –0.023 (0.046) | 0.027 (0.046) | 0.079 (0.054) |
| BW (years) | 2.269 | 1.899 | 4.340 | 2.557 | 3.608 | 2.519 | 4.567 | 2.547 |
| n | 4846 | 4846 | 2059 | 2059 | 5902 | 5902 | 2330 | 2330 |
| (b) | ||||||||
| Depressive symptoms | –0.083 (0.182) | –0.153 (0.252) | 0.017 (0.193) | 0.160 (0.284) | –0.097 (0.111) | –0.061 (0.194) | 0.012 (0.234) | 0.283 (0.294) |
| BW (years) | 4.709 | 2.670 | 6.298 | 2.640 | 14.044 | 3.067 | 3.479 | 2.165 |
| n | 4833 | 4833 | 2057 | 2057 | 5887 | 5887 | 2327 | 2327 |
| (c) | ||||||||
| Binary depressive symptoms | –0.066* (0.039) | –0.081* (0.047) | –0.024 (0.032) | –0.008 (0.049) | –0.033 (0.027) | –0.044 (0.034) | –0.028 (0.032) | –0.002 (0.048) |
| BW (years) | 3.582 | 2.690 | 7.615 | 2.811 | 4.929 | 3.174 | 6.222 | 2.508 |
| n | 4833 | 4833 | 2057 | 2057 | 5887 | 5887 | 2327 | 2327 |
Overall, we conclude that there is substantial variability in the data. Very few models suggest any robust WFP effect on health outcomes. When the effect is precisely estimated, it is not unusual to obtain counterintuitive results. Large p-values are often taken as evidence of no effect, although they can just point to great heterogeneity in the data. With this in mind, we proceed by showing the results for low-income households in Table 19. We define low-income households as those whose income is below the mean or median. In ELSA, mean and median are virtually the same and correspond to log of 2.4 of equivalised total income. Estimates often change sign and their standard errors are often large. Specification curves for this model (not reported but available on request) show that the sign of the point estimate depends very much on the specification utilised. Some specifications for blood pressure find the same counterintuitive result discussed earlier, that is, that the WFP is linked to an increase in blood pressure. A close inspection, however, shows that there are some differences between low-income groups and the full sample. In particular, it is worth noting that there is not much evidence of counterintuitive results for inflammatory markers (this is confirmed by the specification curves, available on request) and chest infections in the low-income portion of the sample, with some evidence of beneficial impact on CRP (the sign is consistently negative and in some cases strongly significant).
| BW choice method | Nurse visits | |||||||
|---|---|---|---|---|---|---|---|---|
| January–March | January–April | |||||||
| Baseline | Beatty12 | Baseline | Beatty12 | |||||
| No Reg | Reg | No Reg | Reg | No Reg | Reg | No Reg | Reg | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Indoor temperature (°C) | –0.169 (0.27) | –0.071 (0.45) | –0.496 (0.486) | –0.191 (0.576) | –0.252 (0.329) | –0.239 (0.402) | –1.096** (0.501) | –1.007* (0.561) |
| BW (years) | 9.247 | 2.814 | 4.271 | 2.560 | 4.005 | 2.500 | 2.535 | 1.997 |
| n | 1962 | 1962 | 859 | 859 | 2351 | 2351 | 1030 | 1030 |
| Blood pressure (mmHg) | 3.388* (1.91) | 3.858 (3.001) | 7.548** (3.22) | 11.192 (6.859) | 4.011** (1.99) | 0.639 (3.345) | 5.689** (2.841) | 5.271 (6.059) |
| BW (years) | 15.994 | 3.450 | 7.485 | 2.550 | 8.774 | 2.882 | 12.980 | 2.781 |
| n | 1777 | 1777 | 779 | 779 | 2121 | 2121 | 932 | 932 |
| Binary blood pressure | 0.125** (0.059) | 0.081 (0.102) | 0.224* (0.117) | 0.301 (0.195) | 0.109 (0.053) | 0.074** (0.09) | 0.164* (0.096) | 0.099 (0.153) |
| BW (years) | 10.369 | 2.901 | 5.357 | 2.588 | 10.392 | 2.842 | 6.095 | 2.486 |
| n | 1777 | 1777 | 779 | 779 | 2121 | 2121 | 932 | 932 |
| Fibrinogen (m/l) | –0.218 (0.144) | –0.276* (0.159) | –0.357 (0.22) | –0.464* (0.248) | 0.015 (0.095) | 0.060 (0.149) | 0.193* (0.114) | 0.157 (0.163) |
| BW (years) | 3.631 | 2.614 | 2.267 | 1.650 | 7.181 | 2.741 | 8.072 | 3.070 |
| n | 1482 | 1482 | 648 | 648 | 1771 | 1771 | 782 | 782 |
| Binary fibrinogen | –0.036 (0.048) | –0.080 (0.074) | –0.119 (0.102) | –0.186 (0.141) | –0.032 (0.04) | –0.032 (0.068) | –0.066 (0.059) | –0.068 (0.059) |
| BW (years) | 7.668 | 3.791 | 3.409 | 1.999 | 11.113 | 2.864 | 3.796 | 3.082 |
| n | 1482 | 1482 | 648 | 648 | 1771 | 1771 | 782 | 782 |
| Log of CRP (mg/l) | –0.825*** (0.311) | –0.910*** (0.343) | –0.833*** (0.315) | –0.935*** (0.326) | –0.317 (0.221) | –0.364 (0.242) | –0.164 (0.191) | –0.180 (0.253) |
| BW (years) | 2.290 | 1.934 | 2.210 | 1.737 | 3.202 | 2.572 | 5.061 | 2.753 |
| n | 1504 | 1504 | 665 | 665 | 1799 | 1799 | 799 | 799 |
| Binary CRP | –0.248** (0.127) | –0.293** (0.144) | –0.801*** (0.192) | –0.822*** (0.199) | –0.054 (0.093) | –0.064 (0.101) | –0.020 (0.106) | –0.046 (0.153) |
| BW (years) | 2.449 | 1.934 | 1.422 | 1.294 | 3.534 | 2.900 | 4.645 | 2.363 |
| n | 1504 | 1504 | 665 | 665 | 1799 | 1799 | 799 | 799 |
| Chest infection | –0.018 (0.068) | 0.006 (0.116) | –0.007 (0.135) | –0.122 (0.224) | 0.011 (0.067) | 0.019 (0.096) | 0.138 (0.088) | 0.084 (0.139) |
| BW (years) | 9.043 | 3.284 | 7.154 | 4.098 | 6.863 | 3.534 | 5.823 | 3.781 |
| n | 1099 | 1099 | 467 | 467 | 1239 | 1239 | 524 | 524 |
| FEV | 0.164 (0.175) | 0.293 (0.212) | 0.474 (0.298) | 0.613* (0.339) | 0.067 (0.088) | 0.100 (0.155) | –0.026 (0.137) | –0.024 (0.247) |
| BW (years) | 3.168 | 2.064 | 1.679 | 1.402 | 10.956 | 3.139 | 6.304 | 2.157 |
| n | 1775 | 1775 | 802 | 802 | 2132 | 2132 | 958 | 958 |
| Binary FEV | –0.121 (0.106) | –0.169 (0.13) | –0.219 (0.305) | –0.240 (0.403) | 0.026** (0.06) | –0.035 (0.083) | 0.075 (0.096) | –0.045 (0.114) |
| BW (years) | 2.655 | 2.002 | 1.663 | 1.254 | 4.876 | 2.653 | 2.688 | 1.724 |
| n | 1768 | 1768 | 799 | 799 | 2124 | 2124 | 955 | 955 |
| Self-rated health | –0.092 (0.079) | –0.165 (0.113) | 0.070 (0.095) | 0.133 (0.111) | –0.064 (0.06) | –0.047 (0.08) | 0.040 (0.1) | 0.058 (0.107) |
| BW (years) | 4.676 | 2.462 | 4.757 | 2.448 | 6.139 | 3.449 | 3.588 | 2.580 |
| n | 1971 | 1971 | 747 | 747 | 2361 | 2361 | 846 | 846 |
| Depressive symptoms | –0.597 (0.352) | –0.332 (0.477) | 0.488 (0.546) | 0.577 (0.555) | –0.331 (0.338) | –0.199 (0.399) | 0.433 (0.487) | 0.533 (0.489) |
| BW (years) | 5.313 | 3.258 | 2.859 | 2.254 | 4.364 | 3.108 | 2.819 | 2.346 |
| n | 1969 | 1969 | 748 | 748 | 2358 | 2358 | 847 | 847 |
| Binary depressive symptoms | –0.141** (0.058) | –0.128 (0.089) | 0.009 (0.096) | 0.014 (0.098) | –0.111** (0.054) | –0.067 (0.078) | 0.003 (0.087) | 0.015 (0.09) |
| BW (years) | 6.462 | 3.406 | 3.122 | 2.577 | 5.632 | 2.827 | 2.974 | 2.310 |
| n | 1969 | 1969 | 748 | 748 | 2358 | 2358 | 847 | 847 |
Chapter 4 Discussion
Winter-related illnesses and mortality represent a salient risk factor for individuals aged > 60 years, who are particularly vulnerable to the health effects of cold weather. 14 This vulnerability is caused by a combination of poor physiological thermoregulation in response to cold stress and a high risk of fuel poverty among older individuals, who tend to have low fixed incomes and live in energy-inefficient homes. The health problems and costs arising from fuel poverty represent a significant public health challenge and issue for policy-makers. The WFP was introduced by policy-makers with the stated aim of ensuring that older people have sufficient funds available to heat their homes throughout the winter months,1 thus attenuating the health and welfare effects of cold weather among at-risk individuals. Labelling this universal cash transfer as a payment for ‘winter fuel’ combined with the timing of the payment (November/December) represents an attempt to shape how the cash is spent. This report builds on initial evidence12 that suggests that such labelling may be an effective policy lever that markedly increases the portion of the payment spent on fuel (47%, compared with 3% if the payment were treated as cash). Specifically, we aimed to ascertain if the WFP has an impact on household temperature levels and whether or not the payment affects a range of health measures thought to be related to ambient temperature levels.
Indoor temperature and health
Prior to assessing the impact of the WFP on health, we aimed to identify which health measures tend to respond to differences in ambient indoor temperature. To do this, we drew on approximately 24,000 temperature measurements on 12,210 individuals which were taken as part of nurse assessments in ELSA. Our analyses provided strong evidence that blood pressure levels are associated with indoor temperature levels. Those living in colder homes experienced higher systolic and diastolic blood pressure levels and were at increased risk of high blood pressure. This association appeared to be linear in nature, with those living in the coldest homes (temperatures of < 17 °C) having blood pressure levels between 2 and 5 points (mmHg) above those living in the warmest homes (temperatures of > 23 °C); the low-temperature group were also at a two-fold increased risk of high systolic blood pressure. Crucially, we moved beyond existing evidence55,56,60 to show that this increased risk could not be attributed to a broad set of demographic and contextual variables (e.g. month of year, region) or to outdoor temperature levels. Furthermore, our fixed-effects analyses demonstrated that the link between colder indoor temperatures and elevated blood pressure was not caused by stable potential confounding factors that were not measured in ELSA.
These analyses also revealed evidence for a graded relationship between indoor temperature and fibrinogen levels, with raised levels identified in colder households. In contrast, our data showed only weak evidence that CRP levels were raised at low temperatures, we did not find consistent support for differences in lung function and the prevalence of chest infections was only marginally reduced at higher indoor temperatures. Participant-reported health measures, such as self-rated health or the presence of depressive symptoms, were also not robustly related to indoor temperature levels.
In summary, our investigation into the association between home temperature and health therefore pointed firmly towards blood pressure and fibrinogen as measures that are likely to respond to a WFP-linked increase in indoor temperature. However, we elected to also examine the link between the WFP and the remainder of the measures we identified a priori as potential indicators that may be affected by the payment. This was chiefly because our measure of indoor temperature was limited in several respects and as such it was not possible to rule out the possibility that these additional measures may be affected by the WFP. The potential limitations associated with how indoor temperature was assessed in ELSA are now discussed at length.
Winter Fuel Payment and health
Our examination of the health effects of the WFP drew on data from ELSA with the aims of identifying whether or not the WFP was linked to increased household temperatures and improved health, and whether or not such potential associations might be most pronounced among those from more disadvantaged backgrounds/those at above average risk of fuel poverty. Our RDD analyses capitalised on the exogenous nature of assignment to the WFP based on the age of the oldest household member in the arbitrary administratively determined qualifying week, as described in detail in Chapter 2. Furthermore, we adjusted for demographic and contextual factors including outdoor temperature. To do this, we drew on the Met Office’s UKCP09 gridded observation data sets103 by matching mean temperatures to survey interviews using participant postcodes (including OS northings and eastings) and exact date of nurse visit. To identify the sensitivity of the results to a range of key factors, such as the timing of the health measurement, household composition and model specification, we estimated a series of RD models. Specifically, across different models, we examined the cold months immediately or for a longer duration after the payment (January–March vs. January–April), we examined either an unrestricted or a restricted sample based on household composition (oldest member is male because of the overlap between WFP eligibility and the female pension age at age 60 years) and we tested whether or not our results were sensitive to different methodologies employed to determine the optimal BW for the analysis. We also produced specification curves showing every possible combination of samples generated from varying these factors.
The results yielded little evidence linking WFP eligibility to increased ambient indoor temperature. Across our key models the point estimates were universally negative, although not statistically significant, and our estimates across all models suggested a point estimate between –0.5 and 0.015 °C. This finding was important as it indicated that if the WFP was linked to health benefits in ELSA these could not be attributed to differences in indoor temperature as measured in the ELSA nurse assessment.
Our examination of key variables, such as blood pressure and inflammation indicators, which appeared to change as a function of household temperature, also did not identify a potential effect of the WFP. We did not find evidence of an effect of the WFP on fibrinogen in any of our main models, and, in some cases in which statistically significant links were found between the WFP and outcomes such as systolic blood pressure, these links were opposite in direction to that anticipated. However, an examination of the more comprehensive specification curves for these two outcomes showed a large degree of heterogeneity in the point estimates generated across different models, suggesting that not much weight should be placed on the small set of statistically significant links identified. Similarly, our results yielded little evidence that the WFP produced changes in the participant-reported outcomes of self-rated health and depressive symptoms. Furthermore, we also do not observe a statistically significant association between WFP eligibility and improved lung functioning.
Finally, we tested whether or not the association between WFP eligibility, indoor temperature and health measures was most pronounced among those from more disadvantaged backgrounds as gauged using household income levels. In order to maintain a relatively large number of observations for examination in these analyses we split the sample into those with income levels below and above the sample median/mean. As in the WFP analyses described above, these models yielded little evidence for an effect of the WFP on either indoor temperature or household member health. Furthermore, although statistically significant effects were identified in some models, these linkages were not clustered among the low-income group specifically, with perhaps only some consistent evidence of lower levels of CRP. Thus, we could conclude that in ELSA the impact of the WFP did not appear to vary systematically between those with low and those with high incomes.
Interpretation
The findings from this project must be interpreted with consideration of several key issues: (1) the validity and reliability of the measurement of ambient indoor temperature in ELSA, (2) the empirical basis for the current project based on existing work examining the impact of the WFP on household energy expenditure, (3) the sensitivity of the RD analyses to identifying potential impacts on health outcomes across different data sets and (4) the sensitivity of the RD analyses to the presence of small temperature effects and effects evident only in low-temperature conditions. We illustrate the importance of the final point through an examination of the potential health effects of the WFP on mortality in the UK during particularly cold weather conditions. First, we discuss each of these points in turn below.
Ambient indoor temperature measurement
In the current study, we could show that certain health measures, such as blood pressure and circulating fibrinogen levels, were linked to household temperature. However, the remaining outcome measures did not follow a gradient of indoor temperature. Furthermore, our WFP analyses did not identify an impact of the payment on indoor temperature despite existing evidence suggesting that almost half of the WFP money received is likely to be spent on increasing energy expenditure in the home. 12
In drawing conclusions from these analyses, it is important to consider the method of measurement of ambient temperature used in ELSA. The assessment is made most often in a single room as part of a scheduled nurse visit to the household. As such, although we have identified evidence that temperature measurements appear to be reliable (based on multiple assessments in a given home throughout the visit, which correlate to ≈0.8), the ecological validity of the temperature assessment is less clear. For instance, it may be the case that individuals are more likely to regulate the temperature in their homes to a comfortable level when it is known that a survey representative will be present in the household on a given day. In this way, the mean indoor temperature level identified in ELSA may be above that which would be observed otherwise and the distribution of temperature levels may be condensed towards the mean.
To evaluate this idea, we consulted four recent studies106–108 (conducted between 2004 and 2010) that examined indoor temperature levels in the UK over prolonged monitoring periods (≤ 1 year) using temperature sensors, high-frequency assessment of temperature (e.g. every second) and data loggers. In ELSA, the mean household temperature was 20.2 °C. This was comparable to the temperatures identified across the four recent UK studies, in which the average living room temperature levels (taken primarily during occupied hours) ranged from 18.7 to 20.5 °C, with an average of 19.6 °C. 107 Thus, these studies suggest that, although there may have been some tendency to increase the temperature of the home during the nurse visit, the indoor temperature level in ELSA is within the range expected based on data collected over several weeks using data loggers in the absence of researchers. In ELSA, temperature recordings also appeared to be normally distributed (see Figure 4), with little evidence that values tended to cluster close to the mean (kurtosis statistic = 1.3), as may be the case if participants tended to adjust their home temperatures to a certain comfortable level because of the presence of a member of the ELSA survey team. Finally, we also observed marked seasonal variation in indoor temperature levels and a moderate correlation between indoor and outdoor temperature levels (r = 0.45), providing some indication of the ecological validity of the ambient indoor temperature data.
However, evidence for the reliability and validity of the temperature assessments remains speculative in the absence of a more extensive empirical assessment of the overlap between the temperature readings taken during the ELSA nurse assessment and those derived from a multisensor, high-frequency assessment of indoor temperature over several weeks or months in the same households. Data from such a study would allow the extent of measurement error present in ELSA temperature data to be quantified and would provide a clearer indication of the validity of the WFP results presented in the current study.
If we do interpret the available evidence as providing sufficient support for the validity of the temperature assessment in ELSA, then this opens the question as to why no impact of the WFP was observed. This question is particularly salient given that available evidence documented in Beatty et al. 12 points to an effect of the WFP on energy expenditure.
The Winter Fuel Payment and household energy expenditure
If the WFP influences energy expenditure then it follows that the payment should lead to an increase in household temperature, particularly in the time period following the receipt of the payment. However, no such effect was observed in the current study. The measurement error in the assessment of indoor temperature in ELSA may exceed the measurement error in the assessment of household energy expenditure in the LCF survey (utilised in Beatty et al. 12) and thus explain why no link between receipt of the WFP and household temperature was identified. This possibility is difficult to evaluate in the absence of information on measurement error in both outcome variables, and existing evidence on the validity of the ELSA temperature measurements remains somewhat speculative, as discussed above.
Another potential reason why we did not identify an impact of the WFP on temperature could be that our study included an insufficient number of observations to detect an effect. The number of observations available for inclusion in our RD analyses was comparable to that available in Beatty et al. 12 within the same age range of the 60 years of age eligibility cut-off point. However, the strength of the link between energy expenditure and household temperature is not clear. If energy expenditure and home temperature are strongly correlated, then an impact of the WFP on home temperature should have been detectable in our models (assuming a relatively high level of validity of the ELSA temperature assessments). Indeed, the standard errors in our RD models indicate that relatively small increases in household temperature (ranging from 0.4 to 1.2 °C) in the months immediately following receipt of the WFP would be identified as statistically significant.
This noted, there are potential reasons why an increase in energy expenditure may not translate into a detectable increase in indoor temperature. One of the potential explanations for this puzzle is that the relationship between energy consumption and home temperature depends on the home energy efficiency performance. The energy efficiency of homes in the UK has been evaluated using the Standard Assessment Procedure (SAP) ratings since 1992. This comprises a score from 0 to 100, where 0 is the lowest energy efficiency score and 100 is the highest. The average score has been increasing from an average of 45–46 to 52–53 in the period considered by this present study. 109 The SAP score is reported on energy performance certificates along with a colour-coded letter grade [A (green)–G (red)] as typically found on electrical appliances, when green is highest energy efficiency. To provide an idea, a score of 45 or 53 places a home on the same letter: E (orange).
The problem of a potential lack of conversion of energy expenditure to household temperature increases may be compounded because elderly households may live in older dwellings that are on average much less energy efficient. 110 Furthermore, SAP scores do not change markedly across income groups: there are few discernible differences in energy efficiency between poor and rich households. An Institute for Fiscal Studies study111 found that the average SAP scores increased for both rich and poor households over the period 2002–10, but were not different across the income distribution. This may partially explain why WFP does not improve indoor temperature across the income distribution in our current report; increases in fuel consumption are lost because of poor insulation, whether the household is rich or poor.
A further possibility is that there was not an increase in energy expenditure as a function of the WFP and this is why no temperature increase was identified. For example, the particular specification employed in the Beatty et al. 12 analysis may have led to an effect of the WFP being uncovered which may not be robust across the broader set of model specifications used in the current study. If the impact of the WFP on energy expenditure is observed only under certain nuanced analytical conditions and fails to appear in many others where an effect should perhaps also be evident, then this would lead our team to question the main channel identified in our conceptual framework – indoor temperature (see Figure 1) – and to put forward alternative avenues of research.
To test the sensitivity of the findings reported in Beatty et al. 12 to variations in RD analysis strategies, we re-examined the LCF survey data used in that study. We constructed a data set using LCF data suitable for RD analysis, comparing the fuel expenditure of thousands of households whose oldest members were born just few months apart, before and after the WFP cut-off date for each cohort. We find evidence (available on request) of a similar ‘nudge’ effect observed in the original analysis, that is, households that just received the payment raise fuel expenditure by more than we would expect from an increase in the level of income from other sources of the same size as WFP. To further test the validity of this conclusion, we subjected our finding to a battery of robustness tests. For instance, one may argue that the relationship could be driven by energy prices in the period of interest rather than a pure nudge effect. Our replication survives the inclusion of energy prices and also changes to the baseline samples.
In sum, we are able to reproduce and extend the Beatty et al. 12 analysis of the impact of the WFP on energy expenditure and we can almost exactly replicate their results. Furthermore, our extensions to their analysis suggest that this effect is likely to be robust and worthy of closer inspection. Given this conclusion, we aimed to extend our examination of the WFP and test the extent to which the conclusions from our ELSA RD analysis would be verified in a separate sample. We therefore estimated the impact of the WFP on health in the British Household Panel Survey (BHPS).
Sensitivity of the regression discontinuity analyses across surveys: regression discontinuity analysis using the British Household Panel Survey
The BHPS is a household-based survey that followed the same representative samples of individuals (adult members of sampled households) over the period between 1991 and 2008. The BHPS also contains detailed questions assessing the health of respondents each year. From these questions, we constructed the following health variables:
-
12-item version of the General Health Questionnaire (GHQ-12)112 scores, which range from 0 to 12 (with higher scores indicating greater psychological problems);
-
a dummy variable indicating whether or not the participant indicated that their health limits their daily activities
-
a dummy variable which indicates whether or not the participant currently suffers from a chest or a breathing problem
-
a dummy variable that takes indications of whether or not the participant suffers any kind of heart or blood pressure problems
-
the number of days the participant has spent at a hospital
-
a categorical life satisfaction variable that takes value 1 if the participant is not at all satisfied with life and takes value 7 if the participant is completely satisfied.
The BHPS does not include information on home temperature. However, in an effort to provide evidence of the potential robustness to our findings with respect to this indicator, we identified a set of questions about home characteristics that should be correlated with indoor temperature. We constructed the following dummy variables that indicate whether or not the house lacks adequate heating, has condensation problems or suffers from damp walls or damp floors.
We analysed all outcomes using a variety of RDD specifications. Each cell of Table 18 shows the results of different estimations. To make the estimates comparable, we report results from RDDs with BW fixed to 5 years on either side of the WFP eligibility cut-off point, so we consider whether or not there is a discontinuity in the relationship between age and each outcome for households whose oldest member is aged 55–65 years. In other words, we fit two linear regressions on either side of the cut-off point using data from 5 years before and after the eligibility age and test whether or not there is a discontinuity in the prediction. This method is often described as parametric RDD. The results do not change if we use quadratic instead of linear regressions.
As we rely here on the RD associated with age to identify the causal effect of eligibility to WFP, we flexibly control for the effect of age on health (and other outcomes) and identify the effect of WFP on outcomes from deviations from this smooth age relationship with outcomes associated with eligibility at age 60 years (and later at age 80 years, when the entitlement level is larger). In all cases, we provide parsimonious estimates with few additional controls in column (1) of Table 20 and add more controls in subsequent columns. As mentioned previously, in RDD models, adding such covariates should not substantially impact on the estimates of the causal parameters. Specification (1) includes just household income and fuel prices; (2) adds marital status, sex, employment status, education dummies, year dummies and region dummies; (3) adds mean winter temperature; (4) adds mean winter temperature interacted with WFP; (5) adds fuel expenditure to 3; (6) adds household tenure and lack of central heating, condensation problems and damp walls and floors; and (7) adds household tenure, lack of central heating and health-limiting illness to 5.
| Model number | Specification | ||||||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| GHQ-12, 0–12 | –0.093 (0.220) | –0.120 (0.212) | –0.118 (0.212) | –0.088 (0.222) | –0.128 (0.215) | –0.137 (0.212) | –0.251 (0.228) |
| Health limits daily activities | 0.027 (0.034) | 0.005 (0.030) | 0.004 (0.030) | 0.012 (0.032) | 0.006 (0.030) | 0.002 (0.029) | 0.000 (0.000) |
| Health condition | |||||||
| Chest/breathing | 0.012 (0.027) | 0.005 (0.026) | 0.005 (0.026) | 0.002 (0.027) | 0.005 (0.027) | –0.000 (0.000) | –0.001 (0.028) |
| Heart/BP | 0.037 (0.034) | 0.030 (0.034) | 0.029 (0.034) | 0.031 (0.035) | 0.021 (0.034) | –0.000 (0.000) | 0.024 (0.037) |
| Days in hospital | –0.013 (0.023) | –0.013 (0.023) | –0.013 (0.023) | –0.004 (0.024) | –0.016 (0.023) | –0.018 (0.023) | –0.020 (0.025) |
| Housing condition | |||||||
| Inadequate heating | 0.001 (0.013) | –0.000 (0.013) | –0.000 (0.013) | 0.002 (0.014) | –0.002 (0.013) | 0.000 (0.000) | –0.000 (0.000) |
| Condensation | –0.019 (0.021) | –0.014 (0.021) | –0.014 (0.021) | –0.013 (0.022) | –0.011 (0.021) | –0.012 (0.021) | –0.024 (0.023) |
| Damp walls, floors | –0.007 (0.018) | –0.006 (0.019) | –0.006 (0.019) | –0.007 (0.019) | –0.010 (0.019) | –0.010 (0.018) | –0.016 (0.020) |
| Life satisfaction 1–7 | –0.122 (0.105) | –0.101 (0.102) | –0.101 (0.102) | –0.154 (0.107) | –0.092 (0.103) | –0.084 (0.102) | –0.057 (0.112) |
The overwhelming impression from Table 20 is that there is not a statistically significant effect of the WFP. In particular, there are no effects on health conditions that we would expect to find if health were part of the downstream effects of the WFP. There are also no effects on housing conditions that we may expect to find if WFP raised indoor temperatures.
In sum, our additional results from the BHPS largely replicate those identified in ELSA: the WFP does not appear to produce robust improvements in health identifiable in either sample. These findings could be considered at odds with our robustness analyses, which suggest that a substantial portion of the WFP is likely to be spent on fuel. However, in both cases, the standard errors in our RD models suggest that the impact of the WFP would need to be large to be detected given the number of observations available in either survey. It may be the case that, because the health consequences of the WFP are at the end of a causal chain (e.g. WFP → energy expenditure increase → home temperature increase → health improvement), detecting such potentially small effects may require a very large number of observations and/or assessments focused on cold exposures in which health effects are potentially most likely to be observed.
Sensitivity of Winter Fuel Payment analyses to the presence of small health effects
To test whether or not drawing on a larger number of observations under specific cold weather conditions would increase the certainty of our estimates of the health impact of the WFP, we conducted an analysis using vital statistics (VS) data at a local authority (LA) level.
An analysis on mortality is interesting in its own right. As discussed in Chapter 1, there is widespread evidence that mortality is affected by weather and, in the context of the UK, much of the literature has focused on cold. The ONS publishes an annual report on the official EWD index, which compares the number of deaths that occurred in the winter period (defined as December–March) with the average number of deaths occurring in the preceding non-winter period (August–November and the following April–July). Data are available from the 1950s onwards and the figures show a clear downward trend, in part because winters have been getting warmer over this period – there is a rise of approximately 1 °C between the start and end of this period (and a rise of approximately 0.5 °C in summer temperatures). 113 Recent time series work114 explores the time series pattern of annual mortality for London from 1949 to 2006 and concludes that a 1 °C colder winter is associated with a 2.3% rise in mortality from all causes, with larger estimates for cardiovascular and respiratory causes. Using weekly data, the estimates were only slightly smaller than the annual data results, suggesting that cold-related mortality affects people who might have been expected to live for some time. In contrast, the annual estimates of the effect of heat were not statistically significant, although the effects found in the weekly data suggested significant mortality displacement – an effect on mortality that is confined to those who are already frail.
We investigated the effect of WFP on monthly mortality at LA level sourced from VS data from 1981 to 2011. Details of the VS database can be found at www.content.digital.nhs.uk/vital (accessed 5 October 2018). We created a pseudo-panel of 455 UK LAs. Each observation is a set of individuals within a cell; a cell is defined by LA, months between 1981 and 2011, age ranges (< 55, 55–59, 60–64, 65–79, ≥ 80 years) and sex. This yields more than 1.4 million cells.
The analysis of the impact of the WFP on mortality used a different empirical method than RD. We conducted difference-in-difference estimation, exploiting the availability of data before and after the introduction of the WFP in 1997 to the population aged ≥ 60 years. This simple estimator allows a before–after comparison of mortality trends, assuming that trends in mortality after 1997 would have followed the same trend as before. To make the estimation more robust, we ran various specifications, with and without LA and year fixed effects:
-
The inclusion of LA fixed effects captures the impact of differences in temperature relative to LA averages (i.e. surprises in temperature), which might be argued to have a bigger mortality effect than cold conditions that could be expected to occur in that LA at that time. However, LAs are not themselves exogenous because location is a choice. It may be the case that frail individuals choose to locate to warm areas – a phenomenon that is thought to be important in the US literature. In any event, the model with LA fixed effects does not make any difference to the results of interest. The results strongly suggest that individuals do not take precautions that affect their mortality based on expected weather.
-
The inclusion of year fixed effects takes account of year specific shocks, such as variations in flu intensity. In addition, the inclusion of fixed effects does not make a substantial difference to our results. The suggestion is that year-to-year events, apart from temperature, are orthogonal to WFP and temperature and, hence, accounting for them does not change our estimates that are our core interest.
Crucially, our investigation on mortality also focuses on the influence of temperature variation at LA level and its interaction with WFP. Monthly temperature data from the MIDAS Land and Marine Surface Station Data [http://catalogue.ceda.ac.uk/uuid/220a65615218d5c9cc9e4785a3234bd0 (accessed 30 August 2018)] were matched to each LA in the overall period.
The validity of the difference-in-difference method depends crucially on the common trends assumption. That is, the effect on mortality of the WFP is identified only if the trend in mortality would have followed the same trend pre and post- 1997 if the WFP had not been introduced. This assumption is not verifiable, but allowing for differential mortality trends across calendar time would capture pre-existing differences. To capture time trends, we generate a linear time trend based on calendar month, that is, the variable takes the value of 1, 2, 3 . . . M, where M is the total number of months in the overall period. The introduction of differential time trends rules out the attribution of changes caused by some pre-existing trends to the WFP. In effect, differential trends control for things like changes in blood pressure medication that might confound the effect of WFP. We also introduce a differential life-cycle pattern by allowing the age effects to interact with this linear trend. This enables us to control for the fact that, say, blood pressure medication might have reduced the mortality rate in the younger age groups relative to older ones, especially for men.
Following from the discussion above and with an eye on saving space, Table 21 reports estimates from difference-in-differences with LA and year fixed effects and the following interactions: (mortality) × (linear time trend in months) and (age) × (linear time trend in months). We consider the role of temperature on mortality as well as WFP in column (1). In column (2), we include an interaction between temperature and the WFP to allow for the possibility, consistent with a transmission effect that is mediated via fuel expenditure, that the WFP affects mortality more when it is cold than when it is not. Subsequent columns attempt to capture non-linearity in the temperature effect by replacing temperature by a count of the number of days in the previous month when the temperature falls below 2 °C (column 3), 0 °C (column 4), –2 °C (column 5), –4 °C (column 6), and –6 °C (column 7).
| Variable (mortality rate) | (1) Include temperature | (2) Include temperature × WFP | (3) Temperature = days < 2 | (4) Temperature = days < 0 | (5) Temperature = days < –2 | (6) Temperature = days < –4 | (7) Temperature = days < –6 |
|---|---|---|---|---|---|---|---|
| WFP | 0.001 (0.001) | –0.005** (0.002) | 0.001 (0.001) | 0.001 (0.001) | 0.001 (0.001) | 0.001 (0.001) | 0.001 (0.001) |
| Temperature | –0.001*** (0.000) | –0.002*** (0.000) | 0.017*** (0.001) | 0.020*** (0.001) | 0.026*** (0.001) | 0.034*** (0.001) | 0.046*** (0.002) |
| Temperature × WFP | 0.001*** (0.000) | –0.006*** (0.002) | –0.011*** (0.002) | –0.020*** (0.002) | –0.031*** (0.002) | –0.045*** (0.004) | |
| Observations | 1,432,094 | 1,432,094 | 1,432,094 | 1,432,094 | 1,432,094 | 1,432,094 | 1,432,094 |
| R-squared | 0.852 | 0.852 | 0.852 | 0.852 | 0.852 | 0.852 | 0.852 |
The independent effect of the WFP on mortality is assessed by looking at the estimates reported in the first row of Table 21. There is no evidence of a robust mortality reducing effect at LA level across the columns reported. The estimated effect is small and has the ‘wrong’ (expected) sign in most of the specifications. This finding is corroborated by other specifications run by the authors and available upon request. It is, however, very interesting to look at temperature and its interaction with the WFP in the subsequent two rows of Table 21.
The estimate in column (1) suggests that a 1 °C rise in average temperature reduces mortality by 0.001. This is a small proportionate effect, approximately 1% of the mean mortality rate of –0.09, but nonetheless statistically significant. As a matter of comparison, this represents only half the size of the Rehill et al. 114 result, albeit one that came from a very different methodology and a very different sample. This small and precisely estimated temperature effect is robust to different specification and in results not reported is larger for men, at –0.002, than for women, at –0.001. In sum, warmth decreases mortality in the UK.
In column (2) we introduce an interaction effect between temperature and the WFP so that the WFP effect is allowed to vary with temperature. We still find similar temperature effects for WFP = 0 (i.e. the period before its introduction) and, when WFP = 1, the interaction effect kicks in and counteracts, to an extent, the temperature effect. We note, however, that when it comes to warmth we are discussing very small effects. In columns (3)–(7) we replace temperature (a measure of warmth) with a count of the number of cold days (a measure of cold) and we vary the intensity of the definition of cold. Our temperature definition is now capturing cold and we therefore expect the effect to be positive – the longer it is cold, the greater the mortality is. An extra day below 2 °C increases mortality by 0.017, which is a large effect relative to the mean of 0.09. An additional very cold day will have a bigger positive effect on mortality, and an extra day below 0 °C (–2 °C, –4 °C, –6 °C) increases mortality by 0.020 (0.026, 0.034, 0.046, respectively). The WFP seems to counteract the effect of warmth and cold. Indeed, the marginal effect of a very cold day (0.046) appears to be completely offset by the WFP, as the interaction coefficient is –0.045. Inspection across results from this data set suggests that this is a general finding – cold kills, but the WFP nullifies that effect.
The investigation into mortality effects suggests that the WFP may act like an insurance against cold spells. This is in conflict with our main analysis in which we do not find any difference in indoor temperature and health outcomes between recipients and non-recipients, irrespective of outdoor temperature.
Future directions and research recommendations
Our investigation into the potential role of the WFP in curtailing the impact of exposure to cold weather on mortality highlights the potential need for very large data sets to identify the health effects of the WFP. Detailed data on biomarkers of human functioning and reported health are now available through the UK Biobank115 on a large sample (n > 500,000). We have acquired access to and linked with Met Office outdoor temperature data103 as part of this project. Incorporating this sample into ongoing work will help establish whether or not the WFP has effects on biomarkers such as blood pressure and inflammation levels and whether or not such effects may be present mainly during particularly cold spells. Similarly, capitalising on administrative data on hospital admissions, health-care use and expenditures on relevant medications (e.g. for influenza, common cold, bronchitis) coupled with information on outdoor temperature levels represents a further avenue for examining the role of the WFP in attenuating the health effects of cold exposure.
To our knowledge, ambient indoor temperature data are currently not available on samples running into hundreds of thousands of observations. However, fewer participants may be required to identify a link between the WFP and indoor temperature because this variable represents an intermediate step in the causal chain from increased energy expenditure to improved health. Furthermore, reducing measurement error in the assessment of temperature would aid in precisely estimating the potential effect of the WFP on ambient temperature within the home. As noted above, there are established methodologies for measuring home temperature,107 which include the use of temperature sensors in multiple rooms and logging temperature for several weeks at a high frequency in order to produce a fine-grained account of home temperature. This information, coupled with fuel expenditure data and survey data on time spent in the home, may be particularly powerful in understanding the impact of the WFP. For example, this type of data would enable researchers to precisely estimate the impact of increased energy expenditure attributable to the WFP on home temperature (as opposed to other forms of energy expenditure, such as the energy expended in cooking/food preparation) and the extent to which householders benefit from this temperature increase. This approach could be further enhanced by measuring the energy efficiency of the home in order to decipher whether or not the potential aggregate benefits of the WFP on home temperature may be driven by a subgroup of those with more energy-efficient homes (where an increase in fuel expenditure is most likely to lead to an increase in temperature). Such data would be further enhanced by sampling households close to the eligibility cut-off point for receipt of the WFP, thus increasing the likelihood that RD analyses could precisely estimate household temperature effects.
Our project also points to the need for more research investigating the real world relationship between money spent on fuel, energy consumption, home temperature and health. As noted above, our temperature analysis was founded on the idea that an increase in energy expenditure should translate into an increase in home temperature, yet the magnitude of this conversion is uncertain. Furthermore, we observed little relationship between indoor temperature and many of our health outcome variables despite our initial ideas to the contrary. Many possibilities remain to be evaluated. For instance, the WFP could be spent on alternative forms on keeping warm, such as warmer clothing. Furthermore, it might be the case that, after a certain home temperature is reached, the relationship between fuel expenditure and temperature could be characterised by non-linearity and tipping points. Although the energy performance of buildings tends to be estimated exante using computer models and theoretical conversion factors, this project shows that further estimation of actual energy fuel consumption and indoor temperature through ex-post studies is warranted. In addition, the literature on the link between ambient indoor temperature and health and how this association varies across outdoor temperature levels remains in its infancy. Advances in this area would further inform the health measures that the WFP is likely to affect and the weather conditions under which such linkages may occur.
Finally, it is important to note that this project was only possible because of two key factors related to the administration of the WFP. The first is the arbitrary nature of WFP eligibility, which is assigned based on the age of the oldest household member on a specific week in a given year. Retaining this administratively determined ‘WFP qualification week’, which cannot be manipulated or influenced by those affected by the policy, is crucial in order to treat the WFP as a natural experiment and examine the payment using a RDD framework. The second is the automatic nature of the payment, whereby the vast majority (95% of cases) do not need to apply for the WFP as they are already in receipt of some form of social security benefits. This meant that our estimates were not markedly affected by heterogeneity in the decision to apply for the payment. We can therefore recommend retaining or expanding the level of automaticity currently associated with the payment of this benefit in order to facilitate future research on the potential impact of the WFP.
Similarly, an extensive investigation into the views and experiences of the public with regard to the WFP (e.g. interviewing a set of individuals born just inside/outside the threshold for WFP eligibility) could provide a more nuanced understanding of the types of weather and financial conditions that lead individuals to consider the WFP when making energy consumption decisions. Furthermore, whereas the current analyses examined the impact of the WFP and indoor temperature on perceived health and depressive symptoms, these are most likely to be an imperfect measure of the potential subjective effects that changes in heating levels may have. In addition, incorporating public involvement could shed important light on additional effects that warrant investigation and gauge whether or not public experiences of the WFP appear to differ markedly between those at risk of fuel poverty and other individuals.
Conclusions
This study capitalised on the sharp assignment rules regarding WFP eligibility to estimate the potential effect of the WFP on household temperature and health in a national sample of English adults. The study showed that lower indoor temperatures are generally related to health problems, as indexed by high blood pressure and inflammation levels. However, the RD design employed did not identify consistent evidence linking the WFP to warmer homes or specific health and well-being benefits. Studies incorporating high-frequency measurement of indoor temperature in multiple rooms over prolonged periods would aid in reducing measurement error in the assessment of home temperature and in precisely identifying the effect of the WFP. Further research utilising larger samples of participants close to the WFP eligibility cut-off point is also needed to identify whether or not the WFP is linked to robust home temperature and health benefits not observed in the current study. The study results suggest that the potential temperature and health benefits of the WFP are unlikely to be large at the aggregate population level. However, the possibility that the WFP may have important implications for population health for certain individuals under certain circumstances cannot be ruled out. In support of this contention, the supplemental analyses examining mortality at the LA level identified initial evidence to suggest that the WFP could attenuate the impact of particularly cold conditions (e.g. temperatures of ≤ 2 °C) on mortality.
Acknowledgements
We are grateful to the ELSA participants and survey team32 and the UK Data Service for providing the main data examined in this study and to NatCen for allowing us to use its London premises to match ELSA data with Met Office gridded daily temperature data at highly sensitive geographical levels.
Contributions of authors
Viola Angelini (Associate Professor in Economics) contributed to the data preparation, scientific background and introduction to the study.
Michael Daly (Associate Professor of Behavioural Science), in close collaboration with Mirko Moro and the other team members, wrote the original grant application, identified relevant measures and data and contributed to the study design and interpretation of the findings. He contributed to several sections of the report, including conducting the analysis and completing the methodology and results sections detailing the linkages between household temperature and health in ELSA.
Mirko Moro (Senior Lecturer in Economics), in close collaboration with Michael Daly and the other team members, wrote the original grant application, developed the analytical strategy and contributed to the study design, the main RD analyses and the interpretation of the findings. He wrote several sections of the report including the methodology and results sections examining the link between the WFP and household temperature and health in ELSA.
Maria Navarro Paniagua (Senior Lecturer in Economics) conducted the replication analysis of Beatty et al. 12 using the LCF and the supplemental analyses of WFP using data from the British Household Panel Study and Vital Statistics from the ONS.
Elanor Sidman (Research Fellow in Epidemiology) was the primary postdoctoral researcher on the project and conducted the key data linkage activities needed to assign WFP eligibility status and the identification of different samples and contributed to the background literature on temperature and health, as well as to the identification, understanding and analysis of the temperature and health variables.
Ian Walker (Professor of Economics) led the integration of outdoor temperature data into the study and oversaw the primary RD analyses and ELSA model specifications. He also contributed to the supplemental analyses of WFP using data from the British Household Panel Study and Vital Statistics from the ONS.
Matthew Weldon (Research Fellow in Mathematics and Statistics) conducted the key data linkage activities needed to assign WFP eligibility status and to link participant location data to Met Office gridded daily temperature data. He also contributed substantially to the analytical strategy and execution of the RD analyses examining the effect of the WFP on indoor temperature and health in ELSA.
Data-sharing statement
The English Longitudinal Study of Ageing data sets32 are available to researchers through the UK Data Service at the following address: https://discover.ukdataservice.ac.uk/series/?sn = 200011.
The questionnaires and general data collection methods are detailed at www.elsa-project.ac.uk.
In the current study, eligibility for the WFP was ascertained using quarter of birth data. Information on outdoor temperature was linked to approximate participant location data. Owing to the potentially identifiable and thus confidential nature of these variables, it was necessary to access and match these data in a secure environment on NatCen Social Research premises. The matched data cannot be shared because of conditions attached to use; however, it can be acquired directly from the NatCen Social Research.
Queries should be submitted to the corresponding authors.
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the PHR programme or the Department of Health and Social Care. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the PHR programme or the Department of Health and Social Care.
References
- Kennedy S, Parkin E. Winter Fuel Payments Update. London: House of Commons Library; 2016.
- Banks J, Mazzonna F. The effect of education on old age cognitive abilities: evidence from a regression discontinuity design. Econ J 2012;122:418-48. https://doi.org/10.1111/j.1468-0297.2012.02499.x.
- Jürges H, Kruk E, Reinhold S. The effect of compulsory schooling on health – evidence from biomarkers. J Popul Econ 2013;26:645-72. https://doi.org/10.1007/s00148-012-0409-9.
- Hajat S, Gasparrini A. The excess winter deaths measure: why its use is misleading for public health understanding of cold-related health impacts. Epidemiology 2016;27:486-91. https://doi.org/10.1097/EDE.0000000000000479.
- Public Health Outcomes Framework for England 2016–19. London: Department of Health and Social Care; n.d.
- Hajat S, Haines A. Associations of cold temperatures with GP consultations for respiratory and cardiovascular disease amongst the elderly in London. Int J Epidemiol 2002;31:825-30. https://doi.org/10.1093/ije/31.4.825.
- Healy JD. Excess winter mortality in Europe: a cross country analysis identifying key risk factors. J Epidemiol Community Health 2003;57:784-9. https://doi.org/10.1136/jech.57.10.784.
- Wilkinson P, Landon M, Armstrong B, Stevenson S, McKee M. Cold Comfort: The Social and Environmental Determinants of Excess Winter Death in England, 1986–96. York: Joseph Rowntree Foundation; 2001.
- Wilkinson P, Smith KR, Beevers S, Tonne C, Oreszczyn T. Energy, energy efficiency, and the built environment. Lancet 2007;370:1175-87. https://doi.org/10.1016/S0140-6736(07)61255-0.
- Liddell C, Morris C. Fuel poverty and human health: a review of recent evidence. Energy Policy 2010;38:2987-97. https://doi.org/10.1016/j.enpol.2010.01.037.
- Housing, Energy and Thermal Comfort: A Review of 10 Countries within the WHO European Region. Denmark: World Health Organization Europe; 2011.
- Beatty TK, Blow L, Crossley TF, O’Dea C. Cash by any other name? Evidence on labeling from the UK Winter Fuel Payment. J Public Econ 2014;118:86-9. https://doi.org/10.1016/j.jpubeco.2014.06.007.
- Annual Report on Fuel Poverty Statistics. London: HMSO; 2013.
- Marmot Review Team . The Health Impacts of Cold Homes and Fuel Poverty 2011. https://friendsoftheearth.uk/sites/default/files/downloads/cold_homes_health.pdf (accessed 30 August 2018).
- Newell RG, Siikamäki J. Nudging energy efficiency behavior: the role of information labels. JAERE 2014;1:555-98.
- Swartz JJ, Braxton D, Viera AJ. Calorie menu labeling on quick-service restaurant menus: an updated systematic review of the literature. Int J Behav Nutr Phys Act 2011;8. https://doi.org/10.1186/1479-5868-8-135.
- Mathios AD. The impact of mandatory disclosure laws on product choices: an analysis of the salad dressing market. J Law Econ 2000;43:651-77. https://doi.org/10.1086/467468.
- Fischer C. Feedback on household electricity consumption: a tool for saving energy?. Energy Efficiency 2008;1:79-104. https://doi.org/10.1007/s12053-008-9009-7.
- Kallbekken S, Sælen H, Hermansen EA. Bridging the energy efficiency gap: a field experiment on lifetime energy costs and household appliances. J Consum Policy 2013;36:1-16. https://doi.org/10.1007/s10603-012-9211-z.
- Hausman DM, Welch B. Debate: to nudge or not to nudge. J Polit Philos 2010;18:123-36. https://doi.org/10.1111/j.1467-9760.2009.00351.x.
- Thaler RH, Sunstein CR. Nudge: Improving Decisions About Health, Wealth, and Happiness. New Haven, CT: Yale University Press; 2008.
- Thaler RH. Mental accounting matters. J Behav Decis Making 1999;12:183-206. https://doi.org/10.1002/(SICI)1099-0771(199909)12:3<183::AID-BDM318>3.0.CO;2-F.
- Kooreman P. The labeling effect of a child benefit system. Am Econ Rev 2000;90:571-83. https://doi.org/10.1257/aer.90.3.571.
- Blow L, Walker I, Zhu Y. Who benefits from child benefit?. Econ Inq 2012;50:153-70. https://doi.org/10.1111/j.1465-7295.2010.00348.x.
- Abeler J, Marklein F. Fungibility, Labels, and Consumption 2008. https://ssrn.com/abstract=1139870 (accessed 30 August 2018).
- Beatty TK, Tuttle CJ. Expenditure response to increases in in-kind transfers: evidence from the Supplemental Nutrition Assistance Program. Am J Agr Econ 2015;97:390-404. https://doi.org/10.1093/ajae/aau097.
- Benhassine N, Devoto F, Duflo E, Dupas P, Pouliquen V. Turning a shove into a nudge? A ‘labeled cash transfer’ for education. Am Econ J Econ Policy 2015;7:86-125. https://doi.org/10.1257/pol.20130225.
- Lawton K, Stanley K, Oppenheim C, Dolphin T. Opportunities in an Age of Austerity: Smart Ways of Dealing with the UK’s Fiscal Deficit. Institute for Public Policy Research; 2009.
- House of Commons Energy and Climate Change Committee 2013. www.publications.parliament.uk/pa/cm201314/cmselect/cmenergy/108/10802.htm (accessed 22 October 2018).
- Lange I, Moro M, Mahbubur Rahman M. Cleaner Nudges? Policy Labels and Investment Decision-Making n.d. http://dea.uib.es/digitalAssets/333/333209_WFP_June.pdf (accessed 4 December 2017).
- Iparraguirre J. Have winter fuel payments reduced excess winter mortality in England and Wales?. J Public Health 2015;37:26-33. https://doi.org/10.1093/pubmed/fdu063.
- Marmot M, Oldfield Z, Clemens S, Blake M, Phelps A, Nazroo J, et al. English Longitudinal Study of Ageing: Waves 0–8, 1998–2017 n.d. http://doi.org/10.5255/UKDA-SN-5050-14 (accessed 4 December 2017).
- Curwen M, Devis T. Winter mortality temperature and influenza: has the relationship changed in recent years?. Population Trends 1988;54:17-20.
- Aylin P, Morris S, Wakefield J, Grossinho A, Jarup L, Elliott P. Temperature, housing, deprivation and their relationship to excess winter mortality in Great Britain, 1986–96. Int J Epidemiol 2001;30:1100-8. https://doi.org/10.1093/ije/30.5.1100.
- Eng H, Mercer JB. Seasonal variations in mortality caused by cardiovascular diseases in Norway and Ireland. J Cardiovasc Risk 1998;5:89-95. https://doi.org/10.1097/00043798-199804000-00004.
- Bull GM, Morton J. Seasonal and short-term relationships of temperature with deaths from myocardial and cerebral infarction. Age Ageing 1975;4:19-31. https://doi.org/10.1093/ageing/4.1.19.
- Keatinge WR. Winter mortality and its causes. Int J Circumpolar Health 2002;61:292-9. https://doi.org/10.3402/ijch.v61i4.17477.
- Eurowinter Group . Cold exposure and winter mortality from ischaemic heart disease, cerebrovascular disease, respiratory disease, and all causes in warm and cold regions of Europe. Lancet 1997;349:1341-6. https://doi.org/10.1016/S0140-6736(96)12338-2.
- Green G, Gilbertson J. Warm Front, Better Health: Health Impact Evaluation of the Warm Front Scheme. Sheffield: Centre for Regional, Economic and Social Research, Sheffield Hallam University; 2008.
- Liu C, Yavar Z, Sun Q. Cardiovascular response to thermoregulatory challenges. Am J Physiol Heart Circ Physiol 2015;309:H1793-812. https://doi.org/10.1152/ajpheart.00199.2015.
- Bøkenes L, Alexandersen TE, Østerud B, Tveita T, Mercer JB. Physiological and haematological responses to cold exposure in the elderly. Int J Circumpolar Health 2000;59:216-21.
- Keatinge WR, Coleshaw SR, Cotter F, Mattock M, Murphy M, Chelliah R. Increases in platelet and red cell counts, blood viscosity, and arterial pressure during mild surface cooling: factors in mortality from coronary and cerebral thrombosis in winter. Br Med J 1984;289:1405-8. https://doi.org/10.1136/bmj.289.6456.1405.
- Collins KJ, Easton JC, Belfield-Smith H, Exton-Smith AN, Pluck RA. Effects of age on body temperature and blood pressure in cold environments. Clin Sci 1985;69:465-70. https://doi.org/10.1042/cs0690465.
- Neild PJ, Syndercombe-Court D, Keatinge WR, Donaldson GC, Mattock M, Caunce M. Cold-induced increases in erythrocyte count, plasma cholesterol and plasma fibrinogen of elderly people without a comparable rise in protein C or factor X. Clin Sci 1994;86:43-8. https://doi.org/10.1042/cs0860043.
- Woodhouse PR, Khaw KT, Plummer M, Foley A, Meade TW. Seasonal variations of plasma fibrinogen and factor VII activity in the elderly: winter infections and death from cardiovascular disease. Lancet 1994;343:435-9. https://doi.org/10.1016/S0140-6736(94)92689-1.
- Haran JP, Suner S, Gardiner F. Correlation of C-reactive protein to severity of symptoms in acute influenza A infection. J Emerg Trauma Shock 2012;5:149-52. https://doi.org/10.4103/0974-2700.96484.
- Health Impacts of Low Indoor Air Temperatures. Report on a WHO meeting: Copenhagen, 11–14 November 1985. Copenhagen: WHO, Regional Office for Europe; 1987.
- Busse WW, Lemanske RF, Gern JE. Role of viral respiratory infections in asthma and asthma exacerbations. Lancet 2010;376:826-34. https://doi.org/10.1016/S0140-6736(10)61380-3.
- Matsumoto K, Inoue H. Viral infections in asthma and COPD. Respir Investig 2014;52:92-100. https://doi.org/10.1016/j.resinv.2013.08.005.
- Koskela HO. Cold air-provoked respiratory symptoms: the mechanisms and management. Int J Circumpolar Health 2007;66:91-100. https://doi.org/10.3402/ijch.v66i2.18237.
- Wells RE, Walker JE, Hickler RB. Effects of cold air on respiratory airflow resistance in patients with respiratory-tract disease. N Engl J Med 1960;263:268-73. https://doi.org/10.1056/NEJM196008112630602.
- Wookey R, Bone A, Carmichael C, Crossley A. Minimum Home Temperature Thresholds for Health in Winter – A Systematic Literature Review. London: Public Health England; 2014.
- Sega R, Cesana G, Bombelli M, Grassi G, Stella ML, Zanchetti A, et al. Seasonal variations in home and ambulatory blood pressure in the PAMELA population. Pressione Arteriose Monitorate E Loro Associazioni. J Hypertens 1998;16:1585-92. https://doi.org/10.1097/00004872-199816110-00004.
- Hopstock LA, Barnett AG, Bønaa KH, Mannsverk J, Njølstad I, Wilsgaard T. Seasonal variation in cardiovascular disease risk factors in a subarctic population: the Tromsø Study 1979–2008. J Epidemiol Community Health 2013;67:113-18. https://doi.org/10.1136/jech-2012-201547.
- Kent ST, Howard G, Crosson WL, Prineas RJ, McClure LA. The association of remotely-sensed outdoor temperature with blood pressure levels in REGARDS: a cross-sectional study of a large, national cohort of African-American and white participants. Environ Health 2011;10. https://doi.org/10.1186/1476-069X-10-7.
- Chen Q, Wang J, Tian J, Tang X, Yu C, Marshall RJ, et al. Association between ambient temperature and blood pressure and blood pressure regulators: 1831 hypertensive patients followed up for three years. PLOS ONE 2013;8. https://doi.org/10.1371/journal.pone.0084522.
- Hong YC, Kim H, Oh SY, Lim YH, Kim SY, Yoon HJ, et al. Association of cold ambient temperature and cardiovascular markers. Sci Total Environ 2012;435–6:74-9. https://doi.org/10.1016/j.scitotenv.2012.02.070.
- Aubinière-Robb L, Jeemon P, Hastie CE, Patel RK, McCallum L, Morrison D, et al. Blood pressure response to patterns of weather fluctuations and effect on mortality. Hypertension 2013;62:190-6. https://doi.org/10.1161/HYPERTENSIONAHA.111.00686.
- Saeki K, Obayashi K, Iwamoto J, Tone N, Okamoto N, Tomioka K, et al. Stronger association of indoor temperature than outdoor temperature with blood pressure in colder months. J Hypertens 2014;32:1582-9. https://doi.org/10.1097/HJH.0000000000000232.
- Shiue I, Shiue M. Indoor temperature below 18 °C accounts for 9% population attributable risk for high blood pressure in Scotland. Int J Cardiol 2014;171:e1-2. https://doi.org/10.1016/j.ijcard.2013.11.040.
- Barnett AG, Sans S, Salomaa V, Kuulasmaa K, Dobson AJ. WHO MONICA Project . The effect of temperature on systolic blood pressure. Blood Press Monit 2007;12:195-203. https://doi.org/10.1097/MBP.0b013e3280b083f4.
- Saeki K, Obayashi K, Iwamoto J, Tone N, Okamoto N, Tomioka K, et al. The relationship between indoor, outdoor and ambient temperatures and morning BP surges from inter-seasonally repeated measurements. J Hum Hypertens 2014;28:482-8. https://doi.org/10.1038/jhh.2014.4.
- Jevons R, Carmichael C, Crossley A, Bone A. Minimum indoor temperature threshold recommendations for English homes in winter – a systematic review. Public Health 2016;136:4-12. https://doi.org/10.1016/j.puhe.2016.02.007.
- Stout RW, Crawford V. Seasonal variations in fibrinogen concentrations among elderly people. Lancet 1991;338:9-13. https://doi.org/10.1016/0140-6736(91)90004-9.
- Elwood PC, Beswick A, O’Brien JR, Renaud S, Fifield R, Limb ES, et al. Temperature and risk factors for ischaemic heart disease in the Caerphilly prospective study. Br Heart J 1993;70:520-3. https://doi.org/10.1136/hrt.70.6.520.
- Yeh CJ, Chan P, Pan WH. Values of blood coagulating factors vary with ambient temperature: the Cardiovascular Disease Risk Factor Two-Township Study in Taiwan. Chin J Physiol 1996;39:111-16.
- Halonen JI, Zanobetti A, Sparrow D, Vokonas PS, Schwartz J. Associations between outdoor temperature and markers of inflammation: a cohort study. Environ Health 2010;9. https://doi.org/10.1186/1476-069X-9-42.
- Horan JT, Francis CW, Falsey AR, Kolassa J, Smith BH, Hall WJ. Prothrombotic changes in hemostatic parameters and C-reactive protein in the elderly with winter acute respiratory tract infections. Thromb Haemost 2001;85:245-9. https://doi.org/10.1055/s-0037-1615704.
- Wilker EH, Yeh G, Wellenius GA, Davis RB, Phillips RS, Mittleman MA. Ambient temperature and biomarkers of heart failure: a repeated measures analysis. Environ Health Perspect 2012;120:1083-7. https://doi.org/10.1289/ehp.1104380.
- Schneider A, Panagiotakos D, Picciotto S, Katsouyanni K, Löwel H, Jacquemin B, et al. Air temperature and inflammatory responses in myocardial infarction survivors. Epidemiology 2008;19:391-400. https://doi.org/10.1097/EDE.0b013e31816a4325.
- Hampel R, Breitner S, Rückerl R, Frampton MW, Koenig W, Phipps RP, et al. Air temperature and inflammatory and coagulation responses in men with coronary or pulmonary disease during the winter season. Occup Environ Med 2010;67:408-16. https://doi.org/10.1136/oem.2009.048660.
- Koh YI, Choi IS. Seasonal difference in the occurrence of exercise-induced bronchospasm in asthmatics: dependence on humidity. Respiration 2002;69:38-45. https://doi.org/10.1159/000049368.
- Donaldson GC, Goldring JJ, Wedzicha JA. Influence of season on exacerbation characteristics in patients with COPD. Chest 2012;141:94-100. https://doi.org/10.1378/chest.11-0281.
- Osman LM, Ayres JG, Garden C, Reglitz K, Lyon J, Douglas JG. Home warmth and health status of COPD patients. Eur J Public Health 2008;18:399-405. https://doi.org/10.1093/eurpub/ckn015.
- Pierse N, Arnold R, Keall M, Howden-Chapman P, Crane J, Cunningham M. Heating Housing and Health Study Group . Modelling the effects of low indoor temperatures on the lung function of children with asthma. J Epidemiol Community Health 2013;67:918-25. https://doi.org/10.1136/jech-2013-202632.
- Howden-Chapman P, Pierse N, Nicholls S, Gillespie-Bennett J, Viggers H, Cunningham M, et al. Effects of improved home heating on asthma in community dwelling children: randomised controlled trial. BMJ 2008;337. https://doi.org/10.1136/bmj.a1411.
- Howden-Chapman P, Matheson A, Crane J, Viggers H, Cunningham M, Blakely T, et al. Effect of insulating existing houses on health inequality: cluster randomised study in the community. BMJ 2007;334. https://doi.org/10.1136/bmj.39070.573032.80.
- Gilbertson J, Grimsley M, Green G. Warm Front Study Group . Psychosocial routes from housing investment to health: evidence from England’s home energy efficiency scheme. Energy Policy 2012;49:122-33. https://doi.org/10.1016/j.enpol.2012.01.053.
- Kearns A, Hiscock R, Ellaway A, Macintyre S. ‘Beyond Four Walls’. The psychosocial benefits of home: evidence from West Central Scotland. Housing Studies 2000;15:387-410. https://doi.org/10.1080/02673030050009249.
- Gilbertson J, Stevens M, Stiell B, Thorogood N. Warm Front Study Group . Home is where the hearth is: grant recipients’ views of England’s home energy efficiency scheme (Warm Front). Soc Sci Med 2006;63:946-56. https://doi.org/10.1016/j.socscimed.2006.02.021.
- Thomson H, Thomas S, Sellstrom E, Petticrew M. Housing improvements for health and associated socio-economic outcomes. Cochrane Database Syst Rev 2013;2. https://doi.org/10.1002/14651858.CD008657.pub2.
- Steptoe A, Breeze E, Banks J, Nazroo J. Cohort profile: the English longitudinal study of ageing. Int J Epidemiol 2013;42:1640-8. https://doi.org/10.1093/ije/dys168.
- Chobanian AV, Bakris GL, Black HR, Cushman WC, Green LA, Izzo JL, et al. The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure: the JNC 7 report. JAMA 2003;289:2560-72. https://doi.org/10.1001/jama.289.19.2560.
- Burt VL, Whelton P, Roccella EJ, Brown C, Cutler JA, Higgins M, et al. Prevalence of hypertension in the US adult population. Results from the Third National Health and Nutrition Examination Survey, 1988-1991. Hypertension 1995;25:305-13. https://doi.org/10.1161/01.HYP.25.3.305.
- Pearson TA, Mensah GA, Alexander RW, Anderson JL, Cannon RO, Criqui M, et al. Markers of inflammation and cardiovascular disease: application to clinical and public health practice: a statement for healthcare professionals from the Centers for Disease Control and Prevention and the American Heart Association. Circulation 2003;107:499-511. https://doi.org/10.1161/01.CIR.0000052939.59093.45.
- Stanojevic S, Wade A, Stocks J. Reference values for lung function: past, present and future. Eur Respir J 2010;36:12-9. https://doi.org/10.1183/09031936.00143209.
- Quanjer PH, Stanojevic S, Cole TJ, Baur X, Hall GL, Culver BH, et al. Multi-ethnic reference values for spirometry for the 3-95-yr age range: the global lung function 2012 equations. Eur Respir J 2012;40:1324-43. https://doi.org/10.1183/09031936.00080312.
- Ganna A, Ingelsson E. 5 year mortality predictors in 498,103 UK Biobank participants: a prospective population-based study. Lancet 2015;386:533-40. https://doi.org/10.1016/S0140-6736(15)60175-1.
- DeSalvo KB, Fan VS, McDonell MB, Fihn SD. Predicting mortality and healthcare utilization with a single question. Health Serv Res 2005;40:1234-46. https://doi.org/10.1111/j.1475-6773.2005.00404.x.
- Radloff LS. The CES-D scale: a self-report depression scale for research in the general population. Appl Psychol Meas 1977;1:385-401. https://doi.org/10.1177/014662167700100306.
- Turvey CL, Wallace RB, Herzog R. A revised CES-D measure of depressive symptoms and a DSM-based measure of major depressive episodes in the elderly. Int Psychogeriatr 1999;11:139-48. https://doi.org/10.1017/S1041610299005694.
- Imbens GW, Lemieux T. Regression discontinuity designs: a guide to practice. J Econom 2008;142:615-35. https://doi.org/10.1016/j.jeconom.2007.05.001.
- Lee DS, Lemieux T. Regression discontinuity designs in economics. J Econ Lit 2010;48:281-355. https://doi.org/10.1257/jel.48.2.281.
- Calonico S, Cattaneo MD, Titiunik R. Robust nonparametric confidence intervals for regression-discontinuity designs. Econometrica 2014;82:2295-326. https://doi.org/10.3982/ECTA11757.
- Calonico S, Cattaneo M, Titiunik R. Robust data-driven inference in the regression-discontinuity design. Stata J 2014;14:909-46.
- Calonico S, Cattaneo M, Farrell M, Titiunik R. Regression discontinuity designs using covariates. Rev Econom Stat 2018. https://doi.org/10.1162/rest_a_00760.
- Calonico S, Cattaneo M, Farrell M, Titiunik R. Rdrobust: software for regression-discontinuity designs. Stata J 2017;17:372-404.
- Skovron C, Titiunik R. A practical guide to regression discontinuity designs in political science. Am J Polit Sci 2019.
- Hahn J, Todd P, Van der Klaauw W. Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica 2001;69:201-9. https://doi.org/10.1111/1468-0262.00183.
- Gelman A, Imbens G. Why high-order polynomials should not be used in regression discontinuity designs. J Bus Econ Stat 2019.
- Imbens G, Kalyanaraman K. Optimal bandwidth choice for the regression discontinuity estimator. Rev Econ Stud 2012;79:933-59. https://doi.org/10.1093/restud/rdr043.
- Blundell R, Bond S. Initial conditions and moment restrictions in dynamic panel data models. J Econom 1998;87:115-43. https://doi.org/10.1016/S0304-4076(98)00009-8.
- Murphy JM, Sexton DM, Jenkins GJ, Booth BB, Brown CC, Clark RT, et al. UK Climate Projections Science Report: Climate Change Projections. Exeter: Met Office Hadley Centre; 2009.
- Cohen J, Cohen P. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. Mahwah, NJ: Lawrence Erlbaum Associates; 1985.
- Simonsohn U, Simmons JP, Nelson LD. Specification Curve: Descriptive and Inferential Statistics on All Reasonable Specifications 2015. https://ssrn.com/abstract=2694998 (accessed 4 December 2017).
- Summerfield AJ, Lowe RJ, Bruhns HR, Caeiro JA, Steadman JP, Oreszczyn T. Milton Keynes Energy Park revisited: changes in internal temperatures and energy usage. Energy Buildings 2007;39:783-91. https://doi.org/10.1016/j.enbuild.2007.02.012.
- Vadodaria K, Loveday DL, Haines V. Measured winter and spring-time indoor temperatures in UK homes over the period 1969–2010: a review and synthesis. Energy Policy 2014;64:252-62. https://doi.org/10.1016/j.enpol.2013.07.062.
- Yohanis YG, Mondol JD. Annual variations of temperature in a sample of UK dwellings. Appl Energy 2010;87:681-90. https://doi.org/10.1016/j.apenergy.2009.08.003.
- Comerford DA, Lange I, Moro M. Proof of concept that requiring energy labels for dwellings can induce retrofitting. Energy Econ 2018;69:204-12. https://doi.org/10.1016/j.eneco.2017.11.013.
- Existing Housing and Climate Change: Seventh Report of Session 2007–08. London: The Stationery Office; 2008.
- Advani A, Johnson P, Leicester A, Stoye G. Household Energy Use in Britain: A Distributional Analysis. London: Institute for Fiscal Studies; 2013.
- Goldberg DP, Williams P. A User’s Guide to the General Health Questionnaire. Windsor: NFER-Nelson; 1988.
- Statistical Bulletin. Excess Winter Mortality in England and Wales: 2015/16 (provisional) and 2014/15 (final). Newport: Office for National Statistics; 2016.
- Rehill N, Armstrong B, Wilkinson P. Clarifying life lost due to cold and heat: a new approach using annual time series. BMJ Open 2015;5. https://doi.org/10.1136/bmjopen-2014-005640.
- Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J, et al. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Medicine 2015;12. https://doi.org/10.1371/journal.pmed.1001779.
List of abbreviations
- BHPS
- British Household Panel Survey
- BMI
- body mass index
- BW
- bandwidth
- CES-D
- Centre for Epidemiological Studies Depression Scale
- CI
- confidence interval
- COPD
- chronic obstructive pulmonary disease
- CRP
- C-reactive protein
- ELSA
- English Longitudinal Study of Ageing
- EWD
- excess winter death
- FEV
- forced expiratory volume
- FEV1
- forced expiratory volume in 1 second
- hs-CRP
- high-sensitivity C-reactive protein
- HSE
- Health Survey England
- ICC
- intraclass correlation coefficient
- GHQ-12
- 12-item version of the General Health Questionnaire
- LA
- local authority
- LCF
- Living Costs and Food Survey
- MSE
- mean squared error
- ONS
- Office for National Statistics
- OR
- odds ratio
- OS
- Ordnance Survey
- RD
- regression discontinuity
- RDD
- regression discontinuity design
- SAP
- standard assessment procedure
- SE
- standard error
- VS
- vital statistics
- WFP
- Winter Fuel Payment
- WHO
- World Health Organization